Что называется реактивной силой: Урок 12. реактивное движение – Физика – 10 класс

Урок 12. реактивное движение – Физика – 10 класс

Физика, 10 класс

Урок 12. Реактивное движение

Перечень вопросов, рассматриваемых на уроке:

1) практическое применение закона сохранения импульса;

2) реактивное движение, реактивная сила;

3) использование реактивного движения в природе и технике;

4) этапы исторического развития освоения космоса;

Глоссарий по теме

Реактивное движение – это движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно него.

Реактивная сила – сила, возникающая при реактивном движении.

Особенность реактивной силы – возникновение без взаимодействия с внешними телами.

Скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы топлива к массе ракеты.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс.

Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 126 – 127;

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2014. – С.47-48.

Открытые электронные ресурсы:

http://kvant.mccme.ru/1971/07/paradoksy_reaktivnogo_dvizheni.htm

Теоретический материал для самостоятельного изучения

Движение тела, которое возникает при отделении с определённой скоростью какой-либо его части, называется реактивным.

Реактивное движение издревле существует в природе. Его для своего перемещения используют некоторые живые существа: кальмары, осьминоги, каракатицы, медузы и т.д. Они всасывают, а затем с силой выталкивают из себя воду, за счёт этого они движутся. Реактивное движение встречается и в быту. Примеры: движение резинового шланга, когда мы включаем воду, салюты и т.д.

Яркий пример реактивного движения в технике – это движение ракеты при истечении из неё струи горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

При реактивном движении возникает сила, которая называется реактивной. Сила – это реактивная сила.

Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Согласно закону сохранения импульса: импульс вырывающихся газов равен импульсу ракеты.

Закон сохранения импульса позволяет оценить скорость ракеты.

Закон сохранения импульса для реактивного движения:

откуда скорость ракеты:

Скорость ракеты тем больше, чем больше скорость выбрасываемых газов и отношение массы топлива к массе ракеты. Эта формула справедлива для случая мгновенного сгорания топлива. На самом деле топливо сгорает постепенно, т.к. мгновенное сгорание приводит к взрыву.

Точная формула для скорости ракеты была получена в 1897 году К.Э. Циолковским.

Первую конструкцию ракеты для космических полётов предложил Константин Эдуардович Циолковский – русский учёный, основоположник теоретической космонавтики. Он обосновал использование ракет для полётов в космос, сделал вывод о необходимости использования многоступенчатых ракет.

Идеи Циолковского воплотил в жизнь советский учёный, инженер-конструктор С.П. Королёв. 4 октября 1957 года считается началом космической эры. В этот день конструкторский коллектив под руководством Королёва осуществил запуск первого искусственного спутника Земли.

12 апреля 1961 г. впервые в мире на орбиту Земли был выведен космический корабль, в котором находился лётчик-космонавт СССР Юрий Алексеевич Гагарин. Он открыл дорогу в космос. В космосе нельзя использовать другие двигатели, кроме реактивных, так как там нет опоры, отталкиваясь от которой космический корабль мог бы получить ускорение. Реактивные двигатели применяют для самолётов и ракет, не выходящих за пределы атмосферы, чтобы максимально увеличить скорость полёта.

Реактивные двигатели делятся на два класса: ракетные и воздушно-реактивные. Воздушно-реактивные в основном используют на самолётах. Современная космическая ракета – это очень сложное и тяжелое устройство, состоящее из оболочки и топлива с окислителем.

Примеры и разбор решения заданий

1. Чему равна реактивная сила тяги двигателя, выбрасывающего каждую секунду 15 кг продуктов сгорания топлива со скоростью 3 км/с относительно ракеты?

Дано: m = 15 кг, v = 3 км/с = 3000 м/с, ∆t = 1 с. Найти F.

Решение:

Записываем 2-й закон Ньютона в импульсной форме: F ∆t = m (v – v₀). Перед стартом скорость ракеты равна 0: = 0. Выразим силу: F = mv/∆t, сделаем расчёт: F = (15 кг·3000 м/с) / 1 с = 45000 кг· м/ с² = 45000 Н. Ответ: F = 45000 Н.

2. Из пороховой ракеты, летящей со скоростью 16 м/с, вылетают продукты сгорания массой 24 г со скоростью 600 м/с. Вычислите массу ракеты.

Дано: v₁ = 16 м / с, m₂ = 24 г = 0,024 кг, v₂ = 600 м/с. Найти m₁.

Решение:

Запишем закон сохранения импульса для реактивного движения: m₁v₁ = m₂v₂, выразим массу ракеты: m₁ = m₂v₂ / v₁.

Делаем расчёт: m₁ = (0,024 кг·600 м/с) / 16 м / с = 0,9 кг. Ответ: m₁ = 0,9 кг.

Реактивная сила – это… Что такое Реактивная сила?

Реактивная сила

Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

• Реактивная мощность
• Реактивная турбина

Полезное

Смотреть что такое “Реактивная сила” в других словарях:

• Реактивная сила — см. Тяга двигателя. Авиация: Энциклопедия. М.: Большая Российская Энциклопедия. Главный редактор Г.П. Свищев. 1994 …   Энциклопедия техники

• реактивная сила — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN reaction force …   Справочник технического переводчика

• реактивная сила — atoveikio jėga statusas T sritis Standartizacija ir metrologija apibrėžtis Veikiamojo kūno atsakomojo poveikio jėga, nukreipta į veikiantįjį kūną. atitikmenys: angl. counter acting force; reactive force vok. Gegenwirkungskraft, f; Rückstosskraft …   Penkiakalbis aiškinamasis metrologijos terminų žodynas

• реактивная сила

  — реактивная сила — см.  Тяга двигателя …   Энциклопедия «Авиация»

• реактивная сила — реактивная сила — см. Тяга двигателя …   Энциклопедия «Авиация»

• реактивная сила ЖРД (камеры ЖРД) — реактивная сила двигателя (камеры) Равнодействующая газо и гидродинамических сил, действующих на внутренние поверхности ЖРД (камеры ЖРД) при истечении продуктов сгоранияю [ГОСТ 17655 89] Тематики двигатели ракетные жидкостные Синонимы реактивная… …   Справочник технического переводчика

• Реактивная тяга — (реактивная сила) сила реакции (отдачи) струи, создаваемая в результате истечения газов (или другого рабочего тела) из сопла реактивного двигателя. Реактивная тяга приложена непосредственно к корпусу ракетного двигателя и без каких либо… …   Морской словарь

• РЕАКТИВНАЯ ТЯГА

  — (реактивная сила) сила реакции (отдачи) струи рабочего тела (напр., газа), вытекающей из сопла реактивного двигателя и приводящей в движение устройство с двигателем в сторону, противоположную направлению истечения рабочего тела …   Большой Энциклопедический словарь

• РЕАКТИВНАЯ ТЯГА — (реактивная сила) сила реакции (отдачи) струи рабочего тела, вытекающей из сопла реактивного двигателя (см. ), приводящая в движение двигатель и связанный с ним аппарат в направлении, противоположном направлению реактивной струи. Принцип… …   Большая политехническая энциклопедия

• Реактивная тяга —         реактивная сила, сила реакции (отдачи) струи газов (или др. рабочего тела (См. Рабочее тело)), вытекающей из сопла реактивного двигателя (См. Реактивный двигатель). Р. т. равнодействующая сил давления рабочего тела на ограничивающие его… …   Большая советская энциклопедия

Что называется реактивной силой – Клуб строителей

Какое движение называется реактивным?

Под реактивным движением понимают движение тела, возникающее при отделении некоторой его части с определенной скоростью относительно тела, например при истечении продуктов сгорания из сопла реактивного летательного аппарата. При этом появляется так называемая реактивная сила, сообщающая телу ускорение.

Наблюдать реактивное движение очень просто. Надуйте детский резиновый шарик и отпустите его. Шарик стремительно взовьется вверх (рис. 5.4). Движение, правда, будет кратковременным. Реактивная сила действует лишь до тех пор, пока продолжается истечение воздуха.

Главная особенность реактивной силы состоит в том, что она возникает без какого-либо взаимодействия с внешними телами. Происходит лишь взаимодействие между ракетой и вытекающей из нее струей вещества.

Сила же, сообщающая ускорение автомобилю или пешеходу на земле, пароходу на воде или винтовому самолету в воздухе, возникает только за счет взаимодействия этих тел с землей, водой или воздухом.

При истечении продуктов сгорания топлива они за счет давления в камере сгорания приобретают некоторую скорость относительно ракеты и, следовательно, некоторый импульс. Поэтому в соответствии с законом сохранения импульса сама ракета получает такой же по модулю импульс, но направленный в противоположную сторону.

Масса ракеты с течением времени убывает. Ракета в полете является телом переменной массы. Для расчета ее движения удобно применить закон сохранения импульса.

Уравнение Мещерского

Выведем уравнение движения ракеты и найдем выражение для реактивной силы. Будем считать, что скорость вытекающих из ракеты газов относительно ракеты постоянна и равна . Внешние силы на ракету не действуют: она находится в космическом пространстве вдали от звезд и планет.

Пусть в некоторый момент времени скорость ракеты относительно инерциальной системы, связанной со звездами, равна (рис. 5.5, а), а масса ракеты равна М. Через малый интервал времени Δt масса ракеты станет равной

где μ — расход топлива(1).

За этот лее промежуток времени скорость ракеты изменится на Δ и станет равной ₁ = + Δ. Скорость истечения газов относительно выбранной инерциальной системы отсчета равна + (рис. 5.5,б), так как до начала сгорания топливо имело ту же скорость, что и ракета.

Запишем закон сохранения импульса для системы ракета — газ:

Раскрыв скобки, получим:

Слагаемым μΔtΔ можно пренебречь по сравнению с остальными, так как оно содержит произведение двух малых величин (это величина, как говорят, второго порядка малости). После приведения подобных членов будем иметь:

Это одно из уравнений Мещерского(2) для движения тела переменной массы, полученное им в 1897 г.

Если ввести обозначение _р = -μ, то уравнение (5.4.1) совпадет по форме записи со вторым законом Ньютона. Однако масса тела М здесь не постоянна, а убывает со временем из-за потери вещества.

Величина _р = -μ носит название реактивной силы. Она появляется вследствие истечения газов из ракеты, приложена к ракете и направлена противоположно скорости газов относительно ракеты. Реактивная сила определяется лишь скоростью истечения газов относительно ракеты и расходом топлива. Существенно, что она не зависит от деталей устройства двигателя. Важно лишь, чтобы двигатель обеспечивал истечение газов из ракеты со скоростью при расходе топлива μ. Реактивная сила космических ракет достигает 1000 кН.

Если на ракету действуют внешние силы, то ее движение определяется реактивной силой и суммой внешних сил. В этом случае уравнение (5.4.1) запишется так:

Принцип реактивного движения основан на том, что истекающие из реактивного двигателя газы получают импульс. Такой же по модулю импульс приобретает ракета.

Вопросы для самопроверки

1. Реактивное движение совершает кальмар (рис. 5.6). Как это ему удается?

Рис. 5.6

Может ли парусная лодка приводиться в движение с помощью компрессора, установленного на лодке, если струя воздуха направлена на паруса? Что произойдет, если поток воздуха будет направлен мимо парусов?

Будет ли увеличиваться скорость ракеты, если скорость истечения газов относительно ракеты меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой?

(1) Расходом топлива называется отношение массы сгоревшего топлива ко времени его сгорания.

(2) Мещерский И. В. (1859—1935) — профессор Петербургского политехнического института. Его труды по механике тел переменной массы стали теоретической основой ракетной техники.

В книжной версии

Том 28. Москва, 2015, стр. 279

Скопировать библиографическую ссылку:

РЕАКТИ́ВНАЯ СИ́ЛА (ре­ак­тив­ная тя­га), си­ла ре­ак­ции ра­бо­че­го те­ла, от­бра­сы­вае­мо­го но­си­те­лем с не­ко­то­рой от­но­си­тель­ной ско­ро­стью $oldsymbol u$ . Яв­ля­ет­ся си­лой тя­ги ре­ак­тив­но­го дви­га­те­ля . По­ня­тие Р. с. вве­де­но в 1897 И. В. Ме­щер­ским . Ве­ли­чи­на Р. с. оп­ре­де­ля­ет­ся фор­му­лой $$F=ufrac

,$$ где $m(t)$ – мас­са но­си­те­ля с ос­тав­шей­ся ча­стью ра­бо­че­го те­ла, $t$ – вре­мя. На­прав­ле­ние Р. с. про­ти­во­по­лож­но на­прав­ле­нию ско­ро­сти $oldsymbol u$ .

• 5 – 9 классы
• Физика
• 5 баллов

Какую силу называю реактивной?

• Попроси больше объяснений
• Следить
• Отметить нарушение

LoveЗайкаlove 03.03.2014

Что ты хочешь узнать?

Ответ

Проверено экспертом

Сила которая возникает как реакция вытекания струи жидкости или газа называют реактивной.

В основе реактивного движения лежит закон сохранения мпульса

“>

Реактивное движение | Физика

Законы Ньютона позволяют объяснить очень важное механическое явление — реактивное движение. Так называют движение тела, возникающее при отделении от него с какой-либо скоростью некоторой его части.

Возьмем, например, детский резиновый шарик, надуем его и отпустим. Мы увидим, что, когда воздух начнет выходить из него в одну сторону, сам шарик полетит в другую. Это и есть реактивное движение.

По принципу реактивного движения передвигаются некоторые представители животного мира, например кальмары и осьминоги. Периодически выбрасывая вбираемую в себя воду, они способны развивать скорость до 60—70 км/ч. Аналогичным образом перемещаются медузы, каракатицы и некоторые другие животные.

Примеры реактивного движения можно обнаружить и в мире растений. Например, созревшие плоды «бешеного» огурца при самом легком прикосновении отскакивают от плодоножки и из отверстия, образовавшегося на месте отделившейся ножки, с силой выбрасывается горькая жидкость с семенами; сами огурцы при этом отлетают в противоположном направлении.

Реактивное движение, возникающее при выбросе воды, можно наблюдать на следующем опыте. Нальем воду в стеклянную воронку, соединенную с резиновой трубкой, имеющей Г-образный наконечник (рис. 20). Мы увидим, что, когда вода начнет выливаться из трубки, сама трубка придет в движение и отклонится в сторону, противоположную направлению вытекания воды.

На принципе реактивного движения основаны полеты ракет. Современная космическая ракета представляет собой очень сложный летательный аппарат, состоящий из сотен тысяч и миллионов деталей. Масса ракеты огромна. Она складывается из массы рабочего тела (т. е. раскаленных газов, образующихся в результате сгорания топлива и выбрасываемых в виде реактивной струи) и конечной или, как говорят, «сухой» массы ракеты, остающейся после выброса из ракеты рабочего тела.

«Сухая» масса ракеты, в свою очередь, состоит из массы конструкции (т. е. оболочки ракеты, ее двигателей и системы управления) и массы полезной нагрузки (т. е. научной аппаратуры, корпуса выводимого на орбиту космического аппарата, экипажа и системы жизнеобеспечения корабля).

По мере истечения рабочего тела освободившиеся баки, лишние части оболочки и т. д. начинают обременять ракету ненужным грузом, затрудняя ее разгон. Поэтому для достижения космических скоростей применяют составные (или многоступенчатые) ракеты (рис. 21). Сначала в таких ракетах работают лишь блоки первой ступени 1. Когда запасы топлива в них кончаются, они отделяются и включается вторая ступень 2; после исчерпания в ней топлива она также отделяется и включается третья ступень 3. Находящийся в головной части ракеты спутник или какой-либо другой космический аппарат укрыт головным обтекателем 4, обтекаемая форма которого способствует уменьшению сопротивления воздуха при полете ракеты в атмосфере Земли.

Когда реактивная газовая струя с большой скоростью выбрасывается из ракеты, сама ракета устремляется в противоположную сторону. Почему это происходит?

Согласно третьему закону Ньютона, сила F, с которой ракета действует на рабочее тело, равна по величине и противоположна по направлению силе F’, с которой рабочее тело действует на корпус ракеты:

        F’ = F.          (12.1)

Сила F’ (которую называют реактивной силой) и разгоняет ракету.

Из равенства (10.1) следует, что сообщаемый телу импульс равен произведению силы на время ее действия. Поэтому одинаковые силы, действующие в течение одного и того же времени, сообщают телам равные импульсы. В данном случае импульс m_рv_р, приобретаемый ракетой, должен пульсу m_газv_газ выброшенных газов:

m_рv_р = m_газv_газ

Отсюда следует, что скорость ракеты

Проанализируем полученное выражение. Мы видим, что скорость ракеты тем больше, чем больше скорость выбрасываемых газов и чем больше отношение массы рабочего тела (т. е. массы топлива) к конечной («сухой») массе ракеты.

Формула (12.2) является приближенной. В ней не учитывается, что по мере сгорания топлива масса летящей ракеты становится все меньше и меньше. Точная формула для скорости ракеты впервые была получена в 1897 г. К. Э. Циолковским и потому носит его имя.

Формула Циолковского позволяет рассчитать запасы топлива, необходимые для сообщения ракете заданной скорости. В таблице 3 приведены отношения начальной массы ракеты m0 к ее конечной массе m, соответствующие разным скоростям ракеты при скорости газовой струи (относительно ракеты) v = 4 км/с.

Например, для сообщения ракете скорости, превышающей скорость истечения газов в 4 раза (v_р=16 км/с), необходимо, чтобы начальная масса ракеты (вместе с топливом) превосходила конечную («сухую») массу ракеты в 55 раз (m₀/m = 55). Это означает, что львиную долю от всей массы ракеты на старте должна составлять именно масса топлива. Полезная же нагрузка по сравнению с ней должна иметь очень малую массу.

Важный вклад в развитие теории реактивного движения внес современник К. Э. Циолковского русский ученый И. В. Мещерский (1859—1935). Его именем названо уравнение движения тела с переменной массой.

1. Что такое реактивное движение? Приведите примеры. 2. В опыте, изображенном на рисунке 22, при вытекании воды через изогнутые трубки ведерко вращается в направлении, указанном стрелкой. Объясните явление. 3. От чего зависит скорость, приобретаемая ракетой после сгорания топлива?

Реактивное движение.

Реактивное движение.

В течение многих веков человечество мечтало о космических полётах. Писатели-фантасты предлагали самые разные средства для достижения этой цели. В XVII веке появился рассказ французского писателя Сирано де Бержерака о полёте на Луну. Герой этого рассказа добрался до Луны в железной повозке, над которой он всё время подбрасывал сильный магнит. Притягиваясь к нему, повозка всё выше поднималась над Землёй, пока не достигла Луны. А барон Мюнхгаузен рассказывал, что забрался на Луну по стеблю боба.

Но ни один учёный, ни один писатель-фантаст за многие века не смог назвать единственного находящегося в распоряжении человека средства, с помощью которого можно преодолеть силу земного притяжения и улететь в космос. Это смог осуществить русский учёный Константин Эдуардович Циолковский (1857-1935). Он показал, что единственный аппарат, способный преодолеть силу тяжести – это ракета, т.е. аппарат с реактивным двигателем, использующим горючее и окислитель, находящиеся на самом аппарате.

Реактивный двигатель – это двигатель, преобразующий химическую энергию топлива в кинетическую энергию газовой струи, при этом двигатель приобретает скорость в обратном направлении. На каких же принципах и физических законах основывается его действие?

Каждый знает, что выстрел из ружья сопровождается отдачей. Если бы вес пули равнялся бы весу ружья, они бы разлетелись с одинаковой скоростью. Отдача происходит потому, что отбрасываемая масса газов создаёт реактивную силу, благодаря которой может быть обеспечено движение как в воздухе, так и в безвоздушном пространстве. И чем больше масса и скорость истекающих газов, тем большую силу отдачи ощущает наше плечо, чем сильнее реакция ружья, тем больше реактивная сила. Это легко объяснить из закона сохранения импульса, который гласит, что геометрическая (т.е. векторная) сумма импульсов тел, составляющих замкнутую систему, остаётся постоянной при любых движениях и взаимодействиях тел системы.

К. Э. Циолковский вывел формулу, позволяющую рассчитать максимальную скорость, которую может развить ракета.

Максимально достижимая скорость зависит в первую очередь от скорости истечения газов из сопла, которая в свою очередь зависит прежде всего от вида топлива и температуры газовой струи. Чем выше температура, тем больше скорость. Значит, для ракеты нужно подбирать самое калорийное топливо, дающее наибольшее количество теплоты. Отношение массы топлива к массе ракеты в конце работы двигателя (т.е. по существу к весу пустой ракеты) называется числом Циолковского.

Основной вывод состоит в том, что в безвоздушном пространстве ракета разовьёт тем большую скорость, чем больше скорость истечения газов и чем больше число Циолковского.

Движения тел переменной массы.
Знание закона сохранения импульса во многих случаях дает возможность найти результат взаимодействия тел, когда значения действующих сил неизвестны.

Рассмотрим в качестве примера действие реактивного двигателя. При сгорании топлива в камере сгорания ракеты образуются газы, нагретые до высокой температуры. При действии двигателя в течение короткого интервала времени t из сопла ракеты выбрасываются со скоростью u относительно ракеты горячие газы массой m. Ракета и выбрасываемые ее двигателем газы взаимодействуют между собой. На основании закона сохранения импульса при отсутствии внешних сил сумма векторов импульсов взаимодействующих тел остается постоянной.

До начала работы двигателей импульс ракеты и горючего был равен нулю, следовательно, и после включения сумма изменений векторов импульса ракеты и импульса истекающих газов равна нулю:

где m – масса ракеты, V – изменение скорости ракеты, m – масса выброшенных газов, u – скорость истечения газов.

Отсюда для векторов импульса получаем:

Разделим обе части равенства на интервал времени t, в течение которого работали двигатели ракеты:

или

Произведение массы ракеты m на ускорение ее движения a по определению равно силе, вызывающей это ускорение:

Таким образом, мы показали, что реактивная сила тяги Fp равна произведению скорости u движения выбрасываемых газов относительно ракеты на секундный расход топлива m/t.

Реактивная сила тяги Fp

действует со стороны газов на ракету и направлена в сторону, противоположную направлению истечения газов.

Выражение

есть уравнение динамики тела переменной массы для случая, когда внешние силы равны нулю. Если же на ракету, кроме реактивной силы Fp, действует внешняя сила F, то уравнение динамики движения примет вид:

Это уравнение получено профессором Петербургского университета
И. В. Мещерским и носит его имя.

Формула Мещерского представляет собой обобщение второго закона Ньютона для движения тел переменной массы. Ускорение тела переменной массы определяется не только внешними силами F, действующими на тело, но и реактивной силой Fp, обусловленной изменением массы движущегося тела:

Ракета. Система двух тел. Корпус топлива.
Корпус – труба с одним открытым концом для выхода отработанных газов. На хвосте ставят сопла (трубки) для направленного выброса газов с большой скоростью.
Топливо – сложное горючее, которое при сжигании превращается в газ большой температуры и большого движения.

V ракеты зависит от m топлива и самой ракеты, а также от V выбросов газов.

В данной формуле не учитывается сопротивление воздуха и F_пр к Земле.

На самом деле выброс газов происходит не мгновенно, а постепенно. Если учесть все условия, то топлива надо брать во много раз больше.

Чтобы сообщить кораблю первую космическую скорость, то

m_т >m_об= в 55 раз

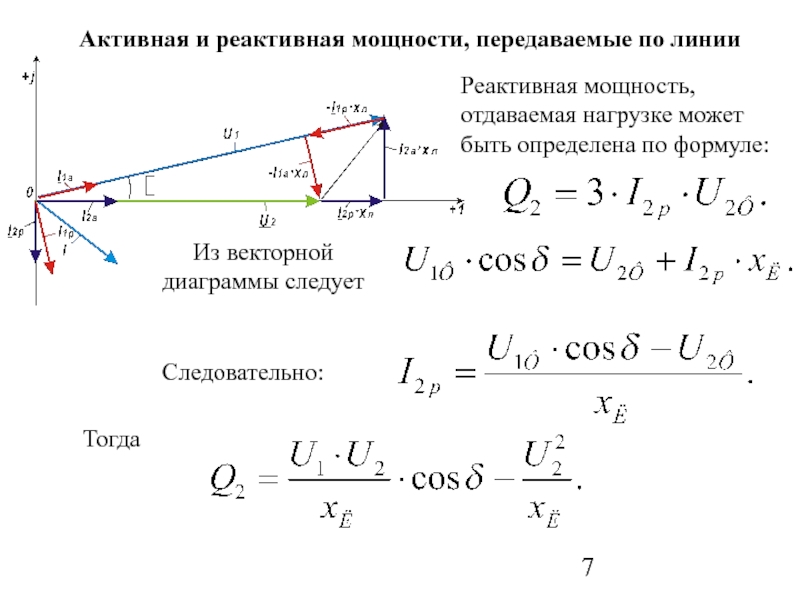
Сила реактивная – Энциклопедия по машиностроению XXL

При сварке на обратной полярности реактивное давление паров меньше, чем на прямой (так как U U ), и струйный перенос металла возникает при меньших силах тока. В. И. Дятловым определена, например, сила реактивного давления паров, действующих на каплю металла при сварке в среде СО2 проволокой Св. 08. Оказалось, что так же, как и сила давления паров на ванну, она пропорциональна квадрату сварочного тока  [c.89]
Решение. Рассмотрим равновесие балки АВ. На балку действуют задаваемые силы вес балки Р и равномерно распределенная нагрузка, равнодействующая которой Q = 2a (рис, 116, б) приложена в середине балки и направлена перпендикулярно к ней. В точке А на балку наложена жесткая связь (заделка), препятствующая этой точке перемещаться в горизонтальном и вертикальном направлениях и лишающая балку возможности поворачиваться вокруг точки А. Действие такой связи на балку эквивалентно действию одной силы реакции и некоторой пары сил — реактивной пары.  [c.56]

Векторные величины Fi и F2 имеют размерность силы. Условимся называть эти величины реактивными силами.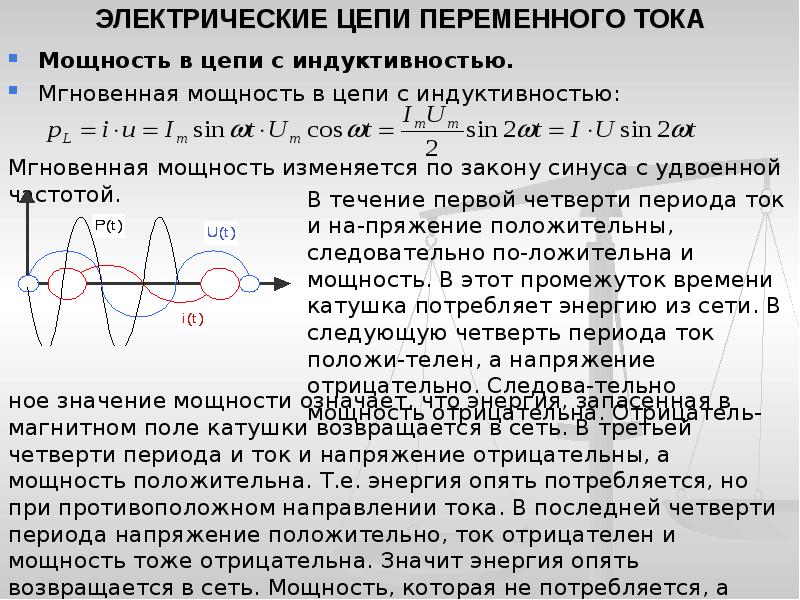 Реактивная сила Fi возникает за счет отделения материальных точек от рассматриваемой системы, а F2 — за счет присоединения точек.  [c.256]

Используя принцип независимости действия сил, реактивное усилие R / можно выразить формулой  [c.593]

По форме уравнение (246) напоминает уравнение движения точки с постоянной массой, но только в правой части уравнения (246) имеется, кроме внешних сил, еще сила реактивная. Однако несмотря на внешнее сходство уравнение (246) отличается своей физической особенностью масса, входяш,ая в левую часть, является переменной величиной и это всегда следует помнить при анализе движения точки с переменной массой и при выводах других уравнений с использованием уравнения (246).  [c.204]

Силы реактивные опор 317— 325  [c.973]

Рассмотрим прямоугольную пластинку, лежащую на сплошном упругом основании и находящуюся под действием поперечной нагрузки интенсивностью (х, у рис. 62). Снизу к пластинке приложены силы реактивного давления упругого основания (отпор основания), представляющего собой неизвестную функцию координат р х, у).  [c.138]

Сила реактивного давления Fp паров испаряющегося металла, соприкасающегося с катодным или анодным пятном, стремится отбросить каплю от этой области.  [c.249]

Для вывода уравнений, определяющих основные параметры муфты, напишем одно из условий равновесия колодки. Если пренебречь трением в пальце, то окажется, что колодка находится под действием сил реактивных давлений на колодку со стороны шкива, центробежных и трения,  [c.306]

Следуя идее Лагранжа, введем аксиому идеальных связен для удара. По определению, идеальными будем называть такие связи, для которых сумма работ сил реактивного удара на любом возможном перемещении системы равна нулю, т. е.  [c.608]

Сила Рг стремится сдвинуть колесо по рельсу влево, однако в результате закона действия и противодействия со стороны рельса на колесо возникает горизонтальная реакция в виде силы /”к, равная силе р2. и направленная в противоположную сторону, но по линии действия, совпадающей с линией действия силы (знак штрих обозначает мгновенное значение появления реактивной силы). Очень важно помнить, что сила является силой реактивной, и она в случае отсутствия скольжения колеса по рельсу может возникнуть количественно лишь в той мере, в какой действует активная сила р2- Следовательно, в каждый момент времени силы и уравновешивают-  [c.8]

В результате действия момента пары сил Хь в точке касания колеса с рельсом сила Ху стремится сдвинуть колесо по рельсу вправо. Колесо нагружено силой Я, передающейся на рельс, и поэтому между ними возникает сила взаимодействия в виде силы сцепления. Эта сила, приложенная от рельса к колесу, направлена влево и удерживает его от скольжения по рельсу. Сила сцепления является силой реактивной (назовем ее В , т. е. ответной реакцией рельса на колесо, и как таковая количественно она может возникнуть лишь в той мере, в какой действует активная сила Х. Поэтому в нормальных условиях торможения силы 5 , и Х равны между собой и взаимно уравновешиваются. Равенство этих сил приводит к тому, что не может быть скольжения колеса по рельсу и точка их касания О в каждый момент времени находится в покое относительно рельса, что является необходимым условием для качения колеса по рельсу. Реактивная сила 5 не может превосходить наибольшую силу сцепления колеса с рельсом фЯ, где Я — нагрузка от колеса на рельс, а гр—коэффициент сцепления между колесом и рельсом, т. е.  [c.97]

Человек, прыгая с лодки на берег, с силой толкает лодку. В свою очередь лодка с такой же силой толкает человека, и эта сила (реактивная сила) выносит его на берег. При этом человек и лодка перемещаются в разные стороны.  [c.18]

Таким образом, если прямолинейное движение точки переменной массы происходит под действием только двух сил реактивной и сопротивления среды, то наивыгоднейший удельный расход должен быть бесконечно малым.  [c.42]

Таким образом, если твердое тело переменной массы имеет одну закрепленную точку и оси Охуг во все время движения остаются главными осями инерции тела, то движение этого тела будет описываться такими же дифференциальными уравнениями, как и для тела постоянной массы, только в правых частях динамических уравнений, кроме моментов внешних сил, нужно прибавить еш,е моменты сил реактивных. Осевые моменты инерции тела будут функциями времени.  [c.107]

Истечение продуктов сгорания в атмосферу со скоростью ш]> у и является источником возникновения реактивной силы. Реактивная сила направлена в сторону, обратную по отношению к скорости ги).  [c.262]

Работа двигателя протекает следующим образом. Из диффузора воздух поступает в компрессор, приводимый в движение газовой турбиной. Турбина работает за счет частичного использования энергии газов, идущих через турбину в выходное сопло. Основная же энергия газов, выходящих через сопло в атмосферу, используется на создание реактивной силы. Реактивная сила определяется по формуле 9-4.  [c.268]

Ротор приводится во вращение парой сил реактивного момента от струи масла, вытекающего с большой скоростью из двух сопел ротора 3. Масло, вытекающее из сопел, стекает в картер двигателя 1. Между ротором центрифуги и главной масляной магистралью установлен дроссель 5.  [c.151]

Ставим задачу определения бокового давления грунта Е на стенку с учетом ее сдвига А (центра подошвы) и поворота на угол а (рис. 74). При действии нагрузки и смещении стенки, определяемом параметрами А и а, возбуждаются следующие силы реактивное давление Е по передней грани, определяемое по (4.24), горизонтальная реакция сдвигу подошвы F =  [c.105]

Силы, действующие на каплю. Характер переноса электродного металла зависит от соотношения сил, действующих на каплю металла на торце электрода. Основные из них сила тяжести, сила поверхностного натяжения, электромагнитная сила, электростатическая сила, сила реактивного давления паров и нейтрализовавшихся на катоде ионов, аэродинамическая сила. Величины отдельных сил и направление их равнодействующей зависят от режима сварки, полярности тока, состава электродного металла и газовой среды, состояния поверхности проволоки и ее диаметра.  [c.72]

При сварке на обратной полярности с увеличением силы тока уменьшается масса переходящей части капли Р р и возрастает число переходящих капель N. Время взаимодействия капель с окружающей средой т р уменьшается. На больших токах дуговой промежуток мал и подвижная сварочная ванна захватывает капли металла на торце электрода, не давая им возможности достигнуть больших размеров. При сварке на прямой полярности масса переходящей части капель и число переходов с ростом силы тока изменяются мало. Объясняется это увеличением плотности тока в активном пятне и возрастанием действия сил реактивного давления паров, которые способствуют удержанию капли на торце электрода (рис. 2-28). Под действием этих сил капли на торце сильно деформируются и вытесняются иногда на его боковую поверхность.  [c.77]

Основной причиной такого переноса является сжатие столба дуги и активных пятен, вызванное диссоциацией углекислого газа. При этом возрастает действие отталкивающих сил реактивного давления паров и осевой составляющей электромагнитной силы, способствующих укрупнению капли и увеличению разбрызгивания металла. Потери металла от разбрызгивания зависят главным образом от режима сварки, диаметра проволоки и характеристик источника питания. С повышением напряжения дуги разбрызгивание повышается.  [c.80]

РЕАКТИВНАЯ СИЛА (реактивная тяга) — сила тяги реактивного двигателя. См. также Динамика ракет.  [c.378]

Р и Рг силы реактивные г , у , х , Уг, Хг Все эти силы  [c.192]

Характер переноса электродного металла зависит от соотношения сил, действующих на каплю металла на торце электрода. К основным из них относят силу тяжести, силу поверхностного натяжения, электромагнитную силу, силу реактивного давления паров, аэродинамическую силу и др. Значения отдельных сил и направление их равнодействующих зависят от режима сварки, полярности тока, состава электродного металла, газовой среды, состояния поверхности и диаметра электрода.  [c.37]

Сила реактивного давления паров — одна из важных сил, оказывающих влияние на характер переноса металла. Испарение металла с поверхности капли и химическое взаимодействие жидкого металла со шлаком или газовой фазой, сопровождаемое образованием и вьщелением газа, приводят к возникновению реактивных сил. Металл испаряется главным образом в области активных пятен, перемещение которых вызывает изменение положения места приложения реактивных сил и значительную подвижность капель. Величина реактивных сил зависит от размеров активных пятен, плотности тока в них и теплофизических свойств материала электрода. Поскольку плотность тока в катодном пятне значительно выше, чем в анодном, влияние реактивного давления в большей мере проявляется на прямой полярности. Сжатие дуги приводит к увеличению плотности тока в пятнах, что вызывает повышение реактивного давления паров. В металлах с высоким давлением паров (магний, цинк) отталкивание капель реактивными силами наблюдается при сварке на обеих полярностях, а в металлах с низким давлением паров — главным образом при сварке на прямой полярности.  [c.38]

Поверхностные силы при переносе материала без коротких замыканий дугового промежутка. Этот вид переноса наблюдается при сварке сравнительно длинной дугой, когда в условиях непрерывной подачи электрода к детали капли успевают сформироваться и отор,ваться от электрода прежде, чем электродный металл войдет в соприкосновение с металлом сварочной ванны. Размеры, форма и поведение капли на конце электрода определяются действием на каплю главным образом сил поверхностного (или межфазного) натяжения, силы тяжести, электромагнитных сил и сил реактивного давления паров и газов, отделяющихся от поверхности капли. При сварке на прямой полярности определенное влияние оказывают реактивные силы нейтрализовавшихся на катоде ионов. Во всех случаях и особенно при сварке в активных средах действуют силы давления газа и пара, образующихся внутри. капель. В некоторой мере действуют силы давления дуговой плазмы. В работе [16] и др. придается важное значение газодинамическим силам, действующим на каплю.  [c.20]

Осевая сила реактивного сопла обычно направлена в сторону движения газа за счет более высоких статических давлений в сечении I—/.  [c.47]

Реактивным двигателем называют двигатель, который создает силу для перемещения аппарата в пространстве путем преобразования энергии собственного или внешнего источника в кинетическую энергию отбрасываемой струи вещества. Для работы реактивного двигателя можно использовать как вещество, размещенное на борту аппарата, так и окружающую среду, т.е. среду, в которой движется аппарат. Струю вещества, истекающую из реактивного двигателя, называют реактивной струей, а силу, которая возникает вследствие ее истечения и передается на аппарат, – реактивной силой. Реактивная сила представляет собой равнодействующую газо- и гидродинамических сил, действующих на внутренние поверхности реактивного двигателя при истечении из него вещества.  [c.5]

Возникновение силы (реактивной) при истечении газа Доплера эффект  [c.182]

Сила реакции струи, вытекающей из резервуаров (рис. 46). Уравнения (37) и (38) применяют к сечениям /—/ (по уровню жидкости в резервуаре) и И—и (по струе, на выходе из резервуара), в которых избыточ21ые давлен я Pi = Pj= О, скорость Vf = 0. Поэтому Рд = = —Aluj, Рст = О (направлена вертикально вниз) Рд и есть сила реактивного воздействия вытекающей струи на резервуар, направленная противоположно скорости t 2 = о (скорости струи) ее значение можно определить по формуле  [c.104]

Сатерленда формула 278 Сила реактивная 51, 553  [c.596]

Переменные нагрузки со случайньши амплитудами, вызываемые воздействиями природных факторов, порывами ветра, ударами волн, случайными колебаниями оснований, случайными неровностями дороги, неоднородностями обрабатываемой среды, воздействием рабочих процессов, в том числе тяговой силы реактивных летательных аппаратов.  [c.8]

На основании полученньпх двух уравнений (4-24) и (4-25) можно достаточно просто написать для рамы конкретные уравнения реактивных моментов и поперечных сил. Реактивные моменты записывают для каждого узла рамы  [c.74]

Усилия, вращаюише диск и вал турбины, обусловлены реактивным действием движущегося канала рабочих лопаток, в котором происходит дальнейшее расширение пара от давления р до Ра. Падение давления сопровождается ускорением пара по отноиюнию к рабочим лопаткам. При этом возникает сила отталкивания — реактивная сила. Реактивная сила направлена против скорости вытекающей струи.  [c.218]

РАКЕТА — летательный аппарат тяжелее воздуха, к-рый приобретает скорость полета за счет сил реакции (сил отдачи) отбрасываемых от аппарата частиц. Результирующая сил реакций — реактивная сила (реактивная тяга) — получается при номощи реактивных двигателей. Реактивная сила обычно параллельна вектору скорости центра масс Р. или образует с ним (при маневре) не-больнгой угол,  [c.333]

Сила реактивного действия газов ( газовое дутье ) возникает за счет частичного превращения электродного металла в пары и расширения их под действием высокой температуры дуги, а также за счет давления газов при сгорании компонентов покрытия электрода. Эта сила направлена по оси электрода и способст ет перемещению образовавшейся капли от электрода к ванне расплавленного металла. При наличии чехольчика на конце толстопокрытого электрода действие этой силы увеличивается.  [c.21]

Воздухоплавательный прибор Кибальчича. Мы помним, что с середины XIX века различными авторами выдвигались самые необыкновенные проекты использования силы реактивной отдачи в транспортных системах. Но в их ряду революционер Николай Кибальчич стоит особняком. Во-первых, он — человек ярчайшей судьбы. Во-вторых, он сформулировал новый и не встречавшийся в других проектах ракетодинамический принцип создания подъемной силы, исключавшей воздух как опорную среду.  [c.204]

---

Основные законы механики (1985) — [ c.77 ]

Курс теоретической механики. Т.1 (1972) — [ c.415 ]

Курс теоретической механики. Т.2 (1983) — [ c.111 ]

Прикладная газовая динамика. Ч.1 (1991) — [ c.51 , c.553 ]

Прикладная механика твердого деформируемого тела Том 3 (1981) — [ c.49 , c.56 ]

Гидрогазодинамика Учебное пособие для вузов (1984) — [ c.239 ]

Краткий курс теоретической механики 1970 (1970) — [ c.357 ]

Курс теоретической механики Том2 Изд2 (1979) — [ c.254 , c.258 ]

Прикладная газовая динамика Издание 2 (1953) — [ c.661 , c.704 ]

Космическая техника (1964) — [ c.399 , c.400 ]

---

Закон сохранения импульса — опредление, формулы, формулировка

Импульс: что это такое

Как-то раз Рене Декарт (это который придумал ту самую декартову систему координат) решил, что каждый раз считать силу, чтобы описать процессы — как-то лень и сложно.

Для этого нужно ускорение, а оно не всегда очевидно. Тогда он придумал такую величину, как импульс. Импульс можно охарактеризовать, как количество движения — это произведение массы на скорость.

Импульс тела → → p = mv p — импульс тела [кг*м/с] m — масса тела [кг] v — скорость [м/с]

Закон сохранения импульса

В физике и правда ничего не исчезает и не появляется из ниоткуда. Импульс — не исключение. В замкнутой изолированной системе (это та, в которой тела взаимодействуют только друг с другом) закон сохранения импульса звучит так:

Закон сохранения импульса Векторная сумма импульсов тел в замкнутой системе постоянна

А выглядит — вот так:

Закон сохранения импульса → → → p1 + p2 + … + pn = const p — импульс тела [кг*м/с]

Простая задачка

Мальчик массой m = 45 кг плыл на лодке массой M = 270 кг в озере и решил искупаться. Остановил лодку (совсем остановил, чтобы она не двигалась) и спрыгнул с нее с горизонтально направленной скоростью 3 м/с. С какой скоростью станет двигаться лодка?

Решение:

Запишем закон сохранения импульса для данного процесса.

→ → →
p0 = p1 + p2

p0 — это импульс системы мальчик + лодка до того, как мальчик спрыгнул,

p1 — это импульс мальчика после прыжка,

p2 — это импульс лодки после прыжка.

Изобразим на рисунке, что происходило до и после прыжка.

Если мы спроецируем импульсы на ось х, то закон сохранения импульса примет вид
0 = p1 — p2
p1 = p2

Подставим формулу импульса.
mV1 = MV2

Выразим скорость лодки V2:
V2 = mV1/M

Подставим значения:
V2 = 45*3/270 = 3/6 = ½ = 0,5 м/с

Ответ: скорость лодки после прыжка равна 0,5 м/с

Задачка посложнее

Тело массы m1 = 800 г движется со скоростью v1 = 3 м/с по гладкой горизонталь- ной поверхности. Навстречу ему движется тело массы m2 = 200 г со скоростью v2 = 13 м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение: Для данной системы выполняется закон сохранения импульса:

Импульс системы до удара — это сумма импульсов тел, а после удара — импульс «получившегося» в результате удара тела.

p1 + p2 = p.

Спроецируем импульсы на ось х:

p1 — p2 = p

После неупругого удара получилось одно тело массы m1 + m2, которое движется с искомой скоростью:

m1v1 — mv2 = (m1 + m2) v

Отсюда находим скорость тела, образовавшегося после удара:

v = (m1v1 — mv2)/(m1 + m2)

Переводим массу в килограммы и подставляем значения:

v = (0,8·3−0,2·13)/(0,8 + 0,2) = 2,4 — 2,6 = -2,6 м/с

В результате мы получили отрицательное значение скорости. Это значит, что в самом начале на рисунке мы направили скорость после удара неправильно.

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси X. Это никак не влияет на значение получившееся значение.

Ответ: скорость системы тел после соударения равна v = 0,2 м/с.

Второй закон Ньютона в импульсной форме

Второй закон Ньютона в импульсной форме можно получить следующим образом. Пусть для определенности векторы скоростей тела и вектор силы направлены вдоль одной прямой линии, т. е. движение прямолинейное.

Запишем второй закон Ньютона, спроецированный на ось х, сонаправленную с направлением движения и ускорением:

a = F/m

Применим выражение для ускорения

a = Δv/Δt

В этих уравнениях слева находится величина a . Так как левые части уравнений равны, можно приравнять правые их части

F/m = Δv/Δt

Полученное выражение является пропорцией. Применив основное свойство пропорции, получим такое выражение:

F⋅Δt = Δv⋅m

В правой части находится Δv =v —v0 — это разница между конечной и начальной скоростью.

Преобразуем правую часть

Δv⋅m = (v —v0)⋅m

Раскрыв скобки, получим

Δv⋅m= v ⋅m—v0⋅m

Заменим произведение массы и скорости на импульс:

v⋅m=p

v0⋅m=p0

Подставляем:

Δv⋅m=p —p0

p —p0 =Δp

Или, сокращенно:

Δv⋅m=Δp

То есть, вектор Δv⋅m – это вектор Δp.

Тогда второй закон Ньютона в импульсной форме запишем так

F⋅Δt =Δp

Вернемся к векторной форме, чтобы данное выражение было справедливо для любого направления вектора ускорения.

→
F⋅Δt =Δp⃗

Задачка про белку отлично описывает смысл второго закона Ньютона в импульсной форме Белка с полными лапками орехов сидит на гладком горизонтальном столе. И вот кто-то бесцеремонно толкает ее к краю стола. Белка понимает законы Ньютона и предотвращает падение. Но как?

Решение:

Чтобы к белке приложить силу, которая будет толкать белку в обратном направлении от края стола, нужно создать соответствующий импульс (вот и второй закон Ньютона в импульсной форме подъехал).

Ну, а чтобы создать импульс, белка может выкинуть орехи в сторону направления движения — тогда по закону сохранения импульса ее собственный импульс будет направлен против направления скорости орехов.

Реактивное движение

В основе движения ракет, салютов и некоторых живых существ: кальмаров, осьминогов, каракатиц и медуз — лежит закон сохранения импульса. В этих случаях движение тела возникает из-за отделения какой-либо его части. Такое движение называется реактивным.

Яркий пример реактивного движения в технике — движение ракеты, когда из нее истекает струя горючего газа, которая образуется при сгорании топлива.

Сила, с которой ракета действует на газы, равна по модулю и противоположна по направлению силе, с которой газы отталкивают от себя ракету:

→ →
F1 = — F2

Сила F2 называется реактивной. Это та сила, которая возникает в процессе отделения части тела. Особенностью реактивной силы является то, что она возникает без взаимодействия с внешними телами.

Закон сохранения импульса позволяет оценить скорость ракеты.

mг vг = mр vр,
где mг — это масса горючего,

vг — скорость горючего,

mр — масса ракеты,

vр — скорость ракеты.

Отсюда можно выразить скорость ракеты:

vр = mг vг / mр

Скорость ракеты при реактивном движении vр = mг vг / mр mг — это масса горючего [кг] vг — скорость горючего [м/с] mр — масса ракеты [кг] v р — скорость ракеты [м/с]

Эта формула справедлива для случая мгновенного сгорания топлива. Мгновенное сгорание — это теоретическая модель. В реальной жизни топливо сгорает постепенно, так как мгновенное сгорание приводит к взрыву.

Что такое центробежные и центростремительные силы?

Центробежная сила повсеместно присутствует в нашей повседневной жизни, но так ли это, как мы думаем?

Мы испытываем это, когда поворачиваем на машине или когда самолет кренится в повороте. Мы видим это в цикле отжима стиральной машины или когда дети катаются на карусели. Однажды он может даже создать искусственную гравитацию для космических кораблей и космических станций.

Но центробежную силу часто путают с ее эквивалентом, центростремительной силой, потому что они очень тесно связаны – по сути, это две стороны одной медали.

Центростремительная сила определяется как «сила, которая необходима для удержания объекта, движущегося по изогнутой траектории и направленная внутрь к центру вращения», в то время как центробежная сила определяется как «кажущаяся сила, которую ощущает объект, движущийся по изогнутой траектории, которая действует наружу от центра вращения », согласно словарю Merriam Webster Dictionary.

Обратите внимание, что хотя центростремительная сила является действительной силой, центробежная сила определяется как кажущаяся сила. Другими словами, при вращении массы на струне струна оказывает на нее внутреннюю центростремительную силу, в то время как масса, кажется, оказывает на струну направленную наружу центробежную силу.

«Разница между центростремительной и центробежной силой связана с разными« системами отсчета », то есть с разными точками зрения, с которых вы что-то измеряете», – сказал Эндрю А. Гансе, физик-исследователь из Вашингтонского университета. «Центростремительная сила и центробежная сила – это на самом деле одна и та же сила, только в противоположных направлениях, потому что они воспринимаются из разных систем отсчета».

Если вы наблюдаете вращающуюся систему снаружи, вы видите направленную внутрь центростремительную силу, ограничивающую вращающееся тело круговой траекторией.Однако, если вы являетесь частью вращающейся системы, вы испытываете очевидную центробежную силу, отталкивающую вас от центра круга, хотя на самом деле вы чувствуете внутреннюю центростремительную силу, которая не дает вам буквально уйти по касательной. .

Силы подчиняются законам движения Ньютона

Эта кажущаяся внешняя сила описывается законами движения Ньютона. Первый закон Ньютона гласит, что «тело в состоянии покоя будет оставаться в покое, а тело в движении будет оставаться в движении, если на него не действует внешняя сила.2 / р.

Третий закон Ньютона гласит, что «на каждое действие есть равное и противоположное противодействие». Точно так же, как гравитация заставляет вас воздействовать на землю, кажется, что земля оказывает равную и противоположную силу на ваши ноги. Когда вы находитесь в ускоряющемся автомобиле, сиденье оказывает на вас прямую силу так же, как вы, кажется, оказывает на сиденье обратную силу.

В случае вращающейся системы центростремительная сила тянет массу внутрь по изогнутой траектории, в то время как масса, кажется, выталкивается наружу из-за своей инерции.Однако в каждом из этих случаев применяется только одна реальная сила, а другая – только кажущаяся сила.

Лабораторные центрифуги быстро вращаются и оказывают центростремительную силу на жидкости, такие как кровь, которые затем разделяются в зависимости от их плотности. (Изображение предоставлено Shutterstock)

Примеры центростремительной силы в действии

Центростремительная сила используется во многих приложениях. Один из них – моделировать ускорение космического запуска для обучения космонавтов.Когда ракета запускается впервые, она настолько загружена горючим и окислителем, что едва может двигаться. Однако по мере подъема он сжигает топливо с огромной скоростью, постоянно теряя массу. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, или F = ma.

В большинстве случаев масса остается постоянной. Однако у ракеты ее масса резко меняется, в то время как сила, в данном случае тяга ракетных двигателей, остается почти постоянной. Это приводит к тому, что к концу фазы наддува ускорение увеличивается в несколько раз по сравнению с ускорением нормальной силы тяжести.НАСА использует большие центрифуги, чтобы подготовить космонавтов к этому экстремальному ускорению. В этом случае центростремительная сила обеспечивается за счет того, что спинка сиденья толкает космонавта внутрь.

Другим примером приложения центростремительной силы является лабораторная центрифуга, которая используется для ускорения осаждения частиц, взвешенных в жидкости. Одним из распространенных способов использования этой технологии является подготовка образцов крови для анализа. Согласно веб-сайту Experimental Biosciences Университета Райса: «Уникальная структура крови позволяет очень легко отделить эритроциты от плазмы и других форменных элементов с помощью дифференциального центрифугирования.”

Под действием нормальной силы тяжести тепловое движение вызывает непрерывное перемешивание, которое предотвращает осаждение клеток крови из образца цельной крови. Однако типичная центрифуга может достигать ускорения, в 600–2000 раз превышающего нормальную силу тяжести. Это заставляет тяжелые эритроциты оседают на дне и расслаивают различные компоненты раствора на слои в соответствии с их плотностью.

Дополнительные ресурсы:

Эта статья была обновлена ​​10 мая 2019 года участником Live Science, Дженнифер Леман .

Центробежные силы – мягкое вещество

Автор Yuhang Jin, AP225 2011 Fall.

Введение

Центробежные силы обычно называют фиктивными силами (инерционными силами), возникающими во вращающейся системе отсчета. Центробежная сила представляет собой инерцию вращающегося тела и направлена ​​от центра оси вращения. Эта концепция может быть обобщена в лагранжевой механике, когда действуют обобщенные координаты. Иногда центробежные силы могут также обозначать силы реакции в ответ на центростремительные силы.

Общая формула центробежных сил как сил инерции

Когда движение тела изучается в неинерциальной системе отсчета, для удобства вводятся фиктивные силы [1]. Связь между скоростью в инерциальной системе отсчета и скоростью в системе, вращающейся с угловой скоростью $\backslash \; mathbf\; \backslash \; Omega$, задается как

$\backslash \; mathbf\; v\; =\; \backslash \; mathbf\; v\; ‘+\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; r$,

где $\backslash \; mathbf\; r\; ‘$ обозначает смещение во вращающейся рамке, $\backslash \; mathbf\; v$ абсолютную скорость (в инерциальной системе отсчета) и $\backslash \; mathbf\; v\; ‘$ скорость во вращающейся рамке.Точно так же отношение ускорения задается как

$\backslash \; mathbf\; a\; =\; \backslash \; mathbf\; a\; ‘+\; \backslash \; dot\; \{\backslash \; mathbf\; \backslash \; Omega\}\; \backslash \; times\; \backslash \; mathbf\; r’\; +\; 2\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; v\; ‘+\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; (\backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; r\; ‘)$.

Применяя второй закон механики Ньютона, мы имеем

$\backslash \; mathbf\; F\; =\; m\; \backslash \; mathbf\; a\; =\; m\; \backslash \; mathbf\; a\; ‘+\; m\; \backslash \; dot\; \{\backslash \; mathbf\; \backslash \; Omega\}\; \backslash \; times\; \backslash \; mathbf\; r’\; +\; 2m\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; v\; ‘+\; m\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; (\backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; r\; ‘)$,

и.е.

$m\; \backslash \; mathbf\; a\; ‘=\; \backslash \; mathbf\; Fm\; \backslash \; dot\; \{\backslash \; mathbf\; \backslash \; Omega\}\; \backslash \; times\; \backslash \; mathbf\; r’-2m\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; v’-m\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; (\backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; r\; ‘)$.

Следовательно, с точки зрения этой вращающейся системы отсчета, члены, отличные от $\backslash \; mathbf\; F$ в правой части уравнения, являются фиктивными силами. В частности, $-m\; \backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; (\backslash \; mathbf\; \backslash \; Omega\; \backslash \; times\; \backslash \; mathbf\; r\; ‘)$ называется центробежной силой, поскольку она направлена ​​наружу перпендикулярно к $\backslash \; mathbf\; \backslash \; Omega\; .Следовательно,\; центробежные\; силы\; пропорциональны\; расстоянию\; до\; оси\; вращения,\; а\; также\; квадрату\; угловой\; скорости\; вращающейся\; рамы.$

Центробежные силы как силы реакции

В некоторых случаях центробежные силы относятся к реактивным силам [2]. Движение вращающегося тела поддерживается центростремительной силой, создаваемой другим объектом. Согласно третьему закону ньютоновской механики, вращающееся тело оказывает на этот объект реактивную силу, называемую центробежной силой.

Приложения

Многие устройства используют центробежные силы, такие как центрифуги и центробежные насосы, которые нашли множество применений в промышленности и академических кругах. Центробежные силы также являются важным фактором в инженерном проектировании железных дорог, спутников и т. Д. В последнее время на космических станциях центробежные силы используются для уравновешивания гравитации, чтобы приблизиться к условиям невесомости.

Список литературы

[1] Грегори Р. Д., «Классическая механика», Cambridge University Press, 2006.

[2] Википедия о центробежных силах

Ключевое слово в ссылках:

Бумага на диске: уравновешивание капиллярного потока и центробежной силы

центростремительная сила и центробежная сила

центростремительная сила и центробежная сила, пара сила действия-противодействия, связанная с круговым движением. Согласно первому закону движения Ньютона, движущееся тело движется по прямой траектории с постоянной скоростью (т. Е. Имеет постоянную скорость), если на него не действует внешняя сила.Чтобы произошло круговое движение, на тело должна действовать постоянная сила, толкающая его к центру круговой траектории. Эта сила является центростремительной ( центростремительной и ) силой. Для планеты, вращающейся вокруг Солнца, сила гравитационная; для объекта, закрученного на веревке, сила механическая; для электрона, вращающегося вокруг атома, он электрический. Величина центростремительной силы F равна массе м тела, умноженной на квадрат его скорости v ² , деленному на радиус r его пути: F = mv ² / г. Согласно третьему закону движения Ньютона, на каждое действие существует равное и противоположное противодействие. Центростремительная сила, действие, уравновешивается силой противодействия, центробежной ( центробежной силы ). Две силы равны по величине и противоположны по направлению. Центробежная сила не действует на движущееся тело; единственная сила, действующая на движущееся тело, – это центростремительная сила. Центробежная сила действует на источник центростремительной силы, смещая его радиально от центра пути.Таким образом, при вращении массы на струне центростремительная сила, передаваемая струной, притягивает массу, удерживая ее на круговом пути, в то время как центробежная сила, передаваемая струной, тянет наружу в точке ее крепления в центре струны. дорожка. Часто ошибочно полагают, что центробежная сила заставляет тело вылетать со своего кругового пути, когда оно высвобождается; скорее, это устранение центростремительной силы, которая позволяет телу двигаться по прямой линии, как того требует первый закон Ньютона.Если бы на самом деле действовала сила, вынуждающая тело отклониться от его круговой траектории, его траектория при высвобождении не была бы прямым касательным курсом, который всегда наблюдается.

Колумбийская электронная энциклопедия, 6-е изд. Авторские права © 2012, Columbia University Press. Все права защищены.

Дополнительные статьи в энциклопедии: Physics

Центростремительная сила, вес, напряжение

и экваториальная выпуклость Земли. Дональд Э.Симанек

Заявление об ограничении ответственности: Этот документ, как и многие другие на этом веб-сайте, является попыткой донести информацию сложная физика на языке, максимально простом, концептуальном и нематематическом. Это, конечно, трудный способ сделать это. Если бы мы использовали полномасштабное векторное исчисление аргументы могли бы быть намного компактнее и точнее. Читатель сильно настоятельно рекомендовал проконсультироваться по таким методам лечения в хороших учебниках.

Центростремительная сила.

Ускорение тела – это изменение его скорости, деленное на длительность этого изменения. a = ΔV / Δt . Поскольку скорость является вектором, любое изменение ее размера или направления , или обоих, требует ускорения. Тело, движущееся по кривой траектории, ускоряется, даже если его скорость постоянна. Следовательно, из закона Ньютона мы знаем, что результирующая сила, действующая на него, не равна нулю.

На схеме показано тело, движущееся с постоянной скоростью V по криволинейной траектории радиусом R . Показаны два положения, во время которых тело переместилось на расстояние S по дуге. В начале временного интервала скорость тела равна В ₁ . В конце интервала это V ₂ . Мы даем им отличительные индексы, потому что они имеют разные направления, даже хоть они и имеют одинаковый размер.За это время тело перемещается на угол на . На справа показана векторная диаграмма связи между этими скоростями и их векторной разностью: ΔV .

Теперь рассмотрим предельный случай, когда временной интервал становится очень маленьким, приближаясь к нулю. Угол также приближается к нулю. На диаграммах есть два одинаковых, очень тонких треугольника. Мы можем написать:

ΔS / R = ΔV / V

Итак: V δS = R ΔV

и: В (ΔS / Δt) = R (ΔV / Δt) .

Но В = ΔS / Δt , и a = ΔV / Δt , поэтому мы можем написать:

V ² = R a , что становится a = V ² / R .

Поскольку угловая скорость тела, движущегося по окружности, равна ω = VR , мы можем записать это ускорение как a = ω ² R . (Эти формулы полезны даже в тех случаях, когда тело движется по извилистой траектории с разными скоростями.В этом случае мы интерпретируем R, V и ω как мгновенные значения () этих величин в заданной точке.)

Из закона Ньютона F = м a мы можем сказать, что сила, вызывающая ускорение, равна F = mV ² / R = mω ² R .

Направление вектора ускорения и силы в любой момент направлено внутрь к центру дуги и, следовательно, перпендикулярно вектору скорости в этот момент, который всегда касается кривой.

В случае извилистого движения мы можем связать эту силу и ускорение с внутренней (радиальной) составляющей любой результирующей силы, действующей на тело (массой м ). Пока это простая физика. Концептуальная проблема возникает, когда мы даем этим силам и ускорениям названия: центростремительное ускорение и центростремительная сила .

Центростремительная сила – это не какой-то новый вид силы, а просто удобное название радиальной составляющей суммы всех реальных сил, действующих на тело.

Более полное рассмотрение показало бы, что это уравнение центростремительной силы полезно для любого вида движения по кривой любого вида. Это не ограничивается кругами. Он также не ограничен постоянной скоростью по пути. Это работает, потому что любой физический путь таков, что достаточно малая его часть очень хорошо аппроксимирует круговую дугу. В расчетах мы берем предел, когда дуга становится нулевой длины, и говорим о связи между мгновенным радиусом дуги в этой точке кривой, мгновенной скоростью в этой точке и мгновенным ускорением в этой точке.Соотношение по-прежнему оказывается a = V ² / R . И если чистая сила имеет касательную к дуге составляющую, это вызывает увеличение или уменьшение скорости тела по этой дуге.

Напряжение.

Упругие тела могут деформироваться под действием приложенных сил. Силы связи, удерживающие молекулы в положении равновесия в твердых и жидких телах действует нечто вроде пружин. Если пружина растягивается, растягивая молекулы дальше друг от друга, эти силы связи увеличиваются в размере.Они также увеличиваются в размере, когда молекулы сближаются. Мы можем смоделировать это поведение, как показано на рисунке, с пружиной, представляющей такой силы, действующие между кусками материи. Для наших ограниченных целей мы можем предположить, что Пружина по поведению примерно гуковская, то есть подчиняется закону Гука. В Закон говорит, что натяжение пружины T изменяется на величину ΔT = – KΔL где k – постоянная упругости пружины, а ΔL – изменение его длины, измеренное от его исходного положения.Если напряжение увеличивается, длина пружины уменьшается. Если натяжение уменьшается, пружина длина увеличивается.

Предположим, что масса самой пружины ничтожно мала по сравнению с массой двух блоков материи. Следовательно, натяжение пружины оказывает равное усилие. размер на каждом из них, как показано.

F ₂ и F ₁ представляют собой силу тяжести на верхних и нижних блоках.В равновесии нижний блок должен испытывать восходящую силу F ₁ + F ₂ (от того, что поддерживает его снизу). Если бы они были равны по размеру, то для равновесия натяжение T также будет такого же размера.

Теперь предположим, что верхний блок стал меньше по массе. Натяжение пружины должно стать пропорционально меньшим для достижения статического равновесия. Поэтому длина пружины должна увеличиваться, немного разделяя два блока.

То же самое произошло бы, если бы было некое дополнительное неоднородное гравитационное поле. прикладывалась к системе, так что она оказывала большую направленную вниз силу на нижний блок, чем на верхний. Натяжение пружины уменьшится, а ее длина увеличится. Но что, если такое внешнее поле вызовет более сильную направленную вверх силу на верхний блок, чем на нижнем? Опять же, натяжение пружины уменьшится, и ее длина уменьшится. увеличивать.Это становится важным, когда обсуждают земные приливы из-за неоднородной гравитационной поля с Луны.

Масса.

Вес может быть определен как сила, необходимая для удержания объекта в относительном состоянии покоя. к его окрестностям. Это определение согласуется с большинством разговорных толкований. слова (сюрприз!).

На рисунке изображен человек массой м , стоящий на весах на поверхности. земли.Весы воздействуют вверх на его ступни силой Вт . Мы называем эту шкалу чтение «веса» человека. Если бы Земля была неподвижной, человек бы быть в равновесии, и у нас будет W = mg , где mg – сила тяжести на мужчину.

Думайте о масштабах как о пружине между массами. Он реагирует на стресс между ноги и пол.

Влияние вращения Земли на вес.

Но если Земля вращается, человек, весы и земля под ней движутся с скорость V по круговой траектории радиусом R , где R – радиус Земли.Эти объекты больше не находятся в статическом равновесии. У всех есть ускорение a = v ² / R к центру Земли. Это центростремительное ускорение изменяет направление скорости, но не меняет своего размера, потому что вектор ускорения всегда направлен к центру круга и, следовательно, перпендикулярно к телу скорость в любое время.

Размер человека относительно радиуса Земли на этой диаграмме сильно преувеличен.Относительные размеры сил тоже.

Закон Ньютона говорит нам, что когда тело массы m имеет ускорение a , чистая сила на корпусе должна составлять F = м a . Таким образом, величина чистой силы, действующей на этого человека, должна быть F = ma = mv ² / R .

На рисунке показаны векторы силы W и м g , которые являются только силы действуют на человека.Вектор F и есть их сумма. W направлена ​​по радиусу Земли. Являясь радиальным компонентом чистой силы (в данном случае это – это чистая сила), ее размер составляет a = v ² / R (центростремительная сила). Теперь сравните эти два случая. На невращающейся Земле вес человека был размером м г . Помните, что вес объекта – это сила, необходимая для его поддержки. я.е. усилие, прилагаемое весами вверх. Когда Земля вращается, это усилие меньше, чем раньше на . Сила контакта между ногами мужчины и масштаб уменьшен. Но все другие подобные стрессовые силы также снижаются внутри человека, в пружинах весов, в теле самой Земли. Это вызывает небольшой декомпрессия этих материалов, расслабление пружины в весах. По факту, все тело земли немного расширяется, и человек и чешуя перемещаются наружу немного от оси вращения, пока силы не придут в равновесие с требованиями вращательной устойчивости на новом радиусе.Это причина экваториальной выпуклости. Земли из-за собственного осевого вращения.

Как мы уже говорили, диаграммы сильно преувеличены. Несложный расчет показывает, что центростремительный разгон всего 0,3% от г. . Таким образом, полезная сила составляет всего 0,3% от Вт . Вес мужчины (учтенный на весах) на 0,3% меньше, чем был бы на один вес. полюсов Земли. Результирующая релаксация напряжений в материалах является причиной экваториальной выпуклости Земля, что делает экваториальный радиус на 43 километра больше полярного.

Дихотомия “причина и следствие”.

Здесь мы можем столкнуться с сложной дилеммой интерпретации. Снижение веса на экватора просто из-за меньшей гравитационной силы на большем радиусе? Либо это просто из-за уменьшения напряжения между ступней и весами? Это еще один неудачное следствие использования языка “причина и следствие” в чем-то, что слишком сложно для такого упрощенного описания. Это также ловушка для учителей, которые позируют вопросы с несколькими вариантами ответов на экзаменах.

Предположим, кто-то говорит, что снижение веса произошло исключительно из-за увеличения радиуса. экватора и немного меньшего гравитационного поля на большем радиусе. Тогда, если бы Земля была идеально твердой и не было бы экваториальной выпуклости, из этого можно сделать логический вывод, что, поскольку радиус не меняется, то вес (зарегистрированный на весах) не меняется. Но это ложь. Вес уменьшится, как и должно быть, из-за радиального ускорения из-за кругового движения и закона Ньютона F = м a .

Если кто-то говорит, что снижение веса связано с уменьшением стресса вызванное растяжением материалов Земли, масштаба и человека, мы должны согласиться, это то, что измеряет механизм весов, и это наше определение веса. Но это снижение стресса также является причиной растяжения. Земли, и для увеличенного радиуса на экваторе. А это, в свою очередь, уменьшает гравитационная сила, создаваемая Землей на большем расстоянии.Суть в том, что сила тяжести уменьшается, а напряжение уменьшается, , но не пропорционально . Сказать, что только одна из этих вещей является «причиной» любой другой, слишком упрощенно. быть полезным. И попытаться объяснить экваториальную выпуклость без упоминания снижение напряжения в материалах – это своего рода обман.

Здесь нужна «центробежная сила»?

Обратите внимание, что в этом обсуждении нам никогда не приходилось вводить термин «центробежная сила».Этот термин полезен только тогда, когда кто-то решает анализировать проблему с использованием вращающейся неинерциальной системы отсчета.

Неинерциальные системы координат

«Инерциальная» система координат не ускоряется. Как мы можем быть уверены, что система координат не ускоряется, когда кажется, что все во Вселенной движется и ускоряется под действием гравитатональных сил других тел? Один из способов – определить все реальные силы, действующие на тело. Если их векторная сумма на теле равна нулю, то тело не ускоряется.Другое определение «инерциальной системы отсчета» – это система отсчета, при которой тело, закрепленное в этой системе координат, строго подчиняется второму закону Ньютона: F = м a .

Но инерционные системы очень редки. Мы действительно сталкиваемся со многими ситуациями, когда «для всех практических целей» система кажется инерциальной системой отсчета. На поверхности Земли лабораторию часто можно рассматривать как инерциальную систему отсчета для чистого ускорения комнаты, поскольку она переносится осевым вращением Земли и ее вращением вокруг Солнца, а также движением солнечной системы в галактике. , так далее., очень мало по сравнению с большими ускорениями, которые мы изучаем. Мы действительно включаем эффект осевого вращения, «корректируя» гравитационную силу, чтобы включить центростремительное ускорение. И если мы имеем дело с очень крупномасштабными движениями воздуха и воды, мы должны также включить эффекты Кориолиса из-за ускорения нашей системы отсчета.

Это сводится к тому, что если чистая сила, действующая на тело в нашей системе отсчета F _{net, действительная} = м a + F _extra , мы пытаемся определить этот дополнительный член силы, а затем вычтите его из «реальных» сил и продолжайте использовать эту «исправленную» форму законов Ньютона.Это эквивалентно определению -F _extra как «фиктивной» силы, добавлению этого к действительному силовому члену и, таким образом, сохранению закона Ньютона, используя его «как если бы» мы решали задачу в инерциальной системе отсчета.

В системе отсчета, центрированной в центре Земли и вращающейся вместе с Землей, одна из этих фиктивных сил, действующих на тело на поверхности земли, называется «центробежной» силой. Это просто отрицательная сила центростремительной силы, действующей на это тело.Он направлен наружу от центра Земли. Другими важными силами на поверхности Земли являются силы Кориолиса, которые имеют большое значение при работе с огромными массами воздуха или воды в метеорологии, океанографии и баллистике на большие расстояния.

Эта длинная преамбула приводит к часто задаваемому вопросу. «Когда мы используем термин центростремительная сила, означает ли это, что мы решаем задачу в неинерциальной системе отсчета?» Нет, это не так. Напротив, центростремительная сила, действующая на объект, – это просто радиальная составляющая суммы действительных сил на него.«Центростремительная сила» используется в первую очередь, когда мы решаем задачу, в которой что-то движется по орбите вокруг фиксированной точки, и мы используем фиксированную (инерциальную) систему координат с центром в этой точке. Мы можем знать, что если векторная сумма всех сил, действующих на тело, зафиксированное в этой системе отсчета, действительно добавляется к нулю. Планетарные орбиты – хороший тому пример. Обычно в этих случаях мы используем инерциальную полярную систему координат.

Но когда мы решаем зафиксировать нашу систему координат на теле, которое, как мы знаем, ускоряется, так что координаты также ускоряются (возможно, претерпевают и вращение, и линейное ускорение), тогда мы обнаруживаем, что действительные силы, которые мы измеряем, действующие на тело, закрепленное в этом (движущаяся) рамка делать , а не прибавлять к нулю.

Большая часть путаницы в отношении приливов возникает из-за того, что мы не можем указать, принимаем ли мы инерциальную систему отсчета или ускоряющуюся систему отсчета. Это также может возникнуть из-за того, что инерциальные системы отсчета могут быть либо декартовыми, либо полярными. Полярные координаты не ограничиваются вращающимися кадрами.

Приложение и резюме

Вопросы о центростремительной и центробежной силе наверняка вызовут споры среди учителей физики, и я сам испытываю к этому сильные чувства.

В Википедии есть две страницы, на которые стоит обратить внимание: Центробежная сила. Обязательно перейдите по ссылке «Центробежная сила (вращающаяся система отсчета)».

Центростремительная сила определяется как радиальная составляющая чистой силы, действующей на тело, когда положение тела представлено в полярной системе координат (координаты представляют собой радиус от фиксированного центра и угол от фиксированного опорного угла). Это просто метка, позволяющая отличить радиальную составляющую от тангенциальной составляющей чистой силы.Но это полезное имя, поскольку оно фигурирует в очень полезном уравнении: F = m v ² / r . Это уравнение не является физическим законом. Это определение.

Центростремительная сила, являющаяся составной частью общей силы, действующей на тело, является «реальной» силой. Реальные силы – это силы, действующие на тело из-за других идентифицируемых материальных объектов: гравитация, электрическое притяжение и отталкивание, магнитные силы, контактные силы (деформация от контакта, а также силы из-за трения и сопротивления качению).

В школьных учебниках иногда можно встретить центробежную силу, «определяемую» как силу реакции на центростремительную силу. Я страстно осуждаю эту вводящую в заблуждение идею, поскольку она ни для чего не нужна и бесполезна. Более того, это вызывает беспокойство и замешательство, когда студенты идут в колледж и изучают определение центробежной силы, используемой при работе с вращающимися системами отсчета.

Почему? Силы реакции определяются в физике третьим законом Ньютона. Сила, которую тело B оказывает на тело A, равна по размеру и противоположна по направлению силе, которую A оказывает на B. Эти силы иногда называют «силами реакции», но из этого определения ничего не следует понимать. Важным моментом является то, что две силы в этом законе действуют на различных тела . Таким образом, в случае качания массы по кругу центростремительная сила – это натяжение струны, действующей внутрь на массу. Сила реакции на это – это сила, которую масса оказывает на струну.Эти двое равны по размеру и противоположны по направлению.

Но учебники, злоупотребляющие этой физикой, заявляют, что сила противодействия центростремительной силе, действующей внутрь на массу, – это центробежная сила, направленная наружу, которую ось (ось вращения) оказывает на струну в центре круга. Если тело A является осью вращения, S – струной, а M – массой, это не соответствует определению третьего закона Ньютона. Ось не оказывает силы на массу; строка делает. Масса не оказывает силы на ось; строка делает.Эта интерпретация полностью игнорирует строку. Для этого может быть оправдание. В задачах, где струна имеет незначительную массу по сравнению с другими элементами в системе, струна в идеале рассматривается как масса нулевого размера. В учебниках инженерного дела это иногда называют «осевой центробежной силой», «реактивной центробежной силой» или «центробежной инерционной реакцией».

Вращающиеся системы отсчета полезны, они используются инженерами-механиками и астрономами или кем-либо, кто должен делать фактические вычисления на основе данных, измеренных во вращающихся системах отсчета.Это практическая стратегия, поскольку преобразование данных в инерциальную систему отсчета перед выполнением физики было бы утомительным и неудобным. Центробежная сила – это фиктивная сила, используемая для упрощения таких расчетов. Этот подход редко используется во вводных курсах, поэтому лучше не упоминать его там. Тем не менее, он нравится наивным студентам (и некоторым авторам учебников), потому что кажется, что он соответствует ощущению «выброшенного наружу», когда кто-то находится на вращающейся платформе, как на карусели, или в автомобиле, движущемся по крутому повороту. .Это «приятное» объяснение для студентов, которым никогда не придется выполнять какие-либо серьезные вычисления, используя эту концепцию.

На самом деле, то, что человек чувствует в такой ситуации, является результатом того, что автомобиль оказывает силу, перпендикулярную вашему движению, которая заставляет ваше собственное движение отклоняться от движения по прямой и превращаться в изогнутую траекторию. Это физиологическое ощущение. Но это, конечно, возникает из-за реальных сил давления в вашем теле, стимулирующих нервы. Эти сенсорные ощущения указывают только на размер сил, но не на их направление.

Центробежная сила – это не реальная сила, действующая на тело из-за какого-либо другого физического объекта. Вот почему мы называем это «фиктивной силой». Решение задачи во вращающейся системе координат не меняет физику задачи. Природе все равно, какую систему координат мы выберем.

Любая задача, решаемая во вращающейся системе координат, может быть решена в фиксированной системе координат без использования концепции центробежной силы. Результаты, полученные двумя методами, конечно, должны быть идентичными.

Предупреждение: полярная система координат может быть фиксированной инерциальной системой координат. Вращающаяся система координат может быть полярной или декартовой. «полярный» и «вращающийся» не синонимы.

Если выбранные вами координаты не вращаются, термин «центробежная сила» не подходит. Если вы не знаете, вращаются ли ваши координаты, вам необходимо изучить основы, чтобы выяснить это, потому что, если вы продолжите, не зная этого факта, у вас есть 50-50 шансов испортить проблему, и любая попытка ее обсудить. приведет к путанице для всех.

Ньютон F = м применяется только в инерциальных (фиксированных, неускоряющих) системах координат. Другими словами, слово «инерциальная» применимо к любой системе координат, для которой верен закон Ньютона. Это также означает «любая система координат, которая не ускоряется». Система координат, движущаяся с ускорением, является неинерциальной системой.

Когда вы решаете задачу во вращающейся неинерциальной системе, вы должны изменить закон Ньютона так, чтобы он читался как F _{реальный} + F _{центробежный} + F _{Кориолис} = m a , где F _{центробежный} и F _Coriolis являются фиктивными «корректирующими» силами для компенсации использования неинерциальной системы координат и представляют собой силы , а не из-за физического воздействия других реальных объектов.(Во вращающейся системе координат , ускоряющей , нужно добавить еще одну фиктивную силу, «силу Эйлера».)

Многие дискуссии, которые я вижу по этому поводу в Интернете, часто являются необдуманными мнениями, которые люди предлагают, не глядя на более широкую картину. Действительно, многие учителя не имели достаточной информации об этом в колледжах и университетах. Обычно он занимает главу в университетском курсе классической механики под названием «Неинерциальные системы». Хорошую трактовку можно найти в превосходной (и классической) книге Джерри Мариона «Классическая динамика частиц и систем» (Academic Press, 1965, и более поздние издания).См. Главу 12 «Движение в неинерциальной системе отсчета». Это должно быть в любой хорошей университетской библиотеке. В Соединенных Штатах (ненавижу признавать) большинство учителей средней школы никогда не проходили такой курс, поэтому совершенно невиновны в стандартных методах решения задач в неинерциальной системе отсчета Земли (часто используемых в гидродинамике океана и метеорологии как а также в дальнобойной баллистике ракет и космических аппаратов) и в астрофизике. Инженеры также используют эти методы при работе с гироскопическими эффектами.

---

Последняя редакция, апрель 2020 г.

---

Вернитесь к Приливным заблуждениям.

Вернитесь на главную страницу Дональда Симанека.

Что такое сила реакции? – Определение из Corrosionpedia

Что означает сила реакции?

Сила противодействия – это сила, которая действует в направлении, противоположном действующей силе. Трение – это сила реакции, возникающая в результате взаимодействия поверхностей и сцепления во время скольжения.Силы реакции и момент реакции обычно являются результатом действия приложенных сил.

Когда силы реакции превышают силы действия, может произойти разрушение конструкции, которое может привести к разрушению, а также к коррозии.

Corrosionpedia объясняет силу реакции

Сила реакции – это сила, приложенная к конструкции, когда она опирается на что-то. При анализе балочной конструкции необходимо вычислить силы реакции на опорах из-за сил, действующих на балку.Схема свободного тела всей балки может использоваться для определения сил реакции.

Балка обладает вертикальными и горизонтальными силами реакции, а также реакционным моментом. Горизонтальная сила реакции равна нулю, пока нет приложенных горизонтальных сил. Консольная балка с одинарной опорой имеет силу реакции и момент реакции. Сила реакции равна сумме сил, приложенных к балке. Если балка сидит на ролике, который позволяет балке свободно перемещаться по горизонтали, ее опора имеет только вертикальную силу реакции.

При сжатии (или любом другом типе напряжения) каждый материал претерпевает некоторую деформацию, даже если она незаметна, что вызывает изменение среднего относительного положения его атомов и молекул. Деформация может быть постоянной или может быть обращена вспять, когда силы сжатия исчезнут. В последнем случае деформация вызывает силы реакции, противодействующие силам сжатия, и в конечном итоге может уравновесить их. Жидкости и газы не могут выдерживать устойчивого одноосного или двухосного сжатия – они деформируются быстро и необратимо и не создают постоянной силы реакции.

Силы реакции могут вызвать коррозию, например, силы реакции подшипников увеличиваются при уменьшении зазоров подшипников с 350 мм до 150 мм из-за повышенной жесткости системы. Силы реакции соотносятся со сжатием различных материалов сердцевины подшипников. Это может вызвать повреждение стержней и отслоение лицевых панелей.

Фермилаб | Наука | Пытливые умы

Вопросы по физике, которые задают люди Фермилаб

Центростремительная или центробежная сила?

Вы написали:
Недавние дебаты закончились ничьей.Это было связано с центробежной силой или ее отсутствием. Обе стороны аргумента выступают за и против этого общего правила физики. Центростремительная сила была единственной силой, действующей на вращающиеся объекты, заявил один из судебных исков. Мой вопрос к вам: существует ли центробежная сила или ее не существует?

Большое спасибо
Ученый-посредник

---

Привет,

спасибо за вопрос, вы правы, немного сложно выяснить, какие силы вызвали данное движение.В своем объяснении я предполагаю, что вы знаете, что такое инерциальные и неинерциальные системы. (Инерционный = движение с постоянной скоростью [включая скорость = 0], неинерциальный = движение с ускорением.) Они будут играть очень важную роль, чтобы различать центростремительные и центробежные силы. (Как видите, я уже сказал вам, что в физике существуют обе силы.)

1) Сядем в ИНЕРЦИОННУЮ систему. Предположим, у нас есть два маленьких шара (маленьких, чтобы исключить их гравитационное взаимодействие).Первый (шар A) покоится в начале координат, а второй (шар B) движется с ПОСТОЯННОЙ СКОРОСТЬЮ в произвольном направлении. (Но НЕ по направлению к центру шара A.) Поскольку B движется с постоянной скоростью, закон Ньютона гласит, что на B нет силы, поэтому он движется по прямой.

1a) Представьте, что мы заряжаем A положительным зарядом, а B – отрицательным. Теперь ситуация кардинально меняется, поскольку на B действует сила A. Эта сила является электрической силой, и направление силы направлено к центру A.Мы говорим, что сила имеет центростремительное направление. НЕТ ДРУГИХ СИЛ, ДЕЙСТВУЮЩИХ НА B! (Заметьте, я еще ничего не сказал о силах, действующих на A. Шар A просто сидит в начале координат, будучи там плотно приклеен). Согласно законам Ньютона (а также согласно вашему повседневному опыту) шар B начинает ВРАЩАТЬСЯ вокруг мяч A и будет делать это, пока не подействует электрическая сила. Это так просто.

2a) Вышеупомянутый мысленный эксперимент можно применить к другим ситуациям. Упомяну несколько.В скобках указываю соответствие с 1а.

• шарик (B) на конце веревки (электрическая сила), вращающийся вокруг вашей руки (A)
• Луна (B) вращается вокруг Земли (A). Вращение вызвано гравитационной силой (электрическая сила).
• автомобиль с американскими горками (B) в круговой петле (A), где центростремительная сила – это сила, действующая петлей на автомобиль,
• школьный автобус (B) на перекрестке с поворотом налево.Дорога является аналогом мяча А, а сила трения между дорогой и шинами – аналогией электрической силы.
• еще много примеров, когда у вас есть объекты в круговом движении.

Теперь мы понимаем, что центростремительная сила, действующая на B, вызывает его круговое движение. Но где центробежная сила ??? Что это? Третий закон Ньютона гласит: если A действует на B посредством силы, B действует на A посредством другой силы, называемой силой реакции, которая имеет ту же величину, но в противоположном направлении.Многие люди путают центробежную силу с этой силой реакции, действующей НА A BY B. (В качестве иллюстрации силы реакции просто помните, что если вы вращаете шар (B) на конце веревки, ваша рука (A) ЧУВСТВУЕТ сила, которая представляет собой силу реакции на центростремительную силу.) Пожалуйста, помните, эта сила реакции не является центробежной силой, введенной физиком. Реагирующая сила не действует на B. Давайте сейчас раскроем эту тайну.

2) Чтобы объяснить понятие центробежной силы, я действую аналогично пункту 1), но давайте теперь представим, что мяч B движется в школьном автобусе, который первоначально движется с постоянной скоростью.Пусть мяч B неподвижно сидит на полу автобуса. Посмотрим, что мы наблюдаем из системы координат автобуса. Первоначально шина была инерциальной системой, но когда автобус поворачивает налево, она становится НЕИНЕРЦИАЛЬНОЙ системой (потому что она ускоряется). Наблюдатель в автобусе видит, что мяч B изначально находится в состоянии покоя, но внезапно (когда автобус начинает разворачиваться) мяч начинает катиться. Таким образом, наблюдатель ДОЛЖЕН ПРИНЯТЬ К ВЫВОДУ, что на мяч действует сила. Если он внимательно наблюдает, то видит, что мяч двигался в радиальном направлении (от центра кривой).Наблюдатель называет эту силу центробежной силой. Однако, как вы, наверное, догадались, эта сила не является реальной силой, мяч движется из-за первого закона инерции Ньютона. Он продолжает двигаться прямо по отношению к любой ИНЕРЦИОННОЙ СИСТЕМЕ, как это было до того, как автобус начал разворачиваться. Центробежная сила возникла исключительно из-за описания мяча с использованием «неправильной», НЕИНЕРЦИАЛЬНОЙ системы отсчета. Конечно, когда мяч ударяется о стенку автобуса, его движение начинает ускоряться центростремительной силой, с помощью которой стена воздействует на мяч.Он повернется вместе с автобусом.

С вышесказанным связано очень интересное явление. В северном полушарии из-за вращения Земли пуля из ружья имеет тенденцию отклоняться вправо. (Что касается направления, в котором был произведен выстрел.) Сила, вызывающая это, называется силой Кориолиса, но это тема для другой истории.

– пока,
Арнольд Помпос

Вернуться на главную страницу вопросов о физике

6.3 Центростремительная сила – Университетская физика, том 1

Цели обучения

К концу раздела вы сможете:

• Объясните уравнение центростремительного ускорения
• Примените второй закон Ньютона, чтобы получить уравнение для центростремительной силы
• Используйте концепции кругового движения при решении задач, связанных с законами движения Ньютона

В «Движении в двух и трех измерениях» мы изучили основные концепции кругового движения.Объект, совершающий круговое движение, например один из гоночных автомобилей, показанных в начале этой главы, должен ускоряться, потому что он меняет направление своей скорости. Мы доказали, что это центрально направленное ускорение, называемое центростремительным ускорением , выражается формулой

.

, где v – скорость объекта, направленная по касательной к кривой в любой момент времени. Если мы знаем угловую скорость

, тогда мы можем использовать

Угловая скорость показывает скорость, с которой объект поворачивает кривую, в рад / с.Это ускорение действует по радиусу криволинейной траектории и поэтому также называется радиальным ускорением.

Ускорение должно производиться силой. Любая сила или комбинация сил могут вызвать центростремительное или радиальное ускорение. Вот лишь несколько примеров: натяжение троса на тросовом шаре, сила притяжения Земли на Луне, трение между роликовыми коньками и полом катка, сила наклона проезжей части, действующая на автомобиль, и силы, действующие на трубу вращающейся центрифуги. . Любая чистая сила, вызывающая равномерное круговое движение, называется центростремительной силой .Направление центростремительной силы – к центру кривизны, то же самое, что и направление центростремительного ускорения. Согласно второму закону движения Ньютона, чистая сила равна массе, умноженной на ускорение:

Для равномерного кругового движения ускорением является центростремительное ускорение: _.

Таким образом, величина центростремительной силы

это

Подставляя выражения для центростремительного ускорения

получаем два выражения для центростремительной силы

по массе, скорости, угловой скорости и радиусу кривизны:

Вы можете использовать любое более удобное выражение для центростремительной силы.Центростремительная сила

всегда перпендикулярно траектории и указывает на центр кривизны, потому что

перпендикулярно скорости и указывает на центр кривизны. Обратите внимание, что если вы решите первое выражение для r , вы получите

Это означает, что для данной массы и скорости большая центростремительная сила вызывает малый радиус кривизны, то есть резкую кривую, как на (Рисунок).

Рисунок 6.20. Сила трения обеспечивает центростремительную силу и численно равна ей. Центростремительная сила перпендикулярна скорости и вызывает равномерное круговое движение. Чем больше

, тем меньше радиус кривизны r и круче кривизна. Вторая кривая имеет то же v, но большее значение

.

дает меньшее r ‘.

Пример

Какой коэффициент трения нужен автомобилям на плоской кривой?

(a) Рассчитайте центростремительную силу, действующую на 900.Автомобиль массой 0 кг, который преодолевает поворот радиусом 500,0 м со скоростью 25,00 м / с. (b) Предполагая, что кривая без кренована, найдите минимальный статический коэффициент трения между шинами и дорогой, при этом статическое трение является причиной, препятствующей скольжению автомобиля ((Рисунок)).

Рисунок 6.21 Этот автомобиль на ровной поверхности движется в сторону и поворачивает налево. Центростремительная сила, заставляющая автомобиль вращаться по круговой траектории, возникает из-за трения между шинами и дорогой. Требуется минимальный коэффициент трения, иначе автомобиль будет двигаться по кривой с большим радиусом и съезжать с проезжей части.

Стратегия

1. Мы знаем, что

   Таким образом,

2. (рисунок) показывает силы, действующие на автомобиль на кривой без кренов (ровной поверхности). Трение направлено влево, предотвращая скольжение автомобиля, и, поскольку это единственная горизонтальная сила, действующая на автомобиль, трение в данном случае является центростремительной силой. Мы знаем, что максимальное статическое трение (при котором шины катятся, но не скользят) составляет

   где

   – статический коэффициент трения, а Н, – нормальная сила.Нормальная сила равна массе автомобиля на ровной поверхности, поэтому

   Таким образом, центростремительная сила в данной ситуации равна

   .

   Теперь у нас есть связь между центростремительной силой и коэффициентом трения. Используя уравнение

   получаем

   Решаем это за

   , отмечая, что масса отменяется, и получаем

   Подстановка известных,

   (Поскольку коэффициенты трения являются приблизительными, ответ дается только двумя цифрами.)

Значение

Коэффициент трения, указанный на (Рисунок) (b), намного меньше, чем обычно наблюдается между шинами и дорогой. Автомобиль все еще движется по кривой, если коэффициент больше 0,13, потому что трение покоя является реактивной силой, которая может принимать значение меньше, но не больше

.

Более высокий коэффициент также позволит автомобилю преодолевать поворот на более высокой скорости, но если коэффициент трения меньше, безопасная скорость будет менее 25 м / с.Обратите внимание, что масса отменяется, подразумевая, что в этом примере не имеет значения, насколько сильно загружена машина для прохождения поворота. Масса сокращается, потому что трение считается пропорциональным нормальной силе, которая, в свою очередь, пропорциональна массе. Если бы поверхность дороги была наклонной, нормальная сила была бы меньше, как обсуждается далее.

Проверьте свое понимание

Автомобиль, движущийся со скоростью 96,8 км / ч, движется по круговой кривой радиусом 182,9 м по ровной проселочной дороге. Какой должен быть минимальный коэффициент статического трения, чтобы автомобиль не скользил?

[показать-ответ q = ”694795 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 694795 ″] 0.40 [/ hidden-answer]

Наклонные кривые

Давайте теперь рассмотрим кривых с наклоном , где уклон дороги помогает вам преодолевать кривую ((рисунок)). Чем больше угол

, тем быстрее вы сможете пройти кривую. Например, гоночные трассы для велосипедов и автомобилей часто имеют крутые повороты. На «кривой с идеальным наклоном» угол

такова, что вы можете преодолевать поворот на определенной скорости без трения между шинами и дорогой.Получим выражение для

для кривой с идеальным наклоном и рассмотрим связанный с ней пример.

Рис. 6.22 Автомобиль на этой кривой с наклоном удаляется и поворачивает налево.

Для perfect bank чистая внешняя сила равна горизонтальной центростремительной силе в отсутствие трения. Составляющие нормальной силы N в горизонтальном и вертикальном направлениях должны равняться центростремительной силе и массе автомобиля соответственно.В случаях, когда силы не параллельны, удобнее всего рассматривать компоненты вдоль перпендикулярных осей – в данном случае вертикального и горизонтального направлений.

(рисунок) показывает диаграмму свободного тела для автомобиля на кривой без трения с наклоном. Если угол

идеально подходит для скорости и радиуса, тогда чистая внешняя сила равна необходимой центростремительной силе. Единственными двумя внешними силами, действующими на автомобиль, являются его вес

кг.

и нормальная сила дороги

(Поверхность без трения может проявлять только силу, перпендикулярную поверхности, то есть нормальную силу.Эти две силы должны складываться, чтобы получить чистую внешнюю силу, горизонтальную по направлению к центру кривизны и имеющую величину

.

Поскольку это решающая сила и она горизонтальна, мы используем систему координат с вертикальной и горизонтальной осями. Только нормальная сила имеет горизонтальную составляющую, поэтому она должна равняться центростремительной силе, то есть

.

Поскольку автомобиль не отрывается от поверхности дороги, чистая вертикальная сила должна быть равна нулю, что означает, что вертикальные составляющие двух внешних сил должны быть равны по величине и противоположны по направлению.Из (Рисунок) мы видим, что вертикальная составляющая нормальной силы равна

.

, а единственная другая вертикальная сила – это вес автомобиля. Они должны быть равны по величине; таким образом,

Теперь мы можем объединить эти два уравнения, чтобы исключить N и получить выражение для

, по желанию. Решение второго уравнения относительно

и подставив его в первое, получим

Взяв арктангенс, получаем

Это выражение можно понять, рассмотрев, как

зависит от v и r .Большой

получается для большого v и маленького r. То есть дороги должны иметь крутой уклон для высоких скоростей и крутых поворотов. Трение помогает, потому что оно позволяет вам двигаться по кривой с большей или меньшей скоростью, чем если бы по кривой не было трения. Обратите внимание, что

не зависит от массы автомобиля.

Пример

Какова идеальная скорость для выхода на крутой крутой поворот?

Кривые на некоторых испытательных треках и гоночных трассах, таких как Международная гоночная трасса Дейтона во Флориде, имеют очень крутой наклон.Этот крен с помощью трения шин и очень стабильной конфигурации автомобиля позволяет преодолевать повороты на очень высокой скорости. Чтобы проиллюстрировать это, рассчитайте скорость, с которой кривая радиусом 100,0 м переходит в

На

следует ездить, если на дороге нет трения.

Стратегия

Прежде всего отметим, что все члены в выражении для идеального угла кривой с наклоном, кроме скорости, известны; таким образом, нам нужно только переставить его так, чтобы скорость появлялась в левой части, а затем подставить известные величины.

Решение

Начиная с

получаем

Отметив, что

получаем

Значение

Это примерно 165 км / ч, что соответствует очень крутому и довольно крутому повороту. Трение в шинах позволяет автомобилю преодолевать поворот на значительно более высоких скоростях.

Самолеты также совершают развороты по крену. Подъемная сила, создаваемая силой воздуха, воздействующего на крыло, действует под прямым углом к ​​крылу.Когда самолет кренится, пилот получает большую подъемную силу, чем необходимо для горизонтального полета. Вертикальная составляющая подъемной силы уравновешивает вес самолета, а горизонтальная составляющая ускоряет самолет. Угол крена, показанный на (Рисунок), равен

.

. Мы анализируем силы так же, как и в случае поворота автомобиля по кривой.

Рис. 6.23 При повороте крена горизонтальная составляющая подъемной силы неуравновешивается и ускоряет самолет.Обычный компонент подъемной силы уравновешивает вес самолета. Угол крена определяется как

. Сравните векторную диаграмму с диаграммой, показанной на (Рисунок).

Силы инерции и неинерционные (ускоренные) рамки: сила Кориолиса

Что общего у взлета на реактивном самолете, поворота на автомобиле, езды на карусели и кругового движения тропического циклона? Каждый из них проявляет силы инерции – силы, которые кажутся просто возникающими в результате движения, потому что система отсчета наблюдателя ускоряется или вращается.Большинство людей согласятся, что при взлете на реактивном самолете создается ощущение, будто вас толкают обратно в кресло, когда самолет ускоряется по взлетно-посадочной полосе. Однако физик сказал бы, что вы, , склонны оставаться неподвижными, в то время как сиденье толкает вас вперед. Еще более распространенный опыт происходит, когда вы делаете крутой поворот на своей машине, скажем, вправо ((рисунок)). Вы чувствуете, как будто вас отбрасывает (то есть принудительно ) влево относительно машины. Опять же, физик сказал бы, что вы, , едете по прямой (вспомните первый закон Ньютона), но автомобиль движется вправо, а не то, что вы испытываете силу слева.

Рис. 6.24 (a) Водитель автомобиля чувствует себя вынужденным влево по отношению к автомобилю при повороте направо. Это инерционная сила, возникающая в результате использования автомобиля в качестве системы отсчета. (б) В земной системе координат водитель движется по прямой, подчиняясь первому закону Ньютона, и машина движется вправо. Слева от водителя относительно Земли нет силы. Вместо этого справа на машине есть сила, заставляющая ее повернуть.

Мы можем согласовать эти точки зрения, исследуя используемые системы координат.Давайте сконцентрируемся на людях в машине. Пассажиры инстинктивно используют автомобиль в качестве ориентира, в то время как физик может использовать Землю. Физик мог бы сделать этот выбор, потому что Земля представляет собой почти инерциальную систему отсчета, в которой все силы имеют идентифицируемое физическое происхождение. В такой системе отсчета законы движения Ньютона принимают форму, данную в Законах движения Ньютона. Автомобиль представляет собой неинерциальную систему отсчета , потому что он ускоряется в сторону. Сила слева, воспринимаемая пассажирами автомобиля, – это сила инерции , не имеющая физического происхождения (она возникает исключительно из-за инерции пассажира, а не из-за какой-либо физической причины, такой как напряжение, трение или гравитация).Автомобиль, как и водитель, действительно ускоряется вправо. Эта сила инерции называется силой инерции, потому что она не имеет физического происхождения, такого как гравитация.

Физик выберет ту систему отсчета, которая наиболее удобна для анализируемой ситуации. Для физика нетрудно включить силы инерции и второй закон Ньютона, как обычно, если это удобнее, например, на карусели или на вращающейся планете. Неинерционные (ускоренные) системы отсчета используются, когда это полезно.При обсуждении движения космонавта в космическом корабле, движущемся со скоростью, близкой к скорости света, необходимо учитывать различные системы отсчета, что вы поймете при изучении специальной теории относительности.

Давайте теперь мысленно прокатимся на карусели, а именно на быстро вращающейся игровой площадке ((Рисунок)). Вы берете карусель в качестве системы отсчета, потому что вы вращаетесь вместе. Вращаясь в этой неинерциальной системе отсчета, вы чувствуете инерционную силу, которая имеет тенденцию сбивать вас с толку; это часто называют центробежной силой (не путать с центростремительной силой).Центробежная сила – это широко используемый термин, но на самом деле его не существует. Вы должны держаться крепче, чтобы противодействовать своей инерции (которую люди часто называют центробежной силой). В системе отсчета Земли нет силы, пытающейся сбить вас с толку; мы подчеркиваем, что центробежная сила – это фикция. Вы должны держаться, чтобы заставить себя двигаться по кругу, потому что в противном случае вы бы пошли по прямой, прямо с карусели, в соответствии с первым законом Ньютона. Но сила, которую вы прикладываете, действует по направлению к центру круга.

Рис. 6.25 (a) Всадник на карусели чувствует себя так, как будто его сбивают с толку. Эту инерционную силу иногда ошибочно называют центробежной силой, пытаясь объяснить движение всадника во вращающейся системе отсчета. (б) В инерциальной системе отсчета и согласно законам Ньютона его уносит инерция (незатененный всадник имеет

и голов по прямой). Сила,

, необходим для создания кругового пути.

Этот инерционный эффект, уносящий вас от центра вращения, если нет центростремительной силы, вызывающей круговое движение, хорошо используется в центрифугах ((Рисунок)). Центрифуга вращает образец очень быстро, как упоминалось ранее в этой главе. Если смотреть из вращающейся системы координат, сила инерции выбрасывает частицы наружу, ускоряя их осаждение. Чем больше угловая скорость, тем больше центробежная сила. Но на самом деле происходит то, что инерция частиц переносит их по касательной к окружности, в то время как пробирка движется по круговой траектории под действием центростремительной силы.

Рис. 6.26. Центрифуги выполняют свою задачу по инерции. Частицы в жидком осадке оседают, потому что их инерция уносит их от центра вращения. Большая угловая скорость центрифуги ускоряет осаждение. В конечном итоге частицы соприкасаются со стенками пробирки, которые затем создают центростремительную силу, необходимую для их движения по кругу постоянного радиуса.

Давайте теперь рассмотрим, что происходит, если что-то движется во вращающейся системе отсчета.Например, что, если вы сдвинете мяч прямо от центра карусели, как показано на (Рисунок)? Мяч движется по прямой относительно Земли (при незначительном трении) и по изогнутой вправо траектории на поверхности карусели. Человек, стоящий рядом с каруселью, видит, как мяч движется прямо, а под ним вращается карусель. В системе отсчета карусели мы объясняем кажущуюся кривую справа с помощью силы инерции, называемой силой Кориолиса , которая заставляет мяч изгибаться вправо.Сила Кориолиса может быть использована любым человеком в этой системе отсчета, чтобы объяснить, почему объекты следуют изогнутыми путями, и позволяет нам применять законы Ньютона в неинерциальных системах отсчета.

Рис. 6.27. Посмотрев вниз на вращение карусели против часовой стрелки, мы видим, что шар, скользящий прямо к краю, следует по изогнутой вправо траектории. Человек перемещает мяч в направлении точки B, начиная с точки A. Обе точки поворачиваются в затемненные положения (A ‘и B’), показанные в то время, когда мяч следует изогнутой траектории во вращающейся рамке и прямой траектории в системе координат Земли. .

До сих пор мы считали Землю инерциальной системой отсчета, почти не беспокоясь о эффектах, возникающих из-за ее вращения. Однако такие эффекты действительно существуют, например, при вращении погодных систем. Большинство последствий вращения Земли качественно можно понять по аналогии с каруселью. Если смотреть сверху на Северный полюс, Земля вращается против часовой стрелки, как и карусель на (рисунок). Как и на карусели, любое движение в Северном полушарии Земли испытывает силу Кориолиса вправо.Прямо противоположное происходит в Южном полушарии; там сила слева. Поскольку угловая скорость Земли мала, силой Кориолиса обычно можно пренебречь, но для крупномасштабных движений, таких как характер ветра, она оказывает существенное влияние.

Сила Кориолиса заставляет ураганы в северном полушарии вращаться против часовой стрелки, тогда как тропические циклоны в южном полушарии вращаются по часовой стрелке. (Термины ураган, тайфун и тропический шторм являются региональными названиями циклонов, которые представляют собой штормовые системы, характеризующиеся центрами низкого давления, сильными ветрами и проливными дождями.) (Рисунок) помогает показать, как происходят эти вращения. Воздух течет в любую область низкого давления, а тропические циклоны имеют особенно низкое давление. Таким образом, ветры движутся к центру тропического циклона или погодной системы низкого давления на поверхности. В Северном полушарии эти внутренние ветры отклоняются вправо, как показано на рисунке, создавая циркуляцию против часовой стрелки на поверхности для зон низкого давления любого типа. Низкое давление у поверхности связано с поднимающимся воздухом, который также вызывает охлаждение и образование облаков, что делает картины низкого давления вполне заметными из космоса.И наоборот, циркуляция ветра вокруг зон высокого давления в Южном полушарии происходит по часовой стрелке, но она менее заметна, потому что высокое давление связано с опусканием воздуха, обеспечивающим чистое небо.

Рис. 6.28 (a) Вращение этого урагана в Северном полушарии против часовой стрелки является главным следствием силы Кориолиса. (б) Без силы Кориолиса воздух поступал бы прямо в зону низкого давления, например, в тропических циклонах. (c) Сила Кориолиса отклоняет ветер вправо, производя вращение против часовой стрелки.(d) Ветер, исходящий из зоны высокого давления, также отклоняется вправо, вызывая вращение по часовой стрелке. (e) Противоположное направление вращения создается силой Кориолиса в Южном полушарии, что приводит к тропическим циклонам. (кредит а и кредит е: модификации работы НАСА)

Вращение тропических циклонов и траектория шара на карусели также могут быть объяснены инерцией и вращением системы под ним. Когда используются неинерциальные системы отсчета, для объяснения искривленной траектории должны быть изобретены силы инерции, такие как сила Кориолиса.Физического источника этих сил инерции нет. В инерциальной системе отсчета инерция объясняет путь, и не обнаруживается сила без идентифицируемого источника. Любая точка зрения позволяет нам описывать природу, но взгляд в инерциальной системе отсчета является самым простым в том смысле, что все силы имеют истоки и объяснения.

Концептуальные вопросы

Если вы хотите уменьшить нагрузку (которая связана с центростремительной силой) на высокоскоростные шины, вы бы использовали шины большого или малого диаметра? Объяснять.

Определите центростремительную силу. Может ли сила любого типа (например, натяжение, сила тяжести, трение и т. Д.) Быть центростремительной силой? Может ли любое сочетание сил быть центростремительной силой?

[показывать-ответ q = ”fs-id1165039453744 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165039453744 ″]

Центростремительная сила определяется как любая чистая сила, вызывающая равномерное круговое движение. Центростремительная сила – не новый вид силы. Обозначение «центростремительная» относится к любой силе , которая заставляет что-то вращаться по кругу.Эта сила может быть напряжением, гравитацией, трением, электрическим притяжением, нормальной силой или любой другой силой. Любая их комбинация может быть источником центростремительной силы, например, центростремительная сила в верхней части траектории троса, проходящего по вертикальному кругу, является результатом как напряжения, так и силы тяжести.

[/ hidden-answer]

Если центростремительная сила направлена ​​к центру, почему вы чувствуете, что вас «отбрасывает» от центра, когда машина движется по кривой? Объяснять.

Водители гоночных автомобилей обычно срезают углы, как показано ниже (Путь 2). Объясните, как это позволяет снимать кривую с максимальной скоростью.

[раскрыть-ответ q = “329939 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 329939 ″] Водитель, который срезает угол (на Пути 2), имеет более плавную кривую с большей радиус. Это будет лучшая гоночная трасса. Если водитель слишком быстро завернет за угол, используя гоночную трассу, он все равно соскользнет с трассы; главное – поддерживать максимальное значение статического трения.Итак, водитель хочет максимально возможной скорости и максимального трения. Рассмотрим уравнение для центростремительной силы:

где v – скорость, а r – радиус кривизны. Таким образом, уменьшая кривизну (1 / r) пути, по которому движется автомобиль, мы уменьшаем силу, которую шины должны оказывать на дорогу, что означает, что теперь мы можем увеличить скорость v. вид водителя на Пути 1, мы можем рассуждать так: чем круче поворот, тем меньше радиус поворота; чем меньше диаметр поворота, тем больше требуется центростремительная сила.Если эта центростремительная сила не приложена, результатом будет занос. [/ Hidden-answer]

Во многих парках развлечений есть аттракционы с вертикальными петлями, как показано ниже. В целях безопасности автомобили прикреплены к рельсам таким образом, чтобы они не могли упасть. Если автомобиль преодолевает вершину с правильной скоростью, только сила тяжести будет обеспечивать центростремительную силу. Какая еще сила действует и в каком направлении, если:

(a) Автомобиль преодолевает вершину быстрее этой скорости?

(b) Автомобиль переваливает через вершину со скоростью ниже этой?

Что заставляет воду удаляться с одежды в центрифуге?

[показывать-ответ q = ”fs-id1165039477270 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165039477270 ″]

Цилиндр сушилки создает центростремительную силу на одежде (включая капли воды), заставляя ее двигаться по круговой траектории.Когда капля воды попадает в одно из отверстий бочки, она перемещается по касательной к окружности.

[/ hidden-answer]

Когда фигурист образует круг, какая сила отвечает за его поворот? Используйте в своем ответе диаграмму свободного тела.

Предположим, что ребенок едет на карусели примерно на полпути между ее центром и краем. У нее есть коробка для завтрака, покоящаяся на вощеной бумаге, так что между ней и каруселью очень мало трения.По какому пути, показанному ниже, пойдет коробка с обедом, когда она отпустит? Ланч-бокс оставляет след в пыли на карусели. Эта тропа прямая, изогнута влево или вправо? Поясните свой ответ.

[раскрыть-ответ q = ”60053 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 60053 ″] Если нет трения, значит и центростремительной силы нет. Это означает, что коробка для завтрака будет двигаться по касательной к кругу и, таким образом, следует по пути B. След пыли будет прямым.Это результат первого закона движения Ньютона. [/ Hidden-answer]

Чувствуете ли вы, что вас бросает в любую сторону, когда вы проезжаете поворот, идеально подходящий для скорости вашего автомобиля? В каком направлении на вас действует сила автокресла?

Предположим, что масса движется по круговой траектории на столе без трения, как показано ниже. В земной системе координат центробежная сила, оттягивающая массу от центра вращения, отсутствует, но есть сила, растягивающая нить, прикрепляющую массу к гвоздю.Используя концепции, связанные с центростремительной силой и третьим законом Ньютона, объясните, какая сила натягивает струну, указав ее физическое происхождение.

[показать-ответ q = ”965193 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 965193 ″] Для поддержания кругового движения необходима центростремительная сила; это обеспечивается гвоздем в центре. Третий закон Ньютона объясняет это явление. Сила воздействия – это сила струны, действующая на массу; сила реакции – это сила массы, действующая на струну.Эта сила реакции заставляет струну растягиваться. [/ Hidden-answer]

Когда сливают воду из туалета или раковину, вода (и другие материалы) по пути вниз начинает вращаться вокруг слива. Предполагая, что начального вращения нет, а поток изначально направлен прямо к водостоку, объясните, что вызывает вращение и какое направление оно имеет в Северном полушарии. (Обратите внимание, что это небольшой эффект, и в большинстве туалетов вращение вызывается направленными водяными струями.) Будет ли направление вращения измениться на противоположное, если вода будет вытесняться в канализацию?

Автомобиль объезжает поворот и наталкивается на кусок льда с очень низким коэффициентом кинетической фиксации.Автомобиль съезжает с дороги. Опишите путь, по которому машина съезжает с дороги.

[показывать-ответ q = ”fs-id116503

62 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id116503

62 ″]

Поскольку радиальное трение с шинами обеспечивает центростремительную силу, а трение почти равно нулю, когда автомобиль сталкивается со льдом, автомобиль подчиняется первому закону Ньютона и съезжает с дороги по прямой, касательной к кривой. Распространенное заблуждение состоит в том, что автомобиль будет двигаться по извилистой дороге за пределами дороги.

[/ hidden-answer]

Во время одной поездки в парке развлечений всадники входят в большую вертикальную бочку и становятся у стены на ее горизонтальном полу. Бочка раскручивается, и пол падает. Всадники чувствуют себя так, как будто они прижаты к стене силой, похожей на силу гравитации. Это сила инерции, которую всадники воспринимают и используют для объяснения событий во вращающейся системе отсчета ствола. Объясните в инерциальной системе отсчета (Земля почти такая), что прижимает всадников к стене, и определите все силы, действующие на них.

Два друга разговаривают. Анна говорит, что спутник на орбите находится в свободном падении, потому что спутник продолжает падать на Землю. Том говорит, что спутник на орбите не находится в свободном падении, потому что ускорение свободного падения не равно

.

. С кем вы согласны и почему?

[show-answer q = ”fs-id11650336 ″] Показать решение [/ show-answer]

[скрытый-ответ a = ”fs-id11650336 ″]

Анна права. Спутник свободно падает на Землю из-за силы тяжести, хотя гравитация слабее на высоте спутника, и g не равно

.Свободное падение не зависит от стоимости г ; то есть вы можете испытать свободное падение на Марсе, если спрыгнете с Олимпа (самого высокого вулкана в Солнечной системе).
[/ hidden-answer]

Невращающаяся система отсчета, помещенная в центр Солнца, очень близка к инерциальной. Почему это не совсем инерциальная система отсчета?

Проблемы

(a) Ребенок весом 22,0 кг катается на детской карусели, вращающейся со скоростью 40,0 об / мин. Какая центростремительная сила действует, если он равен 1.25 м от центра? (b) Какая центростремительная сила действует, если карусель вращается со скоростью 3,00 об / мин и находится на расстоянии 8,00 м от ее центра? (c) Сравните каждую силу с его весом.

[показывать-ответ q = ”fs-id11650311 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id11650311 ″]

а. 483 Н; б. 17,4 Н; c. 2,24, 0,0807

[/ hidden-answer]

Вычислите центростремительную силу на конце лопасти ветряной турбины радиусом 100 м, вращающейся на 0.5 об / с. Предположим, что масса 4 кг.

Каков идеальный угол крена для пологого поворота радиусом 1,20 км на шоссе с ограничением скорости 105 км / ч (около 65 миль / ч), если все едут на пределе?

[показывать-ответ q = ”fs-id1165039344901 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165039344901 ″]

[/ hidden-answer]

Какова идеальная скорость для прохождения кривой радиусом 100,0 м с наклоном

?

угол?

(а) Каков радиус бобслейного поворота с креном

?

и взято на отметке 30.0 м / с при условии идеального наклона? (b) Рассчитайте центростремительное ускорение. (c) Вам кажется это ускорение большим?

[показывать-ответ q = ”fs-id116503

09 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id116503

09 ″]

а. 24,6 м; б.

г. 3,73 раза г
[/ hidden-answer]

Часть езды на велосипеде включает в себя наклон под правильным углом при повороте, как показано ниже. Чтобы быть стабильным, сила, действующая на землю, должна быть на линии, проходящей через центр тяжести.Сила, действующая на колесо велосипеда, может быть разделена на две перпендикулярные составляющие: трение параллельно дороге (оно должно обеспечивать центростремительную силу) и вертикальную нормальную силу (которая должна равняться весу системы). (а) Покажите, что

(как показано на рисунке) относится к скорости v и радиусу кривизны r поворота таким же образом, как и для проезжей части с идеальным уклоном, то есть

(б) Вычислить

для модели 12.0-м / с разворот радиусом 30,0 м (как в гонке).

Если автомобиль движется по крутой кривой на скорости ниже идеальной, необходимо трение, чтобы не допустить скольжения внутрь поворота (проблема на обледенелых горных дорогах). (a) Рассчитайте идеальную скорость для кривой радиусом 100,0 м с наклоном

.

. (b) Какой минимальный коэффициент трения необходим для того, чтобы напуганный водитель проехал по той же кривой на скорости 20,0 км / ч?

[показывать-ответ q = ”fs-id1165038980331 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165038980331 ″]

а.16,2 м / с; б. 0,234

[/ hidden-answer]

Современные американские горки имеют вертикальные петли, подобные показанной здесь. Радиус кривизны вверху меньше, чем по бокам, так что центростремительное ускорение вниз вверху будет больше, чем ускорение силы тяжести, удерживая пассажиров плотно прижатыми к своим сиденьям. (а) Какова скорость американских горок в верхней части петли, если радиус кривизны там 15,0 м, а ускорение машины вниз равно 1.50 г ? (б) На какой высоте над вершиной петли американские горки должны стартовать из состояния покоя, если трение пренебрежимо мало? (c) Если он действительно начинается на 5,00 м выше, чем ваш ответ на вопрос (b), сколько энергии он потерял на трение? Его масса

.

Ребенок массой 40,0 кг находится в машине с американскими горками, которая движется по петле радиусом 7,00 м. В точке А скорость автомобиля составляет 10,0 м / с, а в точке B – 10,5 м / с. Предположим, что ребенок не держится и не пристегнут ремнем безопасности.(а) Какова сила автомобильного кресла, воздействующая на ребенка в точке А? (b) Какое усилие автомобильного кресла действует на ребенка в точке B? (c) Какая минимальная скорость требуется, чтобы удерживать ребенка на сиденье в точке A?

[раскрыть-ответ q = ”484990 ″] Показать решение [/ раскрыть-ответ]
[скрытый-ответ a =” 484990 ″] a. 179 Н; б. 290 Н; c. 8,3 м / с [/ hidden-answer]

В простой модели Бора основного состояния атома водорода электрон движется по круговой орбите вокруг фиксированного протона.Радиус орбиты

и скорость электрона

Масса электрона

. Какая сила действует на электрон?

Железнодорожные пути следуют круговой кривой радиусом 500,0 м и имеют крен под углом

. Для поездов какой скорости предназначены эти пути?

[показывать-ответ q = ”fs-id116503

32 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id116503

32 ″]

20.7 м / с

[/ hidden-answer]

Ускоритель частиц в ЦЕРН имеет форму окружности 7,0 км. (а) Какое ускорение протонов

, которые вращаются вокруг ускорителя на

скорости света? (Скорость света

) (б) Какая сила действует на протоны?

Автомобиль объезжает кривую без кренов радиусом 65 м. Если коэффициент статического трения между дорогой и автомобилем равен 0.70, какова максимальная скорость, с которой автомобиль преодолевает поворот без пробуксовки?

[показывать-ответ q = ”fs-id1165039269152 ″] Показать решение [/ показывать-ответ]

[скрытый-ответ a = ”fs-id1165039269152 ″]

21 м / с

[/ hidden-answer]

Автодорога с наклоном предназначена для движения со скоростью 90,0 км / ч. Радиус поворота 310 м. Какой угол наклона шоссе?

Глоссарий

наклонная кривая

поворот на дороге с уклоном, помогающий транспортному средству преодолевать поворот

центростремительная сила

любая чистая сила, вызывающая равномерное круговое движение

Сила Кориолиса

Сила инерции, вызывающая кажущееся отклонение движущихся объектов при просмотре во вращающейся системе отсчета

Идеальное банковское дело

наклон кривой дороги, где угол наклона позволяет транспортному средству преодолевать поворот с определенной скоростью без помощи трения между шинами и дорогой; чистая внешняя сила на транспортном средстве равна горизонтальной центростремительной силе в отсутствие трения

инерционная сила

сила, не имеющая физического происхождения

неинерциальная система отсчета

ускоренная система отсчета

.