Цифровая обработка звука: Звуковая экосистема, часть 2: Цифровая обработка сигналов

Содержание

Звуковая экосистема, часть 2: Цифровая обработка сигналов

Вы сможете провести встречу без видео, а вот без звука это будет невозможно. 81% IT-специалистов считают, что качество звука оказывает наибольшее влияние на эффективность виртуальных собраний. Часто мы не обращаем внимание на звук, если он хороший. Но плохой звук будет сложно не заметить. Участники будут больше уставать, отвлекаться и меньше понимать контекст дискуссии. Всё это способствует снижению продуктивности и, как следствие, дохода компании.

В этой серии статей мы рассмотрим, как различные части звуковой экосистемы влияют на качество звука. Работа аудиосистемы заключается в том, чтобы захватывать голоса людей в комнате для передачи и воспроизводить голоса людей из других локаций. Чтобы сделать это хорошо, звук должен быть разборчивым (то есть вы можете понять, что говорят другие) и естественным (то есть люди звучат так, как если бы вы разговаривали лицом к лицу). В статье №2 мы обсудим роль цифровой передачи сигнала.

Как DSP-процессор улучшает звук

Работа микрофона заключается в преобразовании звуковых волн, распространяющихся по воздуху, в звуковой сигнал, который можно передавать, усиливать или записывать. За исключением небольших комнат, одного микрофона почти никогда не бывает достаточно. Большинство конференц-залов требуют нескольких микрофонов, которые должны формировать общий микс. Необработанные сигналы от микрофонов похожи на певцов в хоре – независимо от того, насколько они хороши в одиночестве, важно то, как они выступают вместе.

Необходима некоторая пост-обработка, которая полирует и совершенствует каждый отдельный сигнал микрофона, а затем объединяет их в сбалансированный, гармоничный микс. В старые времена для этого требовался рэк, полная коробок с ручками, лампами и счётчиками, которые должны были тщательно настраиваться опытным звукорежиссером для одновременной работы.

К счастью, больше не нужно погружаться в тёмное искусство звуковой инженерии, чтобы выполнить свою работу; теперь все важные процессы могут быть выполнены одним устройством, называемым процессором цифровой обработки сигналов (англ. DSP – Digital Signal Processing). DSP-процессор может быть автономным аппаратным устройством или частью приложения, работающего на ПК, но не каждый DSP-процессор подходит для рабочих мест или университетов. DSP-процессор для видеоконференций имеет дело с видео, управлением вызовами и другими задачами; аудио – это только один из пунктов в списке дел.

Не все DSP-процессоры созданы одинаковыми. DSP-функции, встроенные в приложение для видеоконференций, имеет дело с видео, управлением вызовами и другими задачами; аудио – это только один из пунктов в списке дел.

То, что вам нужно, — это отдельный DSP-процессор для звука, который предназначен для работы с микрофонами и посвящает всё свое внимание тому, чтобы сделать звучание речи настолько естественным, насколько это возможно. Как и швейцарский армейский нож, DSP-процессор для звука оснащён полным набором инструментов для оптимизации слышимости и разборчивости.

Проблемы со звуком, которые может исправить DSP-процессор

В недавнем опросе 80% специалистов назвали проблемы со звуком главными источниками разочарования при проведении виртуальных встреч. Большинство видеоконференций страдают от одного и того же набора хронических проблем. Каждый из инструментов или «блоков обработки» в вашем DSP-процессоре имеет определённую цель и решает одну из следующих проблем:

Проблема №1: Слишком громко или слишком тихо

Одной из самых распространённых проблем со звуком во время видеоконференций является обычное рассогласование по уровням. Иногда люди на одной стороне звонка недостаточно громкие, а иногда они слишком громкие. Решением является автоматическая регулировка усиления (АРУ), которая регулирует уровень каждого канала микрофона (или входного сигнала с удалённой стороны) для обеспечения постоянной громкости. Как хороший звукорежиссер, АРУ немного усиливает голоса тихих спикеров и немного понижает громких. Это идеальный подход для конференц-залов, где расстояние между говорящим и микрофоном различается, поскольку в помещении выступают разные люди.

Проблема №2: Звук как из бочки

Глухой звук – как в банке или бочке – может быть вызван наличием слишком большого количества открытых микрофонов одновременно. Автоматический микшер позаботится об этом, мгновенно активируя ближайший микрофон, когда спикер выступает, и отключая ненужные, неиспользуемые микрофоны. В комнате с восемью микрофонами исключение семи ненужных микрофонов позволяет достигнуть колоссальной разницы в качестве звука.

Проблема №3: Эхо, эхо, эхо…

Во время видеоконференции звук, выходящий из динамика, может быть захвачен микрофоном и повторно передан обратно на дальнюю сторону, что вызывает раздражающее эхо. Акустическое эхоподавление (англ. AEC – Acoustic Echo Canceller) в цифровом виде удаляет входной сигнал удалённой стороны из выходного сигнала, чтобы предотвратить это. Большинство приложений для проведения видеоконференций (например, Microsoft Teams, Zoom или Skype for Business) имеют одноканальный встроенный AEC, который лучше всего подходит, когда вы присоединяетесь к одному из этих собраний с ноутбука. Но для больших переговорных комнат и аудиторий с несколькими участниками и микрофонами для хорошего качества звука требуется внешний DSP-процессор, который выделяет отдельный блок AEC для каждого канала микрофона.

Проблема №4: Отвлекающий шум

В большинстве переговорных комнат присутствует некоторый фоновый шум, вызванный проекторами или компьютерами, системами отопления, вентиляции и кондиционирования воздуха, гулом в здании или окружающим шумом, проникающим извне. Люди в комнате могут не заметить этого, но микрофоны их улавливают. Эквализация может отрегулировать большую часть гула и шипения на низких и высоких частотах, но электронное шумоподавление в цифровом виде удаляет шум, который перекрывает речевой диапазон, поэтому он не слышен участникам собрания. Эффективность DSP-процессора с хорошим шумоподавлением может быть просто удивительной.

Проблема №5: А сейчас слышно?

Чем больше шума и реверберации в аудиосигнале, тем сложнее кодеку видео-конференц-связи (будь то приложение на ПК или отдельное устройство) обеспечить естественную интерактивность. Если проблемы со звуком не будут решены до того, как сигнал достигнет кодека, вам может быть затруднительно прервать другую сторону или им прервать вас. Это замедляет общение и вызывает раздражающие помехи.

Проблема №6: Звук не синхронизирован с видео

Видео обрабатывается немного дольше чем аудио при передаче по обычному Интернет-соединению. Аудиосигнал поступает на дальнюю сторону раньше, чем видео, поэтому вы слышите, как кто-то говорит, прежде чем его губы начнут двигаться. Регулируемая задержка в DSP-процессорах позволяет синхронизировать подачу звука с изображением во время онлайн-конференции.

DSP-процессор: устройство или программа?

DSP-процессор для аудио-конференц-связи должен быть расположен там, где это наиболее целесообразно для вашего использования. В малых помещениях микрофон со встроенным DSP-процессором (например, Microflex Advance MXA710 или MXA910) исключает необходимость использования внешнего оборудования и упрощает настройку. В комнатах среднего и большого размера с несколькими микрофонами и другими источниками сигнала DSP-процессор в виде отдельного устройства (например, IntelliMix P300) обеспечивает большую мощность, гибкость и возможности подключения как к аппаратным, так и программным кодекам. Кроме того, Shure также предлагает программное решение DSP, IntelliMix Room, которое может работать на ПК в помещении или на устройстве для проведения видеоконференций, что упрощает развёртывание и обеспечивает централизованное обслуживание сотрудниками IT-службы. Независимо от форм-фактора, высокопроизводительный DSP-процессор обеспечивает естественный звук, который облегчает общение без лишних усилий и максимизирует отдачу от ваших инвестиций в оборудование и технологии.

Читайте также другие статьи, посвящённые звуковой экосистеме Shure для конференц-связи:

Звуковая экосистема, часть 1: Микрофоны для конференц-связи
Звуковая экосистема, часть 3: Динамики
Звуковая экосистема, часть 4: Программное обеспечение
Звуковая экосистема, часть 5: Технологические партнёры

Цифровые процессоры Shure улучшают и объединяют комнатные микрофоны в аудиосигнал высочайшего качества и доступны на аппаратных или программных платформах. Узнайте больше здесь.

Курс лекций «Основы цифровой обработки сигналов» / Хабр

Всем привет!

Часто ко мне обращаются люди с вопросами по задачам из области цифровой обработки сигналов (ЦОС). Я подробно рассказываю нюансы, подсказываю нужные источники информации. Но всем слушателям, как показало время, не хватает практических задач и примеров в процессе познания этой области. В связи с этим я решил написать краткий интерактивный курс по цифровой обработке сигналов и выложить его в открытый доступ.

Большая часть обучающего материала для наглядного и интерактивного представления реализована с использованием Jupyter Notebook. Предполагается, что читатель имеет базовые знания из области высшей математики, а также немного владеет языком программирования Python.

Список лекций

Этот курс содержит материалы в виде законченных лекций по разным тематикам из области цифровой обработки сигналов. Материалы представлены с использованием библиотек на языке Python (пакеты numpy, scipy, matplotlib, и т.

д.). Основная информация для этого курса взята из моих лекций, которые я, будучи аспирантом, читал студентам Московского Энергетического Института (НИУ МЭИ). Частично информация из этих лекций была использована на обучающих семинарах в

Центре Современной Электроники

, где я выступал в качестве лектора. Кроме того, в этот материал входит перевод различных научных статей, компиляция информации из достоверных источников и литературы по тематике цифровой обработки сигналов, а также официальная документация по прикладным пакетам и встроенным функциям библиотек scipy и numpy языка Python.

Для пользователей MATLAB (GNU Octave) освоение материала с точки зрения программного кода не составит труда, поскольку основные функции и их атрибуты во многом идентичны и схожи с методами из Python-библиотек.

Все материалы сгруппированы по основным тематикам цифровой обработки сигналов:

Сигналы: аналоговые, дискретные, цифровые. Z-преобразование,
Преобразование Фурье: амплитудный и фазовый сигнала, ДПФ и БПФ,
Свертка и корреляция. Линейная и циклическая свертка. Быстрая свёртка,
Случайные процессы. Белый шум. Функция плотности вероятностей,
Детерминированные сигналы. Модуляция: АМ, ЧМ, ФМ, ЛЧМ. Манипуляция,
Фильтрация сигналов: БИХ, КИХ фильтры,
Оконные функции в задачах фильтрации. Детектирование слабых сигналов,
Ресемплинг: децимация и интерполяция. CIC-фильтры, фильтры скользящего среднего,
Непараметрические методы спектрального анализа,
Усреднение по частоте и по времени. Полифазный БПФ.

Список лекций — достаточный ~~но, разумеется, неполный~~ для вводного знакомства с областью ЦОС. При наличии свободного времени я планирую поддерживать и развивать этот проект.

Где найти?

Все материалы —

абсолютно бесплатны

и доступны в виде открытого репозитория на

моем гитхабе как opensource проект

. Материалы представлены в двух форматах — в виде тетрадок Jupyter Notebook для интерактивной работы, изучения и редактирования, и в виде скомпилированных из этих тетрадок HTML-файлов (после скачивания с гитхаба имеют вполне пригодный формат для чтения и для печати).

Ниже приводится очень краткое описание разделов курса с небольшими пояснениями, терминами и определениями. Основная информация доступна в исходных лекциях, здесь представлен лишь краткий обзор!

Сигналы. Z-преобразование

Вводный раздел, в котором содержится основная информация по типам сигналов. Вводится понятие дискретной последовательности, дельта-функции и функции Хевисайда (единичный скачок).

Все сигналы по способу представления на множестве можно разделить на четыре группы:

аналоговые — описываются непрерывными во времени функциями,
дискретные — прерываются во времени с шагом заданным дискретизации,
квантованные — имеют набор конечных уровней (как правило, по амплитуде),
цифровые — комбинация свойств дискретных и квантованных сигналов.

Для правильного восстановления аналогового сигнала из цифрового без искажений и потерь используется теорема отсчетов, известная как Теорема Котельникова (Найквиста-Шеннона).

Любой непрерывный сигнал с ограниченным спектром может быть восстановлен однозначно и без потерь по своим дискретным отсчетам, взятым с частотой строго больше удвоенной верхней частоты спектра непрерывного сигнала.

Такая трактовка справедлива при условии, что непрерывная функция времени занимает полосу частот от 0 до значения верхней частоты. Если шаг квантования и дискретизации выбраны неправильно, преобразование сигнала из аналоговой формы в дискретную будет происходить с искажениями.

Также в этом разделе описывается Z-преобразование и его свойства, показывается представление дискретных последовательностей в Z-форме.

Пример конечной дискретной последовательности:

x(nT) = {2, 1, -2, 0, 2, 3, 1, 0}

Пример этой же последовательности в Z-форме:

X(z) = 2 + z^-1 — 2z^-2 + 2z^-4 + 3z^-5 + 1z^-6

Преобразование Фурье. Свойства. ДПФ и БПФ

В этом разделе описывается понятие временной и частотной области сигнала.

Вводится определение дискретного преобразования Фурье (ДПФ). Рассмотрены прямое и обратное ДПФ, их основные свойства. Показан переход от ДПФ к алгоритму быстрого преобразования Фурье (БПФ) по основанию 2 (алгоритмы децимации по частоте и по времени). Отражена эффективность БПФ в сравнении с ДПФ.

В частности, в этом разделе описывается Python пакет scipy.ffpack для вычисления различных преобразований Фурье (синусное, косинусное, прямое, обратное, многомерное, вещественное).

Преобразование Фурье позволяет представить любую функцию в виде набора гармонических сигналов! Преобразование Фурье лежит в основе методов свертки и проектировании цифровых корреляторов, активно применяется при спектральном анализе, используется при работе с длинными числами.

Особенности спектров дискретных сигналов:
1. Спектральная плотность дискретного сигнала – периодическая функция с периодом, равным частоте дискретизации.
2. Если дискретная последовательность

вещественная, то модуль спектральной плотности такой последовательности есть четная функция, а аргумент – нечетная функция частоты.

Спектр гармонического сигнала:

Сравнение эффективности ДПФ и БПФ

Эффективность алгоритма БПФ и количество выполняемых операций линейно зависит от длины последовательности N:

Как видно, чем больше длина преобразования, тем больше экономия вычислительных ресурсов (по скорости обработки или количеству аппаратных блоков)!

Любой сигнал произвольной формы можно представить в виде набора гармонических сигналов разных частот. Иными словами, сигнал сложной формы во временной области имеет набор комплексных отсчетов в частотной области, которые называются *гармоники*. Эти отсчеты выражают амплитуду и фазу гармонического воздействия на определенной частоте. Чем больше набор гармоник в частотной области, тем точнее представляется сигнал сложной формы.

Свертка и корреляция

В этом разделе вводится понятие корреляции и свертки для дискретных случайных и детерминированных последовательностей. Показана связь автокорреляционной и взаимнокорреляционной функций со сверткой. Описываются свойства свертки, в частности, рассмотрены методы линейной и циклической свертки дискретного сигнала с подробным разбором на примере дискретной последовательности. Кроме того, показан метод вычисления «быстрой» свертки с помощью алгоритмов БПФ.

В реальных задачах часто ставится вопрос о степени похожести одного процесса на другой или же о независимости одного процесса от другого. Иными словами, требуется определить взаимосвязь между сигналами, то есть найти корреляцию. Методы корреляции используются в широком диапазоне задач: поиск сигналов, компьютерное зрение и обработка изображений, в задачах радиолокации для определения характеристик целей и определения расстояния до объекта. Кроме того, с помощью корреляции производится поиск слабых сигналов в шумах.

Свертка описывает взаимодействие сигналов между собой. Если один из сигналов — импульсная характеристика фильтра, то свертка входной последовательности с импульсной характеристикой есть ни что иное, как реакция цепи на входное воздействие.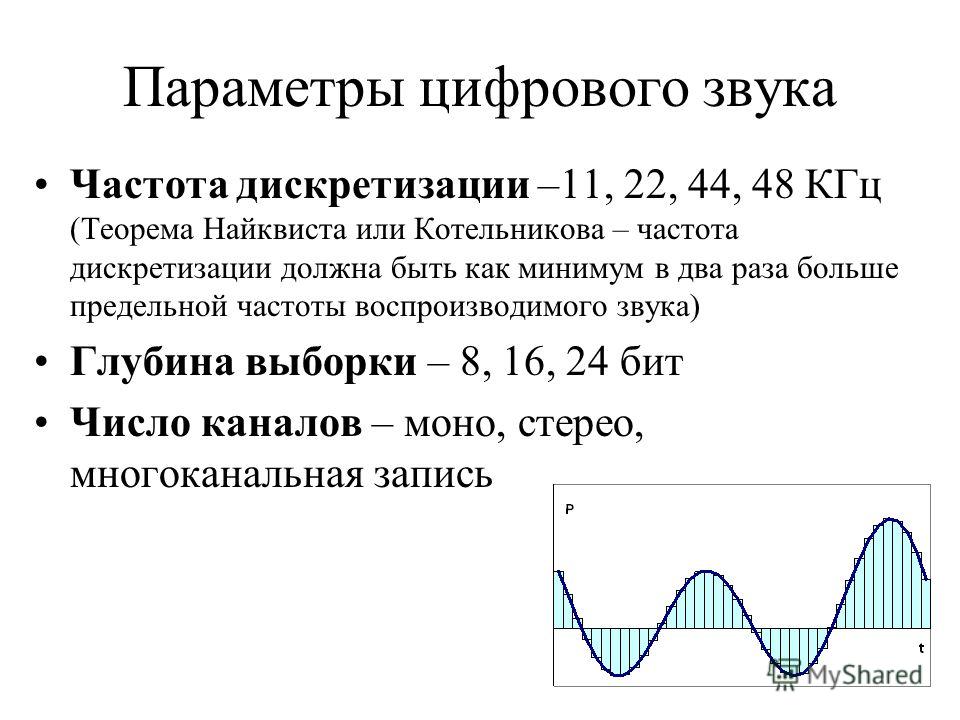 Иными словами, результирующий сигнал отражает прохождение сигнала через фильтр.

Автокорреляционная функция (АКФ) находит применение в кодировании информации. Выбор кодирующей последовательности по параметрам длины, частоты и формы во многом обусловлен корреляционными свойствами этой последовательности. Наилучшая кодовая последовательность обладает наименьшим значением вероятности ложного обнаружения или срабатывания (для детектирования сигналов, для пороговых устройств) или ложной синхронизации (для передачи и приема кодовых последовательностей).

В этом разделе представлена таблица сравнения эффективности быстрой свертки и свертки, вычисляемой по прямой формуле (по числу вещественных умножений).

Как видно, для длин БПФ до 64, быстрая свёртка проигрывает у прямого метода. Однако, при увеличении длины БПФ результаты меняются в обратную сторону — быстрая свертка начинает выигрывать у прямого метода. Очевидно, чем больше длина БПФ, тем лучше выигрыш частотного метода.

Случайные сигналы и шум

В этом разделе вводится понятие случайных сигналов, плотности распределения вероятностей, закона распределения случайной величины. Рассматриваются математические моменты — среднее (математическое ожидание) и дисперсия (или корень этой величины — среднеквадратическое отклонение). Также в этом разделе рассматривается нормальное распределение и связанное с ним понятие

белого шума

, как основного источника шумов (помех) при обработке сигналов.

Случайным сигналом называют функцию времени, значения которой заранее неизвестны и могут быть предсказаны лишь с некоторой вероятностью. К основным характеристикам случайных сигналов относятся:

закон распределения (относительное время пребывания значения сигнала в определенном интервале),
спектральное распределение мощности сигнала.

В задачах ЦОС случайные сигналы делятся на два класса:

шумы — беспорядочные колебания, состоящие из набора разных частот и амплитуд,
сигналы, несущие информацию, для обработки которых требуется прибегать к вероятностным методам.

С помощью случайных величин можно моделировать воздействие реальной среды на прохождение сигнала от источника к приёмнику данных. При прохождении сигнала через какое-то шумящее звено, к сигналу добавляется так называемый белый шум. Как правило, спектральная плотность такого шума равномерно (одинаково) распределена на всех частотах, а значения шума во временной области распределены нормально (Гауссовский закон распределения). Поскольку белый шум физически добавляется к амплитудам сигнала в выбранные отсчеты времени, он называется аддитивный белый гауссовский шум (AWGN — Additive white Gaussian noise).

Сигналы, модуляция и манипуляция

В этом разделе показаны основные способы изменения одного или нескольких параметров гармонического сигнала. Вводятся понятия амплитудной, частотной и фазовой модуляции. В частности, выделяется линейная частотная модуляция, применяемая в задачах радиолокации. Показаны основные характеристики сигналов, спектры модулированных сигналов в зависимости от параметров модуляции.

Для удобства на языке Python создан набор функций, осуществляющих перечисленные виды модуляции. Пример реализации ЛЧМ-сигнала:

def signal_chirp(amp=1.0, freq=0.0, beta=0.25, period=100, **kwargs):
    """
    Create Chirp signal

    Parameters
    ----------
    amp : float
        Signal magnitude
    beta : float
        Modulation bandwidth: beta < N for complex, beta < 0.5N for real
    freq : float or int
        Linear frequency of signal
    period : integer
        Number of points for signal (same as period)
    kwargs : bool
        Complex signal if is_complex = True
        Modulated by half-sine wave if is_modsine = True
    """
    is_complex = kwargs.get('is_complex', False)
    is_modsine = kwargs.get('is_modsine', False)

    t = np.linspace(0, 1, period)
    tt = np.pi * (freq * t + beta * t ** 2)
    
    if is_complex is True:
        res = amp * (np.cos(tt) + 1j * np.sin(tt))
    else:
        res = amp * np.cos(tt)

    if is_modsine is True:
        return res * np. sin(np.pi * t)
    return res

Также в этом разделе из теории передачи дискретных сообщений описаны виды цифровой модуляции — манипуляции. Как и в случае с аналоговыми сигналами, цифровые гармонические последовательности могут быть манипулированы по амплитуде, фазе и частоте (либо по нескольким параметрам сразу).

Цифровые фильтры — БИХ и КИХ

Достаточно большой раздел, посвященный вопросам цифровой фильтрации дискретных последовательностей. В задачах цифровой обработки сигналов данные проходят через цепи, которые называются

фильтрами

. Цифровые фильтры, как и аналоговые, обладают различными характеристиками — частотные: АЧХ, ФЧХ, временная: импульсная характеристика, а также передаточная характеристика фильтра. Цифровые фильтры используются в основном для улучшения качества сигнала — для выделения сигнала из последовательности данных, либо для ухудшения нежелательных сигналов — для подавления определенных сигналов в приходящих последовательностях отсчетов.

В разделе перечислены основные преимущества и недостатки цифровых фильтров (в сравнении с аналоговыми). Вводится понятие импульсной и передаточной характеристик фильтра. Рассматривается два класса фильтров — с бесконечной импульсной характеристикой (БИХ) и конечной импульсной характеристикой (КИХ). Показан способ проектирования фильтров по канонической и прямой форме. Для КИХ фильтров рассматривается вопрос о способе перехода к рекурсивной форме.

Для КИХ фильтров показан процесс проектирования фильтра от стадии разработки технического задания (с указанием основных параметров), до программной и аппаратной реализации — поиска коэффициентов фильтра (с учетом формы представления числа, разрядности данных и т.д.). Вводятся определения симметричных КИХ фильтров, линейной ФЧХ и её связи с понятием групповой задержки.

Оконные функции в задачах фильтрации

В задачах цифровой обработки сигналов используются оконные функции различной формы, которые при наложении на сигнал во временной области, позволяют качественно улучшить его спектральные характеристики. Большое количество всевозможных окон обусловлено в первую очередь одной из главных особенностей любого оконного наложения. Эта особенность выражается во взаимосвязи уровня боковых лепестков и ширины центрального лепестка. Правило:

Чем сильнее подавление боковых лепестков спектра, тем шире главный лепесток спектра и наоборот.

Одно из применений оконных функций: обнаружение слабых сигналов на фоне более сильных путём подавления уровня боковых лепестков. Основные оконные функции в задачах ЦОС — **треугольное, синусоидальное, окно Ланцоша, Ханна, Хэмминга, Блэкмана, Харриса, Блэкмана-Харриса, окно с плоской вершиной, окно Наталла, Гаусса, Кайзера** и множество других. Большая часть из них выражена через конечный ряд путём суммирования гармонических сигналов с определенными весовыми коэффициентами. Такие сигналы отлично реализуются на практике на любых аппаратных устройствах (программируемые логические схемы или сигнальные процессоры).

Ресемплинг.

Децимация и интерполяция

В этом разделе рассматриваются вопросы многоскоростной обработки сигналов — изменения частоты дискретизации. Многоскоростная обработка сигналов (multirate processing) предполагает, что в процессе линейного преобразования цифровых сигналов возможно изменение частоты дискретизации в сторону уменьшения или увеличения, либо в дробное число раз. Это приводит к более эффективной обработке сигналов, так как открывается возможность использования минимально допустимых частот дискретизации и, как следствие, значительного уменьшения требуемой вычислительной производительности проектируемой цифровой системы.

Децимация (прореживание) – понижение частоты дискретизации. Интерполяция – повышение частоты дискретизации.

Также в разделе рассматривается класс однородных КИХ фильтров, которые называются интегрально-гребенчатыми фильтрами (CIC, Cascaded integrator–comb). Показана реализация, основные свойства и особенности CIC фильтров. В силу линейности математических операций, происходящих в CIC фильтре возможно каскадное соединение нескольких фильтров подряд, что дает пропорциональное уменьшение уровня боковых лепестков, но также увеличивает «завал» главного лепестка амплитудно-частотной характеристики.

График АЧХ фильтра в зависимости от коэффициента децимации:

Также в этом разделе обсуждается вопрос увеличения разрядности данных на выходе CIC фильтра в зависимости от его параметров. Это особенно важно в задачах программной реализации, в частности на ПЛИС.

Для практической реализации CIC фильтров на Python разработан отдельный класс CicFilter, реализующий методы децимации и интерполяции. Также показаны примеры изменения частоты дискретизации с помощью встроенных методов из scipy пакета Python.

Python CicFilter Class for Digital Signal Processing

class CicFilter:
    """
    Cascaded Integrator-Comb (CIC) filter is an optimized class of
    finite impulse response (FIR) filter.
    CIC filter combines an interpolator or decimator, so it has some
    parameters:

    R - decimation or interpolation ratio,
    N - number of stages in filter (or filter order)
    M - number of samples per stage (1 or 2)*

    * for this realisation of CIC filter just leave M = 1. 

    CIC filter is used in multi-rate processing. In hardware
    applications CIC filter doesn't need multipliers, just only
    adders / subtractors and delay lines.

    Equation for 1st order CIC filter:
    y[n] = x[n] - x[n-RM] + y[n-1].


    Parameters
    ----------
    x : np.array
        input signal
    """

    def __init__(self, x):
        self.x = x

    def decimator(self, r, n):
        """
        CIC decimator: Integrator + Decimator + Comb

        Parameters
        ----------
        r : int
            decimation rate
        n : int
            filter order
        """

        # integrator
        y = self.x[:]
        for i in range(n):
            y = np.cumsum(y)

        # decimator

        y = y[::r]
        # comb stage
        return np.diff(y, n=n, prepend=np.zeros(n))

    def interpolator(self, r, n, mode=False):
        """
        CIC inteprolator: Comb + Decimator + Integrator

        Parameters
        ----------
        r : int
            interpolation rate
        n : int
            filter order
        mode : bool
            False - zero padding, True - value padding. 
        """

        # comb stage
        y = np.diff(self.x, n=n,
                    prepend=np.zeros(n), append=np.zeros(n))

        # interpolation
        if mode:
            y = np.repeat(y, r)
        else:
            y = np.array([i if j == 0 else 0 for i in y for j in range(r)])

        # integrator
        for i in range(n):
            y = np.cumsum(y)

        if mode:
            return y[1:1 - n * r]
        else:
            return y[r - 1:-n * r + r - 1]

Наконец, в этом разделе приведен особый класс фильтров — скользящего среднего. Показано три способа реализации: через свертку сигналов, с помощью КИХ-фильтра и БИХ-фильтра.

Заключение

Надеюсь, этот курс лекций в совокупности с моими предыдущими статьями по цифровой обработке сигналов на ПЛИС принесет практическую пользу и поможет читателю лучше понять основы цифровой обработки сигналов. Этот проект будет улучшаться и дополняться новым полезным и не менее интересным материалом. Следите за развитием!

Дополнительно к этому материалу я поддерживаю и развиваю свой проект по основным модулям ЦОС (на языке Python). Он содержит пакет генерации различных сигналов, класс CIC фильтров для задач децимации и интерполяции, алгоритм расчета коэффициентов корректирующего КИХ-фильтра, фильтр скользящего среднего, алгоритм вычисления сверх-длинного БПФ через методы двумерного преобразования (последнее очень пригодилось в работе при аппаратной реализации на ПЛИС).

UPD: 20.04.2020

В курс добавлено две лекции:

Непараметрические методы спектрального анализа (Владимир Фадеев)
Усреднение по частоте и по времени. Полифазный БПФ.

Спасибо за внимание!

Цифровая обработка сигналов

Список видео, входящих в плейлист “Цифровая обработка сигналов”:

Введение
Сигналы, шумы и помехи
Решаемые задачи
Знакомство с MATLAB
Создаем аккорд в MATLAB
Выделяем тон из аккорда в MATLAB)
Анализ ЭКГ в MATLAB
Дискретные периодические сигналы
Синусоидальный сигнал как базис
Теорема Котельникова
АЦП и ЦАП
Шум как случайный процесс
Виды шумов, отношение сигнал/шум
Статистическая обработка сигнала
Корреляционная функция
Приближение сигнала функцией
Частотное представление сигнала
Преобразование Фурье
Спектральный анализ
Дискретная свёртка
Линейные стационарные системы
АЧХ и ФЧХ
Цифровые фильтры
КИХ и БИХ фильтры
Многоскоростные системы
Многоскоростные фильтры
Адаптивные фильтры
Активное шумоподавление
Создание приложения в MATLAB
Обработка на Raspberry Pi

01.

Введение

Ролик открывает серию видео, рассказывающих об основах ЦОС. Простота изложения, демонстрация простых примеров и объяснение базовых принципов делают тему доступной даже для новичков в ЦОС, а для опытных практиков помогает взглянуть на привычные вещи свежим взглядом. В данном ролике объясняется, где обработка сигналов встречается в обычной жизни и как применить наши знания на практике. Даем базовые определения – сигнал, представление сигнала, обработка сигналов.

02. Сигналы, шумы и помехи

В ролике доступно объясняется что такое цифровой сигнал и как его создают из аналогового (процесс оцифровки сигнала). Рассказывается о видах шумах, помех и искажений и том, чем эти понятия отличаются друг от друга. Раскрывается понятие «полезного сигнала».

03. Решаемые задачи

Эквализация (исправление) сигнала, фильтрация сигнала, идентификация системы, анализ и оценка параметров сигнала, сжатие сигнала – что это такое, зачем нужно и как проводится? Смотрите наше видео и узнавайте ответы на эти вопросы.

04. Знакомство с MATLAB

Просмотрев это видео, вы узнаете, что же такое MATLAB и как начать в нем работать. И уже меньше, чем через четыре минуты сможете приступить к решению первых конкретных задач ЦОС в MATLAB.

05. Создаем аккорд в MATLAB

В этом видео инженер ЦИТМ Экспонента Марат Усс покажет вам как, при помощи инструментов MATLAB, создать сумму трех синусоидальных колебаний, которые превратятся в аккорд ля-мажор.

06. Выделяем тон из аккорда в MATLAB)

Что такое инструмент Signal Analyzer App и программное расширение Signal Processing Toolbox и какое они имеют отношение к обработке синтезированного сигнала? Смотрите это видео, и вы все узнаете сами.

07. Анализ ЭКГ в MATLAB

Что такое живые скрипты, как импортировать данные в MATLAB и отфильтровать по частоте? В этом видео инженер ЦИТМ Экспонента не только доступно отвечает на эти вопросы, но и наглядно показывает, как подобные действия осуществляются в MATLAB.

08. Дискретные периодические сигналы

В ролике подробно рассказывается о дискретных сигналах и рассматриваются дискретные периодические сигналы.
Если вам интересны ответы на такие вопросы как:
– Что такое сигнал и как он описывается?
– Что такое дискретный сигнал и как получить его из аналогового?
– Что такое периодический сигнал и фундаментальная частота?
– Как тон звука зависит от частоты дискретизации?
смотрите это видео.

09. Синусоидальный сигнал как базис

Посмотрев это видео вы поймете почему именно синусоидальный сигнал является фундаментальным для описания и обработки сигналов. Узнаете как сложные сигналы можно представить сигналами простыми и как из базовых сигналов с различными весовыми коэффициентами можно сформировать сложный сигнал.

10. Теорема Котельникова

Теорема Котельникова описывает основные ограничения при дискретизации аналогового сигнала. В этом видео инженер ЦИТМ Экспонента Марат Усс объясняет при чем тут частота периодического сигнала и рассказывает об эффекте алиасинга.

11. АЦП и ЦАП

В этом ролике кратко рассказывается об устройстве аналого-цифровых преобразователей (АЦП) и цифро-аналоговых преобразователей (ЦАП). Описываются основные характеристики АЦП, а также различные типы ошибок, возникающих при преобразовании аналогового сигнала в цифровой.

12. Шум как случайный процесс

В данном ролике мы знакомимся с математическим описанием шума – случайным процессом, и описанием всех сигналов физического мира моделью «сигнал + шум». Мы начинаем изучать математический аппарат описания случайных процессов, знакомимся с понятием распределения случайной величины и с Центральной Предельной Теоремой теории вероятностей.

13. Виды шумов, отношение сигнал/шум

Этот ролик знакомит нас с основными характеристиками случайных процессов, такими как математическое ожидание, дисперсия, корреляционная функция и спектральная плотность мощности. Мы узнаем о различных видах «цветных» шумов и познакомимся с моделью аддитивного белого гауссовского шума. Также мы определим понятия отношения сигнал/шум, динамического диапазона и чувствительности.

14. Статистическая обработка сигнала

В данном видео мы узнаем о статистических характеристиках сигналов и рассмотрим техники статистического анализа и обработки. Мы рассмотрим задачи выделения постоянной составляющей и поиска локальных экстремумов в сигнале.

15.

Корреляционная функция

Данное видео посвящено рассмотрению взаимно-корреляционной функции и автокорреляционной функции, а также методам корреляционного анализа.

16. Приближение сигнала функцией

В этом видео мы кратко очерчиваем задачу приближения сигнала аналитической функцией, и знакомимся с приложением Curve Fitting, используемого для решения этой задачи.

17. Частотное представление сигнала

В данном видео мы рассматриваем вопросы частотного представления сигнала, а также знакомимся с описанием вещественных сигналов при помощи комплексных величин.

18. Преобразование Фурье

В данном видео мы рассматриваем особенности применения БПФ для спектрального анализа, описываем влияние оконных функций на точность построения спектра, даём определение нелинейным искажениям и демонстрируем пример построения спектрограммы живого сигнала с микрофона.

19. Спектральный анализ

20. Дискретная свёртка

В данном видео рассказывается об одной из ключевых операций в цифровой обработке сигналов – дискретной свёртке, а также демонстрируется принцип поиска сигнала на фоне шума при помощи согласованного фильтра.

21. Линейные стационарные системы

В данном видео мы знакомимся с линейными стационарными дискретными системами, а также со способами их описания – разностными уравнениями, импульсной характеристикой, передаточной функцией, нуль-полюсной диаграммой.

22. АЧХ и ФЧХ



В данном видео рассказывается об амплитудно-частотной характеристике и фазо-частотной характеристике линейной стационарной системы, или фильтра. В видео визуально поясняется зависимость АЧХ системы от её передаточной функции, а также демонстрируется полный анализ фильтра в MATLAB определением большинства характеристик.

23. Цифровые фильтры



В этом видео мы знакомимся с основными параметрами цифровых фильтров, особый упор делая на классификацию по форме их частотной характеристики. Также мы знакомимся с процессом проектирования цифровых фильтров, начиная от формирования спецификации и подсчёта коэффициентов в MATLAB, заканчивая вопросами реализации на целевой платформе.

24. КИХ и БИХ фильтры



Данное видео рассматривает особенности КИХ и БИХ-фильтров, их преимущества и недостатки, методы синтеза, а также примеры разработки в интерактивном приложении Filter Designer App.

25. Многоскоростные системы



В данном видео мы начинаем знакомство с многоскоростными системами, и рассматриваем такие операции, как понижение и повышение частоты дискретизации сигнала в целое число раз.

26. Многоскоростные фильтры



В этом видео мы продолжаем знакомство с многоскоростными системами, рассматриваем значимость фильтрации в задачах понижения и повышения частоты дискретизации, наблюдаем пример изменения частоты в не целое число раз и знакомимся с полифазными структурами многоскоростных фильтров.

27. Адаптивные фильтры



Данное видео знакомит вас с адаптивными фильтрами, то есть фильтрами, коэффициенты которых могут изменять во времени в зависимости от задачи и входного воздействия. Помимо основных параметров, структур и типов подобных систем в видео так же рассматриваются задачи адаптивной фильтрации, и на примере разбирается одна из них – идентификация неизвестной системы.

28. Активное шумоподавление



В этом видео мы рассматриваем одну из задач адаптивной фильтрации – активное шумоподавление. В рамках видео рассматривается принцип формирования «анти-шума» при помощи адаптивного фильтра, а также разбирается практический пример выделения музыки на фоне шума толпы.

29. Создание приложения в MATLAB



Данное практическое видео демонстрирует процесс разработки графического интерфейса пользователя в MATLAB. При помощи App Designer мы создадим приложение цифровой обработки аудио-сигнала.

30. Обработка на Raspberry Pi



В заключительном видео плейлиста мы рассмотрим процессы разработки моделей в среде Simulink, а также реализации алгоритмов ЦОС на Raspberry Pi.

Цифровая обработка звука

Если вы интересуетесь цифровой обработкой звука, следует, в первую очередь, понять, для чего она вам нужна.

Обработка звука — понятие разноплановое. В звук могут попадать разные шумы, что зависит от способа записи звуковой дорожки, наличия студийных или домашних условий, типа используемого оборудования. И вы как раз можете быть заинтересованы в подавлении шумов.

Возможно, вы хотите наложить разные звуковые фильтры. Определенная музыка требует выведения на передний план одних частот и приглушения или переведения на задний план других и пр. Ознакомившись с данной статьей, вы узнаете много нового.

Самой распространенной процедурой, имеющей место при цифровой обработке звука, является подавление шумов. Этот момент заслуживает особого внимания, шумы следует удалять в обязательном порядке, это позволит вашей звуковой дорожке выйти на профессиональный уровень.

Шумы могут быть самыми разными: внешними, случайно записанными на микрофон фоновыми звуками в комнате с посторонними людьми и некачественной звукоизоляцией, и внутрисистемными, которые появились в результате плохого экранирования шнуров и остальной звукозаписывающей аппаратуры.

Шумы, как и все звуки, имеют свои частоты, правда, диапазон у них сравнительно узок, что существенно облегчает их удаление. Существует простой и эффективный метод эквализации, который позволяет устранять частоты с самым большим количеством шума и самым маленьким количеством нужных звуков.

Однако даже при этом следует следить, чтобы это удаление не повредило основную звуковую дорожку. Если в записи шумы занимают сравнительно небольшой диапазон, который не соприкасается с диапазоном других звуков, то она считается чистой. И, наоборот, запись с шумами почти на всех частотах является весьма грязной. Ее очищение от шумов без ущерба для нужных звуков практически невозможно.

Второе место по востребованности при цифровой обработке звука занимает реверберация, которая представляет собой постепенное затухание звука, к примеру, в большом помещении с отличной акустикой.

При небольшой продолжительности она делает звучание вокала или сольного инструмента более глубоким и выразительным. Поэтому неудивительно, что ее так часто используют.

Если простое эхо просто повторяет звук несколько раз, затихая при этом, то реверберация прогрессивно меняет соотношение частот звука, который повторяется, что обеспечивает создание самых разнообразных эффектов.

На третьем месте по популярность находятся, пожалуй, дилэй-эффекты или, простыми словами, задержки звука. Сюда входит и обычное эхо любой частоты затухания, и более изысканные эффекты. При обработке монозвука и необходимости его превращения в псевдостерео большую пользу может принести как раз дилэй.

С этой целью делается совсем маленькая задержка звука в одном из каналов. При этом рекомендуется добавить в один канал немного «сухости» (средних частот), что позволит бывшему монозвуку звучать в разных каналах и слегка по-разному, благодаря чему и появляется эффект псевдостерео.

Прибавление небольшого количества высоких и средних частот и полное отсутствие реверберации и дилэя способствует созданию популярного в последнее время «эффекта присутствия», при котором возникает ощущение, что вокалист находится прямо в вашей комнате.

Фильтры представляют собой эквализационные схемы, накладываемые на существующий записанный звук. Их разделяют на статические и динамические.

С помощью статических фильтров можно убирать некоторые частоты дорожки посредством добавления других. Динамические же предназначены для постоянного изменения соотношения частот по определенной круговой схеме, что способствует созданию эффекта «плавающего» звука.

Мы рассмотрели всего несколько основных моментов, которые заслуживают особого внимания во время самостоятельной цифровой обработки звука.

_______________________

При копировании материала ссылка на сайт www.as-workshop.ru обязательна!

Аналоговая и цифровая обработка звукового сигнала.

Мифы и реальность.

Скачать PDF

Попробуем начать с основ, на которых строятся принципы обработки, анализа и преобразований звука.

Итак, диапазон частот, которые может слышать и различать человек, находится в пределах от 15 Гц до 20 кГц. Человек может слышать только аналоговый звук. Т.е. вне зависимости от того как получен сигнал звука, для того, чтоб он был услышан, он всегда должен быть преобразован в аналоговую форму. Метод представления аналоговой формы выберем классический – waveform, т.е. это такая кривая, которая отображает изменение сигнала во времени. Сразу предположим, что мы имеем громкоговорители близкие к идеалу, и форма звукового давления, которое они создают, максимально повторяет форму сигнала, чтобы исключить фактор акустики, так как это отдельный разговор.

I. Природа тембра и окраса звука.

В звуке все крутится вокруг гармонических колебаний, т.е. колебаний синусоидальной формы. Собственно, абсолютно любая другая форма сигнала может быть представлена суммой различных гармонических колебаний – это и есть та самая основа для «тембра» и «окраса» звука.

Те, для кого это очевидно, могут с легкостью пропустить эту часть, однако, думаю найдутся те, кому это и будет интересно.

Откуда же берутся все эти понятия «теплый ламповый звук», «холодный транзисторный звук» и т.п? Каждый звуковой прибор, будь то обработка или усилитель, вносят определенные изменения в форму сигнала, так как практически все элементы схем являются нелинейными. Представим, что мы имеем идеальный генератор синусоидального сигнала. Вот такого:

Подадим этот сигнал на вход устройства, которое, например, имеет нелинейную передаточную характеристику показанную на рисунке 2 синим цветом, а красным цветом обозначена идеальная линейная передаточная функция (для сравнения).

На выходе устройства будет сигнал отображенный синим цветом на рисунке 3. Красным цветом там отображен входной сигнал для сравнения.

Визуально форма сигнала практически не отличается. Если отобразить ее без сравнения с входной формой, то разница будет практически не заметна. А вот на слух они будут отличаться. Давайте посмотрим на спектр входного и выходного сигнала на рисунке 4, чтобы понять характер различий. Красным цветом обозначен спектр входного сигнала, на котором виден единственный пик на первой гармонике (основной частоте). А вот с выходным сигналом все уже гораздо интересней, там добавились нечетные гармоники (уровень каждой указан на рисунке). Т.е., если мы возьмем 5-ти канальный генератор с частотами кратным гармоникам, и правильно установленными фазами и уровнями и просуммируем их, то мы получим точно такой сигнал как на выходе. И вот эти гармоники и придают тот самый тембр звуку. Собственно, если записать вокалиста берущим какую-то ноту, то мы получим чем-то похожую картину спектра, где будет ярко выражена основная частота ноты и менее выраженные частоты четных и нечетных гармоник. Это и есть то, что называется тембром и окрасом звука.

Т.е. любая периодичная форма сигнала отличная от синусоидальной состоит из суммы синусоидальных колебаний частот кратных основной частоте. И из этого следует то, что для частот 10 кГц и выше, вторая гармоника будет 20 кГц и выше, третья 30 кГц и т.д., но человек не слышит частоты выше 20 кГц, а это означает, что человеческое ухо не в состоянии различить форму сигнала на частотах 10÷20 кГц. Эти факты нам еще пригодится, при рассмотрении цифровых методов обработки сигнала немного позже.

II. Аналог против цифры – что же круче?

Сразу следует сказать, что вопрос сам по себе некорректный, но часто он или его производные становятся предметами споров. Бытует мнение, что «аналог» – это круто и дорого (ну или круто, если дорого), а вот цифра – это такой себе бюджетный ширпотреб. Попробуем разобраться почему существуют такие мнения…

Что есть у аналоговых приборов, чего нет у цифровых или «хуже»:

Управление. Привычное (часто считается, что более удобное) управление. Т.е. на каждом аналоговом приборе есть подписанные ручки, кнопки, переключатели и т.д. которые доступны сразу и чаще всего мгновенно оказывают влияние на сигнал. Другими словами у Вас есть большая рэковая стойка с кучей приборов и к каждому регулируемому параметру Вы имеете мгновенный доступ. У цифровых приборов/программ обычно не все так очевидно и есть меню, кнопки и т.д. и часто, чтобы добраться до регулировки какого-то параметра нужно предварить это несколькими дополнительными манипуляциями, при том, что сами приборы обычно компактней и более функциональны.
Время. Аналоговые приборы обрабатывают звук исключительно при помощи физических процессов. И, как результат, время обработки сигнала находится в порядках скорости света разделенной на физическую длину прохождения сигнала. Т.е. в абсолютном большинстве случаев можно считать его пренебрежимо малым или 0. У цифровых приборов здесь неоспоримая брешь в этой сфере. Как известно, цифровая обработка звука начинается с АЦП (аналогово-цифрового преобразователя) и заканчивается ЦАП (цифро-аналоговым преобразователем) между которыми есть «математика». Но даже, если представить, что математики у нас нет, то прибор с блок-схемой на рисунке 5 будет обеспечивать гарантированную задержку сигнала равную минимум 2 тактам частоты дискретизации (один для АЦП и один для ЦАП). Например, если частота дискретизации 48 кГц, то время задержки будет (1/48000)•2=4.1667•10^-5 или 41.667 микросекунд (соответственно, при повышении частоты дискретизации время будет уменьшаться обратно-пропорционально). И это минимальная задержка только на преобразование сигнала, а его «математическая» обработка в «середине» прибора – это еще дополнительное время. Обычно минимальное время на обработку – 32 сэмпла (такта частоты дискретизации), что составит – 708.339 микросекунды. Это то, от чего цифровым приборам вряд ли удастся избавится в ближайшее время, если вообще удастся. Однако критическое значение это имеет в большинстве случаев только при обработке звука в реальном времени, например живой концерт. (Для справки. При нормальном атмосферном давлении скорость звука составляет 331 м/с, т.е. задержка звука на 41.667 микросекунд будет эквивалентна задержке от звуковых излучателей находящихся примерно на расстоянии 1.4 см от слушателя, а задержка в 708.339 микросекунды – расстоянию 23 см)

На этом реальные и объективные преимущества аналоговых приборов заканчиваются. Маркетинговую и психологическую составляющую мы не учитываем, хотя зачастую они играют решающее значение 🙂

Теперь про цифровой метод. Цифровые приборы могут абсолютно все тоже самое, что могут аналоговые (не учитывая задержку о которой шла речь немного выше). А вот аналоговые могут далеко не все то, что могут цифровые. Например, аналоговым методом (без привлечения механических составляющих) практически невозможно организовать существенную задержку сигнала, как то реверберация или delay, точный pitch и т.п. Аналоговым методом невозможно осуществлять фильтрацию сигнала не внося в него искажения и шум. Любой аналоговый фильтр вызывает сдвиг фазы сигнала. Собственно последняя «проблема» очень часто как раз и является тем самым характером прибора, то что многие называют «звучит». Любой компонент (даже пассивный) аналоговой схемы вносит нелинейные искажения, а именно: электронный шум, добавляет гармоники и сдвиг фазы сигнала. Сумма всех этих искажений вызванная конкретным схемотехническим решением во многих случаях и обеспечивает «фирмовость» прибора при одинаковой функциональности с аналогичными. Когда просто пропустил сигнал через эквалайзер, немного его настроил и все «запело», а в другом аналоговом или цифровом устройстве – повторил все настройки, а оно «сухо» и «никак». Можно ли повторить этот эффект в «цифре»? Да, можно. Математические алгоритмы и современная скорость их обработки позволяют повторять любое поведение сигнала от алгоритмического (когда мы знаем какие трансформации происходят с сигналом и создаем их математическую модель) вплоть до полной имитации работы аналоговой схемы (с помощью таких моделей как SPICE, например). Т.е. разработчик цифрового модуля может заложить и учесть все необходимые сдвиги фаз на разных частотах, добавление гармоник и т.д. вплоть до имитации работы транзистора в каком-то запредельном режиме, в котором реальный транзистор может «прожить» пару минут выдавая особое звучание, или которое сложно реализовать, например, температура охлаждения -10°С. Многие современные цифровые модули (будь то приборы или программы, плагины) делают по принципу аналоговых. Другими словами эквалайзер занимается не просто голой фильтрацией по полосам, а и добавлением своих нюансов, как его аналоговый брат.

Хорошие цифровые плагины стоят не копейки и вот здесь снова часто срабатывает психология материалистов: отдать пачку денег за красивый, увесистый прибор с замечательной табличкой и «звучащий» – это понятно и приемлемо, а отдать не мало, хоть и меньше денег за ссылку по которой можно скачать набор байтов – это вот как-то непонятно. 🙂 Отсюда и произрастает часть мифов про «скупость» звучания «цифры»… Многие, устанавливая программы, для работы со звуком пользуются базовыми инструментами обработки, которые зачастую и не позиционируются как что-то особенное, а часто это как раз инструменты для минимально необходимых манипуляций, как скотч и канцелярский нож в офисе.

III. Как работает «цифра»?

Теперь попробуем заглянуть немного внутрь цифровой обработки сигнала, чтоб иметь хотя бы общее представление что да как.

Как уже говорилось выше «путь» цифровой обработки сигнала начинается с АЦП (ADC). Это одно из ключевых устройств, которое имеет очень сильное влияние на качество процесса и является «необратимым» устройством. Т.е. все искажения которые будут внесены этим устройством на этапе преобразования будут необратимы. Какую-то часть как-то можно компенсировать алгоритмами обработки, однако в целом нужна максимальная точность преобразования.

Есть несколько типов АЦП устройств принципиально различающихся типом выхода цифровых данных, такие как PCM, DSD, PWM и т.д. Мы будем говорить о типе PCM, так как это единственный тип цифровых данных подходящий для полноценной обработки звука, все иные типы преобразовываются в тип PCM для полноценной обработки.

PCM (Pulse code modulation) – это импульсно-кодовая модуляция. Ее смысл заключается в том, что через равные определенные промежутки времени происходит «измерение» (сэмплирование) уровня сигнала и передача цифрового значения этого «замера». Ключевым параметром здесь является частота дискретизации – это частота «замеров» (квантизация). Частота дискретизации определяет предельно возможную частоту преобразовываемого сигнала – она называется частотой Найквиста и равна ровно половине частоты дискретизации. Частота дискретизации определяет возможный частотный диапазон. Стандартными базовыми частотами дискретизации в обработке звука являются 44.1 кГц и 48 кГц, выше кратные им. Наивысшей стандартизированной частотой дискретизации используемой в обработке звука на сейчас является 352.8 кГц.

И вот здесь возникает вопрос: если предел слышимой частоты – 20 кГц, а частотный диапазон при дискретизации в 44.1 кГц выше слышимого и находится на отметке в 22.05 кГц, то зачем нужна частота дискретизации, например, в 192 кГц? Первый логичный ответ который напрашивается из рисунка 5 – это то, что мы сможем иметь больше «точек» описывающих кривую на высоких частотах и получить большую детализацию сигнала и как результат будем ближе к истинному сигналу. Это объяснение весьма логично, однако не имеет особого практичного смысла, так как источники звука выдают сигнал в диапазоне до 20 кГц, а это означает, что в диапазоне 10÷20 кГц присутствуют только синусоидальные составляющие и зная это описывать подробно их форму не имеет особого смысла. На самом деле здесь мяч находится на аналоговой стороне АЦП (извините за тавтологию). Так вот, принципы работы АЦП PCM типа требуют, чтоб входной сигнал находился строго в диапазоне от 0 Гц до частоты Найквиста, иначе в преобразовании будут ошибки, а это в свою очередь означает, что вход АЦП должен быть оборудован фильтром высоких частот, который будет срезать все, что выше частоты Найквиста, но при этом максимально ровно пропускать все что до нее. Т.е. другими словами, при частоте дискретизации 44.1 кГц необходим фильтр который будет иметь пропускную способность 0 дБ на частоте 20 кГц и -150 дБ (для 24 бит) на частоте 22.05 кГц (рисунок 7). Кто хоть немного знаком со схемотехникой понимает, что построение такого фильтра вызывает немало трудностей и приличную его стоимость. А вот при частоте дискретизации в 192 кГц и частоте Найквиста 96 кГц фильтр должен уже обладать куда менее крутой характеристикой и соответственно будет проще и дешевле в реализации. Поэтому при удешевлении технологии производства цифровых схем, со временем, оказалось проще и дешевле поднимать частоту дискретизации, упрощая при этом фильтр и поднимая качество.

Тогда назревает противоположный вопрос, а почему не использовать частоты дискретизации еще выше? Ответ весьма прост – прироста качества это уже не даст, а будет повышать стоимость обработки звука увеличением потока обработок на процессор(ы), удорожанием преобразовывающих чипов, большим количеством места для хранения (на диске)…

Так же бытует мнение о том, что при большей частоте дискретизации качественнее происходит pitching. На самом деле это не совсем верное утверждение, потому как существуют математические алгоритмы, которые позволяют достаточно точно восстанавливать промежуточные значения входного сигнала между сэмплами зная частоту дискретизации, но этот алгоритм создает дополнительную нагрузку, в то время как при высокой частоте дискретизации не редко просто берут ближайшее необходимое значение, что значительно проще.

Еще один параметр АЦП – это его разрядность. Разрядность в данном случае – это прямой показатель возможного динамического диапазона обрабатываемого сигнала. Таким образом, разрядность в 8 бит обеспечивает динамический диапазон примерно в 48 дБ, 12 бит – 72 дБ, 16 бит – 96 дБ, 24 бита – 144 дБ, 32 бита – 192 дБ. Отношение сигнал/шум для большинства высококачественных источников звука находится на уровне 110-120 дБ, т.е. разрядность в 24 бита перекрывает с лихвой этот диапазон.

Все АЦП PCM типа обладают таким неприятным явлением как «шум квантизации». Это явление вызвано тем, что АЦП может воспринимать дискретные (конкретные) уровни сигнала. Рассмотрим на примере 4 битного преобразователя для простоты. Например, амплитуда номинального входного напряжения 1В – это означает, что такой АЦП может выдать значение входного напряжения с интервалом в 62.5 мВ, но что произойдет, если уровень входного напряжения в момент квантизации («замера»), например, 67 мВ? В зависимости от конкретного АЦП он воспримет этот уровень как один из граничных между которыми находится. В данном случае между 62.5 мВ и 125 мВ. Предположим, что рассматриваемым АЦП будет взято ближайшее значение, тогда при обратном преобразовании мы получим 62.5 мВ вместо 67 и, соответсвенно, ошибку в 5.5 мВ. При следующем преобразовании получим новую ошибку и т.д. Величина этой ошибки будет всегда не больше 62.5 мВ в данном случае или эквивалента младшего разряда в общем случае. Однако, не все так страшно, при разрядности в 24 бита получается, что шум квантизации будет находится на уровне -144 дБ, что за пределами сигнал/шум многих источников звука и не будет оказывать влияния на полезный сигнал.

Мы подошли к очередному мифу из серии «аналог vs цифра», что аналоговый сигнал он такой весь гладенький и непрерывный, а цифровой сигнал весь в клеточку – побитый на интервалы во времени частотой дискретизации и амплитуде разрядностью. Так вот, качественно преобразованный цифровой сигнал тоже непрерывный и гладкий на столько, что Вы не заметите эти «клеточки». Например, источник сигнала с соотношением сигнал/шум 120 дБ равнозначен 20 битному звуку, поэтому все, что будет находится между дискретными интервалами в 20 бит – это будет просто шум, таким точно шумом можно заполнить младшие 4 бит в 24 битном звуке и вы не увидите и не услышите никаких «клеточек» и ступенек в сравнении с таким аналоговым источником звука.

Для справки. Обычные качественные компакт-кассеты обладают эквивалентом 5-6 битного диапазона, компакт-кассеты с металлической пленкой 8-10 битного как и катушечные магнитофоны, профессиональные катушечные магнитофоны с профессиональной пленкой 12-14 битного. Именно поэтому многие любят до сих пор использовать пленку как естественный компрессор. К тому же, если Вы посмотрите на АЧХ характеристику пленки, то увидите, что частота там далеко не бесконечна, а заваливается после 12-14 кГц. Это происходит потому, что на пленочных носителях она (частота) тоже дискретизирована. 🙂 Только не «цифровыми выборками», а доменами магнитного материала из которого изготовлена пленка и которые имеют конечную и вполне определенную длину и сохраняют одно положение для магнитного потока, т.е. другими словами, можно взять пленку и абсолютно так же поделить ее на отрезки как рисунок 5. И абсолютно тот же самый эффект и принцип дискретизации происходит при движении пленки вдоль головки магнитофона. Именно поэтому увеличивая скорость на катушечном магнитофоне мы получаем лучшую передачу высоких частот – мы увеличиваем частоту дискретизации.

После преобразования звука в цифровой вид, начинается чистейшая математика и это невероятный объем информации, освещать который не входит в планы этой статьи.

В конце обработанный звук, чаще всего преобразовывается в аналоговый при помощи ЦАП, по принципу противоположному АЦП. Т.е. ЦАП получает значение уровня сигнала с частотой дискретизации и формирует на выходе соответсвующий уровень напряжения. И вот здесь у многих возникает в голове стереотипная картинка со ступеньками 🙂 На самом деле, если Вы подключите осциллограф к качественному ЦАП – Вы не увидите никаких ступенек, а увидите гладенькую, ровненькую аналоговую кривую, да еще и с минимальным уровнем шумов. Почему это происходит? Потому что на выходе ЦАП так же оснащены фильтрами высоких частот, которые срезают все выше нужного для звука диапазона, но, если Вы вспомните начало статьи, то там говорилось, что для резких фронтов (прямоугольного) сигнала нужно присутствие n-кратных гармоник до бесконечности, а наша основная гармоника «ступенек» – это частота дискретизации, т.е. нужны частоты от частоты дискретизации и выше кратные частоте дискретизации, которые благополучно «режутся» сглаживая ступеньки в красивый и чистый звук 🙂

Все описанное распространяется и на аналоговые с псевдоаналоговыми синтезаторами за которыми многие так охотятся. Как раритет, экспонат, моральное наслаждение и кайф на ощупь – да, как источник звука – не сложно полноценно заменяется цифровыми средствами.

Цифровая обработка сигналов – это… Что такое Цифровая обработка сигналов?

Цифрова́я обрабо́тка сигна́лов (ЦОС, DSP — англ. digital signal processing) — преобразование сигналов, представленных в цифровой форме.

Любой непрерывный (аналоговый) сигнал может быть подвергнут дискретизации по времени и квантованию по уровню (оцифровке), то есть представлен в цифровой форме. Если частота дискретизации сигнала не меньше, чем удвоенная наивысшая частота в спектре сигнала (то есть ), то полученный дискретный сигнал эквивалентен сигналу по методу наименьших квадратов (МНК) (см.: Теорема Котельникова).

При помощи математических алгоритмов преобразуется в некоторый другой сигнал , имеющий требуемые свойства. Процесс преобразования сигналов называется фильтрацией, а устройство, выполняющее фильтрацию, называется фильтр. Поскольку отсчёты сигналов поступают с постоянной скоростью , фильтр должен успевать обрабатывать текущий отсчет до поступления следующего (чаще — до поступления следующих n отсчётов, где n — задержка фильтра), то есть обрабатывать сигнал в реальном времени. Для обработки сигналов (фильтрации) в реальном времени применяют специальные вычислительные устройства — цифровые сигнальные процессоры.

Всё это полностью применимо не только к непрерывным сигналам, но и к прерывистым, а также к сигналам, записанным на запоминающие устройства. В последнем случае скорость обработки непринципиальна, так как при медленной обработке данные не будут потеряны.

Различают методы обработки сигналов во временной (англ. time domain) и в частотной (англ. frequency domain) области. Эквивалентность частотно-временных преобразований однозначно определяется через преобразование Фурье.

Обработка сигналов во временной области широко используется в современной электронной осциллографии и в цифровых осциллографах. Для представления сигналов в частотной области используются цифровые анализаторы спектра. Для изучения математических аспектов обработки сигналов используются пакеты расширения (чаще всего под именем Signal Processing) систем компьютерной математики MATLAB, Mathcad, Mathematica, Maple и др.

В последние годы при обработке сигналов и изображений широко используется новый математический базис представления сигналов с помощью «коротких волночек» — вейвлетов. С его помощью могут обрабатываться нестационарные сигналы, сигналы с разрывами и иными особенностями и сигналы в виде пачек.

Основные задачи

Линейная фильтрация — селекция сигнала в частотной области; синтез фильтров, согласованных с сигналами; частотное разделение каналов; цифровые преобразователи Гильберта (Lⁿ(a, b)) и дифференциаторы; корректоры характеристик каналов
Спектральный анализ — обработка речевых, звуковых, сейсмических, гидроакустических сигналов; распознавание образов
Частотно-временной анализ — компрессия изображений, гидро- и радиолокация, разнообразные задачи обнаружения сигнала
Адаптивная фильтрация — обработка речи, изображений, распознавание образов, подавление шумов, адаптивные антенные решетки
Нелинейная обработка — вычисление корреляций, медианная фильтрация; синтез амплитудных, фазовых, частотных детекторов, обработка речи, векторное кодирование
Многоскоростная обработка — интерполяция (увеличение) и децимация (уменьшение) частоты дискретизации в многоскоростных системах телекоммуникации, аудиосистемах
Свертка – традиционные типы
Секционная свертка

Основные преобразования

Цифровая обработка сигнала в передатчике^[1]

Распространение сигналов по каналу связи

Цифровая обработка сигнала в приёмнике^[1]

Приём сигналов
Множественный доступ
Сужение спектра
Демодуляция и дискретизация
Детектирование
Разуплотнение
Канальное декодирование
Дешифрование
Декодирование источника
Форматирование

См. также

Примечания

↑ ¹ ² Скляр Б. Цифровая связь. Теоретические основы и практическое применение. Пер. с англ. — М.: Издательский дом «Вильямс», 2003. — 1104 с. — С. 33. — ISBN 5-8459-0497-8

Литература

Сергиенко А. Б. Цифровая обработка сигналов. — 2-е. — СПб.: Питер, 2007. — С. 751. — ISBN 5-469-00816-9
Гольденберг Л. М. и др. Цифровая обработка сигналов. Справочник. — М.: Радио и связь, 1985. — 312 с.
Гольденберг Л. М. и др. Цифровая обработка сигналов. Учебное пособие для вузов. — М.: Радио и связь, 1990. — 256 с.
Оппенгейм А., Шафер Р. Цифровая обработка сигналов. Изд. 2-е, испр. — М.: Техносфера, 2007. — 856 с. ISBN 978-5-94836-135-2
Оппенгейм А. В., Шафер Р. В. Цифровая обработка сигналов. — М.: Связь, 1979. — 416 с.
Рабинер Л., Гоулд Б. Теория и применение цифровой обработки сигналов. — М.: Мир, 1978. — 848 с.
Глинченко А. С. Цифровая обработка сигналов. В 2 ч. — Красноярск: Изд-во КГТУ, 2001. — 383 с.
Блейхут Р. Быстрые алгоритмы цифровой обработки сигналов. — М.: Мир, 1989. — 448 с.
Даджион Д., Мерсеро Р. Цифровая обработка многомерных сигналов. — М.: Мир, 1988. — 488 с.
Макс Ж. Методы и техника обработки сигналов при физических измерениях. В 2-х тт. — М.: «Мир», 1983.
Марпл-мл. С. Л. Цифровой спектральный анализ и его приложения. — М.: МИР, 1990. — С. 584.
Хемминг Р. В. Цифровые фильтры. — М.: Недра, 1987. — 221 с.
Дьяконов В. П. MATLAB 6.5 SP1/7.0 + Simulink 5/6/ Обработка сигналов и проектирование фильтров. — М.: СОЛОН-Пресс, 2005. — 676 с.
Дьяконов В. П. Вейвлеты. От теории к практике. Изд.е 2-ое дополненное и переработанное. — М.: СОЛОН-Пресс, 2005. — 400 с.
Дьяконов В. П. Современная осциллография и осциллографы. — М.: СОЛОН-Пресс, 2004. — 320 с.
Афонский А. А., Дьяконов В. П. Измерительные приборы и массовые электронные измерения / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2007. — 544 с.
Афонский А. А., Дьяконов В. П. Цифровые анализаторы спектра, сигналов и логики / Под ред. проф. В. П. Дьяконова. — М.: СОЛОН-Пресс, 2009. — 248 с.

Ссылки

Глава 2. Применение цифровой обработки сигналов. Шумоподавление для звука. Технология обработки звука

Обработка аудиосигналов – понимание обработки цифровых и аналоговых аудиосигналов

Современные системы связи полностью изменили мировоззрение аудиоиндустрии. Это также изменило то, как люди общаются, взаимодействуют и взаимодействуют друг с другом. С ростом внедрения умных цифровых аудиотехнологий люди стремятся к автоматизации и подключению домашних аудиосистем. Такие устройства, как умные колонки и порталы Facebook, пользуются большим спросом благодаря своим умным и интеллектуальным функциям.Такие технологии, как распознавание речи, 360-градусное аудио, беспроводное аудио, находятся на переднем крае аудиоиндустрии. Концепция иммерсивного звука сделала общение для слушателей более естественным и сюрреалистичным. За этим высококачественным звуком стоит несколько инструментов и методов, которые улучшают звук и играют важную роль в получении высококачественного звука.

Введение в обработку аудиосигналов

Обработка аудиосигналов – это метод, в котором к аудиосигналам применяются интенсивные алгоритмы и методы.Аудиосигналы – это представление звука в виде цифровых и аналоговых сигналов. Их частоты колеблются от 20 до 20 000 Гц, и это нижний и верхний предел наших ушей. Аналоговые сигналы встречаются в электрических сигналах, а цифровые сигналы – в двоичных представлениях. Этот процесс включает в себя удаление нежелательного шума и балансировку частотно-временных диапазонов путем преобразования цифровых и аналоговых сигналов. Он фокусируется на вычислительных методах изменения звуков. Он удаляет или минимизирует перемодуляцию, эхо, нежелательный шум, применяя к нему различные методы.

Удаленное общение, такое как виртуальная видеоконференцсвязь, становится предпочтительным методом общения по сравнению с личными встречами. Но акустический шум, искажения и эхо неизбежны в любом процессе общения. Предположим, человек разговаривает по телефону или ходит по улице. Его речи будет мешать шум транспорта, шум, производимый людьми вокруг него, шум ветра и т. Д. Становится обязательным устранить такие искажения, чтобы добиться плавного и безупречного качества звука.В процессе улучшения качества звука используются различные методы, которые обсуждаются ниже.

Аналого-цифровой преобразователь (АЦП)
Звуковые эффекты
1. Сжатие / декомпрессия данных
2. Автоматическая регулировка усиления
3. Подавление акустического эха (AEC)
4. Фильтрация / повторная дискретизация
5. Уравнивание
6. Формирование луча
Цифровое в Аналоговый преобразователь (ЦАП)

1. Аналого-цифровое преобразование

Аналоговые аудиосигналы с большей вероятностью подвержены влиянию шума и искажений.Преобразование их в цифровые сигналы позволяет удобно манипулировать, хранить и передавать без ухудшения качества. Он использует заданную частоту дискретизации и преобразует электрические сигналы в двоичное разрешение. Чем выше частота дискретизации и точность измерений, тем выше качество.

Производительность АЦП определяется его полосой пропускания и отношением сигнал / шум (SNR). Полоса пропускания характеризуется частотой дискретизации, а отношение сигнал / шум отличается при изменении разрешения, точности, наложения спектров (происходит, когда кодированный сигнал отличается от исходного сигнала) и т. Д.Считается, что АЦП находится в идеальном состоянии, когда отношение сигнал / шум АЦП превышает отношение сигнал / шум входного сигнала.

2. Звуковые эффекты – методы предварительной / постобработки звука

Алгоритмы постобработки используются для подавления шума и любых артефактов, созданных на первом этапе обработки. Он в первую очередь ориентирован на эхо, удаление искажений и улучшение речи. Эквалайзер и фильтрация – популярные методы постобработки для добавления реверберации и контроля шума.

а.Сжатие / декомпрессия данных

Сжатие – один из самых мощных инструментов микширования, который представляет собой процесс уменьшения динамического диапазона аудиосигналов. Динамический диапазон – это разница между самым высоким и самым низким диапазоном аудиосигнала.

Например, при крике или шепоте высота тона либо слишком высока, либо слишком низка, и в этом случае, если мы запишем его без сжатия, полученный звук будет искажен. Компрессор решает эту проблему, ослабляя самый громкий звук и усиливая самый медленный звук.Это помогает нам найти идеальный баланс звуковой дорожки и дает нам более естественный звук без искажений. Это также уменьшает полосу пропускания цифровых аудиопотоков и размер сохраняемого файла, чтобы сэкономить место для хранения и ускорить передачу.

Существует 2 типа сжатия звука: сжатие без потерь и сжатие с потерями. Наиболее широко используемыми методами сжатия аудиоданных являются методы сжатия с потерями из-за их гораздо более высоких степеней сжатия, чем у исходных данных. Он может исключить не очень актуальную информацию и любое снижение качества.Самыми популярными форматами сжатия аудиоданных являются MP3 и AAC.

б. Автоматическое подавление эха (AEC)
Подавитель акустического эха играет важную роль в обработке аудиосигнала. Он удаляет эхо, реверберацию и нежелательные шумы, вызванные акустической связью между микрофоном и громкоговорителем. Микрофоны улавливают речь на дальнем конце за счет акустической связи.

Предположим, вы во время голосового вызова разговариваете с кем-то по телефону. Речь другого человека, с которым вы разговариваете, называется речью на дальнем конце, которая будет воспроизводиться через громкоговоритель и ваш голос, называемой речью на ближнем конце, которая будет захвачена микрофоном.Если речь на дальнем конце передается обратно на другую сторону вызова, другой абонент услышит их голос после некоторой задержки (сеть + задержка обработки). AEC блокирует передачу на дальнем конце обратно другой стороне вызова.

с. Передискретизация
Передискретизация определяется как общее количество. отсчетов, генерируемых в секунду. Эти отсчеты измеряются в килогерцах (кГц), где одна единица равна 1000 раз в секунду. В разных аудиосистемах используются разные частоты дискретизации и частоты кадров.Он измеряет частоту звуковых сигналов. Он работает по принципу передискретизации и перекодирования, что приводит к меньшему шуму и искажениям. Более высокая частота дискретизации более предпочтительна, поскольку дает более точную информацию о нарастании и падении сигналов, что улучшает качество звука.

г. Фильтрация
Фильтры считаются самой базовой схемой в любой обработке сигналов, используемой почти во всех процессах. Он удаляет нежелательные шумы, эхо, искажения и позволяет отфильтрованным данным проходить через них.Мы будем обсуждать проходные фильтры, которые разрешают только определенные частоты, отклоняя другие.

Фильтр нижних частот

Фильтр высоких частот

Полосовой фильтр

Фильтр подавления / подавления полосы

e. Эквалайзер
Эквалайзеры используются для изменения или настройки частоты, чтобы частота звукового спектра в передатчике совпадала с частотой звукового спектра на приемнике. Частотные диапазоны настраиваются на высокие или низкие с помощью фильтра нижних частот, фильтра верхних частот, полосового фильтра. Он устраняет задержку между различными частотными составляющими и обеспечивает желаемый результат.

ф. Автоматическая регулировка усиления (AGC) или регулировка громкости
Обеспечивает постоянный выходной сигнал, несмотря на наличие различных входных сигналов.Он показывает величину усиления или ослабления, применяемую к входным сигналам для получения целевого входного сигнала. Если входной сигнал выше целевого входа, тогда АРУ вычитает усиление, а если он ниже целевого входного уровня, то АРУ добавляет усиление. Усиление показывает громкость входа канала, который управляет тональностью.

г. Формирование луча
Формирование луча, также известное как пространственная фильтрация, представляет собой метод обработки сигналов, используемый при обработке массива микрофонов. Формирование луча использует пространственное разнесение микрофонов в решетке для обнаружения и извлечения полезных сигналов источников и подавления нежелательных помех.Формирование луча используется для направления и направления луча направленности составных микрофонов в определенном направлении на основе направления источника сигнала. Этот метод помогает расширить составной диапазон микрофонов и увеличивает отношение сигнал / шум (SNR).

Цифро-аналоговое преобразование (DAC)

Современные аудиосигналы чаще всего встречаются в цифровых формах, таких как MP3, но если вы хотите слушать их через динамик, их необходимо преобразовать в аналоговую форму. Он преобразует потоки цифровых данных в аналоговые аудиосигналы, а затем преобразованные аналоговые сигналы отправляются на усилитель.Затем он используется устройствами вывода, такими как динамики, музыкальные плееры. Этот процесс улучшает общее качество звука и улучшает впечатление от прослушивания. Некоторые из устройств с поддержкой ЦАП – это цифровые колонки, проигрыватели компакт-дисков, музыкальные проигрыватели и т. Д.

Заключение

Достижения в цифровых аудиотехнологиях побудили нас создать очень эффективные и высококачественные алгоритмы обработки речи. Эти алгоритмы применяются в процессе записи, хранения и передачи аудиоконтента.Аудиоконтент приносит много нежелательного эха, помех и искажений, которые необходимо удалить, чтобы добиться желаемого качества звука. Он работает по принципу преобразования аудиосигналов между аналоговыми и цифровыми форматами, регулировки частотных диапазонов, удаления нежелательных шумов и добавления звуковых эффектов для получения гладкой и безупречной речи.

PathPartner предоставляет алгоритмы предварительной / постобработки аудиосигнала для различных интеллектуальных аудиоустройств с дополнительными функциями, такими как включение беспроводных и интеллектуальных функций, интеграция голосового помощника, реализация объемного звука 3D и предоставление сертификатов на продукцию Dolby / DTS.Свяжитесь с нами, чтобы узнать больше или получить быструю консультацию, напишите нам по адресу [email protected].

Zölzer, Udo: 9780470997857: Amazon.com: Книги

Полностью обновленное второе издание превосходной цифровой обработки аудиосигналов

Хорошо зарекомендовавшие себя в индустрии бытовой электроники методы цифровой обработки аудиосигналов (DASP) используются в аудио компакт-дисках, компьютерной музыке и мультимедийных компонентах. Кроме того, возможности применения этой универсальной технологии теперь варьируются от обработки сигналов в реальном времени до моделирования помещения.

Обработка цифровых аудиосигналов, второе издание охватывает новейшие алгоритмы обработки аудиосигналов. Каждая глава была полностью переработана с легким для понимания введением в основы, а упражнения включены для самотестирования. Дополнительные файлы Matlab и Java-апплеты были предоставлены на сопутствующем веб-сайте, которые поддерживают книгу легкодоступными примерами приложений.

Ключевые особенности:

Тщательно обновленное и пересмотренное второе издание популярного Digital Audio Signal Processing , всестороннее освещение темы в целом
Предоставляет основные принципы и основы для квантования, фильтров, управления динамическим диапазоном, Моделирование помещения, преобразование частоты дискретизации и кодирование звука
Включает подробные отчеты о студийных технологиях, системах цифровой передачи, носителях и аудиокомпонентах для домашних развлечений
Содержит точное описание алгоритма и приложений
Предоставляет полный отчет о методах DASP демонстрируют их теоретические основы и практические решения.
Включает обновленные компьютерные упражнения, сопутствующий веб-сайт и функции интерактивных JAVA-апплетов на базе Интернета для обработки звука. aud io инженеры, инженеры НИОКР, исследователи в отраслях бытовой электроники и научных кругах, а также разработчики аппаратного и программного обеспечения в ИТ-компаниях.Это руководство также будет интересно студентам продвинутого уровня, изучающим мультимедийные курсы.
Обработка аудиосигналов – обзор
•
Разработанная концепция получила дальнейшее развитие для обнаружения и автоматического анализа сигналов ЭКГ. Для этой цели был исследован комплект обработки звука, разработанный Microchip — dsPIC — 33F — DSC. В MATLAB также реализован дополнительный алгоритм, позволяющий реализовать автоматический анализ отфильтрованного сигнала ЭКГ в реальном времени. Двухканальная конфигурация, описанная выше, используется для одновременного получения пульса сонной артерии и сигнала ЭКГ с целью вычисления параметров, связанных с ВСР, в реальном времени.
•
Разработанная двухканальная система отображает повышенную амплитуду пульсовой волны сонной артерии с повышенным давлением в прямой мышце живота и синхронизируется с данными ВСР во временной области, которые являются результатом данных ЭКГ и сигнала пульса сонной артерии. Анализ ясно показывает, что в критических ситуациях, когда измерение ЭКГ нецелесообразно и недоступно, информация о пульсе сонной артерии может быть подходящей альтернативой для анализа и интерпретации ВСР, поскольку разница была незначительной.Цель состоит в том, чтобы создать местное, экономичное, удобное для пользователя решение для сбора, обработки и мониторинга физиологии человека в реальном времени, которое может принести непосредственную пользу простым людям.
•
Алгоритм MATLAB, созданный для онлайн-параметризации, позволяет определять пик QRS, вычислять интервал RR, частоту сердечных сокращений и оценку спектральной плотности мощности (PSD) формы волны ЭКГ.
•
Анализировались статистические данные ВСР во временной области: средняя частота сердечных сокращений, средний интервал RR, SD-индекс и т. Д.
•
Автономный, платформенно-независимый исполняемый файл для алгоритма был разработан в MATLAB для развертывания в будущих приложениях.
•
Последние системы входных усилителей, разработанные с использованием лучших технологий, используемых в биомедицинских приложениях, имеют высокий CMRR, но все же показывают пятна помех от линий электропередачи 50/60 Гц. В этой работе в P-Spice были исследованы различные концепции проектирования режекторных фильтров на 50 Гц для сравнения и оценки их характеристик.Для аппаратной реализации были выбраны две конструкции фильтров, которые производили резкую метку вместо исключения полосы частот, давали приличную глубину режекции и требуемое минимальное количество высокоточных компонентов. Теоретические и практические кривые частотной характеристики показали отклонения из-за допусков в реальных прецизионных компонентах. Выход фильтра, который близко соответствовал теоретическому результату, был выбран и использован с системой усилителя для устранения эффекта гула линии электропередачи от сигнала ЭКГ и ЭМГ.
•
DSC использовался для улучшения характеристик приобретенной физиологии человека и для создания встроенного решения в реальном времени для биомедицинских приборов.
•
Таким образом, было установлено доказательство концепции двухканальной системы сбора данных на базе ПК для распознавания множества физиологических параметров, согласованных во времени, для сравнения и анализа.
Введение в обработку аудиосигналов | РИТ Пресс
Список рисунков x
Список таблиц xiii
Номенклатура xiv
1 Введение 1
2 аналоговых аудиосигнала 4
2.1 Акустическое давление. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5
2.2 Основные аналоговые сигналы. . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.1 Синусоидальные сигналы. . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.2 Периодические сигналы. . . . . . . . . . . . . . . . . . . . . . . . . . 10
2.2.3 Случайные сигналы. . . . . . . . . . . . . . . . . . . . . . . . . 13
2.3 Обработка аналоговых сигналов. . . . . . . .. . . . . . . . . . . . . . . . 14
2.3.1 Модель импульсного отклика LTIS. . . . . . . . . . . . . . 14
2.3.2 Модель дифференциального уравнения LTIS. . . . . . . . . . . . 20
2.4 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
3 Цифровое кодирование звука 28
3.1 Цифровое представление аналогового сигнала. . . . . . . . . . . . . . 28
3.2 Отбор проб. . . . . . . . . . . . . . . . . . . .. . . . . . . . . . . . . 29
3.2.1 Псевдоним. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2.2 Понижающая и повышающая дискретизация. . . . . . . . . . . . . . . . . . . . . 33
3.2.3 Методы передискретизации. . . . . . . . . . . . . . . . . . . . . . . 34
3.3 Квантование. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
3.3.1 Ошибка квантования. . . . . . . . . . . . . . . . . . . . . . . . 39
3.3.2 Нелинейное квантование.. . . . . . . . . . . . . . . . . . . . 41
3.4 Заключение. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
4 Цифровая обработка аудиосигналов 45
4.1 Основные цифровые сигналы. . . . . . . . . . . . . . . . . . . . . . . . . . . 45
4.1.1 Цифровая импульсная функция. . . . . . . . . . . . . . . . . . . . 45
4.1.2 Шаговая функция цифрового устройства. . . . . . . . . . . . . . . . . . . 46
4.1.3 Цифровой вечный экспоненциальный сигнал.. . . . . . . . . . . . 46
4.1.4 Периодические цифровые функции. . . . . . . . . . . . . . . . . . . . 47
4.2 Цифровой LTIS. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
4.2.1 Цифровая импульсная характеристика LTIS. . . . . . . . . . . . . . . . . 47
4.2.2 Частотная характеристика LTIS. . . . . . . . . . . . . . . . . . . . 49
4.2.3 Z-преобразование. . . . . . . . . . . . . . . . . . . . . . . . . 50
4.2.4 Модель уравнения Диенса.. . . . . . . . . . . . . . . . . . 53
4.2.5 Полюса и нули. . . . . . . . . . . . . . . . . . . . . . . . . . 56
4.3 Фурье-анализ цифровых сигналов и систем. . . . . . . . . . . . 58
4.3.1. Ряд Фурье с дискретным временем. . . . . . . . . . . . . . . . . . 58
4.3.2. Преобразование Фурье с дискретным временем. . . . . . . . . . . . . . . . 62
4.3.3 ДПФ. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
4.3.4 Промежуточное резюме. . . . . . . . . . . . . . . . . . . . . . . . . 64
4.3.5 Круговая свертка. . . . . . . . . . . . . . . . . . . . . . . 64
4.3.6 Быстрая свертка длинных сигналов. . . . . . . . . . . . . . . . 66
4.4 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 68
5 Спектральный анализ звуковых сигналов 70
5.1 Спектры сегментов сигнала. . . . . . . . . . . . . . . . . . . . . . . 70
5.2 Спектральный анализ изменяющихся звуков. . . . . . . . . . . . . . . . . 73
5.3 Спектральный анализ в реальном времени. . . . . . . . . . . . . . . . . . . . . . . 79
5.4 Спектр передискретизированных сигналов. . . . . . . . . . . . . . . . . . . . . 81
5.5 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
6 частотно-формирующих фильтров 84
6.1 Простой фильтр. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
6.2 фильтра второго порядка. . . . . . . . . . . . . . . . . . . . . . . . . . . 87
6.2.1 Пиковый фильтр второго порядка. . . . . . . . . . . . . . . . . . . . 87
6.2.2 Полочные фильтры. . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
6.2.3 Реализация MATLAB. . . . . . . . . . . . . . . . . . . . 90
6.2.4 Аудио эквалайзер. . . . . . . . . . . . . . . . . . . . . . . . . 91
6.3 Конструкция фильтра нижних частот. . . . . . . . . . . . .. . . . . . . . . . . . . 91
6.3.1 Технические характеристики фильтра нижних частот. . . . . . . . . . . . . . . . . . 92
6.3.2 Фильтр нижних частот Баттерворта. . . . . . . . . . . . . . . . . . 92
6.3.3 Другие фильтры нижних частот. . . . . . . . . . . . . . . . . . . . . 96
6.4 Фильтры высоких частот, полосовые и полосовые фильтры. . . . . . . . . . . . . 96
6.5 Фильтры пространства состояний. . . . . . . . . . . . . . . . . . . . . . . . . . . . 98
6.5.1 Модель рекурсивного фильтра в пространстве состояний.. . . . . . . . . . . 99
6.5.2 Полезный фильтр пространства состояний. . . . . . . . . . . . . . . . . . . 100
6.6 Фильтры и модели источников. . . . . . . . . . . . . . . . . . . . . . . . 102
6.7 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 105
7 Генерация звуковых эффектов 106
7.1 Затухание. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
7.1.1 Появление и исчезновение. . . . . . . .. . . . . . . . . . . . . . . . 107
7.1.2 Затухание. . . . . . . . . . . . . . . . . . . . . . . . . . . 108
7.2 Флэнджер. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
7.3 Припев. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 113
7,4 Вау-Вау. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 114
7.5 Контроль динамического диапазона. . . . . . . . . . . . . . . . . . . . .. . . . 116
7.6 Изменение темпа и сдвиг высоты тона. . . . . . . . . . . . . . . . . . . 120
7.6.1 Методы временной области. . . . . . . . . . . . . . . . . . . . . 120
7.6.2 Методы частотной области. . . . . . . . . . . . . . . . . . . 121
7.6.3 Ограничения основных методов изменения темпа и высоты звука. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 122
7.7 Подавление шума. . . . . . . . . . . . . . . . . . . . . . . . .. . . . 123
7.7.1 Шумовой процесс. . . . . . . . . . . . . . . . . . . . . . . . . . . 124
7.7.2 Фильтрация шума. . . . . . . . . . . . . . . . . . . . . . . . . . 126
7.7.3 Реализация MATLAB. . . . . . . . . . . . . . . . . . . . 127
7.8 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 128
8 Реверберация 130
8.1 Измерение импульсной характеристики с разверткой синусоиды. . . . . . . . . . . . . 131
8.2 строительных блока с эффектом реверберации. . . . . . . . . . . . . . . . . . . . . . 134
8.2.1 Линия задержки. . . . . . . . . . . . . . . . . . . . . . . . . . . . 135
8.2.2 Гребенчатые фильтры. . . . . . . . . . . . . . . . . . . . . . . . . . . 136
8.2.3 Всепроходные фильтры. . . . . . . . . . . . . . . . . . . . . . . . . . 138
8.2.4 Матрица рассеяния. . . . . . . . . . . . . . . . . . . . . . . . 139
8.3 Ревербераторы Шредера. . . . . . . . .. . . . . . . . . . . . . . . . 139
8.4 Ревербераторы в пространстве состояний. . . . . . . . . . . . . . . . . . . . . . . . 141
8.5 Ревербераторы с использованием многопортовых элементов. . . . . . . . . . . . . . . . 143
8.6 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 146
9 Сжатие звука 147
9.1 Фильтры для многофазного анализа и синтеза. . . . . . . . . . . . . . . . 148
9.1.1 Фильтр анализа. . . . . .. . . . . . . . . . . . . . . . . . . . 148
9.1.2 Фильтр интерполяции. . . . . . . . . . . . . . . . . . . . . . . . 152
9.1.3 Реализация MPEG Layer 1. . . . . . . . . . . . . . . . . 154
9.2 Психоакустическая модель. . . . . . . . . . . . . . . . . . . . . . . . . . 156
9.2.1 Анализ уровня звукового давления. . . . . . . . . . . . . . . . . 156
9.2.2 Порог слышимости. . . . . . . . . . . . . . . . . . . . . . . 157
9.2.3 Частотная маскировка. . . . . . . . . . . . . . . . . . . . . . . . 158
9.2.4 Глобальный порог маскирования и отношение сигнала к маске. . . . . 162
9.3 Кодирование выборки поддиапазонов. . . . . . . . . . . . . . . . . . . . . . . . . 163
9.4 Резюме. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 163
Библиография 164
Индекс 167
Обработка аудиосигналов для музыкальных приложений
Описание
Обработка аудиосигналов – это инженерная область, в которой основное внимание уделяется вычислительным методам преднамеренного изменения звуков, методам, которые используются во многих музыкальных приложениях.
Мы попытались составить курс, который может быть интересным и доступным для людей разного происхождения, при этом углубляясь в несколько тем, связанных с обработкой сигналов. Мы фокусируемся на методах спектральной обработки, имеющих отношение к описанию и преобразованию звуков, развивая базовые теоретические и практические знания, с помощью которых можно анализировать, синтезировать, преобразовывать и описывать аудиосигналы в контексте музыкальных приложений.
Курс основан на открытом программном обеспечении и содержании.Демонстрации и упражнения по программированию выполняются с использованием Python под Ubuntu, а ссылки и материалы для курса взяты из открытых онлайн-репозиториев. Мы также распространяем по открытым лицензиям программное обеспечение и материалы, разработанные для курса.
Программа курса
Неделя 1: Введение; базовая математика
Неделя 2: Дискретное преобразование Фурье
Неделя 3: Свойства преобразования Фурье
Неделя 4: Кратковременное преобразование Фурье
Неделя 5: Синусоидальная модель
Неделя 6: Гармоническая модель
Неделя 7: Синусоидальная плюс остаточное моделирование
Неделя 8: Звуковые преобразования
Неделя 9: Описание звука / музыки
Неделя 10: Заключительные темы; помимо обработки аудиосигнала
Инструкторы
Ксавье Серра, профессор, кафедраинформационных и коммуникационных технологий, Университет Помпеу Фабра, Барселона,
Профессор Джулиус О. Смит, III, профессор музыки и (любезно) электротехники, CCRMA, Стэнфордский университет
Рекомендуемый фон
Курс предполагает некоторый базовый опыт в области математики и обработки сигналов. Кроме того, поскольку задания выполняются на языке программирования Python, некоторый опыт программирования на любом языке является наиболее полезным.
Рекомендуемая литература
Основные используемые программные инструменты находятся на https: // github.com / MTG / sms-tools и звуки, которые необходимо изучить, взяты с https://freesound.org. Большинство внешних ссылок взято с веб-сайта Julius O Smith, https://ccrma.stanford.edu/~jos или с https://www.wikipedia.org.
FAQ
- Какой уровень программирования необходим для прохождения курса?
  Все задания начинаются с некоторого существующего кода Python, который студент должен понять и изменить. Необходим некоторый опыт программирования.
- Что самое крутое, что я узнаю, если пойду на этот курс?
  Вы будете много экспериментировать со звуками, анализируя их, трансформируя их и создавая новые интересные звуки.
Цифровая обработка аудиосигналов, 2-е издание
Предисловие ко второму изданию.
Предисловие к первому изданию.
1. Введение.
1.1. Студия Технологий.
1.2. Цифровые системы передачи.
1.3. Медиа хранилище.
1.4. Аудио компоненты дома.
2. Квантование.
2.1. Квантование сигнала.
2.2. Дизеринг.
2.3. Формирование спектра квантования – формирование шума.
2.4. Представление числа.
2.5. Java-апплет – квантование, дизеринг и формирование шума.
2.6. Упражнения.
3. Преобразование AD / DA.
3.1. Методы.
3.2. Конвертеры AD.
3.3. Преобразователи DA.
3.4. Java-апплет – передискретизация и квантование.
3.5. Упражнения.
4. Системы обработки звука.
4.1. Цифровые сигнальные процессоры.
4.2. Цифровые аудиоинтерфейсы.
4.3. Однопроцессорные системы.
4.4. Многопроцессорные системы.
5. Эквалайзеры.
5.1. Основы.
5.2. Рекурсивные аудио фильтры.
5.3. Нерекурсивные аудио фильтры.
5.4. Мультикомплементарный банк фильтров.
5.5. Java-апплет – Аудио фильтры.
5.6. Упражнения.
6. Моделирование помещения.
6.1. Основы.
6.2. Ранние размышления.
6.3. Последующая реверберация.
6.4. Аппроксимация импульсных характеристик помещения.
6.5. Java-апплет – быстрая свертка.
6.6. Упражнения.
7. Контроль динамического диапазона.
7.1. Основы.
7.2. Кривая статики.
7.3. Динамическое поведение.
7.4. Реализация.
7,5. Аспекты реализации.
7.6. Java-апплет – Контроль динамического диапазона.
7.7. Упражнения.
8. Преобразование частоты дискретизации.
8.1. Основы.
8.2. Синхронное преобразование.
8.3. Асинхронное преобразование.
8.4. Методы интерполяции.
8.5. Упражнения.
9. Кодирование звука.
9.1. Кодирование звука без потерь.
9.2. Кодирование звука с потерями.
9.3. Психоакустика.
9.4. Кодирование звука ISO-MPEG-1.
9,5. Кодирование звука MPEG-2.
9.6. MPEG-2 Advanced Audio Coding.
9.7. Кодирование звука MPEG-4.
9,8. Воспроизведение спектрального диапазона.
9.9. Java-апплет – Психоакустика.
9.10. Упражнения.
Список литературы.
Индекс.
Цифровая обработка аудиосигналов, второе издание [Книга]
Полностью обновленное второе издание превосходной цифровой обработки аудиосигналов
Хорошо зарекомендовавшие себя в индустрии бытовой электроники методы цифровой обработки аудиосигналов (DASP) используются в аудио CD, компьютерная музыка и мультимедийные компоненты.Кроме того, возможности применения этой универсальной технологии теперь варьируются от обработки сигналов в реальном времени до моделирования помещения.
Цифровая обработка аудиосигналов, второе издание охватывает новейшие алгоритмы обработки аудиосигналов. Каждая глава была полностью переработана с легким для понимания введением в основы, а упражнения включены для самотестирования. Дополнительные файлы Matlab и Java-апплеты были предоставлены на сопутствующем веб-сайте, которые поддерживают книгу легкодоступными примерами приложений.
Ключевые особенности:
- Тщательно обновленное и пересмотренное второе издание популярного Digital Audio Signal Processing , всестороннее освещение темы в целом
- Предоставляет основные принципы и основы для квантования, фильтров, динамических Управление диапазоном, моделирование помещения, преобразование частоты дискретизации и кодирование звука
- Включает подробные отчеты о студийных технологиях, системах цифровой передачи, носителях и аудиокомпонентах для домашних развлечений
- Содержит точное описание алгоритма и приложений
- Предоставляет полный отчет о методах DASP, демонстрируя их теоретические основы и практические решения
- Включает обновленные компьютерные упражнения, сопроводительный веб-сайт и функции интерактивных веб-апплетов JAVA для обработки звука
Это важное руководство к цифровая обработка аудиосигнала послужит бесценным справочником для профессионалов в области звуковой инженерии, инженеров-исследователей, исследователей в отраслях бытовой электроники и научных кругов, а также разработчиков оборудования и программного обеспечения в ИТ-компаниях.

Цифровая обработка звука: Звуковая экосистема, часть 2: Цифровая обработка сигналов

Звуковая экосистема, часть 2: Цифровая обработка сигналов

Как DSP-процессор улучшает звук

Проблемы со звуком, которые может исправить DSP-процессор

DSP-процессор: устройство или программа?

Курс лекций «Основы цифровой обработки сигналов» / Хабр

Список лекций

Где найти?

Сигналы. Z-преобразование

Преобразование Фурье. Свойства. ДПФ и БПФ

Сравнение эффективности ДПФ и БПФ

Свертка и корреляция

Случайные сигналы и шум

Сигналы, модуляция и манипуляция

Цифровые фильтры — БИХ и КИХ

Оконные функции в задачах фильтрации

Ресемплинг.

Заключение

UPD: 20.04.2020

Цифровая обработка сигналов

01.

02. Сигналы, шумы и помехи

03. Решаемые задачи

04. Знакомство с MATLAB

05. Создаем аккорд в MATLAB

06. Выделяем тон из аккорда в MATLAB)

07. Анализ ЭКГ в MATLAB

08. Дискретные периодические сигналы

09. Синусоидальный сигнал как базис

10. Теорема Котельникова

11. АЦП и ЦАП

12. Шум как случайный процесс

13. Виды шумов, отношение сигнал/шум

14. Статистическая обработка сигнала

15.

19. Спектральный анализ

22. АЧХ и ФЧХ

23. Цифровые фильтры

24. КИХ и БИХ фильтры

25. Многоскоростные системы

26. Многоскоростные фильтры

27. Адаптивные фильтры

28. Активное шумоподавление

29. Создание приложения в MATLAB

30. Обработка на Raspberry Pi

Цифровая обработка звука

Аналоговая и цифровая обработка звукового сигнала.

Цифровая обработка сигналов – это… Что такое Цифровая обработка сигналов?

Основные задачи

Основные преобразования

См. также

Примечания

Литература

Ссылки

Глава 2. Применение цифровой обработки сигналов. Шумоподавление для звука. Технология обработки звука

Похожие главы из других работ:

1. Применение Microsoft Office для обработки информации

2.3 Рассмотрение вопросов анализа и способа обработки речевых сигналов

Примеры обработки звука

5.1 Алгоритм обработки звука

1. ПЛИС И СИСТЕМЫ ЦИФРОВОЙ ОБРАБОТКИ СИГНАЛОВ

1.2.3 Блоки цифровой обработки сигналов

2. Программа обработки звука Audacity

1. Основные тенденции обработки звука

1.4 Обзор существующих алгоритмов цифровой обработки образов отпечатка пальца

3.1.4 Средства создания и обработки звука

2.1 Необходимость цифровой обработки

Глава 1. Характеристика сигналов в системах цифровой обработки

3.1 Программа обработки звука Audacity

1. Разъяснения по использованию систем цифровой подписи в связи с введением закона “Об электронной цифровой подписи”

Обработка аудиосигналов – понимание обработки цифровых и аналоговых аудиосигналов

Введение в обработку аудиосигналов

1. Аналого-цифровое преобразование

2. Звуковые эффекты – методы предварительной / постобработки звука

Цифро-аналоговое преобразование (DAC)

Заключение

Zölzer, Udo: 9780470997857: Amazon.com: Книги

Обработка аудиосигналов – обзор

Введение в обработку аудиосигналов | РИТ Пресс

Обработка аудиосигналов для музыкальных приложений