Действующее напряжение – » :

амплитудное значение напряжение | Электрознайка. Домашний Электромастер.

Действующее значение синусоидального
переменного напряжения – тока.

data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>
♦Переменный электрический ток в нашей бытовой электросети представляет собой синусоиду, как на рисунке 1.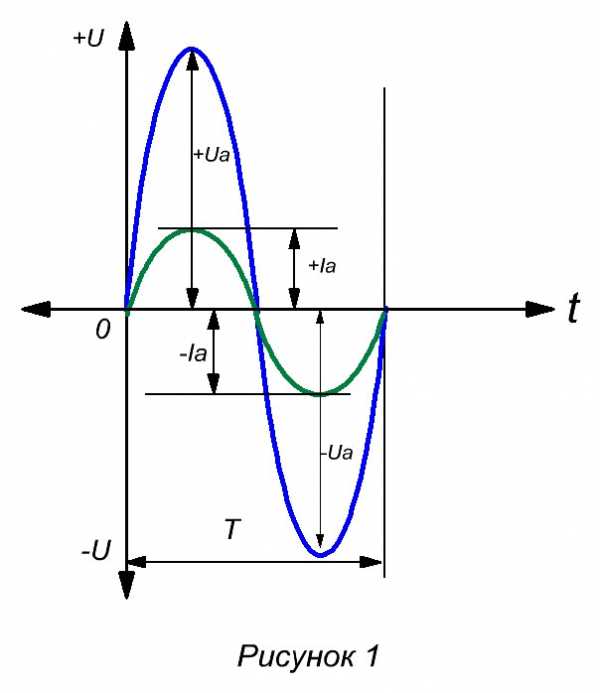

Напряжение меняет свою величину от 0 до + Umax и от 0 до — Umax .  Полный цикл этих изменений называется периодом.
Период измеряется в секундах и обозначается буквой   Т.
Количество периодов переменного тока за 1 секунду, есть частота  f.
Частота переменного тока f измеряется в герцах .

f = 1 / T.

Например.
Частота в нашей электрической сети 50 Гц.  Период этих колебаний будет равен:

T = 1 / f = 1 / 50 = 0,02 сек.

Наибольшее значение изменяющегося переменного напряжения – тока называется амплитудным значением или амплитудой.

Umax = Ua и Imax = Ia

За один период напряжение принимает эти значения два раза: + Ua  и  — Ua .

♦ Если подключить в цепь переменного напряжения какую-нибудь активную нагрузку, например паяльник, в цепи потечет переменный электрический ток, так же принимающий значения +Ia и — Ia, и повторяющий форму синусоиды.
На нагрузке выделяется электрическая мощность в виде тепла. Неважно какой ток течет в цепи — переменный или постоянный. Выделение тепла не зависит от направления тока в цепи.
Выделенное тепло будет равно той энергии, которую затрачивает электрический ток при прохождении по сопротивлению нагрузки.
Введено понятие действующего значения переменного напряжения Uд и тока Iд.

Действующее значение переменного тока — это такое значение величины постоянного тока, который проходя по сопротивлению нагрузки за тот же промежуток времени, выделит такое же количество тепла, что и переменный ток.

♦ Переменный ток оказывает такое же тепловое действие, как и постоянный ток, если амплитуда синусоидального переменного тока превышает величину постоянного тока в 1,41 раз.
Следовательно действующее (или эффективное) значение переменного тока будет равно:

Iд = Ia / 1,41 = 0,707 Ia. – действующее значение переменного тока

Uд = Ua / 1,41 = 0,707 Ua — действующее значение переменного напряжения

На все эти теоретические размышления можно посмотреть иначе!

   ♦Имеем синусоиду переменного напряжения длительностью в 1 период как на рисунке 1.
После выпрямительных диодов оно принимает вид как на рисунке 2.

Нижняя половинка синусоиды перевернута вверх, чтобы удобнее было представить процесс преобразования.

    ♦На рисунке приняты обозначения:

Um = Ua = 1 — амплитудное значение величины переменного напряжения. Значение  Ua примем за единицу.

Из формулы приведенной выше Uд = 1 / 1,41 = 0,707 — действующее напряжение равно 0,707 от амплитудного значения        Ua = 1.
Заштрихованная часть синусоиды обозначает затраченную на нагревание паяльника электрическую энергию. В промежутках между половинками синусоид ток по цепи не протекает, а следовательно и не выделяется электрическая мощность.
♦Проведем линию, обозначающую Uд = 0,707.
Она отсекает верхнюю часть половинок синусоид.
Если эти отсеченные вершинки синусоиды уложить в провалы между полупериодами, получится полностью заполненная площадь соответствующая значениям постоянного напряжения U и тока I.
Получается, что мощность синусоидального переменного тока с амплитудными значениями

Ua и Ia равна мощности действующего значения Uд и Iд переменного тока и равна мощности постоянного тока со значениями U и I.
Одна и та же электрическая мощность, выраженная в трех видах.

P = Ua х Ia = Uд х Iд = U х I

♦ Электрические приборы для измерения переменного напряжения и тока отградуированы на отображение действующих значений Uд и Iд.
В нашей бытовой электросети действующее, эффективное, напряжение переменного тока Uд равно 220 вольт.
Максимальное, амплитудное значение напряжения в сети равно:
Um = Ua = Uд х 1,41 = 220 х 1,41 = 310,2 вольт.

Процесс поэтапного преобразования переменного напряжения в пульсирующее напряжение, а затем в постоянное напряжение, наблюдается в схемах выпрямителей.

data-ad-client=”ca-pub-5076466341839286″
data-ad-slot=”1404500382″>

domasniyelektromaster.ru

Переменный ток — Википедия

     Синусоидальный

Переме́нный ток — электрический ток, который с течением времени изменяется по величине и направлению или, в частном случае, изменяется по величине, сохраняя своё направление в электрической цепи неизменным^[1].

Хотя переменный ток часто переводят на английский как alternating current, эти термины не эквивалентны. Термин alternating current (AC) в узком смысле означает синусоидальный ток, в широком смысле — периодический знакопеременный ток (то есть периодический двунаправленный ток). Условное обозначение на электроприборах: ∼{\displaystyle \thicksim } или ≈{\displaystyle \thickapprox } (знак синусоиды), или латинскими буквами AC{\displaystyle AC}.

Так как переменный ток в общем случае меняется в электрической цепи не только по величине, но и по направлению, то одно из направлений переменного тока в цепи считают условно положительным, а другое, противоположное первому, условно отрицательным. В соответствии с этим и величину мгновенного значения переменного тока в первом случае считают положительной, а во втором случае — отрицательной.

Переменный ток — величина алгебраическая, знак его определяется тем, в каком направлении в рассматриваемый момент времени протекает ток в цепи — в положительном или отрицательном.

Величина переменного тока, соответствующая данному моменту времени, называется мгновенным значением переменного тока.

Максимальное мгновенное значение переменного тока, которое он достигает в процессе своего изменения, называется амплитудой тока Im{\displaystyle I_{m}}.

График зависимости переменного тока от времени называется развёрнутой диаграммой переменного тока.

Развёрнутая диаграмма переменного синусоидального тока

На рисунке приведена развёрнутая диаграмма переменного тока, изменяющегося с течением времени по величине и направлению. На горизонтальной оси 0t{\displaystyle 0t} отложены в определённом масштабе отрезки времени, а по вертикальной оси — величины тока, вверх — от начальной точки 0{\displaystyle 0} — положительные, вниз — отрицательные. Часть развёрнутой диаграммы тока, расположенная выше оси времени 0t{\displaystyle 0t}, характеризует изменение положительных величин во времени, а часть, расположенная ниже оси времени 0t{\displaystyle 0t}, — изменение отрицательных величин.

В начальный момент времени t=0{\displaystyle t=0} ток равен нулю (i=0){\displaystyle (i=0)}. Затем он с течением времени растёт в положительном направлении, в момент времени t=T4{\displaystyle t={\frac {T}{4}}} достигает максимального значения, после чего убывает по величине и в момент времени t=T2{\displaystyle t={\frac {T}{2}}} становится равным нулю. Затем, пройдя через нулевое значение, ток меняет свой знак на противоположный, то есть становится отрицательным, затем растёт по абсолютной величине, затем достигает максимума при t=34T{\displaystyle t={\frac {3}{4}}T}, после чего убывает и при t=T{\displaystyle t=T} становится равным нулю.

Развёрнутая диаграмма периодического переменного тока

Периодическим переменным током называется такой электрический ток, который через равные промежутки времени повторяет полный цикл своих изменений, возвращаясь к своей исходной величине.

На представленной диаграмме мы видим, что через равные промежутки времени T{\displaystyle T} график тока воспроизводится полностью без каких-либо изменений.

Время T{\displaystyle T}, в течение которого переменный периодический ток совершает полный цикл своих изменений, возвращаясь к своей исходной величине, называется периодом переменного тока.

Величина, обратная периоду, называется частотой переменного тока:

f=1T{\displaystyle f={\frac {1}{T}}}, где

f{\displaystyle f} — частота переменного тока;

T{\displaystyle T} — период переменного тока.

Если выразить время T{\displaystyle T} в секундах (sec), то будем иметь:

f=1T[1sec]{\displaystyle f={\frac {1}{T}}\left[{\frac {1}{sec}}\right]}, то есть размерность частоты переменного тока выражается в 1/с.

Частота переменного тока численно равна числу периодов в секунду.

За единицу измерения частоты переменного тока принят 1 герц (1 гц, 1 Гц, 1 Hz).

Герц — единица Международной системы единиц (СИ), названа в честь Генриха Герца. Через основные единицы СИ герц выражается следующим образом: 1 Гц = 1 с⁻¹. Десятичные кратные и дольные единицы образуют с помощью стандартных приставок СИ.

Частота переменного тока равна одному герцу, если период тока равен одной секунде (один полный цикл за одну секунду).

Стандарты частоты[править | править код]

В большинстве стран в электротехнике применяются частоты 50 или 60 Гц (60 Гц — этот вариант принят в США и Канаде). В некоторых странах, например, в Японии, используются оба стандарта

(см. Промышленная частота переменного тока).

Частота 16 ⅔ Гц до сих пор используется в некоторых европейских железнодорожных сетях (Австрия, Германия, Норвегия, Швеция и Швейцария), частота 25 Гц — на старых железнодорожных линиях США. (См. Электрификация железных дорог переменным током пониженной частоты).

В авиации и военной технике для снижения массы устройств или с целью повышения частоты вращения электродвигателей переменного тока применяется частота 400 Гц.

Число оборотов ротора n[1min]{\displaystyle n\left[{\frac {1}{min}}\right]} синхронного электродвигателя определяется по формуле:

n=60fp{\displaystyle n={\frac {60f}{p}}}, где

f{\displaystyle f} — частота переменного тока;

p{\displaystyle p} — число пар полюсов.

Так как минимальное число пар полюсов равно единице, тогда синхронный электродвигатель, работающий на переменном токе частотой 50 герц разовьёт 3 000 оборотов в минуту, а электродвигатель, работающий на переменном токе частотой 400 герц, разовьёт 24 000 оборотов в минуту. Частота вращения ротора асинхронного электродвигателя меньше, чем частота питающего его тока и зависит от нагрузки. Скольжение — разность между частотой вращения вращающегося магнитного поля и частотой вращения ротора.

В технике связи применяются частоты более высокие, и в частности в радиотехнике — порядка миллионов и миллиардов герц.

Синусоидальным током называется периодический переменный ток, который с течением времени изменяется по гармоническому закону синуса.

Синусоидальный ток — элементарный, то есть его невозможно разложить на другие более простые переменные токи^[2].

Переменный синусоидальный ток выражается формулой:

i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t}, где

Im{\displaystyle I_{m}} — амплитуда синусоидального тока;

ωt{\displaystyle \omega t} — некоторый угол, называемый фазой синусоидального тока.

Фаза синусоидального тока ωt{\displaystyle \omega t} изменяется пропорционально времени t{\displaystyle t}.

Множитель ω{\displaystyle \omega }, входящий в выражение фазы ωt{\displaystyle \omega t} — величина постоянная, называемая угловой частотой переменного тока (круговой частотой переменного тока).

Угловая частота ω{\displaystyle \omega } синусоидального тока зависит от частоты f{\displaystyle f} этого тока и определяется формулой:

ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, где

ω{\displaystyle \omega } — угловая (круговая) частота синусоидального тока;

f{\displaystyle f} — частота синусоидального тока;

T{\displaystyle T} — период синусоидального тока;

2π{\displaystyle 2\pi } — центральный угол окружности, выраженный в радианах.

Исходя из формулы ω=2πf=2πT{\displaystyle \omega =2\pi f={\frac {2\pi }{T}}}, можно определить размерность угловой (круговой) частоты:

[ω]=[2πT]=[1sec]{\displaystyle \left[\omega \right]=\left[{2\pi \over T}\right]=\left[{1 \over sec}\right]}, где

sec{\displaystyle sec} — время в секундах,

2π{\displaystyle 2\pi } — угол в радианах, является безразмерной величиной.

Фаза ωt{\displaystyle \omega t} синусоидального тока измеряется радианами.

1 радиан = 57,29° = 57°17′, угол 90° = π2{\displaystyle \pi \over 2} радиан, угол 180° = π{\displaystyle \pi } радиан, угол 270° = 3π2{\displaystyle 3\pi \over 2} радиан, угол 360° = 2π{\displaystyle 2\pi } радиан,
где π=3,14{\displaystyle \pi =3,14} радиан; π{\displaystyle \pi } — число «Пи», ° — угловой градус и ′ — угловая минута.

---

Формула i=Imsin⁡ωt{\displaystyle i=I_{m}\sin \omega t} описывает случай, когда наблюдение за изменением переменного синусоидального тока начинается с момента времени t=0{\displaystyle t=0}. Если начальный момент времени не равен нулю, тогда формула для определения мгновенного значения переменного синусоидального тока принимает следующий вид:

i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )}, где

(ωt+ψ){\displaystyle (\omega t+\psi )} — фаза переменного синусоидального тока;

ψ{\displaystyle \psi } — угол, называемый начальной фазой переменного синусоидального тока.

Если в формуле i=Imsin⁡(ωt+ψ){\displaystyle i=I_{m}\sin(\omega t+\psi )} принять t=0{\displaystyle t=0}, то будем иметь

ωt=0{\displaystyle \omega t=0}, ωt+ψ=ψ{\displaystyle \omega t+\psi =\psi } и it=0=Imsin⁡ψ{\displaystyle i_{t=0}=I_{m}\sin \psi }.

Начальная фаза — это фаза синусоидального тока в момент времени t=0{\displaystyle t=0}.

Начальная фаза переменного синусоидального тока может быть положительной (ψ>0){\displaystyle (\psi >0)} или отрицательной (ψ<0){\displaystyle (\psi <0)} величиной. При ψ>0{\displaystyle \psi >0} мгновенное значение синусоидального тока в момент времени t=0{\displaystyle t=0} положительно, при ψ<0{\displaystyle \psi <0} — отрицательно.

Если начальная фаза ψ=π2{\displaystyle \psi ={\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt+π2){\displaystyle i=I_{m}\sin(\omega t+{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡π2=Im{\displaystyle i_{t=0}=I_{m}\sin {\frac {\pi }{2}}=I_{m}}, то есть равно положительной амплитуде тока.

Если начальная фаза ψ=−π2{\displaystyle \psi =-{\frac {\pi }{2}}}, то ток определяется по формуле i=Imsin⁡(ωt−π2){\displaystyle i=I_{m}\sin(\omega t-{\frac {\pi }{2}})}. Мгновенное значение его в момент времени t=0{\displaystyle t=0} равно

it=0=Imsin⁡(−π2)=−Im{\displaystyle i_{t=0}=I_{m}\sin(-{\frac {\pi }{2}})=-I_{m}}, то есть равно отрицательной амплитуде тока.

Два синусоидальных тока совпадают по фазе друг с другом

Синусоидальные токи сдвинуты по фазе на угол π2{\displaystyle {\frac {\pi }{2}}}

ru.wikipedia.org

Действующее значение переменного тока

Переменный ток долгое время не находил практического применения.  Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.) называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

,

(1)

Величина, обратная периоду, есть частота,  измеряемая в герцах (Гц):

,

(2)

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота  f = 50Гц.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i  – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р– мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m).

 – амплитуда тока;

 – амплитуда напряжения;

 – амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

,

(3)

Аналогично определяются действующие значения ЭДС и напряжения.

 

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е₁ и е₂соответствуют уравнения:

.

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t=0):  и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз.

Для синусоидальных ЭДС е₁ и е₂ угол сдвига фаз:

.

 

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное) с угловой частотой, равной w. Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е₁ и е₂(рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t=0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w. Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

 

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

.

Каждый из этих токов синусоидален и может быть представлен уравнением

и.

Результирующий ток также будет синусоидален:

.

Определение амплитудыи начальной фазыэтого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt=0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

.

Построение векторной диаграммы в масштабе позволяет определить значения ииз диаграммы, после чего может быть записано решение для мгновенного значенияпутем формального учета угловой частоты:.

 

studfile.net

Переменное напряжение и его параметры

Всем доброго времени суток! В прошлой статье я рассказал, как рассчитать индуктивность катушки выполненной на разомкнутом сердечнике (например, ферритовой антенны, контурных катушек радиоприёмников, катушек с построечными сердечниками и т. д.). Сегодняшняя статья посвящена переменному напряжению и параметрам, которые его характеризуют.

Что такое переменное напряжение?

Как известно электрическим током называется упорядоченное движение заряженных частиц, которое возникает под действием разности потенциалов или напряжения. Одной из основных характеристик любого типа напряжения является его зависимость от времени. В зависимости от данной характеристики различают постоянной напряжение, значение которого с течением времени практически не изменяется и переменное напряжение, изменяющееся во времени.

Переменное напряжение в свою очередь бывает периодическим и непериодическим. Периодическим называется такое напряжение, значения которого повторяются через равные промежутки времени. Непериодическое напряжение может изменять своё значение в любой период времени. Данная статья посвящена периодическому переменному напряжению.

Постоянное (слева), периодическое (в центре) и непериодическое (справа) переменное напряжение.

Минимальное время, за которое значение переменного напряжения повторяется, называется периодом. Любое периодическое переменное напряжение можно описать какой-либо функциональной зависимостью. Если время обозначить через t, то такая зависимость будет иметь вид F(t), тогда в любой период времени зависимость будет иметь вид

где Т – период.

Величина обратная периоду Т, называется частотой f. Единицей измерения частоты является Герц, а единицей измерения периода является Секунда

Наиболее часто встречающаяся функциональная зависимость периодического переменного напряжения является синусоидальная зависимость, график которой представлен ниже

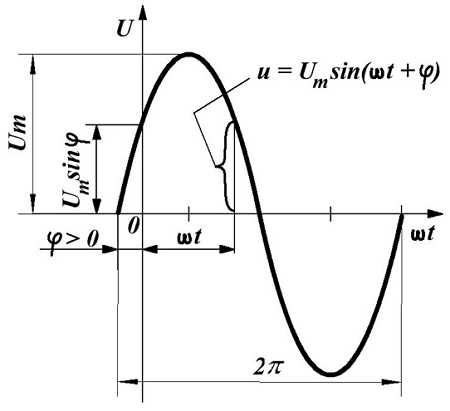Синусоидальное переменное напряжение.

Из математики известно, что синусоида является простейшей периодической функцией, и все другие периодические функции, возможно, представить в виде некоторого количества таких синусоид, имеющих кратные частоты. Поэтому необходимо изначально рассмотреть особенности синусоидального напряжения.

Таким образом, синусоидальное напряжение в любой момент времени, мгновенное напряжение, описывается следующим выражением

где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла),

φ – начальная фаза, определяемая смещением синусоиды относительно начала координат, определяется точкой перехода отрицательной полуволны в положительную полуволну.

Величина (ωt + φ) называется фазой, характеризующая значение напряжения в данный момент времени.

Таким образом, амплитуда U_m, угловая частота ω и начальная фаза φ являются основными параметрами переменного напряжения и определяют его значение в каждый момент времени.

Обычно, при рассмотрении синусоидального напряжения считают, что начальная фаза равна нулю, тогда

В практической деятельности, довольно часто, используют ещё ряд параметров переменного напряжения, такие как, действующее напряжение, среднее напряжение и коэффициент формы, которые мы рассмотрим ниже.

Что такое действующее напряжение переменного тока?

Как я писал выше, одним из основных параметров переменного напряжения является амплитуда U_m, однако использовать в расчётах данную величину не удобно, так как временной интервал в течение, которого значение напряжения u равно амплитудному U_m ничтожно мал, по сравнению с периодом Т напряжения. Использовать мгновенное значение напряжения u, также не очень удобно, вследствие больших объёмов расчётов. Тогда возникает вопрос, какое значение переменного напряжения использовать при расчётах?

Для решения данного вопроса необходимо обратиться к энергии, которая выделяется под воздействием переменного напряжения, и сравнить её с энергией, которая выделяется под воздействием постоянного напряжения. Для решения данного вопроса обратимся к закону Джоуля – Ленца для постоянного напряжения

Для переменного напряжения мгновенное значение выделяемой энергии составит

где u – мгновенное значение напряжения

Тогда количество энергии за полный период от t₀ = 0 до t₁ = T составит

Приравняв выражения для количества энергии при переменном напряжении и постоянном напряжении и выразив полученное выражение через постоянное напряжение, получим действующее значение переменного напряжения

Получившееся выражение, позволяет вычислить действующее значение напряжение U для периодического переменного напряжения любой формы. Из выше изложенного можно сделать вывод, что действующее значение переменного напряжения называется такое постоянное напряжение, которое за такое же время и на таком же сопротивлении выделяет такую же энергию, которая выделяется данным переменным напряжением.

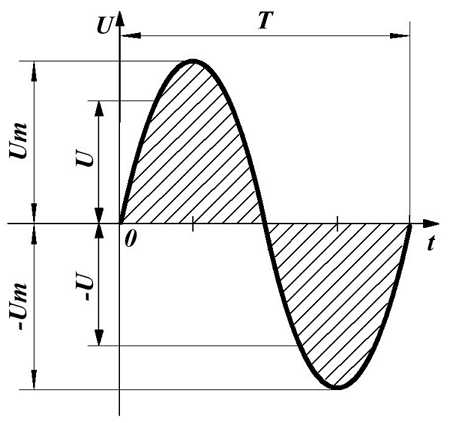
Действующее значение синусоидального напряжения.

Вычислим действующее значение синусоидального напряжения

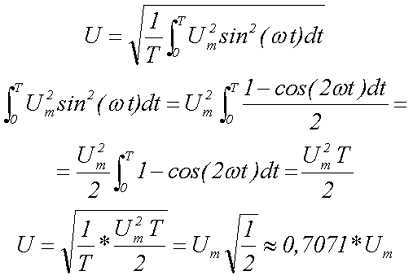
Стоит отметить, все напряжения электротехнических устройств определяются, как правило, действующим значением напряжения.

Для определения амплитудного значения синусоидального напряжения необходимо преобразовать полученное выражение

Таким образом если в розетке у нас U = 230 В, следовательно, амплитудное значение данного напряжения

Действующее напряжение также имеет название эффективного напряжения и среднеквадратичного напряжения.

С действующим напряжением разобрались, теперь рассмотрим среднее значение напряжение.

Что такое среднее значение переменного напряжения?

Ещё одним параметром переменного напряжения, который его характеризует, является средним значением переменного напряжения. В отличие от действующего значения переменного напряжения, которое характеризует работу переменного напряжения, среднее значение напряжения характеризует количество электричества, которое перемещается из одной точки цепи в другую, под действием переменного напряжения. Среднее значение напряжения за период определяется следующим выражением

где Т – период переменного напряжения,

f_u(t) – функциональная зависимость напряжения от времени.

Таким образом, среднее значение переменного напряжения численно будет равно высоте прямоугольника с основанием T, площадь которого равна площади, ограниченной функцией f_u(t) и осью Ox за период Т.

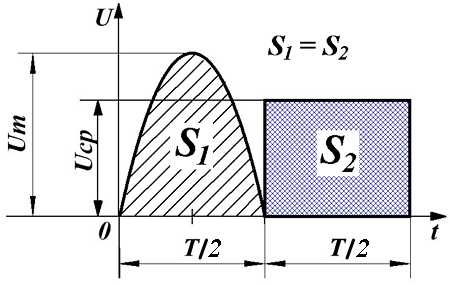
Среднее значение переменного напряжения.

В случае синусоидальной функции, можно говорить только о среднем значении за полупериод, так как в течение всего периода положительная полуволна компенсируется отрицательной полуволной, и тогда среднее за период напряжение будет равно нулю.

Таким образом, среднее за полупериод Т/2 значение переменного напряжения синусоидальной формы будет равно

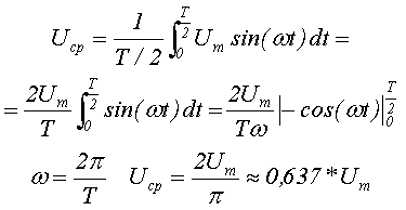
где U_m – максимальное значение напряжения или амплитуда,

ω –угловая частота, скорость изменения аргумента (угла).

Какие коэффициенты, характеризуют переменное напряжение?

Иногда возникает необходимость охарактеризовать форму переменного напряжения. Для этой цели существует ряд параметров данного переменного напряжения:

1. Коэффициент формы переменного напряжения k_ф – показывает как относится действующее значение переменного напряжения U к его среднему значению U_cp.

Так для синусоидального напряжения коэффициент формы составит

2. Коэффициент амплитуды переменного напряжения k_а – показывает как относится амплитудное значение переменного напряжения U_m к его действующему значению U

Так для синусоидального напряжения коэффициент амплитуды составит

На сегодня всё, в следующей статье я рассмотрю прохождение переменного напряжения через сопротивление, индуктивность и емкость.

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

www.electronicsblog.ru

Среднеквадратичное (действующее, эффективное) значение

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор).

Лампочка и постоянное напряжение

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт

Вот ее характеристики:  рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I – сила тока,  можно найти I. Значит  I=P/U=21/12=1,75 Ампер.

Ладно, с лампочкой разобрались. Давайте ее зажжем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

Подаем напряжение с блока питания на лампу и вуаля!

Замеряем напряжение на  клеммах-крокодилах блока питания с помощью мультиметра . Ровнехонько 12 Вольт, как и предполагалось.

К этим же клеммах цепляем и наш осциллограф

Смотрим осциллограмму:

Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени  у нас напряжение остается  таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то  значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

Замеряем  силу тока. Как правильно замерить силу тока в цепи, можно узнать, прочитав статью как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить  на погрешность прибора  или на лампочку 😉

Лампочка и переменное напряжение

Теперь начинается самое интересное. Берем наш ЛАТР

Ставим прибор на измерение переменного напряжения и выставляем с помощью  крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре  находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осциллографе выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

Смотрим, сколько  силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

Среднеквадратичное значение напряжения

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение  зажигали одну и ту же лампочку, которая кушала одну и ту же мощность.  Значит эта осциллограмма

и вот эта осциллограмма

Чем то похожи? Но чем??? 

Среднеквадратичное значение напряжения – это такое  значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении.  То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном.  То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение синусоидального сигнала  любой частоты равняется максимальной его амплитуде, поделенной  на корень из двух

Стоп! Мы ведь не разобрали, что такое максимальная амплитуда! На осциллограмме максимальная амплитуда выглядит примерно вот так:

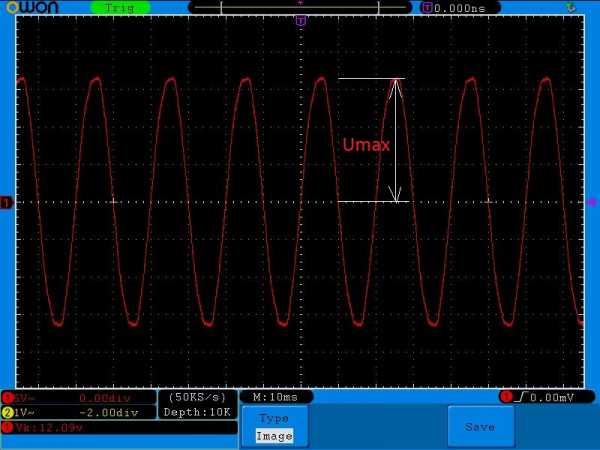
Если даже посчитать по клеточкам и посмотреть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то U_max = 17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение.  Максимальная амплитуда этих  220 Вольт равняется 220х1,41=310 Вольт.

Где же  среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот  же они!

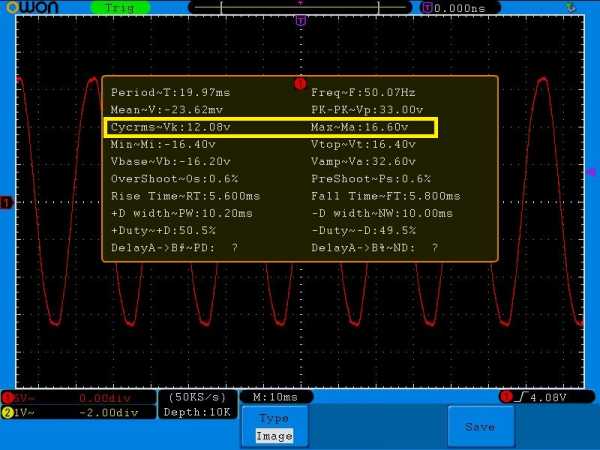
Vk – это и есть среднеквадратичное напряжение этого сигнала.

Ma – это  и есть Umax.

Конечно, 16,6/1,41=11,8  Вольт, а он пишет 12,08 Вольт. Думаю, это связано с тем, что в синусоиде есть небольшие искажения, поэтому измерения немного неточные.

Итак, внимание! Кто первый напишет среднеквадратичное значение  напряжения этого сигнала, получит 100 руб на мобилу 😉

Конкурс уже давненько прошел и первая в комментариях ответила Ирина Молчалина и выиграла 100 руб ;-). Правильный  ответ 1 Вольт. Почему именно так, читаем эту статью.

www.ruselectronic.com

Действующее значение тока и напряжения

Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как го­ворят, по действующей, эффективной его величине.

Действующее или эффективное значение переменного тока рав­но силе такого постоянного тока, который, протекая по дан­ному проводнику, выделяет в нем ежесекундно то же количе­ство энергии в виде тепла, что и переменный ток.

Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых до­стигает переменный ток, но и от формы тока.

Вообще говоря, в электротехнике, и особенно в радиотехни­ке, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы не­скольких синусоидальных токов с различными частотами, ам­плитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.

Если известна амплитуда переменного синусоидального то­ка, то действующее или эффективное его значение определяет­ся по формуле:

то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.

Аналогичная формула применяется и для вычисления эф­фективного значения синусоидального напряжения:

Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эф­фективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

www.sxemotehnika.ru

Эффективные значения тока и напряжения

Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?

Решение:

Среднее значение мощности переменного тока в цепи равно

\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]

где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:

\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2.2\right).\]

Следовательно, можно записать, что:

\[\left\langle P\right\rangle =P_{tR}=\frac{1}{2}{I^2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]

где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.

У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:

\[P=I_{ef}U\ \left(2.4\right),\]

если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:

\[I_{ef}=\frac{I_m}{\sqrt{2}},\ U_{ef}=\frac{U_m}{\sqrt{2}}\left(2.5\right).\]

Следовательно, мощность тока можно записать как:

\[P_{tR}=U_{ef}I_{ef}cos \varphi \left(2.6\right),\]

где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.

Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).

Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$

spravochnick.ru