Действующее значение переменного тока формула: Переменный ток. Формулы и параметры

Содержание

Действующее, среднеквадратичное, эффективное напряжение или ток, что это такое

Электрический ток — направленное (упорядоченное) движение частиц или квазичастиц — носителей электрического заряда.

Среднее значение переменного синусоидального напряжения или тока

Говоря о величине, изменяющейся по синусоидальному (гармоническому) закону, можно за половину периода определить ее среднее значение. Поскольку ток в сети у нас в подавляющем большинстве случаев синусоидальный, то для этого тока также легко может быть найдена средняя его величина (за половину периода), достаточно прибегнуть к операции интегрирования, установив пределы от 0 до Т/2. В результате получим:

Подставив Пи = 3,14, найдем среднюю, за половину периода, величину синусоидального тока в зависимости от его амплитуды. Аналогичным образом находится среднее значение синусоидальной ЭДС или синусоидального напряжения U:

Действующее значение тока I или напряжения U

Однако среднее значение не так широко применяется на практике, как действующее значение синусоидального тока или напряжения. Действующее значение синусоидально меняющейся во времени величины — есть среднеквадратичное, другими словами — эффективное ее значение.

Эффективное (или действующее) значение тока или напряжения находится так же, путем интегрирования, но уже по отношению к квадратам, и с последующим извлечением квадратного корня, причем пределы интегрирования теперь – целый период синусоидальной функции.

Итак, для тока будем иметь:

Подставив значение корня из 2, получим формулу для нахождения эффективного (действующего, среднеквадратичного) значения тока, напряжения, ЭДС — по отношению к амплитудному значению. Эту формулу можно встретить очень часто, ее используют всюду в расчетах, связанных с цепями переменного синусоидального тока:

С практической точки зрения, если сравнить тепловое действие тока переменного синусоидального с тепловым действием тока постоянного непрерывного, на протяжении одного и того же периода времени, на одной и той же активной нагрузке, то выяснится, что выделенная за период синусоидального переменного тока теплота окажется равна выделенной за это же время теплоте от тока постоянного, при условии, что величина постоянного тока будет меньше амплитуды тока переменного в корень из 2 раз:

Это значит, что действующее (эффективное, среднеквадратичное) значение синусоидального переменного тока численно равно такому значению постоянного тока, при котором тепловое действие (выделяемое количество теплоты) этого постоянного тока на активном сопротивлении за один период синусоиды равно тепловому действию данного синусоидального тока за тот же период.

Аналогичным образом находится действующее (эффективное, среднеквадратичное) значение синусоидального напряжения или синусоидальной ЭДС.

Подавляющее большинство современных портативных измерительных приборов, измеряя переменный ток или переменное напряжение, показывают именно действующее значение измеряемой величины, то есть среднеквадратичную величину, а не ее амплитуду и не среднее значение за полпериода.

Если других уточняющих настроек на приборе нет, а стоит значок ~I или ~U – измерены будут действующие значения тока и напряжения. Обозначения для конкретно амплитуды или конкретно действующего — Im (m – maximum – максимум, амплитуда) или Irms (rms – Root Mean Square – среднеквадратичное значение).

Ранее ЭлектроВести писали, что компания Tesla выпустила новое компактное зарядное устройство Wall Connector with 14-50 Plug, которое подключается непосредственно к розетке, благодаря чему ее без проблем можно возить с собой использовать по мере необходимости.

Стоимость новинки составляет те же $500, что и для обычной настенной зарядки Wall Connector.

По материалам: electrik.info.

Действующее значение тока формула. Большая энциклопедия нефти и газа

Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе.

Такое значение постоянного тока называется действующим значением силы переменного тока.

В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.

Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э. д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

а) б)

Рис. 3.4. Пример трехфазной системы переменного тока

а) генератор трёхфазного тока; б) с тремя генераторами;

изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

Соединение звездой

Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы – X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой. Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.

Соединение треугольником.

Рисунок 3.6. Пример соединения треугольником

При использовании данного способа соединения конец X первой обмотки генератора подключают к началу

В второй его обмотки, конец Y второй обмотки – к началу С третьей обмотки, конец Z третьей обмотки – к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл

Контрольные вопросы

1. Перечислите основные параметры, характеризующие переменный ток.

2. Дайте определение частоты и единицы её измерения.

3. Дайте определение амплитуды и единицы её измерения.

4. Дайте определение периода и единицы его измерения.

5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.

6. Что такое фаза?

7. Что представляет собой ротор генератора трёхфазного тока?

8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?

9. Особенность симметричной системы трёх фаз.

10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».

11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».

3.2. Виды сопротивлений в цепях переменного тока

В цепях переменного тока сопротивления разделяют на активные и реактивные.

В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т.д.

В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.

Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.

Активное сопротивление в цепи переменного тока .

При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).

Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.

Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui .

Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма.

Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.

Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность.

Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис.3.8).

При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э. д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока.

Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0.

Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.

Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.

Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в)

Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).

Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).

В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.

В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О.

Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.

В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.

При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны:

Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…

При параллельном соединении катушек:

1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…

Контрольные вопросы

1. Какие виды сопротивления в цепях переменного тока Вы знаете?

2. Что значит активное сопротивление?

3. Что такое реактивное сопротивление?

4. Какие элементы цепи создают реактивное сопротивление?

5. Что такое активная мощность?

1. Дайте определение индуктивности.

2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

4. Дайте определение индуктивного сопротивления.

3.3. Конденсаторы. Ёмкость в цепи переменного тока

Конденсатор – устройство, способное накапливать электрические заряды.

Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.

Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

. Переменный ток можно считать постоянным только в течение очень малых промежутков времени

. Поделим период колебанийна очень большое число малых промежутков времени

. Количество теплоты

, выделяемое на сопротивленииза время

. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло

. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока

. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4.29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

Величину

усреднять не нужно, так как она не зависит от времени, следовательно:

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому

(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то

. Если участок цепи содержит только индуктивность или только ёмкость, то

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением

а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:

. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора

. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Cтраница 2

Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.

Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.

Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.

Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока.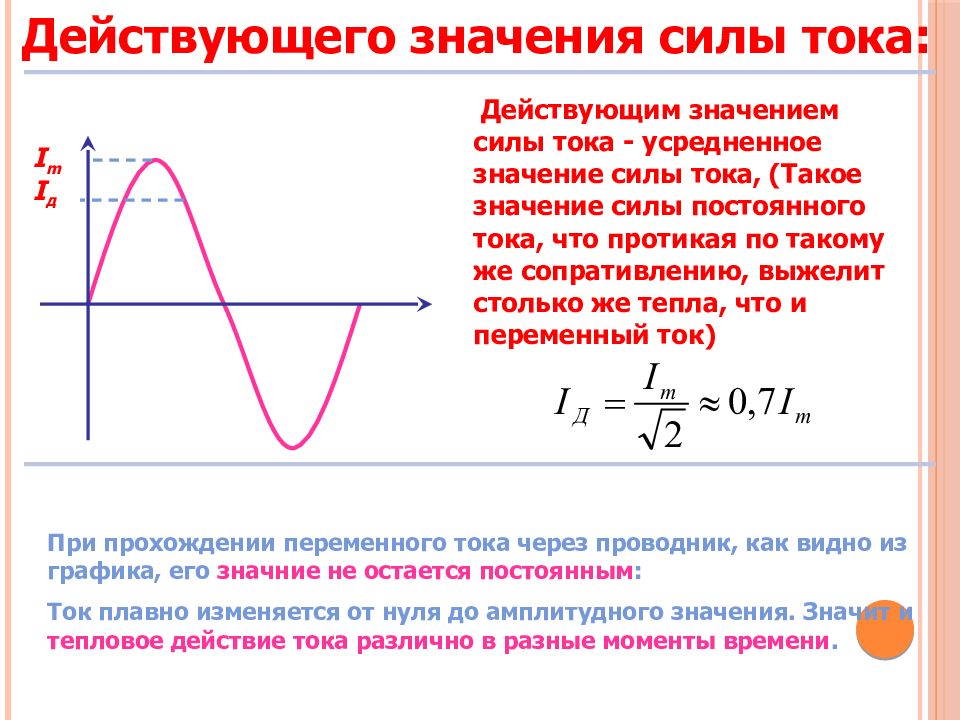 До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Рх o jjFr В слУчае т – н – СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх – / /, где РЯ – мощность eW, ra – активное сопротивление антенны в Q и 1а – действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.

Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 – 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др. Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 – 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.

В данном случае колебания тока являются гармоническими (график колебаний – синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником – генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки – от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность – минус. Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля – Ленца (Q I2Rt), определяем действующее значение силы тока (отв.

Действующее, амплитудное, среднее значение величины на синусоиде

Синусоида (синус) – самый наш идеальный и необходимый вариант. Используется на выходе из генераторов для передачи на расстояния и затем используется вами из розетки (какой ток в розетке?). Самый распространенный сигнал, вероятно, если я чего-то не знаю. Рассмотрим основные элементы графика переменного тока:

Период – это время, через которое функция начинает повторяться, величина обратная частоте. Обозначается буквой Т. Т=2тт/w.

тт – так почему-то в интернетах принято обозначать число “пи”, против толпы не попрешь, так сказать, хотя можно просто 3,14 написать или “пи”. Дело вкуса.

Амплитудное значение (амплитуда) – значения, в которых график синусоиды достигает максимумов. То есть для синусоиды таких значения два на период – положительное и отрицательное.

Действующее значение – это 0,707 от амплитудного значения. Есть у нас цепь – в этой цепи за время Т1 постоянный ток определенной величины I1 выделит определенное количество тепла Q1, если в той же цепи пустить переменный ток, то за тоже время Т1 он выделит такое же количества тепла Q1 при действующем значении равном I1. И это значение I1 для синусоиды будет равно 0,707 от амплитудного – что означает единица делить на корень из двух. Если вам интересно, откуда это такое взялось, то плиз велком:

Мгновенное значение – значение величины в определенный момент времени. Если посмотреть на синусоиду, то видно, что мгновенное значение постоянно передвигается и на протяжении одного периода постоянно меняет свои значения. В следующем периоде опять идет тем же путем. Остановись мгновение =) Значение мгновенного значения определяется как Im*sin(wt) – амплитудное значение умноженное на “синус омега тэ” – где “омега тэ” – произведение угловой скорости на момент времени. Омега равно два пи делить на период Т.

Среднее значение – сумма всех мгновенных значений за полпериода. Для синусоиды равно 0,6366197730950255438113531364418 ~ 0,637 от амплитудного значения. Если вновь стало интересно, откуда число, то ответ ниже на примере переменного тока:

Если амплитудное значение разделить на действующее значение, то мы получим, правильно корень из двух для синусоиды – его еще называют коэффициентом амплитуды. Если же мы разделим действующее значение на среднее – то получим для синусоиды 1,11 – это отношение называется коэффициентом формы кривой.

Сколько инженеров, столько и форм кривых в электронике, а если серьезно, то существуют например такие: Форма сигнала меандр – сигнал, в котором отсутствуют четные гармоники, имеет прямоугольную форму. В отличие от прямоугольного импульса, у которого длительность сигнала и длительность паузы могут отличаться, у меандра они равны. Сигнал такой формы может встречаться в импульсных источниках бесперебойного питания и прочих электронных схемах, ШИМ.

Пилообразный сигнал – сигнал пилообразной формы может идти и в одну сторону и в другую (знак минус в формуле функции). Для создания этой и других форм сигналов применяются генераторы сигналов. Применяются в старых осциллографах, мониторах, как и треугольные.

Треугольный сигнал – у треугольного сигнала длина роста и длина падения равны.

Каждая из этих форм может быть представлена через преобразование фурье, смысл которого в разбиении функции на гармонические составляющие от единицы до бесконечности с набором определенных гармоник – нечетных например, как для меандра. В функциях выше, которые были построены в маткаде, смысл построения в следующем, чем больше составляющих вы берете для построения (ближе к бесконечности), тем красивее получается график.

Самое популярное

Эффективная сила тока. Действующее значение переменного тока

>> Активное сопротивление. Действующие значения силы тока и напряжения

§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

P = i 2 R. (4.19)

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t

Средняя мощность равна, таким образом, первому члену в формуле (4.20):

Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!

Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.

Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э. д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Определение 1

Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.

Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений

Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:

Тогда за один период переменный ток выделяет тепла ($W$):

Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:

Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:

Если сила тока изменяется по синусоидальному закону:

подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:

Следовательно, выражение (6) может быть преобразовано к виду:

где $I_{ef}$ называют эффективным значением силы тока. Аналогично записывают выражения для эффективных (действующих) значений напряжений:

Применение действующих значений тока и напряжения

Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.

Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:

и коэффициент формы ($k_f$):

где $I_{sr\ v}=\frac{2}{\pi }\cdot I_m$ –средневыпрямленное значение силы тока.

Для синусоидального тока $k_a=\sqrt{2},\ k_f=\frac{\pi }{2\sqrt{2}}=1,11.$

Пример 1

Задание: Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?

Решение:

Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220\ В.$ В соответствии с известным соотношением:

найдем амплитудное значение напряжения, как:

Вычислим:

Ответ: $U_m\approx 310,2\ В.$

Пример 2

Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?

Решение:

Среднее значение мощности переменного тока в цепи равно

\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]

где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:

\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2.2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]

где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.

У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:

если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:

Следовательно, мощность тока можно записать как:

где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.

Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).

Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

(4.29)

4.4.5. Мощность в цепи переменного тока

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

С использованием известной тригонометрической формулы

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Переменный синусоидальный ток

Переменный ток – это ток, который периодически изменяется как по модулю, так и по направлению. Появляется переменный ток благодаря электромагнитной индукции. Электромагнитная индукция это явление возникновения тока в замкнутом контуре при изменении магнитного потока проходящего через него. Чтобы понять, как именно возникает ток, представим себе рамку (кусочек проволоки прямоугольной формы), которая находится под воздействием магнитного поля B.

Пока рамка находится в покое, тока в ней нет. Но как только мы начнём её поворачивать, электроны, которые находятся в рамке, начнут перемещаться вместе с ней, то есть двигаться в магнитном поле. Вследствие этого магнитное поле начинает действовать на электроны, заставляя их двигаться по рамке. Чем больше линий магнитного поля пронизывает рамку, тем сила действующая на электроны больше, следовательно, и электрический ток тоже. Получается, что ток достигает максимума в момент, когда рамка перпендикулярна магнитному полю (наибольшее количество линии пронизывает рамку) и равен нулю, когда параллельна (наименьшее количество линии пронизывает рамку). Соответственно и сила, которая действует на электроны, тоже изменяется. После прохождения момента, когда рамка параллельна вектору магнитной индукции B, ток в ней начинает течь в обратную сторону.

Ток, который получается при вращении рамки, изменяясь во времени, описывает синусоиду, то есть является синусоидальным. Переменный синусоидальный ток является частным случаем периодического переменного тока. Закон, описывающий изменение тока, имеет вид:

Амплитуда Im – это наибольшая абсолютная величина, которую принимает периодически изменяющийся ток.

Начальная фаза ψ – аргумент синусоидального тока (угол), отсчитываемый от точки перехода тока через нуль к положительному значению.

Время, за которое ток в проводнике дважды изменяет своё направление, называют периодом T. Период измеряется в секундах.

Циклической частотой f называется величина обратная периоду . Измеряется в Герцах, в домашней розетке циклическая частота тока равна 50 Гц, её также называют промышленной частотой. При такой частоте период тока равен , это значит, что за две сотых секунды ток в нашей розетке меняет свое направление два раза.

Угловая частота ω показывает с какой скоростью изменяется фаза тока и определяется как

Среднее значение Iср синусоидального тока за период Т определяют из геометрических представлений: площадь прямоугольника с основанием T/2 и высотой Iср приравнивают площади ограниченной кривой тока:

После упрощения получаем формулу:

Действующее значение синусоидального тока определяется из энергетических представлений: действующий ток равен по величине такому постоянному току I, который в активном сопротивлении R за период Т выделяет такое количество энергии, как и данный ток i. То есть действующее значение, это своеобразная аналогия между переменным и постоянным током.
Для синусоидального тока действующее значение определяется по формуле:

или

Это основное что нужно знать о переменном синусоидальном токе.

Читайте также – Мгновенная мощность

Действующие значения силы тока и напряжения.

Презентация по физике

Переменный электрический ток. Активное сопротивление. Действующие значения силы тока и напряжения.

Выполняли ученицы 11 «А» класса Радукан Яна, Иванова Алина.

Переменный электрический ток

Как известно, ток (электрический) бывает переменным и постоянным.Переме́нный ток (англ. alternating current — переменный ток) — электрический ток, который периодически изменяется по модулю и направлению.В настоящее время очень широко используется переменный электрический ток. Его можно получить с помощью электрогенераторов переменного тока с применением эффекта электромагнитной индукции. На рисунке изображена примитивная установка для выработки переменного тока.

Принцип действия установки прост. Проволочная рамка вращается в однородном магнитном поле с постоянной скоростью. Своими концами рамка закреплена на кольцах, вращающихся вместе с ней. К кольцам плотно прилегают пружины, выполняющие роль контактов. Через поверхность рамки непрерывно будет протекать изменяющийся магнитный поток, но поток, создаваемый электромагнитом, останется постоянным. В связи с этим в рамке возникнет ЭДС индукции.

Под переменным током также подразумевают ток в обычных одно- и трёхфазных сетях. В этом случае мгновенные значения тока и напряжения изменяются по гармоническому закону.

Ф = BScoswt “

Переменный ток в осветительной сети квартиры, применяемый па заводах и фабриках и т. д., представляет собой не что иное, как вынужденные электромагнитные колебания. Данные колебания напряжения легко обнаружить с помощью осциллографа.(рис. 4.8)

Стандартная частота промышленного переменного тока равна 50 Гц. Это означает, что на протяжении 1 с ток 50 раз идет в одну сторону и 50 раз — в противоположную. Частота 50 Гц принята для промышленного тока во многих странах мира. В США принята частота 60 Гц. Если напряжение на концах цепи меняется по гармоническому закону, то и напряженность электрического поля внутри проводников будет также меняться гармонически.

Переменное напряжение в гнездах розетки осветительной сети создается генераторами на электростанциях. Проволочную рамку, вращающуюся в постоянном однородном магнитном поле, можно рассматривать как простейшую модель генератора переменного тока. Поток магнитной индукции Ф, пронизывающий проволочную рамку площадью S, пропорционален косинусу угла а между нормалью к рамке и вектором магнитной индукции (рис. 4.9):

Ф = BScos а

При равномерном вращении рамки угол а увеличивается прямо пропорционально времени: а=2Пnt , где n – частота вращения.Поэтому поток магнитной индукции меняется гармонически :

Ф = BS cos 2Пnt , Здесь 2Пn число колебаний магнитного потока за 2П с. Это ЦИКЛИЧЕСКАЯ ЧАСТОТА колебаний w=2Пn = Ф = BScoswt

Согласно закону электромагнитной индукции ЭДС индукции в рамке равна взятой со знаком «-» скорости изменения потока магнитной индукции, т. е. производной потока магнитной индукции по времени:

Если к рамке подключить колебательный контур, то угловая скорость w вращения рамки определит частоту w колебаний значений ЭДС, напряжения на paзличныx участках цепи и силы тока.

Если напряжение меняется с циклической частотой , то и сила тока в цепи будет меняться с той же частотой. Но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае сила тока і в любой момент времени (мгновенное значение силы тока) определяется по формуле

Здесь I m – амплитуда силы тока, т. е. максимальное по модулю значение силы тока, а — разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Активное сопротивление .

Действующие значения силы тока и напряжения.

Сопротивление R называется активным, потому что при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников — они нагреваются. Будем считать, что напряжение на зажимах цепи меняется по гармоническому закону:

u = U m cos w t

Как и в случае постоянного тока, мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения. Поэтому для нахождения мгновенного значения силы тока можно применить закон Ома :

Как правило, нам нужно бывает знать среднюю мощность тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найти среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой :

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения (рис. 4.17), а амплитуда силы тока определяется равенством

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой :

P = i 2 R. (4.19)

Средняя мощность

равна первому члену в формуле (4.20)

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем закон Ома для участка цепи переменного тока с резистором

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

P = I 2 R = UI.

Конденсатор в цепи переменного тока

Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.

Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА’) лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ’) лампа загорается, если емкость конденсатора достаточно велика.

Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.

Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Сила тока, представляющая собой производную заряда по времени , равна:

Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).

Следовательно, колебания силы тока опережают по фазе колебания напряжения на конденсаторе на

(рис. 4.15).

Напряжение на конденсаторе

Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.

Амплитуда силы тока равна:

I m = U m C

(4.29)

Если ввести обозначение :

В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение X c . С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим :

Величину X c , обратную произведению

циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением .

Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на

Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.

КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.

Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока.

Соберем цепь из катушки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны.

Объясняется это различие явлением самоиндукции.

Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Определим силу тока в цепи, содержащей катушку, активным сопротивлением которой можно пренебречь (рис. 4.17). Для этого предварительно найдем связь между напряжением на катушке и ЭДС самоиндукции в ней.

–

Из равенства

следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции е і ) равна по модулю и противоположна по знаку удельной работе кулоновского поля. Учитывая, что удельная работа кулоновского поля равна напряжению на концах катушки, можно записать: е і = -u.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю. Иначе сила тока, согласно закону Ома, была бы бесконечно большой. Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля

При изменении силы тока по гармоническому закону :

i = I m sin

ЭДС самоиндукции равна:

порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля

e і = – L i ‘ = – L

l m cos

Так как u = -е і , то напряжение на концах катушки оказывается равным

создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Следовательно, колебания напряжения на катушке опережают по фазе колебания силы тока на

Индуктивное сопротивление зависит от частоты

что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на (рис. 4.18)

Постоянный ток вообще «не замечает» индуктивности катушки. При = 0

индуктивное сопротивление равно нулю (X L = 0).

Амплитуда силы тока в катушке равна:

Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Катушка индуктивности оказывает сопротивление переменному току.

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим:

Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.

Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на

Величину X L , равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Спасибо за внимание!

Источники:https://vk.com/away.php?to=http%3A%2F%2Fselectelement.ru%2Fbasic-concepts%2Felectric-ac.php&cc_key= https://vk.com/away.php?to=https%3A%2F%2Fsites.google.com%2Fsite%2Fopatpofizike%2Fteoria%2Fteoria-11-klass%2Feds-zakon-oma-dla-polnoj-cepi%2Fperemennyj-elektriceskij-tok-aktivnoe-induktivnoe-eemkostnoe-soprotivlenia&cc_

действующие значения силы тока и напряжения

Рассмотрим следующую цепь.

рисунок

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.2)*R = U*I.

Нужна помощь в учебе?

Предыдущая тема: Переменный электрический ток: формулы и примеры
Следующая тема:&nbsp&nbsp&nbspКонденсатор в цепи переменного тока: изменение силы тока в цепи

RMS значение переменного тока | Вывод

В системе постоянного тока напряжение и ток постоянны, поэтому нет проблем с указанием их величины. Но в случае системы переменного тока переменное напряжение меняется от момента к моменту, и поэтому возникает проблема с указанием величины.

Итак, чтобы выразить величины переменного тока в простой и понятной форме, была разработана концепция среднеквадратичного значения. Они также могут быть выражены в виде пикового или среднего значения, но эти значения не отражают эффективность количества переменного тока.

Среднеквадратичное значение переменного тока равно той величине постоянного тока, которая вызывает такой же нагревательный эффект, протекающий через то же сопротивление в течение того же времени.

Термин RMS означает (квадратный) корень из среднего квадратов мгновенных значений тока. Среднеквадратичное значение переменного тока или напряжения можно рассчитать по следующей формуле:

I _RMS = 0,707 x пиковое значение тока
В _RMS = 0.707 x пиковое значение напряжения

Это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию. Например, если мы говорим, что по цепи протекает переменный ток 5 А, это означает, что среднеквадратичное значение переменного тока, протекающего по цепи, составляет 5 А. И он будет производить столько же тепла (энергии), сколько вырабатывается постоянным током 5А.

Все амперметры и вольтметры переменного тока показывают среднеквадратичные значения переменного тока и напряжения соответственно .Все электроприборы оцениваются по среднеквадратичному значению. В Индии внутреннее однофазное электроснабжение переменного тока составляет 230 В, 50 Гц. Здесь 230 В – это действующее значение напряжения питания.

Среднеквадратичное значение AC всегда больше среднего значения, за исключением прямоугольной волны, когда они равны. Его значение никогда не может быть отрицательным.

Управляйте выражением среднеквадратичного значения AC

Пусть i = I _m sinωt будет переменным током, протекающим через сопротивление R Ом в течение времени t секунд и выделяющим такое же тепло, как и выделяемое I _eff (прямой Текущий).

База полупериода делится на n равных частей, как показано на рисунке, так что каждый интервал составляет t / n секунд.

Пусть i ₁, i ₂, i ₃ ……… .i _n – средние ординаты.

Тогда тепло, произведенное в первом интервале = i ₁ ² Rt / n джоулей
Второй интервал = i ₂ ² Rt / n джоулей
Третий интервал = i ₃ ² Rt / n джоулей
n ^th интервал = i _n ² Rt / n джоулей

Общее количество тепла, произведенного за время t

= Rt [(i ₁ 2 + i ₂ ² + i ₃ ² + …… + i _n ²) / n]….. (1)

С I _eff считается действующим значением этого тока.
Тогда тепло, произведенное этим током во времени t = I _eff ² Rt ……. (2)

По определению, уравнения (1) и (2) равны. Следовательно,

I _eff ² Rt = Rt [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n]

Или I _eff ² = [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n]

Или I _eff = [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n] ^1/2

Или I _eff = I _RMS = квадратный корень из среднего квадратов мгновенного тока.

Теперь, используя интегральное исчисление, действующее значение или действующее значение переменного тока за период времени можно рассчитать следующим образом:

Важные термины, относящиеся к среднеквадратическому значению AC

Пиковое значение (I _m) : Максимальное значение, достигаемое переменным током во время полного цикла, называется его пиковым значением. Синусоидальный переменный ток достигает максимального положительного значения при 90 ^o.

Форм-фактор (K _f) : Это отношение среднеквадратичного значения к среднему значению переменной величины.

K _f = среднеквадратичное значение / среднее значение

Для синусоидальной волны это 1,11. Мы можем найти среднеквадратичное значение из среднего значения и наоборот с помощью форм-фактора.

Этот коэффициент показывает «остроту» формы сигнала. Прямоугольная волна, более плоская, чем синусоида, имеет коэффициент формы 1,0. С другой стороны, треугольная волна более «острая», чем синусоида, и имеет форм-фактор 1,15.

Коэффициент пика (Kp) : Это отношение пикового или максимального значения к среднеквадратичному значению переменной величины.

K _p = Пиковое значение / среднеквадратичное значение

Для синусоидальной волны это 1,414. Это очень важно при испытании диэлектрической изоляции, поскольку диэлектрическая нагрузка на изоляционный материал зависит от пикового значения приложенного напряжения. Это также важно при измерении потерь в стали, поскольку эти потери зависят от значения максимального магнитного потока.

Среднее значение переменного тока

Среднее арифметическое всех мгновенных значений, учитываемых в переменном количественном токе за один цикл, называется средним значением переменного тока (I _av).

Это тот постоянный ток, который передает тот же заряд, что и переменный ток, в одно и то же время по любой цепи.

В случае симметричных волн, таких как синусоидальный ток или волна напряжения, положительная половина точно равна отрицательной половине, поэтому среднее значение за полный цикл равно нулю.

Поскольку работа выполняется током как в положительном, так и в отрицательном полупериоде, то среднее значение определяется независимо от знаков или учитывается только положительная половина.

Чтобы определить среднее значение переменного тока, рассмотрите только положительный полупериод и разделите его на n равных частей. Пусть i ₁, i ₂, i ₃ …… in – средние ординаты.

Теперь, среднее значение тока, I _av = Среднее значение средних ординат

= (i ₁ + i ₂ + i ₃ + ……. + I _n) / n

= Площадь полупериода / длина базы полупериода

Теперь, используя интегральное исчисление, мы можем вычислить площадь полупериода и среднее значение переменного тока.После этого расчета мы получаем следующее выражение для синусоидального тока.

I _ср. = 2I _м / π = 0,637 I _м

Основы переменного тока | Все сообщения

Среднеквадратичное значение переменного и переменного тока только через сопротивление | Примечания, видео, контроль качества и тесты | 12 класс> Физика> Переменные токи

Среднеквадратичное значение A.К. и А.С. Только через сопротивление

Среднеквадратичное значение (RMS) или виртуальное значение переменного тока или эффективное значение переменного тока

Это то, что постоянный ток при прохождении через сопротивление в течение заданного времени производит такое же количество тепла, как и переменный ток при том же сопротивлении в в то же время.

Среднеквадратичные значения переменного тока

Чтобы вычислить его значение, пусть переменный ток будет представлен как

$$ I = I_0 \ sin \ omega t $$

Если этот переменный ток протекает через сопротивление R в течение короткого времени dt, затем выделяется небольшое количество тепла, которое дает

\ begin {align *} dH & = I ^ 2R \: dt = (I_0 ^ 2 \ sin ^ 2 \ omega t) R \: dt \\ \ text {или ,} \: dH & = I_o ^ 2 R \ sin ^ 2 \ omega T dt \\ \ end {align *}

Чтобы получить общее количество тепла, произведенного за один цикл, мы должны интегрировать уравнение (i) из t = 0 до t = T.2 RT} {2} \\ \ поэтому \: I_v & = \ frac {I_0} {\ sqrt {2}} = 0.707 \: I_0 \\ \ end {align *}

Отсюда среднеквадратичное значение. значение или виртуальное значение или эффективное значение переменного тока в 0,707 пикового значения переменного тока. то есть 70,7% от пикового значения переменного тока.

Виртуальное значение переменного тока может быть доказано как

$$ E_v = \ frac {E_0} {\ sqrt 2} = 0.707 \: E_0 $$

Переменный ток только через сопротивление

Переменный ток. источник подключен к резистору, известному как резистивная цепь.

\ begin {align *} \ text {Применяемая переменная э.д.с. задается формулой} \\ E & = E_0 \ sin \ omega t \\ \ text {Пусть I будет схемой в любой момент времени t. Итак} \\\ text {Разность потенциалов на резисторе} & = IR \\ \ text {или,} \: E & = IR \\ \ text {или,} \: I & = \ frac ER \\ & = \ frac {E_0 \ sin \ omega t} {R} \\ [\ поэтому E = E_0 \ sin \ omega t \: \ text {в уравнении} \: (i)] \\\ text {или,} \ : I & = I_0 \ sin \ omega T \ dots (ii) \\ \ text {где} \: \ frac {E_0} {R} = I_0 \: \ text {- пиковое значение переменного тока.} \ end {align *}

Сравнивая уравнения (i) и (ii), мы обнаруживаем, что E и I находятся в фазе. Следовательно, в переменном токе цепь, содержащая только R, ток и э.д.с. находятся в фазе.

Ссылка

Ману Кумар Хатри, Манодж Кумар Тапа, Бхеша Радж Адхикари, Арджун Кумар Гаутам, Парашу Рам Пудел. Принципы физики . Катманду: публикация Ayam PVT LTD, 2010.

S.K. Гаутам, Дж. М. Прадхан. Учебник по физике . Катманду: Публикация Сурьи, 2003.

Среднеквадратичное значение, среднее значение, пиковое значение, пик-фактор, форм-фактор в AC

Что такое среднеквадратичное значение, пиковое значение, среднее значение, значение экземпляра, форм-фактор, пик-фактор и другие термины, относящиеся к цепям переменного тока и синусоиде?

Токи постоянного и переменного тока

Известно, что полярность постоянного напряжения и направление постоянного тока всегда одинаковы, то есть это однонаправленное значение, которое не меняет полярность, а также направление, как показано на рис.1.

С другой стороны, (AC) переменный ток или напряжение – это ток, который регулярно меняет свое направление, а также свое значение. Другими словами, переменный ток (AC) – это тип тока, который течет сначала в одном направлении, а во-вторых, он течет в противоположном направлении. В каждом цикле он меняет значение от нуля до максимального и снова достигает нулевого значения.

Значение переменного тока или напряжения может быть выражено в переменном токе (синусоидальном) Синусоидальная волна, как показано на рис. (1) ниже.

Рис. 1 Разница между переменным током и постоянным током

В переменном токе невозможно представить величины, поскольку его амплитуда синусоидальной волны переменного тока непрерывно изменяется со временем.

Таким образом, у нас есть несколько вариантов выражения амплитуды и различных значений, связанных с синусоидальной волной переменного тока, например:

RMS Value
Average Value
Instant Value
Maximum or Peak Value
Peak to Peak Value
Пик-фактор
Форм-фактор
Прочие связанные термины

Мы подробно обсудим их все ниже.

Что такое среднеквадратичное значение?

Значение RMS ( среднеквадратическое значение ) (также известное как эффективное значение или виртуальное значение ) переменного тока (AC) – это значение постоянного тока (DC) при протекании через цепь. или резистор в течение определенного периода времени и производит такое же количество тепла, которое вырабатывается переменным током (AC) при протекании через ту же цепь или резистор в течение определенного времени.

Значение переменного тока, которое при прохождении через нагревательный элемент (например, резистор) будет выделять такое же количество тепла, как и постоянный ток через элемент, называется значением R.M.S.

Короче говоря,

Среднеквадратичное значение переменного тока состоит в том, что по сравнению с постоянным током и переменный, и постоянный ток выделяют одинаковое количество тепла при прохождении через одну и ту же цепь в течение определенного периода времени.

Для синусоидальной волны

или

I _RMS = 0.707 x I _M, E _RMS = 0,707 E _M

Фактически, RMS-значение синусоиды является мерой теплового эффекта синусоидальной волны. Например, когда резистор подключен к источнику переменного напряжения, он выделяет определенное количество тепла (рис. 2 – а). Когда тот же резистор подключен к источнику постоянного напряжения, как показано на (рис. 2 – b). Регулируя значение постоянного напряжения, чтобы получить такое же количество тепла, которое ранее выделялось в источнике переменного напряжения на рис.Это означает, что среднеквадратичное значение синусоидальной волны равно источнику постоянного напряжения, производящему такое же количество тепла, выделяемого источником переменного напряжения.

Рис. 2 – Среднеквадратичные значения тока и напряжения

Говоря более ясными словами, уровень внутреннего напряжения в США составляет 110 В, а в Великобритании – 220 В переменного тока. Этот уровень напряжения показывает эффективное значение (110 В или 220 В R.M.S) и показывает, что домашняя розетка способна обеспечить такое же количество средней положительной мощности, что и напряжение 110 В или 220 В постоянного тока.

Имейте в виду, что амперметры и вольтметры, подключенные к цепям переменного тока, всегда показывают среднеквадратичные значения (тока и напряжения).

Для синусоиды переменного тока среднеквадратичные значения тока и напряжения:

I _RMS = 0,707 x I _M, В _RMS = 0,707 В _M

Чтобы найти среднеквадратичное значение синусоидальной волны, мы можем использовать следующие два метода.

Метод средней ординаты
Метод интегрирования.

Давайте посмотрим, как найти значения R.M.S синусоидальной волны.

Методы определения среднеквадратичного значения синусоиды.

Аналитический метод

Метод 1

Мы знаем, что значение синусоидального переменного тока (AC) =

I _m Sin ω θ = I _m Sin θ

В то время как Среднее квадратическое значение мгновенных значений тока за половину или полный цикл составляет:

Квадратный корень из этого значения:

Следовательно, действующее значение тока равно (если положить I = I _м Sin θ):

Now,

Следовательно, мы можем обнаружить, что для симметричного синусоидального тока:

I _RMS = максимальное значение тока x 0.707

Метод 2.

Пусть i = Sin ω θ = I _м Sin θ

Среднее значение i ₂

Метод 3

Пусть i = Sin ω θ = I _м Sin θ

Графический или средний ординатный метод

Этот метод известен как средний ординатный или графический метод, позволяющий найти значение среднеквадратичного напряжения с использованием средних ординат или нахождения мгновенного значения Форма волны переменного тока.Для ясного понимания ниже пояснения приведен решенный пример.

В синусоидальной волне переменного тока существует множество мгновенных значений напряжения, и это зависит от временного интервала. Как показано на рис. 3 ниже, где число средних ординат равно 12 (чем больше средних ординат, тем точнее будет результат). Он показывает при t = 1, t = 2, t = 3…. tn, мгновенные уровни напряжения равны V ₁, V ₂, V ₃…. V _n соответственно.

Рис. 3 – Среднеординатный или графический метод для RMS

Во-первых, мы найдем мгновенные значения напряжений для каждого периода времени, например t = 1, t = 2… t = n и т. Д.Чтобы найти среднеквадратичное значение, нам нужно будет найти квадратные значения каждого уровня напряжения в форме волны переменного тока, которая показывает квадратную часть среднеквадратичного значения.

V ₁ ² + V ₂ ² + V ₃ ² +… .. V _n ²

Теперь квадратные значения напряжений делятся на количество средних ординат, которое показывает среднее значение среднеквадратичного напряжения.

Например,

Число ординат, использованных на рис. 3 выше, = 12

Предположим, что пиковое значение напряжения (Max Voltage i.е. амплитуда = V _PK или V _Max) составляет 12 В для переменного сигнала. Форма волны разделена на 12 средних ординат, как показано ниже:

4V 905 9005 9005 9005 9005 9005

Напряжение

10V

12V

10V

Угол

15 ^o

30 ^o

45 ^o

60 ^o

105 ^o

120 ^o

135 ^o

150 ^o

165 ^o

180 ^o

Напряжение RMS рассчитывается как следующее напряжение :

Таким образом, значение RMS напряжения равно 6.97 В, используя графический метод или метод средней оси ординат, чтобы найти среднеквадратичное значение напряжения.

Уравнения среднеквадратичного напряжения и тока
Среднеквадратичные значения тока и напряжения, связанные с пиковым значением или максимальным значением (оба одинаковы).
V _RMS = 0,707 x V _PK, I _RMS = 0,707 x I _PK
V _RMS = 0,707 x V _M, I _RMS = 0.707 x I _M
Среднеквадратичные значения тока и напряжения, относящиеся к размаху .
В _RMS = 0,3536 x V _P-P, I _RMS = 0,3536 x I _P-P
Действующие значения тока и напряжения относительно среднего значения.
В _RMS = 1,11 x V _AV, I _RMS = 1,11 x I _AV
Здесь все на одном изображении.
Формулы среднеквадратичного значения напряжения для различных форм волны
В приведенной ниже таблице формулы среднеквадратичного значения напряжения показаны для различных типов синусоидальных форм волны.
96 V ₃
Тип сигнала Формула для среднеквадратичного значения (В _RMS)
Синусоидальная волна В _PK / √2
Половинная выпрямленная волна 905 с _PK / √2
Двухполупериодная выпрямленная синусоида В _PK / √2
Прямоугольная волна V _PK
PK Треугольная форма волны
Пилообразная форма волны В _PK / √3
Калькулятор среднеквадратичного напряжения
В калькуляторе среднеквадратичного значения напряжения вы можете рассчитать значение среднеквадратичного напряжения из различных связанных значений, таких как среднее значение, пиковое значение Значение и максимальное значение.
Что такое среднее значение
Если мы преобразуем синусоидальную волну переменного тока в синусоидальную волну постоянного тока (DC) через выпрямители, то преобразованное значение в постоянный ток будет известно как среднее значение этой синусоиды переменного тока. волна.
Рис. 4 – Среднее значение напряжения
Если максимальное значение переменного тока равно «I _MAX», то значение преобразованного постоянного тока через выпрямитель будет «0,637 I _M», что известно как среднее значение Синусоида переменного тока (I _AV).
Среднее значение тока = I _AV = 0,637 I _M
Среднее значение напряжения = E _AV = 0,637 E _M
Среднее значение (также известное как Среднее значение) переменного тока (AC) выражается тем постоянным током (DC), который передает по любой цепи такое же количество заряда, какое передается этим переменным током (AC) в течение того же времени.
Имейте в виду, что среднее или среднее значение полной синусоидальной волны равно «нулю», значение тока в первой половине (положительное) равно следующему полупериоду (отрицательное) в противоположном направлении.Другими словами, в положительном и отрицательном полупериодах имеется одинаковое количество тока, который течет в противоположном направлении, поэтому среднее значение для полной синусоидальной волны будет «0». По этой причине мы не используем среднее значение для покрытия и зарядки аккумулятора. Если волна переменного тока преобразуется в постоянный ток через выпрямитель, ее можно использовать для электрохимических работ.
Рис. 5 – Среднее значение тока
Короче говоря, среднее значение синусоидальной волны, взятой за полный цикл, всегда равно нулю, потому что положительные значения (выше точки пересечения нуля) смещают или нейтрализуют отрицательные значения (ниже точки пересечения нуля.)
Связанный пост: Соединение звездой (Y): трехфазная мощность, значения напряжения и тока
Методы определения среднего значения синусоиды.
Среднеординатный или графический метод
В этом методе полупериод синусоидальной волны делится на равное количество периодов времени, причем продолжительность каждого периода времени равна «t / n».
Предположим, что средние значения мгновенных токов в каждом временном интервале равны I ₂, 1 ₂, I ₃… I _n.Чтобы найти среднее значение для каждого временного интервала, левая и правая вертикальные линии складываются и делятся на два. То же самое применимо ко всем временным интервалам, чтобы найти среднее значение для каждого экземпляра.
Теперь все средние значения складываются и делятся на числовые средние ординаты (то есть периоды времени), которые показывают общее среднее значение полупериода синусоидальной волны. формула для среднего значения показана ниже:
Пример:
Рис. Текущий i.е. амплитуда = I _PK или I _Max) составляет 12 А для переменного сигнала. Форма волны разделена на 12 средних ординат, как показано ниже:
4A
Ток 2A 4A 6A 8A 10A 12A 10A 2A 0A
Угол 15 ^o 30 ^o 45 ^o 60 ^o 9005 9005 9005 9005 105 ^o 120 ^o 135 ^o 150 ^o 165 ^o 180 ^o
Таким образом, среднее значение тока равно 6A, используя графический метод или метод средней ординаты, чтобы найти среднее значение тока.
Аналитический метод
Мы знаем, что стандартное уравнение переменного тока:
i = Sin ω θ = I _м Sin θ
Максимальное значение тока на синусоиде = I _м
Среднее значение тока на синусоиде = I _AV
Мгновенное значение тока на синусоиде = i
Угол, указанный для « i » после нулевого положения тока = θ
Угол полупериода = Π радиан
Угол полного круга = 2π радиан
(a) Среднее значение полного цикла:
Пусть i = Sin ω θ = I _м Sin θ
Таким образом, среднее значение синусоидальной волны за полный цикл равна нулю.
(b) Среднее значение тока за полупериод
Среднее значение тока (полупериод)
I _AV = 0,637 В _M
Аналогично среднее значение напряжения за полупериод
В _AV = 0,637 В _M
Уравнения среднего напряжения и тока
Среднее значение среднего напряжения или тока равно умножению максимального или пикового значения напряжения и ток соответственно с постоянной 0.637.
Например, если максимальное значение или пиковое значение синусоидальной волны составляет 360 В _PK или 360 В _Макс, используя приведенное выше уравнение, среднее значение напряжения будет:
0,637 x 360 В _PK = 229,32 Av .
Формулы среднего значения и среднеквадратичного значения для различных форм волны
В таблице ниже показаны формулы среднего значения и среднеквадратичного значения напряжения для различных типов синусоидальных форм волны.
Тип сигнала Формула для среднеквадратичного напряжения Формула для среднего напряжения
Синусоидальная волна В _RMS = V _{_{99 AV / √2} = 0}
Полное выпрямленное напряжение В _СКЗ = В _PK / √2 В _AV = 0.637 В _PK
Половина выпрямленного сигнала В _СКЗ = В _PK/2 В _AV = 0,318 В _PK
Синусоидальная волна со смещением по постоянному току В _RMS = √ (VDC ² + V _PK ²/2) V _AV = Vdc
Половина синусоиды с длительностью T и частотой f V _RMS = V _PK x √ (fx T / 2) V _AV = 2f x T x V _PK / π
Положительный прямоугольный сигнал с длительностью T и частотой f V _RMS = V _PK x √ (fx T) V _AV = fx T x V _PK
Волна зубьев пилы с длительностью T и частотой f V _RMS = V _PK x √ (fx T / 3) V _AV = fx T x V _PK/2
Трапециевидная волна e с частотой f, верхним сегментом T и базовым сегментом B. В _RMS = В _PK x √ (fx ((BT) + 3xT) / 3) V _AV = fx V _PK x ((T + B) / 2)
Что такое мгновенное значение
Значение, достигаемое переменной величиной в любой момент времени, называется мгновенным значением. Обозначается буквами «i» и e.
другими словами, значение переменного тока или напряжения в любой конкретный момент мы называем мгновенным значением.
На рис. 7 ниже показаны различные мгновенные значения напряжений или токов в определенный момент и период времени.Значения мгновенного тока или напряжения равны «+» в положительном цикле и «-» в отрицательном цикле в синусоидальной волне. Кривые показывают значения различных мгновенных напряжений, в то время как такая же кривая может быть построена и для тока. На рис. 7 значения мгновенных напряжений составляют 2,5 В при 1 мкс, 5,1 В при 2 мкс, 8,9 В при 3 мкс. В то время как это составляет -2,3 В при 4 мкс, -6,1 В при 5 мкс и -9,2 В при 6 мкс.
Рис. 7 – Мгновенное значение напряжения
Что такое пиковое напряжение или максимальное значение напряжения?
Пиковое значение также известно как Максимальное значение , Пиковое значение или Амплитуда .Это максимальное значение переменного тока или напряжения из положения «0» независимо от положительного или отрицательного полупериода в синусоидальной волне, как показано на рис. 8. Оно выражается как I _M и E _M или В _P и I _M.
Уравнения Пикового значения напряжения составляют:
В _P = √2 x V _RMS = 1,414 В _RMS
V _P = V _PP/2 = 0.5 В _PP
В _P = π / 2 x V _AV = 1,571 x V _AV
Другими словами, это значение напряжения или тока на положительном или отрицательном полюсе. максимум (пики) относительно нуля. Проще говоря, это мгновенное значение с максимальной интенсивностью.
Рис. 8 – Пиковые или максимальные значения напряжений
Пиковое значение Значение
Сумма положительных и отрицательных пиковых значений называется размахом до пика.Выражается как I _PP или V _PP.
Уравнения и формулы для Пиковое напряжение следующие:
В _PP = 2√2 x В _RMS = 2,828 x В _RMS
V _PP = 2 x V _P
V _PP = π x V _AV = 3,141 x V _AV
Другими словами, от пика до пика значение синусоидальной волны – это напряжение или ток от положительного пика до отрицательного пика, и его значение в два раза больше по сравнению с пиковым значением или максимальным значением, как показано на рис. 8 выше.
Что такое пик-фактор
Пик-фактор также известен как пик-фактор или коэффициент амплитуды.
Это соотношение между максимальным значением и среднеквадратичным значением переменной волны.
Для синусоидального переменного напряжения:
Для синусоидального переменного тока:
Что такое форм-фактор
Отношение между среднеквадратичным значением и средним значением переменной величины (ток или напряжение) равно известный как форм-фактор.
В приведенной ниже таблице формулы и значения форм-фактора показаны для различных типов синусоидальных волн.
/ 2 Другие термины, относящиеся к цепям переменного тока
Форма волны
Путь, отслеживаемый величиной (например, напряжением или током), нанесенной на график как функция некоторой переменной (такой как время, градусы, радианы, температура и т. Д.)) называется формой волны.
Цикл
Один полный набор положительных и отрицательных значений переменного качества (таких как напряжение и ток) известен как цикл.
Часть сигнала, содержащаяся в одном периоде времени, называется циклом.
Расстояние между двумя одинаковыми точками, связанное со значением и направлением, называется циклом.
Цикл – это полное чередование.
Период
Время, необходимое переменной величине (например, току или напряжению) для завершения одного цикла, называется ее периодом времени «T».
Он обратно пропорционален частоте « f » и обозначается буквой «T», где единицей измерения периода времени является секунда.
Математически;
T = 1/ f
Частота
Частота – это число, если количество циклов проходит за секунду. Он обозначается буквой «f» и имеет единицу цикла в секунду, то есть Гц (Герты).
Число завершенных циклов за 1 секунду называется частотой.
Это количество циклов переменного количества в секунду в герцах.
Частота – это количество циклов, которые синусоида завершается за одну секунду, или количество циклов, которые происходят за одну секунду.
f = 1 / T
Амплитуда
Максимальное положительное или отрицательное значение переменной величины, такой как напряжение или ток, называется ее амплитудой. Обозначается V _P, I _P или E _MAX и I _MAX.
Чередование
Один полупериод синусоидального сигнала (отрицательного или положительного) известен как чередование, диапазон которого составляет 180 °.
Рис. 9 – Различные термины, используемые в цепях переменного тока и синусоидальной кривой
Связанные сообщения:
Значения переменного тока – Engineer-Educators.com
Существуют три значения переменного тока: мгновенное, пиковое и эффективное (среднее значение квадрат, СКО).
Мгновенное значение
Мгновенное значение напряжения или тока – это индуцированное напряжение или ток, протекающий в любой момент в течение цикла. Синусоидальная волна представляет собой серию этих значений.Мгновенное значение напряжения изменяется от нуля при 0 ° до максимума при 90 °, обратно до нуля при 180 °, до максимума в противоположном направлении при 270 ° и снова до нуля при 360 °. Любая точка на синусоиде считается мгновенным значением напряжения.
Пиковое значение
Пиковое значение – это наибольшее мгновенное значение. Наибольшее одиночное положительное значение возникает, когда синусоидальная волна напряжения находится под углом 90 °, а наибольшее одиночное отрицательное значение возникает, когда оно находится под углом 270 °.Максимальное значение в 1,41 раза превышает эффективное значение. Это так называемые пиковые значения.
Эффективное значение
Эффективное значение также известно как среднеквадратичное значение или среднеквадратичное значение, которое относится к математическому процессу, с помощью которого определяется значение. Большинство вольтметров переменного тока при использовании отображают действующее или среднеквадратичное значение. Действующее значение меньше максимального значения, равное 0,707 максимального значения.
Эффективное значение синусоидальной волны фактически является мерой теплового эффекта синусоидальной волны.На рисунке 107 показано, что происходит, когда резистор подключен к источнику переменного напряжения. На рисунке A определенное количество тепла выделяется мощностью в резисторе. На рисунке B показан тот же резистор, который теперь вставлен в источник постоянного напряжения. Значение источника постоянного напряжения теперь можно отрегулировать так, чтобы резистор рассеивал такое же количество
тепла, как и в цепи переменного тока. Среднеквадратичное или эффективное значение синусоидальной волны равно постоянному напряжению, которое выделяет такое же количество тепла, что и синусоидальное напряжение.
Рисунок 107. Эффективное значение синусоиды.
Пиковое значение синусоидальной волны можно преобразовать в соответствующее среднеквадратичное значение, используя следующее соотношение.
Может применяться как к напряжению, так и к току.
Алгебраически преобразовывая формулу и решая для Vp, можно также определить пиковое напряжение. Результирующая формула:
Таким образом, значение 110 вольт для переменного тока, подаваемого в дома, составляет всего 0,707 от максимального напряжения этого источника.Максимальное напряжение составляет примерно 155 вольт (110 × 1,41 = максимум 155 вольт).
При исследовании переменного тока любые значения, указанные для тока или напряжения, считаются действующими, если не указано иное, и на практике используются только действующие значения напряжения и тока. Аналогичным образом вольтметры и амперметры переменного тока измеряют действующее значение.
Среднее и действующее значение переменного тока и напряжения
Постоянный ток течет только в одном направлении.Переменный ток время от времени меняет направление потока в цепи. В постоянном токе напряжение источника не меняет своей полярности. В переменном токе напряжение источника меняет свою полярность с положительной на отрицательную.
На рисунке 1 показаны величина и полярность переменного напряжения. Начиная с нуля, напряжение возрастает до максимума в положительном направлении. Затем он возвращается к нулю. Затем он возрастает до максимума с противоположной полярностью и возвращается к нулю.
Рисунок 1. Ток и напряжение переменного тока.
Текущая волна также нанесена на график. Он показывает течение тока и направление потока. Выше нулевой линии ток течет в одном направлении. Ниже нулевой линии ток течет в обратном направлении.
График на рис. 1 представляет мгновенные ток и напряжение в любой точке цикла. Но что такое цикл? Цикл – это последовательность или цепочка событий, происходящих в период времени.Цикл переменного тока можно описать как полный набор положительных и отрицательных значений переменного тока.
Переменный ток в вашем доме меняет направление 120 раз в секунду. Он имеет частоту 60 циклов в секунду (60 Гц). Частота , измеряемая в циклах в секунду или герцах (Гц), – это количество полных циклов, происходящих в секунду. Если за одну секунду происходит 60 циклов, то период времени для одного цикла составляет 1/60 секунды или 0,0166 секунды. Это период цикла .Снова обратитесь к , рисунок 1 . Максимальный подъем формы волны показывает амплитуду волны, включая пиковое (самая высокая точка) напряжение и ток.
Мы узнали, что индуцированный ток во вращающемся проводе в магнитном поле течет сначала в одном направлении, а затем в другом. Это было определено как переменный ток. Следует запомнить два момента: :
.
• Частота этого цикла событий увеличивается с увеличением скорости вращения.
• Амплитуда индуцированного напряжения зависит от силы магнитного поля.
Векторы
При решении задач, связанных с переменным током, векторы используются для обозначения величины и направления силы. Вектор – это прямая линия, проведенная в масштабе, который представляет единицы силы. Стрелка на линии показывает направление силы. Длина вектора показывает величину.
Развитие волны переменного тока показано на Рисунке 2 . Эта волна исходит от якоря с одной катушкой, представленного вращающимся вектором, совершающим один оборот через магнитное поле .
Предположим, что пиковое индуцированное напряжение составляет 10 вольт. Если использовать шкалу, в которой один дюйм равен пяти вольт, вектор будет длиться два дюйма или 10 вольт. Предполагается, что векторы такого характера вращаются против часовой стрелки.
Рисунок 2. Развитие синусоидальной волны. Слева вращающийся вектор. Справа – один цикл синусоиды.
Временная база на Рис. 2 – это линия с любым удобным масштабом. Он показывает период одного цикла или оборот вектора.База времени сгруппирована в сегменты, которые представляют время для определенных градусов вращения во время цикла.
Например, при повороте на 90 градусов используется четверть периода времени. При повороте на 270 градусов используются три четверти периода времени. Волна создается путем построения графика амплитуды напряжения в любой момент вращения относительно временного отрезка. Развитая волна называется синусоидой .
Мгновенные наведенные напряжения пропорциональны синусу угла θ (тета), который вектор образует с горизонталью.Затем мгновенное напряжение можно найти в любой точке цикла, используя следующее уравнение:
$ e = {{E} _ {\ max}} \ times \ sin \ theta $
(Обратите внимание, что буква e в нижнем регистре использовалась для представления мгновенного напряжения вместо обычного верхнего регистра. {o}} = 100 В \ times 0.707 = 70,7 В $
Средние и среднеквадратичные значения
Исследование различий между волной переменного тока и постоянным током поднимает ключевой вопрос. Каково действительное значение волны переменного тока? Напряжение и ток постоянно меняются и достигают пикового значения только дважды за цикл.
Часто требуется среднее значение волны. Среднее значение – это математическое среднее всех мгновенных значений в течение одного полупериода переменного тока. Формулы для вычисления среднего значения от пикового значения (макс.) Любых волн переменного тока:
$ \ begin {matrix} {{E} _ {avg}} = 0.637 \ times {{E} _ {\ max}} \\ или \\ {{I} _ {avg}} = 0,637 \ times {{\ operatorname {I}} _ {max}} \\\ end {матрица } $
Если известно E _avg или I _avg, преобразование для нахождения E _max или I _max может быть выполнено с использованием следующих уравнений.
$ \ begin {matrix} {{E} _ {\ max}} = 1,57 \ times {{E} _ {avg}} \\ или \\ {{I} _ {\ max}} = 1,57 \ times { {\ operatorname {I}} _ {avg}} \\\ end {matrix}
долл. США
Более полезным значением переменного тока является эффективное значение .Термин «эффективное значение» был получен от ученых, обнаруживших, что эффект нагрева переменным током эквивалентен постоянному току.
Указанный объем воды был нагрет с использованием заданного уровня постоянного напряжения. Затем такое же количество воды нагревали с помощью переменного тока. Напряжение переменного тока, которое вызывает нагрев, эквивалентный напряжению постоянного тока, было эффективным значением. Формулы для определения эффективного значения любого переменного напряжения или тока:
$ \ begin {matrix} {{E} _ {eff}} = 0,707 \ times {{E} _ {\ max}} \\ или \\ {{I} _ {eff}} = 0.707 \ times {{\ operatorname {I}} _ {\ max}} \\\ end {matrix}
долл. США
Где E _max и I _max – пиковые значения сигнала переменного тока. Если известны E _eff или I _eff, преобразование для нахождения пиковых значений может быть выполнено с использованием следующих уравнений.
$ \ begin {matrix} {{E} _ {\ max}} = 1,414 \ times {{E} _ {eff}} \\ или \\ {{I} _ {\ max}} = 1,414 \ times { {\ operatorname {I}} _ {eff}} \\\ end {matrix}
долларов США
Действующее значение также называется среднеквадратичным значением (среднеквадратичное значение) .Он получил такое название, потому что значение представляет собой квадратный корень из среднего значения всех токов в квадрате между нулем и максимумом волны. Токи возведены в квадрат, поэтому производимую мощность можно сравнить с постоянным током. Закон Ватта гласит: P = I ² R.
Используя коэффициент 0,707, можно найти значение постоянного тока, равное переменному току. Например, , пиковый переменный ток 5 ампер вызывает тот же эффект нагрева в сопротивлении, что и постоянный ток 3.53 ампера. Подставляя значения в уравнение:
I _eff = 0,707 × 5 ампер переменного тока = 3,53 ампера постоянного тока
Обратите внимание, что средние и действующие значения могут применяться как к волнам напряжения, так и к волнам тока.
Смещение фаз
На одной временной основе можно нарисовать несколько форм сигналов, чтобы показать фазовое соотношение между ними. На рис. 3 кривые E и I показывают напряжение и ток в данной цепи. Ток и напряжение растут и падают одновременно.Они пересекают нулевую линию в одной и той же точке. Ток и напряжение совпадают по фазе. Синфазное состояние существует только в чисто резистивной цепи .
Рисунок 3. Эти волны тока и напряжения синфазны.
Часто ток опережает или отстает от напряжения , рисунок 4 . Когда волна тока опережает или отстает от волны напряжения, говорят, что две волны находятся в противофазе. Это создает фазовый сдвиг между двумя волнами.Смещение измеряется в градусах. Сдвиг фазы равен углу θ между двумя полярными векторами.
Рисунок 4. Эти волны тока и напряжения не совпадают по фазе.
Генератор переменного тока
Генератор переменного тока похож на генератор постоянного тока во многих отношениях с одним ключевым исключением. Коммутатор опущен. Концы катушек якоря выдвинуты до контактных колец. Щетки, скользящие по контактным кольцам, обеспечивают постоянное соединение с катушками.Ток во внешне подключенной цепи – это переменный ток.
В крупных промышленных генераторах магнитное поле вращается, и обмотки якоря размещаются в пазах неподвижной рамы или статора генератора. Этот метод позволяет генерировать большие токи в якоре, избегая передачи этих токов через движущиеся или скользящие кольца и щетки.
Вращающееся поле возбуждается через контактные кольца и щетки небольшим генератором постоянного тока, установленным на том же валу, что и вращающееся магнитное поле.Этот небольшой генератор постоянного тока называется возбудителем . Для магнитного поля необходимо постоянное напряжение. Коммерческие генераторы энергии преобразуют множество различных элементов (например, движущуюся воду, уголь, нефть, ветер, ядерную энергию) в электричество. Силовой механизм, который используется для вращения генератора, называется первичным двигателем, Рисунок 5.
Рисунок 5. Первичный двигатель, возбудитель и трехфазный генератор имеют общий вращающийся вал. Возбудитель обеспечивает электрическую энергию для генератора переменного тока.
Генератор переменного тока или генератор переменного тока
Генератор переменного тока (также называемый генератором переменного тока) используется в системе зарядки всех автомобилей США. Рисунок 6 показывает внутреннюю часть устройства, включая встроенный регулятор напряжения для управления выходом. Выходной сигнал выпрямляется с переменного тока на постоянный для зарядки аккумулятора и других электрических устройств в автомобиле.
Производители заявляют, что генератор переменного тока имеет некоторые преимущества перед генератором постоянного тока.Эти преимущества включают более высокую производительность при более низких скоростях, а также безотказное обслуживание.
Рисунок 6. Типичный генератор переменного тока (генератор переменного тока) показан на виде снаружи и в разрезе.
RMS Напряжение сигнала переменного тока
Форма сигнала переменного или переменного тока, связанная с током переменного тока, представляет собой периодический сигнал, который чередуется между положительными и отрицательными значениями. Синусоидальная или синусоидальная волна – это наиболее распространенная изменяющаяся во времени волна, которая используется для представления формы волны переменного тока.
В случае постоянного тока значения напряжения и тока обычно стабильны во времени. Легко выразить величину напряжения или тока, то есть сколько напряжения или тока присутствует в любой части цепи.
В случае переменного тока, в отличие от постоянного тока, их нельзя охарактеризовать одной величиной, поскольку амплитуда формы сигнала переменного тока непрерывно изменяется со временем.
Есть много способов представить величину сигнала переменного тока. Некоторые из них:
Мгновенное значение
Пиковое значение
Пиковое значение
Среднее значение
Действующее значение
В предыдущих разделах мы видели среднее значение напряжения и мгновенные значения формы волны переменного тока.Здесь описывается еще одна важная тема, касающаяся формы сигнала переменного тока, – среднеквадратичное значение напряжения сигнала переменного тока.
RMS напряжение формы сигнала переменного тока
RMS означает «среднеквадратическое значение». Действующее значение напряжения определяется как «квадратный корень из средних квадратов всех мгновенных напряжений в форме волны». Среднеквадратичное значение можно найти следующим образом: входные данные возводятся в квадрат и вычисляется среднее значение.
Это средняя мощность. Для расчета напряжения берется квадратный корень из ранее полученного среднего значения.Следовательно, оно называется среднеквадратичным напряжением.
Среднеквадратичное значение используется для получения эквивалента переменного тока по постоянному току, который рассеивает одинаковое количество тепла при подаче любого из значений на резистор. Переменный ток с максимальным значением 1,4 ампера будет выделять через резистор такое же тепло, как и постоянный ток 1 ампера.
Следовательно, среднеквадратичное значение также иногда называют эквивалентным или эквивалентным значением постоянного тока. Измерение среднеквадратичного значения напряжения или тока формы волны переменного тока – лучший способ соотнести величины переменного и постоянного тока.
Среднеквадратичное значение также называется «эффективным значением», которое эквивалентно значению постоянного тока, тока или напряжения, при котором переменный сигнал производит такую же мощность, как и постоянный ток.
Обычно напряжение сети – это действующее значение. В Индии, например, напряжение питания составляет 220–240 В. Фактически это среднеквадратичное значение переменного тока, которое эквивалентно выработке той же мощности, что и 220–240 В постоянного тока.
RMS используется для обозначения только сигналов переменного тока, т. Е. Изменяющихся во времени синусоидальных сигналов, таких как напряжение переменного тока, переменного тока или других сложных сигналов, величина которых изменяется со временем.Среднеквадратичное значение не применимо к цепям постоянного тока, где величина постоянна во времени.
Процесс определения среднеквадратичного напряжения очень похож на процесс определения среднего значения напряжения. Существует два метода определения среднеквадратичного напряжения сигнала. Это: графический метод и аналитический метод.
Графический метод
В этом методе мы найдем среднеквадратичное значение напряжения, используя средние ординаты или мгновенные значения напряжения переменной формы волны.
Четкое определение среднеквадратичного значения выполняется в несколько этапов, показанных ниже.
STEP 1
В каждой форме волны переменного тока у нас есть много мгновенных напряжений, и количество мгновенных напряжений зависит от длительности синхронизации. Например, если форма волны разделена на n средних ординат, то в момент времени t = 2 мгновенное напряжение формы волны переменного тока равно V2.
Аналогично, в примере t = n, мгновенное напряжение равно van и т. Д. Итак, сначала мы находим мгновенные значения напряжения для каждого экземпляра периодической формы волны, например V1, V2, V3 и Vn.
Чтобы найти среднеквадратичное значение напряжения формы волны, мы должны найти квадратные значения каждого значения напряжения формы волны переменного тока. Это дает «квадратную» часть среднеквадратичного значения.
V1 ² + V2 ² + V3 ² + V4 ² + —-
STEP 2
Нахождение среднего или среднего значения суммы квадратов значений напряжения. Разделим сумму квадратов на количество средних ординат. Это дает «Среднее» значение среднеквадратичного значения.
Усреднение всех значений напряжения формы волны переменного тока периодической формы волны даст нам наиболее точное значение среднеквадратичного напряжения.Как правило, во всех математических приближениях мы устанавливаем средние значения, чтобы избежать значений ошибок и установить наиболее точное значение вычислений.
Если у нас есть значения Vn напряжений в n экземплярах, среднее значение рассчитывается, как показано ниже.
Квадратный корень из этого значения дает нам среднеквадратичное значение формы сигнала переменного тока. Формула для расчета среднеквадратичного значения напряжения показана ниже.
Где n – количество экземпляров,
V1, V2, V3, V4….- мгновенные значения напряжения сигнала.
Пример
Если у нас есть переменный сигнал с максимальной амплитудой 20 В, давайте найдем его действующее значение напряжения.
Мы разделим сигнал на 10 значений по средней ординате следующим образом.
Следовательно, среднеквадратичное значение напряжения формы волны переменного тока с пиком 20 В составляет 14,15 В
Графический метод является очень эффективным методом нахождения среднеквадратичных значений всех типов сигналов, включая сложные формы сигналов.
Аналитический метод
Другой метод, используемый для определения среднеквадратичного значения напряжения (или тока) периодического сигнала переменного тока, – это аналитический или математический метод.Этот метод подходит для сигналов синусоидальной формы.
В этом методе мы рассчитаем среднеквадратичное значение напряжения, проанализировав площадь под кривой формы сигнала переменного тока. Этот метод проще, чем графический, при работе с чисто синусоидальными сигналами.
Периодический синусоидальный сигнал с периодом времени T определяется выражением
V (t) = Vm.cos (ωt)
Где ω = 2π / T
Среднеквадратичное напряжение можно рассчитать как
V _{RMS =} √ [1 / T ∫ ₀ ^t V _m ² cos ² (ωt) dt]
Для одного полного цикла или периода формы волны пределы интегрирования составляют от 0 до 360 ⁰.Таким образом, интегрируя через нижний и верхний пределы, мы получаем
Сложное уравнение можно дополнительно упростить, разделив его на ω = 2π / T. Тогда сокращенное уравнение для среднеквадратичного напряжения составляет
В _RMS = В. _м/2 = В _м * 0,707
Уравнение среднеквадратичного напряжения
Среднеквадратичное напряжение рассчитывается с использованием других значений напряжения формы волны, таких как пиковое напряжение, размах напряжения и среднее напряжение.
Пиковое значение напряжения
Среднеквадратичное значение напряжения переменного тока равно 0.707 раз или 1 / √2 раз от пикового значения напряжения. Среднеквадратичное значение можно рассчитать, разделив пиковое напряжение на квадратный корень из 2 (около 0,707).
В _RMS = V _PEAK x 1 / √2
V _RMS = V _PEAK x 0,707
По размаху напряжения
Среднеквадратичное значение напряжения можно рассчитать умножением значение напряжения от пика до пика с 1/2352 или 0,35355. Пиковое напряжение представлено как V _P-P.
В _RMS = V _PP x 1 / 2√2
V _RMS = V _PP x 0,353
В пересчете на среднее значение напряжения
Среднеквадратичное значение напряжения переменной формы волны составляет 1,1107 раз к среднему значению напряжения.
В _RMS = V _AVG x π / 2√2
V _RMS = V _AVG x 1.1107
Важность среднеквадратичного значения
В случае переменного тока величины тока выражаются в виде значений RMS.
В общем, мы говорим, что напряжение в бытовой сети составляет около 220 Вольт переменного тока. Фактически это означает, что среднеквадратичное значение напряжения бытовой электросети составляет 220 В.
Среднеквадратичное значение дает эквивалентные значения постоянного тока для формы волны переменного тока.
Все измерительное оборудование, такое как амперметры и вольтметры, измеряют только среднеквадратичное значение. В некоторых дорогих вольтметрах сначала рассчитывается пиковое напряжение, а затем, умножая его на 0,707, мы получаем наиболее точное значение среднеквадратичного напряжения.
Среднеквадратичное значение используется для определения пик-фактора и форм-фактора сигнала переменного тока, которые являются ключевыми факторами, определяющими производительность системы.
Форм-фактор и пик-фактор
Для сигнала переменного тока, такого как синусоидальный сигнал, среднеквадратичное значение, пиковое значение и среднее значение – это три важных значения, которые описывают величину. Эти три значения зависят друг от друга.
Помимо этих трех величин, есть некоторые соотношения, которые обычно определяются между этими тремя фундаментальными измерениями. Это форм-фактор и пиковый (или пиковый) фактор.
Форм-фактор
«Форм-фактор – это отношение среднеквадратичного значения напряжения переменного сигнала к его среднему напряжению».Форм-фактор
представлен K _f.
Форм-фактор = среднеквадратичное напряжение / среднее напряжение
K _f = V _RMS / V _AVG
Из отношения между средним значением напряжения и среднеквадратичным значением синусоидальной формы волны переменного тока к пику ) значение, мы можем рассчитать форм-фактор как
K _f = 0,707 В _МАКС / 0,637 В _МАКС
= 1,11
Пик-фактор
“Пик-фактор – это отношение пикового значения напряжения к его действующее значение напряжения ».Мы также называем это «пиковым коэффициентом» или «коэффициентом амплитуды».
Пик-фактор представлен КП.
Пик-фактор = Пиковое напряжение / Среднеквадратичное значение напряжения
KP = В _ПИК (или В _МАКС) / В _RMS
Из соотношения между пиковым значением и среднеквадратичным значением мы можем вычислить пик-фактор как
KP = V _MAX / 0,707 VMAX
= 1,414
Сводка
Формы сигналов, которые периодически чередуются относительно оси, называются «формой волны переменного тока» или «переменной формой волны».
Действующее значение напряжения означает «среднеквадратическое значение» напряжения. Среднеквадратичное значение определяется как «квадратный корень из средних квадратов мгновенных напряжений для изменяющейся во времени формы волны».
Представление среднеквадратичного значения является стандартным способом измерения переменного тока и напряжения, поскольку оно дает эквивалентные значения постоянного тока.
Существует два метода расчета среднеквадратичного напряжения сигнала: графический и аналитический.
Формула для среднеквадратичного напряжения в графическом методе:
Формула для среднеквадратичного напряжения в аналитическом методе:
В _{RMS =} √ [1 / T ∫ ₀ ^t В _м ² cos ² (ωt) dt]
Уравнения RMS для других значений напряжения:
VRMS = Vpeak x 1 / √2
VRMS = Vpeak x 1 / 2√2
VRMS = Vavg x π / 2√2
Мы можем измерить пик-фактор и форм-фактор переменного сигнала, где пик-фактор – это отношение пикового значения к среднеквадратичному значению, а форм-фактор – это отношение среднеквадратичного значения. к среднему значению.
Простая схема измерения среднеквадратичного значения линии питания переменного тока
Среднеквадратичное значение сигнала переменного тока сравнивает теплотворную способность неизвестного сигнала переменного тока с величиной известного сигнала постоянного тока на идентичных нагрузках и равно величине постоянного требуется для производства идентичного количества тепла в нагрузке. Когда мощность, рассеиваемая в нагрузках, равна, известное напряжение постоянного тока равно среднеквадратичному значению неизвестного сигнала переменного тока. Например, если мы подаем среднеквадратичное значение 1 В переменного тока на резистивный нагревательный элемент, он будет производить точно такое же количество тепла, как если бы мы приложили 1 В постоянного тока.
Математически среднеквадратичное значение напряжения определяется как
Эта формула представляет собой стандартное отклонение статистического сигнала с нулевым средним значением.
Более простые отношения включают следующее:
Как правило, для измерения среднеквадратичного значения требуется преобразователь среднеквадратичного значения в постоянный, который обеспечивает выходной сигнал постоянного тока, равный среднеквадратичному значению любой формы входного сигнала. К сожалению, диапазон измеряемых сигналов переменного тока может быть очень большим, в то время как входной диапазон типичных преобразователей среднеквадратичного значения в постоянный составляет всего несколько вольт.Таким образом, чтобы быть полезными для преобразователей среднеквадратичного значения в постоянный, большие входные напряжения должны быть уменьшены. Например, для измерения среднеквадратичного значения домашней линии электропередачи требуется дополнительная схема, которая ослабляет сигнал переменного тока до подходящего значения, которое соответствует входному диапазону преобразователя среднеквадратичного значения в постоянный ток. Это приложение решает проблему измерения среднеквадратичных значений для больших сигналов переменного тока, например, от линии электропередачи.
На рисунке 1 усилитель разности программируемых коэффициентов усиления AD628, настроенный на коэффициент усиления 1/25, масштабирует сигнал линии электропередачи перед подачей его на преобразователь среднеквадратичного значения в постоянный ток AD8436, который может принимать напряжения только в пределах 0.7 В от любого источника. Дифференциальный усилитель имеет синфазный вход ± 120 В и диапазон дифференциального режима, что делает его хорошо подходящим для разделения высоковольтной линии электропередачи. Точный эквивалент постоянного тока среднеквадратичного значения сигнала переменного тока предоставляется на RMS OUT. На рисунке 2 показана домашняя линия электропередачи переменного тока 330 В, частота 60 Гц, масштабированный выходной сигнал разностного усилителя и выходной сигнал постоянного тока преобразователя среднеквадратичного значения в постоянный.
Рисунок 1. Простая схема измерения среднеквадратичного значения линии электропередачи.
Рисунок 2.Входные, промежуточные и выходные сигналы.
Полная конструкция потребляет всего 2 мА, что делает его идеальным для приложений с низким энергопотреблением. Внешний входной резистор, 150 кОм, как показано, можно масштабировать для использования с сигналами, превышающими 400 В (размах). Входной сигнал может превышать мощность источника питания без повреждения устройства, позволяя входному сигналу присутствовать даже при отсутствии напряжения питания. Кроме того, система с защитой от короткого замыкания может работать от двух источников питания напряжением до ± 18 В.
Эта схема вычисляет истинное среднеквадратическое значение комплексного входного сигнала переменного тока (или переменного плюс постоянного тока) и дает эквивалентный выходной уровень постоянного тока.Истинное среднеквадратичное значение сигнала является более полезной величиной, чем среднее выпрямленное значение, поскольку оно является мерой мощности сигнала. Среднеквадратичное значение сигнала, связанного по переменному току, также является его стандартным отклонением.
.
Больше новостей

Навигация по записям
Блок автоматов в квартиру: Квартирный щиток. Установка автоматов и УЗО.Электрощиты. Сборка и проектирование
Пример электролиза: Электролиз – схема, продукты, суть процесса (химия, 11 класс)
Добавить комментарий Отменить ответ
Ваш адрес email не будет опубликован. Обязательные поля помечены *
Комментарий *
Имя *
Email *
Сайт

Найти:
Рубрики
Интересн
Интересные факты
Новинки
Новые
Передатчик
Передатчики
Примеры схем
Простые
Разное
Советы
Схем
Схемы
Электрон
Электроника
© 2019 «Tree of life» — Производство и продажа аксессуаров для iPhone
* iPad, iPhone, iPod, iPod classic, iPod nano, iPod shuffle и iPod touch являются торговыми марками компании Apple Inc, зарегистрированными в США и других странах. Apple Store является торговой маркой компании Apple Inc. PhotoFast является зарегистрированной торговой маркой компании PhotoFast Company Limited.
Вступайте в клуб любителей

Тип сигнала Формула для форм-фактора Значение
Синусоидальная волна π / 2√2 выпрямленная волна 1,5707963
Двухполупериодная выпрямленная синусоида π / 2√2 1.11072073
Прямоугольная волна 1 1
Форма волны треугольника 2 / √3 1,15470054
905 905 905 905

Тип сигнала	Формула для среднеквадратичного значения (В _RMS)
Синусоидальная волна	В _PK / √2
Половинная выпрямленная волна 905 с _PK / √2
Двухполупериодная выпрямленная синусоида	В _PK / √2
Прямоугольная волна	V _PK
PK Треугольная форма волны
Пилообразная форма волны	В _PK / √3

Тип сигнала	Формула для среднеквадратичного напряжения	Формула для среднего напряжения
Синусоидальная волна	В _RMS = V _{_{99 AV / √2} = 0}
Полное выпрямленное напряжение	В _СКЗ = В _PK / √2	В _AV = 0.637 В _PK
Половина выпрямленного сигнала	В _СКЗ = В _PK/2	В _AV = 0,318 В _PK
Синусоидальная волна со смещением по постоянному току	В _RMS = √ (VDC ² + V _PK ²/2)	V _AV = Vdc
Половина синусоиды с длительностью T и частотой f	V _RMS = V _PK x √ (fx T / 2)	V _AV = 2f x T x V _PK / π
Положительный прямоугольный сигнал с длительностью T и частотой f	V _RMS = V _PK x √ (fx T)	V _AV = fx T x V _PK
Волна зубьев пилы с длительностью T и частотой f	V _RMS = V _PK x √ (fx T / 3)	V _AV = fx T x V _PK/2
Трапециевидная волна e с частотой f, верхним сегментом T и базовым сегментом B.	В _RMS = В _PK x √ (fx ((BT) + 3xT) / 3)	V _AV = fx V _PK x ((T + B) / 2)

Тип сигнала	Формула для форм-фактора	Значение
Синусоидальная волна	π / 2√2	выпрямленная волна	1,5707963
Двухполупериодная выпрямленная синусоида	π / 2√2	1.11072073
Прямоугольная волна	1	1
Форма волны треугольника	2 / √3	1,15470054
	905 905 905 905