Дискретный сигнал что это такое: Дискретный сигнал – это… Что такое Дискретный сигнал?

Содержание

Дискретный сигнал – это… Что такое Дискретный сигнал?

Дискретный сигнал

Дискретный сигнал – сигнал, имеющий конечное число значений.
Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

По-английски: Discrete signal

Синонимы: Цифровой сигнал

См. также: Дискретные сигналы Сигналы Дискретные каналы

Финансовый словарь Финам.

Дискретный процессор сигналов
Дискреционная фискальная политика

Смотреть что такое “Дискретный сигнал” в других словарях:

дискретный сигнал — Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени.
[Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика
дискретный сигнал — Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени. [Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика
Дискретный сигнал — У этого термина есть другое (фактически противоположное) определение, смотри [1] и, например, [2] … Википедия
Дискретный сигнал — 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник … Словарь-справочник терминов нормативно-технической документации
дискретный сигнал — diskretusis signalas statusas T sritis automatika atitikmenys: angl. sampled signal vok. abgetastetes Signal, n rus. дискретный сигнал, m pranc. signal échantillonné, m; signal discret, m … Automatikos terminų žodynas
дискретный сигнал — Сигнал, описываемый дискретной функцией времени … Политехнический терминологический толковый словарь
дискретный сигнал времени — diskretinamojo laiko signalas statusas T sritis radioelektronika atitikmenys: angl. discrete time signal vok. diskretes Zeitsignal, n rus. дискретный сигнал времени, m pranc. signal discret de temps, m … Radioelektronikos terminų žodynas
Сигнал (техника) — Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия
Дискретный — (от лат. discretus раздельный, прерывистый). Это прилагательное может употребляться в разных контекстах: В дискретной математике дискретным называется счётное множество, эта концепция также важна в комбинаторике и теории вероятностей. В общей… … Википедия
дискретный — 4.2.6 дискретный: Относящийся к данным, которые состоят из отдельных элементов, таких как символы, или к физическим величинам, имеющим конечное число различных распознаваемых значений, а также к процессам и функциональным блокам, использующим эти … Словарь-справочник терминов нормативно-технической документации

Аналоговые, дискретные и цифровые сигналы

Содержание

Обнаружили ошибку? Выделите ее мышью и нажмите

Вводные понятия

Рисунок 1. Аналоговый, дискретный и цифровой сигналы

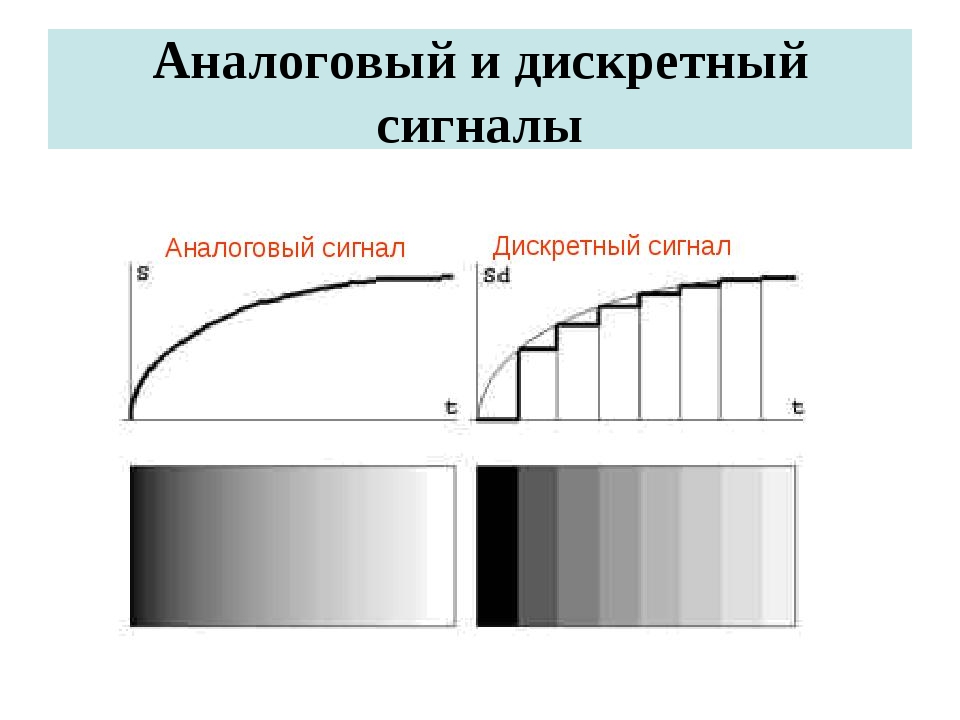
Сигнал называют аналоговым, если он определен на непрерывной оси времени , и в каждый момент может принимать произвольные значения. Аналоговый сигнал может быть представлен непрерывной, или кусочно-непрерывной функции переменной . Пример аналогового сигнала показан на рисунке 1.

Если сигнал принимает произвольные значения только в фиксированные моменты времени , — целое число, то такой сигнал называется дискретным. Наиболее широкое распространение получили дискретные сигналы, определенные на равноотстоящей сетке , где — интервал дискретизации. При этом в моменты дискретизации дискретный сигнал может принимать произвольные значения. Если значения дискретного сигнала также берутся на фиксированной сетке значений, и при этом сами значения могут быть представлены числом конечной разрядности в одной из систем счисления, то такой дискретный сигнал называется цифровым . Часто говорят, что цифровой сигнал представляет собой квантованный по уровню дискретный сигнал. Примеры дискретного и цифрового сигналов также показаны на рисунке 1. Тонкая разница между дискретными и цифровыми сигналами дает возможность их отождествлять практически во всех прикладных задачах. Аналоговый сигнал может быть описан функцией времени, в то время как дискретный и цифровой сигналы могут быть заданы вектором отсчетов :

(1)

Вектор отсчетов цифрового сигнала может быть помещен в память вычислительного устройства с возможность многократной перезаписи и копирования без потери точности, в то время как перезапись и копирование аналоговых сигналов неизбежно сопровождается потерей части информации.

Кроме того, обработка цифровых сигналов позволяет добиться потенциально-возможных характеристик устройств, ввиду возможности выполнения вычислительных операций без потерь, или с пренебрежимо малыми потерями качества.

Указанные преимущества определили повсеместное распространение цифровых систем хранения и обработки сигналов. Но цифровые сигналы также имеют и недостатки по сравнению с аналоговыми.

Во-первых нет возможности передавать цифровые сигналы «как есть», поскольку передача сигналов чаще всего происходит при использовании электромагнитных и акустических волн, которые являются непрерывными во времени. Поэтому для передачи цифровых сигналов требуются дополнительные методы цифровой модуляции, а также цифро-аналоговые преобразователи (ЦАП).

Другим недостатком цифровых сигналов является меньший динамический диапазон сигнала (т.е. отношение самого большого значения к самому маленькому), из-за квантования сигнала на фиксированной сетке значений.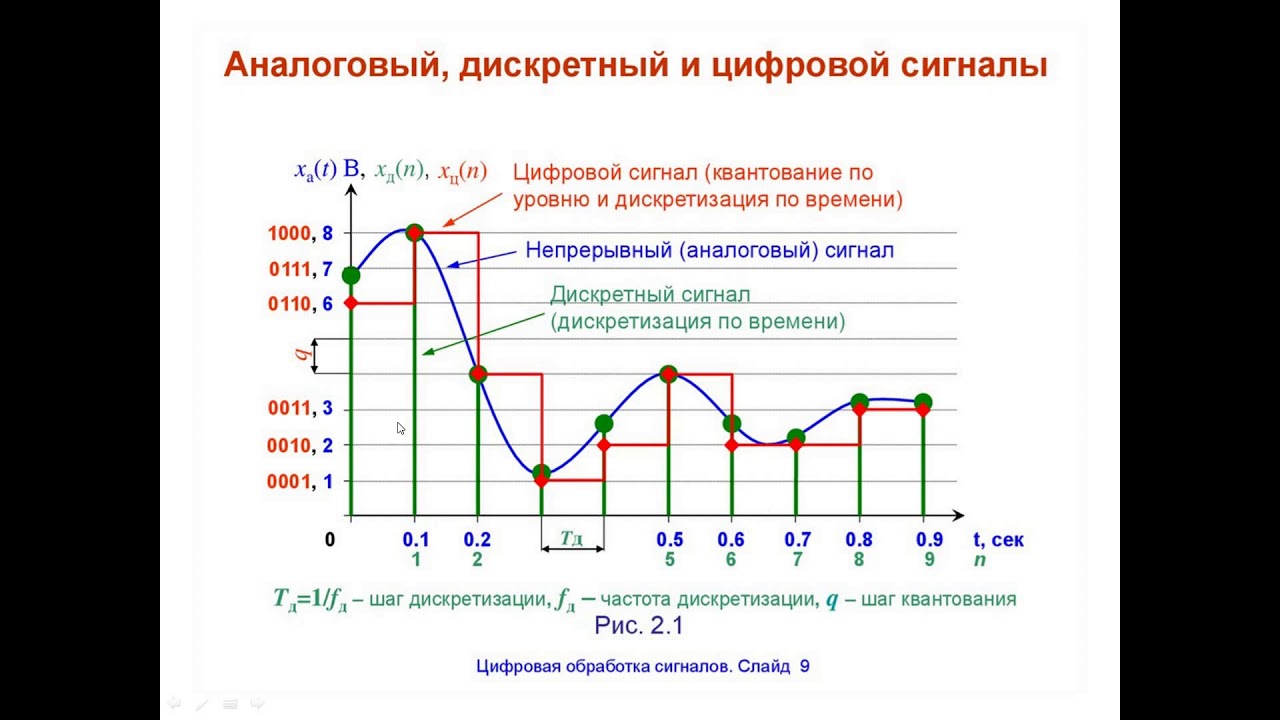

Дискретизация аналоговых сигналов. Математическая модель дискретного сигнала

В данном параграфе мы рассмотрим способ выборки дискретных значений аналогового сигнала. Структурная схема устройства дискретизации показана на рисунке 2. Данное устройство называется аналого-цифровой преобразователь (АЦП), потому что оно преобразует аналоговый сигнал в набор оценок дискретных значений , где — целое число, взятых через равноотстоящие промежутки времени .

Рисунок 2. Структурная схема аналого-цифрового преобразователя

Временны́е осциллограммы, поясняющие принцип работы устройства показаны на рисунке 3 (см. [1, стр. 475–476], или [2, стр. 438]).

Рисунок 3. Временны́е осциллограммы АЦП

На входе АЦП имеется аналоговый сигнал . Генератор импульсов формирует равноотстоящие стробирующие импульсы , которые управляют ключом, в результате чего на вход усилителя подаются короткие выборки сигнала длительности , взятые через интервал дискретизации .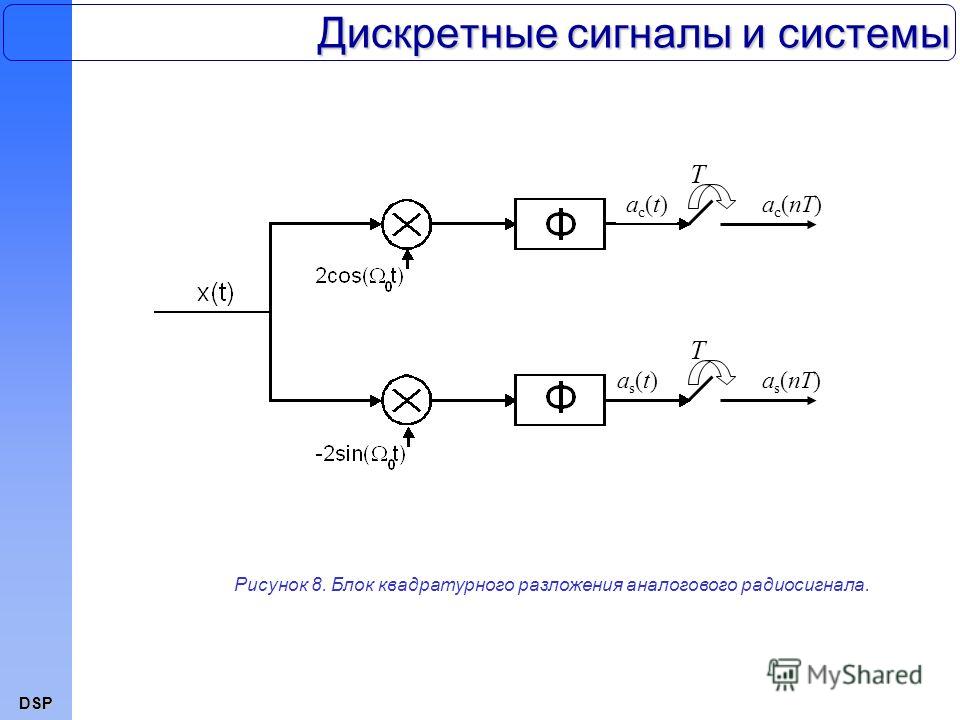

Оценка дискретного сигнала может быть представлена в виде

(2)

где — прямоугольный импульс длительности единичной амплитуды, который мы уже рассматривали в предыдущих разделах.

Интегрируя на каждом интервале длительности стробирующего импульса получим оценку значения сигнала в момент времени . При конечной величине мы можем говорить об оценке значения сигнала в момент времени с некоторой погрешностью, ввиду изменения сигнала на интервале . Поэтому мы используем шапочку над обозначением , чтобы подчеркнуть приближенную оценку.

При уменьшении длительности погрешность оценки будет уменьшаться, и в пределе мы можем получить дискретный сигнал как:

(3)

где — смещенная на дельта-функция Дирака, которую мы подробно рассматривали в одном из предыдущих разделов.

Бесконечная сумма смещенных дельта-функций называется решетчатой функцией и обозначается [3, стр. 77]:

(4)

где индекс указывает временной интервал следования дельта-функций.

Тогда математической моделью дискретного сигнала будет произведение исходного аналогового сигнала на решетчатую функцию:

(5)

Заметим, что (5) уже не является приближенной оценкой, а представляет собой истинную модель дискретного сигнала.

Графически модель дискретного сигнала , с использованием решетчатой функции показана на рисунке 4.

Рисунок 4. Модель дискретного сигнала
на основе решетчатой функции

Для получения численных значений дискретного сигнала необходимо проинтегрировать дискретный сигнал (5) в окрестности :

(6)

где — конечный интервал интегрирования дискретного сигнала в окрестности .

В дальнейшем мы будем широко использовать данную модель дискретного сигнала для перехода от методов анализа и обработки аналоговых сигналов, к цифровым.

Размерность дискретного сигнала

Пусть исходный аналоговый сигнал описывает изменение напряжения во времени и имеет размерность вольт .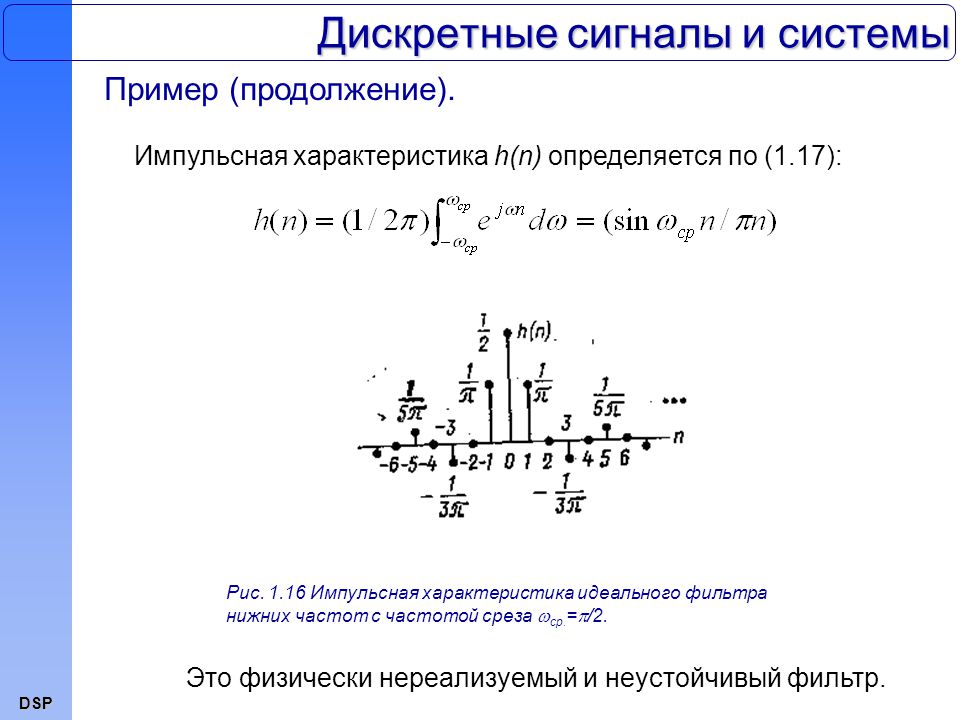 Вспомним, что дельта-функция Дирака имеет размерность, обратную размерности ее аргумента. Тогда решетчатая функция , согласно (4) имеет размерность , а размерность дискретного сигнала (5) будет .

Заметим, что значения дискретного сигнала, полученные из (6) как результат интегрирования дискретного сигнала в окрестности момента времени , будут иметь размерность исходного сигнала .

Преобразование Фурье решетчатой функции

В данном разделе мы проанализируем спектральную плотность решетчатой функции . Для начала рассмотрим как периодический сигнал. Тогда можно представить в виде разложения в ряд Фурье:

(7)

где , рад/с — частота дискретизации,

(8)

Тогда (7) с учетом (8):

(9)

Заметим, что знак аргумента комплексной экспоненты выражения (9) можно изменить, потому что суммирование ведется от минус бесконечности до бесконечности с положительными и отрицательными . Тогда:

(10)

Выражение (10) представляет как бесконечную сумму комплексных экспонент.

Рассмотрим теперь преобразование Фурье решетчатой функции:

(11)

Поменяем операции интегрирования и суммирования и применим фильтрующее свойство дельта-функции:

(12)

Выражение (12) также представляет собой бесконечную сумму комплексных экспонент. Учтем, что и получим:

(13)

Сравнивая (13) с (10) можно заключить, что:

(14)

Таким образом, спектральная плотность решетчатой функции представляет собой также решетчатую функцию.

Период повторения дельта-функций в частотной области равен , при этом дельта-функции масштабируются в раз, как это показно на рисунке 5.

Рисунок 5. Решетчатая функция:
а — временно́е представление; б — спектральная плотность

Заметим, что умножение на в частотной области изменяет размерность спектральной плотности , в результате чего спектральная плотность переходит в безразмерный спектр (что не удивительно, потому что исходная решетчатая функция — периодическая).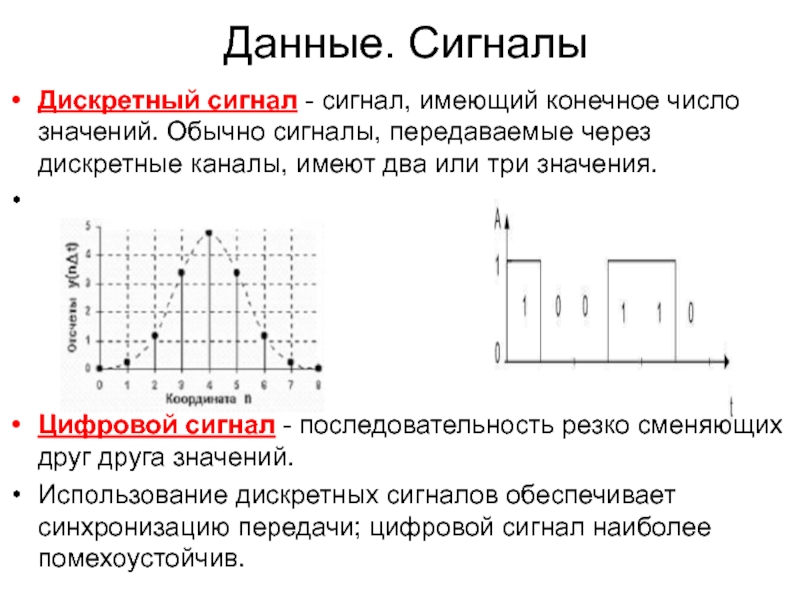

Спектральная плотность дискретного сигнала

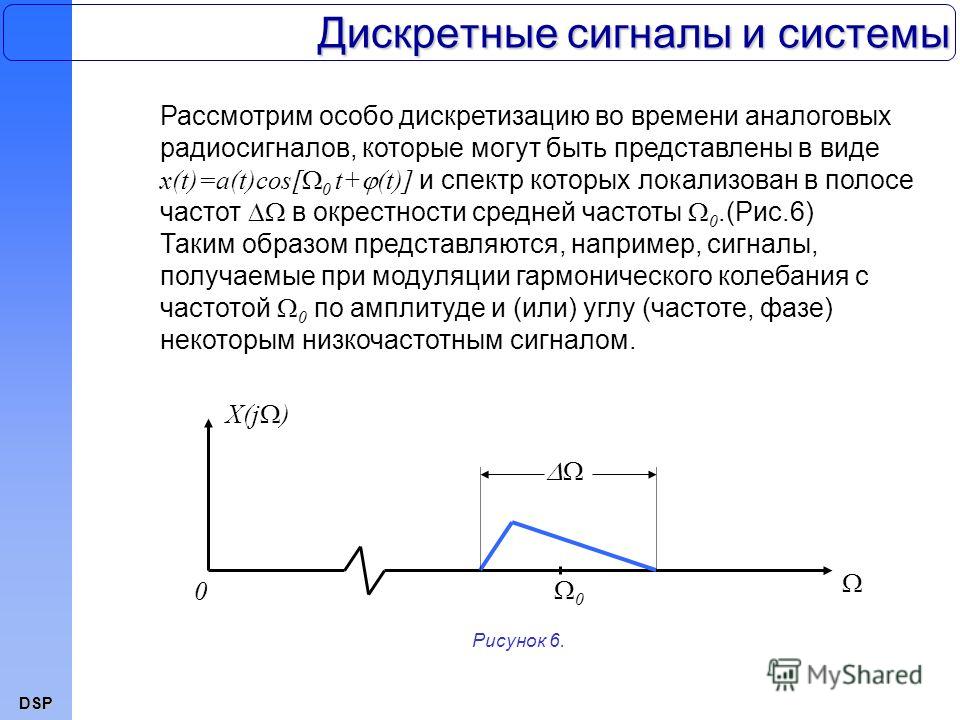
\label{discrete_introduction:ft_discrete} Пусть дан аналоговый сигнал , спектральная плотность которого равна . В данном параграфе мы рассмотрим процесс равноотстоящей дискретизации сигнала в частотной области.

Преобразование Фурье дискретного сигнала (5) равно:

(15)

Применим свойство преобразования Фурье произведения сигналов, тогда представляет собой свертку спектральной плотности решетчатой функции и спектральной плотности исходного сигнала :

(16)

Преобразуем (16), используя фильтрующее свойство дельта-функции:

(17)

Уравнение (17) задает спектральную плотность дискретного сигнала как бесконечную сумму масштабированных копий спектральной плотности , отстоящих друг от друга на рад/с по частоте, как это показано на рисунке 6.

Рисунок 6. Спектральная плотность дискретного сигнала

Заметим, что мы не накладываем никаких ограничений ни на интервал дискретизации , ни на сигнал , ни на спектральную плотность . Вне зависимости от частоты дискретизации рад/с, и формы , спектральная плотность дискретного сигнала всегда будет представлять собой сумму масштабированных копий , отстоящих друг от друга на величину частоты дискретизации рад/с.

Размерность спектра дискретного сигнала

Проанализируем выражение (17) на предмет размерности , в предположении, что исходный аналоговый сигнал имеет размерность :

(18)

Таким образом, из (18) можно заключить, что при дискретизации сигнала, его спектральная плотность переходит в спектр, а размерность спектра дискретного сигнала совпадает с размерностью исходного аналогового сигнала .

Если аналоговый сигнал описывает изменения напряжения во времени и измеряется в единицах вольт, то при дискретизации аналогового сигнала, получим дискретные отсчеты, также измеряемые в вольт, и спектр дискретного сигнала также будет измеряться в единицах вольт. Тогда функцию мы можем назвать спектром, а не спектральной плотностью.

Главный вывод: преобразование Фурье дискретного сигнала не изменяет размерности дискретных отсчетов сигнала, в отличии от преобразования Фурье аналогового сигнала, которое возвращает спектральную плотность .

Выводы

В данном разделе мы ввели понятие дискретного и цифрового сигналов. Мы опеределили, что дискретный сигнал может быть представлен как результат произведения решетчатой функции и аналогового сигнала.

Были детально рассмотрены свойства решетчатой функции и показано, что спектральная плотность решетчатой функции также представляет собой масштабированную по амплитуде решетчатую функцию.

В результате свойств решетчатой функци получили, что спектральная плотность дискретного сигнала представляется бесконечной суммой копий спектральных плотностей исходного сигнала, отставленных дург от друга на величину равную частоте дискретизации.

Смотри также

Представление периодических сигналов рядом Фурье
Некоторые свойства разложения периодических сигналов в ряд Фурье
Свойства преобразования Фурье
Спектральные плотности некоторых сигналов
Информация была полезна? Поделитесь с друзьями!

Facebook

Twitter

Мой мир

Вконтакте

Одноклассники

Список литературы

[1] Гоноровский И. С. Радиотехнические цепи и сигналы Москва, Советское радио, 1977, 608 c.

[2] Баскаков, С.И. Радиотехнические цепи и сигналы. Москва, ЛЕНАНД, 2016, 528 c. ISBN 978-5-9710-2464-4

[3] Bracewell R. The Fourier Transform and Its Applications McGraw-Hills, 1986, 474 c. ISBN 0-07-007-015-6

Последнее изменение страницы: 07.02.2021 (14:06:14)

Страница создана Latex to HTML translator ver. 5.20.11.14

Как аналоговый сигнал преобразуется в цифровой

Телевизионный сигнал — совокупность электрических сигналов, содержащая информацию о телевизионном изображении и звуке. Телевизионный сигнал может передаваться по радио или по кабелю. Термин употребляется в большинстве случаев применительно к аналоговому телевидению, потому что цифровое оперирует таким понятием, как поток данных.

В электронике сигналы делят на: аналоговые, дискретные и цифровые. Начнем с того, что все, что мы чувствуем, видим, слышим в большинстве своем является аналоговым сигналом, а то, что видит процессор компьютера – это цифровой сигнал. Звучит не совсем понятно, поэтому давайте разбираться с этими определениями и с тем как один вид сигналов преобразовывается в другой.

Типы сигналов

В электрическом представлении аналоговый сигнал, судя по его названию, является аналогом реальной величины. Например, вы чувствуете температуру окружающей среды постоянно, на протяжении всей жизни. Нет никаких перерывов. При этом вы чувствуете не только два уровня «горячо» и «холодно», а бесконечное число ощущений, которые описывают эту величину.

Для человека «холодно» может быть по разному, это и осенняя прохлада и зимний мороз, и легкие заморозки, но не всегда «холодно» это отрицательная температура, как и «тепло» – не всегда положительная температура.

Отсюда следует, что у аналогового сигнала две особенности:

1. Непрерывность во времени.

2. Число величин сигнала стремится к бесконечности, т.е. аналоговый сигнал нельзя точно поделить на части или проградуировать, разбив шкалу на конкретные участки. Способы измерения – основаны на единице измерений, и их точность зависит лишь от цены деления шкалы, чем она меньше, тем точнее измерение.

Дискретные сигналы – это сигналы, которые представляют собой последовательность отчетов или измерений какой-либо величины. Измерения таких сигналов не непрерывны, а периодичны.

Попытаюсь объяснить. Если вы установили термометр где-нибудь он измеряет аналоговую величину – это следует из вышеописанного. Но вы, фактически следя за его показаниями, получаете дискретную информацию. Дискретный – значит отдельный.

Например, вы проснулись и узнали, сколько градусов на термометре, в следующий раз вы на него посмотрели на градусник в полдень, и третий раз вечером. Вы не знаете, с какой скоростью изменялась температура, равномерно, или резким скачком, вы знаете только данные в тот момент времени, который наблюдали.

Цифровые сигналы – это набор уровней, типа 1 и 0, высокий и низкий, есть или нет. Глубина отражения информации в цифровом виде ограничена разрядностью цифрового устройства (набора логики, микроконтроллера, процессора etc.) Получается что для хранения булевых данных он подходит идеально. Пример, можно привести следующий, для хранений данных типа «День» и «Ночь», достаточно 1 бита информации.

Бит – это минимальная величина представления информации в цифровом виде, в нём может храниться только два типа значений 1 (логическая единица, высокий уровень), или 0 (логический ноль, низкий уровень).

В электронике бит информации представляется в виде низкого уровня напряжения (близкое к 0) и высокого уровня напряжения (зависит от конкретного устройства, часто совпадает с напряжением питания данного цифрового узла, типовые значения – 1.7, 3.3. 5В, 15В).

Все промежуточные значения между принятыми низким и высоким уровнем являются переходной областью и могут не обладать конкретным значением, в зависимости от схемотехники, как устройства в целом, так и внутренней схемы микроконтроллера (или любого другого цифрового устройства) могут иметь разный переходный уровень, например для 5-тивольтовой логики за ноль могут приниматься значения напряжения от 0 до 0.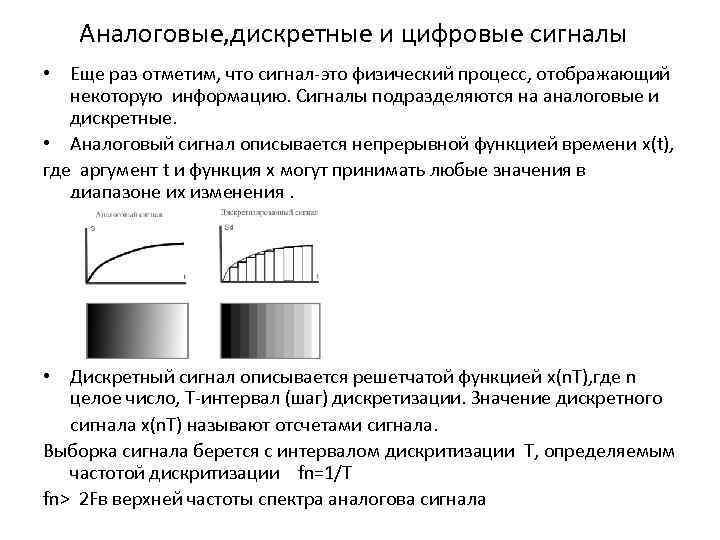 8В, а за единицу от 2В до 5В, при этом промежуток между 0.8 и 2В – это неопределенная зона, фактически с ее помощью отделяется ноль от единицы.

Чем более точные и ёмкие значения нужно хранить, тем больше нужно бит, приведем таблицу-пример с отображением в цифровом виде четырёх значений времени суток:

Ночь – Утро – День – Вечер

Для этого нам нужно уже 2 бита:

Аналогово-цифровое преобразование

В общем случае аналогово-цифровым преобразованием называется процесс перевода физической величины в цифровое значение. Цифровым значением является набор единиц и нолей воспринятых обрабатывающим устройством.

Такое преобразование нужно для взаимодействия цифровой техники с окружающей средой.

Так как аналоговый электрический сигнал повторяет своей формой входной сигнал, он не может быть записан в цифровом виде «так как есть» поскольку он имеет бесконечное число значений. Примером можно привести процесс записи звука. Он в первичном виде выглядит так:

Он представляет собой сумму волн с различными частотами. Которые, при разложении по частотам (подробнее об этом смотрите преобразования Фурье), так или иначе, можно приблизить к похожей картинке:

Теперь попробуйте это представить в виде набора типа «111100101010100», довольно сложно, не так ли?

Другим примером необходимости преобразования аналоговой величины в цифровую, является её измерение: электронные термометры, вольтметры, амперметры и прочие измерительные приборы взаимодействую с аналоговыми величинами.

Как происходит преобразование?

Сначала посмотрите на схему типового преобразования аналогового сигнала в цифровой и обратно. Позже мы к ней вернемся.

Фактически это сложный процесс, который состоит из двух основных этапов:

1. Дискретизация сигнала.

2. Квантование по уровню.

Дискретизация сигнала это определения промежутков времени, на которых измеряется сигнал. Чем короче эти промежутки – тем точнее измерение. Периодом дискретизации (Т) называется отрезок времени от начала считывания данных до его конца.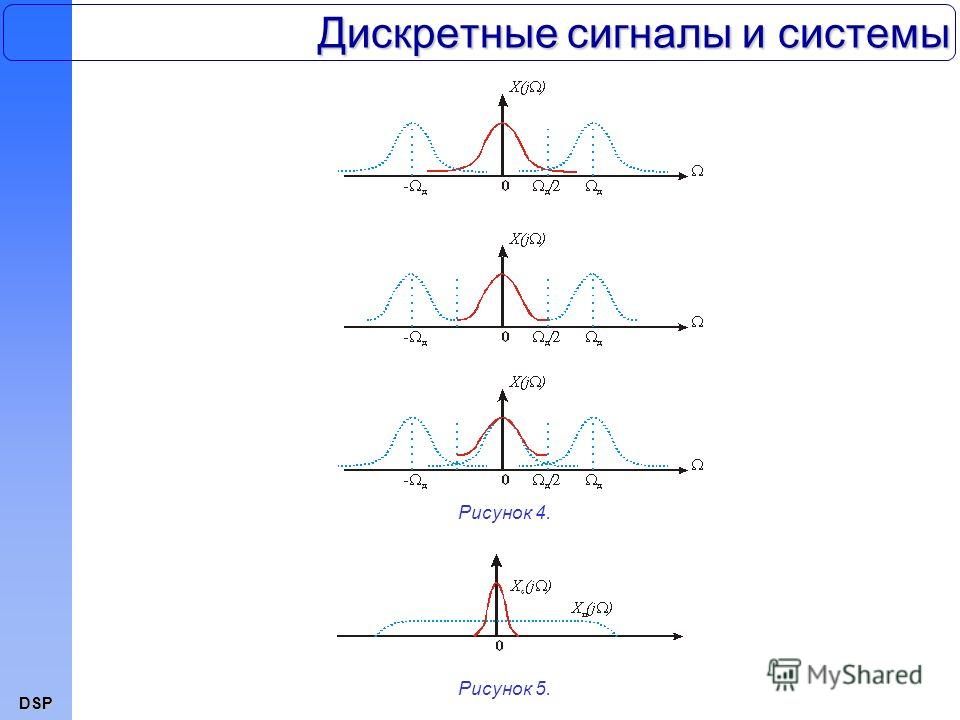 Частота дискретизации (f) – это обратная величина:

fд=1/Т

После считывания сигнала происходит его обработка и сохранение в память.

Получается, что за время, которое считываются и обрабатываются показания сигнала, он может измениться, таким образом, происходит искажение измеряемой величины. Есть такая теорема Котельникова и из нее вытекает такое правило:

Частота дискретизации должны быть как минимум в 2 раза больше чем частота дискретизируемого сигнала.

Это скриншот из википедии, с выдержкой из теоремы.

Для определения численного значение необходимо квантование по уровню. Квант – это определенный промежуток измеряемых значений, усреднено приведенный к определенному числу.

X1…X2=Xy

Т.е. сигналы величиной от X1 до X2, условно приравнивается к определенному значению Xy. Это напоминает цену деления стрелочного измерительного прибора. Когда вы снимаете показания, зачастую вы их равняете по ближайшей отметке на шкале прибора.

Так и с квантованием по уровню, чем больше квантов, тем более точные измерения и тем больше знаков после запятой (сотых, тысячных и так далее значений) они могут содержать.

Точнее сказать число знаков после запятой скорее определяется разрядностью АЦП.

На картинке изображен процесс квантования сигнала с помощью одного бита информации, как я описывал выше, когда при превышении определенного предела принимается значение высокого уровня.

Справа показано квантование сигнала, и запись в виде двух бит данных. Как видите, этот фрагмент сигнала разбит уже на четыре значения. Получается, что в результате плавный аналоговый сигнал превратился в цифровой «ступенчатый» сигнал.

Количество уровней квантования определяется по формуле:

де n — количество разрядов, N — уровень квантования.

Вот пример сигнала разбитого на большее число квантов:

Отсюда очень хорошо видно, что чем чаще снимаются значения сигнала (больше частота дискретизации), тем точнее он измеряется.

На этой картинке изображено преобразование аналогового сигнала в цифровой вид, а слева от оси ординат (вертикальной оси) запись в цифровом 8-битном виде.

Аналогово-цифровые преобразователи

АЦП или Аналогово-цифровой преобразователь может выполняться в виде отдельного устройства или быть встроенным в микроконтроллер.

Ранее в микроконтроллеры, например семейства MCS-51, не содержали в своем составе АЦП, использовалась для этого внешняя микросхема и возникала необходимость писать подпрограмму обработки значений внешней ИМС.

Сейчас они есть в большинстве современных микроконтроллеров, например AVR AtMEGA328, который является основой большинства популярных плат Ардуино, он встроен в сам МК. На языке Arduino чтение аналоговых данных осуществляется просто – командой AnalogRead(). Хотя в микропроцессоре, который установлен в той же не менее популярной Raspberry PI его нет, так что не все так однозначно.

Фактически существует большое число вариантов аналогово-цифровых преобразователей, у каждого из которых есть свои недостатки и преимущества. Описывать которые в пределах этой статьи не имеет особого смысла, так как это большой объём материала. Рассмотрим лишь общую структуру некоторых из них.

Самым старым запатентованным вариантом АЦП, является патент Paul M. Rainey, «Facsimile Telegraph System,» U.S. Patent 1,608,527, Filed July 20, 1921, Issued November 30, 1926. Это 5-ти битный АЦП прямого преобразования. Из названия патента приходят мысли о том, что использование этого прибора было связано с передачей данных через телеграф.

Если говорить о современных АЦП прямого преобразования имеют следующую схему:

Отсюда видно, что вход представляет собой цепочку из компараторов, которые на выходе своем выдают сигнал при пересечении какого-то порогового сигнала. Это и есть разрядность и квантование. Кто хоть немного силен в схемотехнике, увидел этот очевидный факт.

Кто не силен, то входная цепь работает таким образом:

Аналоговый сигнал поступает на вход «+», на все сразу. На выходы с обозначением «-» поступает опорное напряжение, которое раскладывается с помощью цепочки резисторов (резистивного делителя) на ряд опорных напряжений. К примеру, ряд для этой цепи выглядит наподобие такого соотношения:

Urefi=(1/16, 3/16, 5/16, 7/16, 9/16, 11/16, 13/16)*Uref

В скобках через запятую указано, какую часть от общего опорного напряжения Uref подают на вход каждого входного напряжения.

Т.е. каждый из элементов имеет два входа, когда напряжение на входе со знаком «+»превышает напряжение на входе со знаком «-», то на его выходе появляется логическая единица. Когда на положительном (неинвертирующем) входе напряжение меньше, чем на отрицательно (инвертирующем), то на выходе – ноль.

Напряжение делиться таким образом, чтобы входное напряжение разбить на нужное количество разрядов. При достижении напряжения на входе на выходе соответствующего элемента появляется сигнал, схема обработки выводит «правильный» сигнал в цифровом виде.

Такой компаратор хорош скоростью обработки данных, все элементы входной цепи срабатывают параллельно, основная задержка этого вида АЦП формируется из задержки 1 компаратора (все же одновременно параллельно срабатывают) и задержки шифратор.8 компараторов, а это целых 256 штук. Для десятиразрядного (в ардуино 10-разрядный АЦП, кстати, но другого типа) нужно 1024 компаратора. Судите сами о целесообразности такого варианта обработки, и где он может понадобиться.

Есть и другие виды АЦП:

Заключение

Преобразование аналогового сигнала в цифровой нужно для считывания параметров с аналоговых датчиков. Есть отдельный вид цифровых датчиков, они представляют собой либо интегральные микросхемы, например DS18b20 – на его выходе уже цифровой сигнал и его можно обрабатывать любыми микроконтроллерами или микропроцессорами без необходимости применения АЦП, или аналоговый датчик на плате на которой уже размещен свой преобразователь. У каждого типа датчиков есть свои плюсы и минусы, такие как помехоустойчивость и погрешность измерений.

Знание принципов преобразование обязательно для всех кто работает с микроконтроллерами, ведь не в каждой даже современной системе встроены такие преобразователи, приходится использовать внешние микросхемы. Для примера можно привести такую плату, разработанную специально под GPIO-разъём Raspberry PI, с прецизионным АЦП на ADS1256.

Ранее ЭлектроВести писали, что власти Вены запустили тестирование технологии умных камер, которые будут распознавать приближение пешеходов и подавать сигнал на светофор.

По материалам: electrik.info.

Виды дискретных сигналов. Аналоговый, дискретный, цифровой сигналы

Сигналы могут быть: аналоговые (непрерывные) и дискретные.

Дискретный сигнал – информационный сигнал. Сигнал называется дискретным, если он может принимать лишь конечное число значений.

См. также

Дискретный сигнал – сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

Литература

Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. – К. : Вища школа, 1987. – 375 с.

Wikimedia Foundation . 2010 .

Дискретное преобразование Фурье над конечным полем
Дискриминируемые группы населения в Японии

Смотреть что такое “Дискретный сигнал” в других словарях:

Дискретный сигнал – сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи. По английски: Discrete signal Синонимы:… … Финансовый словарь

дискретный сигнал

дискретный сигнал – Cигнал, информативный параметр которого может изменяться только прерывисто и иметь только конечное число значений в заданном диапазоне в течение определенного интервала времени. [Источник] EN discretely timed signal discrete signal a signal… … Справочник технического переводчика

Дискретный сигнал – 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник …

дискретный сигнал – diskretusis signalas statusas T sritis automatika atitikmenys: angl. sampled signal vok. abgetastetes Signal, n rus. дискретный сигнал, m pranc. signal échantillonné, m; signal discret, m … Automatikos terminų žodynas

дискретный сигнал – Сигнал, описываемый дискретной функцией времени … Политехнический терминологический толковый словарь

дискретный сигнал времени – diskretinamojo laiko signalas statusas T sritis radioelektronika atitikmenys: angl. discrete time signal vok. diskretes Zeitsignal, n rus. дискретный сигнал времени, m pranc. signal discret de temps, m … Radioelektronikos terminų žodynas

Сигнал (техника) – Сигнал в теории информации и связи называется материальный носитель информации, используемый для передачи сообщений по системе связи. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым… … Википедия

Дискретный – (от лат. discretus раздельный, прерывистый). Это прилагательное может употребляться в разных контекстах: В дискретной математике дискретным называется счётное множество, эта концепция также важна в комбинаторике и теории вероятностей. В общей… … Википедия

дискретный – 4.2.6 дискретный: Относящийся к данным, которые состоят из отдельных элементов, таких как символы, или к физическим величинам, имеющим конечное число различных распознаваемых значений, а также к процессам и функциональным блокам, использующим эти … Словарь-справочник терминов нормативно-технической документации

Сигналы могут быть: аналоговые (непрерывные) и дискретные.

См. также

Дискретный сигнал – сигнал, имеющий конечное число значений. Обычно сигналы, передаваемые через дискретные каналы, имеют два или три значения. Использование сигналов с тремя значениями обеспечивает синхронизацию передачи.

Литература

Самофалов К.Г., Романкевич А.М., Валуйский В.Н., Каневский Ю.С., Пиневич М.М. Прикладная теория цифровых автоматов. – К. : Вища школа, 1987. – 375 с.

Wikimedia Foundation . 2010 .

Дискретное преобразование Фурье над конечным полем
Дискриминируемые группы населения в Японии

Смотреть что такое “Дискретный сигнал” в других словарях:

дискретный сигнал

Дискретный сигнал – 13. Дискретный сигнал Сигнал, имеющий конечное число значений величин Источник …

Каждый день люди сталкиваются с использованием электронных приборов. Без них невозможна современная жизнь. Ведь речь идет о телевизоре, радио, компьютере, телефоне, мультиварке и прочем. Раньше, еще несколько лет назад, никто не задумывался о том, какой сигнал используется в каждом работоспособном приборе. Сейчас же слова «аналоговый», «цифровой», «дискретный» уже давно на слуху. Некоторые виды сигналов из перечисленных являются качественными и надежными.

Цифровая передача стала использоваться намного позже, чем аналоговая. Это связано с тем, что такой сигнал намного проще обслуживать, да и техника на тот момент не была настолько усовершенствована.

С понятием «дискретность» сталкивается каждый человек постоянно. Если переводить это слово с латинского языка, то означать оно будет «прерывистость». Углубляясь далеко в науку, можно сказать, что дискретный сигнал представляет собой метод передачи информации, который подразумевает изменение во времени среды-переносчика. Последняя принимает любое значение из всех возможных. Сейчас дискретность уходит на второй план, после того, как было принято решение производить системы на чипе. Они являются целостными, а все компоненты тесно взаимодействуют друг с другом. В дискретности же все с точностью наоборот – каждая деталь завершена и связана с другими за счет специальных линий связи.

Сигнал

Сигнал представляет собой специальный код, который передается в пространство одной или несколькими системами. Эта формулировка является общей.

В сфере информации и связи сигналом назван специальный носитель каких-либо данных, который используется для передачи сообщений. Он может быть создан, но не принят, последнее условие не обязательно. Если же сигнал является сообщением, то его «ловля» считается необходимой.

Описываемый код задается математической функцией. Она характеризует все возможные изменения параметров. В радиотехнической теории эта модель считается базовой. В ней же аналогом сигнала был назван шум. Он представляет собой функцию времени, которая свободно взаимодействует с переданным кодом и искажает его.

В статье охарактеризованы виды сигналов: дискретный, аналоговый и цифровой. Также коротко дана основная теория по описываемой теме.

Виды сигналов

Существует несколько имеющихся сигналов. Рассмотрим, какие бывают виды.

По физической среде носителя данных разделяют электрический сигнал, оптический, акустический и электромагнитный. Имеется еще несколько видов, однако они малоизвестны.
По способу задания сигналы делятся на регулярные и нерегулярные. Первые представляют собой детерминированные методы передачи данных, которые задаются аналитической функцией. Случайные же формулируются за счет теории вероятности, а также они принимают любые значения в различные промежутки времени.
В зависимости от функций, которые описывают все параметры сигнала, методы передачи данных могут быть аналоговыми, дискретными, цифровыми (способ, который является квантованным по уровню). Они используются для обеспечения работы многих электрических приборов.

Теперь читателю известны все виды передачи сигналов. Разобраться в них не составит труда любому человеку, главное – немного подумать и вспомнить школьный курс физики.

Для чего обрабатывается сигнал?

Сигнал обрабатывается с целью передачи и получения информации, которая в нем зашифрована. Как только она будет извлечена, ее можно использовать различными способами. В отдельных ситуациях ее переформатируют.

Существует и другая причина обработки всех сигналов. Она заключается в небольшом сжатии частот (чтобы не повредить информацию). После этого ее форматируют и передают на медленных скоростях.

В аналоговом и цифровом сигналах используются особенные методы. В частности, фильтрация, свертка, корреляция. Они необходимы для восстановления сигнала, если он поврежден или имеет шум.

Создание и формирование

Зачастую для формирования сигналов необходим аналого-цифровой (АЦП) и Чаще всего они оба используются лишь в ситуации с применением DSP-технологий. В остальных случаях подойдет только использование ЦАП.

При создании физических аналоговых кодов с дальнейшим применением цифровых методов полагаются на полученную информацию, которая передается со специальных приборов.

Динамический диапазон

Вычисляется разностью большего и меньшего уровня громкости, которые выражены в децибелах. Он полностью зависит от произведения и особенностей исполнения. Речь идет как о музыкальных треках, так и об обычных диалогах между людьми. Если брать, например, диктора, который читает новости, то его динамический диапазон колеблется в районе 25-30 дБ. А во время чтения какого-либо произведения он может вырастать до 50 дБ.

Аналоговый сигнал

Аналоговый сигнал является непрерывным во времени способом передачи данных. Недостатком его можно назвать присутствие шума, который иногда приводит к полной потере информации. Очень часто возникают такие ситуации, что невозможно определить, где в коде важные данные, а где обычные искажения.

Именно из-за этого цифровая обработка сигналов приобрела большую популярность и постепенно вытесняет аналоговую.

Цифровой сигнал

Цифровой сигнал является особым он описывается за счет дискретных функций. Его амплитуда может принять определенное значение из уже заданных. Если аналоговый сигнал способен поступать с огромным количеством шумов, то цифровой отфильтровывает большую часть полученных помех.

Помимо этого, такой вид передачи данных переносит информацию без лишней смысловой нагрузки. Через один физический канал может быть отправлено сразу несколько кодов.

Виды цифрового сигнала не существуют, так как он выделяется как отдельный и самостоятельный метод передачи данных. Он представляет собой двоичный поток. В наше время такой сигнал считается самым популярным. Это связано с простотой использования.

Применение цифрового сигнала

Чем же отличается цифровой электрический сигнал от других? Тем, что он способен совершать в ретрансляторе полную регенерацию. Когда в оборудование связи поступает сигнал, имеющий малейшие помехи, он сразу же меняет свою форму на цифровую. Это позволяет, например, телевышке снова сформировать сигнал, но уже без шумового эффекта.

В том случае, если код поступает уже с большими искажениями, то, к сожалению, восстановлению он не подлежит. Если брать в сравнении аналоговую связь, то в аналогичной ситуации ретранслятор может извлечь часть данных, затрачивая много энергии.

Обсуждая сотовую связь разных форматов, при сильном искажении на цифровой линии разговаривать практически невозможно, так как не слышны слова или целые фразы. Аналоговая связь в таком случае более действенна, ведь можно продолжать вести диалог.

Именно из-за подобных неполадок цифровой сигнал ретрансляторы формируют очень часто для того, чтобы сократить разрыв линии связи.

Дискретный сигнал

Сейчас каждый человек пользуется мобильным телефоном или какой-то «звонилкой» на своем компьютере. Одна из задач приборов или программного обеспечения – это передача сигнала, в данном случае голосового потока. Для переноса непрерывной волны необходим канал, который имел бы пропускную способность высшего уровня. Именно поэтому было предпринято решение использовать дискретный сигнал. Он создает не саму волну, а ее цифровой вид. Почему же? Потому что передача идет от техники (например, телефона или компьютера). В чем плюсы такого вида переноса информации? С его помощью уменьшается общее количество передаваемых данных, а также легче организуется пакетная отправка.

Понятие «дискретизация» уже давно стабильно используется в работе вычислительной техники. Благодаря такому сигналу передается не непрерывная информация, которая полностью закодирована специальными символами и буквами, а данные, собранные в особенные блоки. Они являются отдельными и законченными частицами. Такой метод кодировки уже давно отодвинулся на второй план, однако не исчез полностью. С помощью него можно легко передавать небольшие куски информации.

Сравнение цифрового и аналогового сигналов

Покупая технику, вряд ли кто-то думает о том, какие виды сигналов использованы в том или другом приборе, а об их среде и природе уж тем более. Но иногда все же приходится разбираться с понятиями.

Уже давно стало ясно, что аналоговые технологии теряют спрос, ведь их использование нерационально. Взамен приходит цифровая связь. Нужно понимать, о чем идет речь и от чего отказывается человечество.

Если говорить коротко, то аналоговый сигнал – способ передачи информации, который подразумевает описание данных непрерывными функциями времени. По сути, говоря конкретно, амплитуда колебаний может быть равна любому значению, находящемуся в определенных границах.

Цифровая обработка сигналов описывается дискретными функциями времени. Иначе говоря, амплитуда колебаний этого метода равна строго заданным значениям.

Переходя от теории к практике, надо сказать о том, что аналоговому сигналу характерны помехи. С цифровым же таких проблем нет, потому что он успешно их «сглаживает». За счет новых технологий такой метод передачи данных способен своими силами без вмешательства ученого восстановить всю исходную информацию.

Говоря о телевидении, можно уже с уверенностью сказать: аналоговая передача давно изжила себя. Большинство потребителей переходят на цифровой сигнал. Минус последнего заключается в том, что если аналоговую передачу способен принимать любой прибор, то более современный способ – только специальная техника. Хоть и спрос на устаревший метод уже давно упал, все же такие виды сигналов до сих пор не способны полностью уйти из повседневной жизни.

Существуют аналоговые, дискретные и цифровые сигналы. Аналоговые сигналы описываются непрерывной во времени функцией , которая может принимать любые значения в определенном интервале; дискретные сигналы представляют собой последовательности или отсчеты функции , взятые в определенные дискретные моменты времени nT ; цифровыми являются сигналы, которые в дискретные моменты времени nT принимают конечные дискретные значения – уровни квантования, которые затем кодируются двоичными числами. Если в цепь микрофона (рис. 1), где ток является непрерывной функцией времени, встроить ключ и периодически на короткие мгновения замыкать его, то ток в цепи будет иметь вид узких импульсов с амплитудами, повторяющими форму непрерывного сигнала. Последовательность этих импульсов, которые называют отсчетами непрерывного сигнала, и представляет собой, не что иное, как дискретный сигнал.
Рис. 1 В отличие от непрерывного сигнала дискретный сигнал можно обозначить . Однако, чаще его обозначают , заменяя непрерывное время t дискретными моментами nT , следующими строго через интервал T . Используются и более краткие обозначения: и . Причем, во всех этих записях n – целое число, принимающее как положительные, так и отрицательные значения. Так, на рис. 1 при n . При n = 0 значение равно значению сигнала в момент времени t = 0. При n > 0 отсчеты повторяют форму сигнала , т.к. их амплитуды равны значениям непрерывного сигнала в моменты времени nT . Рис. 2 Дискретные сигналы можно задавать графиками, как это показано на рис. 1, формулами, например, , в виде таблиц дискретных значений или в виде комбинации этих способов. Рассмотрим примеры некоторых дискретных сигналов, полученных из типовых аналоговых сигналов. Все средства связи, которые на сегодняшний день используются в мире, основаны на передаче электрического тока из одной точки в другую. Как работа в сети Internet, так и разговор с другом по телефону обеспечиваются за счет постоянного протекания тока по оборудованию телекоммуникационной инфраструктуры. По каналам связи могут передаваться различные типы сигналов. В этой книге рассматриваются два основных типа сигналов: аналоговые и цифровые. Некоторые виды физической передающей среды, как, например, волоконно-оптический кабель, используются для передачи данных в сети провайдера в виде световых сигналов. Принципы цифровой передачи для такой среды такие же, однако для ее организации используются лазеры и светодиоды. Аналоговые и цифровые сигналы коренным образом отличаются друг от друга. Условно можно сказать, что они находятся на разных концах одного и того же спектра. Из-за таких существенных различий между двумя типами сигналов для организации “моста” между ними приходится использовать промежуточные устройства, наподобие цифро-аналоговых преобразователей (они рассматриваются ниже в текущей главе). Основное различие между аналоговыми и цифровыми сигналами заключается в самой структуре сигнального потока. Аналоговые сигналы представляют собой непрерывный поток, характеризующийся изменениями частоты и амплитуды. Это означает, что форма аналогового сигнала обычно похожа на синусоиду (т.е. гармоническую волну), представленную на рис. 1.2. Зачастую на иллюстрациях, изображающих гармоническую волну, весь сигнал характеризуется одним и тем же соотношением частоты и амплитуды, однако при графическом представлении сложной волны видно, что такое соотношение изменяется в зависимости от частоты.
Цифровым сигналам соответствуют дискретные электрические значения, которые передаются индивидуально по некоторой физической передающей среде. В отличие от аналоговых сигналов, в которых количество возможных значений амплитуды почти бесконечно, для цифровых сигналов она может принимать одно из двух (или четырех) различных значений – как положительных, так и отрицательных. Цифровые сигналы передаются в виде единиц и нулей, которые обычно называют двоичными. Более подробно потоки цифровых сигналов рассматриваются в главе 3, “Аналого-цифровое преобразование”. Как и в любой другой технологии, для описания аналоговых сигналов используются базовые концепции и собственная терминология. Непрерывные аналоговые сигналы имеют три основные характеристики: амплитуду; длину волны; частоту.

ВВЕДЕНИЕ В ЦИФРОВУЮ ОБРАБОТКУ СИГНАЛОВ

Цифровая обработка сигналов (ЦОС или DSP – digital signal processing) является одной из новейших и самых мощных технологий, которая активно внедряется в широкий круг областей науки и техники, таких как коммуникации, метеорология, радиолокация и гидролокация, медицинская визуализация изображений, цифровое аудио- и телевизионное вещание, разведка нефтяных и газовых месторождений и др. Можно сказать, что происходит повсеместное и глубокое проникновение технологий цифровой обработки сигналов во все сферы деятельности человечества. Сегодня технология ЦОС относится к числу базовых знаний, которые необходимы ученым и инженерам всех отраслей без исключения.

Сигналы

Что такое сигнал? В наиболее общей формулировке это зависимость одной величины от другой. Т.е., с математической точки зрения сигнал является функцией. Чаще всего рассматриваются зависимости от времени. Физическая природа сигнала может быть различной. Очень часто это электрическое напряжение, реже – ток.

Формы представления сигнала :

1. временная;

2. спектральная (в частотной области).

Стоимость цифровой обработки данных меньше аналоговой и продолжает снижаться, а производительность вычислительных операций непрерывно возрастает. Немаловажным является и то, что системы ЦОС отличаются высокой гибкостью. Их можно дополнять новыми программами и перепрограммировать на выполнение различных операций без изменения оборудования. Поэтому интерес к научным и к прикладным вопросам цифровой обработки сигналов возрастает во всех отраслях науки и техники.

ПРЕДИСЛОВИЕ К ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ

Дискретные сигналы

Сущность цифровой обработки состоит в том, что физический сигнал (напряжение, ток и др.) преобразуется в последовательность чисел , которая затем подвергается математическим преобразованиям в ВУ.

Аналоговые, дискретные и цифровые сигналы

Исходный физический сигнал является непрерывной функцией времени. Такие сигналы, определенные во все моменты t, называются аналоговыми .

Какой сигнал называется цифровым? Рассмотрим некоторый аналоговый сигнал (рис. 1.1 а). Он задан непрерывно на всем рассматриваемом временном интервале. Считается, что аналоговый сигнал абсолютно точен, если не учитывать погрешности при измерении.

Рис. 1.1 а) Аналоговый сигнал

Рис. 1.1 б) Дискретизированный сигнал

Рис. 1.1 в) Квантованный сигнал

Для того, чтобы получить цифровой сигнал, нужно провести две операции – дискретизацию и квантование . Процесс преобразования аналогового сигнала в последовательность отсчетов называется дискретизацией, а результат такого преобразования – дискретным сигналом .Т. обр., дискретизация заключается в составлении выборки из аналогового сигнала (рис. 1.1 б), каждый элемент которой, называемый отсчетом , будет отстоять по времени от соседних отсчетов на некотором интервале Т , называемом интервалом дискретизации или (поскольку интервал дискретизации чаще неизменен) – периодом дискретизации . Величина, обратная периоду дискретизации называется частотой дискретизации и определяется как:

(1.1)

При обработке сигнала в вычислительном устройстве его отсчеты представляются в виде двоичных чисел, имеющих ограниченное число разрядов. Вследствие этого отсчеты могут принимать лишь конечное множество значений и, следовательно, при представлении сигнала неизбежно происходит его округление. Процесс преобразования отсчетов сигнала в числа называется квантованием . Возникающие при этом ошибки округления называются ошибками или шумами квантования . Т. обр., квантование – это приведение уровней дискретизированного сигнала к некоторой сетке (рис. 1.1 в), чаще обычным округлением в сторону большего. Дискретный во времени и квантованный по уровню сигнал и будет являться цифровым.

Условия, при которых возможно полное восстановление аналогового сигнала по его цифровому эквиваленту с сохранением всей исходно содержавшейся в сигнале информации, выражаются теоремами Найквиста, Котельникова, Шеннона, сущность которых практически одинакова. Для дискретизации аналогового сигнала с полным сохранением информации в его цифровом эквиваленте максимальные частоты в аналоговом сигнале должны быть не менее, чем вдвое меньше, чем частота дискретизации, то есть f max £ (1/2)f d , т.е. на одном периоде максимальной частоты должно быть минимум два отсчета. Если это условие нарушается, в цифровом сигнале возникает эффект маскирования (подмены) действительных частот более низкими частотами. При этом в цифровом сигнале вместо фактической регистрируется “кажущаяся” частота, а, следовательно, восстановление фактической частоты в аналоговом сигнале становится невозможным. Восстановленный сигнал будет выглядеть так, как если бы частоты, лежащие выше половины частоты дискретизации, отразились от частоты (1/2)f d в нижнюю часть спектра и наложились на частоты, уже присутствующие в этой части спектра. Этот эффект называется наложением спектров или алиасингом (aliasing). Наглядным примером алиасинга может служить иллюзия, довольно часто встречающаяся в кино – колесо автомобиля начинает вращаться против его движения, если между последовательными кадрами (аналог частоты дискретизации) колесо совершает более чем пол-оборота.

Преобразование сигнала в цифровую форму выполняется аналого-цифровыми преобразователями (АЦП). Как правило, они используют двоичную систему счисления с определенным числом разрядов в равномерной шкале. Увеличение числа разрядов повышает точность измерений и расширяет динамический диапазон измеряемых сигналов. Потерянная из-за недостатка разрядов АЦП информация невосстановима, и существуют лишь оценки возникающей погрешности «округления» отсчетов, например, через мощность шума, порождаемого ошибкой в последнем разряде АЦП. Для этого используется понятие отношения «сигнал/шум» – отношение мощности сигнала к мощности шума (в децибелах). Наиболее часто применяются 8-, 10-, 12-, 16-, 20- и 24-х разрядные АЦП. Каждый дополнительный разряд улучшает отношение сигнал/шум на 6 децибел. Однако увеличение количества разрядов снижает скорость дискретизации и увеличивает стоимость аппаратуры. Важным аспектом является также динамический диапазон, определяемый максимальным и минимальным значением сигнала.

Обработка цифровых сигналов выполняется либо специальными процессорами, либо на универсальных ЭВМ и компьютерах по специальным программам. Наиболее просты для рассмотрения линейные системы. Линейными называются системы, для которых имеет место принцип суперпозиции (отклик на сумму входных сигналов равен сумме откликов на каждый сигнал в отдельности) и однородность (изменение амплитуды входного сигнала вызывает пропорциональное изменение выходного сигнала).

Если входной сигнал x(t-t 0) порождает однозначный выходной сигнал y(t-t 0) при любом сдвиге t 0 , то систему называют инвариантной во времени . Ее свойства можно исследовать в любые произвольные моменты времени. Для описания линейной системы вводится специальный входной сигнал – единичный импульс (импульсная функция).

Единичный импульс (единичный отсчет) u 0 (n ) (рис. 1.2):

Рис. 1.2. Единичный импульс

В силу свойства суперпозиции и однородности любой входной сигнал можно представить в виде суммы таких импульсов, подаваемых в разные моменты времени и умноженных на соответствующие коэффициенты. Выходной сигнал системы в этом случае представляет собой сумму откликов на эти импульсы. Отклик на единичный импульс (импульс с единичной амплитудой) называют импульсной характеристикой системы h(n). Знание импульсной характеристики позволяет проанализировать прохождение через дискретную систему любого сигнала. Действительно, произвольный сигнал {x(n)} можно представить в виде линейной комбинации единичных отсчетов.

Информация и сигнал (8 класс) Информатика и ИКТ

Информация (от лат. «informatio» -осведомление, разъяснение, изложение) — очень широкое понятие, имеющее множество трактовок. Рассмотрим его с точки зрения субъективного (бытового, человеческого) подхода.

В обыденной жизни под информацией понимают всякого рода сообщения, сведения о чём-либо, которые получают и передают люди. Информация содержится в речи людей, текстах книг, колонках цифр, в звуках и видах природы, в показаниях часов, термометров и других приборов. Каждый материальный объект, с которым происходят изменения, становится источником информации либо об окружающей среде, либо о происходящих в этом объекте процессах. Эту информацию мы получаем в виде сигналов — изменений физических величин (давления, температуры, цвета и др.). Различают световые, звуковые, тепловые, механические, электрические и другие типы сигналов.

Информация для человека — это содержание сигналов (сообщения), воспринимаемых человеком непосредственно или с помощью специальных устройств, расширяющее его знания об окружающем мире и протекающих в нём процессах.

Сигналы могут быть непрерывными или дискретными.

Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.

Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами. Сравните лестницу и наклонную плоскость. В первом случае имеется строго определённое количество фиксированных высот, равное числу ступенек. Все их можно пронумеровать. Наклонная плоскость соответствует бесконечному количеству значений высоты.

В жизни человек чаще всего имеет дело с непрерывными сигналами. Примерами непрерывных сигналов могут служить речь человека, скорость автомобиля, температура в некоторой географической точке в течение определённого периода времени и многое другое. Примером устройства, подающего дискретные сигналы, является светофор. Сигнал светофора может быть красным, жёлтым или зелёным, т. е. принимать всего три значения.

Самое главное:

Информация для человека — это содержание сигналов ( сообщения), которые он получает из различных источников.
Сигналы могут быть непрерывными или дискретными. Непрерывный сигнал принимает бесконечное множество значений из некоторого диапазона. Дискретный сигнал принимает конечное число значений, которые можно пронумеровать.

Вопросы и задания:

Что такое информация для человека? Перечислите источники, из которых вы получаете информацию.
Приведите примеры непрерывных и дискретных сигналов.

Содержание

Что формирует дискретный сигнал. Дискретный сигнал

ВВЕДЕНИЕ В ЦИФРОВУЮ ОБРАБОТКУ СИГНАЛОВ

Сигналы

Формы представления сигнала :

1. временная;

2. спектральная (в частотной области).

ПРЕДИСЛОВИЕ К ЦИФРОВОЙ ОБРАБОТКЕ СИГНАЛОВ

Дискретные сигналы

Аналоговые, дискретные и цифровые сигналы

Рис. 1.1 а) Аналоговый сигнал

Рис. 1.1 б) Дискретизированный сигнал

Рис. 1.1 в) Квантованный сигнал

(1.1)

Единичный импульс (единичный отсчет) u 0 (n ) (рис. 1.2):

Рис. 1.2. Единичный импульс

Лекция № 1

«Аналоговые, дискретные и цифровые сигналы.»

Двумя самыми фундаментальными понятиями в данном курсе являются понятия сигнала и системы.

Под сигналом понимается физический процесс (например, изменяющееся во времени напряжение), отображающий некоторую информацию или сообщение. Математически сигнал описывается функцией определенного типа.

Одномерные сигналы описываются вещественной или комплексной функцией , определенной на интервале вещественной оси (обычно – оси времени) . Примером одномерного сигнала может служить электрический ток в проводе микрофона, несущий информацию о воспринимаемом звуке.

Сигнал x (t ) называется ограниченным если существует положительное число A , такое, что для любого t .

Энергией сигнала x (t ) называется величина

,(1.1)

Если , то говорят, что сигнал x (t ) имеет ограниченную энергию. Сигналы с ограниченной энергией обладают свойством

Если сигнал имеет ограниченную энергию, то он ограничен.

Мощностью сигнала x (t ) называется величина

,(1.2)

Если , то говорят, что сигнал x (t ) имеет ограниченную мощность. Сигналы с ограниченной мощностьюмогут принимать ненулевые значения сколь угодно долго.

В реальной природе сигналов с неограниченной энергией и мощностью не существует. Большинство сигналов, существующих в реальной природе являются аналоговыми.

Аналоговые сигналы описываются непрерывной (или кусочно-непрерывной) функцией , причем сама функция и аргумент t могут принимать любые значения на некоторых интервалах . На рис. 1.1 а представлен пример аналогового сигнала, изменяющегося во времени по закону , где . Другой пример аналогового сигнала, показанный на рис 1.1б, изменяется во времени по закону .

Важным примером аналогового сигнала является сигнал, описываемый т.н. «единичной функцией» , которая описывается выражением

(1.3),

где.

График единичной функции представлен на рис.1.2.

Функцию 1(t ) можно рассматривать как предел семейства непрерывных функций 1(a , t ) при изменении параметра этого семейства a .

(1.4).

Семейство графиков 1(a , t ) при различных значениях a представлено на рис.1.3.

В этом случае функцию 1( t ) можно записать как

(1.5).

Обозначим производную от 1(a , t ) как d (a , t ).

(1.6).

Семейство графиков d (a , t ) представлено на рис.1.4.

Площадь под кривой d (a , t ) не зависит от a и всегда равна 1. Действительно

(1.7).

Функция

(1.8)

называется импульсной функцией Дирака или d – функцией. Значения d – функции равны нулю во всех точках, кроме t =0. При t =0 d -функция равна бесконечности, но так, что площадь под кривой d – функции равна 1. На рис.1.5 представлен график функции d (t ) и d (t – t ).

Отметим некоторые свойства d – функции:

1. (1.9).

Это следует из того, что только при t = t .

2. (1.10) .

В интеграле бесконечные пределы можно заменить конечными, но так, чтобы аргумент функции d (t – t ) обращался в нуль внутри этих пределов.

(1.11).

3. Преобразование Лапласа d -функции

(1.12).

В частности , при t =0

(1.13).

4. Преобразование Фурье d – функции. При p = j v из 1.13 получим

(1.14)

При t =0

(1.15),

т.е. спектр d – функции равен 1.

Аналоговый сигнал f (t ) называется периодическим если существует действительное число T , такое, что f (t + T )= f (t ) для любых t . При этом T называется периодом сигнала. Примером периодического сигнала может служить сигнал, представленный на рис.1.2а, причем T =1/ f . Другим примером периодического сигнала может служить последовательность d – функций, описываемая уравнением

(1.16)

график которой представлен на рис.1.6.

Дискретные сигналы отличаются от аналоговых тем, что их значения известны лишь в дискретные моменты времени.Дискретные сигналы описываются решетчатыми функциями – последовательностями – x д (nT ), где T = const – интервал (период) дискретизации, n =0,1,2,…. Сама функция x д (nT ) может в дискретные моменты принимать произвольные значения на некотором интервале. Эти значения функции называются выборками или отсчетами функции. Другим обозначением решетчатой функции x (nT ) является x (n ) или x n . На рис. 1.7а и 1.7б представлены примеры решетчатых функций и . Последовательность x (n ) может быть конечной или бесконечной, в зависимости от интервала определения функции.

Процесс преобразования аналогового сигнала в дискретный называется временная дискретизация. Математически процесс временной дискретизации можно описать как модуляцию входным аналоговым сигналом последовательности d – функций d T (t )

(1.17)

Процесс восстановления аналогового сигнала из дискретного называется временная экстраполяция.

Для дискретных последовательностей также вводятся понятия энергии и мощности. Энергией последовательности x (n ) называется величина

,(1.18)

Мощностью последовательности x (n ) называется величина

,(1.19)

Для дискретных последовательностей сохраняются те же закономерности, касающиеся ограничения мощности и энергии, что и для непрерывных сигналов.

Периодической называют последовательность x (nT ), удовлетворяющую условию x (nT )= x (nT + mNT ), где m и N – целые числа. При этом N называют периодом последовательности. Периодическую последовательность достаточно задать на интервале периода, например при .

Цифровые сигналы представляют собой дискретные сигналы, которые в дискретные моменты времени могут принимать лишь конечный ряд дискретных значений – уровней квантования. Процесс преобразования дискретного сигнала в цифровой называется квантованием по уровню. Цифровые сигналы описываются квантованными решетчатыми функциями x ц (nT ). Примеры цифровых сигналов представлены на рис. 1.8а и 1.8б.

Связь между решетчатой функцией x д (nT ) и квантованной решетчатой функцией x ц (nT ) определяется нелинейной функцией квантования x ц (nT )= F k (x д (nT )). Каждый из уровней квантования кодируется числом. Обычно для эих целей используется двоичное кодирование, так, что квантованные отсчеты x ц (nT ) кодируются двоичными числами с n разрядами. Число уровней квантования N и наименьшее число двоичных разрядов m , с помощью которых можно закодировать все эти уровни, связаны соотношением

,(1.20)

где int (x ) – наименьшее целое число, не меньшее x .

Т.о., квантование дискретных сигналов состоит в представлении отсчета сигнала x д (nT ) с помощью двоичного числа, содержащего m разрядов. В результате квантования отсчет представляется с ошибкой, которая называется ошибкой квантования

.(1.21)

Шаг квантования Q определяется весом младшего двоичного разряда результирующего числа

.(1.22)

Основными способами квантования являются усечение и округление.

Усечение до m -разрядного двоичного числа состоит в отбрасывании всех младших разрядов числа кроме n старших. При этом ошибка усечения . Для положительных чисел прилюбом способе кодирования . Для отрицательных чисел при использовании прямого кода ошибка усечения неотрицательна , а при использовании дополнительного кода эта ошибка неположительна . Таким образом, во всех случаях абсолютнок значение ошибки усечения не превосходит шага квантования:

.(1.23)

График функции усечения дополнительного кода представлен на рис.1.9, а прямого кода – на рис.1.10.

Округление отличается от усечения тем, что кроме отбрасывания младших разрядов числа модифицируется и m -й (младший неотбрасываемый ) разряд числа. Его модификация заключается в том, что он либо остается неизменным или увеличивается на единицу в зависимости от того, больше или меньше отбрасываемая часть числа величины . Округление можно практически выполнить путем прибавления единицы к ( m +1) – муразряду числа с последующим усечением полученного числа до n разрядов. Ошибка округления при всех способах кодирования лежит в пределах и, следовательно,

.(1.24)

График функции округления представлен на рис. 1.11.

Рассмотрение и использование различных сигналов предполагает возможность измерения значения этих сигналов в заданные моменты времени. Естественно возникает вопрос о достоверности (или наоборот, неопределенности) измерения значения сигналов. Этими вопросами занимается теория информации , основоположником которой является К.Шеннон. Основная идея теории информации состоит в том, что с информацией можно обращаться почти также, как с такими физическими величинами как масса и энергия.

Точность измерений мы обычно характеризуем числовыми значениями полученных при измерении или предполагаемых погрешностей. При этом используются понятия абсолютной и относительной погрешностей. Если измерительное устройство имеет диапазон измерения от x 1 до x 2 , с абсолютной погрешностью ± D , не зависящей от текущего значения x измеряемой величины, то получив результат измерения в виде x n мы записываем его как x n ± D и характеризуем относительной погрешностью .

Рассмотрение этих же самых действий с позиции теории информации носит несколько иной характер, отличающийся тем, что всем перечисленным понятиям придается вероятностный, статистический смысл, а итог проведенного измерения истолковывается как сокращение области неопределенности измеряемой величины. В теории информации тот факт, что измерительный прибор имеет диапазон измерения от x 1 до x 2 означает , что при использовании этого прибора могут бытьполучены показания только в пределах от x 1 до x 2 . Другими словами, вероятность получения отсчетов, меньших x 1 или больших x 2 , равна 0. Вероятность же получения отсчетв где-то в пределах от x 1 до x 2 равна 1.

Если предположить, что все результаты измерения в пределах от x 1 до x 2 равновероятны, т.е. плотность распределения вероятности для различных значений измеряемой величины вдоль всей шкалы прибора одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком распределения плотности вероятности p (x ).

Поскольку полная вероятность получить отсчет где-то в пределах от x 1 до x 2 равна 1, то под кривой должна быть заключена площадь, равная 1, а это значит, что

(1.25).

После проведения измерения получаем показание прибора, равное x n . Однако, вследствие погрешности прибора, равной ± D , мы не можем утверждать, что измеряемая величина точно равна x n . Поэтому мы записывает результат в виде x n ± D . Это означает, что действительное значение измеряемой величины x лежит где-то в пределах от x n – D до x n + D . С точки зрения теории информации результат нашего измерения состоит лишь в том, что область неопределенности сократилась до величины 2 D и характеризуется намного большей плотностью ве5роятности

(1.26).

Получение каой-либо информации об интересующей нас величине заключается, таким образом, в уменьшении неопределенности ее значения.

В качестве характеристики неопределенности значения некоторой случайной величины К.Шеннон ввел понятие энтропии величины x , которая вычисляется как

(1.27).

Единицы измерения энтропии зависят от выбора основания логарифма в приведенных выражениях. При использовании десятичных логарифмов энтропия измеряется в т.н. десятичных единицах или дитах . В случае же использования двоичных логарифмов энтропия выражается в двоичных единицах или битах .

В большинстве случаев неопределенность знания о значении сигнала определяется действием помех или шумов. Дезинформационное действие шума при передаче сигнала определяется энтропией шума как случайной величины. Если шум в вероятностном смысле не зависит от передаваемого сигнала, то независимо от статистики сигнала шуму можно приписывать определенную величину энтропии, которая и характеризует его дезинформационное действие. При этом анализ системы можно проводить раздельно для шума и сигнала, что резко упрощает решение этой задачи.

Теорема Шеннона о количестве информации . Если на вход канала передачи информации подается сигнал с энтропией H ( x ), а шум в канале имеет энтропию H( D ) , то количество информации на выходе канала определяется как

(1.28).

Если кроме основного канала передачи сигнала имеется дополнительный канал, то для исправления ошибок, возникших от шума с энтропией H (D ), по этому каналу необходтмо передать дополнительное количество информации, не меньшее чем

(1.29).

Эти данные можно так закодировать, что будет возможно скорректировать все ошибки, вызванные шумом, за исключением произвольно малой доли этих ошибок.

В нашем случае, для равномерно распределенной случайной величины, энтропия определяется как

(1.30),

а оставшаяся или условная энтропия результата измерения после получения отсчета x n равна

(1.31).

Отсюда полученное количество информации равное разности исходной и оставшейся энтропии равно

(1.32).

При анализе систем с цифровыми сигналами ошибки квантования рассматриваются как стационарный случайный процесс с равномерным распределением вероятности по диапазону распределения ошибки квантования. На рис. 1.12а, б и в приведены плотности вероятности ошибки квантования при округлении дополнительного кода, прямого кода и усечении соответственно.

Очевидно, что квантование является нелинейной операцией. Однако, при анализе используется линейная модель квантования сигналов, представленная на рис. 1.13.

m – разрядный цифровой сигнал, e (nT ) – ошибка квантования.

Вероятностные оценки ошибок квантования делаются с помощью вычисления математического ожидания

(1.33)

и дисперсии

(1.34),

где p e – плотность вероятности ошибки. Для случаев округления и усечения будем иметь

(1.35),

(1.36).

Временная дискретизация и квантование по уровню сигналов являются неотъемлемыми особенностями всех микропроцессорных систем управления, определяемыми ограниченным быстродействием и конечной разрядностью используемых микропроцессоров.

Мы рассматривали различные определения понятия “информация” и пришли к выводу, что информация может быть определена множеством разных способов в зависимости от выбранного подхода. Но об одном мы можем говорить однозначно: информация – знания, данные, сведения, характеристики, отражения и т.д. – категория нематериальная . Но мы живем в мире материальном. Следовательно, для существования и распространения в нашем мире информация должна быть связана с какой-либо материальной основой. Без нее информация не может передаваться и сохраняться.

Тогда материальный объект (или среда), с помощью которого представляется та или иная информация будет являться носителем информации , а изменение какой-либо характеристики носителя мы будем называть сигналом .
Например, представим равномерно горящую лампочку, она не передает никакой информации. Но, если мы будем включать и выключать лампочку (т.е. изменять ее яркость), тогда с помощью чередований вспышек и пауз мы сможем передать какое-нибудь сообщение (например, посредством азбуки Морзе). Аналогично, равномерный гул не дает возможности передать какую-либо информацию, однако, если мы будем изменять высоту и громкость звука, то сможем сформировать некоторое сообщение (что мы и делаем с помощью устной речи).

При этом сигналы могут быть двух видов: непрерывный (или аналоговый ) и дискретный .
В учебнике даны следующие определения.

Непрерывный сигнал принимает множество значений из некоторого диапазона. Между значениями, которые он принимает, нет разрывов.
Дискретный сигнал принимает конечное число значений. Все значения дискретного сигнала можно пронумеровать целыми числами.

Немного уточним эти определения.
Сигнал называется непрерывным (или аналоговым), если его параметр может принимать любое значение в пределах некоторого интервала.

Сигнал называется дискретным , если его параметр может принимать конечное число значений в пределах некоторого интервала.

Графики этих сигналов выглядят следующим образом

Примерами непрерывных сигналов могут быть музыка, речь, изображения, показания термометра (высота столба ртути может быть любой и представляет собой ряд непрерывных значений).

Примерами дискретных сигналов могут быть показания механических или электронных часов, тексты в книгах, показания цифровых измерительных приборов и т.д.

Вернемся к примерам, рассмотренным в начале сообщения – мигающая лампочка и человеческая речь. Какой из этих сигналов является непрерывным, а какой дискретным? Ответьте в комментариях и аргументируйте свой ответ. Можно ли непрерывную информацию преобразовать в дискретную? Если да – приведите примеры.

С дискретностью каждый из нас сталкивается ежедневно. Это одно из свойств, присущее материи. В дословном переводе с латинского языка слово discretus означает прерывистость. Например, дискретный сигнал – это способ передачи информации, когда среда-переносчик изменяется во времени, принимая любое из существующего списка допустимых значений.

Конечно, термин «дискретность» применяется в более широком смысле. В частности, сейчас прогресс в микроэлектронике направлен на создание и развитие технологии SOC – «Система на чипе». Предполагается, что все составляющие устройство компоненты между собой тесно интегрированы на единой подложке. Противоположность такого подхода – дискретные схемы, когда элементы сами являются завершенными изделиями, соединяясь линиями связи.

Пожалуй, сейчас невозможно найти человека, который бы не пользовался мобильным телефоном или программой Скайп на компьютере. Одна из их задач – это передача звукового потока (в частности, голоса). Но так как такой звук представляет собой непрерывную волну, для его непосредственной передачи потребовался бы канал с высокой пропускной способностью. Для решения этого вопроса было предложено использовать дискретный сигнал. Формирует он не волну, а ее цифровое представление (помните, речь идет о мобильных телефонах и компьютерах). С волны через определенные промежутки времени выполняются выборки значений данных. То есть, создается дискретный сигнал. Его преимущество очевидно: меньший суммарный и возможность организации пакетной передачи. Целевое приемное устройство объединяет все выборки в единый блок, генерируя исходную волну. Чем больше промежутки между выборками, тем выше вероятность искажения исходной волны. Дискретизация широко используется в вычислительной технике.

Говоря о том, что такое дискретный сигнал, нельзя не воспользоваться замечательной аналогией с обычной печатной книгой. Человек, читая ее, получает непрерывный поток информации. В то же время, содержащиеся в ней данные «закодированы» в виде определенных последовательностей букв – слов – предложений. Получается, что автор из неделимой мысли формирует своеобразный дискретный сигнал, так как выражает ее разбиением на блоки, используя тот или иной способ кодировки (алфавит, язык). Читатель в данном примере получает возможность воспринимать идею автора только после мысленного объединения слов в поток информации.

Наверняка, вы читаете эту статью с экрана компьютера. А ведь даже экран монитора может служить примером, где проявляется дискретность и непрерывность. Вспомним старые модели, основанные на ЭЛТ. В них изображение формировалось последовательностью кадров, которые необходимо было «отрисовывать» несколько десятков раз в секунду. Очевидно, что данное устройство использует дискретный способ построения картинки.

Дискретный сигнал является полной противоположностью непрерывному. Последний представляет собой функцию интенсивности от времени (если представить его на декартовой плоскости). Как уже указывалось, одним из примеров может служить Она характеризуется частотой и амплитудой, однако естественным образом нигде не прерывается. Большинство природных процессов описываются именно таким способом. Несмотря на то, что, все-таки, существует несколько способов обработки непрерывного (или аналогового) сигнала, позволяющих уменьшить поток данных, в современных цифровых системах распространен именно дискретный. Отчасти благодаря тому, что его можно достаточно просто преобразовать в исходный, независимо от конфигурации последнего. Кстати, стоит отметить, что термины «дискретный» и «цифровой» практически равнозначны.

Page

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

ПРАКТИЧЕСКАЯ ЧАСТЬ

1. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ В ПРОСТРАНСТВЕ СОСТОЯНИЙ

2. ПЕРЕХОД ОТ НЕПРЕРЫВНОЙ СИСТЕМЫ К ЦИФРОВОЙ С ПОМОЩЬЮ ПЕРЕДАТОЧНЫХ ФУНКЦИЙ

3. МОДЕЛИРОВАНИЕ И АНАЛИЗ ЦИФРОВЫХ СИСТЕМ В ПАКЕТЕ SIMULINK СИСТЕМЫ MATLAB

4. ПРЕОБРАЗОВАНИЕ ФОРМ ЛИНЕЙНЫХ МОДЕЛЕЙ ЦИФРОВЫХ СИСТЕМ

Контрольные вопросы

Лабораторная работа № 13

Моделирование и исследование

цифровых систем управления

Цель работы: проанализировать линейные стационарные системы управления с дискретным временем.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Любая система автоматического регулирования и управления представляет собой совокупность элементов, предназначенных для преобразования сигналов, поступающих на ее вход, чтобы обеспечить выполнение цели управления [4]. Если на вход всех элементов системы поступают сигналы, которые могут быть описаны непрерывными функциями времени, система называется непрерывной. Система, содержащая, по крайней мере, один элемент, выходным сигналом которого является дискретный сигнал, называется дискретной.

Дискретный сигнал – это такой сигнал, который определяется последовательностью значений а₀, а₁, а₂, ¼, а_n_,_¼_.Сигналы могут быть дискретными по уровню, по времени, а также одновременно по уровню и по времени.

В зависимости от способов получения дискретных сигналов может быть введена следующая классификация дискретных систем [4, 18]:

1) импульсная система – это система, в которой используются сигналы, дискретные по времени;

2) релейная система – это система, в которой используются сигналы, дискретные по уровню;

3) цифровая система – это система, в которой используются сигналы, дискретные как по времени, так и по уровню.

На рис. 13.1 показана идеализированная амплитудно-импульсная модуляция непрерывного сигнала на основе идеальных импульсов, ширина которых бесконечна малая, а высота равна значениям непрерывного сигнала в дискретные моменты времени. Если f(t) есть непрерывный сигнал, то выделение дискретных значений f(kT) называется квантованием сигнала f(t) по времени с постоянным шагом квантования или периодом дискретизации Т. В то же время f(kT) называют решетчатой функцией. Другим видом импульсной модуляции является широтно-импульсная модуляция, при которой амплитуда импульсов постоянная, а их ширина пропорциональна в некоторых пределах значениям f(kT). Еще возможна фазоимпульсная модуляция сигнала, которая осуществляется за счет смещения импульсов в пределах шага квантования Т. Величина смещения пропорциональна значениям f(kT).

Рис. 13.1. Идеальное квантование непрерывного сигнала по времени

Квантование (дискретизация) непрерывного сигнала по уровню с шагом h показано на рис. 13.2. Оно может быть получено, если преобразовать непрерывный сигнал с помощью многоступенчатого релейного устройства. Дискретный по уровню сигнал, представленный на рис. 13.2, может быть описан в соответствии с выражением [4]:

При квантовании по уровню в произвольные моменты времени выделяются значения непрерывного сигнала при достижении им фиксированных дискретных уровней [18]. Как отмечалось, квантование по уровню характерно для релейных систем автоматического управления, которые представляют собой достаточно большой класс динамических систем, в состав которых входят нелинейные звенья с разрывной характеристикой. Основными достоинствами релейных систем автоматического управления является их простота, связанная с ней высокая надежность, а также экономичность в расходе энергии питания. В то же время к ним не могут быть применены методы анализа и синтеза гладких систем.

Рис. 13.2. Квантование непрерывного сигнала по уровню

Характер квантования по уровню и по времени непрерывного сигнала показан на рис. 13.3. В этом случае непрерывный сигнал f(t) заменяется фиксированными дискретными (по уровню) значениями, ближайшими к значениям непрерывной функции f(t) в дискретные моменты времени 0, Т, 2Т, ¼ . Квантование по уровню и по времени осуществляется в цифровых системах управления при преобразовании непрерывных сигналов в цифровую форму или в коды. Если цифровое устройство оперирует с числовым представлением со значительным количеством разрядов (что характерно для современных компьютеров), то квантованием по уровню можно пренебречь. Тогда цифровую систему можно рассматривать как импульсную систему с амплитудно-импульсной модуляцией.

Рис. 13.3. Квантование сигнала по уровню и по времени

Цифровая система управления включает объект управления (обычно непрерывный объект или процесс), чувствительные элементы (или датчики), аналого-цифровой преобразователь (АЦП), цифровое вычислительное устройство (микропроцессор или компьютер) и цифроаналоговый преобразователь (ЦАП). Функциональная схема цифровой системы управления показана на рис. 13.4.

Discrete Signal – обзор

Periodic-Discrete

Это дискретные сигналы, которые периодически повторяются от отрицательной до положительной бесконечности. Этот класс преобразования Фурье иногда называют дискретным рядом Фурье, но чаще всего его называют дискретным преобразованием Фурье .

Вы могли подумать, что названия, данные этим четырем типам преобразований Фурье, сбивают с толку и плохо организованы. Ты прав; имена эволюционировали довольно бессистемно за 200 лет.Вы ничего не можете сделать, кроме как запомнить их и двигаться дальше.

Все эти четыре класса сигналов простираются до положительной и отрицательной бесконечности . Вы говорите, держитесь! Что, если у вас есть только конечное количество выборок, хранящихся в вашем компьютере, скажем, сигнал, сформированный из 1024 точек. Нет ли версии преобразования Фурье, которая использует сигналы конечной длины? Нет, нет. Волны синуса и косинуса определены как как простирающиеся от отрицательной бесконечности до положительной бесконечности. Вы не можете использовать группу бесконечно длинных сигналов, чтобы синтезировать что-то конечной длины.Чтобы решить эту дилемму, нужно сделать так, чтобы конечные данные выглядели как – сигнал бесконечной длины. Это делается путем представления, что сигнал имеет бесконечное количество выборок слева и справа от фактических точек. Если все эти «воображаемые» выборки имеют нулевое значение, сигнал выглядит дискретным и апериодическим , и применяется дискретное временное преобразование Фурье. В качестве альтернативы воображаемые образцы могут быть дублированием реальных 1024 точек. В этом случае сигнал выглядит дискретным и периодическим с периодом 1024 отсчета.Это требует использования дискретного преобразования Фурье.

Как оказалось, для синтеза сигнала апериодического требуется бесконечное количество синусоид . Это делает невозможным вычисление дискретного преобразования Фурье в компьютерном алгоритме. По исключению единственный тип преобразования Фурье, который может использоваться в DSP, – это DFT. Другими словами, цифровые компьютеры могут работать только с информацией, длина которой составляет дискретных и конечных .Когда вы боретесь с теоретическими проблемами, решаете домашние задания и размышляете над математическими загадками, вы можете обнаружить, что используете первых трех членов семейства преобразований Фурье. Когда вы садитесь за компьютер, вы будете использовать только DFT. Мы кратко рассмотрим эти другие преобразования Фурье в следующих главах. А пока сконцентрируйтесь на понимании дискретного преобразования Фурье.

Вернитесь к примеру разложения ДПФ на рис. 8-1. На первый взгляд, это сигнал из 16 точек, разложенный на 18 синусоид, каждая из которых состоит из 16 точек.Говоря более формально, 16-точечный сигнал, показанный на (а), следует рассматривать как отдельный период бесконечно длинного периодического сигнала. Аналогично, каждая из 18 синусоид, показанных на (b), представляет собой сегмент из 16 точек из бесконечно длинной синусоиды. Имеет ли значение, рассматриваем ли мы это как 16-точечный сигнал, синтезируемый из 16-точечных синусоид, или как бесконечно длинный периодический сигнал, синтезируемый из бесконечно длинных синусоид? Ответ: обычно нет, но иногда да . В следующих главах мы столкнемся со свойствами ДПФ, которые кажутся сбивающими с толку, если рассматривать сигналы как конечные, но станут очевидными, если учесть периодический характер.Ключевым моментом для понимания является то, что эта периодичность вызывается для использования математического инструмента , то есть ДПФ. Обычно это бессмысленно с точки зрения того, где возник сигнал или как он был получен.

Каждое из четырех преобразований Фурье можно разделить на реальных и комплексных версий. Реальная версия является самой простой, с использованием обычных чисел и алгебры для синтеза и разложения. Например, рис. 8-1 представляет собой пример реального ДПФ .Сложные версии четырех преобразований Фурье намного сложнее и требуют использования комплексных чисел . Это такие числа, как: 3+ 4j , где j равно -1 (инженеры-электрики используют переменную j , а математики используют переменную i ). Сложная математика может быстро стать непосильной даже для тех, кто специализируется на DSP. Фактически, основная цель этой книги – представить основы DSP без использования сложных математических вычислений, что позволит более широкому кругу ученых и инженеров понять материал.Сложные преобразования Фурье – это область тех, кто специализируется на DSP и готов погрузиться по шею в болото математики. Если вы так склонны, главы 30–3330313233 доставят вас туда.

Математический термин преобразование широко используется в цифровой обработке сигналов, такой как преобразование Фурье, преобразование Лапласа, преобразование Z, преобразование Гильберта, дискретное косинусное преобразование и т. Д. Что такое преобразование? Чтобы ответить на этот вопрос, вспомните, что такое функция .Функция – это алгоритм или процедура, которые изменяют одно значение на другое значение. Например, y = 2 x + 1 – это функция. Вы выбираете какое-то значение для x , вставляете его в уравнение, и выдает значение y . Функции также могут преобразовывать несколько значений в одно значение, например: y = 2 a + 3 b + 4 c , где a, b и c заменяются на y .

Преобразования

являются прямым продолжением этого, позволяя как входу, так и выходу иметь нескольких значений .Предположим, у вас есть сигнал, состоящий из 100 выборок. Если вы разработаете какое-то уравнение, алгоритм или процедуру для преобразования этих 100 выборок в другие 100 выборок, у вас есть преобразование. Если вы считаете, что он достаточно полезен, у вас есть полное право прикрепить к нему свою фамилию и рассказать коллегам о его достоинствах. (Это лучше всего работает, если вы выдающийся французский математик 18 века.) Преобразования не ограничиваются каким-либо конкретным типом или количеством данных. Например, у вас может быть 100 выборок дискретных данных для входа и 200 выборок дискретных данных для выхода.Точно так же у вас может быть непрерывный сигнал для входа и непрерывный сигнал для выхода. Также разрешены смешанные сигналы, дискретные входящие и непрерывные выходящие и наоборот. Короче говоря, преобразование – это любая фиксированная процедура, которая преобразует один фрагмент данных в другой. Давайте посмотрим, как это применимо к рассматриваемой теме: дискретное преобразование Фурье.

2.4: Сигналы в дискретном времени – Engineering LibreTexts

Цели обучения

Сигналы могут быть представлены дискретными величинами, а не как функция непрерывной переменной.
Эти дискретные временные сигналы не обязательно должны принимать действительные числовые значения.
Многие свойства непрерывных сигналов передаются почти напрямую в дискретную область.

До сих пор мы рассматривали так называемые аналоговые сигналы и системы . Математически аналоговые сигналы – это функции, имеющие в качестве независимых переменных непрерывные величины, такие как пространство и время. Сигналы дискретного времени – это функции, определенные на целых числах; это последовательности.Один из фундаментальных результатов теории сигналов детализирует условия, при которых аналоговый сигнал может быть преобразован в сигнал с дискретным временем и получить без ошибки . Этот результат важен, потому что дискретными сигналами времени можно управлять с помощью систем, созданных как компьютерные программы. Последующие модули описывают, как практически вся обработка аналоговых сигналов может выполняться с помощью программного обеспечения.

Какими бы важными ни были такие результаты, сигналы с дискретным временем носят более общий характер и включают сигналы, полученные из аналоговых сигналов и , которые таковыми не являются.Например, символы, образующие текстовый файл, образуют последовательность, которая также является сигналом дискретного времени. Мы также должны иметь дело с такими символически значимыми сигналами и системами.

Как и в случае с аналоговыми сигналами, мы ищем способы разложения сигналов дискретного времени с действительным знаком на более простые компоненты. Благодаря этому подходу, ведущему к лучшему пониманию структуры сигнала, мы можем использовать эту структуру для представления информации (создавать способы представления информации с помощью сигналов) и для извлечения информации (извлекать информацию, представленную таким образом).Для сигналов с символическими значениями используется другой подход: мы разрабатываем общее представление всех сигналов с символическим значением, чтобы объединить содержащуюся в них информацию. С точки зрения представления информации наиболее важным вопросом становится эффективность как для сигналов с действительным, так и для символьных значений; Каков наиболее экономичный и компактный способ представления информации для последующего извлечения.

Реальные и комплексные сигналы

Сигнал с дискретным временем представлен символически как с (n), , где n = {…, – 1,0,1 …}. Обычно мы рисуем сигналы с дискретным временем в виде основных графиков, чтобы подчеркнуть тот факт, что это функции, определенные только для целых чисел. Мы можем задержать сигнал с дискретным временем на целое число, как и с аналоговыми. Отсроченная единичная выборка имеет выражение

δ (n − m) δ (n − m) \ [\ delta (n-m) \]

и равно единице, если n = m .

Рис. 2.4.1 Косинусоидальный сигнал в дискретном времени отображается в виде основного графика. Можете ли вы найти формулу этого сигнала?

Комплексные экспоненты

Самым важным сигналом, конечно же, является комплексная экспоненциальная последовательность .{i2 \ pi fn} \]

Синусоиды

Синусоиды дискретного времени имеют очевидную форму

\ [s (n) = A \ cos (2 \ pi fn + \ varphi) \]

В отличие от аналоговых комплексных экспонент и синусоид, частота которых может быть любой действительной величиной, частоты их аналогов в дискретном времени дают уникальные формы сигнала только , когда f лежит в интервале (-½, ½). Это свойство можно легко понять, заметив, что добавление целого числа к частоте комплексной экспоненты с дискретным временем не влияет на значение сигнала.{i2 \ pi fn} \]

Этот вывод следует из того, что комплексная экспонента, вычисленная как целое число, кратное 2π , равна единице.

Единица Образец

Вторым по важности сигналом дискретного времени является единичная выборка , которая определена как

\ [\ delta (n) = 1 \; если\; п = 0 \\ \ дельта (п) = 0 \; в противном случае \]

Рис. 2.4.2. Единичная выборка

Исследование графика дискретного сигнала, аналогичного графику косинусоидального сигнала, показанного на рис.{\ infty} s (m) \ delta (n-m) \]

Этот вид разложения уникален для сигналов с дискретным временем и впоследствии окажется полезным.

Системы с дискретным временем могут воздействовать на сигналы с дискретным временем таким же образом, как и в аналоговых сигналах и системах. Из-за роли программного обеспечения в системах с дискретным временем можно представить и «сконструировать» гораздо больше различных систем с помощью программ, чем с помощью аналоговых сигналов. Фактически, особый класс аналоговых сигналов может быть преобразован в сигналы с дискретным временем, обработан с помощью программного обеспечения и преобразован обратно в аналоговый сигнал, и все это без появления ошибки.Для таких сигналов системы могут быть легко созданы в программном обеспечении с эквивалентными аналоговыми реализациями, которые трудно, если не невозможно, спроектировать.

Символьные сигналы

Другой интересный аспект сигналов с дискретным временем состоит в том, что их значения не обязательно должны быть действительными числами. У нас есть действительные сигналы с дискретным временем, такие как синусоида, но у нас также есть сигналы, которые обозначают последовательность символов, набранных на клавиатуре. Такие символы определенно не являются действительными числами, и как набор возможных значений сигналов они имеют небольшую математическую структуру, кроме того, что они являются членами набора.Более формально, каждый элемент символьного сигнала s (n) принимает одно из значений {a ₁, …. a _K} , которые составляют алфавит A . Эта техническая терминология не означает, что мы ограничиваем символы только членами английского или греческого алфавита. Они могут представлять символы клавиатуры, байты (8-битные величины), целые числа, передающие суточную температуру. Независимо от того, управляются ли они программным обеспечением или нет, системы с дискретным временем в конечном итоге состоят из цифровых схем, которые состоят из полностью аналоговых схемных элементов.Кроме того, передача и прием сигналов с дискретным временем, таких как электронная почта, осуществляется с помощью аналоговых сигналов и систем. Понимание того, как взаимосвязаны дискретные и аналоговые сигналы и системы, возможно, является основной целью этого курса.

дискретная связь | теория информации

В теории информации: четыре типа связи

Дискретные сигналы могут представлять только конечное число различных распознаваемых состояний. Например, буквы английского алфавита обычно считаются дискретными сигналами.Непрерывные сигналы, также известные как аналоговые сигналы, обычно используются для передачи величин, которые могут изменяться в пределах… \ n

Подробнее

Бесшумная связь

В теории информации: от алфавита сообщений к алфавиту сигналов
Для бесшумной связи декодер на принимающая сторона получает в точности символы, отправленные кодировщиком. Однако эти передаваемые символы обычно не входят в алфавит исходного сообщения. Например, в азбуке Морзе короткие и длинные электрические импульсы, световые вспышки или звуки с надлежащим интервалом… \ n
Подробнее

шумная связь

В теории информации: коды для исправления и обнаружения ошибок
… работают в область дискретной, зашумленной связи указала на возможность построения кодов с исправлением ошибок.Коды с исправлением ошибок добавляют дополнительные биты для исправления ошибок и, таким образом, работают в направлении, противоположном сжатию. Коды обнаружения ошибок, с другой стороны, указывают на то, что ошибка произошла, но не происходит автоматически… \ n
Подробнее
В теории информации: дискретная, шумная связь и проблема ошибки
\ nВ обсуждении выше это нереально предположить, что все сообщения передаются без ошибок. В реальном мире, однако, ошибки передачи неизбежны – особенно с учетом присутствия в любом канале связи шума, который является суммой… \ n
Подробнее

появление в нервной системе

В теории информации: физиология
После в целом нервная система – это, прежде всего, канал передачи информации, а мозг – это, помимо прочего, центр обработки информации и обмена сообщениями.Поскольку нервные сигналы обычно состоят из импульсов электрической энергии, нервная система является примером… \ n
Подробнее

“,” url “:” Introduction “,” wordCount “: 0,” sequence “: 1} , “imarsData”: {“HAS_REVERTED_TIMELINE”: “false”, “INFINITE_SCROLL”: “”}, “npsAdditionalContents”: {}, “templateHandler”: {“metered”: false, “name”: “INDEX”}, ” paginationInfo “: {” previousPage “: null,” nextPage “: null,” totalPages “: 1},” seoTemplateName “:” PAGINATED INDEX “,” infiniteScrollList “: [{” p “: 1,” t “: 709369} ], “familyPanel”: {“topicLink”: {“title”: “дискретное общение”, “url”: “/ topic / diste-communication”}, “tocPanel”: {“title”: “Directory”, “itemTitle “:” Ссылки “,” toc “: null},” groups “: [],” showCommentButton “: false,” fastFactsItems “: null},” byline “: {” members “: null,” allContributorsUrl “: null, «lastModificationDate»: null, «contentHistoryUrl»: null, «warningMessage»: null, «warningDescription»: null}, «citationInfo»: {«участники»: null, «title»: «дискретное сообщение», «lastModification»: null , “url”: “https: // www.britannica.com/topic/discrete-communication”},”websites”:null,”lastArticle”:false}

Узнайте об этой теме в этих статьях:

дискретных сигналов

В теории информации: четыре типа связи
Дискретные сигналы могут представлять только конечное число различных распознаваемых состояний.Например, буквы английского алфавита обычно считаются дискретными сигналами. Непрерывные сигналы, также известные как аналоговые сигналы, обычно используются для передачи величин, которые могут изменяться в пределах …
Подробнее

Бесшумная связь

Теория информации: От алфавита сообщений к алфавиту сигналов
Для бесшумной связи декодер на принимающей стороне принимает точно символы, отправленные кодировщиком. Однако эти передаваемые символы обычно не входят в алфавит исходного сообщения.Например, в азбуке Морзе короткие и длинные электрические импульсы, световые вспышки или звуки, расположенные надлежащим образом, – это…
Подробнее

шумная связь

В теории информации: Коды исправления и обнаружения ошибок
… работа в области дискретной, зашумленной связи указала на возможность построения кодов исправления ошибок. Коды с исправлением ошибок добавляют дополнительные биты для исправления ошибок и, таким образом, работают в направлении, противоположном сжатию.Коды обнаружения ошибок, с другой стороны, указывают на то, что ошибка произошла, но не …
Подробнее
В теории информации: дискретная, шумная связь и проблема ошибки
В приведенном выше обсуждении нереалистично предполагается, что все сообщения передаются без ошибок. Однако в реальном мире ошибок передачи невозможно избежать – особенно с учетом присутствия в любом канале связи шума, который является суммой…
Подробнее

Возникновение в нервной системе

В теории информации: физиология
В конце концов, нервная система – это, прежде всего, канал для передачи информации, а мозг – это, помимо прочего, информация центр обработки и обмена сообщениями.Поскольку нервные сигналы обычно состоят из импульсов электрической энергии, нервная система кажется примером …
Подробнее

Односкоростные сигналы и системы с дискретным временем: общий обзор: Computer Science & IT Book Chapter

Эта глава представляет собой краткий обзор представлений односкоростных сигналов и систем с дискретным временем во временной области и в области преобразования. Сначала мы рассмотрим представление дискретных сигналов и систем во временной области.Представление в области преобразования включает в себя дискретное преобразование Фурье (DTFT), дискретное преобразование Фурье (DFT) и преобразование z . Кратко описаны основные структуры реализации для систем FIR и IIR. Наконец, приведены соотношения между непрерывными и дискретными сигналами.

ДИСКРЕТНЫЕ ВРЕМЕННЫЕ СИГНАЛЫ

Сигнал является функцией по крайней мере одной независимой переменной. В этой книге мы предполагаем, что независимой переменной является время, даже в тех случаях, когда независимой переменной является величина, отличная от времени.

Мы определяем непрерывный сигнал , x _c ( t ) как сигнал, который существует в каждый момент времени t . Непрерывный сигнал с непрерывной амплитудой также называется аналоговым сигналом . Независимая переменная t является непрерывной переменной, а x _c ( t ) может принимать любое значение в непрерывном диапазоне чисел.

Сигнал дискретного времени представляет собой последовательность чисел, обозначенную как { x [ n ]}, где n называется временным индексом , а x [ n ] обозначает значение элемента n ^-й в последовательности.Сигнал с дискретным временем называется дискретным сигналом . Величина x [ n ] также называется значением выборки , а ее временной индекс n называется индексом выборки . Величина x [ n ] может принимать любое значение в некотором непрерывном диапазоне чисел, x _мин. ≤ x [ n ] ≤ x _max.

Дискретные сигналы могут быть определены только для целых значений n из интервала N ₁ ≤ n ≤ N ₂.Когда значения выборок последовательности { x [ n ]} представлены как двоичные числа с использованием конечного числа битов, сигнал { x [ n ]} представляет собой цифровой сигнал .

Длина последовательности определяется как N ≤ N ₂ – N ₁ + 1. Последовательность { x [ n ]} представляет собой последовательность конечной длины если N имеет конечную длину; в противном случае { x [ n ]} представляет собой последовательность бесконечной длины .

Для целей анализа полезно представить сигналы как комбинацию основных последовательностей. Часто используемые базовые последовательности приведены в таблице 1.

Таблица 1.

Во многих приложениях сигнал дискретного времени { x [ n ]} генерируется путем дискретизации сигнала непрерывного времени x _c ( т ) через единые промежутки времени:

. (1)

Временной интервал T называется интервалом выборки или периодом выборки , а обратное значение

(2) представляет собой частоту выборки или частоту выборки .Обычно единицей частоты дискретизации является количество циклов в секунду, и когда T задается в секундах [с], F _T может быть выражено в герцах [Гц].

Анализ и проектирование дискретных сигналов | Wiley

Предисловие xi

Введение 1

Цели книги

Дискретные сигналы

Преимущества анализа и проектирования дискретных сигналов

DFT и IDFT

Программа Mathcad

MATLAB и менее дорогостоящая программа национальных инструментов 9000isim

9000 Co.

Программа Mathtype

LabVIEW

Поисковые системы

Возможности программного обеспечения Personal Productivity

1 Первые принципы 9

Структура последовательности во временной и частотной областях

Двустороннее преобразование по времени и частоте

Обратное дискретное преобразование Фурье

Масштабирование частоты и времени

Число отсчетов

Комплексные последовательности в частотной области

x (n) по времени и X (k) по сравнению с частотой

2 Синус, косинус и θ 27

Односторонние последовательности

Комбинации двусторонних векторов

Преобразования времени и спектра

Преобразование двухсторонних фазорных последовательностей в односторонние синусоидальные, косинусные, θ

Пример 2-1: нелинейный усилитель и модулятор квадратичного закона

Пример 2-2: Анализ функции линейного изменения

3 Спектральная утечка и искажение 43

Спектральная утечка.Нецелочисленные значения времени x (n) и частоты X (k)

Пример 3-1: Масштабирование частоты для уменьшения наложения утечки в частотной области

Пример 3-2: Анализ наложения наложения частотной области в временная область

4 Сглаживание и создание окон 61

Сглаживание прямоугольного окна без шума и с шумом

Сглаженные последовательности в начале и в конце

Прямоугольное окно

Окно Хэмминга

Окно Хэннинга (

)

Относительные достоинства трех окон

Масштабирование Windows

5 Умножение и свертка 77

Умножение последовательностей

Умножение полиномов

Свертка

Дискретная свертка Базовое уравнение

Связывание с полиномиальным умножением

Связывание

. ”Концепт

Cir Дискретная свертка (старайтесь избегать)

Время последовательности и фазовый сдвиг

ДПФ и ДПФ дискретной свертки

Рис.5-6. Сравните свертку и умножение

Деконволюция

6 Вероятность и корреляция 95

Свойства дискретной последовательности

Ожидаемое значение x (n)

Включить некоторый дополнительный шум

Обнаружение огибающей

Обнаружение огибающей 4 Мощность бесшумной последовательности

Мощность шумной последовательности

Усреднение последовательности

Дисперсия

Гауссово (нормальное) распределение

Кумулятивное распределение

Корреляция и ковариация

Автокорреляция

000 Кросс-корреляция

Коэффициент корреляции

7 Спектр мощности 113

Нахождение спектра мощности

Двусторонний векторный спектр, односторонний спектр мощности

Пример 7-1: Использование уравнения.(7-2)

Случайный гауссовский спектр шума

Измерение спектра мощности

Пример анализатора спектра

Теорема Винера-Хинчина

Передача мощности системы

Спектр перекрестной мощности

Пример расчета фазового шума

90 Преобразование Гильберта 129

Идеальный преобразователь Гильберта

Пример преобразования Гильберта почти прямоугольной волны

Сглаживание примера

Пики прямоугольной волны Гильберта

Математика преобразования Гильберта

Аналитический сигнал

Пример 8-2: Построение аналитического сигнала

Однополосные радиочастотные сигналы

Конструкция SSB

Базовая однопроходная сеть

−90 ^◦ Аудиосеть с каскадным фазовым сдвигом

Почему сеть −90 ^◦ Не эквивалентен трансформатору Гильберта

Phasing Met Передатчик hod SSB Метод фильтрации Передатчик SSB

Метод фазирования Приемник SSB

Метод фильтрации Приемник SSB

Приложение: Дополнительный анализ дискретных сигналов и информация о конструкции 153

Дискретная производная

Решения переменной состояния с использованием дискретной производной

для решения дискретного дифференциального уравнения во временной области

Глоссарий 163

Указатель 171

Введение в сигналы

Определение сигналов
- Типы сигналов
- Свойства сигнала
Пример сигналов
- Различные сигналы
- Свойство периодичности
Дельта функция

Свойства и типы сигналов

Управление сигналами

разворот времени
сдвиг во времени
расширение / сокращение времени
- Разница между CT и DT

Составные сигналы

Почему цифровая обработка сигналов?

Если вы работаете на компьютере или используете компьютер для манипулирования данными, вы почти наверняка работаете с цифровыми сигналами.Все манипуляции с данными являются примерами цифровой обработки сигналов (для наших целей обработка сигналов с дискретным временем как экземпляры цифровой обработки сигналов). Примеры использования DSP:

Фильтрация: устранение шума из сигналов, таких как речевые сигналы и другие аудиоданные, астрономические данные, сейсмические данные, изображения.
Синтез и манипуляции: например, синтез речи, синтез музыки, графика.
Анализ: сейсмические данные, атмосферные данные, анализ фондового рынка.
Голосовая связь: обработка, кодирование и декодирование для хранения и пересылки.
Кодирование голоса, звука и изображений для сжатия.
Активное шумоподавление: наушники, глушители в автомобилях
Обработка изображений, компьютерное зрение
Компьютерная графика
Промышленное применение: анализ вибрации, химический анализ
Biomed: МРТ, сканирование кошек, визуализация, анализы, ЭКГ, ЭМГ и т. Д.
Радар, Эхолот
Сейсмология.

Определение сигналов

Что такое сигнал?

Сигнал – это способ передачи информации. Жесты, семафоры, изображения, звук – все может быть сигналами.

Технически – функция времени, пространства или другой переменной наблюдения, которая передает информацию

Распишем 3 форм сигналов:

Непрерывный / аналоговый сигнал
Дискретно-временной сигнал
Цифровой сигнал

Непрерывный (CT) / аналоговый сигнал

конечная , действительная , гладкая функция $ s (t) $ переменной t , которая обычно представляет время.И s , и t в $ s (t) $ являются непрерывными

Почему с реальной стоимостью ?

Обычно явления реального мира имеют реальную ценность.

Почему конечный ?

Реальные сигналы обычно имеют ограниченную энергию просто потому, что нам не доступен бесконечный источник энергии.
В качестве альтернативы, особенно когда они характеризуют долговременные явления (например, солнечное излучение), они будут ограничены по мощности.
Реальные сигналы также будут ограничены по амплитуде – их значения ни в коем случае не будут бесконечными.

Чтобы утверждать, что сигнал «конечен», нам нужна некоторая характеристика его «размера». Утверждать, что сигнал конечен, значит утверждать, что размер сигнала ограничен – он никогда не стремится к бесконечности.2 (\ тау), д \ тау. $

Амплитуда = $ max | s (t) | $

Почему гладкий ?

Реальные сигналы никогда не меняются резко / мгновенно. Чтобы быть более техническим, у них конечная пропускная способность .

Обратите внимание, что хотя мы делали предположения о сигналах (конечность, реальные, гладкие), при фактическом анализе и разработке методов обработки сигналов эти соображения обычно игнорируются.

Дискретный сигнал (DT)

Сигнал с дискретным временем – это ограниченная последовательность с непрерывными значениями $ s [n] $. С другой стороны, его можно рассматривать как непрерывную функцию от дискретного индекса $ n $. 2 [n].$

Амплитуда = $ max | s [n] |

долл. США

Гладкость неприменима.

Цифровой сигнал

Мы будем работать с цифровыми сигналами , но будем развивать теорию в основном вокруг сигналов с дискретным временем .

Цифровые компьютеры работают с сигналами цифровых , а не с сигналами дискретного времени.Цифровой сигнал представляет собой последовательность $ s [n] $, где index значения $ s [n] $ не только конечны, но могут принимать только конечный набор значений. Например, в цифровом сигнале, где отдельные числа $ s [n] $ хранятся с использованием 16-битных целых чисел, $ s [n] $ может принимать только одно из 2 ¹⁶ значений.

В числовом ряду $ s [n] $ значения s могут принимать только фиксированный набор значений.

Цифровые сигналы – это сигналы с дискретным временем, полученные после «оцифровки». Цифровые сигналы также обычно получают путем измерения от явления реального мира. Однако, в отличие от принятой нормы для аналоговых сигналов, цифровые сигналы могут принимать комплексные значения.

Выше представлены некоторые критерии для реальных сигналов. Теоретические сигналы не ограничены

реальный – это часто нарушается; работаем с комплексными числами

конечное / ограниченное

энергия – ВСЕГДА нарушается
. Сигналы, которые имеют бесконечную временную протяженность, , то есть , которые простираются от $ – \ infty $ до $ \ infty $, могут иметь бесконечную энергию.

мощность – почти никогда: почти все сигналы, с которыми мы столкнемся, имеют ограниченную мощность

плавность – это часто нарушается многими из рассматриваемых нами сигналов непрерывного времени.

Примеры “стандартных” сигналов

Мы перечисляем некоторые основные типы сигналов, которые часто встречаются в DSP. Мы перечисляем их версии для непрерывного и дискретного времени. Обратите внимание, что аналоговые версии с непрерывным временем некоторых из этих сигналов являются искусственными конструкциями – они нарушают некоторые из условий, которые мы указано выше для сигналов реального мира и фактически не может быть реализовано.

Типы сигналов

Мы можем классифицировать сигналы по их свойствам, и все это повлияет на наш анализ этих сигналов позже.

Периодические сигналы

Сигнал является периодическим, если он повторяется ровно через некоторый промежуток времени. Однако значение периодичности различается для сигналов с непрерывным и дискретным временем.Мы рассмотрим каждый из них по очереди.

Сигналы непрерывного времени Таким образом, в непрерывном времени сигнал, если он называется периодическим, если существует какое-либо значение $ T $ такое, что \ [ s (t) = s (t + MT), ~~~~~ – \ infty \ leq M \ leq \ infty, ~~ \ text {integer} ~ M \] Наименьшее значение $ T $, для которого указанное выше соотношение удерживает период сигнала.

Дискретные сигналы времени

Определение периодичности для сигналов с дискретным временем аналогично определению для сигналов с непрерывным временем с одним ключевым отличием: период должен быть целым числом.Как мы увидим, это приводит к некоторым неинтуитивным выводам.

Дискретный сигнал времени $ x [n] $ называется периодическим, если существует положительное целое значение $ N $ такое, что \ [ x [n] = x [n + MN] \] для всех целых $ M $. Наименьшее значение $ N $, для которого справедливо указанное выше, является периодом сигнала.

Четные и нечетные сигналы

Симметический сигнал и даже – это сигнал, который зеркально отражается в момент времени $ t = 0 $.Сигнал считается, даже если он обладает следующим свойством: \ [ \ text {Непрерывное время:} ~ s (t) = s (-t) \\ \ text {Дискретное время:} ~ s [n] = s [-n] \]

Сигнал является нечетным симметическим сигналом, если он имеет следующее свойство: \ [ \ text {Непрерывное время:} ~ s (t) = -s (-t) \\ \ text {Дискретное время:} ~ s [n] = -s [-n] \]

На рисунке ниже показаны примеры четных и нечетных симметричных сигналов.Например, косинус даже симметричен, поскольку $ \ cos (\ theta) = \ cos (- \ theta) $, что приводит к $ \ cos (\ omega t) = \ cos (\ omega (-t)) $ . С другой стороны, синус нечетно симметричен, поскольку $ \ sin (\ theta) = – \ sin (- \ theta) $, что приводит к $ \ sin (\ omega t) = – \ sin (\ omega (-t) ) $.

Разложение сигнала на четные и нечетные составляющие Любой сигнал $ x [n] $ может быть выражен как сумма четного и нечетного сигналов следующим образом. \ [ x [n] = x_ {четное} [n] + x_ {нечетное} [n] \] куда \ [ x_ {даже} [n] = 0.5 (х [п] + х [-n]) \\ x_ {odd} [n] = 0,5 (x [n] – x [-n]) \]

Управляющие сигналы

Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Кратко рассмотрим эти манипуляции.

Масштабирование

Простое масштабирование сигнала вверх или вниз по коэффициенту усиления.

Непрерывное время: $ y (t) = a x (t) $

Дискретное время: $ y [n] = a x [n] $

$ a $ может быть реальным / мнимым, положительным / отрицательным. Когда $ a отрицательно, сигнал переворачивается по оси y.

Разворот времени

Переворот сигнала слева направо.

Непрерывное время: $ y (t) = x (-t) $

Дискретное время: $ y [n] = x [-n] $

Сдвиг во времени

Сигнал смещен вдоль оси индента на $ \ tau $ (или N для дискретного времени). Если $ \ tau $ положительно, сигнал задерживается, а если $ \ tau $ отрицательный сигнал продвигается.

Непрерывное время: $ y (t) = x (t- \ tau) $

Дискретное время: $ y [n] = x [n – N] $

Расширение

Саму временную ось можно масштабировать на $ \ alpha $.

Непрерывное время: $ y (t) = x (\ alpha t) $

Дискретное время: $ y [n] = x [/ alpha n] $

Расширение DT отличается от расширения CT, потому что $ x [n] $ определяется ТОЛЬКО для целого числа n, поэтому для существования $ y [n] = x [\ alpha n] $ «an» должно быть целым числом.

Однако $ x [\ alpha n] $ для $ a \ neq 1 $ проигрывает некоторым семплам. Вы никогда не сможете полностью восстановить x [n] из него. Этот процесс часто называют дециминкацией .

Для сигналов DT $ y [n] = x [\ alpha n] $ для $ \ alpha интерполировать нули для неопределенных значений, если $ an $ не является целым числом.

Составные сигналы

Сигналы могут быть составлены путем манипулирования и комбинирования других сигналов. Есть несколько способов комбинирования сигналов, и мы рассматриваем следующие два:

ПРИЛОЖЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) + x_2 (t) $ Дискретное время: $ y [n] = x_1 [n] + x_2 [n] $

УМНОЖЕНИЕ

Непрерывное время: $ y (t) = x_1 (t) x_2 (t) $ Дискретное время: $ y [n] = y_1 [n] y_2 [n] $

$ x_1 [n] $ и $ x_2 [n] $ сами могут быть получены путем манипулирования другими сигналами.{\ alpha t} u (t) $ для $ \ alpha

На самом деле односторонние сигналы могут быть получены умножением на u [n] (или сдвинутые / обращенные во времени версии u [n] или u (t)).

Получение базовых сигналов друг от друга

Можно получить один сигнал из другого просто с помощью математических манипуляций.{\ infty} u [k] \ delta [n-k] $

На этом завершается введение в сигналы. В обзоре мы обсудили важность DSP, типы сигналов и их свойства, манипуляции с сигналами, и состав сигнала. Далее мы обсудим системы.

Обработка сигналов в дискретном времени | edX

6.341x разработан для обеспечения как глубокого, так и интуитивного понимания теории, лежащей в основе современных систем и приложений обработки сигналов с дискретным временем.Курс начинается с обзора и расширения основ обработки сигналов, включая обсуждение систем с групповой задержкой и минимальной фазой, а также использования систем с дискретным временем (DT) для обработки сигналов с непрерывным временем (CT). В рамках курса разрабатываются структуры блок-схем и блок-схем, включая решетчатые фильтры для реализации систем DT, а также методы проектирования фильтров DT. Обсуждаются и разрабатываются параметрическое моделирование сигналов и эффективная реализация многоскоростных систем DT и систем преобразования частоты дискретизации.Представлено углубленное развитие ДПФ и его вычислений, а также его использование для спектрального анализа и фильтрации. Этот компонент курса включает в себя тщательную и проницательную разработку взаимосвязи между зависящим от времени преобразованием Фурье и использованием банков фильтров как для спектрального анализа, так и для кодирования сигналов.

6.341x состоит из одиннадцати разделов, каждый из которых обычно состоит из двух-четырех тем. Исходный материал для изучения каждой темы включает предлагаемые чтения в тексте курса, поясняющие примечания, прочую связанную литературу и отрывки из видео, а также будет включать интерактивный дискуссионный форум в режиме онлайн.Текст курса – это широко используемый текст Оппенгейма и Шафера (третье издание). Видеосегменты адаптированы на основе видеозаписей в реальном времени курса обучения в Массачусетском технологическом институте.

Каждая тема включает в себя набор автоматически оцениваемых упражнений для самооценки и помощи в усвоении и понимании основ темы, а в некоторых случаях и для предварительного просмотра тем. Типичная часть курса завершается набором более обширных задач, которые помогают интегрировать темы и развивать более глубокое понимание.Будет предоставлена автоматическая оценка ваших ответов на эти проблемы, а также решения.

6.341x и эта свободно доступная версия были разработаны при поддержке и поддержке Департамента электротехники и информатики Массачусетского технологического института, Управления цифрового обучения Массачусетского технологического института и Исследовательской лаборатории электроники Массачусетского технологического института.

Дискретный сигнал что это такое: Дискретный сигнал – это… Что такое Дискретный сигнал?

Дискретный сигнал – это… Что такое Дискретный сигнал?

Смотреть что такое “Дискретный сигнал” в других словарях:

Аналоговые, дискретные и цифровые сигналы

Как аналоговый сигнал преобразуется в цифровой

Виды дискретных сигналов. Аналоговый, дискретный, цифровой сигналы

См. также

Литература

Смотреть что такое “Дискретный сигнал” в других словарях:

См. также

Литература

Смотреть что такое “Дискретный сигнал” в других словарях:

Сигнал

Виды сигналов

Для чего обрабатывается сигнал?

Создание и формирование

Динамический диапазон

Аналоговый сигнал

Цифровой сигнал

Применение цифрового сигнала

Дискретный сигнал

Сравнение цифрового и аналогового сигналов

Информация и сигнал (8 класс) Информатика и ИКТ

Что формирует дискретный сигнал. Дискретный сигнал

Page

Discrete Signal – обзор

Periodic-Discrete

2.4: Сигналы в дискретном времени – Engineering LibreTexts

Реальные и комплексные сигналы

Комплексные экспоненты

Синусоиды

Единица Образец

Символьные сигналы

дискретная связь | теория информации

Бесшумная связь

шумная связь

появление в нервной системе

дискретных сигналов

Бесшумная связь

шумная связь

Возникновение в нервной системе

Односкоростные сигналы и системы с дискретным временем: общий обзор: Computer Science & IT Book Chapter

ДИСКРЕТНЫЕ ВРЕМЕННЫЕ СИГНАЛЫ

Анализ и проектирование дискретных сигналов | Wiley

Введение в сигналы

Почему цифровая обработка сигналов?

Определение сигналов

Примеры “стандартных” сигналов

Типы сигналов

Периодические сигналы

Четные и нечетные сигналы

Управляющие сигналы

Масштабирование

Разворот времени

Сдвиг во времени

Расширение

Составные сигналы

Получение базовых сигналов друг от друга

Обработка сигналов в дискретном времени | edX

Больше новостей

Добавить комментарий Отменить ответ