Эдс формула через силу тока и сопротивление: ЭДС источника 2,4 В. определить внутреннее сопротивление источник электроэнергии,если при включении в цепь резистора сопротивлением…

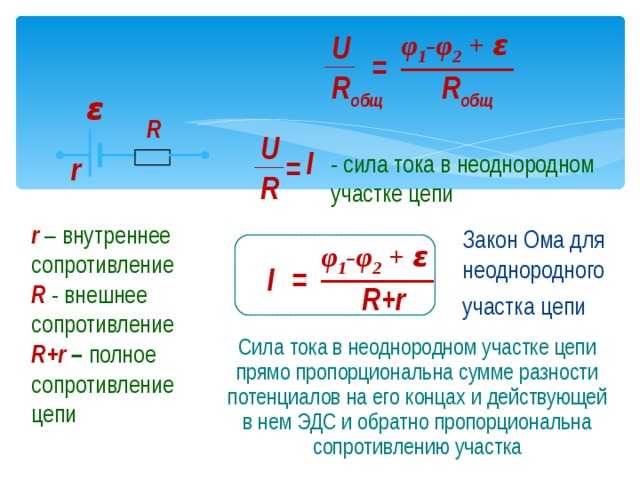
формула через силу тока, индуктивность или площадь, единица измерения в физике

Содержание:

• Что такое ЭДС индукции — когда возникает, при каких условиях
• ЭДС в быту, как обозначается, единицы измерения
• Законы Фарадея и Ленца
• Как рассчитать электродвижущую силу индукции, формулы
  • Через магнитный поток
  • Через силу тока
  • Через сопротивление
  • Через угловую скорость
  • Через площадь

Содержание

• Что такое ЭДС индукции — когда возникает, при каких условиях
• ЭДС в быту, как обозначается, единицы измерения
• Законы Фарадея и Ленца
• Как рассчитать электродвижущую силу индукции, формулы
  • Через магнитный поток
  • Через силу тока
  • Через сопротивление
  • Через угловую скорость
  • Через площадь

Что такое ЭДС индукции — когда возникает, при каких условиях

Определение

Электродвижущая сила, ЭДС — физическая величина, описывающая работу любых сил, которые действуют в квазистационарных цепях постоянного или переменного тока, за исключением диссипативных и электростатических сил.

При замкнутой цепи можно найти ЭДС, воспользовавшись законом Ома:

\(\varepsilon\;=\;I\;\times\;(R\;+\;r).\)

R здесь — сопротивление цепи, r — внутреннее сопротивление источника.

Создание Алессандро Вольтой надежного источника электричества, гальванического элемента, и открытие Хансом Кристианом Эрстедом магнитного действия электрического тока послужили толчком к интенсивному развитию техники электрических измерений в XIX веке.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Выдающаяся роль здесь принадлежит немецкому физику Георгу Симону Ому. Для определения силы тока он использовал принцип крутильных весов Кулона. На длинной тонкой нити подвешено горизонтальное коромысло с заряженным шариком на конце. Второй заряд закреплен на спице, пропущенной сквозь крышку весов.

При их взаимодействии коромысло поворачивается. Вращение головки в верхней части весов закручивало нить, возвращая коромысло в исходное состояние. По углу закручивания можно рассчитать силу взаимодействия зарядов в зависимости от расстояния между ними.

Ом по величине угла закрутки судил о силе тока I в проводнике, т. е. количестве электричества, перенесенном через поперечное сечение проводника за единицу времени.

В качестве основной характеристики источника тока Ом брал величину напряжения \varepsilon на электродах гальванического элемента при разомкнутой цепи. Эту величину \varepsilon он назвал электродвижущей силой, сокращенно ЭДС.

Движущиеся заряды создают вокруг себя магнитное поле. Однако действующая в нем на магнит или другой ток сила отличается от электрической своим направлением — магнитная стрелка старается развернуться перпендикулярно проводу.

Изучение действующей на другой ток силы переросло в отдельное исследование с неожиданным результатом: сила оказалась направленной всегда перпендикулярно внесенному в магнитное поле проводнику, который для простоты исследования был прямолинейным.

Математическое выражение для этой силы, названной силой Ампера, проще всего записать в виде векторного произведения:

\(d\overrightarrow F\;=\;Id\overrightarrow l\;\times\;\overrightarrow B\).

I здесь — сила тока, протекающего через проводник; l — вектор длины проводника, направленный в ту же сторону, куда течет ток; В — характеристика поля. Величина В называется магнитной индукцией и является аналогом электрической напряженности.

Максвелл поставил целью создать теорию эфира, связав его механические характеристики с электрическими и магнитными силами. Тщательно изучив труды Фарадея, он пришел к выводу, что напряженность \(\overrightarrow Е\) электрического поля объясняется упругими напряжениями в эфире, а магнитная индукция \(\overrightarrow B\) — его вихревыми движениями.

Рассматривая замкнутый проводящий контур С, где действует ЭДС индукции \(\varepsilon_i\), Максвелл для получения числа силовых линий магнитного потока \(\triangle Ф\), пересекаемых контуром за время \triangle t, «натягивал» на него некую поверхность S, разбитую на элементарные площадки \(\triangle S\), и отождествлял Ф с магнитным потоком сквозь всю поверхность.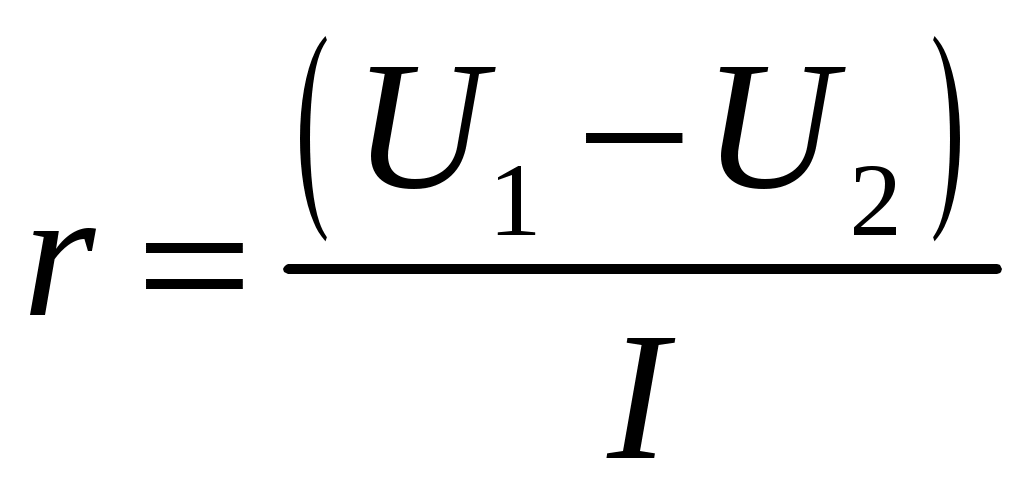 Математически это можно выразить так:

\(Ф\;=\;\sum_{\triangle S}\;\;B\triangle S. \)

Объединив это соотношение с идеей Фарадея, Максвелл пришел к собственной формуле:

\(\varepsilon_i\;=\;-\;\frac1с\;\times\;\frac{dФ}{dt}.\)

Выбор коэффициента пропорциональности \(\alpha\) здесь обусловлен необходимостью согласования формулы с законом Био — Савара — Лапласа, в котором появляется та же электродинамическая постоянная с.

Определение

Электродинамическая постоянная с — универсальная постоянная, равная скорости распространения электромагнитных волн в вакууме.

Но в опытах Фарадея ЭДС индукции регистрировалась как в движущемся, так и в покоящемся проводящем контуре С, если последний находился в переменном магнитном поле. И здесь встал вопрос, что конкретно перемещает заряды в неподвижном проводнике.

Само по себе магнитное поле не воздействует на заряды, находящиеся в покое, из чего следует: условие возникновения индукционного тока — возникающее в контуре электрическое поле \overrightarrow Е.  Так как электростатическое поле в замкнутом контуре не совершает работы, значит, происходит работа вихревого поля, и она равна ЭДС индукции:

\(\varepsilon_i\;=\;\underset С{\oint\;}\;(\overrightarrow{Е\;}\times\;d\overrightarrow l)\)

Определение

Самоиндукция — частный случай магнитной индукции, возникновение ЭДС индукции в проводящем контуре, когда в нем меняется ток.

Источником энергии, возникающей в цепи, является в этом случае запас энергии магнитного поля. Полное количество выделившейся джоулевой теплоты можно вычислить, изобразив на графике зависимость магнитного потока Ф(I) от силы тока I:

Источник: physics.ru

ЭДС в быту, как обозначается, единицы измерения

В быту явление электромагнитной индукции используют для изменения величины напряжения тока в трансформаторах и дросселях. На принципе магнитной индукции работают электрические счетчики, реле мощности, успокоительные системы стрелочных измерительных приборов.

Существуют также магнитные газовые генераторы, в которых благодаря магнитному полю возникает электродвижущая сила, создающая ток.

Электродвижущая сила индукции в системе СИ измеряется в вольтах. Просто электродвижущая сила обозначается греческой буквой \(\varepsilon \), электродвижущая сила индукции —\( \varepsilon_i.\)

Законы Фарадея и Ленца

Фарадей опытным путем выяснил, что при пересечении проводником магнитных силовых линий по нему проходит заряд \(\triangle Q\). Он связан с числом пересеченных силовых линий \( \triangle Ф\) и электрическим сопротивлением контура R, что выражается законом Фарадея:

\(\triangle Q\;=\;\alpha\frac{\triangle Ф}R. \)

Соприкосновение поля и проводника вызвано либо движением проводника, либо изменениями самого магнитного поля. 

Саму электродвижущую силу индукции, связанную с сопротивлением контура и силой тока согласно закону Ома, можно найти по формуле

\(\varepsilon_i\;=\;\alpha\frac{\triangle Ф}{\triangle t}.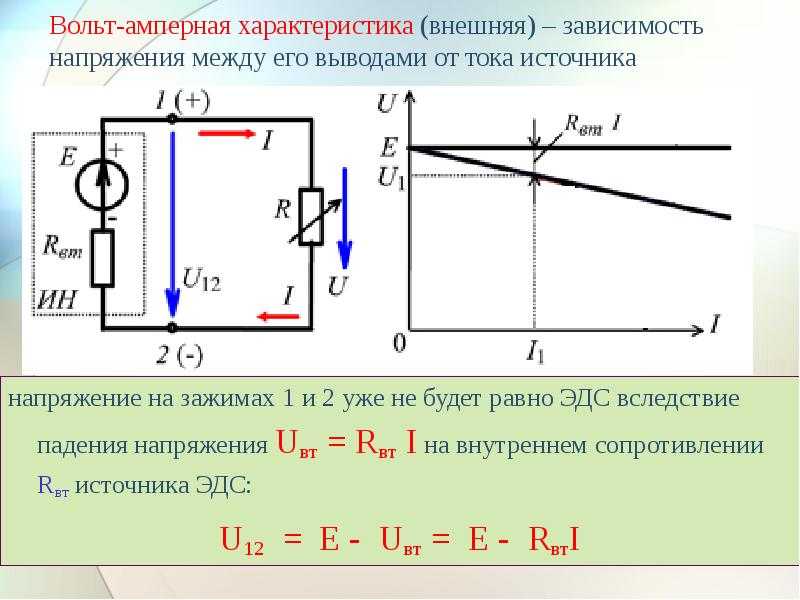

\)

\(\triangle t\) здесь — время, за которое проходит через поперечное сечение проводника количество электричества \(\triangle Q.\)
Ленц доказал, что индукционный ток всегда направлен так, чтобы противодействовать вызвавшей его причине. Согласно правилу Ленца, в вышеприведенном соотношении следует выбрать отрицательный знак, считая коэффициент\( \alpha \) положительным: 

\(\varepsilon_i\;=\;-\;\alpha\frac{\triangle Ф}{\triangle t}.\)

Как рассчитать электродвижущую силу индукции, формулы

Через магнитный поток

\(\varepsilon_i\;=\;-\;\alpha\frac{\triangle Ф}{\triangle t}. \)

Через силу тока

ЭДС самоиндукции зависит от изменения силы тока, при этом магнитный поток собственного поля через цепь пропорционален току в ней:

\(\varepsilon_{is\;}\;=\;-\;L\frac{\triangle I}{\triangle t}. \)

L здесь — индуктивность проводника.

Через сопротивление

Для ЭДС индукции уравнение закона Ома можно переписать в виде:
\(\varepsilon_{i\;}\;=\;IR\;-\;\varepsilon.\)

Через угловую скорость

\(\varepsilon_i\;=\;В\omega SN\sin\left(\alpha\right). \)

B здесь — индукция магнитного поля, \(\omega\) — угловая скорость вращения рамки, S — площадь рамки, N — число витков, \(\alpha\) — угол между векторами индукции магнитного поля и скорости движения проводника.

Через площадь

Если магнитный поток изменяется без деформации витков, т. е. их количество и площадь не меняются, то можно найти электродвижущую силу индукции через площадь.
Угол \alpha между вектором магнитного поля и нормалью к плоскости витков будет равен:

\(2\mathrm\pi\;\times\;\mathrm v\;\times\;\mathrm t. \)Полный магнитный поток в момент времени t будет равен:

\(\psi_B\;=\;N\;\times\;B\;\times\;S\;\times\;\cos\left(\alpha\right)=\;N\;\times\;B\;\times\;S\;\times\;\cos\left(2\mathrm\pi\;\times\;\mathrm v\;\times\;\mathrm t\right). \)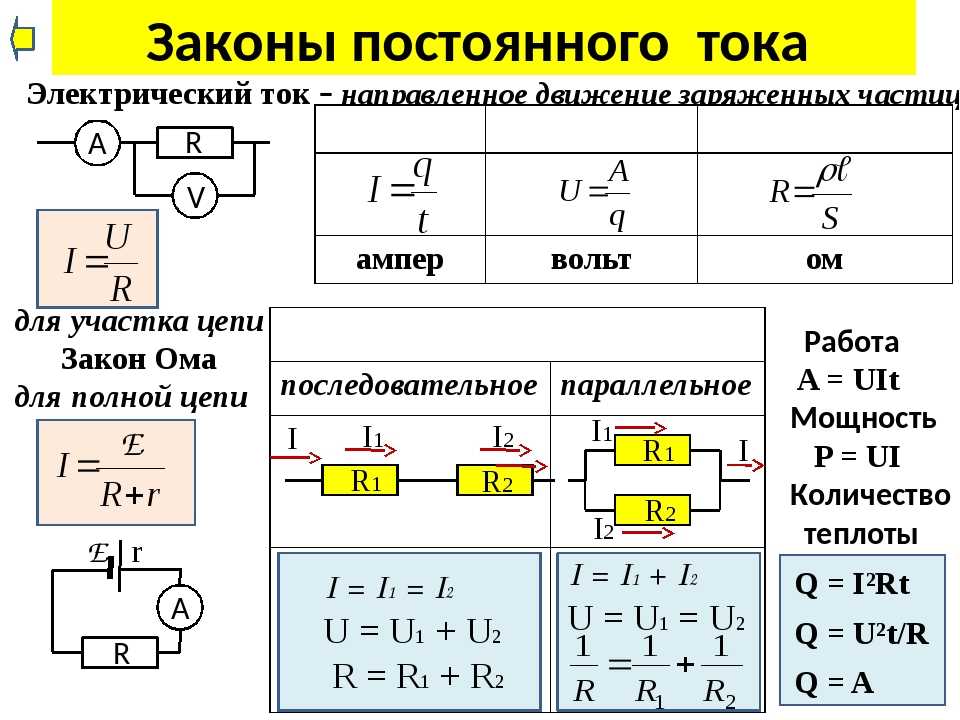

Тогда \(\varepsilon_i\;=\;-\;\frac{d\psi_B}{dt}=\;2\mathrm{pivNBSsin}\left(2\mathrm{pivt}\right).\)

Насколько полезной была для вас статья?

Рейтинг: 5.00 (Голосов: 1)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Поиск по содержимому

простыми словами с примерами для “чайников”

Содержание

Закон Ома для участка цепи

Закон Ома для участка цепи гласит, что сила тока (I) на участке электрической цепи прямо пропорциональна напряжению (U) на концах участка цепи и обратно пропорциональна его сопротивлению (R).

Закон Ома для замкнутой цепи

Если к источнику питания подключить внешнюю цепь сопротивлением R, в цепи пойдёт ток с учётом внутреннего сопротивления источника:

I — Сила тока в цепи. Электродвижущая сила (ЭДС) — величина напряжения источника питания не зависящая от внешней цепи (без нагрузки). Характеризуется потенциальной энергией источника.

r — Внутреннее сопротивление источника питания. Для электродвижущей силы внешнее сопротивление R и внутреннее r соединены последовательно, значит величина тока в цепи определится значением ЭДС и суммой сопротивлений: I =/(R+r) .

Напряжение на выводах внешней цепи определится исходя из силы тока и сопротивления R соотношением, которое уже рассматривалось выше: U = IR.

Напряжение U, при подключении нагрузки R, всегда будет меньше чем ЭДС на величину произведения I*r, которую называют падением напряжения на внутреннем сопротивлении источника питания. С этим явлением мы сталкиваемся достаточно часто, когда видим в работе частично разряженные батарейки или аккумуляторы. По мере разряда, увеличивается их внутреннее сопротивление, следовательно, увеличивается падение напряжение внутри источника, значит уменьшается внешнее напряжение U = — I*r. Чем меньше ток и внутреннее сопротивление источника, тем ближе по значению его ЭДС и напряжение на его выводах U.

Если ток в цепи равен нулю, следовательно, = U. Цепь разомкнута, ЭДС источника равна напряжению на его выводах. В случаях, когда внутренним сопротивлением источника можно пренебречь (r ≈ 0), напряжение на выводах источника будет равно ЭДС (≈ U ) независимо от сопротивления внешней цепи R. Такой источник питания называют источником напряжения.

Закон Ома для переменного тока

При наличии индуктивности или ёмкости в цепи переменного тока необходимо учитывать их реактивное сопротивление. В таком случае запись Закона Ома будет иметь вид: I = U/Z

Здесь Z — полное (комплексное) сопротивление цепи — импеданс. В него входит активная R и реактивная X составляющие. Реактивное сопротивление зависит от номиналов реактивных элементов, от частоты и формы тока в цепи. Более подробно ознакомится с комплексным сопротивлением можно на страничке импеданс.

С учётом сдвига фаз φ, созданного реактивными элементами, для синусоидального переменного тока обычно записывают Закон Ома в комплексной форме.

Нелинейные элементы и цепи

Закон Ома не является фундаментальным законом природы и может быть применим в ограниченных случаях, например, для большинства проводников. Его невозможно использовать для расчёта напряжения и тока в полупроводниковых или электровакуумных приборах, где эта зависимость не является пропорциональной и её можно определять только с помощью вольтамперной характеристики (ВАХ).

К данной категории элементов относятся все полупроводниковые приборы (диоды, транзисторы, стабилитроны, тиристоры, варикапы и т.д.) и электронные лампы. Такие элементы и цепи, в которых они используются, называют нелинейными.

Определение единицы сопротивления — Ом

1 Ом представляет собой электрическое сопротивление участка проводника, по которому при напряжении 1(Вольт) протекает ток 1(Ампер).

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Единицы измерения: вольт, ампер и ом

Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:

Единицы измерения тока, напряжения, сопротивления в таблице:

Величина	Символ	Единица измерения	Сокращение единицы измерения
Ток	I	Ампер	А
Напряжение	V	Вольт	В
Сопротивление	R	Ом	Ом

«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.

Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией».

Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

[E=IR]

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

[I = frac{E}{R}]

[R = frac{E}{I}]

Сила тока, Закон Ома, формула.

Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

[I=frac{U}{R}]

Сила тока, Закон Ома, формула.

Сила тока в проводнике прямо пропорциональна напряжению и обратно пропорциональна сопротивлению.

[I=frac{U}{R}]

Напряжение, Закон Ома, формула

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

[U = IR]

Напряжение, Закон Ома, формула.

Падение напряжения на участке проводника равно произведению силы тока в проводнике на сопротивление этого участка.

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

Какая величина тока (I) в этой цепи?

[I = frac{E}{R} = frac{12 В}{3 Ом} = 4 А]

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

Какое сопротивление (R) оказывает лампа?

[R = frac{E}{I} = frac{36 В}{4 А} = 9 Ом]

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

Какое напряжение обеспечивает батарея?

[E = IR = (2 А)(7 Ом) = 14 В]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Что дает параллельное и последовательное соединение

Теоретические знания — это хорошо, но как их применить на практике? Параллельно и последовательно могут соединяться элементы любого типа. Но мы рассматривали только простейшие формулы, описывающие линейные элементы. Линейные элементы — это сопротивления, которые еще называют «резисторы». Итак, вот как можно использовать полученные знания:

В общем, это наиболее распространенные варианты использования этих соединений.

Параллельное и последовательное соединение

В электрике элементы соединяются либо последовательно — один за другим, либо параллельно — это когда к одной точке подключены несколько входов, к другой — выходы от тех же элементов.

Закон Ома для параллельного и последовательного соединения

Параллельное соединение

Параллельное соединение — это когда начала проводников/элементов сходятся в одной точке, а в другой — соединены их концы. Постараемся объяснить законы, которые справедливы для соединений этого типа. Начнем с тока. Ток какой-то величины подается в точку соединения элементов. Он разделяется, протекая по всем проводникам. Отсюда делаем вывод, что общий ток на участке равен сумме тока на каждом из элементов: I = I1 + I2 + I3.

Теперь относительно напряжения. Если напряжение — это работа по перемещению заряда, тоо работа, которая необходима на перемещение одного заряда будет одинакова на любом элементе. То есть, напряжение на каждом параллельно подключенном элементе будет одинаковым. U = U1=U2=U3. Не так весело и наглядно, как в случае с объяснением закона Ома для участка цепи, но понять можно.

Для сопротивления все несколько сложнее. Давайте введем понятие проводимости. Это характеристика, которая показывает насколько легко или сложно заряду проходить по этому проводнику. Понятно, что чем меньше сопротивление, тем проще току будет проходить. Поэтому проводимость — G — вычисляется как величина обратная сопротивлению. В формуле это выглядит так: G = 1/R.

Законы для параллельного соединения

Для чего мы говорили о проводимости? Потому что общая проводимость участка с параллельным соединением элементов равна сумме проводимости для каждого из участков. G = G1 + G2 + G3 — понять несложно. Насколько легко току будет преодолеть этот узел из параллельных элементов, зависит от проводимости каждого из элементов. Вот и получается, что их надо складывать.

Теперь можем перейти к сопротивлению. Так как проводимость — обратная к сопротивлению величина, можем получить следующую формулу: 1/R = 1/R1 + 1/R2 + 1/R3.

Последовательное соединение

Как работает закон Ома для этих случаев? При последовательном соединении сила тока, протекающая через цепочку элементов, будет одинаковой. Напряжение участка цепи с последовательно подключенными элементами считается как сумма напряжений на каждом участке. Как можно это объяснить? Протекание тока через элемент — это перенос части заряда с одной его части в другую. То есть, это определенная работа. Величина этой работы и есть напряжение. Это физический смысл напряжения. Если с этим понятно, двигаемся дальше.

При последовательном соединении приходится переносить заряд по очереди через каждый элемент. И на каждом элементе это определенный «объем» работы. А чтобы найти объем работы на всем участке цепи, надо работу на каждом элементе сложить. Вот и получается, что общее напряжение — это сумма напряжений на каждом из элементов.

Последовательное соединение и параметры этого участка цепи.

Точно так же — при помощи сложения — находится и общее сопротивление участка цепи. Как можно это себе представить? Ток, протекая по цепочке элементов, последовательно преодолевает все сопротивления. Одно за другим. То есть чтобы найти сопротивление, которое он преодолел, надо сопротивления сложить. Примерно так. Математический вывод более сложен, а так понять механизм действия этого закона проще.

Практическое использование

Собственно, к любому участку цепи можно применить этот закон. Пример приведен на рисунке.

Применяем закон к любому участку цепи.

Используя такой план, можно вычислить все необходимые характеристики для неразветвленного участка. Рассмотрим более детальные примеры.

Находим силу тока

Рассмотрим теперь более определенный пример, допустим, возникла необходимость узнать ток, протекающий через лампу накаливания. Условия:

• Напряжение – 220 В;
• R нити накала – 500 Ом.

Решение задачи будет выглядеть следующим образом: 220В/500Ом=0,44 А.

Рассмотрим еще одну задачу со следующими условиями:

• R=0,2 МОм;
• U=400 В.

В этом случае, в первую очередь, потребуется выполнить преобразование: 0,2 МОм = 200000 Ом,после чего можно приступать к решению: 400 В/200000 Ом=0,002 А (2 мА).
Вычисление напряжения
Для решения мы также воспользуемся законом, составленным Омом. Итак задача:

• R=20 кОм;
• I=10 мА.

Преобразуем исходные данные:

• 20 кОм = 20000 Ом;
• 10 мА=0,01 А.

Решение: 20000 Ом х 0,01 А = 200 В.

Незабываем преобразовывать значения, поскольку довольно часто ток может быть указан в миллиамперах.

Сопротивление

Несмотря на то, что общий вид способа для расчета параметра «R» напоминает нахождение значения «I», между этими вариантами существуют принципиальные различия. Если ток может меняться в зависимости от двух других параметров, то R (на практике) имеет постоянное значение. То есть по своей сути оно представляется в виде неизменной константы.

Если через два разных участка проходит одинаковый ток (I), в то время как приложенное напряжение (U) различается, то, опираясь на рассматриваемый нами закон, можно с уверенностью сказать, что там где низкое напряжение «R» будет наименьшим. Рассмотрим случай когда разные токи и одинаковое напряжение на несвязанных между собой участках. Согласно закону, составленному Омом, большая сила тока будет характерна небольшому параметру «R».

Рассмотрим несколько примеров

Допустим, имеется цепь, к которой подведено напряжение U=50 В, а потребляемый ток I=100 мА. Чтобы найти недостающий параметр, следует 50 В / 0,1 А (100 мА), в итоге решением будет – 500 Ом.

Вольтамперная характеристика позволяет наглядно продемонстрировать пропорциональную (линейную) зависимость закона. На рисунке ниже составлен график для участка с сопротивлением равным одному Ому (почти как математическое представление закона Ома).

Изображение вольт-амперной характеристики, где R=1 Ом

Изображение вольт-амперной характеристики

Вертикальная ось графика отображает ток I (A), горизонтальная – напряжение U(В). Сам график представлен в виде прямой линии, которая наглядно отображает зависимость от сопротивления, которое остается неизменным. Например, при 12 В и 12 А «R» будет равно одному Ому (12 В/12 А).

Обратите внимание, что на приведенной вольтамперной характеристике отображены только положительные значения. Это указывает, что цепь рассчитана на протекание тока в одном направлении. Там где допускается обратное направление, график будет продолжен на отрицательные значения.

Заметим, что оборудование, вольт-амперная характеристика которого отображена в виде прямой линии, именуется — линейным. Этот же термин используется для обозначения и других параметров.

Помимо линейного оборудования, есть различные приборы, параметр «R» которых может меняться в зависимости от силы тока или приложенного напряжения. В этом случая для расчета зависимости нельзя использовать закон Ома. Оборудование такого типа называется нелинейным, соответственно, его вольт-амперные характеристики не будут отображены в виде прямых линий.

Видео: Закон Ома для участка цепи — практика расчета цепей

Источники

• https://poschitat.online/zakon-oma
• https://tel-spb.ru/ohm/
• https://radioprog.ru/post/920
• https://elektroznatok.ru/info/teoriya/zakon-oma
• https://www.asutpp.ru/zakon-oma-dlya-uchastka-cepi.html

10.2: Электродвижущая сила – Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

4407

• OpenStax
• OpenStax

Цели обучения

К концу раздела вы сможете:

• Описывать электродвижущую силу (ЭДС) и внутреннее сопротивление батареи
• Объясните основные принципы работы батареи

Если вы забудете выключить автомобильные фары, они постепенно притухнут по мере разрядки аккумулятора. Почему они не мигают внезапно, когда энергия батареи заканчивается? Их постепенное затемнение означает, что выходное напряжение батареи уменьшается по мере разрядки батареи. Причина снижения выходного напряжения у разряженных аккумуляторов заключается в том, что все источники напряжения имеют две основные части — источник электрической энергии и внутреннее сопротивление. В этом разделе мы исследуем источник энергии и внутреннее сопротивление.

Введение в электродвижущую силу

Напряжение имеет множество источников, некоторые из которых показаны на рисунке \(\PageIndex{2}\). Все такие устройства создают разность потенциалов и могут подавать ток, если подключены к цепи. Особый тип разности потенциалов известен как электродвижущая сила (ЭДС) . ЭДС вообще не является силой, но термин «электродвижущая сила» используется по историческим причинам. Он был придуман Алессандро Вольта в 1800-х годах, когда он изобрел первую батарею, также известную как 9. 0046 вольтова столб . Поскольку электродвижущая сила не является силой, эти источники принято называть просто источниками ЭДС (произносится буквами «э-э-э-э»), а не источниками электродвижущей силы.

Рисунок \(\PageIndex{1}\): различные источники напряжения. а) ветряная электростанция Бразос в Флуванне, штат Техас; (б) Красноярская ГЭС в России; в) солнечная ферма; (d) группа никель-металлогидридных аккумуляторов. Выходное напряжение каждого устройства зависит от его конструкции и нагрузки. Выходное напряжение равно ЭДС только при отсутствии нагрузки. (кредит a: модификация работы «Leaflet»/Wikimedia Commons; кредит b: модификация работы Алекса Полежаева; кредит c: модификация работы Министерства энергетики США; кредит d: модификация работы Тиаа Монто)

Если электродвижущая сила вовсе не сила, то что такое ЭДС и что является источником ЭДС? Чтобы ответить на эти вопросы, рассмотрим простую схему 12-вольтовой лампы, подключенной к 12-вольтовой батарее, как показано на рисунке \(\PageIndex{2}\).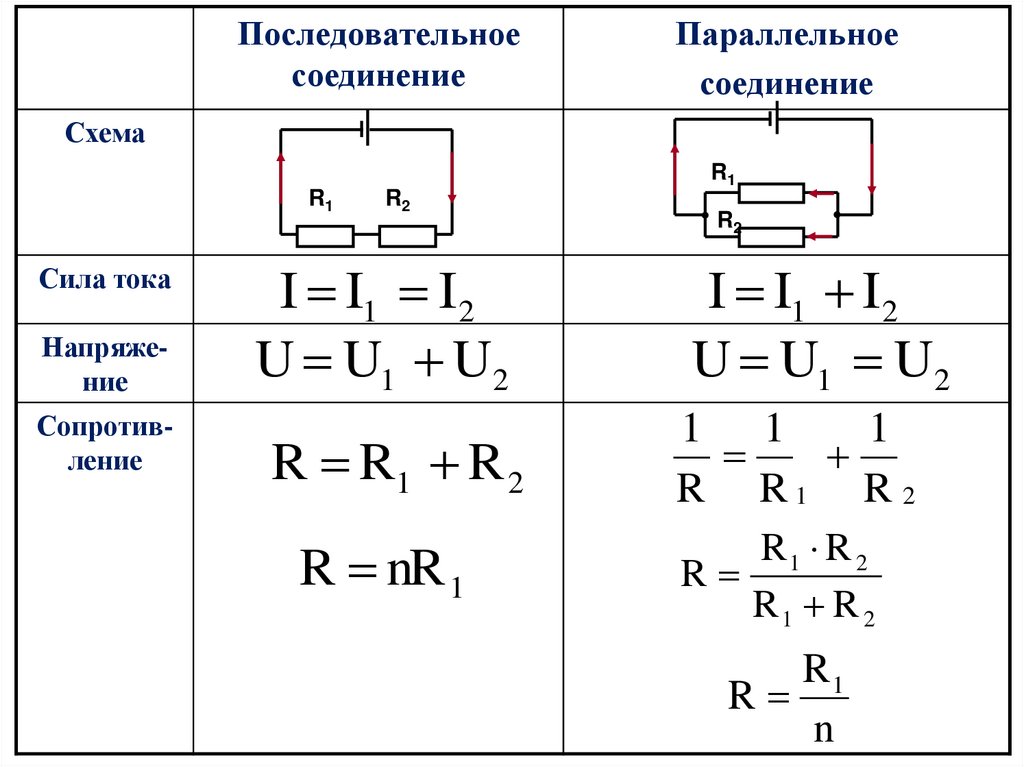 Батарея может быть смоделирована как устройство с двумя выводами, в котором один вывод имеет более высокий электрический потенциал, чем второй вывод. Более высокий электрический потенциал иногда называют положительной клеммой и обозначают знаком плюс. Клемму с более низким потенциалом иногда называют отрицательной клеммой и обозначают знаком минус. Это источник ЭДС.

Рисунок \(\PageIndex{2}\): Источник ЭДС поддерживает на одной клемме более высокий электрический потенциал, чем на другой клемме, действуя как источник тока в цепи.

Если источник ЭДС не подсоединен к лампе, в источнике ЭДС нет чистого потока заряда. Как только батарея подключена к лампе, заряды текут от одной клеммы батареи, через лампу (заставляя лампу загораться) и обратно к другой клемме батареи. Если мы рассмотрим положительный (обычный) ток, положительные заряды покидают положительную клемму, проходят через лампу и входят в отрицательную клемму.

Положительный ток полезен для большинства анализов цепей в этой главе, но в металлических проводах и резисторах наибольший вклад в ток вносят электроны, протекающие в направлении, противоположном положительному току. Поэтому более реалистично рассматривать движение электронов для анализа схемы на рисунке \(\PageIndex{2}\). Электроны покидают отрицательную клемму, проходят через лампу и возвращаются к положительной клемме. Чтобы источник ЭДС поддерживал разность потенциалов между двумя выводами, отрицательные заряды (электроны) должны перемещаться от положительного вывода к отрицательному. Источник ЭДС действует как зарядовый насос, перемещая отрицательные заряды от положительного вывода к отрицательному, чтобы поддерживать разность потенциалов. Это увеличивает потенциальную энергию зарядов и, следовательно, электрический потенциал зарядов.

Сила электрического поля, действующая на отрицательный заряд, действует в направлении, противоположном электрическому полю, как показано на рисунке \(\PageIndex{2}\). Чтобы отрицательные заряды переместились на отрицательный полюс, над отрицательными зарядами должна быть совершена работа. Для этого требуется энергия, которая возникает в результате химических реакций в аккумуляторе. Потенциал поддерживается высоким на положительной клемме и низким на отрицательной клемме, чтобы поддерживать разность потенциалов между двумя клеммами. ЭДС равна работе, совершаемой над зарядом на единицу заряда \(\left(\epsilon = \frac{dW}{dq}\right)\) при отсутствии тока. Поскольку единицей работы является джоуль, а единицей заряда — кулон, единицей ЭДС является вольт \((1 \, V = 1 \, J/C)\).

Напряжение на клеммах \(V_{клемма}\) батареи — это напряжение, измеренное на клеммах батареи, когда к клемме не подключена нагрузка. Идеальная батарея — это источник ЭДС, поддерживающий постоянное напряжение на клеммах, независимо от тока между двумя клеммами. Идеальная батарея не имеет внутреннего сопротивления, а напряжение на клеммах равно ЭДС батареи. В следующем разделе мы покажем, что реальная батарея имеет внутреннее сопротивление и напряжение на клеммах всегда меньше, чем ЭДС батареи.

Происхождение потенциала батареи

Комбинация химических веществ и состав клемм в батарее определяют ее ЭДС. Свинцово-кислотный аккумулятор , используемый в автомобилях и других транспортных средствах, представляет собой одну из наиболее распространенных комбинаций химических веществ. На рисунке \(\PageIndex{3}\) показан один элемент (один из шести) этой батареи. Катодная (положительная) клемма элемента соединена с пластиной из оксида свинца, тогда как анодная (отрицательная) клемма подключена к свинцовой пластине. Обе пластины погружены в серную кислоту, электролит для системы.

Рисунок \(\PageIndex{3}\): Химические реакции в свинцово-кислотном аккумуляторе разделяют заряд, направляя отрицательный заряд на анод, соединенный со свинцовыми пластинами. Пластины оксида свинца соединены с положительным или катодным выводом элемента. Серная кислота проводит заряд, а также участвует в химической реакции.

Знание того, как взаимодействуют химические вещества в свинцово-кислотном аккумуляторе, помогает понять потенциал, создаваемый аккумулятором. На рисунке \(\PageIndex{4}\) показан результат одной химической реакции. Два электрона размещены на анод , что делает его отрицательным, при условии, что катод поставляет два электрона. Это оставляет катод положительно заряженным, потому что он потерял два электрона. Короче говоря, разделение заряда было вызвано химической реакцией.

Обратите внимание, что реакция не происходит, если нет полной цепи, позволяющей подавать два электрона на катод. Во многих случаях эти электроны исходят от анода, проходят через сопротивление и возвращаются к катоду. Заметим также, что поскольку в химических реакциях участвуют вещества, обладающие сопротивлением, невозможно создать ЭДС без внутреннего сопротивления.

Рисунок \(\PageIndex{4}\): В свинцово-кислотном аккумуляторе два электрона направляются на анод элемента, а два электрона удаляются с катода элемента. Химическая реакция в свинцово-кислотном аккумуляторе помещает два электрона на анод и удаляет два электрона с катода. Для продолжения требуется замкнутая цепь, поскольку два электрона должны быть подведены к катоду.

Внутреннее сопротивление и напряжение на клеммах

Величина сопротивления протеканию тока внутри источника напряжения называется внутреннее сопротивление . Внутреннее сопротивление х батареи может вести себя сложным образом. Обычно он увеличивается по мере разрядки аккумулятора из-за окисления пластин или снижения кислотности электролита. Однако внутреннее сопротивление может также зависеть от величины и направления тока через источник напряжения, его температуры и даже его истории. Внутреннее сопротивление перезаряжаемых никель-кадмиевых элементов, например, зависит от того, сколько раз и насколько глубоко они разряжались. Простая модель батареи состоит из идеализированного источника ЭДС \(\эпсилон\) и внутреннего сопротивления r (Рисунок \(\PageIndex{5}\)).

Рисунок \(\PageIndex{5}\): Батарея может быть смоделирована как идеализированная ЭДС \((\эпсилон)\) с внутренним сопротивлением ( r ). Напряжение на клеммах батареи равно \(V_{terminal} = \epsilon – Ir\).

Предположим, внешний резистор, известный как сопротивление нагрузки R , подключен к источнику напряжения, например к батарее, как показано на рисунке \(\PageIndex{6}\). На рисунке представлена ​​модель батареи с ЭДС ε, внутренним сопротивлением Ом и нагрузочный резистор R , подключенный к его клеммам. Используя обычный ток, положительные заряды покидают положительную клемму батареи, проходят через резистор и возвращаются к отрицательной клемме батареи. Напряжение на выводах батареи зависит от ЭДС, внутреннего сопротивления и тока и равно

Примечание

\[V_{клемма} = \эпсилон – Ir\]

При заданных ЭДС и внутреннем сопротивлении , напряжение на клеммах уменьшается по мере увеличения тока из-за падения потенциала Ir внутреннего сопротивления.

Рисунок \(\PageIndex{6}\): Схема источника напряжения и его нагрузочного резистора R . Поскольку внутреннее сопротивление r включено последовательно с нагрузкой, оно может существенно повлиять на напряжение на клеммах и ток, подаваемый на нагрузку.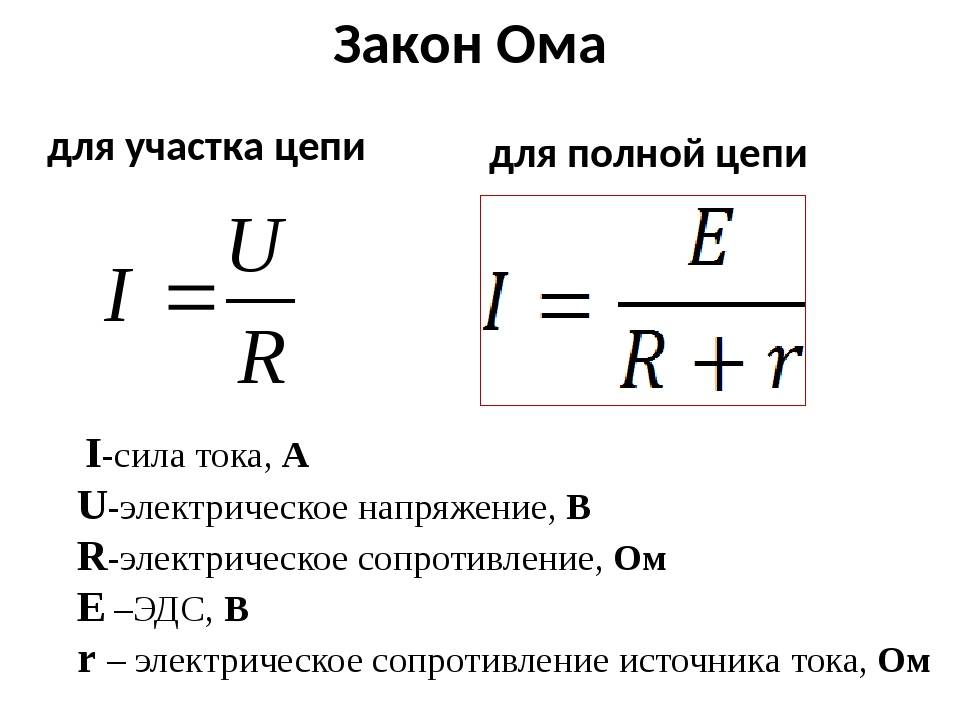

График разности потенциалов на каждом элементе цепи показан на рисунке \(\PageIndex{7}\). По цепи протекает ток I , а падение потенциала на внутреннем резисторе равно Ир . Напряжение на клеммах равно \(\эпсилон – Ir\), что равно падению потенциала на нагрузочном резисторе \(IR = \эпсилон – Ir\). Как и в случае с потенциальной энергией, важно изменение напряжения. Когда используется термин «напряжение», мы предполагаем, что на самом деле это изменение потенциала или \(\Delta V\). Однако \(\Delta\) часто опускается для удобства.

Рисунок \(\PageIndex{7}\): График зависимости напряжения в цепи аккумулятора и сопротивления нагрузки. Электрический потенциал увеличивает ЭДС батареи из-за химических реакций, совершающих работу над зарядами. В аккумуляторе происходит уменьшение электрического потенциала из-за внутреннего сопротивления. Потенциал уменьшается из-за внутреннего сопротивления \(-Ir\), делая напряжение на клеммах батареи равным \((\эпсилон – Ir)\). Затем напряжение уменьшается на ( ИР ). Ток равен \(I = \frac{\epsilon}{r + R}\).

Ток через нагрузочный резистор равен \(I = \frac{\epsilon}{r + R}\). Из этого выражения мы видим, что чем меньше внутреннее сопротивление r , тем больший ток источник напряжения отдает на свою нагрузку R . По мере разрядки батарей r увеличивается. Если r становится значительной долей сопротивления нагрузки, то ток значительно снижается, как показано в следующем примере.

Пример \(\PageIndex{1}\): Анализ цепи с батареей и нагрузкой

Данная батарея имеет ЭДС 12,00 В и внутреннее сопротивление \(0,100 \, \Омега\). (a) Рассчитайте напряжение на его клеммах при подключении к \(10,00 \, \Омега\) нагрузке. (b) Какое напряжение на клеммах при подключении к нагрузке \(0,500 \, \Омега\)? в) Какую мощность рассеивает нагрузка \(0,500\, \Омега\)? (d) Если внутреннее сопротивление возрастает до \(0,500 Ом, \Омега\), найти ток, напряжение на клеммах и мощность, рассеиваемую нагрузкой \(0,500 Ом, \Омега\).

Стратегия

Вышеприведенный анализ дал выражение для тока с учетом внутреннего сопротивления. Как только ток найден, напряжение на клеммах можно рассчитать, используя уравнение \(V_{клемма} = \эпсилон – Ir\). Как только ток найден, мы также можем найти мощность, рассеиваемую резистором.

Решение

1. Ввод заданных значений ЭДС, сопротивления нагрузки и внутреннего сопротивления в приведенное выше выражение дает \[I = \frac{\epsilon}{R + r} = \frac{12,00 \, V }{10,10 \, \Omega} = 1,188 \, A.\] Введите известные значения в уравнение \(V_{клемма} = \epsilon – Ir\), чтобы получить напряжение на клеммах: \[V_{клемма} = \ эпсилон – Ir = 12,00 \, V – (1,188 \, А)(0,100 \, \Омега) = 11,90 \, В. \] Напряжение на клеммах здесь лишь немного ниже, чем ЭДС, что означает, что ток, потребляемый этой легкой нагрузкой, незначителен.
2. Аналогично, при \(R_{нагрузка} = 0,500 \, \Omega\), ток равен \[I = \frac{\epsilon}{R + r} = \frac{12,00 \, V}{0,600 \, \Omega} = 20,00 \, A. 2(0,500 Ом, \Омега) = 72,00 Ом, Вт.\] Мы видим, что увеличение внутреннего сопротивления значительно уменьшило напряжение на клеммах, ток и мощность, подаваемая на нагрузку.

Значение

Внутреннее сопротивление батареи может увеличиваться по многим причинам. Например, внутреннее сопротивление перезаряжаемой батареи увеличивается по мере увеличения количества перезарядок батареи. Повышенное внутреннее сопротивление может иметь два последствия для батареи. Во-первых, напряжение на клеммах уменьшится. Во-вторых, батарея может перегреться из-за увеличения мощности, рассеиваемой внутренним сопротивлением.

Упражнение \(\PageIndex{1}\)

Если вы поместите провод прямо через две клеммы батареи, эффективно закоротив клеммы, батарея начнет нагреваться. Как вы думаете, почему это происходит?

Раствор

Если к клеммам подсоединен провод, сопротивление нагрузки близко к нулю или, по крайней мере, значительно меньше внутреннего сопротивления батареи. 2r)\). Мощность рассеивается в виде тепла.

Тестеры аккумуляторов

Тестеры аккумуляторов, подобные показанным на рис. \(\PageIndex{8}\), используют небольшие нагрузочные резисторы для преднамеренного отбора тока, чтобы определить, падает ли потенциал на клеммах ниже допустимого уровня. Хотя измерить внутреннее сопротивление батареи сложно, тестеры батарей могут обеспечить измерение внутреннего сопротивления батареи. Если внутреннее сопротивление высокое, батарея слабая, о чем свидетельствует низкое напряжение на клеммах.

Рисунок \(\PageIndex{8}\): Тестер батарей измеряет напряжение на клеммах под нагрузкой, чтобы определить состояние батареи. (a) Техник по электронике ВМС США использует тестер батарей для проверки больших батарей на борту авианосца USS Nimitz . Тестер батареи, который она использует, имеет небольшое сопротивление, которое может рассеивать большое количество энергии. (b) Показанное небольшое устройство используется на небольших батареях и имеет цифровой дисплей для индикации допустимого напряжения на клеммах. (кредит a: модификация работы Джейсона А. Джонстона; кредит b: модификация работы Кейта Уильямсона)

Некоторые аккумуляторы можно заряжать, пропуская через них ток в направлении, противоположном току, который они подают в электроприбор. Это обычно делается в автомобилях и в батареях для небольших электроприборов и электронных устройств (рис. \(\PageIndex{9}\)). Выходное напряжение зарядного устройства должно быть больше, чем ЭДС аккумулятора, чтобы ток через него изменил направление. Это приводит к тому, что напряжение на клеммах батареи больше, чем ЭДС, поскольку \(V = \эпсилон – Ir\) и I теперь отрицательный.

Рисунок \(\PageIndex{9}\): Зарядное устройство автомобильного аккумулятора меняет нормальное направление тока через аккумулятор, обращая его химическую реакцию и восстанавливая его химический потенциал.

Важно понимать последствия внутреннего сопротивления источников ЭДС, таких как батареи и солнечные элементы, но часто анализ цепей выполняется с напряжением на клеммах батареи, как мы делали в предыдущих разделах. Напряжение на клеммах обозначается просто как V без нижнего индекса «терминал». Это связано с тем, что внутреннее сопротивление батареи трудно измерить напрямую, и оно может меняться со временем.

Авторы и авторство

Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойолы Мэримаунт) и Билл Моебс со многими сотрудничающими авторами. Эта работа находится под лицензией OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).

---

Эта страница под названием 10.2: Electromotive Force распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Версия лицензии

   4,0

   Программа OER или Publisher

   ОпенСтакс

   Показать оглавление

   нет

2. Теги

   1. электродвижущая сила (эдс)
   2. внутреннее сопротивление
   3. разность потенциалов
   4. падение потенциала
   5. источник@https://openstax. org/details/books/university-physics-volume-2
   6. клеммное напряжение

Как рассчитать ЭДС | наука

Обновлено 2 ноября 2020 г.

Автор Lee Johnson

Электродвижущая сила (ЭДС) — незнакомое большинству людей понятие, но оно тесно связано с более знакомым понятием напряжения. Понимание разницы между ними и того, что означает ЭДС, дает вам инструменты, необходимые для решения многих задач в физике и электронике, и вводит понятие внутреннего сопротивления батареи. ЭДС говорит вам о напряжении батареи без уменьшения внутреннего сопротивления, как это происходит при обычном измерении разности потенциалов. Вы можете рассчитать его несколькими способами, в зависимости от того, какая информация у вас есть.

TL;DR (слишком длинный; не читал)

Рассчитайте ЭДС по формуле:

​ ε = V + Ir ​

ток в цепи и (r) означает внутреннее сопротивление элемента.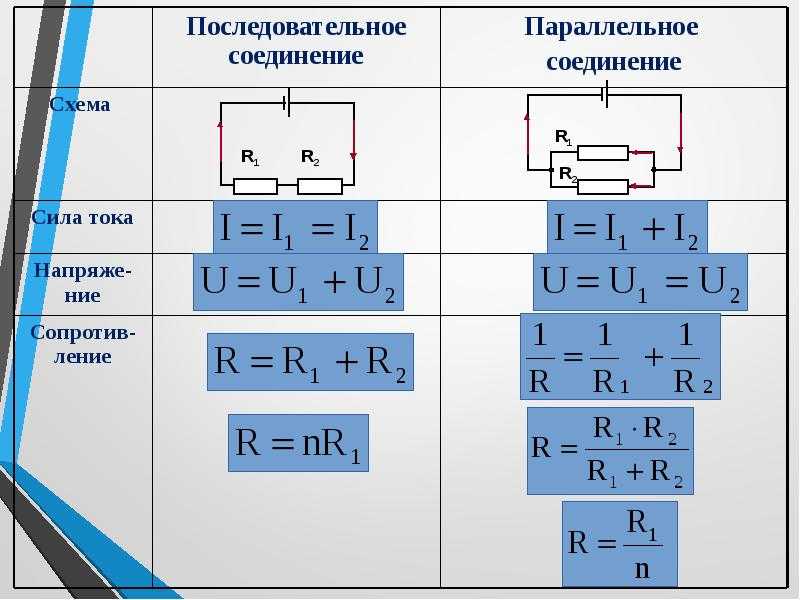

Что такое ЭДС?

Электродвижущая сила представляет собой разность потенциалов (т. е. напряжение) на клеммах батареи при отсутствии тока. Может показаться, что это не имеет значения, но каждая батарея имеет «внутреннее сопротивление». Это похоже на обычное сопротивление, уменьшающее ток в цепи, но оно существует внутри самой батареи. Это связано с тем, что материалы, используемые для изготовления элементов батареи, имеют собственное сопротивление (поскольку практически все материалы имеют его).

Когда через ячейку не протекает ток, это внутреннее сопротивление ничего не меняет, потому что нет тока, который мог бы его замедлить. В некотором смысле, ЭДС можно рассматривать как максимальную разность потенциалов на клеммах в идеализированной ситуации, и на практике она всегда больше, чем напряжение батареи.

Уравнения для расчета ЭДС

Существуют два основных уравнения для расчета ЭДС. Наиболее фундаментальное определение — это количество джоулей энергии (E), которое получает каждый кулон заряда (Q), проходя через ячейку:

Где (ε) — символ электродвижущей силы, (E) — энергия в цепи, а (Q) — заряд цепи. Если вы знаете результирующую энергию и количество заряда, прошедшего через ячейку, это самый простой способ рассчитать ЭДС, но в большинстве случаев у вас не будет этой информации.

Вместо этого вы можете использовать определение, больше похожее на закон Ома (V = IR). Это можно выразить следующим образом:

\epsilon =I(R+r)

Где (I) означает ток, (R) — сопротивление рассматриваемой цепи, а (r) — внутреннее сопротивление ячейки. Расширение этого показывает тесную связь с законом Ома:

\epsilon =IR+Ir=V+Ir

Это показывает, что вы можете рассчитать ЭДС, если знаете напряжение на клеммах (напряжение, используемое в реальных ситуациях), протекающий ток и внутреннее сопротивление клетка.

Как рассчитать ЭДС: пример

В качестве примера представьте, что у вас есть цепь с разностью потенциалов 3,2 В, с текущим током 0,6 А и внутренним сопротивлением батареи 0,5 Ом.