Эффекте холла: что это такое, формулы, применение

что это такое, формулы, применение

В этой статье вы узнаете, что такое эффект Холла и как он применяется на практике. Вы также узнаете, как вывести напряжение Холла, и получите практический пример расчета. Наконец, мы рассмотрим другие варианты эффекта Холла, такие как квантовый эффект Холла.

Простое объяснение

Эффект Холла был продемонстрирован Эдвином Холлом в 1879 году. Как вы, возможно, уже знаете, сила Лоренца действует на движущийся заряд в магнитном поле.

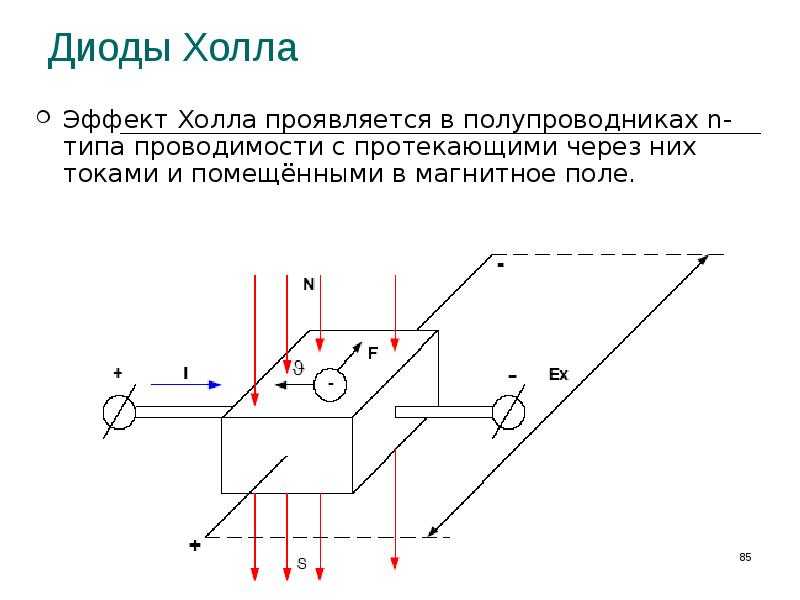
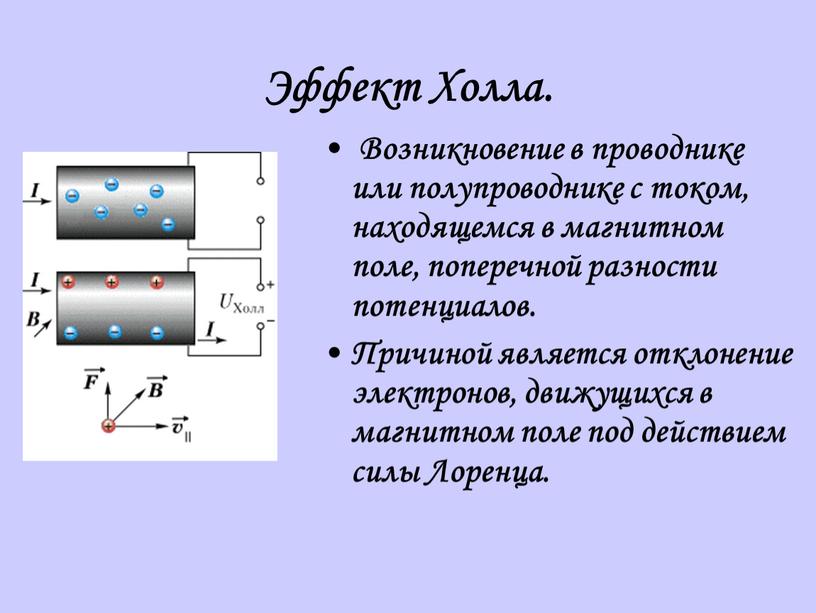
Эффект Холла — это возникновение в электрическом проводнике разности потенциалов на краях образца (напряжения Холла) помещённом в поперечное магнитное поле, при протекании тока, перпендикулярному полю.

Википедия

Это создает электрическое напряжение, которое падает как в направлении протекания электрического тока, так и в направлении магнитного поля на проводнике и называется напряжением Холла.

Физическое объяснение эффекта Холла

Если приложить напряжение к электрическому проводнику, называемому здесь образцом, потечет электрический ток. Электроны движутся по проводнику со средней скоростью v, также называемой скоростью дрейфа. Если держать образец в стационарном магнитном поле, то на электроны действует сила Лоренца. Это вызывает отклонение электронов перпендикулярно движению. Это вызывает избыток электронов на стороне отклонения и соответствующий недостаток электронов на противоположной стороне.

Рис. 1. Эффект Холла: избыток и недостаток электронов

Вы можете представить себе это разделение зарядов как сходное с разделением зарядов в конденсаторе. Поскольку положительно и отрицательно заряженные стороны теперь находятся напротив друг друга, создается электрическое поле. Это электрическое поле оказывает на электроны силу, противоположную силе Лоренца. Если эти две силы компенсируют друг друга в одинаковой степени, то усиление разделения зарядов заканчивается.

Как и в случае с конденсатором, здесь можно отводить напряжение. Это электрическое напряжение называется напряжением Холла. Это напряжение Холла линейно возрастает с увеличением магнитного поля и антипропорционально плотности носителей заряда. Это объясняется тем, что неизменная сила тока при меньшем числе носителей заряда может быть достигнута только за счет большей скорости отдельных носителей заряда. Более сильная сила Лоренца действует на более быстрые носители заряда, что увеличивает напряжение Холла.

Вычисление напряжения Холла

Для того чтобы понять вывод напряжения Холла, необходимо базовое понимание векторного исчисления.

Здесь вы можете увидеть набросок расчета напряжения Холла. Он действителен только для одного типа носителей заряда, например, для металлических образцов.

Сила Лоренца, действующая на проводник в магнитном поле, задается следующим образом:

Где, сила Лоренца F, q — электрический заряд, v — скорость и магнитное поле B. В эффекте Холла возникает электрическое поле E, которое нейтрализует отклоняющую силу магнитного поля. Поэтому:

Для упрощения зададим систему координат так, чтобы носители заряда двигались в направлении x, а магнитное поле действовало в направлении z. Это дает v = ( v_x, 0, 0 ) и B = ( 0, 0, B_z ). После деления на q получается y-компонента:

E_y — v_xB_z = 0

Плотность тока J в проводнике выражается через J = n*q*v, при плотности носителей заряда n. Если преобразовать это уравнение в v_x и подставить его в вышеприведенное уравнение, то получится:

E_y = j_x * B_z * ( 1 / n * q ) = A_H * j_x * B_z.

Мы определили коэффициента Холла A_H, которая характеризует силу эффекта Холла.

Поскольку вы уже знаете, что можно рассматривать разделение зарядов аналогично разделению в конденсаторе, то для упрощения можно использовать следующее обозначение:

E_y = U_H / b

Плотность тока в этом случае может быть выражена через j_x = I / b*d, где I — сила тока, b — ширина проводника и d — толщина проводника. Подставляя оба выражения, получаем для напряжения Холла следующее выражение:

U_H = A_H * ( I * B_z / d )

Расчёт коэффициента Холла

В качестве примера представьте медную пластину (ширина b = 18 мм, толщина d = 0,001 м). Она вносится в магнитное поле с плотностью магнитного потока B = 1,2 Тл. Если через пластину протекает электрический ток I = 15 А, то можно измерить напряжение Холла U_H = — 1,02 * 10^-6 В .

Рис. 2. Расчет коэффициента холла

Если взять приведенную выше формулу и преобразовать ее в A_H, то получится: A_H = U_H * d / I * B .

Подставляя значения, можно вычислить коэффициент Холла, то есть: A_H = — 1,02 * 10^-6 * 0,001 / 15 * 1,2 = — 5,7 * 10^-11 мм³ / Кл

По их отрицательному знаку видно, что это электроны, а не дырки или положительные заряды.

Применение эффекта Холла

Эффект Холла используется в нескольких областях. В электронике, например, он используется для так называемых датчиков Холла. Они используются для измерения магнитных полей. Для этого известен коэффициент Холла конкретного материала, задается необходимый электрический ток и, таким образом, вычисляется напряжение Холла. С помощью приведенной выше формулы датчик Холла может рассчитать магнитное поле.

Кроме того, эффект Холла также используется для расчета плотности носителей заряда. Для этого измеряется коэффициент Холла и уравнение преобразуется соответствующим образом.

Квантовый эффект Холла.

В квантовом эффекте Холла электрический ток не может произвольно изменяться при низких температурах и сильных магнитных полях в двумерных системах путем изменения напряженности магнитного поля. Вместо этого он изменяется ступенчато.

Существуют и другие известные эффекты Холла. Например, спин-эффект Холла, планарный эффект Холла, тепловой эффект Холла и эффект Нернста.

Список использованной литературы

1. Ashcroft Neil W., Mermin N. David. Solid state physics : [англ.]. — New York : Saunders College Publishing, 1976. — ISBN 0-03-083993-9.
2. Введение в физику плазмы и управляемый синтез, Том 1, Физика плазмы, второе издание, 1984, Фрэнсис Ф. Чен
3. Абрикосов А. А. Основы теории металлов. — Москва: «Наука», главная редакция физико-математической литературы, 1987. — 520 с. — ISBN нет, ББК 22.37, УДК 539.21 (075.8).

что это, зачем используется и где применяется / Хабр

Измерять характеристики магнитного поля можно как при помощи элементарных систем, так и посредством весьма сложных технологических решений. Все зависит от того, какие именно измерения выполняются и какие результаты ожидается получить. Самые простые датчики магнитного поля — герконы. Эти элементы изменяют состояние подключенной электрической цепи при воздействии магнитного поля. Герконы используются повсеместно, например, в датчиках открытия двери.

Герконы — очень простые системы. Для получения дополнительной информации о магнитном поле можно использовать еще и компас. Примерно так работали первые магнитометры. Но сейчас возможностей гораздо больше, ведь появились новые системы, включая распространенные датчики, где используется эффект Холла.

Спектр моделей таких датчиков чрезвычайно обширен — от клавиатур до оценки закрытия или открытия клапана. Датчики Холла используются в бесконтактной системе зажигания бензиновых двигателей, они служат для считывания показаний распредвала двигателя, с тем, чтобы определять параметры вращения. Электронный блок управления автомобиля по показаниям датчика определяет исправность системы зажигания и старта.

История появления датчика

Все началось с работы Эдвина Холла, который обнаружил эффект, позже названный его именем, в 1878 году. Основная идея проста: при воздействии магнитного поля на проводник, по которому проходит электрический ток, на концах проводника возникает разность напряжений при протекании тока, перпендикулярного полю.

Этот эффект называют обычным эффектом Холла, поскольку есть и другие явление, которое базируются на взаимодействии проводника, тока и магнитного поля.

Соответственно, датчики, чья работа основывается на эффекте Холла — лишь одна из разновидностей современных магнитометров.

Есть множество разных датчиков других типов, где используются приемные катушки индуктивности. Они могут вращаться ил инет, используются также шкалы или пружины для измерения силы магнитного поля. Обнаружить магнитное поле можно даже при помощи оптических свойств материалов и соответствующих эффектов — например, эффекта Керра или Фарадея.

Есть и весьма специфические датчики, которые можно назвать экзотикой. Они основываются на измерении протонного резонанса в богатых водородом соединениях и веществах вроде керосина, либо определении энергетического состояния молекул газов типа цезия. Есть и датчики со сверхпроводящими катушками.

Но именно датчики на эффекте Холла являются наиболее недорогими, имеют небольшой размер и весьма практичны. Как уже говорилось выше, миниатюрные датчики Холла используются в клавиатурах. Сложно представить клавиатуру, основа которой — сверхпроводящие датчики, прикрепленные к нижней части клавиш.

Датчики Холла — идеальный вариант при создании систем контроля частоты вращения чего-либо, от кулеров до двигателей в технике.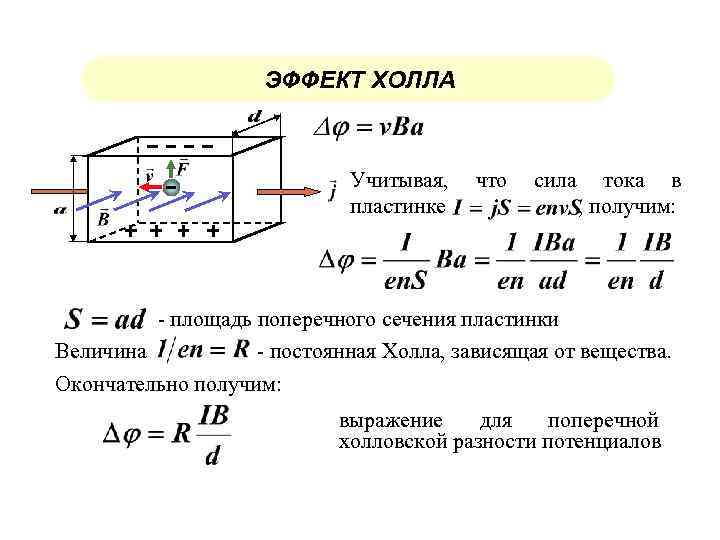 Датчики использовались в видеомагнитофонах и кассетных магнитофонах класса «люкс». Пример — Вега- МП122.

Используются датчики Холла и в смартфонах для решения самых разных задач, включая:

• Работа цифрового компаса, который применятся в навигационных программах и помогает повышать скорость позиционирования.
• Оптимизация взаимодействия девайса с разными аксессуарами, например, магнитными чехлами.
• Применение датчика в моделях с раскладной конструкцией, для включения и отключения экрана при открывании или закрывании крышки.

Как это работает?

В сети есть многочисленные видео, объясняющие физические принципы, лежащие в основе эффекта Холла. Но понять можно и без всяких видео — здесь все относительно просто. Представьте себе проводник размером и формой повторяющий денежную купюру. Левая и правая сторона подключены к источнику постоянного тока, который и проходит через проводник. Если проводник исправен, то без воздействия магнитного поля напряжение в верхней и нижней части проводника будет близким к нулю.

Но если в системе появится магнитное поле, линии которого расположены под прямым углом к течению тока, на электроны и дырки в проводнике начинает воздействовать сила Лоренца. Частицы начинают отклоняться. Соответственно, электроны соберутся на одной стороне проводника, а на другой их не будет.

При помощи мультиметра можно измерить напряжение на верхней и нижней частях проводника. Если убрать магнитное поле, то напряжение снова станет почти равным нулю.

В устройствах, где используется эффект Холла, добавляется еще одна схема, где обычно присутствует усилитель холловского напряжения. Иногда есть регулятор напряжения смещения. У цифрового выходного датчика может быть компаратор и выходной транзистор.

Все датчики — разные

Есть две основные разновидности датчиков Холла — это цифровые датчики, которые, в свою очередь, разделяются на униполярные и биполярные. А также аналоговые датчики.

Если вы хотите использовать датчик Холла в своем проекте, нужно детально разобраться в его базовых характеристиках. У датчиков есть ограничения по частотному диапазону, плюс некоторые могут быть весьма дорогими. Например, у компании Melexis есть девайс на 250 кГц, эта частота гораздо более высокая, чем у большинства похожих систем. Работать оно будет только при 5В и 15 мА.

В примере даташита показано, что есть две разновидности этого датчика — 7,5 mT (миллитесла), второй — 20 mT. Есть даже версия с 60 mT.

Датчики Холла могут быть встроены в электронные схемы. Например, у ESP32 есть собственный датчик Холла, как показано на видео выше.

Разработка систем на основе эффекта Холла

Как и было показано выше, придумать можно много чего. В качестве примера можно привести еще портативный магнетометр, плата которого умещается в пластиковую коробочку из-под Tic Tac. С его помощью можно облегчить задачу отслеживания проложенной в стене или потолке электропроводки. Еще один пример — мониторинг кофе-машин, с целью оценки количества приготовленных чашек кофе.

Эффект Холла

Эффект Холла

Если электрический ток течет по проводнику в магнитном поле, магнитное поле действует на движущиеся носители заряда поперечную силу, которая стремится оттолкнуть их к одной стороне проводника. Это наиболее очевидно в тонком плоском проводнике, как показано на рисунке. Накопление заряда на сторонах проводников уравновешивает это магнитное влияние, создавая измеримое напряжение между двумя сторонами проводника. Наличие этого измеримого поперечного напряжения называется эффектом Холла в честь Э. Х. Холла, открывшего его в 1879 г.. Обратите внимание, что направление тока I на диаграмме совпадает с направлением обычного тока, так что движение электронов происходит в противоположном направлении. Это еще больше сбивает с толку все манипуляции с «правилом правой руки», через которые вам нужно пройти, чтобы получить направление сил. Напряжение Холла определяется как . В Н = IB/нед , где n = плотность мобильных зарядов и e = заряд электрона. Эффект Холла можно использовать для измерения магнитных полей с помощью датчика Холла. Датчик Холла для измерения магнитного поля

Индекс Применение магнитных сил Концепции магнитного поля

Гиперфизика***** Электричество и магнетизм R Ступица

Назад

Поперечное напряжение (эффект Холла), измеренное датчиком Холла, возникает из-за магнитной силы, действующей на движущийся носитель заряда. Магнитная сила равна F м = ev d B, где v d — скорость дрейфа заряда. Ток, выраженный через скорость дрейфа, равен I = neAv d , где n — плотность носителей заряда. Затем F м = eIB/neA В равновесии F м =F e =V H e/W И замена дает В Н = IB/нед	Индекс Электромагнитная сила Магнитная сила Концепции магнитного поля
2 Гиперфизика***** Электричество и магнетизм R 028	Назад

Измерение больших магнитных полей порядка Тесла часто выполняется с использованием эффекта Холла. Тонкопленочный датчик Холла помещают в магнитное поле и измеряют поперечное напряжение (порядка микровольт). 9вольт.

Индекс

Электромагнитная сила

Магнитная сила

Концепции магнитного поля

  2

Гиперфизика***** Электричество и магнетизм

R 028

Назад

Эффект Холла — это явление проводимости, которое различно для разных носителей заряда. В большинстве распространенных электрических приложений обычный ток используется отчасти потому, что не имеет значения, считаете ли вы движущимся положительный или отрицательный заряд. Но напряжение Холла имеет разную полярность для положительных и отрицательных носителей заряда, и его использовали для изучения деталей проводимости в полупроводниках и других материалах, которые демонстрируют комбинацию отрицательных и положительных носителей заряда. Эффект Холла можно использовать для измерения средней скорости дрейфа носителей заряда путем механического перемещения зонда Холла с различными скоростями до тех пор, пока напряжение Холла не исчезнет, ​​показывая, что теперь носители заряда не движутся относительно магнитного поля. Другие типы исследований поведения носителей изучаются в квантовом эффекте Холла.

Указатель Электромагнитная сила Магнитная сила Концепции магнитного поля

Гиперфизика***** Электричество и магнетизм R Ступица

Вернуться

22.6 Эффект Холла – физика в колледже

Глава 22 Магнетизм

Резюме

• Опишите эффект Холла.
• Рассчитайте ЭДС Холла на проводнике с током.

Мы видели влияние магнитного поля на свободно движущиеся заряды. Магнитное поле также влияет на заряды, движущиеся в проводнике. Одним из результатов является эффект Холла, который имеет важные последствия и приложения.

На рис. 1 показано, что происходит с зарядами, движущимися по проводнику в магнитном поле. Поле перпендикулярно скорости дрейфа электронов и ширине проводника. Обратите внимание, что условный ток находится справа в обеих частях рисунка. В части (а) электроны переносят ток и движутся влево. В части (b) положительные заряды переносят ток и движутся вправо. Движущиеся электроны испытывают магнитную силу по направлению к одной стороне проводника, оставляя чистый положительный заряд на другой стороне. Это разделение заряда создает напряжение [latex]{\varepsilon}[/latex] , известное как ЭДС Холла, , на проводнике. Создание напряжения на проводнике с током под действием магнитного поля известно как эффект Холла в честь Эдвина Холла, американского физика, открывшего его в 1879 году.

Рис. 1. Эффект Холла. (а) В этом плоском проводнике электроны движутся влево (условный ток вправо). Магнитное поле находится прямо за пределами страницы и представлено точками в кружках; он воздействует на движущиеся заряды, вызывая напряжение εε, ЭДС Холла, на проводнике. (b) Положительные заряды, движущиеся вправо (обычный ток также вправо), смещаются в сторону, создавая ЭДС Холла противоположного знака, –ε . Таким образом, зная направление поля и тока, можно определить знак носителей заряда по эффекту Холла.

Одним из очень важных применений эффекта Холла является определение того, какие положительные или отрицательные заряды переносят ток. Обратите внимание, что на рисунке 1 (b), где положительные заряды переносят ток, ЭДС Холла имеет знак, противоположный тому, когда отрицательные заряды переносят ток. Исторически эффект Холла использовался, чтобы показать, что электроны переносят ток в металлах, а также показывает, что положительные заряды переносят ток в некоторых полупроводниках. Эффект Холла используется сегодня в качестве инструмента исследования для изучения движения зарядов, их скоростей дрейфа и плотности и т. д. в материалах. В 1980 было обнаружено, что эффект Холла квантуется, что является примером квантового поведения в макроскопическом объекте.

Эффект Холла имеет и другие применения, от определения скорости кровотока до точного измерения напряженности магнитного поля. Чтобы исследовать их количественно, нам нужно выражение для ЭДС Холла [латекс] {\ varepsilon} [/ латекс] на проводнике. Рассмотрим баланс сил на движущийся заряд в ситуации, когда [латекс]{B}[/латекс], [латекс]{v}[/латекс] и [латекс]{l}[/латекс] взаимно перпендикулярны, например, как показано на рисунке 2. Хотя магнитная сила смещает отрицательные заряды в одну сторону, они не могут накапливаться без ограничений. Электрическое поле, вызванное их разделением, противостоит магнитной силе, [латекс]{F = qvB}[/латекс], и электрическая сила, [латекс]{F_e = qE}[/латекс], в конечном итоге вырастает, чтобы сравняться с ней. то есть

[латекс]{qE = qvB}[/латекс]

или

[латекс]{E = vB}.[/латекс]

Обратите внимание, что электрическое поле [латекс]{E}[/латекс] однородно по проводнику, потому что магнитное поле [латекс]{B}[/латекс] однородно, как и проводник. Для однородного электрического поля связь между электрическим полем и напряжением имеет вид [латекс]{Е = \varepsilon /l}[/латекс], где [латекс]{л}[/латекс] — ширина проводника, а [латекс ]{\varepsilon}[/latex] – ЭДС Холла. Ввод этого в последнее выражение дает

[латекс] {\ гидроразрыва {\ varepsilon} {l}} [/латекс] [латекс] {= vB}. [/латекс]

Решение этой задачи для ЭДС Холла дает

[латекс] {\ varepsilon = Blv \; (B, \; v, \;\text{и} \;l, \;\text{взаимно перпендикулярно})},[/latex]

, где [latex]{\varepsilon}[/latex] — напряжение эффекта Холла на проводнике шириной [latex]{l}[/latex], по которому движутся заряды со скоростью [latex]{v}[/latex] .

Рис. 2. ЭДС Холла ε создает электрическую силу, которая уравновешивает магнитную силу движущихся зарядов. Магнитная сила вызывает разделение зарядов, которое накапливается до тех пор, пока не уравновесится электрической силой, равновесие, которое достигается быстро.

Одним из наиболее распространенных применений эффекта Холла является измерение напряженности магнитного поля [латекс]{B}[/латекс]. Такие устройства, называемые датчиками Холла , можно сделать очень маленькими, что позволяет точно отображать положение. Датчики Холла также можно сделать очень точными, что обычно достигается путем тщательной калибровки. Еще одним применением эффекта Холла является измерение расхода жидкости в любой жидкости, которая имеет свободные заряды (большинство из них). (См. Рисунок 3.) Магнитное поле, приложенное перпендикулярно направлению потока, создает ЭДС Холла [латекс] {\ varepsilon} [/латекс], как показано. Обратите внимание, что знак [латекс]{\варепсилон}[/латекс] зависит не от знака зарядов, а только от направлений [латекс]{В}[/латекс] и [латекс]{в}[/ латекс]. Величина ЭДС Холла равна [латекс] {\ varepsilon = Blv} [/латекс], где [латекс] {l} [/латекс] – диаметр трубы, так что средняя скорость [латекс] {v} [/ латекс] может быть определен из [латекс] {\ varepsilon} [/латекс], если известны другие факторы.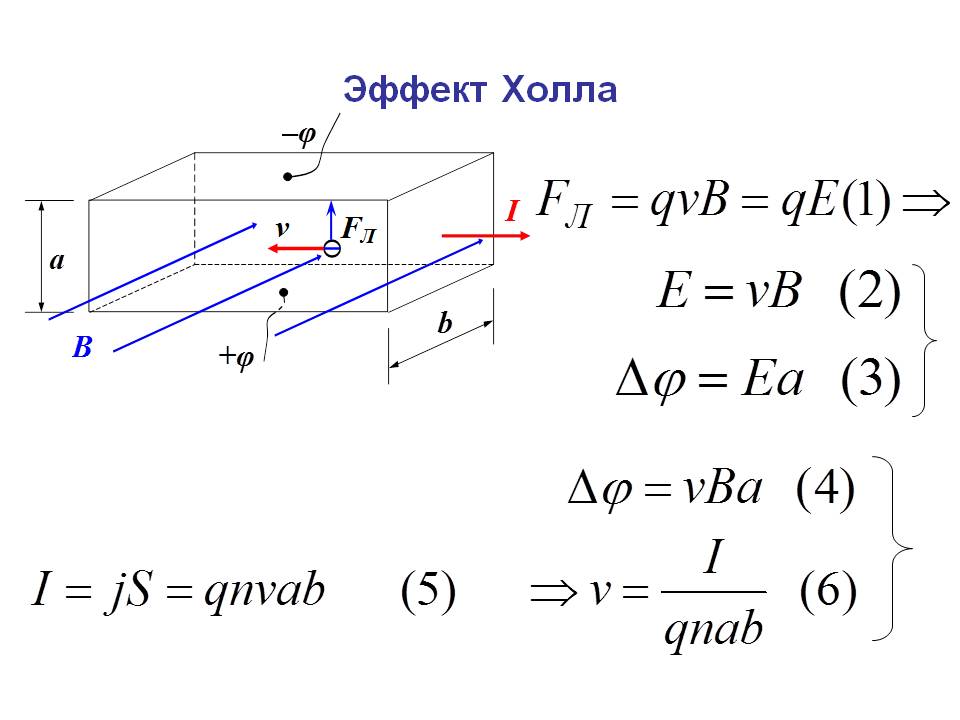

Рисунок 3. Эффект Холла можно использовать для измерения потока любой жидкости, имеющей свободные заряды, например крови. ЭДС Холла ε измеряется поперек трубки перпендикулярно приложенному магнитному полю и пропорциональна средней скорости v .

Расчет ЭДС Холла: эффект Холла для кровотока

Датчик расхода на эффекте Холла помещают на артерию, приложив к ней магнитное поле 0,100 Тл, в установке, аналогичной показанной на рис. 3. Что такое ЭДС Холла, при внутреннем диаметре сосуда 4,00 мм и средней скорости кровотока 20,0 см/с?

Стратегия

Поскольку [латекс]{B}[/латекс], [латекс]{v}[/латекс] и [латекс]{l}[/латекс] взаимно перпендикулярны, уравнение [латекс] {\varepsilon =Blv}[/latex] можно использовать для поиска [латекс]{\varepsilon}[/латекс].

Решение

Ввод заданных значений для [латекс]{B}[/латекс], [латекс]{v}[/латекс] и [латекс]{l}[/латекс] дает

[латекс]\begin{array}{r @{{}={}} l} {\varepsilon} & {Blv = (0,100 \;\textbf{T}) \; (4. {-3} \;\text{m}) \; (0,200 \;\text{м/с})} \\[1em] & {80,0 \;\mu \text{V}} \end{массив}[/latex]

Обсуждение

Это среднее выходное напряжение. Мгновенное напряжение изменяется при пульсирующем токе крови. Напряжение в этом типе измерения мало. Размер εε 12{ε} {} особенно трудно измерить, потому что существуют напряжения, связанные с работой сердца (напряжения ЭКГ), которые имеют порядок милливольт. На практике эта трудность преодолевается приложением переменного магнитного поля, так что ЭДС Холла является переменным с той же частотой. Усилитель может быть очень избирательным, выбирая только подходящую частоту, исключая сигналы и шумы на других частотах.

• Эффект Холла представляет собой создание напряжения [латекс]{\varepsilon}[/латекс], известного как ЭДС Холла, на проводнике с током под действием магнитного поля.
• ЭДС Холла определяется выражением

  [латекс] {\ varepsilon = Blv \; (B, \; v, \;\text{и} \;l, \;\text{взаимно перпендикулярно})}[/latex]

  для проводника шириной [латекс]{l}[/латекс], по которому движутся заряды со скоростью [латекс]{v}[/латекс].