Как найти m2 в физике: Напишите формулу нахождения m2 по закуну всемирного тяготения.

Динамика | Формулы по физике

Инертность, масса, ускорение

Найти

  Известно, что:

     a1a2m2m1 =   

Вычислить ‘a1’

Сила, масса, ускорение

Найти

  Известно, что:

     Fma =   

Вычислить ‘F’

Сила тяжести

Найти

  Известно, что:

     Nmg =   

Вычислить ‘N’

Сила трения

Найти

  Известно, что:

     F_трμN =   

Вычислить ‘F_тр’

Сила трения

Найти

  Известно, что:

     F_трμmg =   

Вычислить ‘F_тр’

Закон всемирного тяготения

Найти

  Известно, что:

     FGm1m2r =   

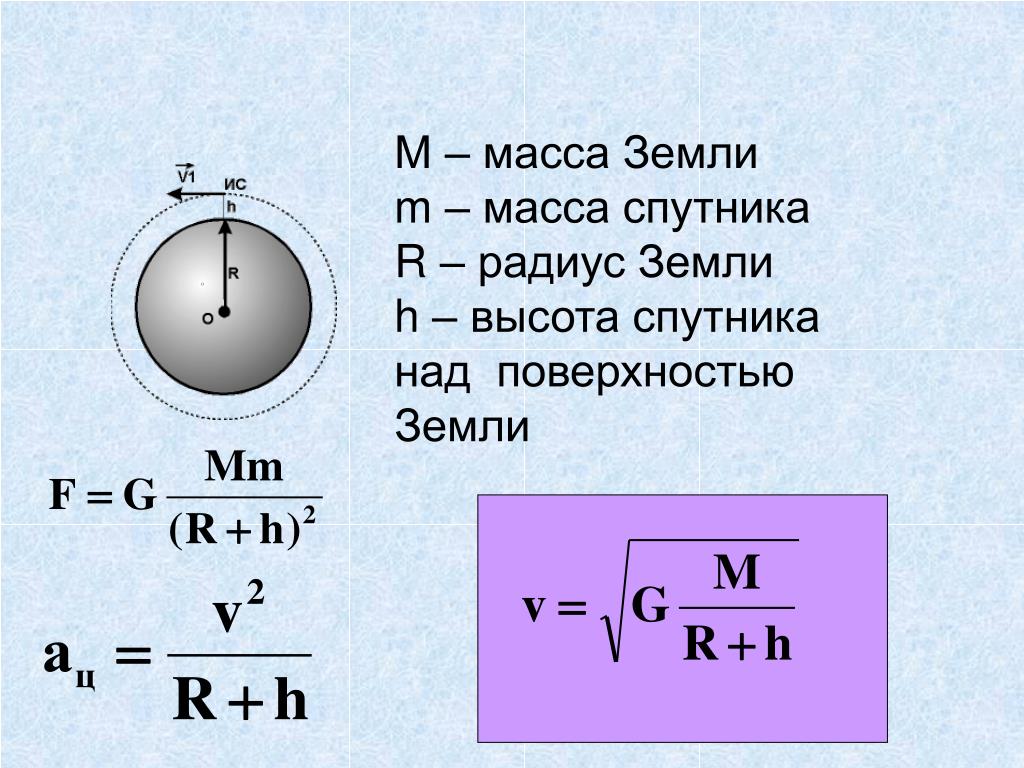
Вычислить ‘F’

Центростремительное ускорение спутника

Найти

  Известно, что:

     avRh =   

Вычислить ‘a’

Скорость спутника

Найти

  Известно, что:

     vGMRh =   

Вычислить ‘v’

Первая космическая скорость (движение по круговой орбите)

Найти

  Известно, что:

     vgR =   

Вычислить ‘v’

Вторая космическая скорость (преодоление гравитации)

Найти

  Известно, что:

     vgR =   

Вычислить ‘v’

Третий закон Кеплера

Найти

  Известно, что:

     T1T2a1a2 =   

Вычислить ‘T1’

Ускорение свободного падения на поверхности земли

Найти

  Известно, что:

     gGMR =   

Вычислить ‘g’

Вес тела

Найти

  Известно, что:

     Pmg =   

Вычислить ‘P’

Вес тела: невесомость

Найти

  Известно, что:

     Pmga =   

Вычислить ‘P’

Вес тела: перегрузка

Найти

  Известно, что:

     Pmga =   

Вычислить ‘P’

Время торможения

Найти

  Известно, что:

     tmvF_тр =   

Вычислить ‘t’

Время торможения

Найти

  Известно, что:

     tvμg =   

Вычислить ‘t’

Путь торможения

Найти

  Известно, что:

     smvF_тр =   

Вычислить ‘s’

Путь торможения

Найти

  Известно, что:

     svμg =   

Вычислить ‘s’

Сила трения качения

Найти

  Известно, что:

     F_трμNR =   

Вычислить ‘F_тр’

Сила упругости

Найти

  Известно, что:

     F_упругkx =   

Вычислить ‘F_упруг’

Кинетическая энергия вращающегося тела

Найти

  Известно, что:

     W_kJω =   

Вычислить ‘W_k’

Формулы по физике 10 класса.

Все формулы по физике за 10 класс с пояснениями и определениями

Закон	Формула	Определение	Единицы измерения
МЕХАНИКА
Вычисление перемещения	АВ2 = АС2 + ВС2	Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещения	Sx = x2 – x1		x1 – начальная координата, [м] x2 – конечная координата, [м] Sx – перемещение, [м]
Формула расчета скорости движения тела	v = s/t	Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.	v – скорость, [м/с] s – путь, [м] t – время, [c]
Уравнение движения	x = x0 + Vxt		x0– начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения тела	a ⃗ = v ⃗- v0⃗ /t	Ускорение – физическая величина, которая характеризует быстроту изменения скорости.	a – ускорение, [м/с2] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] t – время, [c]
Уравнение скорости	v ⃗ = v0 ⃗ + a ⃗t		v – конечная скорость, [м/с] v 0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Уравнение Галилея	S = v0t + at2 / 2		S – перемещение, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движении	x = x0 + v0t + at2/2		x0 – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Первый закон Ньютона		Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютона	a= F ⃗ / m	Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.	a – ускорение, [м/с2] F – сила, [Н] m – масса, [кг]
Третий закон Ньютона	|F1⃗ |=|F2⃗| F1⃗ = -F2⃗	Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое.	F – сила, [Н]
Формула для вычисления высоты, с которой падает тело	H = g*t2/2		Н – высота, [м] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверх	h=v0t -gt2/2		h – высота, [м] v0 – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорением	P = m (g + a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула для вычисления веса тела при движении вниз с ускорением	P = m (g – a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула закона всемирного тяготения	F = Gm1m2/r2	Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.	F – сила, [Н] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная m – масса тела, [кг] r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетах	g = GMпл/Rпл2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м]
Формула расчета ускорения свободного падения	g = GMз/(Rз+H)2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м]
Формула расчета центростремительного ускорения	а = υ2/r		a – центростремительное ускорение, [м/с2] v – скорость, [м/с] r – радиус окружности, [м]
Формула периода движения по окружности	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота вращения, [с-1] t – время, [с] N – число оборотов
Формула расчета угловой скорости	ω = 2π/T = 2πν =υr		ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения,[с-1] r – радиус окружности, [м]
Формула импульса тела	p = mv	Импульсом называют произведение массы тела на его скорость.	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с]
Формула закона сохранения импульса	p1 + p2 =p1’ + p2’ m1v + m2u = m1v’ + m1u’
Формула импульса силы	P = Ft		p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c]
Формула механической работы	A = Fs	Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы.	A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м]
Формула расчета мощности	N = A/t	Мощность – физическая величина, характеризующая быстроту совершения механической работы.	N – мощность, [Вт] A – работа, [Дж] t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)	η = Aп/Aз∙ 100%	КПД – отношение полезной работы к затраченной работе.	Aп – полезная работа, [Дж] Aз – затраченная работа, [Дж]
Формула расчета потенциальной энергии	Eп = mgh	Потенциальная энергия – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.	Eп – потенциальная энергия тела, [Дж] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения h – высота тела над поверхностью земли, [м]
Формула расчета кинетической энергии	Ek= mv2/2	Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.	Ek – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергии	mv12/2 + mgh1=mv22/2 + mgh2	Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.	m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения v1 – скорость тела в начальный момент времени, [м/с] v2 – скорость тела в конечный момент времени, [м/с] h1 – начальная высота, [м] h2 – конечная высота, [м]
Формула силы трения	Fтр = μ mg	Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.	Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения
Уравнение колебаний	x = A cos (ωt + φ0)		А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ0 – начальная фаза, [рад]
Формула периода	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота колебании, [с-1] t – время колебании, [с] N – число колебаний
Формула периода для математического маятника	T= 2π √L/g		Т – период, [с] g ≈ 9,81 м/с2 – ускорение свободного падения L – длина нити, [м]
Формула периода для пружинного маятника	T= 2π √m/K		Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м]
Формула длины волны	λ = υТ = υ/ν		λ – длина волны, [м] Т – период, [с] ν – частота, [с-1] υ – скорость волны, [м/с]
Формула полной механической энергии колебательного движения	E = kA2/2		E – энергия, [Дж] А – амплитуда колебаний, [м] k – жесткость пружины, [Н/м]
Радиус Шварцшильда	R = 2GM/c2	Радиус Шварцшильда – радиус «горизонта событий» черной дыры, из которого ничто не может вырваться.	R – радиус Шварцшильда, [м] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная М – масса черной дыры, [кг]
Собственное время	t = T/√1-v2/c2	Собственное время – время, измеренное наблюдателем, движущимся вместе с часами.	t – собственное время, [с] T – время в движущейся системе отсчета, [с] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Масса покоя	m = M/√1-v2/c22	Масса покоя – масса тела в СО, относительно которой оно покоится.	m – масса тела в СО, относительно которой оно покоится, [кг] M – масса тела в подвижной СО, [кг] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Формула Эйнштейна	E = mc2		E – энергия, [Дж] m – масса, [кг] c – скорость света, [м/с
МОЛЕКУЛЯРНАЯ ФИЗИКА 10 класс
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	МЯ = МА – Z me		MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг]
Формула дефекта масс	∆m = Zmp + Nmn – MЯ	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.	∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг]
Уравнение Менделеева-Клапейрона	pV = m/M RT	Уравнение состояния идеального газа	p – давление, [Па] V – объем, [м3] m – масса, [кг] M – молярная масса, [кг] R = 8,31 [Дж/мольК] – молярная газовая постоянная T – температура, [°С]
Формула давления газа			p – давление, [Па] n – концетрация молекул E – средняя кинетическая энергия молекулы, [Дж] T – температура, [°С] k = 1,38 · 10-23, [Дж/К] – постоянная Больцмана
Закон Бойля-Мариотта	p1V1 = p2V2		p – давление, [Па] V – объем, [м3]
Закон Гей-Люссака	V1/T1 = V2/T2		T – температура, [°С] V – объем, [м3]
Закон Шарля	p1/T1= p2/T2		T – температура, [°С] p – давление, [Па]
Внутренняя энергия идеального газа	U = i/2 pV		U – энергия, [Дж] p – давление, [Па] V – объем, [м3] i – число степеней свободы молекул газа
Работа, совершаемая газом	A = pΔV		p – давление, [Па] V – объем, [м3] А – работа, [Дж]
Первый закон термодинамики	Q = ΔU + A		Q – количество теплоты, [Дж] А – работа, [Дж] U – энергия, [Дж]
Формула для нахождения коэффициента полезного действия (КПД) теплового двигателя	η = A/Q∙100%		А – работа, [Дж] Q – количество теплоты, полученное от нагревателя, [Дж]
Сила поверхностного натяжения	F = ϭl		F – сила поверхностного натяжения, [Н] ϭ – поверхностное натяжение, [Н/м] l – длина участка поверхности слоя, [м]
Закон Гука	ϭ = Eε	При упругой деформации тела напряжение пропорционально относительному удлинению тела.	ϭ – механическое напряжение, [Па] Е – модуль Юнга, [Па] ε – относительное удлинение тела, [м]
ЭЛЕКТРОДИНАМИКА
Закон Кулона	F = kq1q1/r2	Определяет силу электростатического взаимодействия двух точечных зарядов	F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2] q – заряд, [Кл] r – расстояние между зарядами, [м]
Напряженность поля	E = F/q E = kQ/r2		Е – напряженность поля, [Н/Кл] q – пробный положительный заряд, [Кл] F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2]
Потенциал электростатического поля	φ = W/q φ = Q/4πεr		φ – потенциал, [В] W – энергия, [Дж] q – заряд, [Кл]
Потенциальная энергия заряда	W = qφ		W – энергия, [Дж] q – заряд, [Кл] φ – потенциал, [В]
Работа силы электростатического поля	A = qU		А – работа сил, [Дж] q – заряд, [Кл] U – разность потенциалов, [В]
Разность потенциалов в однородном поле	U = Ed		U – разность потенциалов, [В] Е – напряженность поля, [Н/Кл] d – расстояние, [м]
Электроемкость уединенного проводника	C = Q/φ		C – электроемкость, [Ф] φ – потенциал, [В] Q – заряд, [Кл]
Электроемкость конденсатора	C = Q/U		C – электроемкость, [Ф] U – разность потенциалов, [В] Q – заряд, [Кл]
Энергия ЭСП	W = CU2/2		C – электроемкость, [Ф] U – разность потенциалов, [В] W – энергия ЭСП, [Дж

Задачи двух тел

На уроке законов Ньютона была введена тема задач двух тел. Пара стратегий решения проблем была обсуждена и применена для решения трех примеров проблем. Такие задачи двух тел обычно включают решение для ускорения объектов и силы, действующей между объектами. Одна из стратегий решения задач двух тел включает использование системного анализа для определения ускорения в сочетании с анализом отдельных объектов для определения силы, передаваемой между объектами. Вторая стратегия заключалась в использовании анализа двух отдельных объектов для разработки системы двух уравнений для решения двух неизвестных величин. При необходимости найдите время, чтобы просмотреть страницу, посвященную решению задач двух тел. Эта страница будет основываться на уроках, полученных ранее в разделе «Законы Ньютона».

В этом уроке мы будем анализировать задачи двух тел, в которых объекты движутся в разных направлениях. В этих задачах два объекта соединены нитью, которая передает силу одного объекта другому объекту. Струна наматывается на шкив, который изменяет направление действия силы без изменения ее величины. В качестве иллюстрации того, как работает шкив, рассмотрите диаграмму справа. Объект A связан с объектом B цепочкой. Веревка наматывается на шкив в конце стола. Объект А подвешен в воздухе, а объект Б лежит на столе. В этой ситуации объект А упадет вниз под действием силы тяжести, потянув вниз один конец веревки, к которой он подключен. Согласно закону действия-противодействия Ньютона, этот нижний конец нити будет тянуть вверх объект А. Противоположный конец нити соединен с объектом В. Этот конец нити тянет вправо объект В. Таким образом, струна соединение двух объектов означает притяжение обоих объектов с одинаковой силой, но в разных направлениях. Струна тянет вверх объект А и вправо объект В. Блок изменил направление приложения силы.

Задачи, связанные с двумя объектами, соединяющими струны и шкивы, характеризуются объектами, которые движутся (или даже ускоряются) в разных направлениях. Они движутся или ускоряются с одинаковой скоростью, но в разных направлениях. Таким образом, при подходе к таким проблемам становится важным выбрать другую систему отсчета и систему координат для каждого объекта. Следует уделить внимание выбору такой системы координат, чтобы оба объекта ускорялись вдоль оси в положительном направлении. С правильно определенными осями для каждого отдельного объекта можно построить диаграмму свободного тела. Затем к каждой диаграмме можно применить законы Ньютона, чтобы составить систему из двух уравнений для решения двух неизвестных. Этот процесс решения проблем будет продемонстрирован для трех различных примеров задач.

 

Пример задачи 1

Масса 200,0 грамм (m ₁ ) и масса 50,0 грамм (m ₂ ) соединены нитью. Нить натянута на шкив. Определить ускорение масс и натяжение нити.

Как это часто бывает, в этом примере задачи запрашивается информация о двух неизвестных — ускорении объектов и силе, действующей между объектами. В такой ситуации, как эта, с двумя объектами, подвешенными на шкиве, более массивный объект будет ускоряться вниз, а наименее массивный объект будет ускоряться вверх. Величина ускорения будет одинаковой для каждого объекта. Система координат выбрана для m ₁ имеет положительную ось Y, направленную вниз; система координат, выбранная для m ₂ , имеет положительную ось y, направленную вверх. При таком выборе осей направление ускорения будет положительным для каждого объекта. Диаграммы свободного тела для каждой отдельной массы показаны ниже. На каждый объект действует направленная вниз сила тяжести, которая рассчитывается как m ₁ •g и m ₂ •g соответственно. Каждый объект также испытывает восходящую силу натяжения, которая притягивает два объекта друг к другу.

Уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражаться как сила, направленная в направлении ускорения, за вычетом силы, противодействующей ему. Таким образом, для массы 200,0 грамм F _нетто записывается как 1,960 N – F _{десяток} . Для массы 50,0 грамм F _нетто записывается как F _{десятки} – 0,490 Н. Уравнения 1 и 2 являются результатом применения уравнения второго закона Ньютона к массам 200,0 грамм и 50,0 грамм. (Обратите внимание, что перед использованием в уравнениях значения массы преобразуются в стандартные килограммы. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

1,960 – F _{десятков} = 0,2000•a

F _{десятков} – 0,490 = 0,0500•a

С этого момента несколько шагов алгебры приводят к ответам на задачу. Уравнение 2 можно изменить, чтобы получить выражение для F _{десятков} , записанное через ускорение.

F _{десятков} = 0,0500•a + 0,490

Теперь это выражение для F _{десятков} можно подставить в уравнение 1, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

1,96 – (0,0500•а + 0,490) = 0,2000•а
1,96 – 0,0500•а – 0,490 = 0,2000•а
1,47 = 0,2500•а
a = 1,47/0,2500 = 5,88 м/с ²

Теперь, когда ускорение найдено из уравнения 1, его значение можно подставить в уравнение 3, чтобы определить натяжение.

F _{десятки} = 0,0500•(5,88) + 0,490
F _{десятки} = 0,784 N

Рассматриваемую здесь систему шкивов иногда называют машиной Атвуда. Подход к решению проблем — это стандартный подход, который будет использоваться на этой странице для решения двух неизвестных. Это будет повторено в примере задачи 2, чтобы решить то, что обычно называют модифицированной машинной задачей Этвуда.

 

Пример задачи 2

Рассмотрим ситуацию с двумя телами справа. Подвесной груз массой 20,0 грамм (m ₂ ) прикреплен к планеру с воздушной гусеницей массой 250,0 грамм (m ₁ ). Определить ускорение системы и натяжение нити.

Как и в примере задачи 1, эту систему необходимо сначала концептуально проанализировать, чтобы определить направление ускорения двух объектов. Это позволит назначить оси координат для каждого объекта. Так как нечего толкать м ₁ влево, мы думаем, что он ускорится вправо из-за натяжения нити. Подвешенная масса (m ₂ ) будет ускоряться вниз под действием силы тяжести. Таким образом, выбрана система координат для m ₂ с положительной осью ординат, направленной вниз; система координат, выбранная для m ₁ , имеет положительную ось x, направленную вправо. При таком выборе осей направление ускорения будет положительным для каждого объекта.

Диаграмма свободного тела для каждой отдельной массы показана ниже. На каждый объект действует направленная вниз сила тяжести (F _грав ), которая рассчитывается как m ₁ •g и m ₂ •g соответственно. Планер (m ₁ ) испытывает восходящую поддерживающую силу (воздух давит на него), чтобы уравновесить силу тяжести. На планер также действует горизонтальная сила – сила натяжения (F _{десяток} ) вправо. Подвешенная масса (m ₂ ) испытывает направленную вверх силу натяжения (F _{десятков} ), что оказывает некоторое сопротивление нисходящему притяжению гравитации.

Уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F будет выражена как сила в направлении ускорения за вычетом всех сил, противодействующих ему. Для планера весом 250,0 грамм (0,250 кг) F _сеть представляет собой просто неуравновешенную силу натяжения (F _{десяток} ). Для подвесной массы 20,0 г (0,020 кг) F _net записывается как 0,196 N-F _{десяток} . Уравнения 4 и 5 являются результатом применения уравнения второго закона Ньютона к 250,0-граммовому планеру и 20,0-граммовому подвесу. (Обратите внимание, что перед использованием в уравнениях значения массы преобразуются в стандартные килограммы. Также обратите внимание, что единицы измерения были опущены, чтобы уравнения читались более четко.)

F _{десятки} = 0,2500•a

0,196 – F _{десятков} = 0,0200•a

С этого момента несколько шагов алгебры приводят к ответам на задачу. Уравнение 4 выражает F _{десятков} значение с точки зрения ускорения. Это выражение для F _tens можно подставить в уравнение 5, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

0,196 – 0,2500•а = 0,0200•а
0,196 = 0,2700•а
а = 0,196/0,2700 = 0,72593 м/с ²
a = ~0,726 м/с ²

Теперь, когда ускорение найдено из уравнения 5, его значение можно подставить в уравнение 4, чтобы определить натяжение.

F _{десятки} = 0,2500•(0,72593) = 0,18148
F _{десятки} = ~0,181 N

Систему шкивов, проанализированную в примере задачи 2, иногда называют модифицированной машиной Этвуда. Анализ немного сложнее, чем анализ машины Этвуда из примера задачи 1. Последний пример задачи будет представлять собой случай модифицированной машины Этвуда с наклонной поверхностью, как показано ниже. Подход к решению проблемы будет таким же.

 

Пример задачи 3

Рассмотрим ситуацию с двумя телами справа. Ящик размером 2,50×10 ³ кг (m ₁ ) опирается на наклонную плоскость и соединен тросом с массой 4,00×10 ³ кг (m ₂ ). Эта вторая масса (m ₂ ) подвешена на шкиве. Угол наклона составляет 30,0°, поверхность не имеет трения. Определить ускорение системы и натяжение троса.

Как и в предыдущей задаче, первая задача включает анализ ситуации, чтобы определить, в каком направлении будут ускоряться объекты. Такой анализ позволит присвоить каждому объекту систему координатных осей. В этом случае висящая масса (m ₂ ) может быть ускорена вверх или вниз. Направление, в котором он ускоряется, зависит от сравнения его веса (силы тяжести) с противодействующей силой, действующей на другую массу (m ₁ ). Масса на наклонной плоскости сталкивается с тремя силами – силой тяжести, нормальной силой и силой натяжения. Сила тяжести направлена ​​вниз (как обычно) и рассчитывается как m ₁ •г. Нормальная сила направлена ​​перпендикулярно поверхности (как обычно). Сила натяжения направлена ​​вверх и вправо – параллельно наклонной плоскости и вдоль той же ориентации, что и струна, создающая эту силу. Как обсуждалось на предыдущей странице, объекты, расположенные на наклонных плоскостях, анализируются путем разделения силы тяжести на две составляющие. Одна компонента направлена ​​параллельно плоскости (и вниз под этим углом), а другая компонента направлена ​​перпендикулярно плоскости (и вверх под этим углом). Именно параллельная составляющая силы тяжести пытается притянуть m ₁ вниз по наклонной плоскости. Как упоминалось ранее, эту составляющую можно рассчитать, умножив вес объекта (m ₁ •g) на синус угла наклона (30°). Значение для F _{параллельно} составляет

F _{параллельно} = m ₁ •g•sine(θ) = (2500 кг)•(9,8 Н/кг)•sine(30°)
F _{параллельно} = 12250 N

Эта параллельная составляющая силы тяжести пытается тянуть m ₁ вниз по наклонной плоскости. С м ₁ крепится кабелем к m ₂ , с ним будет тянуться подвесная масса. Однако существует противоположное действие силы тяжести, тянущей m ₂ вниз; это противодействующее действие, если оно преобладает, будет тянуть объект m ₁ вверх по наклонной плоскости. Сила тяжести на м ₂ равна

F _грав-2 = м ₂ •g = (4000 кг)•(9,8 Н/кг) = 39200 Н

Эта сила тяжести на м ₂ является доминирующей силой. И так м ₁ ускорит движение вверх по наклонной плоскости, а m ₂ ускорит движение вниз. Оси координат назначаются соответствующим образом, чтобы каждый объект имел положительное ускорение.

На рисунках ниже показаны эти координатные оси и силы, действующие на два объекта. Три силы на m ₁ уже обсуждались. На диаграмме показаны два компонента F _grav . Как упоминалось на предыдущей странице, перпендикулярная составляющая силы тяжести рассчитывается как

F _{перпендикулярно} = м ₁ •g•cosθ = (2500 кг)•(9,8 Н/кг)•cos(30°)
F _{перпендикулярно} = 21218 Н

Нормальная сила (F _норма ), действующая на m ₁ , уравновешивает F _{перпендикулярно} так, что ускорение перпендикулярно наклонной плоскости отсутствует. Значение нормы F _{также равно 21218 Н. Висячая масса (m 2 ) испытывает только две силы — направленную вниз силу тяжести и восходящую силу натяжения.}

Теперь уравнение второго закона Ньютона (F _net = m•a) можно применить к обеим диаграммам свободного тела, чтобы написать два уравнения для двух неизвестных. Сеть F выражается как сила, направленная в направлении ускорения, за вычетом всех сил, противодействующих ему. Для массы 2500 кг на склоне (м ₁ ) F _нетто представляет собой просто силу натяжения (F _{десяток} ) за вычетом параллельной составляющей силы тяжести. Для подвесной массы 4000 кг (м ₂ ), F _net – сила тяжести (39200 Н) минус сила натяжения (F _{десяток} ). Уравнения 6 и 7 являются результатом применения уравнения второго закона Ньютона к m ₁ и m ₂ . (Обратите внимание, что единицы были сброшены, чтобы уравнения прочитали более чистое.)

F _TENS – 12250 = 2500 • A

39200 – F _TENS = 4000 • A

. несколько шагов алгебры приводят к ответам на проблему. Уравнение 6 можно изменить, чтобы создать выражение для F _{десятков} , выраженное через ускорение.

F _{десятков} = 2500•a + 12250

Это выражение для F _{десятков} можно подставить в уравнение 7, чтобы преобразовать его в уравнение с одним неизвестным. Это уравнение и последующие шаги алгебры, ведущие к значению ускорения, показаны ниже.

39200 – (2500•а + 12250) = 4000•а
39200 – 2500•а – 12250 = 4000•а
26950= 6500•а
а = 26950/6500 = 4,1462 м/с ²
a = ~4,15 м/с ²

Теперь, когда ускорение найдено из уравнения 7, его значение можно подставить в уравнение 8, чтобы определить силу натяжения (F _{десяток} ).

F _{десятки} = 2500•a + 12250 = 2500•(4,1462) + 12250 = 22615 N
F _{десятки} = ~2,26 x 10 ^{4 9007 1 N}

 

Задачи двух тел, подобные этим трем примеры проблем могут быть довольно сложной задачей. Наличие системного подхода, применяемого к каждой проблеме, упрощает анализ. Хорошее концептуальное понимание, приверженность использованию диаграмм свободного тела и твердое понимание второго закона Ньютона являются важными составляющими успеха.

 

 

 

Мы хотели бы предложить . ..

Иногда недостаточно просто прочитать об этом. Вы должны взаимодействовать с ним! И это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего симулятора Atwood’s Machine Simulator. Вы можете найти его в разделе Physics Interactives на нашем сайте. Тренажер позволяет исследовать двухмассовые системы, ускоряемые подвешенной массой.

Посетите: Симулятор машины Этвуда

Проверьте свое понимание

1. Рассмотрим ситуацию с двумя телами справа. Подвешенный груз массой 100,0 г (м2) прикреплен к грузу массой 325,0 г (м1), покоящемуся на столе. Коэффициент трения между грузом массой 325,0 грамм и столом равен 0,215. Определить ускорение системы и натяжение нити.

2. Рассмотрим ситуацию с двумя телами справа. А 3,50х10 9Ящик 0070 3 кг (м ₁ ) опирается на наклонную плоскость и соединяется тросом с массой 1,00×10 ³ кг (м ₂ ). Эта вторая масса (m ₂ ) подвешена на шкиве. Угол наклона составляет 30,0°, а поверхность имеет коэффициент трения 0,210. Определить ускорение системы и натяжение троса.

 

Законы движения Ньютона

Теперь, когда мы знать законы движения Ньютона, как мы применять их? Как они могут позволить нам предсказать движение объекта, если мы знаем все силы, действующие на него? Как может они позволяют нам предсказывать силы, действующие на объект, если мы знаем его движение?

Сказать, что остальная часть этого конечно просто ищет окольные способы применить

F = м и

---

Пример 1: Предположим, ящик тянут по трение меньше пол (пока такой пол очень трудно найти, такой еще будет помогите нам понять концепцию и мы можем вернуться к этому ситуация позже, после учитывая трение, и решить ее более реалистично).

Рассмотрим ящик, который тянут по горизонтали, трения меньше пол. Вокруг него привязана веревка, и человек тянет за веревку с силой T. T равно натяжение в веревка. Что происходит с ящиком?

Прежде чем мы сможем применить второй закон Ньютона,

F = м а

мы должны найти чистую силу — вектор сумму все силы — действующие на объект. В добавок к сила T действующая на веревку, какие еще силы действуют на объект ?

Как обсуждалось в классе, на механике мы можем ограничить внимание на «контактные» силы и «гравитацию». Это означает гравитацию тянет вниз на этот ящик с силой, равной его весу, с . Но пол поддерживает ящик. Пол отвечает толкать вверх по ящику с силой, которую мы называем нормой сила . «Нормальный» означает «перпендикулярный». Мы назовем эту силу н ; вы также можете встретить его с маркировкой N или Ф _Н .

Эти силы показаны на «диаграмме свободного тела» выше. Мы нарисовали все силы, действующие на объект. Суммарная сила равна вектору суммы этих сил.

F _нетто = F = T + n + w

где , греческий верхний регистр «сигма» означает «сумма». Помни, хотя, векторная запись всегда элегантная сокращенная запись. Когда мы пишем

F _нетто = F = T + n + w

мы действительно написали

F _{нетто, х} = F _x = T _x + n _x + w _х

и

F _{нетто,у} = F _y = T _y + n _y + w _г

Каковы эти x- и y-компоненты сил T, n, и w ? Для этого первого простого примера мы можем найти — по осмотр — что эти компоненты

Т _х = Т

Т _у = 0

н _х = 0

п _д = п

Вт _х = 0

с _у = – с

Теперь мы готовы применить

F = м а

Но это нужно сначала записать в терминах компонентов,

F _x = F _{нетто, x} = F _x = m a _x

F _x = F _{нетто, x} = F _x = T _x + n _x + w _x = T = m _х

Т = м а _х

а _х = т/м

Ящик имеет горизонтальное ускорение , равное натяжение T разделить на m, массу ящика. Что насчет силы в вертикальном направлении?

F _y = F _{нетто, y} = F _y = m a _y

F _y = F _net,y = F _y = T _y + n _y + w _y = n – w = m _г

н – ш = м а _у

Поскольку мы знаем, что ящик не ускоряется в направлении Y — не вскакивает с пола и не закапывается в пол — мы знаем _у = 0, поэтому

н = ш

Восходящая нормальная сила, действующая со стороны пола на ящик, в этой ситуации, равна весу, направленной вниз силе сила тяжести.

---

Пример 2: Какие силы действуют на книгу, если ее толкнуть вниз на него с силой F пока он сидит на ровной, горизонтальный стол, как показано на рисунке ниже?

Собери все силы. Это называется “свободное тело” диаграмме». В этом курсе механики мы ограничимся «контактные силы» и сила тяжести. Контактные силы, для в этом случае будет «нормальная» сила — перпендикулярная сила — под действием стола — помечен цифрой n на схеме — и сила F , приложенная рукой. Гравитация оказывает силу вниз, называется весом и маркируется w . Так же, как в предыдущий пример, мы можем сразу написать

F = м а

, но это действительно элегантное сокращение для

. F _x = F _{нетто, x} = F _x = м а _х

и

F _y = F _{нетто, y} = F _y = м а _г

В этом примере, хотя ничего не происходит по горизонтали направление. Все силы имеют только вертикаль компоненты, так что все, что у нас есть, это

F _y = F _{нетто, y} = F _y = м а _г

Принимая за положительное, имеем

F _y = F _{нетто, y} = F _г = п – ш – F

Поскольку книга лежит на столе, мы знаем, что она не ускоряется поэтому _y = 0. Это означает

н – ш – Ж = 0

н = ш + Ж

Мы можем использовать законы Ньютона, чтобы определить значение нормального заставить н.

---

Эта же идея и техника могут быть использованы немного по-другому. ситуация,

Пример 3: Рассмотрим лампу, подвешенную на цепи. Что натяжение в цепи?

Как всегда, начнем со “схемы свободного тела”. Натяжение Т воздействует вверх на лампу, в то время как сила тяжести притягивает вниз с силой w , вес светильника. Чистая сила представляет собой векторную сумму этих двух сил. Лампа не ускоряет , поэтому сила должна увеличиться до . равна силе вниз . По величине это означает

Т = ш

---

Напряжение: Напряжение величина силы при помощи цепи, веревки или веревки. Направление этого сила зависит от остальной ситуации и объекта, который мы концентрируемся на данный момент. Если мы сосредоточимся на цепи, показанной ниже, направленная вниз сила T’ — это сила сила, воздействующая на цепь со стороны лампы, в то время как направленная вверх сила Т” сила, действующая на цепь со стороны потолка. Здесь нет заменить хорошие диаграммы свободного тела.

---

Пример 4: Рассмотрим светофор, подвешенный на шнурах, как показано на эскизе ниже. Каково напряжение в каждом из этих шнуры?

Натяжение T ₃ легко, поэтому мы рассмотрим первое. Как мы видели в предыдущих двух примерах; это напряжение в вертикальный шнур, поддерживающий вес, как раз равен весу. В На приведенной ниже схеме мы нарисовали силы, действующие на светофор. На светофор действуют только силы w , вес действует вниз, и T ₃ , восходящая сила из-за вертикального троса. Т ₃ это натяжение этого троса. Ясно

Т ₃ = ш

А как насчет натяжения двух других тросов, T ₂ и Т ₁ ? Чтобы найти их, мы должны посмотреть на перекресток где три кабеля сходятся вместе. Этот перекресток находится в равновесие так

F нетто = 0

F _нетто = F = Т ₁ + Т ₂ + Т ₃ = 0

Однако мы должны помнить, что этот единственный вектор уравнение является элегантным, сокращенная запись для два скаляра уравнения,

F _нетто,x = F _х = Т _{1 х} + Т _{2 х} + Т _{3 х} = 0

F _{нетто,г} = F _г = Т _{1 г} + Т _{2 г} + Т _{3 г} = 0

Итак, мы должны разложить все эти силы на их x- и Y-компоненты,

T _1x = – T ₁ cos 37 ^o = – 0,8 T ₁

T _{1 год} = T ₁ sin 37 ^o = 0,6 Т ₁

T _2x = T ₂ cos 53 ^или = 0,6 Т ₂

T _2y = T ₂ sin 53 ^o = 0,8 Т ₂

Т _3x = 0

T _{3 года} = – T ₃ = – w

знаков важны! Теперь мы можем вернуться к уравнения компонентов и решить для растяжения T ₁ и Т ₂ .

F _нетто,x = F _х = Т _{1 х} + Т _{2 х} + Т _{3 х} = 0

T _{1 x} + T _{2 x} + T _{3 x} = 0

– 0,8 Т ₁ + 0,6 Т ₂ + 0 = 0

Т ₁ = 0,75 Т ₂

F _{нетто, у} = F _г = Т _{1 г} + Т _{2 г} + Т _{3 г} = 0

T _{1 год} + T _{2 года} + T _{3 года} = 0

0,6 Т ₁ + 0,8 Т ₂ 2 – w = 0

0,6 Т ₁ + 0,8 Т ₂ = w

0,6 (0,75 Т ₂ ) + 0,8 Т ₂ = w

1,25 Т ₂ = ш

Т ₂ = 0,8 ш

T ₁ = 0,75 (0,8 Вт)

T ₁ = 0,6 Вт

---

Теперь мы расширяем наши приложения и смотрим на Этвудс Машина

Пример 5 : Рассмотрим показанную здесь машину Этвуда с массы m ₁ и m ₂ . Они прикреплены к легкий шнур над шкивом, как показано на рисунке. Что такое ускорение системы?

	Мы можем сказать “ускорение системы” для масс 1 и 2 будут иметь такое же ускорение , так как они крепятся шнуром. Если m 2 > m 1 и Этвудс машина выходит из состояния покоя, масса m 1 будет ускорение вверх вард в то время как масса m 2 разгоняет вниз на вард. Собственно, это будет их ускорений независимо от того, вышла ли система из состояния покоя или двигается. Вероятно, это легче представить, если вы подумайте о том, что система выходит из состояния покоя. Как мы можем применить F = m a ? Применим F = m a к массам, по одной на a время.
Посмотрите на меньшую массу, m 1 . Какие силы, действующие на эту массу? Натяжение струны создает силу вверх в то время как гравитация оказывает силу вниз . Мы ожидаем этого масса, имеющая ускорение a, равное и . Там горизонтальных сил нет. Возьмем вверх по как положительное . F нетто = F = Т – ш 1 = м 1 а F нетто = F = Т – м 1 г = м 1 а Т – м 1 г = м 1 а Это одно уравнение имеет два неизвестных — напряжение T и ускорение a. Так что нам нужно еще информация .
Мы получаем эту дополнительную информацию, просматривая силы, действующие на более тяжелую массу, м 2 и применяя второй закон Ньютона, F = m a , к эта масса. Горизонтальных сил нет. Натяжение струны создает силу вверх в то время как гравитация оказывает силу вниз . Мы ожидаем этого масса, чтобы иметь ускорение a, которое составляет вниз . Мы можно назвать вниз “положительным” для этой массы или мы можем позвонить до “положительно” и дальше ожидаем эта масса должна иметь ускорение – а. Любой выбор Это хорошо. На этот раз давайте выберем из как “положительное”. F нетто = F = w 2 – T = m 2 а F нетто = F = m 2 г – T = m 2 a м 2 г – Т = м 2 а Конечно, это одно уравнение также имеет два неизвестные — напряжение T и ускорение a.

Но теперь у нас есть два уравнения с двумя неизвестными и этого достаточно. Мы можем найти напряжение T в первое уравнение,

Т – м ₁ г = м ₁ а

T = m ₁ г + m ₁ a

, а затем подставьте это во второе уравнение

. м ₂ г – Т = м ₂ а

м ₂ г – ( м ₁ г + м ₁ а ) = м ₂ а

м ₂ г – м ₁ г – м ₁ а = м ₂ а

м ₂ г – м ₁ г = м ₁ а + м ₂ а

( м ₂ – м ₁ ) г = ( м ₁ + м ₂ ) а

( м ₁ + м ₂ ) а = ( м ₂ – м ₁ ) г

а = ( м ₂ – м ₁ ) г / ( м ₁ + м ₂ )

---

Пример 6: Теперь давайте рассмотрим наклонную машину Этвуда. Массы м ₁ и m ₂ соединены нитью который наезжает на шкив массой m ₂ сидит на гладкой наклонная плоскость. Помните, что «гладкий» — это просто кодовое слово для «без трения»; мы скоро перейдем к трениям. Это наклонно Машина Этвудса нарисована здесь:

Теперь мы хотим применить второй закон Ньютона, F = m и . Второй закон Ньютона описывает действие сил на один объект. Итак, мы должны изолировать все силы от массы м ₁ и примените его. Затем мы изолируем все силы на массу m ₂ и примените еще раз. Это требует хорошего свободного тела диаграммы.

На подвешенный груз m1 действуют только две силы; струна тянет вверх с силой, которую мы обозначаем буквой Т, в то время как гравитация тянет вниз с силой мы маркируем w:

Мы ожидаем, что ускорение будет восходящим, и нарисовали его. рядом с диаграммой свободного тела. Как всегда, мы готовы подать заявку Ф = m a к этим силам, действующим на этот объект.

F _нетто = F = T – m ₁ g = m ₁ а

Т – м ₁ г = м ₁ а

Как мы уже могли ожидать, это одно уравнение имеет два неизвестные — напряжение T и ускорение a — так что надо смотреть в другом месте для получения дополнительной информации. Конечно, где посмотреть находится на другой массе.

Тщательно постройте диаграмму свободного тела, показывающую все силы действующая на массу m ₂ . На тело действуют трех сил. на эту массу — струна действует с силой Тл , (без трения) наклонная плоскость действует на «нормальную» силу n , и гравитация тянет вниз с силой w ₁ = м ₁ г. Чтобы найти чистую силу , мы должны решить эти векторы на их компоненты. Так как ускорение будет быть вдоль направления плоскости, мы выбрали это направление как ось х.

Обратите внимание, что угол в эта диаграмма измерена от оси y 90 395. Это означает, что вес имеет компоненты

w _x = m ₂ g sin

w _y = – m ₂ g cos

А у нас

н _х = 0

п _д = п

и

Т _х = – Т

Т _у = 0

Убедитесь, что вы понимаете знаки и синусы! Не продолжай пока все эти составляющие вам не понятны!

Теперь мы можем применить второй закон Ньютона к этой массе:

F = м а

F = F _нетто = T + n + ш = м а

F _x = F _{нетто, x} = F _x = м ₂ a _x

Ф _х = T _x + n _x + w _x = m ₂ а _х

– Т _{+ 0 + м 2 г синх = m 2 a x = m 2 a}

, где мы использовали

а _х =

, поскольку ускорение происходит только в положительном направлении x.

– Т _{+ м 2 г грех = м 2 и}

Это дает всю информацию, необходимую для решения T и a. Как и раньше, мы можем решить одно из этих уравнений относительно T и подставьте это в другое уравнение и найдите а.

Т = м ₂ г sin – м ₂ а

[м ₂ г sin – м ₂ а] – м ₁ г = м ₁ а

м ₁ а + м ₂ а = м ₂ г sin – м ₁ г

( м ₁ + м ₂ ) а = ( м ₂ sin – м ₁ ) г

а = ( м ₂ грех – м ₁ ) г/( м ₁ + м ₂ )

Как насчет y-компонент сил на массу м ₂ , на наклонной плоскости?

F _y = F _{нетто, y} = F _г = м ₂ а _у

F _у = T _y + n _y + w _y = m ₂ а _у = 0

, где мы использовали

а _у = о

, так как ускорение происходит только в положительном направлении x и ускорение перпендикулярно плоскости отсутствует.

T _y + n _y + w _y = 0

0 + n – m ₂ г cos = 0

n = m ₂ г cos

Из y-компонент сил на массу m ₂ получаем можно найти нормальную силу. Это будет важно, когда мы учитывать трение .

---

Пример 7: Два блока масс m ₁ и m ₂ располагаются в соприкосновении друг с другом на гладкой, горизонтальной плоскости, как показано здесь. Постоянная горизонтальная сила F применяется к m ₁ . Каково ускорение каждая масса?

В каком-то смысле мы можем (почти) решить этот пример интуитивно — в нашей голове. Сила F приложена к телу, масса которого равна m = м ₁ + м ₂ . Значит его ускорение должно быть

а = Ф/м

или

а = F / (м ₁ + м ₂ )

Это правильный ответ! Но больше ничего в этом нет вопрос? Простые вопросы — интуитивно очевидные — заставляют замечательные шаблоны или примеры для более сложных задач.

Посмотреть все силы на m ₁ . Сделать хорошее свободное тело диаграмма сил, действующих на m ₁ .

Конечно, внешняя сила F толкает вправо на масса m ₁ . Гравитация тянет вниз с силой ш ₁ = м ₁ г и самолет отвечает с нормальной силой н ₁ . Но другой масса — m ₂ — действует на массу m 9 с силой0015 1 . Эта сила обозначена как P’ и направлена ​​влево. Мы можем примените второй закон Ньютона к силам, составляющим y, и найдите, что n ₁ = w ₁ 1. Но теперь есть дополнительная и неизвестная сила в x-компоненте второго закона Ньютона,

F _{1, нетто} = F – P’ = m ₁ a

Нам нужно больше информации поэтому обратимся к другой массе, м ₂

Первая масса m1 действует на эту массу с силой P , m2. Применяя y-компоненту F = m a , мы легко найти

п ₂ = ш ₂

Для x-компонент только сила, действующая на м2, равна P так

F _{2, нетто} = P = m ₂ a

Однако из третьего закона Ньютона F ₁₂ = – F ₂₁ , мы знаем, что P = P’, поэтому

F – P’ = м ₁ а

F – м ₂ а = м ₁ а

F = м ₁ а + м ₂ а

F = ( м ₁ + м ₂ ) a

а = F / ( м ₁ + м ₂ )

Это тот же самый ответ, который мы так быстро нашли ранее, но этот может предоставить шаблон для использования в более сложных ситуациях.

---

Пример 8: Этот конкретный пример сформулирован в терминах весом рыба в ускоряющемся лифте. это тоже весело думать о весе себя в разгоняющемся лифте. Когда лифт разгоняется до градусов? Когда лифт разогнаться вниз на кварталов?

Силы, действующие на рыбу, показаны в свободном теле. диаграмма. T – натяжение, обеспечиваемое весами. Это значение шкала читает. Мы можем назвать это кажущимся весом рыба. Чистая сила, действующая на рыбу, равна

F _сетка = T – w

или

F _нетто = T – мг

Суммарная сила ( всегда! ) равна произведению массы на ускорение. Эта рыба движется вместе с лифтом. В этом на диаграмме мы взяли ускорение от до , так что оно положительный.

F _нетто = T – m g = m a

Т = м г+ м а

Т = м (г + а)

Пока лифт ускоряется с до , кажущийся вес рыбы на больше ее истинного веса, мг.