Эффективное напряжение: Действующее значение тока и напряжения

Содержание

Эффективное напряжение переменного тока. Действующие значения силы тока и напряжения

Cтраница 2

Действующим значением силы тока I называется сила постоянного тока, выделяющего в проводнике за то же время такое же количество теплоты, что и переменный ток.

Как видно из рисунка, в каждый момент времени величины напряжения и силы тока принимают различные значения. Поэтому, чтобы судить о величине силы тока и напряжения переменного тока, пользуются действующим значением силы тока и напряжения. Чтобы определить действующее значение силы переменного тока, его приравнивают к силе постоянного тока, которое выделило бы в проводнике такое же количество тепла, как и переменный ток.

Трансформатор, содержащий в первичной обмотке 300 витков, включен в сеть переменного тока с действующим напряжением 220 В. Вторичная цепь трансформатора питает нагрузку с активным сопротивлением 50 Ом. Найти действующее значение силы тока во вторичной цепи, если падение напряжения во вторичной обмотке трансформатора, содержащей 165 витков, равно 50 В.

Таким образом, при замене операции извлечения корня сравнением время, за которое интегрируемый сигнал с ГЛИН станет равен интегралу от квадрата измеренной силы тока, пропорционально действующему значению силы тока. До этого К2 был открыт в течение времени т и пропускал на счетчик СИ импульсы с генератора тактовых импульсов ГТИ. Число импульсов TV / гтит записанное в СЧ, пропорционально действующему значению силы тока. Это число хранится в / 77, а по окончании цикла измерения отображается на ЦИ.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Рх o jjFr В слУчае т – н – СУХОЙ лампы применяют способ термометра, подвешиваемого вблизи генераторной лампы, и отмечают его показание. Затем, разрывая цепь колебательного контура генератора, дают на сетку генераторной лампы положительный потенциал до тех пор, пока термометр не по. Беря в последнем случае величины 1а и Еа как исходные, определяем Рх из соотношения Рх1а Еа. Мощность в антенне определяется по ф-ле Рх – / /, где РЯ – мощность eW, ra – активное сопротивление антенны в Q и 1а – действующее значение силы тока в антенне в А. По скольку по современным международным нормам под мощностью передатчика принято понимать мощность в антенне, то упомянутая выше ф-ла определяет одновременно и мощность передатчика.

Тепловые измерители имеют наиболее широкое практич. Действие тепловых измерителей состоит в удлинении тонкой проволоки при нагревании ее проходящим по ней переменным током высокой частоты. Сам по себе эффект ограничивает пределы применимости таких измерителей токами от нескольких тА до 1 – 3 А в зависимости от материала тонкой проволоки, примененной в измерителе. Применяются сплавы серебра с платиной, платины с иридием и др.

Если сплав применяется в виде проволоки, то она имеет диаметр сотых долей мм. При ленте толщина составляет 0 01 мм, ширина 3 мм и длина 25 – 30 мм. Удлинение нити нагреваемым током пропорционально квадрату действующего значения силы тока. Перемещение по шкале измерителя стрелки, связанной с той же проволокой с помощью особой подвижной системы, обычно пропорционально квадратному корню из действующей силы тока. Из-за этого шкалы тепловых измерителей имеют неравномерные интервалы между делениями.

В данном случае колебания тока являются гармоническими (график колебаний – синусоида) и вынужденными, поскольку параметры колебаний (частота, амплитуда) определяются внешним источником – генератором. Некоторые электротехнические устройства (например, колебательный контур) способны генерировать свободные гармонические колебания электрического тока. По левой ветви рамки – от нас и, поскольку в этом случае через клемму а течет ток в направлении, обратном показанному на рис. 12.1, ее полярность – минус.

Поскольку при данном положении рамки сила тока имеет наибольшее значение, фаза колебаний может быть г / 2 или 3 / 2ir, в зависимости от того, какое направление тока в рамке мы принимаем за положительное. Сравнивая формулу (12.1) и заданную зависимость, нетрудно заметить, что 1т 10 А и ш 4тград / с. Далее, используя формулу (12.2), определяем частоту колебаний (отв. Используя закон Джоуля – Ленца (Q I2Rt), определяем действующее значение силы тока (отв.

Как известно, переменная э.д.с. индукции вызывает в цепи переменный ток. При наибольшем значении э.д.с. сила тока будет иметь максимальное значение и наоборот. Это явление называется совпадением по фазе. Несмотря на то что значения силы тока могут колебаться от нуля и до определенного максимального значения, имеются приборы, с помощью которых можно замерить силу переменного тока.

Характеристикой переменного тока могут быть действия, которые не зависят от направления тока и могут быть такими же, как и при постоянном токе. К таким действиям можно отнести тепловое. К примеру, переменный ток протекает через проводник с заданным сопротивлением. Через определенный промежуток времени в этом проводнике выделится какое-то количество тепла. Можно подобрать такое значение силы постоянного тока, чтобы на этом же проводнике за то же время выделялось этим током такое же количество тепла, что и при переменном токе. Такое значение постоянного тока называется действующим значением силы переменного тока.

В данное время в мировой промышленной практике широко распространен трехфазный переменный ток , который имеет множество преимуществ перед однофазным током. Трехфазной называют такую систему, которая имеет три электрические цепи со своими переменными э.д.с. с одинаковыми амплитудами и частотой, но сдвинутые по фазе относительно друг друга на 120° или на 1/3 периода. Каждая такая цепь называется фазой.

Для получения трехфазной системы нужно взять три одинаковых генератора переменного однофазного тока, соединить их роторы между собой, чтобы они не меняли свое положение при вращении. Статорные обмотки этих генераторов должны быть повернуты относительно друг друга на 120° в сторону вращения ротора. Пример такой системы показан на рис. 3.4.б.

Согласно вышеперечисленным условиям, выясняется, что э.д.с., возникающая во втором генераторе, не будет успевать измениться, по сравнению с э.д.с. первого генератора, т. е. она будет опаздывать на 120°. Э.д.с. третьего генератора также будет опаздывать по отношению ко второму на 120°.

Однако такой способ получения переменного трехфазного тока весьма громоздкий и экономически невыгодный. Чтобы упростить задачу, нужно все статорные обмотки генераторов совместить в одном корпусе. Такой генератор получил название генератор трехфазного тока (рис. 3.4.а). Когда ротор начинает вращаться, в каждой обмотке возникает

а) б)

Рис. 3.4. Пример трехфазной системы переменного тока

а) генератор трёхфазного тока; б) с тремя генераторами;

изменяющаяся э.д.с. индукции. Из-за того что происходит сдвиг обмоток в пространстве, фазы колебаний в них также сдвигаются относительно друг друга на 120°.

Для того чтобы подсоединить трехфазный генератор переменного тока к цепи, нужно иметь 6 проводов. Для уменьшения количества проводов обмотки генератора и приемников нужно соединить между собой, образовав трехфазную систему. Данных соединений два: звезда и треугольник. При использовании и того и другого способа можно сэкономить электропроводку.

Соединение звездой

Обычно генератор трехфазного тока изображают в виде 3 статорных обмоток, которые располагаются друг к другу под углом 120°. Начала обмоток принято обозначать буквами А, В, С , а концы – X, Y, Z . В случае, когда концы статорных обмоток соединены в одну общую точку (нулевая точка генератора), способ соединения называется «звезда». В этом случае к началам обмоток присоединяются провода, называемые линейными (рис. 3.5 слева).

Точно так же можно соединять и приемники (рис. 3.5., справа). В этом случае провод, который соединяет нулевую точку генератора и приемников, называется нулевой.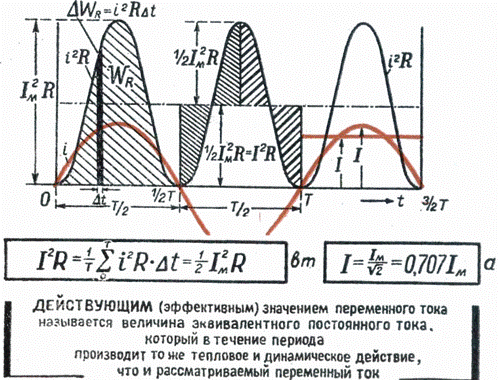

Данная система трехфазного тока имеет два разных напряжения: между линейным и нулевым проводами или, что то же самое, между началом и концом любой обмотки статора. Такая величина называется фазным напряжением (Uл ). Поскольку цепь трехфазная, то линейное напряжение будет в v3 раз больше фазного, т. е.: Uл = v3Uф.

Соединение треугольником.

Рисунок 3.6. Пример соединения треугольником

При использовании данного способа соединения конец X первой обмотки генератора подключают к началу В второй его обмотки, конец Y второй обмотки – к началу С третьей обмотки, конец Z третьей обмотки – к началу А первой обмотки. Пример соединения показан на рис. 3.6. При данном способе соединения фазных обмоток и подключении трехфазного генератора к трехпроводной линии линейное напряжение по своему значению сравнивается с фазным: Uф = Uл

Контрольные вопросы

1. Перечислите основные параметры, характеризующие переменный ток.

2. Дайте определение частоты и единицы её измерения.

3. Дайте определение амплитуды и единицы её измерения.

4. Дайте определение периода и единицы его измерения.

5. Отличие простейшего генератора трёхфазного тока от генератора однофазного тока.

6. Что такое фаза?

7. Что представляет собой ротор генератора трёхфазного тока?

8. Почему сдвинуты по фазе обмотки статора генератора трёхфазного тока?

9. Особенность симметричной системы трёх фаз.

10. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «звезда».

11. Принцип соединения фазных обмоток трёхфазных генераторов и трансформаторов по схеме «треугольник».

3.2. Виды сопротивлений в цепях переменного тока

В цепях переменного тока сопротивления разделяют на активные и реактивные.

В активных сопротивлениях , включенных в цепь переменного тока, электрическая энергия преобразуется в тепловую. Активным сопротивлением R обладают, например, провода электрических линий, обмотки электрических машин и т. д.

В реактивных сопротивлениях электрическая энергия, вырабатываемая источником, не расходуется. При включении реактивного сопротивления в цепь переменного тока возникает лишь обмен энергией между ним и источником электрической энергии. Реактивное сопротивление создают индуктивности и ёмкости.

Если не учитывать взаимное влияние отдельных элементов электрической цепи, то в общем случае электрическая цепь синусоидального тока может быть представлена тремя пассивными элементами: активным сопротивлением R, индуктивностью L и емкостью C.

Активное сопротивление в цепи переменного тока .

При включении в цепь переменного тока активного сопротивления, ток и напряжение совпадают по фазе (рис. 3.7) и изменяются по одному и тому же cинусоидальному закону: u=U m sinωt . Они одновременно достигают своих максимальных значений и одновременно проходят через нуль (рис. 3.7.б).

Для цепи переменного тока, содержащей только активное сопротивление, закон Ома имеет такую же форму, как и для цепи постоянного тока: I=U/R.

Электрическая мощность р в цепи с активным сопротивлением в любой момент времени равна произведению мгновенных значений силы тока i и напряжения u : p=ui .

Рисунок 3.7. Схема включения в цепь переменного тока активного сопротивления R (a), кривые тока i , напряжения u и мощности p (б) и векторная диаграмма.

Из графика видно, что изменение мощности происходит с двойной частотой по отношению к изменению тока и напряжения, т.е. один период изменения мощности соответствует половине периода изменения тока и напряжения. Все значения мощности положительные, это означает, что энергия передается от источника к потребителю.

Средняя мощность Рcp , потребляемая активным сопротивлением, P=UI=I 2 R – это и есть активная мощность.

Под индуктивностью L будем понимать элемент электрической цепи (катушку индуктивности, потерями которой можно пренебречь), способный запасать энергию в своём магнитном поле, который не имеет активного сопротивления и ёмкостиС (рис. 3.8).

При включении в цепь переменного тока индуктивности, изменяющийся ток непрерывно индуцирует в ней э.д.с. самоиндукции e L = LΔi/Δt, где Δi/Δt – скорость изменения тока.

Когда угол ωt равен 90° и 270° скорость изменения тока Δi/Δt =0, поэтому э.д.с. e L =0.

Скорость изменения тока будет наибольшей, когда угол ωt равен 0°, 180° и 360°. В эти минуты времени э.д.с. имеет наибольшее значение.

Кривая мощности представляет собой синусоиду, которая изменяется с двойной частотой по сравнению с частотой изменения тока и напряжения. Мощность имеет положительные и отрицательные значения, т.е. возникает непрерывный колебательный процесс обмена энергией между источником и индуктивностью.

Рисунок 3.8. Схема включения в цепь переменного тока индуктивности (а), кривые тока i , напряжения u , э.д.с. e L (б) и векторная диаграмма (в)

Э.д.с. самоиндукции согласно правилу Ленца направлена так, чтобы препятствовать изменению тока. В первую четверть периода, когда ток увеличивается, э.д.с. имеет отрицательное значение (направлена против тока).

Во вторую четверть периода, когда ток уменьшается, э.д.с. имеет положительное значение (совпадает по направлению с током).

В третью четверть периода ток меняет своё направление и увеличивается, поэтому э.д.с. направлена против тока и имеет положительное значение.

В четвёртую четверть периода ток уменьшается и э.д.с. самоиндукции стремится поддержать прежнее положение тока и имеет отрицательное значение. В результате ток отстает от напряжения по фазе на угол 90 О.

Сопротивление катушки или проводника переменному току, вызванное действием э.д.с. самоиндукции, называется индуктивным сопротивлением Х L [Ом]. Индуктивное сопротивление не зависит от материала катушки и от площади поперечного сечения проводника.

В цепях переменного тока катушки индуктивности соединяют последовательно и параллельно.

При последовательном соединении катушек эквивалентная индуктивностьLэ и эквивалентное индуктивное сопротивление X L э будут равны:

Lэ=L 1 +L 2 +… X L э=X L 1 +X L 2 +…

При параллельном соединении катушек:

1/Lэ=1/L 1 +1/L 2 +… 1/X L э=1/X L 1 +1/X L 2 +…

Контрольные вопросы

1. Какие виды сопротивления в цепях переменного тока Вы знаете?

2. Что значит активное сопротивление?

3. Что такое реактивное сопротивление?

4. Какие элементы цепи создают реактивное сопротивление?

5. Что такое активная мощность?

1. Дайте определение индуктивности.

2. Что происходит в первую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

3. Что происходит во вторую четверть периода колебательного процесса обмена энергией между источником и индуктивностью?

4. Дайте определение индуктивного сопротивления.

3.3. Конденсаторы. Ёмкость в цепи переменного тока

Конденсатор – устройство, способное накапливать электрические заряды.

Простейший конденсатор представляет собой две металлические пластины (электроды), разделенные диэлектриком.

Каждый конденсатор характеризуется номинальной емкостью и допустимым напряжением. Напряжение конденсатора указывают на корпусе, и превышать его нельзя. Конденсаторы различаются формой электродов (плоский), типом диэлектрика и ёмкостью (постоянной и переменной).

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

. Переменный ток можно считать постоянным только в течение очень малых промежутков времени

. Поделим период колебанийна очень большое число малых промежутков времени

. Количество теплоты

, выделяемое на сопротивленииза время

. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло

. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока

. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4.29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

Величину

усреднять не нужно, так как она не зависит от времени, следовательно:

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому

(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то

. Если участок цепи содержит только индуктивность или только ёмкость, то

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением

а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:

. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора

. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Комплексные токи и напряжения. Трехфазное напряжение. Эффективное напряжение. Асинхронный трехфазный двигатель

Экзамен. Комплексные токи и напряжения.

Комплексные токи и напряжения вводят для рассмотрения гармонически изменяющихся токов и напряжений. Комплексные токи и напряжения позволяют заменить дифференциальные уравнения Кирхгофа для токов комплексными уравнениями Кирхгофа.

Рассмотрим вещественное напряжение:

U t( ) =U₀cos(ω ϕt ⁺₀), где U₀ — вещественная амплитуда, ω — циклическая частота, ϕ₀ — начальная фаза.

Будем называть соответствующим комплексным напряжением величину: ^~

_{U t}( )=U e₀i(^ωϕ^t⁺⁰), где волной сверху _U^~ будем обозначать, что величина комплексная.

Тогда U ta f = ReFGHU t~a fIJK

U~ =U eⁱ(ωϕt+ 0) =U e0 iϕ0 ei tω =U e~ 0 i tω , где

U0 ≡U e₀ⁱ^ϕ0 — комплексная амплитуда напряжения, U₀ — вещественная амплитуда, ϕ₀ — начальная фаза или фаза в нулевой момент времени.

~ ~

U t( )=U₀e^{i t}^ω

Гармонически изменяющееся напряжение можно изобразить на комплексной плоскости напряжений.

Напряжение, которое есть на самом деле, — это вещественное напряжение равное проекции комплексного напряжения на вещественную ось ReF^GHU t~a fI^JK =_{U t}a f.

Комплексная амплитуда напряжения тоже может быть изображена на комплексной плоскости — комплексной плоскости амплитуд. В отличие от комплексного напряжения комплексная амплитуда не изменяется во времени и не вращается на комплексной плоскости.

Аналогично комплексным напряжениям вводятся комплексные токи. I t( ) = I₀cos(ω ψt ⁺₀) — вещественный ток.

^~I t( )= I e₀ⁱ(^ωψ^t⁺⁰) — соответствующий ему комплексный ток. I ta f = ReFGH I t~a fIJK

~I t( )= I e0 i(ωψt+ 0) = I e0 iψ0ei tω = ~I e0 i tω =>

I0 ≡ I e₀ⁱ^ψ0 — комплексная амплитуда тока, I₀ — вещественная амплитуда тока, ψ₀ — начальная фаза тока или фаза в нулевой момент времени.

~ ~

I t( )= I e0 i tω

Факультатив. Трехфазное напряжение.

, .

Экзамен. Эффективное напряжение.

Эффективное значение переменного напряжения любой формы равно по величине постоянному напряжению, которое также нагревает сопротивление, как и рассматриваемое переменное напряжение.

Мощность Ленц-Джоулева тепла N = . Согласно определению

эффективного напряжения

U 2 Uэфф2

N = = => R R

Uэфф2 ≡ U 2 ( )t .

Аналогично для тока N = I²R => Iэфф2 ≡ I2 ( )t .

Для гармонически изменяющихся напряжений U t( ) =U₀cos(ω ϕt ⁺₀)

Uэфф2 U2 t U2 2 t U2 2 t U2 =>

Uэфф = U0 .

Аналогично для гармонически изменяющегося тока: I_эфф⁼^I.

Для напряжения (или тока) в форме меандра

——–

Бытовое напряжение сети переменного тока 220 Вольт — эффективное напряжение.

Для трехфазной сети переменного тока есть два стандарта.

1). Сеть 220/127 Вольт. Это сеть с эффективным напряжением 127 Вольт каждой фазы относительно нулевого провода. Эффективное напряжение между фазами —220 Вольт. Бытовые приборы в такой сети включаются между двумя фазами.

2). Сеть 380/220 Вольт. В этой сети эффективное напряжение каждой фазы 200 Вольт, напряжение между фазами 380 Вольт. Бытовые приборы включаются между фазой и нулевым проводом.

Факультатив. Асинхронный трехфазный двигатель.

Двигатель имеет три неподвижных статорных обмотки, на которые подают три фазы трехфазного напряжения.

В пунктирной области между обмотками образуется вращающееся магнитное поле B, так как магнитное поле достигает максимального значения сначала в одной обмотке, затем во второй, затем в третьей.

В эту область вращающегося магнитного поля помещают ротор электродвигателя. Ось вращения ротора перпендикулярна плоскости рисунка. На роторе электродвигателя закреплена короткозамкнутая роторная обмотка.

Для простоты будем считать, что роторная обмотка — это один виток

эффективное напряжение – это… Что такое эффективное напряжение?

эффективное напряжение: net voltage

эффективное наполнение
эффективное обозначение

Смотреть что такое “эффективное напряжение” в других словарях:

Эффективное напряжение — напряжение, действующее в скелете грунта, определяемое как разность между полным напряжением в образце грунта и давлением в поровой жидкости. Источник: ГОСТ 12248 96: Грунты. Методы лабораторного определения характеристик прочности и… … Словарь-справочник терминов нормативно-технической документации
эффективное напряжение — efektinė įtampa statusas T sritis Standartizacija ir metrologija apibrėžtis Apibrėžtį žr. priede. priedas( ai) Grafinis formatas atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
эффективное напряжение — efektinė įtampa statusas T sritis fizika atitikmenys: angl. effective voltage vok. effektive Spannung, f rus. действующее напряжение, n; эффективное напряжение, n pranc. tension efficace, f … Fizikos terminų žodynas
эффективное напряжение — efektyvusis įtempis statusas T sritis fizika atitikmenys: angl. effective stress vok. effektive Spannung, f rus. эффективное напряжение, n pranc. contrainte effective, f … Fizikos terminų žodynas
Эффективное напряжение — Мощность физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу.… … Википедия
эффективное напряжение шума интегральной микросхемы — эффективное напряжение шума Отношение шума на выходе, выраженного в эффективных значениях напряжения в заданной полосе частот, к коэффициенту усиления интегральной микросхемы. Обозначение Uш.эфф Uneff [ГОСТ 19480 89] Тематики микросхемы Синонимы… … Справочник технического переводчика
(эффективное) напряжение прикосновения — ((effective) touch voltage): Напряжение между проводящими частями при одновременном прикосновении к ним человека или животного. 826 11 07 [195 05 02] Источник: ГОСТ Р МЭК 60050 826 2009: Установки электрические. Термины и определения … Словарь-справочник терминов нормативно-технической документации
напряжение прикосновения — Напряжение, появляющееся на теле человека при одновременном прикосновении к двум точкам проводников или проводящих частей, входящих в электрическую цепь, в том числе при повреждении изоляции. [ГОСТ Р 50669 94] напряжение прикосновения Напряжение… … Справочник технического переводчика
Напряжение электронагревательной секции рабочее — Рабочее напряжение электронагревательной секции номинальное эффективное напряжение, при котором предусмотрена эксплуатация электронагревательной секции… Источник: ГОСТ Р 50571.25 2001. Электроустановки зданий. Часть 7. Требования к специальным… … Официальная терминология
эффективное поле зрения ФЭПП — Телесный угол, определяемый соотношением где Uc напряжение фотосигнала ФЭПП; допускается замена параметра Uc на Ic, Iф; θ угол между направлением падающего излучения и нормалью к фоточувствительному элементу; φ азимутальный угол.… … Справочник технического переводчика
напряжение — 3.10 напряжение: Отношение растягивающего усилия к площади поперечного сечения звена при его номинальных размерах. Источник: ГОСТ 30188 97: Цепи грузоподъемные калиброванные высокопрочные. Технические условия … Словарь-справочник терминов нормативно-технической документации

Эффективное, действующее напряжение, сила тока. Значение. Действующие значения силы тока и напряжения

Переменный ток долгое время не находил практического применения. Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи. Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

(4.29)

4.4.5. Мощность в цепи переменного тока

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

С использованием известной тригонометрической формулы

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Рассмотрим следующую цепь.

Она состоит из источника переменного напряжения, соединительных проводов и некоторой нагрузки. Причем индуктивность нагрузки очень мала, а сопротивление R очень велико. Эту нагрузку мы раньше называли сопротивлением. Теперь будем называть её активным сопротивлением.

Активное сопротивление

Сопротивление R называют активным, так как если в цепи будет нагрузка с таким сопротивлением, цепь будет поглощать энергию, поступающую от генератора. Будем считать, что напряжение на зажимах цепи подчиняется гармоническому закону:

U = Um*cos(ω*t).

Мгновенное значение силы тока можем вычислить по закону Ома, оно будет пропорционально мгновенному значению напряжения.

I = u/R = Um*cos(ω*t)/R = Im*cos(ω*t).

Сделаем вывод: в проводнике с активным сопротивлением разность фаз между колебаниями напряжения и силы тока отсутствует.

Действующее значение силы тока

Амплитуда силы тока определяется по следующей формуле:

Среднее значение квадрата силы тока за период вычисляется по следующей формуле:

Здесь Im есть амплитуда колебания силы тока. Если мы теперь вычислим квадратный корень из среднего значения квадрата силы тока, то получим величину, которая называется действующим значением силы переменного тока.2) = Um/√2.

Теперь подставим действующие значения силы тока и напряжения, в выражение Im = Um/R. Получим:

Данное выражение является законом Ома для участка цепи с резистором, по которому течет переменный ток. Как и в случае механических колебаний, в переменном токе нас мало будут интересовать значения силы тока, напряжении в какой-то отдельный момент времени. Гораздо важнее будет знать общие характеристики колебаний – такие, как амплитуда, частота, период, действующие значения силы тока и напряжения.

Кстати, стоит отметить, что вольтметры и амперметры, предназначенные для переменного тока, регистрируют именно действующие значения напряжения и силы тока.

Еще одним преимуществом действующих значений перед мгновенными является то, что их можно сразу использовать для вычисления значения средней мощности P переменного тока.

После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.

Действующее значение переменного тока

Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и – начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Действующее и среднее значения переменного тока и напряжения.

Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:

Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).

Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :

Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.

Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.

Что берется за действующее значение силы переменного тока и переменного напряжения

что берется за действующее значение силы переменного тока и переменного напряжения?

Боевое яйцо

Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.

Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.

Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.

Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.

Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.

Вопрос: напряжение в электросети 220 В, что это значит?

Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.

Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.

Пример: Определить амплитуду напряжения электросети с напряжением 220 В.

Амплитуда равна 220 * 1,41=310,2 В.

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .

Переменный электрический ток – это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

\(~u = U_m \cdot \sin \omega t\) или \(~u = U_m \cdot \cos \omega t\) ,

где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

\(~i = I_m \cdot \sin (\omega t + \varphi_c)\) ,

где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Генератор переменного тока

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.

Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

\(e={\rm E}_{m} \cdot \sin \omega \cdot t,\)

где \({\rm E}_{m} =B\cdot S\cdot \omega\) – амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке

\(i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\)

где \(I_{m} = \dfrac{B\cdot S\cdot \omega }{R}\) – амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

индуктор – электромагнит или постоянный магнит, который создает магнитное поле;
якорь – обмотка, в которой индуцируется переменная ЭДС;
коллектор со щетками – устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

Неподвижная часть генератора называется статором , а подвижная – ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.

На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.

Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.

Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» – спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».

*Принцип действия

Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.

Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией \(\vec{B}\) (см. рис. 1).

При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля \(\vec{B}\) и нормали к плоскости рамки \(\vec{n}\) меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то

\(\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,\)

где ω – угловая скорость вращения рамки, ν – частота ее вращения.

В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом

\(\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.\)

Тогда согласно закону Фарадея индуцируется ЭДС индукции

\(e=-\Phi “(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.\)

Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

\(u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)\)

Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

\(i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)\)

где \(I_m = \dfrac{U_{m}}{R}.\) Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .

Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .

Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой I .

Действующим (эффективным) значением напряжения переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой U .

Действующие (I, U ) и амплитудные (I m , U m ) значения связаны между собой следующими соотношениями:

\(I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}.\)

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

\(P = U\cdot I = I^{2} \cdot R = \dfrac{U^{2}}{R}.\)

Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.

Напряжение эффективное – Энциклопедия по машиностроению XXL

Такая формулировка связана со следующими обстоятельствами. Известные дислокационные модели зарождения микротрещин [4, 25, 170, 247] показывают, что они возникают при некотором критическом значении локальных напряжений в голове дислокационного скопления. Это соответствует критическому значению эффективного напряжения = Эффективное напряжение здесь определяется равенством a ff = ai — оо, в котором величина Оо есть так называемое напряжение трения, являющееся суммой напряжений Пайерлса—Набарро и сопротивления скольжению, обусловленного взаимодействием дислокаций с примесными атомами, точечными дефектами и исходными дислокациями [170]. Иными словами, оо есть напряжение, соответствующее началу пластического течения в зерне. С другой стороны, как известно, при температуре нулевой пластичности Т = = Tq условие наступления пластического течения (2.3) есть одновременно и условие разрушения сг/ = От(7 о) [170, 222]. Очевидно, что в данном случае выполнено условие зарождения микротрещины, и, следовательно, справедливо равенство [c.67]
Для переменных нагрузок допускаемые напряжения понижают с учетом характеристики цикла напряжений, эффективного коэффициента концентрации напряжений в сварных швах, числа циклов нагружения и других факторов. [c.23]

Яа — напряженность эффективного поля магнитной анизотропии [c.653]

Не — напряженность эффективного обменного поля [c.653]

Здесь — напряженность эффективного поля, необ- [c.726]

На прочность пластичных и хрупких материалов концентрация напряжений влияет по-разному. Существенное значение при этом имеет также характер нагрузки. Если материал пластичный (диаграмма напряжений имеет площадку текучести зна чительной протяженности) и нагрузка статическая, то при увеличении последней рост наибольших местных напряжений приостанавливается, как только они достигнут предела текучести. В остальной части поперечного сечения напряжения будут еще возрастать до величины предела текучести Стт, при этом зона пластичности у концентратора будет увеличиваться (рис. 120). Таким образом, пластичность способствует выравниванию напряжений. На этом основании принято считать, что при статической нагрузке пластичные материалы мало чувствительны к концентрации напряжений. Эффективный коэффициент концентрации для таких материалов близок к единице. При ударных и повторно-переменных нагрузках, когда деформации и напряжения быстро изменяются во времени, выравнивание напряжений произойти не успевает и вредное влияние концентрации напряжений сохраняется. Поэтому в расчетах на прочность учитывать концентрацию напряжений необходимо. [c.120]

В отличие от теоретического коэффициента концентрации, зависящего только от формы (геометрии) детали, эффективный коэффициент концентрации зависит также и от свойств материала детали чем менее пластичен материал, тем он чувствительнее к концентрации напряжений. Эффективные коэффициенты концентрации устанавливают опытным путем, но в некоторых случаях при отсутствии экспериментальных данных их вычисляют по известным значениям теоретических коэффициентов концентрации и [c.556]

Выточка — Концентрация напряжений — Эффективный коэфициент 2 — 512 [c.29]

Для оценки действительного понижения усталостной прочности в зависимости от концентрации напряжений при переменных нагрузках вводится эффективный (практический) коэффициент концентрации, представляющий собой отношение предельных номинальных напряжений, вызывающих разрушение деталей, не имеющих и имеющих концентраторы напряжений. Эффективный коэффициент концентрации напряжений меньше теоретического (расчетного) коэффициента и только для высокопрочных материалов с малой пластичностью эффективный коэффициент концентрации почти равен теоретическому. Чем выше прочность стали и хуже пластические свойства, тем сильнее влияние надрезов, причем с увеличением размера образца влияние надреза увеличивается. Чем менее пластичен материал, тем выше эффективный коэффициент концентрации напряжений и наоборот. Пластичные материалы обладают способностью сглаживать неблагоприятные для усталостной прочности пики напряжений концентратора. [c.410]

В том случае, когда прочность образца оценивается не нормальными, а касательными напряжениями, эффективный коэффициент концентрации определяется по формуле [c.354]

С ростом размеров деталей (в особенности содержащих концентраторы напряжений) эффективность наклепа не только не уменьшается, а сохраняется, или дан[c.57]

Ширина образца, мм Диаметр д. отверстия, мм Теоретический коэффициент концентрации напряжений Эффективный коэффициент концентрации напряжений Л(= (аы) Критическая площадь поперечного сечения, мм [c.127]

Автор Материал и свойства Диаметр образца О мм Диаметр отверстия мм Теорети- ческий КОЭф(])И-диент концентрации напряжений Эффективный коэффициент концентрации напряжений А, А Предел выносливости в кГ/лж Расчетный предел выносливости в кГ/ммА [c.140]

Средняя плотность тока, А-см- . . . Запирающее напряжение (эффективное 0,04-0,08 0,1—0,2 80-100 100—200 [c.316]

Литейные напряжения эффективно снижаются путем отжига. [c.431]

Расслоение диаграмм длительной прочности при различных значениях х/а оказалось возможным устранить, аппроксимируя результаты единой кривой, взятой в условных осях — эффективное напряжение — эффективное время At (рис. 64). [c.130]

Здесь Н —напряженность эффективного поля, необходимого для поворота вектора намагниченности в те направления, где меняется только в, аЯ —поле, вращающее вектор намагниченности на поверхности конуса. Значение определяется формулой [c.586]

Если принять, что ползучесть дисперсно упрочненных систем контролируется возвратом, зависящим от объемной диффузии, то высокие значения кажущейся энергии активации ползучести и ее зависимость от температуры следует из влияния температурной зависимости модуля сдвига. Это влияние тем больше, чем выше значение параметра т чувствительности скорости установившейся ползучести к приложенному напряжению. Высокие значения параметра т могут быть объяснены существованием обратного напряжения, создаваемого дисперсными частицами. Обратное напряжение эффективно снижает приложенное напряжение а, поэтому необходимо вместо напряжения а рассматривать разность а – а . Зависимость скорости ползучести от тем- [c.159]

Но — напряженность эффективного поля, связанного с взаимодействием Дзялошинского (см. 28.5) [c.653]

Режим упрочнения выбирают в зависимости от материала детали и требований, предъявляемых к качеству поверхности по глубине и степени наклепа, микрошероховатости и остаточным напряжениям. С увеличением размера дроби шероховатость поверхности ухудшается, но увеличивается глубина наклепа и остаточные напряжения. Эффективность упрочнения возрастает с увеличением скорости и интенсивности (на единицу поверхности) подачи дроби, продолжительности обработки, угла встречи дроби с обрабатываемой поверх-HotTbra. Слишком длительная обработка может привести к шелушению поверхности, перенаклепу и снижению усталостной прочности. [c.106]

Помимо специфичного для крупных высокотемпературных установок устройства температурно-усадочных и компенсационных швов, а также монтажных стыков, обращено виимание на то, чтобы не было никаких обходных путей газа мимо газораспределительной решетки, например через неплотности футеровки под опорным поясом и слой теплоизоляции между футеровкой и кожухом печи. С этой целью к внутренней поверхности кожуха на уровне пояса перед его бетонированием приваривают сетку из арматуры для увеличения сцепления бетона с кожухом. Температурные напряжения в кожухе и, следовательно, бетоне прямо пропорциональны разности температурных деформаций кожуха и бетона. Чтобы уменьшить эти температурные напряжения, эффективным средством, как отмечено в [Л. 199], является повышение температуры кожуха до 200—250° С путем нанесения слоя теплоизоляции на наружную поверхность кожуха в зоне решеток. Как правило, такая мера недостаточна и появляется необходимость предусматривать радиальные компенсационные швы (в бетоне решетки), значительно снижающие напряжения в кожухе печи. Газовая плотность между решеткой и опорным поясом обеспечивается посадкой решетки на конус . [c.236]

Наибольшее применение в промышленности и в бытовых условиях получили электрические паяльники, которые в зависимости от материалоемкости паяемых изделий имеют различные размеры. Рабочая часть паяльника представляет собой стержень из 1меди, медных сплавов и других материалов. Электронагреватель расположен с внешней стороны стержня или внутри его. изготовлен из материала с большим электросопротивлением подачу теплоты в рабочую часть стержня — жала — регулируют изменением входного напряжения. Эффективность электропаяльника зави- [c.192]

Сталь Х16М25М6 очень чувствительна к концентрации напряжений. Эффективный коэффициент концентрации напряжений, установленный при испытании на выносливость цилиндрических образцов с надрезом при температуре 20° С, составил Ка = (см. табл. 50). [c.187]

Уравнения одинаковы по виду, если ввести понятие эффективного поля Яэфф= (Яо-Ио/у), где Яо — напряженность внешнего поля со — частота вращения системы координат вокруг общей для обеих рассматриваемых систем оси 2. При равенстве нулю напряженности эффективного поля магнитный момент во вращающейся системе координат неподвижен Эр/с = [c.171]

М. Н. Степнов исследовал влияние концентрации напряжений на эффект упрочнения алюминиевых сплавов. Согласно данным эксперимента (табл. 9) с увеличением уровня концентрации напряжений эффективность упрочнения повышалась [53]. [c.159]

На электрооптические свойства кристаллов, обладающих размытым фазовым переходом, оказывают влияние ориентационные эффекты. Приложение механического напряжения а в направлении, перпендикулярном электрическому полю Е, вызывает 90°-ные повороты доменов, ориентируя часть из них по направлению электрического поля (aj -домены), а другие по направлению распространения света (яц-домены). В результате совместного действия перпендикулярных друг другу электрического и механического напряжений эффективный показатель преломления в направлении электрического поля уменьшается, а в перпендикулярном направлении увеличивается. Увеличение Ага соответствует увеличению электроопти-ческих коэффициентов. При постепенном увеличении на- [c.88]

Чтобы определить индивидуальность поведения материалов С концентраторами напряжений проводят испытания на усталость образцов с надрезом, позволяющие определить коэффициент чувствительности к концентрацил напряжений Эффективный коэффициент концентрации напряжений/С, связан с а, зависимостью [c.42]

Г руппа Под- группа износостой- кости коррозионной стойкости наличия внутренних напряжений эффективности теплоотвода работоспособности в режиме трения без смазочного материала [c.318]

Размах деформаций 79 Размах коэффициента интенсивности напряжений эффективный 167 Размах напряжений 79 — Поиятие 173 [c.222]

Головная боль напряжения

Головная боль напряжения (ГБН) – какая она и как её лечат? Рассказывает и отвечает на ваши вопросы в комментариях наш врач невролог Нина Владимировна Ващенко.

Головная боль напряжения – как правило, лёгкая или умеренная по интенсивности боль, равномерно распределённая по всей голове. Чаще всего её описывают как ощущение обруча или каски на голове, больше похожее на сжатие и давление, нежели на боль.

Симптомы ГБН могут быть такими:

тупая, ноющая головная боль;
чувство сжатия или давления на лоб, виски и/или затылок;
повышенная чувствительность кожи головы, напряжение в мышцах шеи и плеч.

Это самый распространенный вид первичной головной боли (то есть это сама по себе головная боль, а не симптом другого заболевания), которая периодически возникает почти у всех людей, но у женщин немного чаще. Самый распространенный провокатор этой боли – стресс.

Головные боли напряжения могут быть эпизодическими и хроническими. У этих диагнозов такие критерии:

Эпизодические – беспокоят до 15 дней в месяц как минимум три месяца подряд. Приступ длится от 30 минут до недели.
Хронические – беспокоят от 15 дней в месяц на протяжении более трех месяцев подряд. Приступы могут длиться часами, а могут быть и непрерывными.

Иногда головную боль напряжения трудно отличить от мигрени. К тому же, люди с частой головной болью напряжения могут страдать и мигренью. Но, в отличие от некоторых форм мигрени, головные боли напряжения обычно не связаны со зрительными симптомами, тошнотой или рвотой. Физическая активность, которая обычно усугубляет боль при мигрени, не влияет на головную боль напряжения и может даже улучшать общее состояние. При головной боли напряжения могут возникать повышенная чувствительность к свету или звуку, но это редкие для неё симптомы.

Когда обращаться к врачу?

Если головная боль напряжения нарушает качество жизни.
Если вам необходимо принимать лекарства от головной боли более двух раз в неделю.
Если ваши головные боли стали проявлять себя по-другому (иногда головные боли могут указывать на другие, более серьезные заболевания).

Лечение головной боли напряжения – это баланс между формированием здоровых привычек, поиском эффективного немедикаментозного лечения (например, здесь подходит техника релаксации) и правильно подобранных врачом лекарств.

Сочетание лекарств с расслабляющими техниками может быть более эффективным, чем применение только лекарственных препаратов. Используйте всё, что поможет вам расслабиться и снять эту боль (глубокое дыхание, йога, медитация, майндфулнесс (осознанность) и прогрессирующая мышечная релаксация). Техникам релаксации можно обучиться на занятиях или дома по книгам или видео. НО! Выбирайте источники информации, которым можно доверять, так как “диванных экспертов” сегодня много 🙂

Подписывайтесь на наш Инстаграм, чтобы читать свежие материалы о диагностике и лечении головной боли!

Активное сопротивление. Действующие значения силы тока и напряжения

Подробности: Просмотров: 643

«Физика – 11 класс»

Активное сопротивление

Сила тока в цепи с резистором

Есть цепь, состоящая из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R.

Сопротивление R называется активным сопротивлением, т.к. при наличии нагрузки, обладающей этим сопротивлением, цепь поглощает энергию, поступающую от генератора.
Эта энергия превращается во внутреннюю энергию проводников — они нагреваются.
Напряжение на зажимах цепи меняется по гармоническому закону:

u = U_m cos ωt

Мгновенное значение силы тока прямо пропорционально мгновенному значению напряжения.
По закону Ома мгновенное значение силы тока:

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряжения, а амплитуда силы тока определяется равенством

Мощность в цепи с резистором

В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение меняются.
При прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет меняться во времени.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

Р = I²R

Мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

Р = i²R

Cреднее значение мощности за период (используем формулу для мгновенного значения силы тока и выражение ):

График зависимости мгновенной мощности от времени (рис.а):

Согласно графику (рис.б) среднее за период значение cos 2ωt равно нулю, а значит равно нулю второе слагаемое в формуле для среднего значения мощности за период.

Тогда средняя мощность равна:

Действующие значения силы тока и напряжения.

Среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока.
Действующее значение силы переменного тока обозначается через I:

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично:

Закон Ома для участка цепи переменного тока с резистором в действующих значениях:

В случае электрических колебаний важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность.
Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Действующие значения непосредственно определяют среднее значение мощности Р переменного тока:

р = I²R = UI.

Итак:
Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Что такое принцип эффективного напряжения при проектировании грунтов?

🕑 Время чтения: 1 минута

Принцип эффективного напряжения в почвенной инженерии – одна из важных теорий, выдвинутых Карлом Терзаги в 1936 году. Это разница между общим напряжением и поровым давлением воды. Дополнительные характеристики и определение эффективного напряжения в почве кратко поясняются ниже.

Принцип эффективного напряжения

Принцип эффективного напряжения можно объяснить, изучив пример массива грунта, который находится в полностью насыщенном состоянии, как показано на рисунке 1 ниже.

Рисунок 1. Насыщенная масса почвы

Рассмотрим призму почвы в массиве почвы с площадью поперечного сечения «А». Если P – это вес грунта над призматическим элементом грунта, P определяется по формуле:

P = Вес изделия x (Объем призмы)

, т.е. P = вес устройства x высота призмы (h) x площадь поперечного сечения призмы (A)

Это дает соотношение,

Уравнение 1

1. Определение полного напряжения

Тогда полное напряжение, действующее на призму, равно,

Уравнение2 Уравнение 3

2. Определение давления поровой воды

Давление воды в порах (u) – это давление, вызванное молекулами воды, присутствующими в порах или пустотах почвы. Дается соотношением:

Уравнение 4

Давление поровой воды также можно обозначить как нейтральное давление или нейтральное напряжение, поскольку оно не может противостоять силам сдвига в массиве почвы.

Примечание. Когда давление равно атмосферному, давление поровой воды принимается равным нулю.

3. Определение эффективного напряжения

Эффективное напряжение определяется по формуле:

Уравнение 5

Для насыщенного грунта,

Эффективное напряжение определяется уравнением-5 как:

Важность эффективного стресса

Большинство инженерных свойств почвы контролируются соответствующим действующим напряжением. Скажем, прочность грунта на сжатие и сдвиг зависит от эффективного напряжения грунта и, следовательно, их можно записать как функцию эффективного напряжения, как выражено в приведенном ниже соотношении.

С увеличением эффективного напряжения почвы скорость сжатия почвы также увеличивается. Это приводит к оседанию почвы.

Также читайте: Как улучшить свойства почвы?

Прочность почвы на сдвиг также зависит от изменения эффективного напряжения. Прочность почвы на сдвиг влияет на устойчивость откосов. давление грунта, действующее на подпорные конструкции и несущую способность грунта. Следовательно, на все эти свойства влияет эффективное напряжение почвы.

Проницаемость почвы зависит от коэффициента пустотности почвы. Поскольку изменение эффективного напряжения почвы изменяет коэффициент пустотности почвы, можно сказать, что эффективное напряжение также влияет на проницаемость почвы.

Вертикальное напряжение в грунте

Любое изменение общего вертикального напряжения (s _v) может также привести к изменению общего напряжения по горизонтали (s _h) в той же точке. Взаимосвязь между вертикальным и горизонтальным напряжением сложны.

Чуть выше уровень грунтовых вод почва останется насыщенной из-за капиллярности, но на некотором расстоянии от уровня грунтовых вод почва станет ненасыщенной, с последующим уменьшением удельного веса (ненасыщенный удельный вес = _{г и} г.)

Высота над уровнем грунтовых вод, до которой останется почва насыщенный зависит от размера зерна.
См. Отрицательное поровое давление (всасывание) .

Добавление поверхностной надбавки нагрузка увеличит общие напряжения ниже нее.Если доплата составляет очень широкий, увеличение общего вертикального напряжения ниже его можно рассматривать постоянна с глубиной и равна величине надбавки.

Полное вертикальное напряжение на глубине z,

с _v = г .z + q

Для небольших надбавок, например под ленточным и подушечным фундаментом индуцированное общие вертикальные напряжения будут уменьшаться как с глубиной, так и с горизонтальным расстоянием от груза.В таких случаях необходимо использовать подходящее распределение напряжений. теория – примером является теория Буссинеска.

Вода в порах почвы называется поровой водой . Давление внутри эта поровая вода называется поровым давлением (u). Величина порового давления зависит от:

глубина ниже уровня грунтовых вод
условия фильтрационного потока

Под гидростатическим условиях (отсутствие потока воды) поровое давление в данной точке определяется выражением гидростатическое давление:

u = g _w.в _Вт

где

h _w = глубина ниже уровня грунтовых вод или над поверхностью воды

Поровое давление удобно представить в виде столба воды. в воображаемой колонке; давление снаружи равно давлению внутри.

Естественная статика Уровень воды в грунте называется уровнем грунтовых вод или фреатическим уровнем поверхность (или иногда уровень грунтовых вод ).В условиях отсутствие фильтрационного потока, уровень грунтовых вод будет горизонтальным, как на поверхности озеро. Величина порового давления на уровне грунтовых вод равна нулю. Ниже уровень грунтовых вод, поровые давления положительные.
u = g _w. h _w
В условиях установившегося или переменного фильтрационного потока расчет пор давление становится более сложным.
См. Грунтовые воды

Ниже уровня грунтовых вод, поровое давление положительное .В сухом грунте поровое давление составляет ноль . Выше уровня грунтовых вод, когда почва насыщена, поровое давление будет минус .
u = – g _w .h _w

Высота над уровнем грунтовых вод, до которой насыщается почва, называется капиллярный подъем , и это зависит от размера и типа зерна (и таким образом размер пор):
· На грубых почвах капиллярный подъем очень небольшой
· В илах может достигать 2 м.
· В глинах может быть более 20 м

Между землей поверхность и верх насыщенной зоны, почва часто бывает частично насыщенный, т.е.е. поры содержат смесь воды и воздуха. Поровое давление в частично насыщенном грунте состоит из двух компонентов:
· Давление поровой воды = u _w
· Поровое давление воздуха = u _a
Обратите внимание, что вода несжимаема, но воздух сжимаем. Комбинированный эффект представляет собой сложную взаимосвязь, включающую парциальные давления и степень насыщения почвы. В Европе и других странах с умеренным климатом большинство проектных государств связаны с условиями насыщения, а изучение частично насыщенных почвы считается предметом специализации.

В условиях При просачивании в грунт происходит изменение порового давления. Считайте, что происходит просачивание между двумя точками P и Q.

Гидравлический градиент и между двумя точками – это падение напора на единичная длина между этими точками. Это можно рассматривать как “потенциал” управляя потоком воды.

Гидравлический градиент P-Q,	я = –	dh ds	=	du DS	.	1 г _Вт

Таким образом	du = i. г _ш . DS

Но в установившемся режиме просачивание, i = постоянное
Следовательно, изменение порового давления только за счет фильтрации, du _s = Я.г _ш. s
Для фильтрационного потока вертикально вниз, i отрицательно
Для фильтрационного потока вертикально вверх i положительно.

Колебания грунта и нестабильность могут быть вызваны изменениями общего напряжения. (например, загрузка из-за фундамента или разгрузка из-за раскопок), но они также может быть вызвано изменениями порового давления (склоны могут обрушиться после дождя. увеличивает поровое давление).

Фактически, это совокупный эффект общего напряжения и порового давления, который контролирует поведение почвы, такое как прочность на сдвиг, сжатие и деформацию. Разница между полным напряжением и поровым давлением называется эффективный стресс:

эффективное напряжение = общее напряжение – поровое давление
или s´ = s – ты

Обратите внимание, что штрих (штрих ´) указывает на эффективное напряжение.

Карл Терзаги был родился в Вене и впоследствии стал профессором механики грунтов в СОЕДИНЕННЫЕ ШТАТЫ АМЕРИКИ. Он был первым, кто предложил отношения для эффективного стресса. (в 1936 г.):

Все измеримые эффекты изменения напряжения, такие как сжатие, искажение и изменение сопротивления сдвигу обусловлено исключительно изменениями эффективных стресс. Эффективное напряжение s´ связано с к полному напряжению и поровому давлению на s´ = с – и.

Прилагательное «эффективный» особенно уместно, потому что оно составляет эффективно стресс, который вызывает важные изменения: изменения в силе, изменения объема, изменения формы. Он не представляет собой точного контакта напряжение между частицами, но распределение нагрузки, переносимой почвой по рассматриваемой площади.

Круги Мора можно нарисовать как для полного, так и для эффективного напряжения.Точки E и T представляют собой полное и эффективное напряжения в одной плоскости. В две окружности смещены вдоль оси нормальных напряжений на величину поры. давление (с _n = с _n ‘ + u) , а их диаметры такие же. Полный и эффективный сдвиг напряжения равны (t´ = t) .

Принцип эффективного напряжения имеет фундаментальное значение в механике грунтов.Ее следует рассматривать как основную аксиому, поскольку она определяет поведение почвы. Общие и действующие напряжения должны быть различимы во всех расчетах: алгебраически простое число должно указывать эффективное напряжение, например s´

Изменения уровня воды ниже поверхности (изменения уровня грунтовых вод) приводят к изменения эффективных напряжений ниже уровня грунтовых вод. Изменения уровня воды над землей (например, в озерах, реках и т. Д.) не вызывает изменений в эффективных напряжениях в грунте внизу.

В некоторых анализах лучше работать в изменений количества, точнее чем в абсолютных количествах; тогда выражение эффективного напряжения принимает следующий вид:
Ds´ = Ds – Du

Если и общее напряжение, и поровое давление изменяются на одинаковую величину, эффективное стресс остается постоянным.Изменение эффективного стресса вызовет: изменение в силе и изменении объема.

Критический прочность почвы на сдвиг пропорциональна действующему нормальному напряжению; таким образом, изменение эффективного стресса вызывает изменение силы.

Следовательно, если поровое давление в откосе грунта увеличивается, эффективные напряжения будет уменьшена на Ds, а критическая прочность почвы будет уменьшено Dt – иногда ведущим до отказа.

Морской замок из песка останется нетронутым, пока он сырой, потому что поровое давление отрицательный; по мере высыхания это всасывание порового давления теряется, и он разрушается. Примечание: иногда песочный замок остается неповрежденным, даже когда он почти высох, потому что Соль, отложившаяся в виде морской воды, слегка испаряется и склеивает зерна.

Сразу после строительства фундамента на мелком грунте поры давление увеличивается, но сразу же начинает падать, когда происходит дренаж.

Скорость изменения эффективного напряжения под нагруженным фундаментом после построена, будет такой же, как скорость изменения порового давления, и это контролируется проницаемостью почвы.

Оседание происходит по объему (и, следовательно, по толщине) слоев почвы изменение. Таким образом, оседание происходит быстро в грубых почвах с высокой проницаемостью. и медленно в мелких почвах с низкой проницаемостью.

Расчет вертикального напряжения в грунте

Верх

Приведенные здесь рабочие примеры призваны проиллюстрировать принципы и методы. рассматриваются в Поровое давление, эффективное напряжение и напряжения в грунте. Выбранные примеры типичны и просты.

На рисунке показаны слои почвы на участке.

Масса устройства составляет:: сухой песок: g _d = 16 кН / м³; насыщенный песок: г _г = 20 кН / м³

(a) В верхней части насыщенного песка (z = 2.0 м)
Полное вертикальное напряжение	с _v = 16,0 x 2,0	= 32,0 кПа
Поровое давление	и = 0
Вертикальное эффективное напряжение	s´ _v = s _v – ты	= 32,0 кПа

(b) В верхней части глины (z = 5.0 м)
Полное вертикальное напряжение	с _v = 32,0 + 20,0 x 3,0	= 92,0 кПа
Поровое давление	u = 9,81 x 3,0	= 29,4 кПа
Вертикальное эффективное напряжение	s´ _v = s _v – u = 92,0 – 29,4	= 62.6 кПа

На рисунке показаны слои почвы на участке. Удельный вес содержание илистого песка составляет 19,0 кН / м³ как выше, так и ниже уровня грунтовых вод. Уровень воды в настоящее время находится на поверхности илистого песка, может упасть или может подняться. Следующие расчеты показывают последствия этого:

Из исходного состояния сначала изменяются напряжения под фундаментом. раскопками, т.е. уменьшаются вертикальные напряжения. После постройки нагрузка на фундамент увеличивает напряжения. Другие изменения могут произойти, если вода уровень таблицы изменен.

На рисунке показана отметка фундамента, который должен быть построен в однородной почва. Необходимо рассчитать изменение толщины слоя глины и, таким образом, начальные и конечные действующие напряжения требуются на средней глубине глина.

Вес агрегата: песок выше WT = 16 кН / м³, песок ниже WT = 20 кН / м³, глина = 18 кН / м³.

Расчеты для: начальных напряжений; конечные напряжения

На рисунке показано, как обширный слой заливки будет размещен на определенном сайт.

Вес единицы:: глина и песок = 20 кН / м³,; рулонная шпатлевка 18кН / м³,; предполагается, что вода = 10 кН / м³.

Расчеты производятся для полного и эффективного напряжения на средней глубине песок и средний слой глины для следующих условий: изначально, перед строительством; сразу после строительства; много лет после постройки.

Начальные напряжения на средней глубине глины (z = 2,0 м)
Общее вертикальное напряжение
с _v = 20,0 x 2,0 = 40,0 кПа
Поровое давление
u = 10 x 2,0 = 20,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 20,0 кПа

Начальные напряжения на средней глубине песка (z = 5.0 м)
Общее вертикальное напряжение
с _v = 20,0 x 5,0 = 100,0 кПа
Поровое давление
u = 10 x 5,0 = 50,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 50,0 кПа

При строительстве набережной применяется поверхностная надбавка:
q = 18 x 4 = 72,0 кПа.

Песок осушается (горизонтально или в скалу внизу) и так там нет увеличения порового давления.Глина недренированная и поровое давление увеличивается на 72,0 кПа.

Начальные напряжения на средней глубине глины (z = 2,0 м)
Общее вертикальное напряжение
с _v = 20,0 x 2,0 + 72,0 = 112,0 кПа
Поровое давление
u = 10 x 2,0 + 72,0 = 92,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 20,0 кПа
(я.е. без изменений сразу)

Начальные напряжения на средней глубине песка (z = 5,0 м)
Общее вертикальное напряжение
с _v = 20,0 x 5,0 + 72,0 = 172,0 кПа
Поровое давление
u = 10 x 5,0 = 50,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 122,0 кПа
(т.е. немедленное увеличение)

Через много лет избыточное поровое давление в глине исчезнет.Теперь поровое давление будет таким же, как и было изначально.

Начальные напряжения на средней глубине глины (z = 2,0 м)
Общее вертикальное напряжение
с _v = 20,0 x 2,0 + 72,0 = 112,0 кПа
Поровое давление
u = 10 x 2,0 = 20,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 92,0 кПа
(т.е. долгосрочное увеличение)

Начальные напряжения на средней глубине песка (z = 5.0 м)
Общее вертикальное напряжение
с _v = 20,0 x 5,0 + 72,0 = 172,0 кПа
Поровое давление
u = 10 x 5,0 = 50,0 кПа
Вертикальное эффективное напряжение
s´ _v = s _v – u = 122,0 кПа
(т.е. без дальнейших изменений)

На рисунке показана просачивание вокруг заделанной шпунтовой сваи.
В установившемся режиме гидравлический градиент
i = Dh / Ds = 4 / ( 7 + 3) = 0.4
Тогда эффективные напряжения равны:
s´ _A = 20 x 3 – 2 x 10 + 0,4 x 10 = 44 кПа
с´ _B = 20 x 3 – 2 x 10 – 0,4 x 10 = 36 кПа

Концепция эффективного напряжения в механике грунтов

Скорость потока в непроницаемых грунтах очень низкая, а сжатие происходит постепенно. Давление поровой воды снижается по мере выхода воды из почвенной сети. Рассеяние давления поровой воды передает нагрузку на каркас почвы в виде межкристаллитного давления, которое успешно вызывает деформацию сжатия грунтовой массы.Как следствие, межкристаллитное давление называют концепцией эффективного напряжения.

Приложенное или абсолютное напряжение относится к приложенной извне деформации. Сеть грунта подвергается сжатию только после того, как она разделяет внешнюю нагрузку в виде эффективного напряжения. Уравнение эффективного напряжения зависит от времени.

Примечание : Обозначение σ ’ используется для эффективного напряжения

Разъяснение концепции эффективного напряжения

Рассмотрим волнистую поверхность Y – Y , которая проходит через точки соприкосновения, не рассекая частицы в насыщенной почве.Уровень напряжения в точках контакта настолько высок, что точки контакта деформируются или раздавливаются, что приводит к образованию небольших площадей контакта.

В результате естественные и касательные силы в точках контакта распределяются по площадкам контакта. Когда волнистая поверхность проецируется на горизонтальную (или вертикальную) плоскость, общая площадь A состоит из области контакта Am и водной поверхности Aw , которые в сумме образуют вертикальную часть. В .Как можно видеть, площадь контакта Am очень мала по сравнению с общим поперечным сечением A .

Как показано на рисунке, горизонтальная плоскость в насыщенном грунте может быть рассчитана как:

Здесь
σ = полное напряжение или средн. приложенное напряжение
N = общая сила, переносимая частицами при контакте
Aw = площадь плоскости, проходящей через воду
A = общая проектируемая площадь (Am + Aw)
u = давление воды в порах (= Uw, для насыщенного грунта)

Но площадь контакта очень мала, отсюда

Обычно σ ’= N / A – это напряжение, переносимое частицами при контакте, и известно как эффективное напряжение.Это напряжение рассчитывается на основе общей площади A , а не площади контакта Am .

Приложенное или полное напряжение σ известно из внешней нагрузки, и давление поровой воды может быть фактически измерено или определено.

Эффективное напряжение ( σ ’) рассчитывается как:

Карл Терзаги был первым, кто предложил такое определение эффективного стресса. В механике грунтов это очень важная концепция. Эффективные напряжения влияют на ряд свойств, включая изменение объема, прочность на сдвиг , проницаемость и сжимаемость.

Подводя итог, эффективная теория напряжений выглядит следующим образом:

Полное напряжение за вычетом порового давления равно эффективному напряжению.
Прочность почвы на сдвиг регулируется действующим напряжением.
Сдвиг объема почвы определяется действующим напряжением.

Принцип важности эффективного напряжения

В геотехнических задачах определение эффективного напряжения чрезвычайно важно. Напряжение, приложенное к почвам, не может создавать мгновенных деформаций, как это происходит в стали или бетоне.

Когда к насыщенному грунту прилагается внешняя нагрузка, создается поровое давление, которое затем рассеивается и преобразуется в межкристаллитное или эффективное давление с определенным временным лагом. Скорость рассеивания определяется типом грунта .

Проблемы порового давления в глинистых почвах более серьезны, чем в песчаных.

Ударная нагрузка и вибрация могут вызвать накопление порового давления в песчаных грунтах, что приведет к проблемам с разжижением.Под ударной нагрузкой разжижение относится к превращению насыщенного мелкого песка или ила в жидкую массу из-за потери контактов между частицами.

Эффективное напряжение влияет на прочность на сдвиг и изменение объема грунта. Объем не улучшится, если общее напряжение и поровое давление будут расти с одинаковой скоростью (Δσ = Δu).

С другой стороны, повышенное эффективное напряжение позволяет частицам почвы уплотняться более плотно. Как следствие, эффективные напряжения должны использоваться при оценке устойчивости и расчетах осадки.

При создании эффективного напряжения важным фактором является скорость сдвига.

Отказы системы Земля обычно происходят постепенно, на месяцы или даже годы. В таких обстоятельствах поровое давление может не играть существенной роли. С другой стороны, базовая нагрузка на мягкую глину вызывает поровое давление и низкий дренаж.

Как это:

Нравится Загрузка …

Концепция эффективного напряжения – обзор

1.1 Краткая история механики разрушения континуума

Механика разрушения континуума была введена Качановым [1] в 1958 году и теперь достигла стадии, позволяющей практические инженерные приложения.В отличие от механики разрушения, которая рассматривает процесс зарождения и роста микротрещин как прерывистое явление, механика сплошных повреждений использует непрерывную переменную φ, которая связана с плотностью этих дефектов, как показано на рисунках 1.1 – 1.3 (Ван и др. [2], Беттдж и др. [3], Войиаджис и Венсон [4]), чтобы описать ухудшение материала перед возникновением макротрещин.

Рис 1.1. Полости и микротрещины в границах зерен (Wang et al., [2])

Рис. 1.2. Трещины на поверхности включения (Bettge et al., [3])

Рис. 1.3. Повреждения в композитах с металлической матрицей (Voyiadjis and Venson [4])

На основе переменной повреждения φ разработаны основные уравнения эволюции для прогнозирования возникновения макротрещин для различных типов явлений. Леметр [5] и Шабош [6] использовали его для решения различных типов задач на усталость. Леки и Хайхерст [7], Халт [8] и Леметр и Шабош [9] использовали его для решения задач взаимодействия ползучести и усталости при ползучести.Кроме того, он использовался Леметром для пластического разрушения [10, 11] и для ряда других приложений [12].

Переменная повреждения, основанная на концепции эффективного напряжения, представляет собой среднюю деградацию материала, которая отражает различные типы повреждений на микромасштабном уровне, такие как зарождение и рост пустот, полостей, микротрещин и других микроскопических дефектов, как показано на Рисунки 1.1 – 1.2.

Для случая изотропного повреждения переменная повреждения является скалярной, и уравнения эволюции просты в использовании.Утверждалось [12], что предположение об изотропном повреждении достаточно, чтобы дать хорошие прогнозы несущей способности, количества циклов или времени до местного разрушения в элементах конструкции. Однако развитие анизотропных повреждений и пластичности подтверждено экспериментально [13-15], даже если исходный материал изотропен. Это побудило нескольких исследователей исследовать общий случай анизотропного повреждения.

Теория механики анизотропного разрушения была разработана Сидоровым и Кордебуа [16-18], а затем использована Ли и др. [15], а также Чоу и Вангом [19, 20] для решения простых задач вязкого разрушения.До этой последней разработки Крайчинович и Фонеска [21], Мураками и Оно [22], Мураками [23] и Крайчинович [24] исследовали хрупкое разрушение и разрушение при ползучести, используя соответствующие модели анизотропного повреждения. Хотя эти модели основаны на прочном физическом опыте, им не хватает убедительного математического обоснования и механической согласованности. Следовательно, необходимо проделать большую работу для разработки более сложной теории, способной давать результаты, которые могут быть использованы для практических приложений [21, 25].

Было показано, что в общем случае анизотропного повреждения переменная повреждения имеет тензорную природу [22, 26]. Было показано, что этот тензор повреждений является неприводимым тензором четного ранга [27, 28]. Некоторые другие основные свойства тензора повреждений были описаны Беттеном [29, 30] в строгой математической трактовке с использованием теории тензорных функций.

Леметр [31] резюмировал работу, проделанную за последние пятнадцать лет по описанию поведения трещин, используя теорию механики сплошных повреждений.Также Lemaitre и Dufailly [32] описали восемь различных экспериментальных методов (прямых и косвенных) для измерения повреждений в соответствии с концепцией эффективного напряжения [33].

Чабош [34-36] описал различные определения переменной ущерба, основанные на процедурах косвенного измерения. Примерами являются переменные повреждения, основанные на оставшемся сроке службы, микроструктуре и нескольких физических параметрах, таких как изменение плотности, изменение удельного сопротивления, акустическая эмиссия, изменение предела выносливости и изменение механического поведения посредством концепции эффективного напряжения.

Эффективное напряжение в почве: развитие, важность и принципы

Когда здание строится, его вес передается на землю через его фундамент, вызывая таким образом напряжения в нижележащих слоях. Эти индуцированные напряжения могут вызвать такие проблемы, как чрезмерная осадка или разрушение при сдвиге, и поэтому важны для инженеров-геологов.

Напряжения в недрах почвы:

Напряжения в недрах почвы вызваны:

(i) Собственный вес грунта

(ii) Структурная нагрузка на грунт

Напряжения, развиваемые в насыщенном грунте:

(i) Эффективные напряжения

(ii) Нейтральные напряжения

(iii) Суммарные напряжения.

Эффективное напряжение:

Карл Терзаги был первым, кто осознал важность эффективного стресса. Это напряжение, передаваемое от зерна к зерну в точке контакта с массой почвы. Это также известно как межкристаллитное напряжение. Он обозначается σ ’. При загрузке грунтовой массы. Нагрузка передается на почвы через точку контакта. Если в точке контакта приложенная нагрузка больше, чем сопротивление зерен, то в массиве грунта произойдет сжатие.

Это сжатие частично происходит из-за упругого сжатия зерен в точках контакта, а частично из-за относительного скольжения между частицами. Эта нагрузка на единицу площади грунтового массива, ответственная за деформацию грунтового массива, называется эффективным напряжением.

Нейтральное напряжение:

Это напряжение или давление, передаваемое через поровую жидкость. Его также называют поровым давлением и обозначают буквой u. В насыщенной почве поры почвенной массы заполнены водой.Когда насыщенная почвенная масса загружается, нагрузка не передается через зерна. Нагрузка переносится на поровую воду. Поскольку вода несжимаема, в поровой воде создается давление.

Это давление называется поровым давлением или поровым давлением воды. Поровое давление не оказывает какого-либо измеримого влияния на механические свойства почвы, такие как коэффициент пустотности, прочность на сдвиг и т. Д. Это давление или напряжение называется нейтральным напряжением.

Общее напряжение:

Общее напряжение равно сумме эффективного напряжения и нейтрального напряжения.Обозначается он σ.

σ = σ + u

Эффективное напряжение нельзя измерить в полевых условиях никакими приборами. Его можно рассчитать только после измерения общего напряжения и порового давления. Таким образом, эффективное напряжение не является физическим параметром, а всего лишь очень полезным математическим понятием для определения инженерного поведения грунта.

Важность эффективного напряжения в инженерных задачах:

Эффективное напряжение играет важную роль в:

(i) Осадка почвы

(ii) Прочность грунта на сдвиг

Поселение почв:

Явление постепенного уменьшения объема почвы из-за вытеснения воды из пор почвы называется уплотнением, сжатием или осадкой почвы.На рисунке 5.3 показана кривая сжатия глины. Это кривая между эффективным напряжением σ и коэффициентом пустотности e. Из графика видно, что при увеличении σ e уменьшается, т.е. из-за увеличения эффективного напряжения сжатие грунта будет увеличиваться.

Окончательный расчет консолидации можно рассчитать по формуле

S = м _V H

где m _V – коэффициент объемной сжимаемости

H – толщина сжимаемого слоя

∆σ – среднее увеличение эффективного давления.

Из приведенного выше уравнения ясно, что осадка почвы прямо пропорциональна эффективному давлению. Таким образом, осадка почвы зависит от действующего напряжения или действующего давления. По мере увеличения действующего напряжения оседание почвы также увеличивается.

Прочность почвы на сдвиг:

Многие инженерно-геологические проблемы требуют оценки прочности на сдвиг, в том числе:

(а) Фундаменты:

Нагрузка от конструкции передается на землю через фундамент.Это создает напряжение сдвига и сжимающее напряжение. Если создаваемое напряжение сдвига превышает сопротивление грунта сдвигу, происходит разрушение при сдвиге, которое вызывает обрушение конструкции.

(б) Земные склоны:

На наклонной поверхности гравитация создает в почве напряжения сдвига. Если эти напряжения превышают предел прочности на сдвиг, возникает контактная площадка.

(в) Тротуары:

Колесные нагрузки от транспортных средств передаются через тротуар на землю.Эти нагрузки создают напряжение сдвига, которое вызывает разрушение при сдвиге.

Знаете ли вы?

Значение K в направлении x равно значению K в направлении y для ровной поверхности земли.

Прочность грунта на сдвиг рассчитывается по формуле

S = σ загар ɸ

Где σ = эффективное напряжение

ɸ = эффективный угол трения

Для данной почвы f постоянна. Тогда прочность на сдвиг прямо пропорциональна эффективному напряжению.Так что с увеличением эффективного стресса сила увеличивается. Если прочность почвы на сдвиг больше, разрушение при сдвиге будет меньше.

Принцип эффективного напряжения:

Если насыщенная масса грунта загружена, нагрузка передается на поровую воду. После вытеснения поровой воды она переносится на зерна почвы. Пусть YY – волнистая плоскость, проходящая через точки соприкосновения зерен почвы. Пусть A будет площадью волнистой плоскости YY. Эта площадь A представляет собой сумму площади контакта зерен (A _g) и площади поровой воды (A _w), как показано на рисунке 5.5. Из рисунка 5.6 видно, что площадь контакта зерен (A _g) намного меньше площади поровой воды (A _w), т.е. A _w = A.

Пусть F – общая нагрузка на зону A.

Принцип эффективного напряжения в простейшем виде можно сформулировать как

(i) Эффективное напряжение равно общему напряжению за вычетом порового давления для насыщенного грунта

σ = σ – и

(ii) Эффективное напряжение контролирует определенные аспекты поведения почвы, такие как прочность, деформация и т. Д.

Эффективное напряжение в механике грунта

Здесь вы можете прочитать отрывок из одного из разделов курса «Продвинутая механика грунта», в котором подробно рассматривается концепция эффективного напряжения в механике грунта.

Эффективное напряжение

Нагрузки, прикладываемые к почвенным массам, переносятся либо твердыми зернами, либо водой в порах, а иногда и теми и другими. Как показано на Рисунке 1.5, по мере того, как поровая вода нагружается (посредством приложенного общего напряжения, s), давление внутри нее ( и ) увеличивается, вызывая вытекание воды из почвы, и нагрузка передается на твердые зерна. (s ‘).Вытекание воды под давлением из грунтового массива называется дренажем. Скорость дренажа зависит от водопроницаемости почвы. Технические характеристики, связанные с прочностью и сжимаемостью, зависят от интенсивности напряжений, проходящих через твердую зернистую ткань грунта, то есть эффективных напряжений .

Рисунок 1.5. Нагрузка, которую несут частицы почвы и поровая вода.
Движение грунта и нестабильность могут быть вызваны изменениями общего напряжения; например загрузка из-за фундамента, разгрузка из-за земляных работ.Они также могут быть вызваны изменениями порового давления; например разрушение откосов, возникающее после дождя из-за увеличения порового давления. Фактически, это совокупный эффект общего напряжения и порового давления, который контролирует поведение почвы, такое как прочность на сдвиг, сжатие и деформация.
Этот комбинированный эффект называется эффективным напряжением (s ‘) и выражается как: Эффективное напряжение = Общее напряжение – Давление поровой воды
Продвинутая механика грунтов
Принцип эффективного стресса Терзаги
Карл Терзаги родился в Вене и впоследствии стал профессором механики грунтов в США.В 1936 году он был первым, кто предложил отношения для эффективного стресса. Все измеримые эффекты изменения напряжения, такие как сжатие, деформация и изменение сопротивления сдвигу, обусловлены исключительно изменениями эффективного напряжения.
Прилагательное эффективный особенно подходит, потому что это эффективный стресс, который эффективно вызывает важные изменения: изменения силы, изменения объема и изменения формы.
Дренированная и недренированная почва
На протяжении всей остальной карьеры в гражданском строительстве вы будете слышать выражения осушенный и недренированный применительно к состоянию почвы или условиям нагрузки.
Осушенный не означает, что почва высохла от воды. Точно так же отсутствие дренажа не означает, что каждая пора заполнена водой.
Снова обратитесь к Рисунку 1.5. Когда из-за внешней нагрузки прикладывается нормальное напряжение, поровое давление увеличивается, и это внутреннее давление воды (известное как избыточное давление поровой воды) вызывает вытекание воды из пустот. По мере того, как течет вода с небольшим давлением, оставшаяся вода начинает испытывать снижение избыточного давления поровой воды.В конце концов давление поровой воды возвращается к исходному значению (т.е. избыточное давление поровой воды равно нулю). Скорость, с которой возникает этот поток воды, зависит от типа почвы. Гранулированные грунты (например, пески) имеют гораздо более высокую проницаемость, чем связные грунты (например, глины), поэтому вода стекает намного быстрее в гранулированных грунтах.
Когда избыточное давление поровой воды равно нулю, грунт считается осушенным . До этого момента почва недренированная .
Должно быть достаточно очевидным, что зернистые почвы могут очень быстро стать осушенными .Сообщается, что они находятся в осушенном состоянии . Следовательно, при проведении геотехнического анализа и проектирования зернистых грунтов мы почти всегда будем выполнять анализ осушенных грунтов или рассматривать осушенных условий .
Глины, однако, имеют значительно более низкую проницаемость, чем гранулированные почвы, поэтому дренаж в глине занимает гораздо больше времени (годы, а не минуты / часы). Из-за этого глины остаются в недренированном состоянии в течение длительного времени, поскольку избыточное давление поровой воды очень медленно рассеивается и стремится к нулю.Поэтому при проведении геотехнического анализа и проектирования связных грунтов мы будем учитывать недренированных условий и выполнить недренированный анализ . Проведем и дренированный анализ, так как почва в конце концов достигнет дренированного состояния.
В недренированных анализах мы учитываем влияние общих напряжений , тогда как в анализах осушенных мы работаем с эффективными напряжениями . Таким образом, вы часто будете слышать термины анализ общего напряжения и анализ эффективного напряжения , используемые для описания недренированных и осушенных анализов соответственно.
Теперь, когда мы увидели, как существуют напряжения в земле, давайте посмотрим, что происходит с этими напряжениями, когда к поверхности почвы прилагается нагрузка. Нам нужно знать, что происходит, чтобы (а) установить, сможет ли грунт выдержать приложенную нагрузку (проблема опорного давления) и (б) установить степень сжатия, которое грунт, вероятно, испытает с течением времени ( проблема поселения).
Соотношение напряжение-деформация

Из более ранних исследований мы увидели, что для такого материала, как низкоуглеродистая сталь, соотношение напряжение / деформация показано на Рисунке 1.6 (а).
Рисунок 1.6. Отношения стресс-напряжение.
На Рисунке 1.6 (а) прямолинейная часть графика показывает протяженность упругой области (то есть тот диапазон напряжений, в котором материал ведет себя упруго), а точка А известна как предел упругости. Точка B известна как предел текучести и указывает начало пластической области.
Для низкоуглеродистой стали мы можем идеализировать соотношение, чтобы идентифицировать определенную упругую область и определенную пластическую область, как показано на рисунке 1.6 (б). Однако для грунтов нет определенного предела текучести и, следовательно, нет определенной области упругости и определенной области пластичности, как показано на Рисунке 1.6 (c)
Однако мы обнаружили, что в большинстве работ с грунтом индуцированные напряжения либо достаточно низки, чтобы быть значительно ниже предела текучести грунта, и можно предположить, что грунт будет вести себя упруго (например, немедленные проблемы с осадкой), либо они достаточно высоки. для почвы, чтобы разрушиться из-за пластической текучести (например, проблемы несущей способности).
Напряжения в грунтовом массиве
Когда грунт находится в состоянии напряжения, например, после приложения нагрузки, трехмерный элемент грунта будет иметь 9 компонентов напряжения, действующих на него: 3 нормальных напряжения и 6 касательных напряжений (Рисунок 1.7 (а)). Однако многие геотехнические конструкции работают в состоянии плоской деформации: то есть одно измерение конструкции достаточно велико, чтобы можно было игнорировать концевые эффекты, и тогда проблема рассматривается как одна из двух измерений, как показано на Рисунке 1.7 (b).
Рисунок 1.7. Трех- и двумерные состояния.
33.2: Принцип эффективного стресса Терзаги
Последнее обновление
Сохранить как PDF
Без заголовков
Скалы разрушаются при выветривании.В процессах осадочной геологии, когда реки сбрасывают донные отложения в бассейн, различные сорта зерна почвы откладываются на разных расстояниях от точки сброса. Древняя «мягкая порода», известная как «Кембриджская глина» в городе Кембридж в Англии, представляет собой 20-метровый слой ила или зерен почвы размером с глину, отложенный на дне древнего океана. Сейчас он обнажается вокруг Гертона, к западу от Кембриджа. Выше, когда древнее теплое морское дно было далеко от мест, где реки откладывали наносы, могли расти кораллы.Этот коралл образовал меловую скалу, простирающуюся далеко по всей Европе. Местно недалеко от Кембриджа, он обнажается на холмах Гог-Магог и вдоль линии, проходящей через Ньюмаркет, Ройстон и Лутон. На мелу видна рябь, которая поднимается вверх, образуя Северные холмы, и погружается в Южные холмы. Эта меловая скала образует Белые скалы Дувра. Вертикальные трещины образуются при падении бокового давления в этом мелу. Эти трещины могут привести к тому, что тяжелая поверхность утеса будет опираться на фундамент из морской глины, который, когда он разрушается, позволяет скале упасть в Ла-Манш.
Везде, где накапливается осадок из прочных прочных зерен в виде однородного агрегата из песка или гравия, который можно выкопать для использования в строительстве, такой заполнитель будет смешан с водой и цементным порошком в качестве компонента раствора в кирпичной кладке или в армированном конструкционном бетоне. с стержнями из мягкой стали. Там, где естественный грунт достаточно мягкий, можно выкопать неклассифицированный грунт, вытащить его на площадку и разложить слоями для уплотнения катками для создания крупных насыпей дорог или плотин.В естественном или уплотненном мягком грунте прочные зерна почвы образуют эффективно напряженную агрегатную структуру, в которой силы передаются от зерна к зерну через землю. В объеме грунта часть объема занята твердыми зернами грунта, а поровое пространство между зернами в насыщенном грунте содержит несжимаемую поровую воду. Всякий раз, когда загружается мягкий грунт, возникают градиенты порового давления. Теория первичной консолидации Терзаги проанализировала переходные потоки грунтовых вод и поверхностных поселений.
Принцип эффективного напряжения Терзаги, применяемый к песку, учитывает, что песок должен обладать прочностью, если песчаный склон не оседает. Уклон может быть устойчивым только при наличии межкристаллитных сжимающих напряжений. Общее сжимающее напряжение, приложенное перпендикулярно к конкретной плоскости, σ, равно σ ‘+ u , где σ’ – эффективное сжимающее напряжение, нормальное к плоскости, а u – давление поровой воды. Это принцип эффективного стресса Терзаги.
Этот принцип иллюстрируется поведением песка в двух бутылках, показанных в разделе «Угол естественного откоса», а также ниже.Воздух может легко перемещаться из порового пространства в поровое пространство песчаного заполнителя, но для этого потребуется время.
Эти две бутылки показывают, что если есть время для диффузии порового давления воды (т.е. есть дренаж), такой же наклон в состоянии покоя достигается с присутствием воды и без нее. Если не хватает времени, произойдет ожижение, как это может произойти при раскачивании балкера, то есть торгового судна, предназначенного для перевозки неупакованных навалочных грузов, таких как металлическая руда.
.

Эффективное напряжение: Действующее значение тока и напряжения

Эффективное напряжение переменного тока. Действующие значения силы тока и напряжения

4.4.5. Мощность в цепи переменного тока

Комплексные токи и напряжения. Трехфазное напряжение. Эффективное напряжение. Асинхронный трехфазный двигатель

эффективное напряжение – это… Что такое эффективное напряжение?

Смотреть что такое “эффективное напряжение” в других словарях:

Эффективное, действующее напряжение, сила тока. Значение. Действующие значения силы тока и напряжения

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

4.4.5. Мощность в цепи переменного тока

Активное сопротивление

Действующее значение силы тока

Действующее значение переменного тока

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

Действующее и среднее значения переменного тока и напряжения.

Что берется за действующее значение силы переменного тока и переменного напряжения

Генератор переменного тока

*Принцип действия

Действующие значения силы тока и напряжения

Напряжение эффективное – Энциклопедия по машиностроению XXL

Головная боль напряжения

Активное сопротивление. Действующие значения силы тока и напряжения

Активное сопротивление. Действующие значения силы тока и напряжения

Активное сопротивление

Действующие значения силы тока и напряжения.

Что такое принцип эффективного напряжения при проектировании грунтов?

Принцип эффективного напряжения

1. Определение полного напряжения

2. Определение давления поровой воды

3. Определение эффективного напряжения

Важность эффективного стресса

Вертикальное напряжение в грунте

Расчет вертикального напряжения в грунте

Концепция эффективного напряжения в механике грунтов

Как это:

Концепция эффективного напряжения – обзор

1.1 Краткая история механики разрушения континуума

Эффективное напряжение в почве: развитие, важность и принципы

Эффективное напряжение в механике грунта

Эффективное напряжение

Принцип эффективного стресса Терзаги

Дренированная и недренированная почва

Соотношение напряжение-деформация

Напряжения в грунтовом массиве

33.2: Принцип эффективного стресса Терзаги

Больше новостей

Добавить комментарий Отменить ответ