Эффективные значения тока и напряжения
Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?
Решение:
Среднее значение мощности переменного тока в цепи равно
\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:
\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2.2\right).\]Следовательно, можно записать, что:
\[\left\langle P\right\rangle =P_{tR}=\frac{1}{2}{I^2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.
У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:
\[P=I_{ef}U\ \left(2.4\right),\]если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:
\[I_{ef}=\frac{I_m}{\sqrt{2}},\ U_{ef}=\frac{U_m}{\sqrt{2}}\left(2.5\right).\]Следовательно, мощность тока можно записать как:
\[P_{tR}=U_{ef}I_{ef}cos \varphi \left(2.6\right),\]где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.
Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).
Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$
Действующее значение тока и напряжения
Переменный ток, протекая по проводнику, нагревает его так же, как и постоянный ток. Силу переменного тока удобно оценивать по его тепловому действию (эффекту) или, как говорят, по действующей, эффективной его величине.
Действующее или эффективное значение переменного тока равно силе такого постоянного тока, который, протекая по данному проводнику, выделяет в нем ежесекундно то же количество энергии в виде тепла, что и переменный ток.
Тепловой эффект тока, а значит, и действующие (эффективные) значения переменного тока зависят не только от наибольших значений, которых достигает переменный ток, но и от формы тока.
Вообще говоря, в электротехнике, и особенно в радиотехнике, приходится иметь дело с токами довольно сложной формы. Но все эти токи могут быть представлены в виде суммы нескольких синусоидальных токов с различными частотами, амплитудами и начальными фазами. Поэтому очень важную роль играет связь между амплитудным и действующем значениями для синусоидального тока.
Если известна амплитуда переменного синусоидального тока, то действующее или эффективное его значение определяется по формуле:
то есть эффективное значение синусоидального тока в раз меньше его амплитудного значения.
Аналогичная формула применяется и для вычисления эффективного значения синусоидального напряжения:
Протекая по проводнику, переменный ток создает в нем эффективное падение напряжения, равное произведению эффективного значения силы тока на сопротивление проводника, что эквивалентно закону Ома для постоянного тока, то есть:
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Прописные истины для новичков. – Начинающим – Теория
Как рассчитать шунт для амперметра?
Как измерить, какую мощность выдаёт усилитель низкой частоты?
Такие вопросы порой часто возникают от новичков радиолюбителей. Кратко напомним им, чем нужно руководствоваться в своей практической деятельности.
Закон Ома.
Основным законом, которым руководствуются радиолюбители – является Закон Ома..
Георг Симон ОМ
Georg Simon Ohm, 1787–1854
Немецкий физик. Родился в Эрлангене 16 марта в 1787 году (по другим источникам он родился в 1789-м). Окончил местный университет. Преподавал математику и естественные науки. В академических кругах его признали достаточно поздно. В 1849 году стал профессором Мюнхенского университета, хотя уже в 1827 году он опубликовал закон, который теперь носит его имя. Помимо электричества занимался акустикой и изучением человеческого слуха.
Георг Ом экспериментально установил, что сила тока I, текущего по однородному металлическому проводнику (т. е. проводнику, на который не действуют сторонние силы), пропорционально напряжению U на концах проводника.
Уравнение это выражает закон Ома для участка цепи (не содержащего источника тока). Формулировка этого закона следующая:
Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорционально его сопротивлению.
Единица электрического сопротивления системы СИ называется Ом в честь этого выдающегося ученого. Сопротивление проводника в 1 Ом будет в том случае, если при протекающем по нему токе в 1 Ампер, падение напряжения на нём будет 1 Вольт.
Так же при прохождении тока по проводнику, на нём выделяется мощность(он нагревается), и чем больше протекающий по нему ток, тем больше выделяемая на нём мощность.
Как Вы должны знать U — это работа, выполняемая при перемещении одного кулона, а ток I — количество кулонов, проходящих за 1 сек. Поэтому произведение тока на напряжение показывает полную работу, выполненную за 1 сек, то есть электрическую мощность или мощность электрического тока в Ваттах.
Из всего этого вытекают следующие формулы для расчётов тока, напряжения, сопротивления, мощности.
Величины, проставляемые в этих формулах; напряжение в вольтах, сопротивление в омах, ток в амперах, мощность в ваттах.
Последняя формула определяет мощность тока и выведена на основании практических опытов, проделанных в 1841 году Д. П. Джоулем и независимо от него в 1842 году, опытами Э. Х. Ленца. Называется Законом Джоуля – Ленца. Звучит так;
Количество теплоты, выделяемое в единицу времени в рассматриваемом участке цепи, пропорционально произведению квадрата силы тока на этом участке и сопротивлению участка.
Для определения всех этих величин, есть очень интересная диаграмма (таблица), где отражены все эти формулы.
В центре искомые величины, а в секторах с соответствующими цветами – варианты решений в зависимости от известных величин.
Имеется ещё более упрощённая диаграмма для определения величин, исходя из закона Ома. Называется в простонародье – треугольник Ома.
Выглядит она следующим образом:
В этом треугольнике Ома, нужно закрыть искомую величину, и два других символа дадут формулу для ее вычисления.
Закон Ома также применяется ко всей цепи, но в несколько изменённой форме:
- ,
- — ЭДС цепи,
- I — сила тока в цепи,
- R — сопротивление всех элементов цепи,
Закон Ома для полной цепи звучит так – Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений цепи и внутреннего сопротивления источника.
Электрические измерения.
Нарисуем простейшую электрическую цепь, состоящую из батареи “В” и нагрузки “R”, и рассмотрим, как необходимо измерять протекающий по цепи ток, и напряжение на нагрузке.
Что бы измерить протекающий в цепи ток, необходимо в разрыв источника питания и нагрузки включить измерительный прибор (амперметр).
Для того, что бы на измеряемую цепь было как можно меньше влияний и для повышения точности измерения, амперметры изготавливают с очень малым внутренним сопротивлением, то есть если включить амперметр в разрыв проверяемой цепи, то он практически не добавит к измеряемой цепи дополнительного сопротивления, и протекающий по цепи ток практически не изменится, или уменьшится на очень незначительную величину не оказывающую значительного влияния на конечный результат измерения.
Это равносильно тому, что подключить параллельно нагрузке или источнику питания обычный провод. Попросту сказать – закоротить цепь.
Если источник питания обладает хорошей мощностью – будет очень сильный Б А Х !!! Последствия могут быть самыми разными, от выхода из строя измерительного прибора (амперметра), что обычно и случается, и до выбитых пробок (АЗС) в квартире и обесточивания помещения и возможного поражения током.
Для измерения напряжения на нагрузке необходимо, что бы подключаемый к ней вольтметр не шунтировал нагрузку и не оказывал заметного влияния на результат измерения. Для этого вольтметры изготавливают с очень высоким входным сопротивлением и их наоборот подключают параллельно измеряемой цепи. Благодаря высокому входному сопротивлению вольтметра – сопротивление измеряемой цепи практически не изменяется, или изменяется очень не значительно, не оказывая заметного влияния на результат измерения.
На рисунке выше показан порядок включения амперметра и вольтметра для измерения напряжения на нагрузке и протекающего через неё тока. Так же указана полярность подключения измерительных приборов в измеряемую цепь.
Постоянный и переменный ток.
Кратко напомню – постоянный ток (DC), это такой ток, который в течении определённого промежутка времени не изменяет своей величины и направления.
Переменный ток (AC) – это ток, который в течении определённого промежутка времени периодически изменяется как по величине, так и по направлению.
Промежуток времени, на протяжении которого совершается полный цикл изменения тока, называется периодом. Период обозначается буквой Т и измеряется в секундах.
Промежуток времени, на протяжении которого совершается половина полного цикла изменения тока, называется полупериодом. Следовательно, период изменения тока (ЭДС или напряжения) состоит из двух полупериодов. Совершенно очевидно, что все периоды одного и того же переменного тока равны между собой.
В течение одного периода своего изменения,ток дважды достигает максимального значения.
Максимальное значение переменного тока (ЭДС или напряжения) называется его амплитудой или амплитудным значением тока.
Действующее (эффективное) и амплитудное значение переменного синусоидального тока (напряжения).
Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Возникает вопрос, как же его измерять? Для его измерения и введено понятие – “Действующее (или эффективное) значение” переменного тока.
Что же такое действующее (или эффективное) и амплитудное значение переменного тока?
Как Вам попроще объяснить, чтобы было понятно.
Действующее (эффективное) значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время, выделяет такое же количество энергии.
То есть если к какой либо активной нагрузке (нагревательный элемент, лампа накаливания, резистор и т.д.) подключить переменный ток, который за определённый промежуток времени (например 10 секунд) выделит на активной нагрузке то-же количество энергии, тепла на нагревательном элементе, резисторе, или разогреет спираль лампы накаливания до точно такой же светоотдачи, что и постоянный ток какой-то определённой величины за тот же промежуток времени (тоже 10 секунд) – то тогда действующее (эффективное) значение такого переменного тока будет равняться величине постоянного тока.
Все электроизмерительные приборы (амперметры, вольтметры), отградуированы для измерения действующего значения синусоидального тока или напряжения.
Что такое “Амплитудное значение” переменного тока?
Если объяснять попроще, то это самое максимальное значение (величина) синусоидального тока на самом пике (максимуме) синусоиды.
Амплитудное значение переменного тока можно измерить электронно – лучевым осциллографом, так как все осциллографы откалиброваны на измерение амплитудных значений.
Поскольку действующее значение переменного синусоидального тока пропорционально квадратному корню из площади, то оно получается в 1,41 раза меньше его амплитудного значения.
Проще говоря – если измерить величину переменного тока (напряжения) электроизмерительными приборами, отградуированными для измерения переменного синусоидального тока (напряжения), то есть например замерить величину переменного напряжения на вторичной обмотке трансформатора, – то амплитудное значение напряжения на этой обмотке будет соответственно в 1,41 раз больше замеренного.
Это справедливо только для переменного синусоидального тока (напряжения).
Все конденсаторы в выпрямительных фильтрах соответственно заряжаются до величины амплитудного значения.
Можно посчитать, что при действующем напряжении сети 220 В, амплитудное его значение будет составлять 310 вольт (220 помножить на 1,41).
Отсюда вытекает, что если собрать выпрямитель переменного действующего напряжения 220 вольт, то конденсаторы фильтра необходимо применять на рабочее напряжение не менее чем на 350 вольт, так как они заряжаются до амплитудного (максимального) значения переменного напряжения, а ещё лучше не менее 400 вольт, для обеспечения надёжности работы выпрямителя.
Для действующего значения переменного синусоидального напряжения (тока) – справедливы формулы для расчётов сопротивлений, мощности, действующих токов и напряжений – приведённые выше в Законе Ома для постоянного тока.
Ответим на вопросы в начале статьи;
Как рассчитать шунт для амперметра?
Большинство отечественных измерительных головок для амперметров, рассчитываются на полное отклонение при подведении к ним напряжения в 75 мВ (0,075 вольта). У них на шкале имеется надпись “НШ – 75 мВ”, или “Наружный шунт 75 мв”, или что-то подобное.
Нам стало известно две величины, а именно – необходимый нам ток полного отклонения и напряжение полного отклонения измерительной головки.
Например, нам нужно рассчитать шунт на 20 ампер. По Закону Ома 0,075 делим на 20 = 0,00375 Ом.
Изготовить такой шунт можно из медной проволоки, посмотрев её удельное сопротивление по таблице ЗДЕСЬ . Только необходимо брать проволоку, диаметром желательно не менее 1,5 мм, так как шунт при большом токе будет греться, и показания прибора будет изменяться (при нагреве проволоки увеличится её внутреннее сопротивление).
Почему из 12 вольт переменного напряжения, стало около 16 вольт постоянного – надеюсь Вам стало понятно. У переменного напряжения 12 вольт (действующее его значение) – амплитудное значение будет в 1,41 раз больше, то есть 16,92 вольта, минус около вольта падение напряжения на диодах. В итоге получается около 16 вольт – до которых и заряжаются электролитические конденсаторы фильтра.
Как правильно измерить мощность УНЧ?
Давайте для начала вспомним теорию.
Выходная мощность усилителей НЧ измеряется на синусоидальном сигнале. У идеального двухтактного выходного каскада, максимальное амплитудное значение синусоидального сигнала на выходе может приблизиться к величине равной половине напряжения источника питания.
У каскада по мостовой схеме, выходное напряжение может приблизиться к величине напряжения источника питания.
Говоря другими словами, у автомобильной магнитолы при напряжении питания 13,5 вольт, для двухтактного выходного каскада максимальное выходное напряжение (синус) будет 6,5 вольт, а его действующее значение 4,6 вольта, для мостовой схемы соответственно 13 В. и 9,2 вольта.
Возьмём минимальную нагрузку для этих усилителей 2 Ома, соответственно максимальная выходная мощность (исходя из Закона Джоуля – Ленца) для первой магнитолы, которую она выдаст теоретически – будет 10,6 ватта, для второй – 42,3 ватта (это для нагрузки 2 Ома). На практике не более 10 и не более 40, или и того меньше. Для 4-х Ом соответственно ещё в два раза меньше. Я не говорю уже об искажениях, здесь мы просто измеряем максимальную выходную мощность.
В бытовых условиях измерять выходной сигнала усилителя (при подаче на вход синусоидального сигнала), лучше обычными “цешками” или бытовыми “цифровиками”, так как они сразу измеряют действующее значение синусоидального сигнала. На выход усилителя лучше включать при замерах эквивалент нагрузки, то есть сопротивления с мощностью рассеивания, не менее максимально расчётной мощности усилителя, и с сопротивлением, равному сопротивлению предполагаемой нагрузки (это, что-бы не раздражать себя и соседей звуками во время замеров). Дальше, зная максимальное выходное напряжение и сопротивление нагрузки, рассчитываем мощность по вышеприведённым формулам, то есть напряжение в квадрате делённое на сопротивление нагрузки.
Так, что если Вы в магазине увидите подобный аппарат, и продавец Вас будет уверять, что на канал он выдаёт по 60-80 ватт – это развод, рекламный ход и т.д., если только для питания этого усилителя не применяется повышающий преобразователь.
Эффективное значение напряжения
Действующее значение переменного тока
Действующее (эффективное) значение переменного тока равно величине такого постоянного тока, который за время, равное одному периоду переменного тока, произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток.
В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение переменного тока.
Иначе говоря, действующее значение переменного тока можно определить по формуле:
I = 1 T ∫ 0 T i 2 d t . {\displaystyle I={\sqrt {{\frac {1}{T}}\int _{0}^{T}i^{2}dt}}.}Для синусоидального тока:
I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}где
I m {\displaystyle I_{m}} — амплитудное значение тока.Для тока треугольной и пилообразной формы:
I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}Аналогичным образом определяются действующие значения ЭДС и напряжения.
Дополнительные сведения
В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value — эффективное значение. Также применяется аббревиатура RMS (rms) — root mean square — среднеквадратичное (значение).
В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.
Источники
- «Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
- Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
- «Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 — § 7.10
Ссылки
- Действующие значения тока и напряжения
- Среднеквадратичное значение
| Это заготовка статьи по физике. Вы можете помочь проекту, дополнив её. |
ru.wikipedia.org>
Список параметров напряжения и силы электрического тока
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u ( t ) , i ( t ) {\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.
Амплитудное значение
- Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):
Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.
Среднеквадратичное значение
Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.
U = 1 T ∫ 0 T u 2 ( t ) d t , I = 1 T ∫ 0 T i 2 ( t ) d t {\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температу
4.4.4. Эффективные напряжение и ток
Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.
Действующим илиэффективнымзначением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.
Свяжем
эффективное значение тока с его
амплитудным значением. Для этого
рассчитаем количество теплоты, выделяемое
на активном сопротивлении переменным
током за время, равное периоду колебаний.
Напомним, что по закону Джоуля-Ленца
количество теплоты, выделяющееся на
участке цепи cсопротивлением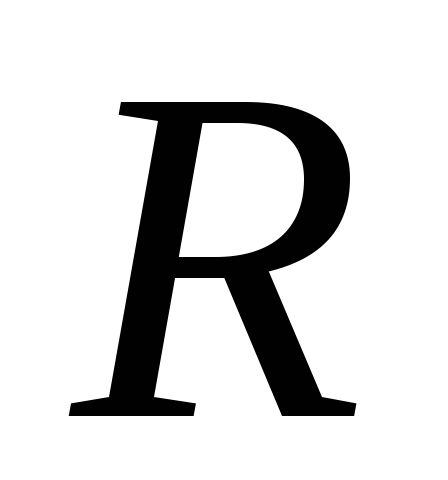 припостоянномтоке
припостоянномтоке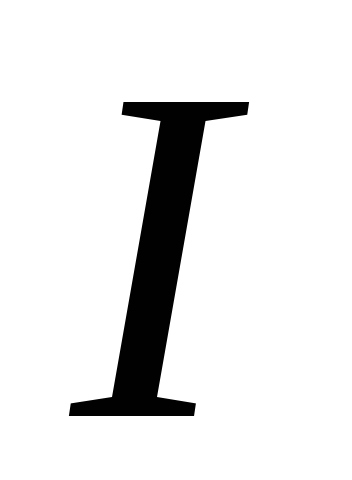 за время
за время ,
определяется по формуле
,
определяется по формуле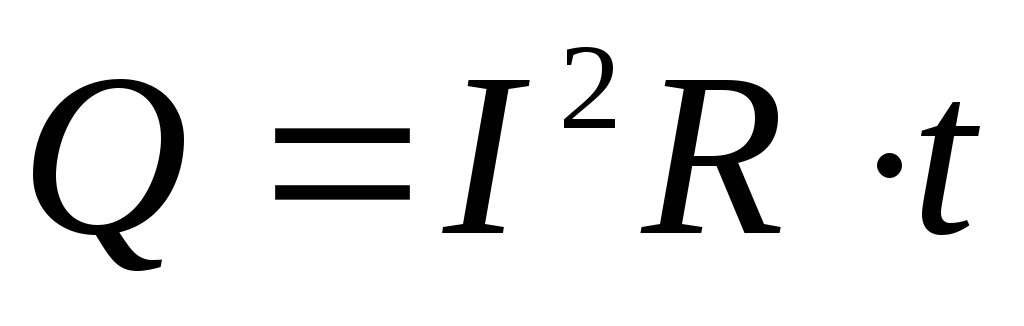 .
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени
.
Переменный ток можно считать постоянным
только в течение очень малых промежутков
времени .
Поделим период колебаний
.
Поделим период колебаний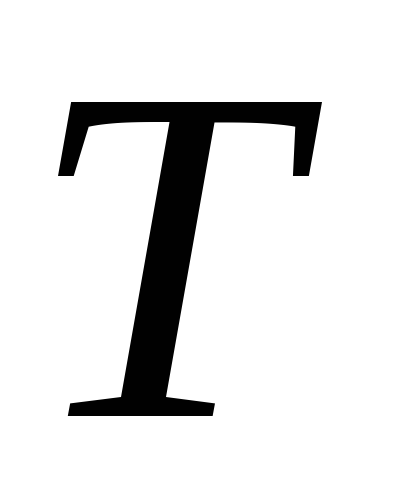 на очень большое число малых промежутков
времени
на очень большое число малых промежутков
времени .
Количество теплоты
.
Количество теплоты ,
выделяемое на сопротивлении
,
выделяемое на сопротивлении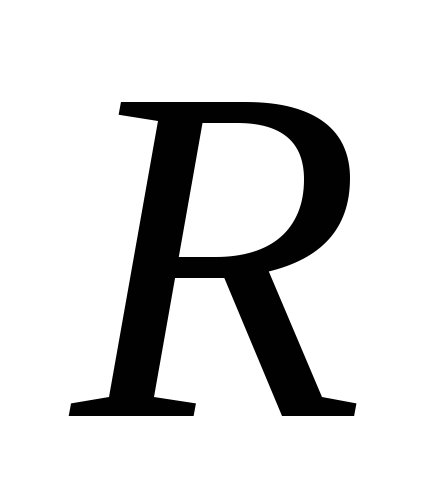 за время
за время :
: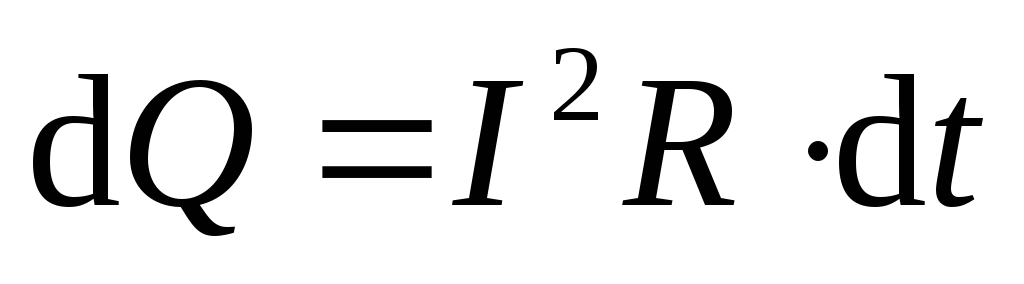 .
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
.
Общее количество теплоты, выделяемое
за период, найдется суммированием
теплот, выделяемых за отдельные малые
промежутки времени, или, другими словами,
интегрированием:
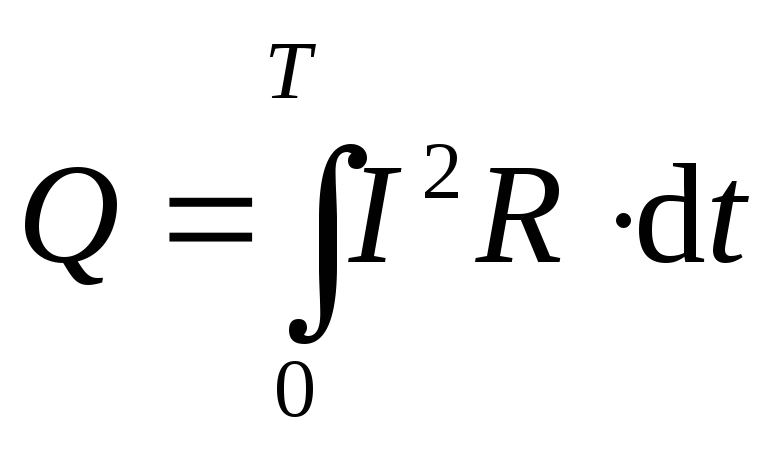 .
.
Сила тока в цепи изменяется по синусоидальному закону
 ,
,
тогда
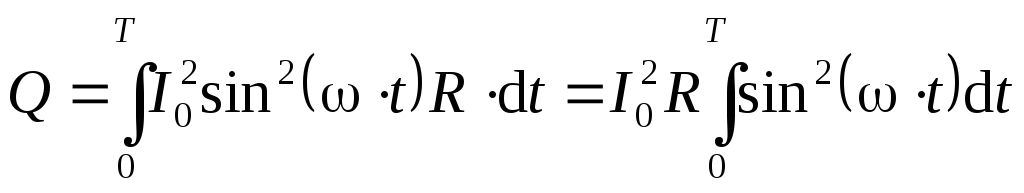 .
.
Опуская вычисления, связанные с интегрированием, запишем окончательный результат
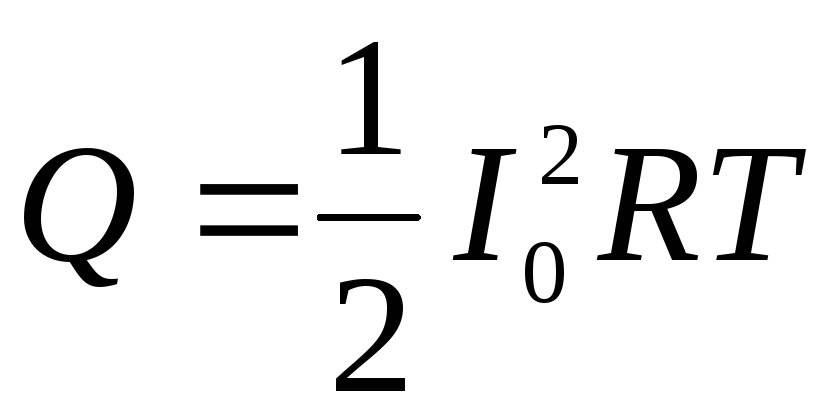 .
.
Если бы по
цепи шёл некоторый постоянный ток 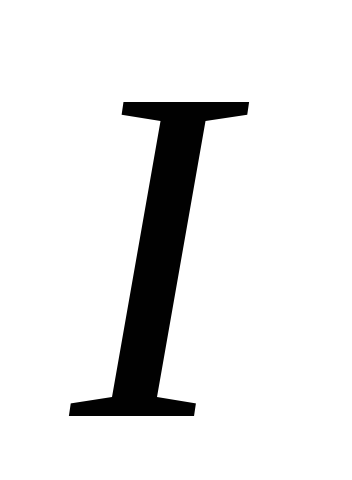 ,
то за время, равное
,
то за время, равное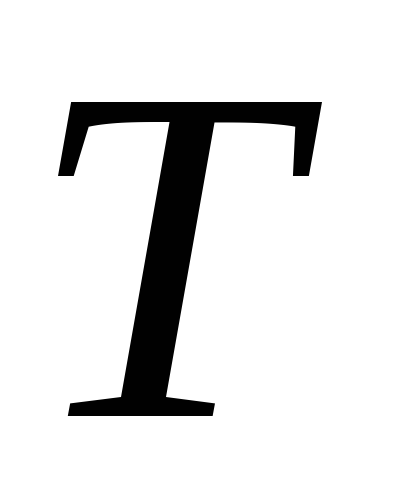 ,
выделилось бы тепло
,
выделилось бы тепло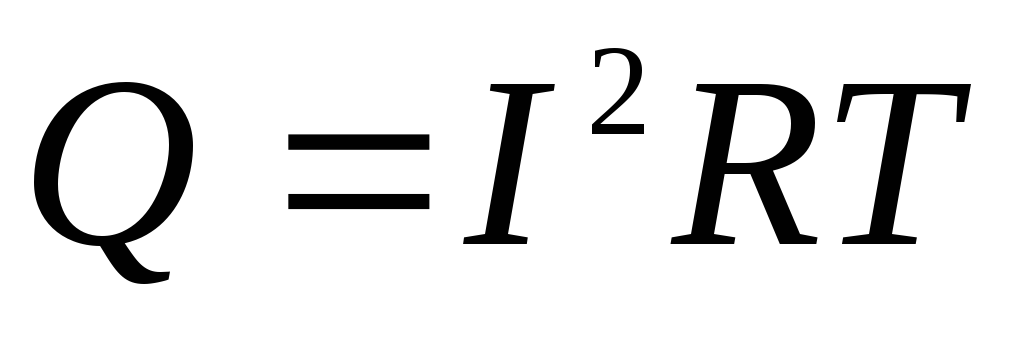 .
По определению постоянный ток
.
По определению постоянный ток ,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока
,
оказывающий такое же тепловое действие,
что и переменный, будет равен эффективному
значению переменного тока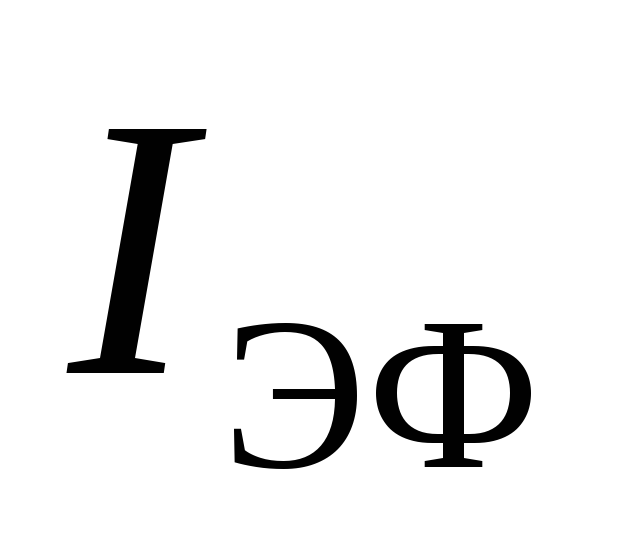 .
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
.
Находим эффективное значение силы
тока, приравнивая теплоты, выделяемые
за период, в случаях постоянного и
переменного токов
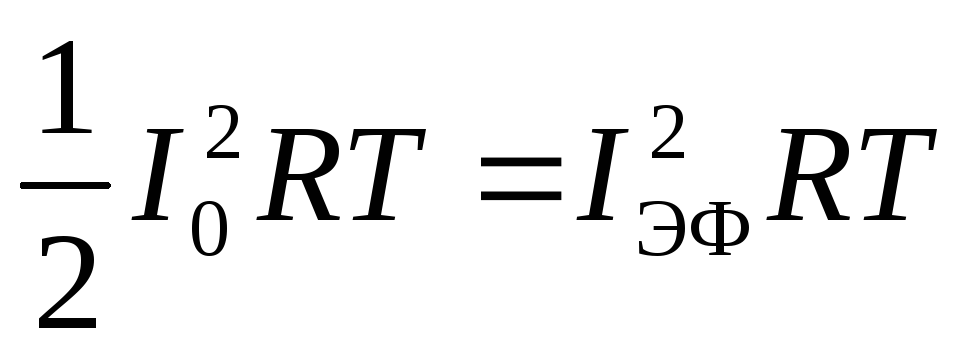

 (4.28)
(4.28)
Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:
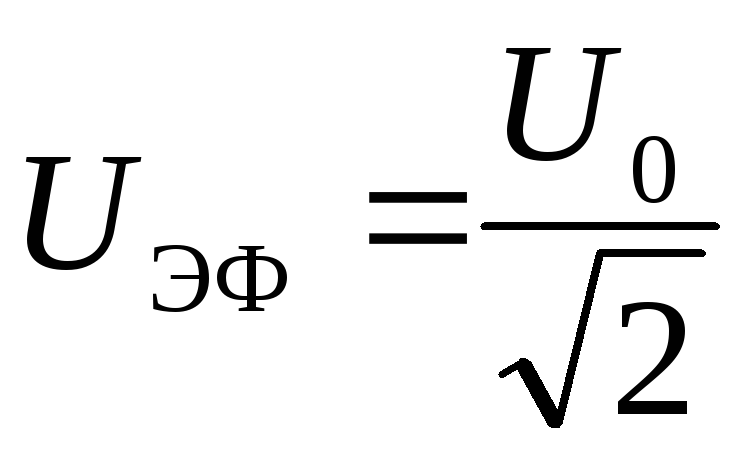 (4.29)
(4.29)
Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.
4.4.5. Мощность в цепи переменного тока
Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:
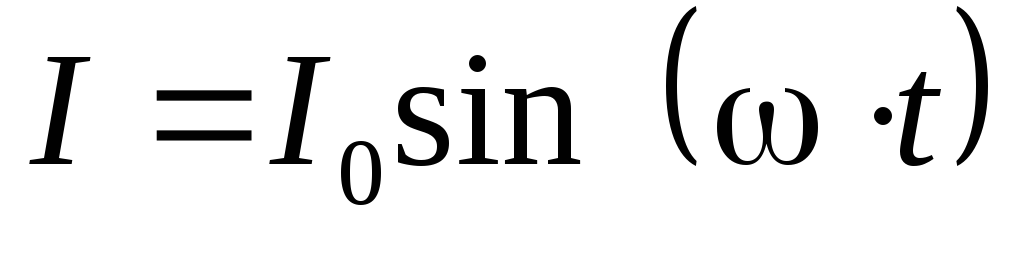 ,
,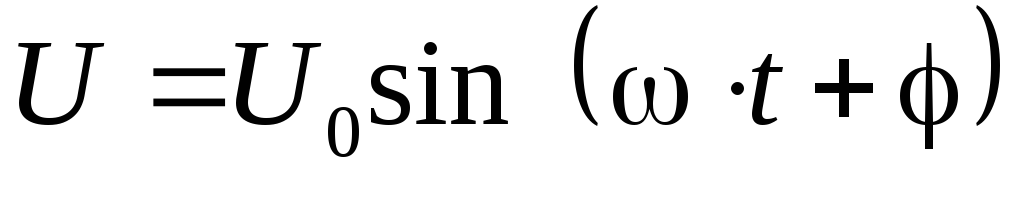 .
.
Тогда мгновенное значение мощности, выделяемой на участке цепи,
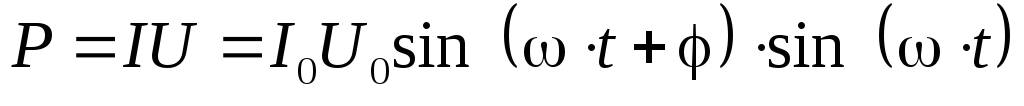 .
.
Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):
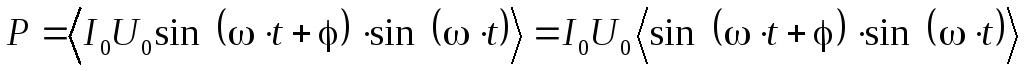 .
.
С использованием известной тригонометрической формулы
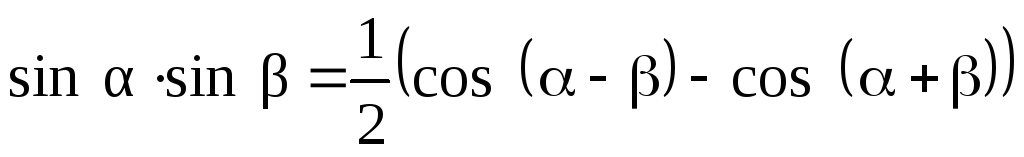
получим
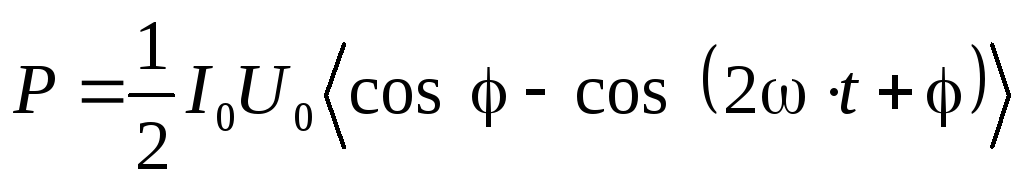 .
.
Величину 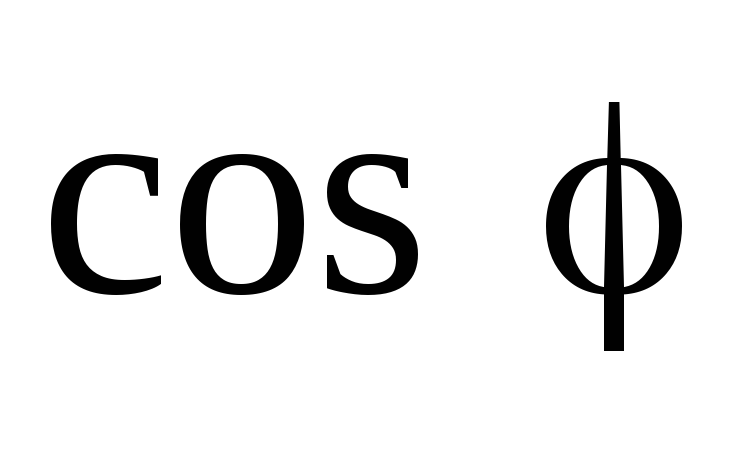 усреднять не нужно, так как она не зависит
от времени, следовательно:
усреднять не нужно, так как она не зависит
от времени, следовательно:
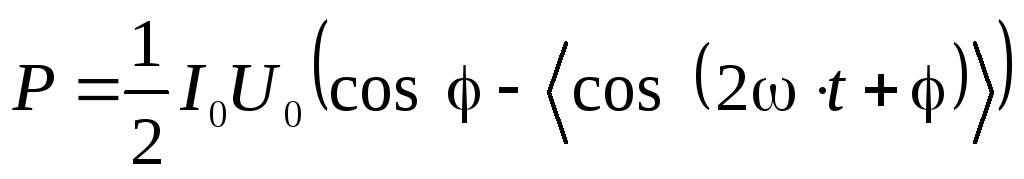 .
.
За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю
 ,
поэтому(4.30)
,
поэтому(4.30)
Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим
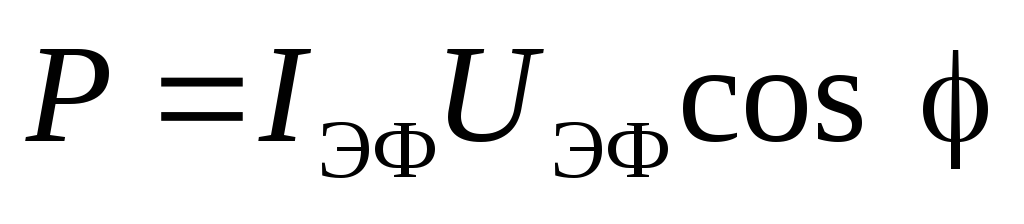 . (4.31)
. (4.31)
Мощность, выделяемая на участке цепи с
переменным током, зависит от эффективных
значений тока и напряжения и сдвига
фаз между током и напряжением. Например,
если участок цепи состоит из одного
только активного сопротивления, то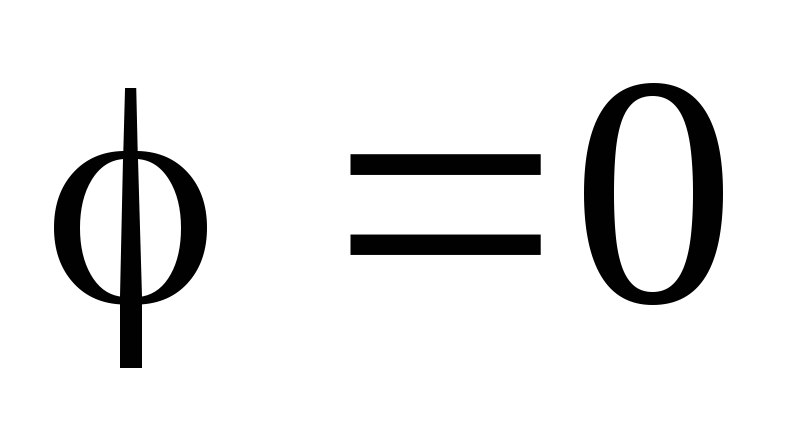 и
и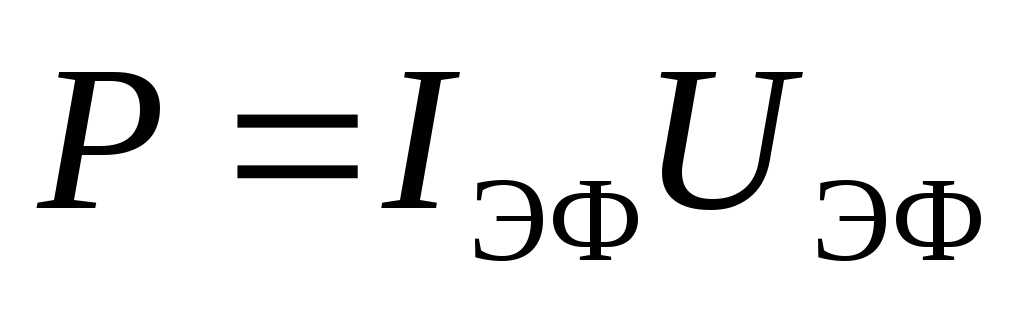 .
Если участок цепи содержит только
индуктивность или только ёмкость, то
.
Если участок цепи содержит только
индуктивность или только ёмкость, то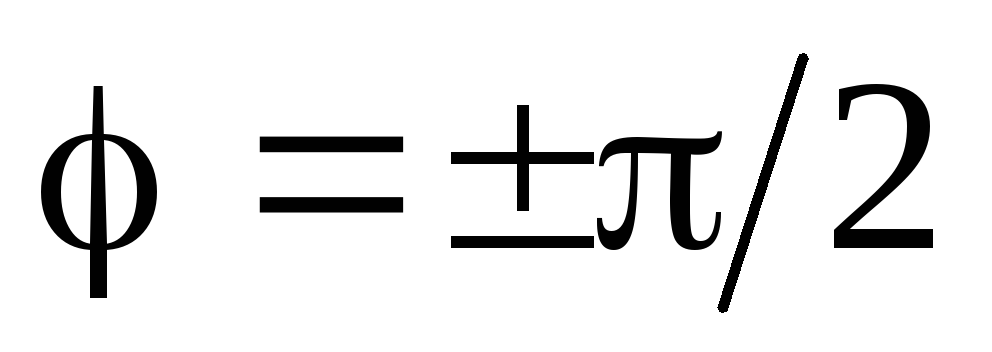 и
и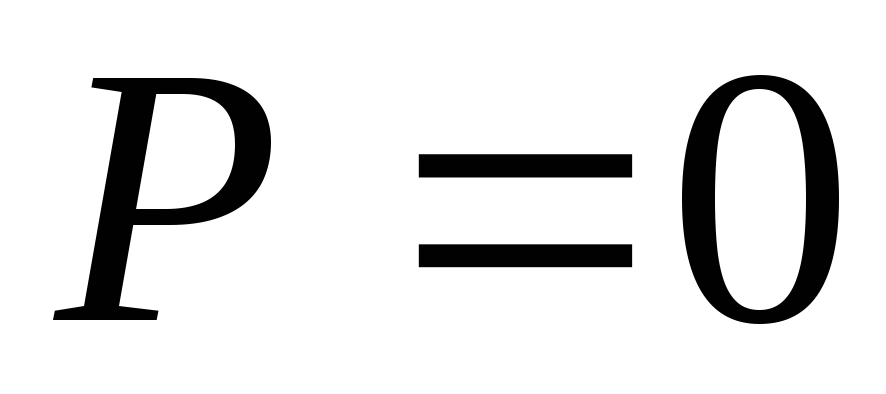 .
.
Объяснить среднее нулевое значение
мощности, выделяемой на индуктивности
и ёмкости можно следующим образом.
Индуктивность и ёмкость лишь заимствуют
энергию у генератора, а затем возвращают
её обратно. Конденсатор заряжается, а
затем разряжается. Сила тока в катушке
увеличивается, затем снова спадает до
нуля и т. д. Именно по той причине, что
на индуктивном и ёмкостном сопротивлениях
средняя расходуемая генератором энергия
равна нулю, их назвали реактивными. На
активном же сопротивлении средняя
мощность отлична от нуля. Другими словами
провод с сопротивлением 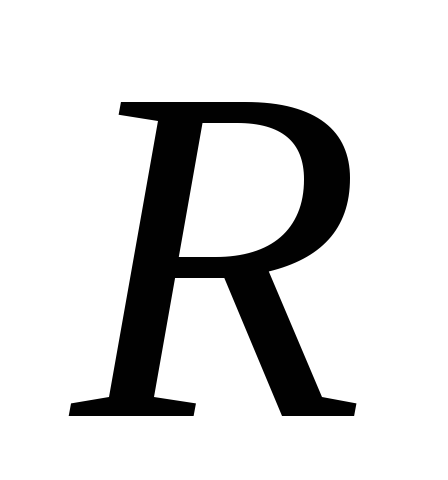 при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
при протекании по нему тока нагревается.
И энергия, выделяемая в виде тепла, назад
в генератор уже не возвращается.
Если участок цепи содержит несколько
элементов, то сдвига фаз 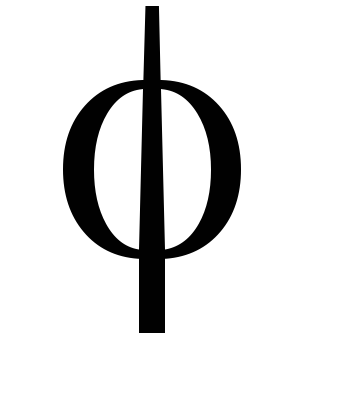 может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).
может быть иным. Например, в случае
участка цепи, изображенного на рис. 4.5,
сдвиг фаз между током и напряжением
определяется по формуле (4.27).
Пример 4.7.К генератору переменного
синусоидального тока подключён резистор
с сопротивлением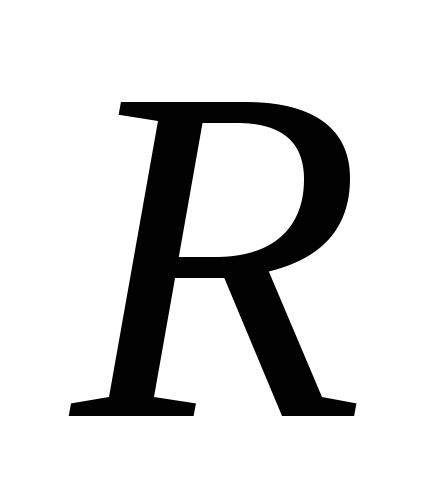 .
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением
.
Во сколько раз изменится средняя
мощность, расходуемая генератором, если
к резистору подключить катушку с
индуктивным сопротивлением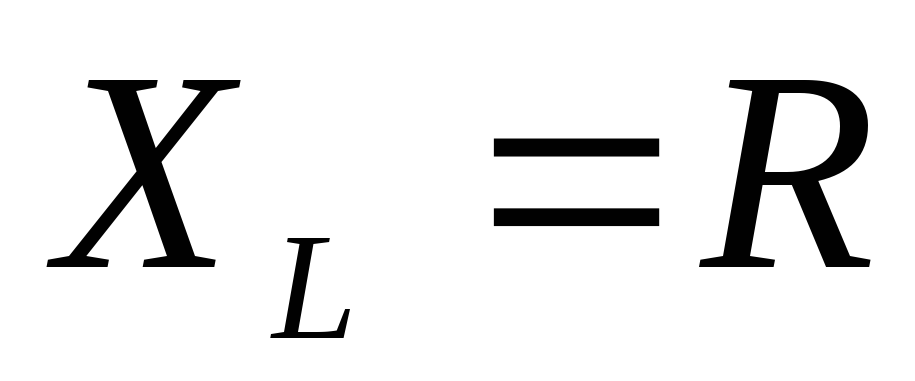 а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
а) последовательно, б) параллельно (рис.
4.10)? Активным сопротивлением катушки
пренебречь.
Решение.Когда к генератору подключено
одно только активное сопротивление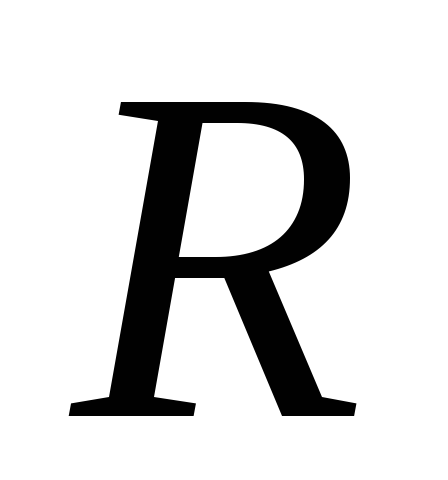 ,
расходуемая мощность
,
расходуемая мощность
 (см. формулу (4.30)).
(см. формулу (4.30)).
Рассмотрим цепь на рис. 4.10, а. В примере
4.6 было определено амплитудное значение
силы тока генератора:  .
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
.
Из векторной диаграммы на рис. 4.11,а
определяем сдвиг фаз между током и
напряжением генератора
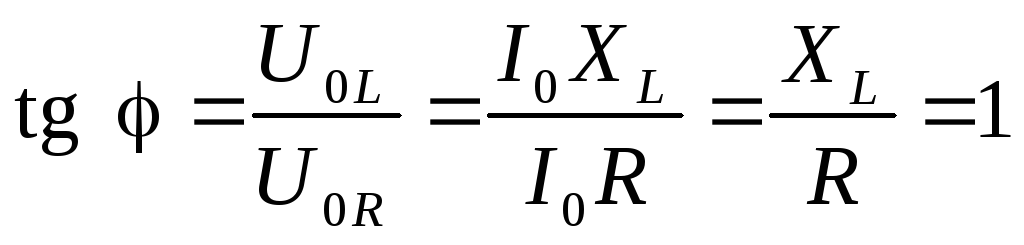

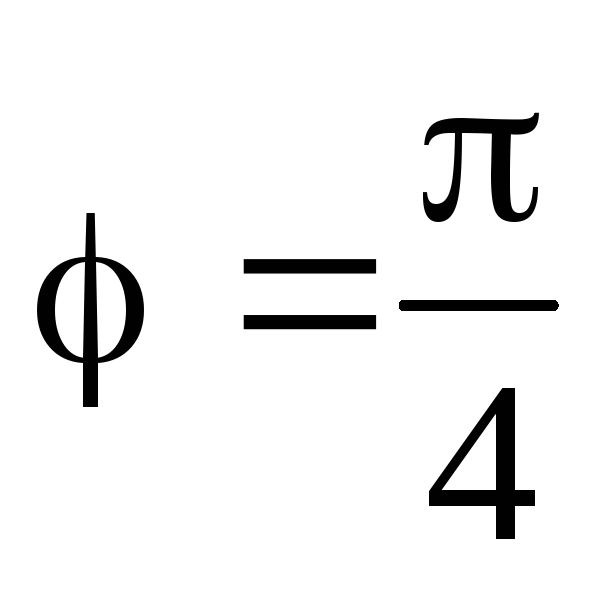 .
.
В результате средняя расходуемая генератором мощность
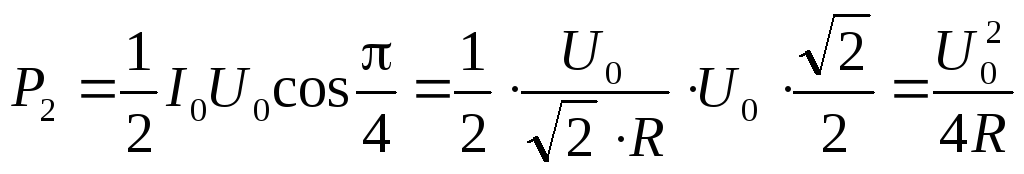 .
.
Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.
Рассмотрим цепь на рис. 4.10,б. В примере
4.6 было определено амплитудное значение
силы тока генератора 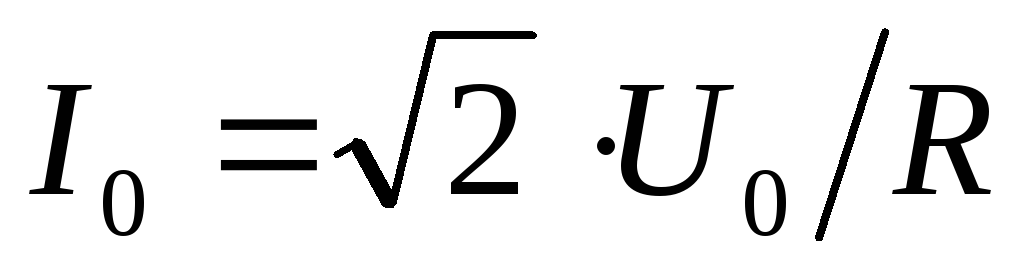 .
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
.
Из векторной диаграммы на рис. 4.11,б
определяем сдвиг фаз между током и
напряжением генератора
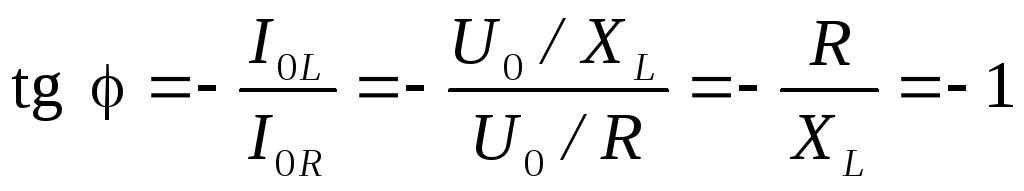

 .
.
Тогда средняя мощность, расходуемая генератором
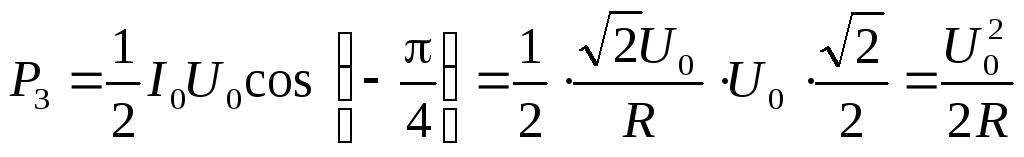 .
.
Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.
Список параметров напряжения и силы электрического тока — Википедия
В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока
Значения переменного напряжения (тока)
Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.
Мгновенное значение
Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является ( u ( t ) , i ( t ) {\displaystyle u(t)~,\quad i(t)} ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.
Амплитудное значение
- Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):
- U M = max ( | u ( t ) | ) , I M = max ( | i ( t ) | ) {\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}
Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.
Среднеквадратичное значение
Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.
- U = 1 T ∫ 0 T u 2 ( t ) d t , I = 1 T ∫ 0 T i 2 ( t ) d t {\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}
Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.
Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.
В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.
Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.
Среднее значение
Среднее значение (смещение) — постоянная составляющая напряжения или силы тока
- U = 1 T ∫ 0 T u ( t ) d t , I = 1 T ∫ 0 T i ( t ) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}
В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.
Средневыпрямленное значение
Средневыпрямленное значение — среднее значение модуля сигнала
- U = 1 T ∫ 0 T ∣ u ( t ) ∣ d t , I = 1 T ∫ 0 T ∣ i ( t ) ∣ d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}
На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.
Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.
Коэффициенты пересчёта значений
- Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .
- Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .
Параметры постоянного тока
- Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени
- Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)
Литература и документация
Литература
Нормативно-техническая документация
Ссылки
См. также
Мощный стабилизатор эффективного значения сетевого напряжения
На моём дачном участке напряжение в электросети в течение суток иногда изменяется от 160 до 250 В. Пришлось приобрести стабилизатор релейного типа “Ресанта” АСН-3000/1-Ц [1]. Он самоотверженно отработал полгода, питая мощный нагреватель (реле нещадно трещали сутками), после чего вышел из строя. На замену ему я сделал фазовый тиристорный регулятор, отличающийся от других подобных тем, что при изменении входного напряжения в широких пределах установленное эффективное (среднеквадратичное) значение выходного напряжения остаётся практически неизменным. В состав стабилизатора входит мощный автотрансформатор от “Ресанты” с номинальным выходным напряжением 300 В.
Основные технические характеристики
Входное синусоидальное напряжение, Вэфф ………….. 165…240
Частота входного напряжения, Гц……………………50
Отклонение эффективного значения выходного напряжения от установленного при изменении входного напряжения в указанных пределах: при выходном напряжении 100…230 Вэфф, %…….±4
при выходном напряжении 200 Вэфф, %…………-2
Максимальный ток нагрузки, А………………………..10
Ввиду несинусоидальности выходного напряжения контролировать его следует вольтметром, измеряющим истинное среднеквадратичное значение такого напряжения. Например, ампервольтомметром Ц4360 или щитовым вольтметром электромагнитной системы. Цифровой или стрелочный мультиметр, если они не имеют функции TrueRMS, не дают в этом случае правильных показаний.
Рис. 1. Схема устройства
Схема устройства показана на рис. 1. При уменьшении сетевого напряжения уменьшается напряжение на конденсаторе C3, которое в сумме с напряжением, стабилизированным стабилитроном VD7, поступает в управляющую цепь генератора импульсов на эквиваленте однопереходного транзистора, собранного из транзисторов VT3 и VT4. При этом зарядка конденсатора C2 происходит быстрее, и импульс, открывающий симистор VS1, работающий в режиме тиристора, и тиристор VS2, в каждом полупериоде генерируется раньше, что приводит к увеличению эффективного напряжения на выходе до прежнего значения. При увеличении напряжения на входе всё происходит в обратном порядке.
Важную роль играет узел плавного пуска. Без него в первый момент после замыкания выключателя SA1 потребителю было бы подано полное вторичное напряжение автотрансформатора T1 амплитудой более 400 В. Работа этого узла подробно описана в [2]. При включении начинает заряжаться конденсатор C1, постепенно полностью открывая составной транзистор VT1VT2.
Переменным резистором R5 устанавливают выходное напряжение, а подстроечным резистором R11 добиваются его наилучшей стабилизации. Цепь R17C5 необходима только при работе на индуктивную нагрузку.
Во время работы стабилизатор должен быть защищён от напряжения в питающей его сети более 250 В. Я применяю для этого защитное устройство “АЛЬБАТРОС-12345” [3]. Тем не менее в своём стабилизаторе я предусмотрел и узел защиты от превышения допустимого напряжения на выходе стабилизатора, которое может случиться, например, при пробое симистора VS1 или тиристора VS2. В таком случае этот узел должен отключить потребителей и включить звуковую сигнализацию.
При превышении выходным напряжением заданного порога (его устанавливают подборкой сопротивления резистора R19) срабатывает реле K1. Соединёнными параллельно контактными группами K1.1 и K1.2 оно отключает от выхода стабилизатора потребителей и подключает к нему звуковой генератор на тиратроне с холодным катодом VL1. Звонок HA1 – от старого проводного телефонного аппарата (ТА56, ТА68, ТА72). Контакты K1.3 при срабатывании реле включают в цепь питания его катушки резистор R18, уменьшая этим ток через неё до значения, достаточного для удержания реле в сработавшем состоянии.
Чертёж печатной платы, на которой размещены маломощные элементы стабилизатора, изображён на рис. 2. Трансформатор Т2 – МИТ-4В. Его можно изготовить самостоятельно, как описано в [4], намотав на кольце типоразмера К10х6х5 из феррита 600НН две обмотки по 50 витков провода ПЭВ-1 диаметром 0,2 мм. Обмотки должны быть хорошо изолированы от кольца и одна от другой. Конденсатор С6 извлечён из энергосберегающей лампы.
Рис. 2. Чертёж печатной платы и элементы на ней
Силовая часть (автотрансформатор T1, тиристор VS2, диодный мост VD8- VD11, демпфирующая цепь R17C5) и устройство защиты от перенапряжения с реле K1 (РП21-003 или РЭК-77/3) и звуковым сигнализатором собраны отдельно с применением проводного монтажа. Также вне платы находятся переменный резистор R5 – СП-I и под-строечный резистор R11 – СП-II, оба с линейной зависимостью сопротивления от угла поворота движка.
Для налаживания подключите стабилизатор к сети через лабораторный автотрансформатор (ЛАТР), рассчитанный на ток, не менее потребляемого нагрузкой, например, лампой накаливания мощностью 100 Вт. Напряжение на ней измеряйте ампервольтомметром Ц4360 или другим прибором, показывающим истинное среднеквадратическое значение напряжения (TrueRMS).
Движки переменного резистора R5 и подстроечного резистора R11 переведите в среднее положение. Установите напряжение на выходе ЛАТР равным 230 В, а переменным резистором R5 – 200 В на выходе стабилизатора. Изменяя напряжение, поступающее с ЛАТР в пределах 165…240 В, добейтесь с помощью подстроечного резистора R11 наилучшей стабильности выходного напряжения стабилизатора. Возможно, чтобы достигнуть наилучшего результата, эти регулировки придётся повторить несколько раз. После этого зафиксируйте в найденном положении движок подстроечного резистора R11 или измерьте сопротивление последнего и замените его постоянным резистором.
При желании можно увеличить задержку включения стабилизатора, увеличив ёмкость конденсатора C1 до 100 мкФ. Если стабилизатор будет применяться только для питания активной нагрузки (электропечи, водонагреватели), из него можно исключить цепь R17C5, а также узел плавного пуска (увеличив номинальное сопротивление резистора R4 до 5,6 кОм).
При малой нагрузке (до 200 Вт) из стабилизатора можно исключить резисторы R15 и R16, тиристор VS2, диодный мост VD8-VD11, а симистор VS1 включить электродами 1 и 2 в разрыв цепи питания потребителей.
При наладке и эксплуатации стабилизатора соблюдайте меры электробезопасности, так как все его элементы находятся под высоким напряжением. Помните, что нельзя питать через него электроприборы, требующие неискажённого синусоидального напряжения.
Литература
1. Стабилизатор напряжения переменного тока электронный с цифровой индикацией. – URL: https://resanta24.ru/files/manuals/ manual_stabi_cifrovie_ver. 13.11.14%2-0red.10.pdf (28.09.2019).
2. Нечаев И. Регулируем яркость светильника. – Радио, 1992, № 1, с. 22, 23.
3. Устройство защиты всего дома или квартиры АЛЬБАТРОС-12345. – URL: https:// bast.ru/products/archive/albatros-12345 (28.09.19).
4. Приймак Д. Низковольтный тринис-торный регулятор напряжения. – Радио, 1989, №5, с. 78-80.
Автор: К. Степанов, г. Таганрог Ростовской обл.
Что такое пиковое значение, среднее значение и среднеквадратичное значение? – определение и объяснение
Пиковое значение
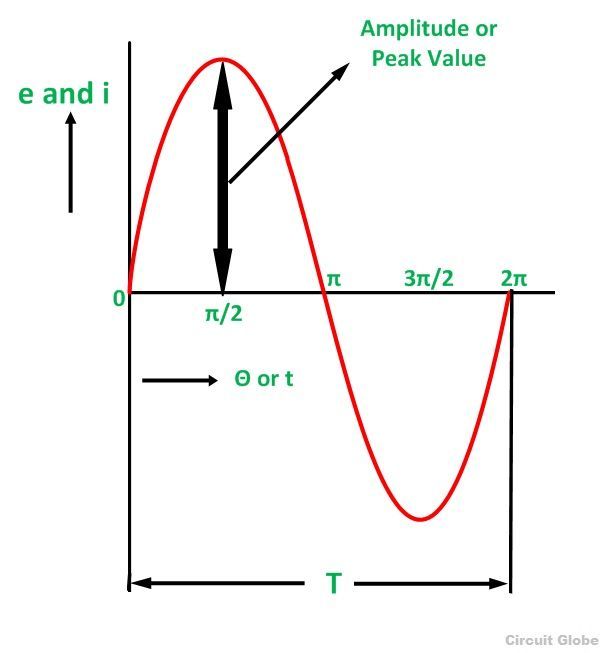
Определение: Максимальное значение, достигаемое переменным количеством в течение одного цикла, называется его значением P eak . Он также известен как максимальное значение, амплитуда или пик. Синусоидальная переменная величина достигает пикового значения под углом 90 градусов, как показано на рисунке ниже.
Пиковые значения переменного напряжения и тока представлены соответственно E m и I m .
 Среднее значение
Среднее значение
Определение: Среднее значение всех мгновенных значений переменного напряжения и токов за один полный цикл называется средним значением .
Если мы рассмотрим симметричные волны, такие как синусоидальный ток или форма волны напряжения, положительный полупериод будет точно равен отрицательному полупериоду. Следовательно, среднее значение за полный цикл будет ноль .
Работа выполняется как по положительному, так и по отрицательному циклу, поэтому среднее значение определяется без учета знаков.
Итак, единственным положительным полупериодом считается определение среднего значения переменных величин синусоидальных волн. Давайте рассмотрим пример, чтобы понять это.
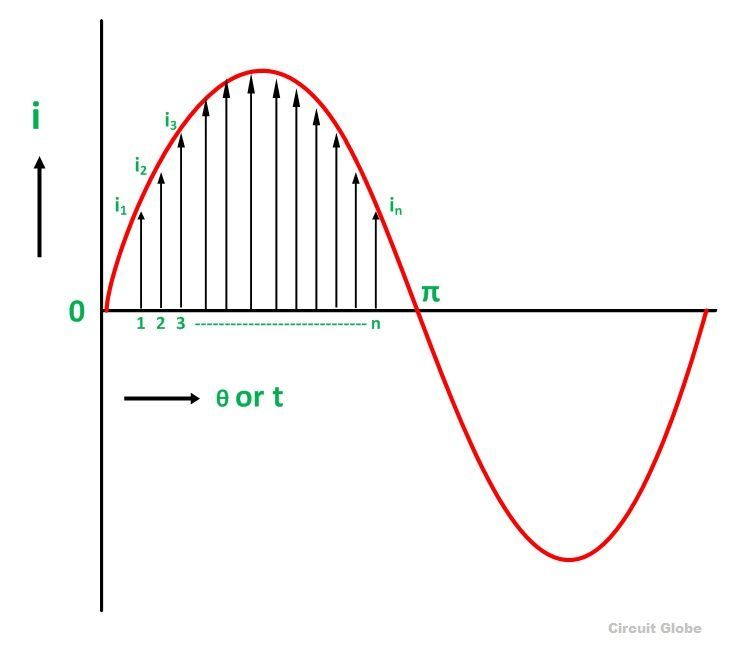 Разделите положительный полупериод на ( n ) количество равных частей, как показано на рисунке выше
Разделите положительный полупериод на ( n ) количество равных частей, как показано на рисунке выше
Пусть i 1 , i 2 , i 3 …… .. i n – средние ординаты
Среднее значение тока I ср = среднее значение средних ординат
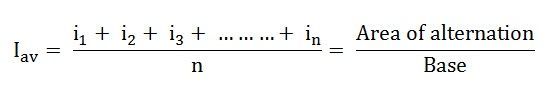 р.Значение M.S
р.Значение M.S
Определение: Тот установившийся ток, который при прохождении через резистор с известным сопротивлением в течение заданного периода времени, в результате такое же количество тепла вырабатывается переменным током, когда он протекает через тот же резистор в течение того же периода времени. время называется RMS или действующим значением переменного тока.
Другими словами, значение R.M.S определяется как квадратный корень из средних квадратов мгновенных значений.
Пусть I будет переменным током, протекающим через резистор R в течение времени t секунд, который производит такое же количество тепла, как и постоянный ток (I eff ).База одного изменения делится на n равных частей, так что каждый интервал составляет t / n секунд, как показано на рисунке ниже.
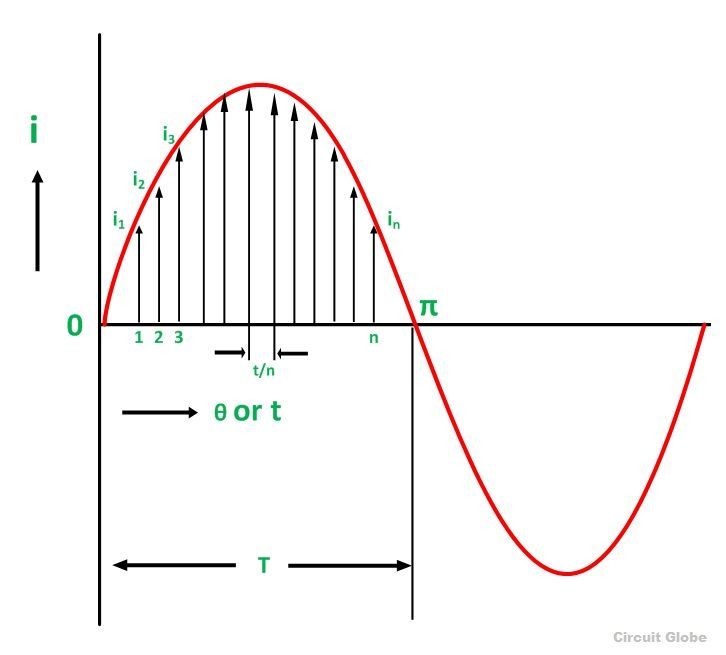 Пусть i 1 , i 2 , i 3 , ……… ..in – средние ординаты
Пусть i 1 , i 2 , i 3 , ……… ..in – средние ординаты
Тогда тепло произведено в
 Так как Ieff рассматривается как эффективное значение этого тока, то общее количество тепла, произведенного этим током, будет
Так как Ieff рассматривается как эффективное значение этого тока, то общее количество тепла, произведенного этим током, будет
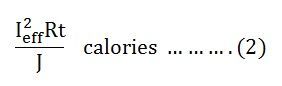
Теперь, приравняв уравнение (1) и (2), получим

I eff = корень квадратный из среднего квадратов мгновенных значений = R.Значение M.S
Среднеквадратическое значение – это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию.
Амперметр регистрирует среднеквадратичное значение переменного тока, а вольтметр записывает среднеквадратичное значение переменного напряжения. Бытовая однофазная сеть переменного тока составляет 230 В, 50 Гц, где 230 В – это среднеквадратичное значение переменного напряжения.
Значения напряжения и тока системы в цепи постоянного тока постоянны, поэтому нет проблем с оценкой их величин, но в системе переменного тока переменное напряжение и ток изменяются время от времени, и, следовательно, необходимо оценивать их магнитуды.
Следующие три способа (пиковое значение, среднее значение и среднеквадратичное значение), приведенные выше, используются для выражения величины напряжения и тока.
,Измерение действующих значений напряжения и тока
ИЗМЕРЕНИЯ НАПРЯЖЕНИЯ (ТОКА)
Стандартные классические измерения значений напряжения (тока) основаны на двух основных методах: «среднее» или «эффективное».«Среднее» значение функции времени – это чистая площадь функции, вычисленная за определенный интервал времени, деленная на этот интервал времени.
В частности,
 (Уравнение 1)
(Уравнение 1)
Если напряжение (ток) является постоянным или периодическим, то измерение его среднего значения не зависит от интервала, в течение которого выполняется измерение.Если, с другой стороны, функция напряжения (тока) растет без ограничения во времени, среднее значение зависит от интервала измерения и не обязательно будет постоянным, то есть никакого среднего значения не существует. К счастью, в практическом мире электричества значения напряжения (тока) не растут безмерно и, следовательно, имеют хорошие средние значения. Это является результатом того факта, что источники реального напряжения (тока), как правило, либо; (1) батареи с постоянными или медленно (экспоненциально) убывающими значениями, (2) ограниченные синусоидальные функции времени или (3) комбинации вышеперечисленного.Синусоидальные функции с постоянной амплитудой имеют чистое нулевое среднее значение за интервалы времени, которые равны целочисленным кратным синусоидального периода. Более того, средние значения могут быть рассчитаны за бесконечное число интервалов, которые не равны синусоидальному периоду. Эти средние также равны нулю. Хотя среднее значение ограниченной синусоидальной функции равно нулю, «эффективное» значение не равно нулю. Например, электрические водонагреватели очень хорошо работают на синусоидальных напряжениях с нулевыми средними значениями.
ЭФФЕКТИВНАЯ СТОИМОСТЬ
«Эффективное» значение симметричных периодических функций напряжения (тока) времени основано на понятии «нагревательная способность». Рассмотрим тестовое приспособление, показанное на рисунке 1.
Рисунок 1: Испытательное приспособление
Этот сосуд изолирован и заполнен некоторой стабильной жидкостью (например, трансформаторным маслом), способной достичь термодинамического равновесия.Если на внутренний нагреватель сосуда подается постоянное напряжение Vx, температура жидкости поднимется. В конце концов, электрическая энергия, подаваемая на этот сосуд, создаст состояние равновесия, при котором подводимая энергия равна потере энергии (тепла) и жидкость сосуда достигнет равновесной температуры, Tx градусов.
Затем в этом экспериментальном сценарии замените источник постоянного напряжения Vx изменяющимся во времени напряжением, которое не увеличивается без ограничений. Со временем, через некоторое время, Tfinal, тепловое равновесие снова будет установлено.Если это условие равновесия устанавливает ту же температуру Tx, которая была достигнута ранее с приложенным напряжением постоянного тока Vx, то можно сказать, что «эффективное» значение этой изменяющейся во времени функции равно Vx.
Отсюда и определение «действующей стоимости». Уравнение 2 иллюстрирует это тепловое равновесие.  (Уравнение 2)
(Уравнение 2)
Если V (t) является периодической функцией времени с периодом цикла Tp, а T final представляет собой целое число «n», умноженное на период (n * Tp), то интеграл по T final равен просто n умноженный на интеграл по Tp.Результаты этих замен показаны в уравнении 3.
 (Уравнение 3)
(Уравнение 3)
Уравнение 3 показывает, что эффективная эквивалентная тепловая способность ограниченной периодической функции напряжения (тока) может быть определена всего за один цикл. Это уравнение признано старой знакомой формой «квадрат R oot из M ean (в среднем) S quared»; отсюда и название « RMS ».
ПРИМЕРЫ ИСПОЛЬЗОВАНИЯ УРАВНЕНИЯ «RMS»
Следующие результаты могут быть получены прямым применением уравнения 3.- Синусоидальная функция, пик Vp

- Симметричная периодическая импульсная волна, пик Vp

- Несимметричная периодическая импульсная волна, все положительные пики Vp, с рабочим циклом D

- Симметричная периодическая треугольная волна, пик Vp

- Двухполупериодная выпрямленная синусоида, пиковое Vp

- Полуволновая выпрямленная синусоида, пиковое Vp

ЭФФЕКТИВНЫЕ (СКЗ) ЗНАЧЕНИЯ КОМПЛЕКСНЫХ ФУНКЦИЙ
Чрезвычайно полезный факт при определении среднеквадратичных значений заключается в том, что любая ограниченная периодическая функция времени с хорошим поведением может быть выражена, например, как среднее значение плюс сумма синусоид (теорема Фурье); (Уравнение 4)
(Уравнение 4) Где ωo – радианная частота V (t), а An, Bn, Ao – коэффициенты амплитуды Фурье.
Когда этот ряд подставляется в интегральное выражение Уравнение 2 для RMS, получается следующее;
 (Уравнение 5)
(Уравнение 5)
Примечание: (A n ) 2 и (B n ) 2 /2 – квадраты среднеквадратичных значений для каждого n -го компонента Sin и косинуса.
Важный вывод:
ПРАКТИЧЕСКИЕ СООБРАЖЕНИЯ
На рисунке 2 показаны составные кривые, образованные добавлением двух синусоид, одна с частотой 60 Гц и одна с частотой 180 Гц. Кривая 1 соответствует нулевой разности фаз, а кривая 2 – разности фаз 90 градусов. Конкретно;
Кривая 1 V (t) = 170 * Sin (377 * t) + 50 * Sin (1131 * t)
Кривая 2 V (t) = 170 * Sin (377 * t) + 50 * Cos (1131 * t)
Примечание: Форма составной кривой определяется гармониками фазы и частоты.

Рисунок 2: Фундаментальный с третьей гармоникой Добавлен
Кривая 2170 * Sin (377 * t) + 50 * Cos (1131 * t)
Кривая 1170 * Sin (377 * t) + 50 * Sin (1131 * t)
Промышленные синусоидальные функции напряжения (тока) часто содержат гармоники, которые влияют на форму волны и пиковые (пиковые) значения.Например, кривая 2 типична для токов намагничивания в трансформаторах и двигателях 60 Гц. В недорогих устройствах для считывания среднеквадратичных значений часто используются схемы выпрямителя, которые фиксируют пиковое значение, которое затем масштабируется на 0,707 и отображается как среднеквадратичное значение. Очевидно, что этот метод может дать неверные показания RMS. В этом примере использование Vpeak ÷ √2 явно дает неверные значения.
Кривая 1: 203 * 0,707 = 144 В, не соответствует действительности
Кривая 2: 155 * 0.707 = 110 вольт, неверно RMS
Правильное среднеквадратичное значение для обеих этих составных синусоидальных функций:
[(170) 2 /2 + (50) 2 /2] 1/2 = 125,3 В (среднеквадратичное значение)
Таблица 1 иллюстрирует два примера вычислений RMS с использованием индивидуальных коэффициентов Фурье и уравнения 5. Примером является двухполупериодная выпрямленная пиковая синусоида 1 вольт. Обратите внимание, что для функции двухполупериодного выпрямления измерительное устройство должно обеспечивать показание RMS в пределах 0.Ошибка 01% требует ширины полосы, которая включает пятую (5) гармонику и разрешение для считывания уровней 10 мВ. Другой пример, проиллюстрированный в Таблице 1, представляет собой пиковую функцию напряжения 1 В. В этом примере измерительному устройству для пилообразной функции, необходимому для получения показаний RMS с погрешностью 0,3%, требуется полоса пропускания, которая включает двадцать пятую (25) гармонику, и разрешение для считывания уровней 10 мВ.
Предположим, в целях иллюстрации, что пульсации переменного тока на выходе постоянного тока выпрямителя могут быть аппроксимированы пилообразной функцией.В таблице 1 показано, что для измерения с погрешностью 0,3% среднеквадратичных пульсаций переменного тока на выходе постоянного тока выпрямителя 20 кГц измерительное устройство должно иметь полосу пропускания более 500 кГц и разрешение для считывания уровней напряжения на 40 дБ (100 микровольт). для пиковой пульсации 10 мВ). Этот пример ясно показывает, что форма сигнала, а также ширина полосы измерения и разрешение чрезвычайно важны для определения точности измерения истинного среднеквадратичного значения.
Любое устройство измерения «истинного среднеквадратичного значения» должно быть способно точно реализовать уравнение 3.Тонкость этого утверждения заключается в том, что электронная реализация уравнения 3 требует, чтобы устройство имело очень большую полосу пропускания и было способно определять малые величины.
КРЕСТ-ФАКТОР
Еще одним показателем качества, часто используемым для характеристики периодической временной функции напряжения (тока), является пик-фактор (CF). Пик-фактор для конкретной формы волны определяется как пиковое значение, деленное на среднеквадратичное значение. В частности, 
ДАННЫЕ ДЛЯ ИЗМЕРЕНИЯ СКЗ
Для истинных измерений среднеквадратичного значения требуются измерительные приборы, которые точно реализуют уравнение 3, «уравнение среднеквадратичного значения».Эти устройства должны иметь широкую полосу пропускания и хорошее разрешение низкого уровня, чтобы поддерживать высокий коэффициент амплитуды. Dataforth разработала три продукта, которые удовлетворяют этим требованиям; модули ввода SCM5B33, DSCA33 и 8B33 True RMS. Эти продукты обеспечивают изоляционный барьер 1500 В среднеквадратичного значения между входом и выходом. SCM5B33 Изолированный модуль ввода True RMS
- Интерфейсы RMS напряжение (0 – 300 В) или ток RMS (0 – 5 A)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 20 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
- ± 0.25% заводская калибровка точности (класс точности 0,2)
- 1500Vrms Изоляция непрерывного трансформатора
- Защита входа от перегрузки до 480 В макс. (Пиковый и постоянный ток) или 10 А среднеквадратичного значения в непрерывном режиме
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- Сертификат CSA, соответствие CE и ATEX

- Интерфейсы RMS напряжение (0 – 300 В) или ток RMS (0 – 5 A)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (работа в расширенном диапазоне до 20 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход 0-1 мА, 0-20 мА, 4-20 мА, 0-5 В или 0-10 В постоянного тока
- ± 0.25% заводская калибровка точности (класс точности 0,2)
- ± 5% Регулируемый ноль и диапазон
- Изоляция трансформатора 1500Vrms
- Защита входа от перегрузки до 480 В (пиковое напряжение переменного и постоянного тока) или 10 А RMS в непрерывном режиме
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- легко устанавливается на стандартную DIN-рейку Внесено в список
- C-UL-US
- Соответствие CE и ATEX

- Интерфейсы для среднеквадратичного напряжения (0-300 В) или среднеквадратичного тока (0-1 А)
- разработан для стандартной работы с частотами от 45 Гц до 1000 Гц (расширенный диапазон до 10 кГц)
- Совместимость со стандартными трансформаторами тока и напряжения
- Промышленный стандартный выход от 0 до 5 В постоянного тока
- ± 0.25% заводская калибровка точности
- Изоляция трансформатора 1500Vrms
- Защита входа от перегрузки до 350 В среднеквадр. Макс. (Пиковый и постоянный ток) или 2 среднекв.
- 120 дБ CMR
- 70 дБ ЯМР при 60 Гц
- ANSI / IEEE C37.90.1 Защита от переходных процессов
- CE соответствует требованиям Внесено в список
- C-UL-US
- Ожидается соответствие ATEX
- Типы модулей Mix and Match на задней панели
Зарядное устройство постоянного тока с постоянным напряжением – Simulink
Выходные характеристики
Выходной ток зарядного устройства составляет
Переменные для выходного тока и соответствующих уравнений:
I out – выход текущая команда, в A.
I ‘ out – это предварительно отфильтрованная команда тока, в A.
k p – фильтр PID пропорциональное усиление.
k i – фильтр ПИД интегральное усиление.
k d – фильтр ПИД дифференциальное усиление.
I выход r % – текущая пульсация на выходе в%.
f out ir – текущая частота пульсаций на выходе в Гц.
t – время в с.
ξ – коэффициент демпфирования, который ограничен значения от
0до0,9.⍵ n – это радиан частота, рад / с.
d % – перерегулирование, в %.
t с – время установления, в с.
I CC – предварительно отфильтрованный текущая регулируемая текущая команда, в A.
I навалом – постоянная текущая команда, в A.
I CV – предварительно отфильтрованный команда тока, регулируемая напряжением, в A.
V ‘ out – напряжение команда, в В.
В ‘ tc – напряжение команда, в V.
V out – температура компенсированное влияние напряжения, В.
Vout ¯ – среднее измеренное выходное напряжение, в В.
T a – окружающее температура, в ° C.
T nom – номинальный температура окружающей среды, ° C.
V tc – напряжение коэффициент компенсации, в В / ° C.
В абс абсорбция напряжение, В.
V float – поплавок напряжение, В.
P – выходная мощность, Вт.
Iout ¯ – средний измеренный выходной ток, А.
Коэффициенты усиления:
Демпфирующий коэффициент это
Когда управление выходом регулируется по току, частота в радианах равна
Когда управление выходом регулируется по напряжению, частота в радианах составляет
Предварительно отфильтрованная команда тока, I ‘ out , предоставляется либо из предварительно отфильтрованная текущая регулируемая текущая команда, I CC , или из предварительно отфильтрованного команда тока с регулируемым напряжением, I CV .На графиках показаны разные фазы цикла зарядки.
Если Режим управления выходом установлен на Только постоянный ток (CC) или Постоянный ток - постоянное напряжение (CCCV) и V out ниже Напряжение холостого хода или Поглощение
напряжение , а конец абсорбции условие не выполняется
Если Режим управления выходом установлен на Только постоянный ток (CC) или Постоянный ток - постоянное напряжение (CCCV) и V out равно Напряжение холостого хода или Поглощение
напряжение , а конец абсорбции условие не выполняется
Когда опция Включить фазу поглощения включена выбирается, и зарядное устройство переключается с постоянного тока на постоянный контроль напряжения, если конец поглощения условие не соблюдается, температура окружающей среды напряжение компенсация, В ‘ tc определяется как
В противном случае компенсация напряжения окружающей температуры, В ‘ tc определяется как
Когда параметр Включить фазу поглощения установлен выбирается, и зарядное устройство переключается с постоянного тока на постоянный контроль напряжения, если конец поглощения условие не соблюдается, температура окружающей среды напряжение компенсация, V ‘ out определяется как
В противном случае компенсация напряжения окружающей температуры, V ‘ out определяется как
Выходная мощность определяется как
Входные характеристики
Входной ток зарядного устройства составляет
Переменные входного тока и соответствующие уравнения:
I in – входной ток команда, в А.
P ‘ – нормализованная выходная мощность.
P – выходная мощность, Вт.
P nom – номинальная выходная мощность, Вт
I ‘ n – нормированное амплитуда гармоники.
f in – входное напряжение частота, в Гц.
f n – гармоника частота, в Гц.
t – время в с.
В inA – вход напряжение, задержанное на пятую часть своего периода, в В.
В в – входное напряжение фазы А, отсроченной на пятую часть своего периода, в V.
I в r % пульсация входного тока в%.
f дюйм ir – частота пульсаций входного тока в Гц.
θ В дюйм – угол входного напряжения в рад.
θ В дюймА угол входного напряжения фазы A, рад.
Где, f eff , – полиномиальная функция, следующая параметры КПД зарядного устройства и КПД коэффициент использования . Этот полиномиальный порядок составляет половину количества данных вошли пары.Для входных значений P ‘, от 0 до 1, полином должен возвращать значения от 0 до 1. В противном случае порядок полиномов уменьшается до тех пор, пока это условие не будет выполнено. Если порядок достигает 0, вывод будет остаются постоянными для среднего значения набора данных.
Где, f THD , – полиномиальная функция, следующая параметры Суммарные гармонические искажения и THD коэффициент использования . Этот полиномиальный порядок составляет половину количества данных вошли пары.Для входных значений P ‘, от 0 до 1, полином должен возвращать значения от 0 до 1. В противном случае порядок полиномов уменьшается до тех пор, пока это условие не будет выполнено. Если порядок достигает 0, вывод будет остаются постоянными для среднего значения набора данных.
Где, f PF , – полиномиальная функция, следующая параметры Коэффициент мощности и PF использование факто р. Этот полиномиальный порядок составляет половину количества пар данных. поступил.Для входных значений P ‘, от 0 до 1, полином должен возвращать значения от 0 до 1. В противном случае порядок полиномов уменьшается до тех пор, пока это условие не будет выполнено. Если порядок достигает 0, вывод будет остаются постоянными для среднего значения набора данных.
Где, f HARMS , – сумма синусов волны, заданные параметрами Амплитуда гармоник и Частота гармоник после выражения
Когда для параметра Type установлено значение DC ,
Когда параметр Type установлен на 1-фазный переменный ток ,
Когда параметр типа установлен на 3-фазный переменный ток
(звезда) :
Когда параметр типа установлен на 3-фазный переменный ток
(дельта) :
Где:
.

