Эффективное значение переменного тока: Действующее значение тока и напряжения

Содержание

Эффективная сила тока. Действующее значение переменного тока

>> Активное сопротивление. Действующие значения силы тока и напряжения

§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.

Сила тока в цени с резистором. Пусть цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением R (рис. 4.10). Эту величину, которую мы до сих пор называли электрическим сопротивлением или просто сопротивлением, теперь будем называть активным сопротивлением.

В проводнике с активным сопротивлением колебания силы тока совпадают по фазе с колебаниями напряже ния (рис. 4.11), а амплитуда силы тока определяется равенством

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро.

Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии , поступающей в цепь за период, к периоду.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

Поэтому мгновенная моoность в цепи переменного тока на участке, имеющем активное сопротивление R, определяется формулой

P = i 2 R. (4.19)

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.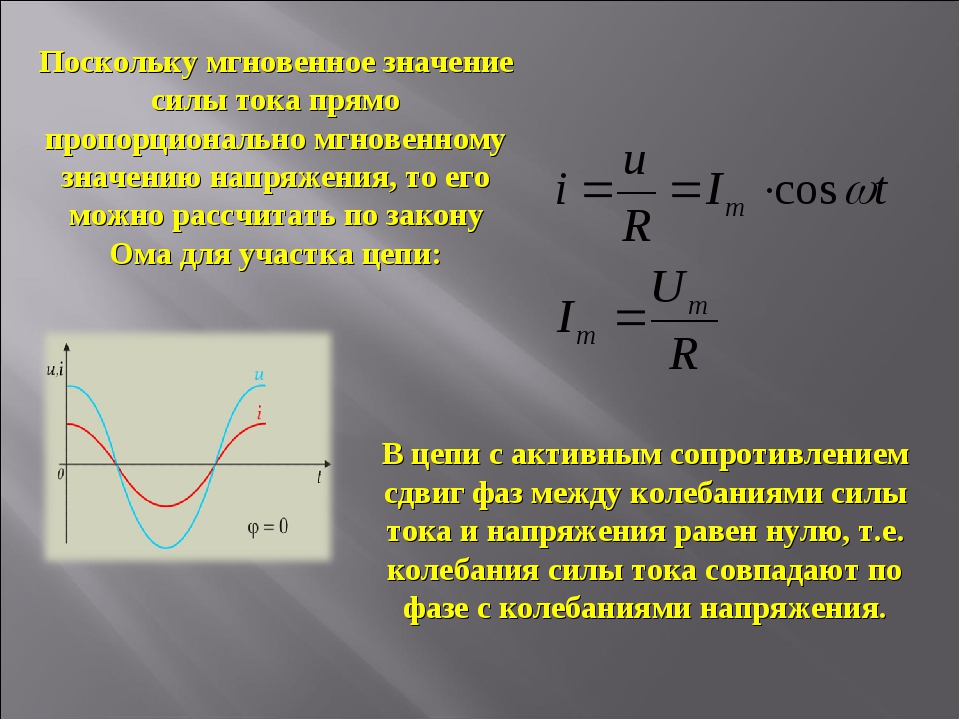

16) для силы тока и используя известное из математики соотношение

График зависимости мгновенной мощности от времени изображен на рисунке 4.12, а. Согласно графику (рис. 4.12, б.), на протяжении одной восьмой периода, когда , мощность в любой момент времени больше, чем . Зато на протяжении следующей восьмой части периода, когда cos 2t

Средняя мощность равна, таким образом, первому члену в формуле (4.20):

Действующие значения силы тока и напряжения . Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока:

Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I:

Действующее значение силы переменного тока

равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4. 17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.

Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока.

Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока:

P = I 2 R = UI.

Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.

1. Чему равна амплитуда напряжения в осветительных сетях переменного тока, рассчитанных на напряжение 220 В!
2. Что называют действующими значениями силы тока и напряжения!

Мякишев Г. Я., Физика. 11 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни / Г. Я. Мякишев, Б. В. Буховцев, В. М. Чаругин; под ред. В. И. Николаева, Н. А. Парфентьевой. – 17-е изд., перераб. и доп. – М. : Просвещение, 2008. – 399 с: ил.

Библиотека с учебниками и книгами на скачку бесплатно онлайн , Физика и астрономия для 11 класса скачать , школьная программа по физике, планы конспектов уроков

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения
Интегрированные уроки

При расчете цепей переменного тока обычно пользуются понятием действующих (эффективных) значений переменного тока, напряжения и э.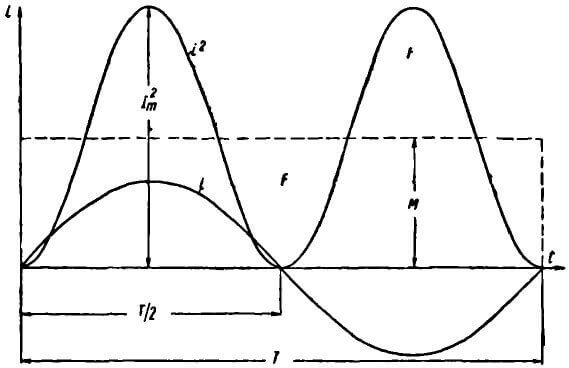 д. с.

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

На шкалах измерительных приборов и технической документации также указываются действующие значения величин.

Действующее значение переменного тока равно значению такого эквивалентного постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет в нем за период то же количество тепла.

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Приравняв Полученное выражение количеству тепла выделенному в том же сопротивлении постоянным током за то же время Т, получим:

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

На рис. 5-8 построена кривая мгновенных значений тока i и кривая квадратов мгновенных значений Площадь, ограниченная последней кривой и осью абсцисс, представляет собой в некотором масштабе величину, определяемую выражением Высота прямоугольника равновеликого площади, ограниченной кривой и осью абсцисс, равная среднему значению ординат кривой представляет собой квадрат действующего значения тока

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

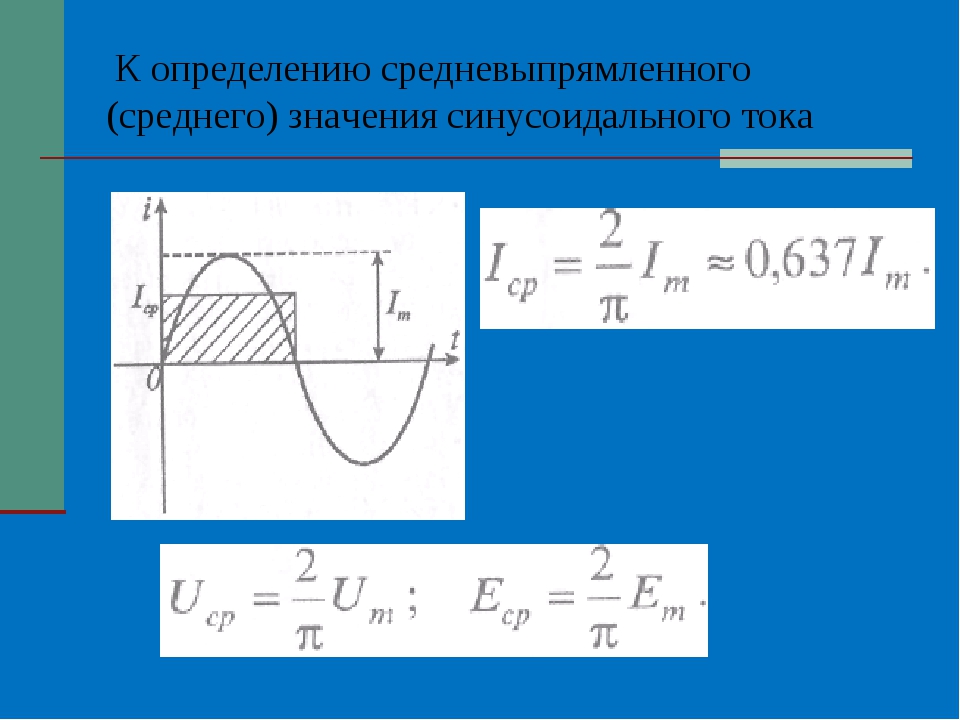
Кроме действующего значения тока и напряжения, иногда пользуются еще понятием среднего значения тбка и напряжения.

Среднее значение синусоидального тока за период равно нулю, так как в течение первой половины периода определенное количество электричества Q проходит через поперечное сечение проводника в прямом направлении. В течение второй половины периода то же количество электричества проходит через сечение проводника в обратном направлении. Следовательно, количество электричества, прошедшее через сечение проводника за период, равно нулю, равно нулю и среднее за период значение синусоидального тока.

Поэтому среднее значение синусоидального тока вычисляют за полупериод, в течение которого ток остается положительным. Среднее значение тока равно отношению количества электричества, прошедшего через сечение проводника за половину периода, к продолжительности этого полупериода.

Определение 1

Эффективным (действующим) называют значение переменного тока равное величине эквивалентного постоянного тока, который при прохождении через такое же сопротивление, что и переменный ток выделяет на нем то же количество тепла за одинаковые промежутки времени.

Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений

Количество тепла, которое выделяется переменным током на сопротивлении $R$ за малый промежуток времени $dt$, равно:

Тогда за один период переменный ток выделяет тепла ($W$):

Обозначим через $I_{ef}$ силу постоянного тока, который на сопротивлении $R$ выделяет такое же количество тепла ($W$), как и переменный ток $I$ за время равное периоду колебаний переменного тока ($T$). Тогда выразим $W$ через постоянный ток и приравняем выражение к правой части уравнения (2), имеем:

Выразим из уравнения (3) силу эквивалентного постоянного тока, получим:

Если сила тока изменяется по синусоидальному закону:

подставим выражение (5) для переменного тока в формулу (4), тогда величина постоянного тока выразится как:

Следовательно, выражение (6) может быть преобразовано к виду:

где $I_{ef}$ называют эффективным значением силы тока.

Аналогично записывают выражения для эффективных (действующих) значений напряжений:

Применение действующих значений тока и напряжения

Когда в электротехнике говорят о силе переменного тока и напряжении, то имеют в виду их эффективные значения. В частности, вольтметры и амперметры градуируют обычно на эффективные значения. Следовательно, максимальное значение напряжения в цепи переменного тока примерно в 1,5 раза больше того, что показывает вольтметр. Этот факт следует учесть при расчете изоляторов, исследовании проблем безопасности.

Эффективные значения используют для характеристики формы сигнала переменного тока (напряжения). Так, вводят коэффициент амплитуды ($k_a$). равный:

и коэффициент формы ($k_f$):

где $I_{sr\ v}=\frac{2}{\pi }\cdot I_m$ –средневыпрямленное значение силы тока.

Для синусоидального тока $k_a=\sqrt{2},\ k_f=\frac{\pi }{2\sqrt{2}}=1,11.$

Пример 1

Задание: Напряжение, которое показал вольтметр равно $U=220 В$. Какова амплитуда напряжения?

Решение:

Как было сказано, вольтметры и амперметры обычно градуируют на действующие значения напряжения (силу тока), следовательно, прибор показывает в наших обозначениях $U_{ef}=220\ В.$ В соответствии с известным соотношением:

найдем амплитудное значение напряжения, как:

Вычислим:

Ответ: $U_m\approx 310,2\ В.$

Пример 2

Задание: Как связана мощность переменного тока на сопротивлении $R$ и эффективные значения тока и напряжения?

Решение:

Среднее значение мощности переменного тока в цепи равно

\[\left\langle P\right\rangle =\frac{A_T}{T}=\frac{U_mI_mcos\varphi }{2}\left(2.1\right),\]

где $cos\varphi $- коэффициент мощности, который показывает эффективность передачи мощности от источника тока к потребителю. С другой стороны средние мощности тока на отдельных элементах цепи $\left\langle P_{tC}\right\rangle =0,\left\langle P_{tL}\right\rangle =0,\left\langle P_{tR}\right\rangle =\frac{1}{2}{I^2}_mR,$ а результирующая мощность может быть найдена как сумма мощностей:

\[\left\langle P\right\rangle =\left\langle P_{tC}\right\rangle +\left\langle P_{tL}\right\rangle +\left\langle P_{tR}\right\rangle \left(2. 2}_mR=\frac{U_mI_mcos \varphi}{2}\left(2.3\right),\]

где $I_m\ $- амплитуда силы тока, $U_m$ — амплитуда внешнего напряжения, $\varphi$ — разность фаз между силой тока и напряжением.

У постоянного тока мгновенная мощность совпадает со средней. Для $I_{ef}$=const можно положить $cos\varphi =1,\ $значит формулу (2.3) можно записать как:

если вместо амплитудных значений ($U_m\ и\ I_m$) использовать их эффективные (действующие) значения:

Следовательно, мощность тока можно записать как:

где $cos \varphi$ — коэффициент мощности. В технике этот коэффициент делают как можно большим. При малом $cos\varphi $ для того, чтобы в цепи выделялась необходимая мощность нужно пропускать большой ток, что ведет к росту потерь в подводящих проводах.

Такую же мощность (как в выражении (2.3)) развивает постоянный ток, сила которого представлена в формуле (2.5).

Ответ: $P_{tR}=U_{ef}I_{ef}cos\varphi .$

Переменный ток долгое время не находил практического применения.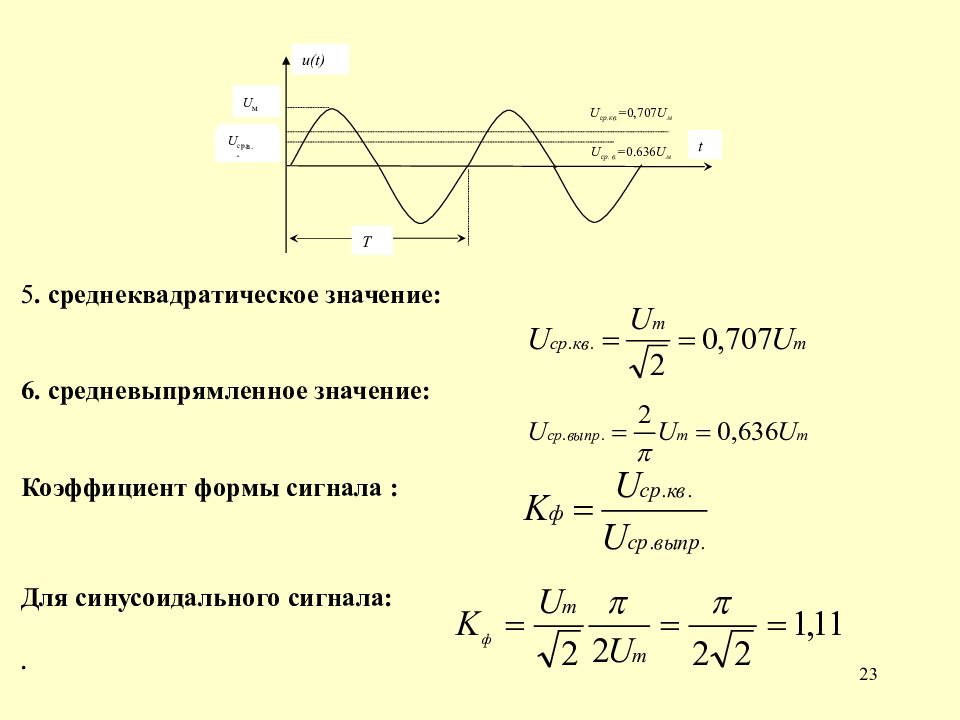 Это было связано с тем, что первые генераторы электрической энергии вырабатывали постоянный ток, который вполне удовлетворял технологическим процессам электрохимии, а двигатели постоянного тока обладают хорошими регулировочными характеристиками. Однако по мере развития производства постоянный ток все менее стал удовлетворять возрастающим требованиям экономичного электроснабжения. Переменный ток дал возможность эффективного дробления электрической энергии и изменения величины напряжения с помощью трансформаторов. Появилась возможность производства электроэнергии на крупных электростанциях с последующим экономичным ее распределением потребителям, увеличился радиус электроснабжения.

В настоящее время центральное производство и распределение электрической энергии осуществляется в основном на переменном токе. Цепи с изменяющимися – переменными – токами по сравнению с цепями постоянного тока имеют ряд особенностей. Переменные токи и напряжения вызывают переменные электрические и магнитные поля. В результате изменения этих полей в цепях возникают явления самоиндукции и взаимной индукции, которые оказывают самое существенное влияние на процессы, протекающие в цепях, усложняя их анализ.

Переменным током (напряжением, ЭДС и т.д.)называется ток (напряжение, ЭДС и т.д.), изменяющийся во времени. Токи, значения которых повторяются через равные промежутки времени в одной и той же последовательности, называются периодическими, а наименьший промежуток времени, через который эти повторения наблюдаются, – периодом Т. Для периодического тока имеем

Диапазон частот, применяемых в технике: от сверхнизких частот (0.01¸10 Гц – в системах автоматического регулирования, в аналоговой вычислительной технике) – до сверхвысоких (3000 ¸ 300000 МГц – миллиметровые волны: радиолокация, радиоастрономия). В РФ промышленная частота f = 50Гц .

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Наибольшее мгновенное значение переменной величины за период называется амплитудой (ее принято обозначать заглавной буквой с индексом m ).

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Значение периодического тока, равное такому значению постоянного тока, который за время одного периода произведет тот же самый тепловой или электродинамический эффект, что и периодический ток, называют действующим значением периодического тока:

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Из всех возможных форм периодических токов наибольшее распространение получил синусоидальный ток. По сравнению с другими видами тока синусоидальный ток имеет то преимущество, что позволяет в общем случае наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Только при использовании синусоидального тока удается сохранить неизменными формы кривых напряжений и токов на всех участках сложной линейной цепи.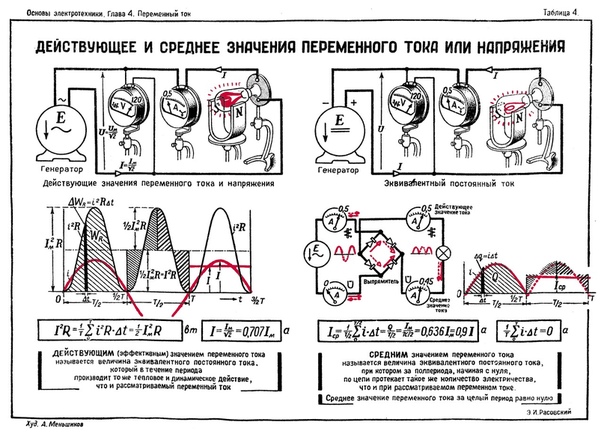 Теория синусоидального тока является ключом к пониманию теории других цепей.

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Синусоидальные токи и напряжения можно изобразить графически, записать при помощи уравнений с тригонометрическими функциями, представить в виде векторов на декартовой плоскости или комплексными числами.

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций иназываютсяфазами синусоид, а значение фазы в начальный момент времени (t =0): и –начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называютугловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть, гдеf– частота.

При совместном рассмотрении двух синусоидальных величин одной частоты разность их фазовых углов, равную разности начальных фаз, называют углом сдвига фаз .

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

На декартовой плоскости из начала координат проводят векторы, равные по модулю амплитудным значениям синусоидальных величин, и вращают эти векторы против часовой стрелки (в ТОЭ данное направление принято за положительное ) с угловой частотой, равной w . Фазовый угол при вращении отсчитывается от положительной полуоси абсцисс. Проекции вращающихся векторов на ось ординат равны мгновенным значениям ЭДС е 1 и е 2 (рис. 3). Совокупность векторов, изображающих синусоидально изменяющиеся ЭДС, напряжения и токи, называют векторными диаграммами. При построении векторных диаграмм векторы удобно располагать для начального момента времени (t =0), что вытекает из равенства угловых частот синусоидальных величин и эквивалентно тому, что система декартовых координат сама вращается против часовой стрелки со скоростью w . Таким образом, в этой системе координат векторы неподвижны (рис. 4). Векторные диаграммы нашли широкое применение при анализе цепей синусоидального тока. Их применение делает расчет цепи более наглядным и простым. Это упрощение заключается в том, что сложение и вычитание мгновенных значений величин можно заменить сложением и вычитанием соответствующих векторов.

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токовидвух ветвей:

Силу переменного тока (напряжения) можно охарактеризовать при помощи амплитуды. Однако амплитудное значение тока непросто измерить экспериментально. Силу переменного тока удобно связать с каким-либо действием, производимым током, не зависящим от его направления. Таковым является, например, тепловое действие тока. Поворот стрелки амперметра, измеряющего переменный ток, вызывается удлинением нити, которая нагревается при прохождении по ней тока.

Действующим илиэффективным значением переменного тока (напряжения) называется такое значение постоянного тока, при котором на активном сопротивлении выделяется за период такое же количество теплоты, как и при переменном токе.

Свяжем эффективное значение тока с его амплитудным значением. Для этого рассчитаем количество теплоты, выделяемое на активном сопротивлении переменным током за время, равное периоду колебаний. Напомним, что по закону Джоуля-Ленца количество теплоты, выделяющееся на участке цепи cсопротивлениемприпостоянном токеза время, определяется по формуле
. Переменный ток можно считать постоянным только в течение очень малых промежутков времени
. Поделим период колебанийна очень большое число малых промежутков времени
. Количество теплоты
, выделяемое на сопротивленииза время
:
. Общее количество теплоты, выделяемое за период, найдется суммированием теплот, выделяемых за отдельные малые промежутки времени, или, другими словами, интегрированием:

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

Если бы по цепи шёл некоторый постоянный ток , то за время, равное, выделилось бы тепло
. По определению постоянный ток, оказывающий такое же тепловое действие, что и переменный, будет равен эффективному значению переменного тока
. Находим эффективное значение силы тока, приравнивая теплоты, выделяемые за период, в случаях постоянного и переменного токов

(4.28)

Очевидно, точно такое же соотношение связывает эффективное и амплитудное значения напряжения в цепи с синусоидальным переменным током:

(4.29)

Например, стандартное напряжение в сети 220 В – это эффективное напряжение. По формуле (4.29) легко посчитать, что амплитудное значение напряжения в этом случае будет равно 311 В.

4.4.5. Мощность в цепи переменного тока

Пусть на некотором участке цепи с переменным током сдвиг фаз между током и напряжением равен , т.е. сила тока и напряжение изменяются по законам:

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

Мощность изменяется со временем. Поэтому можно говорить лишь о ее среднем значении. Определим среднюю мощность, выделяемую в течение достаточно длительного промежутка времени (во много раз превосходящего период колебаний):

С использованием известной тригонометрической формулы

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

За длительное время значение косинуса много раз успевает измениться, принимая как отрицательные, так и положительные значения в пределах от (1) до 1. Понятно, что среднее во времени значение косинуса равно нулю

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Мощность, выделяемая на участке цепи с переменным током, зависит от эффективных значений тока и напряжения и сдвига фаз между током и напряжением . Например, если участок цепи состоит из одного только активного сопротивления, то
и
. Если участок цепи содержит только индуктивность или только ёмкость, то
и
.

Объяснить среднее нулевое значение мощности, выделяемой на индуктивности и ёмкости можно следующим образом. Индуктивность и ёмкость лишь заимствуют энергию у генератора, а затем возвращают её обратно. Конденсатор заряжается, а затем разряжается. Сила тока в катушке увеличивается, затем снова спадает до нуля и т. д. Именно по той причине, что на индуктивном и ёмкостном сопротивлениях средняя расходуемая генератором энергия равна нулю, их назвали реактивными. На активном же сопротивлении средняя мощность отлична от нуля. Другими словами провод с сопротивлением при протекании по нему тока нагревается. И энергия, выделяемая в виде тепла, назад в генератор уже не возвращается.

Если участок цепи содержит несколько элементов, то сдвига фаз может быть иным. Например, в случае участка цепи, изображенного на рис. 4.5, сдвиг фаз между током и напряжением определяется по формуле (4.27).

Пример 4.7. К генератору переменного синусоидального тока подключён резистор с сопротивлением. Во сколько раз изменится средняя мощность, расходуемая генератором, если к резистору подключить катушку с индуктивным сопротивлением
а) последовательно, б) параллельно (рис. 4.10)? Активным сопротивлением катушки пренебречь.

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

Рассмотрим цепь на рис. 4.10, а. В примере 4.6 было определено амплитудное значение силы тока генератора:
. Из векторной диаграммы на рис. 4.11,а определяем сдвиг фаз между током и напряжением генератора

В результате средняя расходуемая генератором мощность

Ответ: при последовательном включении в цепь индуктивности средняя мощность, расходуемая генератором, уменьшится в 2 раза.

Рассмотрим цепь на рис. 4.10,б. В примере 4.6 было определено амплитудное значение силы тока генератора
. Из векторной диаграммы на рис. 4.11,б определяем сдвиг фаз между током и напряжением генератора

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Действующие значения э. д. с., напряжения и силы переменного тока

При синусоидальном переменном токе средние значения напряжения и тока за период равны нулю и не могут служить его характеристиками. Однако среднее значение квадрата силы тока за период отлично от нуля. Следовательно, при включении в цепь переменного тока измерительного прибора, отклонение стрелки которого пропорционально квадрату силы тока, стрелка отклонится и установится на определенном делении шкалы. Каков смысл этого показания?

Вспомним, что количество выделенного в проводнике тепла изменяется пропорционально квадрату силы тока. Представим себе, что в цепь переменного тока включен тепловой амперметр, действие которого основано на выделении тепла электрическим током. Поскольку шкала такого амперметра градуируется на амперы для постоянного тока, можно заключить, что переменный ток по своему тепловому эффекту эквивалентен постоянному току, силу которого указывает на шкале прибора стрелка. Это позволяет ввести понятие эффективного значения силы переменного тока. Эффективным (или действующим) значением силы переменного тока называют силу такого постоянного тока I, который за один период переменного тока выделяет столько же тепла, сколько последний за то же время.

Все амперметры, предназначенные для переменного тока, показывают эффективное значение силы тока. В курсе электротехники доказывается, что оно в √2 раз меньше амплитудного значения силы тока Iм, т. е.

Iм = Iм/√2 ≈ 0,707Iм. (26.5)

Так как деления на шкале вольтметра соответствуют произведению Iвrв, где при переменном токе Iв — эффективное значение тока, протекающего через вольтметр, а rв — сопротивление вольтметра, то U=Iвrв называют эффективным напряжением переменного тока, которое в √2 раз меньше Uм, т. е.

U = Uм/√2 ≈ 0,7O7UM. (26.6)

Аналогично эффективное значение э. д. с. переменного тока Ɛ в √2 раз меньше его амплитудного значения Ɛм:

Ɛ = Ɛм/√2 ≈ 0,707Ɛм. (26.7)

Все вольтметры, предназначенные для переменного тока, показывают эффективные значения э. д. с. и напряжения.

Эффективное напряжение переменного тока. Действующие значения силы тока и напряжения

Переменный синусоидальный ток в течение периода имеет различные мгновенные значения. Естественно поставить вопрос, какое же значение тока будет измеряться амперметром, включенным в цепь? Действия тока не определяются ни амплитудным, ни мгновенным значениями. Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность P постоянного тока I , проходящего через сопротивление r , будет

P = I 2 × r .

Мощность переменного тока выразится как средний эффект мгновенной мощности i 2 × r за целый период или среднее значение от (I m × sin ωt ) 2 × r за то же время.

Пусть среднее значение i 2 за период будет M . Приравнивая мощность постоянного тока и мощность при переменном токе, имеем:

I 2 × r = M × r ,

Величина I называется действующим значением переменного тока.

Среднее значение i 2 при переменном синусоидальном токе определим следующим образом. Построим синусоидальную кривую изменения тока (рисунок 1).

Рисунок 1. Действующее значение синусоидального тока

Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости i 2 от времени. Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i ) во второй половине периода, будучи возведены в квадрат, дают положительные величины. Построим прямоугольник с основанием T и площадью, равной площади, ограниченной кривой i 2 и горизонтальной осью. Высота прямоугольника M будет соответствовать среднему значению i 2 за период. Это значение за период, вычисленное при помощи высшей математики, будет равно .

Следовательно,

Так как действующее значение переменного тока I равно , то окончательно формула примет вид

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и E имеет вид:

Действующие значения переменных величин, то есть действующее значение напряжения, тока и электродвижущей силы, обозначаются прописными буквами без индексов (U , I , E ).

На основании изложенного выше, можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующее значение тока и напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в раз. От этого расположение векторов на диаграмме не изменится.

В механической системе вынужденные колебания возникают при действии на нее внешней периодической силы. Аналогично этому вынужденные электромагнитные колебания в электрической цепи происходят под действием внешней периодически изменяющейся ЭДС или внешнего изменяющегося напряжения.

Вынужденные электромагнитные колебания в электрической цепи представляют собой переменный электрический ток .

Переменный электрический ток – это ток, сила и направление которого периодически меняются.

Мы в дальнейшем будем изучать вынужденные электрические колебания, происходящие в цепях под действием напряжения, гармонически меняющегося с частотой ω по синусоидальному или косинусоидальному закону:

$~u = U_m \cdot \sin \omega t$ или $~u = U_m \cdot \cos \omega t$ ,

где u – мгновенное значение напряжения, U m – амплитуда напряжения, ω – циклическая частота колебаний. Если напряжение меняется с частотой ω, то и сила тока в цепи будет меняться с той же частотой, но колебания силы тока не обязательно должны совпадать по фазе с колебаниями напряжения. Поэтому в общем случае

$~i = I_m \cdot \sin (\omega t + \varphi_c)$ ,

где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Переменный ток обеспечивает работу электрических двигателей в станках на заводах и фабриках, приводит в действие осветительные приборы в наших квартирах и на улице, холодильники и пылесосы, отопительные приборы и т.п. Частота колебаний напряжения в сети равна 50 Гц. Такую же частоту колебаний имеет и сила переменного тока. Это означает, что на протяжении 1 с ток 50 раз поменяет свое направление. Частота 50 Гц принята для промышленного тока во многих странах мира. В США частота промышленного тока 60 Гц.

Генератор переменного тока

Основная часть электроэнергии в мире в настоящее время вырабатывается генераторами переменного тока, создающими гармонические колебания.

Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

$e={\rm E}_{m} \cdot \sin \omega \cdot t,$

где ${\rm E}_{m} =B\cdot S\cdot \omega$ – амплитудное (максимальное) значение ЭДС. При подключении к выводам рамки нагрузки сопротивлением R , через нее будет проходить переменный ток. По закону Ома для участка цепи сила тока в нагрузке

$i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,$

где $I_{m} = \dfrac{B\cdot S\cdot \omega }{R}$ – амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

индуктор – электромагнит или постоянный магнит, который создает магнитное поле;
якорь – обмотка, в которой индуцируется переменная ЭДС;
коллектор со щетками – устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

Неподвижная часть генератора называется статором , а подвижная – ротором . В зависимости от конструкции генератора его якорь может быть как ротором, так и статором. При получении переменных токов большой мощности якорь обычно делают неподвижным, чтобы упростить схему передачи тока в промышленную сеть.

На современных гидроэлектростанциях вода вращает вал электрогенератора с частотой 1-2 оборота в секунду. Таким образом, если бы якорь генератора имел только одну рамку (обмотку), то получался бы переменный ток частотой 1-2 Гц. Поэтому, для получения переменного тока промышленной частоты 50 Гц якорь должен содержать несколько обмоток, позволяющих увеличить частоту вырабатываемого тока. Для паровых турбин, ротор которых вращается очень быстро, используют якорь с одной обмоткой. В этом случае частота вращения ротора совпадает с частотой переменного тока, т.е. ротор должен делать 50 об/с.

Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.

Из истории . Первоначально Фарадей обнаружил лишь едва заметный ток в катушке при движении вблизи нее магнита. «Какая от этого польза?» – спросили его. Фарадей ответил: «Какая может быть польза от новорожденного?» Прошло немногим более половины столетия и, как сказал американский физик Р. Фейнман, «бесполезный новорожденный превратился в чудо-богатыря и изменил облик Земли так, как его гордый отец не мог себе и представить».

*Принцип действия

Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.

Пусть проводящая рамка площадью S вращается с угловой скоростью ω вокруг оси, расположенной в ее плоскости перпендикулярно однородному магнитному полю индукцией $\vec{B}$ (см. рис. 1).

При равномерном вращении рамки угол α между направлениями вектора индукции магнитного поля $\vec{B}$ и нормали к плоскости рамки $\vec{n}$ меняется со временем по линейному закону. Если в момент времени t = 0 угол α 0 = 0 (см. рис. 1), то

$\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,$

где ω – угловая скорость вращения рамки, ν – частота ее вращения.

В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом

$\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.$

Тогда согласно закону Фарадея индуцируется ЭДС индукции

$e=-\Phi “(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.$

Подчеркнем, что ток в цепи проходит в одном направлении в течение полуоборота рамки, а затем меняет направление на противоположное, которое также остается неизменным в течение следующего полуоборота.

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

$u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)$

Согласно закону Ома, сила тока в участке цепи, содержащей только резистор сопротивлением R , подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

$i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)$

где $I_m = \dfrac{U_{m}}{R}.$ Как видим, сила тока в такой цепи также меняется с течением времени по синусоидальному закону. Величины U m , I m называются амплитудными значениями напряжения и силы тока . Зависящие от времени значения напряжения u и силы тока i называют мгновенными .

Кроме этих величин используются еще одна характеристика переменного тока: действующие (эффективные) значения силы тока и напряжения .

Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.{2}dt}}.}

Для синусоидального тока:

I = 1 2 ⋅ I m ≈ 0,707 ⋅ I m , {\displaystyle I={\frac {1}{\sqrt {2}}}\cdot I_{m}\approx 0{,}707\cdot I_{m},}

I m {\displaystyle I_{m}} – амплитудное значение тока.

Для тока треугольной и пилообразной формы:

I = 1 3 ⋅ I m ≈ 0,577 ⋅ I m . {\displaystyle I={\frac {1}{\sqrt {3}}}\cdot I_{m}\approx 0{,}577\cdot I_{m}.}

Аналогичным образом определяются действующие значения ЭДС и напряжения.

Дополнительные сведения

В англоязычной технической литературе для обозначения действующего значения употребляется термин effective value – эффективное значение. Также применяется аббревиатура RMS (rms) – root mean square – среднеквадратичное (значение).

В электротехнике приборы электромагнитной, электродинамической и тепловой систем калибруются на действующее значение.

Источники

«Справочник по физике», Яворский Б. М., Детлаф А. А., изд. «Наука», 1979 г.1
Курс физики. А. А. Детлаф, Б. М. Яворский М.: Высш. шк., 1989. § 28.3, п.5
«Теоретические основы электротехники», Л. А. Бессонов: Высш. шк., 1996. § 7.8 – § 7.10

Ссылки

Действующие значения тока и напряжения
Среднеквадратичное значение

Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока

Мгновенное и максимальное значения. Величину переменной электродвижущей силы, силы тока, напряжения и мощности в любой момент времени называют мгновенными значениями этих величин и обозначают соответственно строчными буквами (e, i, u, p ).
Максимальным значением (амплитудой) переменной э. д. с. (или напряжения или тока) называется та наибольшая величина, которой она достигает за один период. Максимальное значение электродвижущей силы обозначается Е m , напряжения – U m , тока – I m .

Действующим (или эффективным) значением переменного тока называется такая сила постоянного тока, которая, протекая через равное сопротивление и за одно и то же время, что и переменный ток, выделяет одинаковое количество тепла.

Для синусоидального переменного тока действующее значение меньше максимального в 1,41 раз, т. е. в раз.

Аналогично действующие значения переменной электродвижущей силы и напряжения меньше их максимальных значений тоже в 1,41 раза.

По величине измеренных действующих значений силы переменного тока, напряжения или электродвижущей силы можно вычислить их максимальные значения:

E m = E · 1,41; U m = U · 1,41; I m = I · 1,41;

Среднее значение = отношению количества эл энергии прошедшего через сечение проводника за половину периода к величине этого полупериода.

Под средним значением понимают среднеарифметическое ее значение за половину периода.

/ Среднее и действующие значения синусоидальных токов и напряжений

Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за полпериода. Среднее значение тока

т. е. среднее значение синусоидального тока составляет от амплитудного. Аналогично,

Широко применяют понятие действующего значения синусоидально изменяющейся величины (его называют также эффективным или среднеквадратичным). Действующее значение тока

Следовательно, действующее значение синусоидального тока равно 0,707 от амплитудного. Аналогично,

Можно сопоставить тепловое действие синусоидального тока с тепловым действием постоянного тока, текущего то же время по тому же сопротивлению.

Количество теплоты, выделенное за один период синусоидальным током,

Выделенная за то же время постоянным током теплота равна Приравняем их:

Таким образом, действующее значение синусоидального тока численно равно значению такого постоянного тока, который за время, равное периоду синусоидального тока, выделяет такое же количество теплоты, что и синусоидальный ток.

Для установления эквивалентности переменного тока в отношении энергии и мощности, общности методов расчета, а также сокращения вычислительной работы изменяющиеся непрерывно во времени токи. ЭДС и напряжения заменяют эквивалентными неизменными во времени величинами. Действующим или эквивалентным значением называется такой неизменный во времени ток, при котором выделяется в резистивном элементе с активным сопротивлением r за период то же количество энергии, что и при действительном изменяющемся синусоидально токе.

Энергия за период, выделяющаяся в резистивном элементе при синусоидальном токе,


		i 2r dt =		I m 2 sin2 ωt r dt. .

При неизменном во времени токе энергия

W = I 2rT

Приравняв правые части

I m

0,707I m .

Таким образом, действующее значение тока меньше амплитудного в √2 раз.

Аналогично определяют действующие значения ЭДС и напряжения:

Е = E m / √2, U = U m / √2.

Действующему значению тока пропорциональна сила, действующая на ротор двигателя переменного тока, подвижную часть измерительного прибора и т. д. Когда говорят о значениях напряжения, ЭДС и тока в цепях переменного тока, имеют в виду их действующие значения. Шкалы измерительных приборов переменного тока отградуированы соответственно в действующих значениях тока и напряжения. Например, если прибор показывает 10 А, то это значит, что амплитуда тока

I m = √2I = 1,41 10 = 14,1 A,

и мгновенное значение тока

i = I m sin (ωt + ψ) = 14,1 sin (ωt + ψ).

При анализе и расчет выпрямительных устройств пользуются средними значениями тока, ЭДС и напряжения, под которыми понимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, как известно, равно нулю):

	T 2
Е ср =		Е т sin ωt dt =	sin ωt d ωt =	\|cos ωt \| π 0 =	0,637Е т .

Аналогично можно найти средние значения тока и напряжения:

I ср = 2I т /π; U ср = 2U т /π.

Отношение действующего значения к среднему значению какой-либо периодически изменяющейся величины называется коэффициентом формы кривой. Для синусоидального тока

При расчетах цепей переменного тока, а также при электрических измерениях неудобно пользоваться мгновенными или амплитудными значениями токов и напряжений, а их средние значения за период равны нулю. Кроме того, об электрическом эффекте периодически изменяющегося тока (о количестве выделенной теплоты, о совершенной работе и т. д.) нельзя судить по амплитуде этого тока.

Наиболее удобным оказалось введение понятий так называемых действующих значений тока и напряжения . В основу этих понятий положено тепловое (или механическое) действие тока, не зависящее от его направления.

Действующее значение переменного тока – это значение постоянного тока, при котором за период переменного тока в проводнике выделяется столько же теплоты, сколько и при переменном токе.

Для оценки действия, производимого переменным током, мы сравним его действия с тепловым эффектом постоянного тока.

Мощность Р постоянного тока I, проходящего через сопротивление r, будет Р = Р2r.

Мощность переменного тока выразится как средний эффект мгновенной мощности I2r за целый период или среднее значение от (Im х sinωt)2 х rза то же время.

Пусть среднее значение t2 за период будет М. Приравнивая мощность постоянного тока и мощность при переменном токе, имеем: I2r = Mr, откуда I = √M,

Величина I называется действующим значением переменного тока.

Среднее значение i2 при переменном токе определим следующим образом.

Построим синусоидальную кривую изменения тока. Возведя в квадрат каждое мгновенное значение тока, получим кривую зависимости Р от времени.

Действующее значение переменного тока

Обе половины этой кривой лежат выше горизонтальной оси, так как отрицательные значения тока (-i) во второй половине периода, будучи возведены в квадрат, дают положительные величины.

Построим прямоугольник с основанием Т и площадью, равной площади, ограниченной кривой i2 и горизонтальной осью. Высота прямоугольника М будет соответствовать среднему значению Р за период. Это значение за период, вычисленное при помощи высшей математики, будет равно1/2I2m. Следовательно, М = 1/2I2m

Так как действующее значение I переменного тока равно I = √M, то окончательно I = Im / √2

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и Е имеет вид:

U = Um / √2,E= Em / √2

Действующие значения переменных величин обозначаются прописными буквами без индексов (I, U, Е).

На основании сказанного выше можно сказать, что действующее значение переменного тока равно такому постоянному току, который, проходя через то же сопротивление, что и переменный ток, за то же время выделяет такое же количество энергии.

Электроизмерительные приборы (амперметры, вольтметры), включенные в цепь переменного тока, показывают действующие значения тока или напряжения.

При построении векторных диаграмм удобнее откладывать не амплитудные, а действующие значения векторов. Для этого длины векторов уменьшают в √2 раз. От этого расположение векторов на диаграмме не изменяется.

Список параметров напряжения и силы электрического тока

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Мгновенное значение

Мгновенное значение – это значение сигнала в определённый момент времени, функцией которого является (u (t) , i (t) {\displaystyle u(t)~,\quad i(t)}).{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I {\displaystyle I} и U {\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют ввиду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) – постоянная составляющая напряжения или силы тока

U = 1 T ∫ 0 T u (t) d t , I = 1 T ∫ 0 T i (t) d t {\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения).{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

Коэффициент формы кривой переменного напряжения (тока) – величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π / 2 2 ≈ 1.11 {\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11} .

Коэффициент амплитуды кривой переменного напряжения (тока) – величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2 {\displaystyle {\sqrt {2}}} .

Параметры постоянного тока

Размах пульсации напряжения (тока) – величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

Коэффициент пульсации напряжения (тока) – величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
- Коэффициент пульсации напряжения (тока) по действующему значению – величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
- Коэффициент пульсации напряжения (тока) пo среднему значению – величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

Справочник по радиоэлектронным устройствам : В 2-х т.; Под ред. Д. П. Линде – М.: Энергия, 1978
Шульц Ю. Электроизмерительная техника: 1000 понятий для практиков: Справочник: Пер. с нем. М.:Энергоатомиздат, 1989

Нормативно-техническая документация

ГОСТ 16465-70 Сигналы радиотехнические измерительные. Термины и определения
ГОСТ 23875-88 Качество электрической энергии. Термины и определения
ГОСТ 13109-97 Электрическая энергия. Совместимость технических средств. Нормы качества электрической энергии в системах электроснабжения общего назначения

Ссылки

Электрические цепи постоянного тока
Переменный ток. Изображение синусоидальных переменных
Амплитудное, среднее, эффективное
Периодические несинусоидальные ЭДС, токи и напряжения в электрических цепях
Системы тока и номинальные напряжения электроустановок
Электричество
Проблемы высших гармоник в современных системах электропитания

Какой физический смысл имеет действующее значение напряжения и тока

Александр титов

Действующее значение силы ПЕРЕМЕННОГО тока – это такое значение величины ПОСТОЯННОГО тока, действие которого произведёт ту же самую работу (или тепловой эффект) , что и действие переменного тока за время одного периода его действия.2 = Im/2, откуда I = Im / корень из 2. Это и есть действующее значение тока.

То же самое с действующим значением напряжения и ЭДС.

Vitas latish

можно грубо сказать
– напряжение – потенциальная энергия…. расческа- волосы…. напряжение = свечение, искорки, подъем волос… .
– ток это работа, действие, сила.. . тепло, горение, движение выплеск кенетической энергии

Физический смысл данных понятий примерно таков же, как физический смысл средней скорости или других величин, усредненных по времени. В различные моменты времени сила переменного тока и его напряжение принимают разные значения, поэтому говорить о силе переменного тока вообще можно лишь условно.

Вместе с тем совершенно очевидно, что различные токи имеют различные энергетические характеристики – они производят разную работу за один и тот же промежуток времени. Произведенная током работа принята за основу при определении действующего значения силы тока. Задаются определенным промежутком времени и рассчитывают работу, совершенную переменным током за этот промежуток времени. Затем, зная эту работу, производят обратное вычисление: узнают силу постоянного тока, который произвел бы аналогичную работу за тот же промежуток времени. То есть производят усреднение по мощности. Вычисленная сила гипотетически протекающего через тот же проводник постоянного тока, производящего ту же самую работу и есть – действующее значение исходного переменного тока. Аналогично поступают и с напряжением. Данный расчет сводится к определению величины такого интеграла:

Откуда берется данная формула? Из хорошо известной формулы для мощности тока, выражаемой через квадрат его силы.

Действующие значения периодических и синусоидальных токов

Вычислять действующее значение для произвольных токов – занятие малопродуктивное. Зато для периодического сигнала данный параметр может оказаться весьма полезным. Известно, что любой периодический сигнал может быть разложен в спектр. То есть, представлен как конечная или бесконечная сумма синусоидальных сигналов. Поэтому для определения величины действующего значения такого периодического тока нам нужно знать, как вычислять действующее значение простого синусоидального тока. В итоге, сложив действующие значения нескольких первых гармоник с максимальной амплитудой, мы получим приближенное значение действующего значения тока для произвольного периодического сигнала. Подставляя в вышеприведенную формулу выражение для гармонического колебания, получим такую приближенную формулу.

Сила тока в цепи изменяется по синусоидальному закону

Опуская вычисления, связанные с интегрированием, запишем окончательный результат

(4.28)

(4.29)

4.4.5. Мощность в цепи переменного тока

,
.

Тогда мгновенное значение мощности, выделяемой на участке цепи,

С использованием известной тригонометрической формулы

Величину
усреднять не нужно, так как она не зависит от времени, следовательно:

, поэтому
(4.30)

Выражая амплитуды тока и напряжения через их эффективные значения по формулам (4.28) и (4.29), получим

. (4.31)

Решение. Когда к генератору подключено одно только активное сопротивление, расходуемая мощность

(см. формулу (4.30)).

В результате средняя расходуемая генератором мощность

Тогда средняя мощность, расходуемая генератором

Ответ: при параллельном включении индуктивности средняя мощность, расходуемая генератором, не изменяется.

Эффективное (действующее значение переменного тока

Действующее или эффективное значение переменного тока равно такому значению постоянного тока, который за тот же отрезок времени, равный одному или целому числу периодов переменного тока, выделит в некотором сопротивлении такое же количество тепла, как и данный переменный ток [c.519]

Действующее, или эффективное, значение переменного тока равно значению такого постоянного тока, который, проходя через то же сопротивление, что и переменный ток, выделяет за одно и то же время такое же количество тепла. Действующее, или эффективное, значение тока и э. д. с. / и В любой формы [c.498]

Действующим (или эффективным) значением переменного тока (/) называют такой постоянный ток, который на [c.145]

Эффективное (действующее) значение переменного тока 145 [c.208]

Исследуемые металлические образцы, помещенные в вакуум или в среду защитных газов, нагреваются также за счет теплового действия электрического тока, подводимого к ним непосредственно. По характеру передачи электрического тока к образцам можно выделить два основных способа контактный и бесконтактный. При контактном нагреве образец непосредственно присоединяют к источнику переменного тока промышленной частоты (50 Гц) низкого напряжения. Использование постоянного тока нерационально, поскольку вследствие электролиза может происходить перенос содержащихся в образце примесей, в частности углерода, что изменяет химический состав образца по его длине. Скорость контактного нагрева образца зависит от величины его электрического сопротивления и эффективного значения пропускаемого тока /дф, протекающего через образец. Количество выделяющегося в образце тепла может быть определено из уравнения Ленца—Джоуля [c.75]

Эффективное, или действующее, значение синусоидального переменного тока численно равно такому постоянному току, который за промежуток времени, ранный одному периоду, выделяет в сопротивлении такое же количество тепла, как и переменный ток [c.340]

Данные относительно напряжений для машин переменного тока относятся к действующим (эффективным) значениям напряжения. [c.380]

Эффективная нелинейность — изменение эффективной диэлектрической проницаемости бдф в зависимости от амплитуды напряженности переменного электрического поля Е . Эффективную проницаемость е ф, как и эффективную емкость конденсатора Сдф, определяют по действующему значению тока I (несинусоидального), протекающего через конденсатор при заданном действующем напряжении и с угловой частотой со [c.218]

Эффективное или действующее значение синусоидального переменного тока / = 0.707 [c.62]

Во всех случаях технологических расчетов ориентируются на действующее (эффективное) значение сварочного тока. Поэтому интегралы предыдущего параграфа упрощаются, так как вместо функциональной зависимости Р (t) можно оперировать с постоянной величиной эффективного тока. Эта величина весьма просто устанавливается при сварке переменным током длительностью не менее полупериода. Для некоторых особых форм кривых сварочного тока равенство действующих значений тока не обязательно обеспечивает одинаковую картину тепловыделения в контакте. Примером могут служить кривые рис. 48, а и б. Для таких кривых тока, а также для иных, еще более сложных, вполне рационально представлять изменение сварочного тока во времени в виде степенных функций. Обозначим пиковое (максимальное) значение тока через / , мгновенную величину через /j, i , координаты времени возрастания тока через ti и спада тока через /о. Тогда можно написать, например, для любой из кривых рнс. 48 [c.115]

Действующими (эффективными) значениями силы тока (/зфф), электродвижущей силы ( фф) и напряжения переменного тока ( / фф) называются значения этих величин для такого постоянного тока, который на том же актив- [c.311]

Электроконтактный нагрев. Нагрев деталей ДСМ может быть осуществлен также и за счет использования теплового действия электрического тока, пропускаемого по самим деталям. По способу подвода электрического тока к деталям могут быть выделены два основных способа нагрева — контактный и бесконтактный. При контактном нагреве образец непосредственно присоединяют к источнику постоянного или переменного тока. Скорость контактного нагрева образца зависит при этом от величины электросопротивления образца Яд и эффективного значения тока /дф, ср, протекающего по образцу. Количество “тепла (кал), выделяющегося при этом, может быть определено из уравнения Джоуля—Ленца [c.88]

V А). В соответствии с ГОСТ 8.417—81 вар и вольт-ампер не явл. более ед. СИ, но допускаются к применению в электротехнике наравне с ед. СИ. Ватт (вар) равен реактивной мощности электр. цепи с однофазным синусоидальным переменным током при sin = 1 и эффективнь х (действующих значениях напряжения 1 В и силы tok [c.243]

В случае переменного тока Э. н. обычно определяется действующим (эффективным) — среднеквадратичным за период — значением. Напряжение на зажимах источника перем. тока или катушки индуктивности измеряется работой электрич. поля по перемещению единичного положит, заряда вдоль пути, лежащего вне источника или катушки. Вихревое (непотенциальное) электрич. поле на этом пути практически отсутствует, и напряжение равно разности потенциалов. Э. н. обычно измеряют вольтметром. Единица Э. н. в системе СИ — вольт. г. Я. Мяпишев. [c.865]

Стационарные сильноточные П. у. В принципе коаксиальные П. у. можно сделать стационарными (работающими в непрерывном режиме), если поддерживать напряжение ц непрерывно подавать между электродами рабочее вещество. Для оптимизации процесса в случае работы на газе канал надо делать переменной ширины (рис. 4,а). Если анод сделать сплошным, то при пост, подаче рабочего вещества и непрерывном увеличении разрядного тока /р скорость истечения плазмы и кпд ускорителя сначала будут расти (уменьшается уд. вес затрат на ионизацию, нагрев плазмы и потери на стенки). Однако при нек-ром значении /р происходит вынос большой части разрядного тока за срез ускорителя, напряжение резко возрастает, падает кпд, в ускорителе возникают колебания. Наступает т. н. критич. режим. Его физ. причиной является в конечном счёте обеднение ионами прианодной области, к-рое происходит под действием объёмного электрич. поля. Такой критич. решим наиб, эффективно устраняют подачей части рабочего вещества через анод (переход в режи.м ионного токопереноса ), для чего используют не сплошной, а пористый или стержневой анод. Наиб, часто такая схема применяется в квази-стационарных П. у., работающих при мощностях Вт с длительностью импульса —1 мс. [c.611]

Что такое эффективное значение тока и напряжения. Эффективные значения тока и напряжения

Действующие значения тока, напряжения и э. д. с. обозначаются прописными буквами .

Количество тепла, выделенное переменным током в со противлении за бесконечно малый промежуток времени

а за период переменного тока Т

Сократив общий множитель , получим действующее значение тока

Рис. 5-8. График переменного тока и квадрата тока.

Если ток изменяется по закону синуса, т. е.

Аналогично для действующих значений синусоидальных напряжений и э. д. с. можно написать:

Мощность P постоянного тока I , проходящего через сопротивление r , будет

P = I 2 × r .

I 2 × r = M × r ,

Величина I называется действующим значением переменного тока.

Рисунок 1. Действующее значение синусоидального тока

Следовательно,

Так как действующее значение переменного тока I равно , то окончательно формула примет вид

Аналогично зависимость между действующим и амплитудным значениями для напряжения U и E имеет вид:

Переменный электрический ток – это ток, сила и направление которого периодически меняются.

$~u = U_m \cdot \sin \omega t$ или $~u = U_m \cdot \cos \omega t$ ,

$~i = I_m \cdot \sin (\omega t + \varphi_c)$ ,

где φ c – разность (сдвиг) фаз между колебаниями силы тока и напряжения.

Исходя из этого можно дать еще такое определение:

Переменный ток – это электрический ток, который изменяется с течением времени по гармоническому закону.

Генератор переменного тока

Генератором переменного тока называется электротехническое устройство, предназначенное для преобразования механической энергии в энергию переменного тока.

ЭДС индукции генератора изменяется по синусоидальному закону

$e={\rm E}_{m} \cdot \sin \omega \cdot t,$

$i=\dfrac{e}{R} =\dfrac{B \cdot S \cdot \omega }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,$

где $I_{m} = \dfrac{B\cdot S\cdot \omega }{R}$ – амплитудное значение силы тока.

Основными частями генератора являются (рис. 1):

индуктор – электромагнит или постоянный магнит, который создает магнитное поле;
якорь – обмотка, в которой индуцируется переменная ЭДС;
коллектор со щетками – устройство, посредством которого снимается с вращающихся частей или подается по ним ток.

Мощные генераторы вырабатывают напряжение 15-20 кВ и обладают КПД 97-98 %.

*Принцип действия

Принцип действия генератора переменного тока основан на явлении электромагнитной индукции.

$\alpha = \omega \cdot t = 2\pi \cdot \nu \cdot t,$

где ω – угловая скорость вращения рамки, ν – частота ее вращения.

В этом случае магнитный поток, пронизывающий рамку будет изменяться следующим образом

$\Phi \left(t\right)=B\cdot S\cdot \cos \alpha =B\cdot S\cdot \cos \omega \cdot t.$

Тогда согласно закону Фарадея индуцируется ЭДС индукции

$e=-\Phi “(t)=B\cdot S\cdot \omega \cdot \sin \omega \cdot t = {\rm E}_{m} \cdot \sin \omega \cdot t.$

Действующие значения силы тока и напряжения

Пусть источник тока создает переменное гармоническое напряжение

$u=U_{m} \cdot \sin \omega \cdot t.\;\;\;(1)$

$i = \dfrac{u}{R} =\dfrac{U_{m} }{R} \cdot \sin \omega \cdot t = I_{m} \cdot \sin \omega \cdot t,\;\;\; (2)$

Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой I .

Действующим (эффективным) значением напряжения переменного тока называется напряжение такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.

Обозначается буквой U .

Действующие (I, U ) и амплитудные (I m , U m ) значения связаны между собой следующими соотношениями:

$I = \dfrac{I_{m} }{\sqrt{2}}, \; \; \; U =\dfrac{U_{m} }{\sqrt{2}}.$

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

$P = U\cdot I = I^{2} \cdot R = \dfrac{U^{2}}{R}.$

Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R , выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе.

После подстановки значения тока i и последующих преобразований получим, что действующее значение переменного тока равно:

Аналогичные соотношения могут быть получены также для напряжения и ЭДС:

Большинство электроизмерительных приборов измеряют не мгновенные, а действующие значения токов и напряжений.

Учитывая, например, что действующее значение напряжения в нашей сети составляет 220В, можно определить амплитудное значение напряжения в сети: U m =U Ö2=311В. Соотношение между действующим и амплитудным значениями напряжений и токов важно учитывать, например, при проектировании устройств с применением полупроводниковых элементов.

Действующее значение переменного тока

Теория / ТОЭ / Лекция N 3. Представление синусоидальных величин с помощью векторов и комплексных чисел.

Мгновенное значение переменной величины есть функция времени. Ее принято обозначать строчной буквой:

i – мгновенное значение тока ;

u – мгновенное значение напряжения ;

е – мгновенное значение ЭДС ;

р – мгновенное значение мощности .

Амплитуда тока;

Амплитуда напряжения;

Амплитуда ЭДС.

Аналогично определяются действующие значения ЭДС и напряжения.

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Приведенным на рис. 1, 2 графикам двух синусоидальных ЭДС е 1 и е 2 соответствуют уравнения:

Значения аргументов синусоидальных функций и называются фазами синусоид, а значение фазы в начальный момент времени (t =0): и – начальной фазой ( ).

Величину , характеризующую скорость изменения фазового угла, называют угловой частотой. Так как фазовый угол синусоиды за время одного периода Т изменяется на рад., то угловая частота есть , где f– частота.

Для синусоидальных ЭДС е 1 и е 2 угол сдвига фаз:

Векторное изображение синусоидально изменяющихся величин

Пусть, например, в точке разветвления цепи (рис. 5) общий ток равен сумме токов и двух ветвей:

Каждый из этих токов синусоидален и может быть представлен уравнением

Результирующий ток также будет синусоидален:

Определение амплитуды и начальной фазы этого тока путем соответствующих тригонометрических преобразований получается довольно громоздким и мало наглядным, особенно, если суммируется большое число синусоидальных величин. Значительно проще это осуществляется с помощью векторной диаграммы. На рис. 6 изображены начальные положения векторов токов, проекции которых на ось ординат дают мгновенные значения токов дляt =0. При вращении этих векторов с одинаковой угловой скоростью w их взаимное расположение не меняется, и угол сдвига фаз между ними остается равным .

Так как алгебраическая сумма проекций векторов на ось ординат равна мгновенному значению общего тока, вектор общего тока равен геометрической сумме векторов токов:

Построение векторной диаграммы в масштабе позволяет определить значения и из диаграммы, после чего может быть записано решение для мгновенного значения путем формального учета угловой частоты: .

Действующее и среднее значения переменного тока и напряжения.

Среднее или среднеарифметическое значение Fcp произвольной функции времени f (t )за интервал времени Т определяется по формуле:

Численно среднее значение Fср равно высоте прямоугольника, равновеликого по площади фигуре, ограниченной кривой f (t ), осью t и пределами интегрирования 0 – Т (рис. 35).

Для синусоидальной функции среднее значение за полный период Т (или за целое число полных периодов) равно нулю, так как площади положительной и отрицательной полуволн этой функции равны. Для переменного синусоидального напряжения определяют среднее по модулю значение за полный период Т или среднее значение за половину периода (Т /2) между двумя нулевыми значениями (рис. 36) :

Ucp = Um∙ sinwt dt = 2R . Таким образом, количественные параметры электрической энергии на переменном токе (количество энергии, мощность) определяются действующими значениями напряжения U и тока I . По этой причине в электроэнергетике все теоретические расчеты и экспериментальные измерения принято выполнять для действующих значений токов и напряжений. В радиотехнике и в технике связи, наоборот, оперируют максимальными значениями этих функций.

Приведенные выше формулы для энергии и мощности переменного тока полностью совпадают с аналогичными формулами для постоянного тока. На этом основании можно утверждать, что энергетически постоянному току эквивалентно действующее значение переменного тока.

Что берется за действующее значение силы переменного тока и переменного напряжения

что берется за действующее значение силы переменного тока и переменного напряжения?

Боевое яйцо

Переменный ток, в широком смысле электрический ток, изменяющийся во времени. Обычно в технике под П. т. понимают периодический ток, в котором среднее значение за период силы тока и напряжения равно нулю.

Переменные токи и переменные напряжения постоянно изменяются по величине. В каждое другое мгновение у них другая величина. Возникает вопрос, как же их измерять? Для их измерения введено понятие действующее значение.

Действующим или эффективным значением переменного тока называют величину такого постоянного тока, который по своему тепловому действию равноценен данному переменному току.

Действующим или эффективным значением переменного напряжения называют величину такого постоянного напряжения, которое по своему тепловому действию равноценно данному переменному напряжению.

Все переменные токи и напряжения в технике измеряются в действующих значениях. Приборы измеряющие переменные величины показывают их действующее значение.

Вопрос: напряжение в электросети 220 В, что это значит?

Это значит, что источник постоянного напряжения с напряжением 220 В оказывает такое же тепловое действие как и электросеть.

Действующее значение тока или напряжения синусоидальной формы в 1,41 раз меньше амплитуды этого тока или напряжения.

Пример: Определить амплитуду напряжения электросети с напряжением 220 В.

Амплитуда равна 220 * 1,41=310,2 В.

>> Активное сопротивление. Действующие значения силы тока и напряжения

§ 32 АКТИВНОЕ СОПРОТИВЛЕНИЕ. ДЕЙСТВУЮЩИЕ ЗНАЧЕНИЯ СИЛЫ ТОКА И НАПРЯЖЕНИЯ

Мощность в цепи с резистором. В цепи переменного тока промышленной частоты (v = 50 Гц) сила тока и напряжение изменяются сравнительно быстро. Поэтому при прохождении тока по проводнику, например по нити электрической лампочки, количество выделенной энергии также будет быстро меняться со временем. Но этих быстрых изменений мы не замечаем.

Мощность в цепи постоянного тока на участке с сопротивлением R определяется формулой

P = I 2 R. (4.18)

На протяжении очень малого интервала времени переменный ток можно считать практически постоянным.

P = i 2 R. (4.19)

Найдем среднее значение мощности за период. Для этого сначала преобразуем формулу (4.19), подставляя в нее выражение (4.16) для силы тока и используя известное из математики соотношение

Средняя мощность равна, таким образом, первому члену в формуле (4.20):

Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты , что и при переменном токе за то же время.

Действующее значение переменного напряжения определяется аналогично действующему значению силы тока:

Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем

Это закон Ома для участка цепи переменного тока с резистором.

P = I 2 R = UI.

ПЕРЕМЕННЫЙ ТОК

ТЕОРИЯ: ПОНЕМНОГУ – ОБО ВСЕМ

1.3. Переменный ток.

Если заряды движутся периодически то в одном, то в другом направлении, говорят о переменном токе. Часто ток изменяется во времени по простейшему, гармоническому или синусоидальному закону (рис. 3). Проходя через сопротивление, переменный ток, в соответствии с законом Ома, создаст переменное напряжение точно такой же формы. Как его измерить — оно же непрерывно изменяется? Различают амплитудное значение (максимальный размах) переменного напряжения или тока и эффективное значение, численно равное постоянному напряжению или току, развивающему такую же среднюю мощность или такой же тепловой эффект в нагревательных приборах. Большинство электроизмерительных приборов индицирует как раз эффективное значение тока или напряжения.

Рис. 3

    Расчеты показывают, что эффективное значение составляет 0,707 амплитудного. В домашней электросети напряжение 220 В. Это эффективное значение, а амплитудное в 1,41 раза больше и приблизительно равно 310 В. Мгновенное же напряжение изменяется от нуля до +310 В, затем через нуль до -310 В и в обратную сторону — вновь до нуля.
    Цикл, или период, закончен, его длительность Т составляет 0,02 с (для сетевого напряжения). Число циклов, периодов или полных колебаний за секунду в этом случае будет равно 1/0,02=50. Это частота колебаний f (f=1/T), измеряемая в герцах— одно из важнейших понятий в электротехнике (о Генрихе Герце, который открыл электромагнитные волны, мы еще расскажем). В соответствии с общеевропейским стандартом частота промышленного (и бытового) электрического тока во всех сетях составляет 50 Гц, в Америке — 60 Гц. Некоторые маломощные передвижные электростанции, в основном армейские, вырабатывают переменный ток частотой 400 Гц.
    А теперь давайте возьмем микрофон и поговорим в него. На выводах микрофона появится переменное напряжение звуковой частоты. Его амплитуда невелика, всего несколько милливольт (мВ или тысячных долей вольта), но достаточна, чтобы наблюдать этот сигнал на экране осциллографа, — попробуйте, если представится возможность. Получить неподвижную картинку вряд ли удастся — и размах и частота сигнала будут все время изменяться. Амплитуда колебаний определяет громкость, а частота — высоту звукового тона. Басовые колебания имеют низкую частоту, а высокие тона — соответственно высокие частоты. Для удовлетворительной передачи речи нужен диапазон частот от 300 до 3000 Гц, для передачи музыки — примерно от 50 до 10 000 Гц (10 кГц), для высококачественного звуковоспроизведения — от 20 Гц до 20 000 Гц. Человеческое ухо воспринимает частоты в диапазоне 16…16000 Гц.
    Промышленный переменный ток значительно удобнее постоянного из-за того, что его напряжение можно преобразовывать с помощью трансформаторов, а электродвигатели переменного тока не требуют дорогих в изготовлении и ненадежных в эксплуатации коллекторов. Почему это так, мы не сможем разобраться, пока не познакомимся с магнитным действием тока и законом электромагнитной индукции, открытым знаменитым английским физиком-самоучкой и великим экспериментатором Майклом Фарадеем (1791-1867), в честь которого названа единица электрической емкости — фарада.

Радио, 1998

Действующее значение переменного синусоидального тока

Если в цепь переменного синусоидального тока включить прибор, который предназначен для измерения среднего значения тока в цепи, то этот прибор зафиксирует нулевое значение. Действительно, в каждый период ток протекает полпериода в одном направлении и полпериода — в другом.

В цепи такого тока не будет происходить электролиза, то есть осаждения металла на катоде в электролитической ванне. В то же время в сопротивлении, включенном в цепь переменного тока, идет непрерывный процесс выделения тепла независимо от направления тока: и в первый и во второй полупериоды. Поэтому, чтобы судить о силе переменного синусоидального тока, его сравнивают с постоянным током по одинаковому тепловому действию. Полученное путем такого сравнения значение силы переменного тока называют действующим.

Таким образом, действующее (эффективное) значение переменного тока численно равно эквивалентной по тепловому действию силе постоянного тока, то есть такому току, который за то же время,

на том же сопротивлении выделит такое же количество тепла, что и переменный ток одинаковой силы.

В цепи постоянного тока на сопротивлении R за время Т при силе тока I выделяется количество теплоты

Q_–= I²RT. (6.6)

В подобном сопротивлении, включенном в цепь переменного тока, в каждый очень короткий отрезок времени ∆t, в течение которого мгновенное значение силы тока i можно считать практически неизменным, выделяется элементарное количество теплоты:

∆Q_~ = i²R∆t,

то есть количество теплоты, пропорциональное произведению i²R. На рисунке 6.4 построены кривые i и i² для синусоидального переменного тока. Как видно из графика, несмотря на то, что ток i в течение периода меняется по значению и направлению, i² меняется только по значению и остается положительным независимо от направления тока i, то есть в первом полуперирде эта величина имеет положительное значение (+ i)•(+ i) = +i², во втором полупериоде она также остается положительной: (—i)•(—i)= +i².

Разделив площадь, ограниченную кривой i² и осью ωt, на время Т, получим среднюю ординату кривой i² за период, которую обозначим i²_ср.Тогда количество теплоты, которое выделится на сопротивлении в цепи переменного тока за время Т,

Q_~= i²_cр RT. (6.7)

Согласно приведенному выше определению действующего значения переменного тока, Q_~= Q_–, то есть из формул (6.6) и (6.7) следует, что

I²RT=i²_сpRT,

откуда действующее значение переменного тока

I = √i²_сp. (6.8).

Действующее значение переменного тока есть среднеквадратичное за период значение переменного тока.

Величину i², графически представленную на рисунке 6.4, можно определить аналитически через амплитудное значение I_m²:

. 1-cos2ωt I_m²_{I_m²}

i² = I_m² sin²ωt = I_m²—————— = ——— – —— cos2ωt ,

. 2 2 2

где .

. 1-cos2ωt

sin²ωt = ————— ,

. 2

Среднее значение cos2ωt за период Т равно нулю (соответствует сумме площадей, помеченных на рисунке 6.4 знаками + и —). Тогда среднее за период значение квадрата силы синусоидального переменного тока

i_ср²=I_m²/2

а действующее значение синусоидального переменного тока

I = √i_ср² = √I_m²/2 = I_m/2 = I_m/1.414 = 0,707 I_m. (6.9)

Действующее значение переменного синусоидального напряжения может быть найдено из предыдущего как

. I_m

IR = ——— R

. √²

или

. U_m

U = —— = 0,707 U_m.

. √²

Значит, если в сети напряжение U — 220 В, то его максимальное (амплитудное) значение

U_m = 220•1,414 = 311 В.

Амплитуда напряжения 380 В равна 380•1,414 = 538 В. То обстоятельство, что амплитуда значительно превышает действующее значение, дает преимущество переменному току при использовании люминесцентных или дуговых ламп, которые легче зажигаются на переменном токе.

< Предыдущая		Следующая >

значений переменного тока – Engineer-Educators.com

Существует три значения переменного тока: мгновенное, пиковое и эффективное (среднеквадратичное значение, RMS).

Мгновенное значение

Мгновенное значение напряжения или тока – это индуцированное напряжение или ток, протекающий в любой момент в течение цикла. Синусоидальная волна представляет собой серию этих значений. Мгновенное значение напряжения изменяется от нуля при 0 ° до максимума при 90 °, обратно до нуля при 180 °, до максимума в противоположном направлении при 270 ° и снова до нуля при 360 °.Любая точка на синусоиде считается мгновенным значением напряжения.

Пиковое значение

Пиковое значение – это наибольшее мгновенное значение. Наибольшее одиночное положительное значение возникает, когда синусоидальная волна напряжения находится под углом 90 °, а наибольшее одиночное отрицательное значение возникает, когда оно находится под углом 270 °. Максимальное значение в 1,41 раза превышает эффективное значение. Это так называемые пиковые значения.

Эффективное значение

Эффективное значение также известно как среднеквадратичное значение или среднеквадратичное значение, которое относится к математическому процессу, с помощью которого определяется значение.Большинство вольтметров переменного тока при использовании отображают действующее или среднеквадратичное значение. Действующее значение меньше максимального значения, равное 0,707 максимального значения.

Эффективное значение синусоидальной волны фактически является мерой теплового эффекта синусоидальной волны. На рисунке 107 показано, что происходит, когда резистор подключен к источнику переменного напряжения. На рисунке A определенное количество тепла генерируется мощностью в резисторе. На рисунке B показан тот же резистор, который теперь вставлен в источник постоянного напряжения.Значение источника постоянного напряжения теперь можно отрегулировать так, чтобы резистор рассеивал такое же количество
тепла, как и в цепи переменного тока. Среднеквадратичное или эффективное значение синусоидальной волны равно постоянному напряжению, которое выделяет такое же количество тепла, что и синусоидальное напряжение.

Рисунок 107. Эффективное значение синусоиды.

Пиковое значение синусоидальной волны можно преобразовать в соответствующее среднеквадратичное значение, используя следующее соотношение.

Может применяться как к напряжению, так и к току.

Алгебраически преобразовывая формулу и решая для Vp, можно также определить пиковое напряжение. Результирующая формула:

Таким образом, значение 110 вольт для переменного тока, подаваемого в дома, составляет всего 0,707 максимального напряжения этого источника. Максимальное напряжение составляет примерно 155 вольт (110 × 1,41 = максимум 155 вольт).

При исследовании переменного тока любые значения, указанные для тока или напряжения, считаются действующими, если не указано иное, и на практике используются только действующие значения напряжения и тока.Аналогичным образом вольтметры и амперметры переменного тока измеряют действующее значение.

Среднеквадратичное значение переменного тока | Вывод

В системе постоянного тока напряжение и ток постоянны, поэтому нет проблем с указанием их величины. Но в случае системы переменного тока переменное напряжение меняется от момента к моменту, и поэтому возникает проблема с указанием величины.

Итак, чтобы выразить величины переменного тока в простой и понятной форме, была разработана концепция среднеквадратичного значения.Они также могут быть выражены в виде пикового или среднего значения, но эти значения не отражают эффективность количества переменного тока.

Среднеквадратичное значение переменного тока равно той величине постоянного тока, которая вызывает такой же нагревательный эффект, протекающий через то же сопротивление в течение того же времени.

Термин RMS означает (квадратный) корень из среднего квадратов мгновенных значений тока. Среднеквадратичное значение переменного тока или напряжения можно рассчитать по следующей формуле:

I _RMS = 0.707 x пиковое значение тока
В _RMS = 0,707 x пиковое значение напряжения

Это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию. Например, если мы говорим, что по цепи протекает переменный ток 5 А, это означает, что среднеквадратичное значение переменного тока, протекающего по цепи, составляет 5 А. И он будет производить столько же тепла (энергии), сколько вырабатывается постоянным током 5А.

Все амперметры и вольтметры переменного тока показывают среднеквадратичные значения переменного тока и напряжения соответственно .Все электроприборы оцениваются по среднеквадратичному значению. В Индии внутренняя однофазная сеть переменного тока составляет 230 В, 50 Гц. Здесь 230 В – это действующее значение напряжения питания.

Среднеквадратичное значение AC всегда больше среднего значения, за исключением прямоугольной волны, когда они равны. Его значение никогда не может быть отрицательным.

Управляйте выражением среднеквадратичного значения переменного тока

Пусть i = I _m sinωt будет переменным током, протекающим через сопротивление R Ом за время t секунд и выделяющее такое же тепло, как и у I _eff (прямое Текущий).

База полупериода делится на n равных частей, как показано на рисунке, так что каждый интервал составляет t / n секунд.

Пусть i ₁, i ₂, i ₃ ……… .i _n – средние ординаты.

Тогда тепло, произведенное в первом интервале = i ₁ ² Rt / n джоулей
Второй интервал = i ₂ ² Rt / n джоулей
Третий интервал = i ₃ ² Rt / n джоулей
n ^th интервал = i _n ² Rt / n джоулей

Общее количество тепла, произведенного за время t

= Rt [(i ₁ 2 + i ₂ ² + i ₃ ² + …… + i _n ²) / n]….. (1)

Начиная с I _eff считается действующим значением этого тока.
Тогда тепло, произведенное этим током во времени t = I _eff ² Rt ……. (2)

По определению, уравнения (1) и (2) равны. Следовательно,

I _eff ² Rt = Rt [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n]

Или I _eff ² = [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n]

Или I _eff = [(i ₁ ² + i ₂ ² + i ₃ ² + …… + i _n ²) / n] ^1/2

Или I _eff = I _RMS = квадратный корень из среднего квадратов мгновенного тока.

Теперь, используя интегральное исчисление, действующее значение переменного тока или действующее значение переменного тока за период времени можно рассчитать следующим образом:

Важные термины, относящиеся к среднеквадратичному значению AC

Пиковое значение (I _m) : Максимальное значение, достигаемое переменным током во время полного цикла, называется его пиковым значением. Синусоидальный переменный ток достигает своего максимального положительного значения при 90 ^o.

Форм-фактор (K _f) : Это отношение среднеквадратичного значения к среднему значению переменной величины.

K _f = Среднеквадратичное значение / Среднее значение

Для синусоидальной волны это 1,11. Мы можем найти среднеквадратичное значение из среднего значения и наоборот с помощью форм-фактора.

Этот коэффициент показывает «остроту» формы волны. Прямоугольная волна, более плоская, чем синусоида, имеет коэффициент формы 1,0. С другой стороны, треугольная волна более «острая», чем синусоида, и имеет форм-фактор 1,15.

Пик-фактор (Kp) : Это отношение пикового или максимального значения к среднеквадратичному значению переменной величины.

K _p = Пиковое значение / среднеквадратичное значение

Для синусоидальной волны это 1,414. Это очень важно при испытании диэлектрической изоляции, поскольку диэлектрическая нагрузка на изоляционный материал зависит от пикового значения приложенного напряжения. Это также важно при измерении потерь в стали, поскольку эти потери зависят от значения максимального магнитного потока.

Среднее значение переменного тока

Среднее арифметическое всех мгновенных значений, учитываемых в переменном токе величины за один цикл, называется средним значением переменного тока (I _av).

Это тот постоянный ток, который передает тот же заряд, что и переменный ток, в одно и то же время по любой цепи.

В случае симметричных волн, таких как синусоидальный ток или волна напряжения, положительная половина точно равна отрицательной половине, поэтому среднее значение за полный цикл равно нулю.

Поскольку работа выполняется током как в положительном, так и в отрицательном полупериоде, то среднее значение определяется независимо от знаков или учитывается только положительная половина.

Для определения среднего значения переменного тока рассмотрите только положительный полупериод и разделите его на n равных частей. Пусть i ₁, i ₂, i ₃ …… in – средние ординаты.

Теперь, среднее значение тока, I _av = Среднее значение средних ординат

= (i ₁ + i ₂ + i ₃ + ……. + I _n) / n

= Площадь полупериода / длина базы полупериода

Теперь, используя интегральное исчисление, мы можем вычислить площадь полупериода и среднее значение переменного тока.После этого расчета мы получаем следующее выражение для синусоидального тока.

I _ср. = 2I _м / π = 0,637 I _м

Основы переменного тока | Все сообщения

Что такое пиковое значение, среднее значение и среднеквадратичное значение? – определение и объяснение

Пиковое значение

Определение: Максимальное значение, достигаемое переменным количеством в течение одного цикла, называется его значением P eak .Он также известен как максимальное значение, амплитуда или пик. Синусоидальная переменная величина достигает своего пикового значения при 90 градусах, как показано на рисунке ниже.

Пиковые значения переменного напряжения и тока представлены как E _m и I _m соответственно.

Среднее значение

Определение: Среднее значение всех мгновенных значений переменного напряжения и токов за один полный цикл называется средним значением .

Если мы рассмотрим симметричные волны, такие как синусоидальный ток или форма волны напряжения, положительный полупериод будет точно равен отрицательному полупериоду. Следовательно, среднее значение за полный цикл будет ноль .

Работа выполняется как по положительному, так и по отрицательному циклу, поэтому среднее значение определяется без учета знаков.

Итак, единственным положительным полупериодом считается определение среднего значения переменных величин синусоидальных волн.Давайте рассмотрим пример, чтобы понять это.

Разделите положительный полупериод на ( n ) количество равных частей, как показано на рисунке выше

Пусть i ₁, i ₂, i ₃ …… .. i _n – средние ординаты

Среднее значение тока I _ср. = среднее значение средних ординат

R.M.S значение

Определение: Тот установившийся ток, который при прохождении через резистор с известным сопротивлением в течение определенного периода времени, в результате такое же количество тепла выделяется переменным током, когда он протекает через тот же резистор в течение того же периода времени. время называется р.M.S или действующее значение переменного тока.

Другими словами, значение R.M.S определяется как квадратный корень из средних квадратов мгновенных значений.

Пусть I будет переменным током, протекающим через резистор R в течение времени t секунд, который производит такое же количество тепла, как и постоянный ток (I _eff). База одного изменения делится на n равных частей, так что каждый интервал составляет t / n секунд, как показано на рисунке ниже.

Пусть i ₁, i ₂, i ₃, ………..in – средние ординаты

Тогда тепло произведено в

Так как Ieff считается эффективным значением этого тока, то общее количество тепла, произведенного этим током, будет

Теперь, приравняв уравнение (1) и (2), получим

I _eff = квадратный корень из среднего квадратов мгновенных значений = среднеквадратичное значение

Среднеквадратичное значение – это фактическое значение переменной величины, которая говорит нам о способности источника переменного тока передавать энергию.

Амперметр регистрирует среднеквадратичное значение переменного тока, а вольтметр записывает среднеквадратичное значение переменного напряжения. Электропитание однофазного переменного тока в домашних условиях составляет 230 В, 50 Гц, где 230 В – это среднеквадратичное значение переменного напряжения.

Значения напряжения и силы тока в цепи постоянного тока постоянны, поэтому нет проблем с оценкой их величин, но в системе переменного тока переменное напряжение и ток изменяются время от времени, и, следовательно, необходимо оценивать их величины.

Следующие три способа (пиковое значение, среднее значение и среднеквадратичное значение), приведенные выше, используются для выражения величины напряжения и тока.

Эффективное значение синусоиды

E _max, E _avg, I _max и I _avg – используемые значения в измерениях переменного тока. Другое используемое значение – ЭФФЕКТИВНОЕ значение переменного тока. переменное напряжение или ток, которые будут иметь такое же влияние на сопротивление, как и сопоставимые значения постоянного напряжения или тока будут иметь на том же сопротивлении.

В предыдущем обсуждении вам сказали, что когда ток течет в сопротивлении, тепло выделяется. произведено. Когда через сопротивление протекает постоянный ток, количество электроэнергии преобразованная в тепло, равна I ² R Вт. Однако, поскольку переменный ток при максимальном значении 1 ампер не поддерживает постоянное значение, переменный ток не будет выделять столько тепла в сопротивлении, сколько постоянный ток 1 ампер.

На Рисунке 1-15 сравнивается эффект нагрева 1 ампера постоянного тока с эффектом нагрева 1 ампер. ампер переменного тока.

Рисунок 1-15. – Нагревательный эффект переменного и постоянного тока.

Изучите виды A и B на рис. 1-15 и обратите внимание, что тепло (70,7 ° C), производимое 1 ампер переменного тока (то есть переменного тока с максимальным значением 1 ампер) составляет всего лишь 70,7 процента тепла (100 C) вырабатывается 1 ампером постоянного тока. Математически,

Следовательно, для действующего значения переменного тока (I _eff) = 0.707 X I _макс.

Скорость, с которой выделяется тепло в сопротивлении, является удобной основой для установление эффективного значения переменного тока, известное как “нагрев эффект “. Считается, что переменный ток имеет эффективное значение, равное единице. ампер, когда он выделяет тепло с заданным сопротивлением с той же скоростью, что и один ампер постоянный ток.

Вы можете вычислить эффективное значение синусоидального тока с достаточной степенью точности, принимая мгновенные значения тока, равномерно распределенные вдоль кривой, и извлечение квадратного корня из среднего значения суммы квадратов значений.

По этой причине эффективное значение часто называют «среднеквадратическим». (среднеквадратичное) значение. Таким образом,

Другими словами, эффективное или среднеквадратичное значение (I _eff) синусоидальной волны ток составляет 0,707 максимального значения тока (I _max). Таким образом, I _eff = 0,707 X I _макс. Если известен I _eff, вы можете найти I _max по используя формулу I _max = 1.414 X I _эфф. Вы можете задаться вопросом, где постоянная 1,414 происходит от. Чтобы выяснить это, еще раз изучите рисунок 1-15 и прочтите следующее. объяснение. Предположим, что постоянный ток на рисунке 1-15 (A) поддерживается на уровне 1 ампера, а температура резистора на уровне 100С. Также предположим, что переменный ток на рисунке 1-15 (B) увеличен. до тех пор, пока температура резистора не достигнет 100 C. На этом этапе установлено, что максимальное Значение переменного тока 1,414 ампер требуется для того, чтобы иметь такой же нагревательный эффект, как и при прямом подключении. Текущий.Следовательно, в цепи переменного тока максимальный требуемый ток в 1,414 раза больше эффективный ток. Вам важно помнить вышеупомянутые отношения и то, что эффективное значение (I _eff) любой синусоидальной волны тока всегда в 0,707 раза больше максимальное значение (I _max).

Поскольку переменный ток возникает из-за переменного напряжения, соотношение эффективное значение напряжения к максимальному значению напряжения такое же, как отношение эффективное значение тока до максимального значения тока.Другими словами, эффективное или среднеквадратичное значение (E _eff) синусоидального напряжения в 0,707 раз больше максимальное значение напряжения (E _max),

Когда значение переменного тока или напряжения указано в книге или на диаграмме, значение является эффективным, если не указано иное. Помните, что все измерители, если не указано иное, откалиброваны для индикации действующие значения тока и напряжения.

Проблема: известно, что в цепи имеется переменное напряжение 120 В и пиковое или максимальный ток 30 ампер. Каковы значения пикового напряжения и эффективного тока?

На рисунке 1-16 показано соотношение между различными значениями, используемыми для обозначения амплитуда синусоиды. Просмотрите значения на рисунке, чтобы убедиться, что вы понимаете, что каждый значение указывает.

Рисунок 1-16. – Различные значения, используемые для обозначения амплитуды синусоидальной волны.

Q.32 Какая наиболее удобная основа для сравнения переменного и постоянного напряжения и токи?
В.33 Какое значение переменного тока используется для сравнения с постоянным током?
В.34 Какова формула для определения действующего значения переменного тока?
В.35 Если пиковое значение синусоидальной волны составляет 1000 вольт, каково эффективное (E _eff) ценить?
Q.36 Если я _эфф = 4,25 ампера, что я _max?

Среднее и действующее значение переменного тока и напряжения

Постоянный ток течет только в одном направлении.Переменный ток время от времени меняет направление потока в цепи. В постоянном токе напряжение источника не меняет своей полярности. В переменном токе напряжение источника меняет свою полярность с положительной на отрицательную.

На рисунке 1 показаны величина и полярность переменного напряжения. Начиная с нуля, напряжение возрастает до максимума в положительном направлении. Затем он возвращается к нулю. Затем он возрастает до максимума с противоположной полярностью и возвращается к нулю.

Рисунок 1. Ток и напряжение переменного тока.

Текущая волна также нанесена на график. Он показывает течение тока и направление потока. Выше нулевой линии ток течет в одном направлении. Ниже нулевой линии ток течет в обратном направлении.

График на рис. 1 представляет мгновенные значения тока и напряжения в любой точке цикла. Но что такое цикл? Цикл – это последовательность или цепочка событий, происходящих в определенный период времени.Цикл переменного тока можно описать как полный набор положительных и отрицательных значений переменного тока.

Переменный ток в вашем доме меняет направление 120 раз в секунду. Он имеет частоту 60 циклов в секунду (60 Гц). Частота , измеряется в циклах в секунду или герцах (Гц), это количество полных циклов, происходящих в секунду. Если за одну секунду происходит 60 циклов, то период времени для одного цикла составляет 1/60 секунды или 0,0166 секунды. Это период цикла .Снова обратитесь к Рисунок 1 . Максимальный подъем формы волны показывает амплитуду волны, включая пиковое (самая высокая точка) напряжение и ток.

Мы узнали, что индуцированный ток во вращающемся проводе в магнитном поле течет сначала в одном направлении, а затем в другом. Это было определено как переменный ток. Следует запомнить два момента: :

• Частота этого цикла событий увеличивается с увеличением скорости вращения.

• Амплитуда индуцированного напряжения зависит от силы магнитного поля.

Векторы

При решении задач, связанных с переменным током, векторы используются для обозначения величины и направления силы. Вектор – это прямая линия, проведенная в масштабе, который представляет единицы силы. Стрелка на линии показывает направление силы. Длина вектора показывает величину.

Развитие волны переменного тока показано на Рисунке 2 . Эта волна исходит от якоря с одной катушкой, представленного вращающимся вектором, совершающим один оборот через магнитное поле .

Предположим, что пиковое индуцированное напряжение составляет 10 вольт. Используя шкалу, в которой один дюйм равен пяти вольтам, вектор составляет два дюйма или 10 вольт. Предполагается, что векторы такого характера вращаются против часовой стрелки.

Рисунок 2. Развитие синусоидальной волны. Слева вращающийся вектор. Справа – один цикл синусоиды.

Временная база на Рис. 2 – это линия с любым удобным масштабом. Он показывает период одного цикла или оборот вектора.База времени сгруппирована в сегменты, которые представляют время для определенных градусов вращения во время цикла.

Например, при повороте на 90 градусов используется четверть периода времени. При повороте на 270 градусов используются три четверти периода времени. Волна создается путем построения графика амплитуды напряжения в любой момент вращения относительно временного отрезка. Развитая волна называется синусоидой .

Мгновенные наведенные напряжения пропорциональны синусу угла θ (тета), который вектор образует с горизонталью.Затем мгновенное напряжение можно найти в любой точке цикла, используя следующее уравнение:

$ e = {{E} _ {\ max}} \ times \ sin \ theta $

(Обратите внимание, что буква e в нижнем регистре использовалась для обозначения мгновенного напряжения вместо обычного верхнего регистра. По соглашению, мгновенные значения представлены переменными в нижнем регистре.)

Чтобы применить это уравнение, предположим, что генератор переменного тока вырабатывает пиковое напряжение 100 вольт. Каково мгновенное напряжение при повороте на 45 градусов?

$ e = 100 В \ times \ sin {{45} ^ {o}} = 100 В \ times 0.707 = 70,7 В $

Средние и среднеквадратичные значения

Исследование различий между волной переменного тока и постоянным током поднимает ключевой вопрос. Каково действительное значение волны переменного тока? Напряжение и ток постоянно меняются и достигают пикового значения только дважды за цикл.

Часто требуется среднее значение волны. Среднее значение – это математическое среднее всех мгновенных значений в течение одного полупериода переменного тока. Формулы для вычисления среднего значения из пикового значения (макс.) Любых волн переменного тока:

$ \ begin {matrix} {{E} _ {avg}} = 0.637 \ times {{E} _ {\ max}} \\ или \\ {{I} _ {avg}} = 0,637 \ times {{\ operatorname {I}} _ {max}} \\\ end {матрица } $

Если известно E _avg или I _avg, преобразование для нахождения E _max или I _max может быть выполнено с использованием следующих уравнений.

$ \ begin {matrix} {{E} _ {\ max}} = 1,57 \ times {{E} _ {avg}} \\ или \\ {{I} _ {\ max}} = 1,57 \ times { {\ operatorname {I}} _ {avg}} \\\ end {matrix}

долл. США

Более полезным значением переменного тока является эффективное значение .Термин «эффективное значение» был получен от ученых, обнаруживших, что эффект нагрева переменным током эквивалентен постоянному току.

Указанный объем воды был нагрет с использованием заданного уровня постоянного напряжения. Затем такое же количество воды нагревали с помощью переменного тока. Напряжение переменного тока, которое вызывает нагрев, эквивалентный напряжению постоянного тока, было эффективным значением. Формулы для определения эффективного значения любого переменного напряжения или тока:

$ \ begin {matrix} {{E} _ {eff}} = 0,707 \ times {{E} _ {\ max}} \\ или \\ {{I} _ {eff}} = 0.707 \ times {{\ operatorname {I}} _ {\ max}} \\\ end {matrix}

долл. США

Где E _max и I _max – пиковые значения сигнала переменного тока. Если известны E _eff или I _eff, преобразование для нахождения пиковых значений может быть выполнено с использованием следующих уравнений.

$ \ begin {matrix} {{E} _ {\ max}} = 1,414 \ times {{E} _ {eff}} \\ или \\ {{I} _ {\ max}} = 1,414 \ times { {\ operatorname {I}} _ {eff}} \\\ end {matrix}

долл. США

Действующее значение также называется среднеквадратичным значением (среднеквадратичное значение) .Он получил такое название, потому что значение представляет собой квадратный корень из среднего значения всех токов в квадрате между нулем и максимумом волны. Токи возведены в квадрат, поэтому производимую мощность можно сравнить с постоянным током. Закон Ватта гласит: P = I ² R.

Используя коэффициент 0,707, можно найти значение постоянного тока, равное переменному току. Например, , пиковый переменный ток в 5 ампер вызывает тот же эффект нагрева в сопротивлении, что и постоянный ток, равный 3.53 ампера. Подставляя значения в уравнение:

I _eff = 0,707 × 5 ампер переменного тока = 3,53 ампера постоянного тока

Обратите внимание, что средние и действующие значения могут применяться как к волнам напряжения, так и к волнам тока.

Смещение фаз

На одной временной основе можно нарисовать несколько форм сигналов, чтобы показать фазовое соотношение между ними. На рис. 3 формы сигналов E и I показывают напряжение и ток в данной цепи. Ток и напряжение растут и падают одновременно.Они пересекают нулевую линию в одной и той же точке. Ток и напряжение совпадают по фазе. Синфазное состояние существует только в чисто резистивной цепи .

Рисунок 3. Эти волны тока и напряжения синфазны.

Часто ток опережает или отстает от напряжения , рис. 4 . Когда волна тока опережает или отстает от волны напряжения, говорят, что две волны находятся в противофазе. Это создает фазовый сдвиг между двумя волнами.Смещение измеряется в градусах. Сдвиг фазы равен углу θ между двумя полярными векторами.

Рисунок 4. Эти волны тока и напряжения не совпадают по фазе.

Генератор переменного тока

Генератор переменного тока похож на генератор постоянного тока во многих отношениях с одним ключевым исключением. Коммутатор опущен. Концы катушек якоря выдвинуты до контактных колец. Щетки, скользящие по контактным кольцам, обеспечивают постоянное соединение с катушками.Ток во внешне подключенной цепи – это переменный ток.

В крупных промышленных генераторах магнитное поле вращается, и обмотки якоря размещаются в пазах неподвижной рамы или статора генератора. Этот метод позволяет генерировать большие токи в якоре, избегая передачи этих токов через движущиеся или скользящие кольца и щетки.

Вращающееся поле возбуждается через контактные кольца и щетки небольшим генератором постоянного тока, установленным на том же валу, что и вращающееся магнитное поле.Этот небольшой генератор постоянного тока называется возбудителем . Для магнитного поля необходимо постоянное напряжение. Коммерческие генераторы энергии преобразуют множество различных элементов (например, движущуюся воду, уголь, нефть, ветер, ядерную энергию) в электричество. Силовой механизм, который используется для вращения генератора, называется первичным двигателем, Рисунок 5.

Рисунок 5. Первичный двигатель, возбудитель и трехфазный генератор имеют общий вращающийся вал. Возбудитель обеспечивает электрическую энергию для генератора переменного тока.

Генератор переменного тока или генератор переменного тока

Генератор переменного тока (также называемый генератором переменного тока) используется в системе зарядки всех автомобилей США. Рисунок 6 показывает внутреннюю часть устройства, включая встроенный регулятор напряжения для управления выходом. Выходной ток выпрямляется с переменного тока на постоянный для зарядки аккумулятора и других электрических устройств в автомобиле.

Производители говорят, что генератор переменного тока имеет некоторые преимущества перед генератором постоянного тока.Эти преимущества включают более высокую производительность при более низких скоростях, а также безотказное обслуживание.

Рисунок 6. Типичный генератор переменного тока (генератор переменного тока) показан на видах снаружи и в разрезе.

Пиковое напряжение переменного тока (АС), размах напряжения, среднеквадратичное (среднеквадратичное) напряжение

(DC) – постоянный ток

Элементы и батареи вырабатывают электрический ток, который всегда течет по цепи одинаково, это называется постоянным током (DC).

(AC) – переменный ток

В Великобритании электросеть поставляется с напряжением около 230 вольт и подается как (переменный) или переменный ток. Это означает, что ток течет в одном направлении, а затем в другом по цепи. Ток постоянно меняет направление (чередуется), поэтому его называют (переменным) переменным током. В Великобритании частота электросети 50 Гц , то есть 50 циклов в секунду.

Сигналы переменного тока

Мы можем использовать осциллограф для представления сигнала переменного тока.

Мы можем использовать осциллограмму в качестве вольтметра, если мы знаем, какое усиление по оси Y установлено на осциллографе. Используя диаграмму выше и зная, что усиление по оси Y было установлено на 10 В / дел, мы можем это решить;

напряжение от пика до пика = 6 квадратов от самой высокой точки до самой низкой, и каждый квадрат стоит 10В. Таким образом, размах напряжения = 60 В.
пиковое значение напряжение (В _o) = половина пикового напряжения = 60/2 = 30 В

Когда мы знаем пиковое напряжение (V _o) и сопротивление (R) в цепи, мы можем вычислить пиковый ток (I _o) , используя уравнение V = IR.

Среднеквадратичное значение (СКЗ)

Как п.о. и ток непрерывно изменяются в сигнале переменного тока, нам нужно представить среднее значение для p.d. и ток.

Среднеквадратичные значения p.d. (V _rms) и ток (I _rms) представляют собой действующее значение p.d. и ток в цепи переменного тока.

В _{действующее значение} = среднеквадратичная разность потенциалов в вольтах, В
В _o = пиковое напряжение в вольтах, В

I = среднеквадратичный ток в амперах, А
I _o = пиковый ток в амперах, A

Анализ генерации переменного тока: эффективные значения, фазовый угол и частота

Анализ процесса производства электроэнергии переменного тока и переменного тока, который мы используем почти во всех аспектах нашей жизни, необходим для лучшего понимания того, как мощность переменного тока используется в современных технологиях.

Эффективные значения

Выходное напряжение генератора переменного тока можно выразить двумя способами. Один – графически с использованием синусоидальной волны (рис. 3). Второй способ – алгебраически с помощью уравнения e = E _max sin ωt, которое будет рассмотрено позже в тексте.

Рисунок 3: Синусоидальная волна напряжения

Когда напряжение вырабатывается генератором переменного тока, результирующий ток изменяется пропорционально напряжению. Когда катушка генератора вращается на 360 °, выходное напряжение проходит один полный цикл.За один цикл напряжение увеличивается от нуля до E в одном направлении, уменьшается до нуля, увеличивается до E _max в противоположном направлении (отрицательное значение E _max), а затем снова уменьшается до нуля. Значение E _max происходит при 90 ° и называется пиковым напряжением. Время, необходимое генератору для завершения одного цикла, называется периодом, а количество циклов в секунду называется частотой (измеряется в герцах).

Один из способов обозначения переменного напряжения или тока – это пиковое напряжение (E _p) или пиковый ток (I _p).Это максимальное напряжение или ток для синусоидального сигнала переменного тока.

Другое значение, значение размаха (E _p-p или I _p), представляет собой величину напряжения или диапазон тока, охватываемого синусоидальной волной. Однако наиболее часто используемым значением переменного тока является эффективное значение. Эффективное значение переменного тока – это количество переменного тока, которое производит такой же нагревательный эффект, как и такое же количество постоянного тока.

Проще говоря, эффективное значение переменного тока в один ампер будет производить такое же количество тепла в проводнике за заданное время, что и один ампер постоянного тока.Эффект нагрева от данного переменного тока пропорционален квадрату тока. Эффективное значение переменного тока можно вычислить, возведя в квадрат все амплитуды синусоидальной волны за один период, взяв среднее из этих значений, а затем извлекая квадратный корень. Действующее значение, являющееся корнем из среднего (среднего) квадрата токов, известно как среднеквадратичное значение или среднеквадратичное значение. Чтобы понять значение эффективного тока, приложенного к синусоиде, см. Рисунок 4.

Значения I нанесены на верхнюю кривую, а соответствующие значения I ² нанесены на нижнюю кривую.Кривая I ² имеет частоту в два раза большую, чем I, и изменяется выше и ниже новой оси. Новая ось представляет собой среднее значение I ², а квадратный корень из этого значения представляет собой среднеквадратичное или эффективное значение тока. Среднее значение ½ I _max ². Тогда среднеквадратичное значение составляет

Существует шесть основных уравнений, которые используются для преобразования значения переменного напряжения или тока в другое значение, как указано ниже.

Среднее значение = пиковое значение x 0.637
Эффективное значение (RMS) = пиковое значение x 0,707
Пиковое значение = среднее значение x 1,57
Эффективное значение (RMS) = среднее значение x 1,11
Пиковое значение = эффективное значение (RMS) x 1,414
Среднее значение = эффективное (RMS) x 0,9

Значения тока (I) и напряжения (E), которые обычно встречаются, считаются действующими значениями; поэтому нижний индекс не используется.

Рисунок 4: Действующее значение тока

Еще одно полезное значение – это среднее значение амплитуды в течение положительной половины цикла.

Уравнение ниже представляет собой математическое соотношение между I _av, I _max и I.

I _ср. = 0,637 I _макс = 0,9 I

Уравнение ниже представляет собой математическую связь между E _ср., E _макс и E.

E _ср. = 0,637 E _макс = 0,9 E

Пример 1:

Пиковое значение напряжения в цепи переменного тока составляет 200 В. Каково среднеквадратичное значение напряжения?

E = 0.707E _макс

E = 0,707 x 200 = 141,4 В

Пример 2:

Пиковый ток в цепи переменного тока составляет 10 ампер. Какое среднее значение тока в цепи?

I _ср. = 0,637 I _макс

I _ср. = 0,637 x 10 = 6,37 ампер

Фазовый угол

Фазовый угол – это доля цикла в градусах, которая прошла с тех пор, как напряжение или ток прошли через заданное значение.Данное значение обычно равно нулю. Возвращаясь к рисунку 3, возьмите точку 1 как начальную точку или нулевую фазу. Фаза в точке 2 равна 30 °, точке 3 – 60 °, точке 4 – 90 ° и так далее до точки 13, где фаза равна 360 ° или нулю. Чаще используется термин «разность фаз».

Рисунок 5: Соотношение фаз

Разность фаз может использоваться для описания двух разных напряжений с одинаковой частотой, которые проходят через нулевые значения в одном и том же направлении в разное время.На рисунке 5 углы вдоль оси указывают фазы напряжений e ₁ и e ₂ в любой момент времени.

При 120 ° e ₁ проходит через нулевое значение, которое на 60 ° опережает e ₂ (e ₂ равно нулю при 180 °). Считается, что напряжение e ₁ опережает e ₂ на 60 электрических градусов, или можно сказать, что e ₂ отстает от e ₁ на 60 электрических градусов.

Разность фаз также используется для сравнения двух разных токов или тока и напряжения.Если разность фаз между двумя токами, двумя напряжениями или напряжением и током равна нулю, они считаются «синфазными». Если разность фаз отлична от нуля, говорят, что они «не совпадают по фазе».

Расчет напряжения

Приведенное ниже уравнение представляет собой математическое представление напряжения, связанного с любой конкретной ориентацией катушки (индуктора).

e = E _макс sinθ

где

e = наведенная ЭДС
E _max = максимальная наведенная ЭДС
θ = угол от точки отсчета (градусы или радианы)

Пример 1:

Какова наведенная ЭДС в катушке, создающей максимальную ЭДС 120 В, когда угол от точки отсчета составляет 45 °?

e = E _макс sinθ

e = 120 v Sin (45)

е = 84.84 В

Максимальное индуцированное напряжение также можно назвать пиковым напряжением E _p. Если (t) – время, за которое катушка поворачивается на угол (θ), то угловая скорость (ω) катушки равна θ / t и выражается в радианах / сек.

Уравнение ниже представляет собой математическое представление угловой скорости.

θ = ωt

где

ω = угловая скорость (радиан / сек)
t = время поворота на угол от точки отсчета (с)
θ = угол от точки отсчета (радианы)

Используя законы замещения, можно выразить взаимосвязь между наведенным напряжением, максимальным наведенным напряжением и угловой скоростью.

Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между наведенным напряжением, максимальным напряжением и угловой скоростью, и оно равно выходной мощности генератора переменного тока.

e = E _макс sin (ωt)

, где
e = наведенная ЭДС (вольты)
E _max = максимальная наведенная ЭДС (вольт)
ω = угловая скорость (радиан / сек)
t = время поворота на угол от опорной точки (сек)

Текущие расчеты

Максимальный наведенный ток рассчитывается аналогичным образом.Приведенное ниже уравнение представляет собой математическое представление взаимосвязи между максимальным индуцированным током и угловой скоростью.

i = I _макс sin (ωt)

где

i = индуцированный ток (амперы)
I _max = максимальный индуцированный ток (амперы)
ω = угловая скорость (радиан / сек)
t = время поворота на угол от опорного значения (сек)

Расчет частоты

Частота переменного напряжения или тока может быть напрямую связана с угловой скоростью вращающейся катушки.Единицы угловой скорости – радианы в секунду, а 2π радиан – это полный оборот.

Радиан – это угол, образующий дугу, равную радиусу окружности. Один радиан равен 57,3 градуса. Один цикл синусоидальной волны генерируется, когда катушка вращается на 2π радиана.

Уравнение ниже представляет собой математическое соотношение между частотой (f) и угловой скоростью (ω) в цепи переменного тока.

ω = 2πf

где

ω = угловая скорость (радиан / сек)
f = частота (Гц)

Пример 1:

Частота цепи 120 В переменного тока составляет 60 Гц.Найдите следующее: 1. Угловая скорость 2. Угол от точки отсчета через 1 мс 3. Индуцированная ЭДС в этой точке

Решение:

1. ω = 2πf

ω = 2 (3,14) (60 Гц) = 376,8 радиан / сек

2. θ = ωt

θ = (376,8 радиан / сек) (0,001 сек) = 0,3768 радиан

3. e = E _макс sinθ

e = (120 В) (sin 0,3768 радиан)
e = (120 В) (0,3679)
e = 44,15 В

Эффективное значение переменного тока: Действующее значение тока и напряжения

Эффективная сила тока. Действующее значение переменного тока

Количественная связь амплитуд силы и напряжения переменного тока и эффективных значений

Применение действующих значений тока и напряжения

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

4.4.5. Мощность в цепи переменного тока

Действующие значения э. д. с., напряжения и силы переменного тока

Эффективное напряжение переменного тока. Действующие значения силы тока и напряжения

Генератор переменного тока

*Принцип действия

Действующие значения силы тока и напряжения

Дополнительные сведения

Источники

Ссылки

Мгновенные, максимальные, действующие и средние значения электрических величин переменного тока

/ Среднее и действующие значения синусоидальных токов и напряжений

Список параметров напряжения и силы электрического тока

Значения переменного напряжения (тока)

Мгновенное значение

Среднее значение

Коэффициенты пересчёта значений

Параметры постоянного тока

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

Какой физический смысл имеет действующее значение напряжения и тока

Действующие значения периодических и синусоидальных токов

4.4.5. Мощность в цепи переменного тока

Эффективное (действующее значение переменного тока

Что такое эффективное значение тока и напряжения. Эффективные значения тока и напряжения

Генератор переменного тока

*Принцип действия

Действующие значения силы тока и напряжения

Действующее значение переменного тока

Синусоидально изменяющийся ток

Изображение синусоидальных эдс, напряжений и токов на плоскости декартовых координат

Векторное изображение синусоидально изменяющихся величин

Действующее и среднее значения переменного тока и напряжения.

Что берется за действующее значение силы переменного тока и переменного напряжения

ПЕРЕМЕННЫЙ ТОК

ТЕОРИЯ: ПОНЕМНОГУ – ОБО ВСЕМ

Действующее значение переменного синусоидального тока

значений переменного тока – Engineer-Educators.com

Среднеквадратичное значение переменного тока | Вывод

Управляйте выражением среднеквадратичного значения переменного тока

Важные термины, относящиеся к среднеквадратичному значению AC

Среднее значение переменного тока

Основы переменного тока | Все сообщения

Что такое пиковое значение, среднее значение и среднеквадратичное значение? – определение и объяснение

Пиковое значение

Среднее значение

R.M.S значение

Эффективное значение синусоиды

Среднее и действующее значение переменного тока и напряжения

Пиковое напряжение переменного тока (АС), размах напряжения, среднеквадратичное (среднеквадратичное) напряжение

Анализ генерации переменного тока: эффективные значения, фазовый угол и частота

Эффективные значения

Больше новостей

Добавить комментарий Отменить ответ