Формула длины проводника: Длина проводника по сопротивлению

от чего зависит сопротивление проводника, формулы для расчета

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Физический смысл сопротивления

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева , а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью.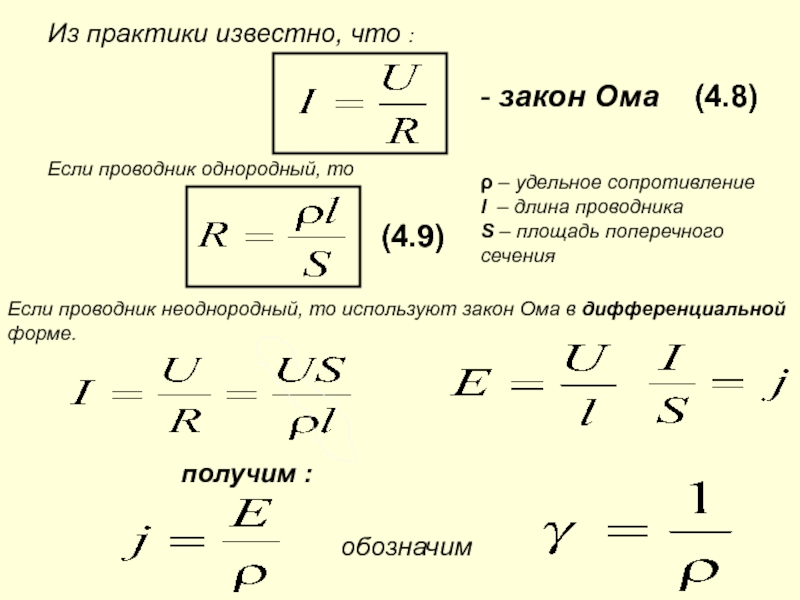

Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

1. Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
2. Полупроводники (могут проводить электрический ток, но при определенных условиях).
3. Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом). Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Зависимость проводимости материала

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

Деформация и удельное сопротивление

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов.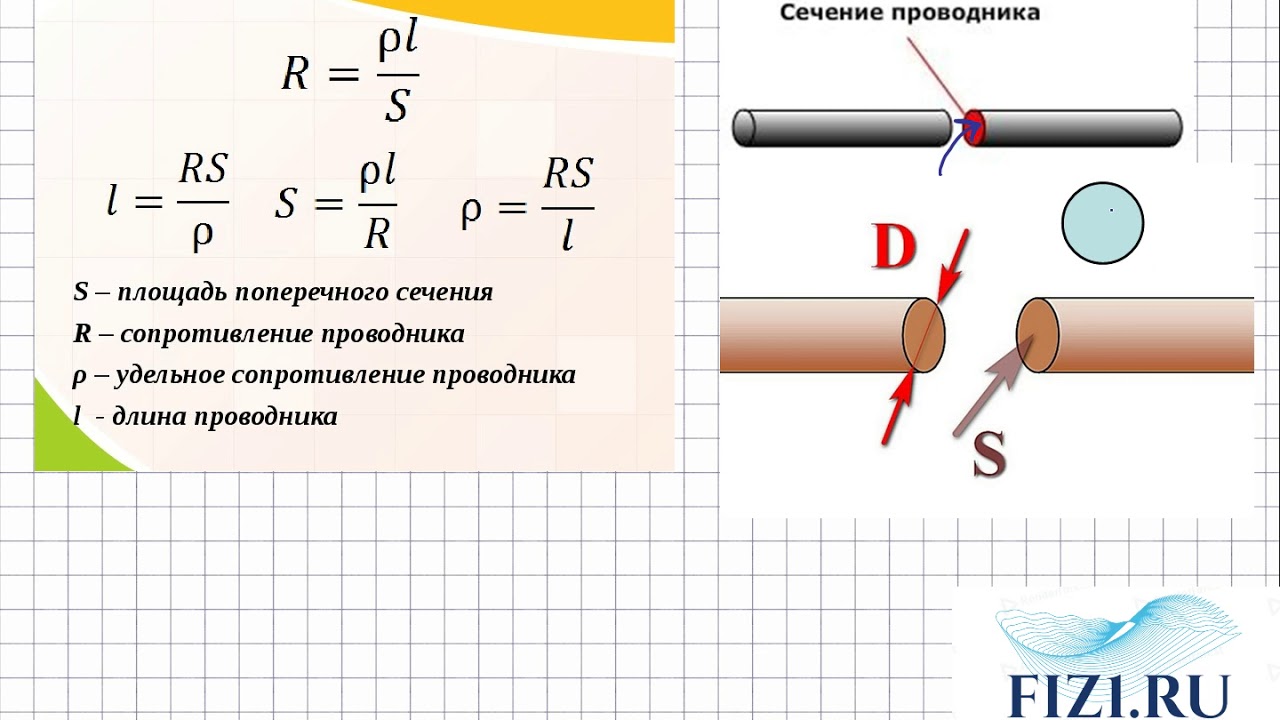 В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться. При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Цепи переменного тока

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

1. Измеряется частота переменного тока (как правило, 50 Гц).
2. Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота.

Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

1. Длины проводника.
2. Площади сечения — S.
3. Температуры.
4. Типа материала.
5. Емкости.
6. Индуктивности.
7. Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z. Меняется и закон для полной цепи.

Измерение электрической проводимости

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы, такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

1. Вытянуть вилку из сети.
2. Включить прибор, при этом произойдет разрядка конденсаторов.
3. Приступить к измерению или прозвонке.
4. Установить переключатель в режим измерения сопротивления.
5. Закоротить щупы прибора, чтобы удостовериться в его работоспособности (покажет очень малое сопротивление).
6. Измерить необходимый участок.

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника. В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Расчет сечения кабеля. По мощности, току, длине

Как рассчитать кабель по току, напряжению и длине. Кабели, как известно, бывают разного сечения, материала и с разным количеством жил. Какой из них надо выбрать, чтобы не переплачивать, и одновременно обеспечить безопасную стабильную работу всех электроприборов в доме. Для этого необходимо произвести расчет кабеля. Расчет сечения проводят, зная мощность приборов, питающихся от сети, и ток, который будет проходить по кабелю. Необходимо также знать несколько других параметров проводки.

Основные правила

При прокладке электросетей в жилых домах, гаражах, квартирах чаще всего используют кабель с резиновой или ПВХ изоляцией, рассчитанный на напряжение не более 1 кВ. Существуют марки, которые можно применять на открытом воздухе, в помещениях, в стенах (штробах) и трубах. Обычно это кабель ВВГ или АВВГ с разной площадью сечения и количеством жил.
Применяют также провода ПВС и шнуры ШВВП для подсоединения электрических приборов.

После расчета выбирается максимально допустимое значение сечения из ряда марок кабеля.

Основные рекомендации по выбору сечения находятся в Правилах устройства электроустановок (ПУЭ). Выпущено 6-е и 7-е издания, в которых подробно описывается, как прокладывать кабели и провода, устанавливать защиту, распределяющие устройства и другие важные моменты.

За нарушение правил предусмотрены административные штрафы. Но самое главное состоит в том, что нарушение правил может привести к выходу из строя электроприборов, возгоранию проводки и серьезным пожарам. Ущерб от пожара измеряется порой не денежной суммой, а человеческими жертвами.

Важность правильного выбора сечения

Почему расчет сечения кабеля так важен? Чтобы ответить, надо вспомнить школьные уроки физики.

Ток протекает по проводам и нагревает их. Чем сильнее мощность, тем больше нагрев. Активная мощность тока вычисляют по формуле:

P=U*I* cos φ=I²*R

R – активное сопротивление.

Как видно, мощность зависит от силы тока и сопротивления. Чем больше сопротивление, тем больше выделяется тепла, то есть тем сильнее провода нагреваются. Аналогично для тока. Чем он больше, тем больше греется проводник.

Сопротивление в свою очередь зависит от материала проводника, его длины и площади поперечного сечения.

R=ρ*l/S

ρ – удельное сопротивление;

l – длина проводника;

S– площадь поперечного сечения.

Видно, что чем меньше площадь, тем больше сопротивление. А чем больше сопротивление, тем проводник сильнее нагревается.

Площадь рассчитывается по формуле:

S=π*d²/4

d – диаметр.

Не стоит также забывать удельное сопротивление. Оно зависит от материала, из которого сделаны провода. Удельное сопротивление алюминия больше, чем меди. Значит, при одинаковой площади сильнее нагреваться будет алюминий. Сразу становится понятно, почему алюминиевые провода рекомендуют брать большего сечения, чем медные.

Чтобы каждый раз не вдаваться в длинный расчет сечения кабеля, были разработаны нормы выбора сечения проводов в таблицах.

Расчет сечения провода по мощности и току

Расчет сечения провода зависит от суммарной мощности, потребляемой электрическими приборами в квартире. Ее можно рассчитать индивидуально, или воспользоваться средними характеристиками.

Для точности расчетов составляют структурную схему, на которой изображены приборы. Узнать мощность каждого можно из инструкции или прочитать на этикетке. Наибольшая мощность у электрических печек, бойлеров, кондиционеров. Суммарная цифра должна получиться в диапазоне приблизительно 5-15 кВт.

Зная мощность, по формуле определяют номинальную силу тока:

I=(P*K)/(U*cos φ)

P – мощность в ваттах

U=220 Вольт

K=0,75 – коэффициент одновременного включения;

cos φ=1 для бытовых электроприборов;

Если сеть трехфазная, то применяют другую формулу:

I=P/(U*√3*cos φ)

U=380 Вольт

Рассчитав ток, надо воспользоваться таблицами, которые представлены в ПУЭ, и определить сечение провода. В таблицах указан допустимый длительный ток для медных и алюминиевых проводов с изоляцией различного типа. Округление всегда производят в большую сторону, чтобы был запас.

Можно также обратиться к таблицам, в которых сечение рекомендуют определять только по мощности.

Разработаны специальные калькуляторы, по которым определяют сечение, зная потребляемую мощность, фазность сети и протяженность кабельной линии. Следует обращать внимание на условия прокладки (в трубе или на открытом воздухе).

Влияние длины проводки на выбор кабеля

Если кабель очень длинный, то возникают дополнительные ограничения по выбору сечения, так как на протяженном участке происходят потери напряжения, которые в свою очередь приводят к дополнительному нагреву. Для расчета потерь напряжения используют понятие «момент нагрузки». Его определяют как произведение мощности в киловаттах на длину в метрах. Далее смотрят значение потерь в таблицах. Например, если потребляемая мощность составляет 2 кВт, а длина кабеля 40 м, то момент равняется 80 кВт*м.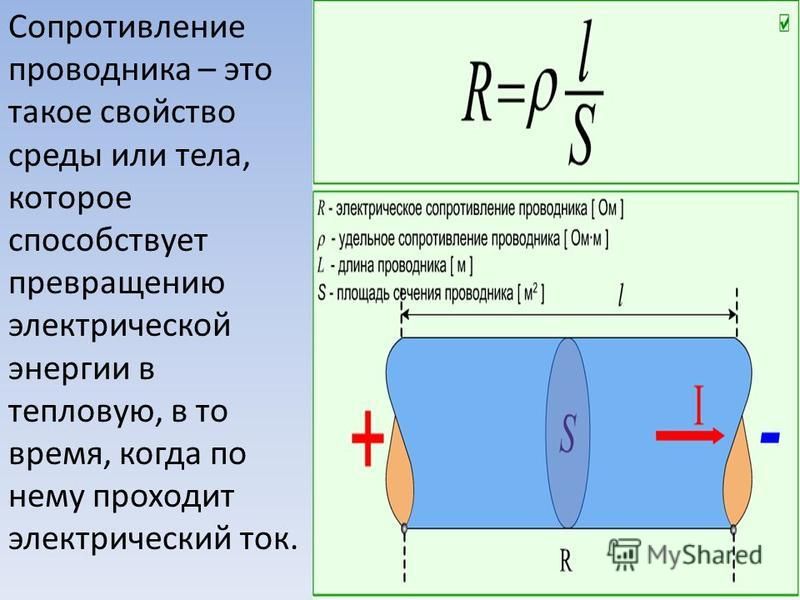 Для медного кабеля сечением 2,5 мм². это означает, что потери напряжения составляют 2-3%.

Если потери будут превышать 5%, то необходимо брать сечение с запасом, больше рекомендованного к использованию при заданном токе.

Расчетные таблицы предусмотрены отдельно для однофазной и трехфазной сети. Для трехфазной момент нагрузки увеличивается, так как мощность нагрузки распределяется по трем фазам. Следовательно, потери уменьшаются, и влияние длины уменьшается.

Потери напряжения важны для низковольтных приборов, в частности, газоразрядных ламп. Если напряжение питания составляет 12 В, то при потерях 3% для сети 220 В падение будет мало заметно, а для низковольтной лампы оно уменьшится почти вдвое. Поэтому важно размещать пускорегулирующие устройства максимально близко к таким лампам.

Расчет потерь напряжения выполняется следующим образом:

∆U = (P∙r0+Q∙x0)∙L/ Uн

P — активная мощность, Вт.

Q — реактивная мощность, Вт.

r0 — активное сопротивление линии, Ом/м.

x0 — реактивное сопротивление линии, Ом/м.

Uн – номинальное напряжение, В. (оно указывается в характеристиках электроприборов).

L — длинна линии, м.

Ну а если попроще для бытовых условий:

ΔU=I*R

R – сопротивление кабеля, рассчитывается по известной формуле R=ρ*l/S;

I – сила тока, находят из закона Ома;

Допустим, у нас получилось, что I=4000 Вт/220 В=18,2 А.

Сопротивление одной жилы медного провода длиной 20 м и площадью 1,5 мм кв. составило R=0,23 Ом. Суммарное сопротивление двух жил равняется 0,46 Ом.

Тогда ΔU=18,2*0,46=8,37 В

В процентном соотношении

8,37*100/220=3,8%

На длинных линиях от перегрузок и коротких замыканий устанавливают автоматические выключатели с тепловыми и электромагнитными расцепителями.

Похожие темы:

Формула удельного сопротивления

Сопротивление проводника

Удельное сопротивление

И вот мы плавно переходим к другому вопросу, что такое сопротивление проводника? Как я уже говорил выше, чем больше свободных электронов в веществе, тем лучше такое вещество проводит электрический ток. Следовательно, сопротивление проводника зависит от того, сколько свободных электронов содержит такой проводник. Поэтому, в физике есть такое понятие, как удельное сопротивление вещества.

Еще раз. Если в каком-либо веществе полно свободных электронов, то такое вещество будет хорошо проводить электрический ток. Если электронов еще меньше, то такое вещество будет плохо проводить электрический ток. А если свободных электронов почти нет, то такое вещество совсем не будет проводить ток. Поэтому, удельное сопротивление вещества показывает способность этого вещества препятствовать электрическому току, проходящему через него.

Удельное сопротивление выражается в единицах Ом × м.

Формула удельного сопротивления проводника

где

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м2

l – длина проводника, м

Площадь поперечного сечения проводника – это что-то типа этого:

площадь поперечного сечения проводника

Формула сопротивления проводника

Итак, мы теперь знаем такую физическую величину, как удельное сопротивление. Теперь мы с легкостью можем найти сопротивление проводника.

где

ρ – это удельное сопротивление, Ом × м

R – сопротивление проводника, Ом

S – площадь поперечного сечения, м2

l – длина проводника, м

Таблица удельных сопротивлений проводников

Материал проводника	Удельное сопротивление ρ в
Серебро Медь Золото Латунь Алюминий Натрий Иридий Вольфрам Цинк Молибден Никель Бронза Железо Сталь Олово Свинец Никелин (сплав меди, никеля и цинка) Манганин (сплав меди, никеля и марганца) Константан (сплав меди, никеля и алюминия) Титан Ртуть Нихром (сплав никеля, хрома, железа и марганца) Фехраль Висмут Хромаль	0,015 0,0175 0,023 0,025… 0,108 0,028 0,047 0,0474 0,05 0,054 0,059 0,087 0,095… 0,1 0,1 0,103… 0,137 0,12 0,22 0,42 0,43… 0,51 0,5 0,6 0,94 1,05… 1,4 1,15… 1,35 1,2 1,3… 1,5

Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм2 обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм2. Серебро — лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм2 обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.

Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.

Сопротивление проводника можно определить по формуле:

где r — сопротивление проводника в омах; ρ — удельное сопротивление проводника; l — длина проводника в м; S — сечение проводника в мм2.

Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм2.

Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм2.

Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.

Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм2. Определить необходимую длину проволоки.

Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.

Пример 5. Проволока сечением 0,5 мм2 и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.

Материал проводника характеризует его удельное сопротивление.

По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.

Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.

У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 — 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.

Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.

температурный коэффициент сопротивления — это изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, обозначается буквой α.

Если при температуре t0 сопротивление проводника равно r0, а при температуре t равно rt, то температурный коэффициент сопротивления

Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).

Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).

Таблица 2

Удельное электрическое сопротивление

Дальнейшие исследования позволили установить связь величины электрического сопротивления с его основными геометрическими размерами. Оказалось, что сопротивление проводника прямо пропорционально длине проводника L и обратно пропорционально площади поперечного сечения проводника S.

Эта функциональная связь хорошо описывается следующей формулой:

$ R = ρ *{ L\over S} $ (4)

Постоянная для каждого вещества величина ρ была названа удельным сопротивлением. Значение этого параметра зависит от плотности вещества, его кристаллической структуры, строения атомов и прочих внутренних характеристик вещества. Из формулы (4) можно получить формулу для расчета удельного сопротивления, если имеются экспериментальные значения для R, L и S:

$ ρ = R*{ S\over L } $ (5)

Для большинства известных веществ измерения были произведены и внесены в справочные таблицы электрических сопротивлений проводников.

Удельное сопротивление металлов, Ом*мм2/м

(при Т = 20С)

Серебро	0,016	Бронза (сплав)	0,1
Медь	0,017	Олово	0,12
Золото	0,024	Сталь (сплав)	0,12
Алюминий	0,028	Свинец	0,21
Иридий	0,047	Никелин (сплав)	0,42
Молибден	0,054	Манганин (сплав)	0,45
Вольфрам	0,055	Константан (сплав)	0,48
Цинк	0,06	Титан	0,58
Латунь (сплав)	0,071	Ртуть	0,958
Никель	0,087	Нихром (сплав)	1,1
Платина	0,1	Висмут	1,2

Экспериментально было обнаружено, что с понижением температуры сопротивление металлов уменьшается. При приближении к температуре абсолютного нуля, которая равна -273С, сопротивление некоторых металлов стремится к нулю. Это явление называется сверхпроводимостью. Атомы и молекулы как бы “замораживаются”, прекращают любое движение и не оказывают сопротивления потоку электронов.

Что мы узнали?

Итак, мы узнали, что способность проводника ограничивать величину электрического тока называется сопротивлением. Величину сопротивления проводника можно определить с помощью закона Ома, измерив напряжение и ток. Если известно удельное сопротивление проводника, его длина и поперечное сечение, то сопротивление можно вычислить с помощью формулы (4), не измеряя ток и напряжение.

Обобщение понятия удельного сопротивления

Кусок резистивного материала с электрическими контактами на обоих концах

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}.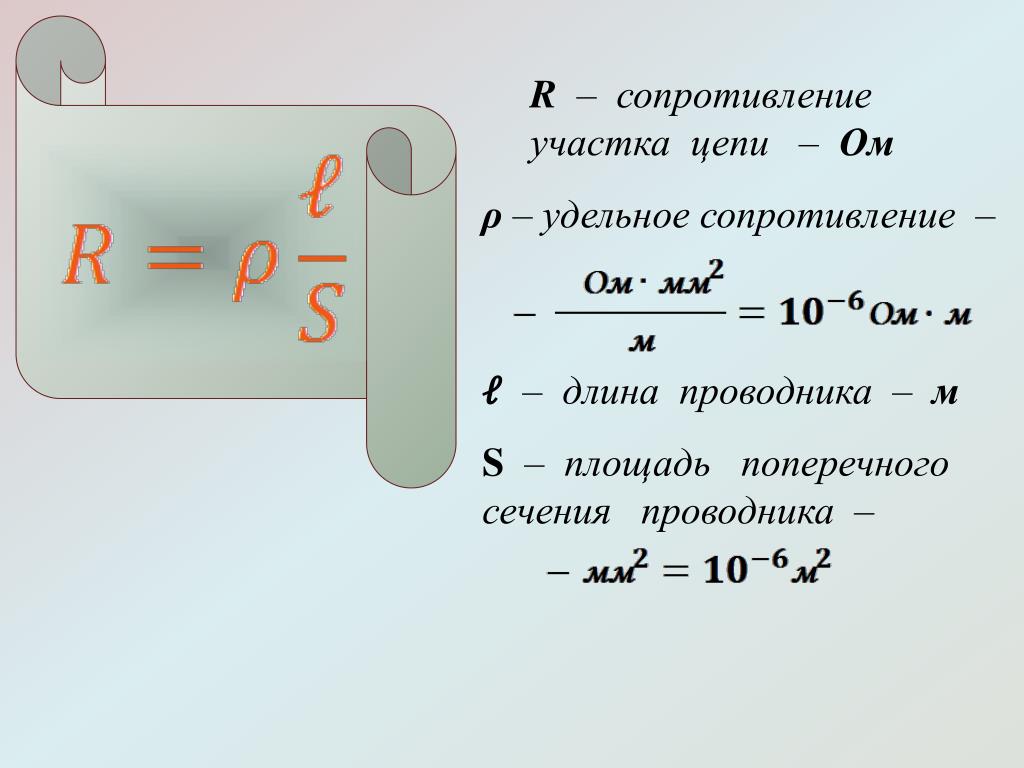 {3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}

В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.

Тензор ρij{\displaystyle \rho _{ij}}симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.

Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать
ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую

Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}

Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.

Обобщение понятия удельного сопротивления[править | править код]

Кусок резистивного материала с электрическими контактами на обоих концах

Удельное сопротивление можно определить также для неоднородного материала, свойства которого меняются от точки к точке. В этом случае оно является не константой, а скалярной функцией координат — коэффициентом, связывающим напряжённость электрического поля E→(r→){\displaystyle {\vec {E}}({\vec {r}})} и плотность тока J→(r→){\displaystyle {\vec {J}}({\vec {r}})} в данной точке r→{\displaystyle {\vec {r}}}. Указанная связь выражается :

E→(r→)=ρ(r→)J→(r→).{\displaystyle {\vec {E}}({\vec {r}})=\rho ({\vec {r}}){\vec {J}}({\vec {r}}).}

Эта формула справедлива для неоднородного, но изотропного вещества. Вещество может быть и анизотропно (большинство кристаллов, намагниченная плазма и т. д.), то есть его свойства могут зависеть от направления. В этом случае удельное сопротивление является зависящим от координат тензором второго ранга, содержащим девять компонент ρij{\displaystyle \rho _{ij}}. {3}\rho _{ij}({\vec {r}})J_{j}({\vec {r}}).}

В анизотропном, но однородном веществе тензор ρij{\displaystyle \rho _{ij}} от координат не зависит.

Тензор ρij{\displaystyle \rho _{ij}}симметричен, то есть для любых i{\displaystyle i} и j{\displaystyle j} выполняется ρij=ρji{\displaystyle \rho _{ij}=\rho _{ji}}.

Как и для всякого симметричного тензора, для ρij{\displaystyle \rho _{ij}} можно выбрать ортогональную систему декартовых координат, в которых матрица ρij{\displaystyle \rho _{ij}} становится диагональной, то есть приобретает вид, при котором из девяти компонент ρij{\displaystyle \rho _{ij}} отличными от нуля являются лишь три: ρ11{\displaystyle \rho _{11}}, ρ22{\displaystyle \rho _{22}} и ρ33{\displaystyle \rho _{33}}. В этом случае, обозначив ρii{\displaystyle \rho _{ii}} как ρi{\displaystyle \rho _{i}}, вместо предыдущей формулы получаем более простую

Ei=ρiJi.{\displaystyle E_{i}=\rho _{i}J_{i}.}

Величины ρi{\displaystyle \rho _{i}} называют главными значениями тензора удельного сопротивления.

Единица измерения электрического сопротивления

Единицу измерения сопротивления назвали в честь Георга Ома. В Международной интернациональной системе единиц СИ электрическое сопротивление 1 Ом имеет участок цепи, на котором падает напряжение равное 1 В при силе тока 1 А:

$ 1 Ом = { 1 В\over 1 A} $ (3)

Для определения сопротивления с помощью закона Ома требуется измерить предварительно напряжение и ток. Двух измерений можно избежать с помощью прибора, разработанного для непосредственного измерения сопротивления. Прибор называется омметром.

Рис. 3. Приборы для измерения сопротивления – омметры.

На практике большинство используемых в электрических схемах и приборах сопротивлений гораздо больше, чем 1 Ом. Поэтому чаще применяются кратные единицы измерений : килоом и мегом:

• 1 кОм = 1000 Ом;
• 1 МОм = 1000 000 Ом.

Последовательное соединение проводников

Сопротивление при последовательном соединении проводников

Последовательное соединение проводников – это когда к одному проводнику мы соединяем другой проводник и так по цепочке. Это и есть последовательное соединение проводников. Их можно соединять с друг другом сколь угодно много.

последовательное соединение резисторов

Чему же будет равняться их общее сопротивление? Оказывается, все просто. Оно будет равняться сумме всех сопротивлений проводников в этой цепи.

Получается, можно записать, что

формула при последовательном соединении резисторов

Пример

У нас есть 3 проводника, которые соединены последовательно. Сопротивление первого 3 Ома, второго 5 Ом, третьего 2 Ома. Найти их общее сопротивление в цепи.

Решение

R_общее =R₁ + R₂ + R₃ = 3+5+2=10 Ом.

То есть, как вы видите, цепочку из 3 резисторов мы просто заменили на один резистор R_AB .

показать на реальном примере с помощью мультиметра

Сила тока через последовательное соединение проводников

Что будет, если мы подадим напряжение на концы такого резистора? Через него сражу же побежит электрический ток, сила которого будет вычисляться по закону Ома I=U/R.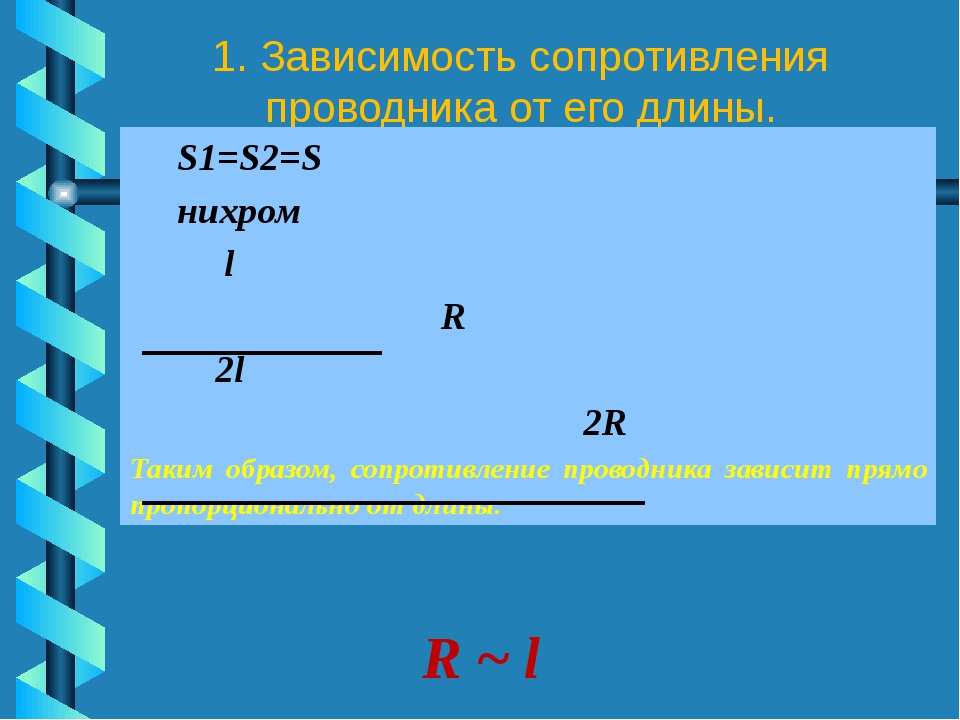

Получается, если через резистор R_AB течет какой-то определенный ток, следовательно, если разложить наш резистор на составляющие R₁ , R₂ , R₃ , то получится, что через них течет та же самая сила тока, которая текла через резистор R_AB .

сила тока через последовательное соединение проводников

Получается, что при последовательном соединении проводников сила тока, которая течет через каждый проводник одинакова. То есть через резистор R₁ течет такая же сила тока, как и через резистор R₂ и такая же сила тока течет через резистор R₃ .

Напряжение при последовательном соединении проводников

Давайте еще раз рассмотрим цепь с тремя резисторами

Как мы уже знаем, при последовательном соединении через каждый резистор проходит одна и та же сила тока. Но вот что будет с напряжением на каждом резисторе и как его найти?

Оказывается, все довольно таки просто. Для этого надо снова вспомнить закон дядюшки Ома и просто вычислить напряжение на  любом резисторе. Давайте так и сделаем.

Пусть у нас будет цепь с такими параметрами.

Мы теперь знаем, что сила тока в такой цепи будет везде одинакова. Но какой ее номинал? Вот в чем загвоздка. Для начала нам надо привести эту цепь к такому виду.

Получается, что в данном случае R_AB =R₁ + R₂ + R₃ = 2+3+5=10 Ом. Отсюда уже находим силу тока по закону Ома I=U/R=10/10=1 Ампер.

Половина дела сделано. Теперь осталось узнать, какое напряжение падает на каждом резисторе. То есть нам надо найти значения U_R1 , U_R2 , U_R3  . Но как это сделать?

Да все также, через закон Ома. Мы знаем, что через каждый резистор проходит сила тока 1 Ампер, мы уже вычислили это значение. Закон ома гласит I=U/R , отсюда получаем, что U=IR.

Следовательно,

U_R1 = IR₁ =1×2=2 Вольта

U_R2 = IR₂ = 1×3=3 Вольта

U_R3 = IR₃ =1×5=5 Вольт

Теперь начинается самое интересное. Если сложить все падения напряжений на резисторах, то можно получить… напряжение источника! Он у нас равен 10 Вольт.

Получается

U=U_R1+U_R2+U_R3

Мы получили самый простой делитель напряжения.

Вывод: сумма падений напряжений при последовательном соединении равняется напряжению питания.

Оцените статью:

Зависимость сопротивления от длины проводника формула. Электросопротивление и удельная электропроводность

Презентация на тему “Расчет сопротивления проводников” по физике в формате powerpoint. Цель данной презентации для школьников 8 класса – научить учащихся измерять сопротивления проводников, устанавливать зависимость сопротивления проводника от его длины, площади поперечного сечения и вещества, из которого он изготовлен. Автор презентации: Нахушева Марита Мухамедовна, учитель физики.

Фрагменты из презентации

Наука начинается с тех пор, как начинают измерять. Точная наука немыслима без меры. Д.И.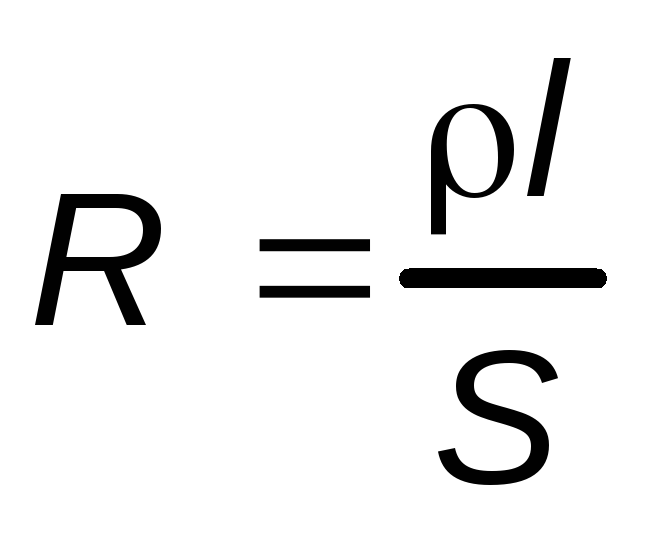 Менделеев

Методы измерения сопротивления проводников

• Авомметр.
• Метод вольтметра и амперметра

Задание 1. Зависимость сопротивления проводника от длины.

Собираем схему 3, нихромовую проволоку (клеммы 1, 2) подключить к источнику тока и амперметру. Меняя длину проводника наблюдать изменение силы тока.

Вывод 1.

• При уменьшении длины нихромовой проволоки сила тока увеличивается, при увеличении длины сила тока уменьшается.
• Следовательно: при L ↓ ~ I ~ R↓ R ~ L

Задание 2. Зависимость сопротивления проводника от площадь сечения.

Собираем схему 3, сперва одну нихромовую проволоку (клеммы 1, 2) подключить к источнику тока и амперметру, затем две нихромовые проволоки (клеммы 1-3, 2-4) подключить к источнику тока и амперметру. Наблюдать изменение силы тока.

Вывод 2.

• При уменьшении площади сечения нихромовой проволоки сила тока уменьшается, при увеличении площади сечения сила тока увеличивается.
• Следовательно: при S ↓ ~ I ↓ ~ R R ~ 1/S

Задание 3. Зависимость сопротивления проводника от рода вещества.

Собираем схему 3, сперва нихромовую проволоку (клеммы 1, 2) подключить к источнику тока и амперметру, затем стальную проволоку (клеммы 5, 6) подключить к источнику тока и амперметру. Наблюдать изменение силы тока.

Вывод 3.

• Сила тока при подключении нихромовой проволоки больше, чем при подключении стальной (железной) проволоки.
• По таблице сравниваем удельные сопротивления этих веществ.
• Следовательно: если I ~ R↓ ~ ρ↓ R ~ ρ

Выводы

• Сопротивление зависит от длины проводника, чем больше длина проводника тем больше его сопротивление.
• Сопротивление проводника зависит от площади поперечного сечения: чем меньше площадь сечения проводника, тем больше сопротивление.
• Сопротивление проводника зависит от рода вещества (материала), из которого он изготовлен.
• Зависимость сопротивления от геометрических размеров проводника (длины и площади поперечного сечения) и вещества, из которого он изготовлен, впервые установил Георг Ом.
• Это выражение позволяет вычислять длину проводника, поперечное сечение и удельное сопротивление проводника.

Последовательное соединение

При последовательном соединении трех проводников, сопротивление увеличивается, так как длина проводника увеличивается (R ~ L, L ~ R ).

Параллельное соединение

При параллельном соединении площадь сечения проводника увеличивается, сопротивление будет уменьшаться (при S ↓ ~ R).

Задача

• Задача. Определите сопротивление телеграфного провода между Южно-Сахалинском и Томари, если расстояние между городами 180 км, а провода сделаны из железной проволоки площадью поперечного сечения 12 мм2
• Задача. Рассчитайте сопротивление медного контактного провода, подвешенного для питания трамвайного двигателя, если длина провода равна 5 км, а площадь поперечного сечения – 0,65 см2 .
• Задача. Какой длины надо взять медную проволоку площадью поперечного сечения 0,5 мм2 , чтобы сопротивление ее было равно 34 Ом?
• Задача. Вычислите, каким сопротивлением обладает нихромовый проводник длиной 5 м и площадью поперечного сечения 0,75 мм2 .

Cтраница 1

Зависимость электрического сопротивления проводников от их геометрических размеров состоит в том, что по мере увеличения длины проводника и уменьшения площади поперечного сечения сопротивление возрастает.  

Термочувствительные преобразователи основаны на зависимости электрического сопротивления проводника (или полупроводника) от температуры.  

В термометрах сопротивления используется зависимость электрического сопротивления проводников от температуры. Стандартизованы платиновый и медный термометры сопротивления.  

Термочувствительные преобразователи основаны на зависимости электрического сопротивления проводника (или полупроводника), от температуры.  

Их действие основано на зависимости электрического сопротивления проводников от температуры. Графики зависимости сопротивления их от температуры показаны на рис. 2.16. Практически – это прямые линии. Значение ТКЭС меди выше, чем платины, поэтому ТСМ чувствительнее к изменению температуры, этим и объясняется большая крутизна графика. Однако верхний температурный предел измерения для ТСМ равен 200 С, а для ТСП – плюс 1100 С. Нижние пределы соответственно равны минус 200 и минус 260 С.  

Принцип действия преобразователей основан на зависимости электрического сопротивления проводников или пвлупроводни-ков от температуры.  

Принцип действия преобразователей основан на зависимости электрического сопротивления проводников или полупроводников от температуры.  

Технические характеристики показывающих манометрических термометров.

Действие этих термометров основано на использовании зависимости электрического сопротивления проводника (тонкой проволоки) от температуры. Термометр сопротивления состоит из обмотки, изготовленной из тонкой проволоки на специальном каркасе, выполненном из изоляционного материала. Чувствительный элемент заключен в защитную гильзу.  

Датчики из термосопротивлений основаны на использовании зависимости электрического сопротивления проводников от температуры. Существуют два способа использования термосопротивлений в виде датчиков. При первом способе температура термосопротивления определяется температурой окружающей среды, гак как ток, протекающий по термосопротивле – Нить нию, выбирается достаточно малым, чтобы выделяемое им тепло не влияло на температуру термосопротивления. Этот способ применяется в датчиках температуры.  

Датчики из термосопротивлений основаны на использовании зависимости электрического сопротивления проводников от темпе ратуры. Существуют два способа использования термосопротивлений ь виде датчиков. При первом способе температура термосопротивления определяется температурой окружающей среды, гак как ток, протекающий по термосопротивлению, выбирается достаточно малым, чтобы выделяемое им тепло не влияло на температуру термосопротивления. Этот способ применяется в датчиках температуры.  

Тензочув-ствительные (проволочные) преобразователи основаны на зависимости электрического сопротивления проводника от вызываемого в нем механического напряжения.  

Тензо-чувствительные (проволочные) преобразователи основаны на зависимости электрического сопротивления проводника от вызываемого в нем механического напряжения.  

Для существования в проводнике постоянного тока, то есть, движения электронов с постоянной скоростью необходимо, чтобы непрерывно действовала внешняя сила ($F$), равная:

где $q_e$ — заряд электрона. Следовательно, электроны в проводнике движутся с трением. Или иначе говорят, что проводники имеют электросопротивление (R). Электросопротивление для различных проводников различно и может зависеть от материала, из которого изготовлен проводник и от его геометрических размеров.

Для измерения сопротивления можно использовать закон Ома. Для этого измеряют напряжение на концах проводника и силу тока, который течет через проводник, используют закон Ома для однородного проводника, вычисляют сопротивление:

Зависимость сопротивления от геометрических размеров и материала проводника

Если провести ряд экспериментов по измерению сопротивления однородного проводника постоянного сечения, но разной длины ($l$), то получится, что его электросопротивление длине ($R\sim l$).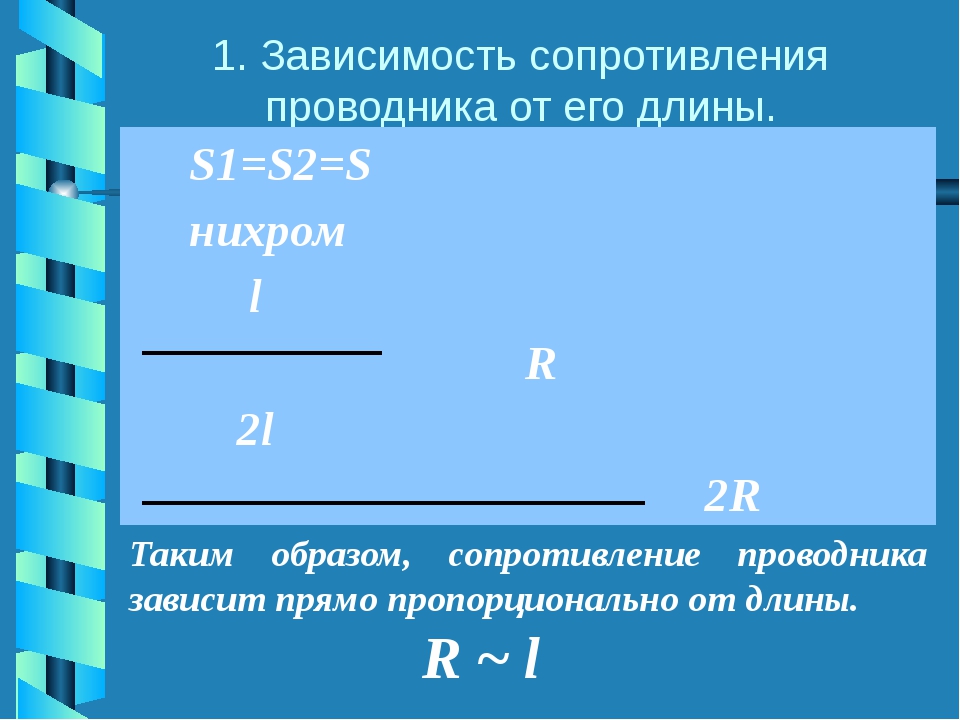

Следующие эксперименты проводим для однородного проводника, одного и того же материала, одной длины, но разного сечения, то получаем, что сопротивление обратно пропорционально площади сечения ($R\sim \frac{1}{S}$).

И третий опыт, по исследованию электросопротивления проводников проводят с проводниками из разных материалов, с одинаковой длиной и сечением. Результат: сопротивление зависит и от материала проводника. Все полученные результаты выражает следующая формула, для вычисления сопротивления:

где $\rho $ — удельное сопротивление материала.

Сопротивлением участка цепи между сечениями 1 и 2 ($R_{12}$) называют интеграл:

Для однородного (с точки зрения удельного сопротивления) цилиндрического проводника ($\rho =const,S=const\ $) сопротивление вычисляется по формуле (3).

Основной единицей измерения сопротивления в СИ является Ом. $1Ом=\frac{1В}{1А}.$

Удельное сопротивление

Удельное сопротивление материала равно сопротивлению из какого то конкретного вещества, высотой 1 м и с площадью поперечного сечения $1 м^2$. {-3}\frac{1}{K}$.

Температурный коэффициент сопротивления данного вещества определен как:

$\alpha $ дает относительное приращение сопротивления при увеличении температуры на один градус. То есть исходя из (6) мы получаем, нелинейную зависимость удельного сопротивления от температуры, однако $\alpha $ изменяется с ростом (падением) температуры не так сильно, и эту нелинейность в большинстве случаев не учитывают. Для металлов $\alpha >0,\ $для $\alpha

Зависимость удельного сопротивления от температуры объясняется, зависимостью средней длинны свободного пробега носителя заряда от температуры. Это свойство используют в разного рода измерительных приборах и автоматических устройствах.

Удельная электропроводность вещества

Величина обратная удельному сопротивлению называется удельной электропроводностью ($\sigma $):

В системе СИ основная единица измерения электропроводности 1 $\frac{сименс}{м}$ ($\frac{См}{м}$). Величина $\sigma $ характеризует способность вещества проводить электрический ток. Электропроводимость зависит от химической природы вещества и условий (например, температуры) при которых это вещество находится. Если мы видели из уравнения (4), что $\rho \sim t$, то, следовательно $\sigma \sim \frac{1}{t}.\ $Надо отметить, что при низких температурах данные зависимости нарушаются. Наблюдается явление сверхпроводимости. При $T\to 0,\ $ у абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле удельная сопротивление должно быть равно нулю, соответственно, удельная проводимость бесконечна.

Пример 1

Задание: Вычислите сопротивление проводника (R), если на одном конце его поддерживается температура $t_1$, на другом $t_2$. Градиент температуры вдоль оси проводника постоянный. Сопротивление этого проводника при температуре равной 00С равно $R_0$.

Исходя из постоянства градиента температуры вдоль оси проводника, запишем, что:

\[\frac{dt}{dx}=k\ \left(1.1\right),\]

где $k=const.$ Следовательно, можно найти закон изменения температуры при движении вдоль проводника, то есть t(x). 4}.$

Удельное сопротивление и электропроводимость: формулы и объяснение

В данной статье мы подробно разберем что такое удельное сопротивление и электропроводность, ясно опишем все формулы с помощью примеров задач, а так же дадим вам таблицу удельных сопротивлений некоторых проводников.

Описание

Закон Ома гласит, что, когда источник напряжения (V) подается между двумя точками в цепи, между ними будет протекать электрический ток (I), вызванный наличием разности потенциалов между этими двумя точками. Количество протекающего электрического тока ограничено величиной присутствующего сопротивления (R). Другими словами, напряжение стимулирует протекание тока (движение заряда), но это сопротивление препятствует этому.

Мы всегда измеряем электрическое сопротивление в Омах, где Ом обозначается греческой буквой Омега, Ω. Так, например: 50 Ом, 10 кОм или 4,7 МОм и т.д. Проводники (например, провода и кабели) обычно имеют очень низкие значения сопротивления (менее 0,1 Ом), и, таким образом, мы можем пренебречь ими, как мы предполагаем в расчетах анализа цепи, что провода имеют ноль сопротивление. С другой стороны, изоляторы (например, пластиковые или воздушные), как правило, имеют очень высокие значения сопротивления (более 50 МОм), поэтому мы можем их игнорировать и для анализа цепи, поскольку их значение слишком велико.

Но электрическое сопротивление между двумя точками может зависеть от многих факторов, таких как длина проводников, площадь их поперечного сечения, температура, а также фактический материал, из которого он изготовлен. Например, давайте предположим, что у нас есть кусок провода (проводник), который имеет длину L, площадь поперечного сечения A и сопротивление R, как показано ниже.

Электрическое сопротивление R этого простого проводника является функцией его длины, L и площади поперечного сечения A. Закон Ома говорит нам, что для данного сопротивления R ток, протекающий через проводник, пропорционален приложенному напряжению, поскольку I = V / R. Теперь предположим, что мы соединяем два одинаковых проводника вместе в последовательной комбинации, как показано на рисунке.

Здесь, соединив два проводника вместе в последовательной комбинации, то есть, к концу, мы фактически удвоили общую длину проводника (2L), в то время как площадь поперечного сечения A остается точно такой же, как и раньше. Но помимо удвоения длины, мы также удвоили общее сопротивление проводника, дав 2R как: 1R + 1R = 2R.

Таким образом , мы можем видеть , что сопротивление проводника пропорционально его длину, то есть: R ∝ L. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально больше, чем оно длиннее.

Отметим также, что, удваивая длину и, следовательно, сопротивление проводника (2R), чтобы заставить тот же ток I, чтобы течь через проводник, как и раньше, нам нужно удвоить (увеличить) приложенное напряжение I = (2 В) / (2R). Далее предположим, что мы соединяем два идентичных проводника вместе в параллельной комбинации, как показано.

Здесь, соединяя два проводника в параллельную комбинацию, мы фактически удвоили общую площадь, дающую 2А, в то время как длина проводников L остается такой же, как у исходного одиночного проводника.  Но помимо удвоения площади, путем параллельного соединения двух проводников мы фактически вдвое сократили общее сопротивление проводника, получив 1 / 2R, поскольку теперь каждая половина тока протекает через каждую ветвь проводника.

Таким образом, сопротивление проводника обратно пропорционально его площади, то есть: R 1 / ∝ A или R ∝ 1 / A. Другими словами, мы ожидаем, что электрическое сопротивление проводника (или провода) будет пропорционально меньше, чем больше его площадь поперечного сечения.

Кроме того, удваивая площадь и, следовательно, вдвое увеличивая суммарное сопротивление ветви проводника (1 / 2R), для того же тока, чтобы I протекал через параллельную ветвь провода, как раньше, нам нужно только наполовину уменьшить приложенное напряжение I = (1 / 2V) / (1 / 2R).

Надеемся, мы увидим, что сопротивление проводника прямо пропорционально длине (L) проводника, то есть: R ∝ L, и обратно пропорционально его площади (A), R ∝ 1 / A.  Таким образом, мы можем правильно сказать, что сопротивление это:

Пропорциональность сопротивления

Но помимо длины и площади проводника, мы также ожидаем, что электрическое сопротивление проводника будет зависеть от фактического материала, из которого он изготовлен, потому что разные проводящие материалы, медь, серебро, алюминий и т.д., имеют разные физические и электрические свойства. Таким образом, мы можем преобразовать знак пропорциональности (∝) вышеприведенного уравнения в знак равенства, просто добавив «пропорциональную константу» в вышеприведенное уравнение, давая:

Уравнение удельного электрического сопротивления

Где: R — сопротивление в омах (Ω), L — длина в метрах (м), A — площадь в квадратных метрах (м ² ), и где известна пропорциональная постоянная ρ (греческая буква «rho») — удельное сопротивление .

Удельное электрическое сопротивление

Удельное электрическое сопротивление конкретного материала проводника является мерой того, насколько сильно материал противостоит потоку электрического тока через него.  Этот коэффициент удельного сопротивления, иногда называемый его «удельным электрическим сопротивлением», позволяет сравнивать сопротивление различных типов проводников друг с другом при определенной температуре в соответствии с их физическими свойствами без учета их длины или площади поперечного сечения. Таким образом, чем выше значение удельного сопротивления ρ, тем больше сопротивление, и наоборот.

Например, удельное сопротивление хорошего проводника, такого как медь, составляет порядка 1,72 х 10 ^-8 Ом (или 17,2 нОм), тогда как удельное сопротивление плохого проводника (изолятора), такого как воздух, может быть значительно выше 1,5 х 10 ¹⁴ или 150 трлн.

Такие материалы, как медь и алюминий, известны низким уровнем удельного сопротивления, благодаря чему электрический ток легко проходит через них, что делает эти материалы идеальными для изготовления электрических проводов и кабелей. Серебро и золото имеют очень низкие значения удельного сопротивления, но по понятным причинам дороже делать из них электрические провода.

Тогда факторы, которые влияют на сопротивление (R) проводника в омах, могут быть перечислены как:

• Удельное сопротивление (ρ) материала, из которого сделан проводник.
• Общая длина (L) проводника.
• Площадь поперечного сечения (А) проводника.
• Температура проводника.

Пример удельного сопротивления № 1

Рассчитайте общее сопротивление постоянному току 100-метрового рулона медного провода 2,5 мм ², если удельное сопротивление меди при 20 ^o C составляет 1,72 x 10 ^-8  Ом метр.

Приведенные данные: удельное сопротивление меди при 20 ^o C составляет 1,72 x 10 ^-8 , длина катушки L = 100 м, площадь поперечного сечения проводника составляет 2,5 мм ², что дает площадь: A = 2,5 x 10 ^-6 м ² .

Ответ: 688 МОм или 0,688 Ом.

Удельное электрическое сопротивление материала

Ранее мы говорили, что удельное сопротивление — это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения проводника, таким образом, показывая, что удельное сопротивление ρ имеет размеры в Ом-метрах или Ом · м, как это обычно пишется. Таким образом, для конкретного материала при определенной температуре его удельное электрическое сопротивление определяется как.

Электрическая проводимость

Хотя как электрическое сопротивление (R), так и удельное сопротивление ρ, являются функцией физической природы используемого материала, а также его физической формы и размера, выраженных его длиной (L) и площадью его сечения ( А), Проводимость или удельная проводимость относится к легкости, с которой электрический ток проходит через материал.

Проводимость (G) является обратной величиной сопротивления (1 / R) с единицей проводимости, являющейся сименсом (S), и ей дается перевернутый символ омов mho, ℧.  Таким образом, когда проводник имеет проводимость 1 сименс (1S), он имеет сопротивление 1 Ом (1 Ом). Таким образом, если его сопротивление удваивается, проводимость уменьшается вдвое, и наоборот, как: Сименс = 1 / Ом, или Ом = 1 / Ом.

В то время как сопротивление проводников дает степень сопротивления потоку электрического тока, проводимость проводника указывает на легкость, с которой он пропускает электрический ток. Таким образом, металлы, такие как медь, алюминий или серебро, имеют очень большие значения проводимости, что означает, что они являются хорошими проводниками.

Проводимость, σ (греческая буква сигма), является обратной величиной удельного сопротивления. Это 1 / ρ и измеряется в сименах на метр (S / m). Поскольку электропроводность σ = 1 / ρ, предыдущее выражение для электрического сопротивления R можно переписать в виде:

Электрическое сопротивление как функция проводимости

Тогда мы можем сказать, что проводимость — это эффективность, посредством которой проводник пропускает электрический ток или сигнал без потери сопротивления.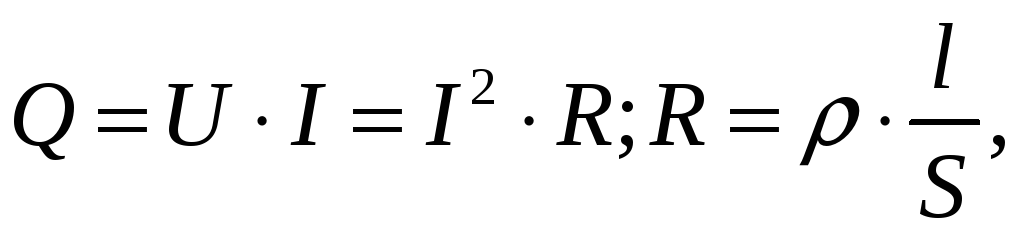 Поэтому материал или проводник, который имеет высокую проводимость, будет иметь низкое удельное сопротивление, и наоборот, поскольку 1 сименс (S) равен 1 Ом ^-1 . Таким образом, медь, которая является хорошим проводником электрического тока, имеет проводимость 58,14 x 10 ⁶ Симен на метр.

Пример удельного сопротивления №2

Кабель длиной 20 метров имеет площадь поперечного сечения 1 мм ² и сопротивление 5 Ом. Рассчитать проводимость кабеля.

Приведенные данные: сопротивление постоянному току, R = 5 Ом, длина кабеля, L = 20 м, а площадь поперечного сечения проводника составляет 1 мм ^{2, что} дает площадь: A = 1 x 10 ^-6 м ² .

Ответ: 4 мега-симена на метр длины.

Таблица удельных сопротивлений проводников

Проводник	Удельное сопротивление ρ	Температурный коэффициент α
Алюминий	0,028	4,2
Бронза	0,095 — 0,1	—
Висмут	1,2	—
Вольфрам	0,05	5
Железо	0,1	6
Золото	0,023	4
Иридий	0,0474	—
Константан	0,5	0,05
Латунь	0,025 — 0,108	0,1-0,4
Магний	0,045	3,9
Манганин	0,43 — 0,51	0,01
Медь	0,0175	4,3
Молибден	0,059	—
Нейзильбер	0,2	0,25
Натрий	0,047	—
Никелин	0,42	0,1
Никель	0,087	6,5
Нихром	1,05 — 1,4	0,1
Олово	0,12	4,4
Платина	0. 107	3,9
Ртуть	0,94	1,0
Свинец	0,22	3,7
Серебро	0,015	4,1
Сталь	0,103 — 0,137	1-4
Титан	0,6	—
Фехраль	1,15 — 1,35	0,1
Хромаль	1,3 — 1,5	—
Цинк	0,054	4,2
Чугун	0,5-1,0	1,0

Где: удельное сопротивление ρ измеряется в Ом*мм²/м и температурный коэффициент электрического сопротивления металлов α измеряется в 10 ^-3*C^-1(или K ^-1) .

Краткое описание удельного сопротивления

Мы поговорили в этой статье об удельном сопротивлении, что удельное сопротивление — это свойство материала или проводника, которое указывает, насколько хорошо материал проводит электрический ток. Мы также видели, что электрическое сопротивление (R) проводника зависит не только от материала, из которого сделан проводник, меди, серебра, алюминия и т.д., но также от его физических размеров.

Сопротивление проводника прямо пропорционально его длине (L) как R ∝ L. Таким образом, удвоение его длины удвоит его сопротивление, в то время как последовательное удвоение проводника уменьшит вдвое его сопротивление. Также сопротивление проводника обратно пропорционально его площади поперечного сечения (A) как R ∝ 1 / A. Таким образом, удвоение его площади поперечного сечения уменьшило бы его сопротивление вдвое, тогда как удвоение его площади поперечного сечения удвоило бы его сопротивление.

Мы также узнали, что удельное сопротивление (символ: ρ) проводника (или материала) связано с физическим свойством, из которого он изготовлен, и варьируется от материала к материалу. Например, удельное сопротивление меди обычно дается как: 1,72 х 10 ^-8 Ом · м. Удельное сопротивление конкретного материала измеряется в единицах Ом-метров (Ом), которое также зависит от температуры.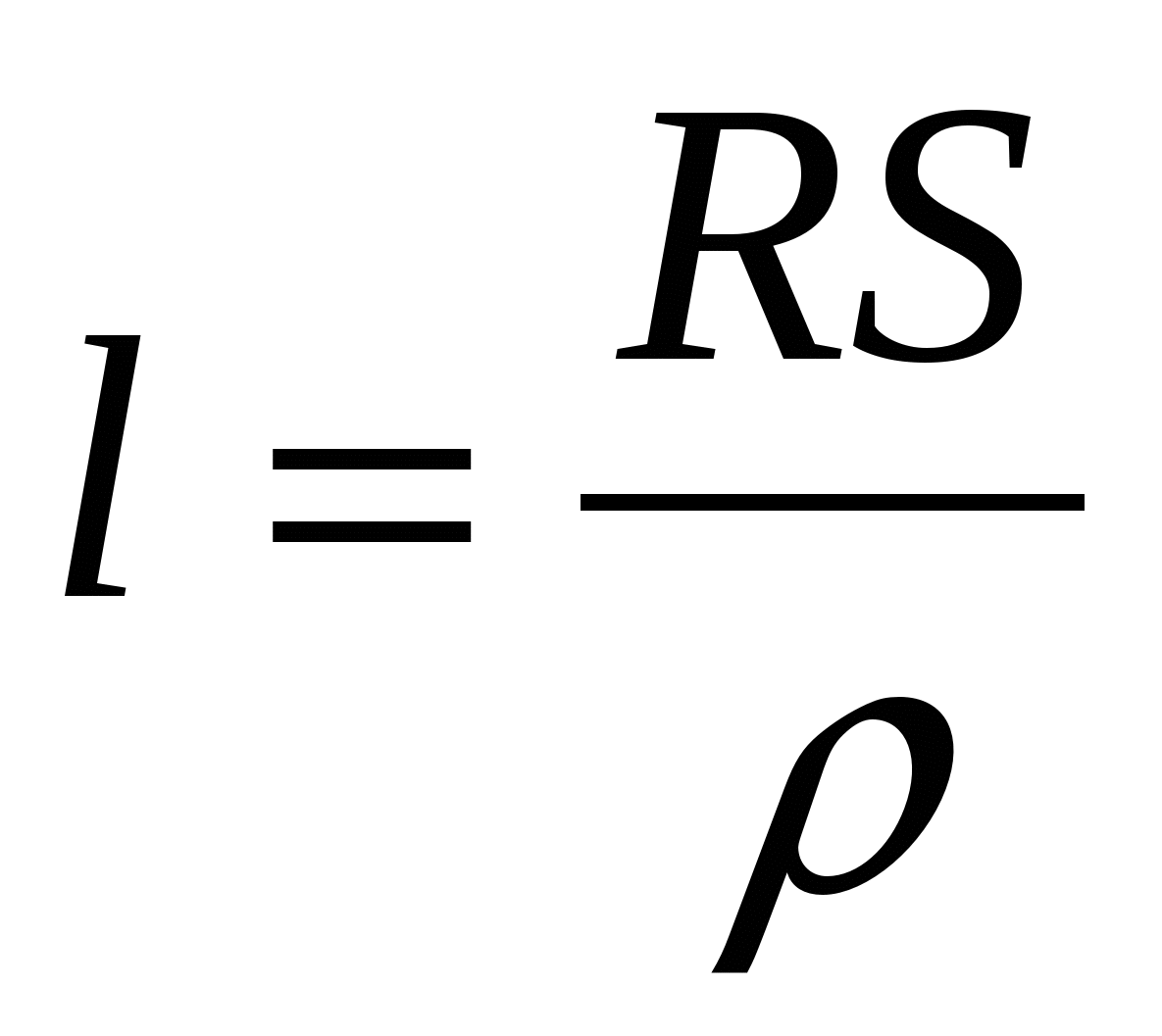

В зависимости от значения удельного электрического сопротивления конкретного материала его можно классифицировать как «проводник», «изолятор» или «полупроводник». Обратите внимание, что полупроводники — это материалы, в которых их проводимость зависит от примесей, добавляемых в материал.

Удельное сопротивление также важно в системах распределения электроэнергии, так как эффективность системы заземления для системы электропитания и распределения сильно зависит от удельного сопротивления земли и материала почвы в месте расположения системы.

Проводимость — это имя, данное движению свободных электронов в форме электрического тока. Проводимость, σ является обратной величиной удельного сопротивления. Это 1 / ρ и имеет единицу измерения сименс на метр, S / m. Проводимость варьируется от нуля (для идеального изолятора) до бесконечности (для идеального проводника). Таким образом, сверхпроводник имеет бесконечную проводимость и практически нулевое омическое сопротивление.

От чего зависит сопротивление

☰

Сила тока в проводнике прямо пропорциональна напряжению на нем. Это значит, что с увеличением напряжения увеличивается и сила тока. Однако при одинаковом напряжении, но использовании разных проводников сила тока различна. Можно сказать по-другому. Если увеличивать напряжение, то хотя сила тока и будет увеличиваться, но везде по-разному, в зависимости от свойств проводника.

Зависимость силы тока от напряжения для данного конкретного проводника представляет собой сопротивление этого проводника. Оно обозначается R и находится по формуле R = U/I. То есть сопротивление определяется как отношение напряжения к силе тока. Чем больше сила тока в проводнике при данном напряжении, тем меньше его сопротивление. Чем больше напряжение при данной силе тока, тем больше сопротивление проводника.

Формулу можно переписать по отношению к силе тока: I = U/R (закон Ома). В таком случае нагляднее, что чем больше сопротивление, тем меньше сила тока.

Можно сказать, что сопротивление как бы мешает напряжению создавать большую силу тока.

Само сопротивление является характеристикой проводника. Оно не зависит от поданного на него напряжения. Если будет подано большое напряжение, то изменится сила тока, но не изменится отношение U/I, т. е. не изменится сопротивление.

От чего же зависит сопротивление проводника? Оно зависти от

• длины проводника,
• площади его поперечного сечения,
• вещества, из которого изготовлен проводник,
• температуры.

Чтобы связать вещество и его сопротивление, вводится такое понятие как удельное сопротивление вещества. Оно показывает, какое будет сопротивление в данном веществе, если проводник из него будет иметь длину 1 м и площадь поперечного сечения 1 м². Проводники такой длины и толщины, изготовленные из разных веществ, будут иметь разные сопротивления. Это связано с тем, что у каждого металла (чаще всего именно они являются проводниками) своя кристаллическая решетка, свое количество свободных электронов.

Чем меньше удельное сопротивление вещества, тем лучшим проводником электрического тока оно является. Маленьким удельным сопротивлением обладают, например, серебро, медь, алюминий; куда большее у железа, вольфрама; очень большое у различных сплавов.

Чем длиннее проводник, тем большее сопротивление он имеет. Это становится понятно, если принять во внимание, что движению электронов в металлах мешают ионы, составляющие кристаллическую решетку. Чем их больше, т. е. чем длиннее проводник, тем больше у электрона шанс замедлить свой путь.

Однако увеличение площади поперечного сечения делает как бы дорогу шире. Электронам легче течь и не сталкиваться с узлами кристаллической решетки. Поэтому чем толще проводник, тем его сопротивление меньше.

Таким образом, сопротивление прямо пропорционально зависит от удельного сопротивления (ρ) и длины (l) проводника и обратно пропорционально зависит от площади (S) его поперечного сечения. Получаем формулу сопротивления:

R = ρl/S

В этой формуле на первый взгляд не отражается зависимость сопротивления проводника от его температуры. Однако удельное сопротивление вещества меряется при определенной температуре (обычно 20 °C). Поэтому температура учитывается. Для вычислений удельные сопротивления берут из специальных таблиц.

Для металлических проводников чем больше температура, тем сопротивление больше. Это связано с тем, что при повышении температуры ионы решетки начинают сильнее колебаться и больше мешать движению электронов. Однако в электролитах (растворах, где заряд несут ионы, а не электроны) с повышением температуры сопротивление уменьшается. Здесь это связано с тем, что чем выше температура, тем больше происходит диссоциация на ионы, и они быстрее двигаются в растворе.

Урок 3. Три друга, один треугольник и много законов

Незнание закона не освобождает от ответственности.
Афоризм

Интересно, о каких законах пойдет речь в уроке под номером три. Неужели в электротехнике этих законов целая гора или даже куча и их все нужно запомнить? Сейчас узнаем. Здравствуйте, уважаемые! Наверное, многие из вас уже с досадой в глазах глядят на очередной урок и думают про себя: «Какая же скукотища!», а, может, даже собираются покинуть наши стройные ряды? Не спешите, всё только начинается! Начальный этап всегда скучный… С этого урока и пойдёт всё самое-самое интересное. Сегодня я расскажу, кто в электротехнике кому друг, а кому и враг, что будет, если студента-электронщика разбудить посреди ночи, и как с помощью одного пальца понять половину всей электротехники. Интересно? Тогда поехали!

С первым нашим другом мы познакомились на прошлом уроке – это сила тока. Она характеризует электричество с точки зрения скорости переноса заряда из одной точки пространства в другую под действием поля. Но, как было замечено, сила тока зависит и от свойств проводника, по которому этот ток «бежит». На силу тока прямо влияет величина удельной электропроводности материала. Теперь представим себе некий проводник (подойдёт такой, как на рисунке 3) с движущимися в нём электронами. Основным недостатком электрона я бы назвал отсутствие у него руля. Из-за этого недостатка движение электронов определяется только воздействующим на них полем и структуры материала, в котором они движутся.

Поскольку электроны «не умеют» поворачивать, некоторые из них могут столкнуться с колеблющимися под действием температуры узлами кристаллической решётки, потерять свою скорость от столкновения, и тем самым снизить скорость переноса заряда, то есть понизить силу тока. Некоторые электроны могут потерять так много энергии, что «прилипнут» к иону и превратят его в нейтральный атом. Теперь, если мы увеличим длину проводника, очевидно, что количество подобных столкновений так же увеличится, и электроны будут отдавать еще больше энергии, то есть сила тока будет снижаться. А вот при увеличении площади поперечного сечения проводника возрастает только количество свободных электронов, а количество столкновений на единицу площади практически не меняется, поэтому с ростом площади растёт и ток. Итак, мы выяснили, что электропроводность (она уже стала не удельной, так как учитывает геометрические размеры конкретного проводника) зависит сразу от трёх характеристик проводника: длины, площади сечения и материала.

Однако, чем лучше материал проводит электрический ток, тем меньше он «сопротивляется» его прохождению. Эти утверждения равнозначны. Пришло время познакомиться с нашим вторым другом – электрическим сопротивлением. Это величина, обратная величине проводимости и зависит от тех же характеристик проводника.

Рисунок 3.1 – От чего зависит сопротивление проводника

Чтобы учесть при численном расчете влияние рода вещества на его электрическое сопротивление, введена величина удельное электрическое сопротивление, характеризующая способность вещества проводить электрический ток. Заметим, что определения электропроводности и электросопротивления идентичны, так же как и утверждения выше. Удельное сопротивление определяется как сопротивление проводника длиной 1м и площадью сечения 1м². Обозначается латинской буквой &#961 («ро») и имеет размерность Ом•м. Ом – единица измерения сопротивления, которая является обратной величине сименс. Так же для определения удельного сопротивления может использоваться размерность Ом•мм²/м, которая в миллион раз меньше основной размерности.
Таким образом, электрическое сопротивление проводника может быть описано через его геометрические и физические свойства следующим образом:

где &#961 – удельное электрическое сопротивление материала проводника;
l – длина проводника;
S – площадь поперечного сечения проводника.

Из зависимости видно, что сопротивление проводника возрастает при увеличении длины проводника и уменьшается при увеличении площади сечения, а так же напрямую зависит от величины удельного сопротивления материала.

А теперь вспомним, что на величину силы тока в проводнике оказывает влияние напряженность электрического поля, под действием которого возникает электрический ток. Ох, сколько миллионов тысяч раз уже упоминалось, что электрический ток возникает под действием электрического поля! Этот факт должен всегда держаться в голове. Есть, конечно, и другие способы создать ток, но пока мы будем рассматривать только этот. Как уже говорилось выше, увеличение напряженности поля приводит к росту тока, а совсем недавно мы выяснили, что чем больше энергии сохранит электрон при движении по проводнику, тем выше значение электрического тока. Из курса механики известно, что энергия тела определяется его кинетической и потенциальной энергией. Так вот, помещённый в электрическое поле точечный заряд обладает в начальный момент времени только потенциальной энергией (поскольку его скорость равна нулю). Для характеристики этой потенциальной энергии поля, которой обладает заряд была введена величина электростатического потенциала, равная отношению потенциальной энергии к величине точечного заряда:

где W_p – потенциальная энергия,
q – величина точечного заряда.

После того, как заряд попадёт под действие электрического поля, он начнёт движение с определённой скоростью и часть его потенциальной энергии перейдёт в кинетическую. Таким образом, в двух точках поля заряд будет обладать различным значением потенциальной энергии, то есть две точки поля можно охарактеризовать различными значениями потенциала. Разность потенциалов определяется как отношение изменения потенциальной энергии (совершённой работы поля) к величине точечного заряда:

Причём работа поля не зависит от пути движения заряда и характеризует только величину изменения потенциальной энергии. Разность потенциалов так же называют электрическим напряжением. Напряжение принято обозначать английской буквой U («у»), единицей измерения напряжения является величина вольт (В), названная в честь итальянского физика и физиолога Алессандро Вольта, который изобрёл первую электрическую батарею.

Ну вот мы и познакомились с тремя неразлучными друзьями в электротехнике: ампер, вольт и ом или ток, напряжение и сопротивление. Любой компонент электрической цепи может быть однозначно охарактеризован при помощи этих трёх электрических характеристик. Первым, кто познакомился и подружился со всеми тремя сразу был Георг Ом, который обнаружил, что напряжение, ток и сопротивление связаны друг с другом определённым соотношением:

которое было впоследствии названо законом Ома.

Сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника.

Данную формулировку необходимо знать от заглавной буквы С до точки в конце. Ходят слухи, что первая фраза любого студент-электронщик, разбуженного среди ночи, будет именно формулировкой закона Ома. Это один из основных законов электротехники. Данная формулировка носит название интегральной. Кроме неё существует так же дифференциальная формулировка, отражающая зависимость плотности тока от характеристик поля и материала проводника:

где &#963 – удельная проводимость проводника,
E – напряженность электрического поля.

Данная формулировка вытекает из формулы, приведённой во втором уроке, и отличается от интегральной тем, что не учитывает геометрические характеристики проводника, принимая во внимание только его физические характеристики. Эта формулировка интересна только с точки зрения теории и на практике не применяется.
Для быстрого запоминания и использования закона Ома можно применить диаграмму, изображённую на рисунке ниже.

Рисунок 3.2 – «Треугольный» закон Ома

Правило использования диаграммы простое: достаточно закрыть искомую величину и два других символа дадут формулу для её вычисления. Например.

Рисунок 3.3 – Как запомнить закон Ома

С треугольником мы закончили. Стоит добавить, что законом Ома называется только одна из представленных выше формул – та, которая отражает зависимость тока от напряжения и сопротивления. Две другие формулы, хотя и являются её следствием, физического смысла не имеют. Так что не перепутайте!
Хорошей интерпретацией закона Ома является рисунок, который наиболее наглядно отражает сущность этого закона:

Рисунок 3.4 – Закон Ома наглядно

Как мы видим, на этом рисунке изображены как раз три наших новых друга: Ом, Ампер и Вольт. Вольт пытается протолкнуть Ампер через сечение проводника(сила тока прямо пропорциональна напряжению), а Ом наоборот – мешает этому (и обратно пропорциональна сопротивлению). И чем сильнее Ом «стягивает» проводник, тем тяжелее Амперу будет пролезть. Но если Вольт посильнее пнёт…

Осталось разобраться, почему в названии урока фигурирует термин «много законов», ведь закон-то у нас один – закон Ома. Ну, во-первых, для него существует две формулировки, во-вторых, мы узнали только так называемый закон Ома для участка цепи, а ведь есть ещё закон Ома для полной цепи, который мы рассмотрим на следующем уроке, в-третьих, мы имеем, по крайней мере, два следствия из закона Ома, позволяющих находить значение сопротивления участка цепи и напряжение на этом участке. Так что закон всего один, а использовать его можно по-разному.

Напоследок расскажу ещё один интересный факт. Через 10 лет после появления «закона Ома» один французский физик (а во Франции работы Ома ещё не были известны) на основе экспериментов пришел к таким же выводам. Но ему было указано, что установленный им закон еще в 1827г. был открыт Омом. Оказывается, что французские школьники и поныне изучают закон Ома под другим именем – для них это закон Пулье. Вот так вот. На этом очередной урок закончен. До новых встреч!

• Любой участок или элемент электрической цепи можно однозначно охарактеризовать при помощи трёх характеристик: тока, напряжения и сопротивления.
• Сопротивление (R) – характеристика проводника, отражающая степень его электропроводности и зависящая от геометрических размеров проводника и рода материала, из которого он изготовлен.
• Напряжение (U) – то же самое, что и разность потенциалов; величина равная отношению работы электрического поля для перемещения точечного заряда из одной точки пространства в другую.
• Ток, напряжение и сопротивление связаны между собой отношением I=U/R, называемым законом Ома (сила электрического тока в проводнике прямо пропорциональна напряжению на концах проводника и обратно пропорциональна сопротивлению проводника).

А также задачки:

• Если длину проволоки вытягиванием увеличить вдвое, то как изменится её сопротивление?
• Какой проводник представляет большее сопротивление: медный сплошной стержень или медная трубка, имеющая внешний диаметр, равный диаметру стержня?
• Разность потенциалов на концах алюминиевого проводника равна 10В. Определить плотность тока, протекающего через проводник, если его длина 3м.

← Урок 2: Как пересчитать электроны | Содержание | Урок 4: Когда есть ток? →

Удельное сопротивление | Физика проводников и изоляторов

Расчет сопротивления проводов

Номинальная допустимая нагрузка проводника – это грубая оценка сопротивления, основанная на потенциальной опасности возникновения пожара по току. Однако мы можем столкнуться с ситуациями, когда падение напряжения, вызванное сопротивлением проводов в цепи, представляет собой другие проблемы, кроме предотвращения возгорания. Например, мы можем проектировать схему, в которой напряжение на компоненте является критическим и не должно опускаться ниже определенного предела.В этом случае падение напряжения из-за сопротивления провода может вызвать техническую проблему, будучи в пределах безопасных (пожарных) пределов допустимой нагрузки:

Если нагрузка в приведенной выше схеме не выдерживает напряжения ниже 220 В при напряжении источника 230 В, то нам лучше убедиться, что проводка не упадет более чем на 10 вольт по пути. Если подсчитать как питающие, так и обратные проводники этой цепи, это оставляет максимально допустимое падение в 5 вольт по длине каждого провода.Используя закон Ома (R = E / I), мы можем определить максимально допустимое сопротивление для каждого отрезка провода:

Мы знаем, что длина провода составляет 2300 футов для каждого отрезка провода, но как определить величину сопротивления для конкретного размера и длины провода? Для этого нам понадобится другая формула:

Эта формула связывает сопротивление проводника с его удельным сопротивлением (греческая буква «ро» (ρ), которая похожа на строчную букву «р»), его длиной («l») и поперечным сечением. площадь сечения («А»).Обратите внимание, что с переменной длины в верхней части дроби значение сопротивления увеличивается по мере увеличения длины (аналогия: труднее протолкнуть жидкость через длинную трубу, чем через короткую), и уменьшается по мере увеличения площади поперечного сечения ( аналогия: жидкость легче течет по толстой трубе, чем по тонкой). Удельное сопротивление является константой для типа рассчитываемого материала проводника.

Удельное сопротивление нескольких проводящих материалов можно найти в следующей таблице.Внизу таблицы мы находим медь, уступающую только серебру по низкому удельному сопротивлению (хорошей проводимости):

Удельное сопротивление при 20 градусах Цельсия

Материал	Элемент / Сплав	(Ом-смил / фут)	(мкОм-см)
нихром	Сплав	675	112,2
Нихром V	Сплав	650	108,1
Манганин	Сплав	290	48.21
Константан	Сплав	272,97	45,38
Сталь *	Сплав	100	16,62
Платина	Элемент	63,16	10,5
Утюг	Элемент	57,81	9,61
Никель	Элемент	41,69	6,93
цинк	Элемент	35.49	5,90
Молибден	Элемент	32,12	5,34
Вольфрам	Элемент	31,76	5,28
Алюминий	Элемент	15,94	2,650
Золото	Элемент	13,32	2,214
Медь	Элемент	10,09	1.678
Серебро	Элемент	9,546	1,587

* = Стальной сплав с содержанием железа 99,5%, углерода 0,5%

Обратите внимание, что значения удельного сопротивления в приведенной выше таблице даны в очень странной единице «Ом-см-мил / фут» (Ом-см-мил / фут). Эта единица указывает, какие единицы мы должны использовать в формуле сопротивления ( R = ρl / A). В этом случае эти значения удельного сопротивления предназначены для использования, когда длина измеряется в футах, а площадь поперечного сечения измеряется в круглых милах.

Метрической единицей измерения удельного сопротивления является ом-метр (Ом-м) или ом-сантиметр (Ом-см), при этом 1,66243 x 10 _-9 Ом-метров на Ом-см-мил / фут (1,66243 x 10 _-7 Ом-см на Ом-см-мил / фут). В столбце таблицы Ом-см цифры фактически масштабированы как мкОм-см из-за их очень малых величин. Например, железо указано как 9,61 мкОм-см, что может быть представлено как 9,61 x 10 _-6 Ом-см.

При использовании единицы измерения удельного сопротивления Ом-метр в формуле R = ρl / A длина должна быть в метрах, а площадь – в квадратных метрах.При использовании единицы Ом-сантиметр (Ом-см) в той же формуле длина должна быть в сантиметрах, а площадь – в квадратных сантиметрах.

Все эти единицы измерения удельного сопротивления действительны для любого материала (Ом-см / фут, Ом-м или Ом-см). Тем не менее, можно предпочесть использовать Ω-cmil / ft при работе с круглой проволокой, площадь поперечного сечения которой уже известна в круглых милах. И наоборот, при работе с шиной нестандартной формы или изготовленной по индивидуальному заказу шиной, вырезанной из металлической заготовки, когда известны только линейные размеры длины, ширины и высоты, более подходящими могут быть единицы измерения удельного сопротивления в Ом-метр или Ом-см.

Решение

Возвращаясь к нашей примерной схеме, мы искали провод с сопротивлением 0,2 Ом или меньше на длине 2300 футов. Предполагая, что мы собираемся использовать медный провод (самый распространенный тип производимого электрического провода), мы можем настроить нашу формулу следующим образом:

Алгебраически решая относительно A, мы получаем значение 116035 круговых милов. Ссылаясь на нашу таблицу размеров сплошных проводов, мы обнаруживаем, что провод «двойной длины» (2/0) с длиной 133 100 см является достаточным, тогда как следующий меньший размер, «одинарный провод» (1/0) с длиной 105 500 см слишком мал. .Имейте в виду, что ток в нашей цепи составляет скромные 25 ампер. Согласно нашей таблице допустимой токовой нагрузки для медного провода на открытом воздухе, достаточно провода калибра 14 (если речь идет о , а не о , вызывающем пожар). Однако с точки зрения падения напряжения провод 14 калибра был бы очень неприемлемым.

Ради интереса, давайте посмотрим, как провод 14 калибра повлияет на характеристики нашей силовой цепи. Глядя на нашу таблицу размеров проводов, мы обнаруживаем, что проволока калибра 14 имеет площадь поперечного сечения 4 107 круглых милов.Если мы все еще используем медь в качестве материала для проволоки (хороший выбор, если только мы не действительно богаты и не можем позволить себе 4600 футов серебряной проволоки 14 калибра!), То наше удельное сопротивление все равно будет 10,09 Ом-см · дюйм / фут. :

Помните, что это 5,651 Ом на 2300 футов медного провода калибра 14, и что у нас есть два участка по 2300 футов во всей цепи, поэтому каждый кусок провода в цепи имеет сопротивление 5,651 Ом:

Полное сопротивление проводов нашей схемы равно 2 умноженным на 5.651 или 11,301 Ом. К сожалению, это сопротивление намного больше, чем , чтобы обеспечить ток в 25 ампер при напряжении источника 230 вольт. Даже если бы сопротивление нагрузки было 0 Ом, сопротивление нашей проводки 11,301 Ом ограничило бы ток в цепи до 20,352 ампер! Как вы можете видеть, «небольшое» сопротивление провода может иметь большое значение в характеристиках схемы, особенно в силовых цепях, где токи намного выше, чем обычно встречаются в электронных схемах.

Давайте рассмотрим пример проблемы сопротивления для отрезка сборной шины, изготовленной по индивидуальному заказу.Предположим, у нас есть кусок сплошного алюминиевого стержня шириной 4 см, высотой 3 см и длиной 125 см, и мы хотим рассчитать сквозное сопротивление по длине (125 см). Во-первых, нам нужно определить площадь поперечного сечения стержня:

Нам также необходимо знать удельное сопротивление алюминия в единицах измерения, соответствующих данному применению (Ом-см). Из нашей таблицы удельных сопротивлений мы видим, что это 2,65 x 10 _-6 Ом-см. Установив нашу формулу R = ρl / A, мы имеем:

Как вы можете видеть, абсолютная толщина шины обеспечивает очень низкое сопротивление по сравнению со стандартными размерами проводов, даже при использовании материала с большим удельным сопротивлением.

Процедура определения сопротивления шины принципиально не отличается от определения сопротивления круглого провода. Нам просто нужно убедиться, что площадь поперечного сечения рассчитана правильно и что все единицы соответствуют друг другу, как должны.

ОБЗОР:

• Сопротивление проводника увеличивается с увеличением длины и уменьшается с увеличением площади поперечного сечения, при прочих равных условиях.
• Удельное сопротивление («ρ») – это свойство любого проводящего материала, показатель, используемый для определения сквозного сопротивления проводника данной длины и площади в этой формуле: R = ρl / A
• Удельное сопротивление материалов указывается в единицах Ом-смил / фут или Ом-метр (метрическая система).Коэффициент преобразования между этими двумя единицами составляет 1,66243 x 10 _-9 Ом-метров на Ом-см-дюйм / фут или 1,66243 x 10 _-7 Ом-см на Ом-см-дюйм / фут.
• Если падение напряжения в цепи критично, перед выбором сечения проводов необходимо произвести точный расчет сопротивления проводов.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Калькулятор сопротивления круглого провода

Калькулятор сопротивления круглого провода

Логотип Chemandy Electronics Логотип Chemandy Electronics CHEMANDY ELECTRONICSПоставщики навигации UnusualShow Скрыть навигацию

Рассчитывает сопротивление постоянному току одиночного круглого провода из обычных проводящих материалов, используя уравнение 2 ниже.

Примечание. Чтобы использовать другие значения удельного сопротивления, выберите «Ввести данные» в текстовом поле выбора материала проводника и затем введите необходимое значение удельного сопротивления (ρ) в поле, выделенное желтым цветом.

Этот калькулятор использует JavaScript и будет работать в большинстве современных браузеров. Для получения дополнительной информации см. О наших калькуляторах

.

Сопротивление проводника постоянному току рассчитывается с использованием удельного сопротивления и площади поперечного сечения: –

Уравнение 1.

Где:

ρ – удельное сопротивление проводника, Ом · м

l Длина в метрах

А – Площадь поперечного сечения в метрах

Круглый провод обычно определяется диаметром, а сопротивление постоянному току, зависящее от диаметра, составляет: –

Уравнение 2.

Где:

ρ – удельное сопротивление проводника, Ом · м

l Длина в метрах

d – диаметр круглого проводника в метрах

Значения ρ взяты из CRC Handbook of Chemistry and Physics 1st Student Edition 1998 page F-88 и относятся к элементам высокой чистоты при 20 ° C.

Таблица «контрольных» измерений, выполненных в нашей лаборатории с использованием эмалированного медного провода
				Измерялся	Вычислено
Диаметр	Длина	Напряжение	Текущий	Сопротивление	Сопротивление
(мм)	(мм)	(В)	(А)	(Ом)	(Ом)
1.0	410	0,0091	1.031	0,008826	0,0087596
0,5	410	0,0359	1.031	0,03482	0,0350385
0,2	410	0,24	1.032	0,2326	0,2189908

Этот калькулятор предоставляется Chemandy Electronics бесплатно для продвижения FLEXI-BOX

Вернуться к калькулятору Указатель

Калькулятор размеров калибра проводов и сопротивления

Вычислите диаметр, площадь поперечного сечения и сопротивление провода с учетом его калибра или найдите калибр провода с учетом диаметра.

Калькулятор калибра провода

Формулы калибра проволоки

Калибр проволоки – это стандартная единица измерения диаметра проволоки, а американский калибр проволоки, или AWG, является стандартом, используемым в Северной Америке. Диаметр и площадь поперечного сечения провода можно определить с помощью калибра провода и нескольких простых формул.

Диаметр проволоки

Формула для определения диаметра проволоки в дюймах:

диаметр (дюйм) =.005 × 92 ^{(36 – AWG) ÷ 39}

Формула для определения диаметра проволоки в миллиметрах:

диаметр (мм) = .127 × 92 ^{(36 – AWG) ÷ 39}

Шаги для определения диаметра

Сначала – найдите показатель степени в уравнении, вычтя калибр проволоки из 36, а затем разделив на 39.

Нахождение экспоненты для проволоки калибра 00, 000 и 0000 немного отличается. Замените -1, -2 и -3 для манометра в приведенной выше формуле вместо значения AWG.

Второй – найти 92 в степени, вычисленной на предыдущем шаге.

Третий – умножьте значение второго шага на 0,005 дюйма или 0,127 мм, чтобы найти диаметр проволоки в дюймах или миллиметрах соответственно.

Площадь поперечного сечения провода

Формула для определения площади поперечного сечения провода в килокруглых милах или килограммах:

площадь (тыс. мил) = 1000 × диаметр ²

Формула для определения площади поперечного сечения провода в квадратных миллиметрах:

площадь (мм ² ) = (π ÷ 4) × диаметр ²

Шаги для определения площади поперечного сечения

Первый – найти диаметр проволоки.Используйте приведенную выше формулу для вычисления ширины, если известно AWG.

Второй – умножьте диаметр на 1000, чтобы найти площадь в километрах, или на (3,1415 ÷ 4), чтобы вычислить квадратные миллиметры.

Диаграмма диаметра, площади и сопротивления проволоки

Значения диаметра, площади поперечного сечения и сопротивления для различных американских калибров провода (AWG).

AWG	Диаметр		Площадь поперечного сечения		Сопротивление
	(дюймы)	(мм)	(тыс. Мил)	(мм 2 )	Ом на 1000 футов	Ом на 1000 м
0000 (4/0)	0.46	11,684	211,6	107,22	0,049	0,1608
000 (3/0)	0,4096	10,405	167,81	85,029	0,0618	0,2028
00 (2/0)	0,3648	9,266	133.08	67,431	0,0779	0,2557
0 (1/0)	0,3249	8.251	105,53	53,475	0,0983	0,3224
1	0,2893	7,348	83,693	42,408	0,1239	0,4066
2	0,2576	6.544	66.371	33,631	0,1563	0,5127
3	0,2294	5,827	52,635	26.67	0,197	0,6464
4	0,2043	5,189	41,741	21,151	0,2485	0,8152
5	0,1819	4,621	33.102	16,773	0,3133	1.028
6	0,162	4,115	26,251	13.302	0,3951	1.296
7	0,1443	3,665	20,818	10,549	0,4982	1,634
8	0,1285	3,264	16,51	8,366	0,6282	2,061
9	0,1144	2,906	13.093	6,634	0,7921	2,599
10	0.1019	2,588	10,383	5.261	0,9988	3,277
11	0,0907	2.305	8,234	4,172	1,26	4,132
12	0,0808	2,053	6.53	3.309	1,588	5,211
13	0,072	1,828	5,178	2.624	2,003	6.571
14	0,0641	1,628	4,107	2,081	2,525	8,285
15	0,0571	1,45	3,257	1,65	3,184	10,448
16	0,0508	1,291	2,583	1,309	4,015	13,174
17	0.0453	1,15	2,048	1.038	5,063	16,612
18	0,0403	1.024	1,624	0,823	6.385	20,948
19	0,0359	0,9116	1,288	0,6527	8,051	26,415
20	0,032	0,8118	1.022	0,5176	10,152	33.308
21	0,0285	0,7229	0,8101	0,4105	12,802	42,001
22	0,0253	0,6438	0,6424	0,3255	16,143	52,962
23	0,0226	0,5733	0,5095	0,2582	20.356	66,784
24	0,0201	0,5106	0,404	0,2047	25,668	84,213
25	0,0179	0,4547	0,3204	0,1624	32,367	106,19
26	0,0159	0,4049	0,2541	0,1288	40,814	133,9
27	0.0142	0,3606	0.2015	0,1021	51,466	168,85
28	0,0126	0,3211	0,1598	0,081	64,897	212,92
29	0,0113	0,2859	0,1267	0,0642	81,833	268,48
30	0,01	0,2546	0.1005	0,0509	103,19	338,55
31	0,008928	0,2268	0,0797	0,0404	130,12	426,9
32	0,00795	0,2019	0,0632	0,032	164,08	538,32
33	0,00708	0,1798	0,0501	0,0254	206.9	678,8
34	0,006305	0,1601	0,0398	0,0201	260,9	855,96
35	0,005615	0,1426	0,0315	0,016	328,98	1 079,3
36	0,005	0,127	0,025	0,0127	414,84	1,361
37	0.004453	0,1131	0,0198	0,01	523,1	1716,2
38	0,003965	0,1007	0,0157	0,007967	659,62	2 164,1
39	0,003531	0,0897	0,0125	0,006318	831,77	2 728,9
40	0,003145	0.0799	0,009888	0,00501	1 048,8	3 441,1

Также ознакомьтесь с нашим калькулятором стоимости электроэнергии и калькулятором стоимости освещения, прежде чем планировать свой следующий электрический проект.

Калькулятор падения напряжения

Калькулятор падения напряжения в проводах / кабелях и способы его расчета.

Калькулятор падения напряжения

* @ 68 ° F или 20 ° C

** Результаты могут отличаться для реальных проволок: различное удельное сопротивление материала и количество жил в проволоке.

*** Для провода длиной 2×10 футов длина провода должна составлять 10 футов.

Калькулятор калибра провода ►

Расчет падения напряжения

DC / однофазный расчет

Падение напряжения V в вольтах (В) равно току провода I в амперах (А), умноженному на 2 умноженной на длину одностороннего провода L в футах (футах), умноженного на сопротивление провода на 1000 футов R в омах (Ом / kft), деленное на 1000:

В _{падение (В)} = I _{провод (A)} × R _{провод (Ом)}

= I _{провод (A)} × (2 × L _(фут) × R _{провод (Ω / kft)} /1000 _{(ft / kft)} )

Падение напряжения V в вольтах (В) равно току провода I в амперах (А), умноженному на 2. длина одностороннего провода L в метрах (м), умноженная на сопротивление провода на 1000 метров R в омах (Ом / км), деленное на 1000:

В _{падение (В)} = I _{провод (A)} × R _{провод (Ом)}

= I _{провод (A)} × (2 × L _(м) × R _{провод (Ом / км)} /1000 _{(м / км)} )

3-фазный расчет

Падение линейного напряжения V в вольтах (В) равно квадратному корню из 3-кратного значения тока провода I в амперах (A), умноженного на односторонняя длина провода L в футах (футах), умноженная на сопротивление провода на 1000 футов R в омах (Ω / kft), деленное на 1000:

V _{падение (V)} = √3 × I _{провод (A)} × R _{провод (Ом)}

= 1.732 × I _{провод (A)} × ( L _(фут) × R _{провод (Ом / кВт)} /1000 _{(фут / кВт)} )

Падение линейного напряжения V в вольтах (В) равно квадратному корню из 3-кратного значения тока провода I в амперах (A), умноженного на длина одностороннего провода L в метрах (м), умноженная на сопротивление провода на 1000 метры R в омах (Ом / км) разделить на 1000:

V _{падение (V)} = √3 × I _{провод (A)} × R _{провод (Ом)}

= 1.732 × I _{провод (A)} × ( L _(м) × R _{провод (Ом / км)} /1000 _{(м / км)} )

Расчет диаметра проволоки

Диаметр проволоки калибра n d _n дюймов (дюймов) равен 0,005 дюйма, умноженному на 92 в степени 36 минус калибр n, деленное на 39:

d _{n (дюйм)} = 0,005 дюйма × 92 ^{(36- n ) / 39}

Диаметр проволоки n калибра d _n в миллиметрах (мм) равен 0.127 мм умножить на 92 в степени 36 минус число n, разделенное на 39:

d _{n (мм)} = 0,127 мм × 92 ^{(36- n ) / 39}

Расчет площади поперечного сечения провода

Площадь поперечного сечения провода калибра n A _n в круговых мил (kcmil) в 1000 раз больше диаметра квадратного провода d в ​​дюймах (дюймах):

A _{n (kcmil)} = 1000 × d _n ² = 0.025 дюйм ² × 92 ^{(36- n ) /19,5}

Площадь поперечного сечения провода калибра n A _n в квадратных дюймах (в ² ) равно пи, деленному на 4 диаметра квадратной проволоки d в дюймах (дюймах):

A _{n (дюйм} 2 ₎ = (π / 4) × d _n ² = 0,000019635 дюйм ² × 92 ^{(36- n ) /19,5}

Площадь поперечного сечения провода калибра n A _n в квадратных миллиметрах ( ² мм) равно pi, деленному на 4, умноженное на диаметр квадратной проволоки d в миллиметрах (мм):

A _{n (мм} 2 ₎ = (π / 4) × d _n ² = 0.012668 мм ² × 92 ^{(36- n ) /19,5}

Расчет сопротивления проводов

Сопротивление провода калибра n R в Ом на килофит (Ом / кфут) равно 0,3048 × 1000000000 удельному сопротивлению провода ρ дюйм Ом-метр (Ом · м), разделенное на 25,4 ² , умноженное на площадь поперечного сечения A _n в квадратных дюймах (в ² ):

R _{n (Ом / kft)} = 0,3048 × 10 ⁹ × ρ _{(Ом · м)} / (25.4 ² × A _{n (в} 2 ₎ )

Сопротивление R провода калибра n в Ом на километр (Ом / км) равно 1000000000 удельному сопротивлению провода ρ дюйм Ом-метры (Ом · м), разделенные на площадь поперечного сечения A _n в квадратных миллиметрах (мм ² ):

R _{n (Ом / км)} = 10 ⁹ × ρ _{(Ом · м)} / A _{n (мм} 2 ₎

Диаграмма AWG

AWG #	Диаметр (дюйм)	Диаметр (мм)	Площадь (тыс. Мил)	Площадь (мм 2 )
0000 (4/0)	0.4600	11,6840	211.6000	107.2193
000 (3/0)	0,4096	10,4049	167.8064	85.0288
00 (2/0)	0,3648	9,2658	133.0765	67.4309
0 (1/0)	0,3249	8,2515	105,5345	53,4751
1	0,2893	7.3481	83,6927	42,4077
2	0,2576	6.5437	66,3713	33,6308
3	0,2294	5,8273	52,6348	26.6705
4	0,2043	5,1894	41,7413	21.1506
5	0,1819	4.6213	33.1024	16.7732
6	0,1620	4,1154	26,2514	13,3018
7	0,1443	3,6649	20,8183	10,5488
8	0,1285	3,2636	16,5097	8,3656
9	0,1144	2,9064	13,0927	6,6342
10	0.1019	2,5882	10,3830	5,2612
11	0,0907	2.3048	8,2341	4,1723
12	0,0808	2,0525	6.5299	3.3088
13	0,0720	1,8278	5,1785	2,6240
14	0,0641	1,6277	4.1067	2,0809
15	0,0571	1.4495	3,2568	1,6502
16	0,0508	1,2908	2,5827	1,3087
17	0,0453	1,1495	2,0482	1.0378
18	0,0403	1.0237	1,6243	0,8230
19	0.0359	0,9116	1,2881	0,6527
20	0,0320	0,8118	1.0215	0,5176
21	0,0285	0,7229	0,8101	0,4105
22	0,0253	0,6438	0,6424	0,3255
23	0,0226	0,5733	0.5095	0,2582
24	0,0201	0,5106	0,4040	0,2047
25	0,0179	0,4547	0,3204	0,1624
26	0,0159	0,4049	0,2541	0,1288
27	0,0142	0,3606	0.2015	0,1021
28	0.0126	0,3211	0,1598	0,0810
29	0,0113	0,2859	0,1267	0,0642
30	0,0100	0,2546	0,1005	0,0509
31	0,0089	0,2268	0,0797	0,0404
32	0,0080	0,2019	0.0632	0,0320
33	0,0071	0,1798	0,0501	0,0254
34	0,0063	0,1601	0,0398	0,0201
35	0,0056	0,1426	0,0315	0,0160
36	0,0050	0,1270	0,0250	0,0127
37	0.0045	0,1131	0,0198	0,0100
38	0,0040	0,1007	0,0157	0,0080
39	0,0035	0,0897	0,0125	0,0063
40	0,0031	0,0799	0,0099	0,0050

---

См. Также

Расчет провисания и натяжения в линии передачи

Расчет прогиба и натяжения в линии передачи зависит от пролета проводника.Пролет с опорами равного уровня называется пролетом уровня, тогда как уровень опор не на одинаковом уровне известен как пролет с разным уровнем. Расчет кондуктора на равном уровне показан ниже.

Рассмотрим проводник AOB, свободно подвешенный между опорами уровня A и B на одном уровне. Самая низкая точка проводника – O. Пусть форма проводника представляет собой параболу.

Лет,

l – длина пролета
w – вес на единицу длины жилы
δ – прогиб жилы
H – натяжение жилы в точке максимального прогиба O
T _B – натяжение жилы в точке опоры B .

Считайте OB – это равновесное натяжение проводника, а сила, действующая на него, – это горизонтальное натяжение H в точке O. Вес (w.OB) проводника OB, действующий вертикально вниз через центр тяжести на расстоянии l / 4 от B. , а натяжение Т _В на опоре В.

Так как OB примерно равно l / 2

Возьмите моменты о B

Приведенное выше уравнение показывает, что прогиб в свободно подвешенном проводнике прямо пропорционален весу на единицу длины проводника и квадрату длины пролета и обратно пропорционален горизонтальному натяжению H.

Расчет прогиба и натяжения на неравном уровне поддерживает

В холмистой местности или на склонах опоры обычно не находятся на одном уровне. Для расчета прогиба и натяжения на неравном уровне опор рассмотрите провод AOB. Участки OA и OB могут рассматриваться как цепные линии половинного пролета x и l-x, соответственно, показанные на рисунке ниже.

Лет,

h – разница в длине пролета между A и B
l – длина горизонтального пролета между A и B
x – горизонтальное расстояние между A и самой нижней точкой O.
l – x – горизонтальное расстояние B от самой низкой точки О.

Провисание в OA и OB выражается уравнениями

Напряжение A и B равно

Максимальное натяжение возникает в точке B, поскольку (l-x) больше x, как показано на рисунке выше.
Вертикальная реакция на верхней опоре – ш. (L-x)
Вертикальная реакция на нижней опоре – ш. X

Для расчетов предполагается, что AOB является параболой.

Но,

Значение x, полученное выше, можно подставить в уравнение (5) для расчета провисания при OA.Уравнение (8) показывает, что самая низкая точка лежит за пределами промежутка AB. Следовательно, проводник в рассматриваемом пролете оказывает направленное вверх усилие, и проводник имеет тенденцию отклоняться от нижней опоры.

Что такое удельное сопротивление – формула и единицы

Удельное электрическое сопротивление – ключевой параметр для любого материала, используемого в электрических цепях, электронных компонентах и ​​многих других предметах.

---

Руководство по сопротивлению Включает:
Что такое сопротивление Закон Ома Удельное сопротивление Таблица удельного сопротивления для обычных материалов Температурный коэффициент сопротивления Электрическая проводимость Последовательные и параллельные резисторы Таблица параллельных резисторов Калькулятор параллельных резисторов

---

Удельное сопротивление – это мера сопротивления определенного размера материала определенного размера электрической проводимости.

Удельное сопротивление также может называться удельным электрическим сопротивлением или объемным сопротивлением, хотя эти термины используются менее широко.

Хотя материалы сопротивляются прохождению электрического тока, некоторые из них проводят его лучше, чем другие.

Удельное сопротивление – это показатель, позволяющий сравнивать то, как разные материалы позволяют или сопротивляются протеканию тока.

Чтобы значения удельного сопротивления были значимыми, для удельного сопротивления используются определенные единицы, и существуют формулы для его расчета и соотнесения с сопротивлением в Ом для данного размера материала.

Материалы, которые легко проводят электрический ток, называются проводниками и имеют низкое удельное сопротивление. Те, которые плохо проводят электричество, называются изоляторами, и эти материалы обладают высоким удельным сопротивлением.

Удельное сопротивление различных материалов играет важную роль при выборе материалов, используемых для электрических проводов во многих электронных компонентах, включая резисторы, интегральные схемы и многие другие.

Определение и единицы удельного сопротивления

Удельное электрическое сопротивление образца материала может быть также известно как его удельное электрическое сопротивление.Это показатель того, насколько сильно материал противостоит прохождению электрического тока.

Определение удельного сопротивления:

Удельное сопротивление вещества – это сопротивление куба этого вещества, имеющего края единичной длины, при том понимании, что ток течет перпендикулярно противоположным граням и равномерно распределяется по ним.

Удельное электрическое сопротивление – это электрическое сопротивление на единицу длины и на единицу площади поперечного сечения при заданной температуре.

В системе СИ единицей удельного электрического сопротивления является омметр (Ом · м). Обычно обозначается греческой буквой ρ, ро.

Несмотря на то, что обычно используется единица измерения удельного сопротивления в системе СИ, омметр, иногда значения могут быть выражены в омах-сантиметрах, Ом⋅см.

В качестве примера, если твердый куб материала размером 1 M ³ имеет листовые контакты на двух противоположных гранях, которые сами по себе не создают никакого сопротивления, а сопротивление между контактами составляет 1 Ом, тогда удельное сопротивление материала называется 1 & Omega: & dot; ⋅m. 2

Из уравнений видно, что сопротивление можно изменять, изменяя множество различных параметров.

Например, сохраняя постоянное удельное сопротивление материала, сопротивление образца можно увеличить, увеличив длину или уменьшив площадь поперечного сечения. Из уравнений удельного сопротивления также видно, что увеличение удельного сопротивления материала приведет к увеличению сопротивления при тех же размерах. Аналогичным образом уменьшение удельного сопротивления уменьшит сопротивление.

Уровни удельного сопротивления материалов

Материалы делятся на разные категории в зависимости от их уровня или удельного сопротивления.-8

Полупроводники

Переменная *

Сверхпроводники

0

* Уровень проводимости полупроводников зависит от уровня легирования. Без легирования они выглядят почти как изоляторы, но с легированием доступны носители заряда, и сопротивление резко падает.Аналогично для электролитов уровень удельного сопротивления широко варьируется.

Практическое значение удельного сопротивления

Удельное сопротивление материалов важно, поскольку оно позволяет использовать правильные материалы в нужных местах в электрических и электронных компонентах.

Материалы, используемые в качестве проводников, например в электрических и общих соединительных проводах, должны иметь низкий уровень удельного сопротивления. Это означает, что для данной площади поперечного сечения сопротивление провода будет низким.Выбор правильного материала зависит от знания его свойств, одним из которых является его удельное сопротивление.

Например, медь является хорошим проводником, поскольку она обеспечивает низкий уровень удельного сопротивления, ее стоимость не слишком высока, а также обеспечивает другие физические характеристики, которые используются во многих электрических и электронных приложениях. Удельное сопротивление меди составляет около 1,7 x 10 ^-8 Ом · м (или 17 нОм), хотя значения могут незначительно отличаться в зависимости от марки меди

.

Такие материалы, как медь и даже алюминий, обеспечивают низкий уровень удельного сопротивления, что делает их идеальными для использования в качестве электрических проводов и кабелей, причем медь часто является фаворитом.Серебро и золото имеют очень низкие значения удельного сопротивления, но, поскольку они значительно дороже, они не получили широкого распространения. Тем не менее, серебро иногда используется для обшивки проводов там, где необходимо его низкое удельное сопротивление, а золотое покрытие используется для сопрягаемых поверхностей многих электронных разъемов, чтобы обеспечить наилучшие контакты. Золото также хорошо подходит для электрических разъемов, поскольку оно не тускнеет и не окисляется, как другие металлы.

Другие материалы должны действовать как изоляторы, пропускающие как можно меньший ток.Удельное сопротивление изолятора будет на много порядков выше. Одним из примеров является воздух, и его удельное сопротивление составляет более 1,5 x 10 ¹⁴ , что, как можно видеть, очень, очень много выше, чем удельное сопротивление меди.

Удельное электрическое сопротивление играет важную роль во многих других электронных компонентах. В резисторах, например, удельное сопротивление различных материалов играет ключевую роль в обеспечении правильного сопротивления резисторов.

Удельное сопротивление также играет ключевую роль в других электронных компонентах.Для интегральных схем очень важно удельное сопротивление материалов в кристалле. Некоторые области должны иметь очень низкое сопротивление и иметь возможность соединять различные области ИС внутри, тогда как другие материалы должны изолировать разные области. Опять же, для этого важно сопротивление.

Удельное сопротивление играет ключевую роль во многих областях электронных компонентов, а также для многих электрических деталей.

Удельное электрическое сопротивление – ключевой параметр для материалов, которые будут использоваться в электрических и электронных системах.Эти вещества с высоким электрическим сопротивлением называются изоляторами и могут использоваться для этой цели. Они с низким уровнем удельного электрического сопротивления являются хорошими проводниками и могут использоваться во множестве приложений, от проводов до электрических соединений и многого другого.

Дополнительные основные понятия:
Напряжение ток Сопротивление Емкость Мощность Трансформеры RF шум Децибел, дБ Q, добротность
Вернуться в меню «Основные понятия».. .

Расчет данных кабеля

Расчетный выход: Диаметр кабеля, общая емкость (мкФ), общий ток зарядки (амперы), параметры заряда на фазу (кВАр), реактивное сопротивление заряда (МОм * 1000 футов), индуктивность (мГн), реактивное сопротивление (Ом), переменный ток Сопротивление, соотношение X / R и импульсное сопротивление (Ом).

Основа расчета

---

Емкость кабелей, зарядный ток и зарядная реактивная мощность

Емкость одножильного экранированного кабеля определяется по следующей формуле:

Где:

C = Общая емкость кабеля (микрофарады)	I заряд = Ток зарядки кабеля
SIC = Диэлектрическая проницаемость изоляции кабеля (Таблица-3)	D = Диаметр над изоляция (дюймы)
d = диаметр проводника (дюймы)	В LL = рабочее напряжение системы в (кВ)
f = рабочая частота системы (Гц)	L = длина Кабель в футах
I заряд = зарядный ток (амперы)	кВАр заряд = однофазный кВАр или зарядный вар на кабель

Индуктивность и реактивность кабеля

Индуктивность и индуктивное сопротивление трех однофазных кабелей рассчитываются по формулам ниже.Формулы предполагают конфигурацию кабеля, показанную на рисунке выше. Кроме того, поскольку индуктивность зависит от окружающего материала, используйте Таблицу 4, чтобы определить соответствующий коэффициент «K» (множитель) для индуктивности.

Где:

X L = Индуктивное сопротивление проводника (Ом)	L C = Индуктивность кабеля (мГн)
L = Длина кабеля в футах	A, B, C = Расстояние на рисунок вверху (дюймы)
K = Коэффициент поправки для установки, указанный в Таблице-4	d = Диаметр проводника (дюймы)

Сопротивление кабеля при рабочей температуре

Сопротивление жилы обеспечивается при 20 град.C в Таблице-1. При работе при другой температуре сопротивление меняется и рассчитывается по следующей формуле:

Где:

R AC = сопротивление переменного тока проводника при рабочей температуре (Ом)

R AC20C = сопротивление переменного тока проводника при 20 ° C (Ом)

T = рабочая температура проводник (° C)

Импеданс перенапряжения

Импеданс кабеля можно рассчитать по следующей формуле:

Где:

Z o = Импеданс кабеля (Ом)

L C = индуктивность проводника (мГн)

C = общая емкость кабеля (микрофарады)

.