Закон Ома. Формула Закона Ома
Закон Ома, основанный на опытах, представляет собой в электротехнике основной закон, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Появление смартфонов, гаджетов, бытовых приборов и прочей электротехники коренным образом изменило облик современного человека. Приложены огромные усилия, направленные на исследование физических закономерностей для улучшения старой и создания новой техники. Одной из таких зависимостей является закон Ома.
Георг Симон ОмЗакон Ома – полученный экспериментальным путём (эмпирический) закон, который устанавливает связь силы тока в проводнике с напряжением на концах проводника и его сопротивлением, был открыт в 1826 году немецким физиком-экспериментатором Георгом Омом.
Строгая формулировка закона Ома может быть записана так: сила тока в проводнике прямо пропорциональна напряжению на его концах (разности потенциалов) и обратно пропорциональна сопротивлению этого проводника.
Формула закона Ома записывается в следующем виде:
где
I – сила тока в проводнике, единица измерения силы тока – ампер [А];
U – электрическое напряжение (разность потенциалов), единица измерения напряжения- вольт [В];
R – электрическое сопротивление проводника, единица измерения электрического сопротивления – ом [Ом].
Согласно закону Ома, увеличение напряжения, например, в два раза при фиксированном сопротивлении проводника, приведёт к увеличению силы тока также в два раза
И напротив, уменьшение тока в два раза при фиксированном напряжении будет означать, что сопротивление увеличилось в два раза.
Рассмотрим простейший случай применения закона Ома. Пусть дан некоторый проводник сопротивлением 3 Ом под напряжением 12 В. Тогда, по определению закона Ома, по данному проводнику течет ток равный:
Существует мнемоническое правило для запоминания этого закона, которое можно назвать треугольник Ома. Изобразим все три характеристики (напряжение, сила тока и сопротивление) в виде треугольника.
Правило работы такое: закрываем пальцем величину в треугольнике, которую нужно найти, тогда две оставшиеся дадут верную формулу для поиска закрытой.
Где и когда можно применять закон Ома?
Нужна помощь в написании работы?
Закон Ома в упомянутой форме справедлив в достаточно широких пределах для металлов. Он выполняется до тех пор, пока металл не начнет плавиться. Менее широкий диапазон применения у растворов (расплавов) электролитов и в сильно ионизированных газах (плазме).
Работая с электрическими схемами, иногда требуется определять падение напряжения на определенном элементе. Если это будет резистор с известной величиной сопротивления (она проставляется на корпусе), а также известен проходящий через него ток, узнать напряжение можно с помощью формулы Ома, не подключая вольтметр.
Значение Закона Ома
Закон Ома определяет силу тока в электрической цепи при заданном напряжении и известном сопротивлении.
Он позволяет рассчитать тепловые, химические и магнитные действия тока, так как они зависят от силы тока.
Закон Ома является чрезвычайно полезным в технике(электронной/электрической), поскольку он касается трех основных электрических величин: тока, напряжения и сопротивления. Он показывает, как эти три величины являются взаимозависимыми на макроскопическом уровне.
Если бы было можно охарактеризовать закон Ома простыми словами, то наглядно это выглядело бы так:
Из закона Ома вытекает, что замыкать обычную осветительную сеть проводником малого сопротивления опасно. Сила тока окажется настолько большой, что это может иметь тяжелые последствия.
Сопротивление при параллельном соединении, формула для расчета сопротивления при параллельном соединении
В этой статье мы разберем, как посчитать общее сопротивление при параллельном соединении сопротивлений. Параллельным соединением сопротивлений называется соединение (рисунок ниже), при котором один зажим каждого из сопротивлений присоединяется к одной точке (узлу) электрической цепи, а другой зажим каждого из тех же сопротивлений присоединяется к другой точке электрической цепи. Таким образом, между двумя точками (узлами) электрической цепи включается несколько сопротивлений, образующих параллельные ветви.
Таким образом, между двумя точками (узлами) электрической цепи включается несколько сопротивлений, образующих параллельные ветви.
При этом напряжение между концами всех ветвей будет одним и тем же, а токи в отдельных ветвях определяются по закону Ома:
I1 = U / r1 ; I2 = U / r2
Напряжение U между узлами (А и Б):
U = I1r1 = I2r2 = I3r3,
откуда
I1 / I2 = R2 / R1 и I2 / I3 = R3 / R2,
т. е.
Токи в параллельных ветвях распределяются обратно пропорционально их сопротивлениям.
Согласно первому правилу Кирхгофа,
I = I1 + I2 + I3
или
U / Rсум = U / R1 + U / R2 + U / R2 = U (1 / R1 + 1 / R2 + 1 / R3).
Произведя сокращение на U, получим:
1 / Rсум = 1 / R1 + 1 / R2 + 1 / R 3
или
g = g1 + g2 + g3 ,
где R и g—сопротивление и проводимость разветвленной цепи или, как их часто называют, общие сопротивление и проводимость цепи.
Из полученной формулы следует, что
Общая проводимость разветвленной цепи равна сумме проводимостей отдельных ветвей.
Формула
1 / Rсум = 1 / R1 + 1 / R2 + 1 / R3
дает возможность определить общее сопротивление цепи. Например, для трех параллельно соединенных сопротивлений, приведя правую часть уравнения к общему знаменателю, получим:
1 / Rсум = R2R3 + R1R3 + R1R2 / R1R2R3
откуда
Rсум = R1R2R3 / R2R3 + R1R3 + R
Если сопротивления R1 = R2 = R3, то общее сопротивление цепи:
Rсум = R1 / 3,
а в общем случае при n параллельных ветвях с равными сопротивлениями R1 :
Rсум = R1 / n
В случае двух параллельных ветвей:
1 / Rсум = 1 / R1 + 1 / R2
откуда
Rсум = R1R2 / R2R3 + R1R3
При параллельном соединении приемников энергии все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных.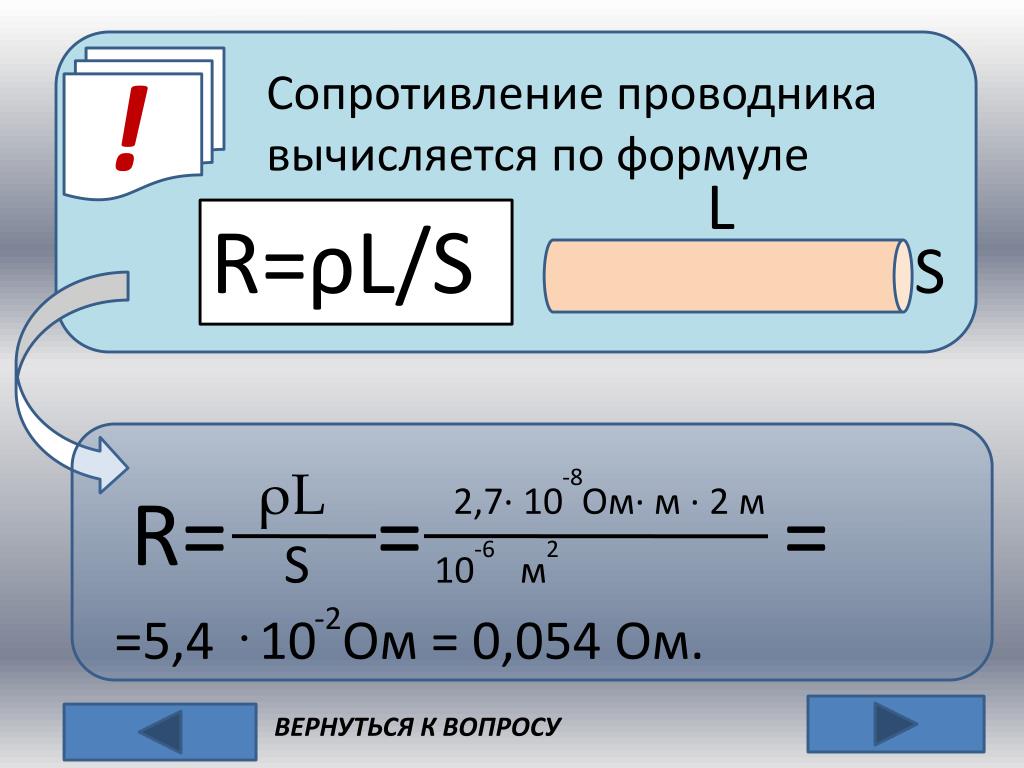 Совершенно иначе обстоит дело при последовательном соединении приемников, при котором изменение сопротивления одного из них тотчас же приводит к изменению напряжения на других, последовательно соединенных с ним. Поэтому электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, включаются параллельно. Одинаковые электрические лампы иногда соединяются последовательно. Пусть, например, напряжение сети U, а напряжение лампы U 0 < U Тогда n ламп соединяются цепочкой друг за другом, причем n > U / U0
Совершенно иначе обстоит дело при последовательном соединении приемников, при котором изменение сопротивления одного из них тотчас же приводит к изменению напряжения на других, последовательно соединенных с ним. Поэтому электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, включаются параллельно. Одинаковые электрические лампы иногда соединяются последовательно. Пусть, например, напряжение сети U, а напряжение лампы U 0 < U Тогда n ламп соединяются цепочкой друг за другом, причем n > U / U0
Такое соединение ламп можно встретить, например, в трамваях, метро и других случаях.
Пример 1:
К сети с напряжением 220 в параллельно подключены двигатель мощностью 1,1 квт и 11 ламп, каждая мощностью 40 вт. Определить ток в главных (подводящих) проводах
Ток двигателя
I1 = P1 / U = 1100 / 220 = 5a.
Ток ламп
I2 = P2 / U = 11 x 40 / 220 = 2a.
Ток в подводящих проводах
I = I1 + I2 = 5 + 2 = 7a.
Пример 2:
Определить общее сопротивление десяти параллельно включенных ламп накаливания, если каждая из них 240 ом:
R = Rл / n = 240 / 10 = 24ом.
3.3.2.10. Расчетные формулы определения основного сопротивления движению
Монография “ТЯГОВЫЕ РАСЧЕТЫ”
3. СИЛЫ, ДЕЙСТВУЮЩИЕ НА ПОЕЗД
3.3. Силы сопротивления движению поезда
3.3.2. Основное сопротивление
3.3.2.10. РАСЧЕТНЫЕ ФОРМУЛЫ ОПРЕДЕЛЕНИЯ ОСНОВНОГО СОПРОТИВЛЕНИЯ ДВИЖЕНИЮ
Несмотря на наличие эмпирических формул для определения всех известных составляющих основного сопротивления (за исключением сопротивления от рассеяния энергии в надрессоренном строении подвижного состава), на практике для конкретной марки локомотива или типа вагонов применяют одну обобщенную формулу определения основного сопротивления. Данная формула определяет зависимость удельного сопротивления движению от скорости движения и нагрузки на рельсы от колесной пары
, (3. 3.2.10-1)
3.2.10-1)где А, В, С, D – коэффициенты.
Для подвижного состава с неизменной (почти неизменной) осевой нагрузкой (локомотивов, электро- и дизель-поездов) формула приобретает вид
wo (wх) = A + B V + C V2. (3.3.2.10-2)
Из-за заметного влияния повышенного воздушного сопротивления головного и хвостового вагонов удельное сопротивление сравнительно коротких поездов (электро- и дизель-поездов) зависит также от числа вагонов в поезде. В связи с этим в ПТР для дизель-поездов ДР1, Д1 и Д приводятся следующие формулы:
а) режим тяги
; (3.3.2.10-3)
б) режим холостого хода
wx = wo + wз, (3.3.2.10-4)
, (3.3.2.10-5)
E, F – коэффициенты;
mдп – общее число вагонов в дизель-поезде;
mм – число моторных вагонов в дизель-поезде.

В общем случае для поезда, состоящего из локомотивов разных марок и вагонов разного типа, основное удельное сопротивление принимается как средневзвешенная (по массе) величина:
а) режим тяги
; (3.3.2.10-6)
б) режим холостого хода
, (3.3.2.10-7)
где Pi – масса локомотивов i-ой марки, т;
Qj – масса вагонов j-ого типа, т.
Для подвижного состава, выпускаемого компанией Siemens, используется формула определения основного сопротивления следующего вида
W’o = k0 + k1 V + k2 m + k3 V m + k4 ktun (V + Vwind)2 + k5 ktun (V + Vwind)2 m , (3.3.2.10-8)
где k0, k1, k2, k3, k4, k5 – коэффициенты;
ktun – коэффициент, учитывающий движение в тоннеле;
m – масса подвижного состава, кг;
V – скорость подвижного состава, м/с;
Vwind – скорость ветра, м/с.
В эту формулу, помимо постоянных (основных) составляющих сопротивления, входят также и временные (дополнительные) – сопротивления от ветра и в тоннеле.
Для тепловозов ER 20, ER 20CF и ER 24 указанная формула при движении на открытой поверхности и отсутствии ветра выглядит следующим образом
W’o = 0 + 486 V + 0.0089333 m + 0 V m + 0 V2 + 0.00000306667 V2. (3.3.2.10-9)
При массе тепловозов m = 138000 кг и скорости, измеряемой в км/ч, формула приобретает стандартный вид
W’o = 1233 + 135 V + 0.03265 V2, (3.3.2.10-10)
w’o = 0.911 + 0.1 V + 0.000024 V2. (3.3.2.10-11)
Аналогичные формулы для двухсистемного 5-вагонного электропоезда Desiro RUS («Ласточка») с массой m = 311700 кг выглядят следующим образом
Wo = 0 + 0 V + 0.0162 m + 0.0002515 V m + 7.739 V2 + 0 V2 m, (3. 3.2.10-12)
3.2.10-12)
Wo = 5050 + 21.776 V + 0.597 V2, (3.3.2.10-13)
wo = 1.65 + 0.007 V + 0.0001953 V2. (3.3.2.10-14)
Для тепловоза Vossloh Euro 4000 испанской фирмы Vossloh в формулу определения основного сопротивления введена зависимость от количества осей (осевой нагрузки)
W’o = 6.5 m + 130 no + 0.1 m V + 0.3 V2, (3.3.2.10-15)
где m – масса подвижного состава, т;
no – количество осей;
V – скорость подвижного состава, км/ч.
При массе тепловоза m = 123 т и количестве осей no = 6 формула приобретает стандартный вид
W’o = 1580 + 12.3 V + 0.3 V2, (3.3.2.10-16)
w’o = 1.3 + 0.01 V + 0.000249 V2. (3.3.2.10-17)
[ТПТР] Приведенные выше формулы (3.3.2.10-1 – 3.3.2.10-4) для определения удельного основного сопротивления действительны только при скорости выше 10 км/ч. При скоростях от 0 (момент трогания поезда с места) до 10 км/ч закономерность изменения сопротивления имеет совершенно другой характер, природа которого рассматривается в следующем разделе.
При скоростях от 0 (момент трогания поезда с места) до 10 км/ч закономерность изменения сопротивления имеет совершенно другой характер, природа которого рассматривается в следующем разделе.
назад вперед
Формулы сопротивления проводника при параллельном соединении
Последовательное соединение сопротивлений
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго — с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1 . Последовательное соединение сопротивлений
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U1 = IR1 U2 = IR2 и U3 = IR3
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В (внутренним сопротивлением источника тока пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи по закону Ома: 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U 1 = 0,75 х 10 = 7,5 В, U 2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Параллельное соединение сопротивлений
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы — в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую — с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (—), заметим, что прибор покажет ту же величину силы тока.
Значит, сила тока в цепи до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Пусть в первой ветви амперметр покажет силу тока I1 , а во второй — I 2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R 1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U — напряжение на зажимах источника тока; U 1 — падение напряжения на сопротивлении R 1 , U2 — падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U 1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1 т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей. Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.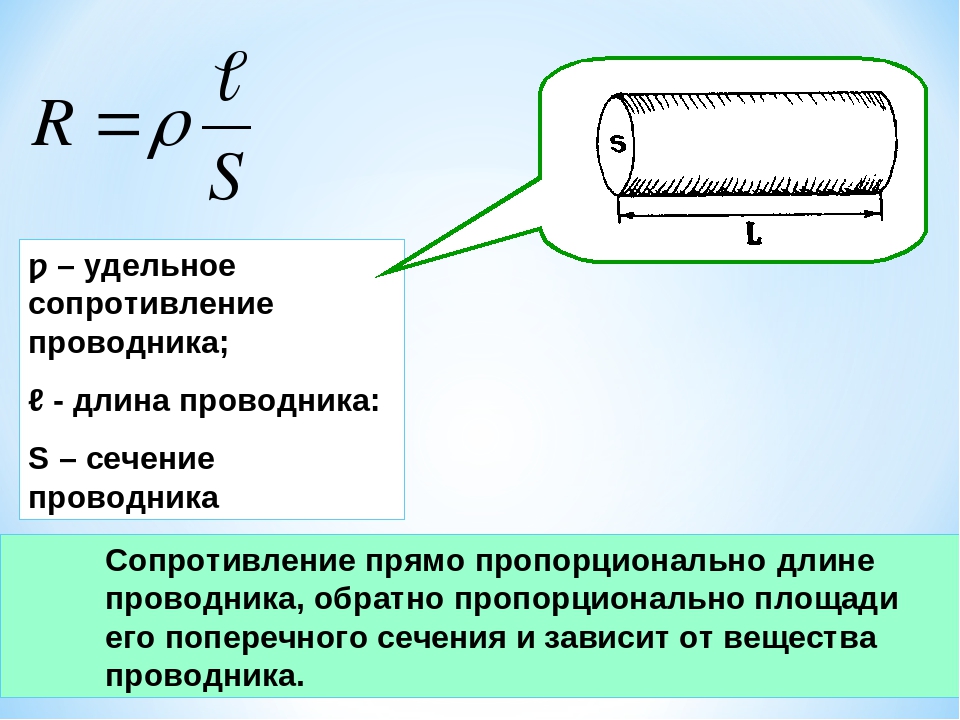
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 + I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть ( I1 = 300 мА) пошла через меньшее сопротивление ( R1 = 10 Ом), а меньшая часть ( R2 = 150 мА) — через большее сопротивление ( R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4 . Через тонкую трубу в один и тот же промежуток времени пройдет воды меньше, чем через толстую
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R , где I — ток во внешней цепи (до точки разветвления), U — напряжение внешней цепи, R — сопротивление внешней цепи, т. е. эквивалентное сопротивление.
е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1 , I2 = U2 / R2 , где I1 и I 2 — токи в ветвях; U 1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R – проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2 = 20 Ом и R3 = 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5 ).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0, 2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 = 1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / ( R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Ток в электроцепи проходит по проводникам от источника напряжения к нагрузке, то есть к лампам, приборам. В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
В большинстве случаев в качестве проводника используются медные провода. В цепи может быть предусмотрено несколько элементов с разными сопротивлениями. В схеме приборов проводники могут быть соединены параллельно или последовательно, также могут быть смешанные типы.
Элемент схемы с сопротивлением называется резистором, напряжение данного элемента является разницей потенциалов между концами резистора. Параллельное и последовательное электрическое соединение проводников характеризуется единым принципом функционирования, согласно которому ток протекает от плюса к минусу, соответственно потенциал уменьшается. На электросхемах сопротивление проводки берется за 0, поскольку оно ничтожно низкое.
Параллельное соединение предполагает, что элементы цепы подсоединены к источнику параллельно и включаются одновременно. Последовательное соединение означает, что проводники сопротивления подключаются в строгой последовательности друг за другом.
При просчете используется метод идеализации, что существенно упрощает понимание. Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Фактически в электрических цепях потенциал постепенно снижается в процессе перемещения по проводке и элементам, которые входят в параллельное или последовательное соединение.
Последовательное соединение проводников
Схема последовательного соединения подразумевает, что они включаются в определенной последовательности один за другим. Причем сила тока во всех из них равна. Данные элементы создают на участке суммарное напряжение. Заряды не накапливаются в узлах электроцепи, поскольку в противном случае наблюдалось бы изменение напряжения и силы тока. При постоянном напряжении ток определяется значением сопротивления цепи, поэтому при последовательной схеме сопротивление меняется в случае изменения одной нагрузки.
Недостатком такой схемы является тот факт, что в случае выхода из строя одного элемента остальные также утрачивают возможность функционировать, поскольку цепь разрывается. Примером может служить гирлянда, которая не работает в случае перегорания одной лампочки.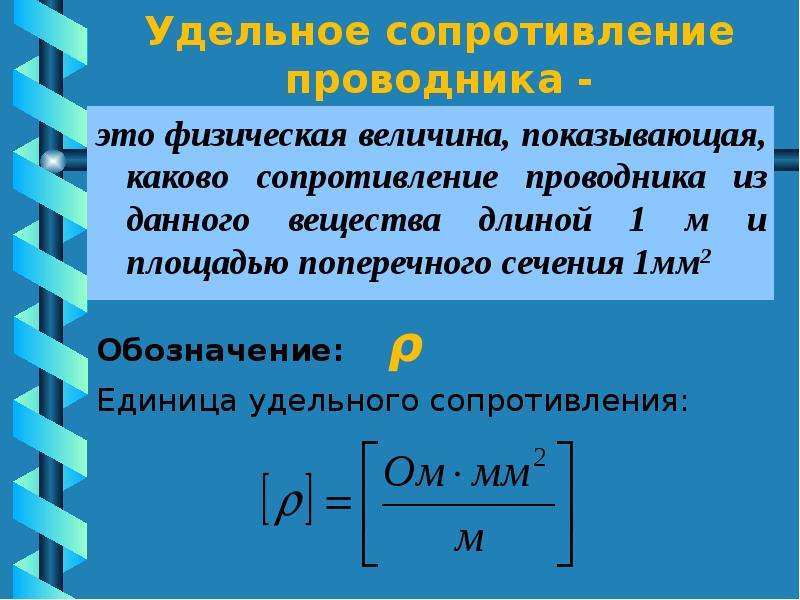 Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Это является ключевым отличием от параллельного соединения, в котором элементы могут функционировать по отдельности.
Последовательная схема предполагает, что по причине одноуровневого подключения проводников их сопротивление в любой точки сети равно. Общее сопротивление равняется сумме уменьшения напряжений отдельных элементов сети.
При данном типе соединения начало одного проводника подсоединяется к концу другого. Ключевая особенность соединения состоит в том, что все проводники находятся на одном проводе без разветвлений, и через каждый из них протекает один электроток. Однако общее напряжение равно сумме напряжений на каждом. Также можно рассмотреть соединение с другой точки зрения – все проводники заменяются одним эквивалентным резистором, и ток на нем совпадает с общим током, который проходит через все резисторы. Эквивалентное совокупное напряжение является суммой значений напряжения по каждому резистору. Так проявляется разность потенциалов на резисторе.
Использование последовательного подключения целесообразно, когда требуется специально включать и выключать определенное устройство. К примеру, электрозвонок может звенеть только в момент, когда присутствует соединение с источником напряжения и кнопкой. Первое правило гласит, что если тока нет хотя бы на одном из элементов цепи, то и на остальных его не будет. Соответственно при наличии тока в одном проводнике он есть и в остальных. Другим примером может служить фонарик на батарейках, который светит только при наличии батарейки, исправной лампочки и нажатой кнопки.
В некоторых случаях последовательная схема нецелесообразна. В квартире, где система освещения состоит из множества светильников, бра, люстр, не стоит организовывать схему такого типа, поскольку нет необходимости включать и выключать освещение во всех комнатах одновременно. С этой целью лучше использовать параллельное соединение, чтобы иметь возможность включения света в отдельно взятых комнатах.
Параллельное соединение проводников
В параллельной схеме проводники представляют собой набор резисторов, одни концы которых собираются в один узел, а другие – во второй узел. Предполагается, что напряжение в параллельном типе соединения одинаковое на всех участках цепи. Параллельные участки электроцепи носят название ветвей и проходят между двумя соединительными узлами, на них имеется одинаковое напряжение. Такое напряжение равно значению на каждом проводнике. Сумма показателей, обратных сопротивлениям ветвей, является обратной и по отношению к сопротивлению отдельного участка цепи параллельной схемы.
При параллельном и последовательном соединениях отличается система расчета сопротивлений отдельных проводников. В случае параллельной схемы ток уходит по ветвям, что способствует повышению проводимости цепи и уменьшает совокупное сопротивление. При параллельном подключении нескольких резисторов с аналогичными значениями совокупное сопротивление такой электроцепи будет меньше одного резистора число раз, равное числу резисторов в схеме.
В каждой ветви предусмотрено по одному резистору, и электроток при достижении точки разветвления делится и расходится к каждому резистору, его итоговое значение равно сумме токов на всех сопротивлениях. Все резисторы заменяются одним эквивалентным резистором. Применяя закон Ома, становится понятным значение сопротивления – при параллельной схеме суммируются значения, обратные сопротивлениям на резисторах.
При данной схеме значение тока обратно пропорционально значению сопротивления. Токи в резисторах не взаимосвязаны, поэтому при отключении одного из них это никоим образом не отразится на остальных. По этой причине такая схема используется во множестве устройств.
Рассматривая возможности применения параллельной схемы в быту, целесообразно отметить систему освещения квартиры. Все лампы и люстры должны быть соединены параллельно, в таком случае включение и отключение одного из них никак не влияет на работу остальных ламп. Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Таким образом, добавляя выключатель каждой лампочки в ветвь цепи, можно включать и отключать соответствующий светильник по необходимости. Все остальные лампы работают независимо.
Все электроприборы объединяются параллельно в электросеть с напряжением 220 В, затем они подключаются к распределительному щитку. То есть все приборы подключаются независимо от подключения прочих устройств.
Законы последовательного и параллельного соединения проводников
Для детального понимания на практике обоих типов соединений, приведем формулы, объясняющие законы данных типов соединений. Расчет мощности при параллельном и последовательном типе соединения отличается.
При последовательной схеме имеется одинаковая сила тока во всех проводниках:
Согласно закону Ома, данные типы соединений проводников в разных случаях объясняются иначе. Так, в случае последовательной схемы, напряжения равны друг другу:
U1 = IR1, U2 = IR2.
Помимо этого, общее напряжение равно сумме напряжений отдельно взятых проводников:
U = U1 + U2 = I(R1 + R2) = IR.
Полное сопротивление электроцепи рассчитывается как сумма активных сопротивлений всех проводников, вне зависимости от их числа.
В случае параллельной схемы совокупное напряжение цепи аналогично напряжению отдельных элементов:
А совокупная сила электротока рассчитывается как сумма токов, которые имеются по всем проводникам, расположенным параллельно:
Чтобы обеспечить максимальную эффективность электрических сетей, необходимо понимать суть обоих типов соединений и применять их целесообразно, используя законы и рассчитывая рациональность практической реализации.
Смешанное соединение проводников
Последовательная и параллельная схема соединения сопротивления могут сочетаться в одной электросхеме при необходимости. К примеру, допускается подключение параллельных резисторов по последовательной схеме к другому резистору или их группе, такое тип считается комбинированным или смешанным.
В таком случае совокупное сопротивление рассчитывается посредством получения сумм значений для параллельного соединения в системе и для последовательного. Сначала необходимо рассчитывать эквивалентные сопротивления резисторов в последовательной схеме, а затем элементов параллельного. Последовательное соединение считается приоритетным, причем схемы такого комбинированного типа часто используются в бытовой технике и приборах.
Итак, рассматривая типы подключений проводников в электроцепях и основываясь на законах их функционирования, можно полностью понять суть организации схем большинства бытовых электроприборов. При параллельном и последовательном соединениях расчет показателей сопротивления и силы тока отличается. Зная принципы расчета и формулы, можно грамотно использовать каждый тип организации цепей для подключения элементов оптимальным способом и с максимальной эффективностью.
В электрических цепях элементы могут соединяться по различным схемам, в том числе они имеют последовательное и параллельное соединение.
При таком соединении проводники соединяются друг с другом последовательно, то есть, начало одного проводника будет соединяться с концом другого. Основная особенность данного соединения заключается в том, что все проводники принадлежат одному проводу, нет никаких разветвлений. Через каждый из проводников будет протекать один и тот же электрический ток. Но суммарное напряжение на проводниках будет равняться вместе взятым напряжениям на каждом из них.
Рассмотрим некоторое количество резисторов, соединенных последовательно. Так как нет разветвлений, то количество проходящего заряда через один проводник, будет равно количеству заряда, прошедшего через другой проводник. Силы тока на всех проводниках будут одинаковыми. Это основная особенность данного соединения.
Это соединение можно рассмотреть иначе. Все резисторы можно заменить одним эквивалентным резистором.
Ток на эквивалентном резисторе будет совпадать с общим током, протекающим через все резисторы. Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Эквивалентное общее напряжение будет складываться из напряжений на каждом резисторе. Это является разностью потенциалов на резисторе.
Если воспользоваться этими правилами и законом Ома, который подходит для каждого резистора, можно доказать, что сопротивление эквивалентного общего резистора будет равно сумме сопротивлений. Следствием первых двух правил будет являться третье правило.
ПрименениеПоследовательное соединение используется, когда нужно целенаправленно включать или выключать какой-либо прибор, выключатель соединяют с ним по последовательной схеме. Например, электрический звонок будет звенеть только тогда, когда он будет последовательно соединен с источником и кнопкой. Согласно первому правилу, если электрический ток отсутствует хотя бы на одном из проводников, то его не будет и на других проводниках. И наоборот, если ток имеется хотя бы на одном проводнике, то он будет и на всех других проводниках. Также работает карманный фонарик, в котором есть кнопка, батарейка и лампочка. Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Все эти элементы необходимо соединить последовательно, так как нужно, чтобы фонарик светил, когда будет нажата кнопка.
Иногда последовательное соединение не приводит к нужным целям. Например, в квартире, где много люстр, лампочек и других устройств, не следует все лампы и устройства соединять последовательно, так как никогда не требуется одновременно включать свет в каждой из комнат квартиры. Для этого последовательное и параллельное соединение рассматривают отдельно, и для подключения осветительных приборов в квартире применяют параллельный вид схемы.
Параллельное соединениеВ этом виде схемы все проводники соединяются параллельно друг с другом. Все начала проводников объединены в одну точку, и все концы также соединены вместе. Рассмотрим некоторое количество однородных проводников (резисторов), соединенных по параллельной схеме.
Этот вид соединения является разветвленным. В каждой ветви содержится по одному резистору. Электрический ток, дойдя до точки разветвления, разделяется на каждый резистор, и будет равняться сумме токов на всех сопротивлениях. Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Напряжение на всех элементах, соединенных параллельно, является одинаковым.
Все резисторы можно заменить одним эквивалентным резистором. Если воспользоваться законом Ома, можно получить выражение сопротивления. Если при последовательном соединении сопротивления складывались, то при параллельном будут складываться величины обратные им, как записано в формуле выше.
ПрименениеЕсли рассматривать соединения в бытовых условиях, то в квартире лампы освещения, люстры должны быть соединены параллельно. Если их соединить последовательно, то при включении одной лампочки мы включим все остальные. При параллельном же соединении мы можем, добавляя соответствующий выключатель в каждую из ветвей, включать соответствующую лампочку по мере желания. При этом такое включение одной лампы не влияет на остальные лампы.
Все электрические бытовые устройства в квартире соединены параллельно в сеть с напряжением 220 В, и подключены к распределительному щитку. Другими словами, параллельное соединение используется при необходимости подключения электрических устройств независимо друг от друга. Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Последовательное и параллельное соединение имеют свои особенности. Существуют также смешанные соединения.
Последовательное и параллельное соединение, рассмотренное ранее, было справедливо для величин напряжения, сопротивления и силы тока, являющихся основными. Работа тока определяется по формуле:
А = I х U х t, где А – работа тока, t – время течения по проводнику.
Для определения работы при последовательной схеме соединения, необходимо заменить в первоначальном выражении напряжение. Получаем:
А=I х (U1 + U2) х t
Раскрываем скобки и получаем, что на всей схеме работа определяется суммой на каждой нагрузке.
Точно также рассматриваем параллельную схему соединения. Только меняем уже не напряжение, а силу тока. Получается результат:
А = А1+А2
Мощность токаПри рассмотрении формулы мощности участка цепи снова необходимо пользоваться формулой:
Р=U х I
После аналогичных рассуждений выходит результат, что последовательное и параллельное соединение можно определить следующей формулой мощности:
Р=Р1 + Р2
Другими словами, при любых схемах общая мощность равна сумме всех мощностей в схеме. Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
Этим можно объяснить, что не рекомендуется включать в квартире сразу несколько мощных электрических устройств, так как проводка может не выдержать такой мощности.
После перегорания одной лампы в гирлянде можно определить вид схемы соединения. Если схема последовательная, то не будет гореть ни одной лампочки, так как сгоревшая лампочка разрывает общую цепь. Чтобы выяснить, какая именно лампочка сгорела, нужно проверять все подряд. Далее, заменить неисправную лампу, гирлянда будет функционировать.
При применении параллельной схемы соединения гирлянда будет продолжать работать, даже если одна или несколько ламп сгорели, так как цепь не разорвана полностью, а только один небольшой параллельный участок. Для восстановления такой гирлянды достаточно увидеть, какие лампы не горят, и заменить их.
Последовательное и параллельное соединение для конденсаторовПри последовательной схеме возникает такая картина: заряды от положительного полюса источника питания идут только на наружные пластины крайних конденсаторов. Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
Конденсаторы, находящиеся между ними, передают заряд по цепи. Этим объясняется появление на всех пластинах равных зарядов с разными знаками. Исходя из этого, заряд любого конденсатора, соединенного по последовательной схеме, можно выразить такой формулой:
qобщ= q1 = q2 = q3
Для определения напряжения на любом конденсаторе, необходима формула:
U= q/С
Где С — емкость. Суммарное напряжение выражается таким же законом, который подходит для сопротивлений. Поэтому получаем формулу емкости:
С= q/(U1 + U2 + U3)
Чтобы сделать эту формулу проще, можно перевернуть дроби и заменить отношение разности потенциалов к заряду емкости. В результате получаем:
1/С= 1/С1 + 1/С2 + 1/C3
Немного иначе рассчитывается параллельное соединение конденсаторов.
Общий заряд вычисляется как сумма всех зарядов, накопившихся на пластинах всех конденсаторов. А величина напряжения также вычисляется по общим законам. В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
В связи с этим формула суммарной емкости при параллельной схеме соединения выглядит так:
С= (q1 + q2 + q3)/U
Это значение рассчитывается как сумма каждого прибора в схеме:
С=С1 + С2 + С3
Смешанное соединение проводниковВ электрической схеме участки цепи могут иметь и последовательное и параллельное соединение, переплетающихся между собой. Но все законы, рассмотренные выше для отдельных видов соединений, справедливы по-прежнему, и используются по этапам.
Сначала нужно мысленно разложить схему на отдельные части. Для лучшего представления ее рисуют на бумаге. Рассмотрим наш пример по изображенной выше схеме.
Удобнее всего ее изобразить, начиная с точек Б и В. Они расставляются на некотором расстоянии между собой и от края листа бумаги. С левой стороны к точке Б подключается один провод, а справа отходят два провода. Точка В наоборот, слева имеет две ветки, а после точки отходит один провод.
Далее нужно изобразить пространство между точками. По верхнему проводнику расположены 3 сопротивления с условными значениями 2, 3, 4. Снизу будет идти ток с индексом 5. Первые 3 сопротивления включены в схему последовательно, а пятый резистор подключен параллельно.
Остальные два сопротивления (первый и шестой) подключены последовательно с рассматриваемым нами участком Б-В. Поэтому схему дополняем 2-мя прямоугольниками по сторонам от выбранных точек.
Теперь используем формулу расчета сопротивления:
- Первая формула для последовательного вида соединения.
- Далее, для параллельной схемы.
- И окончательно для последовательной схемы.
Аналогичным образом можно разложить на отдельные схемы любую сложную схему, включая соединения не только проводников в виде сопротивлений, но и конденсаторов. Чтобы научиться владеть приемами расчета по разным видам схем, необходимо потренироваться на практике, выполнив несколько заданий.
Глава 21.
 Электрический ток. Законы Ома и Джоуля-Ленца
Электрический ток. Законы Ома и Джоуля-ЛенцаДля решения задач ЕГЭ на постоянный ток надо знать определения тока, напряжения, сопротивления, закон Ома для участка цепи и замкнутой цепи, закон Джоуля-Ленца, а также уметь находить эквивалентные сопротивления простейших электрически цепей. Рассмотрим эти вопросы.
Электрическим током называют упорядоченное движение заряженных частиц. Силой тока в некотором сечении проводника называется отношение заряда , протекшего через это сечение за интервал времени , к этому интервалу времени
(21.1) |
Чтобы в проводнике тек электрический ток, в проводнике должно быть электрическое поле, или, другими словами, потенциалы различных точек проводника должны быть разными. Но при движении электрических зарядов по проводнику потенциалы различных точек проводника будут выравниваться (см. гл. 19). Поэтому для протекания тока в течение длительного времени на каких-то участках цепи необходимо обеспечить движение зарядов в направлении противоположном полю. Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Такое движение может быть обеспечено только силами неэлектрической природы, которые в этом контексте принято называть сторонними. В гальванических элементах («батарейках») сторонние силы возникают в результате электрохимических превращений на границах электродов и электролита. Эти превращения обеспечивают перемещение заряда противоположно направлению поля, поддерживая движение зарядов по замкнутому пути.
Сила тока в однородном участке проводника пропорциональна напряженности электрического поля внутри проводника. А поскольку напряженность поля внутри проводника связана с разностью потенциалов его концов (или электрическим напряжением на проводнике ), то
(21.2) |
Коэффициент пропорциональности , который принято записывать в знаменатель формулы (21.2), является характеристикой проводника и называется его сопротивлением. В результате формула (21.2) принимает вид
(21. |
Формула (21.3) называется законом Ома для однородного участка цепи, а сам участок цепи часто называют резистором (от английского слова resistance — сопротивление).
Если проводник является однородным и имеет цилиндрическую форму (провод), то его сопротивление пропорционально длине и обратно пропорционально площади сечения
(21.4) |
где коэффициент пропорциональности зависит только от материала проводника и называется его удельным сопротивлением.
Если участок цепи представляет собой несколько последовательно соединенных однородных проводников с сопротивлениями (см. рисунок), то сила тока через каждый проводник будет одинаковой , электрическое напряжение на всем участке цепи равно сумме напряжений на каждом проводнике , а эквивалентное сопротивление всего участка равно сумме сопротивлений отдельных проводников
(21. |
Если участок цепи представляет собой несколько однородных проводников с сопротивлениями , соединенных параллельно (см. рисунок), то электрическое напряжение на каждом проводнике будет одинаковым , ток через участок будет равен сумме токов, текущих через каждый проводник , а величина, обратная эквивалентному сопротивлению всего участка, равно сумме обратных сопротивлений отдельных проводников
(21.5) |
Рассмотрим теперь закон Ома для замкнутой электрической цепи. Пусть имеется замкнутая электрическая цепь, состоящая из источника сторонних сил с внутренним сопротивлением и внешнего сопротивления . Пусть при прохождении заряда через источник сторонние силы совершают работу . Электродвижущей силой источника (часто используется аббревиатура ЭДС) называется отношение работы сторонних сил к заряду
(21. |
В этом случае сила тока в цепи равна
(21.7) |
Формула (21.7) называется законом Ома для замкнутой электрической цепи.
При прохождении электрического тока через участок цепи электрическое поле совершает работу (часто эту работу называют работой тока, хотя термин этот не очень точный). Очевидно, вся эта работа превращается в тепло. Поэтому если через участок цепи прошел заряд , где — сила тока в цепи, — время, то количество выделившейся теплоты равно
(21.8) |
(для получения последнего и предпоследнего равенств использован закон Ома для участка цепи). Формулы (21.8) называются законом Джоуля-Ленца. Из формулы (21.8) следует, что количество выделившейся при протекании электрического тока теплоты линейно зависит от времени наблюдения. Поэтому отношение
Поэтому отношение
(21.9) |
которое называется мощностью тока, не зависит от времени наблюдения. Формулу (21.9) также называют законом Джоуля-Ленца.
Рассмотрим теперь задачи.
Структура металла кратко обсуждалась в гл. 16: положительно заряженные ионы расположены в узлах кристаллической решетки, образовавшиеся в результате диссоциации валентные электроны могут свободно перемещаться по проводнику (свободные электроны). Они и осуществляют проводимость металла (задача 21.1.1 — ответ 2).
Согласно определению (21.1) находим среднюю силу тока в канале молнии (задача 21.1.2)
(ответ 2).
Если за 1 мин через сечение проводника протекает заряд 60 Кл (задача 21.1.3), то сила тока в этом проводнике равна А. Применяя далее к этому проводнику закон Ома для участка цепи, получаем В (ответ 2).
По закону Ома для участка цепи имеем для силы тока через участок цепи после изменения его сопротивления и электрического напряжения на нем (задача 21.1.4)
Таким образом, сила тока уменьшилась в 4 раза (ответ 3).
Согласно закону Ома для участка цепи сопротивление — это коэффициент пропорциональности между напряжением на этом участке и силой тока в нем. Поэтому в задаче 21.1.5 имеем, например, используя крайнюю точку графика
(ответ 2). Из-за линейной зависимости тока от напряжения вычисления можно было выполнить и по другим точкам графика, ответ был бы таким же.
Согласно формуле (21.4) имеем для первой проволоки в задаче 21.1.6
где — удельное сопротивление меди, — длина проводника, — его радиус. Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
Для медной проволоки с вдвое большей длиной и втрое бóльшим радиусом сечения имеем
(ответ 3).
Как следует из формулы (21.4) при двукратном уменьшении длины проводника вдвое уменьшается его сопротивление. Поэтому из закона Ома для участка цепи (21.3) заключаем, что при двукратном уменьшении напряжения на проводнике и двукратном уменьшении его длины (задача 21.1.7) сила тока в проводнике не изменится (ответ 4).
В задаче 21.1.8 следует использовать закон Ома для замкнутой электрической цепи (21.7). Имеем
где — ЭДС источника, — сопротивлении е внешней цепи, — сопротивление источника (ответ 1).
В задаче 21.1.9 следует применить закон Ома для замкнутой электрической цепи (21.7) к какому-нибудь значению внешнего сопротивления, по графику найти силу тока в цепи, а затем и ЭДС источника. Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
Проще всего применить закон Ома к случаю . Из графика находим силу тока . Поэтому
где — внутреннее сопротивление источника (ответ 3).
Из формулы (21.9) следует, что при фиксированном сопротивлении участка цепи увеличение электрического напряжения в 2 раза (задача 21.1.10) приведет к увеличению мощности тока в 4 раза (ответ 2).
В задаче 21.2.1 удобно использовать вторую из формул (21.9) . Имеем Вт (ответ 3).
Часто школьники не могут ответить на такой вопрос: из формулы для мощности тока следует, что мощность линейно растет с ростом сопротивления, а из формулы — убывает с ростом сопротивления. А как же в действительности мощность зависит от сопротивления? Давайте разберемся в этом вопросе на примере задачи 21.2.2. Конечно, оба предложенных «решения» неправильны: в них молчаливо предполагалось, что сила тока, текущего через это сопротивление, или напряжение на этом сопротивлении не зависят от его величины. А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
А на самом деле эти величины от сопротивления зависят, причем эти зависимости могут быть разными для разных источников тока. Внутреннее сопротивление бытовых электрических сетей очень мало. В этом случае из законов Ома для замкнутой цепи и участка цепи (21.7), (21.3) следует, что напряжение на любом элементе, включенном в такую сеть, не зависит от сопротивления этого элемента и равно номинальному напряжению сети . Поэтому из формулы заключаем, что мощность, которая выделяется на таком элементе обратно пропорциональна его сопротивлению (ответ 3). Отметим, что из проведенного рассуждения следует, что выделяемая мощность будет очень большой (опасная в быту ситуация!) для малого сопротивления внешнего участка цепи, т.е. в случае короткого замыкания, которого, таким образом, необходимо избегать.
Если бы внутреннее сопротивление источника было бы много больше внешнего сопротивления, ток в цепи определялся бы, главным образом, внутренним сопротивлением источника, а от внешнего сопротивления зависел бы слабо. В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
В этом случае мощность тока была бы прямо пропорциональна сопротивлению участка цепи.
Как обсуждалось в решении предыдущей задачи, сопротивление элемента, работающего в бытовой электросети равно , где — номинальная мощность данного элемента, — напряжение в сети. Поэтому отношение сопротивлений ламп мощностью Вт и Вт, рассчитанных на работу в одной и той же бытовой электрической сети (задача 21.2.3) равно
(ответ 2).
Поскольку резисторы в задаче 21.2.4 соединены последовательно, то сила тока в них одинакова. Поэтому из закона Ома для участка цепи заключаем, что
(ответ 2).
При параллельном соединении ламп (задача 21.2.5) напряжение на них одинаково (см. введение к настоящей главе). Поэтому из закона Ома для участка цепи следует, что
(ответ 1).
Рассматриваемый в задаче 21.2.6 участок представляет собой два последовательных соединенных элемента, один из которых есть резистор 6 Ом, второй — два таких же резистора, соединенных параллельно. По правилам сложения сопротивлений находим эквивалентное сопротивление второго участка
а затем и эквивалентное сопротивление всей цепи
(ответ 3).
При разомкнутом ключе сопротивление участка цепи, данного в задаче 21.2.7, можно найти как в предыдущей задаче , где — сопротивление каждого резистора. Если ключ замкнут, то цепь сводится к одному резистору (т.к. параллельно двум резисторам включается проводник с пренебрежимо малым сопротивлением). Поэтому в этом случае сопротивление цепи равно . Таким образом, сопротивление второй цепи составляет две трети от сопротивления первой (ответ 1).
Как обсуждалось в решении задачи 21.2.2, сопротивление элемента номинальной мощности , работающего в бытовой электросети равна
где В — напряжение сети. Из этой формулы следует, что чем больше номинальная мощность элемента, тем меньше должно быть его сопротивление. Если две лампы накаливания включены последовательно (задача 21.2.8), то сила тока в них одинакова и отношение мощностей тока в этих лампах равно отношению их сопротивлений. Отсюда следует, что отношение реально выделяемых в лампах мощностей и обратно отношению номинальных мощностей этих ламп:
(ответ 2).
Работа, совершаемая электрическим полем в проводнике при протекании по нему электрического тока, превращается в энергию тока, которая затем превращается в тепловую энергию. Поэтому работу поля можно найти из закона Джоуля-Ленца. Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
Для работы поля за время получаем . Из этой формулы находим сопротивление проводника в задаче 21.2.9 —
(ответ 1).
Поскольку при последовательном соединении резисторов ток через каждый из них одинаков, из закона Джоуля-Ленца (22.8) заключаем, что из двух сопротивлений и (задача 21.2.10; см. рисунок) наибольшей будет мощность тока на сопротивлении , из двух сопротивлений и — на сопротивлении . Сравним мощности тока на этих сопротивлениях. Учитывая, что при параллельном соединении элементов электрическое напряжение на каждом элементе одинаковое, а при последовательном — складываются значения сопротивлений, получим из законов Ома для верхнего и нижнего участков цепи и закона Джоуля-Ленца
где — электрическое напряжение, приложенное ко всей цепи. Поскольку то в представленной схеме наибольшая мощность будет выделяться на сопротивлении (ответ 2).
Полное сопротивление цепи переменного тока
В предыдущих статьях мы узнали, что всякое сопротивление, поглощающее энергию, называется активным, а сопротивление, не поглощающее энергии, безваттным или реактивным. Кроме того, мы установили, что реактивные сопротивления делятся на два вида — индуктивные и емкостные.
Однако существуют цепи, где сопротивление не является чисто активным или чисто реактивным. То есть цепи, где вместе с активным сопротивлением включены в цепь, как емкости, так и индуктивности.
Введем понятие полного сопротивления цепи переменному току – Z, которое соответствует векторной сумме всех сопротивлений цепи (активных, емкостных и индуктивных). Понятие полного сопротивления цепи нам необходимо для более полного понимания закона Ома для переменного тока
На рисунке 1 представлены варианты электрических цепей и их классификация в зависимости от того какие элементы (активные или реактивные) включены в цепь.
Рисунок 1. Классификация цепей переменного тока.
Полное сопротивление цепи с чисто активными элементами соответствует сумме активных сопротивлений цепи и рассматривалось нами ранее. О чисто емкостном и индуктивном сопротивлении цепи мы тоже с вами говорили, и оно зависит соответственно от общей емкости и индуктивности цепи.
Рассмотрим более сложные варианты цепи, где последовательно с активным сопротивлением в цепь включено индуктивное и реактивное сопротивление.
Полное сопротивление цепи при последовательном соединении активного и реактивного сопротивления.
В любом сечении цепи, изображенной на рисунке 2,а, мгновенные значения тока должны быть одинаковыми, так как в противном случае наблюдались бы скопления и разрежения электронов в каких-либо точках цепи. Иными словами, фазы тока по всей длине цепи должны быть одинаковыми. Кроме того, мы знаем, что фаза напряжения на индуктивном сопротивлении опережает фазу тока на 90°, а фаза напряжения на активном сопротивлении совпадает с фазой тока (рисунок 2,б). Отсюда следует, что радиус-вектор напряжения UL (напряжение на индуктивном сопротивлении) и напряжения UR (напряжение на активном сопротивлении) сдвинуты друг относительно друга на угол в 90°.
Рисунок 2. Полное сопротивление цепи с активным сопротивлением и индуктивностью. а) – схема цепи; б) – сдвиг фаз тока и напряжения; в) – треугольник напряжений; д) – треугольник сопротивлений.
Для получения радиуса-вектора результирующего напряжения на зажимах А и В (рис.2,а) мы произведем геометрическое сложение радиусов-векторов UL и UR. Такое сложение выполнено на рис. 2,в, из которого видно, что результирующий вектор UAB является гипотенузой прямоугольного треугольника.
Из геометрии известно, что квадрат гипотенузы равен сумме квадратов катетов.
По закону Ома напряжение должно равняться силе тока, умноженной на сопротивление.
Так как сила тока во всех точках цепи одинакова, то квадрат полного сопротивления цепи (Z2) будет также равен сумме квадратов активного и индуктивного сопротивлений, т. е.
(1)
Извлекая квадратный корень из обеих частей этого равенства, получим,
(2)
Таким образом, полное сопротивление цепи, изображенной на рис 2,а, равно корню квадратному из суммы квадратов активного и индуктивного сопротивлений
Полное сопротивление можно находить не только путем вычисления, но и путем построения треугольника сопротивлений, аналогичного треугольнику напряжений (рис 2,д), т. е. полное сопротивление цепи переменному току может быть получено путем измерения гипотенузы, прямоугольного треугольника, катетами которого являются активное и реактивное сопротивления. Разумеется, измерения катетов и гипотенузы должны производиться в одном и том же масштабе. Так, например, если мы условились, что 1 см длины катетов соответствует 1 ом, то число омов полного сопротивления будет равно числу сантиметров, укладывающихся на гипотенузе.
Полное сопротивление цепи, изображенной на рис.2,а, не является ни чисто активным, ни чисто реактивным; оно содержит в себе оба эти вида сопротивлений. Поэтому угол сдвига фаз тока и напряжения в этой цепи будет отличаться и от 0° и от 90°, то есть он будет больше 0°, но меньше 90°. К которому из этих двух значений он будет более близок, будет зависеть от того, какое из этих сопротивлений имеет преобладающее значение в цепи. Если индуктивное сопротивление будет больше активного, то угол сдвига фаз будет более близок к 90°, и наоборот, если преобладающим будет активное сопротивление, то угол сдвига фаз будет более близок к 0°.
В цепи, изображенной на рис 3,а, соединены последовательно активное и емкостное сопротивления. Полное сопротивление такой цепи можно определить при помощи треугольника сопротивлений так же, как мы определяли выше полное сопротивление активно-индуктивной цепи.
Рисунок 3. Полное сопротивление цепи с активным сопротивлением и емкостью. а) – схема цепи; б) – треугольник сопротивлений.
Разница между обоими случаями состоит лишь в том, что треугольник сопротивлений для активно-емкостной цепи будет повернут в другую сторону (рис 3,б) вследствие того, что ток в емкостной цепи не отстает от напряжения, а опережает его.
Для данного случая:
(3)
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 4,а), сначала определяется реактивное сопротивление этой цепи, а затем уже полное сопротивление цепи.
Рисунок 4. Полное сопротивление цепи содержащей R, L и C. а) – схема цепи; б) – треугольник сопротивлений.
Реактивное сопротивление этой цепи состоит из индуктивного и емкостного сопротивлений. Так как эти два вида реактивного сопротивления противоположны друг другу по своему характеру, то общее реактивное сопротивление цепи будет равно их разности, т. е.
(4)
Общее реактивное сопротивление цепи может иметь индуктивный или емкостный характер, в зависимости от того, какое из этих двух сопротивлений (XL или XC преобладает).
После того как мы по формуле (4) определили общее реактивное сопротивление цепи, определение полного сопротивления не представит затруднений. Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
(5)
Или
(6)
Способ построения треугольника сопротивлений для этого случая изображен на рис. 4 б.
Полное сопротивление цепи при параллельном соединении активного и реактивного сопротивления.
Полное сопротивление цепи при параллельном соединении активного и реактивного элемента.
Для того чтобы вычислить полное сопротивление цепи, составленной из активного и индуктивного сопротивлений, соединенных между собой параллельно(рис. 5,а), нужно сначала вычислить проводимость каждой из параллельных ветвей, потом определить полную проводимость всей цепи между точками А и В и затем вычислить полное сопротивление цепи между этими точками.
Рисунок 5. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) – параллельное соединение R и L; б) – параллельное соединение R и C.
Проводимость активной ветви, как известно, равна 1/R, аналогично проводимость индуктивной ветви равна 1/ωL , а полная проводимость равна 1/Z
Полная проводимость равна корню квадратному из суммы квадратов активной и реактивной проводимости, т. е.
(7)
Приводя к общему знаменателю подкоренное выражение, получим:
(8)
откуда:
(9)
Формула (9) служит для вычисления полного сопротивления цепи, изображенной на рис. 5а.
Нахождение полного сопротивления для этого случая может быть произведено и геометрическим путем. Для этого нужно построить в соответствующем масштабе треугольник сопротивлений, и затем произведение длин катетов разделить на длину гипотенузы. Полученный результат и будет соответствовать полному сопротивлению.
Аналогично случаю, рассмотренному выше, полное сопротивление при параллельном соединении R и С (рис 5б) будет равно:
(10)
Полное сопротивление может быть найдено также и в этом случае путем построения треугольника сопротивлений.
В радиотехнике наиболее часто встречается случай па¬раллельного соединения индуктивности и емкости, например колебательный контур для настройки приемников и передатчиков. Так как катушка индуктивности всегда обладает кроме индуктивного еще и активным сопротивлением, то эквивалентная (равноценная) схема колебательного контура будет содержать в индуктивной ветви активное сопротивление (рис 7).
Рисунок 6. Эквивалентная схема колебательного контура.
Формула полного сопротивления для этого случая будет:
(11)
Так как обычно активное сопротивление катушки (R) бывает очень мало по сравнению с ее индуктивным сопротивлением (ωL), то мы имеем право формулу (11) переписать в следующем виде:
(12)
В колебательном контуре обычно подбирают величины L и С таким образом, чтобы индуктивное сопротивление равнялось емкостному, т. е. чтобы соблюдалось условие
(13)
При соблюдении этого условия полное сопротивление колебательного контура будет равно:
(14)
где L—индуктивность катушки в Гн;
С—емкость конденсатора в Ф;
R—активное сопротивление катушки в Ом.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Основные расчетные электротехнические формулы
Электрическое сопротивление материала определяется по формулам:
Электрическое сопротивление, Ом, материала
R = U/I, где U — напряжение, В; I — сила тока, А.
Удельное электрическое сопротивление, Ом·м,
ρ=Rs/l. S – сечение проводника, м² ; l – длина проводника, м.
Под удельным электрическим сопротивлением материала понимают сопротивление проводника длиной 1 м и сечением 1 м² при 20°С.
Величина, обратная удельному сопротивлению, называется проводимостью:
v=1/ρ.
Если вместо сечения проводника S задан его диаметр D, то сечение, м², находят по формуле
S= πD²/4, где π =3,14.
Сопротивление материала зависит от температуры. Если материал нагрет до температуры t°С, то его сопротивление, Ом, при этой температуре равно:
Rt= R0[1 + α (t – t0)],
где R0 – сопротивление при начальной температуре t0°С, Ом; α – температурный коэффициент.
Далее приводятся значения α для различных материалов.
| Медь, алюминий, вольфрам | 0,004 |
| Сталь | 0,006 |
| Латунь | 0,002 |
Сопротивление нескольких проводников зависит от способа их соединения. Например, при параллельном соединении сопротивление трех проводников определяется по формуле:
Rоб=R1*R2*R3/(R1R2+R2R3+R3R1)
При последовательном соединении:
Rоб=R1+R2+R3.
Постоянный ток
Постоянный ток применяют для питания устройств связи, транзисторных приборов, стартеров автомобилей, электрокар, а также, для зарядки аккумуляторов.
В качестве источников постоянного тока используют гальванические элементы, солнечные батареи, термоэлектрогенераторы, генераторы постоянного тока.
При параллельном соединении нескольких проводников с током с равными напряжениями:
Iоб = I1+I2+…+In Uоб=U1=U2=…=Un
При последовательном соединении: Iоб = Imin; – где Imin, ток наименьшего по мощности источника тока (генератора, аккумуляторной батареи).
Uоб = U1+U2+…+Un
Основные параметры цепей однофазного переменного тока
Однофазный переменный ток промышленной частоты имеет 50 периодов колебаний в секунду, или 50 Гц. Его применяют для питания небольших вентиляторов, электробытовых приборов, электроинструмента, при электросварке и для питания большинства осветительных приборов.
Частота переменного тока, Гц:
f= 1/T = np/60, где п — частота вращения генератора, мин -1; р – число пар полюсов генератора.
Мощность однофазного переменного тока:
активная, Вт, Ра = IUcosφ;
реактивная, вар, Q = IUsinφ;
кажущаяся, В А, S = IU =√ (P 2α+Q 2)
Если в цепь переменного однофазного тока включено только активное сопротивление (например, нагревательные элементы или электрические лампы), то значение силы тока и мощности в каждый момент времени определяют по закону Ома:
I=U/R; Рa = IU = I²R=U²/R.
Коэффициент мощности в цепи с индуктивной нагрузкой
Cosφ= Рa/IU= Рa/S.
Основные параметры цепей трехфазного переменного тока
Трехфазный переменный ток используют для питания большинства промышленных электроприемников. Частота трехфазного переменного тока 50 Гц.
В трехфазных системах обмотки генератора и электроприемника соединяют по схемам «звезда» или «треугольник». При соединении в звезду концы всех трех обмоток генератора (или электроприемника) объединяют в общую точку, называемую нулевой или нейтралью (рис. 5а).
При соединении в треугольник начало первой обмотки соединяют с концом второй, начало второй обмотки — с концом третьей и начало третьей — с концом первой обмотки (рис. 5б).
Если от генератора отходят только три провода, то такая система называется трехфазной трехпроводной; если от него отходит еще и четвертый нулевой провод, то систему называют трехфазной четырехпроводной.
Трехфазные трехпроводные сети используют для питания трехфазных силовых потребителей, а четырехпроводные сети – для питания преимущественно осветительных и бытовых нагрузок.
В трехфазных системах различают фазные и линейные токи и напряжения. При соединении фаз звездой линейный I и фазный Iφ токи равны:
а напряжение U =√3Uφ
При соединении треугольником
I =√3Iφ
а напряжение U = Uφ.
Мощность переменного трехфазного тока:
генератора:
- активная, Вт, Рг =√3IUcosφ ,
- реактивная, вар, Q=√3IUsinφ
- полная, ВА, S = √3IU.
где φ – угол сдвига фаз между фазным напряжением генератора и током в той же фазе приемника, который равен току в линии при соединении обмоток генератора звездой.
приемника:
- активная, Вт, Рп =3UφIcosφп=√3 IUcosφп ,
- реактивная, вар, Q=√3 UφIsinφп=√3 UIsinφ
- полная, ВА, S = √3UI.
где φ – угол сдвига фаз между фазным напряжением приемника и током в той же фазе приемника, который равен току линейному только при соединении звездой.
Подсчет количества теплоты, выделяемой при протекании электрического тока по проводнику.
Количество теплоты, Дж, выделяемой электрическим током в проводнике,
Q=I²Rt где t — время, с.
При определении теплового действия электрического тока учитывают, что 1 кВт·ч выделяет 864 ккал (3617 кДж).
Если у Вас остались вопросы – обращайтесь к нам, в авторизованный сервисный центр “Эл Ко-сервис” Мы всегда рады помочь Вам в решении возникших у Вас проблем.
Инженерно-технический отдел авторизованного сервисного центра “Эл Ко-сервис”
ЗаконОма: сопротивление и простые схемы
Цели обучения
К концу этого раздела вы сможете:
- Объясните происхождение закона Ома.
- Рассчитывайте напряжения, токи или сопротивления по закону Ома.
- Объясните, что такое омический материал.
- Опишите простую схему.
Что движет током? Мы можем думать о различных устройствах, таких как батареи, генераторы, розетки и т. Д., Которые необходимы для поддержания тока.Все такие устройства создают разность потенциалов и условно называются источниками напряжения. Когда источник напряжения подключен к проводнику, он прикладывает разность потенциалов В, , которая создает электрическое поле. Электрическое поле, в свою очередь, воздействует на заряды, вызывая ток.
Ток, протекающий через большинство веществ, прямо пропорционален приложенному к нему напряжению В, . Немецкий физик Георг Симон Ом (1787–1854) первым экспериментально продемонстрировал, что ток в металлической проволоке прямо пропорционален приложенному напряжению :
.[латекс] I \ propto {V} \\ [/ латекс].
Это важное соотношение известно как закон Ома . Его можно рассматривать как причинно-следственную связь, в которой напряжение является причиной, а ток – следствием. Это эмпирический закон, подобный закону трения – явление, наблюдаемое экспериментально. Такая линейная зависимость возникает не всегда.
Сопротивление и простые схемы
Если напряжение управляет током, что ему мешает? Электрическое свойство, препятствующее току (примерно такое же, как трение и сопротивление воздуха), называется сопротивлением R .Столкновения движущихся зарядов с атомами и молекулами вещества передают энергию веществу и ограничивают ток. Сопротивление обратно пропорционально току, или
[латекс] I \ propto \ frac {1} {R} \\ [/ latex].
Так, например, при удвоении сопротивления ток уменьшается вдвое. Комбинируя отношения тока к напряжению и тока к сопротивлению, получаем
[латекс] I = \ frac {V} {R} \\ [/ латекс].
Это соотношение также называется законом Ома.Закон Ома в такой форме действительно определяет сопротивление определенных материалов. Закон Ома (как и закон Гука) не универсален. Многие вещества, для которых справедлив закон Ома, называются омическими . К ним относятся хорошие проводники, такие как медь и алюминий, и некоторые плохие проводники при определенных обстоятельствах. Омические материалы имеют сопротивление R , которое не зависит от напряжения В и тока I . Объект с простым сопротивлением называется резистором , даже если его сопротивление невелико.Единица измерения сопротивления – Ом, и обозначается символом Ω (греческая омега в верхнем регистре). Перестановка I = V / R дает R = V / I , поэтому единицы сопротивления равны 1 Ом = 1 вольт на ампер:
[латекс] 1 \ Omega = 1 \ frac {V} {A} \\ [/ latex].
На рисунке 1 показана схема простой схемы. Простая схема имеет один источник напряжения и один резистор. Можно предположить, что провода, соединяющие источник напряжения с резистором, имеют незначительное сопротивление, или их сопротивление можно включить в R .
Рис. 1. Простая электрическая цепь, в которой замкнутый путь прохождения тока обеспечивается проводниками (обычно металлическими), соединяющими нагрузку с выводами батареи, представленной красными параллельными линиями. Зигзагообразный символ представляет собой единственный резистор и включает любое сопротивление в соединениях с источником напряжения.
Пример 1. Расчет сопротивления: автомобильная фара
Какое сопротивление проходит у автомобильной фары 2.50 А течет при подаче на него 12,0 В?
СтратегияМы можем изменить закон Ома в соответствии с I = V / R и использовать его для определения сопротивления.
РешениеПерестановка I = V / R и замена известных значений дает
[латекс] R = \ frac {V} {I} = \ frac {\ text {12} \ text {.} \ Text {0 V}} {2 \ text {.} \ Text {50 A}} = \ text {4} \ text {.} \ text {80 \ Omega} \\ [/ latex].
ОбсуждениеЭто относительно небольшое сопротивление, но оно больше, чем хладостойкость фары.Как мы увидим в разделе «Сопротивление и удельное сопротивление», сопротивление обычно увеличивается с температурой, поэтому лампа имеет меньшее сопротивление при первом включении и потребляет значительно больший ток в течение короткого периода прогрева.
Сопротивление может быть разным. Некоторые керамические изоляторы, например те, которые используются для поддержки линий электропередач, имеют сопротивление 10 12 Ом или более. Сопротивление сухого человека может составлять 10 5 Ом, в то время как сопротивление человеческого сердца составляет примерно 10 3 Ом.Кусок медного провода большого диаметра длиной в метр может иметь сопротивление 10 −5 Ом, а сверхпроводники вообще не имеют сопротивления (они неомичны). Сопротивление связано с формой объекта и материалом, из которого он состоит, как будет показано в разделе «Сопротивление и удельное сопротивление». Дополнительное понимание можно получить, решив I = V / R для V , что дает
В = ИК
Это выражение для В, можно интерпретировать как падение напряжения на резисторе, вызванное протеканием тока I .Для этого напряжения часто используется фраза IR drop . Например, у фары в Пример 1 выше падение IR составляет 12,0 В. Если напряжение измеряется в различных точках цепи, будет видно, что оно увеличивается на источнике напряжения и уменьшается на резисторе. Напряжение аналогично давлению жидкости. Источник напряжения подобен насосу, создающему перепад давления, вызывая ток – поток заряда. Резистор похож на трубу, которая снижает давление и ограничивает поток из-за своего сопротивления.Здесь сохранение энергии имеет важные последствия. Источник напряжения подает энергию (вызывая электрическое поле и ток), а резистор преобразует ее в другую форму (например, тепловую энергию). В простой схеме (с одним простым резистором) напряжение, подаваемое источником, равно падению напряжения на резисторе, так как PE = q Δ V , и то же самое q протекает через каждую. Таким образом, энергия, подаваемая источником напряжения, и энергия, преобразуемая резистором, равны.(См. Рисунок 2.)
Рис. 2. Падение напряжения на резисторе в простой цепи равно выходному напряжению батареи.
Подключение: сохранение энергииВ простой электрической цепи единственный резистор преобразует энергию, поступающую от источника, в другую форму. Здесь о сохранении энергии свидетельствует тот факт, что вся энергия, подаваемая источником, преобразуется в другую форму только с помощью резистора. Мы обнаружим, что сохранение энергии имеет другие важные применения в схемах и является мощным инструментом анализа схем.
Исследования PhET: закон ОмаПосмотрите, как уравнение закона Ома соотносится с простой схемой. Отрегулируйте напряжение и сопротивление и посмотрите, как изменяется ток по закону Ома. Размеры символов в уравнении изменяются в соответствии с принципиальной схемой.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Простая схема – это схема , в которой есть один источник напряжения и одно сопротивление.
- Одно из утверждений закона Ома дает соотношение между током I , напряжением В и сопротивлением R в простой схеме как [латекс] I = \ frac {V} {R} \\ [/ latex] .
- Сопротивление выражается в единицах Ом (Ом), относящихся к вольтам и амперам на 1 Ом = 1 В / А.
- Существует падение напряжения IR на резисторе, вызванное протекающим через него током, равным В = IR .
Концептуальные вопросы
- Падение напряжения IR на резисторе означает изменение потенциала или напряжения на резисторе.Изменится ли ток при прохождении через резистор? Объяснять.
- Как падение IR в резисторе похоже на падение давления в жидкости, протекающей по трубе?
Задачи и упражнения
1. Какой ток протекает через лампочку фонаря на 3,00 В, когда ее горячее сопротивление составляет 3,60 Ом?
2. Вычислите эффективное сопротивление карманного калькулятора с батареей на 1,35 В, через которую протекает ток 0,200 мА.
3.Каково эффективное сопротивление стартера автомобиля, когда через него проходит 150 А, когда автомобильный аккумулятор подает на двигатель 11,0 В?
4. Сколько вольт подается для работы светового индикатора DVD-плеера с сопротивлением 140 Ом при прохождении через него 25,0 мА?
5. (a) Найдите падение напряжения в удлинителе с сопротивлением 0,0600 Ом, через который проходит ток 5,00 А. (b) Более дешевый шнур использует более тонкую проволоку и имеет сопротивление 0.300 Ом. Какое в нем падение напряжения при протекании 5.00 А? (c) Почему напряжение на любом используемом приборе снижается на эту величину? Как это повлияет на прибор?
6. ЛЭП подвешена к металлическим опорам со стеклянными изоляторами, имеющими сопротивление 1,00 × 10 9 Ом. Какой ток протекает через изолятор, если напряжение 200 кВ? (Некоторые линии высокого напряжения – постоянного тока.)
Глоссарий
- Закон Ома:
- – эмпирическое соотношение, указывающее, что ток I, пропорционален разности потенциалов В, , ∝ В, ; его часто записывают как I = V / R , где R – сопротивление
- сопротивление:
- электрическое свойство, препятствующее току; для омических материалов это отношение напряжения к току, R = V / I
- Ом:
- единица сопротивления, равная 1Ω = 1 В / A
- омическое:
- тип материала, для которого действует закон Ома
- простая схема:
- схема с одним источником напряжения и одним резистором
Избранные решения проблем и упражнения
1.0,833 А
3. 7,33 × 10 −2 Ом
5. (а) 0,300 В
(б) 1,50 В
(c) Напряжение, подаваемое на любой используемый прибор, снижается, поскольку общее падение напряжения от стены до конечной мощности прибора является фиксированным. Таким образом, если падение напряжения на удлинителе велико, падение напряжения на приборе значительно уменьшается, поэтому выходная мощность прибора может быть значительно уменьшена, что снижает способность прибора работать должным образом.
Что такое закон Ома – формульное уравнение »Электроника Примечания
Закон Ома – один из самых фундаментальных законов теории электричества. Формула или уравнение закона Ома связывает напряжение и ток со свойствами проводника, то есть его сопротивлением в цепи.
Resistance Tutorial:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Удельное сопротивление
Таблица удельного сопротивления для обычных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Закон Ома – один из самых фундаментальных и важных законов, регулирующих электрические и электронные схемы.Он связывает ток, напряжение и сопротивление для линейного устройства, так что, если известны два, можно вычислить третье.
Поскольку ток, напряжение и сопротивление являются тремя основными величинами цепи, это означает, что закон Ома также чрезвычайно важен.
Закон Ома используется во всех областях электротехники и электроники. Он используется для расчета номинала резисторов, необходимых в схемах, а также может использоваться для определения тока, протекающего в цепи, где напряжение может быть легко измерено на известном резисторе, но более того, закон Ома используется в огромное количество вычислений во всех формах электрических и электронных схем – практически везде, где течет ток.
Открытие закона Ома
Существует математическая зависимость, связывающая ток, напряжение и сопротивление. Немецкий ученый Георг Ом провел множество экспериментов, пытаясь показать связь между ними. В те дни, когда он проводил свои эксперименты, не было счетчиков в том виде, в каком мы их знаем сегодня.
Только после значительных усилий и со второй попытки ему удалось разработать то, что мы сегодня знаем как закон Ома.
Примечание о Георге Оме:
Родившийся в Эрлангене, примерно в 50 милях к северу от Мюнхена в 1879 году, Георг Ом стал одним из тех, кто много исследовал новую науку, связанную с электричеством, обнаружив взаимосвязь между напряжением и током в проводнике – теперь этот закон действует. назвал Закон Ома в честь проделанной им работы.
Подробнее о Георг Ом.
Что такое закон Ома?
ЗаконОма описывает способ протекания тока через материал при приложении разных уровней напряжения. Некоторые материалы, такие как электрические провода, имеют небольшое сопротивление току, и этот тип материала называется проводником. Следовательно, если этот провод, например, проложить прямо поперек батареи, будет протекать большой ток.
В других случаях другой материал может препятствовать прохождению тока, но все же пропускать его. В электрических схемах эти компоненты часто называют резисторами. Однако другие материалы практически не пропускают ток, и эти материалы называются изоляторами.
Посмотрите наше видео о законе Ома
Ом посмотрел на то, как ток течет в различных материалах, и смог разработать свой закон, который мы теперь называем законом Ома.
Чтобы получить первое представление о том, что происходит, можно сравнить электрическую ситуацию с потоком воды в трубе.Напряжение представлено давлением воды в трубе, ток представлен количеством воды, протекающей по трубе, и, наконец, сопротивление равно размеру трубы.
Можно представить, что чем шире труба, тем больше воды будет течь. Причина этого в том, что через более широкую трубу легче течь большему количеству воды, чем через более узкую – более узкая труба оказывает большее сопротивление потоку воды. Также, если в e-трубе больше давления, то по той же трубе будет течь больше воды.
Ом определил, что для обычных материалов удвоение напряжения удваивает ток, протекающий для данного компонента. Различные материалы или одни и те же материалы с разной формой будут иметь разные уровни сопротивления току.
Определение закона Ома
Закон Ома гласит, что ток, протекающий в цепи, прямо пропорционален приложенной разности потенциалов и обратно пропорционален сопротивлению в цепи.
Другими словами, удвоив напряжение в цепи, удвоится и ток. Однако если сопротивление увеличится вдвое, ток упадет вдвое.
В этом математическом соотношении единица сопротивления измеряется в Омах.
Формула закона Ома
Формула или уравнение закона Ома очень проста.
Закон Ома можно выразить в математической форме:
Где:V = напряжение, выраженное в вольтах
I = ток, выраженный в амперах
R = сопротивление, выраженное в омах
Формулой можно управлять так, чтобы, если известны любые две величины, можно было вычислить третью.
Треугольник закона Ома
Чтобы помочь запомнить формулу, можно использовать треугольник с одной стороной, горизонтальной, и вершиной наверху в виде пирамиды. Иногда это называют треугольником закона Ома.
В верхнем углу треугольника закона Ома находится буква V, в левом углу – буква I, а в правом нижнем углу – R.
Чтобы использовать треугольник, закройте неизвестное количество, а затем вычислите его по двум другим. Если они выстроены в линию, они умножаются, но если один находится поверх другого, их следует разделить.Другими словами, если необходимо рассчитать ток, напряжение делится на сопротивление, то есть V / R и т. Д.
Если необходимо рассчитать напряжение, оно определяется путем умножения силы тока на сопротивление, т.е. I x R.
Пример расчета закона Ома
Если на резистор 500 Ом подается напряжение 10 В, определите величину тока, который будет протекать.
Глядя на треугольник закона Ома, ток неизвестен, а напряжение и сопротивление остаются известными значениями.
Таким образом, ток определяется делением напряжения на сопротивление.
I = VR = 10500 = 0,02 A = 20 мА
Пример 2
Подобным образом можно использовать закон Ома для определения сопротивления, если известны ток и напряжение. Возьмем, например, напряжение 10 вольт, а ток 0,1 А. Используя треугольник закона Ома, можно увидеть, что:
Пример 3
Наконец, другая комбинация состоит в том, что если сопротивление и ток известны, то можно рассчитать ожидаемое напряжение на сопротивлении.Возьмем, к примеру, расстояние 250 Ом, через которое протекает ток 0,1 А, тогда напряжение можно рассчитать следующим образом:
V = I R = 0,1 × 250 = 25 вольт
Проводники омические и неомические
Используя закон Ома, можно увидеть, что если бы напряжение и ток были построены для фиксированного резистора или отрезка провода и т. Д., То была бы прямая линия.
Видно, что удвоение напряжения удваивает ток, который проходит через конкретный элемент схемы.
График напряжения и тока для линейного сопротивленияНа графике есть две линии, одна для более высокого сопротивления – эта требует приложения большего напряжения для данного протекающего тока. Соответственно, это должно иметь более высокое сопротивление. И наоборот, кривая для более низкого сопротивления показывает компонент, который требует приложения более низкого напряжения для данного тока.
Компоненты, имеющие прямую или прямую линию, подчиняются закону Ома и известны как омические проводники.Однако не все электрические электронные компоненты имеют прямолинейный график для напряжения и тока. По разным причинам они могут иметь разные вольт-амперные характеристики. Эти проводники часто называют неомическими.
Закон Ома – одно из самых основных понятий в электротехнике и электронной технике. Концепция элемента, имеющего определенное сопротивление, которое определяет количество тока, протекающего через него при определенном напряжении, является ключом к работе практически всех цепей.
Дополнительные основные понятия:
Напряжение
Текущий
Сопротивление
Емкость
Мощность
Трансформеры
RF шум
Децибел, дБ
Q, добротность
Вернуться в меню «Основные понятия». . .
Закон Ома для начинающих и новичков
Закон Ома для начинающих и новичковОсновной закон Ома
HTML с: http://www.btinternet.com/~dtemicrosystems/beginner.htm
ЧТО ЭТО. КАК И ГДЕ ПОЛУЧИТЬ ЕГО
Хотя закон Ома применим не только к резисторам – как мы увидим позже – кажется, логично включить его сейчас, так как он обеспечит хорошую точку отсчета для резистора подробности приведены выше.
ЧТО ТАКОЕ ЗАКОН ОМС? :
Используя диаграмму слева, закон Ома определяется как; «При условии, что температура
остается постоянным, отношение разности потенциалов (стр.г) на концах проводника
(R) к току (I), протекающему в этом проводнике, также будет постоянным ». Здесь заканчивается
проповедь!
Из этого мы заключаем, что; Ток равен напряжению, разделенному на сопротивление (I = V / R),
Сопротивление равно напряжению, разделенному на ток (R = V / I), а напряжение равно току, умноженному на
Сопротивление (V = IR).
Важным фактором здесь является температура. Если расчеты по закону Ома должны
давать точные результаты, это должно оставаться постоянным. В «реальном» мире это почти никогда
делает, и с точки зрения новичка вам не нужно беспокоиться об этом.
далее, поскольку схемы, с которыми вы, вероятно, столкнетесь в данный момент, – и около 95%
все те, с которыми вы столкнетесь в будущем – будут работать нормально, даже если они горячие
или холодно!
ЗАКОН ОМС ПРОСТОЙ:
На рисунке 1 слева показан наиболее распространенный треугольник закона Ома.Начиная с любого раздела
треугольник, его можно читать в любом направлении – по часовой стрелке, против часовой стрелки, сверху
вниз или снизу вверх – и он всегда предоставит вам расчет, который вы
требовать.
Если рассматривать (слегка диагональные) горизонтальные линии как знаки разделения, а короткие
вертикальная линия как знак умножения, и всегда начинайте расчет с любого количества
вы ищете, т.е. “V =”, “I =” или “R =” у вас будет все
возможные формулы, основанные на этом конкретном законе Ома.То есть; V = IxR, I = V / R, R = V / I. Это
должно быть очевидно, что формула работает и в обратном направлении, то есть; IxR = V, RxI = V, V / I = R
и V / R = I.
Эти объяснения могут показаться немного сложными, но их легко применить на практике. Как правило, для начинающих будет более понятен полезный пример, а не эти причудливые столы, так что поехали.
ПОЯСНЕНИЕ НА ПРИМЕРЕ:
Допустим, друг просит вас установить красную сигнальную лампу на приборную панель его / ее автомобиля.Будучи энтузиастом электроники, вы решили использовать красный светоизлучающий диод (LED),
поскольку они излучают достаточно чистый красный свет, не выделяют чрезмерного тепла
лампы накаливания, они также дешевы по сравнению и выглядят высокотехнологичными!
С точки зрения принципиальной схемы расположение будет таким, как показано слева.
ОГРАНИЧИТЕЛЬ ТОКА РЕЗИСТОР:
Стандартные светодиоды не могут получать питание напрямую от 12 В без установки ограничения тока
резистор включен последовательно с одним из выводов, но какое значение вы используете? Как общее правило
на практике, вашему среднему светодиоду требуется около 15 мА тока для получения приемлемого света.
выход.Учитывая это, теперь у нас есть две известные величины для использования в наших расчетах:
напряжение и ток. Используя треугольник закона Ома, требуемое сопротивление равно
рассчитывается по формуле «R = V / I», которая дает нам 12 / 0,015 = 800 Ом (см. ниже
для ‘Vf’). Не забывайте, ток измеряется в амперах.
На первый взгляд может показаться, что это проблема, поскольку 800 Ом не является стандартным значением. доступен в диапазоне E12. Однако в этом типе схемы сопротивление не критический, и ближайшего предпочтительного значения будет вполне достаточно, а именно 820 Ом.
НЕ ЗАБЫВАЙТЕ ОБ “Vf”:
Все электронные компоненты демонстрируют – в большей или меньшей степени – то, что известно как
‘выбывать’. Он имеет различные сокращения в зависимости от типа компонента, к которому он
ссылается, но обычно они означают одно и то же. На самом деле это количество напряжения, которое
используется компонентом для функционирования. Для стандартного светодиода это значение находится в диапазоне
около 1,5 – 3 вольт, и для наших целей мы будем считать, что это 2 В.
Это означает, что из ваших 12 вольт от аккумулятора 2 вольта будут израсходованы светодиодом. Сама по себе, поэтому ваш расчет закона Ома должен быть основан на 10 вольт.Истинная формула должно быть на самом деле; (12-Vf) /0.015=666.66 Ом (повторяется для мастеров математики среди ты!). Ближайшее значение в диапазоне E12 составляет 680 Ом, поэтому в идеале это должно быть ценность для использования. В целях безопасности, когда ваши результаты заканчиваются непонятными значениями, такими как при этом всегда выбирайте ближайшее значение выше, а не следующее ниже.
РЕЗИСТОРЫ ПОСЛЕДОВАТЕЛЬНО И ПАРАЛЛЕЛЬНОВозможно “изготовление” стандартных и нестандартных номиналов резисторов на соответствовать вашим потребностям, если требуемое значение отсутствует.Это достигается подключением два или более из них параллельно, последовательно или их комбинация. Однако вам нужно заранее знать, как они взаимодействуют друг с другом в этих конфигурациях.
РЕЗИСТОРЫ СЕРИИ:
На рисунке слева показаны три резистора, соединенные последовательно друг с другом. Это
самый простой способ получить “фабричные” значения. Формула прямой для
расчет окончательного значения; «R» = R1 + R2 + R3. Другими словами, независимо от
количества резисторов или их индивидуальных значений, окончательное значение
«R» всегда будет их суммой.Расчет по ноге изображения
работает для любого количества значений, соединенных последовательно, вы просто продолжаете добавлять их в
список других.
ПАРАЛЛЕЛЬНЫЕ РЕЗИСТОРЫ:
При параллельном соединении резисторов расчеты
посложнее. На рисунке слева показаны три резистора, включенных параллельно. Мы будем
не заботиться о трех отдельных ценностях, а сосредоточиться на том, что
окончательное значение «R» будет с использованием примеров значений.Расчет у подножия
изображение работает для любого количества значений, соединенных параллельно, вы просто продолжаете добавлять их в
список других в скобках. Для наших целей предположим, что R1 – 47K, R2 –
150К, а R3 – 820К. Формула прямой линии для окончательного значения: «R» = 1 / (
(1 / R1) + (1 / R2) + (1 / R3)).
В этой формуле содержится много ненужных скобок (скобок),
и вот в чем причина; почти для всех расчетов электроники вам нужно использовать
калькулятор, который отдает приоритет функциям умножения и деления, а также наиболее научным
калькуляторы работают именно так.К сожалению, многие «простые» калькуляторы этого не делают, поэтому
дополнительные скобки были показаны, чтобы компенсировать те, которые вычисляют цифры в
порядок их ввода. С научным калькулятором вы можете использовать упрощенный
формула прямой линии; «R» = 1 / (1 / R1 + 1 / R2 + 1 / R3).
Важно определить значения в скобках, прежде чем применять окончательный Функция «1 /». В противном случае формула принимает вид 1 / R1 + 1 / R2 + 1 / R3 =? если ты попробуйте это на своем калькуляторе, используя наши примеры значений, вы, вероятно, подумаете, что у вас есть неправильный ответ (0.02916 …), а у вас нет. На самом деле у вас точно есть право ответ, ему просто не хватает последней функции “1 /”.
Если в вашем калькуляторе есть «1 / X» (единица, разделенная на все, что показано в
display), затем нажмите эту кнопку сейчас. Если эта функция недоступна, поместите
результат в памяти (убедившись, что раньше там ничего не было), очистите дисплей
а затем введите «1 MR =» или другую подобную последовательность. Результат должен быть
34,29 кОм (34 290,29005 Ом), что правильно.Итак, итоговое значение всех трех
резисторы, включенные параллельно – 34,29К.
На рис. 2 слева показан второй по величине часто используемый треугольник закона Ома. К этому можно подойти точно так же, как и к выше, только на этот раз он используется для расчета мощности, напряжения и тока. В объяснения здесь таковы; Ток равен мощности, деленной на напряжение (I = P / V), мощность равна Ток, умноженный на напряжение (P = VxI), и напряжение равно мощности, деленной на ток (V = P / I).
ДЕМОНСТРАЦИЯ НА ПРИМЕРЕ:
Чтобы продемонстрировать использование этого треугольника, мы применим его к обычному электрическому / электронному
компонент – трансформатор. Их характеристики обычно цитируются с точки зрения
их выходное напряжение вторичной обмотки, вместе с мощностью – в ВА –
это напряжение. Термин «VA» означает ватты и происходит от формулы
«Вольт на Ампер» (отсюда – ВА). Это обозначается буквой “P” в
треугольник закона Ома.
КАКОЙ ТРАНСФОРМАТОР ДЕЛАТЬ
НЕОБХОДИМОСТЬ ?
Допустим, у вас есть цепь на 9 В, которая потребляет 1.5 ампер тока. Вы хотите знать, если
трансформатор с номиналом 9 В при 25 ВА будет достаточным для питания вашей цепи. Ты
уже есть две величины от трансформатора – напряжение (В) и мощность (P или
VA), и по ним вы хотите узнать, какой будет доступный ток (I).
Используя формулу «I = P / V» из треугольника, результат: 25/9 = 2,77
усилители. Таким образом, этот трансформатор подойдет для ваших нужд на 1,5 А. В целях безопасности
если цепь будет постоянно потреблять определенное количество тока, независимо от
каким может быть этот ток, тогда всегда используйте трансформатор, доступный как минимум на 50%
ток, чем требует ваша схема.Никогда не используйте тот, у которого “ровно” тока,
потому что он станет слишком горячим, что приведет к изменению характеристик напряжения и
текущий указан. Эти изменения сложны, и мы не будем их объяснять в этой статье.
раздел для начинающих, но будьте осторожны при выборе трансформаторов.
Сопротивление резистора | Основы резистора
Сопротивление резистора
Назначение резистора – препятствовать прохождению через него электрического тока.Это называется электрическим сопротивлением и измеряется в омах. Сопротивление можно рассчитать по закону Ома, когда известен ток и измерено падение напряжения:
Сопротивление резистора зависит от его материала и формы. Некоторые материалы имеют более высокое удельное сопротивление, что приводит к более высокому значению. Значение часто печатается на резисторе с номером или в виде цветового кода.
Что такое сопротивление?
Понятия тока, напряжения и сопротивления можно объяснить с помощью гидравлической аналогии.Поток воды по трубе ограничен сужением. Это вызывает падение давления после сужения. Течение воды эквивалентно электрическому току. Падение давления равно падению напряжения. Перетяжка эквивалентна резистору и имеет определенное сопротивление. Сопротивление пропорционально падению напряжения или давления для данного тока.
В гидравлическом примере сопротивление можно увеличить, например, уменьшив диаметр сужения.Для резистора или провода сопротивление обычно зависит от материала и геометрической формы. Влияние геометрической формы можно легко объяснить на примере гидравлики. Длинная и узкая трубка будет иметь более высокое сопротивление, чем короткая и широкая трубка.
Сопротивление резистора прямоугольного сечения площадью А и длиной L.Сопротивление материала называется удельным сопротивлением.-8 Вт · м.
Сопротивление в серии
Эквивалентное сопротивление последовательно подключенных резисторов равно сумме каждого резистора:
Ток, проходящий через все последовательно включенные резисторы, одинаков, а напряжение – нет. Для более подробного объяснения и практических примеров, обратитесь к статье резисторов в серии. Иногда желаемое значение недоступно со стандартными предпочтительными значениями. Вместо этого, чтобы достичь этого значения, два резистора могут быть подключены последовательно или параллельно.
Сопротивление параллельно
Эквивалентное сопротивление резисторов, включенных параллельно, можно рассчитать по следующей формуле:
Напряжение на каждом параллельном резисторе одинаковое, но нет тока. Для более подробного объяснения и практических примеров обратитесь к статье резисторы параллельно.
Как найти сопротивление резистора
Сопротивление резистора либо напечатано на корпусе резистора, либо обозначено цветовым кодом.Комбинация цветов указывала номинал и допуск резистора. Калькулятор или полное объяснение см. В коде резистора.
Электрическое сопротивление – Веб-формулы
По словам физика Джорджа Саймона Ома, напряжение, приложенное извне к двум концам проводника, является постоянным, когда электрический ток течет через него в фиксированных физических условиях. Это называется законом Ома. Напряжение – ток
V œ I
V = RI
Где у нас,
V = Напряжение (В)
I = ток (A)
R = Сопротивление (Ом)
Сопротивление – это не что иное, как препятствие для прохождения заряда.Здесь R называется сопротивлением проводника, единица измерения сопротивления – Ом, а его символ – Ом.
Обратная величина Ома называется проводимостью материала, а единица обратной связи Ом – mho Ω
-1Закон Ома дает информацию о соотношении между разностью потенциалов между проводником и электрическим током, протекающим через него.
Рассмотрим проводник с площадью A и длиной l при заданной температуре, тогда
R œ l и R œ 1 / A
Итак,
R œ l / A
R = p l / A
Где p = удельное сопротивление материала
Единица измерения p = Ом м
Значение p зависит от типа, температуры и давления на проводе.Удельное сопротивление увеличивается с повышением температуры.
Электропроводность равна обратной величине удельного сопротивления, а его символ – 6 , а единица измерения (Ом · м) -1
Ограничение по закону Ома:
- Значение V зависит от значения тока
- Значение V зависит от направления, в котором оно применяется
- Нелинейный.
Сверхпроводимость:
Согласно Камерлинг-Оннесу, сопротивление определенного материала, такого как ртуть, становится почти нулевым, когда его температура опускается выше определенной фиксированной температуры.Материал называется сверхпроводником, а этот процесс – сверхпроводимостью.
Примеры сверхпроводников – Hg, Si, Se, Ge, Te
Примеры расчетов
Пример-1: Разность потенциалов между двумя электродами батареи составляет 10 В и сопротивление 0,5 Ом. Рассчитать ток, протекающий между двумя электродами?
a) 20A b) 0,5A c) 0,05A d) 0,005A
Причина:
Здесь имеем:
R = 0,5 Ом
V = 10 В
Я =?
В = R / I
10 = 0.5 / I
I = 0,5 / 10
I = 0,05 A
Пример 2: Для подключения используется медный провод двенадцатого калибра. Он имеет удельное сопротивление 1,77 × 10 -8 при 20 ° C. Рассчитайте сопротивление проводов длиной 20 м при той же температуре. (Размер 12 = 2,05 × 10 -3 диаметр м)
Причина:
Здесь мы имеем л = 20 м
p = 1,77 × 10 -8
d = размер 12 = 2,05 × 10 -3 м
A = 3,14r 2 = 3,14 × (d / 2) 2 = 3.14 × (2,05 × 10 -3 /2) 2
R = p l / A
R = (1,77 × 10 -8 × 20) / (3,14 × (2,05 × 10 -3 /2) 2 )
R = (1,77 × 10 -8 × 20 × 4) / (3,14 × (2,05 × 10 -3 ) 2 )
R = 10,89 × 10 -2 Ом
Пример 3: Взаимосвязь между разностями потенциалов между проводником и протекающим по нему электрическим током объясняется …………….явление.
a) Удельное сопротивление b) сверхпроводимость c) Проводимость d) Закон Ома
Ответ: Связь между разностью потенциалов между проводником и протекающим по нему электрическим током объясняется законом Ома.
Как рассчитать резисторы, подключенные последовательно и параллельно – Kitronik Ltd
Резисторы серии
Когда резисторы подключаются друг за другом, это называется последовательным соединением. Это показано ниже.Чтобы рассчитать общее общее сопротивление ряда резисторов, подключенных таким образом, вы складываете отдельные сопротивления. Это делается по следующей формуле: Rtotal = R1 + R2 + R3 и так далее. Пример: чтобы рассчитать общее сопротивление для этих трех последовательно соединенных резисторов.| Rtotal = R1 + R2 + R3 = 100 + 82 + 1 Ом = 183 Ом |
Задача 1:
Вычислите общее сопротивление следующего последовательно включенного резистора.| R Итого | = _______________ | |
| = _______________ |
| R Итого | = _______________ | |
| = _______________ |
| R Итого | = _______________ | |
| = _______________ |
Параллельные резисторы
Когда резисторы подключаются друг к другу (бок о бок), это называется параллельным подключением.Это показано ниже.Два параллельных резистора
| Для расчета общего полного сопротивления a двух резисторов, подключенных таким образом, вы можете использовать следующую формулу: |
Задача 2:
Рассчитайте общее сопротивление следующего резистора, включенного параллельно.Три или более резистора, включенных параллельно
Для расчета общего общего сопротивления ряда из трех или более резисторов, подключенных таким образом, вы можете использовать следующую формулу: Пример: Чтобы вычислить общее сопротивление для этих трех резисторов, подключенных параллельноЗадача 3:
Рассчитайте общее сопротивление следующего резистора, включенного параллельно.ответы
Задача 1
1 = 1492 Ом 2 = 2242 Ом 3 = 4847 ОмЗадача 2
1 = 5 Ом 2 = 9,57 Ом 3 = 248,12 ОмЗадача 3
1 = 5,95 Ом 2 = 23,76 Ом Загрузите pdf-версию этой страницы здесь. Подробнее об авторе подробнее »© Kitronik Ltd – Вы можете распечатать эту страницу и дать ссылку на нее, но не должны копировать страницу или ее часть без предварительного письменного согласия Kitronik.
Ом: определение и формула – научный класс
Определение ома
Ом – это единица измерения электрического сопротивления между двумя точками на резисторе, проводнике, устройстве или цепи.Один Ом означает, что разность потенциалов (напряжение) 1 В между этими двумя точками дает ток 1 А. На следующих схемах показаны примеры того, как это может происходить:
В общем, эта взаимосвязь между любым напряжением, током и сопротивлением моделируется законом Ома , который мы определим как уравнение в следующей форме:
Ом Пример простой схемы
Предположим, у неизвестного «черного ящика» есть две электрические клеммы.Вы подключаете батарею 6 В и амперметр (который измеряет ток) последовательно с черным ящиком, как показано. Предположим, что амперметр и провода имеют нулевое сопротивление. В цепи измеряется ток 60 мА (миллиампер или тысячные доли ампера). Какое сопротивление черного ящика в Ом?
Мы применяем закон Ома, чтобы найти:
Действительно плохой юмор
Инженеры и ученые обычно не отличаются особенным юмором, но есть несколько шуток, которыми стоит поделиться.Посмотрите, сможете ли вы определить известные выражения, изображенные на следующих рисунках (A, B и C):
Сдаться? A – это «Ом в диапазоне»; B – «без ома»; C – это «растяжение в омах». Сказал вам, что это был действительно дурной юмор! Ладно, вернемся к уроку.
Ом и мощность
Электрическая мощность (мощность) – это произведение напряжения и тока, поэтому мы можем подставить закон Ома в уравнение мощности и получить соотношение для сопротивления на основе мощности (в ваттах, Вт) и либо напряжение или ток:
Например, если мы знаем, что лампочка мощностью 75 Вт потребляет ток 5 ампер, мы можем найти внутреннее сопротивление лампы:
Другая формула для определения сопротивления
Сопротивление специально разработано в резисторах и интегральных схемах с использованием удельного сопротивления материала. Удельное сопротивление определяется как степень сопротивления материала движению электронов в зависимости от объема. Он измеряется в омах на метр длины материала на квадратный метр площади поперечного сечения материала. Это сводится просто к единицам ом-метрам. Формула для определения удельного сопротивления:
Ниже приведен пример блока кремния с удельным сопротивлением 20 Ом-метров.Мы хотим найти сопротивление в омах, измеренное от одной стороны блока до другой.
Сопротивление будет найдено следующим образом:
Еще плохой юмор
Попробуем еще. Как вы думаете, это что?
Ага, это песня My Old Kentucky Ohm.’
Сводка
Ом – это единица электрического сопротивления, определяемая между двумя точками в цепи или через проводник, резистор или устройство. Один Ом означает, что напряжение в один вольт между двумя точками создает ток в один ампер. Математическая взаимосвязь между сопротивлением, напряжением и током задается законом Ома , который гласит, что сопротивление (в омах) равно напряжению, деленному на ток.


 3)
3) 4)
4)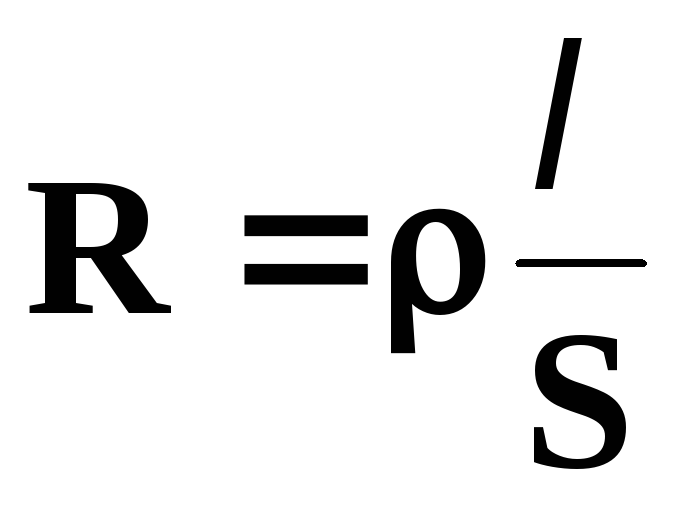 6)
6)