Военно-техническая подготовка
1.3. Переменный ток
1.3.1. Параметры сигналов переменного тока.
Величина переменного тока, как и напряжения, постоянно меняется во времени. Количественными показателями для измерений и расчётов применяются их следующие параметры:
Период T – время, в течении которого происходит один полный цикл изменения тока в оба направления относительно нуля или среднего значения.
Частота f – величина, обратная периоду, равная количеству периодов за одну секунду.
Один период в секунду это один герц (1 Hz)
,
Циклическая частота
,
Обычно используется при расчётах тока и напряжения синусоидальной формы. Тогда в пределах периода можно не рассматривать частоту и время, а исчисления производить в радианах или градусах. T = 2π = 360°
Начальная фаза ψ – величина угла от нуля ( ωt = 0) до начала периода. Измеряется в радианах или градусах. Показана на рисунке для синего графика синусоидального тока.
Начальная фаза может быть положительной или отрицательной величиной, соответственно справа или слева от нуля на графике.
Мгновенное значение – величина напряжения или тока измеренная относительно нуля в любой выбранный момент времени t .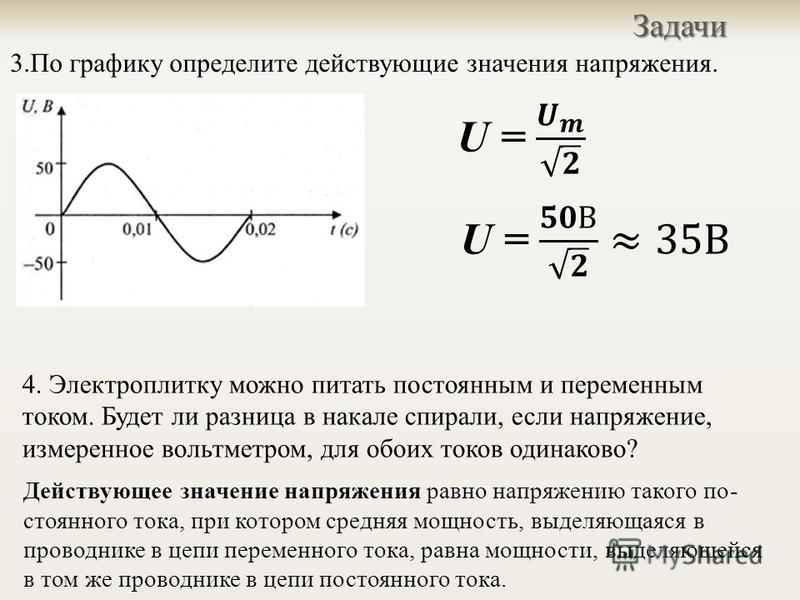
,
Последовательность всех мгновенных значений в любом интервале времени можно рассмотреть как функцию изменения тока или напряжения во времени.
Например, синусоидальный ток или напряжение можно выразить функцией:
,
С учётом начальной фазы:
,
Здесь I amp
Амплитудное значение – максимальное по модулю мгновенное значение за период.
,
Может быть положительным и отрицательным в зависимости от положения относительно нуля.
Часто вместо амплитудного значения применяется термин амплитуда тока (напряжения) – максимальное отклонение от нулевого значения.
Среднее значение (avg) – определяется как среднеарифметическое всех мгновенных значений за период T .
,
Среднее значение является постоянной составляющей DC напряжения и тока.
Для синусоидального тока (напряжения) среднее значение равно нулю.
Средневыпрямленное значение – среднеарифметическое модулей всех мгновенных значений за период.
,
Для синусоидального тока или напряжения средневыпрямленное значение равно среднеарифметическому за положительный полупериод.
,
Среднеквадратичное значение (rms) – определяется как квадратный корень из среднеарифметического квадратов всех мгновенных значений за период.
,
Для синусоидального тока и напряжения амплитудой Iamp ( Uamp ) среднеквадратичное значение определится из расчёта:
,
Среднеквадратичное – это действующее, эффективное значение, наиболее удобное для практических измерений и расчётов. Является объективным количественным показателем для любой формы тока.
В активной нагрузке переменный ток совершает такую же работу за время периода, что и равный по величине его среднеквадратичному значению постоянный ток.
.
1.3.2. Виды модуляции сигналов.
Амплитудная модуляция – вид модуляции, при которой изменяемым параметром несущего сигнала является его амплитуда.
Пусть
S ( t ) — информационный сигнал, | S ( t ) < 1 |,
Uc ( t ) — несущее колебание.
Тогда амплитудно-модулированный сигнал Uam
(1)
Здесь m — некоторая константа, называемая коэффициентом модуляции.
Формула (1) описывает несущий сигнал U c ( t ) , модулированный по амплитуде сигналом S ( t ) с коэффициентом модуляции m . Предполагается также, что выполнены условия:
,
Выполнение условий (2) необходимо для того, чтобы выражение в квадратных скобках в (1) всегда было положительным. Если оно может принимать отрицательные значения в какой-то момент времени, то происходит так называемая перемодуляция (избыточная модуляция). Простые демодуляторы (типа квадратичного детектора) демодулируют такой сигнал с сильными искажениями.
Амплитудной модуляции свойственны следующие существенные недостатки:
1) приему амплитудно-модулированных сигналов сильно мешают индустриальные и атмосферные помехи;
2) в процессе модуляции лампа используется по мощности полностью только при подаче максимального мгновенного модулирующего напряжения, а во все остальное время она недоиспользуется.
Эти недостатки в значительной степени устраняются при частотной и фазовой модуляции.
Рис 1. Амплитудная модуляция с различным коэффициентом модуляции.
Рис 2. Спектр АМ колебания.
Частотная модуляция – вид аналоговой модуляции, при котором информационный сигнал управляет частотой несущего колебания. По сравнению с амплитудной модуляцией здесь амплитуда остаётся постоянной.
Основными характеристиками частотной модуляции являются девиация
(отклонение) и индекс модуляции .Девиация частоты (frequency deviation) – наибольшее отклонение значения модулированного сигнала от значения его несущей частоты. Единицей девиации частоты является герц (Hz), а также кратные ему единицы.
Индекс модуляции (modulation index) – отношение девиации частоты к частоте модулирующего сигнала.
Колебание называют частотно-модулированным (ЧМ), если частота его изменяется пропорционально передаваемому колебанию (например звуковому) S(t).
Следовательно, угловая частота такого колебания должна равняться:
,
где ω 0 и a – некоторые постоянные, которые выбираются так, чтобы частота ω изменялась в желаемых пределах.
Рис 3. Пример частотной модуляции по линейному закону.
Рис 4. Пример частотной модуляции. Вверху — информационный сигнал на фоне несущего колебания. Внизу — результирующий сигнал.
Фазовая модуляция – вид модуляции, при которой фаза несущего колебания управляется информационным сигналом. Фазомодулированный сигнал s(t) имеет следующий вид:
,
где g(t) — огибающая сигнала; φ ( t ) является модулирующим сигналом; f c — частота несущего сигнала; t — время.
Фазовая модуляция, не связанная с начальной фазой несущего сигнала, называется относительной фазовой модуляцией (ОФМ).
Рис 5. Пример фазовой модуляции – двоичная фазовая модуляция BPSK.
Рис 6. AM,FM модуляции.
1.3.3. Особенности цепей переменного тока.
Переменный ток изменяется во времени по синусоидальному закону. Время, за которое совершается полный цикл изменений по величине и направлению, называется периодом. При векторном изображении синусоиды вектор периодически описывает угол а, равный 360° или в дуговом (радианном) измерении равный 2π. Следовательно, первый полупериод оканчивается при α = π, а первое максимальное значение синусоида принимает при π/2. Время, за которое вектор описывает угол 2π [рад], называется периодом и обозначается буквой Т.
Число периодов в секунду называется частотой и обозначается буквой f.
Отсюда
[1/сек] ,
За единицу частоты принят герц (гц). Частота промышленной сети переменною тока обычно равна 50 гц.
В теории переменного тока часто приходится иметь дело с круговой частотой
[1/сек] ,
В течение периода переменный ток, изменяющийся. по синусоидальному закону, достигает максимального значения 2 раза (при π/2 и Зπ/2). Максимальное значение тока или напряжения обозначают соответственно буквами Iмакс и, Uмакс. Действующее значение переменного тока равно величине такого постоянного тока, который, проходя через сопротивление, выделяет в нем (за одинаковое время с переменным током) равное количество тепла:
,
.
Следует иметь в виду, что, например, при расчете токовой нагрузки проводов принимается во внимание действующее значение тока.
Это положение во многих случаях распространяется и на напряжение. Лишь при расчете изоляции на пробой необходимо учитывать максимальное (мгновенное) значение напряжения, так как пробой может произойти во время прохождения напряжения через максимум. На шкалах измерительных приборов указываются, как правило, действующие значения тока или напряжения.
Резистор в цепи переменного тока
| . |
Здесь через IR обозначена амплитуда тока, протекающего через резистор. Связь между амплитудами тока и напряжения на резисторе выражается соотношением
Фазовый сдвиг между током и напряжением на резисторе равен нулю.
Физическая величина R называется активным сопротивлением резистора .
Конденсатор в цепи переменного тока
| , |
. |
Соотношение между амплитудами тока IC и напряжения UC :
.
Ток опережает по фазе напряжение на угол π/2.
Физическая величина
называется емкостным сопротивлением конденсатора .
Катушка в цепи переменного тока
| , |
. |
Соотношение между амплитудами тока IL и напряжения UL :
.
Ток отстает по фазе от напряжения на угол π/2.
Физическая величина XL = ω L называется индуктивным сопротивлением катушки .
Действующее значение напряжения
В проводниках переменного тока основные электродинамические показатели постоянно изменяются. Вследствие этого возникает вопрос: как можно адекватно оценить напряжение и силу тока в конкретной электроцепи? Так как моментальные и простые усредненные значения недостаточны для полной характеристики электротока, в электродинамике вводят такое понятие, как действующее значение тока.
- Что такое действующее значение напряжения
- Действующее значение тока
- Какие коэффициенты характеризуют переменное напряжение
- Параметры переменного тока
- Формула действующего значение тока
Что такое действующее значение напряжения
Изменение значений переменного тока обычно описывается синусоидальной линией с определенным периодом (Т) и амплитудой напряжения (Um). Кроме напряжения, электрический ток также характеризуется силой (I) и мощностью (P). Для постоянного электротока эти параметры складываются в простую формулу:
P = U × I.
При имеющемся сопротивлении в цепи и с учетом закона Ома (I = U / R) мощность, расходуемую электропотребителем. Можно определить как отношение квадрата напряжения к сопротивлению:
P = U2 / R.
В случае же переменного тока не все так однозначно. С изменением напряжения изменяется и мощность — в каждый момент времени (t) значения отличаются друг от друга.
В такой ситуации для оценки электротока удобнее всего использовать его мощностные и тепловые характеристики. Поэтому действующее значение переменного тока приравнивается к работе постоянного тока, производимой за временной промежуток одного периода переменного тока.
При существующей активной нагрузке, независящей от частоты тока и напряжения мгновенная мощность определяется по формуле:
P(t) = U(t) × I(t) = U2 / R
Введя амплитудное значение напряжения, и учитывая период синусоидальной функции, мгновенную мощность можно определить следующим образом:
P(t) = (Um × sin(2π × 1/T))2 / R
Однако этот параметр для переменного тока — не имеет особой важности. Для практических расчетов обычно берут мощность, усредненную за период. Как раз этот показатель указывается на бытовых электроприборах.
Формула усредненной мощности:
Здесь же представлена формула расчета действующего напряжения.
В вышеприведенной формуле интегрирование квадратной величины с последующим извлечением корня дает понять, почему эффективная величина напряжения также носит название «среднеквадратичной». При этом интегральное выражение под корнем является усредненной мощностью, пропорциональной сопротивлению.
Относительно синусоиды напряжение это интегральное выражение упрощается до формулы:
Именно эти цифры показывают вольтметры, настроенные на измерение проводников переменного тока.
Действующее значение тока
Применив метод интегрирования к квадратам амплитудной силы тока и синусу круговой частоты и выведя среднеквадратичные величины, можно получить действующее значение силы тока:
Сравнивая тепловые эффекты постоянного и переменного электротоков, взятые за одинаковый временной отрезок и при одинаковой активной нагрузке, можно обнаружить, что равенство тепловых характеристик проводников того и другого типа достигается в том случае, если сила линейного тока будет меньше максимальных силовых значений в цепи переменного тока в 1,414 раз.
Какие коэффициенты характеризуют переменное напряжение
Помимо базовых параметров переменного тока, в электротехнике принято производить измерения электросигналов, включая выходные напряжения выпрямителей и импульсы различной формы.
Амплитудное значение напряжения
Под амплитудным или пиковым напряжением подразумевают максимальный показатель U за один период синусоиды:
Um = max(|u(t)|)
Для измерения данного параметра обычно используют вольтметр импульсного типа или осциллограф.
Мгновенное значение тока
Параметр обозначает силу тока или напряжение в конкретный временной момент (u(t), i(t)). В зависимости от динамики электрического сигнала, для определения мгновенных значений могут применяться малоинерционные вольтметры, а также шлейфовые или электронно-лучевые осциллографы.
Среднее значение
Показатель является постоянной составляющей переменного тока.
Для напряжения оно рассчитывается по следующей интегральной формуле:
Для синусоидного напряжения с симметричной формой среднее значение равно нулю. Это можно определить с помощью обычного вольтметра. В геометрическом виде это может быть выражено как отношение разности площадей с обеих сторон оси t к периоду. Под названием напряжения смещения величина часто применяется в радиоэлектронике и обозначает напряжение, прилагаемое к электроду для выработки конкретных параметров постоянного электротока.
Среднеквадратичное значение
Среднеквадратичные интегральные величины силы тока и напряжения используются достаточно часто, вследствие их удобства для практического определения электродинамических характеристик в реальных проводниках. Они основываются на сравнении работы постоянного и переменного тока с активной нагрузкой и определенными величинами U и I.
К примеру, лампочка или обогреватель будут выполнять одинаковую работу по освещению или обогреву как в сети переменного тока со стандартным напряжением 220 В, так и в цепи постоянного тока, если на нее подать такое же напряжение.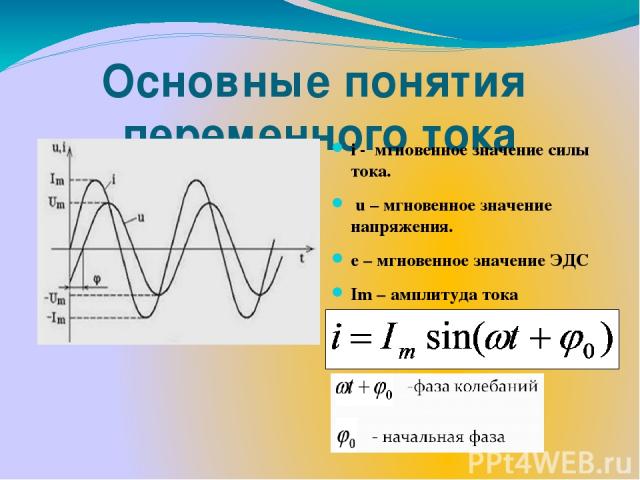
Напряжение в электросети обычно выражают в среднеквадратичном исчислении. Большинство приборов, измеряющих силу тока и напряжение, спроектированы под действующие показатели. Отдельные типы амперметров и вольтметров способны показывать верные эффективные значения только для синусоидального тока. В универсальных устройствах, работающих с любыми формами электросигнала, измерение осуществляется с помощью термопреобразователя. При этом фиксируется температура нагревателя, создающего определенное сопротивление.
Кроме того, в измерительных приборах может быть реализован метод возведения в квадрат мгновенного значения, после чего величина усредняется по временному периоду, а затем выводится квадратный корень.
Средневыпрямленное значение
Величина определяется как взятое по модулю среднеарифметическое всех мгновенных значений напряжения. Для одного периода средневыпрямленная величина равна сумме площадей сверху и снизу оси времени. Хотя параметр не находит практического применения, именно он фиксируется по факту большинством измеряющих устройств магнитоэлектрического принципа действия, несмотря на то, что их шкалы имеют градацию для действительных значений.
При этом эффективные и средневыпрямленные значения оказываются близки друг к другу только в случае синусоидального напряжения.
Параметры переменного тока
Синусоидальные гармоники являются типичной характеристикой переменного тока. В этом отношении по синусоиде происходит изменение электродвижущей силы и тока при определенной нагруженности цепи. При этом динамика ЭДС может быть описана следующими параметрами:
• Период — время, за которое электродинамические показатели изменяются по полному циклу. Он напрямую связан с частотой вращения роторного механизма генератора электротока.
• Частота — определяется как число периодов за одну единицу времени. Современные стандарты для электросетей предписывают частоту переменного тока в 50 герц. Это означает, что за 1 секунду ток меняет направление 50 раз, а один период длится 20 миллисекунд.
• Амплитуда — максимальная величина гармоники переменного тока. В строгом смысле параметр применим исключительно к синусоидальному изменению.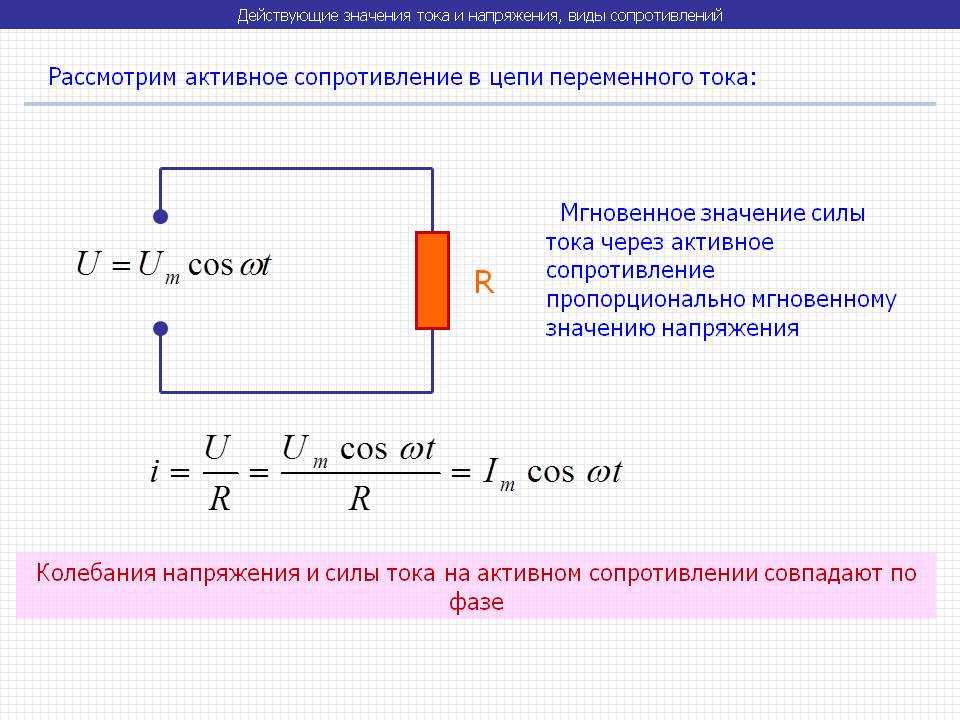
С некоторыми допущениями амплитуда может быть определена и для других форм электросигнала. За один период электродвижущая сила дважды доходит до пиковых значений и обозначается как Em+ и Em- соответственно положению полупериодов.
• Угловая частота — скорость колебательного движения, измеряемая в радианах в секунду. При этом один период синусоиды приравнивается к значению 2π. Общая формула угловой частоты: ω = 2π / Т.
• Фаза колебаний — стадия синусоидальной волны, принимаемая как аргумент функции тока, которая отсчитывается от среднего нулевого значения. Величина фазы колебаний, используемая для определения синуса или косинуса фазового угла, описывается формулой φ = ωt.
Как в случае со среднеквадратичными значениями тока и напряжения, через основные характеристики определяется и среднее значение ЭДС, которое сводится к следующему выражению:
Формула действующего значение тока
Среднеквадратичные показатели переменного тока определяется как отношение амплитудного значения тока к корню из 2.
Схожим образом обозначаются эффективные значения напряжения и ЭДС.
Действительные значения синусоидального тока помогают производить практическую оценку и описание электроцепей. Несмотря на сложность составляющих понятий, эти величины сводятся к простым выражениям. Номинальное напряжение электрических сетей и приборов представляет собой как раз среднеквадратичное значение. Умножив указанный вольтаж на корень из 2, можно узнать амплитудное значение напряжения электроустройств.
Понравилась статья? Расскажите друзьям:
Оцените статью, для нас это очень важно:
Проголосовавших: 1 чел.
Средний рейтинг: 5 из 5.
Внезапная нагрузка – Сопротивление материалов Вопросы и ответы
Этот набор вопросов и ответов с несколькими вариантами ответов (MCQ) по сопротивлению материалов посвящен «Внезапной нагрузке».
1. Какова связь между максимальным напряжением, вызванным внезапной нагрузкой, и максимальным напряжением при постепенной нагрузке?
а) Максимальное напряжение при внезапной нагрузке равно максимальному напряжению при постепенной нагрузке
б) Максимальное напряжение при внезапной нагрузке составляет половину максимального напряжения при постепенной нагрузке
c) Максимальное напряжение при внезапной нагрузке вдвое превышает максимальное напряжение при постепенной нагрузке
d) Максимальное напряжение при внезапной нагрузке в четыре раза превышает максимальное напряжение при постепенной нагрузке
Посмотреть ответ
Ответ: c
Объяснение: Максимальное напряжение при внезапной нагрузке нагрузка = 2P/A
Максимальное напряжение при постепенной нагрузке = P/A.
2. Какая энергия деформации запасается в теле при внезапном приложении нагрузки?
a) σE/V
b) σE 2 /V
c) σV 2 /E
d) σV 2 /2E
Посмотреть ответ
Ответ: d
Пояснение: Энергия деформации при постепенном нагружении = σ 2 V/2E.
3. К круглому стержню диаметром 4 см внезапно приложена растягивающая нагрузка в 60 кН. Каким будет максимальное мгновенное напряжение?
A) 95,493 Н/мм 2
B) 45,25 Н/мм 2
C) 85,64 Н/мм 2
D) 102,45 Н/мм 2
Просмотр Ответ
: А. : Максимальное мгновенное индуцированное напряжение = 2P/A = 2×60000/400π = 95,49 Н/мм 2 .
4. К круглому стержню длиной 4 см и 5 м внезапно прикладывается растягивающая нагрузка 60 кН. Какова будет энергия деформации, поглощенная стержнем, если E=2×105 Н/мм 2 ?
a) 140,5 Н-м
b) 100 Н-м
c) 197,45 Н-м
d) 143,2 Н-м
Просмотреть ответ
Ответ: d
Объяснение: Максимальное мгновенное создаваемое напряжение = 2P/A = 2×604π9/5,0000/90. 2
Энергия деформации = σ 2 В/2E = 95,492 x 2×106π / (2x2x105) = 143238 Н-мм = 143,23 Н-м.
5. Растягивающую нагрузку в 100 кН внезапно приложили к прямоугольному стержню размером 2 см х 4 см.
Каким будет мгновенное напряжение в стержне?
a) 100 Н/мм 2
B) 120 Н/мм 2
C) 150 Н/мм 2
D) 250 Н/мм 2
Посмотреть Ответ
Ответ: D
. : Напряжение = 2x нагрузка / площадь = 2×100 000/(20×40) = 250 Н/мм 2 .
Примечание: присоединяйтесь к бесплатным занятиям по санфаянсу в Telegram или на Youtube
реклама
реклама
6. 2 растягивающая нагрузка 100 кН внезапно приложена к прямоугольному стержню размером 2 см x 4 см и длиной 5 м. Какая энергия деформации будет поглощена стержнем, если E=1×105 Н/мм 2 ?
a) 312,5 Н-м
b) 314500 Н-мм
c) 1250 Н-м
d) 634 Н-м
Посмотреть ответ
Ответ: c
Объяснение: Напряжение = 2xнагрузка / площадь = 2×100 000/ (22540 Н/мм 2
Энергия деформации = σ 2 В/2E = 250x250x20x40x5000/ (2×100000) = 1250000 Н-мм = 1250 Н-м.
7. Стальной стержень длиной 2 м и диаметром 50 мм.
К стержню внезапно прикладывается осевое усилие 100 кН. Каким будет мгновенное напряжение в стержне?
A) 101,89 Н/мм 2
B) 94,25 Н/мм 2
C) 130,45 Н/мм 2
D) 178,63 N/мм 2
. Ответ
. : Площадь = π/4 d2 = 625π
Нагрузка = 100 кН = 100×1000 Н
Напряжение = 2 x нагрузка / площадь = 2x100x1000 / (625π) = 101,86 Н/мм 2 .
реклама
8. Стальной стержень длиной 2 м и диаметром 50 мм. К стержню внезапно прикладывается осевое усилие 100 кН. Какое мгновенное удлинение возникнет в стержне, если Е=22GN/м2?
a) 0,0097 мм
b) 1,0754 мм
c) 1,6354 мм
d) 1,0186 мм
Посмотреть ответ
Ответ: d
Объяснение: Площадь = π/4 d2 = 625π 005 N
Нагрузка = 100k =22GN/м 2 = 200 x 109 / 106 = 200 000 Н/мм 2
Напряжение = 2 x нагрузка/площадь = 2x100x1000 / (625 π)
Удлинение = напряжение x длина / E = 101,86 × 2000 / 200000 = 1,0186 мм.
9. Какое осевое усилие будет приложено к стержню диаметром 4 см, чтобы получить мгновенное значение напряжения 143 Н/мм 2 ?
a) 50 кН
b) 60 кН
c) 70 кН
d) 80 кН
Посмотреть ответ
Ответ: b
Объяснение: Мгновенное напряжение = 2 x нагрузка / площадь
Нагрузка = мгновенное напряжение x площадь / 2
4 = 0043 3,14/2 = 60кН.
реклама
10. Какое мгновенное напряжение возникнет в стержне 10см 2 площадью и длиной 4 м в результате внезапного приложения растягивающей нагрузки неизвестной величины, если удлинение стержня из-за внезапно приложенной нагрузки составляет 1,35 мм, если E = 2×105 Н/мм 2 ?
A) 67,5 Н/мм 2
B) 47 Н/мм 2
C) 55,4 Н/мм 2
D) 78,5 Н/мм 2
Ответ
Ответ:
. : Значение напряжения = нагрузка / площадь, где площадь равна 10 см 2 , а нагрузку можно рассчитать по уравнению напряжения-деформации.
Sanfoundry Global Education & Learning Series – Прочность материалов.
Чтобы практиковать все области сопротивления материалов, здесь полный набор из более чем 1000 вопросов и ответов с несколькими вариантами ответов .
Следующие шаги:
- Получите бесплатную грамоту по сопротивлению материалов
- Участие в конкурсе по сертификации прочности материалов
- Станьте лидером в области сопротивления материалов
- Пройти испытания на прочность материалов
- Практические тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
- Пробные тесты по главам: глава 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
реклама
реклама
Подпишитесь на наши информационные бюллетени (тематические). Участвуйте в конкурсе сертификации Sanfoundry, чтобы получить бесплатный Сертификат отличия.
Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Ютуб | Телеграмма | Линкедин | Инстаграм | Фейсбук | Твиттер | Пинтерест
Маниш Бходжасиа, ветеран технологий с более чем 20-летним стажем работы в Cisco и Wipro, является основателем и техническим директором компании Sanfoundry . Он живет в Бангалоре и занимается разработкой Linux Kernel, SAN Technologies, Advanced C, Data Structures & Alogrithms. Оставайтесь на связи с ним в LinkedIn.
Подпишитесь на его бесплатные мастер-классы на Youtube и технические обсуждения в Telegram SanfoundryClasses.
Калькулятор напряжения
Создано Bogna Szyk
Отредактировано Стивеном Вудингом
Последнее обновление: 30 июня 2022 г.
Содержание:- пример расчетов
- Модуль упругости Единицы
- Часто задаваемые вопросы
Этот калькулятор напряжения поможет вам решить задачи по механике, связанные с напряжением, деформацией и модулем Юнга.
За несколько простых шагов вы узнаете зависимость между напряжением и деформацией для любого материала, который остается эластичным. Мы также научим вас, как рассчитать деформацию и как применять уравнение напряжения.
🔎 Этот калькулятор рассчитан на осевое напряжение. Если вы изучаете поперечный сдвиг, вам следует взглянуть на наши калькуляторы напряжения сдвига и деформации сдвига.
Как рассчитать деформацию и напряжение
Деформация определяется как мера деформации – пропорция между изменением длины и первоначальной длиной объекта. Например, если взять резинку и растянуть ее так, чтобы она стала в два раза длиннее первоначальной, то деформация будет равна 1 (100%).
Формула деформации:
ε = ΔL/L₁ = (L₂ – L₁)/L₁ L₁ обозначает начальную длину, L₂ – конечную длину, а ΔL – изменение длины. Обратите внимание, что деформация безразмерна.
Напряжение, с другой стороны, является мерой давления, которое частицы материала оказывают друг на друга.
Она определяется как сила, действующая на объект на единицу площади. Однако это отличается от давления; при расчете напряжения рассматриваемая площадь должна быть настолько малой, чтобы анализируемые частицы считались однородными. Если принять во внимание большую площадь, расчетное напряжение обычно является средним значением.
Уравнение напряжения:
σ = F/A F обозначает силу, действующую на тело, а A обозначает площадь. Единицы напряжения такие же, как и единицы давления — паскали (обозначение: Па) или ньютоны на квадратный метр.
Положительное напряжение означает, что объект находится в состоянии растяжения – он “хочет” удлиниться. Отрицательное напряжение означает, что находится в сжатии и “хочет” стать короче.
Вы знаете?
Деформация бывает двух видов — инженерная и истинная. Узнайте больше в нашем калькуляторе истинной деформации
Модуль Юнга (напряжение в зависимости от деформации)
Если материал является линейно-упругим , то напряжение и деформация напрямую связаны следующей формулой:
E = σ/ε E – модуль упругости или модуль Юнга .
Это материальная константа, разная для каждого вещества.
Что такое линейно-упругое поведение материала? Если мы прикладываем напряжение к материалу, деформация увеличивается пропорционально. Это может быть верно только для некоторого диапазона напряжений – после того, как мы достигнем определенного значения, материал может сломаться или поддаться. Уступчивость – это увеличение деформации в постоянно напряженном состоянии.
Пример расчета
Предположим, мы хотим найти модуль Юнга стали. Для этого мы подготовили стальной стержень, который тянули с большим усилием.
- Решаем, что сила, приложенная к тяге, будет равна 30 кН (
30*10³ Н). - Определяем размеры штока. Примем длину 2 м (2000 мм) и площадь поперечного сечения 1 см² (
1*10⁻⁴ м²). - Мы заметили, что стержень удлинился на 3 мм.
- Рассчитываем деформацию стержня по формуле:
ε = ΔL/L₁ = 3/2000 = 0,0015. - Мы рассчитываем напряжение, используя формулу напряжения:
σ = F/A = 30*10³ / (1*10⁻⁴) = 300*10⁶ = 300 МПа.
- Наконец, мы делим напряжение на деформацию, чтобы найти модуль Юнга стали:
E = σ/ε = 300*10⁶ / 0,0015 = 200*10⁹ = 200 ГПа.
Единицы модуля упругости
Единицы модуля Юнга такие же, как единицы давления и напряжения: паскали или ньютоны на квадратный метр. В единицах СИ:
1 Па = 1 Н / 1 м² = 1 кг·м / с² / м² = 1 кг / (м·с²)
Если вас интересует механика, воспользуйтесь калькулятором крутящего момента. Или изучите калькулятор круга Мора, чтобы понять различные типы напряжений.
Часто задаваемые вопросы
Что означает высокий модуль Юнга?
Чем выше модуль упругости или модуль Юнга, тем жестче материал. Это означает, что он может выдерживать большее количество нагрузок.
Какой тип напряжения действует на конкретное поперечное сечение стойки из-за сегмента над ней?
Напряжение в поперечном сечении стойки составляет отрицательное или сжимающее напряжение из-за веса сегмента над указанным поперечным сечением.
