Формулы и Задачи (Информатика 10) – Школа N61 г.Ульяновска
Формулы
N = 2i
N – мощность алфавита (количество знаков в алфавите)
i – информационный вес символа алфавита (количество информации в одном символе)
I – количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K – число символов в сообщении
i – информационный вес символа (количество информации в одном символе)
Q – количество разных сообщений
N – количество символов
L – длина сообщения
Формула Хартли:
I = log2N
I – количество информации, содержащееся в выбранном сообщении
N – количество сообщений
Римская система счисления
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
a3a2a1a
Правило перевода числа из любой системы счисления в десятичную систему счисления – умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.
Запись через схему Горнера:
a3a2a1a0 = ((a3 * p + a2) * p + a1) * p + a0
p – основание системы счисления в котором представлено число.
Пример:
637510 = 6 * 103 + 3 * 102 + 7 * 101 + 5 * 100
637510 = ((6 * 10 + 3) * 10 + 7) * 10 + 5
12345 = 1 * 53 + 2 * 52 + 3 * 51 + 4 * 50 = 194 10
12345 = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 19410
Развернутая запись дробного числа:
0,a1a2a3a4 = a1*p-1 + a2*p-2 + a3*p-3 + a4*p-4
Запись через схему Горнера:
0,a1a2a3a4 = p-1 * (a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4)))
p * (0,a1a2a3a4) = a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4))
p – основание системы счисления в котором представлено число.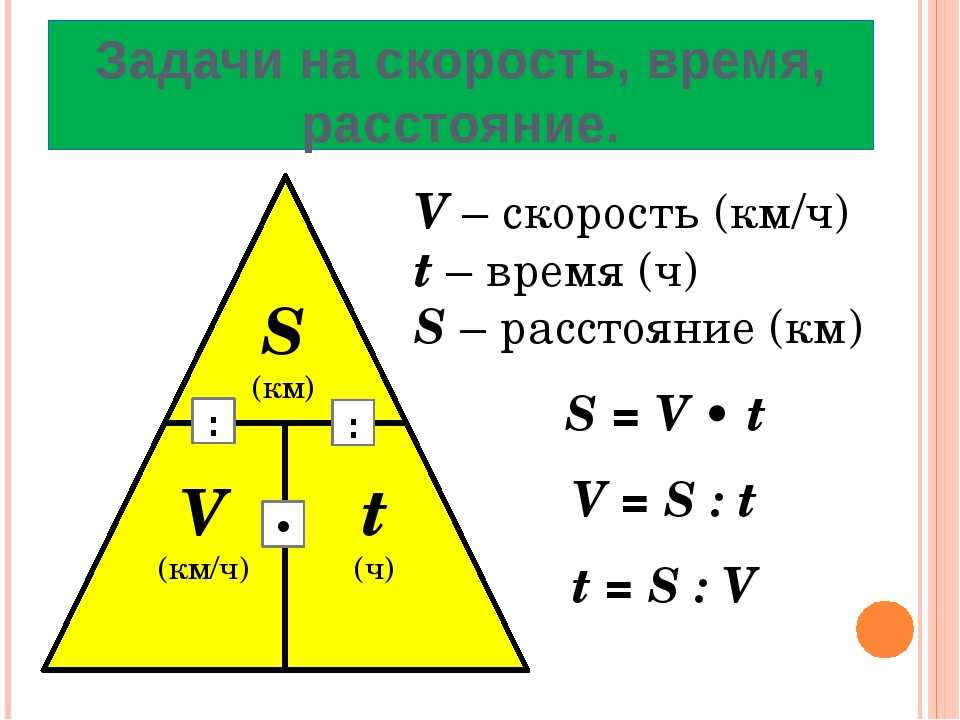
Пример:
0,6375 = 6 * 10
0,6375 = 10-1 * (6 + 10-1 * (3 + 10-1 * (7 + 10-1 * 5)))
0,12345 = 1 * 5-1 + 2 * 5-2 + 3 * 5-3 + 4 * 5-4
0,12345 = 5-1 * (1 + 5-1 * (2 + 5-1 * (3 + 5-1 * 4)))
Задачи
Алфавитный подход к измерению количества информации
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
- информационная ёмкость символа: 256 = 28 =>> i = 8 бит = 1 байт
-
количество символов на странице:
32 * 64 = 25 * 26 = 211 -
общее количество символов:
L = 10 * 211 -
информационный объём сообщения:
I = L * i = 10 * 211 * 1 байт = 20 Кбайт
Системы счисления
X10 X16 X8 X2
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6 6 110
7 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D 15 1101
14 E 16 1110
15 F 17 1111
16 10 20 10000
17 11 21 10001
18 12 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 11110
31 1F 37 11111
32 20 40 100000
Логические операции
Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.
Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.
Таблица истинности для операции НЕ имеет вид:
| A | |
| 0 | 1 |
| 1 | 0 |
Действие, связанное с операцией НЕ можно записать следующим образом:
Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия). B
B
Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.
Таблица истинности для операции ИЛИ имеет вид:
| A | B | X=A v B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Действие, связанное с операцией ИЛИ можно записать следующим образом:
X = A + B = A v B
Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
| A | B | X=AB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:
X = A B
Действие, связанное с операцией Импликации можно записать следующим образом:
X = A → B
Таблица истинности Импликации имеет вид:
| A | A → B | |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция тождество. Операция тождество определяет тождественность аргументов.
Операция тождество определяет тождественность аргументов.
Таблица истинности для операции тождество имеет вид:
| A | B | A Ξ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией тождество можно записать следующим образом:
X = A Ξ B
Диаграммы Венна (круги Эйлера)
Поиск номера сети
Необходимо найти номер сети по IP-адресу 12. 16.196.10 и маске 255.255.224.0.
16.196.10 и маске 255.255.224.0.
| маска сети | 255. | 255. | 224. | 0 | |
| IP-адрес | 12. | 16. | 196. | 10 | – ip-адрес (узла, компьютера и т.п.) |
| IP-адрес | 0000 1100. | 0001 0000. | 1100 0100. | 0000 1010 | |
| маска сети | 1111 1111. | 1111 1111. | 1110 0000. | 0000 0000 | |
| адрес сети | 0000 1100. | 0001 0000. | 110x xxxx. | xxxx xxxx | – эта часть относится к адресу сети – она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее: |
| адрес сети | 0000 1100. | 0001 0000. | 1100 0000. | 0000 0000 | – полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем: |
| адрес сети | 12. | 16. | 192. | 0 | – полный адрес сети (в десятичном виде) |
Формулы по физике 8 класса. Все формулы по физике за 8 класс с пояснениями и определениями
| Закон | Формула | Определение | Единицы измерения |
|---|---|---|---|
| ТЕПЛОВЫЕ ЯВЛЕНИЯ | |||
| Закон сохранения энергии | Qотд = Qприн | Количество теплоты, отданное одним телом другому, равно количеству теплоты, принятому вторым телом. | Q – количество теплоты, [Дж] |
| Формула вычисления количества теплоты | Q = cmΔt | Количество теплоты – физическая величина, показывающая, какая энергия передана телу в результате теплообмена. | Q – количество теплоты, [Дж] c – удельная теплоемкость – физическая величина, численно равная количеству теплоты, которое необходимо сообщить телу массой 1 кг для того, чтобы изменить его температуру на 1 °С, [Дж/кг°С] m – масса тела, [кг] Δt = t2 – ¬t1 – разность температур, [°С] |
| Формула вычисления количества теплоты при сгорании топлива | Q = qm | Топливо – вещество, которое в некоторых процессах выделяет тепло. | Q – количество теплоты, [Дж] q – удельная теплота сгорания топлива – физическая величина, численно равная количеству теплоты, которое выделяется при полном сгорании 1 кг топлива, [Дж/кг] m – масса топлива, [кг] |
| Формула вычисления количества теплоты, необходимого для плавления вещества | Q = λm | Плавление – процесс перехода вещества из твердого состояния в жидкое. | Q – количество теплоты, [Дж] λ – удельная теплота плавления – количество теплоты, которое необходимо сообщить 1 кг вещества, нагретому до температуры плавления, чтобы перевести его из твёрдого состояния в жидкое, [Дж/кг] m – масса вещества, [кг] |
| Формула вычисления количества теплоты при парообразовании и конденсации | Q = Lm | Парообразование – процесс превращения жидкости в пар. Конденсация – переход вещества в жидкое или твёрдое состояние из газообразного. Конденсация – переход вещества в жидкое или твёрдое состояние из газообразного. | Q – количество теплоты, [Дж] L – удельная теплота парообразования и конденсации, [Дж/кг] m – масса вещества, [кг] |
| Формула вычисления абсолютной влажности | ρ=mпара/Vвоздуха | Абсолютная влажность воздуха – количество влаги, содержащейся в одном кубическом метре воздуха. | ρ – абсолютная влажность, [кг/м3] m – масса пара, [кг] V – объем воздуха, [м3] |
| Формула вычисления относительной влажности воздуха | φ=ρ/ρн∙100% | Относительная влажность воздуха – величина, показывающая насколько далек пар от насыщения. | φ – относительная влажность ρ – абсолютная влажность (плотность водяного пара), [кг/м3] ρн – плотность насыщенного пара при данной температуре, [кг/м3] |
| Формула для вычисления КПД тепловой машины | Коэффициент полезного действия (КПД) – характеристика эффективности системы (устройства, машины) в отношении преобразования или передачи энергии.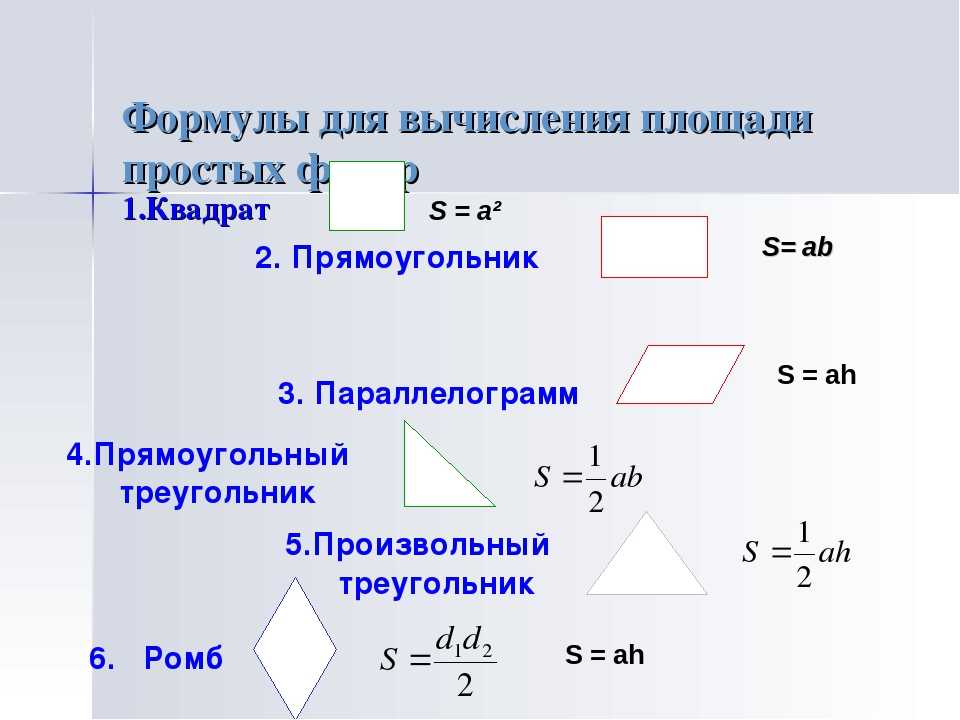 | А – полезная работа, которую совершает рабочее тело, [Дж] Qн – количество теплоты, которое передал рабочему телу нагреватель, [Дж] Qх – количество теплоты, которое рабочее тело передало холодильнику, [Дж] | |
| ЭЛЕКТРИЧЕСКИЕ ЯВЛЕНИЯ | |||
| Закон Ома для участка цепи | I=U/R | Закон Ома: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления удельного сопротивления проводника | R=ρ*L/S ρ=R*S/L | Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник. | ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [мм2] L – длина проводника, [м] |
| Законы последовательного соединения проводников | I = I1 = I2 | Последовательным соединением называется соединение, когда элементы идут друг за другом.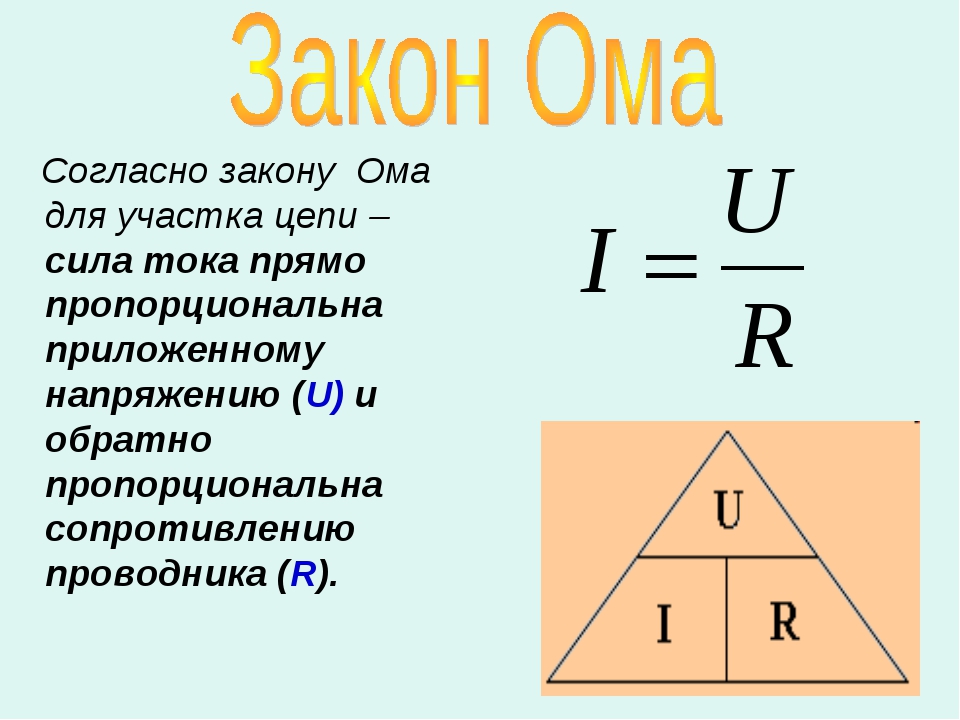 | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Законы параллельного соединения проводников | U = U1 = U2 I = I1 + I2 1/Rобщ=1/R1+1/R2 | Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления величины заряда. | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула для нахождения работы электрического тока. | A = Uq A = UIt | Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. д.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. | A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула электрической мощности | P = A/t P = UI P = U2/R | Мощность – работа, выполненная в единицу времени. | P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом] |
| Формула закона Джоуля-Ленца | Q=I2Rt | Закон Джоуля-Ленца: при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. | Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом]. |
| ЭЛЕКТРОМАГНИТНЫЕ ЯВЛЕНИЯ | |||
| Правило правой руки | Расположим правую руку так, чтобы четыре согнутых пальца совпадали с направлением магнитных линий, тогда большой палец укажет направление тока в проводнике. Или Если направить большой палец правой руки по направлению тока в проводнике, то четыре согнутых пальца укажут направление линий магнитного поля тока. | ||
| Правило буравчика | Если вкручивать буравчик по направлению тока в проводнике, то направление вращения ручки буравчика укажет направление линий магнитного поля тока. | ||
| СВЕТОВЫЕ ЯВЛЕНИЯ | |||
| Закон отражения света | Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча. | ||
| Закон преломления | При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого. | n – показатель преломления одного вещества относительно другого | |
| Формула вычисления абсолютного показателя преломления вещества | n=c/v | Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде. | n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с] |
| Закон Снеллиуса | sinα/sinγ=v1/v2=n | Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления одного вещества относительно другого v – скорость света в данной среде, [м/с] |
| Показатель преломления среды | sinα/sinγ=n | Отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления среды |
| Формула оптической силы линзы | D=1/F | Оптическая сила линзы – способность линзы преломлять лучи. | D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м] |
Простые проценты – определение, формула, примеры
Простые проценты – это метод расчета суммы процентов, начисляемых на сумму по заданной ставке и за определенный период времени. В простых процентах основная сумма всегда одинакова, в отличие от сложных процентов, когда мы добавляем проценты к основной сумме, чтобы найти основную сумму для новой основной суммы на следующий год.
На этом уроке вы познакомитесь с концепцией займа денег и простых процентов, получаемых от займа. Вы также познакомитесь с такими терминами, как основная сумма, сумма, процентная ставка и период времени. С помощью этих терминов вы можете рассчитать простые проценты, используя формулу простых процентов.
| 1. | Что такое простые проценты? |
| 2. | Формула простых процентов |
| 3. | Как найти простые проценты? |
| 4. | Какие типы кредитов используют простые проценты? |
| 5. | Простые проценты против сложных процентов |
| 6. | Часто задаваемые вопросы о простых процентах |
Что такое простые проценты?
Простые проценты — это метод начисления процентов, который всегда применяется к исходной основной сумме с одной и той же процентной ставкой для каждого временного цикла. Когда мы вкладываем наши деньги в любой банк, банк выплачивает нам проценты на нашу сумму. Проценты, применяемые банками, бывают разных типов, и один из них — простой процент. Теперь, прежде чем углубиться в концепцию простых процентов, давайте сначала поймем, что означает кредит.
Кредит – это сумма, которую человек занимает в банке или финансовом органе для удовлетворения своих потребностей. Примеры ссуд включают жилищные ссуды, ссуды на покупку автомобиля, ссуды на образование и личные ссуды. Сумма кредита должна быть возвращена лицом властям вовремя с дополнительной суммой, которая обычно представляет собой проценты, которые вы платите по кредиту.
Формула простых процентов
Простые проценты рассчитываются по следующей формуле: S.I. = (P × R × T)/100, , где P = основная сумма, R = процентная ставка в % годовых и T = время, обычно рассчитываемое как количество лет. Процентная ставка выражается в процентах R% (и должна быть записана как R/100, таким образом, 100 в формуле). Чтобы узнать больше об этой формуле, нажмите здесь.
- Основная сумма: Основная сумма – это сумма, которая была первоначально заимствована (ссуда) в банке или инвестирована. Принципал обозначается P.
- Ставка: Ставка — это процентная ставка, по которой основная сумма предоставляется кому-либо на определенное время, процентная ставка может составлять 5%, 10% или 13% и т.
 д. Процентная ставка обозначается Р.
д. Процентная ставка обозначается Р. - Время: Время — это продолжительность, на которую кому-то дается основная сумма. Время обозначается Т.
Вышеприведенная формула может быть дополнительно решена для любой переменной P, R или T. Например, разделив обе части формулы SI S.I. = (P × R × T)/100 на R × T, мы получим P = (100 × SI) / (R × T). Точно так же мы можем найти либо R, либо T.
Иногда формула простых процентов записывается как просто SI = PRT, где R — десятичная процентная ставка. т. е. если процентная ставка равна 5%, то R можно записать как 5/100 = 0,05.
Сумма: Когда человек берет ссуду в банке, он/она должен вернуть основную сумму займа плюс сумму процентов, и эта возвращаемая сумма называется Сумма.
Сумма = основная сумма + простой процент Как найти простые проценты?
Простые проценты находятся по формуле SI = (PRT)/100, где P — основная сумма долга, R — процентная ставка, а T — дюрация. Значения P, R и T должны быть заменены в этой формуле для расчета простых процентов. Вот пример, чтобы лучше понять процесс для тех же значений P и R, но для разных значений T.
Значения P, R и T должны быть заменены в этой формуле для расчета простых процентов. Вот пример, чтобы лучше понять процесс для тех же значений P и R, но для разных значений T.
Пример:
Отец Майкла занял в банке 1000 долларов под процентную ставку 5%. Каковы будут простые проценты, если сумма займа на 1 год? Аналогичным образом рассчитайте простые проценты, если сумма кредита взята на 2 года, 3 года и 10 лет? Также рассчитайте сумму, которую необходимо вернуть в каждом из этих случаев.
Решение:
Основная сумма = 1000 долларов, процентная ставка = 5% = 5/100. (Добавьте здесь предложение, описывающее данную информацию в вопросе.)
| Продолжительность | Простые проценты |
|---|---|
| 1 год | S.I = (1000 × 5 × 1)/100 = 50 |
| 2 года | S. I = (1000 × 5 × 2)/100 = 100 I = (1000 × 5 × 2)/100 = 100 |
| 3 года | S.I = (1000 × 5 × 3)/100 = 150 |
| 10 Год | S.I = (1000 × 5 × 10)/100 = 500 |
Теперь мы также можем подготовить таблицу для вышеуказанного вопроса, добавив сумму, которая должна быть возвращена по истечении заданного периода времени.
| Простые проценты | Сумма | |
|---|---|---|
| 1 год | S.I = (1000 × 5 × 1)/100 = 50 | А = 1000 + 50 = 1050 |
| 2 года | S.I = (1000 × 5 × 2)/100 = 100 | А = 1000 + 100 = 1100 |
| 3 года | S.I = (1000 × 5 × 3)/100 = 150 | А = 1000 + 150 = 1150 |
| 10 Год | S. I = (1000 × 5 × 10)/100 = 500 I = (1000 × 5 × 10)/100 = 500 | А = 1000 + 500 = 1500 |
Какие типы кредитов используют простые проценты?
Большинство банков в наши дни применяют сложные проценты по кредитам, потому что таким образом банки получают больше денег в виде процентов от своих клиентов, но этот метод более сложен и его трудно объяснить клиентам. С другой стороны, расчеты упрощаются, когда банки применяют простые процентные методы. Простые проценты гораздо полезнее, когда клиент хочет получить кредит на короткий период времени, например, на 1 месяц, 2 месяца или 6 месяцев.
Когда кто-то берет краткосрочный кредит под простые проценты, проценты начисляются ежедневно или еженедельно, а не ежегодно. Учтите, что вы заняли 10 000 долларов под простые проценты по ставке 10 % годовых, поэтому эти 10 % годовых делятся на дневную ставку, равную 10/365 = 0,027 %. Таким образом, вы должны платить 2,73 доллара в день дополнительно на 10 000 долларов.
Простые проценты против сложных процентов
Простые проценты и сложные проценты — это два способа расчета процентов на сумму кредита. Считается, что сложные проценты рассчитать труднее, чем простые проценты, из-за некоторых основных различий в них обоих. Давайте поймем разницу между простыми процентами и сложными процентами через таблицу, приведенную ниже:
| Простые проценты | Сложные проценты |
|---|---|
| Простые проценты каждый раз начисляются на первоначальную основную сумму. | Сложные проценты рассчитываются на накопленную сумму основного долга и процентов. |
| Рассчитывается по следующей формуле: S.I.= P × R × T | Рассчитывается по следующей формуле: C.I.= P × (1 +R) Т – Р |
Равно для каждого года по определенному основному. | Он отличается для каждого периода времени, так как рассчитывается на сумму, а не на основную сумму. |
Важные примечания о простых процентах:
- Если используется процентная ставка в процентах, то формула СИ равна (PRT)/100. Но если процентная ставка используется в виде десятичной дроби (т. е. если мы уже разделили ставку на 100), то формула SI — это просто PRT.
- Процентная ставка — это процент на каждые 100 долларов в течение фиксированного периода времени.
- Проценты всегда больше в случае сложных процентов по сравнению с простыми процентами.
- Формула или методы расчета сложных процентов основаны на методах расчета простых процентов.
Аналитический центр:
- Если проценты, выплачиваемые Майклом, составляют одну пятую от общей суммы, которую он должен выплатить по истечении определенного периода времени, каков период времени, если процентная ставка составляла 25%?
- Проценты на сумму кредита по ставке 10% годовых на срок 20 месяцев равны 1,5-кратному проценту на 3000 долларов США по ставке 5% годовых на 3 года.
 Какова сумма.
Какова сумма.
☛ Связанные темы:
- Будущая стоимость Формула простых процентов
- Формула процентной ставки
- Формула общей суммы процентов
Часто задаваемые вопросы о простых процентах
Что такое определение простых процентов?
Простые проценты — это тип процентов, которые рассчитываются только на первоначальную заемную/инвестированную сумму без учета процентов, начисленных/заработанных в предыдущие периоды. Это фиксированный процент от основной суммы, который взимается или зарабатывается в течение определенного периода времени.
Для чего используются простые проценты?
Простые проценты используются в тех случаях, когда сумма, подлежащая возврату, требует короткого периода времени. Таким образом, ежемесячная амортизация, ипотека, расчет сбережений и образовательные кредиты используют простые проценты.
Что такое формулы сложных и простых процентов?
Для данного основного долга P, времени T и процентной ставки R%,
- формула простых процентов – это PRT.
 Формула сложных процентов
Формула сложных процентов - : P(1 + R) T – P.
Какие бывают виды простых процентов?
Простые проценты бывают двух типов: обычные простые проценты и точные простые проценты. В обычных простых процентах год считается из 365 дней при расчете процентов, в то время как в точных простых процентах год считается 366 дней, если это високосный год. Оба метода используют одну и ту же формулу для расчета простых процентов.
Жилищные кредиты простые или сложные проценты?
Погашение ипотечного кредита занимает много времени, поэтому проценты, добавляемые кредитором, обычно представляют собой сложные проценты.
Где найти простой калькулятор процентов?
Чтобы найти калькулятор простых процентов (калькулятор SI), щелкните здесь. Этот калькулятор позволяет нам вводить значения основного долга, процентной ставки и продолжительности времени (в годах/месяцах/днях) и находит простые проценты, показывая пошаговое решение.
Являются ли автокредиты простыми или сложными процентами?
Автомобильные кредиты или автокредиты используют простые проценты для расчета процентов. Заемщик соглашается вернуть деньги, а также фиксированный процент от суммы займа. Но в случае, если заемщик не погасит сумму вовремя, компания или кредитор могут начать взимать сложные проценты.
Заемщик соглашается вернуть деньги, а также фиксированный процент от суммы займа. Но в случае, если заемщик не погасит сумму вовремя, компания или кредитор могут начать взимать сложные проценты.
В чем разница между простыми и сложными процентами?
Простые проценты — это проценты, выплачиваемые только на основную сумму, тогда как сложные проценты — это проценты, выплачиваемые как на основную сумму, так и на проценты, начисляемые через равные промежутки времени.
Как рассчитать простые проценты?
Простые проценты рассчитываются по следующей формуле: SI = P × R × T, где P = основная сумма, R = процентная ставка и T = период времени. Здесь ставка дается в процентах (r%) и записывается как r/100. А основная сумма — это сумма денег, которая остается неизменной каждый год в случае простых процентов.
Как ежемесячно начислять простые проценты?
Чтобы ежемесячно рассчитывать простые проценты, мы должны разделить годовые проценты, рассчитанные на 12. Таким образом, формула для расчета ежемесячных простых процентов принимает вид (P × R × T) / (100 × 12).
Таким образом, формула для расчета ежемесячных простых процентов принимает вид (P × R × T) / (100 × 12).
Что такое простая формула процентной ставки?
Используя формулу простых процентов, SI = PRT/100. Чтобы найти скорость R из этого, мы просто решаем это уравнение для R. Тогда мы получаем R = (SI × 100) / (P × T).
Формула процентной ставки – Что такое процентная ставка? Примеры
Используя формулу процентной ставки, мы получаем процентную ставку, которая представляет собой процент от основной суммы, взимаемой кредитором или банком с заемщика за использование его активов или денег в течение определенного периода времени. Ставка, которую банк платит своим вкладчикам за хранение денег на сберегательном счете, регулярном депозите или срочном депозите, также называется процентной ставкой, и в этом разделе мы обсудим формулу процентной ставки.
Что такое формула процентной ставки?
Формула процентной ставки помогает рассчитать сумму денег, подлежащую возврату в отношении взятого кредита, и проценты по инвестициям в срочные депозиты, взаимные фонды и т. д. Формула процентной ставки также помогает рассчитать проценты по кредитным картам. Процентная ставка для данной суммы по простым процентам может быть рассчитана по следующей формуле:
д. Формула процентной ставки также помогает рассчитать проценты по кредитным картам. Процентная ставка для данной суммы по простым процентам может быть рассчитана по следующей формуле:
Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время)
Процентная ставка для данной суммы сложных процентов может быть рассчитана по следующей формуле:
Сложная процентная ставка = P (1+i) t – P
63
Формула процентной ставки в терминах простых процентов записывается как:
Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время)
Формула процентной ставки в терминах сложных процентов записывается как:
Сложная процентная ставка = P (1+i) t – P
Где,
- P = основная сумма
- i = r = процентная ставка
- t = период времени
Хотите найти сложные математические решения за считанные секунды?
Воспользуйтесь нашим бесплатным онлайн-калькулятором, чтобы решить сложные вопросы. С Cuemath находите решения простыми и легкими шагами.
С Cuemath находите решения простыми и легкими шагами.
Запись на бесплатный пробный урок
Примеры использования формулы процентной ставки
Пример 1. Если Сэм одолжит 5000 долларов своему другу и через год получит 6000 долларов. Используя формулу процентной ставки, найдите, под какую процентную ставку Сэм одолжил эту сумму своему другу?
Решение:
Основная сумма = 5000 долл. США (дано)
Простой критерий = 6000-5000 долл. США = 1000 долл. США
Время = 1 год
с использованием процентной ставки,
Процентная ставка = (простой процент × 100)
. /(Основная сумма × Время)
Процентная ставка = (1000 × 100)/(5000 × 1)
Процентная ставка = 20%
Следовательно, Сэм будет брать у своего друга процентную ставку 20% через год.
Пример 2: Джеймс занял у банка 600 долларов США по определенной ставке годовых, и эта сумма удвоится за 2 года. Вычислите процентную ставку, по которой Джеймс занял деньги.
Решение:
Основная сумма = 600 долл. США (дано)
Простые проценты = 1200–600 долл. = 600 долл. США
Время = 2 года
9000Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время)
Процентная ставка = (600 × 100)/(600 × 2)
Процентная ставка = 50 %
Следовательно, Джеймс занял деньги по 50 % ставка.
Пример 3. Какова процентная ставка на основную сумму 12 000 через 2 года, если простые проценты равны 1200?
Решение:
Используя простую формулу процентной ставки,
Процентная ставка данной суммы может быть выражена как,
Процентная ставка = (Простой процент × 100)/(Основная сумма × Время)
Процентная ставка = (1200 × 100)/(12000 × 100)
Процентная ставка = 5 %
Таким образом, процентная ставка составляет 5 %
Часто задаваемые вопросы о формуле процентной ставки
Что подразумевается под формулой процентной ставки?
Используя формулу процентной ставки, мы получаем процентную ставку, которая представляет собой процент от основной суммы, взимаемой кредитором или банком с заемщика за использование его активов или денег в течение определенного периода времени. Формула процентной ставки: Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время).
Формула процентной ставки: Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время).
Какая формула используется для расчета процентной ставки?
Процентная ставка для данной суммы простых процентов может быть рассчитана по следующей формуле:
Процентная ставка = (Простые проценты × 100)/(Основная сумма × Время)
Формула процентной ставки в терминах сложных процентов записывается как:
Сложная процентная ставка = P (1+i) t – P
Где,
- P = основная сумма
- i = r = процентная ставка
- t = период времени
Каковы два основных аспекта формулы процентной ставки?
При расчете формулы процентной ставки необходимо учитывать два основных аспекта: простой процент и основную сумму. Простые проценты говорят о сумме, когда берется ссуда, а основная сумма – это точная сумма денег, взятая за ссуду.
Используя формулу процентной ставки, рассчитайте процентную ставку на 1500 долларов США, взятых взаймы в банке и удвоенных за 3 года.



