Формула расчета конденсатора: Как подобрать конденсатор для однофазного электродвигателя или трехфазного

Содержание

Как подобрать конденсатор для однофазного электродвигателя или трехфазного

Что делать, если требуется подключить двигатель к источнику, рассчитанному на другой тип напряжения (например, трехфазный двигатель к однофазной сети)? Такая необходимость может возникнуть, в частности, если нужно подключить двигатель к какому-либо оборудованию (сверлильному или наждачному станку и пр.). В этом случае используются конденсаторы, которые, однако, могут быть разного типа. Соответственно, надо иметь представление о том, какой емкости нужен конденсатор для электродвигателя, и как ее правильно рассчитать.

Что такое конденсатор

Конденсатор состоит из двух пластин, расположенных друг напротив друга. Между ними помещается диэлектрик. Его задача – снимать поляризацию, т.е. заряд близкорасположенных проводников.

Существует три вида конденсаторов:

Полярные. Не рекомендуется использовать их в системах, подключенных к сети переменного тока, т.к. вследствие разрушения слоя диэлектрика происходит нагрев аппарата, вызывающий короткое замыкание.
Неполярные. Работают в любом включении, т.к. их обкладки одинаково взаимодействуют с диэлектриком и с источником.
Электролитические (оксидные). В роли электродов выступает тонкая оксидная пленка. Считаются идеальным вариантом для электродвигателей с низкой частотой, т.к. имеют максимально возможную емкость (до 100000 мкФ).

Как подобрать конденсатор для трехфазного электродвигателя

Задаваясь вопросом: как подобрать конденсатор для трехфазного электродвигателя, нужно принять во внимание ряд параметров.

Чтобы подобрать емкость для рабочего конденсатора, необходимо применить следующую расчетную формулу: Сраб.=k*Iф / U сети, где:

k – специальный коэффициент, равный 4800 для подключения «треугольник» и 2800 для «звезды»;
Iф – номинальное значение тока статора, это значение обычно указывается на самом электродвигателе, если же оно затерто или неразборчиво, то его измеряют специальными клещами;

U сети – напряжение питания сети, т. е. 220 вольт.

Таким образом вы рассчитаете емкость рабочего конденсатора в мкФ.

Еще один вариант расчета – принять во внимание значение мощности двигателя. 100 Ватт мощности соответствуют примерно 7 мкФ емкости конденсатора. Осуществляя расчеты, не забывайте следить за значением тока, поступающего на фазную обмотку статора. Он не должен иметь большего значения, чем номинальный показатель.

В случае, когда пуск двигателя производится под нагрузкой, т.е. его пусковые характеристики достигают максимальных величин, к рабочему конденсатору добавляется пусковой. Его особенность заключается в том, что он работает примерно в течение трех секунд в период пуска агрегата и отключается, когда ротор выходит на уровень номинальной частоты вращения. Рабочее напряжение пускового конденсатора должно быть в полтора раза выше сетевого, а его емкость – в 2,5-3 раза больше рабочего конденсатора. Чтобы создать необходимую емкость, вы можете подключить конденсаторы как последовательно, так и параллельно.

Как подобрать конденсатор для однофазного электродвигателя

Асинхронные двигатели, рассчитанные на работу в однофазной сети, обычно подключаются на 220 вольт. Однако если в трехфазном двигателе момент подключения задается конструктивно (расположение обмоток, смещение фаз трехфазной сети), то в однофазном необходимо создать вращательный момент смещения ротора, для чего при запуске применяется дополнительная пусковая обмотка. Смещение ее фазы тока осуществляется при помощи конденсатора.

Итак, как подобрать конденсатор для однофазного электродвигателя?

Чаще всего значение общей емкости Сраб+Спуск (не отдельного конденсатора) таково: 1 мкФ на каждые 100 ватт.

Есть несколько режимов работы двигателей подобного типа:

Пусковой конденсатор + дополнительная обмотка (подключаются на время запуска). Емкость конденсатора: 70 мкФ на 1 кВт мощности двигателя.
Рабочий конденсатор (емкость 23-35 мкФ) + дополнительная обмотка, которая находится в подключенном состоянии в течение всего времени работы.
Рабочий конденсатор + пусковой конденсатор (подключены параллельно).

Если вы размышляете: как подобрать конденсатор к электродвигателю 220в, стоит исходить из пропорций, приведенных выше. Тем не менее, нужно обязательно проследить за работой и нагревом двигателя после его подключения. Например, при заметном нагревании агрегата в режиме с рабочим конденсатором, следует уменьшить емкость последнего. В целом, рекомендуется выбирать конденсаторы с рабочим напряжением от 450 В.

Как выбрать конденсатор для электродвигателя – вопрос непростой. Для обеспечения эффективной работы агрегата нужно чрезвычайно внимательно рассчитать все параметры и исходить из конкретных условий его работы и нагрузки.

Калькулятор расчета емкости конденсатора

Основная роль такого прибора как конденсатор заключается в том, что он накапливает электрический заряд и одномоментно отдает его. В автомобилях такой заряд тока конденсатор берет у аккумулятора и используется, например, для снабжения автомобильного усилителя нужным зарядом, улучшая, таким образом, звук, доносящийся из аудиосистемы.

Расчет емкости конденсатора с помощью онлайн калькулятора

Расчет конденсатора онлайн, который можно произвести с помощью калькуляторов на специальных ресурсах в Интернете, позволяет в считанные секунды получить результат, просто указав в соответствующих полях нужные данные. С их помощью быстро и легко можно рассчитать емкость, заряд, мощность, ток, энергию, и другие свойства конденсатора, нужные для конкретного устройства.

Среди множества видов конденсаторов существует, так называемый, электролитический тип, который используется в асинхронных электродвигателях. Среди его видов выделяют полярный и неполярный. Электролитический полярный конденсатор отличается от неполярного, прежде всего, большей емкостью. Расчет конденсатора для электродвигателя обязательно необходим перед его подключением. Он позволит, к примеру, узнать нужную емкость для конкретного двигателя.

Расчет конденсатора для трехфазного двигателя требуется ещё и для того, что, обычно, если трехфазный асинхронный двигатель с конденсаторным пуском работает нормально, будучи включенным в однофазную сеть, то емкость конденсатора уменьшается, а частота вращение вала увеличивается.

При правильном подключении, все эти характеристики будут наблюдаться.

Когда запускается асинхронный двигатель, подключением к сети 220В, необходима высокая емкостьфазодвигающего конденсатора. В Интернете всегда можно найти специальный калькулятор конденсаторов онлайн, который, в частности, позволяет рассчитать их емкость. Калькулятор, который позволяет произвести расчет соединения конденсаторов, а именно емкости двух параллельно соединенных приборов: рабочего и пускового, требует указания в соответствующих полях следующих данных:

Соединение обмоток двигателя
Его мощность
Напряжение в сети
Коэффициент мощности
КПД двигателя

После указания всех этих данных, можно получить результаты в виде информации по емкости пускового и рабочего конденсаторов, которая измеряется в мкФ (микроФарадах). Расчет емкости конденсатора для двигателя

, а именно для двух, соединенных между собой конденсаторов, в данном случае, зависит от того, каким был способ соединения их обмоток.

Расчет пускового конденсатора и параллельно рабочего предполагает указание двух таких способов подключения как: подключение звездой и треугольником. Формула расчета емкости конденсатора, подключенного звездой, выглядит так: Cр=2800*I/U, а формула расчета конденсатора, подключенного треугольником – это Cр=4800*I/U. Расчёт ёмкости конденсатора для электродвигателя по таким формулам расшифровывается следующим образом:

Ср означает рабочий конденсатор, пусковой будет обозначаться далее как Сп.
Ток I определен тут соотношением мощности мотора P с произведением 1,73 напряжения U и коэффициента мощности (cosφ ) с коэффициентом поленого действия (η). То есть I=P/1,73Uηcosφ.

Каждый калькулятор емкости конденсаторов использует свой тип расчета. Например, если говорить о соединенных конденсаторах, где емкость пускового прибора должна быть подобрана в 3 раза большая, чем рабочая емкость, то, в конкретном калькуляторе может быть использован расчет Cп=2,5*Cр, где Сп означает пусковой конденсатор, а Ср – рабочий тип.

Расчет заряда конденсатора

После расчета емкости, необходим расчет заряда конденсатора. Начальный заряд прибора равен нулю. Подключением к гальванической батарее или к другому источнику постоянной ЭДС конденсаторы заряжают. Чтобы правильно рассчитать заряд конденсатора от источника постоянной ЭДС, существует также специальный калькулятор конденсаторов онлайн, в котором лишь нужно указать следующие данные:

ЭДС источника в Вольтах,
сопротивление в Омах,
емкость в микроФарадах,
время зарядки в миллисекундах.

Каждый такой калькулятор расчета конденсаторов будет также указывать точность вычисления, с которой будут получены результаты. После нажатия кнопки «Рассчитать», в результатах реально получить:

постоянную времени RC-сети в миллисекундах,
время зарядки в миллисекундах,
требуемый начальный ток в Амперах,
максимальную рассеиваемую мощность в Ваттах,
напряжение в Вольтах,
заряд в микроКулонах,
энергию в микроДжоулях,
а также работу, совершенную источником, в микроДжоулях.

Используя специальные онлайн калькуляторы для расчета конденсатора, вам не придется самостоятельно проводить сложные подсчеты, искать нужные формулы, разбираться и вникать в сложные для вас схемы. Все это сделает калькулятор онлайн за вас.

Расчет емкости конденсатора асинхронного двухфазного двигателя (конденсаторный двигатель) – Help for engineer

Расчет емкости конденсатора асинхронного двухфазного двигателя (конденсаторный двигатель)

Однофазный асинхронный двигатель

Обмотка статора однофазного асинхронного двигателя занимает приблизительно 2/3 окружности, именно по этой причине его мощность на 1/3 меньше мощности трехфазного двигателя таких же габаритов.

Ток, протекая по обмотке статора, создает пульсирующее магнитное поле, которое можно представить как два поля, вращающиеся в разных направлениях. Поле, которое вращается в направлении ротора называется прямым полем, а второе – обратным. Они воздействуют на ротор и создают соответствующие моменты (М_пр и М_обр).

По причине разных направлений вращения эти электрические машины не могут самостоятельно совершить пуск, так как при неподвижном роторе, то есть при S=1, пусковой момент, он же М_рез, равен нолю (смотри Рисунок 1). Однако, если придать движение ротору, то прямой и обратный моменты не будут равны и двигатель продолжит вращение в том же направлении (ток, протекающий по обмотке ротора будет оказывать размагничивающее действие и при этом будет ослабляться обратное поле).

Рисунок 1 – Зависимость механических характеристик от прямого и обратного вращающих полей

Пуск двигателя с помощью пусковых устройств

Для того чтоб запустить однофазный асинхронный двигатель применяют устройства для пуска двигателя:

– Конденсатор – C;

– Резистор – R.

Пуск трехфазных асинхронных двигателей осуществляется более простым способом из-за уже имеющегося в сети сдвига фаз на 120 электрических градусов

Для получения пускового момента используют пусковую обмотку статора, которая по отношению к рабочей обмотке сдвинута на 90 электрических градусов.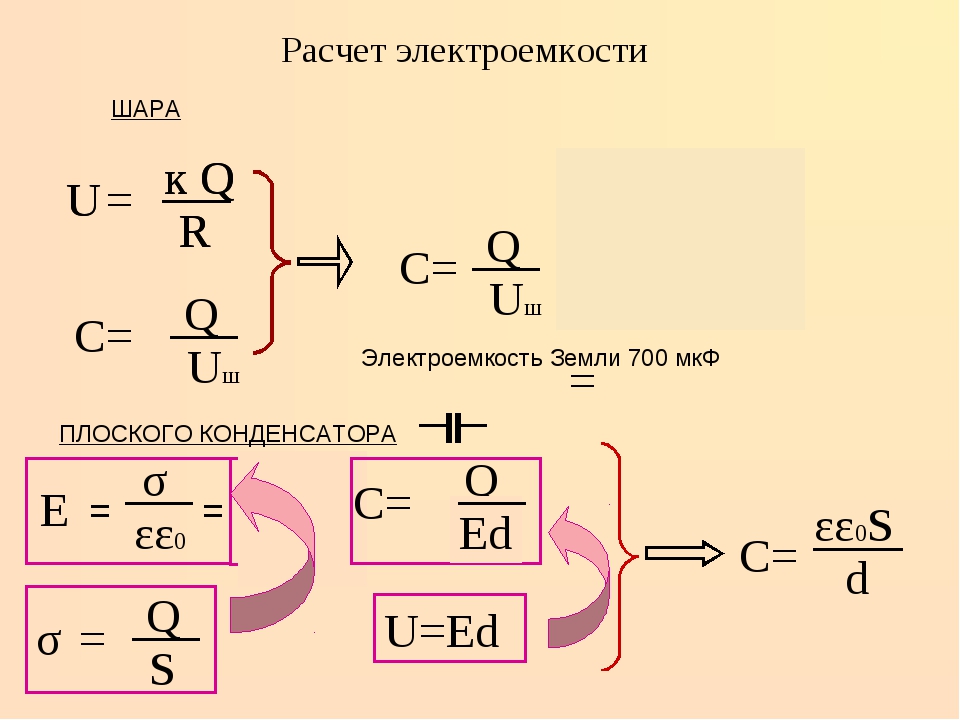 Применяют фазосдвигающие элементы, которые подключают к пусковой обмотке. Эта обмотка работает, обычно, около 3 первых секунд, после чего принудительно отключается вручную или с помощью автоматов. По этой причине ее изготовляют из провода меньшего сечения и с меньшим количеством витков по сравнению с рабочей обмоткой.

Пуск при помощи резистора производится при малых необходимых пусковых моментах, то есть если нагрузка на валу незначительна. Рисунок 2 иллюстрирует применение пускового а) конденсатора и б) резистора; где Р – рабочая обмотка, П – пусковая обмотка.

Рисунок 2 – Схема подключения однофазного асинхронного двигателя

Двухфазные асинхронные двигатели

Наличие конденсатора значительно улучшает характеристики двигателя, по этой причине используются двухфазные асинхронные двигатели. В них две обмотки являются рабочими, в одну из них вводится конденсатор для смещения угла между фазами на 90 градусов и создания кругового магнитного поля. Такие двигатели называют конденсаторными.

Расчет емкости конденсатора для двигателя:

Емкость такого конденсатора определяется по формуле:

где – ток, протекающий в обмотке статора,

sinφ₁ – сдвиг фаз между напряжение и током без конденсатора,

f– частота питающей сети,

U – напряжение сети,

n – коэффициент трансформации.

Где и k_об1,_{k_об2– обмоточные коэффициенты,}

W₁, W₂, – количество витков обмоток статора и ротора.

Напряжение на зажимах конденсатора выше чем напряжение сети и определяется следующей формулой:

Для повышения пусковых характеристик Существуют двигатели в одну обмотку которых ставятся два конденсатора, один из которых пусковой, второй – рабочий. Пусковой конденсатор обычно имеет емкость в разы большую чем рабочий. При этом пусковой отключается при достижении 70-80% номинальной скорости электрической машины.

Рисунок 3 – Пример подключения пары конденсаторов (конденсаторный двигатель)

Преимущества и недостатки конденсаторных двигателей

Недостатки по сравнению с трехфазным двигателем:

– Меньшая мощность;

– Увеличенное скольжение при номинальном режиме;

– Скорость вращения вала при холостом ходу ниже;

– Пониженная кратность пускового момента;

– Повышенная кратность пускового тока.

Преимущества:

– Имеют высокую эксплуатационную надежность;

– Не требуют трехфазного источника тока.

Недостаточно прав для комментирования

РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ

силовой трансформатор радиотехнические расчеты радио калькулятор

РАДИОТЕХНИЧЕСКИЕ РАСЧЕТЫ

Во время конструирования радиолюбителю приходится производить массу расчетов. Один из самых трудоемких - расчет колебательного контура. Рассмотрим методику такого расчета.

Как и при любом расчете нам нужны будут исходные данные. Предположим, нам нужно рассчитать частоту колебательного контура для фиксированных значений емкости конденсатора и индуктивности катушки. Допустим, емкость конденсатора равна 10 пикофарадам, индуктивность катушки – 10 микрогенри. По формуле (1 (А)) определяем частоту. Она равна 15900 килогерц (то есть 15,9 Мегагерца). При расчете индуктивности катушки при известных частоте настройки и емкости контура используем формулу 1(В). Для расчета емкости конденсатора используется формула 1(С).

Статья из журнала “Радио” для упрощенного расчета колебательного контура лежит здесь. Номограмму по расчету числа витков и размера катушек можно скачать по этой ссылке. Обе статьи в формате DjVu – программу для их чтения можно скачать здесь.

Емкости конденсаторов и сопротивления резисторов имеют стандартный числовой ряд, но иногда требуются нестандартные значения. Как можно выйти из такого положения? Можно взять несколько, например, резисторов и соединить их так, чтобы получить нужное значение.

Пользуясь формулой (2) можно рассчитать величину, которую мы получим в результате параллельного (а), либо последовательного (b) соединения резисторов. При последовательном соединении резисторов их номиналы складываются между собой. Параллельное соединение позволяет получить результирующее сопротивление всегда меньшее, чем номинал наименьшего из соединяемых резисторов. При любом способе соединения резисторов (из рассмотренных) общая мощность рассеяния их увеличивается. Кроме того, при параллельном соединении через резисторы можно пропустить больший ток без их порчи.

Соединение конденсаторов:

При последовательном соединении конденсаторов (формула 3(b)) результирующая емкость будет всегда меньше емкости наименьшего из соединяемых конденсаторов. При параллельном соединении (3(a)) результирующая емкость будет равна сумме емкостей конденсаторов.

При работе на переменном токе иногда приходится рассчитывать реактивные сопротивления катушек индуктивности и конденсаторов.

Реактивное сопротивление катушки можно определить, пользуясь формулой (4), сопротивление конденсатора на переменном токе можно вычислить при помощи формулы (5):

В обоих формулах “Pi” – это всем известная математическая константа “Пи”, равная (округленно) 3,14.

В заключении хотелось бы обратить ваше внимание на сноски в формулах. Для того, чтобы получить истинное значение при расчетах не забывайте использовать нужные величины!

В дальнейшем мы с вами рассмотрим формулы расчета катушек индуктивности с сердечником и без сердечника.

Емкость конденсаторов: определение, формулы, примеры.

Определение 1

Конденсатор – это совокупность двух любых проводников, заряды которых одинаковы по значению и противоположны по знаку.

Его конфигурация говорит о том, что поле, созданное зарядами, локализовано между обкладками. Тогда можно записать формулу электроемкости конденсатора:

C=qφ1-φ2=qU.

Значением φ1-φ2=U обозначают разность потенциалов, называемую напряжением, то есть U. По определению емкость положительна. Она зависит только от размерностей обкладок конденсатора их взаиморасположения и диэлектрика. Ее форма и место должны минимизировать воздействие внешнего поля на внутреннее. Силовые линии конденсатора начинаются на проводнике с положительным зарядом, а заканчиваются с отрицательным. Конденсатор может являться проводником, помещенным в полость, окруженным замкнутой оболочкой.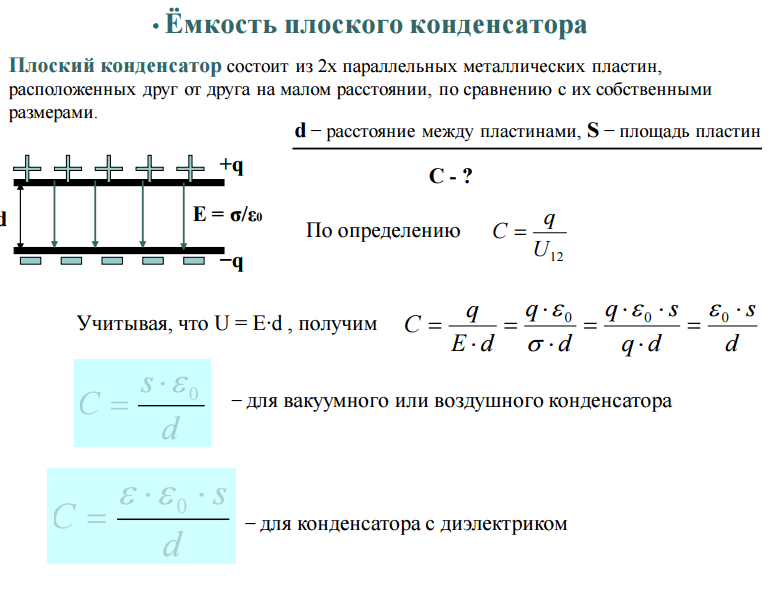

Выделяют три большие группы: плоские, сферические, цилиндрические. Чтобы найти емкость, необходимо обратиться к определению напряжения конденсатора с известными значениями зарядов на обкладках.

Плоский конденсатор

Определение 2

Плоский конденсатор – это две противоположно заряженные пластины, которые разделены тонким слоем диэлектрика, как показано на рисунке 1.

Формула для расчета электроемкости записывается как

C=εε0Sd, где S является площадью обкладки, d – расстоянием между ними, ε – диэлектрической проницаемостью вещества. Меньшее значение d способствует большему совпадению расчетной емкости конденсатора с реальной.

Рисунок 1

При известной электроемкости конденсатора, заполненного N слоями диэлектрика, толщина слоя с номером i равняется di, вычисление диэлектрической проницаемости этого слоя εi выполняется, исходя из формулы:

C=ε0Sd1ε1+d2ε2+…+dNεN.

Сферический конденсатор

Определение 3

Когда проводник имеет форму шара или сферы, тогда внешняя замкнутая оболочка является концентрической сферой, это означает, что конденсатор сферический.

Он состоит из двух концентрических проводящих сферических поверхностей с пространством между обкладками, заполненным диэлектриком, как показано на рисунке 2. Емкость рассчитывается по формуле:

C=4πεε0R1R2R2-R1, где R1 и R2 являются радиусами обкладок.

Рисунок 2

Слишком сложно?

Не парься, мы поможем разобраться и подарим скидку 10% на любую работу

Опиши задание

Цилиндрический конденсатор

Емкость цилиндрического конденсатора равняется:

C=2πεε0llnR2R1, где l – высота цилиндров, R1 и R2 – радиусы обкладок. Данный вид конденсатора имеет две соосные поверхности проводящих цилиндрических поверхности, как показано на рисунке 3.

Рисунок 3

Определение 4

Важной характеристикой конденсаторов считается пробивное напряжение – напряжение, при котором происходит электрический разряд через слой диэлектрика.

Umax находится от зависимости от толщины слоя и свойств диэлектрика, конфигурации конденсатора.

Электроемкость плоского конденсатора. Формулы

Кроме отдельных конденсаторов используются их соединения. Наличие параллельного соединения конденсаторов применяют для увеличения его емкости. Тогда поиск результирующей емкости соединения сводится к записи суммы Ci, где Ci- это емкость конденсатора с номером i:

C=∑i=1NCi.

При последовательном соединении конденсаторов суммарная емкость соединения всегда будет по значению меньше, чем минимальная любого конденсатора, входящего в систему. Для расчета результирующей емкости следует сложить величины, обратные к емкостям отдельных конденсаторов:

Пример 1

Произвести вычисление емкости плоского конденсатора при известной площади обкладок
1 см2 с расстоянием между ними 1 мм. Пространство между обкладками находится в вакууме.

Решение

Чтобы рассчитать электроемкость конденсатора, применяется формула:

C=εε0Sd.

Значения:

ε=1, ε0=8,85·10-12 Фм;S=1 см2=10-4 м2;d=1 мм=10-3 м.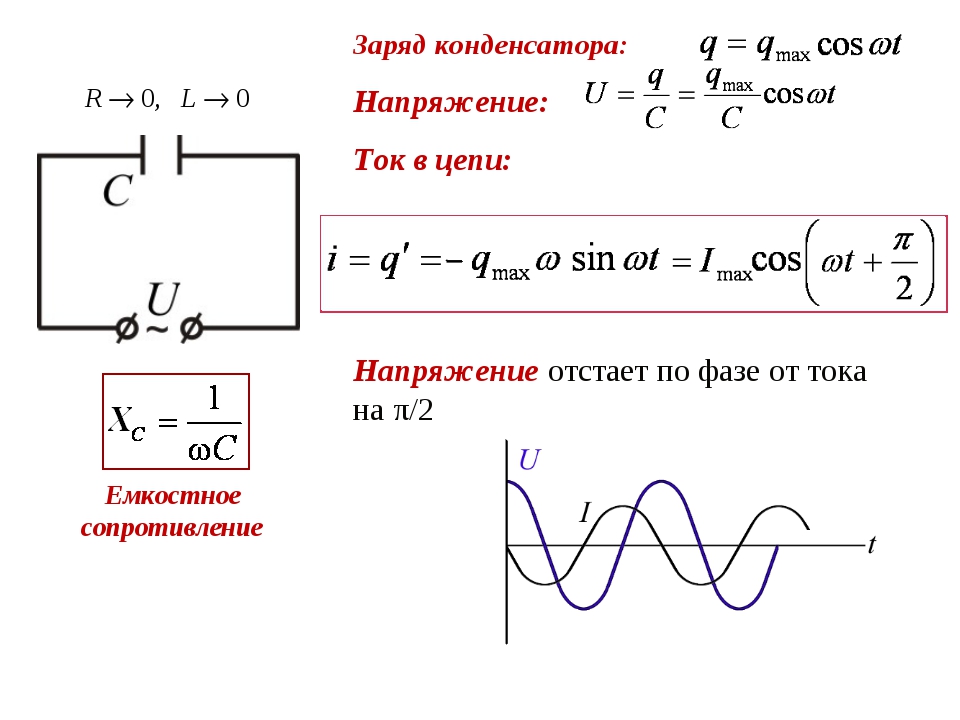

Подставим числовые выражения и вычислим:

C=8,85·10-12·10-410-3=8,85·10-13 (Ф).

Ответ: C≈0,9 пФ.

Пример 2

Найти напряженность электростатического поля у сферического конденсатора на расстоянии x=1 см=10-2 м от поверхности внутренней обкладки при внутреннем радиусе обкладки, равном R1=1 см=10-2 м, внешнем – R2=3 см=3·10-2 м. Значение напряжения – 103 В.

Решение

Производящая заряженная сфера создает напряженность поля. Его значение вычисляется по формуле:

E=14πεε0qr2, где q обозначают заряд внутренней сферы, r=R1+x – расстояние от центра сферы.

Нахождение заряда предполагает применение определения емкости конденсатора С:

q=CU.

Для сферического конденсатора предусмотрена формула вида

C=4πεε0R1R2R2-R1 с радиусами обкладок R1 и R2.

Производим подстановку выражений для получения искомой напряженности:

E=14πεε0U(x+R1)24πεε0R1R2R2-R1=U(x+R1)2R1R2R2-R1.

Данные представлены в системе СИ, поэтому достаточно заменить буквы числовыми выражениями:

E=103(1+1)2·10-4·10-2·3·10-23·10-2-10-2=3·10-18·10-6=3,45·104 Вм.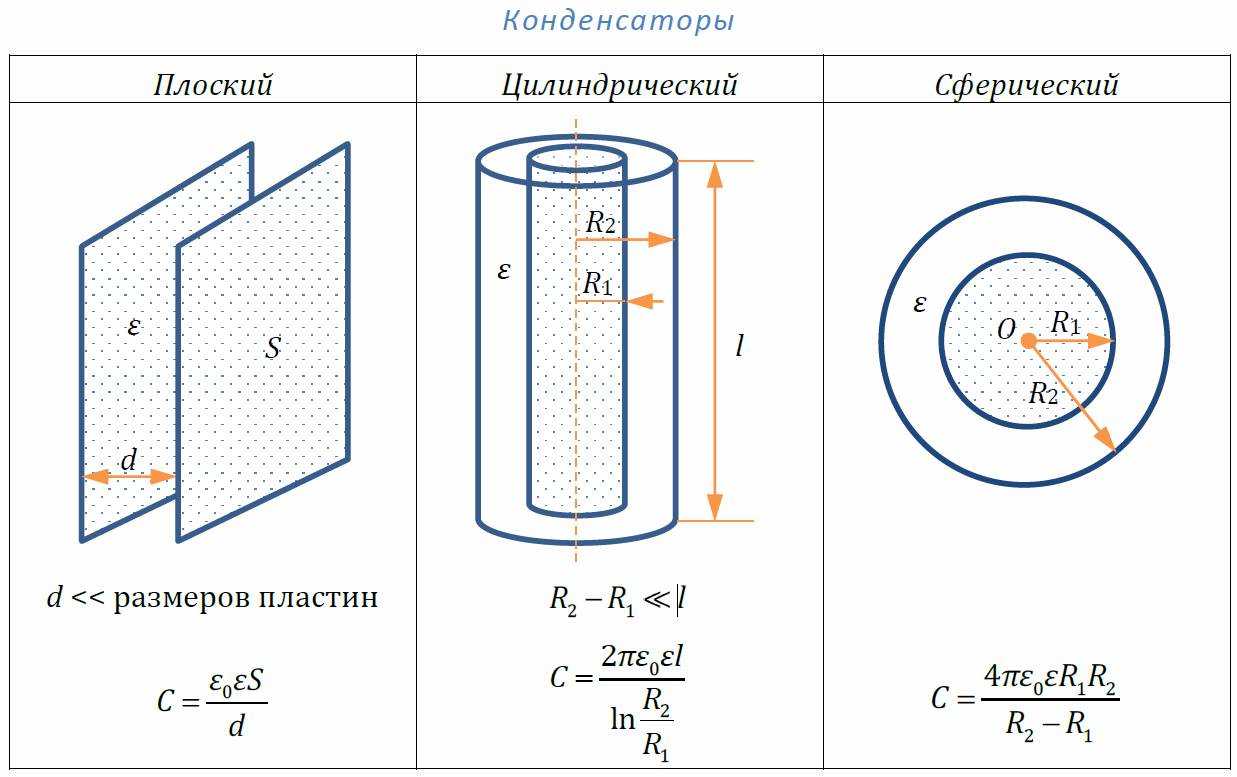

Ответ: E=3,45·104 Вм.

Расчет конденсатора для трехфазного двигателя в однофазной сети

Для включения трехфазного электродвигателя (что такое электродвигатель ➠) в однофазную сеть обмотки статора могут быть соединены в звезду или треугольник.

Напряжение сети подводят к началам двух фаз. К началу третьей фазы и одному из зажимов сети присоединяют рабочий конденсатор 1 и отключаемый (пусковой) конденсатор 2, который необходим для увеличения пускового момента.

Пусковая емкость конденсаторов

Сп = Ср + Со,

где Ср — рабочая емкость,
Со — отключаемая емкость.

После пуска двигателя конденсатор 2 отключают.

Рабочую емкость конденсаторного двигателя для частоты 50 Гц определяют по формулам:

для схемы на рис. а: Ср = 2800 Iном / U;
для схемы на рис. б: Ср = 4800 Iном / U;
для схемы на рис. в: Ср = 1600 Iном / U;
для схемы на рис. г: Ср = 2740 Iном / U,

где Ср — рабочая емкость при номинальной нагрузке, мкФ;
Iном — номинальный ток фазы двигателя, А;
U — напряжение сети, В.

Нагрузка двигателя с конденсатором не должна превышать 65—85% номинальной мощности, указанной на щитке трехфазного двигателя.

Если пуск двигателя происходит без нагрузки, то пусковая емкость не требуется — рабочая емкость будет в то же время пусковой. В этом случае схема включения упрощается.

При пуске двигателя под нагрузкой, близкой к номинальному моменту необходимо иметь пусковую емкость Сп = (2,5 ÷ 3) Ср.

Выбор конденсаторов по номинальному напряжению производят по соотношениям:

для схемы на рис. а, б: Uк = 1,15 U;
для схемы на рис. в: Uк = 2,2 U;
для схемы на рис. г: Uк = 1,3 U,

где Uк и U — напряжения на конденсаторе и в сети.

Купить конденсаторы для запуска двигателя:
CBB60 3/4/5/6/10/12/14/16 мкФ 500 В;
CBB60 20 мкФ 450 В;
CBB60 25 мкФ 450 В;
CBB60 35 мкФ 450 В;
CBB60 50 мкФ 450 В;
CBB60 60 мкФ 450 В;
CBB60 80 мкФ 450 В;
CD60 100 мкФ 450 В;
CBB60 120 мкФ 450 В.

Основные технические данные некоторых конденсаторов приведены в таблице.

Если трехфазный электродвигатель, включенный в однофазную сеть, не достигает номинальной частоты вращения, а застревает на малой скорости, следует увеличить сопротивление клетки ротора проточкой короткозамыкающих колец или увеличить воздушный зазор шлифовкой ротора на 15—20%.

В том случае, если конденсаторы отсутствуют, можно использовать резисторы, которые включаются по тем же схемам, что и при конденсаторном пуске. Резисторы включаются вместо пусковых конденсаторов (рабочие конденсаторы отсутствуют).

Сопротивление (Ом) резистора может быть определено по формуле

где R — сопротивление резистора;
κ и I— кратность пускового тока и линейный ток в трехфазном режиме.

Пример расчета рабочей емкости конденсатора для двигателя

Определить рабочую емкость для двигателя АО 31/2, 0.6 кВт, 127/220 В, 4.2/2.4 А, если двигатель включен по схеме, изображенной на рис. а, а напряжение сети равно 220 В. Пуск двигателя без нагрузки.

Решение

1. Рабочая емкость Ср = 2800 x 2.4 / 220 ≈ 30 мкФ.

2. Напряжение на конденсаторе при выбранной схеме Uк = 1,15 x U = 1,15 x 220 = 253 В.

По таблице выбираем три конденсатора МБГО-2 по 10 мкФ каждый с рабочим напряжением 300 В. Конденсаторы включать параллельно.

Источник: В.И. Дьяков. Типовые расчеты по электрооборудованию.

Видео о том, как подключить электродвигатель на 220 вольт:

Помощь студентам

Онлайн калькулятор расчета параллельного соединения конденсаторов

В устройствах радиоэлектроники конденсаторы представляют собой один из важнейших элементов, способный накапливать и отдавать электрический заряд. В сравнении с другими элементами, конденсатор обладает такими параметрами как емкость и сопротивление. Сопротивление конденсатора обусловлено изолирующим промежутком, который может выйти со строя из-за скачков напряжения или других аварийных процессов в сети. При необходимости заменить какой-либо конденсатор, многие радиолюбители сталкиваются с трудностью достать модель нужной емкости.

В таком случае на помощь придет правило сложения, позволяющее заменить одно устройство несколькими меньшей емкости, чтобы в суме их хватило для компенсации вышедшего со строя конденсатора. В этом месте многие не могут определить, каким способом вычисляется суммарная мощность параллельно соединенных конденсаторов. Следует отметить, что физически для схемы конденсатор представляет собой разрыв.

Рис. 1. Параллельное соединение конденсаторов

Посмотрите на рисунок 1, это принципиальная схема параллельного подключения конденсаторов. Как видите, в этом случае одноименные выводы емкостного элемента подводятся к соответствующей точке электрической цепи.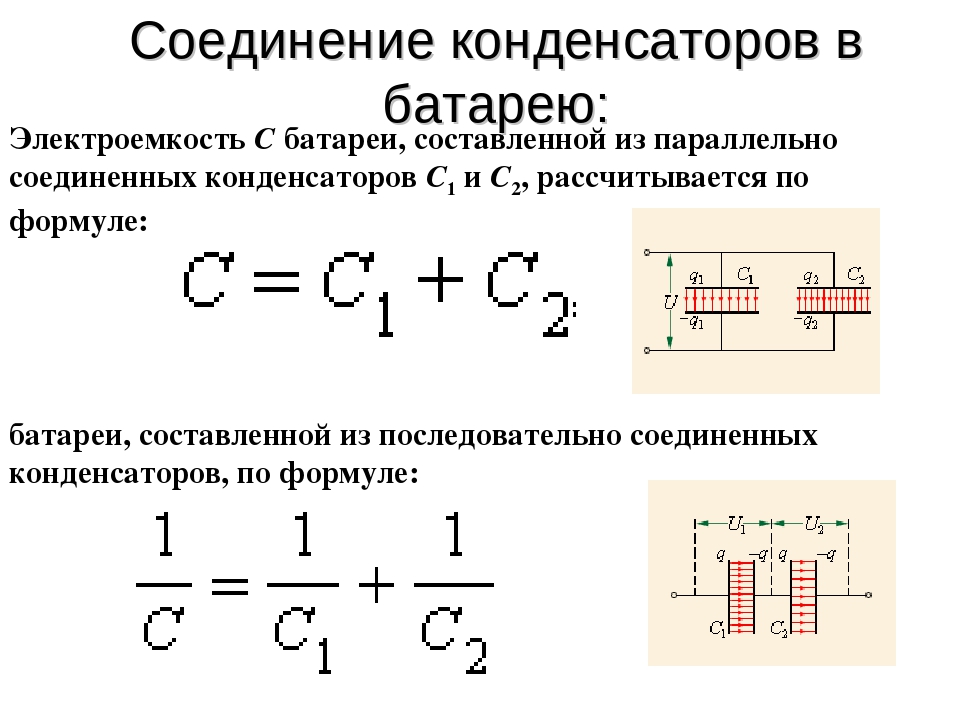 Поэтому и емкость между плоскостями двух и более конденсаторов, соединенных между собой параллельно складывается в одно целое. Исходя из этого, суммарная емкость для параллельно включенных конденсаторов будет вычисляться по формуле:

С₀ = С₁ + С₂ + … + С_n

Где,

С₀ — общая емкость параллельно соединенных конденсаторов
С₁ — емкость первого конденсатора;
С₂ — емкость второго конденсатора.

В данном примере рассматривается ситуация, когда параллельно соединяются только два емкостных элемента, поэтому их результирующая емкость будет равна арифметической сумме емкостей обоих конденсаторов. На практике можно применять и большее число, если вам необходимо получить определенную емкость.

Чтобы рассчитать результирующую емкость при параллельном соединении 2 и более конденсаторов вы можете воспользоваться нашим онлайн калькулятором ниже.

Расчет напряжения и тока | Постоянные времени RC и L / R

Есть надежный способ рассчитать любое из значений в реактивной цепи постоянного тока с течением времени.

Расчет значений в реактивной цепи постоянного тока

Первым шагом является определение начального и конечного значений для любого количества конденсатора или катушки индуктивности, которое препятствует изменению; то есть, какое бы количество реактивный компонент ни пытался поддерживать постоянным. Для конденсаторов это количество составляет , напряжение ; для индукторов это количество равно , ток .Когда переключатель в цепи замкнут (или разомкнут), реактивный компонент будет пытаться поддерживать это количество на том же уровне, что и до переключения переключателя, так что это значение должно использоваться в качестве «начального» значения.

Конечным значением этого количества является то, каким оно будет через бесконечное количество времени. Это может быть определено путем анализа емкостной цепи, как если бы конденсатор был разомкнутой цепью, и индуктивной цепи, как если бы индуктор был коротким замыканием, потому что именно так ведут себя эти компоненты, когда они достигли «полного заряда», через бесконечное количество времени.

Следующим шагом является вычисление постоянной времени схемы: количество времени, необходимое для изменения значений напряжения или тока примерно на 63 процента от их начальных значений до их конечных значений в переходной ситуации.

В последовательной RC-цепи постоянная времени равна полному сопротивлению в омах, умноженному на общую емкость в фарадах. Для последовательной цепи L / R это общая индуктивность в генри, деленная на общее сопротивление в омах.В любом случае постоянная времени выражается в единицах секунд и обозначается греческой буквой «тау» (τ):

Повышение и понижение таких значений схемы, как напряжение и ток, в ответ на переходный процесс, как упоминалось ранее, равны асимптотике . При этом значения начинают быстро меняться вскоре после переходного процесса и со временем стабилизируются. При нанесении на график приближение к конечным значениям напряжения и тока образуют экспоненциальные кривые.

Как было сказано ранее, одна постоянная времени – это количество времени, необходимое для того, чтобы любое из этих значений изменилось примерно на 63 процента от их начальных значений до их (конечных) конечных значений. Для каждой постоянной времени эти значения приближаются (приблизительно) на 63 процента к их конечной цели. Математическая формула для определения точного процента довольно проста:

Буква e обозначает постоянную Эйлера, которая приблизительно равна 2.7182818. Он получен из методов исчисления после математического анализа асимптотического подхода значений схемы. По истечении времени, равного одной постоянной времени, процент изменения от начального значения до конечного значения составляет:

После двух постоянных времени процент изменения от начального значения до конечного значения составляет:

По истечении десяти постоянных времени это процентное соотношение:

Чем больше времени проходит с момента подачи кратковременного напряжения от батареи, тем больше значение знаменателя дроби, что дает меньшее значение для всей дроби, что дает общий итог (1 минус дробь) приближается к 1 или 100 процентам.

Формула универсальной постоянной времени

Из этой формулы можно составить более универсальную формулу для определения значений напряжения и тока в переходных цепях, умножив эту величину на разницу между конечным и пусковым значениями цепи:

Давайте проанализируем рост напряжения в цепи последовательного резистора-конденсатора, показанной в начале главы.

Обратите внимание, что мы решили анализировать напряжение, потому что это количество конденсаторов, как правило, остается постоянным.Хотя формула довольно хорошо работает для тока, начальные и конечные значения тока фактически выводятся из напряжения конденсатора, поэтому расчет напряжения является более прямым методом. Сопротивление составляет 10 кОм, а емкость – 100 мкФ (микрофарад). Поскольку постоянная времени (τ) для RC-цепи является произведением сопротивления и емкости, мы получаем значение в 1 секунду:

Если конденсатор запускается в полностью разряженном состоянии (0 вольт), то мы можем использовать это значение напряжения в качестве «начального» значения. Конечным значением, конечно же, будет напряжение аккумулятора (15 вольт). Наша универсальная формула для напряжения конденсатора в этой схеме выглядит так:

Итак, после 7,25 секунд подачи напряжения через замкнутый переключатель, напряжение конденсатора увеличится на:

Поскольку мы начали с напряжения конденсатора 0 вольт, это увеличение на 14,989 вольт означает, что у нас будет 14,989 вольт после 7.25 секунд.

Та же формула будет работать и для определения тока в этой цепи. Поскольку мы знаем, что разряженный конденсатор изначально действует как короткое замыкание, пусковой ток будет максимально возможным: 15 вольт (от батареи), разделенные на 10 кОм (единственное противодействие току в цепи в начале):

Мы также знаем, что конечный ток будет равен нулю, поскольку конденсатор в конечном итоге будет вести себя как разомкнутая цепь, а это означает, что в конечном итоге электроны не будут течь по цепи.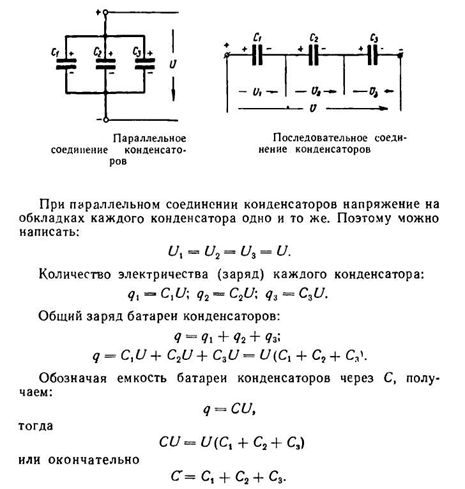 Теперь, когда мы знаем как начальное, так и конечное значения тока, мы можем использовать нашу универсальную формулу для определения тока через 7,25 секунды замыкания переключателя в той же RC-цепи:

Обратите внимание, что полученное значение изменения отрицательное, а не положительное! Это говорит нам о том, что ток уменьшился с течением времени, а не увеличился. Поскольку мы начали с тока 1,5 мА, это уменьшение (-1,4989 мА) означает, что у нас 0.001065 мА (1,065 мкА) через 7,25 секунды.

Мы также могли бы определить ток цепи в момент времени = 7,25 секунды, вычтя напряжение конденсатора (14,989 вольт) из напряжения батареи (15 вольт), чтобы получить падение напряжения на резисторе 10 кОм, а затем рассчитав ток через резистор (и всю последовательную цепь) по закону Ома (I = E / R). В любом случае мы должны получить тот же ответ:

Использование формулы универсальной постоянной времени для анализа индуктивных цепей

Формула универсальной постоянной времени также хорошо подходит для анализа индуктивных цепей. Давайте применим его к нашему примеру цепи L / R в начале главы:

При индуктивности 1 генри и последовательном сопротивлении 1 Ом наша постоянная времени равна 1 секунде:

Поскольку это индукционная цепь, и мы знаем, что индукторы противодействуют изменению тока, мы создадим нашу формулу постоянной времени для начального и конечного значений тока. Если мы начнем с переключателя в разомкнутом положении, ток будет равен нулю, поэтому ноль будет нашим начальным значением тока.

После того, как переключатель оставался замкнутым в течение длительного времени, ток стабилизируется до своего конечного значения, равного напряжению источника, деленному на полное сопротивление цепи (I = E / R), или 15 ампер в этом случае. схема.

Если бы мы хотели определить значение тока через 3,5 секунды, мы бы применили универсальную формулу постоянной времени как таковую:

Учитывая тот факт, что наш пусковой ток был равен нулю, мы получаем ток цепи равный 14. 547 ампер за 3,5 секунды.

Определить напряжение в индуктивной цепи лучше всего, сначала вычислив ток в цепи, а затем вычислив падение напряжения на сопротивлениях, чтобы определить, что осталось упасть на катушке индуктивности. С одним резистором в нашей примерной схеме (имеющим значение 1 Ом) это довольно просто:

Если вычесть из напряжения нашей батареи 15 вольт, на индукторе останется 0,453 вольт за время = 3,5 секунды.

ОБЗОР:

Формула универсальной постоянной времени:
Чтобы проанализировать RC или L / R цепь, выполните следующие действия:
(1): Определите постоянную времени для цепи (RC или L / R).
(2): Укажите величину, которая должна быть вычислена (любая величина, изменение которой прямо противоположно реактивной составляющей. Для конденсаторов это напряжение; для катушек индуктивности это ток).
(3): Определите начальное и конечное значения для этого количества.
(4): Подставьте все эти значения (Конечное, Начало, время, постоянная времени) в универсальную формулу постоянной времени и найдите , измените количества.
(5): Если начальное значение было нулем, то фактическое значение в указанное время равно вычисленному изменению, заданному универсальной формулой.Если нет, добавьте изменение к начальному значению, чтобы узнать, где вы находитесь.

СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:

Ознакомьтесь с нашей коллекцией вычислителей мощности в нашем разделе Инструменты .

конденсаторов последовательно и параллельно

Цели обучения

К концу этого раздела вы сможете:

Выведите выражения для полной емкости последовательно и параллельно.
Обозначение последовательной и параллельной частей в комбинации подключения конденсаторов.
Рассчитайте эффективную емкость последовательно и параллельно с учетом индивидуальных емкостей.

Несколько конденсаторов могут быть соединены вместе в различных приложениях. Несколько соединений конденсаторов действуют как один эквивалентный конденсатор. Общая емкость этого эквивалентного одиночного конденсатора зависит как от отдельных конденсаторов, так и от способа их подключения.Существует два простых и распространенных типа соединений, которые называются серии и параллельно , для которых мы можем легко вычислить общую емкость. Некоторые более сложные соединения также могут быть связаны с комбинациями последовательного и параллельного.

Емкость серии

На рисунке 1а показано последовательное соединение трех конденсаторов с приложенным напряжением. Как и для любого конденсатора, емкость комбинации связана с зарядом и напряжением [латекс] C = \ frac {Q} {V} \\ [/ latex].

Обратите внимание на рис. 1, что противоположные заряды величиной Q протекают по обе стороны от первоначально незаряженной комбинации конденсаторов при приложении напряжения В . Для сохранения заряда необходимо, чтобы на пластинах отдельных конденсаторов были созданы заряды одинаковой величины, поскольку заряд разделяется только в этих изначально нейтральных устройствах. Конечным результатом является то, что комбинация напоминает одиночный конденсатор с эффективным разделением пластин больше, чем у отдельных конденсаторов.(См. Рисунок 1b.) Чем больше расстояние между пластинами, тем меньше емкость. Общей особенностью последовательного соединения конденсаторов является то, что общая емкость меньше любой из отдельных емкостей.

Рис. 1. (a) Конденсаторы, подключенные последовательно. Величина заряда на каждой пластине равна Q. (b) Эквивалентный конденсатор имеет большее расстояние между пластинами d. Последовательные соединения дают общую емкость, которая меньше, чем у любого из отдельных конденсаторов.

Мы можем найти выражение для общей емкости, рассмотрев напряжение на отдельных конденсаторах, показанных на рисунке 1.Решение [latex] C = \ frac {Q} {V} \\ [/ latex] для V дает [latex] V = \ frac {Q} {C} \\ [/ latex]. Таким образом, напряжения на отдельных конденсаторах равны [латексному] V_1 = \ frac {Q} {C_1}, V_2 = \ frac {Q} {C_2}, \ text {и} V_3 = \ frac {Q} {C_3} \\ [/латекс].

Общее напряжение складывается из отдельных напряжений:

В = В ₁ + В ₂ + В ₃.

Теперь, называя общую емкость C _S последовательной емкостью, считайте, что

[латекс] V = \ frac {Q} {C _ {\ text {S}}} = V_1 + V_2 + V_3 \\ [/ latex].

Вводя выражения для V ₁, V ₂ и V ₃, получаем

[латекс] \ frac {Q} {C _ {\ text {S}}} = \ frac {Q} {C_ {1}} + \ frac {Q} {C_ {2}} + \ frac {Q} { C_ {3}} \\ [/ латекс].

Отменяя Q s, мы получаем уравнение для полной емкости в серии C _S, равной

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ точки, \\ [/ latex]

, где «…» означает, что выражение действительно для любого количества конденсаторов, соединенных последовательно. Выражение этой формы всегда приводит к общей емкости C _S, которая меньше любой из отдельных емкостей C ₁, C ₂,…, как показано в примере 1.

Общая емкость в серии,

C _с

Общая емкость в серии:

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} { C_ {3}} + \ dots \\ [/ latex]

Пример 1. Что такое серийная емкость?

Найдите общую емкость для трех последовательно соединенных конденсаторов, учитывая, что их индивидуальные емкости равны 1.000, 5.000 и 8.000 мкФ.

Стратегия

Имея данную информацию, общую емкость можно найти с помощью уравнения для емкости в серии.

Решение

Ввод заданных емкостей в выражение для [latex] \ frac {1} {C _ {\ text {S}}} \\ [/ latex] дает [latex] \ frac {1} {C _ {\ text {S} }} = \ frac {1} {C_ {1}} + \ frac {1} {C_ {2}} + \ frac {1} {C_ {3}} \\ [/ latex].

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {1} {1.000 \ mu \ text {F}} + \ frac {1} {5.000 \ mu \ text {F} } + \ frac {1} {8.000 \ mu \ text {F}} = \ frac {1.325} {\ mu \ text {F}} \\ [/ latex]

Преобразование для нахождения C _S дает [латекс] C _ {\ text {S}} = \ frac {1,325} {\ mu \ text {F}} = 0,755 \ mu \ text {F} \\ [/ латекс].

Обсуждение

Общая последовательная емкость C _с меньше наименьшей индивидуальной емкости, как было обещано. При последовательном соединении конденсаторов сумма меньше деталей. На самом деле это меньше, чем у любого человека. Обратите внимание, что иногда возможно и более удобно решить уравнение, подобное приведенному выше, путем нахождения наименьшего общего знаменателя, который в данном случае (показаны только целочисленные вычисления) равен 40.Таким образом,

[латекс] \ frac {1} {C _ {\ text {S}}} = \ frac {40} {40 \ mu \ text {F}} + \ frac {8} {40 \ mu \ text {F} } + \ frac {5} {40 \ mu \ text {F}} = \ frac {53} {40 \ mu \ text {F}} \\ [/ latex]

, так что

[латекс] C _ {\ text {S}} = \ frac {40 \ mu \ text {F}} {53} = 0,755 \ mu \ text {F} \\ [/ latex]

Параллельные конденсаторы

На рис. 2а показано параллельное соединение трех конденсаторов с приложенным напряжением. Здесь общую емкость найти легче, чем в последовательном случае. Чтобы найти эквивалентную общую емкость C _p, сначала отметим, что напряжение на каждом конденсаторе составляет В, , то же самое, что и у источника, поскольку они подключены к нему напрямую через проводник.(Проводники являются эквипотенциальными, поэтому напряжение на конденсаторах такое же, как и на источнике напряжения.) Таким образом, конденсаторы имеют такие же заряды, как и при индивидуальном подключении к источнику напряжения. Общая сумма начислений Q представляет собой сумму индивидуальных сборов: Q = Q ₁ + Q ₂ + Q ₃.

Рис. 2. (a) Параллельное соединение конденсаторов. Каждый из них подключен непосредственно к источнику напряжения, как если бы он был полностью один, поэтому общая параллельная емкость – это просто сумма отдельных емкостей. (b) Эквивалентный конденсатор имеет большую площадь пластины и поэтому может удерживать больше заряда, чем отдельные конденсаторы.

Используя соотношение Q = CV , мы видим, что общий заряд составляет Q = C _p V , а отдельные сборы составляют Q ₁ = C ₁ V , Q ₂ = C ₂ V , и Q ₃ = C ₃ V Ввод их в предыдущее уравнение дает

C _p V = C ₁ V + C ₂ V + C ₃ V .

Исключая В из уравнения, мы получаем уравнение для полной емкости параллельно

C _p: C _p = C ₁ + C ₂ + C ₃ +….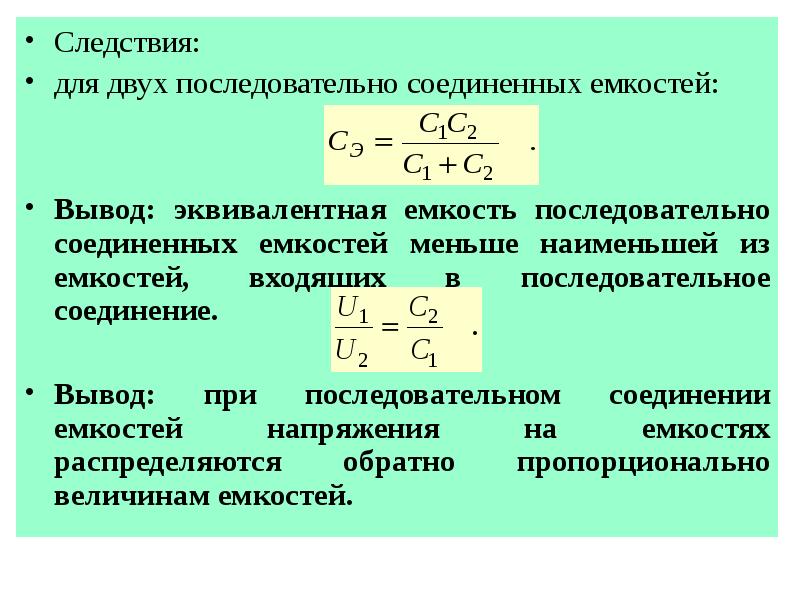

Общая параллельная емкость – это просто сумма отдельных емкостей. (И снова «… » означает, что выражение действительно для любого количества конденсаторов, подключенных параллельно.) Так, например, если конденсаторы в Примере 1 были подключены параллельно, их емкость была бы

C _p = 1.000 мкФ + 5.000 мкФ + 8.000 мкФ = 14000 мкФ.

Эквивалентный конденсатор для параллельного соединения имеет значительно большую площадь пластины и, следовательно, большую емкость, как показано на рисунке 2b.

Общая емкость параллельно,

C _p

Общая емкость параллельно C _p = C ₁ + C ₂ + C ₃ +…

Более сложные соединения конденсаторов иногда могут быть последовательными и параллельными. (См. Рис. 3.) Чтобы найти общую емкость таких комбинаций, мы идентифицируем последовательные и параллельные части, вычисляем их емкости, а затем находим общую.

Рис. 3. (a) Эта схема содержит как последовательные, так и параллельные соединения конденсаторов. См. Пример 2 для расчета общей емкости цепи. (b) C ₁ и C ₂ идут последовательно; их эквивалентная емкость C _S меньше, чем у любого из них. (c) Обратите внимание, что C _S работает параллельно с C ₃. Таким образом, общая емкость равна сумме C _S и C ₃.

Пример 2. Смесь последовательной и параллельной емкостей

Найдите общую емкость комбинации конденсаторов, показанной на рисунке 3. Предположим, что емкости на рисунке 3 известны с точностью до трех десятичных знаков ( C ₁ = 1.000 мкФ, C ₂ = 3.000 мкФ и C ₃ = 8.000 мкФ) и округлите ответ до трех десятичных знаков.