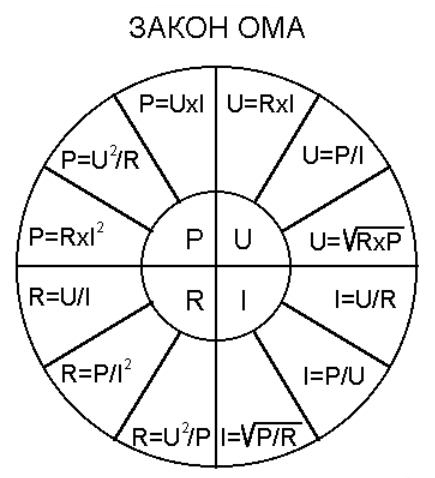
Как рассчитать мощность электрического тока?
Большинство бытовых приборов, подключаемых к сети, характеризуются таким параметром, как электрическая мощность устройства. С физической точки зрения мощность представляет собой количественное выражение совершаемой работы. Поэтому для оценки эффективности того или иного устройства вам необходимо знать нагрузку, которую он будет создавать в цепи. Далее мы рассмотрим особенности самого понятия и как найти мощность тока, обладая различными характеристиками самого устройства и электрической сети.
Понятие электрической мощности и способы ее расчета
С электротехнической точки зрения она представляет собой количественное выражение взаимодействия энергии с материалом проводников и элементами при протекании тока в электрической цепи. Из-за наличия электрического сопротивления во всех деталях, задействованных в проведения электротока, направленное движение заряженных частиц встречает препятствие на пути следования.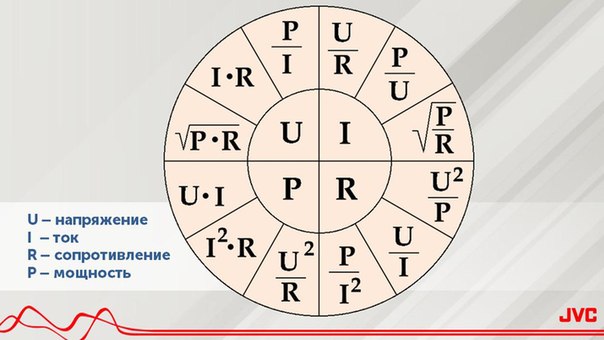
В зависимости от параметров источника тока и напряжения мощность также имеет отличительные характеристики. В электротехнике обозначается S, P и Q, единица измерения согласно международной системы СИ – ватты. Вычислить мощность можно через различные параметры приборов и электрических приборов. Рассмотрим каждый из них более детально.
Через напряжение и ток
Наиболее актуальный способ, чтобы рассчитать мощность в цепях постоянного тока – это использование данных о силе тока и приложенного напряжения. Для этого вам необходимо использовать формулу расчета: P = U*I
Где:
Этот вариант подходит только для активной нагрузки, где постоянный ток не обеспечивает взаимодействия с реактивной составляющей цепи.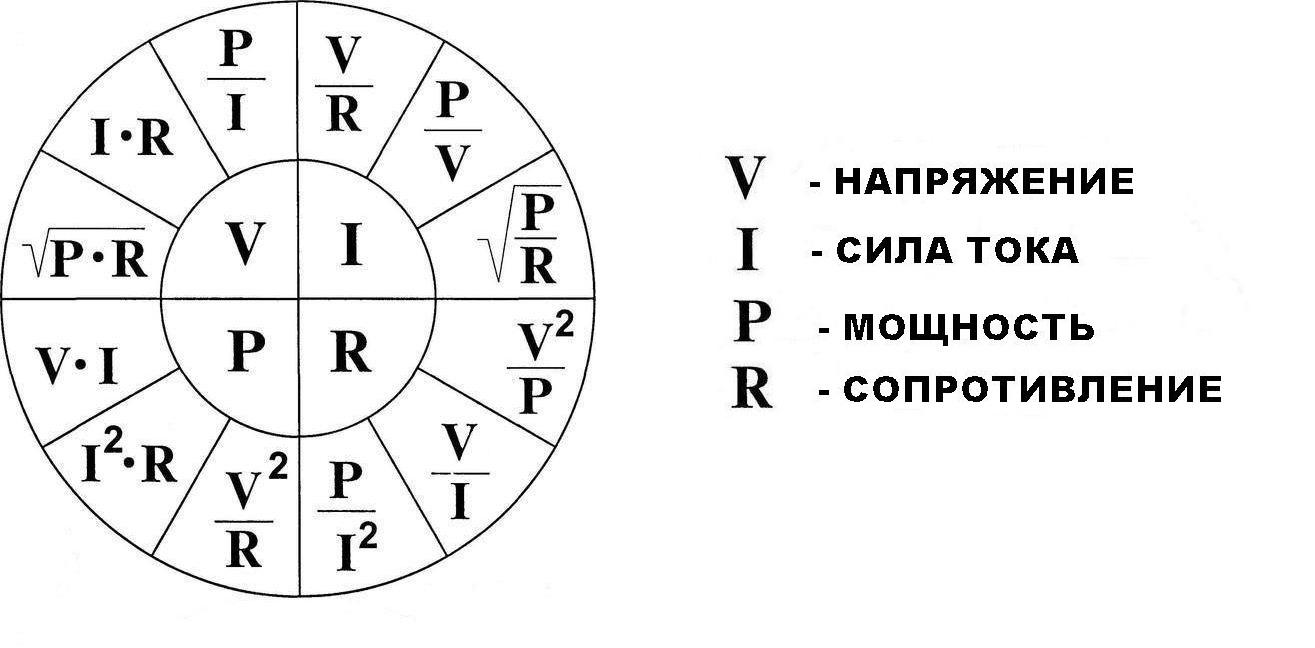
Через напряжение и сопротивление
Для большинства электрических устройств известен такой параметр, как внутреннее сопротивление, которое принимается за константу на весь период их эксплуатации. Так как бытовые или промышленные единицы подключаются к источнику с известным номиналом напряжения, определять мощность достаточно просто. Активная мощность находится из предыдущего соотношения и закона Ома, согласно которого ток на участке прямо пропорционален величине приложенного напряжения и имеет обратную пропорциональность к сопротивлению:
I = U/R
Если выражение для вычисления токовой нагрузки подставить в предыдущую формулу, то получится такое выражение для определения мощности:
P = U*(U/R)=U2/R
Где,
- P – величина нагрузки;
- U – приложенная разность потенциалов;
- R – сопротивление нагрузки.
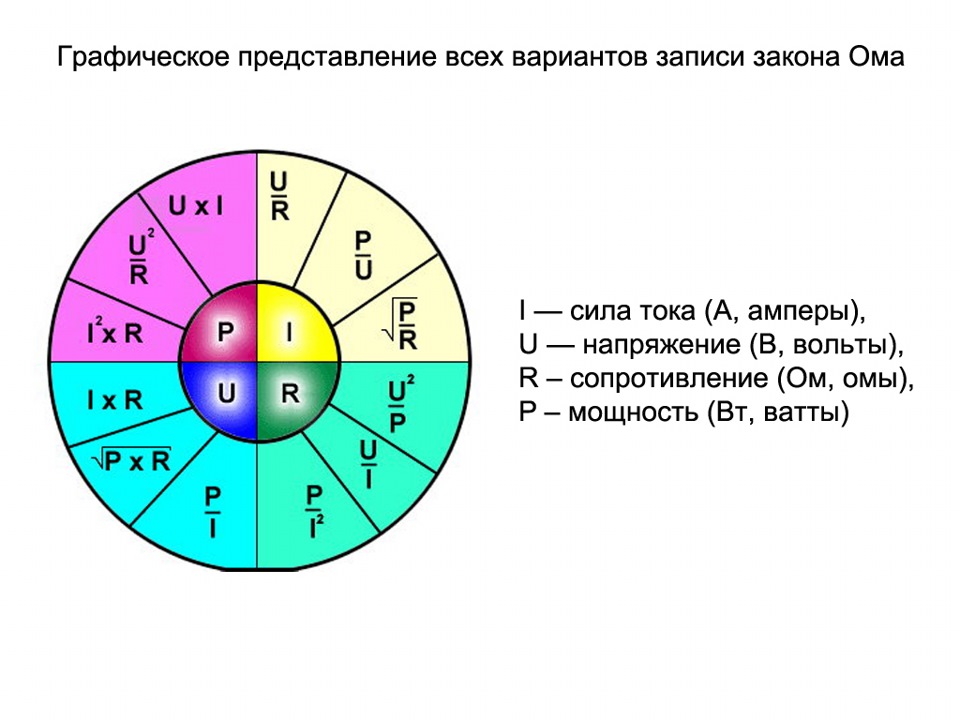
Через ток и сопротивление
Бывает ситуация, когда разность потенциалов, приложенная к электрическому прибору, неизвестна или требует трудоемких вычислений, что не всегда удобно. Особенно актуален данный вопрос, если несколько устройств подключены последовательно и вам неизвестно, каким образом потребляемая электроэнергия распределяется между ними. Подход в определении здесь ничем не отличается от предыдущего способа, за основу берется базовое утверждение, что электрическая нагрузка рассчитывается как P = U×I, с той разницей, что напряжение нам не известно.
Поэтому ее мы также выведем из закона Ома, согласно которого нам известно, что падение напряжения на каком-либо отрезке линии или электроустановки прямо пропорционально току, протекающему по этому участку и сопротивлению отрезка цепи:
U=I*R
после того как выражение подставить в формулу мощности, получим:
P = (I*R)*I =I2*R
Как видите, мощность будет равна квадрату силы тока умноженной на сопротивление.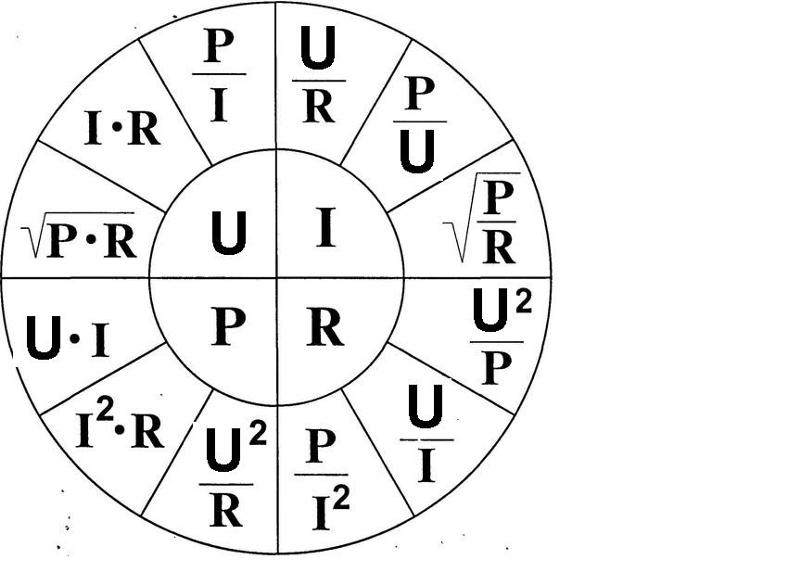
Полная мощность в цепи переменного тока
Сети переменного тока кардинально отличаются от постоянного тем, что изменение электрических величин, приводит к появлению не только активной, но и реактивной составляющей. В итоге суммарная мощность будет также состоять активной и реактивной энергии:
Где,
- S – полная мощность
- P – активная составляющая – возникает при взаимодействии электротока с активным сопротивлением;
- Q – реактивная составляющая – возникает при взаимодействии электротока с реактивным сопротивлением.
Также составляющие вычисляются через тригонометрические функции, так:
P = U*I*cosφ
Q = U*I*sinφ
что активно используется в расчете электрических машин.
Рис. 1. Треугольник мощностейПример расчета полной мощности для электродвигателя
Отдельный интерес представляет собой нагрузка, подключенная к трехфазной сети, так как электрические величины, протекающие в ней, напрямую зависят от номинальной нагрузки каждой из фаз. Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Но для наглядности примера мы не будем рассматривать, как найти мощность несимметричного прибора, так как это довольно сложная задача, а приведем пример расчета трехфазного двигателя.
Особенность питания и асинхронной и синхронной электрической машины заключается в том, что на обмотки может подаваться и фазное и линейное напряжение. Тот или иной вариант, как правило, обуславливается способом соединения обмоток электродвигателя. Тогда мощность будет вычисляться по формуле:
S = 3*Uф*Iф
В случае выполнения расчетов с линейным напряжением, чтобы найти мощность формула примет вид:
Активная и реактивная мощности будут вычисляться по аналогии с сетями переменного тока, как было рассмотрено ранее.
Теперь рассмотрим вычисления на примере конкретной электрической машины асинхронного типа. Следует отметить, что официальная производительность, указываемая в паспортных данных электродвигателя – это полезная мощность, которую двигатель может выдать при совершении оборотов вала. Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Однако полезная кардинально отличается от полной, которую можно вычислить за счет коэффициента мощности.
Как видите, для вычислений с шильда мы возьмем следующую информацию об электродвигателе:
- полезная производительность – 3 кВт, а в переводе на систему измерения – 3000 Вт;
- коэффициент полезного действия – 80%, а в пересчете для вычислений будем пользоваться показателем 0,8;
- тригонометрическая функция соотношения активных и реактивных составляющих – 0,74%;
- напряжение, при соединении обмоток треугольником составит 220 В;
- сила тока при том же способе соединения – 13,3 А.
С таким перечнем характеристик можно воспользоваться несколькими способами:
S = 1,732*220*13,3 = 5067 Вт
Чтобы найти искомую величину, сначала определяем активную составляющую:
P = Pполезная / КПД = 3000/0.8 = 3750 Вт
Далее полную по способу деления активной на коэффициент cos φ:
S = P/cos φ = 3750/0. 74 = 5067 Вт
74 = 5067 Вт
Как видите, и в первом, и во втором случае искомая величина получилась одинакового значения.
Примеры задач
Для примера рассмотрим вычисление на участках электрической цепи с последовательным и параллельным соединением элементов. Первый вариант предусматривает ситуацию, когда все детали соединяются друг за другом от одного полюса источника питания до другого.
Рис. 3. Последовательная расчетная цепьКак видите на рисунке, в качестве источника мы используем батарейку с номинальным напряжением 9 В и три резистора по 10, 20 и 30 Ом соответственно. Так как номинальный ток нам не известен, расчет произведем через напряжение и сопротивление:
P = U2/R = 81 / (10+20+30) = 1.35 Вт
Для параллельной схемы подключения возьмем в качестве примера участок цепи с двумя резисторами и одним источником тока:
Как видите, для удобства расчетов нам нужно привести параллельно подключенные резисторы к схеме замещения, из чего получится:
Rобщ = (R1*R2) / (R1+R2) = (10*15) / (10+15) = 6 Ом
Тогда искомый номинал нагрузки мы можем узнать через значение тока и сопротивления:
P = I2*R = 25*6 = 150 Вт
Видео по теме
как вычислить мощность тока формулой, как рассчитать ампераж
Чтобы электропроводка и все электрическое оборудование, которое имеется в доме, работало исправно и правильно, необходимо правильно сделать вычисление мощности по току и электронапряжению, поскольку при неправильно подобранных показателях может возникнуть короткое замыкание или возгорание. Как сделать расчёт потребляемой мощности по току и напряжению, как вычисляется сила тока, формула через мощность и напряжение и другое, далее.
Как узнать силу тока, зная мощность и напряжения
Чтобы ответить на вопрос, как определить ток, необходимо поделить электронапряжение на общее число ватт. При этом сделать все необходимые вычисления можно самостоятельно, а можно прибегнуть к специальному онлайн-калькулятору.
Узнать потребление электроэнергии по токовой силе резистора можно умножением первой на сопротивление, выражаемое в Омах. В итоге, получится значение, представленное в вольтах, перемноженных на ом. Получится ампер.
Обратите внимание! Если нет сопротивления, нужно поделить ваттный показатель на токовую энергию, то есть следует поделить ватты на амперы и получится значение электроэнергии в вольтах. Понять мощностное показание через величину электричества с электронапряжением, можно умножив соответствующие показания с устройства.
Формулы для расчета тока в трехфазной сети
Подсчитать токовую энергию в трехфазной сети сложно, поскольку вместе одной фазы есть три. К тому же, сложность заключается в использовании нескольких схем соединения. Трудность состоит в симметрии или ее отсутствии во время распределения нагрузки по фазам.
Для определения силы тока в трехфазной сети, нужно общее число ватт поделить на показатель 1,73, перемноженный на напряжение и косинус мощностного коэффициента, который отражает активную и реактивную составляющую сопротивления нагрузки. Что касается однофазной сети, то из выражения для подсчета убирается показатель 1,73. Остается формула I = P/(U*cos φ).
Формула подсчета электротока в трехфазной сетиКак рассчитать ампераж
Ампераж является значением электротока, которое выражена в амперах. Рассчитать ампераж можно так: I=P/U.
Подсчет амперажаРасчет потребляемой мощности
Электромощность является величиной, которая отвечает за факт скорости изменения или передачи электрической энергии. Есть полная и активная мощностная нагрузка, а также активная и реактивная. Полная вычисляется так: S = √ (P2 + Q2), где P является активной частью, а Q реактивной. Для нахождения потребляемого мощностного показателя необходимо знать число электротока, которое потребляется нагрузкой, а также питательное напряжение, которое выдается при помощи источника.
Что касается бытового определения потребляемой электрической энергии, необходимо вычислить общее количество ватт питания электрических приборов и паспортные данные номинальной силы электротока котла. Как правило, все электрические приборы работают с переменным током и напряжением в 220 вольт. Для вычисления тока проще всего воспользоваться амперметром. Зная первый и второй параметры, реально узнать величину потребляемой энергии.
Стоит указать, что измерить мощность через напряжение или сделать расчет мощности по сопротивлению и напряжению возможно не только формулой, но и прибором. Для этого можно воспользоваться мультиметром с токоизмерительными клещами или специализированным измерителем — ваттметром.
Обратите внимание! Оба работают по одному и тому же принципу, указанному в руководстве по их эксплуатации.
Подсчет потребляемой мощностиМощность, ток и напряжение — три составляющие расчета проводки в доме. Узнать все необходимые параметры в любой сети просто при помощи формул, представленных выше. От этих значений будет зависеть исправность работы всей домашней электрики и безопасность ее владельца.
От этих значений будет зависеть исправность работы всей домашней электрики и безопасность ее владельца.
| Содержание: Включение потребителей в бытовые или промышленные электрические сети с использованием кабеля меньшей мощности, чем это необходимо, может вызвать серьезные негативные последствия. В первую очередь это приведет к постоянному срабатыванию автоматических выключателей или перегоранию плавких предохранителей. При отсутствии защиты питающий провод или кабель может перегореть. В результате перегрева изоляция оплавляется, а между проводами возникает короткое замыкание. Чтобы избежать подобных ситуаций, необходимо заранее выполнить расчет тока по мощности и напряжению, в зависимости от имеющейся однофазной или трехфазной электрической сети. Для чего нужен расчет токаРасчет величины тока по мощности и напряжению выполняется еще на стадии проектирования электрических сетей объекта. Полученные данные позволяют правильно выбрать питающий кабель, к которому будут подключаться потребители. Важно Для расчетов силы тока используется значение напряжения сети и полной нагрузки электрических приборов. В соответствии с величиной силы тока выбирается сечение жил кабелей и проводов. Если все потребители в доме или квартире известны заранее, то выполнение расчетов не представляет особой сложности. В дальнейшем проведение электромонтажных работ значительно упрощается. Таким же образом проводятся расчеты для кабелей, питающих промышленное оборудование, преимущественно электрические двигатели и другие механизмы. Расчет тока для однофазной сетиИзмерение силы тока производится в амперах. Для расчета мощности и напряжения используется формула I = P/U, в которой P является мощностью или полной электрической нагрузкой, измеряемой в ваттах. Взаимосвязь силы тока и напряжения хорошо просматривается в таблице:
Таким образом, взаимосвязь мощности и силы тока дает возможность выполнить предварительные расчеты нагрузок в однофазной сети.
Расчет тока для трехфазной сетиВ случае использования трехфазного электроснабжения вычисление силы тока производится по формуле: I = P/1,73U, в которой P означает потребляемую мощность, а U – напряжение в трехфазной сети. Так как напряжение в этом случае составляет 380 вольт, то вся формула будет иметь вид: I = P/657,4. Точно так же, как и в однофазной сети, диаметр и сечение проводников можно определить с помощью таблицы, отражающей зависимости этих параметров от различных нагрузок.
В некоторых случаях расчет тока по напряжению и мощности следует проводить с учетом полной реактивной мощности, присутствующей в электродвигателях, сварочном и другом оборудовании. Как рассчитать мощность тока |
Зависимость мощности от силы тока, формула мощности, физический смысл
Первое упоминание об электричестве встречается в опытах древнегреческого философа Фалеса. Именно он первым обнаружил, что предметы при трении притягиваются. Одноименный термин был введен в начале 17-го века английским физиком Гилбертом, после опытов, проведенных с магнитами. Отцом же науки об электричестве считается французский ученый Кулон – именно после открытия закона, получившего его имя, электротехника начала свою победную поступь, которая продолжается до сих пор. Этот закон утверждает, что два точечных заряда в безвоздушной среде взаимодействуют с силой, прямо пропорциональной их модулям и обратно – расстоянию между ними, возведенному в квадрат.
Выясним, что же представляет собой понятие электричество?
Если коротко, то это – направленное движение потока заряженных частиц. Тела, через которые они проходят, называются проводниками. Каждый проводник имеет определенное сопротивление электрическому току, которое раз
И, перед тем, как перейти к основным законам, несколько слов о заряженных частицах: они бывают, условно говоря, положительными и отрицательными. Одноименные заряды отталкиваются, а разноименные – притягиваются.
Одноименные заряды отталкиваются, а разноименные – притягиваются.
А теперь, перейдем к главному.
Основа-основ науки об электричестве – закон Ома.
Эксперимент, который провел этот немецкий физик, привел его к следующему убеждению: сила тока I, проходящего через металлический проводник, пропорциональна напряжению на его концах, или I = U/R
Здесь напряжением называется разность, образно говоря, «давлений», созданных двумя точками электрической цепи. Измеряют его в вольтах. Электрический ток представляет собой число электронов, которые пропускает участок электрической цепи и измеряется в амперах. Сопротивлением считается свойство цепи помешать этому движению. В честь упомянутого физика, его измеряют в омах. Иначе говоря, проводник, через который проходит ток в 1 ампер при напряжении в 1 вольт, обладает сопротивлением в 1 ом.
Вся остальная электротехника «пляшет» от этого.
О мощности электрического тока
В физике мощностью считают скорость выполнения работы. Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Неважно, какой. Чем эта операция проводится быстрее, тем большей считается мощность того, кто ее исполняет, будь то человек, механическое устройство или что-то еще.
Так же и в случае с электрическим током: ее мощность представляет собой отношение работы, произведенной движущимися электрическими зарядами к промежутку времени, которое для этого понадобилось.
Проще говоря, для того, чтобы получить электрическую мощность в 1 ватт, когда источник тока имеет напряжение 1 вольт, необходимо пропустить через проводник ток в 1 ампер. Другими словами, мощность (P) можно посчитать, перемножив друг на друга электрическое напряжение и ток:
P = U*I.
Запомнив эту нехитрую формулу, на практике можно рассчитать мощность. Например, если известны значения тока и сопротивления, а о напряжении сведений нет, можем воспользоваться законом Ома, подставив в формулу вместо него I*R. Получится, что мощность равна квадрату электрического тока, помноженному на сопротивление.
Этот закон точно так же придет на помощь, если известны величины напряжения и сопротивления. В этом случае подставив вместо значения тока I = U/R, получим значение мощности, равное квадрату напряжения, поделенному на сопротивление.
Вот так – ничего сложного!
Закон Ома.
Закон Ома.Программа КИП и А
В программу «КИП и А», в разделе «Электрика» включен блок расчета закона Ома для постоянного и переменного тока. Сначала немного теории..
Для постоянного тока
Закон Ома определяет зависимость между током (I), напряжением (U) и сопротивлением (R) в участке электрической цепи. Наиболее популярна формулировка:
Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи, т.е.
| I = U / R | где | I – сила тока, измеряемая в Амперах, (A) |
| U – напряжение, измеряемое в Вольтах, (V) | ||
| R – сопротивление, измеряется в Омах, (Ω) |
Закон Ома, является основополагающим в электротехнике и электронике. Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, – “Не знаешь закон Ома, – сиди дома..”.
Без его понимания также не представляется работа подготовленного специалиста в области КИП и А. Когда-то была даже распространена такая поговорка, – “Не знаешь закон Ома, – сиди дома..”.
Помимо закона Ома, важнейшим является понятие электрической мощности, P:
Мощность постоянного тока (P) равна произведению силы тока (I) на напряжение (U), т.е.
| P = I × U | где | P – эл. мощность, измеряемая в Ваттах, (W) |
| I – сила тока, измеряемая в Амперах, (A) | ||
| U – напряжение, измеряемое в Вольтах, (V) |
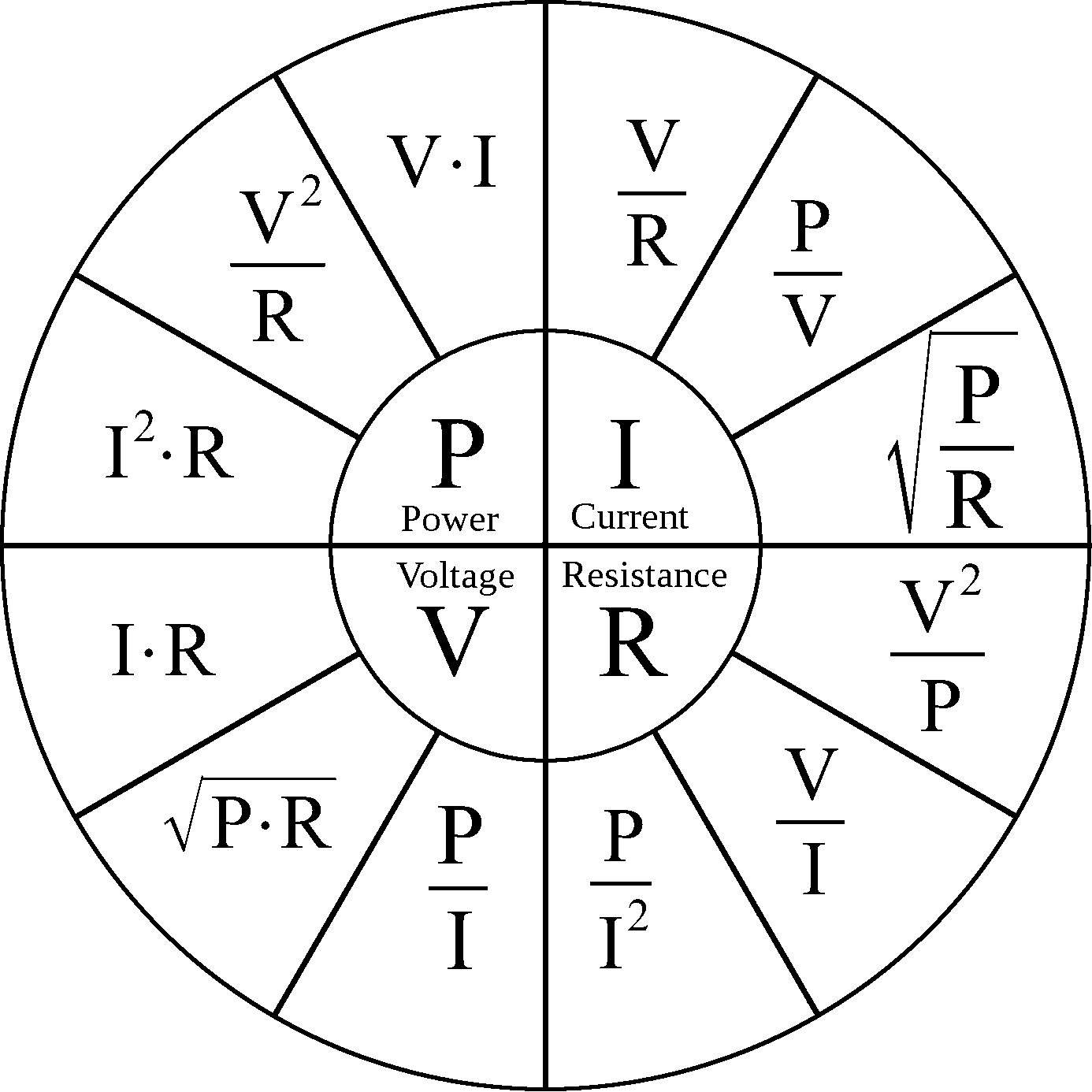
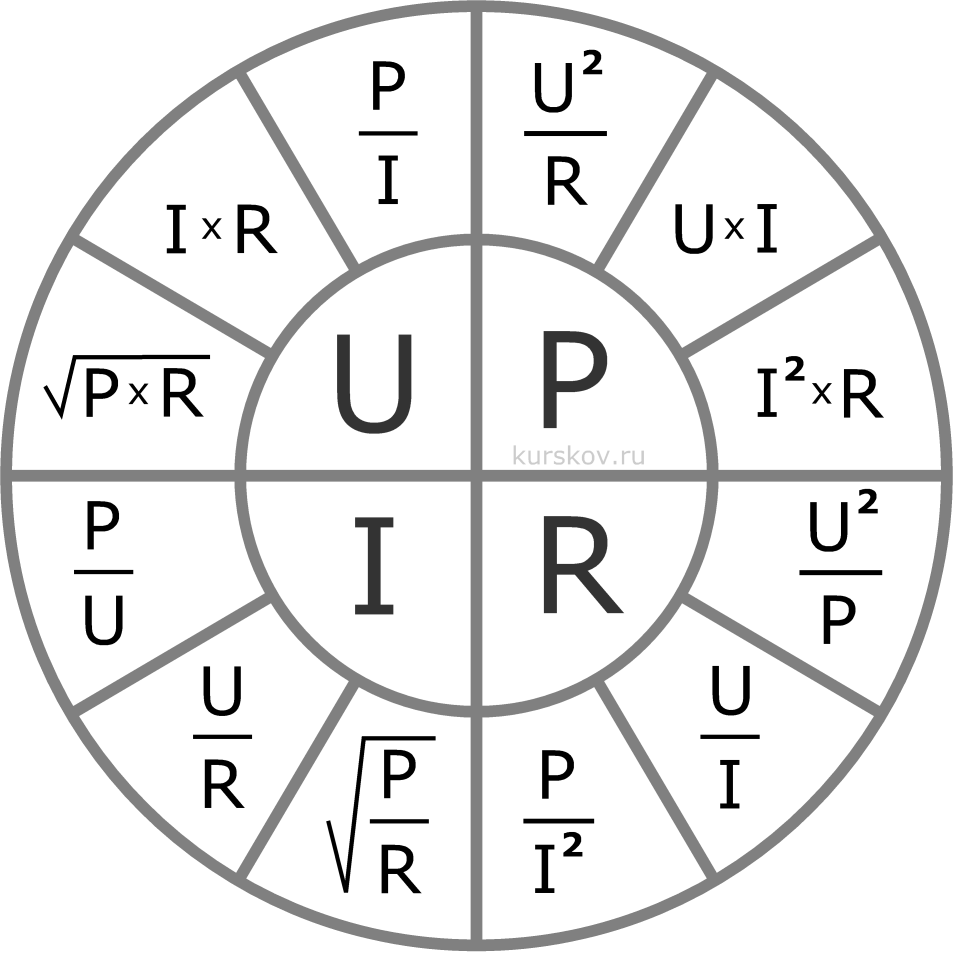
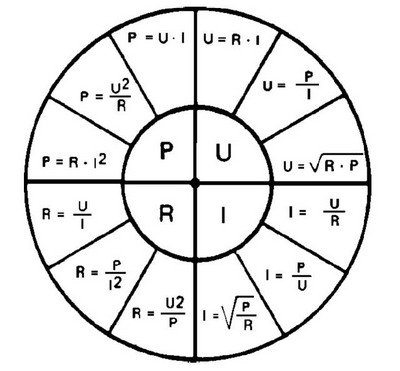
Комбинируя эти две формулы, выведем зависимость между силой тока, напряжением, сопротивлением и мощностью, и создадим таблицу:
| Сила тока, | I= | U/R | P/U | √(P/R) |
| Напряжение, | U= | I×R | P/I | √(P×R) |
| Сопротивление, | R= | U/I | P/I² | U²/P |
| Мощность, | P= | I×U | I²×R | U²/R |
Практический пример использования таблицы: Покупая в магазине утюг, мощностью 1 кВт (1 кВт = 1000 Вт), высчитываем на какой минимальный ток должна быть рассчитана розетка в которую предполагается включать данную покупку:
Несмотря на то, что утюг включается в сеть переменного тока, пренебрегаем его реактивным сопротивлением (см. ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
ниже), и используем упрощенную формулу для постоянного тока. Находим в таблице I = P / U. Получаем: 1000 кВт / 220 В (напряжение сети) = 4,5 Ампера. Это и есть минимальный ток, который должна выдерживать розетка, при подключении к ней нагрузки мощностью 1 кВт.
Наиболее распространенные множительные приставки:
- Сила тока, Амперы (A): 1 килоампер (1 kА) = 1000 А. 1 миллиампер (1 mA) = 0,001 A. 1 микроампер (1 µA) = 0,000001 A.
- Напряжение, Вольты (V): 1 киловольт (1kV) = 1000 V. 1 милливольт (1 mV) = 0,001 V. 1 микровольт (1 µV) = 0,000001 V.
- Сопротивление, Омы (Om): 1 мегаом (1 MOm) = 1000000 Om. 1 килоом (1 kOm) = 1000 Om.
- Мощность, Ватты (W): 1 мегаватт (1 MW) = 1000000 W. 1 киловатт (1 kW) = 1000 W. 1 милливатт (1 mW) = 0,001 W.
Для переменного тока
В цепи переменного тока закон Ома может иметь некоторые особенности, описанные ниже.
Импеданс, Z
В цепи переменного тока, сопротивление кроме активной (R), может иметь как емкостную (C), так и индуктивную (L) составляющие. В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
В этом случае вводится понятие электрического импеданса, Z (полного или комплексного сопротивления для синусоидального сигнала). Упрощенные схемы комплексного сопротивления приведены на рисунках ниже, слева для последовательного, справа для параллельного соединения индуктивной и емкостной составляющих.
Последовательное включение R, L, C
Параллельное включение R, L, C
Также, полное сопротивление, Z зависит не только от емкостной (C), индуктивной (L) и активной (R) составляющих, но и от частоты переменного тока.
| Импеданс, Полное сопротивление, Z | |
| При последовательном включении R, L, C | При параллельном включении R, L, C |
| Z=√(R2+(ωL-1/ωC)2) | Z=1/ √(1/R2+(1/ωL-ωC)2) |
| где, | |
ω = 2πγ – циклическая, угловая частота; γ – частота переменного тока.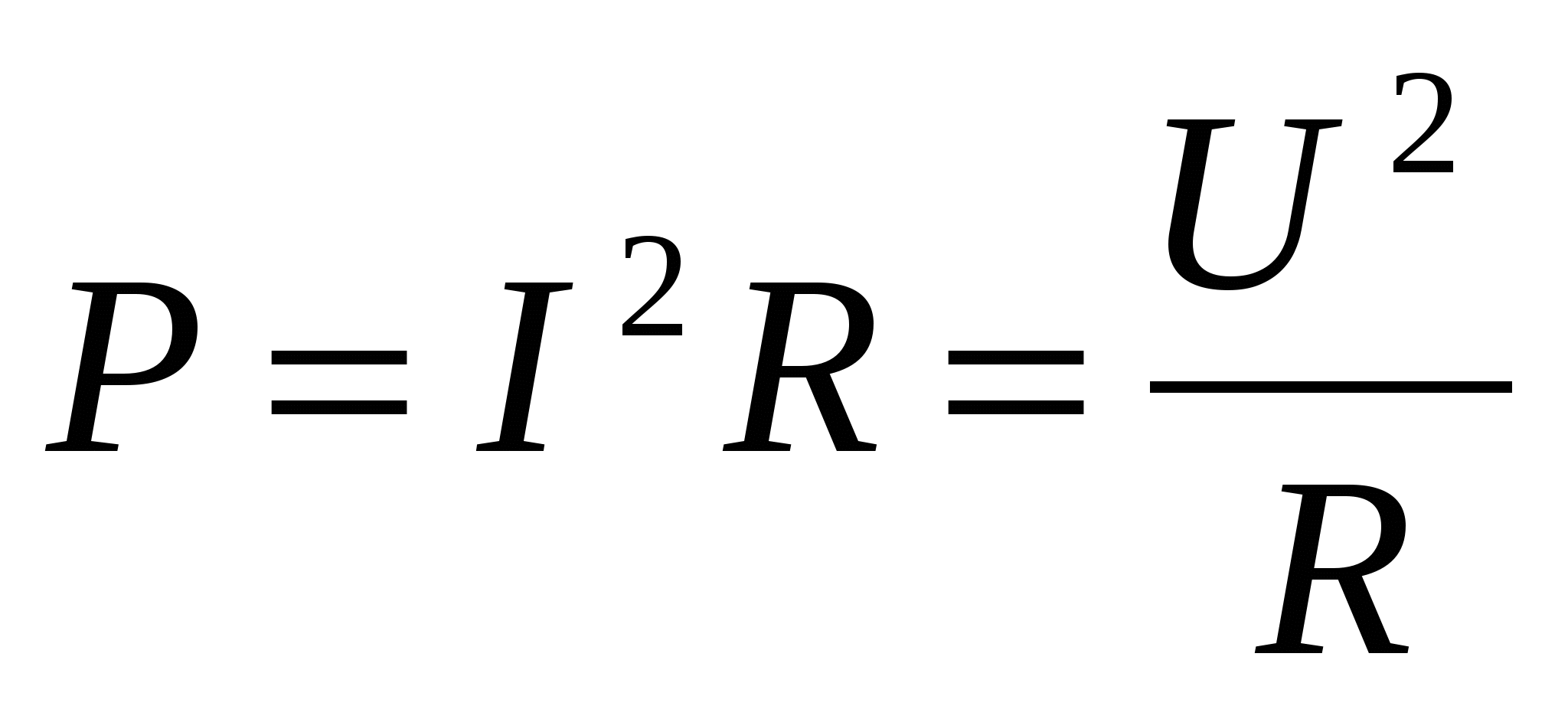 | |
Коэффициент мощности, Cos(φ)
Коэффициент мощности, в самом простом понимании, это отношение активной мощности (P) потребителя электрической энергии к полной (S) потребляемой мощности, т. е.
Cos(φ) = P / S
Он также показывает насколько сдвигается по фазе переменный ток, протекающий через нагрузку, относительно приложенного к ней напряжения.
Изменяется от 0 до 1. Если нагрузка не содержит реактивных составляющих (емкостной и индуктивной), то коэффициент мощности равен единице.
Чем ближе Cos(φ) к единице, тем меньше потерь энергии в электрической цепи.
Исходя из вышеперечисленных понятий импеданса Z и коэффициента мощности Cos(φ), характерных для переменного тока, выведем формулу закона Ома, коэффициента мощности и их производные для цепей переменного тока:
| I = U / Z | где | I – сила переменного тока, измеряемая в Амперах, (A) |
| U – напряжение переменного тока, измеряемое в Вольтах, (V) | ||
| Z – полное сопротивление (импеданс), измеряется в Омах, (Ω) |
Производные формулы:
| Сила тока, | I= | U/Z | P/(U×Cos(φ)) | √(P/Z) |
| Напряжение, | U= | I×Z | P/(I×Cos(φ)) | √(P×Z) |
| Полное сопротивление, импеданс | Z= | U/I | P/I² | U²/P |
| Мощность, | P= | I²×Z | I×U×Cos(φ) | U²/Z |
Программа «КИП и А» имеет в своем составе блок расчета закона Ома как для постоянного и переменного тока, так и для расчета импеданса и коэффициента мощности Cos(φ).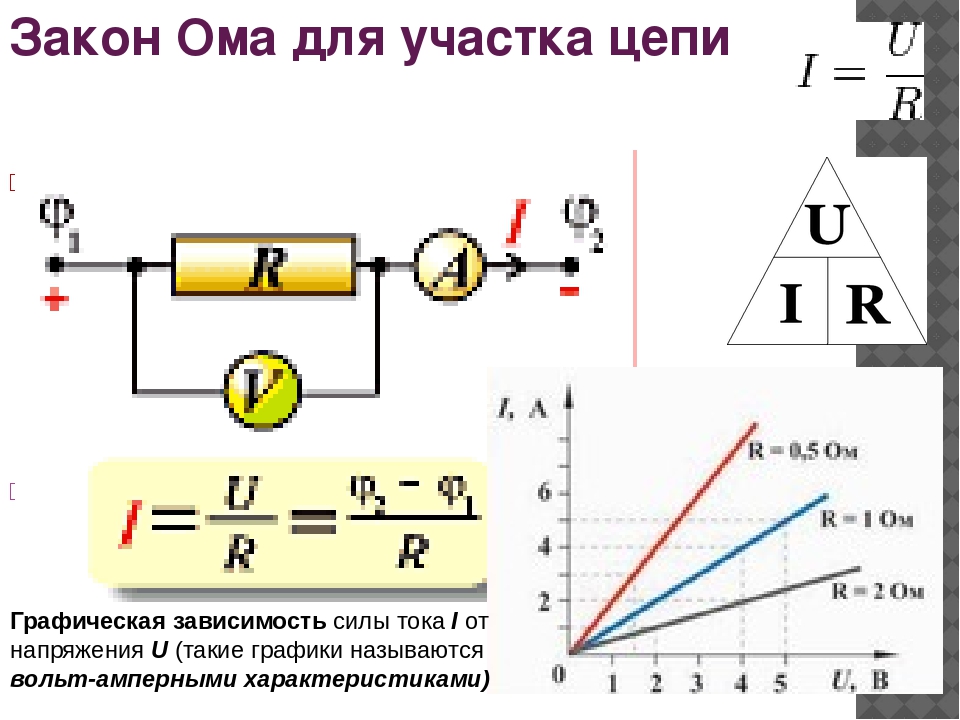 Скриншоты представлены на рисунках внизу:
Скриншоты представлены на рисунках внизу:
Закон Ома для постоянного тока
Закон Ома для переменного тока
Расчет полного сопротивления
Расчет коэффициента мощности Cos(φ)
Расчёт мощности по току и напряжению онлайн
Калькулятор расчёта мощности по току и напряжению
Данный калькулятор позволяет выполнить расчёт мощности по току и напряжению. Параметры необходимо вводить в базовых величинах, ток в амперах (А), напряжение в вольтах (В).
Формула расчёта мощности по току и напряжению
P = I*U ,
- P— мощность потребителя, Вт;
- I— cила тока, А;
- U— напряжение в сети, В;
Обращаем Ваше внимание, что приведённый выше онлайн калькулятор расчёта мощности, производит упрощённый расчёт мощности по току и напряжению, по упрощённой формуле. Онлайн расчёт данным способом позволяет, получить значения близкие к реальным.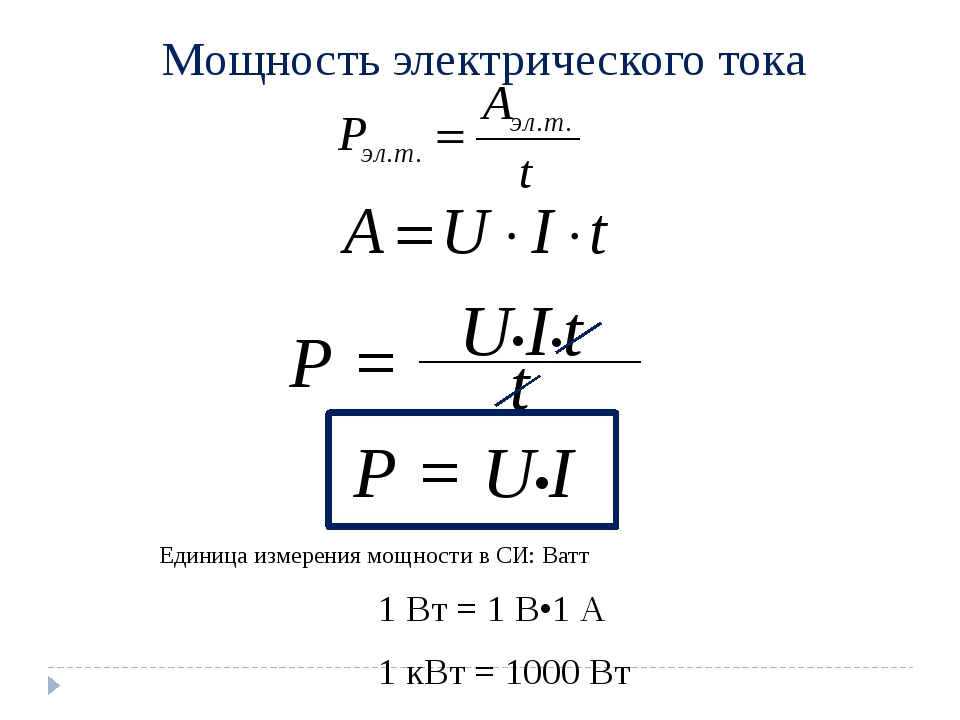
Рекомендуем!
Формула расчёта мощности по току и напряжению для однофазной сети:
Однако, существуют формулы и для более точного расчёта. Если Вы обладаете, всеми необходимыми техническими характеристиками сети и устройства, то более точный расчёт мощности для однофазной сети, Вы можете произвести по формуле:
P = I*U*cosφ ,
- P— мощность потребителя, Вт;
- I— cила тока, А;
- U— напряжение в сети, В;
- cosφ -безразмерная величина, которая равна отношению активной мощности к полной (коэффициент мощности). По умолчанию значение cosφ равно 0,95 для бытовых электросетей и от 0,95 до 0,65 для промышленных.
Формула расчёта мощности по току и напряжению для трёхфазной сети:
P = 1,73*I*U*cosφ ,
- P— мощность потребителя, Вт;
- I— cила тока, А;
- U— напряжение в сети, В;
- cosφ -безразмерная величина, которая равна отношению активной мощности к полной (коэффициент мощности).

По умолчанию значение cosφ равно 0,95 для бытовых электросетей и от 0,95 до 0,65 для промышленных.
Примерные значения cosφ для некоторых типов оборудования:
- лампы накаливания — 1;
- обогреватели, электропечи, электроплиты и т.п. — 0,95;
- электродвигатели — 0,85 ..0,87;
- дрели, отрезные машинки и т.п. — 0,85 ..0,9;
- электродвигатели компрессоров, холодильников, стиральных машин и т.п. — 0,7…0,85
- компьютеры, телевизоры, СВЧ печи, кондиционеры, вентиляторы, энергосберегающие лампы — 0,5 ..0,8
Более точные значения cosφ зачастую можно найти в паспорте прибора или на бирке.
Наши ресурсы в социальных сетях, присоединяйтесь:
[ratings]
Понравилась статья? Поделиться с друзьями:
Расчеты напряжения, силы, сопротивления, нагрузки электрического тока
Современная структура общества такова, что на бытовом и промышленном уровне повсеместно используется электроэнергия. Генераторные установки, вырабатывающие электроэнергию, преобразующие подстанции работают для того, чтобы передать ее потребителям на бытовые электрические приборы и промышленные электроустановки.
Генераторные установки, вырабатывающие электроэнергию, преобразующие подстанции работают для того, чтобы передать ее потребителям на бытовые электрические приборы и промышленные электроустановки.
Общая схема передачи электроэнергии потребителям с учетом мощностей
Что такое мощность электроэнергии
В электросетях, по которым передается энергия, существует ряд основных параметров, которые обязательно учитываются при проектировании и эксплуатации электроустановок.
Одним из таких показателей является электрическая мощность, под этим подразумевается способность электроустановки генерировать, передавать или преобразовывать определенную величину электроэнергии за определенный период времени. Преобразованием считается процесс изменения электрической энергии в тепло, механические движения или другой вид энергии. Чтобы сделать расчет мощности, надо знать, как минимум, величины тока, напряжения и ряда других параметров.
Расчет тока и напряжения, мощности иногда не делают, а измеряют параметры на месте. Но такая возможность не всегда предоставляется. Надо знать, как рассчитать мощность, когда цепь обесточена, при проектировании электроустановок, уметь пользоваться таблицей законов Ома и рассчитать силу тока по известным значениям параметров. Рассчитывать мощность нагрузки и ток нагрузки приходится для того, чтобы правильно выбрать сечение проводов в цепи, величину тока срабатывания для защитных автоматов и других нужд.
Но такая возможность не всегда предоставляется. Надо знать, как рассчитать мощность, когда цепь обесточена, при проектировании электроустановок, уметь пользоваться таблицей законов Ома и рассчитать силу тока по известным значениям параметров. Рассчитывать мощность нагрузки и ток нагрузки приходится для того, чтобы правильно выбрать сечение проводов в цепи, величину тока срабатывания для защитных автоматов и других нужд.
Законы Ома наглядно показывают, как посчитать ток по мощности и напряжению
Физический смысл электрической мощности в цепях переменного и постоянного тока одинаковый, но от условий нагрузки в цепи мощность может выражаться разными соотношениями. Для стандартизации закономерности явлений вводится понятие мгновенное значение, что указывает на зависимость скорости преобразований электроэнергии от фактора времени.
Электрическая мощность – это величина, выражающая скорость преобразования энергии электричества в другой вид энергии, обозначается буквой «Р».
Мгновенное значение электрической мощности
Определение – электрическая мощность тесно связана с другими параметрами цепи, током и напряжением, при изменении величины одного из них изменяются другие. Поэтому показания мощности фиксируются в короткий промежуток времени – ∆t.
Поэтому показания мощности фиксируются в короткий промежуток времени – ∆t.
Напряжение в данном случае обозначают буквой «U» – это выражает разность потенциалов зарядов, перемещенных электрическим полем из одной точки в другую за промежуток времени ∆t.
Сила тока обозначается буквой «I» – это поток, переносимый магнитным полем зарядов, другими словами заряд, перенесенный во временной интервал ∆t.
Исходя из этих определений, просматривается пропорциональная зависимость между этими параметрами:
Р = UxI.
При расчетах можно учитывать зависимость мощности от сопротивления нагрузки «R». По законам Ома для участка цепи с постоянным током мощность выражается как:
Р = I2xR или P = U2|R.
Если поставить в схему питания амперметр и вольтметр, то не придется думать, как вычислить силу тока.
Обратите внимание! Амперметр ставится последовательно в цепь по отношению к сопротивлению нагрузки, а вольтметр – параллельно.
В качестве источника питания используется аккумулятор, как нагрузка установлен прожектор. В данном случае не делается расчет силы тока, параллельно нагрузке подключен вольтметр, для измерения напряжения в Вольтах. Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.
Для участков цепи с переменным током формулы расчетов сложнее – необходимо учитывать характер нагрузки.
Расчеты мощности для электроцепей переменного тока
Переменный ток и напряжение имеют синусоидальный вид, при различных нагрузках происходит смещение фазы между ними на определенный угол. По этой причине направление тока иногда может быть противоположным, от нагрузки к источнику питания. Это бывает в электродвигателях, когда обмотка начинает генерировать энергию, это негативно сказывается на эффективности работы оборудования, снижается мощность. При большом количестве потребителей в электросети характер нагрузки имеет смешанный вид, в идеале выделяют три типа нагрузки:
- Активная нагрузка, ее представляют такие электроприборы, как лампы накаливания, нагревательные тэны, спиральные электроплиты;
- Емкостная нагрузка – это конденсаторы в оборудовании различного назначения;
- Индуктивная нагрузка представлена катушками в электродвигателях, обмотках электромагнитов, дросселями и трансформаторами, другими приборами, где ток протекает через обмотки.
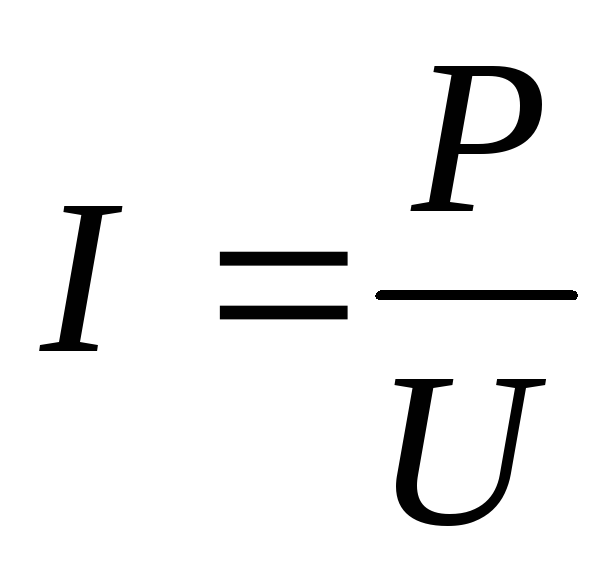
Емкостные и индуктивные виды выделяют как реактивную энергию в электросетях. Зная вид нагрузки, расчет потребляемой мощности делается точнее.
Расчет мощности в цепи с активной нагрузкой
Это классический случай в однофазной сети 220 В, в качестве нагрузки можно использовать обычные резисторы. Мощность рассчитывается как произведение действующих значений тока и напряжения, умноженное на соsϕ. В данном случае ϕ – угол смещения между фазами тока и напряжения.
Р = UI cos ϕ
График зависимости мощности по току и напряжению при активной нагрузке
Из графика можно узнать, что колебания тока и напряжения одинаковы по частоте и фазе, мощность всегда положительная с частотой в два раза больше.
Активная электрическая мощность характеризует процесс преобразования в сетях с переменным током энергии в тепло, механические движения, излучение света, в любой вид другой энергии. Измеряется активная нагрузка в Вт, кВт.
Расчет реактивной мощности
Как найти мощность в цепях с индуктивной и емкостной нагрузками? Это делается аналогичным образом. Расчет потребляемой мощности, как и в случае с активной нагрузкой, означает, что действующие напряжение и ток перемножаются, и результат умножается на sin ϕ. Где ϕ – угол сдвига фаз тока и напряжения.
Расчет потребляемой мощности, как и в случае с активной нагрузкой, означает, что действующие напряжение и ток перемножаются, и результат умножается на sin ϕ. Где ϕ – угол сдвига фаз тока и напряжения.
Р = UI sin ϕ
Диаграмма, показывающая взаимосвязь параметров цепи при индуктивной нагрузке
График показывает, что мощность может принимать отрицательные значения, в этот момент энергия отдается в сторону источника питания, фактически она бесполезна и расходуется на нагрев.
Реактивная составляющая энергии характеризует работу нагрузки в виде электронного оборудования, электротехнических схем, моторов с наличием емкостной и индуктивной нагрузки. Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q».
Треугольник, отображающий отношение мощностей в сети
Зависимость мощности в цепи переменного тока от реактивной и активной составляющих с учетом угла сдвига фаз хорошо отображается на диаграмме, которую называют треугольником мощностей.
Формула расчета полной мощности обозначается буквой «S»
В этом случае учитывается полный импеданс рассчитываемой мощности электрического тока (комплексное сопротивление нагрузки). Тем, кому вычислением заниматься сложно даже на калькуляторе, можно воспользоваться онлайн калькуляторами на сайте https://www.fxyz.ru с вычислением мощности в цепях с различной нагрузкой. Вычисляется все мгновенно, достаточно заполнить таблицу с исходными параметрами. Когда такой калькулятор под рукой, я вычислю быстро нужные мне параметры.
Видео
Оцените статью:Расчет электроэнергии | Закон Ома
Узнайте формулу мощности
Мы видели формулу для определения мощности в электрической цепи: умножая напряжение в «вольтах» на ток в «амперах», мы получаем ответ в «ваттах». Давайте применим это к примеру схемы:
Давайте применим это к примеру схемы:
Как использовать закон Ома для определения силы тока
В приведенной выше схеме мы знаем, что у нас напряжение батареи 18 В и сопротивление лампы 3 Ом.Используя закон Ома для определения силы тока, получаем:
Теперь, когда мы знаем ток, мы можем взять это значение и умножить его на напряжение, чтобы определить мощность:
Это говорит нам о том, что лампа рассеивает (выделяет) 108 Вт мощности, скорее всего, в виде света и тепла.
Повышение напряжения батареи
Давайте попробуем взять ту же схему и увеличить напряжение батареи, чтобы увидеть, что произойдет.Интуиция подсказывает нам, что ток в цепи будет увеличиваться с увеличением напряжения, а сопротивление лампы останется прежним. Так же увеличится и мощность:
Теперь напряжение батареи 36 вольт вместо 18 вольт. Лампа по-прежнему обеспечивает электрическое сопротивление 3 Ом для прохождения тока. Текущий сейчас:
Текущий сейчас:
Это понятно: если I = E / R, и мы удваиваем E, а R остается неизменным, ток должен удвоиться.Действительно, есть: теперь у нас 12 ампер тока вместо 6. А что насчет мощности?
Как повышение напряжения батареи влияет на мощность?
Обратите внимание, что мощность увеличилась, как мы могли подозревать, но она увеличилась немного больше, чем ток. Почему это? Поскольку мощность является функцией напряжения, умноженного на ток, а напряжение и ток удвоены по сравнению с их предыдущими значениями, мощность увеличится в 2 x 2 или 4 раза.
Вы можете проверить это, разделив 432 Вт на 108 Вт и убедившись, что соотношение между ними действительно равно 4. Снова используя алгебру, чтобы манипулировать формулой, мы можем взять нашу исходную формулу мощности и изменить ее для приложений, где мы не знаем обоих напряжение и ток: Если мы знаем только напряжение (E) и сопротивление (R):
Если мы знаем только ток (I) и сопротивление (R):
Закон Джоуля против.
 Закон Ома
Закон ОмаИсторическая справка: именно Джеймс Прескотт Джоуль, а не Георг Саймон Ом первым открыл математическую связь между рассеиваемой мощностью и током через сопротивление. Это открытие, опубликованное в 1841 году, имело форму последнего уравнения (P = I 2 R) и по праву известно как закон Джоуля.
Однако эти уравнения мощности так часто ассоциируются с уравнениями закона Ома, связывающими напряжение, ток и сопротивление (E = IR; I = E / R; и R = E / I), что их часто приписывают Ому.
ОБЗОР:
- Мощность измеряется в Вт , обозначается буквой «W».
- Закон Джоуля: P = I 2 R; P = IE; P = E 2 / R
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Попробуйте наш калькулятор закона Ома в разделе «Инструменты».
Закон Ома
Закон Ома показывает линейную зависимость между напряжением и током в электрической цепи.
Падение напряжения и сопротивление резистора определяют протекание постоянного тока через резистор.
Используя аналогию с потоком воды, мы можем представить электрический ток как ток воды через трубу, а резистор как тонкую трубу, которая ограничивает расход воды, напряжение как разница высот воды, которая обеспечивает течение воды.
Формула закона Ома
Ток I резистора в амперах (A) равен току резистора напряжение V в вольтах (В), деленное на сопротивление R в омах (Ом):
В – падение напряжения на резисторе, измеренное в вольтах (В).В некоторых случаях в законе Ома для обозначения напряжения используется буква E . E обозначает электродвижущую силу.
I – электрический ток, протекающий через резистор, измеренный в амперах (A)
R – сопротивление резистора, измеренное в Ом (Ом)
Расчет напряжения
Зная ток и сопротивление, мы можем рассчитать напряжение.
Напряжение V в вольтах (В) равно току I в амперах (А), умноженному на сопротивление R в омах (Ом):
Расчет сопротивления
Зная напряжение и ток, мы можем рассчитать сопротивление.
Сопротивление R в омах (Ом) равно напряжению V в вольтах (В), деленному на ток I в амперах (A):
Поскольку ток задается значениями напряжения и сопротивления, формула закона Ома может показать, что:
- Если увеличивать напряжение, ток увеличится.
- Если мы увеличим сопротивление, ток уменьшится.
Пример # 1
Найдите ток в электрической цепи с сопротивлением 50 Ом и напряжением питания 5 Вольт.
Решение:
В = 5 В
R = 50 Ом
I = В / R = 5 В / 50 Ом = 0,1 А = 100 мА
Пример # 2
Найдите сопротивление электрической цепи, имеющей напряжение питания 10 В и ток 5 мА.
Решение:
В = 10 В
I = 5 мА = 0,005 А
R = В / I = 10 В / 0,005 A = 2000 Ом = 2 кОм
Закон Ома для цепи переменного тока
Ток нагрузки I в амперах (A) равен напряжению нагрузки V Z = V в вольтах (В), деленному на полное сопротивление Z в омах (Ω):
В – падение напряжения на нагрузке, измеренное в вольтах (В)
I – электрический ток, измеренный в амперах (A)
Z – полное сопротивление нагрузки, измеренное в Ом (Ом)
Пример # 3
Найдите ток в цепи переменного тока, имеющей напряжение питания 110 В ± 70 ° и нагрузку 0. 5кОм∟20 °.
5кОм∟20 °.
Решение:
В = 110 В∟70 °
Z = 0,5 кОм∟20 ° = 500 Ом∟20 °
I = В / Z = 110 В 70 ° / 500 Ом 20 ° = (110 В / 500 Ом) ∟ (70 ° -20 °) = 0,22 А 50 °
Калькулятор закона Ома (краткая форма)
Калькулятор законаОма: вычисляет соотношение между напряжением, током и сопротивлением.
Введите 2 значений, чтобы получить третье значение, и нажмите кнопку Рассчитать :
Калькулятор закона Ома II ►
См. Также
ЗаконОма | Основы резистора
Что такое закон Ома?
ЗаконОма гласит, что электрический ток через проводник пропорционален разности потенциалов на нем.Кроме того, электрическое сопротивление проводника постоянно. Это приводит к математическому уравнению:
где I – ток в амперах, V – напряжение в вольтах, R – сопротивление в омах. Для иллюстрации: резистор сопротивлением 1 Ом, на который действует ток 1 А, имеет разность напряжений на выводах 1 В. Уравнение названо в честь Георга Ома. В 1827 году он опубликовал свои выводы, которые легли в основу формулы, которая используется сегодня. Он провел большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.Следовательно, закон эмпирический. Хотя закон Ома является одной из основ электротехники, на момент публикации он был встречен критикой. Ом принят в качестве официальной единицы измерения электрического сопротивления в системе СИ. Густав Кирхгоф (известный из законов схем Кирхгофа) сделал обобщение, которое больше используется в физике:
Уравнение названо в честь Георга Ома. В 1827 году он опубликовал свои выводы, которые легли в основу формулы, которая используется сегодня. Он провел большую серию экспериментов, которые показали связь между приложенным напряжением и током, протекающим через проводник.Следовательно, закон эмпирический. Хотя закон Ома является одной из основ электротехники, на момент публикации он был встречен критикой. Ом принят в качестве официальной единицы измерения электрического сопротивления в системе СИ. Густав Кирхгоф (известный из законов схем Кирхгофа) сделал обобщение, которое больше используется в физике:
, где σ – параметр проводимости (зависит от материала), J – плотность тока в месте расположения этого материала, а E – электрическое поле в этом месте.
Закон Ома и резисторы
Резисторы – это пассивные элементы, которые создают сопротивление прохождению электрического тока в цепи. Резистор, работающий по закону Ома, называется омическим резистором. Когда ток проходит через омический резистор, падение напряжения на выводах пропорционально величине сопротивления. Формула Ома действительна также для цепей с переменным напряжением или током, поэтому ее можно использовать и для цепей переменного тока. Для конденсаторов и катушек индуктивности этот закон, конечно, не может быть использован, поскольку их ВАХ по своей природе не является линейной (не омической).
Формула Ома действительна также для цепей с переменным напряжением или током, поэтому ее можно использовать и для цепей переменного тока. Для конденсаторов и катушек индуктивности этот закон, конечно, не может быть использован, поскольку их ВАХ по своей природе не является линейной (не омической).
Ома действительна для цепей с несколькими резисторами, которые могут быть подключены последовательно, параллельно или и то, и другое. Группы резисторов, включенных последовательно или параллельно, можно упростить с помощью эквивалентного сопротивления. В статьях «Резисторы в серии» или «Резисторы в параллели» более подробно описано, как это сделать.
Георг Симон Ом (1789-1854)Георг Симон Ом Немецкий физик Георг Симон Ом опубликовал в 1827 году свою полную теорию электричества под названием «Гальваническая цепь, исследованная математически.Он обнаружил, что падение напряжения в части цепи является произведением проходящего через нее тока и сопротивления этой части. |
Уравнения закона Ома
ФормулаОм может использоваться, когда известны две из трех переменных. Связь между сопротивлением, током и напряжением можно записать по-разному. Чтобы запомнить это, может оказаться полезным калькулятор треугольника Ома. Два примера ниже покажут использование калькулятора треугольников.
или
или
Примеры | |
Рассмотрим резистор на 1 Ом в цепи с падением напряжения от 100 В до 10 В на его выводах. Какой ток через резистор? Треугольник напоминает нам, что: Какой ток через резистор? Треугольник напоминает нам, что: | |
| Рассмотрим резистор 10 Ом в цепи, подверженной току 2 Ампера и напряжению 120 В. Какое падение напряжения на резисторе? Использование треугольника показывает нам, что: Таким образом, напряжение на оконечном выводе 120-20 = 100 В. | |
Степенной закон Ома
Резистор рассеивает мощность, когда через него проходит ток.Энергия выделяется в виде тепла. Мощность является функцией тока I и приложенного напряжения V:
, где P – мощность в ваттах. В сочетании с законом Ома степенной закон можно переписать в виде:
или
Идеальные резисторы рассеивают всю энергию и не накапливают электрическую или магнитную энергию. У каждого резистора есть предел мощности, которая может рассеиваться без повреждения. Это называется номинальной мощностью. Окружающие условия могут снизить это значение.Например, корпус вокруг резистора или более высокая температура окружающей среды уменьшат количество энергии, которое резистор может рассеять. Этот эффект называется снижением мощности, и его можно визуализировать с помощью диаграммы снижения мощности. На практике резисторы редко имеют указанную номинальную мощность. Однако большинство резисторов рассчитаны на 1/4 или 1/8 Вт. Круговая диаграмма помогает быстро найти соотношение между электрической мощностью, током, напряжением и сопротивлением. Для каждого из четырех параметров показано, как рассчитать их значение.
Окружающие условия могут снизить это значение.Например, корпус вокруг резистора или более высокая температура окружающей среды уменьшат количество энергии, которое резистор может рассеять. Этот эффект называется снижением мощности, и его можно визуализировать с помощью диаграммы снижения мощности. На практике резисторы редко имеют указанную номинальную мощность. Однако большинство резисторов рассчитаны на 1/4 или 1/8 Вт. Круговая диаграмма помогает быстро найти соотношение между электрической мощностью, током, напряжением и сопротивлением. Для каждого из четырех параметров показано, как рассчитать их значение.
Ниже приведены несколько примеров задач закона Ома. Вы можете попробовать решить проблему самостоятельно, прежде чем читать ответ.
Цветовой код резистора
Значение сопротивления в омах часто обозначается цветовым кодом на резисторе. Комбинация цветов указывает значение, а также допуск резистора. Для получения дополнительной информации по этой теме см. Цветовую маркировку резистора.
Цветовую маркировку резистора.
Шпаргалка по закону Ома и закону Ватта
Закон
Ома устанавливает взаимосвязь между напряжением, током и сопротивлением.Закон Ватта устанавливает взаимосвязь между мощностью, напряжением и током.
Калькулятор закона Ома и закона Ватта
Быстрый старт
- Введите любые два известных значения и нажмите Вычислить , чтобы найти оставшиеся значения.
- Щелкните желаемое значение и выберите Ctrl + C, чтобы скопировать в буфер обмена
- Нажимайте Сброс после каждого расчета.
Важные электрические свойства, о которых следует помнить
- Электродвижущий потенциал : измеряется в вольтах, обозначается как V (или E)
- Ток : измеряется в амперах, обозначается буквой I
- Сопротивление : измеряется в Ом, обозначается буквой R (или греческой буквой ω)
- Мощность : измеряется в ваттах, обозначается буквой W
Рекомендовано: Основные электрические термины и определения
Закон Ома
Закон Ома устанавливает взаимосвязь между напряжением, током и сопротивлением. Учитывая взаимосвязь между этими тремя элементами, если вы знаете любые два из них, можно вычислить третий.
Учитывая взаимосвязь между этими тремя элементами, если вы знаете любые два из них, можно вычислить третий.
В = ИК
I = В / R
R = В / I
- Вольт = Ампер x Ом
- Ампер = Вольт / Ом
- Ом = Вольт / Ампер
Закон Ватта
ЗаконВатта также полезен для выяснения взаимосвязи между мощностью, напряжением и током.
Вт = VI
В = Вт / I
А = Вт / В
- Ватт = Вольт x Ампер
- Вольт = Ватт / Ампер
- Ампер = Ватт / Вольт
Круговая диаграмма упрощенного закона Ома для использования в цепях переменного и постоянного тока. Фотография: Wikimedia
.Комментарии
Войдите или зарегистрируйтесь, чтобы комментировать.Связь мощности и сопротивления – Электротехническая стековая биржа
Я думаю, вы путаете власть с работой. Работа – это количество преобразованной энергии, например сопротивление создает тепло из-за давления или напряжения. Это количество тепла. Мощность – это скорость, с которой создается это тепло, или насколько быстро.
Например, ходьба на милю сжигает 350 калорий, но занимает 30 минут. Спринт на милю также сжигает 350 калорий, но занимает всего 5 минут. Для спринта требуется в 6 раз больше энергии, несмотря на то, что было проделано столько же работы.Итак, мощность состоит из двух составляющих: тепла или затраченной энергии, и времени.
Сопротивление объекта – это не затраченная энергия или период времени. Таким образом, само по себе сопротивление не имеет никакого отношения к работе или временному интервалу. Ни одно из этих устройств не совместимо друг с другом. Это как сравнить прочность стали на сжатие с температурой кипения воды. Они измеряют две совершенно разные вещи. Сами по себе они не имеют отношения. Однако вы добавляете условный компонент, который может совместно использоваться обоими, и сравнительные изменения для каждого могут создавать соединение. Например, добавьте в смесь переменный компонент, например добавление электрического тока как к кипящей воде, так и к стали, затем измерьте прочность стали и точку кипения, чтобы увидеть, изменится ли это одно или оба их измерения. Теперь у вас есть возможность сравнить не друг с другом напрямую, а с тем, как они оба реагируют на этот новый компонент.
Например, добавьте в смесь переменный компонент, например добавление электрического тока как к кипящей воде, так и к стали, затем измерьте прочность стали и точку кипения, чтобы увидеть, изменится ли это одно или оба их измерения. Теперь у вас есть возможность сравнить не друг с другом напрямую, а с тем, как они оба реагируют на этот новый компонент.
Скажем, добавление электрического тока к воде снижает ее точку кипения, а добавление того же электрического тока снижает прочность стали.Что касается электрического тока, то можно сказать, что и температура кипения воды, и прочность стали прямо пропорциональны, потому что они оба падают. Это нереально, но показывает, как могут измениться отношения между двумя единицами измерения.
То же самое верно для сопротивления среды и скорости выделяемого ею тепла. Сопротивление – это статическое измерение, основанное на характеристиках компонента материала. Мощность – это динамическое измерение, основанное на условиях или нескольких компонентах, (количество электрического тока в секунду) в амперах и (дифференциальный заряд проводника) напряжении.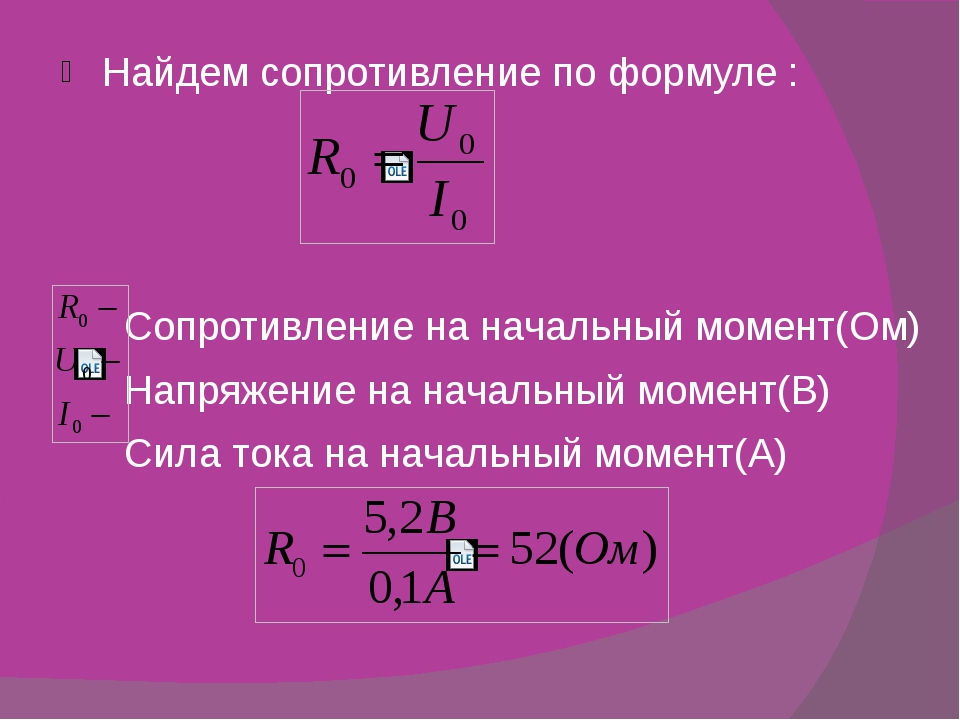 {2}} {\ text {9,8}} \\
& = \ текст {3,67} \ текст {Ω}
\ end {выровнять *}
{2}} {\ text {9,8}} \\
& = \ текст {3,67} \ текст {Ω}
\ end {выровнять *}
Теперь мы можем найти неизвестное сопротивление, сначала вычислив эквивалентное параллельное сопротивление:
\ begin {align *} \ frac {1} {R_ {p}} & = \ frac {1} {R_ {1}} + \ frac {1} {R_ {2}} + \ frac {1} {R_ {3}} \\ & = \ frac {1} {1} + \ frac {1} {5} + \ frac {1} {3} \\ & = \ frac {23} {15} \\ R_ {p} & = \ text {0,65} \ text {Ω} \ end {выровнять *} \ begin {align *} R_ {s} & = R_ {4} + R_ {p} \\ R_ {4} & = R_ {s} – R_ {p} \\ & = \ text {3,67} – \ text {0,65} \\ & = \ текст {3,02} \ текст {Ω} \ end {выровнять *}Теперь мы можем рассчитать общий ток:
\ begin {align *} I & = \ frac {V} {R} \\ & = \ frac {6} {\ text {3,67}} \\ & = \ текст {1,63} \ текст {А} \ end {выровнять *} Это ток в последовательном резисторе и во всем параллельном соединении. {2} (\ text {3,02}) \\
& = \ текст {0,89} \ текст {W}
\ end {выровнять *}
{2} (\ text {3,02}) \\
& = \ текст {0,89} \ текст {W}
\ end {выровнять *}
Затем мы находим напряжение на этих резисторах и используем его, чтобы найти напряжение на параллельной комбинации:
\ begin {align *} V & = IR \\ & = (\ текст {1,63}) (\ текст {3,02}) \\ & = \ текст {4,92} \ текст {V} \ end {выровнять *} \ begin {align *} V_ {T} & = V_ {1} + V_ {p} \\ V_ {p} & = V_ {T} – V_ {1} \\ & = \ text {6} – \ text {4,92} \\ & = \ текст {1,08} \ текст {V} \ end {выровнять *}Это напряжение на каждом из параллельных резисторов.{2}} {\ text {3}} \\ & = \ текст {3,5} \ текст {W} \ end {выровнять *}
Мощность и энергия
- Изучив этот раздел, вы должны уметь:
- Выполните расчеты мощности, напряжения, тока и сопротивления.
- • с использованием соответствующих единиц и подузлов.

- Различают мощность и энергию в электрических цепях.
Мощность резисторов
Когда через резистор протекает ток, электрическая энергия преобразуется в ТЕПЛОВУЮ энергию.Тепло, генерируемое в компонентах схемы, каждый из которых обладает хотя бы некоторым сопротивлением, рассеивается в воздухе вокруг компонентов. Скорость рассеивания тепла называется МОЩНОСТЬЮ, обозначается буквой P и измеряется в ваттах (Вт).
Количество рассеиваемой мощности может быть вычислено с использованием любых двух величин, используемых в расчетах по закону Ома. Помните, как и в любой формуле, в формуле должны использоваться ОСНОВНЫЕ КОЛИЧЕСТВА, то есть ВОЛЬТЫ, ОМЫ и АМПЕРЫ (не милли, мег и т. Д.).
Чтобы найти мощность P, используя V и I
Чтобы найти мощность P, используя V и R
Чтобы найти мощность P, используя I и R
Перед тем, как начать, подумайте об этих нескольких советах, они упростят задачу, если следовать им.
1. Разработайте ответы с помощью карандаша и бумаги; в противном случае легко запутаться на полпути и получить неправильный ответ.
2.Конечно, ответ – это не просто число, это будет определенное количество ватт (или несколько или несколько единиц ватт). Не забудьте указать правильную единицу измерения (например, Вт или мВт и т. Д.), А также число, иначе ответ не имеет смысла.
3. Преобразуйте все вспомогательные единицы, такие как мВ или кОм, в ватты, указав их в соответствующей формуле. Ошибка здесь даст действительно глупые ответы, в тысячи раз слишком большие или слишком маленькие.
4. Хотя структура этих формул мощности кажется очень похожей на формулы закона Ома, есть небольшое различие – они содержат некоторые элементы в квадрате (I 2 и V 2 ).Будьте очень осторожны при использовании трюка с треугольником для транспонирования этих формул. Если вам нужно связать мощность с сопротивлением, то I или V необходимо возвести в квадрат (умножить на себя). Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Однако вы можете построить треугольник, который соответствует любой из формул для получения R, как показано ниже.
Не забудьте загрузить нашу брошюру «Подсказки по математике», в которой показано, как использовать калькулятор с показателями степени и инженерной нотацией, чтобы работать с этими частями и каждый раз получать правильный ответ.
Нет научного калькулятора? Буклет «Подсказки по математике» объясняет, что вам нужно (и что вам не нужно, чтобы не тратить деньги без надобности). Если вы не хотите покупать научный калькулятор, вы всегда можете получить его бесплатно в сети. Пользователи ПК могут попробовать Calc98 на сайте www.calculator.org/download.html. Какой бы калькулятор вы ни выбрали, прочтите инструкции, чтобы ознакомиться с методами работы, которые вам следует использовать, поскольку они варьируются от калькулятора к калькулятору.
Важно помнить о влиянии рассеивания мощности в компонентах: чем больше мощность, тем больше тепла должно рассеиваться компонентом. Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный выход из строя компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с использованием более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут быть даже заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.
Обычно это означает, что компоненты, рассеивающие большое количество энергии, нагреваются, а также они будут значительно больше по размеру, чем типы с низким энергопотреблением. Если компоненту требуется рассеивать больше энергии, чем он предназначен, он не сможет достаточно быстро избавиться от выделяемого тепла. Его температура повысится, и перегрев может вызвать полный выход из строя компонента и, возможно, повреждение других компонентов и самой печатной платы (PCB).В качестве меры предосторожности резисторы большой мощности часто устанавливают вне печатной платы с использованием более длинных выводных проводов, заключенных в керамические гильзы. Резисторы с проволочной обмоткой большой мощности могут быть даже заключены в металлический радиатор и прикреплены болтами к большой металлической поверхности, такой как корпус оборудования, чтобы избавиться от нежелательного тепла. Примеры резисторов большой мощности показаны на странице конструкции резистора.
Компоненты, такие как резисторы, имеют определенную номинальную мощность, указанную производителем (в ваттах или милливаттах). Этот рейтинг (параметр) необходимо проверить при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
Этот рейтинг (параметр) необходимо проверить при замене компонента, чтобы не произошло завышения рейтинга. Это важный фактор безопасности при обслуживании электронного оборудования.
TIP
Тепло, выделяемое резисторами большой мощности, является основной причиной преждевременного выхода из строя многих цепей. Либо сам резистор выходит из строя из-за «разомкнутой цепи», особенно в резисторах с проволочной обмоткой. В резисторах из углеродного состава перегрев в течение длительного периода может вызвать изменение значения. Это может увеличиваться в типах с высоким сопротивлением или более опасно уменьшаться (позволяя увеличить ток) в типах с низким сопротивлением.Увеличение тока, вызванное уменьшением сопротивления, только ускоряет процесс, и в конечном итоге резистор (а иногда и другие связанные компоненты) сгорает!
Энергия в резисторах
Если определенное количество мощности рассеивается в течение заданного времени, то ЭНЕРГИЯ рассеивается. Энергия (мощность x время) измеряется в Джоулях, и, включив время (t) в формулы мощности, можно рассчитать энергию, рассеиваемую компонентом или схемой.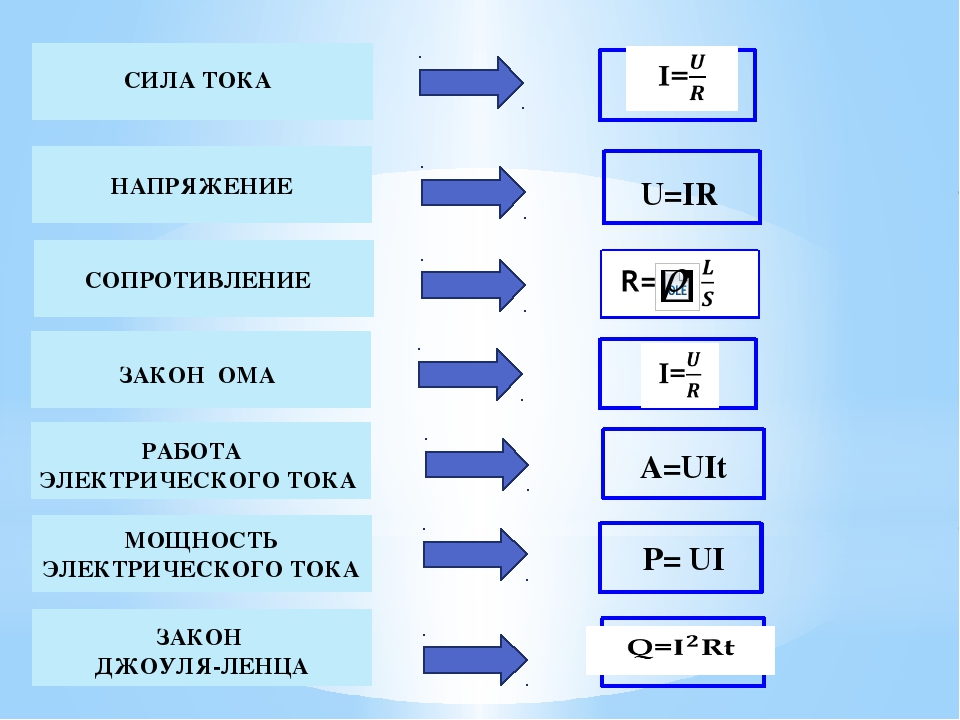
Рассеиваемая энергия = Pt или VIt или V 2 t / R или даже I 2 Rt Джоулей
Обратите внимание, что в формулах для энергии такие величины, как мощность, время, сопротивление, ток и напряжение, должны быть преобразованы в их основные единицы, например.грамм. Ватты, секунды, Ом, Амперы, Вольт и т. Д. Никаких дополнительных единиц или нескольких единиц! Как описано в буклете «Советы по математике».
Все вышеперечисленные единицы являются частью интегрированной системы международно стандартизированных единиц; Система S.I. (Système International d´Unités). Эта система устанавливает основные единицы для любых электрических, механических и физических свойств и их отношения друг к другу. Он также включает стандартную форму кратных и долей кратных, описанную в буклете «Подсказки по математике».
.


 Интересуют пиковые нагрузки на сеть, поэтому для расчета следует использовать максимальную потребляемую мощность, а не среднюю. Эта информация содержится в документации на изделия.
Интересуют пиковые нагрузки на сеть, поэтому для расчета следует использовать максимальную потребляемую мощность, а не среднюю. Эта информация содержится в документации на изделия.

 На его основе производится выбор основных элементов и вычисляется допустимая нагрузка.
На его основе производится выбор основных элементов и вычисляется допустимая нагрузка.
 Такой результат указывает, что ее перемещение происходит в обоих направлениях цепи. То есть, когда увеличивается напряжение, происходит накопление заряда в емкости.
Такой результат указывает, что ее перемещение происходит в обоих направлениях цепи. То есть, когда увеличивается напряжение, происходит накопление заряда в емкости.




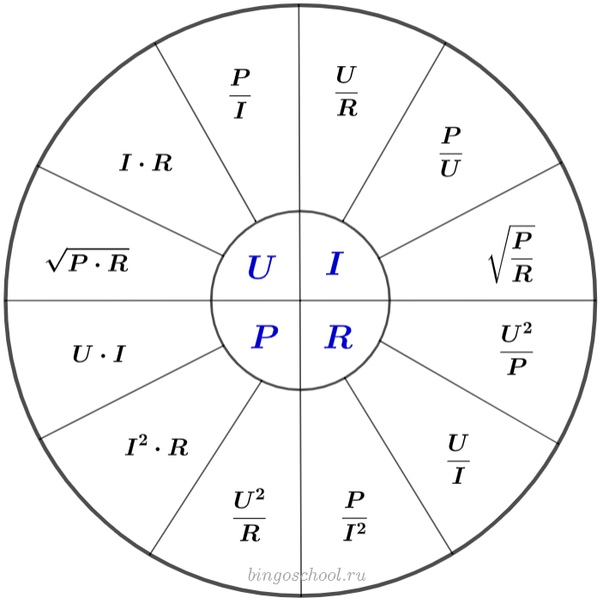
 Правильный и полный расчет тока нагрузки, запитанной переменным U, возможен на основании измеренных данных.
Правильный и полный расчет тока нагрузки, запитанной переменным U, возможен на основании измеренных данных.
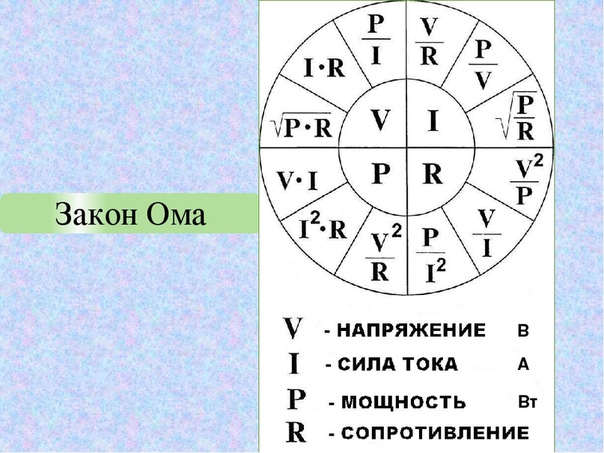 Единицей измерения по Международной системе единиц (СИ) является ватт, в нашей стране обозначается Вт, международное обозначение — W.
Единицей измерения по Международной системе единиц (СИ) является ватт, в нашей стране обозначается Вт, международное обозначение — W.
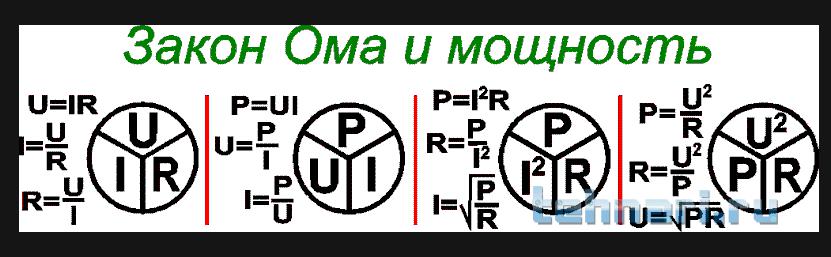

 Даны примеры практического применения законов электротехники.
Даны примеры практического применения законов электротехники.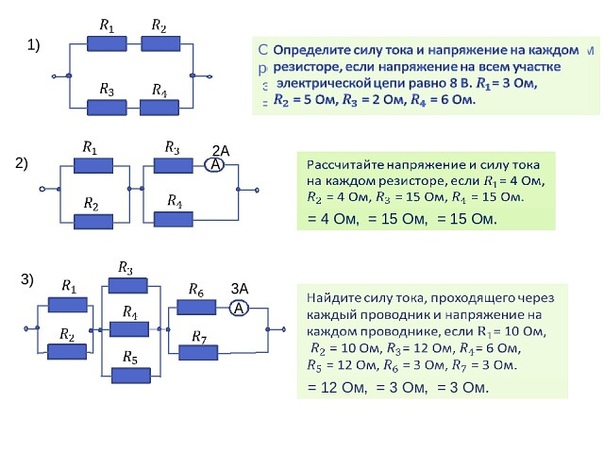

 Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.
Амперметр подключается последовательно для измерения тока в Амперах. Зная показания напряжения и тока по формулам, показанным выше, легко рассчитывается мощность.
 Измеряется активная нагрузка в Вт, кВт.
Измеряется активная нагрузка в Вт, кВт. Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q».
Единица измерения реактивной мощности при подсчете измеряется в Вар, это (Вольт-Ампер реактивный), обозначается буквой «Q». ru/teoriya/raschet-moshhnosti.html
ru/teoriya/raschet-moshhnosti.html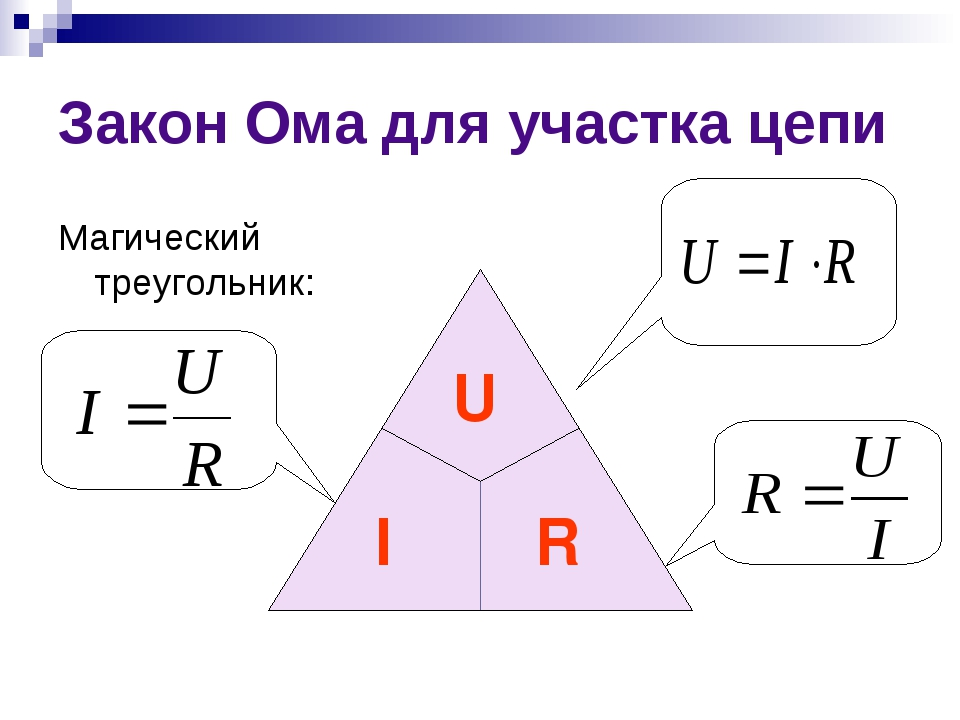 Эти же расчеты можно выполнять и для производственных целей.
Эти же расчеты можно выполнять и для производственных целей.


 Данный параметр обязательно заносится в технический паспорт устройства. U – представляет собой напряжение рассчитываемой сети, измеряемое в вольтах.
Данный параметр обязательно заносится в технический паспорт устройства. U – представляет собой напряжение рассчитываемой сети, измеряемое в вольтах. Таблица расчета поможет подобрать необходимое сечение провода, в зависимости от параметров.
Таблица расчета поможет подобрать необходимое сечение провода, в зависимости от параметров. 1,73 является специальным коэффициентом, применяемым для трехфазных сетей.
1,73 является специальным коэффициентом, применяемым для трехфазных сетей. Для таких устройств коэффициент мощности будет равен 0,8.
Для таких устройств коэффициент мощности будет равен 0,8.
 Не секрет, что в сельской местности сетевое напряжение может колебаться в достаточно широких пределах. Поэтому пи использовании расчетных формул в них необходимо подставлять реальные значения параметров.
Не секрет, что в сельской местности сетевое напряжение может колебаться в достаточно широких пределах. Поэтому пи использовании расчетных формул в них необходимо подставлять реальные значения параметров. Проводка, автоматы с неверно подобранными показателями опасны: может случиться замыкание и пожар.
Проводка, автоматы с неверно подобранными показателями опасны: может случиться замыкание и пожар.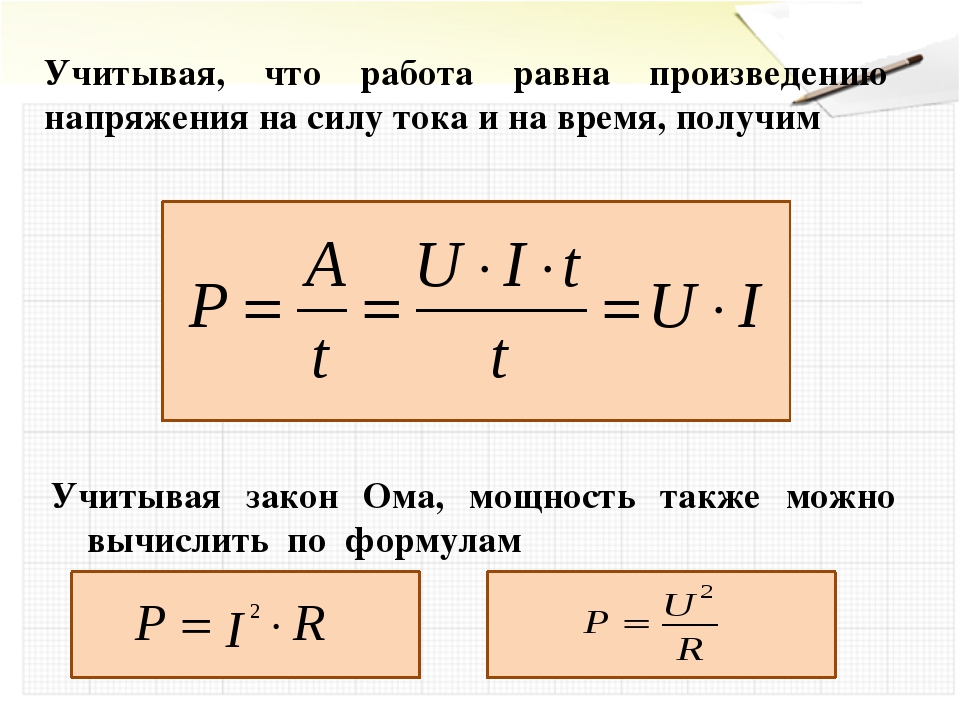 Они выполнены четырьмя проводами: три фазных и нулевой. Если посмотреть на линию электропередач, увидим 4 провода между столбами.
Они выполнены четырьмя проводами: три фазных и нулевой. Если посмотреть на линию электропередач, увидим 4 провода между столбами.

 Подставляя 0,95, для однофазной сети выходит:
Подставляя 0,95, для однофазной сети выходит:

 html
html Это легло в основу того закона, который мы используем сегодня. Закон – одно из основополагающих соотношений для резисторов.
Это легло в основу того закона, который мы используем сегодня. Закон – одно из основополагающих соотношений для резисторов.