Формула v в физике: Все главные формулы по физике – Физика – Теория, тесты, формулы и задачи

Все главные формулы по физике – Физика – Теория, тесты, формулы и задачи

Оглавление:

 

Кинематика

К оглавлению…

Путь при равномерном движении:

Перемещение S (расстояние по прямой между начальной и конечной точкой движения) обычно находится из геометрических соображений. Координата при равномерном прямолинейном движении изменяется по закону (аналогичные уравнения получаются для остальных координатных осей):

Средняя скорость пути:

Средняя скорость перемещения:

Определение ускорения при равноускоренном движении:

Выразив из формулы выше конечную скорость, получаем более распространённый вид предыдущей формулы, которая теперь выражает зависимость скорости от времени при равноускоренном движении:

Средняя скорость при равноускоренном движении:

Перемещение при равноускоренном прямолинейном движении может быть рассчитано по нескольким формулам:

Координата при равноускоренном движении

изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v₀, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

Формула для тормозного пути тела:

Время падения тела при горизонтальном броске с высоты H может быть найдено по формуле:

Дальность полета тела при горизонтальном броске с высоты H:

Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту:

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):

Определение периода вращения при равномерном движении по окружности:

Определение частоты вращения при равномерном движении по окружности:

Связь периода и частоты:

Линейная скорость при равномерном движении по окружности может быть найдена по формулам:

Угловая скорость вращения при равномерном движении по окружности:

Связь линейной и скорости и угловой скорости выражается формулой:

Связь угла поворота и пути при равномерном движении по окружности радиусом

R (фактически, это просто формула для длины дуги из геометрии):

Центростремительное ускорение находится по одной из формул:

 

Динамика

К оглавлению…

Второй закон Ньютона:

Здесь: F – равнодействующая сила, которая равна сумме всех сил действующих на тело:

Второй закон Ньютона в проекциях на оси (именно такая форма записи чаще всего и применяется на практике):

Третий закон Ньютона (сила действия равна силе противодействия):

Сила упругости:

Общий коэффициент жесткости параллельно соединённых пружин:

Общий коэффициент жесткости последовательно соединённых пружин:

Сила трения скольжения (или максимальное значение силы трения покоя):

Закон всемирного тяготения:

Если рассмотреть тело на поверхности планеты и ввести следующее обозначение:

Где: g – ускорение свободного падения на поверхности данной планеты, то получим следующую формулу для силы тяжести:

Ускорение свободного падения на некоторой высоте от поверхности планеты выражается формулой:

Скорость спутника на круговой орбите:

Первая космическая скорость:

Закон Кеплера для периодов обращения двух тел вращающихся вокруг одного притягивающего центра:

 

Статика

К оглавлению. ..

Момент силы определяется с помощью следующей формулы:

Условие при котором тело не будет вращаться:

Координата центра тяжести системы тел (аналогичные уравнения для остальных осей):

 

Гидростатика

К оглавлению…

Определение давления задаётся следующей формулой:

Давление, которое создает столб жидкости находится по формуле:

Но часто нужно учитывать еще и атмосферное давление, тогда формула для общего давления на некоторой глубине h в жидкости приобретает вид:

Идеальный гидравлический пресс:

Любой гидравлический пресс:

КПД для неидеального гидравлического пресса:

Сила Архимеда (выталкивающая сила, V – объем погруженной части тела):

 

Импульс

К оглавлению…

Импульс тела находится по следующей формуле:

Изменение импульса тела или системы тел (обратите внимание, что разность конечного и начального импульсов векторная):

Общий импульс системы тел (важно то, что сумма векторная):

Второй закон Ньютона в импульсной форме может быть записан в виде следующей формулы:

Закон сохранения импульса.

Как следует из предыдущей формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

 

Работа, мощность, энергия

К оглавлению…

Механическая работа рассчитывается по следующей формуле:

Самая общая формула для мощности (если мощность переменная, то по следующей формуле рассчитывается средняя мощность):

Мгновенная механическая мощность:

Коэффициент полезного действия (КПД) может быть рассчитан и через мощности и через работы:

Формула для кинетической энергии:

Потенциальная энергия тела поднятого на высоту:

Потенциальная энергия растянутой (или сжатой) пружины:

Полная механическая энергия:

Связь полной механической энергии тела или системы тел и работы внешних сил:

Закон сохранения механической энергии (далее – ЗСЭ).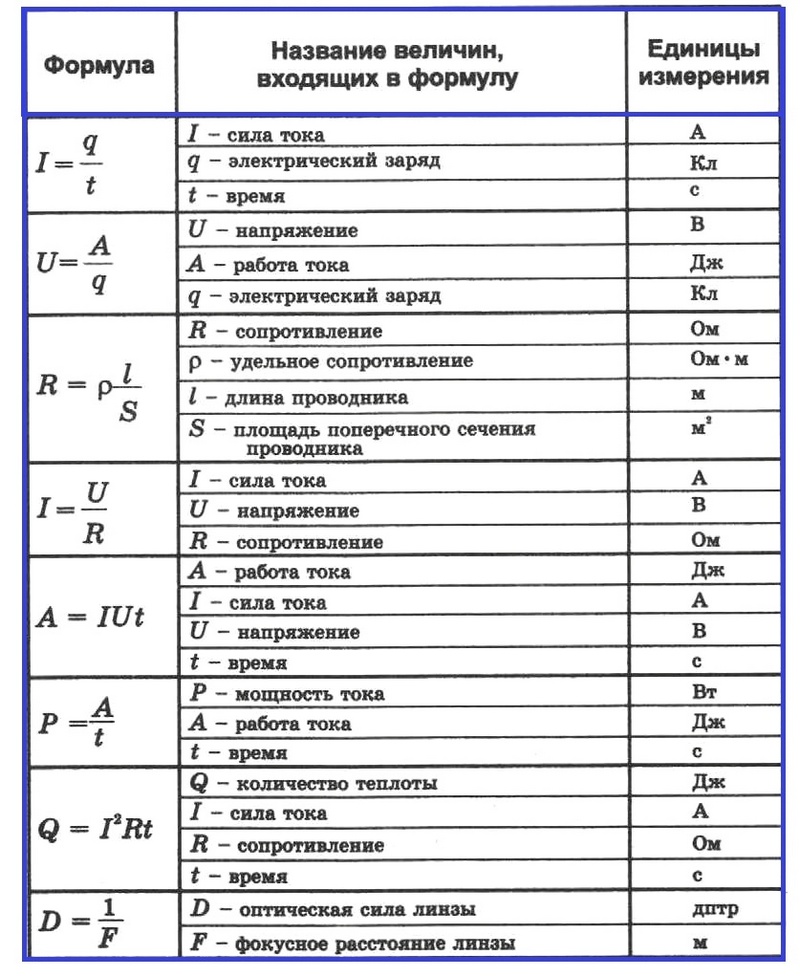 Как следует из предыдущей формулы, если внешние силы не совершают работы над телом (или системой тел), то его (их) общая полная механическая энергия остается постоянной, при этом энергия может перетекать из одного вида в другой (из кинетической в потенциальную или наоборот):

 

Молекулярная физика

К оглавлению…

Химическое количество вещества находится по одной из формул:

Масса одной молекулы вещества может быть найдена по следующей формуле:

Связь массы, плотности и объёма:

Основное уравнение молекулярно-кинетической теории (МКТ) идеального газа:

Определение концентрации задаётся следующей формулой:

Для средней квадратичной скорости молекул имеется две формулы:

Средняя кинетическая энергия поступательного движения одной молекулы:

Постоянная Больцмана, постоянная Авогадро и универсальная газовая постоянная связаны следующим образом:

Следствия из основного уравнения МКТ:

Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева):

Газовые законы.  Закон Бойля-Мариотта:

Закон Гей-Люссака:

Закон Шарля:

Универсальный газовый закон (Клапейрона):

Давление смеси газов (закон Дальтона):

Тепловое расширение тел. Тепловое расширение газов описывается законом Гей-Люссака. Тепловое расширение жидкостей подчиняется следующему закону:

Для расширения твердых тел применяются три формулы, описывающие изменение линейных размеров, площади и объема тела:

 

Термодинамика

К оглавлению…

Количество теплоты (энергии) необходимое для нагревания некоторого тела (или количество теплоты выделяющееся при остывании тела) рассчитывается по формуле:

Теплоемкость (С – большое) тела может быть рассчитана через удельную теплоёмкость (c – маленькое) вещества и массу тела по следующей формуле:

Тогда формула для количества теплоты необходимой для нагревания тела, либо выделившейся при остывании тела может быть переписана следующим образом:

Фазовые превращения.

 При парообразовании поглощается, а при конденсации выделяется количество теплоты равное:

При плавлении поглощается, а при кристаллизации выделяется количество теплоты равное:

При сгорании топлива выделяется количество теплоты равное:

Уравнение теплового баланса (ЗСЭ). Для замкнутой системы тел выполняется следующее (сумма отданных теплот равна сумме полученных):

Если все теплоты записывать с учетом знака, где «+» соответствует получению энергии телом, а «–» выделению, то данное уравнение можно записать в виде:

Работа идеального газа:

Если же давление газа меняется, то работу газа считают, как площадь фигуры под графиком в p–V координатах. Внутренняя энергия идеального одноатомного газа:

Изменение внутренней энергии рассчитывается по формуле:

Первый закон (первое начало) термодинамики (ЗСЭ):

Для различных изопроцессов можно выписать формулы по которым могут быть рассчитаны полученная теплота Q, изменение внутренней энергии ΔU и работа газа A. Изохорный процесс (V = const):

Изобарный процесс (p = const):

Изотермический процесс (T = const):

Адиабатный процесс (Q = 0):

КПД тепловой машины может быть рассчитан по формуле:

Где: Q₁ – количество теплоты полученное рабочим телом за один цикл от нагревателя, Q₂ – количество теплоты переданное рабочим телом за один цикл холодильнику. Работа совершенная тепловой машиной за один цикл:

Наибольший КПД при заданных температурах нагревателя T₁ и холодильника T₂, достигается если тепловая машина работает по циклу Карно. Этот КПД цикла Карно равен:

Абсолютная влажность рассчитывается как плотность водяных паров (из уравнения Клапейрона-Менделеева выражается отношение массы к объему и получается следующая формула):

Относительная влажность воздуха может быть рассчитана по следующим формулам:

Потенциальная энергия поверхности жидкости площадью S:

Сила поверхностного натяжения, действующая на участок границы жидкости длиной L:

Высота столба жидкости в капилляре:

При полном смачивании θ = 0°, cos θ = 1. В этом случае высота столба жидкости в капилляре станет равной:

При полном несмачивании θ = 180°, cos θ = –1 и, следовательно, h < 0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.

 

Электростатика

К оглавлению…

Электрический заряд может быть найден по формуле:

Линейная плотность заряда:

Поверхностная плотность заряда:

Объёмная плотность заряда:

Закон Кулона (сила электростатического взаимодействия двух электрических зарядов):

Где: k – некоторый постоянный электростатический коэффициент, который определяется следующим образом:

Напряжённость электрического поля находится по формуле (хотя чаще эту формулу используют для нахождения силы действующей на заряд в данном электрическом поле):

Принцип суперпозиции для электрических полей (результирующее электрическое поле равно векторной сумме электрических полей составляющих его):

Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра:

Напряженность электрического поля, которую создает заряженная плоскость:

Потенциальная энергия взаимодействия двух электрических зарядов выражается формулой:

Электрическое напряжение это просто разность потенциалов, т.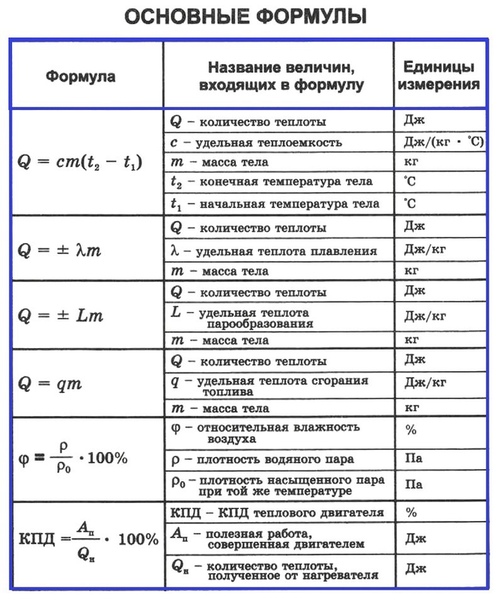 е. определение электрического напряжения может быть задано формулой:

В однородном электрическом поле существует связь между напряженностью поля и напряжением:

Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:

Работа электрического поля в общем случае может быть вычислена также и по одной из формул:

В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:

Определение потенциала задаётся выражением:

Потенциал, который создает точечный заряд или заряженная сфера:

Принцип суперпозиции для электрического потенциала (результирующий потенциал равен скалярной сумме потенциалов полей составляющих итоговое поле):

Для диэлектрической проницаемости вещества верно следующее:

Определение электрической ёмкости задаётся формулой:

Ёмкость плоского конденсатора:

Заряд конденсатора:

Напряжённость электрического поля внутри плоского конденсатора:

Сила притяжения пластин плоского конденсатора:

Энергия конденсатора (вообще говоря, это энергия электрического поля внутри конденсатора):

Объёмная плотность энергии электрического поля:

 

Электрический ток

К оглавлению. ..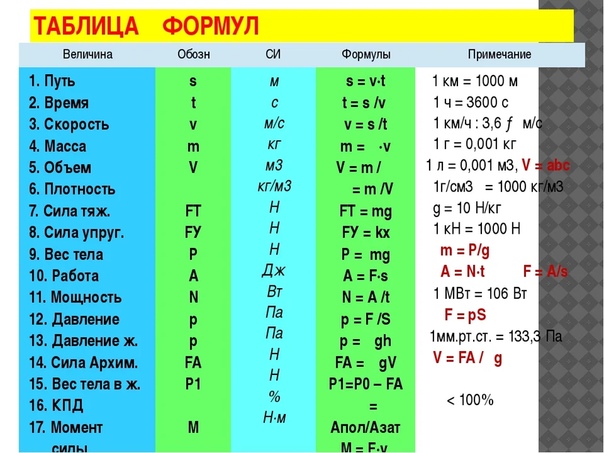

Сила тока может быть найдена с помощью формулы:

Плотность тока:

Сопротивление проводника:

Зависимость сопротивления проводника от температуры задаётся следующей формулой:

Закон Ома (выражает зависимость силы тока от электрического напряжения и сопротивления):

Закономерности последовательного соединения:

Закономерности параллельного соединения:

Электродвижущая сила источника тока (ЭДС) определяется с помощью следующей формулы:

Закон Ома для полной цепи:

Падение напряжения во внешней цепи при этом равно (его еще называют напряжением на клеммах источника):

Сила тока короткого замыкания:

Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока протекающего по проводнику обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике:

Мощность электрического тока:

Энергобаланс замкнутой цепи

Полезная мощность или мощность, выделяемая во внешней цепи:

Максимально возможная полезная мощность источника достигается, если R = r и равна:

Если при подключении к одному и тому же источнику тока разных сопротивлений R₁ и R₂ на них выделяются равные мощности то внутреннее сопротивление этого источника тока может быть найдено по формуле:

Мощность потерь или мощность внутри источника тока:

Полная мощность, развиваемая источником тока:

КПД источника тока:

Электролиз

Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит:

Величину k называют электрохимическим эквивалентом. Он может быть рассчитан по формуле:

Где: n – валентность вещества, N_A – постоянная Авогадро, M – молярная масса вещества, е – элементарный заряд. Иногда также вводят следующее обозначение для постоянной Фарадея:

 

Магнетизм

К оглавлению…

Сила Ампера, действующая на проводник с током помещённый в однородное магнитное поле, рассчитывается по формуле:

Момент сил действующих на рамку с током:

Сила Лоренца, действующая на заряженную частицу движущуюся в однородном магнитном поле, рассчитывается по формуле:

Радиус траектории полета заряженной частицы в магнитном поле:

Модуль индукции B магнитного поля прямолинейного проводника с током I на расстоянии R от него выражается соотношением:

Индукция поля в центре витка с током радиусом R:

Внутри соленоида длиной l и с количеством витков N создается однородное магнитное поле с индукцией:

Магнитная проницаемость вещества выражается следующим образом:

Магнитным потоком Φ через площадь S контура называют величину заданную формулой:

ЭДС индукции рассчитывается по формуле:

При движении проводника длиной l в магнитном поле B со скоростью v также возникает ЭДС индукции (проводник движется в направлении перпендикулярном самому себе):

Максимальное значение ЭДС индукции в контуре состоящем из N витков, площадью S, вращающемся с угловой скоростью ω в магнитном поле с индукцией В:

Индуктивность катушки:

Где: n – концентрация витков на единицу длины катушки:

Связь индуктивности катушки, силы тока протекающего через неё и собственного магнитного потока пронизывающего её, задаётся формулой:

ЭДС самоиндукции возникающая в катушке:

Энергия катушки (вообще говоря, это энергия магнитного поля внутри катушки):

Объемная плотность энергии магнитного поля:

 

Колебания

К оглавлению. ..

Уравнение описывающее физические системы способные совершать гармонические колебания с циклической частотой ω₀:

Решение предыдущего уравнения является уравнением движения для гармонических колебаний и имеет вид:

Период колебаний вычисляется по формуле:

Частота колебаний:

Циклическая частота колебаний:

Зависимость скорости от времени при гармонических механических колебаниях выражается следующей формулой:

Максимальное значение скорости при гармонических механических колебаниях:

Зависимость ускорения от времени при гармонических механических колебаниях:

Максимальное значение ускорения при механических гармонических колебаниях:

Циклическая частота колебаний математического маятника рассчитывается по формуле:

Период колебаний математического маятника:

Циклическая частота колебаний пружинного маятника:

Период колебаний пружинного маятника:

Максимальное значение кинетической энергии при механических гармонических колебаниях задаётся формулой:

Максимальное значение потенциальной энергии при механических гармонических колебаниях пружинного маятника:

Взаимосвязь энергетических характеристик механического колебательного процесса:

Энергетические характеристики и их взаимосвязь при колебаниях в электрическом контуре:

Период гармонических колебаний в электрическом колебательном контуре определяется по формуле:

Циклическая частота колебаний в электрическом колебательном контуре:

Зависимость заряда на конденсаторе от времени при колебаниях в электрическом контуре описывается законом:

Зависимость электрического тока протекающего через катушку индуктивности от времени при колебаниях в электрическом контуре:

Зависимость напряжения на конденсаторе от времени при колебаниях в электрическом контуре:

Максимальное значение силы тока при гармонических колебаниях в электрическом контуре может быть рассчитано по формуле:

Максимальное значение напряжения на конденсаторе при гармонических колебаниях в электрическом контуре:

Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин следующим образом. Действующее значение силы тока:

Действующее значение напряжения:

Мощность в цепи переменного тока:

Трансформатор

Если напряжение на входе в трансформатор равно U₁, а на выходе U₂, при этом число витков в первичной обмотке равно n₁, а во вторичной n₂, то выполняется следующее соотношение:

Коэффициент трансформации вычисляется по формуле:

Если трансформатор идеальный, то выполняется следующее соотношение (мощности на входе и выходе равны):

В неидеальном трансформаторе вводится понятие КПД:

Волны

Длина волны может быть рассчитана по формуле:

Разность фаз колебаний двух точек волны, расстояние между которыми l:

Скорость электромагнитной волны (в т.ч. света) в некоторой среде:

Скорость электромагнитной волны (в т.ч. света) в вакууме постоянна и равна с = 3∙10⁸ м/с, она также может быть вычислена по формуле:

Скорости электромагнитной волны (в т. ч. света) в среде и в вакууме также связаны между собой формулой:

При этом показатель преломления некоторого вещества можно рассчитать используя формулу:

 

Оптика

К оглавлению…

Оптическая длина пути определяется формулой:

Оптическая разность хода двух лучей:

Условие интерференционного максимума:

Условие интерференционного минимума:

Формула дифракционной решетки:

Закон преломления света на границе двух прозрачных сред:

Постоянную величину n₂₁ называют относительным показателем преломления второй среды относительно первой. Если n₁ > n₂, то возможно явление полного внутреннего отражения, при этом:

Формула тонкой линзы:

Линейным увеличением линзы Γ называют отношение линейных размеров изображения и предмета:

 

Атомная и ядерная физика

К оглавлению. ..

Энергия кванта электромагнитной волны (в т.ч. света) или, другими словами, энергия фотона вычисляется по формуле:

Импульс фотона:

Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ):

Максимальная кинетическая энергия вылетающих электронов при фотоэффекте может быть выражена через величину задерживающего напряжение U_з и элементарный заряд е:

Существует граничная частота или длинна волны света (называемая красной границей фотоэффекта) такая, что свет с меньшей частотой или большей длиной волны не может вызвать фотоэффект. Эти значения связаны с величиной работы выхода следующим соотношением:

Второй постулат Бора или правило частот (ЗСЭ):

В атоме водорода выполняются следующие соотношения, связывающие радиус траектории вращающегося вокруг ядра электрона, его скорость и энергию на первой орбите с аналогичными характеристиками на остальных орбитах:

На любой орбите в атоме водорода кинетическая (К) и потенциальная (П) энергии электрона связаны с полной энергией (Е) следующими формулами:

Общее число нуклонов в ядре равно сумме числа протонов и нейтронов:

Дефект массы:

Энергия связи ядра выраженная в единицах СИ:

Энергия связи ядра выраженная в МэВ (где масса берется в атомных единицах):

Формула альфа-распада:

Формула бета-распада:

Закон радиоактивного распада:

Ядерные реакции

Для произвольной ядерной реакции описывающейся формулой вида:

Выполняются следующие условия:

Энергетический выход такой ядерной реакции при этом равен:

 

Основы специальной теории относительности (СТО)

К оглавлению. ..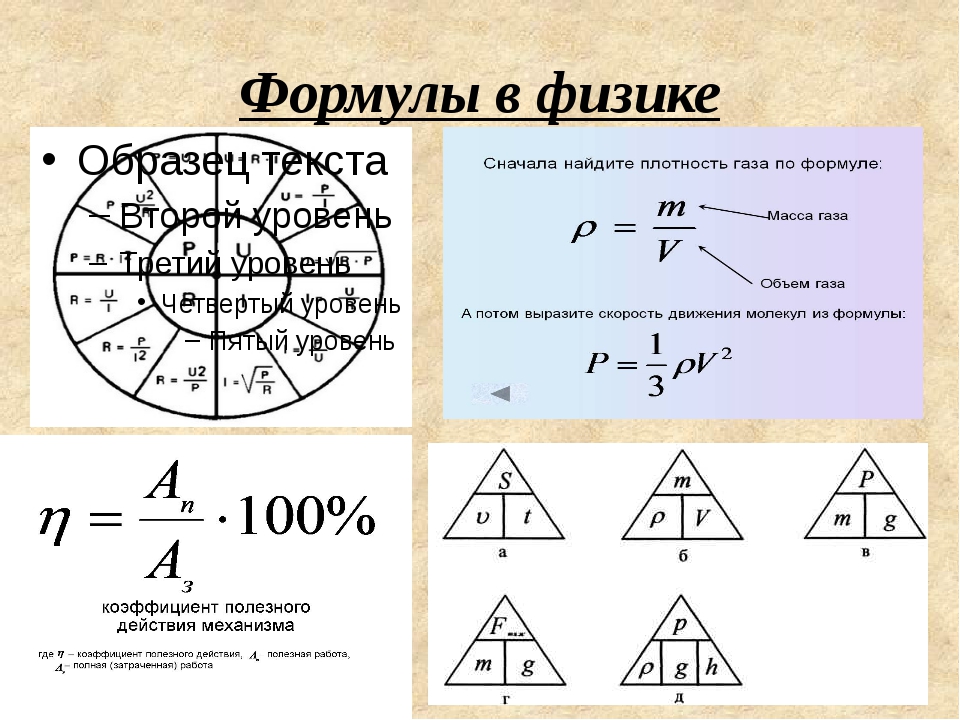

Релятивистское сокращение длины:

Релятивистское удлинение времени события:

Релятивистский закон сложения скоростей. Если два тела движутся навстречу друг другу, то их скорость сближения:

Релятивистский закон сложения скоростей. Если же тела движутся в одном направлении, то их относительная скорость:

Энергия покоя тела:

Любое изменение энергии тела означает изменение массы тела и наоборот:

Полная энергия тела:

Полная энергия тела Е пропорциональна релятивистской массе и зависит от скорости движущегося тела, в этом смысле важны следующие соотношения:

Релятивистское увеличение массы:

Кинетическая энергия тела, движущегося с релятивистской скоростью:

Между полной энергией тела, энергией покоя и импульсом существует зависимость:

 

Равномерное движение по окружности

К оглавлению…

В качестве дополнения, в таблице ниже приводим всевозможные взаимосвязи между характеристиками тела равномерно вращающегося по окружности (T – период, N – количество оборотов, v – частота, R – радиус окружности, ω – угловая скорость, φ – угол поворота (в радианах), υ – линейная скорость тела, a_n – центростремительное ускорение, L – длина дуги окружности, t – время):

 

Расширенная PDF версия документа “Все главные формулы по школьной физике”:

К оглавлению. ..

Формулы по физике для ЕГЭ и 7-11 класса

Рубрика: Подготовка к ЕГЭ по физике

Шпаргалка с формулами по физике для ЕГЭ

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Для начала картинка, которую можно распечатать в компактном виде.

Механика

1. Давление                      Р=F/S
2. Плотность                   ρ=m/V
3. Давление на глубине жидкости   P=ρ∙g∙h
4. Сила тяжести                       Fт=mg
5. 5. Архимедова сила                 Fa=ρ_ж∙g∙Vт
6. Уравнение движения  при равноускоренном  движении

X=X₀+υ₀∙t+(a∙t²)/2                    S= (υ²–υ₀²)^{/2а         S= (υ+υ₀) ∙t /2}

1. Уравнение скорости  при равноускоренном движении υ=υ₀+a∙t
2. Ускорение            a=(υ–υ ₀)/t
3. Скорость при движении по окружности υ=2πR/Т
4. Центростремительное ускорение  a=υ²/R
5. Связь периода с частотой ν=1/T=ω/2π
6. II закон Ньютона                F=ma
7. Закон Гука                          Fy=-kx
8. Закон Всемирного тяготения  F=G∙M∙m/R²
9. Вес тела, движущегося с ускорением а↑      Р=m(g+a)
10. Вес тела, движущегося с ускорением а↓      Р=m(g-a)
11. Сила трения                     Fтр=µN
12. Импульс тела                       p=mυ
13. Импульс силы                     Ft=∆p
14. Момент силы                    M=F∙ℓ
15. Потенциальная энергия тела, поднятого над землей Eп=mgh
16. Потенциальная энергия упруго деформированного тела Eп=kx²/2
17. Кинетическая энергия тела Ek=mυ²/2
18. Работа            A=F∙S∙cosα
19. Мощность     N=A/t=F∙υ
20. Коэффициент полезного действия η=Aп/Аз
21. Период колебаний математического маятника T=2π√ℓ/g
22. Период колебаний пружинного маятника T=2 π √m/k
23. Уравнение гармонических колебаний  Х=Хmax∙cos ωt
24. Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

1. Количество вещества              ν=N/ Na
2. Молярная масса                           М=m/ν
3. Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
4. Основное уравнение МКТ      P=nkT=1/3nm₀υ²
5. Закон Гей – Люссака (изобарный процесс)    V/T =const
6. Закон Шарля (изохорный процесс)    P/T =const
7. Относительная влажность φ=P/P₀∙100%
8. Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
9. Работа газа A=P∙ΔV
10. Закон Бойля – Мариотта (изотермический процесс)    PV=const
11. Количество теплоты при нагревании  Q=Cm(T₂-T₁)
12. Количество теплоты при плавлении   Q=λm
13. Количество теплоты при парообразовании  Q=Lm
14. Количество теплоты при сгорании топлива  Q=qm
15. Уравнение состояния идеального газа PV=m/M∙RT
16. Первый закон термодинамики   ΔU=A+Q
17. КПД тепловых двигателей         η= (Q₁ – Q₂)/ Q₁
18. КПД идеал. двигателей  (цикл Карно)     η= (Т₁ – Т₂)/ Т₁

https://5-ege. ru/formuly-po-fizike-dlya-ege/

Электростатика и электродинамика – формулы по физике

1. Закон Кулона F=k∙q₁∙q₂/R²
2. Напряженность электрического поля E=F/q
3. Напряженность эл. поля точечного заряда E=k∙q/R²
4. Поверхностная плотность зарядов             σ = q/S
5. Напряженность эл. поля бесконечной плоскости E=2πkσ
6. Диэлектрическая проницаемость ε=E₀/E
7. Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R
8. Потенциал φ=W/q
9. Потенциал точечного заряда φ=k∙q/R
10. Напряжение U=A/q
11. Для однородного электрического поля U=E∙d
12. Электроемкость C=q/U
13. Электроемкость плоского конденсатора C=S∙ε∙ε₀/d
14. Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
15. Сила тока I=q/t
16. Сопротивление проводника R=ρ∙ℓ/S
17. Закон Ома для участка цепи I=U/R
18. Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R
19. Законы паралл. соед.   U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R
20. Мощность электрического тока P=I∙U
21. Закон Джоуля-Ленца Q=I²Rt
22. Закон Ома для полной цепи I=ε/(R+r)
23. Ток короткого замыкания (R=0)      I=ε/r
24. Вектор магнитной индукции B=Fmax/ℓ∙I
25. Сила Ампера Fa=IBℓsin α
26. Сила Лоренца Fл=Bqυsin α
27. Магнитный поток Ф=BSсos α      Ф=LI
28. Закон электромагнитной индукции Ei=ΔФ/Δt
29. ЭДС индукции в движ проводнике Ei=Вℓυsinα
30. ЭДС самоиндукции Esi=-L∙ΔI/Δt
31. Энергия магнитного поля катушки Wм=LI²/2
32. Период колебаний кол. контура T=2π ∙√LC
33. Индуктивное сопротивление X_L=ωL=2πLν
34. Емкостное сопротивление Xc=1/ωC
35. Действующее значение силы тока Iд=Imax/√2,
36. Действующее значение напряжения Uд=Umax/√2
37. Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

1. Закон преломления света     n₂₁=n₂/n₁= υ ₁/ υ ₂
2. Показатель преломления      n₂₁=sin α/sin γ
3. Формула тонкой линзы       1/F=1/d + 1/f
4. Оптическая сила линзы       D=1/F
5. max интерференции: Δd=kλ,
6. min интерференции: Δd=(2k+1)λ/2
7. Диф. решетка             d∙sin φ=k λ

Квантовая физика

1. Ф-ла Эйнштейна для фотоэффекта  hν=Aвых+Ek, Ek=U_зе
2. Красная граница фотоэффекта ν_к = Aвых/h
3. Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

1. Закон радиоактивного распада N=N₀∙2^–t/T
2. Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

1. t=t₁/√1-υ²/c²
2. ℓ=ℓ₀∙√1-υ²/c²
3. υ₂=(υ₁+υ)/1+ υ₁∙υ/c²
4. Е = mс²

Скачать эти формулы в doc: formuly-po-fizike-5-ege.ru (файл расположен на 5-ege.ru).

Рекомендуем:

Формула скорости в физике

Содержание:

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $\bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$\bar{v}=\frac{d \bar{r}}{d t}=\dot{\bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=\frac{d s}{d t}=\dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.

Скорость в разных системах координат

Проекции скорости на оси декартовой системы координат запишутся как:

$$v_{x}=\dot{x} ; v_{y}=\dot{y} ; v_{z}=\dot{z}(3)$$

Следовательно, вектор скоростив декартовых координатах можно представить:

$$\bar{v}=\dot{x} \bar{i}+\dot{y} \bar{j}+\dot{z} \bar{k}(4)$$

где $\bar{i}, \bar{j}, \bar{k}$ единичные орты. При этом модуль вектора скорости находят при помощи формулы:

$$v=\sqrt{(\dot{x})^{2}+(\dot{y})^{2}+(\dot{z})^{2}}(5)$$

В цилиндрических координатах модуль скорости вычисляют при помощи формулы:

$$v=\sqrt{(\dot{\rho})^{2}+(\rho \dot{\varphi})^{2}+(\dot{z})^{2}}(6)$$

в сферической системе координат:

$$v=\sqrt{(r)^{2}+(r \dot{\theta})^{2}+(r \dot{\varphi} \sin \theta)^{2}}(7)$$

Частные случаи формул для вычисления скорости

Если модуль скорости не изменяется во времени, то такое движение называют равномерным (v=const). {2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 \mathrm{~m}$ 2) $t_{1}=8,8 \mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Формула скорости в физике

Содержание:

Определение и формула скорости

Определение

Мгновенной скоростью (или чаще просто скоростью) материальной точки называется физическая величина равная первой производной от радиус–вектора $\bar{r}$ точки по времени (t). Обозначают скорость обычно буквой v. Это векторная величина. Математически определение вектора мгновенной скорости записывается как:

$$\bar{v}=\frac{d \bar{r}}{d t}=\dot{\bar{r}}(1)$$

Скорость имеет направление указывающее направление движения материальной точки и лежит на касательной к траектории ее движения. Модуль скорости можно определить как первую производную от длины пути (s) по времени:

$$v=\frac{d s}{d t}=\dot{s}(2)$$

Скорость характеризует быстроту перемещения в направлении движения точки по отношениюк рассматриваемой системе координат.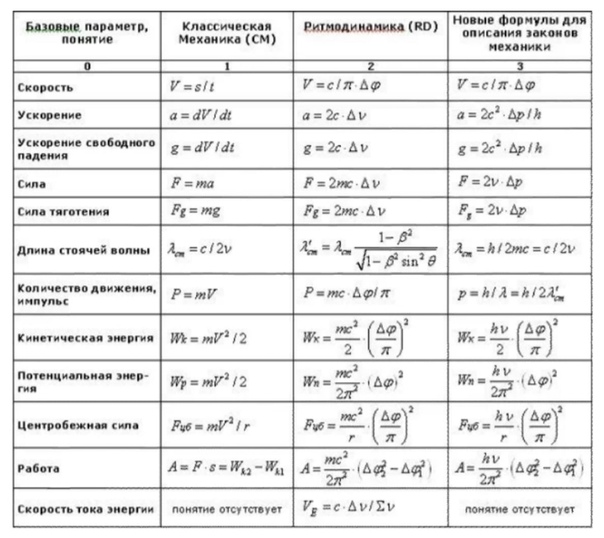 {2}=-10(2.3)$$

При решении уравнения (2.3) нам подойдет корень равный:

$$t_{3}=5+6=11 (c)$$

Ответ. 1) $x=0 \mathrm{~m}$ 2) $t_{1}=8,8 \mathrm{c}, t_{2}=1,13 c, t_{3}=11 c$

Читать дальше: Формула средней скорости.

Формулы кинематики с пояснениями по физике / Блог :: Бингоскул

Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.

Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.

 

Путь, время, скорость

S=v *t

• S – путь
• v – скорость
• t – время

Равномерное движение

x=x_0 + v*t

• x – координата
• x₀ – начальная координата
• v – скорость
• t – время

Равномерно ускоренное движение:

ускорение

a=\frac { v – v_0 } { t }

• a – ускорение
• v – скорость
• v₀ – начальная скорость
• t – время

Равномерно ускоренное движение:

скорость

v=v_0 + at

• v – скорость
• v₀ – начальная скорость
• a – ускорение
• t – время

Равномерно ускоренное движение:

путь

S=vt + \frac { at^2 } { 2 }

• s – путь
• v – скорость
• t – время
• a – ускорение

Равномерно ускоренное движение:

координата

x=x_0 + vt + \frac { at^2 } { 2 }

• x – координата
• x₀ – начальная координата
• v – скорость
• t – время
• a – ускорение

Высота тела, брошенного вертикально вверх (вниз)

h=h_0 + v_ { 0 } t – \frac { gt^2 } { 2 }

• h – высота
• h₀ – начальная высота
• v₀ – начальная скорость
• t – время
• g – ускорение свободного падения

Скорость тела, брошенного вертикально вверх (вниз)

v=v_0 – gt

• v – скорость
• v₀ – начальная скорость
• g – ускорение свободного падения
• t – время

Скорость, ускорение, время

v=at

• v – скорость
• a – ускорение
• t – время

Скорость свободно падающего тела

v=gt

• v – скорость
• g – ускорение свободного падения
• t – время

Центростремительное ускорение

a=\frac { v^2 } { R }

• a – центростремительное ускорение
• v – скорость
• R – радиус

Угловая скорость

\omega=\frac { \phi } { t }

• ω – угловая скорость
• φ – угол
• t – время

Равномерное круговое движение

l=R\phi

• l – длина дуги окружности
• R – радиус
• φ – угол

Равномерное круговое движение: линейная скорость

v=R \omega

• v – линейная скорость
• R – радиус
• ω – угловая скорость

 

Период вращения

T=\frac { t } { N }

• T – период
• t – время
• N – число вращений

T=\frac { 2 \pi R } { v }

• T – период
• R – радиус
• v – линейная скорость

T=\frac { 2 \pi } { \omega }

• T – период
• ω – угловая скорость

Центростремительное ускорение

a=\frac { 4 \pi^ { 2 } R } { T^2 }

• a – центростремительное ускорение
• R – радиус
• T – период вращения

a=4 \pi^ { 2 } Rn^2

• a – центростремительное ускорение
• R – радиус
• n – частота вращения

Частота вращения

n=\frac { 1 } { T }

• n – частота вращения
• T – период вращения

Центростремительное ускорение

a=\omega ^ { 2 } R

• a – центростремительное ускорение
• ω – угловая скорость
• R – радиус

Дальность броска тела, брошенного под углом к горизонту

x=v_0t \cos(\alpha)

• x – координата (дальность)
• v₀ – начальная скорость
• t – время
• α – угол

Высота подъема тела, брошенного под углом к горизонту

y=v_0t \sin (\alpha) – \frac { gt^2 } { 2 }

• y – координата (высота подъема )
• v₀ – начальная скорость
• t – время
• g – ускорение свободного падения
• α – угол

Вертикальная скорость тела, брошенного под углом к горизонту

v_y=v_0* \sin (\alpha) – gt

• v_y – вертикальная скорость
• v₀ – начальная скорость
• α – угол
• g – ускорение свободного падения
• t – время

Максимальная высота подъема тела, брошенного под углом к горизонту

h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }

• h_макс – максимальная высота
• v₀ – начальная скорость
• α – угол
• g – ускорение свободного падения

Общее время движения тела, брошенного под углом к горизонту

t=\frac { 2v_0 * \sin (\alpha) } { g }

• t – время
• v₀ – начальная скорость
• α – угол
• g – ускорение свободного падения

Дальность броска тела, брошенного горизонтально

x=x_0 + vt

• x – координата (дальность)
• x₀ – начальная координата
• v – скорость
• t – время

Высота подъема тела, брошенного горизонтально

y=y_0 – \frac { gt^2 } { 2 }

• y – координата (высота подъема)
• y₀ – начальная координата (высота)
• g – ускорение свободного падения
• t – время

Общее время движения тела, брошенного горизонтально

t_max=\sqrt { \frac { 2h } { g } }

• t_макс – максимальное время
• h – высота
• g – ускорение свободного падения

---

Смотри также:

Основные формулы молекулярной физики – материалы для подготовки к ЕГЭ по Физике

Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

В кодификаторе ЕГЭ нет тем, непосредственно относящихся к содержанию данного листка. Однако без этого вводного материала дальнейшее изучение молекулярной физики невозможно.

Введём основные величины молекулярной физики и соотношения между ними.

— масса вещества, — объём вещества, — плотность вещества (масса единицы объёма). Отсюда

— число частиц вещества (атомов или молекул).
— масса частицы вещества. Тогда

— концентрация вещества (число частиц в единице объёма), . Отсюда

Что получится, если умножить на ? Произведение массы частицы на число частиц в единице объёма даст массу единицы объёма, т. е. плотность. Формально:

Итак,

Массы и размеры частиц невообразимо малы по нашим обычным меркам. Например, масса атома водорода порядка г, размер атома порядка см. Из-за столь малых значений масс и размеров число частиц в макроскопическом теле огромно.

Оперировать столь грандиозными числами, как число частиц, неудобно. Поэтому для измерения количества вещества используют специальную единицу — моль.

Один моль — это количество вещества, в котором содержится столько же атомов или молекул, сколько атомов содержится в граммах углерода. А в граммах углерода содержится примерно атомов. Стало быть, в одном моле вещества содержится частиц. Это число называется постоянной Авогадро: моль.

Количество вещества обозначается . Это число молей данного вещества.

Что получится, если умножить на ? Число молей, умноженное на число частиц в моле, даст общее число частиц:

Масса одного моля вещества называется молярной массой этого вещества и обозначается ( = кг/моль). Ясно, что

Как найти молярную массу химического элемента? Оказывается, для этого достаточно заглянуть в таблицу Менделеева! Нужно просто взять атомную массу (число нуклонов) данного элемента — это будет его молярная масса, выраженная в г/моль. Например, для алюминия , поэтому молярная масса алюминия равна г/моль или кг/моль.

Почему так получается? Очень просто. Молярная масса углерода равна г/моль по определению. В то же время ядро атома углерода содержит нуклонов. Выходит, что каждый нуклон вносит в молярную массу г/моль. Поэтому молярная масса химического элемента с атомной массой оказывается равной г/моль.

Молярная масса вещества, молекула которого состоит из нескольких атомов, получается простым суммированием молярных масс. Так, молярная масса углекислого газа равна г/моль кг/моль.

Будьте внимательны с молярными массами некоторых газов! Так, молярная масса газообразного водорода равна г/моль, поскольку его молекула состоит из двух атомов . То же касается часто встречающихся в задачах азота и кислорода Вместе с тем, наиболее частый персонаж задач — гелий — является одноатомным газом и имеет молярную массу г/моль, предписанную таблицей Менделеева.

Ещё раз предостережение: при расчётах не забывайте переводить молярную массу в кг/моль! Если ваш ответ отличается от правильного на три порядка, то вы наверняка сделали именно эту, очень распространённую ошибку 🙂

Что получится, если умножить на ? Масса частицы, умноженная на число частиц в моле, даст массу моля, т. 2/2.

Скорость и ускорение в “современной” физике.
1. Общее для теоретической физики.
Для запутывания физики научная мафия делает всё возможное. Самый приглянувшийся ей путь – это как можно больше применять математику, но не для конкретных расчётов, собственно, для чего и нужна математика, а для манипулирования буквенными обозначениями. Будет это иметь физический смысл или нет их это не интересует. А школьники и студенты пускай зубрят то, что будет в учебниках.
С помощью математики (математического алгоритма) доказать ничего невозможно. С помощью математики можно только произвести конкретные расчёты. Доказать что-то в физике можно только с помощью эксперимента. Однако и тут могут подстерегать неприятности. Как показывает практика эксперименты не всегда честные, да и объяснения (трактовка) производится под ”нужную“ теорию.
2. Теперь конкретно о скорости и ускорении.
Все думают, что понимают, что такое скорость и ускорение. Сейчас проверим.
При выводе формулы E=mV^2/2 использовалась ошибочная формула a=V/t,
где V – скорость, а t – время. 2
Формула a=V/t ошибочна. Она не имеет физического смысла.
Ускорение – это характеристика скорости на каком-то определённом участке пути. Вот как выглядит формула для ускорения a=(Vк-Vн)/t. Формула a=V/t не имеет физического смысла.
Скорость – это усреднённая характеристика и, соответственно, постоянная величина.
Представьте себе, что машина или поезд едут со скоростью V=70км/час.
Если Вы поделите скорость V=70км/час на время t то:
— во-первых, что Вы хотите этим узнать?
— во-вторых, на какую величину времени t=? Вы собираетесь делить?
— в-третьих, формула a=V/t не имеет физического смысла.
Вы представляете, какая чушь получается, когда, не думая, применяют математику в виде буквенных обозначений. Ведь математика – это наука для конкретных расчётов, а не для манипулирования буквенными обозначениями физических величин.
Итак, Вы поняли отличие ошибочной формулы a=V/t от правильной формулы для ускорения
a=(Vк-Vн)/t,
где a – ускорение,
Vк – конечная скорость,
Vн – начальная скорость. 2/2, у которой всё перепутано (энергия, мощность и размерность).
Что из рассмотренного примера получается?
Оказывается, что выражение dV/dt также не имеет физического смысла.
Скорость величина постоянная, а дифференциал от постоянной величины будет ноль.
Представляете сколько разного рода чепухи горе-физики-математики нагородили в бедной теоретической физике, дифференцируя скорость.
Теперь задумайтесь над причиной: почему Вы этого не замечали?

Используемые источники:
1. Николаев С.А. “Эволюционный круговорот материи во Вселенной”. 6-ое издание,
СПб, 2010 г., 320 с.
2. Николаев С.А. ”Ошибочный перевод Эйлера законов Ньютона“. СПб, 2011 г., 44

09.09.2017

Вы уверены, что хотите удалить вашу публикацию?

Все права на эту публикацую принадлежат автору и охраняются законом.

Kinematic Equations Formula

Кинематика – это исследование движущихся объектов и их взаимосвязей. Существует четыре (4) кинематических уравнения, которые относятся к смещению, D, скорости, v, времени, t и ускорению, a.

a) D = v _i t + 1/2 при ² b) (v _i + v _f ) / 2 = D / t

c) a = (v _f – v _i ) / t d) v _f ² = v _i ² + 2aD

D = смещение

a = ускорение

t = время

v _f = конечная скорость

v _i = начальная скорость

Формула кинематических уравнений.

1) Боб едет на велосипеде в магазин со скоростью 4 м / с, когда перед ним выбегает кошка. Он быстро тормозит до полной остановки, с ускорением – 2м / с ² . Какое у него перемещение?

Ответ: Поскольку Боб остановлен, конечная скорость v _f = 0. Его начальная скорость v _i = 4 м / с. Ускорение, a = -2 м / с ² . Время не указано, поэтому используйте уравнение (d) для смещения D, потому что оно не зависит от времени.

v _f ² = v _i ² + 2aD

(0) ² = (4 м / с) ² +2 (- 2 м / с ² ) D

0 = 16 м ² / с ² + (- 4 м / с ² ) D

-16 м ² / с ² = (- 4 м / с ² ) D

16 м ² / с ² = 4 м / с ² ) D

(16 м ² / с ² ) / (4 м / с ² ) = D

Водоизмещение полное 4 м.

2) Вы путешествуете с постоянной скоростью 11 м / с в течение 5 минут. Как далеко вы уехали?

Ответ: При постоянной скорости v _i = v _f = 11 м / с. Время t = 5 мин или t = (60 сек / мин x 5 мин) = 300 сек. Теперь используйте уравнение (b), чтобы найти смещение D.

(v _i + v _f ) / 2 = D / t

D = [(v _i + v _f ) / 2] t

D = [(11 м / с + 11 м / с) / 2] x 300 с

D = (22 м / с) / 2 x 300 с

D = 11 м / с x 300 с

D = 3,300 м. Водоизмещение полное 3,300 м.

3) Каково ускорение автомобиля, который разгоняется с 11 до 40 м / с за 10 секунд?

Ответ: V _i = 11 м / с. V _f = 40 м / с. Время, t = 10 с. Используйте кинематическое уравнение c), чтобы найти ускорение.

a = (v _f – v _i ) / t

a = (40 м / с – 11 м / с) / 10 с

a = (29 м / с) / 10 с = 2,9 м / с ²

4) Если автомобиль разгоняется на 3.0 м / с ² от полной остановки, сколько времени потребуется, чтобы проехать 3000 м?

Ответ: Ускорение a = 2,9 м / с ² и перемещение D = 3000 м. Автомобиль был неподвижен, поэтому v _i = 0. Используйте уравнение a), чтобы найти время.

D = v _i t + 1/2 при ²

3000 м = 0т + 1/2 (3,0 м / с ² ) т ²

3000 м = 1/2 (3,0 м / с ² ) / т ²

3000 м / 1. 5 м / с ² = t ²

2000 с ² = t ²

t = 44,72 с

Кинематические уравнения

Целью этого первого раздела “Класса физики” было исследование разнообразных средств, с помощью которых можно описать движение объектов. Разнообразие представлений, которые мы исследовали, включает вербальные представления, графические представления, числовые представления и графические представления (графики положения-времени и графики скорости-времени).В Уроке 6 мы исследуем использование уравнений для описания и представления движения объектов. Эти уравнения известны как кинематические уравнения.

Существует множество величин, связанных с движением объектов: смещение (и расстояние), скорость (и скорость), ускорение и время. Знание каждой из этих величин дает описательную информацию о движении объекта. Например, если известно, что автомобиль движется с постоянной скоростью 22.0 м / с, север в течение 12,0 секунд для смещения на север 264 метра, затем движение автомобиля полностью описывается. И если известно, что вторая машина ускоряется из положения покоя с ускорением на восток 3,0 м / с ² в течение 8,0 секунд, обеспечивая конечную скорость 24 м / с, восток и смещение на восток 96 метров. , то полностью описывается движение этой машины. Эти два утверждения обеспечивают полное описание движения объекта. Однако не всегда такая полнота известна.Часто бывает так, что известно лишь несколько параметров движения объекта, а остальные неизвестны. Например, приближаясь к светофору, вы можете узнать, что ваша машина имеет скорость 22 м / с, восток и способна к заносу до 8,0 м / с ² , запад. Однако вы не знаете, какое смещение испытает ваша машина, если вы нажмете на тормоз и резко остановитесь; и вы не знаете, сколько времени потребуется, чтобы остановиться. В таком случае неизвестные параметры могут быть определены с использованием физических принципов и математических уравнений (кинематических уравнений).

БОЛЬШОЙ 4

Кинематические уравнения – это набор из четырех уравнений, которые можно использовать для прогнозирования неизвестной информации о движении объекта, если известна другая информация. Уравнения можно использовать для любого движения, которое можно описать как движение с постоянной скоростью (ускорение 0 м / с / с) или движение с постоянным ускорением. Их нельзя использовать в течение любого периода времени, в течение которого изменяется ускорение.Каждое из кинематических уравнений включает четыре переменные. Если известны значения трех из четырех переменных, то можно рассчитать значение четвертой переменной. Таким образом, кинематические уравнения предоставляют полезные средства прогнозирования информации о движении объекта, если известна другая информация. Например, если известно значение ускорения, а также начальное и конечное значения скорости буксирующего автомобиля, то смещение автомобиля и время можно предсказать с помощью кинематических уравнений.Урок 6 этого модуля будет посвящен использованию кинематических уравнений для прогнозирования числовых значений неизвестных величин для движения объекта.

Четыре кинематических уравнения, описывающие движение объекта:

В приведенных выше уравнениях используются различные символы. Каждый символ имеет свое особое значение. Символ d обозначает смещение объекта. Символ t обозначает время, в течение которого объект двигался.Символ a обозначает ускорение объекта. А символ v обозначает скорость объекта; индекс i после v (как в v _i ) указывает, что значение скорости является начальным значением скорости, а индекс f (как в v _f ) указывает, что значение скорости является окончательным значением скорости.

Каждое из этих четырех уравнений надлежащим образом описывает математическую связь между параметрами движения объекта. Таким образом, они могут использоваться для прогнозирования неизвестной информации о движении объекта, если известна другая информация.В следующей части Урока 6 мы исследуем, как это сделать.

Основы – Простые принципы движения

Расстояние обычно измеряется в метрах (единицы СИ) и часто отображается переменной d .
Время обычно измеряется в секундах и представлено переменной t .
Скорость обычно измеряется в метрах в секунду (м / с) и представляется как v .
Я использую Vi и Vf для обозначения начальной и конечной скорости соответственно.
Помните, что переменные могут быть представлены любой комбинацией букв, они просто названия количеств, например d = 55 м, d = 0,3 см, картофель = 43 м, начальное время = 4 с.

Во всех случаях движение измеряется от «контрольной точки», если вы измеряете расстояние вы идете в школу из дома, вы будете измерять от своего дома – это ориентир В данном случае это точка, с которой вы начинаете измерение.

Международные единицы измерения

При выполнении физических расчетов всегда следует использовать аналогичные типы измерения в тех же единицах. Если вы выполняете расчет с двумя массами которые весят 2 кг и 2000 г, вы должны преобразовать их обоих в один тип устройства, либо перевести их в килограммы или перевести в граммы. Не смешивайте единицы измерения.

Единицы

СИ (международный стандарт) – это специальные условные обозначения для измерения, которые упрощают физические расчеты значительно.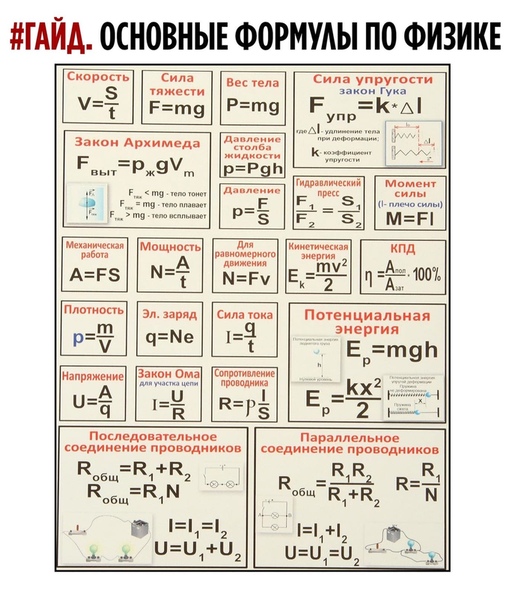 Метр, секунда и килограмм – единицы СИ. если ты Выполните расчет с использованием указанных выше стандартных единиц, которые вы сможете использовать в своих единицы ответа по псевдониму, например 88 кг / м / с² превращается в 88 «Ньютонов».

Кинематике и движению не хватает компактных сокращений для единиц, которые вы, тем не менее, должны по возможности используйте единицы СИ (м, кг, с). Если вы не используете единицы СИ, убедитесь, что что ваши измерения все в тех единицах, которые вы используете.

Основные уравнения

Физика в значительной степени математика.При решении задачи, связанной с физикой вам нужно будет преобразовать слова и события в математические понятия, это преобразование приводит к уравнению.

Скорость Скорость – это скорость изменения расстояния. Сколько единиц расстояния пройдено за каждую единицу времени?
скорость = расстояние / время
v = d / t

Давайте сделаем пример:

Автомобиль проехал 50 км за 120 минут, сохраняя постоянную скорость. Какая у него была скорость? Прежде чем мы начнем решать скорость, нам нужно преобразовать наши единицы в полезные форма.Скорость автомобиля обычно выражается в км / ч, нам нужно преобразовать время поездки в часы. Делаем это делением на 60, 120/60 = 2 часа. Давайте объявим наши переменные
d = 50 км
t = 2h
v =? км / ч Скорость такая «сколько километров пройдено за час» и мы подходим с уравнением для моделирования: v = d / t
Мы вводим наши значения в уравнение:
v = 50/2
v = 25 км / ч Мы всегда формулируем ответ на вопрос в предложении.
«Скорость автомобиля во время поездки составляла 25 км / ч».

Разгон Ускорение – это скорость изменения скорости, как скорость отличается в один момент. к следующему.
ускорение = скорость / время
a = v / t

Кроме того, общее ускорение широко рассматривается как final speed – начальная скорость, деленная на время. Это полезный способ моделировать ускорение, потому что объект мог уже двигаться до начала ускоряется.
a = ( Vfinal – Vinitial ) / т

Пример

Автомобиль разгоняется до 60 км / ч за 6,2 секунды, каково его среднее ускорение? Преобразуйте все измерения в метры и секунды, чтобы избежать путаницы и / или неудобный результат. t = 6,2 с
Vinitial = 0 м / с
Vfinal = 16,6 м / с
a =? м / с² a = 16,6 / 6,2
= 2,677 м / с² Нам нужно округлить ответ до двух значащих цифр (какие значащие цифры?) поэтому наш словесный ответ будет: «Автомобиль ускоряется со скоростью 2.7 м / с² ”

Заключение

Этот раздел веб-сайта служит «напоминанием», если вы не понимаете концепции, изложенные в этом раздел вам следует перечитать материал класса, проконсультироваться с преподавателем или на другом сайте. Этот сайт полагается сильно зависит от вашего понимания всех концепций, содержащихся в этом разделе.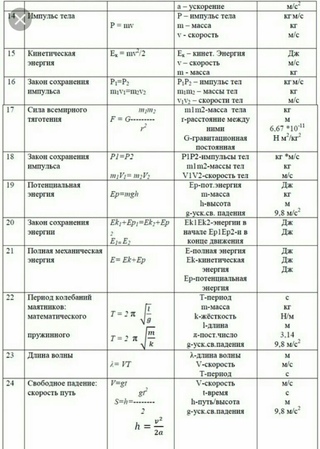

3.4 Движение с постоянным ускорением – University Physics Volume 1

Учебные цели

К концу этого раздела вы сможете:

• Определите, какие уравнения движения следует использовать для решения неизвестных.
• Используйте соответствующие уравнения движения для решения задачи преследования двух тел.

Можно предположить, что чем больше ускорение, скажем, у автомобиля, удаляющегося от знака «Стоп», тем больше смещение автомобиля за данный момент времени. Но мы не разработали конкретное уравнение, которое связывает ускорение и смещение. В этом разделе мы рассмотрим некоторые удобные уравнения кинематических отношений, начиная с определений смещения, скорости и ускорения.Сначала мы исследуем движение одного объекта, называемого движением одного тела. Затем мы исследуем движение двух объектов, называемое задачами преследования двух тел.

Обозначение

Сначала сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Поскольку прошедшее время равно Δt = tf − t0Δt = tf − t0, принятие t0 = 0t0 = 0 означает, что Δt = tfΔt = tf, последнее время на секундомере. Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости.То есть x0x0 – это начальная позиция , а v0v0 – начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t – это конечный момент времени , x – конечная позиция , а v – конечная скорость . Это дает более простое выражение для истекшего времени: Δt = tΔt = t. Это также упрощает выражение для смещения x , которое теперь равно Δx = x − x0Δx = x − x0. Кроме того, это упрощает выражение для изменения скорости, которое теперь равно Δv = v − v0Δv = v − v0. Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,

Δt = tΔx = x − x0Δv = v − v0, Δt = tΔx = x − x0Δv = v − v0,

, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает конечное значение в любом рассматриваемом движении.

Теперь мы делаем важное предположение, что ускорение постоянно . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорение равны, то есть

a– = a = постоянная.a– = a = постоянная.

Таким образом, мы можем использовать символ a для ускорения в любое время. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучать, и не ухудшает точность нашего лечения. Во-первых, ускорение равно постоянным в большом количестве ситуаций. Более того, во многих других ситуациях мы можем точно описать движение, предполагая постоянное ускорение, равное среднему ускорению для этого движения. Наконец, для движения, во время которого ускорение резко изменяется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до полной остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.

Смещение и положение от скорости

Чтобы получить наши первые два уравнения, мы начнем с определения средней скорости:

Замена упрощенных обозначений для ΔxΔx и ΔtΔt дает

v– = x − x0t.v– = x − x0t.

Решение относительно x дает нам

x = x0 + v – t, x = x0 + v – t,

3,10

, где средняя скорость

v– = v0 + v2.v– = v0 + v2.

3,11

Уравнение v– = v0 + v2v– = v0 + v2 отражает тот факт, что при постоянном ускорении v – v– представляет собой простое среднее значение начальной и конечной скоростей. Рисунок 3.18 графически иллюстрирует эту концепцию. В части (а) рисунка ускорение является постоянным, а скорость увеличивается с постоянной скоростью. Средняя скорость в течение 1-часового интервала от 40 км / ч до 80 км / ч составляет 60 км / ч:

v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч v– = v0 + v2 = 40 км / ч + 80 км / ч3 = 60 км / ч.

В части (b) ускорение непостоянно. В течение 1-часового интервала скорость ближе к 80 км / ч, чем к 40 км / ч. Таким образом, средняя скорость больше, чем в части (а).

Рис. 3.18 (a) График зависимости скорости от времени с постоянным ускорением, показывающий начальную и конечную скорости v0andvv0andv.Средняя скорость равна 12 (v0 + v) = 60 км / ч 22 (v0 + v) = 60 км / ч. (б) График зависимости скорости от времени с изменением ускорения со временем. Средняя скорость не равна 12 (v0 + v) 12 (v0 + v), но превышает 60 км / ч.

Решение для окончательной скорости по ускорению и времени

Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения:

Подстановка упрощенных обозначений для ΔvΔv и ΔtΔt дает

a = v − v0t (константа). a = v − v0t (константа).

Решение для v дает

v = v0 + at (constanta). v = v0 + at (constanta).

3,12

Пример 3,7

Расчет конечной скорости

Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с ² в течение 40,0 с. Какова его конечная скорость?

Стратегия

Сначала мы идентифицируем известные: v0 = 70 м / с, a = -1,50 м / с2, t = 40sv0 = 70 м / с, a = -1,50 м / с2, t = 40 с.

Во-вторых, мы идентифицируем неизвестное; в данном случае это конечная скорость vfvf.

Наконец, мы определяем, какое уравнение использовать. Для этого мы выясняем, какое кинематическое уравнение дает неизвестное в терминах известных. Мы вычисляем конечную скорость, используя уравнение 3.12, v = v0 + atv = v0 + at.

Решение

Подставьте известные значения и решите: v = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / сv = v0 + при = 70,0 м / с + (- 1,50 м / с2) (40,0 с) = 10,0 м / с.

Рисунок 3.19 представляет собой эскиз, показывающий векторы ускорения и скорости.

Рис. 3.19 Самолет приземляется с начальной скоростью 70.0 м / с и замедляется до конечной скорости 10,0 м / с, прежде чем направиться к терминалу. Обратите внимание, что ускорение отрицательное, потому что его направление противоположно его скорости, которая положительна.

Значение

Конечная скорость намного меньше начальной скорости, требуемой при замедлении, но все же положительная (см. Рисунок). В реактивных двигателях обратная тяга может поддерживаться достаточно долго, чтобы самолет остановился и начал движение назад, на что указывает отрицательная конечная скорость, но в данном случае это не так.

Уравнение v = v0 + atv = v0 + at не только полезно при решении задач, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем. Мы видим, например, что

• Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
• Если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀ ), как и ожидалось (другими словами, скорость постоянна)
• Если a отрицательное, то конечная скорость меньше начальной скорости

Все эти наблюдения соответствуют нашей интуиции. Обратите внимание, что всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.

Решение для конечного положения с постоянным ускорением

Мы можем объединить предыдущие уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. Начнем с

Добавление v0v0 к каждой стороне этого уравнения и деление на 2 дает

v0 + v2 = v0 + 12at.v0 + v2 = v0 + 12at.

Поскольку v0 + v2 = v – v0 + v2 = v– для постоянного ускорения, имеем

v– = v0 + 12at.v– = v0 + 12at.

Теперь мы подставляем это выражение для v – v– в уравнение для смещения, x = x0 + v – tx = x0 + v – t, что дает

x = x0 + v0t + 12at2 (константа). x = x0 + v0t + 12at2 (константа).

3,13

Пример 3.8

Расчет смещения ускоряющегося объекта

Драгстеры могут развивать среднее ускорение 26,0 м / с ² . Предположим, драгстер ускоряется из состояния покоя на 5.56 с Рисунок 3.20. Как далеко он пролетит за это время?

Рисунок 3.20. Пилот Top Fuel американской армии Тони «Сержант» Шумахер начинает гонку с контролируемого выгорания. (Источник: подполковник Уильям Термонд. Фотография предоставлена ​​армией США)

Стратегия

Сначала нарисуем эскиз, рис. 3.21. Нас просят найти смещение, которое составит x , если мы примем x0x0 равным нулю. (Думайте о x0x0 как о стартовой линии гонки. Она может быть где угодно, но мы называем ее нулевой и измеряем все остальные позиции относительно нее.) Мы можем использовать уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2, когда мы идентифицируем v0v0, aa и t из постановки задачи.

Рис. 3.21. Эскиз разгоняющегося драгстера.

Решение

Во-первых, нам нужно определить известные. Запуск из состояния покоя означает, что v0 = 0v0 = 0, a задается как 26,0 м / с ² и t задается как 5,56 с.

Во-вторых, мы подставляем известные значения в уравнение, чтобы найти неизвестное:

х = х0 + v0t + 12at2.х = х0 + v0t + 12at2.

Поскольку начальное положение и скорость равны нулю, это уравнение упрощается до

Подстановка идентифицированных значений на и t дает

x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м. x = 12 (26,0 м / с2) (5,56 с) 2 = 402 м.

Значение

Если мы переведем 402 м в мили, мы обнаружим, что пройденное расстояние очень близко к четверти мили, стандартному расстоянию для дрэг-рейсинга. Итак, наш ответ разумный. Это впечатляющий объем, который можно покрыть всего за 5.56 с, но первоклассные драгстеры могут проехать четверть мили даже за меньшее время. Если бы драгстеру была присвоена начальная скорость, это добавило бы еще один член в уравнение расстояния. Если в уравнении использовать те же ускорение и время, пройденное расстояние будет намного больше.

Что еще мы можем узнать, исследуя уравнение x = x0 + v0t + 12at2? X = x0 + v0t + 12at2? Мы видим следующие отношения:

• Смещение зависит от квадрата прошедшего времени, когда ускорение не равно нулю. В примере 3.8 драгстер преодолевает только четверть общего расстояния за первую половину прошедшего времени.
• Если ускорение равно нулю, то начальная скорость равна средней скорости (v0 = v -) (v0 = v–), и x = x0 + v0t + 12at2becomesx = x0 + v0t.x = x0 + v0t + 12at2becomesx = x0 + v0t.

Расчет конечной скорости на основе расстояния и ускорения

Четвертое полезное уравнение может быть получено путем другой алгебраической обработки предыдущих уравнений. Если мы решим v = v0 + atv = v0 + at для t , мы получим

Подставляя это и v– = v0 + v2v– = v0 + v2 в x = x0 + v – tx = x0 + v – t, получаем

v2 = v02 + 2a (x − x0) (константа).v2 = v02 + 2a (x − x0) (константа).

3,14

Пример 3.9

Расчет конечной скорости

Рассчитайте окончательную скорость драгстера в Примере 3.8 без использования информации о времени.

Стратегия

Уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) идеально подходит для этой задачи, поскольку оно связывает скорости, ускорение и смещение и не требует информации о времени.

Решение

Сначала мы идентифицируем известные значения. Мы знаем, что v ₀ = 0, поскольку драгстер запускается из состояния покоя.Мы также знаем, что x – x ₀ = 402 м (это был ответ в примере 3.8). Среднее ускорение равнялось a = 26,0 м / с ² .

Во-вторых, мы подставляем известные в уравнение v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) и решаем относительно v :

v2 = 0 + 2 (26,0 м / с2) (402 м). v2 = 0 + 2 (26,0 м / с2) (402 м).

Таким образом,

v2 = 2,09 × 104 м2 / с2 v = 2,09 × 104 м2 / с2 = 145 м / с. v2 = 2,09 × 104 м2 / с2v = 2,09 × 104 м2 / с2 = 145 м / с.

Значение

Скорость 145 м / с составляет около 522 км / ч, или около 324 миль / ч, но даже эта головокружительная скорость отстает от рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.

Изучение уравнения v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0) может дать дополнительное понимание общих соотношений между физическими величинами:

• Окончательная скорость зависит от того, насколько велико ускорение и от расстояния, на котором оно действует.
• При фиксированном ускорении автомобиль, который едет вдвое быстрее, просто не останавливается на удвоенном расстоянии.Чтобы остановиться, нужно гораздо дальше. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)

Объединение уравнений

В следующих примерах мы продолжаем исследовать одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций. Примеры также дают представление о методах решения проблем. Следующее примечание предназначено для облегчения поиска необходимых уравнений. Имейте в виду, что эти уравнения не являются независимыми. Во многих ситуациях у нас есть два неизвестных, и нам нужно два уравнения из набора для решения для неизвестных.Для решения данной ситуации нам нужно столько уравнений, сколько неизвестных.

Сводка кинематических уравнений (константа

a ) х = х0 + v0t + 12at2x = x0 + v0t + 12at2 v2 = v02 + 2a (x − x0) v2 = v02 + 2a (x − x0)

Прежде чем мы перейдем к примерам, давайте более внимательно рассмотрим некоторые уравнения, чтобы увидеть поведение ускорения при экстремальных значениях. Переставляя уравнение 3.12, получаем

Из этого мы видим, что в течение конечного времени, если разница между начальной и конечной скоростями мала, ускорение невелико и приближается к нулю в том пределе, когда начальная и конечная скорости равны.Напротив, в пределе t → 0t → 0 при конечной разности начальной и конечной скоростей ускорение становится бесконечным.

Аналогичным образом, преобразовав уравнение 3. 14, мы можем выразить ускорение в терминах скоростей и смещения:

а = v2-v022 (х-х0). а = v2-v022 (х-х0).

Таким образом, при конечной разнице между начальной и конечной скоростями ускорение становится бесконечным, в пределе смещение приближается к нулю. Ускорение приближается к нулю в пределе, разница в начальной и конечной скоростях приближается к нулю для конечного смещения.

Пример 3.10

Как далеко уезжает машина?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с ² , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м / с ² . Найдите расстояния, необходимые для остановки автомобиля, движущегося со скоростью 30,0 м / с (около 110 км / ч) по (а) сухому бетону и (б) мокрому бетону. (c) Повторите оба вычисления и найдите смещение от точки, где водитель видит, что светофор становится красным, учитывая время его реакции, равное 0.500 с, чтобы нажать на тормоз.

Стратегия

Для начала нам нужно нарисовать набросок Рис.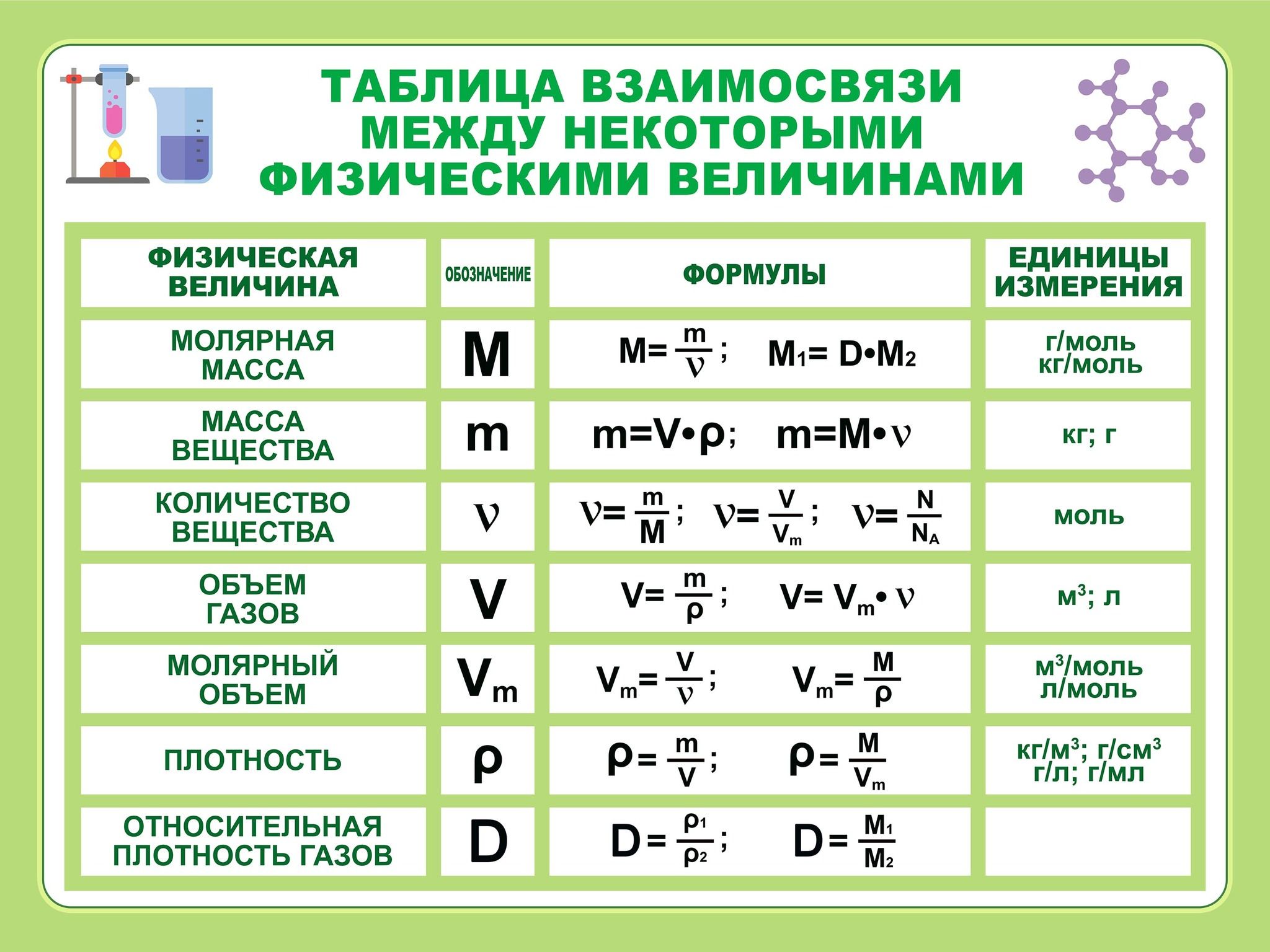 3.22. Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить.

Рис. 3.22. Пример эскиза для визуализации замедления и остановочного пути автомобиля.

Решение

1. Во-первых, нам нужно определить известные и то, что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с, v = 0 и a = −7.00 м / с ² ( и отрицательны, потому что они направлены в направлении, противоположном скорости). Возьмем x ₀ равным нулю. Ищем смещение ΔxΔx, или x – x ₀ .
   Во-вторых, мы определяем уравнение, которое поможет нам решить проблему. Лучшее уравнение для использования – v2 = v02 + 2a (x − x0). v2 = v02 + 2a (x − x0). Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении.(Другие уравнения позволили бы нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)
   В-третьих, мы изменим уравнение, чтобы найти x : x − x0 = v2 − v022ax − x0 = v2 − v022a и подставляем известные значения: x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). x − 0 = 02− (30,0 м / с) 22 (−7,00 м / с2). Таким образом, x = 64,3 м на сухом бетоне. x = 64,3 м на сухом бетоне.
2. Эта часть может быть решена точно так же, как (а).Единственное отличие состоит в том, что ускорение составляет −5,00 м / с ² . Результат xwet = 90,0 м по мокрому бетону. xwet = 90,0 м по мокрому бетону.
3. Когда водитель реагирует, тормозной путь такой же, как в пунктах (a) и (b) для сухого и влажного бетона. Итак, чтобы ответить на этот вопрос, нам нужно вычислить, как далеко проехал автомобиль за время реакции, а затем добавить это значение ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.
   Для этого мы снова определяем известные и то, что мы хотим решить.Мы знаем, что v– = 30,0 м / sv– = 30,0 м / с, treaction = 0,500streaction = 0,500s, а areaction = 0areaction = 0. Примем x0-responsex0-response равным нулю. Ищем xreactionxreaction.
   Во-вторых, как и раньше, мы определяем лучшее уравнение для использования. В этом случае x = x0 + v – tx = x0 + v – t работает хорошо, потому что единственное неизвестное значение – x , что мы и хотим найти.
   В-третьих, мы подставляем известные для решения уравнения: x = 0 + (30,0 м / с) (0,500 с) = 15,0 м. x = 0 + (30,0 м / с) (0,500 с) = 15,0 м.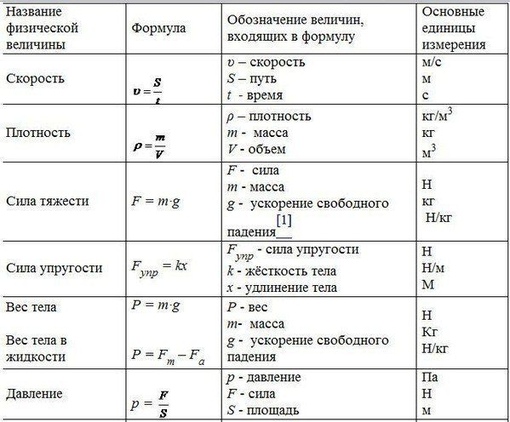 Это значит, что машина едет 15.0 м, в то время как водитель реагирует, в результате чего общее смещение в двух случаях с сухим и мокрым бетоном на 15,0 м больше, чем при мгновенной реакции.
   Наконец, мы добавляем смещение во время реакции к смещению при торможении (рисунок 3.23), xbraking + xreaction = xtotal, xbraking + xreaction = xtotal, и найдите (а) равным 64,3 м + 15,0 м = 79,3 м в сухом состоянии и (б) равным 90,0 м + 15,0 м = 105 м во влажном состоянии.

Рис. 3.23. Расстояние, необходимое для остановки автомобиля, сильно различается в зависимости от дорожных условий и времени реакции водителя.Здесь показан тормозной путь для сухой и мокрой дороги, рассчитанный в этом примере для автомобиля, движущегося со скоростью 30,0 м / с. Также показаны общие расстояния, пройденные от точки, когда водитель впервые видит, что свет загорается красным, при условии, что время реакции составляет 0,500 с.

Значение

Смещения, обнаруженные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.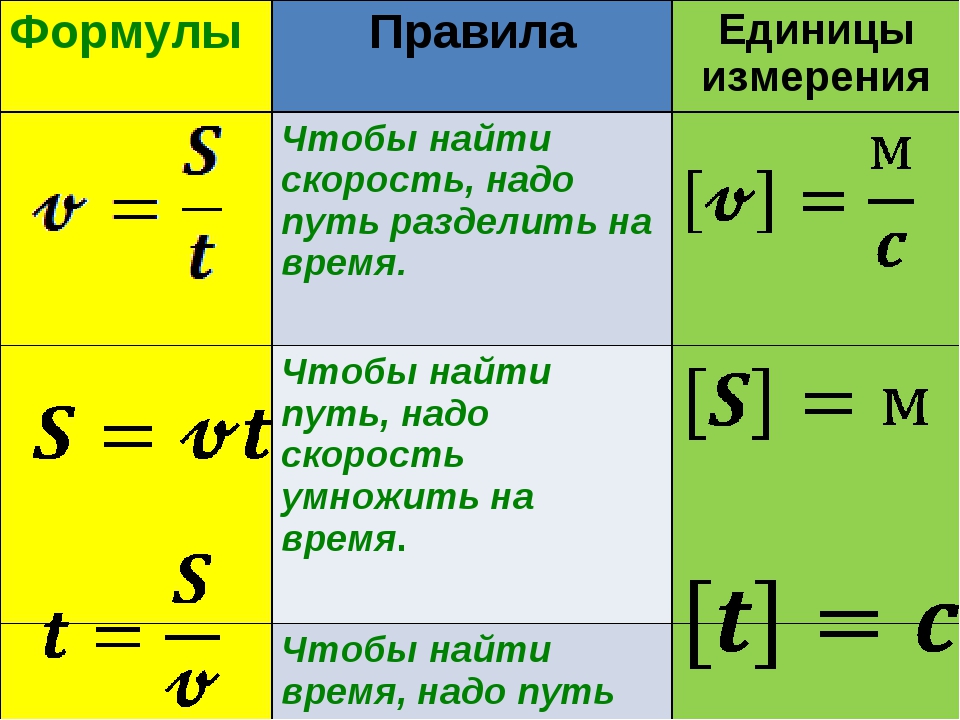 Остановка автомобиля на мокром асфальте должна длиться дольше, чем на сухом. Интересно, что время реакции значительно увеличивает смещения, но более важным является общий подход к решению проблем.Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Если существует более одного неизвестного, нам нужно столько независимых уравнений, сколько неизвестных необходимо решить. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но представленные здесь решения являются самыми короткими.

Пример 3.11

Расчет времени

Предположим, автомобиль въезжает в движение по автостраде на съезде длиной 200 м.Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с ² , сколько времени потребуется автомобилю, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)

Стратегия

Сначала мы рисуем набросок Рис. 3.24. Нам предлагается решить за время т . Как и прежде, мы идентифицируем известные величины, чтобы выбрать удобное физическое соотношение (то есть уравнение с одним неизвестным, t ).

Рис. 3.24. Эскиз автомобиля, ускоряющегося на съезде с автострады.

Решение

Опять же, мы определяем известные и то, что мы хотим решить. Мы знаем, что x0 = 0, x0 = 0,
v0 = 10 м / с, a = 2,00 м / с2v0 = 10 м / с, a = 2,00 м / с2 и x = 200 м.

Надо решить для т . Уравнение x = x0 + v0t + 12at2x = x0 + v0t + 12at2 работает лучше всего, потому что единственной неизвестной в уравнении является переменная t , которую нам нужно решить. Из этого понимания мы видим, что когда мы вводим известные значения в уравнение, мы получаем квадратное уравнение.

Нам нужно изменить уравнение, чтобы найти t , а затем подставив известные значения в уравнение:

200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2. 200 м = 0 м + (10,0 м / с) t + 12 (2,00 м / с2) t2.

Затем мы упрощаем уравнение. Единицы измерения отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = t s, где t – величина времени, а s – единица измерения. Остается

Затем мы используем формулу корней квадратного уравнения, чтобы найти t ,

t2 + 10t − 200 = 0t = −b ± b2−4ac2a, t2 + 10t − 200 = 0t = −b ± b2−4ac2a,

, что дает два решения: t = 10.0 и t = −20,0. Отрицательное значение времени неразумно, так как это означает, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,

Значение

Всякий раз, когда уравнение содержит неизвестный квадрат, есть два решения. В некоторых проблемах имеют смысл оба решения; в других случаях разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.

Проверьте свое понимание 3.5

Ракета ускоряется со скоростью 20 м / с. ² во время пуска.Сколько времени требуется ракете, чтобы достичь скорости 400 м / с?

Пример 3.12

Ускорение космического корабля

Космический корабль покинул орбиту Земли и направляется к Луне. Разгоняется со скоростью 20 м / с ² за 2 мин и преодолевает расстояние в 1000 км. Каковы начальная и конечная скорости космического корабля?

Стратегия

Нас просят найти начальную и конечную скорости космического корабля. Глядя на кинематические уравнения, мы видим, что одно уравнение не дает ответа.Мы должны использовать одно кинематическое уравнение для решения одной из скоростей и подставить его в другое кинематическое уравнение, чтобы получить вторую скорость. Таким образом, мы решаем два кинематических уравнения одновременно.

Решение

Сначала мы решаем для v0v0, используя x = x0 + v0t + 12at2: x = x0 + v0t + 12at2: x − x0 = v0t + 12at2x − x0 = v0t + 12at21.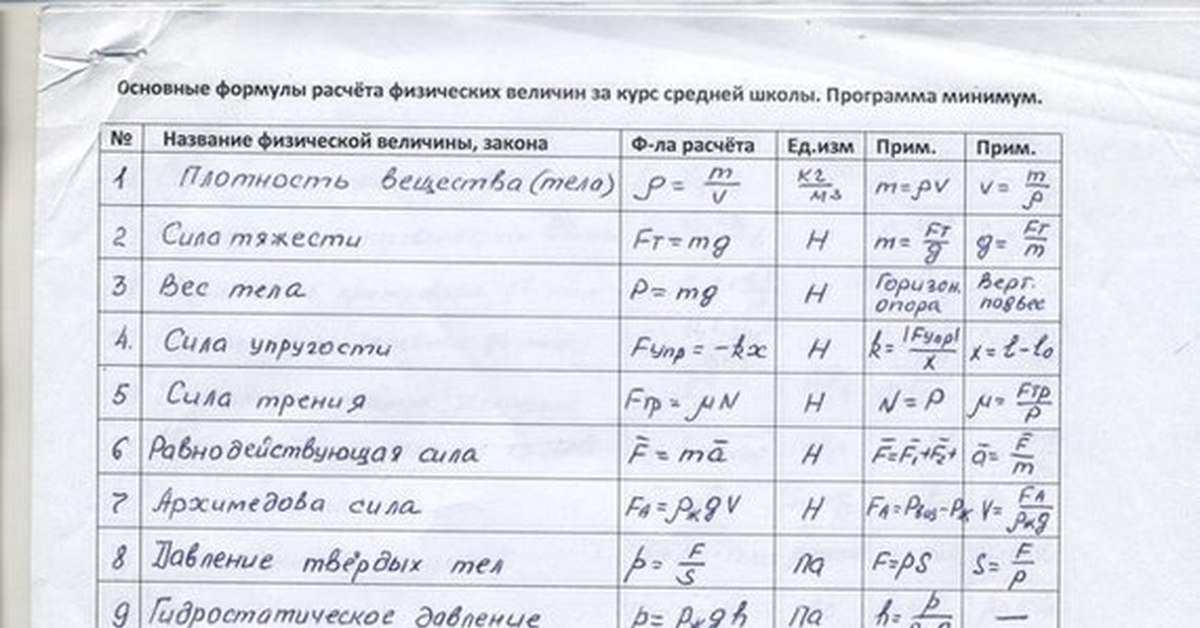 0 × 106m = v0 (120.0s) +12 (20,0 м / с2) (120,0 с) 21,0 × 106 м = v0 (120,0 с) +12 (20,0 м / с2) (120,0 с) 2v0 = 7133,3 м / с. V0 = 7133,3 м / с.

Затем мы подставляем v0v0 в v = v0 + atv = v0 + at, чтобы найти окончательную скорость:

v = v0 + at = 7133.3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с. V = v0 + at = 7133,3 м / с + (20,0 м / с2) (120,0 с) = 9533,3 м / с.

Значение

Есть шесть переменных смещения, времени, скорости и ускорения, которые описывают движение в одном измерении. Начальные условия данной задачи могут быть множеством комбинаций этих переменных. Из-за такого разнообразия решения могут быть не такими простыми, как простая подстановка в одно из уравнений. Этот пример показывает, что решения кинематики могут потребовать решения двух одновременных кинематических уравнений.

Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений.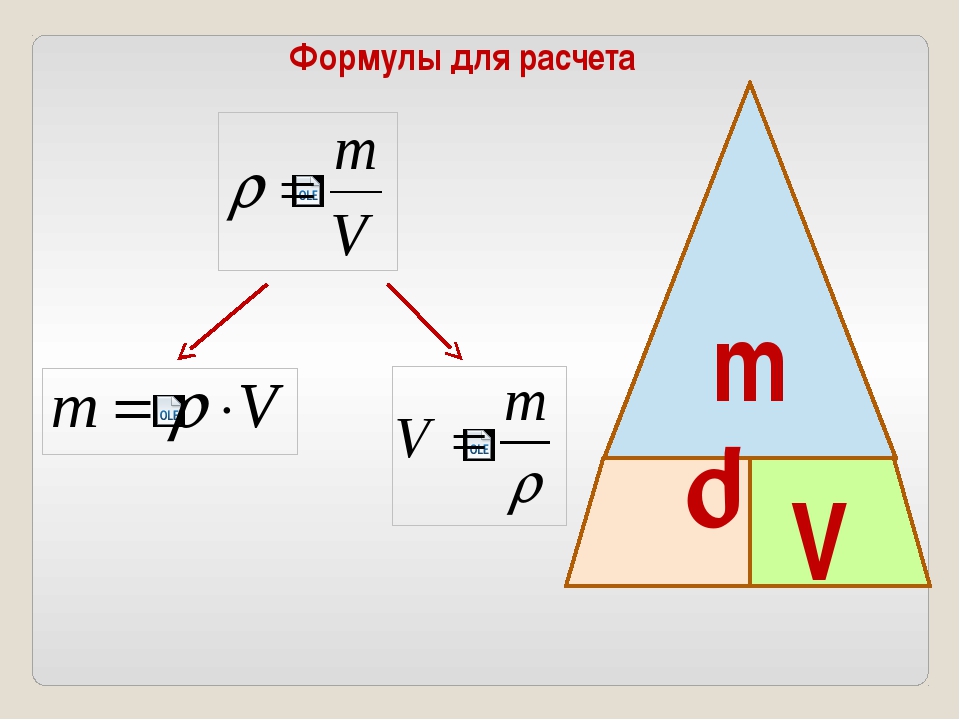 Следующий уровень сложности наших задач кинематики связан с движением двух взаимосвязанных тел, который называется задачами преследования двух тел .

Задачи преследования двух тел

До этого момента мы рассматривали примеры движения с участием одного тела.Даже для задачи с двумя автомобилями и тормозным путем на мокрой и сухой дороге мы разделили эту задачу на две отдельные задачи, чтобы найти ответы. В задаче преследования двух тел движения объектов связаны, то есть искомая неизвестная зависит от движения обоих объектов. Чтобы решить эти проблемы, мы пишем уравнения движения для каждого объекта, а затем решаем их одновременно, чтобы найти неизвестное. Это показано на рисунке 3.25.

Рис. 3.25. Сценарий преследования с двумя телами, в котором автомобиль 2 имеет постоянную скорость, а автомобиль 1 отстает с постоянным ускорением.Автомобиль 1 догонит автомобиль 2 позже.

Время и расстояние, необходимое для того, чтобы автомобиль 1 догнал автомобиль 2, зависят от начального расстояния, на которое автомобиль 1 находится от автомобиля 2, а также от скорости обоих автомобилей и ускорения автомобиля 1. Кинематические уравнения, описывающие движение обоих автомобилей, должны быть решил найти эти неизвестные.

Рассмотрим следующий пример.

Пример 3.13

Гепард ловит газель

Гепард прячется за кустом. Гепард замечает пробегающую мимо газель со скоростью 10 м / с.В тот момент, когда газель проходит мимо гепарда, гепард из состояния покоя ускоряется со скоростью 4 м / с ² , чтобы поймать газель. а) Сколько времени требуется гепарду, чтобы поймать газель? б) Что такое смещение газели и гепарда?

Стратегия

Мы используем систему уравнений для постоянного ускорения, чтобы решить эту проблему. Поскольку есть два движущихся объекта, у нас есть отдельные уравнения движения, описывающие каждое животное. Но то, что связывает уравнения, – это общий параметр, который имеет одинаковое значение для каждого животного.Если мы внимательно посмотрим на проблему, станет ясно, что общим параметром для каждого животного является их положение x , позднее t . Поскольку оба они начинаются в точке x0 = 0x0 = 0, их смещения будут такими же в более позднее время t , когда гепард догонит газель. Если мы выберем уравнение движения, которое решает проблему смещения для каждого животного, мы сможем приравнять уравнения друг к другу и решить неизвестное, то есть время.

Решение

1. Уравнение для газели: Газель имеет постоянную скорость, которая является ее средней скоростью, поскольку она не ускоряется.Поэтому мы используем уравнение 3.10 с x0 = 0x0 = 0: x = x0 + v – t = v – t. x = x0 + v – t = v – t. Уравнение для гепарда: гепард ускоряется из состояния покоя, поэтому мы используем уравнение 3.13 с x0 = 0x0 = 0 и v0 = 0v0 = 0: x = x0 + v0t + 12at2 = 12at2.x = x0 + v0t + 12at2 = 12at2. Теперь у нас есть уравнение движения для каждого животного с общим параметром, который можно исключить, чтобы найти решение. В этом случае мы решаем для t : x = v – t = 12at2t = 2v – a. x = v – t = 12at2t = 2v – a. Газель имеет постоянную скорость 10 м / с, что является ее средней скоростью.Ускорение гепарда составляет 4 м / с ² . Оценивая t , время, за которое гепард достигает газели, получаем t = 2v – a = 2 (10) 4 = 5s. T = 2v – a = 2 (10) 4 = 5s.
2. Чтобы получить смещение, мы используем уравнение движения гепарда или газели, поскольку оба они должны дать одинаковый ответ.
   Смещение гепарда: x = 12at2 = 12 (4) (5) 2 = 50м. X = 12at2 = 12 (4) (5) 2 = 50м. Водоизмещение газели: x = v – t = 10 (5) = 50 м. X = v – t = 10 (5) = 50 м. Мы видим, что оба смещения равны, как и ожидалось.

Значение

Важно анализировать движение каждого объекта и использовать соответствующие кинематические уравнения для описания отдельного движения. Также важно иметь хорошую визуальную перспективу задачи преследования двух тел, чтобы увидеть общий параметр, который связывает движение обоих объектов.

Проверьте свое понимание 3.6

Велосипед имеет постоянную скорость 10 м / с. Человек начинает с отдыха и бежит, чтобы догнать велосипед через 30 секунд, когда велосипед находится в том же положении, что и человек.Какое ускорение у человека?

уравнений движения для постоянного ускорения в одном измерении

Обозначение:

t , x , v , a

Сначала сделаем несколько упрощений в обозначениях. Принятие начального времени равным нулю, как если бы время измерялось секундомером, является большим упрощением. Так как прошедшее время Δ t = t _f – t ₀ , принимая t ₀ = 0 означает, что Δ t = t _f , последнее время на секундомер.Когда начальное время принимается равным нулю, мы используем индекс 0 для обозначения начальных значений положения и скорости. То есть x ₀ – это начальная позиция , а v ₀ – начальная скорость . Мы не ставим нижние индексы на окончательные значения. То есть t – это конечное время , x – конечное положение , а v – конечная скорость . Это дает более простое выражение для прошедшего времени – теперь Δ t = t .Это также упрощает выражение для смещения, которое теперь составляет Δ x = x – x ₀ . Кроме того, это упрощает выражение для изменения скорости, которое теперь составляет Δ v = v – v ₀ . Подводя итог, используя упрощенные обозначения, с начальным временем, принятым равным нулю,

[латекс] \ begin {case} {\ Delta} {t} & = & t \\ {\ Delta} {x} & = & x – {{x} _ {0}} \\ {\ Delta} { v} & = & v – {{v} _ {0}} \ end {case} [/ latex]

, где нижний индекс 0 обозначает начальное значение, а отсутствие нижнего индекса означает окончательное значение в любом рассматриваемом движении.

Теперь мы делаем важное предположение, что ускорение является постоянным . Это предположение позволяет нам избегать использования расчетов для определения мгновенного ускорения. Поскольку ускорение постоянно, среднее и мгновенное ускорения равны. То есть

[латекс] \ bar {a} = a = \ text {constant} [/ latex],

, поэтому мы всегда используем символ a для обозначения ускорения. Предположение, что ускорение является постоянным, не серьезно ограничивает ситуации, которые мы можем изучить, и не ухудшает точность нашего лечения.Во-первых, ускорение равно постоянным в большом количестве ситуаций. Кроме того, во многих других ситуациях мы можем точно описать движение, приняв постоянное ускорение, равное среднему ускорению для этого движения. Наконец, в движениях, когда ускорение резко меняется, например, когда автомобиль разгоняется до максимальной скорости, а затем тормозит до остановки, движение можно рассматривать в отдельных частях, каждая из которых имеет собственное постоянное ускорение.

Решение для смещения (Δ x ) и конечного положения ( x ) из средней скорости, когда ускорение ( a ) является постоянным

Чтобы получить наши первые два новых уравнения, мы начнем с определения средней скорости:

Подставляя упрощенные обозначения для Δ x и Δ t , получаем

[латекс] \ bar {v} = \ frac {x- {x} _ {0}} {t} [/ latex]

Решение для x дает

[латекс] x = {x} _ {0} + \ bar {v} t [/ latex],

, где средняя скорость

[латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} \ left (\ text {constant} a \ right) [/ latex].

Уравнение [латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} [/ latex] отражает тот факт, что при постоянном ускорении v – это просто среднее начальной и конечной скоростей. Например, если вы постоянно увеличиваете скорость (то есть с постоянным ускорением) с 30 до 60 км / ч, тогда ваша средняя скорость во время этого постоянного увеличения составляет 45 км / ч. Используя уравнение [латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} [/ latex], чтобы проверить это, мы видим, что

[латекс] \ bar {v} = \ frac {{v} _ {0} + v} {2} = \ frac {\ text {30 км / ч} + \ text {60 км / ч}} {2 } = \ text {45 км / ч} [/ latex],

, что кажется логичным.

Пример 1. Расчет смещения: как далеко пробегает джоггер?

Бегун бежит по прямому участку дороги со средней скоростью 4,00 м / с в течение 2,00 мин. Какова его конечная позиция, если исходная позиция равна нулю?

Стратегия

Нарисуйте эскиз.

Конечная позиция x задается уравнением

[латекс] x = {x} _ {0} + \ bar {v} t [/ латекс]. {2} [/ latex].На графике линейные функции выглядят как прямые линии с постоянным наклоном.) Например, в автомобильной поездке мы продвинемся вдвое дальше за заданное время, если мы усредним 90 км / ч, чем если бы мы в среднем 45 км / ч.

Решение для окончательной скорости

Мы можем вывести еще одно полезное уравнение, манипулируя определением ускорения.

Подстановка упрощенных обозначений для Δ v и Δ t дает

[латекс] a = \ frac {v- {v} _ {0}} {t} \ text {} \ left (\ text {constant} a \ right) [/ latex]

Решение для v дает

[латекс] v = {v} _ {0} + \ text {at} \ text {} \ left (\ text {constant} a \ right) [/ latex]

Пример 2.Расчет конечной скорости: самолет замедляется после приземления

Самолет приземляется с начальной скоростью 70,0 м / с, а затем замедляется со скоростью 1,50 м / с. ² в течение 40,0 с. Какова его конечная скорость?

Стратегия

Нарисуйте эскиз. Мы рисуем вектор ускорения в направлении, противоположном вектору скорости, потому что самолет замедляется.

Решение

1. Определите известные. v ₀ = 70.{2} \ right) \ left (\ text {40} \ text {.} \ Text {0 s} \ right) = \ text {10} \ text {.} \ Text {0 м / с} [/ latex ]

Обсуждение

Конечная скорость намного меньше начальной скорости, желаемой при замедлении, но все же положительная. С реактивными двигателями обратная тяга могла поддерживаться достаточно долго, чтобы остановить самолет и начать движение назад. На это указывает отрицательная конечная скорость, чего здесь нет.

Уравнение [латекс] v = {v} _ {0} + \ text {at} [/ latex] не только помогает при решении проблем, но и дает нам представление о взаимосвязях между скоростью, ускорением и временем.Из него, например, видно, что

• Конечная скорость зависит от того, насколько велико ускорение и как долго оно длится
• , если ускорение равно нулю, то конечная скорость равна начальной скорости ( v = v ₀ ), как и ожидалось (т.е. скорость постоянна)
• , если a отрицательное, то конечная скорость меньше начальной скорости

(Все эти наблюдения соответствуют нашей интуиции, и всегда полезно исследовать основные уравнения в свете нашей интуиции и опыта, чтобы убедиться, что они действительно точно описывают природу.)

Установление соединений: соединение в реальном мире

Межконтинентальная баллистическая ракета (МБР) имеет большее среднее ускорение, чем космический шаттл, и достигает большей скорости в первые две минуты полета (фактическое время горения межконтинентальной баллистической ракеты засекречено – ракеты с коротким временем горения сложнее для противника. разрушать). Но космический шаттл получает большую конечную скорость, так что он может вращаться вокруг Земли, а не сразу возвращаться вниз, как это делает межконтинентальная баллистическая ракета. Космический шаттл делает это за счет более длительного ускорения.

Решение для конечного положения, когда скорость не постоянна ( a ≠ 0)

Мы можем объединить приведенные выше уравнения, чтобы найти третье уравнение, которое позволяет нам вычислить окончательное положение объекта, испытывающего постоянное ускорение. {2} \ left (\ text {constant} a \ right) \ text {.} [/ латекс]

Пример 3. Расчет смещения ускоряющегося объекта: драгстеры

Драгстеры могут развивать среднее ускорение 26,0 м / с ² . Предположим, такой драгстер ускоряется из состояния покоя за 5,56 с. Как далеко он пролетит за это время?

Стратегия

Нарисуйте эскиз.

Нас просят найти смещение, которое составляет x , если мы примем x ₀ равным нулю. (Подумайте об этом как о стартовой линии гонки.{2} [/ latex] после того, как мы определим v ₀ , a и t из описания проблемы.

Решение

1. Определите известные. Запуск из состояния покоя означает, что v ₀ = 0, a задается как 26,0 м / с ² и t задается как 5,56 с.

2. Подставьте известные значения в уравнение, чтобы найти неизвестное x :

Так как начальное положение и скорость равны нулю, это упрощается до

Подстановка идентифицированных значений на и t дает

дает

x = 402 м.{2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] идеально подходит для этой задачи, потому что он связывает скорости, ускорение и смещение и не требует информации о времени.

Решение

1. Определите известные значения. Мы знаем, что v ₀ = 0, поскольку драгстер запускается из состояния покоя. Затем отметим, что x – x ₀ = 402 м (это был ответ в примере 3). Наконец, было получено среднее ускорение a = 26.{2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] и решите относительно v .

v ² = 0 + 2 (26,0 м / с ² ) (402 м).

Таким образом,

Чтобы получить против , извлекаем квадратный корень:

Обсуждение

145 м / с – это около 522 км / ч или около 324 миль / ч, но даже эта головокружительная скорость отстает от рекорда для четверти мили. Также обратите внимание, что квадратный корень имеет два значения; мы взяли положительное значение, чтобы указать скорость в том же направлении, что и ускорение.{2} + 2a \ left (x- {x} _ {0} \ right) [/ latex] может дать дальнейшее понимание общих отношений между физическими величинами:

• Окончательная скорость зависит от того, насколько велико ускорение и расстояние, на котором оно действует
• При фиксированном замедлении автомобиль, который едет вдвое быстрее, не просто останавливается на удвоенном расстоянии – для остановки требуется гораздо больше времени. (Вот почему у нас есть зоны с пониженной скоростью возле школ.)

Объединение уравнений

В следующих примерах мы дополнительно исследуем одномерное движение, но в ситуациях, требующих немного большего количества алгебраических манипуляций.Примеры также дают представление о методах решения проблем. В рамке ниже приведены ссылки на необходимые уравнения.

Сводка кинематических уравнений (константа a )

Пример 5. Расчет смещения: как далеко уходит автомобиль при остановке?

На сухом бетоне автомобиль может замедляться со скоростью 7,00 м / с ² , тогда как на мокром бетоне он может замедляться только со скоростью 5,00 м / с ² . Найдите расстояния, необходимые для остановки движения машины на отметке 30.0 м / с (около 110 км / ч) (а) на сухом бетоне и (б) на мокром бетоне. (c) Повторите оба вычисления, найдя смещение от точки, где водитель видит, что светофор становится красным, принимая во внимание время его реакции 0,500 с, чтобы нажать ногой на тормоз.

Стратегия

Нарисуйте эскиз.

Чтобы определить, какие уравнения лучше всего использовать, нам нужно перечислить все известные значения и точно определить, что нам нужно решить. Мы сделаем это явно в следующих нескольких примерах, используя таблицы для их выделения.

Решение для (a)

1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что v ₀ = 30,0 м / с; v = 0; a = -7,00 м / с ² ( a отрицательно, потому что он находится в направлении, противоположном скорости). Возьмем x ₀ равным 0. Мы ищем смещение Δ x , или x – x ₀ .

2. Найдите уравнение, которое поможет решить проблему.Лучшее уравнение для использования –

Это уравнение лучше всего, потому что оно включает только одно неизвестное, x . Нам известны значения всех других переменных в этом уравнении. (Существуют и другие уравнения, которые позволят нам решить для x , но они требуют, чтобы мы знали время остановки, t , которое мы не знаем. Мы могли бы использовать их, но это потребовало бы дополнительных вычислений.)

3. Переставьте уравнение, чтобы найти x .

4. Введите известные значения.{2} \ right)} [/ латекс]

Таким образом,

x = 64,3 м на сухом бетоне.

Решение для (b)

Эта часть может быть решена точно так же, как часть A. Единственное отличие состоит в том, что замедление составляет –5,00 м / с ² . Результат

x _мокрый = 90,0 м на мокром бетоне.

Решение для (c)

После реакции водителя тормозной путь будет таким же, как и в частях A и B для сухого и влажного бетона.Итак, чтобы ответить на этот вопрос, нам нужно подсчитать, как далеко проехал автомобиль за время реакции, а затем добавить это значение ко времени остановки. Разумно предположить, что скорость остается постоянной в течение времени реакции водителя.

1. Определите, что мы знаем и что мы хотим решить. Мы знаем, что [латекс] \ bar {v} = 30.0 \ text {m / s} [/ latex]; т _{реакция} = 0,500 с; a _{реакция} = 0. Возьмем x _{0- реакцию} = равным 0.Ищем x _{реакцию} .

2. Определите лучшее уравнение для использования. [latex] x = {x} _ {0} + \ bar {v} t [/ latex] работает хорошо, потому что единственное неизвестное значение – x , что мы и хотим найти.

3. Подключите известные знания, чтобы решить уравнение.

x = 0+ (30,0 м / с) (0,500 с) = 15,0 м.

Это означает, что автомобиль проезжает 15,0 м, в то время как водитель реагирует, создавая общие перемещения в двух случаях: сухой и мокрый бетон 15.0 м больше, чем если бы он среагировал мгновенно.

4. Добавьте смещение за время реакции к смещению при торможении.

x _{торможение} + x _{реакция} = x _всего

1. 64,3 м + 15,0 м = 79,3 м в сухом состоянии
2. 90,0 м + 15,0 м = 105 м во влажном состоянии

Обсуждение

Смещения, найденные в этом примере, кажутся разумными для остановки быстро движущегося автомобиля.Остановка автомобиля на мокром асфальте займет больше времени, чем на сухом. Интересно, что время реакции значительно увеличивает смещения. Но важнее общий подход к решению проблем. Мы определяем известные и определяемые величины, а затем находим соответствующее уравнение. Часто есть несколько способов решить проблему. Фактически, различные части этого примера могут быть решены другими методами, но решения, представленные выше, являются самыми короткими.

Пример 6.Расчет времени: автомобиль сливается с движением

Предположим, автомобиль выезжает на шоссе на съезде длиной 200 м. Если его начальная скорость составляет 10,0 м / с, а ускорение составляет 2,00 м / с ² , сколько времени потребуется, чтобы преодолеть 200 м по рампе? (Такая информация может быть полезна транспортному инженеру.)

Стратегия

Нарисуйте эскиз.

Просят решить за время т . Как и раньше, мы идентифицируем известные величины, чтобы выбрать удобную физическую связь (то есть уравнение с одной неизвестной, t ).{2} [/ латекс]

4. Упростите уравнение. Единицы измерения (м) отменяются, потому что они есть в каждом члене. Мы можем получить единицы секунд для отмены, взяв t = ts , где t – величина времени, а s – единица измерения. Остается

200 = 10 т + т ² .

5. Используйте формулу корней квадратного уравнения, чтобы найти t .

(a) Переставьте уравнение, чтобы получить 0 на одной стороне уравнения.{2} -4 \ text {ac}}} {2a} [/ латекс]

Это дает два решения для т , которые составляют

т = 10,0 и -20,0.

В данном случае время равно t = t в секундах, или

t = 10,0 с и -20,0 с.

Отрицательное значение времени неразумно, так как это будет означать, что событие произошло за 20 секунд до начала движения. Мы можем отказаться от этого решения. Таким образом,

т = 10,0 с.

Обсуждение

Каждый раз, когда уравнение содержит неизвестный квадрат, будет два решения. В некоторых проблемах имеют смысл оба решения, но в других, таких как вышеупомянутое, разумно только одно решение. Ответ 10,0 с кажется разумным для типичной автострады на съезде.

Освоив основы кинематики, мы можем перейти ко многим другим интересным примерам и приложениям. В процессе разработки кинематики мы также познакомились с общим подходом к решению проблем, который дает как правильные ответы, так и понимание физических взаимоотношений.В разделе «Основы решения проблем» обсуждаются основы решения проблем и описывается подход, который поможет вам добиться успеха в этой бесценной задаче.

Задачи и упражнения

1. Спринтер олимпийского класса начинает забег с ускорением 4,50 м / с ² . (а) Какова ее скорость через 2,40 с? (б) Нарисуйте график ее положения в зависимости от времени за этот период.

2. Хорошо брошенный мяч попадает в мягкую перчатку. Если замедление мяча составляет 2,10 × 10 ⁴ м / с ² , и 1.85 мс (1 мс = 10–3 с) проходит с момента первого касания мяча рукавицы до момента остановки. Какова была начальная скорость мяча?

3. Пуля в ружье ускоряется от камеры выстрела до конца ствола со средней скоростью 6,20 × 10 ⁵ м / с ² за 8,10 × 10 ^-4 с. Какова его начальная скорость (то есть конечная скорость)?

4. (a) Пригородный легкорельсовый поезд ускоряется со скоростью 1,35 м / с ² . Сколько времени нужно, чтобы достичь максимальной скорости 80?0 км / ч, трогаться с места? (b) Этот же поезд обычно замедляется со скоростью 1,65 м / с ² . Сколько времени нужно, чтобы остановиться с максимальной скорости? (c) В аварийных ситуациях поезд может замедляться быстрее, останавливаясь на скорости 80,0 км / ч за 8,30 с. Каково его аварийное замедление в м / с ² ?

5. При выезде на автостраду автомобиль ускоряется из состояния покоя со скоростью 2,40 м / с. ² за 12,0 с. (а) Нарисуйте набросок ситуации. (б) Перечислите известных в этой проблеме.(c) Как далеко проехала машина за эти 12,0 с? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали соответствующее уравнение для его решения. После выбора уравнения покажите свои шаги в решении неизвестного, проверьте свои единицы и обсудите, является ли ответ разумным. (d) Какова конечная скорость автомобиля? Решите для этого неизвестного таким же образом, как в части (c), явно показывая все шаги.

6. В конце забега бегун замедляется со скорости 9.00 м / с со скоростью 2,00 м / с ² . а) Как далеко она продвинется в следующие 5,00 с? б) Какова ее конечная скорость? (c) Оцените результат. Имеет ли это смысл?

7. Professional Application: Кровь ускоряется из состояния покоя до 30,0 см / с на расстоянии 1,80 см от левого желудочка сердца. (а) Сделайте набросок ситуации. (б) Перечислите известных в этой проблеме. (c) Как долго длится ускорение? Чтобы решить эту часть, сначала определите неизвестное, а затем обсудите, как вы выбрали соответствующее уравнение для его решения.После выбора уравнения покажите свои шаги в решении неизвестного, проверяя свои единицы. (г) Является ли ответ разумным по сравнению со временем биения сердца?

8. При нанесении удара по воротам хоккеист ускоряет шайбу со скорости 8,00 м / с до 40,0 м / с в том же направлении. Если этот бросок занимает 3,33 × 10 ^-2 , вычислите расстояние, на котором шайба ускоряется.

9. Мощный мотоцикл может разогнаться с места до 26,8 м / с (100 км / ч) всего за 3 секунды.90 с. а) Какое у него среднее ускорение? б) Как далеко он уйдет за это время?

10. Грузовые поезда могут производить только относительно небольшие ускорения и замедления. (a) Какова конечная скорость грузового поезда, который ускоряется со скоростью 0,0500 м / с ² за 8,00 мин, начиная с начальной скорости 4,00 м / с? (b) Если поезд может замедляться со скоростью 0,550 м / с ² , сколько времени потребуется, чтобы остановиться с этой скорости? (c) Как далеко он продвинется в каждом случае?

11.Снаряд салюта ускоряется из состояния покоя до скорости 65,0 м / с на расстояние 0,250 м. а) Как долго длилось ускорение? (b) Рассчитайте ускорение.

12. Лебедь на озере поднимается в воздух, взмахивая крыльями и бегая по воде. (a) Если лебедь для взлета должен достичь скорости 6,00 м / с, и он ускоряется из состояния покоя со средней скоростью 0,350 м / с ² , как далеко он пролетит, прежде чем взлетит? б) Сколько времени это займет?

13. Профессиональное применение: Мозг дятла специально защищен от сильных замедлений с помощью прикрепленных к нему сухожилий внутри черепа. Во время клевания дерева голова дятла останавливается с начальной скорости 0,600 м / с на расстоянии всего 2,00 мм. (a) Найдите ускорение в м / с ² и кратно g ( g = 9,80 м / с ² . (b) Рассчитайте время остановки. (c) Сухожилия, удерживающие мозг, растягиваются , делая его тормозной путь 4.50 мм (больше головы и, следовательно, меньше торможение мозга). Что такое замедление мозга, кратное г ?

14. Неосторожный футболист сталкивается со стойкой ворот с мягкой подкладкой при беге со скоростью 7,50 м / с и полностью останавливается, сжав подушку и свое тело на 0,350 м. а) Каково его замедление? б) Как долго длится столкновение?

15. Во время Второй мировой войны было зарегистрировано несколько случаев, когда летчики прыгали со своих пылающих самолетов без парашюта, чтобы избежать верной смерти.Некоторые упали с высоты около 20000 футов (6000 м), некоторые выжили, получив несколько опасных для жизни травм. Для этих удачливых пилотов ветки деревьев и снежные заносы на земле позволяли снизить их скорость. Если предположить, что скорость пилота при столкновении составляла 123 мили в час (54 м / с), то каково было его замедление? Предположим, что деревья и снег остановили его на расстоянии 3,0 м.

16. Представьте, как серая белка падает с дерева на землю. (а) Если мы проигнорируем сопротивление воздуха в этом случае (только ради этой проблемы), определите скорость белки непосредственно перед ударом о землю, предполагая, что она упала с высоты 3.{2} [/ latex] как проходит. Длина станции 210 м. а) Какова длина носа поезда на станции? б) Как быстро он движется, когда нос покидает станцию? (c) Если длина поезда составляет 130 м, когда конец поезда покидает станцию? г) Какова скорость отходящего поезда?

18. Драгстеры могут развить максимальную скорость 145 м / с всего за 4,45 с – значительно меньше времени, чем указано в Примере 2.10 и Примере 2.11. (а) Рассчитайте среднее ускорение для такого драгстера.(b) Найдите конечную скорость этого драгстера, начиная с состояния покоя и ускоряясь со скоростью, указанной в (a) для 402 м (четверть мили), не используя никакой информации о времени. (c) Почему конечная скорость больше той, которая использовалась для определения среднего ускорения? Подсказка: подумайте, справедливо ли предположение о постоянном ускорении для драгстера. Если нет, обсудите, будет ли ускорение больше в начале или в конце пробега и как это повлияет на конечную скорость.

19.Велогонщик бежит в конце гонки, чтобы одержать победу. Гонщик имеет начальную скорость 11,5 м / с и разгоняется со скоростью 0,500 м / с ² за 7,00 с. а) Какова его конечная скорость? (b) Гонщик продолжает с этой скоростью до финиша. Если он был в 300 м от финиша, когда начал ускоряться, сколько времени он сэкономил? (c) Еще один гонщик был на 5,00 м впереди, когда победитель начал ускоряться, но он не смог ускориться и ехал со скоростью 11,8 м / с до финиша.Насколько далеко от него (в метрах и секундах) финишировал победитель?

20. В 1967 году новозеландец Берт Манро установил мировой рекорд для индийского мотоцикла на соляных равнинах Бонневиль в штате Юта с максимальной скоростью 183,58 миль / ч. Курс в одну сторону длился 5,00 миль. Скорость ускорения часто описывается временем, необходимое для достижения 60,0 миль / ч из состояния покоя. Если на этот раз было 4,00 с, и Берт ускорялся с этой скоростью, пока не достиг максимальной скорости, сколько времени понадобилось Берту, чтобы пройти курс?

21.(а) Мировой рекорд в беге на 100 метров среди мужчин на Олимпийских играх 2008 года в Пекине был установлен Усэйном Болтом из Ямайки. Болт «выбежал» на финиш со временем 9,69 с. Если мы предположим, что Болт ускорялся в течение 3,00 секунд, чтобы достичь своей максимальной скорости, и сохранял эту скорость до конца гонки, рассчитайте его максимальную скорость и его ускорение. (b) Во время той же Олимпиады Болт также установил мировой рекорд в беге на 200 м со временем 19,30 с. Если исходить из тех же предположений, что и для бега на 100 м, какова была его максимальная скорость в этой гонке?

Избранные решения проблем и упражнения

1.10,8 м / с

(б)

2. 38,9 м / с (около 87 миль в час)

4. (а) 16,5 с (б) 13,5 с (в) -2,68 м / с ²

6. (a) 20,0 м (b) -1,00 м / с (c) Этот результат не имеет смысла. Если бегун стартует со скоростью 9,00 м / с и замедляет скорость 2,00 м / с ² , то она остановится через 4,50 с. Если она продолжит замедляться, она будет бежать назад.

8. 0,799 м

10. (a) 28,0 м / с (b) 50,9 с (c) 7,68 км для разгона и 713 м для замедления

12.(а) 51,4 м (б) 17,1 с

14. (а) -80 м / с ² (б) 9,33 × 10 ^{– 2} с

16. (a) 7,7 м / с (b) -15 × 10 ² м / с ² это примерно в 3 раза больше замедления пилотов, падающих с высоты в тысячи метров!

18. (a) 36,2 м / с ² (b) 162 м / с (c) v> v _max , потому что предположение о постоянном ускорении недействительно для драгстера. Драгстер переключает передачи и будет иметь большее ускорение на первой передаче, чем на второй, чем на третьей и т. Д.Ускорение будет наибольшим вначале, поэтому он не будет ускоряться со скоростью 32 м / с ² в течение последних нескольких метров, а будет значительно меньше, а конечная скорость будет меньше 162 м / с.

20. 104 с

21. (а) v = 12/2 м / с; a = 4,07 м / с ² (б) v = 11,2 м / с

Уравнение кинематики v = v_sub_o + at

Уравнение кинематики v = v_sub_o + at

---

[Глава 2 цели]

BHS -> Персонал -> МистерСтэнбро -> Физика -> Механика -> Кинематика -> эта страница

---

Уравнение включает исходные и окончательные показания спидометра объекта (мгновенные скорости), v _o и v , ​​его ускорение, a , ​​и временной интервал между исходным и финальные ситуации,. Если проблема говорит вам о любых трех из этих величин, вы можете использовать это уравнение, чтобы найти четвертое, как показано в примерах ниже.

Вам интересно, откуда взялось это уравнение? из? Вывод этого уравнение доступно.

Пример 1 – Определение конечной скорости:

Автомобиль, первоначально находящийся в состоянии покоя, начинает ускоряться на 4,5 м / с ² . Как быстро, в м / с, он будет идти в 5.0 секунды?

Решение:

Примечание : в этом решении шаги обозначены, чтобы указать шаги, связанные с решением кинематической задачи.При решении реальная проблема, вы обычно не помечаете шаг 1, шаг 2, пр.

Шаг 1. Изучите проблема.

Шаг 2 – Перевести на физика:

v o = 0 м / с

a = 4,5 м / с 2

v =?

= 5.0 с

Шаг 3 – Найдите уравнение кинематики:

Уравнение кинематики, связывающее v, vo, a и является:

Шаг 4 – Решить:

В этом нет необходимости, так как уравнение уже решено для “v”.

Шаг 5 – Замена известна значения:

(Уведомление что единица секунд отменяется в правом члене, чтобы оставить м / с равным Единица.)

Шаг 6 – Сообщить ответ:

Ответ: Автомобиль будет двигаться со скоростью 23 м / с за 5,0 секунд.

Шаг 7 – Проверка:

Если автомобиль разогнался со скоростью 4 м / с ² , его скорость будет меняться на 4 м / с каждую секунду. Через 5 секунд это будет 20 м / с. Если бы он ускорялся со скоростью 5 м / с ² , он бы пошел 25 м / с за 5 сек. 23 м / с кажется правильным.

Вот альтернативный решение этой проблемы.Он использует более простые уравнения, но требует больше размышлений.

---

Пример 2 – Определение ускорения:

Лодка, первоначально движущаяся со скоростью 20 м / с, движется только на скорости 2,0 м / с в том же направлении, спустя 25 секунд. При условии, что ускорение лодки было постоянным, каково было разгон за это время?

Решение:

v o = 20 м / с

v = 2.0 м / с

= 25 с

а =?

Уравнение кинематики, связывающее v, vo, a и это:

решение для ускорения: (Что, если я сначала подставлю значения, тогда решить?)

заменяющий:

Ответ: Ускорение лодки равно 0.72 м / с ² , в направлении, противоположном скорости лодки.

Это разумно? Да. Если бы лодка замедлилась на 18 м / с за 24 часа. секунд (6 переходит в 18 и 24 равномерно …), величина его ускорение будет 18/24 м / с ² = 0,75 м.с ² .

Примечание:

В этой задаче лодка замедляется или замедляется. Помните что нет физического различия между ускорением и замедление – в другими словами, замедление равно ускорению.Иногда заблуждения людей делают это препятствием. Также не падай в ловушку автоматического превращения v _o в меньшее значение, а v – большее значение. Внимательно прочтите проблему и понять, что происходит, прежде чем приступить к решению!

Также то, что ускорение лодки оказалось отрицательный означает, что ускорение лодки противоположное направление от скорости лодки (что положительно).

Вот альтернативный решение для этого примера – работает довольно легко.

---

Пример 3 – Определение временного интервала:

Такси, движущееся со скоростью 28 м / с, задействует тормоза и останавливается. Если его тормоза могут замедлить его со скоростью 3,6 м / с ² , как сколько времени нужно такси, чтобы остановиться?

Решение:

v o = 28 м / с

а = -3.6 м / с 2

v = 0 м / с

= ?

Уравнение кинематики, связывающее v, vo, a и это:

решение для: (Что, если я сначала подставлю значения, тогда решить?)

подставляем значения из таблицы данных:

Ответ: Такси возьмет 7.8 секунд до остановки.

Это разумный ответ? Если бы ускорение кабины было -4 м / с ² , он будет терять 4 м / с скорости каждую секунду, поэтому потеря 28 м / с займет 7 секунд (28/4 = 7). Да ответ разумно.

Вот альтернативный решение этой проблемы.

---

Пример 4 – Нахождение исходной скорости:

Бейсбольный мяч движется вниз со скоростью 65 м / с. 8.5 секунд в свободном падении. Какой был оригинальный бейсбол скорость?

Решение:

v o =?

a = g = 9,8 м / с 2 (вниз)

= 8,5 с

v = 65 м / с

Уравнение кинематики, связывающее v, vo, a и это:

решение для v _o : (Что если я подставлю, то решить?)

подставляющие значения:

Ответ: Исходная скорость бейсбольного мяча составляла 18.3 м / с вверх. (Поскольку знак нисходящей скорости и нисходящей ускорение положительное, отрицательная скорость должна быть направлена вверх.)

Это разумно? Скорость бейсбольного мяча изменилась на около 10 м / с (вниз) каждую секунду в течение 8,5 секунд, поэтому он должен изменились примерно на 85 м / с (8,5 * 10) с момента его запуска. 65 м / с – 85 м / с = -20 м / с. Да, разумный ответ.

Вот альтернативный решение этой проблемы.

---

[Глава 2 цели]

BHS -> Персонал -> Мистер Стэнбро -> Физика -> Механика -> Кинематика -> эта страница

---

последнее обновление 13 августа 2003 г., автор JL Stanbrough

Dynamics | Физика для идиотов

Динамика – это название правил движения. Это то, что, как вы могли подумать, должно было быть выяснено в первую очередь, но не было полностью заблокировано до недавнего времени.При этом правила не сильно изменились и довольно предсказуемы, по крайней мере, в больших масштабах. Кто-то однажды сказал мне, что все, что вам нужно знать для экзамена по динамике, это: и все остальное можно вывести из этого. Я так и не узнал, правы ли они, я узнал и эти, на всякий случай:

Если вы уже знакомы с уравнениями, возможно, вы захотите перейти к следующему разделу, иначе я объясню, откуда они взялись и как их использовать.

При работе с измерениями вы можете использовать скалярные или векторные величины.

Скалярные величины:

• Укажите только величину.
• Энергия, Длина, Масса, Скорость, Температура и Время – все это скалярные величины.

Векторные величины:

• Имеют и величину, и направление
• Смещение, Сила, Скорость, Ускорение и Импульс – все векторные величины.

Иногда может показаться, что скорость и скорость – одно и то же (часто они равны друг другу), но на самом деле они немного отличаются.Скорость – это то, насколько быстро что-то движется, не имеет значения, идет ли он вверх, вниз, влево или вправо, все, что имеет значение, – это то, как далеко он перемещается за установленное время. Вероятно, лучший способ рассмотреть скорость – это если вы думаете или обычная ось x, y. Если тело движется горизонтально по прямой со скоростью 10, затем останавливается и движется в совершенно противоположном направлении, со скоростью 10, очевидно, произошло изменение, однако скорость этого не отражает. Скорость до поворота такая же, как и после.Однако скорость не такая. Если бы мы сказали, что скорость вначале была такой же, как и скорость: 10, тогда, когда тело движется точно в противоположном направлении с той же скоростью, скорость будет -10.

Исаак Ньютон был умным парнем. Мы должны благодарить его за гравитацию (я должен добавить, что он открыл, а не изобрел ее, иначе люди начнут обвинять его каждый раз, когда падают). Больше всего Ньютон известен (кроме случая с яблоком) своими законами движения:

1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.
2. Сила, действующая на объект, равна его массе, умноженной на его ускорение ().
3. Каждое действие имеет равную и противоположную реакцию.

Все это нормально, но что на самом деле означают эти законы?

1. Частица останется в покое или продолжит свое движение, если на нее не будет действовать внешняя сила.

Это просто означает, что если на частицу не действует внешняя сила, она никоим образом не изменит ее движения. Если бы не было трения или сопротивления воздуха, то частица, движущаяся со скоростью 5, продолжалась бы бесконечно.Очевидно, что в реальной жизни этого не происходит, поскольку есть сопротивление воздуха и трение, поэтому практически невозможно иметь внешнюю силу на движущуюся частицу. Однако, если вы думаете о неподвижной частице, это имеет гораздо больший смысл. Если к неподвижной частице не приложить силу, она не начнет двигаться.

2. Сила, действующая на объект, равна его массе, умноженной на его ускорение.

Проще говоря, это, вероятно, одна из самых фундаментальных формул в динамике.Это один из тех, что часто возникают в Dynamics, и его действительно стоит изучить. Это тоже не так сложно понять. Имеет смысл, что если что-то имеет большую массу, потребуется большая сила, чтобы придать ему такое же ускорение, как и что-то с меньшей массой.

3. Каждое действие имеет равную и противоположную реакцию

Этот закон в основном означает, что если вы толкнетесь о стену, это оттолкнет вас назад, что на самом деле является хорошей работой, потому что в противном случае вы бы прошли прямо!

У них так много разных названий, что иногда сложно угнаться за ними.Возможно, вы слышали, что их называют кинематическими уравнениями, уравнениями движения, уравнениями SUVAT, а может быть, вы вообще не слышали о них. Для начала давайте взглянем на них:

(1)

(2)

(3)

(4)

(5)

Может показаться, что там есть о чем вспомнить, но поверьте, это не так сложно, как кажется. Как будто эти уравнения невероятно важны в динамике.

SUVAT Equation 1

Как вы, наверное, уже знаете, скорость, разделенная на время, равна ускорению, а скорость, умноженная на время, равна смещению.Это означает, что на графике зависимости скорости от времени уклон линии равен ускорению, а площадь под линией равна смещению.

Если у вас есть начальная скорость и конечная скорость, график будет выглядеть примерно так:

График, показывающий u против t

Как я уже сказал, уклон линии равен ускорению. Так . Переставив это так, чтобы получился объект, мы получаем нашу первую формулу постоянного ускорения:

SUVAT Equation 2

Ладно, один проиграл, осталось четыре!

Мы знаем, что площадь под графиком равна смещению.Итак, мы знаем, что умножение на дает нам нижний прямоугольник области, а деление на 2 дает нам верхний треугольник. Это дает нам:

Теперь мы уже знаем это, поэтому можем переставить это, чтобы получить, а затем подставить это в наше уравнение для смещения. Из этого у нас есть. Если мы просто умножим скобку, которая дает нам вторую формулу:

Для тех из вас, кто любит находить математику там, где это возможно, вам может быть интересно узнать, что это интеграл по отношению к.Если для вас это не имеет смысла, почему бы не заглянуть в замечательный раздел «Интеграция», где все станет ясно!

SUVAT Equation 3

Те из вас, кто увлечен поиском закономерностей, возможно, заметили, что это уравнение очень похоже на предыдущее. Это потому, что он очень похож на предыдущий. Те из вас, кто решил не переходить на страницу интеграции, могут пожалеть об этом сейчас.

Если переставить, чтобы сделать тему, то получится:

Теперь вам просто нужно интегрировать этот результат относительно времени, чтобы получить наше третье уравнение:

SUVAT Equation 4

Мы уже установили, что площадь под графиком (равная смещению) равна:

Если мы умножим скобку, получим:

, что совпадает с:

Наконец, мы просто разложим это на множители, чтобы получить:

SUVAT Equation 5

Можем переставить, сделать тему:

Затем мы просто подставляем это значение в наше предыдущее уравнение:, что дает нам:

, который можно упростить до

, а затем

это в конечном итоге дает нам окончательную форму

Вот и все! Эти уравнения определенно стоит изучить, поскольку они полезны снова и снова.Есть несколько правил, например, их можно использовать только в случае постоянного ускорения. Это означает, что если ускорение составляет примерно 12 мс ^-2 , они в порядке, но если ускорение составляет 12 мс ^-2 , тогда они не будут работать, поскольку ускорение зависит от.

Большая часть динамики достигается за счет игнорирования сопротивления воздуха, и хотя это значительно упрощает работу, всегда стоит знать, какое влияние это окажет.Для любого объекта, движущегося в жидкости, силу сопротивления можно рассчитать по формуле:

– плотность жидкости (998,2071 кг · м для воды при 30 градусах и 1,204 кг · м для воздуха), – скорость объекта, – площадь поперечного сечения объекта и – коэффициент сопротивления. Коэффициент лобового сопротивления – это число, которое относится к тому, насколько аэродинамическим является объект, с кубом и сферой.

Объект, падающий на Землю, в конечном итоге (если он будет падать достаточно долго) достигнет скорости, при которой сила сопротивления равна силе тяжести, тянущей его вниз.Это называется Конечная скорость , и вы можете получить выражение для этого, приравняв силу сопротивления к, а затем переставив на:

Для человека, падающего в воздухе (сверху), у нас есть 70 кг, площадь 0,5 м и коэффициент лобового сопротивления около 0,8 (приблизительное предположение где-то около углового куба или цилиндра), мы получаем конечную скорость около 53 мс (что оказывается быть довольно хорошей приблизительной оценкой).

Это самый простой экземпляр в динамике.Тело движется по плоской поверхности по прямой. Например:

  1. Преподобный едет на своей машине, как вдруг двигатель перестает работать! Если он едет со скоростью 10 мс  -1 , а его замедление составляет 2 мс  -2 , сколько времени потребуется машине, чтобы остановиться?  

Хорошо, с такими проблемами всегда полезно перечислить то, что вы знаете. Нам даны начальная скорость, и ускорение,. Мы также знаем, что если машина собирается финишировать в состоянии покоя, эта конечная скорость должна быть 0 мс ^-1 .Мы хотим узнать время,. Лично я считаю, что лучше всего изложить эту информацию так:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t =? с

Отсюда видно, какое уравнение нам нужно. В этом случае мы видим, что нам нужно уравнение. Мы переставляем это так, чтобы получился предмет, давая нам

Наконец, мы помещаем числа в уравнение:

.

 2. Майкл выходит на дорогу в 30 метрах от места, где двигатель не работает.Очки преподобного упали, и он не видит Майкла. Остановится ли машина вовремя, чтобы не сбить Майкла? 

Еще раз, лучше всего выложить всю имеющуюся у нас информацию:

u = 10 мс ^-1
v = 0 мс ^-1
a = -2 мс ^-2
t = 5 с
с =? м

На этот раз мы хотим найти смещение s, поэтому нам нужно выбрать уравнение с этим in. Я собираюсь использовать. Я мог бы использовать или, однако, поскольку нам не дали времени, а вместо этого мы разработали это самостоятельно, любая ошибка, сделанная в предыдущих расчетах, будет перенесена в эту.
Опять же, я собираюсь переставить уравнение, на этот раз чтобы дать в качестве объекта. Это хорошая привычка, теперь это может не иметь большого значения, переставляете ли вы уравнение до или после ввода чисел, но с более сложными формулами это может стать действительно беспорядочным, если вы не измените его сначала. Также в экзаменационных ситуациях, если вы допустили ошибку, вы все равно можете получить оценки по методу, если экзаменатор может видеть, что вы сделали.
В любом случае, это дает нам

Подставляя числа в уравнение, получаем:

, чтобы Майкла не ударили! (Уф!)

В приведенном выше примере трение полностью игнорировалось.В реальном мире мы не можем этого сделать (очень удачно, потому что мы все время падали, и люди думали, что мы пьяны). Так что теперь нам лучше взглянуть на ситуацию с трением. Коэффициент трения обозначается символом μ. Результирующая (нормальная) сила веса уравновешивает вес автомобиля (чтобы он не выезжал на дорогу). Сила трения равна μ (или μN).

 3. Машина преподобного сломалась на трассе М1. Ему нужно подтолкнуть его к твердому плечу. Автомобиль весит 5000Н.Rev может выдвинуть около 1800N. Коэффициент трения между автомобилем и дорогой составляет 0,6. Сможет ли Rev подтолкнуть машину к твердой обочине? 

Хорошо, в такой ситуации для начала неплохо нарисовать небольшой набросок того, что происходит.

Диаграмма сил, показывающая, что происходит в примере 3.

Из этого мы знаем, что для того, чтобы машина двигалась, Rev должен толкать с силой не менее μR. Просто умножив коэффициент трения на результирующую силу, мы обнаружим, что сила трения составляет 3000 Н, поэтому Rev не сможет толкнуть автомобиль на обочину дороги.

  4. Бодибилдер случайно проезжает мимо и, пытаясь облегчить заторы на постоянно загруженном M1, он решает помочь. Он может толкать с силой 3200Н. Каким будет ускорение машины с учетом того, что бодибилдер и Rev.  

NB – Принять массу автомобиля 510 кг

Итак, на самом деле ситуация та же, что и раньше, только на этот раз силы не уравновешиваются и будет ускорение. Мы получили это от такого умного Исаака Ньютона.
Помните, что для определения общей силы необходимо убрать силу трения. Итак, это (3200 + 1800) – 3000. Таким образом, общая сила составляет 2000Н. Опять же, нам нужно изменить формулу, чтобы на этот раз в качестве объекта использовались и . Это дает нам. Подставляя числа, получаем:

a = 3.9 мс ^-2 (2 s.f.)

Это очень похоже на движение по плоской поверхности, только одна или две другие переменные … о, и мы больше не будем говорить об автомобиле Rev, так как я не уверен, что это поможет ему подняться в гору!

В любом случае, боюсь, я немного сбился с пути.Введение «наклонной плоскости» или «наклона», как ее называют большинство из нас, означает, что вам придется освежить свою тригонометрию. С другой стороны, вы узнаете, почему люди годами пытались вбить это в вас! Если вы знакомы со старым добрым порядком действий, все будет в порядке.

Итак, давайте начнем с простого простого примера.

Пример наклонной плоскости

На картинке выше показан блок, стоящий на склоне. Хорошее место для начала (вероятно, единственное место, с которого можно начать, если вы хотите получить хоть какой-то шанс получить хоть что-нибудь с вопросом), – это объединить силы.Предполагая, что блок находится в состоянии покоя, мы знаем, что он находится в равновесии, поэтому горизонтальные силы должны быть равны, как и вертикальные силы (если это не один из тех прекрасных левитирующих блоков).

Снаряды

ничем не отличаются от Движения по прямой, просто вместо того, чтобы тело двигалось слева направо, оно также движется вверх или вниз. Сначала рассмотрим типичный пример движения снаряда:

 Мяч брошен под углом 30 °. Имеет начальную скорость 20 мс  -1 .Найдите максимальную высоту, которую может достичь мяч. 

Итак, как обычно, рисуем диаграмму:

Пример движения снаряда

Теперь давайте перечислим то, что мы знаем:

• u = 20 sin30 мс ^-1
• v = 0 мс ^-1
• a = -9,81 мс ^-2
• с =? м

Теперь мы выбираем одну из кинематических формул, которая даст нам результат наиболее прямым путем:, и переставляем ее так, чтобы получился объект:

Затем введите числа в уравнение:

и выскакивает ответ:

Смотри, не так ли сложно было? Вопросы о снарядах иногда могут показаться довольно сложными, но если вы не забудете просто использовать тригонометрию для поиска компонентов x и y, вы не ошибетесь.