Электростатика – Физика – Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Электрический заряд и его свойства
К оглавлению…
Электрический заряд – это физическая величина, характеризующая способность частиц или тел вступать в электромагнитные взаимодействия. Электрический заряд обычно обозначается буквами q или Q. В системе СИ электрический заряд измеряется в Кулонах (Кл). Свободный заряд в 1 Кл – это гигантская величина заряда, практически не встречающаяся в природе. Как правило, Вам придется иметь дело с микрокулонами (1 мкКл = 10–6 Кл), нанокулонами (1 нКл = 10–9 Кл) и пикокулонами (1 пКл = 10–12 Кл). Электрический заряд обладает следующими свойствами:
1. Электрический заряд является видом материи.
2. Электрический заряд не зависит от движения частицы и от ее скорости.
3.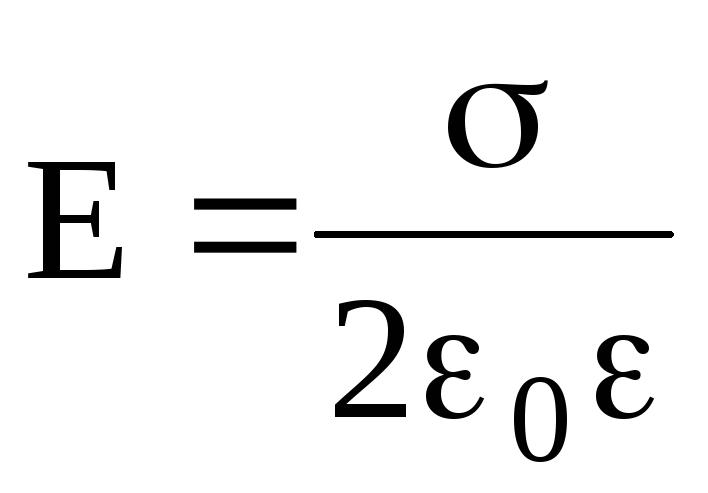
4. Существует два рода электрических зарядов, условно названных положительными и отрицательными.
5. Все заряды взаимодействуют друг с другом. При этом одноименные заряды отталкиваются, разноименные – притягиваются. Силы взаимодействия зарядов являются центральными, то есть лежат на прямой, соединяющей центры зарядов.
6. Существует минимально возможный (по модулю) электрический заряд, называемый элементарным зарядом. Его значение:
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.
Электрический заряд любого тела всегда кратен элементарному заряду:
где: N – целое число.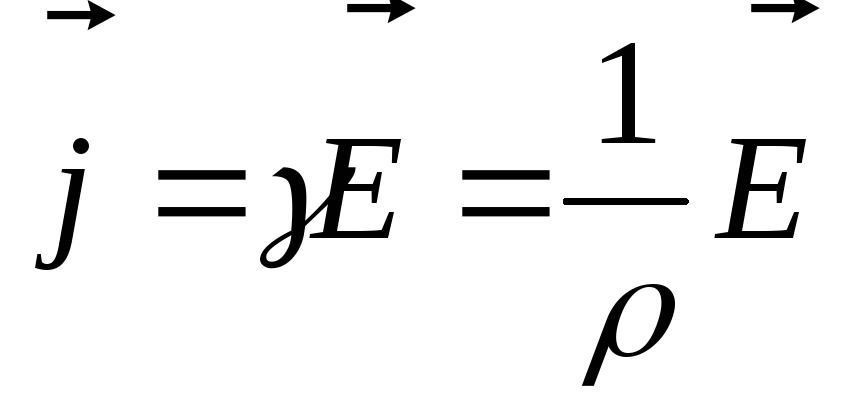
7. Закон сохранения электрического заряда. В изолированной системе алгебраическая сумма зарядов всех тел остается постоянной:
Закон сохранения электрического заряда утверждает, что в замкнутой системе тел не могут наблюдаться процессы рождения или исчезновения зарядов только одного знака. Из закона сохранения заряда так же следует, если два тела одного размера и формы, обладающие зарядами q1 и q2 (совершенно не важно какого знака заряды), привести в соприкосновение, а затем обратно развести, то заряд каждого из тел станет равным:
С современной точки зрения, носителями зарядов являются элементарные частицы. Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
Все обычные тела состоят из атомов, в состав которых входят положительно заряженные протоны, отрицательно заряженные электроны и нейтральные частицы – нейтроны. Протоны и нейтроны входят в состав атомных ядер, электроны образуют электронную оболочку атомов. Электрические заряды протона и электрона по модулю в точности одинаковы и равны элементарному (то есть минимально возможному) заряду e.
В нейтральном атоме число протонов в ядре равно числу электронов в оболочке. Это число называется атомным номером. Атом данного вещества может потерять один или несколько электронов, или приобрести лишний электрон. В этих случаях нейтральный атом превращается в положительно или отрицательно заряженный ион. Обратите внимание, что положительные протоны входят в состав ядра атома, поэтому их число может изменяться только при ядерных реакциях. Очевидно, что при электризации тел ядерных реакций не происходит. Поэтому в любых электрических явлениях число протонов не меняется, изменяется только число электронов.
Иногда в задачах электрический заряд распределен по некоторому телу. Для описания этого распределения вводятся следующие величины:
1. Линейная плотность заряда. Используется для описания распределения заряда по нити:
где: L – длина нити. Измеряется в Кл/м.
2. Поверхностная плотность заряда. Используется для описания распределения заряда по поверхности тела:
где: S – площадь поверхности тела. Измеряется в Кл/м2.
3. Объемная плотность заряда. Используется для описания распределения заряда по объему тела:
где: V – объем тела. Измеряется в Кл/м3.
Обратите внимание на то, что масса электрона равна:
me = 9,11∙10–31 кг.
Закон Кулона
К оглавлению…
Точечным зарядом называют заряженное тело, размерами которого в условиях данной задачи можно пренебречь. На основании многочисленных опытов Кулон установил следующий закон:
Силы взаимодействия неподвижных точечных зарядов прямо пропорциональны произведению модулей зарядов и обратно пропорциональны квадрату расстояния между ними:
где: ε – диэлектрическая проницаемость среды – безразмерная физическая величина, показывающая, во сколько раз сила электростатического взаимодействия в данной среде будет меньше, чем в вакууме (то есть во сколько раз среда ослабляет взаимодействие). Здесь k – коэффициент в законе Кулона, величина, определяющая численное значение силы взаимодействия зарядов. В системе СИ его значение принимается равным:
k = 9∙109 м/Ф.
Силы взаимодействия точечных неподвижных зарядов подчиняются третьему закону Ньютона, и являются силами отталкивания друг от друга при одинаковых знаках зарядов и силами притяжения друг к другу при разных знаках. Взаимодействие неподвижных электрических зарядов называют электростатическим
Закон Кулона справедлив для точечных заряженных тел, равномерно заряженных сфер и шаров. В этом случае за расстояния r берут расстояние между центрами сфер или шаров. На практике закон Кулона хорошо выполняется, если размеры заряженных тел много меньше расстояния между ними. Коэффициент k в системе СИ иногда записывают в виде:
где: ε0 = 8,85∙10–12 Ф/м – электрическая постоянная.
Опыт показывает, что силы кулоновского взаимодействия подчиняются принципу суперпозиции: если заряженное тело взаимодействует одновременно с несколькими заряженными телами, то результирующая сила, действующая на данное тело, равна векторной сумме сил, действующих на это тело со стороны всех других заряженных тел.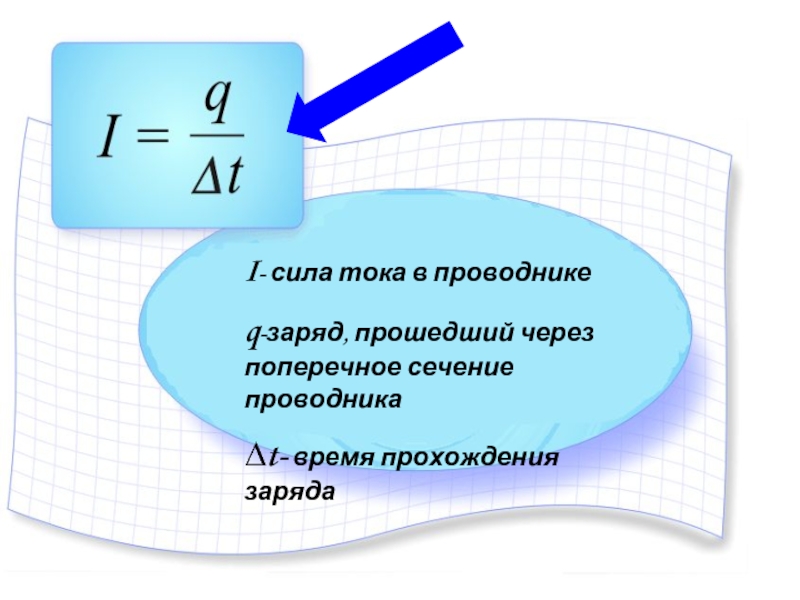
Запомните также два важных определения:
Проводники – вещества, содержащие свободные носители электрического заряда. Внутри проводника возможно свободное движение электронов – носителей заряда (по проводникам может протекать электрический ток). К проводникам относятся металлы, растворы и расплавы электролитов, ионизированные газы, плазма.
Диэлектрики (изоляторы) – вещества, в которых нет свободных носителей заряда. Свободное движение электронов внутри диэлектриков невозможно (по ним не может протекать электрический ток). Именно диэлектрики обладают некоторой не равной единице диэлектрической проницаемостью ε.
Для диэлектрической проницаемости вещества верно следующее (о том, что такое электрическое поле чуть ниже):
Электрическое поле и его напряженность
К оглавлению…
По современным представлениям, электрические заряды не действуют друг на друга непосредственно.
Электрическое поле, окружающее заряженное тело, можно исследовать с помощью так называемого пробного заряда – небольшого по величине точечного заряда, который не вносит заметного перераспределения исследуемых зарядов. Для количественного определения электрического поля вводится силовая характеристика – напряженность электрического поля E.
Напряженностью электрического поля называют физическую величину, равную отношению силы, с которой поле действует на пробный заряд, помещенный в данную точку поля, к величине этого заряда:
Напряженность электрического поля – векторная физическая величина. Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Направление вектора напряженности совпадает в каждой точке пространства с направлением силы, действующей на положительный пробный заряд. Электрическое поле неподвижных и не меняющихся со временем зарядов называется электростатическим.
Для наглядного представления электрического поля используют силовые линии. Эти линии проводятся так, чтобы направление вектора напряженности в каждой точке совпадало с направлением касательной к силовой линии. Силовые линии обладают следующими свойствами.
- Силовые линии электростатического поля никогда не пересекаются.
- Силовые линии электростатического поля всегда направлены от положительных зарядов к отрицательным.
- При изображении электрического поля с помощью силовых линий их густота должна быть пропорциональна модулю вектора напряженности поля.
- Силовые линии начинаются на положительном заряде или бесконечности, а заканчиваются на отрицательном или бесконечности. Густота линий тем больше, чем больше напряжённость.

- В данной точке пространства может проходить только одна силовая линия, т.к. напряжённость электрического поля в данной точке пространства задаётся однозначно.
Электрическое поле называют однородным, если вектор напряжённости одинаков во всех точках поля. Например, однородное поле создаёт плоский конденсатор – две пластины, заряженные равным по величине и противоположным по знаку зарядом, разделённые слоем диэлектрика, причём расстояние между пластинами много меньше размеров пластин.
Во всех точках однородного поля на заряд q, внесённый в однородное поле с напряжённостью E, действует одинаковая по величине и направлению сила, равная F = Eq. Причём, если заряд q положительный, то направление силы совпадает с направлением вектора напряжённости, а если заряд отрицательный, то вектора силы и напряжённости противоположно направлены.
Силовые линии кулоновских полей положительных и отрицательных точечных зарядов изображены на рисунке:
Принцип суперпозиции
К оглавлению. ..
..
Если с помощью пробного заряда исследуется электрическое поле, создаваемое несколькими заряженными телами, то результирующая сила оказывается равной геометрической сумме сил, действующих на пробный заряд со стороны каждого заряженного тела в отдельности. Следовательно, напряженность электрического поля, создаваемого системой зарядов в данной точке пространства, равна векторной сумме напряжённостей электрических полей, создаваемых в той же точке зарядами в отдельности:
Это свойство электрического поля означает, что поле подчиняется принципу суперпозиции. В соответствии с законом Кулона, напряженность электростатического поля, создаваемого точечным зарядом Q на расстоянии r от него, равна по модулю:
Это поле называется кулоновским. В кулоновском поле направление вектора напряженности зависит от знака заряда Q: если Q > 0, то вектор напряженности направлен от заряда, если Q < 0, то вектор напряженности направлен к заряду. Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Величина напряжённости зависит от величины заряда, среды, в которой находится заряд, и уменьшается с увеличением расстояния.
Напряженность электрического поля, которую создает заряженная плоскость вблизи своей поверхности:
Итак, если в задаче требуется определить напряженность поля системы зарядов, то надо действовать по следующему алгоритму:
- Нарисовать рисунок.
- Изобразить напряженность поля каждого заряда по отдельности в нужной точке. Помните, что напряженность направлена к отрицательному заряду и от положительного заряда.
- Вычислить каждую из напряжённостей по соответствующей формуле.
- Сложить вектора напряжённостей геометрически (т.е. векторно).
Потенциальная энергия взаимодействия зарядов
К оглавлению…
Электрические заряды взаимодействуют друг с другом и с электрическим полем. Любое взаимодействие описывается потенциальной энергией. Потенциальная энергия взаимодействия двух точечных электрических зарядов рассчитывается по формуле:
Обратите внимание на отсутствие модулей у зарядов.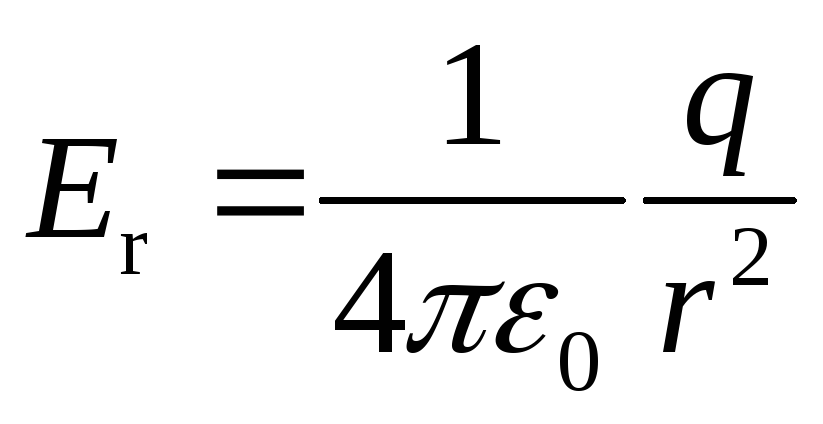 Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Для разноименных зарядов энергия взаимодействия имеет отрицательное значение. Такая же формула справедлива и для энергии взаимодействия равномерно заряженных сфер и шаров. Как обычно, в этом случае расстояние r измеряется между центрами шаров или сфер. Если же зарядов не два, а больше, то энергию их взаимодействия следует считать так: разбить систему зарядов на все возможные пары, рассчитать энергию взаимодействия каждой пары и просуммировать все энергии для всех пар.
Задачи по данной теме решаются, как и задачи на закон сохранения механической энергии: сначала находится начальная энергия взаимодействия, потом конечная. Если в задаче просят найти работу по перемещению зарядов, то она будет равна разнице между начальной и конечной суммарной энергией взаимодействия зарядов. Энергия взаимодействия так же может переходить в кинетическую энергию или в другие виды энергии. Если тела находятся на очень большом расстоянии, то энергия их взаимодействия полагается равной 0.
Обратите внимание: если в задаче требуется найти минимальное или максимальное расстояние между телами (частицами) при движении, то это условие выполнится в тот момент времени, когда частицы движутся в одну сторону с одинаковой скоростью. Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
Поэтому решение надо начинать с записи закона сохранения импульса, из которого и находится эта одинаковая скорость. А далее следует писать закон сохранения энергии с учетом кинетической энергии частиц во втором случае.
Потенциал. Разность потенциалов. Напряжение
К оглавлению…
Электростатическое поле обладает важным свойством: работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только положением начальной и конечной точек и величиной заряда.
Следствием независимости работы от формы траектории является следующее утверждение: работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю.
Свойство потенциальности (независимости работы от формы траектории) электростатического поля позволяет ввести понятие потенциальной энергии заряда в электрическом поле. А физическую величину, равную отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда, называют потенциалом φ электрического поля:
Потенциал φ является энергетической характеристикой электростатического поля. В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал – скалярная величина.
В Международной системе единиц (СИ) единицей потенциала (а значит и разности потенциалов, т.е. напряжения) является вольт [В]. Потенциал – скалярная величина.
Во многих задачах электростатики при вычислении потенциалов за опорную точку, где значения потенциальной энергии и потенциала обращаются в ноль, удобно принять бесконечно удаленную точку. В этом случае понятие потенциала может быть определено следующим образом: потенциал поля в данной точке пространства равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.
Вспомнив формулу для потенциальной энергии взаимодействия двух точечных зарядов и разделив ее на величину одного из зарядов в соответствии с определением потенциала получим, что потенциал φ поля точечного заряда Q на расстоянии r от него относительно бесконечно удаленной точки вычисляется следующим образом:
Потенциал рассчитанный по этой формуле может быть положительным и отрицательным в зависимости от знака заряда создавшего его.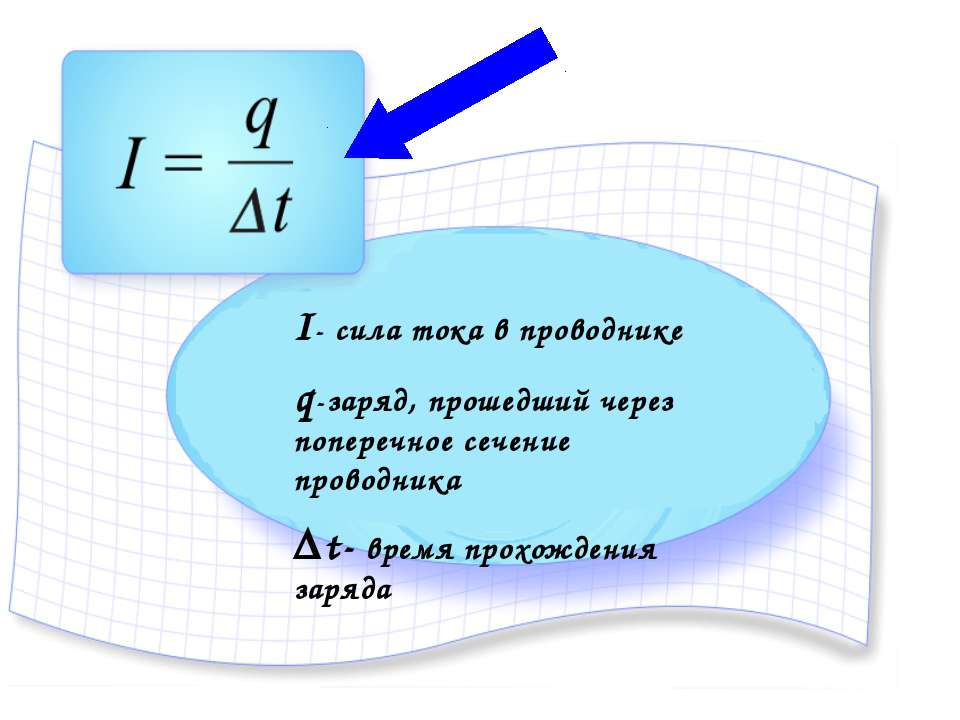 Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Эта же формула выражает потенциал поля однородно заряженного шара (или сферы) при r ≥ R (снаружи от шара или сферы), где R – радиус шара, а расстояние r отсчитывается от центра шара.
Для наглядного представления электрического поля наряду с силовыми линиями используют эквипотенциальные поверхности. Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью или поверхностью равного потенциала. Силовые линии электрического поля всегда перпендикулярны эквипотенциальным поверхностям. Эквипотенциальные поверхности кулоновского поля точечного заряда – концентрические сферы.
Электрическое напряжение это просто разность потенциалов, т.е. определение электрического напряжения может быть задано формулой:
В однородном электрическом поле существует связь между напряженностью поля и напряжением:
Работа электрического поля может быть вычислена как разность начальной и конечной потенциальной энергии системы зарядов:
Работа электрического поля в общем случае может быть вычислена также и по одной из формул:
В однородном поле при перемещении заряда вдоль его силовых линий работа поля может быть также рассчитана по следующей формуле:
В этих формулах:
- φ – потенциал электрического поля.

- ∆φ – разность потенциалов.
- W – потенциальная энергия заряда во внешнем электрическом поле.
- A – работа электрического поля по перемещению заряда (зарядов).
- q – заряд, который перемещают во внешнем электрическом поле.
- U – напряжение.
- E – напряженность электрического поля.
- d или ∆l – расстояние на которое перемещают заряд вдоль силовых линий.
Во всех предыдущих формулах речь шла именно о работе электростатического поля, но если в задаче говорится, что «работу надо совершить», или идет речь о «работе внешних сил», то эту работу следует считать так же, как и работу поля, но с противоположным знаком.
Принцип суперпозиции потенциала
Из принципа суперпозиции напряженностей полей, создаваемых электрическими зарядами, следует принцип суперпозиции для потенциалов (при этом знак потенциала поля зависит от знака заряда, создавшего поле):
Обратите внимание, насколько легче применять принцип суперпозиции потенциала, чем напряженности. Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Потенциал – скалярная величина, не имеющая направления. Складывать потенциалы – это просто суммировать численные значения.
Электрическая емкость. Плоский конденсатор
К оглавлению…
При сообщении проводнику заряда всегда существует некоторый предел, более которого зарядить тело не удастся. Для характеристики способности тела накапливать электрический заряд вводят понятие электрической емкости. Емкостью уединенного проводника называют отношение его заряда к потенциалу:
В системе СИ емкость измеряется в Фарадах [Ф]. 1 Фарад – чрезвычайно большая емкость. Для сравнения, емкость всего земного шара значительно меньше одного фарада. Емкость проводника не зависит ни от его заряда, ни от потенциала тела. Аналогично, плотность не зависит ни от массы, ни от объема тела. Емкость зависит лишь от формы тела, его размеров и свойств окружающей его среды.
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда q одного из проводников к разности потенциалов Δφ между ними:
Величина электроемкости проводников зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.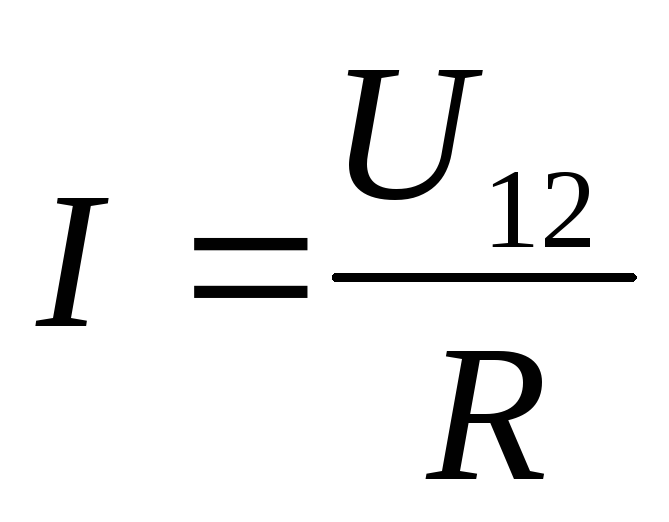 Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, называются обкладками.
Простейший конденсатор – система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика. Такой конденсатор называется плоским. Электрическое поле плоского конденсатора в основном локализовано между пластинами.
Каждая из заряженных пластин плоского конденсатора создает вблизи своей поверхности электрическое поле, модуль напряженности которого выражается соотношением уже приводившимся выше. Тогда модуль напряженности итогового поля внутри конденсатора, создаваемого двумя пластинами, равен:
За пределами конденсатора, электрические поля двух пластин направлены в разные стороны, и поэтому результирующее электростатическое поле E = 0. Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Электроёмкость плоского конденсатора может быть рассчитана по формуле:
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в ε раз. Обратите внимание, что S в этой формуле есть площадь только одной обкладки конденсатора. Когда в задаче говорят о «площади обкладок», то имеют в виду именно эту величину. На 2 умножать или делить её не надо никогда.
Еще раз приведем формулу для заряда конденсатора. Под зарядом конденсатора понимают только заряд его положительной обкладки:
Сила притяжения пластин конденсатора. Сила, действующая на каждую обкладку, определяется не полным полем конденсатора, а полем, созданным противоположной обкладкой (сама на себя обкладка не действует). Напряженность этого поля равна половине напряженности полного поля, и сила взаимодействия пластин:
Энергия конденсатора. Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Ее же называют энергией электрического поля внутри конденсатора. Опыт показывает, что заряженный конденсатор содержит запас энергии. Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор. Существует три эквивалентные формы записи формулы для энергии конденсатора (они следуют одна из другой если воспользоваться соотношением q = CU):
Особое внимание обращайте на фразу: «Конденсатор подключён к источнику». Это означает, что напряжение на конденсаторе не изменяется. А фраза «Конденсатор зарядили и отключили от источника» означает, что заряд конденсатора не изменится.
Энергия электрического поля
Электрическую энергию следует рассматривать как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля. Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Энергия заряженных тел сосредоточена в пространстве, в котором есть электрическое поле, т.е. можно говорить об энергии электрического поля. Например, у конденсатора энергия сосредоточена в пространстве между его обкладками. Таким образом, имеет смысл ввести новую физическую характеристику – объёмную плотность энергии электрического поля. На примере плоского конденсатора, можно получить такую формулу для объёмной плотности энергии (или энергии единицы объёма электрического поля):
Соединения конденсаторов
К оглавлению…
Параллельное соединение конденсаторов – для увеличения ёмкости. Конденсаторы соединены одноименно заряженными обкладками, как бы увеличивая площадь одинаково заряженных пластин. Напряжение на всех конденсаторах одинаковое, общий заряд равен сумме зарядов каждого из конденсаторов, и общая ёмкость также равна сумме емкостей всех конденсаторов соединенных параллельно. Выпишем формулы для параллельного соединения конденсаторов:
При последовательном соединении конденсаторов общая ёмкость батареи конденсаторов всегда меньше, чем ёмкость наименьшего конденсатора, входящего в батарею. Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Применяется последовательное соединение для увеличения напряжения пробоя конденсаторов. Выпишем формулы для последовательного соединения конденсаторов. Общая емкость последовательно соединенных конденсаторов находится из соотношения:
Из закона сохранения заряда следует, что заряды на соседних обкладках равны:
Напряжение равно сумме напряжений на отдельных конденсаторах.
Для двух последовательно соединённых конденсаторов формула выше даст нам следующее выражение для общей емкости:
Для N одинаковых последовательно соединённых конденсаторов:
Проводящая сфера
К оглавлению…
Напряженность поля внутри заряженного проводника равна нулю. В противном случае на свободные заряды внутри проводника действовала бы электрическая сила, которая вынуждала бы эти заряды двигаться внутри проводника. Это движение, в свою очередь, приводило бы к разогреванию заряженного проводника, чего на самом деле не происходит.
Факт того, что внутри проводника нет электрического поля можно понять и по-другому: если бы оно было то заряженные частицы опять таки двигались бы, причем они бы двигались именно так, чтобы свести это поле к нолю своим собственным полем, т.к. вообще-то двигаться им не хотелось бы, ведь всякая система стремится к равновесию. Рано или поздно все двигавшиеся заряды остановились бы именно в том месте, чтобы поле внутри проводника стало равно нолю.
На поверхности проводника напряжённость электрического поля максимальна. Величина напряжённости электрического поля заряженного шара за его пределами убывает по мере удаления от проводника и рассчитывается по формуле, аналогичной формулам для напряженности поля точечного заряда, в которой расстояния отсчитываются от центра шара.
Так как напряженность поля внутри заряженного проводника равна нулю, то потенциал во всех точках внутри и на поверхности проводника одинаков (только в этом случае разность потенциалов, а значит и напряжённость равна нулю). Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Потенциал внутри заряженного шара равен потенциалу на поверхности. Потенциал за пределами шара вычисляется по формуле, аналогичной формулам для потенциала точечного заряда, в которой расстояния отсчитываются от центра шара.
Электрическая емкость шара радиуса R:
Если шар окружен диэлектриком, то:
Свойства проводника в электрическом поле
К оглавлению…
- Внутри проводника напряженность поля всегда равна нулю.
- Потенциал внутри проводника во всех точках одинаков и равен потенциалу поверхности проводника. Когда в задаче говорят, что «проводник заряжен до потенциала … В», то имеют в виду именно потенциал поверхности.
- Снаружи от проводника вблизи от его поверхности напряженность поля всегда перпендикулярна поверхности.
- Если проводнику сообщить заряд, то он весь распределится по очень тонкому слою вблизи поверхности проводника (обычно говорят, что весь заряд проводника распределяется на его поверхности).
 Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся.
Это легко объясняется: дело в том, что сообщая заряд телу, мы передаем ему носители заряда одного знака, т.е. одноименные заряды, которые отталкиваются. А значит они будут стремиться разбежаться друг от друга на максимальное расстояние из всех возможных, т.е. скопятся у самых краев проводника. Как следствие, если из проводника удалить сердцевину, то его электростатические свойства никак не изменятся. - Снаружи проводника напряженность поля тем больше, чем кривее поверхность проводника. Максимальное значение напряженности достигается вблизи остриев и резких изломов поверхности проводника.
Замечания к решению сложных задач
К оглавлению…
1. Заземление чего-либо означает соединение проводником данного объекта с Землей. При этом потенциалы Земли и имеющегося объекта выравниваются, а необходимые для этого заряды перебегают по проводнику с Земли на объект либо наоборот. При этом нужно учитывать несколько факторов, которые следуют из того, что Земля несоизмеримо больше любого объекта находящегося не ней:
- Общий заряд Земли условно равен нолю, поэтому ее потенциал также равен нолю, и он останется равным нолю после соединения объекта с Землей.
 Одним словом, заземлить – означает обнулить потенциал объекта.
Одним словом, заземлить – означает обнулить потенциал объекта. - Для обнуления потенциала (а значит и собственного заряда объекта, который мог быть до этого как положительным так и отрицательным), объекту придется либо принять либо отдать Земле некоторый (возможно даже очень большой) заряд, и Земля всегда сможет обеспечить такую возможность.
2. Еще раз повторимся: расстояние между отталкивающимися телами минимально в тот момент, когда их скорости становятся равны по величине и направлены в одну сторону (относительная скорость зарядов равна нулю). В этот момент потенциальная энергия взаимодействия зарядов максимальна. Расстояние между притягивающимися телами максимально, также в момент равенства скоростей, направленных в одну сторону.
3. Если в задаче имеется система, состоящая из большого количества зарядов, то необходимо рассматривать и расписывать силы, действующие на заряд, который не находится в центре симметрии.
Глава 20. Конденсаторы
Для накопления разноименных электрических зарядов служит устройство, которое называется конденсатором. Конденсатор — система двух изолированных друг от друга проводников (которые часто называют обкладками конденсатора), один из которых заряжен положительным, второй — таким же по величине, но отрицательным зарядом. Если эти проводники представляют собой плоские параллельные пластинки, расположенные на небольшом рас-стоянии друг от друга, то конденсатор называется плоским.
Для характеристики способности конденсатора накапливать заряд вводится понятие электроемкости (часто говорят просто емкости). Емкостью конденсатора называется отношение заряда конденсатора к той разности потенциалов , которая возникает между обкладками при их заряжении зарядами и (эту разность потенциалов проводников часто называют электрическим напряжением между обкладками и обозначают буквой ):
(20. |
Поскольку величины и (или ) в формуле (20.1) зависимы, то емкость (20.1) не зависит от и , а является характеристикой геометрии системы проводников. Действительно, при сообщении проводникам зарядов и проводники приобретут потенциалы, разность которых будет пропорциональна заряду . Поэтому в отношении (20.1) заряд сокращается.
Выведем формулу для емкости плоского конденсатора (эта формула входит в программу школьного курса физики). При заряжении параллельных пластин, расположенных на небольшом расстоянии друг от друга, зарядами и , в пространстве между ними возникает однородное электрическое поле с напряженностью (см. гл. 18):
(20.2) |
Разность потенциалов между пластинами равна
(20.3) |
где — площадь пластин, — расстояние между ними. Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
Отсюда, вычисляя отношение заряда к разности потенциалов (20.3), находим емкость плоского конденсатора
(20.4) |
Если все пространство между обкладками заполнено диэлектриком с диэлектрической проницаемостью , то поле (20.2) и разность потенциалов (20.3) убывает в раз, а емкость конденсатора в раз взрастает
(20.5) |
Для конденсаторов, соединенных в батареи, вводится понятие эквивалентной емкости, как емкости одного конденсатора, который при заряжении его тем же зарядом, что и батарея дает ту же разность потенциалов, что и батарея конденсаторов. Приведем формулы для эквивалентной емкости, а также для заряда и электрического напряжения на каждом конденсаторе при последовательном и параллельном их соединении.
Последовательное соединение (см. рисунок). При сообщении левой пластине левого конденсатора заряда , а правой пластине правого заряда , на внутренних пластинах благодаря поляризации будут индуцироваться заряды (см. рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов
рисунок; значения индуцированных зарядов приведены под пластинами). Можно доказать, что в результате поляризации каждый конденсатор будет заряжен такими же зарядами и , как и заряды крайних пластин, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом, а обратная эквивалентная емкость батареи — сумме обратных емкостей всех конденсаторов
(20.6) |
Параллельное соединение (см. рисунок). В этом случае если сообщить левому проводнику заряд , правому сообщить заряд , заряд распределится между конденсаторами, вообще говоря, не одинаково, но по закону сохранения заряда .
Поскольку правые пластины всех конденсаторов соединены между собой, левые — тоже, то они представляют собой единые проводники, и, следовательно, разность потенциалов между пластинами каждого конденсатора будет одинакова: . Можно доказать, что при таком соединении конденсаторов эквивалентная емкость батареи равна сумме емкостей отдельных конденсаторов
(20. |
Заряженный конденсатор обладает определенной энергией. Если конденсатор емкости заряжен зарядом , то энергия этого конденсатора (можно говорить энергия электрического поля конденсатора) равна
(20.8) |
С помощью определения электрической емкости (20.1) можно переписать формулу (20.8) еще в двух формах:
(20.9) |
Рассмотрим в рамках этого минимума сведений о конденсаторах типичные задачи ЕГЭ по физике, которые были предложены в первой части книги.
Электроемкость конденсатора — его геометрическая характеристика, которая при неизменной геометрии не зависит от заряда конденсатора (задача 20.1.1 — ответ 3). Аналогично не меняется емкость конденсатора при увеличении напряжения на конденсаторе (задача 20.1.2 — ответ 3).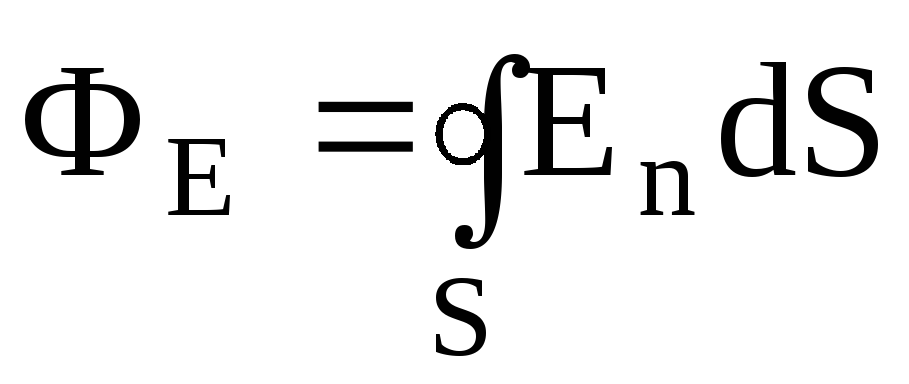
Связь между единицами измерений (задача 20.1.3) следует из определения емкости (20.1). Единица электрической емкости в международной системе единиц измерений СИ называется Фарада. 1 Фарада — это емкость такого конденсатора, между пластинами которого возникает напряжение 1 В при зарядах пластин 1 Кл и -1 Кл (ответ 4).
Поскольку электрическое поле в плоском конденсаторе однородно, то напряженность поля в конденсаторе и напряжение между пластинами связаны соотношением (см. формулу (18.9)) , где — расстояние между пластинами. Отсюда находим напряженность поля между обкладками плоского конденсатора в задаче 20.1.4
(ответ 4).
Согласно определению электрической емкости имеем в задаче 20.1.5
(ответ 2).
Из формулы (20.4) для емкости плоского конденсатора заключаем, что при увеличении площади его пластин в 3 раза (задача 20. 1.6) его емкость увеличивается в 3 раза (ответ 1).
1.6) его емкость увеличивается в 3 раза (ответ 1).
При уменьшении в раз расстояния между пластинами емкость плоского конденсатора возрастет в раз. Поэтому новое напряжение на конденсаторе (задача 20.1.7) можно найти из следующей цепочки формул
где и — новый заряд конденсатора (ответ 3).
Так как конденсатор в задаче 20.1.8 подключен к источнику, то между его пластинами поддерживается постоянное напряжение независимо от расстояния между ними. Поэтому заряд конденсатора изменяется при раздвигании пластин так же, как изменяется его емкость. А поскольку при увеличении расстояния между пластинами вдвое емкость конденсатора уменьшается вдвое (см. формулу (20.4)), то вдвое уменьшается и заряд конденсатора (ответ 2).
В задаче 20.1.9 конденсатор отключен от источника в процессе сближения пластин. Поэтому не меняется их заряд. А поскольку напряженность электрического поля между пластинами определяется соотношением (20. 2)
2)
то напряженность электрического поля между пластинами также не изменяется (ответ 3). Этот же результат можно получить и через определение емкости с учетом того, что
произведение от расстояния между пластинами не зависит (см. формулу (20.4)).
Из формул (20.8), (20.9) видим, что только одно из приведенных в качестве ответов к задаче 20.1.10 соотношений (а именно — 2) определяет энергию конденсатора.
При последовательном соединении конденсаторов (задача 20.2.1) одинаковыми будут их заряды независимо от значений их электрических емкостей (ответ 2). При параллельном соединении конденсаторов (задача 20.2.2) одинаковыми будут напряжения на каждом из них (ответ 3).
Поскольку конденсатор в задаче 20.2.3 отключен от источ-ника напряжения, его заряд не меняется в процессе раздвигания пластин. Поэтому для исследования изменения энергии конденсатора удобно воспользоваться формулой (20.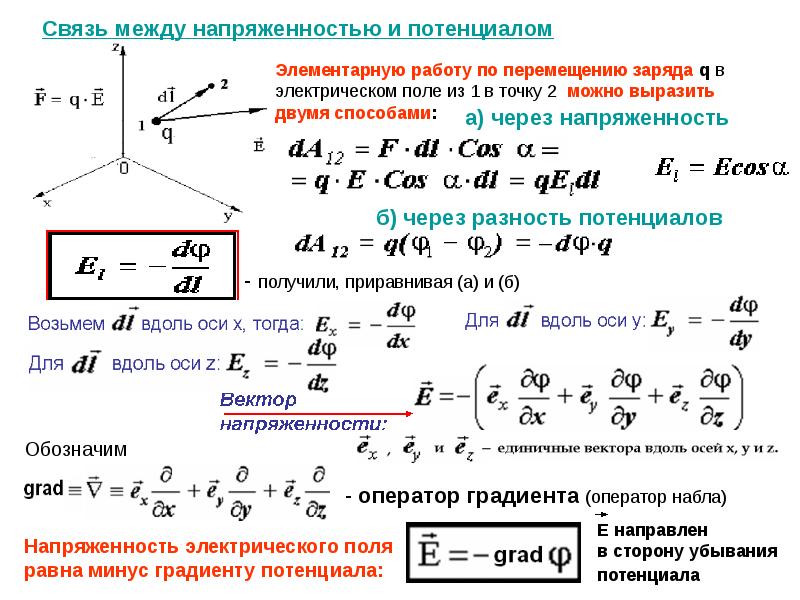 8)
8)
(1) |
Так как при увеличении расстояния между пластинами в раз электрическая емкость конденсатора уменьшается в раз, то согласно формуле (1) энергия конденсатора увеличится в раз (ответ 1).
В задаче 20.2.4 не изменяется напряжение на конденсаторе. Поэтому воспользуемся первой из формул (20.9)
Из этой формулы заключаем, что при увеличении в раз расстояния между пластинами энергия конденсатора уменьшится в раз — ответ 2. (Разница с предыдущей задачей связана с тем, что здесь кроме внешних сил, совершающих работу при раздвигании пластин, совершает работу источник напряжения.)
В задаче 20.2.5 изменяют расстояние между пластинами (и, следовательно, емкость) и заряд конденсатора. Поэтому удобно воспользоваться формулой (20.8)
Из этой формулы заключаем, что при увеличении расстояния между пластинами в 2 раза и увеличении заряда конденсатора в 2 раза его энергия возрастет в 8 раз (ответ 4).
Поскольку в задаче 20.2.6 конденсаторы соединены последовательно, емкость батареи конденсаторов можно найти по формуле (20.6), откуда находим емкость батареи конденсаторов (ответ 2).
В задаче 20.2.7 конденсаторы соединены параллельно, поэтому емкость батареи конденсаторов можно найти по формуле (20.7): (ответ 2).
Основной вопрос, на который нужно ответить в задаче 20.2.8, это как соединены конденсаторы? Последовательно, параллельно, по-другому? Попробуем по-другому расположить в пространстве и изменить длину соединительных проводов, чтобы схема стала более понятной. Очевидно, что можно соединить вершину 1 и вершину 3 («уменьшив» длину провода 1-3), а также вершины 2 и 4. При этом средний конденсатор разворачивается в пространстве, и схема приобретает вид, показанный на рисунке, откуда видно, что конденсаторы соединены параллельно. Поэтому (ответ 1).
Когда в заряженный плоский конденсатор вставляют металлическую пластинку (задача 20.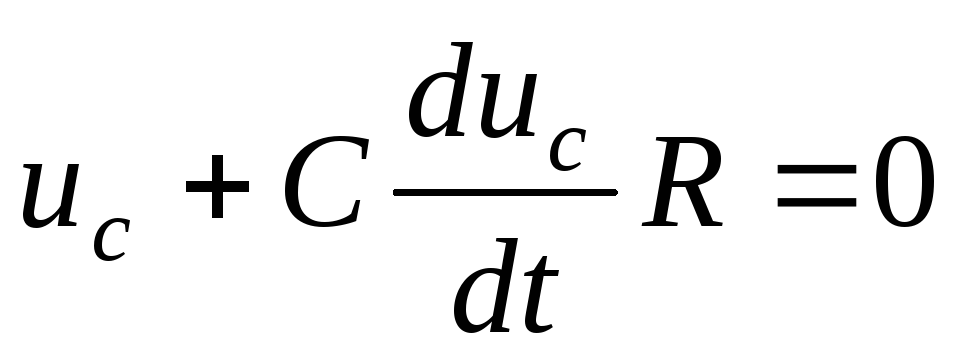 2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:
2.9), параллельную обкладкам конденсатора, напряженность электрического поля внутри пластинки становится равным нулю, вне пластинки между обкладками конденсатора остается таким же, каким оно было в отсутствие пластинки , где — заряд конденсатора, — площадь его пластин. Поэтому напряжение между обкладками конденсатора определяется соотношением:
где — расстояние между обкладками конденсатора, — толщина пластинки. Отсюда находим емкость рассматриваемого конденсатора
(ответ 4).
Чтобы найти емкость сферического конденсатора (задача 20.2.10) сообщим его обкладкам заряды и , найдем напряжение между обкладками, вычислим отношение заряда к напряжению. Разность потенциалов двух концентрических сфер, заряженных зарядами и (напряжение между обкладками сферического конденсатора), определена в задаче 19.2.5., откуда находим электрическую емкость сферического конденсатора (ответ 3):
Потенциал, работа электростатического поля.
 Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулы
Потенциальная энергия, разность потенциалов, принцип суперпозиции. Тесты, формулыТестирование онлайн
Работа электростатического поля
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.
Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.
Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.
В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.
Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q.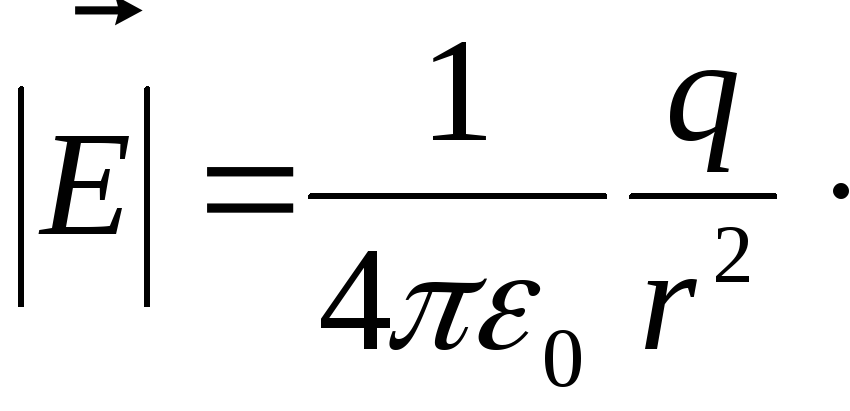 Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциалов
Эту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.
Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.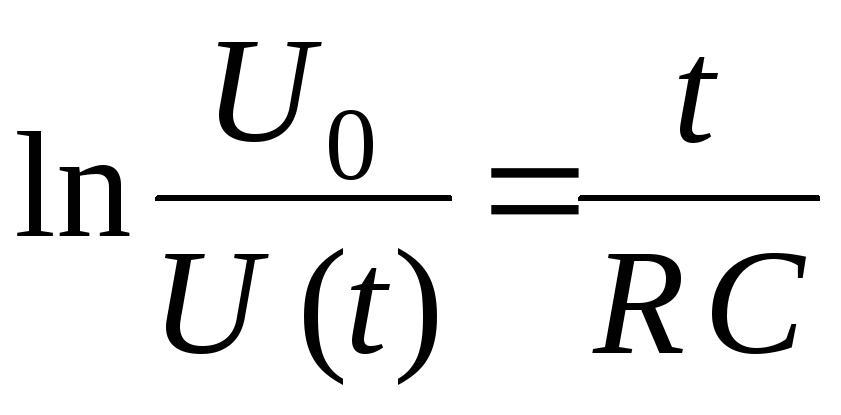
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельности
При решении задач возникает много путаницы при определении знака потенциала, разности потенциалов, работы.
На рисунке изображены линии напряженности. В какой точке поля потенциал больше?
Верный ответ – точка 1. Вспомним, что линии напряженности начинаются на положительном заряде, а значит положительный заряд находится слева, следовательно максимальным потенциалом обладает крайняя левая точка.
Если происходит исследование поля, которое создается отрицательным зарядом, то потенциал поля вблизи заряда имеет отрицательное значение, в этом легко убедиться, если в формулу подставить заряд со знаком “минус”. Чем дальше от отрицательного заряда, тем потенциал поля больше.
Если происходит перемещение положительного заряда вдоль линий напряженности, то разность потенциалов и работа являются положительными. Если вдоль линий напряженности происходит перемещение отрицательного заряда, то разность потенциалов имеет знак “+”, работа имеет знак “-“.
Порассуждайте самостоятельно отрицательные или положительные значения будут принимать работа и разность потенциалов, если заряд перемещать в обратном направлении относительно линий напряженности.
Напряжение в клетках сетчатки глаза при попадания в них света около 0,01 В.
Напряжение в телефонных сетях может достигать 60 В.
Электрический угорь способен создавать напряжение до 650 В.
Из определения потенциала следует, что потенциальная энергия электростатического взаимодействия двух зарядов q1 и q2, находящихся на расстоянии r друг от друга, численно равна работе, которая совершается при перемещении точечного заряда q2 из бесконечности в данную точку поля, созданного зарядом q1
Аналогично Тогда энергия взаимодействия двух точечных зарядов
Энергия взаимодействия n зарядов
Формула заряда через напряжение
В данной статье мы подробно разберем что такое напряжение, как просто его представить и измерить.
Определение
Напряжение — это электродвижущая сила, которая толкает свободные электроны от одного атома к другому в том же направлении.
В первые дни электричества напряжение было известно как электродвижущая сила (ЭДС). Именно поэтому в уравнениях, таких как закон Ома, напряжение представлено символом Е.
Алессандро Вольта
Единицей электрического потенциала является вольт, названный в честь Алессандро Вольта, итальянского физика, жившего между 1745 и 1827 годами.
Алессандро Вольта был одним из пионеров динамического электричества. Исследуя основные свойства электричества, он изобрел первую батарею и углубил понимание электричества.
Представление напряжения
Легче всего понять напряжении, представив давлении в трубе. При более высоком напряжении (давлении) будет течь более сильный ток. Хотя важно понимать, что напряжение (давление) может существовать без тока (потока), но ток не может существовать без напряжения (давления).
Напряжение часто называют разностью потенциалов, потому что между любыми двумя точками в цепи будет существовать разница в потенциальной энергии электронов. Когда электроны протекают через батарею, их потенциальная энергия увеличивается, но когда они протекают через лампочку, их потенциальная энергия будет уменьшаться, эта энергия покинет цепь в виде света и тепла.
Возьмите, например, обычную 1,5-вольтовую батарею AA, между двумя клеммами (+ и -) есть разность потенциалов 1,5 Вольт.
Напряжение или разность потенциалов — это просто измерение количества энергии (в джоулях) на единицу заряда (кулона). Например, в 1,5-вольтовой батарее AA каждый кулон (заряд) будет получать 1,5 вольт или джоулей энергии.
Напряжение = [Джоуль ÷ Кулон]
1 вольт = 1 джоуль на кулон
100 вольт = 100 джоулей на кулон
1 кулон = 6 200 000 000 000 000 000 электронов (6,2 × 10 18 )
В чем измеряется напряжение
Мы измеряем напряжение в единицах «Вольт», которые обычно обозначаются просто буквой «V» на чертежах и технической литературе. Часто необходимо количественно определить величину напряжения, это делается в соответствии с единицами СИ, наиболее распространенные величины напряжения, которые вы увидите:
- мегавольт (мВ)
- киловольт (кВ)
- вольт (В)
- милливольт (мВ)
- микровольт (мкВ)
Напряжение всегда измеряется в двух точках с помощью устройства, называемого вольтметром. Вольтметры являются либо цифровыми, либо аналоговыми, причем последний является наиболее точным. Вольтметры обычно встроены в портативные цифровые мультиметровые устройства, как показано ниже, они являются распространенным и часто важным инструментом для любого электрика или инженера-электрика. Обычно вы найдете аналоговые вольтметры на старых электрических панелях, таких как распределительные щиты и генераторы, но почти все новое оборудование будет поставляться с цифровыми счетчиками в качестве стандарта.
На электрических схемах вы увидите устройства вольтметра, обозначенные буквой V внутри круга, как показано ниже:
Расчет напряжения
В электрических цепях напряжение может быть рассчитано в соответствии с треугольником Ома. Чтобы найти напряжение (V), просто умножьте ток (I) на сопротивление (R).
Напряжение (V) = ток (I) * сопротивление (R)
V = I *R
Пример
Ток в цепи (I) = 10 А
Сопротивление цепи (R) = 2 Ом
Напряжение (V) = 10 А * 2 Ом
Ответ: V = 20В
Резюме
- Напряжение — это сила, которая перемещает электроны от одного атома к другому
- Напряжение также известно как разность потенциалов
- Напряжение измеряется в единицах «вольт» (В)
- Батареи увеличивают потенциальную энергию электронов
- Лампочки и другие нагрузки уменьшают потенциальную энергию электронов
- Напряжение измеряется с помощью вольтметра
- Напряжение цепи можно рассчитать путем умножения тока и сопротивления
Тимеркаев Борис — 68-летний доктор физико-математических наук, профессор из России. Он является заведующим кафедрой общей физики в Казанском национальном исследовательском техническом университете имени А. Н. ТУПОЛЕВА — КАИ
Тема: как рассчитать величину напряжения зная ток, сопротивление, мощность.
Как известно у электрического напряжения должна быть своя мера, которая изначально соответствует той величине, что рассчитана для питания того или иного электротехнического устройства. Превышение или снижение величины этого напряжения питания негативно влияет на электрическую технику, вплоть до полного выхода ее из строя. А что такое напряжение? Это разность электрических потенциалов. То есть, если для простоты понимания его сравнить с водой, то это примерно будет соответствовать давлению. По научному электрическое напряжение — это физическая величина, показывающая, какую работу совершает на данном участке ток при перемещении по этому участку единичного заряда.
Наиболее распространенной формулой напряжения тока является та, в которой имеются три основные электрические величины, а именно это само напряжение, ток и сопротивление. Ну, а формула эта известна под названием закона Ома (нахождение электрического напряжения, разности потенциалов).
Звучит эта формула следующим образом — электрическое напряжение равно произведению силы тока на сопротивление. Напомню, в электротехнике для различных физических величин существуют свои единицы измерения. Единицей измерения напряжения является «Вольт» (в честь ученого Алессандро Вольта, который открыл это явление). Единица измерения силы тока — «Ампер», и сопротивления — «Ом». В итоге мы имеем — электрическое напряжение в 1 вольт будет равно 1 ампер умноженный на 1 ом.
Помимо этого второй наиболее используемой формулой напряжения тока является та, в которой это самое напряжение можно найти зная электрическую мощность и силу тока.
Звучит эта формула следующим образом — электрическое напряжение равно отношению мощности к силе тока (чтобы найти напряжение нужно мощность разделить на ток). Сама же мощность находится путем перемножения тока на напряжение. Ну, и чтобы найти силу тока нужно мощность разделить на напряжение. Все предельно просто. Единицей измерения электрической мощности является «Ватт». Следовательно 1 вольт будет равен 1 ватт деленный на 1 ампер.
Ну, а теперь приведу более научную формулу электрического напряжения, которая содержит в себе «работу» и «заряды».
В этой формуле показывается отношение совершаемой работы по перемещению электрического заряда. На практике же данная формула вам вряд ли понадобится. Наиболее встречаемой будет та, которая содержит в себе ток, сопротивление и мощность (то есть первые две формулы). Но, хочу предупредить, что она будет верна лишь для случая применения активных сопротивлений. То есть, когда расчеты производятся для электрической цепи, у которой имеется сопротивления в виде обычных резисторов, нагревателей (со спиралью нихрома), лампочек накаливания и так далее, то приведенная формула будет работать. В случае использования реактивного сопротивления (наличии в цепи индуктивности или емкости) нужна будет другая формула напряжения тока, которая учитывает также частоту напряжения, индуктивность, емкость.
Электротехника как область науки, занимающаяся использованием электроэнергии, в том числе ее получением, распределением и учетом, оперирует значениями тока, напряжения, мощности и сопротивления. Это основные величины. Кроме этого, имеется множество других характеристик и понятий, но в рамках данной статьи будут рассматриваться именно эти основополагающие понятия.
Электрический ток
Согласно определению, ток представляет собой упорядоченное движение заряженных частиц в среде. Такими частицами могут быть свободные электроны или ионы, частицы вещества, в которых число протонов в ядре не равно количеству электронов, то есть имеющие определенный заряд, положительный или отрицательный. Электроток может быть постоянный или переменный.
Электрическое напряжение
Электрическое напряжение – это разность потенциалов на противоположных участках цепи. Точное определение понятия подразумевает работу по переносу электрического заряда между участками цепи.
Сопротивление
Любой проводник в цепи препятствует прохождению через себя тока. Данная характеристика определяет такую физическую величину, как сопротивление. Исходя из величины сопротивления, все вещества относят к проводникам или изоляторам. Точная граница весьма расплывчата, поэтому при некоторых условиях некоторые вещества можно отнести как к изоляторам, так и к проводникам. Участок электросхемы может иметь элемент с определенным значением величины, который именуется резистор.
Мощность
Скорость преобразования, передачи и потребления электрической энергии определяется мощностью.
Взаимосвязь параметров электрической цепи
Все параметры любой электрической цепи строго взаимосвязаны, поэтому в любой момент времени можно точно определить величину любого из них, зная остальные.
К сведению. Основополагающий закон, по которому производится большинство расчетов, – закон Ома, согласно которому сила тока обратно пропорциональна его сопротивлению и прямо пропорциональна приложенной разности потенциалов.
Формула напряжения тока закона Ома выглядит следующим образом:
Так, цепь с большим напряжением пропускает больший ток, а при одинаковом напряжении ампераж будет больше там, где меньше сопротивление.
Принятые обозначения в формуле расчета напряжения и тока понятны во всем мире:
- I – сила тока;
- U – напряжение;
- R – сопротивление.
Путем простейшего математического преобразования находится формула расчета сопротивления через силу тока и напряжение.
Кроме закона Ома, используется формула расчета мощности:
Символом P здесь обозначена мощность тока.
Любая схема может содержать участки, где имеется последовательное соединение, или есть элемент, подключенный параллельно. Расчеты при этом усложняются, но базовые формулы остаются одинаковыми.
Единицы измерения в формуле
Невозможно выполнять расчеты или измерения, не зная, какими величинами оперировать. Общепринятые обозначения, согласно международной системе измерения СИ:
- Напряжение – Вольт. Обозначается символом В или V в англоязычной литературе;
- Сила тока – Ампер. Обозначается символом А;
- Электрическое сопротивление – Ом. Используется обозначение Ом или Ohm;
- Электрическая мощность – Ватт. Обозначается как Вт или W.
Как работает закон в реальной жизни
Используя совместно формулу расчета мощности и закон Ома, можно производить вычисления, не зная одной из величин. Самый простой пример – для лампы накаливания известны только ее мощность и напряжение. Применяя приведенные выше формулы, можно легко определить параметры нити накаливания и ток через нее.
Сила тока формула через мощность:
Сопротивление:
Такой же результат можно найти из мощности, не прибегая к промежуточным расчетам:
Аналогично можно вычислить любую величину, зная только две из них. Для упрощения преобразований имеется мнемоническое отображение формул, позволяющее находить любые величины.
Внимательно посмотрев на формулы, можно заметить, что, если уменьшить напряжение на лампе в два раза, ожидаемая мощность не снизится аналогично в два раза, а в четыре, согласно формуле:
Это довольно распространенная ошибка среди далеких от электротехники людей, которые неправильно соотносят мощность и напряжение, а также их действие на остальные параметры.
Кстати. Сила тока, найденная через сопротивление и напряжение, справедлива как для постоянного, так и для переменного тока, если в ней не используются такие элементы, как конденсатор или индуктивность.
Облегчить расчеты можно, используя онлайн калькулятор.
Пример с обычной водой
Существуют вещества, которые можно отнести одновременно к проводникам и изоляторам. Самый простой пример – обыкновенная вода. Дистиллированная вода является хорошим изолятором, но наличие в ней практически любых примесей делает ее проводником. Особенно это относится к солям различных металлов. При растворении в воде соли диссоциируются на ионы, их наличие – прямой повод для возникновения тока. Чем больше концентрация солей, тем меньшим сопротивлением будет обладать вода.
Для наглядности можно взять дистиллированную воду для приготовления электролита для автомобильных аккумуляторных батарей. Опустив щупы омметра в воду, можно увидеть, что его показания велики. Добавление всего нескольких кристаллов поваренной соли через некоторое время вызывает резкое уменьшение сопротивления, которое будет тем меньше, чем больше соли перейдет в раствор.
По какой формуле определяется напряжение
Использование той или иной формулы напряжения электрического тока для вычисления зависит от того, какие величины известны:
- Ток и сопротивление – U=I∙R;
- Ток и мощность – U=P/I;
- Мощность и сопротивление – U=√P∙R
Различные используемые величины
Кроме основных величин: вольт, ампер, ом, ватт, используют кратные, большие или меньшие. Для обозначений применяют соответствующие приставки:
- Кило – 1000;
- Мега – 1000000;
- Гига – 1000000000;
- Милли – 0.001.
Таким образом, получается:
- Киловольт (кВ) – тысяча вольт;
- Мегаватт (Мвт) – миллион ватт;
- Миллиом (мОм) – одна тысячная Ом;
- Гигаватт (ГВт) – тысяча мегаватт или миллиард ватт.
Как найти напряжение
Формула нахождения напряжения как разности потенциалов в электрическом поле:
U=ϕA-ϕB, где ϕAи ϕB – потенциалы в точках А и В, соответственно.
Также можно записать напряжение как работу по переносу единицы заряда из точки А в точку В в электрическом поле:
U=A/q, где q – величина заряда.
Работа тем больше, чем выше напряженность электрического поля Е, то есть сила, действующая на неподвижный заряд.
Потенциальную энергию заряда в электростатическом поле называют электростатический потенциал.
Гидравлическая аналогия
Чтобы легче усвоить законы электрических цепей, можно представить себе аналогию с гидравлической системой, в которой соединение насоса и трубопроводов образует замкнутую систему. Для этого нужны следующие соответствия:
- Источник питания – насос;
- Проводники – трубы;
- Электроток – движение воды.
Без особых усилий становится понятнее, что чем меньше диаметр труб, тем медленнее по ним движется вода. Чем мощнее насос, тем большее количество воды он способен перекачать. При одинаковой мощности насоса уменьшение диаметра труб приведет к снижению потока воды.
Измерительные приборы
Для измерения параметров электрических цепей служат измерительные приборы:
Наиболее часто используется класс комбинированных устройств, в которых переключателем выбирается измеряемая величина – ампервольтомметры или авометры.
Типичные напряжения
Для стандартизации и возможности использования различного оборудования в быту и технике применяются электрические сети со стандартными значениями:
- Бытовая сеть –220В;
- Бортовая сеть автомобиля – 12 или 24В;
- Батареи и аккумуляторы – 1.5, 3 или 9В.
Потенциал Гальвани
В электрохимии используется понятие потенциала Гальвани, который означает разность потенциала между различными фазами вещества, например, между электродом и электролитом, между электродами из разнородных металлов.
Видео
чему равно напряжение, как найти сопротивление нагрузки
В наши дни электричество играет в жизни человека очень большую роль, в следствие чего базовые знания в области физики и электротехники нужны практически каждому. Напряжение является одной из главных физических величин, которая позволяет объяснить теорию возникновения электрического поля и методы подбора оптимального сечения кабеля для применения его в повседневной жизни.
Что такое напряжение в сети электричества.
Напряжение – это физическая величина, которая характеризует электрическое поле. Иными словами, оно показывает, какую работу оно совершает при перемещении одного положительного заряда на определённое расстояние.
Показатель напряжения на вольтметреЗа единицу напряжения в международной системе принимается такой показатель на концах проводника, при котором заряд в 1 Кл совершает работу в 1 Дж для перемещения его по этому проводнику. Общепринятой единицей измерения напряжения считается 1 В – Вольт.
Важно! Работа измеряется в Джоулях, заряды в Кулонах, а напряжение в Вольтах, следовательно, 1 Вольт равняется 1 Джоулю, деленному на 1 Кулон.
Чему равно напряжение.
Напряжение напрямую связано с работой тока, зарядом и сопротивлением. Чтобы измерить напряжение непосредственно в электрической цепи, к ней нужно подключить вольтметр. Он присоединяется к цепи параллельно, в отличие от амперметра, который подключается последовательно. Зажимы измерительного прибора крепятся к тем точкам, между которыми нужно вычислить напряжение. Чтобы он правильно показал значение, нужно включить цепь. На схемах вольтметр обозначается буквой V, обведенной в кружок.
Изображение вольтметра и электрической цепиНапряжение обозначается латинской [U], а измеряется в [В]. Оно равно работе, которое совершает поле при перемещении единичного заряда. Формула напряжения тока – это U = A/q, где A – работа тока, q – заряд, а U – само напряжение.
Обратите внимание! В отличие от магнитного поля, где заряды неподвижны, в электрическом поле они находятся в постоянном движении.
Электрическое полеФормула закона Ома
Свои опыты Ом направлял на изучение такой физической величины, как сопротивление, в результате чего в 1826 году он стал автором закона, который не потерял совей актуальность вплоть до сегодняшнего дня. Из своих опытов Ом вывел, что в различных цепях сила тока может возрастать с различной скоростью, и происходит это по мере увеличения напряжения.
Также, Ом сделал вывод, что каждый проводник обладает индивидуальными свойствами проводимости.
Сопротивление обозначается заглавной латинской [R] и измеряется в Омах. Сопротивление – физическая величина, характеризующая свойства проводника оказывать влияние на идущий по нему ток. Оно прямо пропорционально напряжению в сети и обратно пропорционально силе тока. В виде формулы данный закон можно записать как R = U/I, где U – напряжение, а I – сила тока. 1 Ом равняется 1 Вольту, деленному на 1 Ампер.
Запомните! Реостат – прибор, обеспечивающий возможность изменять сопротивление. Прежде всего, он влияет на показатель R в цепи, а, следовательно, на 2 другие величины, описанные в законе Ома. Силу тока может помочь определить амперметр.
Ползунковый реостатИз формулы закона Ома можно вывести практически любую зависимость, связанную с электричеством. Также, существует понятие удельного сопротивления проводника – физической величины, которая демонстрирует, каким сопротивлением будет обладать проводник из определенного вещества. Обозначается эта величина буквой ρ и через неё можно также найти сопротивление в цепи как произведению удельного сопротивления и длины проводника, деленного на площадь его поперечного сечения.
Важно! В виде формулы нахождение сопротивления через удельное сопротивление выглядит так: R = ρ*(l/S), где l – длина проводника, а S – площадь поперечного сечения.
Физический смысл удельного сопротивления показывает, какое влияние будет оказывать проводник длиной в 1 м с площадью поперечного сечения в 1 квадратный мм, изготовленный из определенного вещества. Измеряется в Омах, умноженных на метр: [ρ] = [Ом*м].
Ом и формулаКак найти сопротивление нагрузки
Сопротивление нагрузки обозначается латинскими буквами Rn или Rн. По сути, это является тем же сопротивлением участка цепи и вычисляется также по формулам закона Ома. Нагрузка обозначается символами, которые на электрической схеме изображаются в виде крестиков в кружке – лампочкой; то есть двигатель, лампа, конкретный прибор и т. д.
Каждая нагрузка имеет своё собственное сопротивление. Например, если к сети подключена одна лампочка, то сопротивление нагрузки – показатель этого единственного прибора в цепи. Если к цепи подключено несколько нагрузок, то сопротивление считается суммарно для каждой из них.
Сопротивление нагрузки вычисляется в соответствии с законом Ома, то есть Rn = U/I. Если к сети подключено несколько нагрузок, то оно будет рассчитываться следующим образом: сначала находится сопротивление каждой отдельной «лампочки». Далее Rn вычисляется в зависимости от того, какой тип подключения в цепи: последовательное или параллельное. При параллельном 1/R = 1/R1 + 1/R2 + 1/Rn, где n –количество подключенных приборов. Если же соединение последовательное, общее R равно сумме всех R цепи.
Последовательное/параллельное соединенияКак найти с помощью формулы напряжение
Людей, интересующихся электричеством и физикой, всегда волнует вопрос, как найти напряжения, если известны другие характеристики. Его можно найти через многие формулы: в соответствии с законом Ома, через работу тока, путём сложения всех напряжений в электрической цепи и практическим способом – с помощью вольтметра. Как вычислить показатель с помощью последнего способа было описано выше.
Важно! В цепях с последовательным соединением общее напряжение – сумма значений каждой нагрузки. При параллельном соединении общее напряжение равно значению каждой лампочки, у которых оно также эквивалентно.
Измерение напряженияПо каким формулам вычисляется напряжение через работу и сама сила тока, рассказывают на уроках физики, так как эти величины считаются базовыми. Работа тока равна произведению напряжения и заряда: A = U*q. Также, из этой формулы выводится A = U*I*t, так как заряд – произведение силы тока и времени. Из них следует, что U = A/q или U = A/(I*t). Кроме того, одной из основных является формула напряжения, выведенная из закона Ома: U = R/I.
Важно! Определить напряжение можно и через мощность электрического тока. Мощность [P] равна A/t, и, так как A = U*I*t, конечная формула выглядит, как P = (U*I*t)/t. Здесь t сократится, и останется P = U*I, из которой следует, что U = P/I.
Как найти силу тока через сопротивление и напряжение
Сила тока обозначается латинскими [I] или [Y], и она зависит от количества заряда, перенесенного от одного полюса к другому за определенный промежуток времени, т.е. I = q/t. Измеряется сила тока в амперах, а узнать её значение в цепи можно при помощи амперметра.
Мужчина считает силу токаСуществуют формулы определения силы тока через напряжение и сопротивление. В первом случае произведение силы тока на время равняется работе, деленной на напряжение: I*t = A/U, во втором – по закону Ома, I = U/R. Через мощность сила будет равняться P/U.
При последовательном соединении, сила тока одинакова на всех участках цепи, следовательно, равна общему значению в цепи. В противоположном случае сила электрического тока равняется сумме силы тока всех нагрузок.
Таким образом, существует огромное множество формул для нахождения силы тока, напряжения и сопротивления. Они всегда могут пригодиться для теории, а на практике всегда помогут специальные приборы – амперметр и вольтметр.
Формула и определение электрического напряжения в цепи в физике
В современном быту, строительстве и других сферах жизни человека огромную роль играет энергия, которая необходима для приведения в движение различных механизмов, производственных станков и инструментов. Электрическое напряжение, или как его принято называть в народе ток, занимает первое место среди ресурсов снабжения, поэтому человек во многом зависит от бесперебойной подачи электричества правильного номинала. В данной статье рассмотрено определение электрического напряжения, его формула, а также, от чего зависит и на что влияет данный показатель.
Электрическое напряжение
Что такое напряжение
Электрическое напряжение – это работа, которая необходима для подачи заряда электрическим полем от поставщика до потребляемого прибора по проводам или без них. Проще говоря, это величина силы, потраченной для доставки определенного заряда тока по проводнику от одного конца на другой. Без напряжения не будет перемещения заряженных частиц, а, следовательно, ток не будет поступать к потребителю, номинальная величина в цепи будет равна нулю.
Электрическим током заряжены все элементы и предметы, которые окружают человека, разница лишь в величине напряжения – у некоторых вещей данный показатель минимален и фактически не заметен, у других – наличие тока более выражено. За долгие годы исследований ученые изобрели множество приборов, которые способны вырабатывать электрический ток различного напряжения и силы, начиная от малогабаритных и заканчивая крупными электростанциями, питающими целые города. Электрическое напряжение напрямую связано с силой тока: чем выше напряжение, тем выше будет величина силы тока.
Для более точного понимания определения напряжения тока необходимо разобраться в физике образования электричества в целом. Откуда берется электрический ток?
Все предметы и вещества состоят из атомов с положительным зарядом, число которых равно числу вращающихся вокруг них отрицательно заряженных частиц. Проще говоря, количество электронов равно количеству нейтронов. Чтобы возникло напряжение в сети, из ядра извлекаются некоторые электроны, возникает разряжение, и оставшиеся частицы пытаются восполнить пробел путем притяжения электронов снаружи, возникает положительный заряд. Если же добавить электроны в атом, возникнет переизбыток, и образуется отрицательное энергетическое поле.
В результате такого взаимодействия возникают положительный и отрицательный потенциалы, и чем больше контакта у этих элементов, тем выше сила и напряжение электрического тока. При соединении указанных потенциалов образуется энергетическое поле, которое увеличивается при повышении количества заряженных атомов внутри себя.
Формула для вычисления напряжения тока выглядит следующим образом:
U=A/q, где:
- U – это само напряжение,
- A – работа, необходимая для перемещения заряда,
- Q – отрезок расстояния, на которое перемещается заряженный атом.
Формула напряжения
Таким образом, можно сделать вывод, что сила тока на протяжении всей цепи будет одинаковой, а напряжение на каждом из участков будет разным, в зависимости от нагрузки на данный отрезок. Как известно, энергия не возникает из ниоткуда и не пропадает в неизвестном направлении, поэтому при повышении напряжения на определенном участке провода избыточный ток выражается в тепловой нагрузке, проще говоря, материал, из которого изготовлен проводник, начинает греться.
Влияние температуры проводника на сопротивление
От чего зависит напряжение
Существует три основных фактора, влияющих на норматив напряжения электрических токов, среди которых:
- Материал, из которого выполнен проводник. Для решения определенных задач существуют различные типы проводов, чаще всего можно встретить медные или алюминиевые изделия различного сечения и наружной оболочки. Наружная обмотка таких проводов бывает также из множества материалов, защитных и декоративных, например, ПВХ пленка или резиновая защита. Такая обработка позволяет использовать проводку в любых условиях, в том числе для организации наружного освещения;
- Температуры использования проводника;
- Уровня сопротивления электрического тока на данном участке. Данная величина зависит от свойств проводимости кабеля или иного предмета, подключенного к сети, и способности к беспрепятственному пропуску атомов через себя. Существуют материалы с нулевым сопротивлением или полностью диэлектрические, то есть не способные проводить электрический ток любого напряжения.
Ток и его напряжение напрямую зависят друг от друга, поэтому и их обозначения одинаковы. Напряжение тока измеряется в Вольтах и обозначается буквой В. Вольт выражается в разности положительного и отрицательного потенциалов на двух удаленных от друг друга точках поля, силы которого совершают усилия, равные одному Дж, при доставке заряда от одного отрезка к конечному. Номинал единицы заряда равен одному Кл, таким образом, обозначение 220 Вольт включает в себя понятие, что данная сеть способна потратить энергию в 220 Дж для транспортировки зарядов от входной точки до потребителя, это и называется электрическим напряжением в сети.
Виды напряжения электрического тока
Синусоида постоянного и переменного тока
Что такое электрическое напряжение, описывается в учебниках по физике, там же приводится его классификация на основании временного промежутка подачи энергии. По данному признаку напряжение бывает:
- Постоянное – это когда на одном конце проводника ток и электрическое напряжение положительные, а на другом – отрицательные, и их значение направлено в одну сторону. Чаще всего такая система встречается в автономных батареях слабой и средней мощности;
Важно! Случайная или умышленная замена полярностей может привести к выходу из строя прибора, а также короткому замыканию при соединении нескольких элементов, осуществлять это нужно последовательно, стыкуя минусовый контакт к плюсовому. Синусоида при постоянном токе будет ровной без рывков и волн.
- Переменный ток и электрическое напряжение отличаются от постоянных тем, что у них может быть несколько направлений, например, при частой замене потенциалов полярностей или их перемещении возникает обратное движение заряда, частота данного действия и будет показателем переменного тока. Чаще всего данную систему используют для транспортировки электричества по проводнику на большие расстояния, так как потери тока минимальны, следовательно, и напряжение не уменьшается. Также переменный ток используется в трехфазных двигателях и при доставке постоянного тока на трансформатор для его последующего разделения. Синусоида переменного тока выглядит неровной, волнообразной, с множественными скачками. Существуют формула и механизмы, которые используются для преобразования переменного тока в постоянный, это возможно при наличии конденсаторов и диодного моста.
Между фазами переменного тока также существуют свои показатели, в данном случае напряжение равно 380В, по количеству разности потенциалов в трехфазной сети. В сети напряженностью 220В всего два провода: один – с несущей фазой, второй – с нулем, также для безопасности добавляется кабель заземления. В трехфазной сети имеется четыре жилы, и один дополнительный заземляющий провод, в сумме напряжение всех трех фаз составляет 380В.
Меры предосторожности
Ток и электрическое напряжение являются источником повышенной опасности, поэтому при работе и эксплуатации данного типа энергии необходимо соблюдать нормы и правила безопасности, не допускать аварийных ситуаций и обеспечить все приборы автоматической системой отключения питания.
Запрещается работать с проводкой, находящейся под напряжением, или без устройства для заземления. В случае возникновения короткого замыкания необходимо отключить все приборы от сети и предотвратить возгорание обмотки двигателя или кабеля.
Видео
Оцените статью:Работа электрического поля при перемещении заряда.
??? Вопросы
1. Формула работы электрического поля по перемещению заряда?
2. Единица измерения работы электрического поля?
3. В каких случаях работа электрического поля А=0, А>0, A<0?
4. Зависит ли работа электрического поля по перемещению заряда от формы траектории?
5. Какое электрическое поле называют однородным? Приведите пример?
Рассмотрим ситуацию: заряд q0 попадает в электростатическое поле. Это электростатическое поле тоже создается каким-то заряженным телом или системой тел, но нас это не интересует. На заряд q0 со стороны поля действует сила, которая может совершать работу и перемещать этот заряд в поле.Работа электростатического поля не зависит от траектории. Работа поля при перемещении заряда по замкнутой траектории равна нулю. По этой причине силы электростатического поля называются консервативными, а само поле называется потенциальным.
Потенциал
Система “заряд – электростатическое поле” или “заряд – заряд” обладает потенциальной энергией, подобно тому, как система “гравитационное поле – тело” обладает потенциальной энергией.Физическая скалярная величина, характеризующая энергетическое состояние поля называется потенциалом данной точки поля. В поле помещается заряд q, он обладает потенциальной энергией W. Потенциал – это характеристика электростатического поля.
Вспомним потенциальную энергию в механике. Потенциальная энергия равна нулю, когда тело находится на земле. А когда тело поднимают на некоторую высоту, то говорят, что тело обладает потенциальной энергией.
Касательно потенциальной энергии в электричестве, то здесь нет нулевого уровня потенциальной энергии. Его выбирают произвольно. Поэтому потенциал является относительной физической величиной.
В механике тела стремятся занять положение с наименьшей потенциальной энергией. В электричестве же под действием сил поля положительно заряженное тело стремится переместится из точки с более высоким потенциалом в точку с более низким потенциалом, а отрицательно заряженное тело – наоборот.
Потенциальная энергия поля – это работа, которую выполняет электростатическая сила при перемещении заряда из данной точки поля в точку с нулевым потенциалом.
Рассмотрим частный случай, когда электростатическое поле создается электрическим зарядом Q. Для исследования потенциала такого поля нет необходимости в него вносить заряд q. Можно высчитать потенциал любой точки такого поля, находящейся на расстоянии r от заряда Q.
Диэлектрическая проницаемость среды имеет известное значение (табличное), характеризует среду, в которой существует поле. Для воздуха она равна единице.
Разность потенциалов
Работа поля по перемещению заряда из одной точки в другую, называется разностью потенциаловЭту формулу можно представить в ином виде
Эквипотенциальная поверхность (линия) – поверхность равного потенциала. Работа по перемещению заряда вдоль эквипотенциальной поверхности равна нулю.
Напряжение
Разность потенциалов называют еще электрическим напряжением при условии, что сторонние силы не действуют или их действием можно пренебречь.Напряжение между двумя точками в однородном электрическом поле, расположенными по одной линии напряженности, равно произведению модуля вектора напряженности поля на расстояние между этими точками.
От величины напряжения зависит ток в цепи и энергия заряженной частицы.
Принцип суперпозиции
Потенциал поля, созданного несколькими зарядами, равен алгебраической (с учетом знака потенциала) сумме потенциалов полей каждого поля в отдельностиочков заряда | Безграничная физика
Электрический потенциал из-за точечного заряда
Электрический потенциал точечного заряда Q определяется выражением [латекс] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex].
Цели обучения
Выразите электрический потенциал, генерируемый одиночным точечным зарядом, в форме уравнения
Основные выводы
Ключевые моменты
- Напомним, что электрический потенциал определяется как потенциальная энергия на единицу заряда, т.е.е. [латекс] \ text {V} = \ frac {\ text {PE}} {\ text {q}} [/ latex].
- Разность потенциалов между двумя точками ΔV часто называется напряжением и выражается как [латекс] \ Delta \ text {V} = \ text {V} _ {\ text {B}} – \ text {V} _ {\ текст {A}} = \ frac {\ Delta \ text {PE}} {\ text {q}} [/ latex]. Потенциал на бесконечном расстоянии часто принимается равным нулю.
- Случай электрического потенциала, генерируемого точечным зарядом, важен, потому что он часто встречается. Сферическая сфера заряда создает внешнее поле, как, например, точечный заряд.
- Уравнение электрического потенциала, вызванного точечным зарядом, имеет вид [latex] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex], где k – константа, равная 9,0 × 10 9 Н · м 2 / C 2 .
Ключевые термины
- электрический потенциал : потенциальная энергия на единицу заряда в точке в статическом электрическом поле; Напряжение.
- напряжение : величина электростатического потенциала между двумя точками в пространстве.
Электрический потенциал из-за точечного заряда
Обзор
Напомним, что электрический потенциал определяется как электрическая потенциальная энергия на единицу заряда
[латекс] \ text {V} = \ frac {\ text {PE}} {\ text {q}} [/ latex]
Электрический потенциал говорит вам, сколько потенциальной энергии будет иметь одиночный точечный заряд в данном месте.Электрический потенциал в точке равен электрической потенциальной энергии (измеренной в джоулях) любой заряженной частицы в этом месте, деленной на заряд (измеренный в кулонах) частицы. Поскольку заряд пробной частицы разделен, электрический потенциал является «свойством», относящимся только к самому электрическому полю, а не к пробной частице. Другими словами, поскольку PE зависит от q, q в приведенном выше уравнении будет сокращаться, поэтому V не зависит от q.
Разность потенциалов между двумя точками ΔV часто называется напряжением и выражается как
.[латекс] \ Delta \ text {V} = \ text {V} _ {\ text {B}} – \ text {V} _ {\ text {A}} = \ frac {\ Delta \ text {PE} } {\ text {q}} [/ latex]
Точечных сборов
Точечные заряды, такие как электроны, являются одними из основных строительных блоков материи. Кроме того, сферическое распределение заряда (как на металлической сфере, см. Рисунок ниже) создает внешние электрические поля точно так же, как точечный заряд.Таким образом, нам необходимо рассмотреть электрический потенциал, обусловленный точечным зарядом. Используя расчет для определения работы, необходимой для перемещения пробного заряда q с большого расстояния на расстояние r от точечного заряда Q , и учитывая связь между работой и потенциалом (W = –qΔV), можно показать, что электрический потенциал V точечного заряда равен
[латекс] \ text {V} = \ frac {\ text {kQ}} {\ text {r}} [/ latex] (точечный заряд)
, где k – постоянная, равная 9.0 × 10 9 Нм 2 / C 2 . {2}} [/ latex ]
Электрический потенциал – это скаляр, а электрическое поле – вектор.Обратите внимание на симметрию между электрическим потенциалом и гравитационным потенциалом – оба падают как функция расстояния до первой степени, в то время как электрическое и гравитационное поля снижаются как функция расстояния до второй степени.
Суперпозиция электрического потенциала
Чтобы найти полный электрический потенциал системы точечных зарядов, нужно складывать отдельные напряжения в виде чисел.
Цели обучения
Объясните, как определяется полный электрический потенциал системы точечных зарядов
Основные выводы
Ключевые моменты
- Электрический потенциал V является скаляром и не имеет направления, тогда как электрическое поле E является вектором.
- Чтобы найти напряжение, вызванное комбинацией точечных зарядов, вы складываете отдельные напряжения в виде чисел. Так, например, электрический потенциал в точке L представляет собой сумму потенциальных вкладов зарядов Q 1 , Q 2 , Q 3 , Q 4 и Q 5 , так что [латекс] \ text {V} _ {\ text {L}} = \ text {k} [\ frac {\ text {Q} _ {1}} {\ text {d} _ {1}} + \ frac {\ text {Q} _ {2}} {\ text {d} _ {2}} + \ frac {\ text {Q} _ {3}} {\ text {d} _ {3}} + \ frac {\ text {Q} _ {4}} {\ text {d} _ {4}} + \ frac {\ text {Q} _ {5}} {\ text {d} _ {5}}] [/ latex].
- Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторы, учитывая величину и направление. Это согласуется с тем фактом, что V тесно связан с энергией, скаляром, тогда как E тесно связан с силой, вектором.
- Суммирование всех вкладов напряжения для определения общего потенциального поля называется суперпозицией электрического потенциала. Суммировать скаляры намного проще, чем векторы, поэтому часто предпочтительный метод решения задач с электрическими полями включает суммирование напряжений.
Ключевые термины
- вектор : Направленная величина, имеющая как величину, так и направление; между двумя точками.
- скаляр : величина, имеющая величину, но не направление; сравнить вектор.
- суперпозиция : Суммирование двух или более вкладов полей, занимающих одно и то же пространство.
Суперпозиция электрического потенциала
Мы видели, что электрический потенциал определяется как количество потенциальной энергии на единицу заряда, которое испытывает частица в данном месте в электрическом поле, т.е.{2}} [/ латекс]
с той разницей, что электрическое поле спадает пропорционально квадрату расстояния, в то время как потенциал падает линейно с расстоянием. Это аналогично соотношению между гравитационным полем и гравитационным потенциалом.
Суперпозиция электрического потенциала : Электрический потенциал в точке L представляет собой сумму напряжений от каждого точечного заряда (скаляры).
Напомним, что электрический потенциал V является скаляром и не имеет направления, тогда как электрическое поле E является вектором.Чтобы найти напряжение из-за комбинации точечных зарядов, вы складываете отдельные напряжения в виде чисел. Так, например, на рисунке выше электрический потенциал в точке L представляет собой сумму потенциальных вкладов от зарядов Q 1 , Q 2 , Q 3 , Q 4 и Q 5 , так что
[латекс] \ text {V} _ {\ text {L}} = \ text {k} [\ frac {\ text {Q} _ {1}} {\ text {d} _ {1}} + \ frac {\ text {Q} _ {2}} {\ text {d} _ {2}} + \ frac {\ text {Q} _ {3}} {\ text {d} _ {3}} + \ frac {\ text {Q} _ {4}} {\ text {d} _ {4}} + \ frac {\ text {Q} _ {5}} {\ text {d} _ {5}}] [ / латекс]
Чтобы найти полное электрическое поле, вы должны сложить отдельные поля как векторов , принимая во внимание величину и направление.Это согласуется с тем фактом, что V тесно связан с энергией, скаляром, тогда как E тесно связан с силой, вектором.
Суммирование всех вкладов напряжения для определения полного потенциального поля называется суперпозицией электрического потенциала. Суммирование напряжений вместо суммирования электрических значительно упрощает вычисления, поскольку сложение потенциальных скалярных полей намного проще, чем добавление электрических векторных полей. Обратите внимание, что в некоторых случаях вам может потребоваться суммировать потенциальные взносы из других источников, помимо точечных сборов; однако это выходит за рамки данного раздела.
Электростатика– Почему емкость определяется как заряд, деленный на напряжение?
Мы используем $ C = Q / V $, потому что это полезные вещи для измерения. Часто об этом легко забыть, но многие из используемых нами уравнений выбраны потому, что они работают, и потому, что другие уравнения не работают. Никогда не недооценивайте эту часть реальности.
Мы не используем «плату за единицу объема», потому что это число непостоянно. Вы можете заряжать конденсатор, не меняя его объема. Заряд, разделенный на напряжение, является постоянным.
Думаю, самый важный вопрос, который вы задали:
Или, согласно уравнению $ C = \ frac {Q} {V} $, почему увеличение напряжения при сохранении постоянного заряда будет иметь какое-либо влияние на способность тела накапливать заряд.
Мне нравится этот вопрос, потому что он немного обратный, предполагая, что вы думаете об этом по-другому. Мне нравится, когда люди думают о чем-то задом наперед, потому что это шоу, они действительно думают и хотят попытаться понять, что происходит!
Уловка в том, что вы обнаружите, что не может увеличить напряжение на конденсаторе, сохраняя при этом постоянный заряд, без внесения некоторых физических изменений в сам конденсатор.Реальность вам просто не позволит. Если вы попытаетесь увеличить напряжение, вы обнаружите, что в конденсатор поступает ровно столько заряда, чтобы сбалансировать напряжение.
Более интересно, рассмотрим случай, когда вы мгновенно изменяете напряжение, скажем, с 1 В до 10 В. Теоретически это должно «увеличивать напряжение без увеличения заряда», потому что для протекания тока не было времени. Вы можете нарисовать это в симуляторе схем, таком как PSPICE, и изменить напряжение при t = 0.Похоже, вам нужно изменить емкость.
На самом деле мы видим другой эффект. Мы видим, что даже если мы увеличили напряжение в системе, напряжение на конденсаторе фактически останется таким же! Это имеет смысл из уравнения, потому что мы знаем, что заряд и емкость не изменились, поэтому напряжение не может измениться. Но теперь похоже, что у нас разорвана цепь: как-то у нас на входе 10В, а на конденсаторе только 1В! Все знают, что это не сходится.
В действительности мы обнаруживаем, что в каждом используемом нами устройстве присутствует «паразитное сопротивление». У батареи есть сопротивление, у конденсатора есть сопротивление, даже те провода, которые вы используете для их соединения, имеют сопротивление. Итак, ваша реальная схема – это не просто источник напряжения и конденсатор, это источник напряжения, конденсатор и связка небольших резисторов.
В 99% случаев мы можем игнорировать эти резисторы, потому что они не сильно меняют схему. Однако в этой слегка патологической ситуации они действительно имеют большое значение.Именно они «впитывают» это дополнительное напряжение. В итоге вы получите 1 В на конденсаторе и 9 В на всех резисторах. Теперь начинается самое интересное. поскольку для тока через резистор используется $ V = IR $, мы можем рассчитать ток, проходящий через систему. Чем идеальнее были провода и батареи, тем больший ток нам нужно было использовать для обеспечения 9В. Этот ток представляет собой поток заряда. Куда он течет? Конденсатор. Вы сразу же начнете видеть, как заряд конденсатора возрастает по мере прохождения через него тока, пока в конечном итоге на конденсаторе не накопится достаточно заряда, чтобы создать на нем потенциал 10 В.В этот момент через резисторы больше нет напряжения, поэтому ток падает до 0, а цепь остается постоянной.
(На самом деле там есть несколько экспоненциальных членов, и технически никогда не достигает точно до 10 В, но в реалистичных сценариях мы, как правило, подходим достаточно близко, чтобы отмахнуться от этого набора дополнительных сложностей)
Заряд, ток и разница потенциалов
Обозначения схем – вы встречали эти обозначения схем в GCSE Physics.
Обычный ток течет по цепи от положительной (+) стороны ячейки к отрицательной (-). Однако электронов текут по цепи в противоположном направлении от отрицательной (-) стороны ячейки к положительной (+).
Заряд, ток и разница потенциалов
Заряд (Q) – заряд измеряется в кулонах (Кл).
- Один электрон несет заряд 1,6 x 10 -19 Кл.
Ток (I) – измеряется в амперах (А).
- Ток – это скорость потока заряда . Ток в 1 А означает, что 1 кулон заряда проходит через точку в цепи каждую секунду. (1 A = 1 C s -1 ) Ток в цепи измеряется с помощью амперметра, который включен последовательно с интересующим компонентом в цепи.
- I = ток в амперах, А
- DQ = заряд в кулонах, К
- Dt = время в секундах, с
Разность потенциалов (В) – измеряется в вольтах (В).
- Потенциальная разница – это работа, выполненная на единицу оплаты . Разность потенциалов в 1 В означает, что на один кулон заряда выполняется 1 джоуль работы. (1 В = 1 Дж C -1 ) Разность потенциалов в цепи измеряется с помощью вольтметра, который устанавливается параллельно с интересующим компонентом в цепи.
- В = разность потенциалов в вольтах, В
- Вт = выполненная работа или переданная энергия в джоулях, Дж
- Q = заряд в кулонах, Кл
Сопротивление (Вт) – это отношение разности потенциалов на компоненте к току, протекающему через него, измеряется в омах (Вт).
R = сопротивление в Ом, Вт
В = разность потенциалов в вольтах, В
I = ток в амперах, А
Примеры;
Q1) Если все электроны несут заряд 1,6 x 10 -19 C, сколько электронов потребуется, чтобы получить общий заряд в один кулон?
Q2) Если ток 0.50 ампер протекает через цепь в течение 120 секунд. Сколько заряда будет передано в компонент в цепи?
Q3) Заряд в 4,0 кулонов был перемещен через разность потенциалов 24 вольт, сколько энергии было передано?
Q4) Разность потенциалов на компоненте составляет 12 В, а ток через него составляет 0,37 А. Каково сопротивление компонента?
Как рассчитать кулоны | Sciencing
Обновлено 3 ноября 2020 г.
Автор: Клэр Гиллеспи
Электрический заряд, который проходит через что угодно, от батареи AA до молнии, измеряется в кулонах.Если вы знаете, какой ток в цепи и как долго он течет, вы можете рассчитать электрический заряд в кулонах.
Свойства кулонов
Электроны крошечные и имеют очень маленький заряд. В физике очень большое количество электронов определяется как 1 единица заряда, называемая кулоном. Один кулон эквивалентен 62 × 10 18 электронам. Количество кулонов в секунду называется током (т. Е. Скоростью потока кулонов в цепи).Энергия кулона называется напряжением и измеряется в джоулях.
Как рассчитать электрический заряд
Чтобы определить величину электрического заряда, протекающего в цепи, вам нужно знать, какой ток течет и как долго он протекает. Уравнение:
\ text {заряд в кулонах} = \ text {ток в амперах} \ times \ text {время в секундах}
Например, если ток 20 А течет в течение 40 с, расчет равен 20 × 40. Значит, электрический заряд равен 800 C.
Как рассчитать переданную энергию
Если вы знаете количество электрического заряда в кулонах и напряжение (также известное как разность потенциалов), вы можете вычислить, сколько энергии передается. Уравнение:
\ text {энергия, преобразованная в джоулях} = \ text {разность потенциалов в вольтах} \ times \ text {заряд в кулонах}
Например, если разность потенциалов равна 100 В, а заряд равен 3 Кл. , расчет 100 × 3. Таким образом, передается 300 Дж энергии.
Использование закона Кулона
Произведение электрических зарядов в двух телах (т. Е. Притягиваются они или отталкиваются друг от друга) зависит от заряда каждого тела в кулонах, а также от расстояния между телами. Если полярности одинаковы (обе положительные или обе отрицательные), кулоновская сила отталкивается, но если полярности противоположны (отрицательная / положительная или положительная / отрицательная), кулоновская сила притягивается. Электрический заряд также обратно пропорционален квадрату расстояния между двумя телами.Это известно как закон Кулона, который сформулирован как:
В этом уравнении F – сила, приложенная к зарядам (q 1 ) и (q 2 ), k – постоянная Кулона, а (r) – расстояние между (q 1 ) и (q 2 ). Значение k зависит от среды, в которую погружены заряженные объекты. Например, значение воздуха составляет приблизительно 9,0 × 10 9 Нм 2 / C 2 . Закон Кулона можно использовать для решения многих физических задач, в которых известны все значения, кроме одного.
Электрический потенциал и разность электрических потенциалов (напряжение)
В этой лекции мы узнаем об электрическом потенциале и разнице электрических потенциалов, которая также известна как напряжение.
Вы можете посмотреть следующее видео или прочитать письменное руководство под видео.
В предыдущей лекции мы говорили об электрической потенциальной энергии, которая зависит от заряда объекта, испытывающего электрическое поле.Теперь мы собираемся узнать об электрическом потенциале, который зависит только от положения объекта.
Электрический потенциал (или просто потенциал) – это просто мера электрической потенциальной энергии на единицу заряда.
Формула электрического потенциала
Это основное уравнение для вычисления электрического потенциала, которое показывает, что электрический потенциал V равен электрической потенциальной энергии U, деленной на заряд q, который будет помещен в точку на некотором расстоянии от основного заряда.
Электрическая потенциальная энергия U равна постоянной Кулона k, умноженной на заряд, который создает потенциал большой Q, умноженному на заряд, который будет помещен в точку на некотором расстоянии от основного заряда малого q, и разделенный на это расстояние. р.
Чтобы вычислить электрический потенциал, нам просто нужно разделить потенциальную энергию на малое q.
Мы можем заметить, что маленький q появляется дважды в уравнении, поэтому мы можем его сократить.
Теперь у нас есть это простое уравнение.
Уравнение показывает, что потенциал прямо пропорционален величине заряда Q – по мере увеличения заряда потенциал увеличивается, и наоборот, по мере уменьшения заряда потенциал уменьшается.
С другой стороны, это обратно пропорционально расстоянию r , потому что по мере удаления от заряда потенциал будет уменьшаться, а по мере того, как вы приближаетесь к заряду, потенциал будет увеличиваться. .
Наконец, мы получили бы количество электрической потенциальной энергии, которое в этот момент будет иметь каждая единица заряда.
Связано: Закон Кулона
Единица электрического потенциала
Теперь вернемся к основному уравнению.
Мы знаем, что электрическая потенциальная энергия измеряется в Джоулях, а единица заряда – кулон. Итак, единица измерения электрического потенциала – Джоули на Кулон, или одним словом Вольт.
Имеется точечный заряд, равный +2 мкКл, и мы хотим найти электрический потенциал 15 см (0.15 м) от заряда.
Теперь мы можем использовать это уравнение для вычисления электрического потенциала.
Получили положительный электрический потенциал + 1,2 × 10 5 В.
В случае отрицательного заряда, скажем, -2 мкКл, электрический потенциал в той же точке будет -1,2 × 10 5 В. Мы получили бы то же значение, но со знаком минус.
Давайте взглянем на этот график электрического потенциала.Ось X показывает расстояние от заряда, а ось Y показывает электрический потенциал в определенной точке.
Здесь у нас положительный заряд, а у потенциал вокруг положительного заряда всегда положительный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее положительным и уменьшается, приближаясь к нулю.
С другой стороны, у нас отрицательный заряд, а потенциал вокруг отрицательного заряда всегда отрицательный. По мере того, как вы удаляетесь от заряда, по мере того, как расстояние от заряда увеличивается, потенциал становится менее отрицательным и фактически увеличивается, также приближаясь к нулю.
Если вы находитесь бесконечно далеко от заряда, потенциал будет равен нулю как для положительных, так и для отрицательных зарядов.
Связано: что такое электричество и как работает электричество
Теперь мы можем перейти к разнице электрических потенциалов или напряжению.
По определению, разность электрических потенциалов или напряжение – это разность электрических потенциалов между конечным и начальным положением, когда над зарядом выполняется работа по изменению его потенциальной энергии.
Теперь давайте рассмотрим пример, который поможет нам легко понять термин “напряжение”.
У нас есть положительный заряд + 1,6 × 10 -19 C. Это основной заряд, создающий потенциал.
Первый круг – это первый энергетический уровень на расстоянии 2,5 × 10 -11 м от заряда. Второй кружок – второй энергетический уровень, на расстоянии 4,2 × 10 -12 м от заряда.
Чтобы найти разность электрических потенциалов или напряжение, нам нужно найти потенциал в точке A и потенциал в точке B.
Потенциал в точке A, которая является первым уровнем энергии, будет 57,6 В.
Потенциал в точке B, которая находится на большем расстоянии, будет 34,2 В.
Сначала мы рассчитаем напряжение при переходе от A к B, а затем от B к A.
В первом случае A – это наш начальный потенциал, а B – наш конечный потенциал. Таким образом, разность потенциалов будет конечной минус начальный потенциал, или 34.2–57,6 = -23,4 В. Мы получили отрицательный потенциал, что означает, что при переходе от A к B потенциал уменьшается.
Во втором случае B – это наш начальный потенциал, а A – наш конечный потенциал. Итак, разность потенциалов будет 57,6-34,2 = + 23,4 В. У нас есть положительный потенциал, или по мере перехода от B к A потенциал увеличивается.
Что это значит?По мере того, как мы идем от A к B, электрический потенциал уменьшается из-за того, что у нас есть положительный основной заряд, а его силовые линии электрического поля направлены наружу.Если мы поместим положительный тестовый заряд на первый энергетический уровень, электрическая потенциальная энергия будет больше. Точечный заряд будет отталкивать пробный заряд, потому что плотность силовых линий электрического поля намного сильнее. В B плотность силовых линий электрического поля слабее, а электрическая потенциальная энергия меньше.
Вот и все, что касается электрического потенциала и разности электрических потенциалов. Надеюсь, это было полезно, и вы узнали что-то новое.
Ток, электричество и условный ток
Современное электричество – это движущиеся заряженные частицы. Если вы позволите заряду, который накапливается в статическом электричестве, течь, вы получите ток.
Ток – это скорость потока заряда; – это количество заряда, протекающего через проводник в секунду.
Уравнение для расчета тока:
Где:I = ток (амперы, A)
Q = заряд, протекающий через точку в контуре (кулоны, Кл)
t = время, необходимое для прохождения заряда (секунды, с)
Таким образом, ток в 1 ампер равен 1 кулону заряда, проходящего через точку каждую секунду.
Точно так же кулон – это то же самое, что и ампер-секунда!
( Примечание: , если вы построите график зависимости тока от времени, площадь под графиком будет равна перемещенному заряду.)
Ну, сначала вам нужно иметь проводник, чтобы он протекал через него, а затем вам нужно притягивать или отталкивать заряженные частицы, чтобы заставить их двигаться. Величина вашего притяжения или отталкивания измеряется в вольтах и называется напряжением или разностью потенциалов (стр.d. коротко).
Эти заряженные частицы заставляют их двигаться, поэтому напряжение является мерой количества энергии, выделяемой на один кулон заряда.
1 вольт = 1 джоуль на кулон.
Уравнение для расчета напряжения:
Где:
Вт = количество энергии (джоуль, Дж)
В = напряжение (вольт, В)
Q = заряд (кулон, Кл)
Когда заряженные частицы обтекают контур, они не расходуются; это энергия, которую переносят заряженные частицы, которая уменьшается при движении по цепи.
(Бегуны, идущие по беговой дорожке длиной 400 м, бегают полностью, но при беге теряют энергию).
Таким образом, ток не расходуется. – если у вас остается 12 ампер на выходе из батареи, в цепи будет 12 ампер и 12 ампер возвращаются в батарею.
Напряжение изменяется при перемещении заряда по цепи. Потенциальная энергия, передаваемая заряду, в контуре превращается в тепловую энергию. Электрон может покинуть батарею с напряжением 6 В, но вернется к батарее с напряжением 0 В.Это дает изменение потенциала на 6 В, отсюда и слова «разность потенциалов».
Существует два основных типа схем, о которых вам нужно знать, и для каждой из них есть два правила, упрощающие вычисления:
Последовательные цепи:
В последовательной цепи …
- ток одинаковый по всей цепи.
- напряжение делится между компонентами в цепи.
Параллельные цепи:
В параллельной цепи …
- ток делится, чтобы пройти по каждой петле.
- напряжение в каждом контуре одинаковое.
Первоначально ученые полагали, что в цепях текут положительно заряженные частицы, и поэтому цепи всегда помечены током, протекающим от положительного к отрицательному выводу ячейки в цепи.Мы называем этот ток обычным током. На самом деле электроны текут в противоположном направлении!
Нажмите на кнопки ниже, чтобы увидеть это в действии:
Обычный ток – это поток положительных частиц. Все ссылки на ток в диаграммах и в вопросах на уровне A относятся к обычному току, если в вопросе специально не указано иное.
Для измерения тока используется амперметр . Он включен последовательно в цепь для измерения количества заряда, протекающего через него за секунду. (Вы можете сравнить это с турникетом, подсчитывающим людей на стадионе.)
Для измерения напряжения используем вольтметр. Он размещается параллельно для сравнения потенциала в двух разных точках по обе стороны от компонента. Затем он может измерить разность потенциалов или напряжение на компоненте.
Напряжение – Энергетическое образование
Напряжение часто используется как сокращение для разности напряжений , что является другим названием для разности потенциалов .Напряжение измеряет энергию, которую получит заряд, если он перемещается между двумя точками в пространстве. Единицей измерения напряжения является вольт (В), а 1 вольт = 1 Дж / Кл. [2]
Розетки и батареи имеют связанные с ними напряжения. Фактически, когда электричество доставляется на любое расстояние, между начальной и конечной точками существует напряжение (также известное как разность потенциалов). При приложении напряжения энергетически предпочтительно, чтобы электрический заряд двигался к точке самого низкого напряжения в проводе; это причудливый способ сказать, что положительный электрический заряд приобретает энергию при переходе от точки высокого напряжения к точке низкого напряжения.Отрицательный электрический заряд получит энергию от движения в другом направлении.
Чем больше напряжение, тем больше выигрыш в энергии от перемещения между двумя точками. Кроме того, чем больше заряд проходит через напряжение, тем больше кинетическая энергия, получаемая зарядом. Уравнение, которое моделирует это:
[математика] E = Q \ Delta V [/ математика]
Одна единственная точка не имеет напряжения, поскольку напряжение определяется как разность энергии между двумя точками.Напряжение всегда зависит от некоторой контрольной точки, которая определяется как 0 В. Для удобства Земля почти всегда определяется как 0 В (в классах физики 0 В часто рассматривается как потенциал в точке бесконечно удаленной, но это бесполезен в электронике). Напряжение генерирует поток электронов (электрический ток) через цепь. Специфическое название источника энергии, создающего напряжение для протекания тока, – электродвижущая сила. Это соотношение между напряжением и током задается законом Ома.
Часто бывает полезна аналогия:
Гравитационная потенциальная энергия – это энергия, которую мяч накапливает, сидя на столе. Высота, умноженная на ускорение свободного падения ( g ), дает полную энергию, которая преобразуется в кинетическую энергию, если мяч упадет с этой высоты. Электродвижущая сила – это то, что продолжает поднимать мяч и класть его обратно на стол (это то, что движет потоком мячей, падающих со стола).
Электрическая энергия – это энергия, выделяющаяся, когда заряд «падает» через разность потенциалов (напряжение).Напряжение существует независимо от того, есть заряд или нет.
Для бытового применения
Электрическая розетка в доме имеет напряжение 120 В (в Канаде и США) через два отверстия. Это напряжение присутствует всегда, и когда электрическая нагрузка становится частью цепи (например, путем подключения прибора), это напряжение заставляет ток течь по цепи.
Электрические генераторы перемещают магниты возле катушек с проводами, чтобы создать напряжение в электрической сети.
Генерация постоянного тока создает напряжения, используя энергию света в фотоэлектрических элементах или энергию химических реакций, обычно внутри батарей, и даже разницу температур с помощью термопар.Чтобы узнать больше о физике напряжения, см. Гиперфизику.
Аккумулятор на 9 В имеет напряжение 9 В. Двойные батареи A, AAA, C и D имеют напряжение (разность потенциалов) 1,5 В.
Phet Simulation
Чем больше напряжение, тем больше тока проходит через цепь. Университет Колорадо любезно разрешил нам использовать следующую симуляцию Фета. Используя приведенное ниже моделирование, исследуйте, как увеличение напряжения увеличивает ток в цепи:
Для дальнейшего чтения
Для получения дополнительной информации см. Соответствующие страницы ниже:
Список литературы
- ↑ Это изображение предоставлено кем-то из команды.


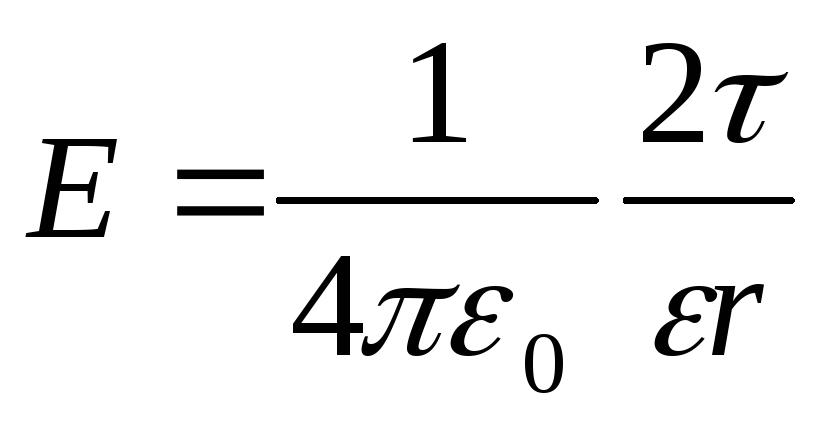 1)
1) 7)
7)