MathSciDoc: архив для математиков
[1] Теорема об исчезающем Ext-ветвлении для (GLn+1(F),GLn(F)) Кей Юэн ЧанТеория представлений mathscidoc:2303.30002
2237–2261, 2021.7
[ Скачать ] [ 2023-03-07 14:01:47 загружено пользователем ] [ 133 загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[2] Ограничение для общих линейных групп: локальная неспокойная гипотеза Гана – Гросса – Прасада (неархимедов случай) Кей Юэн Чан
Теория представлений mathscidoc:2303.
 30001
3000149-94, 2022.2
[Скачать ] [ 2023-03-07 13:58:19 загружено пользователем ] [ 104 загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[3] Изучение моделей разреженных групп с помощью логической релаксации Ицзе Ван Департамент компьютерных наук, Университет Индианы, Блумингтон Юань Чжоу Центр математических наук Яу и факультет математических наук Университета Цинхуа Сяоцин Хуан Департамент биостатистики и медицинских данных, Университет Индианы Кун Хуан Департамент биостатистики и медицинских данных, Университет Индианы Цзе Чжан Департамент медицинской и молекулярной генетики, Университет Индианы Цзянжу Ма Институт исследований индустрии искусственного интеллекта, Университет Цинхуа
Машинное обучение математикаdoc:2302.
 41003
41003Международная конференция по образовательным представительствам (ICLR), 2023.5
[Скачать ] [ 2023-02-27 16:40:04 загружено пользователем ] [ 159 загрузок ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[4] Почти оптимальные границы сожаления для многоэтапного обучения с подкреплением
Машинное обучение математикаdoc:2302.
 41002
41002Конференция по системам обработки нейронной информации (NeurIPS), 2022.12
[Скачать ] [ 2023-02-27 16:35:50 загружено пользователем ] [ 115 загрузок ]
Тезисы не загружены!
[ Реферат ][ Полный ][5] Динамическое ценообразование и управление запасами с фиксированной стоимостью заказа и неполной информацией о спросе Босяо Чен Колледж делового администрирования Иллинойсского университета в Чикаго Давид Симчи-Леви Институт данных, систем и общества, Центр исследования операций, Департамент гражданского строительства и экологии, Массачусетский технологический институт Инин Ван Уоррингтонский колледж бизнеса, Университет Флориды Юань Чжоу Озеро Яньци Пекинский институт математических наук и приложений
Машинное обучение математикаdoc:2302.

Менеджмент, 68, (8), 5684–5703, 2022.8
[Скачать ] [ 2023-02-27 16:32:43 загружено пользователем ] [ 149загрузки ]
Тезисы не загружены!
[ Реферат ][ Полный ]
Самые скачиваемые статьи
Подробнее …
[1] Городской шаблон: проектирование макета с помощью иерархического разделения доменов Юн-Лян Ян КАУСТ Джун Ван КАУСТ Этьен Вуга Колумбийский университет Питер Вонка КАУСТГеометрическое моделирование и обработка математика: 1608.16073
ACM Transactions on Graphics, 32, (6), 181:1 — 181:12, 2013. 12
12
[Скачать ] [ 2016-08-26 00:14:57 загружено пользователем ] [ 14431 загрузок ]
1
Чихан Пэн · Юнлян Ян · Питер Вонка. Вычисление макетов с деформируемыми шаблонами. В транзакциях ACM на графике. Том 33. Выпуск 4.2014.
2
Педринис Ф., Морель М., Гескьер Г. и др. Обнаружение изменений городов[C]., 2015: 123-139.
3
Тесо С., Себастиани Р., Пассерини А. и др. Теории структурированного обучения по модулю[J]. Искусственный интеллект, 2014.
4
Алхалавани С., Ян И., Вонка П. и др. Что заставляет Лондон работать как Лондон[J]. симпозиум по обработке геометрии, 2014, 33(5): 157-165.
5
Ваксман А., Кампен М., Диаманти О. и др. Синтез направленного поля, проектирование и обработка[C]. международная конференция по компьютерной графике и интерактивным технологиям, 2016.
6
Фэн Т., Ю Л., Йенг С. и др. Ориентированный на толпу макет среднего масштаба[J]. ACM Transactions on Graphics, 2016, 35(4).
ACM Transactions on Graphics, 2016, 35(4).
7
Нисида Г., Гарсиадорадо И., Алиага Д. Г. и др. Процедурные городские дороги на основе примеров[J]. Форум компьютерной графики, 2015.
8
Zhou J, Sun Z, Yang K, et al. Стратегия управляемого расположения стежков для вышивания произвольной иглой[J]. Журнал науки Чжэцзянского университета C, 2014, 15 (9): 729-743.
9
Ваксман А., Кампен М., Диаманти О. и др. Синтез направленного поля, проектирование и обработка[C]. международная конференция по компьютерной графике и интерактивным технологиям, 2016.
10
Чихан Пэн · Юнлян Ян · Фань Бао · Даниэль Финк · Дунмин Ян · Питер Вонка · Нилой Дж. Митра. Проектирование вычислительной сети на основе функциональных спецификаций. В транзакциях ACM на графике. Том 35. Выпуск 4. Страница 131.2016.[ Процитировано 14 ]
Мы представляем основу для создания сетей улиц и планировок участков. Наша цель — создание высококачественных макетов, которые можно использовать для городского планирования и виртуальной среды. Мы предлагаем решение, основанное на иерархическом разделении домена с использованием двух типов разделения: разделение на основе линий тока, которое разбивает регион вдоль одной или нескольких линий тока поперечного поля, и разделение на основе шаблона, которое деформирует предварительно разработанные шаблоны в область и использует внутренняя геометрия шаблона в виде линий разделения. Мы объединяем эти два подхода к разделению в иерархическую структуру, предоставляя автоматические и интерактивные инструменты для исследования пространства дизайна.
Наша цель — создание высококачественных макетов, которые можно использовать для городского планирования и виртуальной среды. Мы предлагаем решение, основанное на иерархическом разделении домена с использованием двух типов разделения: разделение на основе линий тока, которое разбивает регион вдоль одной или нескольких линий тока поперечного поля, и разделение на основе шаблона, которое деформирует предварительно разработанные шаблоны в область и использует внутренняя геометрия шаблона в виде линий разделения. Мы объединяем эти два подхода к разделению в иерархическую структуру, предоставляя автоматические и интерактивные инструменты для исследования пространства дизайна.
[ Реферат ][ Полный ]
[2] Обзор дискретизации синего шума и ее приложений Дун-Мин Ян NLPR-CASIA Цзянь-Вэй Го NLPR-CASIA Бин Ван Университет Цинхуа Сяопэн Чжан NLPR-CASIA Питер Вонка КАУСТ
Геометрическое моделирование и обработка математикаdoc:1608.
 16011
16011[ Скачать ] [ 2016-08-19 16:21:46 загружено пользователем ] [ 8163 загрузки ]
1
Чжан С. Ф., Го Дж., Чжан Х. и др. Ограниченная емкость выборки синего шума на поверхностях[J]. Компьютеры и графика, 2016, 55(55): 44-54.
2
Кита Н., Мията К. Мультиклассовая анизотропная выборка синего шума для генерации шаблонов дискретных элементов [J]. Визуальный компьютер, 2016: 1035-1044.
3
Boivin C, Olliviergooch C. Создание треугольной сетки гарантированного качества для областей с искривленными границами [J]. Международный журнал численных методов в технике, 2002 г., 55 (10): 1185-1213.
4
Рушил Анируд · Анаф Масрур · Паван Турага. Разнообразие, способствующее онлайн-семплингу для суммирования потокового видео. 2016.
5
Вейцзе Цюань · Цзяньвэй Го · Дунмин Янь · Вейлян Мэн · Сяопэн Чжан. Анализ шаблонов выборки поверхности с использованием локализованной парной корреляционной функции.
6
Guo J, Yan D, Chen L, et al. Тетраэдрическая сетка с помощью максимальной выборки диска Пуассона [J]. Компьютерное геометрическое проектирование, 2016, 43(43): 186-199.
7
Шицин Синь · Бруно Леви · Чжунгуй Чен · Лей Чу · Яохуэй Юй · Чанхэ Ту · Вэньпин Ван. Диаграммы центроидальной мощности с ограничениями мощности: вычисления, приложения и расширение. 2016.
[ Процитировано 7 ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[3] Квантование гравитации Клаус Герхардт Университет Рупрехта Карла, Институт математических наук Ангеванда
Математическая физика математикаdoc:1609.22008
Доп. Теор. Мат. Phys., 22, (3), 709 – 757, 2018.10
[ Скачать ] [ 2016-09-19 23:54:28 загружено пользователем ] [ 6278 скачиваний ]
В предыдущей статье мы предложили модель квантования гравитации, работая в расслоении $E$, где мы реализовали ограничение Гамильтона как уравнение Уилера-ДеВитта. Однако соответствующий оператор действует только в слоях, а не в базовом пространстве. Поэтому теперь мы отбрасываем уравнение Уилера-ДеВитта и выражаем ограничение Гамильтона по-другому, либо с помощью уравнений Гамильтона, либо используя уравнение геометрической эволюции. Возможны две возможные модификации, каждая из которых эквивалентна ограничению Гамильтона и приводит к двум новым моделям. В первой модели мы получаем гиперболический оператор, действующий как в слоях, так и в базовом пространстве, и мы можем построить симплектическое векторное пространство и систему Вейля. Во второй модели полученное уравнение представляет собой волновое уравнение в $\so \times (0,\infty)$, справедливое в точках $(x,t,\xi)$ в $E$, и мы ищем решения для каждого фиксированного $ \xi$. Эта система уравнений содержит как частный случай уравнение квантованной космологической вселенной Фридмана без материи, но с космологической постоянной, когда мы ищем решения, зависящие только от $t$. Более того, в случае компактности $\so$ доказывается спектральное разрешение уравнения.
Однако соответствующий оператор действует только в слоях, а не в базовом пространстве. Поэтому теперь мы отбрасываем уравнение Уилера-ДеВитта и выражаем ограничение Гамильтона по-другому, либо с помощью уравнений Гамильтона, либо используя уравнение геометрической эволюции. Возможны две возможные модификации, каждая из которых эквивалентна ограничению Гамильтона и приводит к двум новым моделям. В первой модели мы получаем гиперболический оператор, действующий как в слоях, так и в базовом пространстве, и мы можем построить симплектическое векторное пространство и систему Вейля. Во второй модели полученное уравнение представляет собой волновое уравнение в $\so \times (0,\infty)$, справедливое в точках $(x,t,\xi)$ в $E$, и мы ищем решения для каждого фиксированного $ \xi$. Эта система уравнений содержит как частный случай уравнение квантованной космологической вселенной Фридмана без материи, но с космологической постоянной, когда мы ищем решения, зависящие только от $t$. Более того, в случае компактности $\so$ доказывается спектральное разрешение уравнения.
[ Реферат ][ Полный ]
[4] Асимптотическое распределение резонансов для выпуклых препятствий Йоханнес Шёстранд Центр математики, Политехническая школа UMR 7640, CNRS Мацей Зворски Департамент математики, Университет Торонто
подлежит уточнению математикаdoc:1701.331878
Acta Mathematica, 183, (2), 191-253, 1998.5
[Скачать ] [ 2017-01-08 20:33:34 загружено пользователем ] [ 6030 скачиваний ]
[ Процитировано 35 ]
Тезисы не загружены!
[ Реферат ][ Полный ]
[5] Исследование магического шестиугольника порядка 3, его свойств, конструкции и расширений Фаньсин Мэн Тяньцзиньская средняя школа №1
С.
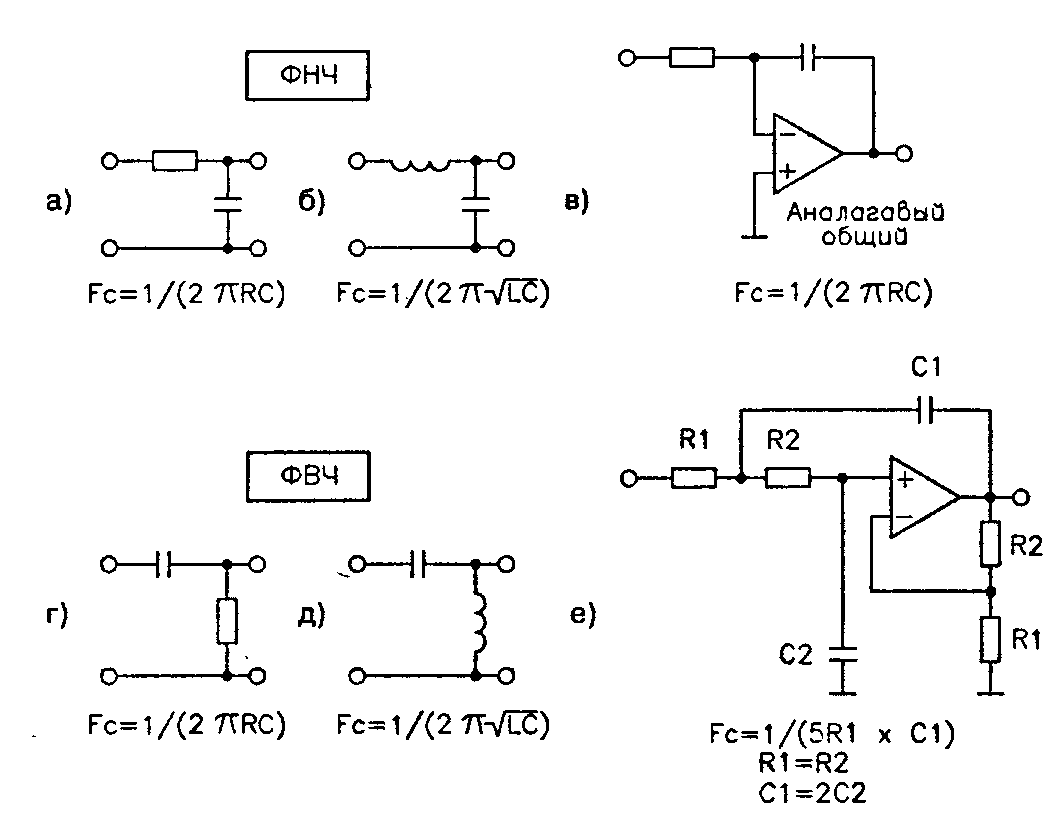 -Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35005
-Т. Награды за научные достижения средней школы Яу
математикаdoc:1608.35005[ Скачать ] [ 2016-08-13 21:51:54 загружено пользователем ] [ 5302 загрузки ]
Магический шестиугольник 3-го порядка напоминает по форме соты с 19 ячейками, расположенными по схеме 3 4 5 4 3. Требование состоит в том, чтобы заполнить числа 1-19 в сетках так, чтобы каждая строка (всего 15) составляла в сумме 38.
Придуманные ранее методы, направленные на решение этой задачи и доказательство ее единственности, были либо недостаточно строгими, либо слишком замысловатыми. Поэтому, анализируя его свойства, я хотел найти комбинаторное решение его конструкции, доказать его уникальность и выяснить, можно ли использовать его математические принципы в реальных приложениях. Сложность зависит от точки зрения, поэтому первым шагом было обозначить каждую сетку удобным способом. Я решил рассматривать магический шестиугольник как сеть, состоящую из центра и колец. Тогда связи и ограничения каждого набора чисел можно было бы найти по формуле
вывод. Аналогичным образом были обнаружены и симметричные свойства. Следующим шагом был анализ возможных распределений нечетных и четных чисел. Из 9конфигурации, только 1 оказался пригодным для использования. Завершающим этапом было строительство. При всех известных свойствах немногие невозможности были легко устранены, и осталось только одно решение, что доказывает его единственность.
Процедуры, используемые для магического шестиугольника порядка 3, могут быть расширены до процедур более высоких порядков, что упрощает их построение. Уникальные свойства магических шестиугольников могут быть использованы в некоторых областях применения, например, в системах паролей, крупномасштабных конструкциях крыш, композитных материалах, системах национальной безопасности и многих других областях.
Тогда связи и ограничения каждого набора чисел можно было бы найти по формуле
вывод. Аналогичным образом были обнаружены и симметричные свойства. Следующим шагом был анализ возможных распределений нечетных и четных чисел. Из 9конфигурации, только 1 оказался пригодным для использования. Завершающим этапом было строительство. При всех известных свойствах немногие невозможности были легко устранены, и осталось только одно решение, что доказывает его единственность.
Процедуры, используемые для магического шестиугольника порядка 3, могут быть расширены до процедур более высоких порядков, что упрощает их построение. Уникальные свойства магических шестиугольников могут быть использованы в некоторых областях применения, например, в системах паролей, крупномасштабных конструкциях крыш, композитных материалах, системах национальной безопасности и многих других областях.
[ Реферат ][ Полный ]
Графический интерфейс пользователя > Окно цепи > Меню выбора > Инструменты энергосистемы
Power System Toolbox состоит из трехфазных компонентов для изучения энергосистемы (анализ коротких замыканий и неисправностей, а также релейная защита).
|
Фундаментальные компоненты
Это стандартные блоки для изучения энергосистем с простым определением неисправностей. Объедините это со стандартными пробниками напряжения и тока со стабильным выходом.
Выбор | Имя объекта | Значок | Плата АТФ | Описание |
Автобус | ШИНА3 | ФИЛИАЛ | Многоузловая (отсеки) точка подключения с дополнительной нагрузкой и разрядником. | |
Линия | ЛИНИЯ3 | ФИЛИАЛ | Компонент LINEPI3S или LINEZT_3 с неисправностями, CB и CT. | |
Нагрузка PQ | НАГРУЗКА | МОДЕЛИ РЛК+СРЦ | Модель нагрузки, зависящая от напряжения. Группа с управляемым источником MODELS на основе векторного расчета | |
Контроллер CB | CTRLCB | МОДЕЛИ ВЫКЛЮЧАТЕЛЬ | Трехфазный переключатель TACS, размыкается при переходе через ноль, управляемом МОДЕЛЯМИ |
Калькуляторы Basic MODELS
Эти калькуляторы принимают трехфазный ток или напряжение, выбранные в диалоговом окне узла ввода (слева).
Выбор | Имя объекта | Значок | Плата АТФ | Описание |
СКЗ | ABC2RMS | МОДЕЛИ | Выходы Среднеквадратичное значение всех 3-фазных входов | |
Векторы +Базовый | ABC2PHR | МОДЕЛИ | Векторы выходов (re, im) для всех 3-фазных входов. | |
Векторы +Инициализировано | ABC2PHRI | МОДЕЛИ | То же, что и ABC2PHR, но с установившейся инициализацией при t=0 | |
Векторы +Част. вариант | ABC2PHRF | МОДЕЛИ | То же, что и ABC2PHR, но с частотой в качестве входа (от PLL) | |
Векторы +1+ч | ABC2PHRh3 | МОДЕЛИ | Расчет векторов (re, im) основной частоты и одной дополнительной гармоники. | |
Векторы +Последовательность 012 | ABC2SEQ | МОДЕЛИ | Рассчитать вектора и преобразовать их в вывод последовательности 012 (re, im). | |
Векторы +Запись/Печать | ЗАПИСЬФАЗОР | МОДЕЛИ | Принимает фазоры (re, im) для просмотра в определенный момент времени | |
Фильтры + Низкочастотный | БЛПФИЛЬТ | МОДЕЛИ | 0-3 Фильтр нижних частот Баттерворта с регулировкой усиления | |
Фильтры +Верхний проход | БХПФИЛЬТ | МОДЕЛИ | 0-3 фильтр верхних частот Баттерворта с регулировкой усиления | |
ПЛЛ | PLLDQ | МОДЕЛИ | Расчет частоты на основе парковочного преобразования трехфазных входов | |
Гармоники | ГАРМОНИКА | МОДЕЛИ | Расчет гармоник 1-26 на основе рекурсивного алгоритма DFT. |
Калькуляторы мощности и RX
Эти калькуляторы требуют ввода 3-фазных токов и напряжений (верхний левый узел — напряжение, нижний левый узел — ток). Обычно два входных узла можно просто подключить и далее к уникальному 3-фазному переключающему узлу, как показано на рис. 4.86. Обратите внимание, что ток можно получить только от коммутаторов, и ATP даст вам ток в первом коммутаторе, подключенном к указанному вами узлу. Чтобы убедиться, что вы получаете правильный ток в случае нескольких коммутаторов, подключенных к одной и той же шине, вы должны подключиться к узлу, который не используется ни одним другим коммутатором, с другим током. Текущий датчик с узлом Добавить текущий добавляет два переключателя последовательно за сценой и дает вам доступ к уникальной средней точке.
Выбор | Имя объекта | Значок | Плата АТФ | Описание |
ПК +PQ 3*1 | UI2PQ | МОДЕЛИ | Расчет активной и реактивной мощности на фазу для трехфазного напряжения и тока. | |
ПК +PQ 3-фазный | UI2PQ3 | МОДЕЛИ | Расчет активной и реактивной 3-фазной мощности. ДПФ+БПФ+DQ алг. | |
ПК +Ваттметр | СЧЕТЧИК | МОДЕЛИ | Расчет средней активной мощности интегральным методом. Без понижения частоты дискретизации. | |
РХ + (Ua-Uб)/(Ia-Iб) | UI2RXL | МОДЕЛИ | Расчет полного сопротивления прямой последовательности (R, X) для междуфазных замыканий. | |
RX + (Ua-Uб)/(Ia-Iб) | UI2RXE | МОДЕЛИ | Расчет полного сопротивления прямой последовательности (R, X) для замыканий на землю. | |
РХ +UA/IA | UI2RX | МОДЕЛИ | Вычисляет импеданс каждой фазы |
Реле защиты
Эти реле должны быть подключены к среднеквадратичным значениям (максимальный ток и минимальное/максимальное напряжение), векторным вычислителям (дифференциал) и вычислителям RX (расстояние). Направленное реле максимальной токовой защиты имеет собственный векторный вычислитель нулевой последовательности, а частотное реле требует ввода частоты. Пользователь должен щелкнуть входной узел моделей, чтобы убедиться, что записываются правильные сигналы. Реле, использующие сигналы от других моделей, по умолчанию имеют вход от моделей и должны быть заказаны после модели, производящей сигналы. Раньше сортировка по порядку была единственной возможностью сделать это, но ATPDraw v7 предлагает опцию «Редактировать | Упорядочить | Сортировать все модели», чтобы помочь правильно упорядочить. Все реле имеют вход сигнала управления блокировкой, выход сигнала отключения и информацию о зоне срабатывания. В диалоговом окне пользователь устанавливает характеристики зон, а также имеется опция «Просмотр», которая отображает зоны и записанные траектории (с дискретизацией) до поездки. Компонент W1RELAY21P также имеет помощник зоны.
Все реле имеют вход сигнала управления блокировкой, выход сигнала отключения и информацию о зоне срабатывания. В диалоговом окне пользователь устанавливает характеристики зон, а также имеется опция «Просмотр», которая отображает зоны и записанные траектории (с дискретизацией) до поездки. Компонент W1RELAY21P также имеет помощник зоны.
Выбор | Имя объекта | Значок | Плата АТФ | Описание |
Реле +Перегрузка по току 50/51 | W1RELAY51 | МОДЕЛИ | На основании входного среднеквадратичного значения и определенного часового пояса выдается сигнал отключения. Доступен вариант блокировки. Выход зоны не актуален. | |
Реле +Время перегрузки по току | W1RELAY51I | МОДЕЛИ | На основе входного среднеквадратичного значения и стандартизированного обратнозависимого часового пояса выдается сигнал отключения. | |
Реле +Реж. Земля 67Н | W1RELAY67N | МОДЕЛИ | Вход тока и напряжения с внутренним расчетом вектора нулевой последовательности. Отключения |V0|>Vlim и I0 в зоне относительно V0. | |
Реле + дистанционный счетверенный 21 | W1RELAY21P | МОДЕЛИ | Ввод с калькулятора RX. Три зоны с задержкой по 4 балла. Доступен помощник зоны. | |
Реле + Расстояние круг 21 | W1RELAY21C | МОДЕЛИ | Ввод с калькулятора RX. Три зоны задержки с характеристикой mho. | |
Реле +Дифф. 87Т | W1RELAY87T | МОДЕЛИ | Ввод текущих векторов 1+h. Ток в блок с обеих сторон. | |
Реле +Линия дифференциала 87L | W1RELAY87L | МОДЕЛИ | Ввод текущих векторов 1+h. Расчет дифференциальный ток с компенсацией временной задержки и блокировкой гармоник. Ток в единицу с обеих сторон. | |
Реле +Пониженное напряжение 27 | W1RELAY27 | МОДЕЛИ | Ввод среднеквадратичного значения напряжения. Две зоны пониженного напряжения с выдержкой времени и 3 различными стандартными характеристиками. | |
Реле +Перенапряжение 59 | W1RELAY59 | МОДЕЛИ | Ввод среднеквадратичного значения напряжения. | |
Реле +Частота 81 | W1RELAY81 | МОДЕЛИ | Ввод с частотного калькулятора. Две зоны для пониженной и повышенной частоты с фиксированной выдержкой времени. |
TACS
Выбор | Имя объекта | Значок | Плата АТФ | Описание |
ТАКС +RMS | TABC2RMS | ТАКС | Трехфазный вычислитель среднеквадратичного значения. УСТРОЙСТВО66 | |
ТАКС +Частота | TABC2FRQ | ТАКС | Трехфазный вычислитель частоты. |


 Ключевыми элементами являются компонент LINE3, который рисуется и редактируется подобно соединениям, а также различные векторные калькуляторы на основе МОДЕЛЕЙ.
Ключевыми элементами являются компонент LINE3, который рисуется и редактируется подобно соединениям, а также различные векторные калькуляторы на основе МОДЕЛЕЙ. Отредактировано как Connections.
Отредактировано как Connections. Рекурсивные методы DFT или методы FFT с понижающей дискретизацией.
Рекурсивные методы DFT или методы FFT с понижающей дискретизацией.
 Старый.
Старый.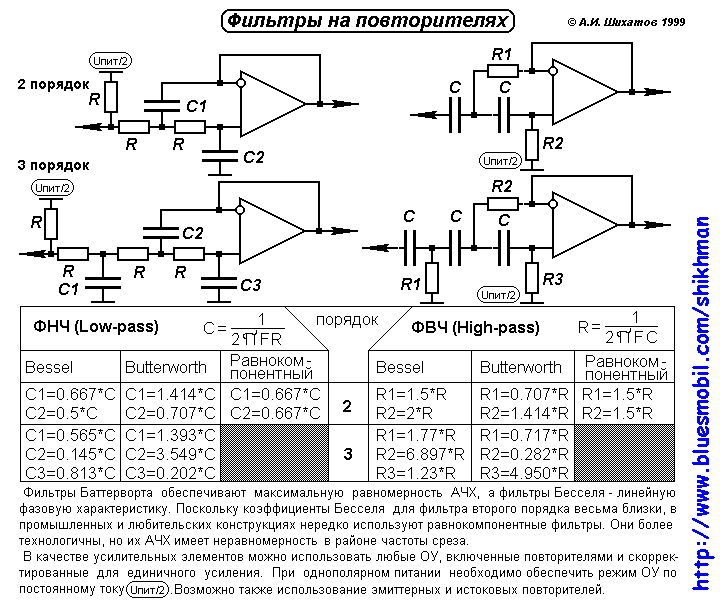


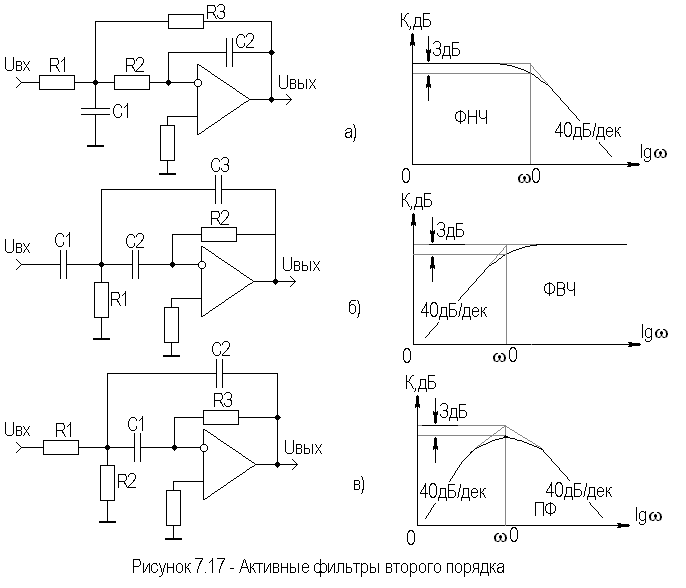 Расчет дифференциальный ток с соотношением витков, масштабированием фазового сдвига и блокировкой гармоник (бросок).
Расчет дифференциальный ток с соотношением витков, масштабированием фазового сдвига и блокировкой гармоник (бросок). Две зоны перенапряжения с выдержкой времени и 3 различными стандартными характеристиками.
Две зоны перенапряжения с выдержкой времени и 3 различными стандартными характеристиками.
