Электрическое сопротивление проводника
Электрическое сопротивление – физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику. Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м . Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
|
Вещество |
p, Ом*мм2/2 |
α,10-3 1/K |
|
Алюминий |
0.0271 |
3.8 |
|
Вольфрам |
0.055 |
4.2 |
|
Железо |
0.098 |
6 |
|
Золото |
0. |
4 |
|
Латунь |
0.025-0.06 |
1 |
|
Манганин |
0.42-0.48 |
0,002-0,05 |
|
Медь |
0.0175 |
4.1 |
|
Никель |
0.1 |
2.7 |
|
Константан |
0.44-0.52 |
0. |
|
Нихром |
1.1 |
0.15 |
|
Серебро |
0.016 |
4 |
|
Цинк |
0.059 |
2.7 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания.
где r это удельное сопротивление после нагрева, r0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t2 – температура до нагрева, t1 – температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.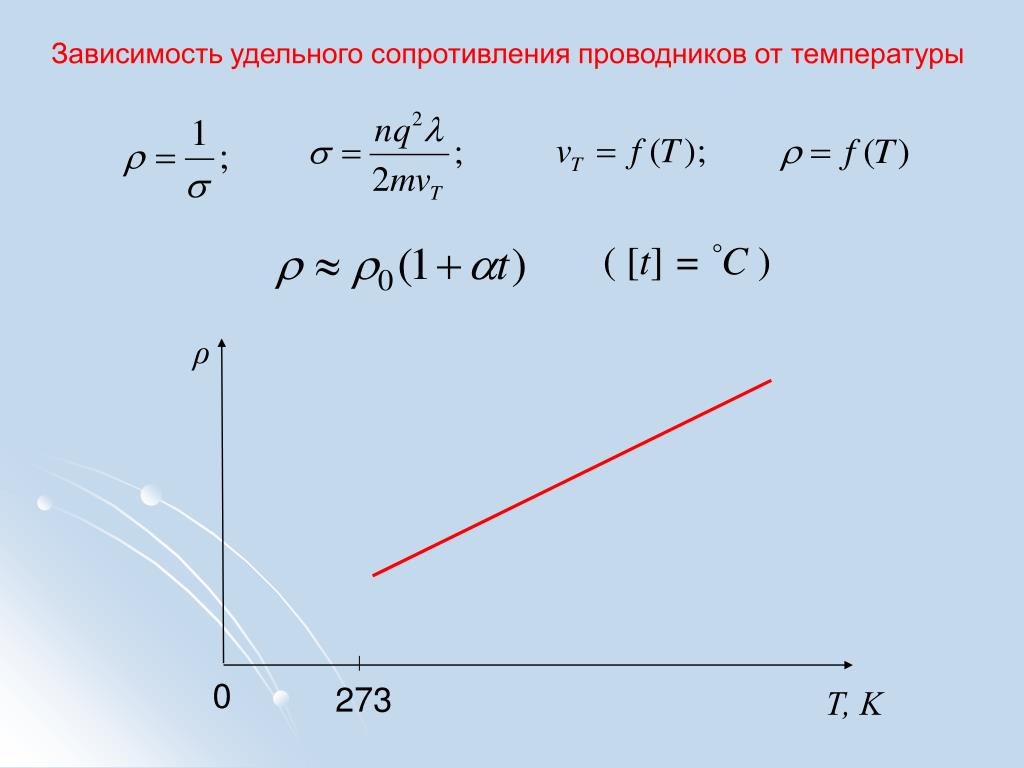
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор.
Зависимость сопротивления проводника от температуры
Практически в электротехнике выло выявлено, что с увеличением температуры сопротивление проводников из металла возрастает, а с понижением уменьшается. Для всех проводников из металла это изменение сопротивления почти одинаково и в среднем равно 0,4% на 1°С.
Если быть точным, то на самом деле при изменении температуры проводника изменяется его удельное сопротивление, которое имеет следующую зависимость:
где ρ и ρ0, R и R0 – соответственно удельные сопротивления и сопротивления проводника при температурах t и 0°С (шкала Цельсия), α – температурный коэффициент сопротивления, [α] = град-1.
Изменение удельного сопротивления проводника приводит к изменения самого сопротивления, что видно из следующего выражения:
Зная электронную теорию строения вещества можно дать следующее объяснение увеличению сопротивления металлических проводников с повышением температуры. При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.
При увеличении температуры проводник получает тепловую энергию, которая несомненно передается всем атомам вещества, в результате чего .возрастает их тепловое движение. Увеличившееся тепловое движение атомов создает большее сопротивление направленному движению свободных электронов (увеличивается вероятность столкновения свободных электронов с атомами), от этого и возрастает сопротивление проводника.
С понижением температуры направленное движение электронов облегчается (уменьшается возможность столкновения свободных электронов с атомами), и сопротивление проводника уменьшается. Этим объясняется интересное явление — сверхпроводимость металлов
График звисимости сопротивления металлического проводника от температуры представлен на рисунке 1.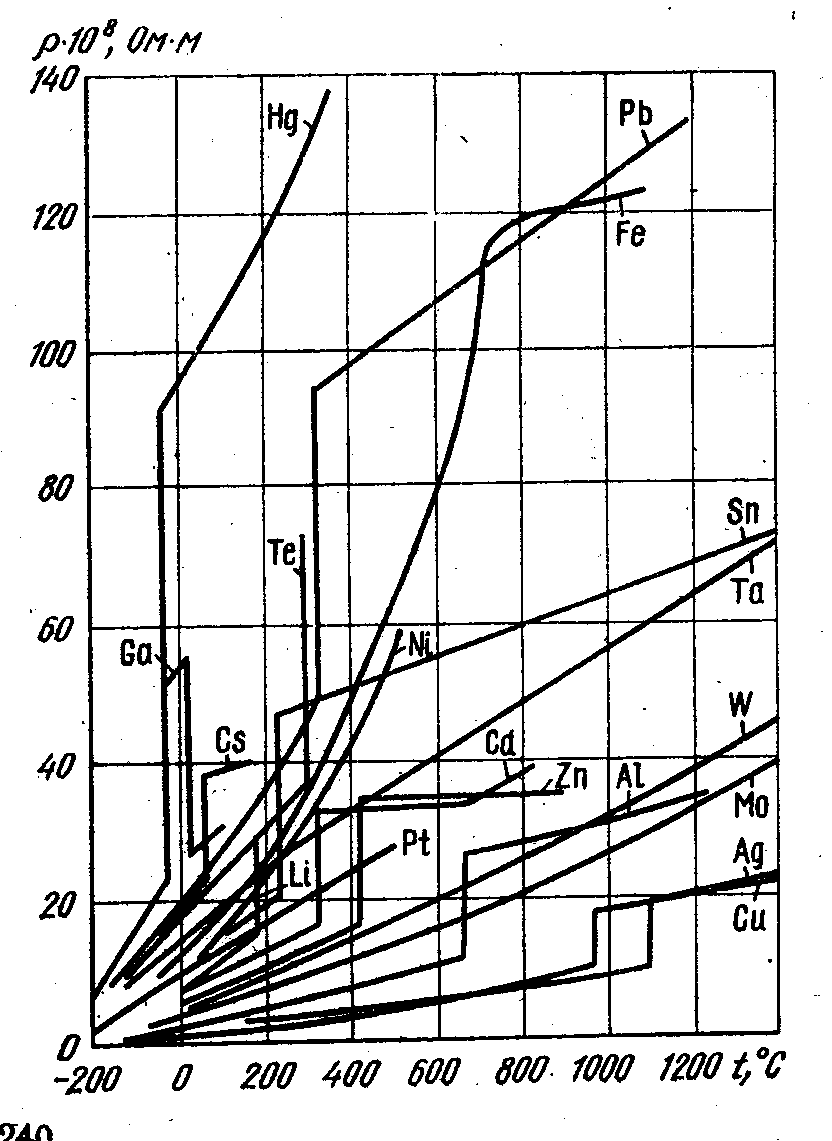
Рисунок 1. График зависимости удельного сопротивления металлического проводника от температуры
Необходимо сказать, что сопротивление электролитов и полупроводников (уголь, селен и другие) с увеличением температуры уменьшается.
Температурная зависимость сопротивления электролита объясняется также в основном изменением удельного сопротивления,однако всегда температурный коэффициент сопротивления – α <0.
Поэтому кривая зависимости сопротивленя электролита от температуры имеет вид, представленый на рисунке 2.
Рисунок 1. График зависимости удельного сопротивления электролита от температуры
Ддя полупроводников характер изменения удельного сопротивления от температуры будет схож с таковым для элетролитов.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
характеристики, свойства и сферы применения
Одним из самых востребованных металлов в отраслях промышленности является медь.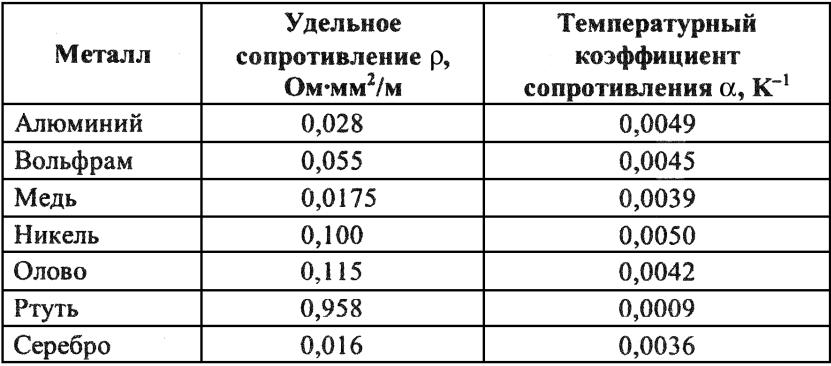 Наиболее широкое распространение она получила в электрике и электронике. Чаще всего ее применяют при изготовлении обмоток для электродвигателей и трансформаторов. Основная причина использования именно этого материала заключается в том, что медь обладает самым низким из существующих в настоящий момент материалов удельным электрическим сопротивлением. Пока не появится новый материал с более низкой величиной этого показателя, можно с уверенностью говорить о том, что замены у меди не будет.
Наиболее широкое распространение она получила в электрике и электронике. Чаще всего ее применяют при изготовлении обмоток для электродвигателей и трансформаторов. Основная причина использования именно этого материала заключается в том, что медь обладает самым низким из существующих в настоящий момент материалов удельным электрическим сопротивлением. Пока не появится новый материал с более низкой величиной этого показателя, можно с уверенностью говорить о том, что замены у меди не будет.Общая характеристика меди
Говоря про медь, необходимо сказать, что еще на заре электрической эры она стала использоваться в производстве электротехники. Применять ее стали во многом по причине уникальных свойств, которыми обладает этот сплав. Сам по себе он представляет материал, отличающийся высокими свойствами в плане пластичности и обладающий хорошей ковкостью.Наряду с теплопроводностью меди, одним из самых главных ее достоинств является высокая электропроводность. Именно благодаря этому свойству медь и получила широкое распространение в энергетических установках, в которых она выступает в качестве универсального проводника.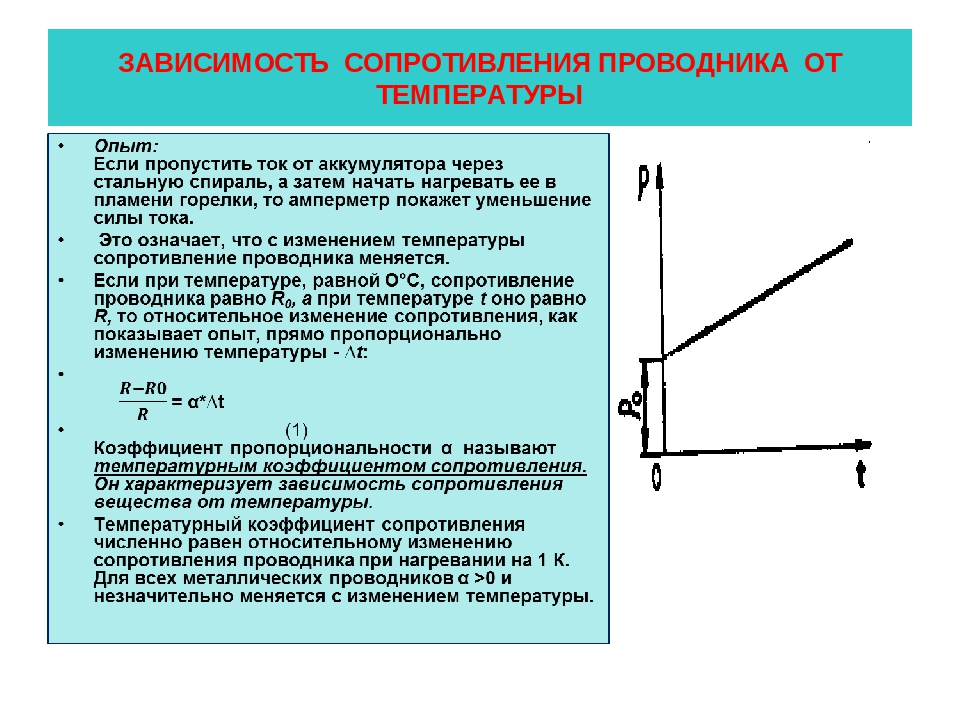 Наиболее ценным материалом является электролитическая медь, обладающая высокой степенью чистоты -99,95%. Благодаря этому материалу появляется возможность для производства кабелей.
Наиболее ценным материалом является электролитическая медь, обладающая высокой степенью чистоты -99,95%. Благодаря этому материалу появляется возможность для производства кабелей.
Плюсы использования электролитической меди
Применение электролитической меди позволяет добиться следующего:- Обеспечить высокую электропроводность;
- Добиться отличной способности к уложению;
- Обеспечить высокую степень пластичности.
Сферы применения
Кабельная продукция, изготавливаемая из электролитической меди, получила широкое распространение в различных отраслях. Чаще всего она применяется в следующих сферах:- электроиндустрия;
- электроприборы;
- автомобилестроение;
- производство компьютерной техники.
Чему равно удельное сопротивление?
Чтобы понимать, что собой представляет медь и его характеристики, необходимо разобраться с основным параметром этого металла — удельным сопротивлением. Его следует знать и использовать при выполнении расчетов.Под удельным сопротивлением принято понимать физическую величину, которая характеризуется как способность металла проводить электрический ток.
Знать эту величину необходимо еще и для того, чтобы правильно произвести расчет электрического сопротивления проводника. При расчетах также ориентируются на его геометрические размеры. При проведении расчетов используют следующую формулу:
R = р l / S
Это формула многим хорошо знакома. Пользуясь ею, можно легко рассчитать сопротивление медного кабеля, ориентируясь только на характеристики электрической сети. Она позволяет вычислить мощность, которая неэффективно расходуется на нагрев сердечника кабеля. Кроме этого, подобная формула позволяет выполнить расчеты сопротивления любого кабеля. При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
При этом не имеет значения, какой материал использовался для изготовления кабеля — медь, алюминий или какой-то другой сплав.
Сименс = 1/ Ом.
У меди любого веса этот параметр состав равен 58 100 000 См/м. Что касается серебра, то величина обратной проводимости у нее равна 62 500 000 См/м.
В нашем мире высоких технологий, когда в каждом доме имеется большое количество электротехнических устройств и установок, значение такого материала, как медь просто неоценимо. Этот материал используют для изготовления проводки, без которой не обходится ни одно помещение. Если бы меди не существовало, тогда человеку пришлось использовать провода из других доступных материалов, например, из алюминия. Однако в этом случае пришлось бы столкнуться с одной проблемой. Все дело в том, что у этого материала удельная проводимость гораздо меньше, чем у медных проводников.
Этот материал используют для изготовления проводки, без которой не обходится ни одно помещение. Если бы меди не существовало, тогда человеку пришлось использовать провода из других доступных материалов, например, из алюминия. Однако в этом случае пришлось бы столкнуться с одной проблемой. Все дело в том, что у этого материала удельная проводимость гораздо меньше, чем у медных проводников.
Удельное сопротивление
Использование материалов с низкой электро- и теплопроводностью любого веса ведет к большим потерям электроэнергии. А это влияет на потерю мощности у используемого оборудования. Большинство специалистов в качестве основного материала для изготовления проводов с изоляцией называют медь. Она является главным материалом, из которого изготавливаются отдельные элементы оборудования, работающего от электрического тока.- Платы, устанавливаемые в компьютерах, оснащаются протравленными медными дорожками.

- Медь также используется для изготовления самых разных элементов, применяемых в электронных устройствах.
- В трансформаторах и электродвигателях она представлена обмоткой, которая изготавливается из этого материала.
Можно не сомневаться, что расширение сфер применения этого материала будет происходить с дальнейшим развитием технического прогресса. Хотя, кроме меди, существуют и другие материалы, но все же конструктора при создании оборудования и различных установок используют медь. Главная причина востребованности этого материала заключается в хорошей электрической и теплопроводности этого металла, которую он обеспечивает в условиях комнатной температуры.
Температурный коэффициент сопротивления
Свойством уменьшения проводимости с повышением температуры обладают все металлы с любой теплопроводностью. При понижении температуры проводимость возрастает. Особенно интересным специалисты называют свойство уменьшения сопротивления с понижением температуры. Ведь в этом случае, когда в комнате температура снижается до определенной величины, у проводника может исчезнуть электрическое сопротивление и он перейдет в класс сверхпроводников.
Особенно интересным специалисты называют свойство уменьшения сопротивления с понижением температуры. Ведь в этом случае, когда в комнате температура снижается до определенной величины, у проводника может исчезнуть электрическое сопротивление и он перейдет в класс сверхпроводников.Для того чтобы определить показатель сопротивления конкретного проводника определенного веса в условиях комнатной температуры, существует коэффициент критического сопротивления. Он представляет собой величину, которая показывает изменение сопротивления участка цепи при изменении температуры на один Кельвин. Для выполнения расчета электрического сопротивления медного проводника в определенном временном промежутке используют следующую формулу:
ΔR = α*R*ΔT, где α — температурный коэффициент электрического сопротивления.
Заключение
Медь — материал, который широко применяют в электронике.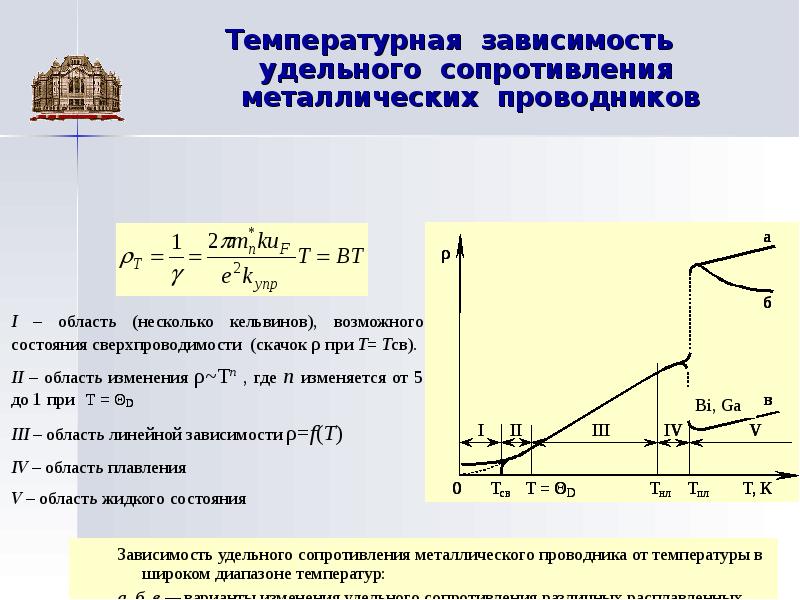 Его используют не только в обмотке и схемах, но и в качестве металла для изготовления кабельной продукции. Чтобы техника и оборудование работали эффективно, необходимо правильно рассчитать удельное сопротивление проводки, прокладываемой в квартире. Для этого существует определенная формула. Зная её, можно произвести расчет, который позволяет узнать оптимальную величину сечения кабеля. В этом случае можно избежать потери мощности оборудования и обеспечить эффективность его использования.
Его используют не только в обмотке и схемах, но и в качестве металла для изготовления кабельной продукции. Чтобы техника и оборудование работали эффективно, необходимо правильно рассчитать удельное сопротивление проводки, прокладываемой в квартире. Для этого существует определенная формула. Зная её, можно произвести расчет, который позволяет узнать оптимальную величину сечения кабеля. В этом случае можно избежать потери мощности оборудования и обеспечить эффективность его использования.
Сопротивление медного провода: таблица, формула расчета сопротивления
Использование меди в электротехнических устройствах обусловлено двумя факторами: хорошей проводимостью и относительной дешевизной. При проектировании или ремонте линий электропередач или электронных приборов, необходимо учитывать сопротивление медных проводов. Пренебрежение данным параметром приведет к поломке электрической системы.
Что такое сопротивление медного провода
В металлах ток образуется при появлении электрического поля. Оно «заставляет» двигаться электроны упорядоченно, в одном направлении. Электроны дальних орбит атома, слабо удерживаемые ядром, формируют ток.
Медные проводаПри прохождении отрицательных частиц сквозь кристаллическую решетку молекул меди, они сталкиваются с атомами и другими электронами. Возникает препятствие или сопротивление направленному движению частиц.
Для оценки противодействия току была введена величина «электрическое сопротивление» или «электрический импеданс». Обозначается она буквой «R» или «r». Вычисляется сопротивление по формуле Георга Ома: R=, где U — разность потенциалов или напряжение, действующее на участке цепи, I — сила тока.
Понятие сопротивленияВажно! Чем выше значение импеданса металла, тем меньший ток проходит по нему, и именно медные проводники так широко распространены в электротехнике, благодаря этому свойству.
Исходя из формулы Ома, на величину тока влияет приложенное напряжение при постоянном R. Но резистентность медных проводов меняется, в зависимости от их физических характеристик и условий эксплуатации.
Что влияет на сопротивление медного провода
Электрический импеданс медного кабеля зависит от нескольких факторов:
- Удельного сопротивления;
- Площади сечения проволоки;
- Длины провода;
- Внешней температуры.
Последним пунктом можно пренебречь в условиях бытового использования кабеля. Заметное изменение импеданса происходит при температурах более 100°C.
Зависимость сопротивленияУдельное сопротивление в системе СИ обозначается буквой ρ. Оно определяется, как величина сопротивления проводника, имеющего сечение 1 м2 и длину 1 м, измеряется в Ом ∙ м2. Такая размерность неудобна в электротехнических расчетах, поэтому часто используется единица измерения Ом ∙ мм2.
Важно! Данный параметр является характеристикой вещества — меди. Он не зависит от формы или площади сечения. Чистота меди, наличие примесей, метод изготовления проволоки, температура проводника — факторы, влияющие на удельное сопротивление.
Зависимость параметра от температуры описывается следующей формулой: ρt= ρ20[1+ α(t−20°C)]. Здесь ρ20— удельное сопротивление меди при 20°C, α— эмпирически найденный коэффициент, от 0°Cдо 100°C для меди имеет значение, равное 0,004 °C-1, t — температура проводника.
Ниже приведена таблица значений ρ для разных металлов при температуре 20°C.
Таблица удельного сопротивленияСогласно таблице, медь имеет низкое удельное сопротивление, ниже только у серебра. Это обуславливает хорошую проводимость металла.
Чем толще провод, тем меньше его резистентность. Зависимость R проводника от сечения называется «обратно пропорциональной».
Важно! При увеличении поперечной площади кабеля, электронам легче проходить сквозь кристаллическую решетку. Поэтому, при увеличении нагрузки и возрастании плотности тока, следует увеличить площадь сечения.
Увеличение длины медного кабеля влечет рост его резистентности. Импеданс прямо пропорционален протяженности провода. Чем длиннее проводник, тем больше атомов встречаются на пути свободных электронов.
ВыводыПоследним элементом, влияющим на резистентность меди, является температура среды. Чем она выше, тем большую амплитуду движения имеют атомы кристаллической решетки. Тем самым, они создают дополнительное препятствие для электронов, участвующих в направленном движении.
Важно! Если понизить температуру до абсолютного нуля, имеющего значение 0° Kили -273°C, то будет наблюдаться обратный эффект — явление сверхпроводимости. В этом состоянии вещество имеет нулевое сопротивление.
Температурная корреляцияКак узнать сопротивление 1 метра медного провода
После выяснения всех факторов, влияющих на резистентность медного провода, можно объединить их в формуле зависимости сопротивления от сечения проводника и узнать, как вычислить этот параметр. Математическое выражение выглядит следующим образом: R= pl/s, где:
- ρ — удельное сопротивление;
- l — длина проводника, при нахождении сопротивления медного проводника длиной 1 м, l = 1;
- S— площадь поперечного сечения.
Для вычисления S, в случае провода цилиндрической формы, используется формула: S = π ∙ r2 = π d2/4 ≈ 0.785 ∙ d2, здесь:
- r — радиус сечения провода;
- d — его диаметр.
Если провод состоит из нескольких жил, то суммарная площадь будет равна: S = n d2/1,27, где n — количество жил.
Если проводник имеет прямоугольную форму, то S = a ∙ b, где a — ширина прямоугольника, b — длина.
Важно! Узнать диаметр сечения можно штангенциркулем. Если его нет под рукой, то намотать на любой стержень измеряемую проволоку, посчитать количество витков, желательно, чтобы их было не меньше 10 для большей точности. После этого измерить намотанную часть проводника, и разделить значение на количество витков.
Вычисление площади сеченияКак правильно рассчитать сопротивление провода по сечению
Проектируя электрическую сеть, необходимо правильно подобрать сечение кабеля, чтобы его резистентность не была высокой. Большой импеданс вызовет падение напряжения выше допустимого значения. В результате подключенное к сети электрическое устройство может не заработать. Также, провода начнут перегреваться.
Для правильного расчета минимального сечения необходимо учесть следующие факторы:
- По стандартам ПУЭ падение напряжения не должно быть больше 5%.
- В бытовых условиях ток проходит по двум проводам. Поэтому, при расчете величину сопротивления нужно умножить на 2.
- Учитывать нужно мощность всех подключенных приборов на линии. Для развития предусмотреть запас по нагрузке.
Как вычислить сопротивление проводника по формуле? Для примера можно рассмотреть задачу. Требуется определить: достаточно ли будет медного кабеля сечением 2,5 мм2 и длиной 30 метров для подключения оборудования мощностью 9 кВт.
Формулы электрической цепиЗадача решается следующим образом:
- Резистентность медного кабеля будет равна:
2 ∙ (ρ ∙ L) / S = 2 ∙ (0,0175 ∙ 30) / 2,5 = 0,42 Ом.
- Для нахождения падения напряжения нужно определить силу тока, по формуле: I= P/U.
Здесь P — суммарная мощность оборудования, U — напряжение в цепи. Тогда сила тока будет равна: I = 9000 / 220 = 40,91 А.
- Используя закон Ома, можно найти падение напряжения по кабелю: ΔU = I ∙ R = 40, 91 ∙ 0,42 = 17,18 В.
- От 220 В процент падения составит: U% = (ΔU / U) ∙ 100% = (17,18 / 220) ∙ 100% = 7, 81%>5%.
Падение напряжение выходит за пределы допустимого значения, значит необходимо использовать кабель большего сечения.
Таблица сопротивления медного провода
Узнать резистентность проводника можно по таблицам. В них содержатся готовые результаты вычислений для разных кабелей.
Таблица меди на метр 1Например, сопротивление меди на метр для различных сечений можно определить без вычислений, из соответствующей таблицы.
Таблица меди на метр 2Важно! Таблицы не содержат данные о всех сечениях. Если нужно узнать величину импеданса для неуказанного кабеля, то находится среднее значение между двумя ближайшими известными сопротивлениями.
Таблица сечений, сопротивлений, силы токаРасчет сопротивления кабеля является важной задачей при проектировании электрической системы. Воспользовавшись формулами или таблицами, можно успешно ее решить.
Удельное сопротивление и сверхпроводимость
Публикации по материалам Д. Джанколи. “Физика в двух томах” 1984 г. Том 2.
На опыте установлено, что сопротивление R металлического проводника прямо пропорционально его длине L и обратно пропорционально площади его поперечного сечения А:
R = ?L/А (26.4)
где коэффициент ? называется удельным сопротивлением и служит характеристикой вещества, из которого изготовлен проводник. Это соответствует здравому смыслу: сопротивление толстого провода должно быть меньше, чем тонкого, поскольку в толстом проводе электроны могут перемещаться по большей площади. И можно ожидать роста сопротивления с увеличением длины проводника, так как увеличивается количество препятствий на пути потока электронов.
Типичные значения ? для разных материалов приведены в первом столбце табл. 26.2. (Реальные значения зависят от чистоты вещества, термической обработки, температуры и других факторов.)
|
Таблица 26.2. Удельное сопротивление и температурный коэффициент сопротивления (ТКС) (при 20 °С) |
||
| Вещество | Удельное сопротивление ?,Ом·м | ТКС ?,°C-1 |
| Проводники | ||
| Серебро | 1,59·10-8 | 0,0061 |
| Медь | 1,68·10-8 | 0,0068 |
| Алюминий | 2,65·10-8 | 0,00429 |
| Вольфрам | 5,6·10-8 | 0,0045 |
| Железо | 9,71·10-8 | 0,00651 |
| Платина | 10,6·10-8 | 0,003927 |
| Ртуть | 98·10-8 | 0,0009 |
| Нихром (сплав Ni, Fe, Сг) | 100·10-8 | 0,0004 |
| Полупроводники 1) | ||
| Углерод (графит) | (3-60)·10-5 | -0,0005 |
| Германий | (1-500)·10-5 | -0,05 |
| Кремний | 0,1 – 60 | -0,07 |
| Диэлектрики | ||
| Стекло | 109 – 1012 | |
| Резина твердая | 1013 – 1015 | |
| 1) Реальные значения сильно зависят от наличия даже малого количества примесей. | ||
Самым низким удельным сопротивлением обладает серебро, которое оказывается, таким образом, наилучшим проводником; однако оно дорого. Немногим уступает серебру медь; ясно, почему провода чаще всего изготовляют из меди.
Удельное сопротивление алюминия выше, чем у меди, однако он имеет гораздо меньшую плотность, и в некоторых случаях ему отдают предпочтение (например, в линиях электропередач), поскольку сопротивление проводов из алюминия той же массы оказывается меньше, чем у медных. Часто пользуются величиной, обратной удельному сопротивлению:
? = 1/? (26.5)
? называемой удельной проводимостью. Удельная проводимость измеряется в единицах (Ом·м) -1.
Удельное сопротивление вещества зависит от температуры. Как правило, сопротивление металлов возрастает с температурой. Этому не следует удивляться: с повышением температуры атомы движутся быстрее, их расположение становится менее упорядоченным, и можно ожидать, что они будут сильнее мешать движению потока электронов. В узких диапазонах изменения температуры удельное сопротивление металла увеличивается с температурой практически линейно:
где ?T – удельное сопротивление при температуре Т, ?0 – удельное сопротивление при стандартной температуре Т0, а ? – температурный коэффициент сопротивления (ТКС). Значения а приведены в табл. 26.2. Заметим, что у полупроводников ТКС может быть отрицательным. Это очевидно, поскольку с ростом температуры увеличивается число свободных электронов и они улучшают проводящие свойства вещества. Таким образом, сопротивление полупроводника с повышением температуры может уменьшаться (хотя и не всегда).
Значения а зависят от температуры, поэтому следует обращать внимание на диапазон температур, в пределах которого справедливо данное значение (например, по справочнику физических величин). Если диапазон изменения температуры окажется широким, то линейность будет нарушаться, и вместо (26.6) надо использовать выражение, содержащее члены, которые зависят от второй и третьей степеней температуры:
?T = ?0(1+?Т+ + ?Т 2 + ?Т 3),
где коэффициенты ? и ? обычно очень малы (мы положили Т0 = 0°С), но при больших Т вклад этих членов становится существенным.
При очень низких температурах удельное сопротивление некоторых металлов, а также сплавов и соединений падает в пределах точности современных измерений до нуля. Это свойство называют сверхпроводимостью; впервые его наблюдал нидерландский физик Гейке Камер-линг-Оннес (1853-1926) в 1911 г. при охлаждении ртути ниже 4,2 К. При этой температуре электрическое сопротивление ртути внезапно падало до нуля.
Сверхпроводники переходят в сверхпроводящее состояние ниже температуры перехода, составляющей обычно несколько градусов Кельвина (чуть выше абсолютного нуля). Наблюдался электрический ток в сверхпроводящем кольце, который практически не ослабевал в отсутствие напряжения в течение нескольких лет.
В последние годы сверхпроводимость интенсивно исследуется с целью выяснить ее механизм и найти материалы, обладающие сверхпроводимостью при более высоких температурах, чтобы уменьшить стоимость и неудобства, обусловленные необходимостью охлаждения до очень низких температур. Первую успешную теорию сверхпроводимости создали Бардин, Купер и Шриффер в 1957 г. Сверхпроводники уже используются в больших магнитах, где магнитное поле создается электрическим током (см. гл. 28), что значительно снижает расход электроэнергии. Разумеется, для поддержания сверхпроводника при низкой температуре тоже затрачивается энергия.
Продолжение следует: Мощность.
Альтернативные статьи: Электрический ток, Закон Ома.
Замечания и предложения принимаются и приветствуются!
Удельное сопротивление меди в системе си. Удельное сопротивление и другие свойства меди
Сопротивление меди действительно меняется с температурой, но сначала нужно определиться, имеется ли в виду удельное электрическое сопротивление проводников (омическое сопротивление), что важно для питания по Ethernet, использующего постоянный ток, или же речь идет о сигналах в сетях передачи данных, и тогда мы говорим о вносимых потерях при распространении электромагнитной волны в среде витой пары и о зависимости затухания от температуры (и частоты, что не менее важно).
Удельное сопротивление меди
В международной системе СИ удельное сопротивление проводников измеряется в Ом∙м. В сфере ИТ чаще используется внесистемная размерность Ом∙мм 2 /м, более удобная для расчетов, поскольку сечения проводников обычно указаны в мм 2 . Величина 1 Ом∙мм 2 /м в миллион раз меньше 1 Ом∙м и характеризует удельное сопротивление вещества, однородный проводник из которого длиной 1 м и с площадью поперечного сечения 1 мм 2 дает сопротивление в 1 Ом.
Удельное сопротивление чистой электротехнической меди при 20°С составляет 0,0172 Ом∙мм 2 /м . В различных источниках можно встретить значения до 0,018 Ом∙мм 2 /м, что тоже может относиться к электротехнической меди. Значения варьируются в зависимости от обработки, которой подвергнут материал. Например, отжиг после вытягивания («волочения») проволоки уменьшает удельное сопротивление меди на несколько процентов, хотя проводится он в первую очередь ради изменения механических, а не электрических свойств.
Удельное сопротивление меди имеет непосредственное значение для реализации приложений питания по Ethernet. Лишь часть исходного постоянного тока, поданного в проводник, достигнет дальнего конца проводника – определенные потери по пути неизбежны. Так, например, PoE Type 1 требует, чтобы из 15,4 Вт, поданных источником, до запитываемого устройства на дальнем конце дошло не менее 12,95 Вт.
Удельное сопротивление меди изменяется с температурой, но для температур, характерных для сферы ИТ, эти изменения невелики. Изменение удельного сопротивления рассчитывается по формулам:
ΔR = α · R · ΔT
R 2 = R 1 · (1 + α · (T 2 – T 1))
где ΔR – изменение удельного сопротивления, R – удельное сопротивление при температуре, принятой в качестве базового уровня (обычно 20°С), ΔT – градиент температур, α – температурный коэффициент удельного сопротивления для данного материала (размерность °С -1). В диапазоне от 0°С до 100°С для меди принят температурный коэффициент 0,004 °С -1 . Рассчитаем удельное сопротивление меди при 60°С.
R 60°С = R 20°С · (1 + α · (60°С – 20°С)) = 0,0172 · (1 + 0,004 · 40) ≈ 0,02 Ом∙мм 2 /м
Удельное сопротивление при увеличении температуры на 40°С возросло на 16%. При эксплуатации кабельных систем, разумеется, витая пара не должна находиться при высоких температурах, этого не следует допускать. При правильно спроектированной и установленной системе температура кабелей мало отличается от обычных 20°С, и тогда изменение удельного сопротивления будет невелико. По требованиям телекоммуникационных стандартов сопротивление медного проводника длиной 100 м в витой паре категорий 5e или 6 не должно превышать 9,38 Ом при 20°С. На практике производители с запасом вписываются в это значение, поэтому даже при температурах 25°С ÷ 30°С сопротивление медного проводника не превышает этого значения.
Затухание сигнала в витой паре / Вносимые потери
При распространении электромагнитной волны в среде медной витой пары часть ее энергии рассеивается по пути от ближнего конца к дальнему. Чем выше температура кабеля, тем сильнее затухает сигнал. На высоких частотах затухание сильнее, чем на низких, и для более высоких категорий допустимые пределы при тестировании вносимых потерь строже. При этом все предельные значения заданы для температуры 20°С. Если при 20°С исходный сигнал приходил на дальний конец сегмента длиной 100 м с уровнем мощности P, то при повышенных температурах такая мощность сигнала будет наблюдаться на более коротких расстояниях. Если необходимо обеспечить на выходе из сегмента ту же мощность сигнала, то либо придется устанавливать более короткий кабель (что не всегда возможно), либо выбирать марки кабелей с более низким затуханием.
- Для экранированных кабелей при температурах выше 20°С изменение температуры на 1 градус приводит к изменению затухания на 0.2%
- Для всех типов кабелей и любых частот при температурах до 40°С изменение температуры на 1 градус приводит к изменению затухания на 0.4%
- Для всех типов кабелей и любых частот при температурах от 40°С до 60°С изменение температуры на 1 градус приводит к изменению затухания на 0.6%
- Для кабелей категории 3 может наблюдаться изменение затухания на уровне 1,5% на каждый градус Цельсия
Уже в начале 2000 гг. стандарт TIA/EIA-568-B.2 рекомендовал уменьшать максимально допустимую длину постоянной линии/канала категории 6, если кабель устанавливался в условиях повышенных температур, и чем выше температура, тем короче должен быть сегмент.
Если учесть, что потолок частот в категории 6А вдвое выше, чем в категории 6, температурные ограничения для таких систем будут еще жестче.
На сегодняшний день при реализации приложений PoE речь идет о максимум 1-гигабитных скоростях. Когда же используются 10-гигабитные приложения, питание по Ethernet не применяется, по крайней мере, пока. Так что в зависимости от ваших потребностей при изменении температуры вам нужно учитывать либо изменение удельного сопротивления меди, либо изменение затухания. Разумнее всего и в том, и в другом случае обеспечить кабелям нахождение при температурах, близких к 20°С.
Электрическое сопротивление, выражаемое в омах, отличается от понятия «удельное сопротивление». Чтобы понять, что такое удельное сопротивление, надо связать его с физическими свойствами материала.
Об удельной проводимости и удельном сопротивлении
Поток электронов не перемещается беспрепятственно через материал. При постоянной температуре элементарные частицы качаются вокруг состояния покоя. Кроме того, электроны в зоне проводимости мешают друг другу взаимным отталкиванием из-за аналогичного заряда. Таким образом возникает сопротивление.
Удельная проводимость является собственной характеристикой материалов и количественно определяет легкость, с которой заряды могут двигаться, когда вещество подвергается воздействию электрического поля. Удельное сопротивление является обратной величиной и характеризуется степенью трудности, которую электроны встречают при своих перемещениях внутри материала, давая представление о том, насколько хорош или плох проводник.
Важно! Удельное электрическое сопротивление с высоким значением указывает на то, что материал плохо проводящий, а с низким значением – определяет хорошее проводящее вещество.
Удельная проводимость обозначается буквой σ и рассчитывается по формуле:
Удельное сопротивление ρ, как обратный показатель, можно найти так:
В этом выражении E является напряженностью создаваемого электрического поля (В/м), а J – плотностью электротока (А/м²). Тогда единица измерения ρ будет:
В/м х м²/А = ом м.
Для удельной проводимости σ единицей, в которой она измеряется, служит См/м или сименс на метр.
Типы материалов
В соответствии с удельным сопротивлением материалов, их можно классифицировать на несколько типов:
- Проводники. К ним относятся все металлы, сплавы, растворы, диссоциированные на ионы, а также термически возбужденные газы, включая плазму. Из неметаллов можно привести в пример графит;
- Полупроводники, фактически представляющие собой непроводящие материалы, кристаллические решетки которых целенаправленно легированы включением чужеродных атомов с большим или меньшим числом связанных электронов. В результате в структуре решетки образуются квазисвободные избыточные электроны или дырки, которые вносят вклад в проводимость тока;
- Диэлектрики или изоляторы диссоциированные – все материалы, которые в нормальных условиях не имеют свободных электронов.
Для транспортировки электрической энергии или в электроустановках бытового и промышленного назначения часто используемый материал – медь в виде одножильных или многожильных кабелей. Альтернативно применяется металл алюминий, хотя удельное сопротивление меди составляет 60% от такого же показателя для алюминия. Но он гораздо легче меди, что предопределило его использование в линиях электропередач сетей высокого напряжения. Золото в качестве проводника применяется в электроцепях специального назначения.
Интересно. Электропроводность чистой меди была принята Международной электротехнической комиссией в 1913 году в качестве стандарта по этой величине. Согласно определению, проводимость меди, измеренная при 20°, равна 0,58108 См/м. Это значение называется 100% LACS, а проводимость остальных материалов выражается как определенный процент LACS.
Большинство металлов имеют значение проводимости меньше 100% LACS. Однако есть исключения, такие как серебро или специальная медь с очень высокой проводимостью, обозначенные С-103 и С-110, соответственно.
Диэлектрики не проводят электричество и используются в качестве изоляторов. Примеры изоляторов:
- стекло,
- керамика,
- пластмасса,
- резина,
- слюда,
- воск,
- бумага,
- сухая древесина,
- фарфор,
- некоторые жиры для промышленного и электротехнического использования и бакелит.
Между тремя группами переходы являются текучими. Известно точно: абсолютно непроводящих сред и материалов нет. Например, воздух – изолятор при комнатной температуре, но в условиях мощного сигнала низкой частоты он может стать проводником.
Определение удельной проводимости
Если сравнивать удельное электрическое сопротивление различных веществ, требуются стандартизированные условия измерения:
- В случае жидкостей, плохих проводников и изоляторов, используют кубические образцы с длиной ребра 10 мм;
- Величины удельного сопротивления почв и геологических образований определяются на кубах с длиной каждого ребра 1 м;
- Проводимость раствора зависит от концентрации его ионов. Концентрированный раствор менее диссоциирован и имеет меньше носителей заряда, что снижает проводимость. По мере увеличения разведения увеличивается число ионных пар. Концентрация растворов устанавливается в 10%;
- Для определения удельного сопротивления металлических проводников используются провода метровой длины и сечения 1 мм².
Если материал, такой как металл, может обеспечить свободные электроны, то когда приложить разность потенциалов, по проводу потечет электрический ток. По мере увеличения напряжения большее количество электронов перемещается через вещество во временную единицу. Если все дополнительные параметры (температура, площадь поперечного сечения, длина и материал провода) неизменны, то отношение силы тока к приложенному напряжению тоже постоянно и именуется проводимостью:
Соответственно, электросопротивление будет:
Результат получается в ом.
В свою очередь, проводник может быть разных длины, размеров сечения и изготавливаться из различных материалов, от чего зависит значение R. Математически эта зависимость выглядит так:
Фактор материала учитывает коэффициент ρ.
Отсюда можно вывести формулу для удельного сопротивления:
Если значения S и l соответствуют заданным условиям сравнительного расчета удельного сопротивления, т. е. 1 мм² и 1 м, то ρ = R. При изменении габаритов проводника количество омов тоже меняется.
Электрическое сопротивление – физическая величина, которая показывает, какое препятствие создается току при его прохождении по проводнику . Единицами измерения служат Омы, в честь Георга Ома. В своем законе он вывел формулу для нахождения сопротивления, которая приведена ниже.
Рассмотрим сопротивление проводников на примере металлов. Металлы имеют внутреннее строение в виде кристаллической решетки. Эта решетка имеет строгую упорядоченность, а её узлами являются положительно заряженные ионы. Носителями заряда в металле выступают “свободные” электроны, которые не принадлежат определенному атому, а хаотично перемещаются между узлами решетки. Из квантовой физики известно, что движение электронов в металле это распространение электромагнитной волны в твердом теле. То есть электрон в проводнике движется со скоростью света (практически), и доказано, что он проявляет свойства не только как частица, но еще и как волна. А сопротивление металла возникает в результате рассеяния электромагнитных волн (то есть электронов) на тепловых колебаниях решетки и её дефектах. При столкновении электронов с узлами кристаллической решетки часть энергии передается узлам, вследствие чего выделяется энергия. Эту энергию можно вычислить при постоянном токе , благодаря закону Джоуля-Ленца – Q=I 2 Rt. Как видите чем больше сопротивление, тем больше энергии выделяется.
Удельное сопротивление
Существует такое важное понятие как удельное сопротивление, это тоже самое сопротивление, только в единице длины. У каждого металла оно свое, например у меди оно равно 0,0175 Ом*мм2/м, у алюминия 0,0271 Ом*мм2/м. Это значит, брусок из меди длиной 1 м и площадью поперечного сечения 1 мм2 будет иметь сопротивление 0,0175 Ом, а такой же брусок, но из алюминия будет иметь сопротивление 0,0271 Ом. Выходит что электропроводность меди выше чем у алюминия. У каждого металла удельное сопротивление свое, а рассчитать сопротивление всего проводника можно по формуле
где p – удельное сопротивление металла, l – длина проводника, s – площадь поперечного сечения.
Значения удельных сопротивлений приведены в таблице удельных сопротивлений металлов (20°C)
Вещество | p , Ом*мм 2 /2 | α,10 -3 1/K |
Алюминий | 0.0271 | |
Вольфрам | 0.055 | |
Железо | 0.098 | |
Золото | 0.023 | |
Латунь | 0.025-0.06 | |
Манганин | 0.42-0.48 | 0,002-0,05 |
Медь | 0.0175 | |
Никель | ||
Константан | 0.44-0.52 | 0.02 |
Нихром | 0.15 | |
Серебро | 0.016 | |
Цинк | 0.059 |
Кроме удельного сопротивления в таблице есть значения ТКС, об этом коэффициенте чуть позже.
Зависимость удельного сопротивления от деформаций
При холодной обработке металлов давлением, металл испытывает пластическую деформацию. При пластической деформации кристаллическая решетка искажается, количество дефектов становится больше. С увеличением дефектов кристаллической решетки, сопротивление течению электронов по проводнику растет, следовательно, удельное сопротивление металла увеличивается. К примеру, проволоку изготавливают методом протяжки, это значит, что металл испытывает пластическую деформацию, в результате чего, удельное сопротивление растет. На практике для уменьшения сопротивления применяют рекристаллизационный отжиг, это сложный технологический процесс, после которого кристаллическая решетка как бы, “расправляется” и количество дефектов уменьшается, следовательно, и сопротивление металла тоже.
При растяжении или сжатии, металл испытывает упругую деформацию. При упругой деформации вызванной растяжением, амплитуды тепловых колебаний узлов кристаллической решетки увеличиваются, следовательно, электроны испытывают большие затруднения, и в связи с этим, увеличивается удельное сопротивление. При упругой деформации вызванной сжатием, амплитуды тепловых колебаний узлов уменьшаются, следовательно, электронам проще двигаться, и удельное сопротивление уменьшается.
Влияние температуры на удельное сопротивление
Как мы уже выяснили выше, причиной сопротивления в металле являются узлы кристаллической решетки и их колебания. Так вот, при увеличении температуры, тепловые колебания узлов увеличиваются, а значит, удельное сопротивление также увеличивается. Существует такая величина как температурный коэффициент сопротивления (ТКС), который показывает насколько увеличивается, или уменьшается удельное сопротивление металла при нагреве или охлаждении. Например, температурный коэффициент меди при 20 градусах по цельсию равен 4.1 · 10 − 3 1/градус. Это означает что при нагреве, к примеру, медной проволоки на 1 градус цельсия, её удельное сопротивление увеличится на 4.1 · 10 − 3 Ом. Удельное сопротивление при изменении температуры можно вычислить по формуле
где r это удельное сопротивление после нагрева, r 0 – удельное сопротивление до нагрева, a – температурный коэффициент сопротивления, t 2 – температура до нагрева, t 1 – температура после нагрева.
Подставив наши значения, мы получим: r=0,0175*(1+0.0041*(154-20))=0,0271 Ом*мм 2 /м. Как видите наш брусок из меди длиной 1 м и площадью поперечного сечения 1 мм 2 , после нагрева до 154 градусов, имел бы сопротивление, как у такого же бруска, только из алюминия и при температуре равной 20 градусов цельсия.
Свойство изменения сопротивления при изменении температуры, используется в термометрах сопротивления. Эти приборы могут измерять температуру основываясь на показаниях сопротивления. У термометров сопротивления высокая точность измерений, но малые диапазоны температур.
На практике, свойства проводников препятствовать прохождению тока используются очень широко. Примером может служить лампа накаливания, где нить из вольфрама, нагревается за счет высокого сопротивления металла, большой длины и узкого сечения. Или любой нагревательный прибор, где спираль разогревается благодаря высокому сопротивлению. В электротехнике, элемент главным свойством которого является сопротивление, называется – резистор . Резистор применяется практически в любой электрической схеме.
При замыкании электрической цепи, на зажимах которой имеется разность потенциалов, возникает электрический ток. Свободные электроны под влиянием электрических сил поля перемещаются вдоль проводника. В своем движении электроны наталкиваются на атомы проводника и отдают им запас своей кинетической энергии. Скорость движения электронов непрерывно изменяется: при столкновении электронов с атомами, молекулами и другими электронами она уменьшается, потом под действием электрического поля увеличивается и снова уменьшается при новом столкновении. В результате этого в проводнике устанавливается равномерное движение потока электронов со скоростью нескольких долей сантиметра в секунду. Следовательно, электроны, проходя по проводнику, всегда встречают с его стороны сопротивление своему движению. При прохождении электрического тока через проводник последний нагревается.
Электрическое сопротивление
Электрическим сопротивлением проводника, которое обозначается латинской буквой r , называется свойство тела или среды превращать электрическую энергию в тепловую при прохождении по нему электрического тока.
На схемах электрическое сопротивление обозначается так, как показано на рисунке 1, а .
Переменное электрическое сопротивление, служащее для изменения тока в цепи, называется реостатом . На схемах реостаты обозначаются как показано на рисунке 1, б . В общем виде реостат изготовляется из проволоки того или иного сопротивления, намотанной на изолирующем основании. Ползунок или рычаг реостата ставится в определенное положение, в результате чего в цепь вводится нужное сопротивление.
Длинный проводник малого поперечного сечения создает току большое сопротивление. Короткие проводники большого поперечного сечения оказывают току малое сопротивление.
Если взять два проводника из разного материала, но одинаковой длины и сечения, то проводники будут проводить ток по-разному. Это показывает, что сопротивление проводника зависит от материала самого проводника.
Температура проводника также оказывает влияние на его сопротивление. С повышением температуры сопротивление металлов увеличивается, а сопротивление жидкостей и угля уменьшается. Только некоторые специальные металлические сплавы (манганин, констаитан, никелин и другие) с увеличением температуры своего сопротивления почти не меняют.
Итак, мы видим, что электрическое сопротивление проводника зависит от: 1) длины проводника, 2) поперечного сечения проводника, 3) материала проводника, 4) температуры проводника.
За единицу сопротивления принят один Ом. Ом часто обозначается греческой прописной буквой Ω (омега). Поэтому вместо того чтобы писать “Сопротивление проводника равно 15 Ом”, можно написать просто: r = 15 Ω.
1 000 Ом называется 1 килоом (1кОм, или 1кΩ),
1 000 000 Ом называется 1 мегаом (1мгОм, или 1МΩ).
При сравнении сопротивления проводников из различных материалов необходимо брать для каждого образца определенную длину и сечение. Тогда мы сможем судить о том, какой материал лучше или хуже проводит электрический ток.
Видео 1. Сопротивление проводников
Удельное электрическое сопротивление
Сопротивление в омах проводника длиной 1 м, сечением 1 мм² называется удельным сопротивлением и обозначается греческой буквой ρ (ро).
В таблице 1 даны удельные сопротивления некоторых проводников.
Таблица 1
Удельные сопротивления различных проводников
Из таблицы видно, что железная проволока длиной 1 м и сечением 1 мм² обладает сопротивлением 0,13 Ом. Чтобы получить 1 Ом сопротивления нужно взять 7,7 м такой проволоки. Наименьшим удельным сопротивлением обладает серебро. 1 Ом сопротивления можно получить, если взять 62,5 м серебряной проволоки сечением 1 мм². Серебро – лучший проводник, но стоимость серебра исключает возможность его массового применения. После серебра в таблице идет медь: 1 м медной проволоки сечением 1 мм² обладает сопротивлением 0,0175 Ом. Чтобы получить сопротивление в 1 Ом, нужно взять 57 м такой проволоки.
Химически чистая, полученная путем рафинирования, медь нашла себе повсеместное применение в электротехнике для изготовления проводов, кабелей, обмоток электрических машин и аппаратов. Широко применяют также в качестве проводников алюминий и железо.
Сопротивление проводника можно определить по формуле:
где r – сопротивление проводника в омах; ρ – удельное сопротивление проводника; l – длина проводника в м; S – сечение проводника в мм².
Пример 1. Определить сопротивление 200 м железной проволоки сечением 5 мм².
Пример 2. Вычислить сопротивление 2 км алюминиевой проволоки сечением 2,5 мм².
Из формулы сопротивления легко можно определить длину, удельное сопротивление и сечение проводника.
Пример 3. Для радиоприемника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки.
Пример 4. Определить сечение 20 м нихромовой проволоки, если сопротивление ее равно 25 Ом.
Пример 5. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом. Определить материал проволоки.
Материал проводника характеризует его удельное сопротивление.
По таблице удельных сопротивлений находим, что таким сопротивлением обладает свинец.
Выше было указано, что сопротивление проводников зависит от температуры. Проделаем следующий опыт. Намотаем в виде спирали несколько метров тонкой металлической проволоки и включим эту спираль в цепь аккумулятора. Для измерения тока в цепь включаем амперметр. При нагревании спирали в пламени горелки можно заметить, что показания амперметра будут уменьшаться. Это показывает, что с нагревом сопротивление металлической проволоки увеличивается.
У некоторых металлов при нагревании на 100° сопротивление увеличивается на 40 – 50 %. Имеются сплавы, которые незначительно меняют свое сопротивление с нагревом. Некоторые специальные сплавы практически не меняют сопротивления при изменении температуры. Сопротивление металлических проводников при повышении температуры увеличивается, сопротивление электролитов (жидких проводников), угля и некоторых твердых веществ, наоборот, уменьшается.
Способность металлов менять свое сопротивление с изменением температуры используется для устройства термометров сопротивления. Такой термометр представляет собой платиновую проволоку, намотанную на слюдяной каркас. Помещая термометр, например, в печь и измеряя сопротивление платиновой проволоки до и после нагрева, можно определить температуру в печи.
Изменение сопротивления проводника при его нагревании, приходящееся на 1 Ом первоначального сопротивления и на 1° температуры, называется температурным коэффициентом сопротивления и обозначается буквой α.
Если при температуре t 0 сопротивление проводника равно r 0 , а при температуре t равно r t , то температурный коэффициент сопротивления
Примечание. Расчет по этой формуле можно производить лишь в определенном интервале температур (примерно до 200°C).
Приводим значения температурного коэффициента сопротивления α для некоторых металлов (таблица 2).
Таблица 2
Значения температурного коэффициента для некоторых металлов
Из формулы температурного коэффициента сопротивления определим r t :
r t = r 0 .
Пример 6. Определить сопротивление железной проволоки, нагретой до 200°C, если сопротивление ее при 0°C было 100 Ом.
r t = r 0 = 100 (1 + 0,0066 × 200) = 232 Ом.
Пример 7. Термометр сопротивления, изготовленный из платиновой проволоки, в помещении с температурой 15°C имел сопротивление 20 Ом. Термометр поместили в печь и через некоторое время было измерено его сопротивление. Оно оказалось равным 29,6 Ом. Определить температуру в печи.
Электрическая проводимость
До сих пор мы рассматривали сопротивление проводника как препятствие, которое оказывает проводник электрическому току. Но все же ток по проводнику проходит. Следовательно, кроме сопротивления (препятствия), проводник обладает также способностью проводить электрический ток, то есть проводимостью.
Чем большим сопротивлением обладает проводник, тем меньшую он имеет проводимость, тем хуже он проводит электрический ток, и, наоборот, чем меньше сопротивление проводника, тем большей проводимостью он обладает, тем легче току пройти по проводнику. Поэтому сопротивление и проводимость проводника есть величины обратные.
Из математики известно, что число, обратное 5, есть 1/5 и, наоборот, число, обратное 1/7, есть 7. Следовательно, если сопротивление проводника обозначается буквой r , то проводимость определяется как 1/r . Обычно проводимость обозначается буквой g.
Электрическая проводимость измеряется в (1/Ом) или в сименсах.
Пример 8. Сопротивление проводника равно 20 Ом. Определить его проводимость.
Если r = 20 Ом, то
Пример 9. Проводимость проводника равна 0,1 (1/Ом). Определить его сопротивление,
Если g = 0,1 (1/Ом), то r = 1 / 0,1 = 10 (Ом)
Электрический ток I в любом веществе создается движением заряженных частиц в определенном направлении за счет приложения внешней энергии (разности потенциалов U). Каждое вещество обладает индивидуальными свойствами, по-разному влияющими на прохождение тока в нем. Эти свойства оцениваются электрическим сопротивлением R.
Георг Ом эмпирическим путем определил факторы, влияющие на величину электрического сопротивления вещества, вывел от напряжения и тока, которая названа его именем. Единица измерения сопротивления в международной системе СИ названа его именем. 1 Ом – это величина сопротивления, замеренного при температуре 0 О С у однородного ртутного столба длиной 106,3 см с площадью поперечного сечения в 1 мм 2 .
Определение
Чтобы оценить и применять на практике материалы для изготовления электротехнических устройств, введен термин «удельное сопротивление проводника» . Добавленное прилагательное «удельное» указывает на фактор использования эталонной величины объема, принятой для рассматриваемого вещества. Это позволяет оценивать электрические параметры разных материалов.
При этом учитывают, что сопротивление проводника возрастает при увеличении его длины и уменьшении поперечного сечения. В системе СИ используется объем однородного проводника с длиной 1 метр и поперечным сечением 1м 2 . В технических расчетах применяется устаревшая, но удобная внесистемная единица объема, состоящая из длины 1 метр и площади 1мм 2 . Формула удельного сопротивления ρ представлена на рисунке.
Для определения электрических свойств веществ, введена еще одна характеристика – удельная проводимость б. Она обратно пропорциональна значению удельного сопротивления, определяет способность материала проводить электрический ток: б =1/ρ.
Как удельное сопротивление зависит от температуры
На величину проводимости материала влияет его температура. Разные группы веществ ведут себя не одинаково при нагреве или охлаждении. Это свойство учитывают в электрических проводах, работающих на открытом воздухе в жару и холод.
Материал и удельное сопротивление провода подбираются с учетом условий его эксплуатации.
Возрастание сопротивления проводников прохождению тока при нагреве объясняется тем, что с повышением температуры металла в нем увеличивается интенсивность передвижения атомов и носителей электрических зарядов во всех направлениях, что создает лишние препятствия для движения заряженных частиц в одну сторону, снижает величину их потока.
Если уменьшать температуру металла, то условия для прохождения тока улучшаются. При охлаждении до критической температуры во многих металлах проявляется явление сверхпроводимости, когда их электрическое сопротивление практически равно нулю. Это свойство широко используется в мощных электромагнитах.
Влияние температуры на проводимость металла используется электротехнической промышленностью при изготовлении обыкновенных ламп накаливания. Их при прохождении тока нагревается до такого состояния, что излучает световой поток. В обычных условиях удельное сопротивление нихрома составляет около 1,05÷1,4 (ом ∙мм 2)/м.
При включении лампочки под напряжение через нить проходит большой ток, который очень быстро разогревает металл. Одновременно возрастает сопротивление электрической цепи, ограничивающее первоначальный ток до номинального значения, необходимого для получения освещения. Таким способом осуществляется простое регулирование силы тока через нихромовую спираль, отпадает необходимость применения сложной пускорегулирующей аппаратуры, используемой в светодиодных и люминесцентных источниках.
Как используется удельное сопротивление материалов в технике
Цветные благородные металлы обладают лучшими свойствами электрической проводимости. Поэтому ответственные контакты в электротехнических устройствах выполняют из серебра. Но это увеличивает конечную стоимость всего изделия. Наиболее приемлемый вариант – использование более дешевых металлов. Например, удельное сопротивление меди, равное 0,0175 (ом ∙мм 2)/м, вполне подходит для таких целей.
Благородные металлы – золото, серебро, платина, палладий, иридий, родий, рутений и осмий, получившие название главным образом благодаря высокой химической стойкости и красивому внешнему виду в ювелирных изделиях. Кроме того, золото, серебро и платина обладают высокой пластичностью, а металлы платиновой группы – тугоплавкостью и, как и золото, химической инертностью. Эти достоинства благородных металлов сочетаются.
Медные сплавы, обладающие хорошей проводимостью, используются для изготовления шунтов, ограничивающих протекание больших токов через измерительную головку мощных амперметров.
Удельное сопротивление алюминия 0,026÷0,029 (ом ∙мм 2)/м чуть выше, чем у меди, но производство и стоимость этого металла ниже. К тому он же легче. Это объясняет его широкое применение в энергетике для изготовления проводов, работающих на открытом воздухе, и жил кабелей.
Удельное сопротивление железа 0,13 (ом ∙мм 2)/м также допускает его применение для передачи электрического тока, но при этом возникают бо́льшие потери мощности. Стальные сплавы обладают повышенной прочностью. Поэтому в алюминиевые воздушные провода высоковольтных линий электропередач вплетают стальные нити, которые предназначены для противостояния нагрузкам, действующим на разрыв.
Особенно актуально это при образовании наледи на проводах или сильных порывах ветра.
Часть сплавов, например, константин и никелин обладают термостабильными резистивными характеристиками в определенном диапазоне. У никелина удельное электрическое сопротивление практически не меняется от 0 до 100 градусов по Цельсию. Поэтому спирали для реостатов изготавливают из никелина.
В измерительных приборах широко применяется свойство строгого изменения значений удельного сопротивления платины от ее температуры. Если через платиновый проводник пропускать электрический ток от стабилизированного источника напряжения и вычислять значение сопротивления, то оно будет указывать температуру платины. Это позволяет градуировать шкалу в градусах, соответствующих значениям Омам. Этот способ позволяет измерять температуру с точностью до долей градусов.
Иногда для решения практических задач требуется узнать полное или удельное сопротивление кабеля . Для этого в справочниках на кабельную продукцию приводятся значения индуктивного и активного сопротивления одной жилы для каждого значения поперечного сечения. С их помощью рассчитываются допустимые нагрузки, выделяемая теплота, определяются допустимые условия эксплуатации и подбираются эффективные защиты.
На удельную проводимость металлов оказывает влияние способ их обработки. Использование давления для пластической деформации нарушает структуру кристаллической решетки, увеличивает число дефектов и повышает сопротивление. Для его уменьшения применяют рекристаллизационный отжиг.
Растяжения или сжатия металлов вызывают в них упругую деформацию, от которой уменьшаются амплитуды тепловых колебаний электронов, а сопротивление несколько снижается.
При проектировании систем заземления необходимо учитывать . Оно имеет отличия в определении от вышеперечисленного метода и измеряется в единицах системы СИ – Ом∙метр. С его помощью оценивают качество растекания электрического тока внутри земли.
На удельную проводимость грунта влияют многие факторы, включая влажность почвы, плотность, размеры ее частиц, температуру, концентрацию солей, кислот и щелочей.
таблица удельного сопротивления меди, алюминия и других металлов
Как нам известно из закона Ома, ток на участке цепи находится в следующей зависимости: I=U/R. Закон был выведен в результате серии экспериментов немецким физиком Георгом Омом в XIX веке. Он заметил закономерность: сила тока на каком-либо участке цепи прямо зависит от напряжения, которое к этому участку приложено, и обратно – от его сопротивления.
Позже было установлено, что сопротивление участка зависит от его геометрических характеристик следующим образом: R=ρl/S,
где l- длина проводника, S – площадь его поперечного сечения, а ρ – некий коэффициент пропорциональности.
Таким образом, сопротивление определяется геометрией проводника, а также таким параметром, как удельное сопротивление (далее – у. с.) – так назвали этот коэффициент. Если взять два проводника с одинаковым сечением и длиной и поставить их в цепь по очереди, то, измеряя силу тока и сопротивление, можно увидеть, что в двух случаях эти показатели будут разными. Таким образом, удельное электрическое сопротивление – это характеристика материала, из которого сделан проводник, а если быть еще более точным, то вещества.
Проводимость и сопротивление
У.с. показывает способность вещества препятствовать прохождению тока. Но в физике есть и обратная величина — проводимость. Она показывает способность проводить электрический ток. Выглядит она так:
σ=1/ρ, где ρ – это и есть удельное сопротивление вещества.
Если говорить о проводимости, то она определяется характеристиками носителей зарядов в этом веществе. Так, в металлах есть свободные электроны. На внешней оболочке их не больше трех, и атому выгоднее их “отдать”, что и происходит при химических реакциях с веществами из правой части таблицы Менделеева. В ситуации же, когда мы располагаем чистым металлом, он имеет кристаллическую структуру, в которой эти наружные электроны общие. Они-то и переносят заряд, если приложить к металлу электрическое поле.
В растворах носителями заряда являются ионы.
Если говорить о таких веществах, как кремний, то по своим свойствам он является полупроводником и работает несколько по иному принципу, но об этом позже.8 Ом.
Между этими двумя классами существуют вещества, называемые полупроводниками. Но выделение их в отдельную группу веществ связано не столько с их промежуточным состоянием в линейке «проводимость – сопротивление», сколько с особенностями этой проводимости в различных условиях.
Зависимость от факторов внешней среды
Проводимость – не совсем постоянная величина. Данные в таблицах, откуда берут ρ для расчетов, существуют для нормальных условий среды, то есть для температуры 20 градусов. В реальности для работы цепи сложно подобрать такие идеальные условия; фактически у.с. (а стало быть, и проводимость) зависят от следующих факторов:
- температура;
- давление;
- наличие магнитных полей;
- свет;
- агрегатное состояние.
Разные вещества имеют свой график изменения этого параметра в разных условиях. Так, ферромагнетики (железо и никель) увеличивают его при совпадении направления тока с направлением силовых линий магнитного поля. Что касается температуры, то зависимость здесь почти линейная (существует даже понятие температурного коэффициента сопротивления, и это тоже табличная величина). Но направление этой зависимости различно: у металлов оно повышается с повышением температуры, а у редкоземельных элементов и растворов электролитов увеличивается – и это в пределах одного агрегатного состояния.
У полупроводников зависимость от температуры не линейная, а гиперболическая и обратная: при повышении температуры их проводимость увеличивается. Это качественно отличает проводники от полупроводников. Вот так выглядит зависимость ρ от температуры у проводников:
Здесь представлены удельное сопротивление меди, платины и железа. Немного другой график у некоторых металлов, например, ртути — при понижении температуры до 4 К она теряет его почти полностью (такое явление называется сверхпроводимостью).
А для полупроводников эта зависимость будет примерно такая:
При переходе в жидкое состояние ρ металла увеличивается, а вот дальше все они ведут себя по-разному. Например, у расплавленного висмута оно ниже, чем при комнатной температуре, а у меди – в 10 раз выше нормального. Никель выходит из линейного графика еще при 400 градусах, после чего ρ падает.
Зато у вольфрама температурная зависимость настолько высока, что это становится причиной перегорания ламп накаливания. При включении ток нагревает спираль, и ее сопротивление увеличивается в несколько раз.
Также у. с. сплавов зависит от технологии их производства. Так, если мы имеем дело с простой механической смесью, то сопротивление такого вещества можно посчитать по среднему, а вот оно же у сплава замещения (это когда два и более элемента складываются в одну кристаллическую решетку) будет иным, как правило, куда большим. Например, нихром, из которого делают спирали для электроплиток, имеет такую цифру этого параметра, что этот проводник при включении в цепь греется до красноты (из-за чего, собственно, и используется).
Вот характеристика ρ углеродистых сталей:
Как видно, при приближении к температуре плавления оно стабилизируется.-8
Как видно из таблицы, лучший проводник – это серебро. И только его стоимость мешает массово применять его в производстве кабеля. У.с. алюминия тоже небольшое, но меньше, чем у золота. Из таблицы становится понятно, почему проводка в домах либо медная, либо алюминиевая.
В таблицу не включен никель, у которого, как мы уже сказали, немного необычный график зависимости у. с. от температуры. Удельное сопротивление никеля после повышения температуры до 400 градусов начинает не расти, а падать. Интересно он ведет себя и в других сплавах замещения. Вот так ведет себя сплав меди и никеля в зависимости от процентного соотношения того и другого:
А этот интересный график показывает сопротивление сплавов Цинк – магний:
В качестве материалов для изготовления реостатов используют высокоомные сплавы, вот их характеристики:
| сплав | удельное сопротивление |
| манганин | 4,82*10^-7 |
| константан | 4,9*10^-7 |
| нихром | 1,1*10^-6 |
| фехраль | 1,2*10^-6 |
| хромаль | 1,2*10^-6 |
Это сложные сплавы, состоящие из железа, алюминия, хрома, марганца, никеля.-7 Ом · м.
Разница между у. с. различных проводников определяет и их применение. Так, медь и алюминий массово применяются при производстве кабеля, а золото и серебро – в качестве контактов в ряде радиотехнических изделий. Высокоомные проводники нашли свое место среди производителей электроприборов (точнее, они и создавались для этого).
Изменчивость этого параметра в зависимости от условий внешней среды легла в основу таких приборов, как датчики магнитного поля, терморезисторы, тензодатчики, фоторезисторы.
Температурный коэффициент сопротивления | Примечания по электронике
Подробная информация о температурном коэффициенте сопротивления вместе с формулой и расчетами, а также таблица распространенных материалов.
Учебное пособие по сопротивлению Включает:
Что такое сопротивление
Закон Ома
Омические и неомические проводники
Сопротивление лампы накаливания
Удельное сопротивление
Таблица удельного сопротивления для распространенных материалов
Температурный коэффициент сопротивления
Электрическая проводимость
Последовательные и параллельные резисторы
Таблица параллельных резисторов
Сопротивление и удельное электрическое сопротивление всех материалов зависит от температуры.
Изменение электрического сопротивления влияет на электрические и электронные цепи. В некоторых это может привести к значительным изменениям. В результате температурный коэффициент сопротивления является важным параметром для многих приложений.
Вследствие важности температурного коэффициента сопротивления указывается для материалов, широко распространенные материалы широко доступны.
Внизу страницы находится таблица температурных коэффициентов сопротивления для многих распространенных материалов, используемых в электротехнической и электронной промышленности.
Температурный коэффициент сопротивления: основы
Есть две основные причины, по которым сопротивление материалов зависит от температуры.
Один эффект возникает из-за количества столкновений между носителями заряда и атомами в материале. По мере увеличения температуры увеличивается количество столкновений, и поэтому можно представить себе, что будет незначительное увеличение сопротивления с температурой.
Это может быть не всегда, потому что некоторые материалы имеют отрицательный температурный коэффициент сопротивления.Это может быть вызвано тем фактом, что с повышением температуры высвобождаются дополнительные носители заряда, что приводит к уменьшению сопротивления с температурой. Как и следовало ожидать, этот эффект часто наблюдается в полупроводниковых материалах.
При рассмотрении температурной зависимости сопротивления обычно предполагается, что температурный коэффициент сопротивления подчиняется линейному закону. Это имеет место при комнатной температуре, а также для металлов и многих других материалов. Однако было обнаружено, что эффекты сопротивления, возникающие в результате количества столкновений, не всегда постоянны, особенно при очень низких температурах для этих материалов.
Было показано, что удельное сопротивление обратно пропорционально длине свободного пробега между столкновениями, то есть это приводит к увеличению удельного сопротивления / сопротивления с увеличением температуры. Для температур выше примерно 15 ° К (то есть выше абсолютного нуля) это ограничено тепловыми колебаниями атомов, и это дает линейную область, которая нам знакома. Ниже этой температуры сопротивление ограничено примесями и доступными носителями.
График сопротивленияТемпературный коэффициент формулы сопротивления
Сопротивление проводника при любой заданной температуре можно рассчитать, зная температуру, его температурный коэффициент сопротивления, его сопротивление при стандартной температуре и рабочую температуру.Формулу этой зависимости сопротивления от температуры в общих чертах можно выразить как:
Где
R = сопротивление при температуре, T
R ref = сопротивление при температуре Tref
α = температурный коэффициент сопротивления материала
T = температура материала в ° C
T ref = – эталонная температура, для которой указан температурный коэффициент.
Температурный коэффициент сопротивления обычно стандартизирован относительно температуры 20 ° C.Эта температура обычно считается нормальной «комнатной температурой». В результате формула для температурного коэффициента сопротивления обычно учитывает это:
Где
R 20 = сопротивление при 20 ° C
α 20 – температурный коэффициент сопротивления при 20 ° C
Таблица температурных коэффициентов сопротивления
В таблице ниже приведены температурные коэффициенты сопротивления для различных веществ, включая температурный коэффициент сопротивления меди, а также температурный коэффициент сопротивления алюминия и многих других материалов.
| Таблица температурных коэффициентов сопротивления для различных веществ | ||
|---|---|---|
| Вещество | Температурный коэффициент ° C -1 | |
| Алюминий | 43 x 10 -4 | |
| Сурьма | 40 x 10 -4 | |
| висмут | 42 x 10 -4 | |
| Латунь | ~ 10 x 10 -4 | |
| Кадмий | 40 x 10 -4 | |
| Кобальт | 7 x 10 -5 | |
| Константан (сплав) | 33 x 10 -4 | |
| Медь | 40 x 10 -4 | |
| Золото | 34 x 10 -4 | |
| Углерод (графит) | -5.6 х 10 -4 | |
| Германий | -4,8 x 10 -2 | |
| Утюг | 56 x 10 -4 | |
| Свинец | 39 x 10 -4 | |
| Манганин | ~ 2 x 10 -5 | |
| Молибден | 46 x 10 -4 | |
| Нихром | 1.7 х 10 -4 | |
| Никель | 59 x 10 -4 | |
| Платина | 38 x 10 -4 | |
| Кремний | -7,5 x 10 24 | |
| Серебро | 40 x 10 -4 | |
| Тантал | 33 x 10 -4 | |
| Олово | 45 x 10 -4 | |
| Вольфрам | 45 x 10 -4 | |
| цинк | 36 x 10 -4 | |
Видно, что большинство материалов, но не те, которые широко используются в электротехнической и электронной промышленности, имеют температурный коэффициент сопротивления примерно от 30 до 50 x 10 -4 , за исключением полупроводников, которые сильно различаются.
Дополнительные концепции и руководства по основам электроники:
Voltage
Текущий
Власть
Сопротивление
Емкость
Индуктивность
Трансформеры
Децибел, дБ
Законы Кирхгофа
Q, добротность
РЧ шум
Вернуться в меню «Основные понятия электроники». . .
Сопротивление и удельное сопротивление | Физика II
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие удельного сопротивления.
- Используйте удельное сопротивление для расчета сопротивления материалов указанной конфигурации.
- Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.
Зависимость сопротивления от материала и формы
Сопротивление объекта зависит от его формы и материала, из которого он сделан. Цилиндрический резистор на Рисунке 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм.Как и следовало ожидать, электрическое сопротивление цилиндра R прямо пропорционально его длине L , подобно сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше зарядов соударяется с его атомами. Чем больше диаметр цилиндра, тем больше тока он может пропускать (опять же, как поток жидкости по трубе). Фактически, R обратно пропорционален площади поперечного сечения цилиндра A .
Рисунок 1.Однородный цилиндр длиной L и площадью поперечного сечения A. Его сопротивление потоку тока аналогично сопротивлению, оказываемому трубой потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше площадь его поперечного сечения A, тем меньше его сопротивление.
Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы обладают разным сопротивлением потоку заряда. Мы определяем сопротивление ρ вещества таким образом, чтобы сопротивление R объекта было прямо пропорционально ρ .Удельное сопротивление ρ – это внутреннее свойство материала, независимо от его формы или размера. Сопротивление R однородного цилиндра длиной L , площадью поперечного сечения A , изготовленного из материала с удельным сопротивлением ρ , составляет
.[латекс] R = \ frac {\ rho L} {A} \\ [/ латекс].
В таблице 1 приведены репрезентативные значения ρ . Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельных сопротивлений.У проводников наименьшее удельное сопротивление, а у изоляторов наибольшее; полупроводники имеют промежуточное удельное сопротивление. Проводники имеют различную, но большую плотность свободных зарядов, тогда как большинство зарядов в изоляторах связаны с атомами и не могут двигаться. Полупроводники являются промежуточными, имеют гораздо меньше свободных зарядов, чем проводники, но обладают свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников находят применение в современной электронике, о чем мы поговорим в следующих главах.
| Материал | Удельное сопротивление ρ ( Ом ⋅ м ) |
|---|---|
| Проводники | |
| Серебро | 1. 59 × 10 −8 |
| Медь | 1. 72 × 10 −8 |
| Золото | 2. 44 × 10 −8 |
| Алюминий | 2.65 × 10 −8 |
| Вольфрам | 5. 6 × 10 −8 |
| Утюг | 9. 71 × 10 −8 |
| Платина | 10. 6 × 10 −8 |
| Сталь | 20 × 10 −8 |
| Свинец | 22 × 10 −8 |
| Манганин (сплав Cu, Mn, Ni) | 44 × 10 −8 |
| Константан (сплав Cu, Ni) | 49 × 10 −8 |
| Меркурий | 96 × 10 −8 |
| Нихром (сплав Ni, Fe, Cr) | 100 × 10 −8 |
| Полупроводники | |
| Углерод (чистый) | 3.5 × 10 5 |
| Углерод | (3,5 – 60) × 10 5 |
| Германий (чистый) | 600 × 10 −3 |
| Германий | (1−600) × 10 −3 |
| Кремний (чистый) | 2300 |
| Кремний | 0,1–2300 |
| Изоляторы | |
| Янтарь | 5 × 10 14 |
| Стекло | 10 9 – 10 14 |
| Люцит | > 10 13 |
| Слюда | 10 11 – 10 15 |
| Кварц (плавленый) | 75 × 10 16 |
| Резина (твердая) | 10 13 – 10 16 |
| Сера | 10 15 |
| тефлон | > 10 13 |
| Дерево | 10 8 – 10 11 |
Пример 1.Расчет диаметра резистора: нить накала фары
Нить накала автомобильной фары изготовлена из вольфрама и имеет сопротивление холоду 0,350 Ом. Если нить представляет собой цилиндр длиной 4,00 см (ее можно свернуть в бухту для экономии места), каков ее диаметр?
СтратегияМы можем переписать уравнение [латекс] R = \ frac {\ rho L} {A} \\ [/ latex], чтобы найти площадь поперечного сечения A нити на основе данной информации. Тогда его диаметр можно определить, предположив, что он имеет круглое поперечное сечение.{-5} \ text {m} \ end {array} \\ [/ latex].
ОбсуждениеДиаметр чуть меньше десятой миллиметра. Он состоит только из двух цифр, потому что ρ известен только из двух цифр.
Температурное изменение сопротивления
Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. Рисунок 2.)
Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах – это сверхпроводник примерно до 4.2 К. Выше этой критической температуры его сопротивление резко возрастает, а затем увеличивается почти линейно с температурой.
И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы колеблются быстрее и на больших расстояниях при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, эффективно увеличивая удельное сопротивление. При относительно небольших изменениях температуры (около 100 ° C или меньше) удельное сопротивление ρ изменяется с изменением температуры Δ T , как выражено в следующем уравнении
ρ = ρ 0 (1 + α Δ T ),
, где ρ 0 – исходное удельное сопротивление, а α – температурный коэффициент сопротивления .(См. Значения α в Таблице 2 ниже.) Для более значительных изменений температуры α может измениться, или может потребоваться нелинейное уравнение, чтобы найти ρ . Обратите внимание, что α положительно для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. У манганина (который состоит из меди, марганца и никеля), например, α близок к нулю (к трем цифрам на шкале в таблице 2), и поэтому его удельное сопротивление лишь незначительно изменяется в зависимости от температуры.Это полезно, например, для создания не зависящего от температуры эталона сопротивления.
| Материал | Коэффициент (1 / ° C) |
|---|---|
| Проводники | |
| Серебро | 3,8 × 10 −3 |
| Медь | 3,9 × 10 −3 |
| Золото | 3.4 × 10 −3 |
| Алюминий | 3,9 × 10 −3 |
| Вольфрам | 4,5 × 10 −3 |
| Утюг | 5,0 × 10 −3 |
| Платина | 3,93 × 10 −3 |
| Свинец | 3,9 × 10 −3 |
| Манганин (сплав Cu, Mn, Ni) | 0,000 × 10 −3 |
| Константан (сплав Cu, Ni) | 0.002 × 10 −3 |
| Меркурий | 0,89 × 10 −3 |
| Нихром (сплав Ni, Fe, Cr) | 0,4 × 10 −3 |
| Полупроводники | |
| Углерод (чистый) | −0,5 × 10 −3 |
| Германий (чистый) | −50 × 10 −3 |
| Кремний (чистый) | −70 × 10 −3 |
Также обратите внимание, что α отрицательно для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с увеличением температуры.Они становятся лучшими проводниками при более высоких температурах, потому что повышенное тепловое перемешивание увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения ρ с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках. Сопротивление объекта также зависит от температуры, поскольку R 0 прямо пропорционально ρ . Для цилиндра мы знаем, что R = ρL / A , и поэтому, если L и A не сильно изменяются с температурой, R будет иметь такую же температурную зависимость, как ρ .(Исследование коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на L и A примерно на два порядка меньше, чем на ρ .) Таким образом,
R = R 0 (1 + α Δ T )
– это температурная зависимость сопротивления объекта, где R 0 – исходное сопротивление, а R – сопротивление после изменения температуры Δ T .Многие термометры основаны на влиянии температуры на сопротивление. (См. Рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для определения его температуры. Устройство небольшое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.
Рис. 3. Эти знакомые термометры основаны на автоматическом измерении сопротивления термистора в зависимости от температуры.(Источник: Biol, Wikimedia Commons)
Пример 2. Расчет сопротивления: сопротивление горячей нити
Хотя следует соблюдать осторожность при применении ρ = ρ 0 (1 + α Δ T ) и R = R 0 (1 + α Δ T ) для изменений температуры более 100 ° C, для вольфрама уравнения достаточно хорошо работают при очень больших изменениях температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температура повышается с комнатной температуры (20ºC) до типичной рабочей температуры 2850ºC?
СтратегияЭто прямое применение R = R 0 (1 + α Δ T ), поскольку исходное сопротивление нити было задано равным R 0 = 0.{-3} / º \ text {C} \ right) \ left (2830º \ text {C} \ right) \ right] \\ & = & {4.8 \ Omega} \ end {array} \\ [/ latex] .
ОбсуждениеЭто значение соответствует примеру сопротивления фары в Законе Ома: сопротивление и простые цепи.
Исследования PhET: сопротивление в проводеУзнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.
Щелкните, чтобы запустить моделирование.
Сводка раздела
- Сопротивление R цилиндра длиной L и площадью поперечного сечения A составляет [латекс] R = \ frac {\ rho L} {A} \ [/ латекс], где ρ – удельное сопротивление материала.
- Значения ρ в таблице 1 показывают, что материалы делятся на три группы – проводников, полупроводников и изоляторов .
- Температура влияет на удельное сопротивление; для относительно небольших изменений температуры Δ T , удельное сопротивление равно [латекс] \ rho = {\ rho} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где ρ 0 – исходное удельное сопротивление, а [латекс] \ text {\ alpha} [/ latex] – температурный коэффициент удельного сопротивления.
- В таблице 2 приведены значения для α , температурного коэффициента удельного сопротивления.
- Сопротивление R объекта также зависит от температуры: [латекс] R = {R} _ {0} \ left (\ text {1} + \ alpha \ Delta T \ right) \\ [/ latex], где R 0 – исходное сопротивление, а R – сопротивление после изменения температуры.
Концептуальные вопросы
1. В каком из трех полупроводниковых материалов, перечисленных в Таблице 1, примеси дают свободные заряды? (Подсказка: изучите диапазон удельного сопротивления для каждого из них и определите, имеет ли чистый полупроводник большую или меньшую проводимость.)
2. Зависит ли сопротивление объекта от пути, через который проходит ток? Рассмотрим, например, прямоугольный стержень – одинаково ли его сопротивление по длине и по ширине? (См. Рисунок 5.)
Рис. 5. Встречается ли ток, проходящий двумя разными путями через один и тот же объект, с разным сопротивлением?
3. Если алюминиевый и медный провода одинаковой длины имеют одинаковое сопротивление, какой из них имеет больший диаметр? Почему?
4. Объясните, почему [латекс] R = {R} _ {0} \ left (1+ \ alpha \ Delta T \ right) \\ [/ latex] для температурного изменения сопротивления R объекта равен не так точен, как [латекс] \ rho = {\ rho} _ {0} \ left ({1} + \ alpha \ Delta T \ right) \\ [/ latex], что дает температурное изменение удельного сопротивления ρ .
Задачи и упражнения
1. Каково сопротивление отрезка медного провода 12-го калибра длиной 20,0 м и диаметром 2,053 мм?
2. Диаметр медного провода нулевого калибра 8,252 мм. Найдите сопротивление такого провода длиной 1,00 км, используемого для передачи энергии.
3. Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление 0,200 Ом при 20 ° C, какой длины она должна быть?
4. Найдите отношение диаметра алюминиевого провода к медному, если они имеют одинаковое сопротивление на единицу длины (как в бытовой электропроводке).
5. Какой ток протекает через стержень из чистого кремния диаметром 2,54 см и длиной 20,0 см при приложении к нему 1,00 × 10 3 В? (Такой стержень может быть использован, например, для изготовления детекторов ядерных частиц.)
6. (a) До какой температуры нужно нагреть медный провод, изначально равный 20,0 ° C, чтобы удвоить его сопротивление, не обращая внимания на любые изменения в размерах? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?
7. Резистор из нихромовой проволоки используется там, где его сопротивление не может изменяться более чем на 1.00% от его значения при 20,0ºC. В каком температурном диапазоне его можно использовать?
8. Из какого материала изготовлен резистор, если его сопротивление на 40,0% больше при 100 ° C, чем при 20,0 ° C?
9. Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0 ° C до 55,0 ° C, содержит резисторы из чистого углерода. В какой степени их сопротивление увеличивается в этом диапазоне?
10. (a) Из какого материала сделана проволока, если она имеет длину 25,0 м, диаметр 0,100 мм и сопротивление 77.7 Ом при 20,0 ° C? (б) Каково его сопротивление при 150 ° C?
11. При условии постоянного температурного коэффициента удельного сопротивления, каков максимальный процент уменьшения сопротивления константановой проволоки, начиная с 20,0 ° C?
12. Через матрицу протягивают проволоку, растягивая ее в четыре раза по сравнению с исходной длиной. По какому фактору увеличивается его сопротивляемость?
13. Медный провод имеет сопротивление 0,500 Ом при 20,0 ° C, а железный провод имеет сопротивление 0,525 Ом при той же температуре.При какой температуре их сопротивления равны?
14. (a) Цифровые медицинские термометры определяют температуру путем измерения сопротивления полупроводникового устройства, называемого термистором (который имеет α, = –0,0600 / ºC), когда он находится при той же температуре, что и пациент. Какова температура пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0 ° C (нормальная температура тела)? (b) Отрицательное значение для α может не поддерживаться при очень низких температурах.Обсудите, почему и так ли здесь. (Подсказка: сопротивление не может стать отрицательным.)
15. Integrated Concepts (a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения 12 × 10 −6 / ºC. б) На какой процент ваш ответ отличается от приведенного в примере?
16. Необоснованные результаты (a) До какой температуры нужно нагреть резистор из константана, чтобы удвоить его сопротивление, при условии постоянного температурного коэффициента удельного сопротивления? б) разрезать пополам? (c) Что необоснованного в этих результатах? (d) Какие допущения необоснованны или какие посылки несовместимы?
Сноски
- 1 Значения сильно зависят от количества и типа примесей
- 2 значения при 20 ° C.
Глоссарий
- удельное сопротивление:
- внутреннее свойство материала, независимо от его формы или размера, прямо пропорциональное сопротивлению, обозначаемое как ρ
- температурный коэффициент удельного сопротивления:
- эмпирическая величина, обозначенная как α , которая описывает изменение сопротивления или удельного сопротивления материала с температурой
Избранные решения проблем и упражнения
1.0,104 Ом
3. 2,8 × 10 −2 м
5. 1,10 × 10 −3 A
7. от −5ºC до 45ºC
9. 1.03
11. 0,06%
13. −17ºC
15. (a) 4,7 Ом (всего) (b) уменьшение на 3,0%
Electric Resistance – The Physics Hypertextbook
Обсуждение
введение
Йех! Что за беспорядок.
Проводимость: С. Грей, 1729 – Сопротивление: Георг Симон Ом, 1827.
Обычная версия…
I ∝ V
| I = | В | ⇒ | .В = ИК | ⇒ | .R = | В |
| R | I |
Variableogy…
- количество: сопротивление R
единица: Ом [Ом] Георг Ом (1787–1854) Германия
Причудливая версия (магнитогидродинамическая версия?)…
Дж ∝ E
| Дж = σ E | ⇐ | ⇒ | .E = ρ Дж |
Добро пожаловать в символический ад…
| количество | символ | единица СИ | символ | собственности… |
|---|---|---|---|---|
| сопротивление | R | Ом | Ом | объектов |
| проводимость | г | siemens | S | |
| удельное сопротивление | ρ | омметр | Ом · м | материалов |
| проводимость | σ | сименс на метр | См / м |
Закон Ома не является серьезным законом.Это непростая физика. Разумные материалы и устройства подчиняются ему, но есть множество мошенников, которые этого не делают.
резисторы
Плохая выпивка портит наши молодые кишки, но водка идет хорошо.
Лучше постройте крышу над гаражом, пока фургон не намок.
| цвет | цифра | множитель | допуск | tcr (10 −6 / К) | |
|---|---|---|---|---|---|
| нет | ± 20% | ||||
| розовый | 10 −3 | ||||
| серебро | 10 −2 | ± 10% | |||
| золото | 10 -1 | ± 5% | |||
| черный | 0 | 10 0+ | ± 250 | ||
| коричневый | 1 | 10 1+ | ± 1% | ± 100 | |
| красный | 2 | 10 2+ | ± 2% | ± 50 | |
| оранжевый | 3 | 10 3+ | ± 0.05% | ± 15 | |
| желтый | 4 | 10 4+ | ± 0,02% | ± 25 | |
| зеленый | 5 | 10 5+ | ± 0,50% | ± 20 | |
| синий | 6 | 10 6+ | ± 0,25% | ± 10 | |
| фиолетовый | 7 | ± 0.10% | ± 5 | ||
| серый | 8 | ± 0,01% | ± 1 | ||
| белый | 9 | ||||
материалы
Сопротивление и удельное сопротивление. Факторы, влияющие на сопротивление в проводящем проводе.
Проводники и изоляторы
Лучшие электрические проводники: серебро, медь, золото, алюминий, кальций, бериллий, вольфрам
Удельное сопротивление и проводимость взаимны.
Электропроводность металлов – это статистическая / термодинамическая величина.
Сопротивление определяется рассеянием электронов. Чем больше рассеяние, тем выше сопротивление.
где…
| σ = | Электропроводность [См / м] |
| n = | плотность свободных электронов [э / м 3 ] |
| e = | заряд электрона (1,60 × 10 −19 Кл) |
| м e = | масса электрона (9.11 × 10 −31 кг) |
| v rms = | Среднеквадратичная скорость электронов [м / с] |
| ℓ = | средняя длина свободного пробега [м] |
Графит
Кому принадлежит эта идея? Нихром был изобретен в 1906 году, что сделало возможным электрические тостеры.
Полимеры электропроводящие.
Удельное сопротивление выбранных материалов (~ 300 K)
(Обратите внимание на разницу в единицах измерения между металлами и неметаллами.)
| металлы | ρ (нОм м) |
|---|---|
| алюминий | 26,5 |
| латунь | 64 |
| хром | 126 |
| медь | 17,1 |
| золото | 22,1 |
| утюг | 96,1 |
| свинец | 208 |
| литий | 92.8 |
| ртуть (0 ° C) | 941 |
| марганец | 1440 |
| нихром | 1500 |
| никель | 69,3 |
| палладий | 105,4 |
| платина | 105 |
| плутоний | 1414 |
| серебро | 15,9 |
| припой | 150 |
| сталь, гладкая | 180 |
| сталь, нержавеющая | 720 |
| тантал | 131 |
| банка (0 ° C) | 115 |
| титан (0 ° C) | 390 |
| вольфрам | 52.8 |
| уран (0 ° C) | 280 |
| цинк | 59 |
| неметаллы | ρ (Ом м) |
|---|---|
| оксид алюминия (14 ° C) | 1 × 10 14 |
| оксид алюминия (300 ° C) | 3 × 10 11 |
| оксид алюминия (800 ° C) | 4 × 10 6 |
| углерод аморфный | 0.35 |
| карбон, алмаз | 2,7 |
| углерод, графит | 650 × 10 −9 |
| Оксид индия и олова, тонкая пленка | 2000 × 10 −9 |
| германий | 0,46 |
| пирекс 7740 | 40 000 |
| кварцевый | 75 × 10 16 |
| кремний | 640 |
| диоксид кремния (20 ° C) | 1 × 10 13 |
| диоксид кремния (600 ° C) | 70 000 |
| диоксид кремния (1300 ° C) | 0.004 |
| вода, жидкость (0 ° C) | 861 900 |
| вода, жидкость (25 ° C) | 181 800 |
| вода, жидкость (100 ° C) | 12 740 |
температура
Общее правило – удельное сопротивление увеличивается с увеличением температуры в проводниках и уменьшается с увеличением температуры в изоляторах. К сожалению, не существует простой математической функции для описания этих отношений.
Температурную зависимость удельного сопротивления (или обратной проводимости) можно понять только с помощью квантовой механики. Точно так же, как материя представляет собой совокупность микроскопических частиц, называемых атомами, а луч света – это поток микроскопических частиц, называемых фотонами, тепловые колебания в твердом теле представляют собой рой микроскопических частиц, называемых фононами . Электроны пытаются дрейфовать к положительному полюсу батареи, но фононы продолжают врезаться в них.Случайное направление этих столкновений нарушает попытку организованного движения электронов против электрического поля. Отклонение или рассеяние электронов на фононах – один из источников сопротивления. С повышением температуры количество фононов увеличивается, а вместе с ним и вероятность столкновения электронов и фононов. Таким образом, когда температура повышается, сопротивление повышается.
Для некоторых материалов удельное сопротивление линейно зависит от температуры.
ρ = ρ 0 (1 + α ( T – T 0 ))
Удельное сопротивление проводника увеличивается с температурой.В случае меди зависимость между удельным сопротивлением и температурой примерно линейна в широком диапазоне температур.
Для других материалов лучше работает соотношение сил.
ρ = ρ 0 ( T / T 0 ) μ
Удельное сопротивление проводника увеличивается с температурой. В случае вольфрама зависимость между удельным сопротивлением и температурой лучше всего описывается соотношением мощности.
см. Также: сверхпроводимость
разное
магнитосопротивление
фотопроводимость
жидкости
электролиты
газы
пробой диэлектрика
плазма
микрофоны
Угольный микрофон – ничто задом наперед
| тип | звуков производят изменений в… | , что вызывает изменений в… | , в результате чего изменений… |
|---|---|---|---|
| углерод | Плотность гранул | сопротивление | напряжение |
| конденсатор | разделение тарелок | емкость | напряжение |
| динамический | Расположение змеевика | флюс | напряжение |
| пьезоэлектрический | сжатие | поляризация | напряжение |
рассчитать температурную зависимость резистора
Формулы температурной зависимости резистора
Сопротивление всех материалов более или менее зависит от температуры.Медь лучше проводит в холоде. Вот почему медь и другие металлы относятся к термисторам PTC. Уголь лучше проводит в тепле. Таким образом, уголь является одним из проводников нагрева.
Температурный коэффициент \ (α \) дает изменение сопротивления за один Сопротивление 1 Ом при нагреве на один \ (К \) (Кельвин) или градус Цельсия.
Пример
Термисторы PTC имеют положительный температурный коэффициент и поэтому называются PTC.
Медь 99.9%: 0,00393
Алюминий 99,9%: 0,004Термисторы NTC имеют отрицательный температурный коэффициент и поэтому называются NTC.
Уголь: -0,00004
Константан: -0,00008 .. + 0,00004
Также в Интернете есть несколько другие значения температурных коэффициентов.Стоимость зависит, помимо прочего, от чистоты материала.
Формулы изменения сопротивления
Изменение сопротивления рассчитывается:
\ (\ Displaystyle ΔR = α · Δ ϑ · R_k \)
Сопротивление в теплом состоянии рассчитывается:
\ (\ Displaystyle R_w = R_k + ΔR \)
или:
\ (\ Displaystyle R_w = R_k (1 + α · Δϑ) \)
Легенда
\ (\ Displaystyle Rk \)
Стойкость при 20 ° C
& ом;
\ (\ Displaystyle α \)
Температурный коэффициент
\ (\ Displaystyle Δϑ \)
Изменение температуры
° C; K
\ (\ Displaystyle ΔR \)
Изменение сопротивления
& ом;
\ (\ Displaystyle R_w \)
Сопротивление в тепле
& ом;
Для некоторых металлов сопротивление близко к абсолютному нулю (-273.16 ° C) при 0 Ом. Мы говорим здесь о сверхпроводниках (например, алюминий, свинец, олово).
Формула \ (\ Displaystyle R_w = R_k (1 + α · Δϑ) \) применяется только до \ (\ displaystyle Δϑ = 200K \)
Изменение температуры и сопротивление | IOPSpark
Температурная зависимость сопротивления
Электричество и магнетизм
Изменение температуры и сопротивление
Практическая деятельность для 14-16
Урок практический
Исследование изменения сопротивления провода при нагревании.
Аппаратура и материалы
- Источник питания, низкое напряжение, постоянный ток, например 12 В, 4 А не менее
- Реостат (10-20 Ом) на 5 А минимум
- Алюминиевый контейнер (например, одноразовый контейнер для пищевых продуктов)
- Амперметр, от 0 до 5 А, постоянный ток
- Вольтметр, от 0 до 10 В, постоянный ток
- Выводы, 4 мм, 6
- Зажимы типа Crocodile, 2
- Катушка медной проволоки (см. Техническое примечание)
Примечания по технике безопасности и охране труда
Проволока с полиуретановым покрытием может выделять опасные пары при перегреве.Окна лаборатории должны быть открыты, чтобы снизить риск.
Прочтите наше стандартное руководство по охране труда
Катушка должна быть свободно намотана из 1 м медной проволоки с полиуретановым покрытием (30 или 33 SWG). Снимите покрытие с концов, чтобы обеспечить электрический контакт через зажимы типа «крокодил».
Процедура
- Создайте простую последовательную цепь с длинными выводами к свободно намотанной катушке медного провода.
- Отрегулируйте источник питания, чтобы в катушке был ток около 4-5 ампер.Как можно скорее выключите цепь.
- Примерно через минуту змеевик остынет до комнатной температуры. Снова включите цепь. Снимите показания амперметра и вольтметра несколько раз в течение следующих полминуты или около того. За это время катушка нагревается, и ток меняется довольно быстро.
- Повторите эксперимент с катушкой из медной проволоки, подвешенной в воде в контейнере. Воду следует держать очень хорошо перемешанной. Будьте осторожны, чтобы избежать короткого замыкания змеевика, используя деревянную палочку на палочке или лопатку в качестве мешалки.
Учебные заметки
- Учащиеся записывают пары показаний разности тока и разности потенциалов, когда катушка находится в воздухе, а затем строят график характеристики разности тока / разности потенциалов. Это не прямая линия, показывающая постоянное сопротивление, а скорее кривая, показывающая, что сопротивление провода увеличивается с температурой.
- Когда эксперимент повторяется с змеевиком в водяной бане, так что его температура остается постоянной, характеристический график представляет собой прямую линию, показывающую, что сопротивление остается постоянным.Чистые металлы подчиняются закону Ома, если их температура остается постоянной. Провода, изготовленные из сплавов, таких как проволока Constantan или Eureka (состоящая из 60% меди и 40% никеля), имеют очень малый температурный коэффициент удельного сопротивления. Поэтому их не нужно помещать в ванну с постоянной температурой, чтобы показать омическое поведение. Как работает наука? Добавочный номер:
- Этот эксперимент может быть использован, чтобы научить понимать достоверность научных результатов. Результаты могут быть признаны недействительными, если на результаты влияет неконтролируемый фактор.В этом случае температура провода является фактором, влияющим на измерения его сопротивления.
- Обсудите, как это можно учесть. Один из подходов (как обсуждалось выше) состоит в том, чтобы поддерживать постоянную температуру проволоки, погружая ее в водяную баню. Альтернативой может быть использование приведенного выше графика p.d./current, чтобы найти сопротивление провода, когда через него не течет ток, потому что тогда не будет эффекта нагрева. Объясните, что сопротивление провода равно p.d. делится на ток; я.е. это градиент линии от начала координат до точки на графике. Поместите линейку на график через начало координат и через самую высокую точку графика. Линейка имеет большой уклон. Двигайтесь вниз по графику от точки к точке, показывая, что градиент уменьшается. Ближе к началу координат график почти прямой (или вы можете использовать идею касательной к графику). Таким образом можно определить сопротивление провода, когда он не нагревается током.
- Этот эксперимент можно расширить, включив в него исследование влияния температуры на сопротивление в диапазоне от 0 ° C до 100 ° C с использованием водяной бани.Если учащиеся знакомы с экспериментальным наблюдением закона Чарльза, вы можете попросить их экстраполировать свой график зависимости сопротивления от температуры, чтобы найти приблизительную температуру, при которой сопротивление провода будет равно нулю. Для чистого металла сопротивление уменьшается примерно линейно по направлению к температуре, близкой к 0 К. (Температурный коэффициент сопротивления многих чистых металлов близок к 0,004 K-1, поэтому график сопротивления / температуры будет экстраполирован обратно до 1 / 0,004 = 250. К.) Вы можете связать это с идеей о том, что сопротивление чистого металла при комнатной температуре зависит от вибрации ионов, и это снизится до нуля близко к 0 К.
Этот эксперимент прошел испытания на безопасность в октябре 2006 г.
Влияние температуры на сопротивление
- Изучив этот раздел, вы сможете:
- • Опишите влияние температуры на сопротивление проводника.
- • Опишите влияние температуры на сопротивление изолятора.
- • Определите отрицательные и положительные температурные коэффициенты.
Как температура изменяет сопротивление
Хотя сопротивление проводника изменяется в зависимости от его размера (например, более толстые провода имеют меньшее сопротивление току, чем более тонкие провода), сопротивление проводника также изменяется с изменением температуры. Этого можно ожидать, потому что при изменении температуры размеры проводника будут изменяться при его расширении или сжатии.
Однако материалы, которые классифицируются как ПРОВОДНИКИ, имеют тенденцию ПОВЫШАТЬ свое сопротивление с повышением температуры. Однако ИЗОЛЯТОРЫ могут УМЕНЬШИТЬ свое сопротивление с повышением температуры. Материалы, используемые для изготовления изоляторов (стекло, пластик и т. Д.), Демонстрируют заметное падение сопротивления только при очень высоких температурах. Они остаются хорошими изоляторами при любых температурах, с которыми они могут столкнуться при использовании.
Таким образом, эти изменения сопротивления нельзя объяснить изменением размеров из-за теплового расширения или сжатия.Фактически, для проводника данного размера изменение сопротивления в основном связано с изменением удельного сопротивления материала и вызвано изменением активности атомов, составляющих материал.
Температура и атомная структура
Причины этих изменений удельного сопротивления можно объяснить, рассмотрев протекание тока через материал. Поток тока – это фактически движение электронов от одного атома к другому под действием электрического поля.Электроны – это очень маленькие отрицательно заряженные частицы, которые отталкиваются отрицательным электрическим зарядом и притягиваются положительным электрическим зарядом. Следовательно, если к проводнику приложен электрический потенциал (положительный на одном конце, отрицательный на другом), электроны будут «мигрировать» от атома к атому к положительному полюсу.
Однако только некоторые электроны могут свободно перемещаться. Остальные внутри каждого атома так сильно привязаны к своему конкретному атому, что даже электрическое поле не сместит их.Таким образом, ток, протекающий в материале, обусловлен движением «свободных электронов», и количество свободных электронов в любом материале по сравнению с теми, которые тесно связаны с их атомами, определяет, является ли материал хорошим проводником (много свободных электронов) или хороший изолятор (почти нет свободных электронов).
Воздействие тепла на атомную структуру материала заставляет атомы колебаться, и чем выше температура, тем сильнее колеблются атомы.
В проводнике, по которому уже протекает большое количество свободных электронов, колебания атомов вызывают множество столкновений между свободными электронами и захваченными электронами.Каждое столкновение использует некоторую энергию свободного электрона и является основной причиной сопротивления. Чем больше атомы толкаются в материале, тем больше возникает столкновений и, следовательно, больше сопротивление току.
Однако в изоляторе ситуация несколько иная. Свободных электронов так мало, что ток почти не протекает. Почти все электроны прочно связаны внутри своего атома. Нагревание изолирующего материала вызывает вибрацию атомов, и при достаточном нагреве атомы вибрируют достаточно сильно, чтобы фактически высвободить часть своих захваченных электронов, создавая свободные электроны, которые становятся носителями тока.Поэтому при высоких температурах сопротивление изолятора может упасть, а в некоторых изоляционных материалах – довольно резко.
В материале, сопротивление которого УВЕЛИЧИВАЕТСЯ с повышением температуры, считается, что материал имеет ПОЛОЖИТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Когда сопротивление ПАДАЕТ с повышением температуры, говорят, что материал имеет ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ.
Как правило, проводники имеют ПОЛОЖИТЕЛЬНЫЙ температурный коэффициент, в то время как (при высоких температурах) изоляторы имеют ОТРИЦАТЕЛЬНЫЙ температурный коэффициент.
У разных материалов внутри каждой группы разные температурные коэффициенты. Материалы, выбранные для изготовления резисторов, используемых в электронных схемах, представляют собой тщательно отобранные проводники с очень низким положительным температурным коэффициентом. При использовании резисторы, изготовленные из таких материалов, будут иметь лишь очень небольшое увеличение удельного сопротивления и, следовательно, их сопротивления. Использование таких материалов для изготовления резисторов создает компоненты, значение которых незначительно изменяется в заданном диапазоне температур.
Материалы, выбранные в качестве изоляторов, будут иметь очень низкий ОТРИЦАТЕЛЬНЫЙ ТЕМПЕРАТУРНЫЙ КОЭФФИЦИЕНТ во всем рабочем диапазоне температур.
Калькулятор сопротивления проводов
Этот калькулятор сопротивления проводов может быстро вычислить электрические свойства конкретного провода – его сопротивление и проводимость. Сопротивление описывает, насколько сильно данный кабель препятствует прохождению электрического тока, а проводимость измеряет способность провода проводить его. С ними также связаны две физические величины – удельное электрическое сопротивление и электропроводность.Прочитав приведенный ниже текст, вы, например, узнаете, как можно оценить сопротивление провода, используя формулу сопротивления (так называемый закон Пуйе).
В настоящее время одним из наиболее часто используемых проводников является медь, которую можно найти почти в каждом электрическом устройстве. Читайте дальше, если вы хотите узнать, каковы проводимость меди и удельное сопротивление меди, а также какие единицы удельного сопротивления и единицы проводимости использовать. Вы также можете рассчитать падение напряжения на конкретном проводе – в этом случае попробуйте наш калькулятор падения напряжения!
Единицы удельного сопротивления и электропроводности
Удельное сопротивление ρ , в отличие от сопротивления, является внутренним свойством материала.Это значит, что неважно, толстая или тонкая, длинная или короткая проволока. Удельное сопротивление всегда будет одинаковым для конкретного материала, а единицы удельного сопротивления – «омметр» ( Ом * м ). Чем выше удельное сопротивление, тем труднее протекать току через провод. Вы можете проверить наш калькулятор скорости дрейфа, чтобы узнать, насколько быстро проходит электричество.
С другой стороны, у нас есть проводимость σ , которая строго связана с удельным сопротивлением.В частности, он определяется как обратное: σ = 1 / ρ . Как и удельное сопротивление, это внутреннее свойство материала, но единицы проводимости – «сименс на метр» ( См / м ). Электрический ток может плавно течь через провод, если проводимость высокая.
В некоторых материалах при очень низких температурах мы можем наблюдать явление, называемое сверхпроводимостью. Сопротивление в сверхпроводнике резко падает до нуля, и, таким образом, проводимость приближается к бесконечности.Можно сказать, что это идеальный дирижер. Сверхпроводимость также связана с левитацией, которую мы описали в нашем калькуляторе магнитной проницаемости.
Формула проводимости и формула сопротивления
И проводимость, и сопротивление зависят от геометрических размеров провода. В нашем калькуляторе сопротивления проводов используется следующая формула сопротивления:
R = ρ * L / A
где
-
R– сопротивление в Ом, -
ρ– удельное сопротивление материала в Ом * м, -
L– длина провода, -
Вы также можете использовать этот калькулятор сопротивления проводов для оценки проводимости, так как:
G = σ * A / L
где
-
G– проводимость в сименсах (S), -
σ– проводимость в См / м, -
LиAсохраняют то же значение.
В расширенном режиме вы можете напрямую изменять значения удельного сопротивления ρ и проводимости σ .Комбинируя два приведенных выше уравнения с соотношением ρ = 1 / σ , мы получаем аналогичную связь между сопротивлением и проводимостью:
R = 1 / G
Вы уже рассчитали сопротивление вашего провода? Попробуйте наш калькулятор последовательных резисторов и параллельный калькулятор резисторов, чтобы узнать, как можно рассчитать эквивалентное сопротивление различных электрических цепей. Вы также можете воспользоваться нашим калькулятором моста Уитстона, чтобы узнать, как измерить неизвестное сопротивление.
Электропроводность меди и удельное сопротивление меди
Такие материалы, как медь и алюминий, имеют низкий уровень удельного сопротивления, что делает эти материалы идеальными для производства электрических проводов и кабелей. Вы должны помнить, что сопротивление (и, следовательно, проводимость) зависит от температуры.


 023
023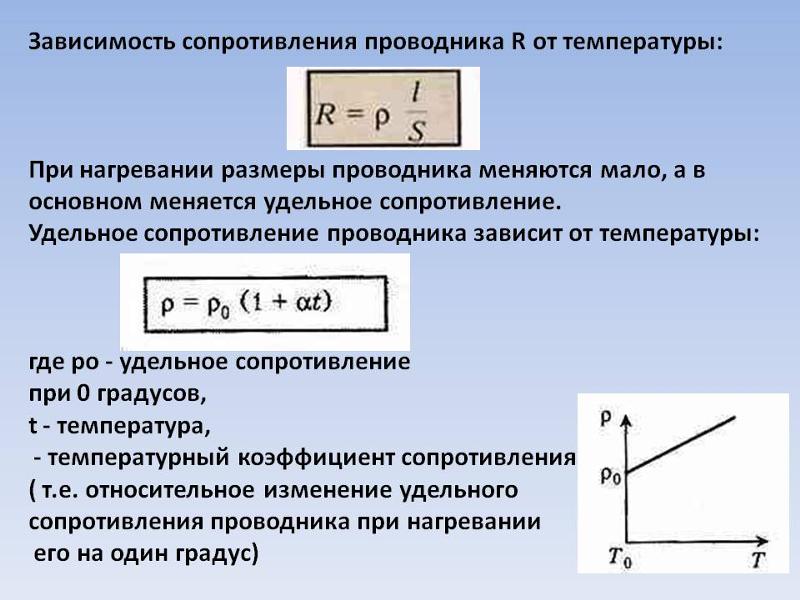 02
02