Схема – полосовой фильтр – Большая Энциклопедия Нефти и Газа, статья, страница 2
Схема – полосовой фильтр
Cтраница 2
Полученная эквивалентная схема с сосредоточенными постоянными относится к числу схем полосовых фильтров, хорошо известных в электротехнике и радиотехнике. Поэтому волновод-ная система рассмотренного типа действительно может быть представлена как волноводный полосовой фильтр. [16]
Он позволяет перейти с помощью известных частотных преобразований к схемам полосовых фильтров или фильтров верхних частот. В общем случае выбор метода расчета определяется постановкой задачи. Однако такой метод синтеза согласующих цепей применительно к системам СВЧ ие всегда эффективен несмотря иа корректность постановки задачи и точность получаемых решений в связи с тем, что иа СВЧ проблема реализуемости становится определяющей, а изложенная выше постановка задачи предполагает единственность решения.
Эквивалентная схема М – контура ( рис. 74, б) отличается от схемы обычного полосового фильтра той особенностью, что в этом М – фильтре внутренняя связь между контурами Ь С и L2C2 избирательная. [18]
Цепи на рис. 8.29 служат иллюстрацией преобразования элементов схемы фильтра нижних частот в схему полосового фильтра. В случае применения преобразования (8.159) значения резисторов и резистивных элементов остаются б ез изменения. [20]
На длинных, средних и коротких волнах наибольшее распространение получили схемы с емкостной, индуктивной и индуктивно-емкостной связью, а также схема двухкон-турного полосового фильтра, индуктивно связанного с антенной. Схема емкостной связи антенны с контуром ( см. рис. 28.1, б) характеризуется тем, что антенна присоединена к контуру через небольшую емкость связи Ссв.
[22]
Схема емкостной связи антенны с контуром ( см. рис. 28.1, б) характеризуется тем, что антенна присоединена к контуру через небольшую емкость связи Ссв.
[22]Чтобы получить требуемую схему полосового фильтра, мы можем реализовать результирующую передаточную функцию H ( s), либо прибегая к различным методам реализации, либо просто используя преобразование цепи. [23]
Эти избиратели позволяют значительно более эффективно использовать полосу частот. На рис. 10.21 приведены схемы полосовых фильтров типа
Для обеспечения высокой избирательности в полосовых усилителях часто используются более сложные резонансные системы. На рис. 4.18 а показана схема полосового фильтра, состоящего из. Крайние пары контуров образуют двухконтур-ные фильтры с индуктивной связью между контурами.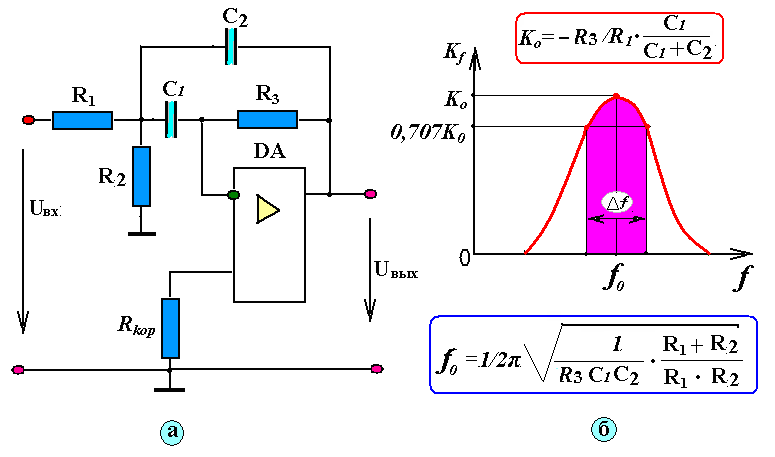 Двухкон-турные фильтры связаны между собой внешнеемкостной связью через конденсатор Ссв, включенный между вторичным контуром левого фильтра и первичным правого.
[26]
Двухкон-турные фильтры связаны между собой внешнеемкостной связью через конденсатор Ссв, включенный между вторичным контуром левого фильтра и первичным правого.
[26]
В качестве усилителей ПЧ в приемниках используются полосовые усилители. Избирательные свойства УПЧ определяются применением в его схеме полосовых фильтров или резонансных нагрузочных контуров, при этом, чем ближе форма резонансной кривой усилителя к прямоугольной, тем выше его избирательность. Это достигается увеличением числа каскадов усилителя. [28]
Таким образом, полоса пропускания исследуемой схемы начинается с частоты со со0 и заканчивается на частоте ср соь. Следовательно, схема рис. 15.6, б является схемой полосового фильтра. [29]
На сверхвысоких частотах, где потери в линии пренебрежимо малы, короткозамкнутые отрезки линии могут быть использованы для построения фильтров.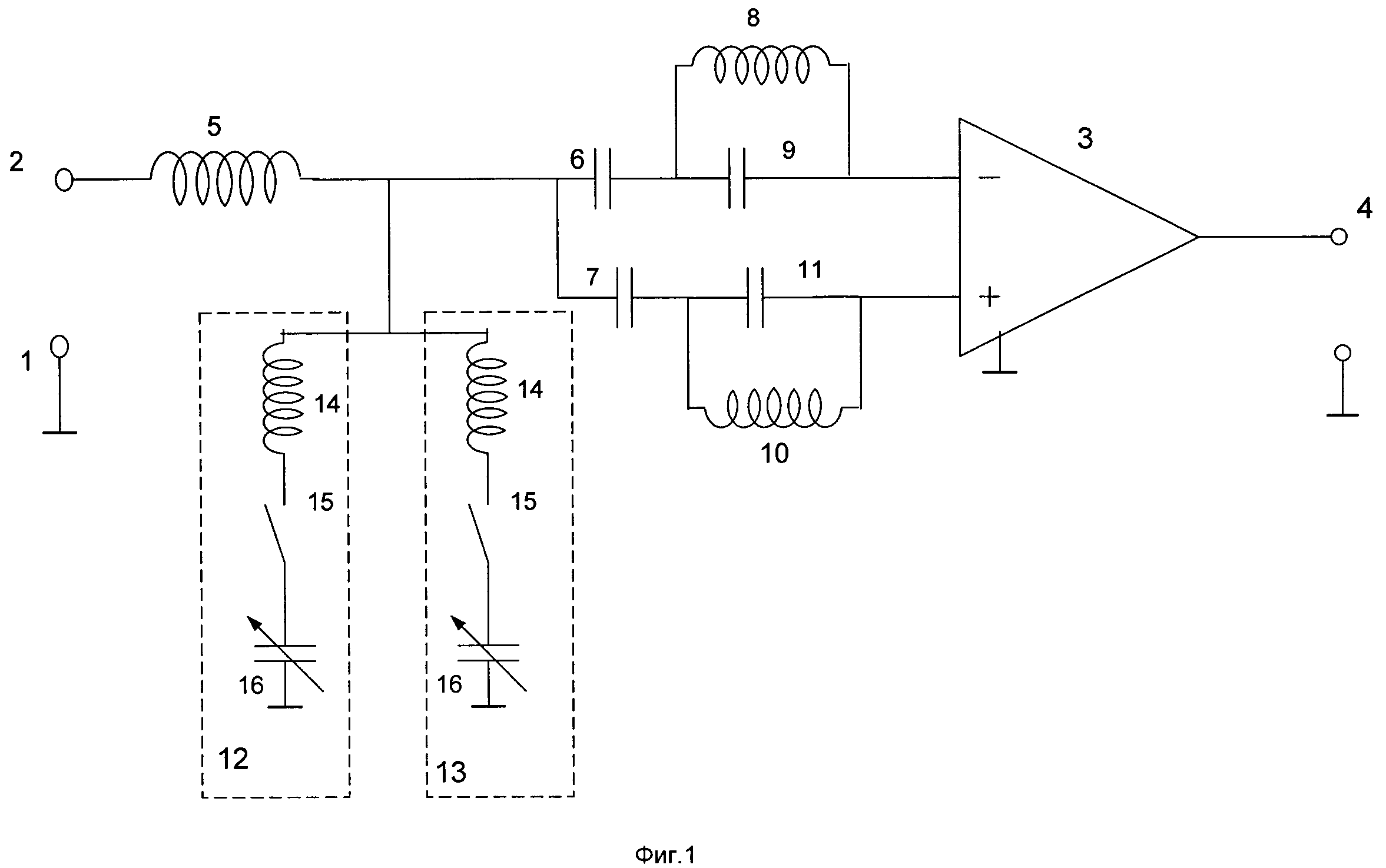 В качестве примера на рис. 11.20, а показана схема полосового фильтра, построенного на двух короткозамкнутых отрезках линии. В продольное плечо схемы включен полуволновый отрезок, в поперечное плечо – четвертьволновый. Первый отрезок имеет входное сопротивление, аналогичное входному сопротивлению последовательного колебательного контура. Второй, четвертьволновый, отрезок играет роль параллельного колебательного контура.
[30]
В качестве примера на рис. 11.20, а показана схема полосового фильтра, построенного на двух короткозамкнутых отрезках линии. В продольное плечо схемы включен полуволновый отрезок, в поперечное плечо – четвертьволновый. Первый отрезок имеет входное сопротивление, аналогичное входному сопротивлению последовательного колебательного контура. Второй, четвертьволновый, отрезок играет роль параллельного колебательного контура.
[30]
Страницы: 1 2 3
4. Полосовые фильтры | 8. Фильтры | Часть2
4. Полосовые фильтры
- Подробности
- Просмотров: 12190
Полосовые фильтры
Существуют устройства, для работы которых необходимо из широкого спектра смешанных частот выделить частоты, находящиеся в определенном диапазоне.
Схема, полученная из последовательного соединения двух фильтрующих схем, обеспечивает прохождение не слишком высоких и не слишком низких частот. Если в показанной выше блок-схеме использовать реальные компоненты, то она примет следующий вид:
capacitive bandpass filter v1 1 0 ac 1 sin r1 1 2 200 c1 2 0 2.5u c2 2 3 1u rload 3 0 1k .ac lin 20 100 500 .plot ac v(3) .end
Помимо конденсаторов, в конструкции полосовых фильтров можно использовать катушки индуктивности. Однако, как упоминалось ранее, реактивная “чистота” конденсаторов дает им преимущество перед катушками индуктивности.
Последовательность включения фильтров нижних и верхних частот не имеет значения: если вы поменяете их местами, то функционирование схемы от этого не изменится. Она по-прежнему будет отфильтровывать слишком низкие и слишком высокие частоты.
Несмотря на то, что идея объединения фильтров верхних и нижних частот для получения полосового фильтра очень хороша, она имеет определенные недостатки. Поскольку этот тип полосового фильтра блокирует нежелательные частоты при помощи двух составляющих его фильтров, спроектировать такой фильтр (позволяющий пропускать нужный диапазон частот) довольно сложно. Совместные усилия низкочастотной и высокочастотной составляющих данного фильтра в лучшем случае ослабят итоговый сигнал (уменьшат его амплитуду) даже на пике частотного диапазона “полосы пропускания”. Обратите внимание на пиковое значение кривой в приведенном выше SPICE анализе: напряжение нагрузки фильтра никогда не поднимается выше 0,59 вольт, хотя напряжения источника питания составляет 1 вольт.
Существуют методы, позволяющие достичь хороших характеристик полосового фильтра без ущерба для амплитуды сигнала в полосе пропускания. Эти методы мы обсудим несколько позже.
Проектирование и расчёт полосного фильтра (стр. 1 из 2)
Проектирование и расчёт полосного фильтра
Реферат
Курсовая работа: 18с., 8 рис., 2 табл., 3 источника.
Объект исследования – активный полосовой фильтр на операционном усилителе.
Цель работы – расчёт и синтез схемы полосового фильтра на интегральном операционном усилителе, анализ амплитудно-частотной характеристики полученного устройства.
Метод исследования – формирование виртуальной модели фильтра, определение электрических параметров (по средствам ЭВМ).
Спроектирован фильтр на операционном усилителе с многопетлевой обратной связью. Устройство характеризуется следующими параметрами: частота среза
Устройство характеризуется следующими параметрами: частота среза
Ключевые слова:
ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ, ПОЛОСОВОЙ ФИЛЬТР, АМПЛИТУДНО-ЧАСТОТНАЯ ХАРАКТЕРИСТИКА, ЧАСТОТА СРЕЗА, ПОЛОСА ПРОПУСКАНИЯ, ОТРИЦАТЕЛЬНАЯ ОБРАТНАЯ СВЯЗЬ.
Содержание
Введение
1 Анализ технического задания
2 Синтез схемы и расчет элементов фильтра
3 Расчет АЧХ фильтра на ЭВМ
4 Подбор элементов для схемы
Выводы
Список использованных источников
Введение
Цепи фильтрации сигналов – важная и неотъемлемая часть многих систем связи и электрических контрольно-измерительных устройств. Они служат для формирования частотных каналов в системах коммутации, разделения и преобразования электрических сигналов.
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство.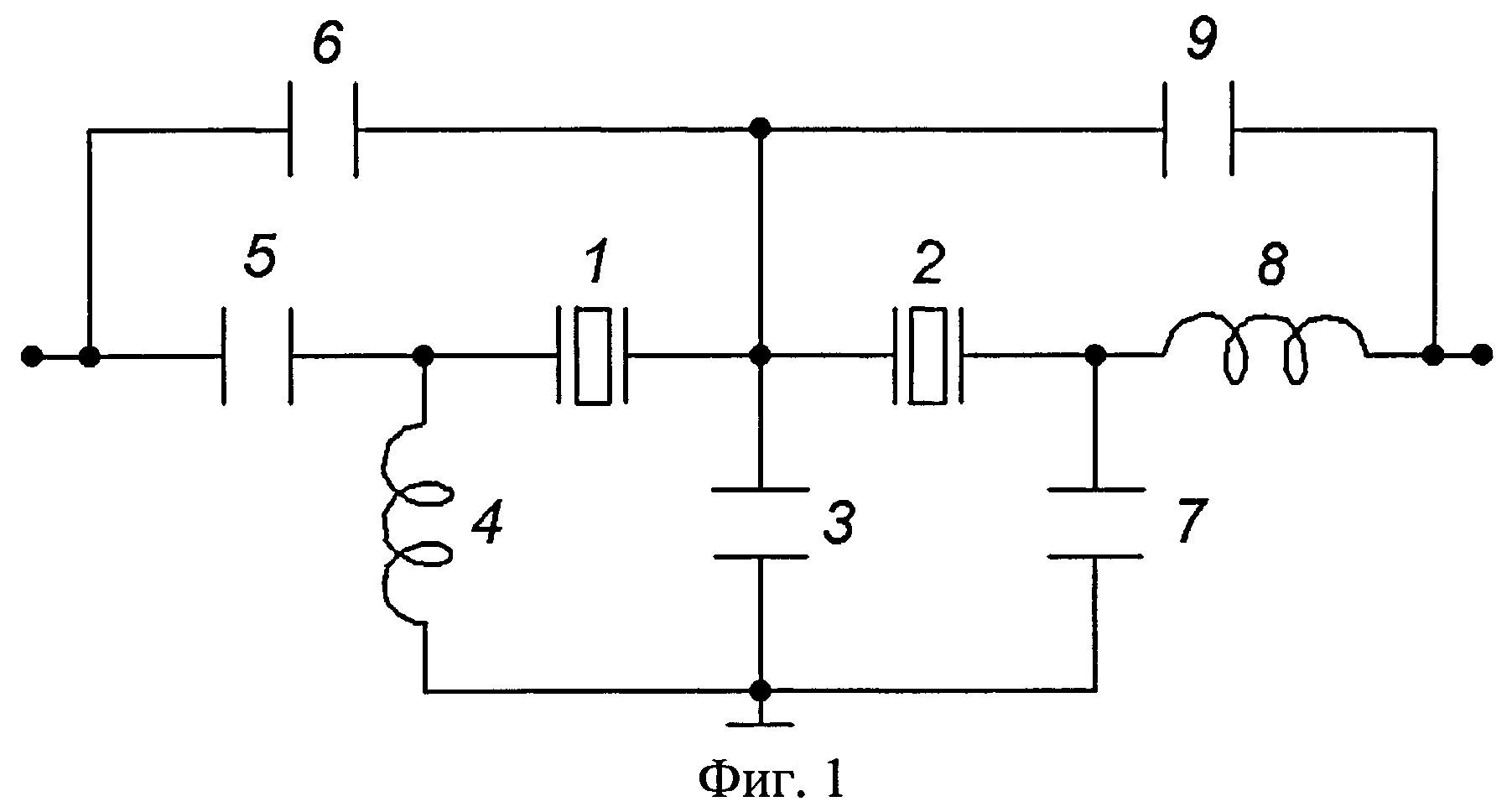 Следовательно, он пропускает сигналы определённых частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше или ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают те частоты, которые расположены выше или ниже этой полосы).
Следовательно, он пропускает сигналы определённых частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше или ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают те частоты, которые расположены выше или ниже этой полосы).
На практике невозможно реализовать идеальную амплитудно-частотную характеристику фильтра, поскольку требуется сформировать очень узкую переходную область. Следовательно, основная проблема при конструировании фильтра заключается в приближении реализованной реальной характеристики с заданной степенью точности к идеальной.
1. Анализ технического задания
Фильтры – это частотно-избирательные устройства, которые пропускают или задерживают сигналы, лежащие в определенных полосах частот. До 60-х годов для реализации фильтров применялись, в основном, пассивные элементы, т.е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и усилители (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приемниках, традиционные пассивные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
До 60-х годов для реализации фильтров применялись, в основном, пассивные элементы, т.е. индуктивности, конденсаторы и резисторы. Основной проблемой при реализации таких фильтров оказывается размер катушек индуктивности (на низких частотах они становятся слишком громоздкими). С разработкой в 60-х годах интегральных операционных усилителей появилось новое направление проектирования активных фильтров на базе ОУ. В активных фильтрах применяются резисторы, конденсаторы и усилители (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1 МГц), за пределами частотного диапазона большинства ОУ широкого применения. Но даже во многих высокочастотных устройствах, например в радиопередатчиках и приемниках, традиционные пассивные RLC-фильтры заменяются кварцевыми фильтрами и фильтрами на поверхностных акустических волнах.
Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах — активных RС-фильтрах.
Работа цифровых фильтров обеспечивается, в основном, программными средствами, поэтому они оказываются значительно более гибкими в применении по сравнению с аналоговыми. С помощью цифровых фильтров можно реализовать такие передаточные функции, которые очень трудно получить обычными методами. Тем не менее, цифровые фильтры пока не могут заменить аналоговые во всех ситуациях, поэтому сохраняется потребность в наиболее популярных аналоговых фильтрах — активных RС-фильтрах.
Фильтры можно классифицировать по их частотным характеристикам, что в условном виде показано на рис. 1.1. На этом рисунке изображены характеристики фильтра нижних частот (ФНЧ), фильтра верхних частот (ФВЧ), полосового фильтра (ПФ), полосно-подавляющего фильтра (ППФ) и фильтра – “пробки” (режекторного фильтра – РФ). Характеристика фазового фильтра (ФФ) на рисунке не показана, т.к. его коэффициент передачи не изменяется с частотой. Основная функция любого фильтра заключается в том, чтобы ослабить сигналы, лежащие в определенных полосах частот, внести в них различные фазовые сдвиги или ввести временную задержку между входным и выходным сигналами.
С помощью активных RС-фильтров нельзя получить идеальные формы частотных характеристик в виде показанных на рис. 1.1 прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации. Это называется “проблемой аппроксимации”. Во многих случаях требования к качеству фильтрации позволяют обойтись простейшимифильтрами первого или второго порядков. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Однако бывают ситуации, когда требования к фильтрации сигнала могут оказаться гораздо более жесткими, и могут потребоваться схемы фильтров с характеристиками более высоких порядков, чем первый или второй.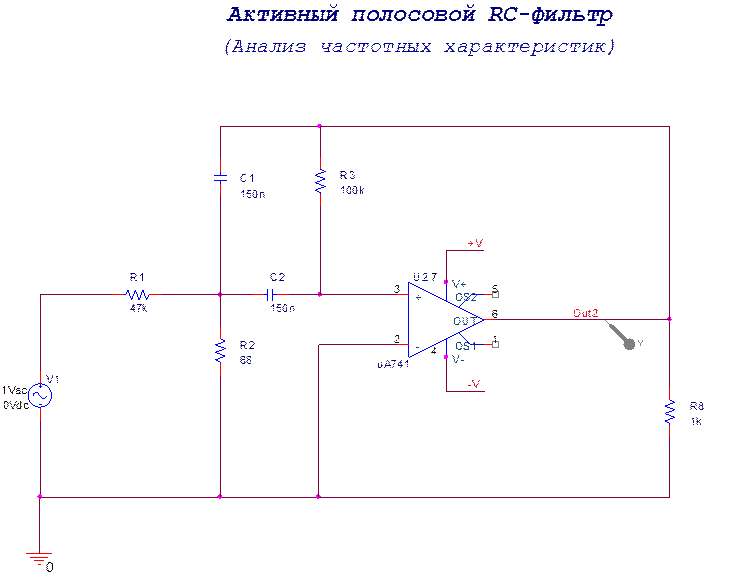
Рисунок 1.1- Основные типы фильтров.
Реальные характеристики фильтров, а именно нижних частот, верхних частот и полосового фильтра, – показаны на рисунке 1.2.
Рисунок 1.2 – АЧХ фильтров.
На этих рисунках сплошными линиями изображены идеальные характеристики фильтров. Пунктирные линии показывают отклонение реальных характеристик от идеальных.Основными параметрами фильтров нижних и верхних частот являются частота среза f0, коэффициент передачи в полосе пропускания Ко, наклон АЧХ в полосе ограничения п и неравномерность АЧХ в полосе пропускания. Дляполосовых фильтров по аналогии с избирательными усилителями вводят понятие добротности Q и усиления Ко на частоте f0.
2. Синтез схемы и расчет элементов фильтра
2.1 Исходные данные и требования для проектирования фильтра
2.2 Разработка функциональной схемы
На рис. 2.1 приведена структурная схема фильтра с многопетлевой обратной связью.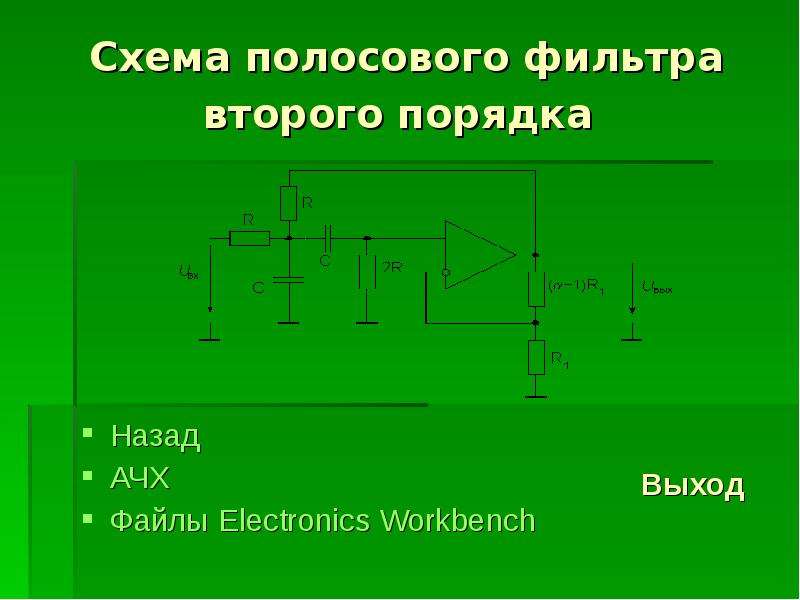 Каждый пассивный двухполюсный элемент в этой схеме может быть либо резистором, либо конденсатором.
Каждый пассивный двухполюсный элемент в этой схеме может быть либо резистором, либо конденсатором.
Рисунок 2.1 – структурная схема фильтра
Передаточная функция для данной схемы имеет вид
(2.1)Для того чтобы схема на рис. 2.1 выделяла полосу частот, передаточную функцию (2.1) необходимо привести к передаточной функции, соответствующей полосовому звену второго порядка:
(2.2)где ωо = 2лf0, H =α·К0.
Сравнивая выражения (2.1) и (2.2), нетрудно заметить, что, для того чтобы числитель не был функцией р, в качестве У1 и У4 должны использоваться резистивные проводимости; для того чтобы получить член с р2 в знаменателе, в качестве У3 и У5 должны использоваться емкостные проводимости; для того чтобы получить в знаменателе член, независимый от р, в качестве У2 должна использоваться резистивная проводимость.
Итак, однозначно определяются пассивные элементы схемы на рис.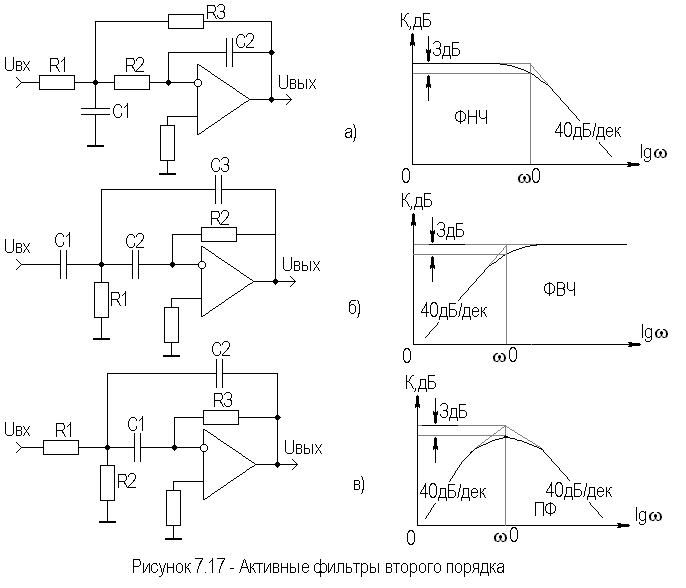 2.1:
2.1:
Y1=1/R1, Y2= pC1, Y3=1/R2, Y4= pC2, Y5=1/R3.
Схема полученного полосового фильтра приведена на рис. 2.2.
Рисунок 2.2 – Схема полосового фильтра
Передаточная функция имеет вид
(2.3)Сравнивая последнее выражение с (2.2), получаем соотношения, необходимые для расчета фильтра:
(2.4)В том случае, если
и , имеем:Кварцевые полосовые фильтры, часть 2
Кварцевые полосовые фильтры, изготовленные нами в прошлый раз, проявили себя не лучшим образом в супергетеродинном приемнике. Суть проблемы, напомню, заключалось в недостаточно крутой АЧХ фильтров. Для приемника это не является такой уж большой проблемой. Но если вы планируете доработать приемник до SSB-трансивера, то кварцевые фильтры однозначно подлежат замене. Спрашивается, существует ли сравнительно простой способ сделать фильтры с более крутой АЧХ?
Статья 9 MHz Filters Built With Inexpensive Crystals [PDF] за авторством известного радиолюбителя-конструктора Wes Hayward, W7ZOI, утверждает, что такой способ есть. В статье предлагается зафиксировать выбор ПЧ на 9 МГц. Если мы согласны на это ограничение, то получаем несколько предварительно рассчитанных и протестированных схем фильтров для телеграфа и SSB.
В статье предлагается зафиксировать выбор ПЧ на 9 МГц. Если мы согласны на это ограничение, то получаем несколько предварительно рассчитанных и протестированных схем фильтров для телеграфа и SSB.
Было решено приобрести 25 кварцев на 9 МГц и опробовать несколько схем из статьи. Использовались кварцы в корпусе HC-49U под брендом «STRONG». В знакомых онлайн-магазинах были только такие кварцы на 9 МГц.
Кварцы были измерены и сгруппированы по Fo. Получилось две группы из 6-и похожих кварцев в каждой, и еще одна группа из 5-и кварцев. В самый раз, чтобы опробовать фильтр, называемый в статье «CW5» (фильтр из 5-и кварцев для CW) и два варианта «SSB6», с полосой 2000 Гц и 2500 Гц.
Усредненные параметры кварцев получились следующими:
C0 = 4 pF
Lm = 16.747 mH
Cm = 18.686 fF
Rm = 9.5 Ohm
Q = 99_650
Эти значения были использованы в LTspice для предварительной проверки схем. Симулятор сообщил, что предложенные схемы должны работать. Добротность меньше 100 000 говорит о том, что кварцы так себе. Но других не имелось, поэтому эксперимент был продолжен.
Но других не имелось, поэтому эксперимент был продолжен.
Фильтр «SSB6» с полосой 2500 Гц вышел таким:
Вот его схема:
Перед нами фильтр Чебышева с рябью в полосе пропускания 0.25 дБ. Он имеет входной и выходной импеданс около 200 Ом. Для согласования с 50 Ом использованы трансформаторы 1:4 на ферритовых кольцах FT37-43. Трансформаторы мотаются бифилярной обмоткой в 10 витков, а затем соединяются, как показано на схеме. Все конденсаторы NP0, емкость в пФ.
Фильтр с полосой 2000 Гц — такой же с точностью до номиналов конденсаторов:
Фильтры получились с первого раза:
У обоих фильтров АЧХ намного круче, чем у фильтра из трех кварцев, сделанного в прошлый раз. По уровню -40 дБ старый фильтр имел полосу 12 кГц, и к уровню -60 дБ шел крайне неспешно. Новый фильтр имеет полосу 4.4 кГц по уровню -40 дБ и 4.6 кГц по уровню -60 дБ. Это цифры для версии с полосой 2500 Гц.
Вносимые потери составили около 5 дБ. Многовато, но ожидаемо, учитывая добротность кварцев и их количество в фильтрах.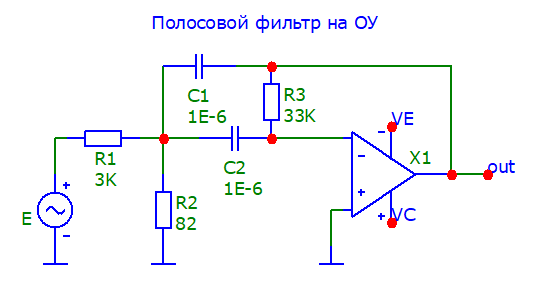 Оба фильтра имеют в полосе пропускания КСВ 1.1-2.0, что говорит о хорошем согласовании импеданса. КСВ измерялся, как ранее было описано в статье Самодельный КСВ-мост и примеры его использования.
Оба фильтра имеют в полосе пропускания КСВ 1.1-2.0, что говорит о хорошем согласовании импеданса. КСВ измерялся, как ранее было описано в статье Самодельный КСВ-мост и примеры его использования.
А вот фильтр «CW5» не получился. Точнее, он как бы заработал, но с вносимыми потерями аж 18 дБ. Были проверены как трансформаторы, так и номиналы всех конденсаторов. Были предприняты попытки поменять порядок кварцевых резонаторов и даже заменять их. Ошибок в схеме обнаружено не было и существенных улучшений добиться не удалось.
Тогда было решено переделать фильтр в более простой, «CW3»:
Схема фильтра:
Это фильтр Баттерворта с заявленной полосой 330 Гц. Фильтр имеет входной и выходной импеданс около 50 Ом, поэтому трансформаторы не используются. Фильтр заработал не сразу. Пришлось подобрать правильные кварцы и правильный их порядок, чтобы получить оптимальную форму АЧХ:
Крутизна АЧХ этого фильтра такая же, как у старого фильтра на ПЧ 12 МГц. Оба фильтра имеют полосу 2.3 кГц по уровню -40 дБ.
Оба фильтра имеют полосу 2.3 кГц по уровню -40 дБ.
Вносимые потери оказались 9 дБ. Много, но с этим можно работать. Измеренный КСВ в полосе пропускания составил ≥ 1.7. Тоже не предел мечтаний. Но если добавить в фильтр пару трансформаторов, то потери на них наверняка превысят потери из-за плохого согласования. Поэтому фильтр было решено оставить, как есть.
SSB-фильтры тестировались в супергетеродинном приемнике, ПЧ которого была изменена с 12 МГц на 9 МГц. На слух заметны существенные улучшения по сравнению с предыдущими фильтрами. На более низкой ПЧ проще добиться высокого усиления и меньше проявляются различные паразитные эффекты. Это тоже следует учитывать.
В целом, фильтры из статьи удалось повторить и работают они нормально. Главное — это где-то найти добротные кварцы на 9 МГц.
Дополнение: В продолжение темы см часть 3 и часть 4.
Метки: Беспроводная связь, Любительское радио, Электроника.
Все про электронику
До сих пор в фильтрах, которые мы сконцентрировали, использовались либо конденсаторы, либо индукторы, но оба они одновременно.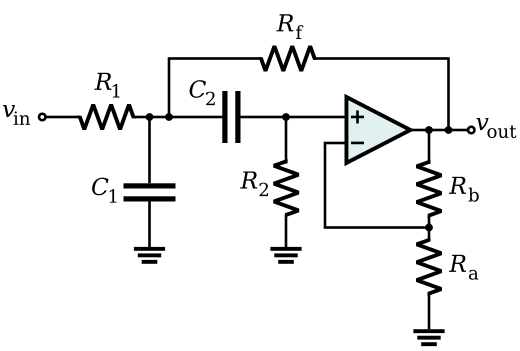 К настоящему времени мы должны знать, что комбинации L и C будут иметь тенденцию резонировать, и это свойство может быть использовано при проектировании полосовых фильтров и полосовых фильтров.
К настоящему времени мы должны знать, что комбинации L и C будут иметь тенденцию резонировать, и это свойство может быть использовано при проектировании полосовых фильтров и полосовых фильтров.
Цепи LC LC дают минимальный импеданс в резонансе, в то время как параллельные схемы LC («tank») обеспечивают максимальный импеданс на их резонансной частоте. Зная это, у нас есть две основные стратегии для проектирования фильтров полосы пропускания или полосы.
Для полосовых фильтров две основные резонансные стратегии: серия LC для передачи сигнала (рисунок ниже ),
Или параллельный LC (рисунок ниже ), чтобы закоротить сигнал. Эти две схемы будут противопоставляться и моделироваться здесь:
Серия резонансный LC полосовой фильтр.
Компоненты серии LC передают сигнал в резонансе и блокируют сигналы любых других частот от попадания на нагрузку. (Рисунок ниже )
Серия резонансный полосовой фильтр V1 1 0 ac 1 sin L1 1 2 1 C1 2 3 1u Rload 3 0 1k .ac lin 20 50 250 .plot ac v (3) .конец
Серийный резонансный полосовой фильтр: пики напряжения на резонансной частоте 159,15 Гц.
Несколько замечаний: посмотрите, как практически отсутствует ослабление сигнала в «полосе пропускания» (диапазон частот вблизи пика напряжения нагрузки), в отличие от полосовых фильтров, выполненных только из конденсаторов или индукторов. Кроме того, поскольку этот фильтр работает по принципу резонанса серии LC, резонансная частота которого не зависит от сопротивления цепи, значение нагрузочного резистора не будет искажать пиковую частоту. Однако разные значения нагрузочного резистора изменят «крутизну» графика Боде («избирательность» фильтра).
В другом базовом стиле резонансных полосовых фильтров используется контур резервуара (параллельная комбинация LC) для коротких сигналов, слишком высоких или слишком низких по частоте от получения до нагрузки: (рисунок ниже )
Параллельный резонансный полосовой фильтр.
Контур резервуара будет иметь большое сопротивление в резонансе, позволяя сигналу доходить до нагрузки с минимальным затуханием. Тем не менее, при резонансной частоте ниже или выше, схема цистерны будет иметь низкий импеданс, замыкание сигнала и падение большей части его через последовательный резистор R 1 . (Рисунок ниже )
Параллельный резонансный полосовой фильтр V1 1 0 ac 1 sin R1 1 2 500 L1 2 0 100 м C1 2 0 10u Rload 2 0 1k .ac lin 20 50 250 .plot ac v (2) .конец
Параллельный резонансный фильтр: напряжение достигает пика резонансной частоты 159,15 Гц.
Подобно низкочастотным и высокочастотным фильтрам, основанным на последовательном сопротивлении и параллельном компоненте «короткого замыкания» для ослабления нежелательных частот, этот резонансный контур никогда не может обеспечить полное входное (исходное) напряжение нагрузки. Это сопротивление серии всегда будет понижать некоторое количество напряжения, пока есть сопротивление нагрузки, подключенное к выходу фильтра.
Это сопротивление серии всегда будет понижать некоторое количество напряжения, пока есть сопротивление нагрузки, подключенное к выходу фильтра.
Следует отметить, что эта схема полосовой фильтрации очень популярна в аналоговой радионастройке, для выбора конкретной радиочастоты из множества частот, доступных от антенны. В большинстве аналоговых схем радиомодуля вращающийся диск для выбора станции перемещает переменный конденсатор в контуре резервуара.
Переменный конденсатор настраивает схему приемника радиоприемника для выбора одной из многих станций вещания.
Переменный конденсатор и индуктор с воздушным сердечником, показанный на рисунке выше, фотографии простой радиостанции содержат основные элементы в фильтрах контура резервуара, используемые для различения сигнала одной радиостанции от другого.
Так же, как мы можем использовать последовательные и параллельные LC-резонансные схемы для пропускания только тех частот в определенном диапазоне, мы также можем использовать их для блокировки частот в определенном диапазоне, создавая фильтр полосы пропускания.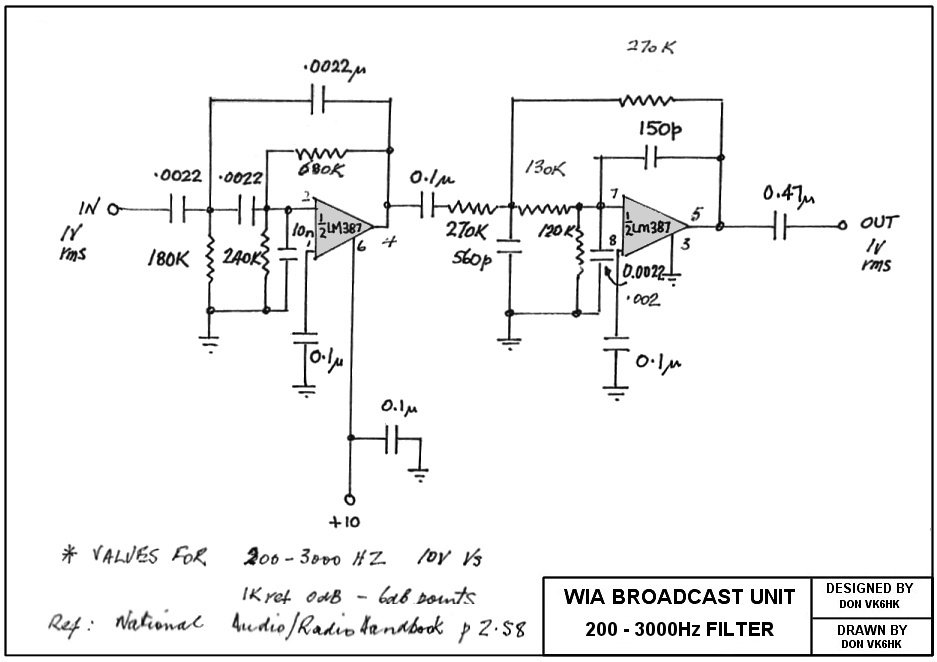 Опять же, у нас есть две основные стратегии, которые следует придерживаться при этом, использовать либо серийный, либо параллельный резонанс. Во-первых, мы рассмотрим ряд серий: (рисунок ниже )
Опять же, у нас есть две основные стратегии, которые следует придерживаться при этом, использовать либо серийный, либо параллельный резонанс. Во-первых, мы рассмотрим ряд серий: (рисунок ниже )
Серийный резонансный полосовой фильтр.
Когда комбинация серии LC достигает резонанса, ее очень низкий импеданс замыкает сигнал, опускает его через резистор R 1 и препятствует его прохождению на нагрузку. (Рисунок ниже )
Серия резонансный полосовой фильтр V1 1 0 ac 1 sin R1 1 2 500 L1 2 3 100 м C1 3 0 10u Rload 2 0 1k .ac lin 20 70 230 .plot ac v (2) .конец
Серийный резонансный лентоопорный фильтр: частота режекции = резонансная частота LC (159,15 Гц).
Затем мы рассмотрим параллельный резонансный ленточный фильтр: (рисунок ниже )
Параллельный резонансный полосовой фильтр.
Параллельные компоненты LC представляют собой высокий импеданс на резонансной частоте, тем самым блокируя сигнал от нагрузки на этой частоте. И наоборот, он передает сигналы нагрузке на любых других частотах. (Рисунок ниже )
Параллельный резонансный полосовой фильтр V1 1 0 ac 1 sin L1 1 2 100 м C1 1 2 10u Rload 2 0 1k .ac lin 20 100 200 .plot ac v (2) .конец
Параллельный резонансный зонный фильтр: частота режекторного резонатора = резонансная частота LC (159,15 Гц).
Еще раз обратите внимание на то, как отсутствие последовательного резистора делает минимальное затухание для всех желаемых (прошедших) сигналов. С другой стороны, амплитуда на частоте выреза очень низка. Другими словами, это очень «избирательный» фильтр.
Во всех этих конструкциях резонансных фильтров селективность сильно зависит от «чистоты» используемой индуктивности и емкости. Если есть какое-либо отклоняющееся сопротивление (особенно вероятно, в индукторе), это уменьшит способность фильтра точно различать частоты, а также введет антирезонансные эффекты, которые будут искажать частоту пика / метки.
Слово предостережения для тех, кто проектирует фильтры нижних частот и верхних частот, находится в порядке на этом этапе. После оценки стандартных моделей фильтров нижних и верхних фильтров RC и LR ученику может показаться, что лучше, более эффективная конструкция фильтра нижних частот или верхних частот может быть реализована путем объединения емкостных и индуктивных элементов вместе, как Рисунок ниже .
Емкостный индуктивный фильтр нижних частот.
Индукторы должны блокировать любые высокие частоты, в то время как конденсатор должен также замыкаться на любых высоких частотах, одновременно работая вместе, чтобы сигналы низкой частоты могли достигнуть нагрузки.
Сначала это кажется хорошей стратегией и устраняет необходимость в последовательном сопротивлении. Тем не менее, более проницательный ученик поймет, что любая комбинация конденсаторов и индукторов вместе в цепи, вероятно, вызовет резонансные эффекты на определенной частоте. Резонанс, как мы видели ранее, может вызвать странные вещи. Давайте построим анализ SPICE и посмотрим, что происходит в широком диапазоне частот: (рисунок ниже )
Lc фильтр нижних частот V1 1 0 ac 1 sin L1 1 2 100 м C1 2 0 1u L2 2 3 100 м Rload 3 0 1k .ac lin 20 100 1k .plot ac v (3) .конец
Неожиданный ответ фильтра нижних частот LC.
То, что должно было быть фильтром нижних частот, оказалось полосовым фильтром с пиком где-то около 526 Гц! Емкость и индуктивность в этой схеме фильтра достигают резонанса в этой точке, создавая большое падение напряжения вокруг C 1 , которое видно на нагрузке, независимо от ослабляющего влияния L 2 . Выходное напряжение на нагрузку в этой точке фактически превышает входное (исходное) напряжение! Немного больше отражений показывает, что если L 1 и C 2 находятся в резонансе, они нанесут очень тяжелую (очень низкий импеданс) нагрузку на источник переменного тока, что тоже может быть не очень хорошим. Мы снова запустим тот же анализ, только на этот раз построим напряжение на C 1 , vm (2) на рисунке ниже , а ток источника I (v1) вместе с напряжением нагрузки vm (3):
Текущие события при нежелательном резонансе низкочастотного фильтра LC.
Разумеется, мы видим напряжение на C 1 и ток источника, поднимающийся до высокой точки на той же частоте, где напряжение нагрузки является максимальным. Если бы мы ожидали, что этот фильтр обеспечит простую функцию низких частот, мы можем быть разочарованы результатами.
Проблема заключается в том, что LC-фильтр имеет входной импеданс и выходной импеданс, которые должны быть согласованы. Импеданс источника напряжения должен соответствовать входному импедансу фильтра, а выходной импеданс фильтра должен соответствовать «rload» для плоского отклика. Входной и выходной импеданс задается квадратным корнем (L / C).
Z = (L / C) 1/2
Принимая значения компонентов из (рис. Ниже ), мы можем найти полное сопротивление фильтра и требуемую нагрузку R g и R для его соответствия.
Для L = 100 мГн, C = 1 мкФ
Z = (L / C) 1/2 = ((100 мГн) / (1 мкФ)) 1/2 = 316 Ом
На рисунке ниже мы добавили R g = 316 Ω к генератору и изменили нагрузку нагрузки R с 1000 до 316 Ом. Обратите внимание, что если нам нужно было управлять нагрузкой 1000 Ом, коэффициент L / C можно было бы скорректировать в соответствии с этим сопротивлением.
Схема источника и нагрузочного фильтра LC нижних частот.
Совместимый с LC фильтр нижних частот V1 1 0 ac 1 SIN Rg 1 4 316 L1 4 2 100 м C1 2 0 1,0u L2 2 3 100 м Rload 3 0 316 .ac lin 20 100 1k .plot ac v (3) .конец
На рисунке ниже показан «плоский» отклик фильтра нижних частот LC, когда импеданс источника и нагрузки соответствует входным и выходным импедансам фильтра.
Ответ полного сопротивления LC-фильтра нижнего фильтра почти плоский до частоты отсечки.
Точка, которую следует выполнить при сравнении ответа несогласованного фильтра (рис. Выше ) с согласованным фильтром (рис. Выше ), заключается в том, что переменная нагрузка на фильтр вызывает значительное изменение напряжения. Это свойство напрямую применимо к источникам питания с фильтром LC – регулирование плохое. Напряжение питания изменяется с изменением нагрузки. Это нежелательно.
Это плохое регулирование нагрузки может быть смягчено качающимся дросселем . Это дроссель , индуктор, предназначенный для насыщения, когда через него проходит большой ток постоянного тока. Под насыщением мы подразумеваем, что постоянный ток создает «слишком высокий» уровень магнитного потока в магнитном сердечнике, так что переменная составляющая тока не может изменять поток. Поскольку индукция пропорциональна dΦ / dt, индуктивность уменьшается на большой ток постоянного тока. Уменьшение индуктивности уменьшает реактивность X L. Уменьшение реактивного сопротивления снижает падение напряжения на индукторе; Таким образом, увеличивая напряжение на выходе фильтра. Это улучшает регулирование напряжения по отношению к переменным нагрузкам.
Несмотря на непреднамеренный резонанс, фильтры нижних частот, состоящие из конденсаторов и катушек индуктивности, часто используются в качестве конечных ступеней в источниках питания переменного / постоянного тока для фильтрации нежелательного переменного напряжения «пульсации» из постоянного тока, преобразованного из переменного тока. Почему это, если этот конкретный дизайн фильтра имеет потенциально неприятную резонансную точку?
Ответ заключается в выборе размеров компонентов фильтра и частот, встречающихся в преобразователе AC / DC (выпрямитель). То, что мы пытаемся сделать в источнике питания переменного / постоянного тока, является отдельным напряжением постоянного тока от небольшого количества относительно высокочастотного переменного напряжения. Индукторы и конденсаторы фильтра, как правило, довольно велики (типичны для нескольких генераторов Henry для индукторов и для тысяч мкФ для конденсаторов), что делает резонансную частоту фильтра очень и очень низкой. DC, конечно, имеет «частоту» нуля, поэтому он не может сделать резонансную схему LC. С другой стороны, напряжение пульсации представляет собой несинусоидальное переменное напряжение, состоящее из основной частоты, по меньшей мере, вдвое превышающей частоту преобразованного переменного напряжения, причем гармоники многократно увеличиваются. Для источников питания с подключением к сети, работающих от 60 Гц переменного тока (60 Гц в США, 50 Гц в Европе), самая низкая частота, которая будет когда-либо наблюдаться, составляет 120 Гц (100 Гц в Европе), что значительно выше Его резонансная точка. Поэтому полностью избежать потенциально затруднительной резонансной точки в таком фильтре.
Следующий анализ SPICE вычисляет выходной сигнал напряжения (AC и DC) для такого фильтра с источниками напряжения постоянного тока и переменного тока (120 Гц), которые обеспечивают приблизительное приближение выходного сигнала смешанной частоты преобразователя AC / DC.
Фильтр питания AC / DC обеспечивает бесперебойную мощность постоянного тока.
Фильтр питания переменного / постоянного тока V1 1 0 ac 1 sin V2 2 1 dc L1 2 3 3 C1 3 0 9500u L2 3 4 2 Rload 4 0 1k .dc v2 12 12 1 .ac lin 1 120 120 .print dc v (4) .print ac v (4) .конец
V2 v (4) 1.200E + 01 1.200E + 01 Напряжение постоянного тока при нагрузке = 12 вольт Freq v (4) 1.200E + 02 3.412E-05 Напряжение переменного тока при нагрузке = 34,12 микровольт
При полном напряжении 12 В постоянного тока при нагрузке и только 34,12 мкВ переменного тока, оставшегося от 1-вольтового источника переменного тока, наложенного на нагрузку, эта схема обеспечивает себя очень эффективным фильтром питания.
Урок, изученный здесь о резонансных эффектах, также относится к разработке фильтров высоких частот с использованием как конденсаторов, так и индукторов. Пока требуемые и нежелательные частоты хорошо подходят по обе стороны от резонансной точки, фильтр будет работать нормально. Но если к входу фильтра применяется какой-либо сигнал значительной величины, близкий к резонансной частоте, странные вещи произойдут!
- ОБЗОР:
- Резонансные комбинации емкостей и индуктивности могут быть использованы для создания очень эффективных полосовых и полосовых фильтров без необходимости дополнительного сопротивления в цепи, которая уменьшала бы прохождение требуемых частот.
Активные фильтры – CoderLessons.com
Фильтры — это электронные схемы, которые допускают определенные частотные компоненты и / или отклоняют некоторые другие. Возможно, вы столкнулись с фильтрами в учебнике по теории сетей. Они являются пассивными и представляют собой электрические цепи или сети, которые состоят из пассивных элементов, таких как резистор, конденсатор и (или) индуктор.
В этой главе подробно рассматриваются активные фильтры .
Типы активных фильтров
Активные фильтры — это электронные схемы, которые состоят из активного элемента, такого как операционный усилитель (и), наряду с пассивными элементами, такими как резистор (ы) и конденсатор (ы).
Активные фильтры в основном подразделяются на следующие четыре типа на основе полосы частот, которые они разрешают и / или отклоняют —
- Активный фильтр нижних частот
- Активный фильтр высоких частот
- Активный полосовой фильтр
- Активный полосовой стоп-фильтр
Активный фильтр нижних частот
Если активный фильтр допускает (пропускает) только низкочастотные компоненты и отклоняет (блокирует) все другие высокочастотные компоненты, то он называется активным фильтром нижних частот .
Принципиальная схема активного фильтра нижних частот показана на следующем рисунке —
Мы знаем, что электрическая сеть, которая подключена к неинвертирующему выводу операционного усилителя, является пассивным фильтром нижних частот . Таким образом, вход неинвертирующего терминала операционного усилителя является выходом пассивного фильтра нижних частот.
Обратите внимание, что вышеуказанная схема напоминает неинвертирующий усилитель . Он имеет выход пассивного фильтра нижних частот в качестве входа на неинвертирующий вывод операционного усилителя. Следовательно, он производит вывод, который в left(1+ fracRfR1 right) умножен на вход, присутствующий на неинвертирующей клемме.
Мы можем выбрать значения Rf и R1, чтобы получить желаемое усиление на выходе. Предположим, если мы рассмотрим значения сопротивления Rf и R1 как ноль и бесконечность, то вышеупомянутая схема выдаст выходной сигнал фильтра нижних частот с единичным усилением .
Активный фильтр высоких частот
Если активный фильтр разрешает (пропускает) только высокочастотные компоненты и отклоняет (блокирует) все остальные низкочастотные компоненты, то он называется активным высокочастотным фильтром .
Принципиальная схема активного фильтра верхних частот показана на следующем рисунке —
Мы знаем, что электрическая сеть, которая подключена к неинвертирующему выводу операционного усилителя, является пассивным фильтром верхних частот . Таким образом, вход неинвертирующего терминала операционного усилителя является выходом пассивного фильтра верхних частот.
Теперь вышеприведенная схема напоминает неинвертирующий усилитель . Он имеет выход пассивного фильтра верхних частот в качестве входа на неинвертирующий вывод операционного усилителя. Следовательно, он производит вывод, который в left(1+ fracRfR1 right) умножен на вход, представленный на его неинвертирующей клемме.
Мы можем выбрать значения Rf и R1 соответствующим образом, чтобы получить желаемое усиление на выходе. Предположим, если мы рассмотрим значения сопротивления Rf и R1 как ноль и бесконечность, то вышеупомянутая схема выдаст выходной сигнал фильтра верхних частот с единичным усилением .
Активный полосовой фильтр
Если активный фильтр допускает (пропускает) только одну полосу частот, то он называется активным полосовым фильтром . В общем, эта полоса частот лежит между диапазоном низких частот и диапазоном высоких частот. Таким образом, активный полосовой фильтр отклоняет (блокирует) как низкочастотные, так и высокочастотные компоненты.
Принципиальная схема активного полосового фильтра показана на следующем рисунке.
Обратите внимание, что на принципиальной схеме активного полосового фильтра есть две части : первая часть — активный фильтр верхних частот, а вторая часть — активный фильтр нижних частот.
Выходной сигнал активного фильтра верхних частот применяется как входной сигнал активного фильтра нижних частот. Это означает, что как активный фильтр верхних частот, так и активный фильтр нижних частот каскадируются , чтобы получить выходные данные таким образом, чтобы он содержал только конкретный диапазон частот.
Активный фильтр верхних частот , который присутствует на первом этапе, допускает частоты, которые превышают нижнюю частоту среза активного полосового фильтра. Таким образом, мы должны выбрать значения RB и CB соответственно, чтобы получить желаемую более низкую частоту среза активного полосового фильтра.
Точно так же активный фильтр нижних частот , который присутствует на втором этапе, допускает частоты, которые меньше, чем более высокая частота среза активного полосового фильтра. Таким образом, мы должны выбрать значения RA и CA соответственно, чтобы получить желаемую более высокую частоту среза активного полосового фильтра.
Следовательно, схема на схеме, рассмотренной выше, будет выдавать активный полосовой фильтр на выходе.
Активный полосовой стоп-фильтр
Если активный фильтр отклоняет (блокирует) определенную полосу частот, то он называется активным полосовым фильтром . В общем, эта полоса частот лежит между диапазоном низких частот и диапазоном высоких частот. Таким образом, фильтр запрета активной полосы позволяет (пропускает) как низкочастотные, так и высокочастотные компоненты
Блок-схема активного фильтра остановки полосы показана на следующем рисунке —
Заметьте, что блок-схема активного полосового фильтра на первом этапе состоит из двух блоков: активного фильтра нижних частот и активного фильтра верхних частот. Выходы этих двух блоков применяются в качестве входов для блока, который присутствует на втором этапе. Таким образом, суммирующий усилитель создает выход, который является усиленной версией суммы выходов активного фильтра нижних частот и активного фильтра верхних частот.
Следовательно, выходные данные вышеуказанной блок-схемы будут выходными сигналами остановки активной полосы , когда мы выбираем частоту среза фильтра низких частот меньше частоты среза фильтра высоких частот.
Принципиальная электрическая схема фильтра запрета активной полосы показана на следующем рисунке —
Мы уже видели принципиальные схемы активного фильтра нижних частот, активного фильтра верхних частот и суммирующего усилителя. Заметьте, что мы получили приведенную выше принципиальную схему фильтра запрета активной полосы, заменив блоки соответствующими схемами в блок-схеме фильтра остановки активной полосы.
Диапазонные полосовые фильтры. Схема ДПФ для трансиверов и радиопрёмников.
А на кой шайтан-узбек сдались нам эти ДПФы?
Возьмём, к примеру, Дегенов, Туксанов и прочих апологетов традиционной китайской цивилизации.
Молодцы ведь – пашут, и не жужжат.
Простенько и со вкусом – без всяких там излишеств!
Две водки, три пива, селёдка и цельная буханка хлеба – скромный спартанский менталитет, воплощённый в схемотехнике и конструктиве.
Так вот. Пашут – и молодцы!
И должны пахать всеми корпусами на полную глубину, оправдывая высокое звание супергетеродинов с двойным преобразованием частоты
и высокой первой промежуточной частотой.
А чтобы вспашка была качественной, нужно следить, чтобы амплитуда сигнала, поступающего на антенный вход электроплуга, не превышала уровня,
отведённого ей динамическим диапазоном.
Динамический диапазон подобных радиоприёмников ограничен цифрой 80дБ, а это значит, что при чувствительности приёмника 1мкВ, максимальная амплитуда входного сигнала, перевариваемая агрегатом, составит величину 1мкВ x 10000 = 10мВ. Подадите больше, начнёт пожужживать. Ещё больше – услышите кашу из интермодуляционных шумов и продуктов искажений.
И не знать бы всего этого геморроя, если бы закон диалектического развития (мать его) не отвернул бы нас от комнатной магнитной рамки в сторону полноразмерной антенны, или, хотя бы, просто длинного куска провода, согласованного с 50-омным входом приёмника.
А тут?
Какие там 10мВ, особенно в условиях города?
Широчайший спектр сигналов, начиная от 50-герцовых сетевых наводок, кончая мощными УКВ ЧМ-станциями, наведут на длинную антенну совокупную
ЭДС, исчисляемую десятками, а то и сотнями милливольт.
Вот, собственно говоря, для того, чтобы очистить, поступающие на вход приёмника сигналы от всякой внеполосной дряни и уменьшить их совокупную амплитуду до приемлемого уровня, не прибегая к помощи аттенюатора, и служат диапазонные фильтры.
Всё вышесказанное относится и к простым приёмникам прямого преобразования с диодными, либо интегральными смесителями.
Несколько другая история связана с SDR-ами и ППП со смесителями на быстродействующих ключевых элементах. Здесь параметр реально достижимого динамического диапазона составляет величину 110-115 дБ, и на первый план выходит функция полосовых фильтров по подавлению паразитных каналов приёма на нечётных гармониках. И функция эта настолько важна, что можно уверенно заявить – без полосовых фильтров приёмник прямого преобразования нормально работать не будет.
Описывать многообразие различных схемотехнических решений диапазонных фильтров в рамках данной статьи я не вижу особого смысла,
поэтому сразу приведу схему ПФ, являющуюся основным, базовым вариантом современных радиоприёмных конструкций высокого класса.
Рис.1
Подробно эти фильтры 3-7 порядков мы рассматривали на странице ссылка на страницу.
Там же можно произвести онлайн расчёт этих фильтров для любых частот и характеристических сопротивлений.
К преимуществам данных фильтров можно отнести минимальные потери и максимально плоскую АЧХ в полосе пропускания.
Крутизна спада АЧХ вне полосы пропускания составляет величину 43 дБ/октаву.
Причём, характеристики подобных фильтров не так сильно зависят от точности подбора номиналов конденсаторов и катушек индуктивности,
как от строгого соблюдения рассчитанных параметров входного и выходного сопротивлений.
В качестве входного у нас выступает сопротивление приёмной антенны, согласованное с волновым сопротивлением коаксиального кабеля.
А теперь давайте прикинем – в каких хуторах и селениях нам искать следы антенны с постоянным и неизменным 50-омным сопротивлением во
всём непрерывном КВ диапазоне?
Ни в каких! Запаришься искать такую антенну, если только она не снабжена активным согласующим устройством.
Чтобы не ограничивать сферу применения наших полосовых диапазонных фильтров исключительно активными антеннами, подобное согласующее
устройство придётся предусмотреть в составе схемы ДПФ.
Причём на первый план здесь выходит ключевая задача – превысить параметры, определяющие динамический диапазон приёмника.
Зададимся цифрой этого параметра – не менее 120 дБ.
В результате получилась следующая схема.
А подробно обсудим её – на следующей странице.
Принципиальная схема полосового фильтра
Теория и эксперимент
Кошмаром каждого разработчика аналоговых устройств было бы столкнуться с шумом в своей схеме. Когда дело доходит до переключающих цепей, аудиоусилителей или цепей частотных сигналов, существует очень высокая вероятность того, что на схему будут воздействовать шумовые сигналы. Из множества способов удаления шума из схемы наиболее часто применяемым является схема фильтра . Как следует из названия, эта схема будет отфильтровывать нежелательные сигналы (шум) из реального сигнала.Существует много типов схем фильтра, но наиболее часто используемым и эффективным является полосовой фильтр , который можно легко сконструировать с использованием пары резистора и конденсаторов. Итак, в этом руководстве мы узнаем об этом полосовом фильтре, теории, лежащей в основе его, и о том, как его можно использовать в практических схемах.
Что такое полосовой фильтр?Схема / устройство полосового фильтра используется для того, чтобы пропускал через него только заранее определенный набор частот.Он будет фильтровать всю частоту, которая ниже установленного значения и выше установленного значения. Это комбинация фильтра высоких частот и фильтра низких частот. Фильтр, который допускает только частоты, которые выше, чем он, называется фильтром верхних частот , а фильтр, который разрешает только частоты ниже, чем он, называется фильтром нижних частот . Полосовой фильтр может быть получен путем каскадного соединения фильтров верхних и нижних частот. Он имеет огромное применение в схемах аудиоусилителей и беспроводных трансиверах, где динамик должен воспроизводить только желаемый набор частот и игнорировать остальные.
Есть два типа полосовых фильтров. Если в схеме используется какой-либо внешний источник питания (активные устройства), например, транзисторы и т. Д., Тогда схема называется Активный полосовой фильтр , и если в схеме нет никаких активных компонентов и она состоит только из пассивных компонентов, таких как резистор, конденсатор и т. Д. индуктор, тогда схема называется Пассивный полосовой фильтр . В этой статье мы поговорим подробнее о пассивном полосовом фильтре. Помимо этой классификации, в этой статье будут кратко описаны другие аспекты, по которым можно классифицировать фильтр.
Цепь полосового фильтраКак уже говорилось ранее, мы обсудим пассивный полосовой фильтр , который построен с использованием резистора и конденсатора. Это комбинация фильтра высоких частот и фильтра низких частот. Примерная принципиальная схема простого пассивного полосового фильтра показана ниже.
Первая половина схемы представляет собой фильтр верхних частот , который фильтрует низкие частоты и допускает только частоту, которая выше установленной высокой частоты среза (fc HIGH ). Значение этой высокой частоты среза можно рассчитать по формуле
fc ВЫСОКАЯ = 1/2 π * R1 * C1
Вторая половина схемы – это схема фильтра низких частот , которая фильтрует более высокие частоты и допускает только частоту, которая ниже установленной частоты среза низкой частоты (fc LOW ) . Значение нижней частоты среза можно рассчитать по формуле
fc LOW = 1/2 π * R2 * C2
Этот тип схемы фильтра называется фильтром порядка 2 и , потому что он имеет два резистора и два конденсатора.Полосовой фильтр может быть фильтром порядка 2 и или более высокого порядка, поскольку для правильного функционирования схемы необходимо минимум два резистора и конденсатор. Теперь, когда частота входного сигнала подается на этот фильтр, он выводит частоту, которая выше, чем fc LOW, и ниже, чем fc HIGH. Другими словами, выходная частота может быть задана как fc HIGH- fc LOW , частота, которая находится между этой областью, называется шириной полосы .Следовательно, пропускную способность фильтра можно рассчитать по
.Пропускная способность = fc HIGH- fc LOWЧастотная характеристика полосового фильтра
Амплитудно-частотная характеристика, также известная как график Боде, для пассивного полосового фильтра порядка 2 и показана ниже.
График построен в зависимости от входной частоты по оси X и выходной частоты в децибелах по оси Y. Когда входная частота меньше, чем нижняя частота среза (f-low), выходная мощность остается ниже -3 дБ, а когда она превышает эту частоту, выход достигает максимума и остается там до тех пор, пока частота не превысит более высокую частоту среза. (ф-высокий).Пик, при котором выходное усиление остается максимальным, называется резонансной частотой . Это просто среднее геометрическое значение верхней верхней частоты среза и нижней частоты среза. Формулы для расчета приведены ниже
.Резонансная частота (Fr) = √ (f - низкий * f - высокий)
Расстояние между нижней и верхней частотой среза называется полосой пропускания. Таким образом, входная частота будет разрешена, только если она находится в пределах полосы пропускания.
Практический пример полосовых фильтровДавайте создадим простой полосовой фильтр, чтобы отфильтровать определенный набор частот и проверить, как он на самом деле работает. Экспериментальная установка, которую я использую для этого урока, показана ниже
.Как видите, фильтр верхних частот построен с использованием конденсатора 0,1 мкФ (C1) и резистора 1K (R1). Таким образом, верхняя частота отсечки на для этой схемы будет
.fc ВЫСОКИЙ = 1 / 2π * R1 * C1 = 1 / (2 * 3.-12) = 7280 Гц
Из приведенных выше расчетов мы можем сделать вывод, что схема допускает частоты только в диапазоне от 1577 Гц до 7280 Гц , и все, что меньше или больше, будет отфильтровано нашим полосовым фильтром. Давайте проверим, работает ли то же самое, построив схему на макете. Моя тестовая установка выглядела примерно так: ниже
Для проверки схемы нам нужен функциональный генератор для генерации сигнала с частотой, которой можно управлять.Поскольку у меня его не было, я решил использовать свой телефон с приложением для Android, которое будет генерировать необходимые частоты через разъем для наушников 3,5 мм. Этот сигнал затем передается в качестве входной частоты в схему с помощью разъема, как показано выше.
Чтобы проверить зависимость приложения, я использовал осциллограф для измерения частоты входного сигнала и обнаружил, что частота генерации является приемлемой. На рисунке ниже показано приложение на моем телефоне, которое генерирует входную частоту около 4819 Гц, а подключенный к нему осциллограф отображает сигнал и измеряет частоту 4.816 кГц, что идеально.
Теперь мы можем подключить осциллограф к выходному сигналу схемы и изменить входную частоту. Схема позволит отображать на осциллографе всю частоту в диапазоне от 1500 до 7000, а остальные будут отфильтрованы или зашумлены. Также имейте в виду, что эта схема предназначена только для понимания цели и, следовательно, подвергается усовершенствованиям, прежде чем применять ее в реальных условиях. Кроме того, поскольку схема построена на макетной плате, выходной сигнал может иметь некоторый шум, поместите конденсатор как можно ближе и уменьшите длину его выводов, чтобы уменьшить проблему.Надеюсь, вы поняли насчет фильтров Band Pass. Если у вас есть какие-либо вопросы, оставьте их в комментариях ниже или воспользуйтесь форумом.
Проектирование и применение схемы активного полосового фильтра
В этом руководстве мы узнаем об активном полосовом фильтре, его частотной характеристике, типах, примерах и многом другом. В предыдущем уроке мы узнали о полосовых фильтрах, но подход к проектированию в этом руководстве был основан на пассивных компонентах.
Полосовой фильтр, как и любой другой фильтр, может быть сконструирован на основе активных компонентов, таких как транзисторы и операционные усилители.Если вам нужна дополнительная информация о пассивных полосовых фильтрах, прочтите « Passive Band Pass RC Filter ».
ВведениеПолосовой фильтр – это схема, которая пропускает через нее только определенную полосу частот. Эта полоса пропускания находится в основном между частотами среза, и это f L и f H, , где f L – нижняя частота среза, а f H – более высокая частота среза.
Центральная частота обозначается «f C », и ее также называют резонансной частотой или пиковой частотой.
Значение f L всегда должно быть меньше значения f H . Полоса пропускания фильтра – это не что иное, как полоса пропускания. Коэффициент усиления фильтра максимален на резонансной или центральной частоте, и это называется общим коэффициентом усиления полосы пропускания. Это усиление полосы пропускания обозначается как «A max ».
Для фильтра нижних частот эта полоса пропускания начинается с 0 Гц и продолжается до тех пор, пока не достигнет значения резонансной частоты на -3 дБ ниже максимального усиления полосы пропускания.
Где, как и в случае фильтра верхних частот, эта полоса пропускания начинается с резонансной частоты -3 дБ и заканчивается на значении максимального усиления контура для активного фильтра.Комбинация низких и высоких частот дает нам полосу пропускания, как показано ниже:
НАЗАД НАЗАД
Активный полосовой фильтрВ зависимости от добротности полосовой фильтр подразделяется на широкополосный фильтр и узкополосный фильтр. Фактор качества также называется «добротностью». Путем каскадирования фильтра высоких частот и фильтра низких частот с усилительным компонентом мы получаем полосовой фильтр.
Схема усилителя между этими фильтрами верхних и нижних частот обеспечивает изоляцию и обеспечивает полное усиление по напряжению схемы. Значения частот среза обоих фильтров должны поддерживаться с минимальной разницей.
Если эта разница очень мала, может существовать возможность взаимодействия каскадов высоких и низких частот. Таким образом, чтобы иметь надлежащие уровни этих частот среза, необходима схема усиления.
Принципиальная схема активного полосового фильтра показана ниже:
НАЗАД НАЗАД
Широкополосный фильтрЕсли значение коэффициента качества меньше десяти, то полоса пропускания широкая, что дает нам большую пропускную способность.Этот полосовой фильтр называется широкополосным фильтром.
В этом фильтре высокая частота среза должна быть больше, чем нижняя частота среза. В его конструкции используются два усилительных элемента (операционные усилители).
Сначала сигнал проходит через фильтр верхних частот, выходной сигнал этого фильтра верхних частот стремится к бесконечности, и, таким образом, сигнал, который стремится к бесконечности, передается в конце фильтра нижних частот.
Этот фильтр нижних частот пропускает высокочастотный сигнал.
Когда фильтр высоких частот соединен с фильтром низких частот, получается простой полосовой фильтр. Чтобы реализовать этот фильтр, порядок цепей нижних и верхних частот должен быть одинаковым.
За счет каскадирования одного фильтра нижних и верхних частот первого порядка получается полосовой фильтр второго порядка, а путем каскадирования двух фильтров нижних частот первого порядка с двумя фильтрами верхних частот формируется полосовой фильтр четвертого порядка.
Из-за этого каскадирования схема имеет низкий коэффициент качества.Конденсатор в фильтре верхних частот первого порядка блокирует любое смещение постоянного тока входного сигнала.
Спад усиления в обеих полосах заграждения составляет ± 20 дБ / декаду в случае фильтра второго порядка (высокий + низкий). Фильтры высоких и низких частот должны быть только в первом порядке.
Аналогично, когда фильтры верхних и нижних частот имеют второй порядок, то спад усиления в обеих полосах заграждения составляет ± 40 дБ / декада.
Выражение усиления напряжения для полосового фильтра имеет вид:
| V из / V из | = [A макс. * (f / f L )] / √ {[1+ (f / f L ) ²] [1+ (f / f H ) ²]}
Он получается индивидуальным усилением как фильтра верхних частот, так и фильтра нижних частот, индивидуальные коэффициенты усиления как фильтра верхних частот, так и фильтра нижних частот приведены ниже.
Коэффициент усиления для фильтра высоких частот:
| V из / V из | = [A max1 * (f / f L )] / √ [1+ (f / f L ) ²]
Коэффициент усиления для фильтра нижних частот:
| V из / V из | = A max2 / √ [1+ (f / f H ) ²]
A макс = A макс1 * A макс2
Где max1 – усиление каскада высоких частот, а max2 – усиление каскада низких частот.
Отклик широкополосного фильтра показан ниже.
НАЗАД НАЗАД
Узкополосный фильтрЕсли значение коэффициента качества больше десяти, тогда полоса пропускания узкая, и полоса пропускания полосы пропускания также меньше. Этот полосовой фильтр называется узкополосным фильтром.
В нем используется только один активный компонент (операционный усилитель), а не два, и этот операционный усилитель имеет инвертирующую конфигурацию. В этом фильтре коэффициент усиления операционного усилителя максимален на центральной частоте f c .
НАЗАД НАЗАД
Цепь узкополосного фильтра
Вход подается на инвертирующую входную клемму. Это показывает, что операционный усилитель находится в инвертирующей конфигурации. Эта схема фильтра обеспечивает отклик узкополосного фильтра.
Коэффициент усиления по напряжению указанной схемы фильтра составляет A В = – R 2 / R 1
Частоты среза схемы фильтра
f C1 = 1 / (2πR 1 C 1 ) и f C2 = 1 / (2πR 2 C 2 )
НАЗАД НАЗАД
Активный полосовой фильтр с множественной обратной связьюЭта схема фильтра создает настроенную схему на основе отрицательной обратной связи фильтра.Важным преимуществом этой множественной обратной связи является то, что без какого-либо изменения максимального усиления на центральной частоте мы можем изменить значение частоты среза. Это изменение частоты среза может быть выполнено с помощью сопротивления «R 3 ».
Рассматривая приведенную ниже схему активного фильтра, давайте рассмотрим измененное значение резистора как R 3 ‘и измененное значение частоты среза как f c ‘, тогда мы можем приравнять новое значение резистора следующим образом:
R 3 ′ = R 3 (f c / f c ′) ²
Он состоит из двух путей обратной связи, из-за наличия нескольких каналов обратной связи его также называют «полосовой схемой с множественной обратной связью».Эта схема создает полосовой фильтр с множественной обратной связью с бесконечным усилением. За счет этой схемы значение добротности увеличивается максимум до 20.
f c = 1 / √ (R 1 R 2 C 1 C 2 )
Q = f c / Полоса пропускания = (½) {√ [R 2 / R 1 ]}
A макс = -R 2 / 2R 1
R 1 = Q / {2πf c CA макс }
R 2 = Q / πf c C
R 3 = Q / {2πf c C (2Q² – A max )}
Усиление на центральной частоте «A max » должно быть меньше 2Q².То есть
A макс <2Q²
Где,
f c = частота среза в Гц
C = емкость, (C 1 = C 2 = C)
Q = коэффициент качества
A max = максимальное усиление
НАЗАД НАЗАД
Частотная характеристика активного полосового фильтраОн имеет две центральные частоты, одна – фильтра высоких частот, а другая – фильтра низких частот.Центральная частота фильтра верхних частот должна быть ниже центральной частоты фильтра нижних частот.
Центральная частота полосового фильтра – это среднее геометрическое для нижней и верхней частоты среза f r 2 = f H * f L.
Коэффициент усиления фильтра составляет 20 log (В на выходе / В на ) дБ / декада. Амплитудный отклик аналогичен отклику фильтра нижних и верхних частот. Кривая отклика зависит от порядка каскадных фильтров.
Нормированная средняя частота задается как f r = 1. Давайте рассмотрим две частоты среза как 300 Гц и 900 Гц, тогда полоса пропускания фильтра составляет 300 Гц -900 Гц = 600 Гц.
НАЗАД НАЗАД
Фактор качестваКоэффициент качества зависит от ширины полосы пропускания. Коэффициент качества обратно пропорционален пропускной способности. Это означает, что при увеличении ширины полосы добротность уменьшается, а при уменьшении ширины полосы добротность увеличивается.
Q = f c / Полоса пропускания
Для широкополосного фильтра коэффициент качества низкий, потому что ширина полосы пропускания велика. Для узкополосного фильтра добротность высока. Селективность и неселективность зависят от ширины полосы пропускания.
Этот коэффициент качества также относится к коэффициенту демпфирования (). Если значение коэффициента демпфирования больше, равномерность выходной характеристики также больше. Это приравнивается следующим образом:
ε = 2 / квартал
Для различных значений коэффициента качества нормализованная характеристика усиления полосового фильтра второго порядка задается как:
По этому графику видно, что селективность больше при более высоком коэффициенте качества.
НАЗАД НАЗАД
Пример активного полосового фильтраРассмотрим схему активного фильтра с множественной обратной связью с усилением на бесконечность, для которой резонансная частота составляет 1,5 кГц, максимальное усиление по напряжению равно 15, а коэффициент качества равен 7. Затем значения компонентов рассчитываются следующим образом:
Для резисторов
Мы считаем, что измененное значение резистора как R 3 ´ и измененное значение частоты среза f c ´ = 2 кГц, тогда мы можем приравнять новое значение резистора следующим образом:
R 3 ´ = R 3 (f c / f c ´) 2 = 447.4 (1,5 / 2) 2 = 251,66 Ом
Таким образом, просто взяв требуемую частоту, мы можем рассчитать новое значение резистора.
НАЗАД НАЗАД
Предыдущий – Активный фильтр высоких частот
Далее – Фильтр Баттерворта
Схема, типы, работа и ее применение
Во время обработки сигнала необходимо устройство, называемое полосовым фильтром или BPF, чтобы разрешить определенный диапазон требуемых частот и избежать нежелательных частотных диапазонов или компонентов.Посредством этой фильтрации шумовой сигнал может быть уменьшен за счет исключения частот, которые не требуются. Различные типы фильтров, такие как линейные и нелинейные, аналоговые, цифровые, активные и пассивные и т. Д., Доступны для использования в зависимости от требований. В этой статье обсуждается обзор полосового фильтра.
Что такое полосовой фильтр?
Полосовой фильтр определяется как устройство, которое пропускает частоты, которые находятся в требуемом диапазоне частот, и отклоняет оставшиеся частоты, которые не находятся в этом конкретном диапазоне.Что касается фильтра верхних частот, этот фильтр будет ослаблять сигналы, которые ниже частоты среза, а фильтр нижних частот ослабляет сигналы, которые имеют частоты выше, чем частота среза. Но если нам нужен только конкретный диапазон частот и мы хотим исключить частоты, которые находятся за пределами этого диапазона, другой фильтр может быть сформирован путем каскадирования фильтра верхних частот и фильтра нижних частот, который можно назвать полосовым фильтром.
В этом полосовом фильтре есть две частоты среза, одна от фильтра высоких частот и его высокая частота среза.Это будет самый высокий частотный предел в этой полосе. Существует еще одна частота среза фильтра нижних частот и его вторая частота среза, известная как нижняя частота среза, которая определяет низкочастотный диапазон этой полосы.
Этот полосовой фильтр пропускает только определенную полосу и ослабляет все остальные сигналы выше или ниже частоты среза.
Схема полосового фильтра
Это принципиальная схема пассивного полосового фильтра RC.
Полосовой фильтр
Каскадирование или комбинация фильтра верхних частот и фильтра нижних частот формирует полосовой фильтр, поскольку он позволяет использовать определенную полосу частот и ослабляет сигналы, которые выше и ниже частот среза.Этот полосовой фильтр пропускает входные сигналы без искажений и шумов. Ширина этой полосы частот называется полосой пропускания. Чтобы четко определить полосу пропускания, это конкретный частотный диапазон, который находится между двумя точками отсечки, то есть высокой и низкой частотой отсечки.
Bw = fH – fL
Разница между самой низкой и самой высокой частотой среза называется полосой пропускания.
Чтобы быть идеальным полосовым фильтром, фильтр должен фильтровать или ослаблять определенные частоты, которые даже лежат в пределах полосы, чтобы устранить шум.Полосовые фильтры также известны как фильтры второго порядка из-за наличия двух конденсаторов, реактивных компонентов в одной цепи. Один конденсатор в цепи верхних частот и другой конденсатор в цепи нижних частот.
Различные типы полосовых фильтров
Эти полосовые фильтры в основном делятся на два типа фильтров. Это
- Широкополосный фильтр
- Узкополосный фильтр
Широкополосный фильтр
Принципиальная схема широкополосного фильтра показана ниже.В этой схеме широкополосного фильтра существует несколько практических схем. Как мы уже обсуждали, этот широкополосный фильтр может быть сформирован каскадом двух секций, то есть высоких и низких частот.
Широкополосный фильтр
Для формирования полосового фильтра + или – 20 дБ / декада две секции верхних частот первого порядка и нижних частот первого порядка соединены каскадом, таким же образом для формирования + или – 4 дБ. / декадный полосовой фильтр секция верхних частот второго порядка и секция нижних частот второго порядка соединены.Это означает, что порядок фильтров нижних и верхних частот будет определять порядок полосового фильтра.
Характеристики полосового фильтра
На изображении выше показаны характеристики полосового фильтра. На рисунке показан широкополосный фильтр, состоящий из фильтра верхних частот первого порядка и фильтра нижних частот первого порядка.
Узкополосный фильтр
Здесь на этой диаграмме показан узкополосный фильтр, использующий множественные обратные связи. В этом фильтре используется только один операционный усилитель.По сравнению с другими фильтрами, этот фильтр обладает некоторыми уникальными функциями, которые очень полезны.
Узкий BPF
- Он называется фильтром множественной обратной связи из-за двух путей обратной связи.
- OP-Amp здесь используется в инвертирующем режиме
- Мы можем видеть частотную характеристику узкополосного фильтра на приведенном выше рисунке. Проектирование узкополосного фильтра выполняется для конкретных значений fc или Q & BW.
Для целей расчета
C1 = C2 = C
R1 = Q / 2π fc CAf
R2 = Q / 2πfc C (2Q2-Af) &
R3 = Q / πfc C
Здесь усиление на центральной частоте определяется как Af
Af = R3 / 2R1
Fc можно изменить на fc ‘без изменения полосы пропускания или усиления.это может быть сформировано простым изменением R2 на R2 ‘
R’2 = R2 [fc / f’c] 2
Расчет калькулятора полосового фильтра
Это схема пассивного полосового фильтра, и с ее помощью можно выполнить расчеты полосы пропускания. схема.
Расчет BPF
Используя формулу, мы можем определить требуемую частоту в этом пассивном полосовом фильтре.
Для высокой частоты среза = 1 / 2ΠR1C1
Для низкой частоты среза = 1 / 2ΠR2C2
Даже мы можем рассчитать требуемые частоты для различных полосовых фильтров, таких как активный инвертирующий ОУ BPF и активный неактивный. инвертирующий операционный усилитель BPF
Применение полосового фильтра
Полосовой фильтр имеет широкий спектр применений
- Он используется в оптике, такой как лидары, лазер и т. д.
- Эти фильтры широко используются в беспроводных передатчиках и приемниках.
- В обработке аудиосигналов эти полосовые фильтры играют жизненно важную роль, разрешая определенные частоты и удаляя нежелательные.
- Эти полосовые фильтры также используются в приборах и приложениях в медицине и сейсмологии.
Одно из лучших применений полосовых фильтров – схемы аудиоусилителей. Мы можем просто наблюдать, как динамики будут воспроизводить желаемый диапазон частот и приглушать остальные. - Полосовой фильтр эффективно используется для оптимизации отношения сигнал / шум, отношения сигнал / шум и даже чувствительности приемника.
- Поскольку эти полосовые фильтры специально разработаны для работы в определенной полосе частот, они широко используются в системах связи.
Итак, это обзор полосовых фильтров, их схемы, типов и применения. Полосовой фильтр имеет широкий спектр применения в современном мире. Вот вам вопрос, что такое полосовой фильтр RLC и фильтр отклонения полосы RLC?
Проектирование схемы пассивного полосового фильтра и его применение
В предыдущих уроках мы видели фильтры низких и высоких частот.В этом руководстве мы узнаем о другой категории фильтров, известной как полосовые фильтры. В частности, мы узнаем о пассивном полосовом RC-фильтре, его базовой схеме, функциональности, частотной характеристике, приложениях и многом другом.
Для получения дополнительной информации о фильтрах нижних или верхних частот прочтите учебные материалы по пассивным RC-фильтрам верхних частот , пассивным RC-фильтрам нижних частот , активным фильтрам верхних частот и активным фильтрам нижних частот .
Введение
Можно сказать, что полосовой фильтр представляет собой комбинацию как фильтра нижних частот, так и фильтра верхних частот.Само название фильтра указывает на то, что он разрешает только определенную полосу частот и блокирует все остальные частоты.
В звуковых приложениях иногда необходимо передать только определенный диапазон частот, этот диапазон частот не начинается с 0 Гц или не заканчивается на очень высокой частоте, но эти частоты находятся в пределах определенного диапазона, широкого или узкого. Эти полосы частот обычно называют полосой пропускания.
Пассивный полосовой фильтр
Полосовой фильтр получается путем каскадного соединения пассивных фильтров нижних частот и пассивных фильтров верхних частот.Такая конструкция обеспечивает селективный фильтр, пропускающий только определенные частоты. Эта новая схема RC-фильтра может пропускать узкий или широкий диапазон частот.
Этот диапазон пропускания частот, который является узким или широким, будет зависеть от способа каскадирования пассивного фильтра нижних частот и фильтра верхних частот. Верхняя и нижняя частоты среза зависят от конструкции фильтра. Этот полосовой фильтр просто выглядит как частотно-избирательный фильтр.
На рисунке выше показана схема полосового фильтра.На входе задан синусоидальный сигнал. Свойства комбинаций низких и высоких частот дают нам полосовой фильтр. При размещении одного набора RC-элементов последовательно, а другого набора RC-элементов параллельно, схема ведет себя как полосовой фильтр.
Это дает нам фильтр второго порядка, потому что схема имеет два реактивных компонента. Один конденсатор относится к фильтру нижних частот, а другой конденсатор относится к фильтру верхних частот. Без каких-либо изменений входного сигнала этот полосовой фильтр пропускает определенный диапазон частот.Этот фильтр не создает дополнительных шумов в сигнале.
Частоту среза цепи можно рассчитать следующим образом:
f C = 1 / (2πRC)
Регулируя частоты среза фильтров высоких и низких частот, мы можем получить подходящую ширину полосы пропускания для полосового фильтра.
Поскольку этот фильтр пропускает полосу частот, он содержит две частоты среза: нижнюю частоту среза «f L » и более высокую частоту среза «f H ».Таким образом, диапазон частот, пропускаемых через фильтр, называется шириной полосы фильтра. Обычно ширина полосы частот схемы может быть рассчитана по частотам «f H и f L ».
BW = f H – f L
Где «f H » – частота среза фильтра высоких частот, а «f L » – частота среза фильтра низких частот. «BW» – это полоса пропускания фильтра. Полосовой фильтр пропускает частоты выше, чем частота среза фильтра высоких частот и ниже, чем частота среза фильтра низких частот.
Это показывает, что частота среза фильтра низких частот должна быть выше, чем частота среза фильтра высоких частот.
Полосовой фильтр с использованием компонентов R, L и C
Конструкция схемы полосового фильтрас использованием катушки индуктивности, конденсатора и резистора приведена ниже.
Центральную частоту полосового фильтра, которую также называют «резонансным пиком», можно сформулировать с помощью следующего уравнения.
f c = 1 / 2π√ (LC)
Где L = индуктивность катушки индуктивности, единицы измерения которой выражены в Генри (Гн).
C = емкость конденсатора, единицы измерения которого указаны в Фарадах (Ф).
Мы также можем разработать полосовой фильтр с катушками индуктивности, но мы знаем, что из-за высокого реактивного сопротивления конденсаторов конструкция полосового фильтра с RC-элементами имеет большее преимущество, чем схемы RL.
Частотная характеристика полосового фильтра
Полюсная частота приблизительно равна частоте максимального усиления.
Кривая частотной характеристики полосового фильтра показана ниже: Идеальные характеристики и практические характеристики полосовых фильтров различаются из-за входного реактивного сопротивления схемы.
Коэффициент усиления входного сигнала можно рассчитать, взяв 20 log (В из / В из ). Диапазон может быть довольно большим в зависимости от характеристик схемы. Сигнал ослабляется на низких частотах с увеличением выходного сигнала с наклоном +20 дБ на декаду или 6 дБ на октаву, пока частота не достигнет более низкой частоты среза «fL».
На этой частоте коэффициент усиления сигнала достигает значения 1 / √2 = 70.7%.
После частоты среза f L выход будет увеличиваться с увеличением частоты со скоростью -20 дБ на декаду и достигает максимального усиления, и это усиление остается постоянным, пока не достигнет более высокой частоты среза ‘f_H ‘. После более высокой частоты среза выходной сигнал уменьшается с наклоном -20 дБ / декада или -6 дБ / октава.
Ранее мы видели, что фазовый сдвиг фильтра первого порядка составляет 90 °. Мы знаем, что полосовой фильтр является фильтром второго порядка, поэтому сдвиг фазы в два раза больше, чем у фильтра первого порядка, который составляет 180 °.Фазовый угол будет изменяться с увеличением частоты. На центральной частоте выходной и входной сигналы синфазны друг с другом.
Ниже резонансной частоты выходной сигнал опережает входной сигнал, а выше резонансной частоты выходной сигнал отстает от входного сигнала. Амплитуда входного сигнала всегда больше выходного сигнала. Чтобы увеличить коэффициент усиления схемы, значение сопротивления R1 должно быть больше, чем сопротивление R2.
Центральная частота полосового фильтра
«Центральная частота» или «Резонансная частота», при которой выходное усиление является максимальным, может быть получена путем вычисления среднего геометрического нижней и верхней частот среза.
f r 2 = f H x f L
fr = √ (f H x f L )
Где fr – резонансная частота или центральная частота
f H – верхняя граничная частота -3 дБ
f L – нижняя граничная частота -3 дБ
Пример полосового фильтра
Предположим, что полосовой фильтр пропускает частоты от 1 кГц до 30 кГц и содержит резистор 10 кОм.Учитывая эти значения, мы можем рассчитать емкость конденсатора.
Мы уже знаем, что значение частоты среза фильтра низких частот должно быть выше, чем фильтра высоких частот. Таким образом, частота среза фильтра высоких частот составляет 1 кГц, а частота среза фильтра низких частот – 30 кГц.
На ступени фильтра высоких частот
f L = 1 кГц и сопротивление R = 10 кОм
C = 1 / (2πf L R) = 1 / (2 * π * 1000 * 1000) = 15.8 нФ
На ступени фильтра нижних частот
f H = 30 кГц и сопротивление R = 10 кОм
C = 1 / (2πf H R) = 1 / (2 * π * 30000 * 10000) = 510 пФ
Из приведенных выше расчетов емкость конденсатора, необходимая для фильтра верхних частот, составляет 15,8 нФ, а емкость конденсатора фильтра нижних частот составляет 510 пФ.
Сводная информация о пассивном полосовом фильтре
Полосовой фильтр получается путем каскадирования фильтров нижних и верхних частот. Это фильтр второго порядка, поскольку он содержит два реактивных элемента.Порядок фильтра зависит от количества каскадных цепей, используемых в цепи.
Коэффициент усиления выходного сигнала всегда меньше входного сигнала. На центральной частоте выходной сигнал синфазен, но ниже центральной частоты выходной сигнал опережает фазу со сдвигом + 90 ° и выше центральной частоты выходной сигнал будет отставать по фазе с фазовым сдвигом -90 °.
Практические характеристики полосового фильтра немного отличаются от идеальных характеристик.Это изменение в основном связано с каскадированием фильтра высоких частот с фильтром низких частот.
Коэффициент усиления на выходе всегда меньше единицы. Когда мы обеспечиваем гальваническую развязку между фильтрами высоких и низких частот, мы можем добиться лучших характеристик фильтра.
Полосовой фильтр оптимизирует чувствительность приемника. Сначала в конструкцию добавляется фильтр высоких частот, а затем добавляется фильтр низких частот. Даже если мы добавим сначала фильтр нижних частот, а затем фильтр верхних частот, он никогда не изменит выходной сигнал.
Добротность фильтра будет зависеть от номинала резистора R1. Если R1 низкий, коэффициент качества низкий, а если значение R1 высокое, то коэффициент качества высокий.
Применение полосового фильтра
- Они используются в беспроводной среде связи в цепях передатчика и приемника. В секции передатчика этот фильтр пропускает только необходимые сигналы и уменьшает помехи сигналов другим станциям. В секции приемника это поможет от проникновения нежелательного сигнала в каналы.
- Они используются для оптимизации отношения сигнал / шум приемника.
- Они используются в области оптической связи, например, в лидарах.
- Они используются в некоторых методах цветовой фильтрации.
- Они также используются в полевых медицинских приборах, таких как ЭЭГ.
- В телефонных приложениях, в DSL для разделения телефонных и широкополосных сигналов.
, типы, калькулятор и его применение
В обработки сигналов фильтры – это один из видов устройств, используемых для разрешения требуемых частотных составляющих, а также для удаления нежелательных частотных составляющих.Фильтрация может быть определена как; фоновый шум интерфейсного сигнала можно уменьшить, удалив некоторые частоты. Схема фильтра может использоваться для объединения свойств LPF и HPF в единственный фильтр, который называется полосовым фильтром. Доступны различные типы фильтров, такие как аналоговые / цифровые, активные / пассивные, линейные / нелинейные, не зависящие от времени / не зависящие от времени. В этой статье обсуждается обзор полосового фильтра с приложениями
Что такое полосовой фильтр?
Определение полосового фильтра – это схема, которая позволяет сигналам проходить между двумя конкретными частотами, хотя и разделяет эти сигналы на других частотах.Эти фильтры доступны в разных типах; часть конструкции полосового фильтра BPF- может быть выполнена с внешним источником питания, а также с активными компонентами, такими как интегральные схемы, транзисторы, которые называются активными полосовыми фильтрами . Точно так же в некоторых фильтрах используются источники питания любого типа, а также пассивные компоненты, такие как конденсаторы и катушки индуктивности, которые называются пассивными полосовыми фильтрами.
Эти фильтры применимы как в беспроводных передатчиках, так и в приемниках.В передатчике BPF может использоваться для ограничения полосы пропускания выходного сигнала до минимально необходимого уровня и передачи данных с предпочтительной скоростью и формой. Точно так же в приемнике этот фильтр позволяет декодировать сигналы в предпочтительном частотном диапазоне, избегая сигналов на ненужных частотах. Отношение сигнал / шум (S / N) приемника можно оптимизировать с помощью BPF.
Цепь полосового фильтра
Лучшим примером схемы полосового фильтра является схема RLC, показанная ниже.Этот фильтр также может быть сконструирован путем объединения ФНЧ и ФВЧ. В BPF Bandpass иллюстрирует своего рода фильтр, иначе процедуру фильтрации. Ее следует отличать от полосы пропускания, которая относится к реальной части спектра, на который воздействуют. Идиллический полосовой фильтр не имеет усиления и затухания, поэтому это полностью ровная полоса пропускания. Это полностью ослабит каждую частоту за пределами полосы пропускания.
Схема полосового фильтраНа практике полосовой фильтр не идеален и не ослабляет полностью каждую из частот за пределами предпочтительного выбора частоты.В частности, есть участок сразу за предлагаемой полосой пропускания, где частоты ослабляются, но не отбрасываются, что называется спадом фильтра, и обычно он указывается в дБ ослабления для каждой октавы, иначе декада частоты. В общем, конструкция фильтра выглядит так, чтобы спад был настолько тонким, насколько это возможно, что позволяет фильтру выполнять предложенную конструкцию. Часто это может быть достигнуто за счет пульсации полосы пропускания, в противном случае пульсации полосы задерживания.
Полоса пропускания фильтра может быть определена как – несходство между верхней и нижней частотами. Форм-фактор – это доля ширины полосы, рассчитанная с двумя разными значениями затухания для определения частоты среза. Например, форм-фактор 2: 1 при 20/2 дБ означает, что ширина полосы, вычисленная среди частот при затухании 20 дБ, удваивается. вычисленное для частот с ослаблением 2 дБ. Оптические BPF обычно используются в фотографии, а также для освещения в театрах.Эти типы фильтров принимают контур прозрачной цветной пленки, иначе лист.
Различные типы полосовых фильтров
Разделение полосового фильтра на категории может быть выполнено по двум типам, например, широкополосный фильтр и узкополосный фильтр .
Широкополосный фильтр
Широкополосный фильтр WBF или (WBF) может быть сформирован путем отбрасывания сегментов низких и высоких частот, что обычно представляет собой другую схему, предназначенную для простой конструкции и действия.
Широкополосный фильтрИзвестен по ряду практических схем. Полосовой фильтр с ± 20 дБ / декаду может быть сформирован с использованием двух секций, таких как низкочастотный фильтр 1-го порядка, а также могут быть исключены секции верхних частот. Точно так же полосовой фильтр с ± 40 дБ / декаду может быть сформирован путем последовательного соединения двух фильтров второго порядка, а именно фильтра нижних частот и фильтра верхних частот (HPF). Это означает, что порядок полосового фильтра (BPF) определяется порядком фильтров нижних и верхних частот.График полосового фильтра показан ниже.
Частотная характеристика BPFПолосовой фильтр с ± 20 дБ / декаду может быть составлен из HPF 1-го порядка (фильтр верхних частот) . Частотная характеристика LPF (фильтр нижних частот) 1-го порядка показана на следующем рисунке.
Узкополосный фильтр
Обычно узкополосный фильтр использует несколько обратных связей. Этот полосовой фильтр использует операционный усилитель , как показано на следующей принципиальной схеме.К основным характеристикам этого фильтра можно отнести следующие.
Узкополосный фильтрДругое название этого фильтра – фильтр множественной обратной связи, поскольку он включает две полосы обратной связи
Операционный усилитель используется в инвертирующем режиме
Частотная характеристика этого фильтра показана на следующем рисунке.
Частотная характеристика NBPFОбычно проектирование этого фильтра может быть выполнено для точных значений центральной частоты (fc) и полосы пропускания или центральной частоты и полосы пропускания.Компоненты этой схемы могут быть определены следующими соотношениями. Каждый из конденсаторов C1 и C2 можно отнести к C для упрощения расчетов конструкции.
R1 = Q / 2∏ fc CAf
R2 = Q / 2∏ fc C (2Q2-Af)
R3 = Q / ∏ fc C
Из приведенных выше уравнений на средней частоте Af обозначает усиление, поэтому Af = R3 / 2R1
Но Af должен удовлетворять этому утверждению Af <2Q2
‘fc (центральная частота) множественных фильтров обратной связи может быть изменен в сторону новой частоты fc без изменения полосы пропускания или усиления.Этого можно достичь, просто изменив R2 на R2 ’, чтобы
R2 ’= R2 * ( fc / fc ) 2
Калькулятор полосового фильтра
Следующая схема представляет собой схему пассивного полосового фильтра. Используя эту схему, мы можем рассчитать пассивный полосовой фильтр. Формула для расчета пассивного полосового фильтра показана ниже.
Калькулятор пассивных полосовых фильтровДля частоты среза низких частот = 1 / 2∏R2C2
Для высокой частоты среза = 1 / 2∏R1C1
Аналогичным образом мы можем рассчитать для активного инвертирующего ОУ BPF и активного неинвертирующего ОУ BPF.
Применение полосового фильтра
Области применения полосовых фильтров включают следующее.
- Эти фильтры широко применяются в беспроводных передатчиках и приемниках.
- Этот фильтр можно использовать для оптимизации отношения сигнал / шум (сигнал / шум), а также для улучшения качества сигнала приемника.
- Основное назначение фильтра в передатчике – ограничить полосу пропускания выходного сигнала выбранной полосой для связи. ПФ
- также широко используются в оптике, такой как лидары , лазеры и т. Д.
- Лучшее применение этого фильтра – обработка аудиосигнала там, где требуется определенный диапазон звуковых частот, но с удалением всего остального.
- Эти фильтры применимы в гидролокаторах, приборах, медицине и приложениях Сейсмология
- Эти фильтры включают систем связи для выбора конкретного сигнала из множества сигналов.
Таким образом, это все о теории полосовых фильтров , которая включает, принципиальную схему с рабочими, типы полосовых фильтров и их применения.Из приведенной выше информации, наконец, мы можем сделать вывод, что другие области применения этих фильтров включают в себя астрономию, эти фильтры пропускают только часть диапазона света в устройство. Эти фильтры могут помочь найти, где звезды лежат в основной серии, распознать красное смещение и т. Д. Вот вам вопрос, , что такое активный полосовой фильтр?
Что такое полосовой фильтр – как его спроектировать?
Что такое полосовой фильтр?
Полосовой фильтр – это электронная схема, которая используется для передачи частот в определенном частотном диапазоне, так что только определенная частота получается для дальнейшей обработки в схеме приложения.
В качестве альтернативы можно сказать, что «Полосовой фильтр ослабляет весь сигнал за пределами определенного частотного диапазона, позволяя принимать только определенные сигналы».
Допустимая частота, этот диапазон этой приемлемой частоты известен как полоса пропускания . Разница между более высокой разрешенной частотой и более низкой разрешенной частотой называется пропускной способностью фильтра.
Эта схема полезна для удаления нежелательных шумовых сигналов путем их блокировки.Полосовой фильтр имеет множество применений, начиная от аудиосхем и кончая радиочастотными схемами.
Обычно полосовые фильтры используются в передатчиках и приемниках, так что мы передаем сигналы данных в требуемое место назначения, не мешая другим сигналам. Поскольку вмешательство в другой сигнал может вызвать путаницу и перекрестные переговоры между передатчиком и приемником.
Важность:
- Фильтрация – один из наиболее часто используемых методов избавления от шума в цепи, помимо техники модуляции и других различных методов.
- Эти схемы являются оружием разработчика электронных схем , который использует их для устранения шума в схемах специальных радиочастотных приемников в устройствах связи.
- Этот тип фильтра можно легко использовать в аудиоусилителе для управления громкоговорителями.
- Здесь вы можете управлять тональностью выходной музыки / звука, управление тоном – это не что иное, как управление частотой прохода к выходному громкоговорителю.
Позже мы кратко обсудим область применения полосового фильтра ниже в разделе приложений.
Работа полосового фильтра:
Мы уже обсуждали работу фильтра нижних частот.Аналогично работает полосовой фильтр, за исключением нескольких дополнительных схем.
Это комбинация фильтра нижних частот и фильтра верхних частот, поэтому формула для частоты среза, которую мы уже обсуждали {здесь}
Основная идея реализации полосового фильтра показана на рисунке:
- Идеальный полосовой фильтр Фильтр и практическая частотная характеристика полосового фильтра показаны на рисунке. Как вы видите, полосовой фильтр имеет бесконечное ослабление для заблокированных частот и нулевое ослабление для частот полосы пропускания.
- Но на практике это невозможно, практический полосовой фильтр предлагает ослабление от нуля от до на один дБ для пассивных фильтров, которое также зависит от типа фильтра, будь то RC-фильтр или LC-фильтр? и / или это пассивный фильтр или активный фильтр, о которых мы поговорим ниже.
Типы полосовых фильтров:
Ультрабазовая классификация – Аналоговый фильтр и Цифровой фильтр . Мы обсуждаем здесь аналоговый (проверьте, наконец, цифровой фильтр ниже).Также основными типами фильтров являются активных фильтров и пассивных фильтров .
Активные фильтры – это фильтры, которые требуют какого-либо внешнего источника питания (и активных компонентов, таких как транзисторы) для получения требуемого результата.
Напротив, вспомогательный фильтр
P не требует каких-либо активных компонентов для выполнения своей работы и поэтому предпочтительнее в недорогих схемах.
Теперь реальный полосовой фильтр классифицируется на два типа в зависимости от его полосы пропускания следующим образом:
1) Широкополосный фильтр.
2) Узкополосный фильтр / настроенный фильтр.
Широкополосный фильтр реализован с использованием одной цепи фильтра нижних частот и фильтра верхних частот.
- Фильтр нижних частот блокирует более низкие частоты, которые не требуются, и пропускает все другие частоты, в то же время фильтр верхних частот блокирует более высокие частоты, чем требуется, и пропускает частоты ниже этих. Взгляните на следующую диаграмму, чтобы лучше понять это.
(BPF с использованием резистора и конденсатора)
- Широкополосный фильтр имеет более низкую добротность. BPF может быть реализован с использованием RC или LC, т.е. с использованием резистора-конденсатора вместо индуктора-конденсатора.
- Лучше всего использовать фильтр с индуктивным конденсатором, так как он имеет низкие потери мощности. Мы обсудили RC-фильтр в фильтре нижних частот, поэтому мы обсудим LC здесь, в примере ниже.
- Его также называют настроенным фильтром.Судя по названию, он будет пропускать через него только узкий диапазон частот. Конструкция узкополосного фильтра совершенно иная.
- Резонансный контур используется для реализации узкополосного фильтра. Это мой любимый фильтр во всех классах фильтров, потому что он использует только два компонента: один – индуктор, а другой – конденсатор, в очень простой конфигурации, как показано на рисунке. Эта конфигурация называется контуром резервуара .
- В этой схеме значение индуктивности и конденсатора выбрано таким образом, чтобы оно резонировало на определенной частоте, точнее говоря, перенос зарядов (ток / энергия) от катушки индуктивности к конденсатору и конденсатора к катушке индуктивности в зависимости от их способность удерживать обвинения.(Это практически используется в различных приложениях, но меньше учитывается в учебной программе)
Важные определения:
1) SNR: Отношение сигнал / шум, это очень важно при проектировании фильтров и радиочастотных схем, особенно передатчиков и приемников, также не менее важен в аудиосхемах. SNR – это отношение мощности сигнала к мощности шума.
- Кроме того, для простоты фактор, используемый для определения качества сигнала, принимаемого на стороне приложения, – это отношение сигнал / шум.
- Мощность сигнала должна быть больше, чем мощность шума, реальный шум – это частоты ненужных сигналов, которые могут быть естественными или искусственными для предполагаемого полного или непреднамеренного.
- Обычно значение на 20 дБ выше, чем это, считается хорошим сетевым сигналом. Точно так же 3 дБ – это минимально допустимое значение, ниже этого значения очень сложно или невозможно точно определить требуемый сигнал.
2) Коэффициент Q: Это аренда, также называемая коэффициентом демпфирования. Это список измерений, который дает информацию о полосе пропускания относительно ее центральной частоты.Он используется в цепи с параллельно включенным LC (контур резервуара).
Пример полосового фильтра (практический):
Спроектировать полосовой фильтр с диапазоном частот
80 МГц от до 120 МГц?Given- fc1 и fc2 (где fc1 = fl = более низкая частота среза & fc2 = fh = более высокая частота среза )
Вышеупомянутая схема разработана с использованием катушки индуктивности и конденсатор, поскольку мы уже обсуждали преимущество LC-фильтра над RC-фильтром, поэтому мы будем спроектировать полосовой фильтр, используя катушку индуктивности.
step1 : для LPF
L2 = 10 нГн (предполагается) и C2 = 0,395 нФ (с использованием формулы).
step2: для HPf
L1 = 10 нФ и C1 = 0,395 нФ
(как для LPF, так и для HPF значения оказались одинаковыми, потому что для LC-фильтров формула для поиска L&C одинакова только положение местами катушки индуктивности и конденсатора см. рис.)
Разработайте узкополосный фильтр с центральной частотой Fc = 100Mhz?
Используйте схему узкополосного фильтра,
Fc = 1 / 2π.sqrt (LC)
Здесь дано только значение частоты , тогда как мы можем вычислить значение L & C?
-Вы должны принять значение любого одного компонента, будь то катушка индуктивности «L» или конденсатор «C».
– Предположим, C = 1,58 нФ (предположим, что стандартное значение , которое вам доступно)
– затем, используя формулу, найдите L , получилось 1,56 нГн.
Значит, цепь замкнута.(см. схему на изображении)
Полосовой фильтр 4-го порядка и полосовой фильтр 5-го порядка:
Влияние порядка фильтров на отклик показано на изображении ниже. Просто наблюдайте за ослаблением проходной и конечной частот.
- Спад затухания каждого из них отличается в разных порядках фильтров.
- На рисунке показан полосовой фильтр 1-го порядка, полосовой фильтр 2-го порядка, полосовой фильтр 4-го порядка, полосовой фильтр 5-го порядка.
- Фильтр 1-го порядка имеет спад усиления -20 дБ / декаду , чем -40 дБ / декада для фильтра 2-го порядка и так далее.
- Порядок фильтра достигается за счет каскадирования количества ступеней одного и того же фильтра, а иногда и с использованием современных топологий.
Применение полосового фильтра:
1) Радиопередатчик и приемник широко используют BPF.
2) Оптимизация отношения сигнал / шум для уменьшения вероятности ошибки в приемнике.
3) Почти в каждой цепи управления Audio Tone для увеличения или уменьшения тональности музыки.
4) Это важная схема в демодуляторах в цепи приемника.
5) Выбор диапазона в FM-радиоприемниках, а также в системах мобильной связи.
6) В схемах предыскажения и снятия выделения для увеличения отношения сигнал / шум.
7) В РАДАРЕ для передачи сигналов в другом спектре.
Калькулятор полосового фильтра – ElectronicBase
Полосовой фильтр пропускает только определенную полосу частот и ослабляет частоты ниже и выше.В этой статье показаны различные варианты схем пассивных полосовых фильтров. В дополнение к формулам вы найдете удобные калькуляторы полосы пропускания для удобного расчета фильтра.
Общие сведения о полосовом фильтре
Схема полосового пропускания или схема полосового фильтра обозначает компонент для фильтрации частот. Название «полоса пропускания» происходит от того факта, что фильтр пропускает определенную полосу частот . Таким образом, он ослабляет частоты выше и ниже полосы частот.Полоса пропускания в своей простейшей форме состоит из комбинации фильтров верхних и нижних частот.
Полоса пропускания используется, например, в конструкции громкоговорителей. Это может ограничить полосу частот среднечастотного динамика. Это помогает улучшить звук, поскольку все частоты за пределами определенного диапазона динамика не могут передаваться чисто. Другой пример применения – приемники радиосигналов, которые ограничены зоной приема с полосой пропускания.
Полосовой фильтр имеет активный и пассивный фильтры.Пассивная полосовая схема присутствует, когда не используется усиливающий элемент. Бэндпасс может выполняться в разных порядках, бэндпасс 1-го порядка составляет базовый вариант. Мы объясняем функциональность полосового фильтра и объясняем , как рассчитать полосовой фильтр . Кроме того, наш калькулятор пропускной способности снижает затраты на это. Это позволяет легко построить полосовой фильтр.
Пассивный полосовой фильтр 1-го порядка
Простая полоса пропускания состоит из RC-цепочки нижних частот и RC-верхних частот, каждый 1-го порядка, то есть двух резисторов и двух конденсаторов.Фильтры высоких и низких частот просто подключаются последовательно. Выходное напряжение \ (V_ {out} \) снимается за обоими фильтрами. Этот вариант также называется RC bandpass .
Если на вход подается низкая частота, часть напряжения на фильтре высоких частот будет падать. Если применяется высокая частота, напряжение падает выше фильтра нижних частот. На средней частоте большая часть входного напряжения \ (V_ {in} \) проходит на выход. Таким образом, частота входного напряжения определяет высоту выходного напряжения.
RC Bandpass – как это работает
Полоса пропускания RC работает через комбинацию фильтров высоких и низких частот, а также этих двух элементов. В секции верхних частот напряжение на резисторе снимается, а в секции нижних частот – через конденсатор. Выходное напряжение \ (V_ {out} \), отводимое параллельно этим двум компонентам, увеличивается по мере приближения входной частоты к центральной частоте. Таким образом, по соотношению резисторов к конденсаторам можно определить полосу частот, которая проходит через фильтр.
Формула – расчет полосового фильтра
Обычно для одной полосы пропускания выбираются два одинаковых резистора и два одинаковых конденсатора. Тогда применяется передаточная функция полосового фильтра :
$$ \ frac {V_ {out}} {V_ {in}} = \ frac {1} {3 + j \ left (\ omega RC – \ frac {1} {\ omega RC} \ right)} $$
\ (\ omega \) – угловая частота \ (2 \ cdot \ pi \ cdot f \). \ (R \) – сопротивление, а \ (C \) – емкость конденсатора. Эту формулу можно использовать для расчета полосы пропускания.Расчет частоты среза полосы пропускания
В зависимости от частоты сопротивления верхних и нижних частот изменяются в противоположном направлении. Другими словами, если сопротивление прохода высоких частот увеличивается, то сопротивление прохода низких частот также падает. Частоты среза обоих фильтров рассчитываются отдельно и помечаются как \ (f_H \) (высокий) и \ (f_L \) (низкий). Затем с помощью этих двух частот среза можно определить центральную частоту \ (\ mathbf {f_0} \) и полосу пропускания \ (\ mathbf {B} \) всего фильтра.
Формула для расчета частот:
$$ f_0 = \ frac {1} {2 \ pi RC} $$
$$ f_0 = \ sqrt {f_H \ cdot f_L} $$
$$ B = f_H – f_L $$
Калькулятор полосового фильтра RC
Калькулятор полосы пропускания RC упрощает создание полосового фильтра.
Калькулятор полосового фильтра RC
Начните расчет
Альтернатива: полосовой LC-фильтр 1-го порядка
Так называемый фильтр Баттерворта просто состоит из катушки индуктивности, с которой последовательно соединен конденсатор.Это самый простой способ построить полосовой фильтр. Эти два компонента отфильтровывают очень высокие и очень низкие частоты.
Формулы для расчета катушки и конденсатора:
$$ C = \ frac {1} {2 \ pi \ cdot Z \ cdot f_L} $$
$$ L = \ frac {Z} {2 \ pi \ cdot f_H} $$
Пассивный полосовой фильтр 2-го порядка
Полоса пропускания 2-го порядка обычно состоит из двух емкостных цепей и двух катушек индуктивности. Схема подключения идентична RC-полосной 1-го порядка, только резисторы заменены на индукторы.Этим усиливается эффект фильтра.
Полосовой фильтр 2-го порядка имеет в два раза большую крутизну фронта, чем фильтр 1-го порядка. Это означает, что он в два раза быстрее реагирует на изменение частоты и, следовательно, фильтрует более сильно. Последовательное соединение нескольких полос, при необходимости порядок может быть дополнительно увеличен.
Работа с полосой пропускания LC
При замене резисторов на индукторы крутизна кромки увеличивается. Резисторы всегда имеют одинаковое значение сопротивления независимо от частоты.Причина изменения в том, что индуктивность намного быстрее реагирует на изменение частоты. С увеличением частоты соответственно увеличивается индуктивное сопротивление \ (X_L \) катушек индуктивности.
Формула– расчет полосы пропускания 2-го порядка
Для соотношения емкостей и индуктивностей:
$$ Z = R_0 = \ sqrt {\ frac {L_1} {C_2}} = \ sqrt {\ frac {L_2} {C_2}} $$
\ (L \) обозначает индуктивность, а \ (C \) емкость конденсатора.Расчет полосы пропускания частоты среза 2-го порядка
Опять же, емкостное и индуктивное реактивное сопротивление изменяются в противоположном направлении.Частота среза – это частота, при которой два значения сопротивления идентичны. Если частота продолжает увеличиваться, \ (X_L \) больше, а \ (X_C \) становится меньше.
Формула для верхней и нижней частот среза:
$$ f_ {H} = \ frac {1} {2 \ pi \ sqrt {L_1 C_1} \ left (- \ frac {1} {2} \ sqrt {\ frac {C_1} {C_2}} + \ sqrt {1 + \ frac {1} {4} \ frac {C_1} {C_2}} \ right)} $$
$$ f_ {L} = \ frac {1} {2 \ pi \ sqrt {L_1 C_1} \ left (+ \ frac {1} {2} \ sqrt {\ frac {C_1} {C_2}} + \ sqrt {1 + \ frac {1} {4} \ frac {C_1} {C_2}} \ right)} $$
Калькулятор полосового фильтра LC
Калькулятор полосы пропускания LC помогает определить размеры компонентов на основе требуемых частот среза.


