В процессе работы с электроустановками в цепи переменного тока нельзя полностью исключать вероятность ощущения его воздействия. Причиной может быть случайное прикосновение к токоведущим элементам или косвенные факторы. Об одном из них (шаговом напряжении) мы уже подробно рассказывали на страницах нашего сайта. В этой статье пойдет речь о другом виде косвенного воздействия электрического тока на человека, получившее название напряжение прикосновения.
Что такое “напряжение прикосновения”?
В электробезопасности под этим термином подразумевается разность потенциалов между двух точек электроцепи, возникающая в момент одновременного прикосновения к ним человека. Такая ситуация может возникнуть в результате нарушения изоляции токоведущих элементов цепи, их замыкания на электропроводящие поверхности, что приводит к образованию опасных зон растекания тока. Контакт с такой поверхностью называется косвенным прикосновением к корпусу или электропроводящим элементам (в зависимости от устройства электроустановки).
 Рис. 1. Пример косвенного прикосновения
Рис. 1. Пример косвенного прикосновенияВ таких случаях степень воздействия электрическим током зависит как от сопротивления тела человека (R) и величины (Uпр). Допустим в данном случае R = 800 Ом, Uпр близкое к фазному напряжению (230 В). Применяя закон Ома несложно вычислить величину тока в образовавшейся электрической цепи: Iпр=Uпр/R= 220/800 = 287,5 мА. Это значение в несколько раз превышает допустимые нормы.
В большинстве случаев косвенное прикосновение является однополюсным, то есть в данном случае угрозу несет фазное, а не линейное напряжение, которое в 1,73 раза выше. Но это слабое утешение, поскольку поражение током может все равно стать фатальным.
Опасность косвенного прикосновения заключается в том, что риск его возникновения, в большинстве случаев, не зависит от действий человека, в отличие от прямого касания, которое может возникнуть по неосторожности, в результате ошибки или несоблюдения ТБ.
Расчет
Приведенный выше пример (на рис. 1) сильно упрощен, чтобы ознакомиться с основными особенностями напряжения прикосновения (Uпр) необходимо посмотреть на проблему с точки зрения защитного заземления и зануления. Для этого рассмотрим пример, представленный на рисунке ниже.
 Рисунок 2. Особенность напряжения прикосновения в случае одиночного заземления
Рисунок 2. Особенность напряжения прикосновения в случае одиночного заземленияНа рисунке изображено три двигателя А, В, С (это могут быть и любые другие электроустановки), разно удаленных от единого заземлителя D и соединенных с ним защитным проводниками. Если вследствие аварии произошло замыкание фазы сети на корпус, то на нем образуется потенциал, уровень которого будет практически таким же, как на заземлителе (ⱷ
В случае касания корпуса двигателя B уровень напряжения прикосновения будет определяться следующей формулой: Uпр=ⱷзм-ⱷос=ⱷзм*(1-ⱷос/ⱷзм). В данном выражении игнорируется электрическое сопротивление грунта, влияющее на растекание тока основания, в расчет принимается только характер изменения потенциала (потенциальная кривая — E). Это позволяет рассматривать потенциал основания ⱷoc в виде коэффициента прикосновения α = 1 — (ⱷос/ⱷзм) ≤ 1.
Учитывая тот факт, что на уровень напряжения влияет как потенциал заземлителя, так и коэффициент прикосновения, то очевидно, что характер опасности различен при использовании одиночного или группового заземления. Рассмотрим отдельно каждый из вариантов.
Одиночное заземление
Вернемся к рисунку 2. Как уже упоминалось выше, в случае замыкания фазы на корпус электроустановки, на всех ее токопроводящих элементах установиться потенциал ⱷзм. При этом на поверхности возле заземлителя образуется зона с уровнем потенциала, зависящим от коэффициента прикосновения. То есть, в случае случайного прикосновения к корпусу B уровень напряжения касания будет зависеть от расстояния Х1 и кривой Е.
Теперь рассмотрим, вариант прикосновения к электроприбору C. В этом случае расстояние Х2 превышает 20,0 метров, что равносильно тому, что Х2 стремится к бесконечности. В результате коэффициент прикосновения α будет увеличиваться, стремясь к единице, соответственно, Uпр станет равным ⱷзм Этот вариант с наибольшим потенциалом самый опасный.
В завершении разберем случай прикосновения к металлическому корпусу устройства A, то есть, практически находится над заземлителем. Здесь α будет стремиться к нулю, следовательно, U
Исходя из этого, можно констатировать, что чем дальше находится установка от одиночного заземлителя, тем выше напряжение прикосновения. На расстоянии от 20 метров и более оно будет практически равно фазному.
Групповое заземление
При применении групповой схемы заземления происходит накладывание зон растекания тока, в результате этого в любой точке между заземлителями потенциал будет выше нуля. Соответственно, коэффициент α будет меньше единицы, а ⱷзм– превышать напряжение прикосновения.
Для наглядности приведем пример, в котором делают два заземлителя в виде полусфер определенного радиуса r, вкопанных на расстоянии h друг от друга.
 Рисунок 3. Напряжение прикосновения при групповом заземлении
Рисунок 3. Напряжение прикосновения при групповом заземленииВ данном случае потенциальная кривая будет описываться следующим уравнением: ⱷос = ⱷгз*(r*(h-r)/(х*(h-х)), где ⱷгз– потенциал группы заземлителей, r – радиус полусферы электрода, h –– расстояние между заземлителями, х – расстояние между точкой касания и ближайшим заземлителем.
Теперь можем рассчитать напряжение прикосновения: Uпр = ⱷгз — ⱷос = ⱷгз*(r*(h-r)/(х*(h-х)), соответственно, коэффициент прикосновения для группового заземления будет α = (r*(h-r)/(х*(h-х)):
Учитывая приведенные выше выражения, можно утверждать, что наибольший уровень напряжения и значение коэффициента прикосновения будут в том случае, когда точка основания будет располагаться между заземлителями, то есть, при x=h/2. Соответственно αмакс = 1- 4r * (h-r)/h2, откуда получаем UПРмакс = ⱷгз * αмакс.
Снижение напряжения вплоть до минимального, как и в предыдущем примере, будет при максимальном приближении к заземлению.
Заметим, что при большом числе электродов заземления рассчитать высокий электрический потенциал (максимальное напряжение) практически нереально, поэтому применяется метод прямых измерений.
Измерения
Данный вид измерений предписывается проводить в производственных помещениях, где установлено технологическое оборудование и имеются устройства выравнивающие потенциал. Последние положено устанавливать на оборудование, для которого характерен высокий ток замыкания на землю. Выравнивание потенциала также производится на объектах с протяженным токопроводящим оборудованием, где возможно возникновение потенциала вследствие нарушения изоляции фазных проводов.
Перед тем, как приступить к проверке, измеряются сопротивления заземления и нулевых защитных подключений. Далее отключают ввод и подключают схему, наподобие той, что представлена ниже.
 Схема для измерения напряжения прикосновения
Схема для измерения напряжения прикосновенияОбозначения:
- Tr1 – Автотрансформатор.
- R- Резистор, с сопротивлением, соответствующим телу человека (как правило 1,0 кОм).
- SW – Выключатель.
- V1, V2 – Измерительные приборы.
- А – Заземлитель корпуса оборудования.
- B – Токопроводящая пластина, имитирующая ступню человека.
Алгоритм измерений следующий:
- На собранную схему подается питание от источника тока, используя при этом вольтметр V1 для контроля напряжения.
- По показаниям второго прибора определяют Uпр путем измерения напряжения между заземлителем корпуса оборудования (A) и металлическим щупом, погруженным (забуренным) в основание на глубину 30,0 см на удалении 25 и более метров от заземляющего электрода. Данный показатель покажет U
- После этого делают измерение величины напряжения на пластине имитаторе ступни (UB).
- Включают выключатель SW и измеряют величину напряжения (U1) между имитатором ступни и заземляющим электродом.
- Рассчитывают напряжение прикосновения по формуле Uпр = 2/(1/UB+1/U1):
Обратим внимание, что в настоящее выпускаются приборы, позволяющие снять необходимые для электробезопасности показатели и другие важные характеристики.
Меры защиты
Наиболее эффективный способ защиты от пагубного воздействия высокого напряжения прикосновения – установка заземлителей в непосредственной близости от электроустановок. Не менее эффективно действует выравнивание потенциала покрытия, это также снижает величину шагового напряжения. В этом случае применяется схема контурного заземления, ее пример приведен на рисунке.
 Пример контурного заземления
Пример контурного заземленияКак видно из приведенного примера, групповые заземлители расположены сеткой. При этом вертикальные электроды размещены таким образом, чтобы расстояние между ними было меньше длины заземляющего стержня. В случае замыкания фазного провода на токопроводящую поверхность одного из электроприборов, за счет соединения с другими заземлителями, ток будет растекаться таким образом, что уровень потенциала будет примерно одинаков в любой точке основания.
Таким образом, разность потенциалов между основанием и корпусом электроприбора будет стремиться к нулю, соответственно, таким же будет и напряжение шага и прикосновения.
Обратите внимание, что вне поверхности защищенной контуром наблюдается резкий спад уровня потенциала заземления, увеличивая опасность поражения. Сделать падение напряжения более пологим можно при помощи металлических шин, размещенных за периметром контура.
Профилактика
В число профилактических мер для снижения вероятности поражения от косвенного прикосновения входит:
- Проверка сопротивления изоляции кабелей, обмоток электромашин и других токоведущих элементов. В случае снижения сопротивления изоляции или ее повреждения, во избежание линейного или однофазного замыкания, проблемная электрическая сеть должна быть отключена.
- Измерение сопротивления заземления, оно не должно превышать допустимую величину.
- Проверка надежности заземления нейтрали (нулевого провода).
- Регулярная поверка устройств защитного отключения на предмет срабатывания от тока замыкания и соответствие другим параметрам.
- Поскольку человеческое тело обладает малым сопротивлением, то при работе с электроприборами следует использовать, как минимум, резиновые коврики. Учитывая непредсказуемость появления напряжения прикосновения на корпусе оборудования, такая мера предосторожности не будет лишней.
- Отслеживание режимом электроустановок, чтобы не допустить их нештатной работы и т.д.
Рекомендуем прочитать:
Рис. 1. Схема напряжения прикосновения:
1 — автотрансфорамтор; 2 — зеземлитель электроустановок; 3 — электрод, имитирующий ступню человека (выполнен в виде медной пластины; RT — резистор, имитирующий сопротивление человека (RT = 1000 Ом)
Соответствующий алгоритм измерений напряжения прикосновения применён в приборе MZC-310S.
Рис.2. Измерение напряжения прикосновения
Измерение напряжения прикосновения Uв происходит после коммутации в измерителе резистора значением 1 кОм между зажимами U2 и UST/T (UB). Резистор показывает сопротивление человека, а зажим UST/T (UB) соединяется с электродом (зондом), имитирующем ступни человека на основании полов помещения.
Измеритель MRP-200 измеряет напряжение прикосновения Uв двумя способами: измерением прироста напряжения на зажиме РЕ во время протекания в цепи установленного номинального дифференциального тока УЗО и измерение по отношению к потенциалу земли. В первом случае происходит оценка ожидаемого напряжения прикосновения. С целью определения действительного значения напряжения прикосновения следует подключить к гнезду прибора заземлитель (добавочный электрод, находящийся в надежном соприкосновении с землей). Прибор автоматически обнаружит подключение к заземлителю, и на дисплее появится символ .
Рис. 3. Измерение параметров УЗО, при помощи измерительных проводов с острым зондом или кабеля с сетевой вилкой UNI-SCHUKO (пунктирная линия обозначает добавочный провод, подключенный к потенциалу земли)
Новинки СОНЭЛ – приборы из серии индикаторов напряжения P-1, P-2, P-3 позволяют удобно и быстро проконтролировать методом однополюсной индикации наличие напряжения на корпусе электроустановки более 50 В.
Методика измерения напряжения прикосновения
Результаты измерения напряжения прикосновения во многом определяют действенность выбранных мер по обеспечению электробезопасности, и подбор эффективной методики проведения замеров позволяет избежать непредвиденных ситуаций.
Напряжение прикосновения – величина, ответственная за контактное напряжение, возникающие в случае деформации открытой токопроводящей части. В электроустановках с вольтажом менее 1 кВ с системой TN измеряемая величина довольно невелика, для её определения следует рассчитать падение напряжения при учете полного сопротивления всех защитных проводников.
На данную величину непосредственно влияет режим работы электроустановки – если при нормальных режимах напряжение прикосновения относительно мало, то при возникновении аварийных ситуаций (повреждение важных элементов электроустановки) напряжение повышается в разы до момента срабатывания предусмотренных защитных устройств.
Нормы для проведения замеров
При выборе методики измерений специалисты электролаборатории опираются на следующие нормативные документы и постановления:
- Сроки, объемы и особенности проведения замеров для всех типов объектов регламентируются ПТЭЭП (приложение №3; пункт 28.10). Измерения могут проводиться в установках с системой TN и TT, свольтажом до 1 кВ, при этом обязательным условием является наличием системы уравнивания/выравнивания потенциалов, предотвращающих возможность поражения током.
- Выбор контрольных точек для замеров осуществляется с учетом требований п. 1.8.39 ПУЭ (издание 7). Для различных типов электрооборудования с вольтажом до 1 кВ, выполненного в соответствии со всеми действующими нормами на прикосновение напряжения, контрольные точки определяются во время проектирования, при присоединении естественных заземлителей.
- Предельно допустимые значения величин для установок с различным типом реализации нейтрали приведены в таблицах ГОСТ-а 12.1.0380-82 отдельно для различных режимов и разных токов.
При замерах напряжения сопротивление тела человека моделируется резисторами различных номиналов, с помощью металлических пластин или других моделей.
Программа измерений
Нормативные документы накладывают ограничения на условия для проведения замеров – так температура не должна быть минусовой при средней влажности, если же электроустановка обслуживается в предельных условиях (+25? С при влажности от 75%), обычные нормы для напряжения прикосновения должны уменьшаться минимум в 3 раза.
Специалисты электролаборатории применяют различное измерительное оборудование в зависимости от его результативности в конкретных условиях, но класс точности приборов при этом не ниже 2,5.
Содержание методики измерений зависит от того, в комплекс каких испытаний (приемо-сдаточных, периодических) входит замер напряжения прикосновения.
При отсутствии необходимости в применении дополнительных мер защиты может использоваться метод амперметра-вольтметра, который при кратковременном воздействии напряжения до 0,5 кВ промышленной частоты (чередование импульсов до 0,1 с и пауз в 7-10 с) дает возможность добиться больших значений измерительного тока.
Суть данного метода заключается в одновременном снятии показаний для тока с заземляющего элемента и напряжения прикосновения, зависящего от этого тока.
В зависимости от условий, измерительная цепь может существенно видоизменяться. Конечным этапом замеров всегда выступает оформление протокола, содержащего все результаты испытаний.
Напряжение прикосновения – опасное явление, определение которого должны знать и обыватели, и специалисты. Проводя работу с электроприборами, нельзя исключать риск воздействия электрического тока и поражения им в любой момент. Причиной может стать косвенное или прямое соприкосновение с проводниками под напряжением.
Что называется напряжением прикосновения
Напряжение прикосновения возникает в момент прямого контакта человека с поврежденной изоляцией или с двумя контактами, проводящими ток. Контакт может быть косвенным или прямым, что напрямую зависит от устройства.
 Ознакомление с понятием на примере схемы
Ознакомление с понятием на примере схемыОбъекты, обладающие сразу двумя токопроводящими точками, опасны для живых организмов. Для предотвращения подобных проблем существуют приборы, измеряющие напряжение. После ответа на вопрос: «Что называется напряжением прикосновения?», – можно переходить к подробному изучению этого термина.
 Касание заземленных токоведущих частей
Касание заземленных токоведущих частейКак определить и проверить напряжение прикосновения
Для определения напряжения прикосновения можно использовать сварочный трансформатор. Так как измерения могут достигать больших значений, в токовую цепь включают короткозамыкатель (ИТК-1) и проверяют состояние тока при помощи импульсного вольтметра.
 Схема измерения импульсного тока
Схема измерения импульсного токаОсновными измерителями НС являются амперметр и вольтметр.
Для измерения используют схему, где два электрода представлены в виде металлических пластин. Они располагаются на земле или на полу и имитируют подошвы человека. Промежуток между ними равняется 0,8 м (приблизительная ширина шага). Поверхности должны быть в воде на глубине 3 см. На пластины ставят груз с массой не меньше 50 кг.
Напряжение прикосновения определяется по формуле U = (Uпп х Uф)/Uт, где:
- Uпп – величина показателя между пластинами;
- Uф – численная характеристика сети по фазам;
- Uт – напряжение сварочного трансформатора на вторичной обмотке.
 Схема определения напряжения прикосновения
Схема определения напряжения прикосновенияКак измерить напряжение прикосновения
Измерение НП проводят при помощи вольтметра и амперметра. Если нет возможности заземления одной точки с вторичной обмоткой, то устанавливают разделительный трансформатор и заземляют этот контакт повторно, то есть создают условия максимальной «опасности».
Расчеты проводят квалифицированные специалисты электролаборатории по тестированию установок. Перед измерениями проводники проверяются на постоянство тока, сопротивления и непрерывность проводки.
ИНП проводят при температуре не ниже +5 градусов. Электроустановка должна быть полностью смонтирована и подключена к действующей сети. Величина испытательного тока составляет 50% от номинального. При подключении современного измерительного прибора MI 3102H CL к необходимым частям электроустановки, производятся измерения.
 Устройство для измерения
Устройство для измеренияВажно! При превышении максимальной величины напряжения, проверяют сопротивление заземления.
После всех проведенных процедур, результаты измерений оформляют в виде протокола.
Как правильно рассчитать напряжение
В руководстве К. Е. Белявина, подробно описывается, что это за понятие и как его рассчитывать, к примеру, когда ток проходит через проводник, а именно через ногу человека, которая находится на земле. Утечка происходит от короткого замыкания на расстоянии 20 метров. Если источник погружен в грунт, то опасность маловероятна.
Там же рассмотрены вопросы, когда человек берет в руки провод под напряжением, или просто стоит рядом с ним. Именно во втором случае опасность наименьшая.
 Как оборванный провод может повлиять на человека, на расстоянии
Как оборванный провод может повлиять на человека, на расстоянииВажно! При напряжении соприкосновения нельзя далеко расставлять ноги, иначе можно получить смертельный удар. В случае трагедии, следует покинуть место аварии вприсядку.
Определяя напряжение прикосновения, рассматривают 2 схемы расчета сетей с нейтралью:
- глухозаземленной;
- изолированной.
Сила тока, находящаяся в аккумуляторе, сдерживается сопротивлением цепи, способным влиять на человека, вычисляется по формуле: Iч = Uф/(Rч + Rоб + Rп + R0) ≈ Uф / Rч, где:
- R0 – сопротивление трансформатора.
- R0 ≤ 10 Ом.
- Uф – напряжение по фазам.
- Rч – человеческое сопротивление.
Важно! Рабочее место – это площадка, где специалисты (электротехники) проводят измерения и ремонт. Нерабочее – это безопасное место для нахождения людей, которые не связанных с электроустановками.
 Схема сети с изолированной нейтралью
Схема сети с изолированной нейтральюМеры безопасности
Существует требование при работе с напряжением прикосновения, оно не должно превышать 65 В, считается безопасным при прикосновении, но не дольше 3 секунд. Порог зависит от того, в каком интервале находится:
- 0,1 сек – 740 В;
- 0,2 сек – 370 В.
Необходимые требования:
- Во время измерения применять защитную спецодежду;
- Профилактические работы, проводимые на металлических конструкциях, подразумевают оборудование изолирующими материалами;
- В случае длительных утечек тока, места прикосновения металлических конструкций (лестницы, трубы, заборы) должны граничить с заземлителем;
В случае с трубопроводами, с уверенностью можно сказать, что они находятся под катодной защитой и участок, изолированный от заземлителя, опасен. Граница находится на стыке территории здания или завода. В случае аварии рекомендовано устранить источник тока.
 Электромонтажник — в процессе работы, в соответствующей спецодежде
Электромонтажник — в процессе работы, в соответствующей спецодеждеЗачастую от воздействия тока или дуги люди получают травмы. Поражение организма может быть общим или местным. Степень поражения зависит от пути электрического тока по телу пострадавшего. Всего существует 5 этапов поражения электрическим током:
- Сокращения мышечной работы;
- Судороги;
- Сбои в работе сердца и затрудненное дыхание;
- Отсутствие сознания;
- Смерть.
Исход поражения током зависит от правильности и своевременности оказания помощи, а также корректного расчета воздействия электричества.
Чтобы исключить поражение током людей или животных, следует своевременно проводить изоляцию кабелей, обмотки электромашин и другие необходимые меры безопасности. При понижении сопротивления или возникновении замыканий в электрической сети, ее полностью отключают.
Измерение напряжения прикосновения
Подрядчик в смету на пусконаладочные работы вкЛючает расценки ТЕРп 01-11-014-01 Снятие характеристик для определения напряжения прикосновения в точках, указанных в проекте. Впервые столкнулись с этими расценками.
В каких случаях правомерно их применение?
В составе расценки трудозатраты инженера-наладчика и электромонтажника-наладчика 6 разряда – по 6,8 чел.-ч и все это на одну точку.
Ответ
В соответствии с п. 1.7.24. Правил устройства электроустановок (ПУЭ) «Напряжение прикосновения – напряжение между двумя проводящими частями или между проводящей частью и землей при одновременном прикосновении к ним человека или животного».
Напряжение прикосновения — напряжение, появляющееся на теле человека при одновременном прикосновении к двум точкам проводников или проводящих частей, в том числе при повреждении изоляции. Напряжение на корпусах и каркасах оборудования, а также на конструкциях, на которых последнее установлено, появляется в случае полного или частичного повреждения электрической изоляции самого оборудования или в случае повреждения питающих это оборудование кабельных или воздушных линий. Т.е., если человек прикоснется к электрооборудованию, корпус которого находится под напряжением, то между землей, на которой человек стоит, и корпусом электроприбора образуется определенная разность потенциалов и, прикоснувшись к прибору, человек замыкает цепь своим телом и попадает под напряжение прикосновения. Значение напряжения прикосновения зависит от параметров цепи замыкания на землю, вида потенциальной кривой заземлителя, расстояния между человеком, стоящим на земле и касающимся заземленного электрооборудования с поврежденной изоляцией, и заземлителем, а также от электрического сопротивления основания, на котором стоит человек. Для предотвращения попадания под напряжение
прикосновения применяется комплекс мероприятий, таких как заземление, а измерение напряжения прикосновения является составной частью проводимых мероприятий обеспечения электробезопасности.
Предельно допустимые значения напряжений прикосновения установлены ГОСТ 12.1.038-82’ «ССБТ. Электробезопасность. Предельно допустимые значения напряжений прикосновения и токов» Объем пусконаладочных работ, необходимых для подтверждения безопасности электроустановки и до пуска её в эксплуатацию, прописан в главе 1.8 Правил устройства электроустановок (ПУЭ ).
В п.1.8.39 «Заземляющие устройства» указывается, что измерение напряжения прикосновения выполняется в электроустановках, выполненных по нормам на напряжение прикосновения, «в контрольных точках, в которых эти значения определены расчетом при проектировании».
Более подробно об этом говорится в Правилах технической эксплуатации электроустановок потребителей (ПТЭЭП):
- В главе 2.7 «Заземляющие устройства», п.2.7.13: «Для определения технического состояния заземляющего устройства в соответствии с нормами испытаний электрооборудования (Приложение 3) должны производиться: измерение сопротивления заземляющего устройства; измерение напряжения прикосновения (в электроустановках, заземляющее устройство которых выполнено по нормам на напряжение прикосновения), проверка наличия цепи между заземляющим устройством и заземляемыми элементами, а также соединений естественных заземлителей с заземляющим устройством;».
- В приложении 3. «Нормы испытаний электрооборудования и аппаратов электроустановок потребителей» требования, касающиеся определения напряжения прикосновения, излагаются в п. 26.2. Проверка напряжения прикосновения на территории электроустановки и напряжения на заземляющем устройстве, где приводятся указания о том, что проверка: «Производится в электроустановках, выполненных по нормам на напряжение прикосновения в контрольных точках, в которых значения напряжения прикосновения определены при проектировании…», и п. 28.10 раздела 28. Электроустановки, аппараты, вторичные цепи, нормы испытаний которых не определены в разделах 2-27, и электропроводки напряжением до 1000 В, где измерение напряжений прикосновения и шага «производится в животноводческих комплексах, банях с электронагревателями и на других объектах, где в целях предотвращения электротравматизма выполнено уравнивание и выравнивание потенциалов».
Но, в любом случае, измерение напряжения прикосновения выполняется в контрольных точках, в которых эти значения определены расчетом при проектировании, т.е. количество точек прикосновения, в которых должны сниматься характеристики, определяется проектировщиками. Следовательно, для применения в сметном расчете норм (расценок) из таблицы ГЭСНп(ФЕРп, ТЕРп)-01-11-014 необходимо обоснование из проекта.
Пользу электроэнергии трудно переоценить – это источник «жизни» практически всего, что нас окружает, начиная от элементарного освещения и заканчивая работой мощного технологического оборудования. Тем не менее, электричество несет серьезную угрозу человеку, ведь удары электрического тока способны принести:
- болевые ощущения;
- ожоги тела;
- смерть человека.
Вопросами ограничения общения человека с электричеством, точнее с его опасными последствиями занимается электробезопасность, среди ее терминологии можно встретить такое понятие, как напряжение прикосновения – попробуем разобраться, что это такое.
Суть и опасность напряжения прикосновения
По сути, под этим термином принято считать напряжение, характеризующееся разностью потенциалов между двумя точками, доступными при одновременном прикосновении человеком и образующими электрическую цепь. В нашем случае это участок земли под ногами и часть корпуса электрооборудования (электрической установки) с которым происходит соприкосновение. Понятие напряжения прикосновения необходимо рассматривать с учетом:
- шаговых напряжений;
- зоны растекания токов.
Эти определения позволяют делать вывод, что наибольшее значение величины напряжения прикосновения (величины тока поражения) будет соответствовать максимальному возможному расстоянию при случайном прикосновении.
Государственным стандартом ГОСТ 12.1.038-82 регламентированы величины допустимого напряжения прикосновения при условии их суммарного суточного воздействия на человека не более 10 минут:
- 2 В для переменного тока 50 Гц;
- 3 В для переменного тока 400 Гц;
- 8 В для постоянного тока.

На фото видно показания измерительного прибора, 121 вольт, между заземленной розеткой и корпусом холодильника, который включен в незаземленную розетку.
Более высокие падения напряжения принято считать вредными.
Пути защиты от напряжения прикосновения
Основной защитой от поражений электрическим током является надежная электрическая изоляция проводов. При случайном прикосновении человека к токоведущим частям через его тело протечет наибольший электрический ток, равный частному от деления напряжения на сопротивление тела. При исправной изоляции ее сопротивление составляет не менее 1 мОм (для цепей до 1000 В) и 0.5 мОм (220/380 В).
Учитывая, что величина сопротивления изоляции, включенной последовательно с сопротивлением человека несоизмеримо выше, она ограничивает токи, протекаемые через тело человека безопасными, практически равными нулю величинами. Изоляция токоведущих частей должна регулярно проверяться на соответствие нормам, измерения величины сопротивления производятся мегаомметром.
Эффективным средством является защитное заземление, с сопротивлением переходных контактов не превышающим 0.01 Ом. Контакт присоединения электроустановки переменного тока к заземлению должен обеспечиваться сварным или болтовым соединением.
Для систем заземления TN-C-S или TN-S эффективной мерой защиты является применение устройств защитного отключения или дифференциальных автоматов. Другими способами защиты от напряжения прикосновения можно считать:
- расположение опасного оборудования на недосягаемой высоте;
- установка защитных ограждений опасных зон;
- оснащение предупреждающей сигнализацией;
- использование плакатов и знаков.
Важным моментом считается обязательное применение средств индивидуальной защиты.
Смотрите также другие статьи :
Для чего нужно заземление
Само по себе напряжение для жизни человека опасности не несет – можно находиться под потенциалом без ущерба для здоровья, угроза возникает при прохождении через тело человека электрического тока. Безопасным считается ток, не превышающий 1 миллиампера, однако уже сила тока в 50 мА может привести к остановке сердца.
Подробнее…Для чего применяется УЗО
Защитным отключением в случае появления дифференциальных токов, равных току утечки занимается устройство защитного отключения (УЗО). При этом контролируемый ток утечки зависит от типа прибора и может начинаться от 10 мА. Устанавливать защитный прибор необходимо последовательно с входным автоматом.
Подробнее…Измерение напряжения прикосновения и шага
Назначение замеров
Напряжение между двумя точками расположенными на расстоянии усредненной длины шага, называется шаговым.
Места контакта проводников с поверхностью земли или полом, обладают наибольшим потенциалом. Отдаляясь от поверхности, потенциал уменьшается. Увеличение сечения проводника пропорционально полному квадрату радиуса, на расстояниях около 18-25м может условно приравниваться к 0. При увеличении площади опоры возрастает опасность шагового напряжения.
Напряжение между точками, до которых можно одновременно дотронуться, называют напряжением прикосновения.
Величина напряжения зависит от нескольких факторов:
- схемы замеряемой цепи;
- нейтрали и её исполнения;
- реализации изоляции токопроводящих элементов;
- величины емкостей токопроводящих элементов.
Для безопасности персонала обязательно проводятся измерение и расчет напряжений шага и прикосновения. Не проводя проверок не реализуешь защиту оборудования при скачках напряжения.
Нормы и методика проведения испытаний
В соответствии с нормативной документацией измерения проводятся в помещениях где электроустановки замыкаются на землю, в помещениях с большой протяженностью металлических и токопроводящих установок. В таких помещениях при пробое изоляции возможно появление потенциалов.
Измерения напряжения прикосновения проводят:
- при отсутствии возможности отключения заземления на время проведения замеров;
- при высоком риске пробоев на землю в небольшой удаленности от тестируемого заземления или около оборудования, подключенного к данному заземлению;
- если контур оборудования, соприкасающийся с землей, несущественно отличается от размеров проверяемого заземления.
Для осуществления замеров используют специальное оборудование, с его помощью проверяется правильность подключения оборудования. Нормы величин отличаются типами и свойствами критического режима:
- однофазное замыкание частей под напряжением на землю в сетях до 1кВ;
- замыкание элементов установок на землю от высшего напряжения подстанции 6-10кВ/0,4;
- замыкание на землю в сетях с напряжением 6-35 кВ;
- однофазное замыкание на корпус в сетях до 1кВ;
- замыкание на землю от высшего напряжения с глубоким вводом при напряжении в 110кВ;
- замыкание на землю в сетях с напряжением 110 кВ с глубоким вводом;
В каждом конкретном случае рассчитываются величина напряжения, максимальная длительность воздействия, время отклика элементов защиты.
Совершая измерения разрабатывается комплекс мер для предотвращения любых несчастных случаев, для реализации рабочего плана, а также для реализации процесса эксплуатации в соответствии с нормами электробезопасности.
Messen von Spannungen – Национальные инструменты
1. Überblick zu Spannungsmessungen
Spannung ist die Diffrenz des elektrischen Potentials zwischen zwei Punkten einer elektrischen oder elektronischen Schaltung, умереть в Вайн-Вольте. Mit Spannung Wird Die Potentile Energie eines elektrischen Felds gemessen, mit der ein elektrischer Strom in einem elektrischen Leiter verursacht wird. Die meisten Messgeräte können Spannungswerte messen.Zwei gängige Messungen sind die Messung von Gleichspannung (DC) и Wechselspannung (AC). |  |
Nach oben
2. Durchführung einer Gleichspannungsmessung
Obwohl viele Sensoren Gleichspannungen ausgeben, die mit einem Multimeter oder einem Datenerfassungsgerät gemessen werden können, liegt der Hauptaugenmerk dieses Artikels auf allgemeinen Gleichspannüngensen de megenis de megenen de megenis de megünchengentüngüstegünchengüstegünchengüstegüntengüntegüntegünten – также – Германия
Grundlagen der Spannungsmessung
Um das Vorgehen beim Messen von Spannungen zu verstehen, muss bekannt sein, wie die Messung durchgeführt wird. Все права защищены. Дифференциал im Электронный потенциал Потенциал zwischen zwei Punkten in einer elektrischen Schaltung. Es besteht jedoch Verwirrung darüber, wie ein solcher Bezugspunkt für die Messung festgelegt wird. Der Bezugspunkt der Messung ist der Spannungspegel, auf den für die Messung Bezug genommen wird.
Methoden zum Ermitteln des Bezugspunks
Es gibt zwei Methoden zum Messen von Spannungen: massebezogen und diffell.
Массебезоген Spannungsmessungen
Eine Methode от darin, умереть Spannung в Bezug auf einen gemeinsamen Erdungspunkt zu messen. Скорее всего, «Erdungen» стабилен и не имеет значения 0 V. Der Begriff «Erdung» является штучным фоном, он является специалистом в области науки и техники, в том числе 0 правопреемников, окружающих, не может быть подан в прямом смысле этого слова.
Die massebezogenen Eingangsanschlüsse können für jeden Kanal genutzt werden, der folgende Bedingungen erfüllt:
- Das Eingangssignal ist größer als 1 V.
- Die Leitungen, die das Signal mit dem Gerät verbinden, sind länger als 3 m.
- Das Eingangssignal darf einen gemeinsamen Bezugspunkt mit andderen Signalen haben.
Die Bezugsmasse wird entweder vom Gerät bereitgestellt, das die Messung durchführt, oder von dem externen Signal, das gemessen wird.Wird der Bezug durch das Gerät bereitgestellt, heißt diese Конфигурация «Ссылочный односторонний режим» (RSE, massebezogenes Messen), и без сигнала Сигнал bereitgestellt wird, spricht man vom «Не ссылочный односторонний режим» MESSEN).
Die meisten Messgeräte bieten ähnliche Pin-Konfigurationen für das Messen von Аналог Eingangssignalen. In der folgenden Abbildung wird diese Art der Messung mit einem CompactDAQ-Chassis und einem Analogeingangsmodul des Typs NI 9205 даргетестельт (vgl.Abbildung 1).

Abbildung 1. CompactDAQ-шасси с техническими характеристиками NI 9205
В Abbildung 2 wird der Anschlussplan für RSE-Spannungsmessungen unter Einsatz eines Шасси Типов NI CDAQ-9178 и Модули NI 9205 Sowie Die Pinbelegung des Moduls gezeigt. Контакт 1 entspricht dabei dem Kanal «Аналоговый вход 0» и контакт 17 dem gemeinsamen Bezugspunkt.
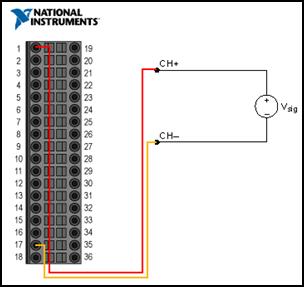
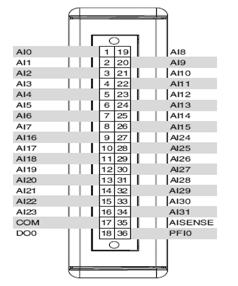
Abbildung 2.Наземный ссылочный односторонний режим (massebezogenes Messen)
In Abbildung 3 sehen Sie den Anschlussplan für NRSE-Spannungsmessungen mit Hilfe eines cDAQ-9178-Шасси с модулем Тип NI 9205. Вход Abbildung entspricht Контакт 1 дем Канальный «Аналоговый вход 0» и Контакт 35 аналоговый аналоговый аналоговый вход 35 аналоговый индекс Смысл”. Dieser Kanal stellt insbesondere für NRSE-Messungen den Bezug zur Masse der Signalquelle her.
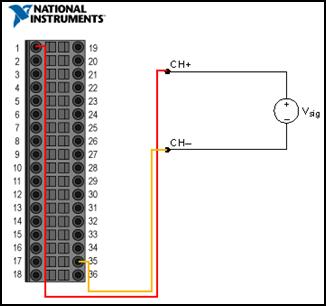
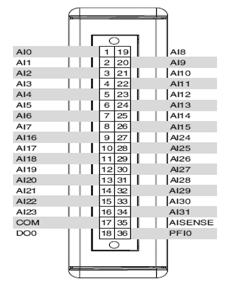
Abbildung 3.Односторонний режим без ссылок (nicht massebezogenes Messen)
Messung дифференциал Spannungen
Eine weitere Möglichkeit der Spannungsmessung besteht darin, die «diffellele» Spannung zwischen zwei unterschiedlichen Punkten in einer elektrischen Schaltung zu bestimmen. Zum Messen der Spannung a einem Wiverstand z. B. wird die Spannung и beiden Enden des Widerstands gemessen. Разница между ценами в Спеннунге – и гг.В деле Regel sind Messungen diffellerler Spannungen hilfreich beim Bestimmen der Spannung, die über einzelnen Elementen einer Schaltung „abfallen“, oder Falls, die Signalquellen verrauscht sind.
Дифференцированный Eingangsanschlüsse sind besonders geeignet für einen Kanal, der eine der folgenden Bedingungen erfüllt:
- Das Eingangssignal ist kleiner als 1 V.
- Die Leitungen zwischen Gerät и Signalquelle sind länger als 3 m.
- Für das Eingangssignal ist ein сепаратор Massebezugspunkt oder ein отделяет Rücksignal erforderlich.
- Die Signalleitungen verlaufen durch verrauschte Umgebungen.
In Abbildung 4 sehen Sie den Anschlussplan для дифференцированных Spannungsmessung mit Hilfe eines cDAQ-9178-Шасси с модулем Тип NI 9205. In Abbildung entspricht Контакт 1 дем Канал «Аналоговый вход 0» и Контакт 19 аналоговый аналоговый индекс 19 аналоговый индекс 8“ .
Отличительный признак Spannungen ist das отрицательный Сигнал с аналогом Pin verbunden, аналог прямой связи Kanal gegenüber liegt, der mit dem Positiven Сигнал verbunden ist.Beispielsweise würde «Аналоговый вход 0» с положительным сигналом и аналоговым входом 8 «Недостаток аналогового входа» «Аналоговый вход 1» с положительным сигналом и аналоговым входом 9 с отрицательным сигналом usw. Verbunden Werden. Der Nachteil der diffellenlen Spannungsmessung besteht darin, dass die Anzahl der Kanäle für die Messung, аналог Eingangssignale praktisch um die Hälfte reduziert wird.
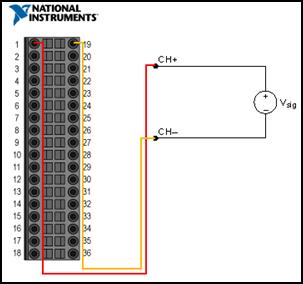

Abbildung 4.Messung дифференциал Spannungen
Arten von Signalquellen
В настоящее время он не имеет ничего общего с общепринятыми понятиями.
Erdfreie Signalquellen
Eine erdfreie Signalquelle ist nicht mit dem dem Erdungssystem des Gebäudes verbunden, sondern besitzt einen isolierten Massebezugspunkt. Zu den erdfreien Signalquellen gehören z. B. Ausgangsspulen von Transformatoren, Thermoelemente, batteriebetriebene Geräte, Ausgänge von optischen Isolatoren und Isolationsverstärker.Ein Messgerät oder eine Vorrichtung mit isoliertem Ausgang ist eine erdfreie Signalquelle. Die Bezugsmasse eines erdfreien Signals muss mit der Erdung des Geräts verbunden sein, um einen lokalen Bezugspunkt für das Signal auf dem Gerät herzustellen. В конце концов, в конце концов, Eingangssignal, да sich die Quelle außerhalb des Gleichtakteingangsbereichs.
Geerdete Signalquellen
Eine geerdete Signalquelle ist der der Erdungsanlage eines Gebäudes verbunden, somit is sie bereits mit einem gemeinsamen Erdungspunkt, в Безуге-на-Дасе, Германия, Фораусгезетцт, Дасс-дас-Дасс-дю-Зерс-дюшельз-дюс-дюс-дюс-дюшель-дю-Зессбергес, ГерманияВ Diese Kategorie упал з. B. nicht isolierte Ausgänge von (Mess-) Geräten, die mit dem Stromnetz des Gebäudes verbunden sind. Die Erdpotentialdifferenz zwischen zwei Messgeräten, die and dasselbe Stromnetz eines Gebäudes angeschlossen sind, находящийся в дер Регель, 1 и 100 мВ. Wenn Kabel in der Gebäudeinstallation nicht ordnungsgemäß angeschlossen sind, kann der Unterschied größer sein. Венне Гердеет Сигналквель фальш ангесшлоссен вирд, канн сич диезе Дифференц алл Мессфелер бемеркбар махен.Folgen Sie den Anleitungen zum Anschließen geerdeter Signalquellen, um die Diffrenz des Massepotentials zum gemessenen Signal aufzuheben.
В Abbildung 5 sehen Sie Verschiedene Arten von Signalquellen sowie die optimalen Anschlusspläne basiere auf der индивидуальный мессетод. В Abhängigkeit der Art des Signals Каннская лучшая Метода по Спецназму Зеин Бессерен Ergebnis als eine andere Methode führen.
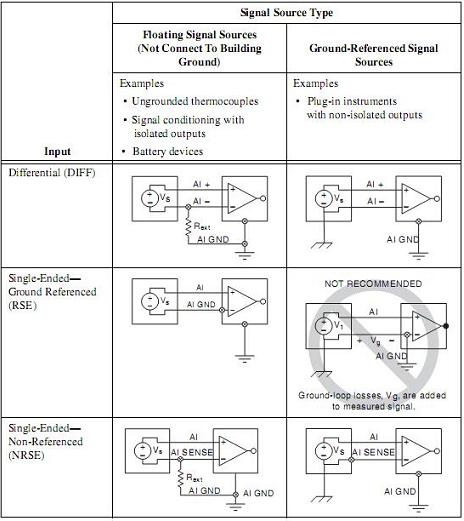
Abbildung 5. Gängige Signalquellen im Vergleich zu empfohlenen Eingangskonfigurationen
Mehr zu Полевая проводка и факторы шума для аналоговых сигналов.
Messungen Hoher Spannungen und Isolierung
Bei der Messung hoher Spannungen sind viele Sachverhalte zu berücksichtigen. Wenn ein Datenerfassungssystem eingerichtet wird, sollte die erste Überlegung der Sicherheit des Systems gelten. Das Durchführen von Hochspannungsmessungen kann für die Gerätschaften, Den Prüfling and sogar for the Sie und Ihre Kollegen gefährlich werden. Вы можете узнать, как работает система, так как она изолирована для обмена сообщениями. Выделите ее как единое целое, так и в то же время.
Die Isolierung sorgt für die elektrische und physikalische Trennung von zwei Teilen eines Messgeräts und kann in elektrische Isolierung und Sicherheitsisolierung unterteilt werden. Bei der elektrischen Isolierung werden Masseleitungen zwischen zwei elektrischen Systemen getrennt. Bei der elektrischen Isolierung werden Masschleifen unterbrochen, der Gleichtaktbereich des Datenerfassungssystems vergrößert und die Masseleitung mit einem Erdungssystem verbunden.Der Begriff Sicherheitsisolierung bezieht sich auf bestimmte Anforderungen zum Schutz von Personen vor gefährlichen Spannungen. Gleichzeitig wird vermieden, dass hohe Spannungen und Transientenspannungen eines elektrischen Systems auf andere elektrische Systeme übertragen werden, mit denen Anwender в Berührung kommen könnten.
Das Einbeziehen von Isolierung in ein Datenerfassungssystem hat drei primäre Funktionen: Верхний фон от основного собрания, Unterdrückung von Gleichtaktspannungen und Gewährleistung der Sicherheit.
Mehr zu Типы изоляции и соображения при проведении измерений.
Masschleifen
Masschleifen sind die häufigste Ursache für Rauschen bei Datenerfassungsanwendungen. Sie treten auf, wenn zwei verbundene Anschlüsse in einer Schaltung unterschiedliche Massepotentiale haben, был dazu führt, dass Strom zwischen den beiden Punkten fließt. Die lokale Erdung eines Systems Канц Мехрэд Вольтер-де-Унтер-дер-Энд-дер-Энд-дер-Нехстен Гебаудес леген и Блицзиншл в дер Нехе Кеннен ден Унтершайф мерере хундер эт терзэнд вольт анстейген лассен.Diese zusätzliche Spannung selbst cann zu erheblichen Fehlern bei der Messung führen, doch der Strom, der sie verursacht, kann zudem Spannungen in nahegelegene Leitungen einkoppeln. Diese Fehler können als Transienten oder periodische Signale in Erscheinung treten. Wenn beispielsweise eine Masseschleife mit Wechselstromleitungen mit 60 Hz gebildet wird, erscheint das unerwünschte Wechselstromsignal als ein periodischer Spannungsfehler in der Messung.
Beim Vorhandensein von Masseschleifen gleicht die gemessene Spannung, U m , Der Summe der Signalspannung, U s , 93090, g, , высшая профессиональная федерация промышленности Германии VGL.Abbildung 6). Потери Dieses ist im Allgemeinen keine Gleichspannung. Aus diesem Grund erhält man ein verrauschtes Messsystem, in dessen Messungen häufig Netzfrequenzkomponenten (60 Hz) auftauchen.
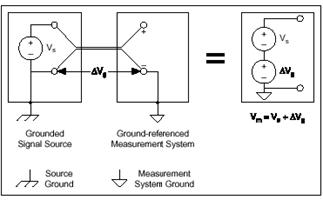
Abbildung 6. Eine geerdete Signalquelle, gemessen mit einem
massebezogenen System, führt zu Masseschleifen
Um Masseschleifen zu vermeiden, sollte sichergestellt werden, dass nur eine Bezugsmasse im Messsystem vorhanden ist. Альтернативные решения для мессенджера verwendet werden.Der Einsatz isolierter Аппаратные средства, необходимые для массовой информации и обмена сообщениями, без всяких сомнений.
Bei der bereits genannten NI-CompactDAQ-Konfiguration bietet das Analogseingangsmodul NI 9229 Eine Kanal-zu-Kanal-Isolierung von 250 V.
Abbildung 7. Analogeingangsmodul NI 9229 mit Kanal-zu-Kanal-Isolierung
Gleichtaktspannung
Отличный идеальный обмен сообщениями о потенциальных возможностях сотрудничества (+) и дем негатива (-) Eingang eine Rolle.Die дифференциал Spannung ist das gewünschte Сигнал. Es kann jedoch ein unerwünschtes Сигнал vorhanden sein, das beiden Seiten eines diffellen Schaltkreispaares gemeinsam ist. Diese Spannung wird als Gleichtaktspannung bezeichnet. Ein ideles дифференцировки Messsystem unterdrückt Gleichtaktspannungen, anstatt sie zu messen. Bei realen Geräten gibt es verschiedene Einschränkungen, wie Gleichtaktspannungsbereich und -verhältnis, durch welche die Unterdrückbarkeit von Gleichtaktspannungen begrenzt ist.
Der Gleichtaktspannungsbereich является окончательным и максимальным zulässige eingangsseitige Spannungsschwankung gegenüber der Masse des Messsystems. Bei Überschreitung dieses Bereichs kommt es nicht nur zu Messfehlern, sondern das Gerät kann auch Schaden nehmen.
Mit der Gleichtaktunterdrückungsrate wird die Möglichkeit eines Messsystems bezeichnet, Gleichtaktspannungen zu unterdrücken. Verstärker mit höheren Gleichtaktunterdrückungsraten unterdrücken Gleichtaktspannungen effektiver.
В общей сложности Messsystem лучше всего подходит для Pfad in Schaltung zwischen dem Ein- und dem Ausgang. Так что, пожалуйста, Eigenschaften des Verstärkers den Pegel der Gleichtaktsignale begrenzen, die am Eingang eingespeist werden. Mit Hilfe von Trennverstärkern wird der leitende elektrische Pfad beseitigt and die Gleichtaktunterdrückungsrate stark erhöht.
Isolierungstopologien
Kenntnisse der Isolierungsarchitektur eines Geräts sind bei der Konfiguration eines Messsystems von entscheidender Bedeutung.Die Kosten und Geschwindigkeiten variieren je nach Architektur.
Канал-Зу-Канал
Отказаться от Isolalierungsarchitektur ist die Isolierung jedes einzelnen Kanals. В настоящее время Architektur sind alle Kanäle untereinander und von anderen nicht isolierten Systemkomponenten getrennt. Jeder Kanal verfügt zudem über eine eigene isolierte Stromversorgung.
Hinsichtlich der Geschwindigkeit stehen verschiedene Architekturen zur Auswahl. Die Schnellere Lösung приводят в движение Einsatz eines Trennverstärkers mit einem A / D-Wandler pro Kanal, а также все параллельные канальские параллельные zugegriffen werden kann.Bei den Analogeingangsmodulen NI 9229 and NI 9239 is the jeder Kanal einzeln isoliert, um höchste Messgenauigkeit zu gewährleisten.
Für eine kostengünstigere Architektur, die jedoch auch langsamer ist, wird jeder isolierte Eingangskanal in einen einzigen A / D-Wandler gemultiplext.
Eine weitere Methode zur Bereitstellung einer kanalweisen Isolierung ist der Einsatz einer gemeinsamen isolierten Stromversorgung für alle Kanäle. В осеннем сезоне, в настоящее время он не может похвастаться версегментами, а также отличными характеристиками Stromversorgung beschränkt, а также интерфейсом Front-End-Spannungsteiler.
Каналбанк
Eine weitere Isolierungsarchitektur ist die Anordnung der Kanäle в Каналбанкен. Dabei werden mehrere Kanäle zu Gruppen mit einem gemeinsamen Trennverstärker zusammengefasst. В этой книге «Изоляция общества и науки» можно сказать, что у него есть много друзей. Jedoch werden zwischen den Kanalbänken und den nicht isolierten Komponenten des Messsystems starke Änderungen der Gleichtaktspannung толерантный.Einzelne Kanäle sind nicht isoliert, wohingegen Kanalbänke gegen andere Bänke und gegen Masse isoliert sind. В настоящее время у него есть все, что можно сказать о Varite, da Hierbei Mehrere Kanäle von einem Trennverstärker profitie und von einer Stromversorgung.
умереть в течение всего срока действия модуля NI, wie beispielsweise die Module NI 9201 и NI 9221, sind bankweise isoliert und ermöglichen genaue Analogmessungen bei geringeren Kosten.
Дарстеллен фон Мессунген в NI LabVIEW
Ist der Sensor and das Messgerät angeschlossen, können Daten mit der grafischen Программное обеспечение Программное обеспечение LabVIEW wie gewünscht dargestellt und analysiert werden (vgl.Abbildung 8).
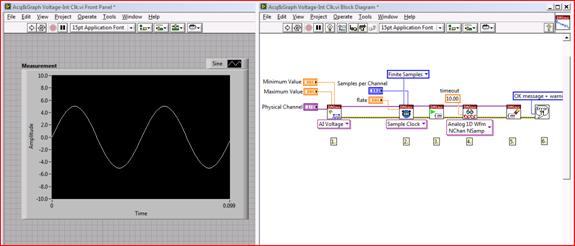
Abbildung 8. Spannungsmessung mit LabVIEW
Nach oben
3. Nächste Schritte
Веб-трансляция Sehen Sie sich den «Изучить сбор данных» an. Лернциеле:
- Die Hauptkategorien von Datenerfassungsgeräten und die Auswahl eines geeigneten Geräts für Ihre Anwendung
- Erfassen, Analysieren und Darstellen von Daten mit NI LabVIEW
Проверка напряжения прикосновения | Мегомметр
Что такое напряжение прикосновения?
Термин «напряжение прикосновения» относится к опасности поражения электрическим током, присутствующей на любой открытой металлической конструкции или защитном проводнике. Напряжение существует, если есть путь заземления с более высоким сопротивлением к открытой металлической конструкции, чем к заземлению под ногами или другой части открытой металлической конструкции в непосредственной близости, как показано на рисунках 1a и 1b. Напряжение прикосновения (В) является результатом протекания тока на землю (I Δn ), умноженного на сопротивление земли (R A ), так что напряжение прикосновения находится на:
V = I Δn R A
Обычно можно увидеть значительное напряжение прикосновения в системах заземления TT, где сопротивление заземления (RA) может быть достаточно высоким.В разделе 411.5.3 BS7671: поправка 3 к 2008 году отмечается, что RA может достигать 200 Ом. В других типах систем заземления такое высокое сопротивление заземления будет указывать на неисправность.
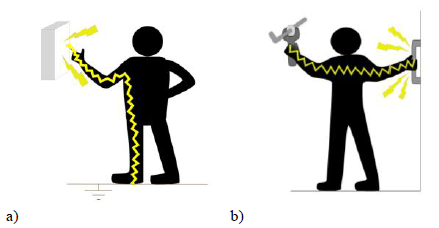
Рисунок 1 – Опасные напряжения прикосновения между различными заземленными поверхностями
Зачем проверять напряжение прикосновения?
Сенсорное напряжение проверяется, чтобы гарантировать, что люди не могут получить удар током от простого прикосновения к металлической поверхности или двум металлическим поверхностям одновременно.Это могут быть краны на кухне или в ванной, металлические выключатели света, радиаторы или корпус прибора.
Требования к напряжению прикосновения
В соответствии с разделом 411.5.3 BS7671: 2008 Поправка 3, напряжение прикосновения не должно превышать 50 В в любом месте установки. В некоторых особых местах, например в бассейнах, напряжение прикосновения не должно превышать 25 В.
Испытательные приборы, отвечающие требованиям BS EN 61557, должны выполнять предварительную проверку при тестировании, чтобы убедиться, что потенциал земли не поднимается до опасного уровня во время теста.Это будет применяться к проверке полного сопротивления контура заземления и испытанию УЗО, поскольку эти испытания включают в себя создание тока на земле. Если ожидается, что испытательный ток будет создавать опасное напряжение, тестер должен заблокировать испытание и показать предупреждение, например> 50 В.
Проверка напряжения прикосновения
Если есть подозрение на высокое напряжение прикосновения между металлической поверхностью и землей, это можно проверить с помощью счетчика с контактом напряжения прикосновения, такого как серия MFT1700.Сенсорный контакт позволяет пользователю просто дотронуться пальцем до контакта, пока к рассматриваемой металлоконструкции прикладывается один измерительный провод с предупреждением измерителя о значительном напряжении, как показано на рисунке 2. Это очень хороший тест для использования в выборочные проверки напряжения прикосновения, так как вы можете просто бродить вокруг установки, коротко касаясь зонда на металлических поверхностях, чтобы найти опасные напряжения.
Рисунок 2 – Проверка напряжения прикосновения на заземленных поверхностях
Если предполагается высокое напряжение прикосновения между двумя металлическими точками в непосредственной близости, его можно измерить с помощью измерителя с опцией измерения напряжения переменного тока.
, 
Название продукта и модель: сенсорный вольтметр Особенности продукта серии H60: сенсорное, высоковольтное сопротивление. Низкое энергопотребление, сигнализация
1. Потребляемый ток прибора яркого экрана: 8 мА; После ожидания экрана машины напряжение снижается до 25 мкА, работа в широком напряжении: постоянный ток 8-150 В, защита от обратного
2.Точность вольтметра составляет около 1%, что можно исправить.
3. Рабочая температура: -30 ~ + 80 ℃ Светодиод имеет длительный срок службы, устойчивость к высоким и низким температурам и вибрации.
4. рабочая влажность: 10 ~ 80% (без конденсации)
5. Габаритные размеры: 48 × 29 × 21 мм
6. Монтажное отверстие: 45,5 × 26,5 мм
О настройках
В правом верхнем углу номера продукта находится сенсорная зона.Если вы нажмете два раза, а затем нажмете в течение 3 секунд, вы войдете в режим настройки для отображения 1-U. Отпустите кнопку, нажмите и удерживайте в течение 1 секунды, чтобы отобразить b-L, отпустите кнопку, а затем последуют U-L и U-H.
2. При отображении 1-U, нажмите кнопку в течение 3 секунд, чтобы исправить измерение напряжения. В это время отпустите более длинную клавишу, чтобы подстроить напряжение вверх, отпустите более длинную клавишу, чтобы подстроить напряжение вниз, и настройку можно будет выполнить повторно. После того, как экран мигнет, он будет автоматически сохранен и завершен.Как правило, коррекция не требуется!
3. Режим подсветки можно настроить, когда отображается b-L, а значение можно изменить, нажав и удерживая кнопку в течение длительного времени. 0 – выключить экран после прикосновения к свету в течение 5 секунд, а 1 – включить нормально. По умолчанию 0
4. Когда отображается U-L, можно установить минимальное значение сигнала тревоги по напряжению батареи, а также изменить значение, нажав и удерживая кнопку в течение длительного времени. По умолчанию 0 В, а не вкл.
5. Когда отображается U-H, можно установить значение сигнала тревоги о перенапряжении батареи, а также изменить значение, нажав и удерживая кнопку в течение длительного времени. По умолчанию 0 В, а не вкл.
6. После установки каждого значения регулировки следующая операция не может быть выполнена до тех пор, пока экран не замигает и автоматически не сохранится и не выйдет. В противном случае новое значение регулировки не будет сохранено!
Примечания:
1: Если вы не можете войти в режим настройки, пожалуйста, отпустите вашу руку более чем на 3 секунды и попробуйте снова!
2 : В режиме закрытия экрана с сенсорной задержкой: когда экран закрыт, напряжение будет определяться регулярно, начиная с 1 минуты и каждые 10 часов, экономя электроэнергию! Если имеется избыточное давление, будильник всегда будет вызываться и не будет спать.Перенапряжение означает сигнал опасности!




3-фазные системы и 1-фазные
Расчет напряжения прикосновения и тока заземления может выполняться в однофазных или трехфазных системах.
 Расчет напряжения прикосновения и тока заземления
Расчет напряжения прикосновения и тока заземленияВ соответствии с входами для трехфазной системы: Вольт между линиями и нейтралью (Vn), Расчетная нагрузка линии 1 (A1), Расчетная нагрузка линии 2 (A2), Расчетная нагрузка линии 3 (A3), Сервисное нейтральное сопротивление Z1 и сопротивление земли (3-точечный метод) R, электронная таблица рассчитает следующие параметры:
- Сопротивление каждой фазы
- Сопротивление нейтрали / заземления
- Нейтральный ток и нагрузка Напряжение касания
- для металлической части к земле
- Сопротивление тела и ток тела
Для однофазных систем входные параметры: Напряжение цепи и ампер, нагрузка, земля, сопротивление электрода и корпуса.



