Как найти c в физике формула: Как найти c из формулы Q=cm(t2-t1)

Содержание

Кинематика | Формулы по физике

Путь, время, скорость

Найти

Известно, что:

Svt =

Вычислить ‘S’

Равномерное движение

Найти

Известно, что:

xx_0vt =

Вычислить ‘x’

Равномерно ускоренное движение: ускорение

Найти

Известно, что:

avv0t =

Вычислить ‘a’

Равномерно ускоренное движение: скорость

Найти

Известно, что:

vv0at =

Вычислить ‘v’

Равномерно ускоренное движение: путь

Найти

Известно, что:

svta =

Вычислить ‘s’

Равномерно ускоренное движение: координата

Найти

Известно, что:

xx0vta =

Вычислить ‘x’

Высота тела, брошенного вертикально вверх (вниз)

Найти

Известно, что:

hh0v0tg =

Вычислить ‘h’

Скорость тела, брошенного вертикально вверх (вниз)

Найти

Известно, что:

vv0gt =

Вычислить ‘v’

Скорость, ускорение, время

Найти

Известно, что:

vat =

Вычислить ‘v’

Скорость свободно падающего тела

Найти

Известно, что:

vgt =

Вычислить ‘v’

Центростремительное ускорение

Найти

Известно, что:

avR =

Вычислить ‘a’

Угловая скорость

Найти

Известно, что:

ωφt =

Вычислить ‘ω’

Равномерное круговое движение

Найти

Известно, что:

lRφ =

Вычислить ‘l’

Равномерное круговое движение: линейная скорость

Найти

Известно, что:

vRω =

Вычислить ‘v’

Период вращения

Найти

Известно, что:

TtN =

Вычислить ‘T’

Период вращения

Найти

Известно, что:

TπRv =

Вычислить ‘T’

Период вращения

Найти

Известно, что:

Tπω =

Вычислить ‘T’

Центростремительное ускорение

Найти

Известно, что:

aπRT =

Вычислить ‘a’

Центростремительное ускорение

Найти

Известно, что:

aπRn =

Вычислить ‘a’

Частота вращения

Найти

Известно, что:

nT =

Вычислить ‘n’

Центростремительное ускорение

Найти

Известно, что:

aωR =

Вычислить ‘a’

Дальность броска тела, брошенного под углом к горизонту

Найти

Известно, что:

xv0tα =

Вычислить ‘x’

Высота подъема тела, брошенного под углом к горизонту

Найти

Известно, что:

yv0tαg =

Вычислить ‘y’

Вертикальная скорость тела, брошенного под углом к горизонту

Найти

Известно, что:

v_yv0αgt =

Вычислить ‘v_y’

Максимальная высота подъема тела, брошенного под углом к горизонту

Найти

Известно, что:

h_максv0αg =

Вычислить ‘h_макс’

Общее время движения тела, брошенного под углом к горизонту

Найти

Известно, что:

tv0αg =

Вычислить ‘t’

Максимальная дальность броска тела, брошенного под углом к горизонту

Найти

Известно, что:

s_максv0g =

Вычислить ‘s_макс’

Дальность броска тела, брошенного горизонтально

Найти

Известно, что:

xx0vt =

Вычислить ‘x’

Высота подъема тела, брошенного горизонтально

Найти

Известно, что:

yy0gt =

Вычислить ‘y’

Общее время движения тела, брошенного горизонтально

Найти

Известно, что:

t_максhg =

Вычислить ‘t_макс’

Все формулы по физике – intmag24.

Все основные формулы по школьной физике, которые помогут для подготовке к ЕГЭ, а также для решения задач в 7, 8, 9, 10 и 11 классах. Все формулы структурированы, что позволит из запомнить гораздо быстрее.

Равномерное движение
S= U∙t, U= S/t, t=S/U	Уравнение движения при равномерном движении? где U-скорость, t-время, S-расстояние
x=x₀+U₀t	Координата при равномерном прямолинейном движении
Равномерное движение по окружности
T=t/N, T=1/v, Т=2π/ω T=2πR/U, T=2π ∙√(R/a)	T – период N – количество оборотов
v=1/T, v=ω/2π, v=U/2πR, v=1/2π ∙√(a/R), v=N/t, v=L/t	v – частота R – радиус окружности
ω=2π/Т, ω=2πv, ω=φ/t ω=U/R, ω=√(a/R)	ω – угловая скорость t – время
υ=2πR/Т, υ=2πvR, U=ωR U=√(a/R), U=L/t	U – линейная скорость тела
a=υ²/R, a=ω²R, a=Uω a=4π²R/T²	a – центростремительное ускорение
L=φR	L – длина дуги окружности (φ – угол поворота (в радианах))
Равноускоренное движение
X=X₀+υ₀∙t+(a∙t²)/2	Уравнение прямолинейного равноускоренного движения
S=U₀t+a∙t²/2 S= (υ²-υ₀²) /2а S= (υ+υ₀) ∙t /2 = U_ср∙t	Расстояние при равноускоренном движении
υ=υ₀+a∙t	Rонечная скорость тела при равноускоренном движении
a=(υ-υ₀)/t	Ускорение
U=√(2gh) t_{падения}=√(2h/g) S=U∙√(2h/g)	— Падение тела с высоты — Горизонтальный бросок (h-высота падения, g – ускорение свободного падения 9,8м/с², t-время падения, S-расстояние)
h_max=U₀²/2g	Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью U₀
t_{подъема}=U₀/g	Время подъема тела на максимальную высоту
t_полета=2U₀/g	Полное время полета (до возвращения в исходную точку)
S_торм=U₀²/2a	Тормозной путь тела двигавшегося до начала торможения со скоростью U₀ , а затем тормозившего с ускорением а
U = √(U₀²+(gt)²) tgβ = U_y/Ux = gt/U₀	Полная скорость в произвольный момент времени при горизонтальном броске, и угол наклона скорости к горизонту
h_max=(U₀∙sinα)²/2g t_{подъема}=(U₀∙sinα)/g	Бросок с земли на землю под углом к горизонту равным α.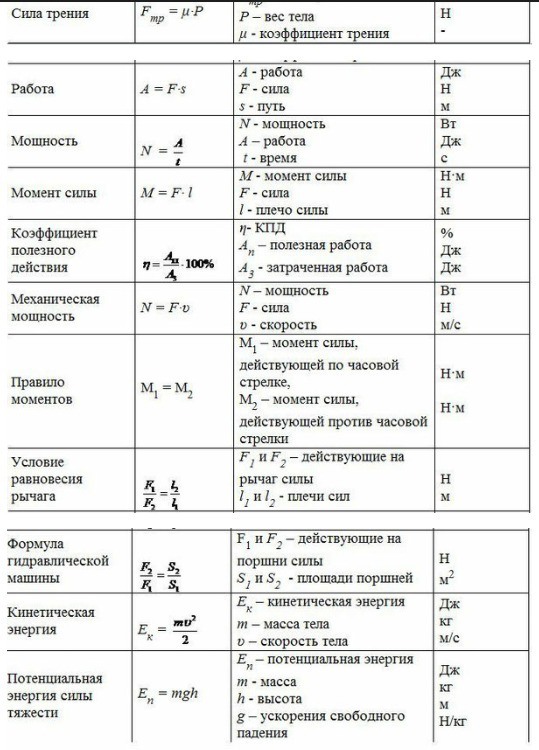 Время подъема до высшей точки и максимальная высота
S_x=U_x∙t_полетаS=U₀∙cosα∙t_полета S=U₀²∙sin2α/g t_полета=2U₀²∙sinα/g	Полное время и дальность полета при броске под углом к горизонту
Импульс
p=mυ	Импульс тела
Ft=∆p	Импульс силы
F=∆p/∆t	Второй закон Ньютона в импульсной форме
p_k=p_n	Закон сохранения импульса: в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется
Энергия
A=F∙S∙cosα	Механическая работа (F – сила, S – путь,  – угол между направлением движения и силой)
P=A/t=F∙υ	Мощность (если мощность переменная, то рассчитывается средняя мощность)
Eп=mgh	Потенциальная энергия тела, поднятого над землей
Eп=kx²/2	Потенциальная энергия упруго деформированного тела
η=Aп/Аз	Коэффициент полезного действия
Ek=mυ²/2	Кинетическая энергия тела
Молекулярная физика
ρ=m/V	Плотность (ρ – его плотность, m – масса вещества, V – объем)
ν=N/ Na = m/M	Количество вещества (N – число частиц вещества, содержащееся в массе вещества m, Na – число Авогадро, m0 – масса одной молекулы вещества, M – молярная масса)
М=m/ν	Молярная масса
m₀=m/N=M/Na	Масса одной молекулы вещества
P=nkT=1/3nm₀υ²pV=NkT	Основное уравнение молекулярно-кинетической теории идеального газа (p – давление газа, n = N/V – концентрация его молекул, m0 – масса одной молекулы, Uкв – средняя квадратичная скорость)
U_кв=√(3kT/m₀), U_кв=√(3RT/M)	Cредняя квадратичная скорость
Ek=3/2∙kT	Средняя кинетическая энергия поступательного движения одной молекулы (k – постоянная Больцмана, T – абсолютная температура)
kNa=R	Связь универсальной газовой постоянной и постоянной Авогадро
PV=m/M∙RT	Уравнение состояния идеального газа (уравнение Клапейрона-Менделеева)
PV=const (m=const и T= const)	Газовые законы. Закон Бойля-Мариотта (изотермический процесс)
V/T=const (m=const и p= const)	Газовые законы. Закон Гей-Люссака (изобарный процесс)
P/T =const (m=const и V= const)	Газовые законы. Закон Шарля (изохорный процесс)
PV/T=const (m=const )	Газовые законы. Универсальный газовый закон (Клапейрона)
V=Vo(1+λt)	Тепловое расширение газов описывается законом Гей-Люссака. (V – объем жидкости при 0 °С, V – при температуре t , λ – коэффициент объемного расширения жидкости)
l=lo(1+αt) S=So(1+2αt) V=Vo(1+3αt)	Изменение линейных размеров, площади и объема тела (lo, So , Vo – соответственно длина, площадь поверхности и объем тела при 0 °С, α – коэффициент линейного расширения тела)
Динамика
Первый закон Ньютона	Существуют такие системы отсчёта, называемые инерциальными, относительно которых материальные точки, когда на них не действуют никакие силы (или действуют силы взаимно уравновешенные), находятся в состоянии покоя или равномерного прямолинейного движения
F=ma	Второй закон Ньютона (F – сила, m – масса, а – ускорение).
F_1-2= — F_2-1	Третий закон Ньютона (сила действия равна силе противодействия)
F_упр = kx	Сила упругости (k – жесткость пружины, х – величина растяжения (или сжатия) пружины, оно равно разности между конечной и начальной длиной деформируемой пружины)
Fy=-kx	Закон Гука
F_{тр.скольжения}=F_{тр.макс} = μТ	Сила трения скольжения ( μ– коэффициент трения, N – сила реакции опоры.)
F=mg F=G∙M∙m/r²g=G∙M/R_n²	Сила тяжести — Закон Всемирного тяготения (G – гравитационная постоянная, F – сила с которой притягивается тело массой m к телу или планете массой M, r – расстояние между центрами этих тел)
g_h= GM/(R_n+h)² = g_h= gR_n²/(R_n+h)²	Ускорение свободного падения на некоторой высоте от поверхности планеты (h – высота над поверхностью планеты)
U= √(GM/(R_n+h)) U= √(gR_n²/(R_n+h))	Скорость спутника на круговой орбите радиусом r = R_n + h
U=√(gR_n)	Первая космическая скорость (скорость движения спутника по орбите вблизи поверхности планеты)
T₁²/T₂²= R₁³/R₂³	Закон Кеплера для периодов обращение T1 и T2 двух тел, вращающихся вокруг одного притягивающего центра на расстояниях R1 и R2 соответственно
Р=m(g+a) Р=m(g-a)	Вес тела, движущегося с ускорением а↑ Вес тела, движущегося с ускорением а↓
Термодинамика
Q=cm(T₂-T₁) C=cm Q=C(T₂-T₁)	Количество теплоты (энергии) необходимое на нагревания некоторого тела (C-теплоемкость, c-удельная теплоемкость, m- масса, t- температура)
Q=λm	Количество теплоты при плавлении (λ – удельная теплота плавления, m – масса расплавившегося тела или кристаллизовавшейся жидкости)
Q=rm	Количество теплоты при парообразовании (r – удельная теплота парообразования, m – масса испарившейся жидкости или конденсировавшегося пара)
Q=qm	Количество теплоты при сгорании топлива (q – удельная теплота сгорания топлива, m – масса сгоревшего топлива)
A=P∙ΔV = m/M∙ R∙ΔT, p = const	Работа идеального газа
U=3/2∙M/µ∙RT	Внутренняя энергия идеального одноатомного газа
ΔU=A+Q	Первый закон (начало) термодинамики (ЗСЭ) (Q – теплота полученная (отданная) газом)
η= (Q₁— Q₂)/ Q₁	КПД тепловых двигателей
η= (Т₁— Т₂)/ Т₁	КПД идеальных двигателей (цикл Карно)
ρ=pM/RT	Абсолютная влажность (ρ — абсолютная влажность, р – парциальное давление водяного пара, М – молярная масса, R – универсальная газовая постоянная, Т – абсолютная температура)
φ=ρ/ρ₀∙100% φ=P/P₀∙100%	Относительная влажность (ρ — абсолютная влажность, ρ₀ -количество водяного пара, которое необходимо для насыщения 1 м3 воздуха при данной температуре) (P — давление водяного пара, Pо — давление насыщенного пара при данной температуре)
E_p = σS	Поверхностное натяжение (σ – коэффициент поверхностного натяжения данной жидкости)
F_н= σL	Сила поверхностного натяжения, действующая на участок границы жидкости длиной L
Статика и Гидростатика
M=F∙ℓ	Момент силы (F – сила, ℓ – плечо силы, т. е. кратчайшее расстояние между точкой опоры, относительно которой происходит вращение и линией действия силы)
Р=F/S	Давление (F – сила, S – площадь на которую распределено действие силы)
P=ρ∙g∙h P=P₀+ρ∙g∙h	Давление на глубине жидкости (p0 – атмосферное давление, ρ – плотность жидкости, g – ускорение свободного падения, h – высота столба жидкости)
Fa=ρ_ж∙g∙V	Закон (сила) Архимеда (V – объем погруженной части тела, который иногда также называют объемом вытесненной жидкости)
Электростатика
q = Ne	Электрический заряд (N – количество элементарных зарядов, е – элементарный заряд)
λ=q/L, σ=q/S, ρ=q/V	Линейная, поверхностная и объемная плотность заряда
F=k∙q₁∙q₂/R²F=k∙q₁∙q₂/εr²	Закон Кулона (сила электростатического взаимодействия двух зарядов величиной q1 и q2, находящихся на расстоянии r друг от друга в веществе с диэлектрической проницаемостью ε):
E=1/(4πεε₀)	Напряженность электрического поля, которую создает заряд Q на расстоянии r от своего центра
E= σ/(2εε₀)	Напряженность электрического поля, которую создает заряженная плоскость
ε=E₀/E	Диэлектрическая проницаемость
E=F/q	Напряженность электрического поля
E=k∙q/R²	Напряженность электрического поля точечного заряда
E=2πkσ	Напряженность электрического поля бесконечной плоскости
W= k∙q₁q₂/R = k∙q₁q₂/εr	Потенциальная энергия взаимодействия двух электрических зарядов
U=Ed, Δφ=E∙ Δl	Cвязь между напряженностью поля и напряжением
A=qU, U=A/q	Работа электрического поля, Напряжение
A= qEd, U=E∙d	Работа электрического поля в однородном поле при перемещении заряда вдоль его силовых линий, Напряжение для однородного электрического поля
φ=W/q	Потенциал
φ=k∙q/R	Потенциал точечного заряда
C=q/U	Электроемкость
C=S∙ε∙ε₀/d	Электроемкость плоского конденсатора
q=CU	Заряд конденсатора
E = U/d = σ/εε₀	Напряженность поля внутри конденсатора
F=qE/2	Сила притяжения пластин конденсатора
W=qU/2=q²/2С=CU²/2	Энергия заряженного конденсатора
Электрический ток
I=q/t	Сила тока (q – заряд, протекший через некоторое поперечное сечение проводника за время t)
R=ρ∙ℓ/S	Сопротивление проводника (l – длина проводника, S – площадь его поперечного сечения, ρ – удельное сопротивление материала проводника)
R=R₀(1+αt)	Сопротивление проводника
I=U/R	Закон Ома для участка цепи (U – электрическое напряжение)
I₁=I₂=I, U₁+U₂=U, R₁+R₂=R	Законы последовательного соединения
U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R	Законы параллельного соединения
ε=A_ст/q	Электродвижущая сила источника тока, ЭДС (Aст – работа сторонних сил по перемещению заряда q)
I=ε/(R+r)	Закон Ома для полной цепи
I=ε/r	Сила тока короткого замыкания (R=0)
Q=A=I²Rt	Работа электрического тока (закон Джоуля-Ленца). Работа А электрического тока, протекающего по проводнику, обладающему сопротивлением преобразуется в теплоту Q выделяющуюся на проводнике
P=IU=U²/R=I²R	Мощность электрического тока
m = kQ = kIt	Электролиз. Масса m вещества, выделившегося на электроде, прямо пропорциональна заряду Q, прошедшему через электролит
Магнетизм
Fa=IBℓsinα	Сила Ампера (В – индукция магнитного поля, I – сила тока в проводнике, l – его длина, α – угол между направлением силы тока (т.е. самим проводником) и вектором индукции магнитного поля)
M = NBIS∙sinα	Момент сил, действующих на рамку с током (N – количество витков, S – площадь рамки, α – угол между нормалью к рамке и вектором магнитной индукции)
Fл=Bqυ∙sinα	Сила Лоренца (q – электрический заряд частицы, υ – её скорость, α – угол между направлением движения частицы и вектором индукции магнитного поля)
R=mU/qB	Радиус траектории полета заряженной частицы в магнитном поле
B=Fmax/ℓ∙I	Вектор магнитной индукции
Ф=BSсos α Ф=LI	Магнитный поток Φ через площадь S
Ei=ΔФ/Δt	Закон электромагнитной индукции
Ei=Вℓυsinα	ЭДС индукции при движении проводника
Esi=-L∙ΔI/Δt	ЭДС самоиндукции
Wм=LI²/2	Энергия магнитного поля катушки
Колебания
a+ω₀²x=0	Уравнение описывает физические системы способные совершать гармонические колебания с циклической частотой ω0
x = A cos (ωt + φ0)	Уравнением движения для гармонических колебаний (x– координата тела в некоторый момент времени t, A – амплитуда колебаний, ω – циклическая частота колебаний, φ0 –начальная фаза колебаний).
Х=Хmax∙cos ωt	Уравнение гармонических колебаний
T=t/N, v=N/t=1/T ω=2πv=2π/T	Связь некоторых характеристик колебательного процесса (T – период, N – количество полных колебаний, v – частота колебаний, ω – циклическая частота)
υ = x'(t) = –Aω sin (ωt + φ0)	Скорость тела при колебательном движении
υ_m = ωA	Максимальное (амплитудное) значение скорости
a = υ'(t) = x»(t) a = –Aω² cos (ωt + φ0)	Ускорение тела при колебательном движении
a_m = Aω²	Максимальное (амплитудное) значение ускорения
ω₀=√(g/ℓ) T=2π√ℓ/g	Циклическая частота и период колебаний математического маятника (l – длина маятника, g – ускорение свободного падения)
ω₀=√(k/m) T=2 π √m/k	Циклическая частота и период колебаний пружинного маятника (m – масса груза, k – коэффициент жесткости пружины маятника)
W=CU²/2+LI²/2 W=CU_max²/2=LI_max²/2	Электрический контур
T=2π ∙√LC ω=2π/T=1/(√LC)	Период колебаний кол. контура и циклическая частота
I_д=I₀/√2, I_д=I_max/√2 U_д=U₀/√2, U_д=U_max/√2	Переменный ток характеризуется действующими значениями силы тока и напряжения, которые связаны с амплитудными значениями соответствующих величин; Действующее значение силы тока и напряжения
P=U_дI_д=I_д²R=U_д²/R	Мощность в цепи переменного тока
U₁/U₂=n₁/n₂	Трансформатор: если напряжение на входе в трансформатор равно U1, а на выходе U2, при этом число витков в первичной обмотке равно n1, а во вторичной n2
λ= υТ=υ/v	Волны. Длина волны (υ – скорость распространения волны, T – период, v – частота)
X_L=ωL=2πLν	Индуктивное сопротивление
Xc=1/ωC	Емкостное сопротивление
Z=√(Xc-X_L)²+R²	Полное сопротивление
Оптика
L_опт=L_n	Оптическая длина пути (L – геометрическая длина траектории, по которой «идет» луч света, n – показатель преломление среды, в которой это происходит)
x=mλL/d	Интерференционная схема Юнга (L – расстояние между экраном и плоскостью в которой расположены две щели, d – расстояние между этими щелями, λ – длина волны света, которым освещаются щели).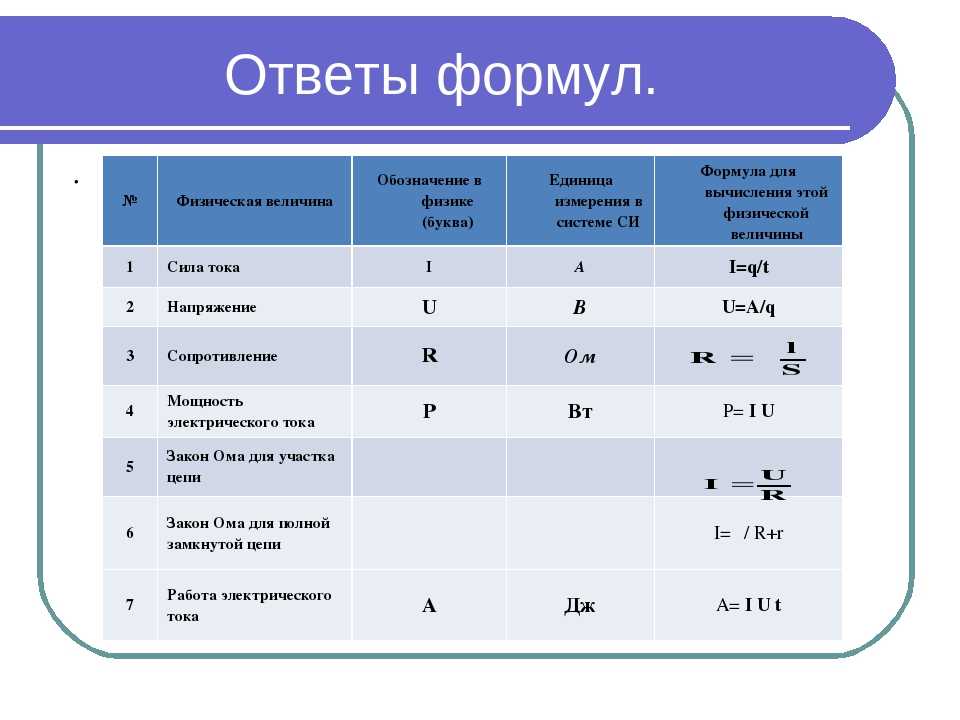
d∙sin φ=k λ	Формула дифракционной решетки (d – период решетки, или расстояние между соседними штрихами, φ – угол под которым наблюдается очередной дифракционный максимум, k – номер (порядок) максимума, λ – длина волны света, падающего на дифракционную решетку)
n₂₁=n₂/n₁= υ₁/ υ₂	Закон преломления света на границе двух прозрачных сред (α – угол падения, β – угол преломления, n1 – показатель преломления первой среды, из которой падает луч, n2 – показатель преломления второй среды, в которую проникает луч)
n₂₁=sinα/sinβ	Показатель преломления
1/F=1/d + 1/f	Формула линзы (d – расстояние от линзы до предмета, f – расстояние от линзы до изображения, F – фокусное расстояние, D – оптическая сила линзы)
D=1/F	Оптическая сила линзы
Δd=kλ, Δd=(2k+1)λ/2	max интерференции, min интерференции
Атомная и ядерная физика
E=hv=hc/λ	Энергия кванта света, т. е. фотона (h – постоянная Планка, λ – длина волны света, v – частота света)
P=mc=h/ λ=Е/с	Импульс фотона
hν=A_вых+(mU²/2)_max hν=A_вых+Ek, Ek=еU_зhν_min=A_вых=hc/λ	Формула Эйнштейна для внешнего фотоэффекта (ЗСЭ) (А_вых – работа выхода, слагаемое в скобках –максимальная кинетическая энергия вылетающих электронов, v – частота падающего света)
(mU²/2)_max=еU_з	Максимальная кинетическая энергия вылетающих электронов
ν_к = A_вых/h	Красная граница фотоэффекта
hν_nm = \|En – Em\|	Второй постулат Бора (правило частот). При переходе атома из одного стационарного состояния с энергией En в другое стационарное состояние с энергией Em излучается или поглощается квант, энергия которого равна разности энергий стационарных состояний
N=N₀∙2^—^t^/^T	Закон радиоактивного распада
E_CB=(Zm_p+Nm_n-Mя)∙c²	Энергия связи атомных ядер
Основы СТО
ℓ=ℓ₀∙√1-υ²/c²	Релятивистское сокращение длины. Длина тела, движущегося со скоростью V в инерциальной системе отсчета уменьшается в направлении движения до длины
t=t₁/√(1-υ²/c²)	Релятивистское удлинение времени события. Время, за которое происходит некоторое событие в движущейся системе отсчета с точки зрения наблюдателя из неподвижной системы отсчета
υ=(υ₁+υ₂)/1+ υ₁∙υ₂/c²	Релятивистский закон сложения скоростей
Е = mс²	Связь энергии и массы тела. Наименьшей энергией Е0 тело обладает в инерциальной системе отсчета относительно которой оно покоится и называется собственной энергией тела (энергия покоя тела)

Уравнения и формулы физики – макеты

Физика заполнена уравнениями и формулами, которые имеют дело с угловым движением, двигателями Карно, жидкостями, силами, моментами инерции, линейным движением, простым гармоническим движением, термодинамикой, работой и энергией.

Вот список некоторых важных физических формул и уравнений, которые следует держать под рукой, упорядоченных по темам, чтобы вам не приходилось искать их.

Угловое движение

Уравнения углового движения применимы везде, где есть вращательные движения вокруг оси. Когда объект повернулся на угол θ с угловой скоростью ω и угловым ускорением α , то вы можете использовать эти уравнения, чтобы связать эти значения вместе.

Для измерения угла необходимо использовать радианы. Кроме того, если вы знаете, что расстояние от оси равно r, , то вы можете вычислить пройденное линейное расстояние, с , скорость, v , центростремительное ускорение, a _c и силу , Ф _с . Когда объект с моментом инерции I (угловой эквивалент массы) имеет угловое ускорение α , тогда возникает чистый крутящий момент Στ.

Двигатели Карно

Тепловая машина берет тепло Q _h от высокотемпературного источника при температуре T _h и перемещает его к низкотемпературному стоку (температура T _{9 по курсу Q _c и при этом выполняет механическую работу, W . (Этот процесс можно обратить вспять, так что можно выполнить работу по перемещению тепла в противоположном направлении — тепловой насос.) Количество работы, выполняемой пропорционально количеству тепла, извлеченного из источника тепла, является КПД двигателя. Двигатель Карно является обратимым и имеет максимально возможный КПД, определяемый следующими уравнениями. Эквивалентом эффективности теплового насоса является коэффициент полезного действия.}

Жидкости

Объем А, В , жидкости с массой, м , имеет плотность, ρ . Сила, F , по площади, A , вызывает давление, P . Давление жидкости на глубине ч зависит от плотности и гравитационной постоянной, г . Объекты, погруженные в жидкость, создающие массу веса, Вт _вода _{вытесненные} , создают направленную вверх выталкивающую силу, F _{плавучесть} . Из-за сохранения массы объемный расход жидкости, движущейся со скоростью v , через площадь поперечного сечения A , является постоянным. Уравнение Бернулли связывает давление и скорость жидкости.

Сил

Масса А, м , ускоряется со скоростью, a , из-за силы, F , действующей. Силы трения, F _F , пропорциональны нормальной силе между материалами, F _Н , с коэффициентом трения мк. Две массы, м ₁ и м ₂ , разделенные расстоянием, r , притягивают друг друга в пропорции гравитационная постоянная Г :

Моменты инерции

Вращательный эквивалент массы — это инерция, I , , которая зависит от того, как масса объекта распределена в пространстве. Здесь показаны моменты инерции для различных форм:

Диск, вращающийся вокруг своего центра:
Полый цилиндр, вращающийся вокруг своего центра: I = mr ²
Полая сфера, вращающаяся с осью, проходящей через ее центр:
Обруч, вращающийся вокруг своего центра: I = mr ²
Точечная масса, вращающаяся на радиусе r: I = mr ²
Прямоугольник, вращающийся вокруг оси вдоль одного края, где другой край имеет длину r :
Прямоугольник, вращающийся вокруг оси, параллельной одному краю и проходящей через центр, где длина другого края равна г :
Стержень, вращающийся вокруг оси, перпендикулярной ему и проходящей через его центр:
Стержень, вращающийся вокруг оси, перпендикулярной ей и через один конец:
Сплошной цилиндр, вращающийся вокруг оси вдоль ее центральной линии:
Кинетическая энергия вращающегося тела с моментом инерции I и угловой скоростью ω :
Угловой момент вращающегося тела с моментом инерции, I , а угловая скорость ω :

Линейное движение

Когда объект в положении x движется со скоростью v , и ускорением a, в результате перемещения s , каждый из этих компонентов связан следующими уравнениями:

Простое гармоническое движение

Определенные виды силы приводят к периодическому движению, когда объект повторяет свое движение с периодом, T , с угловой частотой ω, и амплитудой A . Одним из примеров такой силы является пружина с жесткостью k . Положение x , скорость v и ускорение a, объекта, совершающего простое гармоническое движение, могут быть выражены синусом и косинусом.

Термодинамика

Беспорядочные колебательные и вращательные движения молекул, составляющих объект вещества, обладают энергией; эта энергия называется тепловая энергия. Когда тепловая энергия перемещается из одного места в другое, она называется теплотой, Q . Когда объект получает некоторое количество тепла, его температура T , повышается.

Кельвина ( K ), Цельсия ( C ) и Фаренгейта (F ) — это температурные шкалы. Вы можете использовать эти формулы для преобразования одной температурной шкалы в другую:

Теплота, необходимая для изменения температуры массы, m , увеличивается с константой пропорциональности, c , называется удельной теплоемкостью. В стержне из материала с площадью поперечного сечения A , длиной L и разностью температур на концах ΔT существует тепловой поток за время t , , определяемый выражением эти формулы:

Давление, P , и объем, V , из n молей идеального газа при температуре T определяется по этой формуле, где R — газовая постоянная:

В идеальном газе средняя энергия каждой молекулы KE _avg пропорциональна температуре с постоянной Больцмана k :

Работа и энергия

Когда сила, F , перемещает объект на расстояние с , которое находится под углом Θ ,затем работа, W , выполнена. Импульс p является произведением массы m , и скорости v . Энергия, которой объект обладает благодаря своему движению, называется KE .

25.3: Закон преломления

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 2727

OpenStax
OpenStax

Цели обучения

К концу этого раздела вы сможете:

Определять показатель преломления, зная скорость света в среде.

Заглянув в аквариум, легко заметить некоторые странности. Например, вы можете увидеть одну и ту же рыбу в двух разных местах (рис. \(\PageIndex{1}\)). Это связано с тем, что свет, идущий от рыбы к нам, меняет направление, когда покидает аквариум, и в этом случае он может идти двумя разными путями, чтобы попасть к нашим глазам. Изменение направления светового луча (обобщенно называемое искривлением), когда он проходит через изменения в материи, называется преломление . Преломление отвечает за огромный спектр оптических явлений, от действия линз до передачи голоса по оптическим волокнам.

Определение: ПРЕЛОМЛЕНИЕ

Изменение направления светового луча (приблизительно называемое изгибом), когда он проходит через изменения в материи, называется преломлением.

СКОРОСТЬ СВЕТА

Скорость света \(c\) влияет не только на преломление, это одно из центральных понятий теории относительности Эйнштейна. По мере повышения точности измерений скорости света оказалось, что \(с\) не зависит от скорости источника или наблюдателя. Однако скорость света точно зависит от материала, через который он проходит. Эти факты имеют далеко идущие последствия, как мы увидим в «Специальной теории относительности». Это устанавливает связи между пространством и временем и изменяет наши ожидания, например, что все наблюдатели измеряют одно и то же время для одного и того же события. Скорость света настолько важна, что ее значение в вакууме является одной из самых фундаментальных констант в природе, а также одной из четырех основных единиц СИ.

Рисунок \(\PageIndex{1}\): Глядя на аквариум, как показано на рисунке, мы можем видеть одну и ту же рыбу в двух разных местах, потому что свет меняет направление при переходе из воды в воздух. В этом случае свет может достигать наблюдателя двумя разными путями, и поэтому рыба как бы находится в двух разных местах. Это искривление света называется преломлением и отвечает за многие оптические явления.

Почему свет меняет направление при переходе из одного материала (среды) в другой? Это потому, что свет меняет скорость при переходе от одного материала к другому. Поэтому, прежде чем мы приступим к изучению закона преломления, полезно обсудить скорость света и то, как она меняется в различных средах.

Скорость света

Ранние попытки измерить скорость света, например, сделанные Галилеем, показали, что свет движется чрезвычайно быстро, возможно, мгновенно. Первое реальное свидетельство того, что свет распространяется с конечной скоростью, было получено датским астрономом Оле Ремером в конце 17 века. {8} м/с\) (всего 25% отличается от принятого сегодня значения). В последнее время физики измеряли скорость света различными способами и с возрастающей точностью. Один особенно прямой метод, использованный в 1887 году американским физиком Альбертом Майкельсоном (1852–1819 гг.31), показано на рисунке \(\PageIndex{2}\). Свет, отраженный от вращающегося набора зеркал, отражался от неподвижного зеркала на расстоянии 35 км и возвращался к вращающимся зеркалам. Время прохождения света можно определить по тому, как быстро должны вращаться зеркала, чтобы свет вернулся в глаз наблюдателя.

Рисунок \(\PageIndex{2}\): Схема раннего аппарата, использовавшегося Майкельсоном и другими для определения скорости света. При вращении зеркал отраженный луч лишь кратковременно направляется на неподвижное зеркало. Возвращающийся луч отразится в глаз наблюдателя только в том случае, если следующее зеркало повернулось в правильное положение как раз в тот момент, когда луч возвращается. Измерив правильную скорость вращения, можно измерить время прохождения туда и обратно и рассчитать скорость света.

Рассчитанное Майкельсоном значение скорости света всего на 0,04% отличалось от значения, используемого сегодня. 9{8} м/с\) используется всякий раз, когда достаточно трехзначной точности. Скорость света через вещество меньше, чем в вакууме, потому что свет взаимодействует с атомами в материале. Скорость света сильно зависит от типа материала, поскольку его взаимодействие с различными атомами, кристаллическими решетками и другими субструктурами различается.

Определение: ПОКАЗАТЕЛЬ ПРЕЛОМЛЕНИЯ

Мы определяем показатель преломления \(n\) материала как

\[n = \frac{c}{v}, \label{index}\]

где \(v\) – наблюдаемая скорость света в материале. Так как скорость света всегда меньше \(с\) в веществе и равна \(с\) только в вакууме, показатель преломления всегда больше или равен единице. То есть \(n \gt 1\).

В таблице \(\PageIndex{1}\) приведены показатели преломления некоторых репрезентативных веществ. Значения указаны для определенной длины волны света, потому что они немного меняются в зависимости от длины волны. (Это может иметь важные эффекты, такие как цвета, создаваемые призмой.) Обратите внимание, что для газов \(n\) близко к 1,0. Это кажется разумным, так как атомы в газах далеко друг от друга и свет распространяется со скоростью \(с\) в вакууме между атомами. Обычно для газов принимают \(n = 1\), если не требуется большая точность. Хотя скорость света \(v\) в среде значительно отличается от ее значения \(с\) в вакууме, это все же большая скорость.

Таблица \(\PageIndex{1}\): показатель преломления в различных средах
Средний	п
Газы при \(0ºC, 1 атм\)
Воздух	1.000293
Углекислый газ	1.00045
Водород	1. 000139
Кислород	1.000271
Жидкости при 20ºC
Бензол	1.501
Сероуглерод	1,628
Четыреххлористый углерод	1,461
Этанол	1,361
Глицерин	1,473
Вода пресная	1,333
Твердые вещества при 20ºC
Алмаз	2. 419
Флюорит	1,434
Стекло, заводная головка	1,52
Стекло бесцветное	1,66
Лед при 20ºC	1,309
Полистирол	1,49
Оргстекло	1,51
Кварц кристаллический	1,544
Кварц, плавленый	1,458
Хлорид натрия	1,544
Циркон	1,923

Пример \(\PageIndex{1}\): Скорость света в материи

Рассчитайте скорость света в цирконе, материале, используемом в ювелирных изделиях для имитации алмаза.

Стратегия:

Скорость света в материале \(v\) можно рассчитать на основе показателя преломления \(n\) материала с помощью уравнения \(n = c/v\) .

9{8} м/с. \end{align*}\]

Обсуждение:

Эта скорость чуть больше половины скорости света в вакууме и все еще высока по сравнению со скоростями, с которыми мы обычно сталкиваемся. Единственное вещество, указанное в таблице \(\PageIndex{1}\), которое имеет больший показатель преломления, чем циркон, — это алмаз. Позже мы увидим, что большой показатель преломления циркона заставляет его сверкать больше, чем стекло, но меньше, чем алмаз.

Закон преломления

На рисунке \(\PageIndex{3}\) показано, как луч света меняет направление при переходе из одной среды в другую. Как и прежде, углы измеряются относительно перпендикуляра к поверхности в точке пересечения ее световым лучом. (Некоторая часть падающего света будет отражаться от поверхности, но сейчас мы сосредоточимся на проходящем свете. ) Изменение направления светового луча зависит от того, как изменяется скорость света. Изменение скорости света связано с показателями преломления соответствующих сред. В ситуациях, показанных на рисунке \(\PageIndex{3}\), среда 2 имеет больший показатель преломления, чем среда 1. Это означает, что скорость света в среде 2 меньше, чем в среде 1. Обратите внимание, что, как показано на Рисунок \(\PageIndex{3a}\), направление луча приближается к перпендикуляру, когда он замедляется. И наоборот, как показано на рисунке \(\PageIndex{3b}\), направление луча отклоняется от перпендикуляра, когда он ускоряется. Путь точно обратим. В обоих случаях вы можете себе представить, что происходит, если представить, как вы толкаете газонокосилку с тротуара на траву и наоборот. При переходе с тропинки на траву передние колеса замедляются и тянутся в сторону, как показано на рисунке. Это такое же изменение направления, как и для света, когда он переходит из быстрой среды в медленную. При переходе с травы на пешеходную дорожку передние колеса могут двигаться быстрее, и косилка меняет направление, как показано на рисунке. Это тоже то же изменение направления, что и при переходе света от медленного к быстрому.

Рисунок \(\PageIndex{3}\): Изменение направления светового луча зависит от того, как изменяется скорость света при переходе из одной среды в другую. Скорость света больше в среде 1, чем в среде 2 в показанных здесь ситуациях. а) Луч света движется ближе к перпендикуляру, когда он замедляется. Это аналогично тому, что происходит, когда газонокосилка переходит с тропинки на траву. б) Луч света удаляется от перпендикуляра, когда он ускоряется. Это аналогично тому, что происходит, когда газонокосилка движется от травы к тропинке. Пути точно обратимы.

Величина, на которую луч света меняет свое направление, зависит как от угла падения, так и от величины изменения скорости. Для луча под заданным углом падения большое изменение скорости вызывает большое изменение направления и, следовательно, большое изменение угла. Точное математическое соотношение представляет собой закон преломления , или «закон Снеллиуса», который формулируется в виде уравнения

= n_{2} \sin\theta_{2}.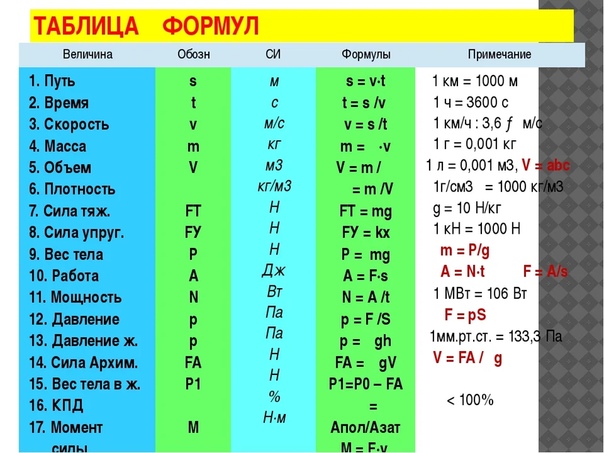 \label{25.4.2}\]

Здесь \(n_{1}\) и \(n_{2}\) – показатели преломления для сред 1 и 2, а \(\theta_{1}\) и \(\theta_{2} \) — это углы между лучами и перпендикуляром в средах 1 и 2, как показано на рисунке \(\PageIndex{3}\). Входящий луч называется падающим лучом, а выходящий луч — преломленным лучом, а связанные с ним углы — углом падения и углом преломления. Закон преломления также называют законом Снелла в честь голландского математика Виллеброрда Снелла (1591–1626), открывшего его в 1621 году. Эксперименты Снелла показали, что закон преломления соблюдается и что характеристический показатель преломления \(n\) может быть отнесены к определенному носителю. Снелл не знал, что скорость света различается в разных средах, но с помощью экспериментов он смог определить показатели преломления по тому, как световые лучи меняют направление.

ДОМАШНИЙ ЭКСПЕРИМЕНТ: СЛОМАННЫЙ КАРАНДАШ

Классическое наблюдение рефракции происходит, когда карандаш помещают в стакан, наполовину наполненный водой. {\circ}\). 9{\circ}}} \\[5pt] &= \frac{0,500}{0,375} \\[5pt] &=1,33. \end{align*}\]

Обсуждение

Это показатель преломления воды, и Снелл мог определить его, измерив углы и выполнив этот расчет. Тогда он нашел бы, что 1,33 является подходящим показателем преломления для воды во всех других ситуациях, например, когда луч проходит из воды в стекло. Сегодня мы можем проверить, что показатель преломления связан со скоростью света в среде, напрямую измерив эту скорость. 9{\circ}\). Мы можем посмотреть показатель преломления алмаза в таблице \(\PageIndex{1}\), найдя \(n_{2} = 2,419\). Единственное неизвестное в законе Снелла — это \(\theta_{2}\), которое мы хотим определить.

Решение

Решение закона Снеллиуса (уравнение \ref{25.4.2}) для \(\sin{\theta_{2}}\) дает

\[ \sin{\theta_{2}} = \ frac{n_{1}}{n_{2}}\sin{\theta_{1}}.\]

Ввод известных значений,

\[ \begin{align*} \sin{\theta_{2}} &= \фракция{1,00}{2,419{8} м/с\)

Показатель преломления \(n = \frac{c}{v}\), где \(v\) — скорость света в веществе, \(c\) — скорость света в вакууме, а \( п\) — показатель преломления.

Закон Снеллиуса, закон преломления, формулируется в виде уравнения \(n_{1} \sin_{\theta_{1}} = n_{2} \sin_{\theta_{2}}\).

Глоссарий

преломление: изменение направления луча света при прохождении через изменения в материи

показатель преломления: для материала, отношение скорости света в вакууме к скорости света в материале

Эта страница под названием 25.3: Закон преломления распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

Вернуться к началу

Была ли эта статья полезной?

Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать оглавление
нет
Метки
1. показатель преломления
2. преломление
3. Закон преломления Снеллиуса
4. источник@https://openstax.

Как найти c в физике формула: Как найти c из формулы Q=c*m*(t2-t1)

Кинематика | Формулы по физике

Все формулы по физике – intmag24.

Уравнения и формулы физики – макеты

Угловое движение

Двигатели Карно

Жидкости

Сил

Моменты инерции

Линейное движение

Простое гармоническое движение

Термодинамика

Работа и энергия

25.3: Закон преломления

Скорость света

Закон преломления

Глоссарий

Больше новостей

Добавить комментарий Отменить ответ

Как найти c в физике формула: Как найти c из формулы Q=cm(t2-t1)