Как найти e в физике: Электростатика | Формулы по физике

Электростатика | Формулы по физике

Электрический заряд

Найти

  Известно, что:

     qne =   

Вычислить ‘q’

Закон Кулона

Найти

  Известно, что:

     Fkq1q2r =   

Вычислить ‘F’

Постоянная Кулона

Найти

  Известно, что:

     kπε_0 =   

Вычислить ‘k’

Относительная диэлектрическая проницаемость

Найти

  Известно, что:

     εF_вакF_окр =   

Вычислить ‘ε’

Электрическое поле

Найти

  Известно, что:

     EFq =   

Вычислить ‘E’

Электрическое поле точечного заряда в вакууме

Найти

  Известно, что:

     Ekq_0r =   

Вычислить ‘E’

Электрическое поле точечного заряда в окружающей среде

Найти

  Известно, что:

     E_окрkq_0εr =   

Вычислить ‘E_окр’

Электрическое поле вне заряженной сферы

Найти

  Известно, что:

     Ekσ4πRr =   

Вычислить ‘E’

Электрическое поле вне заряженной сферы

Найти

  Известно, что:

     Ekqr =   

Вычислить ‘E’

Электрическое поле бесконечной заряженной плоскости

Найти

  Известно, что:

     Ek2πσ =   

Вычислить ‘E’

Электрическое поле бесконечной заряженной плоскости

Найти

  Известно, что:

     Eσε_0 =   

Вычислить ‘E’

Электрическое поле конденсатора

Найти

  Известно, что:

     Ekπσ =   

Вычислить ‘E’

Работа в электрическом поле

Найти

  Известно, что:

     AFΔ_d =   

Вычислить ‘A’

Потенциальная энергия системы двух точечных зарядов

Найти

  Известно, что:

     Wkq0qεr =   

Вычислить ‘W’

Работа в электрическом поле – разность потенциальных энергий

Найти

  Известно, что:

     AW1W2 =   

Вычислить ‘A’

Потенциал электростатического поля

Найти

  Известно, что:

     φWq =   

Вычислить ‘φ’

Напряжение – разность потенциалов

Найти

  Известно, что:

     Uφ1φ2 =   

Вычислить ‘U’

Работа переноса заряда

Найти

  Известно, что:

     AqU =   

Вычислить ‘A’

Потенциал электростатического поля вокруг точечного заряда

Найти

  Известно, что:

     φkq0εr =   

Вычислить ‘φ’

Напряжённость электростатического поля

Найти

  Известно, что:

     EUΔ_d =   

Вычислить ‘E’

Результирующее электрическое поле

Найти

  Известно, что:

     EE0E1 =   

Вычислить ‘E’

Электрический момент

Найти

  Известно, что:

     pql =   

Вычислить ‘p’

Электрическая ёмкость

Найти

  Известно, что:

     Cqφ =   

Вычислить ‘C’

Электрическая ёмкость шара

Найти

  Известно, что:

     CεRk =   

Вычислить ‘C’

Электрическая ёмкость двух проводников

Найти

  Известно, что:

     CqU =   

Вычислить ‘C’

Электрическая ёмкость плоского конденсатора

Найти

  Известно, что:

     Cεε0Sd =   

Вычислить ‘C’

Электрическая ёмкость сферического конденсатора

Найти

  Известно, что:

     Cπεε0R1R2 =   

Вычислить ‘C’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqE1d =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqEd =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqU =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WCU =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     WqC =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     Wεε0EV =   

Вычислить ‘W’

Потенциальная энергия заряженного плоского конденсатора

Найти

  Известно, что:

     Wεε0ESd =   

Вычислить ‘W’

Плотность энергии электрического поля

Найти

  Известно, что:

     ω_pWV =   

Вычислить ‘ω_p’

Плотность энергии электрического поля

Найти

  Известно, что:

     ω_pε0εE =   

Вычислить ‘ω_p’

Формулы по физике 10 класса.

Все формулы по физике за 10 класс с пояснениями и определениями

Закон	Формула	Определение	Единицы измерения
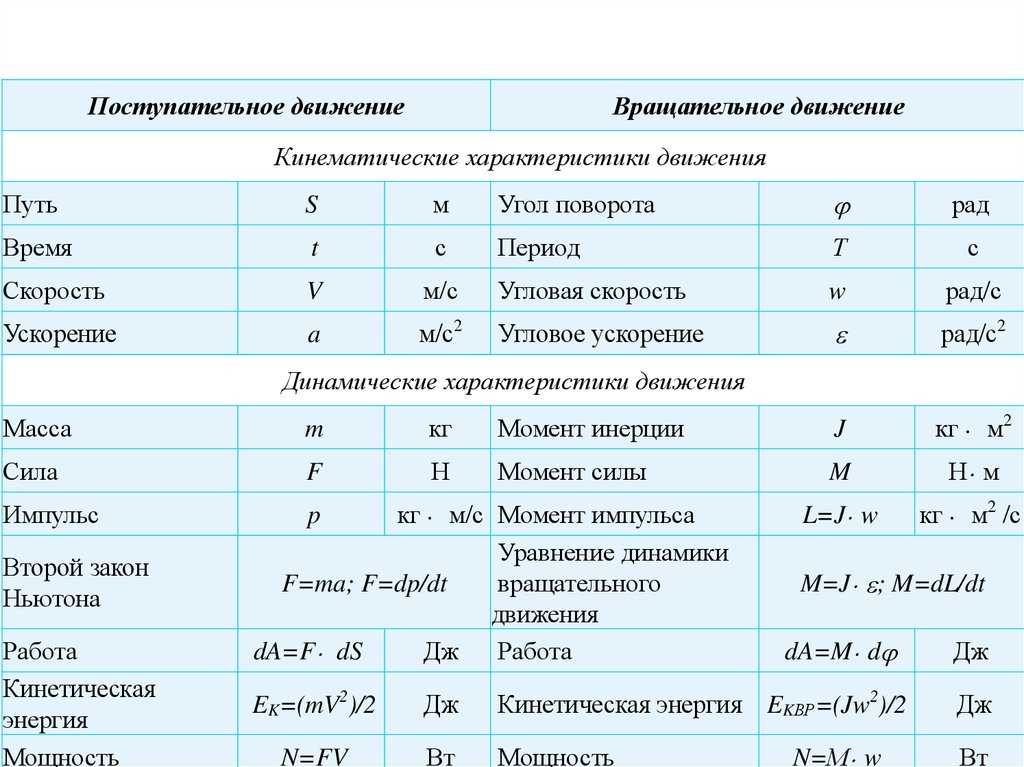
МЕХАНИКА
Вычисление перемещения	АВ2 = АС2 + ВС2	Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой.
Проекция вектора перемещения	Sx = x2 – x1		x1 – начальная координата, [м] x2 – конечная координата, [м] Sx – перемещение, [м]
Формула расчета скорости движения тела	v = s/t	Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло.	v – скорость, [м/с] s – путь, [м] t – время, [c]
Уравнение движения	x = x0 + Vxt		x0– начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c]
Формула для вычисления ускорения движения тела	a ⃗ = v ⃗- v0⃗ /t	Ускорение – физическая величина, которая характеризует быстроту изменения скорости.	a – ускорение, [м/с2] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] t – время, [c]
Уравнение скорости	v ⃗ = v0 ⃗ + a ⃗t		v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Уравнение Галилея	S = v0t + at2 / 2		S – перемещение, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Закон изменения координаты тела при прямолинейном равноускоренном движении	x = x0 + v0t + at2/2		x0 – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c]
Первый закон Ньютона		Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно.
Второй закон Ньютона	a= F ⃗ / m	Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела.	a – ускорение, [м/с2] F – сила, [Н] m – масса, [кг]
Третий закон Ньютона	|F1⃗ |=|F2⃗| F1⃗ = -F2⃗	Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое.	F – сила, [Н]
Формула для вычисления высоты, с которой падает тело	H = g*t2/2		Н – высота, [м] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления высоты при движении вертикально вверх	h=v0t -gt2/2		h – высота, [м] v0 – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения
Формула для вычисления веса тела при движении вверх с ускорением	P = m (g + a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула для вычисления веса тела при движении вниз с ускорением	P = m (g – a)		P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2]
Формула закона всемирного тяготения	F = Gm1m2/r2	Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.	F – сила, [Н] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная m – масса тела, [кг] r – расстояние между телами, [м]
Формула расчета ускорения свободного падения на разных планетах	g = GMпл/Rпл2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м]
Формула расчета ускорения свободного падения	g = GMз/(Rз+H)2		g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м]
Формула расчета центростремительного ускорения	а = υ2/r		a – центростремительное ускорение, [м/с2] v – скорость, [м/с] r – радиус окружности, [м]
Формула периода движения по окружности	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота вращения, [с-1] t – время, [с] N – число оборотов
Формула расчета угловой скорости	ω = 2π/T = 2πν =υr		ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения,[с-1] r – радиус окружности, [м]
Формула импульса тела	p = mv	Импульсом называют произведение массы тела на его скорость.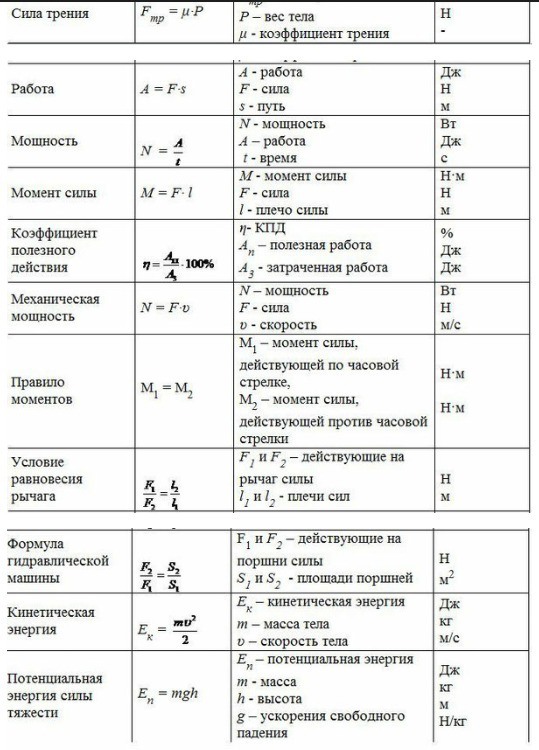	p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с]
Формула закона сохранения импульса	p1 + p2 =p1’ + p2’ m1v + m2u = m1v’ + m1u’
Формула импульса силы	P = Ft		p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c]
Формула механической работы	A = Fs	Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы.	A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м]
Формула расчета мощности	N = A/t	Мощность – физическая величина, характеризующая быстроту совершения механической работы.	N – мощность, [Вт] A – работа, [Дж] t – время, [c]
Формула для нахождения коэффициента полезного действия (КПД)	η = Aп/Aз∙ 100%	КПД – отношение полезной работы к затраченной работе.	Aп – полезная работа, [Дж] Aз – затраченная работа, [Дж]
Формула расчета потенциальной энергии	Eп = mgh	Потенциальная энергия – это энергия, которая определяется взаимным положением взаимодействующих тел или частей одного и того же тела.	Eп – потенциальная энергия тела, [Дж] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения h – высота тела над поверхностью земли, [м]
Формула расчета кинетической энергии	Ek= mv2/2	Кинетическая энергия – энергия, которой обладает тело вследствие своего движения.	Ek – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с]
Формула закона сохранения полной механической энергии	mv12/2 + mgh1=mv22/2 + mgh2	Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной.	m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения v1 – скорость тела в начальный момент времени, [м/с] v2 – скорость тела в конечный момент времени, [м/с] h1 – начальная высота, [м] h2 – конечная высота, [м]
Формула силы трения	Fтр = μ mg	Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению.	Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения
Уравнение колебаний	x = A cos (ωt + φ0)		А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ0 – начальная фаза, [рад]
Формула периода	T = 1/ν = 2πr/υ = t/N		Т – период, [с] ν – частота колебании, [с-1] t – время колебании, [с] N – число колебаний
Формула периода для математического маятника	T= 2π √L/g		Т – период, [с] g ≈ 9,81 м/с2 – ускорение свободного падения L – длина нити, [м]
Формула периода для пружинного маятника	T= 2π √m/K		Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м]
Формула длины волны	λ = υТ = υ/ν		λ – длина волны, [м] Т – период, [с] ν – частота, [с-1] υ – скорость волны, [м/с]
Формула полной механической энергии колебательного движения	E = kA2/2		E – энергия, [Дж] А – амплитуда колебаний, [м] k – жесткость пружины, [Н/м]
Радиус Шварцшильда	R = 2GM/c2	Радиус Шварцшильда – радиус «горизонта событий» черной дыры, из которого ничто не может вырваться.	R – радиус Шварцшильда, [м] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная М – масса черной дыры, [кг]
Собственное время	t = T/√1-v2/c2	Собственное время – время, измеренное наблюдателем, движущимся вместе с часами.	t – собственное время, [с] T – время в движущейся системе отсчета, [с] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Масса покоя	m = M/√1-v2/c22	Масса покоя – масса тела в СО, относительно которой оно покоится.	m – масса тела в СО, относительно которой оно покоится, [кг] M – масса тела в подвижной СО, [кг] v – скорость движущейся системы отсчета, [м/с] c – скорость света, [м/с]
Формула Эйнштейна	E = mc2		E – энергия, [Дж] m – масса, [кг] c – скорость света, [м/с
МОЛЕКУЛЯРНАЯ ФИЗИКА 10 класс
Массовое число	M = Z + N		M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов
Формула массы ядра	МЯ = МА – Z me		MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг]
Формула дефекта масс	∆m = Zmp + Nmn – MЯ	Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.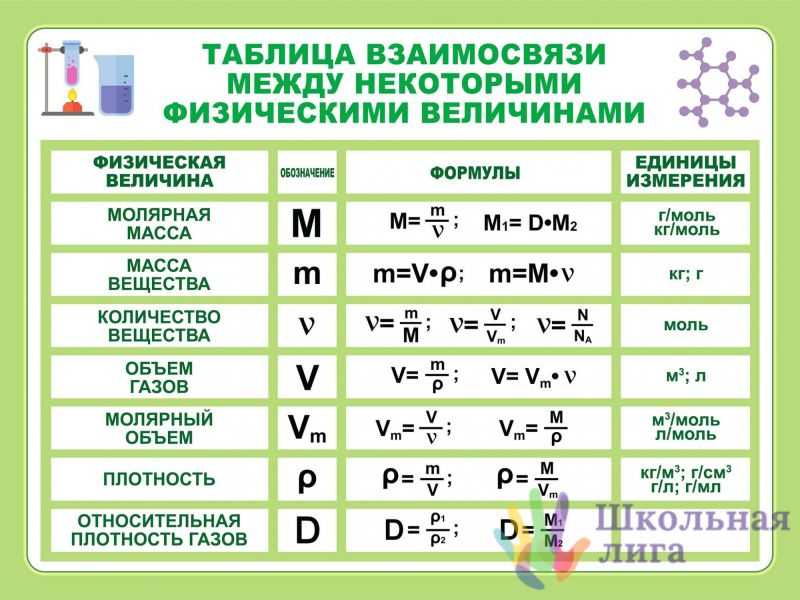	∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг]
Уравнение Менделеева-Клапейрона	pV = m/M RT	Уравнение состояния идеального газа	p – давление, [Па] V – объем, [м3] m – масса, [кг] M – молярная масса, [кг] R = 8,31 [Дж/мольК] – молярная газовая постоянная T – температура, [°С]
Формула давления газа			p – давление, [Па] n – концетрация молекул E – средняя кинетическая энергия молекулы, [Дж] T – температура, [°С] k = 1,38 · 10-23, [Дж/К] – постоянная Больцмана
Закон Бойля-Мариотта	p1V1 = p2V2		p – давление, [Па] V – объем, [м3]
Закон Гей-Люссака	V1/T1 = V2/T2		T – температура, [°С] V – объем, [м3]
Закон Шарля	p1/T1= p2/T2		T – температура, [°С] p – давление, [Па]
Внутренняя энергия идеального газа	U = i/2 pV		U – энергия, [Дж] p – давление, [Па] V – объем, [м3] i – число степеней свободы молекул газа
Работа, совершаемая газом	A = pΔV		p – давление, [Па] V – объем, [м3] А – работа, [Дж]
Первый закон термодинамики	Q = ΔU + A		Q – количество теплоты, [Дж] А – работа, [Дж] U – энергия, [Дж]
Формула для нахождения коэффициента полезного действия (КПД) теплового двигателя	η = A/Q∙100%		А – работа, [Дж] Q – количество теплоты, полученное от нагревателя, [Дж]
Сила поверхностного натяжения	F = ϭl		F – сила поверхностного натяжения, [Н] ϭ – поверхностное натяжение, [Н/м] l – длина участка поверхности слоя, [м]
Закон Гука	ϭ = Eε	При упругой деформации тела напряжение пропорционально относительному удлинению тела.	ϭ – механическое напряжение, [Па] Е – модуль Юнга, [Па] ε – относительное удлинение тела, [м]
ЭЛЕКТРОДИНАМИКА
Закон Кулона	F = kq1q1/r2	Определяет силу электростатического взаимодействия двух точечных зарядов	F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2] q – заряд, [Кл] r – расстояние между зарядами, [м]
Напряженность поля	E = F/q E = kQ/r2		Е – напряженность поля, [Н/Кл] q – пробный положительный заряд, [Кл] F – сила Кулона, [Н] k = 9·109 [Нм2/Кл2]
Потенциал электростатического поля	φ = W/q φ = Q/4πεr		φ – потенциал, [В] W – энергия, [Дж] q – заряд, [Кл]
Потенциальная энергия заряда	W = qφ		W – энергия, [Дж] q – заряд, [Кл] φ – потенциал, [В]
Работа силы электростатического поля	A = qU		А – работа сил, [Дж] q – заряд, [Кл] U – разность потенциалов, [В]
Разность потенциалов в однородном поле	U = Ed		U – разность потенциалов, [В] Е – напряженность поля, [Н/Кл] d – расстояние, [м]
Электроемкость уединенного проводника	C = Q/φ		C – электроемкость, [Ф] φ – потенциал, [В] Q – заряд, [Кл]
Электроемкость конденсатора	C = Q/U		C – электроемкость, [Ф] U – разность потенциалов, [В] Q – заряд, [Кл]
Энергия ЭСП	W = CU2/2		C – электроемкость, [Ф] U – разность потенциалов, [В] W – энергия ЭСП, [Дж

Веб-сайт кабинета физики

Назначение SE10: электрическое поле

Цели:

• Студент должен уметь определять электрическое поле и распознавать переменные, которые влияют (и не влияют) на напряженность электрического поля в данном месте.
• Студент должен уметь использовать уравнения электрического поля и относительно простые числа для определения величины и направления напряженности электрического поля в заданном месте.

Чтение:

Класс физики – Статическое электричество, урок 4, часть a

	Заряд Q создает электрическое поле. Пробным зарядом q измеряют напряженность электрического поля на расстоянии d от Q. На пробный заряд q действует сила F. Напряженность электрического поля в этом месте определяется выражением ___. Перечислите все, что применимо… .
	Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), воздействующее на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Э = Ф/кв
	Напряженность электрического поля ( E ) определяется как количество силы, действующей на пробный заряд на единицу заряда пробного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. F избранный = k • Q 1 • Q 2 / d 2 В приведенном выше уравнении Q 1 может быть исходным зарядом Q , а Q 2 может быть тестовым зарядом q . Если выражение для силы, данное уравнением закона Кулона, подставить вместо F в уравнении напряженности электрического поля, то уравнение для электрического поля принимает вид E = k • Q/d 2
	Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда?

	Заряд Q создает электрическое поле. Пробный заряд q используется для измерения напряженности электрического поля на расстоянии d от Q. Напряженность электрического поля определяется как ____.
	Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Э = Ф/кв
	Легко запутаться в математике напряженности электрического поля. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют Q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Маленький q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите особое внимание количеству заряда — q или q — используемому в каждом уравнении.
	Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда?

	Стандартной метрической единицей напряженности электрического поля является ____.
	Напряженность электрического поля ( E ) в любом месте, окружающем заряд источника, может быть определена путем измерения силы ( F ) при воздействии на испытательный заряд ( q ), помещенный в этом месте. Э = Ф/кв
	Стандартные метрические единицы количества можно понять, подумав о его формуле. Напряженность электрического поля — это отношение силы к заряду (см. раздел Formula Fix выше). Таким образом, единицы напряженности электрического поля — это единицы силы, деленные на единицы заряда. Стандартной метрической единицей силы является ньютон; стандартной метрической единицей заряда является кулон. Таким образом, стандартной метрической единицей напряженности электрического поля является Ньютон/Кулон, сокращенно N/C. 9-9 Кулоновский пробный заряд. Напряженность электрического поля, создаваемая зарядом в 4 мкК, составляет ____ Н/Кл.
	Определение Напряженность электрического поля : Любой источник заряда Q будет создавать электрическое поле в окружающем его пространстве. Напряженность электрического поля ( E ) в любом заданном месте в этом пространстве можно определить, поместив пробный заряд q в пространство и измерив силу ( F ), действующую на него. Напряженность электрического поля определяется как количество силы на единицу заряда испытательного заряда. Э = Ф/кв
	Напряженность электрического поля ( E ) определяется как величина силы, действующей на испытательный заряд на единицу заряда испытательного заряда ( q ). То есть E = F/q . Электрическая сила ( F ) зависит от ряда переменных, как описано законом Кулона. F избранный = k • Q 1 • Q 2 / d 2 В приведенном выше уравнении Q 1 может быть зарядом источника 9.0043 Q и Q 2 может быть пробным зарядом q . Если выражение для силы, данное уравнением закона Кулона, заменить F в уравнении напряженности электрического поля, то уравнение для электрического поля примет вид E = k • Q/d 2
	Легко запутаться в математике напряженности электрического поля. Важно помнить, что в любом электрическом взаимодействии всегда участвуют два заряда. В этом случае начисления составляют Q и q . Большой Q представляет собой исходный заряд, создающий электрическое поле. Little q представляет собой тестовый заряд, который используется для измерения напряженности электрического поля в заданном месте, окружающем заряд источника. Уделите большое внимание количеству заряда – Q или q – используется в каждом уравнении.
	Какие переменные влияют на напряженность электрического поля заряда? Как можно использовать силу пробного заряда для определения напряженности электрического поля другого заряда?

	ИСТИНА или ЛОЖЬ : Величина электрического поля является векторной величиной. (Примечание: ваше фактическое утверждение «Верно-ложно» выбирается случайным образом из набора вариантов и может отличаться от приведенного здесь.)
	Электрическое поле как вектор: Электрическое поле в заданном месте вокруг заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, являются ли Q и q имеют одинаковый или противоположный заряд. При определении направления электрического поля используется условное обозначение, что направление всегда одно и то же, независимо от типа заряда q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
	Является ли электрическое поле скалярной или векторной величиной?

	По соглашению направление электрического поля ____.
	Электрическое поле как вектор: Электрическое поле ( E ) в заданном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется условное обозначение, согласно которому направление зависит от типа заряда исходного заряда 9.0043 В . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
	Как определить направление электрического поля?

	Положительный заряд создает электрическое поле. Направление электрического поля будет ____.
	Электрическое поле как вектор: Электрическое поле ( E ) в данном месте относительно заряда источника ( Q ) — векторная величина. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того, заряжены ли Q и q одинаково или противоположно. заряжен. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля совпадает с направлением положительный тестовый заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
	По соглашению, направление вектора электрического поля в любом данном месте – это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом отталкивания одинаково заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник положительного заряда. Положительный заряд источника и положительный пробный заряд будут отталкивать друг друга. То есть положительный пробный заряд будет отталкиваться от положительного исходного заряда во всех точках пространства, окружающего исходный заряд.
	Как определить направление электрического поля?

	Отрицательный заряд создает электрическое поле. Направление электрического поля будет ____.
	Электрическое поле как вектор: Электрическое поле ( E ) в заданном месте относительно заряда источника ( Q ) является векторной величиной. То есть имеет направление. Сила, действующая на пробный заряд ( q ), может быть силой притяжения (по направлению к исходному заряду) или силой отталкивания (от исходного заряда) в зависимости от того,0043 Q и q заряжены одинаково или противоположно. При определении направления электрического поля используется соглашение, согласно которому направление зависит от типа заряда исходного заряда Q . Согласно соглашению, направление электрического поля соответствует направлению, в котором положительный пробный заряд будет толкаться или тянуться, если его поместить в пространство, окружающее Q .
	По соглашению, направление вектора электрического поля в любом данном месте – это направление, в котором положительный пробный заряд будет выталкиваться или тянуться, если его поместить в это место. Сочетая это соглашение с правилом притяжения противоположно заряженных объектов, можно определить направление электрического поля в пространстве, окружающем источник отрицательного заряда. Отрицательный заряд источника и положительный пробный заряд будут притягиваться друг к другу. То есть положительный пробный заряд будет притягиваться к отрицательному исходному заряду во всех точках пространства, окружающего исходный заряд.
	Как определить направление электрического поля?

Следуйте за нами

18.3 Электрическое поле — физика

Раздел Цели обучения

К концу этого раздела вы сможете делать следующее:

• Вычислять напряженность электрического поля
• Создание и интерпретация рисунков электрических полей

Поддержка учителей

Поддержка учителей

Цели обучения в этом разделе помогут вашим учащимся освоить следующие стандарты:

• (5) Учащийся знает природу сил в физическом мире. Ожидается, что студент:
  • (С) описать и рассчитать, как величина электрической силы между двумя объектами зависит от их зарядов и расстояния между ними.

Основные термины раздела

электрическое поле

испытательный заряд

Поддержка учителей

Поддержка учителей

Спросите учащихся, видели ли они фильмы, в которых используется концепция полей как силовых полей . Попросите их описать, как работают такие поля. Опишите, как можно рассматривать гравитацию как поле, которое окружает массу и с которым взаимодействуют другие массы. Объясните, что электрические поля очень похожи на гравитационные поля.

Возможно, вы слышали о силовом поле в научно-фантастических фильмах, где такие поля применяют силы в определенных точках в космосе, чтобы удержать злодея в ловушке или защитить космический корабль от вражеского огня. Концепция поля очень полезна в физике, хотя она несколько отличается от того, что вы видите в кино.

Поле — это способ концептуализации и отображения силы, которая окружает любой объект и действует на другой объект на расстоянии без видимой физической связи. Например, гравитационное поле, окружающее Землю и все другие массы, представляет собой гравитационную силу, которая возникла бы, если бы в данной точке поля была помещена другая масса. Майкл Фарадей, английский физик девятнадцатого века, предложил концепцию электрического поля. Если вы знаете электрическое поле, то можете легко рассчитать силу (величину и направление), действующую на любой электрический заряд, который вы поместите в поле.

Электрическое поле создается электрическим зарядом и сообщает нам силу на единицу заряда во всех местах в пространстве вокруг распределения заряда. Распределение заряда может быть одноточечным; распределение заряда, скажем, по плоской пластине; или более сложное распределение заряда.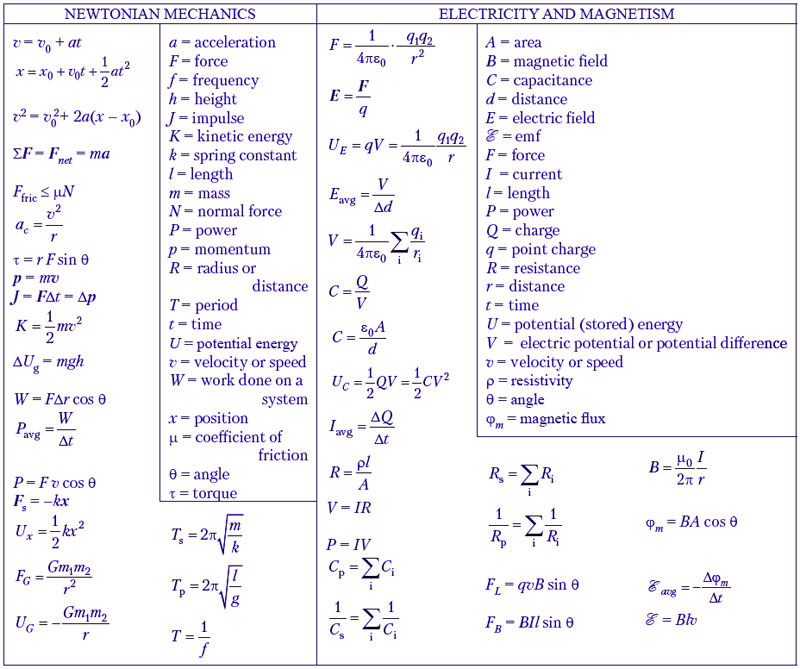 Электрическое поле распространяется в пространстве вокруг распределения заряда. Теперь рассмотрите возможность размещения пробного заряда в поле. Пробный заряд — это положительный электрический заряд, заряд которого настолько мал, что не возмущает существенно заряды, создающие электрическое поле. Электрическое поле действует на пробный заряд в заданном направлении. Приложенная сила пропорциональна заряду пробного заряда. Например, если мы удвоим заряд пробного заряда, сила, действующая на него, удвоится. Математически говоря, что электрическое поле представляет собой силу на единицу заряда, записывается как

E→=F→qtestE→=F→qtest

18.15

где мы рассматриваем только электрические силы. Обратите внимание, что электрическое поле представляет собой векторное поле, направленное в том же направлении, что и сила, действующая на положительный пробный заряд. Единицы электрического поля N/C.

Если электрическое поле создается точечным зарядом или сферой с однородным зарядом, то величина силы между этим точечным зарядом Q и пробным зарядом определяется законом Кулона

F=k|Qqtest|r2F =k|Qqtest|r2

, где используется абсолютное значение, потому что мы учитываем только величину силы. Тогда величина электрического поля равна

E=Fqtest=k|Q|r2.E=Fqtest=k|Q|r2.

18,16

Это уравнение дает величину электрического поля, создаваемого точечным зарядом Q . Расстояние r в знаменателе — это расстояние от точечного заряда Q или от центра сферического заряда до интересующей точки.

Если тестовый заряд удалить из электрического поля, электрическое поле все еще существует. Чтобы создать трехмерную карту электрического поля, представьте себе размещение пробного заряда в разных местах поля. В каждом месте измерьте силу, действующую на заряд, и используйте векторное уравнение E→=F→/qtestE→=F→/qtest для расчета электрического поля. Нарисуйте стрелку в каждой точке, где вы поместите пробный заряд, чтобы представить силу и направление электрического поля. Длина стрелок должна быть пропорциональна напряженности электрического поля. Если вы соедините эти стрелки вместе, вы получите линии. На рис. 18.17 показано изображение трехмерного электрического поля, создаваемого положительным зарядом.

Рисунок 18.17 Трехмерное представление электрического поля, создаваемого положительным зарядом.

Поддержка учителей

Поддержка учителей

[BL][OL]Укажите, что все силовые линии электрического поля берут начало от заряда.

[AL]Обратите внимание, что количество линий, пересекающих воображаемую сферу, окружающую заряд, одинаково независимо от того, какой размер сферы вы выберете. Спросите, могут ли учащиеся использовать это, чтобы показать, что количество силовых линий, пересекающих поверхность на единицу площади, показывает, что напряженность электрического поля уменьшается пропорционально обратному квадрату расстояния.

Простое рисование линий электрического поля в плоскости, пересекающей заряд, дает двумерные карты электрического поля, показанные на рис. 18.18. Слева — электрическое поле, создаваемое положительным зарядом, а справа — электрическое поле, создаваемое отрицательным зарядом.

Обратите внимание, что силовые линии электрического поля направлены от положительного заряда к отрицательному. Таким образом, положительный пробный заряд, помещенный в электрическое поле положительного заряда, будет отталкиваться. Это согласуется с законом Кулона, согласно которому одноименные заряды отталкиваются друг от друга. Если мы поместим положительный заряд в электрическое поле отрицательного заряда, положительный заряд притянется к отрицательному заряду. Противоположное верно для отрицательных тестовых зарядов. Таким образом, направление линий электрического поля согласуется с тем, что мы находим, используя закон Кулона.

Уравнение E=k|Q|/r2E=k|Q|/r2 говорит о том, что электрическое поле становится сильнее по мере приближения к заряду, который его генерирует. Например, на расстоянии 2 см от заряда Q ( r = 2 см) электрическое поле в четыре раза сильнее, чем на расстоянии 4 см от заряда ( r = 4 см). Снова взглянув на рис. 18.17 и рис. 18.18, мы видим, что линии электрического поля становятся более плотными по мере приближения к заряду, который их генерирует. На самом деле плотность линий электрического поля пропорциональна напряженности электрического поля!

Рисунок 18.18 Линии электрического поля от двух точечных зарядов. Красная точка слева несет заряд +1 нКл, а синяя точка справа несет заряд -1 нКл. Стрелки указывают направление, в котором будет двигаться положительный пробный заряд. Линии поля сгущаются по мере приближения к точечному заряду.

Карты электрического поля могут быть составлены для нескольких зарядов или для более сложных распределений зарядов. Электрическое поле от нескольких зарядов можно найти, сложив электрические поля от каждого отдельного заряда. Поскольку эта сумма может быть только одним числом, мы знаем, что только одна линия электрического поля может проходить через любую заданную точку. Другими словами, линии электрического поля не могут пересекаться.

На рис. 18.19(а) показана двухмерная карта электрического поля, создаваемого зарядом + q и соседним зарядом – q . Трехмерная версия этой карты получается путем вращения этой карты вокруг оси, проходящей через оба заряда. Положительный пробный заряд, помещенный в это поле, будет испытывать силу в направлении силовых линий в его местоположении. Таким образом, он будет отталкиваться от положительного заряда и притягиваться к отрицательному заряду. Рисунок 18.19(b) показывает электрическое поле, создаваемое двумя зарядами − q . Обратите внимание, как силовые линии отталкиваются друг от друга и не перекрываются. Положительный пробный заряд, помещенный в это поле, будет притягиваться к обоим зарядам. Если вы находитесь далеко от этих двух зарядов, где далеко означает намного дальше, чем расстояние между зарядами, электрическое поле выглядит как электрическое поле от одного заряда -2 q .

Рисунок 18.19 (а) Электрическое поле, создаваемое точечным положительным зарядом (слева) и точечным отрицательным зарядом той же величины (справа). (б) Электрическое поле, создаваемое двумя равными отрицательными зарядами.

Поддержка учителей

Поддержка учителей

Попросите учащихся интерпретировать карты электрического поля. Где поле сильнее? Где поле слабее? В каком направлении поле увеличивается или уменьшается? Где поле наиболее однородно? Могут ли они проверить, что величина заряда одинакова в данной панели? Чем отличается поле двух отрицательных зарядов от поля положительного и отрицательного зарядов?

Виртуальная физика

Исследование электрического поля

Эта симуляция показывает вам электрическое поле из-за зарядов, которые вы размещаете на экране. Начните с установки верхнего флажка на панели параметров с правой стороны, чтобы отобразить электрическое поле. Перетащите заряды из ведер на экран, перемещайте их и наблюдайте за электрическим полем, которое они образуют. Чтобы более точно увидеть величину и направление электрического поля, перетащите датчик электрического поля или датчик электрического поля из нижнего ведра и перемещайте его по экрану.

Исследования PhET: заряды и поля. Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое.

Нажмите, чтобы просмотреть содержимое

Два положительных заряда размещены на экране. Какое утверждение описывает электрическое поле, создаваемое зарядами?

1. Постоянно везде.

2. Рядом с каждым зарядом ноль.

3. Между зарядками ноль.

4. Наибольшая сила на полпути между зарядами.

Смотреть физику

Электростатика (часть 2): интерпретация электрического поля

В этом видеоролике объясняется, как рассчитать электрическое поле точечного заряда и как интерпретировать карты электрического поля в целом. Обратите внимание, что лектор использует d для расстояния между частицами вместо r . Обратите внимание, что точечные заряды бесконечно малы, поэтому все их заряды сосредоточены в одной точке. Когда рассматриваются более крупные заряженные объекты, расстояние между объектами должно измеряться между центрами объектов.

Проверка захвата

Верно или неверно — если точечный заряд имеет силовые линии электрического поля, которые указывают на него, заряд должен быть положительным.

1. правда
2. ложь

Рабочий пример

Какова плата?

Посмотрите на рисунок электрического поля на рис. 18.20. Какова относительная сила и знак трех зарядов?

Рисунок 18.20 Карта электрического поля трех заряженных частиц.

Стратегия

Мы знаем, что электрическое поле простирается от положительного заряда и заканчивается отрицательным зарядом. Мы также знаем, что количество силовых линий электрического поля, которые касаются заряда, пропорционально заряду. Заряд 1 имеет 12 полей, выходящих из него. В заряд 2 входит шесть силовых линий. В заряд 3 входит 12 силовых линий.

Решение

Линии электрического поля выходят из заряда 1, так что это положительный заряд. Линии электрического поля проходят через заряды 2 и 3, поэтому они являются отрицательными зарядами. Отношение зарядов равно q1:q2:q3=+12:-6:-12q1:q2:q3=+12:-6:-12. Таким образом, величина зарядов 1 и 3 вдвое превышает величину заряда 2.

Обсуждение

Хотя мы не можем определить точный заряд каждой частицы, мы можем получить много информации из электрического поля относительно величины и знака зарядов. и где сила пробного заряда будет наибольшей (или наименьшей).

Рабочий пример

Электрическое поле от дверной ручки

Дверная ручка, которую можно принять за сферический металлический проводник, приобретает заряд статического электричества q=-1,5 нКл. q=-1,5 нКл. Чему равно электрическое поле на расстоянии 1,0 см от дверной ручки? Диаметр дверной ручки 5,0 см.

Стратегия

Поскольку дверная ручка является проводником, весь заряд распределяется по внешней поверхности металла. Кроме того, поскольку дверная ручка считается идеально сферической, заряд на поверхности распределяется равномерно, поэтому мы можем рассматривать дверную ручку так, как если бы весь заряд был сосредоточен в центре дверной ручки. Справедливость этого упрощения будет доказана в следующем курсе физики. Теперь нарисуйте дверную ручку и определите вашу систему координат. Используйте +x+x, чтобы указать внешнее направление, перпендикулярное двери, с x=0x=0 в центре дверной ручки (как показано на рисунке ниже).

Если диаметр дверной ручки 5,0 см, ее радиус 2,5 см. Мы хотим знать электрическое поле на расстоянии 1,0 см от поверхности дверной ручки, что составляет расстояние r = 2,5 см + 1,0 см = 3,5 см, r = 2,5 см + 1,0 см = 3,5 см от центра дверной ручки. Мы можем использовать уравнение E=k|Q|r2E=k|Q|r2, чтобы найти величину электрического поля. Направление электрического поля определяется знаком заряда, который в данном случае отрицателен.

Раствор

Введение заряда Q=-1,5 нКл=-1,5×10-9.

Обсуждение

Похоже на огромное электрическое поле. К счастью, требуется электрическое поле примерно в 100 раз сильнее (3×106 Н/Кл3×106 Н/Кл), чтобы заставить воздух разлагаться и проводить электричество. Кроме того, вес взрослого человека составляет около 70 кг × 9,8 м/с2 ≈ 700 Н70 кг × 9,8 м/с2 ≈ 700 Н, так почему вы не чувствуете силы, действующей на протоны в вашей руке, когда вы тянетесь к дверной ручке? Причина в том, что ваша рука содержит равное количество отрицательного заряда, который отталкивает отрицательный заряд дверной ручки. Из-за поляризации в вашей руке может развиться очень небольшая сила, но вы никогда этого не заметите.

Практические задачи

15.

Какова величина электрического поля на расстоянии 20 см от точечного заряда q = 33 нКл?

1. 7,4 × 10 ³ Н/З
2. 1,48 × 10 ³ Н/З
3. 7,4 × 10 ¹² Н/З
4. 0

16.

Заряд -10 нКл находится в начале. В каком направлении электрическое поле от заряда указывает на x + 10 см?

1. Электрическое поле направлено в сторону от отрицательных зарядов.
2. Электрическое поле указывает на отрицательные заряды.
3. Электрическое поле направлено в сторону положительных зарядов.
4. Электрическое поле направлено в сторону от положительных зарядов.

Проверьте свое понимание

17.

Когда линии электрического поля сближаются, что это говорит вам об электрическом поле?

1. Электрическое поле обратно пропорционально плотности линий электрического поля.
2. Электрическое поле прямо пропорционально плотности линий электрического поля.
3. Электрическое поле не связано с плотностью линий электрического поля.
4. Электрическое поле обратно пропорционально квадратному корню из плотности силовых линий электрического поля.