Как найти индуктивность катушки формула: формула. Измерение индуктивности. Индуктивность контура

Калькулятор импеданса катушки индуктивности • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:

Здесь

X_L — реактивное сопротивление катушки в омах (Ом),

Z_L — импеданс катушки в омах (Ом),

ω = 2πf — угловая частота в рад/с,

f — частота в герцах (Гц),

L — индуктивность в генри (Гн),

j — мнимая единица.

Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.

Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.

Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике

В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока.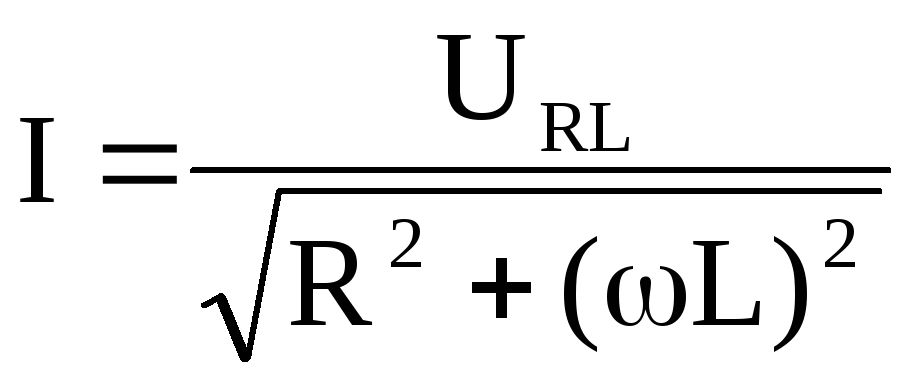 В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.

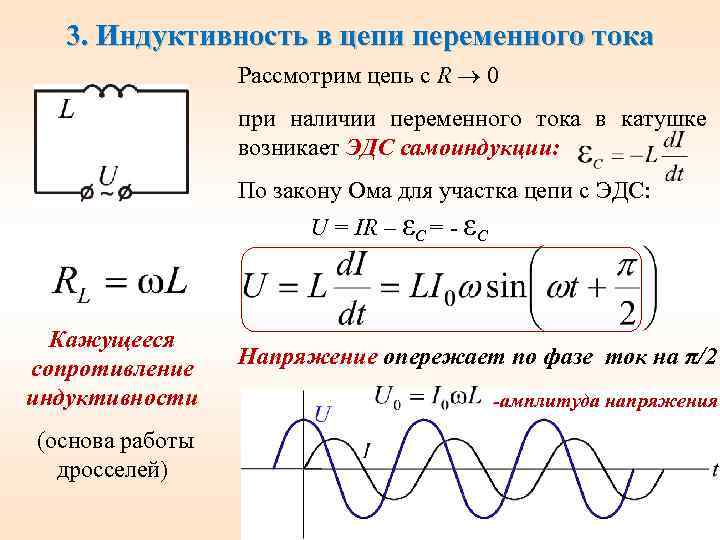
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток.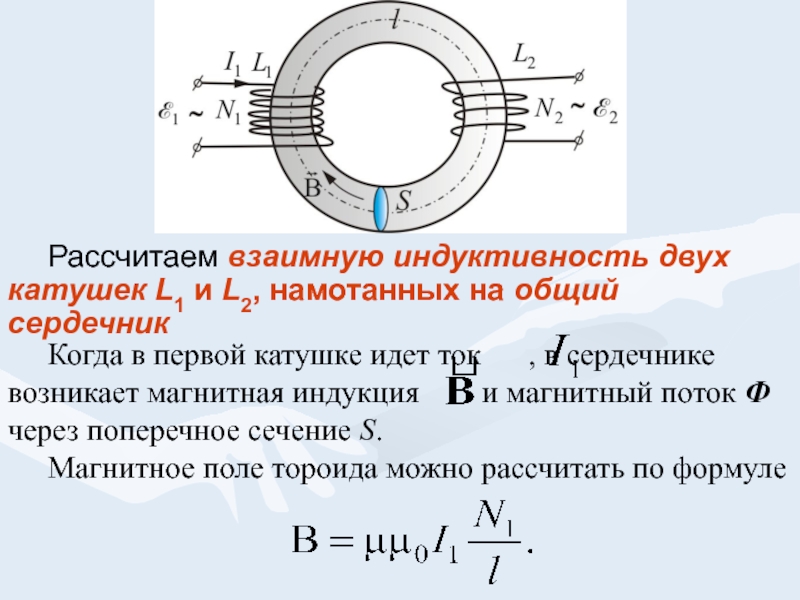 Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.

График зависимости реактивного сопротивления катушки X_L индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока

Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.

Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.

Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.

В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму

Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла.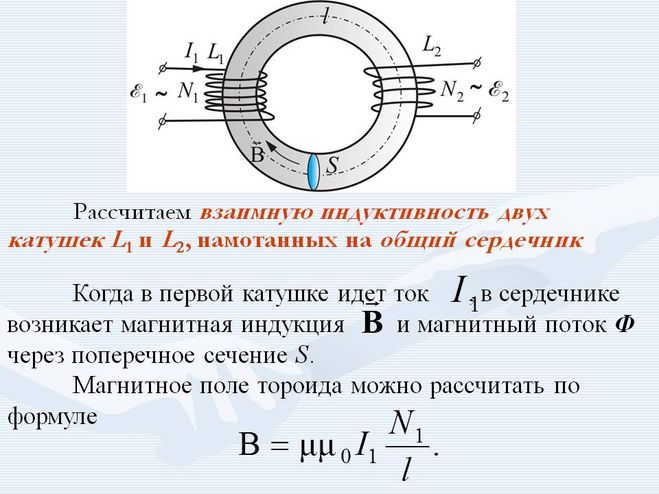 В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.

Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.

День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности

Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности X_L велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот).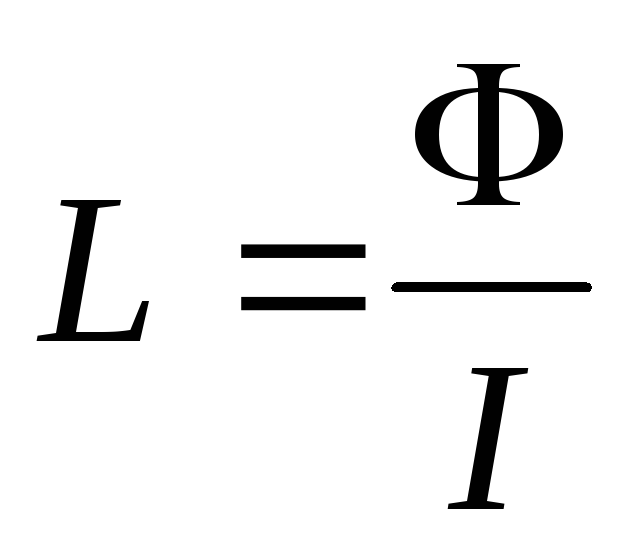 При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.

Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.

Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.

Катушки индуктивности в высокочастотном модуле телевизионного приемника

Автор статьи: Анатолий Золотков

Соединение катушек – Основы электроники

Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.

Последовательное соединение катушек индуктивности.

Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.

Рисунок 1. Последовательное соединение катушект индуктивности.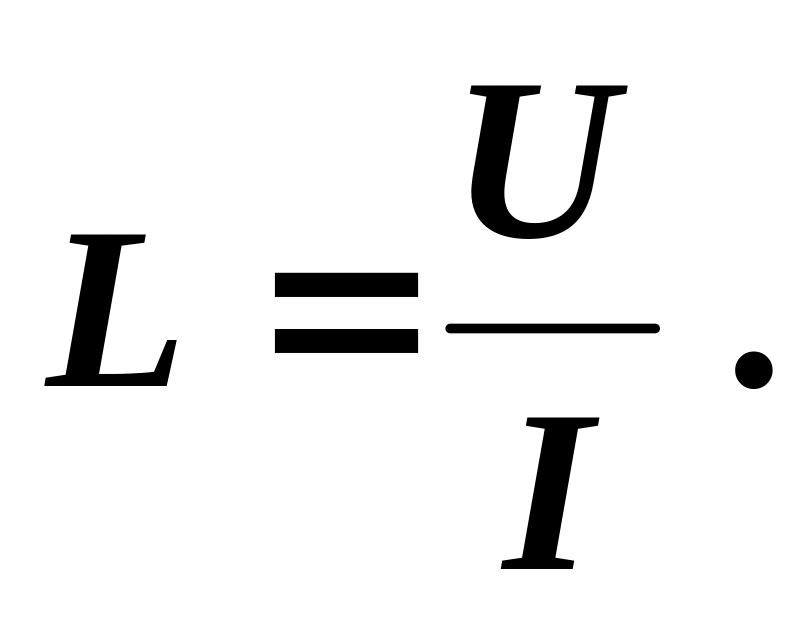

Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:

где L1, L2 и L3 — индуктивности отдельных катушек.

Параллельное соединение катушек индуктивности.

Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же усло­вия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:

Рисунок 2. Параллельное соединение катушек индуктивности.

Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:

Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или парал­лельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопро­тивления цепи при последовательном и параллельном соеди­нении резисторов.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, распо­ложены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше фор­мула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

1. Магнитные потоки обеих катушек имеют одинаковые на­правления
2. Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений то­ков в них.

Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответство­вать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направ­лены в одну сторону. Очевидно, при этих условиях витки каж­дой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в дру­гой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых состав­лена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по фор­муле:

В первом случае ставится знак + (плюс), а во втором слу­чае знак — (минус).

Величина М, называемая коэффициентом взаим­ной индукции, представляет собой добавочную индук­тивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство варио­метров. Вариометр состоит из двух катушек, общая индуктив­ность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передат­чиков.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

3. Факторы, влияющие на индуктивность катушки | 14. Катушки индуктивности | Часть1

3. Факторы, влияющие на индуктивность катушки

Факторы, влияющие на индуктивность катушки

На индуктивность катушки оказывают влияние следующие основные факторы:

Число витков провода в катушке: При прочих равных условиях, увеличение числа витков приводит к увеличению индуктивности; уменьшение числа витков приводит к уменьшению индуктивности.

Пояснение: чем больше количество витков, тем больше будет магнитодвижущая сила для заданной величины тока.

 

 

Площадь поперечного сечения катушки: При прочих равных условиях, катушка с большей площадью поперечного сечения будет иметь большую индуктивность; а катушка с меньшей площадью поперечного сечения – меньшую индуктивность.

Пояснение: Катушка с большей площадью поперечного сечения оказывает меньшее сопротивление формированию магнитного потока для заданной величины магнитодвижущей силы.

 

 

Длина катушки: При прочих равных условиях, чем больше длина катушки, тем меньше ее индуктивность; чем меньше длина катушки, тем больше ее индуктивность.

Пояснение: Чем больше длина катушки, тем большее сопротивление она оказывает формированию магнитного потока для заданной величины магнитодвижущей силы.

 

 

Материал сердечника: При прочих равных условиях, чем больше магнитная проницаемость сердечника, вокруг которого намотана катушка, тем больше индуктивность; чем меньше магнитная проницаемость сердечника – тем меньше индуктивность.

Пояснение: Материал сердечника с большей магнитной проницаемостью способствует формированию большего магнитного потока для заданной величины магнитодвижущей силы.

 

 

Приблизительное значение индуктивности любой катушки можно найти по следующей формуле:

 

 

Следует понимать, что данная формула дает только приблизительные цифры. Одной из причин такого положения дел является изменение величины магнитной проницаемости при изменении напряженности магнитного поля (вспомните нелинейность кривой В/Н для разных материалов). Очевидно, если проницаемость (µ) в уравнении будет непостоянна, то и индуктивность (L) также будет в некоторой степени непостоянна. Если гистерезис материала сердечника будет существенным, то это непременно отразится на индуктивности катушки. Разработчики катушек индуктивности пытаются минимизировать эти эффекты, проектируя сердечник таким образом, чтобы его намагниченность никогда не приближалась к уровням насыщения, и катушка работала в более линейной части кривой B/H.

Если катушку сделать таким образом, что любой из вышеперечисленных факторов у нее можно механически изменить, то получится катушка с регулируемой величиной индуктивности или вариометр. Наиболее часто встречаются вариометры, индуктивность которых регулируется количеством витков или  положением сердечника (который перемещается внутри катушки). Пример вариометра с изменяемым количеством витков можно увидеть на следующей фотографии:

 

 

Это устройство использует подвижные медные контакты, которые подключаются к катушке в различных точках ее длины. Подобные катушки, имеющие воздушный сердечник, применялись в разработке самых первых радиоприемных устройств.

Катушка с фиксированными значениями индуктивности, показанная на следующей фотографии, представляет собой еще одно раритетное устройство, использовавшееся в первых радиостанциях. Здесь вы можете увидеть несколько витков относительно толстого провода, а так же соединительные выводы:

 

 

А это еще одна катушка индуктивности, так же предназначенная для радиостанций.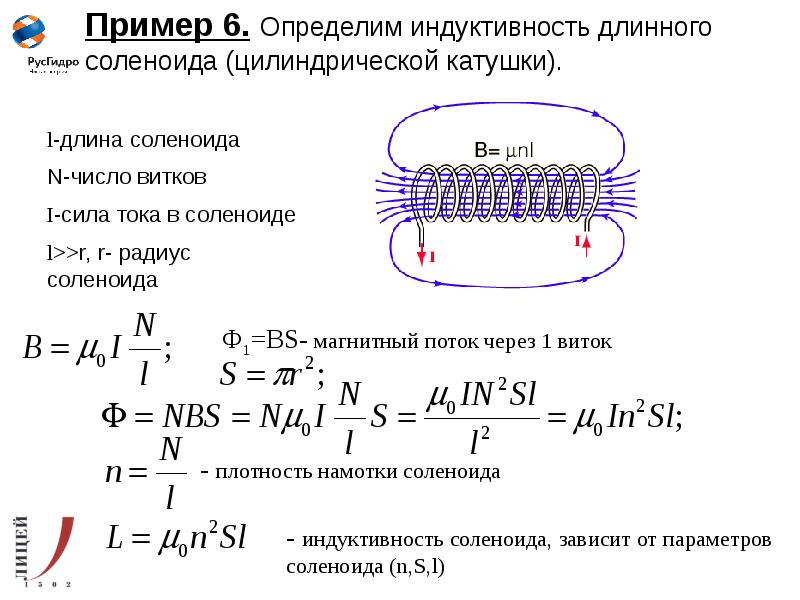 Для большей жесткости ее провод намотан на керамический каркас:

 

 

Многие катушки индуктивности обладают небольшими размерами, что позволяет монтировать их непосредственно на печатные платы. Посмотрев внимательно на следующую фотографию, можно увидеть две расположенные рядом катушки:

 

 

Две катушки индуктивности расположены справа в центре этой платы и имеют обозначения L₁ и L₂. В непосредственной близости от них находятся резистор R₃ и конденсатор С₁₆. Показанные на плате катушки называются “торроидальными”, так как их провод намотан вокруг сердечника, имеющего форму тора.

Как резисторы и конденсаторы, катушки индуктивности могут выполняться в корпусе для поверхностного монтажа (SMD). На следующей фотографии представлено несколько таких катушек:

 

 

Две индуктивности здесь расположены справа в центре платы. Они представляют собой маленькие черные чипы с номером “100”, а над одной из них можно увидеть обозначение L₅.

Катушка индуктивности – это… Что такое Катушка индуктивности?

Обозначение на электрических принципиальных схемах

Катушка индуктивности (жарг. индуктивность) — пассивный двухполюсный компонент электрических и электронных устройств и систем. Основной параметр катушки индуктивности — величина её индуктивности, зависящая только от геометрических размеров и материалов и не зависящая от режима работы (тока и напряжения).

Применяются для подавления помех, сглаживания пульсаций, накопления энергии, ограничения переменного тока, в резонансных (колебательный контур) и частотноизбирательных цепях, в качестве элементов индуктивности искусственных линий задержки с сосредоточенными параметрами, создания магнитных полей, датчиков перемещений и так далее.

Терминология

При использовании для подавления помех, сглаживания пульсаций электрического тока, изоляции (развязки) по высокой частоте разных частей схемы и накопления энергии в магнитном поле сердечника часто называют

дросселем.

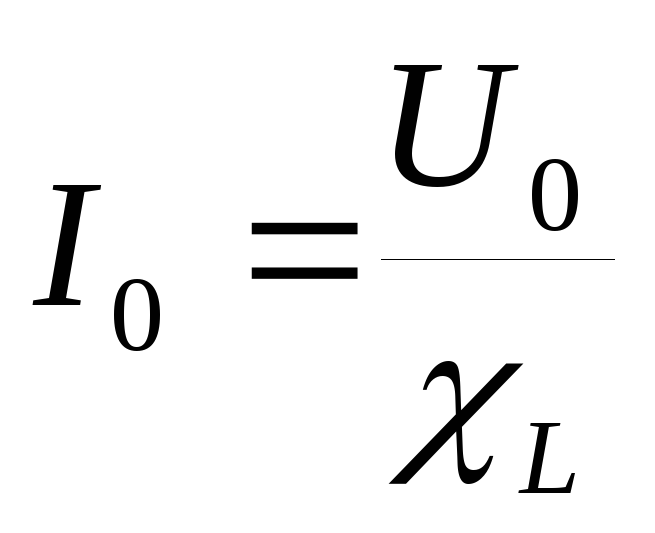
В силовой электротехнике (для ограничения тока при, например, коротком замыкании ЛЭП) называют реактором.

Цилиндрическую катушку индуктивности, длина которой на много превышает диаметр, называют соленоидом, магнитное поле внутри длинного соленоида однородно. Кроме того, зачастую соленоидом называют устройство, выполняющую механическую работу за счёт магнитного поля при втягивании ферромагнитного сердечника, или электромагнитом. В электромагнитных реле называют обмоткой реле, реже — электромагнитом.

Нагревательный индуктор — специальная катушка индуктивности, рабочий орган установок индукционного нагрева.

При использовании для накопления энергии называют индукционным накопителем.

Конструкция

Конструктивно выполняется в виде винтовых, или винтоспиральных (диаметр намотки изменяется по длине катушки) катушек однослойных или многослойных намоток изолированного одножильного или многожильного (литцендрат) проводника на диэлектрическом каркасе круглого, прямоугольного или квадратного сечения, часто на тороидальном каркасе или, при использовании толстого провода и малом числе витков — без каркаса.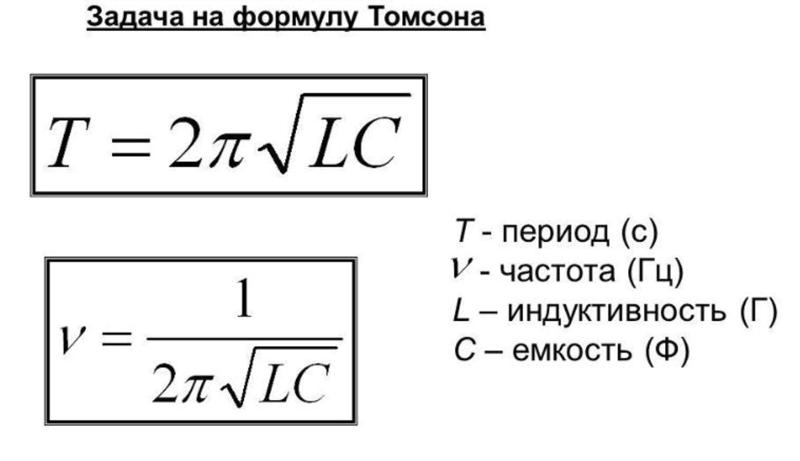 Иногда, для снижения распределённой паразитной ёмкости при использовании в качестве высокочастотного дросселя, однослойные катушки индуктивности наматываются с «прогрессивным» шагом, — шаг намотки плавно изменяется по длине катушки. Намотка может быть как однослойной (рядовая и с шагом), так и многослойная (рядовая, внавал, типа «универсал»). Намотка «универсал» имеет меньшую паразитную ёмкость. Часто, опять же, для снижения паразитной ёмкости, намотку выполняют секционированной, группы витков отделяются пространственно (обычно по длине) друг от друга.

Для увеличения индуктивности часто имеют замкнутый или разомкнутый ферромагнитный сердечник, помехоподавляющие дроссели высокочастотных помех имеют ферродиэлектрические сердечники: ферритовые, флюкстроловые, из карбонильного железа. Дроссели, предназначенные для сглаживания пульсаций промышленной и звуковой частот имеют сердечники из электротехнических сталей или магнитомягких сплавов (пермаллоев). Также сердечники используют для изменения индуктивности катушек в небольших пределах изменением положения сердечника относительно обмотки, как правило, ферромагнитного сердечника. На СВЧ, когда ферродиэлектрики теряют высокую магнитную проницаемость и резко увеличиваются потери, для этой цели применяются металлические (латунные) сердечники.

На печатных платах электронных устройств применяют плоские «катушки» индуктивности — геометрия печатного проводника выполнена в виде круглой или прямоугольной спирали, волнистой, или в виде меандра, линии. Такие «катушки индуктивности» часто используются в сверхбыстродействующих цифровых устройствах для выравнивания времени распространения группы сигналов по разным печатным проводникам от источника до приемника, например, в шинах данных и адреса^[1].

Свойства катушки индуктивности

Свойства катушки индуктивности:

• Скорость изменения тока через катушку ограничена и определяется индуктивностью катушки.
• Сопротивление (модуль импеданса) катушки растет с увеличением частоты текущего через неё тока.
• Катушка индуктивности при протекании тока запасает энергию в своем магнитном поле. При отключении внешнего источника тока катушка отдаст запасенную энергию, стремясь поддержать величину тока в цепи. При этом напряжение на катушке нарастает, вплоть до пробоя изоляции или возникновения дуги на коммутирующем ключе.

Катушка индуктивности в электрической цепи для постоянного тока имеет только собственное омическое сопротивление, но имеет реактивное сопротивление переменному току, нарастающее при увеличении частоты, поскольку при изменении тока в катушке возникает ЭДС самоиндукции, препятствующая этому изменению.

Катушка индуктивности обладает реактивным сопротивлением модуль которого: , где  — индуктивность катушки,  — циклическая частота протекающего тока. Соответственно, чем больше частота тока, протекающего через катушку, тем больше её сопротивление.

Катушка с током запасает энергию в магнитном поле, равную работе, которую необходимо совершить для установления текущего тока . Величина этой энергии равна:

Катушка индуктивности в переменном напряжении — аналог тела с массой, подверженному механическим колебаниям.

При изменении тока в катушке возникает ЭДС самоиндукции, значение которой:

Для идеальной катушки индуктивности (не имеющей паразитных параметров) ЭДС самоиндукции равна по модулю и противоположна по знаку напряжению на концах катушки:

При замыкании катушки с током на резистор ток в цепи экспоненциально уменьшается в соответствие с формулой:

,

где :  — ток в катушке,

 — начальный ток катушки,

 — текущее время,

 — постоянная времени.

Постоянная времени выражается формулой:

,

где :  — сопротивление резистора,

 — омическое сопротивление катушки.

При закорачивании катушки с током процесс характеризуется собственной постоянной времени : катушки:

.

При стремлении к нулю, постоянная времени стремится к бесконечности, именно поэтому в сверхпроводящих контурах ток течёт «вечно».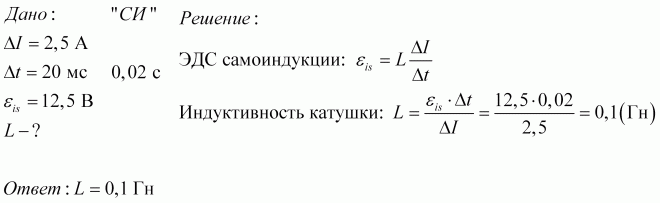

Явление самоиндукции аналогично проявлению инертности тел в механике, если аналогом индуктивности принять массу, тока — скорость, напряжения — силу, то многие формулы механики и поведения индуктивности в цепи принимают похожий вид:

↔ , где

↔ ↔  ; ↔  ; ↔

↔

Характеристики катушки индуктивности

Индуктивность

Основным параметром катушки индуктивности является её индуктивность, численно равная отношению создаваемого током потока магнитного поля, пронизывающего катушку к величине протекающего тока. Типичные значения индуктивностей катушек от десятых долей мкГн до десятков Гн.

Индуктивность катушки пропорциональна линейным размерам катушки, магнитной проницаемости сердечника и квадрату числа витков намотки. Индуктивность катушки, намотанной на тороидальном сердечнике:

где  — магнитная постоянная

 — относительная магнитная проницаемость материала сердечника (зависит от частоты)

 — площадь сечения сердечника

 — длина средней линии сердечника

 — число витков

При последовательном соединении катушек общая индуктивность равна сумме индуктивностей всех соединённых катушек:

При параллельном соединении катушек общая индуктивность равна:

Сопротивление потерь

В катушках индуктивности помимо основного эффекта взаимодействия тока и магнитного поля наблюдаются паразитные эффекты, вследствие которых импеданс катушки не является чисто реактивным. Наличие паразитных эффектов ведёт к появлению потерь в катушке, оцениваемых сопротивлением потерь . Потери складываются из потерь в проводах, диэлектрике, сердечнике и экране:

Потери в проводах

Потери в проводах вызваны тремя причинами:

• Провода обмотки обладают омическим (активным) сопротивлением.
• Сопротивление провода обмотки возрастает с ростом частоты, что обусловлено скин-эффектом. Суть эффекта состоит в вытеснении тока в поверхностные слои провода. Как следствие, уменьшается полезное сечение проводника и растет сопротивление.
• В проводах обмотки, свитой в спираль, проявляется эффект близости, суть которого состоит в вытеснении тока под воздействием вихревых токов и магнитного поля к периферии намотки. В результате сечение, по которому протекает ток, принимает серповидную форму, что ведёт к дополнительному возрастанию сопротивления провода.

Потери в диэлектрике

Потери в диэлектрике (изоляции проводов и каркасе катушки) можно отнести к двум категориям:

• Потери от диэлектрика межвиткового конденсатора (межвитковые утечки и прочие потери характерные для диэлектриков конденсаторов).
• Потери обусловленные магнитными свойствами диэлектрика (эти потери аналогичны потерям в сердечнике).

В общем случае можно заметить, что для современных катушек общего применения потери в диэлектрике чаще всего пренебрежимо малы.

Потери в сердечнике

Потери в сердечнике складываются из потерь на вихревые токи, потерь на перемагничивание ферромагнетика гистерезис.

Потери на вихревые токи

Переменное магнитное поле индуцирует вихревые ЭДС в окружающих проводниках, например в сердечнике, экране и в проводах соседних витков. Возникающие при этом вихревые токи (токи Фуко) становятся источником потерь из-за омического сопротивления проводников.

Добротность

С сопротивлениями потерь тесно связана другая характеристика — добротность. Добротность катушки индуктивности определяет отношение между активным и реактивным сопротивлениями катушки. Добротность равна

Иногда потери в катушке характеризуют тангенсом угла потерь (величина, обратная добротности) — сдвигом фаз тока и напряжения катушки в цепи синусоидального сигнала относительно π/2 — для идеальной катушки.

Практически величина добротности лежит в пределах от 30 до 200. Повышение добротности достигается оптимальным выбором диаметра провода, увеличением размеров катушки индуктивности и применением сердечников с высокой магнитной проницаемостью и малыми потерями, намоткой вида «универсаль», применением посеребрёного провода, применением многожильного провода вида «литцендрат» для снижения потерь, вызванных скин-эффектом.

Паразитная емкость и собственный резонанс

Межвитковая паразитная емкость проводника в составе катушки индуктивности превращает катушку в сложную распределенную цепь. В первом приближении можно принять, что реальная катушка представляет эквивалентно собой идеальную индуктивность с параллельно присоединенным ей конденсатором паразитной емкости. В результате этого катушка индуктивности представляет собой колебательный контур с характерной частотой резонанса. Эта резонансная частота легко может быть измерена и называется собственной частотой резонанса катушки индуктивности. На частотах много ниже частоты собственного резонанса импеданс катушки индуктивный, при частотах вблизи резонанса в основном активный (на частоте резонанса чисто активный) и большой по модулю, на частотах много выше частоты собственного резонанса — ёмкостной. Обычно собственная частота указывается изготовителем в технических данных промышленных катушек индуктивности, либо в явном виде, либо косвенно — в виде рекомендованной максимальной рабочей частоты.

На частотах ниже собственного резонанса этот эффект проявляется в падении добротности с ростом частоты.

Для увеличения частоты собственного резонанса используют сложные схемы намотки катушек, разбиение одной обмотки на разнесённые секции.

Температурный коэффициент индуктивности (ТКИ)

ТКИ — это параметр, характеризующий зависимость индуктивности катушки от температуры.

Температурная нестабильность индуктивности обусловлена целым рядом факторов: при нагреве увеличивается длина и диаметр провода обмотки, увеличивается длина и диаметр каркаса, в результате чего изменяются шаг и диаметр витков; кроме того при изменении температуры изменяются диэлектрическая проницаемость материала каркаса, что ведёт к изменению собственной ёмкости катушки.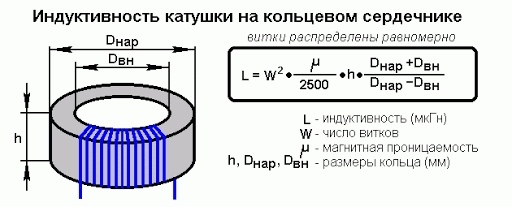 Очень существенно влияние температуры на магнитную проницаемость ферромагнетика сердечника.

Разновидности катушек индуктивности

Контурные катушки индуктивности, используемые в радиотехнике

Эти катушки используются совместно с конденсаторами для организации резонансных контуров. Они должны иметь высокую термо- и долговременную стабильность, и добротность, требования к паразитной ёмкости обычно несущественны.

Катушки связи, или трансформаторы связи

Взаимодействующие магнитными полями пара и более катушек, обычно включаются параллельно конденсаторам для организации колебательных контуров: Такие катушки применяются для обеспечения трансформаторной связи между отдельными цепями и каскадами. Такая связь позволяет разделить по постоянному току, например, цепи базы последующего усилительного каскада от коллектора предыдущего каскада и т. д. К нерезонансным разделительным трансформаторам не предъявляются жёсткие требования на добротность и точность, поэтому они выполняются из тонкого провода в виде двух обмоток небольших габаритов. Основными параметрами этих катушек являются индуктивность и коэффициент связи (коэффициент взаимоиндукции).

Вариометры

Это катушки, индуктивностью которых можно управлять (например, для перестройки частоты резонанса колебательных контуров) изменением взаимного расположения двух катушек, соединённых последовательно. Одна из катушек неподвижная (статор), другая обычно располагается внутри первой и вращается (ротор). Существуют и другие конструкции вариометров. При изменении положения ротора относительно статора изменяется величина взаимоиндукции, а следовательно, индуктивность вариометра. Такая система позволяет изменять индуктивность в 4 − 5 раз. В ферровариометрах индуктивность изменяется перемещением ферромагнитного сердечника относительно обмотки, либо изменением длины воздушного зазора замкнутого магнитопровода.

Дроссели

Это катушки индуктивности, обладающие высоким сопротивлением переменному току и малым сопротивлением постоянному. Применяются в цепях питания радиотехнических устройств в качестве фильтрующего элемента. Для сетей питания с частотами 50-60 Гц выполняются на сердечниках из трансформаторной стали. На более высоких частотах также применяются сердечники из пермаллоя или феррита. Особая разновидность дросселей — помехоподавляющие ферритовые бочонки (бусины или кольца) нанизанные на отдельные провода или группы проводов (кабели) для подавления синфазных высокочастотных помех.

Сдвоенный дроссель

Сдвоенные дроссели

Это две намотанных встречно или согласованно катушки индуктивности, используются в фильтрах питания. За счёт встречной намотки и взаимной индукции более эффективны для фильтрации синфазных помех при тех же габаритах. При согласной намотке эффективны для подавления дифференциальных помех. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания; в дифференциальных сигнальных фильтрах цифровых линий, а также в звуковой технике. ^[2][3] Предназначены как для защиты источников питания от попадания в них наведённых высокочастотных сигналов, из питающей сети, так и во избежание проникновения в питающую сеть электромагнитных помех, генерируемых устройством. На низких частотах используется в фильтрах цепей питания и обычно имеет ферромагнитный (из трансформаторной стали). Для фильтрации высокочастотных помех — ферритовый сердечник.

Применение катушек индуктивности

Балластный дроссель. Ранее применявшаяся в качестве реактивного сопротивления для люминесцентных ламп катушка индуктивности

• Катушки индуктивности (совместно с конденсаторами и/или резисторами) используются для построения различных цепей с частотно-зависимыми свойствами, в частности, фильтров, цепей обратной связи, колебательных контуров и т. п.
• Катушки индуктивности используются в импульсных стабилизаторах как элемент, накапливающий энергию и преобразующий уровни напряжения.
• Две и более индуктивно связанные катушки образуют трансформатор.
• Катушка индуктивности, питаемая импульсным током от транзисторного ключа, иногда применяется в качестве источника высокого напряжения небольшой мощности в слаботочных схемах, когда создание отдельного высокого питающего напряжения в блоке питания невозможно или экономически нецелесообразно. В этом случае на катушке из-за самоиндукции возникают выбросы высокого напряжения, которые можно использовать в схеме, например, выпрямив и сгладив.
• Катушки используются также в качестве электромагнитов — исполнительных механизмов.
• Катушки применяются в качестве источника энергии для нагрева индуктивно-связанной плазмы, а также её диагностики.
• Для радиосвязи — приёма электромагнитных волн, редко — для излучения:
• Для разогрева электропроводящих материалов в индукционных печах.
• Как датчик перемещения: изменение индуктивности катушки может изменяться в широких пределах при перемещении ферромагнитного сердечника относительно обмотки.
• Катушка индуктивности используется в индукционных датчиках магнитного поля в индукционных магнитометрах^[4]
• Для создания магнитных полей в ускорителях элементарных частиц, магнитного удержания плазмы, в научных экспериментах, в ядерно-магнитной томографии. Мощные стационарные магнитные поля, как правило, создаются сверхпроводящими катушками.
• Для накопления энергии.

См. также

Примечания

Ссылки

В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете отредактировать эту статью, добавив ссылки на авторитетные источники. Эта отметка установлена 13 мая 2011.

14.2: Взаимная индуктивность – Physics LibreTexts

ЦЕЛИ ОБУЧЕНИЯ

К концу этого раздела вы сможете:

• Сопоставьте две соседние цепи, которые переносят изменяющиеся во времени токи, с ЭДС, индуцированной в каждой цепи
• Опишите примеры, в которых взаимная индуктивность может быть желательной, а может и нежелательной

Индуктивность – это свойство устройства, которое говорит нам, насколько эффективно оно индуцирует ЭДС в другом устройстве. Другими словами, это физическая величина, которая выражает эффективность данного устройства.

Когда две цепи, несущие изменяющиеся во времени токи, близки друг к другу, магнитный поток через каждую цепь изменяется из-за изменяющегося тока I в другой цепи. Следовательно, ЭДС индуцируется в каждой цепи изменяющимся током в другой. Поэтому этот тип ЭДС называется взаимно индуцированной ЭДС , а возникающее явление известно как взаимная индуктивность ( M ) .В качестве примера рассмотрим две плотно намотанные катушки (рисунок \ (\ PageIndex {1} \)). Катушки 1 и 2 имеют \ (N_1 \) и \ (N_2 \) витки и переносят токи \ (I_1 \) и \ (I_2 \) соответственно. Поток через один виток катушки 2, создаваемый магнитным полем тока в катушке 1, равен \ (\ Phi_ {12} \), тогда как поток через один виток катушки 1 из-за магнитного поля \ (I_2 \) равно \ (\ Phi_ {12} \).

Рисунок \ (\ PageIndex {1} \): Некоторые силовые линии магнитного поля, создаваемые током в катушке 1, проходят через катушку 2.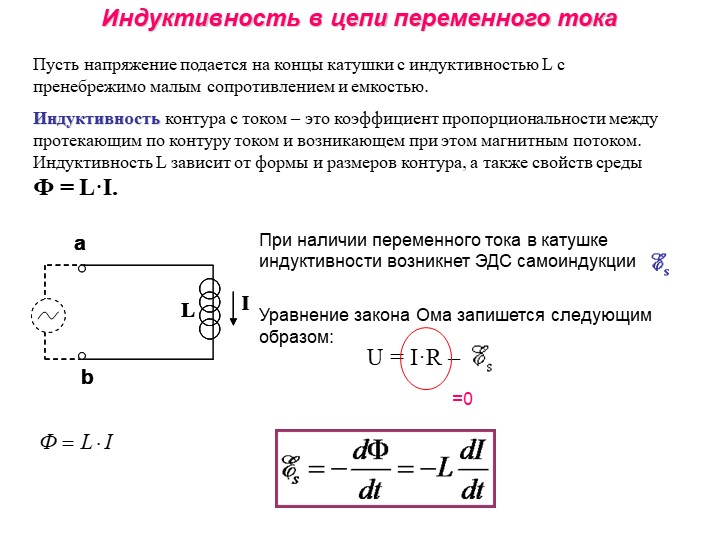

Взаимная индуктивность \ (M_ {21} \) катушки 2 по отношению к катушке 1 – это отношение потока через \ (N_2 \) витков катушки 2, создаваемого магнитным полем тока в катушке 1, разделенным этим током, то есть

\ [M_ {21} = \ dfrac {N_2 \ Phi_ {21}} {I_1}. \ label {12.24} \]

Точно так же взаимная индуктивность катушки 1 относительно катушки 2 составляет

\ [M_ {12} = \ dfrac {N_1 \ Phi_ {12}} {I_2}. \ label {12.25} \]

Как и емкость, взаимная индуктивность является геометрической величиной.Это зависит от формы и относительного положения двух катушек и не зависит от токов в катушках. Единица СИ для взаимной индуктивности M называется henry (H) в честь Джозефа Генри (1799–1878), американского ученого, который открыл наведенную ЭДС независимо от Фарадея. Таким образом, имеем \ (1 \, H = 1 \, V \ cdot s / A \). Из уравнений \ ref {12.24} и \ ref {12.25} мы можем показать, что \ (M_ {21} = M_ {12} \), поэтому мы обычно опускаем индексы, связанные с взаимной индуктивностью, и пишем

\ [M = \ dfrac {N_2 \ Phi_ {21}} {I_1} = \ dfrac {N_1 \ Phi_ {12}} {I_2}. \ label {14.3} \]

ЭДС, возникающая в любой катушке, определяется путем объединения закона Фарадея и определения взаимной индуктивности. Поскольку \ (N_2 \ Phi_ {21} \) – это полный поток через катушку 2 из-за \ (I_1 \), получаем

\ [\ begin {align} \ epsilon_2 & = – \ dfrac {d} {dt} (N_2 \ Phi_ {21}) \\ [4pt] & = – \ dfrac {d} {dt} (MI_1) \\ [4pt] & = – M \ dfrac {dI_1} {dt} \ label {14.4} \ end {align} \]

, где мы использовали тот факт, что \ (M \) не зависит от времени, потому что геометрия не зависит от времени.Аналогично имеем

\ [\ epsilon_1 = – M \ dfrac {dI_2} {dt}. \ label {14.5} \]

В уравнении \ ref {14.5} мы можем увидеть значение предыдущего описания взаимной индуктивности (\ (M \)) как геометрической величины. Значение \ (M \) аккуратно инкапсулирует физические свойства элементов схемы и позволяет отделить физическую схему схемы от динамических величин, таких как ЭДС и ток. Уравнение \ ref {14.5} определяет взаимную индуктивность в терминах свойств в цепи, тогда как предыдущее определение взаимной индуктивности в уравнении \ ref {12. 24} определяется с точки зрения испытываемого магнитного потока, независимо от элементов схемы. Вы должны быть осторожны при использовании формул \ ref {14.4} и \ ref {14.4}, потому что \ (\ epsilon_1 \) и \ (\ epsilon_2 \) не обязательно представляют общие ЭДС в соответствующих катушках. Каждая катушка также может иметь наведенную в ней ЭДС из-за ее самоиндукции (самоиндукция будет обсуждаться более подробно в следующем разделе).

Большая взаимная индуктивность M может быть, а может и не быть желательной.Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на металлический корпус, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность – это использовать катушки противотока, чтобы нейтрализовать создаваемое магнитное поле (Рисунок \ (\ PageIndex {2} \)).

Рисунок \ (\ PageIndex {2} \): Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.

Цифровая обработка сигналов – еще один пример, в котором взаимная индуктивность уменьшается за счет обмотки противообмоток. Быстрая ЭДС включения / выключения, представляющая единицы и нули в цифровой цепи, создает сложное зависящее от времени магнитное поле. ЭДС может возникать в соседних проводниках. Если этот проводник также передает цифровой сигнал, наведенная ЭДС может быть достаточно большой, чтобы переключать единицы и нули, с последствиями от неудобных до катастрофических.

Пример \ (\ PageIndex {1} \): взаимная индуктивность

На рисунке \ (\ PageIndex {3} \) показана катушка из \ (N_2 \) витков и радиуса \ (R_2 \), окружающая длинный соленоид длиной \ (l_1 \), радиусом \ (R_1 \) и \ ( N_1 \) поворотов.

1. Какова взаимная индуктивность двух катушек?
2. Если \ (N_1 = 500 \, витков, \, N_2 = 10 \, витков, \, R_1 = 3.10 \, см, \, l_1 = 75.0 \, см \) и ток в соленоиде изменяется с при скорости 200 А / с, какая ЭДС индуцируется в окружающей катушке?

Рисунок \ (\ PageIndex {3} \): соленоид, окруженный катушкой.

Стратегия

Магнитное поле вне соленоида отсутствует, а поле внутри имеет величину \ (B_1 = \ mu_0 (N_1 / l_1) I_1 \) и направлено параллельно оси соленоида.{-3} В. \ end {align *} \]

Значение

Обратите внимание, что M в части (a) не зависит от радиуса \ (R_2 \) окружающей катушки, потому что магнитное поле соленоида ограничено его внутренней частью. В принципе, мы также можем рассчитать M , найдя магнитный поток через соленоид, создаваемый током в окружающей катушке. Этот подход намного сложнее, потому что \ (\ Phi_ {12} \) очень сложен. Однако, поскольку \ (M_ {12} = M_ {21} \), нам известен результат этого вычисления.{-2} \, V \)

Авторы и указание авторства

• Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4. 0).

Самоиндуктивность

– обзор | Темы ScienceDirect

22.3.3 Зависимость индуктивности

Самоиндуктивность обмоток якоря

Самоиндуктивность любой обмотки якоря периодически изменяется от максимального значения, когда ось полюса совпадает с фазовой осью, до минимума значение, когда ось квадратурного полюса совпадает с фазовой осью.Из-за симметрии ротора синусоидальное распределение обмотки с индуктивностью, имеющей период 180 электрических градусов. Выражения для самоиндукции (рис. 22.7):

Рис. 22.7. Ось ротора и статора.

(22,21) xRR = xRR0 + xRR2cos2qRxyy = xyy0 + xyy2cos2qyxBB = xBB0 + xBB1cos2qB

Взаимная индуктивность обмоток якоря

= (9000R

) xscos2 (θ + 30 градусов)] XyB = XBy = – [xm + xscos2 (θ – 90 градусов)] XBR = XRB = – [xm + xscos (θ + 150 градусов)]

Приведенные выше выражения получены из следующих соображений:

Составляющая взаимного потока фаз якоря не связывает ротор и, следовательно, не зависит от угла

fd = kdcosθR

fq = –kqsinθR

Связь с фазой «y» из-за этих компонентов пропорциональна

fdcosθy –Fdsinθy = kdcosθRcosθy + kqcosθRcosθy

= kdcosθRcos (θ – 120 градусов) + kdsinθRsin (θ – 120 градусов)

= kd + kq4 + kd + kq2cos2 (θ − 9000 градусов 2) (θ −3 + 9000 60 градусов) 9000 = [12A + Bcos2 (θ + 30 градусов)]

Отсюда

xRY = – [xy + xscos (2) (q + 30degrees)] и вскоре

(обратите внимание, что xy = xm, themutu реактивность)

Собственные индуктивности ротора определены как x _ffd , x _{11 d} , x _{22 d} ,… и являются предполагаемыми константами.

Взаимные индуктивности ротора: Из-за симметрии ротора отсутствует взаимная связь между осями d и q ротора.

xf1q = xf2q = xid1q = x1d2q = x1qfd = 0

xf1d = x1fd и т. Д. Для роторного поля и демпфирующей обмотки оси d.

Взаимные индуктивности между статором и потоком ротора

Основные компоненты потока в воздушном зазоре будут связаны с синусодиально распределенным потоком статора. Потоковая связь максимальна, когда две оси катушки находятся на одной линии.

(22,23) xRfd = xfRd = xRfdcosθxyfd = xfyd = xyfdcos (θ − 120 градусов) xBfd = xfBd = xBfdcos (θ + 120 градусов)

(22,24) xR1d = x1cos1dgree (xR1d) = xθBD1D = xR1d = xθBD1D = xR1d = xθBD1 x1Bd = xB1dcos (θ + 120 градусов)

(22,25) xR1q = x1Rq = −xR1qsinθxy1q = x1yq = −xR1qsin (θ − 120 градусов) xB1q = x1Bq = −xB1qsin (θ + 120 градусов) катушка 9000 + 120 градусов наивысшего возможного индуктора (θ + 120 градусов) \ mathbf {Q} $$ Q

Начнем с ответа на вопрос Гаусса об индуктивности постоянного тока. 2 r ‘}, \ end {align} $$

(6)

, где позиции \ ({\ mathbf {r}} = (\ rho, z) \), \ ({\ mathbf {r}} ‘= (\ rho’, z ‘) \) меняются по поперечному сечению катушки, площади \ (A = N / n_2 \).{13/4} / 8 = 3,22 \). Такое отношение среднего радиуса к полувысоте заметно отличается от 3,7 или 3, предложенных, соответственно, Максвеллом и Бруксом, см. Рис. 2а, предполагая, что этот метод слишком груб, чтобы выявить истинную оптимальную геометрию катушки.

Рисунок 2

Сечения оптимальных катушек. ( a ) Конструкции, предложенные Gauss ³ , Maxwell ⁴ и Brooks ⁶ . ( b ) Результаты, полученные в данной работе. Поперечное сечение изменяется от почти круглого до эллиптического и серповидного по мере увеличения \ (\ omega \).2}, \ quad k = \ frac {| {\ mathbf {r}} – {\ mathbf {r}} ‘|} {\ sqrt {4 \ rho \ rho’}} \ end {выровнен} \ end {выровнен } $$

(9)

– взаимная индуктивность коаксиальных линейных токов ⁵ , пронизывающих поперечное сечение в \ ({\ mathbf {r}} \) и \ ({\ mathbf {r}} ‘\); K ( м ) и E ( м ) – полные эллиптические интегралы. 2} {4} \ right], \ end {align} $$

(13)

действительно для \ (k \ ll 1 \) [Ур.{2}} \ frac {\ xi _1} {\ xi _1 + \ xi _2}, \ end {align} $$

(15)

, которая является обобщением формулы Рэлея ¹² для случая \ (b = a \) и является ключевым улучшением по сравнению с (5). Используя эту формулу для L и другую, \ (W = \ pi ab \ bar {\ rho} n_2 \), для ограничения длины, мы смогли легко найти оптимальное значение \ (\ xi _1 \), \ (\ xi _2 \) численно, воспроизводя (10).

Возвращаясь к -фактору Q , мы перепишем (1) в терминах наших характерных масштабов \ (L_c \), \ (Q_c \), \ (\ omega _c \):

$$ \ begin {выровнено } Q = \ frac {\ pi} {2} \ frac {\ omega} {\ omega _c} \ frac {L / L_c} {1 + F (\ omega)} Q_c, \ end {align} $$

(16)

, где мы ввели коэффициент увеличения потерь

$$ \ begin {align} F (\ omega) \ Equiv \ frac {R (\ omega)} {R (0)} – 1. 2}. \ end {align} $$

(18)

На таких частотах \ (F \ ll 1 \) пренебрежимо мало, L практически не отличается от значения постоянного тока, поэтому коэффициент Q является линейным по \ (\ omega \):

$$ \ begin {align} \ frac {Q} {Q_c} = 1.04 \, \ frac {\ omega} {\ omega _c}, \ quad \ omega \ ll \ omega _c, \ end {align} $$

(19)

см. Рис. 3.

Индуктивность

Чтобы увеличить свойство индуктивности, проводник может быть сформирован в виде петли или катушка.Катушку также называют индуктором. На рис. 2-3 показан проводник, сформированный в виде катушки. Ток через одну петлю создает магнитное поле, которое окружает петлю в направление, как показано на рисунке 2-3 (A). По мере увеличения тока магнитное поле расширяется и отрезает все петли, как показано на рисунке 2-3 (B). Ток в каждом контуре влияет на все остальные петли. Поле, пересекающее другую петлю, увеличивает сопротивление текущее изменение.

Рисунок 2-3.- Индуктивность.

Катушки индуктивности классифицируются по типу сердечника. Сердечник – центр индуктора так же, как сердцевина яблока – это центр яблока. Индуктор выполнен путем формирования моток проволоки вокруг сердечника. Материал сердечника обычно бывает двух основных типов: мягкое железо или воздух. Индуктор с железным сердечником и его схематическое обозначение (которое представлено с линиями в верхней части, указывающими на наличие железного сердечника) показаны на рисунок 2-4 (A).Катушка индуктивности с воздушным сердечником может быть не чем иным, как катушкой с проволокой, но она обычно катушка образована вокруг полой формы из какого-либо немагнитного материала, например картона. Этот материал служит только для сохранения формы катушки. Воздушное ядро индуктор и его схематическое обозначение показаны на рисунке 2-4 (B).

Рисунок 2-4. – Типы индукторов и условные обозначения.

Факторы, влияющие на индуктивность катушки Есть несколько физических факторов, которые влияют на индуктивность катушки.Они включают количество витков в катушке, диаметр катушка, длина катушки, тип материала, используемого в сердечнике, и количество слоев обмотка в катушках.

Индуктивность полностью зависит от физической конструкции схемы и может только измеряться специальными лабораторными приборами. Из упомянутых факторов рассмотрим в первую очередь как количество витков влияет на индуктивность катушки. На рисунке 2-5 показаны две катушки. Катушка (A) имеет два витка, а катушка (B) – четыре витка.В катушке (A) магнитное поле, создаваемое одним петля перерезает еще одну петлю. В катушке (B) магнитное поле, создаваемое одним контуром, отсекает три других. петли. Удвоение числа витков в катушке приведет к увеличению поля вдвое, если используется тот же ток. Поле вдвое сильнее, сокращая вдвое больше оборотов, индуцируют в четыре раза большее напряжение. Следовательно, можно сказать, что индуктивность изменяется как квадрат числа витков .

Рисунок 2-5.- Коэффициент индуктивности (витки).

Второй фактор – диаметр катушки. На рисунке 2-6 видно, что катушка в поле зрения Диаметр B в два раза больше диаметра катушки A. Физически требуется больше проволоки, чтобы построить катушку. катушка большего диаметра, чем катушка малого диаметра, с равным числом витков. Следовательно, существует больше силовых линий, чтобы вызвать противоэдс в катушке с большей диаметр. Фактически, индуктивность катушки увеличивается прямо пропорционально поперечному сечению. площадь сердечника увеличивается на .Вспомните формулу площади круга: A = pr ² . Удвоение радиуса катушки увеличивает индуктивность в четыре раза.

Рисунок 2-6. – Коэффициент индуктивности (диаметр).

Третий фактор, влияющий на индуктивность катушки, – это длина катушки. На рис. 2-7 показаны два примера расположения змеевиков. Катушка (A) имеет три витка, довольно широко разнесены, образуя относительно длинную катушку. Катушка этого типа имеет мало потокосцеплений из-за большее расстояние между каждым поворотом.Следовательно, катушка (A) имеет относительно низкую индуктивность. Катушка (B) имеет близкорасположенные витки, что составляет относительно короткую катушку. Это близко расстояние увеличивает потокосцепление, увеличивая индуктивность катушки. Удвоение длина катушки при сохранении того же числа витков уменьшает значение индуктивности вдвое.

Рисунок 2 – 7. – Коэффициент индуктивности (длина катушки). ТЯЖЕЛО РАНО

Четвертый физический фактор – это тип материала сердечника, используемого в катушке.Рисунок 2-8 показаны две катушки: катушка (A) с воздушным сердечником и катушка (B) с сердечником из мягкого железа. В магнитный сердечник катушки (B) – лучший путь для магнитных силовых линий, чем немагнитный сердечник катушки (А). Высокая проницаемость магнитного сердечника из мягкого железа имеет меньшую сопротивление магнитному потоку, что приводит к появлению большего количества магнитных силовых линий. Это увеличение в магнитных силовых линиях увеличивается количество силовых линий, разрезающих каждую петлю катушки, тем самым увеличивая индуктивность катушки.Теперь должно быть очевидно, что индуктивность катушки увеличивается непосредственно по мере увеличения проницаемости материала сердечника .

Рисунок 2-8. – Коэффициент индуктивности (материал сердечника). МЯГКОЕ ЖЕЛЕЗНОЕ ЯДРО

Другой способ увеличения индуктивности – намотать катушку слоями. Рисунок 2-9 показаны три ядра с разным количеством слоев. Катушка на рисунке 2-9 (A) – плохая индуктор по сравнению с другими на рисунке, потому что его витки широко разнесены и наслоения нет.Движение потока, обозначенное пунктирными стрелками, не связывает эффективно, потому что есть только один слой витков. Более индуктивная катушка показана на рисунок 2-9 (B). Витки расположены близко друг к другу, провод намотан в два слоя. В два слоя связывают друг друга с большим количеством петель потока во время всех движений потока. Обратите внимание, что почти все витки, такие как X, находятся рядом с четырьмя другими витками (заштрихованы). Этот вызывает увеличение магнитной связи.

Рисунок 2-9.- Катушки различной индуктивности.

Катушку можно сделать еще более индуктивной, намотав ее в три слоя, как показано на рисунок 2-9 (С). Увеличенное количество слоев (площадь поперечного сечения) улучшает потокосцепление даже больше. Обратите внимание, что некоторые повороты, такие как Y, лежат непосредственно рядом с шестью другими поворотами (заштрихованы). На практике наслоение может продолжаться через намного больше слоев. Важный факт следует помнить, однако, что индуктивность катушки увеличивается с каждым слоем добавил .

Как вы видели, на индуктивность катушки могут влиять несколько факторов, и все они факторы переменные. Многие катушки различной конструкции могут иметь одинаковую индуктивность. В Однако важно помнить, что индуктивность зависит от степень связи между проводником (проводниками) и электромагнитным полем . В прямая длина проводника, между одной частью проводника очень малая магнитная связь. дирижер и другой.Поэтому его индуктивность крайне мала. Было показано, что проводники становятся намного более индуктивными, когда они наматываются на катушки. Это правда, потому что между витками проводника, лежащими бок о бок в катушка.

Q.7 Перечислите пять факторов, влияющих на индуктивность катушки.

Постоянная времени индуктора

• Изучив этот раздел, вы сможете описать:
• • Постоянная времени цепи LR.
• … и провести расчеты по
• • Постоянные времени в простой схеме LR.

Рис. 4.5.1 Постоянная времени LR.

Когда ток подается на катушку индуктивности, требуется некоторое время, чтобы ток достиг своего максимального значения, после чего он будет оставаться в «устойчивом состоянии» до тех пор, пока какое-либо другое событие не приведет к изменению входа. Время, необходимое для повышения тока до установившегося значения в цепи LR, зависит от:

• Сопротивление (R)

Это полное сопротивление цепи, которое включает сопротивление постоянному току самой катушки индуктивности (R _L ) плюс любое сопротивление внешней цепи.

• Индуктивность L

Которая пропорциональна квадрату количества витков, площади поперечного сечения катушки и проницаемости сердечника.

Индуктор противодействует ИЗМЕНЕНИЯМ тока

Рис. 4.5.1 Постоянная времени LR

Когда включается схема на рис. 4.5.1, ток быстро изменяется от нуля, это внезапное изменение создает быстро расширяющееся магнитное поле вокруг катушек индуктивности и тем самым индуцирует напряжение обратно в катушку.Это индуцированное напряжение (называемое обратной ЭДС) создает ток (зеленая стрелка на принципиальной схеме), протекающий в ПРОТИВОПОЛОЖНОМ направлении исходному току (синяя стрелка на принципиальной схеме), подаваемому аккумулятором.

См. Изменение тока обратной ЭДС и тока питания в течение времени, показанного на видео на рис. 4.5.1. Результатом внезапного изменения напряжения при включении цепи является то, что скорость изменения в цепи остается неизменной, а не вызывает внезапное увеличение. при токе от 0 В до максимального ток увеличивается медленнее, чем в полностью резистивной цепи.Если бы начальная скорость изменения тока в цепи LR продолжалась линейно, ток достиг бы своего максимального или устойчивого «значения состояния» за время (T), определяемое по формуле:

T = L / R секунд.

• T – ПОСТОЯННАЯ ВРЕМЯ, измеряется в секундах
• L – ИНДУКТИВНОСТЬ, измеряется в Генри
.
• R – ОБЩЕЕ СОПРОТИВЛЕНИЕ ЦЕПИ, измеряется в Ом.

Секунды и Генри обычно слишком велики для большинства электронных измерений, и обычно используются милли- и микроединицы, но помните при расчетах, чтобы преобразовать любую из этих подединиц в секунды или Генри для использования в формулах.

Однако рост тока не является линейным, а следует изогнутой “экспоненциальной” траекторией, и за одну постоянную времени (обозначенную на рис. 4.5.1 вертикальной пунктирной линией) ток (обозначенный горизонтальной пунктирной линией) будет иметь только поднялся до 63,2% от максимального (установившегося) значения. После двух постоянных времени оно достигнет 86,5%, после 3 постоянных времени 95% и так далее, пока не достигнет 99,5%, что считается максимальным значением после 5 постоянных времени.

Выгрузка

Если цепь выключена, ток теперь не сразу падает до нуля, он снова падает экспоненциально и через один период постоянной времени достигнет 36.8% от предыдущего значения устойчивого состояния (т. Е. Значение устойчивого состояния -63,2%). Считается, что он достигает нуля за пять периодов постоянной времени.

Экспоненциальная кривая

Изменение тока в катушке индуктивности в ответ на скачкообразное изменение входного сигнала является экспоненциальным. В течение ряда равных периодов времени ток заряжает катушку индуктивности до максимального значения на процент от оставшейся разницы между текущим и максимальным значениями. Таким образом, хотя эта разница продолжает сокращаться, дополнительный заряд, накопленный за каждый период времени, также уменьшается.В результате ток никогда не достигнет максимума!

Почему 63,2%?

Если ток никогда не достигает своего установившегося значения, возникает проблема, как измерить время, необходимое для полной зарядки. Вот почему используется идея постоянной времени (время, необходимое для зарядки на 63,2%). Зачем выбирать 63,2%, если есть более простые цифры, например 50%, которые можно использовать? Что ж, 50% было бы неплохо, но создавало бы неудобную формулу для расчета затраченного времени.

Это просто!

Так получилось, что использование 63,2% (что не слишком отличается от 50%) приводит к красивой простой формуле L / R для постоянной времени индуктора и CR для постоянной времени конденсатора. Это значительно упрощает вычисления, и поскольку ток достигнет 99,5% от значения установившегося состояния после 5 постоянных времени, на практике этого достаточно, чтобы считать, что максимальное значение было достигнуто.

Индуктивность

Пример: Метод конечных элементов Magnetics

Дэвид Микер

dmeeker @ ieee.org

Сопутствующий файл: index1a.fem

Введение

Распространенной задачей, к которой может быть применен FEMM, является расчет индуктивности индуктора с зазором. Хотя индуктивность можно оценить с помощью простого магнитного Теория схем, схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ методом конечных элементов может быть заняты. Цель настоящего пример – показать, как рассчитывается индуктивность в моделировании FEMM, и сравните этот результат с приближением, полученным через магнитную цепь подход.

Пример геометрии

Примерная геометрия состоит из ламинированного EI с зазорами. сердечник с поперечным сечением, как показано на рисунке 1. Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного возвратного тракта воздушным зазором. Толщина 0,025 дюйма.

Рисунок 1: Пример геометрии

Обмотка, которая лежит в пазах E, состоит из 66 витки толстой изоляции провода 18 AWG, примерно для 66% меди заполнить фракцию в окошке змеевика.это Предполагается, что сердцевина расширяется на 1 дюйм в направлении страницы. В данной модели материал предполагается, что это линейный ферромагнитный материал с относительной проницаемостью из 2500.

Теория цепей Индуктивность

Для приблизительной оценки индуктивности мы можем предположить, что нет подтеков и окантовки, и что вклад железа секций на сопротивление магнитной цепи тривиально по сравнению с вклады с воздуха.Потом, поток, текущий в магнитной цепи, получается путем решения уравнения цепи:

для φ , полный поток, связанный катушкой. R представляет сопротивление магнитной цепи, которое согласно нашим предположениям можно записать как:

где g = 0,025 дюйма , a _полюс = 0,5 в ² и μ _o = 4 π (10 ^-7 ) H / м. Так как общий поток, связывающий катушку, тогда:

, а полная самоиндукция равна потоку, умноженному на общее количество витков:

так, чтобы самоиндукция была:

Так как в нашем случае витков 66, индуктивность получается равной:

L = 1.39 мГн

Мы ожидаем, что индуктивность получена из конечных элементов. вычисления должны быть в районе 1,39 мГн.

Индуктивность конечного элемента (I)

Для создания решения методом конечных элементов индуктор помещается в центр коробки размером 2 на 2,5 дюйма. На границах области граница условие A = 0 определено. Для Для выполнения анализа методом конечных элементов ток 1 А является допустимым. несколько произвольно применяется к катушкам. Достаточно грубая плотность сетки с ограничением размера ячейки больше 0.05 “определяется везде. Сетка проблемной области изображена на рисунке 2.

Рисунок 2: Проблемная область, нарисованная в FEMM.

После выполнения анализа и запуска постпроцессора, индуктивность можно определить, нажав кнопку «Свойства схемы» в постпроцессор:
Появляется диалоговое окно с рядом свойств обмотки, если смотреть со стороны выводов обмотки. Диалоговое окно “Свойства схемы” для этого примера показано ниже на рисунке 3.

Рисунок 3: Диалоговое окно результатов свойств схемы.

При отсутствии постоянных магнитов или других катушек результат «Поток / Ток» можно интерпретировать напрямую как самоиндукцию:

л = 1,73 мГн

Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и окантовки пренебрежение схемным подходом приводит к небольшому увеличению индуктивности.

Индуктивность конечного элемента (II)

Альтернативный подход – получение энергии через Интеграл «Энергия магнитного поля».Для этого подхода энергия получается через:

, где этот интеграл взят по всей задаче домен, а не просто над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в режим интегрального блока, нажав кнопку на панели задач. Затем выберите каждый регион в проблеме с помощью щелчки левой кнопкой мыши. Когда выделена вся проблемная область, нажмите кнопку Integral и выберите Интеграл «Энергия магнитного поля» из выпадающего списка объемных интегралов.Если W представляет собой интегральный результат, результирующая индуктивность:

Для примера задачи результат из энергии интеграция:

Вт = 0,000865042 Джоулей

Что при подстановке в формулу дает то же результат как метод (I):

л = 1,73 мГн

Выводы

Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получена из двух методы сравнивались друг с другом и с “проверкой работоспособности” оценка индуктивности по теории магнитной цепи.

Хотя результаты двух подходов конечных элементов для получения одинаковых индуктивностей в этом случае обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( то есть асимптотическое граничное условие, используемое для аппроксимации “открытой граничной” задачи) подразумевают, что некоторая энергия хранятся вне смоделированной проблемной области. Внутренне FEMM вычисляет поток связь с использованием метода, который учитывает эту дополнительную энергию, тогда как интеграции B × H по всем элементам нет.

Строго говоря, один коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с учитывались только линейные материалы.

Если проблема связана с нелинейными материалами и есть значительная насыщенность, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному Текущий.В этом случае гармонический анализ может быть запущен в FEMM (, т.е. , когда частота отличается от нуля). указанные в Определении проблемы). FEMM реализует нелинейную формулировку гармоники времени, которая вычисляет амплитуда и фаза основной части магнитного поля для времени гармонические задачи с нелинейными задачами материалов. Для нелинейных задач гармоники по времени свойство Circuit Properties диалоговое окно можно снова использовать для сбора различных оконечных свойств катушки.

.