Формулы по физике 9 класса. Все формулы по физике за 9 класс с пояснениями и определениями
| Закон | Формула | Определение | Единицы измерения |
|---|---|---|---|
| ЗАКОНЫ ВЗАИМОДЕЙСТВИЯ И ДВИЖЕНИЯ ТЕЛ | |||
| Вычисление перемещения | АВ2 = АС2 + ВС2 | Перемещение – вектор, соединяющий начальную точку движения тела с его конечной точкой. | |
| Проекция вектора перемещения | Sx = x2 – x1 | x1 – начальная координата, [м] x2 – конечная координата, [м] Sx – перемещение, [м] | |
| Формула расчета скорости движения тела | v = s/t | Скорость – физическая величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло. | s – путь, [м] t – время, [c] |
| Уравнение движения | x = x0 + vxt | x0 – начальная координата, [м] x – конечная координата, [м] v – скорость, [м/с] t – время, [c] | |
| Формула для вычисления ускорения движения тела | a = v – v0⃗/t | Ускорение – физическая величина, которая характеризует быстроту изменения скорости. | a – ускорение, [м/с2] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] t – время, [c] |
| Уравнение скорости | v = v0⃗+ at | v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c] | |
| Уравнение Галилея | S = v0t + at2/2 | S – перемещение, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c] | |
| Закон изменения координаты тела при прямолинейном равноускоренном движении | x = x0 + v0t + at2/2 | x0 – начальная координата, [м] x – конечная координата, [м] v – конечная скорость, [м/с] v0 – начальная скорость, [м/с] a – ускорение, [м/с2] t – время, [c] | |
| Первый закон Ньютона | Если на тело не действуют никакие тела либо их действие скомпенсировано, то это тело будет находиться в состоянии покоя или двигаться равномерно и прямолинейно. | ||
| Второй закон Ньютона | a = F ⃗/m | Ускорение, приобретаемое телом под действием силы, прямо пропорционально величине этой силы и обратно пропорционально массе тела. | a – ускорение, [м/с F – сила, [Н] m – масса, [кг] |
| Третий закон Ньютона | |F1⃗ |=|F2⃗| F11 ⃗ = -F2⃗ | Сила, с которой первое тело действует на второе, равна по модулю и противоположна по направлению силе, с которой второе тело действует на первое | F – сила, [Н] |
| Формула для вычисления высоты, с которой падает тело | H=gt2/2 | Н – высота, [м] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения | |
| Формула для вычисления высоты при движении вертикально вверх | h=v0t – gt2/2 | h – высота, [м] v0 – начальная скорость, [м/с] t – время, [c] g ≈ 9,81 м/с2 – ускорение свободного падения | |
| Формула для вычисления веса тела при движении вверх с ускорением | P = m (g + a) | P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2] | |
| Формула для вычисления веса тела при движении вниз с ускорением | P = m (g – a) | P – вес тела, [Н] m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения a – ускорение тела, [м/с2] | |
| Формула закона | F = Gm1m2/r2 | Закон всемирного тяготения: два тела притягиваются друг к другу с силой, прямо пропорциональной произведению масс этих тел и обратно пропорциональной квадрату расстояния между ними.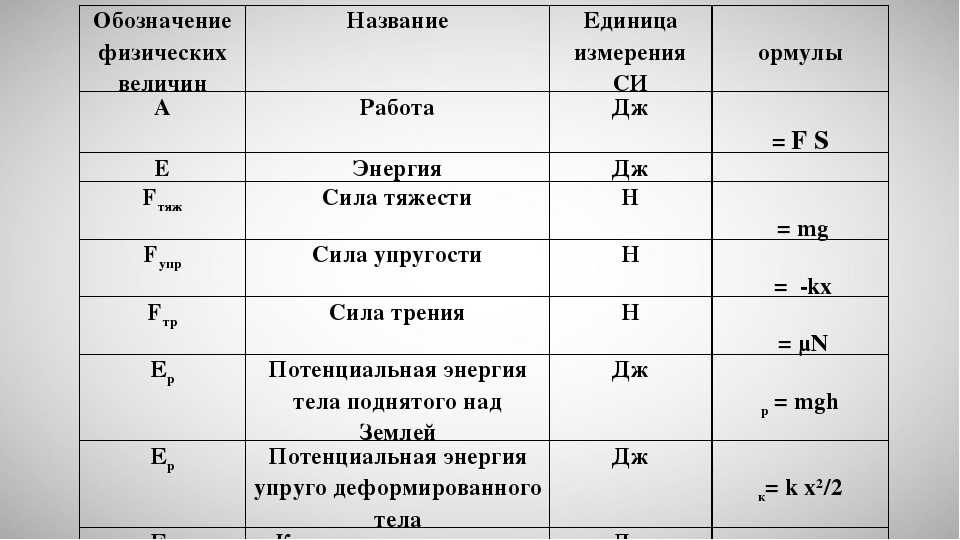 | F – сила, [Н] G = 6,67 · 10-11 [Н·м2/кг2] – гравитационная постоянная m – масса тела, [кг] |
| Формула расчета ускорения свободного падения на разных планетах | g = G Mпл/Rпл2 | g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2 – гравитационная постоянная M – масса планеты, [кг] R – радиус планеты, [м] | |
| Формула расчета ускорения свободного падения | g = GM3/(R3+H)2 | g – ускорение свободного падения, [м/с2] G = 6,67 · 10-11 [Н·м2/кг2 – гравитационная постоянная M – масса Земли, [кг] R – радиус Земли, [м] Н – высота тела над Землей, [м] | |
| Формула расчета центростремительного ускорения | а=υ2/r | a – центростремительное ускорение, [м/с2] v – скорость, [м/с] r – радиус окружности, [м] | |
| Формула периода движения по окружности | T = 1/ν = (2πr)/υ = t/N | Т – период, [с] ν – частота вращения, [с-1] t – время, [с] N – число оборотов | |
| Формула расчета угловой скорости | ω = 2π/T = 2πν = υr | ω – угловая скорость, [рад/с] υ – линейная скорость, [м/с] Т – период, [с] ν – частота вращения, [с-1] r – радиус окружности, [м] | |
| Формула импульса тела | p = mv | Импульсом называют произведение массы тела на его скорость. | p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость, [м/с] |
| Формула закона сохранения импульса | p1 + p2 = p1’ + p2’
m1v + m2u = m | Закон сохранения импульса: в замкнутой системе импульс всех тел остается величиной постоянной. | p – импульс тела, [кг·м/с] m – масса тела, [кг] υ – скорость 1-го тела, [м/с] u – скорость 2-го тела, [м/с] |
| Формула импульса силы | P = Ft | p – импульс тела, [кг·м/с] F – сила, [Н] t – время, [c] | |
| Формула механической работы | A = Fs | Механическая работа – физическая величина, равная произведению модуля силы на величину перемещения тела в направлении действия силы | A – работа, [Дж] F – сила, [Н] s – пройденный путь, [м] |
| Формула расчета мощности | N = A/t | Мощность – физическая величина, характеризующая быстроту совершения механической работы. | N – мощность, [Вт] A – работа, [Дж] t – время, [c] |
| Формула для нахождения коэффициента полезного действия (КПД) | η = Aп/Aз∙100 | КПД – отношение полезной работы к затраченной работе. | Aп – полезная работа, [Дж] Aз – затраченная работа, [Дж] |
| Формула расчета потенциальной энергии | Ek = mv2/2 | Кинетическая энергия – энергия, которой обладает тело вследствие своего движения. | Ek – кинетическая энергия тела, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с] |
| Формула закона сохранения полной механической энергии | mv12/2 + mgh1 = mv22/2 + mgh2 | Закон сохранения полной механической энергии: полная механическая энергия тела, на которое не действуют силы трения и сопротивления, в процессе его движения остается неизменной. | m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения v1 – скорость тела в начальный момент времени, [м/с] v2 – скорость тела в конечный момент времени, [м/с] h1 – начальная высота, [м] h2 – конечная высота, [м] |
| Формула силы трения | Fтр = μmg | Сила трения – сила, возникающая при соприкосновении двух тел и препятствующая их относительному движению. | Fтр – сила трения, [Н] μ – коэффициент трения m – масса тела, [кг] g ≈ 9,81 м/с2 – ускорение свободного падения |
| Уравнение колебаний | x = A cos (ωt + φ0) | А – амплитуда колебаний, [м] х – смещение, [м] t – время, [c] ω – циклическая частота, [рад/с] φ0 – начальная фаза, [рад] | |
| Формула периода | T = 1/ν = 2πr/υ = t/N | Т – период, [с] ν – частота колебании, [с-1] t – время колебании, [с] N – число колебаний | |
| Формула периода для математического маятника | T= 2π √L/g | Т – период, [с] g ≈ 9,81 м/с2 – ускорение свободного падения L – длина нити, [м] | |
| Формула периода для пружинного маятника | T = 2π √m/K | Т – период, [с] m – масса груза, [кг] К – жесткость пружины, [Н/м] | |
| Формула длины волны | λ = υТ = υ/ν | λ – длина волны, [м] Т – период, [с] ν – частота, [с-1] υ – скорость волны, [м/с] | |
| Формула расчета плотности тела | ρ=m/V | Плотность вещества – показывает, чему равна масса вещества в единице объема. | ρ – плотность, [кг/м3] m – масса, [кг] V – объем тела, [м3] |
| Формула гидростатического давления жидкости | p = ρgh | p – давление, [Па], [Н/м] ρ – плотность жидкости, [кг/м3] g ≈ 9,81 м/с2 – ускорение свободного падения h – высота столба жидкости, [м] | |
| Формула силы Архимеда | FA = ρgV | Закон Архимеда: на всякое тело, погруженное в жидкость (газ(, действует выталкивающая сила, равная весу вытесненной жидкости (газа). | FА – сила Архимеда, [Н] ρ – плотность жидкости или газа [кг/м3] g ≈ 9,81 м/с2 – ускорение свободного падения V – объем тела, [м3] |
| ЭЛЕКТРОМАГНИТНОЕ ПОЛЕ | |||
| Формула расчета силы Ампера | FA = BIL sinα | Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником. | FA – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м] |
| Формула расчета силы Лоренца | Fл = q B υ sinα | Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы. | Fл – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] |
| Формула радиуса движения частицы в магнитном поле | r = mυ/qB | r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] | |
| Формула для вычисления магнитного потока | Ф = B S cosα | Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м2] | |
| Формула для вычисления величины заряда | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Закон Ома для участка цепи | I=U/R | Закон Ома: сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления удельного сопротивления проводника | R = ρ * L/S ρ = R * S/L | Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник. | ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [мм2] L – длина проводника, [м] |
| Законы последовательного соединения проводников | I = I1 = I2 U = U1 + U2 Rобщ = R1 + R2 | Последовательным соединением называется соединение, когда элементы идут друг за другом. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Законы параллельного соединения проводников | U = U1 = U2 I = I1 + I2 1/Rобщ = 1/R1 +1/R2 | Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления величины заряда. | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула для нахождения работы электрического тока | A = Uq A = UIt | Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д. д.Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. | A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула электрической мощности | P = A/t P = UI P = U2/R | Мощность – работа, выполненная в единицу времени. | P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом] |
| Формула закона Джоуля-Ленца | Q = I2Rt | Закон Джоуля-Ленца: при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. | Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом]. |
| Закон отражения света | Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча. | ||
| Закон преломления | sinα/sinγ = n2/n1 | При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого. | n – показатель преломления одного вещества относительно другого |
| Формула вычисления абсолютного показателя преломления вещества | n = c/v | Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде. | n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с] |
| Закон Снеллиуса | sinα/sinγ = v1/v2 = n | Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления одного вещества относительно другого v – скорость света в данной среде, [м/с] |
| Показатель преломления среды | sinα/sinγ = n | Отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления среды |
| Формула оптической силы линзы | D = 1/F | Оптическая сила линзы – способность линзы преломлять лучи. | D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м] |
| Формула тонкой линзы | 1/F = 1/d + 1/f | F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м] | |
| СТРОЕНИЕ АТОМА И АТОМНОГО ЯДРА | |||
| Массовое число | M = Z + N | M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов | |
| Формула массы ядра | Мя = МА – Zme | Mя – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг] | |
| Формула дефекта масс | ∆m = Zmp+ Nmn – MЯ | Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида.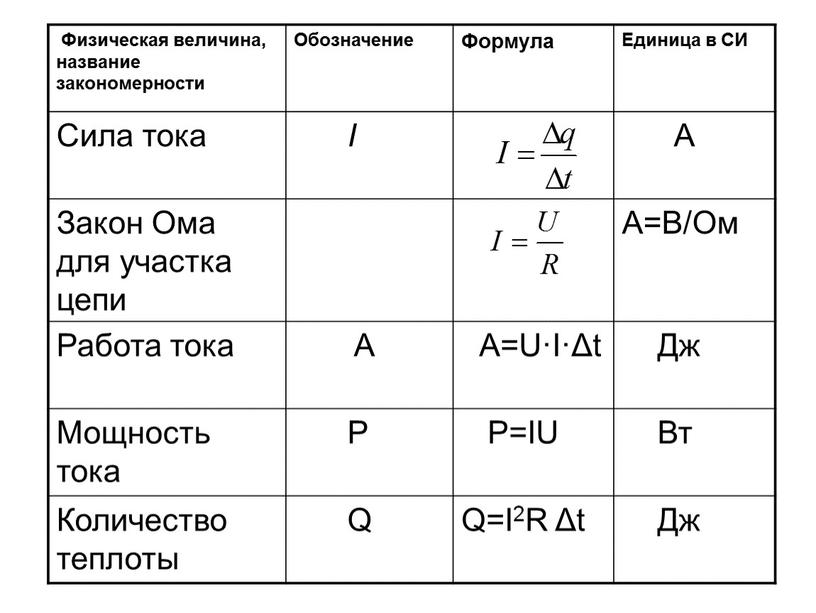 | ∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг] |
| Формула энергии связи | Есвязи = ∆m c2 | Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). | Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·108м/с – скорость света |
| Альфа распад | M/Z * X → 4/2 * α + M/Z – 4/2 * Y | ||
Формулы по физике 11 класса. Все формулы по физике за 11 класс с пояснениями и определениями
| Закон | Формула | Определение | Единицы измерения |
|---|---|---|---|
| Формула расчета силы Ампера | FA = B I L sinα | Закон Ампера: сила действия однородного магнитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником.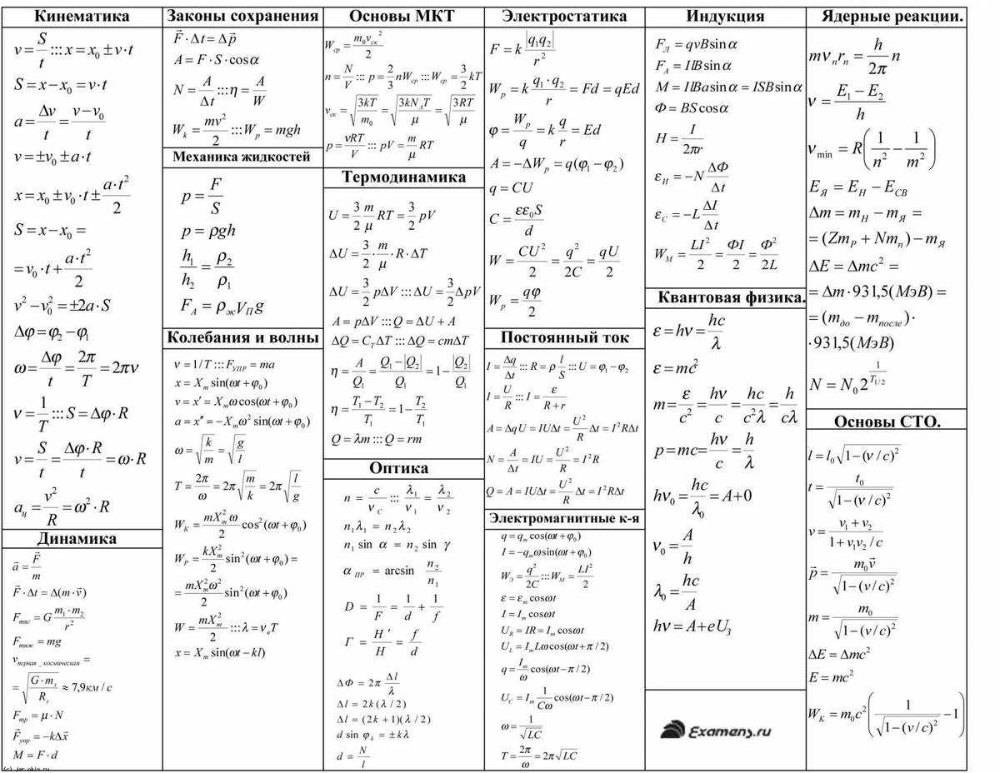 | FA – сила Ампера, [Н] В – магнитная индукция, [Тл] I – сила тока, [А] L – длина проводника, [м] |
| Формула расчета силы Лоренца | Fл= q B υ sinα | Сила Лоренца – сила, действующая на точечную заряженную частицу, движущуюся в магнитном поле. Она равна произведению заряда, модуля скорости частицы, модуля вектора индукции магнитного поля и синуса угла между вектором магнитного поля и скоростью движения частицы. | Fл – сила Лоренца, [Н] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] |
| Формула радиуса движения частицы в магнитном поле | r= mυ/qB | r – радиус окружности, по которой движется частица в магнитном поле, [м] m – масса частицы, [кг] q – заряд, [Кл] В – магнитная индукция, [Тл] υ – скорость движения заряда, [м/с] | |
| Формула для вычисления магнитного потока | Ф = B S cosα | Ф – магнитный поток, [Вб] В – магнитная индукция, [Тл] S – площадь контура, [м2] | |
| Формула для вычисления величины заряда | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Закон Ома для участка цепи | I = U/R | Закон Ома – сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления удельного сопротивления проводника | R = ρ L/S ρ = R S/L | Удельное сопротивление – величина, характеризующая электрические свойства вещества, из которого изготовлен проводник. | ρ – удельное сопротивление вещества, [Ом·мм2/м] R – сопротивление, [Ом] S – площадь поперечного сечения проводника, [ммБ2] L – длина проводника, [м] |
| Законы последовательного соединения проводников | I = I1 = I2 U = U1 + U2 Rобщ = R1 + R2 | Последовательным соединением называется соединение, когда элементы идут друг за другом.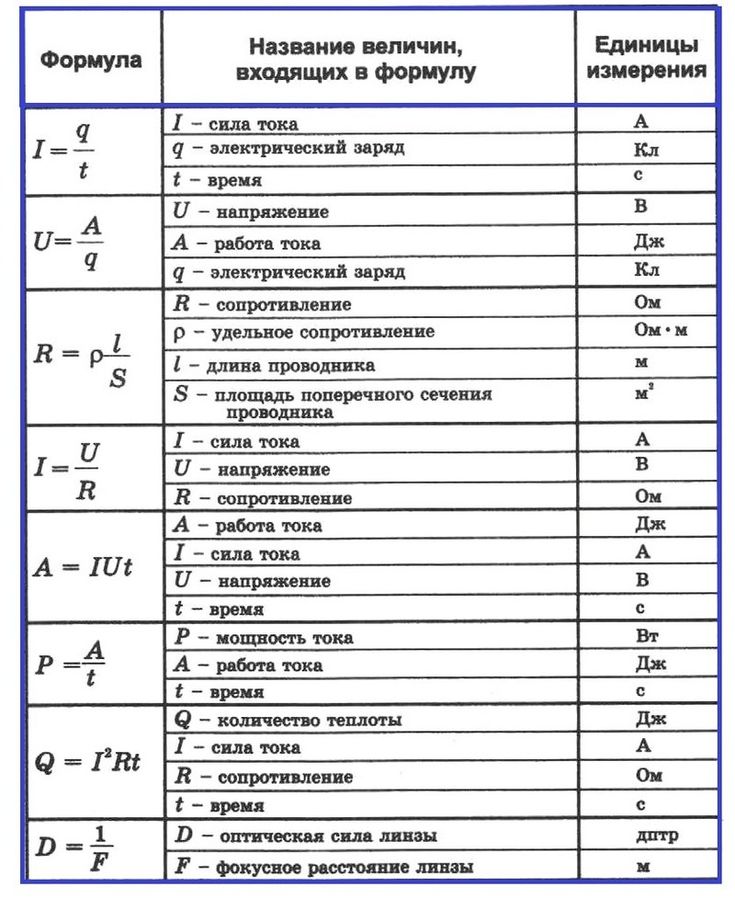 | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Законы параллельного соединения проводников | U = U1 = U2 I = I1 + I2 1/Rобщ =1/R1 +1/R2 | Параллельным соединением проводников называется такое соединение, при котором начала и концы проводников соединяются вместе. | I – сила тока, [А] U – напряжение, [В] R – сопротивление, [Ом] |
| Формула для вычисления величины заряда. | q = It | Заряд – это есть произведение силы тока на время, в течение которого этот заряд протекает по проводнику. | q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула для нахождения работы электрического тока. | A = Uq A = UIt | Работа – это величина, которая характеризует превращение энергии из одного вида в другой, т.е. показывает, как энергия электрического тока, будет превращаться в другие виды энергии – механическую, тепловую и т. д.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. д.
Работа электрического поля – это произведение электрического напряжения на заряд, протекающий по проводнику. Работа, совершаемая для перемещения электрического заряда в электрическом поле. | A – работа электрического тока, [Дж] U – напряжение на концах участка, [В] q – заряд, [Кл] I – сила тока, [А] t – время, [c] |
| Формула электрической мощности | P = A/t P = UI P = U2/R | Мощность – работа, выполненная в единицу времени. | P – электрическая мощность, [Вт] A – работа электрического тока, [Дж] t – время, [c] U – напряжение на концах участка, [В] I – сила тока, [А] R – сопротивление, [Ом] |
| Формула закона Джоуля-Ленца | Q=I2Rt | Закон Джоуля-Ленца при прохождении электрического тока по проводнику количество теплоты, выделяемое в проводнике, прямо пропорционально квадрату тока, сопротивлению проводника и времени, в течение которого электрический ток протекал по проводнику. | Q – количество теплоты, [Дж] I – сила тока, [А]; t – время, [с]. R – сопротивление, [Ом]. |
| ЭЛЕКТРОМАГНИТНОЕ ИЗЛУЧЕНИЕ | |||
| Закон отражения света | Луч падающий, луч отраженный и перпендикуляр, восставленный в точку падения луча, лежат в одной плоскости, при этом угол падения луча равен углу отражения луча. | ||
| Закон преломления | sinα/sinγ = n2/n1 | При увеличении угла падения увеличивается и угол преломления, то есть при угле падения, близком к 90°, преломлённый луч практически исчезает, а вся энергия падающего луча переходит в энергию отражённого. | n – показатель преломления одного вещества относительно другого |
| Формула вычисления абсолютного показателя преломления вещества | n = c/v | Абсолютный показатель преломления вещества – величина, равная отношению скорости света в вакууме к скорости света в данной среде. | n – абсолютный показатель преломления вещества c – скорость света в вакууме, [м/с] v – скорость света в данной среде, [м/с] |
| Закон Снеллиуса | sinα/sinγ = v1/v2=n | Закон Снеллиуса (закон преломления света): отношение синуса угла падения к синусу угла преломления есть величина постоянная. | |
| Показатель преломления среды | sinα/sinγ = n | Отношение синуса угла падения к синусу угла преломления есть величина постоянная. | n – показатель преломления среды |
| Преломляющий угол призмы | δ = α(n – 1) | δ – угол отклонения α – угол падения n – показатель преломления среды | |
| Линейное увеличение оптической системы | Г = H/h | Г – линейное увеличение оптической системы H – размер изображения, [м] h – размер предмета, [м] | |
| Формула оптической силы линзы | D = 1/F | Оптическая сила линзы – способность линзы преломлять лучи. | D – оптическая сила линзы, [дптр] F – фокусное расстояние линзы, [м] |
| Формула тонкой линзы | 1/F = 1/d+1/f | F – фокусное расстояние линзы, [м] d – расстояние от предмета до линзы, [м] f – расстояние от линзы до изображения, [м] | |
| Максимальная результирующая интенсивность | Δt = mT | Δt – максимальная результирующая интенсивность Т – период колебании, [с] | |
| Минимальная результирующая интенсивность | Δt = (2m + 1)T/2 | Δt – минимальная результирующая интенсивность Т – период колебании, [с] | |
| Геометрическая разность хода интерферирующих волн | Δ = mλ | Δ – геометрическая разность хода интерферирующих волн λ – длина волны, [м] | |
| Условие интерференционного минимума | Δ = (2m + 1)λ/2 | λ – длина волны, [м] | |
| Условие дифракционного минимума на щели | Asinα = m λ | A – ширина щели, [м] λ – длина волны, [м] | |
| Условие главных максимумов при дифракции | dsinα = m λ | d – период решетки λ – длина волны, [м] | |
| Энергия кванта излучения | E = hϑ | Е – энергия кванта излучения, [Дж] ϑ – частота излучения h – постоянная Планка | |
| Закон смещения Вина | λT = b | b – постоянная Вина λ – длина волны, [м] Т – температура черного тела | |
| Закон Стефана-Больцмана | R = ϭT4 | ϭ – постоянная Стефана-Больцмана Т – абсолютная температура черного тела R – интегральная светимость абсолютно черного тела | |
| Уравнение Эйнштейна для фотоэффекта | А – работа выхода, [Дж] m – масса тела, [кг] v – скорость движения тела, [м/с] ϑ – частота излучения h – постоянная Планка | ||
| ФИЗИКА ВЫСОКИХ ЭНЕРГИИ | |||
| Массовое число | M = Z + N | M – массовое число Z – число протонов (электронов), зарядовое число N – число нейтронов | |
| Формула массы ядра | МЯ = МА – Z me | MЯ – масса ядра, [кг] МА – масса изотопа , [кг] me – масса электрона, [кг] | |
| Формула дефекта масс | ∆m = Zmp+ Nmn – MЯ | Дефект масс – разность между суммой масс покоя нуклонов, составляющих ядро данного нуклида, и массой покоя атомного ядра этого нуклида. | ∆m – дефект масс, [кг] mp – масса протона, [кг] mn – масса нейтрона, [кг] |
| Формула энергии связи | Есвязи = ∆m c2 | Энергия связи ядра – минимальная энергия, необходимая для того, чтобы разделить ядро на составляющие его нуклоны (протоны и нейтроны). | Есвязи – энергия связи, [Дж] m – масса, [кг] с = 3·108м/с – скорость света |
| Закон радиоактивного распада | N = N02 –t/T1/2 | N0 – первоначальное количество ядер N – конечное количество ядер T – период полураспада, [c] t – время, [c] | |
| Доза поглощенного излучения | D = E/m | D – доза поглощенного излучения, [Гр] E – энергия излучения, [Дж] m – масса тела, [кг] | |
| Эквивалентная доза поглощенного излучения | H = Dk | H – эквивалентная доза поглощенного излучения, [Зв] D – доза поглощенного излучения, [Гр] k – коэффициент качества | |
1.
 4 Размерный анализ | University Physics Volume 1
4 Размерный анализ | University Physics Volume 1Цели обучения
К концу этого раздела вы сможете:
- Находить размерности математического выражения, включающего физические величины.
- Определить, является ли уравнение, включающее физические величины, размерно-согласованным.
Размерность любой физической величины выражает ее зависимость от основных величин как произведение символов (или степеней символов), представляющих основные величины. (Рисунок) перечислены основные величины и символы, используемые для их измерения. Например, говорят, что измерение длины имеет размерность L или L 1 , измерение массы имеет размерность M или M 1 , а измерение времени имеет размерность T или T 1 . Как и единицы, измерения подчиняются правилам алгебры. Таким образом, площадь является произведением двух длин и поэтому имеет размерность L 2 , или длину в квадрате. Точно так же объем является произведением трех длин и имеет размерность L 3 , или длину в кубе. Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
Скорость имеет размерность длины во времени, L/T или LT –1 . Объемная массовая плотность имеет размерность M/L 3 9{0} [/latex]) называется безразмерным (или иногда «размерностью 1», потому что все, что возведено в нулевую степень, равно единице). Физики часто называют безразмерные величины чистыми числами .
| Базовое количество | Символ размера |
|---|---|
| Длина | л |
| Масса | М |
| Время | Т |
| Текущий | я |
| Термодинамическая температура | Θ |
| Количество вещества | Н |
| Сила света | Дж |
Физики часто используют квадратные скобки вокруг символа физической величины, чтобы представить размеры этой величины. Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Например, если [латекс] r [/латекс] — это радиус цилиндра, а [латекс] h [/латекс] — его высота, то мы пишем [латекс] [г]=\текст{L} [/латекс] и [латекс] [ч]=\текст{L} [/латекс] для указания того, что размеры радиуса и высоты совпадают с размерами длины или L. Аналогично, если мы используем символ [латекс] А [/латекс] для площади поверхности цилиндра и [латекс] V [/латекс] для его объема, то [ 9{-3}. [/latex]
Важность концепции размерности возникает из-за того факта, что любое математическое уравнение, связывающее физические величины, должно быть размерно-согласованным, что означает, что уравнение должно подчиняться следующим правилам:
- Каждый член выражения должен иметь одинаковые размеры; нет смысла прибавлять или вычитать количества разной размерности (вспомните старую поговорку: «Нельзя складывать яблоки и апельсины»). В частности, выражения по обе стороны равенства в уравнении должны иметь одинаковые размерности.
- Аргументы любых стандартных математических функций, таких как тригонометрические функции (такие как синус и косинус), логарифмы или экспоненциальные функции, которые появляются в уравнении, должны быть безразмерными.
 Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Эти функции требуют чистых чисел в качестве входных данных и дают чистые числа в качестве выходных данных.
Если какое-либо из этих правил нарушается, уравнение не является размерно-согласованным и не может быть правильной формулировкой физического закона. Этот простой факт можно использовать для проверки опечаток или алгебраических ошибок, чтобы помочь вспомнить различные законы физики и даже предложить форму, которую могут принять новые законы физики. Это последнее использование измерений выходит за рамки этого текста, но вы, несомненно, узнаете об этом позже в своей академической карьере. 9{2} [/латекс] и [латекс] 2\pi r. [/latex] Одно выражение — это длина окружности круга радиусом r , а другое — его площадь. Но что есть что?
Стратегия
Естественная стратегия — искать информацию, но это может занять время, чтобы найти информацию из авторитетного источника. Кроме того, даже если мы считаем источник авторитетным, мы не должны доверять всему, что читаем. Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
Приятно иметь возможность перепроверить, просто подумав об этом. Кроме того, мы можем оказаться в ситуации, в которой мы не можем найти информацию (например, во время теста). Таким образом, стратегия состоит в том, чтобы найти размерности обоих выражений, используя тот факт, что размерности подчиняются правилам алгебры. Если какое-либо из выражений не имеет таких же размеров, как площадь, то оно не может быть правильным уравнением для площади круга. 9{2} [/latex] имеет размерность площади. Точно так же размерность выражения [латекс] 2\pi r [/латекс] равна
[латекс] [2\pi r]=[2]·[\pi ]·[r]=1·1·\text {L}=\text{L,} [/latex]
, так как константы [latex] 2 [/latex] и [latex] \pi [/latex] безразмерны, а радиус [latex] r [/latex ] — это длина. Мы видим, что [латекс] 2\pi r [/латекс] имеет размерность длины, что означает, что он никак не может быть площадью.
Мы исключаем [латекс] 2\pi r [/латекс], потому что его размеры не соответствуют площади. Мы видим, что [латекс] \pi {r}^{2} [/латекс] согласуется по размерам с областью, поэтому, если нам нужно выбирать между этими двумя выражениями, [латекс] \пи {г}^{2} [/latex] — это то, что нужно выбрать. {2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
{2}, [/латекс], то размерные анализ не поможет), но помогает нам запомнить правильную основную форму уравнений. 9{2}\text{/}s). [/latex]
Стратегия
В соответствии с определением размерной согласованности нам необходимо проверить, что каждый член данного уравнения имеет те же размерности, что и другие члены этого уравнения, и что аргументы любых стандартных математических функций безразмерны.
Решение
- В этом уравнении нет ни тригонометрических, ни логарифмических, ни экспоненциальных функций, поэтому нам достаточно посмотреть на размеры каждого члена, входящего в уравнение. Есть три термина, один в левом выражении и два в выражении справа, поэтому мы рассмотрим каждый по очереди: 9{2}}{s})]=1.\hfill \end{массив} [/latex]
Два термина имеют разные размерности — это означает, что уравнение не является размерно-согласованным. Это уравнение — еще один пример «бессмыслицы».
Значение
Если мы доверяем людям, эти виды размерных проверок могут показаться ненужными. Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Но, будьте уверены, любой учебник по количественному предмету, такому как физика (включая этот), почти наверняка содержит некоторые уравнения с опечатками. Регулярная проверка уравнений с помощью размерного анализа избавляет нас от необходимости использовать неверное уравнение. Кроме того, проверка размерностей уравнения, которое мы получаем с помощью алгебраических манипуляций, — отличный способ убедиться, что мы не допустили ошибку (или обнаружить ошибку, если она была допущена).
Проверьте свое понимание
Соответствует ли размерность уравнения v = at ?
Показать решение
Еще один момент, о котором следует упомянуть, — это влияние операций исчисления на размерности. Мы видели, что размеры подчиняются правилам алгебры, как и единицы, но что происходит, когда мы берем производную одной физической величины по отношению к другой или интегрируем физическую величину по другой? Производная функции — это просто наклон линии, касательной к ее графику, а наклоны — это отношения, поэтому для физических величин v и t , мы имеем, что размерность производной v по отношению к t есть просто отношение размерности v к размерности t :
[латекс] [ \frac{dv}{dt}]=\frac{[v]}{[t]}. [/latex]
[/latex]
Аналогично, поскольку интегралы представляют собой просто суммы произведений, размерность интеграла v по отношению к t — это просто размерность v , умноженная на размерность t :
[латекс] [\int vdt]=[v]·[t]. [/latex]
По тем же рассуждениям аналогичные правила справедливы для единиц физических величин, полученных из других величин путем интегрирования или дифференцирования.
Резюме
- Размерность физической величины — это просто выражение основных величин, из которых она получена.
- Все уравнения, выражающие физические законы или принципы, должны быть согласованы по размерам. Этот факт можно использовать как помощь в запоминании физических законов, как способ проверить, возможны ли заявленные соотношения между физическими величинами, и даже для вывода новых физических законов. 9{2}; [/latex] (c) [latex] v=s\text{/}t; [/latex] (d) [latex] a=v\text{/}t. [/latex]
Показать решение
Рассмотрим физические величины [латекс] m, [/латекс] [латекс] s, [/латекс] [латекс] v, [/латекс] [латекс] а, [/латекс] и [латекс] t [/латекс ] с размерами [ м ] = M, [ s ] = L, [ v ] = LT –1 , [ a ] = LT –2 , и [ 2 t 90 ] T.
 Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .
Предполагая, что каждое из следующих уравнений размерно согласовано, найдите размерность величины в левой части уравнения: (a) F = мА ; б) К = 0,5 mv 2 ; в) p = mv ; (г) Вт = мсд ; (e) L = mvr .Предположим, что количество [латекс] s [/латекс] — это длина, а количество [латекс] t [/латекс] — это время. Предположим, что количества [латекс] v [/латекс] и [латекс] а [/латекс] определены как v = ds / dt и a = dv / dt . а) Какова размерность числа 9?{–3}, [/latex] и [t] = T. (a) Какова размерность [latex] \int \rho dV? [/latex] (b) Каков размер dV / dt ? в) Каков размер [латекс] \rho (dV\text{/}dt)? [/latex]
Формула длины дуги говорит, что длина [латекс] s [/латекс] дуги, опирающейся на угол [латекс] Ɵ [/латекс] в окружности радиусом [латекс] r [/латекс], определяется выражением уравнение [латекс] s=rƟ.
 [/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числом
[/latex] Каковы размеры (a) s , (b) r и (c) [latex] \text{Ɵ?} [/latex] 9{0}=1; [/latex] также называется количеством измерения 1 или чистым числомУравнения физики
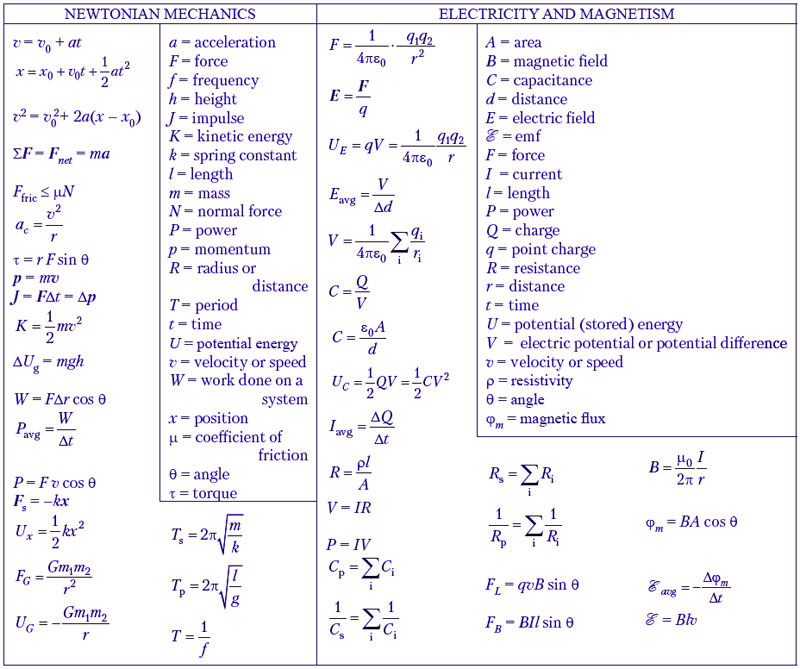
Эти составляют всех уравнений, которые вам приходилось вспоминать на экзаменах по физике… на каждом этапе предполагалось, что вы помните те, что были на предыдущем этап… так что стоило их как следует перенести на свой ментальный “жесткий” водить машину’!
Экзаменационные комиссии по английскому языку теперь ДАЮТ вам уравнения, так что вы больше не будете получать оценки за их запоминание. Однако я бы сказал, что на самом деле знание их облегчает вам объяснение физических принципов.
Например, если вы ЗНАЕТЕ, что F=ma, то, отвечая на вопрос «Что включает в себя наличие действующей силы?», вы знаете, что результирующая сила заставит тело ускоряться.
Имея математический склад ума, я считаю, что изучение уравнений является сокращенным способом изучения физики!
Марка убедитесь, что вы знаете правильные единицы измерения.
 …….. все единицы, которые будут использоваться в уравнениях, должны быть в их основной форме (без префиксов) – ЗА ИСКЛЮЧЕНИЕМ массы – это кг!
…….. все единицы, которые будут использоваться в уравнениях, должны быть в их основной форме (без префиксов) – ЗА ИСКЛЮЧЕНИЕМ массы – это кг!Помнить быть осторожным, когда вы пишете буквы уравнения… это символы НЕ часть вашего почерка!
Особый уход с I для тока спутать с л не должно для длина или 1 (номер один)!Уравнение прописью Символический представительство Год Ключ Сцена
скорость = пройденное расстояние затраченное время
В = д/т Y7 КС3 ускорение = изменение скорости
затраченное время
а = Дв/т Y8 КС3 плотность = масса
объемр = м/В Y7 КС3 сила = масса х ускорение Ф = млн летY9 КС3 работа done = сила x расстояние, пройденное в направлении этой силы Вт = Фс Y9 КС3 импульс = масса х скорость р = мв Y12 КАК мощность = переданной энергии потрачено времени
П = Э/т Y8 KS3 мощность = выполненная работа потрачено времени
П = Вт/т Y9 KS3 вес = масса x гравитационное поле
силаВт = мг Y7 KS3 кинетический энергия = половина x масса x (квадрат скорости) Э К = 1 / 2 МВ 2 Y12 KS4 изменение в гравитационной потенциальной энергии = масса x гравитационное поле сила x разница в росте ДГПЭ = мгдх Y9 KS3 давление = приложенная сила
площадь контактаП = F
AY7 KS3 Газ Закон: давление x объем газа = количество молей x молярная газовая постоянная x абсолютная температура пВ = нРТ Y12 КАК Газ Закон: комбинация закона Бойля и закона Чарльза П 1 В 1 = P 2 V 2
T 1 5 2 9049 9039 5 2 9049 9039NB Температура ДОЛЖНА быть в Кельвинах Y11 КС4 плата = текущее х время ДК = I Dt Y10 KS4 Ом Закон: Разность потенциалов = ток x сопротивление В = I Р Y8 KS3 Ом Закон, применяемый к полной цепи : Электродвижущая сила = ток x (сумма сопротивления цепи и внутреннего сопротивления ячейка) ЭДС = I ( R +р) Y12 КАК мощность = ток x разность потенциалов П = I В Y8 KS3 энергия переданный в компоненте = заряд, прошедший через него x потенциал разница между ними Вт = ГВ Y10 KS4 сопротивление = удельное сопротивление x длина
площадь поперечного сеченияР = r l
AY12 КАК скорость волны = частота x длина волны v = fl
для электромагнитного излучение v = c дает:
c = flY8 KS3 центростремительный сила = масса x скорость 2
радиус путиФ С = мв 2
rY13 А2 Электрика энергия превратилась в тепло = разность потенциалов х ток х время Е = V I т Y9 KS3 Обратный квадратный закон для силы, действующей на массу в гравитационном поле другая масса: сила пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их Ф Г = – G м 1 м 2
r 2НБ знак минус означает, что это ВСЕГДА привлекательно
Y13 А2 Обратный квадратичный закон для силы, действующей на заряд в электрическом поле другого заряд: сила пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними F E = 1 Q 1 Q 2
4PE0391 2
4PE0391 2
4 4PE0391 2 9037 4PE03912 4PE0391 2 4PE0391 2 2 НБ общий знак, указывающий, является ли он привлекательным (отрицательный) или отталкивающее (положительное) происходит от знаков зарядов.
Кроме того, хотя постоянная пропорциональности сложна, это похожее отношение к выше.Y13 А2 емкость = сохраненный заряд
разность потенциаловС = В
ВY13 А2 соотношение напряжения на катушках трансформатора = отношение витков на катушках В 1 = N 1
V 2 N 2
NB 1 может быть P для первичного и 2 может быть s для вторичного – это не имеет значения что есть что!Y11 КС4 LOJ Ноябрь 2000 г.



