Как понять закон ома: Закон ома простым языком. Закон Ома для «чайников»: понятие, формула, объяснение

Закон Ома

Закон Ома – Один из самых применяемых законов в электротехнике. Данный закон раскрывает связь между тремя важнейшими величинами: силой тока, напряжением и сопротивлением. Выявил эту связь Георгом Омом в 1820-е годы именно поэтому этот закон и получил такое название.

Формулировка закона Ома следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

I=U/R

Где I – сила тока, U — напряжение, приложенное к участку цепи, а R — электрическое сопротивление участка цепи.
Так, если известны две из этих величин можно легко вычислить третью.
Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное).

Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.
Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.
Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.
Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 — GB3 — батарейки, S1 — выключатель, HL1 — лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается. Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Что случится с лампочкой?
Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:
чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.

Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Это была обзорная статья. Более подробно об этом законе, мы говорим в следующей статье “Закон Ома для участка цепи”, рассматривая всё на других более сложных примерах.

Если не получается с физикой, английский для детей (http://www. anylang.ru/order-category/?slug=live_language) как вариент альтернативного развития.

---

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

---

Закон Ома понятным языком | Инженерные знания

Рубрики: #электрофизика (inznan) , #основы физики (inznan) , #школьникам (inznan)

Один из фундаментальных законов, который всегда изучают в курсе физике – это закон Ома. Он относительно простой, но при этом весьма важен для корректного понимания. Давайте изучим его в режиме “для чайников”.

С пониманием как такового физического явления, обуславливающего появление закона Ома, обычно проблем не возникает. Но вот с вариантами формулировки и записи самого закона, а также аспектами, связанными с особенностями его применения в разных случаях, сложности частенько появляются.

В основе закона Ома лежит некая физическая штука, которая называется сопротивление.

Понятие сопротивление доходчиво

Электрическое сопротивление – это величина, которая определяет способность проводника пропускать электрический ток. Полезно также освежить знания про электрический ток (писали в этой статье).

Представить это проще всего, исходя из строения металлов.

По классической теории металл состоит из кристаллической решетки, а между структурными элементами этой решетки путешествуют свободные электроны.

Внешнее электрическое поле заставляет их перемещаться и образуется электрический ток, т.е. направленное упорядоченное движение частиц.

Решетка металла мешает им двигаться по своему объему. Электроны трутся об её узлы и не могут протиснуться. Вот это явление и образует сопротивление. Это “сила”, которая мешает перемещению.

Ситуация аналогично ситечку на раковине. Вода проходит, но медленнее, чем проходила бы без ситечка.

Аналогичная ситуация присутствует во всех материалах, правда род и тип частичек может меняться. Тип строения тоже разный. Но условно можно принять, что всегда структура мешает им двигаться что в дереве, что в металле.

В некоторых телах вообще таких частичек не будет, там сопротивление бесконечное (некоторые виды резин, например).

Обратите внимание, что мы не рассматриваем тут понятие электрического тока и напряжения, т.к. это отдельные темы и если есть непонимание, обязательно напишите об этом в комментариях. Правда про электрический ток есть наше видео. Эти вещи нужно четко понимать.

Ну и из сказанного очевидно, что сопротивление будет зависеть от геометрических параметров проводника (т.е. площадь сечения S, длина l) и типа проводника (который тут описывается понятием удельное сопротивление и является табличной величиной). Ещё оно зависит от температуры (чем выше тем больше для большинства тел), но это мы совсем от самого закона уходим. .. Для задачек на закон Ома знаний уже вполне достаточно.

Формулировка закона Ома

В результате множества экспериментов Ом вывел зависимость, которая определяет связь между силой тока в проводнике, напряжением и тем самым сопротивлением, которое мы описали выше.

Звучит закон так: Cила тока на участке электрической цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна его сопротивлению

Вроде как все слова тут понятные, если знать все определения. Сопротивление мы разобрали. Сила тока – это, грубо говоря, количество частичек, которое окажется в проводнике. Понятие сила тока подробно я разбирал в этой статье, обязательно прочитайте её.

Напряжение – это “поток”, который эти частицы несет. Вот вроде бы всё и увязали.

Если рассматривать цепь, то сопротивление по элементам распределяется согласно их техническим характеристикам и вычисляется согласно закону Ома. Т.е. мы не можем утверждать, что на каждом элементе есть одинаковое сопротивление.

Например, если в цепи с последовательным подключением две лампочки, т омы помним что сила тока во всей цепи при таком соединении одинаковая, а вот напряжение на элементах разное. Замеряем его на точках подключения лампочек, записываем и запихиваем в закон Ома. Вот всё и посчитали :)…

Закон Ома для участка цепи

Когда закон ома записан в такой форме, как мы привели выше, то он называется закон ома для участка цепи.

Почему для участка цепи? Для участка, потому что тут не учитывается сопротивление всей цепи. Можно измерить сопротивление на каждом участке исходя из приведенных характеристик.

Закон Ома для полной цепи

Полной цепью (в отличие от участка цепи, применительно к которому мы излагали всё выше) называется цепь с учетом источника тока.

Почему это важно?

Именно потому, что если мы представим себе электрическую цепь условно как систему труб для воды, то участок цепи это будет незамкнутый кусок трубы, а полная цепь – зацикленная система.

Из примера может показаться, что участок цепи есть незамкнутая в электрическом смысле цепь. Нет, пример приведен не для этого. И там, и там электрическая цепь замкнута.

Просто нам нужно обозначить, что без учета источника тока и его внутреннего сопротивления (r) цепь не полная, а расчёт не всегда способен учитывать все значимые характеристики.

Ну а внутреннее сопротивление, как вы наверное догадались – это то сопротивление, которым обладает источник тока. Да, току в цепи сложно проходить и через сам источник! Даже сам источник провоцирует энергетические потери. А вот считать его аналогично расчёту для участка цепи нельзя.

Получается, что в закон Ома добавится ещё и внутренне сопротивление. И всё! Ничего страшного.

Формулировка закона Ома для полной цепи немного изменится. Теперь у нас слово напряжение заменится словом ЭДС (электродвижущая сила), а слово сопротивление заменится суммой внешнего сопротивления цепи и внутреннего сопротивления источника тока. Ну и формула будет такая:

Добавилось понятие электродвижущая сила (ЭДС), обозначенная в формуле E прописное. Что это за зверь?

ЭДС – это, по сути дела, и есть напряжение.

Разница в том, что если мы опять сравним напряжение с напором воды в водопроводе, то напряжением будет являться разница напора между двумя произвольными точками в водопроводе, а ЭДС – это напор на насосе, который качает воду.

При использовании термина ЭДС мы вспоминаем, что у источника есть внутреннее сопротивление, как оно есть и у насоса, который препятствует движению воды через самого себя. Если же мы считали бы именно напряжение источника, то мы бы приняли, что система идеальная и источник движению тока сам не препятствует.

Закон Ома в дифференциальной и интегральной формах

При изучении закона Ома могут выплывать ещё и такие понятия, как закон Ома в дифференциальной и интегральной формах.

Всё это большие темы, поэтому мы рассмотрим их в отдельных статьях.

Тут отметим лишь то, что в дифференциальной форме закон Ома применяется для определения параметров для ничтожно малого участка цепи. Ведь превалирует слово дифференциал или производная.

В интегральной же форме мы рассматриваем цепь с учетом источника тока или без него. Аналогично тому, как мы писали выше. Помним, что интеграл по своей сути – есть сумма.

Если статья оказалась для вас полезной, то обязательно поддержите наш проект лайком и подпиской 😉!

Советую прочитать:

Частные случаи закона ома. Основные электрические законы

Один из самых применяемых законов в электротехнике. Данный закон раскрывает связь между тремя важнейшими величинами: силой тока, напряжением и сопротивлением. Выявил эту связь Георгом Омом в 1820-е годы именно поэтому этот закон и получил такое название.

Формулировка закона Ома следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

Где I – сила тока, U – напряжение, приложенное к участку цепи, а R – электрическое сопротивление участка цепи.
Так, если известны две из этих величин можно легко вычислить третью.
Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное). Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.

Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.
Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.
Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 – GB3 – батарейки, S1 – выключатель, HL1 – лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается.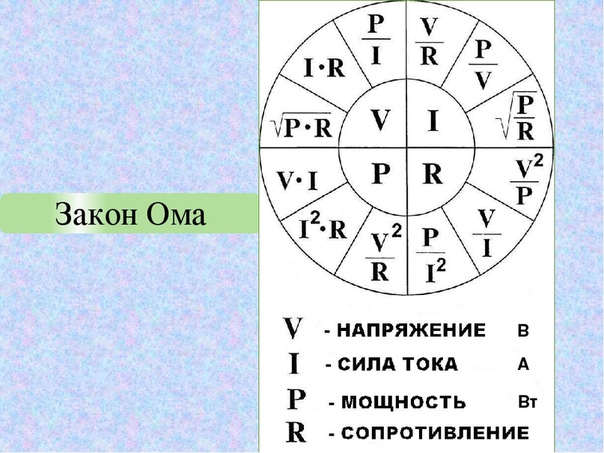 Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Что случится с лампочкой?
Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:
чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.
Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Это была обзорная статья. Более подробно об этом законе, мы говорим в следующей статье ” “, рассматривая всё на других более сложных примерах.

Если не получается с физикой, английский для детей (http://www.anylang.ru/order-category/?slug=live_language) как вариент альтернативного развития.

Такими как электрический ток, напряжение, сопротивление и мощность. Настал черед основных электрических законов, так сказать, базиса, без знания и понимания которых невозможно изучение и понимание электронных схем и устройств.

Закон Ома

Электрический ток, напряжение, сопротивление и мощность, безусловно, между собой связаны. А взаимосвязь между ними описывается, без сомнения, самым главным электрическим законом – законом Ома . В упрощенном виде этот закон называется: закон Ома для участка цепи. И звучит этот закон следующем образом:

«Сила тока в участке цепи прямо пропорциональна напряжению и обратно пропорциональна электрическому сопротивлению данного участка цепи».

Для практического применения формулу закона Ома можно представить в виде вот такого треугольника, который помимо основного представления формулы, поможет определить и остальные величины.

Работает треугольник следующим образом. Чтобы вычислить одну из величин, достаточно закрыть ее пальцем. Например:

В предыдущей статье мы проводили аналогию между электричеством и водой , и выявили взаимосвязь между напряжением, током и сопротивлением. Также хорошей интерпретацией закона Ома может послужить следующий рисунок, наглядно отображающий сущность закона:

На нем мы видим, что человечек «Вольт» (напряжение) проталкивает человечка «Ампера» (ток) через проводник, который стягивает человечек «Ом» (сопротивление). Вот и получается, что чем сильнее сопротивление сжимает проводник, тем тяжелее току через него проходить («сила тока обратно пропорциональна сопротивлению участка цепи» – или чем больше сопротивление, тем хуже приходится току и тем он меньше). Но напряжение не спит и толкает ток изо всех сил (чем выше напряжение, тем больше ток или – «сила тока в участке цепи прямо пропорциональна напряжению»).

Когда фонарик начинает слабо светить, мы говорим – «разрядилась батарейка». Что с ней произошло, что значит разрядилась? А значит это, что напряжение батарейки снизилось и оно больше не в состоянии «помогать» току преодолевать сопротивление цепей фонарика и лампочки. Вот и получается, что чем больше напряжение – тем больше ток.

Последовательное подключение – последовательная цепь

При последовательном подключении потребителей, например обычных лампочек, сила тока в каждом потребителе одинаковая, а вот напряжение будет отличаться. На каждом из потребителей напряжение будет падать (снижаться).

А закон Ома в последовательной цепи будет иметь вид:

При последовательном соединении сопротивления потребителей складываются. Формула для расчета общего сопротивления:

Параллельное подключение – параллельная цепь

При параллельном подключении, к каждому потребителю прикладывается одинаковое напряжение, а вот ток через каждый из потребителей, в случае, если их сопротивление отличается – будет отличаться.

Закон Ома для параллельной цепи, состоящей из трех потребителей, будет иметь вид:

При параллельном соединении общее сопротивление цепи всегда будет меньше значения самого маленького отдельного сопротивления. Или еще говорят, что «сопротивление будет меньше наименьшего».

Общее сопротивление цепи, состоящей из двух потребителей, при параллельном соединении:

Общее сопротивление цепи, состоящей из трех потребителей, при параллельном соединении:

Для большего числа потребителей расчет производится исходя из того, что при параллельном соединении проводимость (величина обратная сопротивлению) рассчитывается как сумма проводимостей каждого потребителя.

Электрическая мощность

Мощность – это физическая величина, характеризующая скорость передачи или преобразования электрической энергии. Рассчитывается мощность по следующей формуле:

Таким образом зная, напряжение источника и измерив потребляемый ток, мы можем определить мощность потребляемую электроприбором. И наоборот, зная мощность электроприбора и напряжение сети, можем определить величину потребляемого тока. Такие вычисления порой необходимы. Например, для защиты электроприборов используются предохранители или автоматические выключатели. Чтобы правильно подобрать средство защиты нужно знать потребляемый ток. Предохранители, применяемые в бытовой технике, как правило подлежат ремонту и для их восстановления достаточно

Зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока . То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток , в свою очередь – это упорядоченное движение частиц под действием электрического поля .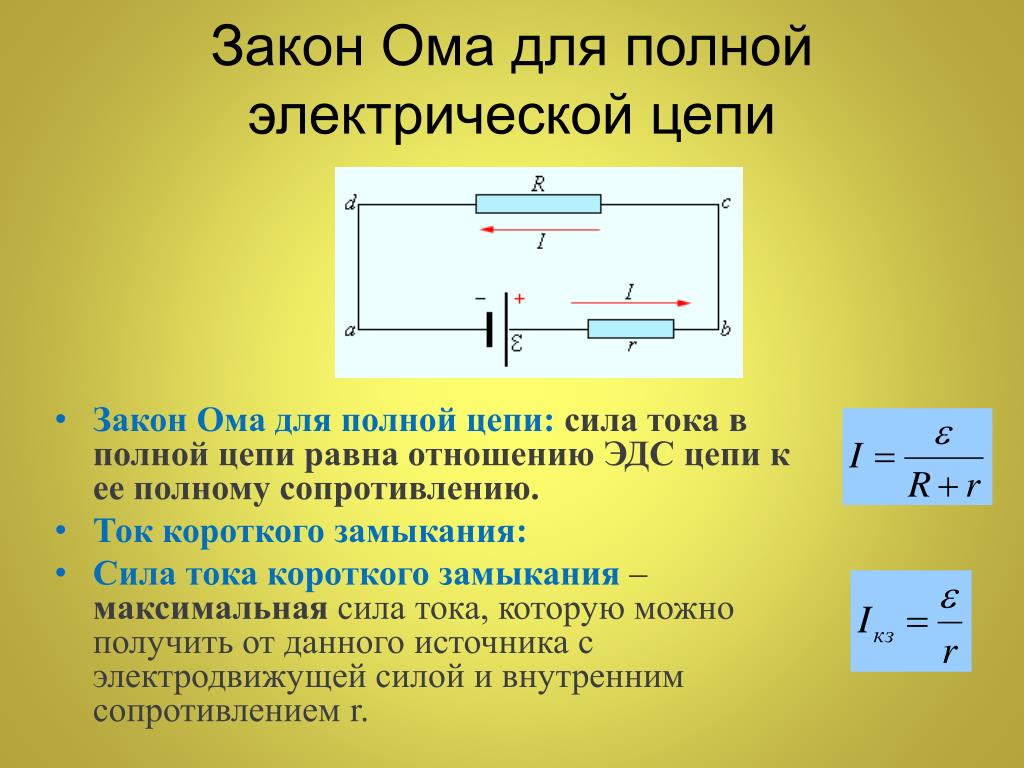

Зависимость силы тока и напряжения

Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением . Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.

И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.

Связь с сопротивлением

Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току . Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.

Формула закона Ома для участка цепи

Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

где I – сила тока,
U – напряжение,
R – сопротивление.

Применение закона Ома

Закон Ома – один из основополагающих законов физики . Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека.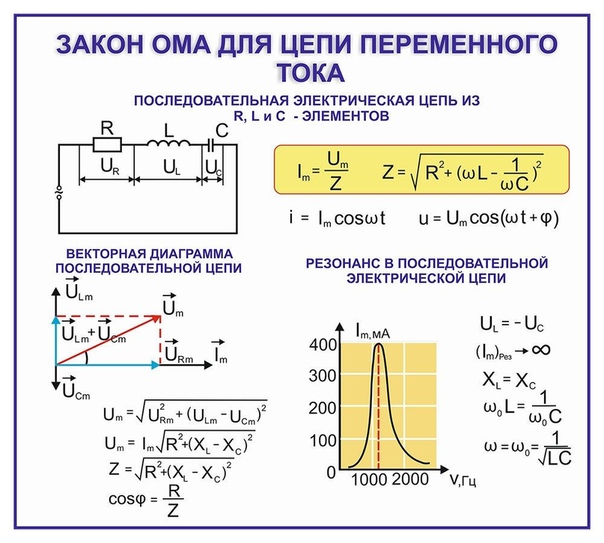 Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».

U=IR и R=U/I

Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.

Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.

Электрическая цепь

Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.

Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.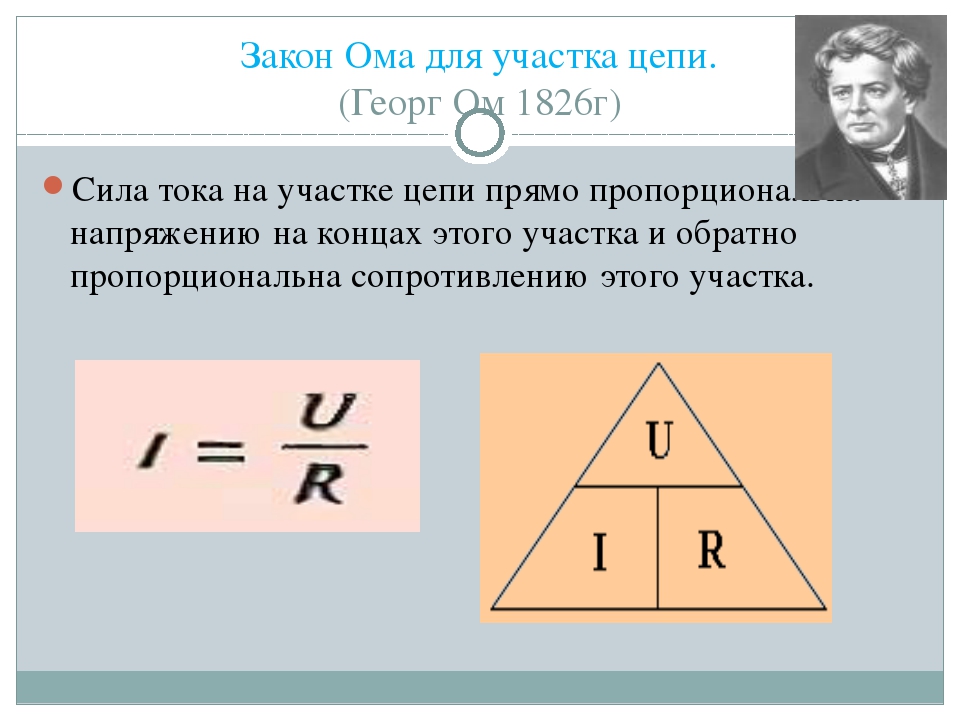

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока , а силы – сторонними силами .

Электрическую цепь, в которой находится источник тока, называют полной электрической цепью . Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.

Параметры электрической цепи

Свой знаменитый закон Ом вывел экспериментальным путём.

Проведём несложный опыт.

Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с помощью ключа электрическую цепь и запишем показания приборов.

Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.

Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.

Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника .

В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению .

Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.

Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».

Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.

Георг Симон Ом

Закон Ома для полной цепи

Между тем, формула, выведенная самим Омом, выглядела так:

Это не что иное, как формула закона Ома для полной электрической цепи: « Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника ».

В опытах Ома величина Х показывала изменение величины тока. В современной формуле ей соответствует сила тока I , протекающего в цепи. Величина а характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε . Значение величины l зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи R . Параметр b характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это r – внутреннее сопротивление источника тока.

Как выводится современная формула закона Ома для полной цепи?

ЭДС источника равна сумме падений напряжений на внешней цепи (U ) и на самом источнике (U 1 ).

ε = U + U 1 .

Из закона Ома I = U / R следует, что U = I · R , а U 1 = I · r .

Подставив эти выражения в предыдущее, получим:

ε = I · R + I · r = I · (R + r) , откуда

По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R . Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r .

Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1 и уменьшается U .

Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.

Короткое замыкание

А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием . Ток, называемый током короткого замыкания , будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.

Закон Ома для переменного тока

В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).

Для таких цепей U = I · Z , где Z – полное сопротивление, включающее в себя активную и реактивную составляющие.

Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:

I = U / R

Мощность и закон Ома

Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:

P = U · I = I 2 · R

Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника.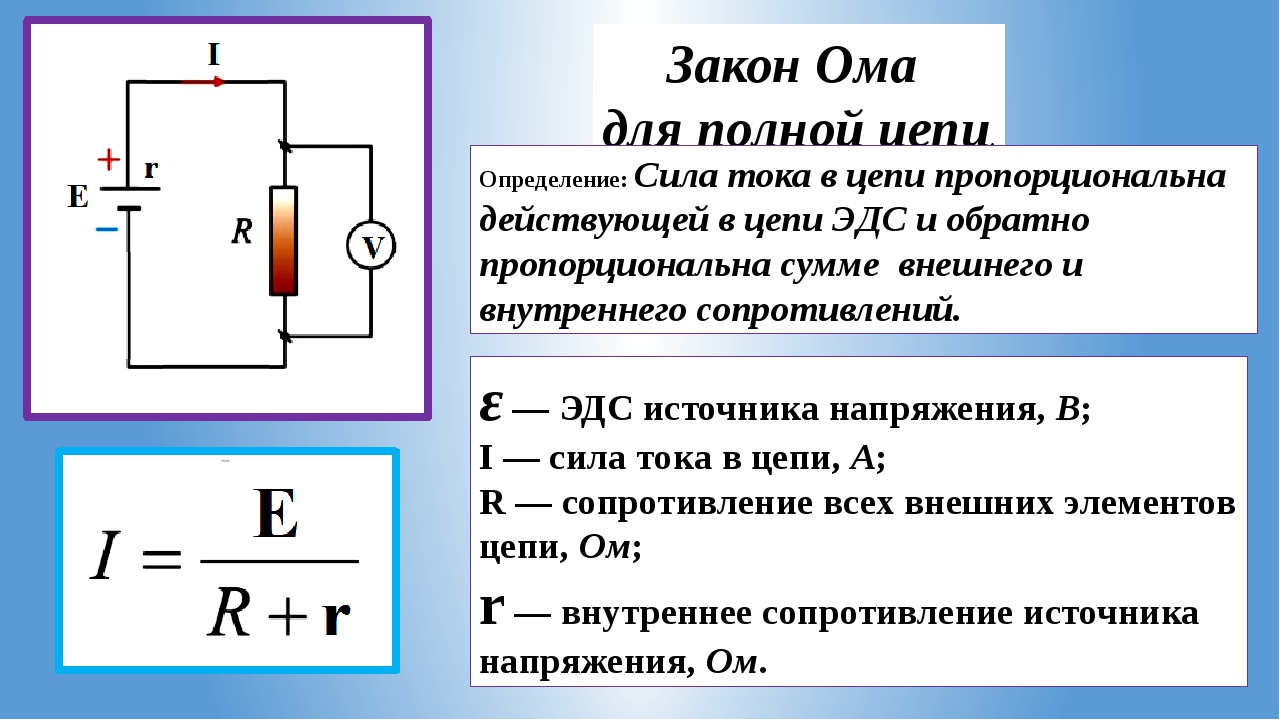 И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.

Вместо эпилога

Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.

Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома – так, как показано на рисунке.

Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.

Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.

Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла».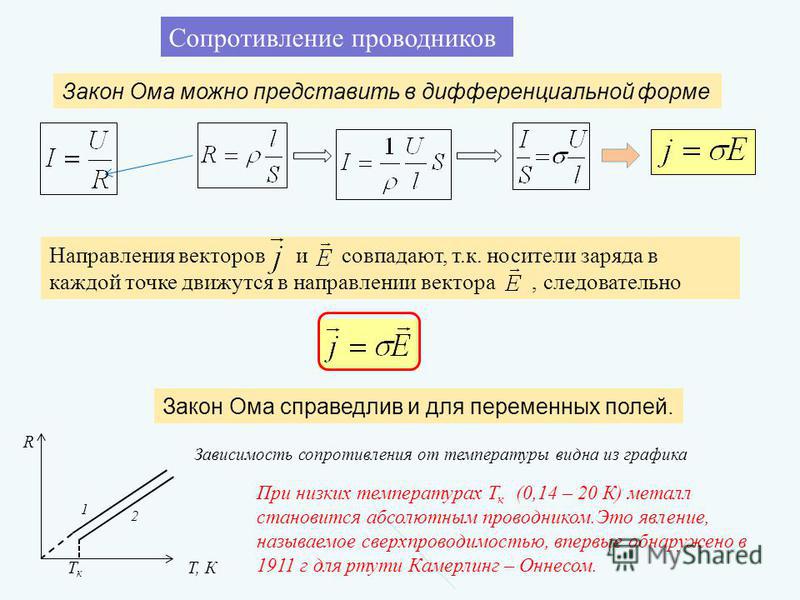 В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.

Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.

Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.

Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.

Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.

В результате нового эксперимента Ом пришел к формуле:

Х = a / b + l

Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.

Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи .

Закон Ома для участка цепи

Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.

I = U / R

Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.

Таким образом формула для расчета сопротивления проводника примет вид:

R = p ⋅ l / s

Закон Ома для полной цепи

Отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:

I = U / R + r

Закон Ома для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Закон ома для участка цепи гласит. Закон Ома для участка цепи

Закон Ома.

I = U/ R

Где U – напряжение концов участка,I– сила тока, R– сопротивление проводника.

R = U / I

Эти формулы справедливы лишь когда сеть испытывает на себе одно сопротивление.

Условием движения электрических зарядов в проводнике является наличие в нем электрического поля, которое создается и поддерживается особыми устройствами, получившими название источников тока .

Основной величиной, характеризующей источник тока, является его электродвижущая сила.

Электродвижущей силой источника (сокращенно ЭДС) называется скалярная физическая величина, характеризующая работу сторонних сил, способных создавать на зажимах источника (полюсах) разность потенциалов.

Она равна работе сторонних сил по перемещению заряженной частицы с положительным единичным зарядом от одного полюса источника к другому, т.е.

В СИ ЭДС измеряется в вольтах (В), т.е. в тех же единицах, что и напряжение.

Сторонние силы источника – это силы, которые осуществляют разделение зарядов в источнике и тем самым создают на его полюсах разность потенциалов. Эти силы могут иметь различную природу, но только не электрическую (отсюда и название) – Механические силы, химическая среда в аккумуляторе; световой поток в фотоэлементах.

Направление ЭДС – это направление принудительного движения положительных зарядов внутри генератора от минуса к плюсу под действием иной, чем электрическая, природы.

Внутреннее сопротивление генератора это сопротивление конструктивных элементов внутри него.

Если электрическую цепь разделить на два участка – внешний, с сопротивлением R , и внутренний, с сопротивлением r , то ЭДС источника тока окажется равной сумме напряжений на внешнем и внутреннем участках цепи:

По закону Ома напряжение на любом участке цепи определяется величиной протекающего тока и его сопротивлением:

Так как , следовательно

, (3)

т.е. напряжение на полюсах источника при замкнутой цепи зависит от соотношения сопротивлений внутреннего и внешнего участков цепи. Если приблизительно равно U .

Электрическое сопротивление.

Свойство материала проводника препятствовать прохождению через него электрического тока называется электрическим сопротивлением.

Из закона Ома: R = U / I

За единицу электрического сопротивления принят 1Ом .

Сопротивлением 1 Ом обладает проводник, в котором при напряжении 1 В проходит ток 1 А.

Величина, обратная сопротивлению, называется электрической проводимостью :

Единицей проводимости является сименс :

Величина, обратная удельной проводимости, называется удельным сопротивлением р, т. е.

Увеличение температуры сопровождается усилением хаотического теплового движения частиц вещества, что приводит к увеличению числа столкновений электронов с ними и затрудняет упорядоченное движение электронов.

Сопротивление – резистор.

Метод узловых потенциалов.

Пример 2.7.4.

Определить значения и направления токов в ветвях методом узловых потенциалов для цепи рис. 2.7.4, если:

Е1=108 В; Е2=90 В; Ri1=2 Ом; Ri2=1 Ом; R1=28 Ом; R2=39 Ом; R3=60 Ом.

Решение.

Определяем токи в ветвях.

Метод двух узлов.

Одним из распространенных методов расчета электрических цепей является метод двух узлов .Этот метод применяется в случае, когда в цепи всего два узла

Метод контурных токов.

Алгоритм действий таков:

По второму закону Кирхгофа, относительно контурных токов, составляем уравнения для всех независимых контуров. При записи равенства считать, что направление обхода контура, для которого составляется уравнение, совпадает с направлением контурного тока данного контура. Следует учитывать и тот факт, что в смежных ветвях, принадлежащих двум контурам, протекают два контурных тока. Падение напряжения на потребителях в таких ветвях надо брать от каждого тока в отдельности.

Произвольно задаемся направлением реальных токов всех ветвей и обозначаем их. Маркировать реальные токи надо таким образом, чтобы не путать с контурными. Для нумерации реальных токов можно использовать одиночные арабские цифры (I1, I2, I3 и т. д.).

При алгебраическом суммировании без изменения знака берется контурный ток, направление которого совпадает с принятым направлением реального тока ветви. В противном случае контурный ток умножается на минус единицу.

Пример расчёта сложной цепи методом контурных токов.

Рис. 1. Схема электрической цепи для примера расчета по методу контурных токов

Решение. Для расчета сложной цепи этим методом достаточно составить два уравнения, по числу независимых контуров. Контурные токи направляем по часовой стрелке и обозначаем I11 и I22 (см. рисунок 1).

По второму закону Кирхгофа относительно контурных токов составляем уравнения:

Решаем систему и получаем контурные токи I11 = I22 = 3 А.

Следует отметить, как положительный факт, что в методе контурных токов по сравнению с решением по законам Кирхгофа приходится решать систему уравнений меньшего порядка. Однако этот метод не позволяет сразу определять реальные токи ветвей.

Закон Ома.

Согласно закону Ома для некоторого участка цепи, сила тока на участке цепи прямо пропорциональна напряжению на концах участка и обратно пропорциональна сопротивлению.

Если увеличить в несколько раз напряжение, действующее в электрической цепи, то ток в этой цепи увеличится во столько же раз. А если увеличить в несколько раз сопротивление цепи, то ток во столько же раз уменьшится. Подобно этому водяной поток в трубе тем больше, чем сильнее давление и чем меньше сопротивление, которое оказывает труба движению воды.

Чтобы выразить закон Ома математически наиболее просто, считают, что сопротивление проводника, в котором при напряжении 1 В проходит ток 1 А, равно 1 Ом.

Ток в амперах можно всегда определить, если разделить напряжение в вольтах на сопротивление в омах. Поэтому закон Ома для участка цепи записывается следующей формулой:

Расчеты, выполняемые с помощью закона Ома для участка цепи, будут правильны в том случае, когда напряжение выражено в вольтах, сопротивление в омах и ток в амперах. Если используются кратные единицы измерений этих величин (например, миллиампер, милливольт, мегаом и т. д.), то их следует перевести соответственно в амперы, вольты и омы. Чтобы подчеркнуть это, иногда формулу закона Ома для участка цепи пишут так:

ампер = вольт/ом

Можно также рассчитывать ток в миллиамперах и микроамперах, при этом напряжение должно быть выражено в вольтах, а сопротивление – в килоомах и мегаомах соответственно.

Закон Ома справедлив для любого участка цепи. Если требуется определить ток в данном участке цепи, то необходимо напряжение, действующее на этом участке (рис. 1), разделить на сопротивление именно этого участка.

Рис 1. Применение закона Ома для участка цепи

Приведем пример расчета тока по закону Ома . Пусть требуется определить ток в лампе, имеющей сопротивление 2,5 Ом, если напряжение, приложенное к лампе, составляет 5 В. Разделив 5 В на 2,5 Ом, получим значение тока, равное 2 А. Во втором примере определим ток, который будет протекать под действием напряжения 500 В в цепи, сопротивление которой равно 0,5 МОм. Для этого выразим сопротивление в омах. Разделив 500 В на 500 000 Ом, найдем значение тока в цепи, которое равно 0,001 А или 1 мА.

Часто, зная ток и сопротивление, определяют с помощью закона Ома напряжение. Запишем формулу для определения напряжения

Из этой формулы видно, что напряжение на концах данного участка цепи прямо пропорционально току и сопротивлению . Смысл этой зависимости понять нетрудно. Если не изменять сопротивление участка цепи, то увеличить ток можно только путем увеличения напряжения. Значит при постоянном сопротивлении большему току соответствует большее напряжение. Если же надо получить один и тот же ток при различных сопротивлениях, то при большем сопротивлении должно быть соответственно большее напряжение.

Напряжение на участке цепи часто называют падением напряжения . Это нередко приводит к недоразумению. Многие думают, что падение напряжения есть какое-то потерянное ненужное напряжение. В действительности же понятия напряжение и падение напряжения равнозначны.

Расчет напряжения с помощью закона Ома можно показать на следующем примере. Пусть через участок цепи с сопротивлением 10 кОм проходит ток 5 мА и требуется определить напряжение на этом участке.

Умножив I = 0,005 А на R -10000 Ом, получим напряжение,равное 50 В. Можно было бы получить тот же результат, умножив 5 мА на 10 кОм: U = 50 В

В электронных устройствах ток обычно выражается в миллиамперах, а сопротивление – в килоомах. Поэтому удобно в расчетах по закону Ома применять именно эти единицы измерений.

По закону Ома рассчитывается также сопротивление, если известно напряжение и ток. Формула для этого случая пишется следующим образом: R = U/I.

Сопротивление всегда представляет собой отношение напряжения к току. Если напряжение увеличить или уменьшить в несколько раз, то ток увеличится или уменьшится в такое же число раз. Отношение напряжения к току, равное сопротивлению, остается неизменным.

Не следует понимать формулу для определения сопротивления в том смысле, что сопротивление данного проводника зависит оттока и напряжения. Известно, что оно зависит от длины, площади сечения и материала проводника. По внешнему виду формула для определения сопротивления напоминает формулу для расчета тока, но между ними имеется принципиальная разница. Ток в данном участке цепи действительно зависит от напряжения и сопротивления и изменяется при их изменении. А сопротивление данного участка цепи является величиной постоянной, не зависящей от изменения напряжения и тока, но равной отношению этих величин.

Когда один и тот же ток проходит в двух участках цепи, а напряжения, приложенные к ним, различны, то ясно, что участок, к которому приложено большее напряжение, имеет соответственно большее сопротивление. А если под действием одного и того же напряжения в двух разных участках цепи проходит различный ток, то меньший ток всегда будет на том участке, который имеет большее сопротивление. Все это вытекает из основной формулировки закона Ома для участка цепи, т. е. из того, что ток тем больше, чем больше напряжение и чем меньше сопротивление.

Расчет сопротивления с помощью закона Ома для участка цепи покажем на следующем примере. Пусть требуется найти сопротивление участка, через который при напряжении 40 В проходит ток 50 мА. Выразив ток в амперах, получим I = 0,05 А. Разделим 40 на 0,05 и найдем, что сопротивление составляет 800 Ом.

Закон Ома можно наглядно представить в виде так называемой вольт-амперной характеристики . Как известно, прямая пропорциональная зависимость между двумя величинами представляет собой прямую линию, проходящую через начало координат. Такую зависимость принято называть линейной .

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах .

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах . Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль .

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах .

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Кстати! Для наших читателей сейчас действует скидка 10% на

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря “участок цепи” мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС , читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего . А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Закон Ома часто называют основным законом электричества. Открывший его в 1826 г. известный немецкий физик Георг Симон Ом установил зависимость между основными физическими величинами электрической цепи – сопротивлением, напряжением и силой тока.

Электрическая цепь

Чтобы лучше понять смысл закона Ома, нужно представлять, как устроена электрическая цепь.

Что же такое электрическая цепь? Это путь, который проходят электрически заряженные частицы (электроны) в электрической схеме.

Чтобы в электрической цепи существовал ток, необходимо наличие в ней устройства, которое создавало бы и поддерживало разность потенциалов на участках цепи за счёт сил неэлектрического происхождения. Такое устройство называется источником постоянного тока , а силы – сторонними силами .

Электрическую цепь, в которой находится источник тока, называют полной электрической цепью . Источник тока в такой цепи выполняет примерно такую же функцию, что и насос, перекачивающий жидкость в замкнутой гидравлической системе.

Простейшая замкнутая электрическая цепь состоит из одного источника и одного потребителя электрической энергии, соединённых между собой проводниками.

Параметры электрической цепи

Свой знаменитый закон Ом вывел экспериментальным путём.

Проведём несложный опыт.

Соберём электрическую цепь, в которой источником тока будет аккумулятор, а прибором для измерения тока – последовательно включенный в цепь амперметр. Нагрузкой служит спираль из проволоки. Напряжение будем измерять с помощью вольтметра, включенного параллельно спирали. Замкнём с помощью ключа электрическую цепь и запишем показания приборов.

Подключим к первому аккумулятору второй с точно таким же параметрами. Снова замкнём цепь. Приборы покажут, что и сила тока, и напряжение увеличились в 2 раза.

Если к 2 аккумуляторам добавить ещё один такой же, сила тока увеличится втрое, напряжение тоже утроится.

Вывод очевиден: сила тока в проводнике прямо пропорциональна напряжению, приложенному к концам проводника .

В нашем опыте величина сопротивления оставалась постоянной. Мы меняли лишь величину тока и напряжения на участке проводника. Оставим лишь один аккумулятор. Но в качестве нагрузки будем использовать спирали из разных материалов. Их сопротивления отличаются. Поочерёдно подключая их, также запишем показания приборов. Мы увидим, что здесь всё наоборот. Чем больше величина сопротивления, тем меньше сила тока. Сила тока в цепи обратно пропорциональна сопротивлению .

Итак, наш опыт позволил нам установить зависимость силы тока от величины напряжения и сопротивления.

Конечно, опыт Ома был другим. В те времена не существовало амперметров, и, чтобы измерить силу тока, Ом использовал крутильные весы Кулона. Источником тока служил элемент Вольта из цинка и меди, которые находились в растворе соляной кислоты. Медные проволоки помещались в чашки со ртутью. Туда же подводились концы проводов от источника тока. Проволоки были одинакового сечения, но разной длины. За счёт этого менялась величина сопротивления. Поочерёдно включая в цепь различные проволоки, наблюдали за углом поворота магнитной стрелки в крутильных весах. Собственно, измерялась не сама сила тока, а изменение магнитного действия тока за счёт включения в цепь проволок различного сопротивления. Ом называл это «потерей силы».

Но так или иначе эксперименты учёного позволили ему вывести свой знаменитый закон.

Георг Симон Ом

Закон Ома для полной цепи

Между тем, формула, выведенная самим Омом, выглядела так:

Это не что иное, как формула закона Ома для полной электрической цепи: « Сила тока в цепи пропорциональна действующей в цепи ЭДС и обратно пропорциональна сумме сопротивлений внешней цепи и внутреннего сопротивления источника ».

В опытах Ома величина Х показывала изменение величины тока. В современной формуле ей соответствует сила тока I , протекающего в цепи. Величина а характеризовала свойства источника напряжения, что соответствует современному обозначению электродвижущей силы (ЭДС) ε . Значение величины l зависело от длины проводников, соединявших элементы электрической цепи. Эта величина являлась аналогией сопротивления внешней электрической цепи R . Параметр b характеризовал свойства всей установки, на которой проводился опыт. В современной обозначении это r – внутреннее сопротивление источника тока.

Как выводится современная формула закона Ома для полной цепи?

ЭДС источника равна сумме падений напряжений на внешней цепи (U ) и на самом источнике (U 1 ).

ε = U + U 1 .

Из закона Ома I = U / R следует, что U = I · R , а U 1 = I · r .

Подставив эти выражения в предыдущее, получим:

ε = I · R + I · r = I · (R + r) , откуда

По закону Ома напряжение во внешней цепи равно произведению силы тока на сопротивление. U = I · R . Оно всегда меньше, чем ЭДС источника. Разница равна величине U 1 = I · r .

Что происходит при работе батарейки или аккумулятора? По мере того, как разряжается батарейка, растёт её внутренне сопротивление. Следовательно, увеличивается U 1 и уменьшается U .

Полный закон Ома превращается в закон Ома для участка цепи, если убрать из него параметры источника.

Короткое замыкание

А что произойдёт, если сопротивление внешней цепи вдруг станет равно нулю? В повседневной жизни мы можем наблюдать это, если, например, повреждается электрическая изоляция проводов, и они замыкаются между собой. Возникает явление, которое называется коротким замыканием . Ток, называемый током короткого замыкания , будет чрезвычайно большим. При этом выделится большое количество теплоты, которое может привести к пожару. Чтобы этого не случилось, в цепи ставят устройства, называемые предохранителями. Они устроены так, что способны разорвать электрическую цепь в момент короткого замыкания.

Закон Ома для переменного тока

В цепи переменного напряжения кроме обычного активного сопротивления встречается реактивное сопротивление (ёмкости, индуктивности).

Для таких цепей U = I · Z , где Z – полное сопротивление, включающее в себя активную и реактивную составляющие.

Но большим реактивным сопротивлением обладают мощные электрические машины и силовые установки. В бытовых приборах, окружающих нас, реактивная составляющая настолько мала, что её можно не учитывать, а для расчётов использовать простую форму записи закона Ома:

I = U / R

Мощность и закон Ома

Ом не только установил зависимость между напряжением, током и сопротивлением электрической цепи, но и вывел уравнение для определения мощности:

P = U · I = I 2 · R

Как видим, чем больше ток или напряжение, тем больше мощность . Так как проводник или резистор не является полезной нагрузкой, то мощность, которая приходится на него, считается мощностью потерь. Она идёт на нагревание проводника. И чем больше сопротивление такого проводника, тем больше теряется на нём мощности. Чтобы уменьшить потери от нагревания, в цепи используют проводники с меньшим сопротивлением. Так делают, например, в мощных звуковых установках.

Вместо эпилога

Небольшая подсказка для тех, кто путается и не может запомнить формулу закона Ома.

Разделим треугольник на 3 части. Причём, каким образом мы это сделаем, совершенно неважно. Впишем в каждую из них величины, входящие в закон Ома – так, как показано на рисунке.

Закроем величину, которую нужно найти. Если оставшиеся величины находятся на одном уровне, то их нужно перемножить. Если же они располагаются на разных уровнях, то величину, расположенную выше, необходимо разделить на нижнюю.

Закон Ома широко применяется на практике при проектировании электрических сетей в производстве и в быту.

Зависит величина воздействия, которое ток может оказывать на проводник, будь то тепловое, химическое или магнитное действие тока . То есть, регулируя силу тока, можно управлять его воздействием. Электрический ток , в свою очередь – это упорядоченное движение частиц под действием электрического поля .

Зависимость силы тока и напряжения

Очевидно, что чем сильнее поле действует на частицы, тем больше будет сила тока в цепи. Электрическое поле характеризуется величиной, называемой напряжением . Следовательно, мы приходит к выводу, что сила тока зависит от напряжения.

И действительно, опытным путем удалось установить, что сила тока связана с напряжением прямо пропорционально. В случаях, когда изменяли величину напряжения в цепи, не меняя всех остальных параметров, сила тока возрастала или уменьшалась во столько же раз, во сколько меняли напряжение.

Связь с сопротивлением

Однако любая цепь или участок цепи характеризуются еще одной немаловажной величиной, называемой сопротивлением электрическому току . Сопротивление связано с силой тока обратно пропорционально. Если на каком-либо участке цепи изменить величину сопротивления, не меняя напряжения на концах этого участка, сила тока также изменится. Причем если мы уменьшим величину сопротивления, то сила тока возрастет во столько же раз. И, наоборот, при увеличении сопротивления сила тока пропорционально уменьшается.

Формула закона Ома для участка цепи

Сопоставив две эти зависимости, можно прийти к такому же выводу, к которому пришел немецкий ученый Георг Ом в 1827 г. Он связал воедино три вышеуказанные физические величины и вывел закон, который назвали его именем. Закон Ома для участка цепи гласит:

Сила тока в участке цепи прямо пропорциональна напряжению на концах этого участка и обратно пропорциональна его сопротивлению.

где I – сила тока,
U – напряжение,
R – сопротивление.

Применение закона Ома

Закон Ома – один из основополагающих законов физики . Открытие его в свое время позволило сделать огромный скачок в науке. В настоящее время невозможно себе представить любой самый элементарный расчет основных электрических величин для любой цепи без использования закона Ома. Представление об этом законе – это не удел исключительно инженеров-электронщиков, а необходимая часть базовых знаний любого мало-мальски образованного человека. Недаром есть поговорка: «Не знаешь закон Ома – сиди дома».

U=IR и R=U/I

Правда, следует понимать, что в собранной цепи величина сопротивления некоторого участка цепи есть величина постоянная, поэтому при изменении силы тока будет изменяться только напряжение и наоборот. Для изменения сопротивления участка цепи следует собрать цепь заново. Расчет же требуемой величины сопротивления при проектировании и сборке цепи можно произвести по закону Ома, исходя из предполагаемых значений силы тока и напряжения, которые будут пропущены через данный участок цепи.

Закон ома для цепи с емкостью. Описание закона ома для электрической цепи переменного тока

Георг Симон Ом начал свои исследования вдохновляясь знаменитым трудом Жана Батиста Фурье «Аналитическая теория тепла». В этой работе Фурье представлял тепловой поток между двумя точками как разницу температур, а изменение теплового потока связывал с его прохождением через препятствие неправильной формы из теплоизолирующего материала. Аналогично этому Ом обуславливал возникновение электрического тока разностью потенциалов.

Исходя из этого Ом стал экспериментировать с разными материалами проводника. Для того, чтобы определить их проводимость он подключал их последовательно и подгонял их длину таким образом, чтобы сила тока была одинаковой во всех случаях.

Важно при таких измерениях было подбирать проводники одного и того же диаметра. Ом, замеряя проводимость серебра и золота, получил результаты, которые по современным данным не отличаются точностью. Так, серебряный проводник у Ома проводил меньше электрического тока, чем золотой. Сам Ом объяснял это тем, что его проводник из серебра был покрыт маслом и из-за этого, по всей видимости, опыт не дал точных результатов.

Однако не только с этим были проблемы у физиков, которые в то время занимались подобными экспериментами с электричеством. Большие трудности с добычей чистых материалов без примесей для опытов, затруднения с калибровкой диаметра проводника искажали результаты тестов. Еще большая загвоздка состояла в том, что сила тока постоянно менялась во время испытаний, поскольку источником тока служили переменные химические элементы. В таких условиях Ом вывел логарифмическую зависимость силы тока от сопротивления провода.

Немногим позже немецкий физик Поггендорф, специализировавшийся на электрохимии, предложил Ому заменить химические элементы на термопару из висмута и меди. Ом начал свои эксперименты заново. В этот раз он пользовался термоэлектрическим устройством, работающем на эффекте Зеебека в качестве батареи. К нему он последовательно подключал 8 проводников из меди одного и того же диаметра, но различной длины. Чтобы измерить силу тока Ом подвешивал с помощью металлической нити над проводниками магнитную стрелку. Ток, шедший параллельно этой стрелке, смещал ее в сторону. Когда это происходило физик закручивал нить до тех пор, пока стрелка не возвращалась в исходное положение. Исходя из угла, на который закручивалась нить можно было судить о значении силы тока.

В результате нового эксперимента Ом пришел к формуле:

Х = a / b + l

Здесь X – интенсивность магнитного поля провода, l – длина провода, a – постоянная величина напряжения источника, b – постоянная сопротивления остальных элементов цепи.

Если обратиться к современным терминам для описания данной формулы, то мы получим, что Х – сила тока, а – ЭДС источника, b + l – общее сопротивление цепи .

Закон Ома для участка цепи

Закон Ома для отдельного участка цепи гласит: сила тока на участке цепи увеличивается при возрастании напряжения и уменьшается при возрастании сопротивления этого участка.

I = U / R

Исходя из этой формулы, мы можем решить, что сопротивление проводника зависит от разности потенциалов. С точки зрения математики, это правильно, но ложно с точки зрения физики. Эта формула применима только для расчета сопротивления на отдельном участке цепи.

Таким образом формула для расчета сопротивления проводника примет вид:

R = p ⋅ l / s

Закон Ома для полной цепи

Отличие закона Ома для полной цепи от закона Ома для участка цепи заключается в том, что теперь мы должны учитывать два вида сопротивления. Это «R» сопротивление всех компонентов системы и «r» внутреннее сопротивление источника электродвижущей силы. Формула таким образом приобретает вид:

I = U / R + r

Закон Ома для переменного тока

Переменный ток отличается от постоянного тем, что он изменяется с определенными временными периодами. Конкретно он изменяет свое значение и направление. Чтобы применить закон Ома здесь нужно учитывать, что сопротивление в цепи с постоянным током может отличатся от сопротивления в цепи с током переменным. И отличается оно в том случае если в цепи применены компоненты с реактивным сопротивлением. Реактивное сопротивление может быть индуктивным (катушки, трансформаторы, дроссели) и емкостными (конденсатор).

Попробуем разобраться, в чем реальная разница между реактивным и активным сопротивлением в цепи с переменным током. Вы уже должны были понять, что значение напряжение и силы тока в такой цепи меняется со временем и имеют, грубо говоря, волновую форму.

Если мы схематически представим, как с течением времени меняются эти два значения, у нас получится синусоида. И напряжение, и сила тока от нуля поднимаются до максимального значения, затем, опускаясь, проходят через нулевое значение и достигают максимального отрицательного значения. После этого снова поднимаются через нуль до максимального значения и так далее. Когда говорится, что сила тока или напряжение имеет отрицательное значение, здесь имеется ввиду, что они движутся в обратном направлении.

Весь процесс происходит с определенной периодичностью. Та точка, где значение напряжения или силы тока из минимального значения поднимаясь к максимальному значению проходит через нуль называется фазой.

На самом деле, это только предисловие. Вернемся к реактивному и активному сопротивлению. Отличие в том, что в цепи с активным сопротивлением фаза тока совпадает с фазой напряжения. То есть, и значение силы тока, и значение напряжения достигают максимума в одном направлении одновременно. В таком случае наша формула для расчета напряжения, сопротивления или силы тока не меняется.

Если же цепь содержит реактивное сопротивление, фазы тока и напряжения сдвигаются друг от друга на ¼ периода. Это означает, что, когда сила тока достигнет максимального значения, напряжение будет равняться нулю и наоборот. Когда применяется индуктивное сопротивление, фаза напряжения «обгоняет» фазу тока. Когда применяется емкостное сопротивление, фаза тока «обгоняет» фазу напряжения.

Формула для расчета падения напряжения на индуктивном сопротивлении:

U = I ⋅ ωL

Где L – индуктивность реактивного сопротивления, а ω – угловая частота (производная по времени от фазы колебания).

Формула для расчета падения напряжения на емкостном сопротивлении:

U = I / ω ⋅ С

С – емкость реактивного сопротивления.

Эти две формулы – частные случаи закона Ома для переменных цепей.

Полный же будет выглядеть следующем образом:

I = U / Z

Здесь Z – полное сопротивление переменной цепи известное как импеданс.

Сфера применения

Закон Ома не является базовым законом в физике, это лишь удобная зависимость одних значений от других, которая подходит почти в любых ситуациях на практике. Поэтому проще будет перечислить ситуации, когда закон может не срабатывать:

• Если есть инерция носителей заряда, например, в некоторых высокочастотных электрических полях;
• В сверхпроводниках;
• Если провод нагревается до такой степени, что вольтамперная характеристика перестает быть линейной. Например, в лампах накаливания;
• В вакуумных и газовых радиолампах;
• В диодах и транзисторах.

Закон ома для переменного тока в общем случае имеет такой же вид, как и для постоянного. То есть при увеличении напряжения в цепи ток также в ней будет увеличиваться. Отличием же является то, что в цепи переменного тока сопротивление ему оказывают такие элементы как катушка индуктивности и емкость. Учитывая этот факт, запишем закон ома для переменного тока.

Формула 1 — закон ома для переменного тока

где z это полное сопротивление цепи.

Формула 2 — полное сопротивление цепи

В общем случае полное сопротивление цепи переменного тока будет состоять из активного емкостного и индуктивного сопротивления. Проще говоря, ток в цепи переменного тока, зависит не только от активного омического сопротивление, но и от величины емкости и индуктивности.

Рисунок 1 — цепь, содержащая омическое индуктивное и емкостное сопротивление

Если, например, в цепь постоянного тока включить конденсатор то тока в цепи не будет, так как конденсатор на постоянном токе является разрывом цепи. Если же в цепи постоянного тока появится индуктивность, то ток не изменится. Строго говоря, изменится, так как катушка будет обладать омическим сопротивлением. Но изменение будет ничтожным.

Если же конденсатор и катушку включить в цепи переменного тока, то они будут оказывать сопротивление току пропорционально величине ёмкости и индуктивности соответственно. Кроме этого в цепи буде наблюдаться сдвиг фаз между напряжением и током. В общем случае ток в конденсаторе опережает напряжение на 90 градусов. В индуктивности же отстает на 90 градусов.

Емкостное сопротивление зависит от величины емкости и частоты переменного тока. Эта зависимость обратно пропорциональна, то есть с увеличением частоты и ёмкости сопротивление будет уменьшаться.

После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.

При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

• I [А] – сила тока,
• U [В] – напряжение,
• Z [Ом] – полное сопротивление цепи.

Полное сопротивление цепи

В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:

где

Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.

Рис.1. Треугольник сопротивлений

Учитывая последние равенства, запишем формулу закона Ома для переменного тока:

– амплитудное значение силы тока.

Рис.2. Последовательная электрическая цепь из R, L, C элементов.

Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора.

Говорят: «не знаешь закон Ома – сиди дома». Так давайте же узнаем (вспомним), что это за закон, и смело пойдем гулять.

Основные понятия закона Ома

Как понять закон Ома? Нужно просто разобраться в том, что есть что в его определении. И начать следует с определения силы тока, напряжения и сопротивления.

Сила тока I

Пусть в каком-то проводнике течет ток. То есть, происходит направленное движение заряженных частиц – допустим, это электроны. Каждый электрон обладает элементарным электрическим зарядом (e= -1,60217662 × 10 -19 Кулона). В таком случае через некоторую поверхность за определенный промежуток времени пройдет конкретный электрический заряд, равный сумме всех зарядов протекших электронов.

Отношение заряда к времени и называется силой тока. Чем больший заряд проходит через проводник за определенное время, тем больше сила тока. Сила тока измеряется в Амперах .

Напряжение U, или разность потенциалов

Это как раз та штука, которая заставляет электроны двигаться. Электрический потенциал характеризует способность поля совершать работу по переносу заряда из одной точки в другую. Так, между двумя точками проводника существует разность потенциалов, и электрическое поле совершает работу по переносу заряда.

Физическая величина, равная работе эффективного электрического поля при переносе электрического заряда, и называется напряжением. Измеряется в Вольтах . Один Вольт – это напряжение, которое при перемещении заряда в 1 Кл совершает работу, равную 1 Джоуль .

Сопротивление R

Ток, как известно, течет в проводнике. Пусть это будет какой-нибудь провод. Двигаясь по проводу под действием поля, электроны сталкиваются с атомами провода, проводник греется, атомы в кристаллической решетке начинают колебаться, создавая электронам еще больше проблем для передвижения. Именно это явление и называется сопротивлением. Оно зависит от температуры, материала, сечения проводника и измеряется в Омах .

Формулировка и объяснение закона Ома

Закон немецкого учителя Георга Ома очень прост. Он гласит:

Сила тока на участке цепи прямо пропорционально напряжению и обратно пропорциональна сопротивлению.

Георг Ом вывел этот закон экспериментально (эмпирически) в 1826 году. Естественно, чем больше сопротивление участка цепи, тем меньше будет сила тока. Соответственно, чем больше напряжение, тем и ток будет больше.

Кстати! Для наших читателей сейчас действует скидка 10% на

Данная формулировка закона Ома – самая простая и подходит для участка цепи. Говоря “участок цепи” мы подразумеваем, что это однородный участок, на котором нет источников тока с ЭДС. Говоря проще, этот участок содержит какое-то сопротивление, но на нем нет батарейки, обеспечивающей сам ток.

Если рассматривать закон Ома для полной цепи, формулировка его будет немного иной.

Пусть у нас есть цепь, в ней есть источник тока, создающий напряжение, и какое-то сопротивление.

Закон запишется в следующем виде:

Объяснение закона Ома для полой цепи принципиально не отличается от объяснения для участка цепи. Как видим, сопротивление складывается из собственно сопротивления и внутреннего сопротивления источника тока, а вместо напряжения в формуле фигурирует электродвижущая сила источника.

Кстати, о том, что такое что такое ЭДС , читайте в нашей отдельной статье.

Как понять закон Ома?

Чтобы интуитивно понять закон Ома, обратимся к аналогии представления тока в виде жидкости. Именно так думал Георг Ом, когда проводил опыты, благодаря которым был открыт закон, названный его именем.

Представим, что ток – это не движение частиц-носителей заряда в проводнике, а движение потока воды в трубе. Сначала воду насосом поднимают на водокачку, а оттуда, под действием потенциальной энергии, она стремиться вниз и течет по трубе. Причем, чем выше насос закачает воду, тем быстрее она потечет в трубе.

Отсюда следует вывод, что скорость потока воды (сила тока в проводе) будет тем больше, чем больше потенциальная энергия воды (разность потенциалов)

Сила тока прямо пропорциональна напряжению.

Теперь обратимся к сопротивлению. Гидравлическое сопротивление – это сопротивление трубы, обусловленное ее диаметром и шероховатостью стенок. Логично предположить, что чем больше диаметр, тем меньше сопротивление трубы, и тем большее количество воды (больший ток) протечет через ее сечение.

Сила тока обратно пропорциональна сопротивлению.

Такую аналогию можно проводить лишь для принципиального понимания закона Ома, так как его первозданный вид – на самом деле довольно грубое приближение, которое, тем не менее, находит отличное применение на практике.

В действительности, сопротивление вещества обусловлено колебанием атомов кристаллической решетки, а ток – движением свободных носителей заряда. В металлах свободными носителями являются электроны, сорвавшиеся с атомных орбит.

В данной статье мы постарались дать простое объяснение закона Ома. Знание этих на первый взгляд простых вещей может сослужить Вам неплохую службу на экзамене. Конечно, мы привели его простейшую формулировку закона Ома и не будем сейчас лезть в дебри высшей физики, разбираясь с активным и реактивным сопротивлениями и прочими тонкостями.

Если у Вас возникнет такая необходимость, Вам с удовольствием помогут сотрудники нашего . А напоследок предлагаем Вам посмотреть интересное видео про закон Ома. Это действительно познавательно!

Цель: экспериментально определить импеданс различных нагрузок и сопоставить экспериментальные значения с теоретическими.

Теоретическая часть

Рассмотрим соотношения между током и напряжением в цепи переменного тока при включении в нее различных нагрузок (рис. 29).

Омическое сопротивление. Под этим термином понимают сопротивление проводника постоянному току. В дальнейшем будем рассматривать квазистационарные токи, для которых мгновенные значения силы тока и напряжения, обозначаемые малыми буквами i и u , подчиняются законам Ома и Джоуля-Ленца. Амплитудные значения тока и напряжения будем обозначать I m и U m .

Пусть к омическому сопротивлению приложено напряжение, меняющееся по гармоническому закону:

U = U m сos wt , (31)

где w – циклическая частота колебаний. Согласно закону Ома через R потечет ток силой i :

i = I m сos wt , (33)

Из соотношений (32) и (33) следует:

1) фазы тока и напряжения на омическом сопротивлении совпадают;

2) амплитуды силы тока и напряжения связаны соотношением

Рис. 29. Омическая, индуктивная и емкостная нагрузки

Индуктивное сопротивление. Подадим на катушку, обладающую индуктивностью L и пренебрежимо малым омическим сопротивлением, напряжение, меняющееся по закону (31). В катушке возникает меняющийся ток, создающий переменное магнитное поле. Изменение магнитного потока Ф = Li этого поля возбудит в витках катушки ЭДС самоиндукции

.

Поскольку подводимое к катушке напряжение играет роль ЭДС, а падение напряжения в цепи отсутствует (R = 0), по второму правилу Кирхгофа для мгновенных значений можем записать:

u + = 0 или .

Последнее перепишем в виде дифференциального уравнения

Или .

Интегрирование этого уравнения дает следующее выражение:

.

,

(35)

Из (31) и (35) следует:

1) ток, проходящий через катушку, отстает от напряжения по фазе на p/2 или, что то же самое, напряжение опережает ток по фазе на p/2;

Из сопоставления (36) с (32) следует, что величина wL в цепи с индуктивностью играет роль сопротивления. Величину

X L = wL (37)

называют индуктивным сопротивлением .

Емкостное сопротивление . Конденсатор представляет собой разрыв проводов, поэтому постоянный ток он не пропускает. При изменении напряжения между обкладками меняется и мгновенное значение заряда конденсатора, определяемого формулой

q = Cu , (38)

для чего в подводящих проводах должен протекать ток, приносящий заряд к обкладкам или уносящий от них. Говорят, что конденсатор пропускает переменный ток, хотя в пространстве между обкладками никакой передачи заряда от одной обкладки к другой не происходит.

Проходящий по проводам заряд скапливается на обкладках конденсатора, поэтому его величина равна i = dq/dt , где q – мгновенное значение заряда обкладки. Учитывая (38) и считая подаваемое напряжение меняющимся по закону (31), получаем:

.

Так как cos (p/2 + wt ) = –sin wt, последнее примет вид:

. (39)

Сопоставляя (31) и (39), имеем:

1) ток в цепи с конденсатором опережает напряжение по фазе на p/2, иначе говоря, напряжение отстает от тока по фазе на p/2;

2) амплитуды тока и напряжения связаны соотношением

. (40)

Величину

называют емкостным сопротивлением .

При измерениях и расчетах цепей переменного тока вместо амплитудных пользуются действующими (эффективными) значениями силы тока I и напряжения U , которые связаны с амплитудными:

Их использование обусловлено тем, что закон Джоуля-Ленца в случае переменного тока принимает такой же вид, как и для постоянного. Соответственно электроизмерительные приборы градуируются на эффективные значения.

Очевидно, что формулы (34), (36) и (40) не изменяются при замене амплитудных значений на эффективные и примут вид:

U R = I × R , U L = I × wL , U C = I /wC , (42)

где индексы R , L и C означают напряжение на соответствующей нагрузке.

Векторные диаграммы . Фазовые соотношения между током и напряжением графически изображены на рис. 30.

Существует и другой способ их представления, позволяющий упростить расчеты цепей со сложной нагрузкой.

Рис. 31

Проведем из некоторой точки О (рис. 31) ось ОХ и отложим из той же точки вектор А под углом j к оси ОХ . Затем приведем этот вектор во вращение вокруг точки О в плоскости рисунка против часовой стрелки с угловой скоростью w. Угол a между А® и ОХ спустя время t будет a = wt + j. Проекция А® на ось ОХ равна

А Х = Х = A cos a

Х = A cos (wt + j). (43)

Вывод: всякое гармоническое колебание можно представить вращением вектора соответствующей длины и ориентации.

Следовательно, если построить вектор U и под соответствующим углом отложить вектор I , то при совместном вращении векторов угол между ними останется неизменным (43). Векторные диаграммы токов и напряжений при различных нагрузках приведены на рис. 32.

Последовательное соединение R , L и С . Для расчета такой цепи воспользуемся методом векторных диаграмм. При последовательном соединении нагрузок мгновенное значение силы тока во всех точках цепи должно быть одинаковым, т.е. фаза тока на всех нагрузках одинакова.

Однако напряжения на нагрузках не совпадают по фазе с током. Напряжение на омическом сопротивлении совпадает по фазе с током, на индуктивном – опережает ток на p/2, на емкостном – отстает на p/2. Таким образом, сложив векторы U R , U L и U C , получим полное напряжение, приложенное к цепи. Поскольку U L и U C противоположны по направлению, удобнее сначала сложить их, а затем вектор U L – U C сложить с U R . В итоге имеем:

.

Подставляя соотношения (42), получим:

. (44)

В этом выражении роль сопротивления выполняет величина

, (45)

называемая полным сопротивлением цепи переменному току или импедансом . С ее использованием (44) примет вид:

U = I × Z. (46)

Это выражение часто называют законом Ома для переменных токов. Величина

(47)

называется реактивным сопротивлением и является комбинацией индуктивного и емкостного сопротивлений.

Векторная диаграмма (рис. 33) также показывает, что приложенное напряжение и протекающий в цепи ток колеблются не в одинаковой фазе, а имеют между собой сдвиг фаз j, величина которого определяется любой из приведенных ниже формул, следующих из диаграммы:

; ;

.

Следует отметить, что формула (46) является общей для любого соединения нагрузок, а формулы (45), (47) и (48) справедливы лишь для частного случая последовательного соединения.

Экспериментальная часть

Оборудование: реостат 1000 Ом, ключ, амперметр, вольтметр, реостат 100 Ом, батарея конденсаторов, катушка.

Порядок выполнения работы

Задание 1. Измерение омического сопротивления.

Схема установки приведена на рис. 34.

В этом опыте в качестве нагрузки применяется низкоомный реостат. Высокоомный реостат используется как потенциометр.

1. Измерить ток через нагрузку при трех различных значениях подаваемого на нее напряжения. Результаты измерения занести в табл. 12.

Задание 2. Измерение емкостного сопротивления.

1. В рабочую схему в качестве нагрузки включить батарею конденсаторов. Ток и напряжение на нагрузке измерить аналогично заданию 1. Результаты измерения также внести в табл. 12.

Примечание. Значение емкости батареи рекомендуется выбрать в интервале 20–40 мкФ.

Задание 3. Измерение импеданса катушки.

1. Измерение импеданса катушки проводится аналогично предыдущим заданиям с использованием катушки в качестве нагрузки.

Задание 4. Измерение импеданса последовательного соединения R , L и С.

1. Нагрузкой будут служить соединенные последовательно реостат, батарея конденсаторов и катушка.

2. Ток и напряжение на нагрузке измерить аналогично заданию 1.

3. По результатам каждого измерения вычислить импедансы Z эксп нагрузок.

4. Сравнить экспериментальные результаты с теоретическими или паспортными значениями. Результаты сравнения привести в выводе.

Таблица 12

Номер задания	Напряжение, U	Сила тока, I	Z эксп, Ом	Z экспср , Ом	Z теор, Ом
цена деления	в делениях	в В	цена деления	в делениях	в А
резистор
конденсатор
катушка
4 последовательное соединение

Примечание. Теоретическим для реостата будет его паспортное значение сопротивления. Для конденсатора Z теор определяется по использованному в опыте значению емкости, расчет производится по формуле (41). Катушка обладает и омическим, и индуктивным сопротивлением, поэтому ее импеданс вычисляется по формуле (45), причем в качестве R должна использоваться сумма омических сопротивлений реостата и катушки.

5. Вычисление погрешностей экспериментальных значений произвести по классам точности амперметра и вольтметра, теоретических – по паспортным данным приборов.

Контрольные вопросы и задания

1. Запишите и поясните закон Ома для переменного тока.

2. Как определяется омическое, реактивное и полное сопротивление в цепи переменного тока?

3. Что понимается под эффективными значениями тока и напряжения?

4. Нарисуйте векторную диаграмму для резистора в цепи переменного тока. Сделайте пояснения.

5. Нарисуйте векторную диаграмму для конденсатора в цепи переменного тока. Сделайте пояснения.

6. Нарисуйте векторные диаграммы для идеальной катушки и катушки с заметным омическим сопротивлением в цепи переменного тока. Сделайте пояснения.

7. Нарисуйте векторную диаграмму для последовательного соединения резистора, конденсатора и катушки в цепи переменного тока. Сделайте пояснения. Получите из векторной диаграммы закон Ома.

Лабораторная работа 9 (11)

ИЗМЕРЕНИЕ МОЩНОСТИ

В ЦЕПИ ПЕРЕМЕННОГО ТОКА

Цель: ознакомиться с измерением мощности в цепи переменного тока методом трех вольтметров.

Теоретическая часть

Как всякий проводник, катушка в цепи постоянного тока потребляет энергию, идущую на нагревание проводов. Свойство проводника превращать энергию электрического тока в тепловую характеризуется его омическим сопротивлением R . Мощность тепловых потерь определяется по формуле

где I – сила тока в проводнике.

При включении катушки в цепь переменного тока у нее также происходит выделение тепла по закону (49), но в этом случае I – эффективное значение силы переменного тока.

Если у катушки имеется ферромагнитный сердечник, то проходящий по катушке переменный ток возбуждает в нем вихревые токи (токи Фуко), ведущие к нагреванию сердечника. Кроме того, происходит непрерывное изменение намагниченности сердечника по величине и направлению (перемагничивание), что также приводит к нагреванию сердечника. Эти дополнительные потери энергии эквивалентны возрастанию сопротивления проводника. Совокупные необратимые потери энергии, идущие на нагревание как проводов, так и сердечника, характеризуются активным сопротивлением катушки, определяемым по формуле

Это сопротивление, в отличие от омического, невозможно измерить, его можно лишь рассчитать.

Падение напряжения на активном сопротивлении считается колеблющимся в фазе с током.

Рис. 35

При отсутствии ваттметра мощность, потребляемая катушкой, может быть определена с использованием трех вольтметров. Если катушка обладает индуктивностью L и активным сопротивлением R а, то между током в катушке и напряжением на ней возникает сдвиг фаз j, что иллюстрируется векторной диаграммой (рис. 35), где I – ток через катушку, U а и U L – падения напряжения на активном и индуктивном сопротивлениях катушки, U к – полное напряжение на катушке.

Потребляемую катушкой мощность можно вычислить либо из (49), либо по формуле

. (51)

I и U к измеряют непосредственно, а для определения коэффициента мощности (сos j) последовательно с катушкой включается омическое сопротивление R .

Из векторной диаграммы (рис. 36) полное напряжение в цепи запишется по теореме косинусов:

. (52)

Рис. 36

В этих выражениях U – подаваемое напряжение, U к – напряжение на катушке, U R – напряжение на омическом сопротивлении. Все три напряжения измеримы непосредственно. Далее, поскольку катушка и омическое сопротивление соединены последовательно, сила тока в них одинакова и определяется по формуле

что позволяет обойтись без амперметра.

Экспериментальная часть

Оборудование: автотрансформатор; катушка; реостат; вольтметр 0-50 В; 2 вольтметра 0-150 В; сплошной и наборный сердечники.

Порядок выполнения работы

Задание 1. Измерение мощности катушки без сердечника.

В схеме на рис. 37 подаваемое в цепь напряжение регулируется автотрансформатором. В качестве омического сопротивления используется реостат.

как связаны между собой напряжение, ток и сопротивление

Добавлено 30 сентября 2020 в 00:30

Сохранить или поделиться

Первая и, возможно, самая важная взаимосвязь между током, напряжением и сопротивлением называется законом Ома, который был открыт Георгом Симоном Омом и опубликован в его статье 1827 года «Гальваническая цепь, исследованная математически».

Напряжение, ток и сопротивление

Электрическая цепь образуется, когда создается проводящий путь, позволяющий электрическому заряду непрерывно перемещаться. Это непрерывное движение электрического заряда по проводникам цепи называется током, и о нем часто говорят как о «потоке», как о потоке жидкости через полую трубу.

Сила, побуждающая носители заряда «течь» по цепи, называется напряжением. Напряжение – это особая мера потенциальной энергии, которая всегда относительна между двумя точками. Когда мы говорим об определенной величине напряжения, присутствующего в цепи, мы имеем в виду измерение потенциальной энергии для перемещения носителей заряда из одной конкретной точки этой цепи в другую конкретную точку. Без упоминания двух конкретных точек термин «напряжение» не имеет значения.

Ток, как правило, проходит через проводники с некоторой степенью трения или противодействия движению. Это противодействие движению правильнее называть сопротивлением. Величина тока в цепи зависит от величины напряжения и величины сопротивления в цепи, препятствующего прохождению тока. Как и напряжение, сопротивление – это величина, измеряемая между двумя точками. По этой причине величины напряжения и сопротивления часто указываются как «между» двумя точками в цепи.

Единицы измерения: вольт, ампер и ом

Чтобы иметь возможность делать осмысленные утверждения об этих величинах в цепях, нам нужно уметь описывать их количества так же, как мы могли бы количественно определить массу, температуру, объем, длину или любые другие физические величины. Для массы мы можем использовать единицы «килограмм» или «грамм». Для температуры мы можем использовать градусы Фаренгейта или градусы Цельсия. В таблице ниже приведены стандартные единицы измерения электрического тока, напряжения и сопротивления:

Единицы измерения тока, напряжения, сопротивления

Величина	Символ	Единица измерения	Сокращение единицы измерения
Ток	I	Ампер	А
Напряжение	V	Вольт	В
Сопротивление	R	Ом	Ом

«Символ», присвоенный каждой величине, представляет собой стандартную букву латинского алфавита, используемую для представления этой величины в формулах. Подобные стандартизированные буквы распространены во всех физических и технических дисциплинах и признаны во всем мире. «Сокращение единицы измерения» для каждой величины представляет собой алфавитный символ(ы), используемый в качестве сокращенного обозначения конкретной единицы измерения.

Каждая единица измерения названа в честь известного экспериментатора в области электричества: ампер в честь француза Андре М. Ампера, вольт в честь итальянца Алессандро Вольта, а ом в честь немца Георга Симона Ома.

Математический символ для каждой величины также имеет значение. «R» для сопротивления и «V» для напряжения говорят сами за себя («Resistance» и «Voltage», соответственно), тогда как «I» для тока кажется немного странным. Предполагается, что буква «I» должна представлять «интенсивность» («Intensity»)(потока заряда). Судя по исследованиям, которые мне удалось провести, кажется, что есть некоторые разногласия по поводу значения слова «I». Другой символ напряжения, «E», означает «электродвижущую силу» («Electromotive force»). Символы «E» и «V» по большей части взаимозаменяемы, хотя в некоторых текстах «E» зарезервировано для обозначения напряжения на источнике (таком как батарея или генератор), а «V»– для обозначения напряжения на любом другом элементе.

Все эти символы выражаются заглавными буквами, за исключением случаев, когда величина (особенно напряжение или ток) описывается в терминах короткого периода времени (так называемые «мгновенные» значения). Например, напряжение батареи, которое стабильно в течение длительного периода времени, будет обозначаться заглавной буквой «E», тогда как пиковое напряжения при ударе молнии в тот самый момент, когда она попадает в линию электропередачи, скорее всего, будет обозначаться строчной буквой «е» (или строчной буквой «v»), чтобы отметить это значение как имеющееся в один момент времени. Это же соглашение о нижнем регистре справедливо и для тока: строчная буква «i» представляет ток в некоторый момент времени. Однако большинство измерений в цепях постоянного тока, которые стабильны во времени, будут обозначаться заглавными буквами.

Кулон и электрический заряд

Одна из основных единиц электрических измерений, которую часто преподают в начале курсов электроники, но нечасто используют впоследствии, – это кулон – единица измерения электрического заряда, пропорциональная количеству электронов в несбалансированном состоянии. Один кулон заряда соответствует 6 250 000 000 000 000 000 электронов. Символом количества электрического заряда является заглавная буква «Q», а единица измерения кулонов обозначается «Кл». Единица измерения тока, ампер, равна 1 кулону заряда, проходящему через заданную точку в цепи за 1 секунду. В этом смысле, ток – это скорость движения электрического заряда через проводник.

Как указывалось ранее, напряжение – это мера потенциальной энергии на единицу заряда, доступная для стимулирования протекания тока из одной точки в другую. Прежде чем мы сможем точно определить, что такое «вольт», мы должны понять, как измерить эту величину, которую мы называем «потенциальной энергией». Общей метрической единицей измерения энергии любого вида является джоуль, равный количеству работы, совершаемой силой в 1 ньютон при движении на 1 метр (в том же направлении). В этих научных терминах 1 вольт равен 1 джоулю электрической потенциальной энергии на (деленному на) 1 кулон заряда. Таким образом, 9-вольтовая батарея выделяет 9 джоулей энергии на каждый кулон заряда, проходящего через цепь.

Эти единицы и символы электрических величин станут очень важны, когда мы начнем исследовать отношения между ними в цепях.

Формула закона Ома

Основное открытие Ома заключалось в том, что величина электрического тока, протекающего через металлический проводник в цепи, при любой заданной температуре прямо пропорциональна напряжению, приложенному к нему. Ом выразил свое открытие в виде простого уравнения, описывающего взаимосвязь напряжения, тока и сопротивления:

\[E=IR\]

В этом алгебраическом выражении напряжение (E) равно току (I), умноженному на сопротивление (R). Используя алгебру, мы можем преобразовать это уравнение в других два варианта, решая его для I и R соответственно:

\[I = \frac{E}{R}\]

\[R = \frac{E}{I}\]

Анализ простых схем с помощью закона Ома

Давайте посмотрим, как эти формулы работают, чтобы помочь нам анализировать простые схемы:

Рисунок 1 – Пример простой схемы

В приведенной выше схеме есть только один источник напряжения (батарея слева) и только один источник сопротивления току (лампа справа). Это позволяет очень легко применить закон Ома. Если мы знаем значения любых двух из трех величин (напряжения, тока и сопротивления) в этой цепи, мы можем использовать закон Ома для определения третьей.

В этом первом примере мы вычислим величину тока (I) в цепи, учитывая значения напряжения (E) и сопротивления (R):

Рисунок 2 – Пример 1. Известны напряжение источника и сопротивление лампы

Какая величина тока (I) в этой цепи?

\[I = \frac{E}{R} = \frac{12 \ В}{3 \ Ом} = 4 \ А\]

Во втором примере мы вычислим величину сопротивления (R) в цепи, учитывая значения напряжения (E) и тока (I):

Рисунок 3 – Пример 2. Известны напряжение источника и ток в цепи

Какое сопротивление (R) оказывает лампа?

\[R = \frac{E}{I} = \frac{36 \ В}{4 \ А} = 9 \ Ом\]

В последнем примере мы рассчитаем величину напряжения, подаваемого батареей, с учетом значений тока (I) и сопротивления (R):

Рисунок 4 – Пример 3. Известны ток в цепи и сопротивление лампы

Какое напряжение обеспечивает батарея?

\[E = IR = (2 \ А)(7 \ Ом) = 14 \ В\]

Метода треугольника закона Ома

Закон Ома – очень простой и полезный инструмент для анализа электрических цепей. Он так часто используется при изучении электричества и электроники, что студент должен запомнить его. Если вы не очень хорошо умеете работать с формулами, то для его запоминания существует простой прием, помогающий использовать его для любой величины, зная две других. Сначала расположите буквы E, I и R в виде треугольника следующим образом:

Рисунок 5 – Треугольник закона Ома

Если вы знаете E и I и хотите определить R, просто удалите R с картинки и посмотрите, что осталось:

Рисунок 6 – Закон Ома для определения R

Если вы знаете E и R и хотите определить I, удалите I и посмотрите, что осталось:

Рисунок 7 – Закон Ома для определения I

Наконец, если вы знаете I и R и хотите определить E, удалите E и посмотрите, что осталось:

Рисунок 8 – Закон Ома для определения E

В конце концов, вам придется научиться работать с формулами, чтобы серьезно изучать электричество и электронику, но этот совет может облегчить запоминание ваших первых вычислений. Если вам удобно работать с формулами, всё, что вам нужно сделать, это зафиксировать в памяти E = IR и вывести из нее две другие формулы, когда они вам понадобятся!

Резюме

• Напряжение измеряется в вольтах, обозначается буквами «E» или «V».
• Сила тока измеряется в амперах, обозначается буквой «I».
• Сопротивление измеряется в омах, обозначается буквой «R».
• Закон Ома: E = IR; I = E/R; R = E/I

Оригинал статьи:

Теги

Закон ОмаЗарядКулонОбучениеСила токаСопротивлениеСхемотехникаЭлектрический токЭлектрическое напряжение

Сохранить или поделиться

(PDF) Закон Ома в первоначальной редакции \\ Ohm’s law in his the initial version

Закон Ома в первоначальной редакции

10

Электростатический электрометр представляет собой воздушный конденсатор (см.

рис. 2), в котором используется феномен притяжения пластин (обкладок) в зависимости от

соотношения количества энергии на них, подробнее, например: [Gibilisco et al., 2016: 59-61].

Если подключить электростатический электрометр параллельно нагрузке, то в этом

случае на одну пластину электрометра поступает поток энергии перед нагрузкой, а на другую

пластину – поток энергии после нагрузки. На пластинах накапливается разное количество

энергии, пропорциональное мощности потоков энергии на входе и выходе из нагрузки, и

пропорционально электроемкости пластин. Таким образом, электростатический электрометр

отражает разность в количестве электроэнергии, входящей в нагрузку и выходящей из нее,

см. рис. 3. Шкалу электрометра можно градуировать так, чтобы он показывал величину

электроэнергии, измеряемую в cal.

Если подключить электростатический электрометр к клеммам источника тока, то он будет

измеряться разность в величине электроэнергии между избыточно заряженной

(«положительной») клеммой источника тока и дефицитно заряженной («отрицательной»)

клеммой источника тока.

7. Электропроводимость и электро-поглощение проводника, элемента цепи

Франц Эпинус (Franz Aepinus, 1759) определял электрическое «сопротивление» как

«непроводимость», свойство определенных веществ (изоляторов, диэлектриков) не

пропускать электрический ток через себя [Эпинус, 1951: 24].

Георг Ом процесс поглощения электроэнергии элементами цепи, называл «потеря

энергии». Это начальное название, как представляется, адекватнее отражает физическую

суть процесса. Ведь проводник не «сопротивляется» прохождению потока электроэнергии, а

«теряет», точнее поглощает и излучает часть ее. При таком понимании логичнее процесс

называть не «электрическим сопротивлением», а эл ектро-поглощением, электро-абсорбцией.

Сам элемент цепи, поглощающий часть электроэнергии, проходящей через него, можно

назвать абсорбером.

Можно говорить, что «сопротивляются» прохождению электрического тока изоляторы

(диэлектрики). Т.е. проводники поглощают электроэнергию, а изоляторы (почти) не

пропускают ток.

Электропроводимость – свойство тела (вещества) пропускать через себя определенную

часть, долю величины потока электроэнергии, проходящего через него. Электропроводимость

зависит от удельной (объемной) электропроводимости среды, т.е. электропроводимости

определенного вещества, определенного объема.

Электропроводимость, как показатель «пропускания» энергии, может измеряться в cal.

Коэффициент электропроводимости (Cconduct) абсорбера, проводника, элемента цепи,

Понимание закона Ома с помощью «хитрого» вопроса

---

На протяжении многих лет мне нравилось изучать различные аспекты нашей Вселенной, такие как электричество, компьютерные системы и физика. Я искренне верю, что нет лучшего форума для игры с этими вещами, чем радиолюбители. За последние пару десятилетий мне посчастливилось работать с различными младшими инженерами, которые работали со мной и научились многим вещам, которые я когда-то стремился усвоить. Я встречал инженеров, которые «только что поняли», и других, которые испытывали трудности из-за неверных предубеждений.Для меня самой важной из этих проблем было действительно полезное понимание Закона Ома.

Большинство (если не все) из нас видели формулы. Они относительно просты, и многие из нас могут легко использовать элементарную школьную алгебру, чтобы вычислить два значения из любых двух, просто манипулируя формулами. Например, если мы знаем напряжение и сопротивление, мы можем рассчитать ток и мощность. Однако то, что мы можем «работать с математикой», не означает, что мы действительно достаточно хорошо понимаем закон Ома, чтобы заставить его работать на нас.

Чтобы заставить электрические заряды выполнять наши заявки, нам нужно понимать, когда и как применять и комбинировать формулы. Нам также может потребоваться отказаться от некоторых концепций, которые у нас есть в настоящее время.

Рисунок 1 хорошо изношен. Значения могут отличаться, но диаграмма часто используется, чтобы начать работу с уравнениями закона Ома.

РИСУНОК 1. Хорошо изношенная схема.

---

Мы видим, что у нас есть источник напряжения, и напряжение подается на резистор, сопротивление которого известно.Одна вещь, о которой я никогда не слышал, это то, что напряжение появляется (измеряется) на объектах, в то время как ток (поток электрического заряда) измеряется от до объектов. Подобно силе и энергии, многие люди (даже некоторые не новички) путают напряжение и ток, и особенно то, что они делают.

Напряжение – это разница между электрическими потенциалами двух отдельных мест. На уроках науки это называется электрическим давлением или электродвижущей силой. Существует довольно обширная аналогия с водой, давлением и потоком, которая иногда помогает людям понять электричество.

С помощью давления воды или воздуха мы не можем говорить о давлении в каком-то месте. Давление должно быть разницей в двух местах. Иногда мы видим манометр, который просто показывает, например, давление в фунтах на квадратный дюйм. Если он не помечен (например) дополнительной буквой, такой как PSIA (фунты на квадратный дюйм абсолютного), мы будем вынуждены предположить, что PSI относится к окружающей среде вокруг метра. Чтобы поднять иглу вверх, по-прежнему должна быть разница давлений.

Как и в случае с давлением, в точке НИКОГДА не может быть напряжения. Вопрос типа “Какое напряжение на этом выводе?” становится чепухой, если нет согласованного «другого места». Часто это место считается землей (например, грязь за пределами вашей хижины или кузов вашей машины). В таких случаях вы услышите, как люди говорят о напряжении в определенной точке. Однако в вашей голове всегда должно быть, что напряжение относится к какой-то другой точке, и этот момент ДОЛЖЕН быть согласован всеми участниками разговора.

In Рисунок 2 ,

РИСУНОК 2. Определены некоторые значения.

---

мы использовали закон Ома для заполнения неизвестных значений:

I = V / R = 10/100 = 0,1 А

Мощность = V x A = 10 x 0,1 = 1 Вт

Ток проходит через резистор, а затем снова и снова через источник напряжения. Резистор – , потому что он имеет сопротивление – будет иметь напряжение на его выводах, вызванное током, протекающим через него.Комбинация тока через устройство и напряжения на устройстве заставляет устройство обрабатывать мощность и превращать ее в тепло.

Имейте в виду:

• Напряжение всегда на чем-то измеряется.
• Ток всегда через что-нибудь измеряется.
• Сопротивление – это характеристика чего-то.
• Мощность – это результат наличия напряжения и тока, протекающего через что-то.

Важно понимать, что в проводах, соединяющих резистор с источником напряжения, протекает тот же ток, что и через резистор.Ток проходит через этот простой цикл. Однако провода имеют очень маленькое сопротивление (в этом идеальном случае мы можем предположить, что у них нет сопротивления). Поскольку провода не имеют сопротивления, они не могут использовать энергию проходящего через них тока.

Вот как электричество «умеет» нагревать нить накаливания в лампе, но не нагревает провода, выключатель и разъемы. Чтобы использовать питание, нам нужны как напряжение, проходящее через что-то, так и ток через одно и то же.То или другое не дает силы. То есть напряжение без тока или ток без напряжения не будут генерировать мощность. Разомкните цепь, и в том, что раньше было цепью, не будет использоваться мощность.

Вопрос с подвохом

На рис. 3 мы разорвали цепь вверху.

РИСУНОК 3. Вопрос.

---

Это то место, где у нас был ток 0,1 ампер непосредственно перед перерывом. Вопрос с подвохом: «Что показывает вольтметр через разрыв цепи?»

Подсказка: Вольтметр хорошего качества будет иметь очень высокое сопротивление.Во время работы он потребляет очень небольшой ток, чтобы минимизировать влияние, которое он оказывает на измеряемое напряжение. В нашем случае вольтметр идеален и имеет бесконечное сопротивление. Никакие обвинения не пройдут; то есть ток равен нулю.

Trains of Thought
Если вы уже уверены в ответе, то эта статья не для вас. Некоторые инженеры и техники сразу поймут, что здесь происходит. Если вы хоть немного не уверены, потерпите меня.Это может иметь некоторую ценность.

Поезд A
«Нет тока, значит, не должно быть напряжения. Счетчик покажет ноль ».

Этот поезд не доставит вас туда. Это наиболее частое обоснование, которое я видел для этой презентации. Проблема в том, что его посылка ложна. У нас может быть напряжение без тока. Это называется статическим электричеством. Статическое электричество – это электричество без потока заряда. Несмотря на то, что батареи будут иметь небольшой ток и, в конечном итоге, саморазрядиться, вы можете купить пакет щелочных батареек, которым исполнился год, и по-прежнему использовать их в качестве источника питания до тех пор, пока они не разрядятся.Напряжение может присутствовать на батареях без протекания тока все время, пока они находятся в упаковке.

Поезд B
«Счетчик замыкает цепь, но я не знаю, каким будет ток».

Этот поезд тоже не доставит вас туда. Если измеритель имеет бесконечный импеданс, он действительно не замыкает цепь. В этой «цепи» отсутствует ток. По сути, это не схема.

Поезд C
«Резистор все еще в цепи.Он должен немного упасть в напряжении. Однако, не зная сопротивления измерителя, мы не можем точно знать, что он показывает ».

Опять же, этот поезд не доставит вас туда. Счетчик имеет бесконечное сопротивление; следовательно, ток через него и резистор равен нулю.

Поезд D
«Сопротивление измерителя намного выше, чем резистор 100 Ом. Все напряжение от источника напряжения должно падать на счетчике. Я говорю 10 вольт ».

Поезд D доставит вас туда.У нас может быть напряжение без тока. Измеритель имеет очень высокий импеданс (намного выше, чем резистор 100 Ом). Счетчик перекрывает весь ток. Напряжение на счетчике должно составлять 10 вольт. Все напряжение питания падает на счетчик.

Реальность

Мы можем лучше понять, почему это правильно, задав вопрос с хитростью в виде делителя напряжения, как показано на Рис. 4 .

РИСУНОК 4. Более реальная схема.

---

Я также взял на себя смелость изменить импеданс измерителя с бесконечного на более реальное значение. Здесь у нас есть резистор в миллион Ом, на котором был установлен измеритель. Мы можем рассчитать ток, который проходит через оба резистора, вычислив эффективное сопротивление. Поскольку резистор на 100 Ом и резистор на 1 миллион Ом включены последовательно, мы можем просто сложить их, чтобы определить эффективное сопротивление цепи. Через оба резистора будет протекать одинаковый ток:

1,000,000 + 100 = 1,000,100 Ом

Обратите внимание, что это все еще очень близко к одному миллиону Ом.

Тогда ток будет:

I = V / R = 10 / 1,000,100 = 0,000009999 ампер

Это довольно мало. Он намного меньше 0,1 А, который был у нас до «перерыва».

Поскольку через оба резистора протекает один и тот же небольшой ток, мы можем вычислить, сколько напряжения падает на каждом резисторе И сколько мощности будет рассеиваться каждым резистором. Да, счетчик рассеивает мощность, но, надеюсь, очень мало:

В ₁₀₀ = I x R = 0,000009999 x 100 = 0.0009999 вольт

Мощность ₁₀₀ = V x I = 0,000000009998 Вт

Напряжение на резисторе 100 Ом теперь составляет 0,0009999 вольт. Не собираюсь никого убивать здесь:

В _1000000 = I x R = 9,999 В
Мощность _1000000 = I x R = 0,00009998 Вт

Напряжение на резисторе сопротивлением 1 миллион Ом теперь составляет 9,999 В. Таким образом, поскольку импеданс измерителя очень высок, напряжение на нем, по сути, является источником напряжения. Здесь мы также видим, что высокое сопротивление может привести к более высокому напряжению.Звучит странно, но это правда.

Также обратите внимание, что общая мощность, используемая обоими резисторами, намного меньше, чем мощность, используемая одним резистором 100 Ом в исходной схеме. Сопротивление растет, напряжение растет, но мощность падает. Опять же, странно, но факт.

На самом деле ни один вольтметр не имеет входа с бесконечным сопротивлением. Однако большинство из них довольно высокие. Даже относительно недорогой измеритель (тот, который иногда предоставляется бесплатно в некоторых магазинах) может иметь входное сопротивление в миллион Ом – намного выше, чем у большинства устройств в цепях, которые мы используем каждый день.

На случай, если есть неверующие, вот несколько фотографий, на которых я проводил эксперимент, чтобы показать, что происходит.

В , рис. 5, я построил схему, разместив свой дешевый (бесплатный) мультиметр поперек разрыва цепи. В данном случае я использовал резистор на 1000 Ом (1 кОм), чтобы доказать свою точку зрения. Даже при 1000 Ом в цепи измеритель по-прежнему считывает, по сути, напряжение источника питания.

РИСУНОК 5. Измерение через разрыв с сопротивлением 1000 Ом.

---

В , рис. 6 , я заменил резистор на 1000 Ом на резистор, который в 10 раз больше (10 000 Ом или 10 кОм).

РИСУНОК 6. Измерение через разрыв с сопротивлением 10 000 Ом.

---

Здесь мы все еще можем видеть, что большая часть напряжения источника питания падает на счетчике. Однако он определенно немного меньше, что означает, что на резисторе 10 кОм падает некоторое напряжение.

Как насчет миллиона Ом?

На одном миллионе Ом (одном МОм) мы видим значительное падение ( Рисунок 7 ).

РИСУНОК 7. Измерение через разрыв с сопротивлением миллиону Ом.

---

Напряжение на измерителе теперь составляет примерно половину напряжения питания. Это означает, что другая половина напряжения ДОЛЖНА быть на резисторе.

Что очень интересно в этой комбинации, так это то, что одинаковый ток течет через счетчик и через резистор. У них обоих примерно одинаковое падение напряжения. Это означает, что измеритель должен иметь такое же сопротивление, что и резистор: один миллион Ом.

По сути, мы измерили входное сопротивление этого бесплатного цифрового мультиметра. Один миллион Ом достаточно для устранения большинства неисправностей. Некоторые измерители более высокого качества будут иметь входное сопротивление 10 миллионов Ом. Некоторые дорогие метры даже выше.

Последний трюк

Есть много других «хитрых» вопросов, которые я использовал, чтобы стимулировать размышления о законе Ома. Мне потребовалось много времени, чтобы разобраться в подобных вещах. Надеюсь, это облегчит вам переход. NV

---

Во время поиска и устранения неисправностей, если два устройства подключены последовательно, мы иногда можем определить неисправное одно, просто измерив напряжение на них. Если напряжение подается на одно устройство, значит, оно предотвращает ток и, возможно, неисправное устройство.

Лампы накаливания при перегорании часто дают разрыв цепи. Если напряжение питания измеряется на лампочке, вероятно, это плохо.

---

Получил два, получил два бесплатно

С помощью закона Ома и уравнения мощности у нас есть две формулы, которые дают представление о том, что происходит с электрическими системами – по крайней мере, с электрическими системами постоянного тока.

Закон Ома можно выразить тремя способами:

В = I x R, I = V / R и R = V / I

где V = напряжение, R = сопротивление и I = ток.

Если мы знаем какую-либо алгебру, мы можем видеть, что каждое из этих уравнений может дать нам два других, просто вычисляя значение, которого у нас нет.

Уравнение мощности:

P = V x I

Где есть и напряжение, и ток, куда-то будет течь энергия.

Используя эти два уравнения, мы можем получить любые два значения с учетом двух других.Например, предположим, что мы знаем напряжение и сопротивление устройства. Устройство может быть любым. Зная эти два значения, мы можем определить два других:

I = V / R

Поместив значение напряжения для V и значение сопротивления для R, мы определили I (ток).

Зная ток и напряжение, мы можем определить мощность, рассеиваемую «вещью»:

P = V x I, = V x V / R = SQR (V) / R

Выучите хотя бы немного алгебры.Затем эти уравнения становятся менее запоминающимися и более понятными.

---

Экранирование электромагнитных помех и закон Ома

При работе с электрическим током важно понимать закон Ома. Между ними существует прямая связь. Этот закон позволяет людям определять основные фундаментальные элементы электрических величин: это сопротивление, ток и напряжение. Основа закона Ома гласит, что ток проводника между двумя точками связан с разностью потенциалов между двумя точками.По сути, ток, протекающий в цепи, прямо пропорционален напряжению, но в то же время обратно пропорционален сопротивлению цепи. Это означает, что когда напряжение повышается, а сопротивление не изменяется, ток будет увеличиваться. Если вместо этого сопротивление увеличивается, то ток будет уменьшаться, но это произойдет только в том случае, если напряжение не изменится. Уравнение работает таким образом, что позволяет найти каждое из трех целых чисел, если два уже известны.С помощью этого уравнения можно анализировать цепи: сюда входят резистивные цепи, реактивные цепи и цепи слабого сигнала.

Для правильной работы экранирующих прокладок необходим закон Ома. Предполагается, что материал прокладки закрывает швы и щели электронного корпуса. Единственный способ, при котором этот материал может работать должным образом, – это знать, какой ток внутри него течет. Это позволяет приобрести подходящую экранирующую прокладку.

Георг Ом основал свою работу на Генри Кавендише, который работал с электрическими токами в конце 1700-х годов.Работа Ома началась только в 1820-х годах, и уравнение было наконец опубликовано в 1827 году. Его работа также была основана на работе Джозефа Фурье. Работа, проделанная Омом, является одним из наиболее важных описаний количественной физики электричества. Странно, что сегодня это уравнение считается само собой разумеющимся, что означает, что мы понимаем текущий поток, но когда оно было опубликовано в 1800-х годах, люди не знали об этом.

Этот закон полезен во многих отраслях промышленности, но особенно полезен в электротехнике.Причина, по которой это необходимо для этой области, состоит в том, чтобы позволить людям смотреть на схемы на макроскопическом уровне.

Уравнение Максвелла было построено на основе закона Ома, но они могут работать вместе. Развитие современной электромагнетизма не противоречит закону Ома. Оба уравнения имеют практическое применение и сегодня.

Экранирование электромагнитных помех

Напряжение, ток, сопротивление и закон Ома | ОРЕЛ

С возвращением, молодой мастер электроники.В нашем предыдущем блоге мы узнали о простой схеме и ее месте в нашем мире электроники. Но чтобы понять истинную сущность электричества, нужно понять, как управлять и измерять напряжение, ток и сопротивление. Вот где приходит этот блог. Мы поднялись на самые высокие вершины, чтобы найти правильную аналогию, объясняющую природу того, как электричество работает в цепи. И вместо того, чтобы проводить еще одну аналогию с водой, мы подумали, что будем более личными, с нашими телами в движении.

Напряжение – все дело в потенциале

Представьте, что вы просыпаетесь утром. Вы лежите в постели, хотите еще несколько часов поспать, но знаете, что настало время для страшной утренней пробежки. Вы знаете, что это хорошо для вас, и вы будете чувствовать себя прекрасно, когда начнете двигаться, но каждое утро вам нужно делать выбор. Вы можете либо остаться в постели и поспать немного дольше, либо встать и начать двигаться.

Это сущность напряжения; все дело в разнице потенциалов.У всех нас есть потенциал, и когда дело доходит до бега, этот потенциал заключается в том, чтобы сделать выбор: бегать или спать. Если вы не решите бегать сегодня утром, ваш потенциал будет бездействовать, но если вы это сделаете, то этот потенциал вырвется наружу, побуждая вас бежать на несколько миль и заряжая энергией остаток дня.

Напряжение в сети

Подобно наличию потенциала движения или отсутствия, напряжение накапливает электрическую энергию с потенциалом движения .Именно эта сила напряжения побуждает электроны течь по цепи и заставляет их работать час за часом.

Voltage просто ждет, пока мы задействуем его потенциал. Посмотрите на каждую неиспользуемую розетку в вашем доме – в розетках гудит напряжение, готовые сделать за вас работу. Но, как и при выборе бежать, у вас есть выбор, подключать ли этот источник напряжения к вашей розетке. Если оставить его в покое, то напряжение останется там, где оно есть, никогда не реализуя свой полный потенциал.

В электрической цепи напряжение измеряется путем определения с помощью мультиметра так называемой разности потенциалов между двумя точками. Возьмем, к примеру, 9-вольтовую батарею. Если вы измеряете положительный и отрицательный полюсы, вы получите разность потенциалов 9 вольт (или близкую к ней). Положительный конец измеряется при 9 В, а отрицательный конец – при 0 В. Минус два числа, и вы получите разность потенциалов.

Вы можете использовать мультиметр, чтобы быстро измерить напряжение или разность потенциалов в батарее.(Источник изображения)

Напряжение бывает двух разных форм: постоянного (постоянного тока) напряжения, которое обеспечивает постоянный поток отрицательного электричества, или переменного (переменного тока) напряжения, которое постоянно переключается с отрицательного на положительное. Вот символы, которые вы хотите найти на схеме для постоянного, переменного напряжения и батареи:

Вот некоторые символы напряжения, на которые следует обратить внимание на следующей схеме: батареи, постоянный и переменный ток.

Отец напряжения – Алессандро Вольта

Человек часа, которому приписывают открытие напряжения – Алессандро Вольта (Источник изображения)

Человеком, первым обнаружившим напряжение, был итальянский физик Алессандро Вольта.Он также обнаружил массу других интересных вещей, в том числе:

• Обнаружение того, что, если вы смешиваете метан с воздухом, вы можете создать электрическую искру, которая положила начало знаменитому ныне двигателю внутреннего сгорания.
• Обнаружение того, что электрический потенциал, хранящийся в конденсаторе, пропорционален его электрическому заряду.
• Volta также приписывают создание первой электрической батареи, названной Voltaic Pile, которая позволила ученым того времени создавать устойчивый поток электронов.

Пример гальванической батареи, впервые созданной Вольтой, позволяющей ученым создавать устойчивый поток электронов. (Источник изображения)

Однако

Volta не был лишен своих причуд. Пока ему не исполнилось четыре года, он не произнес ни слова, и его родители опасались, что он либо умственно отсталый. Хорошо, что они ошибались!

Ток – движение по потоку

Возвращаясь к нашей аналогии с бегом, представьте, что вы сделали выбор в пользу утренней пробежки.Вы в обуви и шортах и ​​выходите за дверь, чтобы отправиться в путь. На этом этапе у вас есть движение, когда вы начинаете бег, поток.

Вот ток, движущийся в наших телах, кто знал, что электричество может быть таким личным?

Может быть, через час пробежки вы начнете бежать, готовые пробежать мили. Когда вы бежите, ваши умные часы точно измеряют, как далеко вы прошли и как быстро вы прошли. Этот процесс запуска и измерения процесса – вот что такое Current .

Ток в электричестве

Как и шаги для завершения утренней пробежки, ток – это постоянное движение или поток электричества в цепи . Электрический ток, протекающий по вашей цепи, всегда измеряется в амперах или амперах. Но что заставляет этот ток двигаться?

Это напряжение, о котором мы говорили ранее. Точно так же, как вам нужно сказать себе, чтобы продолжать бегать, когда вы устали, напряжение является движущей силой тока, которая поддерживает его движение.Есть две школы мысли о том, как ток течет в цепи; Обычный поток или Электронный поток , давайте посмотрим на оба:

Обычный поток – Обычный поток был первым в период научных открытий, когда люди не понимали электроны и то, как они текут в цепи. В рамках этой модели предполагалось, что электричество перетекает с положительного на отрицательный.

Обычный поток с электричеством, протекающим от положительной стороны к отрицательной батареи.

Вы все еще увидите, что этот менталитет используется в схемах и сегодня, и хотя он не совсем точен, его немного легче понять, чем Electron Flow. В конце концов, если мы вернемся к нашей аналогии с бегом, вы начнете с положительного источника энергии и бежите до тех пор, пока энергия не иссякнет. Это отношение положительное к отрицательному, как и многое в жизни.

Электронный поток – Электронный поток был продолжением обычного потока. Эта модель точно описывает электроны как движущиеся в противоположном направлении, от отрицательного к положительному.Поскольку электроны по своей природе отрицательны, они всегда будут выходить из отрицательного и бесконечно пытаться найти свой путь к положительной стороне источника питания с низким напряжением.

И более текущий поток электронов, при этом электроны текут, как в действительности, от отрицательного к положительному.

Имеет ли значение, каким образом вы показываете ток, протекающий в цепи? Не совсем. Вы, вероятно, увидите, что это представлено в обоих направлениях, если взглянуть на множество схем. Взгляните на диоды или транзисторы на следующей схеме, которую вы исследуете; все они будут указывать в направлении обычного потока.

Человек, стоящий за течением – Андре-Мари Ампер

Андре-Мари Ампер, самоучка, человек, совершивший гораздо больше, чем просто открытие Ампера. (Источник изображения)

Ампер был французским физиком и математиком, а также одним из основоположников науки о классическом электромагнетизме. Вы можете поблагодарить Ampere за несколько замечательных вещей, в том числе:

• Его главное открытие – демонстрация того, что провод, по которому проходит электрический ток, может притягивать или отталкивать другой провод, по которому также течет ток, без использования физических магнитов.
• Он был также первым, кто выдвинул идею о существовании частицы, которую мы все признаем электроном.
• Он также организовал химические элементы по их свойствам в периодической таблице за полвека до появления современной периодической таблицы.

Интересный факт об образовании Ампера – у него не было никакого формального образования! Вместо этого отец позволял ему делать то, что ему заблагорассудится, узнавая что угодно. Хотя это могло вызвать лень и чрезмерное увлечение видеоиграми у остальных из нас, Ампер обнаружил естественную любовь к знаниям, пожирая как можно больше книг из семейной библиотеки и даже заучивая страницы из энциклопедии.

Сопротивление – это материальный мир

Наша последняя концепция – Сопротивление. Представьте себя снова на беговой дорожке, по какой поверхности вы бежите? Если вам повезет, то вы, возможно, путешествуете по мягкой траве или грунтовой дороге. Или, может быть, вы предпочитаете твердость улицы или тротуара. Но что, если он начнет литься наружу? Тогда вы можете застрять в густой грязи

Независимо от того, по какой дороге вы бежите, ваши ноги сталкиваются с некоторым сопротивлением, когда вы продолжаете двигаться вперед.Естественно, не все пути сопротивления созданы равными. Бег по грязи значительно снижает вашу способность к бегу по сравнению с бегом по грунтовой дороге или улице. В этом вся суть сопротивления, тяга и тяга материального мира.

Сопротивление электричеству

Какой бы материал ни проходил через электричество, он всегда будет сталкиваться с трением, препятствующим его движению. Проще говоря, сопротивление тормозит ток . Хотя в электрической цепи есть определенные компоненты, такие как резистор, единственная задача которого – сопротивление электричеству, любой физический материал будет оказывать некоторое сопротивление.

Вы обнаружите, что сопротивление измеряется в Ом Ом, и оно напрямую связано с током и напряжением. Вот простой пример: чем больше у вас сопротивление, тем меньше тока может протекать по цепи. Это похоже на бег: чем гуще грязь, тем медленнее ты будешь бежать. Обратное также работает, если вы увеличиваете напряжение, чтобы ваш ток двигался быстрее, чем ваше сопротивление будет иметь меньшее влияние на вашу схему.

Мастер сопротивления – Георг Симон Ом

Георг Ом – Человек, который объединил напряжение, ток , ток и сопротивление в известный ныне закон Ома.(Источник изображения)

Г-н Ом был немецким физиком и математиком, и именно в те годы, когда он был школьным учителем, он начал свои исследования с использованием новой электрической батареи, изобретенной Вольтой. С помощью собственного оборудования Ом смог обнаружить прямую зависимость между напряжением, приложенным к проводнику (например, медному проводу), и возникающим в результате электрическим током. Это стало известно как известный ныне закон Ома, на который мы все сегодня полагаемся.

Интересно отметить, что Ом представил свои открытия в своей первой книге «Гальваническая цепь, исследуемая математически», но колледж, в котором он работал в то время, не заботился об этом.Так что же сделал Ом? Он ушел в отставку и устроился на новую работу в Политехническую школу Нюрнберга. К счастью, именно здесь его работа привлекла заслуженное внимание.

Собираем все вместе с законом Ома

Хорошо, теперь пора объединить все наши концепции. Вот с чем нам предстоит работать:

• Напряжение (В) – это накопленное электричество, имеющее потенциал для движения. Когда этот потенциал активируется, напряжение действует как своего рода давление, проталкивая ток по цепи.
• Ток (I) – Поток электричества в цепи. Его можно измерить непосредственно в амперах, и существует две школы мысли о том, как протекает ток – обычный поток и электронный поток.
• Сопротивление (R) – Сопротивление, с которым электричество сталкивается, просто протекая через какой-то физический материал. Измеряется в Ом.

Собирая все это вместе, мы приходим к закону Ома:

В этом уравнении V = напряжение, I = ток и R = сопротивление.Гибкость закона Ома впечатляет, и его можно использовать для нахождения любого из этих трех значений, когда известны только два из них. Давайте рассмотрим пример, чтобы увидеть, как это работает.

Использование треугольника Ома

Посмотрите на треугольник Ома ниже. Он дает простое и наглядное представление о том, как можно манипулировать законом Ома, чтобы получить нужные ответы. Чтобы использовать его, все, что вам нужно сделать, это скрыть букву значения, которое вам нужно выяснить, а оставшиеся буквы покажут вам, как этого добиться.

Треугольник Ома, ваш удобный инструмент, чтобы точно определить, какой вариант закона Ома необходимо использовать.

Взгляните на схему ниже. У нас есть батарея 9V, подключенная к светодиоду и резистору. Единственная проблема заключается в том, что нам нужно выяснить, каково значение резистора.

Наша тренировочная схема, чтобы познакомиться с законом Ома. Мы можем использовать известные значения ампер и вольт, чтобы получить значение резистора.

Для этого давайте посмотрим на треугольник Ома.Закрыв R, мы видим, что у нас V над I или V, деленное на I. Итак, разделив эти два числа, мы получим номинал нашего резистора. Давайте подставим эти числа в это уравнение: R = V / I.

• Начнем с самого очевидного, у нас напряжение аккумулятора 9 вольт.
• Глядя на техническое описание нашего светодиода, мы можем увидеть рекомендуемый максимальный ток 16 мА (миллиампер), который преобразуется в 0,016 ампер.
• Подставляя эти два числа в наше уравнение, мы получаем R = 9V / 0.016A, что равно 473,68. Это означает, что для включения светодиода нам понадобится резистор на 473 Ом!

Сопротивление бесполезно

Понимать, как напряжение, ток и сопротивление работают вместе, было не так уж сложно, не так ли? Мы надеемся, что в следующий раз, когда вы отправитесь на утреннюю пробежку, у вас будет новый взгляд на электричество. Почувствуйте, как ваши ноги летят по тротуару или грязи, и помните, что это сопротивление. А когда вы проверяете, как далеко вы пробежали, то наблюдаете за движущимся потоком! И та сила, которая вытащила вас из постели и заставила бежать? Напряжение.

Готовы сделать свою первую схему сегодня? Попробуйте Autodesk EAGLE бесплатно!

Понимание закона Ома | BUILD

Закон Ома – это наиболее часто используемая формула для электриков. В его наиболее фундаментальной форме E = I x R, где «E» – электромагнитная сила (вольт), «R» – сопротивление (Ом), а «I» – сила (амперы).

Это тот, который нужно запомнить. Из этой единственной формулы простые алгебраические транспозиции позволяют вам решить для каждого из членов, так что электрические вычисления могут быть легко выполнены.Вам не нужно даже возиться с этой простой задачей, если перед вами колесо закона Ома (см. Рисунок 1).

Как видите, внутренний круг колеса закона Ома содержит четыре элемента: ватты, вольты, амперы и омы. Каждое из них приравнивается к любому из трех выражений в соответствующей четверти внешнего круга. Например, в нижней левой четверти амперы равны ваттам, разделенным на вольты.

Электрики часто используют это уравнение для определения размеров цепей, то есть для определения размера провода на основе допустимой нагрузки.Процедура заключается в обращении к паспортной табличке или документации, относящейся к конкретному прибору или части оборудования, например, обогревателю. Размер нагрузки часто указывается в ваттах, но вам нужно знать токи, чтобы рассчитать схему. Колесо закона Ома говорит вам разделить ватты на вольты, чтобы найти ампер. Используйте номинальное напряжение системы или номинальное напряжение, указанное на паспортной табличке, в отличие от измеренного напряжения, которое может незначительно варьироваться в зависимости от политики энергосистемы, расположения на линии электропередачи и местной нагрузки.

Другой распространенный расчет, выполняемый электриками, особенно при поиске неисправностей неисправного оборудования, также находится в нижней левой четверти колеса закона Ома. Вы не часто будете решать для E (вольт), потому что это предопределено приложением. Вам нужно будет найти I (амперы) или R (омы).

Часто старое моторизованное оборудование подвергается постепенному разрушению изоляции из-за влаги и / или повторяющегося перегрева. Ток (измеренный с помощью накладного омметра) будет иметь аномально высокий уровень или сопротивление (измеренное мультиметром, установленным для функции измерения сопротивления) будет аномально низким.Будет замечено, что оборудование перегревается, а двигатель (особенно под нагрузкой) не достигает своей номинальной скорости или вообще не запускается.

Эти и другие простые вычисления, основанные на колесе закона Ома, облегчат определение размеров схем для новых установок и понимание причин неисправности оборудования.

Конечно, все это зависит от понимания точного значения ампер, омов и вольт.

1A определяется как количество электронов, которое проходит через любую заданную точку в цепи.Излишне говорить, что число очень большое: 628 с 28 нулями. Из этого значения рассчитываются вольты и омы. В частности, один вольт – это величина электромагнитной силы, которая заставит 1 А пройти через сопротивление 1 Ом. Более того, 1 Ом – это величина сопротивления, которая ограничивает протекающий через него ток до одного ампера.

Во всех случаях закон Ома работает, чтобы найти одну из трех величин, которые мы обсуждали, когда известны две другие. На более высоких частотах переменного тока ситуация немного усложняется, и иногда приходится вносить коррективы.Однако при частоте 50 Гц и 60 Гц (циклов в секунду), используемых во всем мире, отклонение от значений постоянного тока не является заметным для большинства приложений.

Мы должны рассмотреть еще один термин: импеданс (Z). Как и сопротивление, импеданс измеряется в омах. Это сумма сопротивления, емкостного реактивного сопротивления и индуктивного реактивного сопротивления. Эти последние термины относятся к противодействию потоку тока, обеспечиваемому конденсатором, и противодействию потоку тока через индуктор, либо простой проводник, либо проводник, намотанный в виде катушки.

Мы часто используем слово «импеданс», когда говорим о противодействии потоку тока в источнике энергии – генераторе, батарее или вторичной обмотке трансформатора. Внутреннее сопротивление действует как резистор, включенный последовательно с источником питания. Источник питания с низким импедансом испытывает меньшее падение напряжения при подключении к относительно большой нагрузке. Максимальная мощность передается, когда импедансы источника и нагрузки равны или согласованы. Если полное сопротивление источника высокое, напряжение падает до более низкого уровня.При высоком импедансе нагрузки ток ограничивается в соответствии с законом Ома. Когда полное сопротивление источника и нагрузки одинаковы, протекает максимальный ток.

Помимо закона Ома, существует множество других теорем и уравнений, применимых к миру электроники. Теорема Тевенина, теорема Нортона, теорема суперпозиции, теорема взаимности, теорема компенсации, теорема Миллмана и другие обращаются к ситуации, когда в цепи имеется несколько источников питания, комбинированные последовательные и параллельные нагрузки и т. Д.Все эти сложные схемы подчиняются закону Ома, но анализ сложен и требует много времени. Приведенные выше теоремы упрощают вычисления, предлагая несколько применимых обобщений. Однако от работающих электриков такие расчеты не требуются. Эти теоремы используются инженерами-энергетиками и электронщиками, которые имеют дело с передовыми схемами.

Один набор формулировок, который очень полезен электрикам, особенно при поиске неисправностей в неисправном оборудовании, известен как законы Кирхгофа.Многие технические специалисты интуитивно понимают принципы, даже если они никогда не слышали о Кирхгофе и не знали о его законах.

В 1847 г. Кирхгоф открыл простую формулировку, которая расширяет закон Ома, так что он применяется к напряжению и току в последовательном контуре.

Проще говоря, в любой момент ток, текущий в любой компонент в цепи, равен току, текущему из этого компонента. Ток в последовательной цепи везде одинаковый.

Если вы визуализируете поток тока в последовательной цепи как однородный поток, который покидает горячую сторону источника и возвращается через заземленный нейтральный проводник или через другую горячую ветвь, вы будете на пути к пониманию схемы и обнаружению любых неисправностей. .

Это некоторые из основных концепций, используемых электриками для отслеживания электрических цепей и поиска неисправностей в неисправном оборудовании. Самый полезный элемент в наборе инструментов электрика – графическая версия колеса закона Ома, которое отображает взаимодействие этих фундаментальных свойств Вселенной.

Закон и крутящий момент

Ом – журнал IAEI

В ходе моих многолетних путешествий стало очевидно, что большинство электриков не понимают закона Ома, ватт и крутящего момента.Все очень просто. Электрические провода и соединения должны работать при температуре не выше 60 ° или 75 ° по Цельсию.

Закон Ома

Единственный способ измерить температуру – это измерить ее термометром. Вы не можете рассчитать это. С другой стороны, вы можете легко измерить вольты и амперы и рассчитать омы и ватты. Это ватты потребляемой мощности. Скорость утечки тепла полностью зависит от температуры окружающего воздуха, количества грязи или стекловолокна.

Алгебра

А теперь самое сложное: алгебра. Я знаю, что большинство парней делают ретроградное движение назад, когда слышат слово «алгебра», но на самом деле это не так уж и сложно. Закон Ома обычно формулируется как E = IR. Это мало что вам говорит. Мы разделим обе стороны на I, чтобы получить E / I = R, потому что вы не можете точно прочитать R от нуля до одного Ом. Если мультиметр показывает, что номинальная 75-ваттная лампа имеет сопротивление 12,5 Ом при 10 ° по Цельсию (50 ° по Фаренгейту), это правда. Но для куска провода или его соединений мы должны ожидать, что Ом будет десятичной точкой, за которой следует группа нулей, прежде чем мы дойдем до значащей цифры.
Есть загвоздка. Вам понадобится вольтметр со шкалой в милливольтах переменного тока. Дешевый счетчик с нижней шкалой от нуля до двух целых вольт просто не подойдет. Мой старый омметр в высшей степени точен с минимальным показанием 0,1 мВ переменного тока. Подойдет любой другой хороший измеритель с минимальным показанием в один или десять мВ переменного тока. Для усилителей точность не требуется. Мой одноразовый нагреватель коробки горит 11,5 ампер. Они могут варьироваться от 11 до 12. Там, где вам нужна точность, это показания мВ AV.

Теперь все, что вам нужно сделать, это взять показание в мВ и разделить на 1000, чтобы получить целые вольты, а затем разделить на 11.5 ампер, чтобы получить Ом. Это число должно быть десятичной точкой, за которой следует множество нулей. В таблице 8 указано, что твердотельный кабель 12 AWG имеет сопротивление 1,93 Ом на тысячу футов. Это длинный круг. Давайте рассмотрим короткое замыкание, – говорится в розетке GFCI на служебном входе с шестью дюймами черного проводника и шестью дюймами белого проводника, всего один фут. Сопротивление провода составляет 1,93 Ом, разделенное на 1000. Это нормально для нагрузки в 20 ампер.

Рисунок 1. Таблица эксперимента

Что недопустимо, так это плохие соединения.У вас есть четыре соединения: черный провод к выключателю, белый провод к заземленной шине и то же самое к латунным и серебряным винтам на устройстве. Эти четыре соединения имеют длину примерно полдюйма каждое. Эти соединения должны иметь примерно такое же сопротивление, как и полдюйма 12 AWG, или 1,93, разделенные на 1000, разделенные на 24.

Надежное соединение обеспечивается правильно откалиброванной динамометрической отверткой.

Эксперимент

Это забавная часть, но сначала вам понадобится еще одна небольшая порция ужасной алгебры.Мощность в ваттах, рабочих джоулях в секунду – это I2R в концепциях, или A2 Ом, или VA в единицах измерения. Вы должны запомнить хотя бы один. Помните, что мы рассчитали сопротивление, измерив милливольты и разделив их на амперы. Теперь мы можем рассчитать ватт, возведя в квадрат 11,5 ампер, умноженных на ом. Не плохо. Но что, если я подключу два обогревателя? Это будет 23 ампера. Чтобы справиться с этой перегрузкой в ​​течение нескольких минут, требуется автоматический выключатель на 20 ампер. А теперь посчитайте. Удвоение тока в квадрате, умноженного на такое же сопротивление, в четыре раза больше тепла в ваттах.Может ли 12 AWG выжить? Может ли связь выжить? Нет, приготовят. Чистые, плотные соединения станут слишком горячими. Неплотные соединения с незащищенным пластиком под винтами могут вызвать возгорание.

Фото 1. Зажимы типа «крокодил» на клемме для измерения падения напряжения.

Еще одна ложка дегтя. Если вы запустите один, два или десять нагревателей на 11,5 ампер в сети на 200 ампер, все должно работать нормально. Мы предполагаем, что сопротивление постоянное. В реальном мире с повышением температуры растет сопротивление.По мере увеличения сопротивления растет и мощность в ваттах. Получается замкнутый круг, как соскальзывание с крыши сарая. Вы начинаете с 20 ° C (68 ° F). Через некоторое время она станет 60 ° C (140 ° F). Для действительно плохой работы это 204 ° C (400 ° F). Это хорошая температура для выпечки печенья. Но красные винтовые соединители становятся бежевыми, а виниловая лента превращается в уголь. Тебе повезло, что дом не сгорел.

В моем первом тесте серебряный винт был ослаблен и покачивался. 12 AWG был закручен вокруг и свободно выдвигался, что он и сделал, в то время как я вставил другой конец в GFCI.Во втором тесте я повернул отвертку большим и указательным пальцами с усилием, превышающим ноль дюймов на фунт, может быть, два, при этом провод все еще мог вращаться. В третьем тесте я набрал около 23 дюймов на фунт. Это было слишком правильно. Двадцать пять разорвали бы винт 8-32.

Обратите внимание, что в табличных результатах значения в омах и ваттах упали до одной десятой, и все это с тем же одноразовым нагревателем, который готовил сам себя несколько лет назад.

Электрические соединения должны быть такими же чистыми.Не угадай; используйте динамометрический ключ. Не используйте 18-дюймовую перемычку.

Примеры закона

Ом – Сборка электронных схем

Обычно я не использую много математики при работе с электроникой, но закон Ома чрезвычайно полезен!

Закон был найден Георгом Омом и основан на том, как связаны напряжение, ток и сопротивление:

Посмотрите на рисунок выше и убедитесь, что для вас это имеет смысл:

• Если вы увеличите напряжение в цепи при неизменном сопротивлении, вы получите больший ток.
• Если вы увеличите сопротивление в цепи при неизменном напряжении, вы получите меньший ток.

Закон Ома – это способ описания взаимосвязи между напряжением, сопротивлением и током с использованием математики:

В = RI

• В – обозначение напряжения.
• I – символ тока.
• R – символ сопротивления.

Использую ОЧЕНЬ часто. Это формула электроники.

Вы можете переключить его и получить R = V / I или I = V / R.Если у вас есть две переменные, вы можете рассчитать последнюю.

Треугольник закона Ома

Вы можете использовать этот треугольник, чтобы запомнить закон Ома:

Как использовать:
Накройте рукой письмо, которое вы хотите найти. Если оставшиеся буквы лежат друг на друге, значит, верхнюю разделите на нижнюю. Если они рядом, значит, умножаются одно на другое.

Пример: напряжение

Найдем формулу для напряжения:

Положите руку на V в треугольнике, затем посмотрите на R и I.I и R находятся рядом друг с другом, поэтому вам нужно умножить. Это означает, что вы получите:

В = I * R

Пример: сопротивление

Найдем формулу сопротивления:

Положите руку на R. Тогда вы увидите, что V находится над I. Это означает, что вам нужно разделить V на I:

R = V / I

Пример: Текущий

Найдем формулу для тока:

Положите руку на I. Затем вы увидите букву V над R, что означает разделение V на R:

I = V / R

Как запомнить закон Ома

Самый простой способ запоминать что-то – создать с ним глупую ассоциацию, чтобы вы запомнили это, потому что это так глупо.

Итак, чтобы помочь вам запомнить закон Ома, позвольте мне представить VRIIIIIIII! правило.

Представьте, что вы ведете машину очень быстро, а затем внезапно резко нажимаете на тормоза. Какой звук вы слышите?

«ВРИИИИИИИИИИИИ!»

И так можно запомнить V = RI;)

Практический пример

Лучший способ научить пользоваться им – это на собственном примере.

Ниже представлена ​​очень простая схема с батареей и резистором. Батарея представляет собой батарею на 12 вольт, а сопротивление резистора составляет 600 Ом.Сколько тока течет по цепи?

Чтобы найти величину тока, вы можете использовать треугольник выше к формуле для тока: I = V / R. Теперь вы можете рассчитать ток, используя напряжение и сопротивление:

I = 12 В / 600 Ом
I = 0,02 A = 20 мА (миллиампер)

Значит ток в цепи 20 мА.

Если вы не любите вычислять вещи самостоятельно, воспользуйтесь этим калькулятором закона Ома.

Другой пример

Попробуем еще один пример.

Ниже мы снова видим схему с резистором и батареей. Но на этот раз мы не знаем напряжение батареи. Вместо этого мы представляем, что измерили ток в цепи и обнаружили, что он составляет 3 мА (миллиампер).

Сопротивление резистора 600 Ом. Какое напряжение у аккумулятора?

Вспоминая «VRIIII!» правило, вы получаете:

В = RI
В = 600 Ом * 3 мА
В = 1,8 В

Значит, напряжение АКБ должно быть 1.8 В.

Возврат от закона Ома к электронным схемам

Вейпинг и закон Ома: руководство для чайников

Последнее обновление 14 января 2020 года

Если вы некоторое время занимались вейпингом, скорее всего, вы столкнулись с принципом закона Ома.

Если вы вейпер, это одно из лучших знаний, которые вы можете получить, особенно если вы увлекаетесь субомингом.

Этот принцип ориентирует вас на причину и следствие, а также на прямое использование и ограничения того, что и как вы вейпируете, и как оставаться в безопасности при этом.

Что такое закон Ома?

Закон Ома был открыт в 19 веке немецким физиком по имени Джордж Саймон Ома, в честь которого назван этот принцип.

В нем говорится, что электрический ток (I), протекающий через проводник, пропорционален напряжению (V), а также обратно пропорционален сопротивлению (R).

Таким образом, если есть увеличение напряжения, ток будет пропорционально увеличиваться до тех пор, пока сопротивление в цепи не изменится.

Как закон Ома соотносится с вейпингом

В вейпинге закон Ома смещает фокус на сопротивление катушек и ток, проходящий через них.

По сути, это количество энергии, необходимое для питания вашей постоянной (также известной как сопротивление) от батареи.

Все катушки не созданы равными и будут иметь разное сопротивление, которое поможет вам определить, насколько ваши непостоянные потребности должны измениться.

Таким образом, вы можете использовать закон Ома для расчета мощности, которую будет выдавать ваше вейп-устройство, на основе напряжения батареи и сопротивления распылителя / катушки.

Если все это звучит немного странно, вам не нужно беспокоиться о законе Ома, если вы используете регулируемое вейп-устройство (как и большинство устройств на рынке), поскольку устройство решает это за вас.

Однако знание закона Ома и техники безопасности при использовании батарей пригодится при использовании нерегулируемого устройства, такого как механический мод.

Высокое и низкое сопротивление

Вообще говоря, катушки, распылители и сборки с более высоким сопротивлением требуют меньше энергии.

Например, если ваша катушка имеет сопротивление 2.1 Ом (сборка выше Ом) вам потребуется всего около 6-12 Вт для его питания. С другой стороны, устройству с меньшим сопротивлением и катушкой менее 1,0 Ом (также известной как катушка субом) может потребоваться немного больше мощности, скажем, 18-25 Вт.

Поскольку проводимость (и долговечность) материалов катушки различается с точки зрения энергии, проходящей через нее, из-за различных материалов катушки может потребоваться использование другой мощности.

Закон Ома для регулируемых модов

Регулируемые испарители или модификаторы – это устройства, которые имеют встроенную защиту для вашего источника питания.В них также есть такие вещи, как индикатор заряда батареи, отображение напряжения и мощности, считыватель сопротивления и т. Д.

Эти устройства упрощают сборку катушек, и у многих компаний есть модели, которые уже включают резервуар или RDA.

Если у вас есть устройство с одной батареей 18650, многие из этих сборок могут легко работать с мощностью от 85 до 100 Вт.

Если вы опускаетесь ниже рекомендуемого уровня катушки (обычно около 0,25 или 0,1 Ом), скорее всего, ваше устройство не сработает до определенной точки, поэтому вы потеряете пар.И если вы это сделаете, это приведет к быстрой разрядке вашей батареи.

Закон Ома для механических модификаций

Теперь предположим, что у вас есть механический мод.

Модификации

Mech обычно не имеют внутренней печатной платы для тех настроек, которые вы найдете на экране регулируемого устройства. Они также не предлагают защиты от короткого замыкания или других встроенных механизмов защиты аккумулятора в случае ошибки пользователя.

Вот почему мехмоды – прерогатива опытных пользователей, хорошо разбирающихся в Законе Ома, безопасности батарей и других важных вещах.

Однако, если у вас негибридный мехмод – механический мод с подключением, похожим на регулируемый мод с 510-контактным контактом, и не находится в прямом контакте с батареей – закон Ома может предоставить вам такую ​​информацию, как идеальная сборка. вы можете иметь на устройстве и 510-контактный контакт, который вы должны использовать на своем атомайзере.

Как вычислить закон Ома

Когда вы хотите вычислить закон Ома, вам не нужно вычислять числа самостоятельно – если, конечно, это не одно из тех занятий, которые заставят вас слиться.

Вместо этого вы можете пропустить математику и воспользоваться одним из многих онлайн-калькуляторов закона Ома, например, вот здесь.

Это даст вам точные числа, и вы сможете получить ключевую информацию, такую ​​как разряд батареи, сопротивление ваших катушек в зависимости от материала, типа сборки и т. Д.

«Понимание закона Ома» поможет вам максимально использовать ваши сеансы вейпинга, понимая, как все работает и как вы можете использовать это, чтобы получить максимум удовольствия.

.