Калькулятор катушки индуктивности без сердечника – Расчет катушки индуктивности | Онлайн калькулятор

Онлайн калькулятор расчета многослойной катушки индуктивности

На практике нередко случаются ситуации, когда при выходе со строя катушки индуктивности, ее необходимо восстановить – намотать новую проволоку взамен старой. При этом вам уже известны геометрические параметры катушки, но требуется узнать, сколько сделать витков, слоев, их толщину и длину необходимого для этого провода. Стоит отметить, что при намотке витки должны ложиться вплотную без зазора.

Для расчета индуктивности многослойной катушки используется такая формула:

Где,

• d – сумма диаметра каркаса и толщины намотки только с одной стороны;
• n – количество витков;
• g – толщина намотанной проволоки;
• h – высота намотанной проволоки;

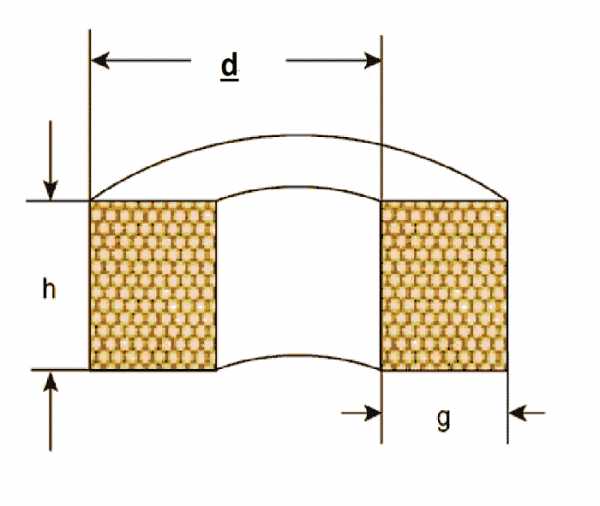
Из этой формулы, зная величину индуктивности, можно вывести толщину намотки:

Для определения количества витков необходимо воспользоваться формулой:

Где,

• d­_пр – диаметр провода
• h – высота катушки;
• g – толщина намотки.

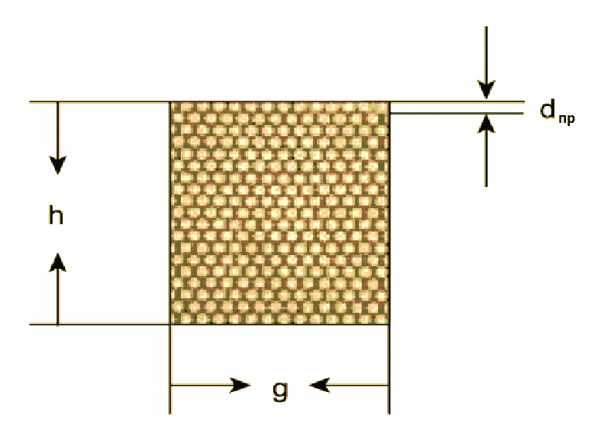Расчет количества витков

Длину одного витка можно определить следующим образом:

l_вит = π * d_вит

Где π – это константа, а d_{вит_}— это диаметр витка.

Тогда, зная общее число витков и принимая, что d – это усредненное значение диаметра для всех витков, длина всего провода будет определяться по формуле:

L_w = n * π * d

Через сопротивление провода можно определить его диаметр, для чего понадобится выразить сопротивление через геометрические параметры устройства.

R = ρ * ( L_w / S ),

где ρ – удельное сопротивление металла, из которого изготовлен проводник, а S – площадь проводника, которая определяется по формуле:

Подставив значение площади и длины провода, получим такое выражение для определения сопротивления:

Из значения сопротивления можно вывести формулу для определения диаметра провода, подставив предварительно формулу для вычисления количества витков:

 

После получения величины диаметра провода, можно определить количество витков, которое подставляется с остальными данными в первую формулу для расчета индуктивности.

Число слоев можно определить, разделив толщину намотки на диаметр провода:

N = g / d_пр

Посредством вышеприведенных вычислений можно определить все параметры многослойной катушки индуктивности, которые помогут вам изготовить устройство с нужными параметрами. Также, чтобы облегчить вычисления вы можете воспользоваться нашим онлайн калькулятором ниже.

www.asutpp.ru

Калькулятор расчета индуктивности катушки с воздушным сердечником

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:

где μ­­₀ – магнитная проницаемость вакуума,  μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки, l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.

Таблица 1

Материал	— µ —  (Гн/м)
Воздух	1.25663753*10−6
Алюминий	1.256665*10−6
Аустенитная нержавеющая сталь	1.260*10−6  — 8.8*10−6
Вакуум (µ0)	4π*10−7
Вода	1.256627*10−6
Водород	1.2566371*10−6
Висмут	1.25643*10−6
Дерево	1.25663760*10−6
Железо (чистота 99.8%)	6.3*10−3
Железо (99.95% чистое Fe отожженное в водороде)	2.5*10−1
Железо-кобальтовые сплавы	2.3*10−2
Медь	1.256629*10−6
Никель-цинковый феррит — магнит	2.0*10−5 – 8.0*10−4
Мартенситная нержавеющая сталь (отожженная)	9.42*10−4 — 1.19*10−3
Мартенситная нержавеющая сталь (закаленная)	5.0*10 −5 — 1.2*10−4
NANOPERM® — магнитомягкий нанокристаллический сплав	1.0*10−1
Неодимовый магнит	1.32*10−6
Никель	1.26*10−4 — 7.54*10−4
Пермаллой (сплав 80% никеля и 20% железа)	1.0*10−2
Платина	1.256970*10−6
Сарфир	1.2566368*10−6
Сверхпроводники	0
Углеродистая сталь	1.26*10−4
Ферритная нержавеющая сталь (отожженная)	1.26*10−3 — 2.26*10−3
Фторопласт 4, Ф-4,   Teflon	1.2567*10−6

Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:

Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.

Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:

Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.

Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.

www.asutpp.ru

Расчет параметров катушки | Онлайн калькулятор

Катушка индуктивности представляет собой электрическую сборную конструкцию, которая может изготавливаться в следующих исполнениях:

1. В виде намотанной на каркас обмотки из провода определенного диаметра.
2. Как витая бескаркасная спираль, предварительно сформированная на твердой основе, а затем снятая с нее.
3. Катушка, намотанная многослойным проводом в специальной матерчатой изоляции.

Особенностью этого электротехнического компонента является наличие у него значительной по величине индуктивности при относительно малой емкостной составляющей и низком активном сопротивлении. Это приводит к тому, что при протекании переменного тока она проявляет себя как элемент, обладающий большой инерционностью.

Обратите внимание: Благодаря этой особенности катушки текущий по ней ток отстает от приложенного напряжения на определенный угол (90 градусов). У профессионалов это явление получило название «отставание по фазе».

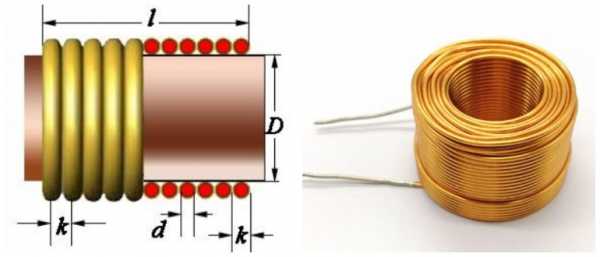
Для того, чтобы получить точные значения индуктивности катушки заданной формы, следует ввести ее основные параметры в онлайн-калькулятор. В нем автоматически рассчитывается такой важный показатель, как число витков в данном изделии. После ввода данных в специальную форму вы мгновенно получите искомое значение.

 

Наш онлайн-калькулятор производит автоматизированный расчет значений катушки индуктивности без сердечника с использованием метода эллиптических интегралов Максвелла. Калькулятор предусматривает расчет значений как однослойных обмоток, так и многослойных.

А вот формула индуктивности:

где,

• L – индуктивность;
• D – диаметр витка;
• N – число витков;
• h – длина намотки;
• g – количество слоев

Преимущества расчета значений параметров катушки с помощью онлайн-калькулятора очевиден.

 

( 1 оценка, среднее 1 из 5 )

Понравилась статья? Поделиться с друзьями:

fishkielektrika.ru

Бесплатная программа расчёта катушек индуктивности Coil32 – Софт для радиолюбителя – Программы

 

Катушки индуктивности практически используются почти в любой радио-аппаратуре, и довольно часто перед радиолюбителями возникает вопрос:

Как рассчитать индуктивность той, или иной катушки? Конечно можно рассчитать индуктивность по определённым формулам, но это требует времени, которого радиолюбителям всегда не хватает.
Бесплатная программа Coil32, автором которой является Кустарев Валерий, позволяет быстро рассчитать индуктивность практически любой катушки.

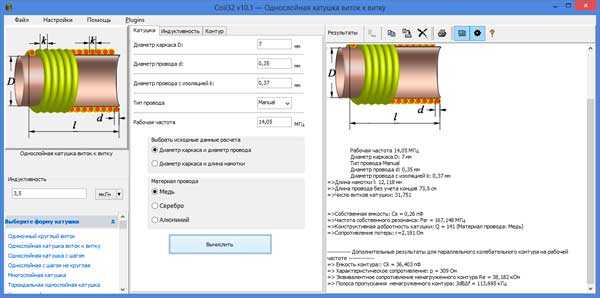
В программе учитываются наиболее распространенные варианты каркасов катушек. Можно рассчитать бескаркасную катушку в виде одиночного витка, на каркасах различной формы, на ферритовых кольцах и в броневых сердечниках, а также плоскую печатную катушку с круглой и квадратной формой витков. Для рассчитанной катушки, так же можно сразу рассчитать и ёмкость конденсатора в колебательном контуре.

Программа бесплатна и свободна для использования и распространения. В последней версии

Coil32 v11.6.1.890 доступны расчёты:

• Одиночный круглый виток
• Однослойная виток к витку
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса и диаметр провода, длина намотки вычисляется.
  2. Известны диаметр каркаса и длина намотки, диаметр провода вычисляется
• Однослойная катушка с шагом
• Катушка с не круглой формой витков
• Многослойная катушка
  В качестве начальных параметров при расчете катушки можно выбрать два варианта:
  1. Известны диаметр каркаса, длина намотки и диаметр провода. Вычисляется число витков, попутно определяется толщина катушки, ее омическое сопротивление постоянному току и приблизительная длина провода для намотки (“сколько надо отрезать”).
  2. Известны диаметр каркаса, длина намотки и предельное омическое сопротивление катушки. Вычисляется число витков, попутно определяется толщина катушки, нужный минимальный диаметр провода  и приблизительная длина провода для намотки.
• Тороидальная однослойная катушка
• Катушка на ферритовом кольце
• Катушка в броневом сердечнике
  (Ферритовом и карбонильном)
• Тонкопленочная катушка
  (Плоская катушка на печатной плате с круглой и квадратной формой витков и в виде одиночного прямого проводника)

Для расчета дополнительных видов индуктивности, которых нет в общем списке программы под заголовком “Выберите форму катушки” – имеется набор дополнительных плагинов “Plugins”. Список плагинов и их краткое описание отображены на рисунке ниже.

 

 

В чем преимущества данной программы перед аналогами?

• Программа рассчитывает индуктивность различных типов катушек под имеющийся каркас.
• Результаты расчетов выводятся в текстовое поле справа, откуда их можно сохранить в файл. Можно открыть этот файл в “MS Word” и распечатать.
• Есть возможность рассчитать добротность для радиочастотных однослойных катушек индуктивности.
• Можно рассчитать основные параметры колебательного контура для однослойной катушки
• Можно рассчитать длину провода для намотки однослойной, многослойной катушки и катушки на ферритовом кольце.
• Для расчёта катушек в броневых сердечниках, есть возможность выбора одного из нескольких стандартных сердечников, что позволяет рассчитать катушку в несколько кликов.
• Для плоских катушек на печатной плате программа подскажет оптимальные размеры для достижения наивысшей добротности.
• Программа имеет мультиязычный интерфейс (20 языков) и дополнительные наборы скинов, которые можно скачать и установить из меню “Настройки”.

Программа распространяется бесплатно в стиле “Portable” и не имеет установщика. Для работы с программой – скачайте архив, распакуйте его в любое удобное для Вас место и запустите файл Coil32.exe. При постоянной работе с программой, желательно создать для нее специальную папку и вынести ярлык Coil32.exe на рабочий стол.

Скачать Coil32.
 

 

 

 

vprl.ru

Coil32 – Однослойная катушка

Расчет индуктивности однослойной катушки

Однослойная катушка индуктивности представляет собой провод, свернутый в спираль. Для придания жесткости, провод обычно наматывают на цилиндрический каркас. Поэтому в Coil32 в качестве исходных параметров приняты размеры каркаса и диаметр провода, т.к. их легче измерить практически. В расчетных формулах, однако, используются геометрические параметры самой спирали. Во избежании путаницы на этой страничке справки можно подробнее ознакомиться с этими тонкостями.

Однослойные катушки получили широкое распространение, особенно для конструкций коротковолнового и средневолнового любительских и радиовещательных диапазонов. Основные свойства однослойных катушек — высокая добротность, относительно небольшая собственная емкость, удобство изготовления. Рассмотрим методы расчета такой катушки без промежутка между витками – “виток к витку“…

---

Начнем с того, что в конце XIX века Х.А.Лоренц вывел формулу с применением эллиптических интегралов для расчета соленоида. Отличием модели Лоренца от модели Максвелла являлся тот момент, что витки соленоида представлялись не бесконечно тонким круговым проводом, а бесконечно тонкой спиральной проводящей лентой с шириной равной реальной толщине провода, без промежутка между витками. Формула имеет высокую точность при расчете реальной катушки в случае если последняя имеет большое количества витков и имеет намотку виток к витку. В 1909 г. японский физик Х.Нагаока преобразовал формулу Лоренца и привел ее к виду из которого следовал важный вывод – индуктивность соленоида зависит исключительно от формы и размеров катушки. Формула Нагаока имеет следующий вид:

[2]

, где

• L_s – индуктивность катушки
• N – число витков катушки
• r – радиус намотки
• l – длина намотки
• k_L – коэффициент Нагаока

Важнейшим выводом из анализа этой формулы был тот, что коэффициент Нагаока зависел только от отношения l/D, который был назван форм-фактором катушки. Коэффициент Нагаока вычислялся с применением эллиптических интегралов. Подробнее на этой формуле останавливаться не будем, т.к. Coil32 ее не использует в расчетах. Стоит только отметить, что в случае длинного соленоида формула упрощается до следующего вида:

[3]

где S – площадь поперечного сечения катушки. Эта формула имеет только академический интерес и не пригодна для расчетов реальных катушек, т.к. справедлива только для бесконечно длинных соленоидов, которых в природе не существует.

---

Однослойную катушку можно рассчитать численным методом, используя формулу Максвелла или формулу Нагаока для соленоида. Однако современные эмпирические формулы дают очень высокую точность расчетов и вполне достаточны для практических целей.

---

Обзор и выбор эмпирических формул начнем с самой известной формулы Г.Вилера. Обычно именно эта формула чаще всего используется в различных программах, онлайн калькуляторах, справочниках и статьях, посвященных расчетам индуктивностей.

В оригинале эта формула выглядит так:

L = a² N² / ( 9 a + 10 b )

где N – число витков, а a и b – соответственно радиус и длина намотки катушки. Размерности в дюймах. Адаптировав эту формулу для метрической системы (вернее сказать для СГС) и поменяв радиус на диаметр, получаем следующее:

[4]

, где

• L – индуктивность катушки [мкГн];
• N – число витков катушки;
• D – диаметр намотки [см];
• l – длина намотки [см];

Это самый известный у нас вариант этой формулы. Раньше на сайте С.-Петербуржского университета телекоммуникаций – sut.ru был довольно информативный ресурс – dvo.sut.ru, на котором можно было найти много информации о катушках индуктивности, включая и эту формулу. Теперь это ресурс к сожалению удален. Но удалось обнаружить клон этого ресурса на qrz.ru, на который перекочевала даже старая ошибка (0,5ё1.0) в формуле 2.37. Там можно найти и формулу Нагаока (формула 2.28) и выражение коэффициента Нагаока через формулу Вилера (формула 2.29).

Формула была предложена Вилером в далеком 1928 году, когда еще о компьютерах только мечтали и была очень полезна в то время, т.к. позволяла “в столбик” на бумажке рассчитать практическую катушку. Формула “укоренилась” в массовом сознании радиолюбителей. Однако мало кто знает, что она, как любая эмпирическая формула, имеет ограничения. Эта формула дает погрешность до 1% при l/D > 0,4, т.е если катушка не слишком короткая. Для коротких катушек эта формула не пригодна.

---

Последовало несколько попыток устранить этот недостаток. В 1985 г. Р.Лундин опубликовал две свои эмпирические формулы, одна – для “длинных”, другая – для “коротких” катушек, позволяющие рассчитать коэффициент Нагаока с точностью не менее чем 3ppM (±0.0003%), что несомненно выше точности изготовления или измерения индуктивности катушки. Вот калькулятор, основанный на этих формулах.
В 1982 г., спустя 54 года, с наступлением эры компьютеров, Вилер опубликовал свою “длинную” формулу, которая рассчитывала однослойную катушку с погрешностью не более ±0.1%, как длинную, так и короткую. В дальнейшем эта формула была усовершенствована Р.Розенбаумом, а в последствии Р.Вивером (Robert Weaver – анализ и вывод формулы у него на сайте).

[5]

где:

• D_k – диаметр намотки
• N – число витков
• k = l/D_k – форм-фактор катушки, отношение длины намотки к ее диаметру

---

В результате мы имеем формулу, позволяющую рассчитать однослойную катушку с точностью не менее 18.5 ppM (в сравнении с формулой Нагаока), что хуже чем по формулам Лундина, но во-первых вполне достаточно для практических расчетов, во-вторых мы имеем одну более простую формулу вместо двух, рассчитывающую однослойную катушку независимо от ее форм-фактора.

Формула [5] и используется в онлайн-калькуляторе однослойной катушки, старых версиях Coil32, а также во всех версиях программы для Linux и в J2ME приложении для мобильных телефонов.

В основной версии Coil32 для Windows, а также начиная с версии 3.0 для Android, применена более сложная методика расчета однослойной катушки, учитывающая спиральную форму витков и произвольный шаг намотки.

---

В 1907 году Э.Роза, сравнивая расчеты по методу Максвелла и по методу Лоренца, вывел таблицу поправок, существенно увеличивающих точность расчета по методу Лоренца, особенно если катушка имеет небольшое число витков. Эти поправки стали именоваться “поправки на круглость провода” – Round Wire Corrections. В дальнейшем эти поправки использовались для увеличения точности расчета коэффициента Нагаока и эмпирических формул Лундина и Вивера. В 2008 г. Р.Вивер создал эмпирический алгоритм, позволяющий численным методом рассчитать “поправки на круглость провода” не прибегая к помощи таблиц. Этот алгоритм применяется в Coil32 начиная с версии 8.0, в онлайн-калькуляторе, а также в версиях Coil32 для Андроид и J2ME, для увеличения точности расчета индуктивности однослойных катушек.

---

Кроме индуктивности, как основного параметра однослойной катушки, программа Coil32 вычисляет и другие параметры:

Этих данных вполне достаточно для создания реалистичной модели катушки в программах схемотехнического моделирования. Например, в популярных RFSim99 или LTSpice IV. В RFSim99 необходимо поставить галочку в чекбоксе “Вкл. физ. модель” и ввести частоту собственного резонанса и добротность. Тип добротности необходимо выбрать третий – Q(f)=Q(F). В LTSpice необходимо задать R_ser – это наше сопротивление потерь (r) и C_par – это собственная емкость катушки Cs.

Кроме того можно рассчитать дополнительные результаты для параллельного колебательного контура на рабочей частоте. Характеристическое сопротивление такого контура равно реактивному сопротивлению катушки на рабочей частоте.

Назад…      Вперед…

coil32.ru

Расчёт индуктивности. Часть 2 | HomeElectronics

Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.

Виды катушек индуктивности

Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности

Расчёт индуктивности катушки.

Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:

D₁ – внутренний диаметр, D₂ – внешний диаметр, D_ср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить

Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:

если l > D_ср – длинная катушка,

если l < D_ср – короткая катушка,

если l << D_ср – очень короткая катушка,

если l = 0 – плоская катушка,

если t ≈ D_ср – толстая катушка,

если t << D_ср – тонкая катушка,

если t = 0 – соленоид.

Особенности расчёта катушек индуктивности

Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением

где L_Р – расчётная индуктивность;

∆L – поправка на «изоляцию», ∆L = ∆₁L + ∆₂L;

∆₁L – поправка учитывающая влияние индуктивности витков;

∆₂L – поправка учитывающая влияние взаимной индуктивности витков.

В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности L_Р, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.

Особенности расчёта круговых катушек индуктивности состоят в следующем:

1. При определении расчётной индуктивности L_P, средний диаметр принимается равным среднему диаметру реальной катушки;

2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении

3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.

4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.

5. Так как величина поправки на взаимную индуктивность ∆₂L в несколько раз меньше, чем поправка на индуктивность витков ∆₁L, то при расчётах можно учитывать только ∆₁L.

Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.

Расчёт индуктивности соленоида

Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.

Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

d – диаметр соленоида, м;

Φ – коэффициент, который зависит от отношения α = l/D;

l – длина соленоида, м;

Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d

Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит

Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит

Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.

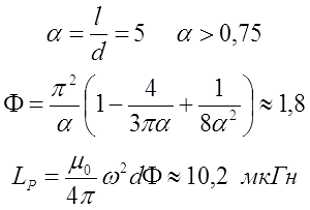
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.

Индуктивность плоской катушки

Определение индуктивности плоской катушки, D₁ – внутренний диаметр, D₂ – внешний диаметр, D – средний диаметр, t – толщина намотки.

В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D – средний диаметр катушки, м;

Ψ – коэффициент, который зависит от отношения ρ = t/D­;

t – толщина намотки катушки.

Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D

При небольшой толщине намотки, когда ρ < 0,5

При большой толщине намотки, когда ρ > 0,5

где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки

Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.

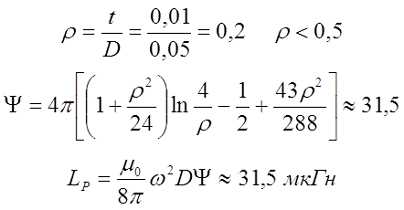
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.

Индуктивность круговой катушки прямоугольного сечения

Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник

Индуктивность прямоугольной катушки.

Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.

Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле

где L₀ – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/D_cp;

l – длина катушки, м;

D_cp – средний диаметр катушки, м;

∆ — поправка на форму катушки.

В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру D_cp, можно разделить на несколько типов:

1. Длинная катушка, у которой α > 0,75.

2. Короткая катушка, имеющая α < 0,75 и γ < 1.

3. Очень короткая катушка, имеет α << 1 и γ > 1.

где

Рассмотрим каждый случай по отдельности.

Индуктивность длинной катушки

Длинная катушка.

Для длинной катушки (α > 0,75) величина L₀ рассчитывается также как для длинного соленоида, где l – длина соленоида, D_cp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

где D₁ – внутренний диаметр, D₂ – внешний диаметр.

Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром D_CP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.

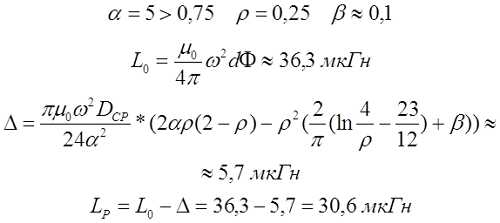
Индуктивность короткой катушки

Короткая катушка.

Для короткой катушки (α < 0,75, t < l) величина L₀ рассчитывается также как для короткого соленоида, где l – длина соленоида, D_СР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;

Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром D_СР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.

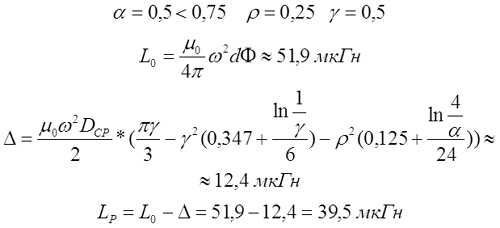
Индуктивность очень короткой катушки

Очень короткая катушка.

Для очень короткой катушки (α << 1, t > l) величина L₀ рассчитывается также как для плоской катушки, где t – толщина намотки, D_cp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению

где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру D_CP;

γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;

ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру D_CP.

Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром D_CP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.

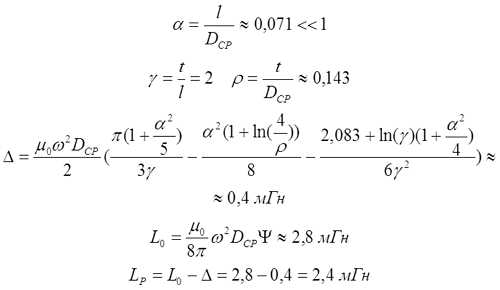
Расчёт поправки на собственную индуктивность витков

Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности L_P и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆₁L и поправки на взаимную индуктивность витков ∆₂L

Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки

Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.

В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

I – коэффициент, зависящий от расположения витков катушки.

Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.

Для варианта а), провод намотан с небольшим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта б), провод намотан с большим коэффициентом заполнения

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки

где s – диаметр провода с изоляцией, s_p – диаметр голого провода (без изоляции).

Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности L_P

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен

где p – шаг намотки по длине катушки, s_p – диаметр голого провода (без изоляции).

Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной диаметру голого провода s_P, то коэффициент I будет равен

— если при вычислении расчётной индуктивности L_P длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен

где q – шаг намотки по толщине катушки, s_p – диаметр голого провода (без изоляции).

Расчёт поправки на взаимную индуктивность витков

В общем случае поправка на взаимную индуктивность витков ∆₂L катушки определяется выражением

где μ₀ – магнитная постоянная, μ₀ = 4π•10^-7 Гн/м;

ω – число витков соленоида;

D_СР – средний диаметр катушки, м;

J – коэффициент, зависящий формы катушки и от числа витков катушки.

1. Для катушки выполненной в один слой по длине катушки (соленоид):

а) при определении расчётной индуктивности L_P толщина намотки t принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит

где ω – количество витков катушки.

2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):

а) при определении расчётной индуктивности L_P длина катушки l принята равной шагу намотки р, то коэффициент J составит

где ω – количество витков катушки.

б) при определении расчётной индуктивности L_P длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит

где ω – количество витков катушки.

На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.

 

Теория это хорошо, но без практического применения это просто слова.Здесь можно всё сделать своими руками.

www.electronicsblog.ru

Расчёт катушки индуктивности под динамик

Данный расчет является примером для определения данных катушки индуктивности на воздушном сердечнике, нагруженной динамиком. В этом примере выбрана катушка без сердечника во избежание искажений, обусловленных перемагничиванием сердечника.

На рисунке показана оптимальная катушка индуктивности в смысле отношения индуктивности катушки и ее активному сопротивлению. Конструкция получается, когда внутренний диаметр цилиндрического слоя обмотки вдвое больше его высоты, а внешний диаметр в четыре раза больше высоты и в два раза больше внутреннего диаметра.

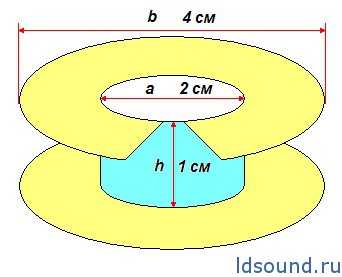
высота 1 см; внутренний диаметр 2 см; внешний диаметр 4 см.

Пример расчета

Современные программы по расчету пассивных фильтров для акустики, дают значение катушек индуктивности в мГн, здесь нужно перевести в мкГн, т.е. умножить на 1000.

Определим данные катушки с индуктивностью 1,25 мГн (или 1250 мкГн) разделительного фильтра, нагруженного динамиком сопротивлением 4 Ом. Активное сопротивление рассчитываемой катушки должно составлять 5% сопротивления динамика. Это соотношение можно считать вполне приемлемым. Активное сопротивление катушки: R = 0,05 х 4 = 0,2 Ом.

1. откуда: L/R = 1250 / 0,2 = 6250 мкГн/Ом;
2. далее имеем: h = √ ((L/R) / 8,6) = √ (6250 / 8,6) = 26,96 мм;
3. длинна жилы: l = 187,3 х √ (L х h) = 187,3 х √ (1250 х 26,96) = 34383 мм = 34,3 м;
4. количество витков: ω = 19,88 √(L / h) = 19,88 х √ (1250 / 26,96) = 135,36 витков;
5. диаметр жилы: d =0,84h / √ω = 0,84 х 26,96 / √ 135,36 = 1,95 мм;
6. масса намотки: m = (h³ х 10^-3) / 21,4 = (26,96³ х 10^-3) / 21,4 = (19595,65 х 0,001) / 21,4= 0,9 кг.

Полученные значения должны быть округлены (в первую очередь диаметр жилы) до ближайшего стандартизированного. Окончательные значения индуктивности подгоняют путем отматывания нескольких витков обмотки, намотанной с некоторым превышением числа витков сравнительно с рассчитанным.

Итак имеем данные, которые понадобятся для расчета будущей катушки:

1. высота намотки h = 26,96 мм;
2. значит внутренний диаметр a = 53,92 мм;
3. соответственно внешний: b = 107,84 мм;
4. длинна жилы: 34,3 м;
5. количество витков: 135;
6. диаметр жилы, соответствует стандартизированному: 1,95 мм (по меди).

Статья специально подготовлена для сайта ldsound.ru

ldsound.ru