Кольца гельмгольца: Кольца Гельмгольца – это… Что такое Кольца Гельмгольца?

Кольца Гельмгольца

Кольца Гельмгольца (катушки Гельмгольца) — две соосно расположенные одинаковые радиальные катушки, расстояние между центрами которых равно их среднему радиусу. В центре системы имеется зона однородного магнитного поля. Используются для получения постоянного, переменного или импульсного магнитного поля с зоной однородности, которое обычно используется в экспериментах, а также для калибровки датчиков магнитной индукции, намагничивания и размагничивания постоянных магнитов, размагничивания стальных заготовок, деталей и инструментов. Область поля с неоднородностью менее 1% является эллипсоидом вращения близким к сфере радиусом 0.3R, что почти в 4 раза больше чем для одного кольца. Эллипсоид немного сжат вдоль оси.

Названы в честь немецкого физика Германа Гельмгольца.

Вывод

Суммарный модуль индукции магнитного поля может быть получен из Закона Био — Савара — Лапласа:

B = μ 0 2 π I R 2 4 π ( R 2 + x 2 ) 3 / 2 {displaystyle B={frac {mu _{0}2pi IR^{2}}{4pi (R^{2}+x^{2})^{3/2}}}} B = μ 0 I R 2 2 ( R 2 + x 2 ) 3 / 2 {displaystyle B={frac {mu _{0}IR^{2}}{2(R^{2}+x^{2})^{3/2}}}} Где: μ 0 {displaystyle mu _{0};} = магнитная постоянная = 4 π × 10 − 7  T ⋅ m/A = 1. {-6}{ ext{ T}}cdot { ext{m/A}}} I {displaystyle I;} = ток через катушку, в амперах R {displaystyle R;} = радиус катушки, в метрах x {displaystyle x;} = расстояние по оси катушек, в метрах

Каждая катушка состоит из n {displaystyle n;} витков. Общий ток: n I {displaystyle nI;} .

Тогда,

B = μ 0 n I R 2 2 ( R 2 + x 2 ) 3 / 2 {displaystyle B={frac {mu _{0}nIR^{2}}{2(R^{2}+x^{2})^{3/2}}}}

Принимая во внимание, что расстояние по оси от катушки до центра x = R/2,

B = μ 0 n I R 2 2 ( R 2 + ( R / 2 ) 2 ) 3 / 2 {displaystyle B={frac {mu _{0}nIR^{2}}{2(R^{2}+(R/2)^{2})^{3/2}}}}

Умножая на 2 (катушки),

B = 2 μ 0 n I R 2 2 ( R 2 + ( R / 2 ) 2 ) 3 / 2 {displaystyle B={frac {2mu _{0}nIR^{2}}{2(R^{2}+(R/2)^{2})^{3/2}}}}

Schwarzbeck HHS 5206-16 – Вспомогательное оборудование

Тип	Описание
HHS 5201-6	кольца Гельмгольца, 2860 A/м 5 MГц для устройств размером до 45 мм.
HHS 5201-98	кольца Гельмгольца, 64 кA/м 200 кГц для устройств размером до 45 мм.
HHS 5202-9	кольца Гельмгольца, диаметр 200 мм, 3053 A/м 2,5 MГц MIL-STD 461E
HHS 5202-81	кольца Гельмгольца, диаметр 200 мм, 3000 A/м 300 кГц MIL-STD 461E
HHS 5204-12	кольца Гельмгольца, диаметр 400 мм, 2500 A/м 500 кГц MIL-STD 461E
HHS 5204-36	кольца Гельмгольца, диаметр 400 мм, 2500 A/м 150 кГц MIL-STD 461E
HHS 5204-144	кольца Гельмгольца, диаметр 400 мм, 10 кA/м, 20 A
HHS 5206-8	кольца Гельмгольца, диаметр 600 мм, 8 витков
HHS 5206-16	кольца Гельмгольца, диаметр 600 мм, 2100 A/м, ток 55 A.
HHS 5206-25	кольца Гельмгольца, диаметр 600 мм, 2700 A/м, ток 46 A.
HHS 5206-132	кольца Гельмгольца, диаметр 600 мм, 4713 A/м, ток 15 A.
HHS 5210	катушки Гельмгольца, 300 A/м, 1 м x 1 м, 10 витков, EN 61000-4-8, VDE 0847 part 4-8
HHS 5210-100	катушки Гельмгольца, 2183 A/м, 1 м x 1 м, 100 витков, EN 61000-4-8, VDE 0847 part 4-8
HHS 5210-100-2,5	катушки Гельмгольца, 1 м, 100 витков с медной проволокой 2,5 мм (меньшие теплопотери)
HHS 5212	катушки Гельмгольца, 250 A/м, 1.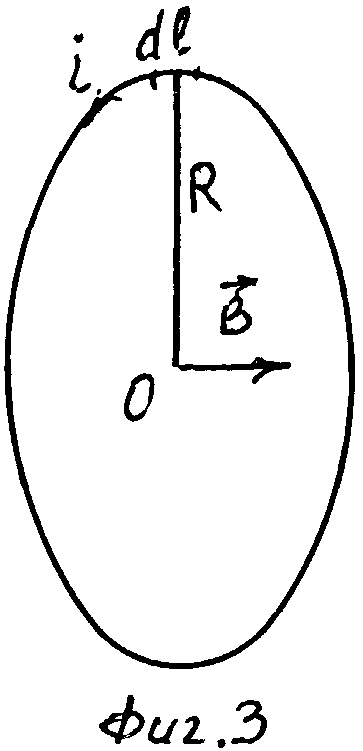 20м x 1.20 м, 10 витков
HHS 5213-50	катушки Гельмгольца, 1.25 м x 1.25 м, 50 витков, EN 55103-2 A.2.1.b)
HHS 5213-100	катушки Гельмгольца,1.29 м x 1.29 м, 100 витков.
HHS 5215	катушки Гельмгольца, 200 A/м, 1,5 м x 1,5 м, 10 витков
HHS 5215-100	катушки Гельмгольца, 2000 A/м, 1,5 м x 1,5 м, 100 витков
HHS 5215-100-2,5	катушки Гельмгольца, 3900 A/м, 1,5 м x 1,5 м, 100 витков, проволока 2,5 мм
HHS 5218	катушки Гельмгольца, 126 A/м, 1,8 м x 1,8 м, 10 витков
HHS 5230-100	катушки Гельмгольца, SAE J551-17: 2 квадратных катушки с длиной стороны 3 м, 100 витков, 650 A/м, подвижная платформа на колесах.

Катушки Гельмгольца. ФДЭ-022 | УЧЕБНАЯ ТЕХНИКА   УЧЕБНАЯ ТЕХНИКА

Демонстрационная установка кольца Гельмгольца  ФДЭ-022м

фдэ-22

          Установка предназначена для проведения демонстраций на лекциях по курсу «Физика», раздел «Электричество и магнетизм» и позволяет получать постоянные и переменные магнитные поля разной величины и направления. Установка состоит из двух плоских одинаковых катушек расположенных параллельно друг другу так, что оси их совпадают. Считается, что по середине между катушками вблизи оси симметрии магнитное поле создаваемое катушками является однородным с достаточной степенью точности. Между катушками находится подъемный столик для размещения демонстрационных элементов.                                      

                                     Катушки подключаются к блоку управления, на котором находятся переключатель режима работы (постоянный ток – переменный ток), переключатель полярности тока и индикатор, показывающий величину тока протекающего через катушки.

 

Данная установка может использоваться в следующих опытах:

• действие магнитного поля на проводник с током;
• контур с током в однородном магнитном поле;
• контур с током в неоднородном магнитном поле;
• явление электромагнитной индукции;
• модель атома в магнитном поле.

Технические характеристики:

Питание от сети сменного тока: 220 В, 50 Гц

Размер столика 160*160

Величина магнитной индукции постоянного магнитного поля создаваемого катушками, не менее, мТл 0,6

Габаритные размеры, мм:

Катушек 510х280х450

Блока управления 260х100х220

Масса установки 15 кг.

 

♦  Рубрика: Демонстрационное оборудование, Измерительные приборы, Каталог, Лабораторные работы, Стенд лабораторный, Физика, Электричество и магнетизм.
♥  Метки: Гельмгольца > Катушки > контур > магнетизм > магнитное > поле > фдэ > электричество

Катушка Гельмгольца – Энциклопедия по машиностроению XXL

Температура сверхпроводящего перехода определяется как средняя точка перехода, которая, по-видимому, не зависит от метода наблюдения по взаимоиндукции, сопротивлению или теплоемкости [72] (рис. 4.22). Общепринятым при воспроизведении температуры перехода является метод взаимоиндукции на переменном токе. В сверхпроводниках первого рода ниже температуры перехода весь магнитный поток выталкивается из металла. Это явление называется эффектом Мейсснера. Выталкивание потока можно наблюдать при использовании моста взаимоиндукции. Для компенсации внешних магнитных полей применяются дополнительные катушки Гельмгольца. Ток в катушках Гельмгольца может устанавливаться по максимальному значению Гс, соответствующему нулевому магнитному полю в сверхпроводнике.  [c.167]
Изучение характера изменения разрядного тока в намагничивающих катушках производят по схеме, изображенной на рис. 3.3. Емкость конденсаторной батареи меняется от 325 до 2600 мкФ, напряжение заряда — от О до 600 В. Намагничивающее устройство соленоидального типа представляет собой две катушки (катушки Гельмгольца), число витков в которых может меняться от 300 до 10. Исследуемые зависимости снимают для параллельного и последовательного включения катушек, расположенных на трубе 0 42 мм на расстоянии 40 мм друг от друга. Длина трубы выбирается с таким расчетом, чтобы влияние ее концов на поле между катушками сводилось к минимуму, т. е. длина трубы должна быть не менее 100 диаметров.  [c.98]

Величина Яц была порядка 0,01 гаусс-, г) в качестве отклоняющей катушки применялась катушка Гельмгольца из одного витка радиусом 12 мм. Угол  

[c.219]

Калий 191, 260 Калориметрия 116 Катушка Гельмгольца 219 Квасцы 6  [c.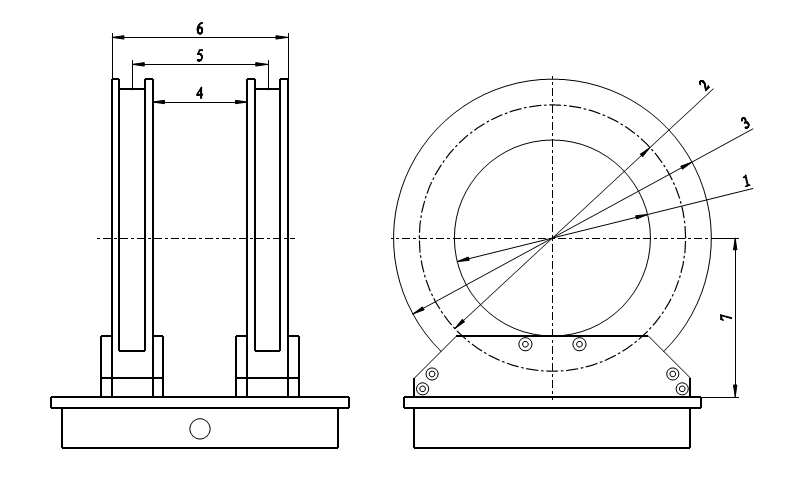 426]

Реальные катушки Гельмгольца представляют собой два параллельных кольца, состоящих из нескольких витков каждое толщина колец должна быть значи.тельно меньше их радиуса.  [c.83]

Для этой же цели применяются кубические катушки, т. е. катушки, состоящие из нескольких квадратных секций, расположенных на определенном расстоянии друг от друга. Такие катушки просты в изготовлении и дают ие худшую однородность поля, чем катушки Гельмгольца.  [c.84]

Рис. 3.9. Схематичное изображение различных типов систем приемных катушек. Для каждого типа буквой с обозначены катушка, связанная по потоку с образцом 5, а с — компенсирующая катушка, имеющая слабую связь по потоку с образцом. а — катушка с плотно намотана вокруг плоского дискообразного образца в его центральной части б — то ) е для цилиндрического образца в — система катушек с образцом малых размеров г — то же, но с иным расположением катушки с (иногда используется вариант типа г, в котором обе катушки разделены надвое, образуя две пары, подобные катушкам Гельмгольца) д — спиральная катушка, осажденная испарением на тонкий образец, нормальный к Н е — то же, что и д, но катушка состоит только из одного кольцевого витка ж — если сам образец (заштрихованная площадь) изготовлен в виде ряда отдельных полосок, осажденных на подложку (показано только четыре полоски, но их число может быть гораздо больше), то катушку можно создать осаждением проводящего слоя вдоль штриховых линий если используются выводы ВВ, то катушка связана по потоку с зазорами между полосками образца, а если АА то она связана по потоку с самими полосками. Заметьте, что для г и ж не показаны виды сбоку и катушки с.

Разновидностью классических катушек Гельмгольца являются квадратные катушки Гельмгольца, расстояние между которыми составляет 0,5445 стороны квадрата (рис. 3.5,6).  [c.60]

Более высокой однородностью поля по сравнению с катушками Гельмгольца обладает катушка Максвелла (рис. 3.5, в), представляющая собой систему из трех кольцевых параллельных катушек, витки которых расположены на общей сфере радиуса Г]. Отношение числа витков ш средней катушки к числу витков Шх каждой из крайних должно быть равно ш/ш1 = б4/49. Радиус  [c.60]

Для испытаний на магнитную чувствительность прибор был установлен внутри катушки Гельмгольца. Ток в 10 А, протекающий по катушке, создавал магнитное поле 12,5 Гс, что в 25 раз интенсивнее магнитного поля Земли. На рис.

12.14 показаны результаты изменения магнитного поля вдоль двух ортогональных осей, перпендикулярных осям чувствительности прибора. Скорость дрейфа изменяется в пределах ранее установленных значений, и нет изменений зависимости скорости дрейфа от изменений магнитного поля. Для этих двух осей магнитная чувствительность по существу равна нулю. На рис. 12.15 показано изменение магнитного поля по  [c.240]

Напряжение на входе X регистратора 12 снимается с резистора R, включенного последовательно с катушками намагничивающего устройства 3. Так как намагничивающее устройство в установке выполнено в виде толстых катушек Гельмгольца, то можно записать  [c.154]

При расчетах катушек Гельмгольца необходимо только примерно определять их постоянную. Более точное определение постоянной катушки производится экспериментально. При правильном исполнении напряженность 6 83  

[c.83]

Наиболее ответственной частью этих установок являются катушечные системы. Известно большое количество таких систем, обеспечивающих однородное поле в некотором рабочем объеме. Об одной из катушек, сферической, уже упоминалось выше Простейшей и наиболее известной катушечной системой однородного поля являются кольца Гельмгольца. В идеальном случае катушки (кольца) Гельмгольца представляют собой два круговых контура одинакового радиуса г, расположенных соосно на расстоянии 2а друг от друга, равном радиусу контура (рис. 3. 5, а). Расчеты показывают, что в центральной области катушек Гельмгольца, занимаемой воображаемым цилиндром радиусом 0,1 г и длиной 0,2 г, поле может отличаться от его значения строго в центре не более чем на 0,02%.  [c.60]

Активная защита от помех осуществляется при помощи компенсирующи.х катушек, создающих маги, поле, равное по величине и противоположное по на)1рав-лению полю помехи. Алгебраически складываясь, эти поля компенсируют друг друга. Наиб, известны катушки Гельмгольца, представляющие собой две одинаковые соосные круговые катупгки с током, раздвинутые на расстояние, равное радиусу катушек. Достаточно однородное магн. ноле создаётся в центре между ними. Для компенсации по трём пространств, комноненгам необходимы минимум три пары катушек. Существует много вариантов таких систем, и выбор их определяется конкретными требованиями.  [c.667]

GSM б) магнитный экран был изготовлен из олова, так как при охлаждении свинца в последнем возникают неоднородности в) величина магнитного поля Яо была сделана намного меньше магнитного поля Земли, что осуществлялось с помощью дополнительной компенсирующей катушки Гельмгольца, которая была соответствующим образом ориентирована и заключена в сверхпроводящую защитную оболочку из олова.  

[c.219]

Классичсскил опособо.м созда)1пя однородного в некотором объеме магнитного поля является использование катушек Гельмгольца. Катушки Гельмгольца в идеальном виде представляют собой два одинаковых кольцевых витка, соединенных последовательно и расположенных иа расстоянии радиуса витка (рис. 3-9).  [c.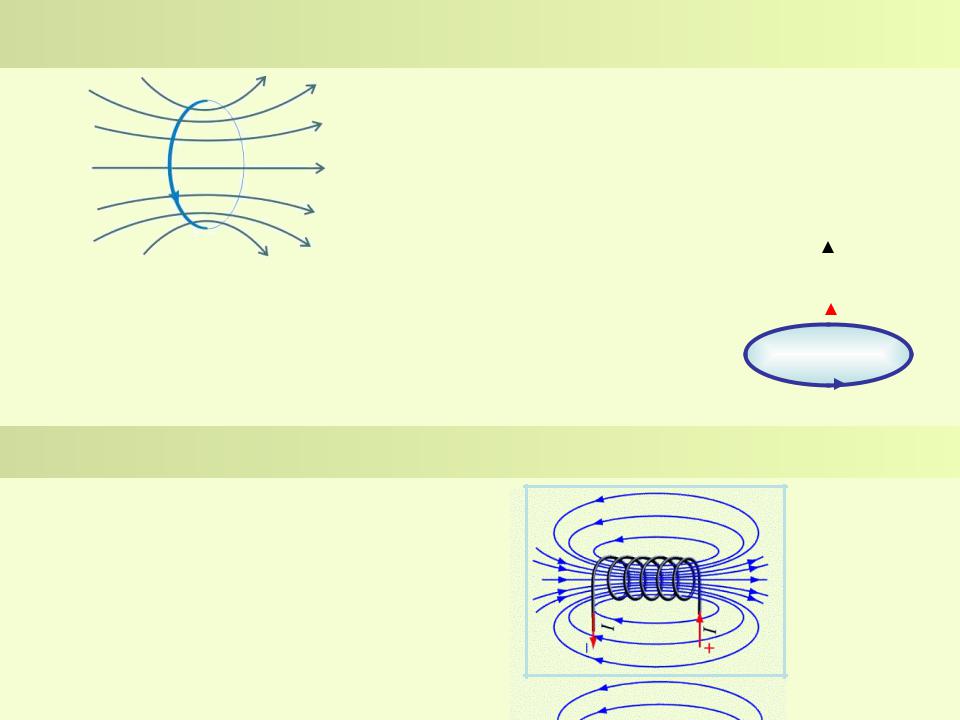 83]

ПОЛЯ катушки Гельмгольца отличается на расстоянии четверти радиуса по оси катушек от ее центра от иа[1ря-женности поля в центре меньше чем па 0,5%. На таком же расстоянии от центра в направлеиип, церпендикуляр-ном оси катушки, эта разность меньше 0,75%.  [c.84]

Кубическая катушка дает несколько лучшую равио-мсрнссть распределения напряженности поля, чем катушки Гельмгольца.  

[c.84]

Гельмгольца б—квадратные катушки Гельмголь ца, в—катушки Максвел ла, г- система трех круг пых катушек, ( —катуш ки Рубенса, е—катушки Браунбека  [c.61]

---

Катушки гельмгольца-ишкова

Предлагаемое изобретение относится к электротехнике и может быть использовано для создания устройств с однородным магнитным полем, протяженность которого сравнима с радиусом возбуждающих обмоток. Технический результат состоит в повышении однородности магнитного поля и эффективности его создания.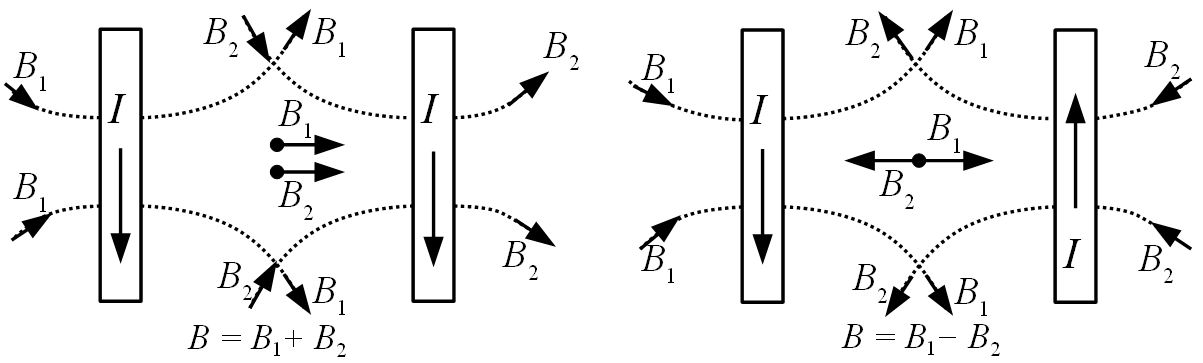 Устройство состоит из катушек Гельмгольца и внешнего магнитопровода. Катушки Гельмгольца типичные круглые. Внешний магнитопровод состоит из двух частей цилиндрической формы с цилиндрическими выемками для размещения катушек Гельмгольца и глухими торцовыми частями. Внешний магнитопровод уменьшает магнитное сопротивление внешней части магнитной цепи, благодаря чему повышается и уровень или однородность магнитного поля между его полосами.

Предлагаемое изобретение относится к области техники магнитных полей и может быть применено для создания эталонных магнитных полей заданного уровня однородности и величины.

Аналогом предлагаемого изобретения являются сами катушки Гельмгольца, которые представляют собой систему двух идентичных круглых катушек, которые размещены соосно на расстоянии радиуса катушек и включены согласно так, что образуются единые магнитные линии магнитного поля и величина магнитного поля на оси системы катушек между плоскостями катушек получается достаточно однородной.

Недостаток аналога состоит в ограниченности однородности поля и эффективности его создания. Для улучшения однородности магнитного поля в рабочей области применяют еще дополнительные пары катушек большого размера со встречным включением дополнительного поля. Это увеличивает габариты лабораторного оборудования и снижает эффективность энергетических затрат на питание, которое должно быть стабильным.

Прототипом предлагаемого изобретения является соленоид Ишкова по патенту RU 2364000. Он состоит из обмотки возбуждения прямоугольного сечения и вешнего магнитопровода в форме цилиндрической оболочки и двух торцевых фланцев, внутренние поверхности которых являются полюсами. Внутри соленоида между полюсами при пропускании электрического тока по обмотке возбуждения создается магнитное поле повышенной однородности.

Недостаток прототипа в свете поставленной цели предлагаемого изобретения состоит в том, что доступ во внутреннее пространство соленоида сопряжен с необходимостью демонтажа фланцев при аксиальном доступе в рабочее пространство соленоида. Особенно сложна проблема радиального доступа в рабочее пространство соленоида.

Техническим решением проблемы свободного доступа в область однородного магнитного поля по оси и радиусу является магнитопровод из двух цилиндрических половинок, из которых нижняя закреплена, а верхняя является съемной частью так, что при поднятой верхней части открывается доступ в рабочее пространство катушек Гельмгольца и по оси, и по радиусу. В качестве примера устройство показано на фиг.1.

Устройство состоит из катушек Гельмгольца 1 и внешнего магнитного провода цилиндрической формы 2, который сам состоит из верхней части 3 и нижней части 4. Торцы магниторовода 2 закреплены по радиусу катушек Гельмгольца 1. По периферии неявных полюсов 5 закреплены обмотки катушек Гельмгольца 1. Исследуемый объект 6 помещается в центральной части устройства. Конструктивно магнитопровод состоит из двух идентичных цилиндрических частей с цилиндрическими выемками для катушек Гельмгольца 1, которые стыкуются плоскими торцами. Отличие верхней подъемной части 3 состоит в наличии конической юбочки 7, которая сопрягается с коническим срезом 8 на нижней неподвижной части магнитопровода 4.

Подъем верхней части 3 и ее фиксация к нижней части 4 осуществляется известными способами.

Действует устройство следующим образом.

При поднятой верхней части 3 в центральную часть устройства помещается исследуемый объект 6, соединительные коммуникации с ним осуществляются через нижнюю часть 4 известными способами. При опускании верхней части 3 она однозначно фиксируется к нижней части 4 посредством конической юбочки 7 и конического среза 8.

При пропускании электрического тока по обмоткам катушек Гельмгольца 1 между полюсами 5 возникает необходимое магнитное поле 9. Величина магнитного поля определяется магнитодвижущей силой катушек, а однородность поля обеспечивается специфическим перераспределением структуры линий магнитного поля во внешнем магнитопроводе 2.

На фиг. 2 представлен ход линий магнитного поля в предлагаемом изобретении. Самая длинная линия магнитного поля проходит в центральной части полюсов и имеет длину 2πR+2R(π+1).

Самая короткая линия поля проходит по периферии полюсов и имеет длину 2R, где R – радиус катушек Гельмгольца.

Для центральной линии магнитного поля отношение длин межполюсной части к магнитопроводной составляет величину ≃ ,

для периферийной линии магнитного поля это отношение будет

.

Из приведенных соотношений следует, что для центральных магнитных линий только восьмая часть проходит между полюсами, а для периферийных магнитных линий только половина. Следовательно, применение внешнего магнититопровода для катушек Гельмгольца деформирует линии магнитного поля так, что уменьшает магнитное сопротивление. Для центральных магнитных линий многократно, а для периферийных магнитных линий – лишь двукратно. Это существенно повысит однородность магнитного поля в предлагаемом изобретении и повысит его уровень при том же токе в катушках Гельмгольца.

В Табл.1 представлена радиальная зависимость отношений длины магнитной линии в магнитопроводе к длине магнитной линии между полюсами магнитопровода l_F, которая определена по вышеприведенной методике. Для простоты записи принято R=1, а r – радиальное удлинение от центра полюсов. Это нелинейная зависимость.

Табл.1 r 0 0,2 0,4 0,6 0,8 1,0 7,28 6,024 4,768 3,512 2,256 1,0

Аналитический расчет магнитиных полей, создаваемых тонким проводником с током, основывается на законе Био-Савара-Лапласа, см. Савельев В.И. «Курс общей физики», т. 2, М., Наука, 1970 с.132.

где µ_о=4·10^-7 _, Гн/м – магнитная постоянная;

i – сила электрического тока, А;

dl – элементарный участок с током I;

_– радиус-вектор из исследуемой точки к элементарному току;

– угол между элементарным током и радиус-вектором _, фиг.3.

Дифференциал магнитного поля в центре кругового тока на его оси,

где

R – радиус кругового тока, м.

Величина магнитного поля в центре кругового тока определяется интегралом

где dl=Rdφ.

Вне плоскости витка магнитное поле имеет две компоненты, фиг.4. Аксиальная компонента магнитного поля зависит от угла β.

B_z=Bsinβ, где sinβ= .

В конечном виде получается формула

где Z – аксиальное расстояние исследуемой точки от центра кругового тока на его оси.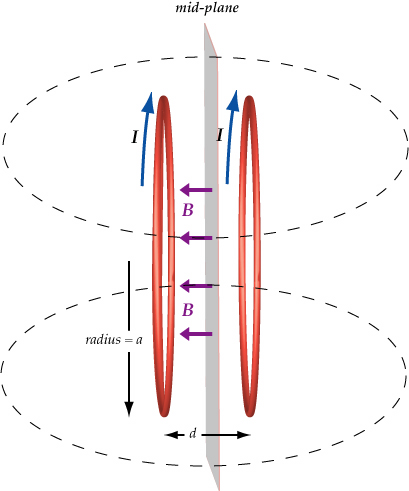 Для случая формула упрощается

Для второй катушки Гельмгольца эта формула примет вид

и в целом на оси катушек Гельмгольца будет

Расчеты по приведенным формулам представлены в табл.2.

Анализ табличных данных показывает, что аксиальное распределение уровня магнитной индукции представляется симметричной криволинейной зависимостью с прогрессивным спадом при удалении от центра кругового тока. Эта же зависимость для катушек Гельмгольца имеет максимум в центре системы катушек с пологим спадом при удалении от него. Поле в центре катушек превышает поля в центрах катушек на 5,3%.

Абсолютный уровень магнитного поля даже во многовитковых катушках невелик, потому что множитель, представляющий магнитную постоянную, имеет порядок 10^-7. Для полей с уровнем Iтл=10⁴ Гс требуются катушки с количеством ампервитков, измеряемых тысячами. Поэтому применение внешнего магнитопровода существенно повышает эффективность питания катушек и снижает энергозатраты на питание и охлаждение электромагнитных установок.

Радиальное распределение магнитного поля в плоскости кругового витка с током можно исследовать по схеме на фиг.5,

где а – радиальное смещение исследуемой точки по диаметру кругового тока,

r – расстояние исследуемой точки от элемента тока , произвольного,

R – радиус кругового тока,

φ – азимут элемента тока .

Для произвольной точки, лежащей на диаметре кругового витка, можно записать

Действительно, h=a·sinφ, b=a·cosφ.

Следовательно, r²=h²+(R-b)²=R²+a²-2Racosφ.

Поскольку угол между элементом тока и вектором то

В результате подстановки полученного выражения в исходную формулу закона БСЛ и последующего интегрирования получаем закон радиального распределения магнитной индукции по диаметру кругового тока

Для случая R=i=1 интеграл упрощается

В табл. 3 представлены результаты числового интегрирования и экспериментального исследования радиального распределения магнитной индукции в плоскости кругового витка с током.

В авторском эксперименте использовался круглый виток диаметром 100 мм из медной проволоки диаметром 1 мм при токе 35 А. При токах большего значения виток нагревался докрасна. Поле измерялось измерительной катушкой диаметром 5 мм и миливольтметром. В последней графе приведены результаты исследования сверхпроводящего короткого соленоида диаметром 1,8 м, см. Хоукинс С.Р. “Сверхпроводящие соленоиды”, изд Мир, 1965, с.238-258.

Анализ табличных данных показывает, что теоретический расчет автора верен и подтвержден экспериментально с достаточной точностью.

Главный вывод состоит в том, что радиальное распределение магнитной индукции в плоскости кругового витка с током неоднородно и его неоднородность растет прогрессивно по мере удаления к периферии витка, где оно возрастает многократно. Эта величина аксиально убывает, а радиально в плоскости витка растет и на центр витка приходится условный максимум типа седла.

Величину магнитной индукции вне плоскости кругового тока можно определить, если исследуемую точку поместить на плоскости, совмещенной с осью симметрии кругового тока, фиг. 6. Координаты этой точки будут: a, z, φ,

где a – расстояние исследуемой точки от оси симметрии кругового тока,

z – расстояние исследуемой точки от плоскости кругового тока,

φ – азимутальный угол.

Теперь аксиальная составляющая магнитной индукции будет определяться углом β по формуле ,

где r²=R²+a²-2Racosφ,

ρ²=R²+a²+z²-2Racosφ.

При R= i=1 расчетная формула примет вид

В табл. 4 представлены результаты расчета по этой интегральной формуле. По горизонтали представлены относительные значения величины магнитной индукции при радиальном переведении расчетной точки, а по вертикали соответственно при аксиальном ее перемещении. За 1 принято значение магнитной индукции в центре кругового тока.

Анализ содержания табл. 4 показывает, что при перемещении расчетной точки только по оси симметрии кругового тока или только по радиусу в плоскости кругового тока числовые значении магнитной индукции повторяются в соответствии с таблицами 2 и 3. Вне плоскости кругового тока радиальном перемещении расчетной точки величина магнитной индукции монотонно убывает.

В табл. 5 в относительных единицах представлено распределение магнитной индукции в диаметральной плоскости катушек Гельмгольца. Анализ содержания этой таблицы показывает, что это поле симметрично относительно плоскости z=0,5. В геометрическом центре катушек Гельмгольца поле имеет условный максимум типа седла, от которого отходят линии хребтов к центрам сечении токовозбуждающих проводников, при приближении к которым расчетная величина магнитной индукции возрастает многократно.

Неоднородность магнитного поля в центре катушек Гельмгольца зависит от размеров выбранной области.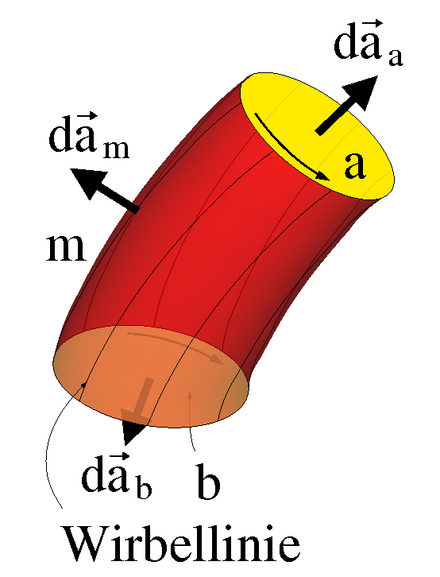 Для цилиндра высотой и диаметром 0,5 R неоднородность составляет 1,5%.

В случае катушек конечного прямоугольного сечения закон БСЛ примет вид

где jdzdr – элемент тока в катушке.

Величина магнитной индукции в точке, отстоящей на а от оси симметрии катушки и на z от медианной плоскости катушки, определится тройным интегралом

где

R₁ – внутренний радиус катушки,

R₂ – внешний радиус катушки,

– половина толщины катушки.

В табл. 6 представлены результаты вычислений для R₁=1, R₂=1, 2, j=30.

Анализ содержании табл. 6 показывает, что в медианной плоскости катушки конечного сечения величина магнитной индукции тоже возрастает при удалении от центра катушки, но крутизна роста слабее, чем в тонкой одновитковой катушке. Аксиальный спад величины магнитной индукции сохраняется, но он тоже слабее.

В табл. 7 представлено диаметральное распределение величины магнитной индукции толстых катушек Гельмгольца.

В центре толстых катушек Гельмгольца магнитная индукция имеет по-прежнему максимум, но он на 15 % выше, чем в тонких при той же магнитодвижущей силе. Общий характер вариации распределения величины магнитной индукции сохраняется. Неоднородность же существенно ухудшилась и для цилиндра высотой и диаметром 0,5 R составила по высоте 3%, а по радиусу 9%.

В качестве общих выводов следует сделать следующее.

Катушки с диаметром сечения обмотки менее 0,1 диаметра катушки можно считать тонкими с достаточной инженерной точностью.

Для катушек конечного сечения обмотки получена универсальная интегральная формула для расчета величины магнитной индукции во внутреннем пространстве катушки.

При создании магнитной системы с однородным магнитным полем не следует увлекаться толстыми катушками.

У Говоркова В. А. “Электрические и магнитное поля”, М., Энергия, 1968 на стр. 205-207 приведен приближенный расчет напряженности магнитного поля внутри кругового тока, на стр. 207-210 приведен расчет аксиального распределения напряженности магнитного поля тонкого соленоида.

Устройство для создания однородного магнитного поля, содержащее катушки Гельмгольца и внешний магнитопровод броневого типа, отличающееся тем, что указанный магнитопровод выполнен из верхней и нижней идентичных состыкованных торцами частей с цилиндрическими полостями для катушек Гельмгольца и исследуемых объектов, оси которых совмещены, внешние торцы магнитопровода скруглены радиусом, равным радиусу катушек Гельмгольца.

52651-13: П1-22 Установки поверочные средств измерений напряженности магнитного поля

Назначение

Установки поверочные средств измерений напряжённости магнитного поля П1-22 предназначены для воспроизведения равномерного переменного магнитного поля в диапазоне частот от 5 Гц до 400 кГ ц.

Описание

Принцип действия установок поверочных средств измерений напряжённости магнитного поля П1-22 основан на возбуждении однородного переменного магнитного поля в пространстве между двумя плоскопараллельными кольцевыми катушками, расположенными на одной оси на расстоянии, равном их радиусу (кольца Гельмгольца). Вектор напряженности магнитного поля в кольцах Гельмгольца перпендикулярен их плоскостям, что позволяет получать однородное магнитное поле необходимой напряженности, задаваемой величиной тока, протекающего через катушки.

Установки поверочные средств измерений напряжённости магнитного поля П1-22 состоит из колец Гельмгольца с преобразователем магнитного поля трансформаторного типа, от-счетного устройства, компаратора магнитного поля и координатного устройства (Рисунок 1).

Кольца Гельмгольца выполнены в виде двух электрически последовательно соединенных плоскопараллельных катушек диаметром 500 мм намотанных на кольцевых каркасах, расположенных горизонтально на расстоянии 250 мм друг от друга.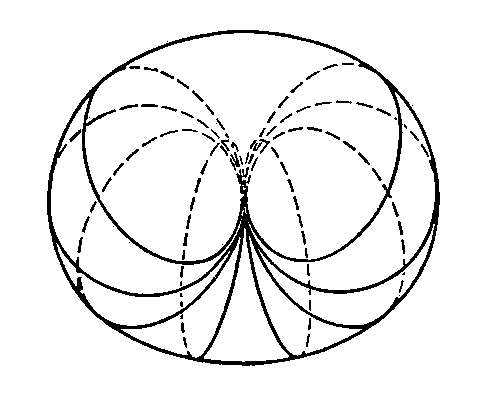

Преобразователь магнитного поля трансформаторного типа выполнен в виде двух последовательно соединенных витков диаметром 300 мм, намотанных экранированным проводом по внутренним образующим каркасов катушек колец Гельмгольца.

Сигнал с преобразователя поступает на вход отсчетного устройства, обрабатывается преобразователем среднеквадратического значения (TRUE RMS), величина выходного сигнала (напряженность воспроизводимого магнитного поля) которого отображается на жидкокристаллическом индикаторе отсчетного устройства.

Кольца ельмгольца с преобразователем

Место нанесения оттиска клейма

От несанкционированного доступа установки поверочные средств измерений напряжённости магнитного поля П1-22 защищены пломбированием в соответствии с рисунками 2 и

3.

Компаратор магнитного поля П3-60 ПМ/2 измеряет и отображает среднеквадратичное значение вектора напряженности переменного магнитного поля.

Поверяемые средства измерений напряженности магнитного поля позиционируются в установке с помощью координатного устройства.

Технические характеристики

Рабочий диапазон частот, кГц	от 0,005 до 400
Диапазон воспроизводимых значений напряжённости магнитного поля, А/м –    на частотах от 0,005 до 2 кГц –    на частотах от 2 до 400 кГц	от 0,04 до 4 от 0,004 до 0,8
Пределы допускаемой относительной погрешности воспроизведения напряженности магнитного поля, %	± 5
Время непрерывной работы, не менее, ч	8
Время установления рабочего режима, мин	1
Г абаритные размеры колец Гельмгольца (длина, ширина, высота), мм, не более	550, 600, 600
Масса установки, кг, не более	10
Потребляемая мощность, В А, не более	10
Средняя наработка на отказ, ч, не менее	5000
Рабочие условия эксплуатации: –    температура окружающего воздуха, °С –    относительная влажность окружающего воздуха, % –    атмосферное давление, кПа (мм рт. ст.) –    напряжение питающей сети, В –    частота питающей сети, Г ц	от 10 до 35 от 30 до 80 от 84 до 106,7 (от 630 до 800) 220 ± 4,4 50 ± 0,5

Знак утверждения типа

Знак утверждения типа наносится на планку фирменную, установленную на боковой стойке, лицевую панель отсчетного устройства методом тампопечати и на титульный лист паспорта ЦКЛМ.411723.002 ПС типографским способом.

Наименование	Обозначение	Количество
Кольца Гельмгольца с преобразователем	ЦКЛМ. 411529.003	1
Отсчетное устройство	ЦКЛМ. 411251.005	1
Компаратор магнитного поля П3-60ПМ/2	ЦКЛМ. 411173.002	1
Блок питания	БПС-А 12-0,35	1
Координатное устройство	–	1
Паспорт	ЦКЛМ. 411723.002.ПС	1
Методика поверки	ЦКЛМ.411723.002. МП	1

Поверка

осуществляется в соответствии с документом «Установка поверочная средств измерений напряженности магнитного поля П1-22. Методика поверки» ЦКЛМ.411723.002 МП», утвержденным руководителем ГЦИ СИ ФГУП «ВНИИФТРИ» 15 октября 2012 года.

Основные средства поверки: рабочий эталон единицы напряженности магнитного поля РЭНМП-05Г/10М, 5о = ± 3 %.

Сведения о методах измерений

«Установка поверочная средств измерений напряженности магнитного поля П1-22. Паспорт» ЦКЛМ.411723.002 ПС. Раздел 9 «Порядок работы».

Нормативные документы, устанавливающие требования к

установкам поверочным средств измерений напряженности магнитного поля П1-22

1    ГОСТ Р 51070-97 Измерители напряженности электрического и магнитного полей. Общие технические требования и методы испытаний.

2    ГОСТ 8. 030-91 ГСИ. Государственный первичный эталон и Государственная поверочная схема для средств измерений магнитной индукции постоянного поля в диапазоне от

12 2

1-10 до 5-10″ Тл, постоянного магнитного потока, магнитной индукции и магнитного момента в интервале частот 0 + 20000 Гц.

3    ГОСТ 8.097-73 Государственный специальный эталон и общесоюзная поверочная схема для средств измерений напряженности магнитного поля в диапазоне частот от 0,01 до 300 МГц.

Рекомендации к применению

Выполнение работ по оценке соответствия промышленной продукции и продукции других видов, а также иных объектов установленным законодательством Российской Федерации обязательным требованиям.

Выполнение работ и услуг по обеспечению единства измерений.

Способность голубей находить дорогу домой все же связана с магнитным полем

Способность голубей находить дорогу домой все же связана с магнитным полем Земли: соответствующие рецепторы ученые обнаружили, подключив к нейронам в мозге голубей множество тончайших электродов и поместив птиц в специальную клетку, окруженную со всех сторон магнитами.

Многие животные на Земле способны ориентироваться по магнитному полю планеты, но то, как именно их мозг получает и обрабатывает данные о магнитном поле, ученым до сих пор не удавалось понять. Были высказаны довольно обоснованные предположения о существовании магнитных рецепторов в сетчатке глаза, клюве, носу и внутреннем ухе различных позвоночных. Генетикам удалось установить несколько областей мозга, активизирующихся под действием магнитного поля.

Но центральный нервный механизм, лежащий в основе приема и обработки магнитного сигнала, оставался неизвестным. Поэтому снова и снова поднимается вопрос, как животные находят дорогу — по магнитному полю Земли, по Солнцу, по плану местности или как-то еще.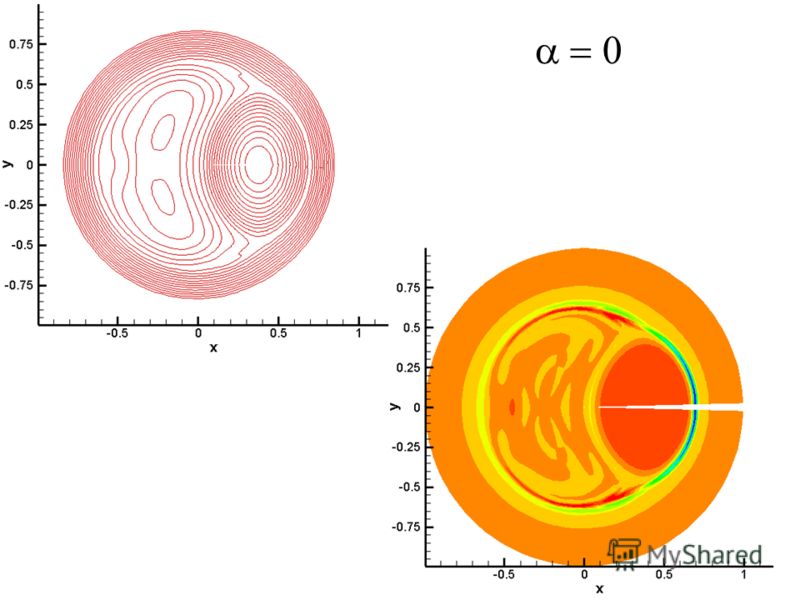

Дейвид Дикман и Ву Лэцин из Бейлорского медицинского колледжа в городе Хьюстон (США) утверждают, что способность птиц ориентироваться связана все же с магнитным полем. Свою работу с результатами в подтверждение этой гипотезы они публикуют в журнале Science.

«Нам удалось найти нервные отклики в стволе головного мозга голубей, которые показывают, как отдельные клетки кодируют направление магнитного поля, его интенсивность и направление.

Эти данные необходимы, чтобы получить внутреннюю модель, позволяющую установить пространственную привязку к местности и ориентироваться в пространстве», — пишут авторы статьи.

Результаты исследования очень обнадеживают, особенно с учетом того, что предыдущая теория ориентации голубей была убедительно развенчана: содержащие железо клетки в клюве птицы оказались не «компасами», а всего лишь макрофагами, перерабатывающими гемоглобин погибших эритроцитов.

Теперь в качестве «компаса» предлагается группа нейронов в головном мозге почтового голубя (Columbia livia). Авторы работы сосредоточили свое внимание на изучении областей мозга голубей, ранее уже подозреваемых в способности к навигации: это задние отделы мозга и вестибулярные ядра — центры ориентации в пространстве и управления движением конечностей.

Задача состояла в том, чтобы локализовать клетки, чувствительные к магнитному полю.

Для этого ученые подключили к нейронам в мозге голубей множество тончайших электродов и поместили птиц в специальную клетку, окруженную со всех сторон магнитами — так называемыми кольцами Гельмгольца.

Кольца Гельмгольца

— две соосно расположенные одинаковые радиальные катушки, расстояние между центрами которых равно их среднему радиусу. В центре системы имеется зона однородного магнитного поля. Используются для получения постоянного, переменного или…

Три пары колец выполняли сразу две функции — они подавляли магнитное поле Земли и генерировали локальное поле, направление и силу которого можно было произвольно менять. Во время эксперимента биологи прикрепляли к голове птицы магнитометр, следили за силой и направлением поля и записывали сигналы, поступающие из мозга голубей.

В результате ученым удалось выделить в вестибулярных ядрах мозга 53 нейрона, которые реагировали на изменение параметров магнитного поля.

Более того, каждая из клеток реагировала только на одно направление магнитного поля. Скорее всего, такая точная настройка и «разделение труда» между клетками и позволяет птицам добиваться такой точности навигации. Кроме того, клетки-сенсоры еще и оценивали величину индукции магнитного поля. Магнитное поле в 20 мкТл, соответствующее магнитному полю Земли у экватора, было нижним порогом чувствительности. Верхним пределом была сила поля в 120 мкТл, что примерно в два раза больше, чем земной максимум в приполярных регионах.

Следует отметить, что, хотя это открытие подтверждает вероятность существования железосодержащих магниторецепторов у позвоночных, оно не сильно приближает ученых к разгадке местонахождения этих рецепторов. Авторы работы склоняются к тому, что эти клетки находятся во внутреннем ухе птицы.

Катушки Гельмгольца пересмотрено: American Journal of Physics: Vol 57, No 1

Два круговых коаксиальных токовых кольца радиусом a , разделенных расстоянием b , обычно называют катушками Гельмгольца, если b = a . Это хорошо известный рецепт наибольшей однородности поля в окрестности центра симметрии. Здесь исследуется магнитное поле пары токовых колец на расстоянии r от центра, большое по сравнению с радиусом кольца a .Расширяя дальнее поле в степенях a / r , каждый член может быть связан с магнитным 2 ^k -полюсным источником и спадом поля как ( a / r ) ^{k +2} . Поле диполя k = 1, уменьшающееся как ( a / r ) ³ , имеет своим источником полный дипольный момент двух колец. В конечном итоге он заглушает вклад высших мультиполей. Член ( a / r ) ⁵ с k = 3 имеет своим источником октупольный (2 ³ ‐полюсный) момент пары колец. Его коэффициент равен нулю, если b = a . Таким образом, пара Гельмгольца, благодаря своей кажущейся несущественной специализации для однородного центрального поля, также наделена нулевым октупольным моментом. Почленная связь между расширением дальнего поля и расширением центрального поля сохраняется для токов, полностью ограниченных поверхностью сферы, что имеет место для пары тонких токовых колец Гельмгольца. Поле диполя можно свести к нулю, вложив пару Гельмгольца в большую пару Гельмгольца, имеющую равную площадь × ампер-витки, но несущую обратный ток.

Ценой незначительного уменьшения центрального поля и без ущерба для однородности центрального поля, общий дипольный момент четырех колец, таким образом, может быть сведен к нулю. Текущая система теперь имеет нулевой дипольный момент a n d нулевой октупольный момент. Поскольку 2 ^k -полюсов с k даже исключаются по симметрии, самый низкий из сохранившихся мультиполей – это 2 ⁵ -полюс, «32-полюсный». Остаточное удаленное поле, из которого оно в настоящее время является доминирующим источником, падает как ( a / r ) ⁷ .Точный расчет отношения магнитуды поля B к центральному полю B ₀ показывает, что B / B ₀ близко пропорционально ( a / r ) ⁷ везде в поле за пределами r ≊5 a . Уже при r ≊6 a , B / B ₀ упало до 10 ^{– 4} . Показано, как эквивалентные результаты могут быть достигнуты с катушками конечного сечения.Эта схема может значительно уменьшить «поле рассеяния» вокруг сверхпроводящего магнита. Фактически, он плотно ограничивает большую часть обратного потока. Другое применение связано с индукцией переменного тока с помощью прецессирующего магнитного момента. Четыре катушки, соединенные последовательно, составляют приемную катушку, прочно связанную с любым колеблющимся диполем в его центре, но практически невосприимчивую к помехам от внешних источников.

Научная лаборатория: Катушки Гельмгольца Магнитное поле

Катушки Гельмгольца

Эти катушки идут парами с одинаковым количеством витков провода на каждой из двух катушек.В конфигурации «истинного Гельмгольца»: (1) катушки соединены последовательно с одинаковыми токами в одном направлении в каждой катушке, и (2) катушки расположены на расстоянии, равном радиусу каждой катушки. В этой конфигурации они создают очень однородное магнитное поле, направленное вдоль их общей центральной оси. Одним из наиболее распространенных применений таких катушек в естественнонаучном образовании является определение отношения заряда к массе электронов, что достигается путем погружения электронной трубки в центральную область катушек и измерения результирующей кривизны электронного луча.

Катушки Гельмгольца

также используются для множества других применений, включая, помимо прочего:

• нейтрализует магнитное поле Земли, позволяя проводить эксперименты с магнитными веществами в среде, свободной от магнитных полей.
• Производство магнитных полей для определения эффективности магнитного экранирования электронного оборудования.
• калибровка магнитометров и калибровка датчика Холла.
• биомагнитных исследований, таких как влияние магнитных полей на прорастание и скорость роста семян.
• Магнитно-резонансная томография (МРТ).

Из-за широкого применения и использования катушек Гельмгольца научные лаборатории с этими катушками были бы весьма поучительны. Хотя катушки Гельмгольца могут стоить от сотен до тысяч долларов, в этом мире производителей, в котором мы сейчас живем, возможно легко и дорого построить их всего за пару часов. Затем пару катушек можно использовать для исследования того, как на индуцированное магнитное поле влияет их расстояние.

Научная лаборатория

На рис. 1 показана экспериментальная установка для этой научной лаборатории. Катушки Гельмгольца были сконструированы из двух венцов из пенополистирола с внешним диаметром 12 дюймов. Снаружи венцов была обернута белая клейкая лента, чтобы обеспечить менее скользкую поверхность для проволоки. Лента также использовалась в четырех местах вокруг венка, чтобы удерживать Проволока от соскальзывания. В качестве проволоки использовали сплошную изолированную проволоку калибра 14, с 10 витками проволоки на каждом витке.Маленькие деревянные бруски 2х4 были прикреплены к боковым сторонам венков, чтобы держать их в вертикальном положении на столешнице и обеспечивать немного большей устойчивости. Пара стержней для привязки (не показаны на рис. 1) была прикреплена к каждому 2×4, и два конца намотанной проволоки были соединены с стержнями для привязки. Две катушки были подключены последовательно к источнику питания и выровнены так, чтобы их центральные оси совпадали. Поскольку использовалась проволока калибра 14, можно было использовать ток около 10 А при небольшом нагреве проволоки. PocketLab Voyager крепился к концу 2-дюймового дюбеля, при этом центр дюбеля находился на одной линии с буквой Z на оранжевой стороне Voyager. (Буква Z находится очень близко к положению магнитометра на внутренней печатной плате Voyager.) Другой конец стержня дюбеля прикреплен к зажиму на кольцевой стойке. Стержень дюбеля визуально совмещен с осью катушек Гельмгольца. Прикрепленная к столу палка из липы позволяет плавно перемещать кольцевую стойку, сохраняя при этом штифт на оси катушки. Вертикальный белый картон за катушками Гельмгольца служит исходной точкой для координат, записанных дальномером «Вояджера».Voyager подключен через BLE (Bluetooth Low Energy) к планшету Samsung Android с программным обеспечением Phyphox. График зависимости магнитной силы от положения создается в режиме реального времени по мере удаления «Вояджера» от белого картона. График, показанный на рисунке 1, был получен, когда катушки были разнесены на расстояние, равное радиусу катушки, то есть в «истинной конфигурации Гельмгольца». Как видно на графике, это привело к созданию очень однородного магнитного поля в области между двумя катушками.

Рис. 1

Альтернативную версию этого научного эксперимента с использованием только приложения PocketLab, а не Phyphox, можно найти, щелкнув здесь.

Программное обеспечение Phyphox

Phyphox ( phy sical pho ne e x periments) – бесплатное приложение, разработанное 2-м Институтом физики Университета Ахена в Германии. Автор этого урока работал с предварительной версией этого приложения для Android, которая поддерживает технологию BLE (Bluetooth Low Energy) для передачи данных от нескольких Voyager в приложение Phyphox.С тех пор была выпущена общедоступная версия приложения Phyphox для Android.

Эксперимент этого урока находится в файле с именем HelmholtzCoils.phyphox и сопровождает этот урок. Затем этот файл можно открыть в Phyphox, и он появится в категории PocketLab Voyager на главном экране, как показано на рисунке 2.

Рис. 2

Прилагаемый файл в формате pdf, Lesson Details.pdf , объясняет, как работать с программным обеспечением Phyphox, и предлагает метод анализа данных.Вот видео, описывающее эту научную лабораторию катушек Гельмгольца.

Катушка Гельмгольца

Герман фон Гельмгольц (1821-1894) Немецкий ученый и философ, внесший фундаментальный вклад в физиологию, оптику, электродинамику, математику и метрологию. Катушки Гельмгольца Пара проводящих круглых катушек, каждая из которых имеет Н витков, каждая из которых несет ток I , разделенные расстоянием, эквивалентным радиусу круговых петель, создают однородное магнитное поле B в средняя плоскость между двумя круговыми катушками.

a = радиус витков a = расстояние между катушками a / 2 = расстояние до средней плоскости B = магнитное поле в средней плоскости

Что создает магнитное поле? Магнитное поле создается всякий раз, когда заряд находится в движении – либо движется в пространстве, либо вращается вокруг себя.Заряд, движущийся в пространстве, называется «током» (обозначается символом I ) и измеряется в кулонах / сек или амперах . Напряженность магнитного поля измеряется в точке пространства (часто называемой точкой поля ) . В случае катушек Гельмгольца интересующие поля расположены в средней плоскости между двумя катушками. Как показано в приведенном выше уравнении, сила магнитного поля зависит от трех величин: текущий I , количество витков Н, в каждой катушке, а радиус а катушки. Суммарный ток в каждой катушке составляет NI .

Насколько однородно магнитное поле? «Претензия на славу» катушки Гельмгольца – это ее очень однородное магнитное поле. Однако возникает закономерный вопрос: «насколько равномерно и на каком расстоянии?». Для определения однородности магнитного поля требуется нечто большее, чем вышеприведенное уравнение, и требуется сложное интегральное исчисление.Тем не менее, мы можем создать некоторые рисунки, которые графически показывают, как магнитное поле изменяется в средней плоскости в зависимости от r (расстояние от оси симметрии, проходящей между центрами двух катушек) и d расстояния между двумя катушками. На рисунках справа мы можем видеть, насколько однородно магнитное поле в средней плоскости, когда расстояние d составляет слишком близко, точно справа, и слишком далеко . Цифры справа рассчитаны для катушек радиусом 20 см (т.е.е., а = 0,20 м). Для получения трех кривых справа был вычислен следующий интеграл.

Расстояние между катушками слишком близко. d = 0,8 а

Расстояние между катушками “в самый раз”.” d = a

Расстояние между катушками слишком велико. d = 1,2 а

где коэффициент «2» в числителе учитывает две катушки, а b = d / 2 – расстояние от каждой катушки до средней плоскости.

Как область однородного магнитного поля зависит от радиуса катушек Гельмгольца? На рисунках ниже показан диапазон однородного магнитного поля в зависимости от радиуса катушки.

Вот лабораторная запись, описывающая процедуру измерения отношения заряда к массе электрона с помощью катушек Гельмгольца.

Повторное посещение катушек Гельмгольца – NASA / ADS

Аннотация

Два круговых коаксиальных токовых кольца радиуса a, разделенных расстоянием b, обычно называют катушками Гельмгольца, если b = a.Это хорошо известный рецепт наибольшей однородности поля в окрестности центра симметрии. Здесь исследуется магнитное поле пары токовых колец на расстоянии r от центра, большом по сравнению с радиусом кольца a. Расширяя удаленное поле по степеням a / r, каждый член может быть связан с магнитным 2 ^k -полюсным источником и спадающим полем как (a / r) ^{k + 2} . Поле диполя k = 1, равное (a / r) ³ , имеет своим источником полный дипольный момент двух колец.В конечном итоге он заглушает вклад высших мультиполей. Член (a / r) ⁵ с k = 3 имеет своим источником октупольный (2 ³ -полюсный) момент пары колец. Его коэффициент обращается в нуль, если b = a. Таким образом, пара Гельмгольца, благодаря своей кажущейся несущественной специализации для однородного центрального поля, также наделена нулевым октупольным моментом. Почленная связь между расширением дальнего поля и расширением центрального поля сохраняется для токов, полностью ограниченных поверхностью сферы, что имеет место для пары тонких токовых колец Гельмгольца.Поле диполя можно свести к нулю, вложив пару Гельмгольца в большую пару Гельмгольца, имеющую равную площадь × ампер-витки, но несущую обратный ток.

Ценой незначительного уменьшения центрального поля и без ущерба для однородности центрального поля, таким образом, общий дипольный момент четырех колец может быть сведен к нулю. Текущая система теперь имеет нулевой дипольный момент и нулевой октупольный момент. Поскольку 2 ^k -полюсов с четным k исключаются из-за симметрии, самым низким из сохранившихся мультиполей является 2 ⁵ -полюсный, 32-полюсный.Остаточное дальнее поле, которое сейчас является доминирующим источником, падает как (a / r) ⁷ . Точный расчет отношения величины поля B к центральному полю B ₀ показывает, что B / B ₀ близко пропорционально (a / r) ⁷ везде в поле за пределами rÀ5a. Уже на r≊6a Ч / Б ₀ упал до 10 ^{– 4} . Показано, как эквивалентные результаты могут быть достигнуты с катушками конечного сечения. Эта схема может резко уменьшить “ поле рассеяния ” вокруг сверхпроводящего магнита.Фактически, он плотно ограничивает большую часть обратного потока. Другое применение связано с индукцией переменного тока с помощью прецессирующего магнитного момента. Четыре катушки, соединенные последовательно, составляют приемную катушку, прочно связанную с любым колеблющимся диполем в его центре, но практически невосприимчивую к помехам от внешних источников.

Моделирование катушек Гельмгольца в COMSOL Multiphysics®

Катушки Гельмгольца используются учеными для создания однородных магнитных полей для изучения электромагнетизма и его характеристик.Эти устройства используются в МРТ, спектроскопии, измерениях магнитосопротивления и калибровке оборудования. Здесь мы рассмотрим, что такое катушки Гельмгольца, почему они важны, и рассмотрим подход, основанный на моделировании, к их проектированию.

Этот пост был первоначально опубликован в 2014 году. С тех пор он был обновлен для обеспечения точности и включения дополнительной информации о магнитном поле катушки Гельмгольца.

Создание однородных магнитных полей с помощью катушек Гельмгольца

Магнитные поля – это силы, которые создаются движущимися электрическими зарядами и могут возникать, когда заряд движется в пространстве или вращается на месте.Когда магнитное поле неоднородно, объекты будут испытывать разные силы в зависимости от их положения. Но благодаря особому расположению двух идентичных катушек, известному как катушка Гельмгольца, можно получить очень однородные магнитные поля.

Катушки

Гельмгольца используются для создания однородных магнитных полей для экспериментов, требующих известного магнитного поля, или для подавления внешних магнитных полей, таких как земные. Другие приложения включают определение эффективности магнитного экранирования, количественную оценку восприимчивости электронного оборудования к магнитным полям и калибровку навигационного оборудования.

Катодные лучи, изогнутые по окружности через катушку Гельмгольца. Изображение Sfu. Под лицензией CC BY-SA 3.0 через Wikimedia Commons.

При разработке катушек Гельмгольца естественно возникает вопрос: насколько однородно магнитное поле и на каком расстоянии? Чтобы ответить на этот вопрос, мы можем обратиться к программному обеспечению COMSOL Multiphysics®.

Анализ магнитного поля катушки Гельмгольца

Геометрия катушки Гельмгольца состоит из двух одинаковых круглых катушек, разнесенных на один радиус.Катушки намотаны так, что ток течет между ними в одном направлении. Это, в свою очередь, создает однородное магнитное поле, в котором первичный компонент параллелен осям двух катушек. Такая однородность может быть объяснена суммой двух составляющих поля, параллельных осям катушек, а также разностью между составляющими, перпендикулярными этим осям.

Схема катушек Гельмгольца.

Для моделирования катушек мы используем встроенный интерфейс 3D Magnetic Fields , который доступен в модуле AC / DC.В этом конкретном примере катушки генерируются 10 витками проводов, и через них проходит ток 0,25 мА.

Геометрия модели для учебного пособия по катушке Гельмгольца.

Из графика ниже мы можем визуализировать плотность магнитного потока между двумя катушками. Обратите внимание, что красные стрелки обозначают силу и направление магнитного поля. Как показывают результаты, плотность магнитного потока в основном однородна в центре двух катушек, с областью около краев катушек, где магнитное поле неоднородно.Компоненты поля, перпендикулярные осям катушек, компенсируют друг друга, в результате чего результирующее поле равно нулю, в то время как компоненты поля, параллельные осям катушек, объединяются друг с другом.

График среза, показывающий плотность магнитного потока между двумя катушками.

Использование методов постобработки позволяет еще более внимательно изучить однородность магнитного поля. И снова мы можем видеть однородный параллельный магнитный поток в центре катушек и неоднородности вблизи самих катушек.

Визуализация однородного магнитного поля катушки Гельмгольца с помощью методов постобработки.

Как показывает этот пример, моделирование еще больше упрощает процесс создания катушек Гельмгольца и расчета их магнитных полей. Такой анализ помогает обеспечить однородность этих полей – часто наиболее востребованную характеристику катушки Гельмгольца – для различных приложений.

Подробнее об анализе конструкций катушек в программном обеспечении COMSOL®

• Для тех, кто новичок в этом программном обеспечении, ознакомьтесь со следующими сообщениями в блоге:
• Если вам нужны более подробные руководства, просмотрите этот список тем:

Синхротронное излучение и накопительные кольца

ffnet в neuem Fenster Открывается в новом окне ffnet externe Seite Открывает внешний сайт ffnet externe Seite в новом Фенстере Открывает внешний сайт в новом окне

Каждый ускоренный заряд излучает электромагнитные волны, описываемые фундаментальными законами электродинамики.Эти электромагнитные волны, возникающие в результате ускорения (например, горизонтального в накопителе), называются синхротронным излучением. Название дано по историческим причинам, поскольку первым ускорителем, на котором наблюдалось это излучение, был так называемый синхротрон. Хотя это уже предсказывалось в начале прошлого века, синхротронное излучение не было доказано до конца 1940-х годов. Это было сделано как косвенно, путем измерения потерь энергии релятивистских электронов в ускорителе, так и напрямую – путем визуального наблюдения.

В источниках света первого поколения синхротронное излучение от ускорительных установок физики высоких энергий использовалось паразитно, где оно создавалось как нежелательный побочный эффект, противодействующий намеченному ускорению.

С первым успешным хранением электронов в кольцах была создана основа для нового поколения источников синхротронного излучения. В начале 1970-х были построены первые специальные накопительные кольца, предназначенные исключительно для генерации синхротронного излучения.BESSY I, установка Soft VUV, работавшая с 1980 по 1999 в Берлине Вильмерсдорф, была одним из этих источников синхротронов второго поколения

В то время как в этих источниках синхротронное излучение производилось только в направляющих дипольных магнитах, началась разработка специальных магнитных структур, так называемых вставных устройств (ID). Эти ID производят более интенсивный свет или сдвигают спектр синхротронного света в сторону более высоких энергий фотонов.

С начала 90-х годов были введены в эксплуатацию источники синхротронного излучения третьего поколения, производящие очень яркое излучение и специально оптимизированные для использования вводных устройств.BESSY II, эксплуатируемая с 1999 года, является одним из примеров.

Синхротронное излучение, генерируемое в накопительных кольцах, имеет ряд привлекательных свойств, которые делают их в целом почти превосходящими любые другие источники излучения:

• Интенсивное, точно рассчитываемое излучение в широком диапазоне,
• излучение, сильно сфокусированное вперед с небольшой площадью источника,
• излучение в плоскости кольца, линейное, поверхностное и поляризованное ниже кругового,
• импульсное излучение, в соответствии с временной структурой электронный луч,
• чистый источник: создается в сверхвысоком вакууме, так что не следует опасаться загрязнения образца и можно отказаться от использования вакуумных окон.

Эти свойства делают синхротронное излучение одним из важнейших универсальных исследовательских инструментов, число пользователей которого постоянно растет. Он находит применение во всех областях науки, от физики, химии и биологии до медицины человека и промышленных приложений (литография, исследования материалов).

Рис .: Свойства синхротронного излучения

Рис .: Одно из вводных устройств BESSY II (Тип: ондулятор)

Однородность магнитного поля катушек Гельмгольца и косинусов θ катушек

Магнитное поле Однородность катушек Гельмгольца < strong> и косинус θ Катушки Тинг-Фай Лам, Департамент физики, Китайский университет из Гонконг РЕЗЮМЕ Изучены однородности магнитного поля катушки Гельмгольца , катушки с косинусом θ и модифицированной катушки с косинусом θ, поскольку однородное магнитное поле необходимо для многих экспериментов, в том числе для эксперимента SNS nEDM.Компьютерное моделирование использовалось для расчета магнитных полей различных катушек. Было обнаружено, что катушка с косинусом θ в целом создает более однородное поле, чем катушка Гельмгольца , следовательно, является лучшим вариантом для экспериментов, требующих более высокой однородности магнитного поля. I. Предпосылки и Введение Катушки Гельмгольца Катушка Гельмгольца – это устройство с двумя одинаковыми круговыми петлями из электрических проводов, параллельных друг другу, с двумя центрами, расположенными на одной воображаемой перпендикулярной оси.Идентичный электрический ток проходит через контуры в параллельном направлении, создавая магнитное поле в направлении центральной оси. Как показано на рис. 1, катушка Гельмгольца – это из десяти, рассматриваемых как комбинация двух колец тока. при незначительной толщине намотки. Таким образом, единственными параметрами в катушке Гельмгольца являются расстояние колец, h, и их радиус.Такая конфигурация имеет нулевую первую производную от напряженности поля на оси относительно z-положения в центральной точке между кольцами. Исходя из закона Био-Савара, можно показать, что радиус колец должен быть отрегулирован так, чтобы он равнялся расстоянию h, чтобы достичь наилучшей однородности поля, определяемой нулевой второй производной of поле в центре катушки. Перекрывающиеся цилиндры Было отмечено, что перекрывающиеся двух токонесущих цилиндров могут создавать область постоянного магнитного поля.В перекрывающемся объеме двух параллельных бесконечно длинных цилиндров, каждый из которых несет постоянную плотность тока J, идущую в противоположном направлении, можно сделать вывод, что магнитное поле является постоянным вектором (рис.