PhysBook:Электронный учебник физики — PhysBook
Содержание
- 1 Учебники
-
2 Механика
- 2.1 Кинематика
- 2.2 Динамика
- 2.3 Законы сохранения
- 2.4 Статика
- 2.5 Механические колебания и волны
-
3 Термодинамика и МКТ
- 3.1 МКТ
 2 Термодинамика
2 Термодинамика
-
4 Электродинамика
- 4.1 Электростатика
- 4.2 Электрический ток
- 4.3 Магнетизм
- 4.4 Электромагнитные колебания и волны
-
5 Оптика. СТО
- 5.1 Геометрическая оптика
- 5.2 Волновая оптика
-
5.
 3 Фотометрия
3 Фотометрия
- 5.4 Квантовая оптика
- 5.5 Излучение и спектры
- 5.6 СТО
-
6 Атомная и ядерная
- 6.1 Атомная физика. Квантовая теория
- 6.2 Ядерная физика
- 8 Новые страницы
Здесь размещена информация по школьной физике:
- материалы из учебников, лекций, рефератов, журналов;
- разработки уроков, тем;
- flash-анимации, фотографии, рисунки различных физических процессов;
- ссылки на другие сайты
и многое другое.
Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.
Учебники
Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –
Механика
Кинематика
Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве
Динамика
Законы Ньютона – Силы в механике – Движение под действием нескольких сил
Законы сохранения
Закон сохранения импульса – Закон сохранения энергии
Статика
Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика
Механические колебания и волны
Механические колебания – Механические волны
Термодинамика и МКТ
МКТ
Основы МКТ – Газовые законы – МКТ идеального газа
Термодинамика
Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение
Электродинамика
Электростатика
Электрическое поле и его параметры – Электроемкость
Электрический ток
Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках
Магнетизм
Магнитное поле – Электромагнитная индукция
Электромагнитные колебания и волны
Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны
Оптика.
 СТО
СТОГеометрическая оптика
Прямолинейное распространение света. Отражение света – Преломление света – Линзы
Волновая оптика
Свет как электромагнитная волна – Интерференция света – Дифракция света
Фотометрия
Фотометрия
Квантовая оптика
Квантовая оптика
Излучение и спектры
Излучение и спектры
СТО
СТО
Атомная и ядерная
Атомная физика. Квантовая теория
Строение атома – Квантовая теория – Излучение атома
Ядерная физика
Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы
Общие темы
Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ – Репетитор по физике
Новые страницы
Запрос не дал результатов.
Физика Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока
Материалы к уроку
12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.doc
55 KBСкачать12. Переменный ток. Активное сопротивление. Конденсатор и катушка индуктивности в цепи переменного тока.ppt
2.78 MBСкачать
Конспект урока
Огромное практическое значение имеют незатухающие вынужденные колебания. Свободные электромагнитные колебания в контуре быстро затухают и поэтому практически не используются. Переменный ток, используемый потребителями, представляет собой не что иное, как вынужденные электромагнитные колебания. Частота переменного тока показывает число колебаний за 1 секунду.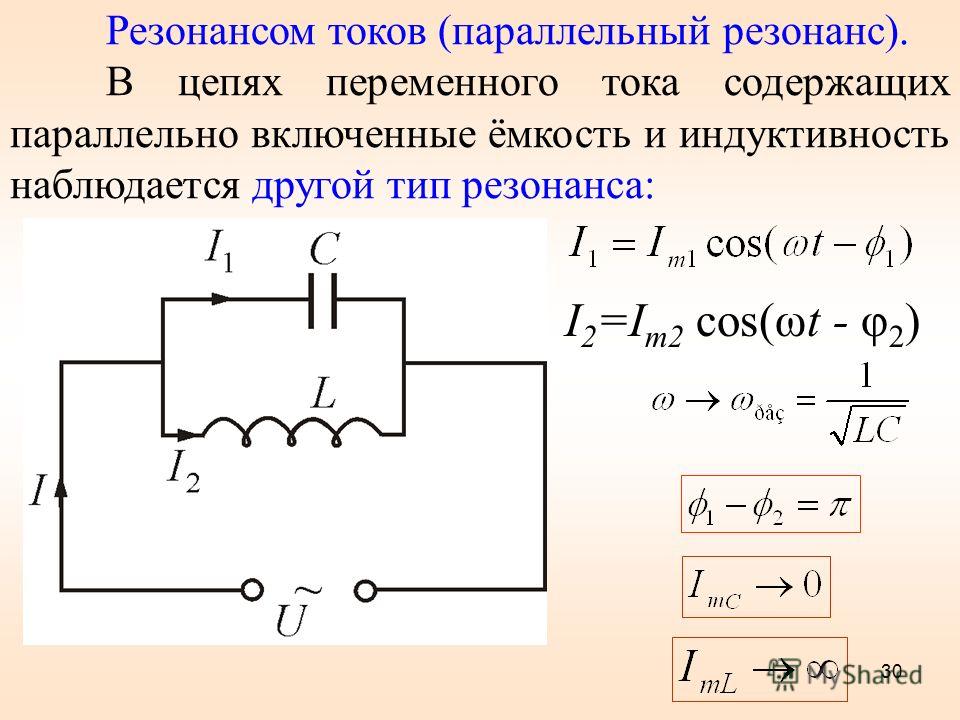
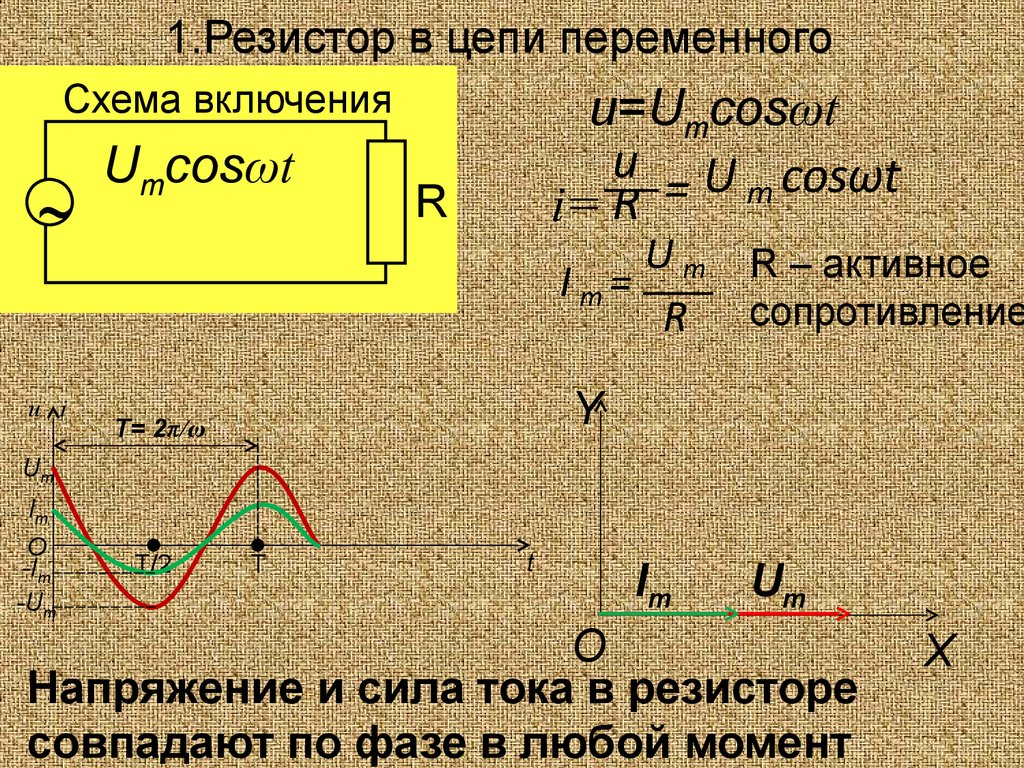
 Цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением, называемым активным сопротивлением. При наличии нагрузки, обладающей активным сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников – они нагреваются. В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения. В цепи переменного тока промышленной частоты, равной 50 Герц, сила тока и напряжение изменяются сравнительно быстро. Мощность в цепи постоянного тока на участке с сопротивлением равна по определению произведению квадрата силы тока на сопротивление. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление, определяется произведением квадрата мгновенного значения силы тока на сопротивление. Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.
Цепь состоит из соединительных проводов и нагрузки с малой индуктивностью и большим сопротивлением, называемым активным сопротивлением. При наличии нагрузки, обладающей активным сопротивлением, цепь поглощает энергию, поступающую от генератора. Эта энергия превращается во внутреннюю энергию проводников – они нагреваются. В проводнике с активным сопротивлением колебания силы тока по фазе совпадают с колебаниями напряжения. В цепи переменного тока промышленной частоты, равной 50 Герц, сила тока и напряжение изменяются сравнительно быстро. Мощность в цепи постоянного тока на участке с сопротивлением равна по определению произведению квадрата силы тока на сопротивление. На протяжении очень малого интервала времени переменный ток можно считать неизменным. Поэтому мгновенная мощность в цепи переменного тока на участке, имеющем активное сопротивление, определяется произведением квадрата мгновенного значения силы тока на сопротивление. Под средней за период мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.
Здесь изображен график зависимости мгновенной мощности от времени. На протяжении одной четверти периода мощность больше половины амплитудного значения. Но на протяжении следующей четверти периода мощность меньше этой величины. На протяжении одной четверти периода эта функция пробегает ряд положительных значений. Половина квадрата амплитуды силы тока в колебательном электромагнитном контуре есть среднее за период значение квадрата силы тока. Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы переменного тока. Всегда можно подобрать такое значение силы постоянного тока, чтобы энергия, выделяемая за некоторое время этим током, равнялась энергии, выделяемой за то же время переменным током. Действующее значение силы переменного тока равно силе постоянного тока, выделяющего в проводнике то же количество теплоты, что и переменный ток за то же время.
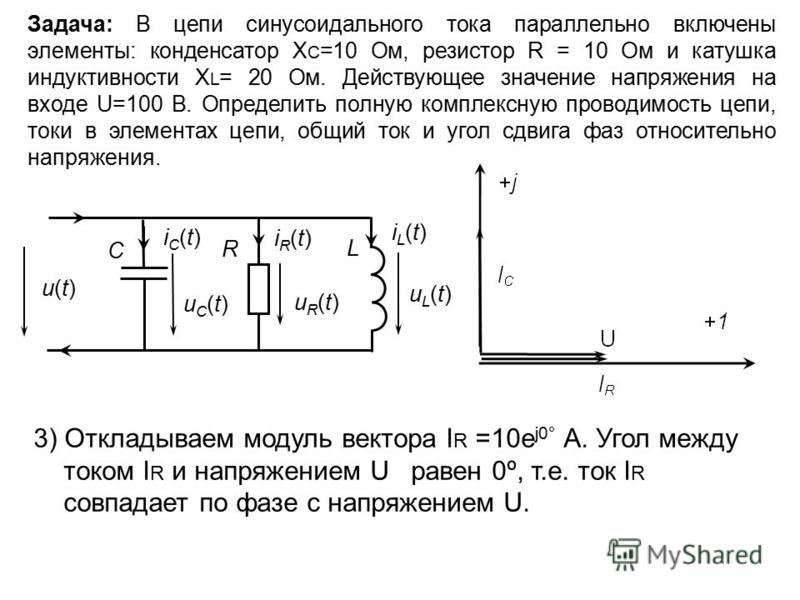
 Нам важны общие характеристики колебаний, такие как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения. Мощность в цепи переменного тока определяется действующими значениями силы тока и напряжения. Мощность равна произведению силы тока и напряжения. Фактически цепь, содержащая конденсатор, оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Поэтому постоянный ток не может существовать в цепи, содержащей конденсатор. Переменный ток способен течь в цепи, содержащей конденсатор. Проведем опыт. Составим последовательную цепь из конденсатора и лампы накаливания. Постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. При включении постоянного напряжения лампа не светится. Но при включении переменного напряжения лампа загорается.
Нам важны общие характеристики колебаний, такие как амплитуда, период, частота, действующие значения силы тока и напряжения и средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры и вольтметры переменного тока. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения. Мощность в цепи переменного тока определяется действующими значениями силы тока и напряжения. Мощность равна произведению силы тока и напряжения. Фактически цепь, содержащая конденсатор, оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком. Поэтому постоянный ток не может существовать в цепи, содержащей конденсатор. Переменный ток способен течь в цепи, содержащей конденсатор. Проведем опыт. Составим последовательную цепь из конденсатора и лампы накаливания. Постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. При включении постоянного напряжения лампа не светится. Но при включении переменного напряжения лампа загорается.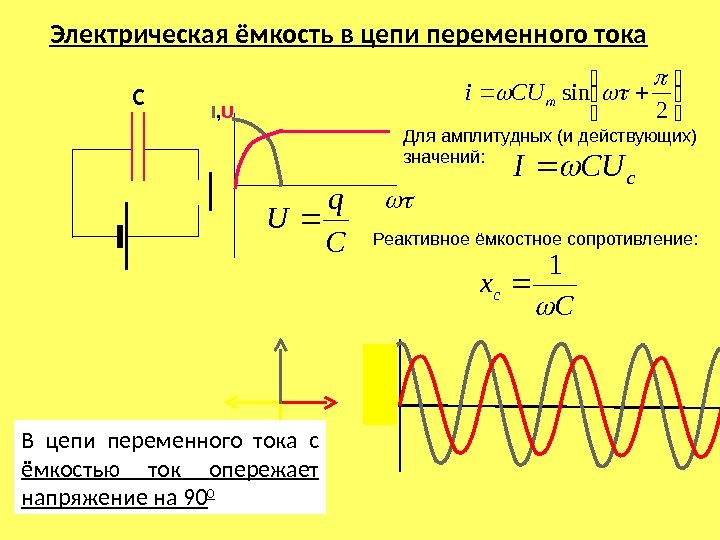

Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта. Составим цепь из катушки большой индуктивности и электрической лампы накаливания. С помощью переключателя можно подключить эту цепь или к источнику постоянного напряжения, или к источнику переменного напряжения с равными значениями. Лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Здесь проявляется самоиндукция. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов.
 Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности. Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура. Следовательно, колебания напряжения на катушке опережают колебания силы тока на пи-пополам. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю. В момент, когда напряжение становится равным нулю, сила тока будет максимальной.
Лишь со временем сила тока достигает наибольшего установившегося значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет достигать тех значений, которые оно бы приобрело с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения. При изменении силы тока по гармоническому закону ЭДС самоиндукции будет равна противоположному значению производной индуктивности. Так как удельная работа кулоновского поля равна напряжению на концах катушки, то напряжение на концах катушки оказывается гармонически связанным с амплитудным значением напряжения контура. Следовательно, колебания напряжения на катушке опережают колебания силы тока на пи-пополам. В момент, когда напряжение на катушке достигает максимума, сила тока равна нулю. В момент, когда напряжение становится равным нулю, сила тока будет максимальной. Величину икс-эл, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Амплитуда силы тока в катушке можно найти отношением амплитуды напряжения на индуктивное сопротивление. Так выглядит закон Ома для цепи постоянного тока с катушкой. Индуктивное сопротивление увеличивается с ростом частоты, значит, катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные, а для постоянного тока оно равно нулю. Рассмотрим использование частотных свойств конденсатора и катушки индуктивности. Реальные электрические цепи содержат все виды сопротивлений: активное, индуктивное, емкостное, поэтому ток в реальной цепи зависит от ее полного эквивалентного сопротивления.
Величину икс-эл, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением. Амплитуда силы тока в катушке можно найти отношением амплитуды напряжения на индуктивное сопротивление. Так выглядит закон Ома для цепи постоянного тока с катушкой. Индуктивное сопротивление увеличивается с ростом частоты, значит, катушка хорошо проводит низкочастотные колебания и плохо – высокочастотные, а для постоянного тока оно равно нулю. Рассмотрим использование частотных свойств конденсатора и катушки индуктивности. Реальные электрические цепи содержат все виды сопротивлений: активное, индуктивное, емкостное, поэтому ток в реальной цепи зависит от ее полного эквивалентного сопротивления.Конденсатор хорошо проводит высокочастотные колебания и плохо – низкочастотные колебания. Катушка наоборот: хорошо проводит низкочастотные колебания и плохо – высокочастотные колебания. Эти свойства позволяют создать различные частотные фильтры – схемы, позволяющие выделить из всего сигнала низкочастотные и высокочастотные составляющие.

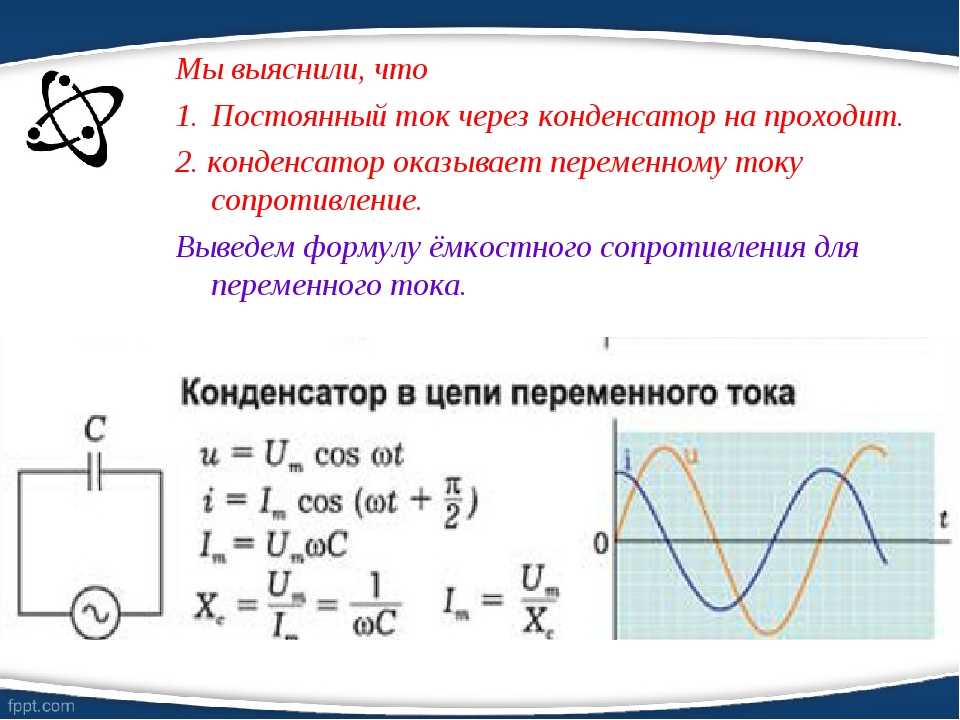
Колебательный контур обладает замечательным свойством – пропускать колебания только определенной частоты, зависящей от емкости конденсатора и индуктивности катушки, под действием резонанса. Эти свойства контура широко применяются в радио- и телеприёмной и передающей аппаратуре для селекции сигналов.
Задача
Конденсатор включен в цепь переменного тока с частотой 200 Герц. Напряжение в цепи 40 Вольт, сила тока 0,64 Ампера. Какова емкость конденсатора?
Вспомнив закон Ома для цепи с колебательным контуром, выразим емкость конденсатора как отношение силы тока к напряжению и циклической частоте. Чтобы определить циклическую частоту, необходимо частоту переменного тока разделить на два-пи. Получаем результат 0,5 микрофарад есть емкость конденсатора.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Электрическое сопротивление– Как протекает ток в цепи с конденсатором?
спросил
Изменено 1 год, 9 месяцев назад
Просмотрено 16 тысяч раз
$\begingroup$
Когда конденсатор подключен к батарее, в цепи начинает течь ток, который заряжает конденсатор до тех пор, пока напряжение между обкладками не станет равным напряжению батареи.
Так как между обкладками конденсатора находится изолятор/диэлектрик, как возможно, что в цепи с конденсатором течет ток, ведь по закону Ома ток обратно пропорционален сопротивлению, а изолятор по определению имеет большое сопротивление, так что у нас в основном разомкнутая цепь?
- электрические цепи
- электрическое сопротивление
- напряжение
- емкость
- диэлектрик
$\endgroup$
$\begingroup$
Так как это физика q и a, объяснение физики в порядке.
Есть два вида тока.
Ток проводимости представляет собой чистый поток зарядов. Это то, о чем люди обычно думают, когда используют слово «ток».
Ток смещения — еще одна форма тока, впервые обнаруженная Максвеллом. Ток смещения играет существенную роль в уравнениях Максвелла. Плотность тока смещения пропорциональна производной по времени от изменения плотности электрического потока.
Когда ток электронов течет в одну сторону конденсатора, электроны накапливаются, так как им некуда деваться. По мере накопления электронов плотность электрического потока изменяется. Это вызывает или, возможно, «является» током смещения.
На противоположной обкладке конденсатора происходит аналогичный процесс, но с противоположной электрической полярностью.
Ток смещения течет от одной пластины к другой через диэлектрик всякий раз, когда ток втекает или выходит из пластин конденсатора, и имеет точно такую же величину, что и ток, протекающий через клеммы конденсатора.
Можно предположить, что этот ток смещения не имеет никакого реального эффекта, кроме «сохранения» тока. Однако ток смещения создает магнитные поля так же, как и ток проводимости.
Этот ответ, возможно, больше, чем хотелось бы знать, но это часть истории электричества, которую стоит рассказать.
$\endgroup$
1
$\begingroup$
как возможно, что ток течет в цепи с конденсатором так как по закону Ома сила тока обратно пропорциональна сопротивление, а изолятор по определению имеет большое сопротивление, поэтому мы в основном есть разомкнутая цепь?
Короткий ответ заключается в том, что электроны могут течь к конденсатору и от него без необходимости прохождения электронов через изоляцию между пластинами. Предлагается следующее качественное объяснение:
Предлагается следующее качественное объяснение:
Если предположить, что конденсатор изначально не заряжен, то перед его подключением к батарее каждая металлическая пластина имеет равное количество протонов (положительный заряд) и высокоподвижных электронов (отрицательный заряд), так что каждая пластина электрически нейтральна и между пластинами нет напряжения (разности потенциалов).
Когда конденсатор подключен к батарее, положительная клемма батареи притягивает электроны от пластины, соединенной с ним, перемещая их к положительной клемме батареи. Это оставляет дефицит электронов на этой пластине, что делает ее положительно заряженной.
В то же время отрицательный полюс батареи подает равное количество электронов на подсоединенную к нему пластину, создавая избыток электронов, делая пластину отрицательно заряженной.
Это перемещение электронов с одной пластины на положительную клемму батареи и с отрицательной клеммы батареи на другую пластину представляет собой ток конденсатора. Обратите внимание, что электроны не проходят через изоляционный материал (диэлектрик) между пластинами.
Обратите внимание, что электроны не проходят через изоляционный материал (диэлектрик) между пластинами.
Вы можете представить себе это примерно как электроны, которые «стягиваются» с одной пластины и «выталкиваются» на другую силой электрического поля, создаваемого батареей, но заряды «застревают» на пластине. пластины, потому что они не могут пройти через изолирующий диэлектрик.
В конце концов, как вы, кажется, уже знаете, батарея перестает перемещать электроны между пластинами, когда разность потенциалов между пластинами становится равной разности потенциалов батареи.
Надеюсь, это поможет.
$\endgroup$
9
$\begingroup$
Удаление электронов с обкладки конденсатора, подключенной к клемме +, представляет собой ток. Поскольку эти электроны удаляются для этой пластины, происходит накопление электронов на другой пластине. Это движение электронов составляет ток.
Это движение электронов составляет ток.
Ток прекращается, когда потенциалы пластин конденсатора становятся равными потенциалам соответствующих клемм батареи. Это не происходит мгновенно, а скорее зависит от времени, потому что транспорт электронов из конденсатора и в него требует времени, а потенциалы зависят от дисбаланса заряда пластин.
$\endgroup$
$\begingroup$
Наличие плоского конденсатора означает, что в части цепи (лишь малая часть; конденсаторы редко имеют такой большой зазор как один миллиметр) нет движения электронов, только накопление поля (в сопровождении электронов, если конденсатор не вакуумный тип). Это проблематично, потому что есть простой способ обнаружения ток, который заключается в наблюдении за магнитным полем, создаваемым током, и ЧАСТЬ цепи больше не имеет тока.
Дело в том, что «поправка» на магнитное поле не
существовать. Соответствующее уравнение Максвелла для тока, создающего магнетизм
имеет член, добавленный к текущему току смещения, который представляет собой скорость изменения
электрическое поле (например, поле внутри диэлектрика конденсатора). Это дополнение к уравнению необходимо не только для цепей,
у него есть дополнительный побочный эффект, заключающийся в том, что изменяющееся электрическое поле создает магнитное поле даже при отсутствии движущихся заряженных частиц.
Это дополнение к уравнению необходимо не только для цепей,
у него есть дополнительный побочный эффект, заключающийся в том, что изменяющееся электрическое поле создает магнитное поле даже при отсутствии движущихся заряженных частиц.
Этот член уравнения объясняет, почему электромагнитные волны (свет) путешествует в вакууме. И, почему зарядка конденсатора (по-нашему измерений) неотличимы от непрерывного течения тока в цепь.
Буквально мы можем видеть, как светит солнце, потому что конденсатор в цепи не отличим от непрерывного тока в цепи.
$\endgroup$
2
$\begingroup$
Конденсатор действительно блокирует постоянный ток (DC). Однако значительный переменный ток (AC) может протекать, когда период колебаний меньше времени зарядки конденсатора.
$\endgroup$
3
$\begingroup$
Накачка электронов в одну пластину конденсатора приводит к тому, что свободные электроны на другой пластине отталкиваются, когда они «видят» входящие другие электроны. другая пластина. Для больших тарелок этот короткий импульс длинный, а для маленьких тарелок короткий импульс.
другая пластина. Для больших тарелок этот короткий импульс длинный, а для маленьких тарелок короткий импульс.
Это означает, что короткие импульсы переменного тока могут легко проходить через конденсатор, в то время как установившийся постоянный ток полностью блокируется.
$\endgroup$
$\begingroup$
Емкость (конденсатор) может первоначально заряжаться при кратковременном накоплении заряда на конденсаторе при замыкании цепи. Обычно:
$𝑡 = 𝑅.𝐶$
С:
$R$: Сопротивление цепи.
$C$: значение емкости.
На самом деле это и есть механизм способности емкости пропускать переменную во времени составляющую сигнала (ток, индуцированный изменением заряда на стенках емкости), блокируя постоянную его компонент.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. В электрическую цепь включен конденсатор
В электрическую цепь включен конденсаторА. Когда клавиша нажата, ток в цепи равен: А. нольБ. максимумС. любое переходное значениеD. зависит от используемого конденсатора
Дата последнего обновления: 20 марта 2023 г.
•
Всего просмотров: 263.1k
•
Просмотров сегодня: 3,42 тыс.
Ответ
Проверено
263,1 тыс.+ просмотров
Подсказка: Когда полностью заряженный конденсатор емкостью C, содержащий резистор, включается в электрическую цепь, ключ R и ключ конденсатор начинает разряжаться. Первоначально ток в цепи максимален, но со временем он уменьшается и, наконец, становится равным нулю.
Полный пошаговый ответ:
Когда полностью заряженный конденсатор емкостью С включен в электрическую цепь, содержащую резистор R, то ток в цепи в цепи при разрядке определяется соотношением 9{\dfrac{{ – t}}{\tau }}}\] , мы получаем \[{I_c} = {I_0}\].


 2 Термодинамика
2 Термодинамика
