Асинхронный двигатель
Если поместить во вращающееся магнитное поле короткозамкнутую медную или алюминиевую рамку на валу электродвигателя, то она вместе с валом придет во вращение по направлению вращения поля. Явление это объясняется следующим образом. Пусть угловая скорость вращения рамки n несколько меньше угловой скорости вращения поля no (асинхронное вращение). В этом случае рамка «проскальзывает» относительно поля. Величину s = (n0—n)/n0 называют скольжением. Относительно магнитного поля рамка вращается с угловой скоростью, пропорциональной скольжению. Поэтому в ней возникает индукционный ток, пропорциональный относительной скорости вращения рамки, т. е. скольжению. По закону Ленца, индуцированный ток взаимодействует с полем так, что рамка увлекается полем.
А так как магнитное поле вращается, то это приводит к вращению рамки. Вращающий момент, действующий на рамку, пропорционален индуцированному току и тем самым скольжению. Этот вращающий момент уравновешивается внешней нагрузкой. Таким образом, в установке данного типа рамка всегда вращается несколько медленнее вращения поля. Такое вращение называют асинхронным (т. е. неодновременным, несогласованным). Сам двигатель получил название асинхронного.
Таким образом, в установке данного типа рамка всегда вращается несколько медленнее вращения поля. Такое вращение называют асинхронным (т. е. неодновременным, несогласованным). Сам двигатель получил название асинхронного.
Асинхронный двигатель наиболее распространен в качестве электропривода различных механизмов благодаря своей простоте и надежности. Их применяют для привода машин и механизмов, не требующих строго постоянной частоты вращения и ее регулировки. Важнейшими достоинствами данного двигателя являются простота его устройства и большая надежность, вызванная отсутствием скользящих контактов. Двигатель имеет достаточный пусковой момент, легко реверсируется (т. е. в нем легко меняется направление вращения ротора). В результате этого асинхронные двигатели являются самыми распространенными в технике электрическими машинами. Более 60 % всей вырабатываемой в мире энергии преобразуется в механическую, в основном, с помощью асинхронных двигателей. Мощность двигателей колеблется от десятков ватт до сотен киловатт.
Асинхронный двигатель изготавливается в однофазном, двухфазном и трехфазном исполнении.
Принцип работы
Рассмотрим вращающееся поле переменного тока трехфазной цепи короткозамкнутого асинхронного двигателя с тремя обмотками, сдвинутыми по окружности на 120° и соединенными звездой .
Обмотки статора питаются симметричным трехфазным напряжением. Начальную фазу тока в обмотке А-х принимаем равной нулю. Тогда:
Конструкция
Асинхронный двигатель состоит из статора и ротора. Статор представляет собой литой корпус (стальной или чугунный) цилиндрической формы. Внутри статора располагается магнитопровод с вырубленными пазами, в которые укладывается статорная обмотка. Концы обмоток выводятся в клеммную коробку и могут быть соединены как треугольником, так и звездой. Корпус статора с торцов закрыт подшипниковыми щитами, в которые запрессовываются подшипники вала ротора. Ротор состоит из стального вала с напрессованным на него магнитопроводом.
По конструкции роторов двигатели делятся на две группы. Первая — с короткозамкнутым ротором и вторая — с фазным. У двигателя с короткозамкнутым ротором в пазы заливаются алюминиевые стержни и накоротко замыкаются по торцам. У фазового ротора имеются три обмотки, соединенные в звезду. Выводы обмоток присоединены к кольцам, закрепленным на валу. К кольцам при пуске прижимаются неподвижные щетки, к которым подключаются сопротивления. В начальный момент пуска ротор находится в заторможенном состоянии, затем сопротивление уменьшается и двигатель плавно запускается, что позволяет снизить пусковой ток.
Первая — с короткозамкнутым ротором и вторая — с фазным. У двигателя с короткозамкнутым ротором в пазы заливаются алюминиевые стержни и накоротко замыкаются по торцам. У фазового ротора имеются три обмотки, соединенные в звезду. Выводы обмоток присоединены к кольцам, закрепленным на валу. К кольцам при пуске прижимаются неподвижные щетки, к которым подключаются сопротивления. В начальный момент пуска ротор находится в заторможенном состоянии, затем сопротивление уменьшается и двигатель плавно запускается, что позволяет снизить пусковой ток.
К обмоткам статора подводится трехфазное напряжение, а ротор вращается посредством вращающегося магнитного поля, создаваемого системой трехфазного тока.
В момент времени t1: . Если ток фазы А положителен, т.е. течет от начала к концу, то, пользуясь правилом правоходового винта, можно найти картину распределения магнитного поля для времени t1.
В момент времени t2 вектор результирующей магнитной индукции Вm развернется на угол α1 и далее по часовой стрелке с периодом обращения 360°. Для данного примера угол α1 = 60°.
Для данного примера угол α1 = 60°.
Таким образом, магнитная индукция представляет собой вращающееся поле с амплитудой
За период поле делает один оборот, , (где f = 50 Гц), и является промышленной частотой питающего переменного напряжения и тока.
При синусоидальном характере вращающегося поля его скорость no равна отношению αf/p (где р — число пар полюсов). В рассматриваемом примере р = 1 и частота вращения равна соответственно 3000 оборотам в минуту. Если число катушек в каждой фазе увеличить в два раза, а сдвиг фаз между токами сохранить 120°, то частота вращения уменьшится в два раза за счет увеличения числа пар полюсов. Особенностью короткозамкнутого асинхронного двигателя является наличие постоянной частоты вращения поля статора, определяемой числом пар полюсов.
Если поменять местами любые две фазы, то возникнет поле обратной последовательности и ротор начнет вращаться в другую сторону. Еще одной особенностью асинхронных двигателей является разность частоты вращения полей статора no и ротора n, что делает возможным их электромагнитное взаимодействие. При этом поле ротора будет как бы скользить относительно поля статора
Еще одной особенностью асинхронных двигателей является разность частоты вращения полей статора no и ротора n, что делает возможным их электромагнитное взаимодействие. При этом поле ротора будет как бы скользить относительно поля статора
где s — скольжение, при номинальной мощности двигателя скольжение составляет 0,01-0,03.
Основное вращающееся магнитное поле индуцирует в обмотках статора и ротора ЭДС, аналогично трансформатору, так как при разомкнутом роторе асинхронный двигатель представляет собой трансформатор в режиме холостого хода:
где индекс 1 относится к параметрам статора, а 2 — к параметрам ротора; Kобм — обмоточные коэффициенты, определяемые способом укладки обмоток (петлевая или волновая). Kобм=0,92-0,98; E2s=E2s; E2 — действующее значение ЭДС неподвижного ротора при s = 1; f2=f1s.
В асинхронном двигателе кроме основного магнитного потока создаются потоки рассеяния. Один охватывает проводники статора, другой — ротора. Потоки рассеяния характеризуются соответствующими индуктивными сопротивлениями X1 и X2s.
Один охватывает проводники статора, другой — ротора. Потоки рассеяния характеризуются соответствующими индуктивными сопротивлениями X1 и X2s.
Уравнения электрического состояния фаз обмоток статора и ротора:
Момент асинхронного двигателя
Вращающий электромагнитный момент двигателя в соответствии с законом электромагнитных сил
где
Cм — конструктивная постоянная;
φ2s — фазовый сдвиг между током и магнитным потоком.
Отношение максимального момента Mmax к номинальному Mн определяет перегрузочную способность двигателя и составляет 2,0-2,2 (дается в каталожных данных). Максимальный момент соответствует критическому скольжению sк, определяемому активными и индуктивными сопротивлениями двигателя, и пропорционален активному сопротивлению цепи ротора.
Потери в асинхронном двигателе
Потери делятся на потери в статоре и в роторе. Потери в статоре состоят из электрических потерь в обмотке Рэ1 и потерь в стали Рст, а потери в роторе — из электрических Рэ2 и механических Рмех плюс добавочные потери на трение и вентиляцию Рдоб.
Потери в статоре состоят из электрических потерь в обмотке Рэ1 и потерь в стали Рст, а потери в роторе — из электрических Рэ2 и механических Рмех плюс добавочные потери на трение и вентиляцию Рдоб.
где К = 2,9-3,6 определяется диаметром статора D1.
Потери в стали в рабочем режиме во много раз меньше электрических потерь в роторе и ими обычно пренебрегают.
КПД асинхронного двигателя составляет от 0,75 до 0,95.
Рабочий момент двигателя пропорционален квадрату напряжения, что необходимо учитывать при включении двигателя в протяженных распределительных сетях. Номинальному моменту соответствует номинальное скольжение, а пусковому — sп.
Зависимость момента двигателя от скольжения М=f(s) приведена на рисунке.
На участке от 0 до Mmax двигатель работает в устойчивом режиме, а участок от Sk называется режимом опрокидывания двигателя, при котором двигатель в результате перегрузки останавливается и не может вернуться в рабочий режим без очередного запуска. Пусковые свойства двигателя определяются соотношением пускового момента Mп и номинального. В соответствии с каталожными данными оно составляет 1,6-1,7. При пуске асинхронного двигателя cosj очень мал и пусковой ток в обмотке статора может возрастать в 5-7 раз по сравнению с номинальным. Ограничение его осуществляется изменением частоты питающего напряжения для двигателя с короткозамкнутым ротором и увеличением активного сопротивления в цепи ротора для двигателя с фазовым ротором. Для механизмов, имеющих тяжелые условия пуска, где желательно использовать асинхронный двигатель с короткозамкнутым ротором, применяются двигатели с улучшенными пусковыми свойствами: с большим пусковым моментом и меньшим пусковым током, чем у двигателей общего назначения.
Пусковые свойства двигателя определяются соотношением пускового момента Mп и номинального. В соответствии с каталожными данными оно составляет 1,6-1,7. При пуске асинхронного двигателя cosj очень мал и пусковой ток в обмотке статора может возрастать в 5-7 раз по сравнению с номинальным. Ограничение его осуществляется изменением частоты питающего напряжения для двигателя с короткозамкнутым ротором и увеличением активного сопротивления в цепи ротора для двигателя с фазовым ротором. Для механизмов, имеющих тяжелые условия пуска, где желательно использовать асинхронный двигатель с короткозамкнутым ротором, применяются двигатели с улучшенными пусковыми свойствами: с большим пусковым моментом и меньшим пусковым током, чем у двигателей общего назначения.
Механическая характеристика асинхронного двигателя
Зависимость скорости вращения от нагрузки на валу двигателя называется механической характеристикой асинхронного двигателя.
Участок АВ механической характеристики соответствует устойчивому режиму работы асинхронного двигателя. Увеличение нагрузки (тормозного момента) ведет к некоторому снижению частоты вращения ротора, что вызывает увеличение вращающего момента. При превышении тормозным моментом критического, двигатель останавливается. Точка В на графике соответствует точке критического или опрокидывающего момента.
Увеличение нагрузки (тормозного момента) ведет к некоторому снижению частоты вращения ротора, что вызывает увеличение вращающего момента. При превышении тормозным моментом критического, двигатель останавливается. Точка В на графике соответствует точке критического или опрокидывающего момента.
Регулирование частоты вращения
Регулирование частоты вращения может быть осуществлено тремя способами: изменением частоты питающего напряжения, переключением числа пар полюсов и изменением скольжения.
Для регулирования частоты вращения двигателей с короткозамкнутым ротором в настоящее время широко используются частотные преобразователи с микропроцессорным управлением.
Тормозные режимы
Тормозные режимы возникают в машине при определенных условиях или создаются искусственно с целью ускорения процесса остановки двигателя. Торможение может быть:
- генераторное с отдачей энергии в сеть;
- противовключением;
- динамическое.
Генераторным тормозным режимом называется режим работы двигателя, когда под действием внешнего момента ротор двигателя вращается в том же направлении, что и магнитное поле, но с большей скоростью.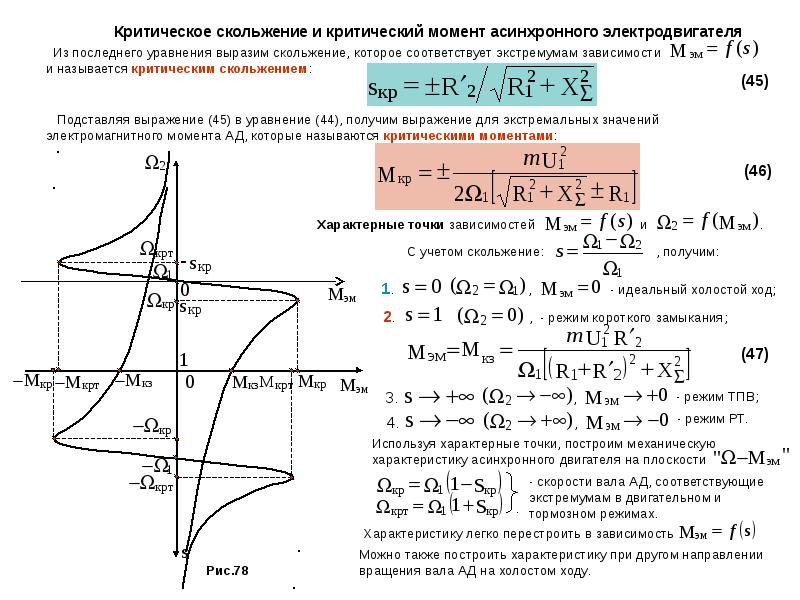
Тормозной режим противовключения возникает в том случае, когда под действием внешнего момента, приложенного к валу двигателя, ротор вращается в противоположную сторону относительно вращающегося магнитного поля.
Динамический тормозной режим получается при отключении обмотки статора от сети трехфазного тока и подключении ее на время торможения к источнику энергии постоянного тока.
Выбор двигателя
Расчетные формулы для выбора двигателя имеют вид:
Выбор двигателя по каталогу осуществляется следующим образом. По заданному моменту рабочего механизма и частоте вращения определяется необходимая мощность. После этого определяются условия окружающей среды, выбирается исполнение по типу монтажа и высоте оси рабочего вала двигателя. Зная эти параметры, по каталогу проверяют необходимую перегрузочную способность, КПД, массу и момент инерции.
Для шахтных условий используются двигатели взрывозащищенного исполнения; для крановых механизмов — двигатели с повышенным скольжением и т. д.
д.
В бытовых приборах используются однофазные двигатели. Однофазный двигатель отличается от трехфазного тем, что его статорная обмотка подключается к однофазному источнику питания. Ротор выполняется короткозамкнутым. На статоре размещаются две обмотки, оси которых смещены друг относительно друга на 90 электрических градусов. Одна называется рабочей, а другая -пусковой.
Рабочие характеристики асинхронного двигателя
Рабочими характеристиками асинхронного двигателя являются зависимости от мощности на валу Р2 таких параметров, как момент, частота вращения, ток статора, КПД и cosφ. Анализ характеристик показывает, что частота вращения ротора падает с увеличением нагрузки, а момент пропорционален ей. Ток статора изменяется по нелинейному закону, что связано с магнитной системой двигателя и при Р2=0 определяется током холостого хода, составляющего до 40% его номинального значения.
В системах управления используются двигатели, в которых одна из обмоток статора постоянно подключена к сети переменного тока (обмотка возбуждения), а ко второй (обмотка управления) подводится напряжение управления. Такие двигатели относятся к классу микромашин.
Такие двигатели относятся к классу микромашин.
Микромашины используются в информационных системах, где они выполняют функции первичных преобразователей для вычислительных операций в системах автоматики и телемеханики.
Одним из примеров является сельсин, предназначенный для передачи на расстояние угловых перемещений валов, механически не связанных друг с другом. По конструкции сельсины делятся на контактные и бесконтактные. Контактные сельсины выполняются в двух вариантах. В одном обмотка возбуждения располагается на роторе, а трехфазная обмотка, называемая обмоткой синхронизации, в пазах статора. В другом варианте наоборот. При включении обмотки возбуждения сельсина на однофазное напряжение ток создает пульсирующее магнитное поле, которое индуцирует в каждой фазе обмотки синхронизации переменную ЭДС. Действующее значение ЭДС каждой фазы зависит от расположения осей этих фаз относительно оси потока возбуждения.
В простейшем случае схема дистанционной передачи угловых перемещений состоит из двух одинаковых сельсинов, у которых одноименные зажимы обмоток синхронизации соединены проводами линии связи, а на обмотки возбуждения подается напряжение сети. Один из сельсинов называют сельсин-датчиком, другой — сельсин-приемником.
Один из сельсинов называют сельсин-датчиком, другой — сельсин-приемником.
Вращающий момент асинхронного электродвигателя
Вращающий момент асинхронного электродвигателя создается, как уже указывалось, за счет взаимодействия между вращающимся магнитным потоком статора и токами в обмотке ротора. Вполне понятно, что при отсутствии тока в обмотке ротора никакого момента создаваться не будет. Скольжение характеризует скорость вращения ротора относительно магнитного поля статора. От величины этой скорости зависит ток в роторе, а от тока—величина вращающего момента электродвигателя, который может быть вычислен по формуле (6). Но выражение (6), несмотря на свою простоту, не дает возможности выяснить влияние различных факторов на величину вращающего момента. Поэтому в курсе электротехники часто используют другое выражение:
где с — постоянная величина, зависящая от конструкции электродвигателя;
?1 —угловая скорость вращающегося магнитного поля.
Выражение (90) показывает, что вращающий момент пропорционален квадрату напряжения сети, в связи с чем даже небольшое уменьшение напряжения в питающей сети приводит к резкому снижению вращающего момента, что отрицательно сказывается на работе электродвигателя.
Кроме того, выражение (90) учитывает зависимость величины вращающего момента от активных и индуктивных сопротивлений электродвигателя, а также от скольжения.
Если обозначить (х1 + сх2) через х и выполнить несложные преобразования в формуле (90), то получим
Величинами r1 s и x2 s2 можно пренебречь, ввиду их малости. Тогда, до некоторого предела
Таким образом доказано, что с увеличением скольжения возрастает и момент электродвигателя.
Более точный анализ выражений (90) и (91) показывает, что момент с увеличением скольжения возрастает лишь до некоторого критического значения Мкрит (так называемый опрокидывающий момент), после чего начинается резкое его снижение.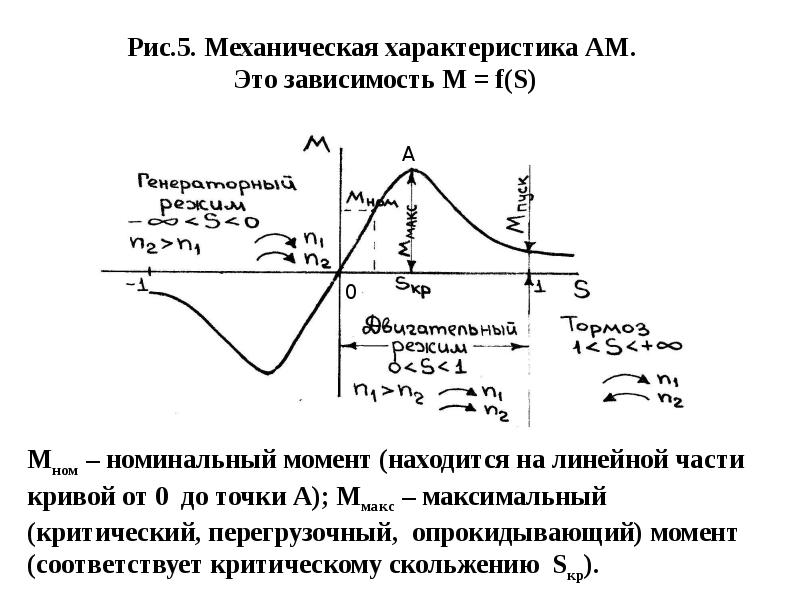
Величина критического скольжения, при которой имеет место опрокидывающий момент,
Подставляя это выражение в уравнение (91), получим
В последних выражениях знак плюс относится к работе электродвигателя в режимах двигательном и торможения противовключением, а знак минус — к работе в генераторном режиме с отдачей энергии в сеть. Очевидно, что критический момент в двигательном режиме меньше, чем в генераторном.
Зависимость
Выражения (93) и (94) показывают, что при изменении активного сопротивления роторной цепи величина опрокидывающего момента Мкрит не изменяется, меняется при этом лишь величина критического скольжения sкрит.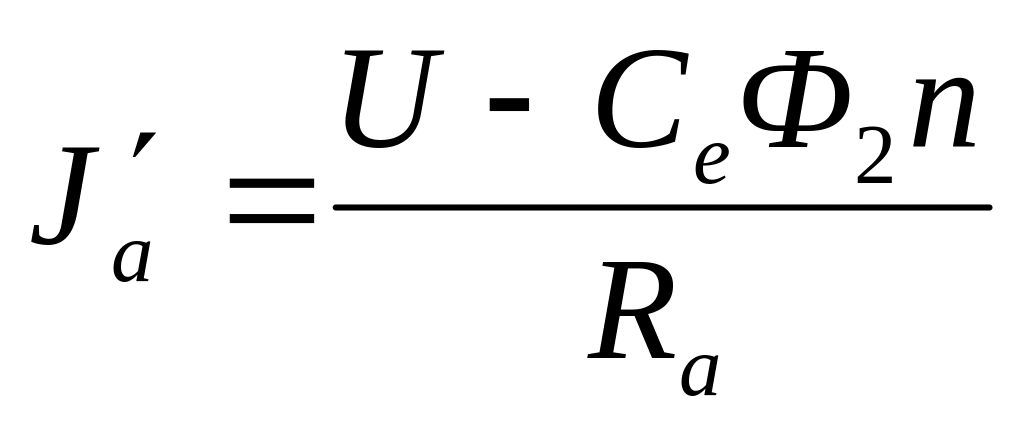 Поэтому при различных активных сопротивлениях роторной цепи кривые М = f(s) имеют различный характер. Эти кривые показывают, что пусковой момент асинхронного электродвигателя с фазным ротором можно искусственным образом изменять, вводя различные активные сопротивления в
Поэтому при различных активных сопротивлениях роторной цепи кривые М = f(s) имеют различный характер. Эти кривые показывают, что пусковой момент асинхронного электродвигателя с фазным ротором можно искусственным образом изменять, вводя различные активные сопротивления в
его роторную цепь. Таким же образом можно регулировать скорость электродвигателя, так как при изменении активного сопротивления роторной цепи меняется величина скольжения (рис. 43), а от скольжения, как показывает выражение (82), зависит число оборотов асинхронного электродвигателя.
| eaDonNTU, Donetsk >
Items in DSpace are protected by copyright, with all rights reserved, unless otherwise indicated.
| |||||||||||||
Расчет и построение естественных электромеханической и механической характеристик двигателя с последовательным возбуждением, страница 3
Данные
двигателя: U1н= 380/220; Pн= 11 кВт; nн= 953 об/мин; R1= 0.415 Ом;
x1 = 0.465 Ом; R2= 0.132 Ом; x2= 0. 27 Ом; Е2н= 200 В; I2н
= 35.4 А; .
27 Ом; Е2н= 200 В; I2н
= 35.4 А; .
Решение
Расчет механических характеристик асинхронного двигателя будем вести по уточненной формуле Клосса:
где Мк – критический момент; Sk – критическое скольжение; .
Коэффициент приведения сопротивлений:
.
Приведенные значения сопротивлений ротора:
Индуктивное сопротивление короткого замыкания:
Ом.
Критический момент двигателя при номинальном значении питающего напряжения:
, где – скорость идеального холостого хода.
Критическое скольжение на естественной характеристике:
Уравнение естественной механической характеристики:
С помощью данного уравнения рассчитана естественная механическая характеристика
асинхронного двигателя (рис.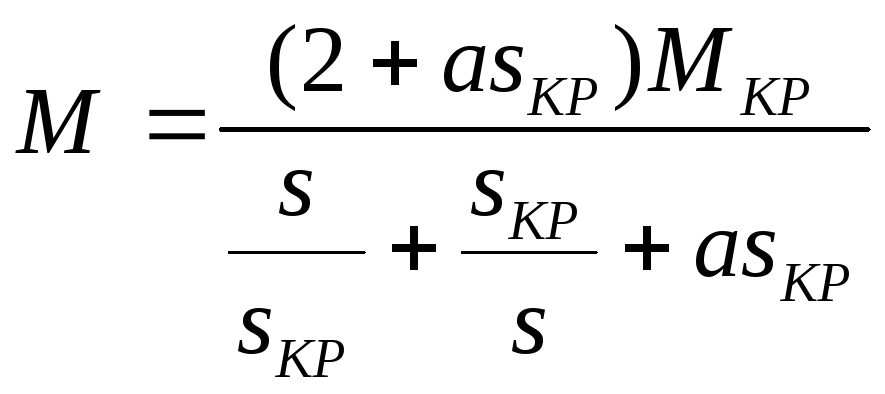 9.23, кривая 1). Для построения реостатной механической
характеристики при R2доб= 0.3 R2Н
определим суммарное приведенное сопротивление роторной цепи:
9.23, кривая 1). Для построения реостатной механической
характеристики при R2доб= 0.3 R2Н
определим суммарное приведенное сопротивление роторной цепи:
, где Ом – величина дополнительного сопротивления, вводимого в цепь ротора.
Критическое скольжение на реостатной характеристике:
.
Уравнение реостатной характеристики:
.
Соответствующая этому уравнению реостатная механическая характеристика иимеет вид (рис. 9.23, кривая 2).
Для построения механической характеристики при U1 = 0.7 U1Н = 0.7 × 220 = 154 В определим критический момент:
.
Уравнение искусственной механической характеристики при U1= 154 В имеет вид:
.
Соответствующая механическая характеристика имеет вид (рис. 9.23, кривая 3).
Пример 17
Для двигателя, рассмотренного в примере 16, рассчитать сопротивления пускового реостата при нормальном режиме пуска в три ступени и при

Решение
Так как режим пуска нормальный, то переключающий момент (М2) должен превышать статический на (10 – 20)%.
Принимаем М2*= 1.2. Отношение максимального момента при пуске (М1) к моменту переключения М2 находим по формуле /2/:
.
Осуществляем проверку на максимальный (пиковый) момент, который должен быть меньше критического:
Сопротивление ступеней пускового реостата при включении их в одинарную звезду:
Пример 18
Для двигателя, рассмотренного в примере 16, рассчитать сопротивления пускового реостата при нормальном режиме пуска в три ступени и при МС = МН, пользуясь приближенным графическим методом.
Решение
При расчете
пусковых сопротивлений приближенным графическим методом исходят из
прямолинейности механической характеристики, и расчет ведется, как для двигателя
постоянного тока с параллельным возбуждением.
На рис. 9.24 построены пусковые характеристики двигателя для указанных условий пуска.
Максимальный момент при пуске:
Переключающий момент:
По графику рис. 9.24 определяем сопротивления ступеней пускового реостата:
Сравнивая результаты расчетов сопротивлений в примерах 17 и 18, видим, что расхождение составляет не более 5 %. Поэтому при практических расчетах можно пользоваться любым из рассмотренных методов.
Пример 19
Для асинхронного двигателя с короткозамкнутым ротором рассчитать и построить естественную и искусственные механические характеристики для двух значений частот тока статора f1 = 35 Гц и f2= 20 Гц, при регулировании напряжения на статоре по пропорциональному закону: U/f = const.
Данные
двигателя: PН= 22 кВт; U1Н= 380/220 В; nН= 727 об/мин; R1= 0. 18 Ом;
18 Ом;
X1 = 0.624 Ом; R`2= 0.153 Ом; X`2= 0.485 Ом.
Решение
Расчет механических характеристик будем вести согласно методике, приведенной в /2, 11/. При пропорциональном законе частотного регулирования U/f = const электромагнитный момент двигателя определяется по формуле:
где m – число фаз статора; U1Н– фазное номинальное напряжение статора при частоте 50 Гц; f* = f/fН – относительная частота; Сf – коэффициент зависящий от частоты f*.
Пусковой момент двигателя. Вращающий момент асинхронного двигателя. Вывод формулы. Номинальный, критический и пусковой моменты
Вращающий момент, развиваемый на валу асинхронного электродвигателя в условиях нулевой скорости вращения ротора (когда ротор еще неподвижен) и установившегося в обмотках статора тока, – называется пусковым моментом асинхронного двигателя.
Пусковой момент иногда называют еще моментом трогания или начальным моментом. При этом подразумевается, что напряжение и частота питающего напряжения приближены к номиналу, причем соединение обмоток выполнено правильно. В номинальном режиме работы данный двигатель будет работать именно так, как предполагали разработчики.
Пусковой момент вычисляется по приведенной формуле. В паспорте электродвигателя (паспорт предоставляется производителем) указана кратность пускового момента.
Обычно значение величины кратности лежит в пределах от 1,5 до 6, в зависимости от типа двигателя. И при выборе электродвигателя для своих нужд, важно убедиться, что пусковой момент окажется больше статического момента планируемой проектной нагрузки на валу. Если это условие не соблюсти, то двигатель попросту не сможет развить рабочий момент при вашей нагрузке, то есть не сможет нормально стартонуть и разогнаться до номинальных оборотов.
Давайте рассмотрим еще одну формулу для нахождения пускового момента.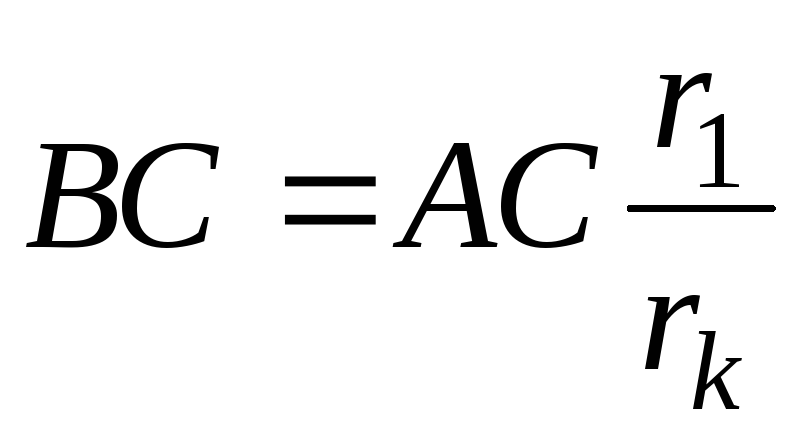 Она будет вам полезной для теоретических расчетов. Здесь достаточно знать мощность на валу в киловаттах и номинальные обороты, – все эти данные указаны на табличке (на шильдике). P2-номинальная мощность, F1-номинальные обороты. Итак, вот эта формула:
Она будет вам полезной для теоретических расчетов. Здесь достаточно знать мощность на валу в киловаттах и номинальные обороты, – все эти данные указаны на табличке (на шильдике). P2-номинальная мощность, F1-номинальные обороты. Итак, вот эта формула:
Для нахождения P2 применяют следующую формулу. Здесь необходимо учесть скольжение, пусковой ток и напряжение питания, все эти данные указаны на шильдике. Как видите, все довольно просто. Из формулы очевидно, что пусковой момент в принципе можно повысить двумя путями: увеличением стартового тока или повышением питающего напряжения.
Попробуем, однако, пойти наиболее простым путем, и рассчитаем значения пусковых моментов для трех двигателей серии АИР. Воспользуемся параметрами кратности пускового момента и величинами номинального момента, то есть пользоваться будем самой первой формулой. Результаты расчетов приведены в таблице:
| Тип двигателя | Номинальный момент, Нм | Отношение пускового момента к номинальному моменту | Пусковой момент, Нм |
| АИРМ132М2 | 36 | 2,5 | 90 |
| АИР180S2 | 72 | 2 | 144 |
| АИР180М2 | 97 | 2,4 | 232,8 |
Роль пускового момента асинхронного электродвигателя (пусковой ток)
Часто двигатели включают напрямую в сеть, осуществляя коммутацию магнитным пускателем: на обмотки подается линейное напряжение, создается вращающееся магнитное поле статора, оборудование начинает работать.
Бросок тока в момент старта в данном случае неизбежен, и он превышает номинальный ток в 5-7 раз, причем длительность превышения зависит от мощности двигателя и от мощности нагрузки: более мощные двигатели стартуют дольше, их обмотки статора дольше принимают токовую перегрузку.
Маломощные двигатели (до 3 кВт) легко переносят данные броски, и сеть так же легко выдерживает эти незначительные кратковременные всплески мощности, ибо у сети всегда есть некоторый мощностный резерв. Вот почему небольшие насосы и вентиляторы, станки и бытовые электроприборы обычно включают напрямую, не заботясь особо о токовых перегрузках. Как правило обмотки статоров двигателей оборудования такого рода соединяются по схеме «звезда» из расчета на трехфазное напряжение 380 вольт или «треугольник» – для 220 вольт.
Если же вы имеете дело с мощным двигателем на 10 и более кВт, то включать напрямую такой двигатель в сеть нельзя. Бросок тока в момент пуска необходимо ограничить, иначе сеть испытает значительную перегрузку, что может привести к опасной «нештатной просадке напряжения».
Пути ограничения пускового тока
Наиболее простой способ ограничения пускового тока – пуск при пониженном напряжении. Обмотки просто переключаются с треугольника на звезду в момент пуска, а затем, когда двигатель набрал какие-то обороты – обратно на треугольник. Переключение осуществляется через несколько секунд после старта с помощью реле времени, например.
В таком решении пусковой момент также понижается, причем зависимость квадратичная: при снижении напряжения в будет в 1,72 раза, момент снизится в 3 раза. По этой причине пуск при пониженном напряжении подходит для такого оборудования, где пуск возможен с минимальной нагрузкой на валу асинхронного двигателя (например пуск многопильного станка).
Мощным нагрузкам, например ленточному конвейеру, необходим другой способ ограничения пускового тока. Здесь лучше подойдет реостатный метод, позволяющий снизить пусковой ток без уменьшения крутящего момента.
Такой способ очень подходит асинхронным двигателям с фазным ротором, где реостат удобно включается в цепь обмотки ротора, и регулировка рабочего тока осуществляется ступенчато, получается очень плавный пуск.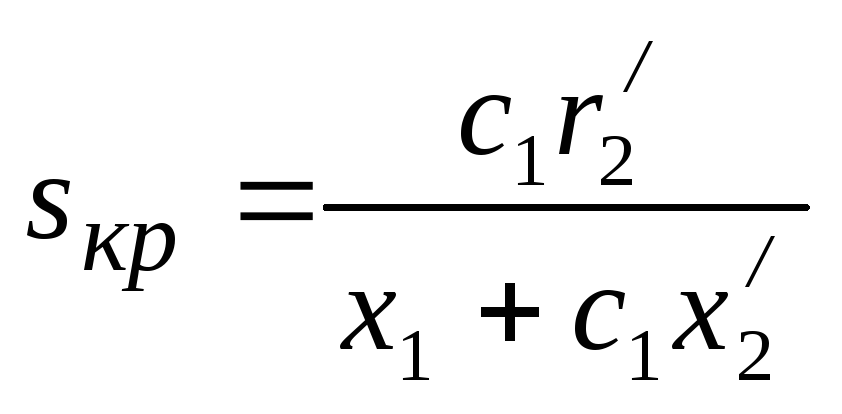 С помощью реостата тут же можно регулировать и рабочую скорость двигателя (не только в момент запуска).
С помощью реостата тут же можно регулировать и рабочую скорость двигателя (не только в момент запуска).
Но наиболее эффективным способом безопасного пуска асинхронных двигателей является все же пуск посредством . Величину напряжения и частоту регулирует сам преобразователь автоматически, создавая оптимальные условия двигателю. Обороты получаются стабильными, при этом броски тока принципиально исключены.
Для каждого асинхронного двигателя может быть определен номинальный режим, т. е. режим длительной работы, при котором двигатель не перегревается сверх установленной температуры. Момент М ном, соответствующий номинальному режиму, называется. номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
n ном = n 0 (1 – s 0)= (0,94…0,98) п 0 .
Отношение максимального момента к номинальному к м = = Mmах/M ном называется перегрузочной способностью асинхронного двигателя. Обычно к т = 1,8.. .2,5.
Обычно к т = 1,8.. .2,5.
При пуске в ход, т. е. при трогании с места и при разгоне, асинхронный двигатель находится в условиях, существенно отличающихся от условий нормальной работы. Момент, развиваемый двигателем, должен превышать момент сопротивления нагрузки, иначе двигатель не сможет разгоняться. Таким образом, с точки зрения пуска двигателя важную роль играет его пусковой момент.
Отношение пускового момента М п развиваемого двигателем в неподвижном состоянии, т. е. при n = 0, к номинальному моменту k п = М п /М ном называется кратностью пускового момента.
Максимальный момент М тах называется критическим моментом асинхронной машины. Работа машины с моментом, превышающим номинальный, возможна лишь кратковременно, в противном случае срок службы машины сокращается из-за ее перегрева.
В результате взаимодействия вращающегося магнитного потока с токами, индуктированными им в проводниках роторной обмотки, возникают силы, действующие на эти проводники в тангенциальном направлении.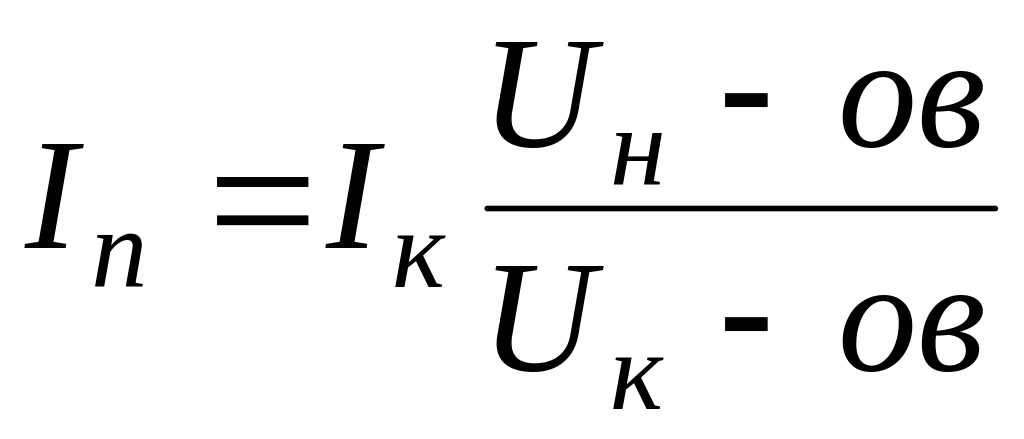 Найдем значение момента, создаваемого этими силами на валу машины.
Найдем значение момента, создаваемого этими силами на валу машины.
Электромагнитная мощность, передаваемая ротору вращающимся магнитным полем, ровна:
где М эм – электромагнитный момент действующий на ротор.
В соответствии со схемой замещения одной фазы машины:
Из этих выражений найдем:
Учитывая действующий ток ротора, ЭДС, индуктивное сопротивление получим:
Введем постоянную и пренебрегая моментом трения, представим выражение момента на валу в виде:
Если магнитный поток Ф выражен в веберах, ток I 2 – в амперах, то вращающий момент получится в ньютон-метрах (Нм).
Вращающий момент машины зависит от изменяющихся при нагрузке ф, I 2 и, но его можно представить в виде функции однойпеременной. В качестве такой переменной для асинхронного двигателя наиболее удобно выбрать скольжениеs.
Полагая, что частота сети неизменна введем
Получим следующее выражение для вращающего момента:
42. Энергетическая диаграмма АД. В электрической машине часть энергии теряется в виде тепла в различных частях – потери в обмотках, в стали, механические потери.
Энергетическая диаграмма АД. В электрической машине часть энергии теряется в виде тепла в различных частях – потери в обмотках, в стали, механические потери.
На диаграмме: Р 1 – мощность, подводимая из сети. Основная часть её за вычетом потерь в статоре, передаётся электромагнитным путём на ротор через зазор; Р эм называется электромагнитной мощностью.
Потери в статоре складываются из потерь в обмотке и в стали:
Рис. 42. Энергетическая диаграмма АД.
р с1 и р с2 . р с1 теряется на вихревые токи и перемагничивание сердечника. Потери в стали имеются и в сердечнике ротора, но они невелики и их можно не учитывать, т.к. n 0 во много раз больше скорости магнитного потока относительно ротора n 0 – n , если n соответствует устойчивой части естественной механической характеристики.
Механическая мощность, развиваемая на валу ротора, меньше Р эм на значение р об2 потерь в обмотке ротораР мх = Р эм – р об2 Мощность на валу Р 2 = Р мх – р мх, где р мх – мощность механических потерь, равная сумме потерь на трение в подшипниках, на трение о воздух и трение щеток о кольца.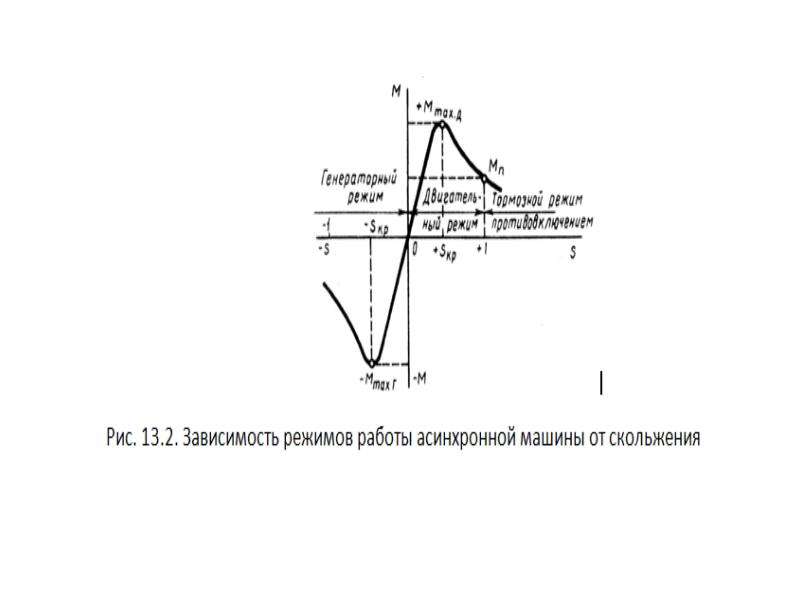
Электромагнитная и механическая Р равныР эм = ω 0 М, Р мх = ωМ , где ω 0 и ω – скорости синхронная и ротора, М – момент, развиваемый двигателей, т.е. момент, с которым вращающееся поле действует на ротор.
Добавочные потери обусловлены зубчатостью ротора и статора, вихревыми токами в различных узлах и другими причинами. При полной нагрузке потери Рд принимаются равными 0,5% его номинальной мощности.
К.п.д. двигателя: h = P 2 /P 1 = / Р 1 .
Т.к. общие потери зависят от нагрузки, то и КПД является функцией нагрузки. Машина конструируется так, чтобы максимум ее коэффициента полезного действия h имел место при нагрузке, несколько меньше номинальной. Для большинства двигателей к.п.д. равен 80-90%, а для мощных двигателей 90-96%.
43. Устройство синхронного двигателя. Схема замещения, уравнения энергетического состояния фазы обмотки статора, векторная диаграмма синхронного дв.
Основными частями статора являются неподвижный пакет магнитопровода и трехфазная обмотка. Пакет магнитопровода изготовлен в виде полого цилиндра, набранного, так же как и магнитопровод трансформатора, из тонких листов электротехнической стали. Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Пакет магнитопровода изготовлен в виде полого цилиндра, набранного, так же как и магнитопровод трансформатора, из тонких листов электротехнической стали. Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Начала и концы фаз обмотки статора присоединены к зажимам, расположенным в коробке выводов, укрепленной на корпусе. Большинство машин имеет коробку выводов с шестью зажимами, что позволяет соединять фазы обмотки треугольником или звездой.
Применяются два типа роторов синхронных машин – неявнопо-люсный, или с неявно выраженными полюсами, и ротор явнополюс-ный, или с явно выраженными полюсами.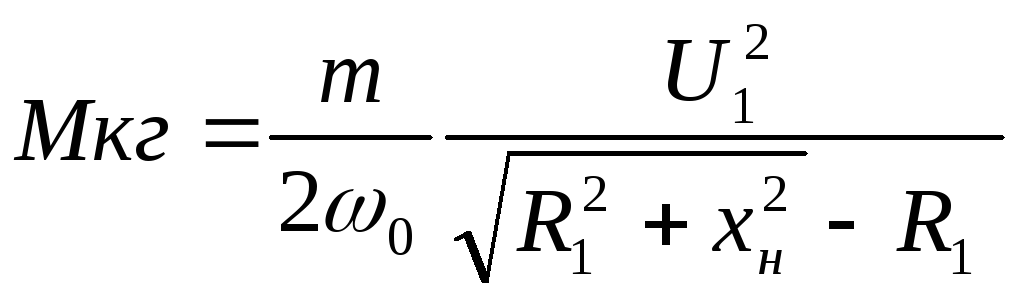 В первом случае сердечник ротора представляет массивное цилиндрическое тело из стали (бочка ротора), вдоль его поверхности выфрезерованы пазы, в которых закладывается обмотка возбуждения. Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
В первом случае сердечник ротора представляет массивное цилиндрическое тело из стали (бочка ротора), вдоль его поверхности выфрезерованы пазы, в которых закладывается обмотка возбуждения. Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
Явнополюсный ротор состоит из массивного стального колеса, посаженного на вал. К его ободу по внешней поверхности крепятся стальные сердечники полюсов. Последние, а иногда и обод выполняются из листовой стали. Для малых машин и при не слишком большом числе полюсов вместо колеса на вал насаживается стальная втулка, к которой крепятся полюса. Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
44. Регулирование реактивной мощности синхронного двигателя осуществляется изменением тока возбуждения Iв
1) Номинальный режим Iв= Iв ном. cosφ=1.
cosφ=1.
2) Iв
реактивная составляющая увеличивается, носит индуктивный характер-режим работы АСД
3) Iв> Iв ном cos φ
ток якоря увеличивается,Емкостной характер
При этом способе реактивная мощность отдается в сеть,что является большим плюсом.
Изменяя ток возбуждения меняем ток якоря.
45. Регулирование активной мощности синхронного двигателя осуществляется изменением угла согласования. При увеличении нагрузки угол увеличивается, при уменьшении- уменьшается. Угол рассогласования определяет перегрузочную способность двигателя.
Отношение максимального момента к номинальному:
46. Устройство, принцип действия двигателя постоянного тока. Способы возбуждения. ЭДС обмотки якоря и электромагнитный момент
Устройство и принцип действия двигателя постоянного тока Двигатель постоянного тока состоит из неподвижной части -статора и вращающейся части – якоря, разделенных воздушным зазором. К внутренней поверхности статора крепятся главные в добавочные полюсы. Главные полюсы с обмотками возбуждения служат для создания в машине основного магнитного потока Ф, а добавочные – для уменьшение искрения.
Главные полюсы с обмотками возбуждения служат для создания в машине основного магнитного потока Ф, а добавочные – для уменьшение искрения.
Якорь состоит из вала, сердечника, обмотки и коллектора. Коллектор содержит изолированные друг от друга медные пластины, которые соединяются с секциями обмотки якоря. На коллектор накладываются неподвижные щётки; соединяющие обмотку якоря с внешней электрической цепью. В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
Напряжение на эажимаx якоря U равно сумме ЭДС и падения напряжения на сопротивлении якорной цепи U=E +RяIя=CеФn, откуда ток якоря Iя=(U-CеФn)/Rя, а частота вращения n=(U- RяIя)/ CеФ/
В зависимости от способа питания обмотки возбуждения генераторы постоянного тока бывают:
Рис.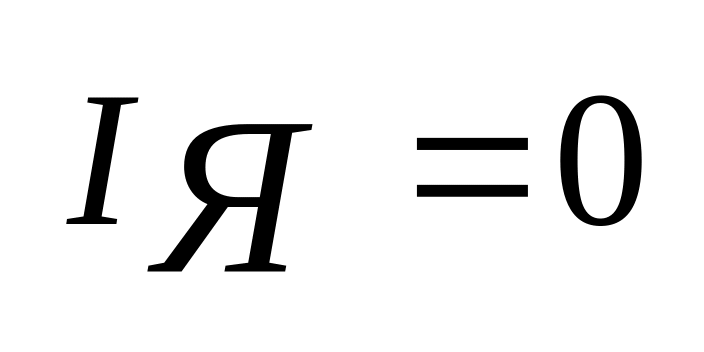 50. Возбуждение генератора: а – независимое, б – параллельное, в – последовательное, г – смешанное.
50. Возбуждение генератора: а – независимое, б – параллельное, в – последовательное, г – смешанное.
При независимом возбуждении ОВ питается от постороннего источника. Применяется в случаях, когда необходимо в широких пределах регулировать ток возбуждения I в и напряжение U на зажимах машины. Ток якоря равен току нагрузки I я = I н (рис. 50, а)
Генераторы с самовозбуждением имеют ОВ, питаемые от самого генератора.
При включении ОВ параллельно с обмоткой якоря имеем генератор с параллельным возбуждением (рис. 50, б), у которого I я = I н + I в. У мощных машин нормального исполнения I в обычно составляет 1-3%, а у малых машин – до нескольких десятков % от тока якоря. У генератора с последовательным возбуждением (рис. 50, в) ОВП включён последовательно с якорем, т.е.
I я = I н = I в.
Генераторы со смешанным возбуждением имеют две обмотки возбуждения, ОВ включёна параллельно якорю, а другая ОВП – последователь но (рис. 50, г). Основной обычно является ОВ. ОВП подмагничивает машину при увеличении тока нагрузки, чем компенсируется падение напряжения U в обмотке якоря и размагничивающее влияние реакции якоря.
ОВП подмагничивает машину при увеличении тока нагрузки, чем компенсируется падение напряжения U в обмотке якоря и размагничивающее влияние реакции якоря.
47. Нагрузочный режим двигателя постоянного тока с параллельным возбуждением. Механическая характеристика. Подадим на зажимы неподвижного якоря напряжение. Напряжение вызовет ток в цепи якоря. При этом возникает электромагнитным момент. Этот момент начнёт вращать якорь, совершая механическую работу. Машина начнет работать в режиме электродвигателя. Чтобы преодолеть сопротивление механической нагрузки на валу, электродвигателя должен потреблять энергию из внешнего источника.
48. Способы пуска двигателя постоянного тока. Нормальная машина постоянного тока имеет цилиндрический ротор с обмоткой, называемый якорем, который вращается в неподвижном магнитном поле. В витках 1-3 и 2-4 обмотки якоря индуктируются переменные ЭДС и для получения постоянного направления тока i в сопротивлении нагрузки r, применяется коллектор К, состоящий из медных изолированных друг от друга пластин, образующих цилиндр, по которому скользят щетки а – B .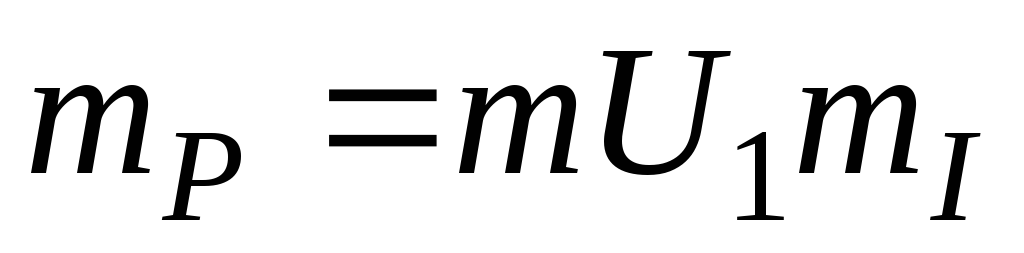 Наличие коллектора, к пластинам которого присоединяются начала и концы витков обмотки якоря, является отличительной особенностью м. п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
Наличие коллектора, к пластинам которого присоединяются начала и концы витков обмотки якоря, является отличительной особенностью м. п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
Рис. 47. Схема генератора постоянного тока с двумя витками и четырьмя коллекторными пластинами.
Конец работы –
Эта тема принадлежит разделу:
Собственная и примесная электропроводность полупроводников
Выпрямителем называется устройство предназначенное для преобразования переменного тока в постоянный Основ ным элементом выпрямителей является…
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
Для каждого асинхронного двигателя может быть определен номинальный режим, т. е. режим длительной работы, при котором двигатель не перегревается сверх установленной температуры. Момент М ном, соответствующий номинальному режиму, называется. номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
е. режим длительной работы, при котором двигатель не перегревается сверх установленной температуры. Момент М ном, соответствующий номинальному режиму, называется. номинальным моментом. Соответствующее ему номинальное скольжение составляет для асинхронных двигателей средней мощности s H0M = 0,02…0,06, т.е. номинальная скорость n иом находится в пределах
n ном = n 0 (1 — s 0)= (0,94…0,98) п 0 .
Отношение максимального момента к номинальному к м = = Mmах/M ном называется перегрузочной способностью асинхронного двигателя. Обычно к т = 1,8.. .2,5.
При пуске в ход, т. е. …
при трогании с места и при разгоне, асинхронный двигатель находится в условиях, существенно отличающихся от условий нормальной работы. Момент, развиваемый двигателем, должен превышать момент сопротивления нагрузки, иначе двигатель не сможет разгоняться. Таким образом, с точки зрения пуска двигателя важную роль играет его пусковой момент.
Отношение пускового момента М п развиваемого двигателем в неподвижном состоянии, т.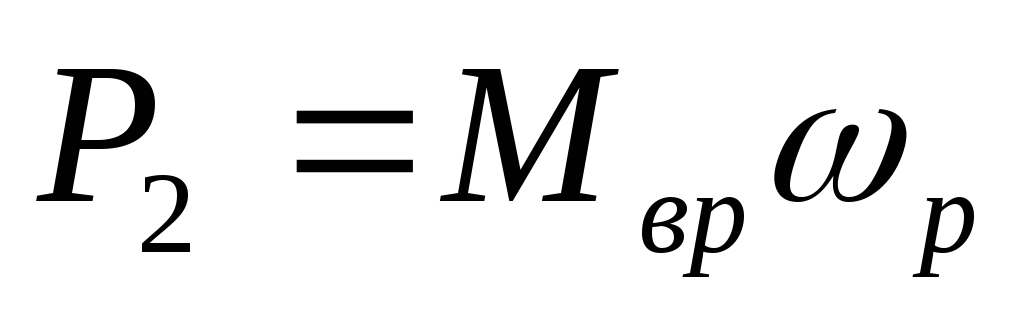 е. при n = 0, к номинальному моменту k п = М п /М ном называется кратностью пускового момента.
е. при n = 0, к номинальному моменту k п = М п /М ном называется кратностью пускового момента.
Максимальный момент М тах называется критическим моментом асинхронной машины. Работа машины с моментом, превышающим номинальный, возможна лишь кратковременно, в противном случае срок службы машины сокращается из-за ее перегрева.
В результате взаимодействия вращающегося магнитного потока с токами, индуктированными им в проводниках роторной обмотки, возникают силы, действующие на эти проводники в тангенциальном направлении. Найдем значение момента, создаваемого этими силами на валу машины.
Электромагнитная мощность, передаваемая ротору вращающимся магнитным полем, ровна:
где М эм — электромагнитный момент действующий на ротор.
В соответствии со схемой замещения одной фазы машины:
Из этих выражений найдем:
Учитывая действующий ток ротора, ЭДС, индуктивное сопротивление получим:
Введем постоянную и пренебрегая моментом трения, представим выражение момента на валу в виде:
Если магнитный поток Ф выражен в веберах, ток I 2 – в амперах, то вращающий момент получится в ньютон-метрах (Нм).
Вращающий момент машины зависит от изменяющихся при нагрузке ф, I 2 и , но его можно представить в виде функции однойпеременной. В качестве такой переменной для асинхронного двигателя наиболее удобно выбрать скольжениеs.
Тогда
Полагая, что частота сети неизменна введем
Получим следующее выражение для вращающего момента:
42. Энергетическая диаграмма АД. В электрической машине часть энергии теряется в виде тепла в различных частях — потери в обмотках, в стали, механические потери.
На диаграмме: Р 1 — мощность, подводимая из сети. Основная часть её за вычетом потерь в статоре, передаётся электромагнитным путём на ротор через зазор; Р эм называется электромагнитной мощностью.
Потери в статоре складываются из потерь в обмотке и в стали:
Рис. 42. Энергетическая диаграмма АД.
р с1 и р с2 . р с1 теряется на вихревые токи и перемагничивание сердечника. Потери в стали имеются и в сердечнике ротора, но они невелики и их можно не учитывать, т.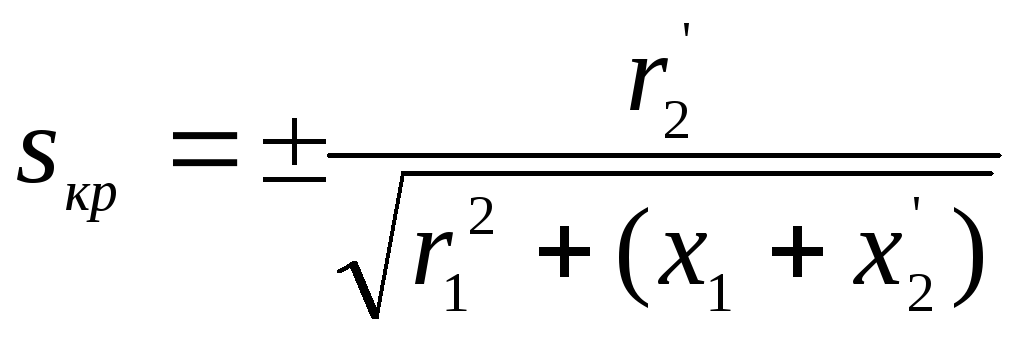 к. n 0 во много раз больше скорости магнитного потока относительно ротора n 0 — n , если n соответствует устойчивой части естественной механической характеристики.
к. n 0 во много раз больше скорости магнитного потока относительно ротора n 0 — n , если n соответствует устойчивой части естественной механической характеристики.
Механическая мощность, развиваемая на валу ротора, меньше Р эм на значение р об2 потерь в обмотке ротораР мх = Р эм — р об2 Мощность на валу Р 2 = Р мх — р мх, где р мх — мощность механических потерь, равная сумме потерь на трение в подшипниках, на трение о воздух и трение щеток о кольца.
Электромагнитная и механическая Р равныР эм = ω 0 М, Р мх = ωМ , где ω 0 и ω — скорости синхронная и ротора, М — момент, развиваемый двигателей, т.е. момент, с которым вращающееся поле действует на ротор.
Добавочные потери обусловлены зубчатостью ротора и статора, вихревыми токами в различных узлах и другими причинами. При полной нагрузке потери Рд принимаются равными 0,5% его номинальной мощности.
К.п.д. двигателя: h = P 2 /P 1 = / Р 1 .
Т.к. общие потери зависят от нагрузки, то и КПД является функцией нагрузки. Машина конструируется так, чтобы максимум ее коэффициента полезного действия h имел место при нагрузке, несколько меньше номинальной. Для большинства двигателей к.п.д. равен 80-90%, а для мощных двигателей 90-96%.
43. Устройство синхронного двигателя. Схема замещения, уравнения энергетического состояния фазы обмотки статора, векторная диаграмма синхронного дв.
Основными частями статора являются неподвижный пакет магнитопровода и трехфазная обмотка. Пакет магнитопровода изготовлен в виде полого цилиндра, набранного, так же как и магнитопровод трансформатора, из тонких листов электротехнической стали. Листы имеют форму колец с пазами, симметрично расположенными вдоль внутренней окружности. В пазы пакета статора уложены стороны многовитковых мягких катушек, образующих три фазы обмотки. Пакет статора с обмоткой запрессован в алюминиевый или чугунный корпус-оболочку, неподвижно закрепляемый при установке машины на фундаментной плите. С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
С корпусом прочно соединены два боковых литых щита со сквозными центральными отверстиями для подшипников, в которых вращается вал ротора.
Начала и концы фаз обмотки статора присоединены к зажимам, расположенным в коробке выводов, укрепленной на корпусе. Большинство машин имеет коробку выводов с шестью зажимами, что позволяет соединять фазы обмотки треугольником или звездой.
Применяются два типа роторов синхронных машин – неявнопо-люсный, или с неявно выраженными полюсами, и ротор явнополюс-ный, или с явно выраженными полюсами. В первом случае сердечник ротора представляет массивное цилиндрическое тело из стали (бочка ротора), вдоль его поверхности выфрезерованы пазы, в которых закладывается обмотка возбуждения. Пазы и обмотка возбуждения размещаются так, чтобы получить по возможности синусоидальное распределение индукции в зазоре между сердечниками ротора и статора. Общий вид неявнополюсного ротора показан на рис.
Явнополюсный ротор состоит из массивного стального колеса, посаженного на вал. К его ободу по внешней поверхности крепятся стальные сердечники полюсов. Последние, а иногда и обод выполняются из листовой стали. Для малых машин и при не слишком большом числе полюсов вместо колеса на вал насаживается стальная втулка, к которой крепятся полюса. Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
К его ободу по внешней поверхности крепятся стальные сердечники полюсов. Последние, а иногда и обод выполняются из листовой стали. Для малых машин и при не слишком большом числе полюсов вместо колеса на вал насаживается стальная втулка, к которой крепятся полюса. Обмотка возбуждения в виде катушек размещается на сердечниках полюсов. Такая конструкция ротора позволяет разместить на нем большое число полюсов, что необходимо для машин с небольшой скоростью вращения.
44. Регулирование реактивной мощности синхронного двигателя осуществляется изменением тока возбуждения Iв
1) Номинальный режим Iв= Iв ном. cosφ=1.
2) Iв
реактивная составляющая увеличивается, носит индуктивный характер-режим работы АСД
3) Iв> Iв ном cos φ
ток якоря увеличивается,Емкостной характер
При этом способе реактивная мощность отдается в сеть,что является большим плюсом.
Изменяя ток возбуждения меняем ток якоря.
45. Регулирование активной мощности синхронного двигателя осуществляется изменением угла согласования.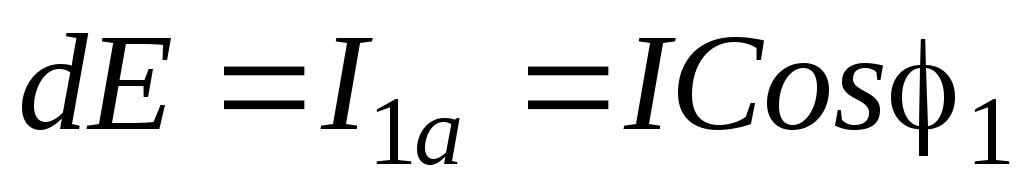 При увеличении нагрузки угол увеличивается, при уменьшении- уменьшается. Угол рассогласования определяет перегрузочную способность двигателя.
При увеличении нагрузки угол увеличивается, при уменьшении- уменьшается. Угол рассогласования определяет перегрузочную способность двигателя.
Отношение максимального момента к номинальному:
46. Устройство, принцип действия двигателя постоянного тока. Способы возбуждения. ЭДС обмотки якоря и электромагнитный момент Устройство и принцип действия двигателя постоянного тока Двигатель постоянного тока состоит из неподвижной части -статора и вращающейся части — якоря, разделенных воздушным зазором. К внутренней поверхности статора крепятся главные в добавочные полюсы. Главные полюсы с обмотками возбуждения служат для создания в машине основного магнитного потока Ф, а добавочные — для уменьшение искрения.
Якорь состоит из вала, сердечника, обмотки и коллектора. Коллектор содержит изолированные друг от друга медные пластины, которые соединяются с секциями обмотки якоря. На коллектор накладываются неподвижные щётки; соединяющие обмотку якоря с внешней электрической цепью. В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
В результата взаимодействия тока якоря Iя И магнитного потока Ф создается вращающий момент, М=СмФIя, где См- постоянная момента, зависящая от конструктивных данных машины. Вращающий момент М, двигателя уравновешивается моментом сопротивления Мс рабочей машины. При вращении якоря с частотой n его обмотка пересекает магнитный поток Ф и в ней, согласно закону электромагнитной индукции, наводится противо-ЭДС E =СеФп, где Се _ конструктивная постоянная.
Напряжение на эажимаx якоря U равно сумме ЭДС и падения напряжения на сопротивлении якорной цепи U=E +RяIя=CеФn, откуда ток якоря Iя=(U-CеФn)/Rя, а частота вращения n=(U- RяIя)/ CеФ/
В зависимости от способа питания обмотки возбуждения генераторы постоянного тока бывают:
Рис. 50. Возбуждение генератора: а — независимое, б — параллельное, в — последовательное, г — смешанное.
При независимом возбуждении ОВ питается от постороннего источника. Применяется в случаях, когда необходимо в широких пределах регулировать ток возбуждения I в и напряжение U на зажимах машины. Ток якоря равен току нагрузки I я = I н (рис. 50, а)
Ток якоря равен току нагрузки I я = I н (рис. 50, а)
Генераторы с самовозбуждением имеют ОВ, питаемые от самого генератора.
При включении ОВ параллельно с обмоткой якоря имеем генератор с параллельным возбуждением (рис. 50, б), у которого I я = I н + I в. У мощных машин нормального исполнения I в обычно составляет 1-3%, а у малых машин — до нескольких десятков % от тока якоря. У генератора с последовательным возбуждением (рис. 50, в) ОВП включён последовательно с якорем, т.е.
I я = I н = I в.
Генераторы со смешанным возбуждением имеют две обмотки возбуждения, ОВ включёна параллельно якорю, а другая ОВП — последователь но (рис. 50, г). Основной обычно является ОВ. ОВП подмагничивает машину при увеличении тока нагрузки, чем компенсируется падение напряжения U в обмотке якоря и размагничивающее влияние реакции якоря.
47. Нагрузочный режим двигателя постоянного тока с параллельным возбуждением. Механическая характеристика. Подадим на зажимы неподвижного якоря напряжение. Напряжение вызовет ток в цепи якоря. При этом возникает электромагнитным момент. Этот момент начнёт вращать якорь, совершая механическую работу. Машина начнет работать в режиме электродвигателя. Чтобы преодолеть сопротивление механической нагрузки на валу, электродвигателя должен потреблять энергию из внешнего источника.
48. Способы пуска двигателя постоянного тока. Нормальная машина постоянного тока имеет цилиндрический ротор с обмоткой, называемый якорем, который вращается в неподвижном магнитном поле. В витках 1-3 и 2-4 обмотки якоря индуктируются переменные ЭДС и для получения постоянного направления тока i в сопротивлении нагрузки r, применяется коллектор К, состоящий из медных изолированных друг от друга пластин, образующих цилиндр, по которому скользят щетки а — B . Наличие коллектора, к пластинам которого присоединяются начала и концы витков обмотки якоря, является отличительной особенностью м. п. т. В положении на рисунке стороны 1-3 витка пересекают магнитные линии перпендикулярно, поэтому между щетками будет Е мах.
Рис. 47. Схема генератора постоянного тока с двумя витками и четырьмя коллекторными пластинами.
(PDF) Анализ классических уравнений асинхронного двигателя с помощью программы Maple
Пакистанский информационный и технологический журнал 2 (2): 173-177, 2003
ISSN 1682-6027
© 2003 Asian Network for Scientific Information
173
Анализ классических уравнений асинхронного двигателя с помощью программы Maple
Эмад Саид Аддаси
Прикладной университет Аль-Балка, Колледж прикладного университета Тафила
Факультет электротехники, П.O. Box 40, Al-Eys-66141, Tafila, Jordan
Аннотация: Теория электрических машин началась в девятнадцатом веке. И многие из их исследований
имеют некоторое приближение и упрощение. Поэтому в теории электрических машин
есть аппроксимативные уравнения, но они используются до сих пор. Поэтому важно убедиться, что такие классические уравнения достаточно точны. В статье
с использованием программы Maple проводится вывод уравнений крутящего момента асинхронного двигателя,
максимального крутящего момента, а также критическое скольжение и сравнение полученных результатов с классическими уравнениями
.
Ключевые слова: электрические машины, асинхронный двигатель, классические уравнения крутящего момента, эквивалент
схема
Введение
Продолжающееся развитие больших высокоскоростных цифровых компьютеров привело к
изменениям в относительной важности различных технологий в решение электрических машин.
Цифровое компьютерное решение зависит от системы уравнений. Поэтому важно понимать формулировку уравнений
, из которых при получении решения выводится программа, за которой следует
, компьютер.
Сегодня широко используется множество различных программ.
наиболее широко используемых программных пакетов – это Mathematica, Mathcad, Matlab, Maple, Macsyma и Dirive [Diaconov, 2001,
Diaconov, 2002, C. D’Aapice, 2000]. Раньше таких программ или компьютеров не было
. Таким образом, некоторые теоретические исследования многих дисциплин имеют много приближений и
упрощений. Поэтому в теории электрических машин есть такие приближенные уравнения.
Многие исследования электрических машин выполняются на основе их схем замещения. Одна из
наиболее распространенных схем замещения для асинхронного двигателя показана на рис. 1, схема замещения
, рекомендованная IEEE [Sen P.C., 1997], где
r! Однофазное сопротивление обмоток статора;
1
х! Однофазное реактивное сопротивление утечки обмоток статора;
1
RT! Сопротивление цепи ротора (для одной фазы), относящееся к стороне статора;
2
Xt! Реактивное сопротивление утечки контура ротора (для одной фазы), относящееся к стороне статора;
2
х! Реактивное сопротивление намагничивания, вызванное взаимной индуктивностью между обмотками статора и ротора;
м
S! Промах.
Определение сопротивления ротора в режиме онлайн асинхронного двигателя с векторным управлением на основе нейронной сети
Определение сопротивления ротора было признано одним из наиболее важных факторов, влияющих на теоретические исследования и применение управления двигателями переменного тока для высокопроизводительной регулировки скорости с регулируемой частотой. В данной статье предлагается новая модель для идентификации параметров сопротивления ротора на основе нейронных сетей Элмана. Рекуррентная нейронная сеть Элмана способна выполнять аппроксимацию нелинейных функций и обладает способностью адаптации характеристик, изменяющихся во времени.Эти факторы, влияющие на указанный параметр, анализируются, соответственно, и рассматриваются различные рабочие состояния, чтобы обеспечить полноту обучающих выборок. Посредством предварительной обработки сигнала на выборках и наборе обучающих данных различные идентификации входных параметров в одной сети сравниваются и анализируются. Обученная нейронная сеть Элмана, применяемая в модели идентификации, способна эффективно прогнозировать сопротивление ротора с высокой точностью. Результаты моделирования и экспериментов показывают, что предложенный метод обладает большой адаптируемостью и очень хорошо работает в применении к асинхронным двигателям с векторным управлением.Этот метод идентификации может улучшить характеристики частотно-регулируемого регулирования скорости асинхронного двигателя.
1. Введение
Ключ к векторному управлению асинхронным двигателем заключается в ориентации магнитного поля, но одним из важных факторов, влияющих на ориентацию поля, является точность параметров ротора. Во время работы двигателя переменного тока его параметры могут изменяться под влиянием внутренних и внешних условий. Изменения температуры двигателя и частоты скольжения могут повлиять на значение сопротивления ротора; он может увеличиваться на 50% с повышением температуры и увеличиваться в несколько раз за счет скин-эффекта, если частота тока ротора высока.Кроме того, индуктивность ротора будет изменяться при магнитном насыщении. Это нелинейная зависимость между этим значением изменения и степенью магнитного насыщения; тогда постоянная времени ротора будет изменяться в зависимости от условий. Когда постоянная времени ротора сильно отклоняется от фактического значения, условия развязки управления магнитным потоком и крутящим моментом нарушаются; таким образом, динамические характеристики системы зависят от онлайн-идентификации и регулировки сопротивления ротора [1, 2]. Чтобы повысить производительность системы векторного управления асинхронным двигателем, необходимо ввести онлайн-идентификацию параметров двигателя.
Существует три основных категории онлайн-идентификации параметров: технология анализа спектра, технология на основе наблюдателя и технология адаптивной идентификации эталонной модели. Спектральный анализ принимает реакцию двигателя на введенный сигнал или информацию о гармонической характеристике на нормальный сигнал напряжения и тока. Требуемые параметры могут быть получены с помощью спектрального анализа сигнала тока или напряжения статора. Как упоминалось в [3], на основе – модели в частотной области осевая составляющая в сигнале обратной последовательности остается нулевой, так что крутящий момент двигателя не нарушается.Быстрое преобразование Фурье используется для анализа основных составляющих тока и напряжения, а также спектральных значений выборок, а результаты используются для определения параметров двигателя.
В технологии на основе наблюдателя параметры двигателя обрабатываются как расширенное состояние системы. Основные методы – это расширение фильтра Калмана (EKF) и расширенный наблюдатель Люенбергера (ELO). При условии нормальной работы асинхронного двигателя расширенная модель двигателя и метод EKF для оценки параметров двигателя описаны в [4].Для этого метода требуется сигнал конца двигателя и измерение скорости ротора. В [5] используется широкополосная гармоника, содержащаяся в выходном напряжении инвертора ШИМ, для оценки постоянной времени ротора с помощью алгоритма EKF. Расширенный обозреватель Люенбергера для оценки критического состояния и параметров двигателя описан в [6–8]. Основная проблема EKF и ELO – расчет на прочность. Чем больше количество оценок параметров расширения, тем быстрее увеличивается расчет прочности.
Характеристики метода адаптивной идентификации эталонной модели просты, но его точность зависит от точности модели. Метод, основанный на реактивной мощности, не чувствителен к изменению сопротивления статора, что является наиболее распространенным эталонным методом адаптивного управления в модели [9, 10]. Чтобы уменьшить изменение других параметров чувствительности, лучше оценить некоторые другие параметры во время адаптивной настройки. Когда рассматривается условие изменения индуктивности намагничивания со степенью насыщения двигателя, точность идентификации статора и сопротивления ротора дополнительно повышается [11–13].
Кроме того, все большее внимание уделяется онлайн-идентификации сопротивления ротора асинхронного двигателя с векторным управлением. В [14] представлен нестационарный алгоритм оценки параметров, который прост и удобен для онлайн-оценки сопротивления ротора асинхронного двигателя с быстрой сходимостью, несмотря на шум измерения, эффекты дискретизации, неопределенности параметров и неточности моделирования. Параметрическая модель выводится с помощью передаточной функции на основе стационарного состояния, и вычисление строится для вычисления множества параметров двигателя [15].Метод нечеткой логики MRAS с формами реализации предложен в [16], в котором эталонная и адаптивная модели выводятся из разных моделей, и все они зависят от гиперстатической теории Попова, но получение эталонной модели всегда сопряжено с трудностями. Система MRAS, состоящая из модели напряжения и тока ротора, представлена в [17], в которой используется ПИ-регулятор, а также подходит только для системы с датчиком.
В последние годы для идентификации параметров все чаще используется искусственная нейронная сеть.Систематически проиллюстрировано, что нейронные сети применяются к системам электропривода в [18] и дают ценные инструкции по их онлайн- и офлайн-реализации. Реализация онлайн-идентификации сопротивления ротора с помощью нейронной сети BP исследуется в [19], что обеспечивает эффективный метод. Метод идентификации параметров на основе нейронной сети Хопфилда представлен в [20], что также дает достаточные условия корректной идентификации с задержкой сигнала датчика. Кроме того, существуют нейросетевые схемы, совмещенные с вейвлет-преобразованием [21] и методом фильтра Калмана [22].Эти исследования доказали применимость нейронной сети для идентификации параметров двигателя теоретически, с помощью моделирования и на практике.
Предлагается модель идентификации сопротивления ротора на основе нейронной сети Эльмана. Нейронная сеть Элмана – это разновидность рекуррентной сети, которая теоретически может аппроксимировать любую функцию с любой точностью. Слой контекста к прямой сети добавляется как фактор задержки для запоминания состояния истории. Таким образом, эта модель обладает способностью адаптироваться к изменяющимся во времени характеристикам, напрямую отражая динамические характеристики системы, и более точным расчетом.Моделирование и эксперименты показали, что нейронная сеть Элмана подходит для решения проблемы идентификации параметров двигателя.
2. Модели асинхронного двигателя
Уравнения асинхронного двигателя в трехфазной статической координате после преобразования могут быть получены в двухфазной стационарной системе координат; также после преобразования его можно измерить в двухфазной вращающейся системе координат на любой математической модели.
Сначала представлена математическая модель в двухфазной синхронно вращающейся системе координат асинхронного двигателя.Двухфазная синхронно вращающаяся система координат является частным случаем двух произвольных координат вращения, вращающихся с синхронной скоростью, также известной как система координат MT. Уравнения математической модели с этой системой асинхронного двигателя показаны следующим образом.
Уравнение напряжения определяется как
Уравнение потока можно записать как
Уравнение крутящего момента выглядит следующим образом:
Уравнение движения может быть выражено как
Во-вторых, описывается векторное управление асинхронным двигателем в соответствии с ориентированным потоком ротора.При использовании ориентации потока ротора ось совпадает с осью потока ротора. Поскольку ось перпендикулярна оси, на оси составляющая равна нулю, а именно, поток ротора, однозначно генерируемый составляющей тока на оси. Итак, уравнения потока показаны следующим образом:
Приведенные выше уравнения преобразуются в уравнение крутящего момента.
Уравнение напряжения в системе координат, ориентированной на поток ротора, имеет вид
Асинхронный двигатель может измерять вектор напряжения, вектор тока и регулируемый регулируемый статор; следовательно, необходимо найти взаимосвязь между каждым компонентом и другими физическими измерениями значения на стороне статора: где
Три уравнения состоят из основных уравнений управления векторной системой управления асинхронным двигателем.Кроме того, для реализации схемы управления необходимы параметры двигателя, включая, и, которые тесно связаны с уровнем производительности и параметрами точности управления асинхронным двигателем.
3. Анализ факторов влияния сопротивления ротора
Основными факторами, влияющими на сопротивление ротора, можно считать ток ротора, время работы, частоту и температуру окружающей среды, и их можно выразить как где – сопротивление ротора, – ток ротора, – время работы, – частота, – температура.
Нагрев – это динамический и высокоинерционный нелинейный процесс; чем больше ток и частота скольжения в течение более длительного рабочего времени, тем больше выделяется тепла. И температура, вызванная этой причиной, в сочетании с температурой окружающей среды определяет температуру ротора. Если рабочее время выбрано в качестве входной переменной, когда двигатель достигает теплового баланса, это больше не влияет на изменение сопротивления ротора, 4 фактора уменьшаются до 3, а другой становится помехой; таким образом, точность не может быть гарантирована.Учитывая, что изменение сопротивления ротора происходит просто из-за повышения температуры, температуру конца обмотки можно выбрать в качестве комплексного ввода. Его также можно использовать в качестве важного справочного материала для диагностики неисправностей двигателя и для мониторинга состояния при выполнении идентификации.
Связь между сопротивлением ротора и температурой выражается в следующем уравнении: где – сопротивление меди при температуре окружающей среды C, – сопротивление при температуре, а – температурный коэффициент при C, который для меди.Скорость его изменения в зависимости от температуры показана на рисунке 1.
Когда переходное значение температуры конца обмотки является постоянным, на сопротивление ротора также могут влиять другие факторы, наиболее очевидным из которых является частота скольжения. Когда двигатель находится в стабильном рабочем состоянии, частота тока ротора в основном определяется сопротивлением скольжению, его значение составляет примерно 1–3 Гц, и скин-эффект, вызванный этой причиной, очень мал, и им можно пренебречь. Когда двигатель запускается или работает с большой нагрузкой, влияние скин-эффекта довольно велико, обычно в 2-3 раза больше нормального значения.Согласно [23], скорость изменения сопротивления ротора в зависимости от частоты скольжения может быть изменена квадратичной функцией в виде следующего уравнения:
Таким образом, скорость изменения сопротивления ротора в зависимости от частоты скольжения показана на рисунке 2.
4. Настройка нейронной сети Элмана и разработка параметров
Для данной задачи, какая структура сети выбрана для ее максимальной скорости обучения и лучшего результата. Эффект предсказать очень сложно. Это зависит от многих факторов, включая входные и выходные переменные, количество обучающих выборок, цель ошибки и взаимосвязь между ними.
4.1. Структура аффилированной сети
Базовая структура нейронной сети Элмана показана на рисунке 3. Ее выражение в нелинейном состоянии: где,, – количество входных переменных, нейронов скрытого слоя и нейронов выходного слоя соответственно; , являются входными и выходными векторами. “ и представляют веса между входным числом и нейроном скрытого слоя, вес между нейроном скрытого слоя и нейроном выходного слоя, а также весовую обратную связь с числом нейрона скрытого слоя., являются передаточными функциями скрытого слоя и выходного слоя соответственно. , – смещение входов разных слоев. , являются вектором вывода и вектором состояния обратной связи контекстного слоя.
Функция корректировки весов сети Элмана имеет медленную скорость сходимости и может быть захвачена на локальных минимальных значениях, и для конкретной проблемы ее алгоритм по умолчанию должен быть изменен; один из оптимизированных алгоритмов можно записать как где – пересмотренное значение на итерации, – коэффициент ускорения, – коэффициенты импульса.Согласно исследованиям, когда = 0,2–0,5, = 0,9–0,98, алгоритм имеет лучшую скорость сходимости и может избежать колебаний взад и вперед, когда поверхность кривой ошибки длинная и узкая.
Поскольку диапазон колебаний входных данных очень велик, когда они используются в качестве входных напрямую, большие входные данные часто размывают меньшие входные данные, что приводит к значительному увеличению времени обучения и снижению точности выходных данных сети. Следовательно, чтобы избежать неотъемлемых характеристик потери данных, необходимо нормализовать входные данные для повышения производительности обучения и моделирования.Характеристики обучения сети до и после нормализации показаны на рисунке 4.
(a) До нормализации
(b) После нормализации
(a) До нормализации
(b) После нормализации
Рисунок 4 (а) показывает, что до нормализации ошибка быстро падает в первые 100 эпох, но скорость ее изменения становится очень медленной; после этого его погрешность не достигла 1% в максимальных точках 1000 эпох. Рисунок 4 (b) показывает, что после нормализации скорость обучения сети значительно увеличивается и достигает цели обучения 0.Точность 1% в эпоху 102. Понятно, что разумный параметр нормализации имеет большое влияние на скорость сходимости и время обучения.
4.2. Обработка обучающих данных
Сложность идентификации параметров двигателя определяется многопараметрическими, нелинейными и сильными связными характеристиками его математической модели. Связь между параметрами, которые должны быть идентифицированы, с переменными рабочего состояния двигателя, трудно выразить функциями, некоторые факторы влияния даже не могут быть полностью изучены.Таким образом, он начинается с факторов, которые имеют четкую взаимосвязь с входной переменной, и после того, как их эффекты сравниваются и проверяются, другие потенциальные факторы влияния могут быть затем постепенно добавлены и проанализированы.
Чтобы обеспечить лучший отклик нейронной сети на различные входные данные, требуется полнота обучающих выборок. Сбор образцов данных должен производиться с учетом различных условий эксплуатации двигателя в реальных условиях, а его мощность должна быть достаточно большой, чтобы включать все характеристики целевой системы.
Здесь в качестве основных условий выбираются температура конца обмотки, частота скольжения и ток ротора, и после объединения переменных на входе определяется состояние обильной работы двигателя.
В классическом или улучшенном методе тестирования параметров двигателя сбор обучающих данных и данных проверки сети занимает очень много времени и почти не может быть завершен. Некоторые методы могут применяться для максимального использования ограниченных данных. Надежный способ – получить серию обучающих выборок традиционными методами, а затем по этим данным настроить эталонную модель сопротивления ротора.В MATLAB / Simulink есть несколько параметров, которые могут быть установлены в модели трехфазного асинхронного двигателя; таким образом, при моделировании можно получить множество данных для обучения сети, комбинируя их с установленной моделью сопротивления ротора.
В настоящий момент на сопротивление ротора влияют не только внешняя среда и внутренние факторы, но и историческое значение, такое как значение в данный момент, и. Если прошлые данные используются для наблюдения за значением в будущем, данные соседних выборок выбираются в качестве скользящего окна и сопоставляются со значениями.Создается некий перекрывающийся сегмент данных выборок. Его принцип показан на рисунке 5.
В процессе нормализации задействуется выбор максимального значения. Значение температуры можно выбрать в соответствии с классом изоляции двигателя, указанным в таблице 1.
| |||||||||||||||||||||||||||||||||||||||
Обычно максимальный пусковой ток асинхронного двигателя пусковой ток примерно в 4–7 раз превышает номинальное значение. Максимальная частота скольжения обычно появляется в момент пуска, то есть переходный процесс, поэтому выбирается максимальная частота скольжения во время работы двигателя.Здесь нормализованный параметр для температуры равен 50, частота скольжения – 25, а сопротивление ротора – 5.
5. Определение сопротивления ротора с помощью нейронной сети Элмана
Сначала температура и частота скольжения ротора используются в качестве входных параметров Элмана. нейронная сеть, чтобы проверить действие этой сети. Затем ток ротора добавляется в качестве входного параметра, чтобы убедиться, улучшились ли результаты идентификации в этой сети, и, наконец, определяется количество входных параметров в этой сети.
Для заметного фактора влияния его внутренняя нелинейная взаимосвязь отображения сильная, количество нейронов скрытого слоя Элмана может быть небольшим, а взаимосвязь между ним и шагами обучения показана в таблице 2.
| ||||||||||||||||||||||
По мере того, как количество нейронов скрытого слоя увеличивается, шаги обучения не сокращаются, а сокращаются до определенной точки, в которой эти шаги имеют тенденцию к увеличению.Разумное объяснение состоит в том, что после того, как структура сети завершает нелинейное отображение от входа к выходу, увеличение числа нейронов приводит к увеличению весов и обратных связей, которые необходимо корректировать. Чтобы достичь того же уровня ошибок, количество и сложность вычислений резко возрастают, поэтому для корректировки требуется больше шагов. Увеличенные нейроны в некоторой степени избыточны, хотя надежность сети увеличивается, но это нежелательно для реализации современных процессоров и электронных устройств.Здесь выбирается сетевая структура 2-7-1.
На рисунке 6 показано, что построенная сеть имеет хорошую производительность на входе, а ошибка в большинстве точек данных составляет менее 1%. На последних 5 пунктах ошибка увеличивается. В частности, в точке 50 он достигает 2%, что достаточно велико, чтобы оказать определенное влияние на высокую эффективность управления, но эти точки данных представляют переходный начальный период, и его ошибка приемлема для общей эффективности управления.
Когда ток добавляется в качестве входа, отношения нелинейного отображения между входом и выходом становятся более сложными, и размер сети следует увеличивать.Начиная с 7 в качестве нейронов скрытого слоя и с всесторонним учетом производительности поезда, количество нейронов скрытого слоя выбрано равным 10. Как показано на рисунке 7, уровни ошибок в большинстве точек данных превышают ± 1% и превышают 3% в последние несколько пунктов.
6. Моделирование и анализ результатов экспериментов
Экспериментальная платформа построена и показана на рисунке 8. Идентификация параметра сопротивления ротора на основе нейронной сети Элмана применяется к инвертору асинхронного двигателя.
(а) Схема системы инвертора асинхронного двигателя
(б) Экспериментальная фотография оборудования
(а) Схема системы инвертора асинхронного двигателя
(б) Экспериментальная фотография оборудования
На этой платформе параметры асинхронного двигателя: кВт, В,,,, мГн, мГн, мГн, и.
Сначала платформа моделирования разрабатывалась с помощью MATLAB / Simulink. Параметр двигателя (сопротивление ротора) определяется с помощью традиционного автономного метода и онлайн-метода нейронной сети Эльмана соответственно.Сравнение этих двух методов показано на рисунке 9.
Очевидно, что результат идентификации традиционным автономным методом не может адаптироваться к повышению температуры и изменению частоты скольжения. Его способности недостаточно для адаптации к требованию высокой производительности системы управления. Однако метод онлайн-идентификации нейронной сети Эльмана – очень хорошее решение. Он также имеет аналогичные результаты для идентификации параметров.
Моделирование изменения параметров двигателя выполняется с помощью модели двигателя на основе Simulink, показанной на рисунке 10.Отверждения потокосцепления и крутящего момента достигаются до и после изменения параметров. Кривые показывают, что изменение параметров оказывает большое влияние на работу системы управления двигателем, основанной на стационарной математической модели. Если эти параметры двигателя могут быть обновлены в реальном времени и использованы в системе управления, точность управления будет в значительной степени улучшена.
Из рисунка 10 видно, что оценка крутящего момента должна достичь стабильного значения около 0.4 секунды с заданным крутящим моментом, начиная с 50. Когда расчетная модель соответствует фактическим параметрам двигателя, пульсации крутящего момента первоначально достигают около 200%, но вскоре они становятся нормальными и более плавными. Однако, если параметры модели оценки крутящего момента отличаются от параметров двигателя, а именно, эти параметры изменяются в процессе работы двигателя и модель оценки не может их обновить, крутящий момент достигает более 450% с большим колебанием. Более того, даже если он, наконец, станет стабильным, все еще есть большие колебания относительно истинного значения в 15%.
На рисунке 11 показано, что изменение сопротивления ротора двигателя влияет на наблюдение потока. Когда модель наблюдения принимает точные параметры двигателя, наблюдаемый поток и результат измерения почти одинаковы, что лучше для отслеживания потока двигателя. Когда значение сопротивления ротора увеличивается вдвое, наблюдаемый магнитный поток имеет большие колебания при запуске двигателя, которые превышают точное значение почти 200% и стремится к точному значению при стабильности скорости с небольшими колебаниями.Когда значение сопротивления ротора увеличивается в три раза, флуктуация наблюдаемого потока все еще велика; это очевидно в стабильной фазе, около 3,5%. Когда значение сопротивления ротора увеличивается в 5 раз, наблюдаемый поток имеет очевидное колебание, достигающее примерно 6,7%. Эта ошибка является большим препятствием для повышения точности системы управления.
На рисунке 12 показаны экспериментальные результаты, включая выходное напряжение и ток инвертора с идентификацией параметра сопротивления ротора. Из этих результатов очевидно, что точность идентификации параметров двигателя играет важную роль для улучшения характеристик в системе привода с регулируемой скоростью.
(а) Форма выходного напряжения
(б) Форма выходного тока
(а) Форма выходного напряжения
(б) Форма выходного тока
7. Заключение
В этой статье рассматривается метод Предложена онлайн-идентификация параметров асинхронного двигателя на основе нейронной сети Эльмана. В качестве нейронной сети с обратной связью ее возможности по аппроксимации нелинейных функций и изменяющейся во времени адаптивности используются для решения проблем идентификации сопротивления ротора.В соответствии с различными условиями работы в реалистичной среде факторы влияния этого параметра анализируются, чтобы гарантировать полноту обучающих выборок.
Результаты моделирования и экспериментов показывают, что этот метод имеет большую применимость для идентификации параметров асинхронных двигателей. С помощью эксперимента по изменению сопротивления ротора получены кривые крутящего момента до и после изменения параметров, которые показывают, что на характеристики асинхронного двигателя с векторным управлением с установившейся математической моделью в значительной степени влияют изменения параметров.Кривые выходного напряжения и тока, полученные с экспериментальной платформы, показывают, что векторное управление с идентификацией сопротивления ротора улучшило характеристики.
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Благодарности
Авторы выражают благодарность за финансовую поддержку Университета Макао, грант No. MYRG079 (Y1-L2) -FST13-YZX. Кроме того, эта работа поддерживается ключевой программой комиссии по образованию в провинции Хэнань Китая (13A470246) и Фондом инновационных наук Хэнаньского университета науки и технологий (2013ZCX019).
Упругий критический момент для анализа бокового продольного изгиба (LTB) структурных стеклянных балок с дискретными механическими боковыми ограничениями
4.1. Проблемы проектирования
Когда подходы к расчету, изложенные в разделе 3, принимаются во внимание при расчетах LTB, открытая проблема для стеклянных элементов, безусловно, связана с фактическим воздействием реальных механических ограничений. Согласно данным, большинство из них на самом деле характеризуются геометрическими и механическими особенностями, которые часто не соответствуют идеализированным узловым упругим пружинам.
Таким образом, предварительная попытка этого проекта была посвящена оценке номинальных характеристик некоторых дискретных ограничителей, которые фактически используются для структурных стеклянных ребер крыш и фасадов. Помимо множества коммерчески доступных решений, внимание было сосредоточено на выбранной конфигурации в. Последний включает устройство из нержавеющей стали (типа сплава AISI 316) и предназначено для стеклянных оребрений общей толщиной до 19 мм. Два отверстия с шагом 100 мм используются для крепления стальных пластин к стеклянной секции.Две боковые жесткие планки для крестовины обеспечивают соединение между стеклянным ребром и ортогональными пластинами (точечное крепление , вращение ). Чтобы избежать локальных пиков напряжения в стекле, на стеклянную балку и металлические детали накладываются шайбы Teflon® (политетрафторэтилен, ПТФЭ). Такое конструктивное решение соответствует практике точечного крепления стеклянных конструкций, где могут использоваться различные низкомодульные мягкие слои. Возможные альтернативы включают нейлон, полиоксиметилен (ПОМ), этилен-пропилендиеновый мономер (EPDM) или другие каучуковые материалы [1].Соответственно, как правило, следует проводить специальные исследования для определения характеристик различных сдерживающих решений. Обычно приведенные выше подробности являются результатом точного проектирования и проверки сопротивления [1]. Учитывая, что используемые материалы с низким модулем упругости могут быть чувствительны к временным нагрузкам и температуре, их механические свойства должны быть надлежащим образом оценены с подтверждением литературных документов или экспериментов [44,45,46,47,48,49]. Однако для предварительных оценок LTB эти свойства мягкого слоя можно принять как эквивалентные линейные упругие члены.
Пример двустороннего механического фиксатора крестовины для стеклянных элементов: ( a ) глобальная сборка с вращающимися элементами; ( b ) деталь аксонометрии; ( c ) номинальные размеры (вид сверху и сбоку, значения в мм).
4.2. Анализ продольного изгиба КЭ и оценка жесткости для стеклянных стержней LR
Чтобы решить вышеуказанную проблему и оценить надежность упрощенных расчетов КЭ на основе пружин, подход к моделированию, описанный в разделе 3.4, был, таким образом, доработан с целью включения более точного описания ограничения. Детали.Пример в, в частности, был разработан на основе файлов. С механической точки зрения последний представляет собой одиночный дискретный фиксатор ( n b = 1), состоящий из двух точечных фиксаторов ( n d = 2) с определенной локальной жесткостью K d .
FE численное моделирование стеклянной балки в LTB ( n b = 1, x b = L /2): ( a ) элемент удержания с подтверждением ( b ) механические характеристики прокладок (деталь «B») и ( c ) пример локальной модели КЭ для анализа жесткости точечного крепления «детали B» (ABAQUS).
Для анализа КЭ, таким образом, использовался набор полнотелых кирпичных элементов для воспроизведения компонентов устройства. Используемые материалы (стекло и сталь) были описаны с помощью линейно-упругих конститутивных законов: E = 70 ГПа, ν = 0,23 для стекла [50] и E s = 197 ГПа, ν s = 0,3 для стали [51]. Две крестообразные пластины, похожие на, были впервые введены в сборку FE (см. A). Болты с шагом 100 мм были воспроизведены с помощью кинематических ограничений (опция «Beam MPC» из библиотеки ABAQUS), способной обеспечить жесткое осевое и вращательное ограничение для задействованных противоположных граней в области отверстий (см. Деталь «A» в).В то же время контактное взаимодействие поверхности без трения было обеспечено на смежных поверхностях стекла и стали (то есть там, где используются мягкие слои прокладки без трения).
Боковые жесткие стержни паук-устройства, наконец, были схематизированы в виде геометрических фигур прямоугольной формы. По сравнению с номинальным устройством в дюймах была принята во внимание средняя площадь поперечного сечения с учетом длины и высоты этих стержней. Над этими стержнями (см. Деталь «B» в a) были фактически введены двухточечные крепления в виде твердых дисков.Для каждого из них средняя ось располагалась на расстоянии 94 мм от внешней грани балки. Стальные пластины и соответствующие боковые стержни были идеально «связаны», что позволяло возможную относительную деформацию.
Особое внимание было уделено описанию механического взаимодействия между распорными стержнями и указанными выше точечными креплениями. С этой целью между каждой крестовиной и соответствующей верхней пластиной был введен комбинированный соединитель « осевой + поворотный » (деталь «B» на a).Такое допущение было выбрано для характеристики номинальной геометрической детали в b, где устройство и отверстие в стекле (закрепленной ортогональной стеклянной пластины) должны взаимодействовать через промежуточный зазор и мягкую прокладку. В этом отношении схематический рисунок в b адекватно воспроизводит теоретическое поведение исследуемой детали точечного крепления и данной стеклянной балки в LTB. Разъем, как обычно, на напряжение не реагирует. В противном случае ожидается, что со стороны сжатия будет постепенно разрешено возможное поперечное смещение балки.Вначале заданный зазор допускает некоторую аккомодацию локальных деформаций ( K d = 0). Когда возникает контакт между устройством болта и прилегающим мягким слоем, действительно обеспечивается определенная жесткость K d против возможных боковых деформаций балки. Этот вклад в локальную жесткость, однако, может быть подвержен локальному раздавливанию мягкого слоя, что требует особого проектирования геометрических деталей.
Надежный расчет M cr, R для данного элемента LR, согласно разделу 3, требует, чтобы в первую очередь была оценена общая упругая жесткость K для крестовины.
Для практических расчетов LTB предполагается, что каждая деталь, согласующаяся с a, b (где n b = 1 и n d = 2), является результатом множественных вкладов локальной жесткости K d (если n d > 1), который может быть размещен в разных положениях x b пролета L для проверки балки LR. Таким образом, ожидается, что совокупная жесткость K из-за механического ограничения в
где уравнение (21),
представляет собой эквивалентную жесткость для крепления в одной точке.Последний зависит от модуля Юнга используемого мягкого слоя ( E soft ), его толщины t soft и контактной поверхности при сжатии ( A soft ) в области взаимодействие между болтом и отверстием в стекле. Соответственно, специализированный экспериментальный анализ или уточненные расчеты КЭ должны поддерживать точную характеристику локального механического поведения (c). Однако до тех пор, пока расчеты ограничиваются линейно-упругим режимом, приблизительный прогноз этой локальной жесткости K d может быть получен как
Kd≈Esoft Asofttsoft,
(22)
с участием
Asoft≈tsoft 0.8Д,
(23)
и D номинальный диаметр болта.
Таким образом, ясно, что, пока изменяются входные параметры в уравнениях (22) и (23), для общей жесткости K в уравнении (20) может быть достигнуто заметно иное предсказание. Последние, кроме того, могут иметь различные эффекты жесткости и эффективность, в зависимости от геометрии проверяемой балки LR.
В этом отношении пример в показывает типичную деформированную форму для выбранной геометрии ( t = 20 мм, b = 200 мм, L = 2000 мм) и одно устройство LR в соответствии с ( n b = 1, n d = 2, x b = L /2, z b = 55 мм).Деформированная форма, в частности, относится к общей упругой жесткости K = 40 кН / м (с K T = 144 кН / м, M cr, 0 = 18,69 кНм и M T = 37,38 кНм).
Пример основной критической формы (ABAQUS) для стеклянной балки в LTB ( n b = 1, x b = L /2) с деталями LR в соответствии с.
Судя по деформированной форме (слабое ограничение), можно заметить, что паук не влияет на общий LTB-отклик стеклянной балки.Другими словами, до тех пор, пока общая жесткость K ограничена, по сравнению с K T , локальные деформации все еще допускаются для закрепленных узлов. Кроме того, можно увидеть изменение оценок критического момента для той же самой геометрии балки, пока K увеличивается. Собранные значения получены с помощью линеаризованного аналитического подхода, инструмента LTBeam и уточненной модели FE в.
Таблица 3
Сравнение изменений критического момента потери устойчивости для выбранной геометрии балки из ( n b = 1 и n d = 2) в зависимости от K (3D = три- размерный).
| M cr, R / M cr, 0 | ||||||
|---|---|---|---|---|---|---|
| K (кН / м) | Аналитический (уравнение (19)) | LTBeam (пружинная модель) | 9060 FE ||||
| 40 | 1,278 | 1,350 | 1,383 | |||
| 80 | 1,554 | 1,632 | 1,655 | 1.658 | 7251,870 | 1,885 |
По мере увеличения K эффект локальных ограничений проявляется в постепенном увеличении на M cr, R , в пределах предельных значений M cr , 0 и M T . Сравнение аналитических, LTBeam и более точных расчетов КЭ в ABAQUS показывает, что первый подход имеет тенденцию недооценивать ожидаемый эффект фиксации, в то время как общая тенденция численных расчетов в основном хорошо коррелирует.Для выбранного примера оценки на основе пружины показывают разброс менее 2% от более точной модели FE с трехмерными (3D) ограничениями.
Соответствующая проблема расчета, таким образом, представлена значением пороговой жесткости K T , описанным в уравнении (19), учитывая, что уравнения (11) – (17) были специально предложены в [32,33] для двойного симметричные стальные элементы двутаврового сечения. Эталонный аналитический подход может быть дополнительно адаптирован к прямоугольным стеклянным секциям t × b , если предполагается, что жесткость коробления в уравнении (13) уменьшается до
Iw≈Iw ∗ = Iz (b2) 4 = b3t348.
(24)
Следовательно (с G ≈ E /3 модуль сдвига стекла) исходное уравнение (13) может быть выражено как
После того, как k оценивается по уравнению (25), окончательное значение K T может быть, таким образом, вычислено с помощью уравнения (11). По сравнению с точной формулировкой (т. Е. Уравнением (13) или итерационными вычислениями с помощью инструмента LTBeam, см. Раздел 3.3), важно отметить, что уравнение (25) может привести к приблизительным прогнозам пороговой жесткости для данного элемента из стекла LR.Таким образом, на этапе проектирования следует тщательно рассмотреть, чтобы учесть эти внутренние приближения.
В этом отношении сравнительные примеры расчетов предлагаются в a для выбранных конфигураций LR, в то время как соответствующий процентный разброс Δ K T (полученный из уравнения (25) или более точных прогнозов) показан на b. Последнее, учитывая предположение уравнения (25), может привести как к положительному, так и к отрицательному разбросу (в зависимости от расстояния a * ) и даже к сильному рассеянию.Комбинация геометрических свойств балки, которую необходимо проверить, а также положение ограничителей могут повлиять на окончательный результат K T . Однако согласно c можно увидеть, что приближение в K T , вычисленное по уравнению (25), может быть эффективно адресовано (для различных геометрий стеклянной балки и положений ограничения), пока предлагаемая функция интерполяции равна учтено.
Сравнительный расчет пороговой жесткости K T для стеклянных балок LR с подтверждением ( a ) ожидаемой точности, ( b ) соответствующего разброса в процентах Δ K T , полученного на основе адаптированного подхода к расчету (Уравнение (25) с выбранными результатами, сгруппированными по L / b и a *) и ( c ) предложение по исправлению.
Крутящий момент в электрических асинхронных двигателях
Крутящий момент – это усилие поворота по радиусу – в единицах измерения Нм, в системе СИ и единицах фунт-фут в британской системе мер.
Крутящий момент, развиваемый асинхронным асинхронным двигателем, изменяется, когда двигатель ускоряется от нуля до максимальной рабочей скорости.
Заблокированный ротор или пусковой крутящий момент
Момент заторможенного ротора или Пусковой момент – это крутящий момент, развиваемый электродвигателем при запуске с нулевой скоростью.
Высокий пусковой момент более важен для приложений или машин, которые трудно запускать – например, поршневых поршневых насосов, кранов и т. Д. Более низкий пусковой момент может быть приемлем для центробежных вентиляторов или насосов, где пусковая нагрузка мала или близка к нулю.
Момент подъема
Момент подъема – это минимальный крутящий момент, развиваемый электродвигателем при его работе от нуля до скорости полной нагрузки (до того, как он достигнет точки крутящего момента срыва).
Когда двигатель запускается и начинает ускоряться, крутящий момент в целом будет уменьшаться, пока не достигнет нижней точки на определенной скорости – крутящий момент – перед тем, как крутящий момент возрастет, пока не достигнет максимального крутящего момента на более высокой скорости – пробивной момент – точка.
Момент затяжки может быть критическим для приложений, которым требуется мощность, чтобы преодолеть некоторые временные препятствия для достижения рабочих условий.
Момент разрушения
Момент разрушения – это самый высокий крутящий момент, доступный до того, как крутящий момент уменьшится, когда машина продолжает ускоряться до рабочих условий.
Крутящий момент при полной нагрузке (номинальный) или тормозной момент
Крутящий момент при полной нагрузке – это крутящий момент, необходимый для выработки номинальной мощности электродвигателя при скорости полной нагрузки.
В британских единицах измерения крутящий момент при полной нагрузке может быть выражен как
T = 5252 P л.с. / n r (1)
, где
T = полная нагрузка крутящий момент (фунт-фут)
P л.с. = номинальная мощность
n r = номинальная частота вращения (об / мин, об / мин)
В метрических единицах номинальный крутящий момент может быть выраженным как
T = 9550 P кВт / n r (2)
где
T = номинальный крутящий момент (Нм)
P кВт = номинальная мощность ( кВт)
n r = номинальная частота вращения (об / мин)
Пример – электродвигатель и тормозной момент
Крутящий момент 908 10 60 л.с. Двигатель , вращающийся со скоростью 1725 об / мин можно рассчитать как:
T fl = 5252 (60 л.с.) / (1725 об / мин)
= 182.7 фунт фут
NEMA Design
NEMA (Национальная ассоциация производителей электрооборудования) классифицировала электродвигатели по четырем различным конструкциям, в которых крутящий момент и инерция пусковой нагрузки являются важными критериями.
Ускоряющий момент
Ускоряющий момент = доступный крутящий момент двигателя – крутящий момент нагрузки
Устройства плавного пуска с пониженным напряжением
Устройства плавного пуска с пониженным напряжением используются для ограничения пускового тока, уменьшая крутящий момент заторможенного ротора или пусковой крутящий момент, и широко используются в приложениях, где трудно запускать или с ним нужно обращаться осторожно – как, например, поршневые насосы, краны, лифты и т. д.
% PDF-1.4 % 66 0 объект > эндобдж xref 66 48 0000000016 00000 н. 0000001325 00000 н. 0000001488 00000 н. 0000002065 00000 н. 0000002514 00000 н. 0000002594 00000 н. 0000002704 00000 н. 0000002807 00000 н. 0000002945 00000 н. 0000003021 00000 н. 0000003144 00000 п. 0000003220 00000 н. 0000003345 00000 н. 0000003420 00000 н. 0000003495 00000 н. 0000003571 00000 н. 0000003842 00000 н. 0000004928 00000 н. 0000005224 00000 н. 0000006325 00000 н. 0000006603 00000 н. 0000007693 00000 н. 0000007981 00000 п. 0000009083 00000 н. 0000009111 00000 п. 0000009140 00000 н. 0000009161 00000 п. 0000009949 00000 н. 0000009970 00000 н. 0000010245 00000 п. 0000011310 00000 п. 0000012136 00000 п. 0000012157 00000 п. 0000013252 00000 п. 0000013539 00000 п. 0000014244 00000 п. 0000014266 00000 п. 0000014989 00000 п. 0000015011 00000 п. 0000015840 00000 п. 0000015862 00000 п. 0000016688 00000 п. 0000016710 00000 п. 0000017498 00000 п. 0000017520 00000 н. 0000017727 00000 п. 0000001639 00000 н. 0000002043 00000 н. трейлер ] >> startxref 0 %% EOF 67 0 объект > / Контуры 70 0 R >> эндобдж 68 0 объект ĄѦk) / U (5OsS’6f ܃ C> эндобдж 112 0 объект > транслировать n6mra] `dU5nyA / yɕ ް ªF7-8V {9gBEçB ^.`6o \ R ƀBR $ I, R +! ty93S ػ DixDGbOyoD8.SQNU7lnk ~ ‘/ CC2 & b} ib * 8’ Ŝ pC28heI ݠ 47} c {F1NfnN ٗ n ܌ V @ 86J6H 쨮 `/ RȀx8 WJP * конечный поток эндобдж 113 0 объект 310 эндобдж 69 0 объект > / Шрифт> / ExtGState> / ProcSet [/ PDF / Text] >> / Содержание [92 0 R 96 0 R 100 0 R 102 0 R 104 0 R 106 0 R 108 0 R 111 0 R] / MediaBox [0 0 612 792] / CropBox [0 0 612 792] / Повернуть 0 >> эндобдж 70 0 объект > эндобдж 71 0 объект EZ \) 皔 Yo) / Родитель 70 0 р / А 80 0 Р / След. 77 0 R / C [0 0 1] >> эндобдж 72 0 объект ] Z) / Родитель 70 0 р / Назад 73 0 руб. / A 74 0 R / C [0 0 1] >> эндобдж 73 0 объект > эндобдж 74 0 объект fJ _- $ \ nJ Խ
Bentley – Документация по продукту
MicroStation
Справка MicroStation
Ознакомительные сведения о MicroStation
Справка MicroStation PowerDraft
Ознакомительные сведения о MicroStation PowerDraft
Краткое руководство по началу работы с MicroStation
Справка по синхронизатору iTwin
ProjectWise
Справка службы автоматизации Bentley
Ознакомительные сведения об услуге Bentley Automation
Сервер композиции Bentley i-model для PDF
Подключаемый модуль службы разметкиPDF для ProjectWise Explorer
Справка администратора ProjectWise
Справка службы загрузки данных ProjectWise Analytics
Коннектор ProjectWise для ArcGIS – Справка по расширению администратора
Коннектор ProjectWise для ArcGIS – Справка по расширению Explorer
Коннектор ProjectWise для ArcGIS Справка
Коннектор ProjectWise для Oracle – Справка по расширению администратора
Коннектор ProjectWise для Oracle – Справка по расширению Explorer
Коннектор ProjectWise для справки Oracle
Коннектор управления результатами ProjectWise для ProjectWise
Справка портала управления результатами ProjectWise
Ознакомительные сведения по управлению поставками ProjectWise
Справка ProjectWise Explorer
Справка по управлению полевыми данными ProjectWise
Справка администратора геопространственного управления ProjectWise
Справка ProjectWise Geospatial Management Explorer
Сведения о геопространственном управлении ProjectWise
Модуль интеграции ProjectWise для Revit Readme
Руководство по настройке управляемой конфигурации ProjectWise
Справка по ProjectWise Project Insights
ProjectWise Plug-in для Bentley Web Services Gateway Readme
ProjectWise ReadMe
Матрица поддержки версий ProjectWise
Веб-справка ProjectWise
Справка по ProjectWise Web View
Справка портала цепочки поставок
Управление эффективностью активов
Справка по AssetWise 4D Analytics
Справка по услугам AssetWise ALIM Linear Referencing Services
AssetWise ALIM Web Help
Руководство по внедрению AssetWise ALIM в Интернете
AssetWise ALIM Web Краткое руководство, сравнительное руководство
Справка по AssetWise CONNECT Edition
AssetWise CONNECT Edition Руководство по внедрению
Справка по AssetWise Director
Руководство по внедрению AssetWise
Справка консоли управления системой AssetWise
Руководство администратора мобильной связи TMA
Справка TMA Mobile
Анализ моста
Справка по OpenBridge Designer
Справка по OpenBridge Modeler
Строительное проектирование
Справка проектировщика зданий AECOsim
Ознакомительные сведения AECOsim Building Designer
AECOsim Building Designer SDK Readme
Генеративные компоненты для справки проектировщика зданий
Ознакомительные сведения о компонентах генерации
Справка по OpenBuildings Designer
Ознакомительные сведения о конструкторе OpenBuildings
Руководство по настройке OpenBuildings Designer
OpenBuildings Designer SDK Readme
Справка по генеративным компонентам OpenBuildings
Ознакомительные сведения по генеративным компонентам OpenBuildings
Справка OpenBuildings Speedikon
Ознакомительные сведения OpenBuildings Speedikon
OpenBuildings StationDesigner Help
OpenBuildings StationDesigner Readme
Гражданское проектирование
Помощь в канализации и коммунальных услугах
Справка OpenRail ConceptStation
Ознакомительные сведения по OpenRail ConceptStation
Справка по OpenRail Designer
Ознакомительные сведения по OpenRail Designer
Справка по конструктору надземных линий OpenRail
Справка OpenRoads ConceptStation
Ознакомительные сведения по OpenRoads ConceptStation
Справка по OpenRoads Designer
Ознакомительные сведения по OpenRoads Designer
Справка по OpenSite Designer
Файл ReadMe OpenSite Designer
Строительство
ConstructSim Справка для руководителей
ConstructSim Исполнительное ReadMe
ConstructSim Справка издателя i-model
Справка по планировщику ConstructSim
ConstructSim Planner ReadMe
Справка стандартного шаблона ConstructSim
ConstructSim Work Package Server Client Руководство по установке
Справка по серверу рабочих пакетов ConstructSim
ConstructSim Work Package Server Руководство по установке
Справка управления SYNCHRO
SYNCHRO Pro Readme
Энергия
Справка по Bentley Coax
Bentley Communications PowerView Help
Ознакомительные сведения о Bentley Communications PowerView
Справка по Bentley Copper
Справка по Bentley Fiber
Bentley Inside Plant Help
Справка конструктора Bentley OpenUtilities
Ознакомительные сведения о Bentley OpenUtilities Designer
Справка по подстанции Bentley
Ознакомительные сведения о подстанции Bentley
Справка по OpenComms Designer
Ознакомительные сведения о конструкторе OpenComms
Справка OpenComms PowerView
Ознакомительные сведения OpenComms PowerView
Справка инженера OpenComms Workprint
OpenComms Workprint Engineer Readme
Справка подстанции OpenUtilities
Ознакомительные сведения о подстанции OpenUtilities
PlantSight AVEVA Diagrams Bridge Help
PlantSight AVEVA PID Bridge Help
Справка по экстрактору мостов PlantSight E3D
Справка по PlantSight Enterprise
Справка по PlantSight Essentials
PlantSight Открыть 3D-модель Справка по мосту
Справка по PlantSight Smart 3D Bridge Extractor
Справка по PlantSight SPPID Bridge
Promis.e Справка
Promis.e Readme
Руководство по установке Promis.e – управляемая конфигурация ProjectWise
Руководство пользователя sisNET
Руководство по настройке подстанции– управляемая конфигурация ProjectWise
Инженерное сотрудничество
Справка рабочего стола Bentley Navigator
Геотехнический анализ
PLAXIS LE Readme
Ознакомительные сведения о PLAXIS 2D
Ознакомительные сведения о программе просмотра вывода PLAXIS 2D
Ознакомительные сведения о PLAXIS 3D
Ознакомительные сведения о программе просмотра 3D-вывода PLAXIS
PLAXIS Monopile Designer Readme
Управление геотехнической информацией
Справка администратора gINT
Справка gINT Civil Tools Pro
Справка gINT Civil Tools Pro Plus
Справка коллекционера gINT
Справка по OpenGround Cloud
Гидравлика и гидрология
Справка Bentley CivilStorm
Справка Bentley HAMMER
Справка Bentley SewerCAD
Справка Bentley SewerGEMS
Справка Bentley StormCAD
Справка Bentley WaterCAD
Справка Bentley WaterGEMS
Дизайн шахты
Помощь по транспортировке материалов MineCycle
Ознакомительные сведения по транспортировке материалов MineCycle
Моделирование мобильности
LEGION 3D Руководство пользователя
Справка по подготовке САПР LEGION
Справка по построителю моделей LEGION
Справка по API симулятора LEGION
Ознакомительные сведения об API симулятора LEGION
Справка по симулятору LEGION
Моделирование
Bentley Посмотреть справку
Ознакомительные сведения о Bentley View
Анализ морских конструкций
SACS Close the Collaboration Gap (электронная книга)
Ознакомительные сведения о SACS
Анализ напряжений в трубах и сосудов
AutoPIPE Accelerated Pipe Design (электронная книга)
Советы новым пользователям AutoPIPE
Краткое руководство по AutoPIPE
AutoPIPE & STAAD.Pro
Завод Дизайн
Ознакомительные сведения об экспортере завода Bentley
Bentley Raceway and Cable Management Help
Bentley Raceway and Cable Management Readme
Bentley Raceway and Cable Management – Руководство по настройке управляемой конфигурации ProjectWise
Справка по OpenPlant Isometrics Manager
Ознакомительные сведения о диспетчере изометрических данных OpenPlant
Справка OpenPlant Modeler
Ознакомительные сведения для OpenPlant Modeler
Справка по OpenPlant Orthographics Manager
Ознакомительные сведения для менеджера орфографии OpenPlant
Справка OpenPlant PID
Ознакомительные сведения о PID OpenPlant
Справка администратора проекта OpenPlant
Ознакомительные сведения для администратора проекта OpenPlant
Техническая поддержка OpenPlant Support
Ознакомительные сведения о технической поддержке OpenPlant
Справка PlantWise
Ознакомительные сведения о PlantWise
Реальность и пространственное моделирование
Справка по карте Bentley
Справка по мобильной публикации Bentley Map
Ознакомительные сведения о карте BentleyСправка консоли облачной обработки ContextCapture
Справка редактора ContextCapture
Файл ознакомительных сведений для редактора ContextCapture
Мобильная справка ContextCapture
Руководство пользователя ContextCapture
Справка Декарта
Ознакомительные сведения о Декарте
Справка карты OpenCities
Ознакомительные сведения о карте OpenCities
OpenCities Map Ultimate для Финляндии Справка
Карта OpenCities Map Ultimate для Финляндии Readme
Структурный анализ
Справка OpenTower iQ
Справка по концепции RAM
Справка по структурной системе RAM
STAAD Close the Collaboration Gap (электронная книга)
STAAD.Pro Help
Ознакомительные сведения о STAAD.Pro
STAAD.Pro Physical Modeler
Расширенная справка по STAAD Foundation
Дополнительные сведения о STAAD Foundation
Детализация конструкций
Справка ProStructures
Ознакомительные сведения о ProStructures
ProStructures CONNECT Edition Руководство по внедрению конфигурации
ProStructures CONNECT Edition Руководство по установке – Управляемая конфигурация ProjectWise
Индукционный генераторкак ветрогенератор
Индукционный генератор как ветроэнергетический генератор
Вращающиеся электрические машины обычно используются в ветроэнергетических системах, и большинство этих электрических машин могут работать как двигатель или как генератор, в зависимости от его конкретное приложение.Но помимо синхронного генератора , который мы рассматривали в предыдущем уроке, существует еще один более популярный тип трехфазной вращающейся машины, который мы можем использовать в качестве генератора ветровой турбины, называемый индукционным генератором .
Как синхронный генератор, так и индукционный генератор имеют аналогичное фиксированное расположение обмоток статора, которое при возбуждении от вращающегося магнитного поля выдает трехфазное (или однофазное) выходное напряжение.
Однако роторы двух машин сильно различаются: ротор асинхронного генератора обычно состоит из двух типов компоновки: «беличья клетка» или «ротор с обмоткой».
Однофазный индукционный генераторИндукционный генератор Конструкция основана на очень распространенном асинхронном двигателе с короткозамкнутым ротором, поскольку они дешевы, надежны и легко доступны в широком диапазоне электрических размеров от машин с дробной мощностью до многоцелевых. -мегаваттные мощности, что делает их идеальными для использования как в бытовых, так и в коммерческих ветроэнергетических установках с использованием возобновляемых источников энергии.
Кроме того, в отличие от предыдущего синхронного генератора, который должен быть «синхронизирован» с электрической сетью, прежде чем он сможет генерировать какую-либо электрическую энергию.Индукционный генератор может быть подключен непосредственно к электросети и приводиться в действие лопастями ротора ветряной турбины при переменной скорости ветра после того, как он будет запущен из состояния покоя.
Для экономии и надежности во многих ветроэнергетических турбинах в качестве генератора используются асинхронные двигатели, приводимые в действие механической коробкой передач для увеличения скорости вращения, производительности и эффективности. Однако индукционным генераторам требуется реактивная мощность, обычно обеспечиваемая шунтирующими конденсаторами в отдельных ветряных турбинах.
Асинхронные машины также известны как Асинхронные машины , то есть они вращаются со скоростью ниже синхронной при использовании в качестве двигателя и выше синхронной скорости при использовании в качестве генератора. Поэтому, когда он вращается быстрее, чем его нормальная рабочая скорость или скорость холостого хода, индукционный генератор вырабатывает электричество переменного тока. Поскольку индукционный генератор синхронизируется непосредственно с основной энергосистемой, то есть вырабатывает электроэнергию с той же частотой и напряжением, выпрямители или инверторы не требуются.
Тем не менее, индукционный генератор может обеспечивать необходимую мощность непосредственно в энергосистему общего пользования, но ему также необходима реактивная мощность, обеспечиваемая электросетью. Автономная (автономная) работа индукционного генератора также возможна, но недостатком здесь является то, что генератор требует дополнительных конденсаторов, подключенных к его обмоткам для самовозбуждения.
Трехфазные индукционные машины очень хорошо подходят для выработки энергии ветра и даже гидроэлектроэнергии.Индукционные машины, работая как генераторы, имеют неподвижный статор и вращающийся ротор, как и у синхронного генератора. Однако возбуждение (создание магнитного поля) ротора выполняется по-другому, и типичная конструкция ротора представляет собой структуру с короткозамкнутым ротором, в которой проводящие стержни встроены в корпус ротора и соединены друг с другом на своих концах посредством закорачивающих колец, как показано на рисунке. .
Конструкция индукционного генератора
Как уже упоминалось в начале, одним из многих преимуществ асинхронной машины является то, что ее можно использовать в качестве генератора без каких-либо дополнительных схем, таких как возбудитель или регулятор напряжения, когда он подключен к трех -фазное питание от сети.Когда неработающий асинхронный генератор подключен к сети переменного тока, в обмотке ротора индуцируется напряжение, аналогичное трансформатору с частотой этого индуцированного напряжения, равной частоте приложенного напряжения.
Поскольку токопроводящие стержни ротора с короткозамкнутым ротором закорочены, вокруг них протекает большой ток, и внутри ротора создается магнитное поле, заставляющее машину вращаться.
Поскольку магнитное поле обоймы ротора следует за магнитным полем статора, ротор ускоряется до синхронной скорости, установленной частотой питания сети.Чем быстрее вращается ротор, тем меньше результирующая относительная разница скоростей между обоймой ротора и вращающимся полем статора и, следовательно, напряжение, наведенное на его обмотку.
Когда ротор приближается к синхронной скорости, он замедляется, поскольку ослабляющее магнитное поле ротора недостаточно для преодоления потерь на трение ротора в режиме холостого хода. В результате ротор теперь вращается медленнее, чем синхронная скорость. Это означает, что асинхронная машина никогда не сможет достичь своей синхронной скорости, поскольку для ее достижения не будет индуцированного тока в короткозамкнутой обойме ротора, магнитного поля и, следовательно, крутящего момента.
Разница в скорости вращения между вращающимся магнитным полем статора и фактической скоростью ротора в асинхронных машинах обычно называется «скольжением».
Для обеспечения крутящего момента на валу ротора необходимо наличие скольжения . Другими словами, «проскальзывание», которое является описательным способом объяснения того, как ротор постоянно «откатывается» от синхронизации, представляет собой разницу в скорости между синхронными скоростями статоров, выражаемую как: n s = ƒ / P в об / мин, а фактическая частота вращения роторов n R также в об / мин и выражается в процентах (скольжение в%).
Тогда дробное скольжение s асинхронной машины определяется как:
Это скольжение означает, что работа индукционных генераторов, таким образом, является «асинхронной» (несинхронизированной), и чем тяжелее нагрузка, подключенная к асинхронному генератору, тем больше это приводит к скольжению, поскольку более высокие нагрузки требуют более сильных магнитных полей. Большее скольжение связано с большим наведенным напряжением, большим током и более сильным магнитным полем.
Таким образом, для того, чтобы асинхронная машина работала как двигатель, ее рабочая скорость всегда будет меньше скорости вращения поля статора, а именно синхронной скорости.Чтобы асинхронная машина работала как генератор, ее рабочая скорость должна быть выше номинальной синхронной скорости, как показано на рисунке.
Характеристики крутящего момента / скорости асинхронной машины
В состоянии покоя вращающееся магнитное поле статора имеет одинаковую скорость вращения по отношению как к статору, так и к ротору, поскольку частота токов ротора и статора одинакова, поэтому в состоянии покоя скольжение положительно и равно единице (s = +1).
При точно синхронной скорости разница между скоростью вращения и частотой ротора и статора будет равна нулю, поэтому при синхронной скорости никакая электрическая энергия не потребляется и не производится, и поэтому скольжение двигателя равно нулю (s = 0 ).
Если частота вращения генератора превышает эту синхронную скорость с помощью внешних средств, результирующий эффект будет заключаться в том, что ротор будет вращаться быстрее, чем вращающееся магнитное поле статора, и полярность индуцированного напряжения и тока ротора будет обратной.
В результате скольжение теперь становится отрицательным (s = -1), и индукционная машина генерирует ток с опережающим коэффициентом мощности обратно в электрическую сеть. Мощность, передаваемая в виде электромагнитной силы от ротора к статору, может быть увеличена простым вращением ротора быстрее, что затем приведет к увеличению количества вырабатываемой электроэнергии.Характеристики крутящего момента асинхронного генератора (s = от 0 до -1) являются отражением характеристик асинхронного двигателя (s = от +1 до 0), как показано.
Скорость индукционного генератора будет изменяться в зависимости от силы вращения (момента или крутящего момента), приложенной к нему энергией ветра, но он будет продолжать вырабатывать электричество до тех пор, пока его скорость вращения не упадет ниже скорости холостого хода. На практике разница между скоростью вращения при пиковой генерирующей мощности и на холостом ходу (синхронная скорость) очень мала, всего несколько процентов от максимальной синхронной скорости.
Например, 4-полюсный генератор с синхронной частотой вращения холостого хода 1500 об / мин, подключенный к электросети с током 50 Гц, может производить свою максимальную генерируемую мощность, вращаясь только на 1–5% выше (от 1515 до 1575). об / мин), что легко достигается с помощью коробки передач.
Это очень полезное механическое свойство: генератор будет немного увеличивать или уменьшать свою скорость при изменении крутящего момента. Это означает, что редуктор будет меньше изнашиваться, что снижает потребность в техническом обслуживании и увеличивает срок службы, и это одна из наиболее важных причин для использования индукционного генератора , а не синхронного генератора на ветряной турбине, которая подключается напрямую. к электросети.
Автономная индукционная машина
Выше мы видели, что индукционный генератор требует намагничивания статора от электросети, прежде чем он сможет вырабатывать электричество. Но вы также можете запустить индукционный генератор в автономной автономной системе, подав необходимый противофазный ток возбуждения или намагничивания от конденсаторов возбуждения, подключенных к клеммам статора машины.
Это также требует наличия некоторого остаточного магнетизма в пластинах железа ротора при запуске турбины.Типичная схема трехфазной индукционной машины с короткозамкнутым ротором для автономного использования показана ниже. Конденсаторы возбуждения показаны звездой (звездой), но также могут быть подключены треугольником (треугольником).
Конденсаторный индукционный генератор с запуском
Конденсаторы возбуждения представляют собой стандартные конденсаторы для запуска двигателя, которые используются для обеспечения необходимой реактивной мощности для возбуждения, которая в противном случае обеспечивалась бы электросетью. Индукционный генератор будет самовозбуждаться при использовании этих внешних конденсаторов только в том случае, если ротор имеет достаточный остаточный магнетизм.
В режиме самовозбуждения на выходную частоту и напряжение генератора влияют частота вращения, нагрузка турбины и значение емкости конденсаторов в фарадах. Затем, чтобы произошло самовозбуждение генератора, должна быть минимальная скорость вращения для значения емкости, используемой на обмотках статора.
«Самовозбуждающийся индукционный генератор» (SEIG) является хорошим кандидатом для использования в ветроэнергетических установках, особенно при переменной скорости ветра и удаленных районах, поскольку им не требуется внешний источник питания для создания магнитного поля.Трехфазный индукционный генератор можно преобразовать в однофазный индукционный генератор с регулируемой скоростью, подключив два конденсатора возбуждения к трехфазным обмоткам. Одно из значений емкости C на одной фазе и другое значение 2C емкости на другой фазе, как показано.
Однофазный выход от трехфазного индукционного генератора
Благодаря этому генератор будет работать более плавно, работая с коэффициентом мощности (PF), близким к единице (100%). В однофазном режиме можно получить КПД, близкий к трехфазному, что составляет примерно 80% от максимального номинала машины.Однако следует соблюдать осторожность при преобразовании трехфазного источника питания в однофазный, поскольку выходное линейное напряжение однофазной сети будет вдвое больше номинального напряжения обмотки.


 donntu.org/handle/123456789/25156
donntu.org/handle/123456789/25156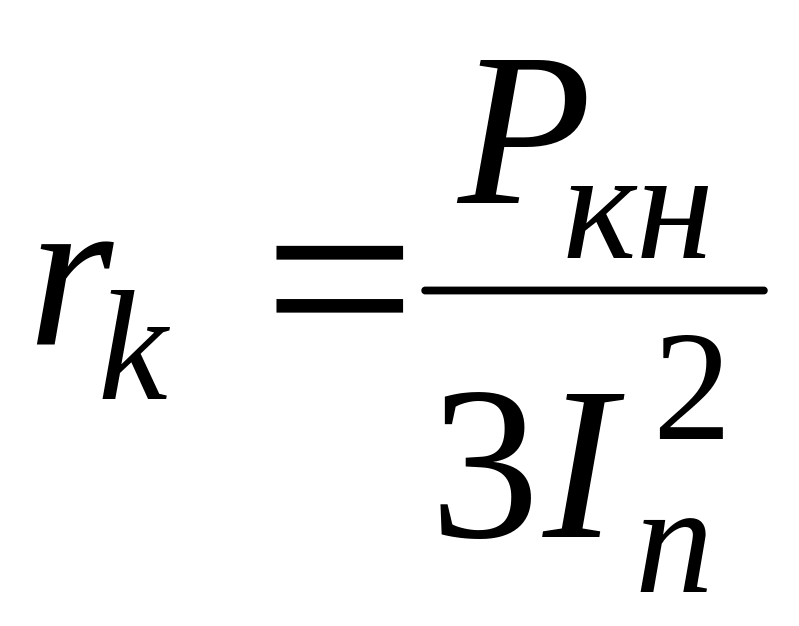 pdf
pdf