Универсальный внешний накопитель для всех iOS-устройств, совместим с PC/Mac, Android
Header Banner
8 800 100 5771 | +7 495 540 4266
c 9:00 до 24:00 пн-пт | c 10:00 до 18:00 сб

Lc фильтр калькулятор онлайн: Расчёт LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.

0 Comments

Содержание

Расчёт LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ.

Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC – фильтров, а также фильтров для акустических систем

LC – фильтры я оставил на десерт, подобно бутылке благородного вина, покрытой слоем вековой пыли. Это антиквариат, причём наиболее древним из семейства фильтров, построенных при помощи индуктивностей и ёмкостей, является параллельный LC колебательный контур, изображённый на Рис.1.
Частотная зависимость коэффициента передачи такого LC контура соответствует характеристике резонансного полосового фильтра. Именно с этого самого простого LC-фильтра мы и начнём расчёт.

Как уже было сказано – LC контур, включённый по схеме, приведённой на Рис.1, представляет собой узкополосный полосовой резонансный фильтр, настроенный на частоту:
fо= 1/(2π√LС).


На резонансной частоте сопротивление контура равно:
Rо = pQ, где р – это характеристическое сопротивление колебательного контура, численно равное: р = √L/C, а
Q = fо/Δf – это параметр добротности LC контура, определяющий полосу пропускания фильтра по уровню 3 дБ.
Рис.1

А рассчитать добротность контура можно по формуле Q = p/Rпот = (√L/C)/Rпот,
где Rпот – это сумма сопротивлений потерь:
а) в катушке индуктивности (в первом приближении = активному сопротивлению катушки) и
б) в конденсаторе (сопротивление потерь в диэлектрике).

На низких частотах конденсаторы практически не вносят потерь, поэтому добротность контура равна добротности катушки индуктивности, величина которой напрямую зависит от активного сопротивления катушки.

Чем ниже частота, тем больше витков и тоньше провод, тем проще его измерить активное сопротивление тестером.
На радиочастотах значение активного сопротивления катушки может составлять доли ома. Поэтому для расчёта добротности надо: либо найти сопротивление катушки в Омах по формуле R= 4ρ*L/(πd²), где ρ — удельное сопротивление меди, равное 0,017 Ом•мм²/м, L – длина в метрах, d – диаметр провода в мм. Либо (и лучше) – вооружиться генератором сигналов, каким-либо измерителем уровня выходного сигнала с высоким внутренним сопротивлением, и определить добротность контура экспериментально.
Это решение является более правильным в связи с тем, что на высоких частотах на сопротивление потерь начинают влиять и другие факторы, в частности потери в конденсаторе, особенно если он окажется варикапом.

Нарисуем табличку с расчётом фильтра для низкочастотных приложений.

ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ НЧ.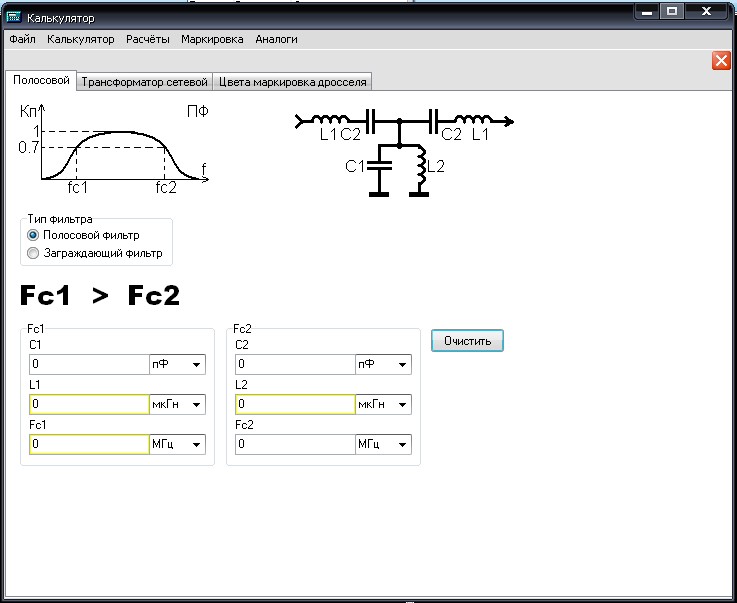

Если параметр активного сопротивления катушки R опущен, его значение принимается равным 100 Омам.
Необходимо отметить, что все полученные в таблице данные верны и для последовательного колебательного контура. При этом, если мы хотим использовать свойства контура полностью, т. е. получить острую резонансную кривую, соответствующую конструктивной добротности, то параллельный контур надо нагружать слабо, выбирая R1 и Rн намного больше Rо (на практике десятки-сотни кОм), для последовательного же контура, сопротивление генератора R1 наоборот должно быть на порядки меньше характеристического сопротивления ρ.

Теперь, нарисуем таблицу для расчёта высокочастотных резонансных контуров.

Тут на добротность влияет не только активное сопротивление катушек, но и другие факторы, такие как – потери в ферритах, наличие экрана, эффект близости витков и т. д. Поэтому вводить этот параметр в качестве входного я не стану – будем считать, что добротность катушки вы измерили, или подсмотрели в документации на готовые катушки. Естественным образом значение добротности катушки должно измеряться на резонансной частоте контура, ввиду прямой зависимости этой величины от рабочей частоты (Q=2πfL/R).
К тому же я добавлю сюда параметр добротности конденсатора, особенно актуальный в случае применения варикапов.
По умолчанию (для желающих оставить эти параметры без внимания), добротность катушки примем равной 100, конденсатора – 1000, а для испытывающих стремление измерить эти параметры в радиолюбительских условиях, рекомендую посетить страницу   ссылка на страницу .

ТАБЛИЦА ДЛЯ LC- РЕЗОНАНСНОГО (ПОЛОСОВОГО) ФИЛЬТРА ДЛЯ ВЧ.

Теперь плавно переходим к LC фильтрам верхних и нижних частот (ФВЧ и ФНЧ).

Рис.2

В полосе пропускания коэффициент передачи по напряжению данных фильтров близок к единице при условии R1 Однако оптимальные параметры, с точки зрения равномерности АЧХ и передачи максимальной мощности в нагрузку, обеспечиваются при R1 = Rн = ρ. В этом случае фильтр является согласованным, правда коэффициент передачи в полосе пропускания становится равным К=0.5.

Номиналы элементов и параметры ФВЧ и ФНЧ вычислим для согласованных LC фильтров. За частоту среза, как водится, примем частоту, на которой ослабление сигнала составляет 3дБ. Крутизна спада АЧХ в полосе подавления таких фильтров составляет 12 дБ/октаву.

Ну да ладно, ближе к делу.

ТАБЛИЦА LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.


А если надо рассчитать L и C при известных значениях Fср и ρ?

ТАБЛИЦА РАСЧЁТА ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.

В последнее время мне на почту приходит всё большее количество вопросов по поводу LC-фильтров для акустических систем. Т. е. фильтров, для которых входным источником является усилитель с практически нулевым внутренним сопротивлением, а нагрузкой – динамическая головка, обладающая неким (условно примем) активным импедансом.
Естественно, что расчёт элементов, выполненный с помощью приведённых выше калькуляторов для согласованных цепей, ожидаемых результатов не даст ни с точки зрения частоты среза фильтра, ни с точки зрения – равномерности его АЧХ. Поэтому вдогонку размещу-ка я и калькулятор для расчёта НЧ-ВЧ фильтров для акустики, либо каких иных приложений, где величина сопротивления источника имеет величину значительно меньшую, чем Rн.

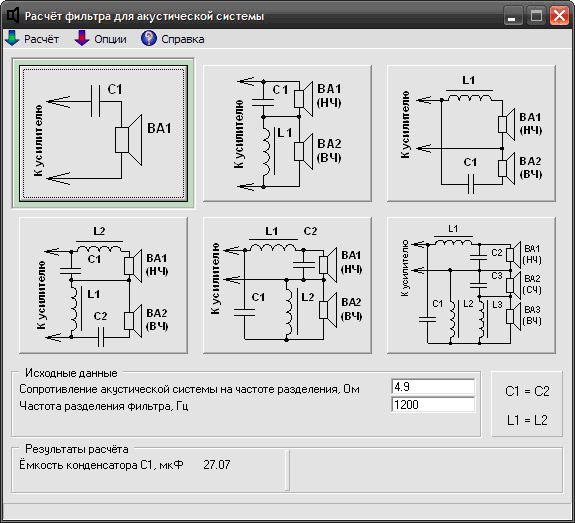
Плюсом этих фильтров является близкий к единице коэффициент передачи сигнала, минусом – меньшая (чем у согласованных) крутизна спада АЧХ в полосе подавления, которая составляет 10 против 12 дБ/октаву.

РАСЧЁТ ЭЛЕМЕНТОВ LC- ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ для АКУСТИКИ и прочего.

Фильтры, посчитанные на последнем калькуляторе, являются фильтрами Баттерворта 2-го порядка. А желающим рассчитать акустические ФВЧ, ФНЧ и ПФ различных типов и порядков предлагаю посетить страницу: ссылка на страницу.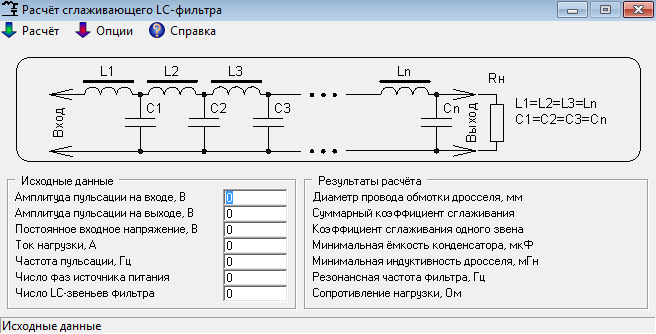

Приведённые выше ФВЧ и ФНЧ называются Г-образными.
Для получения более крутых скатов АЧХ используют два или более согласованных Г-образных звеньев, соединяя их последовательно, чтобы образовать Т-образное звено (на Рис.3 сверху), или П-образное звено (на Рис.3 снизу). При этом получаются ФНЧ третьего порядка. Обычно, ввиду меньшего количества катушек, предпочитают П-образные звенья.


Рис.3

ФВЧ конструируют подобным же образом, лишь катушки заменяются конденсаторами, а конденсаторы – катушками.

Широкополосные полосовые LC – фильтры получают каскадным соединением ФНЧ и ФВЧ.

Что касается многозвенных LC-фильтров высоких порядков, то более грамотным решением (по сравнению с последовательным соединением фильтров низших порядков) будет построение подобных устройств с использованием полиномов товарищей Чебышева или Баттерворта.

Именно такие фильтры 3-го, 5-го и 7-го порядков мы и рассмотрим на следующей странице.

 

Онлайн расчёт многозвенных LC – фильтров. Калькулятор ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков.

Одиночный LC-фильтр, как ни бейся, не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области обычно используют многозвенные LC – фильтры.
Причём фильтры чётных порядков при равенстве сопротивлений источника и нагрузки вообще теряют актуальность, ведь добавлением всего одного конденсатора они превращаются в фильтр более высокого порядка.

В низкочастотной схемотехнике LC-фильтры фильтры решительно теряют позиции в пользу активных фильтров высоких порядков, за исключением, пожалуй, сглаживающих фильтров источников питания, LC-фильтров акустических систем, да изредка НЧ фильтров приёмников прямого преобразования.

Зато на непаханых полях радиочастотных диапазонов свободного пространства хоть отбавляй. То-то раздолье тут земледельцу! По левую руку – входные фильтры приёмников и трансиверов, по правую – фильтры выходных каскадов передатчиков, посередине …
А что, собственно говоря, посередине?
Да всё, что угодно, поля-то – непаханые.

Описания свободных и вынужденных колебаний в электрических цепях, и иже с ними дисперсионные и характеристические уравнения систем различных аппроксимаций оставим бедолагам студентам, а сами играючи воспользуемся таблицами элементов LC фильтров-прототипов, приведённых в справочнике по расчёту фильтров Г. Ханзела.

Как правило, с точки зрения минимизации количества катушек индуктивности, в многозвенных фильтрах используют П-образную схему для ФНЧ и Т-образную для ФВЧ.

На Рис.1 приведены схемы подобных фильтров нижних и верхних частот 3-го, 5-го и 7-го порядков.

Рис. 1

Расчёт поведём доверившись многочленам Пафнутия Львовича нашего Чебышёва.
Почему на сей раз Чебышева, а не вездесущего Баттерворта?

Ответ не сложен – в погоне за максимальным наклоном переходного участка, в жертву некоторой неравномерности АЧХ фильтра в полосе пропускания.

При одном и том же числе элементов схемы у фильтров Чебышева крутизна характеристики ослабления в полосе задерживания значительно больше, чем у фильтров Баттерворта и может составлять величину 8,5дб на октаву (против менее 6 дБ/окт) на каждый порядок фильтра.
Значение же неравномерности в полосе пропускания можно ограничивать, выбирая коэффициенты из таблицы фильтра – прототипа. Я посчитал, что неравномерность 0,28дБ окажется вполне приемлемой.

Ну и хватит, переходим к таблице.

ТАБЛИЦА РАСЧЁТА МНОГОЗВЕННЫХ ФИЛЬТРОВ ВЕРХНИХ и НИЖНИХ ЧАСТОТ.

И как обычно не забываем – многозвенные полосовые LC-фильтры получаются каскадным соединением ФНЧ и ФВЧ, тем более что они отлично друг с другом согласуются.

Ну а если полученный спад амплитудной характеристики не кажется слишком крутым, то нам прямая дорога к эллиптическим фильтрам, которые мы и посчитаем на следующей странице.

 

Фильтр LC. Расчет. Калькулятор. Катушка. Мои закладки.

Фильтр LC. Расчет. Калькулятор. Катушка. Мои закладки.

Фильтр LC. Расчет. Калькулятор. Катушка. Мои закладки.

Расчет LC. Резонанс колебательного контура. Фильтр.

Расчет частоты резонанса колебательного контура … Калькулятор расчета резонанса в контуре … Расчет частоты резонанса колебательного контура. Колебательный контур LC. Свободные электрические колебания в параллельном контуре. Расчёт частоты резонанса LC-контура, простой онлайн-калькулятор …

Coil32 – On-line калькуляторы витков катушки, расчет однослойной индуктивности … Калькулятор расчета однослойной катушки индуктивности .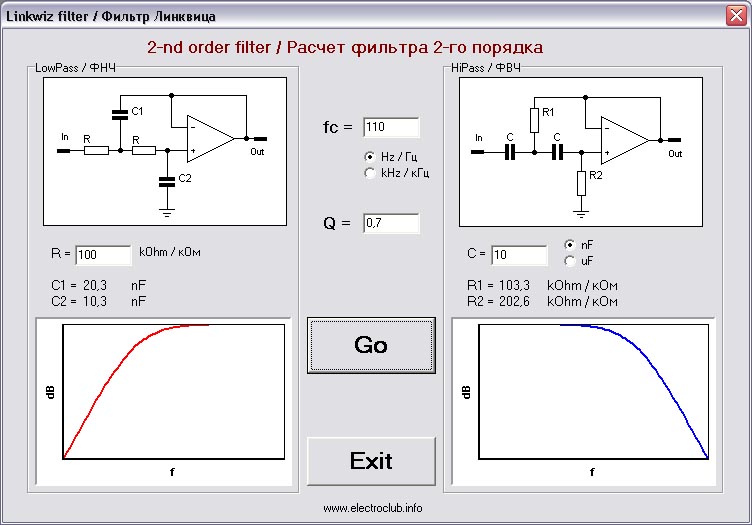 .. Расчет Катушка Индуктивность Витки : On-line калькуляторы. Расчет однослойной катушки …

Свойства катушек индуктивности … Электричество и магнетизм. Общая электротехника и электроника. Расчет Индуктивность Свойства. Свойства катушек индуктивности. Электричество и магнетизм. Общая электротехника и электроника. Накопленная энергия в индуктивности. Гидравлическая модель. Индуктивность в электрических цепях. Схемы соединения катушек индуктивностей. Параллельное соединение индуктивностей. Последовательное соединение индуктивностей. Добротность катушки индуктивности. Катушка индуктивности. Формула индуктивности. Базовая формула индуктивности катушки. Индуктивность прямого проводника. Индуктивность катушки с воздушным сердечником. Индуктивность многослойной катушки с воздушным сердечником. Индуктивность плоской катушки. Конструкция катушки индуктивности. Применение катушек индуктивности. Расчет катушек индуктивности. Метод определения собственной емкости катушек. Расчет и изготовление плоских катушек индуктивности . ..

Емкость. Свойства. Расчет. Электростатика … Электричество и магнетизм. Общая электротехника и электроника. Электростатические машины и лейденская банка. Диэлектрики. Диэлектрическая проницаемость. Проводники. Коммутационные устройства. Удельное сопротивление. Резисторы. Разность потенциалов. Электрическая емкость, конденсаторы. Индуктивные элементы. Свойства катушек индуктивности. Постоянный ток. Источники постоянного тока и напряжения (ЭДС). О реальных явлениях электромагнетизма …

Индуктивные элементы … Электричество и магнетизм. Общая электротехника и электроника. Индуктивные элементы … Расчет Идуктивность Свойства. Индуктивные элементы. Катушки индуктивности и трансформаторы. Катушки контуров. Катушки связи. Дроссели высокой частоты. Дроссели низкой частоты …

Онлайн расчёт RC фильтров … RC-фильтры … Расчет Фильтр ФНЧ ФВЧ. Онлайн расчёт RC фильтров. Схема и частотная характеристика. Частота среза фильтра. RC-фильтры предстваляют собой цепочку, состоящую из резистора и конденсатора. В зависимости от их расположения фильтр пропускает или верхние или нижние частоты …

Расчёт LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ … Онлайн калькулятор LC фильтров … Расчет LC – фильтров. Онлайн калькулятор ПФ, ФВЧ, ФНЧ. Калькуляторы ФНЧ, ФВЧ, резонансных, полосовых LC фильтров. Индуктивность катушки. Активное сопротивление катушки. Емкость конденсатора. Резонансная частота фильтра. Добротность фильтра Q. Характеристическое сопротивление. Полоса пропускания фильтра …

Многозвенные LC фильтры … Онлайн калькулятор многозвенных полосовых LC фильтров … Расчет ФНЧ ФВЧ 3 5 7 порядка – Т и П типа. Онлайн расчёт многозвенных LC – фильтров. Калькулятор ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков. Фильтр Чебышева. Фильтр Баттерворта. Одиночный LC фильтр не может обеспечить достаточного подавления сигналов вне заданного диапазона частот, поэтому для формирования более крутой переходной области обычно используют многозвенные LC фильтры …

Режекторные эллиптические фильтры образуют конденсаторы, установленные катушкам – параллельно в ФНЧ или последовательно в ФВЧ . .. Онлайн калькулятор многозвенных элиптических LC фильтров … Расчет фильтр эллиптический Кауэра. Онлайн расчёт многозвенных эллиптических LC – фильтров Кауэра ПФ, ФВЧ, ФНЧ 3-го, 5-го и 7-го порядков. Крутизна спада амплитудной характеристики линейных фильтров показала себя недостаточно. В отличии от классических линейных аналогов наличие дополнительных конденсаторов, включенных параллельно в ФНЧ (или последовательно в ФВЧ) катушкам индуктивности – образуют режекторные фильтры и формируют дополнительную крутизну спада АЧХ эллиптических фильтров …

Онлайн калькулятор полосовых LC фильтров … Онлайн калькулятор, расчет полосовых LC фильтров 3 / 5 / 7 порядка … Калькулятор полосовых LC фильтров Чебышева … Полосовой, он же полосно-пропускающий фильтр – это фильтр, пропускающий частоты в некоторой полосе, находящейся между нижней и верхней частотами среза … Он может быть легко представлен в виде последовательности, состоящей из ФНЧ / фильтра нижних и ФВЧ / фильтра верхних частот . ..

Калькулятор.

Калькулятор геодезических куполов, 3D дизайн со вращением мышью, расчет размеры … Расчет купольного дома из треугольников … Интересный купольный сферический дом предлагают самостоятельно изготовить из обычных треугольников … Для его расчета можно воспользоваться онлайн калькулятором … Чем больше треугольников – тем, получится, более округлая сфера …

Планета калькуляторов, онлайн калькуляторы … Онлайн калькулятор – Сегмент круга … Вычисление сегмента по хорде и высоте … Площадь сегмента круга по радиусу и высоте … Круговой сегмент – все варианты расчета …

Формулы – геометрия, алгебра, физика … Формулы круга … Все основные формулы для определения длины радиуса окружности. Окружность и круг. Радиус окружности. Длина хорды окружности. Высота сегмента круга. Площадь круга. Длина окружности. Онлайн калькуляторы для расчета …

Сервис бесплатных строительных калькуляторов … Адаптация расчетов под мобильные телефоны и Android . .. Строительные калькуляторы … Общестроительные работы, калькулятор нагрузки, металл, железобетон, дерево, инженерные коммуникации, отделка, расчет размеров, теплотехника, электрика. Перевод единиц измерения …

Некоторые полезные онлайн калькуляторы … Интерактивные утилиты преобразования … Калькулятор / конвертер … Конвертер цифровой базы. Конвертер текущая дата / время GMT. Координаты, современный вариант Lat / Lon в NMEA 0183 dddd.mmmm, HASH строки, Конвертер HEX / DEC / Строка …

Закон Ома. Онлайн калькулятор. Учеба и наука, Физика … Онлайн калькулятор – закон Ома … Закона Ома определяет связь между током, напряжением и сопротивлением в электрических цепях …

Конвертер.

Base64 Decode и Encode – Online … Base64 – декодирование и кодирование … Калькулятор / конвертер Base64 Decode / Encode …

Алфавит Base32 и Base64 … Гари Кесслер Ассошиэйтс … Обучение, образование и консалтинговые услуги … Алфавит Base32 (5-бит), Base64 (6-бит) из RFC4648 . ..

Integer Base конвертер для программистов на C# … Системы счисления на базе 2 10 16, перевод … Если вы программист, вы знаете разные системы счислений. В повседневной жизни нас обычно устраивает система счисления на базе 10. Но компьютерный мир совсем другой. Бинарный характер хранения данных на компьютере двоичная система на базе 2 и числа длинной двоичной строки – читать нелегко. Шестнадцатеричная система на базе 16 делает строки короче – но также непонятно для знакомых нам человеческих десятичных обозначений. Для работы с цифрами, написанными в разных системах позиционных цифр, нужны инструменты для перевода чисел с одной базы на другую …

Конвертер регистров текста – конвертировать онлайн верхний регистр в нижний, нижний регистр в верхний и другие варианты … Текстовые утилиты онлайн … Конвертер регистров текста … Конвертировать онлайн верхний регистр в нижний … Нижний регистр в верхний и другие варианты …

Меню раздела, новости и новые страницы.

Главная страница сайта …

… Фильтр LC. Расчет. Калькулятор. Катушка. Индуктивность. Онлайн. Частота. ФВ … … Земля. Древние книги. Бог. Веды. Енох. Тайные знания. Библия. Христос. Учен … … Фильмы и видео. Альтернативные теории и науки о Земле и Вселенной. Гравитац … … Наука. Теория. Гравитация. Теории заговора. Альтернативные теории. Физика. … … Видео. Мозг. Микробы. Плесень. Земля. Мир. Растения. Сода. Организм. Реальн … … Видео. Право. Битвы экстрасенсов. Сок от рака. Как правильно. Ненависть. Об …

Просто и аскетично. © 2021 ТехСтоп Екатеринбург.

С 2016++ техническая остановка создается вместе с вами и для вас …

Расчет фильтров нижних и верхних частот

Практический расчет фильтров верхних и нижних частот (RC и LC фильтров)

Доброго дня уважаемые радиолюбители!
Сегодня, на сайте “Радиолюбитель”, на очередном занятии “Практикума начинающего радиолюбителя”, мы с вами рассмотрим порядок расчета фильтров  верхних и нижних частот.
Из этой статьи вы узнаете, что фильтровать можно не только “базар”, но и многое другое. А изучив статью, научитесь самостоятельно проводить необходимые расчеты, которые вам помогут при конструировании или наладке различной аппаратуры (в статье много формул, но это не страшно, на самом деле все очень просто).

В первую очередь определимся, что понятия “верхние” и “нижние” частоты относятся к звукотехнике, а понятия “высокие” и “низкие” частоты – относятся к радиотехнике.

Фильтры верхних частот (далее ФВЧ) и фильтры нижних частот (далее ФНЧ) применяются во многих электрических схемах и служат для разных целей. Одним из ярких примеров их применения – цветомузыкальные устройства. К примеру, если вы наберете в поисковике “простая цветомузыка”, то заметите, насколько часто в результатах поиска показывается простейшая цветомузыка на одном транзисторе. Естественно, что такую конструкцию очень трудно назвать цветомузыкой. Зная что такое фильтры верхних и нижних частот и как они рассчитываются, вы сами, самостоятельно, можете переделать такую схему в более полноценное цветомузыкальное устройство. Простейший случай: вы берете две таких одинаковых схемы, но перед каждой ставите фильтр. Перед одним транзистором ФНЧ, а перед вторым – ФВЧ и у вас уже получается двухканальная цветомузыка. А если покумекать, то можно взять еще один транзистор и применив два фильтра (ФНЧ и ФВЧ или один средней частоты) получить третий канал – среднечастотный.

Прежде чем продолжить разговор о фильтрах коснемся очень важной их характеристики – амплитудно-частотная характеристика (АЧХ). Что это за показатель.

АЧХ фильтра показывает как изменяется уровень амплитуду сигнала проходящего через этот фильтр в зависимости от частоты сигнала.
Т.е., на одной частоте входящего на фильтр сигнала уровень амплитуды такой-же как и на выходе, а для другой частоты, фильтр, оказывая сопротивление сигналу, ослабляет амплитуду входящего сигнала.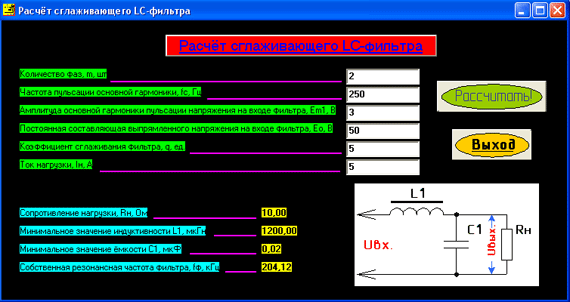

Тут же появляется еще одно определение: частота среза.

Частота среза – это частота, на которой происходит спад амплитуды выходного сигнала до значения равного 0,7 от входного.
Например, если при частоте входного сигнала 1 кГц  амплитудой 1 вольт на выходе фильтра амплитуда входного сигнала уменьшается до 0,7 вольта, то частота 1 кГц является частотой среза данного фильтра.

И последнее определение – крутизна частотной характеристики фильтра.

Крутизна частотной характеристики фильтра – это показатель того, на сколько резко изменяется амплитуда входного сигнала на выходе при изменении его частоты. Чем быстрее происходит спад АЧХ тем лучше.

Фильтры высоких и низких частот – это обыкновенные электрические цепи, состоящие из одного или нескольких элементов, обладающих нелинейной АЧХ, т.е. имеющих разное сопротивление на разных частотах.

Подытоживая вышесказанное можно сделать вывод, что по отношению к звуковому сигналу фильтры являются обыкновенными сопротивлениями, с тем лишь отличием, что их сопротивление меняется в зависимости от частоты звукового сигнала. Такое сопротивление называется реактивным и обозначается как Х.

Частотные фильтры изготавливают из элементов, обладающих реактивным сопротивлением – конденсаторов и катушек индуктивности. Рассчитать реактивное сопротивление конденсатора можно по нижеприведенной формуле:

Xc=1/2пFС   где:
Хс – реактивное сопротивление конденсатора;
п – оно и в Африке “пи”;
F – частота;
С – емкость конденсатора.
То есть, зная емкость конденсатора и частоту сигнала, всегда можно определить какое сопротивление оказывает конденсатор для конкретной частоты.

А реактивное сопротивление катушки индуктивности вот этой формулой:

XL=2пFL    где:
XL – реактивное сопротивление катушки индуктивности;
п – оно и в России “пи”;
F – частота сигнала;
L – индуктивность катушки

Частотные фильтры бывают нескольких типов:
– одноэлементные;
– Г- образные;
– Т – образные;
– П – образные;
– многозвенные.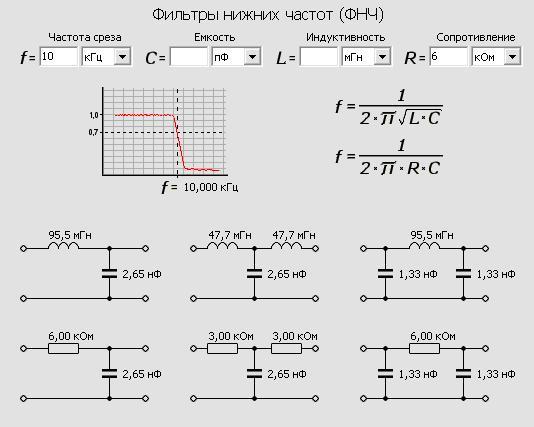

В этой статье мы с вами не будем глубоко опускаться в теорию, а рассмотрим только поверхностные вопросы, и только фильтры состоящие из сопротивлений и конденсаторов (фильтры с катушками индуктивности трогать не будем).

Одноэлементный фильтр

– фильтр состоящий из одного элемента: или конденсатора (для выделения верхних частот), или катушки индуктивности (для выделения нижних частот).

Г – образный фильтр

Г-образный фильтр – это обыкновенный делитель напряжения с нелинейной АЧХ и его можно представить в виде двух сопротивлений:

С помощью делителя напряжения мы можем понизить входное напряжения до необходимого нам уровня.
Формулы для расчета параметров делителя напряжения:

Uвх=Uвых*(R1+R2)/R2
Uвых=Uвх*R2/(R1+R2)
Rобщ=R1+R2
R1=Uвх*R2/Uвых – R2
R2=Uвых*Rобщ/Uвх

К примеру, нам дано:
Rобщ=10 кОм, Uвх=10 В, на выходе делителя надо получить Uвых=7 В
Порядок расчета:
1. Определяем   R2= 7*10000/10= 7000= 7 кОм
2. Определяем  R1= 10*7000/7-7000= 3000= 3 кОм, или R1=Rобщ-R2=10-7= 3 кОм
3. Проверяем     Uвых=10*7000/(3000+7000)= 7 В
Что нам и требовалось.
Знание этих формул необходимо не только для построения делителя напряжения с нужным выходным напряжением, но и для расчета фильтров нижних и верхних частот, в чем вы убедитесь ниже.

ВАЖНО!
Так как сопротивление нагрузки, подключаемой к выходу делителя, влияет на выходное напряжение, то значение R2 должно быть в 100 раз меньше входного сопротивления нагрузки. Если не нужна высокая точность, то это значение можно снизить до 10 раз.
Это правило также справедливо и при расчетах фильтров.

Чтобы из делителя напряжения на двух резисторах получить фильтр применяют конденсатор.
Как вы уже знаете, конденсатор обладает реактивным сопротивлением.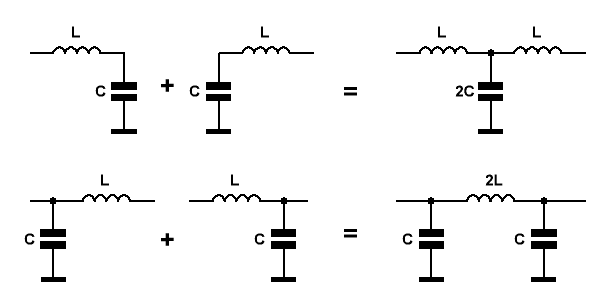 При этом его реактивное сопротивление на высоких частотах минимально, а на низких частотах – максимально.

При замене сопротивления R1 на конденсатор (при этом на высоких частотах ток через него проходит беспрепятственно, а на низких ток через него не проходит) мы получим фильтр верхних частот.
А при замене конденсатором сопротивления R2 (при этом, обладая малым реактивным сопротивлением на высоких частотах, конденсатор шунтирует токи высокой частоты на землю, а на низких частотах его сопротивление велико и ток через него не проходит)- фильтр нижних частот.

Как я уже сказал, уважаемые радиолюбители, мы не будем глубоко нырять в дебри  электротехники, иначе мы заблудимся и забудем о чем шла речь. Поэтому сейчас мы абстрагируемся от сложных взаимосвязей мира электротехники и будем рассматривать эту тему как частный случай, не привязанный ни к чему.
Но продолжим. Не так все плохо. Знание хотя бы элементарных вещей очень большое подспорье в радиолюбительской практике. Ну не рассчитаем мы точно фильтр, а рассчитаем с ошибкой. Ну и ничего страшного, в ходе настройки прибора мы подберем и уточним нужные номиналы радиодеталей.

Порядок  расчета Г-образного фильтра верхней частоты

В приведенных примерах расчет параметров фильтра начинается с того, что нам известно общее сопротивление делителя напряжения, но наверное правильнее, при практическом расчете фильтров, определять сначала сопротивление резистора R2 делителя, значение которого должно быть в 100 раз меньше сопротивления нагрузки к которой фильтр будет подключен. А также следует не забывать что делитель напряжения тоже потребляет ток, так-что в конце, необходимо будет определить и рассеиваемую мощность на резисторах для их правильного выбора.

Пример: Нам надо рассчитать Г-образный фильтр верхней частоты с частотой среза 2 кГц.

Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (можно взять конкретные напряжения, но в нашем случае это никакой роли не играет).
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R1, то реактивное сопротивление конденсатора Хс = R1.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R1 —> C=1/2пFR1:
C=1/2пFR1 = 1/2*3,14*2000*1500 =5,3*10-8 =0,053 мкФ.
Емкость конденсатора также можно определить по формуле: C=1,16/R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR1C= 1/2*3,14*1500*0,000000053 = 2003 Гц.
Таким образом мы определили, что для построения фильтра высокой частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R2= 3,5 кОм и конденсатор емкостью С= 0,053 мкФ.
? Для справки:
? 1 мкФ = 10-6 Ф = 0,000 001 Ф
? 0,1 мкФ = 10-7 Ф = 0,000 000 1 Ф
? 0,01 мкФ = 10-8 Ф = 0,000 000 01 Ф
и так далее…

Порядок  расчета Г-образного фильтра нижней частоты

Пример: Нам надо рассчитать Г-образный фильтр нижней частоты с частотой среза 2 кГц.

Дано: общее сопротивление делителя напряжения – Rобщ= 5 кОм, частота среза фильтра – 2 кГц.
Входное напряжение принимаем за 1, а выходное за 0,7 (как и в предыдущем случае).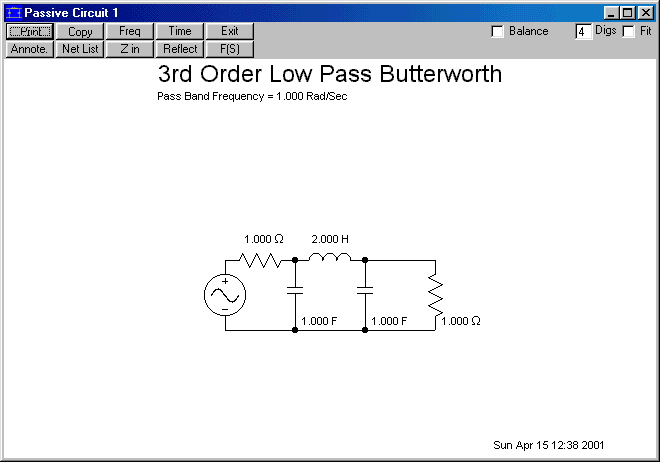
Проводим расчет:
1. Так как мы подключили конденсатор вместо резистор R2, то реактивное сопротивление конденсатора Хс = R2.
2. Определяем по формуле делителя напряжения сопротивление R2:
R2=Uвых*Rобщ/Uвх =0,7*5000/1 = 3500= 3,5 кОм.
3. Определяем сопротивление резистора R1:
R1=Rобщ-R2= 5 – 3,5= 1,5 кОм.
4. Проверяем значение выходного напряжения на выходе фильтра при рассчитанных сопротивлениях:
Uвых=Uвх*R2/(R1+R2) =1*3500/(1500+3500) = 0,7.
5. Определяем емкость конденсатора, которую выводим из формулы: Xc=1/2пFC=R2 —> C=1/2пFR2:
C=1/2пFR2 = 1/2*3,14*2000*3500 =2,3*10-8 =0,023 мкФ.
Емкость конденсатора также можно определить по формуле: C=1/4,66*R2пF.
6. Проверяем частоту среза Fср по формуле, которую также выводим из выше приведенной:
Fср=1/2пR2C= 1/2*3,14*3500*0,000000023 = 1978 Гц.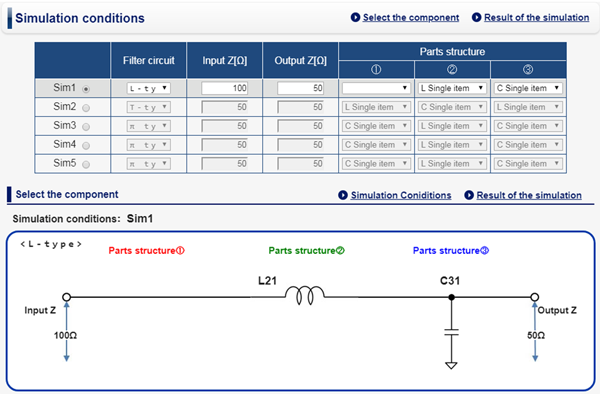
Таким образом мы определили, что для построения фильтра нижней частоты с заданными параметрами (Rобщ= 5 кОм, Fср= 2000 Гц) необходимо применить сопротивление R1= 1,5 кОм и конденсатор емкостью С= 0,023 мкФ.

Т – образный фильтр

Т- образные фильтры высоких и низких частот, это те же Г- образные фильтры, к которым добавляется ещё один элемент. Таким образом, они рассчитываются так же как делитель напряжения, состоящий из двух элементов с нелинейной АЧХ. А после, к расчётному значению суммируется значение реактивного сопротивления третьего элемента. Другой, менее точный способ расчёта Т-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «первого» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента Т-образного фильтра. Если это конденсатор, то значение ёмкости конденсаторов в Т-фильтре увеличивается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек уменьшается в два раза:

П – образный фильтр

П-образные фильтры, это те же Г- образные фильтры, к которым добавляется ещё один элемент впереди фильтра. Всё, что было написано для Т-образных фильтров справедливо для П-образных.
Как и в случае с Т-образными фильтрами, для расчёта П-образных используют формулы делителя напряжения, с добавлением дополнительного шунтирующего сопротивления первого элемента фильтра. Другой, менее точный способ расчёта П-образного фильтра начинается с расчёта Г-образного фильтра, после чего, значение «последнего» рассчитанного элемента Г-образного фильтра увеличивается, или уменьшается в два раза – «распределяется» на два элемента П-образного фильтра. В противоположность Т-образному фильтру, если это конденсатор, то значение ёмкости конденсаторов в П-фильтре уменьшается в два раза, а если это резистор или дроссель, то значение сопротивления, или индуктивности катушек увеличивается в два раза.

Как правило, одноэлементные фильтры применяют в акустических системах. Фильтры верхних частот обычно делают Т-образными, а фильтры нижних частот П-образными. Фильтры средних частот, как правило, делают Г-образными, их двух конденсаторов.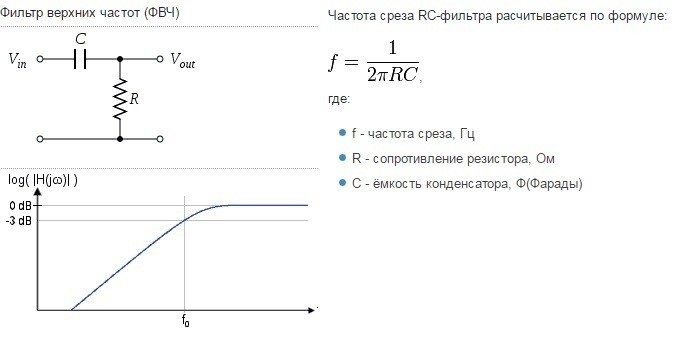

Для написания статьи, кроме всего прочего использовались материалы с сайта www.meanders.ru, автором и владельцем которого является Александр Мельник, за что ему большое и бесконечное (меандровское) спасибо.

Гонконг: фондовый рынок — Investing.com

© 2007-2021 Fusion Media Limited. Все права зарегистрированы. 18+

Предупреждение о риске: Торговля финансовыми инструментами и (или) криптовалютами сопряжена с высокими рисками, включая риск потери части или всей суммы инвестиций, поэтому подходит не всем инвесторам. Цены на криптовалюты чрезвычайно волатильны и могут изменяться под действием внешних факторов, таких как финансовые новости, законодательные решения или политические события. Маржинальная торговля приводит к повышению финансовых рисков.
Прежде чем принимать решение о совершении сделки с финансовым инструментом или криптовалютами, вы должны получить полную информацию о рисках и затратах, связанных с торговлей на финансовых рынках, правильно оценить цели инвестирования, свой опыт и допустимый уровень риска, а при необходимости обратиться за профессиональной консультацией.
Fusion Media напоминает, что информация, представленная на этом веб-сайте, не всегда актуальна или точна. Данные и цены на веб-сайте могут быть указаны не официальными представителями рынка или биржи, а рядовыми участниками. Это означает, что цены бывают неточны и могут отличаться от фактических цен на соответствующем рынке, а следовательно, носят ориентировочный характер и не подходят для использования в целях торговли. Fusion Media и любой поставщик данных, содержащихся на этом веб-сайте, отказываются от ответственности за любые потери или убытки, понесенные в результате осуществления торговых сделок, совершенных с оглядкой на указанную информацию.
При отсутствии явно выраженного предварительного письменного согласия компании Fusion Media и (или) поставщика данных запрещено использовать, хранить, воспроизводить, отображать, изменять, передавать или распространять данные, содержащиеся на этом веб-сайте. Все права на интеллектуальную собственность сохраняются за поставщиками и (или) биржей, которые предоставили указанные данные.
Fusion Media может получать вознаграждение от рекламодателей, упоминаемых на веб-сайте, в случае, если вы перейдете на сайт рекламодателя, свяжитесь с ним или иным образом отреагируете на рекламное объявление.

Калькулятор резистивно-емкостной цепи • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Данный калькулятор позволяет рассчитывать максимальный ток Imax в начале заряда конденсатора, максимальную энергию Emax и максимальный заряд конденсатора Qmax, когда он полностью заряжен при данном напряжении, а также постоянную времени RC-цепи.

Пример. Рассчитать постоянную времени, максимальную энергию, максимальный ток и максимальный заряд для цепи, состоящей из последовательно соединенных резистора 2 кОм и конденсатора 5 мкФ. Цепь подключена к источнику постоянного напряжения 10 V. Обратите внимание: напряжение не нужно для расчета постоянной времени RC-цепи.

Входные данные

Напряжение V

микровольт (мкВ)милливольт (мВ)вольт (В)киловольт (кВ)мегавольт (МВ)

Емкость C

фарад (Ф)микрофарад (мкФ)нанофарад (нФ)пикофарад (пФ)

Сопротивление R

миллиом (мОм)ом (Ом)килоом (кОм)мегаом (МОм)

Выходные данные

Постоянная времени

τ с

Макс. энергия

E Дж

Макс. ток

I А

Макс заряд

Q Кл

Введите величины в поля для ввода, выберите единицы измерения и нажмите кнопку Рассчитать.

Постоянная времени определяется по формуле

где τ — постоянная времени в секундах, R — сопротивление в омах и C — емкость в фарадах. Постоянная времени RC-цепи определяется как время, которое требуется, чтобы конденсатор зарядился до 63,2% его максимально возможного заряда при условии, что начальный заряд нулевой. Отметим, что конденсатор зарядится до 63,2% за время τ и почти полностью (до 99,3%) зарядится за время 5τ.

Энергия E, которую хранит полностью заряженный до напряжения V конденсатор, при условии, что время заряда T ≫ τ, определяется формулой

где C — емкость в фарадах и V — напряжение в вольтах.

Максимальный ток I определяется по закону Ома:

Максимальный заряд Q определяется по формуле

где C — емкость в фарадах и V — напряжение в вольтах.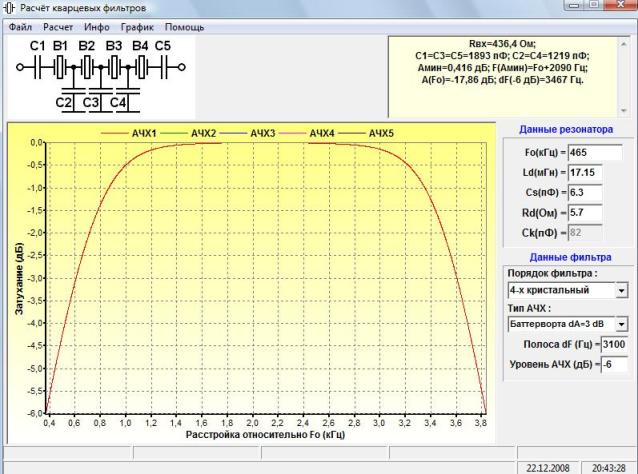

Фильтрующие электролитические конденсаторы на системной плате компьютера

Применение

Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе

Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.

Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.

Резистивно-емкостные фильтры нижних частот

Пример двухкаскадного RC-фильтра нижних частот с неинвертирующим операционным усилителем с единичным коэффициентом передачи, который используется в качестве буфера между двумя каскадами фильтра

Фильтры нижних частот пропускают только низкочастотные сигналы и подавляют высокочастотные сигналы. Частота среза определяется компонентами фильтра.

Такие фильтры широко используются в электронике. Например, их используют в сабвуферах для того, чтобы не подавать на них звуки высоких частот, которые они не могут воспроизводить. Фильтры нижних частот используются также в радиопередатчиках для блокировки нежелательных высокочастотных составляющих в передаваемом сигнале. У тех, кто пользуется ADSL подключением к Интернету, всегда установлены частотные разделители с такими фильтрами нижних частот, которые предотвращают возникновение помех в аналоговых устройствах (телефонах) от сигналов DSL и воздействия помех от аналоговых устройств на оборудование DSL, подключенное к обычной телефонной линии.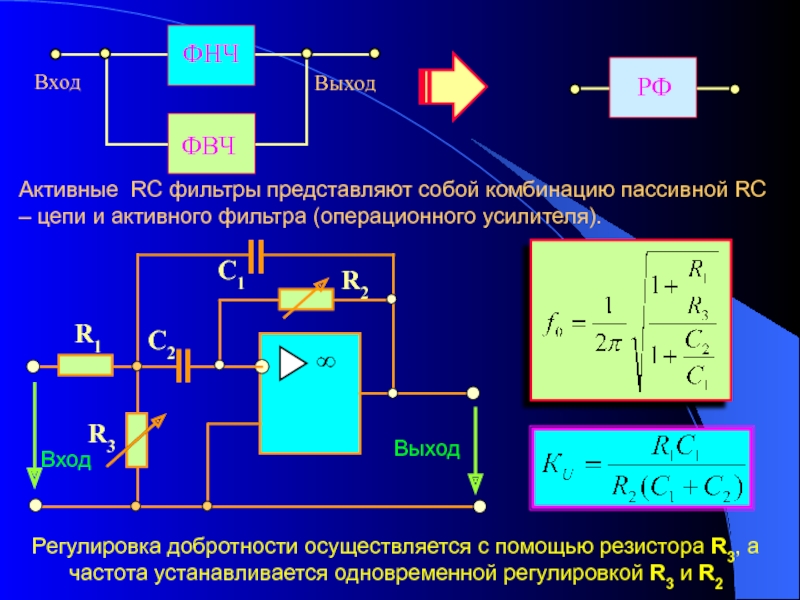

Фильтры нижних частот используются для обработки сигналов перед их аналого-цифровым преобразованием. Такие фильтры улучшают качество аналоговых сигналов при их дискретизации и необходимы для подавления высокочастотных компонентов сигнала выше частоты Найквиста таким образом, чтобы он удовлетворял требованиям теоремы Котельникова для данной частоты дискретизации, то есть максимальная частота не должна быть выше половины частоты выборки.

На верхнем рисунке показан простой фильтр нижних частот. В нем используются только пассивные компоненты, поэтому он называется пассивным фильтром нижних частот (ФНЧ). В более сложных пассивных ФНЧ используются также катушки индуктивности.

В отличие от пассивных фильтров нижних частот, в активных фильтрах используются усилительные устройства, например, транзисторы или операционные усилители. В пассивные фильтрах также часто имеются операционные усилители, применяемые для развязки. В зависимости от количества конденсаторов и катушек индуктивности, влияющих на крутизну частотной характеристики фильтра, они обычно называются «фильтрами первого порядка», «второго порядка» и так далее.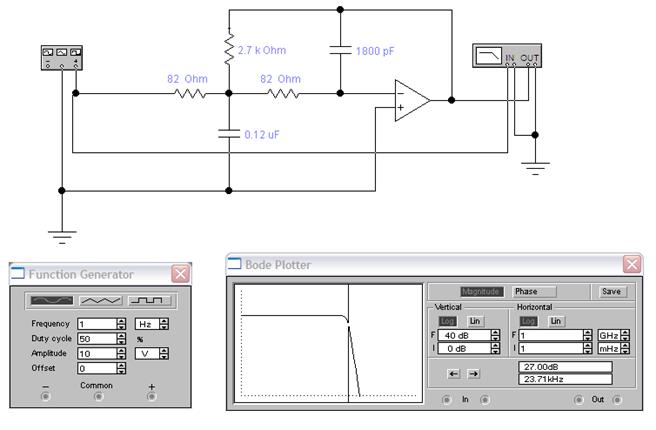 Фильтр, состоящий только из одного резистора и одного конденсатора, называется фильтром первого порядка.

Простой пассивный RC-фильтр верхних частот

RC-фильтры верхних частот

Фильтры верхних частот пропускают только высокочастотные составляющие сигналов и ослабляют низкочастотные составляющие. Фильтры верхних частот используются, например, в разделительных фильтрах звуковых частот (кроссоверах) для подавления низкочастотных составляющих в сигналах, подаваемых на высокочастотные динамики («пищалки»), которые не могут воспроизводить такие сигналы и к тому же обладают малой мощностью по сравнению с мощностью низкочастотных сигналов.

Активный фильтр верхних частот с операционным усилителем

Фильтры верхних частот часто используются для блокировки постоянной составляющей сигналов в тех случаях, когда она нежелательна. Например, в профессиональных микрофонах очень часто используется «фантомное» питание постоянным напряжением, которое подается по микрофонному кабелю.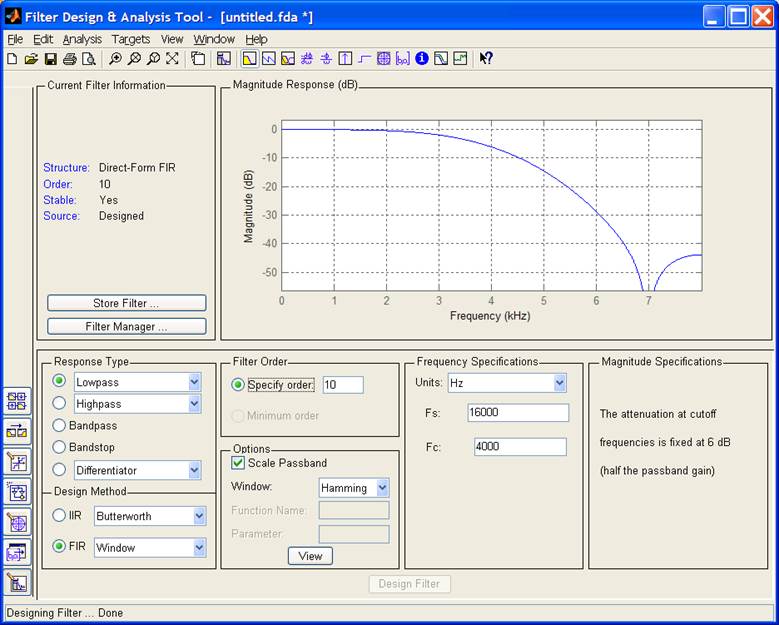 В то же время микрофон записывает переменные сигналы, такие как человеческий голос или музыка. Постоянное напряжение не должно появляться на выходе микрофона и не должно поступать на вход микрофонного усилителя, поэтому для его блокировки используется фильтр верхних частот.

Простой полосовой фильтр, собранный из двух каскадов — фильтра нижних частот (C2, R2) и фильтра высоких частот (C1, R1)

Если фильтр нижних частот и фильтр верхних частот стоят друг за другом, они образуют полосовой фильтр, который пропускает частоты только в определенной полосе частот и не пропускает частоты за пределами этой полосы. Такие фильтры широко используются в радиоприемниках и радиопередатчиках. В приемниках полосовые фильтры используются только для селективного пропускания и усиления сигналов радиостанции в требуемой узкой полосе частот. При этом сигналы других радиостанций за пределами этой полосы подавляются. Передатчики могут передавать радиосигналы только в определенном разрешенном для них диапазоне частот. Поэтому в них используются полосовые фильтры для ограничения полосы передаваемого сигнала таким образом, что он вписывался в допустимые пределы.

Lc фильтр питания расчет

В статье речь пойдёт про расчёт простейших фильтрующих цепей для сглаживания широтно-импульсной модуляции. Что такое ШИМ, где он применяется и как его реализовать читайте в отдельной статье.

Первое, на чём следует заострить внимание — это назначение цепи, для которой вы собрались строить фильтр. Немного упрощая схемы с ШИМ можно поделить на два типа:

  • Сигнальные цепи с ШИМ
  • Силовые цепи с ШИМ

Примером сигнального ШИМ служит, например, простейший ЦАП, под силовым ШИМ чаще всего имеется ввиду ШИМ-сигнал на выходе силовых ключей, например в импульсных источниках питания (ИИП). Строго говоря, в источниках питания сам сигнал ШИМ тоже используется в сигнальной цепи (управление транзисторами) и на выходе таких источников сигнал повторяет форму управляющих сигналов, однако имеет более высокую мощность, потому они требуют фильтров позволяющих пропускать большие мощности.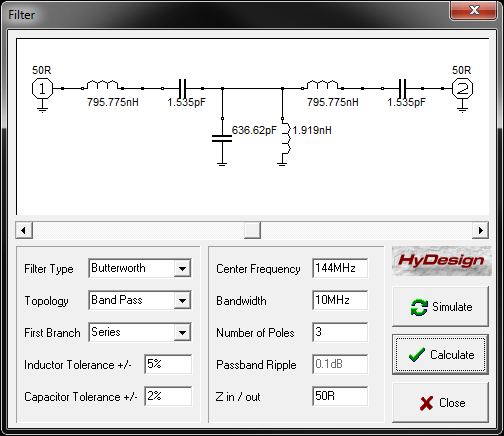

Фильтрация ШИМ в сигнальных цепях


Рис.1. Простейший фильтр нижних частот — интегрирующая RC-цепь и её АЧХ.

Основная характеристика фильтра это частота среза (на рисунке 1 обозначена угловая частота среза — ωс) — амплитуда колебаний данной данной частоты на выходе фильтра ослабляется до уровня

0.707 (-3 Дб) от входного значения. Частота среза определяется по следующей формуле:

Тут R и С — сопротивление резистора в омах и ёмкость конденсатора в фарадах. Необходимо помнить, что для корректной работы сглаживающего фильтра постоянная времени RC-цепочки (τ = R · C) должна быть как можно меньше периода ШИМа, тогда за один период не будет происходить полный заряд-разряд конденсатора.

Следующий важный параметр, позволяющий расчитать ослабление колебаний на заданной частоте это коэффициент передачи фильтра — это отношение K = Uвых/Uвх. Для данной RC-цепочки коэффициент передачи рассчитывается следующим образом:

Зная эти формулы и учтя постоянное падение напряжения на резисторе можно приближённо рассчитать фильтр с нужными характеристиками — например, задавшись имеющейся ёмкостью, либо необходимым уровнем пульсаций.

Калькулятор ШИМ-фильтра на RC-цепочке

Входные данные:Расчётные значения:
Частота ШИМГц
Коэффициент заполнения ШИМ
(duty cycle)		%
Напряжение на входеВ
Сопротивление резистора фильтраОм
Сопротивление нагрузки RнОм
Ёмкость конденсаторамкФ
Частота среза RC-фильтра— ГцАмплитуда пульсаций на частоте ШИМ— ВКоэффициент пульсаций на выходе— %Напряжение на выходе
(с учётом потерь на резисторе фильтра)— В

Постоянная времени RC-цепи

Постоянная времени цепи (R · C) не должна быть сильно меньше периода ШИМ!

Потери на резисторе фильтра
(не менее)— Вт

Обратите внимание — если вы хотите получать из ШИМ-сигнала сглаженный синусоидальный сигнал, необходимо чтобы частота среза фильтра была выше максимальной частоты сигнала, а значит частота ШИМ должна быть ещё выше.

Фильтрация ШИМ в силовых цепях


Рис.2. Фильтр нижних частот на LC-контуре и его АЧХ.

LC-фильтр представляет из себя элементарный колебательный контур, который имеет собственную частоту резонанса, поэтому его реальная АЧХ будет несколько отличаться от АЧХ, приведённой на рисунке 2.

Поскольку речь в данной статье идёт о фильтре для силовых цепей, при расчёте фильтра нужно учитывать, что основная гармоника входящего напряжения тоже должна ослабляться фильтром, следовательно, его резонансная частота должна быть ниже частоты ШИМ.

Формула для расчёта частоты резонанса LC-контура:

f = 1/(2 · π · (L · C) 0.5 )

Если частота резонанса контура совпадёт с частотой ШИМ, LC-контур может перейти в режим генерации, тогда на выходе может случиться конфуз, посему предлагаю вам данного недоразумения тщательно избегать. Кроме того, при проектировании данного фильтра есть ещё несколько нюансов, которые неплохо бы соблюдать для получения желаемого результата, а именно:

    Для исключения резонансных явлений на одной из высокочастотных гармонических составляющих ёмкость конденсатора желательно находить из условия равенства волнового сопротивления фильтра сопротивлению нагрузки:
  • Для сглаживания пульсаций таким фильтром желательно, чтобы ёмкостное сопротивление конденсатора для низшей частоты пульсации было как можно меньше сопротивления нагрузки, а также много меньше индуктивного сопротивления дросселя для первой гармоники.

    • Комплексный коэффициент передачи LC-фильтра рассчитывается по следующей формуле:

    где n — номер гармонической составляющей входного сигнала, i — мнимая единица, ω = 2πf, L — индуктивность дросселя (Гн), C — ёмкость конденсатора (Ф), R — сопротивление нагрузки (Ом).

    Из формулы очевидно, что чем выше гармоника, тем лучше она подавляется фильтром, следовательно, достаточно рассчитывать уровень только для первой гармоники.

    Чтобы перейти от комплексного представления коэффициента передачи к показательному, нужно найти модуль комплексного числа. Для тех, кто (как и я) спал на парах матана в институте, напомню, модуль комплексного числа считается очень просто:

    r = |Z| = (x 2 + y 2 ) 0.5

    Так как у нас в формуле коэффициента дробь, просто так сходу посчитать модуль не получится и проще всего посчитать это всё, например в MathCad’е. А для тех, кому лень делать всё самим, я запилил весь расчёт в этот прекрасный калькулятор. Пользуйтесь:

    Калькулятор силового ШИМ-фильтра на LC-контуре

    Частота ШИМГц
    Коэффициент заполнения ШИМ
    (duty cycle)    		%
    Напряжение на входеВ
    Сопротивление нагрузкиОм
    Индуктивность катушкимГн
    Ёмкость конденсаторамкФ
    Амплитуда пульсаций на частоте ШИМВ
    Резонансная частота контураГц
    Напряжение на выходе
    (потери не учитываются)    		В

    Обратите внимание — при использовании LC-фильтра следует помнить, что из-за наличия в цепи индуктивности, на выходе могут появляться выбросы обратной полярности. Если полярность импульсов на входе не изменяется (например для изменения направления вращения двигателя) для ограничения амлитуды отрицательных выбросов параллельно конденсатору (?) можно включать диод Шоттки.

    Расчет LC фильтров начинают с определения порядка и сопротивления нагрузки, затем элементы LC фильтра определяют умножением значений фильтра-прототипа на частоту среза. Элементы фильтров-прототипов рассчитаны заранее и сведены в таблицы. Наиболее полные таблицы приведены в справочнике по расчету LC фильтров Р. Зааля [3] В таблице 1 приведены элементы фильтра Баттерворта с частотой среза, равной 1 Гц и сопротивлением 1 Ом.

    Таблица 1. Элементы ФНЧ прототипа Баттерворта

    Порядок
    фильтра    		C1
    (мФ)    		L1
    (мГн)    		C2
    (мФ)    		L2
    (мГн)    		C3
    (мФ)    		L3
    (мГн)    		C4
    (мФ)    		L4
    (мГн)    		C5
    (мФ)    		L5
    (мГн)
    2225,08225,08————————
    3159,15318,31159,15———————
    4121,81294,08294,08121,81——————
    598,363257,52318,31257,5298,363—————
    682,385225,08307,46307,46225,0882,385————
    770,831198,46286,79318,31286,79198,4670,831———
    862,099176,84264,67312,19312,19264,67176,8462,099——
    955,274159,15243,84299,11318,31299,11243,84159,1555,274—
    1049,795144,51225,08283,62314,39314,39283,62225,08144,5149,795

    Схемы LC фильтров Баттерворта от второго до пятого порядка приведены на рисунке 1.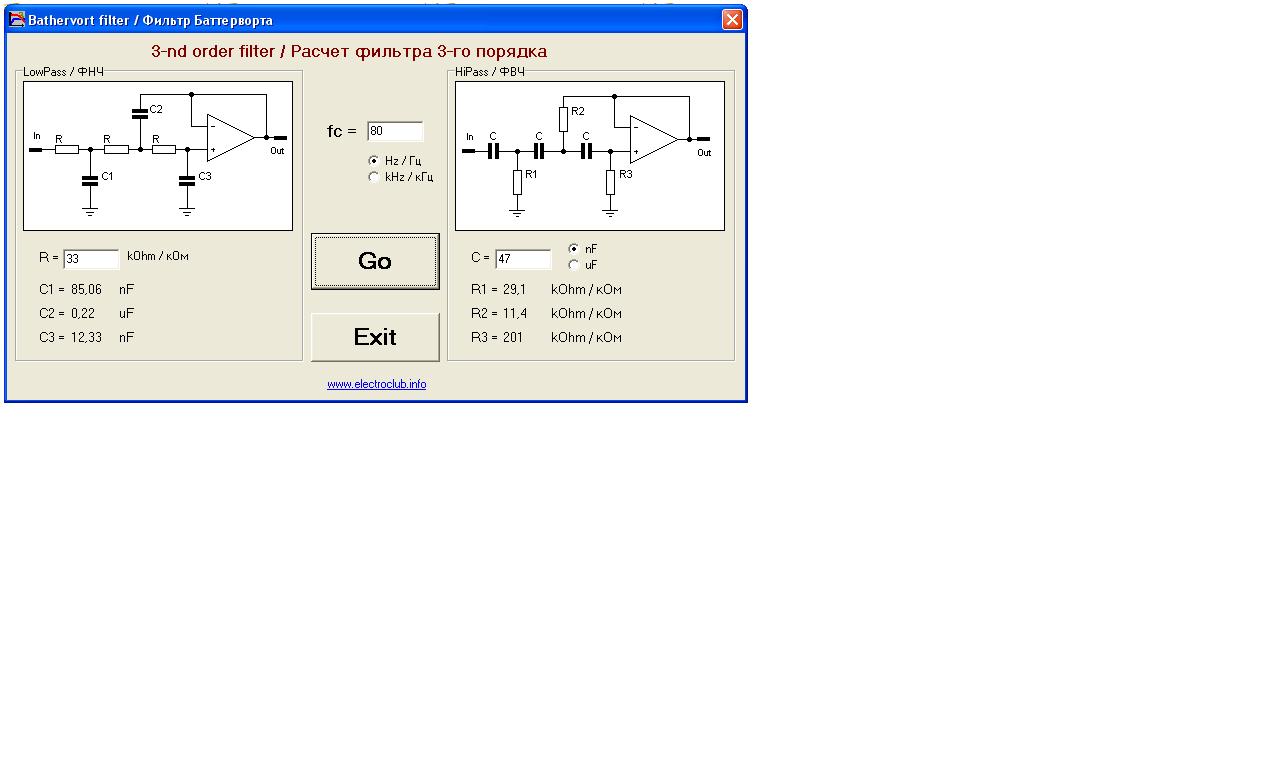 Номиналы их элементов соответствуют частоте 1 Гц.





    Рисунок 1. Схемы П-образных фильтров Баттерворта

    После определения фильтра-прототипа производится преобразование входного и выходного сопротивления фильтра. Для увеличения сопротивления LC фильтра значения индуктивностей увеличиваются, а значения емкостей конденсаторов уменьшаются, как это показано в следующей формуле:

    (1),

    где KZ это отношение сопротивлений рассчитываемого LC фильтра и фильтра-прототипа

    И завершается расчет LC фильтра увеличением частоты среза до требуемой величины. Для этого значения индуктивностей и конденсаторов уменьшаются на соответствующий коэффициент:

    (2),

    Точно таким же образом можно рассчитать и LC фильтр Чебышева. Таблицы L и C элементов фильтров Чебышева с полосой пропускания 1 Гц и сопротивлением 1 Ом приведены ниже:

    Таблица 2. Элементы ФНЧ прототипа Чебышева с неравномерностью 0.1 дБ

    Порядок
    фильтра    		C1
    (мФ)    		L1
    (мГн)    		C2
    (мФ)    		L2
    (мГн)    		C3
    (мФ)    		L3
    (мГн)    		C4
    (мФ)    		L4
    (мГн)    		C5
    (мФ)
    3164,18182,61164,18——————
    5182,52218.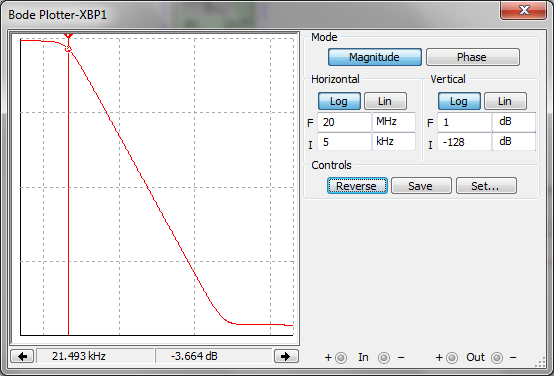 23314.33218.23182,52————
    7187,99226,45333,70250.41333,70226,45187,99——
    9190.30229,60339.73257.31351.00257.31339.73229,60190.30

    Таблица 3. Элементы ФНЧ прототипа Чебышева с неравномерностью 0.5 дБ

    Порядок
    фильтра    		C1
    (мФ)    		L1
    (мГн)    		C2
    (мФ)    		L2
    (мГн)    		C3
    (мФ)    		L3
    (мГн)    		C4
    (мФ)    		L4
    (мГн)    		C5
    (мФ)
    3254,06174,54254,06——————
    5271,50195.70404.39195. 70271,50————
    7276,51200,25419,91213.95419,91200,25276,51——
    9278.60201,97424.60217.61433.53217.61424.60201,97278.60

    Таблица 4. Элементы ФНЧ прототипа Чебышева с неравномерностью 3 дБ

    Порядок
    фильтра    		C1
    (мФ)    		L1
    (мГн)    		C2
    (мФ)    		L2
    (мГн)    		C3
    (мФ)    		L3
    (мГн)    		C4
    (мФ)    		L4
    (мГн)    		C5
    (мФ)
    3533,00113,27533,00——————
    5554,10121.26722.21121.26554,10————
    7560,02122,89738,35127. 92738,35122,89560,02——
    9562.48123,50743.14129.20752.37129.20743.14123,50562.48

    В таблицах приведены только фильтры нечетных порядков. Это связано с тем, что у LC фильтров Чебышева четных порядков входное и выходное сопротивление не могут быть равны. Рассмотрим пример проектирования LC фильтра.

    Пример 1 Расчет LC фильтра низких частот

    Задание Спроектировать фильтр нижних частот, пропускающий сигнал с частотами ниже и подавляющий помехи с частотами выше на . Неравномерность АЧХ в полосе пропускания . Входное и выходное сопротивление фильтра должно быть равно . Подобные фильтры часто применяются в качестве антиалиайсинговых фильтров на входе аналого-цифровых преобразователей.

    1) Рассчитаем расстройку по частоте на частоте подавления помех.

    ,

    2) Определим порядок фильтра и тип аппроксимации АЧХ. Так как дополнительных требований к фильтру не задано, выберем фильтр с максимальной крутизной АЧХ — фильтр Чебышева с неравномерностью 3 дБ. Фильтр Чебышева третьего порядка обеспечит при отстройке по частоте ξ=2 подавление сигнала на 28 дБ, что недостаточно (аппроксимация по Чебышеву, рисунок 6). Фильтр Чебышева пятого порядка обеспечит подавление помех на , поэтому именно его и выберем. Схема фильтра-прототипа Чебышева 5-порядка показана на рисунке 2.


    Рисунок 2. Схема фильтра-прототипа на LC элементах

    3) Согласуем вход и выход фильтра с волновым сопротивлением . Для этого воспользуемся выражением (1). Новые значения емкостей уменьшатся в , а значения индуктивностей увеличатся на это же значение. Преобразованная схема фильтра приведена на рисунке 3.


    Рисунок 3. Схема 50-омного фильтра низких частот с частотой среза 1 Гц

    И, наконец, уменьшим значения индуктивностей и емкостей в миллион раз, чтобы частота среза фильтра стала равной . Окончательная схема разработанного фильтра низкой частоты, пропускающего сигналы в полосе и подавляющего помехи в полосе непропускания на приведена на рисунке 4.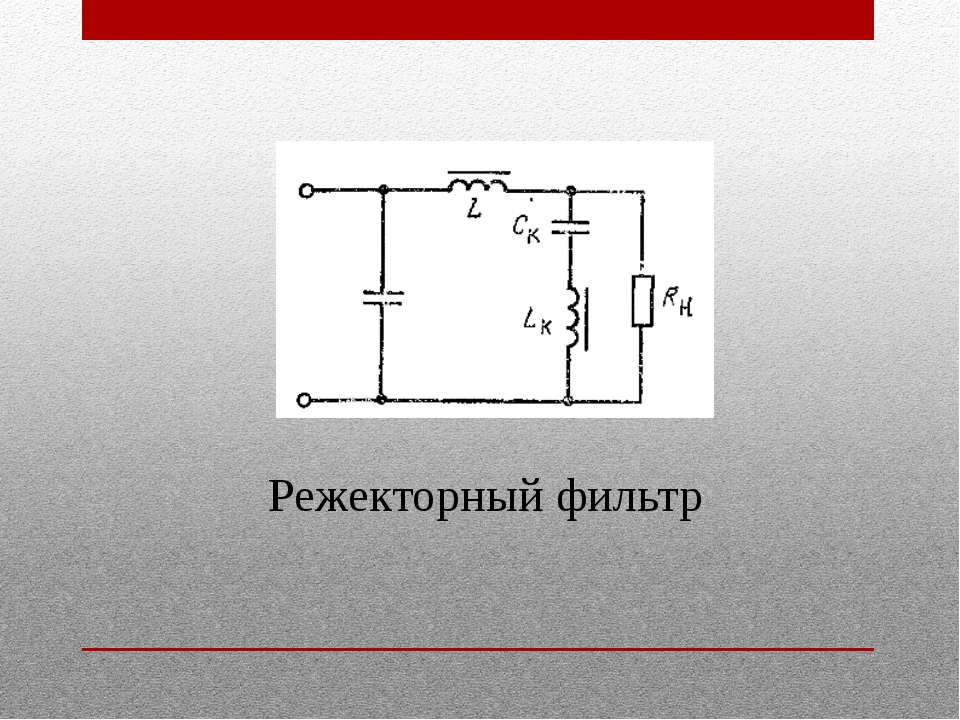


    Рисунок 4. Схема рассчитанного LC фильтра низких частот с частотой среза 1 МГц

    После этого можно приступать к проектированию конструкции фильтра. До недавнего времени при проектировании фильтра выбирались только конденсаторы, а индуктивности изготавливались самостоятельно. В последнее время появилась возможность покупать не только конденсаторы, но и индуктивности. Ряд фирм предоставляет готовые индуктивности с заданными параметрами.

    Пример 2 Расчет полосового LC фильтра

    Задание Спроектировать полосовой фильтр с центральной частотой f, равной . Полоса пропускания равна , неравномерность в полосе пропускания . Коэффициент прямоугольности равен 2, подавление в полосе непропускания . Входное и выходное сопротивление фильтра должно быть равно . Подобные фильтры часто применяются в качестве входных фильтров радиоприемников.

    1) Сначала определим узкополосный или широкополосный полосовой фильтр нам задан. Для этого поделим полосу пропускания фильтра на его центральную частоту.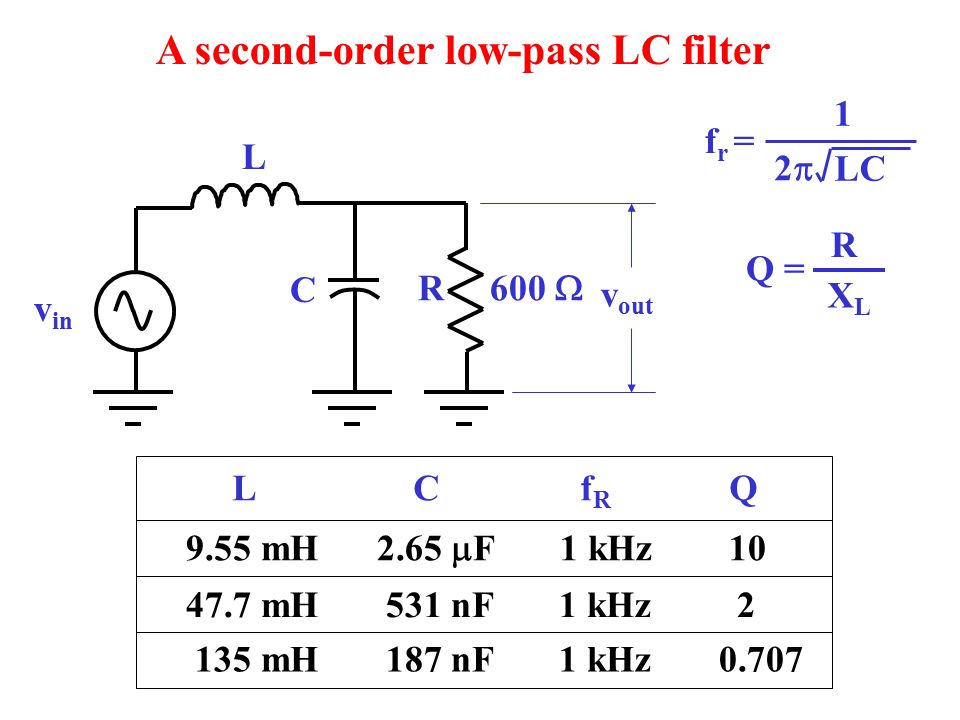

    ,

    Так как относительная ширина полосы пропускания получилась меньше 10%, то полосовой фильтр узкополосный, и его не имеет смысла выполнять в виде отдельных ФНЧ и ФВЧ.

    2) Формула определения коэффициента прямоугольности фильтра совпадает с формулой определения отстройки по частоте для полосы задерживания ФНЧ прототипа, поэтому запишем ξз=2.

    3) Теперь определим порядок фильтра-прототипа, необходимый для обеспечения подавления мешающего сигнала на . По графику амплитудно-частотной характеристики фильтра Чебышева пятого порядка определим, что он на частоте отстройки, равной двум, как раз обеспечивает подавление . Поэтому схема фильтра-прототипа будет выглядеть так же, как и в предыдущем примере:


    Рисунок 5. Схема фильтра-прототипа пятого порядка

    4) Следующий этап — это увеличение полосы пропускания фильтра до и увеличение входного и выходного сопротивления до . Для этого нужно пересчитать индуктивности и конденсаторы фильтра:

    ,

    Дата последнего обновления файла 08.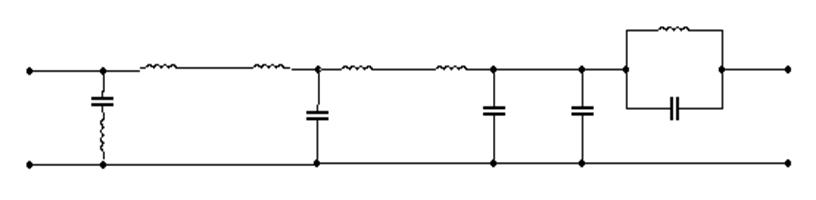 04.2019

    Вместе со статьёй “Расчет LC фильтров” читают:

    Ёмкостные, индуктивно-ёмкостные, активные сглаживающие фильтры.
    Схемы, свойства, онлайн калькулятор.

    Потолковали мы основательно на предыдущей странице про разные виды диодных выпрямителей, перебросились парой фраз на тему простейших ёмкостных фильтров, а вопрос достижения параметра коэффициента пульсаций Кп в пределах 10 -5 . 10 -4 так и повис в воздухе — уж очень немалым получается номинал ёмкости сглаживающего конденсатора.

    Коэффициент пульсаций выпрямленного напряжения Кп является важнейшим параметром выпрямителя. Его численное значение равно отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей.
    Напомню выдержку из печатного издания, приведённую на предыдущей странице:

    «Коэффициент пульсаций выбирают самостоятельно в зависимости от предполагаемой нагрузки, допускающей питание постоянным током вполне определённой “чистоты”:
    10 -3 . 10 -2 (0,1-1%) — малогабаритные транзисторные радиоприёмники и магнитофоны,
    10 -4 . 10 -3 (0,01-0,1%) — усилители радио и промежуточной частоты,
    10 -5 . 10 -4 (0,001-0,01%) — предварительные каскады усилителей звуковой частоты и микрофонных усилителей.»

    Помимо этого в характеристиках выпрямителей может использоваться и понятие коэффициента фильтрации (коэффициента сглаживания).
    Коэффициент фильтрации, он же коэффициент сглаживания — величина, численно равная отношению коэффициента пульсаций на входе фильтра к коэффициенту пульсаций на выходе фильтра Кс = Кп-вх/Кп-вых .
    Для многозвенных фильтров коэффициент фильтрации равен произведению коэффициентов фильтрации отдельных звеньев.

    В слаботочных цепях вопрос снижения пульсаций решается легко и кардинально — применением интегральных стабилизаторов. Параметр подавления пульсаций (Ripple Rejection) у подобных массовых ИМС составляет не менее 50дБ (в 360раз по напряжению), что при высокой “чистоте” выходного напряжения позволяет уменьшить ёмкости электролитов в 5-10 раз.

    Если же у разработчика нет возможности (либо желания) включать в состав устройства стабилизаторы напряжения, то реальным подспорьем окажутся индуктивно-ёмкостные или активные сглаживающие фильтры.

    Начнём с фильтров, выполненных из индуктивных элементов – дросселей и из ёмкостных элементов – конденсаторов.

    Рис.1

    На Рис.1а приведена схема простейшего ёмкостного сглаживающего фильтра. Принцип действия заключается в накоплении электрической энергии конденсатором фильтра и последующей отдачи этой энергии в нагрузку.

    Для того чтобы не ограничиваться 50-ти герцовыми блоками питания, но и иметь возможность расчёта фильтров импульсных ИБП, приведу универсальные формулы, учитывающие частоту входного сигнала F :
    С1 = Iн/(3,14×Uн×F×Кп) для однополупериодных выпрямителей и
    С1 = Iн/(6,28×Uн×F×Кп) — для двухполупериодных.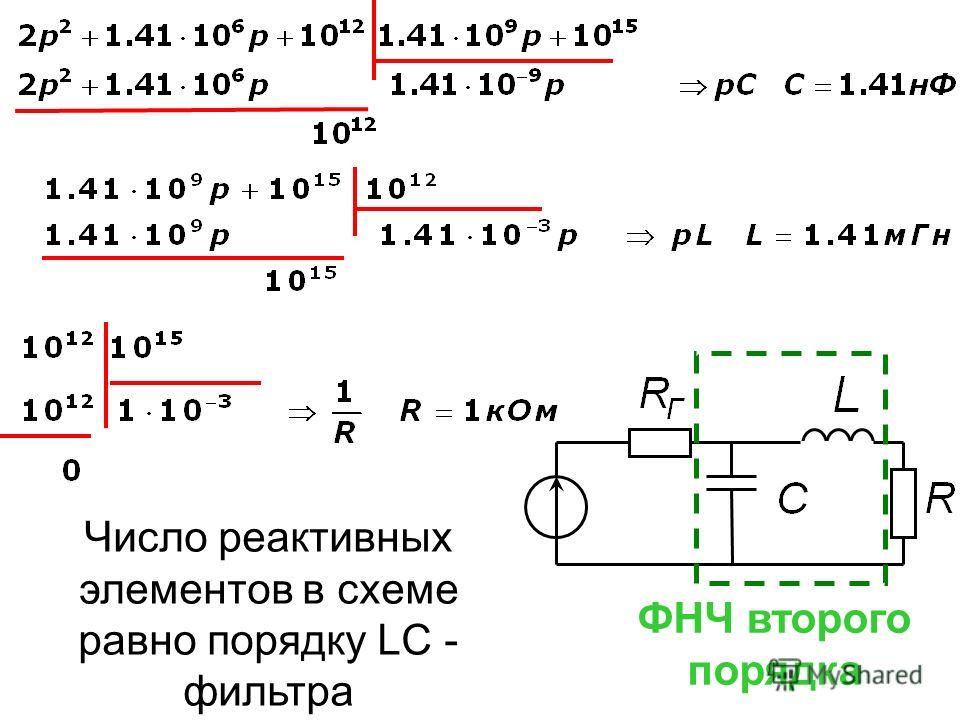
    Кп — это коэффициент пульсаций, равный отношению амплитудного значения пульсирующего напряжения к его постоянной составляющей, а
    F — частота переменного напряжения на входе диодного выпрямителя.

    Переходим к индуктивно-ёмкостным LC фильтрам.
    ВНИМАНИЕ.     Потребность в такого рода цепях возникает исключительно в случаях необходимости получить низкий уровень пульсаций в достаточно мощных сетевых блоках питания, либо в высокочастотных импульсных ИБП. Связано это с тем, что для эффективной работы LC-фильтра, индуктивное сопротивление катушки XL на частоте подавления стремятся сделать значительно больше Rн. А это, в свою очередь, приводит к тому, что в условиях низких частот и малых токов (высоких Rн) индуктивность дросселя получается необоснованно высокой.

    Г-образный индуктивно-ёмкостной LC фильтр 2-го порядка (Рис.1б) обладает значительно лучшими фильтрующими свойствами по сравнению с обычным ёмкостным.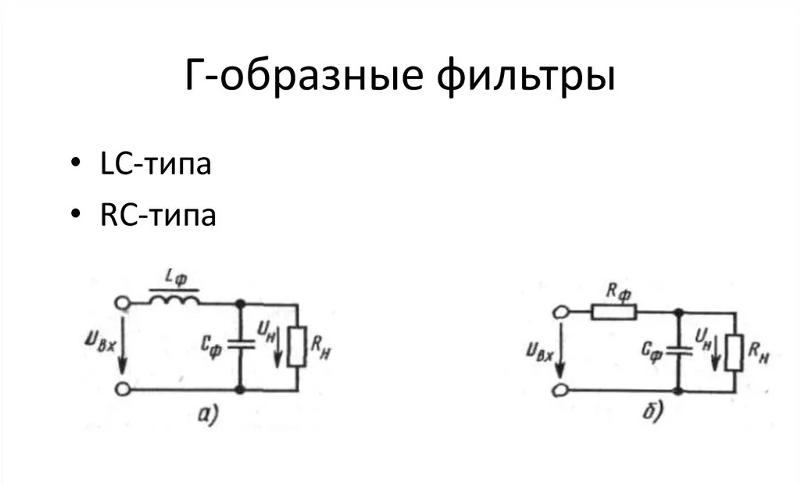
    Произведение LC (Гн*мкФ) зависит от необходимого коэффициента сглаживания фильтра и определяется по приближенной формуле:
    L1(Гн)×С1(МкФ) = 25000/(F 2 (Гц)×Кп) для однополупериодных выпрямителей и
    L1×С1 = 12500/(F 2 ×Кп) — для двухполупериодных, где
    С1(МкФ)/L1(мГн) = 1000/Rн 2 (Ом) .

    Схема П-образного LC-фильтра приведена на Рис.1в. Сглаживающее действие П-образного LC-фильтра можно упрощённо представить как совместное действие двух фильтров, описанных выше, а коэффициент сглаживания — как произведение коэффициентов сглаживания звеньев: ёмкостного и Г-образного индуктивно-ёмкостного.
    Наилучшими фильтрующими свойствами обладают LC-фильтры Чебышева. Напишем формулу, исходя из рекомендаций, изложенных на странице ссылка на страницу:
    С1 = С2 ; С1(МкФ)/L1(мГн) = 1176/Rн 2 (Ом) .

    Уменьшить напряжение пульсаций на выходе однозвенного П-образного LC-фильтра можно, включив параллельно дросселю L1 неполярный конденсатор С3 (Рис. 1г), который вместе с индуктивностью катушки образует режекторный фильтр. Если ёмкость конденсатора С3 выбрать такой, чтобы резонансная частота контура L1-С3 равнялась частоте пульсаций (F при однополупериодном выпрямлении или 2F при двухполупериодном), то большая часть напряжения пульсаций задержится этим контуром и лишь незначительная перейдёт в нагрузку.
    Итак: С3 = 1/(39,44×L1×F 2 ) для однополупериодных выпрямителей и
    С3 = 1/(9,86×L1×F 2 ) — для двухполупериодных.
    Все остальные номиналы элементов — такие же, как в предыдущей схеме.

    Давайте сдобрим пройденный материал онлайн таблицей.

    КАЛЬКУЛЯТОР РАСЧЁТА ЭЛЕМЕНТОВ СЛАЖИВАЮЩЕГО ФИЛЬТРА БЛОКА ПИТАНИЯ.

    Выбор схемы фильтра&nbsp Тип выпрямителя&nbsp Частота напряжения с обмотки трансформатора (Гц) Выходное постоянное напряжение Uн (В) Максимальный ток нагрузки Iн (А) Пульсации выходного напряжения (%) Минимальное сопротивление нагрузки Rн (Ом) Ёмкость конденсатора С1 (МкФ) Индуктивность дросселя L1 (мГн) Ёмкость конденсатора С3 (МкФ)

    Транзисторные фильтры по сравнению с ёмкостными сглаживающими фильтрами имеют меньшие габариты, массу и более высокий коэффициент сглаживания пульсаций.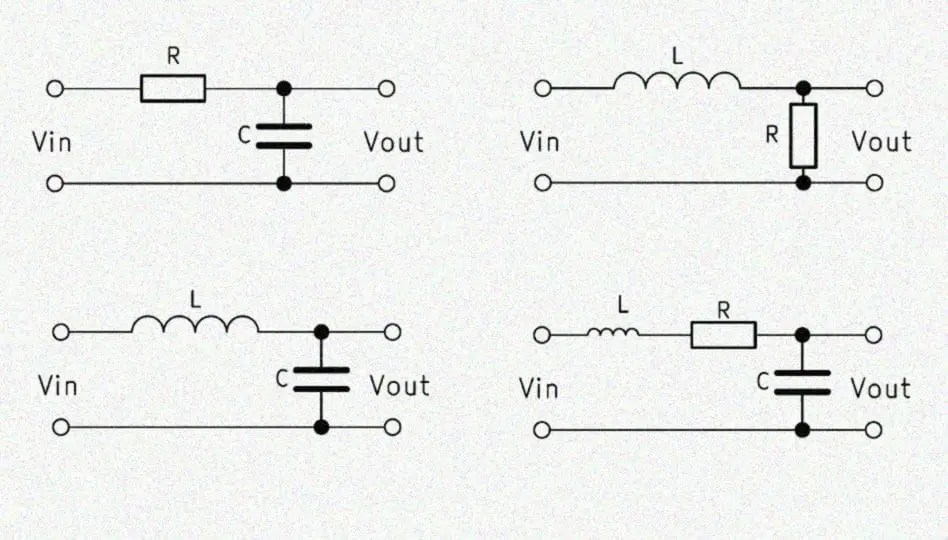 Они позволяют уменьшить в десяток раз (при том же уровне пульсаций) номинал сглаживающего конденсатора, либо уменьшить в аналогичное количество раз амплитуду пульсаций при неизменном значении ёмкости.

    Рис.2

    На Рис.2а представлена схема наиболее распространённого транзисторного фильтра.

    Напряжение с высокой амплитудой пульсаций, поступающее на коллектор транзистора, по сути, является напряжением питания эмиттерного повторителя, образованного Т1.
    В это же самое время цепь базы питается через резисторы смещения и интегрирующую цепь R1C1, которая сглаживает пульсации напряжения на базе. Чем больше постоянная времени T=R1C1, тем меньше пульсации напряжения на базе, а так как устройство представляет собой эмиттерный повторитель, то на выходе фильтра пульсации будут столь же малыми, как и на базе.
    Для того, чтобы снизить зависимость напряжения на выходе фильтра от уровня передаваемой мощности, ток через делитель R1R2 выбирают в 5…10 раз большим, чем ток, ответвляющийся в базу при минимальном сопротивлении нагрузки.
    При расчёте номиналов элементов делителя, следует исходить из напряжения на базе транзистора:
    Uб = Uвх — Uвх пульсаций — (2,5. 3В) .
    В этом случае будет обеспечена работа регулирующего транзистора в активном режиме, а падение напряжения на нём составит величину:
    Uкэ = Uвх пульсаций + (3,1. 3,6В) .
    Коэффициент полезного действия транзисторного фильтра будет тем больше, чем меньше падание постоянного напряжения на силовом транзисторе. Из формулы видно, что для обеспечения высокого КПД активного сглаживающего фильтра, на вход устройства следует подавать уже отфильтрованное до определённого уровня напряжение.
    На практике это делается включением на вход простейшего ёмкостного фильтра (Рис.1а), уровень пульсаций которого можно посчитать на приведённом выше калькуляторе.

    Эффективность активных сглаживающих фильтров напрямую зависит от величины коэффициента усиления транзистора. Чем выше h31 полупроводника, тем больших величин можно выбрать номиналы резисторов R1, R2 — тем лучшими фильтрующими свойствами будет обладать схема. Поэтому в данной ситуации не стоит даже рассматривать транзисторы с h31<50. Но при этом и составные транзисторы, обладающие высоким усилением — также не являются оптимальным выбором в силу повышенных падений напряжений на p-n переходах, значительно снижающих КПД транзисторных устройств.

    Для дальнейшего улучшения фильтрующих свойств сглаживающего фильтра можно применить двухзвенный RC-фильтр в цепи базы транзистора (Рис.2б).
    Здесь сумма значений сопротивления резисторов R1 и R2 равна сопротивлению резистора R1 в предыдущем устройстве, а сопротивление резистора R3 равно сопротивлению резистора R2 в фильтре (Рис.2а).

    Ещё эффективней будет работать транзисторный фильтр, у которого в цепь базы транзистора вместо R2 (Рис.1а), либо R3 (Рис.1б) включить стабилитрон с напряжением пробоя, равным значению, рассчитанному для резистивного делителя.

    RF Инструменты | Инструмент проектирования LC-фильтров

    RF Tools | Инструмент проектирования LC-фильтров

    Рассчитайте значения схемы LC-фильтров с низкочастотной, высокочастотной, полосовой или полосовой характеристикой.
    Выберите тип фильтра Чебышева, Эллиптический, Баттерворта или Бесселя с порядком фильтрации до 20 и произвольным входным и выходным импедансами.

    Больше информации Свойства фильтра

    Ответ

    Тип

    Фильтр нижних частот, верхний фильтр, полосовой пропуск, полосовой выключатель

    ЧебышевЭллиптическийБуттервортИнверсный ЧебышевБессельЛежандр

    Шунт FirstSeries First

    Обычный, сначала шунтирующий, Обычный, Серия Первый, с прямой связью, последовательный конденсатор, с прямой связью, шунтирующий конденсатор, с прямой связью, с последовательным индуктором, с прямой связью, шунтирующий индуктор, трубчатый

    1234567891011121314151617181920

    Нижняя частота среза

    Верхняя частота среза

    Пульсация полосы пропускания (дБ)

    Stopband Atten.(дБ)

    Входное сопротивление (Ом)

    Выходное сопротивление (Ом)

    Емкость конденсатора с прямой связью

    Значение индуктивности с прямой связью

    Дополнительные настройки

    Значения компонентов

    Значения конденсатора

    Мин.Конденсатор Значение

    E6 (допуск 20%) E12 (допуск 10%) E24 (допуск 5%) E48 (допуск 2%) E96 (допуск 1%)

    Значения индуктивности

    Мин.Индуктор Значение

    E6 (допуск 20%) E12 (допуск 10%) E24 (допуск 5%) E48 (допуск 2%) E96 (допуск 1%)

    © 2017-2021 РФ Инструменты | Отображается в 0.14333s | Политика конфиденциальности

    Калькулятор фильтра нижних частот

    – ElectronicBase

    Фильтр нижних частот пропускает только сигналы ниже своей частоты среза и ослабляет компоненты над ней. Вот как рассчитать различные варианты пассивных фильтров нижних частот. В дополнение к формулам вам могут помочь несколько калькуляторов нижних частот.

    Общие сведения о фильтре нижних частот

    Низкий проход обозначает компонент в электротехнике, который ослабляет или блокирует высокие частоты и позволяет низким частотам проходить в значительной степени беспрепятственно.Также широко используется термин фильтр нижних частот. Термин пассивный просто означает, что схема фильтра нижних частот построена без усилительного элемента. При использовании операционного усилителя имеем активный НЧ.

    Фильтр нижних частот используется, когда нежелательны быстрые и резкие изменения напряжения на выходе. Он используется, например, в конструкции низкочастотных динамиков для улучшения их акустики. Также в сетевых фильтрах часто используется фильтр нижних частот для удаления передаваемых паразитных частот из энергосистемы.

    Специалисты различают ФНЧ 1-го порядка и ФНЧ 2-го порядка. Мы объясняем элементы каждого фильтра нижних частот, как он работает и как рассчитать фильтр нижних частот. Поскольку это очень сложные вычисления, мы также предоставляем калькулятор фильтра нижних частот .

    Пассивный ФНЧ 1-го порядка

    Фильтр нижних частот первого порядка состоит из последовательно соединенных резистора и конденсатора . Следовательно, термин RC low pass является общим, где \ (R \) обозначает резистор, а \ (C \) обозначает конденсатор.Параллельно конденсатору снимается выходное напряжение \ (V_ {out} \). Это важно, потому что в противном случае это фильтр высоких частот.

    В случае резких изменений входного напряжения \ (V_ {in} \) практически не падает напряжение на конденсаторе, в результате чего выходное напряжение \ (V_ {out} \) также приближается к нулю. С другой стороны, если есть медленное изменение напряжения \ (V_ {in} \), часть напряжения на конденсаторе падает. Выходное напряжение \ (V_ {out} \) изменяется с задержкой по времени.В следующем разделе мы хотим рассчитать RC-фильтр нижних частот и пролить свет на передаточную функцию фильтра нижних частот первого порядка.

    RC low pass – как это работает

    Выходное напряжение \ (V_ {out} \) следует неустойчивому входному напряжению \ (V_ {in} \), задержанному во времени на той же высоте скачка. Это связано с тем, что измененное входное напряжение на короткое время проходит через конденсатор, потому что сначала нарастает емкостное сопротивление конденсатора. Как только емкостное реактивное сопротивление достигает нового значения, выходное напряжение больше не изменяется.2}} $$

    Здесь \ (V_ {in} \) обозначает входное напряжение, а \ (V_ {out} \) – выходное напряжение. \ (\ Omega \) – это угловая частота, то есть произведение \ (2 \ cdot \ pi \ cdot f \) (частота). \ (C \) – емкость конденсатора, а \ (R \) – омическое сопротивление.

    Рассчитать частоту среза фильтра нижних частот

    Омическое сопротивление \ (R \) остается неизменным, в то время как емкостное реактивное сопротивление \ (X_C \) изменяется в зависимости от частоты. Частота среза обозначает частоту, на которой два значения равны, то есть \ (R = X_C \).Таким образом, на частоте выше частоты среза \ (X_C \) меньше, чем \ (R \), на более низкой частоте \ (X_C \) больше, чем \ (R \). При работе с частотой среза выводится 70,71% входного напряжения из-за пик-фактора \ (\ sqrt {2} \).

    Расчет частоты среза для RC-фильтра нижних частот выполняется по следующей формуле:

    $$ f_c = \ frac {1} {2 \ pi R C} $$

    Калькулятор низких частот RC

    С помощью онлайн-калькулятора вы можете рассчитать необходимые компоненты для желаемой частоты среза.

    Калькулятор фильтра нижних частот RC

    Начните расчет

    Альтернатива: RL low pass

    Если вместо конденсатора используется катушка, можно также построить фильтр нижних частот первого порядка. 2}} $$

    Частота среза рассчитывается по следующей формуле для нижних частот LR:

    $$ f_c = \ frac {R} {2 \ pi L} $$

    Калькулятор низких частот RL

    Онлайн-калькулятор помогает рассчитать необходимые элементы конструкции для соответствующей частоты среза.

    Калькулятор фильтра низких частот RL

    Начните расчет

    Пассивный фильтр нижних частот 2-го порядка

    Низкочастотный фильтр второго порядка также состоит из двух компонентов. В фильтре нижних частот 2-го порядка катушка последовательно соединена с конденсатором, поэтому этот фильтр нижних частот также называется LC-фильтром нижних частот . Опять же, выходное напряжение \ (V_ {out} \) отводится параллельно конденсатору. Таким образом, структура идентична низкочастотному фильтру 1-го порядка, это только омическое сопротивление, замененное на катушку.

    Низкочастотный проход 2-го порядка в основном выполняет ту же функцию, что и его аналог 1-го порядка, но имеет вдвое больший наклон. Так низкие частоты могут возникать, в то время как высокие частоты фильтруются вдвое эффективнее. Разница вызвана катушкой. Как индуктивная нагрузка, она намного быстрее реагирует на изменения напряжения, чем омическое сопротивление.

    LC low pass – как это работает

    Функция конденсатора точно такая же, как и в ФНЧ 1-го порядка. Он расположен точно в том же месте, и выходное напряжение отводится идентично.Реакция на единичное случайное изменение входного напряжения также сопоставима. Катушка имеет сопротивление, близкое к нулю, пока подается постоянное напряжение.

    Разница становится очевидной только при подаче изменяющегося напряжения. Катушка более чувствительна к увеличению частоты, чем омическое сопротивление. С увеличением частоты индуктивное сопротивление катушки \ (X_L \) увеличивается, а емкость \ (X_C \) конденсатора уменьшается. Таким образом, изменение частоты на входе еще более четко отражается на уровне выходного напряжения.2 LC} $$

    В расчет \ (L \) добавляется индуктивность катушки. Омическое сопротивление \ (R \) не имеет значения. Мы предоставили калькулятор нижних частот LC , чтобы упростить расчет нижних частот.

    Рассчитать частоту среза на нижнем проходе LC

    Индуктивное сопротивление \ (X_L \) увеличивается с частотой, в то время как емкостное реактивное сопротивление \ (X_C \) обратно пропорционально ему – оно уменьшается с увеличением частоты. Частота среза – это частота, при которой \ (X_C = X_L \).Таким образом, на частоте, большей, чем частота среза, \ (X_C \) меньше, чем \ (X_L \). При более низкой частоте \ (X_C \) больше, чем \ (X_L \).

    Частота среза для низкочастотного фильтра LC рассчитывается по следующей формуле:

    $$ f_c = \ frac {1} {2 \ pi \ sqrt {LC}} $$

    Калькулятор низких частот LC

    Здесь вы можете рассчитать желаемую частоту среза, а также необходимые компоненты.

    Калькулятор фильтра нижних частот LC

    Начните расчет

    Фильтры LC

    Design (версия 4.0 15 июня 2018 г.)


    Это веб-приложение позволяет пользователю создавать простые радиочастотные фильтры. с индукторами и конденсаторами. Эти фильтры наиболее эффективны в диапазоне от 50 кГц до 50 кГц. 500 мГц. Активные фильтры ниже 50 кГц обычно более рентабельны и выше Обычно используются полосковые линии 500 МГц.

    Источники индуктивности:
    CoilCraft
    DigiKey

    Создайте свой собственный:
    Калькулятор индуктивности для радиолюбителей
    DIY Аудио калькулятор индуктора
    Калькулятор индуктивности многослойного воздушного сердечника
    Калькулятор индуктивности для Windows
    Используйте Google, чтобы найти больше.

    Формулы и таблицы, используемые в этой программе, взяты из Руководства по проектированию электронных фильтров Артура Б. Уильямса. Открытый исходный код здесь.

    Пользователь выбирает основной тип (Lowpass или Highpass), количество полюсов, 3 дБ отсечки частота и импеданс ввода / вывода. Приложение генерирует значения частей для трех форм отклика: Баттерворта, Бесселя и 0,1 дБ пульсации Чебышева. Две разные конфигурации со схемами генерируются. Графики частотной характеристики являются приблизительными и предполагают идеальные компоненты и конструкцию.Результаты в реальном мире не будут такими хорошими. Точность графиков Бесселя составляет только 2-кратную частоту среза (1/2 для фильтра верхних частот).

    Пользователь выбирает базовый тип, Bandpass или Bandstop, количество полюсов, полосу пропускания 3 дБ и импеданс ввода / вывода. Приложение генерирует значения деталей для трех форм отклика: Баттерворта, Бесселя. и 0,1 дБ пульсации Чебышева. Две разные конфигурации со схемами также генерируются.

    Примечание. Эти фильтры чувствительны к паразитной емкости, индуктивности и добротности компонентов.Имейте в виду, что конденсаторы имеют последовательную индуктивность, а индукторы имеют параллельную емкость и последовательное сопротивление, которое в некоторых случаях может быть очень значительным.

    Я получил электронные письма от людей, у которых возникли проблемы с программой, вычисляющей нулевые или очень низкие значения индуктивности или конденсатора. Это вызвано тем, что пользователь задает параметры, которые трудно или невозможно достичь с помощью LC-фильтров. У вас могут возникнуть проблемы с центральными частотами выше 250 МГц или полосой пропускания менее 10% от центральной частоты.Высокие частоты требуют небольших конденсаторов и катушек индуктивности. Паразитная индуктивность и емкость в цепи добавляют к значениям компонентов, а в крайних случаях могут даже превышать их. Полосовые фильтры с узкой полосой пропускания требуют компонентов с высокой точностью и добротностью. Полосы пропускания менее 10% от центральной частоты могут быть трудными или даже невозможными для реализации с дискретными ЖК-компонентами. Ваш пробег может отличаться.

    Полосовые фильтры с полосой пропускания более одной октавы могут не работать должным образом.Если вам требуется полоса пропускания более одной октавы, вам необходимо каскадировать фильтр нижних частот и фильтр верхних частот.

    Если LC-фильтр не может сделать то, что вам нужно, потому что частота слишком высока, я предлагаю взглянуть на встречно-штыревой полосовой фильтр.

    15 июня 2018 года в этой программе были исправлены некоторые ошибки, чтобы исправить плохие графики для широкополосных фильтров. Пожалуйста, сообщайте об оставшихся ошибках на моей странице контактов.

    Проектирование и расчет схемы простого LC-фильтра нижних частот »Электроника

    Соображения по конструкции, схема и формулы для 3-полюсного ЖК-фильтра нижних частот с постоянным k для ВЧ приложений.

    Фильтр постоянного K Включает:
    Фильтр постоянного k Простая конструкция LC LPF Конструкция LC HPF Конструкция полосового фильтра LC

    Основные сведения о фильтрах: : RF фильтры – основы Характеристики фильтра Основы проектирования ВЧ-фильтров Конструкция фильтра высоких и низких частот Постоянный k-фильтр Фильтр Баттерворта Чебычевский фильтр Фильтр Бесселя Эллиптический фильтр

    Часто бывает сложно разработать простой ЖК-фильтр нижних частот, поскольку вычисления могут быть трудными для выполнения или таблицы нормализованных значений могут быть недоступны.

    Несмотря на то, что в Интернете есть несколько калькуляторов фильтров, с уравнениями для простого фильтра легко работать, и они дают представление о работе фильтра.

    Основы проектирования ФНЧ

    Фильтры нижних частот используются в большом количестве приложений. В частности, в радиочастотных приложениях фильтры нижних частот изготавливаются в форме LC с использованием катушек индуктивности и конденсаторов. Обычно они могут использоваться для фильтрации нежелательных сигналов, которые могут присутствовать в полосе частот выше желаемой полосы пропускания.Таким образом, этот вид фильтра принимает только сигналы ниже частоты среза.

    Фильтры нижних частот обычно состоят из нескольких секций. Они могут иметь конфигурацию Pi (Π) или T. Для фильтра Π секции каждая секция имеет одну последовательную катушку индуктивности и конденсатор с каждой стороны, соединенный с землей.

    Типовой 3-полюсный Π LC-фильтр нижних частот RF

    Сетевой фильтр нижних частот T имеет один конденсатор между линией RF и землей, а в сигнальной линии есть две катушки индуктивности, по одному конденсатору с каждой стороны.Т-образная секция не всегда так удобна, потому что даже при наличии дополнительных секций все равно требуется больше индукторов, которые дороже покупать или требуют отдельной обмотки.

    Типовой трехполюсный ВЧ фильтр нижних частот T LC

    Расчетные уравнения фильтра нижних частот

    Существует множество различных вариантов фильтра, которые могут использоваться в зависимости от требований с точки зрения пульсации в полосе, скорости, с которой достигается окончательный спад, и т. Д. Используемый здесь тип – константа-k, и это дает некоторые управляемые уравнения :

    L = Z0π fc Генри

    C = 1Zo π fc Фарады

    fc = 1πL C Гц

    Где:
    Z 0 = характеристическое сопротивление в омах
    C = емкость в фарадах
    L = индуктивность в единицах Генри
    f c = частота среза в герцах

    Дополнительные детали дизайна

    Есть несколько идей и указателей, которые можно учесть при разработке и реализации конструкции фильтра нижних частот.

    • Каскадирование секций для большего спада: Чтобы обеспечить больший наклон или спад, можно каскадировать несколько секций фильтра нижних частот. При этом фильтрующие элементы из соседних секций можно комбинировать. Например, если два Т-образных фильтра соединены каскадом, и каждая Т-образная секция имеет индуктор 1 мкГн в каждой ветви Т, их можно объединить в смежных секциях и использовать индуктор 2 мкГн.
    • Выбор компонентов: Выбор компонентов для любого фильтра, и в данном случае для конструкции фильтра нижних частот, важен.Следует использовать компоненты с жесткими допусками, чтобы гарантировать получение требуемых характеристик. Также необходимо проверить температурную стабильность, чтобы убедиться, что компоненты фильтра не изменяются значительно в зависимости от температуры, что приводит к изменению рабочих характеристик.
    • Расположение фильтра: Следует соблюдать осторожность при размещении фильтра. Это следует делать не только для частот полосы пропускания, но, что более важно, для частот в полосе заграждения, которые могут значительно превышать частоту среза фильтра нижних частот.Емкостная и индуктивная связь являются основными элементами, которые ухудшают характеристики фильтра. Соответственно, вход и выход фильтра должны быть разделены. Следует использовать короткие провода и дорожки, компоненты из соседних секций фильтра должны быть разнесены. При необходимости используются экраны, а на входе и выходе используются качественные разъемы и коаксиальный кабель, если применимо.

    Эти уравнения дают очень простой метод разработки трехполюсного фильтра нижних частот.Хотя они могут не обеспечивать точный требуемый отклик, например, Бесселя, Чебышева и т. Д., Они, тем не менее, очень просты в использовании и представляют собой идеальное решение для большинства конструкций фильтров нижних частот. Рисунки или даже сами уравнения также можно преобразовать, чтобы получить конструкцию фильтра верхних частот.

    Другие важные темы по радио:
    Радиосигналы Типы и методы модуляции Амплитудная модуляция Модуляция частоты OFDM ВЧ микширование Петли фазовой автоподстройки частоты Синтезаторы частот Пассивная интермодуляция ВЧ аттенюаторы RF фильтры Радиочастотный циркулятор Типы радиоприемников Радио Superhet Избирательность приемника Чувствительность приемника Обработка сильного сигнала приемника Динамический диапазон приемника
    Вернуться в меню тем радио.. .

    Калькулятор резонансной частоты | LC Calculator

    Этот калькулятор резонансной частоты использует значения емкости (C) и индуктивности (L) LC-контура (также известного как резонансный контур, резервуарный контур или настроенный контур) для определения его резонансной частоты (f).

    Вы можете использовать калькулятор в три простых шага:

    1. Введите любые два параметра для резонансного контура.
    2. Выберите единицы измерения, которые вы хотите использовать.
    3. Нажмите «Рассчитать», и калькулятор резонансной частоты вычислит третий недостающий параметр.

    Ссылка

    В области электроники LC-цепь используется либо для генерации сигналов с определенной частотой, либо для выбора одного сигнала из более сложного сигнала с определенной частотой. LC-схемы играют фундаментальную роль в работе многих электронных устройств, включая радиооборудование, и используются в таких схемах, как фильтры, генераторы, тюнеры и смесители частот.

    LC-цепи состоят из двух соединенных между собой электронных компонентов: индуктора (L) и конденсатора (C).

    Когда L и C размещены параллельно или последовательно, они имеют резонансную частоту. Эта резонансная частота представлена ​​следующим уравнением:

    f = 1 / (2π √LC)

    Где: f – резонансная частота в герцах (Гц), L – индуктивность в генри (H ), C – емкость в фарадах (Ф), π – постоянная (3.(-6)))

    f = 1677,64 Гц ≈ 1,678 кГц.

    Формулы

    В этом калькуляторе резонансной частоты используются следующие формулы:

    f = 1 / (2π √LC) Резонансная частота [Гц]

    L = 1 / (4π 2 f 2 C) Индуктивность [H]

    C = 1 / (4π 2 f 2 L) Емкость [F]

    Вас также может заинтересовать наш бесплатный калькулятор кроссовера

    Калькулятор резонансной частоты

    для LC-контура

    Если вы хотите рассчитать резонансную частоту LC-контура, не смотрите дальше – этот калькулятор резонансной частоты – инструмент для вас.Введите индуктивность и емкость, и вы сразу же найдете резонансную и угловую частоту. Мы также предлагаем некоторую теорию, поскольку это может быть удобно – ниже вы узнаете, как рассчитать резонансную частоту, а также дадим краткое определение того, что такое резонансная частота на самом деле.

    Если вас интересуют электронные схемы, вы, вероятно, хотели бы знать, как получить некоторую долю входного напряжения – наш калькулятор делителя напряжения просто необходим для этой задачи.

    Что такое контур LC (контур резервуара)?

    LC-контур (также называемый резонансным контуром, резервуарным контуром или настроенным контуром) представляет собой идеализированный контур RLC с нулевым сопротивлением.Он содержит только катушку индуктивности и конденсатор в параллельной или последовательной конфигурации:

    Параллельная цепь LC Последовательный контур LC
    Цепи

    Tank обычно используются в качестве генераторов сигналов и полосовых фильтров – это означает, что они выбирают сигнал определенной частоты из более сложного сигнала.Они широко применяются в электронике – LC-схемы можно найти в усилителях, генераторах, тюнерах, радиопередатчиках и приемниках. Цепи LC и RC могут использоваться для фильтрации сигнала путем блокировки определенных частот.

    Что такое резонансная частота?

    Резонансная частота – это естественная незатухающая частота системы. Если мы применяем резонансную частоту, тогда колебания становятся максимальной амплитудой, и даже относительно небольшие силы могут создавать большие амплитуды.Однако, если выбрана любая другая частота, этот сигнал ослабляется. Есть много разных типов резонансов, например

    • механические и акустические,
    • электрика,
    • оптический,
    • орбитальный,
    • молекулярный.

    Для LC-контуров резонансная частота определяется емкостью C и импедансом L.

    Как рассчитать резонансную частоту?

    Следующая формула описывает взаимосвязь в цепи LC:

    f = 1 / (2 * π * √ (L * C))

    Где:

    • f – резонансная частота
    • L – индуктивность цепи
    • С – емкость цепи

    Откуда взялась эта формула? Резонанс в LC-цепи возникает, когда индуктивное сопротивление катушки индуктивности становится равным емкостному сопротивлению конденсатора.Итак:

    • xL = 2 * π * f * L
    • xC = 1 / (2 * π * f * C)

    Тогда, преобразовав уравнение, находим:

    • xL = xC
    • 2 * π * f * L = 1 / (2 * π * f * C)
      так:
    • f² = 1 / (4 * π² * L * C)
      и наконец:
    • f = 1 / (2 * π * √ (L * C))

    Также угловая частота может быть вычислена по следующей известной формуле:

    ω = 2 * π * f

    Как пользоваться вычислителем резонансной частоты

    С помощью нашего инструмента прогулка по парку:

    1. Введите значение конденсатора .Например, у нас емкость равна 1 мкФ.
    2. Тип индуктивности . Наша индуктивность в нашей LC-цепи равна 0,18 мГн.
    3. Вычислитель резонансной частоты сделал свое дело! Мы быстро выяснили, что такое резонансная частота: 11,863 кГц. Если вы хотите проверить также и угловую частоту, просто нажмите кнопку расширенного режима , и результат появится внизу.

    Калькулятор резонансной частоты – это гибкий инструмент, поэтому, как обычно, вы можете ввести любые две переменные, и недостающая переменная будет вычислена в мгновение ока.

    Калькулятор импеданса LC-цепи серии

    • Электрические, радиочастотные и электронные калькуляторы • Онлайн-преобразователи единиц

    Этот последовательный калькулятор импеданса LC-цепи определяет импеданс и угол сдвига фаз идеальной катушки индуктивности и идеального конденсатора, соединенных последовательно для заданной частоты синусоидальный сигнал. Также определяется угловая частота.

    Пример: Рассчитайте полное сопротивление катушки индуктивности 100 мГн и конденсатора 800 нФ на частоте 562 Гц.Этот пример показывает очень низкий импеданс, близкий к резонансному, около 0,9 Ом. Если вы хотите проверить импеданс при почти точном резонансе, введите 562,6977 Гц вместо 562 Гц. На этой частоте сопротивление слегка индуктивное. Если вы введете немного более низкую частоту 562,6976 Гц, импеданс изменится на слегка емкостный, и вы заметите, что угол разности фаз изменился с 90 ° на –90 °.

    Входной

    Индуктивность, л

    генри (H) миллигенри (мГн) микрогенри (мкГн) наногенри (нГн) пикогенри (pH)

    Емкость, C

    фарад (F) мкФ (нанофарад) мкФ (нФ) пикофарад (пФ)

    Частота, f

    герц (Гц) миллигерц (МГц) килогерц (кГц) мегагерц (МГц) гигагерц (ГГц)

    Выход

    Угловая частота рад / ω

    Емкостное реактивное сопротивление X C = Ом

    Индуктивное реактивное сопротивление X L = Ом

    Общее полное сопротивление LC | Z LC | = Ом

    Разность фаз φ = ° = рад

    Резонансная частота

    f 0 = Гц ω 0 = рад / с

    Введите значения емкости, индуктивности и частоты, выберите единиц и нажмите или коснитесь кнопки Calculate .Попробуйте ввести нулевые или бесконечно большие значения, чтобы увидеть, как ведет себя эта схема. Бесконечная частота не поддерживается. Чтобы ввести значение Infinity , просто введите inf в поле ввода.

    Для расчета используются следующие формулы:

    φ = 90 °, если 1/2 πfC <2 πfL

    90 φ если 1/2 πfC > 2 πfL

    φ = 0 °, если 1/2 πfC = 2 πfL

    , где

    LC Z 3 сопротивление цепи в омах (Ом),

    ω = 2πf – угловая частота в рад / с,

    f – частота в герцах (Гц),

    L – индуктивность в генри (H ),

    C – емкость в фарадах (F),

    ω 0 = резонансная угловая частота в радианах в секунду (рад / с),

    f 0 = резонансная частота в герц (Г),

    X C i s реактивное сопротивление конденсатора в Ом (Ом),

    X L – реактивное сопротивление катушки индуктивности в Ом (Ом),

    φ – фазовый сдвиг между общим напряжением В T и общим ток I T и

    j – мнимая единица.

    Для расчета введите индуктивность, емкость и частоту, выберите единицы измерения, и результат для полного сопротивления LC будет показан в омах, а для разности фаз – в градусах. Также будут рассчитаны реактивные сопротивления C и L, а также резонансная частота. Щелкните или коснитесь Расчет на резонансной частоте , чтобы увидеть, что произойдет при резонансе.

    Последовательная LC-цепь состоит из последовательно соединенных катушек индуктивности L и конденсатора C. Контур LC может резонировать на резонансной частоте.Резонанс возникает на частоте, на которой полное сопротивление цепи минимально, то есть, если в цепи нет реактивного сопротивления. Это явление возникает, когда реактивные сопротивления катушки индуктивности и конденсатора равны и из-за их противоположных знаков они компенсируют друг друга (подавление можно увидеть на правой векторной диаграмме ниже).

    Несколько графиков полного сопротивления последовательного LC-контура Z LC в зависимости от частоты f для заданной индуктивности и емкости показывают нулевое сопротивление на резонансных частотах.Когда частота увеличивается, реактивное сопротивление катушки индуктивности увеличивается, а реактивное сопротивление конденсатора уменьшается. Однако, если частота приближается к нулю (или постоянному току), реактивное сопротивление катушки индуктивности уменьшается до нуля, а реактивное сопротивление конденсатора увеличивается до бесконечности. При нулевой частоте последовательный LC-контур действует как разомкнутый контур. Обратите внимание, что импеданс является индуктивным справа от резонанса и емкостным слева от резонанса.

    Калькулятор определяет резонансную частоту LC-контура, и вы можете ввести эту частоту или значение немного выше или ниже ее, чтобы посмотрите, что произойдет с другими расчетными значениями при резонансе.

    Векторная диаграмма теоретически идеальной последовательной LC-цепи. Слева – емкостное реактивное сопротивление, то есть схема выполняет роль конденсатора; в центре – индуктивное реактивное сопротивление, то есть цепь действует как индуктор; справа – нулевое реактивное сопротивление при резонансе, и цепь действует как короткое замыкание.

    В последовательной цепи через катушку индуктивности и конденсатор протекает один и тот же ток, но отдельные напряжения на конденсаторе и на катушке индуктивности различаются. На векторной диаграмме показано напряжение V T идеального источника синусоидального напряжения.Поскольку сопротивление отсутствует, на резисторе нет падения напряжения в фазе с током, протекающим по цепи. Вектор напряжения индуктивности V L отстает от тока в векторе индуктивности на 90 °, поэтому он нарисован под + 90 °. Вектор напряжения емкости V C опережает вектор тока в конденсаторе на 90 ° и проходит под углом –90 °. Векторная сумма двух противоположных векторов может быть направлена ​​вниз или вверх в зависимости от падения напряжения на катушке индуктивности и конденсаторе.

    На резонансной частоте емкостное и индуктивное реактивные сопротивления равны, и если мы посмотрим на уравнение для | Z | выше, мы увидим, что эффективное сопротивление равно нулю, потому что два противоположных напряжения просто компенсируют друг друга. Ток, протекающий через катушку индуктивности и конденсатор, одинаков, а напряжения на них равны и противоположны. Таким образом, на резонансной частоте ток, потребляемый от источника, становится теоретически бесконечным, и идеальный последовательный LC-контур на резонансной частоте, подключенный к источнику напряжения, действует как короткое замыкание.В реальной жизни индукторы всегда имеют сопротивление, ограничивающее ток. Настоящие источники питания также не могут обеспечивать бесконечно большой ток, поскольку он ограничен внутренним сопротивлением источника питания.

    Резонансная частота последовательного LC-контура определяется с учетом того, что

    Умножая обе части уравнения на частоту f , мы получим

    Разделив обе части на 2 πL , взяв извлекая квадратный корень из обеих частей уравнения и упрощая, мы получим резонансную частоту:

    Катушки индуктивности в радиочастотном модуле телевизионного приемника

    Режимы отказа

    Что, если что-то пойдет не так в этой цепи? Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных режимах отказа:

    Специальные режимы

    Щелкните или коснитесь соответствующей ссылки, чтобы просмотреть калькулятор в различных специальных режимах:

    Различные режимы постоянного тока

    Короткое замыкание

    Обрыв цепи

    Чисто емкостная цепь

    Резонансная цепь

    Чисто индуктивная цепь

    Индуктивная цепь

    Примечания

    • В наших объяснениях поведения этой цепи нулевая частота означает постоянный ток.

    Больше новостей

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *