Напряжение на конденсаторе в цепи переменного: Attention Required! | Cloudflare

Конденсатор в цепи переменного тока

Господа, в сегодняшней статье я хотел бы рассмотреть такой интересный вопрос, как конденсатор в цепи переменного тока. Эта тема весьма важна в электричестве, поскольку на практике конденсаторы повсеместно присутствуют в цепях с переменным током и, в связи с этим, весьма полезно иметь четкое представление, по каким законам изменяются в этом случае сигналы. Эти законы мы сегодня и рассмотрим, а в конце решим одну практическую задачу определения тока через конденсатор.

Господа, сейчас для нас наиболее интересным моментом является то, как связаны между собой напряжение на конденсаторе и ток через конденсатор для случая, когда конденсатор находится в цепи переменного сигнала.

Почему сразу переменного? Да просто потому, что конденсатор в цепи постоянного тока ничем не примечателен. Через него течет ток только в первый момент, пока конденсатор разряжен. Потом конденсатор заряжается и все, тока нет (да-да, слышу, уже начали кричать, что заряд конденсатора теоретически длится бесконечно долгое время, да еще у него может быть сопротивление утечки, но пока что мы этим пренебрегаем). Заряженный конденсатор для

постоянного тока – это как разрыв цепи. Когда же у нас случай переменного тока – тут все намного интереснее. Оказывается, в этом случае через конденсатор может протекать ток и конденсатор в этом случае как бы эквивалентен резистору с некоторым вполне определенным сопротивлением (если пока забить забыть про всякие там сдвиги фазы, об этом ниже). Нам надо каким-нибудь образом получить связь между током и напряжением на конденсаторе.

Пока мы будем исходить из того, что в цепи переменного тока находится только конденсатор и все. Без каких-либо других компонентов типа резисторов или индуктивностей. Напомню, что в случае, когда у нас в цепи находится исключительно одни только резисторы, подобная задача решается очень просто: ток и напряжения оказываются связанными между собой через закон Ома. Мы про это уже не один раз говорили. Там все очень просто: делим напряжение на сопротивление и получаем ток. А как же быть в случае конденсатора? Ведь конденсатор-то это не резистор. Там совсем иная физика протекания процессов, поэтому вот так вот с наскока не получится просто связать между собой ток и напряжение. Тем не менее, сделать это надо, поэтому давайте попробуем порассуждать.

Сперва давайте вернемся назад. Далеко назад. Даже очень далеко. К самой-самой первой моей статье на этом сайте. Старожилы должно быть помнят, что это была статья про силу тока. Вот в этой самой статье было одно интересное выражение, которое связывало между собой силу тока и заряд, протекающий через сечение проводника. Вот это самое выражение

Кто-нибудь может возразить, что в той статье про силу тока запись была через Δq и Δt – некоторые весьма малые величины заряда и времени, за которое этот заряд проходит через сечение проводника. Однако здесь мы будем применять запись через

dq и dt – через дифференциалы. Такое представление нам потребуется в дальнейшем. Если не лезть глубоко в дебри матана, то по сути dq и dt здесь особо ничем не отличаются от Δq и Δt. Безусловно, глубоко сведущие в высшей математике люди могут поспорить с этим утверждением, но да сейчас я не хочу концентрировать внимание на данных вещах.

Итак, выражение для силы тока мы вспомнили. Давайте теперь вспомним, как связаны между собой емкость конденсатора С, заряд q, который он в себе накопил, и напряжение U на конденсаторе, которое при этом образовалось. Ну, мы же помним, что если конденсатор накопил в себе какой-то заряд, то на его обкладках неизбежно возникнет напряжение. Про это все мы тоже говорили раньше, вот в этой вот статье. Нам будет нужна вот эта формула, которая как раз и связывает заряд с напряжением

Давайте-ка выразим из этой формулы заряд конденсатора:

А теперь есть очень большой соблазн подставить это выражение для заряда конденсатора в предыдущую формулу для силы тока. Приглядитесь-ка повнимательнее – у нас ведь тогда окажутся связанными между собой сила тока, емкость конденсатора и напряжение на конденсаторе! Сделаем эту подстановку без промедлений:

Емкость конденсатора у нас является величиной постоянной. Она определяется исключительно самим конденсатором, его внутренним устройством, типом диэлектрика и всем таким прочим. Про все это подробно мы говорили в одной из прошлых статей. Следовательно, емкость С конденсатора, поскольку это константа, можно смело вынести за знак дифференциала (такие вот правила работы с этими самыми дифференциалами). А вот с напряжением U нельзя так поступить! Напряжение на конденсаторе будет изменяться со временем

. Почему это происходит? Ответ элементарный: по мере протекания тока на обкладках конденсатора, очевидно, заряд будет изменяться. А изменение заряда непременно приведет к изменению напряжения на конденсаторе. Поэтому напряжение можно рассматривать как некоторую функцию времени и его нельзя выносить из-под дифференциала. Итак, проведя оговоренные выше преобразования, получаем вот такую вот запись:

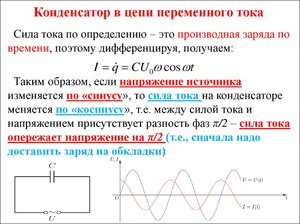
Господа, спешу вас поздравить – только что мы получили полезнейшее выражение, которое связывает между собой напряжение, приложенное к конденсатору, и ток, который течет через него. Таким образом, если мы знаем закон изменения напряжения, мы легко сможем найти закон изменения тока через конденсатор путем простого нахождения производной.

А как быть в обратном случае? Допустим, нам известен закон изменения тока через конденсатор и мы хотим найти закон изменения напряжения на нем. Читатели, сведущие в математике, наверняка уже догадались, что для решения этой задачи достаточно просто проинтегрировать написанное выше выражение. То есть, результат будет выглядеть как-то так:

По сути оба этих выражений про одно и тоже. Просто первое применяется в случае, когда нам известен закон изменения напряжения на конденсаторе и мы хотим найти закон изменения тока через него, а второе – когда нам известно, каким образом меняется ток через конденсатор и мы хотим найти закон изменения напряжения. Для лучшего запоминания всего этого дела, господа, я приготовил для вас поясняющую картинку. Она изображена на рисунке 1.

Рисунок 1 – Поясняющая картинка

На ней, по сути, в сжатой форме изображены выводы, которые хорошо бы запомнить.

Господа, обратите внимание – полученные выражения справедливы для любого закона изменения тока и напряжения. Здесь не обязательно должен быть синус, косинус, меандр или что-то другое. Если у вас есть какой-то совершенно произвольный, пусть даже совершенно дикий, не описанный ни в какой литературе, закон изменения напряжения

U(t), поданного на конденсатор, вы, путем его дифференцирования можете определить закон изменения тока через конденсатор. И аналогично если вы знаете закон изменения тока через конденсатор I(t) то, найдя интеграл, сможете найти, каким же образом будет меняться напряжение.

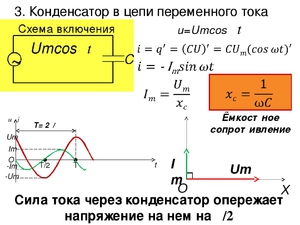
Итак, мы выяснили как связать между собой ток и напряжение для абсолютно любых, даже самых безумных вариантов их изменения. Но не менее интересны и некоторые частные случаи. Например, случай успевшего уже нам всем полюбиться синусоидального тока. Давайте теперь разбираться с ним.

Пусть напряжение на конденсаторе емкостью C изменяется по закону синуса вот таким вот образом

Какая физическая величина стоит за каждой буковкой в этом выражении мы подробно разбирали чуть раньше. Как же в таком случае будет меняться ток? Используя уже полученные знания, давайте просто тупо подставим это выражение в нашу общую формулу и найдем производную

Или можно записать вот так

Господа, хочу вам напомнить, что синус ведь только тем и отличается от косинуса, что один сдвинут относительно другого по фазе на 90 градусов. Ну, или, если выражаться на языке математики, то . Не понятно, откуда взялось это выражение? Погуглите формулы приведения . Штука полезная, знать не помешает. А еще лучше, если вы хорошо знакомы с тригонометрическим кругом, на нем все это видно очень наглядно.

Господа, отмечу сразу один момент. В своих статьях я не буду рассказывать про правила нахождения производных и взятия интегралов. Надеюсь, хотя бы общее понимание этих моментов у вас есть. Однако даже если вы не знаете, как это делать, я буду стараться излагать материал таким образом, чтобы суть вещей была понятна и без этих промежуточных выкладок. Итак, сейчас мы получили немаловажный вывод –

если напряжение на конденсаторе изменяется по закону синуса, то ток через него будет изменяться по закону косинуса. То есть ток и напряжение на конденсаторе сдвинуты друг относительно друга по фазе на 90 градусов. Кроме того, мы можем относительно легко найти и амплитудное значение тока (это множители, которые стоят перед синусом). Ну то есть тот пик, тот максимум, которого ток достигает. Как видим, оно зависит от емкости C конденсатора, амплитуды приложенного к нему напряжения U_m и частоты ω. То есть чем больше приложенное напряжение, чем больше емкость конденсатора и чем больше частота изменения напряжения, тем большей амплитуды достигает ток через конденсатор. Давайте построим график, изобразив на одном поле ток через конденсатор и напряжение на конденсаторе. Пока без конкретных цифр, просто покажем качественный характер. Этот график представлен на рисунке 2 (картинка кликабельна).

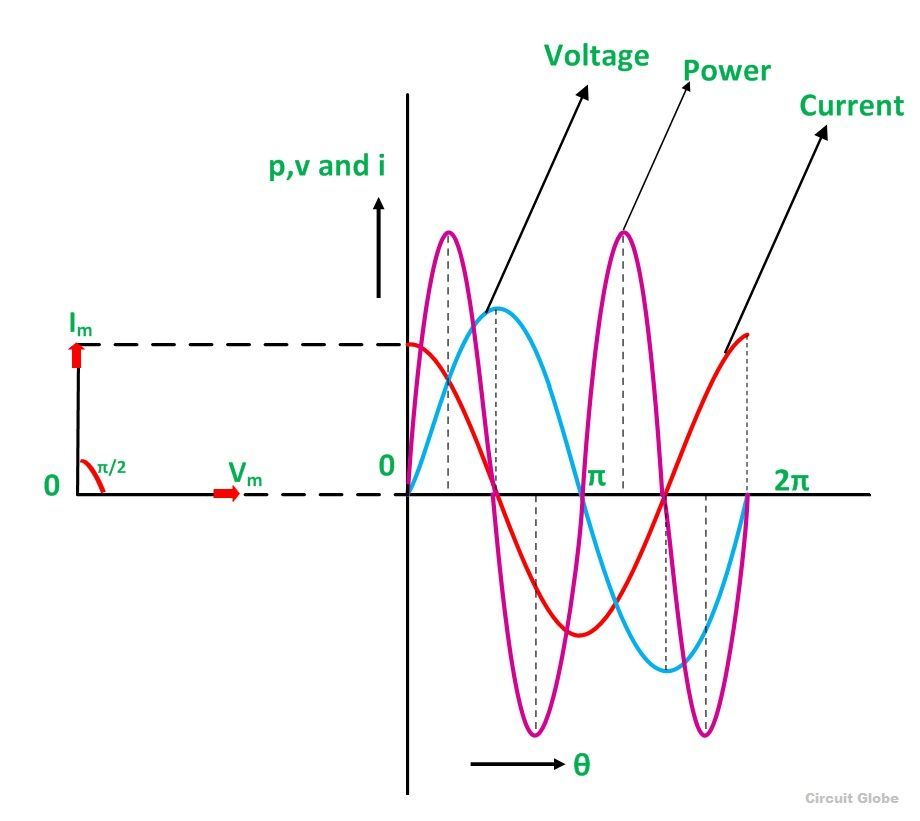
Рисунок 2 – Ток через конденсатор и напряжение на конденсаторе

На рисунке 2 синий график – это синусоидальный ток через конденсатор, а красный – синусоидальное напряжение на конденсаторе. По этому рисунку как раз очень хорошо видно, что ток опережает напряжение (пики синусоиды тока находятся левее соответствующих пиков синусоиды напряжения, то есть наступают раньше).

Давайте теперь проделаем работу наоборот. Пусть нам известен закон изменения тока I(t) через конденсатор емкостью C. И закон этот пусть тоже будет синусоидальным

Давайте определим, как в таком случае будет меняться напряжение на конденсаторе. Воспользуемся нашей общей формулой с интегральчиком:

По абсолютнейшей аналогии с уже написанными выкладками, напряжение можно представить вот таким вот образом

Здесь мы снова воспользовались интересными сведениями из тригонометрии, что . И снова формулы приведения

придут вам на помощь, если не понятно, почему получилось именно так.

Какой же вывод мы можем сделать из данных расчетов? А вывод все тот же самый, какой уже был сделан: ток через конденсатор и напряжение на конденсаторе сдвинуты по фазе друг относительно друга на 90 градусов. Более того, они не просто так сдвинуты. Ток опережает напряжение. Почему это так? Какая за этим стоит физика процесса? Давайте разберемся.

Представим, что незаряженный конденсатор мы подсоединили к источнику напряжения. В первый момент никаких зарядов в конденсаторе вообще нет: он же разряжен. А раз нет зарядов, то нет и напряжения. Зато ток есть, он возникает сразу при подсоединении конденсатора к источнику. Замечаете, господа? Напряжения еще нет (оно не успело нарасти), а ток уже есть. И кроме того, в этот самый момент подключения ток в цепи максимален (разряженный конденсатор ведь по сути эквивалентен короткому замыканию цепи). Вот вам и отставание напряжения от тока. По мере протекания тока, на обкладках конденсатора начинает накапливаться заряд, то есть напряжение начинает расти а ток постепенно уменьшаться. И через некоторое время накопится столько заряда на обкладках, что напряжение на конденсаторе сравняется с напряжением источника и ток в цепи совсем прекратится.

Теперь давайте этот самый заряженный конденсатор отцепим от источника и закоротим накоротко. Что получим? А практически то же самое. В самый первый момент ток будет максимален, а напряжение на конденсаторе останется таким же, какое оно и было без изменений. То есть снова ток впереди, а напряжение изменяется вслед за ним. По мере протекания тока напряжение начнет постепенно уменьшаться и когда ток совсем прекратится, оно тоже станет равным нулю.

Для лучшего понимания физики протекающих процессов можно в который раз уже использовать водопроводную аналогию. Представим себе, что заряженный конденсатор – это некоторый бачок, полный воды. У этого бачка есть внизу краник, через который можно спустить воду. Давайте этот краник откроем. Как только мы его откроем, вода потечет сразу же. А давление в бачке будет падать постепенно, по мере того, как вода будет вытекать. То есть, грубо говоря, ручеек воды из краника опережает изменение давления, подобно тому, как ток в конденсаторе опережает изменение напряжения на нем. 

Подобные рассуждения можно провести и для синусоидального сигнала, когда ток и напряжения меняются по закону синуса, да и вообще для любого. Суть, надеюсь, понятна.

Давайте проведем небольшой практический расчет переменного тока через конденсатор и построим графики.

Пусть у нас имеется источник синусоидального напряжения, действующее значение равно 220 В, а частота 50 Гц. Ну, то есть все ровно так же, как у нас в розетках. К этому напряжению подключают конденсатор емкостью 1 мкФ. Например, пленочный конденсатор К73-17, рассчитанный на максимальное напряжение 400 В (а на меньшее напряжение конденсаторы ни в коем случае нельзя подключать в сети 220 В), выпускается с емкостью 1 мкФ. Чтобы вы имели представление, с чем мы имеем дело, на рисунке 3 я разместил фотографию этого зверька (спасибо Diamond за фото )

Рисунок 3 – Ищем ток через этот конденсатор

Требуется определить, какая амплитуда тока будет протекать через этот конденсатор и построить графики тока и напряжения.

Сперва нам надо записать закон изменения напряжения в розетке. Если вы помните, амплитудное значение напряжения в этом случае равно около 311 В. Почему это так, откуда получилось, и как записать закон изменения напряжения в розетке, можно прочитать вот в этой статье. Мы же сразу приведем результат. Итак, напряжение в розетке будет изменяться по закону

Теперь мы можем воспользоваться полученной ранее формулой, которая свяжет напряжение в розетке с током через конденсатор. Выглядеть результат будет так

Мы просто подставили в общую формулу емкость конденсатора, заданную в условии, амплитудное значение напряжения и круговую частоту напряжения сети. В результате после перемножения всех множителей имеем вот такой вот закон изменения тока

Вот так вот, господа. Получается, что амплитудное значение тока через конденсатор чуть меньше 100 мА. Много это или мало? Вопрос нельзя назвать корректным. По меркам промышленной техники, где фигурируют сотни ампер тока, очень мало. Да и для бытовых приборов, где десятки ампер не редкость – тоже. Однако для человека даже такой ток представляет большую опасность! Отсюда следует вывод, что хвататься за такой конденсатор, подключенный к сети 220 В не следует . Однако на этом принципе возможно изготовление так называемых источников питания с гасящим конденсатором. Ну да это тема для отдельной статьи и здесь мы не будем ее затрагивать.

Все это хорошо, но мы чуть не забыли про графики, которые должны построить. Надо срочно исправляться! Итак, они представлены на рисунке 4 и рисунке 5. На рисунке 4 вы можете наблюдать график напряжения в розетке, а на рисунке 5 – закон изменения тока через конденсатор, включенный в такую розетку.

Рисунок 4 – График напряжения в розетке

Рисунок 5 – График тока через конденсатор

Как мы можем видеть из этих рисунков, ток и напряжение сдвинуты на 90 градусов, как и должно быть. И, возможно, у читателя возникла мысль – если через конденсатор течет ток и на нем падает какое-то напряжение, вероятно, на нем должна выделяться и некоторая мощность. Однако спешу предупредить вас – для конденсатора дело обстоит совершенно не так. Если рассматривать идеальный конденсатор, то мощность на нем не будет вообще выделяться, даже при протекании тока и падении на нем напряжения. Почему? Как же так? Об этом – в будущих статьях. А на сегодня все. Спасибо что читали, удачи, и до новых встреч!

Вступайте в нашу группу Вконтакте

Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.

Конденсатор в цепи переменного тока

Мы знаем, что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.

Совершенно иначе ведет себя конденсатор в цепи переменного тока (Рис 1,а).

Рисунок 1. Сравнение конденсатора в цепи переменного тока с пружиной, на которую воздействует внешняя сила.

 

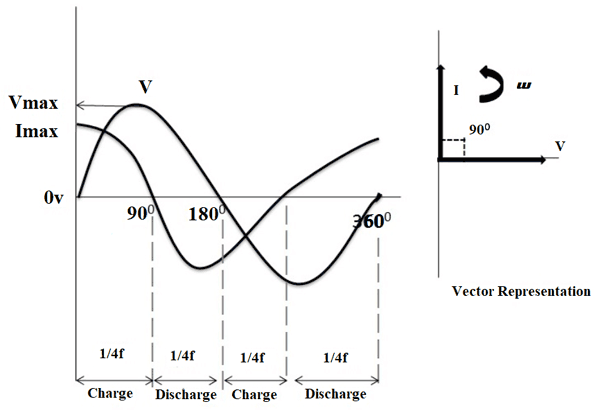
В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться. Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС пе-рестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.

После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.

Итак, к концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.

С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т. е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.

Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.

Итак, к концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.

В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.

Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рис. 1,а, который мы построили на основании наших рассуждений, видно, что в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°.

Отметим, что в цепи с индуктивностью ток отставал от напряжения, а в цепи с емкостью ток опережает напряжение. И в том и в другом случае между фазами тока и напряжения имеется сдвиг, но знаки этих сдвигов противоположны

 

Емкостное сопротивление конденсатора

Мы уже заметили, что ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС

Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление. Величина емкостного сопротивления тем меньше, чем больше емкость и чем выше частота переменного тока. И наоборот, сопротивление конденсатора переменному току увеличивается с уменьшением его емкости и понижением частоты.

Рисунок 2. Зависимость емкостного сопротивления конденсатра от частоты.

Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.

Величина емкостного сопротивления определяется по следующей формуле:

где Хс — емкостное сопротивление конденсатора в ом;

f—частота переменного тока в гц;

ω — угловая частота переменного тока;

С — емкость конденсатора в ф.

При включении конденсатора в цепь переменного тока, в последнем, как и в индуктивности, не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление, как и индуктивное, является реактивным или безваттным.

Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается большая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому се называют мощностью потерь.

Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.

Ранее мы сравнивали электрическую емкость с вместимостью герметически (наглухо) закрытого сосуда или с площадью дна открытого сосуда, имеющего вертикальные стенки.

Конденсатор в цепи переменного тока целесообразно сравнивать с гиб-костью пружины. При этом во избежание возможных недоразумений условимся под гибкостью понимать не упругость («твердость») пружины, а величину, ей обратную, т. е. «мягкость» или «податливость» пружины.

Представим себе, что мы периодически сжимаем и растягиваем спиральную пружину, прикрепленную одним концом наглухо к стене. Время, в течение которого мы будем производить полный цикл сжатия и растяжения пружины, будет соответствовать периоду переменного тока.

Таким образом, мы в течение первой четверти периода будем сжимать пружину, в течение второй четверти периода отпускать ее, в течение третьей четверти периода растягивать и в течение четвертой четверти снова отпускать.

Кроме того, условимся, что наши усилия в течение периода будут неравномерными, а именно: они будут нарастать от нуля до максимума в течение первой и третьей четвертей периода и уменьшаться от максимума до нуля в течение второй и четвертой четвертей.

Сжимая и растягивая пружину таким образом, мы заметим, что в начале первой четверти периода незакрепленный конец пружины будет двигаться довольно быстро при сравнительно малых усилиях с нашей стороны.

В конце первой четверти периода (когда пружина сожмется), наоборот, несмотря на возросшие усилия, незакрепленный конец пружины будет двигаться очень медленно.

В продолжение второй четверти периода, когда мы будем постепенно ослаблять давление на пружину, ее незакрепленный конец будет двигаться по направлению от стены к нам, хотя наши задерживающие усилия направлены по направлению к стене. При этом наши усилия в начале второй четверти периода будут наибольшими, а скорость движения незакрепленного конца пружины наименьшей. В конце же второй четверти периода, когда наши усилия будут наименьшими, скорость движения пружины будет наибольшей и т. д.

Продолжив аналогичные рассуждения для второй половины периода (для третьей и четвертой четвертей) и построив графики (рис. 1,б) изменения наших усилий и скорости движения незакрепленного конца пружины, мы убедимся, что эти графики в точности соответствуют графикам ЭДС и тока в емкостной цепи (рис 1,а), причем график усилий будет соответствовать графику ЭДС , а график скорости — графику силы тока.

 

Рисунок 3. а)Процессы в цепи переменного тока с конденсатором и б)сравнение конденсатора с пружиной.

Нетрудно, заметить, что пружина, так же как и конденсатор, в течение одной четверти периода накапливает энергию, а в течение другой четверти периода отдает ее обратно.

Вполне очевидно также, что чем меньше гибкость пружины,- т е. чем она более упруга, тем большее противодействие она будет оказывать нашим усилиям. Точно так же и в электрической цепи: чем меньше емкость, тем больше будет сопротивление цепи при данной частоте.

И наконец, чем медленнее мы будем сжимать и растягивать пружину, тем меньше будет скорость движения ее незакрепленного конца. Аналогично этому, чем меньше частота, тем меньше сила тока при данной ЭДС.

При постоянном давлении пружина только сожмется и на этом прекратит свое движение, так же как при постоянной ЭДС конденсатор только зарядится и на этом прекратится дальнейшее движение электронов в цепи.

А теперь как ведет себя конденсатор в цепи переменного тока вы можете посмотреть в следующем видео:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Конденсатор в цепи переменного тока

Конденсатор в цепи переменного тока

Подробности

Просмотров: 358

«Физика – 11 класс»

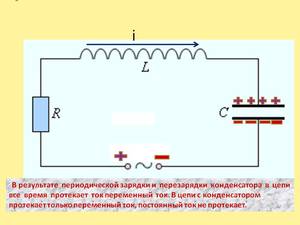
Постоянный ток не может идти по цепи, содержащей конденсатор, так как обкладки конденсатора разделены диэлектриком.
Переменный же ток может идти по цепи, содержащей конденсатор.

Есть источники постоянного и переменного напряжений, в которых постоянное напряжение на зажимах источника равно действующему значению переменного напряжения.
Цепь состоит из конденсатора и лампы накаливания, соединенных последовательно.
При включении постоянного напряжения (переключатель влево) лампа не светится.
При включении переменного напряжения (переключатель вправо) лампа загорается, если емкость конденсатора достаточно велика.

Под действием переменного напряжения происходит периодическая зарядка и разрядка конденсатора.
Ток, идущий в цепи при перезарядке конденсатора, нагревает нить лампы.

Если сопротивлением проводов и обкладок конденсатора можно пренебречь,

то напряжение на конденсаторе равно напряжению на концах цепи.

Следовательно,

Заряд конденсатора меняется по гармоническому закону:

q = CU_m cos ωt

Сила тока, представляющая собой производную заряда по времени, равна:

Колебания силы тока опережают по фазе колебания напряжения на конденсаторе на .

Амплитуда силы тока равна:

I_m = U_mCω

Если ввести обозначение

и вместо амплитуд силы тока и напряжения использовать их действующие значения, то получим

Величину Х_с, обратную произведению ωС циклической частоты на электрическую емкость конденсатора, называют емкостным сопротивлением.
Роль этой величины аналогична роли активного сопротивления R в законе Ома.
Действующее значение силы тока связано с действующим значением напряжения на конденсаторе точно так же, как связаны согласно закону Ома сила тока и напряжение для участка цепи постоянного тока.
Это и позволяет рассматривать величину Х_с как сопротивление конденсатора переменному току (емкостное сопротивление).

Чем больше емкость конденсатора, тем больше ток перезарядки.
Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора.
В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Х_с.
С увеличением емкости оно уменьшается.
Уменьшается оно и с увеличением частоты ω.

На протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергии электрического поля.
В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.

Итак,
сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .

Источник: «Физика – 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса – Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

принцип работы устройства, реактивная электроэнергия

Конденсатор в цепи переменного тока или постоянного, который нередко называется попросту кондёром, состоит из пары обкладок, покрытых слоем изоляции. Если на это устройство будет подаваться ток, оно будет получать заряд и сохранять его в себе некоторое время. Емкость его во многом зависит от промежутка между обкладками.

Принцип работы

Конденсатор может быть выполнен по-разному, но суть работы и основные его элементы остаются неизменными в любом случае. Чтобы понять принцип работы, необходимо рассмотреть самую простую его модель.

У простейшего устройства имеются две обкладки: одна из них заряжена положительно, другая — наоборот, отрицательно. Заряды эти хоть и противоположны, но равны. Они притягиваются с определенной силой, которая зависит от расстояния. Чем ближе друг к другу располагаются обкладки, тем больше между ними сила притяжения. Благодаря этому притяжению заряженное устройство не разряжается.

Однако достаточно проложить какой-либо проводник между двумя обкладками и устройство мгновенно разрядится. Все электроны от отрицательно заряженной обкладки сразу же перейдут на положительно заряженную, в результате чего заряд уравняется. Иными словами, чтобы снять заряд с конденсатора, необходимо лишь замкнуть две его обкладки.

Описание конденсатора постоянного тока

Электрические цепи бывают двух видов — постоянными или переменными. Все зависит от того, как в них протекает электроток. Устройства в этих цепях ведут себя по-разному.

Чтобы рассмотреть, как будет вести себя конденсатор в цепи постоянного тока, нужно:

1. Взять блок питания постоянного напряжения и определить значение напряжения. Например, «12 Вольт».
2. Установить лампочку, рассчитанную на такое же напряжение.
3. В сеть установить конденсатор.

Никакого эффекта не будет: лампочка так и не засветится, а если убрать из цепи конденсатор, то свет появится. Если устройство будет включено в сеть переменного тока, то она попросту не будет замыкаться, поэтому и никакой электроток здесь пройти не сможет. Постоянный — не способен проходить по сети, в которую включен конденсатор. Всему виной обкладки этого устройства, а точнее, диэлектрик, который разделяет эти обкладки.

Убедиться в отсутствии напряжения в сети постоянного электротока можно и другими способами. Подключать к сети можно, что угодно, главное, чтобы в цепь был включен источник постоянного электротока. Элементом же, который будет сигнализировать об отсутствии напряжения в сети или, наоборот, о его присутствии, также может быть любой электроприбор. Лучше всего для этих целей использовать лампочку: она будет светиться, если электроток есть, и не будет гореть при отсутствии напряжения в сети.

Можно сделать вывод, что конденсатор не способен проводить через себя постоянный ток, однако это заключение неправильное. На самом деле электроток сразу после подачи напряжения появляется, но мгновенно и исчезает. В этом случае он проходит в течение лишь нескольких долей секунды. Точная продолжительность зависит от того, насколько емким является устройство, но это, как правило, в расчет не берется.

Особенности устройства с переменным электротоком

Чтобы определить, будет ли проходить переменный электроток, необходимо устройство подключить в соответствующую цепь. Основным источником электроэнергии в таком случае должно являться устройство, генерирующее именно переменный электроток.

Постоянный электрический ток не идет через конденсатор, а вот переменный, наоборот, протекает, причем устройство постоянно оказывает сопротивление проходящему через него электротоку. Величина этого сопротивления связана с частотой. Зависимость здесь обратно пропорциональная: чем ниже частота, тем выше сопротивление. Если к источнику переменного электротока подключить кондер, то наибольшее значение напряжения здесь будет зависеть от силы тока.

Убедиться в том, что конденсатор может проводить переменный электроток, наглядно поможет простейшая цепь, составленная из:

• Источника тока. Он должен быть переменным.
• Конденсатора.
• Потребителя электротока. Лучше всего использовать лампу.

Однако стоит помнить об одном: лампа загорится лишь в том случае, если устройство имеет довольно большую емкость. Переменный ток оказывает на конденсатор такое влияние, что устройство начинает заряжаться и разряжаться. А ток, который проходит по сети во время перезарядки, повышает температуру нити накаливания лампы. В результате она и светится.

От емкости устройства, подключенного к сети переменного тока, во многом зависит электроток перезарядки. Зависимость прямо пропорциональная: чем большей емкостью обладает, тем больше величина, характеризующая силу тока перезарядки. Чтобы в этом убедиться, достаточно лишь повысить емкость. Сразу после этого лампа начнет светиться ярче, так как нити ее будут больше накалены. Как видно, конденсатор, который выступает в качестве одного из элементов цепи переменного тока, ведет себя иначе, нежели постоянный резистор.

При подключении конденсатора переменного тока начинают происходить более сложные процессы. Лучше их понять поможет такой инструмент, как вектор. Главная идея вектора в этом случае будет заключаться в том, что можно представить значение изменяющегося во времени сигнала как произведение комплексного сигнала, который является функцией оси, отображающей время и комплексного числа, которое, наоборот, не связано со временем.

Поскольку векторы представляются некоторой величиной и некоторым углом, начертить их можно в виде стрелки, которая вращается в координатной плоскости. Напряжение на устройстве немного отстает от тока, а оба вектора, которыми они обозначаются, вращаются на плоскости против часовых стрелок.

Конденсатор в сети переменного тока может периодически перезаряжаться: он то приобретает какой-то заряд, то, наоборот, отдает его. Это означает, что кондер и источник переменного электротока в сети постоянно обмениваются друг с другом электрической энергией. Такой вид электроэнергии в электротехнике носит название реактивной.

Конденсатор не позволяет проходить по сети постоянному электротоку. В таком случае он будет иметь сопротивление, приравнивающееся к бесконечности. Переменный же электроток способен проходить через это устройство. В этом случае сопротивление имеет конечное значение.

Конденсатор в цепи переменного тока

Если конденсатор включить в цепь постоянного тока, то такая цепь будет разомкнутой, так как обкладки конденсатора разделяет диэлектрик, и ток в цепи идти не будет. Иначе происходит в цепи переменного тока. Переменный ток способен течь в цепи, если она содержит конденсатор. Это происходит не из-за того, что заряды вдруг получили возможность перемещаться между пластинами конденсатора. В цепи переменного тока происходит периодическая зарядка и разрядка конденсатора, который в нее включен благодаря действию переменного напряжения.

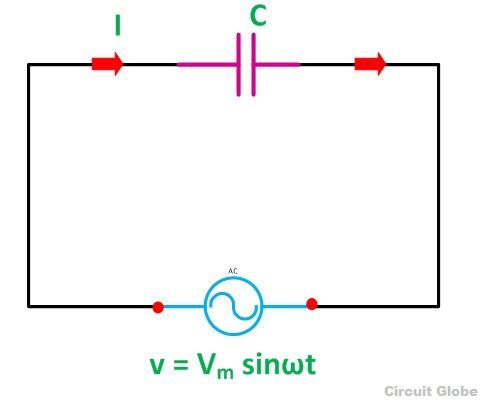
Рассмотрим цепь на рис.1, которая включает конденсатор. Будем считать, что сопротивление проводов и обкладок конденсатора не существенно, напряжение переменного тока изменяется по гармоническому закону:

   

По определению емкость на конденсаторе равна:

   

Следовательно, напряжение на конденсаторе:

   

Из выражения (3), очевидно, что заряд на конденсаторе будет изменяться по гармоническому закону:

   

Сила тока равна:

   

Сравнивая законы колебаний напряжения на конденсаторе и силы тока, видим, что колебания тока опережают напряжение на . Этот факт отражает то, что в момент начала зарядки конденсатора сила тока в цепи является максимальной при равенстве нулю напряжения. В момент времени, когда напряжение достигает максимума, сила тока падает до нуля.

В течение периода, при зарядке конденсатора до максимального напряжения, энергия, поступающая в цепь, запасается на конденсаторе, в виде энергии электрического поля. За следующую четверть периода данная энергия возвращается обратно в цепь, когда конденсатор разряжается.

Амплитуда силы тока (), исходя из выражения (5), равна:

   

Емкостное сопротивление конденсатора

Физическую величину, равную обратному произведению циклической частоты на емкость конденсатора называют его емкостным сопротивлением ():

   

Роль емкостного сопротивления уподобляют роли активного сопротивления (R) в законе Ома:

   

где – амплитудное значение силы тока; – амплитуда напряжения. Для емкостного сопротивления действующая величина силы тока имеет связь с действующим значением напряжения аналогичную выражению (8) (как сила тока и напряжение для постоянного тока):

   

На основании (9) говорят, что сопротивление конденсатора переменному току.

При увеличении емкости конденсатора растет ток перезарядки. Тогда как сопротивление конденсатора постоянному току является бесконечно большим (в идеальном случае), ёмкостное сопротивление конечно. С увеличением емкости и (или) частоты уменьшается.

Примеры решения задач

Конденсатор в цепи переменного тока

Физика > Конденсаторы в цепях переменного тока: емкостное сопротивление и фазовые диаграммы

 

Изучите колебание, емкость, сопротивление и напряжение конденсатора в цепи переменного тока: использование фазового вектора, диаграмма, закон Ома, уравнения.

Напряжение на конденсаторе отстает от тока. Из-за разности фаз лучше всего ввести фазоры, чтобы охарактеризовать схемы.

Задача обучения

• Разобраться в преимуществе применения фазора.

Основные пункты

• Если конденсатор присоединен к переменному напряжению, то максимальное выступает пропорциональным максимальному току. Но они не возникают одновременно.
• Если питание переменного тока присоединено к резистору, то ток и напряжение выступают пропорциональными по отношению друг к другу. То есть, они достигнут пика в одно время.
• Среднеквадратичный ток в цепи с конденсатором определяется версией закона Ома: I_rms = V_rms/X_C, где X_С – емкостное сопротивление.

Термины

• RMS – среднеквадратичное число; статическая мера величины.

Фазор

Благодаря фазовым векторам сложный и меняющийся во времени сигнал можно представить в виде комплексного числа (не зависит от времени) и сложного сигнала (зависит от времени). Фазоры делятся на основе А (амплитуды), v (частоты) и θ (фазы). Это приносит большую пользу, ведь частотный коэффициент часто выступает общим для всех компонентов линейной комбинации синусоид. В подобных ситуациях факторы исключают факультативную характеристику и основываются лишь на A и θ.

К примеру, можно представить A⋅cos (2πνt + θ) просто как комплексную постоянную Ae^iθ. Из-за того, что фазовые векторы передаются величиной и углом, наглядно изображаются вектором в плоскости x-y.

Фазор можно рассматривать с позиции вектора, вращающегося вокруг начала координат. Косинусная функция – проекция вектора на ось. Амплитуда выступает модулем вектора. Постоянная фазы – угол, сформированный вектором и осью при t = 0

Конденсаторы в цепях переменного тока

Если питание переменного тока присоединено к резистору, то ток и напряжение выступают пропорциональными. То есть, достигают пика в одно время. Если к переменному напряжению подключен конденсатор, то максимальные ток и напряжение пропорциональны. Ток достигает максимума в точке ¼ цикла пикового напряжения (приводит к 90°).

Максимумы тока на ¼ цикла напряжения, в случаях, когда к переменному напряжению присоединен конденсатор

Для схемы с конденсатором значение V/I не выступает постоянным. Но V_max/I_max полезное и именуется емкостью сопротивления. Это все еще напряжение, деленное на ток, а единица – Ом. Значение X_C основывается на емкости и частоте: 

Конденсатор влияет на ток и при полном заряде способен полностью его остановить. Напряжение переменного тока поступает постоянно, поэтому есть среднеквадратичный ток, ограниченный конденсатором. Это эффективное сопротивление конденсатора к переменному току, поэтому среднеквадратичное (I_rms) определяется версией закона Ома:

(V_rms – среднеквадратичное напряжение).

Фазовое представление

Напряжение на конденсаторе в цепи переменного тока не поспевает за током, поэтому фазовый вектор повторяет его движение. На диаграмме стрелки совершают обороты против часовой стрелки в частоте v.

Схема фазора для цепи переменного тока с конденсатором

---

Цепь переменного тока с конденсатором

При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.

Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.

Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0).

Схема замещения конденсатора с параллельным соединением элементов

Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной B_с проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/U_c², а емкость — конструкцией конденсатора. Предположим, что проводимости G и В_с для такой цепи известны, а напряжение имеет уравнение

u = Umsinωt.

Требуется определить токи в цепи и мощность. Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и В_с , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

i = i_G + i_c,                                                      (13.30)

Учитывая, что ток i_G совпадает по фазе с напряжением, а ток i_c опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:

 

Векторная диаграмма токов в цепи с конденсатором

Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению

I = I_G + I_C

 

Действующие величины составляющих тока:

 

I_G = GU                                                       (13.31)

 

I_C = B_CU                                                      (13.32)

Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φ_a =0). Вектор I_G совпадает по направлению с вектором U, а вектор I_C направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы I_G и I_C : При напряжении u = U_msinωt соответствии с векторной диаграммой уравнение тока

i = I_msin(ωt + φ)

 

Треугольник проводимостей для конденсатора

Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = I_G/U и емкостная В_с = I_с/U проводимости, а гипотенузой — полная проводимость цепи Y = I/U. Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами

I = UY

 

U = I/Y                                                        (13.35)

 

Из треугольников токов и проводимостей определяют величины

 

cosφ = I_G/I = G/Y;                sinφ = I_c/I = B_c/Y;              tgφ = I_C/I_G = B_c/G.               (13.36)

 

Мощность цепи с конденсатором

Выражение мгновенной мощности реального конденсатора

p = ui = U_msinωt * I_msin(ωt+φ)

совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная

 P = UI_G = UIcosφ

реактивная

Q = UI_C = UIsinφ

полная

 

Схема замещения конденсатора с последовательным соединением элементов

Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Х_с сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е. емкостью С[B_C = ωC, X_c = 1/(ωC)] Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.

Конденсатор

в последовательной, параллельной и цепи переменного тока

Конденсатор – один из наиболее часто используемых электронных компонентов. Он имеет способность накапливать энергию внутри себя в виде электрического заряда, создающего статическое напряжение (разность потенциалов) на его пластинах. Проще говоря, конденсатор похож на небольшую аккумуляторную батарею. Конденсатор представляет собой просто комбинацию двух проводящих или металлических пластин, расположенных параллельно друг другу и электрически разделенных хорошим изолирующим слоем (также называемым диэлектриком ) , состоящим из вощеной бумаги, слюды, керамики, пластика и т. Д.

Существует множество применений конденсатора в электронике, некоторые из них перечислены ниже:

• Накопитель энергии
• Кондиционирование питания
• Коррекция коэффициента мощности
• Фильтрация
• Осцилляторы

Теперь дело в , как конденсатор работает ? Когда вы подключаете источник питания к конденсатору, он блокирует постоянный ток из-за изолирующего слоя и позволяет напряжению присутствовать на пластинах в виде электрического заряда.Итак, вы знаете, как работает конденсатор и каково его использование или применение, но вы должны научиться этому, как использовать конденсатор в электронных схемах.

Как подключить конденсатор в электронную схему?

Здесь мы собираемся продемонстрировать вам подключение конденсатора и связанный с ним эффект на примерах.

• Конденсатор серии
• Параллельный конденсатор
• Конденсатор в цепи переменного тока

Конденсатор в последовательной цепи

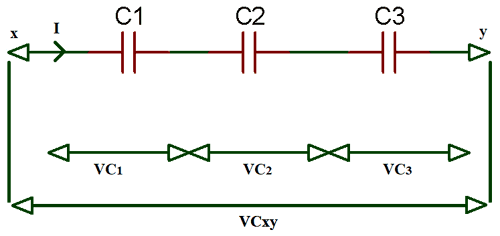
В схеме, когда вы соединяете конденсаторы последовательно, как показано на изображении выше, общая емкость уменьшается.Ток через конденсаторы, соединенные последовательно, равен (т.е. _T = ₁ = ₂ = _{3 = n} ). Следовательно, заряд, накопленный конденсаторами, также одинаков (то есть Q _T = Q ₁ = Q ₂ = Q ₃ ), потому что заряд, накопленный пластиной любого конденсатора, исходит от пластины соседнего конденсатор в цепи.

Применяя Закон Кирхгофа (KVL) о напряжении в цепи, мы получаем

  V  T  = V  C1  + V  C2  + V  C3 … уравнение (1)  

Как известно,

  Q =  CV
  Итак, V = Q / C  

Где, V _C1 = Q / C ₁ ; V _C2 = Q / C ₂ ; V _C3 = Q / C ₃

Теперь, подставив вышеуказанные значения в уравнение (1)

   (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 )  

Для n последовательно подключенных конденсаторов уравнение будет

.

  (1 / C  T ) = (1 / C  1 ) + (1 / C  2 ) + (1 / C  3 ) +….+ (1 / Cn)  

Следовательно, приведенное выше уравнение является уравнением конденсаторов серии .

Где, C _T = Общая емкость цепи

C ₁ … n = емкость конденсаторов

Уравнение емкости для двух особых случаев определено ниже:

Случай I: , если два конденсатора соединены последовательно, с разными значениями емкость будет выражена как:

  (1 / C  T ) = (C  1  + C  2 ) / (C  1  * C  2 ) 
  Или, C  T  = (C  1  * C  2 ) / (C  1  + C  2 )… уравнение (2)  

Вариант II: , если два конденсатора включены последовательно, с одинаковым значением емкость будет выражаться как:

  (1 / C  T ) = 2 / C  2  = 2 / C 
  Или, C  T  = C / 2  

Пример цепи последовательного конденсатора:

Теперь в приведенном ниже примере мы покажем вам, как рассчитать общую емкость и индивидуальное среднеквадратичное падение напряжения на каждом конденсаторе.

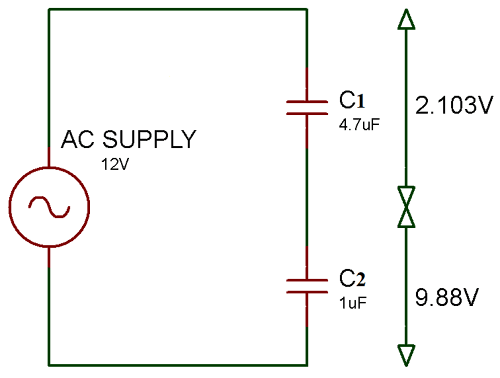
Как показано на приведенной выше принципиальной схеме, есть два конденсатора , соединенных последовательно с разными номиналами. Значит, падение напряжения на конденсаторах также неодинаково. Если мы подключим два конденсатора с одинаковым значением, падение напряжения также будет одинаковым.

Теперь для определения общего значения емкости воспользуемся формулой из уравнения (2)

  Итак, C  T  = (C  1  * C  2 ) / (C  1  + C  2 ) 
  Здесь C  1  = 4.7 мкФ и C  2  = 1 мкФ 
  C  T  = (4,7 мкФ * 1 мкФ) / (4,7 мкФ + 1 мкФ) 
  C  T  = 4,7 мкФ / 5,7 мкФ 
  C  T  = 0,824 мкФ  

Теперь падение напряжения на конденсаторе C ₁ составляет:

  VC  1  = (C  T  / C  1 ) * V  T  
  VC  1  = (0,824 мкФ / 4,7 мкФ) * 12 
  VC  1  = 2,103V  

Теперь падение напряжения на конденсаторе C ₂ составляет:

  VC  2  = (C  T  / C  2 ) * V  T  
  VC  2  = (0.824 мкФ / 1 мкФ) * 12 
  VC  2  = 9,88 В  

Конденсатор в параллельной цепи

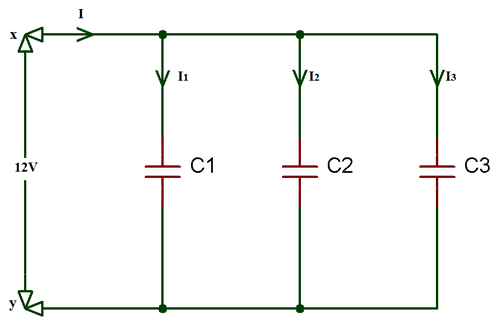
При параллельном подключении конденсаторов общая емкость будет равна сумме емкостей всех конденсаторов. Потому что верхняя пластина всех конденсаторов соединена вместе, как и нижняя пластина. Таким образом, при соприкосновении друг с другом эффективная площадь пластин также увеличивается. Следовательно, емкость пропорциональна отношению площади и расстояния.

Применяя Текущий закон Кирхгофа (KCL) в вышеуказанной схеме,

  i  T  = i  1  + i  2  + i  3   

Как известно, ток через конденсатор выражается как;

  i = C (dV /   dt  ) 
  So, i  T  = C  1  (dV /   dt  ) + C  2  (dV /   dt  ) + C  3  (dV /   dt  ) 
  А,
   i    T     = (C  1  + C  2  + C  3 ) * (dV /   dt  ) 
  i  T  = C  T  (dV /   dt  )… уравнение (3)  

Из уравнения (3) уравнение параллельной емкости:

  C  T  = C  1  + C  2  + C  3   

Для числа n конденсаторов, соединенных параллельно, уравнение выше выражается как:

  C  T  = C  1  + C  2  + C  3  +… + Cn  

Пример параллельной цепи конденсатора

На приведенной ниже принципиальной схеме три конденсатора подключены параллельно .Поскольку эти конденсаторы подключены параллельно, эквивалентная или полная емкость будет равна сумме отдельной емкости.

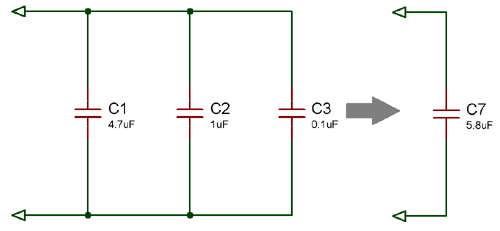
  C  T  = C  1  + C  2  + C  3  
  Где, C  1  = 4,7 мкФ; C  2  = 1 мкФ и C  3  = 0,1 мкФ 
  Так, C  T  = (4,7 +1 + 0,1) мкФ 
  C  T  = 5,8 мкФ  

Конденсатор в цепях переменного тока

Когда конденсатор подключен к источнику постоянного тока, конденсатор начинает медленно заряжаться.И, когда напряжение зарядного тока конденсатора равно напряжению питания, считается, что он полностью заряжен. Здесь в этом состоянии конденсатор работает как источник энергии, пока подается напряжение. Также конденсаторы не позволяют току проходить через него после полной зарядки.

Каждый раз, когда на конденсатор подается переменное напряжение, как показано в чисто емкостной схеме выше. Затем конденсатор непрерывно заряжается и разряжается до каждого нового уровня напряжения (заряжается при положительном уровне напряжения и разряжается при отрицательном уровне напряжения).Емкость конденсатора в цепях переменного тока зависит от частоты входного напряжения, подаваемого в цепь. Сила тока прямо пропорциональна скорости изменения напряжения, приложенного к цепи.

  i = dQ /   dt   = C (dV /   dt  )  

Векторная диаграмма конденсатора в цепи переменного тока

Как вы видите на векторной диаграмме конденсатора переменного тока на изображении ниже, ток и напряжение представлены в виде синусоидальной волны.При наблюдении при 0 ° зарядный ток достигает своего пикового значения из-за постоянного увеличения напряжения в положительном направлении.

Теперь при 90 ° нет тока через конденсатор, потому что напряжение питания достигает максимального значения. При 180 ° напряжение начинает медленно снижаться до нуля, а ток достигает максимального значения в отрицательном направлении. И снова заряд достигает своего пикового значения на 360 °, потому что напряжение питания находится на минимальном значении.

Таким образом, из приведенного выше сигнала мы можем видеть, что ток опережает напряжение на 90 °.Итак, мы можем сказать, что напряжение переменного тока отстает от тока на 90⁰ в идеальной конденсаторной цепи .

Реактивное сопротивление конденсатора (Xc) в цепи переменного тока

Рассмотрим приведенную выше принципиальную схему, поскольку мы знаем, что входное напряжение переменного тока выражается как

  V = V  м  Sin  wt   

А, заряд конденсатора Q = CV,

Итак, Q = CV _м Sin _wt

А, ток через конденсатор, i = dQ / dt

Итак,

  i = d (CV  м  Sin  wt ) / dt 
  i = C * d (V  м  Sin  wt ) / dt 
  i = C * V  м  Cos  wt  * w 
  i = w * C * V  м  Sin (wt + π / 2) 
  ат, wt = 0 
  sin (вес + π / 2) = 1 
 , следовательно, i  м  = wCV  м  
  V  м  / i  м  = 1 / wC  

Как известно, w = 2πf

Итак,

  Емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC  

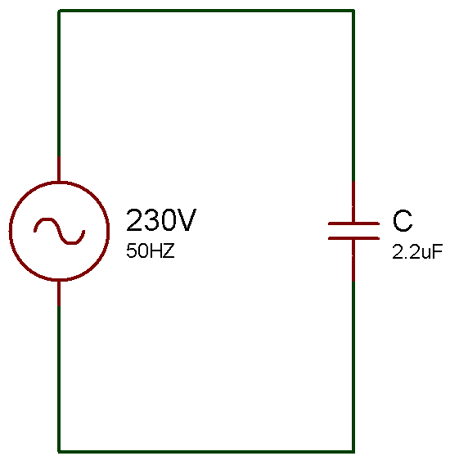
Пример емкостного реактивного сопротивления в цепи переменного тока

диаграмма

Рассмотрим значение C = 2.2uf и напряжение питания V = 230 В, 50 Гц

  Теперь емкостное реактивное сопротивление (Xc) = V  м  / i  м  = 1 / 2πfC 
  Здесь C = 2,2 мкФ и f = 50 Гц 
  Итак, Xc = 1/2 * 3.1414 * 50 * 2.2 * 10 -6  
  Xc = 1446,86 Ом  

.

Что такое цепь чистого конденсатора? – Фазорная диаграмма и форма волны

Цепь, содержащая только чистый конденсатор емкостью C фарад, известна как цепь чистого конденсатора . Конденсаторы накапливают электроэнергию в электрическом поле, их эффект известен как емкость. Его еще называют конденсатор .

Конденсатор состоит из двух проводящих пластин, разделенных диэлектрической средой. Диэлектрический материал состоит из стекла, бумаги, слюды, оксидных слоев и т. Д.В чистой цепи конденсатора переменного тока ток опережает напряжение на угол 90 градусов.

В комплекте:

Когда на конденсатор подается напряжение, электрическое поле создается на пластинах конденсатора, и между ними не протекает ток. Если источник переменного напряжения приложен к пластинам конденсатора, то текущий ток течет через источник из-за зарядки и разрядки конденсатора.

Объяснение и происхождение конденсаторной цепи

Конденсатор состоит из двух изолирующих пластин, разделенных диэлектрической средой.Он хранит энергию в электрической форме. Конденсатор работает как запоминающее устройство и заряжается, когда питание в ВКЛ , и разряжается, когда питание ВЫКЛ . Если он подключен к прямому источнику питания, он заряжается равным значению приложенного напряжения.

Принципиальная электрическая схема чистого конденсатора

Пусть переменное напряжение, приложенное к цепи, задается уравнением:

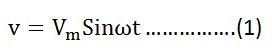
Заряд конденсатора в любой момент времени определяется как:

Ток, протекающий по цепи, определяется уравнением:

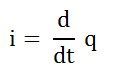
Подставив значение q из уравнения (2) в уравнение (3), мы получим

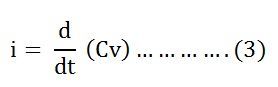
Теперь, подставив значение v из уравнения (1) в уравнение (3), мы получим

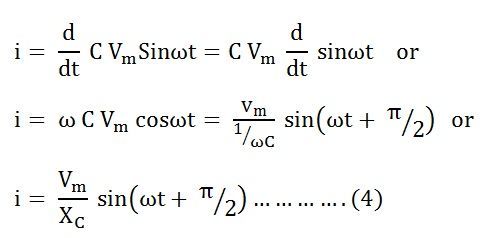
Где Xc = 1 / ωC – сопротивление протеканию переменного тока чистым конденсатором и называется емкостным реактивным сопротивлением.

Значение тока будет максимальным, когда sin (ωt + π / 2) = 1. Следовательно, значение максимального тока I _м будет представлено как:

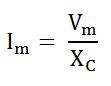
Подставив значение I _м в уравнение (4), получим:

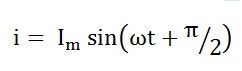
Диаграмма фазора и кривая мощности

В цепи чистого конденсатора ток, протекающий через конденсатор, опережает напряжение на угол 90 градусов. Векторная диаграмма и осциллограмма напряжения, тока и мощности показаны ниже:

Тел.

.

Что такое конденсатор (C)

Что такое конденсатор и расчет конденсатора.

Что такое конденсатор

Конденсатор – это электронный компонент, который хранит электрический заряд. Конденсатор состоит из двух закрытых проводников (обычно пластин), которые разделены диэлектрическим материалом. Пластины накапливаются электрический заряд при подключении к источнику питания. Одна тарелка накапливает положительный заряд, а другая пластина накапливает отрицательный заряд.

Емкость – это количество электрического заряда, который хранится в конденсаторе при напряжении 1 Вольт.

Емкость измеряется в единицах Фарад (Ф).

Конденсатор отключает ток в цепях постоянного (DC) и короткое замыкание в цепях переменного (AC).

Фотографии конденсатора

Символы конденсаторов

Емкость

Емкость (C) конденсатора равна электрическому заряду (Q), деленному на напряжение (В):

C – емкость в фарадах (Ф)

Q – это электрический заряд в кулонах (C), накопленный на конденсаторе

В – напряжение между пластинами конденсатора в вольтах (В)

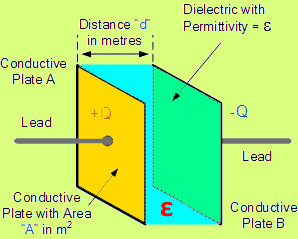
Емкость пластин конденсатора

Емкость (C) пластин конденсатора равна диэлектрической проницаемости (ε), умноженной на площадь пластины (A), деленную на зазор или расстояние между пластинами (d):

C – емкость конденсатора в фарадах (Ф).

ε – диэлектрическая проницаемость диалектического материала конденсатора в фарадах на метр (Ф / м).

А – площадь пластины конденсатора в квадратных метрах ( ² м).

d – расстояние между пластинами конденсатора в метрах (м).

Конденсаторы серии

Суммарная емкость конденсаторов, включенных последовательно, C1, C2, C3, ..:

Конденсаторы параллельно

Суммарная емкость конденсаторов, включенных параллельно, C1, C2, C3 ,., :

C _Итого = C ₁ + C ₂ + C ₃ + …

Ток конденсатора

Мгновенный ток конденсатора i _c (t) равен емкости конденсатора

раз производная мгновенного напряжения конденсатора v _c (t):

Напряжение конденсатора

Мгновенное напряжение конденсатора v _c (t) равно начальному напряжению конденсатора

плюс 1 / C, умноженный на интеграл мгновенного тока конденсатора i _c (t) за время t:

Энергия конденсатора

Накопленная энергия конденсатора E _C в джоулях (Дж) равна емкости C в фарадах (Ф)

раз больше напряжения конденсатора квадратной формы В _C в вольтах (В) разделенных на 2:

E _C = C × V _C ² /2

Цепи переменного тока

Угловая частота

ω = 2 π f

ω – угловая скорость, измеренная в радианах в секунду (рад / с)

f – частота, измеренная в герцах (Гц).

Реактивное сопротивление конденсатора

Импеданс конденсатора

Декартова форма:

Полярная форма:

Z _C = X _C ∟-90º

Типы конденсаторов

Конденсатор переменной емкости	Конденсатор переменной емкости с изменяемой емкостью
Конденсатор электролитический	Электролитические конденсаторы используются, когда требуется высокая емкость.Большинство электролитических конденсаторов поляризованы
Конденсатор сферический	Сферический конденсатор сферической формы
Конденсатор силовой	Силовые конденсаторы используются в высоковольтных энергосистемах.
Конденсатор керамический	Керамический конденсатор имеет керамический диэлектрический материал. Имеет функцию высокого напряжения.
Конденсатор танталовый	Диэлектрический материал из оксида тантала. Имеет высокую емкость
Слюдяной конденсатор	Конденсаторы высокой точности
Конденсатор бумажный	Бумажный диэлектрический материал

---

См. Также:

,

Почему конденсаторный блок пропускает постоянный ток? Электрические технологии

Почему конденсатор допускает переменный ток и блокирует постоянный ток?

Один из наиболее частых вопросов, которые студенты-электрики задают снова и снова: почему конденсаторы блокируют постоянный ток и допускают переменный ток ?. Чтобы узнать точную причину, давайте узнаем, что такое конденсатор и как он работает при подключении к источнику постоянного, а затем переменного тока.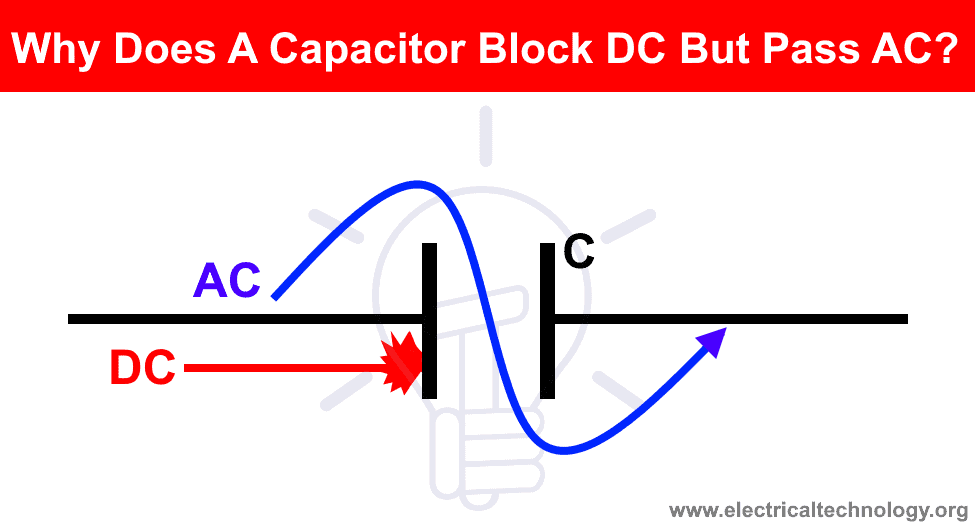

Что такое конденсатор?

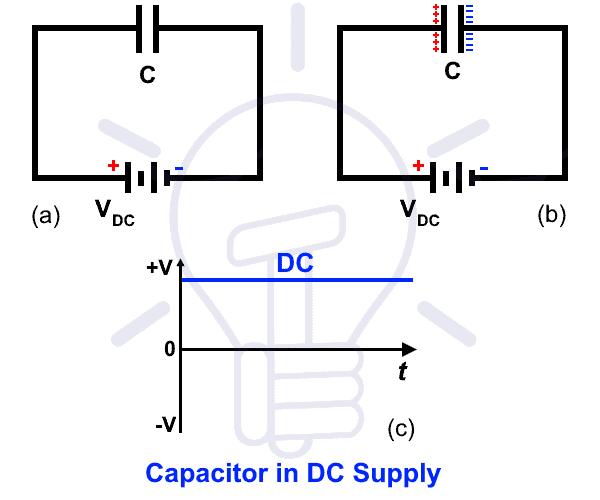
Конденсатор (также известный как конденсатор) представляет собой устройство из двух металлических пластин, разделенных изолирующей средой, такой как фольга, ламинированная бумага, воздух и т. Д.Он накапливает энергию в виде электростатического поля и передается в цепь при необходимости в случае переменного тока. Его способность к хранению измеряется в фарадах. Для конденсаторов малой емкости используются единицы «мкФ» или «нФ». Имейте в виду, что конденсатор работает как разомкнутая цепь при постоянном токе, то есть он работает только при переменном напряжении.

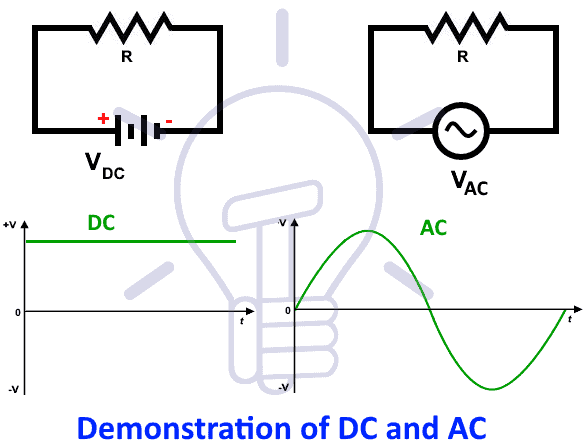
Разница между переменным током и постоянным током

Постоянный ток является постоянным значением, т.е. он не меняет полярность (направление) и величину, в то время как переменный ток постоянно меняет свое направление и амплитуду в зависимости от своей частоты, как показано на рисунке ниже ,

Теперь давайте подключим конденсатор к постоянному току, а затем к переменному току и посмотрим, что произойдет?

Почему конденсаторный блок постоянного тока?

Имейте в виду, что конденсатор действует как короткое замыкание на начальной стадии, а полностью заряженный конденсатор ведет себя как разомкнутая цепь. Конденсаторы сопротивляются изменениям напряжения , в то время как индуктивности сопротивляются изменению тока и действуют как короткое замыкание в постоянном токе .

На начальном этапе, когда мы подключаем конденсатор к источнику постоянного тока, будет возникать небольшой ток, пока пластины не станут насыщенными.Другими словами, положительный вывод источника питания постоянного тока будет всасывать электроны с одного вывода и подталкивать электроны ко второму выводу, пока первая пластина не станет заряжаться положительно, а вторая – отрицательно, как показано на рис. На этом этапе приложенное напряжение, равное напряжению на конденсаторе и обкладках конденсатора, становится насыщенным, и ток больше не протекает. На этом этапе конденсатор ведет себя как разомкнутая цепь, и если мы увеличим значение приложенного постоянного напряжения, конденсатор может повредиться и взорваться.

Давайте посмотрим на решенном примере конденсатора, подключенного к постоянному току.

Мы знаем, что в источнике постоянного тока нет частоты, то есть частоты 0 Гц.

Если мы положим частоту « f = 0» в формулу индуктивного реактивного сопротивления (которое является сопротивлением переменного тока в емкостной цепи).

X _C = 1 / 2π f C

Положим f = 0

X _C = 1 / 2π 0 C

X _C = 1/0 = Infinity

Это означает Теоретически конденсатор обеспечит бесконечное сопротивление протеканию тока в соответствии со своим номиналом.Следовательно, ток не будет протекать, поскольку ток в емкостных цепях равен:

I = V / X _C

Если мы положим X _C как бесконечность, значение тока будет равно нулю.

I = 0 A

Это точная причина, почему конденсаторный блок постоянного тока.

Почему конденсатор проходит переменный ток?

Когда мы подключаем конденсатор к источнику переменного тока, он начинает заряжаться и разряжаться непрерывно из-за постоянного изменения напряжения питания.Это происходит из-за изменений в напряжении переменного тока, т.е. переменный ток положительный в начальном цикле для «t = 1» и отрицательный во втором цикле «t = 2», как показано на рисунке ниже.

На рис. 2 (а) происходит то же самое, что и в конденсаторе, подключенном по постоянному току, на начальной стадии, то есть положительный вывод источника всасывает электроны из подключенной пластины конденсатора и проталкивается обратно ко второму выводу. Первая пластина становится положительной, а другая отрицательной из-за большого количества электронов. Этот процесс известен как зарядка конденсатора i.е. он хранит энергию в виде электрического поля.

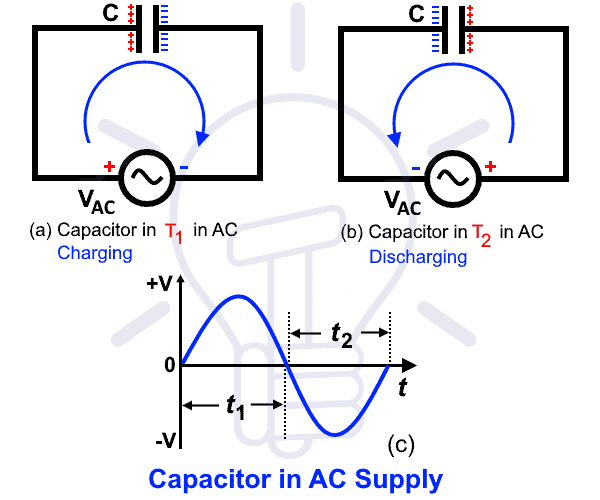
Заряд конденсатора определяется по формуле:

В _C = V _S (1− e ^{(−t / RC)} )

или

В _C = В _S (1 – e ^{-t / τ} )

Где:

• В _C = Напряжение на конденсаторе
• В _S = Напряжение источника или приложенного напряжения
• e = 2,718 ( Экспоненциальная i.e основание натурального логарифма)
• τ = R / C = постоянная времени «тау» в секундах

Теперь полярность приложенного напряжения меняется на противоположную, т.е. положительное становится отрицательным и наоборот, как показано на рис. 2 (b) , Теперь отрицательный вывод источника притягивается к дыркам и отталкивает электроны к дыркам в противоположном направлении. Процесс остается непрерывным, и ток течет из-за непрерывного потока электронов. Этот процесс известен как разряд конденсатора, то есть он восстанавливает накопленную энергию в цепи.

Разрядка конденсатора определяется по формуле:

В _C = В _S x e ^{(−t / RC)} )

Почему тогда конденсатор рассчитан на постоянный ток?

Мы знаем, что существуют разные конденсаторы с разной маркировкой на паспортных табличках, то есть 400 В постоянного тока или 400 В переменного тока. Если конденсатор блокирует постоянный ток, почему номинал указан в постоянном токе?

Ну, это не значит, что мы не можем использовать конденсаторы в цепях постоянного тока (вы их уже видели). Значение постоянного тока, указанное на паспортной табличке конденсатора, является максимальным значением постоянного напряжения, которое может быть безопасно подключено к нему.Имейте в виду, что это не значение емкости зарядки. Поляризованные конденсаторы в основном используются в цепях постоянного тока, а неполяризованные – в цепях переменного тока.

Как показывает опыт;

• Конденсаторы с маркировкой AC могут использоваться на постоянном токе.
• Конденсаторы с маркировкой DC не могут использоваться с переменным током.

Потому что напряжения переменного тока показывают среднеквадратичное значение, где пиковое значение переменного тока в 1,414 раза больше, чем постоянного тока.

Связанное сообщение: AC или DC – какой из них более опасен и почему?

Применение конденсаторов в постоянном токе

• Фильтры
• Выпрямители (преобразование переменного тока в постоянный)
• Кондиционирование питания
• Конденсатор связи и конденсатор развязки и т. Д.

Применение конденсаторов в сети переменного тока

Связанные сообщения:

.