изменение силы тока в цепи
При изучении постоянного тока мы узнали, что он не может проходить в цепи, в которой есть конденсатор. Так как конденсатор – это две пластины, разделенные слоем диэлектрика. Для цепи постоянного тока конденсатор будет, как разрыв в цепи. Если конденсатор пропускает постоянный ток, значит, он неисправен.
Конденсатор в цепи переменного тока
В отличии от постоянного переменный ток может идти и через цепь, в которой присутствует конденсатор. Рассмотрим следующий опыт.
Возьмем два источника питания. Один из них пусть будет источником постоянного напряжения, а второй – переменного. Причем подберем источники так, чтобы постоянное значение напряжения равнялось действующему значению переменного напряжения.
Подключим к ним с помощью переключателя цепь, состоящую из лампочки и конденсатора. Причем лампочка и конденсатор подключены последовательно.
рисунок
При включении питания от источника постоянного тока (АА’) лампочка не загорится.
В цепи происходит периодическая зарядка и разрядка конденсатора. В то время, когда конденсатор перезаряжается, ток проходит по цепи и нагревает нить накаливания лампочки.
Рассмотрим, как будет меняться сила тока в цепи, содержащей конденсатор, с течением времени. При этом будем пренебрегать сопротивлением соединяющих проводов и обкладок конденсатора.
рисунок
Напряжение на конденсаторе будет равняться напряжению на концах цепи. Значит, мы можем приравнять эти две величины.
u = φ1-φ2 = q/C,
u = Um*cos(ω*t).
Имеем:
q/C = Um*cos(ω*t).
Выражаем заряд:
q = C*Um*cos(ω*t).
Видим, что заряд будет изменяться по гармоническому закону. Сила тока – это скорость изменения заряда. Значит, если возьмем производную от заряда, получим выражение для силы тока.
I = q’ = Um*C*ω*cos(ω*t+pi/2).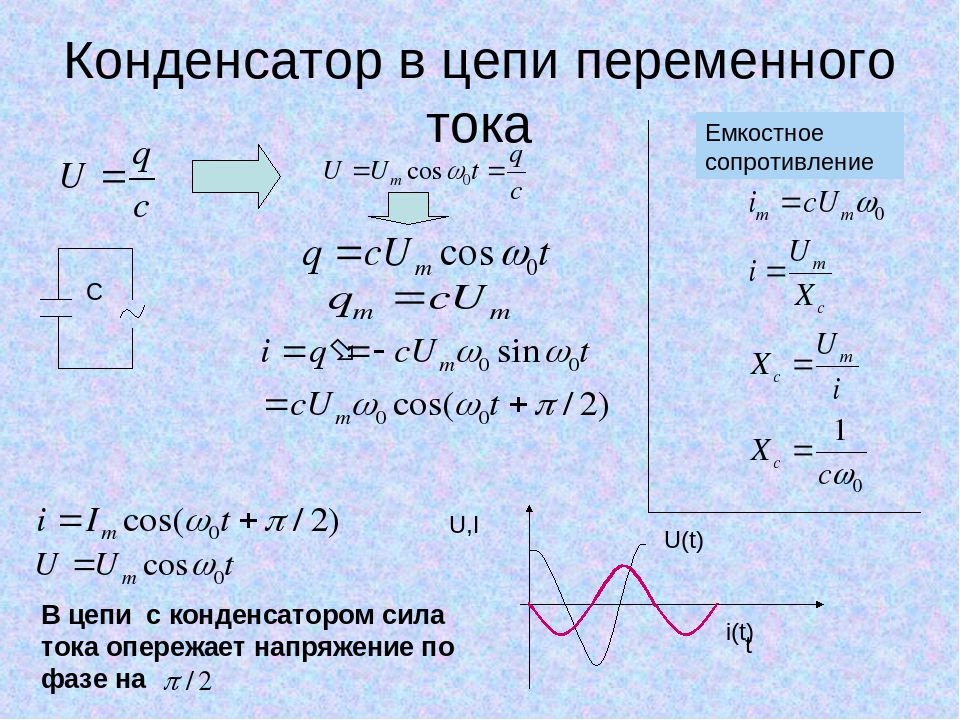
Разность фаз между колебаниями силы тока и заряда, а также напряжения, получилась равной pi/2. Получается, что колебания силы тока опережают по фазе колебания напряжения на pi/2. Это представлено на следующем рисунке.
рисунок
Из уравнения колебаний силы тока получаем выражение для амплитуды силы тока:
Im = Um*C*ω.
Введем следующее обозначение:
Xc = 1/(C*ω).
Запишем следующее выражение закона Ома, используя Xc и действующие значения силы тока и напряжения:
I = U/Xc.
Xc – величина, называемая емкостным сопротивлением.
Нужна помощь в учебе?
Предыдущая тема: Активное сопротивление: действующие значения силы тока и напряжения
Следующая тема:   Катушка индуктивности в цепи переменного тока: индуктивное сопротивление
Конденсатор в цепях переменного тока
Чтобы понять, как работает конденсатор в цепях переменного тока, вам потребуется хотя бы
минимальное представление об этом самом переменном токе.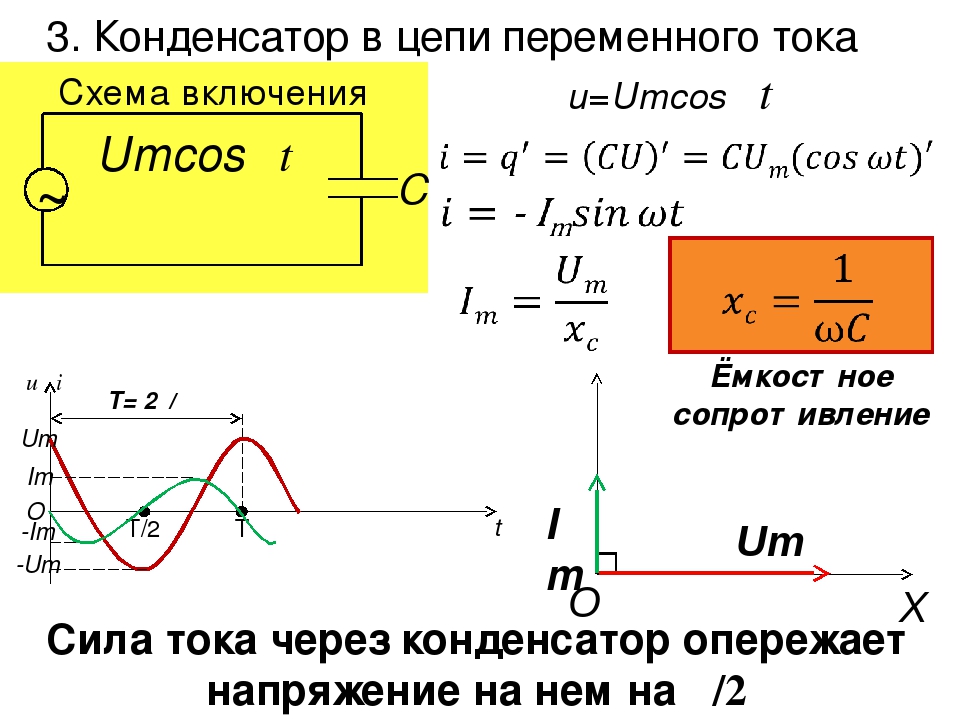 Будем считать, что эти знания у вас есть,
поэтому здесь приведём только информацию, касающуюся работы конденсатора.
Будем считать, что эти знания у вас есть,
поэтому здесь приведём только информацию, касающуюся работы конденсатора.
На рис. 1 приведены графики изменения силы тока и напряжения во времени для ёмкостной нагрузки, то есть для конденсатора.
Рис. 1. Изменения силы тока и напряжения во времени для ёмкостной нагрузки.
Здесь Uc(t) – напряжение на конденсаторе, I(t) – ток в цепи, Ug(t) – напряжение на выходе источника переменного напряжения.
Итак, при подключении конденсатора к источнику переменного напряжения (перед подключением конденсатор разряжен), ток в цепи максимальный (см. рис. 1), а напряжение Uc на конденсаторе равно нулю. Ёмкость конденсатора влияет на ток, но нас пока это не интересует.
В первой четверти периода напряжение источника увеличивается, напряжение на конденсаторе также увеличивается. Конденсатор заряжается, а ток в цепи уменьшается. По прошествии 1/4 периода конденсатор полностью заряжен и ток в цепи равен нулю.
Во второй четверти происходит разряд конденсатора, ток в цепи увеличивается. И так далее.
И так далее.
Таким образом, ток, протекающий через конденсатор, отстаёт от напряжения на его обкладках на одну четверть периода.
Закон Ома для действующих значений имеет вид:
I = CUω = U / XcГде С – ёмкость конденсатора, Ф, U – напряжение, В, Хс – ёмкостное сопротивление цепи, Ом, которое равно
Xc = 1 /ωC = 1 / 2πfCГде f – частота переменного тока, Гц.
Отсюда можно сделать вывод, что ёмкостное сопротивление зависит не только от ёмкости конденсатора, но и от частоты переменного тока. Чем выше частота, тем меньше ёмкостное сопротивление конденсатора, и наоборот.
Исходя из вышесказанного напрашивается первое применение конденсатора в цепях
переменного тока – работа в качестве гасящего элемента в делителях напряжения.
Конечно, проще и удобнее использовать в качестве такого элемента резистор.
Однако, если требуется существенное падение напряжения на
гасящем резисторе, то даже небольшие токи потребуют применения резистора большой мощности и,
соответственно, габаритов.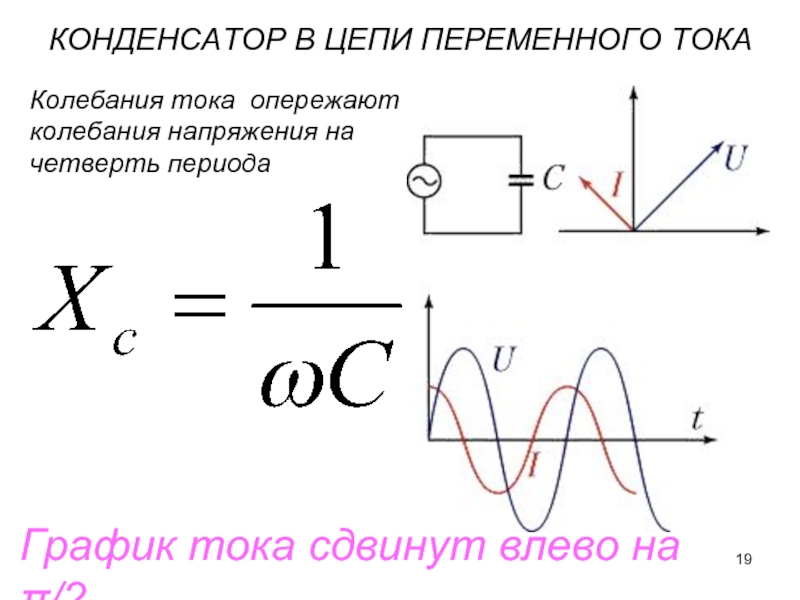
Конденсатор в цепях переменного тока не рассеивает энергию, а значит и не нагревается. Почему? Потому что, как мы выяснили, ток и напряжение в конденсаторе смещены относительно друг друга на 90o. То есть в момент, когда напряжение максимально, ток равен нулю, соответственно, и мощность равна нулю в этот момент (см. рис. 1). Работа не совершается, нагрев не происходит.
Именно поэтому вместо резистора часто применяют конденсаторы. Основной недостаток такого использования конденсатора заключается в том, что при изменении тока в цепи изменяется и напряжение на нагрузке. Второй недостаток (по сравнению с применением трансформаторов) – отсутствие гальванической развязки. По этим и другим причинам применение конденсаторов в качестве гасящих элементов ограничено и используется обычно в тех случаях, когда сопротивление нагрузки относительно стабильно. Например, в цепях питания нагревательных элементов.
Однако частотно-зависимые делители напряжения применяются очень широко. Свойства конденсаторов
используются, например, при создании различных фильтров и резонансных схем.
Свойства конденсаторов
используются, например, при создании различных фильтров и резонансных схем.
Частотный фильтр – это устройство, которое пропускает сигналы одной частоты и не пропускает другие. Или наоборот – пропускает все частоты кроме одного диапазона. Работа частотных фильтров основана на способности конденсатора изменять ёмкостное сопротивление в зависимости от частоты. Например, нам нужно подавить в усилителе фон переменного тока частотой 50 Гц. В таком случае можно использовать фильтр – схему из конденсаторов и резисторов, которая будет подавлять сигнал с частотой 50 Гц и пропускать все остальные сигналы. Расчёт и конструирование фильтров – занятие непростое и здесь не рассматривается.
Резонансные схемы используют резонанс, который возникает при последовательном или
параллельном включении конденсатора и катушки индуктивности. Поскольку сопротивление этих элементов зависит от
частоты, то при некоторой частоте общее сопротивление цепи будет максимальным, а при некоторых –
минимальным. Эти эффекты и используются в резонансных схемах. Например, резонанс используется
в радиоприёмниках при настройке на станцию.
Эти эффекты и используются в резонансных схемах. Например, резонанс используется
в радиоприёмниках при настройке на станцию.
Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока – Физика – 11 класс
Физика, 11 класс
Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока
Перечень вопросов, рассматриваемых на уроке:
Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;
Устройство и принцип действия генератора переменного тока и трансформатора;
Автоколебания;
Проблемы передачи электроэнергии и способы повышения эффективности её использования.
Глоссарий по теме
Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами.
Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.
Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.
Рымкевич А.П. Сборник задач по физике. 10-11 класс. – М.: Дрофа, 2014. – С. 128 – 132.
Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.
Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004
Основное содержание урока
Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.
В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.
Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:
N- число витков.
Возникает ЭДС индукции который меняется по гармоническому закону.
ЭДС индукции в рамке равна:
Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.
В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.
Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.
Величину ХC, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.
Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.
Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.
Величину ХL, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.
Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.
Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.
Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.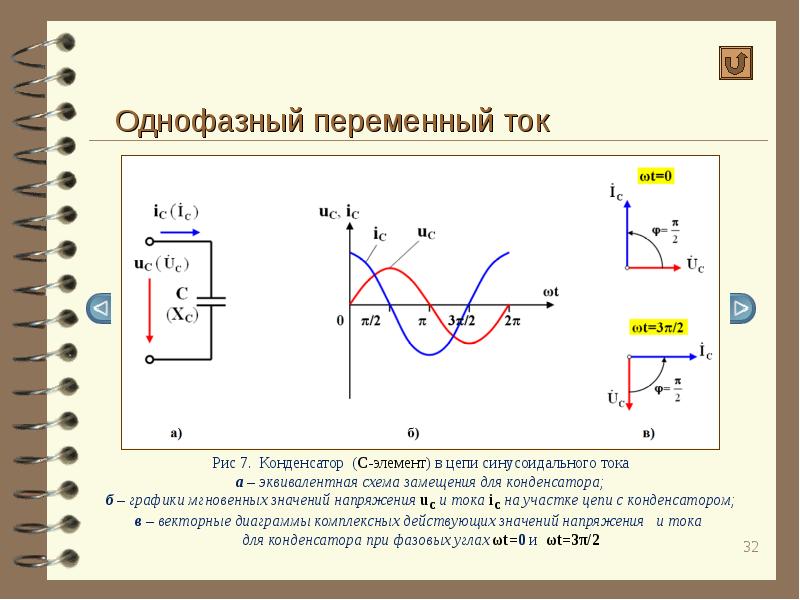
Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.
Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:
Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.
Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.
Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».
k– коэффициент трансформации.
U1 иU2 – напряжения на первичной и на вторичной обмотке.
N1 и N2– число витков на первичной и на вторичной обмотке.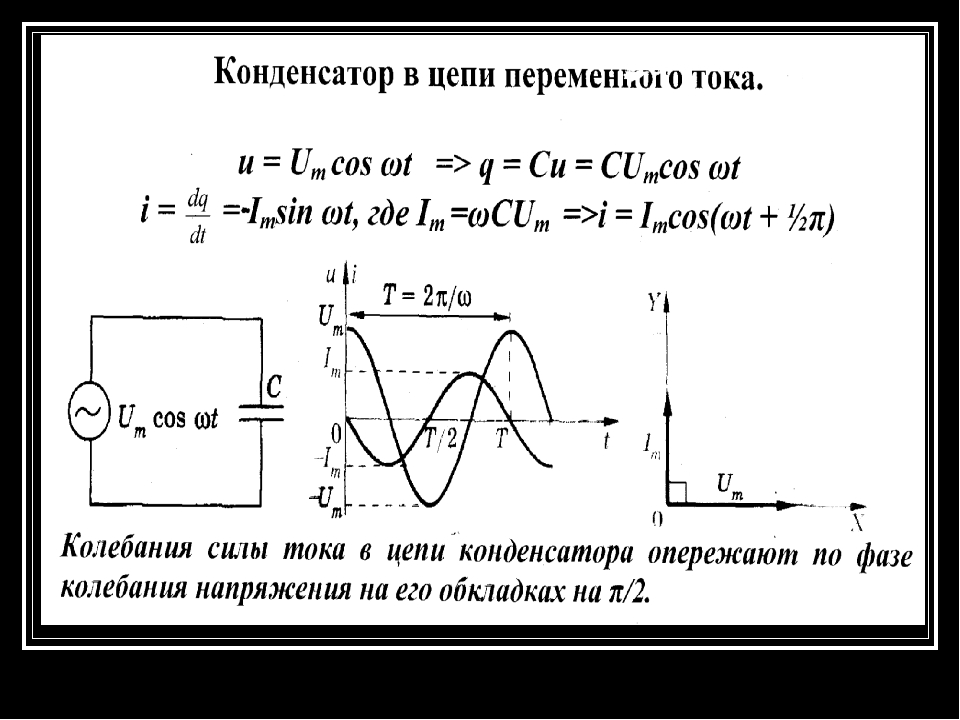
Если k < 1 – трансформатор повышающий,
k > 1 – трансформатор понижающий.
КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:
Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления – понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.
Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.
Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.
В этом заключается условие возникновения резонанса в электрической цепи.
Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.
Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция
Разбор тренировочных заданий
1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м2.
Дано:
N=50
ω=180 рад/с
B=0,4 Тл
S=0,02 м2
_________
Ԑm=?
Решение:
Ответ: 72 В.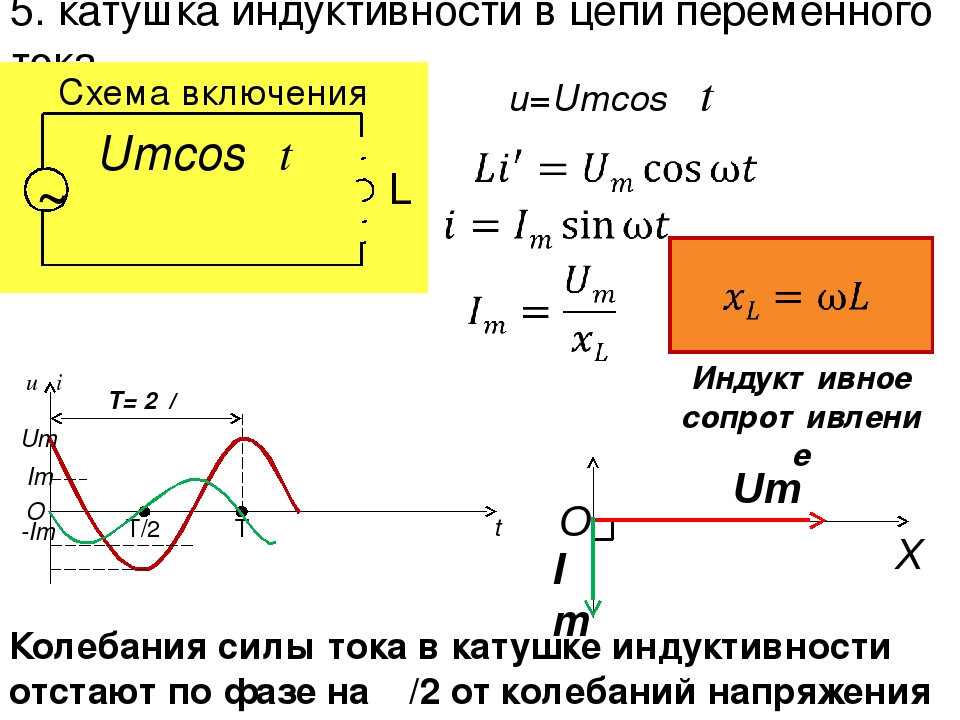
2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.
Дано:
L=0,08 Гн
ν= 1000 Гц
U=100 В
__________
Im=?
Решение:
Напишем закон Ома для переменного тока
Т.к. ХC и R равны нулю, то
Учитывая, что , получаем:
Найдем амплитудное значение напряжения:
Подставим числовые данные в формулу для расчета амплитуды силы тока:
Ответ: Im = 0,3 А.
Зависимость тока от напряжения на конденсаторе. Как ведет себя конденсатор в цепи переменного тока
На рис. 4.11 показана цепь электрического генератора, содержащая конденсатор. После включения цепи вольтметр, включенный в цепь, покажет полное напряжение генератора. Стрелка амперметра установится на нуле – ток через изоляцию конденсатора протекать не может.
Но проследим внимательно за стрелкой амперметра при включении незаряженного конденсатора. Если амперметр достаточно чувствителен, а емкость конденсатора велика, то нетрудно обнаружить колебание стрелки: сразу после включения стрелка сойдет с нуля, а затем быстро вернется в исходное положение.
Рис. 4.11. Цепь электрического генератора, содержащая конденсатор
Этот опыт показывает, что при включении конденсатора (при его зарядке) в цепи протекал ток – в ней происходило передвижение зарядов: электроны с пластины, присоединенной к положительному полюсу источника, перешли на пластину, присоединенную к отрицательному полюсу.
Как только конденсатор зарядится, движение зарядов прекращается.
Отключая генератор и повторно замыкая его на конденсатор, мы уже не обнаружим движения стрелки: конденсатор остается заряженным, и при повторном включении движения зарядов в цепи не происходит.
Для того чтобы вновь наблюдать отклонение стрелки, нужно замыкать генератор на разряженный конденсатор. С этой целью, предварительно отключив генератор, замкнем пластины конденсатора проволокой, при этом между зажимами конденсатора и подносимой к ним проволокой проскочит искра, тем самым легко убедиться, что при разряде конденсатора в его цепи опять протекал ток.
С этой целью, предварительно отключив генератор, замкнем пластины конденсатора проволокой, при этом между зажимами конденсатора и подносимой к ним проволокой проскочит искра, тем самым легко убедиться, что при разряде конденсатора в его цепи опять протекал ток.
Если замыкание проволокой произвести так, чтобы путь зарядов проходил через амперметр, то легко увидеть, что его стрелка кратковременно отклонится. Отклонение стрелки теперь должно происходить, конечно, в другую сторону.
После разряда конденсатора можно повторить первый опыт – стрелка амперметра вновь покажет, что в цепи конденсатора передвигаются электрические заряды (проходит ток).
Попытаемся вычислить ток, протекающий в проводах, присоединенных к конденсатору.
Если за промежуток времени напряжение конденсатора увеличивается на , то, значит, за это же время его заряд увеличится на
т. е. заряд конденсатора возрастает на произведение емкости и приращения напряжения.
Предположим, что напряжение на конденсаторе емкостью возросло на 50 В за время в одну десятую долю секунды . В таком случае за это же время заряд положительной пластины конденсатора увеличился на
В таком случае за это же время заряд положительной пластины конденсатора увеличился на
Но для того чтобы такой заряд прошел по проводам за время с, нужно, чтобы по ним протекал средний ток
Заряд конденсатора через резистор. Представим себе, что генератор с постоянным напряжением замыкается через резистор с сопротивлением на незаряженный конденсатор емкостью (рис. 4.12, а).
В начальный момент, пока еще конденсатор не заряжен, его напряжение равно нулю.
Значит все напряжение источника приходится на сопротивление R. А это значит, что по закону Ома в цепи будет протекать ток
С течением времени, напротив, конденсатор зарядится, его напряжение будет равно напряжению генератора, в цепи не будет тока, на резисторе не будет никакого напряжения.
Рис. 4.12. а – заряд конденсатора С через резистор с сопротивлением Слева показана электрическая схема, на которой применено общепринятое изображение конденсатора, справа показано, как с течением времени нарастает напряжение на конденсаторе «с и как постепенно убывает ток г. Эти графики построены в предположении, что конденсатор емкостью 100 мкФ заряжается от источника постоянного напряжения 100 В через сопротивление 10 000 Ом. В этом случае заряд происходит очень медленно. Если бы емкость составила всего 1 мкФ, а сопротивление 1 Ом, все происходило бы в миллион раз скорее. Для того чтобы приведенные графики оказались пригодными и для второго случая, нужно считать, что время выражено не в секундах, а в миллионных долях секунды (в общем случае при любых R и С указанные на графике значения времени следует умножить на произведение С и Я). Если напряжение источника остается 100 В, то значения тока должны быть увеличены в 10 000 раз. Например, в начальный момент будет протекать ток не 10 мА, а 100 А. Длительность и характер процесса не зависят от напряжения источника; б – разряд конденсатора С через резистор сопротивлением R. Слева показана электрическая схема. После заряда конденсатор отключается. Справа показано, как изменяются ток и напряжение конденсатора с течением времени.
Эти графики построены в предположении, что конденсатор емкостью 100 мкФ заряжается от источника постоянного напряжения 100 В через сопротивление 10 000 Ом. В этом случае заряд происходит очень медленно. Если бы емкость составила всего 1 мкФ, а сопротивление 1 Ом, все происходило бы в миллион раз скорее. Для того чтобы приведенные графики оказались пригодными и для второго случая, нужно считать, что время выражено не в секундах, а в миллионных долях секунды (в общем случае при любых R и С указанные на графике значения времени следует умножить на произведение С и Я). Если напряжение источника остается 100 В, то значения тока должны быть увеличены в 10 000 раз. Например, в начальный момент будет протекать ток не 10 мА, а 100 А. Длительность и характер процесса не зависят от напряжения источника; б – разряд конденсатора С через резистор сопротивлением R. Слева показана электрическая схема. После заряда конденсатор отключается. Справа показано, как изменяются ток и напряжение конденсатора с течением времени. Графики построены для случая . Уменьшение емкости и сопротивления до значений и 1 Ом увеличило бы скорость разряда в миллион раз. Начальное; значение тока (при неизменности начального напряжения) при этом возросло бы в 10 000 раз и составило бы 100 А вместо 10 мА. При других значениях R и С время, показанное на графике, нужно умножить на произведение
Графики построены для случая . Уменьшение емкости и сопротивления до значений и 1 Ом увеличило бы скорость разряда в миллион раз. Начальное; значение тока (при неизменности начального напряжения) при этом возросло бы в 10 000 раз и составило бы 100 А вместо 10 мА. При других значениях R и С время, показанное на графике, нужно умножить на произведение
При этом заряд конденсатора должен быть равен
Поставим такой вопрос: как скоро заряд в одну сотую кулона может быть сообщен конденсатору?
Если бы в цепи ток не уменьшался, а оставался равным т. е. 10 мА, то для этого потребовалось бы время, равное всего лишь 1 с:
Но сообразим, может ли долго протекать такой ток, как Если бы такой ток протекал четверть секунды, он уже сообщил бы конденсатору четверть полного заряда, а значит, поднял бы его напряжение до четверти от полных 100 В.
Но когда напряжение конденсатора возрастет до 25 В, ток должен уменьшиться до 7,5 мА. В самом деле, если напряжение генератора 100 В, а напряжение на конденсаторе 25 В, то разность между ними приходится на резистор.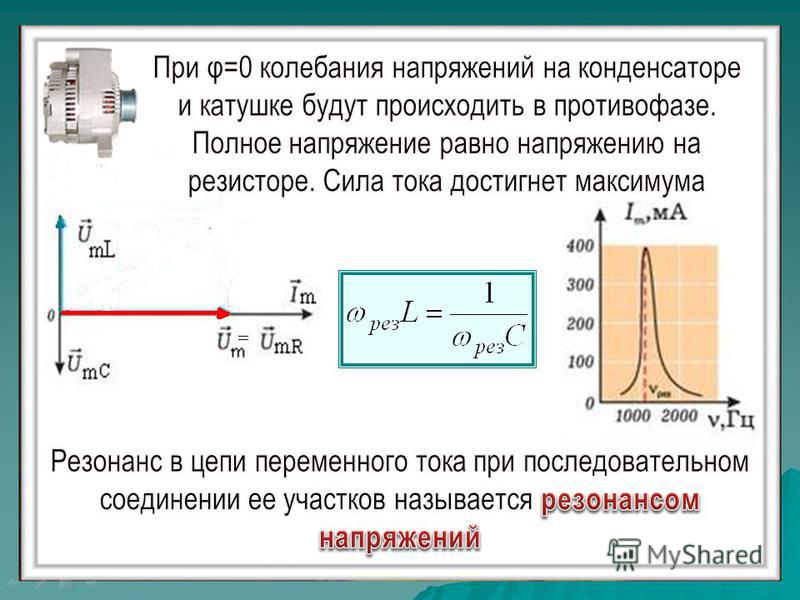
Опять же по закону Ома
Но такой ток будет заряжать конденсатор медленнее, чем его заряжал ток в 10 мА.
Из приведенного рассуждения ясно, что:
нарастание напряжения на конденсаторе будет происходить, постепенно замедляясь;
ток, достигнув наибольшего значения в начальный момент, потом постепенно уменьшится;
чем больше емкость (больше заряд) и чем больше сопротивление цепи, тем медленнее происходит заряд конденсатора.
Разряд конденсатора на резистор. Если отключить генератор и через резистор с сопротивлением R замкнуть пластины конденсатора, начнется процесс его разряда. На рис. 4.12, б приведены кривые тока и напряжения конденсатора при его разряде.
Энергия электрического поля в конденсаторе. Заряженный конденсатор обладает определенным запасом энергии, заключенной в его электрическом поле.
Об этом можно судить по тому, что заряженный конденсатор, отключенный от сети, способен некоторое время поддерживать электрический ток – об этом можно судить и по искре, наблюдаемой при разряде конденсаторов.
Энергия, заключенная в конденсаторе, подводится к нему в то время, когда он заряжается от генератора. В самом деле, во время его заряда в цепи течет ток и к его зажимам приложено напряжение, а это значит, что ему сообщается энергия. Полное количество энергии, запасенной конденсатором, может быть выражено формулой
Энергия равна половине квадрата напряжения, умноженного на емкость.
Если напряжение выражено в вольтах, а емкость – в фарадах, то энергия окажется выраженной в джоулях.
Так, энергия, запасенная в конденсаторе емкостью 100 мкФ при напряжении 1000 В,
Это, конечно, не очень большая энергия (такая энергия поглощается лампочкой 50 Вт за каждую секунду). Но если конденсатор быстро разряжается (скажем, за одну тысячную долю секунды), то мощность происходящего разряда энергии, конечно, очень велика:
Поэтому понятно, что при разряде большого конденсатора звук похож на выстрел.
Быстрым разрядом энергии, запасенной в конденсаторе, иногда пользуются для сварки маленьких металлических изделий.
При разряде конденсатора на резистор энергия, заключавшаяся в электрическом конденсаторе, переходит в тепло нагреваемого резистора.
Применение конденсаторов. Применения конденсаторов в электротехнике очень разнообразны.
Рассмотрим здесь некоторые из них.
1. Конденсаторы широко применяют для целей изоляции двух цепей по постоянному напряжению при сохранении связи между ними на переменном токе. Конденсаторы изолируют постоянное напряжение, не пропуская постоянный ток. В то же время малейшее изменение напряжения изменяет их заряд и, следовательно, пропускает через них соответствующий переменный ток (рис. 4.13).
Рис. 4.13. На входе схемы между точками а и б приложено постоянное напряжение и маленькое, изменяющееся во времени напряжение – его форма Соответствует передаваемому сигналу. Конденсатор не пропускает постоянный ток (соответствующий ). Маленькое изменяющееся напряжение А и меняет заряд конденсатора. Протекающий зарядный ток создает падение напряжения на большом сопротивлении цепи. Это падение напряжения очень близко к значению переменного напряжения Таким образом, напряжение на выходе схемы между точками в и г приблизительно равно
Это падение напряжения очень близко к значению переменного напряжения Таким образом, напряжение на выходе схемы между точками в и г приблизительно равно
2. На свойствах конденсатора пропускать ток под действием изменяющегося напряжения и не пропускать ток под действием постоянного напряжения основаны сглаживающие устройства (фильтры, не пропускающие переменное напряжение). На рис. 4.14 показано такое устройство – переменный ток проходит через первый резистор и конденсатор, но благодаря большой емкости конденсатора колебание напряжения на нем очень мало. На выходе схемы напряжение сглажено – оно близко к постоянному.
Еще более сильное сглаживание можно получить, включая вместо резисторов индуктивные катушки L.
Рис. 4.14. Сглаживающее устройство, содержащее R и С. Колебания напряжения на входе схемы не передаются на выход. Напряжение на выходе близко к постоянному
Как было показано в гл. 2, при протекании изменяющегося тока в них наводится ЭДС, препятствующая колебаниям тока. Такое сглаживающее устройство показано на рис. 4.15.
Такое сглаживающее устройство показано на рис. 4.15.
3. На рис. 4.16 схематически показано устройство для зажигания горючей смеси в цилиндрах автомобильного двигателя.
Рис. 4.15. Сглаживающее устройство, содержащее L и С. На вход подано напряжение, заметно колеблющееся во времени. Напряжение на нагрузке почти постоянно
Ток от батареи проходит через первичную обмотку катушки. В нужный момент он прерывается специальными подвижными контактами. Быстрое изменение тока наводит ЭДС взаимоиндукции во вторичной обмотке катушки. Число витков вторичной обмотки очень велико, и разрыв тока производится быстро. Поэтому ЭДС, наводимая во вторичной обмотке, может достигать 10-12 тыс. В. При таком напряжении происходит искровой разряд между электродами «свечи», воспламеняющей рабочую смесь в цилиндре. Прерывание контакта происходит очень часто: так, в четырехцилиндровом двигателе один разрыв контактов происходит за каждый оборот двигателя.
На схеме на рис. 4.16 показан конденсатор, присоединенный к зажимам прерывателя.
Объясним его назначение.
При отсутствии конденсатора разрыв цепи сопровождался бы образованием искры между контактами прерывателя.
Рис. 4.16. Схема цепи, служащей для электрического зажигания горючей смеси в цилиндрах автомобильного двигателя: – прерыватель. Внизу показан разрез цилиндра с поршнем, над которым смесь воздуха с бензином воспламеняется электрической искрой, проскакивающей между электродами свечи
Не говоря уже о том, что часто появляющаяся искра быстро привела бы к износу контактов, наличие искры препятствует резкому разрыву тока: ток, после того как контакты разойдутся, еще остается замкнутым через искру и лишь постепенно спадает до нуля.
Если между контактами прерывателя включен конденсатор (как это показано на рис. 4.16), картина будет иной. Когда контакты начинают расходиться, цепь тока не разрывается – ток замыкается через еще не заряженный конденсатор. Но конденсатор быстро заряжается, и дальнейшее протекание тока оказывается невозможным.
Напряжение на заряженном конденсаторе может намного превысить 12 В, так как уменьшение тока в первичной обмотке катушки наводит в ней большую ЭДС самоиндукции.
Несмотря на это между контактами прерывателя искра уже не возникает, так как к этому моменту контакты прерывателя успевают достаточно далеко отойти один от другого.
Когда контакты прерывателя вновь замкнутся, конденсатор быстро разрядится и будет готов к работе при новом разрыве контактов.
Таким образом, конденсатор предохраняет контакты от обгорания и улучшает работу системы зажигания.
На схеме на рис. 4.16 рядом с конденсатором может быть включено добавочное сопротивление. Его назначение станет ясным после того, как мы рассмотрим электрические колебания в системе индуктивность – конденсатор.
Рис. 4.17. Разряд конденсатора на индуктивность. В такой цепи возникают электрические колебания (см. рис., 4.18)
4. Одно из очень важных применений конденсаторы находят в цепях переменного тока (улучшение «косинуса фи»).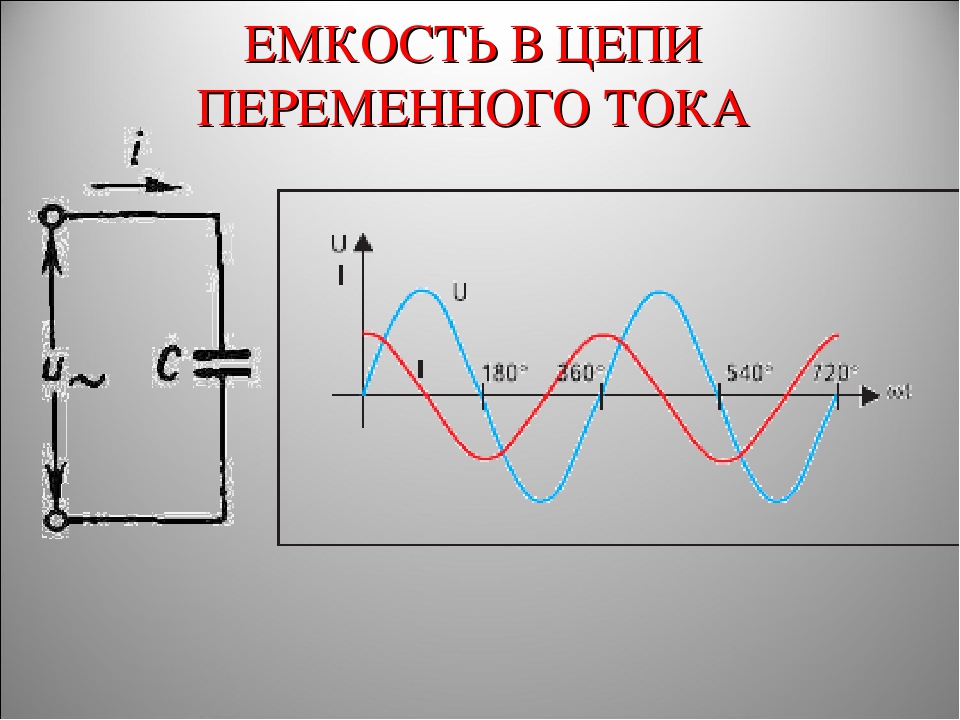 Оно рассмотрено в гл. 6.
Оно рассмотрено в гл. 6.
О применении конденсаторов в колебательных контурах генераторов рассказано в гл. 8.
Эти применения конденсаторов основаны на электрических колебаниях в системе LC (индуктивность и емкость).
Разряд конденсатора на индуктивность. Электрические колебания. Рассмотрим, что произойдет, если заряженный конденсатор замкнуть на катушку, обладающую индуктивностью и очень малым сопротивлением (рис. 4.17).
Возьмем конденсатор С, заряженный до напряжения в его электрическом поле при этом запасена энергия
Замкнем конденсатор на индуктивную катушку. Очевидно, что конденсатор начнет разряжаться. Однако благодаря возникающей ЭДС самоиндукции ток в катушке возрастает постепенно (§ 2.16 и 2.18). Ток первоначально был равен нулю, постепенно он возрастает. По мере протекания тока разряжается конденсатор; его напряжение при этом уменьшается.
Но мы знаем, что скорость нарастания тока – или вообще скорость изменения тока – в индуктивности пропорциональна приложенному к ней напряжению (внимательно рассмотрите, если нужно, § 2.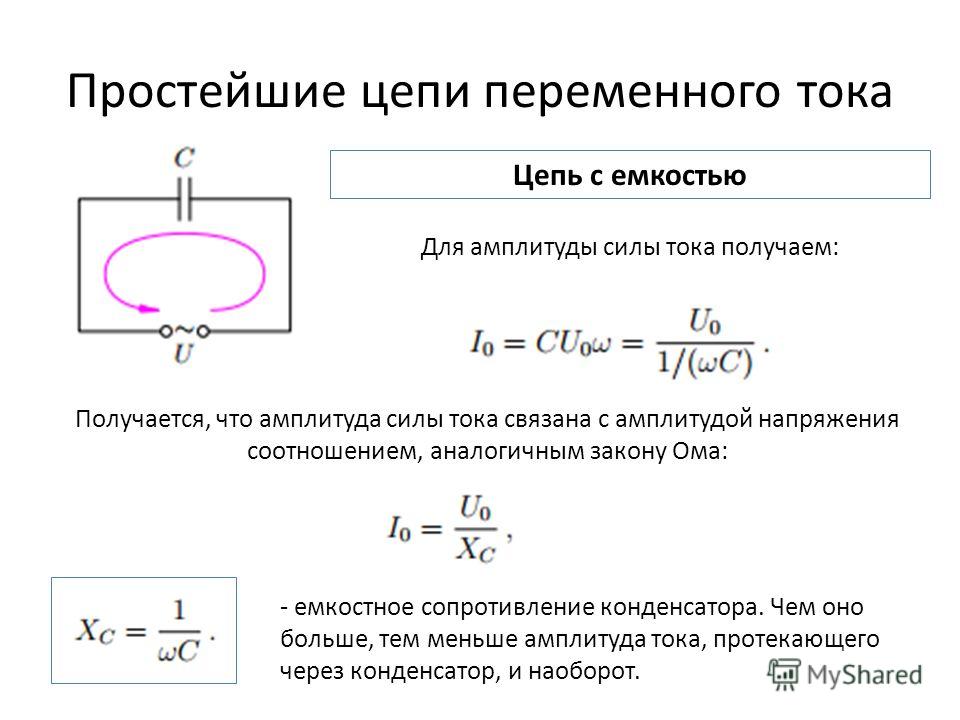 16).
16).
По мере уменьшения напряжения на конденсаторе уменьшеется скорость нарастания тока.
Мы сказали, что уменьшается скорость нарастания тока, но это вовсе не значит, что уменьшается сам ток.
Рис. 4.18. Изменения напряжения на конденсаторе и разрядного тока в цепи, изображенной на рис. 4.17. Приведенные здесь значения тока и напряжения соответствуют разряду конденсатора емкостью С=4мкФ, предварительно заряженного до напряжения . Индуктивность катушки L = 1,6 мГн. Этим данным соответствует период
Действительно, рассмотрим графики напряжения на конденсаторе и тока, представленные на рис. 4.18.
Сначал ток был равен нулю, но возрастал он очень быстро (это видно по крутизне подъема кривой линии, изображающей зависимость тока от времени). В конце разряда конденсатора, когда его напряжение стало равным нулю, ток перестал возрастать – он достиг наибольшего значения и уже не возрастает дальше.
Мы можем всё сказанное выразить таким уравнением:
Напряжение на конденсаторе всегда равное напряжению на индуктивности, равно скорости нарастания тока умноженной на индуктивность L.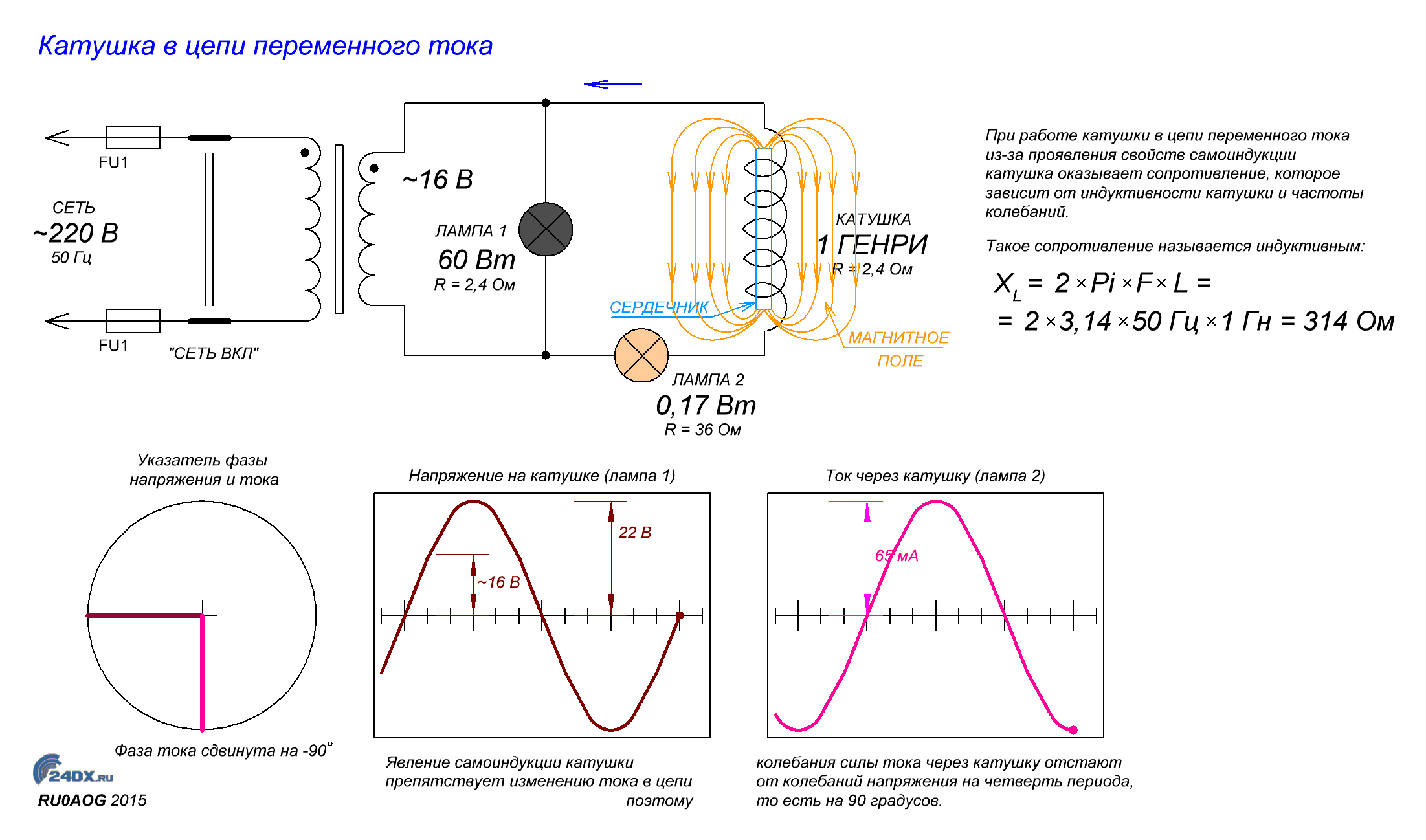
Конденсатор разрядился.
Энергия, заключенная в электрическом поле конденсатора, покинула конденсатор. Но куда она перешла?
В случае разряда конденсатора на сопротивление энергия перешла в тепло нагретого сопротивления. Но в рассматриваемом сейчас примере сопротивление цепи ничтожно (мы пренебрегли им вовсе). Где же теперь энергия, заключавшаяся в конденсаторе?
Энергия перешла из электрического поля конденсатора в магнитное поле индуктивности.
В самом деле, в начале процесса тока в индуктивности не было; когда ток в индуктивности достиг величины в ее магнитном поле появилась энергия
На основании закона сохранения энергии нетрудно найти то наибольшее значение которое достигается током в момент равенства нулю напряжения на конденсаторе.
В этот момент в конденсаторе нет энергии, значит, вся первоначально запасенная в нем энергия перешла в энергию магнитного поля. Приравнивая их выражения, находим
Очевидно, что в любой момент времени, когда напряжение на конденсаторе меньше, чем а ток меньше, чем общая энергия равна сумме энергий электрического и магнитного полей:
Итак, мы объяснили, что происходит за промежуток времени, понадобившийся для полного разряда конденсатора.
На рис. 4.18 этому соответствуют кривые тока и напряжения, относящиеся к промежутку, обозначенному цифрой I (время от 0 до 125 мкс).
Но дело на этом не кончается. Хотя конденсатор разрядился полностью, в цепи протекает большой ток. Этот ток не может сразу исчезнуть, так как его существование связано с энергией магнитного поля.
Этот ток продолжает протекать в цепи и перезаряжает конденсатор: он продолжает уносить электроны с отрицательных пластин и переносить их на пластины положительные, точнее – переносить с пластин, которые были отрицательными, на пластины, которые были положительными. Знак заряда на пластинах теперь изменяется.
На конденсаторе появляется напряжение, препятствующее дальнейшему протеканию тока, и ток постепенно начинает уменьшаться.
К концу промежутка времени, обозначенного цифрой II (к моменту времени 250 мкс), ток спадает до нуля. Но к этому моменту конденсатор опять окажется полностью заряженным; вся энергия, перешедшая в магнитное поле, теперь вновь превратилась в энергию электрического поля.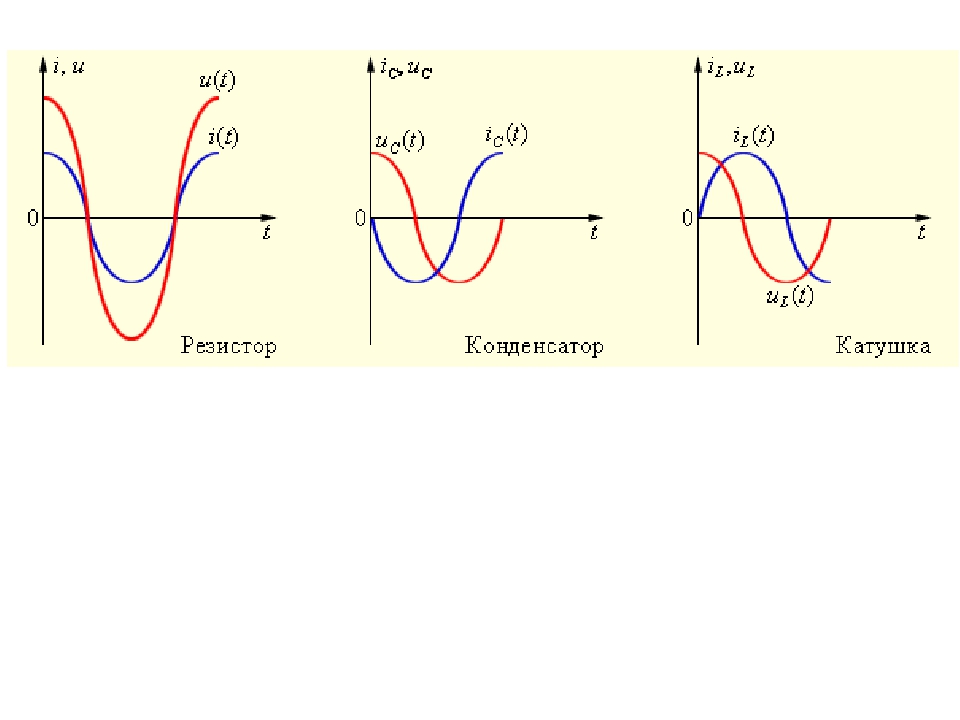
Ток равен нулю. Конденсатор имеет такое же напряжение, как вначале (только другого знака). Все начинается снова, так, как было рассказано: конденсатор начинает разряжаться, ток начинает возрастать и т. д.
Разница только в знаке напряжения на конденсаторе и соответственно в направлении тока: ток остается отрицательным в течение промежутков времени, обозначенных цифрами III и IV.
В конце промежутка IV (т. е. после того как пройдет 500 мкс) все вернется к исходному состоянию – конденсатор заряжен положительно и тока нет.
Начиная с этого момента все повторяется сначала.
Рассмотренная картина и представляет собой электрические колебания в цепи LC.
Время, требующееся на то, чтобы после начала разряда все вернулось к исходному состоянию, называется периодом (Т).
При значениях емкости и индуктивности, для которых построены графики на рис. 4.18, один период составляет 500 мкс. Чем больше индуктивность и емкость, тем больше период колебаний.
Связь между этими тремя величинами выражается равенством
Рассмотренные колебания называют свободными (в отличие от вынужденных), так как они происходят при отсутствии постороннего источника энергии, который мог бы заставить изменяться напряжение по какому-либо другому закону.
Такие колебания будут рассмотрены ниже, в.гл. 5 и 6. Там будет показано следующее: один источник (генератор) дает напряжение, изменяющееся по закону, подобному показанному на рис. 4.18, и если к источнику подключена катушка индуктивности, то в ней будет протекать ток
Это равенство имеет тот же смысл, что и равенство (А).
Небольшой приведенный здесь расчет показывает, до какой степени электрику нужно знать математику и иметь сноровку в проведении алгебраических действий.
Мы рассмотрели колебания, происходящие при разряде конденсатора, пренебрегая сопротивлением цепи. На самом деле в любом колебательном контуре сопротивление нельзя считать равным нулю.
Наличие небольшого сопротивления цепи приводит к постепенному затуханию колебаний, так как в сопротивлении происходит рассеяние энергии электромагнитного поля – она превращается в тепло в соответствии с законом Джоуля – Ленца.
Рис. 4.19. Затухающий колебательный разряд. Приведенный график напряжения на конденсаторе соответствует данным: , начальное напряжение на конденсаторе .
Поэтому каждый раз, когда вся энергия вновь сосредоточивается в электрическом поле конденсатора, напряжение на конденсаторе оказывается меньше:
На рис. 4.19 показана кривая напряжения на конденсаторе в цепи RLC (т. е. в цепи, содержащей кроме индуктивности и емкости также и сопротивление).
При достаточно большом сопротивлении в цепи колебания вообще не возникают. Разряд конденсатора происходит, как говорят, апериодически. Такой разряд показан на рис. 4.20. Разряд может быть сделан апёриодическйм и посредством подключения сопротивления параллельно конденсатору.
Понятие о разнообразных применениях колебательной системы (колебательного контура) будет дано в гл. 6 и 8.
Рис. 4.20. Апериодический разряд конденсатора. На графике изображены напряжения и ток в цепи конденсатора при тех же индуктивности и емкости (L = 1,6 МГн, С=4 мкФ) и при сопротивлении цепи, равном 64 Ом
Сейчас мы ограничимся указанием на то, что наличие конденсатора между контактами прерывателя в автомобиле (рис.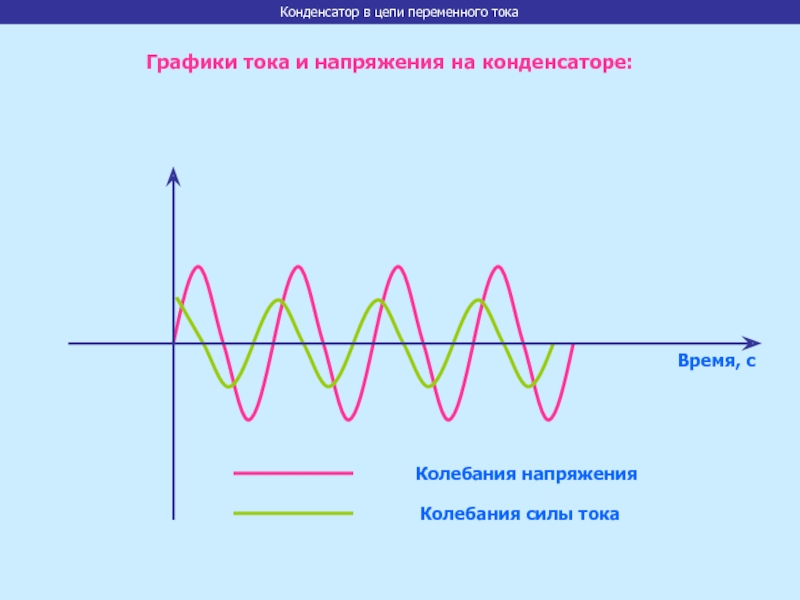 4.16) может служить источником колебаний, мешающих радиоприему. Эти колебания могут «гаситься», если ввести добавочный резистор (в соответствии со схемой на рис. 4.20).
4.16) может служить источником колебаний, мешающих радиоприему. Эти колебания могут «гаситься», если ввести добавочный резистор (в соответствии со схемой на рис. 4.20).
VI. Зависимость емкости конденсаторов от времени и от температуры
V. Поляризация диэлектриков
IV. Номинальная емкость и допускаемые отклонения
III. Емкость
Система условных обозначений и маркировка конденсаторов
II. Классификация конденсаторов
В зависимости от назначения различают конденсаторы общего и специального назначения. Группа общего назначения включает в себя широко применяемые конденсаторы, используемые в большинстве видов и классов аппаратуры (низковольтные конденсаторы). Все остальные конденсаторы являются специальными. К ним относятся высоковольтные, импульсные, помехоподавляющие, пусковые, дозиметрические и др.
По характеру изменения емкости различают конденсаторы постоянной емкости, переменной емкости и подстроечные.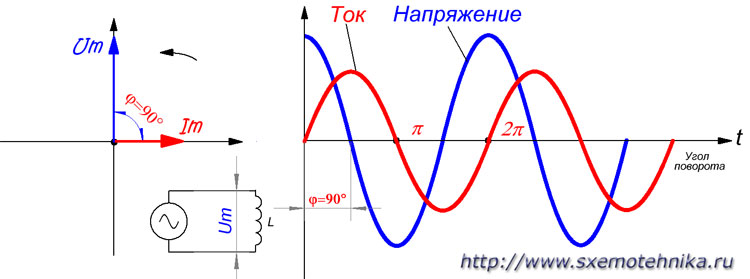 У конденсаторов постояннойемкости – емкость является фиксированной, и в процессе эксплуатации не изменяется. Конденсаторы переменной емкости – допускают изменение емкости в процессе функционирования аппаратуры. Управление емкостью может осуществляться механически, электрическим напряжением (вариконды) и температурой (термоконденсаторы). Емкость подстроечных конденсаторов изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры.
У конденсаторов постояннойемкости – емкость является фиксированной, и в процессе эксплуатации не изменяется. Конденсаторы переменной емкости – допускают изменение емкости в процессе функционирования аппаратуры. Управление емкостью может осуществляться механически, электрическим напряжением (вариконды) и температурой (термоконденсаторы). Емкость подстроечных конденсаторов изменяется при разовой или периодической регулировке и не изменяется в процессе функционирования аппаратуры.
По характеру защиты от внешних факторов конденсаторы выполняются незащищенные, защищенные, неизолированные, изолированные, уплотненные и герметизированные. Незащищенные конденсаторы допускают эксплуатацию в условиях повышенной влажности только в составе герметизированной аппаратуры. Защищенные конденсаторы допускают эксплуатацию в аппаратуре любого исполнения. Неизолированные конденсаторы – не допускают касания своим корпусом шасси аппаратуры. Изолированные конденсаторы имеют хорошее изоляционное покрытие (компаунды, пластмассы и т.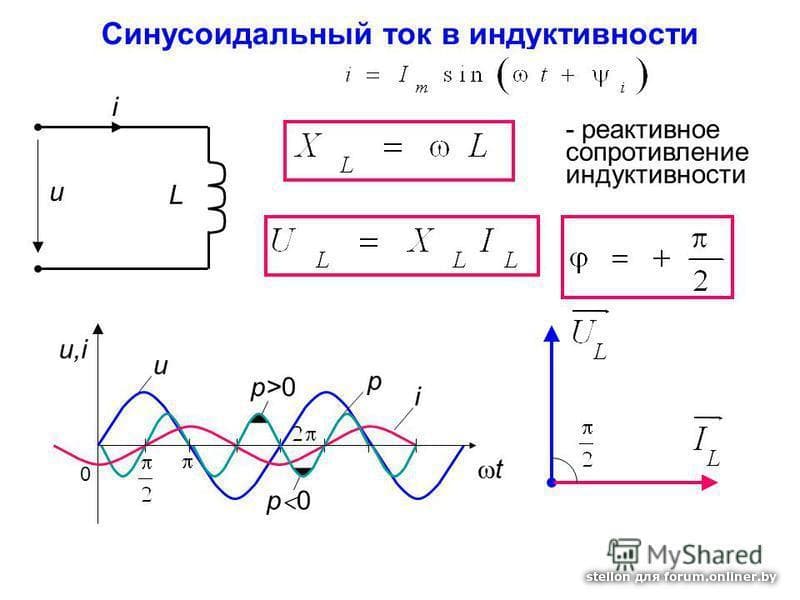 д.) и допускают касания корпусом шасси или токоведущих частей аппаратуры. Уплотненные конденсаторы – имеют уплотненную органическими материалами конструкцию корпуса. Герметизированные конденсаторы – имеют герметичную конструкцию корпуса, который исключает возможность сообщения окружающей среды с его внутренним пространством. Герметизация осуществляется с помощью керамических и металлических корпусов или стеклянных колб.
д.) и допускают касания корпусом шасси или токоведущих частей аппаратуры. Уплотненные конденсаторы – имеют уплотненную органическими материалами конструкцию корпуса. Герметизированные конденсаторы – имеют герметичную конструкцию корпуса, который исключает возможность сообщения окружающей среды с его внутренним пространством. Герметизация осуществляется с помощью керамических и металлических корпусов или стеклянных колб.
Система условных обозначений и маркировка конденсаторов может быть сокращенной и полной.
В соответствии с действующей системой сокращенное условное обозначение состоит из букв и цифр.
Первый элемент – буква или сочетание букв, обозначающее подкласс конденсаторов: К – постоянной емкости; КТ – подстроечные; КП – переменной емкости; КС – конденсаторные сборки.
Второй элемент – цифра, обозначает группу конденсатора в зависимости от материала диэлектрика.
Третий элемент – цифра, пишется через дефис и обозначает регистрационный номер конкретного типа конденсатора.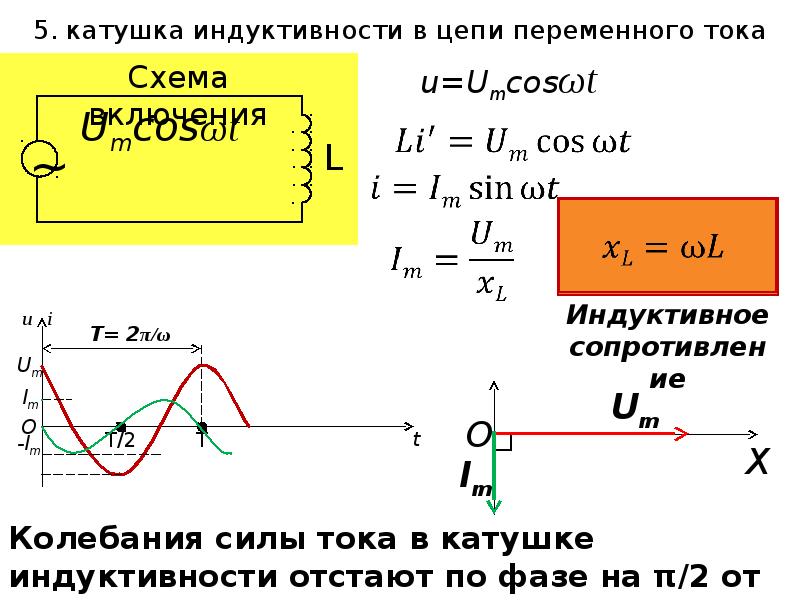 В состав третьего элемента может входить так же буквенное обозначение.
В состав третьего элемента может входить так же буквенное обозначение.
Полное условное обозначение конденсатора состоит из сокращенного обозначения, обозначения и величины основных параметров и характеристик, необходимых для заказа и записи конструкторской документации, обозначения климатического исполнения и документа на поставку.
Например:
Керамический конденсатор постоянной емкости на номинальное напряжение до 1600 В с регистрационным номером 17 имеет сокращенное условное обозначение К10-17;
Подстроечный керамический конденсатор с регистрационным номером 25 сокращенно обозначается КТ4-25;
Конденсатор керамический К10-7В, всеклиматического исполнения с температурным коэффициентом емкости равным , номинальной емкостью 27пФ, с допуском ±10%, поставляемый по ГОСТ 5.621-70 имеет полное условное обозначение:
К10-7В-М47-27пФ±10% ГОСТ 5.621-70
Кодированные обозначения предназначены для маркировки малогабаритных конденсаторов и для записи на малоформатных многоэлементных электрических схемах.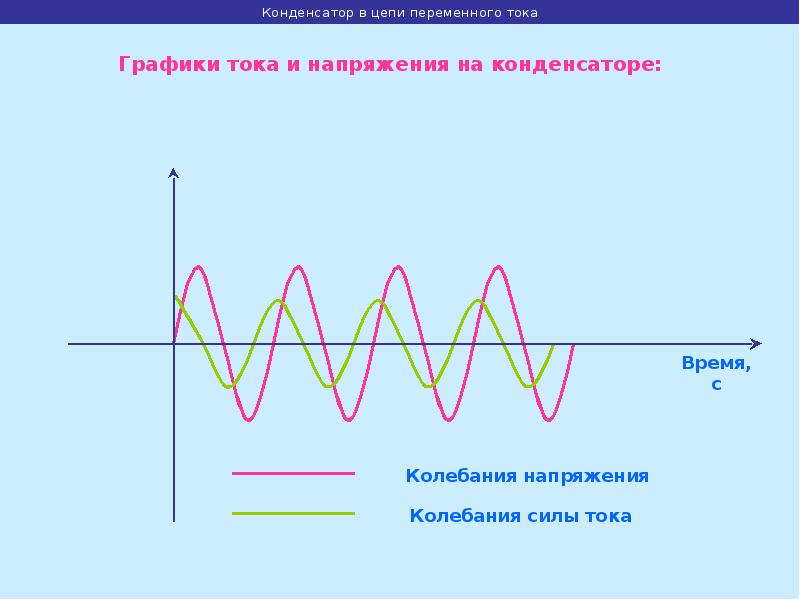 Полное обозначение состоит из значения номинальной емкости (цифра) и обозначения единицы измерения (пФ, мкФ, Ф). Например: 1.5 пФ (1П5 или 1p5), 0.1 мкФ, 10 Ф.
Полное обозначение состоит из значения номинальной емкости (цифра) и обозначения единицы измерения (пФ, мкФ, Ф). Например: 1.5 пФ (1П5 или 1p5), 0.1 мкФ, 10 Ф.
Основное свойство конденсатора – его емкость, то есть способность накапливать на обкладках электрический заряд. Выражается соотношением:
N Для шарового конденсатора:
[Ф] ,
где r – радиус сферического конденсатора [м].
Эти формулы справедливы для однородного поля, и не учитывают его искажения у края конденсаторных обкладок. Если учитывать искажения, то вводят поправку на краевую емкость .
Конденсаторы соединяют в группы – параллельно, последовательно и смешанно.
При параллельном соединении конденсаторов общая емкость равна сумме емкостей:
При последовательном соединении величина обратная общей емкости группы равна сумме обратных величин отдельных емкостей.
Во всех радиотехнических и электронных устройствах кроме транзисторов и микросхем применяются конденсаторы. В одних схемах их больше, в других меньше, но совсем без конденсаторов не бывает практически ни одной электронной схемы.
В одних схемах их больше, в других меньше, но совсем без конденсаторов не бывает практически ни одной электронной схемы.
При этом конденсаторы могут выполнять в устройствах самые разные задачи. Прежде всего, это емкости в фильтрах выпрямителей и стабилизаторов. С помощью конденсаторов передается сигнал между усилительными каскадами, строятся фильтры низких и высоких частот, задаются временные интервалы в выдержках времени и подбирается частота колебаний в различных генераторах.
Свою родословную конденсаторы ведут от , которую в середине XVIII века в своих опытах использовал голландский ученый Питер ван Мушенбрук. Жил он в городе Лейдене, так что нетрудно догадаться, почему так называлась эта банка.
Собственно это и была обыкновенная стеклянная банка, выложенная внутри и снаружи оловянной фольгой – станиолем. Использовалась она в тех же целях, как и современная алюминиевая, но тогда алюминий открыт еще не был.
Единственным источником электричества в те времена была электрофорная машина, способная развивать напряжение до нескольких сотен киловольт.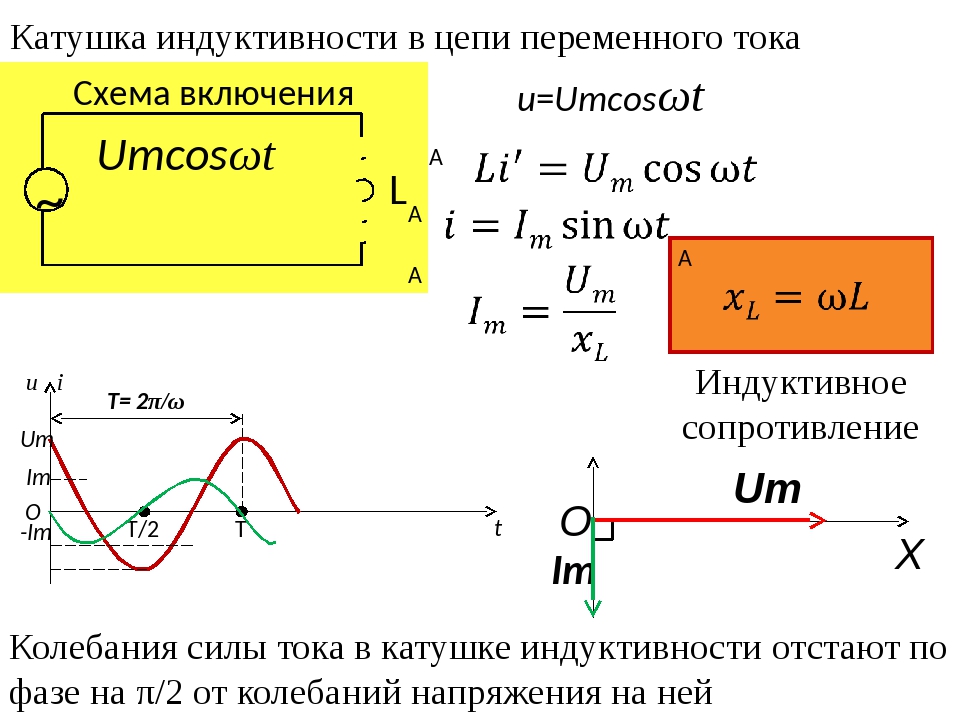 Вот от нее и заряжали лейденскую банку. В учебниках физики описан случай, когда Мушенбрук разрядил свою банку через цепь из десяти гвардейцев взявшихся за руки.
Вот от нее и заряжали лейденскую банку. В учебниках физики описан случай, когда Мушенбрук разрядил свою банку через цепь из десяти гвардейцев взявшихся за руки.
В то время никто не знал, что последствия могут быть трагическими. Удар получился достаточно чувствительным, но не смертельным. До этого не дошло, ведь емкость лейденской банки была незначительной, импульс получился очень кратковременным, поэтому мощность разряда была невелика.
Как устроен конденсатор
Устройство конденсатора практически ничем не отличается от лейденской банки: все те же две обкладки, разделенные диэлектриком. Именно так на современных электрических схемах изображаются конденсаторы. На рисунке 1 показано схематичное устройство плоского конденсатора и формула для его расчета.
Рисунок 1. Устройство плоского конденсатора
Здесь S – площадь пластин в квадратных метрах, d – расстояние между пластинами в метрах, C – емкость в фарадах, ε – диэлектрическая проницаемость среды. Все величины, входящие в формулу, указаны в системе СИ. Эта формула справедлива для простейшего плоского конденсатора: можно просто расположить рядом две металлические пластины, от которых сделаны выводы. Диэлектриком может служить воздух.
Все величины, входящие в формулу, указаны в системе СИ. Эта формула справедлива для простейшего плоского конденсатора: можно просто расположить рядом две металлические пластины, от которых сделаны выводы. Диэлектриком может служить воздух.
Из этой формулы можно понять, что емкость конденсатора тем больше, чем больше площадь пластин и чем меньше расстояние между ними. Для конденсаторов с другой геометрией формула может быть иной, например, для емкости одиночного проводника или . Но зависимость емкости от площади пластин и расстояния между ними та же, что и у плоского конденсатора: чем больше площадь и чем меньше расстояние, тем больше емкость.
На самом деле пластины не всегда делаются плоскими. У многих конденсаторов, например металлобумажных, обкладки представляют собой алюминиевую фольгу свернутую вместе с бумажным диэлектриком в плотный клубок, по форме металлического корпуса.
Для увеличения электрической прочности тонкая конденсаторная бумага пропитывается изолирующими составами, чаще всего трансформаторным маслом.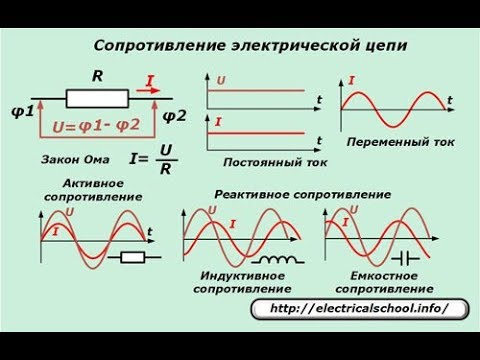 Такая конструкция позволяет делать конденсаторы с емкостью до нескольких сотен микрофарад. Примерно так же устроены конденсаторы и с другими диэлектриками.
Такая конструкция позволяет делать конденсаторы с емкостью до нескольких сотен микрофарад. Примерно так же устроены конденсаторы и с другими диэлектриками.
Формула не содержит никаких ограничений на площадь пластин S и расстояние между пластинами d. Если предположить, что пластины можно развести очень далеко, и при этом площадь пластин сделать совсем незначительной, то какая-то емкость, пусть небольшая, все равно останется. Подобное рассуждение говорит о том, что даже просто два проводника, расположенные по соседству, обладают электрической емкостью.
Этим обстоятельством широко пользуются в высокочастотной технике: в некоторых случаях конденсаторы делаются просто в виде дорожек печатного монтажа, а то и просто двух скрученных вместе проводков в полиэтиленовой изоляции. Обычный провод-лапша или кабель также обладают емкостью, причем с увеличением длины она увеличивается.
Кроме емкости C, любой кабель обладает еще и сопротивлением R. Оба этих физических свойства распределены по длине кабеля, и при передаче импульсных сигналов работают как интегрирующая RC – цепочка, показанная на рисунке 2.
Рисунок 2.
На рисунке все просто: вот схема, вот входной сигнал, а вот он же на выходе. Импульс искажается до неузнаваемости, но это сделано специально, для чего и собрана схема. Пока же речь идет о влиянии емкости кабеля на импульсный сигнал. Вместо импульса на другом конце кабеля появится вот такой «колокол», а если импульс короткий, то он может и вовсе не дойти до другого конца кабеля, вовсе пропасть.
Исторический факт
Здесь вполне уместно вспомнить историю о том, как прокладывали трансатлантический кабель. Первая попытка в 1857 году потерпела неудачу: телеграфные точки – тире (прямоугольные импульсы) искажались так, что на другом конце линии длиной 4000 км разобрать ничего не удалось.
Вторая попытка была предпринята в 1865 году. К этому времени английский физик У. Томпсон разработал теорию передачи данных по длинным линиям. В свете этой теории прокладка кабеля оказалась более удачной, сигналы принять удалось.
За этот научный подвиг королева Виктория пожаловала ученого рыцарством и титулом лорда Кельвина. Именно так назывался небольшой город на побережье Ирландии, где начиналась прокладка кабеля. Но это просто к слову, а теперь вернемся к последней букве в формуле, а именно, к диэлектрической проницаемости среды ε.
Именно так назывался небольшой город на побережье Ирландии, где начиналась прокладка кабеля. Но это просто к слову, а теперь вернемся к последней букве в формуле, а именно, к диэлектрической проницаемости среды ε.
Немножко о диэлектриках
Эта ε стоит в знаменателе формулы, следовательно, ее увеличение повлечет за собой возрастание емкости. Для большинства используемых диэлектриков, таких как воздух, лавсан, полиэтилен, фторопласт эта константа практически такая же, как у вакуума. Но вместе с тем существует много веществ, диэлектрическая проницаемость которых намного выше. Если воздушный конденсатор залить ацетоном или спиртом, то его емкость возрастет раз в 15…20.
Но подобные вещества обладают кроме высокой ε еще и достаточно высокой проводимостью, поэтому такой конденсатор заряд держать будет плохо, он быстро разрядится сам через себя. Это вредное явление называется током утечки. Поэтому для диэлектриков разрабатываются специальные материалы, которые позволяют при высокой удельной емкости конденсаторов обеспечивать приемлемые токи утечки.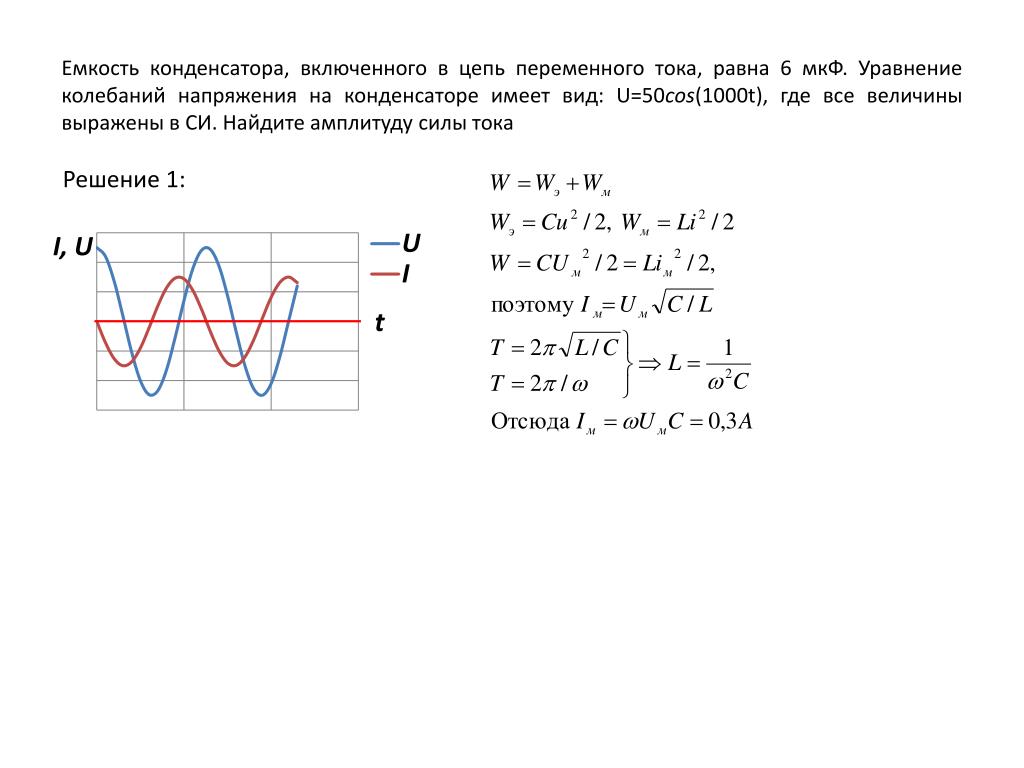 Именно этим и объясняется такое разнообразие видов и типов конденсаторов, каждый из которых предназначен для конкретных условий.
Именно этим и объясняется такое разнообразие видов и типов конденсаторов, каждый из которых предназначен для конкретных условий.
Наибольшей удельной емкостью (соотношение емкость / объем) обладают . Емкость «электролитов» достигает до 100 000 мкФ, рабочее напряжение до 600В. Такие конденсаторы работают хорошо только на низких частотах, чаще всего в фильтрах источников питания. Электролитические конденсаторы включаются с соблюдением полярности.
Электродами в таких конденсаторах является тонкая пленка из оксида металлов, поэтому часто эти конденсаторы называют оксидными. Тонкий слой воздуха между такими электродами не очень надежный изолятор, поэтому между оксидными обкладками вводится слой электролита. Чаще всего это концентрированные растворы кислот или щелочей.
На рисунке 3 показан один из таких конденсаторов.
Рисунок 3. Электролитический конденсатор
Чтобы оценить размеры конденсатора рядом с ним сфотографировался простой спичечный коробок. Кроме достаточно большой емкости на рисунке можно разглядеть еще и допуск в процентах: ни много ни мало 70% от номинальной.
В те времена, когда компьютеры были большими и назывались ЭВМ, такие конденсаторы стояли в дисководах (по-современному HDD). Информационная емкость таких накопителей теперь может вызвать лишь улыбку: на двух дисках диаметром 350 мм хранилось 5 мегабайт информации, а само устройство весило 54 кг.
Основным назначением показанных на рисунке суперконденсаторов был вывод магнитных головок из рабочей зоны диска при внезапном отключении электроэнергии. Такие конденсаторы могли хранить заряд несколько лет, что было проверено на практике.
Чуть ниже с электролитическими конденсаторами будет предложено проделать несколько простых опытов, чтобы понять, что может делать конденсатор.
Для работы в цепях переменного тока выпускаются неполярные электролитические конденсаторы, вот только достать их почему-то очень непросто. Чтобы как-то эту проблему обойти, обычные полярные «электролиты» включают встречно-последовательно: плюс-минус-минус-плюс.
Если полярный электролитический конденсатор включить в цепь переменного тока, то сначала он будет греться, а потом раздастся взрыв. Отечественные старые конденсаторы разлетались во все стороны, импортные же имеют специальное приспособление, позволяющее избежать громких выстрелов. Это, как правило, либо крестовая насечка на донышке конденсатора, либо отверстие с резиновой пробкой, расположенное там же.
Отечественные старые конденсаторы разлетались во все стороны, импортные же имеют специальное приспособление, позволяющее избежать громких выстрелов. Это, как правило, либо крестовая насечка на донышке конденсатора, либо отверстие с резиновой пробкой, расположенное там же.
Очень не любят электролитические конденсаторы повышенного напряжения, даже если полярность соблюдена. Поэтому никогда не надо ставить «электролиты» в цепь, где предвидится напряжение близкое к максимальному для данного конденсатора.
Иногда в некоторых, даже солидных форумах, начинающие задают вопрос: «На схеме означен конденсатор 470µF * 16V, а у меня есть 470µF * 50V, можно ли его поставить?». Да, конечно можно, вот обратная замена недопустима.
Конденсатор может накапливать энергию
Разобраться с этим утверждением поможет простая схема, показанная на рисунке 4.
Рисунок 4. Схема с конденсатором
Главным действующим лицом этой схемы является электролитический конденсатор C достаточно большой емкости, чтобы процессы заряда – разряда протекали медленно, и даже очень наглядно. Это дает возможность наблюдать работу схемы визуально с помощью обычной лампочки от карманного фонаря. Фонари эти давно уступили место современным светодиодным, но лампочки для них продаются до сих пор. Поэтому, собрать схему и провести простые опыты очень даже просто.
Это дает возможность наблюдать работу схемы визуально с помощью обычной лампочки от карманного фонаря. Фонари эти давно уступили место современным светодиодным, но лампочки для них продаются до сих пор. Поэтому, собрать схему и провести простые опыты очень даже просто.
Может быть, кто-то скажет: «А зачем? Ведь и так все очевидно, да если еще и описание почитать…». Возразить тут, вроде, нечего, но любая, даже самая простая вещь остается в голове надолго, если ее понимание пришло через руки.
Итак, схема собрана. Как она работает?
В положении переключателя SA, показанном на схеме, конденсатор C заряжается от источника питания GB через резистор R по цепи: +GB __ R __ SA __ C __ -GB. Зарядный ток на схеме показан стрелкой с индексом iз. Процесс заряда конденсатора показан на рисунке 5.
Рисунок 5. Процесс заряда конденсатора
На рисунке видно, что напряжение на конденсаторе возрастает по кривой линии, в математике называемой экспонентой. Ток заряда прямо-таки зеркально отражает напряжение заряда. По мере того, как напряжение на конденсаторе растет, ток заряда становится все меньше. И только в начальный момент соответствует формуле, показанной на рисунке.
По мере того, как напряжение на конденсаторе растет, ток заряда становится все меньше. И только в начальный момент соответствует формуле, показанной на рисунке.
Через некоторое время конденсатор зарядится от 0В до напряжения источника питания, в нашей схеме до 4,5В. Весь вопрос в том, как это время определить, сколько ждать, когда же конденсатор зарядится?
Постоянная времени «тау» τ = R*C
В этой формуле просто перемножаются сопротивление и емкость последовательно соединенных резистора и конденсатора. Если, не пренебрегая системой СИ, подставить сопротивление в Омах, емкость в Фарадах, то результат получится в секундах. Именно это время необходимо для того, чтобы конденсатор зарядился до 36,8% напряжения источника питания. Соответственно для заряда практически до 100% потребуется время 5* τ.
Часто, пренебрегая системой СИ, подставляют в формулу сопротивление в Омах, а емкость в микрофарадах, тогда время получится в микросекундах. В нашем случае результат удобнее получить в секундах, для чего придется микросекунды просто умножить на миллион, а проще говоря, переместить запятую на шесть знаков влево.
Для схемы, показанной на рисунке 4, при емкости конденсатора 2000мкФ и сопротивлении резистора 500Ω постоянная времени получится τ = R*C = 500 * 2000 = 1000000 микросекунд или ровно одна секунда. Таким образом, придется подождать приблизительно 5 секунд, пока конденсатор зарядится полностью.
Если по истечении указанного времени переключатель SA перевести в правое положение, то конденсатор C разрядится через лампочку EL. В этот момент получится короткая вспышка, конденсатор разрядится и лампочка погаснет. Направление разряда конденсатора показано стрелкой с индексом iр. Время разряда также определяется постоянной времени τ. График разряда показан на рисунке 6.
Рисунок 6. График разряда конденсатора
Конденсатор не пропускает постоянный ток
Убедиться в этом утверждении поможет еще более простая схема, показанная на рисунке 7.
Рисунок 7. Схема с конденсатором в цепи постоянного тока
Если замкнуть переключатель SA, то последует кратковременная вспышка лампочки, что свидетельствует о том, что конденсатор C зарядился через лампочку.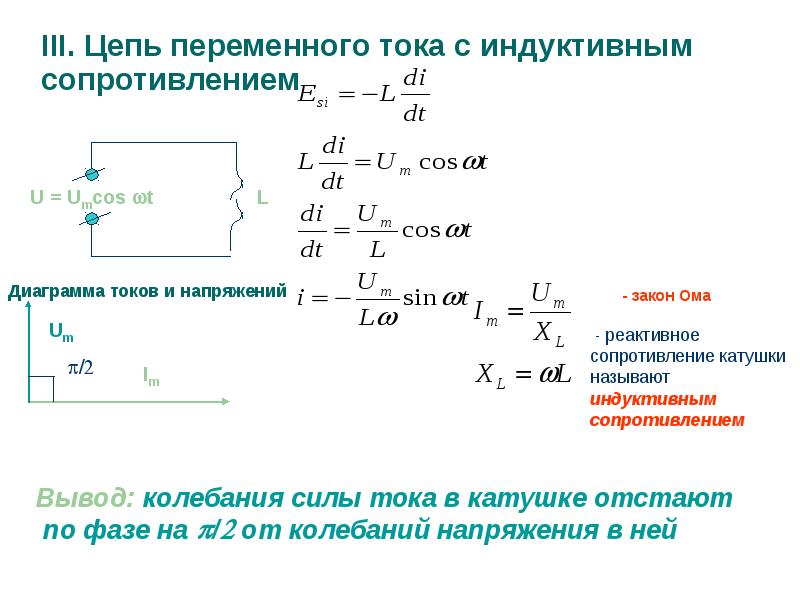 Здесь же показан и график заряда: в момент замыкания переключателя ток максимальный, по мере заряда конденсатора уменьшается, а через некоторое время прекращается совсем.
Здесь же показан и график заряда: в момент замыкания переключателя ток максимальный, по мере заряда конденсатора уменьшается, а через некоторое время прекращается совсем.
Если конденсатор хорошего качества, т.е. с малым током утечки (саморазряда) повторное замыкание выключателя к вспышке не приведет. Для получения еще одной вспышки конденсатор придется разрядить.
Конденсатор в фильтрах питания
Конденсатор ставится, как правило, после выпрямителя. Чаще всего выпрямители делаются двухполупериодными. Наиболее распространенные схемы выпрямителей показаны на рисунке 8.
Рисунок 8. Схемы выпрямителей
Однополупериодные выпрямители также применяются достаточно часто, как правило, в тех случаях, когда мощность нагрузки незначительна. Самым ценным качеством таких выпрямителей является простота: всего один диод и обмотка трансформатора.
Для двухполупериодного выпрямителя емкость конденсатора фильтра можно рассчитать по формуле
C = 1000000 * Po / 2*U*f*dU, где C емкость конденсатора мкФ, Po мощность нагрузки Вт, U напряжение на выходе выпрямителя В, f частота переменного напряжения Гц, dU амплитуда пульсаций В.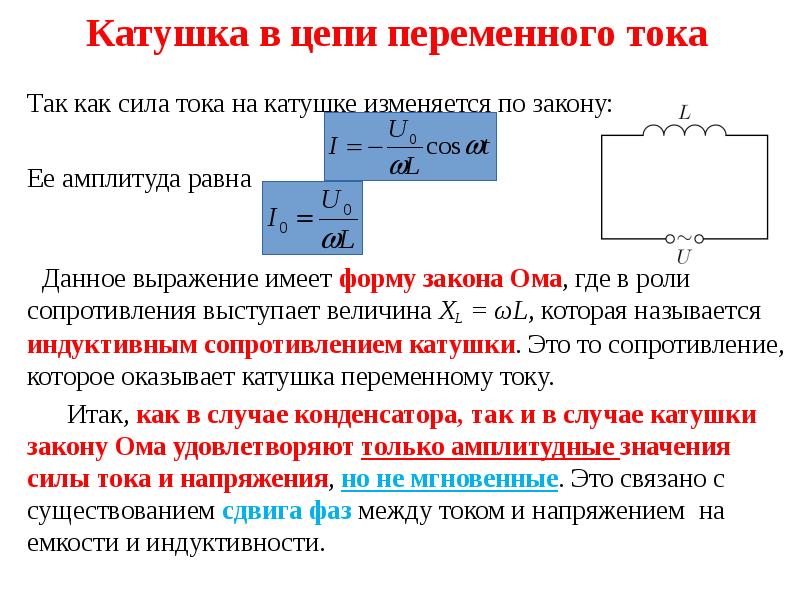
Большое число в числителе 1000000 переводит емкость конденсатора из системных Фарад в микрофарады. Двойка в знаменателе представляет собой число полупериодов выпрямителя: для однополупериодного на ее месте появится единица
C = 1000000 * Po / U*f*dU,
а для трехфазного выпрямителя формула примет вид C = 1000000 * Po / 3*U*f*dU.
Суперконденсатор – ионистор
В последнее время появился новый класс электролитических конденсаторов, так называемый . По своим свойствам он похож на аккумулятор, правда, с несколькими ограничениями.
Заряд ионистора до номинального напряжения происходит в течение короткого времени, буквально за несколько минут, поэтому его целесообразно использовать в качестве резервного источника питания. По сути ионистор прибор неполярный, единственное, чем определяется его полярность это зарядкой на заводе – изготовителе. Чтобы в дальнейшем эту полярность не перепутать она указывается знаком +.
Большую роль играют условия эксплуатации ионисторов. При температуре 70˚C при напряжении 0,8 от номинального гарантированная долговечность не более 500 часов. Если же прибор будет работать при напряжении 0,6 от номинального, а температура не превысит 40 градусов, то исправная работа возможна в течение 40 000 часов и более.
При температуре 70˚C при напряжении 0,8 от номинального гарантированная долговечность не более 500 часов. Если же прибор будет работать при напряжении 0,6 от номинального, а температура не превысит 40 градусов, то исправная работа возможна в течение 40 000 часов и более.
Наиболее распространенное применение ионистора это источники резервного питания. В основном это микросхемы памяти или электронные часы. В этом случае основным параметром ионистора является малый ток утечки, его саморазряд.
Достаточно перспективным является использование ионисторов совместно с солнечными батареями. Здесь также сказывается некритичность к условию заряда и практически неограниченное число циклов заряд-разряд. Еще одно ценное свойство в том, что ионистор не нуждается в обслуживании.
Пока получилось рассказать, как и где работают электролитические конденсаторы, причем, в основном в цепях постоянного тока. О работе конденсаторов в цепях переменного тока будет рассказано в другой статье – .
Цепь переменного тока с ёмкостью
Поскольку после того, как конденсатор зарядился полностью, он не пропускает через себя электрический ток, и поэтому идеальный конденсатор (ёмкость), установленный в цепи постоянного тока, обладает бесконечно большим сопротивлением.
Цепь переменного тока с ёмкостью
Если же произвести подключение конденсатора к источнику переменного тока, то процесс его заряда и разряда будет осуществляться непрерывно. Это означает, что через ёмкость будет проходить переменный электрический ток.
Ток i при условии включения в цепь переменного тока некоторой ёмкости будет определяется количеством электричества q, протекающего по этой цепи в единицу времени. Из этого следует, что:
где Δq – это изменение заряда q (то есть количества электричества) в течение времени Δt.
Что касается заряда q, который накоплен при изменениях напряжения u в конденсаторе, то он также подвержен непрерывному изменению, которое выражается формулой:
где Δu – это изменение напряжения u в течение промежутка времени Δt.
Та скорость, с которой изменяется напряжение (она выражается отношением Δu/Δt) будет иметь свои наибольшие значения тогда, когда угол ωt равняется 360°, 180° и 0°. Из этого следует, что значение тока i принимает свои наибольшие величины именно в эти моменты времени. Если же угол ωt равняется 270° и 90°, то i = 0, поскольку скорость изменения напряжения Δu/Δt = 0.
Ток и напряжение в цепи переменного тока с ёмкостью
Ток заряда, который принято считать положительным, в цепи течет тогда, когда происходит заряд конденсатора, то есть на протяжение первой четверти периода. По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока
По мере того, как разница потенциалов на электродах ёмкости растет вследствие накопления ею электрического заряда, значение тока i падает. Когда ωt = 90°, наступает полный заряд емкости, значение i = 0, а разность потенциалов между электродами конденсатора обретает то же самое значение, что и напряжение источника тока.
Значение тока i становится отрицательным тогда, когда он меняет свое направление. Это происходит тогда, когда ёмкость начинает разряжаться, то есть во второй четверти периода. Тогда, когда u = 0 а ωt = 180°, значение тока i становится максимальным. В этот же самый момент ток i начинает течь в обратном направлении (его принято считать отрицательным), начинается процесс перезарядки емкости, а полярность напряжения u источника также меняется на противоположную. Когда ωt = 270° значение тока i становится равным нулю, и поэтому процесс заряда прекращается. После чего начинается разряд при первоначальном (то есть положительном) направлении тока.
После чего начинается разряд при первоначальном (то есть положительном) направлении тока.
Получается, что ёмкость и заряжается, и разряжается два раза на протяжении одного периода изменения напряжения. Из этого следует, что переменный ток i протекает в цепи непрерывно. Когда ёмкость включается в цепь переменного тока, то ток i опережает напряжение u по фазе на угол, равный 90°. Можно также сказать, что напряжение u отстает по фазе от тока i на угол, равный 90°.
Емкостное сопротивление
Сопротивление, которое проявляет ёмкость к переменному току, носит название емкостного.
Единицей измерения этой величины является Ом, а обозначается оно Хс. Физическая природа емкостного сопротивления заключается в том, что оно обусловлено возникающей в конденсаторе ЭДС ес. Направление этой электродвижущей силы противоположно приложенному напряжению u, поскольку заряженная ёмкость рассматривается в качестве источника, у которого между пластинами действует некоторая ЭДС ес. Именно она препятствует тому, чтобы под действием напряжения u происходило изменение тока, то есть оказывает определенное сопротивление его прохождению.
Именно она препятствует тому, чтобы под действием напряжения u происходило изменение тока, то есть оказывает определенное сопротивление его прохождению.
Поведение конденсатора в цепи переменного тока
Если говорить строго, то через конденсатор не проходит ни постоянный, ни переменный ток, так как между обкладками находится изолятор, в котором свободные электрические заряды двигаться не могут.
Включение конденсатора в цепь постоянного тока равносильно разрыву этой цепи. Что же касается переменного тока, то он будет протекать по цепи, в которую включен конденсатор, благодаря периодическому заряду и разряду этого конденсатора. Действительно, когда происходит заряд конденсатора, то электрические заряды, например электроны, на одной обкладке накапливаются, а с другой обкладки уходят. При этом они, конечно, двигаются по соединительным проводам, подключенным к обкладкам конденсатора. Такое же движение зарядов, только в противоположном направлении, происходит и при разряде конденсатора.
Если включить конденсатор в цепь переменного тока, то он будет периодически заряжаться то в одной полярности, то в противоположной. Это значит, что электроны будут накапливаться то на одной, то на другой обкладке, и каждый раз при заряде и разряде свободные электроны будут двигаться по цепи, в которую включен конденсатор, не попадая, однако, в изолятор, включенный между обкладками. А поскольку под действием переменного напряжения в цепи конденсатора двигаются заряды, то мы считаем, что конденсатор пропускает переменный ток, хотя и в этом случае заряды не проходят через изолятор.
Конденсатор влияет на величину переменного тока в цепи, и поэтому (по аналогии с законом Ома) его часто рассматривают как сопротивление. Это так называемое емкостное сопротивление обозначается буквой хс и так же, как и обычное сопротивление, измеряется в омах. Величина хс зависит от частоты переменного тока и от емкости С конденсатора: с уменьшением емкости конденсатора, так же как и с уменьшением частоты переменного тока, емкостное сопротивление конденсатора увеличивается (рис. 80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:
80, 81, лист 87). Эту зависимость удобно записать в виде простой формулы:
Смысл этой формулы весьма прост: чем меньше емкость С, тем меньше зарядов будет двигаться к обкладкам при каждом заряде и разряде конденсатора; чем меньше частота переменного тока, тем реже будет заряжаться и разряжаться конденсатор. Отсюда следует, что с уменьшением f и С уменьшается ток в цепи, или, иными словами, растет сопротивление конденсатора.
Этот вывод имеет огромное практическое значение. Так, например, если нам понадобится включить в цепь конденсатор с очень маленьким емкостным сопротивлением, то емкость этого конденсатора нужно будет выбирать с учетом частоты переменного тока в цепи. Для высоких частот можно будет взять конденсатор небольшой емкости, а вот для низких частот емкость конденсатора придется взять большой. Это хорошо иллюстрируется простым примером. На частоте 100 кгц конденсатор емкостью 100 пф обладает емкостным сопротивлением хс=16 ком. При уменьшении частоты в 1000 раз, то есть на частоте 100 гц, сопротивление конденсатора возрастет в 1000 раз и станет равным 16 000 ком (16 Мом). Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).
Для того чтобы при уменьшении частоты емкостное сопротивление не изменилось, нужно увеличить емкость конденсатора. Сопротивление 16 ком на частоте 100 гц будет иметь конденсатор емкостью 100 000 пф (0,1 мкф).
Из приведенной выше формулы следует также, что уменьшение емкости конденсатора связи Ссв (лист 85) приведет к росту сопротивления этого конденсатора, а следовательно, к уменьшению тока в цепи антенны. Поэтому емкость Ссв нельзя брать слишком малой.
Сказанное можно пояснить еще иначе. Конденсатор связи и колебательный контур Lк Ск можно рассматривать как делитель напряжения, к которому приложена э. д. с, действующая между зажимами А («антенна») и З («земля»). Мы не будем пока говорить о том, чему равно сопротивление колебательного контура – даже без этого ясно: чем больше емкостное сопротивление конденсатора связи, тем меньшая часть э. д. с. будет действовать на нижней части делителя – на контуре и подключенной к нему цепи детектор – телефон.
2. Конденсатор в цепи переменного тока | 4. Реактивное сопротивление и импеданс — Емкость | Часть2
2. Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока
Конденсатор в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то конденсаторы противостоят изменению напряжения (“тормозя” или добавляя ток во время зарядки или разрядки до нового уровня напряжения). Проходящий через конденсатор ток прямопропорционален скорости изменения напряжения. Это противостояние изменению напряжения является еще одной формой реактивного сопротивления, которое по своему действию противоположно реактивному сопротивлению катушки индуктивности.
Математическая взаимосвязь между проходящим через конденсатор током и скоростью изменения напряжения на нем выглядит следующим образом:
Отношение du/dt представляет собой скорость изменения мгновенного напряжения (u) с течением времени, и измеряется в вольтах в секунду. Емкость (С) измеряется в Фарадах, а мгновенный ток (i) – в амперах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую емкостную схему:
Емкость (С) измеряется в Фарадах, а мгновенный ток (i) – в амперах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую емкостную схему:
Простая емкостная цепь: напряжение конденсатора отстает от тока на 90o.
Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:
Как вы помните, проходящий через конденсатор ток является реакцией на изменение напряжения на этом конденсаторе. Отсюда можно сделать вывод, что мгновенный ток равен нулю всякий раз, когда мгновенное значение напряжения находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны напряжения), и мгновенный ток равен своему пиковому значению всякий раз, когда мгновенное напряжение находится в точках максимального изменения (точки самого крутого наклона волны напряжения, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на -90o не совпадает по фазе с волной тока. На графике видно, как волна тока дает “фору” волне напряжения: ток “ведет” напряжение, а напряжение “запаздывает” за током.
На графике видно, как волна тока дает “фору” волне напряжения: ток “ведет” напряжение, а напряжение “запаздывает” за током.
Как вы уже догадались, такая же необычная волна мощности, которую мы видели в простой индуктивной цепи, присутствует и в простой емкостной цепи:
Как и в случае с простой индуктивной цепью, фазовый сдвиг 90 градусов между напряжением и током приводит к равномерному чередованию волны мощности между положительными и отрицательными значениями. Это означает, что конденсатор не рассеивает мощность (когда реагирует на изменения напряжения), а просто поглощает и высвобождает ее (поочередно).
Сопротивление конденсатора, изменяющее напряжение, интерпретируется как сопротивление переменному напряжению в целом, у которого по определению постоянно меняется мгновенная величина и направление. Для любой заданной величины переменного напряжения на заданной частоте, конденсатор заданного размера будет “проводить” определенную величину переменного тока. Так же, как ток через резистор является функцией напряжения на этом резисторе и его сопротивления, переменный ток через конденсатор является функцией переменного напряжения на этом конденсаторе и его реактивного сопротивления. Как и в случае с катушками индуктивности, реактивное сопротивление конденсатора измеряется в Омах, и обозначается буквой Х (или ХС, если быть более точным).
Так же, как ток через резистор является функцией напряжения на этом резисторе и его сопротивления, переменный ток через конденсатор является функцией переменного напряжения на этом конденсаторе и его реактивного сопротивления. Как и в случае с катушками индуктивности, реактивное сопротивление конденсатора измеряется в Омах, и обозначается буквой Х (или ХС, если быть более точным).
Поскольку проходящий через конденсатор ток пропорционален скорости изменения напряжения, он будет больше для быстро меняющихся напряжений, и меньше – для напряжений с более медленным изменением. Это означает, что реактивное сопротивление любого конденсатора (в Омах) обратно пропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления конденсатора выглядит следующим образом:
Если на конденсатор емкостью 100 мкФ воздействовать частотами 60, 120 и 2500 Гц, то его реактивное сопротивление примет следующие значения:
| Частота (Гц) | Реактивное сопротивление (Ом) |
|---|---|
| 60 | 26.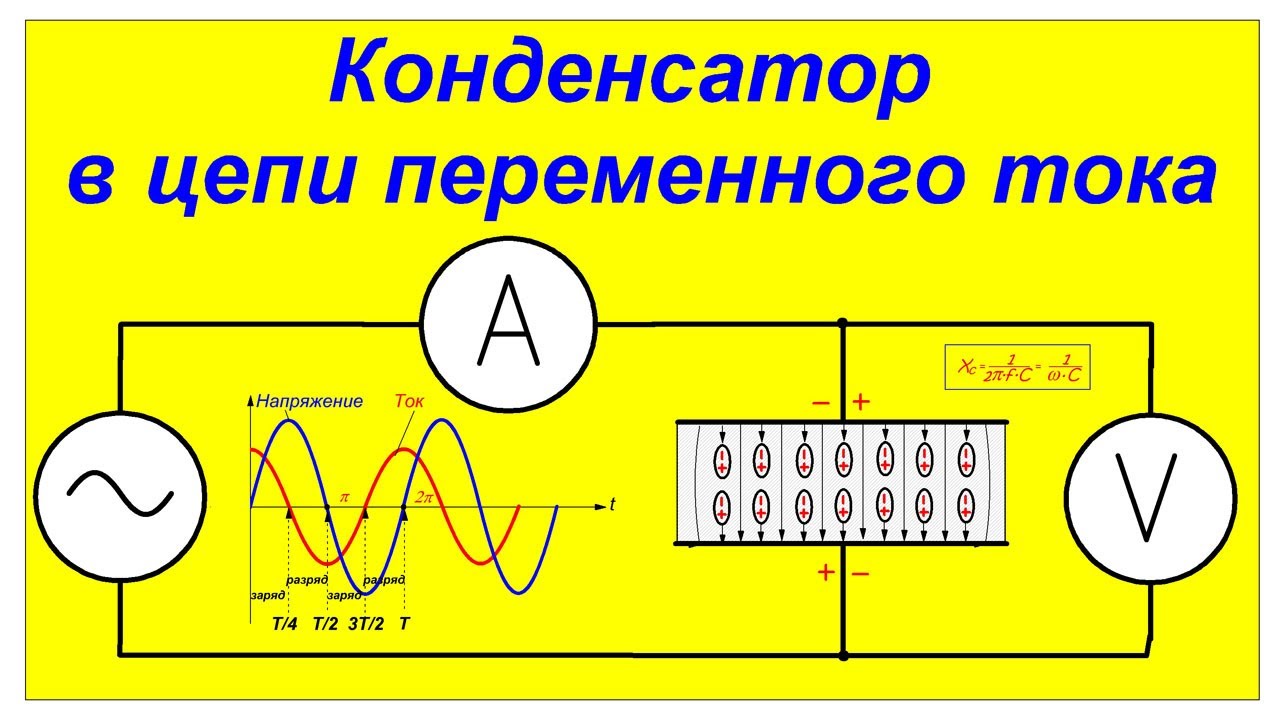 5258 5258 |
| 120 | 13.2629 |
| 2500 | 0.6366 |
Обратите внимание на то, что отношение емкостного реактивного сопротивления к частотам точно противоположно отношению индуктивного реактивного сопротивления к тем же частотам. Емкостное реактивное сопротивление уменьшается с увеличением частоты переменного тока, а индуктивное реактивное сопротивление наоборот, увеличивается с ростом частоты переменного тока. Если катушки индуктивности выступают против быстрого изменения тока, производя большее напряжение, то конденсаторы выступают против быстрого изменения напряжения, производя больший ток.
По аналогии с катушками индуктивности, выражение 2πf в уравнении реактивного сопротивления конденсатора может быть заменено на строчную греческую букву ω (Омега), которую иначе называют угловой (циклической) частотой переменного тока. Таким образом, уравнение XC = 1/(2πfC) может быть записано как XC = 1/(ωC), где ω выражается в радианах в секунду.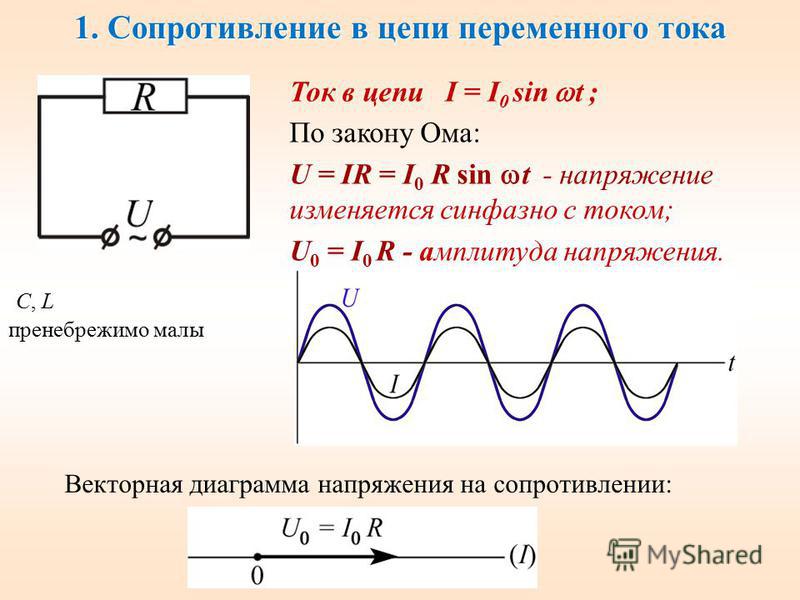
Переменный ток в простой емкостной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление конденсатора (в Омах). Это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:
Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, ток имеет фазовый сдвиг +90o по отношению к напряжению. Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что реактивное сопротивление конденсатора переменному току обладает следующим фазовым углом:
Математически можно сказать, что фазовый угол сопротивления конденсатора переменному току составляет -90o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом.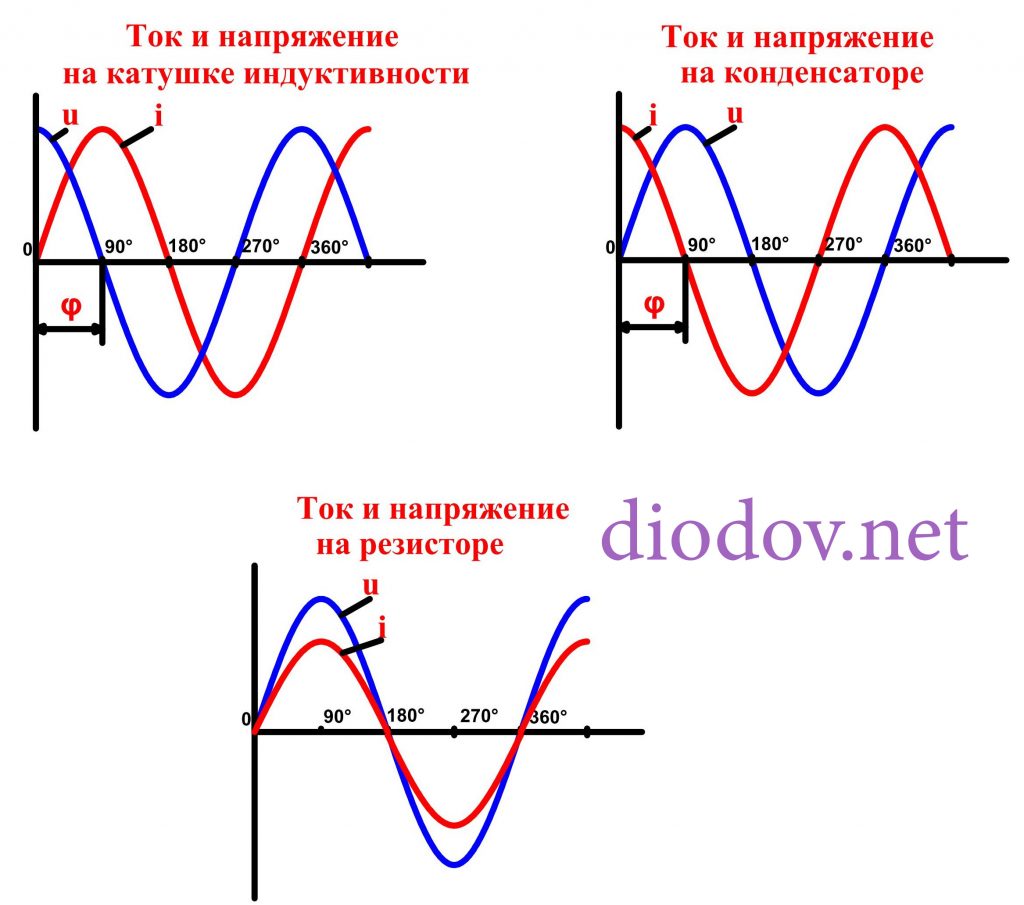 Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).
Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).
| Реактивное сопротивление и импеданс – емкостный
Конденсаторы Vs. Резисторы
Конденсаторы ведут себя не так, как резисторы. В то время как резисторы пропускают через себя поток электронов, прямо пропорциональный падению напряжения, конденсаторы противодействуют изменениям напряжения, потребляя или подавая ток при зарядке или разрядке до нового уровня напряжения.
Поток электронов «через» конденсатор прямо пропорционален скорости изменения напряжения на конденсаторе.Это противодействие изменению напряжения представляет собой другую форму реактивного сопротивления , но оно прямо противоположно тому, которое демонстрируют индукторы.
Характеристики цепи конденсатора
Выражаясь математически, соотношение между током, протекающим через конденсатор, и скоростью изменения напряжения на конденсаторе как таковое:
Выражение de / dt – это выражение из расчетов, означающее скорость изменения мгновенного напряжения (e) во времени в вольтах в секунду.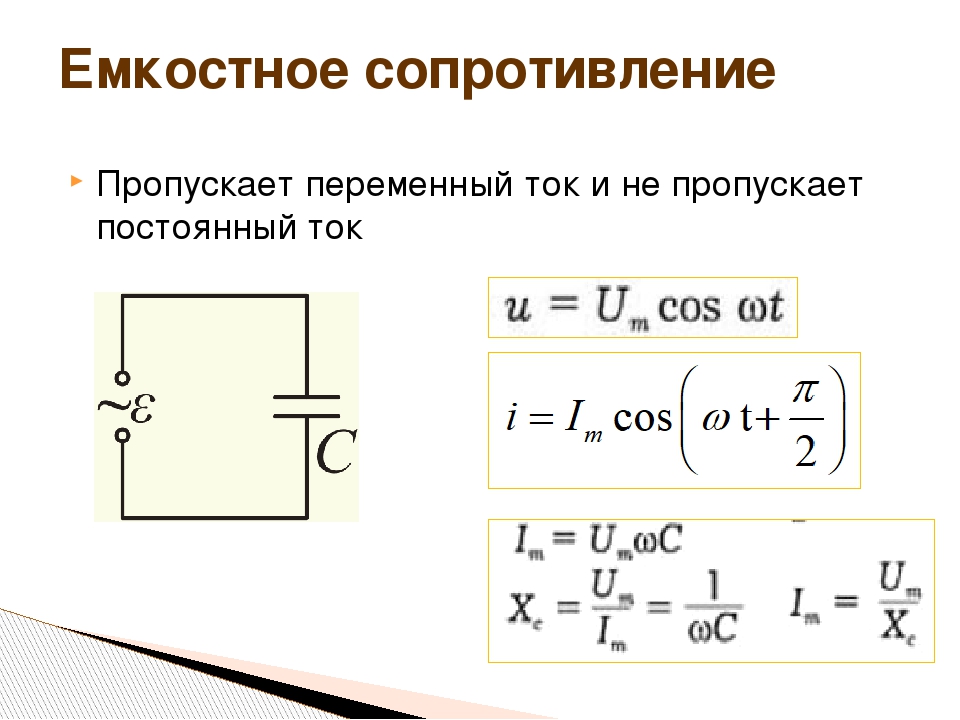 Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.
Емкость (C) выражается в фарадах, а мгновенный ток (i), конечно, выражается в амперах.
Иногда можно встретить скорость мгновенного изменения напряжения с течением времени, выраженную как dv / dt вместо de / dt: вместо напряжения используется строчная буква «v» или «e», но это означает то же самое. Чтобы показать, что происходит с переменным током, давайте проанализируем простую схему конденсатора:
Чистая емкостная цепь: напряжение конденсатора отстает от тока конденсатора на 90 °
Если бы мы изобразили ток и напряжение для этой очень простой схемы, это выглядело бы примерно так:
Формы сигналов чисто емкостной цепи.
Помните, что ток через конденсатор – это реакция на изменение напряжения на нем.
Следовательно, мгновенный ток равен нулю всякий раз, когда мгновенное напряжение достигает пика (нулевое изменение или наклон уровня синусоидальной волны напряжения), а мгновенный ток находится на пике везде, где мгновенное напряжение имеет максимальное изменение (точки крутизны на волне напряжения, где она пересекает нулевую линию).
Это приводит к появлению волны напряжения, сдвинутой по фазе на -90 ° с волной тока.Глядя на график, кажется, что волна тока имеет «фору» по сравнению с волной напряжения; ток «опережает» напряжение, а напряжение «отстает» от тока.
Напряжение отстает от тока на 90 ° в чисто емкостной цепи.
Как вы могли догадаться, та же необычная волна мощности, которую мы видели в простой цепи индуктивности, присутствует и в простой цепи конденсатора:
В чисто емкостной цепи мгновенная мощность может быть положительной или отрицательной.
Как и в случае с простой схемой индуктивности, сдвиг фазы на 90 градусов между напряжением и током приводит к появлению волны мощности, которая в равной степени чередуется между положительной и отрицательной полярностью. Это означает, что конденсатор не рассеивает мощность, поскольку он реагирует на изменения напряжения; он просто поочередно поглощает и высвобождает энергию.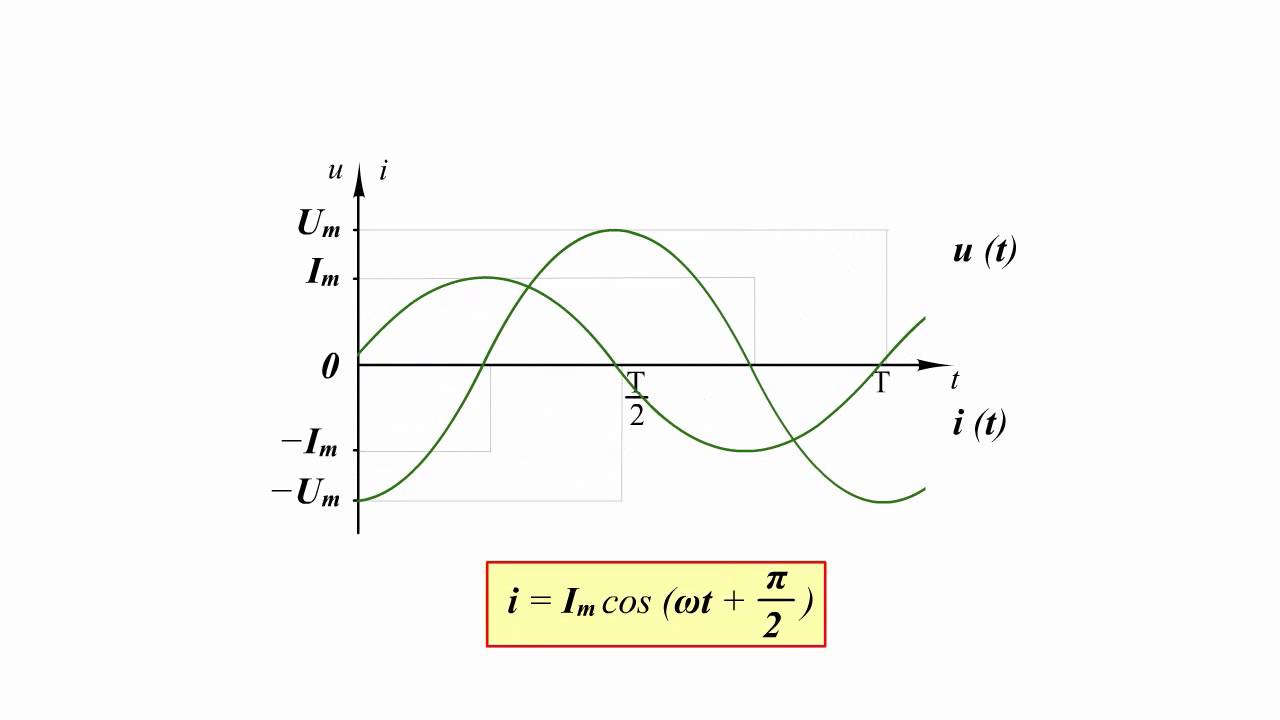
Реактивное сопротивление конденсатора
Противодействие конденсатора изменению напряжения означает сопротивление переменному напряжению в целом, которое по определению всегда изменяется по мгновенной величине и направлению.
Для любой заданной величины переменного напряжения и заданной частоты конденсатор заданного размера будет «проводить» определенную величину переменного тока.
Точно так же, как ток через резистор является функцией напряжения на резисторе и сопротивления, предлагаемого резистором, переменный ток через конденсатор является функцией переменного напряжения на нем, и реактивного сопротивления , обеспечиваемого конденсатором. .
Как и в случае катушек индуктивности, реактивное сопротивление конденсатора выражается в омах и обозначается буквой X (или, точнее, XC).
Поскольку конденсаторы «проводят» ток пропорционально скорости изменения напряжения, они будут пропускать больше тока при более быстром изменении напряжения (поскольку они заряжаются и разряжаются до тех же пиков напряжения за меньшее время) и меньший ток при более медленном изменении напряжения. .
.
Это означает, что реактивное сопротивление в Ом для любого конденсатора равно , обратно пропорционально частоте переменного тока.
Реактивное сопротивление конденсатора 100 мкФ:
| Частота (Герцы) | Реактивное сопротивление (Ом) |
| 60 | 26.5258 |
| 120 | 13,2629 |
| 2500 | 0,6366 |
Обратите внимание, что отношение емкостного реактивного сопротивления к частоте прямо противоположно отношению индуктивного реактивного сопротивления.
Емкостное реактивное сопротивление (в омах) уменьшается с увеличением частоты переменного тока. И наоборот, индуктивное реактивное сопротивление (в омах) увеличивается с увеличением частоты переменного тока. Индукторы противодействуют более быстрому изменению токов, производя большие падения напряжения; Конденсаторы противодействуют более быстрому изменению падений напряжения за счет увеличения тока.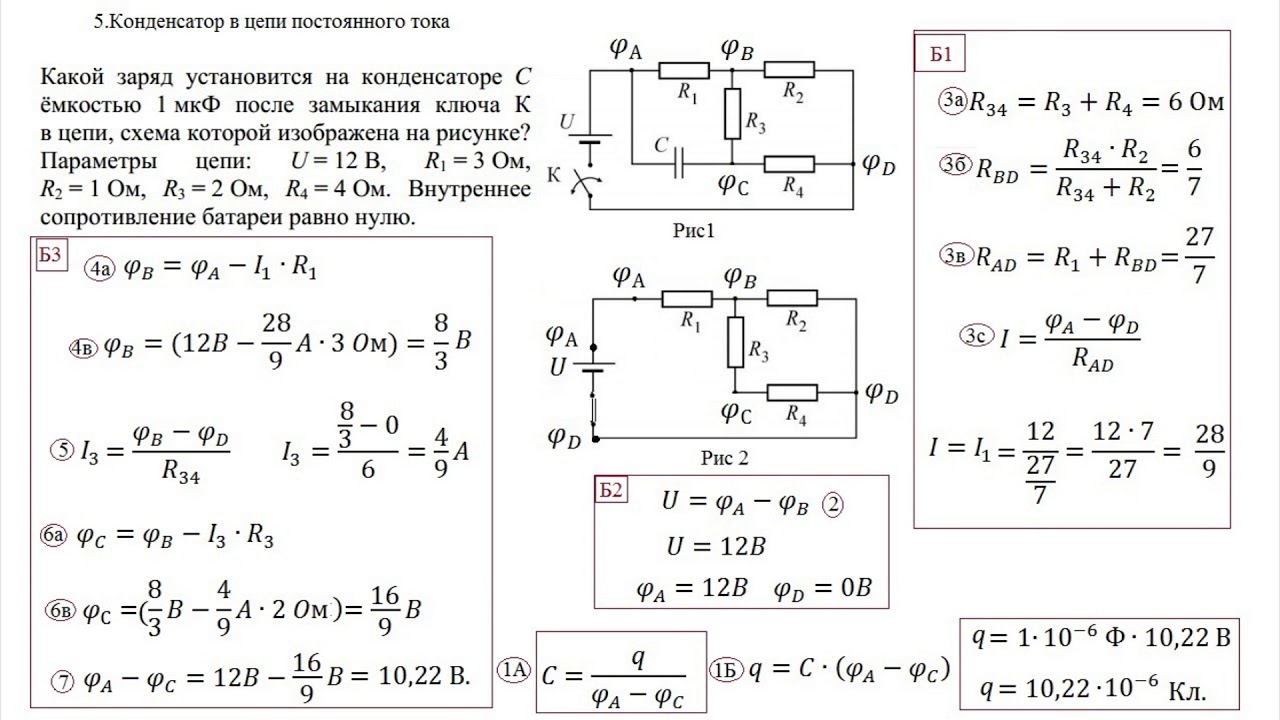
Как и в случае катушек индуктивности, член 2πf в уравнении реактивного сопротивления может быть заменен строчной греческой буквой Омега (ω), которая обозначается как угловая скорость цепи переменного тока. Таким образом, уравнение XC = 1 / (2πfC) также может быть записано как XC = 1 / (ωC), где ω приводится в единицах радиан в секунду .
Переменный ток в простой емкостной цепи равен напряжению (в вольтах), деленному на емкостное реактивное сопротивление (в омах), точно так же, как переменный или постоянный ток в простой резистивной цепи равен напряжению (в вольтах), деленному на сопротивление (в Ом).Следующая схема иллюстрирует это математическое соотношение на примере:
Емкостное реактивное сопротивление.
Однако мы должны помнить, что здесь напряжение и ток не совпадают по фазе. Как было показано ранее, ток имеет фазовый сдвиг + 90 ° по отношению к напряжению. Если мы математически представим эти фазовые углы напряжения и тока, мы сможем вычислить фазовый угол реактивного сопротивления конденсатора току.
Напряжение в конденсаторе отстает от тока на 90 °.
Математически мы говорим, что фазовый угол сопротивления конденсатора току равен -90 °, что означает, что сопротивление конденсатора току является отрицательной мнимой величиной. (См. Рисунок выше). Этот фазовый угол реактивного противодействия току становится критически важным при анализе цепей, особенно для сложных цепей переменного тока, где реактивное сопротивление и сопротивление взаимодействуют.
Будет полезно представить любое сопротивление компонента току в виде комплексных чисел, а не только скалярных величин сопротивления и реактивного сопротивления.
ОБЗОР:
- Емкостное реактивное сопротивление – это противодействие, которое конденсатор предлагает переменному току из-за его сдвинутого по фазе накопления и выделения энергии в его электрическом поле. Реактивное сопротивление обозначается заглавной буквой «X» и измеряется в омах, как и сопротивление (R).
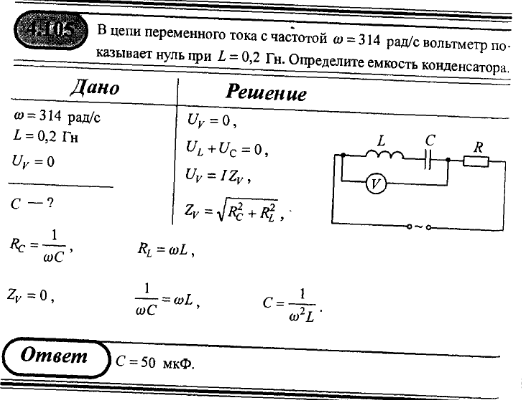
- Емкостное реактивное сопротивление можно рассчитать по следующей формуле: XC = 1 / (2πfC)
- Емкостное реактивное сопротивление уменьшается с увеличением частоты . Другими словами, чем выше частота, тем меньше он сопротивляется (тем больше «проводит») переменному току.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Емкостные цепи переменного тока
Когда две проводящие пластины разделены диэлектрической или изолирующей средой, образуется конденсатор. Основное свойство конденсатора – накапливать электрический заряд.Если к конденсатору подключен источник напряжения, две пластины приобретают противоположный электрический заряд, что означает, что одна пластина накапливает положительный заряд, а другая – отрицательный.
Это вызывает перетекание электронов от одной пластины к другой, пока напряжение на конденсаторе не станет равным приложенному напряжению. Скорость изменения напряжения на конденсаторе определяет протекание тока через конденсатор.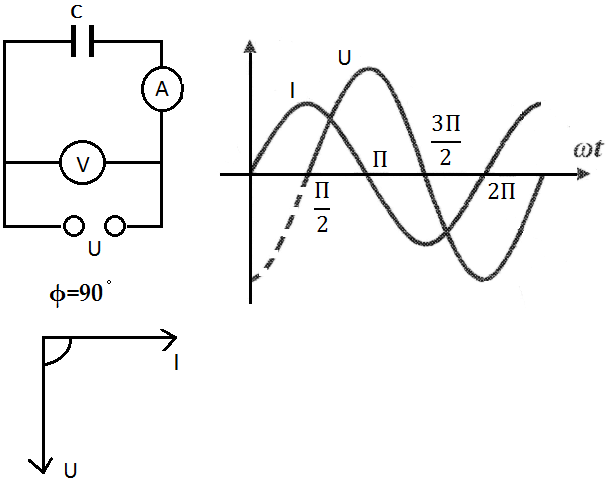
наряду с резисторами и индукторами помогают создавать очень сложные цепи переменного тока во многих электронных устройствах.Обсудим вкратце поведение цепи переменного тока с емкостью.
Переменный ток, приложенный через чистый конденсатор
Когда чистый конденсатор подключен к источнику переменного тока, изменяющееся значение приложенного напряжения заставляет конденсатор попеременно заряжаться и разряжаться. Заряд, протекающий через конденсатор, пропорционален емкости (размеру конденсатора) и приложенному напряжению на конденсаторе. Его можно выразить как
Q = C V
В = Q / C
Где
В = приложенное напряжение в вольтах
Q = заряд конденсатора в кулонах
C = емкость конденсатора в фарадах
Рассмотрим приведенную выше схему, в которой чистый конденсатор подключен к источнику переменного напряжения v = Vm sin ωt.Источник напряжения вызывает прохождение тока через цепь. Ток пропорционален скорости изменения заряда конденсатора во времени.
Ток в цепи, i = d (q) / dt
Подставляя q = C v = C Vm sin ωt в уравнение выше, мы получаем
i = d / dt (C V м sin ωt) = ωC V м cos ωt
или i = ω C V м sin (ωt + π / 2)
Когда член sin (ωt + π / 2) равен единице, значение тока будет максимальным, т.е.е.,
i м = ωC Vm
Подставляя это текущее значение, получаем
i = i м sin (ωt + π / 2)
Из приведенных выше уравнений ясно, что в чисто емкостной цепи ток опережает напряжение на 900. Это означает, что когда чистый конденсатор подключен к источнику переменного тока, максимальный ток протекает через конденсатор, когда скорость изменения напряжение максимальное (в положении нулевого напряжения). И этот ток уменьшается, когда скорость изменения напряжения минимальна.
Другим способом из-за разряженного состояния конденсатора ток в цепи достигает максимума, когда напряжение на конденсаторе начинает расти.
Когда конденсатор полностью заряжается до максимального значения напряжения, зарядный ток падает до нуля. Когда напряжение начинает падать, конденсатор начинает заряжаться. Таким образом, соотношение между напряжением и током описывается как сдвинутое по фазе на 90 градусов.
Следовательно, ток конденсатора опережает приложенное напряжение на угол 90 градусов.Векторная диаграмма емкостной цепи переменного тока приведена ниже.
Емкостное реактивное сопротивление
Из приведенного выше вывода уравнение максимального тока дается как
i м = ωC V м
V м / i м = (1 / wC)
Это отношение напряжения к току является противодействием емкостной цепи протеканию тока. Эта величина (1 / w C) называется емкостным реактивным сопротивлением и обозначается как XC и измеряется в Ом.
Емкостное реактивное сопротивление цепи переменного тока можно представить как
.XC = (1 / ω C) = (1 / 2πf C) (так как ω = 2Πf)
Где
XC – емкостное сопротивление в омах
f – частота питающего напряжения
C – емкость конденсатора в фарадах
Из приведенного выше уравнения емкостное сопротивление конденсатора в цепи переменного тока является функцией частоты и емкости. Емкостное реактивное сопротивление уменьшается с увеличением частоты, что приводит к протеканию большего тока через цепь.
Емкостное реактивное сопротивление уменьшается с увеличением частоты, что приводит к протеканию большего тока через цепь.
Точно так же при уменьшении частоты увеличивается реактивное сопротивление, что приводит к уменьшению тока. Соотношение между емкостным реактивным сопротивлением и частотой показано на рисунке ниже.
Мощность и коэффициент мощности в емкостной цепи переменного тока
Мощность в цепи переменного тока является произведением мгновенного напряжения и тока. Это может быть указано как
.P = v × i
P = V м sin ωt × I м sin (ωt + 90)
Принимая интегрирование по циклу, получаем,
P = V м sin ωt × I м sin (ωt + 90)
P = 1 / 2π (∫ 0 2π V м sin ωt × I м sin (ωt + 90) dwt)
= (V м I м / 2π) (∫ 0 2π sin ωt cos ωt dwt)
= (V м I м / 4π) (∫ 0 2π (sin 2 ωt) / 2 dwt)
= (V м I м / 8π) (- cos 4π + cos 0)
= (V м I м / 8π) (- 1 + 1)
P = 0
Таким образом, аналогично индуктивной схеме, мощность, потребляемая в чистой емкости, равна нулю, поскольку мощность, потребляемая и возвращаемая в течение каждого полупериода. На рисунке ниже показаны формы сигналов напряжения, тока и мощности емкостной цепи переменного тока.
На рисунке ниже показаны формы сигналов напряжения, тока и мощности емкостной цепи переменного тока.
Во время положительного полупериода сигнала мощности энергия накапливается в конденсаторе во время его зарядки. А во время отрицательного полупериода накопленная энергия возвращается обратно источнику во время его разряда. Следует отметить, что площади обоих циклов равны, и, следовательно, средняя мощность, потребляемая цепью, равна нулю.
В этой чисто емкостной цепи разность фаз между формами сигналов напряжения и тока составляет 900 (опережающая).Тогда коэффициент мощности станет
.Коэффициент мощности, cos θ = cos 90 0 = 0
Следовательно, коэффициент мощности в чисто емкостной цепи является нулевым опережением, то есть чисто опережающим коэффициентом мощности.
Цепь серии RC
Этот тип схемы аналогичен последовательной цепи R L , но вместо индуктора используется конденсатор. На рисунке ниже к источнику переменного тока подключено последовательное соединение сопротивления и конденсатора.
Падение напряжения на сопротивлении синфазно с током, в то время как ток опережает падение напряжения на конденсаторе на 900, как показано на рисунке ниже.
Падение напряжения на резисторе, VR = IR
Напряжение на чистом конденсаторе, VC = I × X C (где X C = 1 / 2πfC)
Таким образом, V = √ (V R 2 + V C 2 ) = √ (IR) 2 + (I X C ) 2 )
= I √ (R 2 + X C 2) = IZ
Где Z – импеданс в последовательной цепи RC, равный √ (R 2 + X C 2 ).
Треугольник с сопротивлением
Из векторной диаграммы серии RC,
тангенс угла ϕ = V C / V C = X C / R
cos ϕ = V C / V = R / Z
sin ϕ = V C / V = X C / Z
Из треугольника импеданса R, XC и полное сопротивление в последовательной цепи RC можно выразить как
R = Z cos ϕ
X C = Z sin ϕ
Z = √ (R 2 + X C 2 )
А ϕ = загар -1 (-X C / R)
Цепь серии RLC
В этой схеме резистор, катушка индуктивности и конденсатор последовательно соединены через источник переменного тока. В зависимости от результирующего значения от комбинаций емкостного и индуктивного реактивных сопротивлений, схема будет работать либо по схеме RL, либо по RC. Путем вычитания большего реактивного сопротивления из меньшего реактивного сопротивления получается полное реактивное сопротивление.
В зависимости от результирующего значения от комбинаций емкостного и индуктивного реактивных сопротивлений, схема будет работать либо по схеме RL, либо по RC. Путем вычитания большего реактивного сопротивления из меньшего реактивного сопротивления получается полное реактивное сопротивление.
Напряжение на резисторе, В R = I R
Напряжение на катушке индуктивности, В L = I X L
Напряжение на чистом конденсаторе, В С = I X С
Векторная диаграмма этой цепи зависит от значений X L и X C , рассмотрим разные значения этих реактивных сопротивлений.
(1) X L > X C
Если X L > X C , то V L (= I X L ) больше, чем VC (= I X C ). Следовательно, схема является индуктивной по своей природе, поскольку результирующая V L и V C направлена в сторону VL.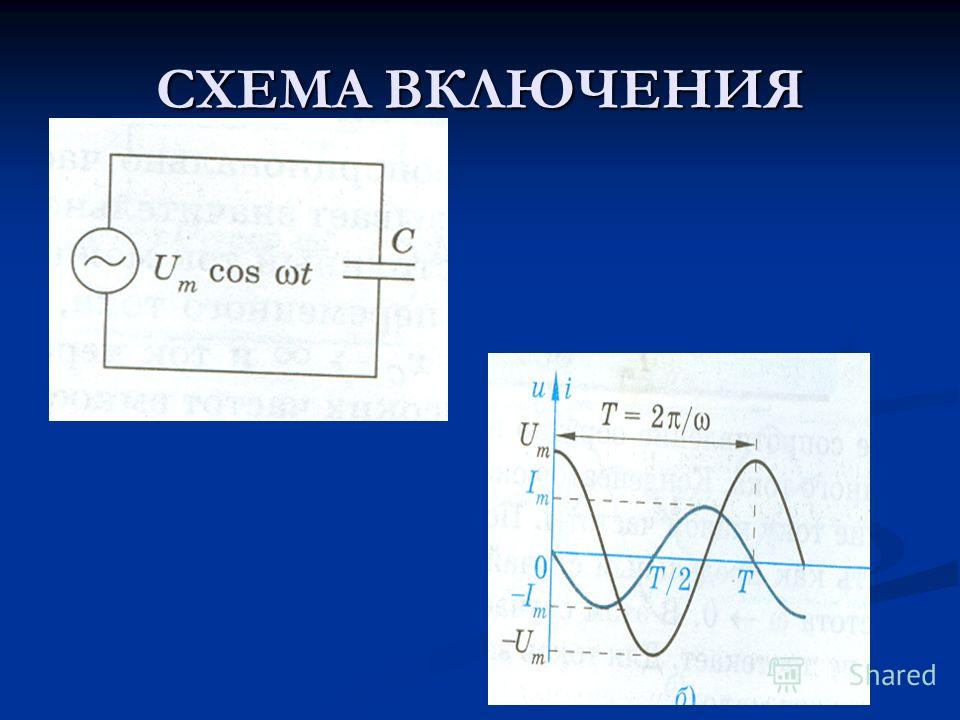 Таким образом, схема ведет себя как последовательная цепь RL.
Таким образом, схема ведет себя как последовательная цепь RL.
Таким образом, напряжение питания V = √ ((V R 2 + (V L – V C ) 2 ) = √ ((I R ) 2 + (IX ) L – IX C ) 2 )
V = I √ ((R) 2 + (X L – X C ) 2 )
В = ИЗ
Где Z = √ ((R) 2 + (X L – X C ) 2 )
(2) X L
Если X L
Таким образом, напряжение питания V = √ ((V 2 R + (V C – V L ) 2 ) = √ ((IR) 2 + (IX C – IX L ) 2 )
V = I √ ((R) 2 + (X C – X L ) 2 )
В = ИЗ
Где Z = √ ((R) 2 + (X L – X C ) 2 )
(3) X L = X C
Если X L = X C , то V L = V C . В таком случае результирующее напряжение равно нулю. Следовательно, V R = V. Следовательно, схема ведет себя как резистивная схема.
В таком случае результирующее напряжение равно нулю. Следовательно, V R = V. Следовательно, схема ведет себя как резистивная схема.
Сформируйте векторную диаграмму,
В = В R
В = I R
В = I Z
Где Z = R.
Пример
Однофазное синусоидальное напряжение переменного тока v = 283 sin 314t подключено к чистому конденсатору 100 мкФ. Затем найдите ток, протекающий через конденсатор.
Преобразуя напряжение из временной области в полярную форму, получаем
v = 283 sin 314t = 283∠0 0
Емкостное реактивное сопротивление можно определить как
.X C = (1 / j w C) = (1/314 × 100µ) = 31.8 ∠– 90 0
Согласно закону Ома ток, протекающий по цепи, можно получить как
Ic = (V / j X Ic = (283∠0 0 / 31,8 ∠– 90 0 ) Ic = 8,8 ∠ + 90 0 ) Проблемы в цепях переменного тока определяются автоматически. Наиболее распространенные цепи переменного тока приводятся в действие синусоидальной переменной ЭДС, Δ v = V sinω t , которую удобно представить в виде вращающегося вектора длиной V , вращающегося с угловой скоростью ω.В таких цепях переменного тока компоненты R, L и C имеют мгновенные значения разности потенциалов Δ v R , Δ v L , и Δ v C , векторы которых V R , V L , и V C имеют разные фазовые отношения (фазовые углы) с соответствующими токами, i R , i L , и i C . В частности, Δ v R и i R синфазны, Δ v L выводов i L на 90 °, и Δ v C отстает i C на 90 °. В цепи переменного тока реактивное сопротивление емкости C или индуктивности L является мерой способности этого компонента препятствовать прохождению заряда в этой цепи. Реактивное сопротивление зависит от частоты v переменного тока. Реактивное сопротивление X C емкости C равно 1 / ω C = 1/2 (π vC ). Реактивное сопротивление X L индуктивности L равно ω L = 2π vL .Чистое реактивное сопротивление X цепи переменного тока определяется как X = X L – X C . Мы начинаем анализ последовательной цепи переменного тока, комбинируя аналогичные компоненты, когда это необходимо. Если эквивалентные компоненты находятся в цепи серии RLC , то в каждый момент в каждом компоненте будет одинаковый ток. Поэтому удобно соотнести векторы компонентов схемы с вектором тока I . Импеданс Z = В / I цепи переменного тока играет ту же роль, что и сопротивление цепи в цепи постоянного тока. Для данной последовательной цепи переменного тока полное сопротивление Z = R2 + (XL-XC) 2 зависит от сопротивления и реактивного сопротивления цепи. Поскольку X L и X C зависят от частоты ЭДС, импеданс зависит от частоты. Частота, при которой импеданс минимален, называется резонансной частотой v o контура.Резонанс возникает, когда частота такова, что чистое реактивное сопротивление, X L – X C , равно нулю, то есть когда X L = X C . Резонансная частота v o может быть выражена через индуктивность L и емкость C цепи как v o = 1 / (2π√ LC ). Измерения мощности в цепях переменного тока удобно описывать в терминах среднеквадратичных (среднеквадратичных) значений ЭДС и тока. Используя В, среднеквадратичное значение = В, / √2 и I среднеквадратичное значение = I / √2, мы можем выразить среднюю мощность P среднеквадратического значения , подаваемую в цепь переменного тока посредством P av = В среднеквадратичное значение I среднеквадратическое значение cosϕ, где cosϕ называется коэффициентом мощности цепи. И снова ϕ – это фазовый угол между вектором ЭДС V и вектором тока I .Величина ϕ связана с общим сопротивлением R и импедансом Z цепи переменного тока соотношением cosϕ = R / Z . Электромагнитные (ЭМ) волны состоят из взаимно перпендикулярных электрических и магнитных полей, которые распространяются в свободном пространстве со скоростью света ( c = 3,0 × 10 8 м / с). Длина волны λ электромагнитной волны – это расстояние между соседними максимумами электрического поля (или магнитного поля), измеренное вдоль направления распространения волны.Длина волны λ и частота v электромагнитной волны в свободном пространстве связаны со скоростью распространения c соотношением c = v λ. Таким образом, указание длины волны ЭМ, по сути, определяет ее частоту; аналогично, указав его частоту, вы получите длину волны. Диапазон известных длин (или частот) электромагнитных волн называется электромагнитным спектром. Радио- и телевизионные волны, микроволны, инфракрасное излучение, видимый свет, ультрафиолетовое излучение, рентгеновские лучи и гамма-лучи составляют электромагнитный спектр.Хотя эти излучения возникают по-разному и очень по-разному взаимодействуют с веществом, существенное различие между этими электромагнитными излучениями заключается в их длине волны (или частоте). Где я не прав? Мне жаль сообщать, что вы ошибаетесь до конца. Вы упускаете из виду весь анализ (формулировка книги тоже не помогает). «P.D. на пластинах конденсатора = приложенная ЭДС» – это просто причудливый (и сбивающий с толку любого новичка) способ сказать: «Давайте подадим напряжение переменного тока на конденсатор и посмотрим, что произойдет тогда с другими величинами, такими как ток через него». смоделировать эту схему – Схема создана с помощью CircuitLab Таким образом, легко ответить на ваш вопрос: […], как может быть верно, что данное утверждение (1) истинно в любой момент? Что ж, это правда, потому что мы заставляем его быть таким же, как , чтобы мы могли видеть, что происходит тогда с током через конденсатор. Следующий шаг – выяснить, как V и я связаны.Можно было ожидать, что если мы заставим потенциал между пластинами конденсатора изменяться со временем, то ток через конденсатор будет каким-то образом аналогичным образом. Мы напоминаем, как и книга, что: $
Q = CV и $
I = \ dfrac {dQ} {dt} Итак, с помощью небольшой математики, наконец, мы приходим к: $
I = {\ omega} {C} {\ xi_0} \ sin ({\ omega} t + \ frac {\ pi} 2) Что в математическом смысле означает, что ток также является синусоидальным и что существует \ $ \ dfrac {\ pi} 2 \ $ разность фаз между V и I. Однако, что означает в физическом смысле ? Что ж, как-то твоя интуиция все-таки неплохая: Ток равен 0 при π / 2 и нечетных кратных π / 2, где приложенная ЭДС соответствует своему пиковому значению. Таким образом, конденсатор полностью заряжается в этих случаях Вот и все! Когда конденсатор полностью заряжен, ток к нему не течет. Когда он полностью разряжен, к нему течет максимальный ток для зарядки.И конденсатор колеблется в этих состояниях все время, пока мы подаем на него переменное напряжение. РЕДАКТИРОВАТЬ: Прочитав ваш комментарий к моему ответу, я понял, в чем ваша проблема: ваш математический подход ошибочен. Вы смотрите на мгновенное значение \ $ V \ $ и думаете, что можно взять интервал времени \ $ {\ Delta} t \ $ достаточно малым, чтобы \ $ V \ $ можно было считать постоянным, то есть \ $ {\ Delta} V {\ приблизительно} 0 \ $. Затем вы ассимилируете эту ситуацию с постоянным током (что также неверно, потому что в постоянном токе вы заряжаете конденсатор через резистор, который здесь отсутствует) и заключаете, что если \ $ {\ Delta} V = 0 \ $, то \ $ I = 0 \ $ так что ток не течет. Ну, это математически неверно по ряду причин: Если вы имеете дело с интервалами, примените их к ВСЕМ задействованным величинам . Ваш недостаток заключается в том, что вы рассматриваете \ $ I = 0 \ $ вместо того, чтобы рассматривать \ $ {\ Delta} I = 0 \ $ (что тоже неверно, продолжайте читать, чтобы понять, почему). Если посмотреть, что происходит в произвольный момент времени \ $ t_1 \ $, ваш \ $ {\ Delta} t \ $ является приращением к \ $ t_1 \ $. То же самое касается \ $ V \ $ и \ $ I \ $: ваш \ $ {\ Delta} V \ $ будет приращением к \ $ V_1 = V (t_1) \ $ и \ $ {\ Delta} I \ $ будет приращением к \ $ I_1 = I (t_1) \ $. Думайте о \ $ V_1 \ $ и \ $ I_1 \ $ как о начальных условиях в начале интервала \ $ {\ Delta} t \ $. Ошибочно считать, что \ $ V_1 \ $ и \ $ I_1 \ $ равны нулю. Для очень маленьких интервалов \ $ {\ Delta} t \ $ у вас будут \ $ {\ Delta} V {\ приблизительно} 0 \ $ и \ $ {\ Delta} I {\ приблизительно} 0 \ $. Но это вовсе не означает, что конкатенация временных интервалов, где \ $ {\ Delta} I {\ приблизительно} 0 \ $ даст \ $ I = 0 \ $ и отсюда сделает вывод, что “ток не течет, поэтому конденсатор должен быть заряжен и \ $ V \ $ должен быть постоянным ». Так думать неправильно.Дифференциальное исчисление и исчисление бесконечно малых говорят нам, как поступать, когда \ $ {\ Delta} t {\ rightarrow} 0 \ $. И кто-то более умный, чем вы и я, уже использовал их, чтобы разработать его, чтобы мы построили его: $$
I = \ dfrac {dQ} {dt} В этом месяце мы обсудим функции конденсатора в цепи переменного тока, включая заряд и разряд, приложения и соединения в силовых цепях, а также безопасность конденсаторов. Электрический конденсатор – это электрическое устройство, которое накапливает электричество или электрическую энергию и улучшает коэффициент мощности цепи переменного тока. Он состоит из трех основных частей. Две обычно представляют собой металлические пластины, разделенные и изолированные третьей частью, известной как диэлектрик. Заряд конденсатора зависит от размера и расстояния между проводящими пластинами, а также от типа изолирующей или диэлектрической среды между пластинами. Все конденсаторы, независимо от типа, обозначаются по их зарядной емкости.Для цепей электроприборов, таких как двигатели и разрядное освещение высокой интенсивности, конденсаторы обозначаются фарадом, единицей электрической емкости, названной в честь британского ученого Майкла Фарадея. В распределительной сети конденсаторы обозначаются в киловольт-амперах реактивной мощности, или кВАр, для простоты применения. Измерители потребления измеряют потребность в коэффициенте мощности в кВАр. Если нагрузка двигателя потребителя вызывает индуктивное напряжение 700 кВАр на линии, это можно исправить, подключив к линии емкостное напряжение 700 кВАр. Зарядка и разрядка конденсатора в цепи переменного тока Например, когда вы видите в небе молнию, вы видите огромный конденсатор. Одна пластина – это облако, другая пластина – это земля, а молния – это заряд, высвобождающийся между этими двумя пластинами. Очевидно, что в таком большом конденсаторе вы можете удерживать огромное количество заряда. Применения в цепях питания Подключения в цепях питания Распределительные конденсаторы с двумя изолированными вводами обычно подключаются между фазами, но могут быть соединены фазой с землей. Вам также следует знать о конденсаторах постоянной и переключаемой емкости. Эти термины просто относятся к способу подачи напряжения на конденсатор. Если он зафиксирован, проходной изолятор, подключенный к источнику, напрямую попадает в плавкий вырез. Этот предохранитель является единственным средством включения или выключения конденсатора.В случае переключаемого конденсатора ввод, подключенный к источнику, идет к переключающему устройству, включенному последовательно между предохранителем и конденсатором. Назначение этого переключающего устройства – позволить конденсатору работать в то время, когда это больше всего необходимо. Безопасность конденсаторов При выводе конденсаторов из эксплуатации нельзя выделить следующие шаги: Об авторе: Джон Мортон, CUSP, начал свою карьеру в электротехнической промышленности в 1970 году в качестве земляка в компании Houston Lighting and Power, ныне известной как CenterPoint Energy. В 1997 году он принял должность инструктора по вопросам электротехники и связи в отделе распространения знаний Техасского университета A&M, а в 2004 году занял свою нынешнюю должность директора по безопасности и обучению в Willbros T&D Services в Техасе. В предыдущем разделе «Резисторы в цепях переменного тока» мы представили источник питания переменного тока и изучили, как резисторы ведут себя в цепях переменного тока. Ключевая идея представления вектора заключается в том, что сложный, изменяющийся во времени сигнал может быть представлен как произведение комплексного числа (которое не зависит от времени) и сложного сигнала (которое зависит от времени). Фазоры разделяют зависимости от A (амплитуда), $ \ nu $ (частота) и θ (фаза) на три независимых фактора. Это может быть особенно полезно, потому что частотный коэффициент (который включает временную зависимость синусоиды) часто является общим для всех компонентов линейной комбинации синусоид.{i \ theta} $. Так как векторы представлены величиной (или модулем) и углом, он наглядно представлен вращающейся стрелкой (или вектором) в плоскости x-y. Вектор можно рассматривать как вектор, вращающийся вокруг начала координат в комплексной плоскости. Функция косинуса – это проекция вектора на действительную ось. Его амплитуда – это модуль вектора, а его аргумент – полная фаза \ omega t + \ theta. Фазовая постоянная \ theta представляет собой угол, который вектор образует с действительной осью при t = 0. Ранее в предыдущем Atom мы изучали, как напряжение и ток меняются во времени. Если источник переменного тока подключен к резистору, то ток и напряжение будут пропорциональны друг другу. Это означает, что ток и напряжение будут «пиковыми» одновременно. Мы говорим, что ток и напряжение совпадают по фазе. Когда конденсатор подключен к переменному напряжению, максимальное напряжение пропорционально максимальному току, но максимальное напряжение не возникает одновременно с максимальным током.Ток имеет максимум (пик) за четверть цикла до пика напряжения. Инженеры говорят, что «ток опережает напряжение на 90 ». Это показано в. Пик тока (имеет максимум) за четверть волны до напряжения, когда конденсатор подключен к переменному напряжению. Для цепи с конденсатором мгновенное значение V / I непостоянно. Однако значение V max / I max полезно и называется емкостным реактивным сопротивлением (X C ) компонента.Поскольку это все еще напряжение, деленное на ток (например, сопротивление), его единицей является ом. Значение X C (C означает конденсатор) зависит от его емкости (C) и частоты (f) переменного тока. $ X_C = \ frac {1} {2 \ pi \ nu C} $. Конденсатор влияет на ток, имея возможность полностью его отключить при полной зарядке. Поскольку подается переменное напряжение, возникает среднеквадратичный ток, но он ограничивается конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичный ток I rms в цепи, содержащей только конденсатор C, определяется другой версией закона Ома как $ I_ {rms} = \ frac { V_ {rms}} {X_C} $, где V rms, – среднеквадратичное значение напряжения.Обратите внимание, что X C заменяет R в версии закона Ома для постоянного тока. Поскольку напряжение на конденсаторе отстает от тока, вектор, представляющий ток и напряжение, будет иметь вид. На схеме стрелки вращаются против часовой стрелки с частотой $ \ nu $. (Следовательно, ток ведет к напряжению.) В следующих разделах «Атомы» мы увидим, как эти векторы можно использовать для анализа цепей RC, RL, LC и RLC. Диаграмма цепи переменного тока с конденсатором Предложения или отзывы? – обзор
18.
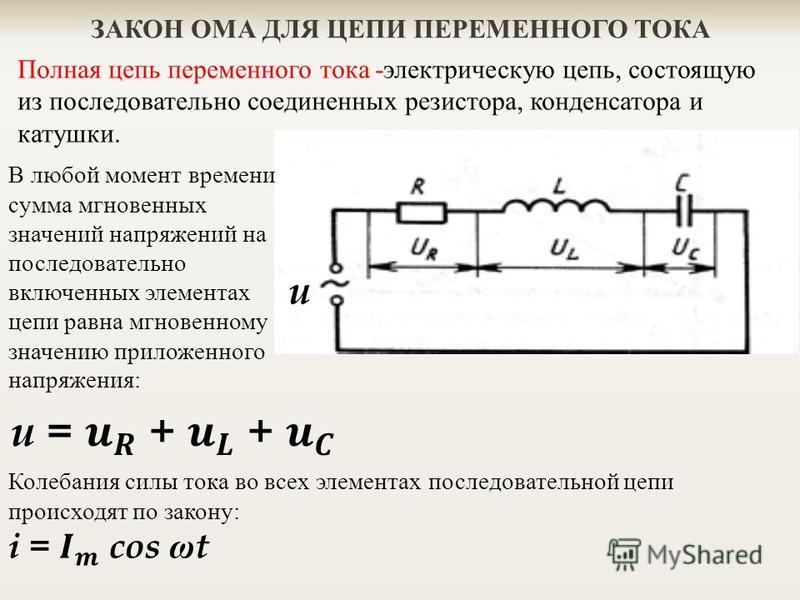 4 Краткое изложение решения проблем
4 Краткое изложение решения проблем
 В частности, вектор разности потенциалов, V R = IR , для сопротивления R находится в фазе с I , а вектор V R находится в том же направлении, что и ток вектор I .Вектор разности потенциалов В L = IX L , для индуктивности L выводов I на 90 °, а вектор разности потенциалов В C = IX C , для емкостных лагов I на 90 °. Затем мы можем построить векторную диаграмму с I , нарисованным в произвольный момент времени t , так что I образует угол ω t с осью, соответствующей направлению I при t = 0.Затем, нарисовав векторы V R , V L , и V C , в их соответствующих направлениях, мы можем построить вектор разности потенциалов V ЭДС. Величина и направление вектора V равны векторной сумме векторов, V R , V L и V C .
В частности, вектор разности потенциалов, V R = IR , для сопротивления R находится в фазе с I , а вектор V R находится в том же направлении, что и ток вектор I .Вектор разности потенциалов В L = IX L , для индуктивности L выводов I на 90 °, а вектор разности потенциалов В C = IX C , для емкостных лагов I на 90 °. Затем мы можем построить векторную диаграмму с I , нарисованным в произвольный момент времени t , так что I образует угол ω t с осью, соответствующей направлению I при t = 0.Затем, нарисовав векторы V R , V L , и V C , в их соответствующих направлениях, мы можем построить вектор разности потенциалов V ЭДС. Величина и направление вектора V равны векторной сумме векторов, V R , V L и V C .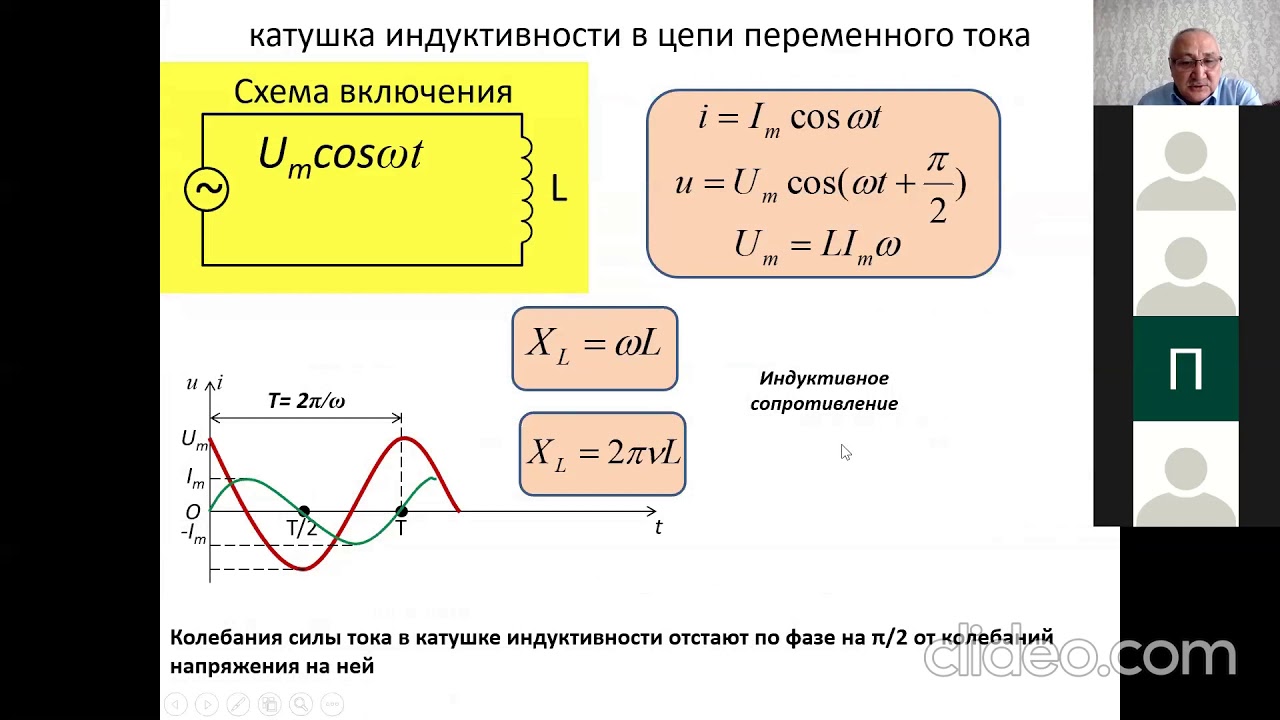 Фазовый угол ϕ между ЭДС и током в цепи – это угол между векторами V и I , а величина ϕ определяется как ϕ = tan -1 ( X / R ).
Фазовый угол ϕ между ЭДС и током в цепи – это угол между векторами V и I , а величина ϕ определяется как ϕ = tan -1 ( X / R ).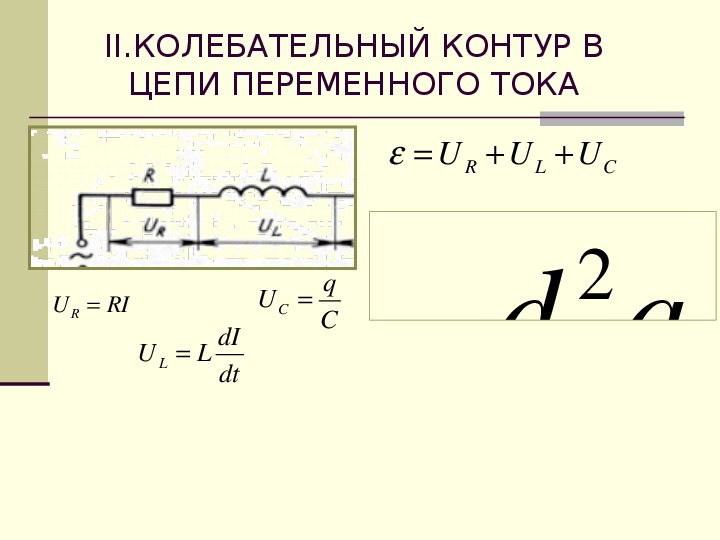 На резонансной частоте ток в цепи переменного тока достигает максимальной амплитуды.
На резонансной частоте ток в цепи переменного тока достигает максимальной амплитуды.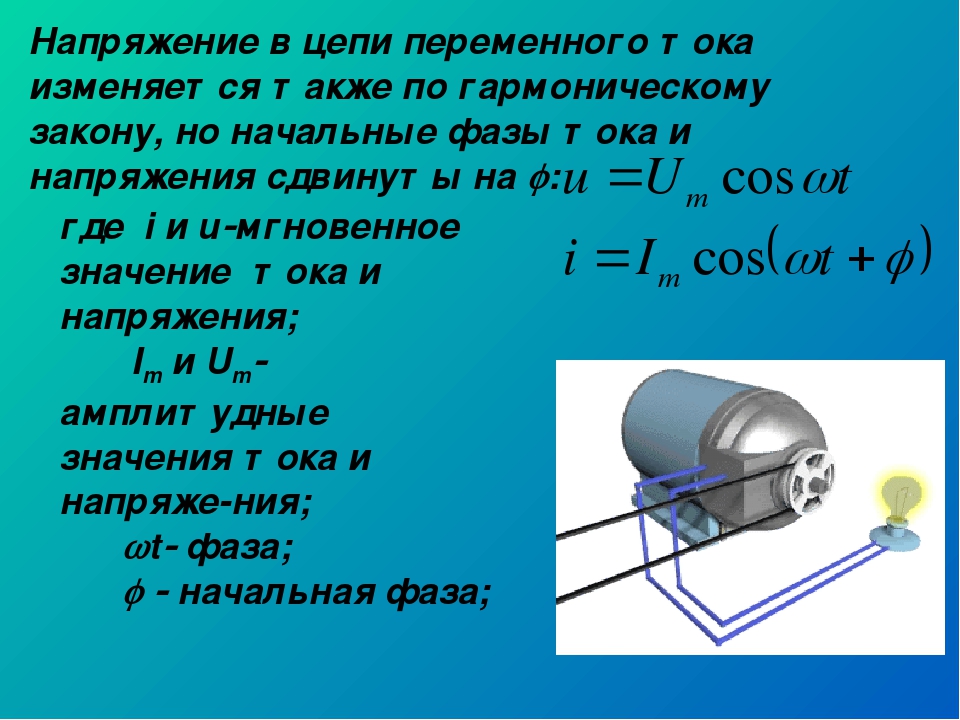 Как электрическое поле E , так и магнитное поле B электромагнитной волны перпендикулярны направлению распространения волны.Направление распространения в каждой точке волны соответствует направлению, заданному как E × B . Вектор Пойнтинга, S = (1 / μ o ) E × B , дает величину и направление энергии, переносимой электромагнитной волной через единицу площади за единицу времени. Таким образом, величина S представляет мощность, которую электромагнитная волна передает через единицу площади.
Как электрическое поле E , так и магнитное поле B электромагнитной волны перпендикулярны направлению распространения волны.Направление распространения в каждой точке волны соответствует направлению, заданному как E × B . Вектор Пойнтинга, S = (1 / μ o ) E × B , дает величину и направление энергии, переносимой электромагнитной волной через единицу площади за единицу времени. Таким образом, величина S представляет мощность, которую электромагнитная волна передает через единицу площади.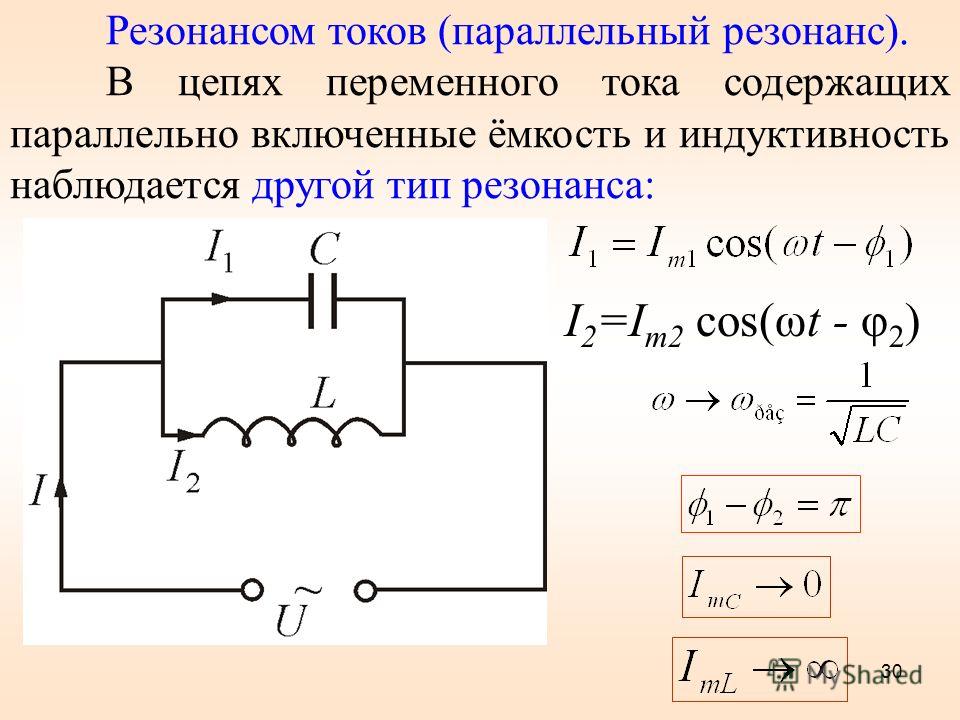
– цепь переменного тока, имеющая только конденсатор
 Т.е.:
Т.е.:
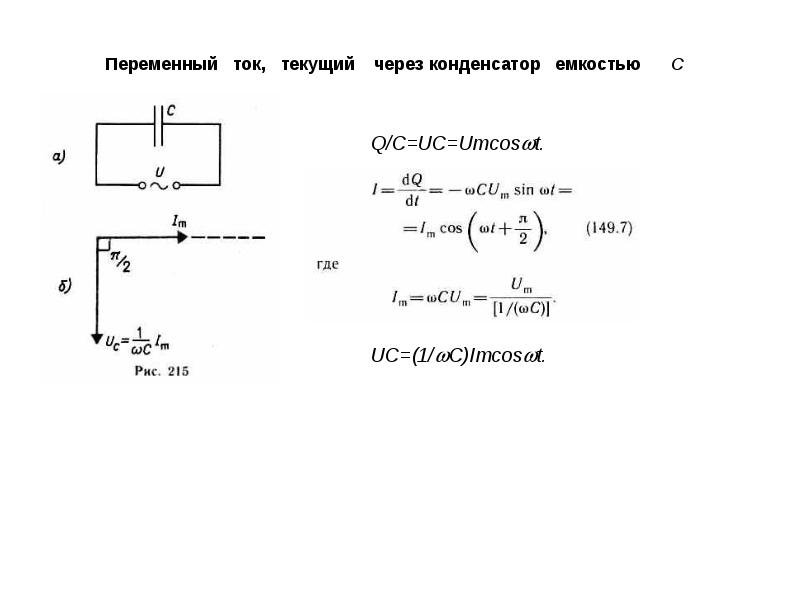 Затем вы экстраполируете этот вывод на все возможные \ $ t \ $ и заключаете, что ток вообще не течет и что конденсатор должен быть всегда полностью заряжен при пиковом значении приложенной ЭДС.
Затем вы экстраполируете этот вывод на все возможные \ $ t \ $ и заключаете, что ток вообще не течет и что конденсатор должен быть всегда полностью заряжен при пиковом значении приложенной ЭДС.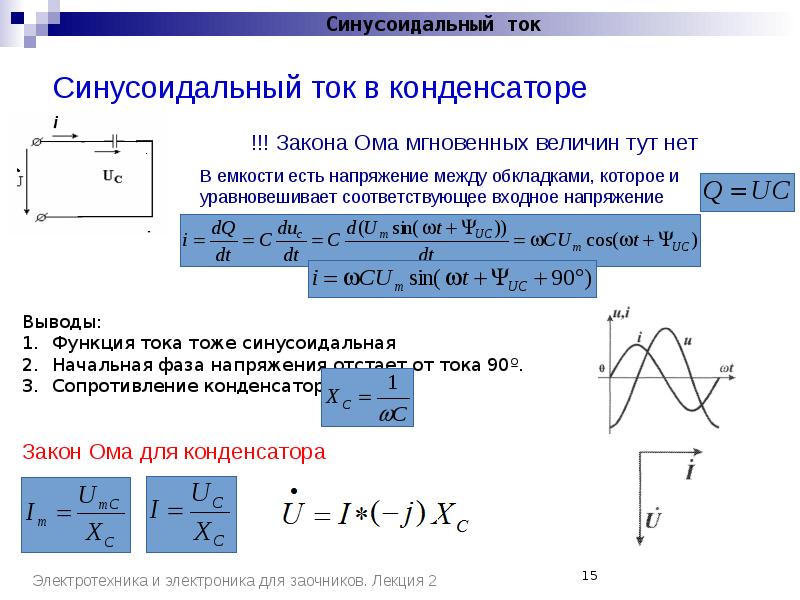 Также неправильно думать о \ $ {\ Delta} V \ $ как о разнице между приложенной ЭДС и напряжением на конденсаторе.Как уже было сказано, нет разницы между приложенной ЭДС и напряжением на конденсаторе, просто оно должно быть равным.
Также неправильно думать о \ $ {\ Delta} V \ $ как о разнице между приложенной ЭДС и напряжением на конденсаторе.Как уже было сказано, нет разницы между приложенной ЭДС и напряжением на конденсаторе, просто оно должно быть равным. Электрические конденсаторы в цепях переменного тока – Предотвращение инцидентов

 Это не так просто, но идею вы поняли.
Это не так просто, но идею вы поняли.
Конденсатор немного похож на батарею. Хотя они работают совершенно по-разному, конденсаторы и батареи хранят электрическую энергию. Вы знаете, что аккумулятор имеет две клеммы. Внутри батареи химические реакции производят электроны на одном выводе и поглощают электроны на другом. Конденсатор – гораздо более простое устройство, и он не может производить новые электроны – он только хранит их.
Конденсаторы должны применяться аккуратно и правильно. Как было сказано ранее, конденсатор предназначен для улучшения коэффициента мощности схемы.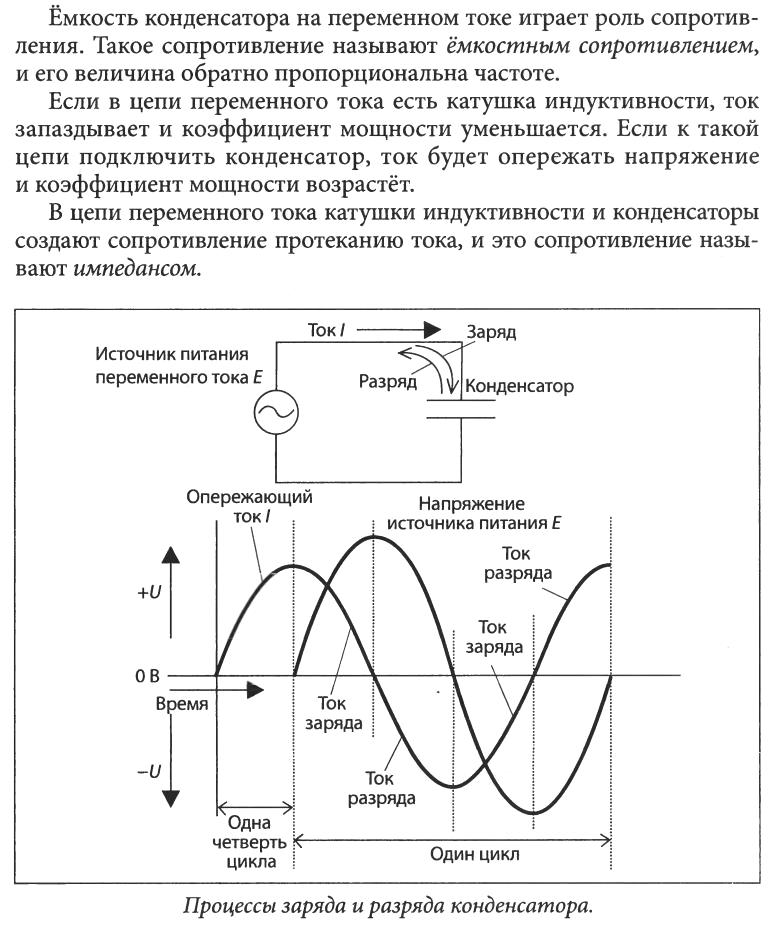 Конденсатор только корректирует коэффициент мощности от конденсатора обратно в систему. Конденсаторы не влияют на коэффициент мощности между конденсатором и реактивной нагрузкой, вызывая коэффициент мощности. Неправильно установленные конденсаторы могут обеспечивать больший реактивный ток, чем требуется нагрузке, что приводит к опережающему коэффициенту мощности и увеличению потерь вместо уменьшения. Вот почему конденсаторы находятся после тщательного изучения системы квалифицированными инженерами.
Конденсатор только корректирует коэффициент мощности от конденсатора обратно в систему. Конденсаторы не влияют на коэффициент мощности между конденсатором и реактивной нагрузкой, вызывая коэффициент мощности. Неправильно установленные конденсаторы могут обеспечивать больший реактивный ток, чем требуется нагрузке, что приводит к опережающему коэффициенту мощности и увеличению потерь вместо уменьшения. Вот почему конденсаторы находятся после тщательного изучения системы квалифицированными инженерами.
Установка одного конденсатора или батареи конденсаторов является простой процедурой после определения правильного размера и места установки.Во многих отношениях конденсатор установить намного проще, чем трансформатор, потому что нет вторичных вводов, а конденсатор представляет собой герметичный блок. У одних агрегатов две втулки, у других – одна. Конденсаторы с одним изолированным вводом обычно соединяют фазой с изолированным вводом, а корпус – с землей. В подстанциях конденсаторы распределительного напряжения подключаются параллельно, разделяя фазные напряжения передачи.Они установлены на изолированном каркасе, который является частью межсоединения, работающего при фазном напряжении передачи. Любой, кто работает с любым конденсатором, должен хорошо знать, как он подключен и при каком напряжении работает.
Конденсаторы с одним изолированным вводом обычно соединяют фазой с изолированным вводом, а корпус – с землей. В подстанциях конденсаторы распределительного напряжения подключаются параллельно, разделяя фазные напряжения передачи.Они установлены на изолированном каркасе, который является частью межсоединения, работающего при фазном напряжении передачи. Любой, кто работает с любым конденсатором, должен хорошо знать, как он подключен и при каком напряжении работает. Существует много типов элементов управления, которые определяют, должен ли конденсатор быть включен или выключен в зависимости от требований системы. Ниже приведены примеры средств контроля и то, для чего они чаще всего используются:
Существует много типов элементов управления, которые определяют, должен ли конденсатор быть включен или выключен в зависимости от требований системы. Ниже приведены примеры средств контроля и то, для чего они чаще всего используются:
• Контроль времени используется в областях, где известно, что нагрузка возникает через определенные промежутки времени либо из-за промышленного использования, либо из-за требований жилых помещений.
• Текущее управление используется в областях, где нагрузка клиента является прерывистой и не всегда присутствует в одно и то же время дня.
• Контроль температуры используется в тех областях, где сезонные изменения увеличивают индуктивную нагрузку на систему (например, кондиционирование воздуха). В основном доступны два основных контроля температуры: включение при 85 градусах и выключение при 65 градусах или включение при 90 градусах и выключение при 70 градусах.
• Контроль напряжения используется в областях, где нагрузка вызывает падение напряжения в системе, которое можно легко контролировать. Регуляторы напряжения также часто используются вместе с регуляторами времени, тока и температуры.
Регуляторы напряжения также часто используются вместе с регуляторами времени, тока и температуры.
• Ручное управление используется для более простого отключения переключаемого банка, который часто используется для сезонной нагрузки.
Хотя конденсаторы являются простыми устройствами, они чрезвычайно опасны после отключения от обслуживания, поскольку могут сохранять заряд. Они должны быть построены с резисторами утечки, которые снижают их напряжение до менее чем 50 вольт через пять минут.Однако никогда не принимайте ничего как должное. Обязательно выждите пять минут после отсоединения, а затем закоротите втулки перемычкой с помощью рукоятки для дробовика. Перед началом работы с любым конденсатором, установленным на опоре, всегда выполняйте эти процедуры, потому что конденсатор может удерживать заряд без каких-либо признаков того, что он это делает.
• Отключите от источника.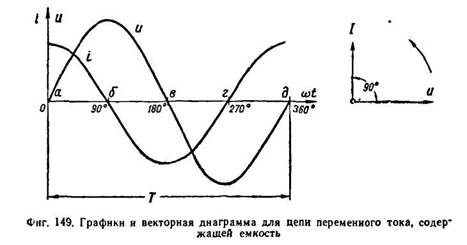
• Подождите пять минут, пока разрядится заряд.
• Замкните накоротко вводы или, в случае конденсаторов с одним выводом, короткое замыкание между вводом и корпусом.
• Сохраняйте соединение короткого замыкания на месте до тех пор, пока конденсатор не будет подключен для обслуживания. Емкостное реактивное сопротивление и фазовые диаграммы
 Там мы использовали закон Ома (V = IR), чтобы вывести соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и индукторы. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора.
Там мы использовали закон Ома (V = IR), чтобы вывести соотношение между напряжением и током в цепях переменного тока. В этом и последующих разделах «Атомы» мы обобщим закон Ома, чтобы мы могли использовать его, даже если в цепи присутствуют конденсаторы и индукторы. Чтобы добраться туда, мы сначала представим очень общий графический способ представления синусоидальной волны с помощью фазора. Phasor
Рис 3
Конденсаторы в цепях переменного тока
Рис 2
Фазовое представление
Рис 4
Страница не найдена | MIT
Перейти к содержанию ↓
Меню ↓
Поиск Меню
Ой, похоже, мы не смогли найти то, что вы искали!
Попробуйте поискать что-нибудь еще!
Что вы ищете?
Увидеть больше результатов


