Параллельное соединение — урок. Физика, 8 класс.
При параллельном соединении все потребители подключены к источнику тока независимо друг от друга и образуют разветвлённую цепь.
При параллельном соединении все потребители подключены к одному источнику тока, между клеммами которого имеется определённое напряжение.
Каждый потребитель получает полное напряжение цепи.
U=U1=U2=U3=…
При параллельном соединении общий ток является суммой токов, протекающих через отдельные потребители.
I=I1+I2+I3+…
Общее сопротивление потребителей, находящихся в параллельном соединении, будет наименьшим (меньше, чем наименьшее из сопротивлений параллельно подключённых потребителей).
Если параллельно соединены \(n\) потребителей, а сопротивление каждого из них одинаково и равно \(R\), тогда общее сопротивление цепи будет равно \(R : n\).
Можно сделать вывод о том, что при увеличении числа потребителей общая сила тока неограниченно возрастает, что может привести к пожару.
Обрати внимание!
В одну розетку нельзя включать несколько мощных потребителей, так как перенагруженные провода нагреваются и могут загореться.
Электрический кабель, который используется в электрической цепи квартиры, имеет три провода. Третий провод является заземлением.
Преимуществом параллельного соединения является то, что при отключении одного из потребителей, остальные продолжают работать.
Источники:
Fizika 9. klasei/Ilgonis Vilks. — Rīga: Zvaigzne ABC, 2008. — 159 lpp.: izmantotā literatūra: 117, lpp.
(Физика для 9 класса// Илгонис Вилкс. — Рига: Zvaigzne ABC, 2008. — 159 стр.: использованная литература: 117. стр.)
Fizika pamatskolai 2. daļa// V. Rasmane, A. Vītols, Ā. Cacāne. — Rīga: RAKA, 2006. — 136 lpp.: il.-izmantotā literatūra: 84, lpp.
(Физика для начальной школы, 2 часть// Расмане В., Витолс А., Цацане А. — Рига: RAKA, 2006. — 136 стр.: ил.-использованная литература: 84. стр.)
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
http://www.goerudio.com/demo/paralelais_slegums
http://www.ndg.lv/latvian/Macibas/FizInter/b2.2.4.htm
Напряжение при параллельном соединении двух резисторов. Формула для расчета параллельного соединения сопротивлений. Мощность при паралл ельном соединение
Последовательное и параллельное соединение резисторов
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.
Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
Параллельное соединение резисторов
Параллельное соединение
–
это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.
Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.
Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:
Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.
Общее сопротивление Rобщ
o Цепь разбивают на участки с только пареллельным или только последовательным соединением. o Вычисляют общее сопротивление для каждого отдельного участка.
o Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:
Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
Можно, в соответствии схеме, сразу записывать формулу следующим образом:
o Если резисторы соединяются последоватеьно – складывать.
o Если резисторы соединяются параллельно – использовать условное обозначение “||”. o Подставлять формулу для параллельного соединения где стоит символ “||”.
Так это будет выглядеть для схемы 1.
Параллельное соединение резисторов. При параллельном соединении резисторов нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются включенными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
Эквивалентные преобразования электрических схем.
Определение последовательного соединения элементов
Последовательное соединение элементов электрической цепи – это такое соединение, когда вывод одного элемента подключен к выводу другого элемента. В этом месте подключения нет узлов. Следующий элемент так же подключен к выводу другого элемента и т.д…
На рисунке ниже показано последовательное подключение четырех сопротивлений.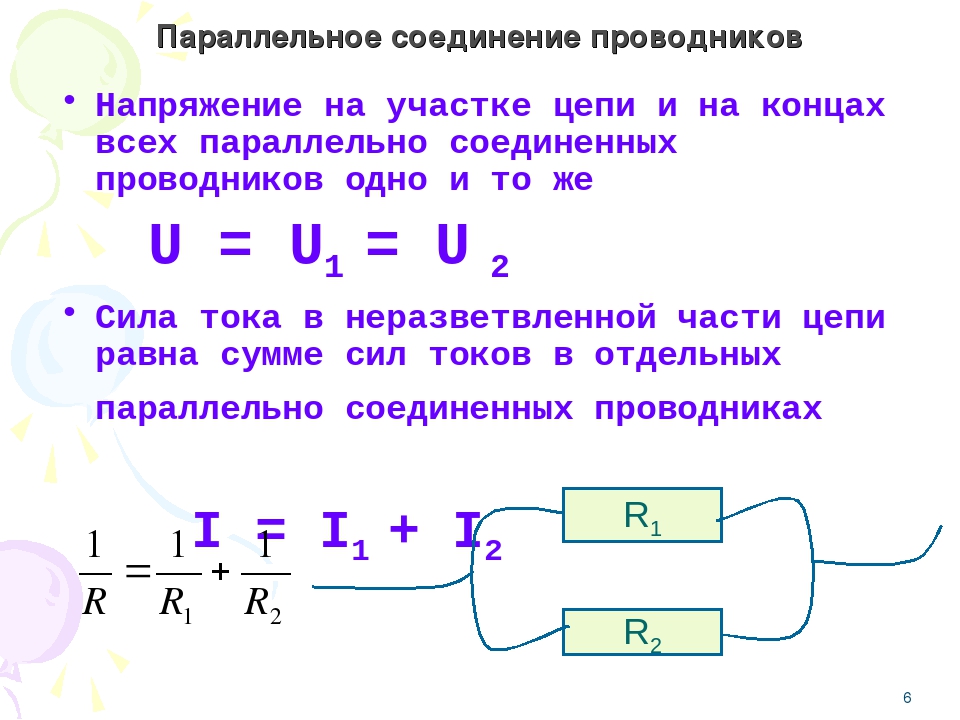
Формулы для расчета эквивалентного сопротивления при последовательном подключении элементов
При последовательном подключении сопротивлений их эквивалентное сопротивление равно сумме сопротивлений.
R экв =ΣR i =R1 + R2 + R3 +…+Rn
При последовательном соединении индуктивностей их эквивалентное сопротивление равно сумме индуктивностей (без учета взаимной индуктивности).
L экв =ΣL i =L1 + L2 + L3 +…+Ln
При последовательном подключении емкостей обратная величина от эквивалентной емкости равна сумме обратных величин емкостей.
1/С экв =Σ(1/C i)=1/С1+1/С2+1/С3+…+1/Cn
Свойства последовательного соединения элементов
При последовательном подключении элементов через них протекает одинаковый ток.
Согласно закону Ома и второму закону Кирхгофа экивалентное (суммарное) напряжение на участке последовательно соединенных сопротивлений равно сумме напряжений на каждом элементе. U общ = U1+U2+U3+U4 = I·(R1+R2+R3+R4). На данном принципе построены простейшие делители напряжения.
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) – это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения “n” одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Смешанное соединение . Это сочетание последовательного и параллельного соединения элементов.
Эквивалентное сопротивление для последовательно-параллельного соединения элементов:
R экв = R 1 +R 2 R 3 / (R 2 +R 3)
Сложное соединение . Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.
Формулы преобразования треугольника сопротивлений в эквивалентную трехлучевую звезду имеют вид:
Формулы обратного преобразования ветвей трехлучевой звезды в эквивалентный треугольник:
,
РЕЖИМЫ РАБОТЫ ИСТОЧНИКОВ ПИТАНИЯ
Различают четыре режима работы источников питания. Е
Режим холостого хода . В режиме холостого хода концы источника разомкнуты: (R х = ∞).
Этот режим используют для измерения ЭДС источника. Параметры режима холостого хода: I х = 0; R х = ∞; U х = E; (U х =E-Ir; r= 0; U х = E)
Режим короткого замыкания . В режиме короткого замыкания концы источника соединены накоротко: (R к = 0).
Номинальный режим . Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения приводятся в паспорте источника питания.
Согласованный режим . Это режим работы источника питания с максимальной мощностью Р=Р mах. Такое возможно при условии, когда R вн =R вш. Формула мощности для согласованного режима:
P max = I 2 R = E 2 / 4R.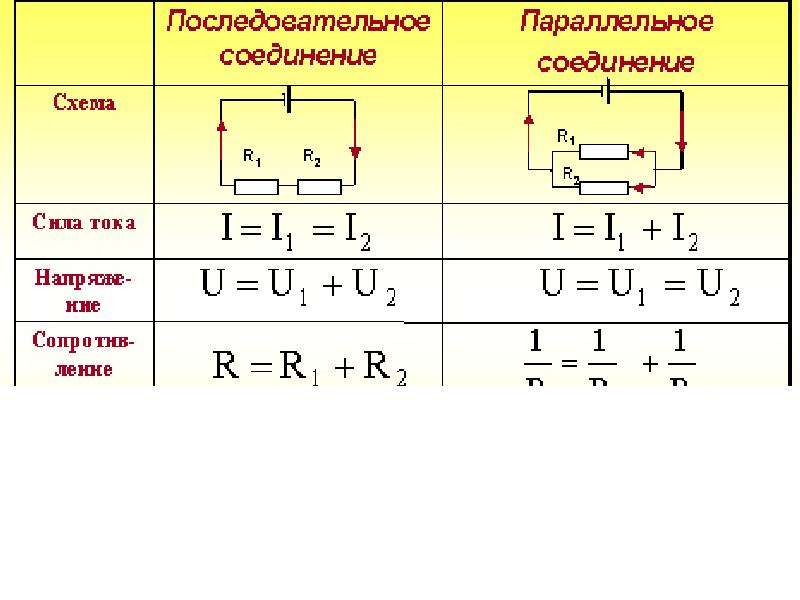
Параллельное и последовательное соединение проводников – способы коммутации электрической цепи. Электрические схемы любой сложности можно представить посредством указанных абстракций.
Определения
Существует два способа соединения проводников, становится возможным упростить расчет цепи произвольной сложности:
- Конец предыдущего проводника соединен непосредственно с началом следующего — подключение называют последовательным. Образуется цепочка. Чтобы включить очередное звено, нужно электрическую схему разорвать, вставив туда новый проводник.
- Начала проводников соединены одной точкой, концы – другой, подключение называется параллельным. Связку принято называть разветвлением. Каждый отдельный проводник образует ветвь. Общие точки именуются узлами электрической сети.
На практике чаще встречается смешанное включение проводников, часть соединена последовательно, часть – параллельно. Нужно разбить цепь простыми сегментами, решать задачу для каждого отдельно. Сколь угодно сложную электрическую схему можно описать параллельным, последовательным соединением проводников. Так делается на практике.
Использование параллельного и последовательного соединения проводников
Термины, применяемые к электрическим цепям
Теория выступает базисом формирования прочных знаний, немногие знают, чем напряжение (разность потенциалов) отличается от падения напряжения. В терминах физики внутренней цепью называют источник тока, находящееся вне – именуется внешней. Разграничение помогает правильно описать распределение поля. Ток совершает работу. В простейшем случае генерация тепла согласно закону Джоуля-Ленца. Заряженные частицы, передвигаясь в сторону меньшего потенциала, сталкиваются с кристаллической решеткой, отдают энергию. Происходит нагрев сопротивлений.
Для обеспечения движения нужно на концах проводника поддерживать разность потенциалов. Это называется напряжением участка цепи. Если просто поместить проводник в поле вдоль силовых линий, ток потечет, будет очень кратковременным. Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Процесс завершится наступлением равновесия. Внешнее поле будет уравновешено собственным полем зарядов, противоположным направлением. Ток прекратится. Чтобы процесс стал непрерывным, нужна внешняя сила.
Таким приводом движения электрической цепи выступает источник тока. Чтобы поддерживать потенциал, внутри совершается работа. Химическая реакция, как в гальваническом элементе, механические силы – генератор ГЭС. Заряды внутри источника движутся в противоположную полю сторону. Над этим совершается работа сторонних сил. Можно перефразировать приведенные выше формулировки, сказать:
- Внешняя часть цепи, где заряды движутся, увлекаемые полем.
- Внутренняя часть цепи, где заряды движутся против напряженности.
Генератор (источник тока) снабжен двумя полюсами. Обладающий меньшим потенциалом называется отрицательным, другой – положительным. В случае переменного тока полюсы непрерывно меняются местами. Непостоянно направление движения зарядов. Ток течет от положительного полюса к отрицательному. Движение положительных зарядов идет в направлении убывания потенциала. Согласно этому факту вводится понятие падения потенциала:
Падением потенциала участка цепи называется убыль потенциала в пределах отрезка. Формально это напряжение. Для ветвей параллельной цепи одинаково.
Под падением напряжения понимается и нечто иное. Величина, характеризующая тепловые потери, численно равна произведению тока на активное сопротивление участка. Законы Ома, Кирхгофа, рассмотренные ниже, формулируются для этого случая. В электрических двигателях, трансформаторах разница потенциалов может значительно отличаться от падения напряжения. Последнее характеризует потери на активном сопротивлении, тогда как первое учитывает полную работу источника тока.
При решение физических задач для упрощения двигатель может включать в свой состав ЭДС, направление действия которой противоположно эффекту источника питания. Учитывается факт потери энергии через реактивную часть импеданса. Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Школьный и вузовский курс физики отличается оторванностью от реальности. Вот почему студенты, раскрыв рот, слушают о явлениях, имеющих место в электротехнике. В период, предшествующий эпохе промышленной революции, открывались главные законы, ученый должен объединять роль теоретика и талантливого экспериментатора. Об этом открыто говорят предисловия к трудам Кирхгофа (работы Георга Ома на русский язык не переведены). Преподаватели буквально завлекали люд дополнительными лекциями, сдобренными наглядными, удивительными экспериментами.
Законы Ома и Кирхгофа применительно к последовательному и параллельному соединению проводников
Для решения реальных задач используются законы Ома и Кирхгофа. Первый выводил равенство чисто эмпирическим путем – экспериментально – второй начал математическим анализом задачи, потом проверил догадки практикой. Приведем некоторые сведения, помогающие решению задачи:
Посчитать сопротивления элементов при последовательном и параллельном соединении
Алгоритм расчета реальных цепей прост. Приведем некоторые тезисы касательно рассматриваемой тематики:
- При последовательном включении суммируются сопротивления, при параллельном — проводимости:
- Для резисторов закон переписывается в неизменной форме. При параллельном соединении итоговое сопротивление равняется произведению исходных, деленному на общую сумму. При последовательном – номиналы суммируются.
- Индуктивность выступает реактивным сопротивлением (j*ω*L), ведет себя, как обычный резистор. В плане написания формулы ничем не отличается. Нюанс, для всякого чисто мнимого импеданса, что нужно умножить результат на оператор j, круговую частоту ω (2*Пи*f). При последовательном соединении катушек индуктивности номиналы суммируются, при параллельном – складываются обратные величины.
- Мнимое сопротивление емкости записывается в виде: -j/ω*С. Легко заметить: складывая величины последовательного соединения, получим формулу, в точности как для резисторов и индуктивностей было при параллельном.
Для конденсаторов все наоборот. При параллельном включении номиналы складываются, при последовательном – суммируются обратные величины.
Тезисы легко распространяются на произвольные случаи. Падение напряжения на двух открытых кремниевых диодах равно сумме. На практике составляет 1 вольт, точное значение зависит от типа полупроводникового элемента, характеристик. Аналогичным образом рассматривают источники питания: при последовательном включении номиналы складываются. Параллельное часто встречается на подстанциях, где трансформаторы ставят рядком. Напряжение будет одно (контролируются аппаратурой), делятся между ветвями. Коэффициент трансформации строго равен, блокируя возникновение негативных эффектов.
У некоторых вызывает затруднение случай: две батарейки разного номинала включены параллельно. Случай описывается вторым законом Кирхгофа, никакой сложности представить физику не может. При неравенстве номиналов двух источников берется среднее арифметическое, если пренебречь внутренним сопротивлением обоих. В противном случае решаются уравнения Кирхгофа для всех контуров. Неизвестными будут токи (всего три), общее количество которых равно числу уравнений. Для полного понимания привели рисунок.
Пример решения уравнений Кирхгофа
Посмотрим изображение: по условию задачи, источник Е1 сильнее, нежели Е2. Направление токов в контуре берем из здравых соображений. Но если бы проставили неправильно, после решения задачи один получился бы с отрицательным знаком. Следовало тогда изменить направление. Очевидно, во внешней цепи ток течет, как показано на рисунке. Составляем уравнения Кирхгофа для трех контуров, вот что следует:
- Работа первого (сильного) источника тратится на создание тока во внешней цепи, преодоление слабости соседа (ток I2).
- Второй источник не совершает полезной работы в нагрузке, борется с первым. Иначе не скажешь.
Включение батареек разного номинала параллельно является безусловно вредным. Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Что наблюдается на подстанции при использовании трансформаторов с разным передаточным коэффициентом. Уравнительные токи не выполняют никакой полезной работы. Включенные параллельно разные батарейки начнут эффективно функционировать, когда сильная просядет до уровня слабой.
Возьмем три постоянных сопротивления R1, R2 и R3 и включим их в цепь так, чтобы конец первого сопротивления R1 был соединен с началом второго сопротивления R 2, конец второго – с началом третьего R 3, а к началу первого сопротивления и к концу третьего подведем проводники от источника тока (рис. 1 ).
Такое соединение сопротивлений называется последовательным. Очевидно, что ток в такой цепи будет во всех ее точках один и тот же.
Рис 1
Как определить общее сопротивление цепи, если все включенные в нее последовательно сопротивления мы уже знаем? Используя положение, что напряжение U на зажимах источника тока равно сумме падений напряжений на участках цепи, мы можем написать:
U = U1 + U2 + U3
где
U1 = IR1 U2 = IR2 и U3 = IR3
или
IR = IR1 + IR2 + IR3
Вынеся в правой части равенства I за скобки, получим IR = I(R1 + R2 + R3) .
Поделив теперь обе части равенства на I , будем окончательно иметь R = R1 + R2 + R3
Таким образом, мы пришли к выводу, что при последовательном соединении сопротивлений общее сопротивление всей цепи равно сумме сопротивлений отдельных участков.
Проверим этот вывод на следующем примере. Возьмем три постоянных сопротивления, величины которых известны (например, R1 == 10 Ом, R 2 = 20 Ом и R 3 = 50 Ом). Соединим их последовательно (рис. 2 ) и подключим к источнику тока, ЭДС которого равна 60 В ( пренебрегаем).
Рис. 2. Пример последовательного соединения трех сопротивлений
Подсчитаем, какие показания должны дать приборы, включенные, как показано на схеме, если замкнуть цепь. Определим внешнее сопротивление цепи: R = 10 + 20 + 50 = 80 Ом.
Найдем ток в цепи : 60 / 80 = 0 ,75 А
Зная ток в цепи и сопротивления ее участков, определим падение напряжения на каждое участке цепи U
1 = 0,75х 10 = 7,5 В, U
2 = 0,75 х 20=15 В, U3 = 0,75 х 50 = 37,5 В.
Зная падение напряжений на участках, определим общее падение напряжения во внешней цепи, т. е. напряжение на зажимах источника тока U = 7,5+15 + 37,5 = 60 В.
Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Объясняется это тем, что мы пренебрегли внутренним сопротивлением источника тока.
Замкнув теперь ключ выключатель К, можно убедиться по приборам, что наши подсчеты примерно верны.
Возьмем два постоянных сопротивления R1 и R2 и соединим их так, чтобы начала этих сопротивлений были включены в одну общую точку а, а концы – в другую общую точку б. Соединив затем точки а и б с источником тока, получим замкнутую электрическую цепь. Такое соединение сопротивлений называется параллельным соединением.
Рис 3. Параллельное соединение сопротивлений
Проследим течение тока в этой цепи. От положительного полюса источника тока по соединительному проводнику ток дойдет до точки а. В точке а он разветвится, так как здесь сама цепь разветвляется на две отдельные ветви: первую ветвь с сопротивлением R1 и вторую – с сопротивлением R2. Обозначим токи в этих ветвях соответственно через I1 и I 2. Каждый из этих токов пойдет по своей ветви до точки б. В этой точке произойдет слияние токов в один общий ток, который и придет к отрицательному полюсу источника тока.
Таким образом, при параллельном соединении сопротивлений получается разветвленная цепь. Посмотрим, какое же будет соотношение между токами в составленной нами цепи.
Включим амперметр между положительным полюсом источника тока (+) и точкой а и заметим его показания. Включив затем амперметр (показанный «а рисунке пунктиром) в провод, соединяющий точку б с отрицательным полюсом источника тока (-), заметим, что прибор покажет ту же величину силы тока.
Значит, до ее разветвления (до точки а) равна силе тока после разветвления цепи (после точки б).
Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора.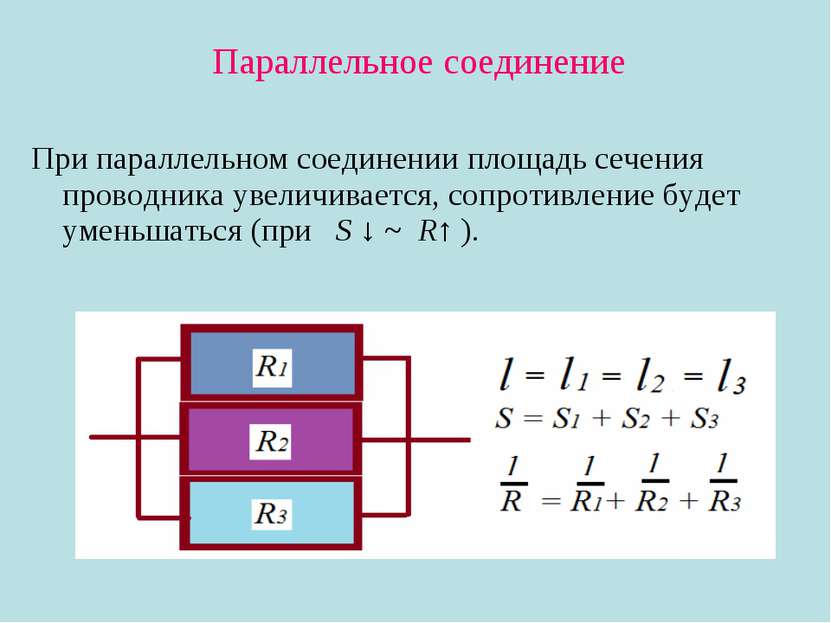 Пусть в первой ветви амперметр покажет силу тока I1
, а во второй – I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Пусть в первой ветви амперметр покажет силу тока I1
, а во второй – I
2. Сложив эти два показания амперметра, мы получим суммарный ток, по величине равный току I до разветвления (до точки а).
Следовательно, сила тока, протекающего до точки разветвления, равна сумме сил токов, утекающих от этой точки. I = I1 + I2 Выражая это формулой, получим
Это соотношение, имеющее большое практическое значение, носит название закона разветвленной цепи .
Рассмотрим теперь, каково будет соотношение между токами в ветвях.
Включим между точками а и б вольтметр и посмотрим, что он нам покажет. Во-первых, вольтметр покажет напряжение источника тока, так как он подключен, как это видно из рис. 3 , непосредственно к зажимам источника тока. Во-вторых, вольтметр покажет падения напряжений U1 и U2 на сопротивлениях R1 и R2, так как он соединен с началом и концом каждого сопротивления.
Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Это дает нам право написать, что U = U1 = U2 ,
где U – напряжение на зажимах источника тока; U1 – падение напряжения на сопротивлении R1 , U2 – падение напряжения на сопротивлении R2. Вспомним, что падение напряжения на участке цепи численно равно произведению силы тока, протекающего через этот участок, на сопротивление участка U = IR .
Поэтому для каждой ветви можно написать: U1 = I1R1 и U2 = I2R2 , но так как U1 = U2, то и I1R1 = I2R2 .
Применяя к этому выражению правило пропорции, получим I1/ I2 = U2 / U1
т. е. ток в первой ветви будет во столько раз больше (или меньше) тока во второй ветви, во сколько раз сопротивление первой ветви меньше (или больше) сопротивления второй ветви.
Итак, мы пришли к важному выводу, заключающемуся в том, что при параллельном соединении сопротивлений общий ток цепи разветвляется на токи, обратно пропорциональные величинам сопротивлении параллельных ветвей.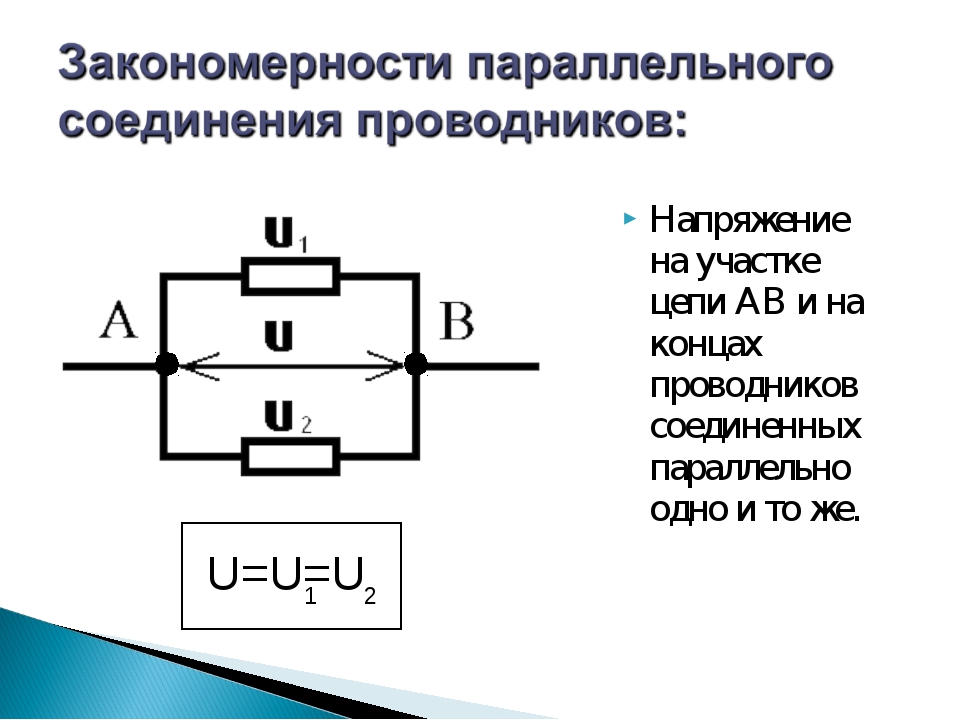 Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Иначе говоря, чем больше сопротивление ветви, тем меньший ток потечет через нее, и, наоборот, чем меньше сопротивление ветви, тем больший ток потечет через эту ветвь.
Убедимся в правильности этой зависимости на следующем примере. Соберем схему, состоящую из двух параллельно соединенных сопротивлений R1 и R 2, подключенных к источнику тока. Пусть R1 = 10 Ом, R2 = 20 Ом и U = 3 В.
Подсчитаем сначала, что покажет нам амперметр, включенный в каждую ветвь:
I1 = U / R1 = 3 / 10 = 0 ,3 А = 300 мА
I 2 = U / R 2 = 3 / 20 = 0,15 А = 150 мА
Общий ток в цепи I = I1 +I2 = 300 + 150 = 450 мА
Проделанный нами расчет подтверждает, что при параллельном соединении сопротивлений ток в цепи разветвляется обратно пропорционально сопротивлениям.
Действительно, R1 == 10 Ом вдвое меньше R 2 = 20 Ом, при этом I1 = 300 мА вдвое больше I2 = 150 мА. Общий ток в цепи I = 450 мА разветвился на две части так, что большая его часть (I1 = 300 мА) пошла через меньшее сопротивление (R1 = 10 Ом), а меньшая часть (R2 = 150 мА) -через большее сопротивление (R 2 = 20 Ом).
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Представьте себе трубу А, которая в каком-то месте разветвляется на две трубы Б и В различного диаметра (рис. 4). Так как диаметр трубы Б больше диаметра трубок В, то через трубу Б в одно и то же время пройдет больше воды, чем через трубу В, которая оказывает потоку воды большее сопротивление.
Рис. 4
Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Под этим общим сопротивлением внешней цепи надо понимать такое сопротивление, которым можно было бы заменить при данном напряжении цепи оба параллельно включенных сопротивления, не изменяя при этом тока до разветвления. Такое сопротивление называется эквивалентным сопротивлением.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
– ток во внешней цепи (до точки разветвления), U – напряжение внешней цепи, R – сопротивление внешней цепи, т. е. эквивалентное сопротивление.
3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Применяя к этой цепи закон Ома, мы можем написать: I = U/R
, где I
– ток во внешней цепи (до точки разветвления), U – напряжение внешней цепи, R – сопротивление внешней цепи, т. е. эквивалентное сопротивление.
Точно так же для каждой ветви I1 = U1 / R1
, I2 = U2 / R2
, где I1
и I
2 – токи в ветвях; U1
и U2 – напряжение на ветвях; R1
и R2
– сопротивления ветвей.
По закону разветвленной цепи: I = I1 + I2
Подставляя значения токов, получим U / R = U1 / R1 + U2 / R2
Так как при параллельном соединении U = U1 = U2 , то можем написать U / R = U / R1 + U / R2
Вынеся U в правой части равенства за скобки, получим U / R = U (1 / R1 + 1 / R2 )
Разделив теперь обе части равенства на U , будем окончательно иметь 1 / R = 1 / R1 + 1 / R2
Помня, что проводимостью называется величина, обратная сопротивлению , мы можем сказать, что в полученной формуле 1 / R – проводимость внешней цепи; 1 / R1 проводимость первой ветви; 1 / R2- проводимость второй ветви.
На основании этой формулы делаем вывод: при параллельном соединении проводимость внешней цепи равна сумме проводимостей отдельных ветвей.
Следовательно, чтобы определить эквивалентное сопротивление включенных параллельно сопротивлений, надо определить проводимость цепи и взять величину, ей обратную.
Из формулы также следует, что проводимость цепи больше проводимости каждой ветви, а это значит, что эквивалентное сопротивление внешней цепи меньше наименьшего из включенных параллельно сопротивлений.
Рассматривая случай параллельного соединения сопротивлений, мы взяли наиболее простую цепь, состоящую из двух ветвей. Однако на практике могут встретиться случаи, когда цепь состоит из трех и более параллельных ветвей. Как же поступать в этих случаях?
Оказывается, все полученные нами соотношения остаются справедливыми и для цепи, состоящей из любого числа параллельно соединенных сопротивлений.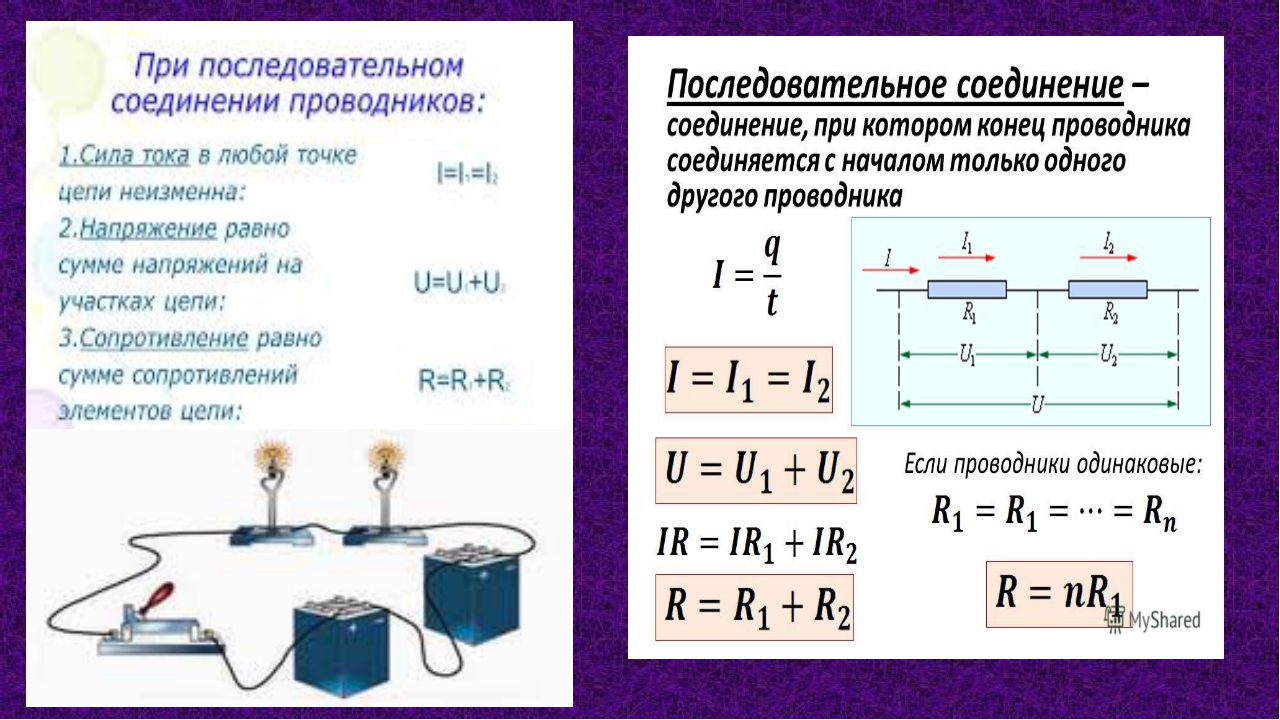
Чтобы убедиться в этом, рассмотрим следующий пример.
Возьмем три сопротивления R1 = 10 Ом, R2
= 20 Ом и R3
= 60 Ом и соединим их параллельно. Определим эквивалентное сопротивление цепи (рис. 5
).
Рис. 5. Цепь с тремя параллельно соединенными сопротивлениями
Применяя для этой цепи формулу 1 / R = 1 / R1 + 1 / R2 , можем написать 1 / R = 1 / R1 + 1 / R2 + 1 / R3 и, подставляя известные величины, получим 1 / R = 1 / 10 + 1 / 20 + 1 / 60
Сложим эта дроби: 1/R = 10 / 60 = 1 / 6, т. е.. проводимость цепи 1 / R = 1 / 6 Следовательно, эквивалентное сопротивление R = 6 Ом.
Таким образом, эквивалентное сопротивление меньше наименьшего из включенных параллельно в цепь сопротивлений , т. е. меньше сопротивления R1.
Посмотрим теперь, действительно ли это сопротивление является эквивалентным, т. е. таким, которое могло бы заменить включенные параллельно сопротивления в 10, 20 и 60 Ом, не изменяя при этом силы тока до разветвления цепи.
Допустим, что напряжение внешней цепи, а следовательно, и напряжение на сопротивлениях R1, R2, R3 равно 12 В. Тогда сила токов в ветвях будет: I1 = U/R1 = 12 / 10 = 1 ,2 А I 2 = U/R 2 = 12 / 20 = 1 ,6 А I 3 = U/R1 = 12 / 60 = 0,2 А
Общий ток в цепи получим, пользуясь формулой I = I1 + I2 + I3 =1,2 + 0,6 + 0,2 = 2 А.
Проверим по формуле закона Ома, получится ли в цепи ток силой 2 А, если вместо трех параллельно включенных известных нам сопротивлений включено одно эквивалентное им сопротивление 6 Ом.
I = U / R = 12 / 6 = 2 А
Как видим, найденное нами сопротивление R = 6 Ом действительно является для данной цепи эквивалентным.
В этом можно убедиться и на измерительных приборах, если собрать схему с взятыми нами сопротивлениями, измерить ток во внешней цепи (до разветвления), затем заменить параллельно включенные сопротивления одним сопротивлением 6 Ом и снова измерить ток. Показания амперметра и в том и в другом случае будут примерно одинаковыми.
На практике могут встретиться также параллельные соединения, для которых рассчитать эквивалентное сопротивление можно проще, т. е. не определяя предварительно проводимостей, сразу найти сопротивление.
Например, если соединены параллельно два сопротивления R1 и R2 , то формулу 1 / R = 1 / R1 + 1 / R2 можно преобразовать так: 1/R = (R2 + R1) / R1 R2 и, решая равенство относительно R, получить R = R1 х R2 / (R1 + R2 ), т. е. при параллельном соединении двух сопротивлений эквивалентное сопротивление цепи равно произведению включенных параллельно сопротивлений, деленному на их сумму.
Количество теплоты, выделившееся при прохождении электрического тока по проводнику, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени, в течение которого шел ток: | Последовательное соединение. 1. Сила тока во всех последовательно соединенных участках цепи одинакова: I1=I2=I3=…=In=… 2. Напряжение в цепи, состоящей из нескольких последовательно соединенных участков, равно сумме напряжений на каждом участке: U=U1+U2+…+Un+… 3. Сопротивление цепи, состоящей из нескольких последовательно соединенных участков, равно сумме сопротивлений каждого участка: R=R1+R2+…+Rn+… Если все сопротивления в цепи одинаковы, то: R=R1. При последовательном соединении общее сопротивление увеличивается (больше большего). | Параллельное соединение. 1. Сила тока в неразветвленном участке цепи равна сумме сил токов во всех параллельно соединенных участках. I=I1+I2+…+In+… | 2. Напряжение на всех параллельно соединенных участках цепи одинаково: U1=U2=U3=…=Un=… 3. При параллельном соединении проводников проводимости складываются (складываются величины, обратные сопротивлению): Если все сопротивления в цепи одинаковы, то: При параллельном соединении общее сопротивление уменьшается (меньше меньшего). | 4. Работа электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+…+An+… т.к. A=I2Rt=I2(R1+R2+…+Rn+…)t. 5. Мощность электрического тока в цепи, состоящей из последовательно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. силы тока во всех участках одинаковы, то: U1:U2:…:Un:… = R1:R2:…:Rn:… Для двух резисторов: – чем больше сопротивление, тем больше напряжение. | 4. Работа электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме работ на отдельных участках: A=A1+A2+. т.к. .
5. Мощность электрического тока в цепи, состоящей из параллельно соединенных участков, равна сумме мощностей на отдельных участках: P=P1+P2+…+Pn+… 6. Т.к. напряжения на всех участках одинаковы, то: I1R1= I2R2=…= I3R3=… Для двух резисторов: – чем больше сопротивление, тем меньше сила тока. |
Параллельное соединение проводников | Физика
При параллельном соединении все проводники (резисторы, лампы и т.д.) подключаются к одной и той же паре точек A и B (рис. 43). Связь между общими значениями силы тока, напряжения и сопротивления с их значениями на отдельных участках цепи при этом отличается от той, что была при последовательном соединении. Теперь соответствующие формулы имеют вид
I = I1 + I2, (17.1) U = U1 = U2, (17.2) R = (R1R2) / (R1 + R2). (17.3)
Чтобы убедиться в справедливости этих соотношений, следует собрать цепь и с помощью амперметра и вольтметра произвести необходимые измерения.
Итак, при параллельном соединении проводников напряжение на всех участках цепи одно и то же, общая сила тока равна сумме сил токов на отдельных проводниках, а общее сопротивление двух проводников находится как отношение произведения их сопротивлений к их сумме.
Первые две из этих закономерностей справедливы для любого числа параллельно соединенных проводников, последняя — только для двух.
Если R1 = R2, то
R = (R1R2) / (R1 + R2) = R12/2R1 = R1/2 (17.4)
Мы видим, что общее сопротивление двух одинаковых проводников в 2 раза меньше сопротивления одного проводника.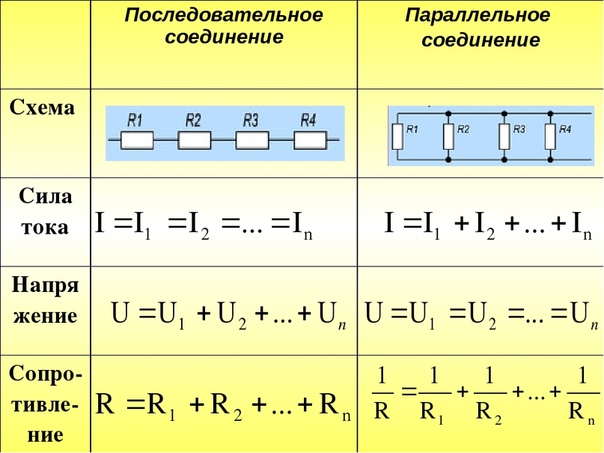 Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:
Эта закономерность допускает обобщение: если параллельно соединено n одинаковых потребителей электроэнергии (резисторов, ламп и т.д.), то их общее сопротивление в n раз меньше сопротивления каждого из них:
R = R1/n (17.5)
Отсюда следует, что с увеличением числа проводников общее сопротивление будет становиться все меньше и меньше. Это может показаться странным. На самом деле ничего удивительного в этом нет: ведь при параллельном соединении проводников происходит как бы увеличение общей площади их поперечного сечения, а с увеличением площади сечения проводника, как известно, его сопротивление уменьшается.
Отличительной особенностью параллельного соединения нескольких потребителей является то, что при выключении одного из них остальные продолжают работать. Так, например, вывернув одну лампу в цепи, изображенной на рисунке 44, мы увидим, что другая будет по-прежнему гореть.
Большинство потребителей электроэнергии — электронагревательные приборы, холодильники, швейные машины, магнитофоны, телевизоры и т. д. — рассчитаны на напряжение сети 220 В. Поэтому все они должны включаться в сеть параллельно, ибо только в этом случае они окажутся под одним и тем же напряжением (220 В) и будут продолжать работать при выключении одного из них.
На рисунке 45 приведена упрощенная схема квартирной электропроводки. Провода сети, между которыми существует напряжение 220 В, обозначены буквами Ф и О. Первый из них называют фазным, второй — нулевым. Нулевой провод соединен с землей. Именно с ним соединяют все потребители. И наоборот, все выключатели соединяют с фазным проводом. Такой порядок подключения потребителей и выключателей обеспечивает наибольшую безопасность человека.
??? 1. Какое соединение называют параллельным? 2. Начертите схему цепи, изображенной на рисунке 44. 3. Какие три закономерности справедливы для параллельного соединения проводников? 4. Как находится общее сопротивление параллельно соединенных проводников, когда они одинаковые? 5.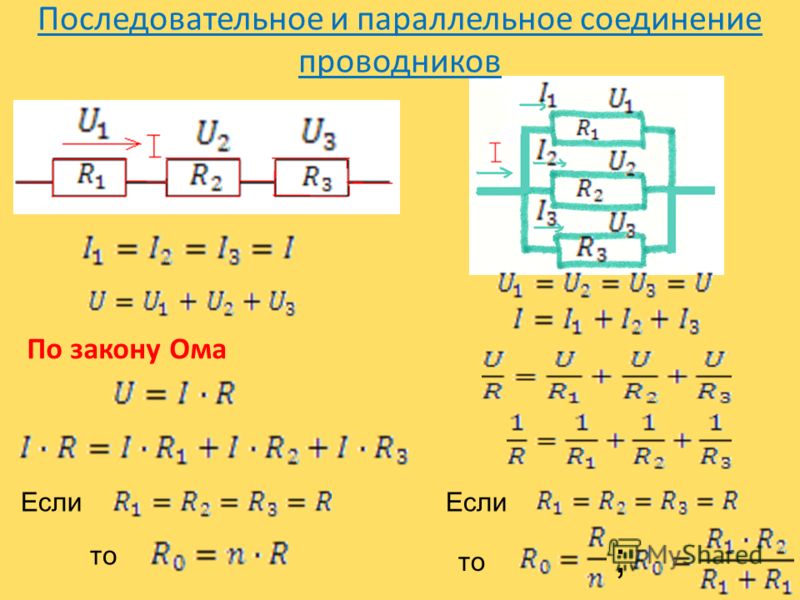 Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?
Перечислите все элементы электрической цепи, изображенной на рисунке 45. 6. Предположим, что при замене лампы человек случайно коснулся металлического контакта в патроне лампы и одновременно с этим какой-либо заземленной части здания (например, батареи отопления). Под каким напряжением он окажется? Рассмотрите ситуацию, когда лампа и выключатель подсоединены к проводам сети так, как это показано на рисунке 45. Что произойдет, если лампу и выключатель поменять местами? 7. Почему у вольтметров делают большое внутреннее сопротивление, а у амперметров — малое?
Падение напряжения при параллельном соединении резисторов. Параллельное соединение проводников
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений – считая одно соединение курицей, а другое – яйцом, то сомнений вообще нет никаких.
Потому что закон Ома – это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, – все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое – ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое – ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек – они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R – сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине – то есть 1,5 В.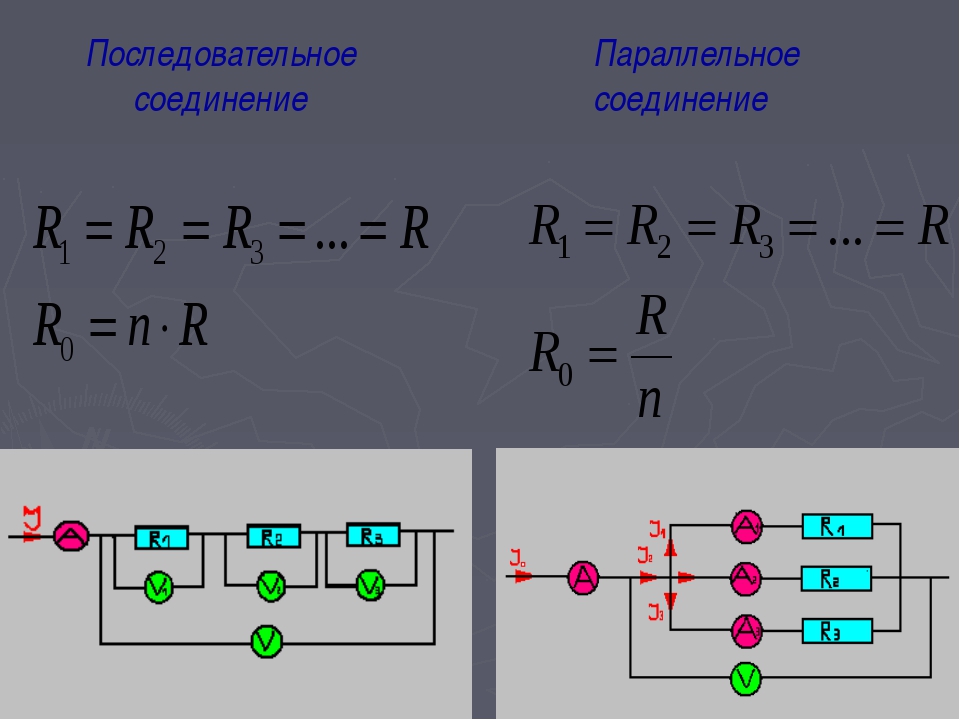 И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе – 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А – ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается – это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая – которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений.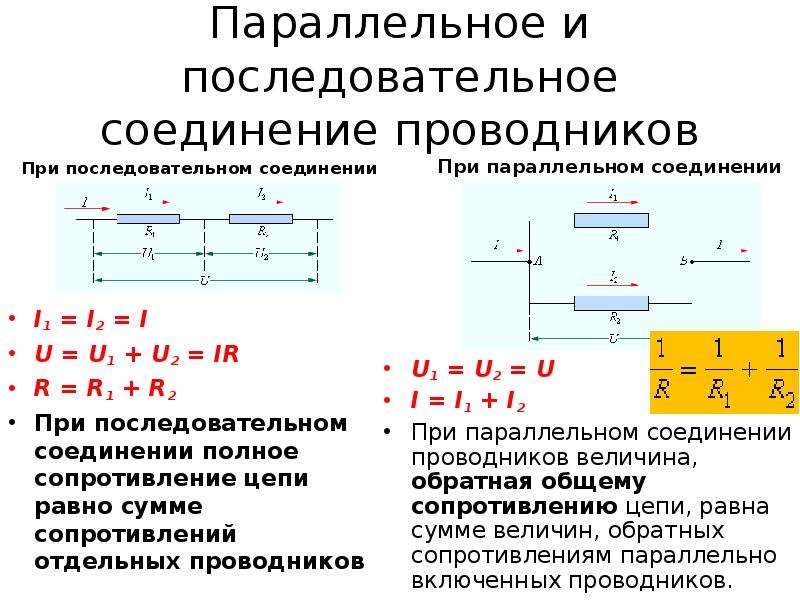 Это могут быть лампочки или что-то другое.
Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Сопротивление проводников. Параллельное и последовательное соединение проводников.
Электри́ческое сопротивле́ние – физическая величина, характеризующая свойства проводника препятствовать прохождению электрического тока и равная отношениюнапряжения на концах проводника к силе тока, протекающего по нему . Сопротивление для цепей переменного тока и для переменных электромагнитных полей описывается понятиями импеданса и волнового сопротивления. Сопротивлением (резистором) также называют радиодеталь, предназначенную для введения в электрические цепи активного сопротивления.
Сопротивление (часто обозначается буквой R или r ) считается, в определённых пределах, постоянной величиной для данного проводника; её можно рассчитать как
R – сопротивление;
U – разность электрических потенциалов (напряжение) на концах проводника;
I – сила тока, протекающего между концами проводника под действием разности потенциалов.
При последовательном соединении проводников (рис. 1.9.1) сила тока во всех проводниках одинакова:
По закону Ома, напряжения U 1 и U 2 на проводниках равны
При последовательном соединении полное сопротивление цепи равно сумме сопротивлений отдельных проводников.
Этот результат справедлив для любого числа последовательно соединенных проводников.
При параллельном соединении (рис. 1.9.2) напряжения U 1 и U 2 на обоих проводниках одинаковы:
Этот результат
следует из того, что в точках разветвления
токов (узлы A и B )
в цепи постоянного тока не могут
накапливаться заряды. Например, к
узлу A за
время Δt подтекает
заряд I Δt ,
а утекает от узла за то же время
заряд I 1 Δt + I 2 Δt .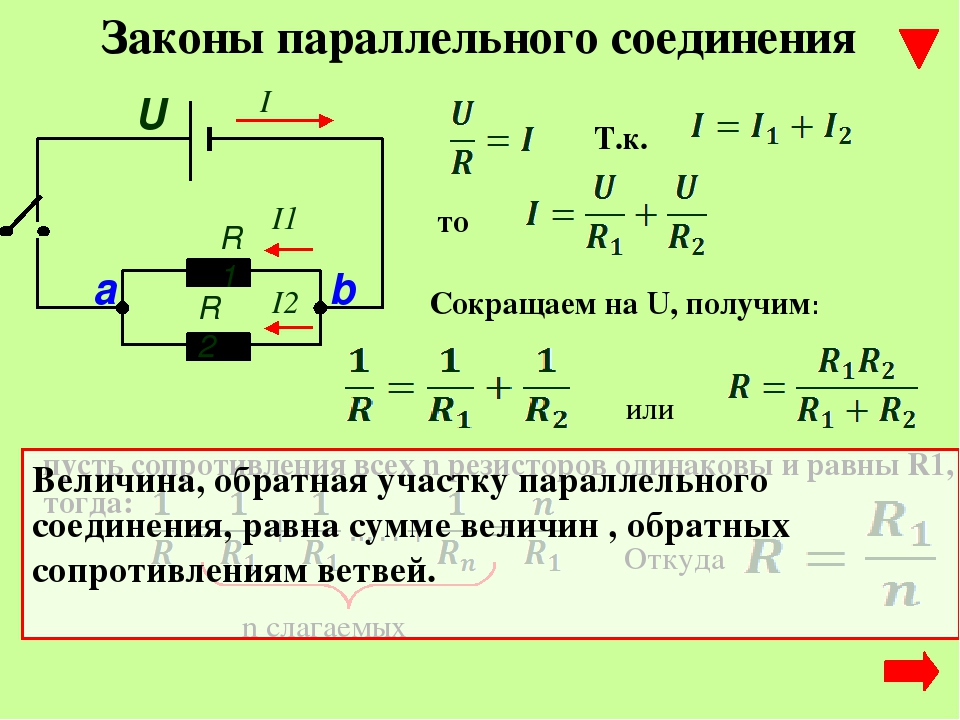 Следовательно,I = I 1 + I 2 .
Следовательно,I = I 1 + I 2 .
Записывая на основании закона Ома
При параллельном соединении проводников величина, обратная общему сопротивлению цепи, равна сумме величин, обратных сопротивлениям параллельно включенных проводников.
Этот результат справедлив для любого числа параллельно включенных проводников.
Формулы для последовательного и параллельного соединения проводников позволяют во многих случаях рассчитывать сопротивление сложной цепи, состоящей из многих резисторов. На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений.
Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения. На рис. 1.9.4 приведен пример электрической цепи, которую нельзя рассчитать указанным выше методом.
Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).
Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:
Применяя закон Ома для каждого участка цепи, получим:
где R – общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем
Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:
Если сопротивления отдельных резисторов равны между собой, т.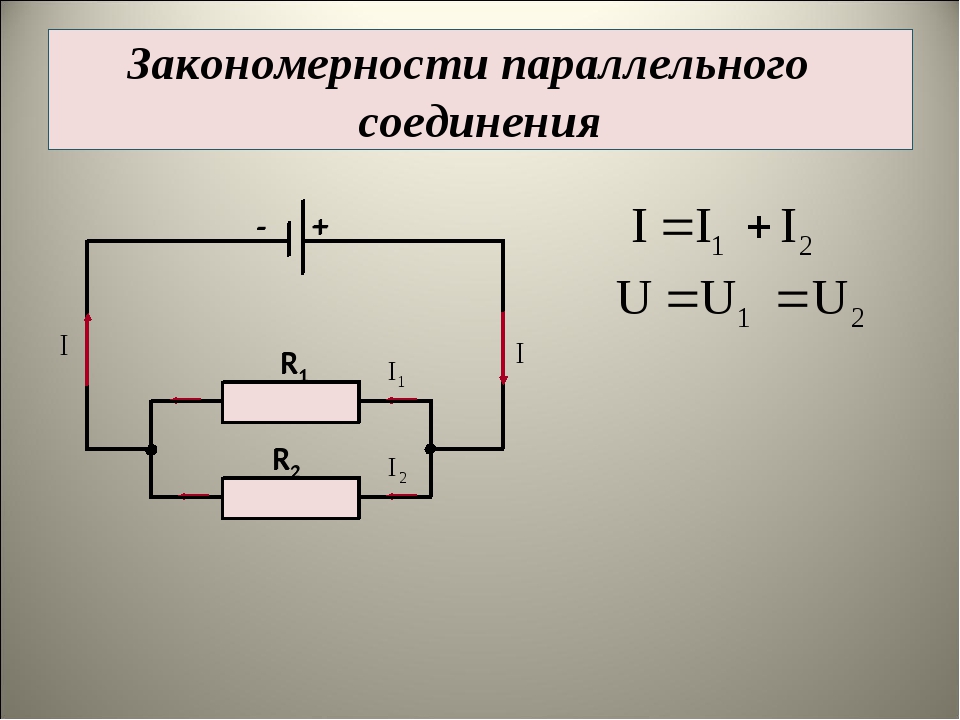 е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .
е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .
При последовательном соединении резисторов справедливо соотношение
т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы – в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:
Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:
Подставляя I, I 1 и I 2 в формулу (2), получим.
Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).
Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U . n \frac{1}{R_i} .\)
n \frac{1}{R_i} .\)
Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. – Мн.: Адукацыя i выхаванне, 2004. – C. 257-259.
Темы кодификатора ЕГЭ : параллельное и последовательное соединение проводников, смешанное соединение проводников.Есть два основных способа соединения проводников друг с другом – это последовательное и параллельное соединения. Различные комбинации последовательного и параллельного соединений приводят к смешанному соединению проводников.
Мы будем изучать свойства этих соединений, но сначала нам понадобится некоторая вводная информация.
Проводник, обладающий сопротивлением , мы называем резистором и изображаем следующим образом (рис. 1 ):
Рис. 1. Резистор
Напряжение на резисторе – это разность потенциалов стационарного электрического поля между концами резистора. Между какими именно концами? В общем-то, это неважно, но обычно удобно согласовывать разность потенциалов с направлением тока.
Ток в цепи течёт от «плюса» источника к «минусу». В этом направлении потенциал стационарного поля убывает. Напомним ещё раз, почему это так.
Пусть положительный заряд перемещается по цепи из точки в точку , проходя через резистор (рис. 2 ):
Рис.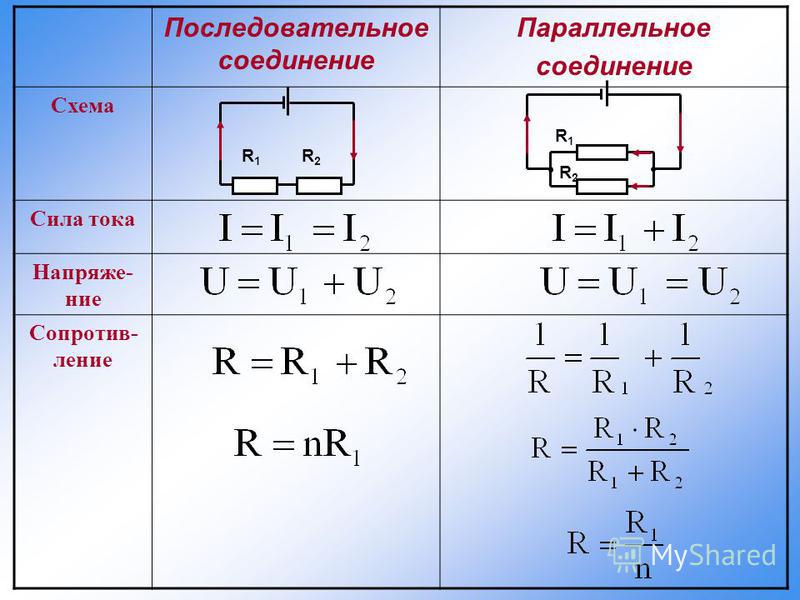 2.
2.
Стационарное поле совершает при этом положительную работу .
Так как alt=”q > 0″> и alt=”A > 0″> , то и alt=”\varphi_a – \varphi_b > 0″> , т. е. alt=”\varphi_a > \varphi_b”> .
Поэтому напряжение на резисторе мы вычисляем как разность потенциалов в направлении тока: .
Сопротивление подводящих проводов обычно пренебрежимо мало; на электрических схемах оно считается равным нулю. Из закона Ома следует тогда, что потенциал не меняется вдоль провода: ведь если и , то . (рис. 3 ):
Рис. 3.
Таким образом, при рассмотрении электрических цепей мы пользуемся идеализацией, которая сильно упрощает их изучение. А именно, мы считаем, что потенциал стационарного поля изменяется лишь при переходе через отдельные элементы цепи, а вдоль каждого соединительного провода остаётся неизменным . В реальных цепях потенциал монотонно убывает при движении от положительной клеммы источника к отрицательной.
Последовательное соединение
При последовательном соединении проводников конец каждого проводника соединяется с началом следующего за ним проводника.
Рассмотрим два резистора и , соединённых последовательно и подключённых к источнику постоянного напряжения (рис. 4 ). Напомним, что положительная клемма источника обозначается более длинной чертой, так что ток в данной схеме течёт по часовой стрелке.
Рис. 4. Последовательное соединение
Сформулируем основные свойства последовательного соединения и проиллюстрируем их на этом простом примере.
1. При последовательном соединении проводников сила тока в них одинакова.
В самом деле, через любое поперечное сечение любого проводника за одну секунду будет проходить один и тот же заряд. Ведь заряды нигде не накапливаются, из цепи наружу не уходят и не поступают в цепь извне.
2. Напряжение на участке, состоящем из последовательно соединённых проводников, равно сумме напряжений на каждом проводнике .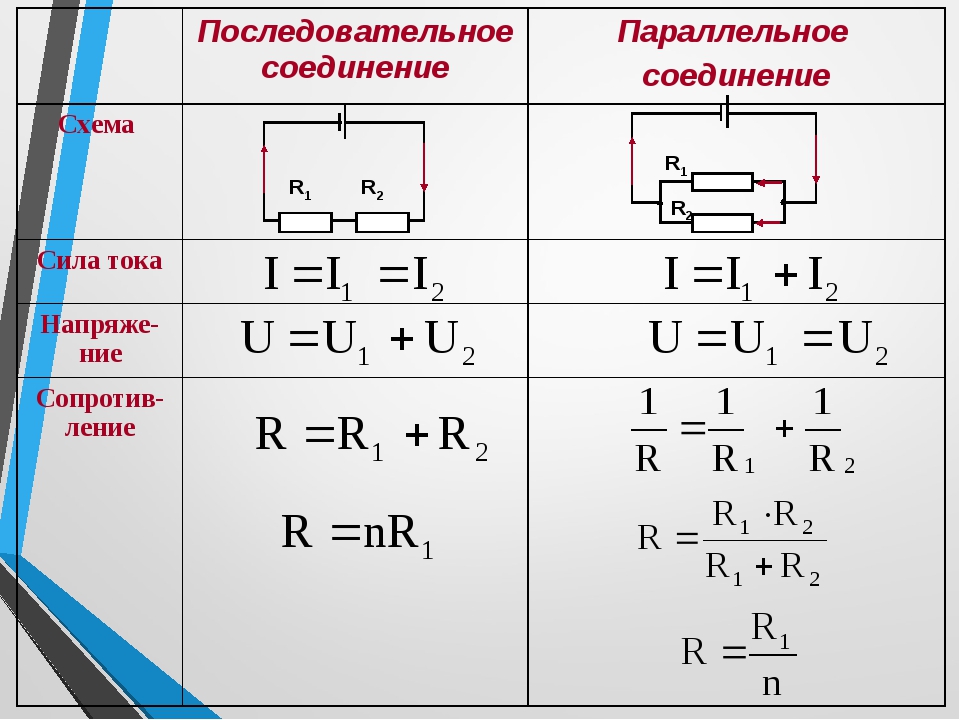
Действительно, напряжение на участке – это работа поля по переносу единичного заряда из точки в точку ; напряжение на участке – это работа поля по переносу единичного заряда из точки в точку . Складываясь, эти две работы дадут работу поля по переносу единичного заряда из точки в точку , то есть напряжение на всём участке:
Можно и более формально, без всяких словесных объяснений:
3. Сопротивление участка, состоящего из последовательно соединённых проводников, равно сумме сопротивлений каждого проводника.
Пусть – сопротивление участка . По закону Ома имеем:
что и требовалось.
Можно дать интуитивно понятное объяснение правила сложения сопротивлений на одном частном примере. Пусть последовательно соединены два проводника из одинакового вещества и с одинаковой площадью поперечного сечения , но с разными длинами и .
Сопротивления проводников равны:
Эти два проводника образуют единый проводник длиной и сопротивлением
Но это, повторяем, лишь частный пример. Сопротивления будут складываться и в самом общем случае – если различны также вещества проводников и их поперечные сечения.
Доказательство этого даётся с помощью закона Ома, как показано выше.
Наши доказательства свойств последовательного соединения, приведённые для двух проводников, переносятся без существенных изменений на случай произвольного числа проводников.
Параллельное соединение
При параллельном соединении проводников их начала подсоединяются к одной точке цепи, а концы – к другой точке.
Снова рассматриваем два резистора, на сей раз соединённые параллельно (рис. 5 ).
Рис. 5. Параллельное соединение
Резисторы подсоединены к двум точкам: и . Эти точки называются узлами или точками разветвления цепи. Параллельные участки называются также ветвями ; участок от к (по направлению тока) называется неразветвлённой частью цепи.
Теперь сформулируем свойства параллельного соединения и докажем их для изображённого выше случая двух резисторов.
1. Напряжение на каждой ветви одинаково и равно напряжению на неразветвлённой части цепи.
В самом деле, оба напряжения и на резисторах и равны разности потенциалов между точками подключения:
Этот факт служит наиболее отчётливым проявлением потенциальности стационарного электрического поля движущихся зарядов.
2. Сила тока в неразветвлённой части цепи равна сумме сил токов в каждой ветви.
Пусть, например, в точку за время из неразветвлённого участка поступает заряд . За это же время из точки к резистору уходит заряд , а к резистору – заряд .
Ясно, что . В противном случае в точке накапливался бы заряд, меняя потенциал данной точки, что невозможно (ведь ток постоянный, поле движущихся зарядов стационарно, и потенциал каждой точки цепи не меняется со временем). Тогда имеем:
что и требовалось.
3. Величина, обратная сопротивлению участка параллельного соединения, равна сумме величин, обратных сопротивлениям ветвей.
Пусть – сопротивление разветвлённого участка . Напряжение на участке равно ; ток, текущий через этот участок, равен . Поэтому:
Сокращая на , получим:
(1)
что и требовалось.
Как и в случае последовательного соединения, можно дать объяснение данного правила на частном примере, не обращаясь к закону Ома.
Пусть параллельно соединены проводники из одного вещества с одинаковыми длинами , но разными поперечными сечениями и . Тогда это соединение можно рассматривать как проводник той же длины , но с площадью сечения . Имеем:
Приведённые доказательства свойств параллельного соединения без существенных изменений переносятся на случай любого числа проводников.
Из соотношения (1) можно найти :
(2)
К сожалению, в общем случае параллельно соединённых проводников компактного аналога формулы (2) не получается, и приходится довольствоваться соотношением
(3)
Тем не менее, один полезный вывод из формулы (3)
сделать можно. Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
Именно, пусть сопротивления всех резисторов одинаковы и равны . Тогда:
Мы видим, что сопротивление участка из параллельно соединённых одинаковых проводников в раз меньше сопротивления одного проводника.
Смешанное соединение
Смешанное сединение проводников, как следует из названия, может являться совокупностью любых комбинаций последовательного и параллельного соединений, причём в состав этих соединений могут входить как отдельные резисторы, так и более сложные составные участки.
Расчёт смешанного соединения опирается на уже известные свойства последовательного и параллельного соединений. Ничего нового тут уже нет: нужно только аккуратно расчленить данную схему на более простые участки, соединённые последовательно или параллельно.
Рассмотрим пример смешанного соединения проводников (рис. 6 ).
Рис. 6. Смешанное соединение
Пусть В, Ом, Ом, Ом, Ом, Ом. Найдём силу тока в цепи и в каждом из резисторов.
Наша цепь состоит из двух последовательно соединённых участков и . Сопротивление участка :
Ом.
Участок является параллельным соединением: два последовательно включённых резистора и подключены параллельно к резистору . Тогда:
Ом.
Сопротивление цепи:
Ом.
Теперь находим силу тока в цепи:
Для нахождения тока в каждом резисторе вычислим напряжения на обоих участках:
(Заметим попутно, что сумма этих напряжений равна В, т. е. напряжению в цепи, как и должно быть при последовательном соединении.)
Оба резистора и находятся под напряжением , поэтому:
(В сумме имеем А, как и должно быть при параллельном соединении.)
Сила тока в резисторах и одинакова, так как они соединены последовательно:
Стало быть, через резистор течёт ток A.
Последовательное и параллельное соединения проводников – FIZI4KA
1. Потребители электрической энергии: электрические лампочки, резисторы и пр. — могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
— могут по-разному соединяться друг с другом в электрической цепи. Существует два основных типа соединения проводников: последовательное и параллельное. При последовательном соединении проводников конец одного проводника соединяется с началом другого проводника, а его конец — с началом третьего и т.д. (рис. 85).
Примером последовательного соединения проводников может служить соединение электрических лампочек в ёлочной гирлянде.
При последовательном соединении проводников ток проходит через все лампочки, при этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд, т.е. заряд не скапливается ни в какой части проводника. Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: \( I_1=I_2=I \).
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений: \( R_1=R_2=R \). Это следует из того, что при последовательном соединении проводников их общая длина увеличивается, она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: \( U_1=IR_1 \), \( U_2=IR_2 \), а общее напряжение равно \( U=I(R_1+R_2) \). Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике: \( U=U_1+U_2 \).
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
2. Примером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи (А), а вторым концом к другой точке цепи (В) (рис. 86).
86).
Поэтому вольтметр, подключенный к этим точкам, покажет напряжение как на проводнике 1, так и на проводнике 2. Таким образом, напряжение на концах всех параллельно соединённых проводников одно и то же: \( U_1=U_2=U \).
При параллельном соединении проводников электрическая цепь разветвляется, в данном случае в точке В. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: \( I=I_1+I_2 \).
В соответствии с законом Ома \( I=\frac{U}{R} \), \( I_1=\frac{U_1}{R_1} \), \( I_2=\frac{U_2}{R_2} \). Отсюда следует: \( \frac{U}{R}=\frac{U_1}{R_1}+\frac{U_2}{R_2} \). Так как \( U_1=U_2=U \), \( \frac{1}{R}=\frac{1}{R_1}+\frac{1}{R_2} \). Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление \( r \), то их общее сопротивление равно: \( R=r/2 \). Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения, соответственно уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно: они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них и соответствие суммарной силы тока предельно допустимой силе тока.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. На рисунке изображёна схема участка электрической цепи АВ. В эту цепь параллельно включены два резистора сопротивлением \( R_1 \) и \( R_2 \). 2 \)
2 \)
2) \( R=2R_1 \)
3) \( R=\frac{R_1}{2} \)
4) \( R=\sqrt{R_1} \)
6. Общее сопротивление участка цепи, изображённого на рисунке, равно 9 Ом. Сопротивления резисторов \( R_1 \) и \( R_2 \) равны. Чему равно сопротивление каждого резистора?
1) 81 Ом
2) 18 Ом
3) 9 Ом
4) 4,5 Ом
7. Чему равно сопротивление участка цепи, содержащего три последовательно соединенных резистора сопротивлением по 9 Ом каждый?
1) 1/3 Ом
2) 3 Ом
3) 9 Ом
4) 27 Ом
8. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 10 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 5 Ом?
1) 9 Ом
2) 11 Ом
3) 16 Ом
4) 26 Ом
9. Чему равно общее сопротивление участка цепи, изображённого на рисунке, если \( R_1 \) = 1 Ом, \( R_2 \) = 3 Ом, \( R_3 \) = 10 Ом, \( R_4 \) = 10 Ом?
1) 9 Ом
2) 10 Ом
3) 14 Ом
4) 24 Ом
10. Если ползунок реостата (см. схему) переместить влево, то сила тока
1) в резисторе \( R_1 \) уменьшится, а в резисторе \( R_2 \) увеличится
2) увеличится в обоих резисторах
3) в резисторе \( R_1 \) увеличится, а в резисторе \( R_2 \) уменьшится
4) уменьшится в обоих резисторах
11. На рисунке изображена электрическая цепь, состоящая из источника тока, резистора и реостата. Как изменяются при передвижении ползунка реостата вправо его сопротивление, сила тока в цепи и напряжение на резисторе 1?
Для каждой физической величины определите соответствующий характер изменения. Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) сопротивление реостата 2
Б) сила тока в цепи
B) напряжение на резисторе 1
ХАРАКТЕР ИЗМЕНЕНИЯ
1) увеличивается
2) уменьшается
3) не изменяется
12. Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов \( R_1 \) и \( R_2 \). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
Установите соответствие между физическими величинами и правильной электрической схемой для измерения этих величин при последовательном соединении двух резисторов \( R_1 \) и \( R_2 \). Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) сила тока в резисторе \( R_1 \) и \( R_2 \)
Б) напряжение на резисторе \( R_2 \)
B) общее напряжение на резисторах \( R_1 \) и \( R_2 \)
Часть 2
13. Три резистора соединены, как показано на рисунке. Сопротивления резисторов \( R_1 \) = 10 Ом, \( R_2 \) = 5 Ом, \( R_3 \) = 5 Ом. Каково напряжение на резисторе 1, если амперметр показывает силу тока 2 А?
Ответы
Последовательное и параллельное соединения проводников
3.3 (65%) 4 votesПараллельное соединение сопротивлений в электрической цепи. Параллельное соединение конденсаторов и катушек.
Определение параллельного соединения
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) – это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения “n” одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
При параллельном подключении индуктивностей, эквивалентная индуктивность рассчитывается так же, как и эквивалентное сопротивление при параллельном соединении:
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к источнику ЭДС E1. R1 – одним концом подключено к R5, а не к узлу. R5 – одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Рассчитать эквивалентное сопротивлений R14 можно по формуле для двух сопротивлений.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
простых параллельных схем | Последовательные и параллельные схемы
На этой странице мы изложим три принципа, которые вы должны понимать в отношении параллельных цепей:
- Напряжение: Напряжение одинаково на всех компонентах параллельной цепи.
- Ток: Полный ток цепи равен сумме токов отдельных ответвлений.
- Сопротивление: Отдельные сопротивления уменьшают , чтобы равняться меньшему общему сопротивлению, вместо прибавляют , чтобы получить общее.
Давайте взглянем на несколько примеров параллельных цепей, демонстрирующих эти принципы.
Начнем с параллельной схемы, состоящей из трех резисторов и одной батареи:
Напряжение в параллельных цепях
Первый принцип для понимания параллельных цепей заключается в том, что напряжение одинаково на всех компонентах в цепи . Это связано с тем, что в параллельной цепи есть только два набора электрически общих точек, и напряжение, измеренное между наборами общих точек, всегда должно быть одинаковым в любой момент времени.
Следовательно, в приведенной выше схеме напряжение на R 1 равно напряжению на R 2 , которое равно напряжению на R 3 , которое равно напряжению на батарее.
Это равенство напряжений можно представить в другой таблице для наших начальных значений:
Применение закона Ома для простых параллельных схем
Как и в случае с последовательными цепями, применимо то же предостережение для закона Ома: значения напряжения, тока и сопротивления должны быть в одном контексте, чтобы вычисления работали правильно.
Однако в приведенной выше примерной схеме мы можем немедленно применить закон Ома к каждому резистору, чтобы найти его ток, потому что мы знаем напряжение на каждом резисторе (9 вольт) и сопротивление каждого резистора:
На данный момент мы все еще не знаем, каков полный ток или полное сопротивление для этой параллельной цепи, поэтому мы не можем применить закон Ома к крайнему правому столбцу («Всего»). Однако, если мы внимательно подумаем о том, что происходит, должно стать очевидным, что общий ток должен равняться сумме всех токов отдельных резисторов («ответвлений»):
По мере того, как полный ток выходит из положительной (+) клеммы батареи в точке 1 и проходит через цепь, часть потока разделяется в точке 2, чтобы пройти через R 1 , еще часть разделяется в точке 3, чтобы пройти через R 2 , а оставшаяся часть идет через R 3 .Подобно реке, разветвляющейся на несколько более мелких ручьев, общий расход всех потоков должен равняться расходу всей реки.
То же самое происходит, когда токи через R 1 , R 2 и R 3 соединяются, чтобы течь обратно к отрицательной клемме батареи (-) в направлении точки 8: поток тока из точки 7 до точки 8 должно равняться сумме токов (ответвлений) через R 1 , R 2 и R 3 .
Это второй принцип параллельных цепей: полный ток цепи равен сумме токов отдельных ветвей .
Используя этот принцип, мы можем заполнить место ИТ на нашем столе суммой I R1 , I R2 и I R3 :
Как рассчитать полное сопротивление в параллельных цепях
Наконец, применив закон Ома к крайнему правому столбцу («Общее»), мы можем вычислить полное сопротивление цепи:
Уравнение сопротивления в параллельных цепях
Обратите внимание на кое-что очень важное. Общее сопротивление цепи составляет всего 625 Ом: на меньше , чем у любого из отдельных резисторов. В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше , чем у любого из резисторов по отдельности.
В последовательной цепи, где полное сопротивление было суммой отдельных сопротивлений, общее сопротивление должно было быть на больше , чем у любого из резисторов по отдельности.
Здесь, в параллельной цепи, наоборот: мы говорим, что отдельных сопротивлений уменьшают , а не прибавляют , чтобы получить общее .
Этот принцип завершает нашу триаду «правил» для параллельных цепей, точно так же, как было обнаружено, что у последовательных цепей есть три правила для напряжения, тока и сопротивления.
Математически соотношение между общим сопротивлением и отдельными сопротивлениями в параллельной цепи выглядит следующим образом:
Как изменить схемы нумерации параллельных цепей для SPICE
Та же основная форма уравнения работает для любого числа резисторов, соединенных вместе параллельно, просто добавьте столько членов 1 / R к знаменателю дроби, сколько необходимо для размещения всех параллельных резисторов в цепи.
Как и в случае с последовательной схемой, мы можем использовать компьютерный анализ для перепроверки наших расчетов.Во-первых, конечно, мы должны описать нашу примерную схему компьютеру в понятных ему терминах. Я начну с рисования схемы:
И снова мы обнаруживаем, что исходная схема нумерации, используемая для идентификации точек в цепи, должна быть изменена в интересах SPICE.
В SPICE все электрически общие точки должны иметь одинаковые номера узлов. Так SPICE узнает, что с чем связано и как.
В простой параллельной схеме все точки электрически являются общими в одном из двух наборов точек.В нашей примерной схеме провод, соединяющий верхние части всех компонентов, будет иметь один номер узла, а провод, соединяющий низ компонентов, будет иметь другой номер.
Оставаясь верным соглашению о включении нуля в качестве номера узла, я выбираю числа 0 и 1:
Пример, подобный этому, делает обоснование номеров узлов в SPICE довольно ясным для понимания. Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они подключены параллельно друг другу.
Поскольку все компоненты имеют общие наборы чисел, компьютер «знает», что все они подключены параллельно друг другу.
Чтобы отобразить токи ответвлений в SPICE, нам нужно вставить источники нулевого напряжения последовательно (последовательно) с каждым резистором, а затем привязать наши измерения тока к этим источникам.
По какой-то причине создатели программы SPICE сделали так, чтобы ток мог быть рассчитан только с по от источника напряжения. Это несколько раздражающее требование программы моделирования SPICE. После добавления каждого из этих «фиктивных» источников напряжения необходимо создать несколько новых номеров узлов, чтобы подключить их к соответствующим резисторам ответвления:
Как проверить результаты компьютерного анализа
Все фиктивные источники напряжения настроены на 0 В, чтобы не влиять на работу схемы.
Файл описания схемы или список цепей выглядит так:
Параллельная схема v1 1 0 r1 2 0 10к r2 3 0 2k r3 4 0 1k vr1 1 2 постоянного тока 0 vr2 1 3 постоянного тока 0 vr3 1 4 постоянного тока 0 .dc v1 9 9 1 .print dc v (2,0) v (3,0) v (4,0) .print dc i (vr1) i (vr2) i (vr3) .конец
Запустив компьютерный анализ, мы получили следующие результаты (я снабдил распечатку описательными этикетками):
| версия 1 | v (2) | v (3) | v (4) |
|---|---|---|---|
| 9.000E + 00 | 9.000E + 00 | 9.000E + 00 | 9.000E + 00 |
| аккумулятор | Напряжение R1 | Напряжение R2 | Напряжение R3 |
Напряжение
| версия 1 | я (vr1) | я (vr2) | я (vr3) |
|---|---|---|---|
| 9.000E + 00 | 9.000E-04 | 4.500E-03 | 9.000E-03 |
| аккумулятор | R1 ток | R2 ток | R3 ток |
Напряжение
Эти значения действительно совпадают со значениями, вычисленными ранее по закону Ома: 0.9 мА для I R1 , 4,5 мА для I R2 и 9 мА для I R3 . При параллельном подключении, естественно, все резисторы имеют одинаковое падение напряжения на них (9 вольт, как у батареи).
Три правила параллельных цепей
Таким образом, параллельная цепь определяется как цепь, в которой все компоненты подключены между одним и тем же набором электрически общих точек. Другими словами, все компоненты подключены друг к другу через клеммы.Из этого определения следуют три правила параллельных цепей:
- Все компоненты имеют одинаковое напряжение.
- Сопротивления уменьшаются до меньшего общего сопротивления.
- Токи ответвления в сумме равняются большему общему току.
Как и в случае с последовательными цепями, все эти правила находят корень в определении параллельной цепи. Если вы полностью понимаете это определение, то правила – не более чем сноски к определению.
ОБЗОР:
- Компоненты в параллельной цепи имеют одинаковое напряжение: E Всего = E 1 = E 2 =. . . E n
- Общее сопротивление в параллельной цепи на меньше , чем любое из отдельных сопротивлений: R Всего = 1 / (1 / R 1 + 1 / R 2 +… 1 / R n )
- Общий ток в параллельной цепи равен сумме токов отдельных ответвлений: I Всего = I 1 + I 2 +.. . Я н. .
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Напряжение в параллельных цепях (источники, формулы и как сложить)
Что такое параллельные напряжения?
Параллельная схема или Параллельное соединение относится к случаю, когда два или более электрических устройства соединены вместе в схеме, расположенной рядом друг с другом. В связи с этим каждое устройство находится в своей отдельной ветке. Напряжение (т.е. разность потенциалов) является причиной того, что ток проходит по замкнутой цепи.В этой статье будет подробно рассмотрено напряжений в параллельной цепи .
Цепь с источником напряжения и 3 параллельными резисторамиМножественные ответвления в цепи означают, что существует несколько путей для перехода заряда во внешнюю цепь. Когда заряд достигает узла или места разветвления, он выбирает, через какую ветвь он должен пройти во время поездки, чтобы вернуться к низкопотенциальному терминалу.
Рассмотрим замкнутую цепь источника напряжения и резистора.В этой цепи ток будет проходить по единственному доступному пути. Затем в той же схеме мы добавляем еще два резистора параллельно первому резистору.
Это приводит к тому, что ток проходит по нескольким путям, а не по одному пути, чтобы достичь терминала с низким потенциалом. Итак, с увеличением количества ветвей общее сопротивление уменьшается и очевидно, что ток в цепи увеличивается.
То есть, весь ток будет суммой различных токов, протекающих через три резистора.Здесь, в параллельной схеме, мы видим, что имеется не более двух наборов электрически общих точек. То есть; A и H, B и G, C и F, D и E в схеме, показанной ниже. Напряжение, которое измеряется в общих точках за все время, должно быть одинаковым.
На двух приведенных выше рисунках сначала показана замкнутая цепь с источником напряжения и одним резистором. Второй – параллельная схема из 3-х резисторов и источника напряжения.
Напряжение в этой цепи одинаково для всех без исключения трех ветвей, а также равно напряжению источника.Формально, то есть:
Полный ток в данной параллельной цепи представлен как I total . Формула для этого представлена как.
Полное или эффективное сопротивление данной параллельной цепи описано в формуле ниже.
Таким образом, мы можем сделать вывод, что добавление дополнительных ветвей в конкретной параллельной цепи увеличивает общий ток и цепь перегружается.
Преимущества параллельных цепей
Когда мы хотим подключить две лампочки к одной батарее, у нас есть два варианта.Либо он может быть подключен массивом или параллельно. Если мы соединим их в массив, две лампочки будут находиться на одном и том же проводящем пути между двумя выводами батареи. Проблемы с этим подключением следующие:
- Мы не можем включить или использовать одну лампочку.
- Обе лампы будут тусклыми, поскольку они используют один и тот же источник.
- Если неисправна одна лампочка, это повлияет на всю цепь.
Затем, если мы подключим две лампочки рядом или параллельно, две лампочки получат полное напряжение батареи.Так что в результате будут следующие преимущества.
- Обе лампочки получают полное напряжение аккумулятора.
- Мы можем управлять двумя лампами по отдельности.
- При включении обе лампочки будут яркими.
- Если неисправна одна лампочка, ее можно удалить или отремонтировать. Таким образом, это не повлияет на всю схему.
Параллельные цепи в доме
Все наши домашние устройства подключаются параллельно друг другу. Вот почему мы можем управлять каждым прибором отдельно, не затрагивая других.Например, мы можем включить стиральную машину, не включая микроволновую печь или телевизор.
Мы знаем, что в нашем доме электрические кабели состоят из трех проводов: под напряжением, нейтрали и заземления. На данный момент мы игнорируем землю и просто концентрируемся на проводе под напряжением и нулевом проводе.
Напряжение присутствует на токоведущем и нейтральном проводе, который в конечном итоге подключен к электростанции. Каждая розетка в нашем доме подключена к этим живым и нейтральным. Когда мы вставляем металлический штифт прибора в эту розетку, он создает электрическое соединение с этой розеткой.
Каждый прибор имеет собственное соединение между токоведущим и нулевым проводом. Итак, когда мы включаем устройство, все напряжение будет присутствовать на нем, и им можно будет управлять отдельно.
Подача напряжения параллельно
Применения напряжения параллельно включают:
электричество – Почему напряжение остается неизменным в параллельной цепи
Это заблуждение можно устранить с помощью самого определения.
Напряжение – это энергия, приходящаяся на один свободный электрон (которая способствует протеканию тока в проводнике), тогда как ток – это скорость потока свободных электронов через площадь поперечного сечения проводника.Другими словами, ток – это количество материала, который проходит через поперечное сечение в течение заданного периода времени, а напряжение – это то, что движет материалом.
Начисление – это сохраняемая величина. То, что вы воспринимаете как тепло, – это энергия частиц 1 , движущихся со скоростью дрейфа (около нескольких миллиметров в секунду). Это просто напряжение, которое преобразуется в тепло. Свободные электроны не могут учуять и делиться соответственно в зависимости от сопротивления на каждом пути цепи. Это просто случайный поток.Они просто ходят по кругу, и когда встречается разделение пути, некоторые проходят одним путем, а некоторые – другим.
Чтобы копнуть глубже, давайте рассмотрим параллельную сеть, подобную этой (ABCDEFA). Батарея (DC) поддерживает разность потенциалов (насколько сейчас не имеет значения), которой достаточно для того, чтобы заряды 2 начали течь. Эти заряды встречаются по пути на перекрестке B. Как уже говорилось ранее, нет никаких особых условий, которые перенаправляют платежи в какое-либо предпочтительное направление.Это просто случайно. Следовательно, некоторые идут по пути BE, а остальные идут через CD, чтобы добраться до батареи.
Скажите сопротивление $ R_2> R_1 $. Что случилось бы? Время, затрачиваемое зарядами на прохождение через $ R_2 $, больше, чем через $ R_1 $. Таким образом, в течение определенного периода времени из $ R_1 $ может быть снято много расходов, в то время как в случае $ R_2 $ их количество будет меньше. И это происходит в течение нескольких секунд после установления разности потенциалов, и поэтому мы понимаем, что ток через $ R_2 $ меньше, чем через $ R_1 $ (что является причиной того, что «ток делит в параллельных цепях). .
Как только заряды выходят из резисторов, электрического поля батареи достаточно, чтобы свести их с ума (поскольку провод имеет относительно более низкое сопротивление). И заряды снова получают свою энергию. Вот почему мы говорим, что напряжение в параллельных цепях одинаковое 3 .
1: Я упомянул «частицы» просто потому, что свободные электроны не обязательно движутся со скоростью дрейфа (что может привести к другому заблуждению). Они всегда на релятивистской скорости.Скорость дрейфа – это просто представление их вклада в текущий поток в макромасштабе …
2: Грубо говоря, я просто использовал «заряды», потому что обычный ток течет от положительного к отрицательному, тогда как поток электронов – наоборот (что мне довольно трудно выразить). Под зарядами я имел в виду заряженные частицы.
3: Также обратите внимание, что напряжение и ток остаются одинаковыми для резисторов с одинаковым сопротивлением независимо от того, подключены они параллельно или последовательно…
Основные операции, уход и обслуживание, а также расширенное устранение неисправностей для квалифицированных специалистов
Как и в последовательных цепях, электрический ток течет «от отрицательного к положительному» через каждый из компонентов нагрузки в параллельной цепи. Как показано на рисунке 6, электроны покидают отрицательный вывод источника и перетекают с отрицательного полюса на положительный через каждый из нагрузочных резисторов. Обратите внимание, что полярность каждого из резисторов такая же, как полярность источника.
Рисунок 6 – Полярность в параллельной цепи
Полярность всегда выражается от одной точки цепи относительно другой точки с другим электрическим потенциалом. Обратите внимание, что на рисунке 6 верхняя сторона каждого резистора, отмеченная отрицательным знаком, фактически находится в одной точке. Между этими подобными клеммами нет разницы в потенциале.
Также обратите внимание, что отдельные токи через каждый резистор (I 1 , I 2 , I 3 ) вместе составляют полный ток (I T ), потребляемый от источника.Когда общий ток, необходимый для работы каждой из этих параллельных нагрузок, превышает номинальный выходной ток одного источника, вам необходимо увеличить выходную мощность источника.
Проверка полярности параллельных источников напряжения
Источники напряжения подключаются параллельно всякий раз, когда необходимо обеспечить выходной ток, превышающий выходной ток, который может обеспечить один источник питания, без увеличения напряжения на нагрузке.
- Источники питания подключены последовательно для увеличения выходного напряжения.
- И наоборот, источники питания подключаются параллельно для увеличения текущей мощности.
Преимущество параллельно подключенных источников питания состоит в том, что один источник может быть отключен для обслуживания или ремонта при сохранении пониженной мощности нагрузки. Если батарея на 6 В имеет максимальный выходной ток 1 А, и если необходимо запитать нагрузку, требующую 2 А, то вы можете подключить вторую батарею на 6 В параллельно первой.
Если есть какие-либо сомнения относительно полярности двух батареек, вы можете провести простой вольтметр для проверки правильности полярности.
- Свяжите одну сторону источников питания вместе.
- Перед тем, как подключить перемычку параллельного включения между двумя оставшимися клеммами, вставьте вольтметр между этими двумя точками. См. Рисунок 7.
- Если полярность неправильная (рисунок 7b), вольтметр показывает удвоенное напряжение источника, потому что одинаковые ЭДС помогают друг другу. НЕ подключайте через эти клеммы.
ВНИМАНИЕ! Поскольку между этими двумя точками существует разность потенциалов, подключение перемычки для параллельного включения между ними приведет к короткому замыканию!
Если полярность правильная (рисунок 7a), то вольтметр показывает 0 В, потому что ЭДС противостоят друг другу.Вы можете подключить перемычку параллельно между этими двумя точками.
Рисунок 7: Проверка полярности
Удвойте выходной ток с помощью параллельных регуляторов напряжения
Для повышения эффективности в мощных приложениях можно использовать регуляторы напряжения параллельно, чтобы удвоить выходной ток – если предусмотрены средства принудительного разделения тока.
В одном схемном подходе используются резисторы считывания, включенные последовательно с нагрузкой, и он применим к регуляторам любого типа. С небольшими изменениями он может быть размещен перед регуляторами входного тока.Другой метод наиболее применим к синхронным переключателям, поскольку он требует наличия чувствительных элементов нижнего уровня, которые могут быть резисторами или полевыми транзисторами.
Бывают случаи, когда разработчикам может потребоваться параллельное включение регуляторов, чтобы удвоить ток или повысить эффективность. К ним относятся случаи, когда:
1. Кто-то хочет использовать линейный регулятор или IC-переключатель со встроенными силовыми полевыми транзисторами, но его максимальный номинальный ток превышен.
2. Повышение температуры отдельной ИС превышает допустимое значение для поверхностного монтажа.
3. Повышение эффективности оправдано снижением общей стоимости или увеличением срока службы батареи.
4. Требование к высокому выходному току требует двухфазной конструкции. Преимущества двухфазных переключателей для сильноточных приложений широко известны. Но многие двухфазные контроллеры IC не обеспечивают возможности простого параллельного вывода. Это особенно верно для контроллеров, работающих в режиме напряжения.
На рисунках 1a и 1b показаны регулируемые блоки регуляторов, подключенные параллельно. Напряжения обратной связи (FB) на Рисунке 1a относятся к Gnd, а на Рисунке 1b показаны трехконтактные устройства, у которых FB привязан к V OUT .На данном этапе обсуждения блоки регуляторов могут быть как линейными, так и переключателями.
Большинство регуляторов напряжения использовать контур обратной связи с высоким коэффициентом усиления к подчиненному V OUT к внутреннему источнику опорного напряжения, так что сигнал ошибки на обратном штифте всего нескольких милливольт приведет к изменению полномасштабного на V OUT . Отрицательная обратная связь с высоким коэффициентом усиления вынуждает V OUT быть линейной функцией от V REF и соотношения резисторов обратной связи, как определено:
(для рис.1а)
V OUT = V REF (R F2 / R F1 + 1), где V REF равно V FB (напряжение на FB) (1)
(для рис. 1b)
V OUT = V REF (R F1 / R F2 + 1), где V REF равно V OUT V FB (2)
Ошибкипостоянного тока в основном определяются точностью V REF и допусками резисторов обратной связи.Когда два одинаковых регулятора соединены параллельно, небольшая разница в V REF заставит один регулятор генерировать почти весь ток нагрузки, пока он не достигнет предела тока. Затем его V OUT будет снижаться до тех пор, пока второй регулятор с немного более низким V REF не начнет подавать оставшийся ток нагрузки. Работа таким образом может быть приемлемой, если рассеивание тепла и температура устройства остаются достаточно низкими, чтобы избежать термоциклирования.
По мере увеличения тока нагрузки и рассеяния регулятора, регуляторы должны делить ток, поэтому для этого необходимо добавить некоторые схемы.На рисунках 2a и 2b показаны резисторы R SHARE , включенные последовательно с каждым выходом для обеспечения предсказуемого распределения при максимальном токе нагрузки. R SHARE выбрано таким образом, чтобы падение напряжения на нем при полной нагрузке в несколько раз превышало максимальную разницу напряжений между регуляторами. Тогда:
V OUT = V REG1 (I REG1 × R SHARE ) = V REG2 (I REG2 × R SHARE ) (3)
Разница тока при полной нагрузке = (В REG1 V REG2 ) / R SHARE (4)
Выбрав ток разницы при полной нагрузке I OUT × 10%, определив Tolerance = T и установив максимальное (V REG1 V REG2 ) значение на 2 × T × V REG , мы получим:
R SHARE = (V REG1 V REG2 ) / (I OUT × 10%) = 20 × T × V REG / I OUT (5)
Пример 1:
Для I OUT = 2 A с использованием двух регуляторов 1-A с допуском ± 3% и V REG = 5 В, R SHARE = 10 × 0.3 В / 2 А = 1,5 Ом. Совместное использование хорошее, но падение напряжения при полной нагрузке составляет 1,5 В или 30%, что слишком много для большинства нагрузок.
При параллельном подключении регуляторов напряжения основные цели хорошего регулирования и предсказуемого распределения тока могут быть достигнуты путем добавления последовательного резистора для измерения тока в каждом канале, а также операционного усилителя для усиления и интеграции сигнала ошибки. Сигнал ошибки используется для подчинения одного канала другому путем регулировки напряжения обратной связи подчиненного устройства до тех пор, пока напряжение на каждом измерительном резисторе не станет равным.Этот метод, как показано на рисунках 3a и 3b, прост и относительно эффективен для токов от нуля до нескольких ампер. И он одинаково хорошо работает для синхронных и несинхронных переключателей и линейных регуляторов.
Выделенные серым цветом схемы на обоих рисунках состоят из резисторов считывания, R S1 , R S2 и дифференциального интегратора. Для регуляторов без возможности приема тока, которые должны работать при малой нагрузке, добавляется R OS для обеспечения небольшого смещения холостого хода интегратору.Без R OS , поскольку ток нагрузки падает настолько, чтобы напряжение на R S1 или R S2 было меньше, чем напряжение смещения операционного усилителя, напряжение ведомого устройства V REG2 может возрасти. R F3 устанавливает диапазон регулирования V REG2 . Конфигурация совместного использования, показанная на рисунке 3b, работает со всеми типами регуляторов, включая трехполюсные регуляторы.
Выбор номинала резистора считывания – это компромисс между эффективностью и повышенными затратами на определение операционного усилителя с малым смещением.Выберите U1, чтобы обеспечить низкое напряжение смещения и возможность подключения к сети. На рисунке 3a операционный усилитель может быть LMV931M5 и питаться от V OUT в диапазоне от 1,5 до 5,5 В. Или это может быть часть, подобная LM7301M5 в диапазоне V OUT от 2,2 до 30 В. Оба доступны в пакетах SOT23-5 с V OS IN, при условии, что V IN V OUT больше 1,5 В.
На рисунке 3b U1 питается от V IN и должен иметь активный входной синфазный диапазон на положительной шине, как и LMV931M5, LM7301M5, LMC7101M5 и LMC8101M5.Выберите R OS для подачи небольшого падения напряжения на входном резисторе интегратора, равного напряжению смещения операционного усилителя. Уравнения 6 и 7 используются для выбора R S для каждого регулятора на основе меньшей из максимальной мощности, которую он готов рассеять при полном токе в каждом R S . Или максимально допустимое падение напряжения на каждом R S . Уравнение 8 используется для выбора максимального напряжения смещения, допустимого для операционного усилителя, выбранного для допустимого разностного тока I OUT , ID, при полной нагрузке:
R S = 4 × (Мощность, рассеиваемая в каждом R S ) / I OUT2 (6)
R S = 2 × V RS / I OUT , где V RS – падение напряжения на каждом R S (7)
В OSmax = I D × R S /2 (8)
Минимальное значение для каждого R S основано на точности, требуемой для текущего соответствия.Максимальное значение для R S определяется либо доступным падением напряжения, либо рассеиваемой мощностью. Требуемая разность токов 10% или меньше (I D ¾ I OUTMAX /10) требует, чтобы V RS как минимум в 10 раз превышал напряжение смещения U1.
Пример 2:
Для I OUT = 2 А с использованием двух регуляторов 1 А с допуском ± 3% и V REG = 5 В, давайте выберем рассеивание R S при 100 мВт. Тогда R S = 4 × 0.1 Вт / 4 = 0,1 (омега). И, V OSmax = 2/10 × 0,1 / 2 = 10 мВ. Для схемы на Рисунке 1a выбран R OS для подачи тока, достаточного для падения 10 мВ на резисторе 1 кОм, или 10 мкА. Таким образом, его значение составляет 5 В / 10 мкА = 500 кОм. R F3 должен обеспечивать достаточно большой диапазон регулирования, чтобы заставить V REG2 выйти на полный диапазон выходного тока. Выберите его значение с выходом U1 на нуле и его током больше, чем (V OUT × 2 × допуск%) / (R F1 + R F2 ), в результате получится:
R F3 > = V FB (R F1 + R F2 ) / (2 × V OUT × допуск%), где V FB – напряжение на FB (9)
На рисунке 4 показан более подробный вид рисунка 3a с V REG1 и V REG2 , изображенными как синхронные переключатели.Поскольку синхронные переключатели потребляют и истока ток, R OS можно не использовать, а требования V OS к операционному усилителю можно снизить на 50%. Уравнение 8 принимает вид V OSmax = I D × R S .
Пример 3:
Для I OUT = 10 А с использованием двух регуляторов 5 А с допуском ± 3% и V REG = 5 В, давайте выберем рассеивание R S при 250 мОм. Тогда R S = 4 × 0,25 Вт / 100 = 10 мО и V OS max = 10/10 × 0.01 = 10 мВ. Потери можно дополнительно уменьшить в три раза, если выбрать лучший операционный усилитель, такой как LMV711M5, который имеет максимальное напряжение 3 мВ V OS , уменьшив минимальные значения R S до 3 мОм.
При более высоком токе, например, 33 А, даже 1 мВт последовательного сопротивления добавляет 1 Вт рассеиваемой мощности. В этом случае последовательные резисторы имеют тенденцию быть относительно большими и дорогими, добавляют значительные потери и вызывают нежелательное повышение температуры. При использовании полевых транзисторов нижнего плеча R DS (ON) в качестве токоизмерительных резисторов не требуется дополнительных потерь.Точность распределения тока будет несколько отличаться из-за несоответствия R DS (ON) . Но это будет в приемлемом диапазоне, если полевые транзисторы установлены на одном радиаторе или на медной поверхности печатной платы.
Измерение небольших падений напряжения на R DS (ON) нижних полевых транзисторов при наличии амплитуды сигнала переключения, которая в 100–1000 раз больше, на первый взгляд кажется трудным. Схема на Рисунке 5 показывает один из способов относительно точно сделать это с помощью недорогих деталей.Измерения не требуют абсолютной точности, поскольку в качестве сигнала ошибки используется интегральная разность напряжений.
В серой схеме измерения тока на рис. 5 используется сдвоенный операционный усилитель U1 для измерения и усиления (× 10) небольшого отрицательного напряжения, присутствующего на каждом нижнем полевом транзисторе в период его проводимости. Для этого метода измерения требуется полевой транзистор нижнего уровня, что делает его применимым к синхронным переключателям.
Диоды D1 и D2 на рис. 5 предотвращают сильное колебание сигнала в каждом узле переключения от перегрузки входов операционного усилителя.Это позволяет U1 быть низковольтным двойным усилителем с однополярным питанием. Его наиболее важные характеристики – низкое напряжение смещения и широкая полоса пропускания, поскольку он измеряет сигналы
Выбранная деталь, LMV722MM, обеспечивает полосу пропускания 10 МГц с максимальным смещением 3 мВ. Он может питаться от широкого диапазона источников, часто включая выход регулятора, если он находится в пределах необходимого диапазона питания от 2,2 до 5,5 В. В этом примере он легко запитывается от источника питания 5-вольтового драйвера затвора.
U2 используется для интегрирования разности напряжений с выходов U1 для формирования сигнала ошибки с очень высоким коэффициентом усиления по постоянному току.На рисунке 5 показан сигнал ошибки, суммированный в узле обратной связи подчиненного канала R F3 . R F3 выбирается намного больше, чем R F1 и R F2 , чтобы диапазон регулировки сигнала ошибки составлял
.Четвертый пример, который объясняет, как схема на Рисунке 5 может объединить каналы 30-А, 1,2-В в один выход 60-А, см. В разделе «Удвоение выходного тока с помощью параллельных регуляторов напряжения (часть 2)» на www. elecdesign.com , Drill Deeper 9279 ED Online 9270 .
Как я могу рассчитать падение напряжения в параллельной цепи?
Что ж, для этого вам понадобится схема, чтобы показать мне, тем не менее, я даю вам два примера того, как работать.
См. Схему ниже,
Понятно, что Омега # 2 # параллельна другой Омега # 2 #, и их результирующее соединение последовательно с # 1 Ом # и # 3 Ом #, поэтому общее сопротивление цепи равно # (2 * 2) / (2 + 2) + 1 + 3 = 5 Ом #
Итак, ток, протекающий по цепи, равен # 20/5 = 4 А #
, поэтому падение потенциала на каждом сопротивлении можно рассчитать, просто умножив их значение сопротивления на ток, протекающий через них.
таким образом #V_ (1Ohm) = 1 * 4 = 4V #
#V_ (3 Ом) = 3 * 4 = 12 В #
и, #V_ (2 || 2 Ом) = (20-12-4) = 4 В #
или, вы могли бы умножить ток, протекающий через них, на их эквивалентное сопротивление, то есть # (2 * 2) / (2 + 2) * 4 = 1 * 4 = 4V #
В приведенном ниже примере в верхнем проводе # 1 Omega # параллельно # 1Omega #, их результирующее сопротивление последовательно с # 0.5 Omega #, и эквивалентное сопротивление снова параллельно эквивалентному сопротивлению # 4 Omega. # и # 4 Омега # в параллельной комбинации.
Итак, чистое сопротивление верхнего провода составляет # (1 * 1) / (1 + 1) + 0,5 = 1 Омега #
., а нижний провод – # (4 * 4) / (4 + 4) = 2 Omega #
.Итак, сопротивление цепи равно # (1 * 2) / (1 + 2) = 2/3 Омега #
.Итак, ток, протекающий по цепи, равен # 14 / (2/3) = 21 А #
, падение напряжения на параллельной комбинации двух резисторов # 4 Omega # аналогично падению напряжения на батарее, то есть # 14 В #
на верхний провод упало такое же напряжение, поскольку оба соединены параллельно.
Итак, мы должны найти ток, протекающий через верхнюю цепь, чтобы вычислить это.
Итак, ток, протекающий по нижнему проводу, равен # 14/2 = 7A # (поскольку чистое сопротивление нижнего провода составляет # 2 Омега #
, таким образом, ток, протекающий через верхнюю цепь, равен # (21-7) = 14 A #
Итак, падение потенциала на # 0,5 Омега # составляет # 14 * 0,5 = 7 В #
Итак, остальные, то есть # (14-7) = 7 V #, должны были упасть на параллельную комбинацию резисторов # 1 Omega #.
10.3: Последовательные и параллельные резисторы
Цели обучения
К концу раздела вы сможете:
- Определите термин эквивалентное сопротивление
- Рассчитайте эквивалентное сопротивление резисторов, включенных последовательно
- Рассчитайте эквивалентное сопротивление резисторов, включенных параллельно
В статье «Ток и сопротивление» мы описали термин «сопротивление» и объяснили основную конструкцию резистора. По сути, резистор ограничивает поток заряда в цепи и представляет собой омическое устройство, где \ (V = IR \).В большинстве схем имеется более одного резистора. Если несколько резисторов соединены вместе и подключены к батарее, ток, подаваемый батареей, зависит от эквивалентного сопротивления цепи.
Эквивалентное сопротивление комбинации резисторов зависит как от их индивидуальных значений, так и от способа их подключения. Самыми простыми комбинациями резисторов являются последовательное и параллельное соединение (Рисунок \ (\ PageIndex {1} \)). В схеме серии выходной ток первого резистора течет на вход второго резистора; следовательно, ток одинаков в каждом резисторе.В параллельной схеме все выводы резистора на одной стороне резисторов соединены вместе, а все выводы на другой стороне соединены вместе. В случае параллельной конфигурации каждый резистор имеет одинаковое падение потенциала на нем, и токи через каждый резистор могут быть разными, в зависимости от резистора. Сумма отдельных токов равна току, протекающему по параллельным соединениям.
Рисунок \ (\ PageIndex {1} \): (a) При последовательном соединении резисторов ток одинаков в каждом резисторе.(b) При параллельном соединении резисторов напряжение на каждом резисторе одинаковое. Резисторысерии
Считается, что резисторывключены последовательно, если ток течет через резисторы последовательно. Рассмотрим рисунок \ (\ PageIndex {2} \), на котором показаны три последовательно включенных резистора с приложенным напряжением, равным \ (V_ {ab} \). Поскольку заряды проходят только по одному пути, ток через каждый резистор одинаков. Эквивалентное сопротивление набора резисторов при последовательном соединении равно алгебраической сумме отдельных сопротивлений.
Рисунок \ (\ PageIndex {2} \): (a) Три резистора, подключенные последовательно к источнику напряжения. (b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения. N R_i.\ label {серия эквивалентных сопротивлений} \]Одним из результатов подключения компонентов в последовательную цепь является то, что если что-то происходит с одним компонентом, это влияет на все остальные компоненты. Например, если несколько ламп подключены последовательно и одна лампа перегорела, все остальные лампы погаснут.
Пример \ (\ PageIndex {1} \): эквивалентное сопротивление, ток и мощность в последовательной цепи
Батарея с напряжением на клеммах 9 В подключена к цепи, состоящей из четырех последовательно соединенных резисторов \ (20 \, \ Omega \) и одного \ (10 \, \ Omega \) (Рисунок \ (\ PageIndex {3 } \)).Предположим, что батарея имеет незначительное внутреннее сопротивление.
- Рассчитайте эквивалентное сопротивление цепи.
- Рассчитайте ток через каждый резистор.
- Рассчитайте падение потенциала на каждом резисторе.
- Определите общую мощность, рассеиваемую резисторами, и мощность, потребляемую батареей.
Стратегия
В последовательной цепи эквивалентное сопротивление представляет собой алгебраическую сумму сопротивлений.2R \), а общая мощность, рассеиваемая резисторами, равна сумме мощности, рассеиваемой каждым резистором. Мощность, подаваемая батареей, можно найти с помощью \ (P = I \ epsilon \).
Решение
- Эквивалентное сопротивление – это алгебраическая сумма сопротивлений (Уравнение \ ref {серия эквивалентных сопротивлений}): \ [\ begin {align *} R_ {S} & = R_1 + R_2 + R_3 + R_4 + R_5 \\ [4pt ] & = 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 20 \, \ Омега + 10 \, \ Омега = 90 \, \ Омега.2 (10 \, \ Omega) = 0,1 \, W, \ nonumber \] \ [P_ {рассеивается} = 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,2 \, W + 0,1 \, W = 0,9 \, W, \ nonumber \] \ [P_ {источник} = I \ epsilon = (0,1 \, A) (9 \, V) = 0,9 \, W. \ nonumber \]
Значение
Есть несколько причин, по которым мы могли бы использовать несколько резисторов вместо одного резистора с сопротивлением, равным эквивалентному сопротивлению цепи. Возможно, резистора необходимого размера нет в наличии, или нам нужно отводить выделяемое тепло, или мы хотим минимизировать стоимость резисторов.Каждый резистор может стоить от нескольких центов до нескольких долларов, но при умножении на тысячи единиц экономия затрат может быть значительной.
Упражнение \ (\ PageIndex {1} \)
Некоторые гирлянды миниатюрных праздничных огней закорачиваются при перегорании лампочки. Устройство, вызывающее короткое замыкание, называется шунтом, который позволяет току течь по разомкнутой цепи. «Короткое замыкание» похоже на протягивание куска проволоки через компонент. Луковицы обычно сгруппированы в серию по девять луковиц.Если перегорает слишком много лампочек, в конце концов открываются шунты. Что вызывает это?
- Ответ
Эквивалентное сопротивление девяти последовательно соединенных лампочек составляет 9 R . Ток равен \ (I = V / 9 \, R \). Если одна лампочка перегорит, эквивалентное сопротивление будет 8 R , и напряжение не изменится, но ток возрастет \ ((I = V / 8 \, R \). Чем больше лампочек перегорят, ток станет равным. В конце концов, ток становится слишком большим, что приводит к сгоранию шунта.№ Р_и. \]
- Одинаковый ток протекает последовательно через каждый резистор.
- Отдельные последовательно включенные резисторы не получают полное напряжение источника, а делят его. Общее падение потенциала на последовательной конфигурации резисторов равно сумме падений потенциала на каждом резисторе.
Параллельные резисторы
На рисунке \ (\ PageIndex {4} \) показаны резисторы, включенные параллельно, подключенные к источнику напряжения. Резисторы включены параллельно, когда один конец всех резисторов соединен непрерывным проводом с незначительным сопротивлением, а другой конец всех резисторов также соединен друг с другом непрерывным проводом с незначительным сопротивлением.Падение потенциала на каждом резисторе одинаковое. Ток через каждый резистор можно найти с помощью закона Ома \ (I = V / R \), где напряжение на каждом резисторе постоянно. Например, автомобильные фары, радио и другие системы подключены параллельно, так что каждая подсистема использует полное напряжение источника и может работать полностью независимо. То же самое и с электропроводкой в вашем доме или любом здании.
Рисунок \ (\ PageIndex {4} \): Два резистора, подключенных параллельно источнику напряжения.(b) Исходная схема сокращается до эквивалентного сопротивления и источника напряжения.Ток, протекающий от источника напряжения на рисунке \ (\ PageIndex {4} \), зависит от напряжения, подаваемого источником напряжения, и эквивалентного сопротивления цепи. В этом случае ток течет от источника напряжения и попадает в переход или узел, где цепь разделяется, протекая через резисторы \ (R_1 \) и \ (R_2 \). По мере того, как заряды идут от аккумулятора, некоторые проходят через резистор \ (R_1 \), а некоторые – через резистор \ (R_2 \).Сумма токов, текущих в переход, должна быть равна сумме токов, текущих из перехода:
\ [\ sum I_ {in} = \ sum I_ {out}. \ nonumber \]
Это уравнение называется правилом соединения Кирхгофа и будет подробно обсуждено в следующем разделе. На рисунке \ (\ PageIndex {4} \) правило соединения дает \ (I = I_1 + I_2 \). В этой схеме есть два контура, которые приводят к уравнениям \ (V = I_1R_1 \) и \ (I_1R_1 = I_2R_2 \). Обратите внимание, что напряжение на резисторах, включенных параллельно, одинаковое (\ (V = V_1 = V_2 \)), а ток – аддитивный:
\ [\ begin {align *} I & = I_1 + I_2 \\ [4pt] & = \ frac {V_1} {R_1} + \ frac {V_2} {R_2} \\ [4pt] & = \ frac {V } {R_1} + \ frac {V} {R_2} \\ [4pt] & = V \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) = \ frac {V} {R_ {P}} \ end {align *} \]
Решение для \ (R_ {P} \)
\ [R_ {P} = \ left (\ frac {1} {R_1} + \ frac {1} {R_2} \ right) ^ {- 1}.{-1}. \ label {10.3} \]
Это соотношение приводит к эквивалентному сопротивлению \ (R_ {P} \), которое меньше наименьшего из отдельных сопротивлений. Когда резисторы подключены параллельно, от источника течет больше тока, чем протекает для любого из них по отдельности, поэтому общее сопротивление ниже.
Пример \ (\ PageIndex {2} \): Анализ параллельной цепи
Три резистора \ (R_1 = 1,00 \, \ Omega \), \ (R_2 = 2,00 \, \ Omega \) и \ (R_3 = 2,00 \, \ Omega \) подключены параллельно.Параллельное соединение подключается к источнику напряжения \ (V = 3,00 \, V \).
- Какое эквивалентное сопротивление?
- Найдите ток, подаваемый источником в параллельную цепь.
- Рассчитайте токи в каждом резисторе и покажите, что в сумме они равны выходному току источника.
- Рассчитайте мощность, рассеиваемую каждым резистором.
- Найдите выходную мощность источника и покажите, что она равна общей мощности, рассеиваемой резисторами.
Стратегия
(a) Общее сопротивление для параллельной комбинации резисторов определяется с помощью уравнения \ ref {10.3}. (Обратите внимание, что в этих расчетах каждый промежуточный ответ отображается с дополнительной цифрой.)
(b) Ток, подаваемый источником, можно найти из закона Ома, заменив \ (R_ {P} \) на полное сопротивление \ (I = \ frac {V} {R_ {P}} \).
(c) Отдельные токи легко вычислить по закону Ома \ (\ left (I_i = \ frac {V_i} {R_i} \ right) \), поскольку каждый резистор получает полное напряжение.{-1} = 0,50 \, \ Omega. \ Nonumber \] Общее сопротивление с правильным количеством значащих цифр равно \ (R_ {eq} = 0,50 \, \ Omega \). Как и предполагалось, \ (R_ {P} \) меньше наименьшего индивидуального сопротивления.
- Полный ток можно найти из закона Ома, заменив полное сопротивление \ (R_ {P} \). Это дает \ [I = \ frac {V} {R_ {P}} = \ frac {3.00 \, V} {0.50 \, \ Omega} = 6.00 \, A. \ nonumber \] Текущий I для каждого устройства намного больше, чем для тех же устройств, подключенных последовательно (см. предыдущий пример).Схема с параллельным соединением имеет меньшее общее сопротивление, чем резисторы, включенные последовательно.
- Отдельные токи легко вычислить по закону Ома, поскольку каждый резистор получает полное напряжение. Таким образом, \ [I_1 = \ frac {V} {R_1} = \ frac {3.00 \, V} {1.00 \, \ Omega} = 3.00 \, A. \ nonumber \] Аналогично, \ [I_2 = \ frac {V } {R_2} = \ frac {3.00 \, V} {2.00 \, \ Omega} = 1.50 \, A \ nonumber \] и \ [I_3 = \ frac {V} {R_3} = \ frac {3.00 \, V } {2.00 \, \ Omega} = 1.50 \, A. \ nonumber \] Полный ток – это сумма отдельных токов: \ [I_1 + I_2 + I_3 = 6.2} {2.00 \, \ Omega} = 4.50 \, W. \ nonumber \]
- Общую мощность также можно рассчитать несколькими способами. Выбор \ (P = IV \) и ввод общей текущей доходности \ [P = IV = (6.00 \, A) (3.00 \, V) = 18.00 \, W. \ nonumber \]
Значение
Общая мощность, рассеиваемая резисторами, также 18,00 Вт:
\ [P_1 + P_2 + P_3 = 9,00 \, W + 4,50 \, W + 4,50 \, W = 18,00 \, W. \ nonumber \]
Обратите внимание, что общая мощность, рассеиваемая резисторами, равна мощности, подаваемой источником.
Упражнение \ (\ PageIndex {2A} \)
Рассмотрим одну и ту же разность потенциалов \ ((V = 3,00 \, V) \), приложенную к одним и тем же трем последовательно включенным резисторам. Будет ли эквивалентное сопротивление последовательной цепи больше, меньше или равно трем резисторам, включенным параллельно? Будет ли ток в последовательной цепи выше, ниже или равен току, обеспечиваемому тем же напряжением, приложенным к параллельной цепи? Как мощность, рассеиваемая последовательно подключенными резисторами, будет сравниваться с мощностью, рассеиваемой параллельно резисторами?
- Решение
Эквивалент последовательной схемы будет \ (R_ {eq} = 1.00 \, \ Omega + 2.00 \, \ Omega + 2.00 \, \ Omega = 5.00 \, \ Omega \), что выше эквивалентного сопротивления параллельной цепи \ (R_ {eq} = 0.50 \, \ Omega \ ). Эквивалентное сопротивление любого количества резисторов всегда выше, чем эквивалентное сопротивление тех же резисторов, соединенных параллельно. Ток через последовательную цепь будет равен \ (I = \ frac {3.00 \, V} {5.00 \, \ Omega} = 0.60 \, A \), что меньше суммы токов через каждый резистор в параллельная цепь, \ (I = 6.00 \, А \). Это неудивительно, поскольку эквивалентное сопротивление последовательной цепи выше. Ток при последовательном соединении любого количества резисторов всегда будет ниже, чем ток при параллельном соединении тех же резисторов, поскольку эквивалентное сопротивление последовательной цепи будет выше, чем параллельной цепи. Мощность, рассеиваемая последовательно подключенными резисторами, будет равна \ (P = 1,800 \, Вт \), что ниже мощности, рассеиваемой в параллельной цепи \ (P = 18.00 \, Вт \).
Упражнение \ (\ PageIndex {2B} \)
Как бы вы использовали реку и два водопада, чтобы смоделировать параллельную конфигурацию двух резисторов? Как разрушается эта аналогия?
- Решение
Река, текущая горизонтально с постоянной скоростью, разделяется на две части и течет через два водопада. Молекулы воды аналогичны электронам в параллельных цепях. Количество молекул воды, которые текут в реке и падает, должно быть равно количеству молекул, которые текут над каждым водопадом, точно так же, как сумма тока через каждый резистор должна быть равна току, текущему в параллельном контуре.Молекулы воды в реке обладают энергией благодаря своему движению и высоте. Потенциальная энергия молекул воды в реке постоянна из-за их одинаковой высоты. Это аналогично постоянному изменению напряжения в параллельной цепи. Напряжение – это потенциальная энергия на каждом резисторе.
При рассмотрении энергии аналогия быстро разрушается. В водопаде потенциальная энергия преобразуется в кинетическую энергию молекул воды. В случае прохождения электронов через резистор падение потенциала преобразуется в тепло и свет, а не в кинетическую энергию электронов.
Суммируем основные характеристики резисторов параллельно:
- Эквивалентное сопротивление находится по формуле \ ref {10.3} и меньше любого отдельного сопротивления в комбинации.
- Падение потенциала на каждом параллельном резисторе одинаковое.
- Параллельные резисторы не получают суммарный ток каждый; они делят это. Ток, поступающий в параллельную комбинацию резисторов, равен сумме токов, протекающих через каждый резистор, включенный параллельно.
В этой главе мы представили эквивалентное сопротивление резисторов, соединенных последовательно, и резисторов, соединенных параллельно. Как вы помните, в разделе «Емкость» мы ввели эквивалентную емкость конденсаторов, соединенных последовательно и параллельно. Цепи часто содержат как конденсаторы, так и резисторы. Таблица \ (\ PageIndex {1} \) суммирует уравнения, используемые для эквивалентного сопротивления и эквивалентной емкости для последовательных и параллельных соединений.
Таблица
\ (\ PageIndex {1} \): Сводка по эквивалентному сопротивлению и емкости в последовательной и параллельной комбинациях Комбинация серий Параллельная комбинация Эквивалентная емкость \ [\ frac {1} {C_ {S}} = \ frac {1} {C_1} + \ frac {1} {C_2} + \ frac {1} {C_3} +.N R_i \ nonumber \] \ [\ frac {1} {R_ {P}} = \ frac {1} {R_1} + \ frac {1} {R_2} + \ frac {1} {R_3} +. . . \ nonumber \] Сочетания последовательного и параллельного
Более сложные соединения резисторов часто представляют собой просто комбинации последовательного и параллельного соединения. Такие комбинации обычны, особенно если учесть сопротивление проводов. В этом случае сопротивление провода включено последовательно с другими сопротивлениями, включенными параллельно.
Комбинации последовательного и параллельного соединения можно уменьшить до одного эквивалентного сопротивления, используя метод, показанный на рисунке \ (\ PageIndex {5} \).Различные части могут быть идентифицированы как последовательные или параллельные соединения, уменьшенные до их эквивалентных сопротивлений, а затем уменьшенные до тех пор, пока не останется единственное эквивалентное сопротивление. Процесс занимает больше времени, чем труден. Здесь мы отмечаем эквивалентное сопротивление как \ (R_ {eq} \).
Рисунок \ (\ PageIndex {5} \): (а) Исходная схема из четырех резисторов. (b) Шаг 1: резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, и эквивалентное сопротивление равно \ (R_ {34} = 10 \, \ Omega \). (c) Шаг 2: сокращенная схема показывает, что резисторы \ (R_2 \) и \ (R_ {34} \) включены параллельно, с эквивалентным сопротивлением \ (R_ {234} = 5 \, \ Omega \).(d) Шаг 3: сокращенная схема показывает, что \ (R_1 \) и \ (R_ {234} \) включены последовательно с эквивалентным сопротивлением \ (R_ {1234} = 12 \, \ Omega \), которое является эквивалентное сопротивление \ (R_ {eq} \). (e) Уменьшенная схема с источником напряжения \ (V = 24 \, V \) с эквивалентным сопротивлением \ (R_ {eq} = 12 \, \ Omega \). Это приводит к току \ (I = 2 \, A \) от источника напряжения.Обратите внимание, что резисторы \ (R_3 \) и \ (R_4 \) включены последовательно. Их можно объединить в одно эквивалентное сопротивление.Один из методов отслеживания процесса – включить резисторы в качестве индексов. Здесь эквивалентное сопротивление \ (R_3 \) и \ (R_4 \) равно
.\ [R_ {34} = R_3 + R_4 = 6 \, \ Omega + 4 \, \ Omega = 10 \, \ Omega. \ nonumber \]
Схема теперь сокращается до трех резисторов, как показано на рисунке \ (\ PageIndex {5c} \). Перерисовывая, мы теперь видим, что резисторы \ (R_2 \) и \ (R_ {34} \) составляют параллельную цепь. {- 1} = 5 \, \ Omega.\ nonumber \]
Этот шаг процесса сокращает схему до двух резисторов, показанных на рисунке \ (\ PageIndex {5d} \). Здесь схема сводится к двум резисторам, которые в данном случае включены последовательно. Эти два резистора можно уменьшить до эквивалентного сопротивления, которое является эквивалентным сопротивлением цепи:
\ [R_ {eq} = R_ {1234} = R_1 + R_ {234} = 7 \, \ Omega + 5 \ Omega = 12 \, \ Omega. \ nonumber \]
Основная цель этого анализа схемы достигнута, и теперь схема сводится к одному резистору и одному источнику напряжения.
Теперь мы можем проанализировать схему. Ток, обеспечиваемый источником напряжения, равен \ (I = \ frac {V} {R_ {eq}} = \ frac {24 \, V} {12 \, \ Omega} = 2 \, A \). Этот ток проходит через резистор \ (R_1 \) и обозначается как \ (I_1 \). Падение потенциала на \ (R_1 \) можно найти с помощью закона Ома:
\ [V_1 = I_1R_1 = (2 \, A) (7 \, \ Omega) = 14 \, V. \ nonumber \]
Глядя на рисунок \ (\ PageIndex {5c} \), это оставляет \ (24 \, V – 14 \, V = 10 \, V \) отбрасывать через параллельную комбинацию \ (R_2 \) и \ ( R_ {34} \).Ток через \ (R_2 \) можно найти по закону Ома:
\ [I_2 = \ frac {V_2} {R_2} = \ frac {10 \, V} {10 \, \ Omega} = 1 \, A. \ nonumber \]
Резисторы \ (R_3 \) и \ (R_4 \) включены последовательно, поэтому токи \ (I_3 \) и \ (I_4 \) равны
.\ [I_3 = I_4 = I – I_2 = 2 \, A – 1 \, A = 1 \, A. \ nonumber \]
Используя закон Ома, мы можем найти падение потенциала на двух последних резисторах. Потенциальные капли равны \ (V_3 = I_3R_3 = 6 \, V \) и \ (V_4 = I_4R_4 = 4 \, V \).2 (4 \, \ Omega) = 4 \, W, \\ [4pt] P_ {рассеивается} & = P_1 + P_2 + P_3 + P_4 = 48 \, W. \ end {align *} \]
Полная энергия постоянна в любом процессе. Следовательно, мощность, подаваемая источником напряжения, составляет
\ [\ begin {align *} P_s & = IV \\ [4pt] & = (2 \, A) (24 \, V) = 48 \, W \ end {align *} \]
Анализ мощности, подаваемой в схему, и мощности, рассеиваемой резисторами, является хорошей проверкой достоверности анализа; они должны быть равны.
Пример \ (\ PageIndex {3} \): объединение последовательных и параллельных цепей
На рисунке \ (\ PageIndex {6} \) показаны резисторы, подключенные последовательно и параллельно.Мы можем считать \ (R_1 \) сопротивлением проводов, ведущих к \ (R_2 \) и \ (R_3 \).
- Найдите эквивалентное сопротивление цепи.
- Какое падение потенциала \ (V_1 \) на резисторе \ (R_1 \)?
- Найдите ток \ (I_2 \) через резистор \ (R_2 \).
- Какую мощность рассеивает \ (R_2 \)?
Стратегия
(a) Чтобы найти эквивалентное сопротивление, сначала найдите эквивалентное сопротивление параллельного соединения \ (R_2 \) и \ (R_3 \). Затем используйте этот результат, чтобы найти эквивалентное сопротивление последовательного соединения с \ (R_1 \).
(b) Ток через \ (R_1 \) можно найти с помощью закона Ома и приложенного напряжения. Ток через \ (R_1 \) равен току от батареи. Падение потенциала \ (V_1 \) на резисторе \ (R_1 \) (которое представляет собой сопротивление в соединительных проводах) можно найти с помощью закона Ома.{-1} = 5.10 \, \ Omega. \ Nonumber \] Общее сопротивление этой комбинации является промежуточным между значениями чистой серии и чисто параллельной (\ (20.0 \, \ Omega \) и \ (0.804 \, \ Omega \) ), соответственно).
- Ток через \ (R_1 \) равен току, обеспечиваемому батареей: \ [I_1 = I = \ frac {V} {R_ {eq}} = \ frac {12.0 \, V} {5.10 \, \ Omega} = 2.35 \, A. \ nonumber \] Напряжение на \ (R_1 \) равно \ [V_1 = I_1R_1 = (2.35 \, A) (1 \, \ Omega) = 2.35 \, V. \ nonumber \] Напряжение, приложенное к \ (R_2 \) и \ (R_3 \), меньше напряжения, подаваемого батареей, на величину \ (V_1 \).Когда сопротивление провода велико, это может существенно повлиять на работу устройств, представленных \ (R_2 \) и \ (R_3 \).
- Чтобы найти ток через \ (R_2 \), мы должны сначала найти приложенное к нему напряжение. Напряжение на двух параллельных резисторах одинаково: \ [V_2 = V_3 = V – V_1 = 12.0 \, V – 2.35 \, V = 9.65 \, V. \ nonumber \] Теперь мы можем найти ток \ (I_2 \) через сопротивление \ (R_2 \) по закону Ома: \ [I_2 = \ frac {V_2} {R_2} = \ frac {9.65 \, V} {6.00 \, \ Omega} = 1.2 (6.00 \, \ Omega) = 15.5 \, W. \ nonumber \]
Значение
Анализ сложных схем часто можно упростить, сведя схему к источнику напряжения и эквивалентному сопротивлению. Даже если вся схема не может быть сведена к одному источнику напряжения и одному эквивалентному сопротивлению, части схемы могут быть уменьшены, что значительно упрощает анализ.
Упражнение \ (\ PageIndex {3} \)
Рассмотрите электрические цепи в вашем доме.Приведите по крайней мере два примера схем, которые должны использовать комбинацию последовательных и параллельных схем для эффективной работы.
- Решение
Все цепи верхнего освещения параллельны и подключены к основному питанию, поэтому при перегорании одной лампочки все верхнее освещение не гаснет. У каждого верхнего света будет по крайней мере один переключатель, включенный последовательно с источником света, так что вы можете включать и выключать его.
В холодильнике есть компрессор и лампа, которая загорается при открытии дверцы.Обычно для подключения холодильника к стене используется только один шнур. Цепь, содержащая компрессор, и цепь, содержащая цепь освещения, параллельны, но есть переключатель, включенный последовательно со светом. Термостат управляет переключателем, включенным последовательно с компрессором, чтобы контролировать температуру холодильника.
Практическое применение
Одним из следствий этого последнего примера является то, что сопротивление в проводах снижает ток и мощность, подаваемую на резистор.Если сопротивление провода относительно велико, как в изношенном (или очень длинном) удлинителе, то эти потери могут быть значительными. Если потребляется большой ток, падение IR в проводах также может быть значительным и может проявляться из-за тепла, выделяемого в шнуре.
Например, когда вы роетесь в холодильнике и включается мотор, свет холодильника на мгновение гаснет. Точно так же вы можете увидеть тусклый свет в салоне, когда вы запускаете двигатель вашего автомобиля (хотя это может быть связано с сопротивлением внутри самой батареи).
Что происходит в этих сильноточных ситуациях, показано на рисунке \ (\ PageIndex {7} \). Устройство, обозначенное символом \ (R_3 \), имеет очень низкое сопротивление, поэтому при его включении протекает большой ток. Этот увеличенный ток вызывает большее падение IR в проводах, обозначенных \ (R_1 \), уменьшая напряжение на лампочке (которое составляет \ (R_2 \)), которое затем заметно гаснет.
Рисунок \ (\ PageIndex {7} \): Почему свет тускнеет, когда включен большой прибор? Ответ заключается в том, что большой ток, потребляемый двигателем прибора, вызывает значительное падение IR в проводах и снижает напряжение на свету.Стратегия решения проблем: последовательные и параллельные резисторы
- Нарисуйте четкую принципиальную схему, пометив все резисторы и источники напряжения. Этот шаг включает список известных значений проблемы, поскольку они отмечены на вашей принципиальной схеме.
- Определите, что именно необходимо определить в проблеме (определите неизвестные). Письменный список полезен.
- Определите, включены ли резисторы последовательно, параллельно или в комбинации последовательно и параллельно.Изучите принципиальную схему, чтобы сделать эту оценку. Резисторы включены последовательно, если через них должен последовательно проходить один и тот же ток.
- Используйте соответствующий список основных функций для последовательных или параллельных подключений, чтобы найти неизвестные. Есть один список для серий, а другой – для параллелей.
- Проверьте, являются ли ответы разумными и последовательными.
Пример \ (\ PageIndex {4} \): объединение последовательных и параллельных цепей
Два резистора, соединенных последовательно \ ((R_1, \, R_2) \), соединены с двумя резисторами, включенными параллельно \ ((R_3, \, R_4) \).Последовательно-параллельная комбинация подключается к батарее. Каждый резистор имеет сопротивление 10,00 Ом. Провода, соединяющие резисторы и аккумулятор, имеют незначительное сопротивление. Через резистор \ (R_1 \) проходит ток 2,00 А. Какое напряжение подается от источника напряжения?
Стратегия
Используйте шаги предыдущей стратегии решения проблем, чтобы найти решение для этого примера.
Решение
Рисунок \ (\ PageIndex {8} \): Чтобы найти неизвестное напряжение, мы должны сначала найти эквивалентное сопротивление цепи.- Нарисуйте четкую принципиальную схему (рисунок \ (\ PageIndex {8} \)).
- Неизвестно напряжение аккумулятора. Чтобы определить напряжение, подаваемое батареей, необходимо найти эквивалентное сопротивление.
- В этой схеме мы уже знаем, что резисторы \ (R_1 \) и \ (R_2 \) включены последовательно, а резисторы \ (R_3 \) и \ (R_4 \) включены параллельно. Эквивалентное сопротивление параллельной конфигурации резисторов \ (R_3 \) и \ (R_4 \) последовательно с последовательной конфигурацией резисторов \ (R_1 \) и \ (R_2 \).{-1} = 5,00 \, \ Омега. \ nonumber \] Эта параллельная комбинация включена последовательно с двумя другими резисторами, поэтому эквивалентное сопротивление схемы равно \ (R_ {eq} = R_1 + R_2 + R_ {34} = (25.00 \, \ Omega \). поэтому напряжение, подаваемое батареей, равно \ (V = IR_ {eq} = 2.00 \, A (25.00 \, \ Omega) = 50.00 \, V \).
- Один из способов проверить соответствие ваших результатов – это рассчитать мощность, подаваемую батареей, и мощность, рассеиваемую резисторами.


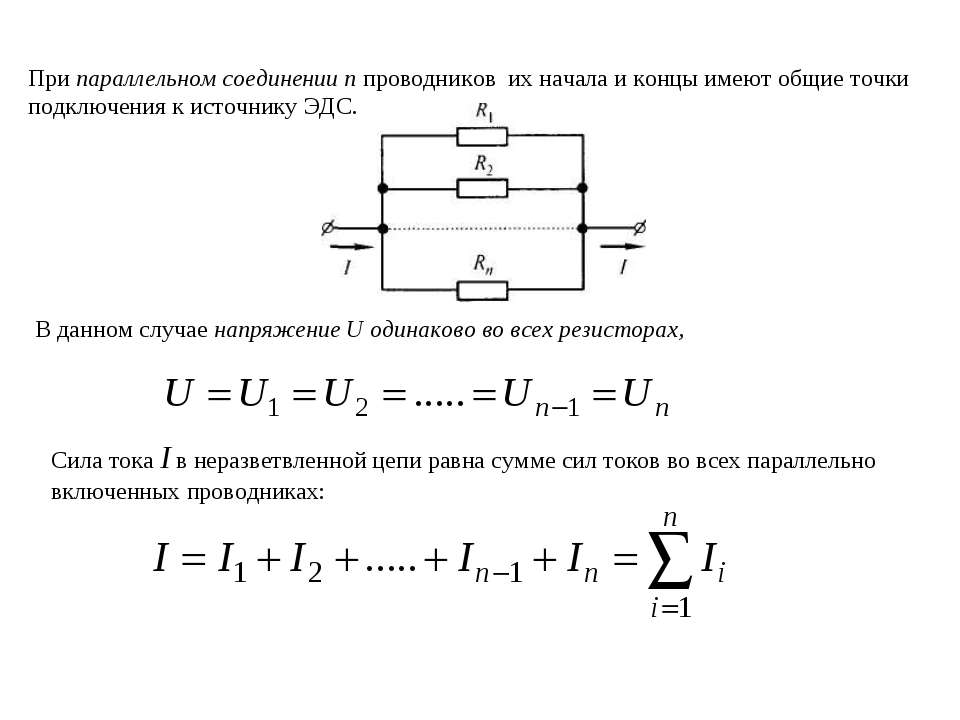 N
N ..+An+…
..+An+… 