Как определить емкость конденсатора: 4 рабочих способа
Основной характеристикой конденсатора является его емкость. Очень часто замеры емкости требуется проводить в электролитическом конденсаторе. В отличие от керамических и оксидных конденсаторов, которые редко выходят из строя (разве что в результате пробоя диэлектрика), электролитическим деталям свойственна потеря ёмкости из-за высыхания электролита. Поскольку работа электронных схем сильно зависит от емкостных характеристик, то необходимо знать, как определить емкость конденсатора.
Существуют разные способы определения ёмкости:
- по кодовой или цветной маркировке деталей;
- с помощью измерительных приборов;
- с использованием формулы.
Измерить емкость проще всего с помощью измерителя C и ESR. Для этого контакты измерительных щупов подсоединяют к выводам конденсатора, соблюдая полярность электролитических деталей. При этом результаты измерений выводятся на дисплей.
С использованием мультиметра и формул
Если в вашем распоряжении есть мультиметр с функцией измерения параметра «Cx», то измерить ёмкость конденсатора довольно просто: следует переключить прибор в режим «Сх», после чего выбрать оптимальный диапазон измерения, соответствующий параметрам конденсатора. Ножки конденсатора вставляем в соответствующее гнездо (соблюдая полярность подключения) и считываем его параметры.
Режим «Сх» в мультиметреМенее точно можно определить ёмкость с помощью тестера, у которого нет режима «Сх». Для этого потребуется источник питания, к которому подключают конденсатор по простой схеме (рис. 2).
Рис. 2. Схема подключения конденсатораАлгоритм измерения следующий:
- Измерьте напряжение источника питания щупами контактов измерительного прибора.

- Образуйте RC-цепочку с конденсатором и выводами резистора номиналом 1 – 10 кОм.
- Закоротите выводы конденсатора и подключите RC-цепочку к источнику питания.
- Замерьте напряжение образованной цепи с помощью мультиметра.
- Если напряжение изменилось, необходимо подогнать его до значения, близкого к тому, которое вы получили на выходе источника питания.
- Вычислите 95% от полученного значения. Запишите показатели измерений.
- Возьмите секундомер и включите его одновременно с убиранием закоротки.
- Как только мультиметр покажет значение напряжения, которое вы вычислили (95%), остановите секундомер.
- По формуле С = t/3R, где t – время падения напряжения, вычисляем ёмкость конденсатора в фарадах, если единицы измерения сопротивление резистора выразили в омах, а время в секундах.
Подчеркнём ещё раз, что точность измерения ёмкости данным способом не слишком высока, но определить работоспособность радиоэлемента на основании такого измерения вполне возможно. Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.
Некоторые узлы электронных приборов исправно работают, если есть небольшие отклонения от номинальных емкостей, главное, чтобы не было электрического пробоя.
Таким же методом можно вычислить параметры керамического радиоэлемента. Для этого необходимо подключить RC-цепочку через трансформатор и подать переменное напряжение. Значение ёмкости в данном случае определяем по формуле: C = 0.5*π*f*Xc , где f – частота тока, а Xc – ёмкостное сопротивление.
Осциллографом
С приемлемой точностью можно определить ёмкость конденсатора с помощью цифрового или обычного электронного осциллографа. Принцип похож на метод измерения ёмкости тестером. Разница только в том, что не потребуется секундомер, так как с высокой точностью время зарядки конденсатора отображается на экране осциллографа. Если применить генератор частоты и последовательную RC-цепочку (рис. 4), то ёмкость можно рассчитать по простой формуле: C = U R / UC* ( 1 / 2*π*f*R ).
Алгоритм вычисления простой:
- Подключите осциллограф к электрической схеме. При подключении щупов прибора к электролитам соблюдайте полярность электрического тока.
- Измерьте амплитуды напряжений на конденсаторе и на резисторе.
- Путём подстройки частоты генератора добивайтесь, чтобы значения амплитуд на обоих элементах сравнялись (хотя бы приблизительно).
- Подставьте полученные значения в формулу и вычислите ёмкость конденсатора.
При измерении ёмкостей неполярных конденсаторов часто вместо RC-цепочки собирают мостовую схему с частотным генератором (показано на рис. 5), а также другие сборки. Сопротивления резисторов подбирают в зависимости от параметров номинальных напряжений измеряемых деталей. Ёмкость вычисляют из соотношения: r4 / Cx = r2 / C0.
Рисунок 5. Мостовая схемаГальванометром
При наличии баллистического гальванометра также можно определить ёмкость конденсатора. Для этого используют формулу:
Для этого используют формулу:
C = α * Cq / U , где α – угол отклонения гальванометра, Cq – баллистическая постоянная прибора, U – показания гальванометра.
Из-за падения сопротивления утечки ёмкость конденсаторов уменьшается. Энергия теряется вместе с током утечки.
Описанные выше методики определения ёмкости позволяют определить исправность конденсаторов. Значительное отклонение от номиналов говорит, что конденсаторы неисправны. Пробитый электролитический радиоэлемент легко определяется путём измерения сопротивления. Если сопротивление стремится к 0 – изделие закорочено, а если к бесконечности – значит, есть обрыв.
Следует опасаться сильного электрического разряда при подключениях щупов к большим электролитам. Они могут накапливать мощный электрический заряд от постоянного тока, который молниеносно высвобождается током разряда.
По маркировке
Напомним, что единицей емкости в системе СИ является фарада ( обозначается F или Ф).
- миллифарады (mF, мФ ) = 10
- микрофарады (µF, uF, mF, мкФ) = 10-3 мФ = 10-6 Ф;
- нанофарады (nF, нФ) = 10-3 мкФ =10-9 Ф;
- пикофарады (pF, mmF, uuF) = 1 пФ = 10-3 нФ = 10-12 Ф.
Мы перечислили название единиц и их сокращённое обозначение потому, что они часто встречаются в маркировке крупных конденсаторов (см. рис. 6).
Рис. 6. Маркировка крупных конденсаторовОбратите внимание на маркировку плоского конденсатора (второй сверху): после трёхзначной цифры стоит буква М. Данная буква не обозначает единицы измерения «мегафарад» – таких просто не существует. Буквами обозначены допуски, то есть, процент отклонения от ёмкости, обозначенной на корпусе. В нашем случае отклонение составляет 20% в любую сторону.
Теперь расшифруем надпись на корпусе третьего изделия. 118 – 130 MFD обозначает, что перед нами конденсатор, ёмкость которого находится в пределах 118 – 130 микрофарад. В данном примере буква М уже обозначает «микро». FD – обозначает «фарады», сокращение английского слова «farad».
На этом простом примере видно, какая большая путаница в маркировке. Особенно запутана кодовая маркировка, применяемая для крохотных конденсаторов. Дело в том, что можно встретить конденсаторы, маркировка которых выполнена старым способом и детали с современной кодировкой, в соответствии со стандартом EIA. Одни и те же символы можно по-разному интерпретировать.
По стандарту EIA:
- Две цифры и одна буква. Цифры обозначают ёмкость, обычно в пикофарадах, а буква – допуски.
- Если буква стоит на первом или втором месте, то она обозначает либо десятичную запятую (символ R), либо указывает на название единицы измерения («p» – пикофарад, «n» – нанофарад, «u» – микрофарад).

- Маркировка тремя цифрами. В данном коде обращайте внимание на третью цифру. Если её значение от 0 до 6, то умножайте первые две на 10 в соответствующей степени. При этом 100 =1; 101 = 10; 102 = 100 и т. д. до 106.
Цифры от 7 до 9 указывают на показатель степени со знаком «минус»: 7 условно = 10-3; 8 = 10-2; 9 = 10-1.
Пример:
- 256 обозначает: 25× 105 = 2500 000 пФ = 2,5 мкФ;
- 507 обозначает: 50 × 10-3 = 50 000 пФ = 0, 05 мкФ.
Возможна и такая надпись: «1B253». При расшифровке необходимо разбить код на две части – «1B» (значение напряжения) и 253 = 25 × 10 3 = 25 000 пФ = 0,025 мкФ.
В кодовой маркировке используются прописные буквы латинского алфавита, указывающие допуски. Один пример мы рассмотрели, анализируя маркировку на рис. 6.
Приводим полный список символов:
- B = ± 0,1 пФ;
- C = ± 0,25 пФ;
- D = ± 0,5 пФ или ± 0,5% (если емкость превышает 10 пФ).

- F = ± 1 пФ или ± 1% (если емкость превышает 10 пФ).
- G = ± 2 пФ или ± 2% (для конденсаторов от 10 пФ»).
- J = ± 5%.
- K = ± 10%.
- M = ± 20%.
- Z = от –20% до + 80%.
Изделия с кодовой маркировкой изображены на рис. 7.
Рис. 7. Пример кодовой маркировкиЕсли в кодировке отсутствует символ из приведённого выше списка, а стоит другая буква, то она может единицу измерения емкости.
Важным параметром является его рабочее напряжение конденсатора. Но так как в данной статье мы ставим задачу по определению ёмкости, то пропустим описание маркировки напряжений.
Отличить электролитический конденсатор от неполярного можно по наличию символа «+» или «–» на его корпусе.
Цветовая маркировка
Описывать значение каждого цвета не имеет смысла, так как это понятно из следующей таблицы (рис. 8):
Рис. 8. Цветовая маркировкаЗапомнить символику кодовой и цветовой маркировки довольно трудно. Если вам не приходится постоянно заниматься подбором конденсаторов, то проще пользоваться справочниками или обратиться к информации, изложенной в данной статье.
Видео в помощь
Электрическая емкость. Конденсаторы. | |
Емкость уединенного проводника. Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. эта величина не зависит ни от заряда, ни от потенциала и определяется только размерами шара (радиусом) и диэлектрической проницаемостью среды. Этот вывод справедлив для проводника любой формы. |
|
Электрической емкостью проводника наз. отношение заряда проводника к его потенциалу: . | |
Емкость определяется геометрической формой, размерами проводника и свойствами среды (от материала проводника не зависит). Чем больше емкость проводника, тем меньше меняется потенциал при изменении заряда. | Емкость шара в СИ: – |
Единицы емкости. Емкостью 1Ф (фарад) обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл. Емкостью 1Ф обладал бы уединенный шар, радиус которого был бы равен 13 радиусам Солнца. Емкость Земли 700 мкФ Если проводник не уединенный, то потенциалы складываются по правилу суперпозиции и емкость проводника меняется. | 1 мкФ=10-6Ф 1нФ=10-9Ф 1пФ=10-12Ф |
Конденсаторы (condensare – сгущение) . Можно создать систему проводников, емкость которой не зависит от окружающих тел. Первые конденсаторы – лейденская банка (Мушенбрук, сер. XVII в.). |
|
Конденсатор представляет собой систему из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники наз. обкладками конденсатора. Если заряды пластин конденсатора одинаковы по модулю и противоположны по знаку, то под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. | |
На рисунке – плоский и сферический конденсаторы. Поле плоского конденсатора почти все сосредоточено внутри (у идеального – все). Усферического – все поле сосредоточено между обкладками. |
|
Электроемкостью конденсатора называют отношение заряда конденсатора к разности потенциалов между обкладками: . | |
При подключении конденсатора к батарее аккумуляторов происходит поляризация диэлектрика внутри конденсатора и на обкладках появляютсязаряды – конденсатор заряжается. |
|
Емкость плоского конденсатора. , т.о. емкость плоского конденсатора зависит только от его размеров, формы и диэлектрической проницаемости. Для создания конденсатора большой емкости необходимо увеличить площадь пластин и уменьшить толщину слоя диэлектрика. | |
Емкость сферического конденсатора . Если зазор между обкладками мал по сравнению с радиусами, то формула переходит в формулу емкости плоского конденсатора. | |
Виды конденсаторов | |
При подключении электролитического конденсатора необходимо соблюдать полярность. | |
Назначение конденсаторов
|
|
Формула емкости конденсатора, С
Если q – величина заряда одной из обкладок конденсатора, а – разность потенциалов между его обкладками, то величина C, равная:
называется емкостью конденсатора. Это постоянная величина, которая зависит то размеров и устройства конденсатора.
Рассмотрим два одинаковых конденсатора, разница между которым заключается только в том, что между обкладками одного вакуум (или часто говорят воздух), между обкладками другого находится диэлектрик. В таком случае при равных зарядах на конденсаторах разность потенциалов воздушного конденсатора будет в раз меньше, чем между обкладками второго. Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
Значит емкость конденсатора с диэлектриком (C) в раз больше, чем воздушного ():
где – диэлектрическая проницаемость диэлектрика.
За единицу емкости конденсатора принимают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) служит фарад (Ф).
Формула электрической емкости плоского конденсатора
Поле между обкладками плоского конденсатора обычно считают однородным. Его однородность нарушается только около краев. При вычислении емкости плоского конденсатора этими краевыми эффектами часто пренебрегают. Это следует делать, если расстояние между пластинами мало в сравнении с их линейными размерами. Для расчета емкости плоского конденсатора применяют формулу:
где – электрическая постоянная; S – площадь каждой (или наименьшей) пластины; d – расстояние между пластинами.
Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:
Формула электрической емкости цилиндрического конденсатора
Цилиндрический конденсатор представляется собой две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость цилиндрического конденсатора вычисляется как:
где l – высота цилиндров; – радиус внешней обкладки; – радиус внутренней обкладки.
Формула электрической емкости сферического конденсатора
Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:
где – радиусы обкладок конденсатора.
Примеры решения задач по теме «Емкость конденсатора»
Емкость конденсатора, теория и примеры задач
Емкость в Международной системе единиц (СИ) измеряется в фарадах (Ф). Фарад – это большая емкость, поэтому на практике часто применяют пико фарады (пФ), нано фарады (нФ), микро фарады (мкФ).
Фарад – это большая емкость, поэтому на практике часто применяют пико фарады (пФ), нано фарады (нФ), микро фарады (мкФ).
Емкость плоского конденсатора
Получим формулу для расчета ёмкости плоского конденсатора, который состоит из двух параллельных проводящих пластин, площадь которых равна S (каждая). Пластины расположены на расстоянии d друг от друга. Одна пластина имеет заряд а другая . Будем считать, что расстояние между пластинами конденсатора много меньше, чем их линейные размеры. В таком случае краевые эффекты можно не принимать в расчет и электрическое поле между обкладками будем считать однородным. Поле (E), которое создают две бесконечные плоскости, несущие одинаковый по модулю и противоположный по знаку заряд, разделенные диэлектриком с диэлектрической проницаемостью , можно определить при помощи формулы:
где — плотность распределения заряда по поверхности пластины. В таком случае, разность потенциалов между рассматриваемыми обкладками конденсатора, находящимися на расстоянии d будет равна:
Подставим правую часть выражения (3) вместо разности потенциалов в (1) и учитывая, что , получаем:
Емкости цилиндрического и сферического конденсаторов получают по аналогичной схеме.
Емкости цилиндрического и сферического конденсаторов
Цилиндрическим называют конденсатор, который представляет собой две соосные цилиндрические поверхности из проводника, разного радиуса, пространство между которыми заполнено диэлектриком. Емкость такого конденсатора находят как:
где l – высота цилиндров; – радиус внешнего цилиндра; – радиус внутреннего цилиндра. По формуле (5) вычисляют емкость коаксиального кабеля.
Сферическим конденсатором является конденсатор, обкладки которого две концентрические сферические поверхности из проводника, пространство между ними заполняет диэлектрик. Емкость сферического конденсатора определяют как:
где – радиусы обкладок конденсатора.
Примеры решения задач
По какой формуле найти ёмкость (объем) конденсаторов
Во всех электронных устройствах используются конденсаторы. При их конструировании или изготовлении своими руками параметры устройств рассчитываются по специальным формулам.
Конденсаторы
Расчёт конденсаторов
Один из главных параметров таких устройств – ёмкость. Рассчитать её можно по следующей формуле:
C=q/U, где:
- C – ёмкость,
- q – заряд одной из обкладок элемента,
- U – разность потенциалов между обкладками.
В электротехнике вместо понятия «разность потенциалов между обкладками» используется «напряжение на конденсаторе».
Ёмкость элемента не зависит от конструкции и размеров устройства, а только от напряжения на нём и заряда обкладок. Но эти параметры могут изменяться в зависимости от расстояния между ними и материала диэлектрика. Это учитывается в формуле:
С=Co*ε, где:
- С – реальная ёмкость,
- Со – идеальная, при условии, что между пластинами вакуум или воздух,
- ε – диэлектрическая проницаемость материала между ними.
Например, если в качестве диэлектрика используется слюда, «ε» которой 6, то ёмкость такого устройства в 6 раз больше, чем воздушного, а при изменении количества диэлектрика меняются параметры конструкции. На этом принципе основана работа ёмкостного датчика положения.
На этом принципе основана работа ёмкостного датчика положения.
Устройство конденсатора
Единицей ёмкости в системе СИ является 1 фарад (F). Это большая величина, поэтому чаще применяются микрофарады (1000000mkF=1F) и пикофарады (1000000pF=1mkF).
Расчет плоской конструкции
Если нужно рассчитать плоский конденсатор, то необходимо учесть площадь обкладок и расстояние между ними. Это отражено в формуле, по которой рассчитывается ёмкость плоского конденсатора:
C=ε/d, где:
- ε – диэлектрическая проницаемость изолирующего материала,
- d – расстояние между пластинами.
Расчет конструкции цилиндрической формы
Цилиндрический конденсатор – это две соосные трубки различного диаметра, вставленные друг в друга. Между ними находится диэлектрик. При радиусе цилиндров, близком друг к другу и намного большем, чем расстояние между ними, цилиндрической формой можно пренебречь и свести расчёт к формуле, аналогичной той, по которой рассчитывается плоский конденсатор.
Вычисляются параметры такого устройства по формуле:
C=(2π*l*R*ε)/d, где:
- l – длина устройства,
- R – радиус цилиндра,
- ε – диэлектрическая проницаемость изолятора,
- d – его толщина.
Расчёт сферической конструкции
Есть устройства, обкладки которых представляют собой два шара, вложенные друг в друга. Формула ёмкости такого прибора:
C=(4π*l*R1*R2*ε)/(R2-R1), где:
- R1 – радиус внутренней сферы,
- R2 – радиус внешней сферы,
- ε – диэлектрическая проницаемость.
Формулы ёмкости конденсаторов различной формы
Ёмкость одиночного проводника
Кроме конденсаторов, способностью накапливать заряд обладают отдельные проводники. Одиночным проводником считается такой проводник, который бесконечно далёк от других проводников. Параметры заряженного элемента рассчитывается по формуле:
C=Q/φ, где:
- Q – заряд,
- φ – потенциал проводника.
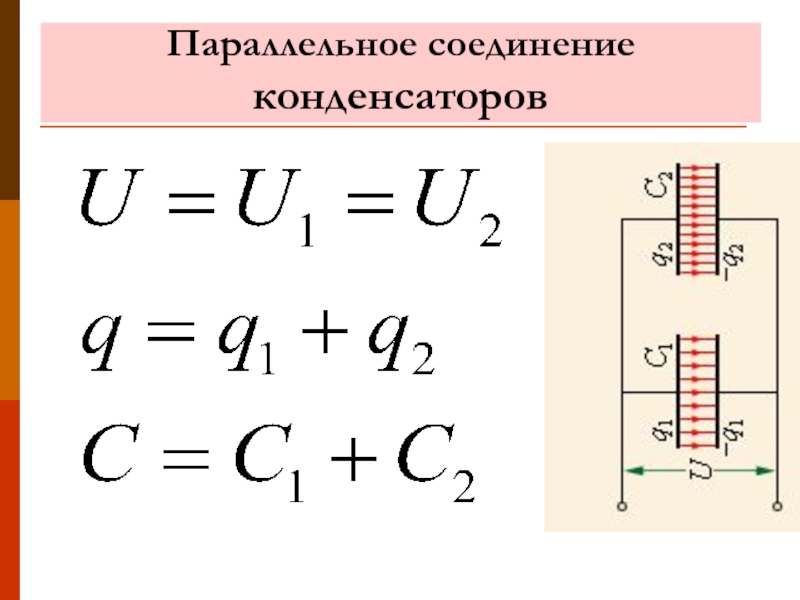
Объём заряда определяется размером и формой устройства, а также окружающей средой. Материал прибора значения не имеет.
Способы соединения элементов
Не всегда есть в наличии элементы с необходимыми параметрами. Приходится соединять их различными способами.
Соединение конденсаторов
Параллельное соединение
Это такое соединение деталей, при котором к одной клемме или контакту присоединяются первые обкладки каждого конденсатора. При этом вторые обкладки присоединяются к другой клемме.
При таком соединении напряжение на контактах всех элементов будет одинаковым. Заряд каждого из них происходит независимо от остальных, поэтому общая ёмкость равна сумме всех величин. Её находят по формуле:
C=C1+C2+…Cn,
где C1-Cn – параметры деталей, участвующих в параллельном соединении.
Важно! Конденсаторы имеют предельное допустимое напряжение, превышение которого приведёт к выходу элемента из строя. При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.
При параллельном соединении устройств с различным допустимым напряжением этот параметр получившейся сборки равен элементу с наименьшим значением.
Последовательное соединение
Это такое соединение, при котором к клемме присоединяется только одна пластина первого элемента. Вторая пластина присоединяется к первой пластине второго элемента, вторая пластина второго – к первой пластине третьего и так далее. Ко второй клемме присоединяется только вторая обкладка последнего элемента.
При таком соединении заряд на обкладках конденсатора в каждом приборе будет равен остальным, однако напряжение на них будет разным: для зарядки устройств большей ёмкости тем же зарядом требуется меньшая разность потенциалов. Поэтому вся цепочка представляет собой одну конструкцию, разность потенциалов которой равна сумме напряжений на всех элементах, а заряд конденсатора равен сумме зарядов.
Последовательное соединение увеличивает допустимое напряжение и уменьшает общую ёмкость, которая меньше самого меньшего элемента.
Рассчитываются эти параметры следующим образом:
- Допустимое напряжение:
Uобщ=U1+U2+U3+…Un, где U1-Un – напряжение на конденсаторе;
- Общая ёмкость:
1/Собщ=1/С1+1/С2+1/С3+…1/Сn, где С1-Сn – параметры каждого устройства.
Интересно. Если в цепи только два элемента, то можно воспользоваться упрощённой формулой: Собщ=(С1*С2)/(С1+С2).
Смешанное соединение
Это такое соединение, в котором есть детали, соединённые последовательно, и есть соединённые параллельно. Параметры всей цепи рассчитывается в следующей последовательности:
- определяются группы элементов, соединённые параллельно;
- для каждой группы в отдельности рассчитывается эквивалентные значения;
- рядом с каждой группой параллельно соединённых деталей пишутся получившиеся величины;
- получившаяся схема эквивалентна последовательной схеме и рассчитывается по соответствующим формулам.

Знание формул, по которым можно найти емкость при изготовлении конденсаторов или их соединении необходимо при конструировании электронных схем.
Видео
Оцените статью:Как определить емкость конденсатора – Стройпортал Biokamin-Doma.ru
Иногда, когда на конденсаторе отсутствует маркировка или нет доверия к указанным на его корпусе параметрам, требуется как-то узнать реальную емкость. Но как это сделать, не имея специального оборудования?
Безусловно, если под рукой есть мультиметр с возможностью измерения емкости или C-метр с подходящим диапазоном измерения емкостей, то проблема перестает быть таковой. Но что же делать, если в наличии только простой бытовой мультиметр и какой-нибудь блок питания, а измерить емкость конденсатора необходимо здесь и сейчас? На помощь в этом случае придут известные законы физики, которые позволят с достаточной степенью точности измерить емкость.
Рассмотрим сначала простой способ измерения емкости электролитического конденсатора подручными средствами. Как известно, при заряде конденсатора от источника постоянного напряжения через резистор, имеет место закономерность, по которой напряжение на конденсаторе станет экспоненциально приближаться к напряжению источника, и в пределе когда-нибудь, наконец, его достигнет.
Но чтобы долго не ждать, можно задачу себе упростить. Известно, что за время, равное 3*RC, напряжение на конденсаторе в процессе зарядки достигнет 95% напряжения, приложенного к RC-цепочке. Значит, зная напряжение блока питания, номинал резистора, и вооружившись секундомером, можно легко измерить постоянную времени, а точнее — троекратную постоянную времени для большей точности, и вычислить затем емкость конденсатора по известной формуле.
Для примера рассмотрим далее эксперимент. Допустим, есть у нас электролитический конденсатор, на котором присутствует какая-то маркировка, но мы ей не особо доверяем, так как конденсатор давно валялся в закромах, и мало ли высох, в общем нужно измерить его емкость. Например, на конденсаторе написано 6800мкф 50в, но нужно узнать точно.
Например, на конденсаторе написано 6800мкф 50в, но нужно узнать точно.
Шаг №1. Берем резистор номиналом 10кОм, измеряем его сопротивление мультиметром, поскольку своему мультиметру в этом эксперименте мы будем изначально доверять. Например, получилось сопротивление 9840 Ом.
Шаг №2. Включаем блок питания. Поскольку мультиметру мы доверяем больше, чем калибровке шкалы (если таковая имеется) блока питания, переводим мультиметр в режим измерения постоянного напряжения, и подключаем его к выводам блока питания. Выставляем напряжение блока питания на 12 вольт, чтобы мультиметр точно показал 12,00 В. Если напряжение блока питания не регулируется, то просто замеряем его и записываем.
Шаг №3. Собираем RC-цепочку из резистора и конденсатора, емкость которого нужно измерить. Конденсатор закорачиваем на время так, чтобы его легко можно было раскоротить.
Шаг №4. Подключаем RC-цепочку к блоку питания. Конденсатор все еще закорочен. Измеряем мультиметром еще раз напряжение, подаваемое на RC-цепочку, и фиксируем это значение для верности на бумаге. К примеру, оно так и осталось 12,00 В, или таким же, каким было в начале.
К примеру, оно так и осталось 12,00 В, или таким же, каким было в начале.
Шаг №5. Вычисляем 95% от этого напряжения, например если 12 вольт, то 95% — это 11,4 вольта. Теперь мы знаем, что за время, равное 3*RC, конденсатор зарядится до 11,4 В.
Шаг №6. Берем в руки секундомер, и раскорачиваем конденсатор, начинаем одновременно отсчет времени. Фиксируем время, за которое напряжение на конденсаторе достигло 11,4 В, это и будет 3*RC.
Шаг №7. Производим вычисления. Получившееся время в секундах делим на сопротивление резистора в омах, и на 3. Получаем значение емкости конденсатора в фарадах.
Например: время получилось 220 секунд (3 минуты и 40 секунд). Делим 220 на 3 и на 9840, получаем емкость в фарадах. В нашем примере получилось 0,007452 Ф, то есть 7452 мкф, а на конденсаторе написано 6800 мкф. Таким образом, в допустимые 20% отклонение емкости уложилось, поскольку составило примерно 9,6%.
Но как быть с неполярными конденсаторами малых емкостей? Если конденсатор керамический или полипропиленовый, то здесь поможет переменный ток и знание о емкостном сопротивлении.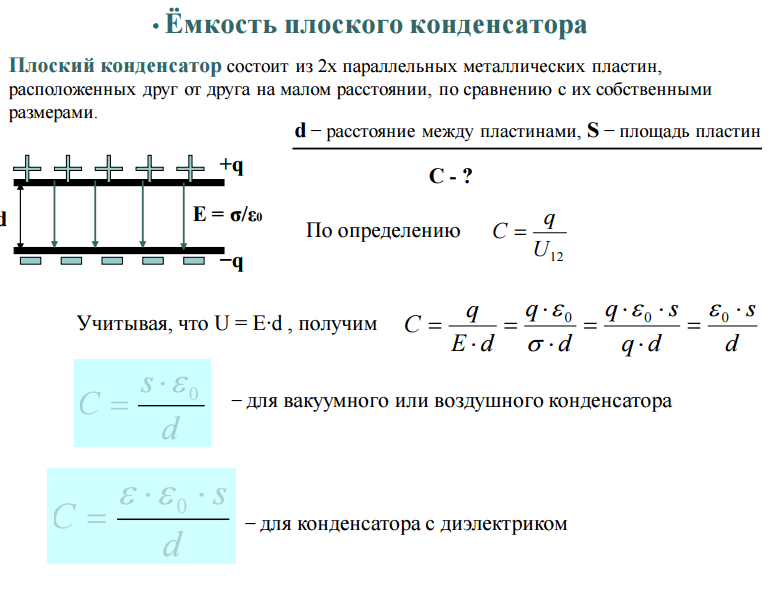
К примеру, есть конденсатор, емкость его предположительно несколько нанофарад, и известно, что в цепи переменного тока работать он может. Для выполнения измерений потребуется сетевой трансформатор со вторичной обмоткой, скажем, на 12 вольт, мультиметр, и все тот же резистор на 10 кОм.
Шаг №1. Собираем RC-цепь, и подключаем ее ко вторичной обмотке трансформатора. Затем включаем трансформатор в сеть.
Шаг №2. Измеряем мультиметром переменное напряжение на конденсаторе, затем — на резисторе.
Шаг №3. Производим вычисления. Сначала вычисляем ток через резистор, — делим напряжение на нем на значение его сопротивление. Поскольку цепь последовательная, то переменный ток через конденсатор точно такой же величины. Делим напряжение на конденсаторе на ток через резистор (ток через конденсатор такой же), получаем значение емкостного сопротивления Хс. Зная емкостное сопротивление и частоту тока (50 Гц), вычисляем емкость нашего конденсатора.
Например: на резисторе 7 вольт, а на конденсаторе 5 вольт. Мы посчитали, что ток через резистор в этом случае 700 мкА, следовательно и через конденсатор — такой же. Значит емкостное сопротивление конденсатора на частоте 50 Гц составляет 5/0,0007 = 7142,8 Ом. Емкостное сопротивление Xc = 1/6,28fC, следовательно C = 445 нф, то есть номинал 470 нф.
Мы посчитали, что ток через резистор в этом случае 700 мкА, следовательно и через конденсатор — такой же. Значит емкостное сопротивление конденсатора на частоте 50 Гц составляет 5/0,0007 = 7142,8 Ом. Емкостное сопротивление Xc = 1/6,28fC, следовательно C = 445 нф, то есть номинал 470 нф.
Описанные здесь способы являются весьма грубыми, поэтому применять их можно только тогда, когда других вариантов просто нет. В иных случаях лучше пользоваться специальными измерительными приборами.
Способы определения емкости конденсатора
Использование режима «Cx»
После того, как контакты закоротили, можно осуществлять определение сопротивления. Если элемент исправлен, то сразу после подключения он начнет заряжаться постоянным током. В этом случае сопротивление отобразиться минимальное и будет продолжать расти.
В случае если конденсатор неисправен, то мультиметр будет сразу указывать бесконечность или будет указывать нулевое сопротивление и при этом пищать. Такая проверка осуществляется, если конструкция полярная.
Для того чтобы узнать емкость необходимо иметь мультиметр с функцией измерения параметра «Сх».
Определить емкость с помощью такого мультиметра просто: установить его в режим «Сх» и указать минимальный предел измерения, которым должен обладать данный конденсатор. В таких мультиметрах есть специальные гнезда с определенными пределами измерения. В эти гнезда вставляется конденсатор согласно его пределу измерения и происходит определение его параметров.
Если в тестере таких гнезд нет, то определить емкость можно с помощью измерительных щупов, как показано на фото ниже:
Важно! В отдельной статье мы рассказывали о том, как проверить исправность конденсатора. Рекомендуем также ознакомиться с этим материалом!
Применение формул
Что делать, если под рукой нет такого мультиметра с гнездами измерения, а есть только обычный бытовой прибор? В таком случае необходимо вспомнить законы физики, которые помогут определить емкость.
Для начала вспомним, что в случае, когда конденсатор заряжается от источника неизменного напряжения через резистор, то существует закономерность, согласно которой напряжение на устройстве будет подходить к напряжению источника и в конечном итоге сравняется с ним.
Но для того чтобы этого не ожидать, можно процесс упростить. Например, за определенное время, которое равняется 3*RC, во время заряжения элемент достигает напряжения 95% примененного к RC цепи. Таким образом, по току и напряжению можно определить константу времени. А правильнее, если знать вольтаж в блоке питания, номинал самого резистора, происходит определение постоянной времени, а затем и емкости устройства.
Например, есть электролитический конденсатор, узнать емкость которого можно по маркировке, где прописывается 6800 мкф 50в. Но что если устройство давно лежало без дела, а по надписи сложно определить его рабочее состояние? В этом случае лучше проверить его емкость, чтобы знать наверняка.
Для этого необходимо выполнить следующее:
- С помощью мультиметра измерить сопротивление резистора в 10 кОм. Например, оно получилось равно 9880 Ом.
- Подключаем блок питания. Мультиметр переводим в режим замера постоянного напряжения. Затем подключаем его к блоку питания (через его выводы).
 После этого в блоке устанавливается 12 вольт (на мультиметре должна появиться цифра 12,00 В). Если же не удалось отрегулировать напряжение в блоке питание, то тогда записываем те результаты, которые получились.
После этого в блоке устанавливается 12 вольт (на мультиметре должна появиться цифра 12,00 В). Если же не удалось отрегулировать напряжение в блоке питание, то тогда записываем те результаты, которые получились. - С помощью конденсатора и резистора собираем электрическую RC-цепь. На схеме ниже указана простая RC-цепочка:
- Закоротить конденсатор и подключить цепь к питанию. С помощью прибора еще раз определить напряжение, которое подается на цепь, и записать это значение.
- Затем необходимо высчитать 95% от полученного значения. К примеру, если это 12 Вольт, то это будет 11,4 В. То есть, за определенное время, которое равняется 3*RC, конденсатор получит напряжение в 11,4 В. Формула выглядит следующим образом:
- Осталось определить время. Для этого устройство раскорачиваем и с помощью секундомера производим отсчет. Определение 3*RC будет вычисляться таким образом: как только напряжение на устройстве будет равно 11,4 В, то это и будет означать нужное время.
- Производим определение.
 Для этого полученное время (в секундах) делим на сопротивление в резисторе и на три. Например, получилось 210 секунд. Эту цифру делим на 9880 и на 3. Получилось значение 0,007085. Это величина указывается в фарадах, или 7085 мкф. Допустимое отклонение может быть не более 20%. Если учитывать, что на изделии указано 6800 мкф, наши расчеты подтверждаются и укладываются в норматив.
Для этого полученное время (в секундах) делим на сопротивление в резисторе и на три. Например, получилось 210 секунд. Эту цифру делим на 9880 и на 3. Получилось значение 0,007085. Это величина указывается в фарадах, или 7085 мкф. Допустимое отклонение может быть не более 20%. Если учитывать, что на изделии указано 6800 мкф, наши расчеты подтверждаются и укладываются в норматив.
А как определить емкость керамического конденсатора? В этом случае можно сделать определение с помощью сетевого трансформатора. Для этого RC-цепочку подсоединяем ко вторичной обмотке трансформатора, и его подсоединяют в сеть. Далее с помощью мультиметра осуществляется замер напряжения на конденсаторе и на резисторе. После этого необходимо сделать подсчеты: высчитывается ток, что проходит через резистор, затем его напряжение делится на сопротивление. Получается емкостное сопротивление Хс.
Если есть частота тока и Хс, можно определить емкость по формуле:
Другие методики
Также емкость можно определить и с помощью баллистического гальванометра. Для этого используется формула:
Для этого используется формула:
- Cq — баллистическая постоянная гальванометра;
- U2 — показания вольтметра;
- a2 — угол отклонения гальванометра.
Определение значения методом амперметра вольтметра осуществляется следующим образом: измеряется напряжение и ток в цепи, после чего значение емкости определяется по формуле:
Напряжение при таком методе определения должно быть синусоидальным.
Измерение значения возможно и при помощи мостиковой схемы. В этом случае схема моста переменного тока указывается ниже:
Здесь одно плечо моста образуется за счет элемента, который необходимо измерить (Cx). Следующее плечо состоит из конденсатора без потерь и магазина сопротивлений. Оставшиеся два плеча состоят из магазинов сопротивлений. Подключаем в одну диагональ источник питания, в другую – нулевой индикатор. И рассчитываем значение по формуле:
Напоследок рекомендуем просмотреть полезное видео по теме:
Это все, что мы хотели рассказать вам о том, как определить емкость конденсатора мультиметром. Надеемся, предоставленная информация была для вас полезной и интересной!
Надеемся, предоставленная информация была для вас полезной и интересной!
Наверняка вы не знаете:
Как измерить емкость конденсатора своими руками
Конденсатор — элемент электрической цепи, состоящий из проводящих электродов (обкладок), разделённых диэлектриком. Предназначен для использования его электрической ёмкости. Конденсатор, ёмкостью С, к которому приложено напряжение U, накапливает заряд Q на одной стороне и — Q — на другой. Ёмкость здесь в фарадах, напряжение — вольтах, заряд — кулоны. Когда ток силой 1 А протекает через конденсатор ёмкостью 1 Ф напряжение изменяется на 1 В за 1 с.
Одна фарада ёмкость огромная, поэтому обычно применяются микрофарады (мкФ) или пикофарады (пФ). 1Ф = 106 мкФ = 109 нФ = 1012 пФ. На практике используются значения от нескольких пикофарад до десятков тысяч микрофарад. Зарядный ток конденсатора отличается от тока через резистор. Он зависит не от величины напряжения, а от скорости изменения последнего. По этой причине для измерения ёмкости требуются специальные схемные решения, применительно к особенностям конденсатора.
По этой причине для измерения ёмкости требуются специальные схемные решения, применительно к особенностям конденсатора.
Обозначения на конденсаторах
Проще всего определить значение ёмкости по маркировке, нанесённой на корпус конденсатора.
Электролитический (оксидный) полярный конденсатор, ёмкостью 22000 мкФ, рассчитанный на номинальное напряжение 50 В постоянного тока. Встречается обозначение WV — рабочее напряжение. В маркировке неполярного конденсатора обязательно указывается возможность работы в цепях переменного тока высокого напряжения (220 VAC).
Плёночный конденсатор ёмкостью 330000 пФ (0.33 мкФ). Значение в этом случае, определяется последней цифрой трёхзначного числа, обозначающей количество нолей. Далее буквой указана допустимая погрешность, здесь — 5 %. Третьей цифрой может быть 8 или 9. Тогда первые две умножаются на 0.01 или 0.1 соответственно.
Ёмкости до 100 пФ маркируются, за редкими исключениями, соответствующим числом. Этого достаточно для получения данных об изделии, так маркируется подавляющее число конденсаторов. Производитель может придумать свои, уникальные обозначения, расшифровать которые не всегда удаётся. Особенно это относится к цветовому коду отечественной продукции. По стёртой маркировке узнать ёмкость невозможно, в такой ситуации не обойтись без измерений.
Производитель может придумать свои, уникальные обозначения, расшифровать которые не всегда удаётся. Особенно это относится к цветовому коду отечественной продукции. По стёртой маркировке узнать ёмкость невозможно, в такой ситуации не обойтись без измерений.
Вычисления с помощью формул электротехники
Простейшая RC — цепь состоит из параллельно включённых резистора и конденсатора.
Выполнив математические преобразования (здесь не приводятся), определяются свойства цепи, из которых следует, что если заряженный конденсатор подключить к резистору, то он будет разряжаться так, как показано на графике.
Произведение RC называют постоянной времени цепи. При значениях R в омах, а C — в фарадах, произведение RC соответствует секундам. Для ёмкости 1 мкФ и сопротивления 1 кОм, постоянная времени — 1 мс, если конденсатор был заряжен до напряжения 1 В, при подключении резистора ток в цепи будет 1 мА. При зарядке напряжение на конденсаторе достигнет Vo за время t ≥ RC. На практике применяется следующее правило: за время 5 RC, конденсатор зарядится или разрядится на 99%. При других значениях напряжение будет изменяться по экспоненциальному закону. При 2.2 RC это будет 90 %, при 3 RC — 95 %. Этих сведений достаточно для расчёта ёмкости с помощью простейших приспособлений.
При других значениях напряжение будет изменяться по экспоненциальному закону. При 2.2 RC это будет 90 %, при 3 RC — 95 %. Этих сведений достаточно для расчёта ёмкости с помощью простейших приспособлений.
Схема измерения
Для определения ёмкости неизвестного конденсатора следует включить его в цепь из резистора и источника питания. Входное напряжение выбирается несколько меньшим номинального напряжения конденсатора, если оно неизвестно — достаточно будет 10–12 вольт. Ещё необходим секундомер. Для исключения влияния внутреннего сопротивления источника питания на параметры цепи, на входе надо установить выключатель.
Сопротивление подбирается экспериментально, больше для удобства отсчёта времени, в большинстве случаев в пределах пяти — десяти килоом. Напряжение на конденсаторе контролируется вольтметром. Время отсчитывается с момента включения питания — при зарядке и выключении, если контролируется разряд. Имея известные величины сопротивления и времени, по формуле t = RC вычисляется ёмкость.
Удобнее отсчитывать время разрядки конденсатора и отмечать значения в 90 % или 95 % от начального напряжения, в этом случае расчёт ведётся по формулам 2.2t = 2.2RC и 3t = 3RC. Таким способом можно узнать ёмкость электролитических конденсаторов с точностью, определяемой погрешностями измерений времени, напряжения и сопротивления. Применение его для керамических и других малой ёмкости, с использованием трансформатора 50 Hz, вычислением емкостного сопротивления — даёт непрогнозируемую погрешность.
Измерительные приборы
Самым доступным методом замера ёмкости является широко распространённый мультиметр с такой возможностью.
В большинстве случаев, подобные устройства имеют верхний предел измерений в десятки микрофарад, что достаточно для стандартных применений. Погрешность показаний не превышает 1% и пропорциональна ёмкости. Для проверки достаточно вставить выводы конденсатора в предназначенные гнёзда и прочитать показания, весь процесс занимает минимум времени. Такая функция присутствует не у всех моделей мультиметров, но встречается часто с разными пределами измерений и способами подключения конденсатора. Для определения более подробных характеристик конденсатора (тангенса угла потерь и прочих), используются другие устройства, сконструированные для конкретной задачи, не редко являются стационарными приборами.
Для определения более подробных характеристик конденсатора (тангенса угла потерь и прочих), используются другие устройства, сконструированные для конкретной задачи, не редко являются стационарными приборами.
В схеме измерения, в основном, реализован мостовой метод. Применяются ограничено в специальных профессиональных областях и широкого распространения не имеют.
Самодельный С — метр
Не принимая во внимание разные экзотические решения, такие как баллистический гальванометр и мостовые схемы с магазином сопротивлений, изготовить простой прибор или приставку к мультиметру по силам и начинающему радиолюбителю. Широко распространённая микросхема серии 555 вполне подходит для этих целей. Это таймер реального времени со встроенным цифровым компаратором, в данном случае используется как генератор.
Частота прямоугольных импульсов задаётся выбором резисторов R1–R8 и конденсаторов С1, С2 переключателем SA1 и равняется: 25 kHz, 2.5 kHz, 250 Hz, 25Hz — соответственно положениям переключателя 1, 2, 3 и 4–8.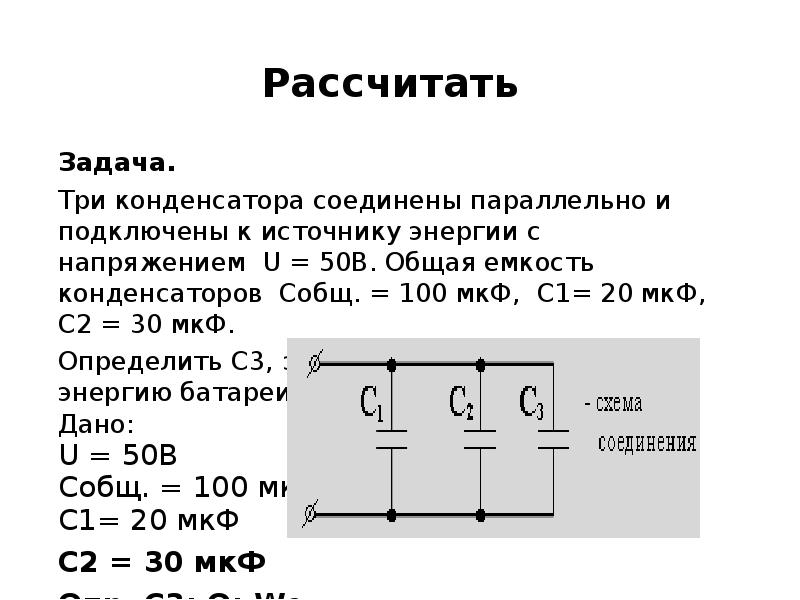 Конденсатор Сх заряжается с частотой следования импульсов через диод VD1, до фиксированного напряжения. Разряд происходит во время паузы через сопротивления R10, R12–R15. В это время образуется импульс длительностью, зависимой от емкости Сх (больше ёмкость — длиннее импульс). После прохождения интегрирующей цепи R11 C3 на выходе появляется напряжение, соответствующее длине импульса и пропорциональное величине ёмкости Сх. Сюда и подключается (Х 1) мультиметр для измерения напряжения на пределе 200 mV. Положения переключателя SA1 (начиная с первого) соответствуют пределам: 20 пФ, 200 пФ, 2 нФ, 20 нФ, 0.2 мкФ, 2 мкФ, 20 мкФ, 200 мкФ.
Конденсатор Сх заряжается с частотой следования импульсов через диод VD1, до фиксированного напряжения. Разряд происходит во время паузы через сопротивления R10, R12–R15. В это время образуется импульс длительностью, зависимой от емкости Сх (больше ёмкость — длиннее импульс). После прохождения интегрирующей цепи R11 C3 на выходе появляется напряжение, соответствующее длине импульса и пропорциональное величине ёмкости Сх. Сюда и подключается (Х 1) мультиметр для измерения напряжения на пределе 200 mV. Положения переключателя SA1 (начиная с первого) соответствуют пределам: 20 пФ, 200 пФ, 2 нФ, 20 нФ, 0.2 мкФ, 2 мкФ, 20 мкФ, 200 мкФ.
Наладку конструкции необходимо делать с прибором, который будет применяться в дальнейшем. Конденсаторы для наладки надо подобрать с ёмкостью, равной поддиапазонам измерений и как можно точнее, от этого будет зависеть погрешность. Отобранные конденсаторы поочерёдно подключаются к Х1. В первую очередь настраиваются поддиапазоны 20 пФ–20 нФ, для этого соответствующими подстроечными резисторами R1, R3, R5, R7 добиваются соответствующих показаний мультиметра, возможно придётся несколько изменить номиналы последовательно включённых сопротивлений. На других поддиапазонах (0.2 мкФ–200 мкФ) калибровка проводится резисторами R12–R15.
На других поддиапазонах (0.2 мкФ–200 мкФ) калибровка проводится резисторами R12–R15.
Провода, соединяющие резисторы с переключателем должны быть как можно короче, а если позволяет конструкция — размещены на его выводах. Переменные желательно использовать многооборотные, лучше вообще — постоянные, но это не всегда возможно. Тщательнейшим образом необходимо отмыть печатную плату от флюса и другой грязи, иначе паразитные ёмкости и сопротивления между проводниками могут привести к полной неработоспособности изделия.
При выборе источника питания следует учитывать, что амплитуда импульсов напрямую зависит от его стабильности. Интегральные стабилизаторы серии 78хх вполне здесь применимы Схема потребляет ток не более 20–30 миллиампер и конденсатора фильтра ёмкостью 47–100 микрофарад будет достаточно. Погрешность измерений, при соблюдении всех условий, может составить около 5 %, на первом и последнем поддиапазонах, по причине влияния ёмкости самой конструкции и выходного сопротивления таймера, возрастает до 20 %. Это надо учитывать при работе на крайних пределах.
Это надо учитывать при работе на крайних пределах.
Конструкция и детали
R1, R5 6,8k R12 12k R10 100k C1 47nF
R2, R6 51k R13 1,2k R11 100k C2 470pF
R3, R7 68k R14 120 C3 0,47mkF
R4, R8 510k R15 13
Диод VD1 — любой маломощный импульсный, конденсаторы плёночные, с малым током утечки. Микросхема — любая из серии 555 (LM555, NE555 и другие), русский аналог — КР1006ВИ1. Измерителем может быть практически любой вольтметр с высоким входным сопротивлением, под который проведена калибровка. Источник питания должен иметь на выходе 5–15 вольт при токе 0.1 А. Подойдут стабилизаторы с фиксированным напряжением: 7805, 7809, 7812, 78Lxx.
Вариант печатной платы и расположение компонентов
Видео по теме
Как проверить конденсатор мультиметром
Мультиметр – это электроизмерительное устройство с различными функциями. С его помощью можно проверять напряжение, силу тока, а также производные от этих величин – сопротивление и емкость. С помощью мультиметра можно проверить и работоспособность различных электронных компонентов. В этой статье мы с вами узнаем, как проверить мультиметром конденсатор и его емкость.
С помощью мультиметра можно проверить и работоспособность различных электронных компонентов. В этой статье мы с вами узнаем, как проверить мультиметром конденсатор и его емкость.
Конденсатор и емкость
Конденсаторы используются практически во всех микросхемах и являются частой причиной ее неработоспособности. Так что в случае неисправности устройства следует проверять в первую очередь именно этот элемент.
Виды конденсаторов по типу диэлектрика:
- вакуумные;
- с газообразным диэлектриком;
- с неорганическим диэлектриком;
- с органическим диэлектриком;
- электролитические;
- твердотельные.
Основные неисправности конденсаторов:
- Электрический пробой. Обычно вызван превышением допустимого напряжения.
- Обрыв. Связан с механическими повреждениями, встрясками, вибрациями. Причиной может служить некачественная конструкция и нарушение эксплуатационных условий.

- Повышенные утечки. Сопротивление между обкладками изменяется, и это приводит к низкой емкости конденсатора, которая не способна сохранять заряд.
Все эти причины приводят к тому, кто конденсатор становится непригодным для дальнейшего использования.
В данном случае присутствует протечка электролитаПеред проверкой конденсатора
Т.к. конденсаторы накапливают электрический заряд, перед проверкой их следует разряжать. Это можно сделать отверткой – жалом нужно прикоснуться к выводам, чтобы образовалась искра. Затем можно прозванивать компонент. Проверку конденсатора можно сделать как мультитестером, так и при помощи лампочек и проводов. Первый способ является более надежным и дает более точные сведения об электронном элементе.
До начала проверки следует осмотреть конденсатор. Если он имеет трещины, нарушение изоляции, подтеки или вздутие, поврежден внутренний электролит и прибор сломан. Его нужно поменять на работающее устройство. При отсутствии внешних повреждений придется использовать мультиметр.
Перед проведением измерений нужно определить вид конденсатора – полярный или неполярный. У первого обязательно должна соблюдаться полярность, иначе прибор выйдет из строя. Во втором случае определение плюсового и минусового выходов не требуется, но измерения будут проводиться по другой технологии.
Определить полярность можно по метке на корпусе. На детали должна быть черная полоса с обозначением нуля. Со стороны этой ножки расположен отрицательный контакт, а с противоположной – положительный.
Измерение емкости в режиме сопротивления
Переключатель мультиметра следует установить в режим сопротивления (омметра). В этом режиме можно посмотреть, есть ли внутри конденсатора обрыв или короткое замыкание. Для проверки неполярного конденсатора выставляется диапазон измерений 2 МОм. Для полярного изделия ставится сопротивление 200 Ом, так как при 2 МОм зарядка будет производиться быстро.
Сам конденсатор нужно отпаять от схемы и поместить его на стол. Щупами мультиметра нужно коснуться выводов конденсатора, соблюдая полярность. В неполярной детали соблюдать плюс и минус не обязательно.
В неполярной детали соблюдать плюс и минус не обязательно.
Когда щупы прикоснутся к ножкам, на дисплее появится значение, которое будет возрастать. Это вызвано тем, что мультитестер будет заряжать компонент. Через некоторое время значение на экране достигнет единицы – это значит, что прибор исправен. Если при проверке сразу же загорается 1, внутри устройства произошел обрыв и его следует заменить. Нулевое значение на дисплее говорит о том, что внутри конденсатора произошло короткое замыкание.
Если проверяется неполярный конденсатор, значение должно быть выше 2. В ином случае прибор является не рабочим.
Аналоговое устройство
Вышеописанный алгоритм подходит для цифрового тестера. При использовании аналогового устройства проверка производится еще проще – нужно наблюдать лишь за ходом стрелки. Щупы подключаются так же, режим – проверка сопротивления. Плавное перемещение стрелки свидетельствует о том, что конденсатор исправен. Минимальное и максимальное значение при подключении говорят о поломке электронной детали.
Важно отметить, что проверка в режиме омметра производится для деталей с емкостью выше 0Ю25 мкФ. Для меньших номиналов используются специальные LC-метры или тестеры с высоким разрешением.
Измерение емкости конденсатора
Емкость является основной характеристикой конденсатора. Она указывается на внешней оболочке прибора, и при наличии тестера можно замерить реальное значение и сравнить его с номиналом.
Переключатель мультиметра переводится в диапазон измерений. Значение ставится равное или близкое к номиналу, указанному на компоненте. Сам конденсатор устанавливается в специальные отверстия –CX+ (если они есть на мультиметре) или с помощью щупов. Подключаются щупы так же, как и при измерении в режиме сопротивления.
При подключении щупов на мониторе должно появиться значение сопротивления. Если оно близко к номинальной характеристике, конденсатор исправен. Когда расхождение полученного и номинального значений отличаются более чем на 20% , устройство пробито, и его нужно поменять.
Измерение емкости через напряжение
Проверка работоспособности детали может производиться и при помощи вольтметра. Значение на мониторе сравнивается с номиналом, и из этого делается вывод об исправности устройства. Для проверки нужен источник питания с меньшим напряжением, чем у конденсатора.
Соблюдая полярность, нужно подключить щупы к выводам на несколько секунд для зарядки. Затем мультиметр переводится в режим вольтметра и проверяется работоспособность. На дисплее тестера должно появиться значение, схожее с номинальным. В ином случае прибор сломан.
Другие способы проверки
Можно проверить конденсатор, не выпаивая его из микросхемы. Для этого нужно параллельно подключить заведомо исправный конденсатор с такой же емкостью. Если устройство будет работать, то проблема в первом элементе, и его следует поменять. Такой способ применим только в схемах с небольшим напряжением!
Иногда проверяют конденсатор на искру. Его нужно зарядить и металлическим инструментом с заизолированной рукояткой замкнуть выводы. Должна появиться яркая искра с характерным звуком. При малом разряде можно сделать вывод, что деталь пора менять. Проводить данное измерение нужно в резиновых перчатках. К этому методу прибегают для проверки мощных конденсаторов, в том числе пусковых, которые рассчитаны на напряжение более 200 Вольт.
Должна появиться яркая искра с характерным звуком. При малом разряде можно сделать вывод, что деталь пора менять. Проводить данное измерение нужно в резиновых перчатках. К этому методу прибегают для проверки мощных конденсаторов, в том числе пусковых, которые рассчитаны на напряжение более 200 Вольт.
Использовать способы проверки без специальных приборов нежелательно. Они небезопасны – при малейшей неосторожности можно получить электрический удар. Также будет нарушена объективность картины – точные значения не будут получены.
Сложности проверки
Основной сложностью при определении работоспособности конденсатора мультиметром является его выпаивание из схемы. Если оставить компонент на плате, на измерение будут влиять другие элементы цепи. Они будут искажать показания.
В продаже существуют специальные тестеры с пониженным напряжением на щупах, которые позволяют проверять конденсатор прямо на плате. Малое напряжение сводит к минимуму риск повреждения других элементов в цепи.
Как проверить емкость – видео ролики в Youtube
Отличное видео с описанием процесса проверки конденсаторов и поиска неисправностей от популярных ютуб-блогеров.
Как измерить ёмкость конденсатора мультиметром?
Ёмкость – это мера способности конденсатора накапливать заряды. Ёмкость измеряется в фарадах, по имени почетного члена Петербургского университета английского физика Майкла Фарадея.
Что такое емкость?
Если удалить одиночный электропроводник бесконечно далеко, исключить влияние заряженных тел друг на друга, то потенциал удаленного проводника станет пропорционален заряду. Но у отличающихся по размеру проводников потенциалы не совпадают.
Единицей емкости конденсатора в СИ является фарад. Коэффициент пропорциональности обозначают буквой С – это емкость, на которую влияет размер и внешняя структура проводника. Материал, фазовое состояние вещества электрода роли не играют – заряды распределяются на поверхности. Поэтому в международных правилах СГС ёмкость измеряется не в фарадах, а в сантиметрах.
Материал, фазовое состояние вещества электрода роли не играют – заряды распределяются на поверхности. Поэтому в международных правилах СГС ёмкость измеряется не в фарадах, а в сантиметрах.
Уединенный шар радиусом 9 млн км (1400 радиусов Земли) содержит 1 фарад. Отдельный проводящий элемент удерживает заряды в недостаточных для применения в технике количествах. По технологиям XXI в. создается ёмкость конденсаторов с единицами измерений выше 1 фарада.
Накапливать требуемое для работы электронных схем количество электричества способна структура из минимум 2 электродов и разделяющего диэлектрика. В такой конструкции положительные и отрицательные частицы взаимно притягиваются и сами себя держат. Диэлектрик между электронно-позитронной парой не допускает аннигиляции. Подобное состояние зарядов называется связанным.
Раньше для измерения электрических величин применяли громоздкое оборудование, не отличающееся точностью. Теперь, как измерить ёмкость тестером, знает даже начинающий радиолюбитель.
Маркировка на конденсаторах
Знать характеристики электронных приборов требуется для точной и безопасной работы.
Определение ёмкости конденсатора включает измерение величины приборами и чтение маркировки на корпусе. Обозначенные значения и полученные при измерениях отличаются. Это вызвано несовершенством производственных технологий и эксплуатационным разбросом параметров (износ, влияние температур).
На корпусе указана номинальная емкость и параметры допустимых отклонений. В бытовых устройствах используют приборы с отклонением до 20%. В космической отрасли, военном оборудовании и в автоматике опасных объектов разрешают разброс характеристик в 5-10%. Рабочие схемы не содержат значений допусков.
Номинальная емкость кодируется по стандартам IEC – Международной электротехнической комиссии, которая объединяет национальные организации по стандартам 60 стран.
Стандарт IEC использует обозначения:
- Кодировка из 3 цифр. 2 знака в начале – количество пФ, третий – число нулей, 9 в конце – номинал меньше 10 пФ, 0 спереди – не больше 1 пФ.
 Код 689 – 6,8 пФ, 152 – 1500 пФ, 333 – 33000 пФ или 33 нФ, или 0,033 мкФ. Для облегчения чтения десятичная запятая в коде заменяется буквой “R”. R8=0,8 пФ, 2R5 – 2,5 пФ.
Код 689 – 6,8 пФ, 152 – 1500 пФ, 333 – 33000 пФ или 33 нФ, или 0,033 мкФ. Для облегчения чтения десятичная запятая в коде заменяется буквой “R”. R8=0,8 пФ, 2R5 – 2,5 пФ. - 4 цифры в маркировке. Последняя – число нулей. 3 первых – величина в пФ. 3353 – 335000 пФ, 335 нФ или 0,335 мкФ.
- Использование букв в коде. Буква µ – мкФ, n – нанофарад, p – пФ. 34p5 – 34,5 пФ, 1µ5 – 1,5 мкФ.
- Планерные керамические изделия кодируют буквами A-Z в 2 регистрах и цифрой, обозначающей степень числа 10. K3 – 2400 пФ.
- Электролитические SMD приборы маркируются 2 способами: цифры – номинальная емкость в пФ и рядом или во 2 строчке при наличии места – значение номинального напряжения; буква, кодирующая напряжение и рядом 3 цифры, 2 определяют емкость, а последняя – количество нулей. А205 значит 10 В и 2 мкФ.
- Изделия для поверхностного монтажа маркируются кодом из букв и чисел: СА7 – 10 мкФ и 16 В.
- Кодировки – цветом корпуса.
Маркировка IEC, национальные обозначения и кодировки брендов делают запоминание кодов бессмысленным. Разработчикам аппаратуры и мастерам-ремонтникам требуются справочные источники.
Разработчикам аппаратуры и мастерам-ремонтникам требуются справочные источники.
Вычисление с помощью формул
Вычисление номинальной емкости элемента требуется в 2 случаях:
- Конструкторы электронной аппаратуры рассчитывают параметр при создании схем.
- Мастера при отсутствии конденсаторов подходящей мощности и емкости используют расчет элемента для подбора из доступных деталей.
RC цепи рассчитывают с применением величины импеданса – комплексного сопротивления (Z). Rа – потери тока на нагревание участников цепи. Ri и Rе – учитывают влияние индуктивности и ёмкости элементов. На выводах резистора в RC цепи напряжение Uр обратно пропорционально Z.
Тепловое сопротивление увеличивает потенциал на нагрузке, а реактивное уменьшает. Работа конденсатора на частотах выше резонансных, когда растет реактивная составляющая комплексного сопротивления, приводит к потерям напряжения.
Частота резонанса обратно пропорциональна способности накапливать заряд. Из формулы для определения Fр вычисляют, какие значения Ск (емкости конденсатора) требуются для работы цепи.
Из формулы для определения Fр вычисляют, какие значения Ск (емкости конденсатора) требуются для работы цепи.
Для расчета импульсных схем используют постоянную времени цепи, определяющую воздействие RC на структуру импульса. Если знают сопротивление цепи и время заряда конденсатора, по формуле постоянной времени вычисляют емкость. На истинность результата влияет человеческий фактор.
Мастера используют параллельные и последовательные соединения конденсаторов. Формулы расчета обратны формулам для резисторов.
Последовательное соединение делает емкость меньше меньшей в соединении элементов, параллельная схема суммирует величины.
Как измерить ёмкость конденсатора мультиметром?
Измеряя параметры, конденсатор предварительно разряжают, замкнув выводы между собой отверткой с изоляцией на ручке. Если этого не сделать, маломощный мультиметр выйдет из строя.
Ответ на вопрос, как проверить емкость конденсатора мультиметром с режимом “Сх” такой:
- Включить режим “Сх” и подобрать предел замера – 2000 пФ – 20 мкФ в стандартном приборе;
- Вставить конденсатор в гнезда в приборе или приложить щупы к выводам конденсатора и посмотреть значение на шкале прибора.

Амперовольтметром или мультиметром определяют наличие внутри корпуса короткого замыкания или обрыва.
Полярный конденсатор включают в цепь прибора с учетом направления тока. Электроды изделия производители маркируют. Конденсатор, рассчитанный для напряжения 1-3 В, при обратном токе выше нормы выйдет из строя.
Перед тем как измерить характеристики, полярный электролитический конденсатор выпаивают из платы. Включают мультиметр в режим измерения сопротивления или проверки полупроводников. Прикладывают щупы к электродам полярного конденсатора – плюс к плюсу, минус к минусу. Исправная емкость покажет плавный рост сопротивления. По мере заряда ток уменьшается, ЭДС растет и достигает напряжения источника питания.
Обрыв в конденсаторе будет выглядеть на мультиметре как бесконечное сопротивление. Прибор не отреагирует или стрелка на аналоговом экземпляре едва шевельнется.
При пробое элемента измеряемый параметр не соответствует номинальному значению в меньшую сторону, пропорционально величине пробоя.
Если задаться вопросом, как измерить мультиметром комплексное или эквивалентное последовательное сопротивление (ESR конденсатора), то без приставки сделать это проблематично. Реактивные свойства конденсатор проявляет при высокочастотном токе.
Прочие способы измерения
Измеритель емкости конденсаторов своими руками собирают по схемам импульсных устройств. Последовательности RC цепей с переменными резисторами создают на выходе изделия серии сигналов со ступенчатым изменением частоты. Для наладки устройства используют мультиметр, с которым будет применяться приставка.
Набор проверенных конденсаторов поочередно подключают к конструкции и настраивают точность работы в каждом поддиапазоне.
Измеритель ёмкости полярных электролитических элементов своими руками схематически реализуется и настраивается, как часть приставки без колебательного контура. На выходе вместо импульсного – постоянное напряжение.
В цифровых измерителях ёмкости источник питания – высокостабильный. “Плавающие” параметры элементов, из которых собирается схема, дадут неприемлемую для точности измерений погрешность.
На логических элементах создаются источники переменного импульсного тока для замеров ESR.
Недорогие приборы для измерения емкости конденсатора, типа мостовых RLC устройств с дополнительной функцией проверки SMD сопротивлений, сетевой зарядкой и жидкокристаллическим дисплеем, сами размером с палец. Выполняют функции профессионального метрологического комплекса. Способны выступать в роли измерителя емкости электролитических конденсаторов, как полярных, так и переменных.
Как проверить конденсатор мультиметром
Одной из самых распространённых причин неисправности электронной техники, это выход из строя конденсатора. Любая электроника, бытовая техника и цифровые процессоры все имеют в своем оборудовании конденсаторы и достаточно одной незначительной неисправности конденсатора, что бы весь механизм прекратил выполнять свои функции.
Я рад снова видеть все вас на страницах сайта «Электрик в доме». Сегодня мы познакомимся и изучим одну из самых используемых деталей в электронике – конденсатор. История создания первого конденсатора относит нас назад в 1745 год («лейденская банка»).
В наше время, в век технологий нас со всех сторон окружает электротехнические машины и оборудование. Вы конечно хорошо знакомы с конденсатором и если не сталкивались технически, то слышали о нем однозначно.
Одной из самых распространённых причин неисправности электронной техники, это выход из строя конденсатора. Любая электроника, бытовая техника и цифровые процессоры все имеют в своем оборудовании конденсаторы и достаточно одной незначительной неисправности конденсатора, что бы весь механизм прекратил выполнять свои функции.
Вот почему, в случае неисправности оборудования, первым делом необходимо обратить ваше внимание на работоспособность в схеме конденсаторов. И сделать это можно только при помощи электронного прибора, так как визуально определить состояние невозможно, если нет внешних повреждений.
И сделать это можно только при помощи электронного прибора, так как визуально определить состояние невозможно, если нет внешних повреждений.
Для этих целей и предназначен недорогой прибор мультиметр, выполняющий многие функции. Об одной из них — проверки сопротивления, я уже знакомил вас в своей предыдущей статье. Этот же материал предназначен для изучения методики проверки конденсатора мультиметром.
С этой проблемой ко мне обратился один из моих подписчиков. Следуя уже своей традиции, я как всегда, буду излагать материал просто и доступно для легко понимания всем желающим.
Проверка конденсатора мультиметромДля лучшего усвоения материала, начнем с небольшой теории:
- Устройство и принцип работы мультиметра;
- Виды и особенности конденсаторов.
Устройство (прибор) предназначенное для накопления электрического заряда – это основное определение конденсатора. Конструктивно он состоит из определенного корпуса, внутри которого расположены две параллельные металлические пластины.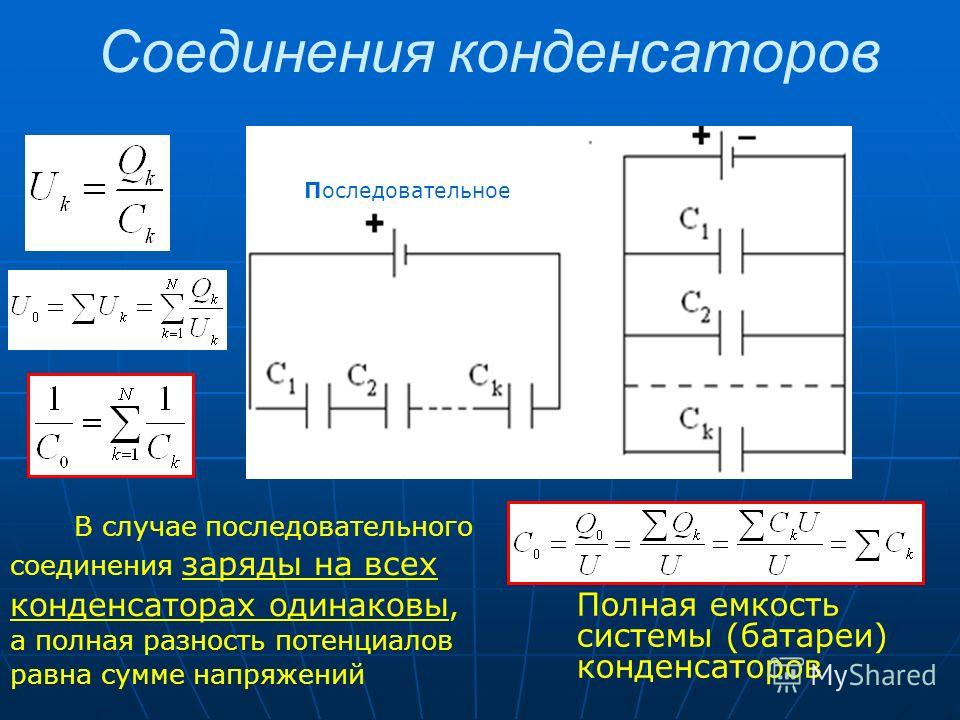 Между пластинами установлена прокладка (диэлектрик). Площадь пластин напрямую влияет на величину электрического заряда. Чем больше площадь пластин, тем больше величина накопленного заряда.
Между пластинами установлена прокладка (диэлектрик). Площадь пластин напрямую влияет на величину электрического заряда. Чем больше площадь пластин, тем больше величина накопленного заряда.
Конденсаторы могут быть двух видов: полярными и неполярными.
Конденсаторы полярные.
Определить какой вид конденсаторов достаточно не сложно, уже название вам дает подсказку, что «полярные» должны иметь полярность, то есть иметь (+ плюс) и (- минус). Их подключение в электросхему строго регламентировано в соответствие полярности. Плюс подключается к плюсу, минус к минусу. При нарушении этого правила — конденсатор не будет работать, а вместе с ним и вся схема.
Все полярные конденсаторы заполнены электролитом (твердым или жидким), поэтому их классифицируют как электролитические. Их физические параметры (емкость) находится в следующих параметрах 0.1 ÷ 100000 мкФ.
Конденсаторы неполярные
Неполярные конденсаторы, как вы уже поняли, не имеют полярности и не требуют строгого соблюдения условий подключений. У них нет ни плюса, ни минуса. Роль диэлектрика у них могут выполнять: бумага, стекло, керамика и слюда. Их физические параметры (емкость) незначительна и находится в следующем диапазоне (от нескольких микрофарад до нескольких пикофарад).
У них нет ни плюса, ни минуса. Роль диэлектрика у них могут выполнять: бумага, стекло, керамика и слюда. Их физические параметры (емкость) незначительна и находится в следующем диапазоне (от нескольких микрофарад до нескольких пикофарад).
Забегая вперед, сразу хочу ответить на ваши вопросы, зачем нам с вами необходимо знать эти технические тонкости. Это очень важно, так как к каждому типу конденсаторов применима своя методика проверки мультиметром. И пред началом проверки, мы должны первым делом, установить тип конденсатора. Это очень важный момент. Прошу вас обратить на это внимание!
Как проверить конденсатор с помощью приборовЛюбую проверку конденсаторов необходимо начинать с внешнего осмотра, на наличие внешних признаков повреждений корпуса (трещин, вздутия). Достаточно часто происходит повреждение электролита, что приводит к повышению давления на внутреннюю поверхность оболочки и последующее ее вздутие.
После того как визуальный осмотр окончен и мы не установили внешних повреждений конденсатора, необходимо продолжить проверку специальным прибором, в нашем случае мультиметром. Этот простейший прибор поможет нам установить емкость конденсатора и обрывы внутри.
Этот простейший прибор поможет нам установить емкость конденсатора и обрывы внутри.
Перед проверкой незабываем, установить тип конденсатора, более подробно об этом написано выше. Продолжаем процесс проверки с соблюдением полярности, для этого подключаем плюсовой щуп к плюсовому контакту конденсатора и соответственно минусовой щуп к контакту минус.
Проверяя неполярный конденсатор, подключение мультиметра проводим произвольно без соблюдения правила полярности. Единственное, что здесь необходимо выполнить, это выставить переключатель мультиметра на отметку 2 Мом. Это важно, так как при меньшем значении дисплей прибора отобразит — «1» (единицу), что укажет на неисправность конденсатора.
Проверяем конденсатор мультиметром в режиме омметраДля примера мы свами выполним проверку четырех конденсаторов: два полярных (диэлектрических) и два неполярных (керамических).
Но перед проверкой мы должны обязательно разрядить конденсатор , при этом достаточно замкнуть его контакты при помощи любого металла.
Для того чтобы перейти в режим (омметра) сопротивления, мы перемещаем переключатель в группу измерения сопротивления, для того чтобы установить наличие обрыва или короткого замыкания.
Итак, первым делом проверим полярные кондиционеры (5.6 мкФ и 3.3 мкФ), установленных ранее у неработающих энергосберегающих лампочек
Разряжаем конденсаторы путем замыкания их контактов обычной отверткой. Вы можете использовать, удобный для вас, любой другой металлический предмет. Главное чтобы к нему плотно прилегали контакты. Это позволит нам получить точные показания прибора.
Следующим шагом выставляем переключатель на шкалу 2 МОм и соединяем контакты конденсатора и щупы прибора. Далее наблюдаем на дисплее быстро увиливающие параметры сопротивления.
Вы спросите меня, в чем дело и почему на дисплее мы наблюдаем «плавающие показатели» сопротивления? Это объяснить довольно просто, поскольку питание прибора (батарейка) имеет постоянное напряжение и за счет этого происходит зарядка конденсатора.
С течением времени конденсатор все больше и больше накапливает заряд (заряжается), тем самым увеличивая сопротивление. Емкость конденсатора влияет на скорость зарядки. Как только конденсатор получит полную зарядку, значение его сопротивления будет соответствовать значению бесконечности, а мультиметр на дисплее покажет «1». Это параметры рабочего конденсатора.
Нет возможности показать картинку на фотографии. Так для следующего экземпляра емкостью 5.6 мкФ, показатели сопротивления начинаются с 200 кОм и плавно возрастают до тех пор, пока не преодолеют показатель 2 МОм. Эта процедура не занимает более -10 сек.
Для следующего конденсатора емкостью 3.3 мкФ происходит все аналогично, но время процесса занимает менее — 5 сек.
Проверить следующую пару неполярных конденсаторов можно точно также по аналогии с предыдущими конденсаторами. Соединяем щупы прибора и контакты, следим за состоянием сопротивления на дисплее прибора.
Рассмотрим первый «150nК». Вначале его сопротивление несколько снизится примерно до 900 кОм, затем следует его плавное увеличение до определенной отметки. Время процесса занимает — 30 сек.
Время процесса занимает — 30 сек.
При этом на мультиметре модели МБГО переключатель устанавливаем на шкалу 20 МОм (сопротивление приличное, очень быстро идет зарядка)
Процедура классическая, снимаем заряд при помощи замыкания контактов отверткой:
Смотрим на дисплей, отслеживая показатели сопротивления:
Делаем вывод, что в результате проверки все представленные конденсаторы исправны.
Как проверить емкость конденсатораГлавный показатель, основная характеристика всех конденсаторов — это «емкость». Измеряя эту характеристику и сравнивая ее с указанными параметрами на корпусе, мы сможем выяснить, исправен кондиционер или нет. Есть приборы, которые легко позволят вам выполнить эту проверку.
Но можно ли проверить емкость конденсатора, как в нашем случае, мультиметром . Если вы будет проверять емкость при помощи щупов, вы не получите желаемого результата. Как же быть?
В этом нам помогут разъемы «гнезда» -CX+(«-» и «+» — это полярность подключения)
Для этого примера мы будем использовать кондер «150нФ». Маркировка 150nK:
Маркировка 150nK:
Устанавливаем переключатель на отметку – ближайшее большее значение. В нашем случае это 200 нФ. Следующим шагом вставляем ножки конденсатора в разъемы -CX+. (не обращаем внимание на полярность, наш кондер неполярный). Дисплей показывает значение емкости– 160.3 нФ, что совпадает с номинальными показателями.
Продолжаем проверку конденсатора с емкостью 4700 пФ. Устанавливаем переключатель на шкале в положение 20 n.
Теперь вставляем ножки в разъёмы прибора и наблюдаем на дисплее параметры 4750 пФ. Вы это можете увидеть на фото. Параметры точно соответствуют параметрам заявленным производителем.
Запомните, если показатели сильно отличаются от номинальных параметров или вообще равны нулю, это говорит нам, что конденсатор не рабочий и его необходимо заменить.
Как проверить конденсатор при помощи прибора ESR-METR
Недавно я приобрел ESR-METR и я решил выполнить им ту же самую проверку.
Методика проверки очень проста. Прибор необходимо откалибровать, в моем случае в комплекте идет специальная перемычка, при помощи которой замыкается нужная группа контактов на колодке 1-4. Нажимаем кнопку и прибор автоматический калибруется, сообщив нам об этом на своем экране. После калибровки не забываем разрядить конденсатор и подключаем его к нужным нам разъемам. и производим измерение.
Прибор необходимо откалибровать, в моем случае в комплекте идет специальная перемычка, при помощи которой замыкается нужная группа контактов на колодке 1-4. Нажимаем кнопку и прибор автоматический калибруется, сообщив нам об этом на своем экране. После калибровки не забываем разрядить конденсатор и подключаем его к нужным нам разъемам. и производим измерение.
На этом все. Если у Вас есть замечания или предложения по данной статье, прошу написать администратору сайта.
Как проверить конденсатор мультиметром на работоспособность
По сути ремонт любой радиоэлектронной аппаратуры сводится к поиску и замене неисправных деталей. И, возможно, вы удивитесь тому, насколько часто выходят из строя такие, казалось бы, простые компоненты как конденсаторы. В то время как нежные диоды, чувствительные транзисторы и сложные микросхемы остаются целыми и невредимыми.
И, возможно, вы удивитесь тому, насколько часто выходят из строя такие, казалось бы, простые компоненты как конденсаторы. В то время как нежные диоды, чувствительные транзисторы и сложные микросхемы остаются целыми и невредимыми.
Типичные неисправности конденсаторов:
- КЗ между обкладками. Как правило, это следствие механического повреждения, перегрева или превышения рабочего напряжения (пробой). Самый простой случай, т.к. легко выявляется любым мультиметром в режиме прозвонки;
- внутренний обрыв с полной потерей емкости (вот почему нельзя коротить отвертками). В случае с конденсаторами большой емкости этот дефект достаточно просто диагностируется. Выявление обрыва у мелких кондеров (менее 500 пФ) является довольно трудоемкой задачей и осуществляется только при помощи спец. приборов;
- частичная потеря емкости. Для электролитических конденсаторов потеря емкости с годами практически неизбежна, однако это не всегда приводит к неисправности устройства (но может ухудшать его характеристики).
 Керамические, пленочные и прочие с твердым диэлектриком, как правило, более стабильны, но могут потерять емкость в результате механического повреждения;
Керамические, пленочные и прочие с твердым диэлектриком, как правило, более стабильны, но могут потерять емкость в результате механического повреждения; - слишком низкое сопротивление утечки (конденсатор “не держит” заряд). В основном это свойственно электролитическим конденсаторам. Хотя танталовые в этом плане очень хороши;
- слишком большое эквивалентное последовательное сопротивление (ЕПС или ESR). Проблема по большей части касается “электролитов” и проявляется только при работе с высокочастотными или импульсными токами.
Существует масса способов как проверить конденсатор мультиметром на работоспособность. Пойдем по-порядку.
Содержание статьи:
Внешний осмотр
Иногда достаточно одного взгляда, чтобы определить неисправный конденсатор на плате. В таких случаях нет смысла проверять его какими-либо приборами.Конденсатор подлежит замене, если визуальный осмотр показал наличие:
- даже незначительного вздутия, следов подтеков;
- механических повреждений, вмятин;
- трещин, сколов (актуально для керамики).

Конденсаторы, имеющие любой из указанных признаков, эксплуатировать НЕЛЬЗЯ.
Измерение емкости конденсатора мультиметром и специальными приборами
Некоторые мультиметры имеют функцию измерения емкости. Взять хотя бы эти распространенные модели: M890D, AM-1083, DT9205A, UT139C и т.д.Также в продаже есть цифровые измерители емкости, например, XC6013L или A6013L.
С помощью любого из этих приборов можно не только узнать точную емкость конденсатора, но и убедиться в отсутствии короткого замыкания между обкладками или внутреннего обрыва одного из выводов.
Некоторые производители даже уверяют, что их мультиметры способны проверить емкость конденсатора не выпаивая его с платы. Что, конечно же, противоречит здравому смыслу.
К сожалению, проверка конденсатора мультиметром не поможет определить такие наиважнейшие параметры, как ток утечки и эквивалентное последовательное сопротивление (ESR). Их измерить только с помощью специализированных тестеров. Например, с помощью весьма недорогого LC-метра.
Например, с помощью весьма недорогого LC-метра.
Проверка на короткое замыкание
Способ №1: определение КЗ в режиме прозвонки
Как прозванивать конденсаторы мультиметром? Нужно включить мультиметр в режим прозвонки или измерения сопротивления и приложить щупы к выводам конденсатора.
В зависимости от емкости мультиметр либо сразу же покажет бесконечное сопротивление, либо через какое-то время (от нескольких секунд до десятков секунд).
Если же прибор постоянно пищит в режиме прозвонки (или показывает очень низкое сопротивление в режиме измерения сопротивления), то конденсатор можно смело выкидывать.
Способ №2: определение КЗ конденсатора с помощью светодиода и батарейки
Если нет мультиметра (и даже старой советской “цешки” нету), то можно попробовать подключить светодиод или лампочку к батарейке через исследуемый конденсатор.
Т.к. исправный конденсатор имеет ооочень большое сопротивление постоянному току, лампочка гореть не должна. Хотя, если емкость конденсатора достаточно большая, лампочка может вспыхнуть на короткое время (пока конденсатор не зарядится).
Хотя, если емкость конденсатора достаточно большая, лампочка может вспыхнуть на короткое время (пока конденсатор не зарядится).
Если же светодиод горит постоянно, конденсатор 100% неисправен.
Если при проверке конденсатора наблюдается эффект постепенного роста сопротивления вплоть до бесконечности (ну или светодиод на какое-то время вспыхивает и гаснет) то конденсатор совершенно точно имеет какую-то емкость. Следовательно, проверку на обрыв можно не делать.Способ №3: проверка конденсатора лампочкой на 220В
Подходит для высоковольтных неполярных конденсаторов (например, пусковые конденсаторы из стиральных машин, насосов, различных станков и т.п.).
Все что нужно сделать – просто подключить лампу накаливания небольшой мощности (25-40 Вт) через конденсатор. Полярность конденсатора не имеет значения:
Способ позволяет одним выстрелом убить двух зайцев: обнаружить КЗ, если оно есть, и убедиться в том, что конденсатор имеет ненулевую емкость (не находится в обрыве).
При исправном конденсаторе лампочка будет гореть в полнакала. Чем меньше емкость – тем тусклее будет гореть лампочка.
Если лампа горит в полную мощность (точно также как и без конденсатора), значит конденсатор “пробит” и подлежит замене. Если лампочка совсем не светится – внутри конденсатора обрыв.
Способ №3 очень наглядно продемонстрирован в этом видео:
Проверка на отсутствие внутреннего обрыва
Обрыв – распространенный дефект конденсатора, при котором один из его электродов теряет электрическое соединение с обкладкой и фактически превращается в короткий, ни с чем не соединенный (висящий в воздухе), проводник.
Чаще всего обрыв происходит из-за превышения рабочего напряжения конденсатора. Этим грешат не только электролитические конденсаторы, но и специальные помехоподавляющие конденсаторы типа Y (они, кстати говоря, специально так спроектированы, чтобы уходить в отрыв, а не в КЗ).
Конденсатор с внутренним обрывом внешне ничем не отличается от исправного, кроме случаев, когда ножку физически оторвали от корпуса 🙂
Разумеется, в случае отрыва одного из выводов от обкладки конденсатора, емкость такого конденсатора становится равной нулю. Поэтому суть проверки на обрыв состоит в том, чтобы уловить хоть малейшие признаки наличия емкости у проверяемого конденсатора.
Как это сделать? Есть три способа.
Способ №1: исключение обрыва через звуковой сигнал в режиме прозвонки
Включить мультиметр в режим прозвонки, прикоснуться щупами к выводам конденсатора и в этот момент мультиметр должен издать непродолжительный писк. Иногда звук настолько короткий (зависит от емкости конденсатора), что больше похож на щелчок и нужно очень постараться, чтобы его услышать.
Небольшой лайфхак: чтобы увеличить продолжительность звукового сигнала при прозвонке совсем маленьких конденсаторов, нужно предварительно зарядить их отрицательным напряжением, приложив щупы мультиметра в обратном порядке.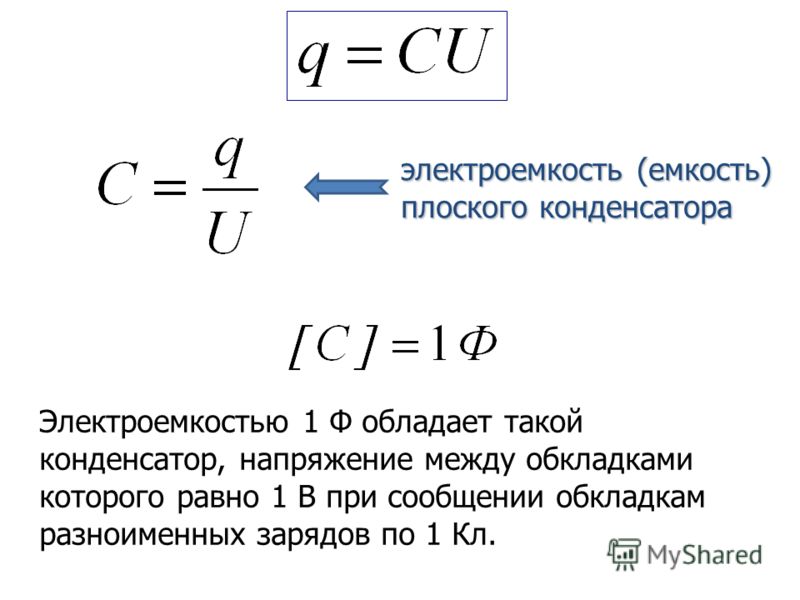 Тогда при последующей прозвонке мультиметру сначала придется перезарядить конденсатор от какого-то отрицательного напряжения до нуля, и только потом – от нуля до момента отключения пищалки. На все это уйдет значительно больше времени, а значит сигнал будет звучать дольше и его проще будет расслышать.
Тогда при последующей прозвонке мультиметру сначала придется перезарядить конденсатор от какого-то отрицательного напряжения до нуля, и только потом – от нуля до момента отключения пищалки. На все это уйдет значительно больше времени, а значит сигнал будет звучать дольше и его проще будет расслышать.
Вот какой-то чувак, сам того не подозревая, применяет этот лайфхак на видео:
Из своей практике могу сказать, что с помощью уловки, описанной выше, мне удавалось уловить реакцию мультиметра на конденсатор емкостью всего лишь 0.1 мкФ (или 100 нФ)!
Способ №2: увеличение сопротивления постоянному току как признак отсутствия обрыва
Если предыдущий способ не помог и вообще не понятно, как проверить конденсатор тестером, то вот вам более чувствительный метод проверки.
Необходимо переключить мультиметр в режим измерения сопротивления. Выбрать максимально доступный предел измерения (20 или лучше 200 МОм). Приложить щупы к выводам конденсатора и наблюдать за показаниями мультиметра.
Приложить щупы к выводам конденсатора и наблюдать за показаниями мультиметра.
По мере заряда конденсатора от внутреннего источника мультиметра, его сопротивление будет постоянно расти до тех пор, пока не выйдет за пределы диапазона измерения. Если такой эффект наблюдается, значит обрыва нет.
Кстати говоря, может так оказаться, что рост сопротивления остановится на значении от единиц до пары десятков МОм – для конденсаторов с жидким электролитом (кроме танталовых) это абсолютно нормально. Для остальных конденсаторов сопротивление утечки должно быть больше, как минимум, на порядок.
При измерении таких высоких сопротивлений необходимо следить за тем, чтобы не касаться пальцами сразу обоих измерительных щупов. Иначе сопротивление кожи внесет свои коррективы и исказит все результаты.
С помощью измерения сопротивления на пределе 200 МОм мне удавалось однозначно определить отсутствие обрыва в конденсаторах емкостью всего 0.001 мкФ (или 1000 пФ).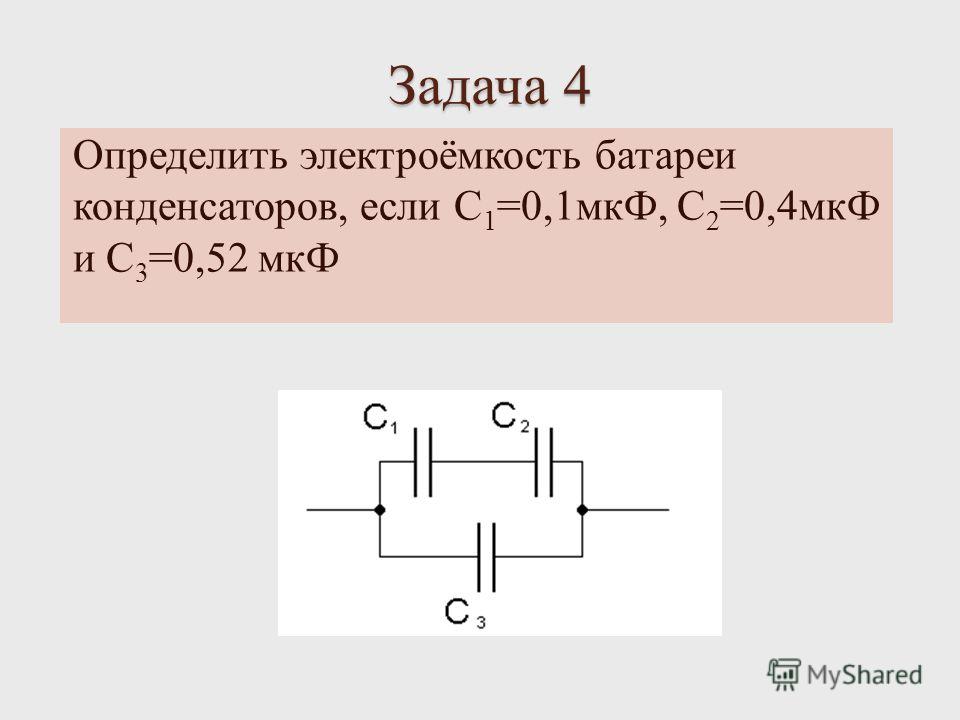
Вот видео для наглядности:
Способ №3: измерение остаточного напряжения для исключения внутреннего обрыва
Это самый чувствительный способ, позволяющий убедиться в отсутствии обрыва конденсатора даже тогда, когда все предыдущие способы не помогли.
Берется мультиметр в режиме прозвонки или в режиме измерения сопротивления (не важно в каком диапазоне) и на пару секунд прикладываем щупы к выводам испытуемого конденсатора. В этот момент конденсатор зарядится от мультиметра до какого-то небольшого напряжения (обычно 2.8 В).
Затем мы быстро переключаем мультиметр в режим измерения постоянного напряжения на самом чувствительном диапазоне и, не мешкая слишком долго, снова прикладываем щупы к конденсатору, чтобы измерить на нем напряжение. Если у кондера есть хоть какая-нибудь вразумительная емкость, то мультиметр успеет показать напряжение, до которого был заряжен конденсатор.
Этим способом мне удавалось с помощью обычного цифрового мультиметра M890D отловить емкость вплоть до 470 пФ (0.00047 мкФ)! А это очень маленькая емкость.
Вообще говоря, это наиболее эффективный метод прозвонки конденсаторов. Таким способ можно проверять кондеры любой емкости – от малюсеньких до самых больших, а также любого типа – полярные, неполярные, электролитические, пленочные, керамические, оксидные, воздушные, металло-бумажные и т.д.
Правда, если конденсатор имеет совсем маленькую емкость, до 470 пФ, то, увы, проверить его на обрыв без специального прибора, вроде упомянутого ранее LC-метра, никак не получится.
Определение рабочего напряжения конденсатора
Строго говоря, если на конденсаторе нет маркировки и не известна схема, в которой он стоял, то узнать его рабочее напряжение неразрушающими методами НЕВОЗМОЖНО.
Однако, имея некоторый опыт, можно оооочень приблизительно прикинуть “на глазок” рабочее напряжение исходя из габаритов конденсатора. Естественно, чем больше размеры конденсатора и чем меньше при этом его емкость, тем на большее напряжение он расчитан.
Естественно, чем больше размеры конденсатора и чем меньше при этом его емкость, тем на большее напряжение он расчитан.
Способ №1: определение рабочего напряжения через напряжения пробоя
Если имеется несколько одинаковых конденсаторов и одним из них не жалко пожертвовать, то можно определить напряжение пробоя, которое обычно раза в 2-3 выше рабочего напряжения.
Напряжение пробоя конденсатора измеряется следующим образом. Конденсатор подключается через токоограничительный резистор к регулируемому источнику напряжения, способного выдавать заведомо больше, чем напряжение пробоя. Напряжение на конденсаторе контроллируется вольтметром.
Затем напряжение плавно повышают до тех пор, пока не произойдет пробой (момент, когда напряжение на конденсаторе резко упадет до нуля).
За рабочее напряжение можно принять значение, в 2-3 раза меньше, чем напряжение пробоя. Но это такое… Вы можете иметь свое мнение на этот счет.
Внимание! Обязательно соблюдайте все меры предосторожности! При проверке конденсатора на пробой необходимо использовать защищенный стенд, а также индивидуальные средства защиты зрения.
Энергии заряженного конденсатора бывает достаточно, чтобы устроить небольшой ядерный взрыв прямо на рабочем столе. Вот, можно посмотреть, как это бывает:
А некоторые типы керамических конденсаторов при электрическом пробое способны разлетаться на очень мелкие, но твердые осколки, без труда пробивающие кожу (не говоря уже о глазах).
Способ №2: нахождение рабочего напряжения конденсатора через ток утечки
Этот способ узнать рабочее напряжение конденсатора подходит для алюминиевых электролитических конденсаторов (полярных и неполярных). А таких конденсаторов большинство.
Суть заключается в том, чтобы отловить момент, при котором его ток утечки начинает нелинейно возрастать. Для этого собираем простейшую схему:
и делаем замеры тока утечки при различных значениях приложенного напряжения (начиная с 5 вольт и далее). Напряжение следует повышать постепенно, одинаковыми порциями, записывая показания вольтметра и микроампераметра в таблицу.
У меня получилась такая табличка (моя чуйка подсказала мне, что это довольно высоковольтный конденсатор, так что я сразу начал прибавлять по 10В):
| Напряжение на конденсаторе, В | Ток утечки, мкА | Прирост тока, мкА |
|---|---|---|
| 10 | 1.1 | 1.1 |
| 20 | 2.2 | 1.1 |
| 30 | 3.3 | 1.1 |
| 40 | 4.5 | 1.2 |
| 50 | 5.8 | 1.3 |
| 60 | 7.2 | 1.4 |
| 70 | 8.9 | 1.7 |
| 80 | 11.0 | 2.1 |
| 90 | 13.4 | 2.4 |
| 100 | 16.0 | 2.6 |
Как только станет заметно, что одинаковый прирост напряжения каждый раз приводит к непропорционально бОльшему приросту тока утечки, эксперимент следует остановить, так как перед нами не стоит задача довести конденсатор до электрического пробоя.
Если из полученных значений построить график, то он будет иметь следующий вид:
Видно, что начиная с 50-60 вольт, график зависимости тока утечки от напряжения обретает явно выраженную нелинейность. А если принять во внимание стандартный ряд напряжений:
| Стандартный ряд номинальных рабочих напряжений конденсаторов, В | |||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 6.3 | 10 | 16 | 20 | 25 | 32 | 40 | 50 | 63 | 80 | 100 | 125 | 160 | 200 | 250 | 315 | 350 | 400 | 450 | 500 |
то можно предположить, что для данного конденсатора рабочее напряжение составляет либо 50 либо 63 В.
Согласен, метод достаточно трудоемкий, но не сказать о нем было бы ошибкой.
Как измерить ток утечки конденсатора?
Чуть выше уже была описана методика измерения тока утечки. Хотелось бы только добавить, что Iут измеряется либо при максимальном рабочем напряжении конденсатора либо при таком напряжении, при котором конденсатор планируется использовать.
Также можно вычислить ток утечки конденсатора косвенным методом – через падение напряжения на заранее известном сопротивлении:
При проверке полярных конденсаторов на утечку необходимо соблюдать полярность их подключения. В противном случае будут получены некорректные результаты.
При измерении тока утечки электролитических конденсаторов после подачи напряжения очень важно выждать какое-то время (минут 5-10) для того, чтобы все электрохимические процессы завершились. Особенно это актуально для конденсаторов, которые в течение длительного времени были выведены из эксплуатации.
Вот видео с наглядной демонстрацией описанного метода измерения тока утечки конденсатора:
Определение емкости неизвестного конденсатора
Способ №1: измерение емкости специальными приборами
Самый просто способ – измерить емкость с помощью прибора, имеющего функцию измерения емкостей. Это и так понятно, и об этом уже говорилсь в начале статьи и тут нечего больше добавить.Если с приборами совсем туган, можно попробовать собрать простенький самодельный тестер. В интернете можно найти неплохие схемы (посложнее, попроще, совсем простая).
Ну или раскошелиться, наконец, на универсальный тестер, который измеряет емкость до 100000 мкФ, ESR, сопротивление, индуктивность, позволяет проверять диоды и измерять параметры транзисторов. Сколько раз он меня выручал!
Способ №2: измерение емкости двух последовательно включенных конденсаторов
Иногда бывает так, что имеется мультиметр с измерялкой емкости, но его предела не хватает. Обычно верхний порог мультиметров – это 20 или 200 мкФ, а нам нужно измерить емкость, например, в 1200 мкФ. Как тогда быть?
На помощь приходит формула емкости двух последовательно соединенных конденсаторов:Суть в том, что результирующая емкость Cрез двух последовательных кондеров будет всегда меньше емкости самого маленького из этих конденсаторов. Другими словами, если взять конденсатор на 20 мкФ, то какой бы большой емкостью не обладал бы второй конденсатор, результирующая емкость все равно будет меньше, чем 20 мкФ.
Таким образом, если предел измерения нашего мультиметра 20 мкФ, то неизвестный конденсатор нужно последовательно с конденсатором не более 20 мкФ.Остается только измерить общую емкость цепочки из двух последовательно включенных конденсаторов. Емкость неизвестного конденсатора рассчитывается по формуле:Давайте для примера рассчитаем емкость большого конденсатора Сх с фотографии выше. Для проведения измерения последовательно с этим конденсатором включен конденсатор С1 на 10.06 мкФ (он был предварительно измерен). Видно, что результирующая емкость составила Cрез = 9.97 мкФ.
Подставляем эти цифры в формулу и получаем:
Способ №3: измерение емкости через постоянную времени цепи
Как известно, постоянная времени RC-цепи зависит от величины сопротивления R и значения емкости Cх:Постоянная времени – это время, за которое напряжение на конденсаторе уменьшится в е раз (где е – это основание натурального логарифма, приблизительно равное 2,718).
Таким образом, если засечь за какое время разрядится конденсатор через известное сопротивление, рассчитать его емкость не составит труда.Для повышения точности измерения необходимо взять резистор с минимальным отклонением сопротивления. Думаю, 0.005% будет нормально =)Хотя можно взять обычный резистор с 5-10%-ой погрешностью и тупо измерить его реальное сопротивление мультиметром. Резистор желательно выбирать такой, чтобы время разряда конденсатора было более-менее вменяемым (секунд 10-30).
Вот какой-то чел очень хорошо все рассказал на видео:
Другие способы измерения емкости
Также можно очень приблизительно оценить емкость конденсатора через скорость роста его сопротивления постоянному току в режиме прозвонки. Об этом уже упоминалось, когда шла речь про проверку на обрыв.
Яркость свечения лампочки (см. метод поиска КЗ) также дает весьма приблизительную оценку емкости, но тем не менее такое способ имеет право на существование.
Существует также метод измерения емкости посредством измерения ее сопротивления переменному току. Примером реализации данного метода служит простейшая мостовая схема:Вращением ротора переменного конденсатора С2 добиваются баланса моста (балансировка определяется по минимальным показаниям вольтметра). Шкала заранее проградуирована в значениях емкости измеряемого конденсатора. Переключатель SA1 служит для переключения диапазона измерения. Замкнутое положение соответствует шкале 40…85 пФ. Конденсаторы С3 и С4 можно заменить одинаковыми резисторами.
Недостаток схемы – необходим генератор переменного напряжения, плюс требуется предварительная калиброка.
Можно ли проверить конденсатор мультиметром не выпаивая его с платы?
Не существует однозначного ответа на вопрос как проверить конденсатор мультиметром не выпаивая: все зависит о схемы, в которой стоит конденсатор.
Все дело в том, что принципиальные схемы, как правило, состоят из множества элементов, которые могут быть соединены с исследуемым конденсатором самым замысловатым образом.
Например, несколько конденсаторов могут быть соединены параллельно и тогда прибор покажет их суммарную емкость. Если при этом один из конденсаторов будет в обрыве, то это будет очень сложно заметить.
Или, например, довольно часто параллельно электролитическому конденсатору устанавливают керамический. В этом случае нет ни малейшей возможности прозвонить конденсатор мультиметром на плате и определить внутренний обрыв.В колебательных контурах, вообще, параллельно кондеру может оказаться катушка индуктивности. Тогда прозвонка конденсатора покажет короткое замыкание, хотя на самом деле его нет.
Вот пример, когда все пять конденсаторов покажут ложное КЗ:
Таким образом, проверка конденсаторов мультиметром без выпаивания вообще невозможна.В схемах импульсных блоков питания очень часто встречаются контура, состоящие из вторичной обмотки трансформатора, диода и выпрямительного конденсатора. Так вот любая “прозвонка” конденсатора при пробитом диоде покажет КЗ. А на самом деле конденсатор может быть вполне исправен.Вообще-то, проверить электролитический конденсатор мультиметром не выпаивая можно, но это только для кондеров ощутимой емкости (>1 мкФ) и только проверить наличие емкости и отсутствие коротыша. Ни о каком измерении емкости и речи быть не может. К тому же, если прибор покажет КЗ, то выпаивать все-таки придется, так как коротить может что угодно на плате.
Мелкие кондеры проверяются только на отсутствие КЗ, обрыв и нулевую емкость таким образом не проверишь.
Вот очень правильный и понятный видос на эту тему:
Примеры выше (а также доходчивое видео) не оставляют никаких сомнений, что проверка конденсаторов не выпаивая из схемы – это фантастика.
Если какой-либо конденсатор вызывает сомнения, лучше сразу заменить его на заведомо исправный. Или хотя бы временно подпаять хороший конденсатор параллельно сомнительному, чтобы подтвердить или опровергнуть подозрения.
Конденсаторы и емкость – Университетская физика, том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие конденсатора и его емкости
- Опишите, как оценить емкость системы проводов
Конденсатор – это устройство, используемое для хранения электрического заряда и электрической энергии. Он состоит как минимум из двух электрических проводников, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, это «обкладки конденсатора».Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор называется «вакуумным конденсатором». Однако пространство обычно заполнено изоляционным материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем накопителя в конденсаторе определяется свойством, называемым емкостью , , о котором вы узнаете больше чуть позже в этом разделе.
Конденсаторымогут применяться в самых разных областях – от фильтрации статического электричества от радиоприема до накопления энергии в дефибрилляторах сердца.Как правило, у промышленных конденсаторов две проводящие части расположены близко друг к другу, но не соприкасаются, как показано на (Рисунок). В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной Q с положительной пластины на отрицательную. Конденсатор в целом остается нейтральным, но заряжается и находится на противоположных пластинах.
Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее.Теперь у них есть заряды и (соответственно) на своих тарелках. (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A, , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами ((Рисунок)). Величина электрического поля в пространстве между параллельными пластинами равна, где обозначает поверхностную плотность заряда на одной пластине (напомним, что это заряд Q на площадь поверхности A ).Таким образом, величина поля прямо пропорциональна Q .
Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности обкладок конденсатора. Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.
Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах.Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В, на его пластинах. Другими словами, емкость – это наибольшая величина заряда на вольт, которая может храниться на устройстве:
Единица измерения емкости в системе СИ – фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость – это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или
.По определению, 1.Конденсатор 0-F может хранить 1,0 Кл заряда (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад – это очень большая емкость. Типичные значения емкости находятся в диапазоне от пикофарад до миллифарад, включая микрофарады (). Конденсаторы могут быть изготовлены различных форм и размеров ((рисунок)).
Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости.(Источник: Windell Oskay)
Расчет емкости
Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.
Стратегия решения проблем: расчет емкости
- Предположим, что конденсатор имеет заряд Q .
- Определите электрическое поле между проводниками. Если симметрия присутствует в расположении проводников, вы можете использовать закон Гаусса для этого расчета.
- Найдите разность потенциалов между проводниками из
, где путь интеграции ведет от одного проводника к другому. Тогда величина разности потенциалов. - При известном В емкость можно получить непосредственно из (Рисунок).
Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.
Конденсатор с параллельными пластинами
Конденсатор с параллельными пластинами ((рисунок)) имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A, , разделенных расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними.Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить. Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины друг к другу, тем больше на них притяжения противоположных зарядов. Следовательно, C должно быть больше для меньшего d .
В конденсаторе с параллельными пластинами, разделенными обкладками на расстояние d , каждая пластина имеет одинаковую площадь поверхности A .
Определим поверхностную плотность заряда на пластинах как
Из предыдущих глав мы знаем, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как
, где константа – это диэлектрическая проницаемость свободного пространства, единица измерения Ф / м в системе СИ эквивалентна так как электрическое поле между пластинами однородно, разность потенциалов между пластинами равна
.Следовательно (рисунок) дает емкость конденсатора с параллельными пластинами как
Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или В . Если заряд изменяется, потенциал изменяется соответственно, так что Q / V остается постоянным.
Емкость и заряд, накопленный в конденсаторе с параллельными пластинами (a) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, площадь каждой из которых составляет 1,00 мм? (б) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение?
Стратегия Определение емкости C является простым приложением (Рисунок).Найдя C , мы сможем найти накопленный заряд, используя (Рисунок).
Решение
- Ввод данных значений в (рисунок) дает
Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. - Инвертирование (рисунок) и ввод известных значений в это уравнение дает
Значение Этот заряд лишь немного больше, чем в типичных приложениях статического электричества.Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3,0 МВ / м, на этом конденсаторе больше не может храниться заряд при увеличении напряжения.
A 1-F конденсатор с параллельными пластинами. Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь необходимо использовать для каждой пластины, если пластины разделены на 1,0 мм?
Переставляя решение (рисунок), получаем
Каждая квадратная пластина должна быть 10 км в поперечнике. Раньше было обычным розыгрышем – попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.
Проверьте свое понимание Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины равна, каково расстояние между пластинами?
Проверьте свое понимание Убедитесь в этом и используйте те же физические единицы.
Цилиндрический конденсатор
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров ((Рисунок)). Внутренний цилиндр радиуса может быть либо оболочкой, либо полностью твердым.Внешний цилиндр представляет собой оболочку внутреннего радиуса. Мы предполагаем, что длина каждого цилиндра составляет l и что избыточные заряды и находятся на внутреннем и внешнем цилиндрах, соответственно.
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров. Здесь заряд на внешней поверхности внутреннего цилиндра положительный (обозначен значком), а заряд на внутренней поверхности внешнего цилиндра отрицательный (обозначен значком).Без учета краевых эффектов электрическое поле между проводниками направлено радиально наружу от общей оси цилиндров.Используя гауссову поверхность, показанную на (Рисунок), мы имеем
Следовательно, электрическое поле между цилиндрами равно
Здесь – единичный радиальный вектор по радиусу цилиндра. Можно подставить в (рисунок) и найти разность потенциалов между цилиндрами:
Таким образом, емкость цилиндрического конденсатора
Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением (рисунок) является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов.Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом. (Здесь мы предполагаем наличие вакуума между проводниками, но физика практически такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация защищает электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен.Теперь, как показано на рисунке, емкость коаксиального кабеля на единицу длины равна
.В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.
Проверьте свое понимание Когда цилиндрическому конденсатору дают заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В.а) Какова емкость этой системы? (b) Если длина цилиндров составляет 1,0 м, каково соотношение их радиусов?
Несколько типов практических конденсаторов показаны на (Рисунок). Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. (Рисунок) (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы – это слюда, керамика, бумага и антипригарное покрытие Teflon ™.
Другой популярный тип конденсатора – электролитический конденсатор. Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста.Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку. Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).
Воздушный конденсатор переменной емкости ((Рисунок)) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»).Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение. Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую радиостанцию, думайте об емкости.
В переменном воздушном конденсаторе емкость можно настраивать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроул)
Обозначения, показанные на (Рисунок), представляют собой схемы различных типов конденсаторов.Обычно мы используем символ, показанный на (Рисунок) (а). Символ на (Рисунок) (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор частично представлен символом (Рисунок) (b), где изогнутая пластина обозначает отрицательный вывод.
Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор.Символ в (c) представляет конденсатор переменной емкости.
Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки ((рисунок)). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм. Рассматривая клеточную мембрану как конденсатор наноразмеров, оценка наименьшей напряженности электрического поля на ее «пластинах» дает значение.
Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.
Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней. Диффузия перемещает ионы (калия) и (хлорида) в показанных направлениях, пока кулоновская сила не остановит дальнейшую передачу. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране.Мембрана обычно непроницаема для Na + (ионов натрия).Сводка
- Конденсатор – это устройство, которое накапливает электрический заряд и электрическую энергию. Количество заряда, которое может хранить вакуумный конденсатор, зависит от двух основных факторов: приложенного напряжения и физических характеристик конденсатора, таких как его размер и геометрия.
- Емкость конденсатора – это параметр, который говорит нам, сколько заряда может храниться в конденсаторе на единицу разности потенциалов между его пластинами.Емкость системы проводников зависит только от геометрии их расположения и физических свойств изоляционного материала, заполняющего пространство между проводниками. Единицей измерения емкости является фарад, где
Концептуальные вопросы
Зависит ли емкость устройства от приложенного напряжения? Зависит ли емкость устройства от заряда, находящегося на нем?
Не могли бы вы разместить пластины конденсатора с параллельными пластинами ближе друг к другу или дальше друг от друга, чтобы увеличить их емкость?
Значение емкости равно нулю, если пластины не заряжены.Правда или ложь?
Если пластины конденсатора имеют разные площади, получат ли они одинаковый заряд, когда конденсатор подключен к батарее?
Зависит ли емкость сферического конденсатора от того, какая сфера заряжена положительно или отрицательно?
Проблемы
Какой заряд сохраняется в конденсаторе, когда к нему приложено 120,0 В?
Найдите заряд, накопленный при приложении 5,50 В к конденсатору 8,00 пФ.
Рассчитайте напряжение, приложенное к конденсатору, когда он сохраняет заряд.
Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ, чтобы накопить заряд 0,160 мкКл?
Какая емкость необходима для хранения заряда при напряжении 120 В?
Какова емкость вывода большого генератора Ван-де-Граафа, если он хранит 8,00 мКл заряда при напряжении 12,0 МВ?
Пластины пустого плоского конденсатора емкостью 5,0 пФ находятся на расстоянии 2,0 мм друг от друга. Какова площадь каждой пластины?
А 60.Вакуумный конденсатор 0 пФ имеет плоскую обкладку. Какое расстояние между его пластинами?
Набор параллельных пластин имеет емкость. Какой заряд нужно добавить к пластинам, чтобы разность потенциалов между ними увеличилась на 100 В?
Считайте Землю сферическим проводником радиусом 6400 км и вычислите ее емкость.
Если емкость на единицу длины цилиндрического конденсатора составляет 20 пФ / м, каково отношение радиусов двух цилиндров?
Пустой конденсатор с параллельными пластинами имеет емкость.Сколько заряда должно стечь с пластин, прежде чем напряжение на них снизится на 100 В?
Глоссарий
- емкость
- количество хранимого заряда на единицу вольт
- конденсатор
- Устройство для хранения электрического заряда и электрической энергии
- диэлектрик
- изоляционный материал, используемый для заполнения пространства между двумя пластинами
- конденсатор с параллельными пластинами
- система двух идентичных параллельных проводящих пластин, разделенных расстоянием
Как измерить емкость с помощью цифрового мультиметра
Мультиметр определяет емкость, заряжая конденсатор известным током, измеряя результирующее напряжение и затем вычисляя емкость.
Предупреждение: Хороший конденсатор сохраняет электрический заряд и может оставаться под напряжением после отключения питания. Перед тем, как дотронуться до него или провести измерение, а) выключите все питание, б) используйте мультиметр, чтобы убедиться, что питание отключено, и в) осторожно разрядите конденсатор, подключив резистор к его проводам (как указано в следующем абзаце). Обязательно используйте соответствующие средства индивидуальной защиты.
Для безопасной разрядки конденсатора: После отключения питания подключите 5-ваттный резистор 20 000 Ом к клеммам конденсатора на пять секунд.Используйте мультиметр, чтобы убедиться, что конденсатор полностью разряжен.
- Используйте цифровой мультиметр (DMM), чтобы убедиться, что питание цепи отключено. Если конденсатор используется в цепи переменного тока, настройте мультиметр на измерение переменного напряжения. Если он используется в цепи постоянного тока, установите цифровой мультиметр на измерение постоянного напряжения.
- Осмотрите конденсатор. Если утечки, трещины, выпуклости или другие признаки износа очевидны, замените конденсатор.
- Поверните циферблат в режим измерения емкости.Символ часто разделяет точку на циферблате с другой функцией. Помимо регулировки шкалы, для активации измерения обычно необходимо нажать функциональную кнопку. За инструкциями обратитесь к руководству пользователя мультиметра.
4. Для правильного измерения необходимо удалить конденсатор из цепи. Разрядите конденсатор, как описано в предупреждении выше.
Примечание: Некоторые мультиметры поддерживают относительный (REL) режим. При измерении низких значений емкости можно использовать относительный режим для удаления емкости измерительных проводов.Чтобы перевести мультиметр в относительный режим измерения емкости, оставьте измерительные провода открытыми и нажмите кнопку REL. Это удаляет значение остаточной емкости измерительных проводов.
- Подключите измерительные провода к клеммам конденсатора. Оставьте измерительные провода подключенными на несколько секунд, чтобы мультиметр автоматически выбрал правильный диапазон.
- Считайте отображаемое измерение. Если значение емкости находится в пределах диапазона измерения, мультиметр отобразит значение конденсатора.Он будет отображать OL, если а) значение емкости выше диапазона измерения или б) конденсатор неисправен.
Обзор измерения емкости
Устранение неисправностей однофазных двигателей – одно из наиболее практических применений функции емкости цифрового мультиметра.
Однофазный двигатель с конденсаторным пуском, который не запускается, является признаком неисправного конденсатора. Такие двигатели будут продолжать работать после запуска, что затрудняет поиск и устранение неисправностей. Выход из строя конденсатора жесткого пуска компрессоров HVAC является хорошим примером этой проблемы.Двигатель компрессора может запуститься, но вскоре перегреется, что приведет к срабатыванию выключателя.
Однофазные двигатели с такими проблемами и шумные однофазные двигатели с конденсаторами нуждаются в мультиметре для проверки правильного функционирования конденсаторов. Почти все моторные конденсаторы имеют значение в микрофарадах, указанное на конденсаторе.
Трехфазные конденсаторы коррекции коэффициента мощности обычно защищены плавкими предохранителями. Если один или несколько из этих конденсаторов выйдут из строя, это приведет к неэффективности системы, скорее всего, увеличатся счета за коммунальные услуги и могут произойти непреднамеренные отключения оборудования.Если предохранитель конденсатора перегорел, необходимо измерить предполагаемое значение микрофарад конденсатора и убедиться, что оно находится в пределах диапазона, указанного на конденсаторе.
Стоит знать о некоторых дополнительных факторах, связанных с емкостью:
- Конденсаторы имеют ограниченный срок службы и часто являются причиной неисправности.
- Неисправные конденсаторы могут иметь короткое замыкание, разрыв цепи или могут физически выйти из строя до точки отказа.
- При коротком замыкании конденсатора может перегореть предохранитель или повредить другие компоненты.
- Когда конденсатор размыкается или выходит из строя, цепь или ее компоненты могут не работать.
- Износ может также изменить значение емкости конденсатора, что может вызвать проблемы.
Ссылка: Принципы цифрового мультиметра Глена А. Мазура, American Technical Publishers.
Связанные ресурсы
8.1 Конденсаторы и емкость – Университетская физика, Том 2
Цели обучения
К концу этого раздела вы сможете:
- Объясните понятие конденсатора и его емкости
- Опишите, как оценить емкость системы проводов
Конденсатор – это устройство, используемое для хранения электрического заряда и электрической энергии.Он состоит как минимум из двух электрических проводников, разделенных расстоянием. (Обратите внимание, что такие электрические проводники иногда называют «электродами», но, точнее, они «обкладки конденсатора».) Пространство между конденсаторами может быть просто вакуумом, и в этом случае конденсатор будет известен как «Вакуумный конденсатор». Однако пространство обычно заполнено изоляционным материалом, известным как диэлектрик. (Вы узнаете больше о диэлектриках в разделах, посвященных диэлектрикам, далее в этой главе.) Объем конденсатора определяется свойством , емкостью , о котором вы узнаете больше чуть позже в этом разделе.
Конденсаторымогут применяться в самых разных областях – от фильтрации статического электричества от радиоприема до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как показано на рисунке 8.2. В большинстве случаев между двумя пластинами используется диэлектрик. Когда клеммы батареи подключены к первоначально незаряженному конденсатору, потенциал батареи перемещает небольшое количество заряда величиной Q с положительной пластины на отрицательную.Конденсатор в целом остается нейтральным, но с зарядами + Q + Q и −Q − Q, расположенными на противоположных пластинах.
Рисунок 8.2 Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь на их тарелках есть заряды + Q + Q и −Q − Q (соответственно). (a) Конденсатор с параллельными пластинами состоит из двух пластин противоположного заряда с площадью A, , разделенных расстоянием d . (b) Катаный конденсатор имеет диэлектрический материал между двумя проводящими листами (пластинами).Система, состоящая из двух идентичных параллельно проводящих пластин, разделенных расстоянием, называется конденсатором с параллельными пластинами (рисунок 8.3). Величина электрического поля в пространстве между параллельными пластинами составляет E = σ / ε0E = σ / ε0, где σσ обозначает поверхностную плотность заряда на одной пластине (напомним, что σσ – это заряд Q на площадь поверхности A ). Таким образом, величина поля прямо пропорциональна Q .
Рис. 8.3 Разделение зарядов в конденсаторе показывает, что заряды остаются на поверхности пластин конденсатора.Линии электрического поля в конденсаторе с параллельными пластинами начинаются с положительных зарядов и заканчиваются отрицательными зарядами. Величина электрического поля в пространстве между пластинами прямо пропорциональна количеству заряда на конденсаторе.
Конденсаторы с разными физическими характеристиками (такими как форма и размер пластин) накапливают разное количество заряда для одного и того же приложенного напряжения В на своих пластинах. Емкость C конденсатора определяется как отношение максимального заряда Q , который может храниться в конденсаторе, к приложенному напряжению В, на его пластинах.Другими словами, емкость – это наибольшая величина заряда на вольт, которая может храниться на устройстве:
Единица измерения емкости в системе СИ – фарад (Ф), названная в честь Майкла Фарадея (1791–1867). Поскольку емкость – это заряд на единицу напряжения, один фарад равен одному кулону на один вольт, или
.По определению, конденсатор емкостью 1,0 мкФ может сохранять заряд 1,0 К (очень большой заряд), когда разность потенциалов между его пластинами составляет всего 1,0 В. Следовательно, один фарад – это очень большая емкость.Типичные значения емкости варьируются от пикофарад (1пФ = 10−12Ф) (1пФ = 10−12Ф) до миллифарад (1мФ = 10−3Ф) (1мФ = 10−3Ф), что также включает микрофарады (1мкФ = 10−6F1мкФ = 10− 6F). Конденсаторы могут быть разных форм и размеров (рис. 8.4).
Рис. 8.4 Это некоторые типичные конденсаторы, используемые в электронных устройствах. Размер конденсатора не обязательно зависит от его емкости. (кредит: Windell Oskay)
Расчет емкости
Мы можем рассчитать емкость пары проводов с помощью следующего стандартного подхода.
Стратегия решения проблем
Расчет емкости
- Предположим, что конденсатор заряжен Q .
- Определить электрическое поле E → E → между проводниками. Если симметрия присутствует в расположении проводников, вы можете использовать закон Гаусса для этого расчета.
- Найдите разность потенциалов между проводниками из
VB − VA = −ABE → · dl →, VB − VA = −ABE → · dl →,
8,2
где путь интегрирования ведет от одного проводника к другому.Тогда величина разности потенциалов равна V = | VB-VA | V = | VB-VA |. - Зная В, , определите емкость непосредственно из уравнения 8.1.
Чтобы показать, как работает эта процедура, мы теперь вычисляем емкости параллельных пластин, сферических и цилиндрических конденсаторов. Во всех случаях мы предполагаем вакуумные конденсаторы (пустые конденсаторы) без диэлектрического вещества в пространстве между проводниками.
Конденсатор с параллельными пластинами
Конденсатор с параллельными пластинами (рисунок 8.5) имеет две идентичные токопроводящие пластины, каждая с площадью поверхности A, , разделенными расстоянием d . Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость может зависеть от A и d , рассматривая характеристики кулоновской силы. Мы знаем, что сила между зарядами увеличивается с увеличением заряда и уменьшается с расстоянием между ними. Следует ожидать, что чем больше пластины, тем больше заряда они могут хранить.Таким образом, C должно быть больше для большего значения A . Точно так же, чем ближе пластины друг к другу, тем больше на них притяжения противоположных зарядов. Следовательно, C должно быть больше для меньшего d .
Рис. 8.5 В конденсаторе с параллельными пластинами с пластинами, разнесенными на расстояние d , каждая пластина имеет одинаковую площадь поверхности A .
Определим плотность поверхностного заряда σσ на пластинах как
Из предыдущих глав мы знаем, что когда d мало, электрическое поле между пластинами довольно однородно (без учета краевых эффектов) и что его величина определяется как
где постоянная ε0ε0 – диэлектрическая проницаемость свободного пространства, ε0 = 8.85 × 10–12Ф / м. Ε0 = 8,85 × 10–12Ф / м. Единица СИ в Ф / м эквивалентна C2 / N · m2.C2 / N · m2. Поскольку электрическое поле E → E → между пластинами однородно, разность потенциалов между пластинами составляет
V = Ed = σdε0 = Qdε0A.V = Ed = σdε0 = Qdε0A.Следовательно, уравнение 8.1 дает емкость конденсатора с параллельными пластинами как
C = QV = QQd / ε0A = ε0Ad.C = QV = QQd / ε0A = ε0Ad.8,3
Обратите внимание на это уравнение, что емкость является функцией только геометрии и того, какой материал заполняет пространство между пластинами (в данном случае вакуум) этого конденсатора.Фактически, это верно не только для конденсатора с параллельными пластинами, но и для всех конденсаторов: емкость не зависит от Q или В . Если заряд изменяется, потенциал изменяется соответственно, так что Q / V остается постоянным.
Пример 8.1
Емкость и заряд в конденсаторе с параллельными пластинами
(a) Какова емкость пустого конденсатора с параллельными пластинами с металлическими пластинами, каждая из которых имеет площадь 1,00 м 21.00м2, разделенных расстоянием 1,00 мм? (b) Сколько заряда хранится в этом конденсаторе, если к нему приложено напряжение 3,00 × 103 В3,00 × 103 В?Стратегия
Определение емкости C представляет собой прямое применение уравнения 8.3. Найдя C , мы сможем найти накопленный заряд, используя уравнение 8.1.Решение
- Ввод заданных значений в уравнение 8.3 дает C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3м = 8,85 × 10−9F = 8,85nF.C = ε0Ad = (8,85 × 10−12Fm) 1,00м21,00 × 10−3m = 8 .85 × 10−9F = 8,85 нФ. Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью.
- Обращение уравнения 8.1 и ввод известных значений в это уравнение дает Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл. Q = CV = (8,85 × 10–9F) (3,00 × 103 В) = 26,6 мкКл.
Значение
Этот заряд лишь немного больше, чем в типичных приложениях статического электричества. Поскольку воздух разрушается (становится проводящим) при напряженности электрического поля около 3.0 МВ / м, на этом конденсаторе больше нельзя накапливать заряд при увеличении напряжения.Пример 8.2
Конденсатор с параллельными пластинами, 1 Ф
Предположим, вы хотите сконструировать конденсатор с параллельными пластинами емкостью 1,0 F. Какую площадь вы должны использовать для каждой пластины, если пластины разделены на 1,0 мм?Решение
Преобразуя уравнение 8.3, получаем A = Cdε0 = (1.0F) (1.0 × 10−3m) 8.85 × 10−12F / m = 1.1 × 108m2 A = Cdε0 = (1.0F) (1.0 × 10−3m) 8,85 × 10−12F / m = 1,1 × 108м2.Каждая квадратная пластина должна быть 10 км в поперечнике.Раньше было обычным розыгрышем – попросить студента пойти в склад лаборатории и попросить конденсатор с параллельными пластинами 1F, пока обслуживающий персонал не устанет от шуток.
Проверьте свое понимание 8.1
Емкость конденсатора с параллельными пластинами составляет 2,0 пФ. Если площадь каждой пластины составляет 2,4 см 22,4 см2, каково расстояние между пластинами?
Проверьте свое понимание 8.2
Убедитесь, что σ / Vσ / V и ε0 / dε0 / d имеют одинаковые физические единицы.
Сферический конденсатор
Сферический конденсатор – это еще один набор проводников, емкость которых можно легко определить (Рисунок 8.dr) = Q4πε0∫R1R2drr2 = Q4πε0 (1R1−1R2).
В этом уравнении разность потенциалов между пластинами равна V = – (V2 − V1) = V1 − V2V = – (V2 − V1) = V1 − V2. Мы подставляем этот результат в уравнение 8.1, чтобы найти емкость сферического конденсатора:
C = QV = 4πε0R1R2R2 − R1.C = QV = 4πε0R1R2R2 − R1.8,4
Рисунок 8.6 Сферический конденсатор состоит из двух концентрических проводящих сфер. Обратите внимание, что заряды на проводнике находятся на его поверхности.
Пример 8.3
Емкость изолированной сферы
Вычислите емкость одиночной изолированной проводящей сферы радиуса R1R1 и сравните ее с уравнением 8.dr) = Q4πε0∫R1 + ∞drr2 = 14πε0QR1.Следовательно, емкость изолированного шара составляет
. C = QV = Q4πε0R1Q = 4πε0R1.C = QV = Q4πε0R1Q = 4πε0R1.Значение
Тот же результат можно получить, взяв предел уравнения 8.4 при R2 → ∞R2 → ∞. Таким образом, одиночная изолированная сфера эквивалентна сферическому конденсатору, внешняя оболочка которого имеет бесконечно большой радиус.Проверьте свое понимание 8.3
Радиус внешней сферы сферического конденсатора в пять раз превышает радиус его внутренней оболочки.Каковы размеры этого конденсатора, если его емкость 5,00 пФ?
Цилиндрический конденсатор
Цилиндрический конденсатор состоит из двух концентрических проводящих цилиндров (рисунок 8.7). Внутренний цилиндр радиуса R1R1 может быть оболочкой или полностью твердым. Внешний цилиндр представляет собой оболочку внутреннего радиуса R2R2. Мы предполагаем, что длина каждого цилиндра составляет l и что избыточные заряды + Q + Q и −Q − Q находятся на внутреннем и внешнем цилиндрах соответственно.dr) = Q2πε0l∫R1R2drr = Q2πε0llnr | R1R2 = Q2πε0llnR2R1.
Таким образом, емкость цилиндрического конденсатора
C = QV = 2πε0lln (R2 / R1). C = QV = 2πε0lln (R2 / R1).8,6
Как и в других случаях, эта емкость зависит только от геометрии расположения проводников. Важным применением уравнения 8.6 является определение емкости на единицу длины коаксиального кабеля , который обычно используется для передачи изменяющихся во времени электрических сигналов. Коаксиальный кабель состоит из двух концентрических цилиндрических проводников, разделенных изоляционным материалом.(Здесь мы предполагаем наличие вакуума между проводниками, но физика практически такая же, когда пространство между проводниками заполнено диэлектриком.) Эта конфигурация защищает электрический сигнал, распространяющийся по внутреннему проводнику, от паразитных электрических полей, внешних по отношению к проводнику. кабель. Ток течет в противоположных направлениях во внутреннем и внешнем проводниках, при этом внешний проводник обычно заземлен. Теперь из уравнения 8.6 емкость на единицу длины коаксиального кабеля равна
. Cl = 2πε0ln (R2 / R1).Cl = 2πε0ln (R2 / R1).В практических приложениях важно выбирать конкретные значения C / l . Это может быть достигнуто за счет соответствующего выбора радиусов проводников и изоляционного материала между ними.
Проверьте свое понимание 8.4
Когда цилиндрическому конденсатору дают заряд 0,500 нКл, между цилиндрами измеряется разность потенциалов 20,0 В. а) Какова емкость этой системы? (b) Если цилиндры 1.Длина 0 м, каково соотношение их радиусов?
Несколько типов конденсаторов, которые можно использовать на практике, показаны на рис. 8.4. Обычные конденсаторы часто состоят из двух небольших кусочков металлической фольги, разделенных двумя небольшими кусочками изоляции (см. Рисунок 8.2 (b)). Металлическая фольга и изоляция покрыты защитным покрытием, а два металлических вывода используются для подключения фольги к внешней цепи. Некоторые распространенные изоляционные материалы – это слюда, керамика, бумага и антипригарное покрытие Teflon ™.
Другой популярный тип конденсатора – электролитический конденсатор.Он состоит из окисленного металла в проводящей пасте. Основным преимуществом электролитического конденсатора является его высокая емкость по сравнению с другими распространенными типами конденсаторов. Например, емкость одного типа алюминиевого электролитического конденсатора может достигать 1,0 F. Однако вы должны быть осторожны при использовании электролитического конденсатора в цепи, потому что он работает правильно только тогда, когда металлическая фольга находится под более высоким потенциалом, чем проводящая паста. Когда возникает обратная поляризация, электролитическое действие разрушает оксидную пленку.Этот тип конденсатора не может быть подключен к источнику переменного тока, потому что в половине случаев переменное напряжение будет иметь неправильную полярность, поскольку переменный ток меняет свою полярность (см. Схемы переменного тока в цепях переменного тока).
Воздушный конденсатор переменной емкости (рисунок 8.8) имеет два набора параллельных пластин. Один набор пластин закреплен (обозначен как «статор»), а другой набор пластин прикреплен к валу, который может вращаться (обозначается как «ротор»). Поворачивая вал, можно изменять площадь поперечного сечения в перекрытии пластин; следовательно, емкость этой системы может быть настроена на желаемое значение.Настройка конденсатора находит применение в любом типе радиопередачи и при приеме радиосигналов от электронных устройств. Каждый раз, когда вы настраиваете автомобильное радио на любимую радиостанцию, думайте об емкости.
Рисунок 8.8 В конденсаторе переменного тока емкость можно регулировать, изменяя эффективную площадь пластин. (кредит: модификация работы Робби Спроул)
Обозначения, показанные на рисунке 8.9, представляют собой схемные изображения различных типов конденсаторов. Обычно мы используем символ, показанный на рисунке 8.9 (а). Символ на Рисунке 8.9 (c) представляет конденсатор переменной емкости. Обратите внимание на сходство этих символов с симметрией конденсатора с параллельными пластинами. Электролитический конденсатор представлен символом на рис. 8.9 (b), где изогнутая пластина обозначает отрицательный вывод.
Рисунок 8.9 Здесь показаны три различных схемных представления конденсаторов. Символ в (а) является наиболее часто используемым. Символ в (b) представляет собой электролитический конденсатор. Символ в (c) представляет конденсатор переменной емкости.
Интересный прикладной пример модели конденсатора взят из клеточной биологии и имеет дело с электрическим потенциалом в плазматической мембране живой клетки (рис. 8.10). Клеточные мембраны отделяют клетки от их окружения, но позволяют некоторым отобранным ионам проходить внутрь или из клетки. Разность потенциалов на мембране составляет около 70 мВ. Клеточная мембрана может иметь толщину от 7 до 10 нм. Рассматривая клеточную мембрану как наноразмерный конденсатор, оценка наименьшей напряженности электрического поля на ее “ пластинах ” дает значение E = Vd = 70 × 10−3V · 10 · 10−9m = 7 · 106V / m> 3MV / mE. = Vd = 70 × 10−3V10 × 10−9m = 7 × 106V / m> 3MV / m.
Этой величины электрического поля достаточно, чтобы вызвать электрическую искру в воздухе.
Рис. 8.10. Полупроницаемая мембрана биологической клетки имеет разные концентрации ионов на внутренней поверхности, чем на внешней. Диффузия перемещает ионы K + K + (калий) и Cl – Cl– (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Таким образом, внешняя поверхность мембраны приобретает положительный заряд, а ее внутренняя поверхность приобретает отрицательный заряд, создавая разность потенциалов на мембране.Мембрана обычно непроницаема для Na + (ионов натрия).Конденсаторы и диэлектрики | Физика
Цели обучения
К концу этого раздела вы сможете:
- Опишите действие конденсатора и определите емкость.
- Объясните, почему конденсаторы с параллельными пластинами и их емкости.
- Обсудите процесс увеличения емкости диэлектрика.
- Определите емкость с учетом заряда и напряжения.
Конденсатор – это устройство, используемое для хранения электрического заряда. Конденсаторы имеют различные применения: от фильтрации статического электричества при радиосигнале до накопления энергии в дефибрилляторах сердца. Обычно в промышленных конденсаторах две токопроводящие части расположены близко друг к другу, но не соприкасаются, как, например, на рисунке 1. (В большинстве случаев между двумя пластинами используется изолятор для обеспечения разделения – см. Обсуждение диэлектриков ниже). Клеммы батареи подключены к изначально незаряженному конденсатору, равные количества положительного и отрицательного заряда, + Q и – Q , разделены на его две пластины.Конденсатор в целом остается нейтральным, но в этом случае мы называем его хранящим заряд Q .
Рис. 1. Оба конденсатора, показанные здесь, были изначально разряжены перед подключением к батарее. Теперь у них разделены заряды + Q и – Q на двух половинах. (а) Конденсатор с параллельными пластинами. (b) Скрученный конденсатор с изоляционным материалом между двумя проводящими листами.
Конденсатор
Конденсатор – это устройство для хранения электрического заряда.
Количество заряда Q , который может хранить конденсатор , зависит от двух основных факторов – приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Количество заряда
Q Конденсатор может хранитьКоличество заряда Q , которое может хранить конденсатор , зависит от двух основных факторов – приложенного напряжения и физических характеристик конденсатора, таких как его размер.
Рис. 2. Линии электрического поля в этом конденсаторе с параллельными пластинами, как всегда, начинаются с положительных зарядов и заканчиваются отрицательными.Поскольку напряженность электрического поля пропорциональна плотности силовых линий, она также пропорциональна количеству заряда на конденсаторе.
Система, состоящая из двух идентичных параллельных проводящих пластин, разделенных расстоянием, как на Рисунке 2, называется конденсатором с параллельными пластинами . Легко увидеть взаимосвязь между напряжением и накопленным зарядом для конденсатора с параллельными пластинами, как показано на рисунке 2. Каждая линия электрического поля начинается с отдельного положительного заряда и заканчивается отрицательным, так что поля будет больше. линий, если больше заряда.(Рисование одной линии поля для каждого заряда – это только удобство. Мы можем нарисовать множество линий поля для каждого заряда, но их общее количество пропорционально количеству зарядов.) Таким образом, напряженность электрического поля прямо пропорциональна Ом. .
Поле пропорционально начислению:
E ∝ Q ,
, где символ ∝ означает «пропорционально». Из обсуждения в разделе «Электрический потенциал в однородном электрическом поле» мы знаем, что напряжение на параллельных пластинах равно
.V = Ed .
Таким образом, V ∝ E . Отсюда следует, что V ∝ Q , и, наоборот,
Q ∝ V .
В целом это верно: чем больше напряжение, приложенное к любому конденсатору, тем больше в нем хранится заряд.
Различные конденсаторы будут накапливать разное количество заряда для одного и того же приложенного напряжения в зависимости от их физических характеристик. Мы определяем их емкость C как такую, что заряд Q , хранящийся в конденсаторе, пропорционален C .Заряд, накопленный в конденсаторе, равен
.Q = CV .
Это уравнение выражает два основных фактора, влияющих на количество накопленного заряда. Этими факторами являются физические характеристики конденсатора C и напряжение В . Изменив уравнение, мы видим, что емкость , C, , – это количество накопленного заряда на вольт, или
.[латекс] C = \ frac {Q} {V} \\ [/ латекс].
Емкость
Емкость C – величина накопленного заряда на вольт, или
[латекс] C = \ frac {Q} {V} \\ [/ latex]
Единица измерения емкости – фарад (Ф), названная в честь Майкла Фарадея (1791–1867), английского ученого, внесшего вклад в области электромагнетизма и электрохимии. Поскольку емкость – это заряд на единицу напряжения, мы видим, что фарад – это кулон на вольт, или
.[латекс] 1 \ text {F} = \ frac {1 \ text {C}} {1 \ text {V}} \\ [/ latex].
Конденсатор емкостью 1 фарад может хранить 1 кулон (очень большое количество заряда) при подаче всего 1 вольт. Таким образом, одна фарада – это очень большая емкость. Типичный диапазон конденсаторов составляет от долей пикофарада (1 пФ = 10 −12 Ф) до миллифарадов (1 мФ = 10 −3 Ф).
На рисунке 3 показаны некоторые распространенные конденсаторы. Конденсаторы в основном изготавливаются из керамики, стекла или пластика, в зависимости от назначения и размера. В их конструкции обычно используются изоляционные материалы, называемые диэлектриками, как обсуждается ниже.
Рисунок 3. Некоторые типичные конденсаторы. Размер и значение емкости не обязательно связаны. (Источник: Windell Oskay)
Конденсатор с параллельными пластинами
Рис. 4. Конденсатор с параллельными пластинами, разделенные пластинами на расстояние d. Каждая пластина имеет площадь A.
Конденсатор с параллельными пластинами, показанный на рис. 4, имеет две идентичные проводящие пластины, каждая из которых имеет площадь поверхности A , разделенных расстоянием d (без материала между пластинами).Когда на конденсатор подается напряжение В, , он сохраняет заряд Q , как показано. Мы можем увидеть, как его емкость зависит от A и d , рассмотрев характеристики кулоновской силы. Мы знаем, что одинаковые заряды отталкиваются, в отличие от зарядов притягиваются, и сила между зарядами уменьшается с расстоянием. Поэтому кажется вполне разумным, что чем больше пластины, тем больше заряда они могут хранить, потому что заряды могут расходиться больше. Таким образом, C должен быть больше для большего A .Точно так же, чем ближе пластины друг к другу, тем больше на них притяжения противоположных зарядов. Таким образом, C должен быть больше для меньшего d .
Можно показать, что для конденсатора с параллельными пластинами есть только два фактора ( A, и d ), которые влияют на его емкость C . Емкость конденсатора с параллельными пластинами в форме уравнения равна
.[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].
Емкость параллельного пластинчатого конденсатора
[латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex]
A – это площадь одной пластины в квадратных метрах, а d – это расстояние между пластинами в метрах.Константа ε 0 – диэлектрическая проницаемость свободного пространства; его числовое значение в единицах СИ составляет ε 0 = 8,85 × 10 −12 Ф / м. Единицы измерения Ф / м эквивалентны C 2 / Н · м 2 . Небольшое числовое значение ε 0 связано с большим размером фарада. Конденсатор с параллельными пластинами должен иметь большую площадь, чтобы его емкость приближалась к фараду. (Обратите внимание, что приведенное выше уравнение действительно, когда параллельные пластины разделены воздухом или свободным пространством.Когда между пластинами помещается другой материал, уравнение изменяется, как описано ниже.)
Пример 1. Емкость и заряд, накопленный в параллельном пластинчатом конденсаторе
- Какова емкость конденсатора с параллельными пластинами, каждая из которых имеет площадь 1,00 м 2 , разделенных расстоянием 1,00 мм?
- Какой заряд хранится в этом конденсаторе, если на него приложено напряжение 3,00 × 10 3 В?
Стратегия
Определение емкости C представляет собой прямое приложение уравнения [латекс] C = \ epsilon_ {o} \ frac {A} {d} \\ [/ latex].{-9} \ text {F} = 8.85 \ text {nF} \ end {array} \\ [/ latex]
Обсуждение части 1
Это небольшое значение емкости указывает на то, насколько сложно изготовить устройство с большой емкостью. Помогают специальные методы, например, использование тонких пленок очень большой площади, расположенных близко друг к другу.
Решение для Части 2
Заряд любого конденсатора определяется уравнением Q = CV . Ввод известных значений в это уравнение дает
[латекс] \ begin {array} {lll} Q & = & CV = \ left (8.{3} \ text {V} \ right) \\\ text {} & = & 26.6 \ mu \ text {C} \ end {array} \\ [/ latex]
Обсуждение части 2
Этот заряд лишь немного больше, чем при обычном статическом электричестве. Поскольку воздух разрывается при примерно 3,00 × 10 6 В / м, на этом конденсаторе не может быть накоплено больше заряда за счет увеличения напряжения.
Другой интересный биологический пример, связанный с электрическим потенциалом, обнаружен в плазматической мембране клетки. Мембрана отделяет клетку от окружающей среды, а также позволяет ионам выборочно входить и выходить из клетки.Существует разность потенциалов на мембране около –70 мВ. Это связано с преобладанием в клетке отрицательно заряженных ионов и преобладанием положительно заряженных ионов натрия (Na + ) снаружи. {6} \ text {V / m} \\ [/ latex]
Этого электрического поля достаточно, чтобы вызвать пробой в воздухе.
Диэлектрик
Предыдущий пример подчеркивает сложность сохранения большого количества заряда в конденсаторах. Если d сделать меньше, чтобы обеспечить большую емкость, то максимальное напряжение должно быть уменьшено пропорционально, чтобы избежать пробоя (поскольку [латекс] E = \ frac {V} {d} \\ [/ latex]). Важным решением этой проблемы является размещение изоляционного материала, называемого диэлектриком , между пластинами конденсатора и обеспечение минимально возможного размера d .Мало того, что меньший d увеличивает емкость, многие изоляторы могут выдерживать более сильные электрические поля, чем воздух, перед тем как сломаться.
Есть еще одно преимущество использования диэлектрика в конденсаторе. В зависимости от используемого материала емкость больше, чем заданная уравнением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], на коэффициент κ , называемый диэлектрическая постоянная . Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex] (конденсатор с параллельными пластинами с диэлектриком).
Значения диэлектрической проницаемости κ для различных материалов приведены в таблице 1. Обратите внимание, что κ для вакуума точно равно 1, и поэтому приведенное выше уравнение справедливо и в этом случае. Если использовать диэлектрик, например, поместив тефлон между пластинами конденсатора в примере 1, то емкость будет больше в κ раз, что для тефлона составляет 2,1.
Эксперимент на вынос: создание конденсатора
Насколько большой конденсатор можно сделать с помощью обертки от жевательной резинки? Пластины будут из алюминиевой фольги, а разделитель (диэлектрик) между ними – из бумаги.
| Таблица 1. Диэлектрическая проницаемость и диэлектрическая прочность для различных материалов при 20ºC | ||
|---|---|---|
| Материал | Диэлектрическая проницаемость κ | Электрическая прочность (В / м) |
| Вакуум | 1,00000 | – |
| Воздух | 1.00059 | 3 × 10 6 |
| Бакелит | 4,9 | 24 × 10 6 |
| Плавленый кварц | 3.78 | 8 × 10 6 |
| Неопреновый каучук | 6,7 | 12 × 10 6 |
| Нейлон | 3,4 | 14 × 10 6 |
| Бумага | 3,7 | 16 × 10 6 |
| полистирол | 2,56 | 24 × 10 6 |
| Стекло Pyrex | 5,6 | 14 × 10 6 |
| Кремниевое масло | 2.5 | 15 × 10 6 |
| титанат стронция | 233 | 8 × 10 6 |
| тефлон | 2,1 | 60 × 10 6 |
| Вода | 80 | – |
Обратите внимание, что диэлектрическая проницаемость воздуха очень близка к 1, так что конденсаторы, заполненные воздухом, действуют так же, как конденсаторы с вакуумом между пластинами , за исключением , что воздух может стать проводящим, если напряженность электрического поля становится равной. слишком большой.(Напомним, что [латекс] E = \ frac {V} {d} \\ [/ latex] для конденсатора с параллельными пластинами.) В таблице 1 также показаны максимальные напряженности электрического поля в В / м, которые называются диэлектрической прочностью , для нескольких материалов. Это поля, над которыми материал начинает разрушаться и проводить. Диэлектрическая прочность накладывает ограничение на напряжение, которое может быть приложено для данного расстояния между пластинами. 6 \ text {V / m} \ right) \ left ( 1.{-3} \ text {m} \ right) \\\ text {} & = & 3000 \ text {V} \ end {array} \\ [/ latex]
Однако предел для расстояния в 1,00 мм, заполненного тефлоном, составляет 60 000 В, поскольку электрическая прочность тефлона составляет 60 × 10 6 В / м. Таким образом, тот же конденсатор, заполненный тефлоном, имеет большую емкость и может подвергаться гораздо большему напряжению. Используя емкость, которую мы рассчитали в приведенном выше примере для конденсатора с параллельными пластинами, заполненного воздухом, мы обнаружили, что конденсатор с тефлоновым заполнением может хранить максимальный заряд
[латекс] \ begin {array} {lll} Q & = & CV \\\ text {} & = & \ kappa {C} _ {\ text {air}} V \\\ text {} & = & (2.4 \ text {V}) \\\ text {} & = & 1.1 \ text {mC} \ end {array} \\ [/ latex]
Это в 42 раза больше заряда того же конденсатора, заполненного воздухом.
Диэлектрическая прочность
Максимальная напряженность электрического поля, при превышении которой изоляционный материал начинает разрушаться и становится проводником, называется его диэлектрической прочностью.
Микроскопически, как диэлектрик увеличивает емкость? За это отвечает поляризация изолятора. Чем легче он поляризуется, тем больше его диэлектрическая проницаемость κ .Вода, например, представляет собой полярную молекулу , потому что один конец молекулы имеет небольшой положительный заряд, а другой конец имеет небольшой отрицательный заряд. Полярность воды обуславливает ее относительно большую диэлектрическую проницаемость, равную 80. Эффект поляризации лучше всего можно объяснить с помощью характеристик кулоновской силы. На рис. 5 схематично показано разделение зарядов в молекулах диэлектрического материала, помещенных между заряженными пластинами конденсатора. Кулоновская сила между ближайшими концами молекул и зарядом на пластинах притягивает и очень сильна, поскольку они расположены очень близко друг к другу.Это притягивает больше заряда к пластинам, чем если бы пространство было пустым, а противоположные заряды были на расстоянии d от.
Рис. 5. (a) Молекулы изоляционного материала между пластинами конденсатора поляризованы заряженными пластинами. Это создает слой противоположного заряда на поверхности диэлектрика, который притягивает больше заряда к пластине, увеличивая ее емкость. (б) Диэлектрик снижает напряженность электрического поля внутри конденсатора, что приводит к уменьшению напряжения между пластинами при одинаковом заряде.Конденсатор сохраняет тот же заряд при меньшем напряжении, что означает, что он имеет большую емкость из-за диэлектрика.
Другой способ понять, как диэлектрик увеличивает емкость, – это рассмотреть его влияние на электрическое поле внутри конденсатора. На рис. 5 (б) показаны силовые линии электрического поля с установленным диэлектриком. Поскольку силовые линии заканчиваются зарядами в диэлектрике, их меньше, идущих от одной стороны конденсатора к другой. Таким образом, напряженность электрического поля меньше, чем если бы между пластинами был вакуум, даже если бы на пластинах был одинаковый заряд.Напряжение между пластинами составляет В, = Ед, , поэтому оно тоже уменьшается за счет диэлектрика. Таким образом существует меньшее напряжение В, для того же заряда Q ; поскольку [латекс] C = \ frac {Q} {V} \\ [/ latex], емкость C больше.
Диэлектрическая постоянная обычно определяется как [латекс] \ kappa = \ frac {E_0} {E} \\ [/ latex], или отношение электрического поля в вакууме к электрическому полю в диэлектрическом материале, и в конечном итоге связанных с поляризуемостью материала.
Большое и маленькое: субмикроскопическое происхождение поляризации
Поляризация – это разделение зарядов в атоме или молекуле. Как уже отмечалось, планетарная модель атома описывает его как имеющее положительное ядро, вращающееся вокруг отрицательных электронов, аналогично планетам, вращающимся вокруг Солнца. Хотя эта модель не совсем точна, она очень полезна для объяснения широкого круга явлений и будет уточнена в других местах, например, в атомной физике. Субмикроскопическое происхождение поляризации можно смоделировать, как показано на рисунке 6.
Рис. 6. Художественное представление о поляризованном атоме. Орбиты электронов вокруг ядра немного смещены внешними зарядами (показаны в преувеличении). Получающееся разделение зарядов внутри атома означает, что он поляризован. Обратите внимание, что непохожий заряд теперь ближе к внешним зарядам, вызывая поляризацию.
В атомной физике мы обнаружим, что орбиты электронов более правильно рассматривать как электронные облака с плотностью облака, связанной с вероятностью нахождения электрона в этом месте (в отличие от определенных местоположений и путей планет на их орбитах). вокруг Солнца).Это облако сдвигается кулоновской силой, так что атом в среднем имеет разделенный заряд. Хотя атом остается нейтральным, теперь он может быть источником кулоновской силы, поскольку заряд, поднесенный к атому, будет ближе к одному типу заряда, чем к другому.
Некоторым молекулам, например молекулам воды, присуще разделение зарядов, поэтому они называются полярными молекулами. На рисунке 7 показано разделение зарядов в молекуле воды, которая имеет два атома водорода и один атом кислорода (H 2 O).Молекула воды несимметрична – атомы водорода отталкиваются в одну сторону, придавая молекуле форму бумеранга. Электроны в молекуле воды больше сконцентрированы вокруг более заряженного ядра кислорода, чем вокруг ядер водорода. Это делает кислородный конец молекулы слегка отрицательным, а водородный конец слегка положительным. Собственное разделение зарядов в полярных молекулах облегчает их выравнивание с внешними полями и зарядами. Следовательно, полярные молекулы проявляют более сильные поляризационные эффекты и имеют более высокие диэлектрические проницаемости.Те, кто изучает химию, обнаружат, что полярная природа воды имеет множество эффектов. Например, молекулы воды собирают ионы гораздо эффективнее, потому что у них есть электрическое поле и разделение зарядов, чтобы притягивать заряды обоих знаков. Кроме того, как указывалось в предыдущей главе, полярная вода обеспечивает защиту или экранирование электрических полей в сильно заряженных молекулах, представляющих интерес в биологических системах.
Рис. 7. Художественная концепция молекулы воды. Существует внутреннее разделение зарядов, поэтому вода – полярная молекула.Электроны в молекуле притягиваются к ядру кислорода и оставляют избыток положительного заряда около двух ядер водорода. (Обратите внимание, что схема справа является приблизительной иллюстрацией распределения электронов в молекуле воды. На ней не показано фактическое количество протонов и электронов, участвующих в структуре.)
Исследования PhET: лаборатория конденсаторов
Узнайте, как работает конденсатор! Измените размер пластин и добавьте диэлектрик, чтобы увидеть влияние на емкость.Измените напряжение и посмотрите, как на пластинах накапливаются заряды. Наблюдайте за электрическим полем в конденсаторе. Измерьте напряжение и электрическое поле.
Щелкните, чтобы загрузить симуляцию. Запускать на Java.
Сводка раздела
- Конденсатор – это устройство для хранения заряда.
- Количество заряда Q , которое может хранить конденсатор, зависит от двух основных факторов – приложенного напряжения и физических характеристик конденсатора, таких как его размер.
- Емкость C – это количество заряда, накопленного на вольт, или [латекс] C = \ frac {Q} {V} \\ [/ latex].
- Емкость конденсатора с параллельными пластинами составляет [латекс] C = {\ epsilon} _ {0} \ frac {A} {d} \\ [/ latex], когда пластины разделены воздухом или свободным пространством. [latex] {\ epsilon} _ {\ text {0}} [/ latex] называется диэлектрической проницаемостью свободного пространства.
- Конденсатор с параллельными пластинами с диэлектриком между пластинами имеет емкость, определяемую выражением [латекс] C = \ kappa \ epsilon_ {0} \ frac {A} {d} \\ [/ latex], где κ – диэлектрик. постоянная материала.
- Максимальная напряженность электрического поля, выше которой изолирующий материал начинает разрушаться и становится проводником, называется электрической прочностью.
Концептуальные вопросы
- Зависит ли емкость устройства от приложенного напряжения? А как насчет хранящегося в нем заряда?
- Используйте характеристики кулоновской силы, чтобы объяснить, почему емкость должна быть пропорциональна площади пластины конденсатора. Точно так же объясните, почему емкость должна быть обратно пропорциональна расстоянию между пластинами.
- Объясните причину, по которой диэлектрический материал увеличивает емкость по сравнению с тем, что было бы с воздухом между пластинами конденсатора.Какова независимая причина того, что диэлектрический материал также позволяет приложить большее напряжение к конденсатору? (Таким образом, диэлектрик увеличивает C и допускает более В .)
- Как полярный характер молекул воды помогает объяснить относительно большую диэлектрическую проницаемость воды? (См. Рисунок 7.)
- Искры возникают между пластинами заполненного воздухом конденсатора при более низком напряжении, когда воздух влажный, чем когда сухой. Объясните почему, учитывая полярный характер молекул воды.
- Вода имеет большую диэлектрическую проницаемость, но редко используется в конденсаторах. Объяснить, почему.
- Мембраны в живых клетках, в том числе в человеческих, характеризуются разделением заряда через мембрану. Таким образом, мембраны представляют собой заряженные конденсаторы, важные функции которых связаны с разностью потенциалов на мембране. Требуется ли энергия для разделения этих зарядов в живых мембранах, и если да, то является ли ее источником метаболизм пищевой энергии или каким-либо другим источником?
Рисунок 8.Полупроницаемая мембрана клетки имеет разную концентрацию ионов внутри и снаружи. Диффузия перемещает ионы K + (калий) и Cl – (хлорид) в показанных направлениях, пока кулоновская сила не остановит дальнейший перенос. Это приводит к слою положительного заряда снаружи, слою отрицательного заряда внутри и, следовательно, к напряжению на клеточной мембране. Мембрана обычно непроницаема для Na + (ионы натрия).
Задачи и упражнения
- Какой заряд сохраняется в конденсаторе 180 мкФ, когда к нему приложено 120 В?
- Найдите накопленный заряд, когда 5.На конденсатор емкостью 8,00 пФ подается 50 В.
- Какой заряд хранится в конденсаторе в примере 1?
- Вычислите напряжение, приложенное к конденсатору 2,00 мкФ, когда он имеет заряд 3,10 мкКл.
- Какое напряжение необходимо подать на конденсатор емкостью 8,00 нФ для накопления заряда 0,160 мкКл?
- Какая емкость необходима для хранения 3,00 мкКл заряда при напряжении 120 В?
- Какая емкость терминала большого генератора Ван-де-Граафа, учитывая, что он хранит 8?00 мкКл заряда при напряжении 12,0 МВ?
- Найдите емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 5,00 м 2 , разделенных слоем тефлона 0,100 мм.
- (a) Какова емкость конденсатора с параллельными пластинами, площадь пластин которого составляет 1,50 м 2 , разделенных 0,0200 мм неопреновой резины? (b) Какой заряд он держит, когда к нему приложено 9,00 В?
- Комплексные концепции. Шутник подает 450 В на 80.Конденсатор 0 мкФ, а затем бросает его ничего не подозревающей жертве. Палец пострадавшего обгорел от разряда конденсатора через 0,200 г мяса. Какое повышение температуры мяса? Разумно ли предполагать отсутствие изменения фазы?
- Необоснованные результаты. (a) Конденсатор с параллельными пластинами имеет пластины площадью 4,00 м 2 , разделенные нейлоном толщиной 0,0100 мм, и накапливает 0,170 Кл заряда. Какое приложенное напряжение? б) Что неразумного в этом результате? (c) Какие предположения являются ответственными или противоречивыми?
Глоссарий
конденсатор: устройство, накапливающее электрический заряд
емкость: количество заряда на единицу вольт
диэлектрик: изоляционный материал
диэлектрическая прочность: максимальное электрическое поле, выше которого изолирующий материал начинает разрушаться и проводить
конденсатор с параллельными пластинами: две идентичные проводящие пластины, разделенные расстоянием
полярная молекула: молекула с внутренним разделением заряда
Избранные решения проблем и упражнения
1.21,6 мК
3. 80.0 мС
5. 20,0 кВ
7. 667 пФ
9. (а) 4,4 мкФ; (б) 4.0 × 10 −5 C
11. (а) 14,2 кВ; (b) Напряжение неоправданно велико, более чем в 100 раз больше напряжения пробоя нейлона; (c) Предполагаемый заряд неоправданно велик и не может храниться в конденсаторе таких размеров.
факторов, влияющих на емкость | Конденсаторы
В конструкции конденсатора есть три основных фактора, определяющих величину создаваемой емкости.Все эти факторы определяют емкость, влияя на то, какой поток электрического поля (относительная разница электронов между пластинами) будет развиваться для данной величины силы электрического поля (напряжения между двумя пластинами):
ПЛОЩАДЬ ПЛАСТИНЫ : При прочих равных условиях большая площадь пластины дает большую емкость; меньшая площадь пластины дает меньшую емкость.
Пояснение: Чем больше площадь пластины, тем больше магнитный поток (заряд, собранный на пластинах) для данной силы поля (напряжение на пластинах).
РАССТОЯНИЕ ПЛАСТИН : При прочих равных условиях большее расстояние между пластинами дает меньшую емкость; меньшее расстояние между пластинами дает большую емкость.
Пояснение: Более близкое расстояние приводит к большей силе поля (напряжение на конденсаторе, деленное на расстояние между пластинами), что приводит к большему потоку поля (заряд, накопленный на пластинах) для любого заданного напряжения, приложенного к пластинам.
ДИЭЛЕКТРИЧЕСКИЙ МАТЕРИАЛ : При прочих равных условиях большая диэлектрическая проницаемость диэлектрика дает большую емкость; меньшая диэлектрическая проницаемость диэлектрика дает меньшую емкость.
Пояснение: Хотя это сложно объяснить, некоторые материалы предлагают меньшую оппозицию потоку поля для данной величины силы поля. Материалы с большей диэлектрической проницаемостью допускают больший поток поля (предлагают меньшее сопротивление) и, следовательно, больший накопленный заряд для любой заданной величины силы поля (приложенного напряжения).
«Относительная» диэлектрическая проницаемость означает диэлектрическую проницаемость материала относительно диэлектрической проницаемости чистого вакуума. Чем больше число, тем больше диэлектрическая проницаемость материала.Стекло, например, с относительной диэлектрической проницаемостью 7, имеет в семь раз большую диэлектрическую проницаемость чистого вакуума и, следовательно, позволяет создать поток электрического поля, в семь раз более сильный, чем у вакуума, при прочих равных условиях. В следующей таблице перечислены относительные диэлектрические проницаемости (также известные как «диэлектрическая проницаемость») различных распространенных веществ:
Материал | Относительная диэлектрическая проницаемость (диэлектрическая проницаемость) |
|---|---|
| Вакуум | 1.0000 |
| Воздух | 1.0006 |
| PTFE, FEP («тефлон») | 2,0 |
| Полипропилен | от 2,20 до 2,28 |
| Смола АБС | от 2,4 до 3,2 |
| полистирол | от 2,45 до 4,0 |
| Вощеная бумага | 2,5 |
| Масло трансформаторное | от 2,5 до 4 |
| Твердая резина | 2.5 до 4,80 |
| Дерево (Дуб) | 3,3 |
| Силиконы | от 3,4 до 4,3 |
| Бакелит | от 3,5 до 6,0 |
| Кварц плавленый | 3,8 |
| Дерево (клен) | 4,4 |
| Стекло | от 4,9 до 7,5 |
| Касторовое масло | 5,0 |
| Дерево (береза) | 5,2 |
| Слюда, мусковит | 5.От 0 до 8,7 |
| Стекловолоконная слюда | от 6,3 до 9,3 |
| Фарфор, стеатит | 6,5 |
| Глинозем | от 8,0 до 10,0 |
| Дистиллированная вода | 80,0 |
| Барий-стронций-титанит | 7500 |
Приблизительное значение емкости для любой пары разделенных проводов можно найти по следующей формуле:
Конденсатор можно сделать переменным, а не фиксированным, путем изменения любого из физических факторов, определяющих емкость.Одним из относительно простых факторов, которые можно изменить в конструкции конденсатора, является площадь пластины или, точнее, величина перекрытия пластин.
На следующей фотографии показан пример переменного конденсатора, использующего набор чередующихся металлических пластин и воздушный зазор в качестве диэлектрического материала:
По мере вращения вала степень перекрытия наборов пластин друг с другом будет изменяться, изменяя эффективную площадь пластин, между которыми может быть установлено концентрированное электрическое поле.Этот конкретный конденсатор имеет емкость в пикофарадном диапазоне и находит применение в радиосхемах.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
Лаборатория 4 – Зарядка и разрядка конденсатора
Введение
Конденсаторы – это устройства, которые могут накапливать электрический заряд и энергию. Конденсаторы имеют несколько применений, например, в качестве фильтров в источниках питания постоянного тока и в качестве аккумуляторов энергии для импульсных лазеров. Конденсаторы пропускают переменный ток, но не постоянный, поэтому они используются для блокировки постоянной составляющей сигнала, чтобы можно было измерить переменную составляющую.Физика плазмы использует способность конденсаторов накапливать энергию. В физике плазмы часто необходимы короткие импульсы энергии при чрезвычайно высоких напряжениях и токах. Конденсатор можно медленно заряжать до необходимого напряжения, а затем быстро разряжать для обеспечения необходимой энергии. Можно даже зарядить несколько конденсаторов до определенного напряжения, а затем разрядить их таким образом, чтобы получить от системы большее напряжение (но не больше энергии), чем было вложено. В этом эксперименте используется схема RC , которая является одной из простейших схем, в которой используется конденсатор.Вы изучите эту схему и способы изменения ее эффективной емкости, комбинируя конденсаторы последовательно и параллельно.Обсуждение принципов
Конденсатор состоит из двух проводов, разделенных небольшим расстоянием. Когда проводники подключены к зарядному устройству (например, к батарее), заряд передается от одного проводника к другому до тех пор, пока разность потенциалов между проводниками из-за их равного, но противоположного заряда не станет равной разности потенциалов между клеммами. зарядного устройства.Количество заряда, накопленного на любом проводнике, прямо пропорционально напряжению, а константа пропорциональности известна как емкость , . Это записывается алгебраически как Заряд C измеряется в единицах кулонов (C), напряжениеΔV
в вольт (В) и емкость C в единицах фарад (F). Конденсаторы – физические устройства; Емкость является собственностью устройства.Зарядка и разрядка
В простой RC-цепи резистор и конденсатор соединены последовательно с батареей и переключателем. См. Рис.1.Рисунок 1 : Простая RC-цепь
Когда переключатель находится в положении 1, как показано на рис. 1 (а), заряд на проводниках через некоторое время достигает максимального значения. Когда переключатель переведен в положение 2, как показано на рис. 1 (b), аккумулятор больше не является частью цепи и, следовательно, заряд конденсатора не может быть восполнен.В результате конденсатор разряжается через резистор. Если мы хотим исследовать зарядку и разрядку конденсатора, нас интересует, что происходит сразу, после того, как переключатель перемещается в положение 1 или положение 2, а не дальнейшее поведение схемы в ее устойчивом состоянии. Для схемы, показанной на рис. 1 (а), уравнение петли Кирхгофа может быть записано как Решение уравнения. (2) является(3)
Q = Q fQ f
представляет собой окончательный заряд на конденсаторе, который накапливается через бесконечное время, R – сопротивление цепи, а C – емкость конденсатора.Из этого выражения вы можете видеть, что заряд растет экспоненциально во время процесса зарядки. См. Рис. 2 (а). Когда переключатель перемещается в положение 2, для схемы, показанной на рис. 1 (b), уравнение петли Кирхгофа теперь имеет вид Решение уравнения. (4) является(5)
Q = Q 0 e (−t / RC)
гдеQ 0
представляет начальный заряд на конденсаторе в начале разряда, то есть приt = 0.
Из этого выражения видно, что заряд экспоненциально спадает при разряде конденсатора и что для полной разрядки требуется бесконечное количество времени. См. Рис. 2 (b).Рисунок 2 : График изменения во времени
Постоянная времени
τ ПродуктRC
(имеющий единицы времени) имеет особое значение; это называется постоянной времени цепи. Постоянная времени – это время, необходимое для повышения заряда зарядного конденсатора до 63% от его конечного значения.Другими словами, когдаt = RC,
(6)
Q = Q f(7)
1 – e −1 = 0,632.
Другой способ описать постоянную времени – сказать, что это количество секунд, необходимое для того, чтобы заряд на разряжающемся конденсаторе упал до 36,8%(e -1 = 0,368)
от своего начального значения.Мы можем использовать определение(I = dQ / dt)
тока через резистор и уравнение. (3) Q = Q fQ = Q 0 e (−t / RC)
, чтобы получить выражение для тока во время процессов зарядки и разрядки.(8)
зарядка: I = + I 0 e −t / RC
(9)
разгрузка: I = −I 0 e −t / RC
где в формуле.(8)зарядка: I = + I 0 e −t / RC
и уравнение. (9)разряд: I = −I 0 e −t / RC
– максимальный ток в цепи в момент времени t = 0. Тогда разность потенциалов на резисторе будет выражена следующим образом.(10)
зарядка: ΔV = + ΔV f e −t / RC
(11)
нагнетание: ΔV = – ΔV 0 e −t / RC
Обратите внимание, что во время процесса разряда ток будет течь через резистор в обратном направлении.Следовательно, I иΔV
в уравнении. (9)разряда: I = −I 0 e −t / RC
и уравнение. (11)разряд: ΔV = – ΔV 0 e −t / RC
отрицательны. Это напряжение как функция времени показано на рис.3.Рисунок 3 : Напряжение на резисторе как функция времени
Полезно описывать зарядку и разрядку в терминах разности потенциалов между проводниками (т.е.е., «напряжение на конденсаторе»), поскольку напряжение на конденсаторе можно измерить непосредственно в лаборатории. Используя соотношениеQ = C ΔV,
Eq. (3) Q = Q fQ = Q 0 e (−t / RC)
, которые описывают зарядку и разрядку конденсатора, можно переписать в терминах напряжения. Просто разделите оба уравнения наC,
, и отношения станут следующими.(12)
зарядка: ΔV = ΔV f(13)
нагнетание: ΔV = ΔV 0 e (−t / RC)
Обратите внимание, что эти два уравнения похожи по форме на формулу. (3) Q = Q fQ = Q 0 e (−t / RC)
.График зависимости напряжения на конденсаторе от времени показан на рисунке 4 ниже.Рисунок 4 : Напряжение на конденсаторе как функция времени
Переставляя уравнение. (12) зарядка: ΔV = ΔV f(15)
−ln−ln ((ΔV f – ΔV) / ΔV f )
от времени даст прямолинейный график с наклоном 1/ RC . Точно так же для процесса разряда уравнение. 13разрядка: ΔV = ΔV 0 e (−t / RC)
можно переписать, чтобы получить Возьмите натуральный логарифм (ln) от обеих частей этого выражения и умножьте на –1, чтобы получить(17)
−ln−ln (ΔV) / ΔV 0 )
от времени даст прямолинейный график с наклоном 1/ RC .Использование прямоугольной волны для имитации роли коммутатора
В этом эксперименте мы будем использовать не переключатель, а генератор сигналов, который может генерировать периодические формы волн различной формы, такие как синусоидальная волна, треугольная волна и прямоугольная волна. Также можно отрегулировать как частоту, так и амплитуду формы волны. Здесь мы будем использовать генератор сигналов для создания изменяющегося во времени напряжения прямоугольной формы на конденсаторе, аналогичного показанному на рис.5.Рисунок 5 : Прямоугольная волна с периодом Τ
Выходное напряжение генератора сигналов изменяется назад и вперед от постоянного положительного значения до постоянного нуля вольт через равные интервалы времени t . ВремяT = 2t
– это период прямоугольной волны. В течение первой половины цикла, когда напряжение положительное, это похоже на то, что переключатель находится в положении 1. Во второй половине цикла, когда напряжение равно нулю, это то же самое, что переключатель находится в положении 2. .Таким образом, прямоугольная волна, представляющая собой постоянное напряжение, которое периодически включается и выключается, служит одновременно аккумулятором и переключателем в схеме на рис. Генератор сигналов позволяет выполнять это переключение многократно, и можно оптимизировать сбор данных, регулируя частоту повторения. Эта частота будет зависеть от постоянной времени RC-цепи. Когда время t больше, чем постоянная времени τ RC-цепи, у конденсатора будет достаточно времени для заряда и разряда, и напряжение на конденсаторе будет таким, как показано на рис.4.Цель
В этом эксперименте (смоделированный компьютером) осциллограф будет использоваться для наблюдения за разностью потенциалов и, таким образом, косвенно за зарядом конденсатора. Измерения напряжения будут использоваться двумя разными способами для вычисления постоянной времени цепи. Наконец, конденсаторы будут подключены параллельно, чтобы проверить их эквивалентную емкость.Оборудование
- Печатная плата PASCO
- Сигнальный интерфейс с выходной мощностью
- Соединительные провода
- Программное обеспечение Capstone
Процедура
Распечатайте лист для этой лабораторной работы.Этот лист понадобится вам для записи ваших данных.Настройка RC-цепи
Печатная плата RLC, которую вы будете использовать, среди других элементов состоит из трех резисторов и двух конденсаторов. См. Рис. 6 ниже. Теоретически вы можете использовать разные комбинации резисторов и конденсаторов. В этом эксперименте вы будете использовать резисторы 33 и 100 Ом и два конденсатора.Рисунок 6 : Печатная плата RLC
1
Подключите крайнюю правую выходную клемму сигнального интерфейса к резистору 33 Ом в точке 2.2
Чтобы обойти индуктор, подключите провод от точки 8 к точке 9.3
Подключите точку 6 ко второй выходной клемме сигнального интерфейса, чтобы замкнуть цепь.4
Подключите пробник напряжения к аналоговому каналу A.5
Чтобы измерить напряжение на конденсаторе, подключите черный провод датчика напряжения к точке 6, а красный провод – к точке 9. Убедитесь, что заземление интерфейса (вывод «-») подключено к той же стороне конденсатора, что и заземление генератора сигналов (выход мощности).Схема подключения должна выглядеть так, как показано на рис.7.Рисунок 7 : Принципиальная схема
Контрольная точка 1:
Попросите своего технического специалиста проверить соединения вашей цепи.
Процедура A: Постоянная времени контура
Мы будем использовать компьютер для эмуляции осциллографа в этом эксперименте.6
Откройте файл Capstone, связанный с этой лабораторной работой.Отобразится экран, аналогичный показанному на рис. 8.Рисунок 8 : Начальный экран файла Capstone
7
Настройте генератор сигналов на создание положительной прямоугольной волны, выбрав положительную прямоугольную волну в окне генератора сигналов, как показано на рисунке 9 ниже.Рисунок 9 : Окно генератора сигналов
8
Если это еще не установлено при открытии файла Capstone, настройте генератор сигналов на создание прямоугольной волны амплитудой 5 В с частотой 20 Гц и установите смещение напряжения на 5 В.9
Включите генератор сигналов, щелкнув ON в окне генератора сигналов.10
Чтобы контролировать сигнал, нажмите кнопку START в главном окне. Потребуется настроить шкалу времени и напряжения, чтобы получить кривую сигнала, подобную показанной на рис. 10. Это позволит вам наблюдать, как напряжение на конденсаторе изменяется в зависимости от времени. Для этого установите курсор на любое значение вдоль оси, которую вы хотите увеличить, и переместите курсор влево-вправо или вверх-вниз по мере необходимости.При правильном увеличении у вас будет только одна длина волны на графике, как на кривой на рис.10.Рисунок 10 : Трасса сигнала
Если в любой момент вы захотите удалить записанный набор данных, нажмите кнопку Delete Last Run под графиком.11
Нажмите кнопку Показать координаты из кнопок над графиком. См. Рис.11.Рисунок 11 : Показать координаты
Когда активна функция отображения координат, показания напряжения и времени отображаются, куда бы вы их ни перетащили, как на рис.11. Используя этот инструмент, определите и запишите время начала (то есть, когда кривая начиналась от 0 вольт) на рабочем листе.12
Вычислите 63,2% от максимального напряжения,ΔV f ,
(которое должно быть 5 В), настройку амплитуды генератора сигналов. Используя Показать координаты , определите и запишите время начала (то есть, когда кривая начиналась вверх с 0 вольт) на рабочем листе.13
Из этих двух значений времени определите и запишите время, необходимое для перехода сигнала от Δ V = 0 до Δ V = 0.632ΔV f .
Это ваше экспериментальное значение для RC .14
Заполните рабочий лист принятыми значениями сопротивления и емкости, которые указаны на печатной плате.15
Вычислите экспериментальное значение емкости, используя свое экспериментальное значение для RC и принятое значение R . Запишите это на листе.16
Вычислите ошибку в процентах, используя два значения емкости.См. Приложение Б. Контрольная точка 2:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Процедура B: Расчет емкости графическими методами
17
Запишите максимальное напряжение на листе.18
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, когда Δ В, = 1, 2, 3 и 4 В на восходящей части кривой.Запишите эту информацию в таблицу данных 1 на рабочем листе. Примечание : Возможно, вам придется сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента.19
Выполните необходимые вычисления, чтобы заполнить таблицу данных 1.20
Используя Excel, постройте график−ln ((ΔV f – ΔV) / ΔV f )
в зависимости от времени. См. Приложение G.21
Используйте опцию линии тренда в Excel, чтобы нарисовать наиболее подходящую линию для ваших данных, определить наклон линии и записать это значение на листе.См. Приложение H.22
По значению крутизны определите постоянную времени и емкость. Запишите эти значения в рабочий лист.23
Вычислите погрешность в процентах между этим значением емкости и принятым значением. Контрольная точка 3:
Попросите своего технического специалиста проверить ваши данные, график и расчеты, прежде чем продолжить.
Процедура C: Измерение эффективной емкости
Емкость увеличивается непосредственно при параллельном подключении конденсаторов и обратно при последовательном подключении.Это противоположно правилу для резисторов. Для конденсаторов, подключенных параллельно, эффективная емкость определяется как(18)
C eff = C 1 + C 2 + C 3 +. . .
а для конденсаторов, включенных последовательно, эффективная емкость равна24
Подключите второй конденсатор (330 μ Ф) параллельно конденсатору, используемому в процедуре A, подключив провод от точки 6 к точке 7.25
Переключите резистор на резистор 10 Ом, переместив соединение из точки 2 в точку 1.26
Запишите другой набор данных, щелкнув START в главном окне. После того, как вы записали второй набор данных, вы можете захотеть отобразить только эти данные на графике и удалить набор данных 1. Для этого удалите первый прогон (см. Примечание к шагу 10). На графике вы будете видеть только одну длину волны.27
В этой части эксперимента вы будете рассматривать разрядную часть кривой. Теперь начальное напряжениеΔV 0
будет самым высоким значением пика перед тем, как график начнет спадать.Запишите это значение на листе.28
Из записанных данных найдите с помощью интеллектуального инструмента моменты времени, когда Δ В, = 1, 2, 3 и 4 вольта на спадающей части кривой. ( Примечание : вам может потребоваться сильно увеличить масштаб, чтобы получить необходимую точность при использовании интеллектуального инструмента). Запишите эту информацию в таблицу данных 2 на рабочем листе.29
Выполните необходимые вычисления, чтобы заполнить Таблицу данных 2.30
Используя Excel, постройте график зависимости−ln (ΔV) / ΔV 0 )
от времени.31
Используйте опцию линии тренда в Excel, чтобы нарисовать наиболее подходящую линию для ваших данных, определить наклон линии и записать это значение на листе.32
По значению наклона определите постоянную времени и запишите это значение в рабочий лист.33
ВычислитеC eff ,
эффективную емкость параллельной комбинации, используя принятое значение для R .34
Сравните это экспериментальное значение с тем, что вы получили из уравнения.18C eff = C 1 + C 2 + C 3 +. . .
и принятые значения емкости путем вычисления ошибки в процентах между двумя значениями. Контрольная точка 4:
Попросите своего технического специалиста проверить ваши данные и расчеты, прежде чем продолжить.
Copyright © 2012 Advanced Instructional Systems, Inc. и Государственный университет Северной Каролины | Кредиты
Конденсаторы: все, что вам нужно знать | EAGLE
Нет, мы здесь не говорим о Grand Theft Auto! Открывать крышку в мире электроники – это плохо, если вам не нравится видеть, как ваш электролитический конденсатор горит в огне.Конденсаторы играют важную роль в семействе пассивных электронных компонентов, и их можно найти повсюду.
Помните вспышку в вашей цифровой камере? Конденсаторы делают это возможным. Или возможность переключать канал на телевизоре? Опять конденсаторы. Эти ребята – маленькие батарейки, которые «могут», и вам нужно знать все, что о них известно, прежде чем вы начнете работать над своим первым электронным проектом.
Это как бутерброд с мороженым
Для простоты – конденсатор накапливает электрический заряд , очень похоже на батарею.Также называемые caps , вы найдете этих парней в приложениях, требующих накопления энергии, подавления напряжения и даже фильтрации сигналов. А как они выглядят? Ну бутерброд с мороженым!
Что бы вы сделали с баром «Клондайк»? Сравните это, конечно, с конденсатором! (Источник изображения)
Подумайте о том восхитительном бутерброде с мороженым, который вам понравился в тот знойный летний день. У вас есть вкусная корочка с двух сторон и кремовый кусок ванильного мороженого посередине.Эта композиция из двух внешних слоев и одного внутреннего слоя – это то, как выглядит конденсатор. Вот из чего они сделаны:
- Начиная снаружи. Сверху и снизу конденсатора вы найдете набор металлических пластин, также называемых проводниками. Электрический заряд находит эти металлические пластины очень привлекательными.
- Посередине. Среди этих двух металлических пластин вы найдете изолятор или материал, к которому не притягивается электричество.Этот изолятор обычно называют диэлектриком и может быть изготовлен из бумаги, стекла, резины, пластика и т. Д.
- Соединяем вместе. Две металлические пластины сверху и снизу крышки соединены двумя электрическими клеммами, которые соединяют ее с остальной частью цепи. Один конец конденсатора подключается к источнику питания, а другой – к земле.
Внутренняя структура конденсатора, у нас есть две металлические пластины, внутренний диэлектрик и соединительные клеммы.
Конденсаторы всех форм и размеров
Конденсаторыбывают разных форм и размеров, каждый из которых определяет, насколько хорошо они могут удерживать заряд. Три наиболее распространенных типа конденсаторов, с которыми вы столкнетесь, включают керамический конденсатор, электролитический конденсатор и суперконденсатор:
Конденсаторы керамические
Это конденсаторы, с которыми вы, вероятно, будете работать в своем первом электронном проекте с использованием макета. В отличие от своих электролитических аналогов, керамические конденсаторы удерживают меньший заряд, но и меньше пропускают ток.Они также оказываются самыми дешевыми конденсаторами из всей группы, так что запасайтесь! Вы можете быстро определить керамический конденсатор со сквозным отверстием, посмотрев на маленькие желтые или красные лампочки с двумя торчащими из них клеммами.
Три типа керамических конденсаторов, вы будете использовать их на макетных платах. (Источник изображения)
Конденсаторы электролитические
Эти парни выглядят как маленькие консервные банки, которые вы найдете на печатной плате, и в их крошечном следе могут удерживаться огромные электрические разряды.Это также единственный тип конденсатора, который поляризован, а это означает, что они будут работать только при подключении с определенной ориентацией. На этих электролитических конденсаторах есть положительный вывод, называемый анодом, и отрицательный вывод, называемый катодом. Анод всегда нужно подключать к более высокому напряжению. Если вы подключите его наоборот, когда на катоде будет более высокое напряжение, приготовьтесь к взрыву крышки!
Электролитический конденсатор, обратите внимание на положительный вывод и более длинный вывод (анод) и более короткий отрицательный вывод (катод).(Источник изображения)
Несмотря на то, что электролитические колпачки способны удерживать большое количество электрического заряда, они также хорошо известны тем, что пропускают ток быстрее, чем керамические колпачки. Из-за этого они не лучший выбор, когда вам нужно хранить энергию.
Суперконденсаторы
Supercaps – супергерои семейства конденсаторных, они могут хранить большое количество энергии! К сожалению, суперкапс не очень хорошо справляется с избыточным напряжением, и вы окажетесь без колпачка, если превысите максимальное напряжение, указанное в таблице данных.ПОП!
В отличие от электролитических конденсаторов, вы обнаружите, что суперконденсаторы используются для хранения и разряда энергии, как и батареи. Но в отличие от батареи, суперкаперы высвобождают свой заряд сразу, и вы никогда не получите такой же срок службы, как обычный аккумулятор.
Посмотрите на этот мощный supercap ! Он имеет огромную емкость 3000F. (Источник изображения)
Обозначения конденсаторов
Определить конденсатор на вашей первой схеме очень просто, поскольку они бывают только двух типов: стандартные и поляризованные.Обратите внимание на символ стандартного конденсатора ниже. Вы заметите, что это всего лишь две простые линии с пробелом между ними. Это две металлические пластины, которые вы найдете сверху и снизу физического конденсатора.
Поляризованный конденсатор выглядит немного иначе и имеет дугообразную линию в нижней части, а также положительный вывод наверху. Этот положительный вывод очень важен и указывает, как этот поляризованный конденсатор должен быть подключен. Положительная сторона всегда подключается к источнику питания, а сторона дуги подключается к земле.
Два наиболее распространенных типа конденсаторов, которые вы увидите на схеме для США, стандартные и поляризованные.
Кто изобрел эти вещи?
Хотя многие считают английского химика Майкла Фарадея пионером современного конденсатора, он не был первым, кто его изобрел. То, что сделал Фарадей, было важно – в своих экспериментах он продемонстрировал первые практические примеры конденсатора и способы его использования для хранения электрического заряда. И благодаря Фарадею у нас также есть способ измерить заряд, который может удерживать конденсатор, известный как емкость, который измеряется в Фарадах!
Гениальный английский химик Майкл Фарадей, пионер конденсаторов, которые мы используем сегодня.(Источник изображения)
До Майкла Фарадея некоторые записи указывают на то, что покойный немецкий ученый Эвальд Георг фон Клейст изобрел первый конденсатор в 1745 году. Спустя несколько месяцев голландский профессор по имени Питер ван Мушенбрук придумал похожий дизайн, теперь известный как Лейденская банка. Странное время, правда? Однако все это было просто совпадением, и оба ученых в равной степени получили признание за их первоначальные изобретения конденсатора.
Самый ранний образец конденсатора, лейденская банка.(Источник изображения)
Знаменитый Benjamin Franklin позже стал усовершенствованием конструкции Лейденской банки, созданной Musschenbroek. Франклин также смог обнаружить, что использование плоского куска стекла было отличной альтернативой целой банке. Так родился первый плоский конденсатор, получивший название площади Франклина.
Колпачки в действии – как они работают
Давайте подробно рассмотрим, как работают эти мощные конденсаторы, на практическом примере. Вы ведь раньше пользовались цифровой камерой? Тогда вы знаете, что между нажатием кнопки, чтобы сделать снимок, и моментом срабатывания вспышки есть несколько коротких моментов.
Что здесь происходит? К вспышке прикреплен конденсатор, который заряжается после того, как вы нажмете кнопку, чтобы сделать снимок. Как только этот конденсатор полностью заряжен аккумулятором камеры, вся эта энергия взрывается наружу в ослепительной вспышке света!
Обратите внимание, конденсатор, который делает возможной вспышку в этой камере. (Источник изображения)
Так как же все это произошло? Заглянем изнутри в загадочный мир конденсатора:
- Начинается с зарядки. Электрический ток от источника питания сначала течет в конденсатор и застревает на первой пластине. Почему застревает? Потому что есть изолятор, который не пропускает отрицательно заряженную электронику.
- Накопление сборов. По мере того, как все больше и больше электронов прилипает к этой первой пластине, она становится отрицательно заряженной и в конечном итоге отталкивает все лишние электроны, с которыми она не может справиться, к другой пластине. Затем эта вторая пластина становится положительно заряженной.
- Заряд сохраняется. По мере того, как две пластины конденсатора продолжают заряжаться, отрицательные и положительные электроны отчаянно пытаются соединиться, но этот надоедливый изолятор в центре не позволяет им, создавая электрическое поле. Вот почему колпачок продолжает удерживать и накапливать заряд, потому что существует бесконечный источник напряжения между отрицательной и положительной сторонами двух пластин, которые не разрешены.
- Заряд высвобождается. Рано или поздно две пластины в нашем конденсаторе не смогут удерживать заряд, так как они на пределе емкости.Но что происходит сейчас? Если в вашей цепи есть путь, по которому электрический заряд может течь в другом месте, то все электроны в вашей крышке разрядятся, и , наконец, прекратят свое напряжение, когда они будут искать другой путь друг к другу.
Измерение заряда
Как можно измерить, сколько заряда хранится в конденсаторе? Каждый колпачок рассчитан на определенную емкость. Он измеряется в фарадах по английскому химику Майклу Фарадею. Поскольку в одном фараде содержится тонна электрического заряда, вы обычно видите конденсаторы, измеряемые в пикофарадах или микрофарадах.Вот полезная таблица, которая показывает, как разбиваются эти измерения:
| Имя | Сокращение | Фарады |
| Пикофарад | пФ | 0,000000000001 Факс |
| нанофарад | нФ | 0,000000001 Факс |
| Микрофарад | мкФ | 0,000001 Факс |
| Милифарад | мФ | 0.001 F |
| Килофарад | кФ | 1000 Факс |
Теперь, чтобы выяснить, сколько заряда в настоящее время хранит конденсатор, вам понадобится это уравнение:
В этом уравнении общий заряд представлен как (Q) , и соотношение этого заряда можно найти, умножив емкость конденсатора ( C ) на приложенное к нему напряжение ( В ). Следует отметить, что емкость конденсатора напрямую зависит от его напряжения.Таким образом, чем больше вы увеличиваете или уменьшаете источник напряжения в цепи, тем больший или меньший заряд будет у вашего конденсатора.
Емкость в параллельных и последовательных цепях
Когда вы размещаете конденсаторы в цепи параллельно, вы можете определить общую емкость, сложив вместе все отдельные емкости.
Получить общую емкость в параллельной цепи так же просто, как 1 + 1, просто сложите их все вместе! (Источник изображения)
При последовательном размещении конденсаторов общая емкость вашей цепи является обратной величиной всех ваших суммированных емкостей.Вот краткий пример. Если у вас есть два конденсатора по 10 Ф, соединенные последовательно, то они будут давать общую емкость 5 Ф.
Получить полную емкость в последовательной цепи немного сложнее. Емкость уменьшается вдвое. (Источник изображения)
Начало работы
Теперь, когда у нас есть твердое представление о том, что такое конденсаторы, как они работают и как измеряются, давайте рассмотрим три распространенных применения конденсаторов. Сюда входят такие приложения, как развязывающие конденсаторы, накопители энергии и емкостные сенсорные датчики.
Конденсатор развязки
В наши дни вам будет сложно найти схему, в которой нет интегральной схемы или ИС. В этих типах схем конденсаторы должны выполнять важную работу, удаляя весь высокочастотный шум, обнаруживаемый в сигналах источника питания, питающих ИС.
Почему это необходимая работа для нашего конденсатора? Любые колебания напряжения могут быть фатальными для ИС и даже привести к неожиданному отключению питания микросхемы. Помещая конденсаторы между ИС и источником питания, они успокаивают колебания напряжения, а также действуют как второй источник питания, если первичная мощность падает до уровня, достаточного для выключения ИС.
Конденсатор развязки для контроля колебаний напряжения.
Накопитель энергии
Конденсаторыимеют много общих характеристик с батареями, включая их способность накапливать энергию. Однако, в отличие от батареи, конденсаторы не выдерживают такой большой мощности. Но хотя они и не успевают за количеством, они стараются разрядиться как можно быстрее! Конденсаторы могут передавать энергию намного быстрее, чем аккумулятор, что делает их идеальным выбором для питания вспышки в камере, настройки радиостанции или переключения каналов на телевизоре.
Емкостные сенсорные датчики
Одно из последних достижений в области применения конденсаторов связано с бурным ростом технологий сенсорных экранов. Стеклянные экраны, из которых состоят эти сенсорные датчики, имеют очень тонкое прозрачное металлическое покрытие. Когда ваш палец касается экрана, это вызывает падение напряжения, определяющее точное местоположение вашего пальца!
Емкостные сенсорные датчики в действии с защитной накладкой и печатной платой. (Источник изображения)
Практика – выбор конденсатора
Давайте перейдем к сфере практичности и поговорим о том, на что обращать внимание при выборе следующего конденсатора.Необходимо учитывать пять переменных, в том числе:
- Размер – включает как физический размер вашего конденсатора, так и его общую емкость. Не удивляйтесь, если выбранный вами конденсатор будет самой большой частью вашей печатной платы, так как чем больше вам потребуется емкости, тем больше они станут.
- Допуск – Конденсаторы, как и их аналоги с резисторами, имеют переменный допуск. Вы найдете допуск для конденсаторов в диапазоне от ± 1% до ± 20% от заявленного значения.
- Максимальное напряжение – Каждый конденсатор имеет максимальное напряжение, с которым он может работать. В противном случае он взорвется! Вы найдете максимальное напряжение от 1,5 до 100 В.
- Эквивалентное последовательное сопротивление (ESR) – Как и любой другой физический материал, выводы конденсатора имеют очень маленькое сопротивление. Это может стать проблемой, если вам нужно помнить о потерях тепла и энергии.
- Leakage Current – В отличие от наших батарей, в конденсаторах происходит утечка накопленного заряда.И пока он истощается медленно, вам стоит обратить внимание на то, насколько сильно протекает ваш конденсатор, если его основная функция – накопление энергии.
Все заряжено
Вот и все, что вам нужно знать о конденсаторах, чтобы полностью зарядиться для вашего следующего электронного проекта! Конденсаторы – это очаровательная небольшая группа, способная накапливать электрический заряд для множества применений, и они даже могут выступать в качестве вторичного источника питания для этих чувствительных интегральных схем.При работе с конденсаторами внимательно следите за максимально возможным напряжением. В противном случае вы получите несколько взрывающихся крышек, как вы увидите на видео:
Знаете ли вы, что Autodesk EAGLE бесплатно включает в себя массу библиотек конденсаторов? Начните со своего следующего проекта в области электроники и забудьте о создании собственных деталей! Попробуйте Autodesk EAGLE бесплатно сегодня.
.

 Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: , где e – диэлектрическая проницаемость окружающей среды. Следовательно:
Пусть это будет шар радиусом r. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара равен: , где e – диэлектрическая проницаемость окружающей среды. Следовательно: 

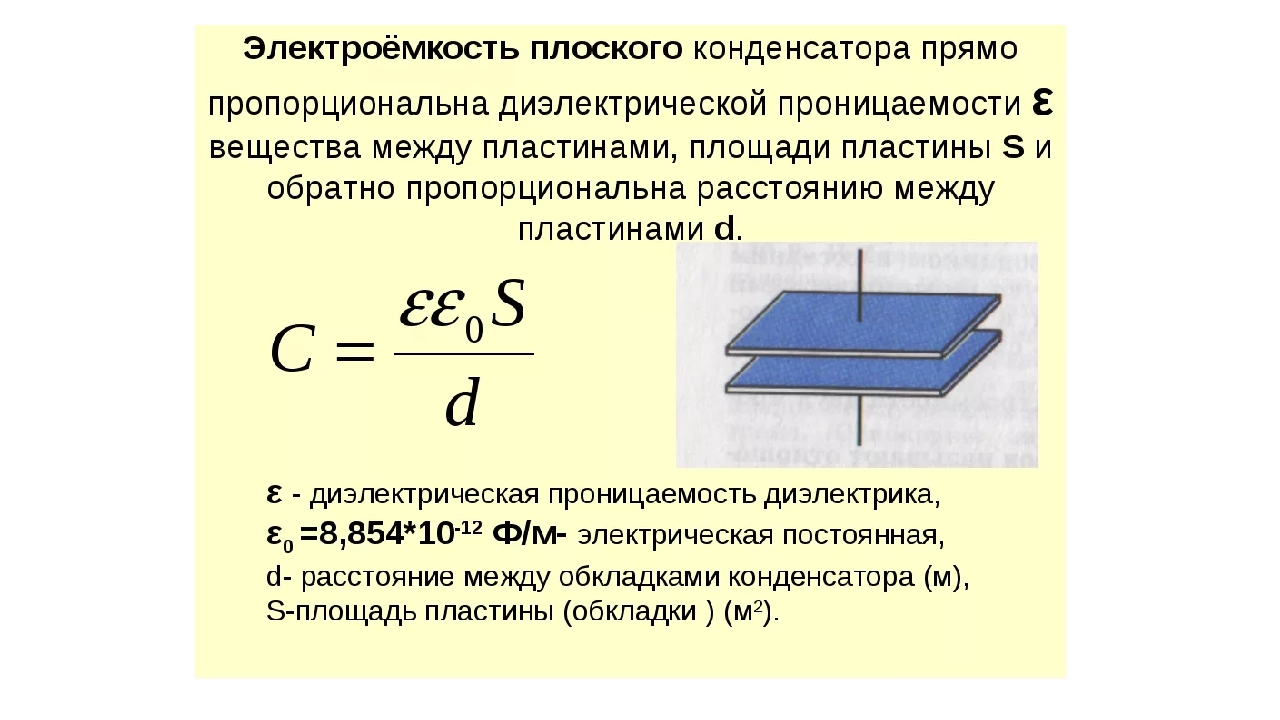 Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними.
Электрические поля окружающих тел почти не проникают через металлические обкладки и не влияют на разность потенциалов между ними.
