Расчёт фильтра нижних частот
Rin – Входное сопротивление ФНЧ
Rout – Выходное сопротивление ФНЧ
| Расчёт фильтра нижних частот | |||||
|---|---|---|---|---|---|
|
|
|||||
|
Частота сигнала: |
МГц |
||||
|
Входное сопротивление фильтра: |
Ом |
||||
|
Выходное сопротивление фильтра: |
Ом |
||||
|
Добротность фильтра: |
|||||
|
|||||
|
|
Индуктивности: |
Ёмкости: |
|||
|
L1: |
мкГн |
C1: |
пФ |
||
|
L2: |
мкГн |
C2: |
пФ |
||
|
|
C3: |
пФ |
|||
|
|
|||||
|
*Формат ввода – х. |
|||||
|
Пожелания, замечания, рекомендации по улучшению раздела расчётов на нашем сайте просьба присылать по электронной почте [email protected] Разрешается копирование java-скриптов при условии ссылки на источник. |
ВСЕ РАСЧЁТЫ
Расчет фильтра нижних частот
Название: Расчет фильтра нижних частот
Вид работы: курсовая работа
Рубрика: Коммуникации и связь
Размер файла: 777,63 Kb
Скачать файл: referat.me-170615.docx
Содержание
Введение
1 Физические основы и принцип действия широкополосных фильтров
2 Пример расчета фильтра нижних частот на заданные параметры
Заключение
Список использованной литературы
Введение
Во многих радиотехнических устройствах часто возникает необходимость выделения заданных частотных диапазонов из имеющегося спектра частот. Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами.
Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами.
В начале нашего столетия электрические фильтры, составленные из ряда катушек индуктивности и конденсаторов, получили широкое применение в технике. Благодаря их применению оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.
Известный интерес представляют пассивные цепочные, или лестничные фильтры, состоящие из комбинаций элементов L и C и не требующие источника питания. Пассивные фильтры могут обладать как широкими полосами пропускания, так и очень узкими.
При расчете фильтра, с одной стороны, необходимо определить, с какими допустимыми искажениями передается входной сигнал, являющийся функцией частоты или времени, на выход фильтра, и, с другой стороны, из каких конкретных элементов должен состоять этот фильтр. Получение наивыгоднейших выходных характеристик с минимальными искажениями и создание принципиальной схемы фильтра с минимальным числом элементов, осуществляющей требуемую передачу сигнала, является содержанием расчета фильтров.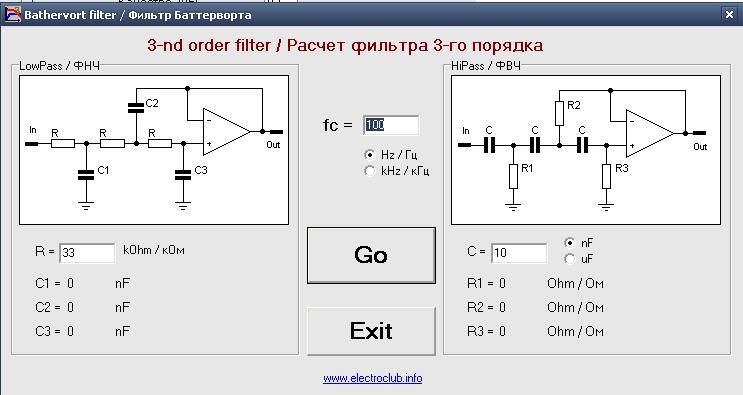
1 Физические основы и принцип действия широкополосных фильтров
В электрических, радиотехнических и телемеханических установках часто решается задача: из совокупного сигнала, занимающего широкую полосу частот, выделить один или несколько составляющих сигналов с более узкой полосой. Сигналы заданной полосы выделяют при помощи частотных электрических фильтров.
К частотным электрическим фильтрам различной аппаратуры предъявляются разные, порой противоречивые требования. В одной области частот, которая называется полосой пропускания, сигналы не должны ослабляться, а в другой, называемой полосой задерживания, ослабление сигналов не должно быть меньше определенного значения. Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление сигналов и фазо-частотная характеристика линейна (нет искажения формы сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.
Фильтры могут быть однозвенные (первого порядка), двухзвенные (второго порядка) и многозвенные (n- го).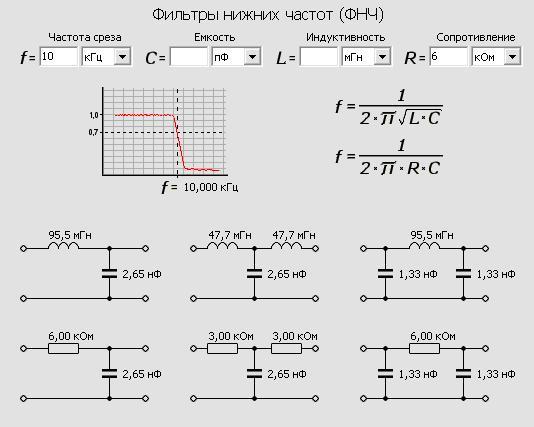
Электрический фильтр представляет собой четырехполюсник, предназначенный для выделения из состава сложного электрического колебания частотных составляющих, расположенных в заданной полосе частот, и подавления тех составляющих, которые расположены в других полосах частот. Первая из названных полос представляет собой полосу пропускания, а вторая – полосу задерживания.
По взаимному расположению полос пропускания и полос задерживания различают фильтры нижних частот, фильтры верхних частот, полосовые и режекторные фильтры.
Фильтры нижних частот (ФНЧ) пропускают сигналы частот от 0 до и задерживающей колебания любых белее высоких частот (рис.1).
LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до
.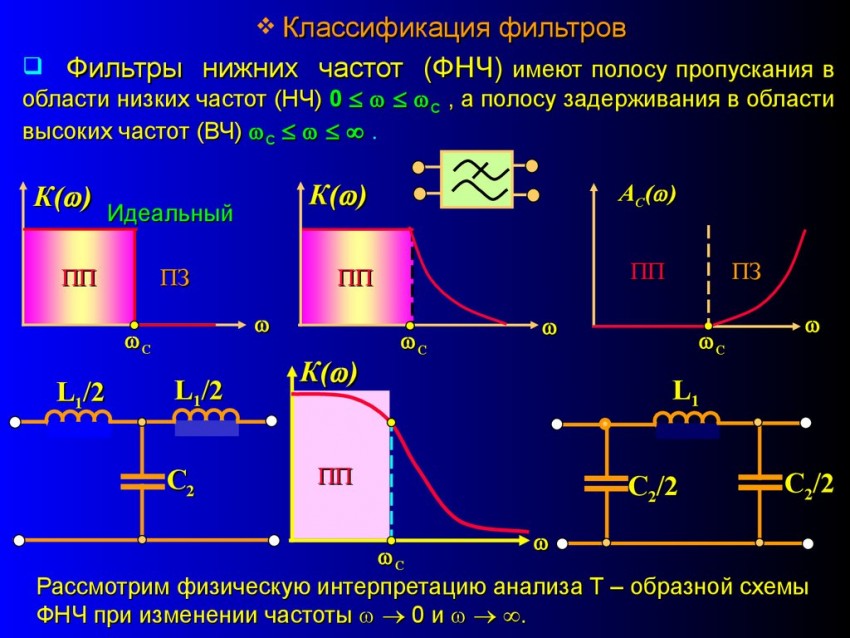
Это объясняется тем, что на низких частотах сопротивление индуктивного элемента XL фильтра мало, а емкостного XC – велико и электрические колебания проходят со входа на выход почти без ослабления. С увеличением частоты сопротивление индуктивного элемента возрастает, а емкостного – снижается и коэффициент передачи фильтра уменьшается (рисунок 1–б).
Фильтры верхних частот (ФВЧ), напротив, пропускают сигналы, частоты которых простираются от до , и задерживают сигналы более низких частот(рис.2).
Полосовые фильтры (ПФ) пропускают сигналы в полосе частот от до (рис.3).
Режекторные (заграждающие) фильтры (РФ) задерживают сигналы в полосе частот от до (рис.4).
(а)
(б)
Рисунок – 1 Фильтры нижних частот (а) и его АЧХ (б).
Рисунок – 2 Фильтры верхних частот
Рисунок – 3 Полосовые фильтры
Рисунок – 4 Заграждающие фильтры
Широкополосный фильтр состоит из звеньев, включающих в себя только элементарные контуры. Поэтому механизм фильтрации в широкополосных фильтрах определяется в основном процессами, происходящими в элементарны контурах, т. е. в двухэлементных двухполюсниках, имеющих одну резонансную частоту.
Поэтому механизм фильтрации в широкополосных фильтрах определяется в основном процессами, происходящими в элементарны контурах, т. е. в двухэлементных двухполюсниках, имеющих одну резонансную частоту.
Полное сопротивление Z любого элементарного контура состоит из активной R и реактивной Xсоставляющих:
Z = R + jX(1)
или
Y = G + jB(2)
где Y – полная проводимость
G – активная составляющая полной проводимости
B – реактивная составляющая поной проводимости
Реактивное сопротивление последовательного контура на частоте = равно нулю, активное сопротивление при этом мало, так как оно определяется только потерями в контуре; полное сопротивление контура близко к нулю. Поэтому последовательные контуры применяются в параллельных плечах Т-образных звеньев фильтров верхних частот (рис.5)., так как они оказывают сильное шунтирующее действие на частотах, близких к резонансной.
Рисунок – 5 Схема звена ФВЧ и резонансные характеристики последовательного контура
Реактивная проводимость = равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев =. Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания ( >), а для ФВЧ – ниже (<). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.
Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев =. Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания ( >), а для ФВЧ – ниже (<). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.
Рисунок – 6 Схема звена ФНЧ и резонансные характеристики параллельного контура
Благодаря этому через фильтр беспрепятственно проходят частоты полосы пропускания. В этой связи становится понятным, почему в широкополосных фильтрах все звенья настраиваются на частоты полосы задерживания.
Крутизна частотной характеристики фильтра в переходной области зависит от числа звеньев. Широкополосный фильтр всегда состоит из фильтра нижних частот и фильтра верхних частот. Полоса пропускания широкополосный фильтра – образуется благодаря перекрытию полос пропускания ФНЧ (0 -) и ФИЧ (- ) – (рис.7)
Рисунок – 7 Образование полосы пропускания широкополосного фильтра
2 Пример расчета фильтра нижних частот на заданные параметры
Аналитический метод расчета цепочных фильтров основан на нахождении оптимальных параметров фильтра по заданной характеристике собственного или рабочего затухания. При этом реализуется фильтр, удовлетворяющий заданным условиям, при минимальном числе элементов, что гарантирует минимальное искажение в полосе пропускания. Отметим, что, так как последовательно и параллельно-производные звенья фильтров являются дуальными, т.е. взаимообратными, а свойства таких схем в отношении передачи энергии аналогичны, то количество расчетных формул, используемых для расчета фильтров, будет вдвое уменьшено.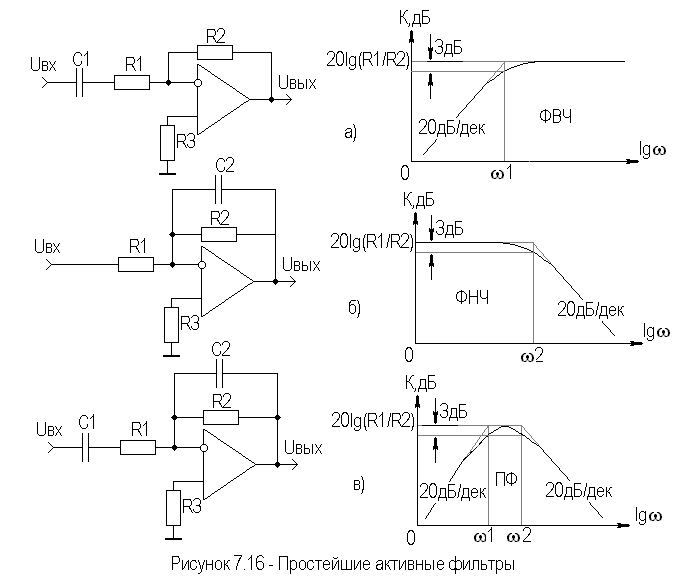 Поэтому ведется единый расчет фильтра.
Поэтому ведется единый расчет фильтра.
Требуется рассчитать фильтр, удовлетворяющий следующим техническим требованиям:
1. Полоса пропускания
= 50 кГц, = 100 кГц,
где и соответственно нижняя и верхняя граничные полосы пропускания.
2. Полоса задерживания
От = 115 кГц и выше
где и соответственно верхняя и нижняя граничные полосы задерживания.
3. Рабочее затухание в полосе пропускания
7дБ = =0,805 неп
4. Рабочее затухание в полосе задерживания
50 дБ = =5,75 неп
5.Фильтр включается между сопротивлением нагрузок
= 1000 Ом
6.Отклонение характеристического сопротивления от номинального в полосе пропускания (коэффициент несогласованности)
= 10 % =0,1
7. Амплитуда входного сигнала
= 5 В
9. Коэффициент использования полосы пропускания.
8. Рекомендуется выполнить катушки индуктивностей на альсиферовых сердечниках.
Прежде чем приступить к расчету фильтра, необходимо определить критерий полосности
=
Так как n < 2, рассчитываем фильтр как полосовой.
Зная вычислим ,затем определим затухание несогласованности
Выбрав класс фильтра по сопротивлению (обычно 2-ой), т.е. =2, найти параметр
Далее определить расчетный параметр полосы пропускания
и затем расчетный параметр
Найдем коэффициент использования полосы пропускания
И только потом можно определить коэффициент использования полосы задерживания и теоретическую частоту среза. Для реальных фильтров . Заданные параметры и = 100 кГц, определим теоретическую частоту среза
Так как теоретическая частота среза лежит в пределах переходной области, она удовлетворяет предъявленным условиям. Исходя из этого, определяем предварительный коэффициент использования полосы пропускания
Поскольку величина не превышает предельно достижимого в реальных фильтрах значения 0,98, останавливаемся на этих значениях и . Определяем коэффициент использования полосы задерживания и расчетные параметры – расчетный параметр и – расчетный параметр полосы задерживания:
Зная , определяем затухание одного звена фильтра с учетом потерь в полосе задерживания
Далее находим минимальное собственное затухание всего фильтра в полосе задерживания, которое необходимо для обеспечения гарантируемого минимума затухания
По найденным значениям и определяем число звеньев N (или, что то же самое, класс фильтра по затуханию)
Для выбранного округленного числа звеньев N=4 пересчитываем величины , , , а также . Уточнив все эти параметры проверяем отклонение характеристического сопротивления от номинального.
Уточнив все эти параметры проверяем отклонение характеристического сопротивления от номинального.
Зная , пересчитываем коэффициент использования полосы задерживания
,
используя который, определяем уточненную верхнюю теоретическую частоту среза
Полученное значение теоретической частоты среза удовлетворяет исходным требованиям, так как находится в переходной области. Далее определяем уточненный коэффициент использования полосы пропускания
,
Теперь по сути дела возвращаемся в начало расчета. Для проверки отклонения характеристического сопротивления фильтра от номинального сопротивления нагрузки в полосе пропускания рассчитываем параметры , и (по данным полосы пропускания):
Выбираем заранее фильтр 2-го класса по сопротивлению и определяем затухание несогласованности в полосе пропускания
и затухание эха
После определяем величину отклонения характеристического сопротивления от номинального в полосе пропускания
Что удовлетворяет исходным техническим требованиям.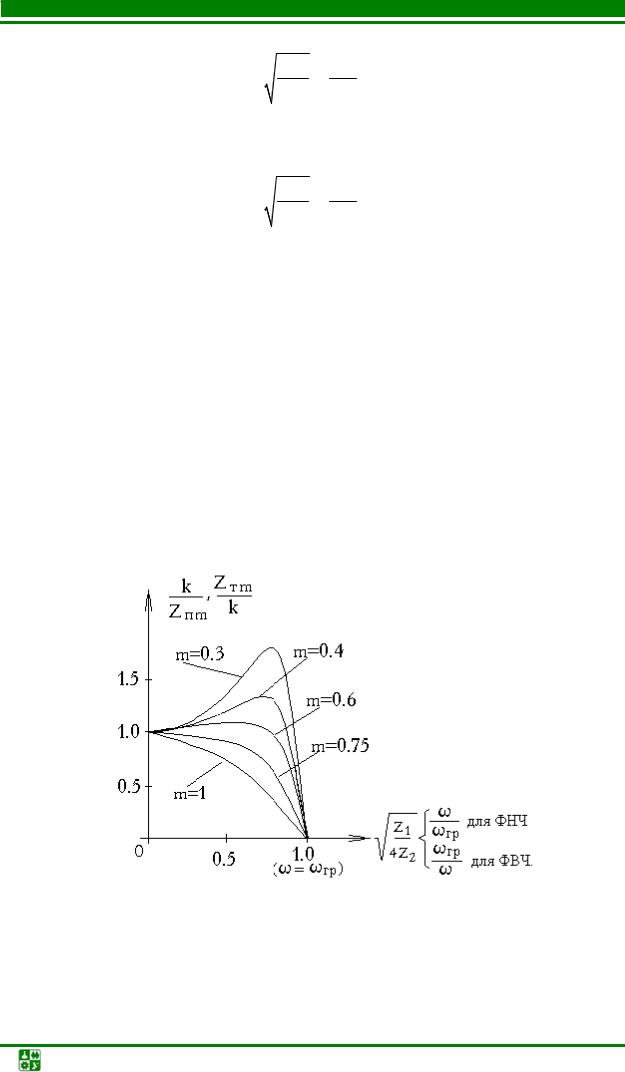 Таким образом, на основании проведенного расчета выбран фильтр 2-го класса по сопротивлению с числом звеньев N=4. Отклонение характеристического сопротивления от номинального в полосе пропускания составляет 3,558 %, коэффициент использования полосы пропускания =0,885, теоретическая частота среза =113,016 кгц.
Таким образом, на основании проведенного расчета выбран фильтр 2-го класса по сопротивлению с числом звеньев N=4. Отклонение характеристического сопротивления от номинального в полосе пропускания составляет 3,558 %, коэффициент использования полосы пропускания =0,885, теоретическая частота среза =113,016 кгц.
Расчетные параметры необходимые в дальнейшем,
=0,43 =0,4659=113,016 кгц.
Так как фильтр состоит из четырех звеньев, то для каждого звена рассчитываем коэффициент и соответственно расчетный параметр m.
где
=1,2,3,4 – № звена
N= 4 – число звена
Таким образом
Проверкой правильности расчета при четном числе звеньев служит соблюдение следующих соотношений:
, и т.д.
т.е. в рассматриваемом примере и т.д.
Для расчета коэффициентов m полагаем, что =0,43, тогда
Затем определяем
Для получения наилучшего согласования фильтра с нагрузкой начинаем и оканчиваем фильтр полузвеньями, у которых значение коэффициента m ближе к .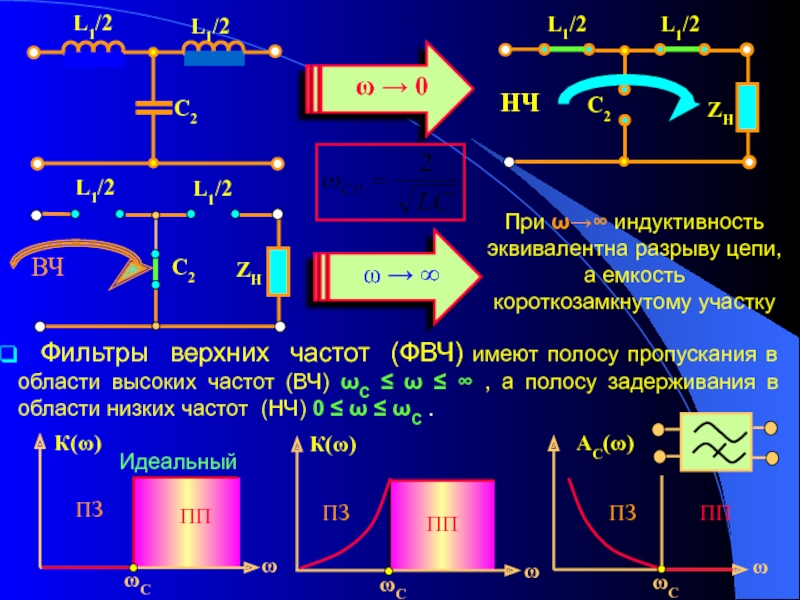 В рассматриваемом примере этому требованию удовлетворяет коэффициент .
В рассматриваемом примере этому требованию удовлетворяет коэффициент .
Внутри фильтра звенья с различными коэффициентами могут соединяться в произвольном порядке, но при условии соблюдения согласования.
Затем приступаем к выбору конкретной схемы фильтра нижних частот. При этом нужно стремиться к выбору звеньев с наименьшим числом катушек индуктивности, поскольку именно эти элементы наиболее усложняют производство и настройку фильтра. Так как класс фильтра определяется классом конечных полузвеньев, то для них выбираем звено типа 2А1н (звено Т-образного вида, 2-го класса по сопротивлению, с одной стороной среза фильтра нижних частот) и делим его пополам, для того, чтобы не увеличивать общее число звеньев. При этом получаются оконечные полузвенья Г-образного вида. В качестве промежуточных звеньев используем звенья типа 1В1н (звено П-образного вида, первого класса по сопротивлению, с одной частотой среза, фильтра нижних частот). Далее составляем полную принципиальную схему всего фильтра нижних частот рисунок 8.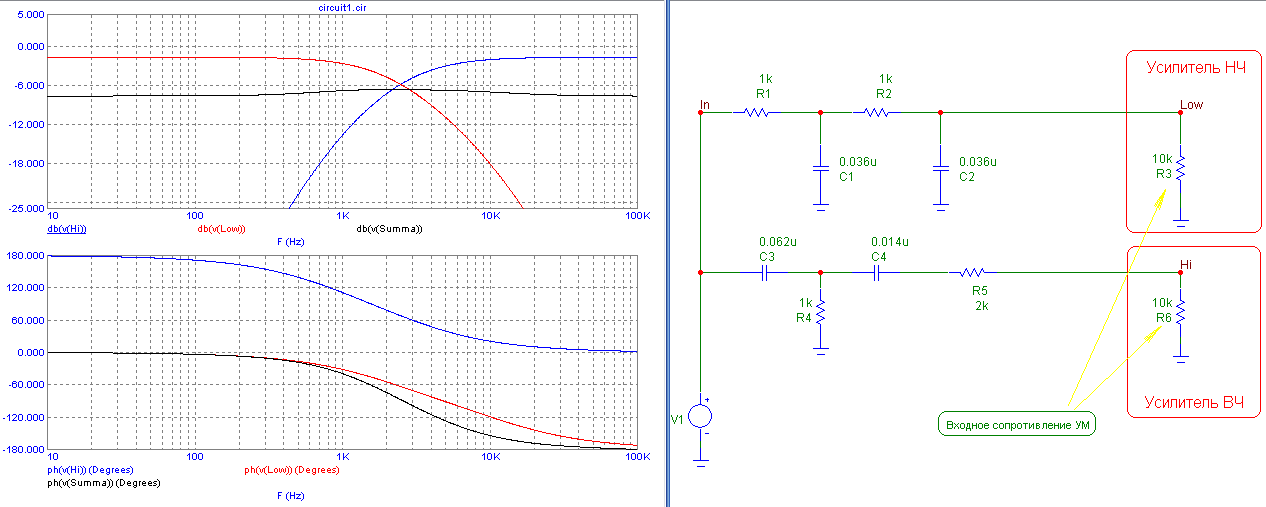
звена 2А1н 1В1н 1В1н1В1нзвена 2А1н
Рисунок 8 – Полная принципиальная схема фильтра нижних частот
Первый этап расчета заканчиваем вычислением частот минимального затухания, лежащих в полосе задерживания.
соответственно
Формула для расчета частот минимального затухания
Аналогично формуле для расчета с той лишь разницей, что вместо параметра подставляется . Коэффициент , аналогичный коэффициенту , рассчитывается по формуле
где=1,2,3,4 – № звена
N= 4 – число звеньев
=0,3986 – ранее определенный параметр
Таким образом
Проверка правильности расчета коэффициентов :
, и т.д.
где
т.е. в рассматриваемом примере и т.д.
Далее для каждого звена определяем параметр и частоту минимального затухания:
Частота последнего минимума затухания должна совпадать с верхней граничной частотой полосы задерживания. Кроме того должно соблюдаться строгое чередование частот бесконечного и минимального затухания. Правильность расчета подтверждается в рассматриваемом примере равенством и таблицей 1.
Кроме того должно соблюдаться строгое чередование частот бесконечного и минимального затухания. Правильность расчета подтверждается в рассматриваемом примере равенством и таблицей 1.
Таблица 1
Заметим, что наибольшему значению m соответствует наиболее удаленная от полосы пропускания частота бесконечного затухания, а наименьшему значению m соответствует ближайшая к переходной области частота бесконечного затухания. Все частоты и находятся в полосе задерживания. Не допускается расположение частот и в полосе пропускания.
Определив частоты бесконечного и минимального затухания, а так же значения коэффициентов для всех звеньев и составив полную принципиальную схему фильтра нижних частот (ФНЧ состоит из трех звеньев типа 1В1н и двух полузвеньев типа 2А1н), приступаем к расчету номинальных значений элементы схемы ФНЧ. Начинаем с определения величины расчетного сопротивления , а затем единичной индуктивности и единичной емкости .
Коэффициент нагрузки рассчитывается графоаналитическим способом.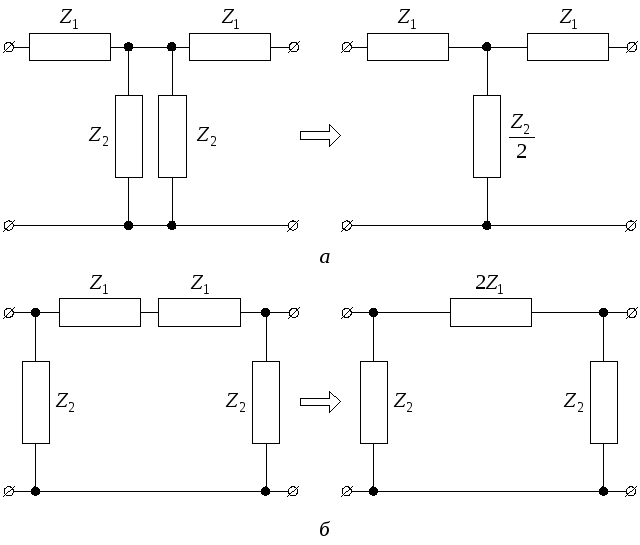 Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).
Суть расчета сводится к тому, что выбирается такое соотношение между сопротивлением нагрузки и номинальным характеристическим сопротивлением, при котором в заданной полосе частот обеспечивается наилучшее согласование. Расчет характеристического сопротивления ведется только для оконечного полузвена, ибо если выполняются условия согласования характеристического сопротивления с сопротивлением нагрузки для оконечного полузвена на всех частотах полосы пропускания, то они выполняются и для всех промежуточных звеньев (данные расчета приведены в таблице 2).
Таблица 2
| Оконечное полузвено Ом =113,016 кгц. | ||||||
| f, кгц | ||||||
| 50 | 0,4424 | 0,8968 | 0,87128 | 1,02929 | 1029,29 | 1,03592 |
| 55 | 0,4867 | 0,8736 | 0,84421 | 1,0348 | 1034,8 | 1,0415 |
| 60 | 0,5309 | 0,8474 | 0,8146 | 1,04027 | 1040,27 | 1,04697 |
| 65 | 0,5751 | 0,81805 | 0,7825 | 1,0454 | 1045,4 | 1,0521 |
| 70 | 0,6194 | 0,7851 | 0,7477 | 1,0500 | 1050,0 | 1,0568 |
| 75 | 0,6636 | 0,7481 | 0,71037 | 1,05311 | 1053,11 | 1,053865 |
| 80 | 0,7079 | 0,7064 | 0,6704 | 1,05369 | 1053,69 | 1,0605 |
| 85 | 0,7521 | 0,6590 | 0,62797 | 1,0494 | 1049,4 | 1,0562 |
| 90 | 0,7964 | 0,6048 | 0,58285 | 1,03766 | 1037,66 | 1,0443 |
| 95 | 0,8406 | 0,5417 | 0,53526 | 1,01203 | 1012,03 | 1,01855 |
| 100 | 0,8848 | 0,4659 | 0,48511 | 0,9604 | 960,4 | 0,9666 |
Коэффициент согласования – это отношение характеристического сопротивления к сопротивлению нагрузки, т. е. . Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой относительно значения (т.е. уравнивания наибольшего и наименьшего значений в полосе пропускания).
е. . Чем меньше коэффициент согласования отличается от единицы, тем лучше согласованы характеристическое сопротивление и сопротивление нагрузки. Графоаналитический метод заключается в симметрировании кривой относительно значения (т.е. уравнивания наибольшего и наименьшего значений в полосе пропускания).
Исходя из этого, определяется коэффициент нагрузки , позволяющий затем вычислить как оптимальное номинальное характеристическое сопротивление. Проводя симметрирование, перемещаем кривую вдоль оси ординат относительно значения (в рассматриваемом примере вниз) так, чтобы максимальное положительное и максимальное отрицательное отклонения функции от значения были приблизительно равны.
Рисунок 9 – График симметрирования характеристического сопротивления ФНЧ
В рассматриваемом примере экспериментальное значение функции соответствует значениям и . На частоте коэффициент согласования . На частоте коэффициент согласования .
Из этого обобщенного графика можно сделать заключение о форме характеристики затухания фильтра нижних частот. Положительное отклонение от значения свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот и ; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).
Положительное отклонение от значения свидетельствует об обеспечении неискаженной передачи частот полосы пропускания в диапазоне частот и ; отрицательное отклонение свидетельствует о наличие искажений для некоторых частот полосы пропускания (наблюдается так называемый завал фронтов амплитудно-частотной характеристики).
Максимально положительное и максимально отрицательное отклонение на этих частотах составляют соответственно ()
Разность отклонений
Среднее отклонение
Новое значение коэффициента согласования на частоте с учетом среднего отклонения
Коэффициент несогласованности и коэффициент нагрузки на частоте соответственно равны
Полагая коэффициент нагрузки на частотах и одинаковым, находим коэффициент согласования и коэффициент несогласованности на частоте :
Так как значения и ничтожно мало отличаются друг от друга, коэффициент нагрузки выбираем окончательно .
Определяем расчетное характеристическое сопротивление
Ом
Следует отметить, что, так как и мало отличается от , можно было бы пренебречь несогласованностью при расчете и полагать Ом.
Вычисляем величины единичной индуктивности и единичной емкости исходного звена типа .
, ,
Рисунок 10 – Расчетные соотношения для П-образного звена типа 1В1н фильтра нижних частот.
Учитывая составленную полную принципиальную схему фильтра нижних частот (см. рисунок 8), рассчитываем номинальные величины элементов каждого звена схемы. Звено типа 1В1н рассчитывается следующим образом:
Зная коэффициенты и можно рассчитать элементы всех звеньев (рисунок 10), учитывая при этом, что для каждого звена требуются свои значения m, а значения и постоянны для всех звеньев. Расчет дается для одного типового промежуточного звена и оконечного полузвена. Значения элементов остальных звеньев сведены в таблице 3.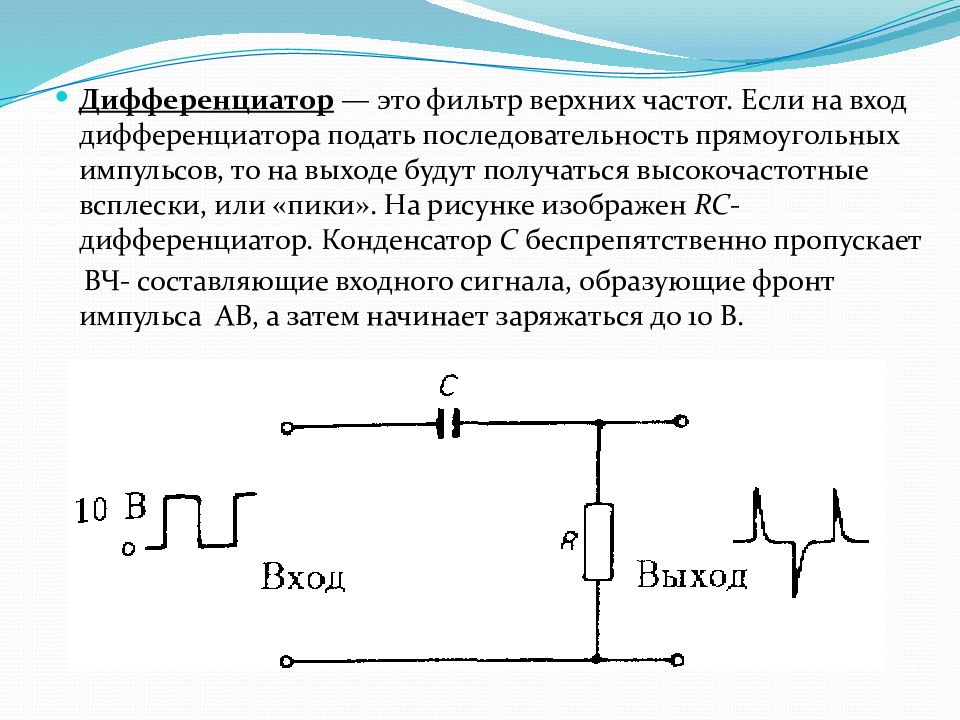
Расчет промежуточного полузвена
,,,
,
,
,
Сразу же проверяем резонансную частоту контура, значение которой должно совпадать со значением частоты бесконечного затухания при том же значении m.
()
Таблица 3
№ звена |
Расчетный коэффициент |
, кГц |
||||||
| 0,31642 | 1,4099 | 0,63284 | 0,8974 | 1973,8 | 442,97 | 119,65 | ||
| 0,19862 | 2,4181 | 0,39742 | 0,56329 | 3385,22 | 278,06 | 115,31 |
Расчет оконечного полузвена.
Четвертое звено состоит из двух полузвеньев, включенных на входе и на выходе фильтра. Для того, чтобы рассчитать номинальные величины Г-образных полузвеньев по приведенным формулам, необходимо пересчитать величину , так как оконечные полузвенья образуются путем деления пополам Т-образного звена типа 2А1н (линия а-а на рисунке 11).
Для того, чтобы рассчитать номинальные величины Г-образных полузвеньев по приведенным формулам, необходимо пересчитать величину , так как оконечные полузвенья образуются путем деления пополам Т-образного звена типа 2А1н (линия а-а на рисунке 11).
Рисунок 11 – Преобразование звена типа 2А1н в оконечные полузвенья ФНЧ и расчетные соотношения.
Проверяем резонансную частоту контура
()
Имея полную схему фильтра (см. рисунок 8), можно составить его приведенную схему, отличающуюся от полной тем, что параллельно соединенные элементы заменим одним эквивалентным элементом (см.рисунок 12). Это внесет упрощение в изготовление фильтра и также удешевит его. В приведенной схеме изменены обозначения. Поэтому приведем нумерацию и расчет эквивалентных элементов (обозначения полной схемы в скобках):
, ,
,,
,,
,,
,
Рисунок 12 – Приведенная схема фильтра нижних частот
Построение полной характеристики затухания ФНЧ. Необходимо рассчитать затухание в полосе задерживания и в полосе пропуская. Так же учтем, что общее собственное затухание как в полосе задерживания, так и в полосе пропускания равняется сумме затуханий всех звеньев . Поэтому рассчитаем затухания отдельно для каждого звена, и затем просуммируем их.
Необходимо рассчитать затухание в полосе задерживания и в полосе пропуская. Так же учтем, что общее собственное затухание как в полосе задерживания, так и в полосе пропускания равняется сумме затуханий всех звеньев . Поэтому рассчитаем затухания отдельно для каждого звена, и затем просуммируем их.
Расчет характеристики затухания фильтра нижних частот начинаем с расчета собственного затухания каждого звена на частотах , где учитываем что Q – добротность катушек индуктивности (для выбранных мною альсиферовых сердечников она обычно берется равной 60) и – рассчитанные ранее коэффициенты звеньев.
Таким образом
Далее считаем собственное затухание в полосе задерживания без учета потерь, так как потери в полосе задерживания не сказываются существенно на затухании.
,
где
Рассчитываем собственное затухание в полосе задерживания на всех частотах и , кроме частоты бесконечного затухания данного звена, так как оно рассчитано ранее. Полный расчет для звена I () приведен в таблице 4. Для всех остальных звеньев в таблице 5 приведены расчетные значения частот и и величины соответствующих им затуханий, там же приводится собственное затухание всего ФНЧ в полосе задерживания.
Полный расчет для звена I () приведен в таблице 4. Для всех остальных звеньев в таблице 5 приведены расчетные значения частот и и величины соответствующих им затуханий, там же приводится собственное затухание всего ФНЧ в полосе задерживания.
Таблица 4
| I звено | |||||
| f,кГц | |||||
| 115,00 | 1,0176 | 5,4001 | 6,0296 | 4,0296 | 0,40301 |
| 115,313 | 1,0203 | 5,0385 | 5,6928 | 3,0928 | 0,43282 |
| 116,419 | 1,0301 | 4,1056 | 4,8239 | 2,8239 | 0,5346 |
| 119,137 | 1,0542 | 3,1594 | 3,9426 | 1,9426 | 0,7048 |
| 125,179 | 1,1076 | 2,3259 | 3,1663 | 1,1663 | 0,9987 |
| 139,356 | 1,2331 | 1,7091 | 2,5918 | 0,5918 | 1,4769 |
| 176,369 | 1,5606 | 1,3026 | 2,2132 | 0,2132 | 2,3399 |
Таблица 5
| f,кГц | I звено | II звено | III звено | IV звено | |
| 310,442 | 9,381 | 1,47681 | 0,7077 | 0,4333 | 11,99881 |
| 176,369 | 2,3399 | 2,00241 | 0,8765 | 0,5294 | 5,74821 |
| 139,356 | 1,4769 | 5,247 | 1,21056 | 0,7071 | 8,64156 |
| 125,179 | 0,9987 | 1,87846 | 1,8832 | 0,9997 | 5,76006 |
| 119,137 | 0,7078 | 1,21113 | 2,328 | 1,4738 | 5,72073 |
| 116,419 | 0,53546 | 0,88646 | 2,0395 | 2,2865 | 5,74792 |
| 115,313 | 0,43282 | 0,70645 | 1,4737 | 3,39 | 6,00297 |
| 115 | 0,40301 | 0,6556 | 1,34079 | 1,04941 | 3,44881 |
Для получения рабочего затухания в полосе задерживания рассчитаем затухание задерживания , так как оно существенно влияет в этой области частот на рабочее затухание.
,
где
Затухание отражения считаем только для оконечного полузвена со значением , так как затухание отражения получается за счет несогласованности характеристического сопротивления с сопротивлением нагрузки. Окончательные результаты сведены в таблице 6.
Таблица 6
| f, кГц | , неп | f, кГц | , неп |
| 115,000 | –0,5637 | 125,179 | –0,3235 |
| 115,3013 | –0,5972 | 139,356 | 7,45 |
| 116,419 | –0,674 | 176,369 | –0,467 |
| 119,137 | –0,6806 | 310,442 | –0,602 |
Далее находим рабочее затухание всего фильтра в полосе задерживания (таблица 7).
Таблица 7
| f, кГц | , дБ |
, неп |
||||
| 115,00 | 1,0176 | 3,44881 | –0,5637 | 2,88511 | 28,14 | 2,89 |
| 115,313 | 1,0203 | 6,00297 | –0,5972 | 5,40577 | 47,07 | 5,41 |
| 116,419 | 1,0301 | 5,74792 | –0,674 | 5,07392 | 44,11 | 5,07 |
| 119,137 | 1,0542 | 5,72073 | –0,6806 | 5,04013 | 43,85 | 5,04 |
| 125,179 | 1,1076 | 5,76006 | –0,3235 | 5,43656 | 47,33 | 5,44 |
| 139,356 | 1,2331 | 8,64156 | 7,45 | 16,0916 | 139,98 | 16,09 |
| 176,369 | 1,5606 | 5,74821 | –0,467 | 5,28121 | 45,94 | 5,28 |
| 310,442 | 2,75 | 11,99881 | –0,602 | 11,3968 | 99,15 | 11,39 |
Рассчитываем фазовый сдвиг, вносимый одним звеном ФНЧ.
где – фазовый сдвиг, вносимый каждым звеном;
= 1,2,3,4 – № звена
Общий фазовый сдвиг представляет собой сумму фазовых сдвигов звеньев. Расчеты фазового сдвига каждого звена и всего фильтра приведены в таблицах 8 и 9. Как видно из таблицы 9 фазовый сдвиг вырастает при приближении к частоте среза. Для ФНЧ эта частотой является наивысшей частотой полосы пропускания.
Для получения полной характеристики затухания ФНЧ рассчитываем для каждого звена в отдельности затухание в полосе пропускания с учетом потерь по следующей формуле:
Таблица 8
| I звено | |||||||
| f, кГц | f, кГц | ||||||
| 50 | 0,4424 | 0,4595 | 80 | 0,7079 | 0,9334 | ||
| 55 | 0,4867 | 0,5189 | 85 | 0,7521 | 1,0629 | ||
| 60 | 0,5309 | 0,5835 | 90 | 0,7964 | 1,2264 | ||
| 65 | 0,5751 | 0,6548 | 95 | 0,8406 | 1,4453 | ||
| 70 | 0,6194 | 0,7348 | 100 | 0,8848 | 1,7688 | ||
| 75 | 0,6636 | 0,8262 | |||||
Расчет собственного затухания в полосе пропускания, вносимого I звеном, отражен в таблице 10. Окончательные результаты аналогичных расчетов затухания полосы пропускания для остальных звеньев сведены в таблице 11. В этой же таблице приведено суммарное собственное затухание фильтра в полосе пропускания .
Окончательные результаты аналогичных расчетов затухания полосы пропускания для остальных звеньев сведены в таблице 11. В этой же таблице приведено суммарное собственное затухание фильтра в полосе пропускания .
Таблица 9
Таблица10
| I звено Q=60 | ||||||
| f, кГц | , неп | , дБ | ||||
| 50 | 0,4424 | 0,21114 | 1,21114 | 0,37939 | 0,002797 | 0,02433 |
| 55 | 0,4867 | 0,26926 | 1,6926 | 0,30657 | 0,002487 | 0,02164 |
| 60 | 0,5309 | 0,34047 | 1,3047 | 0,44723 | 0,003957 | 0,03443 |
| 65 | 0,5751 | 0,42876 | 1,42876 | 0,45829 | 0,004393 | 0,03822 |
| 70 | 0,6194 | 0,53993 | 1,53993 | 0,47716 | 0,004926 | 0,04286 |
| 75 | 0,6636 | 0,68261 | 1,68261 | 0,49102 | 0,005431 | 0,04725 |
| 80 | 0,7079 | 0,87124 | 1,87124 | 0,49881 | 0,005885 | 0,05120 |
| 85 | 0,7521 | 1,12976 | 2,12976 | 0,49907 | 0,006256 | 0,05443 |
| 90 | 0,7964 | 1,50406 | 2,50406 | 0,48976 | 0,006501 | 0,05657 |
| 95 | 0,8406 | 2,08889 | 3,08889 | 0,46790 | 0,006555 | 0,05703 |
| 100 | 0,8848 | 3,12865 | 4,12865 | 0,42842 | 0,063178 | 0,05496 |
За счет потерь энергии в катушках индуктивности и конденсаторах собственное затухание фильтра не равно нулю, а имеет некоторое конечное значение, возрастающее по мере приближения к предельной частоте.
На основании ранее полученных данных о затухании фильтра составляем таблицу для расчета выходного напряжения в полосе пропускания и полосе задерживания фильтра нижних частот, помня, что и (таблица 12).
Рисунок 13 – Фазовая характеристика ФНЧ с полосой
пропускания 50–100 кГц
Таблица 12
| f, кГц | , дБ | , В | f, кГц | , дБ | , В |
| 50 | 0,057409 | 4,967 | 100 | 0,217759 | 4,876 |
| 55 | 0,062213 | 4,964 | 115,00 | 28,14 | 0,196 |
| 60 | 0,083417 | 4,952 | 115,313 | 47,07 | 0,0222 |
| 65 | 0,096649 | 4,945 | 116,419 | 44,11 | 0,03115 |
| 70 | 0,111872 | 4,936 | 119,137 | 43,85 | 0,0321 |
| 75 | 0,128068 | 4,927 | 125,179 | 47,33 | 0,0215 |
| 80 | 0,145215 | 4,917 | 139,356 | 139,98 | 0 |
| 85 | 0,163141 | 4,907 | 176,369 | 45,94 | 0,0252 |
| 90 | 0,181667 | 4,896 | 310,442 | 99,15 | 0,000055 |
| 95 | 0,200216 | 4,886 | |||
Таблица 11
| f, кГц | I звено |
II звено |
III звено |
IV звено |
, неп |
, дБ |
||||
| , неп | , дБ | , неп | , дБ | , неп | , дБ | , неп | , дБ | |||
| 50 | 0,002797 | 0,02433 | 0,001964 | 0,01709 | 0,001124 | 0,009775 | 0,000714 | 0,006214 | 0,006599 | 0,057409 |
| 55 | 0,002487 | 0,02164 | 0,00239 | 0,020792 | 0,001387 | 0,012067 | 0,000887 | 0,007714 | 0,007151 | 0,062213 |
| 60 | 0,003957 | 0,03443 | 0,002859 | 0,024873 | 0,001687 | 0,014681 | 0,001084 | 0,009433 | 0,009587 | 0,083417 |
| 65 | 0,004393 | 0,03822 | 0,003372 | 0,029336 | 0,002031 | 0,017672 | 0,001313 | 0,011421 | 0,011109 | 0,096649 |
| 70 | 0,004926 | 0,04286 | 0,003928 | 0,034175 | 0,002426 | 0,021102 | 0,001579 | 0,013735 | 0,012859 | 0,111872 |
| 75 | 0,005431 | 0,04725 | 0,004522 | 0,039338 | 0,002878 | 0,025037 | 0,00189 | 0,016443 | 0,014721 | 0,128068 |
| 80 | 0,005885 | 0,05120 | 0,005148 | 0,044789 | 0,003399 | 0,029574 | 0,002259 | 0,019652 | 0,016691 | 0,145215 |
| 85 | 0,006256 | 0,05443 | 0,005789 | 0,050363 | 0,004004 | 0,034836 | 0,002703 | 0,023512 | 0,018752 | 0,163141 |
| 90 | 0,006501 | 0,05657 | 0,006419 | 0,055829 | 0,004713 | 0,041 | 0,003249 | 0,028268 | 0,020882 | 0,181667 |
| 95 | 0,006555 | 0,05703 | 0,006973 | 0,060658 | 0,005543 | 0,048221 | 0,003943 | 0,034307 | 0,023014 | 0,200216 |
| 100 | 0,063178 | 0,05496 | 0,007332 | 0,063794 | 0,00651 | 0,05664 | 0,00487 | 0,042365 | 0,08189 | 0,217759 |
Рисунок – 14 Амплитудно-частотная характеристика ФНЧ с полосой пропускания 50–100 кГц
Окончательной проверкой правильности расчета фильтра является близкое совпадение расчетной характеристики с экспериментальной (рисунок 15).
1–теоретическая характеристика; 2– расчетная характеристика
Рисунок – 15 Амплитудно-частотная характеристика ФНЧ с полосой пропускания 50–100 кГц
В заключении расчета приведем общую схему фильтра нижних частот, сопротивление нагрузки ставим в конце схемы.
; ; ; ;
; ; ; ; ; ; ; ; ;
Рисунок –16 Общая схема ФНЧ с рассчитанными значениями емкостей и индуктивностей
Так как в расчете использованы катушки индуктивности с альсиферовыми тороидальными сердечниками, то рекомендуется расположение всех катушек на общей оси и воспользоваться изолирующими прокладками между ними. Монтаж конденсатора может быть осуществлен подобно монтажу сопротивлений, на общей плате. Кожух фильтра выполняется из алюминия, дюраля либо пермаллоя, или другого материала, играющего роль электрического экрана (рисунок 17). Выводы осуществляются через разъемы, которые могут быть и герметичными. Если требуется герметичность всего фильтра, можно рекомендовать заливку компаундами, например эпоксидной смолой. При этом катушки индуктивности должны пройти предварительную пропитку церезином.
Если требуется герметичность всего фильтра, можно рекомендовать заливку компаундами, например эпоксидной смолой. При этом катушки индуктивности должны пройти предварительную пропитку церезином.
При монтаже всех деталей требуется тщательная и надежная пайка, потому что в большинстве случаев неисправности фильтре связаны с плохой пайкой контактов.
Рисунок 17 – Наружный вид фильтра нижних частот 120 80 60
Заключение
В результате выполнения курсового проекта был рассчитан фильтр нижних частот 2-го порядка по сопротивлению, с полосой пропускания 50–100кГц. Характеристики затуханий, построенные по рассчитанным частотам, отвечают требованиям к полосам задержания и пропускания. Проведенное моделирование показало, что характеристики рассчитанных фильтров близки к идеальным, что подтверждает точность расчёта и возможность использования этого фильтра на практике. Преобразование общей схемы фильтра, т.е. уменьшение общего количества необходимых емкостей и индуктивностей позволило удешевить и уменьшить вес конструкции фильтра.
Следует отметить, чторассчитанный мною фильтр может использоваться как все L C -фильтры: в силовых электрических цепях для гашения помех и для сглаживания пульсаций напряжения после выпрямителя; в каскадах радиоэлектронной аппаратуры, включенный на входе средневолнового радиоприёмника обеспечивая настройку на определённую радиостанцию; в звуковой аппаратуре в многополосных эквалайзерах для корректировки АЧХ; для разделения сигналов низких, средних и высоких звуковых частот в многополосных акустических системах; в схемах частотной коррекции магнитофонов и др.
Список использованной литературы
1. Богданов Н.Г. Расчёт электрических фильтров. – Пособие по курсовому и дипломному проектированию – М.: ВИПС, 2000 г.,352 с.
2. Зааль Р., Справочник по расчетам фильтров – М.: Радио и связь, 1983 г., 753 с.
3. Куцко Т. Ю. Расчет полосовых фильтров – М.: Энергия 1985 г., 193 с.
4. Босый К. Д. Электрические фильтры – М.: Гостехиздат 1960 г., 350 с.
Расчет фильтра нижних частот (Курсовая работа)
Содержание
Введение
1 Физические основы и принцип действия широкополосных фильтров
2 Пример расчета фильтра нижних частот на заданные параметры
Заключение
Список использованной литературы
Введение
Во многих радиотехнических устройствах часто возникает необходимость выделения заданных частотных диапазонов из имеющегося спектра частот. Выделение требуемой полосы частот с очень малым затуханием осуществляется фильтрами.
В начале нашего столетия электрические фильтры, составленные из ряда катушек индуктивности и конденсаторов, получили широкое применение в технике. Благодаря их применению оказалось возможным осуществление многих магистралей дальней телефонной, телеграфной и других видов связи.
Известный интерес представляют пассивные цепочные, или лестничные фильтры, состоящие из комбинаций элементов L и C и не требующие источника питания. Пассивные фильтры могут обладать как широкими полосами пропускания, так и очень узкими.
При расчете фильтра, с одной стороны, необходимо определить, с какими допустимыми искажениями передается входной сигнал, являющийся функцией частоты или времени, на выход фильтра, и, с другой стороны, из каких конкретных элементов должен состоять этот фильтр. Получение наивыгоднейших выходных характеристик с минимальными искажениями и создание принципиальной схемы фильтра с минимальным числом элементов, осуществляющей требуемую передачу сигнала, является содержанием расчета фильтров.
1 Физические основы и принцип действия широкополосных фильтров
В электрических, радиотехнических и телемеханических установках часто решается задача: из совокупного сигнала, занимающего широкую полосу частот, выделить один или несколько составляющих сигналов с более узкой полосой. Сигналы заданной полосы выделяют при помощи частотных электрических фильтров.
К частотным электрическим фильтрам различной аппаратуры предъявляются разные, порой противоречивые требования. В одной области частот, которая называется полосой пропускания, сигналы не должны ослабляться, а в другой, называемой полосой задерживания, ослабление сигналов не должно быть меньше определенного значения. Фильтр считают идеальным, если в полосе пропускания отсутствует ослабление сигналов и фазо-частотная характеристика линейна (нет искажения формы сигналов), а вне полосы пропускания сигналы на выходе фильтра отсутствуют.
Фильтры могут быть однозвенные (первого порядка), двухзвенные (второго порядка) и многозвенные (n- го). Чем выше порядок фильтра, тем круче его амплитудно-частотная характеристика и тем более она похожа на его идеальную характеристику. Фильтр любого порядка можно построить путем каскадного соединения фильтров первого и второго порядков.
Электрический фильтр представляет собой четырехполюсник, предназначенный для выделения из состава сложного электрического колебания частотных составляющих, расположенных в заданной полосе частот, и подавления тех составляющих, которые расположены в других полосах частот. Первая из названных полос представляет собой полосу пропускания, а вторая – полосу задерживания.
По взаимному расположению полос пропускания и полос задерживания различают фильтры нижних частот, фильтры верхних частот, полосовые и режекторные фильтры.
Фильтры нижних частот (ФНЧ) пропускают сигналы частот от 0 до и задерживающей колебания любых белее высоких частот (рис.1).
LC–фильтр нижних частот (рис. 6.3,а) пропускает электрические колебания в полосе частот от 0 до
.
Это объясняется тем, что на низких частотах сопротивление индуктивного элемента XL фильтра мало, а емкостного XC – велико и электрические колебания проходят со входа на выход почти без ослабления. С увеличением частоты сопротивление индуктивного элемента возрастает, а емкостного – снижается и коэффициент передачи фильтра уменьшается (рисунок 1–б).
Фильтры верхних частот (ФВЧ), напротив, пропускают сигналы, частоты которых простираются от до , и задерживают сигналы более низких частот(рис.2).
Полосовые фильтры (ПФ) пропускают сигналы в полосе частот от до (рис.3).
Режекторные (заграждающие) фильтры (РФ) задерживают сигналы в полосе частот от до (рис.4).
(а)
(б)
Рисунок – 1 Фильтры нижних частот (а) и его АЧХ (б).
Рисунок – 2 Фильтры верхних частот
Рисунок – 3 Полосовые фильтры
Рисунок – 4 Заграждающие фильтры
Широкополосный фильтр состоит из звеньев, включающих в себя только элементарные контуры. Поэтому механизм фильтрации в широкополосных фильтрах определяется в основном процессами, происходящими в элементарны контурах, т. е. в двухэлементных двухполюсниках, имеющих одну резонансную частоту.
Полное сопротивление Z любого элементарного контура состоит из активной R и реактивной X составляющих:
Z = R + jX (1)
или
Y = G + jB (2)
где Y – полная проводимость
G – активная составляющая полной проводимости
B – реактивная составляющая поной проводимости
Реактивное сопротивление последовательного контура на частоте = равно нулю, активное сопротивление при этом мало, так как оно определяется только потерями в контуре; полное сопротивление контура близко к нулю. Поэтому последовательные контуры применяются в параллельных плечах Т-образных звеньев фильтров верхних частот (рис.5)., так как они оказывают сильное шунтирующее действие на частотах, близких к резонансной.
Рисунок – 5 Схема звена ФВЧ и резонансные характеристики последовательного контура
Реактивная проводимость = равна нулю. Следовательно, такой контур является фильтром-пробкой для частот, близких к резонансной. Поэтому параллельные контуры применяются в последовательных плечах П-образных звеньев фильтров нижних частот (рис.6). Резонансные частоты элементарных контуров равны частотам бесконечного затухания соответствующих звеньев =. Резонансные частоты контуров, или частоты бесконечного затухания, для ФНЧ располагаются выше частот полосы пропускания ( >), а для ФВЧ – ниже (<). Параллельные плечи фильтра шунтируют частоты полосы задерживания в то время, как последовательные являются для них пробкой. В полосе пропускания сопротивление параллельных плеч фильтра , напротив, велико, а сопротивление последовательных плеч близко к нулю.
Расчет фильтра верхних частот
В качестве фильтра высоких частот используем пассивный RC-фильтр:
Рисунок 3 – Фильтр верхних частот
Так как для промежуточной части входное сопротивление приблизительно равно
R6= 2 кОм, сопротивление фильтра R5 << R6 можно не учитывать. За сопротивление фильтра принимаем R6=2 кОм.
=
Емкость выбираем из номинального ряда Е24
Расчет фильтра нижних частот
В качестве фильтра низких частот используем пассивный RC-фильтр (Рисунок 5).
Рисунок 5 – Фильтр нижних частот
Емкость выбираем из номинального ряда Е24
С2=2,7 нФ.
Гц.
Проектирование выходной части
Выходной каскад выполняется на инвертирующем ОУ К140УД26 и на биполярных транзисторах КТ502А (p-n-p) (обозначение на схеме VT3 и VT7) и КТ503А (n-p-n) (обозначение на схеме VT4 и VT8), а так же на КТ8131А (n-p-n) (обозначение на схеме VT5) и КТ8130А (p-n-p) (обозначение на схеме VT6) составляющих комплементарную пару. И одну не комплементарную пару: КТ216А (p-n-p) (обозначение на схеме VT2) и КТ301 (n-p-n) (обозначение на схеме VT1) Стабилитроны КС170А.
По техническому заданию выходная часть должна обеспечивать следующие требования – выходное напряжение U вых.mах = 50 В; нижняя граница диапазона частот 100 Гц; верхняя граница диапазона частот 10000 Гц; минимальное сопротивление нагрузки 15 Ом.
Так как ОУ не обеспечивает необходимую амплитуду выходного напряжения, то на его выходе необходимо установить дополнительный усилительный каскад, который позволяет получить усиление по напряжению.
Каскад по рисунку 6 использует свойство ОУ, что их ток питания зависит от сопротивления нагрузки (потребляемый ток по форме полностью повторяет входной сигнал). Поэтому, если обеспечить неизменное напряжение питания ОУ, а изменения тока преобразовать в напряжение с помощью резисторов, то легко получить требуемое дополнительное изменение выходного напряжения ОУ.
Выходной ток при максимальной нагрузке:
Максимальная амплитуда выходного тока ОУ:
Коэффициент усиления по току для транзисторного каскада:
Коэффициент усиления по напряжении:
Пусть выбираем равным 4.
тогда Из ряда Е192 выбираем номиналы ,
Напряжение питания ОУ стабилизировано с помощью транзисторов VT1 и VT2. Для этого на их базы подан потенциал, снимаемый с параметрических стабилизаторов напряжения и . Транзисторы VT1 и VT2 включены по схеме с ОБ. Изменение тока, потребляемого ОУ, создает на резисторе падение напряжения, повторяющее входной сигнал. Соответствующая полуволна напряжение усиливается транзисторами VT3 и VT4, включенными в схему с ОЭ. Коэффициент их усиления:
.
В данном случае роль играют резисторы , а входное сопротивление транзисторов VT5, VT6 с подключенным к их входу сопротивлением нагрузки. Мощные транзисторы VT5, VT6 обеспечивают получение в нагрузке требуемого значения тока и уменьшают влияние ее подключения на усилитель.
Транзисторы VT7, VT8 выполняют функции защиты усилителя мощности от перегрузок. Как только падение напряжение на резисторах на резисторах превысит значение порогового напряжения этих транзисторов, они открываются и шунтируют цепь источника входного сигнала. Происходит ограничение тока транзисторов VT5, VT6 на том уровне, при которых VT7, VT8 открылись.
Резисторы выбираем из ряда Е24 по 1 кОм.
Рассчитываем входное сопротивление транзистора VT5:
где, – выходное сопротивление ОУ, – омическое сопротивление тела базы транзистора VT5 (50 ÷ 100 Ом), – коэффициент передачи базового тока транзистора VT5 (= 750 ÷15000).
Так как VT5 работает в режиме В, то резистор выбираем исходя из условия:
Выберем из ряда Е24 номинал резистора
Эквивалентное сопротивление в цепи коллектора VT3:
Ток транзистора VT3 на этом сопротивлении должен создать падение напряжения , где – коэффициент передачи эмиттерного повторителя. Возьмем UK3 с запасом UK3=55 В. Тогда амплитуда переменной составляющей тока коллектора через RЭ равна:
При максимальном токе коллектора падение напряжения UКЭ3 следует брать порядка 1,5-2 В, что существенно больше UКЭнас. При этом транзистор VT3 будет работать в активном режиме. Следовательно, для него можно записать уравнение
.
Ориентировочное значение коэффициента усиления каскада с ОЭ на VT3 можно оценить:
Так как ОУ имеет выходное напряжение 12 В, то для получения требуемой амплитуды необходимо 14. Возьмем c запасом равный 20. Тогда
Из ряда Е24 выбираем Тогда напряжение питания:
Входной сигнал, снимаемый с резистора , должен быть равен:
Если изменения тока ОУ при наличии входного сигнала составляет 4,7 мА, то
Выберем из ряда Е24 номинал резистора .
Резистор определяем исходя из уровня тока, на котором необходимо ограничить выходной сигнал, и порогового напряжения транзисторов VT7 и VT8.
.
Выберем из ряда Е24 номинал .
Выходной усилительный каскад представим как на рисунке 7.
Рисунок 7 – Упрощенная схема выходного усилительного каскада
Эквивалентное сопротивление последовательного соединения усилителя и первой ступени каскада:
Эквивалентное сопротивление всей выходной части:
Сопротивление выходной части с нагрузкой
Дополнительная погрешностьпри подключении нагрузки:
Дополнительная погрешность не превышает установленного значения 1,5%.
Рассчитываем коэффициент частотных искажений:
Глубина обратной связи:
.
.
Погрешность коэффициента усиления в полосе рабочих частот:
.
Коэффициент частотных искажений:
Общий коэффициент усиления измерительного усилителя
Наибольший возможный коэффициент усиления измерительного усилителя :
.
Наименьший возможный коэффициент усиления измерительного усилителя:
Погрешность коэффициента усиления не превышает заданного значения 3%.
Общий коэффициент частотных искажений измерительного усилителя:
Погрешность коэффициента преобразования в рабочем диапазоне частот:
()*100%=0,4915795%
Расчет дрейфа температурного нуля:
Расчет и моделирование фильтров — Мегаобучалка
Диапазон частот реосигнала лежит в пределах от 0,05 Гц до 30 Гц [Полищук В.И., Терехова Л.Г. Техника и методика реографии и реоплетизмографии. – М.: Медицина, 1983].
Фильтр верхних частот. Расчет и моделирование.
Зададим частоту среза fc=0,05 Гц. Выбирем неинвертирующий фильтр верхних частот второго порядка.
Коэффициент усиления фильтра примем 20.
Рассчитаем элементы схемы. Основные соотношения:
Выберем (в соответствии с «ГОСТ 28884-90 Ряды предпочтительных значений для резисторов и конденсаторов»):
R1=100 [кОм];
R2=1 [кОм];
R3=1 [кОм];
R4=18 [кОм];
C1=33 [мкФ].
C2=33 [мкФ].
Проверим подобранные параметры:
Промоделируем выбранный ФВЧ в среде MicroCap.
Рис.7. Неинвертирубщий фильтр верхних частот в среде MicroCap.
Рис.8. Частотный анализ ФВЧ в среде MicroCap.
Фильтр нижних частот. Расчет и моделирование
Частоту среза фильтра нижних частот выберем, исходя из полосы частот исследуемого сигнала. Примем частоту среза равную fc=30 Гц.
Для реализации выберем фильтр Баттерворта второго порядка.
Основные соотношения:
ФНЧ1
Коэффициент усиления: 20.
Определим номиналы элементов схемы (в соответствии с «ГОСТ 28884-90 Ряды предпочтительных значений для резисторов и конденсаторов»):
R1=1 [кОм];
R2=245 [кОм];
R3=1 [кОм];
R4=18 [кОм];
C1=0,1 [мкФ];
C2=1 [мкФ].
Проверим, подходят ли выбранные элементы:
Промоделируем рассчитанный фильтр в среде MicroCap.
Рис.9. Фильтр нижних частот второго порядка в среде MicroCap.
Рис.10. Частотный анализ ФНЧ в среде MicroCap.
ФНЧ2
Коэффициент усиления данного фильтра: 5.
Определим номиналы элементов схемы (в соответствии с «ГОСТ 28884-90 Ряды предпочтительных значений для резисторов и конденсаторов»):
R1=2 [кОм];
R2=200 [кОм];
R3=1 [кОм];
R4=3,9 [кОм];
C1=0,01 [мкФ];
C2=1 [мкФ].
Проверим, подходят ли выбранные элементы:
Промоделируем рассчитанный фильтр в среде MicroCap.
Рис.11. Фильтр нижних частот второго порядка в среде MicroCap.
Рис.12. Частотный анализ ФНЧ в среде MicroCap.
Выводы.
В данной курсовой работе были разработаны структурная и принципиальная схема одноканального реографа.
Были использованы электронные компоненты фирм AnalogDevices для реализации поставленной задачи – разработки системы регистрации, сбора и передачи данных. Аналоговыми устройствами происходит разделение сигналов и первичное подавление помех, в результате чего на АЦП поступает сигнал, который дискритизируется и передается на микроконтроллер для последующей передачи на компьютер через USB, цифровой фильтрации и обработки.
В соответствии с техническим заданием в курсовой работе были реализованы следующие задачи:
1. Проведен обзор методов неинвазивной оценки параметров гемодинамики.
2. Рассмотрены биофизические основы метода реографии.
3. Проведен обзор существующих приборов и систем для реографии.
4. По ГОСТ 15.013.-94 и по ГОСТ 50267.0-92 были разработаны медико-технические требования на одноканальный реограф.
5. Разработана структурная схема реографа.
6. Был проведен расчет основных элементов принципиальной схемы биоусилителя.
7. В соответствии со структурной схемой, разработана принципиальная схема биоусилителя.
Разработанный биоусилитель одноканального стационарного реографа обладает следующими характеристиками:
- Диапазон измерения базового сопротивления 10 – 200 Ом, дифференциального сопротивления 0,01 – 2 Ом.
- Частота воздействующего тока 100 кГц, действующее значение 1 мА.
- Коэффициент подавления синфазного сигнала – 80 дБ.
- Диапазон частот реосигнала от 0,1 Гц до 25 Гц.
Список используемой литературы:
1. Пейтон А. Дж, Волш В. Аналоговая электроника на операционных усилителях. Издательство: Бином, 1994.
2. Д. Джонсон, Дж. Джонсон, Г. Мур. Справочник по активным фильтрам Москва, Энергоатомиздат 1983 Рецензент В. А. Силаев D. JOHNSON, J. JOHNSON, H. MOORE A handbook of active filters Prentice-Hall, Inc., Englewood Cliffs, New Jersey
3. Полищук В.И., Терехова Л.Г. Техника и методика реографии и реоплетизмографии. – М.: Медицина, 1983.
4. Сергеев И.К. Определение параметров центральной гемодинамики методом трансторакальной реографии. Часть 1. – Москва: Издательство МГТУ им. Н.Э.Баумана, 2007.
5. П. Хоровиц, У. Хилл Искусство схемотехники. – М.: издательство «Мир», 1998.
6. Электронный ресурс http://www.analog.com
Фильтр нижних частот – это… Что такое Фильтр нижних частот?
Фильтр ни́жних часто́т (ФНЧ) — один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой частоты зависит от вида фильтра.
В отличие от фильтра нижних частот (НЧ), фильтр верхних частот пропускает частоты сигнала выше частоты среза, подавляя низкие частоты.
Реализация фильтров нижних частот может быть разнообразной, включая электронные схемы, программные алгоритмы, акустические барьеры, механические системы и т. д.
Типы
Осциллограмма простейшего RC фильтра нижних частот Осциллограмма низкочастотного фильтра БесселяВ схемах пассивных аналоговых фильтров используют реактивные элементы, такие как катушки индуктивности и конденсаторы. Сопротивление реактивных элементов зависит от частоты сигнала, поэтому, комбинируя такие элементы, можно добиться усиления или ослабления гармоник с нужными частотами.
Идеальный фильтр нижних частот
Идеальный фильтр нижних частот (sinc-фильтр) полностью подавляет все частоты входного сигнала выше частоты среза и пропускает без изменений все частоты ниже частоты среза. Переходной зоны между частотами полосы подавления и полосы пропускания не существует. Идеальный фильтр нижних частот может быть реализован лишь теоретически с помощью умножения входного сигнала на прямоугольную функцию в частотной области, или, что даёт тот же эффект, свёртки сигнала во временно́й области с sinc-функцией.
Однако такой фильтр практически нереализуем для большинства сигналов, так как sinc-функция имеет ненулевые значения для всех моментов времени вплоть до бесконечности. Его можно использовать только для уже записанных цифровых сигналов либо для идеально периодических сигналов.
Реальные фильтры для приложений реального времени могут лишь приближаться к идеальному фильтру.
Фильтр Бесселя
Один из наиболее распространённых типов линейных фильтров, отличительной особенностью которого является максимально гладкая групповая задержка (линейная фазо-частотная характеристика).
Применение
Для звуковых волн твёрдый барьер играет роль фильтра нижних частот — например, в музыке, играющей в другой комнате, легко различимы басы, а высокие частоты отфильтровываются (звук «оглушается»). Точно так же ухом воспринимается музыка, играющая в закрытой машине.
Электронные фильтры нижних частот используются для подавления пульсаций напряжения на выходе выпрямителей переменного тока, для разделения частотных полос в акустических системах, в системах передачи данных для подавления высокочастотных помех и ограничения спектра сигнала, а также имеют большое число других применений.
Радиопередатчики используют ФНЧ для блокировки гармонических излучений, которые могут взаимодействовать с низкочастотным полезным сигналом и создавать помехи другим радиоэлектронным средствам.
Механические низкочастотные фильтры часто используют в контурах АВМ непрерывных систем управления в качестве корректирующих звеньев.
В обработке изображений низкочастотные фильтры используются для очистки картинки от шума и создания спецэффектов, а также при сжатии изображений.
См. также
Ссылки
Расчёт фильтра с характеристикой Баттерворта
Страница 1 из 2
Задание
- Рассчитать ФНЧ с характеристикой Баттерворта.
- Частота среза fc = 4 кГц, ослабление на частоте 8 кГц не менее 24 дБ.
- Коэффициент передачи 10.
Порядок фильтра
Определим порядок фильтра исходя из требуемых условий по графику для затухания в полосе задерживания в книге Г.Лэм «Аналоговые и цифровые фильтры» гл.8.1 стр.215.
Понятно, что для необходимого затухания достаточно фильтра 4 порядка. График приведён для случая, когда wс=1 рад/с, а соответственно частота, на которой нужно необходимое затухание – 2 рад/с (соответственно 4 и 8 кГц). Общий график для передаточной функции фильтра Баттерворта:
Определяем схемную реализацию фильтра:
активный фильтр нижних частот четвёртого порядка со сложной отрицательной обратной связью:
Чтобы желаемая схема имела желаемую амплитудно-частотную характеристику, входящие в неё элементы могут быть подобраны с не очень высокой точностью, что является плюсом данной схемы.
активный фильтр нижних частот четвёртого порядка с положительной обратной связью:
В данной схеме коэффициент усиления операционного усилителя должен иметь строго определённое значение, а коэффициент передачи данной схемы будет не больше 3. Поэтому данную схему можно отбросить.
активный фильтр нижних частот четвёртого порядка с омической отрицательной обратной связью
Данный фильтр построен на четырех операционниках, что увеличивает помехи и сложность расчёта данной схемы, поэтому её мы также отбрасываем.
Из рассмотренных схем мы выбираем фильтр со сложной отрицательной обратной связью.
Расчёт фильтра
Определение передаточной функции
Записываем табличные значения коэффициентов для фильтра Баттерворта четвёртого порядка:
a1=1.8478 b1=1
a2=0.7654 b2=1
(см. У.Титце, К.Шенк «Полупроводниковая схемотехника» табл.13.6 стр. 195)
Общее выражение передаточной функции для ФНЧ четвёртого порядка:
(см. У.Титце, К.Шенк «Полупроводниковая схемотехника» табл.13.2 стр. 190 и форм. 13.4 стр. 186).
Далее используются формулы из У.Титце, К.Шенк «Полупроводниковая схемотехника» п.13.4.2 стр.204:
Передаточная функция первого звена имеет вид:
Передаточная функция второго звена имеет вид:
где wс – круговая частота среза фильтра, wс=2pfc.
Расчёт номиналов деталей
Приравняв коэффициенты выражений (2) и (3) коэффициентам выражения (1) получим:
-коэффициенты передачи постоянного сигнала для каскадов, их произведение А0 должно быть равно 10 по заданию. Они отрицательные, так как данные каскады являются инвертирующими, однако их произведение даёт положительный коэффициент передачи.
Для расчёта схемы лучше задаться емкостями конденсаторов, при этом для того, чтобы значение R2 было действительным, должно выполняться условие
и соответственно
Далее мы задаёмся коэффициентами передачи первого и второго каскадов.
Исходя из этих условий выбирается С1=С3=1 нФ, С2=10 нФ, С4=33 нФ.
Рассчитываем значения сопротивлений для первого каскада:
Значения сопротивлений второго каскада:
Выбор ОУ
При выборе ОУ необходимо учитывать диапазон частот фильтра: частота единичного усиления ОУ (на которой коэффициент усиления равен единице) должна быть больше произведения частоты среза и коэффициента усиления фильтра Kу.
Поскольку максимальный коэффициент усиления равен 3.33, а частота среза 4 кГц, то этому условию удовлетворяют почти все существующие ОУ.
Другим важным параметром ОУ является его входное сопротивление. Оно должно быть больше десятикратного максимального сопротивления резистора схемы.
Максимальное сопротивление в схеме равно 99.6 кОм, следовательно входное сопротивление ОУ должно быть не менее 996 кОм.
Так же необходимо учитывать нагрузочную способность ОУ. Для современных ОУ минимальное сопротивление нагрузки составляет 2 кОм. Учитывая, что сопротивление R1 и R4 равны соответственно 33.2 и 3.09 кОм, выходной ток операционного усилителя будет заведомо меньше максимально допустимого.
В соответствии с вышеприведёнными требованиями выбираем ОУ К140УД601 со следующими паспортными данными (характеристиками):
Uп = ±15 В
Kу.min= 50 000
Rвх = 1 МОм
Fед.ус. = 0.3 МГц
НачалоПредыдущая 1 2 Следующая > Последняя >>
2}} \)
\ (\ Displaystyle X_C = \ гидроразрыва {1} {2 π · е · C} \)
Затухание в децибелах
На резонансной частоте затухание составляет 3 дБ. Если входное и выходное напряжение известны, затухание для всех частот можно легко рассчитать по следующей формуле.
\ (\ Displaystyle V_u = 20 · lg \ влево (\ гидроразрыва {U_2} {U_1} \ right) \)
Если напряжения неизвестны, используется следующая формула.2}} \ справа) \)
Фазовый сдвиг
В нижнем проходе RC выходное напряжение отстает от входного на 0 ° – 90 °, в зависимости от частоты. На резонансной частоте фазовый сдвиг -45 °. На низких частотах он стремится к 0. На высоких частотах сдвиг фазы в сторону -90 °. Фазовый сдвиг можно рассчитать по следующей формуле.
\ (\ Displaystyle φ = acos \ влево (\ гидроразрыва {U_2} {U_1} \ вправо)) \)
\ (\ Displaystyle φ = arctan (ω · R · C) \)
Частота среза
На предельной частоте f g bzw.ω g значение амплитудно-частотной характеристики (т.е. величина передаточной функции) составляет 0,707. Это соответствует -3 дБ.
\ (\ Displaystyle 0.707 = \ гидроразрыва {1} {\ sqrt {2}} \)
Формулы частоты среза
\ (\ Displaystyle ω_g = \ гидроразрыва {1} {R · C} ⇒ \)
\ (\ Displaystyle f_g = \ гидроразрыва {1} {2 · π · R · C} \)
\ (\ Displaystyle R = \ гидроразрыва {1} {2 · π · f_g · C} \)
\ (\ Displaystyle С = \ гидроразрыва {1} {2 · π · f_g · R} \)
Импеданс
\ (\ Displaystyle Z = \ sqrt {X_C ^ 2 + R ^ 2} \)
Текущий
\ (\ Displaystyle I = \ гидроразрыва {U} {Z} \)
Напряжение рестистора
\ (\ Displaystyle U_R = R · I \)
Пассивные низкочастотные фильтры первого и второго порядка
В этом руководстве мы узнаем о пассивных RC-фильтрах нижних частот.Как следует из названия, это фильтр нижних частот, разработанный с использованием пассивных компонентов. В следующих разделах вы можете узнать об основной схеме пассивных RC-фильтров нижних частот, ее частотной характеристике, выходном напряжении, приложениях и многом другом.
Чтобы получить информацию о пассивных RC-фильтрах верхних частот, прочтите руководство «Пассивные RC-фильтры высоких частот ».
Введение
Фильтр – это схема, которая используется для фильтрации сигналов, то есть пропускает только необходимые сигналы и избегает нежелательных сигналов.Обычно фильтры состоят из пассивных или активных компонентов.
- Пассивными компонентами являются резисторы, катушки индуктивности и конденсаторы.
- Активные компоненты: транзисторы, полевые транзисторы и операционные усилители.
Фильтр нижних частот – это фильтр, который пропускает только низкочастотные сигналы и ослабляет или останавливает высокочастотные сигналы. Он позволяет сигналам только от 0 Гц до частоты среза «fc». Это значение частоты среза будет зависеть от номинала компонентов, используемых в схеме.
Обычно эти фильтры предпочтительнее ниже частоты 100 кГц. Частота среза также называется частотой отключения или частотой переключения.
Пассивный фильтр нижних частот
Схема фильтра нижних частот, состоящая из пассивных компонентов, называется пассивным фильтром нижних частот.
На следующем рисунке показана простая схема RC-фильтра нижних частот, показанная ниже.
Просто подключив резистор «R» последовательно с конденсатором «C», можно получить RC-фильтр нижних частот.Его можно просто назвать фильтром низких частот (LPF). Резистор не зависит от изменений приложенных частот в цепи, но конденсатор является чувствительным компонентом, что означает, что он реагирует на изменения в цепи.
Поскольку она имеет только один реактивный компонент, эту схему также можно назвать «однополюсным фильтром» или «фильтром первого порядка». Входное напряжение Vin подается последовательно на резистор, а выходное напряжение снимается только на конденсаторе.
Так как конденсатор является чувствительным компонентом, основная наблюдаемая концентрация связана с «емкостным реактивным сопротивлением».Емкостное реактивное сопротивление – это противодействие, создаваемое конденсатором в цепи.
Чтобы сохранить емкость конденсатора, конденсатор будет препятствовать протеканию небольшого количества тока в цепи. Это противодействие току в цепи называется сопротивлением. Таким образом, емкостное реактивное сопротивление уменьшается с увеличением встречного тока.
Этим мы можем сказать, что емкостное реактивное сопротивление обратно пропорционально частоте, приложенной к цепи.Значение сопротивления резистора стабильно, тогда как значение емкостного реактивного сопротивления меняется. Падение напряжения на конденсаторе намного меньше по сравнению с потенциалом напряжения конденсатора.
Это означает, что на низких частотах падение напряжения невелико, а потенциал напряжения велик, но на высоких частотах падение напряжения очень велико, а потенциал напряжения меньше. По этому явлению мы можем сказать, что вышеупомянутая схема может действовать как схема «частотно-регулируемого делителя напряжения».
Емкостное реактивное сопротивление можно сформулировать следующим образом:
Расчет выходного напряжения
Чтобы получить уравнение делителя потенциала, мы должны учитывать полное сопротивление, емкостное реактивное сопротивление, входное и выходное напряжение. Используя эти термины, мы можем сформулировать уравнение для RC потенциального делителя следующим образом:
Используя это уравнение, мы можем вычислить значение выхода на любой приложенной частоте.
Пример фильтра нижних частот
Давайте исследуем эти значения выходного напряжения и значения емкостного реактивного сопротивления, рассматривая значения резистора и конденсатора.Пусть номинал резистора R равен 4,7 кОм, а емкость конденсатора 47 нФ. Входное напряжение переменного тока составляет 10 В. Значения частот, для которых мы собираемся вычислить, составляют 1 кГц и 10 кГц.
Этим мы можем четко сказать, что с увеличением частоты емкостное реактивное сопротивление уменьшается. Уменьшается не только емкостное реактивное сопротивление, но и выходное напряжение.
Из приведенного выше примера видно, что емкостное реактивное сопротивление уменьшилось с 3386,27 Ом до 338.62 Ом, тогда как выходное напряжение уменьшилось с 5,84 вольт до 0,718 вольт с увеличением частоты с 1 кГц до 10 кГц.
Частотная характеристика фильтра нижних частот
Из введения в фильтры мы уже видели, что величина | H (jω) | фильтра принимается за коэффициент усиления схемы. Это усиление измеряется как 20 log (V на выходе / V на ), и для любой RC-цепи угол наклона «спада» составляет -20 дБ / декаду.
Полоса частот ниже области среза называется «полосой пропускания», а полоса частот после частоты среза называется «полосой пропускания».Из графика видно, что полоса пропускания – это ширина полосы пропускания фильтра.
Из этого графика видно, что до тех пор, пока частота среза не изменяется, усиление остается постоянным, поскольку выходное напряжение пропорционально значению частоты на низких частотах. Это связано с емкостным реактивным сопротивлением, которое действует как разомкнутая цепь на низких частотах и пропускает через цепь максимальный ток на высоких частотах. Значение емкостного реактивного сопротивления очень велико на низких частотах, поэтому оно имеет большую способность блокировать ток, протекающий через цепь.
По достижении значения частоты среза выходное напряжение постепенно уменьшается и достигает нуля. Коэффициент усиления также уменьшается вместе с выходным напряжением. После частоты среза характеристика наклона схемы достигнет точки спада, которая происходит при -20 дБ / декаду.
Это происходит главным образом из-за увеличения частоты, когда частота увеличивается, значение емкостного реактивного сопротивления уменьшается и, таким образом, способность блокировать ток через конденсатор уменьшается.Когда ток в цепи увеличивается и из-за ограниченной емкости конденсатора, цепь действует как короткое замыкание. Таким образом, выходное напряжение фильтра на высоких частотах равно нулю.
Единственный способ избежать этой проблемы – выбрать диапазоны частот, до которых могут выдерживать эти резистор и конденсатор. Значения конденсатора и резистора играют основную роль, потому что от этих значений будет зависеть только частота среза «fc». Если частотные диапазоны находятся в пределах диапазона частот среза, тогда мы можем преодолеть проблему короткого замыкания.
Эта точка отсечки возникает, когда значение сопротивления и значение емкостного реактивного сопротивления совпадают, что означает, что векторная сумма сопротивления и реактивной емкости равны. Это когда R = X c , и в этой ситуации входной сигнал ослабляется на -3 дБ / декаду.
Это затухание составляет примерно 70,7% входного сигнала. Время, необходимое для зарядки и разрядки пластин конденсатора, зависит от синусоиды. Из-за этого фазовый угол (ø) выходного сигнала отстает от входного сигнала после частоты среза.На частоте среза выходной сигнал сдвинут по фазе на -45 °.
Если входная частота фильтра увеличивается, увеличивается угол запаздывания выходного сигнала схемы. Просто для большего значения частоты схема больше не совпадает по фазе.
У конденсатора больше времени для заряда и разряда пластин на низких частотах, потому что время переключения синусоидальной волны больше. Но с увеличением частоты время переключения на следующий импульс постепенно уменьшается. Из-за этого происходят временные изменения, которые приводят к сдвигу фазы выходной волны.
Частота среза пассивного фильтра нижних частот в основном зависит от номиналов резистора и конденсатора, используемых в цепи фильтра. Эта частота среза обратно пропорциональна номиналам резистора и конденсатора. Частота среза пассивного фильтра нижних частот задается как
f C = 1 / (2πRC)
Фазовый сдвиг пассивного фильтра нижних частот задается как
Сдвиг фазы (ø) = – tan -1 (2πfRc)
Постоянная времени (τ)
Как мы уже видели, время, затрачиваемое конденсатором на зарядку и разрядку пластин по отношению к входной синусоидальной волне, приводит к разности фаз.Последовательное соединение резистора и конденсатора будет производить этот эффект зарядки и разрядки.
Постоянная времени последовательной RC-цепи определяется как время, необходимое конденсатору для зарядки до 63,2% от конечного значения установившегося состояния, а также определяется как время, необходимое конденсатору для разряда до 36,8% от установившегося значения. государственное значение. Эта постоянная времени представлена символом «τ».
Связь между постоянной времени и частотой отсечки выглядит следующим образом:
Постоянная времени τ = RC = 1 / 2πfc и ω c = 1 / τ = 1 / RC
Мы также можем переписать в терминах отсечки частота как
Таким образом, мы можем сказать, что выходной сигнал фильтра зависит от частот, подаваемых на вход, и от постоянной времени.
Пример 2 пассивного фильтра нижних частот
Давайте вычислим частоту среза фильтра нижних частот, который имеет сопротивление 4,7 кОм и емкость 47 нФ.
Мы знаем, что уравнение для частоты среза:
fc = 1 / 2πRC = 1 / (2π x 4700 x 47 x 10 -9 ) = 720 Гц
Пассивный фильтр нижних частот второго порядка
Till Теперь мы изучили фильтр нижних частот первого порядка, который состоит из последовательного соединения резистора и конденсатора. Однако иногда одной ступени может быть недостаточно для удаления всех нежелательных частот, тогда используется фильтр второго порядка, как показано ниже.
RC-фильтр нижних частот второго порядка может быть получен простым добавлением еще одного каскада к фильтру нижних частот первого порядка. Этот фильтр дает наклон -40 дБ / декаду или -12 дБ / октаву, а фильтр четвертого порядка дает наклон -80 дБ / октаву и так далее.
Пассивный фильтр нижних частот Усиление на частоте среза задается как
A = (1 / √2) n
Где n – порядок или количество ступеней
Частота среза нижних частот второго порядка пропускной фильтр задается как
fc = 1 / (2π√ (R1C1R2C2))
Фильтр нижних частот второго порядка -3 дБ Частота задается как
f (-3dB) = fc √ (2 (1 / n ) – 1)
Где fc – частота среза, n – количество ступеней, а ƒ -3 дБ – частота полосы пропускания -3 дБ.
Сводка по фильтру низких частот
Фильтр низких частот состоит из резистора и конденсатора. Не только конденсатор, но и любой реактивный компонент с резистором дает фильтр нижних частот. Это фильтр, который пропускает только низкие частоты и ослабляет высокие частоты.
Частоты ниже частоты среза называются частотами полосы пропускания, а частоты выше частоты среза называются частотами полосы задерживания. Полоса пропускания – это ширина полосы фильтра.
Частота среза фильтра зависит от значений компонентов, выбранных для схемы.Частоту среза можно рассчитать с помощью приведенной ниже формулы.
f C = 1 / (2πRC)
Коэффициент усиления фильтра принимается как величина фильтра, и коэффициент усиления можно рассчитать по формуле 20 log (V из / V из ). Выходной сигнал фильтра постоянен, пока уровни частоты не достигнут частоты среза.
На частоте среза выходной сигнал составляет 70,7% входного сигнала, а после частоты среза выходной сигнал постепенно уменьшается до нуля.Фазовый угол выходного сигнала отстает от входного сигнала после частоты среза.
На частоте среза фазовый сдвиг выходного сигнала составляет 45 °.
Если мы поменяем местами резистор и конденсатор в схеме фильтра нижних частот, то схема будет вести себя как фильтр верхних частот.
Для синусоидальных входных волн схема ведет себя как фильтр нижних частот первого порядка. Мы уже изучили работу фильтра первого порядка, но при изменении типа входного сигнала необходимо наблюдать за тем, что происходит с выходом фильтра.
Когда мы меняем тип входного сигнала либо на режим переключения (ВКЛ / ВЫКЛ), либо на прямоугольную форму, схема ведет себя как интегратор, который обсуждается ниже.
Фильтр нижних частот как схема формирования волны
На приведенном выше рисунке показаны характеристики фильтра для прямоугольного входа. Когда вход фильтра нижних частот представляет собой прямоугольную волну, полученный выходной сигнал фильтра будет иметь треугольную форму.
Это связано с тем, что конденсатор не может работать как переключатель ВКЛ или ВЫКЛ.На низких частотах, когда на входе фильтра используется прямоугольная волна, на выходе также будет только прямоугольная волна.
Когда частота увеличивается, выходной сигнал фильтра выглядит как треугольная волна. Тем не менее, если мы увеличим частоту, то амплитуда выходного сигнала уменьшится.
Треугольная волна генерируется из-за действия конденсаторов или просто схема зарядки и разрядки конденсатора приводит к треугольной волне.
Применения фильтра нижних частот
- Основное применение схем фильтра нижних частот – избежать A.C. пульсации на выходе выпрямителя.
Фильтр нижних частот используется в схемах усилителя звука. - Используя этот пассивный фильтр нижних частот, мы можем напрямую снизить высокочастотный шум до уровня небольших помех в стереосистемах. Фильтр нижних частот
- в качестве интегратора может использоваться в схемах формирования и генерации волн из-за легкого преобразования одного типа электрического сигнала в другую форму.
- Они также используются в схемах демодулятора для извлечения требуемых параметров из модулированных сигналов.
Пассивный фильтр нижних частот
Это руководство посвящено пассивному фильтру нижних частот , широко используемому термину в электронике. Вы будете слышать или использовать этот «технический» термин почти каждый раз во время учебы или в своей профессиональной карьере. Давайте разберемся, в чем особенность этого технического термина.
Что это, Схема, формулы, кривая?Начнем с названия. Вы знаете, что такое пассивный ? Что такое низкий ? Что проходит , а что Фильтр ? Если вы понимаете значение этих четырех слов « Passive Low Pass Filter », вы поймете 50% « Passive Low Pass Filter », остальные 50%, которые мы изучим далее.
« Пассивный » – в словаре это означает разрешение или принятие того, что происходит или что делают другие, без активного ответа.
« Фильтр нижних частот » – это означает пропуск того, что является low , что также означает блокирование того, что high . Он действует так же, как традиционный фильтр для воды, который есть у нас дома / в офисе, который блокирует загрязнения и пропускает только чистую воду.
Фильтр нижних частот пропускает низкую частоту и блокирует верхнюю .Традиционная частота пропускания фильтра нижних частот в диапазоне от 30 до 300 кГц (низкая частота) и блокировка выше этой частоты, если используется в аудио приложении.
С фильтром нижних частот связано много вещей. Как было описано ранее, он будет отфильтровывать нежелательные элементы (сигнал) синусоидального сигнала (AC) .
В качестве пассивного средства мы обычно не применяем какой-либо внешний источник к отфильтрованному выходному сигналу, это может быть сделано с использованием пассивных компонентов, которые не требуют мощности, поэтому отфильтрованный сигнал не усиливается, амплитуда выходного сигнала не будет увеличиваться ни при каких условиях. Стоимость.
Фильтры нижних частот сделаны с использованием комбинации резистора и конденсатора (RC) для фильтрации до 100 кГц, но для остальных 100 кГц – 300 кГц используются резистор, конденсатор и индуктор (RLC).
Вот схема на этом изображении:
Это RC-фильтр. Обычно входной сигнал подается на эту комбинацию резистора и неполяризованного конденсатора . Это фильтр первого порядка, поскольку в схеме есть только один реактивный компонент – конденсатор.Отфильтрованный выход будет доступен через конденсатор.
Что на самом деле происходит внутри схемы, довольно интересно.
На низких частотах реактивное сопротивление конденсатора будет очень большим, чем сопротивление резистора. Таким образом, потенциал напряжения сигнала на конденсаторе будет намного больше, чем падение напряжения на резисторе.
На более высоких частотах произойдет прямо противоположное. Сопротивление резистора увеличивается, и из-за влияния реактивного сопротивления конденсатора напряжение на конденсаторе становится меньше.
Вот такая кривая на выходе конденсатора: –
Частотная характеристика и частота среза
Давайте разберемся с этой кривой дальше
f c – частота среза фильтра. Сигнальная линия от 0dB / 118Hz до 100 KHz почти плоская.
Формула расчета прироста:
Прирост = 20log (Vout / Vin)
Если мы введем эти значения, мы увидим результат усиления до тех пор, пока частота среза не станет почти 1.1 единица усиления или 1x усиления называется единичным усилением .
После сигнала отсечки ответ схемы постепенно уменьшается до 0 (ноль), и это уменьшение происходит со скоростью -20 дБ / декада . Если мы посчитаем уменьшение на октаву, оно составит -6 дБ. В технической терминологии он называется « прокатка ».
На низких частотах высокое реактивное сопротивление конденсатора останавливает прохождение тока через конденсатор.
Если мы применяем высокие частоты выше предела отсечки, реактивное сопротивление конденсатора уменьшается пропорционально увеличению частоты сигнала, в результате чего меньшее реактивное сопротивление на выходе будет равно 0 в результате короткого замыкания конденсатора.
Это фильтр нижних частот. Выбрав соответствующий резистор и соответствующий конденсатор, мы можем остановить частоту, ограничить сигнал, не влияя на сигнал, поскольку нет активной реакции.
На изображении выше есть слово Полоса пропускания . Это означает, к чему будет применено единичное усиление и сигнал будет заблокирован. Таким образом, если это фильтр нижних частот 150 кГц, то полоса пропускания будет 150 кГц. После этой полосы пропускания сигнал будет ослабевать и перестанет проходить через схему.
Также есть -3 дБ, это важно, на частоте среза мы получим усиление -3 дБ, где сигнал ослаблен до 70,7%, а емкостное реактивное сопротивление и сопротивление равны R = Xc.
Какова формула частоты среза?
f c = 1 / 2πRC
Итак, R – сопротивление, а C – емкость. Если мы поставим значение, мы будем знать частоту среза.
Расчет выходного напряженияДавайте посмотрим на первое изображение схемы, в которой 1 резистор и один конденсатор используются для формирования фильтра нижних частот или RC-цепи.
Когда сигнал постоянного тока подается на цепь, это сопротивление цепи, которое создает падение при протекании тока, но в случае сигнала переменного тока это импеданс, который также измеряется в Ом.
В RC-цепи две резистивные штуки . Один из них – это сопротивление, а другой – емкостное реактивное сопротивление конденсатора. Итак, нам нужно сначала измерить емкостное реактивное сопротивление конденсатора, поскольку это потребуется для расчета импеданса схемы.
Первое сопротивление – емкостное реактивное сопротивление , формула: –
Xc = 1 / 2π f c
Выход формулы будет в Ом, поскольку Ом – единица емкостного реактивного сопротивления, поскольку это противоположность означает сопротивление.
Вторая оппозиция – это сам резистор . Величина резистора также является сопротивлением.
Итак, объединив эти два противостояния, мы получим общее сопротивление , которое является импедансом в цепи RC (вход сигнала переменного тока).
Импеданс обозначается как Z.
RC-фильтр действует как схема «, частота, , , делитель напряжения с зависимой переменной, ».
Выходное напряжение этого делителя =
Vout = Vin * (R2 / R1 + R2) R1 + R2 = R T
R1 + R2 – полное сопротивление цепи, оно равно импедансу.
Итак, сложив это общее уравнение, мы получим
Решая приведенную выше формулу, получаем окончательную: –
Vout = Vin * (Xc / Z)
Пример с расчетом
Поскольку мы уже знаем, что на самом деле происходит внутри схемы и как узнать значение. Выберем практические значения .
Давайте рассмотрим наиболее распространенные значения резистора и конденсатора, 4,7 кОм и 47 нФ. Мы выбрали это значение, поскольку оно широко доступно и его легче вычислить.Посмотрим, какой будет частота среза и выходное напряжение .
Частота среза будет: –
Решив это уравнение, частота среза равна 720 Гц.
Так это правда или нет…
Это схема. Как и в частотной характеристике, описанной ранее, на частоте среза дБ будет -3 дБ, независимо от частот. Мы будем искать -3 дБ в выходном сигнале и смотреть, составляет ли он 720 Гц или нет.Вот АЧХ: –
Как вы можете видеть частотную характеристику (также называемую графиком Боде ), мы устанавливаем курсор на -3 дБ (красная стрелка) и получаем 720 Гц (зеленая стрелка) угол или частоту полосы пропускания .
Если мы подадим сигнал 500 Гц, то емкостное реактивное сопротивление будет
Тогда Vout при подаче напряжения 5V Vin при 500 Гц: –
Фазовый сдвиг
Поскольку с фильтром нижних частот связан один конденсатор, и это сигнал переменного тока, фазовый угол на выходе обозначается как φ (Phi), что не совпадает по фазе -45 при -3 дБ или частоте среза.Почему?
Когда входное напряжение изменяет время заряда конденсатора и из-за этого выходное напряжение отстает от входного сигнала или имеет синусоидальную форму.
Соотношение следующее: –
Увеличение входной частоты = увеличение запаса по фазе . Все эти двое пропорциональны друг другу.
Формула фазового сдвига:
Фазовый сдвиг φ = -arctan (2πfRC)
Рассмотрим фазовый сдвиг схемы
.Это кривая фазового сдвига.Устанавливаем курсор на -45 (красная стрелка) и получаем результат частоты среза 720 Гц (зеленая стрелка).
Постоянная времени
Как мы уже узнали ранее о фазовом сдвиге и частотной характеристике, конденсатор получает эффект заряда и разряда от частот входного сигнала. Этот эффект зарядки и разрядки составляет Постоянная времени обозначается как τ (тау). Это также связано с частотой среза.
Как?
τ = RC = 1 / 2π f c
Иногда нам нужно знать частоту среза, когда у нас есть значение постоянной времени, в таком случае, изменяя формулу, мы можем легко получить, что: –
f c = 1 / 2πRC Где RC = τ f c = 1 / 2πτ
Благодаря этому Постоянная времени RC-фильтр создает зубчатую волну, треугольную волну, если мы изменим входной сигнал с синусоидальной на прямоугольную.Это называется схемой интегратора .
Фильтр нижних частот второго порядка: формулы, расчеты и частотные кривые
Когда два каскада RC-каскада нижних частот первого порядка соединены каскадом, это называется фильтром второго порядка, поскольку имеется две RC-цепи каскада.
Вот схема: –
Это фильтр нижних частот второго порядка. R1 C1 – это первый порядок, а R2 C2 – второй порядок. Каскадно они образуют фильтр нижних частот второго порядка.
Фильтр второго порядка играет роль крутизны 2 x -20 дБ / декада или -40 дБ (-12 дБ / октава).
Вот кривая отклика: –
Курсор, показывающий точку отсечки -3 дБ в зеленом сигнале, который находится в первом порядке (R1 C1), наклон при этом был замечен ранее -20 дБ / декада, а красный – на конечном выходе, который имеет наклон -40 дБ / Десятилетие.
Формулы: –
Усиление при f c : –
Это позволит вычислить усиление цепи нижних частот второго порядка.
Частота среза: –
На практике крутизна спада увеличивается в соответствии с каскадом добавления фильтра, точка -3 дБ и частота полосы пропускания изменяются от своего фактического расчетного значения, указанного выше, на определенную величину.
Эта определенная сумма рассчитывается по следующей формуле: –
Не так хорошо каскадировать два пассивных фильтра, поскольку динамический импеданс каждого порядка фильтров влияет на другую сеть в той же схеме.
Приложения
Фильтр нижних частот – широко используемая схема в электронике.
Вот несколько приложений: –
- Аудиоприемник и эквалайзер
- Фильтр камеры Осциллограф
- Система управления музыкой и частотной модуляцией низких частот
- Функциональный генератор
- Блок питания
Фильтры – Практические EE
Мы обсудили ряды Фурье и то, как электромагнитные сигналы можно рассматривать как совокупность частотных компонентов.Фильтр – это схема, которая ослабляет компоненты сигнала в зависимости от их частот. Фильтры характеризуются диапазоном частот, на который они влияют, и их порядком, который представляет степень ослабления.
Диапазоны частот фильтров
| Low-Pass | Ослабляет частотные компоненты выше определенного порога |
| High-Pass | Ослабляет частотные компоненты ниже определенного порога |
| Bandpass | Проходит непрерывный диапазон (полосу) частот частоты вне этой полосы |
| Band-Reject или Notch | Ослабляет полосу частот |
Конструкции фильтров
| Пассивный | Состоит из пассивных компонентов (резисторы, конденсаторы и катушки индуктивности) |
| Активный | Содержит активные компоненты, такие как транзисторы и операционные усилители. |
| Цифровой | Сигналы оцифровываются и обрабатываются как наборы цифровых значений с помощью логических схем или микропрограмм, запущенных на процессоре. |
Пассивные фильтры
Пассивные фильтры состоят из пассивных компонентов: резисторов, конденсаторов и катушек индуктивности. Быстрый способ определить, какой диапазон частот будет ослабляться расположением пассивных компонентов, – это учесть, что конденсаторы действуют как короткое замыкание для высокочастотных компонентов и действуют как разомкнутые цепи для низкочастотных компонентов.Индукторы все наоборот. И резисторы одинаково влияют на все частотные составляющие. Посмотрите схему ниже.
Пассивный фильтр нижних частотПассивный фильтр нижних частот
Схема имеет только один реактивный компонент, конденсатор C1, а R1 и C1 образуют делитель напряжения. По формуле делителя напряжения Vout = Vin * Z C1 / (Z R1 + Z C1 ). Итак, передаточная функция Vout / Vin равна:
Конденсатор C1 имеет высокое сопротивление по отношению к низкочастотным компонентам.Таким образом, на низкой частоте его импеданс будет большим, что приведет к значению передаточной функции. Это означает, что фильтр пропускает низкочастотные составляющие. На высокой частоте конденсатор имеет тенденцию к короткому замыканию, поэтому значение передаточной функции будет минимальным на высокой частоте, что означает, что фильтр ослабляет высокочастотные компоненты. Это фильтр нижних частот.
А теперь давайте рассмотрим подробнее. Импеданс конденсатора составляет 1 / сС, а сопротивление резистора – R.
Фильтр нижних частот в частотной областиТогда передаточная функция Vout / Vin равна:
Обратите внимание на пару моментов об этой функции передачи. Во-первых, оно не может быть больше единицы, потому что сопротивление и емкость компонентов являются положительными числами. Когда передаточная функция имеет диапазон значений 1 или меньше, она только ослабляется, а не усиливается. Это всегда будет иметь место с пассивными фильтрами, они только ослабляют, а их передаточные функции всегда имеют значение меньше 1.
Во-вторых, обратите внимание, что числитель является константой, а знаменатель – многочленом одного порядка от s. Это означает, что это фильтр 1-го порядка, поскольку порядок фильтра – это наивысший порядок полинома (наивысшая степень s) либо в числителе, либо в знаменателе его передаточной функции. Передаточные функции схем, состоящих из пассивных компонентов, всегда будут отношениями полиномов. Этот фильтр не имеет нулей и имеет один полюс -1 / RC, потому что это значение s, которое делает знаменатель равным нулю.
Порядок фильтра: Наивысший полиномиальный порядок числителя или знаменателя передаточной функции
Как я сказал ранее, полюса и нули передаточной функции схемы являются ключевыми для поведения схемы, и эти значения можно использовать как ярлыки для работы со схемой. Полюс -1 / RC определяет пороговую частоту, выше которой этот фильтр ослабляет частотные составляющие. Другими словами, он определяет частоту среза, которая является разделительной линией между полосой пропускания и полосой заграждения.Частота среза в радианах – это просто абсолютное значение полюса.
Частота среза:
Анализ переменного тока с фильтром нижних частот
Анализ переменного тока – это анализ частотной характеристики системы, которая является постоянной, а не временной. Математически анализ переменного тока касается части jω переменной Лапласа (s = σ + jω) , а не σ , которая связана с переходной характеристикой.Замените jω на s в передаточной функции, чтобы определить частотную характеристику. Затем преобразуйте в полярную форму, чтобы получить величину и фазу передаточной функции.
Частотная характеристика: замените
jω на s в передаточной функцииНа практике мы используем компьютерный инструмент для выполнения анализа переменного тока. SPICE – это стандартизированная платформа для моделирования схем, и существует пара отличных бесплатных программ SPICE. Я настоятельно рекомендую вам установить оба из них и потратить время на их тщательное изучение.
SPICE Программ:
Я буду использовать LT Spice для анализа фильтра нижних частот. Анализ переменного тока в SPICE создает график частотной характеристики передаточной функции, показывающий ее величину и фазу. Масштаб может показаться странным. Горизонтальная шкала является логарифмической в декадах (субтики представляют x1, x2,…, x9 и расположены неравномерно). Вертикальная шкала величины также логарифмическая, но в децибелах (дБ). Децибелы для передаточных функций, включающих напряжение и / или ток, равны 20 • log (H (s)), где H (s) – передаточная функция.Децибелы для передаточных функций, включающих мощность, равны 10 • log (H (s)). Вертикальная шкала фазы является линейной и выражается в градусах.
Горизонтальная шкала анализа переменного тока: логарифмическая шкала в десятилетиях, единицы: Гц.
Величина анализа переменного тока Вертикальная шкала: 20 • log (H (s)), единицы: дБ.
Фаза анализа переменного тока Вертикальная шкала: линейная шкала, единицы: градусы.
Анализ переменного тока с фильтром нижних частотПунктирная линия – фаза, а сплошная линия – величина. Этот фильтр нижних частот имеет резистор 10 Ом и конденсатор 100 мкФ, поэтому частота среза составляет 1 / (2 * pi * R * C) = 159 Гц.Частота среза также называется частотой 3 дБ, потому что на этой частоте величина на 3 дБ ниже максимального значения (3 дБ = 1 / sqrt (2) или 0,707). Частота среза находится где-то между 100 Гц на графике и следующей субтикой, и да, действительно, величина там действительно составляет около -3 дБ. И фаза составляет -45 градусов на частоте среза, что означает, что выходной сигнал будет задержан на 45 градусов относительно входного.
При частоте среза фильтра нижних частот:
– Величина составляет 3 дБ (или.707) ниже макс.
– Фаза -45 градусов.
Давайте проведем анализ переходных процессов, чтобы увидеть, что делает вывод в реальном времени. Я настрою функцию входного напряжения как знаковую волну с величиной 10 В и частотой 159 Гц (на частоте среза).
Анализ переходных процессов с помощью фильтра нижних частотВот и все. На частоте среза амплитуда выходного сигнала в 0,707 раз превышает входную амплитуду. И выходная фаза отстает от входной фазы на 45 градусов. Видите, как прекрасна SPICE?
Эффект нижних частот на прямоугольной волне
Ниже представлена симуляция SPICE, показывающая влияние фильтра нижних частот на прямоугольную волну.Нарастающие и спадающие фронты выходного сигнала замедляются и асимптотически приближаются к своим конечным значениям (экспоненциальный спад).
Влияние фильтра нижних частот на прямоугольную волнуПассивный фильтр высоких частот
Теперь давайте посмотрим на фильтр верхних частот, который пропускает высокочастотные компоненты и задерживает низкочастотные компоненты. Если мы поменяем местами резистор и конденсатор так, чтобы конденсатор теперь был включен последовательно с сигналом, мы преобразуемся в фильтр верхних частот.
Пассивный фильтр высоких частотПередаточная функция:
На основе передаточной функции это фильтр первого порядка, поскольку нет степени s выше 1.Кроме того, он имеет один ноль при S = 0 и один полюс при s = -1 / RC. Частота среза определяется полюсом и поэтому такая же, как для фильтра нижних частот.
Частота среза =
Фильтр высоких частот Анализ переменного тока
Анализ переменного тока с фильтром высоких частот Анализпеременного тока с помощью SPICE показывает, что величина передаточной функции мала на низкой частоте и увеличивается до частоты среза 1 / (2 * pi * RC) = 159 Гц, где она выравнивается. Как и ожидалось, фильтр верхних частот ослабляет низкочастотные сигналы и пропускает высокочастотные сигналы.
Анализ переходных процессов фильтра высоких частот
Анализ переходных процессов с помощью фильтра верхних частотАнализ переходных процессов входного сигнала, настроенного на синусоидальную волну с частотой, равной частоте среза, дает выходной сигнал, фаза которого предшествует входу на 45 градусов (или запаздывает на 315 градусов), а величина которого составляет 0,707 раза. входная величина.
Схема, типы, калькуляторы и их применение
В электронных устройствах фильтры – это схемы, которые разрешают желаемые частотные компоненты и блокируют все другие частотные компоненты сигнала.Например, в радио или телевидении схема настраивающего фильтра отклоняет нежелательные частоты, разрешая только желаемый канал. Цепи фильтров делятся на четыре типа в зависимости от диапазона частот, который позволяет схема при блокировании всех остальных частот. Это фильтры нижних частот, фильтры верхних частот, полосовые фильтры и полосовые фильтры. Эти типы цепей фильтров подпадают под категорию пассивных фильтров, потому что в цепи используются резистор пассивных элементов, конденсатор и катушки индуктивности.В этой статье описывается фильтр нижних частот, использующий операционный усилитель (активный элемент), который также называют активным ФНЧ.
Что такое фильтр низких частот?
Определение: Схема фильтра, которая допускает только низкочастотные компоненты и блокирует все другие высокочастотные компоненты, называется фильтром нижних частот. Само название LPF указывает на частоту нижнего диапазона.
Этот тип схемы фильтра позволяет использовать частотные составляющие сигнала меньше, чем вырезка частотного диапазона сигнала.Коэффициент усиления фильтра нижних частот обратно пропорционален частоте. Если частота входного сигнала увеличивается, коэффициент усиления схемы уменьшается и также становится равным нулю на конечной стадии переходной полосы. Таким образом, пропускная способность также ограничена. Но на практике LPF позволяет использовать низкочастотные компоненты сигнала, даже если он достигает частоты среза.
Цепь фильтра нижних частот
Схема цепи фильтра нижних частот показана ниже. Он содержит пассивные элементы, резистор и конденсатор, соединенные последовательно с приложенным входным напряжением на резисторе, а его выходное напряжение получается на конденсаторе.
Схема фильтра нижних частот
ФНЧ первого порядка
Фильтр нижних частот первого порядка бывает двух типов. Это
Индуктивный тип LPF
Этот тип представляет собой простую цепь RL, как показано ниже. Когда частота сигнала увеличивается, сопротивление катушки индуктивности увеличивается. Это приводит к блокировке высокочастотных сигналов и пропускает только низкие частоты сигнала через цепь.
Индуктивный LPF
Емкостный LPF
Этот тип представляет собой простую RC-цепочку LPF, как показано на рисунке выше.Ее также называют простой схемой фильтра нижних частот. Когда частота сигнала увеличивается, тогда сопротивление конденсатора уменьшается, что приводит к блокировке высоких частот сигнала и пропускает только низкие частоты сигнала через цепь.
ФНЧ второго порядка
Схема фильтра нижних частот второго порядка представляет собой схему RLC, как показано на диаграмме ниже. Выходное напряжение получается на конденсаторе. Этот тип LPF работает более эффективно, чем LPF первого порядка, потому что два пассивных элемента – индуктор и конденсатор – используются для блокировки высоких частот входного сигнала.
Фильтр низких частот второго порядка
Фильтр низких частот с ОУ
ФНЧ с ОУ называется активным фильтром низких частот. Очень легко спроектировать схему фильтра нижних частот с использованием операционного усилителя без использования электрических компонентов, таких как индуктор, который очень сложно спроектировать, а также является дорогостоящим. Операционные усилители (операционные усилители) используются в схемах фильтров для усиления сигнала, а также для управления усилением. Операционные усилители изменяют частотную характеристику и обеспечивают лучшее усиление напряжения в своей обратной связи.Он также имеет более высокий входной импеданс, более низкий выходной импеданс, низкий уровень шума и высокий уровень производительности.
Фильтр нижних частот с использованием операционного усилителя
Работа базовой схемы LPF (пассивного фильтра) и фильтра нижних частот с использованием операционного усилителя (активного фильтра) одинакова, за исключением того, что операционный усилитель подключен к цепи RC-фильтра. . Это может быть инвертирующий или неинвертирующий операционный усилитель. Принципиальная схема фильтра нижних частот с использованием операционного усилителя показана ниже.
Схема активного LPF первого порядка с использованием операционного усилителя
Активная схема LPC первого порядка спроектирована с конденсатором, резистором и операционным усилителем, как показано ниже.Инвертирующий или неинвертирующий операционный усилитель подключается к RC-цепи, чтобы получить активную схему LPF. Амплитуда выходного сигнала, полученного от схемы RC-фильтра нижних частот, меньше амплитуды входного сигнала. Этот низкочастотный сигнал RC-цепи LPF подается на операционный усилитель в качестве входа для достижения усиления, высокого усиления по мощности и стабильности фильтра. Здесь операционный усилитель действует как буферная схема, как повторитель напряжения с коэффициентом усиления постоянного тока = 1.
Активный ФНЧ первого порядка
По мере увеличения частоты входного сигнала он проходит через конденсатор, увеличивая амплитуду выходного сигнала для усиление, связанное с усилением полосы пропускания.На низких частотах выходной сигнал RC-цепи проходит непосредственно через операционный усилитель для усиления.
Коэффициент усиления по напряжению определяется как DC = 1 + R2 / R1
Схема активного LPF второго порядка с ОУ
Схема активного LPF второго порядка спроектирована путем каскадного соединения двух RC цепей фильтра нижних частот с операционный усилитель. Здесь операционный усилитель действует как усилитель источника с управляемым напряжением. Частотная характеристика такая же, как у активного LPF первого порядка, за исключением того, что усиление полосы задерживания в два раза больше, чем у активного LPF i первого порядка.е, 40 дБ / декада. Каскадирование цепей фильтров формирует фильтры более высокого порядка, усиление которых является произведением каждой RC-цепи LPF.
Активный фильтр нижних частот второго порядка
Мы знаем, что усиление активного ФНЧ первого порядка составляет -3 дБ на частоте среза. Таким образом, усиление активного ФНЧ второго порядка составляет -6 дБ на частоте среза, то есть усиление увеличилось вдвое.
Коэффициент усиления рассчитывается как
Av = Av1 x Av2
Общий коэффициент усиления в дБ
Av = Av1 + Av2
Принципиальная схема активного LPF второго порядка показана ниже.
Калькулятор ФНЧ
Калькулятор ФНЧ вычисляет частоту среза, усиление по напряжению и фазовый сдвиг цепи ФНЧ.
Из принципиальной схемы LPF (RC-цепи) мы можем заметить, что Vi – это приложенное входное напряжение
Vo – выходное напряжение
Используя передаточную функцию схемы, мы получаем
H ( s) = V₀ (s) / Vᵢ (s) = (1 / sC) / (R + (1 / sC))
Поскольку Vo (s) = 1 / sC
Vi (s) = R + 1 / с
H (s) = 1 / (1 + sCR)
Пусть s = jω
Тогда приведенное выше уравнение принимает вид
H (jω) = 1 / (1 + jωCR)
Мы можем вычислить величину передаточной функции из приведенного выше уравнения. 2]
Поскольку общее усиление напряжения равно
Av = 20log10 (Vout / Vin) в дБ
Рассмотрим f = рабочая частота и fc = частота среза
Фазовый сдвиг цепи LPF составляет
Φ = tan⁻¹ (ω / ωc)
Отсечка частота цепи LPF составляет,
fc = 1 / 2πRC
Следовательно,
Сдвиг фазы равен, 90 009
Φ ⁼ tan⁻¹ (2πfRC)
Уравнение емкостного реактивного сопротивления в омах цепи LPF дается как
Xc = 1 / 2πfC
Где C = емкость в Фарадах
f = рабочая частота в Гц
Характеристики частотной характеристики представлены между усилением (дБ) и частотой (Гц).
Частотная характеристика
На низких частотах усиление LPF выше, чем усиление полосы пропускания фильтра
На высоких частотах усиление LPF меньше, чем его усиление полосы пропускания, и оно падает до -20 дБ
По мере увеличения частоты выходное напряжение падает на 70,71% ниже входного.
Приложения
Приложения с фильтром нижних частот включают следующее.
- Используется для удаления шума высокочастотных сигналов
- Используется в аудиоприложениях
- Используется в биомедицинских приложениях
- Используется в электронных приложениях, таких как громкоговорители, сабвуферы и т. Д.
- Используется в цифроаналоговых преобразователях
- Используется как анти -анализирующие фильтры
- Используются в анализаторах волн, усилителях звука и эквалайзерах.
Таким образом, это все об обзоре схемы фильтра нижних частот с использованием операционного усилителя, базовой схемы LPF, активного LPF первого порядка, активного LPF второго порядка, вычислителя фильтра нижних частот и приложений. Назначение LPF – пропускать только низкочастотные сигналы и блокировать высокочастотные сигналы. Вот вам вопрос: «Каковы преимущества LPF с ОУ?»
RC и фильтр нижних частот RL
Простые схемы RC и RL могут использоваться как фильтры нижних и верхних частот.В этом разделе мы рассмотрим фильтры нижних частот RC и RL.
RC-фильтры нижних частотRC-цепь действует как фильтр нижних частот, если сконструирована, как показано на рис. 1 . В показанной схеме резистор расположен непосредственно на пути прохождения сигнала, то есть непосредственно между источником (E) и нагрузкой. Конденсатор подключается по пути прохождения сигнала к земле параллельно нагрузке. Следовательно, V RL = V C (как показано на рисунке).Когда конденсатор (или другой компонент) подключается по пути прохождения сигнала к земле, он называется шунтирующим компонентом.
Рисунок 1: RC-фильтр нижних частот
Фильтрующее действие схемы на рисунке 1 является результатом реакции конденсаторов на увеличение частоты. Этот отклик можно объяснить, используя кривую и схемы на рисунке 2.
Кривая на рисунке 2a показывает взаимосвязь между емкостным реактивным сопротивлением (X C ) и рабочей частотой (f).Как показывает кривая, конденсатор имеет почти бесконечное реактивное сопротивление, когда его рабочая частота равна 0 Гц. Имея это в виду, посмотрите на схему, показанную на рис. 2b . Предполагая, что входная частота равна 0 Гц, конденсатор эффективно действует как разомкнутая цепь, поэтому он не используется в эквивалентной схеме. В этом случае напряжение на нагрузке равно разнице между E и V RF.
На противоположном конце кривой реактивного сопротивления значение X C приближается к 0 Ом.В этом случае фильтр имеет эквивалентную схему, показанную на Рис. 2c . Как видите, конденсатор представлен в виде короткого замыкания параллельно нагрузке. В этом случае V L = 0 В.
Между крайними значениями, показанными на Рис. 2 лежит диапазон частот, в котором уменьшается V RL , как и выходная мощность схемы. В результате схема имеет кривую частотной характеристики.
Рисунок 2: Работа фильтра нижних частот RC
Верхняя частота среза (f C )Верхняя частота среза RC-фильтра нижних частот определяется номиналами резистора цепи и конденсатора.По формуле
\ [\ begin {matrix} {{f} _ {C}} = \ frac {1} {2 \ pi RC} & {} & \ left (1 \ right) \\\ end {matrix } \]
Где
f C = частота среза цепи
R = полное сопротивление цепи
C = значение конденсатора фильтра
Рисунок 3: Сопротивление в фильтре нижних частот RL
Значение R, используемое в уравнении, представляет собой полное сопротивление конденсатора. Общее сопротивление (видимое через конденсатор) в , рис. 3a, можно измерить, подключив омметр к разомкнутым клеммам конденсатора, как показано на , рис. 3b, .Общее сопротивление конденсатора (R EQ ) имеет значение:
\ [\ begin {matrix} {{R} _ {EQ}} = {{R} _ {F}} || {{ R} _ {L}} & {} & \ left (2 \ right) \\\ end {matrix} \]
и
\ [\ begin {matrix} {{f} _ {C}} = \ frac {1} {2 \ pi {{R} _ {EQ}} C} & {} & \ left (3 \ right) \\\ end {matrix} \]
Помните, что || символ в уравнении 2 указывает, что значения решены как параллельные резисторы. Для расчета стоимости EQ можно использовать либо взаимный подход, либо подход произведения на сумму. Пример 1 демонстрирует процедуру вычисления частоты среза RC-фильтра нижних частот.
Пример 1
Определите частоту среза для схемы, показанной на рисунке 3a.
Рисунок 3a
Решение
Во-первых, сопротивление цепи (видимое через конденсатор) определяется как:
\ [{{R} _ {EQ}} = {{R} _ {F}} || {{R} _ {L}} = \ frac {100 \ times 910} {100 + 910} = 90,1 \ Omega \]
Теперь частота среза схемы может быть найдена как:
\ [{{f} _ {C}} = \ frac {1} {2 \ pi {{R} _ {EQ}} C} = \ frac {1} {2 \ pi \ times 90.1 \ Omega \ times 10 \ mu F} = 177 Гц \]
Этот результат показывает, что коэффициент усиления схемы снижается до 50% от максимального значения, когда рабочая частота достигает 177 Гц. Кривая частотной характеристики схемы показана на рис. 3b .
Рисунок 3b: Кривая частотной характеристики
Фильтры нижних частот RLСхема RL действует как фильтр нижних частот, если сконструирована, как показано на рис. В показанной схеме катушка индуктивности является последовательным компонентом, а резистор – шунтирующим элементом.
Рисунок 4: RL фильтр нижних частот
Фильтрующее действие схемы на рисунке 4 является результатом реакции катушек индуктивности на увеличение рабочей частоты. Этот отклик можно объяснить с помощью кривой и эквивалентных схем на рис. 5а .
рис. 5: Работа фильтра нижних частот RL
Кривая на рис. L ) и рабочих частот (е).Как показывает кривая, реактивное сопротивление катушки индуктивности составляет 0 Ом, когда входная частота равна 0 Гц. Имея это в виду, посмотрите на эквивалентную схему, показанную на рис. 5b . Предполагая, что входная частота равна 0 Гц, индуктивное реактивное сопротивление равно 0 Ом. Однако индуктор имеет некоторое сопротивление обмотки (R W ). Поэтому в эквивалентную схему включен резистор, представляющий сопротивление обмотки катушки. В этом случае напряжение нагрузки равно разнице между напряжением источника (E) и напряжением на R W.
Как показано на кривой реактивного сопротивления, увеличение рабочей частоты вызывает пропорциональное увеличение значения X L . Теоретически рабочая частота может стать достаточно высокой, чтобы индуктор мог эффективно работать как разомкнутый. В этом случае фильтр имеет эквивалентную схему, показанную на Рис. 5c . Как показано на схеме, индуктор представлен как разрыв проводника (из-за его почти бесконечного реактивного сопротивления). В этом случае V RL = 0V.Между крайними значениями, представленными на рисунке 5, находится диапазон частот, в котором V RL уменьшается с E – V RW до 0 В.
Верхняя частота среза (f C )Верхняя частота среза для фильтра нижних частот RL определяется индуктором и параллельной комбинацией R F и R L . По формуле
\ [\ begin {matrix} {{f} _ {C}} = \ frac {{{R} _ {EQ}}} {2 \ pi L} & {} & \ left (4 \ справа) \\\ end {matrix} \]
Где
R EQ = R F || R L
Пример 2 демонстрирует расчет f C для RL Low- Пропустить фильтр.
Пример 2
Рассчитайте частоту среза для схемы, показанной на рис. 6 .
Рисунок 6
Решение
Во-первых, значение R EQ находится как:
\ [{{R} _ {EQ}} = {{R} _ {F} } || {{R} _ {L}} = \ frac {51 \ times 750} {51 + 750} = 47,8 \ Omega \]
Теперь частота среза схемы может быть найдена как:
\ [{{f} _ {C}} = \ frac {{{R} _ {EQ}}} {2 \ pi L} = \ frac {47.8 \ Omega} {2 \ pi \ times 10mH} = 761 Гц \]
Этот результат показывает, что прирост мощности схемы снижается до 50% от максимального значения, когда рабочая частота достигает 761 Гц. Кривая частотной характеристики схемы показана на рис. 7 .
Рисунок 7: Кривая частотной характеристики
Взгляд вперед
Теперь мы обсудили работу и анализ RC и RL фильтров нижних частот. В следующем разделе мы аналогичным образом рассмотрим фильтры высоких частот RC и RL .Как вы увидите, большинство принципов, обсуждаемых в этом разделе, также применимы к этим схемам.
Фильтры низких и высоких частот [Analog Devices Wiki]
Цель:
Целью этой лабораторной работы является изучение характеристик пассивных фильтров путем получения частотной характеристики RC-фильтра нижних частот и RL-фильтра верхних частот.
Примечания:
Как и во всех лабораториях ALM, мы используем следующую терминологию при описании подключений к разъему M1000 и настройке оборудования.Зеленые заштрихованные прямоугольники обозначают подключения к разъему аналогового ввода-вывода M1000. Контакты аналогового канала ввода / вывода обозначаются как CA и CB. При настройке для принудительного измерения напряжения / измерения тока – В добавляется , как в CA- V , или при настройке для принудительного измерения тока / измерения напряжения добавляется -I, как в CA-I. Когда канал настроен в режиме высокого импеданса только для измерения напряжения, -H добавляется как CA-H.
Следы осциллографа аналогичным образом обозначаются по каналу и напряжению / току.Например, CA- V , CB- V для сигналов напряжения и CA-I, CB-I для сигналов тока.
Фон:
Импеданс катушки индуктивности пропорционален частоте, а импеданс конденсатора обратно пропорционален частоте. Эти характеристики могут использоваться для выбора или отклонения определенных частот входного сигнала. Этот выбор и отклонение частот называется фильтрацией, а схема, которая выполняет это, называется фильтром.
Рисунок 1: RC-фильтр нижних частот.
Рисунок 2: фильтр верхних частот RL.
Если фильтр пропускает высокие частоты и отклоняет низкие частоты, то это фильтр верхних частот. И наоборот, если он пропускает низкие частоты и отклоняет высокие, это фильтр нижних частот. Фильтры, как и большинство вещей, не идеальны. Они абсолютно не пропускают одни частоты и абсолютно отвергают другие. Частота считается пройденной, если ее величина (амплитуда напряжения) находится в пределах 70% или 1 / sqrt (2) от максимальной пройденной амплитуды, и отклоняется в противном случае.Частота 70% называется угловой частотой, частотой спада или частотой половинной мощности.
Граничные частоты для RC-фильтра и RL-фильтра следующие:
Для фильтров RC:
(1)
Для фильтров RL:
(2)
Частотная характеристика: это график зависимости выходного напряжения фильтра от частоты. Обычно он используется для характеристики диапазона частот, в котором предназначен фильтр.
Рисунок 3: Частотная характеристика типичного фильтра нижних частот с частотой среза f c
Материалы:
Аппаратный модуль ADALM1000
Резисторы (1 кОм)
Конденсатор (1 мкФ)
Индуктор (22 мГн)
Процедура:
A. RC фильтр нижних частот:
Рисунок 4: Соединения макетной платы низкочастотного RC-фильтра.
1. Настройте RC-цепь, как показано на рисунке 1, на беспаечной макетной плате со значениями компонентов R 1 = 1 кОм, C 1 = 1 мкФ.
2. Установите минимальное значение AWG канала A на 0,5 и максимальное значение на 4,5 В, чтобы подать синусоидальную волну 4 В (размах) с центром на 2,5 В в качестве входного напряжения в схему. В раскрывающемся меню AWG A Mode выберите режим SVMI. В раскрывающемся меню AWG A Shape выберите Sine. В раскрывающемся меню AWG B Mode выберите режим Hi-Z.
3. В раскрывающемся меню «Кривые ALICE» выберите CA- V и CB- V для отображения. В раскрывающемся меню «Триггер» выберите CA- V и Auto Level.Установите Hold Off на 2 (мсек). Отрегулируйте развертку до тех пор, пока на сетке дисплея не будет примерно двух периодов синусоидальной волны. В раскрывающемся меню Meas CA выберите P-P в разделе CA- V и сделайте то же самое для CB. Также в меню Meas CA выберите A-B Phase.
4. Начните с низкой частоты, 50 Гц, и измерьте выходное напряжение CB- V от пика до пика на экране осциллографа. Он должен быть таким же, как выход канала А. Увеличивайте частоту канала A небольшими приращениями, пока пиковое напряжение канала B не станет примерно 0.В 7 раз больше напряжения от пика до пика для канала A. Вычислите 70% от Vp-p и получите частоту, при которой это происходит на осциллографе. Это дает частоту среза (спада) для сконструированного RC-фильтра нижних частот.
Б. Фильтр верхних частот RL
Рисунок 5: Соединения макетной платы фильтра верхних частот RL.
1. Настройте цепь RL, как показано на рисунке 2, на беспаечной макетной плате со значениями компонентов R 1 = 1 кОм, L = 20 мГн.
2. Повторите шаги 2 и 3, как в Части A, чтобы получить осциллограф.
3. Начните с высокой частоты 20 кГц и измерьте выходное напряжение CB- V от пика до пика на экране осциллографа. Он должен быть таким же, как выход канала А. Уменьшайте частоту канала A небольшими приращениями до тех пор, пока пиковое напряжение канала B не станет примерно в 0,7 раза больше пикового напряжения для канала A. Вычислите 70% от Vp-p и получите частоту, при которой это происходит на Осциллограф.Это дает частоту среза (спада) для сконструированного фильтра верхних частот RL.
Вопросы:
Рассчитайте частоты среза для RC-фильтра нижних частот и RL-фильтра верхних частот, используя уравнения (1) и (2). Сравните вычисленные теоретические значения с полученными в результате экспериментальных измерений и дайте подходящее объяснение любых различий.
Приложение, Графики частотных характеристик с плоттером ALICE Bode Plotter
Настольное программное обеспечение для построения графиков Боде ALICE может значительно упростить построение графиков частотных и фазовых характеристик.Используя RC-схему нижних частот на рисунке 1, с R 1 = 100 Ом и C 1 = 1,0 мкФ, мы можем развернуть входную частоту от 10 Гц до 5000 Гц и построить график амплитуды сигнала обоих каналов A и B. и относительный фазовый угол между каналами B и A.
Со схемой, подключенной к ALM1000, как показано на рисунке 1, запустите программное обеспечение рабочего стола ALICE. Откройте плоттер Боде.
В меню Curves выберите CA-dBV, CB-dBV и Phase B-A.
В раскрывающемся меню «Параметры» нажмите Cut-DC, чтобы выбрать его.
Установите минимальное значение канала A AWG на 1,086 и максимальное значение на 3,914. Это будет амплитуда 1 В (среднеквадр.) (0 дБВ) с центром в середине 2,5 В диапазона аналогового входа. Установите режим AWG A на SVMI и Shape на Sine. Установите канал B AWG в режим Hi-Z. Убедитесь, что установлен флажок Sync AWG.
Используйте запись Start Frequency, чтобы установить развертку частоты, чтобы она начиналась с 100 Гц, и используйте запись Stop Frequency, чтобы развернуть развертку, чтобы остановиться на 20000 Гц. Выберите CHA в качестве канала для развертки.Также используйте кнопку Sweep Steps, чтобы ввести количество шагов частоты, используйте 100 в качестве числа.
Теперь вы должны иметь возможность нажать зеленую кнопку Run и запустить развертку частоты. После завершения развертки вы должны увидеть что-то вроде снимка экрана на рисунке A1.


 хх (разделитель – точка)
хх (разделитель – точка)