Расчет индуктивности катушки с сердечником: Расчет катушки на ферритовом стержне

Как рассчитать сердечник и витки самодельных катушек индуктивности

Катушки индуктивности предназначены для фильтрации токов высокой частоты. Они устанавливаются в колебательных контурах и используются для других целей в электрических и электронных схемах. Готовое устройство заводского изготовления надёжнее в работе, но дороже, чем изготовленное своими руками. Кроме того, не всегда удаётся приобрести элемент с необходимыми характеристиками. В этом случае расчёт катушки  индуктивности и само устройство можно сделать самостоятельно.

Устройство катушки индуктивности

Конструкция катушки

Каркас устройства изготавливается из диэлектрика. Это может быть тонкий (нефольгированный) гетинакс, текстолит, а на тороидальных сердечниках –просто обмотка из лакоткани или аналогичного материала.

Обмотка выполняется из одножильного или многожильного изолированного провода.

Внутрь обмотки вставляется сердечник. Он изготавливается из железа, трансформаторной стали, феррита и других материалов.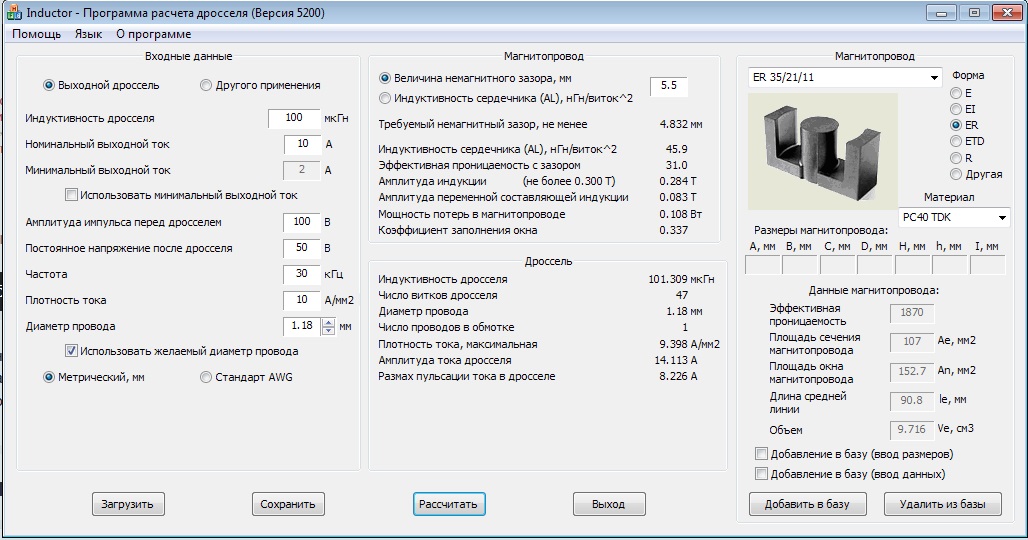 Он может быть замкнутым, тороидальным (бублик), квадратным или незамкнутым (стержень). Выбор материала зависит от условий работы: частоты, магнитного потока и других параметров.

Кроме того, есть приборы, в которых сердечник отсутствует. Они характеризуются большой линейностью импеданса, но при намотке тороидальной формы обладают паразитной ёмкостью.

Расчет параметров катушки индуктивности

Протекающий по проводу электрический ток создаёт вокруг него электромагнитное поле. Соотношение величины поля к силе тока называется индуктивностью. Если провод свернуть кольцом или намотать на каркас, то получится катушка индуктивности. Её параметры рассчитывают по определённым формулам.

Расчёт индуктивности прямого провода

Индуктивность прямого стержня – 1-2мкГн на метр. Она зависит от его диаметра. Точнее можно рассчитать по формуле:

L=0.2l(logl/d-1), где:

• d – диаметр провода,
• l – длина провода.

Эти величины нужно измерять в метрах (м). При этом результат будет иметь размерность микрогенри (мкГн). Вместо натурального логарифма ln допустимо использовать десятичный lg, который в 2,3 раза меньше.

Предположим, что какая-то деталь подключена проводами длиной 4 см и диаметром 0,4 мм. Произведя при помощи калькулятора расчет по выше приведённой формуле, получаем, что индуктивность каждого из этих проводов составит (округлённо) 0,03 мкГн, а двух – 0,06 мкГн.

Ёмкость монтажа составляет порядка 4,5пФ. При этом резонансная частота получившегося контура составит 300 МГц. Это диапазон УКВ.

Важно! Поэтому при монтаже устройств, работающих в частотах УКВ, длину выводов деталей нужно делать минимальной.

Расчёт однослойной намотки

Для увеличения индуктивности провод сворачивается кольцом. Величина магнитного потока внутри кольца выше примерно в три раза. Рассчитать её можно при помощи следующего выражения:

L = 0,27D(ln8D/d-2), где D – диаметр кольца, измеренный в метрах.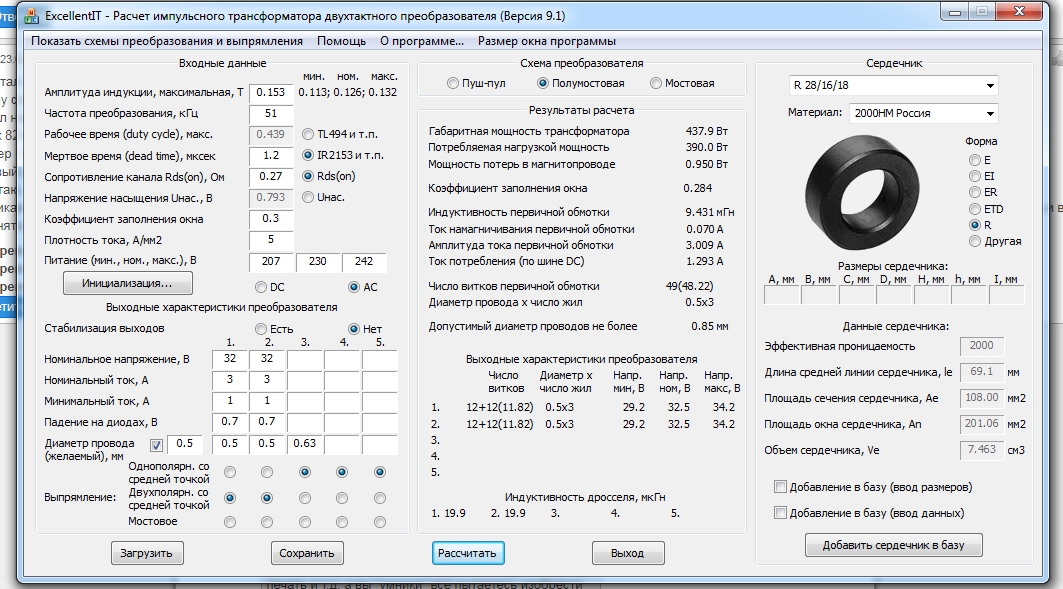

При увеличении количества витков индуктивность продолжает расти. При этом индукция отдельных витков влияет на соседние, поэтому получившиеся параметры пропорциональны не количеству витков N, а их квадрату.

Однослойная намотка

Дроссель с сердечником

Параметры обмотки, намотанной на каркас, диаметром намного меньше длины рассчитывается по формуле:

L=*0*N2*S.

Она справедлива для устройства большой длины или большого тора.

Размерность в ней дана в метрах (м) и генри (Гн). Здесь:

• 0 = 4•10-7 Гн/м – магнитная константа,
• S = D2/4 – площадь поперечного сечения обмотки, магнитная проницаемость магнитопровода, которая меньше проницаемости самого материала и учитывает длину сердечника; в разомкнутой конструкции она намного меньше, чем у материала.

Например, если стержень антенны изготовить из феррита с проницаемостью 600 (марки 600НН), то у получившегося изделия она будет равна 150. При отсутствии магнитного сердечника = 1.

Для того чтобы использовать это выражение для расчёта обмоток, намотанных на тороидальном сердечнике, его необходимо измерять по средней линии «бублика». При расчёте обмоток, намотанных на железе Ш-образной формы без воздушного зазора, длину пути магнитного потока измеряют по средней линии сердечника.

Катушка с Ш-образным сердечником

В расчёте диаметр провода не учитывается, поэтому в низкочастотных конструкциях сечение провода выбирается по таблицам, исходя из допустимого нагрева проводника.

В высокочастотных устройствах, так же как и в остальных, стремятся свести омическое сопротивление к минимуму для достижения максимальной добротности прибора. Простое повышение сечения провода не помогает. Это приводит к необходимости наматывать обмотку в несколько слоёв. Но ток ВЧ идёт преимущественно по поверхности, что приводит к увеличению сопротивления. Добротность в высокочастотных элементах растёт вместе с увеличением всех размеров: длины и диаметров обмотки и провода.

Максимальная добротность получается в короткой обмотке большого диаметра, с соотношением диаметр/длина, равным 2,5. Параметры такого устройства вычисляются по формуле:

L=0.08D2N2/(3D+9b+10c).

В этой формуле все параметры измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

По этой формуле рассчитывается также плоская катушка. Диаметр «D» измеряется по среднему витку, а длина «l» по ширине:

l=Dmax-Dmin.

Плоская катушка

Многослойная намотка

Многослойная намотка без сердечника вычисляется по формуле:

L=0.08D2N2/(3D+9b+10c).

Размеры здесь измеряются в сантиметрах (см), а результат получается в микрогенри (мкГн).

Добротность такого устройства зависит от способа намотки:

• обычная плотная намотка – самая плохая, не более 30-50;
• внавал и универсал;
• «сотовая».

Многослойная катушка

Для увеличения добротности при частоте до 10 мГц вместо обычного, одножильного провода, можно взять литцендрат или посеребренный проводник.

Справка. Литцендрат – это провод, скрученный из большого количества тонких изолированных друг от друга жил.

Литцендрат имеет большую поверхность, по сравнению с одножильным проводником того же сечения, поэтому на высоких частотах его сопротивление ниже.

Использование сердечника в высокочастотных устройствах повышает индуктивность и добротность катушки. Особенно большой эффект даёт использование замкнутых сердечников. При этом добротность дросселя зависит не от активного сопротивления провода, а от проницаемости магнитопровода. Рассчитывается такой прибор по обычным формулам для низкочастотных устройств.

Сделать катушку или дроссель можно самостоятельно. Перед тем, как её изготавливать, необходимо рассчитать индуктивность катушки по формулам или при помощи онлайн-калькулятора.

Видео

Оцените статью:

Расчет катушек индуктивности | Микросхема

Крайне полезная программа для любого радиолюбителя. Позволяет в считанные секунды подсчитать индуктивность любой катушки, контура или отрезка провода. Нередко на схемах можно увидеть катушки и рядом с ними надпись, обозначающую её индуктивность (Гн – Генри, 1 Гн=10⁹ см). Но часто количество витков и размеры катушки не указывают. Так вот, с помощью данной программы можно быстро подобрать необходимое количество витков на уже имеющийся каркас катушки или любой сердечник. Все возможности показаны на картинках ниже.

В первое низпадающее меню входят следующие виды расчетов: “Предельная нагрузка провода”, “Отрезок круглого провода”, “Отрезок провода прямоугольного сечения”, “Одиночный круглый виток”, “Тонкопленочный круглый виток”, “Тонкопленочный квадратный виток”.

Во втором меню можно подсчитать следующие виды катушек: “Однослойная круглого сечения”, “Однослойная квадратного сечения”, “Многослойная цилиндрическая короткая”, “Плоская круглая спиральная”, “Плоская квадратная спиральная”, “Тороидальная однослойная квадратного сечения”, “Тороидальная однослойная круглого сечения”, “Тороидальная многослойная”.

В третьем пункте только катушки на ферритах: “Катушка на тороидальном ферромагнитном сердечнике прямоугольной формы с плотной намоткой”, “Катушка на П-, Ш-образном ферромагнитном замкнутом сердечнике”, “Катушка в броневом цилиндрическом сердечнике”. И ещё приведу пример работы программы. По радиусу, длине катушки и количеству витков легко расчитывается индуктивность. Главное смотрите единицы измерения.

Скачать

Огромное спасибо автору Струкову И.В.

Обсуждайте в социальных сетях и микроблогах

Метки: справка

Радиолюбителей интересуют электрические схемы:

Расчет количества витков в катушке
Электронное ухо

РАСЧЕТ ИНДУКТИВНОГО ДАТЧИКА С РАЗОМКНУТОЙ МАГНИТНОЙ ЦЕПЬЮ

ИНДУКТИВНО-ЧАСТОТНЫЕ ПРЕОБРАЗОВАТЕЛИ НЕЭЛЕКТРИЧЕСКИХ ВЕЛИЧИН

Выше отмечалось, что методы определения индуктивности ка­тушек различных поперечных сечений без сердечников хорошо известны.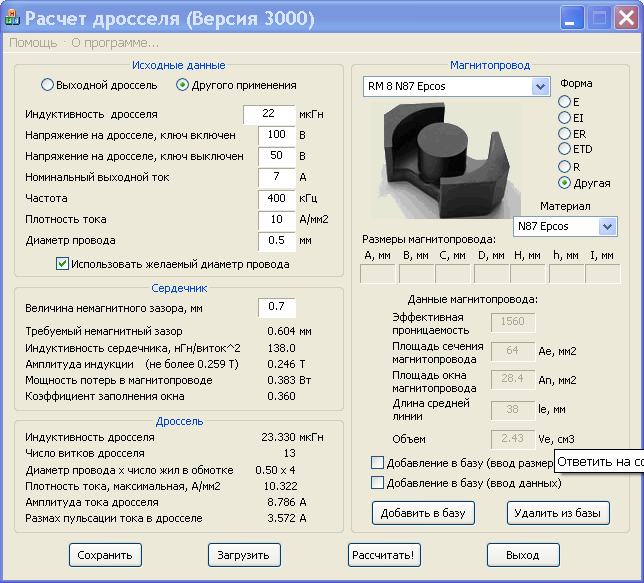 Между тем расчет катушек с разомкнутыми ферромагнит­ными сердечниками связан со значительными трудностями и почти не разработан. Трудности расчета вызваны в основном наличием ферромагнитного тела ограниченных размеров в поле короткой ка­тушки. Формулы (2-18)—(2-20) позволяют приблизительно учесть влияние неподвижного сердечника на индуктивность катушки в слу­чае, когда катушка занимает симметричное положение относительно концов сердечника. В датчиках измерительных устройств это усло­вие не выполняется: под воздействием входной величины положе­ние феррита относительно катушки меняется В общем случае фер­рит только частично вдвинут в катушку. При движении феррита изменяется магнитное сопротивление потоку и распределение маг­нитных силовых линий поля катушки. Таким образом, каждому положению феррита соответствует вполне определенная картина поля, и расчет индуктивности датчика классическими методами ста­новится практически неосуществимым.

В конечном счете представляет интерес интегральный эффект, заключающийся в изменении индуктивности при перемещении сер­дечника. внутр и толщина обмотки /кат — у обеих катушек одинаковы.

При изменениях входной величины, приводящих к изменению положения феррита, длины и числа витков катушек 1 и 2 также не остаются постоянными. Так, при вдвижении ст/ержня /j и wt уменьшаются, а /2 и w2 возрастают. При обратном движении стерж­ня картина изменения параметров меняется на противоположную. Суммарная индуктивность катушек 1 и 2 равна:

L — L– L2–2M2.

Поскольку обе катушки примыкают друг к другу, нельзя не учитывать влияния ферритового стержня второй катушки на индук­тивность первой. Это влияние проявляется в увеличении индуктив­ности катушки 1 по сравнению с тем ее значением L01, которое

имело бы место при отсутствии феррита, и может быть учтено вве­дением некоторого коэффициента

В свою очередь на индуктивность катушки 2 влияет участок длины ферритового сердечника, выступающий за ее край.

Обозначив через Lm2 индуктивность катушки 2 с сердечником, длина которого равна длине катушки, запишем:

L2=Lmyk,2,

где k2>, a L2 определяется из соотношения

Для коэффициента взаимоиндукции М12 справедлива формула

Мм = 2 (^i+2

которая непосредственно следует из (2-38). Очевидно, что восполь­зоваться ей не представляется возможным, поскольку:

1) Li+2 — индуктивность катушки, составленной из катушек / и 2, в данном случае является конечной целью нашего расчета;

2) ввиду наличия ферромагнитного сердечника среда, в которой находятся катушки 1 и 2, не является изотропной. Область, занятая обмотками катушек и лежащая снаружи их, имеет магнитную про­ницаемость р-о*, эквивалентная проницаемость области внутри катуш­ки 2 равна » а внутри катушки 1 — &іЦо.

Для определения МХ2 воспользуемся искусственным приемам: заменим катушку с сердечником, находящуюся в среде с const, катушкой без сердечника. Последнюю будем рассматривать в среде

с магнитной проницаемостью ц0. При данном преобразовании необ­ходимо, чтобы Lu L2 и Afj2 остались без изменения.

Для того чтобы при произведенном преобразовании осталось неизменным значение М12, недостаточно выполнения этих условий. Необходимо, чтобы неизменным осталось и общее потокосцепление катушек.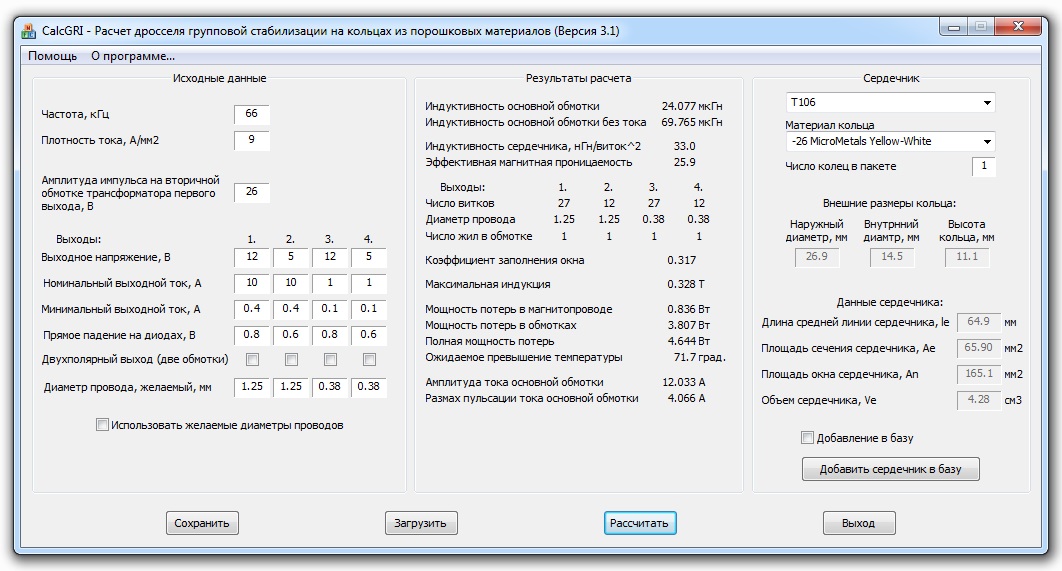 Последнее требование, очевидно, не может быть выполне­но со всей строгостью, так как картина поля новых катушек без сердечника в изотропной среде отличается от картины поля исход­ных катушек, находящихся в среде с лфconst и содержащих сер­дечник. Из сказанного следует, что предлагаемый метод нельзя рекомендовать для расчета картин поля катушек с сердечником.

В то же время при расчете интегральных параметров катушек он дает вполне удовлетворительные результаты, поскольку для слу­чая коротких и достаточно тонких катушек эта погрешность неве­лика, так как соответствующее увеличение эквивалентной плотности витков способствует примерно такой же концентрации магнитных силовых линий поля, как и при наличии ферромагнитного сердеч­ника. Кроме того, М12 входит в выражение для L в качестве одно­го из слагаемых.

1. Для получения максимальной чувствительности датчика при данных его габаритах витки катушки должны как можно блил£е примыкать к сердечнику. Поэтому увеличение диаметра катушки за счет с? Внутр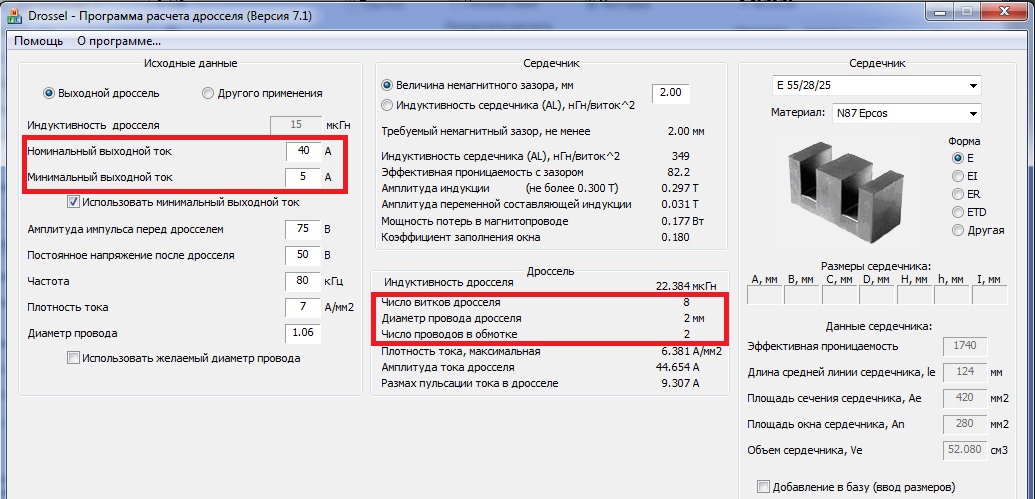, т. ст

*<о

Ф-1000

9,91

4,21

Ф-600

9,86

4,20

Ф-400

9,80

4,17

Таблица 2-3 хорошо иллю­стрирует этот факт: при отноше­нии lddc = 2,5 изменение магнит­ной проницаемости материала в 2,5 раза изменяет коэффициент и, следовательно, индуктив­ность Lm только на 0,95%. Влия­ние же коэффициентов k и &2 на индуктивность меньше, чем влия­ние IV

Отношение tK/dK для кату­шек, используемых в датчиках индуктивно-частотных преобразователей, колеблется в небольших пределах. Экспериментальные исследования показали, что влияние его на ki и &2 можно не учитывать, так как оно соизмеримо с раз­бросом значений этйх коэффициентов, вызванным погрешностями

изготовления катушек и погрешностями эксперимента. Методика

определения коэффициентов k и k2 позволяет учесть изменение кар­тины поля катушек датчика при движении сердечника.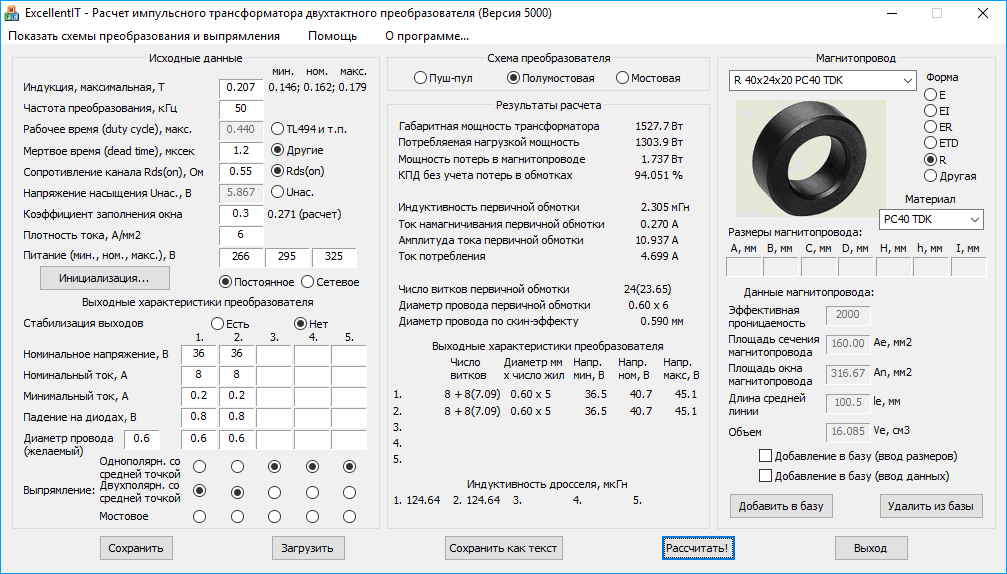

Значения коэффициентов k и k2 приведены на рис. 2-4. Пред­ложенный метод расчета может оказаться полезным при проекти­ровании индуктивных датчиков с разомкнутой магнитной цепью не только с катушками прямоугольного поперечного сечения, но и с профилированной обмоткой. В этом случае число слагаемых в (2-48) увеличивается в соответствии с количеством элементов, на которые будет разбита исходная катушка датчика. Точность метода ограничивается следующими факторами:

1) точностью используемых выражений для N/4n; Ф;

2) точностью определения поправочных коэффициентов kx и к2. В серии катушек, изготавливаемых для этой цели, неизбежны коле­бания lK/dK и tK/dK по сравнению с заданными значениями. Практи­чески индуктивность катушки рассчитывается с точностью до 3—5%.

Рис. 2-4. Кривые для определения коэффициентов kj и k2.

Рассмотрим пример расчета индуктивности катушки с несим­метрично расположенным сердечником. —=0,442;

dK

Из рис. 2-2 находим: Фі (1,33; 0,221) = 4,6; Ф2 (0,442; 0,221) = 8,5; Ф-(1,78; 0,221) =3,76.

Стабилизаторы напряжения для котлов и другой бытовой техники Контакты для заказов: +38 050 457 1330 [email protected] Технические характеристики АСН-250 – 615 грн. Номинальная мощность 250 Вт Рабочий диапазон (1) вх) …

Прибор предназначен для измерения различных физиологиче­ских параметров с регистрацией результатов измерений на электро­термической бумаге шириной 100 мм. Прибор имеет три датчика, с помощью которых осуществляется одновременное измерение арте­риального и венозного …

В последние годы за рубежом для измерения кровяного давле­ния стали применяться электрические манометры. Описываемый ниже прибор является электроманометром, построенным на прин­ципе индуктивно-частотного преобразования сигнала. Принципиальная схема манометра показана на рис. …

Расчет катушки на цилиндрическом сердечнике: pkuz — LiveJournal

Раз уж сегодня день космонавтики, то и тема космическая…….а именно расчет катушки на цилиндрическом сердечнике, если быть точным то разомкнутый сердечник (не думал что такая сложная тематика J).

Расчетные данные не точны, желающие могут проверить, других методик мне неизвестно.

Расчетные величины буду просчитывать для контура ПЧ от ЧБ телевизоров (мне больше нравятся  с круглым экраном).

Справочные данные на них мне не попадались, однако известно, что подстроичные сердечники из карбонильного железа, назывались СЦР.

В литературе, пятилеток и прочего, нашей промышленности, очень много рассказывалось о достижениях,  в качестве материала сердечника используют карбонильное железо марок Р-10, Р-20, Р-100.

Однако в справочной литературе лишь мельком проскакивал материал и якобы проницаемость 10,но тогда не понятно их широкое использование  в ТВ, где частоты ПЧ около 30-20мГц.

В пользу большей проницаемости говорит  частота измерений-15мГц. Марку сто встретить мне не удавалось и где она применялась неизвестно.

Порывшись в предложениях сегодняшнего дня, было сделано открытие, что теперь сердечники СЦР-1(М6*0,75*10) называются ПР6х0.75х10 . Самое интересное, в подтверждение предположения о проницаемости, мы их делаем, можем сделать на заказ из стандартного материала Р-20.Однако в размерах явно путаница с диаметром тела (или мы их штампуем с такой глубиной резьбы?).

С материалом все выбрано, данные есть, можно начинать расчет.

Многослойная нас не интересует.
Мои данные: Диаметр каркаса-8,2мм,экрана 24мм,Проницаемость 20, сердечник 4,5мм*10мм,поэтому приведу расчет для длин от 1-12мм.
В таблице последние две строки- результат расчета в Coil32,для индуктивности со штрихом(расчетная с учетом действия экрана,а начальная была 2мкгн и емкости 110пф,провод ПЭТВ-2 0,2мм).Во второй таблице просчет для проницаемости 10.


Намотанный контур с 9 витками……очень мало,резонанс где-то 12мГц,оптимальный результат 14 витков.Если кто сможет измерить индуктивность….то буду благодарен.

Расчет числа витков катушки на тороидальном ферритовом сердечнике | Радиотехника

Маркировка размеров кольцевых сердечников

Сначала цифрами указывается величина начальной магнитной проницаемости, затем марка используемого материала, и потом размер кольца в миллиметрах:

2000НН D x d x h

Где — 2000 величина начальной магнитной проницаемости, НН – марка материала, D – внешний диаметр, d – внутренний диаметр, h – толщина кольца, все размеры в миллиметрах.

Для более простых расчетов стоит воспользоваться оценочными формулами, позволяющими получить приближенные значения параметров катушки по известным характеристикам:

где: ω – число витков катушки, намотанной на кольце, L— индуктивность мкГн, µ — магнитная проницаемость, D1-наружный диаметр кольца, D2-внутренний диаметр кольца, h-высота кольца (все в мм).

Для упрощения расчета можно воспользоваться онлайн калькуляторами на странице https://rcl-radio.ru/?p=20475

Онлайн калькуляторы позволяют рассчитать число витков катушки на тороидальном ферритовом сердечнике, индуктивность катушки на тороидальном ферритовом сердечнике и начальную магнитную проницаемость ферритовых колец по пробной обмотке.

В качестве эксперимента был взят тороидальный ферритовый сердечник с магнитной проницаемостью 2000 с внешним диаметром 46 мм, внутренним диаметром 28, высотой 8 мм. Намотав равномерно по всему кольцу 17 витков провода была получена индуктивность 444 мкГн (измерена при помощи Е7-21).

Вот результаты расчета по данному примеру:

Расчет числа витков катушки на тороидальном ферритовом сердечникеРасчет числа витков катушки на тороидальном ферритовом сердечникеРасчет числа витков катушки на тороидальном ферритовом сердечникеРасчет числа витков катушки на тороидальном ферритовом сердечникеРасчет числа витков катушки на тороидальном ферритовом сердечнике

Как видно на скриншотах, расчетная индуктивность с небольшой погрешностью совпадает с измеренной прибором индуктивностью катушки.

Расчет числа витков катушки на тороидальном ферритовом сердечнике на сайте rcl-radio.ru

Собственная паразитная ёмкость катушки индуктивности. Онлайн расчёт.

Собственная ёмкость – это паразитный параметр катушки индуктивности. Паразитный, но не так, чтобы уж очень: не домашнее животное в виде таракана, не нежданный гость в виде татарина, а так… мелкий, но важный аспект, требующий учёта и внимания.
Возникновение собственной ёмкости обусловлено наличием ёмкостей между отдельными витками катушки, между витками и сердечником, витками и экраном, а также витками и близлежащими элементами конструкции. Все эти распределённые ёмкости суммируются и называются собственной ёмкостью катушки C

L.
Паразитная собственная ёмкость всегда подключена параллельно катушке и образует с её собственной индуктивностью параллельный колебательный контур, резонансная частота которого является частотой собственного резонанса катушки.

Несмотря на кажущуюся простоту, точный расчёт этого параметра – это вовсе: не плёвое дело, не поиск халявы и не комариная плешь, по крайней мере, практически все отечественные авторы справочной литературы, дружно повернулись спиной к суровой правде бытия, выдавая за истину теорию, никак не подкреплённую экспериментом.
Для примера приведу выдержку из подобного умного справочника.

Совсем другое дело – буржуйские пытливые умы, преимущественно американской этнической национальности. Эти ребята копают и вглубь и вширь похлеще азиатских хунвейбинов, восполняя нехватку теоретических обоснований многочисленными практическими экспериментами.

Вот как, к примеру, у них выглядит незамысловатая измерительная приблуда для определения собственной резонансной частоты катушки.

В результате всех этих раскопок из глубины на поверхность была извлечена совсем уж до неприличия простая формула определения собственной ёмкости катушки:
C_L(пф) ≈ 0,5×D_кат(см).

Казалось бы, вот оно – добро пожаловать “за грань добра и зла”. Однако не всё так плохо – формула обеспечивает вполне приемлемую точность вычислений и может быть использована для оценки собственных ёмкостей однослойных конструкций катушек с соотношением длины намотки к диаметру:
0.5 нам/D_кат

А как посчитать нам величину собственной ёмкости при другом форм-факторе катушки?

Найти всеобъемлющую формулу, позволяющую рассчитать этот параметр для любых вариаций (включая частотную зависимость) оказалось делом нереальным – по крайней мере мне этого сделать не удалось. Поэтому самым простым и точным методом, позволяющим оценить собственную ёмкость катушки, я посчитал интерполяцию графика экспериментальной зависимости, полученной англичанином R.G.Medhurst-ом, в лаборатории компании General Electric.

По шкале X – отношение длины к диаметру катушки;
По шкале Y – коэффициент H, равный отношению собственной ёмкости к диаметру катушки;
Шкала зависимости – логарифмическая.

Формула значения собственной ёмкости катушки в данном случае выглядит следующим образом:
C_L(пф) = H×D_кат(см).
Зависимость снята для однослойных бескаркасных катушек в диапазоне частот, находящихся ниже частоты собственного резонанса катушки.

В этом же источнике приведена и удобная таблица, отражающая изменение коэффициента H в зависимости от форм-фактора катушки.

И, как результат – формула, позволяющая с 2-3% точностью описать полученные экспериментальные зависимости:
H = 0,1126×L/D+0,08+0,27/√L/D.

Это то, что касается бескаркасных катушек. При наличии гладкого каркаса расчётная ёмкость изделия увеличится на величину ≈10×ε (%), где ε – относительная диэлектрическая проницаемость материала каркаса. Для катушек, намотанных на каркасах с нарезкой для фиксации витков, коэффициент увеличения ёмкости уже может составлять величину ≈20×ε (%).

И в завершении мероприятия просуммируем вышеизложенные идеи калькулятором.

ТАБЛИЦА РАСЧЁТА ЗНАЧЕНИЯ СОБСТВЕННОЙ ЁМКОСТИ БЕСКАРКАСНОЙ КАТУШКИ.

Будьте внимательны – в качестве значения межвиткового расстояния принято считать расстояние между центрами соседних витков, а не зазор между ними, поэтому данное расстояние никак не может быть меньше величины диаметра провода.

Значение собственной ёмкости многослойной катушки значительно больше и может достигать нескольких десятков пФ. Здесь, помимо всего прочего, вступают в сложное взаимодействие и ёмкости между соседними витками, и ёмкости между слоями, и разные другие факторы, значительно усложняющие структуру длинной линии, описывающей свойства моточного изделия.
Наверно по этой причине никто никому и не выносит мозг, все отдыхают на расслабоне. Формул – нет!
Или я чего-то пропустил в этой жизни…

 

Расчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM

Расчет индукторов, дросселей, катушек индуктивности методом численного моделирования FEM.

Современный подход к разработке сложной электронной и электротехнической продукции предполагает точное проектирование силовых элементов схемы. С ростом мощностей разрабатываемого оборудования, цена ошибок и неточностей в расчетах растет в геометрической прогрессии. А особенно это становится заметно, когда разрабатывается уникальное оборудование.

Безусловно, существует масса литературы по расчету и проектированию трансформаторов, дросселей, катушек индуктивности с сердечником и без сердечника, где рассмотрены большинство стандартных применений.

Для студентов, которые только начинают заниматься электроникой и электротехникой, я всегда рекомендовал замечательную книгу –

Семенов Б.Ю. Силовая электроника: от простого к сложному. 2005г.

Ясное и понятное изложение для начинающих.

Далее, по расчету катушек индуктивности, есть не менее полезная книга-

Калантаров П.Л., Цейтлин Л.А. Расчет индуктивностей. 1986г.

По расчету трансформаторов напряжения (тока) и дросселей существует масса литературы.

Приводить их нет смысла. Интернет велик. Все можно найти.

Особняком стоят книги по расчету, разработке и конструированию индукторов для технологий индукционного нагрева.

Тут Слухоцкого А.Е. вне конкуренции. Хотя, в последнее время, появилось достаточно много статей и книг, где подробно и более глубоко рассмотрены проблемы проектирования индукторов для конкретных видов технологий индукционного нагрева ТВЧ.

Для простейших случаев существует множество on-line калькуляторов, которые позволяют прикинуть или даже рассчитать простые варианты катушек индуктивности, дросселей, трансформаторов.

Например, очень хорошая программа Coil32. Сайт – http://coil32.narod.ru/

Позволяет определить основные параметры катушек индуктивности различной формы.

Для простейшего расчета трансформаторов, например, калькулятор радиолюбителя.

Сайт – http://www.radioamcalc.narod.ru/

Но все это расчеты для устройств, в лучшем случае, до 1кВт.

Дальше начинается своя специфика. Особенно если эти устройства работают на частотах выше нескольких десяток кГц.

В мощных высокочастотных дросселях, катушках индуктивности, индукторах, трансформаторах существенно возрастают потери от поверхностных эффектов протекания тока. Высокочастотный ток может легко концентрироваться и перегревать локальные участки силового устройства.

На высокой частоте существенно возрастает сложность точного расчета потерь мощности в магнитопроводе и обмоточном проводе или шинах. Существенно увеличивается влияние на потери многослойность катушки. Учет влияния зазора в магнитопроводе также становится достаточно сложной задачей.

Использование программ численного моделирования FEM позволяет решить большинство технических вопросов, возникающих при расчете и проектировании индукторов, дросселей, катушек индуктивности, трансформаторов, шиносборок и т.д., а также существенно повысить точность расчета и провести оптимизацию проектируемого устройства в кратчайшие сроки во многих случаях без создания натурального макета, что особенно важно для мощных и дорогих устройств.

Несколько слов хотел сказать о индукционных водонагревателях.

Индукционные водонагреватели, индукционные котлы, индукционные парогенераторы – это технически сложные устройства, требующие особенно тщательной проработки и проектирования индукционной системы. В качестве источника питания обычно используется промышленная частота 50Гц с напряжением 220В или 380В. 

Основной проблемой при проектировании индукционных водонагревателей является оптимальное конфигурировании индуцирующей обмотки. Т. е. проектирование геометрии обмотки, числа витков, сечения провода. Необходимо учитывать, что индукционная система имеет cosφ существенно отличный от 1. Поэтому, без установки дополнительного конденсатора, параллельно обмотки, от сети будет потребляться дополнительный реактивный ток. 

Выбор и расчет требуемого компенсирующего конденсатора является обязательным требованием для получения максимального КПД водонагревательного устройства. Также многие путают электрический и тепловой КПД нагревательного устройства. Тепловой КПД для таких устройств действительно может составлять почти 100%.

Принцип работы индукционного котла показан на рисунках:

Одной из лучших программ FEM моделирования электротехнических устройств является программа Jmag-Designer. Сайт – http://www.jmag-international.com/

Несколько примеров расчетов и моделирования индукторв для разных технологий:

1. Расчет и моделирование индукционной системы тигель-индуктор-магнитопровод.

Определение параметров индукционной системы, КПД, распределение тока в индукторе, определение потерь в магнитопроводе.

 

2. Расчет и моделирование процесса нагрева шестерни в индукторе под закалку.

Решалась совместная электромагнитная и тепловая задача.

В результате моделирования были определены параметры индукционной системы, КПД, требуемая мощность, частота и время нагрева под закалку.

 

 

3. Ресчет и моделирование нагрева шейки коленчатого вала под закалку.

Решалась электромагнитная и тепловая задача в 3D с вращением нагреваемой детали (коленчатого вала).

В результате моделирования определены параметры индукционной системы, КПД, требуемая мощность и время нагрева под закалку.

 

4. Еще один вариант расчета и моделирования шейки коленчатого вала под закалку.

Вращение детали присутствует.

 

Несколько примеров расчетов катушек индуктивности и трансформаторов:

– Трансформатор тока.

Частота около 100кГц. Сердечник феррит 2500НМС1. Обмотка задана, как FEM Coil с распределенными витками по геометрии заданной области.

Задается в параметрах число витков и общее сопротивление обмотки.

Моделировалось распределение тока в медной шине и магнитной индукциии в магнитопроводе. Проверялось отсутствие насыщения магнитопровода для различных режимов работы трансформатора тока. Оптимизировалассь конструкция трансформатора тока для ВЧ применений.

 

– Расчет и моделирование трехфазного трансформатора с кожухом.

На рисунке справа показана расчетная схема и схема включения обмоток и нагрузки трансформатора.

Определялся КПД трансформатра (потери в обмотках, сердечнике, кожухе) и рассеяние в различных режимах работы.  

– Расчет, моделирование и анализ потерь в трансформаторе с плоскими обмотками.

Оценивалось распределение потерь в сердечнике и обмотках трансформатора.

Индуктивность, импеданс и потери – Блог о пассивных компонентах

L.1.7 Индуктивность L

Не только магнитные материалы обладают магнитным полем, каждый проводник с током сам создает магнитное поле.

Рис. 1.23: Магнитные поля токоведущих проводов

Энергия может временно храниться в магнитном поле. Этот эффект технически используется в катушках, состоящих из одной или нескольких проволочных обмоток.Синонимичный термин «индуктор» утвердился.

Существуют различные типы индукторов или катушек:

• Воздушные змеевики (без феррита)
• Дроссельные катушки с сердечником из железного порошка или ферритовым сердечником
• Катушка с тороидальным сердечником
• Катушка стержневого сердечника
Типы
• SMD становятся все более важными из-за их небольшого размера. Помимо индукторов SMD с намоткой, все большее распространение получают индукторы для многопользовательской игры.

Все катушки имеют особое поведение, более подробно описанное в следующих определениях.

1.7.1 Определение индуктивности L

Элемент схемы, который реагирует на изменение тока противодавлением, проявляет индуктивные свойства. Катушка индуктивности – это пассивный компонент, который, как сопротивление переменному току, создает противодействующее напряжение – напряжение самоиндукции.

Напряжение самоиндукции (U _ind ) на выводах индуктора зависит от скорости изменения тока (di / dt) и константы пропорциональности, индуктивности (L):

Индуктивность (L ) катушки зависит от материала сердечника, геометрии материала сердечника, витков обмотки и типа обмоток.Следующее уравнение обычно применяется для расчета индуктивности (L):

Единицей измерения индуктивности (L) является Генри (H) = Vs / A .

Индуктивность сердечников со вставленным воздушным зазором может быть рассчитана по следующей формуле:

l _{среднее значение} = средняя длина магнитного пути в сердечнике (без воздушного зазора)
l _зазор = длина пути воздушный зазор (с)
μ _r = относительная проницаемость

Эта формула, вставленная в формулу для расчета общей индуктивности, дает:

Это также позволяет определить ширину воздушного зазора, если известны требуемая индуктивность L и другие параметры.Здесь необходимо иметь в виду, что приведенная выше формула применима только в том случае, если μ _r велико, а длина воздушного зазора намного меньше средней длины в сердечнике.

Чтобы учесть паразитные эффекты и их влияние на индуктивность, МакЛайман предлагает следующую форму расчета паразитных эффектов F:

w _h = высота обмотки
l _зазор = длина пути воздушного зазора ( s)
A _зазор = площадь поперечного сечения воздушного зазора
F = коэффициент рассеяния

В результате индуктивность L _F изменяется на расчетное значение L _{зазора в} раз больше, чем коэффициент рассеяния F:

Положительное влияние воздушного зазора заключается в увеличении тока насыщения для сердечника того же размера.Недостатком является то, что для достижения заданного значения L теперь необходимо увеличить количество витков, и поэтому, если для обмотки нет свободного места, для более толстого или более одного провода в бифилярной или трехзаходной обмотке сопротивление постоянному току обмотки также увеличивается.

Ни при каких обстоятельствах не следует уменьшать количество витков для компенсации паразитного эффекта – это дополнительно увеличивает индукцию и может привести к преждевременному насыщению.

Требуемая ширина воздушного зазора для данной индуктивности L с учетом паразитного фактора F может быть рассчитана в первом приближении следующим образом:

1.7.2 Определение значения A _L

Чтобы избавить пользователя от расчета эффективной магнитной длины (l _eff ) и площади (A _eff ), для тороидальных сердечников и гильз указано соответствующее значение A _L . Он представляет собой эффективную индуктивность для одной обмотки и должен быть умножен на квадрат витков обмотки (N), чтобы получить фактическую индуктивность (L).

Величина (A _L ) представляет собой индуктивность (L) при условии N = 1 витков обмотки.Таким образом, учитывая значение A _L , необходимое количество обмоток катушки может быть найдено без необходимости проделывать долгий путь с учетом геометрических данных сердечника:

Пример:
Требуемая индуктивность 100 мкГн; сердечник имеет значение A _L , равное 250 нГн / Н ²

Результат:
Для создания индуктивности 100 мкГн сердечник должен иметь 20 обмоток.

1.7.3 Импеданс Z

Если катушка индуктивности работает от переменного напряжения, очевидно, что она имеет другое сопротивление, чем при работе на постоянном токе.

Сопротивление переменного напряжения, приложенного к клеммам катушки, называется импедансом (Z) .

Рис. 1.24: Взаимосвязь между импедансом, реактивным сопротивлением и сопротивлением

Полное сопротивление (Z) зависит от частоты и складывается из геометрической суммы сопротивления потерь (R) и реактивного сопротивления (X _L ) идеальной катушки (L).

Реактивное сопротивление X _L определяется следующим образом:

Наблюдение:

Импеданс растет с увеличением частоты.

Эта линейная зависимость продолжается до бесконечно высоких частот для идеальной катушки.

Рис. 1.25: Кривая импеданса для реальных катушек индуктивности

Однако из-за частотной зависимости проницаемости и конструкции катушки и паразитной емкости применимость катушек на высоких частотах ограничена.

Импеданс быстро уменьшается от собственной резонансной частоты; индуктивный характер катушки исчезает.

1.7.4 Собственная резонансная частота (SFR)

Рис. 1.26: Эквивалентная схема реальной индуктивности

Каждая катушка индуктивности также имеет емкостную связь, возникающую из ее обмоток или многослойных элементов. Эти паразитные емкости обозначены конденсатором (C) в эквивалентной схеме. Этот конденсатор в катушке образует параллельный резонансный контур с индуктивностью.

На собственной резонансной частоте входная энергия колеблется между элементами индуктивности и емкости.Внешняя энергия больше не поглощается (идеальная катушка).

Если катушка работает выше своего резонанса, она становится все более емкостной. На практике катушки должны работать намного ниже их резонансной частоты.

1,7,5 R потери

Активная мощность (тепловые потери) не рассеивается в реактивном сопротивлении X _L из-за сдвига фаз 90 ° между напряжением и током. Общие потери в катушке можно объединить в сопротивление потерь (R), которое последовательно соединено с идеальной индуктивностью (L).В результате получается эквивалентная схема реальной индуктивности (см. Рисунок 1.26).

Поскольку потери в R зависят от частоты, сопротивление постоянному току (DCR) также всегда определяется в технических характеристиках. Это зависит от материала используемого провода или типа конструкции индукторов SMD и определяется при комнатной температуре путем простого измерения сопротивления.

Размер сопротивления постоянному току DCR имеет прямое влияние на повышение температуры катушки. Поэтому следует избегать длительного превышения текущего номинального значения.Общие потери в катушке состоят как из потерь в сопротивлении постоянному току DCR, так и из следующих частотно-зависимых компонентов:

• Потери в материале сердечника (потери на магнитный гистерезис, вихретоковые потери)
• Дополнительные потери в проводнике от скин-эффекта (смещение тока на высоких частотах)
• Потери магнитного поля соседних обмоток (эффект близости)
• Радиационные потери
• Потери от дополнительной магнитной защиты (WE-MI)

Все эти компоненты потерь можно объединить в сопротивление потерь (R).Это сопротивление потерь в первую очередь отвечает за определение качества катушки индуктивности. К сожалению, математическое определение сопротивления потерь R невозможно.

Следовательно, индукторы обычно измеряются во всем частотном диапазоне с помощью анализатора импеданса. Это измерение обеспечивает отдельные компоненты X _L (f), R (f) и Z (f). Добротность определяется как характеристика качества индуктора.

1.7.6 Потери меди

Потери в меди для индуктивных компонентов состоят из потерь на постоянный ток и потерь на вихревые токи.Потери постоянного тока рассчитываются по закону Ома:

P _В = потеря мощности
R = сопротивление постоянному току
I _RMS = эффективный ток

На более высоких частотах также есть потери из-за скин-эффекта и эффекта близости. Эти потери от вихревых токов можно напрямую объяснить законом Фарадея. Ток, протекающий по проводнику, создает вокруг него магнитное поле.

Это магнитное поле быстро изменяется из-за высокой частоты, так что в проводнике и в соседних проводниках индуцируется напряжение.Это напряжение генерирует ток, противодействующий исходному току. Таким образом, в проводнике, а также в соседних проводниках возникают дополнительные токи.

Рассматривая одиночный проводник, говорят о скин-эффекте. Для проводников, по которым протекают токи высокой частоты, ток течет только по внешней обшивке проводника (рисунок 1.27). Глубина проникновения, при которой плотность тока упала до значения 1 / e, определяется как:

δ = глубина проникновения
ρ = удельное сопротивление
ω = угловая частота 2 πf
μ = проницаемость проводника (для меди μ ₀ )

Глубина проникновения при 50 Гц равна 9.38 мм, при 10 кГц – 0,66 мм.

Рис. 1.27: Распределение тока в проводнике на высокой частоте. В качестве примера приведен диаметр проволоки, в 7 раз превышающий глубину проплавления.

Эффект близости играет гораздо большую роль для трансформаторов, когда соседние проводники генерируют поля, смещенные током. Возможность расчета потерь на вихревые токи для простых геометрий описана Доуэллом. Теория была развита Карстеном. Математическое описание выходит далеко за рамки этой книги.

Здесь гораздо важнее описать имеющиеся варианты ограничения потерь на вихревые токи. Потери на вихревые токи зависят от величины магнитного поля. Таким образом, способ ограничения потерь на вихревые токи заключается в ограничении напряженности магнитного поля.

Это может быть достигнуто, например, путем чередования обмоток, т.е. наматывается половина первичной обмотки, затем вторичная обмотка, а затем вторая половина первичной обмотки. Это снижает абсолютное значение магнитного поля и, следовательно, потери на вихревые токи.На рисунке 1.28 показан профиль поля H в обмотке из медной фольги со структурой обмотки первичная – вторичная и половина первичной вторичной обмоток – половина первичной.

Напряженность магнитного поля внутри обмотки возрастает изнутри наружу, потому что все больше витков (все большие токи) ограничиваются силовыми линиями. Магнитное поле вторичной обмотки противоположно исходному полю. Это снова служит для уменьшения магнитного поля. Уменьшение величины поля H очевидно.

Рис. 1.28: Профиль магнитного поля в трансформаторе с различными конфигурациями обмоток.

Тонкие плоские проводники, например медная фольга, также может использоваться для намотки. Толщина должна быть порядка глубины проникновения. Это следует использовать только для небольшого числа витков, потому что при большем количестве обмоток большое количество слоев вызывает более высокие потери на вихревые токи.

Еще одним вариантом уменьшения вихревых токов является намотка более тонкими изолированными проводами, а не толстыми.Здесь необходимо следить за тем, чтобы отдельные провода, подключенные параллельно, имели одинаковое распределение тока. Здесь можно использовать высокочастотные литц-провода, при которых отдельные провода скручиваются друг с другом, так что в среднем каждый провод имеет одинаковое положение в магнитном поле. С этим вариантом также нужно следить, чтобы количество слоев не было слишком большим.

1.7.7 Определение добротности Q

Компонент входящей извне энергии, преобразованной в тепло в сопротивлении потерь R, не вносит вклад в энергию, запасенную в магнитном поле.Чем больше эти потери, тем хуже индуктор действует как буфер.

Это определяет качество как фактор качества Q следующим образом:

Практические значения:

• Воздушный змеевик Q до 400
• Ферритовый дроссель Q до 150
• Многопользовательские индукторы SMD Q до 60

График качество-частота помогает выбрать лучшую конструкцию индуктора для конкретного применения.

Фиг.1.29: График добротности – частота

Наблюдения:

• Качество повышается до максимального значения, а затем снижается.
• Допускаются постоянные малые потери в сопротивлении R индуктора вплоть до пикового значения качества.
• За пределами пикового значения становятся очевидными значительные потери, а также изменяется индуктивность из-за нелинейности ферритового материала.
• Рабочий диапазон с наименьшими потерями может быть определен до критической точки качества.Если индуктор используется на более высоких частотах, потери быстро увеличиваются.

1.7.8 Температурный режим

Рис. 1.30: Температурный дрейф многослойного индуктора

Катушки с ферромагнитным сердечником демонстрируют переменную индуктивность в зависимости от температуры окружающей среды. Если к стабильности цепей фильтров, построенных с использованием катушек индуктивности
, предъявляются высокие требования (например, в измерительной технике), целесообразно выбрать катушку с почти линейной температурной кривой.В этом случае изменение индуктивности ΔL относительно номинальной индуктивности L катушки является наименьшим. На рисунке 1.30 показан этот график для многослойной катушки индуктивности.

1.7.9 Номинальный ток

Номинальный ток, который может выдерживать индуктор, более точно определен в главе о компонентах для различных продуктов.

Номинальный ток обычно связан с заявлением о самонагреве компонента. Если компонент работает при номинальном токе, он нагревается выше температуры окружающей среды на температуру, указанную в техническом паспорте.

Затем необходимо выяснить, подходит ли полученная температура компонента для данного применения. В противном случае необходимо выбрать компонент с более высокой номинальной допустимой нагрузкой по току. Необходимо убедиться, что при работе при номинальном токе деталь не превышает рабочую температуру (в противном случае необходимо снижение номинальных характеристик).

Пример:
Экранированный многослойный индуктор (WE-MI) Максимальное значение номинального тока достигается, если повышение температуры компонента превышает 20 ° C для выбранного испытательного тока.

1.7.10 Ток насыщения

Ток насыщения катушки индуктивности – это ток, при котором значение индуктивности упало на процент, указанный в таблице данных.

Пример:
Дроссели для накопителей серии WE-PD

Здесь ток насыщения определяет ток, при котором индуктивность упала на 10%.

Примечание!
Специально для приложений с коммутационным контроллером или приложений с высокими емкостными нагрузками или высокими пусковыми токами, пиковый ток, протекающий через катушку индуктивности, может быть значительно выше в момент включения, чем при нормальной работе.Это может привести к полному насыщению компонента и, следовательно, к возможным последующим неисправностям электроники. Желательно понимать и ограничивать ток или активировать функции плавного пуска.

Рис. 1.31: График индуктивности-тока

---

ABC CLR: Глава L Индукторы

Индуктивность, импеданс и потери

Лицензионный контент EPCI: Würth Elektronik eiSos, Trilogy of Magnetics, распечатки справочника можно заказать здесь.

Содержание этой страницы находится под международной лицензией Creative Commons Attribution-ShareAlike 4.0.

Ссылки для намотки рулонов Страница

Сделай сам К4ЗАД Калькулятор намотки катушки Ссылки

Радио домашние пивовары легко справляются с работой с резисторами и конденсаторами; они поставляются в аккуратных маленьких упаковках, и их ценность легко решительно, но работать с индукторами не так просто.Чтобы получить индуктивность и другие желаемые характеристики, катушки часто не могут быть куплены и должны быть намотаны на заказ. Катушка дизайн / создание включает выбор правильной формы катушки, размера провода и материал сердечника (если не воздух), все составляющие процесс немного сложный. к счастью несколько авторы / веб-программисты взяли основные формулы для конструкции индуктора и создали онлайн-калькуляторы, которые помогают определить физический параметры, необходимые для катушки с желаемой электрической характеристики.Ниже приведены ссылки на онлайн-калькуляторы. полезен при разработке катушек для радиоприложений. Посмотрите на этих сайтах, так как некоторые из них перечисляют другие полезные калькуляторы.

Кому насколько мне известно во время создание этой страницы все ссылки к бесплатным калькуляторам без регистрации, необходимой для использования. Как и я использовал только некоторые из них я не давать никаких рекомендаций, и порядок листинга не указывает предпочтение. Информация о каждом может помочь вам выбрать лучшие удовлетворяя ваши потребности.Стоит отметить, что авторы некоторых критически относятся к точности используемых формул другими.

Большое спасибо авторам за их работу в создание этого браузерного дизайна вспомогательные средства доступны.

### Указывает на калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.

Несколько Расчеты или конфигурации катушек:

Три Калькуляторы индуктивности – Единицы: nHenrys, uHenrys & mHenrys – вычисляет количество витков, индуктивность катушки AL и L
и многое другое – Несколько вариантов единиц измерения – Выходная индуктивность – Калькуляторы для доступно несколько форм без катушки.
Калькулятор индуктивности катушки – Несколько выбор единиц – вычисляет индуктивность для однослойных / многослойных соленоидов и плоские спиральные катушки
Find L для катушек и других форм – Несколько вариантов юнитов + Проницаемость – Выходная индуктивность
Калькулятор индуктивности с двумя катушками – Входы в дюймах – Делает однослойные и многорядные многослойные катушки.Вычисляет L
Пять Калькуляторы катушки / индуктивности – Несколько калькуляторов индуктивности использование различных знаний для входных данных – Размеры в мм
Калькулятор с тремя катушками / индуктивностью – Вводятся в см или дюймах – Делает однослойный и многорядные многослойные катушки. Вычисляет L
Еще три калькулятора катушек / индуктивностей – Выбор единиц для входов – 2 выхода – индуктивность – другое – реактивность

Одноместный Катушки с воздушным сердечником слоя:

Калькулятор индуктивности с воздушным сердечником – Широкий выбор единиц размера катушки – Вычисляет индуктивность с выбором единицы измерения
Воздух Разработчик сердечника индуктора – Калькулятор – Ввод в миллигенах и дюймах – расширенный вывод на новую страницу Калькулятор индуктора с воздушным сердечником
– включает Q – Размеры в мм – Вычисляет Индуктивность, добротность и длина провода Калькулятор индуктивности
AL ### – Введите два значения и получите третье – Единицы индуктивности: mHenrys, uHenrys, nHenrys Калькулятор индуктивности катушки
– Размеры в дюймах -Вычисляет индуктивность в uHenrys и длина провода в дюймах и футах
Калькулятор с двумя катушками – Входные размеры в миллиметрах или дюймах и количество оборотов – Вычисляет индуктивность и количество витков
Helical Coil Calculator – Input размер в мм или дюймах – вычисляет индуктивность и провод длина – включает собственная емкость
Многоступенчатая конструкция катушки -Входной размер в мм – Расчеты для несколько свойств змеевика – с примерами
LF Калькулятор индуктивности – Размеры в мМетрах и МГц (для Q) – Результат в микроГенри и Q
Одноместный Слой, воздушный сердечник, калькулятор индуктивности – размеры указаны в мм МГц (для Q) – Вычисляет L в нескольких единицах и длине провода Калькулятор индуктивности сердечника
– Размеры в дюймах – Выход в uHenrys
Индуктивность однослойных катушек на цилиндрические формы – введите радиус, длину, проницаемость и количество витков – вычисляет калькуляторы индуктивности uH
LC – Входные витки, диаметры катушек и проводов в дюймах – Вычисляет uHenrys и провод и катушку длина Калькулятор индуктивности катушки с воздушным сердечником
– Входные обороты, диаметр и длина рулона в дюймах – Расчет L в uHenrys
однослойный Калькулятор воздушной катушки – Широкий выбор единиц – Входная длина, диаметры катушек и проводов – Вычисления Обороты и длина рулона
Одноместный Калькулятор слоев воздушного змеевика – ### – Поля ввода: обороты, диаметр, длина и L – введите 3, получите 4-е.- С примерами
Еще одна однослойная воздушная катушка Калькулятор – Выбор единиц – Входная длина, диаметры катушки и проволоки – Вычисление оборотов и длина рулона
Калькулятор цилиндрической катушки профессора Койла – Закрывает ли катушки намотки и намотки пространства – Прочтите инструкции первый
Два Калькуляторы катушек – выбор единиц – один рассчитывает L, другой витков и длину намотки

Одноместный Слой катушек поверх магнитного материала:

Универсальный однослойный калькулятор – ### – Ввод: 4 параметра и 5-й – банка использоваться для поиска неизвестного ядра Проницаемость
Комплексный калькулятор катушек – Слишком обширно, чтобы резюмировать – Взгляните на это – Включает собственная емкость Конструкция катушки
и калькулятор индуктивности – Ввод: размеры в метрических единицах или дюймах – Вычисляет индуктивность в единицах Генри
Индуктивность однослойных катушек – вход: Обороты, размеры в мметрах и перм.- Рассчитывает L на новой странице
вычисляет индуктивность круговой петли – Ввод: витки, размеры в миллиметрах и перми. – Рассчитывает L в Генри
определяет индуктивность однооборотного соленоида – Выбор единиц – Ввод: число оборотов, радиус длины и допустимость. – Выход L в нескольких единицах
Цилиндрическая катушка индуктивности Калькулятор дизайна – ### – через 4 калькулятора – выбор единиц – Вычисляет L, повороты, допуск, площадь и длину

Тороид Катушки:

Калькулятор Amidon Toroid (Железный порошок) – Введите желаемый размер ядра uHenrys и Amidon и цвет в найти L, повороты и т. д.
Калькулятор тороида Amidon (феррит) – Введите желаемый размер ядра uHenrys и Amidon и цвет в найти L, повороты и т. д. Калькулятор индуктивности с ферритовым сердечником
– Введите количество витков и AL, чтобы найти индуктивность катушки.
Индуктивность тороида – вход размеры сердечника в см, количество витков и проницаемость для поиска катушки Индуктивность Калькулятор индуктивности тороида
– Вход размеры сердечника в мм или мил, количество витков и проницаемость, чтобы найти катушку Индуктивность
Калькулятор индуктивности тороида на оборот – Широкий выбор единиц ввода и количества оборотов – Выходы L и другие характеристики
Калькулятор индуктивности с двумя тороидами – Широкий выбор устройств ввода / вывода & количество витков – Выходы L и другие характеристики
Калькулятор намотки тороида – Находит количество витков для питаемых железных и ферритовых сердечников. известный размер и состав материала
Некоторый помогите работать с тороидами: (также см. последний раздел Дополнительные Катушка Информация ниже)

Тороид Таблица спецификаций – для тороидов 88 – с гибким калькулятор
Тороид Графики характеристик – Восемь диаграмм данных по тороидам
G-QRP Информация о клубном тороиде – для обычных тороидов – включает AL данные Таблица индуктивности тороида
G-QRP Club – PDF-файл значений mHenrys для много цветов тороиды с 1-50 оборотами
Что это за материал? – Мой PDF Сборник методов идентификации материала тороида
Тороиды – некоторые практические соображения – Подробная статья – с номинальной мощностью (Ватт) для многих общие тороиды
Собственная емкость тороида Индукторы – возможно, больше, чем вам нужно знать. собственная емкость в конструкции катушки

Спираль (Плоские) Катушки

Плоские спиральные индукторы с воздушным сердечником – Большой выбор единиц измерения – Находит индуктивность – Пять других Калькуляторы катушек здесь
Калькулятор плоских спиральных катушек – Принимает вводимые размеры в дюймах или мм – вывод в uHenrys
Плоская спиральная катушка Калькулятор индуктивности – Размеры в мкм – Имеет несколько плоских форм – Другое калькулятор ссылки здесь
однослойный Калькулятор плоской воздушной катушки – принимает вводимые размеры в дюймах или мм – вывод в uHenrys или nHenrys Калькулятор спирального индуктора
– Размеры в мметрах – Девять выходы, для различных форм и формул, рассчитываются Калькулятор спиральной катушки
– Габаритные размеры в мм и количество оборотов – Выход в uHenrys – Использует формулу Уиллера
Калькулятор спирали профессора Койла из паутины – Красиво – Включает в себя таблицу проводов и калькулятор резонанса – Прочтите инструкции ниже

Соленоид – Многослойные катушки:

Многослойный Калькулятор индуктивности с воздушным сердечником – Выбор единиц – Входы: L, Катушка диаметр и длина, калибр провода – несколько выходов
Калькулятор индуктивности многослойного воздушного сердечника – Выбор единиц – Сложные входы из-за слоев – Только полезные ниже 3 МГц Калькулятор индуктивности многослойной катушки
– Air Core – мм или дюймы – сложные входы из-за слоев – несколько выходов
Калькулятор физических свойств катушки – Для катушек соленоидов реле – Не для RF

проницаемость – Найти Проходимость неизвестного ядра

Определите проницаемость тороида – Вводятся в mHenrys к nHenrys и мм или же см размеры жилы – Выпуск Пермь.& AL
Как определить проницаемость неизвестного Ядра – Входы в uHenrys & размеры в мм – Также калькулятор индуктивности
Видеть также: Универсальный однослойный калькулятор ###

Реактивное сопротивление:

Калькулятор индуктивного сопротивления

– Принимает входные данные в герцах до ГГц и от нГенри до Генри. Калькулятор импеданса индуктора
– Принимает входные сигналы в герцах до МГц и Калькулятор реактивного сопротивления от pHenrys до Henrys
R L C ### – Единицы измерения исправлены: uFarads, mHenrys & Hertz – Ссылки на емкостной Калькулятор реактивного сопротивления
Реактивное сопротивление Калькулятор для обоих аккредитивов -& Единицы измерения фиксированы: pFarads, uHenrys и MHz

Другой Калькуляторы:

Калькулятор взаимной индуктивности – Вычисляет взаимную индуктивность для 2 катушек индуктивности (в mHenrys) и их коэффициент связи.
Другой калькулятор взаимной индуктивности – То же, что и выше, но предлагает выбор единиц.
Сайт разработки радиочастотных фильтров WA4DSY – Есть несколько типов фильтров с выходными графиками – Действительно полезный; a keeper
Калькулятор коэффициента поворотов – Возводит ли отношение поворотов в квадрат. Калькулятор глубины кожи
RF Cafe – Нечасто требуется, но с отличного сайта для радиотехников и радиолюбителей. Калькулятор самоиндукции провода
– Выбор входных единиц – вычисляет L в нГенри длина провода
Комплексная конструкция катушки Тесла – Нет полезно для РФ?
Больше калькуляторов катушек Тесла – Не подходит для РФ

Дополнительный Информация о катушке:

Балун и выбор сердечника трансформатора – много полезной информации и ссылки из W8JI
Провода, тороиды и трансформаторы – много полезного информация – Включает таблицу сечения проводов и многое другое.
PDF – Измерение свойств мягкого ферритового сердечника – Четырехстраничный PDF-файл с информацией об измерениях.
Все о феррите из гаек & Volts Magazine – Хорошее образование со ссылками в конце

### калькуляторы которые выходят за рамки простого решения уравнения для одного заявленного отсутствующее значение, найдя недостающее значение при условии, что другие значения введены.

Пожалуйста контакт мне о других приложениях этого типа и о любые исправления информации на этой странице.

Назад к странице указателя

Главный Сайт – Архив истории морского радио

Создано 11.11.2018 – Код страницы обновлен 26.02.2021

Индуктор

Индуктор

Подборка недорогих катушек индуктивности

Тип: пассивный

Принцип работы: Электромагнитная индукция

Первая постановка: Майкл Фарадей (1831)

Электронный символ:

Индуктор, также называемый катушкой, дросселем или реактором, представляет собой пассивный двухконтактный электрический компонент, который сопротивляется изменениям электрического тока, проходящего через него.Он состоит из проводника, такого как провод, обычно намотанный в катушку. Когда через него протекает ток, энергия временно сохраняется в магнитном поле в катушке. Когда ток, протекающий через катушку индуктивности, изменяется, изменяющееся во времени магнитное поле индуцирует в проводнике напряжение в соответствии с законом электромагнитной индукции Фарадея. Согласно закону Ленца направление индуцированной ЭДС всегда таково, что оно противодействует изменению тока, создавшему ее. В результате индукторы всегда противодействуют изменению тока, так же как маховик противодействует изменению скорости вращения.Следует проявлять осторожность, чтобы не путать это с сопротивлением, обеспечиваемым резистором.

Катушка индуктивности характеризуется своей индуктивностью, отношением напряжения к скорости изменения тока, которое имеет единицы генри (Гн). Индукторы имеют значения, которые обычно находятся в диапазоне от 1 мкГн (10-6Гн) до 1 Гн. Многие индукторы имеют магнитный сердечник из железа или феррита внутри катушки, который служит для увеличения магнитного поля и, следовательно, индуктивности. Наряду с конденсаторами и резисторами, индукторы являются одним из трех пассивных элементов линейной цепи, составляющих электрические цепи.Индукторы широко используются в электронном оборудовании переменного тока (AC), особенно в радиооборудовании. Они используются для блокировки переменного тока, позволяя проходить постоянному току; индукторы, предназначенные для этой цели, называются дросселями. Они также используются в электронных фильтрах для разделения сигналов разных частот и в сочетании с конденсаторами для создания настраиваемых схем, используемых для настройки радио и ТВ-приемников.

Осевые свинцовые индукторы (100 мкГн)

Содержание

1 Обзор

1.1 Материальное уравнение

1.2 Закон Ленца

1.3 Идеальные и настоящие индукторы

2 Приложения

3 Конструкция индуктора

4 типа индуктора

4.1 Индуктор с воздушным сердечником

4.1.1 Радиочастотный индуктор

4.2 Индуктор с ферромагнитным сердечником

4.2.1 Индуктор с ламинированным сердечником

4.2.2 Индуктор с ферритовым сердечником

4.2.3 Индуктор с тороидальным сердечником

4.2.4 Дроссель

4.3 Переменный индуктор

5 Теория схем

5.1 Реактивное сопротивление

5.2 Анализ цепи Лапласа (s-область)

5.3 Индукторные сети

5,4 Накопленная энергия

6 Q-фактор

7 Формулы индуктивности

Обзор

Индуктивность (L) возникает из-за магнитного поля вокруг проводника с током; электрический ток через проводник создает магнитный поток.С математической точки зрения индуктивность определяется тем, какой магнитный поток φ через цепь создается заданным током i

.

Катушки индуктивности с ферромагнитными сердечниками нелинейны; индуктивность изменяется с током, в этом более общем случае индуктивность определяется как

Любой провод или другой проводник будет генерировать магнитное поле, когда через него протекает ток, поэтому каждый проводник имеет некоторую индуктивность. Индуктивность цепи зависит от геометрии пути тока, а также от магнитной проницаемости соседних материалов.Индуктор – это компонент, состоящий из проволоки или другого проводника, имеющего форму для увеличения магнитного потока через цепь, обычно в форме катушки или спирали. Намотка провода в катушку увеличивает количество раз, когда линии магнитного потока связывают цепь, увеличивая поле и, следовательно, индуктивность. Чем больше витков, тем выше индуктивность. Индуктивность также зависит от формы катушки, расстояния между витками и многих других факторов. При добавлении «магнитного сердечника», сделанного из ферромагнитного материала, такого как железо, внутрь катушки, намагничивающее поле катушки будет индуцировать намагничивание в материале, увеличивая магнитный поток.Высокая магнитная проницаемость ферромагнитного сердечника может увеличить индуктивность катушки в несколько тысяч раз по сравнению с тем, что было бы без нее.

Материальное уравнение

Любое изменение тока через катушку индуктивности создает изменяющийся магнитный поток, вызывая напряжение на катушке индуктивности. Согласно закону индукции Фарадея, напряжение, вызванное любым изменением магнитного потока в цепи, равно

.

сверху

Таким образом, индуктивность также является мерой величины электродвижущей силы (напряжения), генерируемой при заданной скорости изменения тока.Например, катушка индуктивности с индуктивностью 1 генри создает ЭДС 1 вольт, когда ток через катушку индуктивности изменяется со скоростью 1 ампер в секунду. Обычно это считается определяющим соотношением (определяющим уравнением) индуктора.

Двойной индуктор – это конденсатор, который накапливает энергию в электрическом поле, а не в магнитном поле. Его отношение тока к напряжению получается путем обмена током и напряжением в уравнениях катушки индуктивности и замены L емкостью C.

Закон Ленца

Полярность (направление) индуцированного напряжения задается законом Ленца, который гласит, что оно будет таким, чтобы препятствовать изменению тока. Например, если ток через катушку индуктивности увеличивается, индуцированное напряжение будет положительным на клемме, через которую ток входит, и отрицательной на клемме, через которую он выходит, стремясь противодействовать дополнительному току. Энергия внешней цепи, необходимая для преодоления этого потенциального «холма», сохраняется в магнитном поле индуктора; индуктор называется «заряжающим» или «возбуждающим».Если ток уменьшается, индуцированное напряжение будет отрицательным на выводе, через который ток входит, и положительным на выводе, через который он выходит, стремясь поддерживать ток. Энергия магнитного поля возвращается в цепь; индуктор называется “разряжающимся”.

Идеальные и настоящие индукторы

В теории цепей индукторы идеализируются как точно подчиняющиеся приведенному выше математическому соотношению. «Идеальная катушка индуктивности» имеет индуктивность, но не имеет сопротивления или емкости и не рассеивает и не излучает энергию.Однако у реальных индукторов есть побочные эффекты, которые заставляют их поведение отличаться от этой простой модели. У них есть сопротивление (из-за сопротивления провода и потерь энергии в материале сердечника) и паразитная емкость (из-за электрического поля между витками провода, которые имеют немного разные потенциалы). На высоких частотах емкость начинает влиять на поведение катушки индуктивности; на некоторой частоте настоящие катушки индуктивности ведут себя как резонансные цепи, становясь саморезонансными. Выше резонансной частоты емкостное реактивное сопротивление становится доминирующей частью импеданса.На более высоких частотах резистивные потери в обмотках увеличиваются из-за скин-эффекта и эффекта близости.

Катушки индуктивности с ферромагнитными сердечниками имеют дополнительные потери энергии из-за гистерезиса и вихревых токов в сердечнике, которые увеличиваются с увеличением частоты. При высоких токах индукторы с железным сердечником также показывают постепенное отклонение от идеального поведения из-за нелинейности, вызванной магнитным насыщением сердечника. Индуктор может излучать электромагнитную энергию в окружающее пространство и цепи и может поглощать электромагнитные излучения от других цепей, вызывая электромагнитные помехи (EMI).В реальных приложениях индуктивности эти паразитные параметры могут считаться такими же важными, как и индуктивность.

Приложения

Большой трехфазный индуктор нагрузки с железным сердечником мощностью 50 МВАр на австрийской подстанции

Ферритовый дроссель, состоящий из ферритового цилиндра, удаляет электронные помехи из кабеля питания компьютера.

Пример фильтрации сигнала. В этой конфигурации катушка индуктивности блокирует переменный ток, позволяя проходить постоянному току.

Пример фильтрации сигнала. В этой конфигурации катушка индуктивности разъединяет постоянный ток, позволяя проходить переменному току.

Катушки индуктивности широко используются в аналоговых схемах и обработке сигналов. Применения варьируются от использования больших катушек индуктивности в источниках питания, которые в сочетании с фильтрующими конденсаторами удаляют остаточный шум, известный как сетевой гул или другие колебания от выхода постоянного тока, до небольшой индуктивности ферритового шарика или тора, установленного вокруг кабеля, чтобы предотвратить передачу радиочастотных помех по проводам.Индукторы используются в качестве накопителя энергии во многих импульсных источниках питания для выработки постоянного тока. Катушка индуктивности подает энергию в цепь для поддержания протекания тока в периоды выключения.

Катушка индуктивности, подключенная к конденсатору, образует настроенный контур, который действует как резонатор для колебательного тока. Настроенные схемы широко используются в радиочастотном оборудовании, таком как радиопередатчики и приемники, в качестве узкополосных фильтров для выбора одной частоты из составного сигнала и в электронных генераторах для генерации синусоидальных сигналов.

Два (или более) расположенных рядом индуктора, которые имеют связанный магнитный поток (взаимную индуктивность), образуют трансформатор, который является основным компонентом каждой энергосистемы общего пользования. Эффективность трансформатора может снизиться с увеличением частоты из-за вихревых токов в материале сердечника и скин-эффекта на обмотки. Размер ядра можно уменьшить на более высоких частотах. По этой причине в самолетах используется переменный ток 400 Гц вместо обычных 50 или 60 Гц, что позволяет значительно сэкономить в весе за счет использования трансформаторов меньшего размера.

Катушки индуктивности

также используются в системах электропередачи, где они используются для ограничения коммутируемых токов и токов короткого замыкания. В этой области их чаще называют реакторами.

Поскольку индукторы имеют сложные побочные эффекты (подробно описаны ниже), которые заставляют их отклоняться от идеального поведения, потому что они могут излучать электромагнитные помехи (EMI), и, прежде всего, из-за их большого размера, который не позволяет их интегрировать в полупроводниковые микросхемы, использование катушек индуктивности в современных электронных устройствах, особенно в компактных портативных устройствах, уменьшается.Настоящие катушки индуктивности все чаще заменяются активными цепями, такими как гиратор, который может синтезировать индуктивность с помощью конденсаторов.

Конструкция индуктора

Катушка индуктивности с ферритовым сердечником и двумя обмотками по 47 мГн.

Катушка индуктивности обычно состоит из катушки из проводящего материала, обычно изолированного медного провода, обернутого вокруг сердечника из пластика или ферромагнитного (или ферримагнитного) материала; последний называется индуктором с «железным сердечником».Высокая магнитная проницаемость ферромагнитного сердечника увеличивает магнитное поле и ограничивает его плотностью к индуктору, тем самым увеличивая индуктивность. Низкочастотные индукторы сконструированы как трансформаторы, с сердечниками из электротехнической стали, ламинированными для предотвращения возникновения вихревых токов. «Мягкие» ферриты широко используются для сердечников, превышающих звуковые частоты, поскольку они не вызывают больших потерь энергии на высоких частотах, как обычные сплавы железа. Индукторы бывают разных форм. Большинство из них построено в виде эмалированной проволоки (магнитной проволоки), обернутой вокруг ферритовой катушки с проволокой, открытой снаружи, в то время как некоторые полностью покрывают провод ферритом и называются «экранированными».Некоторые индукторы имеют регулируемый сердечник, который позволяет изменять индуктивность. Индукторы, используемые для блокировки очень высоких частот, иногда изготавливаются путем нанизывания ферритовой бусины на провод.

Небольшие катушки индуктивности можно выгравировать прямо на печатной плате, расположив след по спирали. В некоторых таких плоских индукторах используется плоский сердечник.

Катушки индуктивности

могут также быть построены на интегральных схемах с использованием тех же процессов, которые используются для изготовления транзисторов. Обычно используются алюминиевые межсоединения, расположенные в виде спиральной катушки.Однако небольшие размеры ограничивают индуктивность, и гораздо чаще используется схема, называемая «гиратором», в которой конденсатор и активные компоненты действуют аналогично катушке индуктивности.

Типы индукторов

Индуктор с воздушным сердечником

Трансформатор резонансных колебаний от передатчика искрового разрядника. Сцепление можно регулировать, перемещая верхнюю катушку на опорной штанге. Демонстрирует конструкцию с высоким коэффициентом добротности с разнесенными витками трубок большого диаметра.

Термин «катушка с воздушным сердечником» описывает индуктор, в котором не используется магнитный сердечник, сделанный из ферромагнитного материала. Этот термин относится к катушкам, намотанным на пластмассовые, керамические или другие немагнитные формы, а также к катушкам, внутри обмоток которых находится только воздух. Катушки с воздушным сердечником имеют более низкую индуктивность, чем катушки с ферромагнитным сердечником, но часто используются на высоких частотах, потому что они свободны от потерь энергии, называемых потерями в сердечнике, которые возникают в ферромагнитных сердечниках, которые увеличиваются с частотой. Побочный эффект, который может возникать в катушках с воздушным сердечником, в которых обмотка не имеет жесткой опоры на форму, – это «микрофонность»: механическая вибрация обмоток может вызывать колебания индуктивности.

Радиочастотный индуктор

Коллекция радиочастотных индукторов, показывающая методы снижения потерь. Три вверху слева и ферритовая петля или стержневая антенна внизу имеют обмотки корзины.

На высоких частотах, особенно радиочастотах (RF), индукторы имеют более высокое сопротивление и другие потери. Помимо потери мощности, в резонансных цепях это может снизить добротность цепи, расширяя полосу пропускания. В ВЧ-индукторах, которые в основном представляют собой типы с воздушным сердечником, используются специальные методы изготовления, чтобы минимизировать эти потери.Убытки из-за этих эффектов:

• Скин-эффект: сопротивление провода высокочастотному току выше, чем его сопротивление постоянному току из-за скин-эффекта. Радиочастотный переменный ток не проникает глубоко в тело проводника, а проходит по его поверхности. Следовательно, в сплошном проводе большая часть поперечного сечения провода не используется для проведения тока, который находится в узком кольцевом пространстве на поверхности. Этот эффект увеличивает сопротивление провода в катушке, который уже может иметь относительно высокое сопротивление из-за его длины и небольшого диаметра.
• Эффект близости: Другой подобный эффект, который также увеличивает сопротивление провода на высоких частотах, – это эффект близости, который возникает в параллельных проводах, лежащих близко друг к другу. Индивидуальное магнитное поле соседних витков индуцирует вихревые токи в проводе катушки, в результате чего ток в проводнике концентрируется в тонкой полосе на стороне рядом с соседним проводом. Как и скин-эффект, это уменьшает эффективную площадь поперечного сечения провода, проводящего ток, увеличивая его сопротивление.

Катушка резервуара High Q в коротковолновом передатчике

Катушка паутины

Регулируемая ферритовая радиочастотная катушка с сетчатой ​​обмоткой и литц-проволокой

• Диэлектрические потери: Высокочастотное электрическое поле около проводников в катушке резервуара может вызывать движение полярных молекул в соседних изоляционных материалах, рассеивая энергию в виде тепла. Таким образом, катушки, используемые для настроенных схем, часто не наматываются на формы катушек, а подвешены в воздухе, поддержанные узкими пластиковыми или керамическими полосками.
• Паразитная емкость: емкость между отдельными витками катушки, называемая паразитной емкостью, не вызывает потерь энергии, но может изменить поведение катушки. Каждый виток катушки имеет немного другой потенциал, поэтому электрическое поле между соседними витками накапливает заряд на проводе, поэтому катушка действует так, как будто у нее есть конденсатор, параллельный ей. На достаточно высокой частоте эта емкость может резонировать с индуктивностью катушки, образуя настроенный контур, в результате чего катушка становится саморезонансной.

Чтобы уменьшить паразитную емкость и эффект близости, высокодобротные ВЧ-катушки сконструированы таким образом, чтобы не было большого количества витков, лежащих близко друг к другу, параллельно друг другу. Обмотки радиочастотных катушек часто ограничиваются одним слоем, а витки разнесены друг от друга. Чтобы уменьшить сопротивление из-за скин-эффекта, в мощных индукторах, таких как те, которые используются в передатчиках, обмотки иногда изготавливаются из металлической полосы или трубки с большей площадью поверхности, а поверхность покрывается серебром.

• Катушки с плетением корзины: для уменьшения эффекта близости и паразитной емкости многослойные РЧ-катушки намотаны в виде рисунка, в котором последовательные витки не параллельны, а перекрещены под углом; их часто называют сотовыми или корзиночными катушками. Иногда их наматывают на вертикальные изолирующие опоры с помощью дюбелей или пазов, при этом проволока вплетается и выходит через пазы.
• Бухты паутины: Другой конструкторский метод с аналогичными преимуществами – это плоские спиральные бухты.Их часто наматывают на плоскую изолирующую опору с радиальными спицами или прорезями, при этом проволока вплетается и выходит через прорези; их называют спиралями паутины. Форма имеет нечетное количество прорезей, поэтому последовательные витки спирали лежат на противоположных сторонах формы, увеличивая разделение.
• Литц-провод: для уменьшения потерь на скин-эффект некоторые катушки намотаны специальным радиочастотным проводом, называемым литц-проводом. Вместо одного сплошного проводника литц-провод состоит из нескольких более мелких проволочных жил, по которым проходит ток.В отличие от обычного многожильного провода, жилы изолированы друг от друга, чтобы ток на поверхность не передавался через скин-эффект, и скручены или сплетены вместе. Схема скручивания гарантирует, что каждая жила провода тратит одинаковое количество своей длины на внешней стороне жгута проводов, поэтому скин-эффект распределяет ток равномерно между жилами, в результате чего площадь поперечного сечения проводимости больше, чем у эквивалентного одиночного провода.

Индуктор с ферромагнитным сердечником

Различные типы индукторов и трансформаторов с ферритовым сердечником

Катушки индуктивности

с ферромагнитным сердечником или железным сердечником используют магнитный сердечник, сделанный из ферромагнитного или ферримагнитного материала, такого как железо или феррит, для увеличения индуктивности.Магнитопровод может увеличить индуктивность катушки в несколько тысяч раз за счет увеличения магнитного поля из-за его более высокой магнитной проницаемости. Однако магнитные свойства материала сердечника вызывают несколько побочных эффектов, которые изменяют поведение индуктора и требуют специальной конструкции:

• Потери в сердечнике: изменяющийся во времени ток в ферромагнитном индукторе, который вызывает изменяющееся во времени магнитное поле в его сердечнике, вызывает потери энергии в материале сердечника, которые рассеиваются в виде тепла за счет двух процессов:
  
  • Вихревые токи : Согласно закону индукции Фарадея, изменяющееся магнитное поле может индуцировать циркулирующие петли электрического тока в проводящем металлическом сердечнике.Энергия этих токов рассеивается в виде тепла в сопротивлении материала сердечника. Количество потерянной энергии увеличивается с увеличением площади внутри контура тока.
  • Гистерезис: изменение или реверсирование магнитного поля в сердечнике также вызывает потери из-за движения крошечных магнитных доменов, из которых он состоит. Потери энергии пропорциональны площади петли гистерезиса на графике BH материала сердечника. Материалы с низкой коэрцитивной силой имеют узкие петли гистерезиса и, следовательно, низкие гистерезисные потери.

Для обоих этих процессов потери энергии за цикл переменного тока постоянны, поэтому потери в сердечнике линейно увеличиваются с частотой. Для расчета потерь энергии доступны онлайн-калькуляторы потерь в сердечнике. Используя такие входные данные, как входное напряжение, выходное напряжение, выходной ток, частота, температура окружающей среды и индуктивность, эти калькуляторы могут прогнозировать потери в сердечнике катушек индуктивности и переменном / постоянном токе в зависимости от рабочего состояния используемой цепи.

• Нелинейность: Если ток через катушку с ферромагнитным сердечником достаточно высок, чтобы магнитный сердечник насыщался, индуктивность не останется постоянной, а будет изменяться вместе с током, протекающим через устройство.Это называется нелинейностью и приводит к искажению сигнала. Например, аудиосигналы могут страдать от интермодуляционных искажений в насыщенных индукторах. Чтобы предотвратить это, в линейных цепях ток через индукторы с железным сердечником должен быть ограничен ниже уровня насыщения. Некоторые слоистые сердечники имеют для этой цели узкий воздушный зазор, а сердечники из порошкового железа имеют распределенный воздушный зазор. Это позволяет более высокий уровень магнитного потока и, следовательно, более высокие токи через индуктор до его насыщения.

Индуктор с ламинированным сердечником

Индуктор балласта с ламинированным железным сердечником для металлогалогенной лампы

Низкочастотные катушки индуктивности часто изготавливаются с многослойными сердечниками для предотвращения возникновения вихревых токов и имеют конструкцию, аналогичную трансформаторам. Сердечник состоит из стопок тонких стальных листов или пластин, ориентированных параллельно полю, с изолирующим покрытием на поверхности. Изоляция предотвращает возникновение вихревых токов между листами, поэтому любые оставшиеся токи должны находиться в пределах площади поперечного сечения отдельных пластин, уменьшая площадь контура и, таким образом, значительно снижая потери энергии.Пластины изготовлены из кремнистой стали с низкой коэрцитивной силой для уменьшения потерь на гистерезис.

Индуктор с ферритовым сердечником

Для более высоких частот индукторы изготавливаются с сердечниками из феррита. Феррит – это керамический ферримагнитный материал, который не проводит ток, поэтому вихревые токи не могут течь внутри него. Состав феррита – xxFe2O4, где xx представляет собой различные металлы. Для сердечников индукторов используются мягкие ферриты, которые имеют низкую коэрцитивную силу и, следовательно, низкие гистерезисные потери. Другой аналогичный материал – железный порошок, цементированный связующим.

Индуктор с тороидальным сердечником

Тороидальный индуктор в блоке питания беспроводного маршрутизатора

В индукторе, намотанном на стержнеобразный стержень с прямым сердечником, силовые линии магнитного поля, выходящие из одного конца сердечника, должны проходить через воздух, чтобы снова войти в сердечник на другом конце. Это уменьшает поле, потому что большая часть пути магнитного поля находится в воздухе, а не в материале сердечника с более высокой проницаемостью. Более высокое магнитное поле и индуктивность может быть достигнуто за счет формирования сердечника в замкнутой магнитной цепи.Силовые линии магнитного поля образуют замкнутые петли внутри сердечника, не покидая его материала. Часто используется форма тороидального или кольцевого ферритового сердечника. Из-за своей симметрии тороидальные сердечники позволяют минимуму магнитного потока выходить за пределы сердечника (так называемый поток утечки), поэтому они излучают меньше электромагнитных помех, чем другие формы. Катушки с тороидальным сердечником изготавливаются из различных материалов, в первую очередь из феррита, порошкового железа и ламинированных сердечников.

Дроссель

СЧ- или ВЧ-дроссель на десятые доли ампера и УКВ-дроссель с ферритовым шариком на несколько ампер.

Дроссель разработан специально для блокировки высокочастотного переменного тока (AC) в электрической цепи, при этом пропуская более низкую частоту или постоянный ток. Обычно он состоит из катушки из изолированного провода, часто намотанного на магнитный сердечник, хотя некоторые из них состоят из бусинки из ферритового материала в форме пончика, нанизанной на провод. Подобно другим индукторам, дроссели сопротивляются изменениям тока, проходящего через них, и поэтому переменным токам более высокой частоты, которые быстро меняют направление, сопротивление больше, чем токам более низкой частоты; сопротивление дросселя увеличивается с частотой.Его низкое электрическое сопротивление позволяет проходить как переменному, так и постоянному току с небольшими потерями мощности, но может ограничивать количество переменного тока, проходящего через него из-за его реактивного сопротивления.

Переменный индуктор

Индуктор с ферритовым стержнем с резьбой (виден вверху), который можно повернуть, чтобы вставить или вывести из катушки. Высота 4,2 см.

Вариометр, используемый в радиоприемниках в 1920-е годы

Роликовая катушка, регулируемый ВЧ-индуктор с воздушным сердечником, используемый в настроенных схемах радиопередатчиков.Один из контактов с катушкой представляет собой маленькое рифленое колесо, которое движется по проводу. Вращение вала вращает катушку, перемещая контактное колесо вверх или вниз по катушке, позволяя большему или меньшему количеству витков катушки войти в цепь, чтобы изменить индуктивность.

Вероятно, наиболее распространенный тип переменного индуктора сегодня – это индуктор с подвижным ферритовым магнитным сердечником, который можно сдвигать или ввинчивать в катушку или вынимать из нее. Перемещение сердечника дальше в катушку увеличивает проницаемость, увеличивая магнитное поле и индуктивность.Во многих индукторах, используемых в радиоприложениях (обычно менее 100 МГц), используются регулируемые сердечники, чтобы настроить такие индукторы на желаемое значение, поскольку производственные процессы имеют определенные допуски (неточности). Иногда такие сердечники для частот выше 100 МГц изготавливаются из немагнитного материала с высокой проводимостью, такого как алюминий. Они уменьшают индуктивность, потому что магнитное поле должно их обходить.

Катушки индуктивности

с воздушным сердечником могут использовать скользящие контакты или несколько ответвлений для увеличения или уменьшения количества витков, включенных в цепь, для изменения индуктивности.Тип, который часто использовался в прошлом, но в основном устаревший сегодня, имеет пружинный контакт, который может скользить по оголенной поверхности обмоток. Недостатком этого типа является то, что контакт обычно замыкает один или несколько витков. Эти витки действуют как короткозамкнутая вторичная обмотка одновиткового трансформатора; индуцируемые в них большие токи вызывают потери мощности.

Типом бесступенчатого индуктора с воздушным сердечником является вариометр. Он состоит из двух катушек с одинаковым количеством витков, соединенных последовательно один внутри другого.Внутренняя катушка установлена ​​на валу, поэтому ее ось может поворачиваться относительно внешней катушки. Когда оси двух катушек коллинеарны, а магнитные поля направлены в одном направлении, поля складываются и индуктивность максимальна. Когда внутренняя катушка повернута так, что ее ось находится под углом к ​​внешней, взаимная индуктивность между ними меньше, поэтому общая индуктивность меньше. Когда внутренняя катушка повернута на 180 °, так что катушки коллинеарны с противоположными магнитными полями, два поля компенсируют друг друга, и индуктивность очень мала.Преимущество этого типа в том, что он может плавно изменяться в широком диапазоне. Он используется в антенных тюнерах и согласующих схемах для согласования низкочастотных передатчиков с их антеннами.

Другой метод управления индуктивностью без каких-либо движущихся частей требует дополнительной обмотки смещения постоянного тока, которая контролирует проницаемость легко насыщаемого материала сердечника. См. Магнитный усилитель.

Теория схем

Действие катушки индуктивности в цепи состоит в том, чтобы противодействовать изменениям тока через нее, создавая на ней напряжение, пропорциональное скорости изменения тока.Идеальный индуктор не имел бы сопротивления постоянному постоянному току; однако только сверхпроводящие катушки индуктивности действительно имеют нулевое электрическое сопротивление.

Связь между изменяющимся во времени напряжением v (t) на катушке индуктивности с индуктивностью L и изменяющимся во времени током i (t), проходящим через нее, описывается дифференциальным уравнением:

При прохождении через индуктор синусоидального переменного тока (AC) индуцируется синусоидальное напряжение. Амплитуда напряжения пропорциональна произведению амплитуды (IP) тока и частоты (f) тока.

В этой ситуации фаза тока отстает от фазы напряжения на π / 2 (90 °). Для синусоид, когда напряжение на катушке индуктивности достигает максимального значения, ток становится равным нулю, а когда напряжение на катушке индуктивности стремится к нулю, ток через нее достигает максимального значения.

Если индуктор подключен к источнику постоянного тока со значением I через сопротивление R, а затем происходит короткое замыкание источника тока, приведенное выше дифференциальное соотношение показывает, что ток через индуктор будет разряжаться с экспоненциальным затуханием:

Реактивное сопротивление

Отношение пикового напряжения к пиковому току в катушке индуктивности, питаемой от синусоидального источника, называется реактивным сопротивлением и обозначается XL.Суффикс предназначен для различения индуктивного реактивного сопротивления от емкостного реактивного сопротивления, обусловленного емкостью.

Таким образом,

Реактивное сопротивление измеряется в тех же единицах, что и сопротивление (Ом), но на самом деле это не сопротивление. Сопротивление будет рассеивать энергию в виде тепла при прохождении тока. Этого не происходит с индуктором; скорее, энергия накапливается в магнитном поле по мере нарастания тока и позже возвращается в цепь, когда ток падает. Индуктивное реактивное сопротивление сильно зависит от частоты.На низкой частоте реактивное сопротивление падает, а при установившемся токе (нулевая частота) индуктор ведет себя как короткое замыкание. С другой стороны, при увеличении частоты реактивное сопротивление увеличивается, и при достаточно высокой частоте индуктор приближается к разомкнутой цепи.

Анализ цепи Лапласа (s-домен)

При использовании преобразования Лапласа в анализе цепей полное сопротивление идеальной катушки индуктивности без начального тока представляется в области s как:

где

– индуктивность, а

– комплексная частота.

Если в катушке индуктивности есть начальный ток, он может быть представлен как:

• Добавление источника напряжения последовательно с катушкой индуктивности, имеющее значение:

где

– индуктивность, а

– начальный ток в катушке индуктивности.

(обратите внимание, что источник должен иметь полярность, соответствующую начальному току)

• или добавлением источника тока параллельно катушке индуктивности, имеющего значение:

где

– начальный ток в катушке индуктивности.

– комплексная частота.

Индукторные сети

Катушки индуктивности в параллельной конфигурации имеют одинаковую разность потенциалов (напряжение). Чтобы найти их общую эквивалентную индуктивность (Leq):

Ток, проходящий через последовательно включенные индукторы, остается неизменным, но напряжение на каждой катушке индуктивности может быть разным. Сумма разностей потенциалов (напряжения) равна общему напряжению. Чтобы найти их общую индуктивность:

Эти простые соотношения справедливы только тогда, когда нет взаимной связи магнитных полей между отдельными индукторами.

Накопленная энергия

Пренебрегая потерями, энергия (измеряемая в джоулях в СИ), запасенная индуктором, равна количеству работы, необходимой для установления тока через индуктор и, следовательно, магнитного поля. Это дает:

где L – индуктивность, а I – ток через катушку индуктивности.

Эта зависимость действительна только для линейных (ненасыщенных) областей связи магнитного потока и тока.В общем, если кто-то решает найти энергию, запасенную в катушке индуктивности LTI, которая имеет начальный ток в определенное время между и и может использовать это:

Коэффициент добротности

Идеальный индуктор не имел бы сопротивления или потерь энергии. Однако настоящие катушки индуктивности имеют сопротивление обмотки из металлической проволоки, образующей катушки. Поскольку сопротивление обмотки появляется как сопротивление, включенное последовательно с индуктором, его часто называют последовательным сопротивлением.Последовательное сопротивление индуктора преобразует электрический ток, проходящий через катушки, в тепло, что приводит к потере качества индукции. Добротность (или Q) индуктора – это отношение его индуктивного реактивного сопротивления к его сопротивлению на данной частоте и является мерой его эффективности. Чем выше добротность индуктора, тем ближе он к поведению идеального индуктора без потерь. Индукторы с высокой добротностью используются с конденсаторами для создания резонансных цепей в радиопередатчиках и приемниках.Чем выше добротность, тем уже полоса пропускания резонансного контура.

Коэффициент добротности катушки индуктивности можно найти по следующей формуле, где L – индуктивность, R – эффективное последовательное сопротивление катушки индуктивности, ω – рабочая частота в радианах, а произведение ωL – индуктивное реактивное сопротивление:

Обратите внимание, что Q увеличивается линейно с частотой, если L и R постоянны. Хотя они постоянны на низких частотах, параметры меняются с частотой.Например, скин-эффект, эффект близости и потери в сердечнике увеличивают R с частотой; Емкость обмотки и изменение магнитной проницаемости в зависимости от частоты влияют на L.

Качественно, на низких частотах и ​​в определенных пределах, увеличение числа витков N улучшает Q, потому что L изменяется как N², в то время как R изменяется линейно с N. Аналогично, увеличение радиуса r индуктора улучшает Q, поскольку L изменяется как r², а R изменяется линейно. с р. Катушки индуктивности с воздушным сердечником с таким высоким Q часто имеют большой диаметр и много витков.Оба этих примера предполагают, что диаметр проволоки остается неизменным, поэтому в обоих примерах используется пропорционально больше проволоки (меди). Если общая масса провода остается постоянной, тогда не будет преимуществ в увеличении количества витков или радиуса витков, потому что провод должен быть пропорционально тоньше.

Использование ферромагнитного сердечника с высокой магнитной проницаемостью может значительно увеличить индуктивность для того же количества меди, поэтому сердечник также может увеличить добротность. Однако сердечники также вносят потери, которые увеличиваются с частотой.Материал сердечника выбран для получения наилучших результатов для диапазона частот. На УКВ или более высоких частотах, вероятно, будет использоваться воздушный сердечник.

Катушки индуктивности, намотанные на ферромагнитный сердечник, могут насыщаться при высоких токах, вызывая резкое снижение индуктивности (и добротности). Этого явления можно избежать, используя индуктор с воздушным сердечником (физически большего размера). Хорошо спроектированный индуктор с воздушным сердечником может иметь добротность в несколько сотен.

Формулы индуктивности

В таблице ниже перечислены некоторые распространенные упрощенные формулы для расчета приблизительной индуктивности некоторых конструкций индукторов.

Строительство	Формула	Банкноты
Цилиндрическая катушка с воздушным сердечником	L = индуктивность в генри (Гн) мкм 0 = проницаемость свободного пространства = K = коэффициент Нагаока N = количество витков A = площадь поперечного сечения змеевика в квадратных метрах (м 2 ) l = длина змеевика в метрах (м)	Точный расчет K сложен. K составляет приблизительно единицу для катушки, которая намного длиннее ее диаметра и плотно намотана с использованием проволоки небольшого калибра (так что она приближается к токовому слою).
Прямой провод	L = индуктивность л = длина баллона c = радиус цилиндра мкм 0 = проницаемость свободного пространства = μ = проницаемость проводника p = удельное сопротивление ω = фазовая скорость	Точно, если ω = 0 или ω = ∞
	(при d ² f ≫ 1 мм² МГц) (при d ² f ≪ 1 мм² МГц) L = индуктивность (нГн) l = длина проводника (мм) d = диаметр жилы (мм) f = частота	Cu или Al (т.е.е., относительная проницаемость – единица) л > 100 г
Цилиндрическая катушка с коротким сердечником	L = индуктивность (мкГн) r = внешний радиус катушки (дюймы) l = длина змеевика (дюймы) N = количество витков
Многослойная катушка с воздушным сердечником	L = индуктивность (мкГн) r = средний радиус рулона (дюйм) l = физическая длина обмотки катушки (дюймы) N = количество витков d = глубина витка (внешний радиус минус внутренний радиус) (дюймы)
Плоская спиральная катушка с воздушным сердечником	L = индуктивность (мкГн) r = средний радиус катушки (см) N = количество витков d = глубина бухты (внешний радиус минус внутренний радиус) (см)
	L = индуктивность (мкГн) r = средний радиус рулона (дюйм) N = количество витков d = глубина витка (внешний радиус минус внутренний радиус) (дюймы)	с точностью до 5 процентов для d > 0.2 р .
Тороидальный сердечник (круглое сечение)	L = индуктивность (мкГн) d = диаметр намотки катушки (дюйм) N = количество витков D = 2 * радиус вращения (дюймы)
	L = индуктивность (мкГн) d = диаметр намотки катушки (дюйм) N = количество витков D = 2 * радиус вращения (дюймы)	, когда d <0.1 Д
Тороидальный сердечник (прямоугольное сечение)	L = индуктивность (мкГн) d 1 = внутренний диаметр тороида (дюйм) d 2 = внешний диаметр тороида (дюйм) N = количество витков h = высота тороида (дюйм)

Источник: www.wikipedia.com

Конструкция индуктора

с сердечниками из магнитного порошка

Чтобы получить помощь в выборе сердечника (сердечников) Magnetics для использования в конкретных конструкциях индукторов, загрузите наш инструмент для проектирования индукторов или обратитесь в Magnetics с запросом на проектирование нестандартных индукторов.

Для выбора сердечника индуктора с ограничением тока необходимо знать только два параметра проектного приложения; индуктивность требуется при постоянном смещении и постоянном токе. Используйте следующую процедуру, чтобы определить размер сердечника и количество витков.

1. Вычислить произведение LI ² где:

L = требуемая индуктивность при смещении постоянного тока (мГн)
I = постоянный ток (A)
l _e = длина магнитного пути сердечника (мм)
N = количество витков
H = напряженность магнитного поля (А • Тл / см)

2. Найдите значение LI ² на диаграмме выбора сердечника. Следуйте по этой координате до пересечения с первым размером керна, который лежит выше диагональной линии проницаемости.Это наименьший размер сердечника, который можно использовать.

3. Линия проницаемости разделена на стандартные доступные значения проницаемости керна. Выбор указанной проницаемости будет лучшим компромиссом между A _L и смещением постоянного тока.

4. Теперь известны индуктивность, размер сердечника и проницаемость. Рассчитайте количество оборотов, используя следующую процедуру:

(a) Коэффициент индуктивности (A _L в нГн / Т ² ) для сердечника определяется из его технических характеристик.Определите минимальное значение A _L , используя отрицательный допуск наихудшего случая (обычно -8%). Используя эту информацию, рассчитайте количество витков, необходимое для получения требуемой индуктивности:

Где требуется L, индуктивность (мкГн)

(b) Рассчитайте смещение в A • T / см из:

(c) Из кривых зависимости проницаемости от смещения постоянного тока определите спад на единицу начальной проницаемости для ранее рассчитанного уровня смещения.Уравнения подбора кривой, представленные в каталоге, могут упростить этот шаг.

(d) Умножьте требуемую индуктивность на спад на единицу, чтобы найти индуктивность с приложенным током смещения.

(e) Увеличьте количество витков, разделив начальное количество витков (из шага 4 (a)) на начальное значение проницаемости на единицу. Это даст индуктивность, близкую к требуемому значению, после повторения шагов 4 (b), (c) и (d).

(f) Повторите шаги 4 (b), (c) и (d), если необходимо, чтобы отрегулировать смещенную индуктивность вверх или вниз, пока она не станет достаточно близко к цели.

5. Выберите правильный размер провода с помощью таблицы проводов. Продолжительность включения ниже 100% допускает меньшие размеры проводов и меньшие коэффициенты намотки, но не допускает меньших размеров сердечников.

6. Для расчета коэффициента намотки умножьте количество витков на площадь провода, указанную в таблице проводов, чтобы найти общую площадь провода. Разделите общую площадь провода на площадь окна сердечника, чтобы получить коэффициент намотки конструкции. Убедитесь, что коэффициент намотки приемлем, обратившись к различным подходам к намотке, описанным здесь.(Область ядра и область окна можно найти в таблице данных ядра или на странице каталога.)

7. Если будет присутствовать значительный пульсирующий ток, оцените потери в сердечнике с помощью процедуры расчета потерь в сердечнике. Если потери в сердечнике переменного тока приведут к слишком большому нагреву или к КПД ниже требуемого, тогда индуктор может быть ограничен потерями, а не насыщением. Варианты конструкции этого сердечника должны учитывать более крупный сердечник, материал с более низкой проницаемостью, материал с меньшими потерями или некоторую комбинацию этих трех.

Пример выбора сердечника

Определите размер сердечника и количество витков для соответствия следующему требованию:

(a) Минимальная индуктивность при смещении постоянного тока 0,6 мГн (600 мкГн)

(б) Постоянный ток 5,0 А

1. LI ² = 0,6 X 5,0 ² = 15,0 мГн • A ²

2. Используя диаграмму Kool Mμ Toroids LI ² , найдите 15 мГн • A ² на нижней оси.Следование этой координате по вертикали приводит к выбору 0077083A7 в качестве соответствующего ядра для вышеуказанных требований.

3. Из данных сердечника 0077083A7 коэффициент индуктивности (A _L ) этого сердечника составляет 81 нГн / Тл ² ± 8%. Минимальное значение A _L этого ядра составляет 74,6 нГн / т ² .

4. Количество витков, необходимое для получения 600 мкГн без нагрузки, составляет 90 витков. Чтобы рассчитать количество оборотов, необходимых при полной нагрузке, определите уровень смещения постоянного тока: H = N • I / l _e = A • T / см, где l _e – длина пути в см.Смещение постоянного тока составляет 45,7 А • Тл / см, что дает 71% начальной проницаемости по кривой смещения постоянного тока 60 мкм Kool Mµ. Скорректированные обороты составляют 90 / 0,71 = 127 оборотов.

5. Пересчитайте уровень смещения постоянного тока в А • Тл / см: кривая зависимости проницаемости от смещения постоянного тока показывает 57% от начальной проницаемости при 64,5 А • Т / см.

6. Умножьте минимальное значение A _L 74,6 нГн / т ² на 0,57, чтобы получить эффективное значение A _L = 42,5 нГн / т ² . Индуктивность этого сердечника 127 витков и 64.5 А • Тл / см будет минимум 685 мкГн. Требование индуктивности соблюдено.

7. Таблица проводов показывает, что для передачи 5,0 А при плотности тока 500 А / см требуется 17 AWG. ² . 127 витков 17 AWG (площадь провода = 1,177 мм ² ) равняется общей площади провода 149,5 мм ² . Площадь окна 0077083A7 составляет 427 мм ² . Расчет заполнения окна, 149,5 мм ² /427 мм ² соответствует приблизительному коэффициенту намотки 35%.0077083A7 со 127 витками 17 AWG представляет собой конструкцию, которую можно изготовить.

Загрузить Инструмент проектирования индукторовContact Magnetics

Как сконструировать катушку

Каждый любитель, желающий заняться радио, должен – в какой-то момент – намотать катушку или две, будь то антенная катушка AM-радио, катушка на тороидальном сердечнике для полосового фильтра в приемопередатчик связи или катушка с центральным отводом для использования в генераторе Хартли.Намотка катушек несложная, но довольно трудоемкая. Существуют разные методы изготовления катушек в зависимости от области применения и необходимой индуктивности. Воздушные сердечники являются наиболее широкополосными, но получение высокой индуктивности означает использование большого количества проводов, они также не являются наиболее эффективным средством для устранения магнитного поля, выходящего из катушки – это выходящее магнитное поле может вызывать помехи, наводясь в соседних проводах и других катушках.

Намотка катушки на ферромагнитную катушку фокусирует магнитное поле, увеличивая индуктивность.Отношение индуктивностей после и до того, как сердечник с диаметром катушки был вставлен внутрь, называется относительной проницаемостью (обозначается μ _r ). Различные обычно используемые материалы имеют разную относительную проницаемость: от 4000 для электротехнической стали, используемой в сетевых трансформаторах, до около 300 для ферритов, используемых в трансформаторах SMPS, и около 20 для сердечников из железного порошка, используемых на УКВ. Каждый материал сердечника следует использовать только в указанном диапазоне частот, за пределами которого сердечник начинает демонстрировать высокие потери.Тороидальные сердечники с несколькими отверстиями, горшок и другие закрытые сердечники заключают магнитное поле внутри сердечника, повышая эффективность и практически сводя к нулю помехи. Чтобы узнать больше об индукторах и их работе, перейдите по ссылке.

Индукторы с воздушным сердечником Катушки

с воздушным сердечником подходят для катушек с низкой индуктивностью, где помехи не имеют особого значения. Катушки с небольшим количеством витков и относительно толстой проволокой наматываются на цилиндрический объект, такой как сверло или банка , которые затем удаляются, и катушка поддерживает себя, иногда катушка покрыта смолой для большей механической устойчивости.Катушки большего размера с большим количеством витков обычно наматываются на неферромагнитный каркас, такой как полая пластиковая трубка или керамический каркас (для мощных РЧ катушек), а затем прикрепляются к каркасу с помощью клея. Чтобы намотать их, вам сначала нужно рассчитать требуемый диаметр проволоки, потому что он сильно влияет на общую длину катушки.

Формула для диаметра проволоки :

(√I) * 0,6 = d, где I - среднеквадратичный или постоянный ток, а d - диаметр проволоки. 

Если катушки используются на низких уровнях мощности, диаметр провода не имеет большого значения, 0.3 мм подходит для большинства применений, а 0,12 мм подходит для консервов, если катушки используются в транзисторных радиоприемниках. Если катушка используется в генераторе, провод должен быть жестким, чтобы предотвратить эффекты коробления, поскольку они могут в некоторой степени изменить индуктивность и вызвать нестабильность частоты (возбуждение).

Далее необходимо знать, какой диаметр должен быть у катушки. Рекомендуется, чтобы диаметр катушки составлял от 50% до 80% длины катушки для оптимальной добротности, и это зависит от того, сколько места может занимать катушка.Если катушка будет самонесущей, вы можете использовать болт или винт, намотать витки внутри канавок и удалить болт, открутив его, удерживая провод катушки, это делает катушку очень ровной и воспроизводимой.

Ниже приведена формула индуктивности для цилиндрической катушки

L = µ _r (n ² . ᴫ ² . R ² / л) 0,00000126

L - индуктивность в генри,
μ  r  - относительная проницаемость сердечника (1 для воздуха, пластика, керамики и т. д.катушки),
n - количество витков,
π - это пи,
r - радиус катушки в  метра  (от середины слоя разводки до середины обмотки) или
половина диаметра (от середины слоя разводки через середину до середины слоя разводки на другой стороне),
l - длина намотки в  метра, 
а длинное число на обороте - проницаемость свободного пространства.

 

Еще одна формула индуктивности.

  L = (n  2 .d  2 ) / 18d + 40l  

Эта формула используется при намотке однослойной однородной катушки, когда все витки намотаны плотно, без промежутков между ними. Единицы такие же, как в приведенной выше формуле, за исключением d, который представляет собой диаметр рулона в метрах.

Очень хороший калькулятор для катушки сделал Serge Y. Stroobandt, позывной ON4AA здесь.

Как сделать индуктор с воздушным сердечником

На намотайте обычную катушку с воздушным сердечником. вам понадобится формирователь, источник проволоки, мелкая наждачная бумага или нож для моделирования (не показан) и немного суперклея или двусторонней ленты, чтобы удерживать провод на месте.

После проектирования катушки пора наматывать ее . Если вы делаете катушку с воздушным сердечником, рекомендуется использовать пластиковый формирователь для намотки, так как пластиковый формирователь неферромагнитен и не проводит электричество, это не повлияет на работу катушки при низкой мощности. уровни. Затем отрежьте полоску двустороннего скотча по длине катушки и приклейте ее к каркасу, затем просверлите отверстия в каркасе там, где заканчивается виток и на отводах, снимите защитный слой с ленты и начните наматывать сначала пропуская его через просверленное отверстие, а затем наматывая его, как обычно, провод будет удерживаться двусторонней лентой, в качестве альтернативы вы можете приклеить начало катушки к каркасу, намотав несколько витков цианакрилатным клеем, намотайте оставшуюся часть катушки и клей через каждые 1 см (также называемый суперклеем, используйте перчатки, его очень трудно удалить с кожи и вызывает раздражение).Для метчиков скрутите вместе кусок проволоки, пропустите ее через отверстие в образце и продолжайте как обычно. Попробуйте намотать витки поближе, после намотки снимите эмаль мелкой наждачной бумагой или лепочным ножом и залудите концы паяльником. Вы можете использовать измеритель LCR для измерения индуктивности или GDM, чтобы использовать GDM в качестве устройства для измерения индуктивности, см. Связанную статью.

Рисунки ниже объясняют процесс намотки индуктора с воздушным сердечником :

Шаг 1: На двух рисунках ниже показано устройство Former с кусочком ленты, куда будет наматываться провод. и Отверстия для удержания провода на месте.

Шаг 2: На рисунке ниже защитная пленка снята, намотка началась, и провод для отвода согнут и скручен .

Шаг 3: Затем проденьте отверстие в первой и вытащите другую сторону.

Шаг 4: Провода готовой катушки лужены путем погружения их в припой на куске ламината печатной платы.

Шаг 5: Наконец, индуктивность катушки измеряется с помощью измерителя LCR. Вы также можете использовать Arduino для измерения индуктивности катушки или использовать Grid Dip Meter (GDM) .

Катушки обмотки на ферритовых стержнях

Обмотка на ферритовых стержнях (например, антенны с ферритовыми стержнями в радиоприемниках) аналогична намотке катушек с воздушным сердечником, но с вы не можете просверлить ферритовый стержень , вам придется полагаться на двустороннюю ленту или клей крепко держать провод.Поскольку лента не всегда прилипает к ферриту, рекомендуется сначала покрыть стержень одним-тремя слоями бумажной малярной ленты прямо под тем местом, где должна проходить катушка, и наклеить ленту поверх него. Вы можете использовать суперклей, чтобы удерживать проволоку на месте вместо двусторонней.

Для расчета катушки используйте формулу индуктивности для цилиндрической катушки, приведенную выше, для μ _r введите относительную магнитную проницаемость, указанную в таблице данных или онлайн-калькуляторе катушки. Если вы разработали катушку , вы можете наматывать ее так же, как катушки с воздушным сердечником, но есть другой метод, более быстрый метод !

Поместите ферритовый стержень в электродрель, как сверло, и медленно вращайте его, стержень будет вращаться сам по себе, таким образом вы можете очень быстро изготавливать высококачественные катушки с высокой индуктивностью с большим количеством оборотов! Если у вас есть пластиковые формирователи для стержня, сначала намотайте их, а затем наденьте на катушку и приклейте на место.

Слева – заводская антенная катушка в радиовещательном приемнике, где катушка намотана на каркас, который прикреплен к стержню с помощью пластиковых элементов. Проволока закреплена эпоксидной смолой. Справа небольшая катушка на ферритовом стержне , изготовленная описанными выше методами.

Тороидальная обмотка сердечника

Тороидальные катушки довольно легко рассчитать, но немного сложнее.Тороидальные сердечники имеют широкий спектр применений, таких как индукторы фильтров в импульсных источниках питания, дроссели радиопомех, силовые трансформаторы импульсных источников питания, входные радиочастотные фильтры, балуны, трансформаторы тока и другие.

Индуктивность тороидальной катушки в наногенри (когда индекс индуктивности AL указан в нГн / Н ² ) можно рассчитать по следующей формуле:

  л (нГн) = A  л  (нГн / н  2 ) * Обороты  2   

После преобразования получаем формулу количества витков, необходимых для необходимой индуктивности:

  Необходимое количество оборотов = [L (нГн) / A  L  (нГн / Н  2 )]  1/2   

Чтобы намотать тороидальную катушку, вам понадобится тороидальный сердечник, источник провода (хорошим источником являются отклоняющие катушки от старых ЭЛТ-телевизоров), мелкая наждачная бумага и немного суперклея.

Чтобы намотать тороид, вам сначала нужно отрезать проволоку соответствующей длины, потому что вы не можете пропустить катушку проволоки через отверстие. Чтобы рассчитать необходимый провод, умножьте длину окружности поперечного сечения кольца на количество необходимых витков. Иногда это указывается в таблице данных как mlt (средняя длина на оборот). На этом веб-сайте есть онлайн-калькулятор, который помогает в проектировании тороидальных катушек, просто выберите свой сердечник, подключите необходимую индуктивность, и он даст необходимое количество проводов и витков.

Шаг 1: Сначала пропустите один конец провода через отверстие, убедитесь, что он выступает примерно на 4 см – этот кусочек называется косичкой.

Шаг 2: Оберните косичку вокруг сердечника, оставьте на расстоянии 1–2 см и закрепите оставшуюся часть суперклеем.

Шаг 3: Используйте оставшуюся длину проволоки, чтобы намотать оставшуюся часть катушки, прикрепите более длинный конец к гвоздю или гвоздю для облегчения наматывания.

Поскольку ожидается, что катушка будет иметь низкую индуктивность (около 3,6 мкГн) в отсутствие профессионального измерителя LCR, лучше использовать GDM, поскольку обычные измерители на основе микроконтроллера имеют очень низкую точность при измерении малых индуктивностей. Конденсатор 680 пФ был подключен к катушке параллельно вместе с небольшой петлей связи. Эта схема имеет частоту 3,5 МГц (справа), помещая эти значения в вычислитель резонанса, мы получаем около 3 мкГн. Слева измеритель настроен на другую частоту вне резонанса контура.

Расчетные катушки могут давать очень разные результаты в реальных условиях из-за паразитных емкостей и вызванного ими параллельного саморезонанса.

Пример расчета индуктивности

Индуктивность Пример расчета

Дэвид Микер

[email protected]

Сопутствующий файл: index1a.fem

Введение

Распространенной задачей, к которой может быть применен FEMM, является расчет индуктивности индуктора с зазором.Хотя индуктивность можно оценить с помощью простого магнитного Теория схем, схемный подход обычно игнорирует утечку потока и окантовочные эффекты. Чтобы решить эти неидеальные эффекты более подробно анализ методом конечных элементов может быть заняты. Цель настоящего пример – показать, как рассчитывается индуктивность в моделировании FEMM, и сравните этот результат с приближением, полученным через магнитную цепь подход.

Пример геометрии

Примерная геометрия состоит из ламинированного EI с зазором. сердечник с поперечным сечением, как показано на рисунке 1.Сердечник E с центральным полюсом шириной 0,5 дюйма и внешними полюсами Ширина 0,25 дюйма отделена от I-образного возвратного тракта воздушным зазором. Толщина 0,025 дюйма.

Рисунок 1: Пример геометрии

Обмотка, которая лежит в пазах E, состоит из 66 витки толстой изоляции провода 18 AWG, примерно для 66% меди заполните фракцию в окне змеевика. это Предполагается, что сердцевина расширяется на 1 дюйм в направлении страницы.В данной модели материал считается линейным ферромагнитным материалом с относительной проницаемостью из 2500.

Теория цепей Индуктивность

Для приблизительной оценки индуктивности мы можем предположить, что нет подтеков и окантовки, и что вклад железа секций на сопротивление магнитной цепи тривиально по сравнению с вклады с воздуха.Потом, поток, текущий в магнитной цепи, получается путем решения уравнения цепи:

для f , всего поток, связанный катушкой. Модель R представляет собой сопротивление магнитной цепи, которое согласно нашим предположениям можно записать как:

, где g = 0,025 дюйма , a _полюс = 0.5 в ² и м _o = 4 p (10 ^-7 ) H / м. Так как общий поток, связывающий катушку, тогда:

, а общая самоиндукция равна потоку, умноженному на общее количество витков:

, так что самоиндукция равна:

Так как в нашем случае витков 66, индуктивность работает из:

L = 1.39 мГн

Мы ожидаем, что индуктивность получена из конечных элементов. вычисления должны быть в районе 1,39 мГн.

Индуктивность конечного элемента (I)

Для создания решения методом конечных элементов индуктор помещается в центр коробки размером 2 на 2,5 дюйма. На границах области граница условие A = 0 определено. Для Для выполнения анализа методом конечных элементов ток 1 А является допустимым. несколько произвольно применяется к катушкам.Достаточно грубая плотность ячеек с ограничением размера ячейки больше 0,05 дюйма определяется везде. Сетка проблемной области изображена на рисунке 2.

Рисунок 2: Проблемная область, нарисованная в FEMM.

После выполнения анализа и запуска постпроцессора, индуктивность можно определить, нажав кнопку «Свойства схемы» в постпроцессор:
Появляется диалоговое окно с рядом свойств обмотки, если смотреть со стороны выводов обмотки.Диалоговое окно “Свойства схемы” для этого примера показано ниже на рисунке 3.

Рисунок 3: Схема Диалог результатов свойств.

При отсутствии постоянных магнитов или других катушек, Результат потока / тока можно интерпретировать напрямую как собственную индуктивность:

L = 1,73 м вод. Ст.

Этот результат выше, чем 1,39 мГн, предсказанный простой подход теории цепей, потому что эффекты утечки и окантовки пренебрежение схемным подходом приводит к небольшому увеличению индуктивности.

Индуктивность конечного элемента (II)

Альтернативный подход – получение энергии через Интеграл «Энергия магнитного поля». Для этого подхода энергия получается через:

, где этот интеграл берется по всей задаче домен, а не просто над катушками. Чтобы выполнить эту интеграцию в постпроцессор, переключитесь в режим интегрального блока, нажав кнопку на панели задач.Затем выберите каждый регион в проблеме с помощью щелчки левой кнопкой мыши. Когда выделена вся проблемная область, нажмите кнопку Integral и выберите Интеграл энергии магнитного поля из выпадающего списка объемных интегралов. Если W представляет собой интегральный результат, результирующая индуктивность:

Для примера задачи результат из энергии интеграция:

Вт = 0.000865042 Джоули

Что при подстановке в формулу дает то же результат как метод (I):

L = 1,73 м вод. Ст.

Выводы

Был представлен простой пример, демонстрирующий, как FEMM можно использовать для получения индуктивности. Была рассмотрена двумерная плоская задача, и индуктивность получена из двух методы сравнивались друг с другом и с “проверкой работоспособности” оценка индуктивности по теории магнитной цепи.

Хотя результаты двух подходов конечных элементов для получения одинаковых индуктивностей в этом случае обычно лучше использовать метод (I). Причина в том, что некоторые граничные условия ( т.е. асимптотическое граничное условие, используемое для аппроксимации “открытой граничной” задачи) подразумевают, что некоторая энергия хранятся вне смоделированной проблемной области. Внутренне FEMM вычисляет поток связь с использованием метода, который учитывает эту дополнительную энергию, тогда как интегрирования B * H по всем элементам нет.

Строго говоря, единственный коэффициент индуктивности подразумевает линейная зависимость между приложенным током и результирующим потоком. По этой причине пример проблемы с учитывались только линейные материалы.

Если проблема связана с нелинейными материалами и есть значительная насыщенность, больше нет линейной зависимости между ток и поток. Однако есть много ситуаций, в которых применяется синусоидальный ток, и хотелось бы знать амплитуду основной гармоники потока, соответствующую приложенному Текущий.В этом случае гармонический анализ может быть запущен в FEMM (, т.е. , когда частота, отличная от нуля, указанные в Определении проблемы). FEMM реализует нелинейную формулировку гармоники времени, которая вычисляет амплитуда и фаза основной части магнитного поля для времени гармонические задачи с нелинейными материалами. Для нелинейных задач гармоники по времени свойство Circuit Properties Диалог снова может быть использован для сбора различных свойств терминала катушек.

Калькулятор катушек и трансформаторов

Калькулятор катушек и трансформаторов

Вернуться к оглавлению.

Калькулятор катушек и трансформаторов.

С помощью этого калькулятора катушек вы можете спроектировать и рассчитать свойства катушки. или трансформатор.
Введите параметры в поля желтого цвета и затем нажмите кнопки расчета.

Ниже калькулятора вы найдете более подробное описание расчетов.
Используйте десятичную точку (не запятую), если вы хотите ввести десятичные дроби.

рекомендую вы также можете прочитать эту веб-страницу по поводу катушек и трансформаторов, многие вещи, которые я использую в этом калькуляторе, имеют Я там учился.
Он объясняет это очень ясно.

Пояснения к некоторым терминам, используемым в этом калькуляторе

Индуктивность: L

Индуктивность катушки – это свойство, которое описывает соотношение между напряжением, индуцированным в катушке, и изменением тока через катушку.

L = V _L / (di / dt)

Где:
L = индуктивность катушки в Генри (Гн).
В _L = Напряжение, индуцированное в катушке в Вольтах
di / dt = изменение тока через катушку в Амперах в секунду.

Магнитный поток: Φ

Магнитный поток, обычно обозначаемый как Φ, равен измеряется в единицах Вебера (Вб).
Если у вас есть петля из провода, и вы подаете на нее 1 Вольт в течение 1 секунды, магнитный поток в петле изменится на 1 Вебер.
Неважно, какого размера или формы петля, или из какого материала внутри петля есть.
Вы можете представить себе единицу Wb как количество силовых линий магнитного поля, проходящих через петля.

Для одиночного контура применяется:
Φ = Vt

Если катушка имеет более одного витка, мы можем использовать следующую формулу:
Φ = Vt / N

Где:
Φ = изменение магнитного потока в катушке в Weber
V = напряжение на катушке в вольтах
t = время в секундах
N = количество витков катушки

Плотность магнитного потока: B

Плотность магнитного потока B измеряется в единицах Тесла (Т).
Плотность магнитного потока указывает магнитный поток через определенную область.

Один Tesla – это один Вебер на квадратный метр
Или в формуле:
B = Φ / A

Где:
B = плотность магнитного потока в теслах
Φ = магнитный поток в Weber
A = площадь в квадратных метрах

Максимальная плотность магнитного потока при низкой частота: Bmax = Bsat

Магнитные материалы, используемые в сердечниках катушек и трансформаторов, могут использоваться до определенная максимальная плотность магнитного потока.
Для низкочастотных приложений (включая постоянный ток) максимальная плотность потока ограничена магнитным насыщение материала сердечника, эта плотность потока называется: Bsat.
В насыщенном состоянии все магнитные области в материале направлены одинаково. направление.

Однако теоретически возможно увеличить плотность потока выше насыщения, из-за проницаемости вакуума.
Но для этого требуется большой ток через катушку и чрезмерные потери мощности в обмотки.
Выше насыщения катушка потеряет большую часть своей индуктивности и запустится. действует как катушка без материала катушки.
Итак, держите плотность потока ниже Bsat.
Значение Bsat указано в спецификации материала керна.
Например, Bsat составляет около 0,3 Тл для ферритового материала и около 1,3 Тл для кремнистая сталь.

Значение Bsat зависит от температуры, чем выше температура, тем в большинстве случаев ниже Bsat.
В этом калькуляторе я использую значение Bsat при 100 ° C, который автоматически появляется в поле Bmax при выборе материала сердцевины.
Итак, это наиболее безопасное значение, при более низкой температуре, однако Bsat может быть выше.

Максимальная плотность магнитного потока на более высокой частоте: Bmax
Для высокочастотных приложений максимальный поток плотность в ядре ограничена потерями мощности в ядре, а не ядром насыщенность.
На более высоких частотах нам нужно уменьшить значение Bmax ниже Значение Bsat, чтобы избежать перегрева ядра из-за потери собственной мощности.
Чем выше частота, тем меньше значение Bmax.

Для сердечников большего размера необходимо соблюдать плотность потока Bmax. ниже, чем для сердечников меньшего размера, чтобы избежать перегрева сердечника.
Это потому, что объем ядра (который производит тепло) увеличивается. быстрее, чем внешняя часть сердечника (которая должна рассеивать тепло).

Мой калькулятор катушек и трансформаторов не рассчитывает для вас потери в сердечнике.
Вместо этого вы должны ввести определенную максимальную плотность потока в калькулятор, что сохранит потери в сердечнике ниже желаемого уровня.

Потери в сердечнике в сердечниках из кремнистой стали

На следующих рисунках показаны некоторые примеры потерь в сердечнике в кремнистой стали (также называется: электротехническая сталь или трансформаторная сталь).

Рисунок 1. Потери в сердечнике в кремнистой стали.

На рисунке 1 приведены некоторые примеры потерь в сердечнике при различной толщине ламинирования. и частоты.
Чем выше частота, тем больше потери.
А более толстая ламинация дает большие потери.
Чтобы преобразовать толщину ламинирования из “мил” в “мм”, умножьте на 0,0254.
Однако потери в сердечнике (в ватт / кг) выше на более высоких частотах, Сердечник трансформатора можно сделать меньше на более высоких частотах.
И вы можете получить высокочастотный трансформатор с меньшими потерями в сердечнике (в ваттах), по сравнению с низкочастотным трансформатором той же номинальной мощности.

Для силовых трансформаторов при 50 или 60 Гц потери в сердечнике обычно значительны. ниже потери в обмотках при полной нагрузке.
При 50 или 60 Гц вы можете использовать в конструкции трансформатора, плотность потока в ядро равно: Bsat.

Для аудиопреобразователя вы разрабатываете самую низкую частоту звука. сигнал, если он не превышает примерно 100 Гц, вы можете использовать Bsat в качестве максимальная плотность потока в сердечнике.
Для более высоких звуковых частот ток намагничивания и плотность потока в ядро автоматически уменьшается.

Рисунок 2, потери в сердечнике в кремнистой стали при различных частотах.
Эти данные относятся к неориентированной кремнистой стали марки М-19 толщиной 14 мил или Толщина 0,36 мм.
О, а 1 фунт равен 0,45359 кг.

Потери в ферритовых сердечниках

Ферритовые сердечники имеют гораздо меньшие потери мощности на высоких частотах, чем кремниевые стальные сердечники.
Информация о максимальной плотности потока на определенной частоте может быть найдено в техническом описании ферритового материала, вот два примера:

Рисунок 3. Потери в сердечнике феррита N27.

На рисунке 3 показано соотношение между частотой, плотностью потока и потерями мощности в сердечник для ферритового материала N27, который насыщается при 0,41 Тл при 100 C.
Предположим, мы хотим, чтобы максимальная потеря мощности в активной зоне составляла 100 кВт / м. , что равно 100 мВт / см, я обозначил это значение красной линией.
Для сигнала 10 кГц (зеленая линия) мы находим максимальное пиковое значение для поток 300 мТл (= 0,3 Тл) при 100 C.
А для 200 кГц (синяя линия) мы находим максимум 50 мТл (= 0.05 Тесла).

Рисунок 4. Потери в сердечнике феррита 3C90.

На рисунке 4 показаны потери в сердечнике для ферритового материала 3C90, здесь данные представлен немного иначе.
Для потерь в сердечнике 100 кВт / м (= 100 мВт / см) мы найдите на частоте 200 кГц максимальную пиковую плотность потока 70 мТл (= 0,07 Тл).

Эффективная площадь поперечного сечения сердечника: Ae

Эффективная площадь поперечного сечения сердечника может быть найдена в лист данных ядра, это предпочтительный метод.
Или можете измерить.
Но только магнитный материал является частью эффективной площади поперечного сечения, поэтому любое изолирующее покрытие, которое может покрывать сердцевину.

Рисунок 5: В сердечнике трансформатора EI эффективная площадь поперечного сечения (Ae), это площадь центральной ножки.
Обе внешние ноги обычно имеют площадь 1/2 Ae.

Когда вы уложили несколько жил, общая эффективная площадь поперечного сечения Ae (всего), равно значению Ae одного ядра, умноженному на количество ядра

Максимальный магнитный поток в сердечнике: Φmax

Максимальный магнитный поток в сердечнике рассчитывается по формуле:
Φmax = Bmax.Ae (всего)

Где:
Φmax = максимальный магнитный поток в сердечнике в Weber
Bmax = максимальная плотность магнитного потока в сердечнике в Tesla
Ae (total) = Общая эффективная площадь поперечного сечения сердечника в квадратных метрах

Относительная проницаемость керна: μr.

Относительная проницаемость мкр жилы Материал показывает, насколько больше индуктивности будет у вашей катушки по сравнению с катушка с вакуумом в сердечнике.
Вакуум имеет проницаемость (μ0) около 1.2566. 10 ^-6 Гн / м (Генри на метр).
Относительная проницаемость не имеет единиц измерения.
Air имеет значение μr 1.00000037, поэтому практически равняется вакууму.
Относительная проницаемость материала керна μr часто зависит от плотности магнитного потока в сердечнике.
В этом калькуляторе я использую значение μr, близкое к нулю. плотность потока, в таблицах это обозначается как μi (относительная начальная проницаемость).
Еще один параметр, который вы можете найти в таблицах данных: μa (относительная амплитудная проницаемость), которая является значением μr при более высокой плотности потока.

Эффективная проницаемость керна: мкэ

Если у вас есть катушка, намотанная на кольцевой сердечник, сердечник полностью состоит из сердечника. материал, и полностью закрыт ..
Тогда эффективная проницаемость равна относительной проницаемости основной материал.

Но многие сердечники состоят из двух частей, которые соединены вокруг катушки. бывший с обмотками на нем.
Две основные части всегда будут иметь некоторый промежуток или воздушный зазор в между ними, что, кажется, снижает проницаемость ядра.
У вас есть керн с эффективной проницаемостью, которая меньше, чем относительная проницаемость материала сердечника.

Иногда в сердечнике намеренно делают воздушный зазор, чтобы уменьшить эффективная проницаемость.
При этом увеличивается максимальный ток через катушку, но не магнитный поток. плотность в ядре.
Это дает тот же эффект, что и при использовании другого материала сердцевины с более низкой проницаемостью.

Эффективная проницаемость сердечника с воздушным зазором составляет:

мкэ = мкр.le / (le + (g .μr))

Где:
μe = эффективная проницаемость керна.
мкм = относительная проницаемость материала сердечника.
le = эффективная длина магнитного пути в сердечнике
g = длина воздушного зазора (измеряется в тех же единицах, что и le)

Эффективная длина магнитного пути в сердечнике: le

Эффективная длина магнитного путь в ядре можно найти в даташит ядра.
Или можно прикинуть по габаритам сердечника.
Это длина линии магнитного поля в центре материала сердечника. поедет.
Не включайте воздушный зазор в эту длину пути, а только путь в сердечнике сам материал.

Воздушный зазор: g

Воздушный зазор – это слой воздуха на магнитном пути сердечника.

Рисунок 6: воздушный зазор в центральной ножке сердечника трансформатора EI.

На рисунке 6 показан воздушный зазор, вызванный укорочением центральной стойки трансформатора. затем две внешние ножки.
Пунктирными линиями обозначены силовые линии магнитного поля длиной: le

Рисунок 7: Воздушный зазор во всех выводах сердечника трансформатора EI.

На рисунке 7 показан еще один сердечник трансформатора ЭУ с воздушным зазором.
Здесь все ножки трансформатора имеют одинаковую длину, а воздушный зазор создается слегка раздвинув части «E» и «I».
Видите ли, теперь силовые линии должны дважды перепрыгивать через слой воздуха, чтобы сформировать замкнутый цикл.
Это означает, что мы должны рассчитывать с воздушным зазором, который вдвое превышает расстояние между частями «Е» и «И».

Воздушный зазор необязательно заполнять воздухом или другими немагнитными материалами. как бумага или пластик, тоже пригодятся.
В трансформаторах воздушный зазор в сердечнике приведет к снижению связи между обмотки, которые могут быть нежелательными.

Коэффициент индуктивности: AL.

Коэффициент индуктивности AL сердечника – это индуктивность одной обмотки вокруг этого сердечника.
Если у вас более одной обмотки, индуктивность катушки будет:

L = N.AL

Где:
L = индуктивность катушки
N = количество витков
AL = коэффициент индуктивности сердечника

Если вам неизвестен коэффициент AL сердечника, это может быть рассчитано из эффективной проницаемости и размеров керна:

AL = μ0. мкэ. Ae (всего) / le

Где:
AL = коэффициент индуктивности в H / N
μ0 = проницаемость вакуума = 1,2566. 10 ^-6 H / м
μe = эффективная проницаемость сердечника
Ae (total) = общая эффективная площадь поперечного сечения сердечника в м
le = эффективная длина магнитного пути в сердечнике в м.

Объединение сердечников

Объединение сердечников означает использование более одной жилы и пропускание обмоток через все эти ядра.
По сравнению с катушкой с одним сердечником, индуктивность умножается на количество ядра сложены.

Рисунок 8: катушка на стопке из 5 сердечников

Сопротивление провода

Провод, который вы используете для наматывания катушки или трансформатора, будет иметь некоторое сопротивление.
Это сопротивление рассчитывается по формуле:

R = ρ.l / A

Где:
R = сопротивление провода
ρ = удельное сопротивление материала провода в Ом · м, для меди это примерно 1,75. 10 ^-8 Ом · м
l = длина провода в метрах
A = площадь поперечного сечения провода в квадратных метрах

Общая площадь котла обмотки.

Расчетное значение площади меди, как говорится, только для меди обмотки.
На практике также приходится иметь дело с изоляцией проводов, воздух между витками и, вероятно, формирователь катушки.
Итак, на практике вам нужно больше места для обмотки, скажем в 2,5 или 3 раза расчетное значение для меди.

Максимальный ток (пиковое значение постоянного или переменного тока) через катушку

Максимальный ток через катушку – это ток, который дает максимальное значение. допустимый магнитный поток в сердечнике.

Imax = Φmax. Н / д

Где:
Imax = максимальный ток через катушку (пик постоянного или переменного тока)
Φmax = максимальный магнитный поток в сердечнике в Weber
N = количество витков
L = индуктивность катушки в Генри

Зарядка время до максимального тока.

Когда вы подключаете катушку к источнику постоянного напряжения V, ток I будет увеличиваться с время.
Другими словами, вы заряжаете катушку.
Пока катушка не имеет сопротивления, ток увеличивается линейно, и время достижения определенного тока определяется по формуле:

t = L.I / V

Если катушка имеет сопротивление, увеличение тока больше не является линейным.
Максимальный ток через катушку ограничен значением: I = V / R.
Время зарядки катушки с сопротивлением рассчитывается по формуле:

т = -L / R.LN (1- (I.R / V))

Где:
t = время в секундах для увеличения тока от нуля до значения I.
L = индуктивность катушки в Генри.
R = сопротивление катушки в Ом.
LN = Натуральный логарифм.
I = ток в амперах, для которого вы рассчитываете время зарядки.
В = напряжение на катушке.

В этом калькуляторе рассчитывается время, чтобы зарядить до максимальной катушки. ток, то есть ток, который дает в сердечнике плотность потока Bmax.

Накопленная энергия в катушке

Когда через катушку проходит ток, определенное количество энергии хранится в катушке.
Накопленная энергия рассчитывается по формуле:

E = 1/2. (L. I)

Где:
E = накопленная энергия в катушке в джоулях
L = индуктивность катушки в Генри
I = ток через катушку в амперах

Максимальное напряжение переменного тока на катушке

Максимальное напряжение переменного тока (синусоида), которое вы можете приложить к катушке, составляет рассчитано по формуле:

Vmax = 4,44. Φмакс. N. f

Где:
Vmax = максимальное синусоидальное напряжение переменного тока на катушке в вольтах RMS
Φmax = максимальный магнитный поток в сердечнике в Weber
N = количество витков на катушке
f = частота напряжения в герцах

Фактор 4.44 – это произведение двух коэффициенты, которыми являются:
4, поток изменяется от нуля до + Φmax в 1/4 цикла, следующая 1/4 цикла он возвращается к нулю, следующие две 1/4 цикла до -Φmax и обратно до нуль.
Таким образом, за один цикл поток изменяется в 4 раза по Φmax.
Умноженный на:
1,11, это форм-фактор синусоидальной волны, который представляет собой отношение среднеквадратичного значения к среднее значение.

Вот еще один способ вычисления максимального переменного напряжения на катушке:
Vmax = Imax.2. пи. f .L / √2
Здесь мы умножаем максимальный ток через катушку на полное сопротивление катушки при частоту f, а затем разделите ее на √2, чтобы преобразовать пиковое значение в среднеквадратичное значение.

---

Число витков первичной обмотки трансформатора.

Из формулы для максимального напряжения на катушке (см. Выше) мы легко можем найти формулу количества витков первичной обмотки трансформатора.

Np = Vp / (4.44. Φmax. F) Эта формула предназначена для синусоидальной волны. напряжения.

Где:
Np = количество витков первичной обмотки
Vp = первичное напряжение (= входное напряжение) трансформатора, действующее значение
Φmax = максимальный магнитный поток в сердечнике в Weber
f = частота напряжения в Гц

Если вы используете трансформатор для прямоугольных напряжений, форм-фактор для напряжение равно 1 (вместо 1,11 для синусоид),
, а количество витков трансформатора должно быть в 1,11 раза больше.

Количество витков, которое мы теперь рассчитали, является минимальным количеством первичных повороты.
Если уменьшить количество витков первичной обмотки, сердечник трансформатора войдет в магнитное насыщение, которого необходимо избегать.
Однако разрешено делать количество витков (как первичных, так и вторичных). выше, но это увеличит сопротивление обмоток, и тем самым потеря мощности трансформатора.
Для трансформаторов линий электропередачи обычно сохраняется количество витков на минимально возможное значение, достаточное для предотвращения насыщения сердечника при максимальном вводе Напряжение.

Число витков вторичной обмотки трансформатора

В идеальном трансформаторе без потерь соотношение напряжений между вторичной и первичной обмотками стороны, такое же, как отношение витков между вторичной и первичной сторонами.
Или в формуле:
Vs / Vp = Ns / Np

Где:
Vs = Напряжение на вторичной стороне
Vp = Напряжение на первичной стороне
Ns = Число витков вторичной обмотки
Np = Число витков первичной обмотки

Отсюда следует:
Ns = Np. Vs / Vp

Мы также могли бы рассчитать его по формуле, очень похожей на формулу первичные витки:
Ns = Vs / (4.44. Φmax. f) Эта формула предназначена для синусоидальной волны. напряжения.

Индуктивность первичной обмотки трансформатора

Это индуктивность первичной обмотки трансформатора.
Вы можете измерить индуктивность первичной обмотки с помощью измерителя индуктивности.
При этом вторичная обмотка ни к чему не должна подключаться.

Или, если вы знаете количество витков первичной обмотки и коэффициент AL, первичный индуктивность можно рассчитать с помощью:

Lp = Np. AL

Где:
Lp = первичная индуктивность
Np = количество витков первичной обмотки
AL = коэффициент индуктивности сердечника

Значение первичной индуктивности необходимо для расчета намагничивания ток трансформатора.

Ток намагничивания

Ток намагничивания – это небольшой ток, который протекает через первичную обмотку. обмотка трансформатора, даже если выход трансформатора не нагружен.
Ток намагничивания создает магнитный поток в трансформаторе. основной.
Амплитуда тока намагничивания рассчитывается по формуле:

Im = Vp / (2.pi.f.Lp)

Где:
Im = ток намагничивания в амперах RMS
Vp = первичное напряжение в RMS вольтах
f = частота в герцах
Lp = первичная индуктивность трансформатора в Генри

Ток намагничивания фактически такой же, как максимальный ток, который мы рассчитали для катушки.
Но для максимального тока катушки мы вычислили пиковое значение, в ток намагничивания трансформатора мы вычисляем действующее значение, поэтому есть коэффициент 1.414 между.

Если мы собираемся нагружать вторичную обмотку трансформатора, ток через первичная обмотка поднимется.
Но поток в сердечнике останется прежним.
Это потому, что ток во вторичной обмотке дает противоположный поток, который нейтрализует весь дополнительный поток первичной обмотки.
Итак, в конце мы сохраняем только поток, вызванный током намагничивания, как бы тяжело мы ни нагружали трансформатор.

Ну так должно быть, если обмотки трансформатора имеют нулевое сопротивление.
Однако на практике обмотки трансформатора имеют некоторое сопротивление.
Ток через первичную обмотку дает определенное падение напряжения на сопротивление первичной обмотки.
Это вызывает уменьшение напряжения на первичной индуктивности (Lp), и это уменьшит ток намагничивания (Im) и магнитный поток в сердечнике.

Итак, для практических трансформаторов (с некоторым сопротивлением в обмотках) ток намагничивания и магнитный поток в сердечнике уменьшатся при загрузке трансформатор более тяжелый.
Это вызвано не сердечником трансформатора, а сопротивлением первичной обмотки. обмотка.

Номинальная мощность

Мощность, которую может выдать трансформатор, ограничена сопротивлением обмотки, а не сам сердечник.

Сопротивление обмоток приведет к понижению напряжения вторичного трансформатора. падение при более высоких токах нагрузки.
Это один из ограничивающих факторов, насколько допустимое падение напряжения для вашего заявление?

Другой ограничивающий фактор: потери мощности в первичной и вторичной обмотке.
означает больший ток нагрузки на вторичной обмотке, большие потери мощности в первичной обмотке. и вторичные обмотки.
Потеря мощности приведет к нагреву обмоток трансформатора.
Во избежание перегрева трансформатора выходной ток трансформатора должен быть ограниченным ниже некоторого максимума.

Чтобы сделать трансформатор с высокой номинальной мощностью, мы должны сохранить сопротивление как можно ниже обмотки.
В первую очередь это делают: сохраняя как можно меньшее количество витков, делая магнитный поток плотность в ядре как можно выше, чуть ниже насыщения.
Еще одна полезная вещь: использование большого сердечника трансформатора, а не потому, что сердечник ограничивает мощность, а потому что:

– Большой сердечник дает больше места для обмоток, поэтому мы можем использовать более толстую проволоку, чтобы уменьшить сопротивление.
– Большая площадь сердечника означает, что вы можете увеличить поток (не поток плотность) за счет уменьшения количества витков.
– Трансформатор большего размера может лучше рассеивать тепло, вызванное потерей мощности.

Калькулятор трансформаторов рассчитает для вас падение напряжения на вторичной обмотке и потери мощности в обмотках.
Вам решать, сколько падения напряжения и потери мощности приемлемы для ваш трансформатор.

Ток первичной обмотки трансформатора

Ток, идущий в первичную обмотку трансформатора (Ip), складывается из следующие токи:
Ток намагничивания (Im), который составляет 90 за первичным напряжением.
Ток, вызванный током вторичной нагрузки (Is), появляется ток нагрузки. на первичной обмотке величиной: Is. Ns / Np.

Ip = √ (Im + (Is.Ns / Np))

На самом деле существует также некоторый первичный ток, вызванный потерями в сердечнике, но я игнорирую это.
Не то чтобы этот ток обязательно был незначительным, но я тоже его обнаружил. сложно реализовать потери в сердечнике в калькуляторе.
Так что я просто опускаю его.
Так или иначе, первичный ток трансформатора при полной нагрузке почти только в зависимости от вторичного тока нагрузки.

Потери в трансформаторе

В этом калькуляторе потери в трансформаторе рассчитываются на основе ток нагрузки, ток намагничивания и сопротивление обмоток постоянному току.

Однако есть и другие причины потерь в трансформаторе, такие как:
– Потери в сердечнике (потери на гистерезис и потери на вихревые токи).
– Емкость внутри и между обмотками.
– Скин-эффект и эффект близости, увеличивающие сопротивление провода при более высоких частоты.
Но я их опускаю, поэтому вам не нужно указывать все правильные параметры для эти эффекты, и для меня калькулятор не стал слишком сложным в изготовлении.

Ток намагничивания играет незначительную роль в потерях трансформатора, но I реализовали это в калькуляторе, потому что это было довольно легко сделать.

Рисунок 9

Рисунок 9 показывает эквивалентную схему для трансформатора с первичной обмоткой. сопротивление (Rp), вторичное сопротивление (Rs) и первичная индуктивность (Lp).
Резистор RL – это нагрузочный резистор, который вы подключаете к трансформатору. выход.
«Идеальный трансформатор» в схеме – это воображаемое устройство без потерь, с бесконечная индуктивность и нулевое сопротивление.

Рисунок 10: упрощение рисунка 9.

На рисунке 10 показаны идеальные трансформаторы Rs и RL из рисунка 9. заменен одним резистором номиналом (Rs + RL). (Np / Ns).
Теперь можно рассчитать напряжение на катушке Lp, а затем ток намагничивания.
Я не буду подробно объяснять, как проходит этот расчет, калькулятор делаем расчет за вас.
Напряжение на Lp можно умножить на Ns / Np, чтобы получить напряжение на Rs + RL.
Таким образом мы можем определить мощность всех резисторов.

Вернуться к оглавлению.

.