Расчет однослойной катушки индуктивности: Coil32 – Расчет однослойной катушки индуктивности

Coil32 – Расчет однослойной катушки индуктивности

Информация о материале

Опубликовано: 25 августа 2012

Обновлено: 08 января 2023

Просмотров: 114273

Для работы этого калькулятора необходимо включить JavaScript в вашем браузере!

---

Об особенностях расчета однослойных катушек можно узнать здесь.

Программа Coil64 ведет расчет по другой методике и результат, полученный в ней, может незначительно отличаться от результата этого калькулятора. Кроме того Coil64 также позволяет рассчитать конструктивную добротность катушки и ее собственную емкость.

Расчет числа витков по заданной индуктивности

ВВЕСТИ ДАННЫЕ:

---

---

L	= мГнμГннГн	– Требуемая индуктивность
D	= ммсм	– Диаметр каркаса
d	= ммсм	– Диаметр провода без изоляции
k	= ммсм	– Диаметр провода с изоляцией	Автоматически

---

Рассчитать

РЕЗУЛЬТАТ:

---

N	=	– Число витков
l	= ммсм	– Длина намотки

Очистить все

 

Расчет индуктивности по числу витков и размерам катушки

ВВЕСТИ ДАННЫЕ:

---

N	=	– Число витков
D	=ммсм	– Диаметр каркаса
l	=ммсм	– Длина намотки

---

Рассчитать

РЕЗУЛЬТАТ:

---

L

=мГнμГннГн

– Индуктивность

Очистить все

---

Ссылки по теме:

1. Single-layer Coil Inductance calculator by IN3OTD
2. RF Inductance Calculator by ON4AA
3. Round Coil Inductance Calculator by R. Weaver

 

Калькулятор расчета индуктивности катушки с воздушным сердечником

Катушка индуктивности является неотъемлемым элементом большинства современных приборов. При этом она используется для различных целей в работе электрических цепей. В случае необходимости замены можно использовать как заводскую, так и изготовленную самостоятельно катушку. Но при этом необходимо учитывать ее основной параметр – индуктивность. Для того чтобы рассчитать индуктивность катушки без сердечника можно воспользоваться универсальной формулой:

где μ­­₀ – магнитная проницаемость вакуума,  μ – магнитная проницаемость сердечника (можно взять из таблицы 1), N – число витков, S – площадь сечения катушки, l – длина намотки. Такой способ является универсальным и может использоваться, как для полых катушек, так и для имеющих сердечник.

Таблица 1

Материал	— µ —  (Гн/м)
Воздух	1. 25663753*10−6
Алюминий	1.256665*10−6
Аустенитная нержавеющая сталь	1.260*10−6  — 8.8*10−6
Вакуум (µ0)	4π*10−7
Вода	1.256627*10−6
Водород	1.2566371*10−6
Висмут	1.25643*10−6
Дерево	1.25663760*10−6
Железо (чистота 99.8%)	6.3*10−3
Железо (99.95% чистое Fe отожженное в водороде)	2.5*10−1
Железо-кобальтовые сплавы	2.3*10−2
Медь	1.256629*10−6
Никель-цинковый феррит — магнит	2.0*10−5 – 8.0*10−4
Мартенситная нержавеющая сталь (отожженная)	9.42*10−4 — 1.19*10−3
Мартенситная нержавеющая сталь (закаленная)	5. 0*10−5 — 1.2*10−4
NANOPERM® — магнитомягкий нанокристаллический сплав	1.0*10−1
Неодимовый магнит	1.32*10−6
Никель	1.26*10−4 — 7.54*10−4
Пермаллой (сплав 80% никеля и 20% железа)	1.0*10−2
Платина	1.256970*10−6
Сарфир	1.2566368*10−6
Сверхпроводники	0
Углеродистая сталь	1.26*10−4
Ферритная нержавеющая сталь (отожженная)	1.26*10−3 — 2.26*10−3
Фторопласт 4, Ф-4,   Teflon	1.2567*10−6

Если рассматривать частный вариант – катушку с воздушным сердечником, то для расчета ее индуктивности можно использовать формулу:

Где D – диаметр катушки, n – количество витков, а l – длина ее намотки.

Такой способ расчета будет справедливым для катушек, имеющих однослойную структуру, набираемых в один уровень. В случае если катушка наматывается в несколько слоев, то их толщина вносит дополнительные изменения в расчет. При этом формула расчета преобразится к виду:

Где D – диаметр катушки, n – количество витков, h – высота самой катушки, g – толщина слоя намотки.

Для упрощения процесса расчета индуктивности катушки без сердечника можно воспользоваться онлайн калькулятором. Здесь вы указываете ее основные параметры – диаметр, длину и количество витков, после чего нажать кнопку «Рассчитать» и вы получите значение индуктивности без лишних вычислений и затрат времени.

Электроника | Бесплатный полнотекстовый | Расчет индуктивности однослойной планарной спиральной катушки

1. Введение

Благодаря простоте реализации спиральная катушка нашла широкое применение во многих электромагнитных приложениях, начиная от высокочастотной радиочастотной идентификации (RFID) [1] и заканчивая относительно низкочастотная беспроводная передача энергии [2,3,4]. Для успешного применения в этих приложениях требуется точное моделирование спиральной катушки. Для решения этой проблемы было проделано много работ. Некоторые из них кратко рассмотрены в этой статье.

В [5,6,7] собственная индуктивность плоской спиральной катушки вычисляется путем рассмотрения ее как группы концентрических окружностей. Поэтому всегда существует некоторая погрешность между вычисленным и результатом измерения. Кроме того, для получения собственной индуктивности плоской спиральной катушки требуется вычисление индуктивностей каждой окружности и взаимных индуктивностей между ними. Следовательно, вычислительная сложность увеличивается.

Собственная индуктивность спиральной катушки аппроксимируется с помощью формулы Уилера или ее модифицированной формы [8,9]. Однако в этих формулах не учитывался один из параметров, влияющих на индуктивность: диаметр провода. Поэтому точность формул снижается при изменении диаметра проволоки спирального витка. Более того, точная деталь их вывода не установлена, и вместо аналитического метода индуктивность вычисляется эмпирически.

Программное обеспечение ANSYS Maxwell 3-D — один из лучших методов определения собственной индуктивности спиральной катушки любой формы; однако моделирование требует значительного времени расчета.

Для решения этого вопроса в статье предложено точное выражение собственной индуктивности плоской спиральной катушки, включающее все параметры, влияющие на индуктивность. Кроме того, используя интегральную формулу Неймана, этот метод вычисляет индуктивность плоской спиральной катушки, рассматривая всю спираль, не предполагая ее как группу концентрических окружностей. В результате вычислительная сложность формулы снижается.

Для проверки точности предложенного метода результаты расчета сравниваются с результатом моделирования и общепринятыми формулами, которые показывают хорошее совпадение. Для экспериментальной проверки несколько катушек с разными геометрическими параметрами изготавливаются на бобине, специально разработанной с помощью 3D-принтера. Наконец, сравнение результатов расчета и измерений подтверждает точность предложенного метода.

Структура документа следующая: Расчет собственной индуктивности плоской катушки обсуждается в Разделе 2. Раздел 3 проверяет результаты расчета с помощью другого традиционного метода и моделирования с использованием метода конечных элементов (МКЭ). Экспериментальная проверка результата расчета показана в разделе 4. Наконец, в разделе 5 подводятся итоги.

2. Расчет собственной индуктивности плоской спиральной катушки

Самоиндукция круглой плоской спиральной катушки может быть рассчитана путем решения интегральной формулы Неймана для взаимной индуктивности между двумя катушками [10]. Геометрические параметры плоской спирали, лежащие в плоскости x–y, показаны на рис. 1. Предполагается, что по спиральной катушке течет постоянный ток.

На рис. 1 R — внешний радиус спиральной катушки. θ — угол поворота R относительно оси x. w показывает диаметр провода, а s — расстояние между витками.

Внешний радиус R определяется по уравнению плоской спиральной катушки.

где R _i — внутренний радиус катушки, а — коэффициент шага, влияющий на расстояние между каждым витком.

Н – количество витков спиральной катушки.

Когда радиус кривизны спиральной катушки с одинаковой площадью поперечного сечения больше радиуса проводника катушки, самоиндукция плоской спиральной катушки будет равна взаимной индуктивности между исходной спиральной катушкой и ее фиктивной катушка размещена на расстоянии среднего геометрического расстояния (GMD) проводника [11]. Среднее геометрическое расстояние для литцендрата круглого сечения приведено в уравнении (4)

g представляет собой среднее геометрическое расстояние, а r — радиус проводника.

Радиус кривизны (внешний радиус) исходного R ₁ и его фиктивного спирального витка R ₂ показан в уравнениях (5) и (6).

θ ₁ и θ ₂ — угол поворота исходного и его фиктивного спирального витка соответственно.

Интегральная формула Неймана может быть представлена ​​уравнением (7).

где μ ₀ — вакуумная проницаемость, dl ₁ и dl ₂ — составляющие линии, а R — расстояние между dl ₁ и dl ₂ . Индуктивность плоской катушки можно рассчитать, оценив параметры в уравнении (7).

Скалярное произведение между dl ₁ и dl ₂ дано в уравнении (10).

Расстояние R можно представить с помощью формулы косинуса.

Подставляя уравнения (10) и (11) в уравнение (7), получаем точное уравнение собственной индуктивности плоской спиральной катушки, как показано в уравнении (12)

Уравнение (11) содержит все параметры, влияющие на индуктивность, такие как внутренний и внешний радиус спиральной катушки, число витков, диаметр провода и расстояние между витками.

Влияние каждого параметра на индуктивность подробно обсуждается в следующих разделах.

3. Сравнение с моделированием и традиционными методами

Для проверки предлагаемого метода индуктивности нескольких спиральных катушек с различными геометрическими параметрами рассчитываются с использованием уравнения (12). Индуктивности также рассчитываются с использованием обычного метода и метода конечных элементов (МКЭ). По отношению к результату моделирования вычисляются погрешность расчета и условные результаты. Ошибка вычисляется как RFem-RcRFem×100, где R _Fem представляет результат моделирования, а R _c показывает расчетный или обычный результат.

Моделирование МКЭ проводится с использованием программного обеспечения ANSYS Maxwell 15. Тип решения — магнетостатический. Сетка назначается как длина на основе катушки и ее границы. Длина элемента является значением по умолчанию. Ток назначается равномерно по поперечному сечению катушки для простоты.

Существует множество традиционных методов расчета спиральной катушки [8,9].,12]. В большинстве этих методов использовалась модифицированная формула Уилера для расчета собственной индуктивности спиральной катушки. Некоторые из этих формул были выбраны для сравнения в данной работе и обсуждаются ниже.

В [8] собственная индуктивность спиральной катушки аппроксимирована с использованием понятия среднего диаметра катушки, как показано в уравнении (13).

Собственная индуктивность спиральной катушки определяется исходя из эквивалентных плотностей тока и аппроксимации спирали [9]. Уравнение этого метода аппроксимации индуктивности спиральной катушки приведено в уравнении (16).

C _i – зависимый коэффициент. Для спиральной катушки круглой формы значение C ₁ равно 1, C ₂ равно 2,46, C ₃ равно 0,00 и C ₄ равно 0,20.

Методом приближения Уилера вычисляется собственная индуктивность спиральной катушки [12]. Эта формула недействительна, когда расстояние между витками меньше диаметра проволоки и катушка имеет меньшее количество витков. Эта формула аппроксимации математически обозначена в уравнении (17) и представлена ​​графически на рисунке 2.

Для расчета индуктивности однослойной круглой спиральной катушки в уравнении (18) используется модифицированная формула Гарольда А. Уилера.

где N — общее количество витков, w — диаметр провода, s — зазор между витками, а d _в и d _вых — внутренний и наружный диаметр провода соответственно.

Уравнения (13), (16)–(18) получены с использованием формулы Уилера или ее модифицированной формы для расчета индуктивности спиральной катушки. Следовательно, собственная индуктивность плоской спиральной катушки будет одинаковой при использовании любой из этих формул, а значит, и их погрешность относительно предлагаемого метода будет одинаковой. Любая из этих формул может быть выбрана для сравнения с предлагаемым методом.

Сравнение индуктивности путем изменения каждого геометрического параметра обсуждается в следующем подразделе.

3.1. Изменение внешнего радиуса

Для различного внешнего радиуса поведение самоиндукции спирали сравнивается для провода радиусом r = 1,8 мм, числом витков N = 10 и зазором между витками s = 4 мм. . Подробное сравнение показано на рисунке 3. На приведенном выше рисунке показано, что индуктивность катушки увеличивается, когда увеличивается внешний радиус или внешний диаметр катушки. Это можно объяснить определением индуктивности катушки.

Одним из факторов, от которых зависит индуктивность, является размер катушки. С увеличением размера катушки увеличивается и индуктивность. Индуктивность, полученная традиционным методом, ниже, чем результат расчета и моделирования. Таким образом, относительно результата моделирования ошибка традиционного метода выше, которая составляет около 16 %, по сравнению с ошибкой результата расчета, которая составляет менее 4 %. Таким образом, предлагаемый метод обеспечивает хорошую точность в отношении изменения внешнего радиуса.

3.2. Изменение диаметра провода

На рис. 4 показано поведение индуктивности для диаметров провода 3 мм и 3,6 мм. Значения остальных параметров такие же, как показано в разделе 3.1. По сравнению с проводом большого диаметра индуктивность катушки меньшего диаметра выше в результате расчета и моделирования. Однако индуктивность остается постоянной при изменении диаметра провода во многих традиционных формулах, потому что эти формулы не учитывают диаметр провода. При использовании обычного метода для расчета индуктивности ошибка составляет менее 17 % для диаметра провода 3,6 мм и 20 % для w = 3,0 мм по сравнению с результатом моделирования, и ошибка увеличивается по мере уменьшения диаметра провода. Однако погрешность результата расчета для всех случаев составляет менее 4%, что подтверждает его точность.

3.3. Изменение числа витков

На рис. 5 показано сравнение расчета собственной индуктивности и обычных результатов при различном числе витков для R _i = 10 мм, s = 4 мм и w = 3,6 мм. При увеличении числа витков катушки индуктивность возрастает. В обычных методах ошибка увеличивается с увеличением числа витков; однако он показал лучшую точность для меньшего количества витков по сравнению с результатом расчета. Можно сделать вывод, что обычная формула подходит для приложений, где требуется катушка с меньшим количеством витков. С другой стороны, погрешность результата расчета относительно результата МКЭ составляет менее 6 %, и точность сохраняется для всех случаев.

3.4. Изменение зазора между витками

На рис. 6 показано поведение индуктивности спиральной катушки при различных зазорах между витками при w = 3,6 мм, R _i = 10 мм и N = 10. Геометрия катушка расходуется с увеличением зазора между витками, увеличивая таким образом индуктивность. Погрешность резко возрастает с увеличением зазора между витками при использовании обычного метода. Однако результат расчета имеет погрешность менее 5% для увеличения зазора между витками. Таким образом, эти сравнения подтверждают справедливость результата расчета при различных вариациях геометрического параметра спирального витка.

4. Экспериментальная проверка

Для экспериментальной проверки предлагаемого метода необходимо рассчитать некоторые параметры изготовления спиральной катушки, такие как длина провода и сопротивления постоянному току. Кроме того, необходимо учитывать тип проволоки, качество пайки и катушку для удержания проволоки. Каждый из этих факторов кратко обсуждается в следующем подразделе.

4.1. Выбор провода

Для изготовления катушки используются различные типы проводов, но в этом исследовании выбран литцендратный провод из-за его огромных преимуществ и многократного использования во многих приложениях, таких как кристаллическое радио, рамочная антенна, высокодобротные катушки, коммутация. электроснабжение и индукционное нагревательное оборудование. Литцендрат изготавливается путем соединения нескольких жил тонкой изолированной проволоки рядом друг с другом. Каждая изолированная жила несет часть тока, уменьшая воздействие на кожу и близость. Благодаря этим эффектам литцендраты уменьшают увеличение сопротивления на более высоких частотах [13]. Этот провод можно использовать примерно до 1 МГц. В этой работе для изготовления спиральных катушек используется 500 прядей литцендрата, каждая прядь диаметром 0,1 мм. Диаметр проволоки составляет около 3,6 мм, что определяется эмпирическим путем по уравнению (19).).

где D _e — расчетный диаметр литцендрата, D _s — диаметр одной жилы, а N _s — общее количество прядей.

4.2. Качество пайки

Диаметр провода, который является одним из факторов, влияющих на индуктивность, может быть уменьшен во время пайки. Поэтому для качественной пайки необходимы надлежащий процесс и меры предосторожности. Температура припоя (свинца) должна равномерно распределяться внутри паяльной ванны, при этом лучше выбирать припой с меньшим количеством примесей. Температура пайки зависит от типа и ширины проволоки. Таким образом, температуру следует регулировать и проверять термометром. Наконец, требуется специальное приспособление и соответствующий набор для пайки, как показано на рис. 7.

4.3. Расчет длины провода и сопротивления провода

Длина провода пропорциональна его сопротивлению постоянному току. Поэтому важно рассчитать длину провода и сопротивление. Общая длина и сопротивление провода могут быть рассчитаны по уравнениям (20) и (21). Кроме того, расчетная и фактическая длина и сопротивление постоянному току провода показаны на рис. 8а,б. Сопротивление постоянному току измеряется с помощью Gwinstek LCR-6020.

где l длина провода; σ постоянная, ее значение равно 58 000; n – количество прядей; r — радиус одной нити.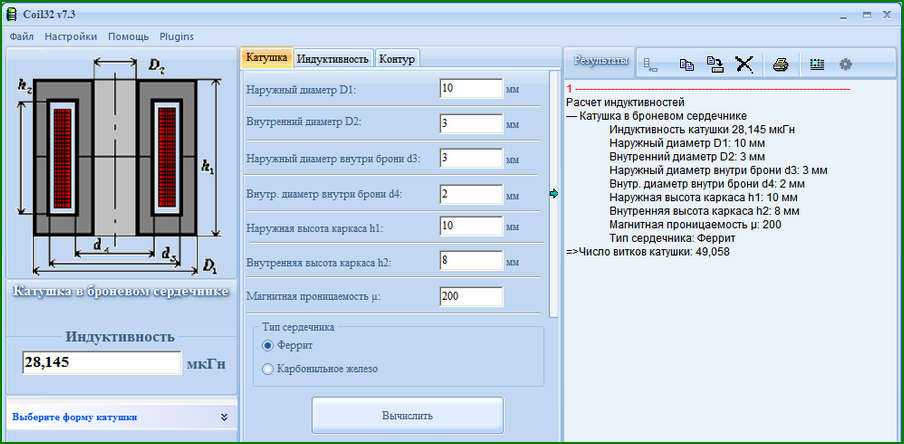

4.4. Бобина

Для крепления проволоки спиральной катушки с помощью 3D-принтера изготавливаются различные бобины с различным диаметром проволоки, количеством витков, расстоянием между витками и внешним радиусом. Нить для печати была PLA (полимолочная кислота). На рис. 9а,б показаны катушка и спиральная катушка с катушкой.

4.5. Экспериментальный результат

Для проверки предлагаемого метода изготавливаются три случайные катушки разных размеров, и их индуктивность измеряется с помощью Gwinstek LCR-6020 m. Частота тестирования для этого измерения составляет 20 кГц. Наконец, результаты измерений сравниваются с результатом расчета, и их результаты представлены в таблице 1. Кроме того, результаты измерений также показаны на рисунке 10.

Из таблицы 1 видно, что результаты расчета хорошо согласуются с результатом измерений. Относительная ошибка составляет менее 5%.

5. Выводы

В этой статье представлен новый способ вычисления индуктивности однослойной плоской спирали. Используя принцип среднего геометрического расстояния, предлагаемый метод определяется путем решения формулы Неймана для взаимной индуктивности между двумя катушками. Численно рассчитаны индуктивности различных размеров спиральных катушек с различными внешними радиусами, числом витков, диаметром проволоки и зазором между витками. Результаты расчетов проверяются моделированием, экспериментальными и общепринятыми формулами. Погрешность результатов расчета составляет менее 5 % для всех случаев по сравнению с общепринятой формулой, которая составляла более 20 %. Более того, предлагаемый метод содержит все параметры, влияющие на индуктивность. Однако традиционные формулы не учитывали все параметры, что приводило к ошибочным результатам.

В этом исследовании индуктивность однослойной спиральной катушки рассчитывается для равномерного протекания тока в проводе. Однако индуктивность может быть разной для неоднородных токов. В этом случае она требует дальнейшего исследования и может быть учтена в дальнейшей работе.

Вклад авторов

И.Х. предложил теоретическую модель и провел эксперимент; Д.-К.В. пересмотрела проект и дала указания. Все авторы прочитали и согласились с опубликованной версией рукописи.

Финансирование

Это исследование не получило внешнего финансирования.

Конфликт интересов

Авторы заявляют об отсутствии конфликта интересов.

Ссылки

1. Лю, Ю.; Терри, Т.Ю. Антенна с сопряженной планарной катушкой (CPC) в качестве датчика смещения для меток NFC или HF RFID. В материалах Международной конференции IEEE по RFID (RFID) 2020 г., Орландо, Флорида, США, 5–9 октября 2020 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2020 г.; стр. 1–6. [Google Scholar]
2. Ифтихар Х.; Ву, Д.-К. Упрощенный расчет взаимной индуктивности плоской спиральной катушки для беспроводных приложений питания. Датчики 2022 , 22, 1537. [Google Scholar] [CrossRef] [PubMed]
3. Шахид, Х. ; Мохамед, А .; Ахмед, К.-Б.Л.; Ким, Ю.К. Весовая схема зарядки с нечеткой логикой для оптимального распределения мощности зарядки между электромобилями на стоянке. Энергии 2020 , 13, 3119. [Google Scholar] [CrossRef]
4. Янг, Д.Дж. Беспроводное питание и телеметрия данных для биомедицинских имплантатов. В материалах ежегодной международной конференции IEEE Engineering in Medicine and Biology Society 2009 г., Миннеаполис, Миннесота, США, 3–6 сентября 2009 г.; IEEE: Манхэттен, штат Нью-Йорк, США, 2009 г.; стр. 3221–3224. [Google Scholar]
5. Чан, Х.Л.; Ченг, KWE; Сутанто, Д. Упрощенная формула Неймана для расчета индуктивности спиральной катушки. В материалах Восьмой международной конференции по силовой электронике и приводам с регулируемой скоростью 2000 г. (публикация IEE Conf. No.475), Лондон, Великобритания, 18–19 сентября 2000 г.; стр. 69–73. [Google Scholar]
6. Рам Рахьяни, А.К.; Шахриар, М .; Mu, C. Проектирование и оптимизация эффективных беспроводных систем подачи энергии на основе резонанса для биомедицинских имплантатов. IEEE транс. Биомед. Цепи Сист. 2010 , 5, 48–63. [Google Scholar] [CrossRef] [PubMed]
7. Li, X.; Ханру, З .; Фей, П.; Ян, Л .; Тяньян, Ю .; Поклон.; Dongming, F. Беспроводная магнитно-резонансная система передачи энергии для микроимплантируемых медицинских датчиков. Датчики 2012 , 12, 10292–10308. [Google Scholar] [CrossRef] [PubMed]
8. Jie, L.; Костинетт, Д. Анализ и разработка последовательной саморезонансной катушки для беспроводной передачи энергии. В материалах конференции и выставки IEEE Applied Power Electronics Conference and Exposition (APEC) 2018 г., Сан-Антонио, Техас, США, 4–8 марта 2018 г.; стр. 1052–1059.. [Google Scholar]
9. Тао, Л.; Вэй, З .; Чи, Х .; Инь, Б. Расчет индуктивности многослойных круглых печатных спиральных катушек. Дж. Физ. конф. сер. 2019 , 1176, 062045. [Google Scholar]
10. Инан, Инженерная электромагнетика США; Pearson Education: Noida, India, 1998. [Google Scholar]
11. Калантаров П.Л. расчет индуктивности; National Power Press: Москва, Россия, 1955. [Google Scholar]
12. Чаттерджи, С.; Айер, А .; Бхаратираджа, К.; Вагасия, И.; Валивети, Р. Оптимизация конструкции эффективной беспроводной системы передачи энергии для электромобилей. Энергетическая процедура 2017 , 117, 1015–1023. [Google Scholar] [CrossRef]
13. Вяйсянен, В.; Хилтунен, Дж.; Нерг, Дж.; Сильвентойнен, П. Методы расчета сопротивления переменному току и практические соображения по проектированию при использовании литцендрата. В материалах IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Вена, Австрия, 10–13 ноября 2013 г.; стр. 368–375. [Google Scholar]

Рисунок 1. Плоская спиральная катушка.

Рисунок 1.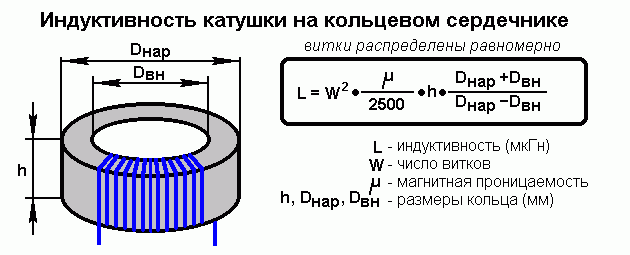 Плоская спиральная катушка.

Рисунок 2. Поперечный разрез спиральной катушки.

Рисунок 2. Поперечный разрез спиральной катушки.

Рисунок 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.

Рисунок 3. Поведение собственной индуктивности спиральной катушки в зависимости от внешнего радиуса.

Рисунок 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.

Рисунок 4. Влияние изменения диаметра проволоки на самоиндукцию спиральной катушки.

Рисунок 5. Влияние изменения числа витков на индуктивность спиральной катушки.

Рисунок 5. Влияние изменения числа витков на индуктивность спиральной катушки.

Рисунок 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.

Рисунок 6. Влияние изменения зазора между витками на индуктивность спиральной катушки.

Рисунок 7. Настройка пайки.

Рис. 7. Настройка пайки.

Рисунок 8. Сравнение расчетной и измеренной длины и DCR. ( a ) Сравнение длины. ( b ) Сравнение DCR.

Рис. 8. Сравнение расчетной и измеренной длины и DCR. ( а ) Сравнение длин. ( b ) Сравнение DCR.

Рисунок 9. Спиральная катушка и бобина. ( a ) Бобина. ( b ) Спиральная катушка, намотанная на бобины.

Рис. 9. Спиральная катушка и бобина. ( a ) Бобина. ( b ) Спиральная катушка, намотанная на бобины.

Рисунок 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( с ) 16 витков.

Рис. 10. Измерены индуктивности спиральной катушки разных размеров. ( и ) 7 витков. ( б ) 10 витков. ( c ) 16 витков.

Таблица 1. Сравнение результата расчета и измерения.

Таблица 1. Сравнение результата расчета и измерения.

Параметры					Результаты
N	R i (mm)	s (mm)	w (mm)	R o (mm)	Inductance (μH) (Calculated)	Inductance (μH) (Measured)	Error (%)
7	12	4	3.6	40	2. 25	2.17	3.56
10	10	3.8	3.6	48	5,68	5.50	3.16
16	8	4	3.6	72	20.10	19.55	2.73

Publisher’s Note: MDPI stays neutral with regard к юрисдикционным требованиям в опубликованных картах и ​​институциональной принадлежности.

© 2022 авторами. Лицензиат MDPI, Базель, Швейцария. Эта статья находится в открытом доступе и распространяется на условиях лицензии Creative Commons Attribution (CC BY) (https://creativecommons.org/licenses/by/4.0/).

[PDF] Расчет индуктивности однослойной спиральной катушки

• ID корпуса: 157063379

  title={Расчет индуктивности однослойной спиральной катушки},
  автор={Mat{\'u}{\vs} Ocilka},
  год = {2012}
} 

• Матуш Оцилка
• Опубликовано в 2012 г.
• Физика

Целью данной статьи является оценка индуктивности однослойной плоской спиральной (блинчатой) катушки. Сначала применяется аналитический подход однослойного, затем производится расчет индуктивности методом конечных элементов решения. Для этого был использован программный комплекс COMSOL Multiphysics с модулем AC-DC. Спроектированная катушка создается в двумерном осесимметричном пространственном измерении и результаты сравниваются с аналитическим решением. Наконец, были проведены экспериментальные измерения индуктивности, чтобы… 

Mechatronika.polsl.pl

с показателем 1-10 из 13 ссылок

Сорт Byrelevancemost, влияющий на PapersRecency

Математическое моделирование системы электромагнитной формирования с плоской спиралью As Actuator

• M.R. Joyson Luiz Pacheco, E. Paese

• Physics

• 2010

В этом исследовании представлено математическое моделирование и процедура расчета для задач электромагнитного формования тонких круглых металлических листов с использованием плоской спиральной катушки в качестве привода. Метод фокусируется на…

Расчет индуктивности спиральных индукторов различной формы

В этой статье получены простые коэффициенты формы для расчета индуктивности спиральных индукторов различной формы. По сравнению с численными результатами (например, IE3D) средняя ошибка составляет менее 2%, при этом… индукторы дешевле, чем индукторы на микросхемах или катушках для конструкций на основе печатных плат (печатных плат). Точность при проектировании спирального индуктора важна, потому что это…

Простые точные выражения для индуктивностей плоской спирали

Мы представляем несколько новых простых и точных выражений для индуктивности постоянного тока квадратных, шестиугольных, восьмиугольных и круглых спиральных индукторов. Мы оцениваем точность наших выражений, а также…

Промышленная электротехника – Моделирование преобразователей, 1-я часть, книга

• 2011

Промышленная электротехника – Моделирование преобразователей, 2-я часть, книга

• 2011

Электромагнитная совместимость -измерение

• 2009

Промышленное электрическое интрэлексирование -моделирование конвертеров, 1 -я часть, книга, опубликованная TU of KoShice

961
91919191919101019191919191919 гг.