Расчёт сопротивления проводника. Удельное сопротивление.
Цель: исследовать зависимость сопротивления проводника от его характеристик.
Задачи
обучающие:
- исследовать зависимость сопротивления проводника от его длины, площади поперечного сечения и вещества, из которого он изготовлен;
- сформировать первичные представления знаний о новой физической величине « удельное электрическое сопротивление»;
- продолжить формирование умений решать задачи;
развивающие:
- работать над формированием исследовательских компетенций учащихся путем организации фронтального виртуального мини-исследования с использованием электронных ресурсов;
- работать над формированием умений учащихся воспринимать и представлять информацию в словесной и символической формах через обсуждение результатов демонстрационного эксперимента и самостоятельных виртуальных экспериментов;
- формировать умения делать выводы на основе проведенного анализа;
- работать над формированием коммуникативных компетенций учащихся;
воспитательные:
- знакомить с экспериментальным методом научного познания природы; создать условия для развития самостоятельности учащихся;
- развивать познавательный интерес учащихся к предмету.
Тип урока: комбинированный.
Формы работы учащихся:
- групповая (исследовательская самостоятельная работа с электронными ресурсами)
- коллективное обсуждение результатов виртуальных экспериментов;
- индивидуальная (текущий контроль, самостоятельная работа с ЭОР К-типа)
Методы обучения, используемые на уроке: словесные, наглядные, практические.
Демонстрационное оборудование: источник питания ВС-24М, лампочки на 3В и 12 В, ключ, цифровой амперметр, реохорд, соединительные провода.
Средства ИКТ: ПК (для учителя), видеопроектор, интерактивная доска, нетбук (на индивидуальном рабочем месте каждого учащегося).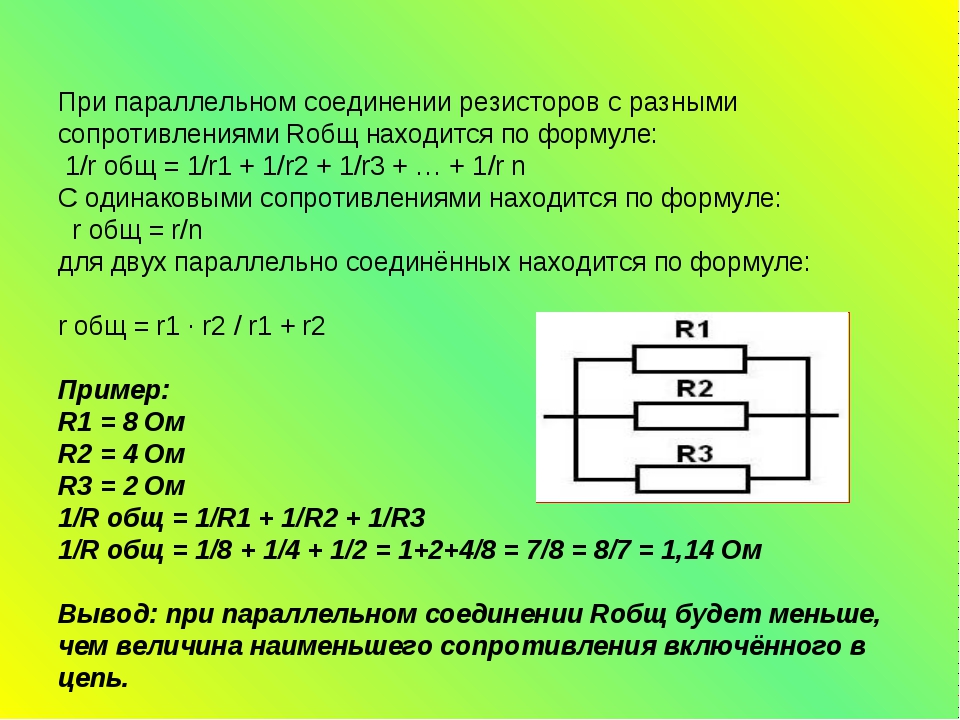 Презентация SMART Notebook по теме «Расчет сопротивления проводников. Удельное сопротивление».
Презентация SMART Notebook по теме «Расчет сопротивления проводников. Удельное сопротивление».
Структура и ход урока
1.Организационный этап
|
Деятельность учителя |
Деятельность ученика |
|
Приветствует учащихся. Проверяет готовность учащихся к занятию. |
Приветствуют учителя. Проверяют готовность к уроку. |
2. Проверка домашнего задания
|
Деятельность учителя |
Деятельность ученика |
|
Проводит проверку домашнего задания. (Приложение 1) |
Выполняют тест (варианты разного уровня сложности) |
3. Актуализация знаний
|
Деятельность учителя |
Деятельность ученика |
|
Готовит учащихся к восприятию новых знаний. Предлагает разгадать анаграммы, сопоставить текст – изображение.
Давайте вспомним, что является причиной сопротивления проводника? Зависит ли сила тока от сопротивления проводника? Как зависит? Зависит ли сопротивление от силы тока и напряжения? |
Выполняют интерактивные задания. Составляют название приборов, правила их подключения для измерения физических величин. Сопоставляют условное обозначение прибора на схеме с его названием.
Отвечают на вопросы учителя |
4. Создание проблемной ситуации
|
Деятельность учителя |
Деятельность ученика |
|
1.Предлагает вниманию учащихся следующий эксперимент:
К источнику тока с напряжением 3 В включают поочерёдно лампочки на 3В и 12 В. Почему лампочка на 12 В не светится.
2. Проверяет исправность лампы, увеличив напряжение источника тока. |
Выдвигают предположения:
|
5. Постановка цели урока. Изучение новой темы
|
Деятельность учителя |
Деятельность ученика |
|
1.Подводит учащихся к цели урока. Разные потребители тока имеют разное сопротивление, что необходимо знать, чтобы изготовить проводник с необходимым сопротивлением? Зависимость сопротивления от геометрических размеров проводника (длины и площади поперечного сечения) и вещества, из которого он изготовлен, впервые установил Георг Ом. |
1. |
|
2. Выясните: от чего и зависит сопротивление проводника? Краткие рекомендации по работе над учебным модулем (Расчет сопротивления проводника. Удельное сопротивление. Реостаты). Разделяет учащихся по группам и предлагает самостоятельно решить поставленную задачу, сделать выводы и поделиться выводами со всем классом.
|
2. Слушают рекомендации учителя для выполнения практического задания. Работают с учебным модулем (1-5 пункты). Проводят исследования и составляют краткий конспект. Делают выводы по результатам выполнения каждого задания в отдельности. Обобщают результаты трех виртуальных экспериментов и формулируют общий вывод.
|
|
3.
|
3.Совместно с учителем проводят эксперимент подтверждающий справедливость сделанных выводов.
|
|
4. Предлагает учащимся продолжить работу с учебным модулем. Выясните: какая физическая величина характеризует зависимость сопротивления проводника от материала, из которого изготовлен проводник. |
4. Продолжают работу с учебным модулем (6 пункт) и выполняют записи в тетрадях. |
|
5.Предлагает учащимся поработать с таблицей удельного сопротивления некоторых веществ(стр.105 учебник физика 8 класс, автор А.В.Пёрышкин) и ответить на вопросы:
|
5. Работают с таблицей удельного сопротивления (учебник) и отвечают на вопросы учителя. Работают с таблицей удельного сопротивления (учебник) и отвечают на вопросы учителя.
|
|
6. Предлагает учащимся обобщить полученные закономерности и составить формулу для нахождения сопротивления проводника. Провести проверку.
|
6. Анализируют полученные результаты и составляют формулу сопротивления. Используя, учебный модуль (7пункт) проводят проверку полученной формулы. |
|
7. Предлагает получить дополнительные формулы.
|
7. Сравнивают полученные формулы.
|
6. Этап первичного освоения знаний
|
Деятельность учителя |
Деятельность ученика |
|
1. (Удельное электрическое сопротивление веществ) В практический модуль включены 7 интерактивных заданий различных типов с возможностью автоматизированной проверки для закрепления знаний. Модуль относится к II уровню интерактивности Отвечает на вопросы учащихся по разъяснению правил выполнения работы. |
1.Слушают рекомендации учителя по выполнению задания. Задают организационные вопросы учителю. Выполняют практическое задание. |
|
2.Определяет успешность выполнения задания. Интересуется возникшими трудностями. Определяет задания, с которыми учащиеся не смогли справиться. |
2. |
|
3.Организует работу учащихся по демонстрации верных решений. |
3.Объясняют решение заданий.
|
7. Этап закрепления полученного материала
|
Деятельность учителя |
Деятельность ученика |
|
1. Учитель приглашает ученика к доске записать решение задачи и проверить ответ. Чему равно сопротивление 100 м медного провода сечением 1 мм2?
2.Предлагает учащимся для закрепления нового материала выполнение практического модуля, для решения которого необходимы новые знания. |
1.Учащиеся записывают условие и решение задачи в тетрадь.
|
|
2.Определяет успешность выполнения заданий. Фиксирует результаты. Отмечает (для себя) учащихся, которые наиболее (наименее) успешно справились с заданием. |
2.Выполняют тест. Сообщают результаты учителю.
|
8. Рефлексия (Подведение итогов)
|
Деятельность учителя |
Деятельность ученика |
|
Предлагает учащимся вернуться к цели и задачам урока, проанализировать степень их достижения, объяснить результаты эксперимента, поставленного в начале урока с использованием новой терминологии, сделать выводы. Сообщает оценки за урок. |
Вспоминают цель урока. Анализируют степень ее достижения. Формулируют выводы. Оценивают успешность своей работы на уроке и уровень усвоения знаний. |
9. Домашнее задание
|
Деятельность учителя |
Деятельность ученика |
|
Сообщает домашнее задание: 1.§45, 46; упражнение 20 № 2 (а), 4. 2.Интерактивная лекция для тех, кто плохо разобрался с материалом 3.Тест |
Записывают в дневниках домашнее задание. |
|
Ø типоразмер мм |
Электрическое сопротивление нихрома (теория) Ом |
||
| Нихромовая нить Ø 0,01 | 13000 | ||
| Нихромовая нить Ø 0,02 | 3340 | ||
| Нихромовая нить Ø 0,03 | 1510 | ||
| Нихромовая нить Ø 0,04 | 852 | ||
| Нихромовая нить Ø 0,05 | 546 | ||
| Нихромовая нить Ø 0,06 | 379 | ||
| Нихромовая нить Ø 0,07 | 279 | ||
| Нихромовая нить Ø 0,08 | 214 | ||
| Нихромовая нить Ø 0,09 | 169 | ||
|
Нихромовая нить Ø 0,1 |
137 | ||
| Нихромовая нить Ø 0,2 | 34,60 | ||
| Нихромовая нить Ø 0,3 | 15,71 | ||
| Нихромовая нить Ø 0,4 | 8,75 | ||
| Нихромовая нить Ø 0,5 | 5,60 | ||
| Нихромовая нить Ø 0,6 | 3,93 | ||
| Нихромовая нить Ø 0,7 | 2,89 | ||
| Нихромовая нить Ø 0,8 | 2,2 | ||
| Нихромовая нить Ø 0,9 | 1,70 | ||
| Нихромовая проволока Ø 1,0 | 1. 40 40 |
||
| Нихромовая проволока Ø 1,2 | 0,97 | ||
| Нихромовая проволока Ø 1,5 | 0,62 | ||
| Нихромовая проволока Ø 2,0 | 0.35 | ||
| Нихромовая проволока Ø 2,2 | 0,31 | ||
| Нихромовая проволока Ø 2,5 | 0,22 | ||
| Нихромовая проволока Ø 3,0 | 0,16 | ||
| Нихромовая проволока Ø 3,5 | 0,11 | ||
| Нихромовая проволока Ø 4,0 | 0,087 | ||
| Нихромовая проволока Ø 4,5 | 0,069 | ||
| Нихромовая проволока Ø 5,0 | 0,056 | ||
| Нихромовая проволока Ø 5,5 | 0,046 | ||
| Нихромовая проволока Ø 6,0 | 0,039 | ||
| Нихромовая проволока Ø 6,5 | 0,0333 | ||
| Нихромовая проволока Ø 7,0 | 0,029 | ||
| Нихромовая проволока Ø 7,5 | 0,025 | ||
| Нихромовая проволока Ø 8,0 | 0,022 | ||
| Нихромовая проволока Ø 8,5 | 0,019 | ||
| Нихромовая проволока Ø 9,0 | 0,017 | ||
| Нихромовая проволока Ø 10,0 | 0,014 | ||
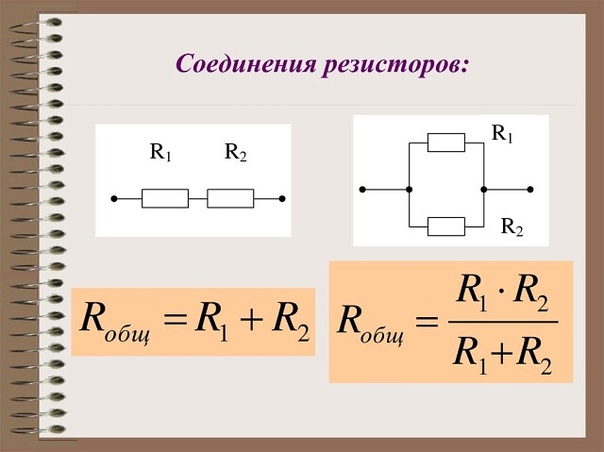
Калькулятор параллельных сопротивлений • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет сопротивление нескольких параллельно соединенных резисторов.
Пример. Рассчитать эквивалентное сопротивление двух резисторов 20 Ом and 30 Ом, соединенных параллельно.
Входные данные
Добавить резистор
Выходные данные
Эквивалентное сопротивление
R ом (Ом)
Введите величины сопротивлений в поля R1, R2 и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы сопротивления в миллиомах (мОм), омах (Ом), килоомах (кОм) или мегаомах (МОм) и нажмите кнопку Рассчитать.
1 мОм = 0,001 Ом. 1 кОм = 1 000 = 10³ Ом. 1 МОм = 1 000 000 = 10⁶ Ом.
Эквивалентное сопротивление Req группы параллельно соединенных резисторов является величиной, обратной сумме величин, обратно пропорциональных сопротивлениям этих резисторов.
или
Иными словами, проводимость G параллельно соединенных резисторов равна сумме проводимостей этих резисторов:
Эта формула для Req и используется в данном калькуляторе для расчетов. Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Например, общее сопротивление трех резисторов 10, 15 и 20 ом, соединенных параллельно, равно 4.62 Ом:
Если параллельно соединены только два резистора, формула упрощается:
или
Если имеется n соединенных параллельно одинаковых резисторов R, то их эквивалентное сопротивление будет равно
Отметим, что общее сопротивление группы из любого количества соединенных параллельно резисторов всегда будет меньше, чем наименьшее сопротивление резистора в группе и добавление нового резистора всегда приведет к уменьшению эквивалентного сопротивления.
Отметим также, что все резисторы, соединенные параллельно находятся под одним и тем же напряжением. Однако токи, протекающие через отдельные резисторы, отличаются и зависят от их сопротивления. Общий ток через группу резисторов равен сумме токов в отдельных резисторах.
При соединении нескольких резисторов параллельно всегда нужно учитывать их допуски и рассеиваемую мощность.
Различные постоянные и переменные резисторы
Примеры применения параллельного соединения резисторов
Одним из примеров параллельного соединения резисторов является шунт в приборе для измерения токов, которые слишком велики для того, чтобы быть напрямую измеренными прибором, предназначенным для измерения небольших токов или напряжений. Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Для измерения тока параллельно гальванометру или электронному прибору, измеряющему напряжение, подключается резистор с очень маленьким точно известным сопротивлением, изготовленный из материала со стабильными характеристиками. Этот резистор называется шунтом. Измеряемый ток протекает через шунт. В результате на нем падает небольшое напряжение, которое и измеряется вольтметром. Поскольку падение напряжения пропорционально току, протекающему через шунт с известным и точным сопротивлением, вольтметр, подключенный параллельно шунту, можно проградуировать непосредственно в единицах тока (амперах).
Установленный в мультиметре шунт для измерения ток до 20 ампер. Отметим, что если этим мультиметром измеряется большой ток непрерывно более 10 секунд, шунт перегреется и его сопротивление изменится, что приведет к ошибке измерения
Параллельные и последовательные схемы часто используются для получения точного сопротивления или если резистора с требуемым сопротивлением нет или он слишком дорог, если его приобретать в небольших количествах для массового производства. Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Например, если устройство содержит много резисторов по 20 кОм и необходим только один резистор 10 кОм. Конечно, несложно найти резистор на 10 кОм. Однако для массового производства иногда бывает лучше поставить два резистора на 20 кОм параллельно, чтобы получить необходимые 10 кОм. Это приведет к снижению себестоимости печатной платы, так как будет снижена оптовая цена компонентов, а также стоимость монтажа, так как будет уменьшено количество типоразмеров элементов, которые должен установить на плату автомат установки компонентов.
Резисторы поверхностного монтажа на печатной плате
Расчет заземления,сопротивление заземления,как рассчитать сопротивление заземления
Кроме качества материалов, используемых при монтаже заземления, главным показателем качества заземления является значение сопротивления заземляющего устройства растеканию электрического тока.
В теории расчет значения сопротивления заземляющего устройства (ЗУ) в определенном грунте и с определенным видом заземляющего устройства производится по следующей формуле:где
ρ –
удельное сопротивление грунта (Ом*м)
L –
длина заземлителя (м)
d –
диаметр заземлителя (м)
T -
заглубление заземлителя (расстояние от поверхности земли до середины
заземлителя) (м)
Π -
математическая константа Пи (3,141592)
Ln -
натуральный логарифм
Данная формула используется при
проектирования заземляющих устройств. С помощью этой формулы на стадии
проектирования закладывается количество материалов, которые будут использованы
при реальном монтаже заземления, а так же форма заземляющего устройства.
С помощью этой формулы на стадии
проектирования закладывается количество материалов, которые будут использованы
при реальном монтаже заземления, а так же форма заземляющего устройства.
Но когда настает этап реального монтажа заземления, как правило, расчетные данные оказываются неверны. Либо запланированного материала не хватает, либо остается много лишних комплектующих.
Поэтому с определенного момента мы перестали пользоваться расчетными данными. После анализа грунта на монтируемой местности мы приступали к монтажу. Для большей доли вероятности достижения требуемого значения сопротивления заземляющего устройства мы используем универсальный комплект заземления ZandZ ZZ-000-015. В процессе монтажа заглубляем 4-5 1.5 метровых омеднённых штыря, производим замер сопротивления. На основе полученного значения делаем вывод о дальнейших действиях.
Как правило если заземление монтируется
для электросети дома с системой заземления TT, то 4-5 забитых штырей для этого
достаточно с вероятностью 100%.
Что касается конкретно требуемого значения сопротивления заземления как, например, для заземляющего устройства газового котла(часто газовые службы, принимающие газовое хозяйство, требуют значение <10 Ом), то в этом случае 5 штырей и заземляющего устройства из одного электрода может не хватить.
И тут необходимо анализировать значения
сопротивления, полученные после монтажа 5 штырей. Если после монтажа 5 штырей
значение составляет <20-30 Ом и монтаж идет без затруднений, то можно
продолжать монтаж, проверяя динамику снижения значения сопротивления заземления
при погружении каждого штыря, если значение уменьшается в 1.5-2 раза то
монтировать до нужного значения. Если значение уменьшается не значительно, а
порой может немного возрастать, то будет целесообразно монтировать еще один
электрод, на расстоянии от первого и соединить их горизонтальным заземлителем (
либо стальная пластина 4х40 либо омеднённая проволока.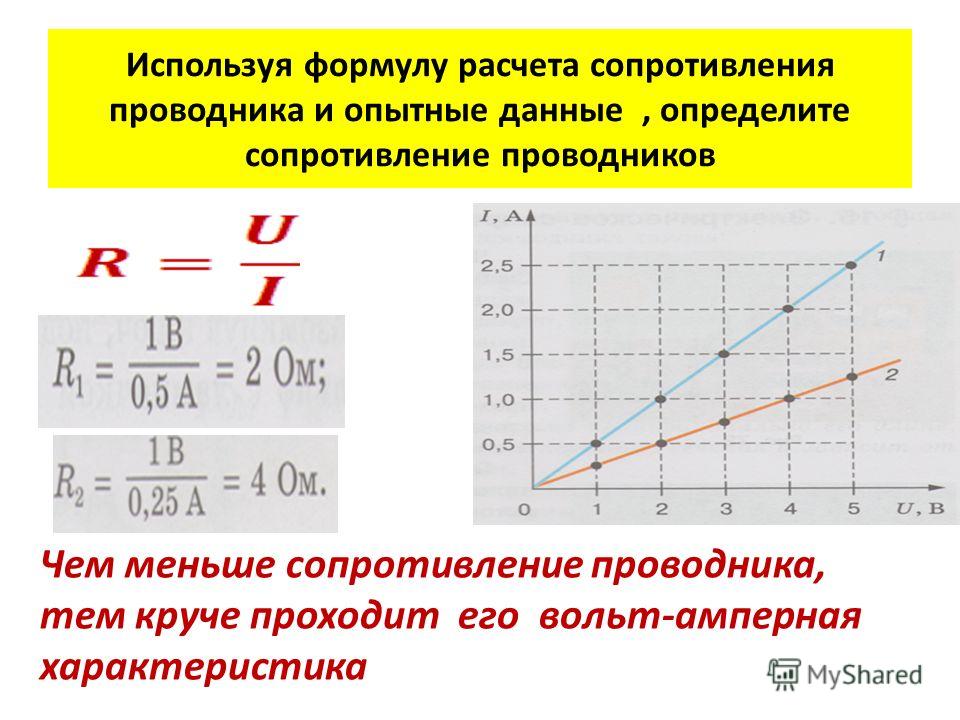 Расстояние между электродами в идеале, должно быть равно глубине забитого электрода умноженного на 2, но на дачных участках редко имеется такие просторы и копать такую траншею не легко и поэтому можно обойтись расстоянием равным глубине забитого электрода. И продолжать монтаж до нужного значения. В этом случае горизонтальный заземлитель (закопанный в траншею глубиной от 50-70 см), соединяющий электроды будет также уменьшать сопротивление заземляющего устройства.
Расстояние между электродами в идеале, должно быть равно глубине забитого электрода умноженного на 2, но на дачных участках редко имеется такие просторы и копать такую траншею не легко и поэтому можно обойтись расстоянием равным глубине забитого электрода. И продолжать монтаж до нужного значения. В этом случае горизонтальный заземлитель (закопанный в траншею глубиной от 50-70 см), соединяющий электроды будет также уменьшать сопротивление заземляющего устройства.
С случае песчаного, сухого или смешанного грунта можно делать заземляющие устройства более сложного типа – в виде треугольника, квадрата, прямоугольника, с количеством вертикальных и горизонтальных заземлителей необходимых для достижения нужного значения сопротивления заземляющего устройства(здесь можно посмотреть варианты и формы заземляющих устройств). Если же грунт промёрзший или сильно сухой, то можно использовать электролитическое заземление, разработанное специально для сухих и вечномёрзлых грунтов.
Эта статья сугубо субъективная и не
претендует на правила монтажа заземляющих устройств «по умолчанию» Хотим
поделиться опытом монтажа заземляющих устройств с использованием модульного
заземления модульного типа. Заземление из стальных уголков является также
полноценным заземляющим устройством, только уступает модульному заземлению ZandZ сложностью монтажа и меньшим сроком эксплуатации.
Заземление из стальных уголков является также
полноценным заземляющим устройством, только уступает модульному заземлению ZandZ сложностью монтажа и меньшим сроком эксплуатации.
Расчёт сопротивления проводника. Удельное сопротивление. Примеры расчетов
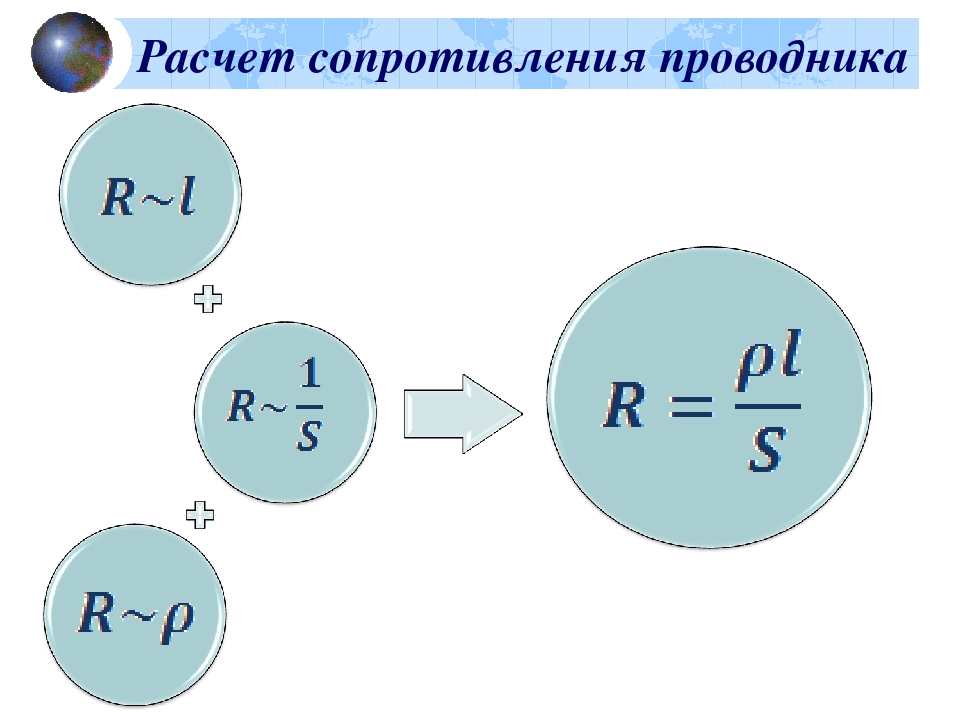
Сопротивление в проводниках возникает из-за взаимодействия электронов с ионами кристаллической решетки. Если вдуматься, то можно заметить, что чем длиннее проводник, тем больше такое взаимодействие.
Также, логично предположить, что чем толще проводник, тем больший поток электронов может пройти через поперечное сечение.
И, конечно, мы знаем, что разные вещества по-разному проводят ток. Исходя из этих знаний, мы можем установить следующее:
Чем длиннее проводник, тем больше его сопротивление.
Чем толще проводник, тем меньше его сопротивление.
Сопротивления проводников одинаковой длины
и толщины могут быть различны, в зависимости от вещества.
Ну а как именно зависит сопротивление проводника от его размеров, можно узнать только с помощью опытов. Мы уже немного знакомы с методикой проведения подобных экспериментов: нам нужно провести некоторые измерения, и, построив график, установить зависимость сопротивления от тех или иных величин. Данные опыты были проведены Георгом Омом.
Подключим проводник к источнику тока и, с помощью
амперметра и вольтметра, измерим силу тока и напряжение. Мы используем, так
называемый, мультиметр — современный прибор, который выполняет функции
амперметра и вольтметра, в зависимости от настроек. Но, тем не менее, мы
по-прежнему должны следовать правилам: когда мы хотим измерить силу тока,
мультиметр подключается последовательно. На мультиметре есть переключатель
между режимами измерения той или иной величины. Также, когда мы хотим измерить
напряжение, мультиметр подключается параллельно. Используя закон Ома, мы можем
вычислить сопротивление данного проводника.
Подобным способом, мы можем вычислить сопротивление проводников разной длины, но той же толщины, сделанных из того же материала. Проведя несколько измерений, выясним, что сопротивление проводника увеличивается ровно во столько раз, во сколько увеличивается его длина.
В таблице с данными можно увидеть незначительные несоответствия. Однако, мелкие погрешности в измерениях, при проведении любого опыта, неизбежны. Тем не менее, закономерность очевидна: сопротивление проводника прямо пропорционально длине проводника. Это подтверждается и графиком, который является прямой линией.
Проведем несколько иной опыт: сравним сопротивления проводников из того же материала, одинаковой длины, но разной толщины. Поскольку роль играет не сама толщина, а площадь поперечного сечения проводника, то мы попытаемся выяснять, как зависит сопротивление именно от этого параметра.
Полученные данные показывают, что на этот раз сопротивление
проводника обратно пропорционально площади поперечного сечения проводника. Наш график зависимости сопротивления от поперечного сечения имеет форму ветви
гиперболы.
Наш график зависимости сопротивления от поперечного сечения имеет форму ветви
гиперболы.
Как вы уже, наверное, догадались, удельное сопротивление проводников из того или иного материала тоже вычисляется экспериментальным путём. На этот раз, все проводники имеют одну и ту же длину и толщину, но состоят из разного вещества.
Удельное сопротивление проводника — это сопротивление проводника из данного вещества с площадью поперечного сечения 1 м2 и длиной 1 м. В таблице даны значения удельного сопротивления для некоторых веществ.
Однако, площадь поперечного сечения проводника удобнее измерять в квадратных миллиметрах, поскольку это больше соответствует размерам реальных проводников.
Итак, исходя из наших опытов, сопротивление проводника прямо пропорционально длине проводника, обратно пропорционально площади поперечного сечения и зависит от вещества:
Из формулы мы можем выразить удельное сопротивление и определить его единицы измерения:
Упражнения.
Задача 1. Железный провод длиной 250 м имеет площадь поперечного сечения 2 мм2. Найдите сопротивление данного провода.
Задача 2. Какое напряжение должно быть на эбонитовом диске толщиной 1 мм, чтобы через него прошел ток в 1 мкА? Диаметр диска составляет 1 см.
Мы видим, что даже для того, чтобы через эбонит прошел очень маленький ток, нужно просто огромное напряжение. Такое напряжение создать практически невозможно. Даже в современных ускорителях частиц достигалось напряжение не больше нескольких ТВ. Поэтому, можно сказать, что мы не можем провести ток через эбонит. Этого следовало ожидать, поскольку удельное сопротивление эбонита огромно, и он является непроводником.
Задача 3. На рисунке показан график зависимости силы тока на участке цепи от неизвестной величины. Можете ли вы определить, что это за величина?
Итак, давайте вспомним, от чего вообще может зависеть
сила тока. В первую очередь, сила тока — это количество заряда, прошедшего
через поперечное сечение за единицу времени. Из формулы видно, что сила тока
находится в линейной зависимости от количества заряда в единицу времени, а на
рисунке мы видим график функции, который показывает нелинейную зависимость. Мы
знаем, что график функции, описывающий любую линейную зависимость, будет
являться прямой. Из формулы, описывающей закон Ома, мы видим, что сила тока
прямо пропорциональна напряжению. Значит, неизвестная величина не является ни
количеством заряда, ни напряжением. Сила тока обратно пропорциональна
сопротивлению. Однако, мы уже знаем, что график функции зависимости силы тока
от сопротивления представляет собой ветвь гиперболы, а на рисунке мы видим
другой график.
Тогда следует заметить, что сила тока зависит от
величин, которые, в свою очередь, зависят от других величин. Напряжение связано
с работой по переносу заряда, но эта зависимость тоже линейная. Рассмотрим, от чего
зависит сопротивление: от удельного сопротивления, от длины проводника и от
площади поперечного сечения. Удельное сопротивление для каждого проводника —
есть величина постоянная. Сопротивление находится в линейной зависимости от
длины проводника, длина проводника — это независимая величина. Остается площадь
поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата
радиуса проводника, что приводит нас к нелинейной зависимости. Если мы
преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим,
что сила тока прямо пропорциональна квадрату радиуса проводника. Это
единственная величина, которая могла привести к построению графика квадратичной
функции. Действительно, если мы внимательно изучим график, то убедимся, что это
парабола. Следует заметить, что это может быть график зависимости силы тока не
от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна
дополнительная информация.
Рассмотрим, от чего
зависит сопротивление: от удельного сопротивления, от длины проводника и от
площади поперечного сечения. Удельное сопротивление для каждого проводника —
есть величина постоянная. Сопротивление находится в линейной зависимости от
длины проводника, длина проводника — это независимая величина. Остается площадь
поперечного сечения. Как раз-таки, она зависит не от радиуса, а от квадрата
радиуса проводника, что приводит нас к нелинейной зависимости. Если мы
преобразуем формулу, по которой вычисляется сила тока в проводнике, то увидим,
что сила тока прямо пропорциональна квадрату радиуса проводника. Это
единственная величина, которая могла привести к построению графика квадратичной
функции. Действительно, если мы внимательно изучим график, то убедимся, что это
парабола. Следует заметить, что это может быть график зависимости силы тока не
от радиуса, а от диаметра. Однако, для того, чтобы это проверить, нам нужна
дополнительная информация. Тем не менее, мы с уверенностью можем сказать, что
это график зависимости силы тока либо от радиуса, либо от диаметра проводника
(по форме эти два графика ничем не отличаются — существуют лишь числовые
отличия).
Тем не менее, мы с уверенностью можем сказать, что
это график зависимости силы тока либо от радиуса, либо от диаметра проводника
(по форме эти два графика ничем не отличаются — существуют лишь числовые
отличия).
схема и расчёт [Амперка / Вики]
Для того, чтобы получить из исходного напряжения лишь его часть используется делитель напряжения (voltage divider). Это схема, строящаяся на основе пары резисторов.
В примере, на вход подаются стандартные 9 В. Но какое напряжение получится на выходе Vout? Или эквивалентный вопрос: какое напряжение покажет вольтметр?
Ток, протекающий через R1 и R2 одинаков пока к выходу Vout ничего не подключено. А суммарное сопротивление пары резисторов при последовательном соединении:
Таким образом, сила тока протекающая через резисторы
Теперь, когда нам известен ток в R2, расчитаем напряжение вокруг него:
Или если отавить формулу в общем виде:
Так с помощью пары резисторов мы изменили значение входного напряжения с 9 до 5 В. Это простой способ получить несколько различных напряжений в одной схеме, оставив при
этом только один источник питания.
Это простой способ получить несколько различных напряжений в одной схеме, оставив при
этом только один источник питания.
Применение делителя для считывания показаний датчика
Другое применение делителя напряжения — это снятие показаний с датчиков. Существует множество компонентов, которые меняют своё сопротивление в зависимости от внешних условий. Так термисторы меняют сопротивление от нуля до определённого значения в зависимости от температуры, фоторезисторы меняют сопротивление в зависимости от интенсивности попадающего на них света и т.д.
Если в приведённой выше схеме заменить R1 или R2 на один из таких компонентов, Vout будет меняться в зависимости от внешних условий, влияющих на датчик. Подключив это выходное напряжение к аналоговому входу Ардуино, можно получать информацию о температуре, уровне освещённости и других параметрах среды.
Значение выходного напряжения при определённых параметрах среды можно расчитать, сопоставив документацию
на переменный компонент и общую формулу расчёта Vout.
Подключение нагрузки
С делителем напряжения не всё так просто, когда к выходному подключения подключается какой-либо потребитель тока, который ещё называют нагрузкой (load):
В этом случае Vout уже не может быть расчитано лишь на основе значений Vin, R1 и R2: сама нагрузка провоцирует дополнительное падение напряжения (voltage drop). Пусть нагрузкой является нечто, что потребляет ток в 10 мА при предоставленных 5 В. Тогда её сопротивление
В случае с подключеной нагрузкой следует рассматривать нижнюю часть делителя, как два резистора соединённых параллельно:
Подставив значение в общую формулу расчёта Vout, получим:
Как видно, мы потеряли более полутора вольт напряжения из-за подключения нагрузки.
И тем ощутимее будут потери,
чем больше номинал R2 по отношению к сопротивлению L. Чтобы нивелировать этот эффект мы могли
бы использовать в качестве R1 и R2 резисторы, например, в 10 раз меньших
номиналов.
Пропорция сохраняется, Vout не меняется:
А потери уменьшатся:
Однако, у снижения сопротивления делящих резисторов есть обратная сторона медали. Большое количество энергии от источника питания будет уходить в землю. В том числе при отсоединённой нагрузке. Это небольшая проблема, если устройство питается от сети, но — нерациональное расточительство в случае питания от батарейки.
Кроме того, нужно помнить, что резисторы расчитаны на определённую предельную мощьность. В нашем случае нагрузка на R1 равна:
А это в 4-8 раз выше максимальной мощности самых распространённых резисторов! Попытка воспользоваться описанной схемой со сниженными номиналами и стандартными 0.25 или 0.5 Вт резисторами ничем хорошим не закончится. Очень вероятно, что результатом будет возгарание.
Применимость
Делитель напряжения подходит для получения необходимого заниженного напряжения в случаях, когда подключенная
нагрузка потребляет небольшой ток (доли или единицы миллиампер). Примером подходящего использования является
считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.
Примером подходящего использования является
считывание напряжения аналоговым входом микроконтроллера, управление базой/затвором транзистора.
Делитель не подходит для подачи напряжения на мощных потребителей вроде моторов или светодиодных лент.
Чем меньшие номиналы выбраны для делящих резисторов, тем больше энергии расходуется впустую и тем выше нагрузка на сами резисторы. Чем номиналы больше, тем больше и дополнительное (нежелательное) падение напряжения, провоцируемое самой нагрузкой.
Если потребление тока нагрузкой неравномерно во времени, Vout также будет неравномерным.
какие формулы помогут вычислить сопротивление
В наше время светодиоды используются если не во всех, то в очень многих сферах деятельности. И несмотря на это, многие потребители едва ли понимают принципы работы светодиодов. Как и почему вообще работают светодиоды? И какую роль в этом процессе играют резисторы? Как произвести расчет резистора для светодиода? Постараемся разобраться.
Что такое резистор и сопротивление светодиода?
Резистором называется компонент электрической цепи, который характеризуется пассивностью и в лучшем случае обладает сопротивлением электрическому току. Другими словами, для такого устройства в любое время должен действовать закон Ома.
Главная функция резистора – энергичное сопротивление электротоку. Именно это качество делает резисторы необходимыми при создании систем искусственного освещения, в том числе и с применением светодиодов.
В каких случаях возможно подключение светодиода с помощью резистора?
Подключать светодиод с помощью резистора можно при условии, что эффективность схемы не является первостепенной целью. Самый простой пример – применение светодиода для индикации подсветки выключателя в электроприборе. В таком случае мощность потребления едва достигает 0.1 Вт, а яркость не ставится во главу угла. А вот при использовании светодиода с энергопотреблением более 1 Вт нужно обязательно убедиться, что блок питания обеспечивает стабилизированное напряжение. Если же напряжение схемы не стабилизировано, то все скачки и помехи будут негативно сказываться на работе светодиода.
Если же напряжение схемы не стабилизировано, то все скачки и помехи будут негативно сказываться на работе светодиода.
Не менее актуальна схема питания через резистор в лабораторных условиях, когда есть задача тестирования новой модели светодиода.
Виды резисторов
Существует несколько классификаций резисторов, каждая из которых отличается признаков, по которому сравниваются разные виды устройств.
В зависимости от материала резистивного элемента выделяют следующие типы резисторов:
- Металлофольговые;
- Непроволочные;
- Проволочные.
По способы защиты резисторы бывают:
- Неизолированными;
- Изолированными;
- Вакуумными;
- Герметизированными.
Назначение резисторов группирует устройства следующим образом:
- Резисторы общего предназначения;
- Высокочастотные;
- Высокомегаомные;
- Высоковольтные.
Расчет резистора для светодиода
Осуществить расчет резисторов по силам не только специалистам. Достаточно базовых знаний и понимания физики процесса. Чтобы определить необходимое сопротивление резисторов, нужно учитывать следующие важные факторы:
Достаточно базовых знаний и понимания физики процесса. Чтобы определить необходимое сопротивление резисторов, нужно учитывать следующие важные факторы:
- Маркировка на устройстве отображает так называемое напряжение падения, которое необходимо для расчета необходимого напряжения и для подбора резисторов.
- Числовое значение напряжения определяется в виде разницы между напряжением агрегата и напряжением питания светодиода;
- Чтобы рассчитать необходимое сопротивление, нужно разделить остаточное напряжение на величину тока, необходимую для бесперебойной работы системы.
Математический расчет сопротивления резистора
Согласно второму правилу Кирхгофа, можно составить равенство U = Ur + Uled, которое можно интерпретировать таким образом: U = I x R + I x Rled, где Rled – это дифференциальное сопротивление.
Значение Rled меняется вместе с изменением работы полупроводника. В данном случае соотношение переменных величин тока и напряжения определяет величину сопротивления.
Также есть смысл вывести формулу для вычисления сопротивления резистора: R = (U – Uled) / I, Ом. В данной формуле Uled – это паспортная величина для конкретного типа светодиода.
Как рассчитать резистор графическим способом?
При наличии ВАХ светодиода расчет резистора для светодиодов можно осуществить графическим методом, хотя такой способ и не очень распространен. Зная ток нагрузки, можно с помощью графика определить прямое напряжение. Необходимо с оси ординат (I) провести прямую до пересечения с кривой и опустить на ось абсцисс.
Особенности расчета
Каким бы ни было подключение резистора, всегда есть свои тонкости и нюансы. Постараемся разобраться, в чем особенности последовательного, параллельного и смешанного способов соединения.
Последовательное соединение
При последовательной схеме светодиоды расставляются друг за другом, и обычно достаточно одного резистора, если удастся корректно произвести расчет сопротивления. Это можно объяснить тем, что в электроцепи в каждом месте установки электроприбора имеется один и тот же ток, значение которого не изменяется.
Это можно объяснить тем, что в электроцепи в каждом месте установки электроприбора имеется один и тот же ток, значение которого не изменяется.
Параллельное соединение
Часто бывает необходимость в подключении нескольких диодов к одному и тому же источнику. В теории можно использовать один токоограничивающий резистордля питания нескольких LED, соединенных параллельно.
Стоит отметить, что даже в «китайских» моделях производитель устанавливает отдельный ограничительный резистор. При общем балласте для нескольких LED значительно растет вероятность поломки диодов, излучающих свет.
Смешанное соединение
При выборе смешанного соединения схему следует рассчитывать отдельно для каждой последовательной цепи. Если количество и типы светодиодов одинаковы в каждой из последовательных цепей, расчет можно произвести единожды для любой группы диодов. Важно, чтобы все светодиоды были однотипными, как минимум, в пределах общей цепи.
Примеры расчетов сопротивления и мощности резистора
Рассмотрим пример расчета сопротивления резистора LED SMD 5050, при работе с которой следует учитывать некоторые конструкционные особенности светодиода, который включает три независимых кристалла.
При условии, что LED SMD 5050 одноцветный, напряжение на кристалле будет отличаться максимум на 0.1 В. Таким образом, светодиод может быть запитан от одного резистора, а три анода можно объединить в одну группу, три катода – соответственно, в другую. Для подключения SMD 5050 с параметрами ULED=3,3 В и ILED=0,02 А.
R = (5 – 3.3) / (0.02 х 3) = 28.3 Ом. Ближайший стандартный показатель составляет 30 Ом. К установке принимаем резистор с сопротивлением 30 Ом и мощностью 0.25 Вт.
Для максимального удобства и скорости проведения расчетов можно использовать специальный онлайн калькулятор расчет резистора. Этот инструмент дает возможность произвести расчет резисторов в кратчайшие сроки с минимальными затратами времени и сил.
Расчет сопротивления – Закон Ома – Ток, напряжение и сопротивление – Редакция GCSE Physics (Single Science) – Другое
Сопротивление электрического компонента можно определить путем измерения электрического тока, протекающего через него, и разности потенциалов на нем.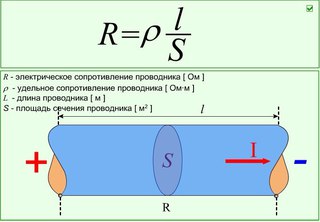
Это уравнение, называемое законом Ома , показывает взаимосвязь между разностью потенциалов, током и сопротивлением:
напряжение = ток × сопротивление
В = I × R
где:
В – разность потенциалов в вольт, В
I – ток в амперах (амперах), A
R – сопротивление в омах, Ом
Уравнение можно переставить, чтобы найти сопротивление:
1bdmw94x7ke.0.0.0.1:0.1.0.$0.$1.$9″> R = V ÷ I
- Вопрос
Через лампу на 240 В проходит 3 А.Какое сопротивление лампы?
- Выявить ответ
Сопротивление = 240 ÷ 3 = 80 Ом
Для расчета сопротивления электрического компонента используется амперметр для измерения тока и 1bdmw94x7ke.0.0.0.1:0.1.0.$0.$1.$11.$3″> вольтметр для измерения потенциала разница. Затем сопротивление можно рассчитать по закону Ома.
Закон Ома | Клуб электроники
Закон Ома | Клуб электроникиСледующая страница: Power and Energy
См. Также: Напряжение и ток | Сопротивление
Закон Ома показывает взаимосвязь между напряжением, током и сопротивлением
Чтобы ток протекал через сопротивление, на этом сопротивлении должно быть напряжение.Закон Ома показывает взаимосвязь между тремя величинами: напряжением, током и сопротивлением.
Закон Ома можно записать в виде словарного уравнения :
| напряжение = ток × сопротивление |
Или используя символы для обозначения величин напряжения (В), тока (I) и сопротивления (R):
На самом деле это можно записать тремя способами, и вы можете выбрать версию, которая лучше всего подходит для ваших целей:
Треугольник ВИР – способ запомнить закон Ома
Вы можете использовать треугольник VIR, чтобы помочь вам запомнить три версии закона Ома.
- Для расчета напряжения, В : приложите палец к В, это оставляет I R, поэтому уравнение V = I × R
- Чтобы рассчитать ток , I : положите палец на I, это оставляет V над R, поэтому уравнение I = V / R
- Чтобы рассчитать сопротивление , R : положите палец на R, это оставляет V над I, поэтому уравнение R = V / I
Расчет по закону Ома
Используйте этот метод для проведения расчетов:
- Запишите значения , при необходимости преобразовав единицы.
- Выберите необходимое Equation (используйте треугольник VIR).
- Введите числа в уравнение и вычислите ответ.
Должно быть V ery E asy N ow! См. Примеры ниже:
Пример 3:
Резистор 1,2 кОм пропускает ток 0,2 А, какое напряжение на нем?
Пример 4:
9 В подается на резистор 15 кОм, какой ток?
- V alues: V = 9V, I =?, R = 15k
- E предложение: I = V / R
- N единиц: Ток, I = 9 / 15 = 0.
 6 мА
6 мА
(использование k для сопротивления означает, что расчет дает ток в мА)
Следующая страница: Энергетика | Исследование
Политика конфиденциальности и файлы cookie
Этот сайт не собирает личную информацию.
Если вы отправите электронное письмо, ваш адрес электронной почты и любая личная информация будет
используется только для ответа на ваше сообщение, оно не будет передано никому.
На этом веб-сайте отображается реклама, если вы нажмете на
рекламодатель может знать, что вы пришли с этого сайта, и я могу быть вознагражден.Рекламодателям не передается никакая личная информация.
Этот веб-сайт использует некоторые файлы cookie, которые классифицируются как «строго необходимые», они необходимы для работы веб-сайта и не могут быть отклонены, но они не содержат никакой личной информации.
Этот веб-сайт использует службу Google AdSense, которая использует файлы cookie для показа рекламы на основе использования вами веб-сайтов. (включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
(включая этот), как объяснил Google.
Чтобы узнать, как удалить файлы cookie и управлять ими в своем браузере, пожалуйста
посетите AboutCookies.org.
клуб электроники.инфо © Джон Хьюс 2021
Веб-сайт размещен на Tsohost
Расчет сопротивления– документация Stimfit 0.15.8
| Авторы: | Хосе Гусман |
|---|---|
| Обновлено: | 20 февраля 2019 |
Сопротивление можно рассчитать по закону Ома. Токи, проходящие через пипетку, будут пропорциональны приложенной разнице напряжений. Этот пропорциональный коэффициент и есть сопротивление.
В зажимах напряжения сопротивление можно рассчитать, записав ток, если известна разность напряжений. Эта подпрограмма Python должна вычислить разницу токов, а сопротивление будет рассчитано с учетом амплитуды напряжения.
Функция сопротивления
Примечание
Вы можете найти различные процедуры для расчета сопротивления в файле charlie. py . Этот файл можно найти в каталоге программы Stimfit (C: \ Program Files \ Stimfit в Windows или / usr / lib / python2.5 / site-packages / Stimfit в GNU / Linux, при условии, что python2.5 является вашей текущей средой Python). Название charlie.py дано в знак признательности Чарли за ее вклад в развитие данных программ.
py . Этот файл можно найти в каталоге программы Stimfit (C: \ Program Files \ Stimfit в Windows или / usr / lib / python2.5 / site-packages / Stimfit в GNU / Linux, при условии, что python2.5 является вашей текущей средой Python). Название charlie.py дано в знак признательности Чарли за ее вклад в развитие данных программ.
Обратите внимание, что эта функция предполагает, что ток записывается в пА. Он устанавливает курсоры stf (пик и базовая линия) для расчета отклонения тока в ответ на разность напряжений. Наконец, необходимо ввести амплитуду напряжения в мВ.
импортировать numpy как np
Модуль python optimfit:
импорт stf
сопротивление def (base_start, base_end, peak_start, peak_end, амплитуда):
"" "Вычисляет сопротивление по серии кривых зажимов напряжения.Аргументы ключевого слова:
base_start - Начальный индекс (отсчитываемый от нуля) курсоров базовой линии.
base_end - Конечный индекс (отсчитываемый от нуля) курсоров базовой линии. peak_start - Начальный индекс (отсчитываемый от нуля) курсоров пиков.
peak_end - конечный индекс (отсчитываемый от нуля) курсоров пиков.
амплитуда - Амплитуда команды напряжения.
Возврат:
Сопротивление.
"" "
если не stf.check_doc ():
print "Не удалось найти открытый файл; сейчас прерывается."
возврат 0
# Временный массив для вычисления среднего:
установить = np.пустой ((stf.get_size_channel (), stf.get_size_trace ()))
для n в диапазоне (0, stf.get_size_channel ()):
# Добавьте эту трассировку, чтобы установить:
set [n] = stf.get_trace (n)
# вычислить среднее и создать из него новый раздел:
stf.new_window (np.average (набор, 0))
# установить пиковые курсоры:
если не stf.set_peak_mean (-1): return 0 # -1 означает все точки в пределах окна пика.
если не stf.set_peak_start (peak_start): вернуть 0
если не stf.set_peak_end (peak_end): вернуть 0
# установить базовые курсоры:
если не stf.
peak_start - Начальный индекс (отсчитываемый от нуля) курсоров пиков.
peak_end - конечный индекс (отсчитываемый от нуля) курсоров пиков.
амплитуда - Амплитуда команды напряжения.
Возврат:
Сопротивление.
"" "
если не stf.check_doc ():
print "Не удалось найти открытый файл; сейчас прерывается."
возврат 0
# Временный массив для вычисления среднего:
установить = np.пустой ((stf.get_size_channel (), stf.get_size_trace ()))
для n в диапазоне (0, stf.get_size_channel ()):
# Добавьте эту трассировку, чтобы установить:
set [n] = stf.get_trace (n)
# вычислить среднее и создать из него новый раздел:
stf.new_window (np.average (набор, 0))
# установить пиковые курсоры:
если не stf.set_peak_mean (-1): return 0 # -1 означает все точки в пределах окна пика.
если не stf.set_peak_start (peak_start): вернуть 0
если не stf.set_peak_end (peak_end): вернуть 0
# установить базовые курсоры:
если не stf.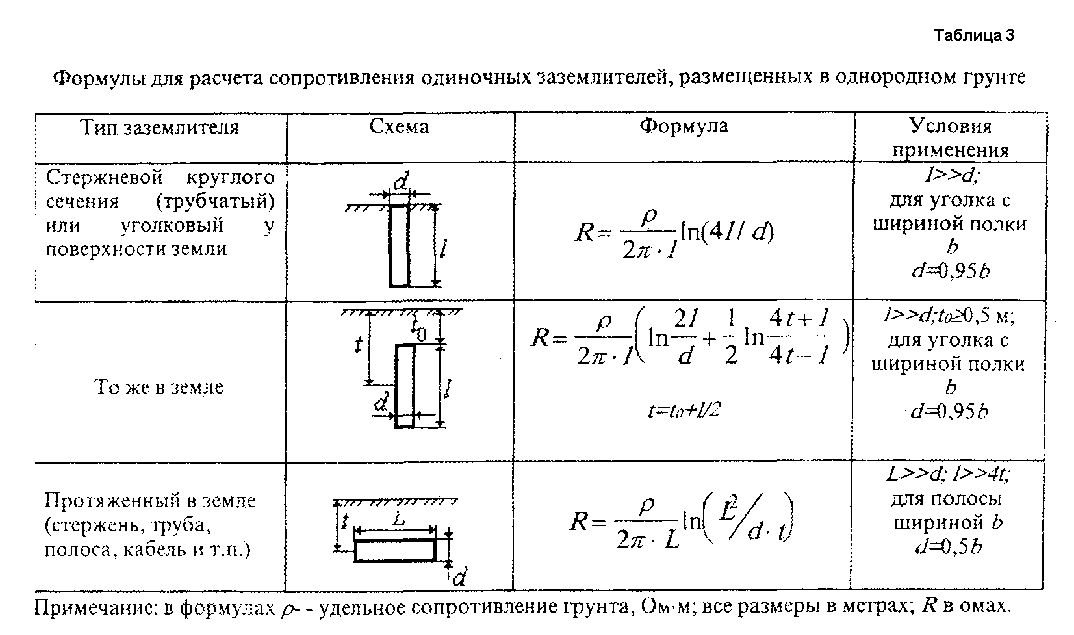 set_base_start (base_start): вернуть 0
если не stf.set_base_end (base_end): вернуть 0
# все измерить:
stf.measure ()
# вычислить r_seal и вернуть:
вернуть амплитуду / (stf.get_peak () - stf.get_base ())
set_base_start (base_start): вернуть 0
если не stf.set_base_end (base_end): вернуть 0
# все измерить:
stf.measure ()
# вычислить r_seal и вернуть:
вернуть амплитуду / (stf.get_peak () - stf.get_base ())
Использование
Теперь вы можете использовать эту функцию для разных целей. Например, вы можете захотеть проверить значение последовательного сопротивления в ответ на гиперполяризующий импульс 5 мВ. Во-первых, предположим, что ваша запись имеет текущий пик между 10700 и 10999 точками выборки.Вы должны установить базовую линию (например, от 0 до 999), а затем пик между 10700 и 10999. После этого, учитывая, что разница напряжений составляет 5 мВ, вы вводите:
>>> заклинания. Сопротивление (0,999,10700,1999, -5)
Обратите внимание, что charlie.py имеет подпрограмму r_in (амплитуда = -5) , которая делает именно это.
Таким же образом, если вы хотите рассчитать значение сопротивления уплотнения (при условии, что это наименьшее сопротивление в цепи, поэтому ток не будет проходить через любое другое сопротивление), вы можете проверить его с помощью большего импульса напряжения.
>>> заклинания. Сопротивление (0,199,1050,1199,50)
Опять же, файл charlie.py имеет процедуру под названием r_seal (50) для расчета сопротивления уплотнения. Просто измените параметры (базовый уровень и пики), чтобы адаптировать его к вашим записям.
Учебное пособие по физике: Комбинированные схемы
Ранее в Уроке 4 упоминалось, что существует два разных способа соединения двух или более электрических устройств в цепь.Они могут быть соединены последовательным или параллельным соединением. Когда все устройства в цепи соединены последовательным соединением, тогда схема называется последовательной схемой. Когда все устройства в цепи соединены параллельными соединениями, тогда цепь называется параллельной цепью. Третий тип схемы предполагает двойное использование последовательного и параллельного соединений в схеме; такие схемы называются составными схемами или комбинированными схемами.Схема, изображенная справа, является примером использования как последовательного, так и параллельного соединения в одной цепи. В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
В этом случае лампочки A и B подключаются параллельно, а лампочки C и D подключаются последовательно. Это пример комбинированной схемы .
При анализе комбинированных схем критически важно иметь твердое понимание концепций, относящихся как к последовательным, так и к параллельным схемам.Поскольку оба типа соединений используются в комбинированных схемах, концепции, связанные с обоими типами схем, применяются к соответствующим частям схемы. Основные понятия, связанные с последовательными и параллельными цепями, представлены в таблице ниже.
Цепи серии
 .. .. | Параллельные схемы
|
Каждое из приведенных выше понятий имеет математическое выражение. Объединение математических выражений вышеуказанных понятий с уравнением закона Ома (ΔV = I • R) позволяет провести полный анализ комбинированной схемы.
Анализ комбинированных схем Основная стратегия анализа комбинированных схем включает использование значения эквивалентного сопротивления для параллельных ветвей для преобразования комбинированной схемы в последовательную. После преобразования в последовательную схему анализ можно проводить обычным образом. Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем полное или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Ранее в Уроке 4 описывался метод определения эквивалентного параллельного сопротивления, затем полное или эквивалентное сопротивление этих ветвей равно сопротивлению одной ветви, деленному на количество ветвей.
Этот метод соответствует формуле
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 + …, где R 1 , R 2 и R 3 – значения сопротивления отдельных резисторов, подключенных параллельно. Если два или более резистора, находящихся в параллельных ветвях, не имеют одинакового сопротивления, следует использовать приведенную выше формулу.Пример этого метода был представлен в предыдущем разделе Урока 4.
Применяя свое понимание эквивалентного сопротивления параллельных ветвей к комбинированной цепи, комбинированную схему можно преобразовать в последовательную. Затем понимание эквивалентного сопротивления последовательной цепи можно использовать для определения общего сопротивления цепи. Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , помещенными в параллельные ветви.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
Рассмотрим следующие диаграммы ниже. Схема A представляет собой комбинированную схему с резисторами R 2 и R 3 , помещенными в параллельные ветви.Два параллельных резистора 4 Ом эквивалентны сопротивлению 2 Ом. Таким образом, две ветви можно заменить одним резистором с сопротивлением 2 Ом. Это показано на диаграмме B. Теперь, когда все резисторы включены последовательно, можно использовать формулу для общего сопротивления последовательных резисторов для определения общего сопротивления этой цепи: Формула для последовательного сопротивления составляет
Итак, на схеме B полное сопротивление цепи составляет 10 Ом.
После определения общего сопротивления цепи анализ продолжается с использованием закона Ома и значений напряжения и сопротивления для определения значений тока в различных местах. Весь метод проиллюстрирован ниже на двух примерах.
Первый пример – самый простой – резисторы, включенные параллельно, имеют одинаковое сопротивление. Цель анализа – определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением. Два последовательно подключенных резистора 8 Ом эквивалентны одному резистору 4 Ом. Таким образом, два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 4 Ом. Этот резистор 4 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
. R до = R 1 + 4 Ом + R 4 = 5 Ом + 4 Ом + 6 ОмR до = 15 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи. При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I до = 4 А
Расчет тока 4 А представляет собой ток в месте расположения батареи. Тем не менее, резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 4 А Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 4 ампер. Существует бесконечное количество возможных значений I 2 и I 3 , которые удовлетворяют этому уравнению. Поскольку значения сопротивления равны, значения тока в этих двух резисторах также равны.Следовательно, ток в резисторах 2 и 3 равен 2 ампер.
Теперь, когда известен ток в каждом отдельном месте резистора, можно использовать уравнение закона Ома (ΔV = I • R) для определения падения напряжения на каждом резисторе. Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (4 А) • (5 Ом)ΔV 1 = 20 ВΔV 2 = I 2 • R 2 = (2 А) • (8 Ом)
ΔV 2 = 16 ВΔV 3 = I 3 • R 3 = (2 А) • (8 Ом)
ΔV 3 = 16 ВΔV 4 = I 4 • R 4 = (4 А) • (6 Ом)
ΔV 4 = 24 В
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Второй пример – более сложный – резисторы, включенные параллельно, имеют другое сопротивление. Цель анализа та же – определить ток и падение напряжения на каждом резисторе.
Как обсуждалось выше, первым шагом является упрощение схемы путем замены двух параллельных резисторов одним резистором с эквивалентным сопротивлением.Эквивалентное сопротивление резистора 4 Ом и 12 Ом, включенного параллельно, можно определить по обычной формуле для эквивалентного сопротивления параллельных ветвей:
1 / R экв. = 1 / R 1 + 1 / R 2 + 1 / R 3 …1 / R экв = 1 / (4 Ом) + 1 / (12 Ом)
1 / R экв. = 0,333 Ом -1
R экв = 1 / (0,333 Ом -1 )
R экв = 3.00 Ом
На основании этого расчета можно сказать, что два резистора ответвления (R 2 и R 3 ) можно заменить одним резистором с сопротивлением 3 Ом. Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
Этот резистор 3 Ом включен последовательно с R 1 и R 4 . Таким образом, общее сопротивление составляет
R до = 16 Ом
Теперь уравнение закона Ома (ΔV = I • R) можно использовать для определения полного тока в цепи.При этом необходимо использовать общее сопротивление и общее напряжение (или напряжение батареи).
I общ = ΔV общ / R общ = (24 В) / (16 Ом)I до = 1,5 А
Расчет тока 1,5 А представляет собой ток в месте расположения батареи. Тем не менее, резисторы R 1 и R 4 включены последовательно, и ток в последовательно соединенных резисторах везде одинаков.Таким образом,
I до = I 1 = I 4 = 1,5 А Для параллельных ветвей сумма тока в каждой отдельной ветви равна току вне ветвей. Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неодинаковый ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Таким образом, I 2 + I 3 должно равняться 1,5 А. Существует бесконечное множество значений I 2 и I 3 , которые удовлетворяют этому уравнению. В предыдущем примере два параллельно включенных резистора имели одинаковое сопротивление; таким образом, ток распределялся поровну между двумя ветвями.В этом примере неодинаковый ток в двух резисторах усложняет анализ. Ветвь с наименьшим сопротивлением будет иметь наибольший ток. Для определения силы тока потребуется использовать уравнение закона Ома. Но для его использования сначала необходимо знать падение напряжения на ветвях. Таким образом, направление решения в этом примере будет немного отличаться от более простого случая, проиллюстрированного в предыдущем примере.
Чтобы определить падение напряжения на параллельных ветвях, сначала необходимо определить падение напряжения на двух последовательно соединенных резисторах (R 1 и R 4 ).Уравнение закона Ома (ΔV = I • R) может использоваться для определения падения напряжения на каждом резисторе.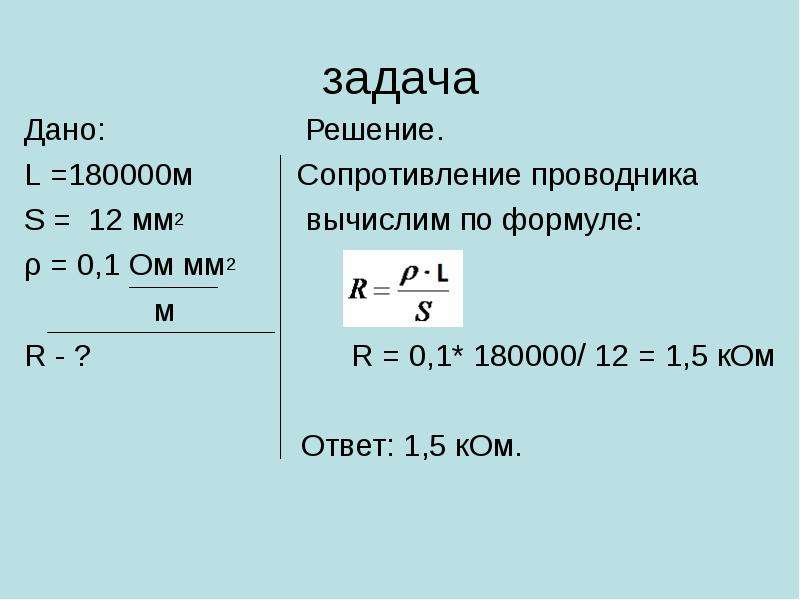 Эти расчеты показаны ниже.
Эти расчеты показаны ниже.
ΔV 1 = I 1 • R 1 = (1,5 А) • (5 Ом)ΔV 1 = 7,5 ВΔV 4 = I 4 • R 4 = (1,5 А) • (8 Ом)
ΔV 4 = 12 В
Эта схема питается от источника 24 В.Таким образом, совокупное падение напряжения заряда, проходящего по контуру цепи, составляет 24 вольта. Произойдет падение 19,5 В (7,5 В + 12 В) в результате прохождения через два последовательно соединенных резистора (R 1 и R 4 ). Падение напряжения на ответвлениях должно составлять 4,5 В, чтобы компенсировать разницу между общим значением 24 В и падением 19,5 В на R 1 и 4 R. Таким образом,
ΔV 2 = V 3 = 4,5 В Зная падение напряжения на параллельно соединенных резисторах (R 1 и R 4 ), можно использовать уравнение закона Ома (ΔV = I • R) для определения тока в двух ветвях.
I 2 = ΔV 2 / R 2 = (4,5 В) / (4 Ом)I 2 = 1,125 AI 3 = ΔV 3 / R 3 = (4,5 В) / (12 Ом)
I 3 = 0,375 A
На этом анализ завершен, и его результаты представлены на диаграмме ниже.
Разработка стратегии Два приведенных выше примера иллюстрируют эффективную концептуально-ориентированную стратегию анализа комбинированных схем.Этот подход требовал твердого понимания концепций последовательностей и параллелей, обсуждавшихся ранее. Такие анализы часто проводятся, чтобы решить физическую проблему для указанного неизвестного. В таких ситуациях неизвестное обычно меняется от проблемы к проблеме. В одной задаче значения резистора могут быть заданы, а ток во всех ветвях неизвестен. В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
В другой задаче могут быть указаны ток в батарее и несколько значений резистора, и неизвестная величина становится сопротивлением одного из резисторов.Очевидно, что разные проблемные ситуации потребуют небольших изменений в подходах. Тем не менее, каждый подход к решению проблем будет использовать те же принципы, что и при подходе к двум приведенным выше примерам проблем.
Начинающему студенту предлагаются следующие предложения по решению задач комбинированной схемы:
- Если схематическая диаграмма не предоставлена, найдите время, чтобы построить ее. Используйте условные обозначения, такие как показанные в примере выше.
- При приближении к проблеме, связанной с комбинированной схемой, найдите время, чтобы организовать себя, записав известные значения и приравняв их к символу, например I – , I 1 , R 3 , ΔV 2 и т. Д. Схема организации, использованная в двух приведенных выше примерах, является эффективной отправной точкой.

- Знать и использовать соответствующие формулы для эквивалентного сопротивления последовательно соединенных и параллельно соединенных резисторов. Использование неправильных формул гарантирует неудачу.
- Преобразуйте комбинированную схему в строго последовательную, заменив (на ваш взгляд) параллельную часть на один резистор, значение сопротивления которого равно эквивалентному сопротивлению параллельной части.
- Используйте уравнение закона Ома (ΔV = I • R) часто и надлежащим образом. Большинство ответов будет определено с использованием этого уравнения. При его использовании важно подставлять соответствующие значения в уравнение. Например, при вычислении I 2 важно подставить в уравнение значения ΔV 2 и R 2 .
Для дальнейшей практики анализа комбинированных схем рассмотрите возможность анализа проблем в разделе «Проверьте свое понимание» ниже.
Мы хотели бы предложить . .. Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажав на резистор или источник напряжения, вы можете изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванной).
.. Зачем просто читать об этом и когда можно с этим взаимодействовать? Взаимодействие – это именно то, что вы делаете, когда используете одну из интерактивных функций The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства построения цепей постоянного тока.Вы можете найти его в разделе Physics Interactives на нашем сайте. Построитель цепей постоянного тока предоставляет учащемуся набор для построения виртуальных цепей. Вы можете легко перетащить источники напряжения, резисторы и провода на рабочее место, а также расположить и подключить их так, как хотите. Вольтметры и амперметры позволяют измерять ток и падение напряжения. Нажав на резистор или источник напряжения, вы можете изменить сопротивление или входное напряжение. Это просто. Это весело. И это безопасно (если вы не используете его в ванной).
1. Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
Комбинированная схема показана на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы.
а. Ток в точке A равен _____ (больше, равен, меньше) ток в точке B.
г. Ток в точке B равен _____ (больше, равен, меньше) ток в точке E.
с. Ток в точке G равен _____ (больше, равен, меньше) ток в точке F.
г. Ток в точке E равен _____ (больше, равен, меньше) току в точке G.
e. Ток в точке B равен _____ (больше, равен, меньше) ток в точке F.
ф. Ток в точке A равен _____ (больше, равен, меньше) ток в точке L.
г. Ток в точке H равен _____ (больше, равен, меньше) ток в точке I.
2. Рассмотрим комбинированную схему на схеме справа. Используйте диаграмму, чтобы ответить на следующие вопросы. (Предположим, что падение напряжения в самих проводах пренебрежимо мало.)
а. Разность электрических потенциалов (падение напряжения) между точками B и C составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками J и K.
г. Разность электрических потенциалов (падение напряжения) между точками B и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
с. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками G и H.
г. Разность электрических потенциалов (падение напряжения) между точками E и F составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
e. Разность электрических потенциалов (падение напряжения) между точками J и K составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками D и I.
ф. Разность электрических потенциалов между точками L и A составляет _____ (больше, равно, меньше) разности электрических потенциалов (падение напряжения) между точками B и K.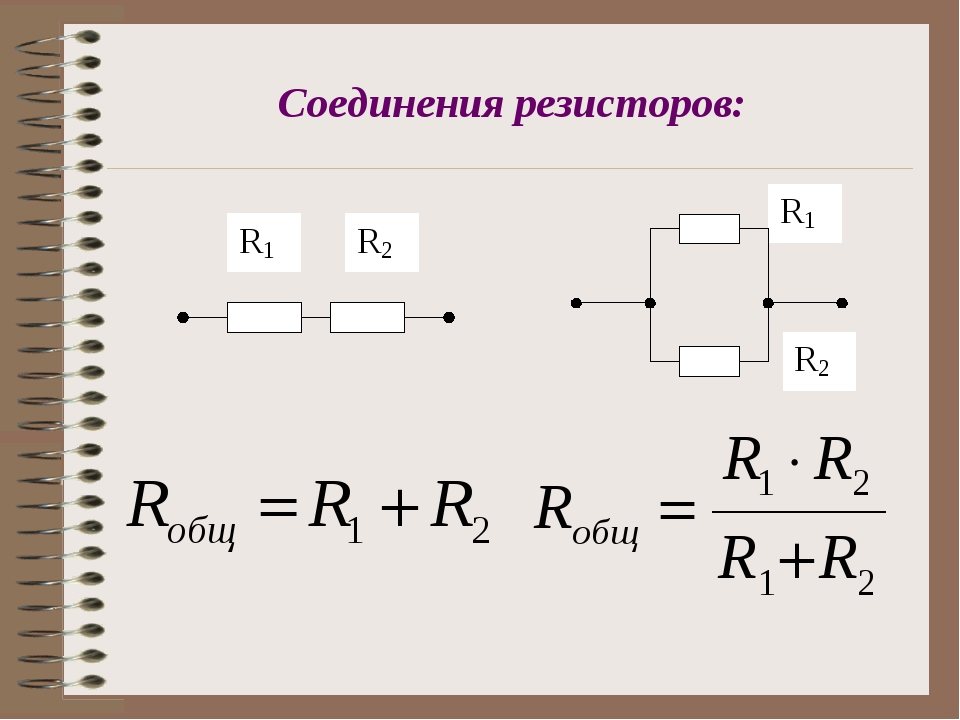
3.Используйте концепцию эквивалентного сопротивления, чтобы определить неизвестное сопротивление идентифицированного резистора, которое сделало бы схемы эквивалентными.
4. Проанализируйте следующую схему и определите значения общего сопротивления, общего тока, а также тока и падения напряжения на каждом отдельном резисторе.
5. Обращаясь к диаграмме в вопросе №4, определите …
а. … номинальная мощность резистора 4.г. … скорость, с которой энергия потребляется резистором 3.
Сопротивление листа и расчет удельного сопротивления или толщины относительно полупроводниковых приложений
В приборах на основе четырехточечного датчика используется давно зарекомендовавший себя метод измерения среднего сопротивления тонкого слоя или листа путем пропускания тока через две внешние точки датчика и измерение напряжения во внутренних двух точках.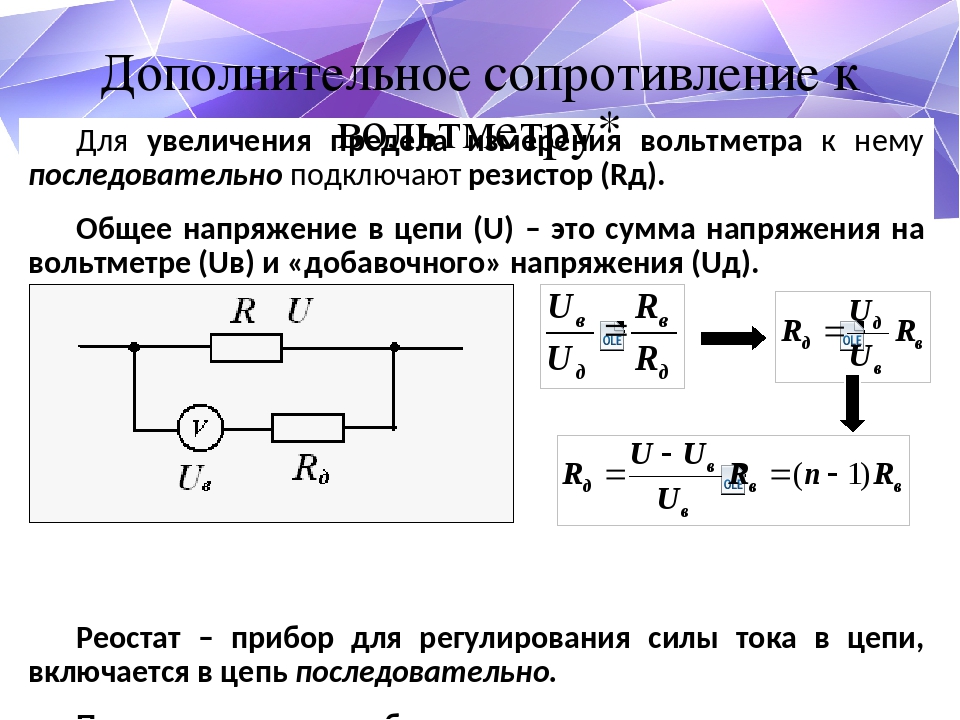
Если расстояние между точками зонда постоянное, а толщина проводящей пленки меньше 40% расстояния, а края пленки более чем в 4 раза больше расстояния от точки измерения, среднее сопротивление пленки или сопротивление листа определяется как:
Rs = 4,53 x V / I
Толщина пленки (в см) и ее удельное сопротивление (в Ом · см) связаны с Rs соотношением:
Rs = удельное сопротивление / толщина
Следовательно, можно вычислить удельное сопротивление, если известна толщина пленки, или можно вычислить толщину, если известно удельное сопротивление.
Глоссарий терминов
Ом на квадрат: Единица измерения при измерении сопротивления тонкой пленки материала с использованием метода четырехточечного зонда. Оно равно сопротивлению между двумя электродами на противоположных сторонах теоретического квадрата. Размер квадрата не имеет значения.
Подробнее читайте здесь, в Википедии: http://en. wikipedia.org/wiki/Sheet_resistance
wikipedia.org/wiki/Sheet_resistance
Ом-сантиметр (Ом-см): Единица измерения при измерении объемного или объемного удельного сопротивления толстых или однородных материалов, таких как голые кремниевые пластины или кремниевые слитки, с использованием метода четырехточечного зонда.
В. Является ли сопротивление листа «неотъемлемым» свойством материала или оно зависит от толщины?
СОПРОТИВЛЕНИЕ – это неотъемлемое свойство материала, которое придает ему электрическое сопротивление. Иногда его называют удельным сопротивлением. Сопротивление листа – это сопротивление тонкого листа материала, которое при умножении на толщину (в см) дает значение удельного сопротивления.
В. Как мне преобразовать из омов на квадрат в ом-сантиметр?
Термин Ом-см (Ом-сантиметр) относится к измерению «объемного» или «объемного» удельного сопротивления полупроводящего материала.Ом-см используется для измерения проводимости трехмерного материала, такого как слиток кремния или толстый слой материала. Термин «Ом на квадрат» используется при измерении сопротивления листа, то есть значения сопротивления тонкого слоя полупроводящего материала.
Термин «Ом на квадрат» используется при измерении сопротивления листа, то есть значения сопротивления тонкого слоя полупроводящего материала.
Чтобы рассчитать Ом-см с помощью четырехточечного зонда, необходимо знать толщину пластины (если это однородная пластина) или толщину измеряемого верхнего слоя, чтобы иметь возможность рассчитать Ом-см.Метод четырехточечного зонда используется для измерения одного слоя или одного однородного материала. При измерении образца с двумя или более проводящими слоями результатом будет какое-то бессмысленное среднее значение всех подключенных проводников.
Как упоминалось выше, поскольку метод четырехточечного зонда не позволяет напрямую измерять толщину тонких пленок, если известны две из следующих трех характеристик для данного образца, четырехточечный зонд можно использовать для определения третьей характеристики: 1) объемное сопротивление в Ом-см, 2) сопротивление листа в Ом-квадрат, 3) толщина образца.Подробнее об этом можно прочитать здесь: http://www.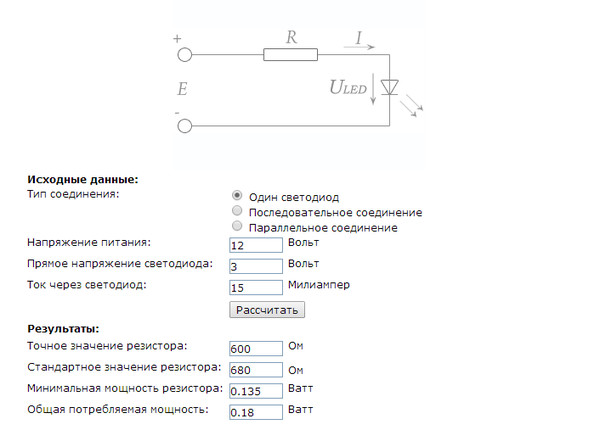 fourpointprobes.com/understanding-volume-resistivity-measurements/
fourpointprobes.com/understanding-volume-resistivity-measurements/
Уравнения для расчета объемного сопротивления отличаются от тех, которые используются для расчета сопротивления листа, однако, если сопротивление листа уже известно, объемное сопротивление можно рассчитать, умножив сопротивление листа в Ом на квадрат на толщину материала в сантиметры.
В. В какой момент вы перестаете умножать сопротивление листа на толщину в сантиметрах, чтобы получить Ом-см?
Когда толщина превышает 0.1 расстояния между двумя иглами – после которого сопротивление листа не применяется. Итак, 0,1 мм для головки зонда с расстоянием между иглами 1 мм. Однако, из-за исправлений, подойдет до 0,3 мм.
Если толщина равна или превышает пятикратное расстояние между датчиками, поправочный коэффициент, применяемый к формуле удельного сопротивления (rho) = 2 x pi x s x V / I, составляет менее 0,1%. С точки зрения удельного сопротивления листа, таблицы поправочных коэффициентов, которые у нас есть, начинаются с отношения толщины к расстоянию между зондами, равного 0. 3, где поправочный коэффициент равен единице, до отношения 2, где поправочный коэффициент равен x0,6337.
3, где поправочный коэффициент равен единице, до отношения 2, где поправочный коэффициент равен x0,6337.
Я ожидаю, что эти таблицы можно расширить до большего соотношения, но ясно, что от толщины в 2 раза до 5-кратного расстояния – это немного нейтральная зона, но если предположить, что ситуация “ большая ”, есть поправочные коэффициенты, охватывающие отношение толщины к интервалу от 10 до 0,4, где поправочный коэффициент равен x0,288.
Дополнительная информация: Взаимосвязь между сопротивлением листа (Ом на квадрат), толщиной пленки и объемным сопротивлением (Ом-см)
Подробнее здесь, в Википедии: http: // en.wikipedia.org/wiki/Resistivity
Четырехточечные зонды – это подразделение компании Bridge Technology. Чтобы запросить дополнительную информацию, позвоните в Bridge Technology по телефону (480) 988-2256 или отправьте электронное письмо Ларри Бриджу по адресу: [email protected]
Сопротивление серии| PVEducation
Последовательное сопротивление в солнечном элементе имеет три причины: во-первых, движение тока через эмиттер и основание солнечного элемента; во-вторых, контактное сопротивление между металлическим контактом и кремнием; и наконец сопротивление верхних и задних металлических контактов. Основное влияние последовательного сопротивления заключается в снижении коэффициента заполнения, хотя слишком высокие значения могут также снизить ток короткого замыкания.
Основное влияние последовательного сопротивления заключается в снижении коэффициента заполнения, хотя слишком высокие значения могут также снизить ток короткого замыкания.
Схема солнечного элемента с последовательным сопротивлением.
I = IL-I0exp [q (V + IRS) nkT]
где: I – выходной ток элемента, I L – ток, генерируемый светом, В, – напряжение на выводах элемента, T – температура, q и k – константы, n – это коэффициент идеальности, а R S – последовательное сопротивление элементов.Формула является примером неявной функции из-за появления тока, I , в обеих частях уравнения, и для ее решения требуются численные методы.
Влияние последовательного сопротивления на ВАХ показано ниже. Для построения графика изменяется напряжение на диоде, что позволяет избежать необходимости решать неявное уравнение.
Влияние последовательного сопротивления на коэффициент заполнения. Площадь солнечного элемента составляет 1 см 2 , так что единицы сопротивления могут быть ом или ом см 2 .На ток короткого замыкания (I SC ) не влияет последовательное сопротивление, пока оно не станет очень большим.
Площадь солнечного элемента составляет 1 см 2 , так что единицы сопротивления могут быть ом или ом см 2 .На ток короткого замыкания (I SC ) не влияет последовательное сопротивление, пока оно не станет очень большим.
не влияет на солнечный элемент при напряжении холостого хода, поскольку общий ток, протекающий через солнечный элемент, и, следовательно, через последовательное сопротивление равен нулю. Однако вблизи напряжения холостого хода на ВАХ сильно влияет последовательное сопротивление. Простой метод оценки последовательного сопротивления солнечного элемента состоит в том, чтобы найти наклон ВАХ в точке напряжения холостого хода.
Уравнение для FF как функции последовательного сопротивления можно определить, отметив, что для умеренных значений последовательного сопротивления максимальная мощность может быть аппроксимирована как мощность при отсутствии последовательного сопротивления минус мощность, потерянная при последовательном сопротивлении. Уравнение для максимальной мощности от солнечного элемента тогда принимает следующий вид:
Уравнение для максимальной мощности от солнечного элемента тогда принимает следующий вид:
, определяя нормированное последовательное сопротивление как;
дает следующее уравнение, которое аппроксимирует влияние последовательного сопротивления на выходную мощность солнечного элемента;
Предполагая, что на напряжение холостого хода и ток короткого замыкания не влияет последовательное сопротивление, можно определить влияние последовательного сопротивления на FF;
В приведенном выше уравнении коэффициент заполнения, на который не влияет последовательное сопротивление, обозначен FF 0 , а FF ‘называется FF S .Тогда уравнение становится;
Эмпирическое уравнение, которое немного точнее для связи между FF 0 и FF S :
, который действителен для r s <0,4 и v oc > 10.
Следующий калькулятор определяет влияние R s на коэффициент заполнения солнечного элемента. Типичные значения последовательного сопротивления, нормированного по площади, находятся между 0.5 Ом · см 2 для солнечных батарей лабораторного типа и до 1,3 0,5 Ом · см 2 для коммерческих солнечных батарей. Уровни тока в солнечном элементе имеют большое влияние на потери из-за последовательного сопротивления, и в следующем калькуляторе изучите влияние повышения тока на FF.
Калькулятор последовательного сопротивленияРезультаты
Характеристическое сопротивление элемента, R CH X (Ом)
Нормализованное V oc , v oc X (единицы)
Нормированное последовательное сопротивление, r s X (единицы)
Приблизительное заполнение коэффициент, FF, с R с FF приблизительно X
Более точный FF действителен для r с <0.4 и v oc > 10 FF s X
Разница между поверхностным сопротивлением и поверхностным сопротивлением
Что такое разница между удельным поверхностным сопротивлением и поверхностным сопротивлением? Хотя вокруг этих параметров было много дискуссий, они, вероятно, являются одними из наименее понятных в индустрии ESD. Специалисты по ОУР должны четко понимать, в чем заключаются различия, чтобы делать осознанный выбор материалов в своей рабочей среде.
Начнем с основ. Удельное поверхностное сопротивление в Ом / квадрат используется для оценки изоляционных материалов, где желательны высокие характеристики сопротивления. Поверхностное сопротивление в омах – это измерение для оценки рассеивающих статическое электричество упаковочных материалов, где требуются более низкие характеристики сопротивления. Теперь давайте рассмотрим стандарты и тесты, которые касаются этих измерений.
ASTM D-257 Удельное сопротивление поверхности
В течение многих лет измерения удельного поверхностного сопротивления использовались для классификации упаковочных материалов, контролируемых электростатическим разрядом.Основным эталоном для этого измерения был ASTM D-257 Standard Test Methods for D-C Resistance or Conduct of изоляционных материалов . ASTM D-257 измеряет резистивные или проводящие свойства изоляционных материалов, а не рассеивающие характеристики материалов для защиты от электростатического разряда. Независимо от названия, ASTM D-257 использовался повсюду в военном и коммерческом мире для классификации характеристик упаковочных материалов с контролем статического электричества.
Устранение неправильного использования ASTM D-257
В конце 1980-х комитет ASTM D-9 уведомил Комитет по упаковке электронных продуктов для отгрузки (PEPS) Ассоциации электронной промышленности (EIA), что использование ASTM D-257 для оценки упаковочных материалов было технически некорректным.Комитет D-9 заявил, что его использование для оценки рассеивающих материалов привело к ошибкам, и потребовал, чтобы Стандарт EIA 541 на упаковочные материалы для ESD-чувствительных предметов исключил ASTM D-257 в качестве метода испытаний для материалов с контролируемым статическим электричеством.
Рекомендация комитета по изменению была вполне правильной. ASTM D-257 содержит несколько процедур для измерения и оценки изоляционных материалов с высоким сопротивлением и обеспечивает наихудший сценарий для оценки самого низкого удельного поверхностного сопротивления изоляционного материала, которое указывает на самые низкие изоляционные свойства материала.Метод испытания определяет высокие испытательные напряжения, относительную влажность (RH) от умеренной до высокой и высокое давление испытательного приспособления для уменьшения контактного сопротивления, что обеспечивает измерения более низкого сопротивления изоляторов.
При оценке материалов, рассеивающих статический заряд, необходимо знать максимальное сопротивление, которое может предотвратить перемещение статического заряда к земле. Другими словами, метод ASTM D-257 для оценки изоляционных свойств дает оптимистичное представление о характеристиках материала, контролируемого электростатическим разрядом, а также о несогласованных измерениях рассеиваемых продуктов.
Чтобы подтвердить мнение комитета, рабочая группа № 1 по ОУР Комитета EIA PEPS провела круговой тест среди пяти лабораторий с использованием пяти идентичных наборов образцов. Каждая лаборатория тестировала наборы образцов в контролируемых условиях, используя свою интерпретацию ASTM D-257. Анализ данных испытаний в лабораториях показал, что использование ASTM D-257 для оценки материалов с контролируемым статическим электричеством привело к разнице между лабораториями на 4-й порядок. Оперативная группа № 1 приступила к работе, чтобы исправить ситуацию.
Оценка проблемы
Первой целью было определить, что измеряется, и почему была обнаружена такая большая разница. Рабочая группа пришла к выводу, что изоляторы представляют собой однородные материалы с высоким сопротивлением, предназначенные для предотвращения прохождения электронов через их поверхность; статические рассеивающие материалы были материалами с более низким сопротивлением, предназначенными для того, чтобы позволить электронам проходить через и под их поверхностью.
Рассеивающие материалы неоднородны, потому что они могут состоять из любой комбинации проводников, органических химикатов или металлов.Эти добавки стимулируют поток электронов. Хотя изоляторы изготовлены из чисто непроводящих материалов, метод ASTM позволяет оценивать характеристики удельного поверхностного сопротивления однородных изоляторов и не подходит для оценки сложных неоднородных рассеивателей, содержащих проводящие элементы. Это ошибка применения отличного инструмента, аналогичного тому, как плотник режет дерево молотком.
Влияние влажности
ASTM D-257 рекомендует испытывать материалы при относительной влажности 50% или выше.Влажность создает проводящий слой на поверхности материала, снижая защитные свойства изолятора за счет увеличения потока электронов и характеристик материалов, рассеивающих статическое электричество. И наоборот, низкая относительная влажность увеличивает резистивные характеристики изолятора и снижает функцию рассеивающего материала.
Рекомендации по креплению
ASTM D-257 обсуждает несколько конструкций приспособлений. Цель конструкции приспособления – обеспечить определенное сопротивление квадратной части поверхности материала; то есть удельное сопротивление в Ом / квадрат.Можно использовать любое приспособление, если определены его конфигурация и размеры. Целевая группа № 1 EIA нашла преимущество в использовании концентрических колец для измерения материалов, рассеивающих статическое электричество, но различные конструкции и состав материалов создавали несоответствия при оценке материалов, рассеивающих статическое электричество.
Давление на приспособление
Высокое давление (от 20 до 100 фунтов на кв. Дюйм) прикладывается к концентрическому кольцу или лопастным испытательным приспособлениям для уменьшения контактного сопротивления между электродами и испытуемым изолятором и для оценки его наиболее проводящих свойств.Электронные устройства, защищенные материалами, контролируемыми электростатическим разрядом, относительно легкие и часто имеют дополнительное контактное сопротивление из-за своей конфигурации. В результате высокое давление в арматуре искажает функциональное сопротивление рассеивающих материалов, часто преувеличивая характеристики материалов.
Испытательное напряжение и ток
Перед расчетом удельного сопротивления поверхности к материалу на длительное время прикладывают испытательное напряжение 500 В или выше. Эти более высокие испытательные напряжения необходимы для точного измерения изоляторов и обеспечения более низких значений сопротивления, чем низкие испытательные напряжения.
Высокие испытательные напряжения, приложенные к материалам ESD со сравнительно низким сопротивлением, создают значительный ток, который легко изменяет характеристики материала и обеспечивает более низкое сопротивление. Если 500 В применяется к рассеивающему материалу, как указано в ASTM D-257, ток в миллионы раз превышает ток через изолятор.
Сильный ток вызывает разрушение материала или образование углеродных следов между проводящими элементами и слоями ламинирования. Это приводит к неправильным измерениям, повреждению материала и ложному указанию на его полезные свойства.
Период электрификации
Подача испытательного напряжения на приспособление в течение некоторого времени перед записью измерения называется периодом электрификации. При измерениях изолятора длительные периоды электрификации дают более низкое сопротивление. При измерении рассеивающих материалов длительные периоды электрификации могут повлиять на характеристики поверхности и изменить предполагаемые характеристики.
Период электрификации четко не определен в ASTM D-257, и практикующие специалисты используют разные периоды для измерения материалов.Результат – несовместимые значения измерений.
Модифицированный подход
После рассмотрения данных испытаний ASTM D-257 и обсуждения цели измерения, рабочая группа № 1 разработала модифицированный подход к измерению сопротивления материалов, рассеивающих статическое электричество. В первых пяти лабораториях была разработана и протестирована определенная процедура.
Окончательная версия процедуры снизила общую дисперсию до ± 0,25 от 1 порядка величины между лабораториями, или до степени достоверности менее половины порядка.Это было сочтено неплохим, и новая методика была в конечном итоге представлена в отрасли в 1993 году Ассоциацией ESD как Измерение поверхностного сопротивления статически-рассеивающих плоских материалов , EOS / ESD S11.11-1993.
Поверхностное сопротивление согласно S11.11
S11.11 определяет процедуру измерения поверхностного сопротивления для плоского (плоского) материала, рассеивающего статическое электричество. Это критические элементы:
Сборка электродов и сопутствующее оборудование
Конструкция приспособления для сборки электродов основана на концентрическом кольце ( Рисунок 1 ).Электродная сборка S11.11 определяется ее размером, материалом поверхности электрода и общим весом. Любая лаборатория, измеряющая характеристики поверхностного сопротивления рассеивающего материала, должна использовать такую же конфигурацию.
Циклические испытания показали, что поверхностное сопротивление материала, рассеивающего статическое электричество, значительно варьировалось, если испытательный образец измерялся на проводящем испытательном стенде. Эта переменная была устранена путем указания изолятор в качестве опорной поверхности образца.
Приборы, используемые для измерения поверхностного сопротивления, могут состоять либо из источника питания и амперметра, либо из интегрированного устройства, которое объединяет эти функции прибора.Приборы должны иметь размеры от 1,0 x 10 3 до 1,0 x 10 13 Вт и иметь возможности испытательного напряжения 10 и 100 В (± 5%). Поскольку все системы разные, S11.11 использует две процедуры для проверки и характеристики возможностей каждой системы.
Проверка системы в диапазоне низких сопротивлений
Критические переменные с низким сопротивлением при измерении поверхности были исключены в S11.11. Первой задачей было обеспечить равномерный контакт узла электрода с испытываемым материалом при низком напряжении (10 В).Второй заключался в том, чтобы подтвердить, что вся система провела точное измерение низкого сопротивления (1,0 x 10 6 Вт) при 10 В. Если электродный узел не был выровнен или испытательное напряжение системы было аномально низким, результат был неточным. измерения высокого сопротивления.
Прецизионное калибровочное кольцо (приспособление для проверки системы низкого сопротивления) используется для подтверждения совмещения электродного узла. Если электродная сборка верна и полностью контактирует с поверочным приспособлением, измеренное сопротивление системы будет равно 5.0 x 10 5 Вт, ± 1% при 10 В. При точном выравнивании поворот узла электрода на 90 ° снова даст 5,0 x 10 5 Вт, ± 1%.
Проверка системы в диапазоне высоких сопротивлений
Аналогичным образом была подтверждена способность системы измерять высокое сопротивление (1,0 x 10 12 Вт) и определять соответствующий период электрификации. Каждая система может отличаться и иметь различные варианты подключения источника питания, измерения тока, кабелей и электродов.Чтобы оценить эти переменные, используется приспособление для проверки системы верхнего диапазона сопротивления, чтобы подтвердить работу системы при высоком сопротивлении.
Это второе калибровочное приспособление имеет два кольца, которые соответствуют поверхности контакта с материалом электродного узла. Резистор 1,0 x 10 12 Вт (± 5%) установлен между внутренним и внешним кольцами. Эта конфигурация позволяет определить период электрификации системы с помощью следующей процедуры:
Электродный узел помещается на приспособление для проверки верхнего диапазона и подключается к контрольно-измерительным приборам.
100 В подается на систему и электродный узел для измерения сопротивления поверочного приспособления. Фактическое сопротивление определяется как верхнее стабильное измерение сопротивления системы, которое должно составлять 1,0 x 10 12 , ± 5%. Как только определено верхнее стабильное измерение сопротивления, оно используется для определения периода электрификации.
Выполняется пять измерений (в секундах) с точностью до 10% от стабильного измерения сопротивления.
Пять времен измерения усредняются и добавляются к нему 5 с.Результатом является период электрификации этой конкретной системы.
Расчетный период электрификации позволяет системе производить измерение максимального сопротивления без чрезмерного воздействия на образец высокого напряжения. Период электрификации используется для всех измерений сопротивления, превышающих 1,0 x 10 6 Вт, и обеспечивает согласованность измерений.
Размер образца и предварительная подготовка
S11.11 указывает, что измерения поверхностного сопротивления должны выполняться на образцах, размер которых не менее 3 ″ x 5 ″.Образцы должны быть немного больше, чем электродный узел; и при сравнении различных материалов все образцы для испытаний должны быть одного размера.
Перед испытанием образцы выдерживают от 48 до 72 часов при определенной температуре и низкой относительной влажности; то есть 23 ° C (± 3 ° C) и 12% относительной влажности (± 3% относительной влажности). Измерение образцов одинакового размера при определенной температуре и относительной влажности дополнительно увеличивает повторяемость и повышает согласованность измерений.
Basic S11.11 Процедура измерения
Измеряется не менее шести образцов одного и того же материала для обеспечения минимального уровня статистической надежности.После того, как образец для испытаний помещается на изолированный испытательный стенд и электродный узел помещается в его центральную точку, на электродный узел подается напряжение 10 В.
Если указанное сопротивление материала меньше 1,0 x 10 6 Вт через 5 с, сопротивление регистрируется. Если указанное сопротивление равно или больше 1,0 x 10 6 Вт, испытательное напряжение отключается и 100 В используется для повторного включения электродного узла. Указанное сопротивление после завершения расчетного периода электрификации системы считается поверхностным сопротивлением образца в Ом на S11.11.
Все шесть образцов измерены, и данные представлены:
Минимальное, максимальное и среднее поверхностное сопротивление всех образцов.
Период кондиционирования, относительная влажность и температура.
Период электрификации диапазона испытательных напряжений и верхнего сопротивления.
Сравнение данных S11.11 с данными ASTM D-257
Многие организации по-прежнему ссылаются на ASTM D-257 и указывают, что резистивные характеристики материала должны указываться в Ом / квадрат. Хотя это может показаться проблемой, но S11.Геометрия электродного узла 11 имеет коэффициент преобразования 10, который коррелирует с измерениями ASTM D-257. Чтобы преобразовать измерения S11.11 в удельное сопротивление поверхности в Ом / квадрат, просто умножьте на 10, потому что измерения S11.11 на 1 порядок ниже, чем полученные с использованием ASTM D-257, как показано на Рис. 2 .
S11.11 предупреждает, что преобразование измерений в удельное сопротивление в Ом / квадрат может быть недопустимым для многих типов материалов. Сюда входят ламинированные, гальванические, металлизированные и другие материалы, содержащие проводящие элементы.
Сводка
Новая процедура S11.11 принимает во внимание многие переменные измерения сопротивления и является намного более совершенным методом оценки и классификации материалов ESD от 1,0 x 10 4 до 1,0 x 10 11 Вт. Это повышает повторяемость измерений и может значительно уменьшить путаницу среди поставщиков, переработчиков и пользователей материалов ESD.
Об авторе
Стивен А. Гальперин – основатель и президент Stephen Halperin & Associates, независимой лаборатории и консалтинговой фирмы, специализирующейся на электростатических технологиях.Он известен своей работой в области разработки стандартов с EIA и ESD Association, а также своими оригинальными концепциями по оценке объектов в условиях, чувствительных к статическому электричеству. Г-н Гальперин получил B.S.B.A. Получил степень в Университете Рузвельта, а также закончил аспирантуру в области наук об организационной коммуникации, а также несколько курсов военной подготовки и программ AMA. Stephen Halperin & Associates, 1072 Tower Lane, Bensenville, IL 60106, (708) 238-8883.
БОКОВАЯ ПАНЕЛЬ
Объяснение Ом на квадрат
Тех, кто плохо знаком с измерениями, связанными с электростатическим разрядом, часто путают с термином «Ом на квадрат».Любопытные всегда спрашивают: «Что за квадрат? Дюймы? Ноги? Ярды? » Ответ: на любой квадрат, если измерение относится к квадрату.
Простая красота ASTM D-257 заключается в том, что удельное сопротивление поверхности является расчетом сопротивления области, а не измерением от точки к точке. Фактически, измерения в омах / квадрате всегда будут одинаковыми независимо от размера материального квадрата.
Для иллюстрации, предположим, что у нас есть квадрат материала 2 ″ x 2 ″, и мы используем стержневые электроды 2 ″ для измерения удельного сопротивления этого образца.Омметр показывает 5 Вт. Так как мы точно измерили этот квадрат 2 дюйма, мы выражаем результат как 5 Вт / кв.
Теперь давайте прикрепим еще 2 ″ квадрат материала к первому квадрату и переместим стержень электрода 2 ″ к концу второго квадрата. По сути, это похоже на измерение двух последовательно соединенных резисторов, потому что теперь у нас есть два материала мощностью 5 Вт, образующие прямоугольник 2 x 4 дюйма. Это больше не квадрат, и наш прибор покажет примерно 10 Вт на 4 ″ длине материала.
R Tseries = R 1 + R 2
и
R Серия = 5 Вт + 5 Вт
R Серия = 10 Вт
Если еще два куска материала 2 ″ x 2 ″ прикреплены к нижней части нашего прямоугольника 2 ″ x 4 ″, мы получим два прямоугольника 10 Вт, которые образуют один квадрат 4 ″ x 4 ″.Согласно расчету основного сопротивления для двух параллельно подключенных резисторов, если бы у нас было два 4-дюймовых электрода, размещенных вдоль края нашего нового квадрата, мы должны измерить 5 Вт / кв. На большом образце, потому что:
R T Параллельно = R 1 x R 2
———-
R 1 + R 2
где: R T параллельно = общее сопротивление двух резисторов, включенных параллельно
R 1 = сопротивление верхнего прямоугольника
R 2 = сопротивление нижнего прямоугольника
следовательно:
10 Вт x 10 Вт 100 Вт 2
R T Параллельно = —————- = ——— = 5 Вт
10 Вт + 10 Вт 20 Вт
Квадрат любого размера из того же изоляционного материала будет измерять примерно одинаковое сопротивление.





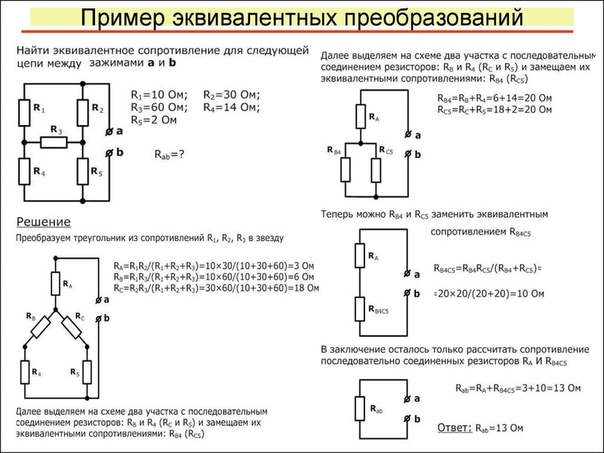 Формулируют с учителем цель урока.
Формулируют с учителем цель урока.
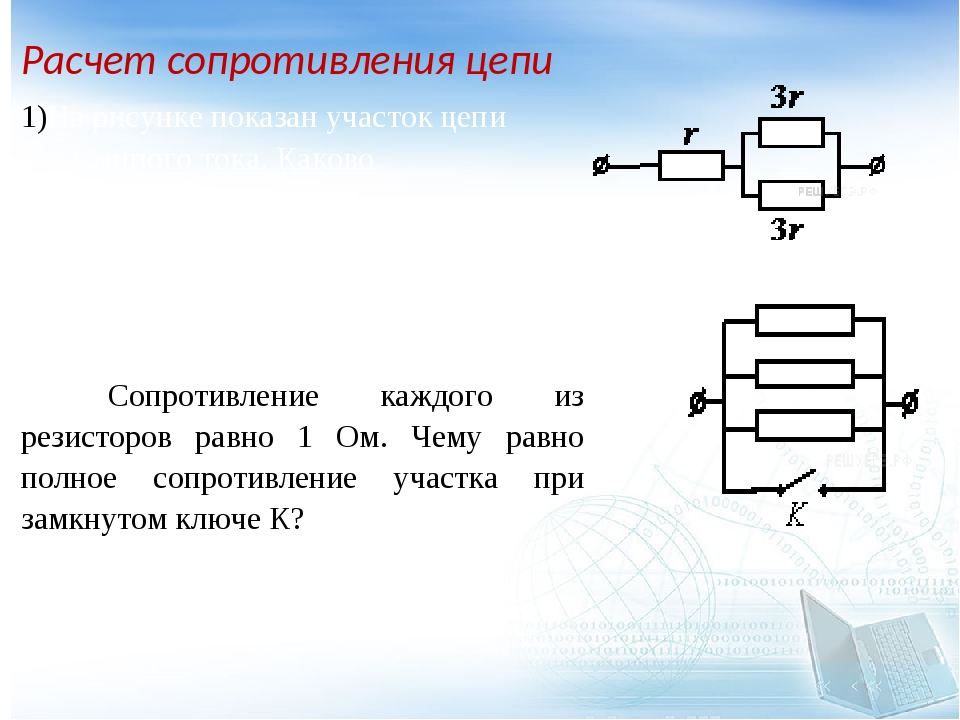 Предлагает проверить результаты исследований на экспериментальной установке.
Предлагает проверить результаты исследований на экспериментальной установке.
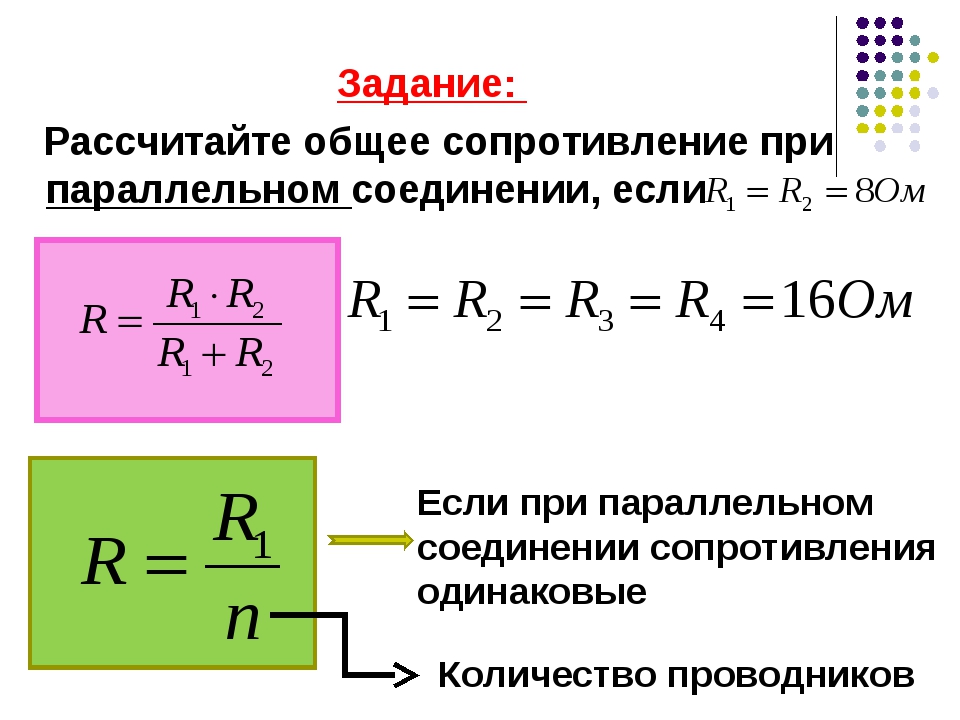 Дает задание учащимся по работе с тестом для первичной диагностики уровня освоения знаний.
Дает задание учащимся по работе с тестом для первичной диагностики уровня освоения знаний.
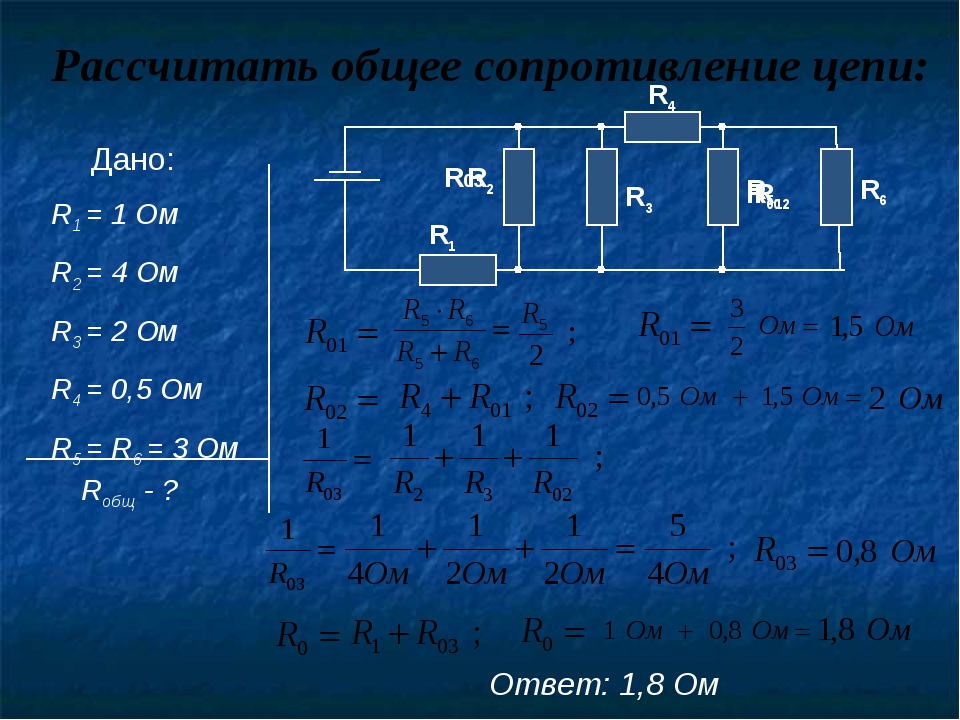 Сообщают, какие задания теста вызвали затруднения.
Сообщают, какие задания теста вызвали затруднения.
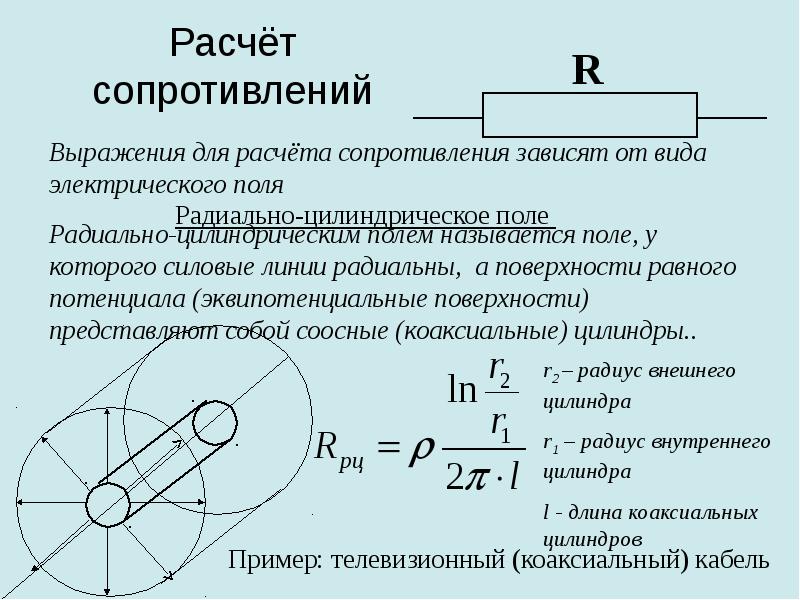 Для сильных учащихся тестирование из 9 вопросов, для слабых учащихся – три расчетных задачи.
Для сильных учащихся тестирование из 9 вопросов, для слабых учащихся – три расчетных задачи.