Расчет сопротивление: Онлайн калькулятор – закон Ома (ток, напряжение, сопротивление) + Мощность :: АвтоМотоГараж

При проектировании электрических схем возникает необходимость использования последовательного и параллельного соединений резисторов. Соединения применяются также и при ремонтах электрооборудования, поскольку в некоторых ситуациях невозможно найти эквивалентный номинал резистора. Выполнить расчет просто, и справиться с этой операцией может каждый.

Типы проводников

Проводимость веществом электрического тока связана с наличием в нем свободных носителей заряда. Их количество определяется по электронной конфигурации. Для этого необходима химическая формула вещества, при помощи которой можно вычислить их общее число. Значение для каждого элемента берется из периодической системы Дмитрия Ивановича Менделеева.

Электрический ток — упорядоченное движение свободных носителей заряда, на которые воздействует электромагнитное поле. При протекании тока по веществу происходит взаимодействие потока заряженных частиц с узлами кристаллической решетки, при этом часть кинетической энергии частицы превращается в тепловую энергию. Иными словами, частица «ударяется» об атом, а затем снова продолжает движение, набирая скорость под действием электромагнитного поля.

Процесс взаимодействия частиц с узлами кристаллической решетки называется электрической проводимостью или сопротивлением материала. Единицей измерения является Ом, а определить его можно при помощи омметра или расчитать. Согласно свойству проводимости, вещества можно разделить на 3 группы:

1. Проводники (все металлы, ионизированный газ и электролитические растворы).
2. Полупроводники (Si, Ge, GaAs, InP и InSb).
3. Непроводники (диэлектрики или изоляторы).

Проводники всегда проводят электрический ток, поскольку содержат в своем атомарном строении свободные электроны, анионы, катионы и ионы. Полупроводники проводят электричество только при определенных условиях, которые влияют на наличие или отсутствие свободных электронов и дырок. К факторам, влияющим на проводимость, относятся следующие: температура, освещенность и т. д. Диэлектрики вообще не проводят электричество, поскольку в их структуре вообще отсутствуют свободные носители заряда. При выполнении расчетов каждый радиолюбитель должен знать зависимость сопротивления от некоторых физических величин.

Зависимость сопротивления

Значение электропроводимости зависит от нескольких факторов, которые необходимо учитывать при расчетах, изготовлении элементов резистивной нагрузки (резисторов), ремонте и проектировании устройств. К этим факторам необходимо отнести следующие:

1. Температура окружающей среды и материала.
2. Электрические величины.
3. Геометрические свойства вещества.
4. Тип материала, из которого изготовлен проводник (полупроводник).

К электрическим величинам можно отнести разность потенциалов (напряжение), электродвижущую силу (ЭДС) и силу тока. Геометрией проводника является его длина и площадь поперечного сечения.

Электрические величины

Зависимость величины электропроводимости от параметров электричества определяется законом Ома. Существует две формулировки: одна — для участка, а другая — для полной цепи. В первом случае соотношение определяются, исходя из значений силы тока (I) и напряжения (U) простой формулой: I = U / R. Из соотношения видна прямо пропорциональная зависимость тока от величины напряжения, а также обратно пропорциональная от сопротивления. Можно выразить R: R = U / I.

Для расчета электропроводимости всего участка следует воспользоваться соотношением между ЭДС (e), силой тока (i), а также внутренним сопротивлением источника питания (Rвн): i = e / (R+Rвн). В этом случае величина R вычисляется по формуле: R = (e / i) — Rвн. Однако при выполнении расчетов необходимо учитывать также геометрические параметры и тип проводника, поскольку они могут существенно повлиять на вычисления.

Тип и геометрические параметры

Свойство вещества к проводимости электричества определяется структурой кристаллической решетки, а также количеством свободных носителей. Исходя из этого, тип вещества является ключевым фактором, который определяет величину электропроводимости. В науке коэффициент, определяющий тип вещества, обозначается литерой «р» и называется удельным сопротивлением. Его значение для различных материалов (при температуре +20 градусов по Цельсию) можно найти в специальных таблицах.

Иногда для удобства расчетов используется обратная величина, которая называется удельной проводимостью (σ). Она связана с удельным сопротивлением следующим соотношением: p = 1 / σ. Площадь поперечного сечения (S) влияет на электрическое сопротивление. С физической точки зрения, зависимость можно понять следующим образом: при малом сечении происходят более частые взаимодействия частиц электрического тока с узлами кристаллической решетки. Поперечное сечение можно вычислить по специальному алгоритму:

1. Измерение геометрических параметров проводника (диаметр или длину сторон) при помощи штангенциркуля.
2. Визуально определить форму материала.
3. Вычислить площадь поперечного сечения по формуле, найденной в справочнике или интернете.

В случае когда проводник имеет сложную структуру, необходимо вычислить величину S одного элемента, а затем умножить результат на количество элементов, входящих в его состав. Например, если провод является многожильным, то следует вычислить S для одной жилы. После этого нужно умножить, полученную величину S, на количество жил. Зависимость R от вышеперечисленных величин можно записать в виде соотношения: R = p * L / S. Литера «L» является длиной проводника. Однако для получения точных расчетов необходимо учитывать температурные показатели внешней среды и проводника.

Температурные показатели

Существует доказательство зависимости удельного сопротивления материала от температуры, основанное на физическом эксперименте. Для проведения опыта нужно собрать электрическую цепь, состоящую из следующих элементов: источника питания, нихромовой спирали, соединительных проводов амперметра и вольтметра. Приборы нужны для измерения значений силы тока и напряжения соответственно. При протекании электричества происходит нагревание нихромовой пружины. По мере ее нагревания, показания амперметра уменьшаются. При этом происходит существенное падение напряжения на участке цепи, о котором свидетельствуют показания вольтметра.

В радиотехнике уменьшение величины напряжение называется просадкой или падением. Формула зависимости р от температуры имеет следующий вид: p = p0 * [1 + a * (t — 20)]. Значение p0 — удельное сопротивление материала, взятого из таблицы, а литера «t» — температура проводника.

Температурный коэффициент «а» принимает следующие значения: для металлов — a>0, а для электролитических растворов — a<0. Для получения формулы, определяющей все зависимости, необходимо подставить все соотношения в общую формулу зависимости R от типа материала, температуры, длины и сечения: R = p0 * [1 + a * (t — 20)] * L / S. Формулы используются только для расчетов и изготовления резисторов. Для быстрого измерения величины сопротивления применяется омметр.

Объединение резистивных радиокомпонентов

Для получения необходимого номинала сопротивления применяются два типа соединения резисторов: параллельное и последовательное. Если их соединить параллельно, то нужно два вывода одного резистора подключить к двум выводам другого. Если соединение является последовательным, то один вывод резистора соединяется с одним выводом другого резистора. Соединения используются для получения необходимых номиналов сопротивлений, а также для увеличения рассеивания мощности тока, протекающего по цепи.

Каждое из соединений обладает определенными характеристиками. Кроме того, последовательно или параллельно могут объединяться несколько резисторов. Соединения также могут быть смешанными, т. е. применяться оба типа объединения радиокомпонентов.

Параллельное соединение

При параллельном подключении значение напряжения на всех резисторах одинаковое, а сила тока — обратно пропорциональна их общему сопротивлению. В интернете web-разработчики создали для расчета величины общего сопротивления параллельного соединения резисторов онлайн-калькулятор.

Рассчитывается общее сопротивление при параллельном соединении по формуле: 1 / Rобщ = (1 / R1) + (1 / R2) + …+ (1 / Rn). Если выполнить математические преобразования и привести к общему знаменателю, то получится удобная формула параллельного соединения для расчета Rобщ. Она имеет следующий вид: Rобщ = (R1 * R2 * … * Rn) / (R1 + R2 + … + Rn). Если необходимо рассчитать величину Rобщ только для двух радиокомпонентов, то формула параллельного сопротивления имеет следующий вид: Rобщ = (R1 * R2) / (R1 + R2).

При ремонте или проектировании схемы устройства возникает задача объединения нескольких резистивных элементов для получения конкретной величины сопротивления. Например, значение Rобщ для определенной цепочки элементов равно 8 Ом, которое получено при расчетах. Перед радиолюбителем стоит задача, какие нужно подобрать номиналы для получения нужного значения (в стандартном ряду резисторов отсутствует радиокомпонент с номиналом в 8 Ом, а только 7,5 и 8,2). В этом случае нужно найти сопротивление при параллельном соединении резистивных элементов. Посчитать значение Rобщ для двух элементов можно следующим образом:

1. Номинал резистора в 16 Ом подойдет.
2. Подставить в формулу: R = (16 * 16) / (16 + 16) = 256 / 32 = 8 (Ом).

В некоторых случаях следует потратить больше времени на подбор необходимых номиналов. Можно применять не только два, но и три элемента. Сила тока вычисляется с использованием первого закона Кирхгофа. Формулировка закона следующая: общее значение тока, входящего и протекающего по цепи, равен выходному его значению. Величина силы тока для цепи, состоящей из двух резисторов (параллельное соединение) рассчитывается по такому алгоритму:

1. Ток, протекающий через R1 и R2: I1 = U / R1 и I2 = U / R2 соответственно.
2. Общий ток — сложение токов на резисторах: Iобщ = I1 + I2.

Например, если цепь состоит из 2 резисторов, соединенных параллельно, с номиналами в 16 и 7,5 Ом. Они запитаны от источника питания напряжением в 12 В. Значение силы тока на первом резисторе вычисляется следующим способом: I1 = 12 / 16 = 0,75 (А). На втором резисторе ток будет равен: I2 = 12 / 7,5 = 1,6 (А). Общий ток определяется по закону Кирхгофа: I = I1 + I2 = 1,6 + 0,75 = 2,35 (А).

Последовательное подключение

Последовательное включение резисторов также применяется в радиотехнике. Методы нахождения общего сопротивления, напряжения и тока отличаются от параллельного подключения. Основные правила соединения следующие:

1. Ток не изменяется на участке цепи.
2. Общее напряжение равно сумме падений напряжений на каждом резисторе.
3. Rобщ = R1 + R2 + … + Rn.

Пример задачи следующий: цепочка, состоящая из 2 резисторов (16 и 7,5 Ом), питается от источника напряжением 12 В и током в 0,5 А. Необходимо рассчитать электрические параметры для каждого элемента. Порядок расчета следующий:

1. I = I1 = I2 = 0,5 (А).
2. Rобщ = R1 + R2 = 16 + 7,5 = 23,5 (Ом).
3. Падения напряжения: U1 = I * R1 = 0,5 * 16 = 8 (В) и U2 = I * R2 = 0,5 * 7,5 = 3,75 (В).

Не всегда выполняется равенство напряжений (12 В не равно 8 + 3,75 = 11,75 В), поскольку при этом расчете не учитывается сопротивление соединительных проводов. Если схема является сложной, и в ней встречается два типа соединений, то нужно выполнять расчеты по участкам. В первую очередь, рассчитать для параллельного соединения, а затем для последовательного.

Таким образом, параллельное и последовательное соединения резисторов применяются для получения более точных значений сопротивлений, а также при отсутствии необходимого номинала радиокомпонента при проектировании или ремонте устройств.

Параллельное соединение резисторов. Калькулятор для расчета

Параллельное соединение резисторов — одно из двух видов электрических соединений, когда оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов. Зачастую резисторы соединяют последовательно или параллельно для того, чтобы создать более сложные электронные схемы.

Схема параллельного соединения резисторов показан на рисунке ниже. При параллельном соединении резисторов, напряжение на всех резисторах будет одинаковым, а протекающий через них ток будет пропорционален их сопротивлению:

Формула параллельного соединения резисторов

Общее сопротивление нескольких резисторов соединенных параллельно определяется по следующей формуле:

Ток, протекающий через отдельно взятый резистор, согласно закону Ома, можно найти по формуле:

Параллельное соединение резисторов — расчет

Пример  №1

При разработке устройства, возникла необходимость установить резистор с сопротивлением 8 Ом. Если мы просмотрим весь номинальный ряд стандартных значений резисторов, то мы увидим, что резистора с сопротивлением в 8 Ом в нем нет.

Выходом из данной ситуации будет использование двух параллельно соединенных резисторов. Эквивалентное значение сопротивления для двух резисторов соединенных параллельно рассчитывается следующим образом:

Данное уравнение показывает, что если R1 равен R2, то сопротивление R составляет половину сопротивления одного из двух резисторов. При R = 8 Ом, R1 и R2 должны, следовательно, иметь значение 2 × 8 = 16 Ом.
Теперь проведем проверку, рассчитав общее сопротивление двух резисторов:

Таким образом, мы получили необходимое сопротивление 8 Ом, соединив параллельно два резистора по 16 Ом.

Пример расчета №2

Найти общее сопротивление  R из трех параллельно соединенных резисторов:

Общее сопротивление R рассчитывается по формуле:

Этот метод расчета может быть использованы для расчета любого количества отдельных сопротивлений соединенных параллельно.

Один важный момент, который необходимо запомнить при расчете параллельно соединенных резисторов – это то, что общее сопротивление всегда будет меньше, чем значение наименьшего сопротивления в этой комбинации.

Как рассчитать сложные схемы соединения резисторов

Более сложные соединения резисторов могут быть рассчитаны путем систематической группировки резисторов. На рисунке ниже необходимо посчитать общее сопротивление цепи, состоящей из трех резисторов:

Для простоты расчета, сначала сгруппируем резисторы по параллельному и последовательному типу соединения.
Резисторы R2 и R3 соединены последовательно (группа 2). Они в свою очередь соединены параллельно с резистором R1 (группа 1).

Последовательное соединение резисторов группы 2 вычисляется как сумма сопротивлений R2 и R3:

В результате мы упрощаем схему в виде двух параллельных резисторов. Теперь общее сопротивление всей схемы можно посчитать следующим образом:

Расчет более сложных соединений резисторов можно выполнить используя законы Кирхгофа.

Ток, протекающий в цепи параллельно соединенных резисторах

Общий ток I протекающий в цепи параллельных резисторов равняется сумме отдельных токов, протекающих во всех параллельных ветвях, причем ток в отдельно взятой ветви не обязательно должен быть равен току в соседних ветвях.

Несмотря на параллельное соединение, к каждому резистору приложено одно и то же напряжение. А поскольку величина сопротивлений в параллельной цепи может быть разной, то и величина протекающего тока через каждый резистор тоже будет отличаться (по определению закона Ома).

Рассмотрим это на примере двух параллельно соединенных резисторов. Ток, который течет через каждый из резисторов ( I1 и I2 ) будет отличаться друг от друга поскольку сопротивления резисторов R1 и R2 не равны.
Однако мы знаем, что ток, который поступает в цепь в точке «А» должен выйти из цепи в точке «B» .

Первое правило Кирхгофа гласит: «Общий ток, выходящий из цепи равен току входящий в цепь».

Таким образом, протекающий общий ток в цепи  можно определить как:

I = I1 + I2

Затем с помощью закона Ома можно вычислить ток, который протекает через каждый резистор:

Ток, протекающий в R1 = U ÷ R1 = 12 ÷ 22 кОм = 0,545 мА

Ток, протекающий в R 2 = U ÷ R2 = 12 ÷ 47 кОм = 0,255 мА

Таким образом, общий ток будет равен:

I = 0,545 мА + 0,255 мА = 0,8 мА

Это также можно проверить, используя закон Ома:

I = U ÷ R = 12 В ÷ 15 кОм = 0,8 мА (то же самое)

где 15кОм — это общее сопротивление двух параллельно соединенных резисторов (22 кОм и 47 кОм)

И в завершении хочется отметить, что большинство современных резисторов маркируются цветными полосками и назначение ее можно узнать здесь.

Параллельное соединение резисторов — онлайн калькулятор

Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных параллельно, вы можете воспользоваться следующим онлайн калькулятором:

Подведем итог

Когда два или более резистора соединены так, что оба вывода одного резистора соединены с соответствующими выводами другого резистора или резисторов, то говорят, что они соединены между собой параллельно. Напряжение на каждом резисторе внутри параллельной комбинации одинаковое, но токи, протекающие через них, могут отличаться друг от друга, в зависимости от величины сопротивлений каждого резистора.

Эквивалентное или полное сопротивление параллельной комбинации всегда будет меньше минимального сопротивления резистора, входящего в параллельное соединение.

Расчет сопротивления электрической цепи: резисторов

Многие люди, которые изучают электрику, сталкиваются с таким понятием, как расчет сопротивления. Что собой представляет эта величина, в каких единицах измеряется сопротивление проводника, от чего зависит и как его вычислить — далее.

Описание явления

Электрическим сопротивлением называется физическая величина, которая характеризует проводниковое свойство препятствовать электротоку. Она равна напряжению, поделенному на силу тока, которое проходит по проводниковому элементу.

Расчет сопротивляемости

Электросопротивление бывает активным, реактивным и удельным. Активным является часть полного, находящегося в электроцепи. В нем энергия целиком преобразовывается во все энергетические виды. Бывает тепловой, механической и химической. Отличительным свойством является процесс полного потребления всей электрической энергии.

Обратите внимание! Согласно международной системе единиц, измеряется величина в омах, умноженных на метр. В некоторых случаях применяется единица ом, умноженная на миллиметр в квадрате, поделенная на метр. Это обозначение для проводника, имеющего метровую длину и миллиметровую площадь сечения в квадрате.

Определение из учебного пособия

Зачем нужно рассчитывать сопротивление

Рассчитывать сопротивление нужно, чтобы избежать появления короткого замыкания. Резисторы, образующие его, преобразовывают ток в напряжение, ограничивают протекающий электроток и получают заданную величину. Они создают делители напряжения в измерительном оборудовании и решают другие специальные задачи, к примеру, уменьшают радиопомехи.

Рассчитывать сопротивление нужно, чтобы сохранялась работоспособность резисторов и их нормальная регулировочная функция. Если будут находиться в целости резисторы, в которых преобразовывается энергия, то будут работать все электрические приборы.

Защита от короткого замыкания

Факторы влияния

Сопротивляемость зависит от температуры. Она увеличивается, когда повышается столбик термометра. Это поясняется физиками так, что при росте температуры атомные колебания в кристаллической проводниковой решетке повышаются. Это препятствует тому, чтобы свободные электроны двигались. Что касается полупроводников и диэлектриков, то там величина понижается из-за того, что увеличивается структура концентрации зарядных носителей.

Сопротивление у металлических монокристаллов с металлами и сплавами разные. Их вычисления, соответственно, неодинаковые. Значения различаются из-за химической металлической чистоты, способов создания составов и их непостоянства. Также стоит иметь в виду, что значения меняются при изменении температуры. Иногда сопротивляемость падает до нуля. В таком случае явление называется сверхпроводимостью. Под термической обработкой, например, отжигом меди, значение вырастает в 3 раза, несмотря на то, что доля примесей в антикоррозийном и легком составе, как правило, равна не больше 0,1 %.

Зависимость от температуры

Электрические величины

Электрическое сопротивление является физической величиной, которая равна напряжению, поделенному на силу тока. Сила тока в участке цепи является прямо пропорциональной величиной напряжению на окончаниях данного участка и обратно пропорциональной его сопротивляемости. Последнее значение имеет прямую пропорциональность проводниковой длине и обратную пропорциональность площади его сечения. Оно зависит от проводникового вещества.

Обратите внимание! Все представленные свойства сопротивляемости выражены в соответствующих формулах, которые даны ниже.

Формулы нахождения единицы

Тип и геометрические параметры

Бывают резисторы постоянными, переменными, подстрочными по типу сопротивляемости и термическими. Имеют свои геометрические обозначения и параметры. Как правило, первые цифры обозначают материал, вторые — стержневую, дисковую или микромодульную конструкцию, а третьи — порядковый разработочный номер.

Температурные показатели

Каждый резистор, полупроводник и проводник, образующий сопротивляемость, имеет свой температурный коэффициент. Он равен удельной сопротивляемости вещества на единицу времени. Температурный коэффициент проводимости — тот коэффициент, который идет с обратным знаком.

Расчет сопротивления электрической цепи резисторов

Перед тем как рассчитать общее сопротивление электрической цепи, нужно изучить формулу ниже. Также это можно сделать при помощи специального измерительного прибора под названием омметр или мультиметр.

Формулы для расчета

Сопротивление — важный параметр, без которого работа электрооборудования невозможна. Его нужно научиться рассчитывать, чтобы правильно составлять электросхему и не допускать короткого замыкания. Зависит оно, прежде всего, от температуры, что и выражается в формулах измерения.

Онлайн калькулятор расчета последовательного соединения резисторов

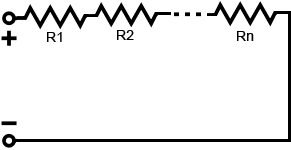
При последовательном соединении резисторов конец одного из них соединяется с началом следующего. В такой схеме через все резистивные элементы протекает одинаковый ток I, но падение напряжения на каждом из них пропорционально величине сопротивления. Для расчета электрических величин в схемах используется сложение сопротивлений всех элементов в последовательной цепи для получения суммарной величины, как показано на рисунке:

Последовательное соединение резисторов

Данный онлайн калькулятор позволяет выполнять расчет суммарного сопротивления для последовательно соединенных элементов цепи.

Чтобы воспользоваться калькулятором расчета вам необходимо:

• В окошке «количество резисторов» укажите число последовательно соединенных элементов, в данном случае, в схеме представлено три резистора, но может быть и другое количество;
• После этого в поле ниже появится несколько окошек, в которые вам необходимо внести значение сопротивления каждого резистора, к примеру, 10, 20 и 45 Ом;
• Нажмите кнопку «рассчитать» и в окошке «сопротивление» вы получите значение сопротивления в 75 Ом.

Для перехода к расчету следующей цепи или при необходимости подобрать другие элементы, нажмите кнопку «сбросить», чтобы обнулить значение последовательно включенных элементов калькулятора.

В работе калькулятора для определения сопротивления цепи последовательно соединенных резисторов используется принцип арифметического сложения. Поэтому формулу для определения суммарного значения можно представить следующим образом:

R_сум = R₁ + R₂ + R₃ +…+ R_n

Где,

• R_сум — суммарное сопротивление последовательно соединенных элементов
• R₁ — сопротивление первого резистора;
• R₂ — сопротивление второго резистора;
• R₃ — сопротивление третьего резистора;
• R_n — сопротивление n-ого элемента.

Так как в рассматриваемом примере включено только три элемента, то формула примет такой вид:

R_сум = R₁ + R₂ + R₃

Подставив значение омического сопротивления каждого из элементов, получим:

R_сум = 10 + 20 + 45 = 75 Ом

Использование калькулятора для вычисления суммарного сопротивления в цепи последовательно соединенных резисторов наиболее актуально для схем с большим количеством элементов и дробными величинами.

Следует отметить, если вам известно омическое сопротивление каждого элемента в разных единицах измерения (Ом, кОм, МОм), то их следует привести к одной, к примеру, к Омам, так как калькулятор выполняет расчет для всех резисторов в одинаковой единице.

Расчёт реактивного сопротивления

Реактивное сопротивление – электрическое сопротивление переменному току, обусловленное передачей энергии магнитным полем в индуктивностях или электрическим полем в конденсаторах.

Элементы, обладающие реактивным сопротивлением, называют реактивными.

Реактивное сопротивление катушки индуктивности.

При протекании переменного тока I в катушке, магнитное поле создаёт в её витках ЭДС, которая препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении – положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.

В результате созданного противодействия, на выводах катушки индуктивности в противофазе формируется напряжение U, подавляющее ЭДС, равное ей по амплитуде и противоположное по знаку.

При прохождении тока через нуль, амплитуда ЭДС достигает максимального значения, что образует расхождение во времени тока и напряжения в 1/4 периода.

Если приложить к выводам катушки индуктивности напряжение U, ток не может начаться мгновенно по причине противодействия ЭДС, равного -U, поэтому ток в индуктивности всегда будет отставать от напряжения на угол 90°. Сдвиг при отстающем токе называют положительным.

Запишем выражение мгновенного значения напряжения u исходя из ЭДС (ε), которая пропорциональна индуктивности L и скорости изменения тока: u = -ε = L(di/dt).
Отсюда выразим синусоидальный ток .

Интегралом функции sin(t) будет -соs(t), либо равная ей функция sin(t-π/2).
Дифференциал dt функции sin(ωt) выйдет из под знака интеграла множителем 1/ω.
В результате получим выражение мгновенного значения тока со сдвигом от функции напряжения на угол π/2 (90°).
Для среднеквадратичных значений U и I в таком случае можно записать .

В итоге имеем зависимость синусоидального тока от напряжения согласно Закону Ома, где в знаменателе вместо R выражение ωL, которое и является реактивным сопротивлением:

Реактивное сопротивлениие индуктивностей называют индуктивным.

Реактивное сопротивление конденсатора.

Электрический ток в конденсаторе представляет собой часть или совокупность процессов его заряда и разряда – накопления и отдачи энергии электрическим полем между его обкладками.

В цепи переменного тока, конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное. Следовательно, в моменты амплитудного значения напряжения на конденсаторе, ток в нём будет равен нулю. Таким образом, напряжение на конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.

В результате ток в цепи будет ограничен падением напряжения на конденсаторе, что создаёт реактивное сопротивление переменному току, обратно-пропорциональное скорости изменения тока (частоте) и ёмкости конденсатора.

Если приложить к конденсатору напряжение U, мгновенно начнётся ток от максимального значения, далее уменьшаясь до нуля. В это время напряжение на его выводах будет расти от нуля до максимума. Следовательно, напряжение на обкладках конденсатора по фазе отстаёт от тока на угол 90 °. Такой сдвиг фаз называют отрицательным.

Ток в конденсаторе является производной функцией его заряда i = dQ/dt = C(du/dt).
Производной от sin(t) будет cos(t) либо равная ей функция sin(t+π/2).
Тогда для синусоидального напряжения u = U_ampsin(ωt) запишем выражение мгновенного значения тока следующим образом:

i = U_ampωCsin(ωt+π/2).

Отсюда выразим соотношение среднеквадратичных значений .

Закон Ома подсказывает, что 1/ωC есть не что иное, как реактивное сопротивление для синусоидального тока:

Реактивное сопротивление конденсатора в технической литературе часто называют ёмкостным. Может применяться, например, в организации ёмкостных делителей в цепях переменного тока.

---

Онлайн-калькулятор расчёта реактивного сопротивления

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

Реактивное сопротивление ёмкости XC = 1 /(2πƒC)

Реактивное сопротивление индуктивности XL = 2πƒL

Расчитать ёмкость или индуктивность для реактивного сопротивления:

Расчёт ёмкости: C = 1 /(2πƒXC)

Расчёт индуктивности: L = XL /(2πƒ)

---

Похожие страницы с расчётами:

Расcчитать импеданс.
Расcчитать частоту резонанса колебательного контура LC.
Расcчитать реактивную мощность и компенсацию.

Резистор

Калькулятор

Ниже приведены инструменты для расчета значения и допуска в омах на основе цветовых кодов резисторов, общего сопротивления группы резисторов, включенных параллельно или последовательно, а также сопротивления проводника на основе размера и проводимости.

Резистор калькулятор кодов цвета

Используйте этот калькулятор, чтобы узнать значение ома и допуск на основе цветовых кодов резистора.

Параллельный резисторный калькулятор

Укажите все значения сопротивления параллельно, разделенные запятой “,” и нажмите кнопку “Рассчитать”, чтобы определить общее сопротивление.

Резисторы в последовательном калькуляторе

Укажите все значения сопротивления последовательно, разделенные запятой “,” и нажмите кнопку “Рассчитать”, чтобы определить общее сопротивление.

Сопротивление проводника

Используйте следующее для расчета сопротивления проводника. Этот калькулятор предполагает, что проводник круглый.

Законодательный калькулятор
Резистор

Цветовой код

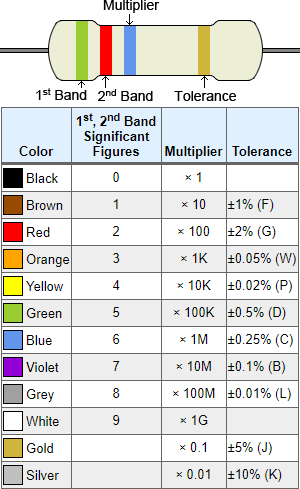
Электронный цветовой код – это код, который используется для указания номинальных характеристик определенных электрических компонентов, таких как сопротивление в омах резистора.Электронные цветовые коды также используются для оценки конденсаторов, катушек индуктивности, диодов и других электронных компонентов, но чаще всего используются для резисторов. Только резисторы адресованы этим калькулятором.

Как работает цветовое кодирование:

Цветовое кодирование для резисторов является международным стандартом, который определен в МЭК 60062. Цветовой код резистора, показанный в таблице ниже, включает различные цвета, которые представляют значащие цифры, множитель, допуск, надежность и температурный коэффициент.К какому из этих цветов относится цвет, зависит от положения цветовой полосы на резисторе. В типичном четырехполосном резисторе имеется промежуток между третьей и четвертой полосой, чтобы указать, как должен считываться резистор (слева направо, с одиночной полосой после интервала, являющейся самой правой полосой). В приведенном ниже объяснении будет использоваться четырехполосный резистор (тот, который конкретно показан ниже). Другие возможные варианты резисторов будут описаны позже.

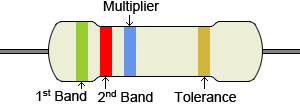
Значимая составляющая фигуры:

В типичном четырехполосном резисторе первая и вторая полосы представляют значимые цифры.Для этого примера обратитесь к рисунку выше с зеленой, красной, синей и золотой полосой. Используя приведенную ниже таблицу, зеленая полоса представляет число 5, а красная полоса – 2.

Множитель:

Третья синяя полоса – множитель. Таким образом, используя таблицу, множитель составляет 1 000 000. Этот множитель умножается на значащие цифры, определенные из предыдущих полос, в данном случае 52, что приводит к значению 52 000 000 Ом или 52 МОм.

Допуск:

Четвертая полоса присутствует не всегда, но когда она есть, представляет собой допуск.Это процент, на который значение резистора может меняться. Золотая полоса в этом примере показывает допуск ± 5%, который можно обозначить буквой J. Это означает, что значение 52 МОм может изменяться на 5% в любом направлении, поэтому значение резистора составляет 49,4 МОм. 54,6 МОм.

Надежность, температурный коэффициент и другие вариации:

Кодированные компоненты имеют как минимум три полосы: две значимые полосы цифр и множитель, но возможны и другие варианты.Например, компоненты, изготовленные по военным спецификациям, обычно представляют собой четырехполосные резисторы, которые могут иметь пятую полосу, которая указывает на надежность резистора с точки зрения процента отказов на 1000 часов работы. Также возможно иметь диапазон 5 ^th , который является температурным коэффициентом, который указывает на изменение сопротивления компонента в зависимости от температуры окружающей среды в пересчете на ppm / K.

Чаще всего существуют пятиполосные резисторы, более точные из-за третьего значащего диапазона цифр.Это смещает положение множителя и диапазона допусков в положение 4 ^th и 5 ^th по сравнению с типичным четырехполосным резистором.

На самых точных резисторах может присутствовать полоса 6 ^тыс. . Первые три полосы будут значимыми полосами цифр, 4 ^-й – множителем, 5 ^-й – допуском, а 6 ^-й – либо надежностью, либо температурным коэффициентом. Есть и другие возможные варианты, но это некоторые из наиболее распространенных конфигураций.

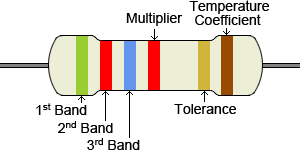
Цвет	1 st , 2 и , 3 и Значимые цифры диапазона	Множитель	Допуск	Температурный коэффициент
Черный	0	× 1		250 ppm / K (U)
Коричневый	1	× 10	± 1% (F)	100 ppm / K (S)
Красный	2	× 100	± 2% (G)	50 ppm / K (R)
Оранжевый	3	× 1K	± 0.05% (Ш)	15 ppm / K (P)
Желтый	4	× 10К	± 0,02% (P)	25 ppm / K (Q)
Зеленый	5	× 100К	± 0,5% (D)	20 ppm / K (Z)
Синий	6	× 1M	± 0.25% (С)	10 ppm / K (Z)
Фиолетовый	7	× 10М	± 0,1% (В)	5 промилле / К (М)
Серый	8	× 100М	± 0,01% (л)	1 ppm / K (K)
Белый	9	× 1G
Золото		× 0.1	± 5% (Дж)
Серебро		× 0,01	± 10% (К)
Нет			± 20% (М)

Резисторы – это элементы схемы, которые придают электрическое сопротивление.Хотя схемы могут быть очень сложными, и существует множество различных способов, которыми резисторы могут быть расположены в цепи, резисторы в сложных цепях обычно могут быть разбиты и классифицированы как соединенные последовательно или параллельно.

Резистор параллельно:

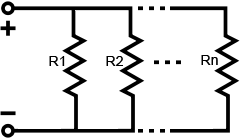
Общее сопротивление параллельных резисторов равно обратной величине суммы обратных величин каждого отдельного резистора. Обратитесь к уравнению ниже для уточнения:

R всего =

1 + + +… +

Резистор в серии:

Общее сопротивление параллельных резисторов – это просто сумма сопротивлений каждого резистора. Обратитесь к уравнению ниже для уточнения:

R _всего = R ₁ + R ₂ + R ₃ … + R _n

Сопротивление проводника:

Где:
L – длина проводника
А – площадь поперечного сечения проводника
С – проводимость материала

,

параллельного резисторного калькулятора R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллельный Параллельный резисторный калькулятор R1 + R2 = эквивалентный резистор R сопротивление цепи в эквиваленте суммарный резистор искатель легко сделать контрейлер = параллель – sengpielaudio Sengpiel Berlin

R всего

Формула: R всего = R1 × R2 / (R1 + R2)

Пожалуйста, введите два значения резистора , будет рассчитано третье значение параллельной цепи.
Вы даже можете ввести общее сопротивление R _всего и одно известное сопротивление R ₁ или R ₂ .

Формула (уравнение) для расчета двух сопротивлений R ₁ и R ₂ , соединенных параллельно:

Расчет необходимого параллельного резистора R ₂ , когда R ₁ и полное сопротивление R _всего дается:

Решение по формуле R всего = ( R 1 × R 2 ) / ( R 1 + R 2 ) для R 1 : Первый шаг – очистить все дроби, умножив на самое низкое значение . общий знаменатель, то есть R т × R 1 × R 2 … так мы получаем: 1/ R всего = 1/ R 1 + 1/ R 2 R всего × R 1 × R 2 [1/ R всего = 1/ R 1 + 1/ R 2 ] R 1 × R 2 = R всего × R 2 + R всего × R 1 , затем соберите члены с R 1 и решить R 1 × R 2 – R всего × R 1 = R всего × R 2 R 1 ( R 2 – R всего ) = R 2 × R всего Последний шаг: R 1 = R 2 × R всего / ( R 2 – R всего ) или: R 2 = R 1 × R всего / ( R 1 – R всего )

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно составляет
точно так же, как расчеты, необходимые для параллельных индукторов или последовательно соединенных конденсаторов.

Два резистора параллельно и полученное суммарное сопротивление: два одинаковых значения, также покажите уравнение, что результаты всегда наполовину. Это облегчает, когда проектирование схем или прототипирование. С заглавными буквами он всегда двойной, потом опять заглавные буквы просто просто сложить параллельно.

• Поисковые сопротивления R ₁ и R ₂ , когда известно целевое сопротивление (эквивалентное сопротивление) •

Расчет: резисторные пары – обратный инженерный калькулятор
Поиск R ₁ и R ₂ с известным сопротивлением цели

● Рассчитать много резисторов параллельно ●

Этот калькулятор определяет сопротивление от до 10 резисторов параллельно . Введите сопротивления в поля ниже и, когда все значения были введены, нажмите на кнопку «Рассчитать», и результат появится в поле под этой кнопкой. В качестве теста, если мы введем сопротивления 4, 6 и 12 Ом, ответ должен быть 2 Ом. Примечание: очистка полей вручную не сбрасывает сохраненные значения. Используйте «сброс».

закон Ома – калькулятор и формулы

Два резистора параллельно и полученное суммарное сопротивление
Сопротивление в диапазоне от 1 Ом до 100 Ом

R2	R1
	1	1.5	2,2	3,3	4,7	6,8	10	15	22	33	47	68
1	0,5	0,6	0.69	0,77	0,83	0,87	0,91	0,93	0,95	0,97	0,98	0,99
1,5	0,6	0,75	0,89	1,03	1,14	1,22	1,30	1,36	1,40	1.43	1,45	1,46
2,2	0,69	0,89	1,1	1,32	1,50	1,66	1,82	1,92	2,0	2,06	2,10	2,13
3,3	0,77	1.03	1,32	1,65	1,94	2,22	2,48	2,70	2,87	3,00	3,08	3,14
4,7	0,83	1,14	1,50	1,94	2,35	2,78	3,20	3,58	3.87	4,12	4,27	4,39
6,8	0,87	1,22	1,66	2,22	2,78	3,40	4,05	4,68	5,19	5,64	5,94	6,18
10	0.91	1,30	1,82	2,48	3,20	4,05	5,0	6,0	6,9	7,7	8,3	8,7
15	0,93	1,36	1,92	2,70	3,58	4,68	6,0	7.50	8,9	10,3	11,4	12,2
22	0,95	1,40	2,00	2,87	3,87	5,19	6,9	8,9	11,0	13,2	15.0	16,6
33	0.97	1,43	2,06	3,0	4,12	5,64	7,7	10,3	13,2	16,5	19,4	22,2
47	0,98	1,45	2,1	3,08	4,27	5,94	8,3	11.4	15,0	19,4	23,5	27,8
68	0,99	1,46	2,13	3,14	4,39	6,18	8,7	12,2	16,6	22,2	27,8	34,0

Примечание: Этот калькулятор также может решать другие математические задачи.Расчет резисторов параллельно составляет
точно так же, как расчеты, необходимые для параллельных индукторов или последовательно соединенных конденсаторов.

Мощность, рассеиваемая в резисторе: P = В × I , P = В 2 / R , P = I 2 × R .

Примечание: Для последовательно включенных резисторов ток для каждого резистора равен , и для параллельных резисторов напряжение одинаково для каждого резистора.

,

Сопротивление напряжению тока и электрической энергии Общие основные электрические формулы Математические расчеты Калькулятор Формула для расчета мощности Уравнение мощности Энергетический закон Ватты понимают общие электрические круговые диаграммы Расчет электричества Электрические ЭДС Напряжение Формула питания Уравнение Два различных уравнения для расчета мощности Общий закон Ома Аудио Физика Электроэнергия Электроника формула колесо формулы ампер ватты вольт кумуляция уравнение аудиоинжиниринг звуковая техника круговая диаграмма заряд физика мощность звукозапись calc электротехника формула мощность математика пи физика отношение отношение Сопротивление напряжению по току и электрической энергии общие основные электрические формулы математические расчеты калькулятор формула для расчета мощности уравнение работы энергии степенной закон ватты понимают общее вычисление электрической круговой диаграммы электричество электрическая эдс напряжение формулы мощности уравнение два различных уравнения для расчета мощности общий закон Ома аудио физика электричество электроника формула формулы колес амперы ватты вольты омы косинусное уравнение аудиоинженерия круговая диаграмма заряд физика мощность звукозапись calc электротехника формула мощность математика пи физика отношение отношения – sengpielaudio Sengpiel Berlin

Электрический ток , Электроэнергия , Электрическое напряжение

Электричество и Электрическая зарядка

Наиболее распространенные общие формулы, используемые в электротехнике

● Основные формулы и Расчеты ●

Взаимосвязь физических и электрических величин (параметров)
Электрическое напряжение В , сила тока I , удельное сопротивление R , импеданс Z , Мощность и Мощность P
Вольт В , ампер A, сопротивление и импеданс Ом Ом и Вт Вт

Номинальное полное сопротивление Z = 4, 8 и 16 Ом (громкоговорители) часто принимается за сопротивление R . Уравнение закона Ома (формула): В = I × R и уравнение степенного закона (формула): P = I × В . P = мощность, I или J = латиница: влияние, международный ампера или интенсивность и R = сопротивление. В = напряжение, разность электрических потенциалов ΔV или E = электродвижущая сила (эдс = напряжение).

Введите любые два известных значения и нажмите «рассчитать», чтобы решить для двух других. Пожалуйста, введите только два значения.

Используемый браузер, к сожалению, не поддерживает Javascript. Программа указана, но фактическая функция отсутствует.

Формула Колеса Электротехники

В происходит от “напряжения” и E от “электродвижущей силы (ЭДС)”. E означает также энергию , поэтому мы выбираем V . Энергия = напряжение × заряд. E = V × Q . Некоторым нравится лучше придерживаться E вместо V , так что сделайте это. Для R принять Z .

12 самых важных формул: Напряжение В = I × R = P / I = √ ( P × R ) в вольтах В Ток I = В / R = P / V = √ ( P / R ) в амперах A Сопротивление R = В / I = P / I 2 = В 2 / P в Ом Ω Мощность P = В × I = R × I 2 = В 2 / R Вт, Вт

См. Также: Формула Колеса Акустики (Аудио)

Большой Power Formulas Расчет электрической и механической мощности (прочность)

Мощность Формула 1 – Уравнение электрической мощности: Мощность P = I × V = R × I 2 = V 2 ⁄ R где мощность P в ваттах, напряжение В в вольтах и ​​ток I в амперах (DC). Если есть переменный ток, посмотрите также на коэффициент мощности PF = cos φ и φ = угол коэффициента мощности (фазовый угол) между напряжением и силой тока. Электрический Энергия составляет E = P × т – измеряется в ватт-часах или также в кВтч. 1J = 1N × м = 1 Вт × с Формула мощности 2 – Уравнение механической мощности: Мощность P = E ⁄ т , где мощность P в ваттах, Мощность P = работа / время ( Вт 000 т ). Энергия E в джоулях, а время т в секундах. 1 Вт = 1 Дж / с. Мощность = сила, умноженная на смещение, деленное на время P = F × с / т или Мощность = сила, умноженная на скорость (скорость) P = F × v. Неискаженный мощный звук не встречается в этих формулах. Пожалуйста, берегите уши! Диафрагмы барабанной перепонки и микрофона действительно двигаются только волнами звуковое давление .Это не влияет ни на интенсивность, ни на мощность, ни на энергию. Если вы занимаетесь аудиозаписью, разумно не заботиться об энергии, мощность и интенсивность, поскольку вызывают , больше заботятся об эффекте звукового давления p и уровень звукового давления в ушах и на микрофонах и посмотреть на соответствующие звуковое напряжение В ~ п ; см .: Звуковое давление и мощность звука – следствие и причина Динамики с очень громким звучанием будут иметь большую мощность, но лучше присмотреться к самой важно , эффективность динамиков.Это включает в себя типичный вопрос: Сколько децибел (дБ) на самом деле в два или три раза громче? Там действительно нет RMS власти. Слова «среднеквадратичная мощность» неверны. Есть расчет мощности, которая является умножением среднеквадратичного напряжения и среднеквадратичного тока. Watts RMS не имеет смысла. На самом деле, мы используем этот термин как крайнюю стенографию власти в Ватты, рассчитанные из измерения среднеквадратичного напряжения. Пожалуйста, прочитайте здесь: Почему нет такой вещи, как «среднеквадратичная мощность» или «среднеквадратичная мощность ватт», и никогда не было. Сила “RMS” – довольно глупый термин, который собрал деньги среди аудио людей. Мощность – это количество энергии, которое преобразуется в единицу времени. Ожидайте платить больше, когда требуя высшей силы.

Andr-Marie Ampre был французский физик и математик. Единица измерения электрического тока СИ, ампер, , была названа его именем. Алессандро Джузеппе Антонио Анастасио Вольта был итальянским физиком. Единица измерения электрического напряжения СИ, вольт , была названа в его честь. Георг Симон Ом был немецкий физик и математик. Единица измерения электрического сопротивления СИ, Ом, , была названа его именем. Джеймс Уотт был шотландским изобретателем и инженером-механиком. Единица измерения электрической мощности (мощности) СИ, Вт, , была названа его именем.

Мощность, как и все размеры энергии, в первую очередь, расчетное значение.

Слово «усилитель мощности» является неправильным, особенно в звуковой инженерии. Напряжение и ток могут быть усилены. Странный термин «усилитель мощности» Понятно, что усилитель предназначен для управления нагрузкой такой как громкоговоритель. Мы называем произведение усиления тока и усиления напряжения «усиление мощности».

Совет : треугольник электрического напряжения В = I × R (закон Ома VIR)
Пожалуйста, введите два значения , третье значение будет рассчитано. Треугольник электроэнергии P = I × В (Степенной закон PIV)
Пожалуйста, введите два значения , третье значение будет рассчитано.

Волшебный треугольник может быть использован для расчета всех формул легко. Вы прячетесь с
палец значение, которое будет рассчитано. Два других значения показывают, как выполнить расчет.

Расчеты: закон Ома – магический треугольник Ома
Измерение входного и выходного сопротивления

ТОК ИЗМЕНЕНИЯ (AC) ~

В _л = напряжение сети (вольт), В _р = напряжение фазы (вольт), I _л = ток линии (ампер), I _р = ток фазы ( ампер)
Z = полное сопротивление (Ом), P = мощность (Вт), φ = угол коэффициента мощности, VAR = вольт-ампер (реактивный)

Ток (однофазный): I = P / V p × cos φ	Ток (3 фазы): I = P / √3 В л × cos φ или I = P /3 В p × cos φ
Мощность (однофазная): P = В p × I p × cos φ	Мощность (3 фазы): P = √3 В л × I л × cos φ или P = √3 В p × I p × cos φ

Коэффициент мощности PF = cos φ = R / (R2 + X2) ^1/2 , φ = угол коэффициента мощности.Для чисто резистивной схемы PF = 1 (идеально).
Полная мощность S рассчитывается по Пифагору, активная мощность P и реактивная мощность Q . S = √ ( P ² + Q ² )

формулы питания постоянного тока Напряжение В, В (В), расчет по току I, В (А) и сопротивлению R, В (Ом): В (В) = I (А) × R (Ом) Мощность P в (Вт), расчет от напряжения В, в (В) и тока I, в (А): P (Ш) = В (В) × I (А) = В 2 (В) / R (Ω) = I 2 (A) R (Ω) формулы переменного тока Напряжение В в вольт (В) равно току I в амперах (A), умноженному на полное сопротивление Z в Ом (Ом): В (В) = I (A) Z ((Ω) = (| I | × | Z |) и ( θ I + θ Z ) Полная мощность S в вольт-ампер (ВА) равна напряжению В, в вольт (В), умноженному на ток I в амперах (A): S (ВА) = В (В) I (A) = (| В | × | I |) и ( θ В – θ I ) Реальная мощность P в ваттах (Вт) равна напряжению В, в вольт (В), умноженному на ток, I, в амперах (A), умноженному на коэффициент мощности (cos φ ): P (Ш) = В (В) × I (А) × cos φ Реактивная мощность Q в вольт-ампер реактивного (VAR) равна напряжению В в вольт (В), умноженному на ток I в амперах (A) синус комплексного фазового угла мощности ( φ ): Q (VAR) = В (V) × I (A) × sin φ Коэффициент мощности (FP) равен абсолютному значению косинуса комплексного фазового угла мощности ( φ ): ПФ = | cos φ |

Фактический коэффициент мощности, а не обычный коэффициент мощности смещения 50/60 Гц

Определения электрических измерений
Количество	Имя	Определение
частота ф	герц (Гц)	1 / с
сила F	ньютон (N)	кг · м / с²
давление р	паскаль (Па) = Н / м²	кг / м · с²
энергия E	Джоулей (J) = N · м	кг · м² / с²
мощность P	Вт (Вт) = Дж / с	кг · м² / с³
электрический заряд Q	кулонов (C) = A · с	A · с
напряжение В	вольт (В) = W / A	кг · м² / A · с³
ток I	ампер (А) = Q / с	A
Емкость C	фарад (F) = C / V = ​​A · с / V = ​​с / Ω	A² · с 4 / кг · м²
индуктивность L	Генри (H) = Wb / A = V · с / A	кг · м² / A² · с²
сопротивление R	Ом (Ом) = V / A	кг · м²A² · с³
Проводимость G	сименс (S) = A / V	A² · с³ / кг · м²
магнитный поток Φ	Вебер (Wb) = V · с	кг · м² / A · с²
плотность потока B	тесла (Т) = Wb / м² = V · с / м²	кг / А · с²

Поток электрического заряда Q упоминается как электрический ток I. Сумма сбора за единицу времени это изменение электрического тока. Ток течет с постоянным значением I. за время т. , он транспортирует . заряд Q = I × t . Для постоянной во времени мощности соотношение между зарядом и током: I = Q / т или Q = I × t. Благодаря этим отношениям, основные единицы ампер и второй кулон в Международная система единиц установлена.Кулоновская единица может быть представлена ​​как 1 C = 1 A × s. Заряд Q , (единица измерения в ампер-часах Ач), ток разряда I , (единица измерения в амперах A), время т , (единица измерения в часах).

В акустике у нас есть “ Акустический эквивалент для закона Ома ”

Соотношения акустических размеров, связанных с плоскими прогрессивными звуковыми волнами

Преобразование многих единиц, таких как мощность и энергия

префиксы | длина | площадь | объем | вес | давление | температура | время | энергия | мощность | плотность | скорость | ускорение | сила

[начало страницы]

,

Round Wire AC Калькулятор сопротивления переменного тока Round Wire AC Калькулятор сопротивления Логотип Chemandy Electronics Логотип Chemandy Electronics CHEMANDY ELECTRONICS Поставщики необычного Показать навигацию Скрыть навигацию

Вычисляет сопротивление переменного тока круглой прямой проволоки для обычных проводящих материалов, используя уравнение и данные, указанные ниже, или введенные вручную данные материала.

Примечание. Чтобы использовать разные значения для удельного сопротивления и относительной проницаемости, выберите «Ввести данные» в текстовом поле «Выбор материала проводника», а затем введите соответствующие значения в поля, выделенные желтым цветом.

Этот калькулятор использует JavaScript и будет работать в большинстве современных браузеров. Для получения дополнительной информации см. О наших калькуляторах

.

г.в. Сопротивление для длины круглого прямого провода рассчитывается с использованием удельного сопротивления проводника, длины проводника и эффективной площади поперечного сечения, используемой скин-эффектом.

где ρ – удельное сопротивление проводника в Ом.м

л – Длина проводника в мм

A _eff – эффективная площадь поперечного сечения, используемая в мм

Площадь поперечного сечения, используемая скин-эффектом, определяется путем первого расчета номинальной глубины проникновения для проводника.

Из линий электропередачи и сетей Уолтер С. Джонсон, McGraw-Hill 1963 p58.

Где ρ – удельное сопротивление проводника в Ом.м

f – частота в герцах

μ – абсолютная магнитная проницаемость проводника

Абсолютная магнитная проницаемость (μ) = μ _o x μ _r

µ _o = 4π x 10 ^-7 H / m

Значения µ _r взяты из Справочника по проектированию линий электропередачи , автор Brian C Wadell, Artech House 1991 Таблица 9.3.2. 446.

Значения для ρ взяты из Справочника по химии и физике CRC, 1-е издание для студентов, , 1998, стр. F-88, и предназначены для элементов высокой чистоты при 20 ° C.

Фактическая площадь поперечного сечения, используемая из-за скин-эффекта, может быть рассчитана несколькими методами с различной степенью точности. Самый простой способ – умножить глубину оболочки на окружность проводника.

Где d – диаметр проводника

Этот метод делает используемую площадь поперечного сечения слишком большой от высоких частот вплоть до точки, где глубина обшивки становится примерно половиной радиуса проводника, и в этот момент неточности увеличиваются, и в конечном итоге расчетная используемая площадь становится больше, чем фактический проводник.Делая метод расчета только приближенным, а затем применимым только при r >> δ.

Второй простой метод состоит в том, чтобы вычислить общую площадь проводника и затем вычесть область круга, представляющую центральную область, в которой не используется скин-эффект.

где r – радиус проводника

Этот метод более точен в первом методе, когда r >> δ, но становится очень неточным ниже точки, где d / δ = π, и может иметь огромные положительные или отрицательные колебания в значении.

Гораздо более точный метод описан Дэвидом Найтом в очень подробной статье под названием Zint.pdf, которую можно найти по адресу http://www.g3ynh.info/zdocs/comps/part_1.html. В этом методе используется метод усеченного экспоненциального убывания. устранить ошибки, вызванные тем, что фактическая площадь проводника становится меньше расчетной площади глубины скин-слоя в простом способе, описанном выше, и модифицированную коррекцию Лоренца, которая устраняет ошибку, возникающую при приближении расчетной площади глубины скин-слоя к фактической площади проводника.Автор называет это уравнение Rac – TED – ML и указывает максимальную ошибку 0,09%.

Метод расчета предполагает наличие одиночного изолированного проводника и не учитывает путь возврата. Это делает довольно сложным измерение сквозных измерений, и поэтому результаты этого калькулятора сравнивались с данными, приведенными в оригинальной статье, чтобы доказать точность.

W J Highton 30/9/2011

Этот калькулятор предоставляется компанией Chemandy Electronics для продвижения FLEXI-BOX

Вернуться к индексу калькулятора

,