Исследование пассивных RC-фильтров (Отчет по лабораторной работе) | ЛАБЫ
Цель работы: изучение свойств RC-фильтров низких частот, а также полосовых фильтров, приобретение навыков работы с генератором сигналов специальной формы и цифровым осциллографом.
1. Теоретический расчет выражений для АЧХ и ФЧХ фильтров
Если собрать делитель напряжения из пары пассивных двухполюсников разного типа, например из резистора и конденсатора, то возникает цепь, попадающая под понятие пассивный четырехполюсник.
Очевидно, что выходное напряжение должно зависеть от частоты входного напряжения в результате изменения емкости конденсатора.
Фаза выходного напряжения при изменении частоты также не останется неизменной, так как вклад в полное сопротивление цепи со стороны компонента (конденсатора), у которого имеется фазовый сдвиг между током и напряжением, будет разным для разных частот.
1.1. Однозвенный фильтр нижних частот
Данный фильтр (рис. 1, а) является делителем напряжения, к которому не подключена никакая нагрузка. Такой делитель называют идеальным делителем напряжения (ИДН). Выходное напряжение U2 представляет собой в данном ИДН падение напряжения на конденсаторе C и поэтому зависит от частоты.
Рис. 1. Исследуемые однозвенный (а) и двухзвенный (б) фильтры нижних частот,
фильтр Вина (в)
Согласно формуле делителя напряжения, отношение выходного к входному напряжений можно выразить через комплексные сопротивления, аналогично резистивному делителю напряжений:
|
. |
(1) |
Произведение RC выражается в секундах, тогда единицей измерения 1/ RC как и для угловой частоты будет секунда в минус первой степени. Обозначим тогда эту величину как w0 и подставим в формулу (1):
|
. |
(2) |
Для устранения мнимого числа в знаменателе умножим числитель и знаменатель в (2) на сопряженное знаменателю комплексное число:
|
|
(3) |
Из (3) можно найти АЧХ, как модуль данного выражения, и ФЧХ как арктангенс отношения аргументов мнимой и вещественной части:
|
; . |
(4) |
Графическое представление полученных амплитудно-частотной и фазо-частотной характеристик представлено совместно с практическими результатами на рис.
1.2. Двухзвенный фильтр нижних частот
Для данного фильтра (рис. 1, б) мы можем воспользоваться тем фактом, что для исследуемых синусоидальных сигналов из правила перемножения экспоненциальных зависимостей вытекают два важных свойства последовательных соединений двух и более четырехполюсников – результирующая АЧХ получается путем перемножения АЧХ отдельных четырехполюсников, а результирующая ФЧХ образуется сложением ФЧХ последовательных четырехполюсников:
|
; . |
(5) |
В предыдущем пункте мы рассчитали АЧХ и ФЧХ для одного звена. Воспользовавшись правилами (5), получим:
|
; . |
(6) |
Стоит сказать, что поскольку в данном фильтре всего два звена, выражения (5) описывают его довольно хорошо, что подтверждают рис. 5 и 6. В случае большего числа звеньев делители напряжения еще более неидеальны, так как их выходы шунтируются выходами последующих звеньев, но на примере двухзвенного фильтра таким образом мы показали простой способ оценки усиления.
1.3. Фильтр Вина
Аналогично начальным выкладкам, данный фильтр (рис. 1, в) можно рассматривать как делитель напряжения с комплексными сопротивлениями, представленными последовательным и параллельным соединением резистора и конденсатора. Поэтому:
Как и ранее, произведение обозначаем величину 1/ RC как w0 и, подставляя, получаем:
|
. |
(7) |
Из (7) можно найти АЧХ, как модуль данного выражения, и ФЧХ как арктангенс отношения аргументов мнимой и вещественной части:
|
; . |
(8) |
2.1. Характеристики однозвенного фильтра нижних частот
|
Рис. 2. Теоретическая (1) и экспериментально полученная (2) AЧХ однозвенного RC-фильтра нижних частот |
|
Рис. 3. Теоретическая (1) и экспериментально полученная (2) ФЧХ однозвенного RC-фильтра нижних частот |
2.2. Характеристики для двухзвенного фильтра нижних частот
|
Рис. 4. Теоретическая (1) и экспериментально полученная (2) AЧХ двухзвенного RC-фильтра нижних частот |
|
Рис. 5. Теоретическая (1) и экспериментально полученная (2) ФЧХ двухзвенного RC-фильтра нижних частот |
2.3. Характеристики фильтра Вина
|
Рис. 6 Теоретическая (1) и экспериментально полученная (2) AЧХ фильтра Вина |
|
Рис. 7. Теоретическая (1) и экспериментально полученная (2) ФЧХ фильтра Вина |
Выводы
1. Фильтр нижних частот пропускает только низкочастотные сигналы (рис. 2 и 4). Как видно из сравнения полученных графиков, крутизну амплитудно-частотной характеристики можно увеличить за счет применения каскадного включения однозвенных фильтров, в нашем случае – двух. При этом граничная частота остается той же, а подавление высоких частот происходит лучше. Фазовый сдвиг при этом за счет вклада второй емкости увеличивается до двух раз (рис. 3 и 5).
2. Комбинации фильтров нижних и верхних частот позволяют создавать полосовые фильтры, с помощью которых их всего спектра выделяется только определенная область частот. Эта возможность продемонстрирована на приме фильтра Вина (рис. 6). Максимальный коэффициент усиления, в отличие от ФНЧ, равен 1/3.
3. Простые фильтры хорошо поддаются теоретическому описанию, как видно из полученных экспериментальных характеристик и сравнения с математическими выкладками. Неравномерность погрешностей связана с нелинейными законами распределения частот и измерительной шкалы.
mc-plc.ru
9.Активные RC фильтры
9.
АКТИВНЫЕ RC-ФИЛЬТРЫ
Общие положения
Фильтром называют четырехполюсник, предназначенный для выделения из состава подведенного к его входу сложного электрического колебания частотных составляющих, расположенных в заданной области, и для подавления частотных составляющих, расположенных во всех других областях частот.
Область частот, где фильтр усиливает или мало ослабляет сигнал, называют полосой пропускания, а область частот, где ослабление сигнала велико, – полосой задержания. Чем больше разница между усилением и ослаблением, тем сильнее выражены фильтрующие свойства цепи.
Низкочастотные (до 100 кГц) активные фильтры используют в системах управления и передачи речевых сообщений и данных для выделения полезного сигнала из помех, имеющих частотный спектр, отличающийся от спектра сигнала. Для этого диапазона частот в настоящее время наиболее целесообразно применять фильтры, построенные на пассивных RC-цепях с активными приборами (чаще всего ОУ).
В зависимости от взаимного расположения полосы пропускания и полосы задержания различают (рис. 9.1):
1. Фильтр верхних частот (ФВЧ) – фильтр с полосой пропускания от некоторой частоты 1 до бесконечности и полосой задержания от 0 до з1 < 1.
2. Фильтр нижних частот (ФНЧ) – фильтр с полосой пропускания от 0 до некоторой частоты 2 и полосой задержания от 0 до з2 > 2 до бесконечности.
3. Полосовой фильтр (ПФ) – фильтр с полосой пропускания от некоторой частоты 1 до другой частоты 2 > 1 и полосами задержания от 0 до з1 < 1 и от з2 > 2 до бесконечности.
4. Режекторный (заграждающий) фильтр (РФ) – фильтр с полосой пропускания от 0 до частоты 1 и от частоты 2 > 1 до бесконечности и полосой задержания от з1 до з2 > з1.
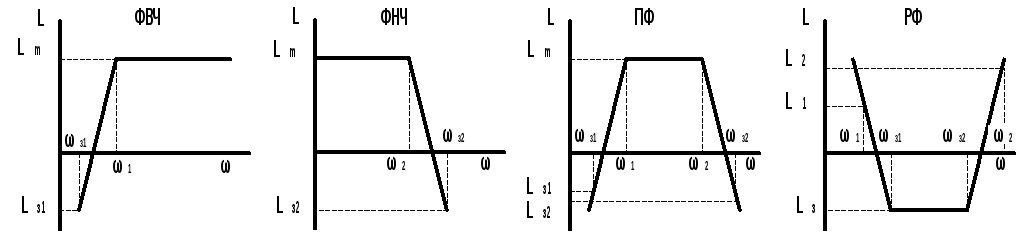
Рис.9.1
Здесь приведены лишь основные типы характеристик фильтров, комбинируя их можно сформировать практически любую АЧХ.
Кроме формы АЧХ, при проектировании фильтра, учитывают стабильность параметров фильтра, шумы, экономичность, технологичность, массогабаритные показатели, настраиваемость и возможность электрического управления параметрами фильтра.
Перечисленные условия часто противоречивы. Поэтому перед разработчиком обычно стоит задача ранжирования показателей качества между собой и, опираясь на имеющийся опыт, окончательный выбор схемного решения в наибольшей степени удовлетворяющего техническому заданию.
Частотные характеристики реальных фильтров нельзя изобразить в виде простых ломаных линий. Их АЧХ могут существенно различаться (иметь монотонный характер или содержать большое количество локальных экстремумов). Поэтому процесс проектирования фильтров делят на несколько этапов.
1. Конструируют математическую модель (передаточную функцию) проектируемого устройства, АЧХ которого удовлетворяет заданию. Этот этап носит название аппроксимации.
2. Выбирают принцип построения фильтра и по передаточной функции либо производят синтез схемы, либо по имеющимся каталогам осуществляют выбор схемы. Отметим, что основным принципом построения фильтров, является каскадно-развязанная реализация на основе простых звеньев не выше третьего порядка.
3. Производят расчет параметров элементов с учетом технологических ограничений на параметры элементов.
Частотные характеристики фильтров и их аппроксимация
На практике наиболее часто применяют аппроксимацию АЧХ полиномами Баттерворта, Чебышёва и Бесселя. Для унификации общепринято применять нормирование по частоте, приводящее расчет различных типов фильтров (ФВЧ, ФНЧ, ПФ, РФ), работающих на различных частотах, к расчету нормированного фильтра нижних частот (прототипа), у которого нормированная граничная частота полосы пропускания принимается равной единице. Применение различных методов аппроксимации приводит к различным видам АЧХ и ФЧХ, а также к разному времени нарастания сигнала.
Полиномы Баттерворта обеспечивают монотонное изменение АЧХ в полосе пропускания и резкий спад ее за граничной частотой.
Полиномы Чебышёва дают равноволновое приближение к характеристике в полосе пропускания и более резкий спад за частотой среза, чем полиномы Баттерворта. В обоих этих случаях переходная характеристика имеет колебательный характер.
Полиномы Бесселя обеспечивают ещё более пологий спад АЧХ по сравнению с полиномами Баттерворта и у них переходная характеристика практически не имеет колебаний.
Использование в расчетах принципа нормированного фильтра нижних частот позволяет по относительным требованиям, таким как: коэффициент прямоугольности kп =г/з; где г – граничная частота полосы пропускания ФНЧ, з – частота начала полосы задержания; H – неравномерность АЧХ в полосе пропускания; Hз – уровень затухания АЧХ на частоте з, используя программы аппроксимации из системы MatLAB, получают численные значения коэффициентов передаточной функции ФНЧ прототипа
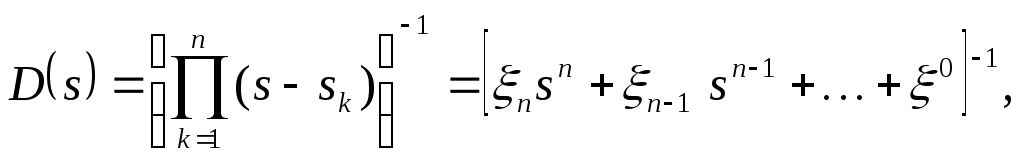
где 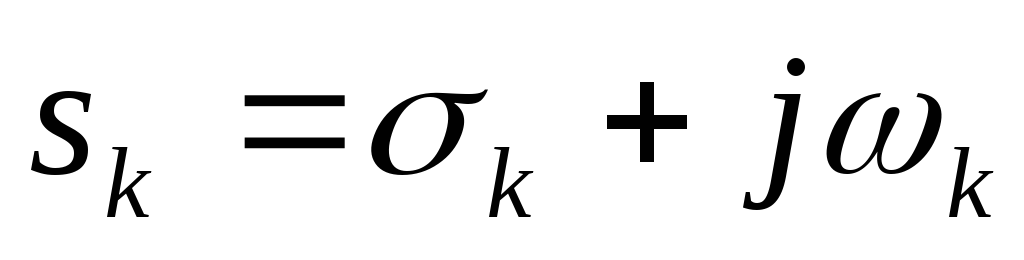 корни аппроксимирующего полинома.
Последующие преобразования [ 2] позволяют
получить аналогичные выражения для
фильтров иных типов.
корни аппроксимирующего полинома.
Последующие преобразования [ 2] позволяют
получить аналогичные выражения для
фильтров иных типов.
Наиболее ярко выраженными избирательными свойствами обладают звенья, имеющие пару комплексно сопряженных корней знаменателя передаточной функции. Именно для таких звеньев можно говорить о явлении аналогичному резонансу в колебательном контуре. В дальнейшем такой эффект будем называть квазирезонансом. Рассмотрим его на примере звена полосового фильтра второго порядка с передаточной функцией вида
K(s)=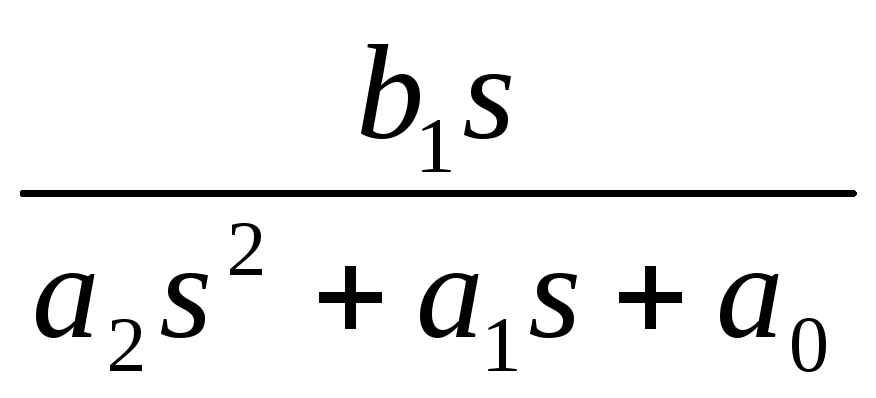 .
.
Откуда ЛАЧХ описывается выражением
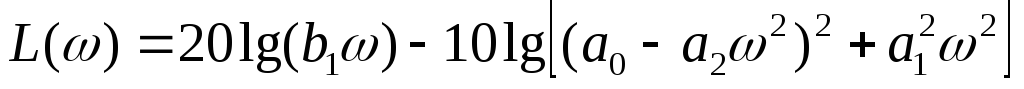 ,
,
а
максимум достигается при  р=(а0/а2)1/2 названной частотой квазирезонанса.
Величина =(а1/а2)
определяет полосу пропускания фильтра
и находится графически по ЛАЧХ (рис.9.2),
отсчитывая от максимума уровень в 3 дБ.
Относительная избирательность фильтра
характеризуется добротностью Q=р./
и связана с коэффициентами передаточной
функции выражением Q=(а0а2/а12)1/2.
р=(а0/а2)1/2 названной частотой квазирезонанса.
Величина =(а1/а2)
определяет полосу пропускания фильтра
и находится графически по ЛАЧХ (рис.9.2),
отсчитывая от максимума уровень в 3 дБ.
Относительная избирательность фильтра
характеризуется добротностью Q=р./
и связана с коэффициентами передаточной
функции выражением Q=(а0а2/а12)1/2.
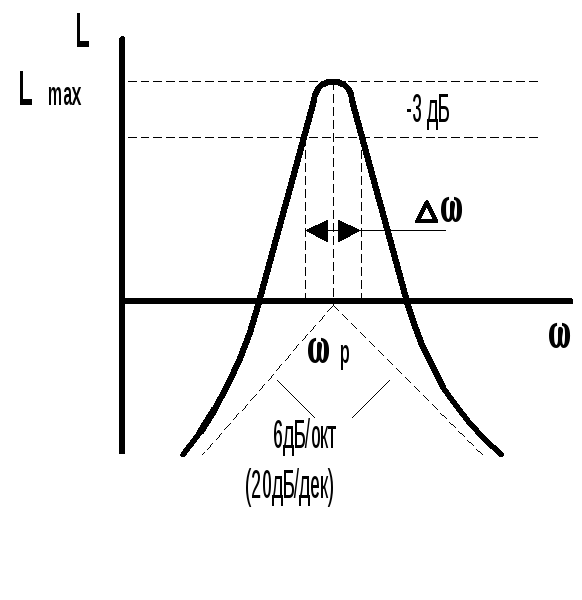
Рис.9.2
ЛАЧХ (рис.9.3) и их характерные точки для ФНЧ,ФВЧ, и РФ звеньев фильтра второго порядка могут быть получены из следующих выражений для передаточных функций:
K(s)=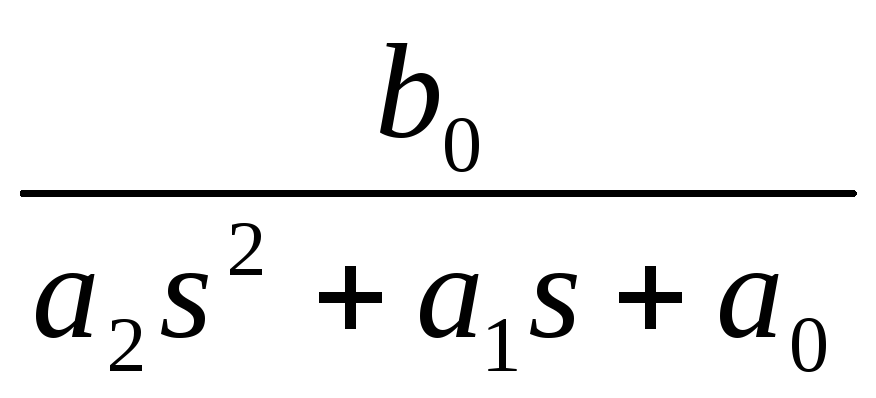 , ФНЧ
, ФНЧ
K(s)=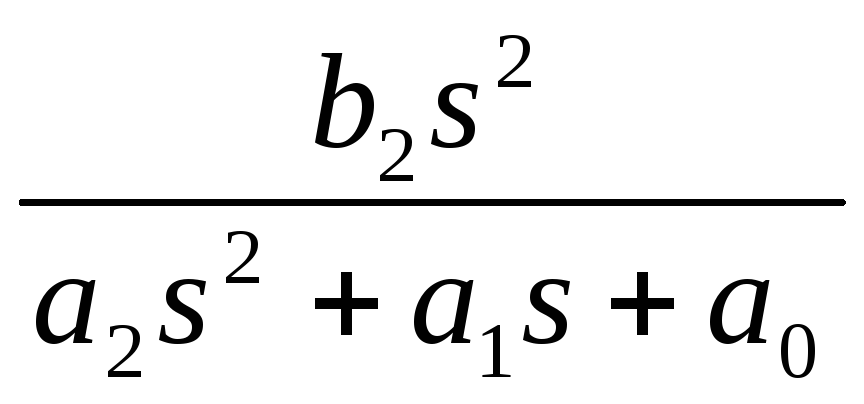 , ФВЧ
, ФВЧ
K(s)=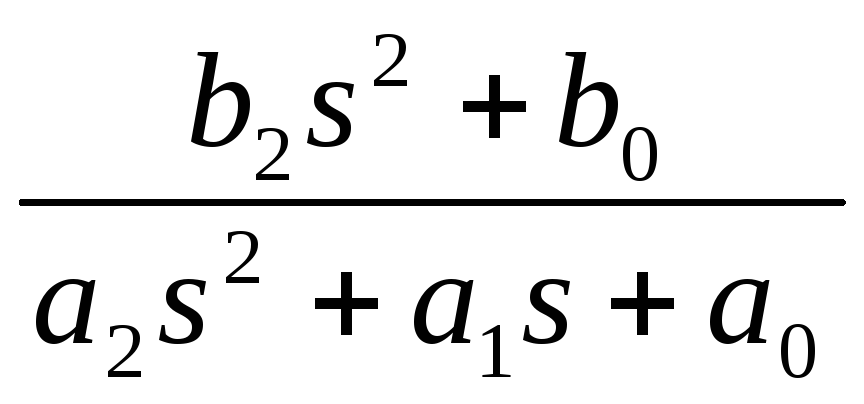 . РФ.
. РФ.
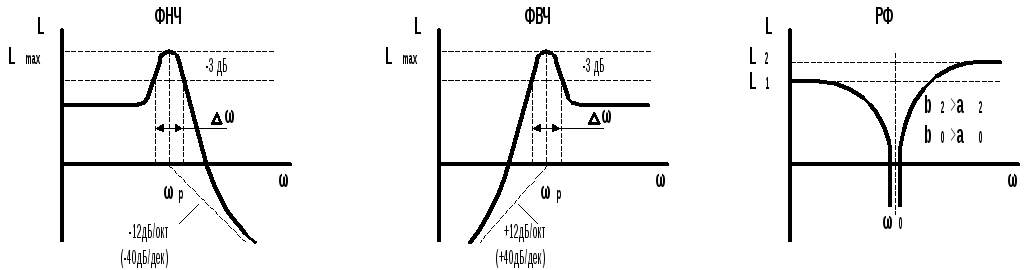
Рис.9.3
Для
определения связи характерных точек
ЛАЧХ с коэффициентами передаточной
функции могут быть использованы выражения
для полосового фильтра (за исключением
РФ звена, у которого частота нуля передачи
определяется выражением 0=(b0/b2)1/2). Однако надо помнить, что они будут иметь
приближенный характер, а их точность
будет повышаться с ростом добротности.
Так для Q>5
погрешность не превысит 5%. В случае
расчета низко добротных звеньев, следует
использовать точные выражения, приведенные
в работе [1].
0=(b0/b2)1/2). Однако надо помнить, что они будут иметь
приближенный характер, а их точность
будет повышаться с ростом добротности.
Так для Q>5
погрешность не превысит 5%. В случае
расчета низко добротных звеньев, следует
использовать точные выражения, приведенные
в работе [1].
Схемные реализации звеньев фильтров второго порядка
Простейшими устройствами, выполняющими операцию фильтрации, являются пассивные RC-цепи. Так интегрирующая RC-цепочка может трактоваться как простейший ФНЧ, дифференцирующая – ФВЧ, а последовательное их соединение – ПФ. При этом, интегрирующая и дифференцирующая RC-цепи имеют передаточные функции первого порядка, их последовательное соединение – передаточную функцию второго порядка, а корни характеристического уравнения (знаменателя передаточной функции) чисто действительные. Не трудно показать, что максимально достижимая добротность таких звеньев Q (степень избирательности) не превосходит 1/2.
Дальнейшее повышение добротности возможно за счет перехода к схемным реализациям, предполагающим наличие пары комплексно сопряженных корней знаменателя передаточной функции. В схемотехническом плане это означает такую трансформацию пассивной RC-цепи второго порядка, при которой обеспечивается потенциальный рост некоторых коэффициентов передаточной функции приводящих к увеличению Q. Из выражения для добротности
Q=(а0а2/а12)1/2
следует, что увеличение Q достижимо при увеличении а0,а2, уменьшении а1, либо комбинации этих действий.
Изменение соотношений между коэффициентами передаточной функции обеспечивается введением активного прибора (усилителя). Рассмотрим некоторые основные случаи:
а0*= а0п + kuа0’, а1*= а1п, а2*= а2п;
а0*= а0п, а1*= а1п, а2*= а2п+ kuа2’;
а0*= а0п, а1*= а1п– kuа1’, а2*= а2п;
а0*= а0п + kuа0’, а1*= а1п+ kuа1’, а2*= а2п+ kuа2’; ku,
где: аi*– коэффициенты передаточной функции проектируемого активного RC- фильтра, аiп – коэффициенты передаточной функции пассивной цепи второго порядка, ku– коэффициент усиления активного прибора.
Первый и второй способы формирования коэффициентов ориентированы на использование усилителя с конечным коэффициентом усиления. При этом усилитель охвачен отрицательной обратной связью. Стабильность основных параметров звена фильтра (частоты резонанса, полосы пропускания и добротности) определяется стабильностью параметров пассивных элементов и коэффициента усиления усилителя. Эти два варианта могут оказаться предпочтительными в случае необходимости организации управления частотой резонанса за счет изменения ku.
Третий способ так же ориентирован на использования усилителя с конечным коэффициентом усиления. Однако присутствие отрицательного слагаемого в выражении для а1* свидетельствует о наличии положительной обратной связи.
Этот способ удобен для организации непосредственного управления полосой пропускания фильтра, а значит и добротностью. Однако при существенном уменьшении коэффициента а1* возникает опасность потери устойчивости процессов происходящих в цепи второго порядка.
Напомним, что в соответствии с алгебраическим критерием устойчивости Гурвица, процессы в звене второго порядка устойчивы при положительности всех коэффициентов знаменателя передаточной функции (это эквивалентно необходимому и достаточному условию отрицательности действительных частей корней характеристического уравнения для цепи второго порядка).
Опасность потери устойчивости при реализации этого способа из-за возможной нестабильности ku ограничивает на практике область его применения низкими величинами добротности Q<5.
Четвертый способ повышения добротности фильтра ориентирован на использование ОУ. Он предполагает охват ОУ таким количеством отрицательных обратных связей, при котором организуются дополнительные слагаемые во всех коэффициентах знаменателя передаточной функции. При этом требуется обеспечить относительно меньший прирост коэффициента а1* по сравнению с остальными.
Такая организация структуры коэффициентов позволяет обеспечить увеличение добротности звена в совокупности с высокими показателями стабильности основных параметров фильтров. Так как, при использовании ОУ (приближающемуся по своим параметрам к идеальной модели), стабильность характеристик устройства определяется стабильностью параметрами только пассивных элементов цепи.
Основные этапы синтеза структуры звена фильтра предполагают:
перечисление графов, начиная от простейшего, обеспечивающего достаточное количество ребер для реализации звена;
На каждом из этапов осуществляется направленный перебор всех возможных комбинаций. Кроме того, алгоритм расширен для случая с произвольным количеством активных приборов. Поэтому, принципиально данный подход позволяет синтезировать полный каталог звеньев фильтров с самыми разнообразными свойствами.
Рассмотрим несколько конкретных реализаций звеньев фильтров второго порядка, начиная с, так называемой канонической (простейшей), приведенной на рис. 9.4.
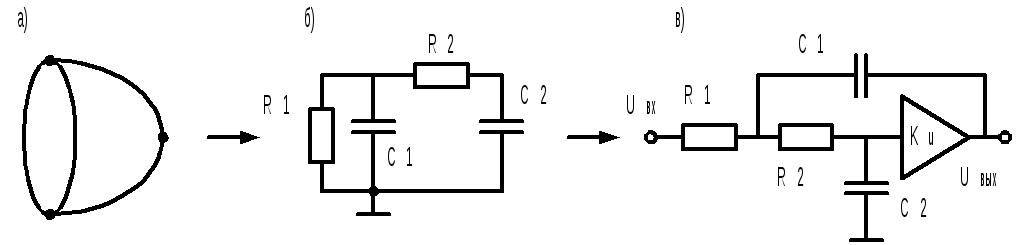
Рис.9.4
Основой для построения этого звена является канонический граф с четырьмя ребрами и тремя вершинами (рис.9.4, а). Выбор в качестве пассивной RC-цепи конфигурации показанной на рис.9.4, б. и последующее подключение активного элемента, как показано на рис.9.4, в, реализует звено активного RC-фильтра со структурой коэффициентов знаменателя передаточной функции соответствующей третьему способу повышения добротности. Его передаточная функция имеет вид
K(s)=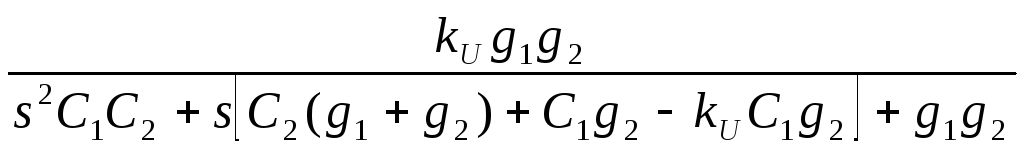 .
.
Отсюда находим частоту резонанса и полосу пропускания фильтра:
р=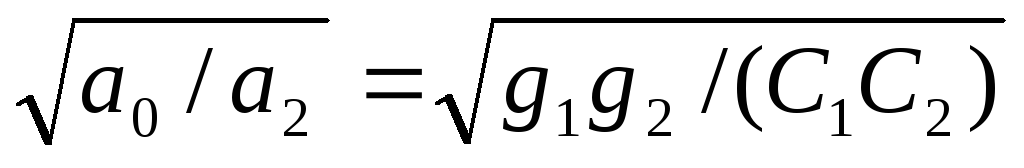 ,
,
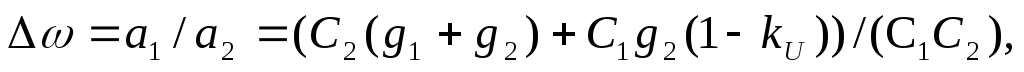
а при равно номинальных параметрах резисторов и конденсаторов величина добротности описывается выражением
Qi=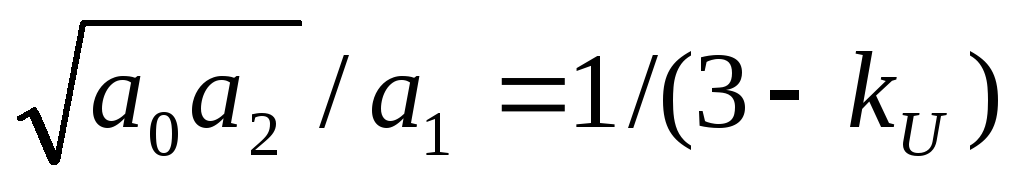 .
.
Вид передаточной функции свидетельствует о том, что звено реализует фильтр нижних частот. Из данной схемы путем замены резисторов на конденсаторы и наоборот можно получить каноническую схему фильтра верхних частот.
Для реализации полосового звена требуется дополнительный элемент – резистор (рис.9.5).
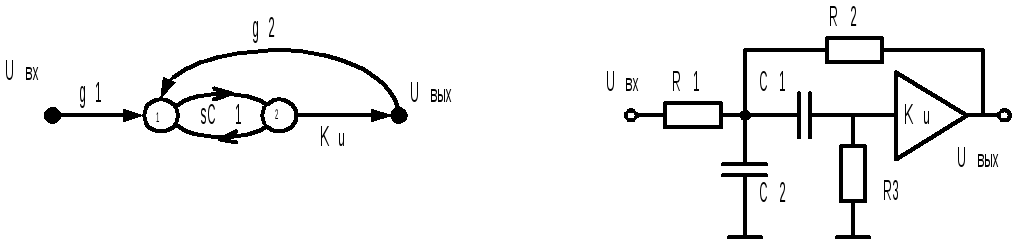
Рис. 9.5
Звенья фильтров, построенные на основе ОУ, отличаются большим количеством и разнообразием отрицательных обратных связей. В качестве примера можно привести схему ФНЧ на рис.9.6.
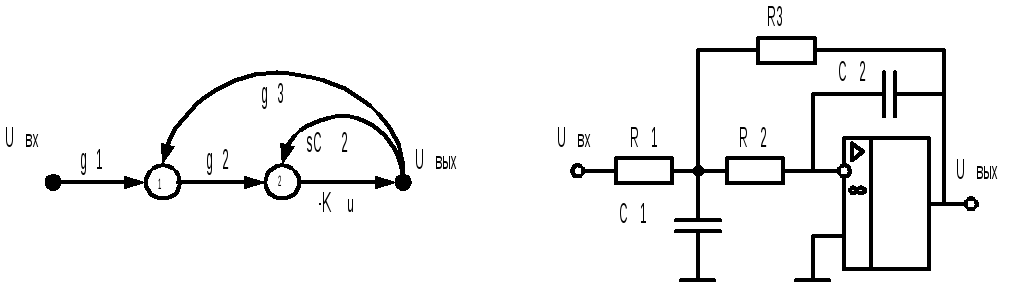
Рис.9.6.
Передаточная функция такого звена имеет вид:
K(s)=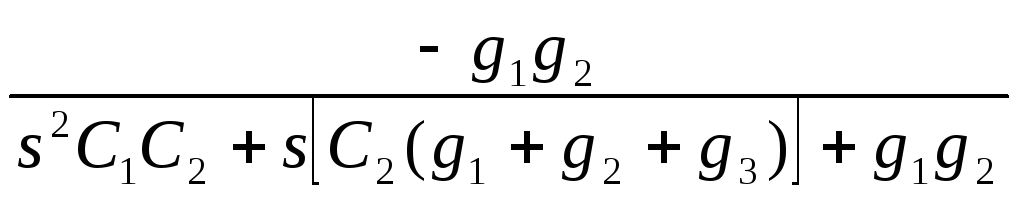 ,
,
а частота резонанса и полоса пропускания описываются выражениями:
р=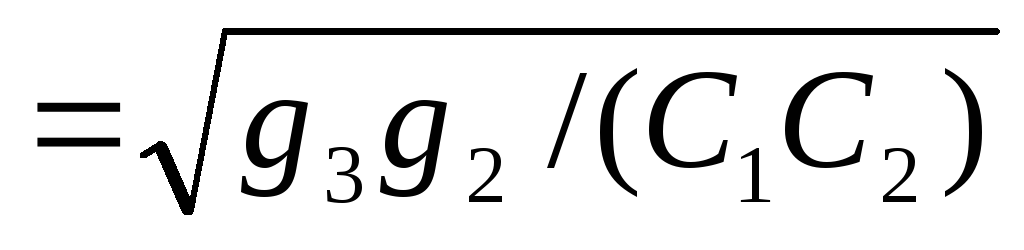 ,
,
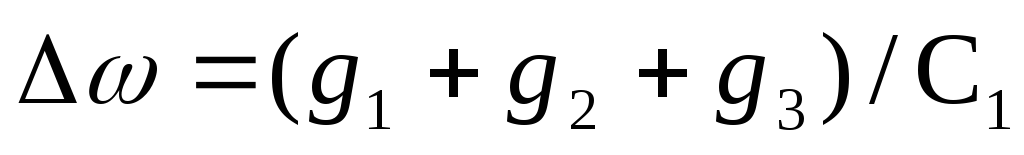 .
.
Следует обратить внимание на тот факт, что в итоговых выражениях для полосы пропускания и частоты резонанса в явном виде отсутствует коэффициент передачи ОУ. Это обеспечивает стабильность характеристик, определяемую только стабильностью пассивных элементов.
Анализ символьных выражений для основных параметров фильтров позволяет детализировать требования к конкретным схемным реализациям. Например, наличие проводимости резистора R3 в выражении для частоты резонанса и ее отсутствие в выражении для полосы пропускания позволяет сделать вывод о целесообразности использования данного элемента для организации независимой настройки или перестройки параметров звена.
Многообразие схемных решений звеньев фильтров второго порядка не ограничивается использование одного активного прибора. Существуют и активно применяются схемы на двух – четырех ОУ. Это объясняется возможностью реализации больших добротностей, а так же расширением их функциональных возможностей. В качестве примера можно привести схему рис.9.7. Она может рассматриваться как универсальный фильтр, одновременно реализующий три четырех основных операций фильтрации. Кроме того, некоторое избыточное количество пассивных элементов позволяет получить высокие величины добротности приближающиеся к 100.
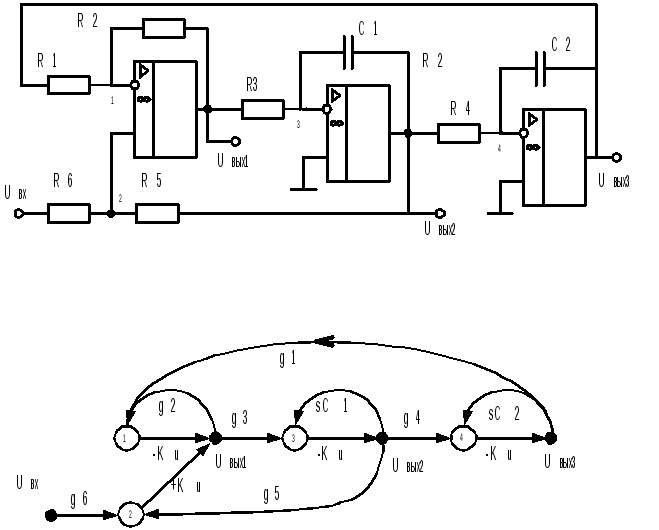
Рис.9.7
K1(s)=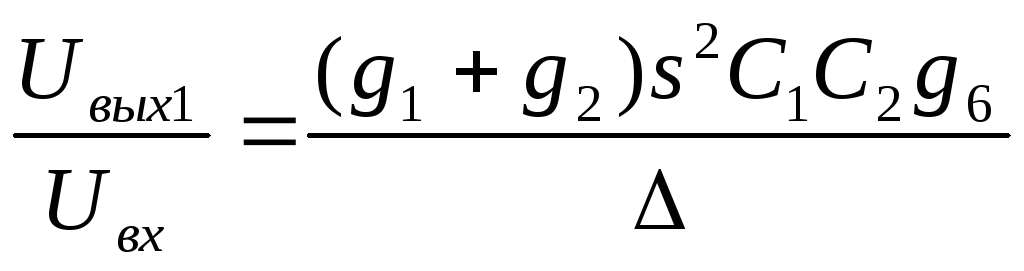 , ФВЧ
, ФВЧ
K2(s)= 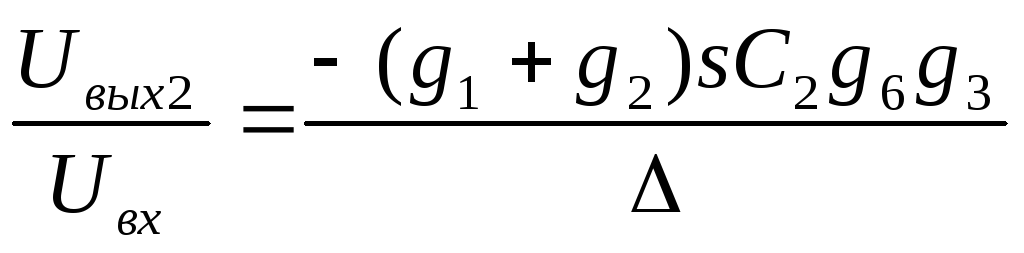 , ПФ
, ПФ
K3(s)= 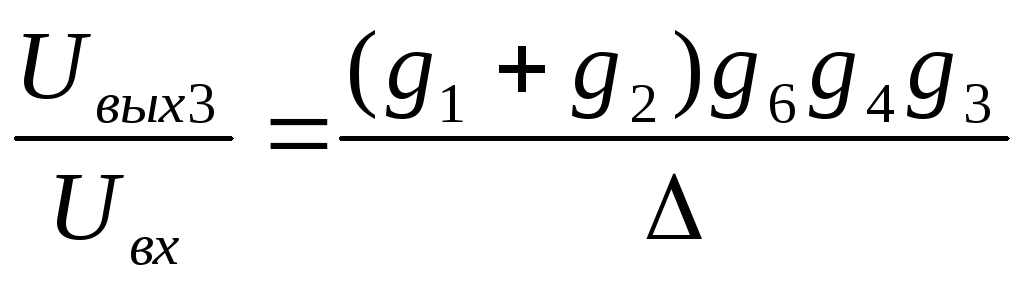 , ФНЧ
, ФНЧ
где 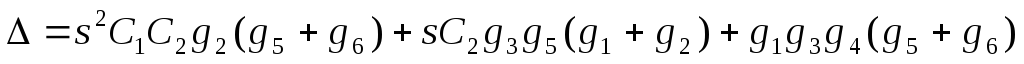 .
.
studfile.net
RC фильтр – это… Что такое RC фильтр?
Фильтр – получить на Академике рабочий купон на скидку ЗооПассаж или выгодно фильтр купить с бесплатной доставкой на распродаже в ЗооПассаж
Фильтр Чебышёва — Линейные электронные фильтры Фильтр Баттерворта Фильтр Чебышёва Эллиптический фильтр Фильтр Бесселя Фильтр Гаусса Фильтр Лежандра Фильтр Габора Править Фильтр Чебышёв … Википедия
Фильтр-пресс — Фильтр прессы мануфактуры Джонсона, 1884 г. Фильтр пресс (англ. filter press) аппарат периодического действия для разделения под давлением жидких неоднородных систем (суспензий, пульп) на жидкую фазу (фильтрат) и твердую… … Википедия
Фильтр нижних частот — (ФНЧ) один из видов аналоговых или электронных фильтров, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой… … Википедия
Фильтр — Фильтр (от лат. filtrum «войлок») понятия, устройства, механизмы, выделяющие (или удаляющие) из исходного объекта некоторую часть с заданными свойствами. Содержание 1 Фильтры жидкости 2 Фильтры газа … Википедия
Фильтр — аппарат, задерживающий твёрдые и жидкие радиоактивные частицы, находящиеся во взвешенном состоянии в воздухе или газе; существуют инерционные, пористые, смачиваемые, масляные, пенные, бумажные, электрические и др. фильтры. в радиологии… … Термины атомной энергетики
Фильтр низких частот — Фильтр нижних частот (ФНЧ) электронный или любой другой фильтр, эффективно пропускающий частотный спектр сигнала ниже некоторой частоты (частоты среза), и уменьшающий (или подавляющий) частоты сигнала выше этой частоты. Степень подавления каждой… … Википедия
Фильтр — в обогащении полезных ископаемыx (франц. filtre, от лат. filtrum, букв. войлок * a. filter; н. Filter; ф. filtre; и. filtro, filtrante, filtrador) устройство (аппарат) для разделения, сгущения или осветления неоднородной системы,… … Геологическая энциклопедия
Фильтр высоких частот — Фильтр верхних частот (ФВЧ) электронный или любой другой фильтр, пропускающий высокие частоты входного сигнала, при этом подавляя частоты сигнала меньше, чем частота среза. Степень подавления зависит от конкретного типа фильтра. В отличие от ФВЧ … Википедия
Фильтр с бесконечной импульсной характеристикой — (Рекурсивный фильтр, БИХ фильтр) или IIR фильтр (IIR сокр. от infinite impulse response бесконечная импульсная характеристика) линейный электронный фильтр, использующий один или более своих выходов в качестве входа, то есть… … Википедия
Фильтр — для очистки воздуха от взвешенных частиц Фильтр, карманный Фильтр, многослойный Фильтр, складчатый Фильтр, смоченный Фильтр, сухой Фильтр, рулонный Фильтр, самоочищающийся Фильтр, электрический Фильтр, электростатический Фильтр, ячейковый Фильтр … Словарь ГОСТированной лексики
Фильтр с конечной импульсной характеристикой — (Нерекурсивный фильтр, КИХ фильтр) или FIR фильтр (FIR сокр. от finite impulse response конечная импульсная характеристика) один из видов линейных цифровых фильтров, характерной особенностью которого является ограниченность по времени … Википедия
dic.academic.ru
Полосовой rc-фильтр
Полосовой RC-фильтр может быть образован при последовательном соединении RC-фильтров нижних и верхних частот. На рис. 5 показана схема этого фильтра и его векторная диаграмма.
В полосовом фильтре первое звено (ФНЧ) не
пропускает колебаний высоких частот,
а второе звено (ФВЧ) не пропускает
колебаний низких частот. Где-то в области
перехода от полосы прозрачности к полосе
задержки обоих звеньев и лежит максимальное
значение коэффициента передачи фильтра
(рис. 6).
полосовом фильтре первое звено (ФНЧ) не
пропускает колебаний высоких частот,
а второе звено (ФВЧ) не пропускает
колебаний низких частот. Где-то в области
перехода от полосы прозрачности к полосе
задержки обоих звеньев и лежит максимальное
значение коэффициента передачи фильтра
(рис. 6).

Рис. 5
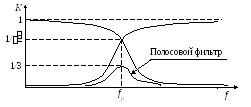
Рис. 6
Выражение для коэффициента передачи по напряжению для полосового фильтра при R1=R2=R и C1=C2=Cимеет вид
| (8) |
Из соотношения (8) для модуля коэффициента передачи (АЧХ) полосового фильтра следует:
| (9) |
Максимальная
величина модуля коэффициента передачи
выражения (9) наблюдается
при 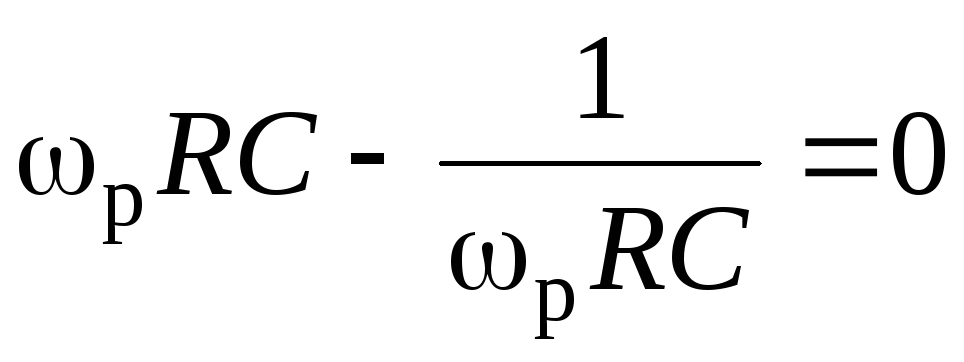 и принимает значение
и принимает значение
График зависимости
(9) показан на рис. 6. Как видно на данном
рисунке, АЧХ полосового фильтра напоминает
резонансную кривую колебательного
контура. Поэтому соответствующую частоту 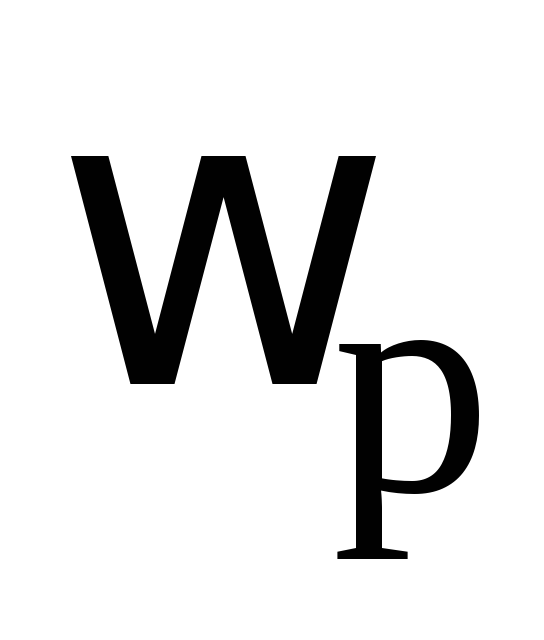 называют квазирезонансной. Ее значение
может быть получено из выражения (9) с
учетом соотношения (10)
называют квазирезонансной. Ее значение
может быть получено из выражения (9) с
учетом соотношения (10)
| (11) |
Заградительный rc-фильтр
З аградительныйRC-фильтр
часто называют двойным Т-образным
мостом. Он представляет собой параллельное
соединение Т-образных фильтров верхних
и нижних частот (рис. 7, а).
Качественно
работу заградительного фильтра можно
объяснить, перерисовав схему более
наглядно, как это показано на рис. 7,б.
В данном случае считаем, что сопротивление
нагрузки Rн не влияет на работу фильтра, т. е. что Rн имеет достаточно большую величину.
Слева и справа подведено переменное
входное напряжение от одного и того же
источника сигнала. В этом случае можно
заметить, что при 0 K1 и при K1.
аградительныйRC-фильтр
часто называют двойным Т-образным
мостом. Он представляет собой параллельное
соединение Т-образных фильтров верхних
и нижних частот (рис. 7, а).
Качественно
работу заградительного фильтра можно
объяснить, перерисовав схему более
наглядно, как это показано на рис. 7,б.
В данном случае считаем, что сопротивление
нагрузки Rн не влияет на работу фильтра, т. е. что Rн имеет достаточно большую величину.
Слева и справа подведено переменное
входное напряжение от одного и того же
источника сигнала. В этом случае можно
заметить, что при 0 K1 и при K1.
а б
Рис. 7
Это означает, что в области нулевой частоты и бесконечно больших частот коэффициент передачи фильтра равен 1. Векторные диаграммы для левой и правой части преобразованной схемы приведены на рис. 8, а, б.
Если
направить векторы напряжений 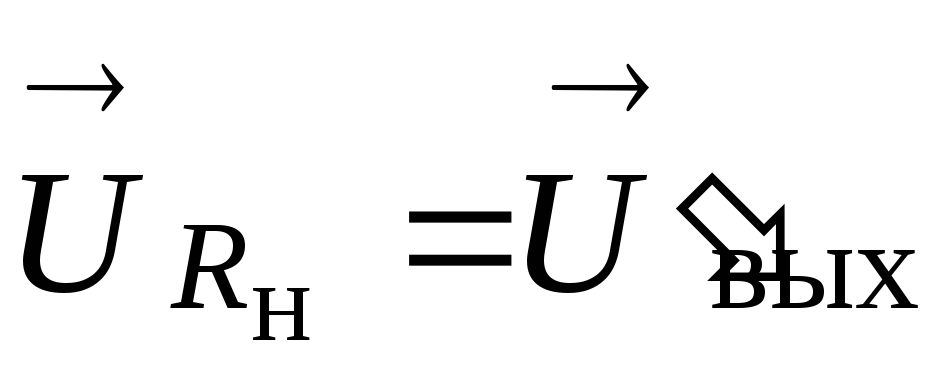 и
и 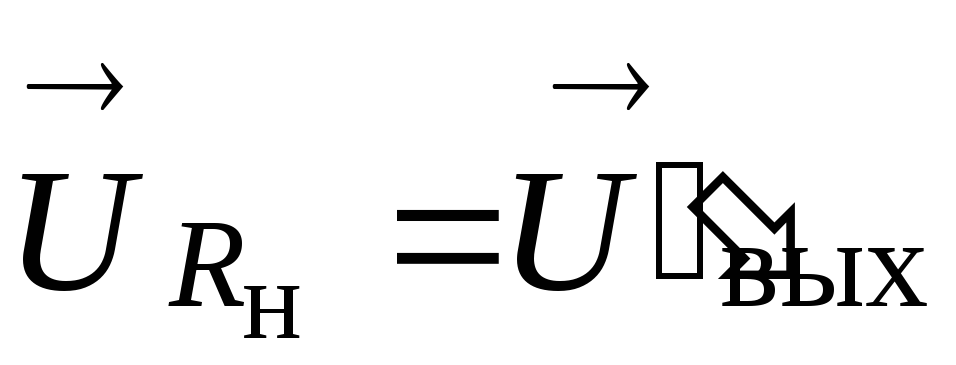 из одной точки (рис. 8, в),
то видно, что они при определенной
частоте сигнала могут быть равны друг
другу по величине и противоположны по
фазе. На этой частоте, называемой так
же, как и в случае полосового фильтра,
квазирезонансной, коэффициент передачи
фильтра будет равен нулю, а фаза меняется
скачком на .
Графики зависимостей K(f)
и (f) представлены
на рис. 9. Если в рассматриваемом
заградительном фильтре положить R1=R2=R, C1=C2=C, R3=R/2,
и C3=2C,
то выражения для его АЧХ и ФЧХ будут
иметь вид соответственно
из одной точки (рис. 8, в),
то видно, что они при определенной
частоте сигнала могут быть равны друг
другу по величине и противоположны по
фазе. На этой частоте, называемой так
же, как и в случае полосового фильтра,
квазирезонансной, коэффициент передачи
фильтра будет равен нулю, а фаза меняется
скачком на .
Графики зависимостей K(f)
и (f) представлены
на рис. 9. Если в рассматриваемом
заградительном фильтре положить R1=R2=R, C1=C2=C, R3=R/2,
и C3=2C,
то выражения для его АЧХ и ФЧХ будут
иметь вид соответственно
| (12) |
а значение квазирезонансной частоты будет равно
| (13) |
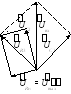


а
б в
Р ис.
8
ис.
8
а б
Рис. 9
Расчетное задание
Рассчитать величины R и С для фильтров нижних и верхних частот, а также полосового и заградительного. Указать на схемах номинальные значения R и С. Данные для частоты fс (или fр), по которой рассчитываются фильтры, приведены по вариантам в таблице.
Вариант | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
fс (fр), кГц | 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 2,2 | 2,4 | 2,6 | 2,8 |
Рассчитать и построить графики АЧХ и ФЧХ фильтров верхних и нижних частот. Расчеты выполнить для коэффициентов передачи K, равных соответственно 0,2; 0,4; 0,7; 0,8; 1,0. Hа графике частоту f откладывать в логарифмическом масштабе.
Нарисовать схемы рассчитанных фильтров и указать на них номинальные значения элементов.
studfile.net


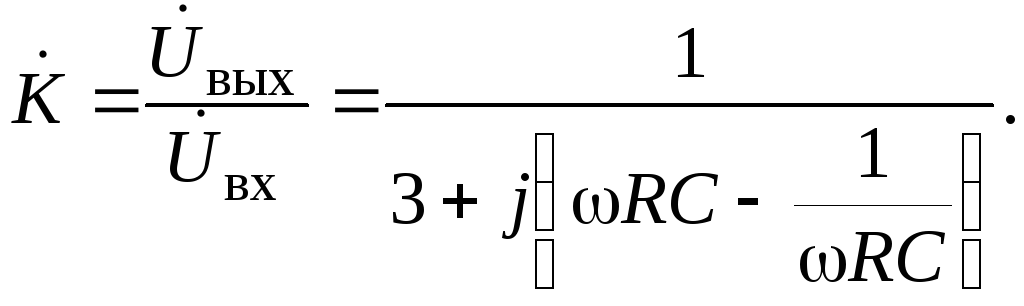
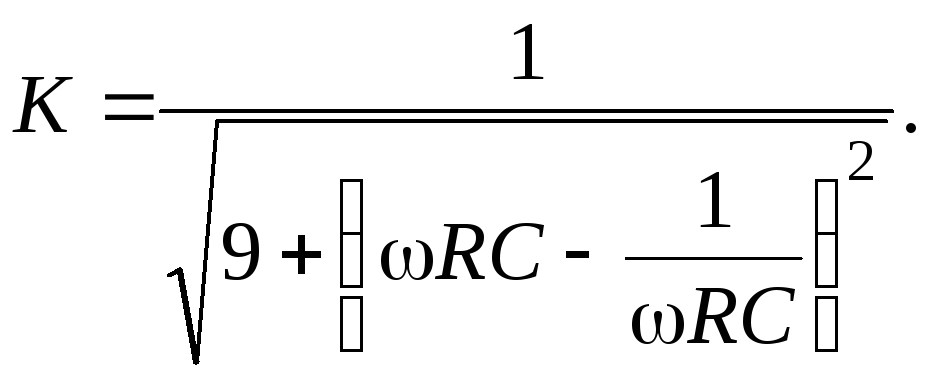
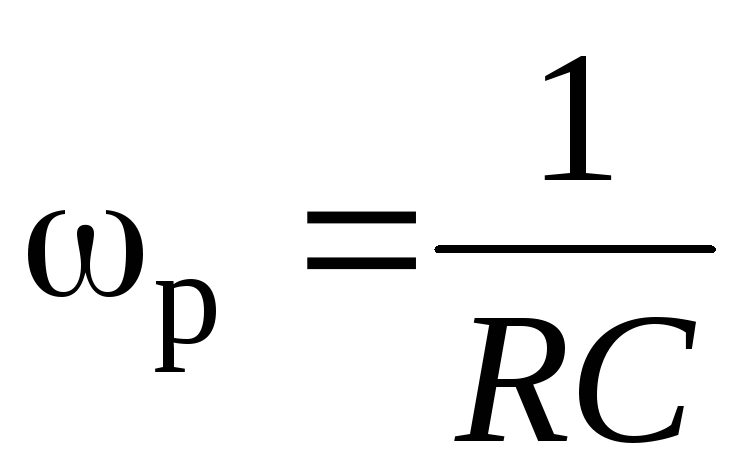 или
или 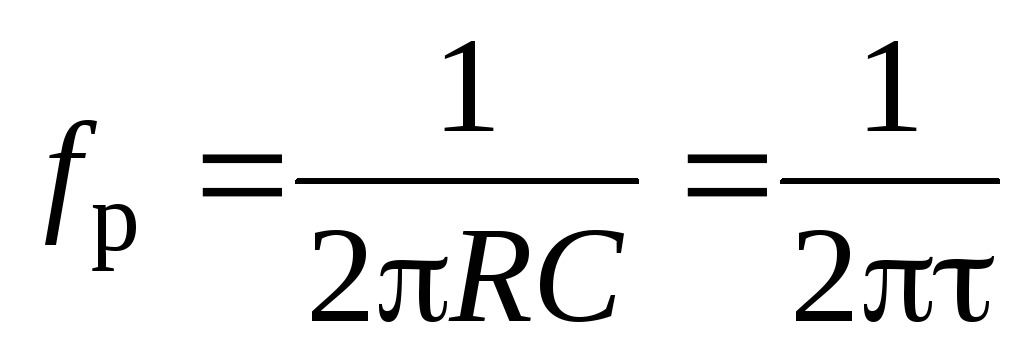 .
.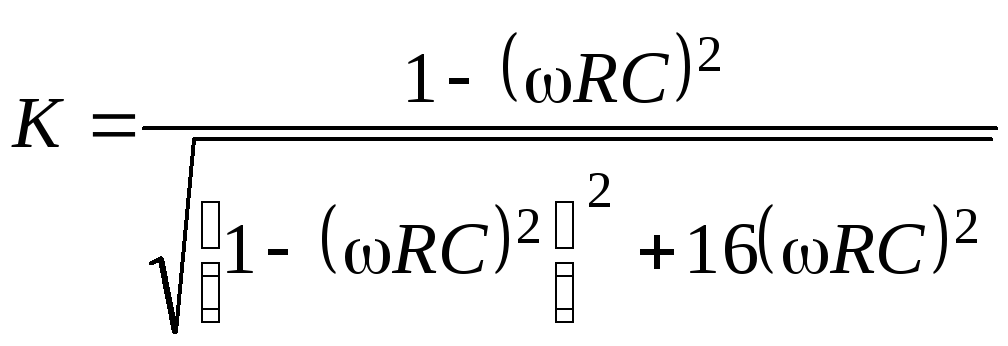 ,
, 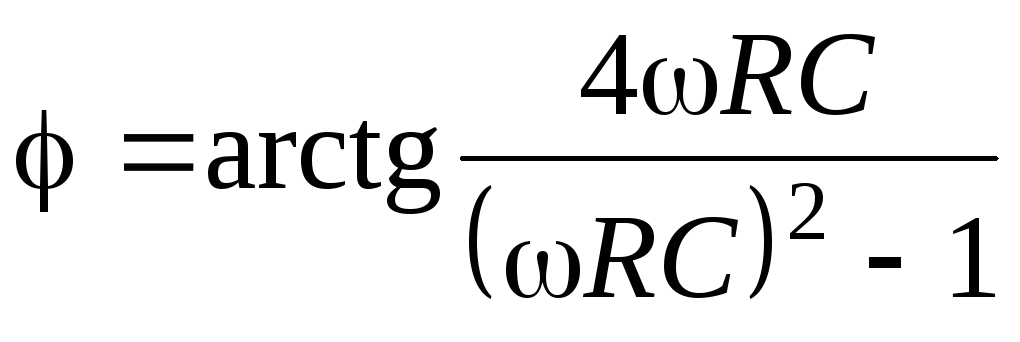 ,
,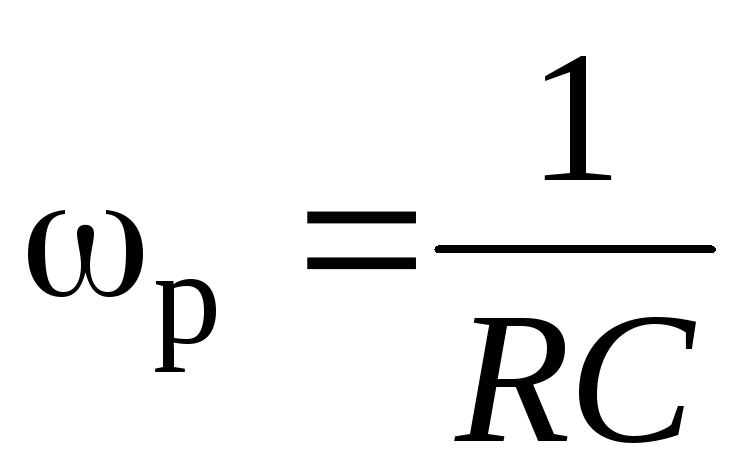 или
или