Найдено решение канонической задачи дифракции на открытом конце волновода с диэлектриком
Дифракция в простом понимании — это отклонение направления распространения волны от прямолинейного при прохождении мимо какого-либо объекта. Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное. Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.
Волноводные и резонаторные структуры — одни из ключевых элементов современных ускорителей частиц. В классических ускорителях эти структуры являются чисто вакуумными. Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова.
В интернете можно найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Однако это лишь то, что мы можем видеть глазом. На самом деле эффект Вавилова-Черенкова проявляется в очень широком диапазоне частот электромагнитного спектра, лишь малая часть которого доступна человеческому глазу. В частности, этот эффект имеет место и в диапазонах гига- и терагерцовых частот, которые наиболее интересны для данной работы. В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны.
Для развития описанных выше технологий крайне полезно иметь математический метод для строгого решения задачи дифракции электромагнитных волн и задачи дифракции поля движущегося сгустка заряженных частиц на открытом конце круглого волновода со слоем диэлектрика. Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений.
«Мы, конечно, не изобрели этот метод с нуля. В теории дифракции на таких структурах известно достаточно подходов и решено много канонических задач, но как раз нужная в данный момент оказалась нерешенной. Наиболее близко к нашей стоит работа московских физиков Воскресенского и Журава конца 1970-х годов.
По большому счету, нам просто удалось понять, как обобщить их подход на случай цилиндрической геометрии, а также мы апробировали полученные результаты современными численными средствами. Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка, — говорит
Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ. — Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным. К решению этих задач мы и планируем приступить в ближайшем будущем».
Каковы правильные резонансные структуры закиси азота?
Чтобы добавить хороший ответ Ринго и добавить более глубокое понимание ситуации с привязкой, я выполнил расчет на уровне теории DF-BP86/def2-SVP.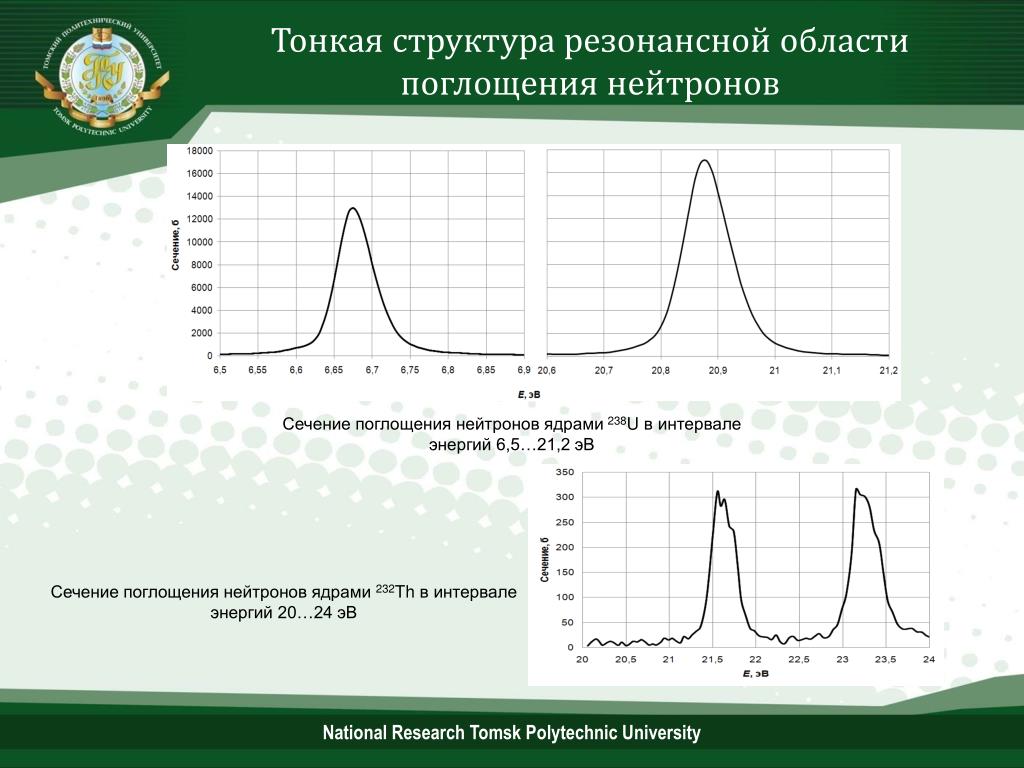
Орбиталы 1-3 представляют собой орбитали ядра (1s) в соответствующих элементах. MO 4 соответствует $ \ ce {O-N} ~ \ sigma $ -связью. Следует отметить, что эта связь делокализуется, а также описывает часть $ \ ce {N-N} ~ \ sigma $ -связы. Аналогично это справедливо для МО 5, но наоборот. В МО 6 мы видим присутствие одиночной пары в кислороде. МО 7 и 8 описывают две делокализованные $ \ pi $ -связки, связывающие по отношению ко всем атомам соединения. MO 9 имеет в основном одиночный парный характер и находится в конечном азоте. То HOMOs также являются $ \ pi $ орбиталями, связанными с $ \ ce {N-N} $ и антисвязывающимися относительно $ \ ce {O-N} $. Это несколько подразумевает одиночный парасимвол для этих орбиталей.
Я дополнительно проанализировал волновую функцию с теорией орбитальных уравнений естественной связи. Этот метод локализует орбитали (и плотность электронов) и сравнивает его с идеальной электронной плотностью данной структуры Льюиса. Высокие проценты означают, что конфигурация хорошо согласуется с концепцией Льюиса.
Я включил структуры, которые вы предложили. Вы можете видеть, что, хотя конфигурация 1 не является идеальной структурой Льюиса, она по-прежнему согласуется с определенной точкой с концепцией Льюиса. Если бы кто-то сделал более строгий подход с теорией Валанса Бонда, я бы ожидал, что эта структура будет иметь (хотя бы незначительный) вклад в общую ситуацию с привязкой. Основным недостатком этой структуры является электронный секстет на концевом азоте, о котором уже упоминал Ринго. Положительным аспектом этой структуры является то, что она не требует официальных обвинений.
Однако вторая структура неверна. Это может существовать только в возбужденном состоянии. Азот не может содержать более восьми электронов. Третья структура – идеальная структура, то есть та, которая имеет наивысшее согласие. Я ожидаю, что он будет иметь самый высокий вклад в общее соединение.
Структура 3 учитывает эффекты делокализации и является одним из основных вкладов в общую резонансную стабилизацию молекулы. В основном вы можете увидеть характер этого в MO 7 и 8 выше.
Последняя структура ( 5 ) пробует то же самое, но, на мой вкус, это немного далека. Он по-прежнему несколько согласен с концепцией Льюиса, но, как конфигурация 1 , я ожидал бы меньшего вклада.
Решена задача о дифракции на открытом конце волновода с диэлектриком
 Этот результат может послужить дальнейшему развитию пучковых методов генерации излучения, а также методов диагностики пучков заряженных частиц и управления их структурой. Исследование выполнено при финансовой поддержке Президентской программы Российского научного фонда (РНФ).
Этот результат может послужить дальнейшему развитию пучковых методов генерации излучения, а также методов диагностики пучков заряженных частиц и управления их структурой. Исследование выполнено при финансовой поддержке Президентской программы Российского научного фонда (РНФ).Дифракция в простом понимании — это отклонение направления распространения волны от прямолинейного при прохождении мимо какого-либо объекта. Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное. Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.
Волноводные и резонаторные структуры — одни из ключевых элементов современных ускорителей частиц. В классических ускорителях эти структуры являются чисто вакуумными. Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова. Он возникает при движении заряженной частицы со скоростью, превышающей фазовую скорость распространения волн в среде (в данном случае — в диэлектрике). Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.
Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова. Он возникает при движении заряженной частицы со скоростью, превышающей фазовую скорость распространения волн в среде (в данном случае — в диэлектрике). Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.
В интернете можно найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Однако это лишь то, что мы можем видеть глазом. На самом деле эффект Вавилова-Черенкова проявляется в очень широком диапазоне частот электромагнитного спектра, лишь малая часть которого доступна человеческому глазу. В частности, этот эффект имеет место и в диапазонах гига- и терагерцовых частот, которые наиболее интересны для данной работы. В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Она подобна той, что возникает за идущими по воде кораблями — правда, в данном случае она имеет электромагнитную природу, а роль «корабля» выполняет движущийся сгусток электронов. Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений — как сугубо прикладных, например в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.
В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Она подобна той, что возникает за идущими по воде кораблями — правда, в данном случае она имеет электромагнитную природу, а роль «корабля» выполняет движущийся сгусток электронов. Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений — как сугубо прикладных, например в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.
Для развития описанных выше технологий крайне полезно иметь математический метод для строгого решения задачи дифракции электромагнитных волн и задачи дифракции поля движущегося сгустка заряженных частиц на открытом конце круглого волновода со слоем диэлектрика. Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений.
Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений.
Ученые кафедры радиофизики Санкт-Петербургского государственного университета (СПбГУ) посвятили свою работу строгому аналитическому решению такой канонической задачи. Свой подход они продемонстрировали на примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. Формально задача состояла в решении одного известного уравнения математической физики, но нужно было наиболее удобным образом выбрать представление для электромагнитного поля в каждой области пространства (волноводные стенки и их продолжения, а также торец волновода являются естественными границами, которые разбивают все пространство на ряд таких областей) и удовлетворить граничным условиям на всех отмеченных границах.
«Мы, конечно, не изобрели этот метод с нуля. В теории дифракции на таких структурах известно достаточно подходов и решено много канонических задач, но как раз нужная в данный момент оказалась нерешенной. Наиболее близко к нашей стоит работа московских физиков Воскресенского и Журава конца 1970-х годов. По большому счету нам просто удалось понять, как обобщить их подход на случай цилиндрической геометрии, а также мы апробировали полученные результаты современными численными средствами. Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка,— говорит Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ.— Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным.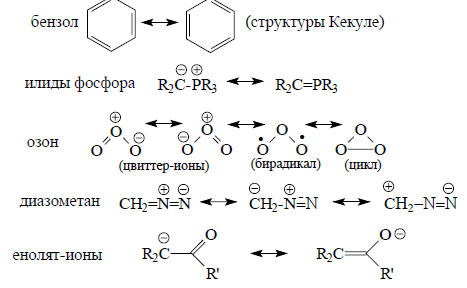 К решению этих задач мы и планируем приступить в ближайшем будущем».
К решению этих задач мы и планируем приступить в ближайшем будущем».
Использованы материалы статьи Diffraction at the Open-Ended Dielectric-Loaded Circular Waveguide: Rigorous Approach; Sergey N. Galyamin; Victor V. Vorobev, Andrey V. Tyukhti, журнал IEEE Explore, март 2021 г.
Найдено решение канонической задачи дифракции на открытом конце волновода с диэлектриком – Газета.Ru
Российские ученые построили строгое аналитическое решение канонической задачи дифракции волноводной моды на открытом конце круглого волновода с диэлектрическим заполнением. Этот результат может послужить дальнейшему развитию пучковых методов генерации излучения, а также методов диагностики пучков заряженных частиц и управления их структурой. Исследование выполнено при финансовой поддержке Президентской программы Российского научного фонда (РНФ) и опубликовано в IEEE Transactions on Microwave Theory and Techniques.
Дифракция в простом понимании — это отклонение направления распространения волны от прямолинейного при прохождении мимо какого-либо объекта.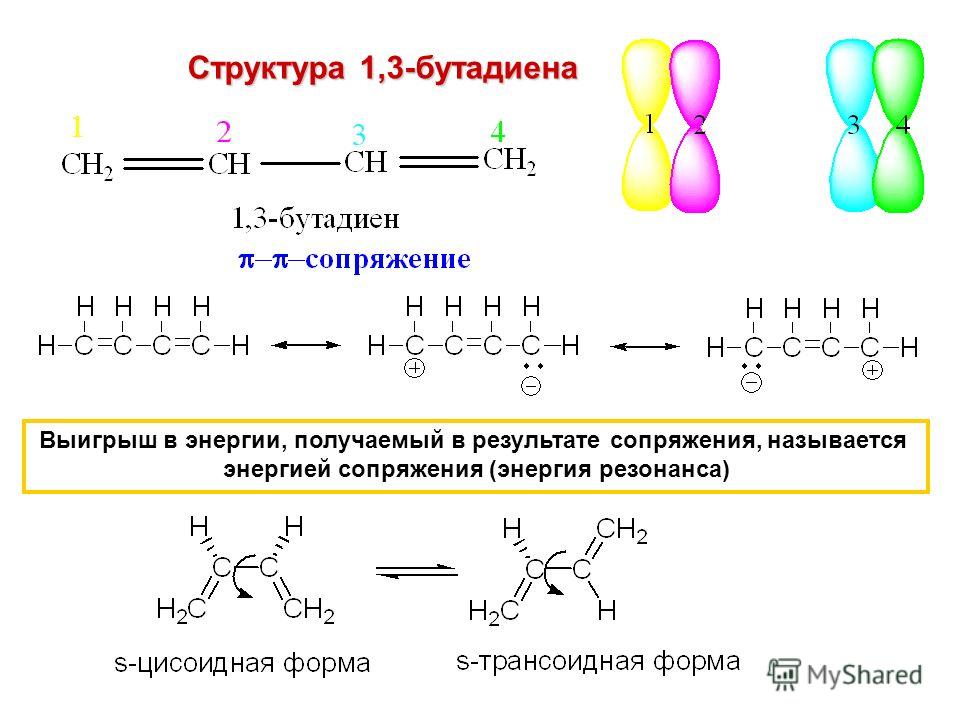 Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное. Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.
Теория дифракции, которая рассматривает это явление более широко и с помощью математических методов, обычно имеет дело с так называемыми каноническими задачами, то есть задачами взаимодействия относительно простых волн со сравнительно простыми геометрическими объектами, такими как, например, бесконечно тонкое ребро, клин, шар, цилиндр и тому подобное. Отдельный класс канонических задач связан с дифракцией волн в резонаторах и на открытом конце волноводов.
Волноводные и резонаторные структуры — одни из ключевых элементов современных ускорителей частиц. В классических ускорителях эти структуры являются чисто вакуумными. Однако в последние годы большое внимание уделяется волноводам и резонаторам с различным диэлектрическим заполнением, так как это открывает перспективы для использования в ускорительной физике эффекта Вавилова-Черенкова. Он возникает при движении заряженной частицы со скоростью, превышающей фазовую скорость распространения волн в среде (в данном случае — в диэлектрике). Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.
Излучение расходится конусом от траектории движения частицы, и, поскольку угол при вершине конуса зависит от скорости частицы и скорости света в среде, физики могут определять скорость заряженной частицы и обнаруживать ее в экспериментах.
В интернете можно найти многочисленные фотографии излучения Вавилова-Черенкова в виде голубого свечения. Однако это лишь то, что мы можем видеть глазом. На самом деле эффект Вавилова-Черенкова проявляется в очень широком диапазоне частот электромагнитного спектра, лишь малая часть которого доступна человеческому глазу. В частности, этот эффект имеет место и в диапазонах гига- и терагерцовых частот, которые наиболее интересны для данной работы. В этой связи следует отметить значительные успехи, достигнутые в последнее время в методе кильватерного ускорения заряженных частиц. В этом методе используется излучение Вавилова-Черенкова на гига- или терагерцовых частотах, генерируемое в волноводе с диэлектриком в виде кильватерной волны. Она подобна той, что возникает за идущими по воде кораблями — правда, в данном случае она имеет электромагнитную природу, а роль «корабля» выполняет движущийся сгусток электронов.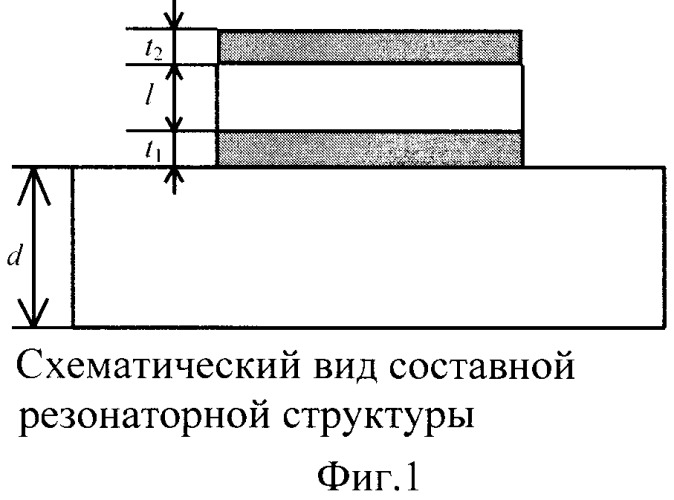 Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений, как сугубо прикладных, например, в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.
Так как частота этой волны может попадать в терагерцовый диапазон, физики обсуждают возможность создания на базе таких кильватерных структур генераторов терагерцового излучения. Его уникальные свойства имеют целый ряд перспективных применений, как сугубо прикладных, например, в системах безопасности, так и чисто научных, связанных с исследованиями структуры материи.
Для развития описанных выше технологий крайне полезно иметь математический метод для строгого решения задачи дифракции электромагнитных волн и задачи дифракции поля движущегося сгустка заряженных частиц на открытом конце круглого волновода со слоем диэлектрика. Другими словами, желательно иметь решение соответствующей канонической задачи. Однако до настоящего момента оно отсутствовало, что, вероятно, связано с математическими сложностями, к которым приводит наличие диэлектрического слоя в волноводе: решение не строится в замкнутом виде, возникают бесконечные линейные или нелинейные системы уравнений. Поэтому ученые кафедры радиофизики Санкт-Петербургского государственного университета (СПбГУ) посвятили свою работу строгому аналитическому решению такой канонической задачи. Свой подход они продемонстрировали на примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. Формально задача состояла в решении одного известного уравнения математической физики, но нужно было наиболее удобным образом выбрать представление для электромагнитного поля в каждой области пространства (волноводные стенки и их продолжения, а также торец волновода являются естественными границами, которые разбивают все пространство на ряд таких областей) и удовлетворить граничным условиям на всех отмеченных границах.
Свой подход они продемонстрировали на примере сплошного заполнения волновода диэлектриком и возбуждения в виде набегающей волноводной моды. Формально задача состояла в решении одного известного уравнения математической физики, но нужно было наиболее удобным образом выбрать представление для электромагнитного поля в каждой области пространства (волноводные стенки и их продолжения, а также торец волновода являются естественными границами, которые разбивают все пространство на ряд таких областей) и удовлетворить граничным условиям на всех отмеченных границах.
«Мы, конечно, не изобрели этот метод с нуля. В теории дифракции на таких структурах известно достаточно подходов и решено много канонических задач, но как раз нужная в данный момент оказалась нерешенной. Наиболее близко к нашей стоит работа московских физиков Воскресенского и Журава конца 1970-х годов. По большому счету, нам просто удалось понять, как обобщить их подход на случай цилиндрической геометрии, а также мы апробировали полученные результаты современными численными средствами. Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка, — говорит Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ. — Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным. К решению этих задач мы и планируем приступить в ближайшем будущем».
Разработанный в итоге метод может применяться для решения более сложных и практически значимых задач со слоистым заполнением, при этом возбуждение может быть и в виде свободной волны, и в виде движущегося заряженного сгустка, — говорит Сергей Галямин, руководитель гранта РНФ, кандидат физико-математических наук, доцент кафедры радиофизики СПбГУ. — Кроме того, полученные нами результаты могут применяться для улучшения существующих приближенных подходов и контроля корректности численного моделирования, что особенно важно в случаях, когда моделирование оказывается ресурсозатратным. К решению этих задач мы и планируем приступить в ближайшем будущем».
Химическая связь – Резонансные структуры
Описание плоского гексагонального Молекула бензола , C 6 H 6 , иллюстрирует другой аспект теории VB. Считается, что каждый из шести атомов углерода гибридизован s p 2 . Две гибридные орбитали используются для образования σ-связей с соседними атомами углерода, а одна используется для образования σ-связи с атомом водорода. Негибридизированные углеродные 2 p- орбитали могут перекрываться и образовывать π-связи со своими соседями ( рис. 12 ). Однако есть несколько возможностей для создания пары; два из них:
Негибридизированные углеродные 2 p- орбитали могут перекрываться и образовывать π-связи со своими соседями ( рис. 12 ). Однако есть несколько возможностей для создания пары; два из них:
Рисунок 12: Описание валентной связи молекулы бензола. В ы р 2 гибридизированных атомы углерода образуют сг связи со своими соседями, и негибридизированные р – орбитали перекрываются с образованием π связей. Этот образец склеивания соответствует одной из структур Кекуле (см. Текст).
Британская энциклопедия, Inc.Для каждого из этих так называемых Структуры Кекуле . (Они названы так в честь Фридриха Августа Кекуле , которому обычно приписывают впервые предложенную гексагональную структуру для бензола в 1865 году; однако циклическая структура уже была предложена Джозефом Лошмидтом четырьмя годами ранее.) Фактическая структура представляет собой суперпозицию ( сумма) двух волновых функций: в терминах VB структура бензола представляет собойрезонансный гибрид двух канонических структур. С точки зрения квантовой механики, эффект смешения резонанса в подходе Льюиса к связыванию – это суперпозиция волновых функций для каждой вносящей вклад канонической структуры. Эффект резонанса заключается в разделении характера двойной связи вокруг кольца, так что каждая связь углерод-углерод имеет смешанный характер одинарной и двойной связи. Резонанс также (по причинам квантовой механики) снижает энергию молекулы относительно любой из канонических структур. Действительно, бензол – это молекула, которая удивительно устойчива к химическому воздействию (двойные связи, а не источник молекулярной прочности и стабильности, обычно являются объектами химической атаки) и более стабильна, чем предполагает ее структура.
Одной из трудностей, сделавших VB непривлекательным с точки зрения вычислений, является большое количество канонических структур, как ковалентных, так и ионных, которые необходимо использовать для достижения количественно надежных результатов; в некоторых случаях необходимо использовать десятки тысяч конструкций.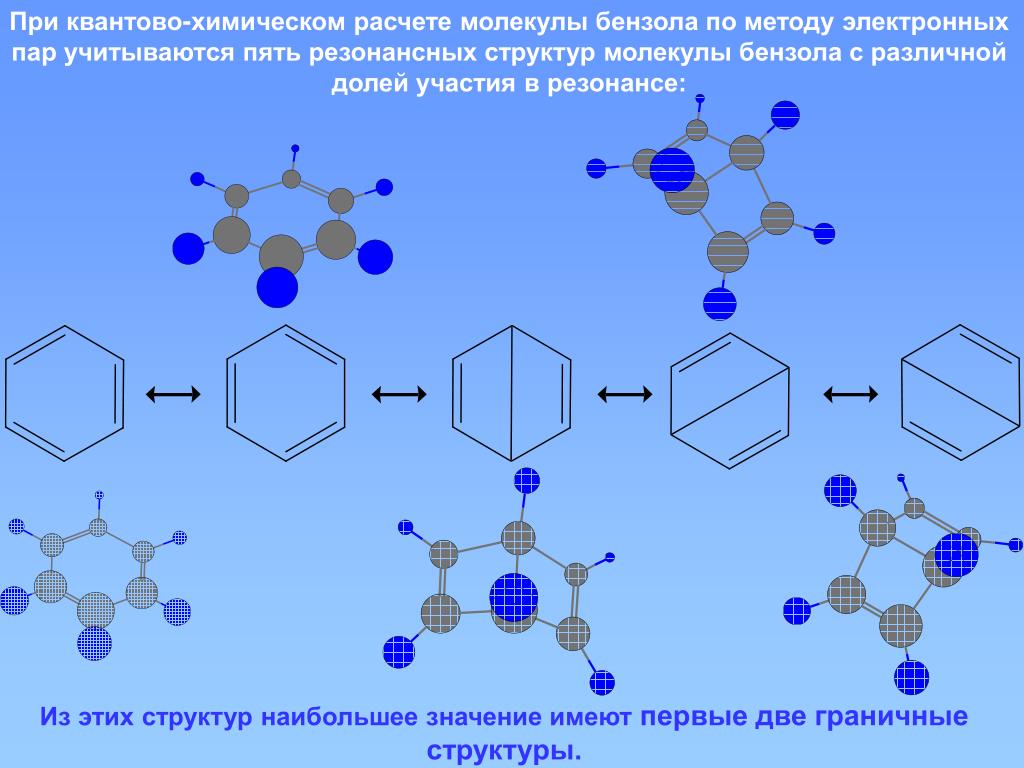 Тем не менее, теория VB сильно повлияла на язык химии, и концепции σ- и π-связей, гибридизации и резонанса являются частью повседневного словаря предмета.
Тем не менее, теория VB сильно повлияла на язык химии, и концепции σ- и π-связей, гибридизации и резонанса являются частью повседневного словаря предмета.
Альтернативной квантово-механической теорией электронного строения молекул является теория МО. Этот подход был введен примерно в то же время, что и теория VB, но оказался более подходящим для количественной реализации на компьютерах . В настоящее время это практически единственный метод, применяемый в вычислительном исследовании молекул. Подобно теории VB, она ввела язык, который широко используется в химии, и многие химики обсуждают химические связи в терминах, сочетающих обе теории.
Как атомная орбиталь – это волновая функция , описывающая распределение электрона вокруг ядра атома, так и атомная орбиталь – это волновая функция , описывающая распределение электрона вокруг ядра атома.молекулярная орбиталь (МО) – это волновая функция, описывающая распределение электрона по всем ядрам молекулы. Если амплитуда волновой функции МО велика в окрестности конкретного атома, то электрон с большой вероятностью может там оказаться.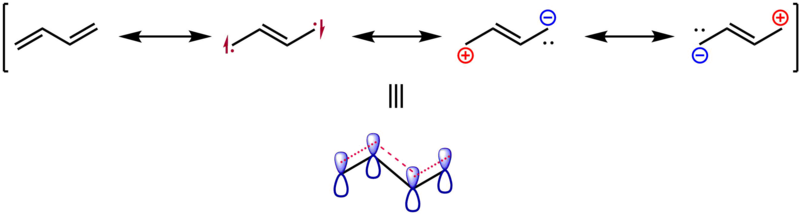 Если волновая функция МО равна нулю в определенной области, то электрон там не будет.
Если волновая функция МО равна нулю в определенной области, то электрон там не будет.
Хотя МО может быть в принципе определена путем решения уравнения Шредингера для электрона в электростатическом поле массива ядер, на практике всегда принимается приближение. В этом приближении, известном какВ приближении линейной комбинации атомных орбиталей (ЛКАО) каждая МО строится из суперпозиции атомных орбиталей, принадлежащих атомам в молекуле . Размер вклада орбитали от конкретного атома указывает вероятность того, что электрон будет найден на этом атоме. Фактическая форма молекулярной орбитали (и косвенно ее энергия) является отражением степени, в которой отдельные атомные орбитали взаимодействуют друг с другом конструктивно или деструктивно.
Резонансные структуры в органической химии примеры. Органическая химия. канонические структкры резонансная структура
Часто, а точнее всегда, электроны размазаны по молекуле так, что нет возможности изобразить её электронную структуру в понятных человеку символах одним схематическим рисунком.
 Можно конечно с помощью компьютера показать электронную плотность, но даже опытному химику далеко не всегда будет понятно что это за молекула и какой реактивности от неё ожидать (а именно для этого вся схематичность и придуманна). Дабы как-то разрулить ситуёвину придумали понятие “резонансные структуры ” – эдакие костыли для саванных обезьяноподобных трупоедов, которые бананы считать научились, но всё, что не выглядит как банан понять затрудняются. Рисуют вобщем несколько схематических структур и говорят, что молекула описывается одновременно всеми этими структурами, находящимися в суперпозиции (и там всякие уравнения Шредингера, о которых тут не будем, но самого ещё ниже вспомним). У большинства студентов на этой теме случается взрыв мозга, а многие так и заканчивают степень, не поняв чозафигня.
Можно конечно с помощью компьютера показать электронную плотность, но даже опытному химику далеко не всегда будет понятно что это за молекула и какой реактивности от неё ожидать (а именно для этого вся схематичность и придуманна). Дабы как-то разрулить ситуёвину придумали понятие “резонансные структуры ” – эдакие костыли для саванных обезьяноподобных трупоедов, которые бананы считать научились, но всё, что не выглядит как банан понять затрудняются. Рисуют вобщем несколько схематических структур и говорят, что молекула описывается одновременно всеми этими структурами, находящимися в суперпозиции (и там всякие уравнения Шредингера, о которых тут не будем, но самого ещё ниже вспомним). У большинства студентов на этой теме случается взрыв мозга, а многие так и заканчивают степень, не поняв чозафигня.Таких резонансных структур на самом деле для каждой молекулы можно нарисовать огромное количество, но используют обычно в простых случаях (коих основная масса) одну, в случаях посложнее две и очень редко три и более. Забавно, что люди дошли до такого искуства строгания костылей, что даже научились вычислять процентный вклад каждой выдуманной структуры. Естественно, почти никакой информативной нагрузки, кроме интуитивной, информация о процентном вкладе не несёт, но немного успокаивает обеспокоенных сложностью мира трупоедов.
Забавно, что люди дошли до такого искуства строгания костылей, что даже научились вычислять процентный вклад каждой выдуманной структуры. Естественно, почти никакой информативной нагрузки, кроме интуитивной, информация о процентном вкладе не несёт, но немного успокаивает обеспокоенных сложностью мира трупоедов.
Ну вот например двe резонансные структуры (по ~50% каждая) всем известного озона:
Моим самым большим отрытием (топик по ссылке писал не я – честно-честно) до сих пор был синтез вот такой молекулы: R2SiFLi, которая, как утверждают говно теоретики, является на ~75% (R2SiF)- Li+ (формально anion) и на ~7% (R2Si:) FLi (формально silylene). Oстальные 18% распределены примерно поровну между ещё сотней-другой структур. Реагирует она кстати с равной охотой как первая и как вторая структура. То есть можно предположить, что при взаимодействии с реагентом А структура “коллапсирует” к одной, а с реагентом Б – ко второй. Открыл коробку с котегом вышеупомянутого с одной стороны – он жив, с другой – мёртв.
Конец химического вступления.
Похоже мотивы для принятия людьми того или иного решения или мнения можно описать подобным способом. Родился ребёнок открытый ко всем возможным мнениям – а потом подрос, столкнулся с А или Б – и коллапснул, да так – что не вытащишь. А способность к коллапсируемости/вытаскиваемости – (эпи)генетически обусловлена.
Или вот из другой области: противники политика Х говорят, что он сделал то, что сделал потому что хотел нобелевской премии мира/спасался от левацкого суда, а его сторонники – что он искренне заботился о благе страны и выполнял волю большинства народа. На самом деле правы и те и другие. Всё это (и ещё много чего) было в суперпозиции. А уж в каком процентном отношении – каждый решает сам. Между прочим из этого предположения следует, что если что-то из уравнения убрать – например упразднить нобелевскую премию, убрать вероятность преследования или как-то доказать, что блага не будет, будет один вред, а большинство народа против – решение в том самом виде вероятно принято не будет. И вообще любой человек при принятии любого решения руководствуется миллионом как сознательных так и подсознательных причин, находящимися в суперпозиции.
Или верующие учёные. С одной стороны им известно, что истина определяется только научным методом. Им также понятно, что существование высшей сущности никак научно не подтверждено и возможно не может быть подтверждено в принципе, что теоретически показана возможность существования вселенной без высшего разума, и что святое писание входит в противоречие с наблюдаемым миром. Но с другой стороны ” ” уже коллапснулось, и приходится их мозгам жить в суперпозиции науки и религии. Спросишь про науку – реагируют соответственно. Заговоришь про религию – другие отделы мозга работают. И друг другу не мешают.
Из этого описания может показаться, что мы по идее можем расчитать в каком случае какова будет реакция. В химии это так. Но в психологии совсем не факт, потому что выше всего этого вероятно стоит случайность, чьё влияние пока полностью не исключено.
РЕЗОНАНСА ТЕОРИЯ , теория
электронного строения хим. соединений, в основе к-рой лежит представление о
том, что электронное распределение, геометрия и все др. физ. и хим. св-ва молекул
должны быть описаны не одной возможной структурной ф-лой, а сочетанием (резонансом)
всех альтернативных структур. Идея такого способа описания электронного строения
принадлежит Л. Полингу (1928). Р. т. является развитием классич. теории хим.
строения для молекул, ионов, радикалов, строение к-рых можно представить в виде
неск. разл. структурных ф-л, отличающихся способом распределения электронных
пар между атомными ядрами. Согласно Р. т., строение таких соед. является промежуточным
между отдельными возможными классич. структурами, причем вклад каждой отдельной
структуры можно учесть при помощи разл. модификаций квантовомех. метода валентных
связей (см. Валентных связей метод).
Для соед. с сопряженными
связями из всех возможных структур с разложением типами спаривания электронов кратных
связей достаточно рассмотреть лишь структуры с неперекрещивающимися связями
(канонич. структуры). Электронное строение бензола описывается резонансом пяти
канонич. структур:
Волновая ф-ция молекулы
бензола по Полингу представляет линейную комбинацию:
Y
= 0,624(Y
I
+ Y
II) + 0,271(Y
III + Y
IV +
Y
V).
Откуда следует, что осн.
вклад (примерно 80%) в волновую ф-цию вносят кекулевские структуры I и II. Их
эквивалентность и эквивалентность структур III-V объясняют вырав-ненность всех
углерод-углеродных связей в молекуле бензола и их промежуточный (примерно полуторный)
характер между простой и двойной связями углерод-углерод. Это предсказание
находится в полном соответствии с экспериментально найденными длиной связи С-С
в бензоле (0,1397 нм) и св-вами симметрии его молекулы (группа симметрии D 6h).
Р. т. с успехом применяют
для описания строения и св-в ионов и радикалов. Так, строение карбонат-иона
представляют как резонанс (обозначается двусторонней стрелкой) трех структур,
каждая из к-рых вносит одинаковый вклад в волновую ф-цию:
Поэтому ион
обладает тригональной симметрией (группа
симметрии V 3h ), и каждая связь С-О имеет на
1 / 3 характер двойной связи.
Строение аллильного радикала
не соответствует ни одной из классич. структур VI и VII и должно описываться
их резонансом:
Спектр ЭПР аллильного радикала
свидетельствует о том, что неспаренный электрон не локализован ни на одной из
концевых метиленовых групп, а распределен между ними так, что радикал имеет
группу симметрии С 2h , причем энергетич. барьер вращения концевых
метиленовых групп (63 кДж/моль) имеет промежуточный значение между величинами, характерными
для барьеров вращения вокруг простой и двойной связи С-С.
В соед., включающих связи
между атомами с существенно разл. электроотрицательностями, значит. вклад в
волновую ф-цию вносят резонансные структуры ионного типа. Строение СО 2
в рамках Р. т. описывается резонансом трех структур:
Длина связи между атомами
С и О в этой молекуле меньше, чем длина двойной связи С=О.
Поляризация связей в молекуле
формамида, приводящая к потере мн. св-в, характерных для карбонильной группы,
объясняется резонансом:
Резонанс структур ведет
к стабилизации осн. состояния молекулы, иона или радикала. Мерой этой стабилизации
служит энергия резонанса, к-рая тем больше, чем больше число возможных резонансных
структур и чем больше число резонирующих низкоэнергетич. эквивалентных структур.
Энергию резонанса можно рассчитать при помощи метода валентных связей или метода
мол. орбиталей (см. Молекулярных орбиталей методы )как разность энергий
осн. состояния молекулы и ее изолир. связей или осн. состояния молекулы и структуры,
моделирующей одну из устойчивых резонансных форм.
По своей осн. идее Р. т.
очень близка к теории мезомерии (см. Мезомерия ), однако носит
более количеств. характер, ее символика вытекает непосредственно из классич.
структурной теории, а квантовомех. метод валентных связей служит прямым продолжением
Р. т. В силу этого Р. т. продолжает сохранять определенное значение как удобная
и наглядная система структурных представлений.
Лит.: Паулинг Л.,
Природа химической связи, пер. с англ., М.-Л., 1947; Уэланд Дж., Теория резонанса
и ее применение в органической химии, пер. с
англ., М., 1948; Полинг Л., “Ж. Весе. Хим. об-ва им. Д. И. Менделеева”,
1962 т. 7, № 4, с. 462-67. В. И. Минкин.
Полезные интернет ресурсы:
Основные положения координационной теории
В молекуле любого комплексного соединения один из ионов, обычно положительно заряженный занимает центральное положение и называется комплексообразователем или центральным ионом. Нельзя сказать, что комплексные соединения построены всегда из ионов; в деиствительности эффективные заряды атомов и молекул, входящих в состав комплекса, обычно невелики. Более правильно, поэтому, пользоваться термином центральный атом. Вокруг него в непосредственной близости расположено, или, как говорят, координировано некоторое число противоположно заряженных ионов или электронейтральных молекул, называемых лигандами (или аддендами ) и образующих внутреннюю координационную сферу . Число лигандов, окружающих центральный ион, называется координационным числом (кч.)
Внутренняя сфера комплекса в значительной степени сохраняет стабильность при растворении. Её границы обозначают квадратными скобками . Ионы, находящиеся во внешней сфере , в растворах легко отщепляются. Поэтому говорят, что во внутренней сфере ионы связаны неионогенно , а во внешней − ионогенно. Например:
Стрелки на схеме символически изображают координационные или донорно-акцепторные связи.
Простые лиганды, например H 2 O, NH 3 , CN – , и Сl – называются монодентантными, поскольку каждый из них способен образовывать только одну координационную связь (занимают во внутренней координационной сфере одно место). Существуют лиганды, образующие с центральным атомом 2 и более координационные связи. Такие лиганды называются би- и полидентантными. Примером бидентантных лигандов могут служить
оксалатный ион С 2 О 4 2- и молекула этилендиамина C 2 N 2 H 8
Способностью образовывать комплексные ионы обладают, как правило, d − элементы, но и не только; Al и B также образуют комплексные ионы. Комплексные ионы, образуемые d−элементами, могут быть электронейтральными, положительно или отрицательно заряженными:
В анионных комплексах для обозначения центрального атома металла используется его латинское название, а в катионных − русское.
Заряды, имеющиеся на комплексном ионе, делокализованы по всему иону. Для описания
химической связи в подобных ионах используется резонансная структура, представляющая собой гибрид из всевозможных распределений электронов. Различные распределения называются каноническими структурами.
Например, нитрат-ион имеет следующие канонические и резонансные структуры:
канонические структкры резонансная структура
Заряд комплексного иона равен алгебраической сумме заряда центрального атома и зарядов лигандов, например:
4- → заряд = (+2) + 6(-1) = -4
3+ → заряд = (+3) + 6(0) = +3
Некоторые лиганды способны образовывать циклические структуры с центральным атомом. Это свойство лигандов называется их хелатообразующей способностью, а образуемые такими лигандами соединения называются хелатными соединениями (клешневидными). Они содержат би- и полидентантный лиганд, который как бы захватывает центральный атом подобно клешням рака:
К группе хелатов относятся и внутрикомплексные соединения, в которых центральный атом входит в состав цикла, образуя ковалентные связи с лигандами разными способами донорно-акцепторным и за счёт неспаренных электронов (обменный механизм). Комплексы такого рода характерны для аминокислот. Так, глицин (аминоуксусная кислота) образует хелаты с ионами Cu 2+ , Pt 2+ , Rh 3+ , например:
металла при крашении и изготовлении цветной пленки. Большое применение они находят в аналитической химии, велико их место и в природе. Так, гемоглобин состоит из комплекса-гема, связанного с белком-глобином. В геме центральным ионом является Fe +2 , вокруг которого координированы 4 атома азота, принадлежащие к сложному лиганду с циклическими группировками. Гемоглобин обратимо присоединяет кислород и доставляет его из легких по кровеносной системе ко всем тканям.
Хлорофилл, участвующий в процессах фотосинтеза в растениях, построен аналогично, но в качестве центрального иона, содержит Mg 2+ .
Заряд центрального иона (точнее степень окисления центрального атома) является основным фактором, влияющим на координационное число.
| +1 +2 +3 +4 | → → → → | 4;6 6;4 |
Красным отмечены наиболее часто встречающиеся координационные числа. Координационное число не является неизменной величиной для данного комплексообразователя, а обусловлено также и природой лиганда, его электронными свойствами. Даже для одних и тех же комплексообразователей или лигандов координационное число зависит от агрегатного состояния, от концентрации компонентов и температуры раствора.
Геометрическая форма комплексного иона зависит от координационного числа его центрального атома. Комплексы с кч = 2 имеют линейную структуру, с кч = 4 –обычно тетраэдрическую, однако некоторые комплексы с кч = 4 имеют плоскую квадратную структуру. Комплексные ионы с кч = 6 чаще всего имеют октаэдрическую структуру.
кч = 2 кч = 4 кч = 4
кч=6
Иногда можно записать несколько правильных формул Льюиса, которые различаются характером связей между одними и теми же атомами. Например:
В каждом случае существует два пути выполнения правила октета для всех атомов. Если молекулу можно представить двумя или более такими формулами, в которых атомы соединены в одной и той же последовательности, эти формулы называются резонансными формами или классическими резонансными структурами.
Резонансные структуры принято соединять обоюдоострыми стрелками, как это сделано выше.
Реальная структура частицы не совпадает ни с одной из резонансных структур. Не происходит и непрерьюного превращения одной структуры в другую и обратно. На самом деле истинная структура есть нечто среднее между двумя предельными формами. Эта реальная структура носит название резонансного гибрида.
В первом случае резонансный гибрид к первой структуре значительно ближе, чем ко второй. Однако реальная молекула имеет и некоторые черты второй структуры с зарядами на атомах азота и кислорода. В двух Других случаях обе предельные структуры вносят одинаковый вклад в резонансный гибрид. Кратность связей в обоих случаях равна Все три резонансных гибрида изображены ниже (пунктирными линиями показаны частично двойные связи):
Соединения, для которых возможны резонансные структуры, обычно более стабильны. Скажем, во втором примере отрицательный заряд распределен по двум атомам кислорода, а не сконцентрирован только на одном из них. Такая делокализация заряда является стабилизирующим фактором. В первом примере связь ведет себя не как обычная простая связь, а электронная пара атома азота не склонна участвовать в образовании новых связей. Наличие второй (правой) резонансной структуры объясняет эти факты.
Вообще надо помнить, что польза любой теории определяется способностью этой теории объяснять уже известные факты и предсказывать новые.
Резонанс – это делокализация электронов внутри ковалентно связанной частицы, приводящая к дополнительной стабилизации этой частицы. Резонанс изображается с помощью резонансных структур, соединяемых обоюдоострыми стрелками или с помощью резонансных гибридов.
Теория резонанса – теория электронного строения химических соединений, в соответствии с которой распределение электронов в молекулах (в том числе сложных ионах или радикалах), является комбинацией (резонансом) канонических структур с различной конфигурацией двухэлектронных ковалентных связей . Резонансная волновая функция , описывающая электронную структуру молекулы, является линейной комбинацией волновых функций канонических структур .
Иными словами, молекулярная структура описывается не одной возможной структурной формулой, а сочетанием (резонансом) всех альтернативных структур. Теория резонанса – это способ посредством химической терминологии и классических структурных формул визуализировать чисто математическую процедуру построения приближенной волновой функции сложной молекулы.
Следствием резонанса канонических структур является стабилизация основного состояния молекулы; мерой такой резонансной стабилизации является энергия резонанса – разность между наблюдаемой энергией основного состояния молекулы и расчетной энергией основного состояния канонической структуры с минимальной энергией . С позиций квантовой механики это означает, что более сложная волновая функция, представляющая собой линейную комбинацию волновых функций, каждая из которых соответствует одной из канонических структур, точнее описывает молекулу, чем волновая функция структуры с минимальной энергией.
Энциклопедичный YouTube
1 / 3
Теория Резонанса
Резонансные структуры, часть I
Мезомерный эффект (эффект сопряжения). Часть 1.
Субтитры
Нарисуем молекулу бензола. И подумаем, какие интересные для нас процессы происходят в этой молекуле. Итак, бензол. В цикле шесть атомов углерода. Первый, второй, третий, четвертый, пятый и шестой углероды в цикле. Что делает бензол таким особенным? Что отличает его от циклогексана? Конечно же, речь идет о трех двойных связях в цикле. Будем считать, что двойной связью соединены эти два углерода, между этими атомами также двойная связь, как и между этими углеродами. Водороды нарисуем только для того, чтобы помнить, что они вообще здесь есть. Нарисуем их едва заметными. Итак, сколько водородов будет присоединено к этому углероду? Один, два, три валентных электрона уже задействованы. А потому углерод связан только с один водородом. Здесь все тоже самое. Только один водород. Всего четыре валентных электрона. Здесь аналогично. Думаю, вы уже поняли систему. Всего у каждого углерода три связи с атомами углерода: две одинарные связи с двумя атомами углерода и еще одна двойная связь. Соответственно, четвертая связь образуется с водородом. Давайте я нарисую здесь все атомы водорода. Изобразим их темным цветом, чтобы они нас не отвлекали. Вот теперь мы нарисовали бензол. В будущем мы еще не раз с ним столкнемся. Но в этом видео мы рассмотрим или, по крайней мере, попытаемся рассмотреть любопытное свойство бензола, и это, конечно же, резонанс. Это свойство не конкретно бензола, это свойство многих органических молекул. Просто бензол из них, пожалуй, самый занятный. Итак, давайте поразмыслим, что такого может происходить с этой молекулой. Начнем с этого электрона. Выделим его другим цветом. Выберем для этого электрона синий. Итак, вот этот электрон. Что, если этот электрон сместится к этому углероду? У этого углерода связь не разрывается, он сохраняет электрон, который просто переместится сюда. Итак, этот электрон сместился сюда. Теперь у этого углерода появился ненужный пятый электрон. Следовательно, один электрон сместился сюда. Теперь у этого углерода пять электронов. А потому этот электрон вернется к первоначальному атому углерода, который потерял первый электрон. В итоге все атомы углерода остались при своем. Если это произойдет, то мы получим структуру, которая выглядит вот так. Нарисую двойную стрелку, так как процесс может протекать в обоих направлениях. Начнем с углеродной цепочки. Итак, первый углерод, второй, третий, четвертый, пятый и, наконец, шестой углерод. На рисунке слева двойная связь была здесь, значит теперь она сдвинулась сюда. Давайте нарисуем эту двойную связь синим цветом, чтобы подчеркнуть разницу. Теперь двойная связь здесь. Этот синий электрон сместился сюда. Этот синий электрон сместился наверх. Давайте изобразим их разными цветами, для большей наглядности. Скажем, этот электрон будет зеленым. Зеленый электрон мигрировал с этого атома углерода на этот атом углерода. Мы можем представить как это произошло. Теперь рассмотрим этот пурпурный электрон, который был у этого атома углерода, но теперь сместился и перешел к другому углероду сюда. Соответственно, двойная связь также сместилась, на что нам указывает эта стрелка. Осталось рассмотреть синий электрон. Этот синий электрон смещается к первому углероду. А двойная связь, в свою очередь, смещается сюда. Естественно, мы получили две очень и очень схожих молекулы. На самом деле это та же молекула, только перевернутая. Нас больше должно интересовать то, что эти двойные связи постепенно перемещаются то туда, то обратно, образуя то эту структуру, то эту. И они делают это все время. Двойные связи постоянно двигаются. И реальность бензола такова, что ни одна из этих структур не отображает то, что происходит в действительности. Бензол находится в неком переходном состоянии. Реальная структура бензола выглядит скорее вот так. Я сейчас не буду рисовать углероды и водороды. Давайте, разве что, нарисуем водороды вот здесь, раз уж я начал их изображать на первом рисунке. Итак, водороды рисуем здесь. Не забываем о них. Хотя наличие этих водородов всегда подразумевается. Закончили с водородами. Повторюсь, на примере этого кольца мы можем не рисовать углероды и водороды, поскольку они подразумеваются. Итак, реальная структура бензола находится между этой и этой. И в действительности, между каждым углеродом будет по половине двойной связи. То есть на самом деле, структура выглядит как-то так. Здесь будет половина двойной связи, здесь половина двойной связи, здесь половина двойной связи, здесь тоже самое и здесь половина двойной связи. Почти закончили. И вот тут половина двойной связи. В действительности, в молекуле бензола электроны постоянно перемещаются по всему кольцу. И я не имею ввиду переход от одной структуры к другой. Настоящая структура, энергия которой минимальна, представлена вот здесь. Итак, эти структуры Льюиса, хотя, правильнее было бы назвать их каноническими структурами, потому что я нарисовал не все электроны. Мы часто рисуем бензол подобным образом, когда, например, рассматриваем механизм. Но важно понимать, что в результате резонанса этих двух структур, мы получаем переходную структуру, которая и соответствует действительности. Подобное происходит не только с бензолом. Можно привести большое количество примеров. Но мы разберем еще один, чтобы набить руку. Возьмем карбонат-ион. Довольно яркий пример для демонстрации резонансных структур. Итак, карбонат-ион. Углерод соединен двойной связью с одним из атомов кислорода и двумя одинарными связями с другими атомами кислорода. И у этих двух кислородов есть дополнительные электроны. У этого атома кислорода будет один, два, три, четыре пять, шесть валентных… На самом деле, конечно же, семь валентных электронов. Давайте еще раз. Один, два, три, четыре, пять, шесть, семь валентных электронов. И один дополнительный электрон приводит к возникновению отрицательного заряда. Тоже самое справедливо для этого атома. У него один, два, три, четыре, пять, шесть, семь валентных электронов. Один лишний. Значит будет отрицательный заряд. Давайте присмотримся повнимательнее к этой резонансной структуре или же канонической структуре. Как мы уже заметили, этот кислород нейтральный. И у него шесть валентных электронов. Один, два, три, четыре, пять, шесть. Представим себе, что один из этих электронов перейдет к углероду, в результате чего углерод передаст свой электрон верхнему кислороду. Итак, мы можем вообразить ситуацию, в которой этот электрон сместится вот сюда к углероду. И когда углерод получит еще один электрон, то одновременно с этим, атом углерода передаст свой электрон верхнему кислороду, вот сюда. Как изменится структура, если произойдет такой процесс? Итак, если электроны переместятся подобным образом, то вот, что мы увидим. Начнем с углерода. Теперь у углерода здесь только одинарная связь. Здесь рисуем кислород. У кислорода шесть валентных электронов. Один, два, три, четыре, пять, шесть электронов. Но теперь у него появился еще один, вот этот синий. Итак, поскольку у кислорода теперь появился дополнительный седьмой электрон, мы рисуем у кислорода отрицательный заряд. Вот этот кислород, который отдал свой электрон углероду, образует с атомом углерода двойную связь. Нарисуем новую связь вот таким цветом. Итак, двойная связь углерода с этим кислородом внизу. Один электрон кислород отдал, так что у него теперь шесть валентных электронов. Один, два, три, четыре, пять, шесть. И теперь заряд у кислорода нейтральный. С этим кислородом слева ничего не произошло. Поэтому просто скопируем и вставим его. Сначала копируем, а теперь вставляем. Этот кислород остается здесь. Представим ситуацию, при которой вот этот кислород с дополнительным электроном, который, в свою очередь, мог прийти от другого кислорода сверху, будет отдавать свой дополнительный электрон атому углерода. И тогда углерод разорвет двойную связь с другим кислородом. В данном случае вот с этим. Давайте я нарисую это. Возможно ситуация, в которой этот электрон перейдет к углероду… Сформируется двойная связь. И затем углерод отдаст один из своих электронов. Вот этот электрон вернется обратно к кислороду. Что же получится? Если это произойдет, конечная структура будет выглядеть вот так. Начнем с углерода, связанного одинарной связью с кислородом, у которого один, два, три, четыре, пять, шесть, семь валентных электронов. Здесь все по-прежнему. Вы можете назвать это резонансной реакцией, а можете назвать иначе. Здесь по-прежнему отрицательный заряд. Перейдем к этому кислороду. Он вернул себе электрон. И теперь у него опять семь валентных электронов. Один, два, три, четыре, пять, шесть, семь валентных электронов снова. Давайте обозначим тот электрон, который вернулся к кислороду. Сделаем его фиолетовым. И теперь у кислорода отрицательный заряд. Этот кислород, в свою очередь, отдал электрон углероду. И он сформировал новую двойную связь. Вот двойная связь этого кислорода с углеродом. Один электрон кислород отдал, поэтому у него теперь один, два, три, четыре, пять, шесть валентных электронов и нейтральный заряд. Все эти структуры переходят друг в друга. Мы даже можем получить из этой эту структуру. Начав с одной из этих структур, мы можем получить любую другую. Именно это в карбонат-ионе и происходит. Давайте я запишу, что это карбонат-ион. Итак, реальная его структура представляет из себя нечто среднее между этими тремя. Структура карбонат-ион в действительности выглядит вот так. Здесь углерод, связанный с тремя кислородами. Между каждым из трех кислородов и углеродом рисуем связь. И затем еще каждая связь C-O будет иметь на одну треть характер двойной связи. Одна треть связи. Не совсем привычная запись, но максимально приближенная к реальности. Треть всего времени электрон будет находиться здесь. Оставшиеся две трети времени атомы кислорода поровну будут владеть этим электроном. Считается, что у каждого кислорода заряд −2/3. Обычно, конечно же, рисуют одну из этих структур, потому что целыми числами оперировать удобно. Но в действительности карбонат-ионы подвержены резонансу. Электроны, на самом деле, постоянно перемещаются от одной С-О связи к другой. Это и делает молекулу более стабильной. Энергия этой структуры меньше энергии любой из тех, что приведены выше. Тоже самое справедливо и для бензола. Энергия вот этой переходной структуры ниже энергии любой из этих, и потому такая форма бензола стабильнее тех, что нарисованы выше. Subtitles by the Amara.org community
История
Идея резонанса был введена в квантовую механику Вернером Гейзенбергом в 1926 году при обсуждении квантовых состояний атома гелия . Он сравнил структуру атома гелия с классической системой резонирующего гармонического осциллятора .
Модель Гейзенберга была применена Лайнусом Полингом (1928 год) к описанию электронной структуры молекулярных структур. В рамках метода валентных схем Полинг успешно объяснил геометрию и физико-химические свойства целого ряда молекул через механизм делокализации электронной плотности π-связей.
Сходные идеи для описания электронной структуры ароматических соединений были предложены Кристофером Ингольдом . В 1926-1934 годах Ингольд заложил основы физической органической химии, развив альтернативную теорию электронных смещений (теорию мезомерии), призванную объяснить структуру молекул сложных органических соединений, не укладывающуюся в обычные валентные представления. Предложенный Ингольдом для обозначения явления делокализации электронной плотности термин «мезомеризм » (1938), используется преиущественно в немецкой и французской литературе, а английской и русской преобладает «резонанс ». Представления Ингольда о мезомерном эффекте стали важной составной частью теории резонанса. Благодаря немецкому химику Фрицу Арндту были введены, ставшие общепринятыми обозначения мезомерных структур при помощи двунаправленных стрелок.
СССР 40-50 гг.
В послевоенном СССР теория резонанса стала объектом гонения в рамках идеологических кампаний и была объявлена «идеалистической», чуждой диалектическому материализму – и поэтому неприемлемой для использования в науке и образовании:
«Теория резонанса», будучи идеалистической и агностической, противостоит материалистической теории Бутлерова, как несовместимая и непримиримая с ней;… сторонники «теории резонанса» игнорировали её и извращали её существо. «Теория резонанса», будучи насквозь механистической. отрицает качественные, специфические особенности органического вещества и совершенно ложно пытается сводить закономерности органической химии к закономерностям квантовой механики…
…Мезомерийно-резонансная теория в органической химии представляет собою такое же проявление общей реакционной идеологии, как и вейсманизм-морганизм в биологии, как и современный «физический» идеализм, с которыми она тесно связана.
Хотя гонения на теорию резонанса иногда называют «лысенковщиной в химии», история этих гонений имеет ряд отличий от гонений на генетику в биологии . Как отмечает Лорен Грэхэм : «Химики сумели отразить эту серьёзную атаку. Модификации теории носили скорее терминологический характер». В 50-х гг. химики, не опровергая критики теории резонанса, развивали аналогичные теоретические (в том числе – квантовохимические) построения, используя термин «
Способ измерения коэффициента затухания акустических волн в резонаторной структуре и ее добротности
Изобретение относится к области измерительной техники и может быть использовано при физических исследованиях механизмов затухания акустических волн в твердых телах и в технике при разработке и производстве акустических ВЧ и СВЧ резонаторов и фильтров.
Известен эхо – метод измерения затухания акустических волн в твердых телах (Р.Труэлл, Ч.Эльбаум, Б.Чик, Ультразвуковые методы в физике твердого тела. Издательство «Мир», Москва, 1972, глава 2). Этот метод основан на измерении и сравнении амплитуд акустических волн, совершающих многократные пробеги по кристаллу с плоскопараллельными отражающими гранями, с последующим вычислением коэффициента затухания. Недостаток метода – необходимость в использовании достаточно длинных образцов – от единиц мм до нескольких см, что необходимо для надежного временного разделения эхоимпульсов.
Известен способ измерения добротности резонатора (Патент РФ RU 2312368 (С2), дата публикации 2007.12.10). В этом способе измерения добротности в резонаторе возбуждают колебания с линейно изменяющейся частотой, измеряют резонансную частоту и ширину резонансной кривой на уровне половинной мощности и определяют добротность. Метод отличается тем, что при измерениях контролируют моменты равенства амплитуды колебаний в резонаторе ее заданному пороговому значению, меняют в эти моменты направление изменения частоты сигнала возбуждения на противоположное и измеряют среднюю частоту сигнала возбуждения fcp и частоту модуляции этого сигнала fм, а добротность резонатора определяют по формуле Q=Kfcpfм, где K – постоянный коэффициент. Недостаток метода состоит в необходимости создания для его реализации специализированной установки с достаточно сложным электронным узлом управления параметрами зондирующего сигнала, а также подбора коэффициента K.
При исследовании свойств пьезоэлектрических резонаторов, обладающих частотами резонанса и антирезонанса, для измерения добротности используется весьма точный, но технически громоздкий метод (С.Г.Алексеев, Г.Д.Мансфельд, Простой способ измерения добротности и затухания в акустических резонаторах. // Радиотехника и электроника. 2008. Т.53. №1, С.122). Он включает следующую последовательность действий: измеряют частотные зависимости действительной и мнимой частей электрического импеданса структуры, из измеренных значений импеданса в частотном промежутке между обертонами экстраполяцией находят значения импеданса, задаваемого емкостью преобразователя, эти значения вычитают из исходного массива экспериментальных данных. Результат вычитания в точности соответствует резонансным кривым соответствующего параллельного колебательного контура в электрической эквивалентной схеме резонатора. Далее полосу пропускания и, соответственно, добротность Q находят по уровню половинной мощности модуля импеданса этого контура, или по крутизне его фазово-частотной характеристики на резонансной частоте f. Зная добротность, коэффициент поглощения акустических волн в структуре находят стандартным способом по формуле α=πf/Q.
Наиболее близким к заявленному техническому решению (прототипом) является способ измерения коэффициента затухания акустических волн и добротности в резонаторной структуре, основанный на измерении разности Δn(φ) между частотами экстремумов на фазово-частотной характеристике коэффициента отражения электромагнитных волн от резонаторной структуры или пьезоэлектрического, например, кварцевого, резонатора (G.D.Mansfeld, A.D.Freik, M.Mourey Characterization of losses in quartz resonator using electromagnetic wave reflection coefficient measurements, Proc. Of European Frequency and Time Forum EFTF-95, 8-10 March, 1995, Besancon, France, Actes Proc., p.20-23).
Для определения добротности Qn и коэффициента затухания αn на частоте резонанса (или обертона с номером n) fn измеряют частотную зависимость фазы коэффициента отражения электромагнитной волны от резонаторной структуры, на частоте возбуждаемого в структуре обертона фиксируют частоты, соответствующие экстремумам на этой характеристике, и вычисляют разность Δn(φ) между этими частотами, измеряют частотную зависимость модуля импеданса для того же номера обертона и фиксируют величину сопротивления в точке минимума на кривой, которая равна последовательному сопротивлению резонаторной структуры Rn. Затем вычисляют добротность по формуле
где R – волновое сопротивление измерительного тракта.
В случае выражение для Qn упрощается:
При этом коэффициент затухания волн в структуре может быть определен по приближенной формуле:
αn≈π·Δfn(φ)
Недостатками прототипа являются:
– Недостаточно высокая точность измерений, поскольку на величину Rn могут влиять паразитные сопротивления подводящих проводов и электродов;
– Ограниченность метода – этот способ неприменим, в частности, для измерении при , что как раз часто имеет место на достаточно высоких частотах;
– Необходимость дополнительно измерять частотную характеристику модуля электрического импеданса структуры.
Целью изобретения является повышение точности измерения величины коэффициента поглощения акустических волн и добротности в резонаторных структурах на объемных акустических волнах, расширение области частот измерений, а также упрощение способа.
Данная цель достигается тем, что в предлагаемом способе измерения коэффициента поглощения акустических волн в резонаторной структуре и ее добротности, основанном на измерении частотной характеристики электрического импеданса резонаторной структуры, измеряют частотную зависимость мнимой части ее электрического импеданса для выбранного номера обертона, фиксируют положения экстремумов на измеренной зависимости, вычисляют разность между частотами экстремумов Δn(Im z). Затем производят вычисления коэффициента затухания αn и добротности Qn на частоте fn обертона с номером n по формулам:
αn=π·Δfn(Im z)
Здесь fn – частота обертона с номером n.
Новым в предложенном способе по сравнению с прототипом является измерение разности Δf(Imz) между частотами экстремумов на частотных зависимостях мнимой части электрического импеданса и определение Qn и αn по формулам, адекватно описывающим работу тонких слоев и пленок в резонаторной структуре.
Фиг.1 – структура составного акустического резонатора на объемных акустических волнах, состоящего из пластины – подложки (1) толщиной d, электродов (3, 4) толщиной t, пьезоэлектрика (2) толщиной l.
Фиг.2 – частотная зависимость модуля импеданса резонатора с резонансами и антирезонансами. n-1, n, n+1 – номера обертонов.
и – частоты резонанса и антирезонанса для обертона с номером n.
Фиг.3 – частотная характеристика мнимой части входного электрического импеданса резонаторной структуры. Δfn-1(Imz) и Δfn(Im z), Δfn+1(Im z) – разности частот между экстремумами на обертонах с номерами n-1, n, n+1.
и – частоты экстремумов для обертона с номером n.
Фиг.4 – пример экспериментальной частотной зависимости мнимой части электрического импеданса. f1 и f2 – частоты экстремумов для выбранного обертона.
Сущность изобретения состоит в следующем. С помощью электроакустического преобразователя, образованного пьезоэлектрической пленкой и электродами, в резонаторной структуре, показанной на Фиг.1, возбуждаются и регистрируются акустические волны. В случае, когда набег фазы акустической волны равен nπ, где n – целое число, амплитуды всех отраженных волн складываются в фазе, и имеет место стоячая акустическая волна, т.е. возникает резонанс. Спектр собственных резонансных частот структуры оказывается многочастотным, как это видно на частотной характеристике модуля импеданса, показанной на Фиг.2. Резонансы расположены в частотной области почти эквидистантно. Обычно резонансные пики наблюдаются в широком интервале частот, от долей до нескольких ГГц. В гигагерцовом диапазоне при толщине резонатора порядка единиц мм номера обертонов доходят до нескольких сотен и даже тысяч.
Выражения, используемые для вычисления коэффициента затухания акустических волн и связанной с ним добротности, получаются из анализа формул для входного электрического импеданса резонатора Ze, описывающего его уточненную полную эквивалентную схему (Т.Д.Мансфельд, С.Г.Алексеев, Н.И.Ползикова, Эквивалентная электрическая схема составного акустического резонатора для радиотехнических устройств СВЧ-диапазона, Акустический журнал, №4, том 54, год 2008, стр.552-558).
где
r=1+cosωnl/νl+sin(ωnl/νl+2ωnt/νt)
y=sinβl·(1-cos(ωnl/νl+2ωnt/νt))/πN,
ω=2πf – частота, N – номер обертона, ωn=2πfn – частота обертона с номером N, l – толщина пленки пьезоэлектрика, t – толщина верхнего электрода, С0 – статическая электрическая емкость между электродами, β – волновой вектор для волны в пьезоэлектрической пленке, νl и νt – скорости акустических волн в материалах электрода и пьезоэлектрической пленки, соответственно, Qn – добротность резонатора на частоте обертона с номером N, – эффективная константа электромеханической связи на частоте обертона.
Исследуя частотную зависимость мнимой части входного электрического импеданса на минимум и максимум, можно найти выражения для соответствующих частот и и затем найти их разности
Опуская громоздкие выкладки, приведем окончательные выражения для коэффициента поглощения акустических волн:
Используя стандартную связь между коэффициентом поглощения акустических волн и добротностью, получим:
Типичный ход частотной зависимости мнимой части импеданса, содержащей упомянутые экстремумы, показан на Фиг.3.
Способ осуществляется следующим образом. Электроды резонаторной структуры, содержащие пьезоэлектрическую пленку или пьезоэлектрический слой, подключаются к векторному измерителю импеданса, позволяющему измерять мнимую часть ее электрического импеданса. На экране прибора наблюдается частотная зависимость мнимой части электрического импеданса, как показано на Фиг.3. Из этой частотной зависимости находятся значения частот, соответствующих экстремумам. Вычисляется разность этих частот Δn(Im z). Далее с помощью вышеприведенных формул вычисляют αn и Qn
Пример реализации способа
Производились измерения добротности и коэффициента затухания для резонаторной структуры, схематически показанной на Фиг.1 со следующими размерами: толщина подложки из лангасита – 745 мкм, толщина пленки окиси цинка – 0.82 мкм, толщина электродов из алюминия – 150 нм, диаметр электродов – 150 мкм. Измерения производились с помощью СВЧ анализатора цепей HP 8753ES.
На Фиг.4 показан пример экспериментальной частотной зависимости мнимой части электрического импеданса структуры.
Получены следующие результаты: на частоте f=ω/2π=399900 кГц измеренная разность между частотами экстремумов мнимой части импеданса Δf=f2-f1=369,375кГц, коэффициент затухания, выраженный в дБ/мкс, равен α=8,68πΔf(Im Ze,) (МГц)=8,68·π·0,369375=9.95 дБ/мкс, соответственно, вычисленное значение добротности:
Значение добротности, полученное методом, описанным в работе С.Г.Алексеева, Г.Д.Мансфельда (Простой способ измерения добротности и затухания в акустических резонаторах. // Радиотехника и электроника. 2008. Т.53. №1, С.122), являющимся точным, но весьма технически сложным и громоздким, равно 10830. Таким образом, данные, полученные известным и предлагаемым способами, практически совпадают. В то же время способ-прототип оказывается вообще неприменимым, поскольку Rn составляет единицы Ом, a R=50 Ом, и условие применимости метода не выполняется.
Таким образом, технический результат предлагаемого изобретения заключается в повышении точности измерения поглощения и добротности в резонаторных структурах, обеспечении возможности измерений в более широком диапазоне частот и существенном упрощении способа, поскольку при использовании предлагаемого способа снимаются какие-либо ограничения на соотношение между Rn и R.
Предлагаемый способ позволяет проводить измерения в тонких слоях, когда прямое использование эхометода наталкивается на технические трудности.
Способ измерения коэффициента затухания акустических волн в резонаторной структуре и ее добротности, основанный на измерении частотной зависимости импеданса резонаторной структуры, отличающийся тем, что измеряют частотную зависимость мнимой части электрического импеданса структуры для выбранного номера обертона, фиксируют положения экстремумов на измеренной зависимости, вычисляют разность между частотами экстремумов Δf(Imz) и вычисляют значения коэффициента затухания α и добротности Q на частоте f обертона с номером n по формулам:α=π·Δf(Imz), где – разность между частотами экстремумов и на частотных зависимостях мнимой части импеданса, f – частота обертона с номером n.Новые резонаторные структуры для применения гребенчатых фильтров: WestminsterResearch
Настройка характеристик фильтра с помощью резонаторов на основе графена
Илич, А.З., Буквич, Б.М., Будимир, Д. и Илич, М.М. 2019. Настройка отклика фильтров с помощью резонаторов на основе графена. ICEAA (Международная конференция по электромагнетизму в передовых приложениях) – IEEE APWC (Тематическая конференция IEEE-APS по антеннам и распространению в беспроводной связи. Гранада, Испания 09-13 сентября 2019 IEEE.
Недорогие гибридные полосовые фильтры с волноводом и вставным диэлектриком, напечатанным на 3D-принтере
Янкович, У., Мохоттиге, Н., Басу, А. и Будимир, Д. 2019. Недорогие гибридные полосовые фильтры с волноводом с 3D-печатью Вставьте диэлектрик. European Microwave Conference (EuMC2019), часть European Microwave Week (EuMW2019). Париж, Франция 29 сентября – 4 октября 2019 г. IEEE.
Влияние сигналов 5G на производительность выпрямителя сбора энергии
Olukoya, O., Млачич, Б. и Будимир, Д. 2019. Влияние форм волны 5G на производительность выпрямителя, собирающего энергию. IEEE MTT-S Wireless Power Transfer Conference (WPTC), часть Wireless Power Week (WPW2019). Лондон, Великобритания 17–21 июня 2019 г., IEEE. https://doi.org/10.1109/WPTC45513.2019.
35
Оценка кандидатов формы сигнала для беспроводной связи 5G
Олукойя, О. и Будимир, Д. 2019. Оценка кандидатов формы сигнала для беспроводной связи 5G. Европейская микроволновая конференция в Центральной Европе (EuMCE2019). Прага 13-15 мая 2019 IEEE.
Методология проектирования графеновых настраиваемых фильтров на частотах субмиллиметровых волн
Илич, А.З., Буквич, Б.М., Будимир, Д. и Илич, М.М. 2019. Методика проектирования графеновых перестраиваемых фильтров субмиллиметрового диапазона частот. Твердотельная электроника. 157, стр. 34-41. https://doi.org/10.1016/j.sse.2019.04.003
Миниатюрные квадратурные гибридные муфты на основе новых U-образных линий передачи
Olukoya, O., Илич А.З., Басу А. и Будимир Д. 2019. Миниатюрные квадратурные гибридные ответвители на основе новых U-образных линий передачи. Письма о микроволновых и оптических технологиях. 61 (2), стр. 509-512. https://doi.org/10.1002/mop.31555
Планарные переходы коаксиальных линий с интегрированной подложкой в однослойные линии передачи и волноводы
Янкович, У., Басу, А. и Будимир, Д. 2018. Интегрированная подложка Планарные переходы коаксиальных линий в однослойные линии передачи и волноводы.Будимир Д. (ред.) IEEE MTT-S International Microwave and RF Conference (IMaRC2018). Калькутта, Индия, 28-30 ноября 2018 г., IEEE.
Влияние нелинейности выпрямителя на беспроводные системы 4G и 5G
Олукойя, О. и Будимир, Д. 2018. Влияние нелинейности выпрямителя на беспроводные системы 4G и 5G. Будимир, Д. (ред.) IEEE MTT-S International Microwave and RF Conference (IMaRC2018). Калькутта, Индия, 28-30 ноября 2018 г., IEEE.
Выпрямители на основе квадратурного гибридного ответвителя с улучшенными характеристиками для сбора энергии
Unich, G., Олукойя, О. и Будимир, Д. 2018. Выпрямители на основе квадратурного гибридного соединителя с улучшенными характеристиками для сбора энергии. IEEE Wireless Power Transfer Conference (WPTC2018). Монреаль, Квебек, Канада. 07 июн – 03 июл 2018 IEEE. https://doi.org/10.1109/WPT.2018.8639267
Широкополосный датчик с широкополосным зондовым датчиком на основе полностью плоской подложки
Янкович, У. и Будимир, Д. 2018. Полностью плоский субстрат, интегрированный широкополосный зондовый режим Преобразователь. 12-я Европейская конференция по антеннам и распространению радиоволн (EUCAP2018). Excel, Лондон, Великобритания, 9–13 апреля 2018 г. IEEE. https://doi.org/10.1049/cp.2018.0427
Импульсный отклик с исследованием корреляции широкополосной изогнутой носимой монопольной антенны
Захран, С.Р., Абдалла, М.А., Будимир, Д. 2018. Импульсный отклик с корреляционным исследованием Широкополосная изогнутая носимая монопольная антенна. 12-я Европейская конференция по антеннам и распространению радиоволн (EUCAP). Excel, Лондон, 09–13 апреля 2018 г., IEEE.https://doi.org/10.1049/cp.2018.1216
Высокоэффективные сбалансированные усилители мощности для приложений 4G
Олукойя О., Кодогианнис В. и Будимир Д. 2018. Высокоэффективные сбалансированные усилители мощности для приложений 4G . 41-я Международная конференция по телекоммуникациям и обработке сигналов. Афины, 4–6 июля 2018 г., IEEE. https://doi.org/10.1109/TSP.2018.8441354
Высокоэффективные симметричные усилители мощности для агрегации несущих
Olukoya, O.и Будимир, Д. 2018. Высокоэффективные сбалансированные усилители мощности для агрегирования несущих. Письма о микроволновых и оптических технологиях. 60 (3), стр. 529-534. https://doi.org/10.1002/mop.31014
Адаптивная система с нечеткой логикой для компенсации нелинейных искажений в беспроводных усилителях мощности
Кодогианнис В., Васкович М. и Будимир Д. 2018. An Адаптивная система нечеткой логики для компенсации нелинейных искажений в беспроводных усилителях мощности. Нейронные вычисления и приложения. 30 (8), с. 2539–2554. https://doi.org/10.1007/s00521-017-2849-3
Гибридные волноводные резонаторы и фильтры для миллиметровых волн
Янкович У., Мохоттиге Н., Глубоков О. и Будимир, D. 2017. Гибридные волноводные резонаторы и фильтры для миллиметровых волн. 2017 Серия международных семинаров по СВЧ IEEE MTT-S по усовершенствованным материалам и процессам для приложений RF и THz. Павия, Италия, 22–24 сентября 2017 г., IEEE. https: // doi.org / 10.1109 / IMWS-AMP.2017.8247360
Спаренные линии передачи CRLH для компактных и высокоселективных полосовых фильтров
Ибрагим, А.А., Абдалла, Массачусетс, и Будимир, Д. 2017. Спаренные линии передачи CRLH для компактных полосовых фильтров с высокой избирательностью . Письма о микроволновых и оптических технологиях. 59 (6), стр. 1248-1251. https://doi.org/10.1002/mop.30518
Миниатюрные квадратурные гибридные ответвители для струйной печати для многодиапазонных беспроводных систем
Olukoya, O., Tarczynski, A. и Budimir, D. 2017. Миниатюрные квадратурные гибридные ответвители для многополосных беспроводных систем, напечатанные на струйной печати. 2017 Симпозиум IEEE AP-S по антеннам и распространению радиоволн и конференция USNC-URSI Radio Science Meeting. Сан-Диего, Калифорния, США, 09–14 июля 2017 г. IEEE. https://doi.org/10.1109/USNC-URSI.2017.8074908
Конструкция монопольных антенн для приложений СШП
Ахмад, В., Тарчинский, А. и Будимир, Д. 2017. Проектирование монопольных антенн для приложений СШП . 2017 Симпозиум IEEE AP-S по антеннам и распространению радиоволн и конференция USNC-URSI Radio Science Meeting (APS2017). Сан-Диего, Калифорния, США, 09–14 июля 2017 г. IEEE. https://doi.org/10.1109/APUSNCURSINRSM.2017.8073204
СШП-фильтры с двойной полосой пропускания для диапазонов WiMAX и WLAN с использованием круглых и квадратных резонаторов
Ахмад В. и Будимир Д. 2016. СШП-фильтры с двойной полосой пропускания для Диапазоны WiMAX и WLAN с использованием круглых и квадратных резонаторов. Конференция IET по активным и пассивным радиочастотным устройствам, 2016 г. Лондон, Великобритания 17–17 февраля 2016 г. Институт инженерии и технологий (IET). https://doi.org/10.1049/ic.2016.0004
Компактные линейные волноводные резонаторы в плоскости E и полосовые фильтры с I-образными резонансными вставками
Янкович, У. и Будимир, Д. 2016. Компактные линейные волноводные резонаторы в плоскости E и полосовые фильтры с I-образными резонансными вставками. IEEE Азиатско-Тихоокеанская конференция по СВЧ (APMC2016). Нью-Дели, Индия, 5–9 декабря 2016 г. IEEE. https://doi.org/10.1109 / APMC.2016.7
3
Полосные фильтры для струйной печати для подавления помех в многостандартных беспроводных системах
Олукойя, О. и Будимир, Д. 2016. Полосовые фильтры для струйной печати для подавления помех в многостандартных беспроводных системах. IEEE Азиатско-Тихоокеанская конференция по СВЧ (APMC2016). Нью-Дели, Индия, 5–9 декабря 2016 г. IEEE. https://doi.org/10.1109/APMC.2016.7
Компактные фильтры UWB MIMO с двойной полосой пропускания, высокой изоляцией и большим разнообразием
Ahmad, W., Ташич, М. и Будимир, Д. 2016. Компактные СШП-фильтры MIMO с двойной полосой пропускания, высокой изоляцией и большим разнообразием. Азиатско-Тихоокеанская конференция по микроволновой печи IEEE 2016 (APMC2016). Нью-Дели, Индия, 5–9 декабря 2016 г. IEEE. https://doi.org/10.1109/APMC.2016.7
Антенны с струйной печатью для приложений 5G 28 ГГц
Ахмад В. и Будимир Д. 2016. Антенны с струйной печатью для приложений 5G 28 ГГц. Азиатско-Тихоокеанская конференция по микроволновой печи IEEE 2016 (APMC2016). Нью-Дели, Индия, 5–9 декабря 2016 г. IEEE. https://doi.org/10.1109/APMC.2016.75
Переключаемые фильтенны с острым двойным полосным вырезом с использованием петлевых резонаторов
Ахмад, В. и Будимир, Д. 2016. Переключаемые фильтры с острым двойным полосным вырезом с использованием петлевых резонаторов. 46-я Европейская микроволновая конференция (EuMC2016). ExCel, Лондон, Великобритания, 4–6 октября 2016 г. IEEE. https://doi.org/10.1109/EuMC.2016.7824375
Компактные широкополосные фильтры для струйной печати с тройной полосой
Ahmad, W.и Будимир, Д. 2016. Компактные широкополосные фильтры для струйной печати с тройной полосой. 46-я Европейская микроволновая конференция (EuMC2016). ExCel, Лондон, Великобритания, 4–6 октября 2016 г. IEEE. https://doi.org/10.1109/EuMC.2016.7824282
Волноводные резонаторы на основе графена для субмиллиметровых волн
Илич, А.З., Буквич, Б., Илич, М.М. и Будимир, Д. 2016. Волноводные резонаторы на основе графена для приложений субмиллиметрового диапазона. Физический журнал D: Прикладная физика. 49 (32), стр. 325105 325105. https://doi.org/10.1088/0022-3727/49/32/325105
Высоколинейные реконфигурируемые фильтры СШП с независимо управляемым двойным полосным узлом
Ахмад В. и Будимир Д. 2016. Очень линейный Реконфигурируемые фильтры СШП с независимо управляемым двухдиапазонным режектором. Письма о микроволновых и оптических технологиях. 58 (11), стр. 2639–2643. https://doi.org/10.1002/mop.30113
Переход из интегрированного волновода со ступенчатой подложкой в прямоугольный волновод
Янкович, У.и Будимир, Д. 2016. Переход со ступенчатым изгибом подложки из интегрированного волновода в прямоугольный волновод. 2016 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное собрание радионауки USNC-URSI. Пуэрто-Рико, США 26 июня – 1 июля 2016 г. IEEE. https://doi.org/10.1109/APS.2016.7696323
Фильтры для струйной печати с тройной полосой
Ахмад, В., Будимир, Д. и Злебич, К. 2016. Фильтры для струйной печати с тройной полосой. 2016 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное совещание по радионауке USNC-URSI (APS2016). Фахардо, Пуэрто-Рико, 26 июня – 1 июля 2016 г., IEEE. https://doi.org/10.1109/APS.2016.7696121
Реконфигурируемые фильтры СШП с двойной полосой пропускания для нежелательных полос с использованием коммутаторов на основе графена
Ахмад, В. и Будимир, Д. 2016. Реконфигурируемые фильтры СШП для нежелательных полос с двойной полосой пропускания Полосы с использованием переключателей на основе графена. 2016 Международный симпозиум IEEE по антеннам и распространению радиоволн и конференция USNC-URSI Radio Science Meeting (APS2016). Пуэрто-Рико, США 26 июня – 1 июля 2016 г. IEEE.https://doi.org/10.1109/APS.2016.7696768
Ухудшение оборудования влияет на производительность ретрансляции AF с фиксированным усилением при замирании Накагами
Cabarkapa, M., Neskovic, N., Budimir, D. and Maletic , N. 2016. Ухудшение оборудования влияет на производительность ретрансляции AF с фиксированным усилением при замираниях Накагами-м. Электронные письма. 52 (2), стр. 121–122. https://doi.org/10.1049/el.2015.3378
Двухдиапазонная антенная решетка для приложений WLAN
Ahmad, W.и Будимир, Д. 2016. Двухдиапазонный решетчатый фильтр для приложений WLAN. Письма о микроволновых и оптических технологиях. 58 (2), стр. 477-481. https://doi.org/10.1002/mop.29597
Ультракомпактные линейные полосовые фильтры с волноводом E-Plane с перекрестной связью
Мохоттиге, Н., Глубоков, О., Янкович, У. и Будимир, Д. 2016 Ультракомпактные линейные полосовые волноводные фильтры E-Plane с перекрестной связью. IEEE Transactions по теории и методам микроволнового излучения. 64 (8), с.2561–2571. https://doi.org/10.1109/TMTT.2016.2578329
Моделирование и компенсация искажений совместных усилителей мощности и I / Q-модулятора для передатчиков LTE с использованием искусственных нейронных сетей
Анастасиевич, А., Кожа, Д., Нескович, Н. ., Нескович, А. и Будимир, Д. 2015. Моделирование и компенсация ухудшения совместных усилителей мощности и I / Q-модулятора для передатчиков LTE с использованием искусственных нейронных сетей. Международный журнал электроники и связи (AEÜ). 69 (2), стр. 529-538. https://doi.org/10.1016/j.aeue.2014.11.005
Реконфигурируемые согласующие сети для РЧ-усилителей
Будимир Д. и Буквич Б. 2015. Реконфигурируемые согласующие сети для РЧ-усилителей. Письма о микроволновых и оптических технологиях. 57 (6), стр. 1487-1491. https://doi.org/10.1002/mop.29126
Совместная компенсация искажений I / Q и нелинейности PA для параллельных двухдиапазонных передатчиков с использованием двухкорпусной модели
Bozic, M.и Будимир, Д. 2015. Совместная компенсация искажений I / Q и нелинейности PA для параллельных двухдиапазонных передатчиков с использованием модели с двумя блоками. Письма о компонентах СВЧ и беспроводной связи IEEE. 25 (5), стр. 340-342. https://doi.org/10.1109/LMWC.2015.2409771
Магнитно-смещенные переключатели на основе графена для микроволновых приложений
Буквич, Б. и Будимир, Д. 2015. Магнитно-смещенные переключатели на основе графена для микроволновых приложений. Письма о микроволновых и оптических технологиях. 57 (12), стр. 2956-2958. https://doi.org/10.1002/mop.29468
Предыскажение и постискажение беспроводных усилителей мощности для беспроводных систем 4G и B4G
Кодогианнис, В., Васкович, М., Миюскович, Дж. и Будимир, Д. 2015. Предыскажение и постискажение беспроводных усилителей мощности для беспроводных систем 4G и B4G. Конференция: Симпозиум IEEE по компьютерам и коммуникациям. Кипр, июль 2015 г.
Реконфигурируемые фильтры UWB с двойной полосой пропускания Sharp WLAN
Ahmad, W.и Будимир, Д. 2015. Реконфигурируемые фильтры UWB с двойным полосным вырезом Sharp WLAN. 45-я Европейская микроволновая конференция (EuMC2015). Париж, Франция, 7–10 сентября 2015 г. IEEE. https://doi.org/10.1109/EuMC.2015.7345991
Полосовые фильтры и фильтры для струйной печати с использованием чернил с наночастицами серебра на гибкой подложке
Ахмад В., Будимир Д., Марич А. и Иванишевич Н. 2015. Полосовые фильтры и фильтры для струйной печати с использованием чернил с наночастицами серебра на гибкой подложке. Международный симпозиум AP-S по антеннам и распространению радиоволн (APS2015). Ванкувер, Британская Колумбия, Канада 19–24 июля 2015 г. IEEE. https://doi.org/10.1109/APS.2015.7304458
Двухдиапазонная антенная решетка WLAN со встроенными полосовыми фильтрами для подавления гармоник
Ahmad, W. и Budimir, D. 2015. Двухдиапазонная антенная решетка WLAN со встроенной Полосовые фильтры для подавления гармоник. Международный симпозиум AP-S по антеннам и распространению радиоволн (APS2015). Ванкувер, Британская Колумбия, Канада 19–24 июля 2015 г. IEEE.https://doi.org/10.1109/APS.2015.7304696
Компенсация нелинейных искажений ВЧ мощности усилители для приложений LTE
Васкович М. и Будимир Д. 2014. Компенсация нелинейных искажений в ВЧ мощности усилители для приложений LTE. Письма о микроволновых и оптических технологиях. 56 (8), стр. 1910-1013. https://doi.org/10.1002/mop.28480
Высокоселективный реконфигурируемый фильтр для систем СШП
Раввин, К.М.Ф. и Будимир, Д.2014. Высокоселективный реконфигурируемый фильтр для СШП систем. Письма о компонентах СВЧ и беспроводной связи IEEE. 24 (3), стр. 146-148. https://doi.org/10.1109/LMWC.2013.22
Сверхкомпактные псевдоэллиптические полосовые фильтры с линейным волноводом с байпасной связью
Mohottige, N., Jankovic, U. and Budimir, D. 2014. Сверхкомпактные псевдо- эллиптические линейные волноводные полосовые фильтры с байпасной связью. Международный симпозиум IEEE MTT по микроволновому излучению (IMS2014). Тампа, Флорида, США, 1–6 июня 2014 г., IEEE. https://doi.org/10.1109/MWSYM.2014.6848392
Реконфигурируемые волноводные резонаторы в E-плоскости для применения в фильтрах
Mohottige, N., Bukvic, B. и Budimir, D. 2014. Реконфигурируемые волноводные резонаторы в E-плоскости для фильтровать приложения. 44-я Европейская микроволновая конференция (EuMC2014). Рим, Италия 5-10 октября 2014 г.
Реконфигурируемый вырез WLAN для фильтров UWB
Ахмад В. и Будимир Д.2014. Реконфигурируемый вырез WLAN для фильтров UWB. 44-я Европейская микроволновая конференция (EuMC2014). Рим, Италия, 6–9 октября 2014 г., IEEE. https://doi.org/10.1109/EuMC.2014.6986742
Двухдиапазонная антенная решетка WLAN со встроенными фильтрами для подавления гармоник
Ахмад, В. и Будимир, Д. 2014. Двухдиапазонная антенная решетка WLAN со встроенными фильтрами для подавления гармоник. Конференция по активным и пассивным радиочастотным устройствам IET, 2014 г. Бирмингем, Великобритания, 29–29 октября 2014 г. Институт инженерии и технологий (IET).https://doi.org/10.1049/ic.2014.0181
Оценка нелинейных искажений в оптически переключаемых фильтрах UWB
Чакрабарти, К., Раввин, KMF, Панагамува, К., Кодогианнис, В. и Будимир, Д. 2014. Оценка нелинейных искажений в оптически переключаемых СШП-фильтрах. Письма о микроволновых и оптических технологиях. 56 (5), стр. 1092-1094. https://doi.org/10.1002/mop.28277
Электромагнитный анализ перестраиваемых волноводных резонаторов на основе графена
Илич, А.З. и Будимир, Д. 2014. Электромагнитный анализ настраиваемых волноводных резонаторов на основе графена. Письма о микроволновых и оптических технологиях. 56 (10), стр. 2385-2388. https://doi.org/10.1002/mop.28603
Обобщенная двумерная архитектура улучшения линейности для одновременных двухдиапазонных беспроводных передатчиков
Кабаркапа, М., Нескович, Н. и Будимир, Д. 2013. A Обобщенная двумерная архитектура улучшения линейности для одновременных двухдиапазонных беспроводных передатчиков. IEEE Transactions по теории и методам микроволнового излучения. 61 (12), стр. 4579-4590. https://doi.org/10.1109/TMTT.2013.2287679
Сверхкомпактный линейный полосовой фильтр в плоскости E с извлеченными полюсами
Мохоттидж, Н., Глубоков, О. и Будимир, Д. 2013. Сверхкомпактный линейный E- плоские волноводные полосовые фильтры с извлеченными полюсами. Письма о компонентах СВЧ и беспроводной связи IEEE. 23 (8), стр. 409-411. https://doi.org/10.1109/LMWC.2013.2270431
Высоколинейный микрополосковый широкополосный полосовой фильтр с переключаемой полосой пропускания для беспроводных приложений
Rabbi, K.M.F., Athukorala, L., Panagamuwa, C., Vardaxoglou, J.C. и Budimir, D. 2013. Высоколинейный широкополосный полосовой фильтр с переключаемой полосой пропускания для беспроводных приложений. Письма о микроволновых и оптических технологиях. 55 (6), стр. 1331-1335. https://doi.org/10.1002/mop.27585
Компактный полосовой фильтр СШП с реконфигурируемой режущей полосой
Rabbi, KMF, Athukorala, L., Panagamuwa, C., Vardaxoglou, JC and Budimir, D. 2013. Компактный полосовой фильтр СШП с перестраиваемой режекторной полосой. Электронные письма. 49 (11), с. 709-711. https://doi.org/10.1049/el.2012.3555
Микрополосковый полосовой фильтр высокой линейности с электронно настраиваемым режектором
Rabbi, KMF, Athukorala, L. и Budimir, D. 2013. Микрополосковый полосовой фильтр высокой линейности с электронно настраиваемой выемка. Письма о микроволновых и оптических технологиях. 55 (2), стр. 418-421. https://doi.org/10.1002/mop.27312
Миниатюрные двухрежимные микрополосковые полосовые фильтры с реконфигурируемой полосой с режущей кромкой для приложений UWB
Rabbi, K.М.Ф. и Будимир, Д. 2013. Миниатюрные двухрежимные микрополосковые полосовые фильтры с реконфигурируемой полосой с режектором для приложений СШП. 2013 Международный симпозиум IEEE MTT-S по микроволновому излучению (IMS2013). Сиэтл, Вашингтон, США 2-7 июня 2013 г. https://doi.org/10.1109/MWSYM.2013.6697586
Миниатюрный полосовой фильтр резкого подавления с изменяемой полосой пропускания для приложений UWB
Rabbi, K.M.F. и Будимир, Д. 2013. Миниатюрный полосовой фильтр с резким режектором и настраиваемой полосой пропускания для приложений СШП. 43-я Европейская микроволновая конференция (EuMC2013). Нюрнберг, Германия 6-11 октября 2013 г. стр. 1023-1026
Оптически реконфигурируемые волноводные резонаторы и фильтры в E-плоскости
Mohottige, N., Panagamuwa, C. и Budimir, D. 2013. Оптически реконфигурируемая E-плоскость волноводные резонаторы и фильтры. 43-я Европейская микроволновая конференция (EuMC2013). Нюрнберг, Германия 6-11 октября 2013 г. стр. 798-801
Компактные полосовые фильтры с настройкой варактора E-plane
Mohottige, N., Янкович, У. и Будимир, Д. 2013. Компактные полосовые фильтры, настроенные на варактор E-плоскости. 2013 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное совещание USNC-URSI по радионауке. Лейк-Буэна-Виста, Флорида, США. 7-12 июля 2013 г.
Электромагнитное моделирование решетчатых фильтров волноводных антенн с диэлектриком
Янкович У., Мохоттидж Н., Петрович В. и Будимир Д. 2013. Электромагнитное моделирование волноводных антенн с диэлектриком массивы фильтров. 2013 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное совещание USNC-URSI по радионауке. Лейк-Буэна-Виста, Флорида, США. 7-12 июля 2013 г., стр. 2121-2122 https://doi.org/10.1109/APS.2013.6711719
Оценка линейности оптически реконфигурируемого микрополоскового полосового фильтра UWB
Чакрабарти, К., Раввин, KMF, Панагамува, С. ., Vardaxoglou, JC и Budimir, D. 2013. Оценка линейности оптически реконфигурируемого микрополоскового полосового фильтра UWB. 2013 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное совещание USNC-URSI по радионауке. Лейк-Буэна-Виста, Флорида, США. 7-12 июля 2013 г.
Оценка нелинейных искажений реконфигурируемых РЧ-цепей в системах беспроводной связи
Чакрабарти, К., Буквич, Б., Мохоттидж, Н. и Будимир, Д. 2013. Оценка нелинейных искажений реконфигурируемых РЧ-цепей в системах беспроводной связи. SBMO / IEEE MTT-S Международная конференция по микроволновой и оптоэлектронике (IMOC2013). Рио-де-Жанейро, Бразилия 4-7 августа 2013 г.
Компактные настраиваемые полосовые фильтры с дефектной микрополосковой структурой для мультистандартных беспроводных систем
Чакрабарти, К. и Будимир, Д. 2013. Компактные настраиваемые полосовые фильтры с дефектной микрополосковой структурой для мультистандартные беспроводные системы. 43-я Европейская микроволновая конференция (EuMC2013). Нюрнберг, Германия 6-11 октября 2013 г. стр. 1031-1034
Метод компенсации двумерной нелинейности для параллельных двухдиапазонных беспроводных передатчиков
Cabarkapa, M., Нескович, Н. и Будимир, Д. 2013. Метод компенсации двумерной нелинейности для одновременных двухдиапазонных беспроводных передатчиков. 2013 Международный симпозиум IEEE MTT-S по микроволновому излучению (IMS2013). Сиэтл, Вашингтон, США 2–7 июня 2013 г.
Реконфигурируемые согласующие сети для беспроводных передатчиков
Буквич Б., Нескович Н. и Будимир Д. 2013. Реконфигурируемые согласующие сети для беспроводных передатчиков. 2013 Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное совещание USNC-URSI по радионауке. Лейк-Буэна-Виста, Флорида, США. 7-12 июля 2013 г. стр. 796-797 https://doi.org/10.1109/APS.2013.6711057
Компактные волноводные фильтры и диплексеры с диэлектрическим заполнением
Мохоттидж Н. и Будимир Д. 2012. Компактный диэлектрик -наполненные волноводные фильтры и диплексеры. Международный симпозиум IEEE по антеннам, распространению и ЧПУ // Национальное собрание радионауки USNC / URSI (APS2012). Чикаго, Иллинойс, США, 8–14 июля 2012 г. IEEE. https://doi.org/10.1109/APS.2012.6348788
Планарная сверхширокополосная антенна с режекторными полосами с фотонным управлением
Драшкович, Д., Фернандес, Дж. Р.О., Бризо-Родригес, К. и Будимир, Д. 2012. Планарная сверхширокополосная антенна с режекторными полосами, управляемыми фотонами. Международный симпозиум IEEE по антеннам, распространению и ЧПУ // Национальное собрание радионауки USNC / URSI (APS2012). Чикаго, Иллинойс, США, 8–14 июля 2012 г. IEEE. https://doi.org/10.1109/APS.2012.6348541
Компенсация нежелательных эффектов в беспроводных трансиверах MIMO
Cabarkapa, M., Божич, М., Нескович, Н., Нескович, А. и Будимир, Д. 2012. Компенсация нежелательных эффектов в беспроводных трансиверах MIMO. Международный симпозиум IEEE по антеннам, распространению и ЧПУ // Национальное собрание радионауки USNC / URSI (APS2012). Чикаго, Иллинойс, США, 8–14 июля 2012 г. IEEE. https://doi.org/10.1109/APS.2012.6348077
Компактные конфигурации фильтров с использованием концентрических микрополосковых резонаторов с разомкнутым контуром
Athukorala, L. и Budimir, D. 2012. Компактные конфигурации фильтров с использованием концентрических микрополосковых резонаторов с разомкнутым контуром. Письма о компонентах СВЧ и беспроводной связи IEEE. 22 (5), стр. 245-247. https://doi.org/10.1109/LMWC.2012.21
Реконфигурируемый пятидиапазонный PIFA для небольших и тонких мобильных телефонов
AbuTarboush, H.F., Nilavalan, R., Peter, T., Cheung, S.W. и Будимир, Д. 2012. Реконфигурируемый пятидиапазонный PIFA для небольших и тонких мобильных телефонов. Письма о микроволновых и оптических технологиях. 54 (3), стр. 725-729. https://doi.org/10.1002/mop.26640
Локализация нескольких систем и нескольких операторов в PLMN с использованием нейронных сетей
Боренович, М., Нескович, А. и Будимир, Д. 2012. Локализация нескольких систем и нескольких операторов в PLMN с использованием нейронных сетей. Международный журнал коммуникационных систем. 25 (2), стр. 67-83. https://doi.org/10.1002/dac.1252
Компактные фильтры с металло-диэлектрическими вставками
Глубоков О., Будимир Д. 2012. Компактные фильтры с металло-диэлектрическими вставками. 42-я Европейская микроволновая конференция (EuMC2012). Амстердам, Нидерланды 28 октября – 2 ноября 2012 г. IEEE.
Оценка нелинейных искажений в передатчиках MIMO
Божич, М., Кабаркапа, М., Нескович, Н., Нескович, А. и Будимир, Д. 2012. Оценка нелинейных искажений в передатчиках MIMO. 42-я Европейская микроволновая конференция (EuMC2012). Амстердам, Нидерланды 28 октября – 2 ноября 2012 г. IEEE.
Перестраиваемые резонаторы и фильтры с разомкнутым контуром и постоянной полосой пропускания
Athukorala, L. и Budimir, D. 2012. Перестраиваемые резонаторы и фильтры с разомкнутым контуром и постоянной шириной полосы. IET Микроволны, антенны и распространение. 6 (7), с. 800-806. https://doi.org/10.1049/iet-map.2010.0426
Реконфигурируемая широкополосная и многодиапазонная антенна с использованием элементов двойного патча для компактных беспроводных устройств
AbuTarboush, HF, Nilavalan, R., Cheung, SW, Nasr, К.М., Питер, Т., Будимир, Д. и Аль-Равешиди, Х.С. 2012. Реконфигурируемая широкополосная и многодиапазонная антенна с использованием элементов с двойным патчем для компактных беспроводных устройств. Транзакции IEEE по антеннам и распространению. 60 (1), стр. 36-43. https://doi.org/10.1109/TAP.2011.2167925
Оптически реконфигурируемые фильтры CPW для приложений UWB
Rabbi, K.M.F. и Будимир, Д. 2012. Оптически реконфигурируемые фильтры CPW для приложений СШП. Международный симпозиум IEEE по антеннам, распространению и ЧПУ // Национальное собрание радионауки USNC / URSI (APS2012). Чикаго, Иллинойс, США, 8–14 июля 2012 г. IEEE. https://doi.org/10.1109/APS.2012.6348654
Извлечение обобщенных коэффициентов связи для линейных фильтров с извлеченными полюсами с нерезонирующими узлами
Глубоков, О.и Будимир, Д. 2011. Извлечение обобщенных коэффициентов связи для встроенных фильтров с извлеченными полюсами с нерезонирующими узлами. IEEE Transactions по теории и методам микроволнового излучения. 59 (12), стр. 3023-3029. https://doi.org/10.1109/TMTT.2011.2168967
Компактные двухрежимные микрополосковые полосовые фильтры с высокой линейностью переключаемые
Chakrabarty, K., Athukorala, L. и Budimir, D. 2011. Компактные переключаемые двойные фильтры с высокой линейностью режим микрополосковых полосовых фильтров. IEEE Азиатско-Тихоокеанская конференция по СВЧ (APMC2011). Мельбурн, Австралия 5-8 декабря 2011 г. стр. 2214-2220
Настраиваемые фазовращатели EBG для антенн
Vardaxoglou, JC, Chauraya, L., Athukorala, L. и Budimir, D. 2011. Настраиваемые фазовращатели EBG для антенных приложений. Конференция по антеннам и распространению радиоволн в Лафборо (LAPC2011). Loughborough, UK 14-15 Noc 2011
Интегрированные волноводные фильтры с перекрестной связью на складчатой подложке со структурой отрицательной связи для беспроводных систем
Глубоков, О., Нагандирам, С., Тарчински, А. и Будимир, Д. 2011. Интегрированные волноводные фильтры с перекрестной связью на складчатой подложке со структурой отрицательной связи для беспроводных систем. Письма о микроволновых и оптических технологиях. 53 (11), стр. 2521-2526. https://doi.org/10.1002/mop.2634
Реконфигурируемая трехдиапазонная H-образная антенна с функцией частотной избирательности для компактных систем беспроводной связи
AbuTarboush, HF, Nilavalan, R., Cheung, SW, Nasr, К.М., Петр, Т., Аль-Равешиди, Х.С. и Будимир, Д. 2011. Реконфигурируемая трехдиапазонная H-образная антенна с функцией частотной избирательности для компактных систем беспроводной связи. IET Микроволны, антенны и распространение. 5 (14), стр. 1675-1682. https://doi.org/10.1049/iet-map.2010.0518
Робастная оценка коэффициентов нелинейной модели для беспроводных усилителей мощности
Васкович М., Джурович З., Тарчинский А. и Будимир Д. 2011 • Робастная оценка коэффициентов нелинейной модели для беспроводных усилителей мощности. 10-я Международная конференция IEEE по телекоммуникациям в современных услугах спутникового, кабельного и вещания (TELSIKS 2011). Ниш, Сербия. 5-8 октября 2011 г. С. 222-225 https://doi.org/10.1109/TELSKS.2011.6112037
Новые линейные волноводные фильтры Е-плоскости с использованием двухмодовой выделенной полюсной секции
Глубоковы О. и Будимир Д. 2011. Новые линейные волноводные фильтры E-plane, использующие двухрежимную извлеченную полюсную секцию. 41-я Европейская микроволновая конференция (EuMC). Манчестер, Великобритания 09–14 октября 2011 г.
Улучшенные беспроводные передатчики с использованием межкаскадного режекторного фильтра
Chakrabarty, K., Athukorala, L., Golubicic, Z. и Budimir, D. 2011. Улучшенные беспроводные передатчики с использованием межкаскадный режекторный фильтр. 10-я Международная конференция IEEE по телекоммуникациям в современных услугах спутникового, кабельного и вещания (TELSIK2011). Ниш, Сербия 05-08 октября 2011
Компактные высоколинейные двухрежимные фильтры второго порядка с варакторной настройкой и постоянной полосой пропускания
Athukorala, L.и Будимир, Д. 2011. Компактные высоколинейные двухрежимные фильтры второго порядка с настройкой на варактор и постоянной полосой пропускания. IEEE Transactions по теории и методам микроволнового излучения. 59 (9), стр. 2214-2220. https://doi.org/10.1109/TMTT.2011.2160279
Стратегии разделения пространства для позиционирования WLAN внутри помещений с каскадными структурами ИНС
Боренович, М., Нескович, А. и Будимир, Д. 2011. Стратегии разделения пространства для позиционирования WLAN внутри помещений с каскадно подключенными структурами ANN. Международный журнал нейронных систем. 21 (1), стр. 1-15. https://doi.org/10.1142/S01211002614
Новые волноводные фильтры с Т-образными резонаторами
Будимир Д., Глубоков О. и Потребич М. 2011. Новые волноводные фильтры с Т-образными резонаторами. Электронные письма. 47 (1), стр. 38-40. https://doi.org/10.1049/el.2010.2958
Реконфигурируемые микрополосковые СШП-фильтры с высокой линейностью
Rabbi, K.M.F., Athukorala, L., Панагамува, К., Вардаксоглу, Дж. К. и Будимир, Д. 2011. Реконфигурируемые микрополосковые сверхширокополосные полосовые фильтры с высокой линейностью. 41-я Европейская микроволновая конференция (EuMC). Манчестер, Великобритания, 09–14 октября 2011 г. стр. 172-175
Моделирование реконфигурируемой режекции WLAN для UWB-фильтров
Раввин, KMF, Ананд, А., Атукоорала, Л. и Будимир, Д. 2011. Моделирование реконфигурируемого Вырез WLAN для фильтров UWB. Международный симпозиум IEEE по антеннам и распространению радиоволн (AP-S) и Национальная конференция по радионауке USNC / CNC / URSI 2011 г. Спокан, Вашингтон, США 3–8 июля 2011 г.
Электромагнитное моделирование волноводных фильтров с диэлектрическим наполнением для диплексеров
Мохиттиге, Н., Потребич, М., Голубичич, З. и Будимир, Д. 2011. Электромагнитное моделирование диэлектрических волноводных фильтров для диплексоров. Международный симпозиум IEEE по антеннам и распространению радиоволн (AP-S) и Национальная конференция по радионауке USNC / CNC / URSI 2011 г. Спокан, Вашингтон, США 03 – 08 июля 2011
Субстратные интегрированные волноводные кросс-связанные фильтры для беспроводных приложений
Глубоков, О., Нагандирам, С., Тарчински, А. и Будимир, Д. 2011. Интегрированные на подложке волноводные фильтры с перекрестной связью для беспроводных приложений. Международный симпозиум IEEE по антеннам и распространению радиоволн (AP-S) и Национальная конференция по радионауке USNC / CNC / URSI 2011 г. Спокан, Вашингтон, США 3–8 июля 2011 г.
Программа Всемирной службы Би-би-си по микроволнам
Будимир Д., Атукорала Л. и Чакрабарти К. 2010. Программа Всемирной службы Би-би-си по микроволнам.
Конструкция компактных двухрежимных микрополосковых фильтров
Athukorala, L.и Будимир, Д. 2010. Разработка компактных двухрежимных микрополосковых фильтров. IEEE Transactions по теории и методам микроволнового излучения. 58 (11), стр. 2888-2895. https://doi.org/10.1109/TMTT.2010.2079110
Миниатюрные полосовые фильтры с использованием замкнутого микрополоскового кольцевого резонатора с параллельной подачей
Athukorala, L. и Budimir, D. 2010. Миниатюрная полосовая фильтрация фильтры с использованием замкнутого микрополоскового кольцевого резонатора с параллельной подачей. Письма о микроволновых и оптических технологиях. 52 (6), стр. 1277-1280. https://doi.org/10.1002/mop.25188
Патч-антенна с двумя U-образными пазами для трехдиапазонных беспроводных систем
АбуТарбуш, Х.Ф., Нилавалан, Р., Будимир, Д. и Аль-Равешиди, Х.С. 2010. Патч-антенна с двойным U-образным пазом для трехдиапазонных беспроводных систем. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 20 (3), стр. 279-285. https://doi.org/10.1002/mmce.20431
Диплексеры интегрированные микрополосковые антенны
Зайниев Д.и Будимир, Д. 2010. Диплексеры со встроенной микрополосковой антенной. Четвертая Европейская конференция по антеннам и распространению радиоволн (EuCAP2010). Барселона, Испания 12–16 апреля 2010 г. IEEE.
Двухдиапазонный микрополосковый антенный фильтр для беспроводной связи
Зайниев Д. и Будимир Д. 2010. Двухдиапазонный микрополосковый антенный фильтр для беспроводной связи. в: 2010 Международный симпозиум IEEE Antennas and Propagation Society (APSURSI), Торонто, Канада, 11-17 июля IEEE.
Микрополосковые антенные диплексеры для беспроводной связи
Зайниев, Д., АбуТарбуш, Х.Ф. и Будимир, Д. 2010. Диплексеры с микрополосковой антенной для беспроводной связи. в: European Microwave Conference (EuMC 2009), 28 сентября – 2 октября 2009 г., Рим, Италия IEEE. С. 1508-1510
Электромагнитное моделирование полосовых полосовых фильтров, нагруженных гребенчатым волноводным резонатором
Сунтералингам, Н., Мохоттидж, Н. и Будимир, Д. 2010. Электромагнитное моделирование полосовых фильтров, нагруженных гребенчатым волноводным резонатором. в: 2010 Международный симпозиум IEEE Antennas and Propagation Society (APSURSI), Торонто, Канада, 11-17 июля IEEE.
Электромагнитный анализ SRR и фильтров с S-образным резонатором
Глубоков О., Сунтералингам Н., Будимир Д. и Мохоттидж Н. 2010. Электромагнитный анализ SRR и S-образных фильтров с резонатором. Четвертая Европейская конференция по антеннам и распространению радиоволн (EuCAP2010). Барселона, Испания 12–16 апреля 2010 г. IEEE.
Компактный встроенный в подложку интегрированный волноводный фильтр с нулями пропускания
Глубоков О., Шелковников А.Б. и Будимир, Д. 2010. Компактный встроенный волноводный фильтр со встроенной подложкой с нулями передачи. в: 2010 IEEE Antennas and Propagation Society International Symposium (APSURSI), Торонто, Канада, 11-17 июля 2010 IEEE.
Интегрированные полосовые фильтры на многослойной подложке
Глубоков О., Потребич М. и Будимир Д. 2010. Интегрированные полосовые фильтры на многослойной подложке. 5-я Европейская конференция по схемам и системам связи (ECCSC’10). Белград, Сербия 23 – 25 ноября 2010 г.
Компактные дублетные структуры E-плоскости для модульного проектирования фильтров
Глубоков О. и Будимир Д. 2010. Компактные дублетные структуры E-плоскости для модульного проектирования фильтров. в: 40-я Европейская микроволновая конференция (EuMC), 29 сентября – 1 октября 2010 г., Париж, Франция IEEE. С. 1253-1256
Оптически реконфигурируемые радиочастотные схемы
Драшкович Д., Христодулу Г. и Будимир Д. 2010. Оптически реконфигурируемые радиочастотные схемы.in: Материалы Четвертой Европейской конференции по антеннам и распространению радиоволн (EuCAP2010), 12–16 апреля 2010 г., Барселона, Испания, IEEE. С. 1-3
Межсистемная локализация в PLMN с использованием нейронных сетей
Боренович М., Нескович А. и Будимир Д. 2010. Межсистемная локализация в PLMN с использованием нейронных сетей. в: IEEE Radio and Wireless Symposium (RWS 2010), 10–14 января 2010 г., отель Sheraton, Новый Орлеан, Лос-Анджелес IEEE. С. 168-171
Линеаризация высокоэффективных усилителей мощности с использованием цифрового предыскажения основной полосы частот с итеративной инжекцией
Бондарь Д., Лопес, Н.Д., Попович, З. и Будимир, Д. 2010. Линеаризация высокоэффективных усилителей мощности с использованием цифрового предыскажения основной полосы частот с итеративной инжекцией. в: IEEE Radio and Wireless Symposium (RWS 2010), 10–14 января 2010 г., отель Sheraton, Новый Орлеан, Лос-Анджелес IEEE. стр. 148-151
Новое цифровое предыскажение для улучшения линейности и подавления эффектов памяти
Бондарь Д. и Будимир Д. 2010. Новое цифровое предыскажение для улучшения линейности и подавления эффектов памяти.в: European Microwave Conference (EuMC 2009), 28 сентября – 2 октября 2009 г., Рим, Италия IEEE. С. 1437-1440
Оптически реконфигурируемые микрополосковые полосовые фильтры UWB
Athukorala, L., Rabbi, KMF, Panagamuwa, C., Vardaxoglou, JC, Philippakis, M. и Budimir, D. 2010. Оптически реконфигурируемая микрополосковая полоса UWB фильтры. в: IEEE Loughborough Antennas and Propagation Conference (LAPC2010), 8-9 ноября 2010 г., Loughborough IEEE. С. 617-620
Конструкция двухрежимных микрополосковых фильтров с разомкнутым контуром
Athukorala, L., Потребич, М. и Будимир, Д. 2010. Разработка двухрежимных микрополосковых фильтров с разомкнутым контуром. 18-й телекоммуникационный форум TELFOR 2010. 23–25 ноября 2010 г. Белград, Сербия
Дизайн двухрежимных микрополосковых фильтров с разомкнутым контуром
Athukorala, L., Budimir, D. и Potrebic, M. 2010. Дизайн открытого -контурные двухрежимные микрополосковые фильтры. Progress in Electromagnetics Research Letters. 19, стр. 179–185. https://doi.org/10.2528/PIERL10102007
Компактные настраиваемые двухрежимные микрополосковые фильтры с высокой линейностью
Athukorala, L., Бондарь, Д. и Будимир, Д. 2010. Компактные перестраиваемые двухмодовые микрополосковые фильтры с высокой линейностью. в: 40-я Европейская микроволновая конференция (EuMC), 29 сентября – 1 октября 2010 г., Париж, Франция IEEE. стр. 834-837
Компактная печатная антенна для многодиапазонных беспроводных приложений
AbuTarboush, HF, Nilavalan, R., Nasr, KM, Al-Raweshidy, HS, Budimir, D. and Alexander, MJ 2010. Компактная печатная антенна для многодиапазонных беспроводных приложений. в: 6-й Международный семинар IEEE по антенной технологии (iWAT), Лиссабон, Португалия IEEE.
Реконфигурируемая H-образная антенна для беспроводных приложений
AbuTarboush, H.F., Nilavalan, R., Nasr, K.M., Al-Raweshidy, H.S. и Будимир, Д. 2010. Реконфигурируемая Н-образная антенна для беспроводных приложений. in: Материалы Четвертой Европейской конференции по антеннам и распространению радиоволн (EuCAP2010), 12–16 апреля 2010 г., Барселона, Испания, IEEE. стр. 1-4
Широко настраиваемая многополосная реконфигурируемая патч-антенна для беспроводных приложений
AbuTarboush, H.Ф., Нилаван, Р., Наср, К.М., Аль-Равешиди, Х.С. и Будимир, Д. 2010. Широко настраиваемая многополосная реконфигурируемая патч-антенна для беспроводных приложений. in: Материалы Четвертой Европейской конференции по антеннам и распространению радиоволн (EuCAP2010), 12–16 апреля 2010 г., Барселона, Испания, IEEE. С. 1-3
Широкополосная плоская перевернутая F-антенна для когнитивного радио
АбуТарбуш, Х.Ф., Будимир, Д., Нилавалан, Р. и Аль-Равешиди, Х.С. 2010. Широкополосная планарная перевернутая F-антенна для когнитивного радио.в: European Microwave Conference (EuMC 2009), 28 сентября – 2 октября 2009 г., Рим, Италия IEEE. С. 1504-1507
ВЧ-схемы с изменяемой частотой с использованием фотопроводящих переключателей
Драшкович, Д., Панагамува, К., Вардаксоглу, Дж. К. и Будимир, Д. 2010. ВЧ-схемы с изменяемой частотой с использованием фотопроводящих переключателей. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 20 (1), стр. 15-21. https://doi.org/10.1002/mmce.20415
Усовершенствованные волноводные полосовые фильтры с S-образными резонаторами
Бондарь, Д.и Будимир, Д. 2009. Усовершенствованные волноводные полосовые фильтры с использованием S-образных резонаторов. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 19 (6), стр. 627-633. https://doi.org/10.1002/mmce.20373
Компактные двухрежимные микрополосковые резонаторы и фильтры с открытым контуром
Athukorala, L. и Budimir, D. 2009. Компактные двухрежимные микрополосковые резонаторы с открытым контуром и фильтры. Письма о компонентах СВЧ и беспроводной связи IEEE. 19 (11), с. 698-700.https://doi.org/10.1109/LMWC.2009.2032003
Цифровой предыскажитель для беспроводных передатчиков
Бондарь Д. и Будимир Д. 2009. Цифровой предыскажитель для беспроводных передатчиков. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 19 (4), стр. 453-459. https://doi.org/10.1002/mmce.20367
Ответвитель уменьшенного размера для улучшенных балансных усилителей мощности LDMOS
Драшкович, Д., Кулузис, Х. и Будимир, Д.2009. Ответвитель уменьшенного размера для улучшенных балансных усилителей мощности LDMOS. Письма о микроволновых и оптических технологиях. 51 (2), стр. 445-448. https://doi.org/10.1002/mop.24058
Компактные микрополосковые псевдо-встречно-штыревые полосовые фильтры с ступенчатым импедансом с улучшенными характеристиками полосы задерживания
Зайниев Д. и Будимир Д. 2009. Компактные микрополосковые псевдо-встречно-штыревые полосовые фильтры с ступенчатым импедансом фильтры с улучшенными характеристиками полосы задерживания. в: 10-я ежегодная конференция IEEE по беспроводным и микроволновым технологиям, 2009 г.(WAMICON ’09), 20–21 апреля 2009 г., Клируотер, Флорида, IEEE. стр. 1-2
Компактные микрополосковые двухдиапазонные псевдо-встречно-штыревые полосовые фильтры со ступенчатым сопротивлением для беспроводных приложений
Зайниев, Д., Будимир, Д. 2009. Компактные микрополосковые двухдиапазонные псевдо-встречно-штыревые полосовые фильтры с ступенчатым сопротивлением для беспроводных сетей Приложения. в: Международный симпозиум IEEE Antennas and Propagation Society (APSURSI ’09), Чарлстон, Южная Каролина, США, 1-5 июня 2009 г. IEEE.
Интегрированная антенна-фильтр с подавлением гармоник
Зайниев Д.и Будимир, Д. 2009. Интегрированный антенный фильтр с подавлением гармоник. EUCAP 2009: 3-я Европейская конференция по антеннам и распространению радиоволн. Берлин, Германия 23 – 27 марта 2009 г.
Компактный S-образный резонатор с волноводными полосовыми фильтрами
Сунтералингам, Н. и Будимир, Д. 2009. Компактный S-образный резонатор с нагруженным волноводным полосовым фильтром. AP-S 2009, Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное собрание радионауки USNC / URSI. Северный Чарльстон, Южная Каролина 01 – 05 июня 2009
Интегрированный в подложку фильтр с перекрестной связью в виде складчатых волноводов и структурой отрицательной связи
Глубоков, О. и Будимир, Д. 2009. Интегрированный в подложку фильтр с перекрестными связями в виде складчатых волноводов и структура отрицательной связи. AP-S 2009, Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное собрание радионауки USNC / URSI. Северный Чарльстон, Южная Каролина 01 – 05 июня 2009
Компактный квазигребристый резонатор на 28 ГГц, интегрированный на подложке LCP
Глубоков, О.и Будимир, Д. 2009. Компактный квазигребристый резонатор на 28 ГГц, интегрированный на подложку LCP. в: 10-я ежегодная конференция IEEE по беспроводным и микроволновым технологиям, 2009 г. (WAMICON ’09), 20–21 апреля 2009 г., Клируотер, Флорида IEEE. С. 1-3
Компактные интегрированные волноводные резонаторы на подложке с CSRR на подложке LCP
Глубоков О., Будимир Д. 2009. Компактные интегрированные волноводные резонаторы с CSRR-подложкой на подложке LCP. EUCAP 2009: 3-я Европейская конференция по антеннам и распространению радиоволн. Берлин, Германия 23–27 марта 2009 г.
Двухдиапазонный ответвитель с переключением частоты
Draskovic, D., Budimir, D., Panagamuwa, C. и Vardaxoglou, JC 2009. Двухдиапазонный ответвитель с переключением частоты- линейный соединитель. 39-я Европейская микроволновая конференция 2009. Рим, Италия 28 сентября – 02 октября 2009 г.
Двухдиапазонный делитель мощности Вилкинсона, настроенный на варактор
Драшкович, Д. и Будимир, Д. 2009. Двухдиапазонный делитель мощности Вилкинсона, настроенный на варактор. AP-S 2009, Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное собрание радионауки USNC / URSI. Северный Чарльстон, Южная Каролина 01–5 июня 2009 г.
Четырехдиапазонный делитель мощности с обобщенными линиями передачи из метаматериала NRI
Драшкович, Д. и Будимир, Д. 2009. Четырехдиапазонный делитель мощности с обобщенными линиями передачи из метаматериала NRI. AP-S 2009, Международный симпозиум IEEE по антеннам и распространению радиоволн и Национальное собрание радионауки USNC / URSI. Северный Чарльстон, Южная Каролина 01–5 июня 2009 г.
Оптически реконфигурируемые линии передачи с отрицательным показателем преломления
Драшкович, Д. и Будимир, Д. 2009. Оптически реконфигурируемые линии передачи с отрицательным показателем преломления. EUCAP 2009: 3-я Европейская конференция по антеннам и распространению радиоволн. Берлин, Германия 23 – 27 марта 2009 г.
Волноводные конструкции и фильтры для миллиметровых волн
Будимир Д. и Глубоков О.2009. Волноводные конструкции и фильтры для миллиметровых волн. 5-й семинар ЕКА по технологиям и приложениям миллиметрового диапазона и 31-й семинар ЕКА по антеннам. ESTEC, Нордвейк, Нидерланды 18–20 мая 2009 г.
Каскадные структуры ANN для позиционирования WLAN внутри помещений
Боренович, М., Нескович, А. и Будимир, Д. 2009. Структуры ANN с каскадом для внутренней WLAN позиционирование. в: Корчадо, Э. и Инь, Х. (ред.) Интеллектуальная разработка данных и автоматизированное обучение – IDEAL 2009: Материалы 10-й Международной конференции, Бургос, Испания, 23–26 сентября 2009 г., Springer.
Метод итерационной инжекции составляющих искажения для линеаризации усилителей мощности
Бондарь Д., Будимир Д., Шелковников А.Б. 2009. Метод итерационной инжекции компонентов искажения для линеаризации усилителей мощности. в: Материалы 19-й Международной Крымской конференции «СВЧ и телекоммуникационные технологии», CriMiCo 2009, 14-18 сентября 2009 г., Севастополь, Украина IEEE. С. 115-118
Улучшение искажений усилителей мощности с цифровым предыскажением
Бондарь, Д.и Будимир, Д. 2009. Улучшение искажений усилителей мощности с цифровым предыскажением. в: 10-я ежегодная конференция IEEE по беспроводным и микроволновым технологиям, 2009 г. (WAMICON ’09), 20–21 апреля 2009 г., Клируотер, Флорида IEEE. стр. 1-2
Цифровое предыскажение основной полосы частот широкополосных усилителей мощности с улучшенными эффектами памяти
Бондарь Д. и Будимир Д. 2009. Цифровое предыскажение основной полосы частот широкополосных усилителей мощности с улучшенными эффектами памяти. IEEE Radio and Wireless Symposium 2009 (RWS’2009). Сан-Диего, Калифорния 19–22 января 2009 г.
Микрополосковые резонаторы и фильтры с регулируемой частотой
Athukorala, L. и Budimir, D. 2009. Микрополосковые резонаторы и фильтры с регулируемой частотой. in: Европейская неделя микроволнового излучения «Наука, прогресс и качество в радиочастотах», Материалы конференции, 28 сентября – 2 октября 2009 г., Рим, Италия IEEE. стр. 1239-1242
Двухрежимные микрополосковые фильтры с обратной связью для беспроводных приложений
Athukorala, L.и Будимир, Д. 2009. Двухрежимные микрополосковые фильтры с обратной связью для беспроводных приложений. в: 9-я Международная конференция по электросвязи в современных услугах спутникового, кабельного и вещания (TELSIKS ’09), 7–9 октября 2009 г., Ниш, Сербия IEEE. стр. 151-153
Дизайн плоских перевернутых F-антенн (PIFA) для многодиапазонных беспроводных приложений
АбуТарбуш, Х.Ф., Нилаван, Р., Будимир, Д. и Аль-Равешиди, Х.С. 2009. Разработка плоских перевернутых F-антенн (PIFA) для многополосных беспроводных приложений.в: Международная конференция IEEE по электромагнетизму в передовых приложениях (ICEAA ’09), Турин, Италия, 14–18 сентября 2009 г. IEEE. С. 78-81
Компактная плоская перевернутая F-антенна (PIFA) для приложения WiMAX
АбуТарбуш, Х.Ф., Нилавалан, Р., Будимир, Д. и Аль-Равешиди, Х.С. 2009. Компактная планарная перевернутая F-антенна (PIFA) для приложений WiMAX. в: Международный симпозиум IEEE Antennas and Propagation Society (APSURSI ’09), Чарлстон, Южная Каролина, США, 1-5 июня 2009 г. IEEE.
Реконфигурируемая широкополосная патч-антенна для когнитивного радио
AbuTarboush, H.F., Khan, S., Nilavalan, R., Al-Raweshidy, H.S. и Будимир, Д. 2009. Реконфигурируемая широкополосная патч-антенна для когнитивного радио. в: IEEE Loughborough Antennas & Propagation Conference (LAPC 2009). Лафборо, Великобритания, 16-17 ноября 2009 г., IEEE. С. 141-144
Миниатюрные микрополосковые фильтры и диплексеры для систем беспроводной связи
Зайниев Д., Будимир Д.и Зуганелис, Г. 2008. Миниатюрные микрополосковые фильтры и диплексеры для систем беспроводной связи. Письма о микроволновых и оптических технологиях. 50 (10), стр. 2701-2702. https://doi.org/10.1002/mop.23733
Микрополосковые трехпортовые 4-канальные мультиплексоры с использованием двухдиапазонных полосовых фильтров для беспроводных приложений
Зайниев Д. и Будимир Д. 2008. Трехпортовые микрополосковые 4-канальные мультиплексоры, использующие двухполосные полосовые фильтры для беспроводных приложений. в: 2008 Международный симпозиум IEEE Antennas and Propagation Society, 5-11 июля 2008 г., Сан-Диего, Калифорния, Лос-Аламитос, США IEEE.стр. 1-4
Новые полосовые волноводные фильтры со складчатым SRR
Сунтералингам, Н. и Будимир, Д. 2008. Новые полосовые волноводные фильтры со складчатым SRR. в: 2008 Международный симпозиум IEEE Antennas and Propagation Society, 5-11 июля 2008 г., Сан-Диего, Калифорния, Лос-Аламитос, США IEEE. стр. 1-4
Компактные волноводные полосовые фильтры с улучшенными характеристиками полосы задерживания
Сунтералингам, Н. и Будимир, Д. 2008. Компактные волноводные полосовые фильтры с улучшенными характеристиками полосы задерживания. Азиатско-Тихоокеанская конференция по СВЧ 2008 (APMC’08). Гонконг 15 – 19 декабря 2008 г.
Новые компактные интегрированные волноводные резонаторы на подложке на 60 ГГц для LCP
Глубоков О., Будимир Д., Шелковников А. 2008. Новые компактные интегрированные в подложку волноводные резонаторы на 60 ГГц для LCP. в: 18-я Крымская международная конференция «СВЧ и телекоммуникационные технологии» (CriMiCo’2008). 8-12 сентября, Севастополь, Крым, Украина Лос-Аламитос, США IEEE.С. 537-538
Компактная подложка интегрированных волноводных резонаторов на подложке LCP для беспроводных систем миллиметрового диапазона
Глубоков О., Будимир Д. 2008. Компактная подложка интегрированных волноводных резонаторов на подложке LCP для беспроводных систем миллиметрового диапазона. Азиатско-Тихоокеанская конференция по СВЧ 2008 (APMC’08). Гонконг 15 – 19 декабря 2008 г.
Компактные многослойные интегральные волноводные фильтры с SRR-нагрузкой на жидкокристаллической полимерной подложке
Глубоков, О.и Будимир, Д. 2008. Компактные многослойные интегрированные волноводные фильтры с SRR на жидкокристаллической полимерной подложке. в: 2008 Международный симпозиум IEEE Antennas and Propagation Society, 5-11 июля 2008 г., Сан-Диего, Калифорния, Лос-Аламитос, США IEEE. стр. 1-4
Оптически реконфигурируемый двухдиапазонный ответвитель с искусственными линиями передачи
Драшкович Д. и Будимир Д. 2008. Оптически реконфигурируемый двухдиапазонный ответвитель с искусственными линиями передачи.в: 2008 Международный симпозиум IEEE Antennas and Propagation Society, 5-11 июля 2008 г., Сан-Диего, Калифорния, Лос-Аламитос, США IEEE. Стр. 1-4
Оптически реконфигурируемая согласующая схема входа
Драшкович Д. и Будимир Д. 2008. Оптически реконфигурируемая входная согласующая сеть. 2008 Тематическое совещание IEEE по микроволновой фотонике, проведенное совместно с Азиатско-Тихоокеанской конференцией по микроволновой фотонике 2008 года. Голд-Кост, Австралия 30 сентября – 3 октября 2008 г.
Многочастотное беспроводное радиоуправляемое судно Tesla
Budimir, D.и Маринчич, А. 2008. Многочастотное беспроводное радиоуправляемое судно Теслы. в: Конференция IEEE по истории электротехнологии (HISTELCON 2008), 11–12 сентября 2008 г., Париж, Франция IEEE. С. 24-27
Миниатюрные микрополосковые диплексоры для приложений WiMAX
Будимир Д. и Атукорала Л. 2008. Миниатюрные микрополосковые диплексоры для приложений WiMAX. в: 2008 Международный симпозиум IEEE Antennas and Propagation Society, 5-11 июля 2008 г., Сан-Диего, Калифорния, Лос-Аламитос, США IEEE.стр. 1-4
Использование искусственных нейронных сетей для позиционирования WLAN
Боренович, М., Нескович, А., Будимир, Д. и Зезель, Л. 2008. Использование искусственных нейронных сетей для позиционирования WLAN. 19-й Международный симпозиум IEEE по персональной, внутренней и мобильной радиосвязи (PIMRC’08). Канны, Франция, 15–18 сентября 2008 г. IEEE. https://doi.org/10.1109/PIMRC.2008.4699620
Новый подход к нелинейному анализу усилителей мощности
Бондарь, Д., Будимир Д., Шелковников А. 2008. Новый подход к нелинейному анализу усилителей мощности. в: 18-я Крымская международная конференция «СВЧ и телекоммуникационные технологии» (CriMiCo’2008). 8-12 сентября, Севастополь, Крым, Украина Лос-Аламитос, США IEEE. С. 125-128
Снижение роста спектра в усилителях мощности с использованием цифровой инжекции модулирующего сигнала
Бондарь Д., Будимир Д., Шелковников А.Б. 2008. Снижение роста спектра усилителей мощности с использованием цифровой инжекции модулирующего сигнала. Азиатско-Тихоокеанская конференция по СВЧ 2008 (APMC’08). Гонконг 15 – 19 декабря 2008 г.
Минимизация эффектов памяти в передатчиках OFDM с использованием адаптивной коррекции основной полосы частот
Бондарь Д., Будимир Д. и Шелковников А. 2008. Минимизация эффектов памяти в передатчиках OFDM с помощью адаптивной коррекции основной полосы частот. в: 18-я Крымская международная конференция «СВЧ и телекоммуникационные технологии» (CriMiCo’2008). 8-12 сентября, Севастополь, Крым, Украина Лос-Аламитос, США IEEE.С. 272-275
Линеаризация усилителей мощности с помощью цифрового предыскажения основной полосы частот для передатчиков OFDM
Бондарь Д., Будимир Д., Шелковников А.Б. 2008. Линеаризация усилителей мощности с помощью цифрового предыскажения в основной полосе частот для передатчиков OFDM. в: 18-я Крымская международная конференция «СВЧ и телекоммуникационные технологии» (CriMiCo’2008). 8-12 сентября, Севастополь, Крым, Украина Лос-Аламитос, США IEEE. С. 270-271
Эффективная диэлектрическая проницаемость и конструкция нарезанной линзы Люнеберга
Zouganelis, G.и Будимир, Д. 2007. Эффективная диэлектрическая проницаемость и конструкция разрезной линзы Люнеберга. Письма о микроволновых и оптических технологиях. 49 (10), стр. 2332-2337. https://doi.org/10.1002/mop.22751
Миниатюрные прямоугольные волноводные фильтры
Шелковников, А. и Будимир, Д. 2007. Миниатюрные прямоугольные волноводные фильтры. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 17 (4), стр. 398-403. https://doi.org/10.1002/mmce.20238
Кремниевый микрополосковый щелевой тетрагональный резонатор с зазором под действием ИК-излучения
Зуганелис, Г.и Будимир, Д. 2007. Кремниевый микрополосковый щелевой тетрагональный резонатор с зазором под действием ИК-излучения. Письма о микроволновых и оптических технологиях. 49 (3), стр. 699-702. https://doi.org/10.1002/mop.22240
Эффективный метод линеаризации усилителей, работающих близко к насыщению
Мальс-Илич, Н., Милованович, Б. и Будимир, Д. 2007. Эффективный метод линеаризации усилителей работает близко к насыщению. Международный журнал компьютерной инженерии в области радиочастот и сверхвысоких частот. 17 (2), стр. 169-178. https://doi.org/10.1002/mmce.20211
Сверхкомпактные микрополосковые псевдо-встречно-штыревые полосовые фильтры
Зайниев Д., Будимир Д. и Зуганелис Г. 2007. Сверхкомпактные микрополосковые псевдо-встречно-штыревые полосовые фильтры . 11-й Международный симпозиум по микроволновой и оптической технологии (ISMOT-2007). Villa Mondragone, Монте-Порцио-Катоне, Италия 17-21 декабря 2007 г.
Новые метаволноводные резонаторы и фильтры миллиметрового диапазона
Suntheralingam, N., Шелковников, А. и Будимир, Д. 2007. Новые метаволноводные резонаторы и фильтры миллиметрового диапазона. 37-я Европейская микроволновая конференция 2007. Мюнхен, Германия 08 – 12 октября 2007 г.
Компактные полосовые волноводные фильтры с SRR-нагрузкой
Шелковников А.Б., Будимир Д. и Сунтералингам Н. 2007. Компактные волноводные полосовые фильтры с SRR-нагрузкой. 11-й Международный симпозиум по микроволновой и оптической технологии (ISMOT-2007). Villa Mondragone, Монте-Порцио-Катоне, Италия 17-21 декабря 2007 г.
Конструкция балансных LDMOS-усилителей мощности с улучшенными характеристиками интермодуляционных искажений и уменьшением размеров
Koulouzis, H., Драшкович, Д. и Будимир, Д. 2007. Разработка балансных LDMOS-усилителей мощности с улучшенными характеристиками интермодуляционных искажений и уменьшением размеров. Азиатско-Тихоокеанская конференция по СВЧ 2007 (APMC’07). Бангкок, Таиланд 11–14 декабря 2007 г.
Оптически реконфигурируемые двухдиапазонные компактные ответвители ответвлений
Драшкович, Д. и Будимир, Д. 2007. Оптически реконфигурируемые двухдиапазонные компактные ответвители ответвлений. Вторая европейская конференция по антеннам и распространению радиоволн (EuCAP 2007). EICC, Эдинбург, Великобритания 11–16 ноября 2007 г.
Интегрированные в подложку безызлучательные диэлектрические волноводные резонаторы для миллиметровых волн
Будимир, Д. и Сунтералингам, Н. 2007. Интегрированные в подложку неизлучающие диэлектрические волноводные резонаторы для миллиметровых волн Приложения. Вторая европейская конференция по антеннам и распространению радиоволн (EuCAP 2007). EICC, Эдинбург, Великобритания 11–16 ноября 2007 г.
Новые полосовые фильтры metawaveguide
Budimir, D.и Камаль Ф. 2007. Новые полосовые фильтры с метаволноводом. Вторая европейская конференция по антеннам и распространению радиоволн (EuCAP 2007). EICC, Эдинбург, Великобритания 11–16 ноября 2007 г.
Линеаризация усилителя мощности WiMax посредством введения компонента основной полосы
Бондарь, Д. и Будимир, Д. 2007. Линеаризация усилителя мощности WiMax путем введения компонента основной полосы частот. 11-й Международный симпозиум по микроволновой и оптической технологии (ISMOT-2007). Villa Mondragone, Монте-Порцио-Катоне, Италия 17-21 декабря 2007 г.
Левые прямоугольные волноводные заграждающие фильтры
Шелковников, А.Б. и Будимир, Д. 2006. Правосторонние прямоугольные волноводные заграждающие фильтры. Письма о микроволновых и оптических технологиях. 48 (5), стр. 846-848. https://doi.org/10.1002/mop.21494
Полосовые фильтры с использованием периодически загружаемых гребенчатых резонаторов
Шен, Г. и Будимир, Д. 2006. Полосовые фильтры с использованием периодически загружаемых гребенчатых резонаторов. Международный журнал научно-исследовательской и микроволновой компьютерной инженерии. 16 (2), стр. 171-180. https://doi.org/10.1002 / mmce.20123
Новые электромагнитные резонаторы и фильтры на основе периодичности магнитной проницаемости
Зуганелис Г. и Будимир Д. 2006. Новые электромагнитные резонаторы и фильтры на основе периодичности магнитной проницаемости. MMA’2006: 4-я Международная конференция по микроволновым материалам и их применению. Оулу, Финляндия 12-15 июня 2006 г.
Новые s-образные SRR волноводные резонаторы с нагрузкой в E-плоскости
Suntheralingam, N.и Будимир, Д. 2006. Новые s-образные SRR-нагруженные E-плоские волноводные резонаторы. in: Proceedings of the European Conference on Antennas and Propagation: EuCAP 2006, 6-10 November 2006, Nice, France Noordwijk, The Netherlands ESA Publications.
Новые заграждающие фильтры с волноводом с нагрузкой SRR
Шелковников А.Б., Сунтералингам Н. и Будимир Д. 2006. Новые заградительные фильтры с волноводом с нагрузкой SRR. в: IEEE Antennas and Propagation Society International Symposium 2006 Los Alamitos, USA IEEE.С. 4523-4526
Малогабаритные волноводные диплексеры SRR
Шелковников, А.Б. и Будимир, Д. 2006. Компактные волноводные диплексеры SRR с нагрузкой. in: Proceedings of the European Conference on Antennas and Propagation: EuCAP 2006, 6-10 November 2006, Nice, France Noordwijk, The Netherlands ESA Publications.
LDMOS-усилители мощности с CRLH-сумматорами для передатчиков LINC
Кулузис, Х. и Будимир, Д. 2006. LDMOS-усилители мощности с CRLH-сумматорами для LINC-передатчиков.в: 36-я Европейская конференция по микроволновому излучению, 2006 г., Лос-Аламитос, США, IEEE. стр. 1181-1184
Коррекция искажений в усилителях мощности LDMOS с использованием гибридной инжекции второй ВЧ гармоники / цифровой линеаризации предыскажений
Кулузис, Х. и Будимир, Д. 2006. Коррекция искажений в усилителях мощности LDMOS с использованием гибридной инжекции второй ВЧ гармоники / цифровая линеаризация предыскажений. в: Средиземноморская электротехническая конференция IEEE, 2006. MELECON 2006. Лос-Аламитос, США IEEE.С. 177-179
Составные правые / левые объединители для передатчиков LINC
Кулузис, Х. и Будимир, Д. 2006. Составные правые / левые объединители для передатчиков LINC. 15-й Саммит IST по мобильной и беспроводной связи. Миконос, Греция 04-08 июня 2006 г.
Структуры метавоволноводного резонатора для миллиметровых волн
Будимир, Д., Сунтералингам, Н. и Камаль, Ф. 2006. Структуры метавоволноводного резонатора для приложений миллиметрового диапазона.в: Семинар IET по продуктам и технологиям MM-Wave, Лондон, Институт инженерии и технологий Великобритании (IET).
Исследования и будущие тенденции в области беспроводной микроволновой передачи энергии
Будимир Д. и Маринчич А. 2006. Исследовательская деятельность и будущие тенденции в области беспроводной микроволновой передачи энергии. 6-й Международный симпозиум Никола Тесла. Белград, Сербия 18-20 октября 2006 г.
ВЧ усилители мощности и гребенчатые фильтры для беспроводных базовых станций
Будимир, Д.и Кулузис, Х. 2006. ВЧ-усилители мощности и гребенчатые фильтры для беспроводных базовых станций. 13-я Международная конференция по телекоммуникациям (ICT 2006). Фуншал, остров Мадейра, Португалия 09-12 мая 2006 г.
ВЧ-усилители мощности LDMOS с улучшенными характеристиками с использованием дефектной конструкции заземления
Кулузис, Х. и Будимир, Д. 2006. ВЧ-усилители мощности LDMOS с улучшенными характеристиками с использованием дефектных наземная конструкция. Письма о микроволновых и оптических технологиях. 48 (1), стр. 50-53. https://doi.org/10.1002/mop.21257
Волноводные полосовые фильтры для приложений MMIC
Лалехпарвар, Л. и Будимир, Д. 2005. Волноводные полосовые фильтры для приложений MMIC. Письма о микроволновых и оптических технологиях. 46 (5), стр. 471-473. https://doi.org/10.1002/mop.21020
Новые трехмерные микрополосковые резонаторы Гильберта
Црноевич-Бенгин В. и Будимир Д. 2005. Новые трехмерные микрополосковые резонаторы Гильберта. Письма о микроволновых и оптических технологиях. 46 (3), стр. 195–197. https://doi.org/10.1002/mop.20943
Компактный гребенчатый волноводный фильтр с параллельными и последовательно соединенными резонаторами
Goussetis, G., Feresidis, AP, Budimir, D. и Vardaxoglou, JC 2005. Компактный гребень волноводный фильтр с параллельными и последовательно включенными резонаторами. Письма о микроволновых и оптических технологиях. 45 (1), стр. 22-23. https://doi.org/10.1002/mop.20711
Новые конструкции гребенчатого резонатора
Шен, Г.и Будимир, Д. 2005. Новые конструкции гребенчатого резонатора. Средиземноморский симпозиум по микроволновому излучению (MMS2005). Афины, Греция 06-08 сентября 2005 г.
Коэффициенты связи гребенчатых резонаторов
Шен Г. и Будимир Д. 2005. Коэффициенты связи гребенчатых резонаторов. в: 2005 SBMO / IEEE MTT-S Международная конференция по СВЧ и оптоэлектронике США IEEE. С. 400-402
Новые компактные волноводные резонаторы EBG в планарной форме
Шелковников, А.Б. и Будимир Д. 2005. Новые компактные волноводные резонаторы EBG в плоской форме. 35-я Европейская микроволновая конференция. Париж, Франция 04-06 октября 2005 г.
Новые полосовые фильтры в плоской форме для систем СВЧ связи
Шелковников, А. и Будимир, Д. 2005. Новые полосовые фильтры в плоской форме для микроволновых систем связи. Конференция аспирантов по электронике, фотонике, коммуникациям и сетям, а также вычислительной технике (PREP’05). Ланкастер, Великобритания 29 марта – 01 апреля
Левосторонние прямоугольные волноводные резонаторные структуры
Шелковников, А. и Будимир, Д. 2005. Левосторонние прямоугольные волноводные резонаторные структуры. Мастерская по метаматериалам для СВЧ и оптических технологий. Сан-Себастьян, Испания 18-20 июля 2005 г.
Коррекция искажений в усилителях мощности LDMOS RF с использованием цифрового предыскажения
Кулузис, Х. и Будимир, Д. 2005. Коррекция искажений усилителей мощности LDMOS RF с использованием цифрового предыскажения. Средиземноморский симпозиум по микроволновому излучению (MMS2005). Афины, Греция 06-08 сентября 2005 г.
Компоненты волновода
Будимир Д. 2005. Компоненты волновода. in: Chang, K. (ed.) Энциклопедия радиочастотной и микроволновой техники Хобокен, США Wiley.
Новые компактные резонаторы с множественными двумерными фрактальными кривыми Гильберта
Бенгин-Црноевич В. и Будимир Д. 2005. Новые компактные резонаторы с множественными двумерными фрактальными кривыми Гильберта. 35-я Европейская микроволновая конференция. Париж, Франция 04-06 октября 2005 г.
Компактные полосовые фильтры и диплексеры с гребенчатым волноводом
Шелковников А.Б., Гуссетис Г. и Будимир Д. 2004. Компактные полосовые фильтры с гребенчатым волноводом и диплексеры. Письма о микроволновых и оптических технологиях. 41 (6), стр. 465-467. https://doi.org/10.1002/mop.20173
Влияние производственных допусков на центральную частоту узкополосного волноводного фильтра E-плоскости
Ракич М., Йоканович Б.и Будимир, Д. 2004. Влияние допусков производства на центральную частоту узкополосного волноводного фильтра E-плоскости. Микроволновая техника. 10 (1), стр. 14-19.
Интегрированные волноводные полосовые фильтры с использованием толстопленочной технологии
Bengin-Crnojevic, V. и Budimir, D. 2004. Интегрированные волноводные полосовые фильтры с использованием толстопленочной технологии. Микроволновая техника. 10 (1).
Комбинированные фильтры с периодически нагружаемыми резонаторами
Шен, Г.и Будимир, Д. 2004. Комбинированные фильтры, использующие периодически нагружаемые резонаторы. Письма о микроволновых и оптических технологиях. 40 (3), стр. 189-191. https://doi.org/10.1002/mop.11324
Диэлектрические гребенчатые резонаторы
Шен Г. и Будимир Д. 2004. Диэлектрические гребенчатые резонаторы. 2004 Азиатско-Тихоокеанская конференция по СВЧ. Нью-Дели, Индия 15-18 декабря 2004 г.
Полосовые фильтры с использованием периодически загружаемых гребенчатых резонаторов
Шен, Г.и Будимир, Д. 2004. Полосовые фильтры, использующие периодически нагружаемые гребенчатые резонаторы. 2004 Азиатско-Тихоокеанская конференция по СВЧ. Нью-Дели, Индия 15-18 декабря 2004 г.
Прямоугольные волноводные резонаторы в плоской форме для применения в фильтрах
Шелковников, А.Б. и Будимир, Д. 2004. Прямоугольные волноводные резонаторы в плоской форме для применения в фильтрах. в: Международный симпозиум IEEE Antennas and Propagation Society, 2004 г., Лос-Аламитос, США, IEEE.
Новые фильтры и диплексоры Е-плоскости на прямоугольном волноводе планарной формы
Шелковников, А.Б. и Будимир, Д. 2004. Новые фильтры и диплексоры в плоскости Е, использующие прямоугольный волновод в плоской форме. 2004 Азиатско-Тихоокеанская конференция по СВЧ. Нью-Дели, Индия 15-18 декабря 2004 г.
Электромагнитное моделирование новых диплексеров в плоскости Е
Шелковников, А. и Будимир, Д. 2004. Электромагнитное моделирование новых диплексеров в плоскости Е. EPSRC PREP 2004. Хартфордшир, Великобритания 05-07 апреля 2004
Ребристый волноводный фильтр 3-го порядка с параллельно связанными резонаторами
Goussetis, G., Фересидис, А.П., Будимир, Д., Вардаксоглу, Дж. К. 2004. Гребневый волноводный фильтр 3-го порядка с параллельно связанными резонаторами. в: 2004 IEEE MTT-S International Microwave Symposium Digest Los Alamitos, USA IEEE.
Новые микрополосковые резонаторы со встроенными трехмерными кривыми
Црноевич-Бенгин В. и Будимир Д. 2004. Новые микрополосковые резонаторы со встроенными трехмерными кривыми. 2004 Азиатско-Тихоокеанская конференция по СВЧ. Нью-Дели, Индия 15-18 декабря 2004 г.
ВЧ-усилители мощности LDMOS с улучшенными характеристиками интермодуляционных искажений
Будимир, Д., Кулузис, Х. и Уильямс, С. 2004. ВЧ-усилители мощности LDMOS с улучшенными характеристиками интермодуляционных искажений. in: 34-я Европейская микроволновая конференция, 2004 г., Лондон, Великобритания, Horizon House Publications Ltd.
Усовершенствование техники линеаризации второй гармоники для многоканальных усилителей
Мальс-Илич, Н., Милованович, Б. и Будимир, Д. 2003. Улучшение в метод линеаризации второй гармоники для многоканальных усилителей. Письма о микроволновых и оптических технологиях. 38 (2), стр.150-153. https://doi.org/10.1002/mop.11000
Трехмерные копланарные волноводные фильтры нижних частот для приложений MMIC
Лалехпарвар, Л. и Будимир, Д. 2003. Трехмерные копланарные волноводные фильтры нижних частот для приложений MMIC. Письма о микроволновых и оптических технологиях. 37 (6), стр. 403-405. https://doi.org/10.1002/mop.10931
Новые периодически загружаемые фильтры E-plane
Goussetis, G. и Budimir, D. 2003. Новые фильтры E-plane с периодической загрузкой. Письма о компонентах СВЧ и беспроводной связи IEEE. 13 (6), стр. 193–195. https://doi.org/10.1109/LMWC.2003.811046
Новые периодически нагружаемые гребенчатые волноводные резонаторы
Гуссетис Г. и Будимир Д. 2003. Новые периодически нагружаемые гребенчатые волноводные резонаторы. Письма о микроволновых и оптических технологиях. 37 (4), стр. 266-268. https://doi.org/10.1002/mop.10890
Разработка асимметричных полосовых фильтров ВЧ и СВЧ методом компьютерной оптимизации
Будимир, Д.и Goussetis, Г. 2003. Разработка асимметричных полосовых фильтров ВЧ и СВЧ путем компьютерной оптимизации. IEEE Transactions по теории и методам микроволнового излучения. 51 (4, п.), Стр. 1174-1178. https://doi.org/10.1109/TMTT.2003.809623
Многослойные гребенчатые резонаторы с высокой добротностью
Шен Г. и Будимир Д. 2003. Многослойные гребенчатые резонаторы с высокой добротностью. 2003 Азиатско-Тихоокеанская конференция по СВЧ. Сеул, Южная Корея 04-07 ноября 2003 г.
Новые комбинированные резонаторные конструкции для беспроводных систем
Шен, Г.и Будимир, Д. 2003. Новые конструкции комбинированного резонатора для беспроводных систем. in: Proceedings of the International Multiconference on Circuits, Systems, Communications and Computers (CSCS 2003), Корфу, Греция, 07-10 июля 2003 г. WSEAS.
Высокодобротный диэлектрический гребенчатый резонатор с широкими характеристиками без паразитных составляющих
Шен, Г. и Будимир, Д. 2003. Высокодобротный диэлектрический гребенчатый резонатор с широкими характеристиками без паразитных составляющих. in: Proceedings of the 2003 SBMO / IEEE MTT-S International Microwave and Optoelectronics Conference, 2003.IMOC 2003 Лос-Аламитос, США IEEE.
Системы широкополосного беспроводного доступа
Шелковников А.Б., Шелковников Б.Н. и Будимир, Д. 2003. Системы широкополосного беспроводного доступа. 11-й Телекоммуникационный Форум (TELFOR 2003). Белград, Сербия и Черногория 25-27 ноября 2003 г.
Новые волноводные полосовые фильтры в плоскости Е в планарной форме
Шелковников, А. и Будимир, Д. 2003. Новые волноводные полосовые фильтры в плоскости Е в планарной форме. 2003 Азиатско-Тихоокеанская конференция по СВЧ. Сеул, Южная Корея 04-07 ноября 2003 г.
Электромагнитное моделирование структур плоских прямоугольных волноводных резонаторов
Лалехпарвар Л., Будимир Д. и Кулузис Х. 2003. Электромагнитное моделирование структур плоских прямоугольных волноводных резонаторов. EPSRC PREP 2003. Эксетер, Великобритания 14-16 апреля 2003 г.
Планарные волноводные резонаторы для генераторов и фильтров
Кулузис, Х., Лалехпарвар, Л. и Будимир, Д. 2003.Волноводные резонаторы планарной формы для генераторов и фильтров. в: 11-й Международный симпозиум IEEE по электронным устройствам для микроволновых и оптоэлектронных приложений, 2003 г. EDMO 2003 г. Лос-Аламитос, США IEEE. С. 71-75
Ребристые волноводные мультиплексоры с улучшенными характеристиками
Гуссетис Г., Шелковников А.Б. и Будимир, Д. 2003. Мультиплексоры с ребристыми волноводными коллекторами с улучшенными характеристиками. в: 33-я Европейская микроволновая конференция, 2003 г., Лос-Аламитос, США, IEEE.
Компактные гребенчатые волноводные фильтры с улучшенными характеристиками полосы задерживания
Гуссетис, Г. и Будимир, Д. 2003. Компактные гребенчатые волноводные фильтры с улучшенными характеристиками полосы задерживания. в: Дайджест Международного симпозиума микроволнового излучения IEEE MTT-S, Лос-Аламитос, США, США, IEEE, 2003.
Толстые микрополосковые резонаторы с торцевыми соединениями и периодической щелевой загрузкой.
Црноевич-Бенгин, В. и Будимир, Д. 2003. Толстые микрополосковые резонаторы с торцевыми соединениями и периодической щелевой нагрузкой. 11-й Телекоммуникационный Форум (TELFOR 2003). Белград, Сербия и Черногория 25-27 ноября 2003 г.
Разработка толстопленочных микрополосковых фильтров нижних частот
Црноевич-Бенгин, В. и Будимир, Д. 2003. Разработка толстопленочных микрополосковых фильтров нижних частот. в: 6-я Международная конференция по телекоммуникациям в современной спутниковой, кабельной и радиовещательной службе, 2003 г. TELSIKS 2003. Лос-Аламитос, США IEEE.
Линеаризация многоканальных усилителей с инжекцией вторых гармоник в усилитель и схема предыскажений
Будимир, Д., Малес-Илич, Н., Милованович, Б. и Томич, М. 2003. Линеаризация многоканальных усилителей с вводом второй гармоники в усилитель и цепь предыскажений. в: 6-я Международная конференция по телекоммуникациям в современной спутниковой, кабельной и радиовещательной службе, 2003 г. TELSIKS 2003 г. Лос-Аламитос, США IEEE.
Новые периодически нагружаемые гребенчатые волноводные резонаторы
Гуссетис Г. и Будимир Д. 2002. Новые периодически нагружаемые гребенчатые волноводные резонаторы. Письма о микроволновых и оптических технологиях. 37 (4), стр. 266-268. https://doi.org/10.1002/mop.10890
Микроволновые диэлектрические свойства соединений R2BAZNO5 и EU2BAZN075CU025O5 с использованием резонатора микроволнового резонатора
Шен Г., Зуганелис Г., Будимир Д., Кан А. , Огава, Х. и Осато, Х. 2002. Микроволновые диэлектрические свойства соединений R2BAZNO5 и EU2BAZN075CU025O5 с использованием полости микроволнового резонатора. Конференция по микроволновым материалам и их применению. York, UK 01-03 сентября 2002 г.
Пониженная чувствительность к изменению фазы в методе линеаризации второй гармоники для многоканальных усилителей
Мальс-Илич, Н., Милованович, Б. и Будимир, Д. 2002. Пониженная чувствительность к фазе изменение метода линеаризации введенной второй гармоники для многоканальных усилителей. 2002 Азиатско-Тихоокеанская конференция по СВЧ. Киото, Япония 19-22 ноября 2002 г.
Усилители с улучшенными характеристиками IMD для многоканальных беспроводных систем
Males-Ilic, N., Милованович Б. и Будимир Д. 2002. Усилители с улучшенными характеристиками IMD для многоканальных беспроводных систем. в: 32-я Европейская конференция по СВЧ (EUMC 2002) Fiera di Milano, Италия, Европа.
Интеграция фильтров нижних частот в полосовые фильтры для улучшения полосы задерживания
Гуссетис Г. и Будимир Д. 2002. Интеграция фильтров нижних частот в полосовые фильтры для улучшения полосы задерживания. в: 32-я Европейская конференция по СВЧ (EUMC 2002) Fiera di Milano, Италия, Европа.
Антенные фильтры для систем беспроводной связи
Гуссетис Г. и Будимир Д. 2002. Антенные фильтры для систем беспроводной связи. в: 32-я Европейская конференция по СВЧ (EUMC 2002) Fiera di Milano, Италия, Европа.
Характеристический импеданс в волноводе с тройным гребнем
Казануева, Дж. А., Медиавилла, А., Маккей, М., Каплин, М., Будимир, Д., Переда, Дж. А. и Helszajn, J. 2002. Характеристический импеданс в волноводе с тройным гребнем. Microwave Engineering Europe.
САПР радиочастотных и микроволновых фильтров для беспроводной связи
Будимир Д., Шен Г. и Гуссетис Г. 2002. САПР радиочастотных и микроволновых фильтров для беспроводной связи. в: Материалы 1-й Международной конференции IEEE по схемам и системам связи, 2002 г. ICCSC ’02. Лос-Аламитос, США IEEE. С. 308-311
Диэлектрические резонаторы для приложений мобильной связи
Будимир, Д., Николич, Н. и Шен, Г. 2002. Диэлектрические резонаторы для приложений мобильной связи. in: Материалы 6-й Международной конференции WSEAS по схемам, системам, коммуникациям и компьютерам (CSCC 2002), Ретимно, Крит, Греция, 7-14 июля 2002 г. WSEAS. С. 476-479
Разработка усилителей с низкой интермодуляцией для беспроводных многоканальных приложений
Будимир Д., Малес-Илич Н. и Милованович Б. 2002. Разработка усилителей с низкой интермодуляцией для беспроводных многоканальных приложений. Средиземноморский симпозиум по микроволновому излучению 2002 г. (MMS2002). Cacares, Испания 26-28 июня 2002 г.
Разработка обобщенных фильтров Чебышева с сосредоточенными элементами путем компьютерной оптимизации
Будимир Д., Лалехпарвар Л. и Николич Н. 2002. Разработка обобщенных фильтров Чебышева с сосредоточенными элементами путем компьютерной оптимизации . в: 11-я Средиземноморская электротехническая конференция, 2002 г. MELECON 2002. Лос-Аламитос, США IEEE. С. 475-478
Оптимизация асимметричных полосовых фильтров
Будимир Д.и Goussetis, Г. 2002. Оптимизация асимметричных полосовых фильтров. в: 32-я Европейская конференция по СВЧ (EUMC 2002) Fiera di Milano, Италия, Европа.
Толстопленочная технология и конструкция фильтра нижних частот
Бенгин-Црноевич В. и Будимир Д. 2002. Технология толстой пленки и конструкция фильтра нижних частот. Средиземноморский симпозиум по микроволновому излучению 2003 (MMS2003). Каир, Египет 06-08 мая 2003 г.
Верхняя и нижняя границы единичного элемента на 180 градусов гребневого волновода: расчеты и измерения
Goussetis, G., Будимир, Д. и Хелшайн, Дж. 2001. Верхняя и нижняя границы 180-градусного единичного элемента гребневого волновода: расчеты и измерения. Письма о микроволновых и оптических технологиях. 31 (4), стр. 260-261. https://doi.org/10.1002/mop.10004
Вклад Теслы в распространение радиоволн
Маринчич А. и Будимир Д. 2001. Вклад Теслы в распространение радиоволн. Обзор СВЧ. 7 (2), стр. 24-28.
Усилитель с несколькими несущими, линеаризованный посредством второй гармоники и обратной связи IM второго порядка
Milanovic, B., Males-Ilic, N. и Budimir, D. 2001. Конструкция усилителя с несколькими несущими, линеаризованная посредством второй гармоники и обратной связи IM второго порядка. Facta Universitatis Серия: Электроника и энергетика. 14 (2), стр. 243-252.
Конструкция гибридного усилителя мощности MIC, линеаризованного с помощью обратной связи по второй гармонике.
Будимир, Д., Малес-Илич, Н. и Милованович, Б. 2001. Разработка гибридного усилителя мощности MIC, линеаризованного с помощью обратной связи по второй гармонике. Обзор СВЧ. 7 (1), стр. 13-18.
Улучшение продукта интермодуляции третьего порядка усилителей РЧ и СВЧ путем инжекции
Aitchison, CS, Mbabele, M., Moazzam, MR, Budimir, D. и Ali, F. 2001. Улучшение продукта интермодуляции третьего порядка усилителей ВЧ и СВЧ методом инжекции. IEEE Transactions по теории и методам микроволнового излучения. 49 (6, п.), Стр. 1148-1154. https://doi.org/10.1109/22.
8
Программное обеспечение для проектирования беспроводных широкополосных систем
Шелковников, Б.Н., Шелковников, А. и Будимир, Д. 2001. Программное обеспечение для проектирования беспроводных широкополосных систем. в: 11-я Международная конференция по микроволновым и телекоммуникационным технологиям (CriMiCo 2001). 10-14 сентября, Севастаполь, Крым, Украина Лос-Аламитос, США IEEE. С. 45-49
САПР проектирования кабельного телевидения
Шелковников, А.Б. и Будимир, Д. 2001. САПР для проектирования кабельного телевидения. в: 5-я Международная конференция по телекоммуникациям в современной спутниковой, кабельной и радиовещательной службе, 2001 г. (TELSIKS 2001) Лос-Аламитос, США IEEE.
Конструкция усилителя с несколькими несущими, линеаризованная через вторые гармоники и обратную связь IM второго порядка
Милованович, Б., Малес-Илич, Н. и Будимир, Д. 2001. Конструкция усилителя с несколькими несущими, линеаризованная через вторые гармоники и IM второго порядка Обратная связь. в: 5-я Международная конференция по телекоммуникациям в современной спутниковой, кабельной и радиовещательной службе (TELSIKS 2001) Лос-Аламитос, США IEEE.
Усилители с низкой интермодуляцией для радиочастотных и микроволновых беспроводных систем
Males-Ilic, N., Милованович Б. и Будимир Д. 2001. Усилители с низкой интермодуляцией для радиочастотных и микроволновых беспроводных систем. в: 2001 Азиатско-Тихоокеанская конференция по СВЧ. APMC 2001. Лос-Аламитос, США IEEE. С. 984-987
Усилители интермодуляционных искажений
Малес-Илич Н., Милованович Б. и Будимир Д. 2001. Усилители интермодуляционных искажений. XLV Конференция по электронике, телекоммуникациям, компьютерам, автоматизации и ядерной инженерии. Аранджеловац, Югославия 04-07 июня 2001
Разработка усилителей с низкой интермодуляцией для беспроводных многоканальных приложений
Males-Ilic, N., Милованович, Б. и Будимир, Д. 2001. Разработка усилителей с низкой интермодуляцией для беспроводных многоканальных приложений. 31-я Европейская микроволновая конференция. Лондон, Великобритания 24-28 сентября 2001 г.
Электромагнитное моделирование многослойного CPW на подложке GaAs для MMIC
Lalehparvar, L., Budimir, D. и Koulouzis, H. 2001. Электромагнитное моделирование многослойного CPW на подложке GaAs для MMIC . Конференция EPSRC. Кил, Великобритания, апрель 2001 г.
Электромагнитное моделирование многослойного CPW на подложке GaAs для MMIC
Lalehparvar, L.и Будимир, Д. 2001. Электромагнитное моделирование многослойного CPW на подложке GaAs для MMIC. 7-й Международный симпозиум по последним достижениям в микроволновой технологии (ISRAMT2001). Монреаль, Канада 19-23 июня 2001 г.
Электромагнитное моделирование трехмерных многослойных линий передачи CPW на подложках GaAs / Si для MMIC
Лалехпарвар, Л. и Будимир, Д. 2001. Электромагнитное моделирование трехмерных многослойных линий передачи CPW на GaAs / Si подложки для MMIC. in: Proceedings of the 2001 SBMO / IEEE MTT-S International Microwave and Optoelectronics Conference, 2001.IMOC 2001. Лос-Аламитос, США IEEE.
Сравнение многослойного CPW на подложке GaAs и Si для MMIC
Лалехпарвар Л. и Будимир Д. 2001. Сравнение многослойного CPW на подложке GaAs и Si для MMIC. 8-я Международная конференция по телекоммуникациям (ICT2001). Бухарест, Румыния 4–7 июня 2001 г.
Трехмерные копланарные волноводные структуры на подложках из GaAs / Si для MMIC
Лалехпарвар, Л. и Будимир, Д. 2001. Трехмерные копланарные волноводные структуры на подложках из GaAs / Si для MMIC.в: 2001 Азиатско-Тихоокеанская конференция по СВЧ, 2001. APMC 2001. Лос-Аламитос, США IEEE.
Простая процедура настройки фильтров со связанными резонаторами
Гуссетис Г. и Будимир Д. 2001. Простая процедура настройки фильтров со связанными резонаторами. в: 2001 Азиатско-Тихоокеанская конференция по СВЧ, 2001. APMC 2001. Лос-Аламитос, США IEEE.
Электромагнитное моделирование гребневого волновода
Гуссетис Г. и Будимир Д. 2001. Электромагнитное моделирование гребневого волновода. Конференция EPSRC. Кил, Великобритания, апрель 2001 г.
Электромагнитный анализ и проектирование ребристых волноводных Т-образных переходов для мультиплексоров
Гуссетис, Г. и Будимир, Д. 2001. Электромагнитный анализ и разработка ребристых волноводных Т-образных переходов для мультиплексорных приложений. in: Материалы Международной конференции по электромагнетизму в передовых приложениях (ICEAA 01), 10–14 сентября, Турин, Италия Турин, Италия Политехнический университет Турина.
Мультиплексоры-манифольды E-plane с улучшенной полосой пропускания
Goussetis, G.и Будимир, Д. 2001. Мультиплексоры на E-плоскости с улучшенной полосой пропускания. 31-я Европейская микроволновая конференция. Лондон, Великобритания 24-28 сентября 2001 г.
Двухреберные волноводные фильтры и диплексеры в плоскости Е для систем связи
Гуссетис, Г. и Будимир, Д. 2001. Двухреберные волноводные фильтры и диплексеры в плоскости Е для систем связи. 31-я Европейская микроволновая конференция. Лондон, Великобритания 24-28 сентября 2001 г.
CAD для проектирования широкополосного беспроводного доступа
Будимир, Д.и Шелковников, А. 2001. САПР для проектирования широкополосного беспроводного доступа. в: 5-я Международная конференция по телекоммуникациям в современной спутниковой, кабельной и радиовещательной службе, 2001 г. (TELSIKS 2001) Лос-Аламитос, США IEEE.
Периодически нагружаемые волноводные структуры
Будимир Д. 2001. Периодически нагружаемые волноводные структуры. в: 11-я Международная конференция по микроволновым и телекоммуникационным технологиям (CriMiCo 2001). 10-14 сентября, Севастаполь, Крым, Украина Лос-Аламитос, США IEEE.С. 470-471
Усилители для многоканальных радиочастотных и микроволновых систем.
Будимир, Д. 2001. Усилители для радиочастотных и микроволновых многоканальных беспроводных систем. в: 2001 Международный симпозиум по электронным устройствам для микроволновых и оптоэлектронных приложений Лос-Аламитос, США IEEE. стр. 261-265
EPFIL: программное обеспечение для проектирования волноводных фильтров E-Plane и руководство пользователя
Budimir, D. 1999. EPFIL: программное обеспечение для проектирования волноводных фильтров E-Plane и руководство пользователя. Artech House.
Обобщенный дизайн фильтра с помощью компьютерной оптимизации
Будимир, Д. 1998. Обобщенный дизайн фильтра с помощью компьютерной оптимизации. Artech House.
A 2 × 2 антенны с фильтрующими подрешетками с использованием полностью резонаторных структур – Махмуд – 2021 – Микроволны, антенны и распространение IET
1 ВВЕДЕНИЕ
Компактность и многофункциональность – особенности антенн, которые привлекают внимание исследователей современных систем беспроводной связи.Кроме того, прием и / или передача сигналов в четко определенном, более широком частотном диапазоне является одной из проблем в области применения антенн с высоким коэффициентом усиления. Волноводная антенна с прорезями является хорошим кандидатом для применения в антеннах с высоким коэффициентом усиления из-за ее способности легко создавать высокое усиление путем добавления дополнительных прорезей на стенках волновода [1]. Кроме того, на него не влияют ни диэлектрические потери, ни потери паразитного излучения по сравнению с микрополосковыми антенными решетками [2]. Однако схема последовательного питания, которая широко используется в антенных решетках с щелевым волноводом и высоким коэффициентом усиления, ограничивает полосу пропускания из-за эффектов длинной линии, которые перемещают луч с рабочей частотой [3].
Чтобы свести к минимуму эту проблему, были предложены различные типы питающей сети, например, сеть с центральным питанием [4] или сеть с частичным корпоративным питанием [5]. В этих сетях, хотя ширина полосы частот увеличена, излучающие элементы находятся на том же месте, что и излучающие элементы, и, следовательно, обеспечивают меньшую гибкость в позиционировании и обычно ухудшают диаграмму направленности. Позднее идея структуры двойного волноводного слоя обсуждалась в исследовании для более крупного массива [6].Это придает гибкость конструкции, поскольку один слой волновода выделяется только для конструкции питающей сети, а второй слой размещается сверху и содержит излучающие щели. Это обеспечивает большую гибкость в размещении излучающих элементов и дает разработчику гораздо большее пространство для сети питания с превосходными характеристиками. Это улучшает диаграмму направленности, увеличивает полосу пропускания и преодолевает эффекты протяженности. Исходя из этого, в [6] была представлена решетка волноводов с прорезями 24 × 24.
В последнее время элемент субматрицы с резонатором, который также имеет два волноводных слоя, стал интересным конструктивным элементом большой антенной решетки. Он был разработан для достижения более широкой полосы пропускания излучающих элементов и минимизации отражений, возникающих в сети питания массива. Основываясь на этой идее, элементы подматрицы 2 × 4 и 2 × 2, поддерживаемые резонатором, были широко исследованы в [3, 7-12]. Несмотря на то, что элементы подрешетки с подкладкой из резонатора обладают потенциалом для увеличения полосы пропускания всей антенной решетки, они увеличивают объем решеток и могут усугублять проблему несовпадения между слоями волновода.
Впервые мы предлагаем новые топологии для конструкции двух фильтрующих подмассивов 2 × 2, основанных исключительно на резонаторах. Топологии, показанные на рисунке 1, позволяют построить две подрешетки 2 × 2 из одного волноводного слоя, сохраняя при этом хорошие диаграммы направленности и контролируемую полосу пропускания. Здесь резонаторы используются как для питающей сети, так и в качестве излучателей, образуя компактную фильтрующую подрешетку антенн. Кроме того, они дают хорошую гибкость при выборе шага выхода излучателя, чтобы не ухудшать диаграммы направленности.Кроме того, теория матрицы связи, используемая в массивах, добавляет конструктивную функцию частотной фильтрации массива, которая может устранить необходимость размещения полосового фильтра (BPF) после антенны. Поскольку использование резонаторов таким образом устраняет необходимость в отдельной питающей сети, это особенно полезно при применении этой идеи к большим массивам и может в конечном итоге уменьшить громкость внешнего интерфейса системы связи. Для дополнительного пояснения было проведено сравнение между субматрицей 2 × 2, поддерживаемой резонаторами, и предлагаемой субматрицей фильтрации 2 × 2.
Представлены две новые топологии для фильтрующих подрешеточных антенн 2 × 2 на основе всех резонаторов: (a) топология I, фильтрующая подрешеточная антенна 2×2 с использованием семи резонаторов и (b) топология II, фильтрующая подматричная антенна 2×2 с шестью резонаторами
Традиционно теория матрицы связи использовалась при проектировании двухпортовых схем ПФ с использованием n -связанных резонаторов [13].Позже он был использован при создании многопортовых схем, таких как мультиплексоры на основе всех резонаторных структур [14-17]. Эта концепция получила дальнейшее развитие при разработке других многопортовых фильтрующих СВЧ-компонентов, таких как планарные антенны, усилители, смесители и умножители частоты, которые также были полностью резонаторными [1, 18-21].
Это исследование организовано следующим образом. Матрицы связи, физические схемы и результаты моделирования двух подмассивов фильтрации 2 × 2 приведены в разделе 2.В разделе 3 приведены сравнения двух предлагаемых фильтрующих подмассивов 2 × 2 и подмассивов с резонатором, а также методы повышения внеполосной селективности. В разделе 4 описывается изготовление и измерения, за которыми следуют выводы в разделе 5.
2 СОЕДИНИТЕЛЬНАЯ МАТРИЦА И ФИЗИЧЕСКАЯ УСТАНОВКА
Матрица связи фильтрующей подмассивы 2 × 2, которая основана на полностью резонаторных структурах, может быть получена аналогично матрице мультиплексора.Детальное проектирование фильтрующих антенных решеток описано в [1, 22]. Для расчета используется общая матрица [ A ], которая определяется как:[A] = [1qe1 ⋯ 00 ⋮ ⋱ ⋮⋮ 0 ⋯ 1qr (n − 1) ⋮ 0 ⋯ ⋮ 1qrn] + p [1 ⋯ 00 ⋮ ⋱ ⋮⋮ 0 ⋯ 1 ⋮ 0 ⋯ ⋮ 1] −j [m11 ⋯ m1 (n − 1) m1n ⋮ ⋱ ⋮⋮ m (n − 1) 1 ⋯ m (n − 1) (n − 1) m (n − 1) nmn1 ⋯ ⋮ mnn] (1)
Здесь q e 1 ( q e 1 = Q e 1 FBW ) – это нормализованная внешняя добротность резонатора 1, подключенного к входному электрическому порту (рисунок 1). квартал e 1 – ненормированный внешний коэффициент качества. FBW – это относительная полоса пропускания, которая выбрана равной 10% для предлагаемых топологий подматриц. В уравнении (1) q r n ( q r n = Q r n FBW ) – нормализованная добротность излучения излучающего резонатора, связанного со свободным пространством (рисунок 1). квартал r n – ненормированный коэффициент качества излучения. p ( p = j / FBW ( ω / ω 0 – ω 0 / ω )) – комплексная частотная переменная, а ω и ω 0 – угловая и центральная угловые частоты соответственно. Предлагаемые фильтрующие подмассивы 2 × 2 предназначены для центрирования на частоте 10 ГГц.А также м ij ( м ij = млн ij / FBW ) – нормированный коэффициент связи между резонаторами i и j . м ij – ненормированный коэффициент связи. Следует отметить, что внешняя добротность ( q e 1 ) и коэффициенты качества излучения ( q r n ) должны быть равны друг другу (т.е. кв e 1 = q r 1 = q r 2 …. = q r n ), чтобы поддерживать соответствие между портами ввода и портами вывода излучения. Это аналогично полностью резонаторным фильтрующим мультиплексорам [15].
Коэффициент отражения ( S 11 ) фильтрующих антенн подрешетки 2 × 2 можно выразить как функцию от [ A ] как:S11 = (1−2qe1 [A] 11−1) (2)
Для определения S 11 с использованием матрицы [ A ], параметры q e 1 , q r n и m ij Сначала необходимо рассчитать .Это зависит от спецификаций предлагаемых топологий массивов, которые подробно обсуждаются в следующих подразделах.
2.1 Топология I
На рис. 1 (а) показана топология I фильтрующей подрешеточной антенны 2 × 2. Он состоит из семи резонаторов, которые делят входную мощность на четыре равных излучающих выхода. Есть только три неизлучающих резонатора, которые образуют питающую сеть к четырем выходам излучающих резонаторов. Такое небольшое количество питающих резонаторов можно считать новым значительным достижением с точки зрения простоты и уменьшения размера схемы фильтрующих антенн.Следует отметить, что каждый резонатор в топологии I связан не более чем с двумя резонаторами. Это сводит к минимуму эффект перекрестных связей между питающими резонаторами и упрощает конструкцию физической структуры. Взаимосвязь между излучающими выходами в данной работе не учитывается. Примерная структура, использующая эту топологию, предназначена для работы на центральной частоте f . 0 = 10 ГГц с FBW = 10% и S 11 = -20 дБ в полосе пропускания.С этими спецификациями нормализованные коэффициенты связи и коэффициенты качества могут быть получены с использованием метода оптимизации на основе градиента [1, 15]. Они м 12 = м 13 = м 24 = м 25 = м 36 = м 37 = 0,729 и q e 1 = q r 1 = q r 2 = q r 3 = q r 4 = 0.8516.
С точки зрения физической реализации используются резонаторы с прямоугольным волноводом, работающие в режиме TE 101 , и их расположение показано на рисунке 2. Для наглядности окружающий проводник настроен прозрачным, а воздух внутри конструкции – показано. Существует симметрия как в электрическом (E), так и в магнитном (H) полях, что дает значительные преимущества с точки зрения времени расчета поля, необходимого для разделения структуры на четыре симметричных участка.Резонаторы связаны друг с другом емкостными диафрагмами. Расстояние между излучающими выходами как в E-, так и в H-плоскости рассчитано на 24,32 мм (0,81 λ 0 ) на центральной частоте 10 ГГц. Его можно уменьшить, уменьшив стандартный размер b резонаторов волноводной полости, что также поможет подавить уровни боковых лепестков. Это рассматривается в топологии II раздела 2.2. Однако здесь стандартное значение волновода b ( b = 10.16 мм).
Физическая реализация топологии I. Размеры в мм: a = 22,86, b = 10,16, l 0 = 8, л 1 = 19,76, л 2 = 23,90, л r = 20,10, л a = 17.65, т = 2, т г = 10, д 0 = 17,70, д к 12 = 1,14, д г = 3,55, x = 69,56, y = 58,48, z = 40,86, l х = л л = 24.32 и радиус скругления углов = 1,6
Используется проектный подход, представленный в [1] для извлечения размеров. Физические размеры конструкции напрямую связаны со значениями коэффициентов межрезонаторной связи ( M ij ), а также к внешним и радиационным факторам качества ( Q e 1 , Q r n ) в матрице.Размеры диафрагмы находятся путем рассмотрения всего двух резонаторов и их настройки до получения желаемого значения матрицы. Во время этого процесса частота поддерживается постоянной за счет небольшого изменения размера резонаторов. Аналогичный процесс с одним резонатором позволяет получить размер диафрагмы на входе для правильного Q . e 1 . Размер одиночной излучающей апертуры настраивается для получения желаемого Q r n для излучающих резонаторов.Затем вся структура собирается с этими начальными размерами и оптимизируется. Все полученные оптимизированные размеры приведены в подписи к рисунку 2.
Отклики S-параметров, которые рассчитываются как из матрицы связи в уравнении (2), так и моделируются с использованием имитатора технологии компьютерного моделирования (CST) [23], показаны на рисунке 3. И моделирование, и расчет S 11 ответов хорошо согласуются между собой.Кроме того, смоделированный реализованный коэффициент усиления сравнивается с коэффициентом передачи, рассчитанным по матрице связи S . 21 и в целом хорошо согласуется. В смоделированном реализованном усилении присутствует, по крайней мере, один ноль передачи, который отчетливо виден в начале полосы частот. Это происходит из-за паразитных связей между резонаторами, не учтенных в матрице связи [24-26]. Например, существует небольшая связь между резонатором 2 и резонаторами 4 и 5, а также между резонатором 3 и резонаторами 6 и 7.При моделировании получены 10% FBW и возвратные потери -20 дБ в полосе пропускания (9,5–10,5 ГГц). Реальное усиление колеблется от 13,79 дБи до 14,23 дБи во всей полосе пропускания, а ширина полосы усиления по 3 дБ составляет 17,7%. Стоит отметить, что подматрица моделируется в CST с использованием материала алюминиевого сплава 6082 с проводимостью 3,56 × 10 7 См / м. Смоделированная общая эффективность составляет более 95% в полосе пропускания.
S – откликов параметров топологии, полученной из матрицы связи.Реализованный прирост и S 11 получено из КНТ
2.2 Топология II
На рисунке 1 (b) показана вторая топология фильтрующей подрешеточной антенны 2 × 2. Новизна здесь заключается в том, что размер схемы уменьшен по сравнению с топологией I на рисунке 1 (а), за счет использования только двух резонаторов для построения питающей сети и для питания четырех излучающих резонаторов. Опять же, метод оптимизации на основе градиента [15] используется для получения м ij , q e 1 и q r n .Они рассчитаны на м 12 = 1.032, м 23 = м 24 = м 25 = м 26 = 0,516 и q e 1 = q r 1 = q r 2 = q r 3 = q r 4 = 0.8516. Электрические характеристики снова составляют 10% FBW на центральной частоте 10 ГГц и с обратными потерями -20 дБ в интересующей полосе частот.
Физическая конфигурация топологии II проиллюстрирована на рисунке 4. Для связи резонаторов снова выбираются емкостные диафрагмы. Модель b 1 Размер для питания резонаторов 1 и 2 теперь составляет 7 мм, чтобы уменьшить расстояние между элементами до л л = 0.7 λ 0 в плоскости yz и минимизируйте уровни боковых лепестков, как описано в разделе 2.1. Следует отметить, что подмассив питается от той же плоскости, что и излучающие выходы. Это позволяет построить более крупную фильтрующую планарную решетку, если используются несколько блоков, и по-прежнему использовать только слой с одним волноводом. Звездообразный переход с пятью связями с резонатором 2 используется для уменьшения общего количества резонаторов, необходимых для построения подрешетки.Физические размеры взяты для каждого из M . ij , квартал e 1 и Q r n значений с использованием подхода проектирования, представленного выше и в [1]. Здесь интересно отметить, что хотя значение коэффициента связи между резонаторами 2 и 3 ( M 23 ) то же, что и между резонаторами 2 и 5 ( M 25 ) в матрице, их эквивалентная ширина апертуры ( d к 23 и д к 25 ) не совпадают.Это связано с тем, что электрическое поле в резонаторе 2 не является симметричным из-за асимметричной связи с резонатором 1. Все полученные оптимизированные размеры приведены в подписи к рисунку 4.
Физическая реализация топологии II. Размеры в мм: a = 22,86, b = 10,16, b . 1 = 7,0, л 0 = 8, л 1 = 26.55, л 2 = 26,47, л г = 20,21, л а = 18,60, т = 2, т г = 10, д 0 = 4.80, д к 12 = 1.45, д к 23 = 3,12, д к 25 = 2,95, x 1 = 8,138, x = 72,12, y = 35,32, z = 35,86, l х = 23,04, л л = 21.16 и радиус скругления углов = 1,6
Результаты моделирования сравниваются с рассчитанными откликами S-параметра на рисунке 5. Можно видеть, что затухание в реализованном усилении около начала полосы хуже, чем рассчитанное S 21 . Это могло быть результатом емкостных диафрагм, используемых для связи резонаторов друг с другом. Эти диафрагмы обеспечивают более низкое затухание на нижней частоте полосы из-за резонанса диафрагмы на частоте среза [16].Смоделированный S 11 хорошо согласуется с расчетом по полосе пропускания. Ширина полосы усиления по 3 дБ составляет около 15,7% на центральной частоте 10 ГГц, с пиковым усилением 12,94 дБи на частоте 9,55 ГГц. Общая эффективность фильтрующего подмассива превышает 95% в полосе пропускания.
S-параметров отклика топологии II, полученных из матрицы связи. Модель S 11 и реализованный выигрыш, полученный от CST
3 СРАВНЕНИЕ С ПОДСТАВКОЙ 2 × 2 С ПОЛОСТЬЮ
Для сравнения и демонстрации преимуществ предлагаемых фильтрующих подрешеток 2 × 2, конструкция подрешетки 2 × 2 с волноводным резонатором, описанная в [3], которая работает на центральной частоте 60 ГГц, теперь переработана на 10 ГГц.На рис. 6 показана структура субматричной волноводной антенны 2 × 2 с подкладкой из резонатора. Он состоит из волновода питания, размещенного в нижней части конструкции, с размерами a и b . Питающий волновод соединен с резонатором с размерами ( a c , л c ) через паз муфты размером w и и л r . Волновод с модой TE 101 используется в качестве источника питания для подрешетки.Чтобы прервать линии тока на стенках волновода питания и соответствующим образом возбудить паз связи, паз смещен от центральной линии волновода питания на величину x . Кроме того, паз связи расположен примерно на четверть длины волны волновода ( λ г ) от конца волновода, чтобы получить соответствующую связь. Имеются четыре одинаковых излучающих щели с размерами ( b а , л a ), распределенные в верхней части полости с равным интервалом ( d х = д л ).Они одинаково возбуждены и совпадают по фазе. Структура моделируется и оптимизируется с помощью симулятора CST. Размеры, указанные в подписи к рисунку 6, определены в соответствии с этапами процедуры проектирования, представленными в [3]. Производительность аналогична таковой в [3].
Субмассив 2 × 2 с гнездом с подложкой. Размеры в мм: a = 22,86, b = 10,16, a . с = 27, б с = 12.4, л с = 33,5, т = 2, л а = 15,75, б а = 9,25, л i 1 = 2, л i 2 = 9,125, d х = д л = 17.75, д z = 56,5, л f = 38, л г = 15,25, Вт а = 5,43, x = 8,43 мм и л = 65 мм
Моделируемый S 11 и реализованное усиление субматричной антенны с резонатором 2 × 2 сравниваются с предлагаемыми фильтрующими субматричными антеннами 2 × 2 на рисунке 7.Что касается S 11 , фильтрующие подмассивы 2 × 2 имеют 10% FBW чуть ниже -20 дБ с сильными спадами по краям полосы, в то время как подмассив 2 × 2 с полостями имеет около 10% FBW при – 10 дБ. Три полюса в S 11 ответов фильтрующих подмассивов. Однако в S всего два полюса. 11 Наблюдается отклик субматрицы с полостью.Стоит отметить, что модель S 11 подматрицы 2 × 2 с резервным резонатором можно улучшить до уровня ниже -20 дБ, как описано в [3]. Однако это будет происходить за счет сужения полосы пропускания. С точки зрения реализованного усиления подрешетка 2 × 2 с подкладкой из резонатора имеет усиление 12,76 дБи на центральной частоте 10 ГГц, что на ≈1,5 дБи ниже, чем усиление первой предложенной топологии (топология I). Это связано с большей физической апертурой ( A p ) размеры фильтрующих подмассивов, рассчитанные и сравниваемые следующим образом.Общий размер диафрагмы ( А, п = 4 ( л a × a )) предлагаемых фильтрующих подматриц 2 × 2 составляет 717,3 мм 2 и 755,9 мм 2 . В то время как A p субматрицы 2 × 2 с полостями составляет 582,8 мм 2 . Высота ( z ) топологии I составляет 40,86 мм, что больше, чем z = 35,86 мм топологии II из-за подачи снизу.Субмассив с полостями немного тоньше, z = 29 мм, чем фильтрующие субмассивы. С точки зрения физических структур предлагаемые фильтрующие подрешеточные антенны 2 × 2 могут быть построены с использованием одного волноводного слоя вместо использования питающего волноводного слоя и большего слоя резонатора. Предлагаемые схемы фильтрующих подмассивов облегчают процесс изготовления ЧПУ, где они могут быть сделаны только из двух частей, как будет показано в следующем разделе.
Сравнение смоделированных S 11 и реализованное усиление двух предложенных подматриц фильтрации 2 × 2 и подматрицы 2 × 2 с резервным резонатором
Ослабление реализованного усиления наших новых фильтрующих подмассивов 2 × 2 из полосы пропускания намного сильнее, чем у элементов подмассивов 2 × 2, поддерживаемых резонатором, особенно в первой топологии (топология I).Это одна из особенностей фильтрующих антенн подрешеток 2 × 2, которая устраняет необходимость размещать BPF после антенны на переднем конце системы. В соответствии с предлагаемым подходом с фильтрующей матрицей связи, использование большего количества резонаторов в схеме может дополнительно улучшить внеполосное затухание.
Чтобы исследовать это, мы можем рассмотреть различные варианты топологии II. На топологии II (рис. 1 (b)) можно увидеть, что имеется шесть резонаторов, используемых для проектирования подрешетки 2 × 2, где три резонатора участвовали в создании каждого из излучающих путей.Внеполосное затухание составляет -37 дБ на частотах полосы запуска и остановки, как показано на рисунке 5. Еще три версии топологии II, использующие большее количество резонаторов в их питающих цепях, представлены на рисунке 8. На рисунке 8 (a), один резонатор добавлен к основной линии питания, в то время как на рисунке 8 (b) один резонатор добавлен рядом с каждым из излучающих резонаторов. Однако на рисунке 8 (c) один резонатор добавлен к основной линии питания, а также один резонатор добавлен рядом с каждым из излучающих выходов одновременно.Что касается внеполосного затухания, топологии, показанные на рис. 8 (a) и (b), имеют одинаковые отклики из-за совместного использования четырех резонаторов на каждом из излучающих путей, как показано на рис. 8 (d). Кроме того, они имеют лучшее внеполосное затухание, чем топология II, на величину 19 дБ на частоте 8 ГГц по сравнению с рисунком 8 (d). Топология II (c) имеет даже лучшее затухание, чем топология II (a) и (b) из-за совместного использования пяти резонаторов в каждом из излучающих выходов. Следует отметить, что хотя топология II (a), (b) и (c) имеет лучшие характеристики внеполосного затухания, чем топология II, они не изготавливаются и будут намного больше.Другой способ улучшить затухание внеполосного усиления – ввести перекрестные связи между резонаторами, которые могут привести к введению нулей передачи вокруг частот полосы начала и остановки.
Различные варианты топологии II с их расчетными характеристиками
4 ИЗГОТОВЛЕНИЕ И ИЗМЕРЕНИЯ
Фильтрующие антенны подрешетки 2 × 2 изготовлены из алюминиевого сплава 6082 с использованием фрезерного станка с ЧПУ и показаны на рисунках 9 (а) и 10 (а).Они разделены вдоль E-плоскости на две части, чтобы облегчить процесс изготовления. Когда волновод разделен в центре E-плоскости (линия нулевого тока), это сводит к минимуму эффект дополнительных потерь, возникающих из-за несовершенных стыков между частями [22]. Установочные штифты используются во избежание больших перекосов. Металлические винты используются для сборки деталей и вставляются снизу, чтобы уменьшить влияние головки винта на характеристики излучения.
Изготовление и выполнение фильтрующих элементов подмассива 2 × 2 на основе топологии I
Изготовление и выполнение фильтрующих элементов подмассива 2 × 2 на основе топологии II
Измеренные возвратные потери и реализованная прибыль сравниваются с результатами моделирования на рисунках 9 (b) и 10 (b), и они очень хорошо согласуются.Эти небольшие различия связаны с ошибками в процессе производства. Смоделированные и измеренные диаграммы направленности для обеих плоскостей E и H на центральной частоте 10 ГГц показаны на рисунках 9 (c) и 10 (c). Получено очень хорошее согласие между результатами моделирования и измерениями. Следует отметить, что диаграммы H-плоскости обоих подматриц имеют более низкие уровни боковых лепестков, чем диаграммы E-плоскости, особенно в топологии II. Это связано с разным расстоянием между элементами. Кросс-поляризованное усиление для обоих подрешеток измерено, и они ниже -25 дБ в полосе пропускания.
5 ЗАКЛЮЧЕНИЕ
Были представлены две новые топологии для проектирования фильтрующих подрешеточных антенн 2 × 2 с использованием всех резонаторных структур. Топология I включала семь резонаторов, а в топологии II использовалось шесть резонаторов. В дополнение к использованию меньшего количества резонаторов, была также введена топология II, чтобы обеспечить боковой подвод, который позволяет расширить структуру до большой решетки, используя только один волноводный слой.Топологии были изготовлены с использованием резонаторов с прямоугольным волноводом, работающих на центральной частоте 10 ГГц, с использованием фрезерования с ЧПУ. Выполненные измерения очень хорошо согласуются с результатами моделирования.
ПОДТВЕРЖДЕНИЕ
Авторы хотели бы поблагодарить W. Hay из Физической школы Университета Бирмингема, Эджбастон, Бирмингем, Великобритания, за изготовление компонентов волновода.
ССЫЛКИ
- 1 Махмуд, Р.Х., Ланкастер, М.Д .: Планарная антенная решетка с высоким коэффициентом усиления и широкополосной фильтрацией, основанная исключительно на резонаторах. IEEE Trans. Антенны Propag . 65, 2367–2375 (2017).
- 2 Левин, Э. и др.: Исследование антенн с микрополосковой решеткой с питающей сетью. IEEE Trans. Антенны Propag . 37, 426–434 (1989)
- 3 Миура, Ю.и др.: Двухслойная щелевая антенная решетка с полым волноводом и полным корпоративным питанием в диапазоне 60 ГГц. IEEE Trans. Антенны Propag . 59, 2844–2851 (2011).
- 4 Парк, С. и др.: Однослойный щелевой волноводный массив с центральным питанием. IEEE Trans. Антенны Propag . 54, 1474–1480 (2006).
- 5 Фуджи, С., и др .: Широкополосная однослойная волноводная решетка с прорезями и встроенным частично корпоративным фидом. Труды Международного симпозиума по антеннам и распространению радиоволн. с. TP-C27-5 (2008). https://doi.org/10.34385/proc.35.3C28-5
- 6 О, С.-С. и др.: Двухслойная антенная решетка с щелевым волноводом с широкой полосой отражения / усиления на частотах миллиметрового диапазона. IEE Proc. Микроу. Антенны Propag . 151, 393–398 (2004).
- 7 Юнг, К. и др .: Планарная щелевая антенная решетка с резонатором и одной подрешеткой с волноводным питанием. В: Антенны IEEE и симпозиум общества распространения радиоволн, стр. 3273–3276 (2004).
- 8 Ли, Б., Юнг, К., Ян, С.H .: Высокоэффективная планарная щелевая антенная решетка с одиночным волноводом и подрешеткой. Микроу. Опт. Technol. Lett . 43, 228–231 (2004).
- 9 Гуан-Лонг, Х. и др.: Широкополосная щелевая антенная решетка с волноводным питанием и высоким коэффициентом усиления в Ku-диапазоне. IET Microw. Антенны Propag . 8, 1041–1046 (2014).
- 10 Хирокава, Дж.: Пластинчато-слоистые волноводные щелевые антенные решетки и их слои преобразования поляризации. Automatika: časopis za automatiku, mjerenje, elektroniku, računarstvo i komunikacije . 53, 9–19 (2012).
- 11 Ким, Д. и др.: 4х4-элементная волноводная щелевая антенная решетка корпоративного типа с полостями для диапазона 120 ГГц. IEEE Trans. Антенны Propag . 61, 5968–5975 (2013).
- 12 Чен, З., Чжоу, С.-Г., Чио, Т.-Х .: Класс цельнометаллической решетки пазов с полостью и прямым лазерным спеканием металла. Доступ IEEE . 6. 69650–69659 (2018).
- 13 Хонг, Дж.-С.Г., Ланкастер, М.Дж .: Микрополосковые фильтры для ВЧ / СВЧ-приложений, т. 167. Джон Вили и сыновья, Хобокен (2004). https://onlinelibrary.wiley.com/doi/book/10.1002/0471221619
- 14 Ланкастер, М.: Радиочастотный фильтр (2001). Патент ВОИС WO / 01/69712
- 15 Скайк, Т.Ф., Ланкастер, М., Хуанг, Ф .: Синтез схем с несколькими выходами связанных резонаторов с использованием оптимизации матрицы связи. IET Microw. Антенны Propag . 5, 1081–1088 (2011).
- 16 Шанг, X., et al.: Разработка многополосных фильтров с использованием оптимизации матрицы связи. IET Microw. Антенны Propag . 6, 24–30 (2012)
- 17 Шанг, X., и др .: Новые топологии мультиплексора, основанные на полностью резонаторных структурах. IEEE Trans. Микроу. Теория Техн . 61, 3838–3845 (2013).
- 18 Гао, Ю.и др.: Конструкция усилителей с волноводными фильтрами на основе матрицы связи. IEEE Trans. Микроу. Теория Техн . 66, 5300–5309 (2018).
- 19 Гуо, К. и др .: утроитель частоты 135–150 ГГц с согласованием волноводного фильтра. IEEE Trans. Микроу. Теория Техн . 66, 4608–4616 (2018).
- 20 Го, К.и др .: Смеситель с одной боковой полосой на 290–310 ГГц со встроенными волноводными фильтрами. IEEE Trans. Terahertz Sci. Технол . 8, 446–454 (2018)
- 21 Гао, Ю. и др.: Усилитель с интегрированным волноводным фильтром, использующий метод матрицы связи. IEEE Microw. Wirel. Компон. Lett . 29, 267–269 (2019)
- 22 Махмуд, Р.Н .: Синтез волноводных антенных решеток с использованием подхода матрицы связи, кандидатская диссертация. Бирмингемский университет (2016)
- 23 MWS, C. Computer Simulation Technology Std (2011). Технология компьютерного моделирования: Microwave studio.
- 24 Коголлос С. и др.: Новые прямоугольные волноводные структуры для улучшенных характеристик фильтров.В: Международный симпозиум IEEE MTT-S, посвященный микроволновому излучению, 2014 г., стр. 1–4 (2014 г.). IMS2014
- 25 Сото П., Боря В. и др.: Практическая конструкция прямоугольных волноводных фильтров с емкостным строительным блоком, обеспечивающим дополнительный ноль передачи. В: Международный микроволновый симпозиум IEEE MTT-S, 2015 г., стр. 1–4 (2015).
- 26 Карселлер, К.и др .: Разработка компактных широкополосных мультиплексоров с мультиплексной связью. IEEE Trans. Микроу. Теория Техн . 63, 3398–3407 (2015).
Сверхширокополосный когерентный поглотитель из метаматериала терагерцового диапазона с использованием многослойных электрических кольцевых резонаторных структур на основе просветляющего покрытия
* Соответствующие авторы
a Лаборатория исследования электронных материалов, Ключевая лаборатория Министерства образования и Международного центра диэлектрических исследований, Школа электронных наук и инженерии, Сианьский университет Цзяотун, Сиань, Китай
Электронная почта: zhoudi1220 @ gmail.ком
б Школа информационных и коммуникационных технологий, Сианьский университет Цзяотун, Сиань, Китай
с Государственная ключевая лаборатория электроизоляции и энергетического оборудования, Сианьский университет Цзяотун, Сиань 710049, Шэньси, Китай
д Международный исследовательский центр возобновляемых источников энергии, Государственная ключевая лаборатория многофазных потоков в энергетике, Сианьский университет Цзяотун, Сиань, Шэньси 710049, Китай
и Школа электроники и коммуникаций, Прекрасный профессиональный университет, Джаландхар, Пенджаб, Индия
f Национальный исследовательский технологический университет «МИСиС», Ленинский просп., 4, Москва, Россия
г Южно-Уральский государственный университет, пр. Ленина, 76, г. Челябинск, Россия
ч Научно-практический центр материаловедения НАН Беларуси, П.Бровки, 19, Минск, Беларусь
| [1] | Джейкоб Б. Хургин и С. Такер. Родни ред. Медленный свет: наука и приложения. CRC press, 2008. |
| [2] | A. Canciamilla et al., «Настраиваемые линии задержки в кремниевой фотонике: связанные резонаторы и фотонные кристаллы, настраиваемые линии задержки в кремниевой фотонике: связанные резонаторы и фотоника», т. 2, вып. 2, 2010. |
| [3] | M. Davenport et al. , «Гетерогенный перестраиваемый кремниевый лазер III – V на основе связанных резонаторов и зеркал», т. 7, вып. 3, 2015. |
| [4] | Р. В. Бойд, Д. Дж. Готье и А. Л. Гаэта, «Применение медленного света в телекоммуникациях», № 3, с.Апрель, стр. 18–23, 2006 г. |
| [5] | М. С. Бигелоу, Н. Н. Лепешкин, Р. В. Бойд, «Наблюдение сверхмедленного распространения света в кристалле рубина при комнатной температуре», № 4, с. March, pp. 7–10, 2003. |
| [6] | J. E. Sharping, Y. Okawachi и A. L. Gaeta, «Широкополосный медленный свет с использованием рамановского волоконного усилителя», т. 1, вып. 16, pp. 6092–6098, 2005. |
| [7] | K. Y. Song, M. G. Herráez, L. Thévenaz, «Наблюдение за задержкой и продвижением импульсов в оптических волокнах с использованием вынужденного рассеяния Бриллюэна», т.13, вып. 1, pp. 82–88, 2005. |
| [8] | Y. Okawachi et al. , «Настраиваемые полностью оптические задержки с помощью медленного света Бриллюэна в оптическом волокне», т. 153902, нет. April, pp. 1–4, 2005. |
| [9] | LV Hau, SE Harris, Z. Dutton, CH Behroozi и EHL Boulevard, «Снижение скорости света до 17 метров в секунду в ультрахолодном атомном газе. , ”Т. 397, нет. Февраль, стр. 594–598, 1999. |
| [10] | Y.C. Fiber, H. Shahoei, S. Member и J. Yao, «Непрерывно настраиваемый медленный и быстрый свет с помощью наклонной волоконной брэгговской решетки с оптической накачкой», т. 24, вып. 10, стр. 818–820, 2012. |
| [11] | Фиготин А., Витебский И. Медленный свет в фотонных кристаллах. 16, нет. 3. С. 293–382, 2006. |
| [12] | К. Тоцука, М. Томита, «Медленный и быстрый свет в системе микросфера – оптическое волокно», т. 23, нет. 10. С. 2194–2199, 2006. |
| [13] | Д. Сю и др., «Широкополосные кольцевые фотонные проволочные резонаторы КНИ с использованием соединителей MMI Аннотация:», т. 15, нет. 6, pp. 3149–3155, 2007. |
| [14] | Б. Э. Литтл, С. Т. Чу, Х. А. Хаус, Дж. Фореси и Дж. Лэйн, «Микрокольцевые резонаторные фильтры на канале», т. 15, вып. 6, pp. 998–1005, 1997. |
| [15] | T. A. Ibrahim et al. , «Полностью оптическое нелинейное переключение в микрокольцевых резонаторах GaAs – AlGaAs», т. 9, с.14, вып. 1, pp. 74–76, 2002. |
| [16] | S. Member et al. , «Оптическое зондирование биомолекул с помощью микрокольцевых резонаторов», т. 12, вып. 1, pp. 148–155, 2006. |
| [17] | Б. Бабагорбани и Х. Каатузян, «Разработка и исследование устройства медленного света на эллиптическом микрокольцевом резонаторе», принято и представлено в ICEE.2017 , Май 2017 г. |
| [18] | JKS Poon, J. Scheuer, S. Mookherjea, T.Джордж, Ю. Хуанг, А. Ярив, “Матричный анализ микрокольцевых оптических волноводов со связанными резонаторами”, т. 12, вып. 1, pp. 2140–2143, 2004. |
| [19] | Дж. Э. Хибнер и Р. У. Бойд, «Медленный» и «быстрый» свет в волноводах, связанных с резонаторами », т. 1, с. 49, нет. 14. С. 2629–2636, 2002. |
| [20] | А. Ярив, “Универсальные соотношения для связи оптической мощности между микрорезонаторами и диэлектрическими волноводами”, Электрон. Lett., Vol. 36, нет.4, pp. 321–322, февраль 2000 г. |
| [21] | Х. Каатузян, «Фотоника», том 2, 3-е издание, AKU Press 2017 |
| [22] | Х. Шахоеи, С. Член, Д. Сю и Дж. Х. Шмид, «Непрерывная медленная и быстрая генерация света с использованием микрокольцевого резонатора кремния на изоляторе, включающего … Непрерывную медленную и быструю генерацию света с использованием кремния на изоляторе. Микрокольцевой резонатор с многомодовым интерференционным ответвителем », № Ноябрь 2014 г. |
| [23] | A. Optics, LR Xi, F. Mechanics и KR Xi, «Медленный и быстрый свет в двойном узловом резонаторе из микрофибры с параллельной структурой. Медленный свет и быстрый свет в двойном узле из микрофибры. резонатор с параллельной структурой », № 2, с. Ноябрь, 2016 г. |
| [24] | М. Дайнес, М. Цю, З. Чжан, М. Дайнес, Л. Восински и М. Цю, «Резонансное расщепление и увеличенная глубина выемки в кольцевых резонаторах КНИ. с взаимной связью мод. Резонансное расщепление и увеличенная глубина зазоров в кольцевых резонаторах КНИ с взаимной связью мод.Август 2014 года. |
Дизайн резонатора, объяснение в энциклопедии RP Photonics; конструкция резонатора, размеры мод, области устойчивости, чувствительность юстировки
Энциклопедия> буква R> конструкция резонатора
можно найти в Руководстве покупателя RP Photonics. Среди них:
Найдите более подробную информацию о поставщиках в конце этой статьи энциклопедии или посетите наш
Вас еще нет в списке? Получите свою запись!
Используя наш рекламный пакет, вы можете разместить свой логотип и далее под описанием продукта.
Анализ и оптимизация лазерных резонаторов
Программное обеспечение RP Resonator – это особенно гибкий инструмент для анализа и оптимизации лазерных резонаторов. Например, его можно использовать для расчета и минимизации чувствительности юстировки лазерных резонаторов.
RP Photonics также предлагает компетентные услуги по проектированию резонаторов, позволяющие создавать самые современные конструкции.
Определение: описание оптических компонентов, из которых изготовлен оптический резонатор, и их точное расположение.
Альтернативный термин: конструкция с полостью
Немецкий язык: Resonatordesign
Категории: оптические резонаторы, методы
Как цитировать статью; предложить дополнительную литературу
Автор: Dr.Rüdiger Paschotta
URL: https://www.rp-photonics.com/resonator_design.html
Термин конструкция резонатора (или конструкция резонатора ) чаще всего используется в контексте лазерных резонаторов для твердотельных объемных лазеров, но иногда также и для более простых резонаторов, например для использования в спектрометрах высокого разрешения. Конструкция оптического резонатора в основном означает определение расположения оптических элементов (например, лазерных зеркал), включая их точные расстояния, чтобы моды резонатора имели желаемые свойства.Механический дизайн также может быть важным аспектом.
В простых случаях базовая конструкция резонатора ясна с самого начала (например, двухзеркальный резонатор), и нужно только настроить определенные конструктивные параметры, такие как радиусы кривизны зеркал или расстояния между элементами. В других случаях также необходимо будет определиться с основной архитектурой резонатора – например:
- Резонатор линейный или кольцевой?
- Следует ли размещать лазерный кристалл рядом с торцевым зеркалом или лучше где-то между двумя фокусирующими зеркалами?
- Где следует разместить элемент настройки длины волны или насыщающийся поглотитель?
- Полезно ли где-нибудь вставить изогнутое складывающееся зеркало?
Не всегда можно ответить на такие вопросы в начале процесса проектирования.Можно начать с определенной архитектуры резонатора, но позже придется изменить ее, осознав определенные фундаментальные ограничения.
Рисунок 1: Два простых лазерных резонатора с лазерным кристаллом в качестве активной среды. Выходные лучи генерируются там, где зеркала резонатора частично пропускают.Важные свойства резонатора
Цели проектирования резонаторов, особенно лазерных резонаторов, могут включать в себя большое количество аспектов, которые могут влиять на различные характеристики производительности:
- Часто встречающимся требованием является требование подходящих размеров мод в определенных оптических компонентах, таких как усиливающая среда (в лазерном резонаторе), насыщающийся поглотитель (в лазере с синхронизацией мод) или зеркало.
- Во многих случаях важно избегать чрезмерной чувствительности размеров мод к механическим допускам (отклонения по длине или несовпадение), а также к эффектам теплового линзирования (включая оптические аберрации). Для лазера это может помочь добиться хорошего качества луча в широком диапазоне мощностей накачки.
- Зоны стабильности относительно диоптрической силы тепловой линзы в усиливающей среде должны быть как можно шире, но это свойство связано с минимальным размером моды e.грамм. в среде усиления лазера.
- Резонатор должен иметь подходящую длину, например короткая длина для генерации коротких импульсов с переключением добротности или для простого одночастотного режима, или определенная длина для подходящей частоты следования импульсов лазера с синхронизацией мод. В некоторых случаях резонатор должен иметь потенциал для работы с переменной длиной резонатора, например для получения настраиваемой частоты следования импульсов.
- Во многих случаях потери при передаче туда и обратно должны быть минимизированы, e.грамм. для низкой пороговой мощности накачки и низкого уровня шума лазера.
- Часто желательно минимальное количество оптических компонентов.
- Можно оптимизировать общий размер, а также механическую стабильность и простоту изготовления.
Нельзя недооценивать важность этих критериев. Бывают случаи, когда с помощью оптимизированного резонатора можно добиться очень значительного улучшения характеристик лазера, а также значительного снижения чувствительности юстировки.
Роль режимов резонатора
Обратите внимание, что большинство важных свойств резонатора, как обсуждалось выше, относятся к свойствам мод резонатора.Таким образом, процесс проектирования резонатора обычно состоит из двух отдельных этапов:
- Во-первых, необходимо определить, какие свойства режима важны для производительности и какие значения они должны иметь.
- После этого можно попытаться найти конструкцию резонатора, имеющую моды с такими свойствами.
Первый шаг часто должен основываться на некоторых расчетах физики лазера. Например, может потребоваться сконструировать резонатор для соответствующего отношения оптической интенсивности к интенсивности насыщения усиливающей среды.
Для второго шага часто требуется программное обеспечение для численного расчета резонатора.
Без концепции режимов резонатора, свойства резонатора и их оптимизацию было бы гораздо труднее понять.
Пример: лазер с одной поперечной модой
Простым примером является твердотельный лазер непрерывного действия с торцевой накачкой, который должен иметь высокое (ограниченное дифракцией) качество луча. Здесь радиус моды в лазерном кристалле должен приблизительно соответствовать радиусу луча накачки, поскольку это приводит к оптимизированной эффективности преобразования энергии.Кроме того, это приводит к подавлению генерации на поперечных модах более высокого порядка, которые в этом случае имеют меньшее усиление по сравнению с основными (гауссовыми) модами из-за их меньшего пространственного перекрытия.
Соответствующие радиусы накачки и лазерного луча следует рассчитывать исходя из желаемого лазерного порога.Радиус луча накачки и радиус моды обычно следует выбирать таким образом, чтобы при предполагаемом уровне мощности накачки лазер работал в несколько раз выше лазерного порога. Для четырехуровневой среды усиления это означает, что интенсивность внутрирезонаторного лазера должна в несколько раз превышать интенсивность насыщения лазерного усиления.(Для квазитрехуровневых лазерных усиливающих сред расчет немного сложнее.) Тогда потребуется определенное качество пучка накачки для поддержания соответствующего радиуса пучка накачки по всему кристаллу.
Обычно следует избегать работы вблизи края зоны устойчивости резонатора!Обратите внимание, что радиусы мод обычно зависят от силы тепловой линзы. Таким образом, особенно для мощных лазеров, необходимо оценить силу (диоптрическую силу) тепловой линзы и спроектировать резонатор таким образом, чтобы он хорошо работал в определенном диапазоне этого значения.Например, радиусы мод внутри лазерного кристалла и на выходе лазера не должны слишком сильно изменяться, и нигде радиус моды не должен становиться достаточно малым, чтобы привести к оптическому повреждению или другим проблемам, связанным с чрезмерной оптической интенсивностью. Обычно это достигается за счет такой конструкции резонатора, что для ожидаемой диоптрической силы тепловой линзы один будет хорошо работать в зоне стабильности, то есть не близко к краю зоны стабилизации, где модовые радиусы могут расходиться или стремиться к нулю.
Не забывайте о чувствительности юстировки!Также необходимо проверить чувствительность юстировки. Обратите внимание, что конструкции резонаторов с одинаковыми радиусами мод в лазерном кристалле могут очень сильно различаться с точки зрения чувствительности юстировки, и это может затруднить работу с некоторыми конструкциями на практике. Обратите внимание, что чувствительность настройки расходится на одном из четырех краев двух областей устойчивости линейного резонатора.
Иногда лучше пожертвовать качеством луча ради более широких диапазонов стабильности и меньшей чувствительности юстировки.Ширина зоны стабильности относительно диоптрической силы тепловой линзы обратно пропорциональна минимальному радиусу моды, что указывает на проблемы для мощных лазеров, требующих больших мод. Кроме того, чувствительность совмещения в этом случае обычно будет выше. Поэтому иногда проектируют резонаторы для существенно меньших мод, так что диапазоны стабильности намного шире, а юстировка менее чувствительна, хотя при этом жертвуют качеством луча: тогда вся область накачки в лазерном кристалле может быть покрыта только некоторой комбинацией поперечных режимы.(Полученное качество луча затем можно оценить по соотношению площади накачки и площади основной моды резонатора.) Достигаемая эффективность преобразования мощности такого многомодового лазера часто несколько выше, чем с резонатором, обеспечивающим одиночный поперечный режим работы, по существу потому, что профиль интенсивности лазера может тогда более гибко подстраиваться под имеющееся усиление.
Дополнительные ограничения в импульсных лазерах
В лазере с активной модуляцией добротности требуется какой-то оптический модулятор.Следовательно, конструкция резонатора должна обеспечивать для этого некоторое пространство, и он должен иметь соответствующий радиус моды в этом месте, чтобы не было ни обрезания луча на апертуре модулятора, ни слишком сильной фокусировки луча, которая может привести к повреждать.
Аналогичным образом, пассивный Q-переключатель (насыщающийся поглотитель) должен работать с соответствующим радиусом луча, чтобы можно было получить соответствующую степень насыщения поглотителя. В противном случае поглотитель может выйти из строя или вызвать чрезмерные потери мощности.
Аналогичные соображения применимы к лазерам с пассивной синхронизацией мод. Дополнительным аспектом является то, что можно получить нестабильность модуляции добротности, если насыщение поглотителя слишком мало. Также обратите внимание, что стабильная работа с одной поперечной модой является жизненно важным условием синхронизации мод, поэтому правильные размеры мод особенно важны. Другой проблемой может быть компенсация дисперсии, для которой может потребоваться интеграция пары призм и / или некоторых дисперсионных зеркал в конструкцию.
Общая длина резонатора, определяющая время прохождения света в резонаторе, также является важным показателем в импульсном лазере.Для лазера с модуляцией добротности он оказывает важное влияние на получаемую длительность импульса, в то время как в случае синхронизации мод он определяет частоту следования импульсов.
Внутрирезонаторное удвоение частоты
В случае удвоения частоты внутри резонатора, резонатор, конечно, должен обеспечивать некоторое пространство и соответствующий радиус луча для нелинейного кристалла, так что достигается разумная величина однопроходного преобразования (например, несколько процентов). Кроме того, необходимо направить свет с удвоенной частотой в подходящем месте – предпочтительно так, чтобы получить единый выходной луч при использовании нелинейного преобразования в обоих направлениях.Обычно выходное соединение выбирают на складывающемся зеркале, а не на торцевом.
Частоты поперечной моды
В некоторых случаях следует также учитывать оптические частоты поперечных мод. Например, это может быть важно для пассивного резонатора, используемого в качестве частотного фильтра, когда нельзя гарантировать идеальное согласование мод с основной модой. Существуют также случаи, когда необходимо избегать связи мод с модами более высокого порядка в лазерном резонаторе, обеспечивая, чтобы те моды, с которыми возможна существенная связь на основе свойств пространственных мод, имели оптические частоты, которые существенно отличаются от частот фундаментальных колебаний. режимы [5].
Типичные компромиссы в конструкции резонатора
Часто невозможно идеально удовлетворить все требования к конструкции резонатора, потому что существуют определенные фундаментальные ограничения или недостаточно много свободных параметров в конструкции. Следовательно, оптимизация резонатора может включать в себя различные компромиссы:
- Особенно компактная конструкция резонатора может быть не идеальной с точки зрения качества луча или чувствительности юстировки.
- Работа в зоне стабильности I может сильно снизить чувствительность юстировки, но для этого может потребоваться более длинный резонатор и / или меньшие размеры пятна на зеркалах резонатора, что может вызвать проблемы. E.грамм. в случае лазеров с модуляцией добротности.
- Мощный лазер может быть разработан для качества луча с ограничением дифракции, но тогда он будет иметь меньший допуск на несовпадение.
Таким образом, успешная оптимизация возможна только на основе твердого понимания конкретных требований, соответствующих физических эффектов и сопутствующих компромиссов.
Проблема дизайна
Найти хороший дизайн зачастую намного сложнее, чем анализировать дизайн.В то время как обычно не очень сложно оценить модовые свойства данного резонатора, может быть гораздо сложнее найти конструкцию резонатора, которая имеет требуемые модовые свойства – особенно в случаях, когда несколько условий должны выполняться одновременно.Также обратите внимание, что любое изменение дизайна, например направленный на улучшение одного свойства резонатора, может в то же время влиять на все другие свойства. Поэтому процесс проектирования резонатора обычно не может работать так, чтобы решать различные проблемы шаг за шагом. Как правило, проектирование лазера, в котором различные проблемы решаются только шаг за шагом, требует много времени и неэффективно.
Иногда определенные цели проектирования не известны заранее, например потому что сила термолинзы пока точно не известна.Тогда может быть хорошо иметь дизайн, который можно будет соответствующим образом скорректировать.
Можно использовать предварительный испытательный резонатор, например, для точного измерения прочности термолинзы.Также есть случаи, когда сначала может потребоваться спроектировать и сконструировать испытательный резонатор, который позволяет точно измерить силу тепловой линзы, прежде чем реализовывать фактический лазерный резонатор для оптимальной работы. Полезный тестовый резонатор может, например, имеют четко выраженный край устойчивости, например, где радиусы мод быстро (а не постепенно) увеличиваются при достижении определенной диоптрической силы.
Во многих случаях для поиска хорошего решения требуется
- глубокое понимание физики резонатора
- гибкое программное обеспечение для проектирования резонаторов с возможностью численной оптимизации с произвольно заданной добротностью (см. Ниже)
- значительный опыт работы с различными типами конструкций резонаторов и их характеристиками (не только при работе с некоторым программным обеспечением)
Мощный численный метод для проектирования резонатора состоит в том, чтобы определить показатель качества , рассчитанный как сумму «штрафов» за все неидеальные свойства, и минимизировать его численными методами путем изменения длины плеча резонатора и, возможно, кривизны зеркала. .Поскольку показатель качества часто имеет огромное количество локальных экстремумов, метод Монте-Карло иногда используется для поиска глобального оптимума или, по крайней мере, хорошего решения. Обратите внимание, что процедура начинается с некоторой базовой структуры резонатора, которую, возможно, придется изменить, если не удастся найти хорошее решение.
Особенно сложные задачи проектирования резонаторов возникают в контексте лазеров с синхронизацией мод, с комбинациями различных размеров мод, ограничений длины резонатора и других сложностей.
Вопросы и комментарии пользователей
Здесь вы можете оставлять вопросы и комментарии. Если они будут приняты автором, они появятся над этим абзацем вместе с ответом автора. Автор примет решение о приеме на основании определенных критериев. По сути, вопрос должен представлять достаточно широкий интерес.
Пожалуйста, не вводите здесь личные данные; в противном случае мы бы скоро удалили его. (См. Также наше заявление о конфиденциальности.) Если вы хотите получить личный отзыв или консультацию от автора, свяжитесь с ним e.грамм. по электронной почте.
Отправляя информацию, вы даете свое согласие на возможную публикацию ваших материалов на нашем веб-сайте в соответствии с нашими правилами. (Если вы позже откажетесь от своего согласия, мы удалим эти данные.) Поскольку ваши материалы сначала проверяются автором, они могут быть опубликованы с некоторой задержкой.
Библиография
| [1] | D. Metcalf et al. , «Лазерные резонаторы, содержащие элементы самофокусировки», Прил. Опт. 26 (21), 4508 (1987), DOI: 10.1364 / AO.26.004508 |
| [2] | A. E. Siegman, «Новые разработки в лазерных резонаторах», Proc. SPIE 1224, 2 (1990), DOI: 10.1117 / 12.18425 |
| [3] | V. Magni et al. , «Последние разработки в области проектирования лазерных резонаторов», Опт. Квантовая электроника. 23, 1105 (1991), DOI: 10.1007 / BF00619980 |
| [4] | G. Cerullo et al. , «Резонаторы для фемтосекундных Ti: сапфировых лазеров с синхронизацией мод с использованием керровской линзы», Опт.Lett. 19 (11), 807 (1994), DOI: 10.1364 / OL.19.000807 |
| [5] | Р. Пашотта, «Ухудшение качества луча лазеров из-за внутрирезонаторных искажений луча», Опт. Express 14 (13), 6069 (2006), doi: 10.1364 / OE.14.006069 |
| [6] | С. Ефет и А. Пеер, «Обзор конструкции резонатора для твердотельного тела с линзой Керра с синхронизацией мод. -государственные лазеры », Прил. Sci. 3 (4), 694 (2013), DOI: 10.3390 / app3040694 |
| [7] | AE Siegman, Lasers , University Science Books, Mill Valley, CA (1986) |
| [8] | Н.Ходжсон и Х. Вебер, Лазерные резонаторы и распространение луча , 2-е изд., Спрингер, Берлин (2005) |
(Предложите дополнительную литературу!)
См. Также: оптические резонаторы, лазеры, лазерные резонаторы, резонаторы усиления, зоны устойчивости оптических резонаторов, чувствительность юстировки оптических резонаторов, конструкция лазера, The Photonics Spotlight 2011-06-10
и другие статьи в категориях оптические резонаторы, методы
Если вам понравилась эта страница, поделитесь ссылкой со своими друзьями и коллегами, e.грамм. через соцсети: Эти кнопки обмена реализованы с учетом конфиденциальности! |
Код для ссылок на других сайтах
Если вы хотите разместить ссылку на эту статью на каком-либо другом ресурсе (например, на своем веб-сайте, в социальных сетях, дискуссионном форуме, Википедии), вы можете получить здесь требуемый код.
HTML-ссылка на эту статью:
Статья о конструкции резонатора
в
Энциклопедия фотоники RP С изображением для предварительного просмотра (см. Рамку чуть выше):
 alt = "article">
alt = "article"> Для Википедии, например в разделе «== Внешние ссылки ==»:
* [https://www.rp-photonics.com/resonator_design.html
статья о конструкции резонатора в энциклопедии RP Photonics] Поставщики и ресурсы беспроводной связи RF
О компании RF Wireless World
Веб-сайт RF Wireless World является домом для поставщиков и ресурсов радиочастотной и беспроводной связи.На сайте представлены статьи, руководства, поставщики, терминология, исходный код (VHDL, Verilog, MATLAB, Labview), тестирование и измерения, калькуляторы, новости, книги, загрузки и многое другое.
Сайт RF Wireless World охватывает ресурсы по различным темам, таким как RF, беспроводная связь, vsat, спутник, радар, волоконная оптика, микроволновая печь, wimax, wlan, zigbee, LTE, 5G NR, GSM, GPRS, GPS, WCDMA, UMTS, TDSCDMA, Bluetooth, Lightwave RF, z-wave, Интернет вещей (IoT), M2M, Ethernet и т. Д. Эти ресурсы основаны на стандартах IEEE и 3GPP.Он также имеет академический раздел, который охватывает колледжи и университеты по инженерным дисциплинам и MBA.
Статьи о системах на основе Интернета вещей
Система обнаружения падений для пожилых людей на основе Интернета вещей : В статье рассматривается архитектура системы обнаружения падений, используемой для пожилых людей.
В нем упоминаются преимущества или преимущества системы обнаружения падений Интернета вещей.
Узнать больше➤
Также обратитесь к другим статьям о системах на основе Интернета вещей следующим образом:
• Система очистки туалетов самолета.
• Система измерения столкновений
• Система отслеживания скоропортящихся продуктов и овощей
• Система помощи водителю
• Система умной торговли
• Система мониторинга качества воды.
• Система Smart Grid
• Система умного освещения на базе Zigbee
• Умная парковка на базе Zigbee
• Система умной парковки на основе LoRaWAN
Статьи о беспроводной связи РФ
В этом разделе статей представлены статьи о физическом уровне (PHY), уровне MAC, стеке протоколов и сетевой архитектуре на основе WLAN, WiMAX, zigbee, GSM, GPRS, TD-SCDMA, LTE, 5G NR, VSAT, Gigabit Ethernet на основе IEEE / 3GPP и т. Д. .стандарты. Он также охватывает статьи, относящиеся к испытаниям и измерениям, по тестированию на соответствие, используемым для испытаний устройств на соответствие RF / PHY. УКАЗАТЕЛЬ СТАТЬИ ДЛЯ ССЫЛКИ >>.
Физический уровень 5G NR : Обработка физического уровня для канала 5G NR PDSCH и канала 5G NR PUSCH рассмотрена поэтапно. Это описание физического уровня 5G соответствует спецификациям физического уровня 3GPP. Читать дальше➤
Основы повторителей и типы повторителей : В нем объясняются функции различных типов ретрансляторов, используемых в беспроводных технологиях.Читать дальше➤
Основы и типы замирания : В этой статье описываются мелкомасштабные замирания, крупномасштабные замирания, медленные, быстрые и т. Д., Используемые в беспроводной связи. Читать дальше➤
Архитектура сотового телефона 5G : В этой статье рассматривается блок-схема сотового телефона 5G с внутренними модулями 5G Архитектура сотового телефона. Читать дальше➤
Основы помех и типы помех: В этой статье рассматриваются помехи в соседнем канале, помехи в совмещенном канале, Электромагнитные помехи, ICI, ISI, световые помехи, звуковые помехи и т. Д.Читать дальше➤
5G NR Раздел
В этом разделе рассматриваются функции 5G NR (New Radio), нумерология, диапазоны, архитектура, развертывание, стек протоколов (PHY, MAC, RLC, PDCP, RRC) и т. Д.
5G NR Краткий указатель ссылок >>
• Мини-слот 5G NR
• Часть полосы пропускания 5G NR
• 5G NR CORESET
• Форматы DCI 5G NR
• 5G NR UCI
• Форматы слотов 5G NR
• IE 5G NR RRC
• 5G NR SSB, SS, PBCH
• 5G NR PRACH
• 5G NR PDCCH
• 5G NR PUCCH
• Эталонные сигналы 5G NR
• 5G NR m-последовательность
• Золотая последовательность 5G NR
• 5G NR Zadoff Chu Sequence
• Физический уровень 5G NR
• Уровень MAC 5G NR
• Уровень 5G NR RLC
• Уровень 5G NR PDCP
Учебные пособия по беспроводным технологиям
В этом разделе рассматриваются учебные пособия по радиочастотам и беспроводной связи.Он охватывает учебные пособия по таким темам, как сотовая связь, WLAN (11ac, 11ad), wimax, bluetooth, zigbee, zwave, LTE, DSP, GSM, GPRS, GPS, UMTS, CDMA, UWB, RFID, радар, VSAT, спутник, WLAN, волновод, антенна, фемтосота, тестирование и измерения, IoT и т. Д. См. УКАЗАТЕЛЬ >>
Учебное пособие по 5G – В этом учебном пособии по 5G также рассматриваются следующие подтемы по технологии 5G:
Учебное пособие по основам 5G.
Частотные диапазоны
руководство по миллиметровым волнам
Волновая рама 5G мм
Зондирование волнового канала 5G мм
4G против 5G
Испытательное оборудование 5G
Сетевая архитектура 5G
Сетевые интерфейсы 5G NR
канальное зондирование
Типы каналов
5G FDD против TDD
Разделение сети 5G NR
Что такое 5G NR
Режимы развертывания 5G NR
Что такое 5G TF
Этот учебник GSM охватывает основы GSM, архитектуру сети, элементы сети, системные спецификации, приложения,
Типы пакетов GSM, структура или иерархия кадров GSM, логические каналы, физические каналы,
Физический уровень GSM или обработка речи, вход в сеть мобильного телефона GSM, установка вызова или процедура включения питания,
MO-вызов, MT-вызов, VAMOS, AMR, MSK, модуляция GMSK, физический уровень, стек протоколов, основы работы с мобильным телефоном,
Планирование RF, нисходящая линия связи PS-вызовов и восходящая линия связи PS-вызовов.
➤Подробнее.
LTE Tutorial , охватывающий архитектуру системы LTE, охватывающий основы LTE EUTRAN и LTE Evolved Packet Core (EPC). Он обеспечивает связь с обзором системы LTE, радиоинтерфейсом LTE, терминологией LTE, категориями LTE UE, структурой кадра LTE, физическим уровнем LTE, Стек протоколов LTE, каналы LTE (логические, транспортные, физические), пропускная способность LTE, агрегация несущих LTE, передача голоса по LTE, расширенный LTE, Поставщики LTE и LTE vs LTE продвинутые.➤Подробнее.
RF Technology Stuff
Эта страница мира беспроводной радиосвязи описывает пошаговое проектирование преобразователя частоты RF на примере преобразователя RF UP от 70 МГц до диапазона C.
для микрополосковой платы с использованием дискретных радиочастотных компонентов, а именно. Смесители, гетеродин, MMIC, синтезатор, опорный генератор OCXO,
колодки аттенюатора. ➤Подробнее.
➤Проектирование и разработка радиочастотного трансивера
➤Конструкция RF-фильтра
➤Система VSAT
➤Типы и основы микрополосковой печати
➤ОсновыWaveguide
Секция испытаний и измерений
В этом разделе рассматриваются контрольно-измерительные ресурсы, испытательное и измерительное оборудование для тестирования DUT на основе
Стандарты WLAN, WiMAX, Zigbee, Bluetooth, GSM, UMTS, LTE.ИНДЕКС испытаний и измерений >>
➤Система PXI для T&M.
➤ Генерация и анализ сигналов
➤Измерения слоя PHY
➤Тест устройства на соответствие WiMAX
➤ Тест на соответствие Zigbee
➤ Тест на соответствие LTE UE
➤Тест на соответствие TD-SCDMA
Волоконно-оптическая технология
Оптоволоконный компонент , основы, включая детектор, оптический соединитель, изолятор, циркулятор, переключатели, усилитель,
фильтр, эквалайзер, мультиплексор, разъемы, демультиплексор и т. д.Эти компоненты используются в оптоволоконной связи.
Оптические компоненты INDEX >>
➤Учебник по оптоволоконной связи
➤APS в SDH
➤SONET основы
➤SDH Каркасная конструкция
➤SONET против SDH
Поставщики, производители радиочастотной беспроводной связи
Сайт RF Wireless World охватывает производителей и поставщиков различных радиочастотных компонентов, систем и подсистем для ярких приложений, см. ИНДЕКС поставщиков >>.
Поставщики радиочастотных компонентов, включая радиочастотный изолятор, радиочастотный циркулятор, радиочастотный смеситель, радиочастотный усилитель, радиочастотный адаптер, радиочастотный разъем, радиочастотный модулятор, радиочастотный трансивер, PLL, VCO, синтезатор, антенну, генератор, делитель мощности, сумматор мощности, фильтр, аттенюатор, диплексор, дуплексер, микросхема резистора, микросхема конденсатора, микросхема индуктивности, ответвитель, оборудование ЭМС, программное обеспечение для проектирования радиочастот, диэлектрический материал, диод и т. д.Поставщики радиокомпонентов >>
➤Базовая станция LTE
➤RF Циркулятор
➤RF Изолятор
➤Кристаллический осциллятор
MATLAB, Labview, встроенные исходные коды
Раздел исходного кода RF Wireless World охватывает коды, связанные с языками программирования MATLAB, VHDL, VERILOG и LABVIEW.
Эти коды полезны для новичков в этих языках.
ИНДЕКС ИСХОДНОГО КОДА >>
➤3-8 декодер кода VHDL
➤Код MATLAB для дескремблера
➤32-битный код ALU Verilog
➤T, D, JK, SR триггеры labview коды
* Общая информация о здравоохранении *
Выполните эти пять простых действий, чтобы остановить коронавирус (COVID-19).
СДЕЛАЙТЕ ПЯТЬ
1. РУКИ: часто мойте их
2. КОЛЕНО: Откашляйтесь
3. ЛИЦО: Не трогай его
4. НОГИ: держитесь на расстоянии более 3 футов (1 м) друг от друга
5. ЧУВСТВОВАТЬ: Болен? Оставайся дома
Используйте технологию отслеживания контактов >>, соблюдайте >> рекомендации по социальному дистанцированию и установить систему видеонаблюдения >> чтобы спасти сотни жизней. Использование концепции телемедицины стало очень популярным в таким странам, как США и Китай, остановить распространение COVID-19, поскольку это заразное заболевание.
RF Беспроводные калькуляторы и преобразователи
Раздел «Калькуляторы и преобразователи» охватывает ВЧ-калькуляторы, беспроводные калькуляторы, а также преобразователи единиц.
Сюда входят такие беспроводные технологии, как GSM, UMTS, LTE, 5G NR и т. Д.
СПРАВОЧНЫЕ КАЛЬКУЛЯТОРЫ Указатель >>.
➤ Калькулятор пропускной способности 5G NR
➤5G NR ARFCN против преобразования частоты
➤Калькулятор скорости передачи данных LoRa
➤LTE EARFCN для преобразования частоты
➤ Калькулятор антенн Яги
➤ Калькулятор времени выборки 5G NR
IoT-Интернет вещей Беспроводные технологии
Раздел IoT охватывает беспроводные технологии Интернета вещей, такие как WLAN, WiMAX, Zigbee, Z-wave, UMTS, LTE, GSM, GPRS, THREAD, EnOcean, LoRa, SIGFOX, WHDI, Ethernet,
6LoWPAN, RF4CE, Bluetooth, Bluetooth Low Power (BLE), NFC, RFID, INSTEON, X10, KNX, ANT +, Wavenis, Dash7, HomePlug и другие.Он также охватывает датчики Интернета вещей, компоненты Интернета вещей и компании Интернета вещей.
См. Главную страницу IoT >> и следующие ссылки.
➤ НИТЬ
➤EnOcean
➤Учебник по LoRa
➤Учебник по SIGFOX
➤WHDI
➤6LoWPAN
➤Zigbee RF4CE
➤NFC
➤Lonworks
➤CEBus
➤UPB
СВЯЗАННЫЕ ЗАПИСИ
RF Wireless Tutorials
Датчики разных типов
Поделиться страницей
Перевести страницу
Новый оптический резонатор может отслеживать движение наночастиц в космосе – ScienceDaily
Обычные микроскопы позволяют получать увеличенные изображения небольших структур или объектов с помощью света.Однако наночастицы настолько малы, что почти не поглощают и не рассеивают свет и, следовательно, остаются невидимыми. Оптические резонаторы увеличивают взаимодействие между светом и наночастицами: они захватывают свет в минимальном пространстве, тысячи раз отражая его между двумя зеркалами. Если наночастица находится в захваченном световом поле, она тысячи раз взаимодействует со светом, так что изменение интенсивности света можно измерить. «Световое поле имеет разную интенсивность в разных точках пространства.Это позволяет делать выводы относительно положения наночастицы в трехмерном пространстве », – говорит д-р Лариса Колер из Physikalisches Institut KIT.
Резонатор делает движение наночастиц видимым
И не только это: «Если наночастица находится в воде, она сталкивается с молекулами воды, которые движутся в произвольных направлениях из-за тепловой энергии. Эти столкновения заставляют наночастицу перемещаться беспорядочно. Это броуновское движение теперь также можно обнаружить», эксперты добавляют.«До сих пор для оптического резонатора было невозможно отследить движение наночастицы в космосе. Можно было только установить, находится ли частица в световом поле», – объясняет Колер. В новом волоконном резонаторе Фабри-Перо зеркала с высокой отражающей способностью расположены на концах стеклянных волокон. Это позволяет нам определить гидродинамический радиус частицы, то есть толщину воды, окружающей частицу, исходя из ее трехмерного движения. Это важно, потому что такая толщина изменяет свойства наночастицы.«Благодаря гидратной оболочке можно обнаружить наночастицы, которые без нее были бы слишком маленькими», – говорит Колер. Более того, гидратная оболочка вокруг белков или других биологических наночастиц может влиять на биологические процессы.
Датчик обеспечивает понимание биологических процессов
Потенциальным применением резонатора может быть обнаружение трехмерного движения с высоким временным разрешением и определение оптических свойств биологических наночастиц, таких как белки, ДНК оригами или вирусы.Таким образом, датчик может дать представление о еще не изученных биологических процессах. (Мексика)
История Источник:
Материалы предоставлены Karlsruher Institut für Technologie (KIT) . Примечание.


