Синусоид это – Синусоида – это… Что такое Синусоида?

Графики тригонометрических функций. Синусоида | Подготовка к ЕГЭ по математике

Категория: Справочные материалыФункции и графики

Смешное видео по теме 

График функции y=sinx

Если вы умеете работать с тригонометрическим кругом, то вам не составит труда построить график функции .

Переносим  все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.

По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

.

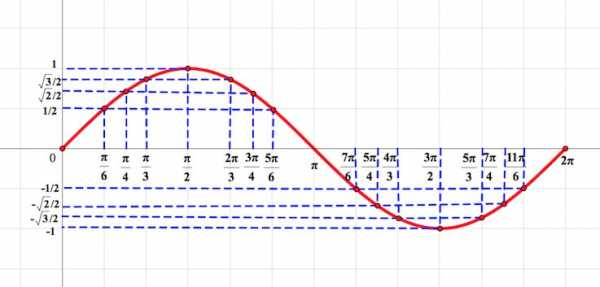Переносим  все основные значения углов, представленные на круге, и соответствующие им значения синуса на координатную плоскость.

По оси абсцисс откладываем угол в радианах, по оси ординат — значения синуса угла.

 

Нанесенные на координатную плоскость точки подсказывают нам плавную кривую.  Это и есть график функции на

Поскольку на тригонометрическом круге значения синуса повторяются через каждый круг (несколько кругов), то не составит труда построить график функции и на всей числовой прямой.

Указанный выше фрагмент графика синуса будет для нас являться как бы штампом. Тиражируя этот фрагмент, мы и получим вот такой график функции :

График функции называется синусоидой. График симметричен относительно начала координат.

График функции y=cosx

Точно также, как мы строили график при помощи тригонометрического круга, мы могли бы построить и .

Поступим несколько иначе.

Согласно формулам приведения .

Из чего мы делаем вывод, что график функции будет получен смещением графика функции на   единиц влево.

То  есть график функции  – это все таже синусоида, но теперь уже, симметричная относительно оси ординат.

 

Преобразования синусоиды

Приглашаю посмотреть  небольшой видеоролик о том, как  меняется поведение синусоиды в зависимости от  умножения аргумента или функции на некоторое число или от прибавления к аргументу или функции некоторого числа.

egemaximum.ru

синусоид – это… Что такое синусоид?

Синусоид, Капилляр Синусоидный (Sinusoid) — разновидность кровеносных капилляров диаметром 25 30 мкм, имеющихся в некоторых органах, например, в печени или надпочечниках. Особенно большое количество синусоидов можно обнаружить в печени. Синусоидные капилляры начинаются от вокругдольковой… …   Медицинские термины

СИНУСОИД, КАПИЛЛЯР СИНУСОИДНЫЙ — (sinusoid) разновидность кровеносных капилляров диаметром 25 30 мкм, имеющихся в некоторых органах, например, в печени или надпочечниках. Особенно большое количество синусоидов можно обнаружить в печени. Синусоидные капилляры начинаются от… …   Толковый словарь по медицине

синусоидальный — синусоид альный …   Русский орфографический словарь

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.… …   Википедия

МОЩНОСТЬ ЭЛЕКТРИЧЕСКАЯ — величина, характеризующая скорость изменения (преобразования, рассеяния, передачи и т. п.) электрич. энергии. В цепях пост. тока М. э. равна произведению Напряжения и силы тока. В цепях перем. тока различают мгновенную, активную, реактивную и… …   Большой энциклопедический политехнический словарь

Формула Эйлера — У этого термина существуют и другие значения, см. Список объектов, названных в честь Леонарда Эйлера#Формулы. Геометрический смысл формулы Эйлера Формула Эйлера на …   Википедия

Метод стационарной фазы — Метод стационарной фазы  метод, использующийся для аппроксимации интегралов вида: Содержание 1 Основы 2 Пример 3 Книги …   Википедия

Амплитудно-частотная характеристика —         зависимость амплитуды синусоид, колебания от его частоты на выходе устройства. Измеряется при постоянной амплитуде изменяемого по частоте колебания на входе устройства и линейном режиме его работы. Часто А. ч. х. упрощённо называют… …   Большая советская энциклопедия

Волны —         изменения состояния среды (возмущения), распространяющиеся в этой среде и несущие с собой энергию. Например, удар по концу стального стержня вызывает на этом конце местное сжатие, которое распространяется затем вдоль стержня со скоростью… …   Большая советская энциклопедия

Гармонический синтезатор —         специализированное вычислительное устройство для получения сложной функции, образуемой суммированием кратных по частоте и различных по амплитуде и фазе простых синусоидальных функций. Применяется главным образом в лабораторных… …   Большая советская энциклопедия

dic.academic.ru

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

Графики тригонометрических функций.

Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд – углы в радианах.

Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0^o до 360^o, показаны на рисунках ниже.

График функции y=sinA (синусоида)	График функции y=cosA (косинусоида)
График функции y=tgA (тангенсоида)

Из графиков видно что:

1. Графики синуса и косинуса колеблются в пределах между -1 и 1
2. Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90^o
3. Кривые синуса и косинуса непрерывны и повторяются с периодом 360^o , кривая тангенса имеет разрывы и повторяется с периодом 180^o .

Углы произвольной величины

На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О – отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке – отрицательным.

График. Положительное или отрицательное
направление при движении по окружности.

Пусть ОА вращается против часовой стрелки таким образом, что Θ₁ – любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ₂ – любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ₂=+/+ = +; cos Θ₂=+/- = -; tg Θ₂=+/- = -. Пусть ОА вращается дальше таким образом, что Θ₃ – любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ

3= -/+ = -; cos Θ₃= -/+ = -; tg Θ₃ = -/- =+ .

График. Поcтроение углов в
различных квадрантах.

Пусть ОА вращается дальше таким образом, что Θ₄– любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ₄= -/+= -; cos Θ₄=+/+=+; tg Θ₄= -/+= -.

В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем – только тангенс, в четвертом только косинус, что и показано на рис. слева.

График. Положительные и отрицательные
значения синусов, косинусов и тангенсов.

Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0^o и 360^o , синус которых равен, скажем, 0,3261. Если ввести в калькулятор 0,3261 и нажать кнопку sin

-1, получим ответ 19,03^o . Однако существует второй угол между 0^o и 360^o , который калькулятор не покажет. Синус также положителен во втором квадранте. Другой угол показан на рис. ниже как угол Θ, где Θ=180^o – 19,03^o = 160,97^o . Таким образом, 19,03^o и 160,97^o – это углы в диапазоне от 0^o до 360^o , синус которых равен 0,3261.

Будьте внимательны! Калькулятор дает только одно из этих значений. Второе значение следует определить согласно теории углов произвольной величины.
График. Нахождение всех углов по
заданному значению синуса (пример)

Пример 1

Найти все углы в диапазоне от 0

o до 360^o , синус которых равен -0,7071

Решение:
Углы, синус которых равен -0,7071^o находятся в третьем и четвертом квадранте, поскольку синус отрицателен в этих квадрантах (смотри рис. слева).

График. Нахождение всех углов по
заданному значению синуса (пример)

Из следующего рисунка Θ = arcsin 0,7071 = 45^o. Два угла в диапазоне от 0^o до 360^o, синус которых равен -0,7071, это 180^o +45^o =225^o и 360^o – 45 ^o = 315^o .

Примечание. Калькулятор дает только один ответ.
График. Нахождение всех углов по
заданному значению синуса (пример)

Пример 2 

Найти все углы между 0^o и 360^o , тангенс которых равен 1, 327.

Решение:
Тангенс положителен в первом и третьем квадрантах – рис. слева.

График. Нахождение всех углов по
заданному значению тангенса (пример)

Из рис ниже Θ = arctg1,327= 53^o .
Два угла в диапазоне от 0^o до 360^o , тангенс которых равен 1,327, это 53^o и 180^o + 53 ^o, т.е. 233^o .
График. Нахождение всех углов по
заданному значению тангенса (пример)

Построение синусоиды и косинусоиды

Пусть ОR на рис. слева- это вектор единичной длины, свободно вращающийся против часовой стрелки вокруг О. За один оборот получается круг, показанный на рис. и разделенный секторами по 15 ^o. Каждый радиус имеет горизонтальную и вертикальную составляющую. Например, для 30^o вертикальная составляющая – это ТS, а горизонтальная – ОS.

 

График. Построение синусоиды.

Из определения тригонометрических функций
sin30^o=TS/TO=TS/1, т.е. TS= sin30^o и cos30^o=OS/TO=OS/1, т.e. OS=cos30^o

 

Вертикальную составляющую TS можно перенести на график в виде T’S’, что равно значению, соответствующему углу 30^o на графике зависимости y от угла х. Если все вертикальные составляющие, подобно TS, перенести на график, то получится синусоида, показанная на рис. выше.

Если все горизонтальные составляющие, подобные OS, спроецировать на график зависимости у от угла х, получится косинусоида. Эти проекции легко визуализировать, перерисовывая круг с радиусом OR и началом отсчета углов от вертикали, как показано на рисунке слева.
Из рис. слева видно, что синусоида имеет ту же форму, что и косинусоида, но смещенная на 90^o.
График. Построение косинусоиды.

Синусоидальные и косинусоидальные графики

График. y=sinA и y=sin2A (синусоиды).	График. y=sinA и y=sin(1/2)A (синусоиды).
График. y=cosA и y=cos2A (косинусоиды).	График. y=cosA и y=cos(1/2)A (косинусоиды).

Периодические функции и период
Каждый из графиков функций, показанных на четырех рис. выше, повторяется при увеличении угла А, поэтому их называют периодическими функциями.
Функции y=sinA и y=cosA повторяются через каждые 360^o (или 2π радиан), поэтому 360^o называется периодом этих функций. Функции y=sin2A и y=cos2A повторяются через каждые 180^o (или π радиан),поэтому 180^o – это период для данных функций.
В общем случае если y=sinpA и y=cospA (где р – константа), то период функции равен 360^o/p (или 2π/p радиан ). Следовательно, если y=sin3A, то период этой функции равен 360^o/3= 120^o, если y=cos4A, то период этой функции равен 360^o/4= 90^o.

Амплитуда
Амплитудой называется максимальное значение синусоиды. Каждый из графиков 1-4 имеет амплитуду +1 (т.е. они колеблются между +1 и -1). Однако, если y=4sinA, каждая из величин sinA умножается на 4, таким образом, максимальная величина амплитуды – 4. Аналогично для y=5cos2A амплитуда равна 5, а период – 360^o/2= 180^o.

Пример 3.
Построить y=3sin2A в диапазоне от А= 0^o до А=360^o.

 Решение:
 Амплитуда =3, период = 360^o/2 =180^o.
График. Построение y=3sin2A (синусоида).

Пример 4.
Построить график y=4cos2x в диапазоне от х=0^o до х=360^o

Решение:
Амплитуда = 4. период = 360^o/2 =180^o.

График. Построение y=4cos2x (косинусоида).

 

Углы запаздывания и опережения
Кривые синуса и косинуса не всегда начинаются в 0^o . Чтобы учесть это обстоятельство, периодическая функция представляется в виде y=sin(A± α), где α – сдвиг фазы относительно y=sinA и y=cosA.

Составив таблицу значений, можно построить график функции y=sin(A-60^o), показанный на рис. слева. Если кривая y=sinA начинается в 0^o, то кривая y=sin(A-60^o) начинается в 60^o (т.е. ее нулевое значение на 60^o правее ). Таким образом, говорят, что y=sin(A-60^o) запаздывает относительно y=sinA на 60^o.
График. y=sin(A-60^o) (синусоида).

  Составив таблицу значений, можно построить график функции y=cos(A+45^o), показанный на рис. ниже.
  Если кривая y=cosA начинается в 0^o, то кривая y=cos(A+45^o) начинается на 45^o левее (т.е. ее нулевая величина   находится на 45^o раньше ).
  Таким образом, говорят, что график y=cos(A+45^o) опережает график y=cosA на 45^o.
График. y=cos(A+45^o) (косинусоида).

В общем виде, график y=sin(A-α) запаздывает относительно y=sinAна угол α.
Косинусоида имеет ту же форму, что и синусоида, но начинается на 90^o левее, т.е. опережает ее на 90^o. Следовательно, cosA=sin(A+90^o).

Пример 5.
Построить график y=5sin(A+30^o) в диапазоне от А=0^o до А=360^o

  Решение:
  Амплитуда = 5, период = 360^o/1 = 360^o. 
  5sin(A+30^o) опережает 5sinA на 30^o т.е. начинается на 30^o раньше.
График y=5sin(A+30^o) (синусоида).

Пример 6.
Построить график y=7sin(2A-π/3) в диапазоне от А=0^o до А=360^o.

   Решение:
  Амплитуда = 7, период =2π/2= π радиан
  В общем случае y=sin(pt-α) запаздывает относительно y=sinpt на α/p, следовательно 7sin(2A-π/3) запаздывает  относительно 7sin2A на ( π/3)/2, т.е. на π/6 радиан или на 30^o
График. y=7sin2A и y=7sin(2A-п/3) (синусоиды).

Синусоида вида Asin(ωt±α). Фазовый угол. Сдвиг по фазе.

Пусть OR на рис. слева представляет собой вектор, свободно вращающийся против часовой стрелки вокруг О со скоростью ω радиан/с. Вращающийся вектор называется фазовым вектором. Через время t секунд OR повернется на угол ωt радиан (на рис. слева это угол TOR). Если перпендикулярно к OR построить ST, то sinωt=ST/OT, т.e. ST=OTsinωt.
Если все подобные вертикальные составляющие спроецировать на график зависимости у от ωt, получится синусоида с амплитудой OR.
График. Фазовый угол. Сдвиг по фазе.

 

Если фазовый вектор OR делает один оборот (т.е. 2π радиан) за Т секунд, то угловая скорость ω=2π/Т рад/с, откуда
Т=2π/ ω (с), где
Т – это период
Число полных периодов, проходящих за 1 секунду, называется частотой f.
Частота = (количество периодов)/(секунда) = 1/ T = ω/2π Гц, т.е. f= ω/2π Гц
Следовательно, угловая скорость
ω=2πf рад/с.

Если в общем виде синусоидальная функция выглядит, как y=sin(ωt± α), то
А – амплитуда
ω – угловая скорость
2π/ ω – период Т, с
ω/2π – частота f, Гц
α – угол опережения или запаздывания (относительно y=Аsinωt ) в радианах, он называется также фазовым углом.

Пример 7.
Переменный ток задается как i=20sin(90πt+0,26) ампер. Определить амплитуду, период, частоту и фазовый угол (в градусах)

Решение:
i=20sin(90πt+0,26)А, следовательно,
амплитуда равна 20 А
угловая скорость ω=90π, следовательно,
период Т = 2π/ ω = 2π/ 90π = 0,022 с = 22мс
частота f = 1/Т = 1/0,022 = 45,46 Гц
фазовый угол α = 0,26 рад. = (0,26*180/π)^o = 14,9^o.

Пример 8.
Колебательный механизм имеет максимальное смещение 3 м и частоту 55 Гц. Во время t=0 смещение составляет 100см. Выразить смещение в общем виде Аsin(ωt± α).

Решение
Амплитуда = максимальное смещение = 3м
Угловая скорость ω=2πf = 2π(55) = 110 πрад./с
Следовательно, смещение 3sin(110πt + α) м.
При t=0 смещение = 100см=1м.
Следовательно, 1= 3sin(0 + α), т.е. sinα=1/3=0,33
Следовательно α=arcsin0,33=19^o
Итак, смещение равно 3sin(110 πt + 0,33).

Пример 9.
Значение мгновенного напржения в схеме переменного тока в любые t секунд задается в виде v=350sin(40πt-0,542)В. Найти:
а) Амплитуду, период, частоту и фазовый угол (в градусах)
б) значение напряжения при t =0
в) значение напряжения при t =10 мс
г) время, за которое напряжение впервые достигнет значения 200 В.
Решение:
а) Амплитуда равна 350 В, угловая скорость равна ω=40π
Следовательно,
период Т=2π/ ω=2π/40π=0,05 с =50мс
частота f=1/Т=1/0,05=20 Гц
фазовый угол = 0,542 рад (0,542*180/π) = 31^oс запаздыванием относительно v=350sin(40πt)
б) Если t =0, то v=350sin(0-0,542)=350sin(-31^o)=-180,25 В
в) Если t =10 мс, то v=350sin(40π10/10³-0,542)=350sin(0,714)=350sin41^o =229,6 В
г) Если v=200 И, то 200=350sin(40πt-0,542) 200/350=sin(40πt-0,542)

График. Колебательный механизм
(пример, синусоида).

v=350sin(40πt-0,542) Следовательно, (40πt-0,542)=arcsin200/350=35^o или 0,611 рад.
40πt= 0,611+0,542=1,153.
Следовательно, если v=200В, то время t=1,153/40π=9,179 мс

tehtab.ru

синусоид — Викисловарь

Морфологические и синтаксические свойства[править]

падеж	ед. ч.	мн. ч.
Им.	синусо́ид	синусо́иды
Р.	синусо́ида	синусо́идов
Д.	синусо́иду	синусо́идам
В.	синусо́ид	синусо́иды
Тв.	синусо́идом	синусо́идами
Пр.	синусо́иде	синусо́идах

си-ну-со́-и-д

Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).

Корень: -синус-; суффикс: -оид.

Произношение[править]

• МФА: ед. ч. [sʲɪnʊˈsoɪt], мн. ч. [sʲɪnʊˈsoɪdɨ]

Семантические свойства[править]

Значение[править]

1. анат. тип капилляра, имеющий в стенке щели (синусы) столь большого размера, что они пропускают эритроциты ◆ В синусоидах наряду с эритроцитами, не отличающимися от нормы, встречались эритроциты, имеющие в цитоплазме митохондрии, везикулы, липидные капли. М. М. Калашникова, Е. О. Фадеева, «Особенности ультраструктуры клеток печени грачей, обитающих в экологически неблагоприятных зонах», 2006 г. // «Известия Российской академии наук»

Синонимы[править]

1. синусоидный капилляр

Антонимы[править]

1. —

Гиперонимы[править]

1. капилляр, кровеносный сосуд

Гипонимы[править]

1. —

Родственные слова[править]

Этимология[править]

Суффиксное производное от существительного синус, далее от лат. sinus «полость, изгиб, складка, залив».

Фразеологизмы и устойчивые сочетания[править]

Перевод[править]

Библиография[править]

си-ну-со́-ид

• форма родительного падежа множественного числа существительного синусоида ◆ Оказалось, под действием набегающих волн в пластине возникают сложные пространственные механические колебания, которые представляют собой сумму синусоид с разными амплитудами, периодами и фазами. Алексей Андрианов, Игорь Андрианов, «Ещё одно предсказание Жюля Верна сбывается?», 2009 г. // «Наука и жизнь» (цитата из Национального корпуса русского языка, см. Список литературы)

ru.wiktionary.org

Свойства функций синуса, косинуса, тангенса и котангенса и их графики

Свойства функции y=sin(x) и ее график. 

График функции (синусоида)

Свойства функции

1.  Область определения: R (x — любое действительное число) т.е. 
2. Область значений:

3. Функция нечетная:

   (график симметричен относительно начала координат).

4. Функция периодическая с периодом 
5. Точки пересечения с осями координат:  
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания:   
   

 

Объяснение и обоснование

Описывая свойства функций, мы будем чаще всего выделять такие их характеристики: 1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями координат; 6)   промежутки знакопостоянства; 7) промежутки возрастания и убывания; 8) наибольшее и наименьшее значения функции.

Замечание. Абсциссы точек пересечения графика функции с осью Ох (то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.

Напомним, что значение синуса — это ордината соответствующей точки единичной окружности (рис. 1).

 

 Рис.1.

Поскольку ординату можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности всегда можно провести единственную прямую, перпендикулярную оси ординат), то область определения функции — все действительные числа. Это можно записать так:

Для точек единичной окружности ординаты находятся в промежутке [—1; 1] и принимают все значения от —1 до 1, поскольку через любую точку отрезка [—1; 1] оси ординат (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси орди­нат, и получить точку окружности, которая имеет рассматриваемую орди­нату. Таким образом, для функции область значений: . Это можно записать так:.Как видим, наибольшее значение функции sin x равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при Наименьшее значение функции равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при.

Синус — нечетная функция: , поэтому ее график симметричен относительно начала координат.

Синус — периодическая функция с наименьшим положительным периодом : , таким образом, через промежутки длиной вид графика функции повторя­ется. Поэтому при построении графика этой функции достаточно построить график на любом промежутке длиной , а потом полученную линию парал­лельно перенести вправо и влево вдоль оси Ox на расстояние , где k — любое натуральное число.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение , то есть график функции проходит через начало координат.

На оси значение . Поэтому необходимо найти такие значения , при которых , то есть ордината соответствующей точки единичной окруж­ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж­ности будут выбраны точки C или D, то есть при (см. рис. 1).

Промежутки знакопостоянства. Значения функции синус положительны (то есть ордината соответствующей точки единичной окружности положительна) в I и II четвертях (рис. 2). Таким образом, при всех , а также, учитывая период, при всех .

Значения функции синус отрицательны (то есть ордината соответствую­щей точки единичной окружности отрицательна) в III и IV четвертях, поэто­му при .

Промежутки возрастания и убывания. Учитывая периодичность функции с периодом , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке . 

Если (рис. 3, а), то при увеличении аргумента  ордината соответствующей точки единичной окружности увеличивается (то есть , следовательно, на этом промежутке функция возрас­тает. Учитывая периодичность функции , делаем вывод, что она также возрастает на каждом из промежутков 

Рис.2                                                                            Рис.3

Если  (рис.3,б), то при увеличении аргумента  ордината соответствующей точки единичной окружности уменьшается (то есть ), таким образом, на этом промежутке функция убыва­ет. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков 

Проведенное исследование позволяет обоснованно построить график функции . Учитывая периодичность этой функции (с периодом ), достаточно сначала построить график на любом промежутке длиной , на­пример на промежутке . Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината соответствующей точки единичной окружности. На рисунке 4 показано построение графика функции на промежутке . Учитывая нечетность функции  (ее график симметричен относительно начала координат), для построения графика на промежутке отображаем полученную кривую симметрич­но относительно начала координат (рис. 5).

Рис.4

Рис.5

 

Поскольку мы построили график на промежутке длиной , то, учитывая периодичность синуса (с периодом ), повторяем вид графика на каждом промежутке длиной (то есть переносим параллельно график вдоль оси на , где k — целое число). Получаем график, который называется синусоидой .(Рис.6)

Рис.6

Замечание. Тригонометрические функции широко применяются в ма­тематике, физике и технике. Например, множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п., описываются функцией, которая задается формулой . Та­кие процессы называют гармоническими колебаниями.

График функции можно получить из синусоиды сжатием или растяжением ее вдоль координатных осей и параллельным пере­носом вдоль оси . Чаще всего гармоническое колебание является функцией времени t. Тогда оно задается формулой , где А — амплитуда

колебания, — частота, — начальная фаза, — период колебания.

 

СВОЙСТВА ФУНКЦИИ И ЕЕ ГРАФИК

График функции  (косинусоида).

Свойства функции 

1. Область определения: R (x — любое действительное число).
2. Область значений: 

3. Функция четная:

   (график симметричен относительно оси ).

4. Функция периодическая с периодом  : 
5. Точки пересечения с осями координат 
6. Промежутки знакопостоянства: 
7. Промежутки возрастания и убывания: 
   

Объяснение и обоснование

Напомним, что значение косинуса — это абсцисса соответствующей точки единичной окружности (рис.7). Поскольку абсциссу можно найти для любой точки единичной окружности (в силу того, что через любую точку окружности, всегда можно провести единственную прямую, перпендикулярную оси абсцисс), то область определения функции — все действительные числа. Это можно записать так:
.

Рис.7

Для точек единичной окружности абсциссы находятся в промежутке и принимают все значения от -1 до 1, поскольку через любую точку отрезка оси абсцисс (который является диаметром единичной окружности) всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следовательно, область значений функции . Это можно записать так: .

Как видим, наибольшее значение функции равно единице. Это зна­чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при .

Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда соответствующей точкой единичной окруж­ности является точка B, то есть при .

Косинус — четная функция: , поэтому ее график симметричен относительно оси .

Косинус — периодическая функция с наименьшим положительным периодом : . Таким об­разом, через промежутки длиной вид графика функции повторяется.

Чтобы найти точки пересечения графика функции с осями координат, напомним, что на оси значение . Тогда соответствующее значение . На оси значение . Поэтому необходимо найти такие значения , при которых , то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только тогда, когда на единичной окружности будут выбраны точки C или D, то есть при .

Промежутки знакопостоянства. Значения функции косинус положительны (то есть абсцисса соответствующей точки единичной окружности положительна) в I и IV четвертях (рис. 8). Следова­тельно, 0 при , а также, учитывая период, при всех .

Значения функции косинус отрицательны (то есть абсцисса соответству­ющей точки единичной окружности отрицательна) во II и III четвертях, поэтому  при 

Промежутки возрастания и убывания. Учитывая периодичность функции , достаточно исследовать ее на возрастание и убывание на любом промежутке длиной , например на промежутке .

Если (рис. 9, а), то при увеличении аргумента  абсцис­са соответствующей точки единичной окружности уменьшается (то есть ), следовательно, на этом промежутке функция убывает. Учитывая периодичность функции , делаем вывод, что она также убывает на каждом из промежутков .

Если (рис. 9, б), то при увеличении аргумента  аб­сцисса соответствующей точки единичной окружности увеличивается (то есть ), таким образом, на этом промежутке функция  возрастает. Учитывая периодичность функции , делаем вывод, что она возрастает также на каждом из промежутков . 

Рис.8                                                                                                                          Рис.9

Проведенное исследование позволяет построить график функции аналогично тому, как был построен график функции . Но график функции можно также получить с помощью геометрических преобразований графика функции , используя формулу

Рис.10

Эту формулу можно обосновать, например, так. Рассмотрим единичную окружность (рис. 10), отметим на ней точки а также

абсциссы и ординаты этих точек. Так как , то при повороте

прямоугольника  около точки на угол — против часовой стрел­ки он перейдет в прямоугольник . Но тогда . Следовательно, 00.

Укажем также формулы, которые нам понадобятся далее:.

Тогда,

Таким образом, .

Учитывая, что , график функции можно полу­чить из графика функции его параллельным переносом вдоль оси на  (рис. 11). Полученный график называется косинусоидой (рис. 12).

Рис.11

Рис.12

График функции  (тангенсоида) 

Свойства функции :

1. Область определения: 

2. Область значений: 

3. Функция нечетная: 

4. Функция периодическая с периодом 

5. Точки пересечения с осями координат:   

6. Промежутки знакопостоянства:

7. Промежутки возрастания и убывания:

8. Наибольшего и наименьшего значений функция не имеет.

График функции  (котангенсоида)

Свойства функции :

1. Область определения:

2. Область значений:

3. Функция нечетная: 

4. Функция переодическая с периодом 
5. Точки пересечения с осями координат: 

6. Промежутки знакопостоянства: 

7. Промежутки возрастания и убывания:

 

8. Наибольшего и наименьшего значений функция не имеет.

 

ya-znau.ru

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

Тригонометрические кривые. Синусоида. Косинусоида. Тангенсоида. Котангенсоида.

Графики тригонометрических функций.

Все углы А по умолчанию приведены в градусах. Все таблицы значений и формулы синусов, косинусов, тангенсов, котангенсов (здесь). Во всех формулах пределов и разложений в ряд – углы в радианах.

Графики функций y=sinA, y=cosA, y=tgA,построенные для диапазона от 0^o до 360^o, показаны на рисунках ниже.

График функции y=sinA (синусоида)	График функции y=cosA (косинусоида)
График функции y=tgA (тангенсоида)

Из графиков видно что:

1. Графики синуса и косинуса колеблются в пределах между -1 и 1
2. Кривая косинуса имеет ту же форму, что и кривая синуса, но сдвинута относительно нее на 90^o
3. Кривые синуса и косинуса непрерывны и повторяются с периодом 360^o , кривая тангенса имеет разрывы и повторяется с периодом 180^o .

Углы произвольной величины

На рис. слева показаны перпендикулярные оси ХХ’ и YY’; пересекающиеся в начале координат О. При работе с графиками измерения вправо и вверх от О считаются положительными, влево и вниз от О – отрицательными. Пусть ОА свободно вращается относительно О. При повороте ОА против часовой стрелки измеряемый угол считается положительным, а при повороте по часовой стрелке – отрицательным.

График. Положительное или отрицательное направление при движении по окружности.

Пусть ОА вращается против часовой стрелки таким образом, что Θ₁ – любой угол в первом квадранте, и построим перпендикуляр АВ для получения прямоугольного треугольника ОАВ на рис. слева. Поскольку все три стороны треугольника положительны, тригонометрические функции синус, косинус и тангенс в первом квадранте будут положительны. (Отметим, что длина ОА всегда положительна, поскольку является радиусом круга.)
Пусть ОА вращается дальше таким образом, что Θ₂ – любой угол во втором квадранте, и построим АС так, чтобы образовался прямоугольный треугольник ОАС. Тогда sin Θ₂=+/+ = +; cos Θ₂=+/- = -; tg Θ₂=+/- = -. Пусть ОА вращается дальше таким образом, что Θ₃ – любой угол в третьем квадранте, и построим АD так, чтобы образовался прямоугольный треугольник ОАD. Тогда sin Θ₃= -/+ = -; cos Θ₃= -/+ = -; tg Θ₃ = -/- =+ .

График. Поcтроение углов в различных квадрантах.

Пусть ОА вращается дальше таким образом, что Θ₄– любой угол в четвертом квадранте, и построим АЕ так, чтобы образовался прямоугольный треугольник ОАЕ. Тогда sin Θ₄= -/+= -; cos Θ₄=+/+=+; tg Θ₄= -/+= -.

В первом квадранте все тригонометрические функции имеют положительные значения, во втором положителен только синус, в третьем – только тангенс, в четвертом только косинус, что и показано на рис. слева.

График. Положительные и отрицательные значения синусов, косинусов и тангенсов.

Знание углов произвольной величины необходимо при нахождении, например, всех углов между 0^o и 360^o , синус которых равен, скажем, 0,3261.

dpva.ru

Синусоидальный – это… Что такое Синусоидальный?



Синусоидальный

синусоида́льный

прил.
1.
2.

Свойственный синусоиде, характерный для нее.

Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000.

.

Синонимы:

• Синусоида
• Синхронизатор

Смотреть что такое “Синусоидальный” в других словарях:

• СИНУСОИДАЛЬНЫЙ — СИНУСОИДАЛЬНЫЙ, синусоидальная, синусоидальное (мат.). прил. к синусоида; являющийся синусоидой. Толковый словарь Ушакова. Д.Н. Ушаков. 1935 1940 …   Толковый словарь Ушакова

• синусоидальный — прил., кол во синонимов: 1 • синусоидоподобный (1) Словарь синонимов ASIS. В.Н. Тришин. 2013 …   Словарь синонимов

• синусоидальный — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN sinusoidal …   Справочник технического переводчика

• синусоидальный — синусоидальный, синусоидальная, синусоидальное, синусоидальные, синусоидального, синусоидальной, синусоидального, синусоидальных, синусоидальному, синусоидальной, синусоидальному, синусоидальным, синусоидальный, синусоидальную, синусоидальное,… …   Формы слов

• синусоидальный — синусоид альный …   Русский орфографический словарь

• синусоидальный — …   Орфографический словарь русского языка

• синусоидальный — ая, ое. 1. Матем. Являющийся синусоидой. 2. Физ., техн. Изменяющийся по синусоиде. С ые колебания. С. ток …   Энциклопедический словарь

• синусоидальный — ая, ое. 1) матем. Являющийся синусоидой. 2) физ., техн. Изменяющийся по синусоиде. С ые колебания. Синусоида/льный ток …   Словарь многих выражений

• синусоидальный — синус/оид/альн/ый …   Морфемно-орфографический словарь

• синусоидальный ток — Периодический электрический ток, являющийся синусоидальной функцией времени. Примечание — Аналогично определяют синусоидальные электрическое напряжение, электродвижущую силу, магнитный поток и т. д. [ГОСТ Р 52002 2003] Тематики… …   Справочник технического переводчика

dic.academic.ru