Сопротивление резистора в цепи эмиттера.
Резистор в цепи эмиттера биполярного транзистора задает нагрузочную прямую усилителя наряду с резистором в цепи коллектора. Схема усилителя показана на рисунке1.Рисунок 1 – Схема усилителя
На рисунке 2 а показано семейство выходных вольт амперных характеристик биполярного транзистора подключенного по схеме с общим эмиттером. На этой характеристике показаны две нагрузочные прямые. Верхняя – нагрузочная прямая для случая когда в схеме отсутствует резистор Rэ, нижняя когда присутствует.Рисунок 2 – а) семейство выходных характеристик, б) входная характеристика
Нагрузочная прямая показывает как может изменяться ток коллектора и напряжение коллектор-эмиттер транзистора. В один момент времени, в зависимости от тока базы Iб, ток коллектора Iк (как и напряжение коллектор-эмиттер Uкэ) имеет одно значение. Это значение Iк и соответствующее ему значение Uкэ называется рабочей точкой. Рабочая точка может находится только на нагрузочной прямой и не выше той точки которой соответствует напряжение насыщения и не ниже той точки которой соответствует напряжение отсечки.
При увеличении температуры увеличивается ток эмиттера Iэ. При увеличении тока эмиттера Iэ увеличивается напряжение на резисторе в цепи эмиттера URэ (т.к. URэ=Iэ·Rэ). Напряжение база-эмиттер Uбэ связано с напряжением на резисторе в цепи эмиттера URэ соотношением: Uбэ=Uвх-URэ. Это соотношение показывает что чем больше напряжение на резисторе в цепи эмиттера URэ тем меньше напряжение база-эмиттер при неизменном напряжении на входе Uвх.
Биполярные транзисторы
3.9. Биполярные транзисторы
1. Общие сведения. Характеристики
Биполярный транзистор – это полупроводниковый прибор с двумя р-n
переходами и тремя выводами, служащий для усиления мощности. В транзисторе
имеется три области – эмиттер (э), база (б) и коллектор (к). В зависимости от
типа проводимости этих областей различают транзисторы n-p-n
и p-n-p
типа.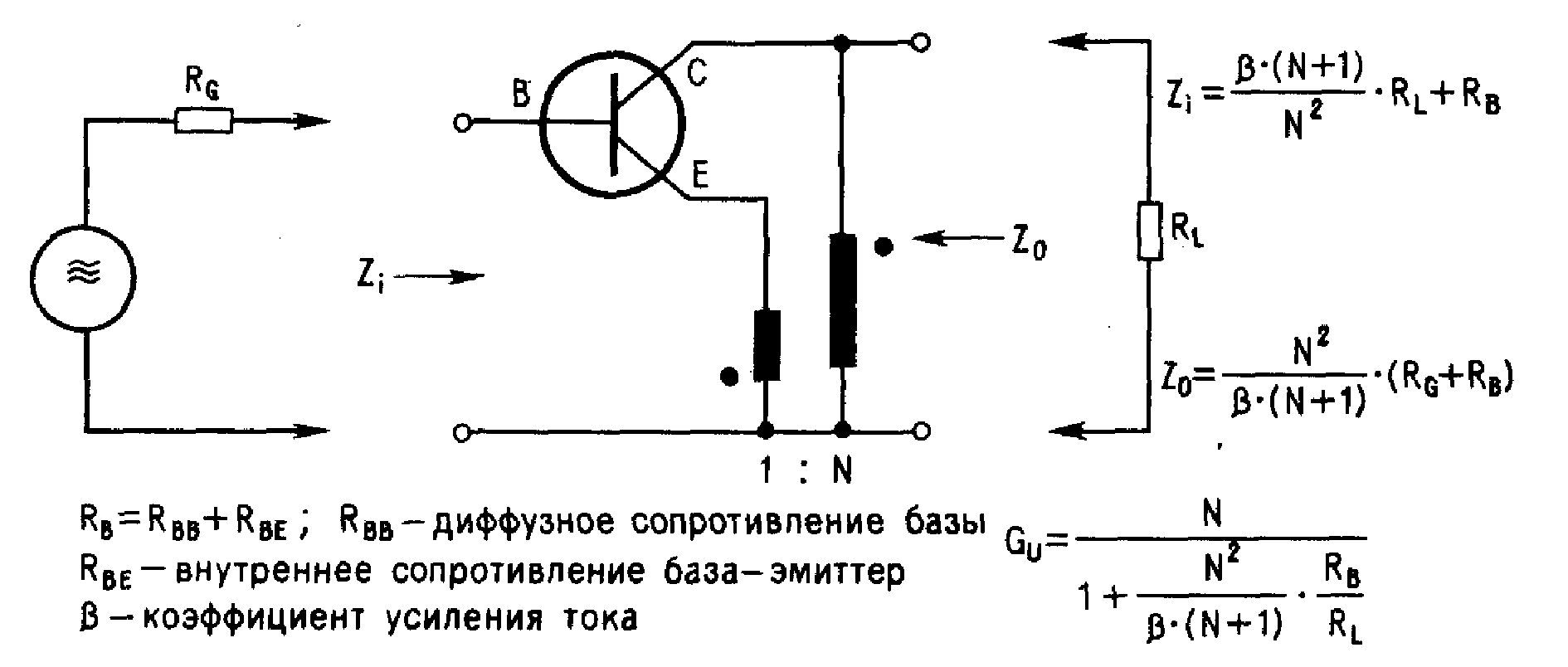 Таким образом, в транзисторе имеется два p-n
перехода: эмиттер-база (эмиттерный) и коллектор-база (коллекторный). Стрелка на
условных обозначениях транзисторов (см. в начале главы) указывает направление от
p области к n области.
Принцип работы обоих типов транзисторов одинаков.
Таким образом, в транзисторе имеется два p-n
перехода: эмиттер-база (эмиттерный) и коллектор-база (коллекторный). Стрелка на
условных обозначениях транзисторов (см. в начале главы) указывает направление от
p области к n области.
Принцип работы обоих типов транзисторов одинаков.
Толщина базы делается значительно меньше длины свободного пробега неосновных носителей тока, попадающих в нее из эмиттера, а концентрация основных носителей в базе много меньше концентрации основных носителей в эмиттере. В результате в базе сводится до минимума рекомбинация неосновных носителей с основными, пришедшими из эмиттера.
Площадь коллекторного перехода (перехода база-коллектор) значительно
больше площади эмиттерного перехода (перехода база-эмиттер). Это делается для
того, чтобы перехватить весь поток носителей, идущих от эмиттера, а также
потому, что на коллекторном переходе выделяется большая мощность. Концентрация
же основных носителей в коллекторе несколько меньше, чем в эмиттере.
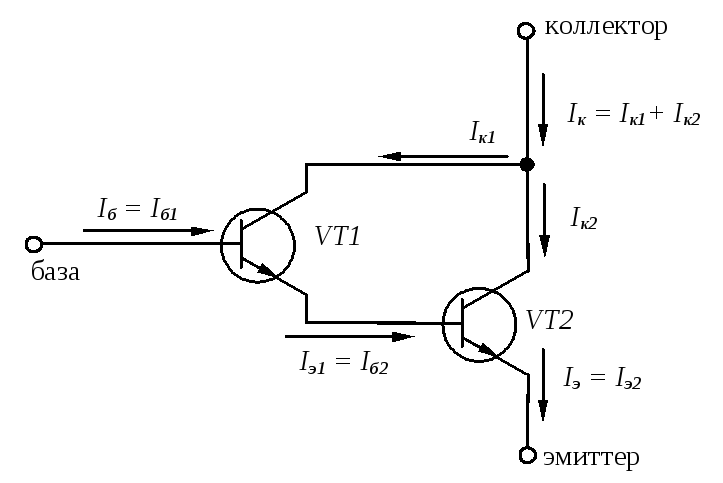
В зависимости от того, какое напряжение (прямое или обратное) подано на переходы транзистора, выделяют четыре режима работы транзистора. В активном режиме (он является основным) напряжение на эмиттерном переходе прямое, на коллекторном – обратное. В режиме отсечки (запирания) на оба перехода подается обратное напряжение. В режиме насыщения напряжение на обоих переходах прямое. В
Рассмотрим работу транзистора n-p-n
типа в активном режиме без нагрузки (рис. 3.30). На рисунке
темными кружками изображены электроны, светлыми – дырки. Поскольку на переход
база-эмиттер подано прямое напряжение, то сопротивление эмиттерного перехода
мало и для получения тока на этом переходе достаточно напряжения Е1 в
десятые доли вольта. Сопротивление коллекторного перехода велико (на него подано
обратное напряжение) и напряжение Е2 обычно составляет единицы и
десятки вольт.
При увеличении прямого напряжения на эмиттерном переходе электроны из эмиттера переходят в базу. Благодаря малой толщине базы и малой концентрации в ней дырок лишь незначительная часть электронов рекомбинирует с дырками базы, образуя ток базы (его стараются сделать как можно меньше). Основная часть электронов достигает коллекторного перехода и под действием его обратного напряжения втягивается в коллектор (электроны являются неосновными носителями для базы и поле запирающего слоя на переходе коллектор-база является для них ускоряющим). Поэтому ток коллектора лишь немного меньше тока эмиттера: i э=iк+iб.
Когда на эмиттерный переход не подано прямое напряжение, то через коллектроный
переход протекает только небольшой обратный ток, созданный неосновными
носителями. Таким образом, прямое напряжение эмиттерного перехода существенно
влияет на токи эмиттера и коллектора: чем больше это напряжение, тем больше токи
эмиттера и коллектора. Такое свойство транзистора позволяет использовать его в
качестве электронного ключа, а также для усиления электрического тока.
Такое свойство транзистора позволяет использовать его в
качестве электронного ключа, а также для усиления электрического тока.
Для расчета схем с транзисторами необходимо знать их характеристики (зависимости между токами и напряжениями). Для схемы включения транзистора с общим эмиттером (рис. 3.30) входная характеристика представляет собой зависимость силы тока базы от напряжения база-эмиттер при постоянном напряжении коллектр-эмиттер. Она имеет такой же вид, как прямая ветвь ВАХ полупроводникового диода. Выходные характеристики биполярного транзистора при схеме включения с общим эмиттером представляют собой зависимости силы тока коллектора от напряжения коллектор-эмиттер при различных постоянных значениях тока базы (рис. 3.31).
Самая нижняя
выходная характеристика построена для
iб=0.
Она похожа на обратную ветвь вольт-амперной характеристики полупроводникового
диода. Чем больше сила тока базы, тем выше расположена выходная характеристика.
Активная область на семействе выходных характеристик транзистора (рис. 3.32) ограничена максимально допустимым током коллектора, максимально допустимым напряжением коллектор-эмиттер, гиперболой максимально допустимой мощности рассеяния и неуправляемым током коллектора (ток коллектора при iб=0). Для уменьшения нелинейных искажений рабочую область ограничивают также слева (см. штриховую линию на рис. 3.32).
Характеристики транзисторов, как и всех полупроводниковых элементов, очень сильно зависит от температуры. При увеличении температуры сопротивление полупроводников уменьшается и токи в них увеличиваются. Поэтому семейство выходных характеристик при увеличении температуры смещается вверх (рис. 3.33).
2. Определение структуры и выводов биполярных транзисторов
В последнее время
все чаще используют транзисторы, извлеченные из неработающих электронных
приборов.
При экспериментальном определении структуры транзистора (р-n-р или n-р-n) его можно рассматривать состоящим из двух диодов, соединенных в зависимости от структуры анодами или катодами (рис. 3.34 а, б), причем точка соединения диодов соответствует выводу базы транзистора. Для определения структуры и вывода базы транзистора воспользуемся омметром с известной полярностью напряжения, подаваемого на гнезда омметра от внутреннего источника питания. Обычно положительный полюс внутреннего источника питания омметра соединен с гнездом “общий”.
Следует отметить, что существуют омметры и с другой полярностью напряжения на
гнездах. Так, например, авометр Ц20-05 выпускается в двух модификациях: в одной
из них на общее гнездо омметра выведен плюс внутреннего источника питания, а в
другой – минус.
Поэтому перед экспериментальным определением структуры и вывода
базы транзистора следует с помощью диода с маркированной полярностью проверить,
какой полюс внутреннего источника питания омметра соединен с общим гнездом.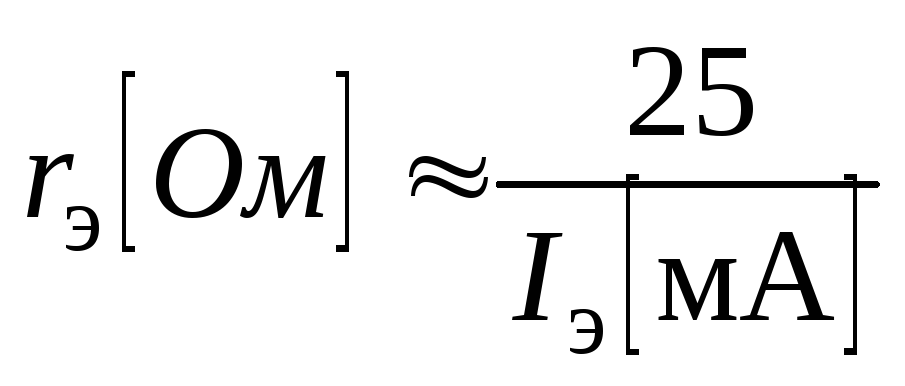
При одной полярности щупов омметра, подключаемых к переходу транзистора, сопротивление перехода оказывается малым (прямое подключение), а при другой – большим (обратное подключение). Если при малом сопротивлении переходов транзистора плюсовой щуп омметра касался одного и того же вывода, значит это вывод базы и транзистор имеет структуру n-р-n. Если в этой же ситуации минусовой щуп омметра касался одного и того же вывода (базы), то транзистор р-n-р типа.
После того, как определена структура транзистора и найден вывод базы
транзистора, приступают к определению выводов эмиттера и коллектора. На
рисунках, поясняющих принцип работы биполярного транзистора, области эмиттера и
коллектора выглядят симметрично и, казалось бы, что выводы коллектора и эмиттера
можно поменять местами. Однако конструктивно эмиттер и коллектор выполняются
по-разному (имеют неодинаковую концентрацию носителей заряда и площадь
поверхности). Поэтому менять их
местами не следует, так как получится
существенно меньший коэффициент усиления по току и меньшая мощность рассеяния
транзистора.
Существует несколько вариантов экспериментального определения выводов эмиттера и коллектора. Рассмотрим два из них.
Возьмем резистор сопротивлением 10-100 кОм и включим его между выводом базы и
предполагаемым выводом коллектора. К выводам эмиттера и коллектора омметр
можно подключить так, как показано на
рисунках 3.36а и 3.36б для транзистора n-р-n типа, а на рисунках 3.37а и 3.37б – для
транзистора р-n-р типа. На всех рисунках предполагаемый вывод коллектора
расположен вверху (по рисунку). Правильному выбору выводов коллектора и эмиттера
соответствует меньшее сопротивление, фиксируемое омметром, т. е. подключение по
схемам рисунков 3.36а, 3.37а.
е. подключение по
схемам рисунков 3.36а, 3.37а.
Рассмотрим второй вариант определения выводов коллектора и эмиттера. В качестве источника питания используют любой источник постоянного напряжения (3-9 В). Миллиамперметр включают между положительным полюсом источника и предполагаемым выводом коллектора для транзисторов n-р-n типа (рис. 3.38а и 3.38б), между отрицательным полюсом источника и предполагаемым выводом коллектора для транзисторов р-n-р типа (рис. 3.39а и 3.39б). Предполагаемый вывод коллектора, как и в предыдущем случае, расположен на рисунке вверху. Правильно выбранному выводу коллектора соответствует больший ток, фиксируемый миллиамперметром.
В этом варианте можно определить не только выводы транзистора, но и приблизительно определить коэффициент усиления транзистора по току: , где Iк – сила тока коллектора, Iб – сила тока базы.
Ток базы можно рассчитать по формуле
, где Uп – напряжение источника
питания, Uбэ – напряжение между базой и эмиттером транзистора.
Для кремниевых транзисторов напряжение база-эмиттер составляет примерно 0,6 В. Выберем напряжение питания 4,5 В и сопротивление резистора 390 кОм. Тогда Iб = 10-2 мА, и коэффициент усиления определяется из формулы: , где Iк – сила тока коллектора в мА.
Транзистор – принцип работы.Основные параметры.
Как устроен транзистор.
Вне зависимости от принципа работы, полупроводниковый транзистор содержит в себе монокристалл из основного полупроводникового материала, чаще всего это – кремний, германий, арсенид галлия. В основной материал добавлены, легирующие добавки для формирования p-n перехода(переходов), металлические выводы.
Кристалл помещается в металлический, пластиковый или керамический корпус, для защиты от внешних воздействий. Однако, существуют также и бескорпусные транзисторы.
Принцип работы биполярного транзистора.

Биполярный транзистор может быть либо p-n-p, либо n-p-n в зависимости от чередования слоев полупроводника в кристалле. В любом случае выводы называются – база, коллектор и эмиттер. Слой полупроводника, соответствующий базе заключен между слоями эмиттера и коллектора. Он имеет принципиально очень малую ширину. Носители заряда движутся от эмиттера через базу – к коллектору. Условием возникновения тока между коллектором и эмиттером является наличие свободных носителей в области базы. Эти носители проникают туда при возникновении тока эмиттер-база. причиной которого может являться разность напряжения между этими электродами.
Т.е. – для нормальной работы биполярного транзистора в качестве усилителя сигнала
всегда необходимо присутствие напряжения некого минимального уровня, для смещения перехода эмиттер-база в
прямом направлении.
Прямое смещение перехода база-эмиттер приоткрывая транзистор, задает
так называемую – рабочую точку режима. Для гармоничного усиления сигнала по напряжению и току используют
режим – А. В этом режиме напряжение между коллектором
и нагрузкой, примерно равно половине питающего напряжения – т. е выходное сопротивление транзистора
и нагрузки примерно равны . Если подавать теперь на переход база – эмиттер
сигнал переменного тока, СОПРОТИВЛЕНИЕ эмиттер – коллектор будет изменяться, графически повторяя
форму входного сигнала. Соответственно, то же будет происходить и с током через эмиттер к коллектору
протекающим. Причем амплитуда тока будет большей, нежели амплитуда
входного сигнала – будет происходить усиление сигнала.
Для гармоничного усиления сигнала по напряжению и току используют
режим – А. В этом режиме напряжение между коллектором
и нагрузкой, примерно равно половине питающего напряжения – т. е выходное сопротивление транзистора
и нагрузки примерно равны . Если подавать теперь на переход база – эмиттер
сигнал переменного тока, СОПРОТИВЛЕНИЕ эмиттер – коллектор будет изменяться, графически повторяя
форму входного сигнала. Соответственно, то же будет происходить и с током через эмиттер к коллектору
протекающим. Причем амплитуда тока будет большей, нежели амплитуда
входного сигнала – будет происходить усиление сигнала.
Если увеличивать напряжение смещения база – эмиттер дальше, это приведет к росту
тока в этой цепи, и как результат – еще большему росту тока эмиттер – коллектор.
В конце, концов ток перестает расти – транзистор переходит в полностью открытое
состояние(насыщения). Если затем убрать напряжение смещения – транзистор закроется,
ток эмиттер – коллектор уменьшится, почти исчезнет. Так транзистор может работать
в качестве электронного ключа. Этот режим наиболее эффективен в отношении
управления мощностями, при протекании тока через полностью открытый транзистор величина падения напряжения
минимальна. Соответственно малы потери тока и нагрев переходов транзистора.
Так транзистор может работать
в качестве электронного ключа. Этот режим наиболее эффективен в отношении
управления мощностями, при протекании тока через полностью открытый транзистор величина падения напряжения
минимальна. Соответственно малы потери тока и нагрев переходов транзистора.
Существует три вида подключения биполярного транзистора.
С общим эмиттером (ОЭ) — осуществляется усиление как по току, так и по напряжению — наиболее
часто применяемая схема.
Усилительные каскады построенные подобным образом, легче согласуются между собой,
так как значения их входного и выходного сопротивления относительно близки, если
сравнивать с двумя остальными видами включения (хотя иногда и отличаются в десятки раз).
С общим коллектором (ОК) осуществляется усиление только по току — применяется для согласования
источников сигнала с высоким внутренним сопротивлением(импендансом) и низкоомными сопротивлениями нагрузок. Например, в выходных каскадах усилителей и контроллеров.
Например, в выходных каскадах усилителей и контроллеров.
С общей базой (ОБ) осуществляется усиление только по напряжению. Имеет низкое входное и высокое выходное сопротивление и более широкий частотный диапазон. Это позволяет использовать подобное включение для согласования источников сигнала с низким внутренним сопротивлением(импендансом) с последующим каскадом усиления. Например – в входных цепях радиоприемных устройств.
Принцип работы полевого транзистора.
Полевой транзистор, как и биполярный имеет три электрода. Они носят названия – сток, исток и затвор. Если на затворе отсутствует напряжение, а на сток подано положительное напряжение относительно истока, то между истоком и стоком через канал течет максимальный ток.
Т. е. – транзистор полностью открыт.
Для того, что бы его изменить, на затвор подают отрицательное напряжение, относительно истока.
Под действием электрического поля (отсюда и название транзистора) канал сужается,
его сопротивление растет, а ток через него уменьшается. При определенном значении напряжения канал сужается до такой степени, что ток
практически исчезает – транзистор закрывается.
При определенном значении напряжения канал сужается до такой степени, что ток
практически исчезает – транзистор закрывается.
На рисунке изображено устройство полевого транзистора с изолированным затвором(МДП).
Если на затвор этого прибора не подано положительное напряжение, то канал между истоком и стоком отсутствует и ток равен нулю. Транзистор полностью закрыт. Канал возникает при некотором минимальном напряжении на затворе(напряжение порога). Затем сопротивление канала уменьшается, до полного открывания транзистора.
Полевые транзисторы, как с p-n переходом (канальные), так и МОП (МДП) имеют следующие схемы включения: с общим истоком (ОИ) — аналог ОЭ биполярного транзистора; с общим стоком (ОС) — аналог ОК биполярного транзистора; с общим затвором (ОЗ) — аналог ОБ биполярного транзистора.
По рассеиваемой в виде тепла мощности различают:
маломощные транзисторы – до 100 мВт ;
транзисторы средней мощности – от 0,1 до 1 Вт;
мощные транзисторы – больше 1 Вт.
Важные параметры биполярных транзисторов.
1. Коэффициент передачи тока(коэффициент усиления) –
от 1 до 1000 при постоянном токе. С увеличением частоты постепенно снижается.
2. Максимальное напряжение между коллектором и эмиттером(при разомкнутой базе)
У специальных высоковольтных транзисторов, достигает десятков тысяч вольт.
3.Предельная частота, до которой коэффициент передачи тока выше 1.
До 100000 гц. у низкочастотных транзисторов, свыше 100000 гц. – у высокочастотных.
4.Напряжение насыщения эмиттер-коллектор – величина падения напряжения между этими
электродами у полностью открытого транзистора.
Важные параметры полевых транзисторов.
Усилительные свойства полевого транзистора определяются отношением приращения тока стока к вызвавшему его приращению напряжения затвор – исток, т. е.
ΔId /ΔUGS Это отношение принято называть крутизной прибора, а по сути дела оно является передаточной проводимостью и
измеряется в миллиамперах на вольт(мА /В).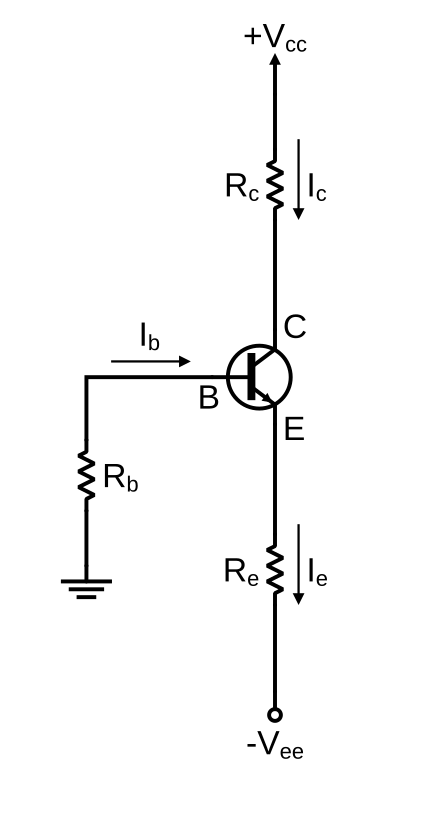
Другие важнейшие параметры полевых транзисторов приведены ниже:
1. IDmax – максимальный ток стока.
2.UDSmax – максимальное напряжение сток-исток.
3.UGSmax – максимальное напряжение затвор-исток.
4.РDmax – максимальна мощность, которая может выделяться на приборе.
5.ton – типовое время нарастания тока стока при идеально прямоугольной форме входного сигнала.
6.toff – типовое время спада тока стока при идеально прямоугольной форме входного сигнала.
7.RDS(on)max – максимальное значение сопротивления исток – сток в включенном(открытом) состоянии.
На главную страницу
Использование каких – либо материалов этой страницы, допускается при наличии ссылки на сайт “Электрика это просто”.
До сих пор мы рассматривали влияние цепей обратной связи только на режим работы транзистора по постоянному току (как средства обеспечения стабильного положения исходной рабочей точки при наличии внешних дестабилизирующих факторов). В схеме на рис. 5.1 имеет место отрицательная обратная связь по току нагрузки. Она обеспечивается включением в эмиттерную цепь транзистора сопротивления \(R_Э\). Увеличение тока нагрузки приводит к повышению падения напряжения на этом резисторе, что, в свою очередь, вызывает уменьшение напряжения, прикладываемого к эмиттерному переходу, т.е. входного напряжения транзисторного звена. В рабочей полосе частот для переменного входного сигнала действие данной обратной связи оказывается довольно существенным. Во-первых, из формулы (5.1) видно, что входное сопротивление транзистора rвх увеличивается на величину, равную \((1+ \beta) R_Э\). Учитывая, что значение коэффициента передачи тока базы \(\beta\), как правило, достаточно велико, то даже при относительно незначительной величине сопротивления \(R_Э\) входное сопротивление транзистора rвх для сигнала в рабочей полосе частот увеличивается настолько, что часто перестает оказывать определяющее влияние на полное входное сопротивление усилительного каскада \(R_{вх}\), которое теперь в основном зависит от сопротивления цепи делителя напряжения \(R_Б\). Как видно из формул (5.2), (5.3), рассматриваемый вид обратной связи не оказывает влияния на выходное сопротивление, а также на коэффицент усиления по току в рабочей полосе частот усилительного каскада с ОЭ (на самом деле выходное сопротивление все-таки незначительно увеличивается). Если увеличение входного сопротивления мы сочли скорее полезным, чем вредным, то падение коэффициента усиления по напряжению однозначно можно считать нежелательным эффектом. Правда, он все-таки сопровождается рядом явлений, которые положительно влияют на другие параметры усилителя. А именно: увеличивается динамический диапазон, уменьшаются линейные и нелинейные искажения, расширяется полоса пропускания. На практике разработчик довольно часто встает перед дилеммой: либо повышать коэффициент усиления, либо снижать уровень искажений. Каково бы ни было значение резистора \(R_Э\), которое выбирается исходя из требований к температурной стабильности рабочей точки каскада по постоянному току, мы всегда (если только речь не идет об усилителе постоянного тока) можем скорректировать его влияние в рабочей полосе частот. Достигается это включением разнообразных \(RC\)-цепочек вместо одиночного сопротивления \(R_Э\). Если мы шунтируем это сопротивление конденсатором \(C_Э\) (как показано на рис. 5.1), чье эквивалентное сопротивление в рабочей полосе частот пренебрежимо мало, то оказывается, что действие обратной связи на частоте полезного сигнала полностью блокируется (отсюда и название — блокировочный конденсатор), эмиттер транзистора на эквивалентной схеме оказывается заземленным и схема становится полностью отвечающей своему названию — схема с общим эмиттером.
Рис. 5.3. Варианты включения RC-цепочек в эмиттерную цепь транзистора в каскаде с ОЭ
До сих пор мы подразумевали, что емкость блокировочного конденсатора выбирается из такого расчета, чтобы его эквивалентное сопротивление в рабочей полосе частот усилителя было ничтожно мало. Но иногда может потребоваться коррекция частотной характеристики усилителя, а делать это особенно удобно, включая корректирующие элементы в цепи обратной связи. Например, если нам необходимо скорректировать частотную характеристику апериодического усилителя с целью придания ей более линейного вида, мы можем так подобрать емкость блокировочного конденсатора, чтобы его эквивалентное сопротивление в рабочем диапазоне частот было сравнимо по величине с сопротивлением резистора \(R_Э\). В звено обратной связи могут включаться и гораздо более сложные конструкции, чем были описаны выше. Очень удобно иногда оказывается использовать данную возможность формирования полосы пропускания при построении разнообразных узкополосных усилителей. Включая вместо одиночного блокировочного конденсатора последовательный резонансный контур, мы обеспечиваем большой коэффицент усиления каскада (малое эквивалентное сопротивление в цепи эмиттера) на частотах вблизи резонансной частоты контура и малый коэффициент усиления (большое эквивалентное сопротивление в цепи эмиттера) на всех остальных частотах.
Рис. 5.4. Оконечный каскад усилителя записи кассетного магнитофона
|
Транзисторные конфигурации – CoderLessons.com
Любой транзистор имеет три клеммы: эмиттер , базу и коллектор . Используя эти 3 клеммы, транзистор может быть подключен в цепи с одной клеммой, общей для обоих входов и выходов в трех различных возможных конфигурациях.
Три типа конфигураций — это конфигурации Common Base, Common Emitter и Common Collector . В каждой конфигурации эмиттерный контакт смещен в прямом направлении, а коллекторный контакт — в обратном направлении.
Общая база (CB) Конфигурация
Само название подразумевает, что базовая клемма используется как общая клемма для входа и выхода транзистора. Общее базовое соединение для транзисторов NPN и PNP показано на следующем рисунке.
Для понимания рассмотрим NPN-транзистор в CB-конфигурации. Когда на эмиттер подается напряжение, поскольку оно смещено в прямом направлении, электроны от отрицательного вывода отталкивают электроны эмиттера, и ток течет через эмиттер и основание к коллектору, чтобы внести ток коллектора. Напряжение коллектора V CB поддерживается постоянным на протяжении всего этого.
В конфигурации CB входной ток — это ток эмиттера I E, а выходной ток — ток коллектора I C.
Коэффициент усиления тока (α)
Отношение изменения тока коллектора (ΔI C ) к изменению тока эмиттера (ΔI E ), когда напряжение коллектора V CB поддерживается постоянным, называется коэффициентом усиления тока . Обозначается через α .
$ \ alpha = \ frac {\ Delta I_C} {\ Delta I_E} $ при постоянной V CB
Выражение для тока коллектора
Используя приведенную выше идею, давайте попробуем нарисовать некоторое выражение для тока коллектора.
Наряду с протекающим током эмиттера существует некоторая величина базового тока I B, который протекает через базовый вывод из-за рекомбинации электронных дырок. Поскольку соединение коллектор-база имеет обратное смещение, существует другой ток, который протекает из-за неосновных носителей заряда. Это ток утечки, который можно понимать как утечка . Это связано с меньшим количеством носителей заряда и, следовательно, очень мало.
Ток эмиттера, который достигает коллектора, равен
$$ \ alpha I_E $$
Общий ток коллектора
$$ I_C = \ alpha I_E + I_ {утечка} $$
Если напряжение на базе эмиттера V EB = 0, то даже тогда протекает небольшой ток утечки, который можно назвать I CBO (ток на базе коллектора с открытым выходом).
Следовательно, ток коллектора может быть выражен как
$$ I_C = \ alpha I_E + I_ {CBO} $$
$$ I_E = I_C + I_B $$
$$ I_C = \ alpha (I_C + I_B) + I_ {CBO} $$
$$ I_C (1 — \ alpha) = \ alpha I_B + I_ {CBO} $$
$$ I_C = \ frac {\ alpha} {1 — \ alpha} I_B + \ frac {I_ {CBO}} {1 — \ alpha} $$
$$ I_C = \ left (\ frac {\ alpha} {1 — \ alpha} \ right) I_B + \ left (\ frac {1} {1 — \ alpha} \ right) I_ {CBO} $$
Следовательно, полученное выше выражение является выражением для тока коллектора. Значение тока коллектора зависит от тока базы и тока утечки, а также от коэффициента усиления тока используемого транзистора.
Характеристики конфигурации CB
Эта конфигурация обеспечивает усиление напряжения, но не дает усиления по току.
При постоянном значении V CB при небольшом увеличении напряжения на базе эмиттера V EB ток эмиттера I E увеличивается.
Ток эмиттера I E не зависит от напряжения коллектора V CB .
Напряжение коллектора V CB может влиять на ток коллектора I C только при низких напряжениях, когда V EB поддерживается постоянным.
Входное сопротивление R i представляет собой отношение изменения базового напряжения эмиттера (ΔV EB ) к изменению тока эмиттера (ΔI E ) при постоянном базовом напряжении коллектора V CB .
Эта конфигурация обеспечивает усиление напряжения, но не дает усиления по току.
При постоянном значении V CB при небольшом увеличении напряжения на базе эмиттера V EB ток эмиттера I E увеличивается.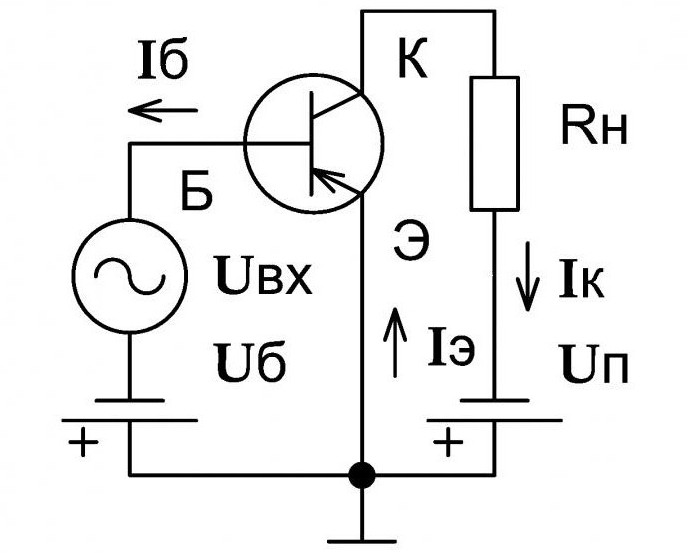
Ток эмиттера I E не зависит от напряжения коллектора V CB .
Напряжение коллектора V CB может влиять на ток коллектора I C только при низких напряжениях, когда V EB поддерживается постоянным.
Входное сопротивление R i представляет собой отношение изменения базового напряжения эмиттера (ΔV EB ) к изменению тока эмиттера (ΔI E ) при постоянном базовом напряжении коллектора V CB .
$ R_i = \ frac {\ Delta V_ {EB}} {\ Delta I_E} $ при постоянной V CB
Поскольку входное сопротивление имеет очень низкое значение, достаточно небольшого значения V EB , чтобы создать большой ток тока эмиттерного тока I E.
Выходное сопротивление R o представляет собой отношение изменения базового напряжения коллектора (ΔV CB ) к изменению тока коллектора (ΔI C ) при постоянном токе эмиттера IE.
Поскольку входное сопротивление имеет очень низкое значение, достаточно небольшого значения V EB , чтобы создать большой ток тока эмиттерного тока I E.
Выходное сопротивление R o представляет собой отношение изменения базового напряжения коллектора (ΔV CB ) к изменению тока коллектора (ΔI C ) при постоянном токе эмиттера IE.
$ R_o = \ frac {\ Delta V_ {CB}} {\ Delta I_C} $ при постоянной I E
Поскольку выходное сопротивление имеет очень высокое значение, большое изменение V CB приводит к очень небольшому изменению тока коллектора I C.
Эта конфигурация обеспечивает хорошую стабильность против повышения температуры.
Конфигурация CB используется для высокочастотных применений.
Поскольку выходное сопротивление имеет очень высокое значение, большое изменение V CB приводит к очень небольшому изменению тока коллектора I C.
Эта конфигурация обеспечивает хорошую стабильность против повышения температуры.
Конфигурация CB используется для высокочастотных применений.
Конфигурация с общим эмиттером (CE)
Само название подразумевает, что клемма эмиттера используется как общая клемма для входа и выхода транзистора. Общее подключение эмиттера для транзисторов NPN и PNP показано на следующем рисунке.
Как и в конфигурации CB, эмиттерный контакт смещен в прямом направлении, а коллекторный контакт — в обратном направлении. Поток электронов контролируется таким же образом. Входной ток — это базовый ток I B, а выходной ток — ток коллектора I C здесь.
Базовый коэффициент усиления тока (β)
Отношение изменения тока коллектора (ΔI C ) к изменению базового тока (ΔI B ) известно как коэффициент усиления базового тока . Обозначается через β.
$$ \ beta = \ frac {\ Delta I_C} {\ Delta I_B} $$
Связь между β и α
Попробуем вывести соотношение между коэффициентом усиления базового тока и коэффициентом усиления тока эмиттера.
$$ \ beta = \ frac {\ Delta I_C} {\ Delta I_B} $$
$$ \ alpha = \ frac {\ Delta I_C} {\ Delta I_E} $$
$$ I_E = I_B + I_C $$
$$ \ Delta I_E = \ Delta I_B + \ Delta I_C $$
$$ \ Delta I_B = \ Delta I_E — \ Delta I_C $$
Мы можем написать
$$ \ beta = \ frac {\ Delta I_C} {\ Delta I_E — \ Delta I_C} $$
Деление на ΔI E
$$ \ beta = \ frac {\ Delta I_C / \ Delta I_E} {\ frac {\ Delta I_E} {\ Delta I_E} — \ frac {\ Delta I_C} {\ Delta I_E}} $$
У нас есть
$$ \ alpha = \ Delta I_C / \ Delta I_E $$
Следовательно,
$$ \ beta = \ frac {\ alpha} {1 — \ alpha} $$
Из приведенного выше уравнения очевидно, что при приближении α к 1, β достигает бесконечности.
Следовательно, коэффициент усиления по току в соединении с общим эмиттером очень высок . По этой причине это схемное соединение в основном используется во всех транзисторных приложениях.
Выражение для тока коллектора
В конфигурации с общим эмиттером I B — входной ток, а I C — выходной ток.
Мы знаем
$$ I_E = I_B + I_C $$
А также
$$ I_C = \ alpha I_E + I_ {CBO} $$
$$ = \ alpha (I_B + I_C) + I_ {CBO} $$
$$ I_C (1 — \ alpha) = \ alpha I_B + I_ {CBO} $$
$$ I_C = \ frac {\ alpha} {1 — \ alpha} I_B + \ frac {1} {1 — \ alpha} I_ {CBO} $$
Если базовая цепь разомкнута, т.е. если I B = 0,
Коллектор эмиттер тока с открытой базой генерального директора
$$ I_ {CEO} = \ frac {1} {1 — \ alpha} I_ {CBO} $$
Подставляя значение этого в предыдущее уравнение, получим
$$ I_C = \ frac {\ alpha} {1 — \ alpha} I_B + I_ {CEO} $$
$$ I_C = \ beta I_B + I_ {CEO} $$
Отсюда получается уравнение для тока коллектора.
Колено Напряжение
В конфигурации CE, поддерживая постоянный ток I B базы, если V CE изменяется, I C увеличивается почти до 1 В от V CE и остается постоянным после этого. Это значение V CE, до которого ток коллектора I C изменяется с V CE , называется напряжением на колене . Транзисторы, работая в конфигурации CE, работают с напряжением выше колена.
Это значение V CE, до которого ток коллектора I C изменяется с V CE , называется напряжением на колене . Транзисторы, работая в конфигурации CE, работают с напряжением выше колена.
Характеристики конфигурации CE
Эта конфигурация обеспечивает хорошее усиление тока и напряжения.
Сохраняя V CE постоянным, при небольшом увеличении V BE базовый ток I B увеличивается быстрее, чем в конфигурациях CB.
Для любого значения V CE выше напряжения колена I C приблизительно равно βI B.
Входное сопротивление R i представляет собой отношение изменения базового напряжения эмиттера (ΔV BE ) к изменению базового тока (ΔI B ) при постоянном напряжении эмиттера коллектора V CE .
Эта конфигурация обеспечивает хорошее усиление тока и напряжения.
Сохраняя V CE постоянным, при небольшом увеличении V BE базовый ток I B увеличивается быстрее, чем в конфигурациях CB.
Для любого значения V CE выше напряжения колена I C приблизительно равно βI B.
Входное сопротивление R i представляет собой отношение изменения базового напряжения эмиттера (ΔV BE ) к изменению базового тока (ΔI B ) при постоянном напряжении эмиттера коллектора V CE .
$ R_i = \ frac {\ Delta V_ {BE}} {\ Delta I_B} $ при постоянной V CE
Поскольку входное сопротивление имеет очень низкое значение, достаточно небольшого значения V BE , чтобы создать большой ток базового тока I B.
Выходное сопротивление R o представляет собой отношение изменения напряжения эмиттера коллектора (ΔV CE ) к изменению тока коллектора (ΔI C ) при постоянной I B.
Поскольку входное сопротивление имеет очень низкое значение, достаточно небольшого значения V BE , чтобы создать большой ток базового тока I B.
Выходное сопротивление R o представляет собой отношение изменения напряжения эмиттера коллектора (ΔV CE ) к изменению тока коллектора (ΔI C ) при постоянной I B.
$ R_o = \ frac {\ Delta V_ {CE}} {\ Delta I_C} $ при постоянной I B
Поскольку выходное сопротивление цепи CE меньше, чем сопротивление цепи CB.
Эта конфигурация обычно используется для методов стабилизации смещения и применения звуковых частот.
Поскольку выходное сопротивление цепи CE меньше, чем сопротивление цепи CB.
Эта конфигурация обычно используется для методов стабилизации смещения и применения звуковых частот.
Конфигурация Common Collector (CC)
Само название подразумевает, что клемма коллектора используется как общая клемма для входа и выхода транзистора. Подключение общего коллектора для транзисторов NPN и PNP показано на следующем рисунке.
Подключение общего коллектора для транзисторов NPN и PNP показано на следующем рисунке.
Как и в конфигурациях CB и CE, эмиттерный контакт смещен в прямом направлении, а коллекторный контакт — в обратном направлении. Поток электронов контролируется таким же образом. Входной ток — это базовый ток I B, а выходной ток — это ток эмиттера I E.
Коэффициент усиления тока (γ)
Отношение изменения тока эмиттера (I E ) к изменению базового тока (I B ) известно как коэффициент усиления тока в конфигурации с общим коллектором (CC). Обозначается через γ.
$$ \ gamma = \ frac {\ Delta I_E} {\ Delta I_B} $$
- Коэффициент усиления по току в конфигурации CC такой же, как в конфигурации CE.
- Коэффициент усиления по напряжению в конфигурации CC всегда меньше 1.
Связь между γ и α
Попробуем нарисовать некоторую связь между γ и α
$$ \ gamma = \ frac {\ Delta I_E} {\ Delta I_B} $$
$$ \ alpha = \ frac {\ Delta I_C} {\ Delta I_E} $$
$$ I_E = I_B + I_C $$
$$ \ Delta I_E = \ Delta I_B + \ Delta I_C $$
$$ \ Delta I_B = \ Delta I_E — \ Delta I_C $$
Подставляя значение I B , получаем
$$ \ gamma = \ frac {\ Delta I_E} {\ Delta I_E — \ Delta I_C} $$
Деление на ΔI E
$$ \ gamma = \ frac {\ Delta I_E / \ Delta I_E} {\ frac {\ Delta I_E} {\ Delta I_E} — \ frac {\ Delta I_C} {\ Delta I_E}} $$
$$ = \ frac {1} {1 — \ alpha} $$
$$ \ gamma = \ frac {1} {1 — \ alpha} $$
Выражение для тока коллектора
Мы знаем
$$ I_C = \ alpha I_E + I_ {CBO} $$
$$ I_E = I_B + I_C = I_B + (\ alpha I_E + I_ {CBO}) $$
$$ I_E (1 — \ alpha) = I_B + I_ {CBO} $$
$$ I_E = \ frac {I_B} {1 — \ alpha} + \ frac {I_ {CBO}} {1 — \ alpha} $$
$$ I_C \ cong I_E = (\ beta + 1) I_B + (\ beta + 1) I_ {CBO} $$
Выше приведено выражение для тока коллектора.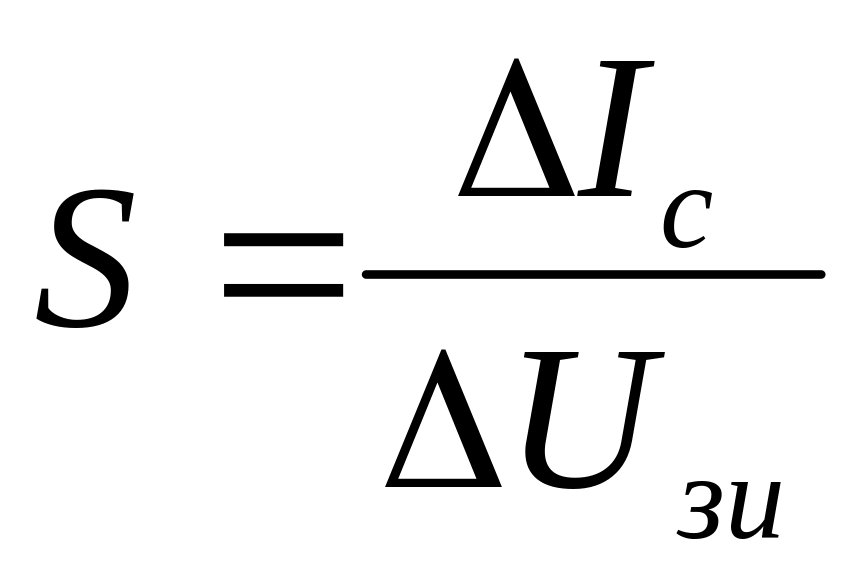
Эта конфигурация обеспечивает усиление по току, но без усиления по напряжению.
В конфигурации CC входное сопротивление высокое, а выходное сопротивление низкое.
Усиление напряжения, обеспечиваемое этой схемой, составляет менее 1.
Сумма тока коллектора и тока базы равна току эмиттера.
Входные и выходные сигналы находятся в фазе.
Эта конфигурация работает как выход неинвертирующего усилителя.
Эта схема в основном используется для согласования импедансов. Это означает, что необходимо управлять нагрузкой с низким импедансом от источника с высоким импедансом.
Каскад с общим коллектором эмиттерный повторитель
Схему рис. 1.23а называют каскадом с общим коллектором (ОК), потому что коллекторный вывод транзистора по переменному току является общим электродом для входной и выходной цепей каскада. Схема также называется эмиттерным повторителем, т.к. выходное напряжение, снимаемое с эмиттера транзистора близко по величине входному напряжению ( Uвых = Uвх + Uбэ Uвх ) и совпадает с ним по фазе.
Рисунок 1.23 – Схема усилительного каскада ОК (а) и его схема замещения (б)
Расчет каскада по постоянному току проводят аналогично со схемой ОЭ. Резистор Rэ в схеме выполняет ту же функцию, что и резистор Rк в схеме ОЭ – создание изменяющегося напряжения в выходной цепи за счет протекания в ней тока, по цепи базы. Конденсаторы Ср1 и Ср2 являются разделительными, а резисторы R1 и R2 предназначены для задания рабочей точки, причем для повышения входного сопротивления резистор R2 в схему часто на вводят.
Входное сопротивление каскада ОК определяется параллельно включенными сопротивлениями R1, R2 и сопротивлением входной цепи транзистора rвх:
Rвх = R1 || R2 || rвх
Из эквивалентной схемы замещения рис.1.23б можно найти: Uвх = Iб [rб + (1 + )(rэ + Rэ || Rн)]
а разделив левую и правую часть уравнения на Iб получим: rвх = rб + (1 + )(rэ + Rэ || Rн)
Если принять, что rэ и rб значительно меньше других составляющих полученного выражения, то входное сопротивление транзистора , включенного по схеме ОЭ rвх (1 + )(Rэ || Rн),
а входное сопротивление каскада ОК: Rвх R1 || R2 || (1 + )(Rэ || Rн)
При достаточно высокоомном входном делителе и транзисторе с высоким входное сопротивление каскада может достигать десятков-сотен кОм, что является одним из важнейших достоинств каскада ОК.
Коэффициент усиления по току можно определить , используя эквивалентную схему замещения, аналогично каскаду ОК
Ток нагрузки является частью эмиттерного тока транзистора, поэтому:
откуда:
Выразив аналогично схеме ОЭ ток базы через входной ток каскада получаем:
Разделив левую и правую часть уравнения на Iвх имеем:
т.е. коэффициент усиления каскада ОК зависит от соотношений Rвх и rвх, а также Rэ и Rн. Если предположить, что Rвх rвх, имеем;
Таким образом, каскад ОК обеспечивает усиление по току, причем при Rэ = Rк и одинаковых значениях Rн коэффициенты усиления по току в схемах ОК и ОЭ примерно одинаковы. Коэффициент усиления по напряжению аналогично схеме ОЭ может быть определен как:
После подстановки значения КI:
Для оценки коэффициента усиления каскада ОК по напряжению примем Rвх >> Rг и считаем делитель в цепи базы достаточно высокоомным.
 Это позволяет принять
и получить КU 1.
Точный расчет дает КU
Это позволяет принять
и получить КU 1.
Точный расчет дает КUВыходное сопротивление каскада ОК представляет собой сопротивление со стороны эмиттера, которое из эквивалентной схемы замещения определяется как:
Выходное сопротивление каскада ОК мало и составляет 10 – 50 Ом, поэтому каскад ОК целесообразно использовать при необходимости согласования выходной цепи усилителя с низкоомным сопротивлением нагрузки.
Расчет биполярного транзистора в ключевом режиме с резистивной нагрузкой
Расчет биполярного транзистора в ключевом режиме с резистивной нагрузкойУпрощенный расчет транзистора для работы в ключевом режиме на резистивную нагрузку.
Ключевой режим работы характеризуется тем, что транзистор находится в одном из двух состояний: в полностью открытом (режим насыщения), или полностью закрытом (состояние отсечки).
Рассмотрим пример, где в
качестве нагрузки выступает контактор типа КНЕ030 на напряжение 27В с катушкой
сопротивлением 150 Ом. Индуктивным характером катушки в данном примере
пренебрежем, считая, что реле будет включено раз и надолго.
Индуктивным характером катушки в данном примере
пренебрежем, считая, что реле будет включено раз и надолго.
Рассчитываем ток коллектора:
Ik=(Ucc–Uкэнас)/Rн , где
Ik –ток коллектора
Ucc- напряжение питания (27В)
Uкэнас- напряжение насыщения биполярного транзистора (типично от 0.2 до 0.8В, хотя и может прилично различаться для разных транзисторов), в нашем случае примем 0.4В
Rн- сопротивление нагрузки (150 Ом)
Итак,
Ik= (27-0.4)/150 = 0.18A = 180мА
На практике из соображений надежности элементы всегда необходимо выбирать с запасом. Возьмем коэффициент 1.5
Таким образом, нужен транзистор с допустимым током коллектора не менее 1.5*0.18=0.27А и максимальным напряжением коллектор-эмиттер не менее 1.5*27=40В.
Открываем
справочник по биполярным транзисторам .
По заданным параметрам подходит
КТ815А (Ikмакс=1. 5А
Uкэ=40В)
5А
Uкэ=40В)
Следующим этапом рассчитываем ток базы, который нужно создать, чтобы обеспечить ток коллектора 0.18А.
Как известно, ток коллектора связан с током базы соотношением
Ik=Iб*h21э,
где h31э – статический коэффициент передачи тока.
При отсутствии дополнительных данных можно взять табличное гарантированное минимальное значение для КТ815А (40). Но для КТ815 есть график зависимости h31э от тока эмиттера. В нашем случае ток эмиттера 180мА, этому значению соответствует h31э=60. Разница невелика, но для чистоты эксперимента возьмем графические данные.
Итак,
Iб=180/60=3мА
Для
расчета базового резистора R1
смотрим второй график, где приведена зависимость напряжения насыщения
база-эмиттер (Uбэнас)
от тока коллектора. При токе коллектора 180мА напряжение насыщения базы будет
0.78В (При отсутствии такого графика можно использовать допущение, что ВАХ
перехода база-эмиттер подобна ВАХ диода и в диапазоне рабочих токов напряжение
база-эмиттер находится в пределах 0. 6-0.8 В)
6-0.8 В)
Следовательно, сопротивление резистора R1 должно быть равно:
R1=(Uвх-Uбэнас)/Iб = (5-0.78)/0.003 = 1407 Ом = 1.407 кОм.
Из стандартного ряда сопротивлений выбираем ближайшее в меньшую сторону (1.3 кОм)
Если к базе подключен шунтирующий резистор (вводится для более быстрого выключения транзистора или для повышения помехоустойчивости) нужно учитывать, что часть входного тока уйдет в этот резистор, и тогда формула примет вид:
R1= (Uвх-Uбэнас)/(Iб+IR2) = (Uвх-Uбэнас)/(Iб+ Uбэнас/R2)
Так, если R2=1 кОм, то
R1=
(5-0.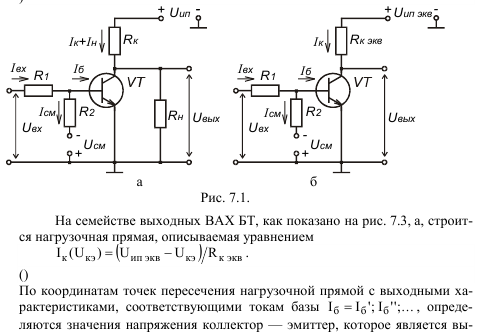 78)/(0.003+0.78/1000) = 1116 Ом = 1.1 кОм
78)/(0.003+0.78/1000) = 1116 Ом = 1.1 кОм
Рассчитываем потери мощности на транзисторе:
P=Ik*Uкэнас
Uкэнас берем из графика: при 180мА оно составляет 0.07В
P= 0.07*0.18= 0.013 Вт
Мощность смешная, радиатора не потребуется.
Сопротивление эмиттера переменного тока – WhatsWho.com
Что такое сопротивление эмиттера переменного тока?Переменное сопротивление или динамическое сопротивление диода перехода эмиттер-база транзистора равно , которое называется сопротивлением эмиттера переменного тока. Он определяется как изменение напряжения база-эмиттер, деленное на изменение соответствующего тока эмиттера. [См. Рис. 10.23] , т.е.
Например, предположим, что изменение базового напряжения переменного тока на 1 мВ вызывает изменение переменного тока эмиттера на 50 мкА. Тогда эмиттерный диод имеет сопротивление переменному току
Тогда эмиттерный диод имеет сопротивление переменному току
Математически можно показать, что сопротивление эмиттерного диода переменному току определяется выражением;
Обратите внимание на значение этой формулы.Это означает, что сопротивление эмиттера переменного тока можно найти, просто подставив в уравнение значение тока эмиттера в состоянии покоя. Нет необходимости в наличии характеристик. Важно помнить, что эта формула верна только для работы в режиме слабого сигнала. Обычно сопротивление эмиттера переменного тока обозначается как re ‘.
Нижний индекс e указывает на эмиттер. Строчная буква r используется для обозначения сопротивления переменному току. Штрих показывает, что это внутреннее сопротивление.
Пример 10.13. Определите сопротивление эмиттера переменного тока для схемы транзистора, показанной на Рис. 10.24.
Коэффициент усиления по напряжению усилителя CE Коэффициент усиления по напряжению (Av) усилителя равен переменному току. выходное напряжение (vout) деленное на переменный ток. входное напряжение (vin), т.е. Av = vout / vin. Мы уже видели, что коэффициент усиления по напряжению усилителя CE определяется выражением;
выходное напряжение (vout) деленное на переменный ток. входное напряжение (vin), т.е. Av = vout / vin. Мы уже видели, что коэффициент усиления по напряжению усилителя CE определяется выражением;
Вышеупомянутая формула для Av может использоваться, если нам известны значения RC (или RAC), β и Rin.Как правило, все эти значения неизвестны. В этом случае мы можем найти значение Av в виде общего переменного тока. сопротивление коллектора и общий переменный ток сопротивление эмиттера. Для схемы, показанной в Рис. 10.25 (с CE, подключенным к RE), можно доказать, что коэффициент усиления по напряжению определяется выражением;
Усиление напряжения ненагруженного усилителя CE На рис. 10.25 показана схема ненагруженного усилителя CE (т. Е. К цепи не подключена нагрузка RL). Обратите внимание, что конденсатор обхода эмиттера CE подключен параллельно с сопротивлением эмиттера RE .Конденсатор CE действует как * замыкающий на переменный ток. сигнал, чтобы он обходил переменный ток. сигнал на землю. Следовательно, эмиттер фактически находится на переменном токе. земля. Важно отметить, что CE играет важную роль в определении коэффициента усиления по напряжению (Av) усилителя CE. Если его снять, то усиление усилителя по напряжению сильно снизится (скоро вы увидите причину этого).
сигнал, чтобы он обходил переменный ток. сигнал на землю. Следовательно, эмиттер фактически находится на переменном токе. земля. Важно отметить, что CE играет важную роль в определении коэффициента усиления по напряжению (Av) усилителя CE. Если его снять, то усиление усилителя по напряжению сильно снизится (скоро вы увидите причину этого).
Вывод. На рис. 10.25 показан усилитель с общим эмиттером. Эквивалентная схема усилителя по переменному току показана на рис. .10.26. (я). Заменяя транзистор на его эквивалентную схему *, мы получаем схему, показанную на рис. 10.26 (ii) . Обратите внимание, что источник тока по-прежнему подключен между клеммами коллектора и базы, а диод – между клеммами базы и эмиттера. Кроме того, входной ток – это базовый ток (ib), в то время как выходной ток остается ic. Обратите внимание, что входное напряжение (Vin) приложено к диоду и re ‘. Если предположить, что диод идеален (чтобы его можно было заменить на провод), то переменный ток эмиттера определяется как:
Рис. 10.27 показывает простой переменный ток. модель усилителя CE с подключением CE через RE. Обратите внимание, что CE ведет себя как короткое замыкание, поэтому RE отключен от цепи эмиттера для переменного тока. сигнал. Следовательно, что касается as a.c. сигнал, общий переменный ток сопротивление эмиттера re ′. Коэффициент усиления по напряжению для нагруженного усилителя. Рис. 10.28 (i) показывает часть переменного тока. эквивалентная схема 0В переменного тока
10.27 показывает простой переменный ток. модель усилителя CE с подключением CE через RE. Обратите внимание, что CE ведет себя как короткое замыкание, поэтому RE отключен от цепи эмиттера для переменного тока. сигнал. Следовательно, что касается as a.c. сигнал, общий переменный ток сопротивление эмиттера re ′. Коэффициент усиления по напряжению для нагруженного усилителя. Рис. 10.28 (i) показывает часть переменного тока. эквивалентная схема 0В переменного тока
Усилитель CE. Обратите внимание, что нагрузка RL подключена к цепи. Помните, что для файла.c. анализ, VCC = 0 В, т.е. на земле. Так как RC и RL подключены к коллектору с одной стороны и заземлены с другой, два резистора включены * параллельно, как показано на рис. 10.28 (ii).
Коэффициент усиления по напряжению усилителя CE без CE Когда мы убираем конденсатор обхода эмиттера с усилителя CE, показанного на рис. 10.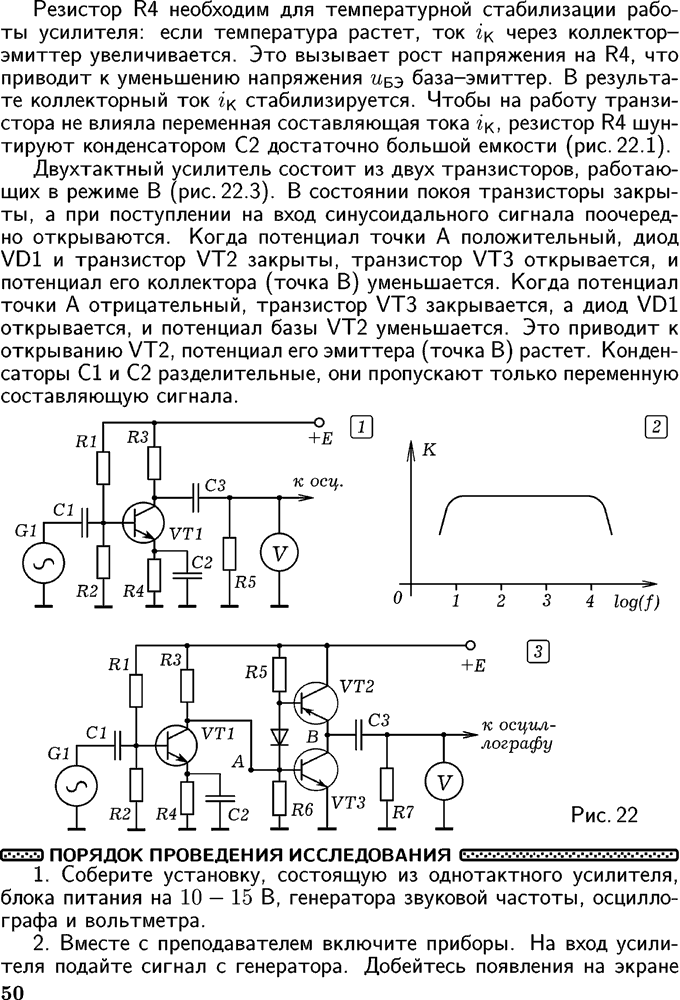 25, , усиление напряжения схемы значительно уменьшается. Причина проста. Без шунтирующего конденсатора эмиттера CE эмиттер больше не находится на земле переменного тока, как показано на Рис.10.29. Следовательно, для переменного тока сигнал, оба e r ‘и RE идут последовательно. В результате коэффициент усиления по напряжению усилителя составит:
25, , усиление напряжения схемы значительно уменьшается. Причина проста. Без шунтирующего конденсатора эмиттера CE эмиттер больше не находится на земле переменного тока, как показано на Рис.10.29. Следовательно, для переменного тока сигнал, оба e r ‘и RE идут последовательно. В результате коэффициент усиления по напряжению усилителя составит:
Пример 10.14. Для схемы усилителя, показанной на рис. 10.30, найдите коэффициент усиления по напряжению усилителя с (i) CE, подключенным в схему (ii) CE, удаленным из схемы.
Решение. Сначала мы найдем DC IE и, следовательно, re
Какая разница, которую имеет конденсатор шунтирования эмиттера CE! При подключенном CE Av = 360, а при удалении CE коэффициент усиления по напряжению снижается до 5.38.
Пример 10.15. Если в приведенном выше примере нагрузка 6 кОм подключена (с подключенным CE) к клемме коллектора через конденсатор, каков будет коэффициент усиления по напряжению усилителя?
Решение.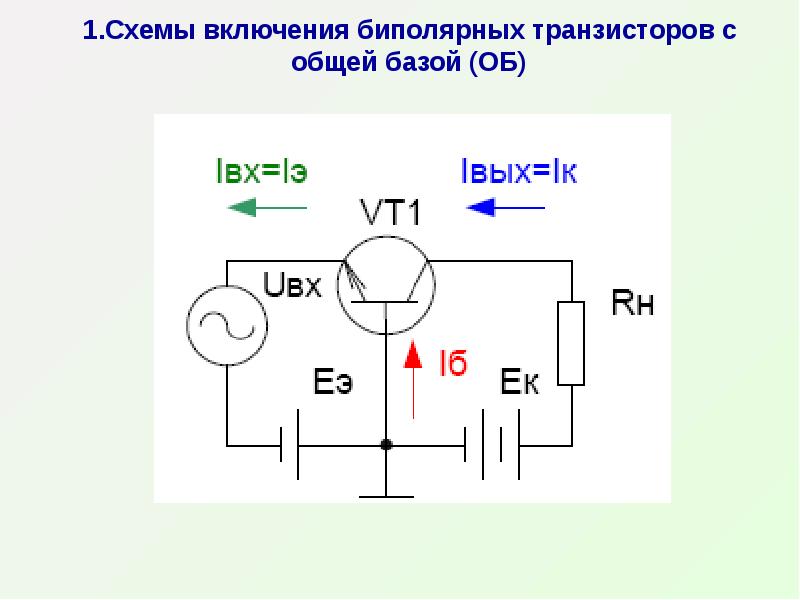 Усилители используются для подачи переменного тока на нагрузку. Когда нагрузка RL подключается к клемме коллектора через конденсатор, общее сопротивление коллектора переменному току изменяется на: ‘.
Усилители используются для подачи переменного тока на нагрузку. Когда нагрузка RL подключается к клемме коллектора через конденсатор, общее сопротивление коллектора переменному току изменяется на: ‘.
Таким образом, коэффициент усиления по напряжению усилителя уменьшается с 360 до 120 при подключении нагрузки к цепи.Комментарии. Этот пример показывает, что коэффициент усиления по напряжению усилителя уменьшается при подключении к нему нагрузки. И наоборот, если с усилителя снять нагрузку, коэффициент усиления по напряжению увеличится. Если нагрузка отключается, эффект будет таким же, как и при полном отключении нагрузки. Таким образом, основным признаком разомкнутой нагрузки в усилителе является увеличение коэффициента усиления схемы.
Пример 10.16. Для схемы, показанной на рис. 10.31, найдите (i) a.c. сопротивление эмиттера (ii) коэффициент усиления по напряжению (iii) постоянного тока напряжение на обоих конденсаторах
Решение. (i) Чтобы найти переменный ток сопротивление эмиттера re ′, сначала найдем постоянный ток эмиттера IE. Чтобы найти IE, мы действуем следующим образом:
(i) Чтобы найти переменный ток сопротивление эмиттера re ′, сначала найдем постоянный ток эмиттера IE. Чтобы найти IE, мы действуем следующим образом:
(iii) The d.c. напряжение на входном конденсаторе равно постоянному току. напряжение на базе транзистора V2 = 1V. Следовательно, d.c. напряжение на Cin составляет 1 В. Точно так же d.c. напряжение на CE = d.c напряжение на эмиттере = VE = 0,3В.
Пример 10.17. Для схемы, показанной на рис. 10.32, найдите (i) постоянного тока. уровни смещения (ii) d.c. напряжения на конденсаторах (iii) перем. сопротивление эмиттера (iv) усиление по напряжению и (v) состояние транзистора.
Решение.
(i) уровней смещения постоянного тока. Постоянный ток уровни смещения означают различные значения постоянного тока. токи и постоянный ток напряжения.
токи и постоянный ток напряжения.
Пример 10.18. Усилитель имеет коэффициент усиления по напряжению 132 и β = 200. Определите коэффициент усиления по мощности и выходную мощность усилителя, если входная мощность составляет 60 мкВт.
Решение.
Прирост мощности, Ap = усиление по току × усиление по напряжению
= β × Av = 200 × 132 = 26400
Выходная мощность, Pout = Ap × Pin = (26400) (60 мкВт) = 1,584 Вт
Пример 10.19. Для схемы, показанной на рис.10.33, определяют (i) усиление по току, (ii) усиление по напряжению и (iii) усиление мощности. Пренебрегайте переменным током. сопротивление эмиттера для транзистора.
Решение. В большинстве практических схем значение переменного тока Сопротивление эмиттера re ‘для транзистора обычно довольно мало по сравнению с RE, и им можно пренебречь при расчетах схемы с разумной точностью
Входное сопротивление усилителя CE Когда один усилитель CE используется для управления другим, входное сопротивление второго усилителя будет служить сопротивлением нагрузки первого.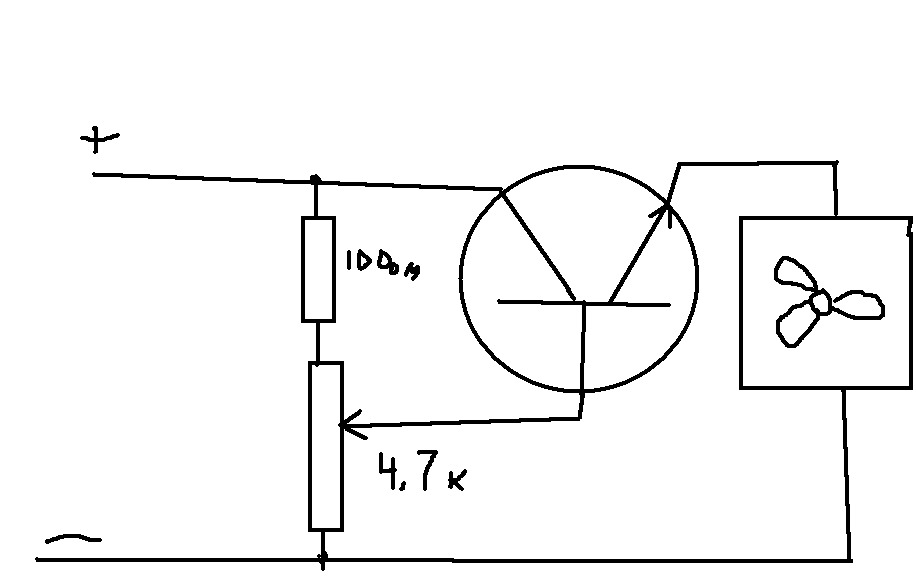 Следовательно, чтобы правильно рассчитать коэффициент усиления по напряжению (Av) первого каскада усилителя, мы должны вычислить входное сопротивление второго каскада. Входной импеданс усилителя можно найти, используя эквивалентную схему усилителя на переменном токе, как показано на рис. 10.34.
Следовательно, чтобы правильно рассчитать коэффициент усиления по напряжению (Av) первого каскада усилителя, мы должны вычислить входное сопротивление второго каскада. Входной импеданс усилителя можно найти, используя эквивалентную схему усилителя на переменном токе, как показано на рис. 10.34.
Zin = R1 || R2 | | Zin (база)
, где Zin = входное сопротивление усилителя
Zin (база) = входное сопротивление базы транзистора
Теперь Zin (база) = * β re ‘
Входное сопротивление [Zin] всегда меньше, чем входное сопротивление база [Zin (база)].
Пример 10.20. Определите входной импеданс цепи усилителя, показанной на рис. 10.35.
Стабильность усиления по напряжению Одним из важных факторов, учитываемых при выборе усилителя, является стабильность его усиления по напряжению. Усилитель должен иметь стабильные значения усиления по напряжению, чтобы выходной сигнал схемы был предсказуем во всех нормальных условиях. В стандартном усилителе CE весь постоянный ток сопротивление эмиттера RE шунтируется конденсатором эмиттера шунтирования CE.Следовательно, общий переменный ток сопротивление эмиттера re ′. Коэффициент усиления по напряжению такого усилителя без нагрузки определяется выражением;
В стандартном усилителе CE весь постоянный ток сопротивление эмиттера RE шунтируется конденсатором эмиттера шунтирования CE.Следовательно, общий переменный ток сопротивление эмиттера re ′. Коэффициент усиления по напряжению такого усилителя без нагрузки определяется выражением;
Коэффициент усиления по напряжению стандартного усилителя CE довольно велик. Однако недостатком схемы является то, что ее коэффициент усиления по напряжению изменяется в зависимости от тока эмиттера IE, колебаний температуры и замены транзистора. Например, если ток IE эмиттера увеличивается, переменный ток сопротивление эмиттера re ′ уменьшается. Это изменяет коэффициент усиления по напряжению усилителя. Аналогичным образом, при изменении температуры или при замене транзистора параметр a.c. текущий коэффициент усиления β изменяется. Это также приведет к изменению коэффициента усиления по напряжению. Чтобы стабилизировать коэффициент усиления по напряжению, сопротивление эмиттера RE частично обходится CE. Такой усилитель называется заболоченным.
Такой усилитель называется заболоченным.
Рис. 10.36 (i) показывает эмиттерную ветвь стандартного усилителя CE, а Рис. 10.36 (ii) показывает эмиттерную ветвь затопленного усилителя. В усиленном усилителе сопротивление RE разделено на две части, а именно. RE1 и RE2. CE обходит только RE2, а RE1 – нет.
Щелкните здесь, чтобы загрузить приложение WhatsWho
Сопротивление излучателя переменного тока Природа окружающей среды | Типы Сопротивление излучателя переменного тока
Сопротивление излучателя переменного тока Что такое частота и длина волны? Сопротивление эмиттера переменного тока
Сопротивление эмиттера переменного тока Что такое анализ линии нагрузки | Усиление напряжения Сопротивление эмиттера переменного тока
Сопротивление эмиттера переменного тока Вопрос об электронной связи Сопротивление эмиттера переменного тока
1) НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОЧИТАТЬ СВЯЗАННЫЕ СТАТЬИ (эмиттерный диод и сопротивление переменному току эмиттерного диода)
2). НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОЧИТАТЬ СВЯЗАННЫЕ СТАТЬИ (эмиттерный диод и сопротивление по переменному току эмиттерного диода)
НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОЧИТАТЬ СВЯЗАННЫЕ СТАТЬИ (эмиттерный диод и сопротивление по переменному току эмиттерного диода)
3). НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОЧИТАТЬ СВЯЗАННЫЕ СТАТЬИ (эмиттерный диод и сопротивление эмиттерного диода по переменному току)
4). НАЖМИТЕ ЗДЕСЬ, ЧТОБЫ ПРОЧИТАТЬ СВЯЗАННЫЕ СТАТЬИ (эмиттерный диод и сопротивление эмиттерного диода по переменному току)
Сопротивление эмиттера | PVEducation
На основе удельного сопротивления листа потери мощности из-за сопротивления эмиттера могут быть рассчитаны как функция расстояния между пальцами в верхнем контакте.Однако расстояние, на котором ток течет в эмиттере, не является постоянным. Ток может собираться от основания близко к пальцу, и поэтому он имеет лишь небольшое расстояние, чтобы протекать к пальцу, или, в качестве альтернативы, если ток входит в эмиттер между пальцами, то длина резистивного пути, видимого таким носителем, равна половина шага сетки.
Идеальное прохождение тока от точки генерации до внешнего контакта в солнечном элементе.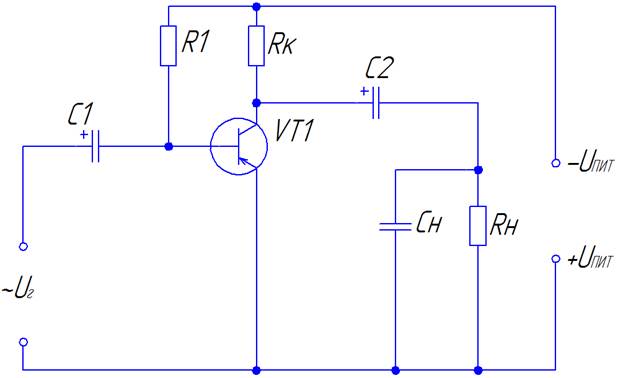 Излучатель обычно намного тоньше, чем показано на схеме.{2} d R $$
Излучатель обычно намного тоньше, чем показано на схеме.{2} d R $$
Дифференциальное сопротивление определяется по формуле:
$$ d R = \ frac {\ rho} {b} d y $$
где
ρ – удельное сопротивление листа в Ом / кв.
b – расстояние вдоль пальца; и
y расстояние между двумя пальцами сетки, как показано ниже.
Размеры, необходимые для расчета потерь мощности из-за бокового сопротивления верхнего слоя.
Ток также зависит от y, а I (y) – это боковой ток, который равен нулю в средней точке между линиями решетки и линейно возрастает до своего максимума на линии решетки при равномерном освещении.{2} J_ {M P}} {12 V_ {M P}} $$
Следовательно, можно рассчитать минимальный интервал для верхней контактной сетки. Например, для типичного кремниевого солнечного элемента, где ρ = 40 Ом / кв., Дж mp = 30 мА / см 2 , В mp = 450 мВ, чтобы иметь потерю мощности в у излучателя менее 4% расстояние между пальцами должно быть менее 4 мм.
| Биполярные переходные транзисторы
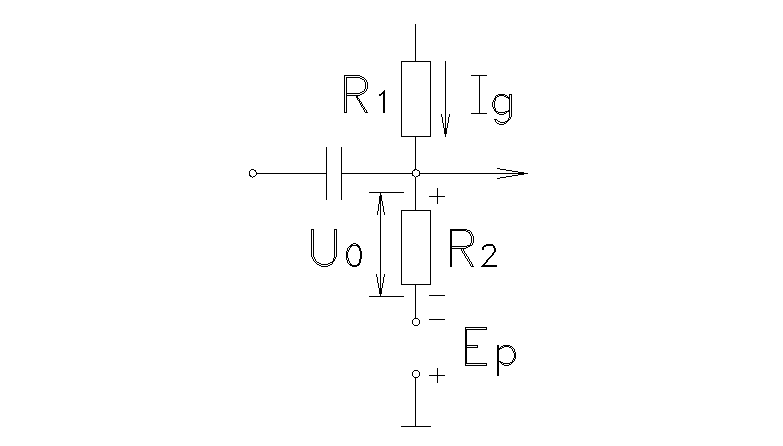
Хотя схемы переключения транзисторов работают без смещения, для аналоговых схем необычно работать без смещения.Один из немногих примеров – «TR One, одно транзисторное радио» TR One, Ch 9 с усиленным детектором AM (амплитудной модуляцией). Обратите внимание на отсутствие резистора смещения на базе в этой схеме. В этом разделе мы рассмотрим несколько основных схем смещения, которые могут установить выбранный IE тока эмиттера. При желаемом токе эмиттера IE, какие требуются резисторы смещения, RB, RE и т. Д.?
Базовый резистор смещения
В простейшем смещении используется резистор смещения базы между базой и базовой батареей V BB . Удобно использовать существующий источник питания VCC вместо нового источника смещения. Примером каскада звукового усилителя, использующего смещение базы, является «Кристаллический радиоприемник с одним транзистором. . . Кристалл радиоприемника, Ch 9. Обратите внимание на резистор от базы до клеммы аккумулятора. Аналогичная схема изображена на рисунке ниже. Напишите уравнение KVL (закон напряжения Кирхгофа) для контура, содержащего батарею, RB и падение диода VBE на транзисторе, как показано на рисунке ниже. Обратите внимание, что мы используем VBB для базового питания, хотя на самом деле это VCC.Если β велико, мы можем сделать приближение IC = IE. Для кремниевых транзисторов ВБЭ≅0,7В.
. . Кристалл радиоприемника, Ch 9. Обратите внимание на резистор от базы до клеммы аккумулятора. Аналогичная схема изображена на рисунке ниже. Напишите уравнение KVL (закон напряжения Кирхгофа) для контура, содержащего батарею, RB и падение диода VBE на транзисторе, как показано на рисунке ниже. Обратите внимание, что мы используем VBB для базового питания, хотя на самом деле это VCC.Если β велико, мы можем сделать приближение IC = IE. Для кремниевых транзисторов ВБЭ≅0,7В.
Базовое смещение
Кремниевые малосигнальные транзисторы обычно имеют β в диапазоне 100–300.
Пример расчета:
Предполагая, что у нас есть транзистор с β = 100, какое значение резистора смещения базы требуется, чтобы обеспечить ток эмиттера 1 мА? Решение уравнения базового смещения IE для RB и замена β, VBB, VBE и IE дает 930 кОм.Ближайшее стандартное значение – 910 кОм.
Какой ток эмиттера с резистором 910 кОм? Каков ток эмиттера, если мы случайно получим транзистор β = 300?
Ток эмиттера мало изменяется при использовании резистора стандартного номинала 910 кОм. Однако при изменении β от 100 до 300 ток эмиттера утроился. Это неприемлемо для усилителя мощности, если мы ожидаем, что напряжение коллектора будет колебаться от около VCC до около земли. Однако для сигналов низкого уровня от микровольт до примерно вольта точка смещения может быть центрирована для β квадратного корня из (100 · 300) = 173.Точка смещения все равно будет сильно смещаться. Однако сигналы низкого уровня не будут обрезаться.
Однако при изменении β от 100 до 300 ток эмиттера утроился. Это неприемлемо для усилителя мощности, если мы ожидаем, что напряжение коллектора будет колебаться от около VCC до около земли. Однако для сигналов низкого уровня от микровольт до примерно вольта точка смещения может быть центрирована для β квадратного корня из (100 · 300) = 173.Точка смещения все равно будет сильно смещаться. Однако сигналы низкого уровня не будут обрезаться.
Базовое смещение не подходит для высоких эмиттерных токов, используемых в усилителях мощности. Ток эмиттера, смещенный к базе, нестабилен по температуре.
Термический разгон является результатом высокого эмиттерного тока, вызывающего повышение температуры, которое вызывает увеличение эмиттерного тока, что еще больше увеличивает температуру.
Смещение коллектора-обратной связи
Изменения смещения из-за температуры и бета можно уменьшить, переместив конец VBB резистора смещения базы на коллектор, как показано на рисунке ниже.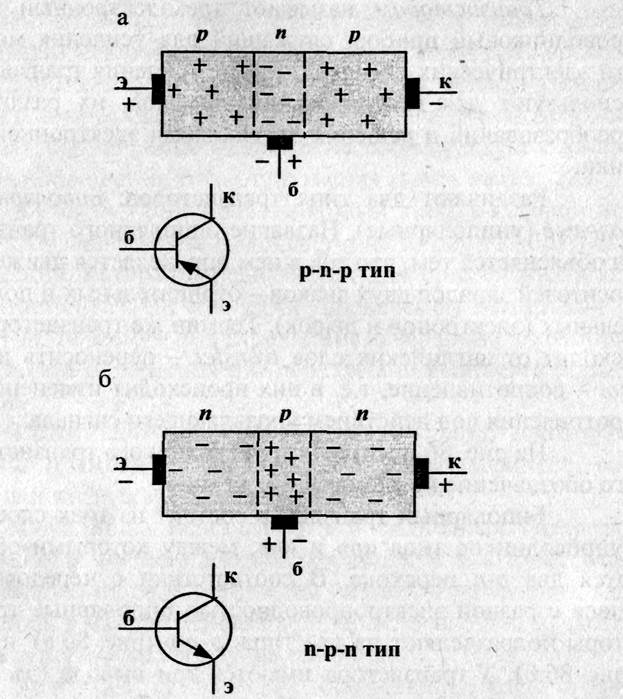 Если ток эмиттера увеличится, падение напряжения на RC увеличится, уменьшится VC и уменьшится IB, возвращаемый на базу. Это, в свою очередь, снижает ток эмиттера, корректируя первоначальное увеличение.
Если ток эмиттера увеличится, падение напряжения на RC увеличится, уменьшится VC и уменьшится IB, возвращаемый на базу. Это, в свою очередь, снижает ток эмиттера, корректируя первоначальное увеличение.
Напишите уравнение KVL для контура, содержащего батарею, RC, RB и каплю VBE. Заменить IC≅IE и IB≅IE / β. Решение для IE дает уравнение смещения IE CFB. Решение IB дает уравнение IB CFB-bias.
Смещение обратной связи коллектора.
Пример расчета:
Найдите требуемый резистор смещения обратной связи коллектора для тока эмиттера 1 мА, a 4.Коллекторный нагрузочный резистор 7К, а транзистор с β = 100. Найдите напряжение коллектора VC. Это должно быть примерно посередине между VCC и землей.
Ближайшее стандартное значение резистора смещения обратной связи коллектора 460 кОм составляет 470 кОм. Найдите ток эмиттера IE с резистором 470 кОм. Пересчитайте ток эмиттера для транзистора с β = 100 и β = 300.
Мы видим, что при изменении бета от 100 до 300 ток эмиттера увеличивается с 0,989 мА до 1.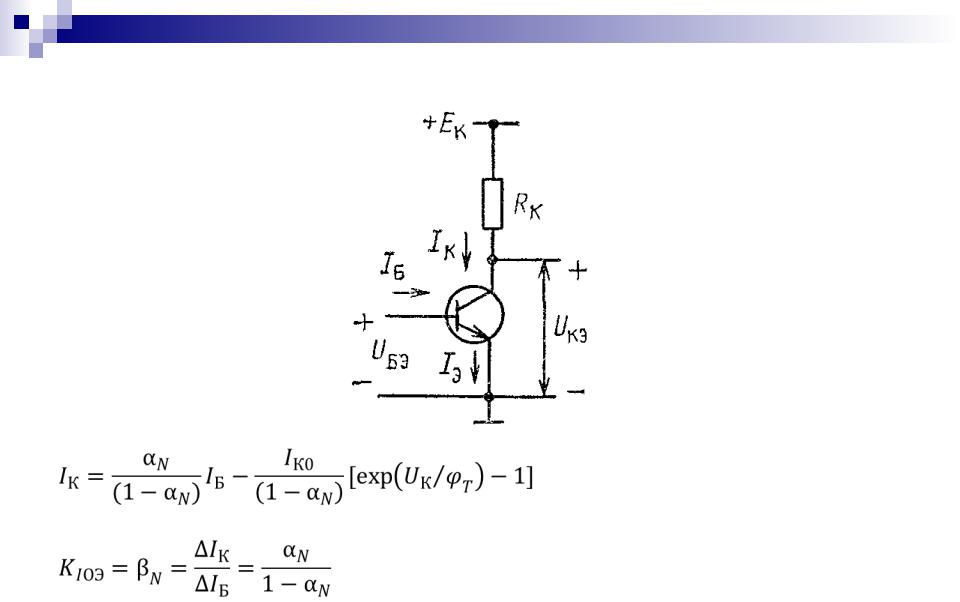 48 мА. Это улучшение по сравнению с предыдущей схемой базового смещения, которая увеличилась с 1,02 мА до 3,07 мА. Смещение обратной связи коллектора в два раза стабильнее, чем смещение базы, в отношении бета-вариации.
48 мА. Это улучшение по сравнению с предыдущей схемой базового смещения, которая увеличилась с 1,02 мА до 3,07 мА. Смещение обратной связи коллектора в два раза стабильнее, чем смещение базы, в отношении бета-вариации.
Эмиттер-смещение
Вставка резистора RE в схему эмиттера, как показано на рисунке ниже, вызывает дегенерацию , также известную как отрицательная обратная связь . Это препятствует изменению тока IE эмиттера из-за изменений температуры, допусков резистора, бета-изменения или допуска источника питания.Типовые допуски следующие: резистор – 5%, бета – 100-300, блок питания – 5%. Почему эмиттерный резистор может стабилизировать изменение тока? Полярность падения напряжения на RE обусловлена VCC коллекторной батареи. Конец резистора, ближайший к (-) клемме батареи, – (-), конец, ближайший к клемме (+), – это (+). Обратите внимание, что (-) конец RE подключен через батарею VBB и RB к базе. Любое увеличение тока, протекающего через RE, увеличит величину отрицательного напряжения, приложенного к схеме базы, уменьшив ток базы, уменьшив ток эмиттера.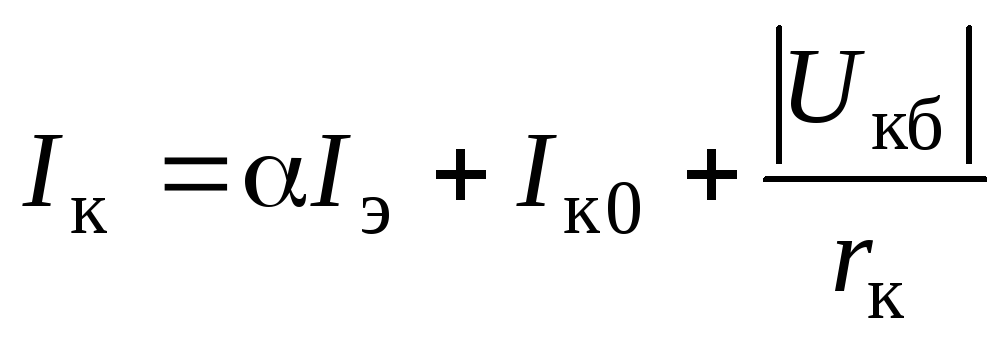 Этот уменьшающийся ток эмиттера частично компенсирует первоначальное увеличение.
Этот уменьшающийся ток эмиттера частично компенсирует первоначальное увеличение.
Эмиттер-смещение
Обратите внимание, что батарея VBB с базовым смещением используется вместо VCC для смещения базы на рисунке выше. Позже мы покажем, что смещение эмиттера более эффективно при использовании батареи с более низким базовым смещением. Между тем, мы пишем уравнение КВЛ для контура через цепь база-эмиттер, обращая внимание на полярность компонентов. Подставляем IB≅IE / β и решаем ток эмиттера IE.Это уравнение может быть решено для RB, уравнение: RB emitter-bias, рисунок выше.
Перед применением уравнений: RB emitter-bias и IE emitter-bias, рисунок выше, нам нужно выбрать значения для RC и RE. RC связан с питанием коллектора VCC и желаемым током коллектора IC, который, как мы предполагаем, приблизительно равен току эмиттера IE.
Обычно точка смещения для VC устанавливается равной половине VCC. Хотя его можно установить выше, чтобы компенсировать падение напряжения на эмиттерном резисторе RE. Ток коллектора – это то, что мы требуем или выбираем. Он может варьироваться от микроампер до ампер в зависимости от приложения и номинала транзистора. Выбираем IC = 1 мА, что типично для схемы на малосигнальном транзисторе.
Ток коллектора – это то, что мы требуем или выбираем. Он может варьироваться от микроампер до ампер в зависимости от приложения и номинала транзистора. Выбираем IC = 1 мА, что типично для схемы на малосигнальном транзисторе.
Пример расчета:
Рассчитываем значение RC и выбираем близкое стандартное значение. Эмиттерный резистор, который составляет 10-50% резистора нагрузки коллектора, обычно работает хорошо.
Для RB был рассчитан резистор 883 кОм, выбрано 870 кОм.При β = 100 IE составляет 1,01 мА.
Для β = 300 токи эмиттера показаны в таблице ниже.
Сравнение тока эмиттера для β = 100, β = 300.
| Цепь смещения | IC β = 100 | IC β = 300 |
|---|---|---|
| базовое смещение | 1,02 мА | 3,07 мА |
| смещение обратной связи коллектора | 0,989 мА | 1,48 мА |
| эмиттер-смещение, В BB = 10 В | 1. 01 мА 01 мА | 2,76 мА |
Таблица выше показывает, что для VBB = 10 В смещение эмиттера не очень хорошо стабилизирует ток эмиттера. Пример смещения эмиттера лучше, чем предыдущий пример смещения базы, но не намного. Ключом к эффективному смещению эмиттера является снижение базового напряжения VBB ближе к величине смещения эмиттера.
Округление, которое означает время эмиттерного тока на резистор эмиттера: IERE = (1 мА) (470) = 0,47 В. Кроме того, нам нужно преодолеть VBE = 0.7В. Таким образом, нам нужен VBB> (0,47 + 0,7) В или> 1,17 В. Если ток эмиттера отклоняется, это число изменится по сравнению с постоянным базовым питанием VBB, вызывая коррекцию базового тока IB и эмиттерного тока IE. Хорошее значение для VB> 1,17 В – 2 В.
Расчетный базовый резистор 83 кОм намного ниже, чем у предыдущего 883 кОм. Выбираем 82к из списка стандартных значений. Токи эмиттера с РБ 82 кОм для β = 100 и β = 300 составляют:
Сравнивая токи эмиттера для смещения эмиттера с VBB = 2 В при β = 100 и β = 300 с предыдущими примерами схемы смещения в таблице ниже, мы видим значительное улучшение при 1.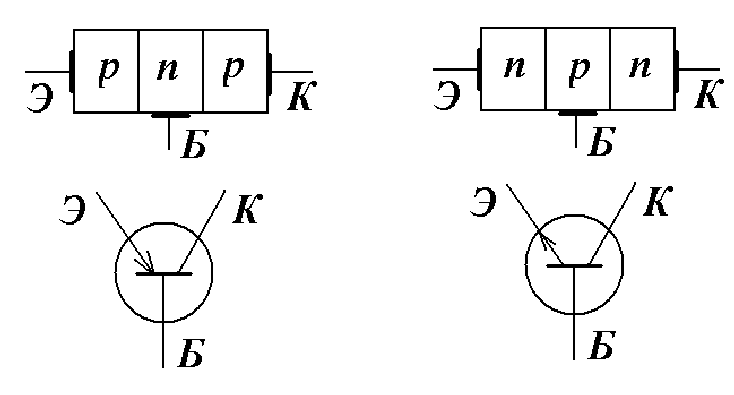 75 мА, однако, не так хорошо, как 1,48 мА обратной связи коллектора.
75 мА, однако, не так хорошо, как 1,48 мА обратной связи коллектора.
Сравнение тока эмиттера для β = 100, β = 300.
| Цепь смещения | IC β = 100 | IC β = 300 |
|---|---|---|
| базовое смещение | 1,02 мА | 3,07 мА |
| смещение обратной связи коллектора | 0,989 мА | 1,48 мА |
| эмиттер-смещение, В BB = 10 В | 1,01 мА | 2.76 мА |
| эмиттер-смещение, В BB = 2 В | 1,01 мА | 1,75 мА |
Чтобы улучшить характеристики эмиттерного смещения, либо увеличьте резистор эмиттера RE, либо уменьшите подачу базового смещения VBB, либо и то, и другое.
В качестве примера мы удвоим резистор эмиттера до ближайшего стандартного значения 910 Ом.
Вычисленное RB = 39 кОм – резистор стандартного номинала. Нет необходимости пересчитывать IE для β = 100. Для β = 300 это:
Нет необходимости пересчитывать IE для β = 100. Для β = 300 это:
Эффективность схемы смещения эмиттера с эмиттерным резистором 910 значительно улучшена.См. Таблицу ниже.
Сравнение тока эмиттера для β = 100, β = 300.
| Цепь смещения | IC β = 100 | IC β = 300 |
|---|---|---|
| базовое смещение | 1,02 мА | 3,07 мА |
| смещение обратной связи коллектора | 0,989 мА | 1,48 мА |
| эмиттер-смещение, В BB = 10 В | 1,01 мА | 2,76 мА |
| эмиттер-смещение, В BB = 2 В, R E = 470 | 1.01 мА | 1,75 мА |
| эмиттер-смещение, В BB = 2 В, R E = 910 | 1,00 мА | 1,25 мА |
В качестве упражнения переработайте пример смещения эмиттера с резистором эмиттера, возвращенным обратно на 470 Ом, а напряжение смещения базы уменьшено до 1,5 В.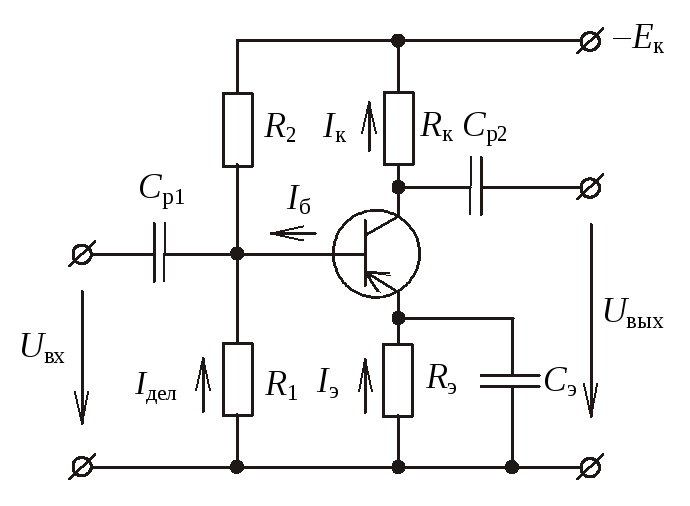
Базовый резистор 33 кОм – стандартное значение, ток эмиттера при β = 100 в порядке. Ток эмиттера при β = 300 составляет:
В таблице ниже сравниваются результаты упражнений 1 мА и 1.38 мА к предыдущим примерам.
Сравнение тока эмиттера для β = 100, β = 300.
| Цепь смещения | IC β = 100 | IC β = 300 |
|---|---|---|
| базовое смещение | 1,02 мА | 3,07 мА |
| смещение обратной связи коллектора | 0,989 мА | 1,48 мА |
| эмиттер-смещение, В BB = 10 В | 1,01 мА | 2,76 мА |
| эмиттер-смещение, В BB = 2 В, R B = 470 | 1.01 мА | 1,75 мА |
| эмиттер-смещение, В BB = 2 В, R B = 910 | 1,00 мА | 1,25 мА |
| эмиттер-смещение, В BB = 1,5 В, R B = 470 | 1,00 мА | 1,38 мА |
Уравнения смещения эмиттера повторены на рисунке ниже с включенным внутренним сопротивлением эмиттера для большей точности. Внутреннее сопротивление эмиттера – это сопротивление в цепи эмиттера внутри корпуса транзистора.Это внутреннее сопротивление rEE является значительным, когда (внешний) эмиттерный резистор RE мал или даже равен нулю. Значение внутреннего сопротивления REE является функцией тока эмиттера IE, таблица ниже.
Внутреннее сопротивление эмиттера – это сопротивление в цепи эмиттера внутри корпуса транзистора.Это внутреннее сопротивление rEE является значительным, когда (внешний) эмиттерный резистор RE мал или даже равен нулю. Значение внутреннего сопротивления REE является функцией тока эмиттера IE, таблица ниже.
Получение r EE
r EE = KT / I E m где: K = 1,38 × 10 -23 ватт-сек / o C, постоянная Больцмана T = температура в Кельвинах ≅300. I E = ток эмиттера m = изменяется от 1 до 2 для кремния r EE ≅ 0.026V / I E = 26 мВ / I E
Для справки, приближение 26 мВ указано как уравнение rEE на рисунке ниже.
Уравнения смещения эмиттера с внутренним сопротивлением эмиттера rEE.
Более точные уравнения смещения эмиттера на рисунке выше могут быть получены путем записи уравнения KVL. В качестве альтернативы, начните с уравнений IE emitter-bias и RB emitter-bias на рисунке выше, заменив RE на rEE + RE.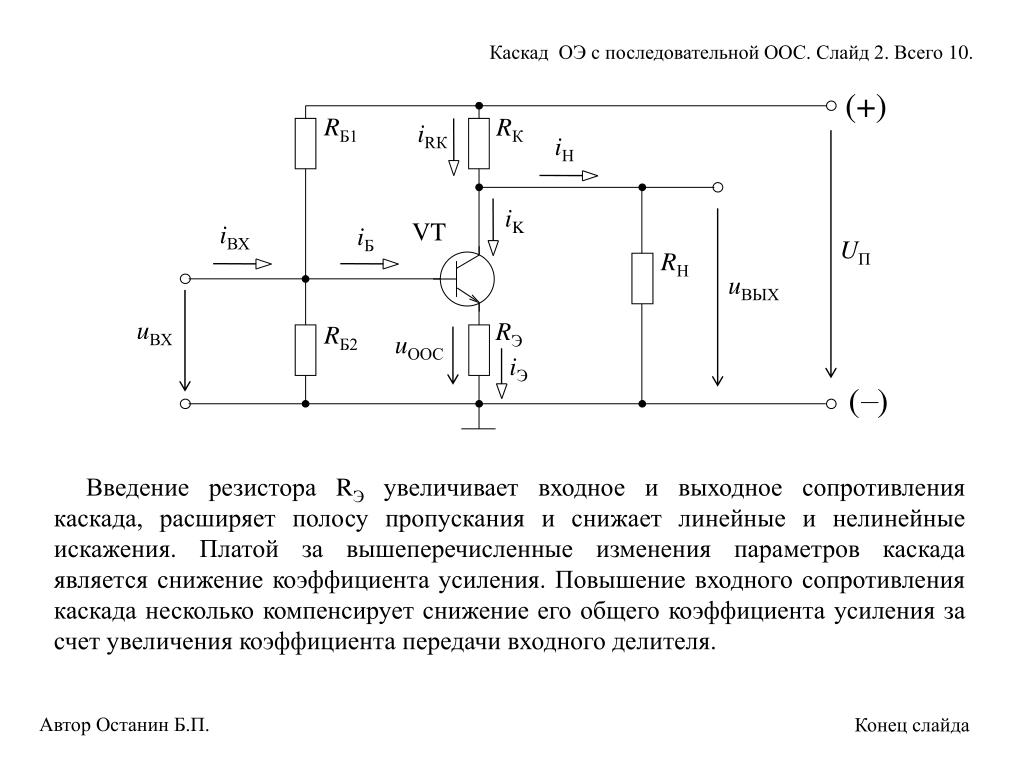 Результатом являются уравнения IE EB и RB EB соответственно на рисунке выше.
Результатом являются уравнения IE EB и RB EB соответственно на рисунке выше.
Повторите вычисление RB в предыдущем примере смещения эмиттера с включением rEE и сравните результаты.
Учет rEE в расчетах приводит к более низкому значению базового резистора RB, как показано в таблице ниже. Он падает ниже стандартного значения резистора 82 кОм, а не выше.
Влияние включения РЭЭ на расчетную РБ
| r EE ? | r EE Значение |
|---|---|
| Без r EE | 83к |
| С r EE | 80.4к |
Байпасный конденсатор для RE
Одна из проблем со смещением эмиттера заключается в том, что значительная часть выходного сигнала падает на эмиттерный резистор RE (рисунок ниже). Это падение напряжения на эмиттерном резисторе идет последовательно с базой и имеет противоположную полярность по сравнению с входным сигналом. (Это похоже на обычную конфигурацию коллектора с коэффициентом усиления <1). Это ухудшение сильно снижает коэффициент усиления от базы к коллектору. Решением для усилителей сигналов переменного тока является обход эмиттерного резистора конденсатором.Это восстанавливает усиление переменного тока, поскольку конденсатор не подходит для сигналов переменного тока. Постоянный ток эмиттера все еще испытывает вырождение в эмиттерном резисторе, таким образом, стабилизируя постоянный ток.
(Это похоже на обычную конфигурацию коллектора с коэффициентом усиления <1). Это ухудшение сильно снижает коэффициент усиления от базы к коллектору. Решением для усилителей сигналов переменного тока является обход эмиттерного резистора конденсатором.Это восстанавливает усиление переменного тока, поскольку конденсатор не подходит для сигналов переменного тока. Постоянный ток эмиттера все еще испытывает вырождение в эмиттерном резисторе, таким образом, стабилизируя постоянный ток.
Cbypass требуется для предотвращения снижения усиления переменного тока.
Величина байпасного конденсатора зависит от самой низкой частоты, которую нужно усилить.
Для радиочастот Cbpass было бы маленьким. Для аудиоусилителя с диапазоном частот до 20 Гц он будет большим.«Практическое правило» для байпасного конденсатора состоит в том, что реактивное сопротивление должно быть 1/10 сопротивления эмиттера или меньше. Конденсатор должен быть спроектирован таким образом, чтобы выдерживать самую низкую частоту усиления. Конденсатор для аудиоусилителя с диапазоном частот от 20 Гц до 20 кГц:
Конденсатор для аудиоусилителя с диапазоном частот от 20 Гц до 20 кГц:
Обратите внимание, что внутреннее сопротивление эмиттера rEE не шунтируется шунтирующим конденсатором.
Смещение делителя напряжения
Для стабильного смещения эмиттера требуется источник смещения базы низкого напряжения, как показано на рисунке ниже.Альтернативой базовому источнику питания VBB является делитель напряжения, основанный на питании коллектора VCC.
Делитель напряжения смещения заменяет базовую батарею делителем напряжения.
Методика проектирования состоит в том, чтобы сначала разработать схему смещения эмиттера, а затем преобразовать ее в конфигурацию смещения делителя напряжения с помощью теоремы Тевенина. [TK1] Шаги графически показаны на рисунке ниже. Изобразите делитель напряжения без назначения значений. Отделите перегородку от основания.(База транзистора – это нагрузка.) Примените теорему Тевенина, чтобы получить одно эквивалентное сопротивление Тевенина Rth и источник напряжения Vth.
Теорема Тевенина преобразует делитель напряжения на однополярное питание Vth и сопротивление Rth.
Эквивалентное сопротивление Тевенина – это сопротивление от точки нагрузки (стрелка) с аккумулятором (VCC), уменьшенным до 0 (земля). Другими словами, R1 || R2. Эквивалентное напряжение Тевенина – это напряжение холостого хода (нагрузка снята). Этот расчет выполняется методом коэффициента делителя напряжения.R1 получается путем исключения R2 из пары уравнений для Rth и Vth. Уравнение R1 выражается в известных величинах Rth, Vth, Vcc. Обратите внимание, что Rth – это RB, резистор смещения из конструкции эмиттерного смещения. Уравнение для R2 выражается через R1 и Rth.
Преобразуйте этот предыдущий пример смещения эмиттера в смещение делителя напряжения.
Пример преобразования эмиттерного смещения в смещение делителя напряжения.
Эти значения были ранее выбраны или рассчитаны для примера смещения эмиттера
Замена VCC, VBB, RB дает R1 и R2 для конфигурации смещения делителя напряжения.
R1 – стандартное значение 220К. Ближайшее стандартное значение R2, соответствующее 38,8k, составляет 39k. Это не меняет IE настолько, чтобы мы могли его вычислить. Примеры проблем 1. Рассчитайте резисторы смещения для каскодного усилителя, показанного на рисунке ниже. VB2 – напряжение смещения для каскада с общим эмиттером. VB1 – это довольно высокое напряжение 11,5, потому что мы хотим, чтобы каскад с общей базой удерживал эмиттер при 11,5-0,7 = 10,8 В, около 11 В. (Это будет 10 В с учетом падения напряжения на RB1.То есть каскад с общей базой является нагрузкой, заменяющей резистор, для коллектора каскада с общим эмиттером. Нам нужен ток эмиттера 1 мА.
Смещение для каскодного усилителя.
2. Преобразуйте базовые резисторы смещения для каскодного усилителя в резисторы смещения делителя напряжения, управляемые напряжением VCC 20 В.
Окончательная принципиальная схема показана в главе «Практические аналоговые схемы», «Каскодный усилитель класса А.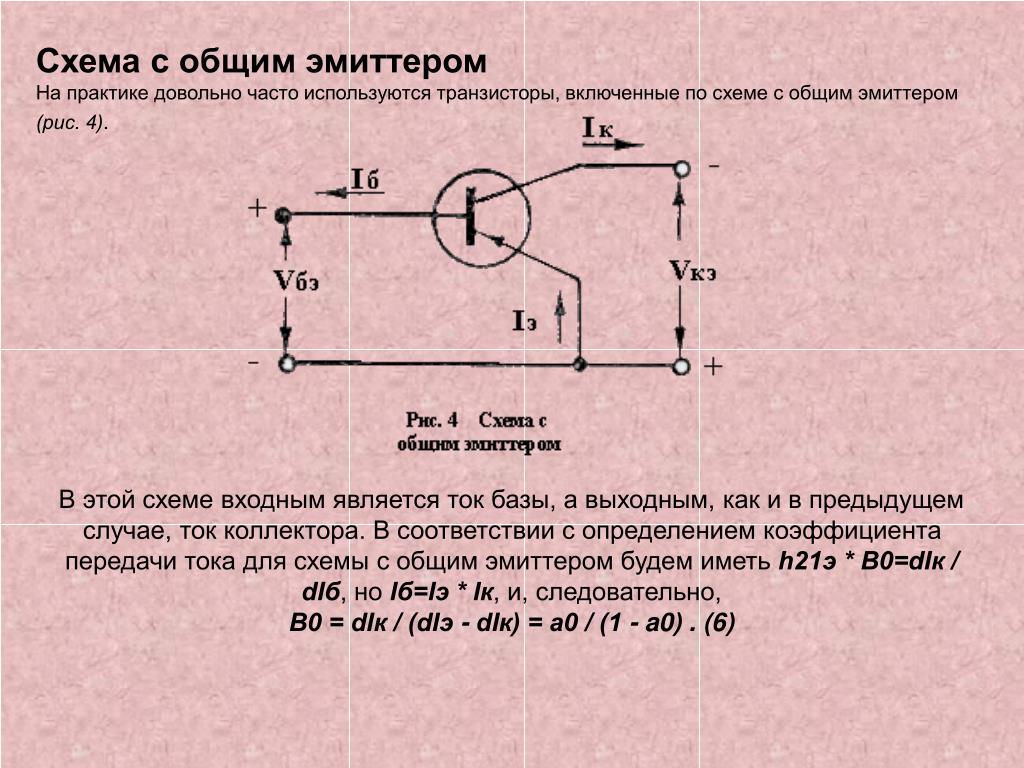 . . ”Каскод, гл. 9.
. . ”Каскод, гл. 9.
ОБЗОР:
- См. Рисунок ниже.
- Выбор конфигурации цепи смещения
- Выберите RC и IE для предполагаемого приложения. Значения RC и IE обычно должны устанавливать напряжение коллектора VC равным 1/2 от VCC.
- Рассчитайте базовый резистор RB для достижения желаемого тока эмиттера.
- При необходимости пересчитайте ток эмиттера IE для резисторов стандартного номинала.
- Для смещения делителя напряжения сначала выполните расчеты смещения эмиттера, а затем определите R1 и R2.
- Для усилителей переменного тока байпасный конденсатор, включенный параллельно с RE, улучшает усиление переменного тока.Установите XC≤0,10RE для минимальной частоты.
Сводка уравнений смещения.
СВЯЗАННЫЕ РАБОЧИЕ ЛИСТЫ:
(PDF) Извлечение сопротивления базы и эмиттера BJT из данных постоянного тока
Рис. 3 Сопротивление эмиттера из данных FG
Рис.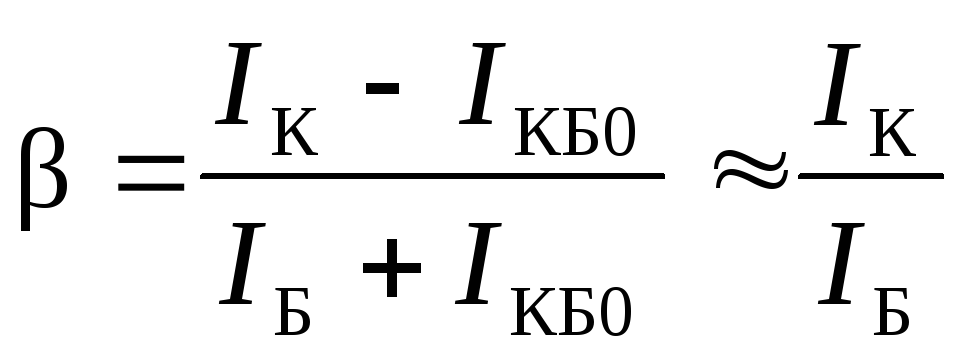 4 Сопротивление базы постоянного и переменного тока из данных FG
4 Сопротивление базы постоянного и переменного тока из данных FG
6. ДОПОЛНИТЕЛЬНЫЕ КОММЕНТАРИИ
Большинство моделей предполагают, что e
r не зависит от смещения. Если
это не так, зависимость от смещения e
r может быть включена в анализ
аналогично тому, как это используется для b
r.Если
(24) reeeee VgeiVIgI ==) () (
, то при возбуждении слабым сигналом
(25)) log () log (,
eeeeereee IgdidVgi ∂∂ = + =.
Это может быть учтено для в (6) путем замены
ee
ac
erdr) 1 (- = для e
r (при условии, что его можно смоделировать как функцию
от e
I).
Хотя o
g здесь явно не используется (кроме
его вклад в
и
π
G предполагается пренебрежимо малым
), его можно рассчитать из (8) или (10).Этот
позволит оценить точность некоторых из предположений
, которые лежат в основе процедур, определенных выше
(хотя c
r необходимо знать, чтобы полностью оценить
терминов, которые не включены в анализ).
7. ВЫВОДЫ
В этой статье представлен анализ разницы между внутренней и внешней проводимостью БЮТ
для слабого сигнала, для
с целью определения сопротивления базы и эмиттера.
То, что разница между внутренней и внешней крутизной
может быть использована для расчета e
r, было
, отмеченное ранее [5], однако анализ, представленный здесь
, основан на более точной модели слабого сигнала. .
Важно отметить, что зависимость b
r от смещения учитывается при анализе проводимости слабого сигнала;
это делается путем введения эффективной базы переменного тока
сопротивления)) log () 1log (1 (bbb
ac
bIrrr ∂∂− =.Это имеет существенное влияние на моделирование переменного тока; Предыдущие анализы слабого сигнала
для извлечения сопротивления BJT не включали этот компонент
. Простота представленного анализа заключается в части
за счет того, что b
I рассматривается как количество, от которого зависят другие параметры
.
Когда правильное сопротивление базы переменного тока включено в анализ слабых сигналов
, показано, что это дает
по существу те же результаты, что и анализ постоянного тока.Априори
может показаться, что до тех пор, пока
π
β
gg m
≠ в данных проводимости будет
дополнительной информации; анализ
показывает, что это неверно.
Представлена простая оценка e
r, основанная на данных FG
и без схем смещения, полностью отличных от схем
, используемых в реальных схемах. Это выражение (22) для e
r –
, основанное исключительно на измеренных данных, оно не требует подгонки
модели a) (bb vI.
БЛАГОДАРНОСТИ
Я хотел бы поблагодарить Тамару Беттингер и Чжун Лу
за данные измерений и обсуждения этой работы.
СПИСОК ЛИТЕРАТУРЫ
[1] Т. Х. Нинг и Д. Д. Тан, «Метод определения последовательного сопротивления эмиттера и базы
биполярных транзисторов
», IEEE Trans.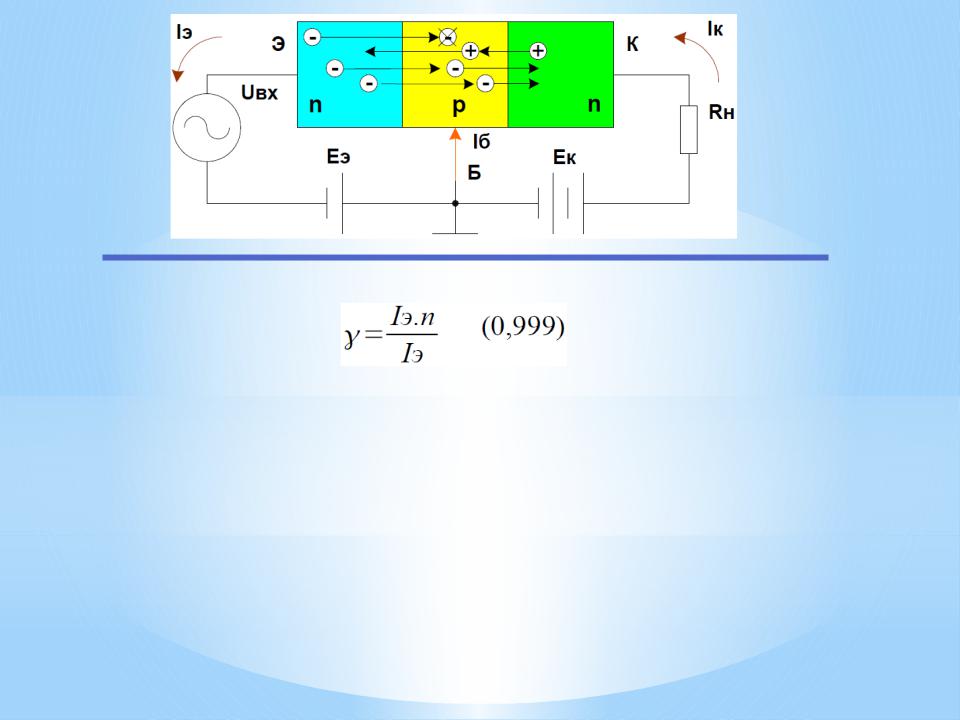 Электрон Дев., Т. ЭД-31, вып. 4,
Электрон Дев., Т. ЭД-31, вып. 4,
pp. 409-412, Apr. 1984.
[2] Л. Дж. Джаколетто, «Измерение сопротивлений эмиттера и коллектора серии
», IEEE Trans.Электронные устройства, т.
ED-19, стр. 692-693, 1972.
[3] Р. Габл, М. Райш и М. Поль, «Улучшенный метод извлечения.
Метод определения эмиттерного сопротивления биполярных транзисторов»,
Proc. . IEEE BCTM, стр. 211-214, 1998.
[4] WMC Sansen и RG Meyer, «Определение характеристик и
измерение сопротивления базы и эмиттера биполярных транзисторов
», IEEE J. Solid-State Circuits, vol. . SC-
7, no. 6, pp. 492-498, Dec.1972.
[5] У. Дж. Клоостерман, Дж. К. Дж. Паасшенс и Д. Б. М.
Клаассен, «Улучшенное извлечение базы и эмиттера
сопротивления из слабых сигналов высокой пропускной способности
Измерения», Proc. IEEE BCTM, pp. 93-96, 1999.
[6] М. Линдер, Ф. Ингварсон, К. О. Джеппсон, Дж. В. Гран, С.-Л.
Чжан и М. Остлинг, «Извлечение сопротивлений эмиттера и базы биполярных транзисторов серии
Остлинг, «Извлечение сопротивлений эмиттера и базы биполярных транзисторов серии
из одного измерения постоянного тока
», IEEE Trans.Сем. Производство, т. 13,
нет. 2, pp. 119-126, May 2000.
[7] W. Z. Cai, G.H. Loechelt, S. Shastri, «Новый метод
для извлечения базового сопротивления в биполярных транзисторах
», IEEE Trans. Электрон Дев., Т. 52, нет.
4, pp. 626-629, апрель 2005 г.
IEEE BCTM 5.2
Лучшая в Индии платформа для индивидуального обучения и подготовки к экзаменам для GATE-IES, IIT-JEE, NEET, БАНКОВСКОГО ХОЗЯЙСТВА ← nthexam.com
Узнайте о nthexam
Vision
Упрощение сложной системы образования путем предоставления учащимся и преподавателям возможности упрощенного и персонализированного обучения и сделать обучение доступным для широких масс наиболее экономичным способом.Мы стремимся предоставить персонализированный опыт обучения всем школам, колледжам, профессионально-техническим, подготовительным и профессиональным школам путем кураторства преподавателей и опытных кандидатов.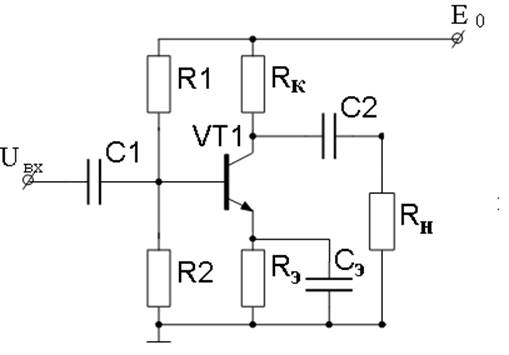
Около
Nthexam уделяет основное внимание повышению качества образования с помощью алгоритмов машинного обучения, разработке интеллектуальной платформы и продуктов помимо аналитики, которые позволяют как учащимся, так и преподавателям взаимодействовать, взаимодействовать и добиваться наилучших результатов вместе с устранением пиратства.
Nthexam – высокоразвитая технологическая компания в области образования и создатель первого в Индии приложения для персонализированного обучения памяти.
Запущенная в 2017 году, Nthexam предлагает персонализированные и эффективные программы обучения для соискателей конкурсных экзаменов, таких как JEE, NEET, GATE, BANK и т. Д. Nthexam стала одной из наиболее предпочтительных платформ для персонализированного обучения в Индии.
Nthexam Personalized Learning
Мы пытаемся решить самую большую проблему бурного образования, которая заключается в том, что «один размер подходит всем» для предоставления образования, будь то онлайн или офлайн.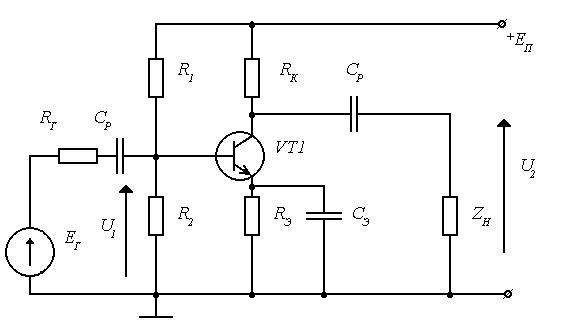 Студенты не получают целенаправленной персонализации и тратят 50% времени на то, что и как учить, а Институту не хватает внимания и 60% времени они проводят в микроменеджменте.
Студенты не получают целенаправленной персонализации и тратят 50% времени на то, что и как учить, а Институту не хватает внимания и 60% времени они проводят в микроменеджменте.
Персонализация – это сложная функция, которую необходимо предоставить в образовании, она различается в зависимости от возрастных групп, различных сценариев и условий обучения. У каждого ученика разная память, и обучение никогда не прекращается, в разные моменты времени мы продолжаем изучать что-то новое и соединяем вещи с тем, что мы узнали в прошлом.
В отличие от других аналитиков, предоставляющих информационные технологии, мы фокусируемся на взвешенной аналитике и продукте, выходящем за рамки аналитики, который создается как побочный продукт персонализации. Мы предоставляем неограниченное количество тренировочных наборов, которые создаются на основе вашей относительной, абсолютной производительности, анализа памяти и времени, скорости и микроуровня обучения для каждой концепции и сложности. Межтематическое обучение, зависимость и постоянство исполнения.
Выходное сопротивление с общим эмиттером – 2N3904Blog
В этом посте будет разработана эквивалентная схема выходного сопротивления усилителя с общим эмиттером.Для начала будет решена низкочастотная безреактивная модель выходного сопротивления усилителя с общим эмиттером (CE). В следующие модели будут входить емкостные элементы усилителя CE. Разделение высокочастотной (HF) модели на два различных случая позволит провести анализ схемы, который целесообразно выполнять вручную. Первая модель HF будет для случая, когда база заземлена по переменному току, а эмиттер видит резистор дегенерации. Вторая модель ВЧ разработана с заземленным эмиттером и сопротивлением источника к входному (базовому) выводу.Завершение поста симуляцией специй для сравнения / проверки разработанных эквивалентных моделей схем. Желаемый результат этого поста – получить интуитивное представление о том, как «это выглядит», говоря электрически, на выходе усилителя CE.
Схема:
– Обзор выходного сопротивления / импеданса
– Низкочастотная модель
– Высокочастотная модель – Заземленная база
– Высокочастотная модель – Заземленный эмиттер
– Spice Simulation
Обзор выходного сопротивления / импеданса
Из теории элементарных схем можно вспомнить, что любую линейную схему можно упростить относительно двух произвольных узлов схемы.Одним из наиболее часто используемых узлов является общий узел схемы (обычно заземляющий). Второй узел выбирается как обычно входной или выходной узел для несимметричных цепей. В случае дифференциальных схем упрощение сделано в отношении положительной и отрицательной ветвей портов ввода / вывода. Для любой нелинейной схемы, такой как транзисторный усилитель, нелинейное поведение может быть линеаризовано относительно рабочей точки для слабых сигналов. На рисунке ниже показано упрощение этой схемы.Здесь произвольное тестируемое устройство (DUT) или тестируемая цепь (CUT) можно упростить до одной из двух основных схем. С левой стороны, источник напряжения с последовательным сопротивлением называется эквивалентной схемой Тевенина. Справа источник тока, зашунтированный резистором, обозначен как эквивалентная схема Нортона.
Выбор упрощения схемы до эквивалентной схемы Нортона или Тевенина является совершенно произвольным, при этом обычно предпочтение отдается той, которая обеспечивает аналитическое удобство.Если посмотреть на клеммы эквивалентной схемы Norton или Thévenin, невозможно было различить, какой стиль был выбран.
Электрический импеданс (\ (Z \)) может быть применен эквивалентно электрическому сопротивлению с включением комплексного члена \ (X \) (реактивное сопротивление). Для некоторой конкретной частоты \ (\ omega = 2 \ pi f \) полное сопротивление составляет
\ [Z (\ omega) = R + j X (\ omega) \]
Импеданс можно использовать как прямую замену сопротивлению, но математические вычисления должны выполняться со сложной арифметикой.Здесь стоит подчеркнуть, что реактивное сопротивление равно ортогонально сопротивлению. При синусоидальном возбуждении в установившемся режиме реактивный ток составляет ортогонально напряжению источника и не генерирует и не расходует полезную энергию.
Импеданс также можно удобно анализировать в s-области (частотной области). Подробное объяснение преобразования Лапласа выходит за рамки этого блога, пожалуйста, обратитесь к альтернативной ссылке по использованию преобразования Лапласа для схем.Идеальный конденсатор не имеет последовательного или параллельного сопротивления и является исключительно реактивным элементом с реактивным сопротивлением
.\ [X_C = \ frac {-1} {\ omega C} \]
его импеданс
\ [Z_C (\ omega) = 0 + \ frac {1} {j \ omega C} \]
в s-области, его импеданс
\ [Z_C (s) | _ {j \ omega = s} = \ frac {1} {sC} \]
Транзистор – это нелинейный элемент схемы, но его можно линеаризовать вокруг рабочей точки. Возьмем, например, схему ниже, база смещена постоянным током \ (I_b \), а коллектор приводится в движение источником напряжения V1.
В качестве примера моделирования источник напряжения изменяется от 0 В постоянного тока до 5 В постоянного тока. Ток коллектора Ic показан на рисунке ниже. В течение первых 200 мВ развертки переход база-коллектор сильно смещен в прямом направлении, что приводит к насыщению транзистора. Во время насыщения ток коллектора сильно зависит от потенциала коллектора. Область насыщения можно наблюдать на графике ниже, когда ток коллектора быстро нарастает от 0 мА до 1,4 мА в течение первых 200 мВ.Это аналогично низкому выходному сопротивлению, которое также можно увидеть в виде зеленой кривой на графике.
Когда переход база-коллектор смещен в обратном направлении, транзистор работает в «активной области». Как видно на графике выше, от 500 мВ до 5 В постоянного тока ток коллектора очень слабо зависит от потенциала коллектора. Поскольку переход база-коллектор все больше смещается в обратном направлении, область отклонения расширяется, тем самым сужая область базового заряда, что приводит к модуляции ширины базы.Как можно вспомнить, ток течет от коллектора к эмиттеру в транзисторе из-за неосновного градиента концентрации в области базы. Когда базовый заряд остается постоянным, а его ширина сужается, градиент концентрации увеличивается, что приводит к большему току коллектора.
Когда линия наилучшего соответствия соответствует току коллектора в активной области в зависимости от потенциала коллектора, точка пересечения оси x рассматривается как раннее напряжение. На двух графиках ниже показан пример моделирования пряностей, иллюстрирующий зависимость тока коллектора Ic от потенциала Vce коллектора.Здесь NPN-транзистор смещен с источником тока на базу, а источник напряжения качает потенциал коллектора, одновременно регистрируя ток коллектора. Базовый ток увеличивается при каждом изменении напряжения коллектора. На левом графике все три линии наилучшего соответствия пересекают ось x примерно при -100 В для начального напряжения | 100 | V.
Уравнения для каждой из линий наилучшего соответствия следующие:
\ begin {align *}
I_c \ left (V_ {CE}, I_b = 2 \; \ mathrm {\ mu A} \ right) & = 6 \; \ mathrm {\ frac {\ mu A} {V} } \ cdot V_ {CE} + 595 \; \ mathrm {\ mu A} \\
I_c \ left (V_ {CE}, I_b = 5 \; \ mathrm {\ mu A} \ right) & = 15 \; \ mathrm {\ frac {\ mu A} { V}} \ cdot V_ {CE} + 1484 \; \ mathrm {\ mu A} \\
I_c \ left (V_ {CE}, I_b = 10 \; \ mathrm {\ mu A} \ right) & = 30 \; \ mathrm {\ frac {\ mu A} { V}} \ cdot V_ {CE} + 2957 \; \ mathrm {\ mu A}
\ end {align *}
Что важно из этого сделать, так это то, что ток коллектора имеет зависимость от напряжения примерно \ (1 / V_A \).Для приведенного выше примера моделирования это коэффициент напряжения \ (1 \% / V \). Следовательно, отношение протекающего тока к приложенному напряжению – это проводимость, а обратная зависимость – сопротивление. Тем самым позволяя моделировать коэффициент напряжения тока коллектора как выходное сопротивление относительно рабочей точки постоянного тока для тока коллектора.
\ [r_o = \ frac {1} {I_C \ cdot 1 / V_A} = \ frac {V_A} {I_C} \]
Модифицированная модель малосигнального транзистора NPN показана ниже. Эта модель называется гибридной – \ (\ pi \) моделью.Целый пост в блоге может быть посвящен его происхождению и не будет рассматриваться в этом посте. Модель ниже представляет собой упрощение полной гибридной модели – \ (\ pi \). В полной модели все клеммы устройства будут иметь последовательное сопротивление и индуктивность. Для выводов коллектора и эмиттера последовательное сопротивление на порядок ниже, чем эквивалентное последовательное сопротивление на выводе базы. Во всех будущих сообщениях в блогах паразитные соединения между коллекторами и эмиттерами будут опускаться.
В этом блоге элементы гибридной модели – \ (\ pi \) следующие:
\ [g_m = \ frac {Ic} {V_ {Thermal}} \]
\ [R_b = \ rm {constant} = 0 \]
\ [C_ \ pi = C_ {be, d} + C_ {be, j} \ simeq C_ {be, 0} \ sqrt {2} + g_m \ tau_f \]
\ [r_ \ pi = \ frac {\ beta} {g_m} \]
\ [C _ {\ mu} = C_ {bc, 0} \ sqrt {2} \]
Чтобы применить гибридную модель – \ (\ pi \) к базовому усилителю CE, все элементы схемы должны быть заменены их эквивалентами для слабого сигнала.Вывод эмиттера связан с общим потенциалом или заземлением переменного тока. Если истоковый элемент на входе усилителя CE является источником напряжения, то он закорочен по переменному току, оставляя только сопротивление его последовательного источника относительно земли переменного тока. В случае, когда источник тока управляет входом усилителя CE, источник тока «открывается», оставляя только шунтированное выходное сопротивление. Схема слабого сигнала усилителя CE без емкостных элементов показана на рисунке ниже
В простейшем случае, когда эмиттер подключен непосредственно к земле, на \ (r_ \ pi \) никогда не может развиться напряжение.В результате получается выходное сопротивление, которое всегда равно внутреннему выходному сопротивлению транзистора \ (r_o \), независимо от величины \ (R_S \). Обратите внимание, что чрезвычайно большое сопротивление источника – это не что иное, как идеализированный источник тока.
Низкая частота – (безреактивная модель)
Для низкочастотных (НЧ) слабых сигналов модель гибридного Пи может быть упрощена, включив только нереактивные элементы (то есть без катушек индуктивности или конденсаторов). После удаления паразитной емкости на переходах база-эмиттер и база-коллектор, а также после удаления динамической емкости база-эмиттер, результирующая цепь слабого сигнала показана на рисунке ниже.Чтобы аналитически определить выходное сопротивление (не импеданс, поскольку реактивные элементы исключены), мы можем либо подать тестовое напряжение, либо тестовый ток на выход и найти соответствующий ток или напряжение соответственно. Выбор приложения испытательного напряжения по сравнению с испытательным током не зависит от значения. Для этой схемы предпочтительным является испытательный ток, поскольку общий ток через оба зависимых источника тока \ (g_m V_ \ pi \) и \ (r_o \) должен равняться приложенному испытательному току. В узле эмиттера входящий ток \ (I_T \) будет делиться между \ (r_ \ pi \) и \ (R_E \) в качестве текущего делителя.Позволяя легко решить \ (V_ \ pi \) как функцию \ (I_T \).
Для начала мы устанавливаем, что испытательный ток \ (I_T \) будет поступать на клемму коллектора, и результирующее испытательное напряжение \ (V_T \) вырабатывается относительно земли слабого сигнала. Поскольку коллектор модели слабого сигнала имеет соединение только с выводом эмиттера, ток, входящий в узел эмиттера, должен быть равен току, выходящему из узла коллектора. Ток через резистор \ (r_ \ pi \) можно решить как делитель тока
\ [I_ {r_ \ pi} = \ frac {I_T R_E} {R_E + r_ \ pi + R_S} \]
Отмечая, что потенциал схемы \ (V_ \ pi \) упоминается как положительный в базовом узле и отрицательный в узле эмиттера.
\ [V_ \ pi = -r_ \ pi I_ {r_ \ pi} \]
Замена \ (I_ {r_ \ pi} \) дает
\ [V_ \ pi = \ frac {- r_ \ pi R_E} {R_E + r_ \ pi + R_S} I_T \]
Потенциал эмиттера \ (V_E \) – это ток, разделенный на \ (R_E \), умноженный на \ (R_E \), который равен
\ [V_E = \ frac {R_E \ left (r_ \ pi + R_S \ right)} {R_E + r_ \ pi + R_S} I_T \]
Наконец, испытательное напряжение \ (V_T \) должно быть равно потенциалу, развиваемому на \ (R_E \) и \ (r_0 \).
\ [V_T = V_E + \ left (I_T – g_m V_ \ pi \ right) r_o \]
\ [V_T = \ frac {R_E \ left (r_ \ pi + R_S \ right)} {R_E + r_ \ pi + R_S} I_T + r_o I_T + \ frac {g_m r_o r_ \ pi R_E} {R_E + r_ \ pi + R_S} I_T \]
Тогда выходное сопротивление будет просто
\ [R_ {out} = \ frac {V_T} {I_T} \]
\ begin {Equation}
R_ {out} = \ frac {R_E \ left (r_ \ pi + R_S \ right)} {R_E + r_ \ pi + R_S} + \ left [1 + \ beta \ frac {R_E} {R_S + r_ \ pi + R_E} \ right] r_o \ tag {LF.1} \ label {LF.1}
\ end {формула}
Здесь важно понимать, что когда \ (R_E \) велико, а \ (R_S \) мало, любое постепенное изменение испытательного тока шунтируется через \ (r_ \ pi \). Которая в ответ управляет дополнительным \ (\ beta \) умноженным на возрастающий ток через \ (r_o \). В результате выходное сопротивление оказывается в \ (\ beta \) раз большим, чем собственное выходное сопротивление \ (r_o \).
Если \ (R_S >> \ {R_E, r_ \ pi \} \), то
\ [R_ {out} \ simeq R_E + r_o \]
Если \ (R_E >> r_ \ pi \) и \ (R_S << r_ \ pi \)
\ begin {align *}
R_ {out} & = r_ \ pi + \ left [1 + \ beta \ right] r_o \\
R_ {out} & \ simeq \ beta r_o
\ end {align *}
Из уравнения (\ ref {LF.1}) эквивалентную модель схемы можно построить в виде последовательной цепочки из трех резисторов. Начиная с первого резистора в виде параллельной комбинации \ (R_E || \ left (r_ \ pi + R_s \ right) \). Второй резистор равен собственному выходному сопротивлению \ (r_o \). В-третьих, резистор с обратной связью \ (R_ {fo} \). Ниже представлено схематическое изображение эквивалентной модели схемы.
Приравнивая выходное сопротивление эквивалентной модели схемы к (LF.1), можно определить значение \ (R_ {fo} \).
\ begin {align *}
R_ {out} & = R_E || \ left (r_ \ pi + R_S \ right) + r_o + R_ {fo} \\
R_ {out} & = \ frac {R_E \ left (r_ \ pi + R_S \ right)} {R_E + r_ \ pi + R_S} + \ left [1 + \ beta \ frac {R_E} {R_S + r_ \ pi + R_E} \ right] r_o \\ \\
R_ {fo} = \ beta \ frac {R_E} {R_S + r_ \ pi + R_E}
\ end {align *}
Заземленный излучатель – высокая частота
Включая емкостные элементы \ (C_ \ pi \) и \ (C_ \ mu \), теперь существует обратная связь по переменному току от выходной клеммы к входной через \ (C_ \ mu \).В отличие от ранее разработанной нереактивной модели, когда эмиттер заземлен, выход возвращается обратно на входной терминал. Модель слабосигнального усилителя CE с заземленным эмиттером показана ниже
Для определения выходного импеданса на выходную клемму усилителя CE подается испытательный ток \ (I_T \). Применение KCL в узле \ (V_T \) дает
\ [\ frac {V_T} {r_o} + g_mV_ \ pi + \ left (V_T – V_ \ pi \ right) sC_ \ mu = I_T \ tag {GE.1} \]
Применение KCL на узле \ (V_ \ pi \) дает
\ [\ frac {V_ \ pi} {R_S} + \ frac {V_ \ pi} {r_ \ pi} + V_ \ pi s C_ \ pi + \ left (V_ \ pi – V_T \ right) sC_ \ mu = 0 \ tag {GE.2} \]
Упрощение (GE.2)
\ [V_T s C_ \ mu = V_ \ pi \ left (\ frac {1} {R_S} + \ frac {1} {r_ \ pi} + sC_ \ pi + sC_ \ mu \ right) \ tag {GE. 3} \]
\ [V_T = V_ \ pi \ left (\ dfrac {r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {sR_Sr_ \ pi C_ \ mu} \ right) \ тег {GE.4} \]
Упрощение (GE.1)
\ [V_T \ left (\ frac {1} {r_o} + sC_ \ mu \ right) + V_ \ pi \ left (g_m – sC_ \ mu \ right) = I_T \ tag {GE.5} \]
\ [V_ \ pi = \ dfrac {I_T – V_T \ left (\ frac {1 + s r_o C_ \ mu} {r_o} \ right)} {g_m – s C_ \ mu} \ tag {GE.6} \]
Замена (GE.6) на (GE.4) дает
\ [V_T = \ left (\ dfrac {I_T – V_T \ left (\ frac {1 + s r_o C_ \ mu} {r_o} \ right)} {g_m – s C_ \ mu} \ right) \ left (\ dfrac {r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {sR_Sr_ \ pi C_ \ mu} \ right) \ tag {GE.7} \]
Решение для \ (V_T \)
\ [V_T \ left [1 + \ dfrac {\ left (\ frac {1 + s r_o C_ \ mu} {r_o} \ right) \ left (r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right) \ right)} {\ left (g_m – s C_ \ mu \ right) \ left (sR_Sr_ \ pi C_ \ mu \ right)} \ right] = \ dfrac {r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {\ left (g_m – s C_ \ mu \ right) \ left (sR_Sr_ \ pi C_ \ mu \ right)} \ tag {GE.8} \]
\ [V_T = \ dfrac {r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {\ left (g_m – s C_ \ mu \ right) \ left (sR_Sr_ \ pi C_ \ mu \ right) + \ left (\ frac {1 + s r_o C_ \ mu} {r_o} \ right) \ left (r_ \ pi + R_S + sr_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right) \ right)} I_T \ tag {GE. 2} \ tag {GE.2 \\
b_2 & = r_ \ pi R_S C_ \ pi C_ \ mu
\ end {align *}
Ноль (корень числителя) находится в
\ begin {align *}
z_1 & = \ dfrac {-a_0} {a_1} = \ dfrac {- \ left (r_ \ pi + R_S \ right)} {r_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} \\
z_1 & \ simeq \ dfrac {- \ left (r_ \ pi + R_S \ right)} {r_ \ pi R_S C_ \ pi}
\ end {align *}
Чтобы найти полюса Z (s), мы могли бы попытаться: разложить знаменатель на множители, применить квадратное уравнение или предположить, что два полюса хорошо разделены.2} {p_1 p_2} \\ \\
p_1 & = \; – \ dfrac {b_0} {b_1} \ tag {GE.12} \\ \\
p_2 & = \ dfrac {b_0} {b_2 p_1} \ тег {GE.13}
\ end {align *}
Доминирующий полюс \ (p_1 \) из \ (Z (s) \) равен
\ begin {align *}
p_1 & \ simeq – \ dfrac {b_0} {b_1} \\
p_1 & = \ left (\ dfrac {-1} {g_m R_S r_ \ pi C_ \ mu + \ frac {r_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {r_o} + C_ \ mu \ left (r_ \ pi + R_S \ right)} \ right) \ left (\ dfrac {r_ \ pi + R_S } {r_o} \ right) \\
p_1 & = \ dfrac {- \ left (r_ \ pi + R_S \ right)} {g_m R_S r_ \ pi r_o C_ \ mu}
\ end {align *}
Второй полюс \ (p_2 \) –
\ begin {align *}
p_2 & \ simeq \ dfrac {b_0} {b_2 p_1} \\
p_2 & = \ dfrac {\ left (-g_m R_S r_ \ pi r_o C_ \ mu \ right) \ left (r_ \ pi + R_S \ right)} {\ left (r_ \ pi + R_S \ right) r_o r_ \ pi C_ \ mu C_ \ pi} \\
p_2 & = \ dfrac {-g_m} {C_ \ pi}
\ конец {align *}
Когда \ (Rs << r_ \ pi \), полюса и нули следующие:
\ begin {align *}
z_1 & = \ dfrac {-a_0} {a_1} = \ dfrac {- \ left (r_ \ pi + R_S \ right)} {r_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} \\
z_1 & \ simeq – \ dfrac {1} {R_S C_ \ pi}
\ end {align *}
Доминирующий полюс \ (p_1 \) из \ (Z (s) \) равен
\ begin {align *}
p_1 & \ simeq – \ dfrac {b_0} {b_1} \\
p_1 & = \ dfrac {-1} {g_m R_S r_ \ pi C_ \ mu + \ frac {r_ \ pi R_S \ left (C_ \ pi + C_ \ mu \ right)} {r_o} + C_ \ mu \ left (r_ \ pi + R_S \ right)} \ dfrac {r_ \ pi + R_S} {r_o} \\
p_1 & = – \ dfrac {1} {r_o C_ \ mu}
\ end {align *}
Второй полюс \ (p_2 \) –
\ begin {align *}
p_2 & \ simeq \ dfrac {b_0} {b_2 p_1} \\
p_2 & = \ dfrac {\ left (-roC_ \ mu \ right) \ left (r_ \ pi + R_S \ right )} {\ left (r_ \ pi R_SC_ \ pi C_ \ mu \ right) r_o} \\
p_2 & = – \ dfrac {1} {R_SC_ \ pi}
\ end {align *}
Когда сопротивление источника низкое по сравнению с \ (r_ \ pi \), \ (Z (s) \) является приблизительно однополюсной функцией.Поскольку \ (p_2 \ simeq z_1 \), полюс \ (p_2 \) «отменяет» ноль \ (z_1 \), оставляя только доминирующий полюс \ (p_1 \). Выходной сигнал тогда выглядит как просто внутренние элементы \ (ro \) и \ (c_ \ mu \), параллельные земле.
Эквивалентная модель цепиЧтобы разработать эквивалентную модель схемы для уравнения (\ ref {GE.10}), мы начнем с параллельных внутренних элементов \ (r_o \) и \ (C_ \ mu \). Чтобы добавить дополнительный полюс и ноль, последовательно к внутренним элементам добавляются последовательный резистор и конденсатор.Схема эквивалентной модели схемы следующая:
Два полюса созданы
\ [p_a = \ frac {-1} {r_o \ left (C_f + C_ \ mu \ right)} \; \; \; \; \; p_b = \ frac {-1} {R_Z C_ \ mu} \]
Если предположить, что \ (C_f >> C_ \ mu \), тогда полюс \ (p_a \) становится
\ [p_a = \ frac {-1} {r_o C_f} \]
Приравнивание полюса \ (p_a \) к полюсу \ (p_1 \) из \ (Z (s) \) и решение для эквивалентного элемента схемы \ (C_f \)
\ begin {align *}
\ frac {1} {r_o C_f} & = \ dfrac {- \ left (r_ \ pi + R_S \ right)} {g_m R_S r_ \ pi r_o C_ \ mu} \\\\
C_f & = \ left (\ dfrac {R_S} {r_ \ pi + R_S} \ right) \ beta C_ \ mu
\ end {align *}
Для эквивалентной модели схемы, ноль создается в
\ [z_a = \ frac {-1} {R_z C_f} \]
Приравнивание нуля \ (z_a \) к нулю \ (z_1 \) из \ (Z (s) \) и решение для эквивалентного элемента схемы \ (R_z \)
\ begin {align *}
\ frac {-1} {R_z C_f} & = \ dfrac {- \ left (r_ \ pi + R_S \ right)} {r_ \ pi R_S C_ \ pi} \\
R_z & = \ dfrac {r_ \ pi R_S C_ \ pi} {\ left (r_ \ pi + R_S \ right)} \ left (\ dfrac {r_ \ pi + R_S} {R_S \ beta C_ \ mu} \ right) \\
R_z & = \ left (\ dfrac {C_ \ pi} {C_ \ mu} \ right) \ dfrac {1} {g_m} \\
\ end {align *}
Когда транзистор смещен для больших токов коллектора, \ (C_ \ pi \ simeq g_m \ tau_f \), в результате эквивалентный параметр схемы \ (R_z \) приближается к константе устройства
\ [R_z = \ left (\ dfrac {\ tau_f} {C_ \ mu} \ right) \]
Если Rs большой, то
\ [C_f \ simeq \ beta C_ \ mu \]
Когда \ (R_S << r_ \ pi \) эквивалентная модель схемы упрощается до только внутренних элементов \ (r_o \) и \ (C_ \ mu \)
Сравнение эквивалентной модели схемы с выходным импедансом \ (Z (s) \) можно проиллюстрировать с помощью графика Боде \ (Z (s) \).График Боде для большого сопротивления источника показан на рисунке ниже. Импеданс собственных элементов \ (r_o \) и \ (c_ \ mu \) включен, в дополнение к двум эквивалентным элементам схемы \ (R_z \) (показано зеленым) и \ (C_f \) (показано голубым. ). Как вычислено выше, для \ (Z (s) \) видны два полюса и один ноль. По мере увеличения сопротивления источника частота полюса и нуля на голубой дорожке понижается. Полюс и ноль перемещаются не более чем в \ (1 / \ beta \) раз (примерно два десятилетия).
График Боде для Z (s, gm = 0,01, ro = 420k, beta = 300, Cpi = 16pF, Cu = 2pF)Заземленная база – высокая частота
Когда клемма базы подключена к заземлению, обратная связь от выхода к входу происходит путем измерения выходного тока через резистор \ (R_E \) и создания последовательного потенциала по отношению к входу. Чтобы решить вопрос о выходном сопротивлении усилителя CE, который приводится в действие источником с низким сопротивлением (заземленная по переменному току база), мы могли бы сначала упростить схему слабого сигнала как две независимые цепи.Конденсатор \ (C_ \ mu \) в гибридной модели – \ (\ pi \) может быть разделен на вторую цепь, чтобы в конечном итоге повторно объединиться. Поскольку \ (C_ \ mu \) не влияет на тракт обратной связи усилителя.
Поскольку общее уравнение \ (Z (s) \) желательно сравнить с симуляцией специй, \ (C_ \ mu \) включается с самого начала анализа (честный ответ: не думал об этом, когда писал от руки план поста). Установление отношения испытательного тока \ (I_T \) и испытательного напряжения \ (V_T \) можно увидеть на схеме слабого сигнала ниже
Применение KCL к узлу \ (V_T \) дает
\ [\ dfrac {V_T – (-V_ \ pi)} {r_o} + g_mV_ \ pi + V_T s C_ \ mu = I_T \ tag {GB.1} \]
Применение KCL к узлу \ (-V_ \ pi \) дает
\ [\ dfrac {(- V_ \ pi)} {R_E} + \ dfrac {(- V_ \ pi)} {r_ \ pi} + (-V_ \ pi) sC_ \ pi – g_mV_ \ pi + \ dfrac { (-V_ \ pi) – V_T} {r_o} = 0 \ tag {GB.2} \]
Условия сбора (GB.1)
\ [V_T \ left (\ frac {1} {r_o} + sC_ \ mu \ right) + V_ \ pi \ left (\ frac {1} {r_o} + g_m \ right) = I_T \ tag {GB.3 } \]
Условия сбора (GB.2)
\ [V_T \ left (\ frac {-1} {r_o} \ right) + V_ \ pi \ left (- \ frac {1} {R_E} – \ frac {1} {r_ \ pi} – sC_ \ pi – g_m – \ frac {1} {r_o} \ right) = 0 \ tag {ГБ.4} \]
Решение для \ (V_ \ pi \) из (GB.3)
\ [V_ \ pi = \ dfrac {I_T – V_T \ left (\ frac {1} {r_o} + s C_ \ mu \ right)} {\ frac {1} {r_o} + g_m} \ tag {ГБ. 5} \]
\ [V_ \ pi = \ dfrac {I_T} {g_m} – V_T \ dfrac {\ left (\ frac {1} {r_o} + s C_ \ mu \ right)} {g_m} \ tag {GB.6} \]
Замена (GB.6) на (GB.4)
\ [\ frac {V_T} {r_o} + \ left [\ dfrac {I_T} {g_m} – V_T \ dfrac {\ left (\ frac {1} {r_o} + s C_ \ mu \ right)} {g_m } \ right] \ left [\ frac {r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o \ left (sC_ \ pi + g_m \ right)} {R_E r_ \ pi r_o} \ right] = 0 \ tag {ГБ.7} \]
Сроки разложения и сбора
\ [V_T \ left [… \ right] = – \ frac {I_T} {g_m} \ left [… \ right] \]
\ [V_T = \ frac {I_T} {g_m} \ left [\ dfrac {\ left (r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o \ left (sC_ \ pi + g_m \ right ) \ right) \ left (g_m R_E r_ \ pi r_o \ right)} {\ left (R_E r_ \ pi r_o \ right) \ left (g_mR_E r_ \ pi – \ left (\ frac {1} {r_o} + sC_ \ mu \ right) \ left (r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o \ left (sC_ \ pi + g_m \ right) \ right) \ right)} \ right] \ tag { ГБ. 2 R_E r_ \ pi r_o C_u C_ \ pi} \ tag {ГБ.10}
\ end {формула}
В качестве проверки работоспособности уравнение (GB.10) можно оценить как \ (s = j \ omega = 0 \) и сравнить с низкочастотной моделью, полученной ранее.
\ begin {align *}
Z_ {out} (s = 0) & \ simeq \ dfrac {r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o g_m} {r_ \ pi + R_E} \\
& = \ frac {r_ \ pi R_E} {r_ \ pi + R_E} + \ left [1 + \ frac {g_m R_E r_ \ pi} {r_ \ pi + R_E} \ right] r_o \ tag {ГБ .11}
\ end {align *}
Уравнение (GB.11) действительно соответствует уравнению (LF.2} \ tag {GB.12}
\ end {формула}
Где коэффициенты \ (a_n \) и \ (b_n \) следующие
\ begin {align *}
a_0 & = r_ \ pi r_o + R_E r_o + R_E r_ \ pi + g_m R_E r_ \ pi r_o \\
a_1 & = R_E r_ \ pi r_o C_ \ pi \\
b_0 & = r_ \ pi + R_E \\
b_1 & = C_u \ left [r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o g_m + \ left (\ frac {C_ \ pi} {C_u} \ right ) R_E r_ \ pi \ right] \\
b_2 & = R_E r_ \ pi r_o C_u C_ \ pi \\
\ end {align *}
Решение относительно нуля \ (z_1 \)
\ begin {уравнение *}
z_1 = \ dfrac {- a_0} {a_1} \ приблизительно – \ dfrac {r_o + R_E + g_m R_E r_o} {R_E r_o C_ \ pi}
\ end {уравнение *}
Решение для доминирующего полюса \ (p_1 \)
\ begin {align *}
p_1 & = \ dfrac {- b_0} {b_1} \\
p_1 & = – \ dfrac {r_ \ pi + R_E} {C_u \ left [r_ \ pi r_o + R_E r_o + R_E r_ \ pi + R_E r_ \ pi r_o g_m + \ left (\ frac {C_ \ pi} {C_u} \ right) R_E r_ \ pi \ right]} \\
p_1 & = \ dfrac {-1} {C_u \ left [1 + \ dfrac {g_m r_ \ pi R_E} {r_ \ pi + R_E} \ right] r_o} \\
p_1 & = \ dfrac {-1} {C_u \ left [1 + \ beta \ left (\ frac {R_E} {r_ \ pi + R_E} \ right) \ right] r_o}
\ end {align *}
Решение для второго полюса \ (p_2 \)
\ begin {align *}
p_2 & = \ dfrac {b_0} {b_2 p_1} \\
p_2 & = \ dfrac {\ left (r_ \ pi + R_E \ right) C_u \ left [1 + \ dfrac {g_m] r_ \ pi R_E} {r_ \ pi + R_E} \ right] r_o} {R_E r_ \ pi r_o C_u C \ pi} \\
p_2 & = – \ dfrac {r_o + R_E + g_m R_E r_o} {R_E r_o C_ \ pi}
\ end {align *}
Удобно, чтобы полюс \ (p_2 \) приблизительно равнялся нулю \ (z_1 \), оставляя \ (Z (s) \) приблизительно однополюсной функцией.
Эквивалентная модель цепиКогда клемма базы связана с заземлением переменного тока, выходное сопротивление усилителя CE всегда является однополюсным. Эквивалентная модель схемы должна иметь высокое выходное сопротивление на низких частотах, а затем отключение и спад как однополюсной системы. Одна схема, которая удовлетворяет этим ограничениям, показана на рисунке ниже. В настоящее время единственным определенным элементом схемы является \ (r_o \), необходимо будет определить некоторый последовательный резистор \ (R_ {fo} \) и параллельный конденсатор \ (C_x \).
При осмотре выходное сопротивление низкой частоты составляет
\ [R_ {out} = r_o + R_ {fo} \]
Решение относительно \ (R_ {fo} \) с использованием уравнения (GB.11) дает
\ [R_ {fo} = \ frac {r_ \ pi R_E} {r_ \ pi + R_E} + \ left [1 + \ frac {g_m R_E r_ \ pi} {r_ \ pi + R_E} \ right] r_o – р_о \]
\ [R_ {fo} \ simeq \ left [\ frac {R_E} {r_ \ pi + R_E} \ right] \ beta r_o \]
Полюс модели эквивалентной схемы будет находиться на
\ [p_a = \ frac {-1} {\ left (r_o + R_ {fo} \ right) C_x} \]
Приравнивание \ (p_a \) к доминирующему полюсу \ (p_1 \) и решение для \ (C_x \)
\ [\ frac {-1} {\ left (r_o + R_ {fo} \ right) C_x} = \ dfrac {-1} {C_u \ left [1 + \ beta \ left (\ frac {R_E} {r_ \ pi + R_E} \ right) \ right] r_o} \]
\ [C_x = C_ \ mu \]
Сравнение \ (Z (s) \) с импедансом эквивалентной модели схемы можно увидеть на графике Боде ниже.Выходное сопротивление \ (Z (s) \) усилителя CE с источником с низким импедансом показано синим цветом. Также нанесены импеданс каждого из внутренних элементов и эквивалентного элемента обратной связи \ (R_ {fo} \). Когда сопротивление эмиттера \ (R_E \) увеличивается, низкочастотный выходной импеданс поднимается от \ (r_o \) к максимуму \ (\ beta r_o \).
Хотя это не рассматривается аналитически в этом посте, если байпасный конденсатор будет добавлен параллельно \ (R_E \) (при условии, что байпасный конденсатор большой), произойдет разрыв низкочастотного выходного импеданса.Когда импеданс \ (| Z_ {C, bypass} | \) равен \ (R_E \), низкочастотный выходной импеданс начнет падать до -20 дБ / дек. Это продолжается до тех пор, пока выходное сопротивление не достигнет собственного выходного сопротивления транзистора \ (r_o \). После этого выходной импеданс выглядит как \ (R_E = 0 \).
Исследование моделирования специй
Одной из проблем параметрического исследования влияния Re и Rs на выходной импеданс CE-усилителя является потенциальный сдвиг точки смещения постоянного тока.Если бы кто-то использовал источники напряжения или тока, которые не зависели от выбора Re и Rs, точка смещения постоянного тока, скорее всего, будет изменяться при изменении Re или Rs. Ниже приведен образец приспособления для испытания специй для решения этой проблемы:
Здесь источник тока I1 и источник напряжения V2 обеспечивают требуемую рабочую точку как ток коллектора Ic и потенциал Vbc база-коллектор соответственно. Усилитель U1 управляет базовым напряжением, чтобы получить желаемую рабочую точку Ic и Vcb.U1 – это идеальный операционный усилитель с усилением без обратной связи 120 дБ и шириной полосы пропускания (GBW) 1 Гц. Произведение GBW в 1 Гц выбрано в качестве чрезвычайно доминирующей стратегии компенсации полюсов. Выходное сопротивление испытательного стенда, представленного в тестируемой цепи, является идеальным заземлением по переменному току (0 Ом). Параметры слабого сигнала gm, ro, Cu, Cpi все являются функцией рабочей точки постоянного тока Ic и Vbc. Когда gm, ro, Cu, Cpi все поддерживаются постоянными, выходной импеданс как функция Re, Rs или обоих можно легко наблюдать в моделировании специй.Стабильность смещения тока коллектора для этого испытательного стенда можно увидеть в таблице ниже для Ic = 250uA и различных комбинаций Re и Rs:
Re [Ом] | |||||||||||
| 1 | 10 | 100 | 1к | 10к | 100 тыс. | 400к | 1 мес. | 10 мес. | 100 млн | ||
Rb [Ом | 1 | 10 па | 0 | 0 | 10 па | 0 | 0 | 0 | 0 | 0 | 0 |
| 10 | 10 па | -10 па | 0 | -10 па | 0 | 0 | 0 | 0 | 0 | 0 | |
| 100 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1к | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 10к | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 100 тыс. | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
Вариант \ (\ pm 0.Коллекторный ток 25 \) ppm наблюдался при Ic = 250 мкА. Обратите внимание, что для Ic = 250 мкА и Re = 100 МОм резистор Re смещен на 25 кВ постоянного тока. Конечно, это идеализированный сценарий, поскольку такие большие значения Re не будут получены с реальным резистором, а с активной нагрузкой, такой как источник тока с высоким выходным сопротивлением. К счастью, при симуляции специй 25 кВ на резисторе не проблема (ну, может быть, немного для арифметики с одинарной точностью). Смещение соединения база-коллектор также поддерживалось на уровне 5 В постоянного тока с точностью до доли ppm, независимо от выбора Re или Rs.oC]} \]
Ток коллектора выбирается таким, чтобы \ (g_m = 1/100 \) [A / V]
\ [I_C = VT g_m = 250 \; \ mathrm {[\ mu A]} \; = 1/4000 \; \ mathrm {[A]} \]
Остальные параметры малых сигналов также можно легко обрабатывать с помощью мысленной арифметики.
\ [r_ \ pi = \ frac {1} {g_m} \ beta = 100 \ cdot 300 = 30 \; \ mathrm {k \ Omega} \]
\ [r_o = \ frac {| VA |} {I_C} = 100 \ cdot 4000 = 400 \; \ mathrm {k \ Omega} \]
Обратите внимание, что собственное выходное сопротивление иногда моделируется как
\ [r_o = \ frac {| VA | + V_ {cb}} {I_C} = 105 \ cdot 4000 = 420 \; \ mathrm {k \ Omega} \]
Полная рабочая точка постоянного тока для тестируемого устройства (DUT) Q_DUT:
| Имя: | Кдут |
|---|---|
| Модель: | 2n3904_a |
| Ib: | 8.36e-07 |
| Ic: | 2,50e-04 |
| Vbe: | 6.37e-01 |
| Vbc: | -5.00e + 00 |
| Vce: | 5.64e + 00 |
| BetaDC: | 2.99e + 02 |
| Гм: | 9.99e-03 |
| Rpi: | 2.99e + 04 |
| Rx: | 0,00e + 00 |
| Ro: | 4.20e + 05 |
| Cbe: | 1.62e-11 |
| КБК: | 2.04e-12 |
| Cjs: | 0,00e + 00 |
| BetaAC: | 2.99e + 02 |
| CBX: | 0,00e + 00 |
| фут: | 8.73e + 07 |
Источник переменного напряжения V1 управляет коллектором тестируемой цепи, в результате чего возникает переменный ток, напрямую связанный с выходным сопротивлением.Выходное сопротивление тестируемой цепи тогда будет следующим:
\ [Z_ {out} = V (C) / I_C (DUT) \]
Примерный график выходного сопротивления выглядит следующим образом:
Ic = 250 мкА, Vbc = 5 В постоянного тока, Re = {10 100 1k 10k 100k 400k 1MEG 10MEG 100MEG} ОмКрасный график соответствует наименьшему значению Re = 10 Ом, а серый график показывает наибольшее значение Re = 100 МОм. В соответствии с предыдущим анализом, выходное сопротивление достигает максимального значения \ (\ beta r_o \) для очень больших значений Re.График выходного сопротивления в линейном масштабе был сделан, чтобы подчеркнуть важность Re для выходного сопротивления. На следующем рисунке выходное сопротивление нанесено в логарифмическом масштабе для одной точечной частоты 1 Гц.
Ось y: 20log10 (| Zo (f = 1 Гц) |) [дБОм], ось x: сопротивление Re [Ом], Ic = 250 мкА, Vbc = 5 В постоянного токаСобственное выходное сопротивление \ (r_o \) ИУ при 1 Гц составляет Va / Ic = 112 дБОм, что совпадает с выходным сопротивлением для Re ~ 0. Для чрезвычайно больших значений Re примерно на 50 дБ увеличивается выходное сопротивление вблизи постоянного тока (\ (f_ {test} \) = 1 Гц) можно наблюдать на графике.{(50/20)} \ simeq \ beta \]
Ссылаясь на приведенную выше таблицу рабочих точек постоянного тока для Spice, для этой симуляции \ (beta = 299 \). Полное сравнение низкочастотной модели (\ ref {LF.1}) с симуляцией специй показано на рисунке ниже.
Вспоминая, что \ (1 / gm = 100 \) Ом, глядя на рисунок выше, для каждого кратного \ (1 / g_m \) достигается 1x улучшение выходного сопротивления. Для \ (Re = 100 \) Ом выходное сопротивление увеличивается вдвое. Для \ (Re = 10 \ cdot 100 \) Ом выходное сопротивление увеличивается в 10 или 20 дБ.
Интересно, что если второй транзистор соединен последовательно с выходом усилителя CE (что приводит к конфигурации каскода), второй транзистор будет смещен примерно таким же током коллектора.
Точно так же, имея примерно одинаковые параметры слабого сигнала. Для второго транзистора его база связана с заземлением переменного тока, а его эмиттер видит выходное сопротивление усилителя CE. Собственное выходное сопротивление \ (r_o \) примерно в 4000 раз больше, чем \ (1 / gm \), для любого значения тока коллектора.Значение использования \ (r_o \) для дегенерации эмиттера можно увидеть на рисунке выше, глядя на точку данных для \ (Re = r_o = 400 \) кОм, здесь выходное сопротивление составляет всего 5% процентов от максимально возможного. выходное сопротивление (когда \ (Re = \ infty \)). Формально второй транзистор работает как усилитель с общей базой, однако представленный здесь анализ полностью применим.
Излучатель с заземлением переменного токаМоделирование специй с параметрической разверткой сопротивления источника показано на рисунке ниже.Сопротивление источника изменялось логарифмически от 1 Ом до 100 МОм с шагом в 1 декаду.
При графическом анализе выходного импеданса существуют два полюса и один ноль, причем второй полюс всегда находится на частоте около 100 МГц. Первый полюс и одиночный ноль переводятся ниже по частоте при увеличении сопротивления источника. Сравнение полюсов и нулей, оцененных из Z (s) (GE.10), с теми, которые были оценены при моделировании специй, можно наблюдать на рисунке ниже.
Напоминая, что приблизительные значения полюсов и нулей
\ [z_1 \ simeq \ dfrac {- \ left (r_ \ pi + R_S \ right)} {r_ \ pi R_S C_ \ pi}, \; \; \; p_1 \ simeq \ dfrac {- \ left (r_ \ pi + R_S \ right)} {g_m R_S r_ \ pi r_o C_ \ mu}, \; \; \; p_2 \ simeq \ dfrac {-g_m} {C_ \ pi} \]
Сравнение эквивалентной модели схемы, созданной для случая заземленного эмиттера, с симуляцией Spice показано на рисунке ниже.
Когда пара полюс-нуль расположены близко, они приблизительно сокращаются, что затрудняет численное решение точного абсолютного значения. Когда полюс и ноль начинают разделяться, численная оценка, полученная при моделировании пряностей, показывает хорошее согласие с полюсами и нулем эквивалентной модели схемы.
Основание с заземлением переменного токаИспользуя то же приспособление для тестирования специй, что и выше, выполняется параметрическая развертка сопротивления эмиттера. Сопротивление эмиттера изменяется логарифмически от 1 Ом до 100 МОм с шагом в 1 декаду.По результатам моделирования, выходной импеданс как функция сопротивления эмиттера показан на рисунке ниже.
Отмечая, что выходной импеданс нарушается на одной частоте и продолжает бесконечно снижаться на -20 дБ / дек, что означает, что Z (s) является приблизительно однополюсной функцией. Напомним, что из сечения заземленного основания, примерные полюса и ноль оказались равными
\ [p_1 \ simeq \ dfrac {-1} {C_u \ left [1 + \ beta \ left (\ frac {R_E} {r_ \ pi + R_E} \ right) \ right] r_o}, \; \; \ ; \; p_2 = z_1 \ simeq – \ dfrac {r_o + R_E + g_m R_E r_o} {R_E r_o C_ \ pi} \]
На рисунке ниже показано сравнение полюсов, аппроксимированных вручную, и нуля \ (Z (s) \) с полюсами, полученными при моделировании специй.
Эквивалентная модель схемы для заземленной базы имеет только один полюс и не имеет нулей. Сравнение доминирующего полюса CEM с полюсами и нулями, наблюдаемыми при моделировании специй, показано на рисунке ниже.
chet_paynter_introduct_6 | Усилители с общим эмиттером | Краткое содержание главы
Усилитель с общим эмиттером (CE) обеспечивает выходное напряжение 180 ° не совпадает по фазе с входным напряжением, как показано на рисунке 9-1.Этот сдвиг фазы напряжения можно объяснить следующим образом:
- Входное напряжение и ток синфазны.
- Входной и выходной токи синфазны. Следовательно, выходной ток находится в фазе с входным напряжением.
- Увеличение выходного тока приводит к уменьшению выходного напряжения и наоборот (как указано).
Поскольку выходной ток находится в фазе с входным напряжением, входное и выходное напряжения составляют 180 ° не в фазе.
Рисунок 9-1. Входное и выходное напряжение с общим эмиттером.Сопротивление эмиттера переменного тока () транзистора – это динамическое значение (например, импеданс стабилитрона), которое используется только в расчетах переменного тока. Для усилителя слабого сигнала значение. может быть аппроксимировано с помощью
Процесс, используемый для определения значения, показан в Примере 9.1 текста.
Коэффициент усиления по переменному току транзистора отличается от его коэффициента усиления по постоянному току.Это связано с тем, что эти два значения измеряются по-разному, как показано на рисунке 9.4 текста. Как показано на этом рисунке,
иОбратите внимание, что в спецификациях транзисторов указаны как и как.
Конденсаторы связи и байпаса
Усилители часто подключаются каскадом (последовательно) для увеличения усиления. Каждый усилитель в каскаде называется каскадом , а вся схема упоминается как многокаскадный усилитель .
Конденсаторы связи используются для обеспечения связи по переменному току и изоляции по постоянному току между каскадами усилителя. Они также используются для подключения усилителя к его источнику сигнала и нагрузке, как показано на рисунке 9-2. Конденсаторы связи предотвращают влияние источника и нагрузки на смещение постоянного тока транзистора. Обратите внимание, что конденсаторы связи обычно представляют собой компоненты с высокой стоимостью, которые обеспечивают небольшое реактивное сопротивление на самой низкой рабочей частоте схемы.
Рисунок 9-2.Конденсаторы связи и байпаса.Перепускной конденсатор (показанный на рисунке 9-2) подключен параллельно эмиттерному резистору. Результатом этого соединения является обеспечение заземления переменного тока на выводе эмиттера транзистора. Это приводит к увеличению коэффициента усиления по напряжению цепи (как описано далее в этой главе). Обратите внимание, что байпасный конденсатор обычно представляет собой компонент с высокой стоимостью, который обеспечивает небольшое реактивное сопротивление на самой низкой рабочей частоте цепи.
Типичные формы сигналов с общим эмиттером показаны на рисунке 9.10 текста. Обратите внимание, что нет никаких изменений из-за наличия шунтирующего конденсатора (который эффективно замыкает переменную составляющую напряжения эмиттера на землю).
Эквивалентные схемы переменного тока
Эквивалент переменного тока любого усилителя определяется следующим образом:
- Замыкание соединительных и байпасных конденсаторов
- Замена всех источников постоянного тока символом заземления
Полный процесс продемонстрировано в Примере 9.2 текста.
Усиление усилителя
Коэффициент усиления по напряжению – это коэффициент, на который увеличивается напряжение сигнала переменного тока от входа усилителя к выходу усилителя. Выражается математически:
Поскольку коэффициент усиления по напряжению усилителя CE также равен отношению сопротивления коллектора переменного тока к сопротивлению эмиттера переменного тока .
Эквивалент усилителя по переменному току на Рисунке 9-2 показан на Рисунке 9-3.Как показано на рисунке, полное сопротивление переменному току в цепи коллектора равно. Поскольку резистор эмиттера закорочен в эквивалентной схеме переменного тока, полное сопротивление эмиттера переменного тока равно. Следовательно, коэффициент усиления по напряжению усилителя можно найти как
где. Полная процедура расчета усиления по напряжению усилителя CE продемонстрирована в Примере 9.4 текста.
Рисунок 9-3. Эквивалент переменного тока на рис. 9-2.
На сопротивление эмиттера транзистора () может влиять изменение температуры.В результате на усиление напряжения CE-усилителя также может влиять повышение (или снижение) рабочей температуры. Метод построения схемы, известный как с заменой , иногда используется для стабилизации усиления напряжения. (Затухание усилителя рассматривается в разделе 9.6 текста.)
Коэффициент усиления по току () усилителя CE ниже, чем значение для транзистора, из-за делителей тока в цепях базы и коллектора. Коэффициент усиления по мощности усилителя CE равен произведению коэффициента усиления по току () и усиления по напряжению ().
Расчеты усиления и импеданса
Если нагрузка на усилителе размыкает , сопротивление переменного тока в цепи коллектора увеличивается. В результате коэффициент усиления схемы по напряжению увеличивается. Эта концепция проиллюстрирована на рисунке 9.16 текста.
Входной импеданс CE-усилителя равен параллельной комбинации резистора (-ов) смещения базы и входного сопротивления базы транзистора. Например, входной импеданс усилителя на Рисунке 9-3 находится как
где.Обратите внимание, что значение указано в спецификации транзистора. Расчет для усилителя CE показан в Примере 9.9 текста.
Когда значения и для усилителя CE известны, коэффициент усиления схемы по току можно найти с помощью
Расчет для усилителя CE продемонстрирован в Примере 9.10.
Чтобы рассчитать общий коэффициент усиления многокаскадного усилителя, необходимо сначала определить значения и для каждого каскада.Затем общий коэффициент усиления по току () находится как произведение коэффициентов усиления отдельного каскада. То же самое верно и для общего усиления по напряжению (). Наконец, общий прирост мощности можно найти с помощью
. Расчеты многокаскадного усиления напряжения показаны в примерах 9.11 и 9.12 текста.
Усилители с затоплением
Усилитель с затуханием уменьшает колебания коэффициента усиления напряжения за счет увеличения сопротивления цепи эмиттера по переменному току.Затопленный усилитель также называется усилителем со стабилизированным усилением.
Затянутый усилитель показан на Рисунке 9-4. Обозначенный резистор не шунтируется, поэтому он является частью эквивалентной схемы переменного тока для усилителя. Для показанной схемы полное сопротивление эмиттера переменного тока равно ().
Рисунок 9-4. Заболоченный (стабилизированный по усилению) усилитель.Когда усилитель спроектирован таким образом, чтобы минимизировать влияние любых изменений на усиление напряжения.Этот принцип продемонстрирован в Примере 9.14 текста. Обратите внимание, что добавление затухающего резистора также приводит к увеличению входного сопротивления базы транзистора, как показано в следующем соотношении:
Влияние затухания на входное сопротивление усилителя продемонстрировано в примерах 9.15 и 9.16. текст.
H-параметры
Гибридные параметры или h-параметры – это характеристики транзисторов, которые измеряются при определенных условиях.Четыре параметра h , которые перечислены в большинстве спецификаций транзисторов, сведены в Таблицу 9-1.
ТАБЛИЦА 9-1
| Обозначение параметра | Параметр | Условия измерения |
Базовое входное сопротивление | Короткое замыкание на выходе | |
Коэффициент усиления по току база-коллектор | Короткое замыкание выхода | |
Входная полость | Вход открыт | |
Коэффициент обратной связи по обратному напряжению | Вход открыт |
Перечисленные параметры измерены, как показано на рисунке 9.23 текста.
Значения и могут использоваться для получения более точного значения, как показано ниже:
Когда параметры указаны как максимальное и минимальное значений, используется среднее геометрическое из двух. Во многих случаях параметры h предоставляются с помощью графиков, подобных тем, которые показаны на рисунке 9.26 текста. При использовании этих графиков:
Анализ параметров CE усилителя h показан в Примере 9.19.
Поиск и устранение неисправностей усилителя
Существует несколько способов устранения неисправностей многокаскадных усилителей. Один из таких подходов состоит в том, чтобы начинался на выходе конечного этапа и возвращался к входу . (Этот подход имеет смысл, если учесть, что многие электронные системы содержат два или более сигнальных тракта, которые объединяются на более поздних этапах.



 Теперь, проведя подробный анализ, мы можем сделать некоторые выводы о влиянии обратной связи на усилительные и другие свойства каскада с ОЭ.
Теперь, проведя подробный анализ, мы можем сделать некоторые выводы о влиянии обратной связи на усилительные и другие свойства каскада с ОЭ.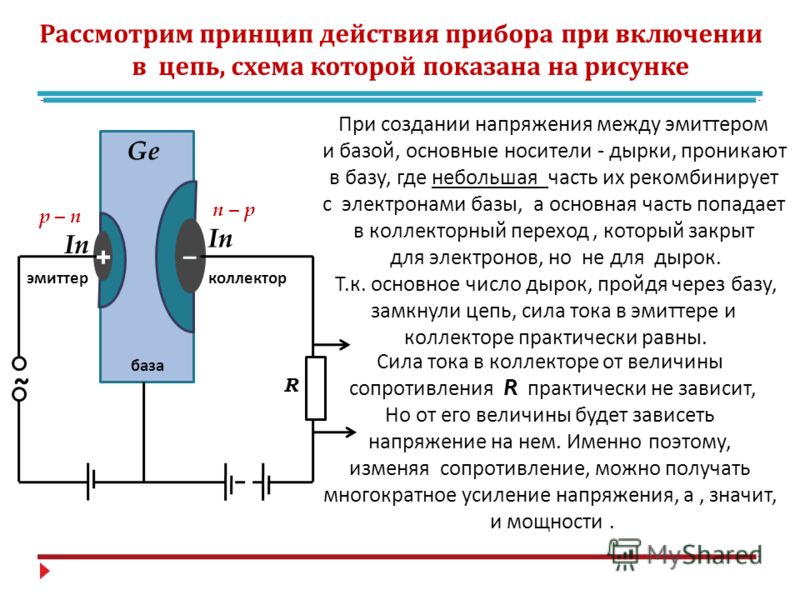 Нельзя сказать, что это явление вредное. Ведь высокое входное сопротивление означает, что данный каскад будет оказывать минимальное влияние на режимы работы и параметры каскада усиления, предшествующего ему. Кроме того, увеличится чувствительность, поскольку теперь слабые сигналы будут наводить бóльшие по амплитуде напряжения на входе каскада, выделяясь из общего шумового фона. Однако в диапазоне СВЧ, когда требуется точное согласование импедансов, рост входного сопротивления полезен далеко не всегда и может привести к потере устойчивости усилителя. Да и упомянутое выше повышение чувствительности также необязательно является положительным явлением. Ведь если в схеме уровень полезного сигнала наверняка превышает уровень помех и является оптимальным при некоторой известной чувствительности усилительного каскада, то повышение чувствительности ведет только к бóльшему усилению сигналов помех, но не полезного сигнала.
Нельзя сказать, что это явление вредное. Ведь высокое входное сопротивление означает, что данный каскад будет оказывать минимальное влияние на режимы работы и параметры каскада усиления, предшествующего ему. Кроме того, увеличится чувствительность, поскольку теперь слабые сигналы будут наводить бóльшие по амплитуде напряжения на входе каскада, выделяясь из общего шумового фона. Однако в диапазоне СВЧ, когда требуется точное согласование импедансов, рост входного сопротивления полезен далеко не всегда и может привести к потере устойчивости усилителя. Да и упомянутое выше повышение чувствительности также необязательно является положительным явлением. Ведь если в схеме уровень полезного сигнала наверняка превышает уровень помех и является оптимальным при некоторой известной чувствительности усилительного каскада, то повышение чувствительности ведет только к бóльшему усилению сигналов помех, но не полезного сигнала.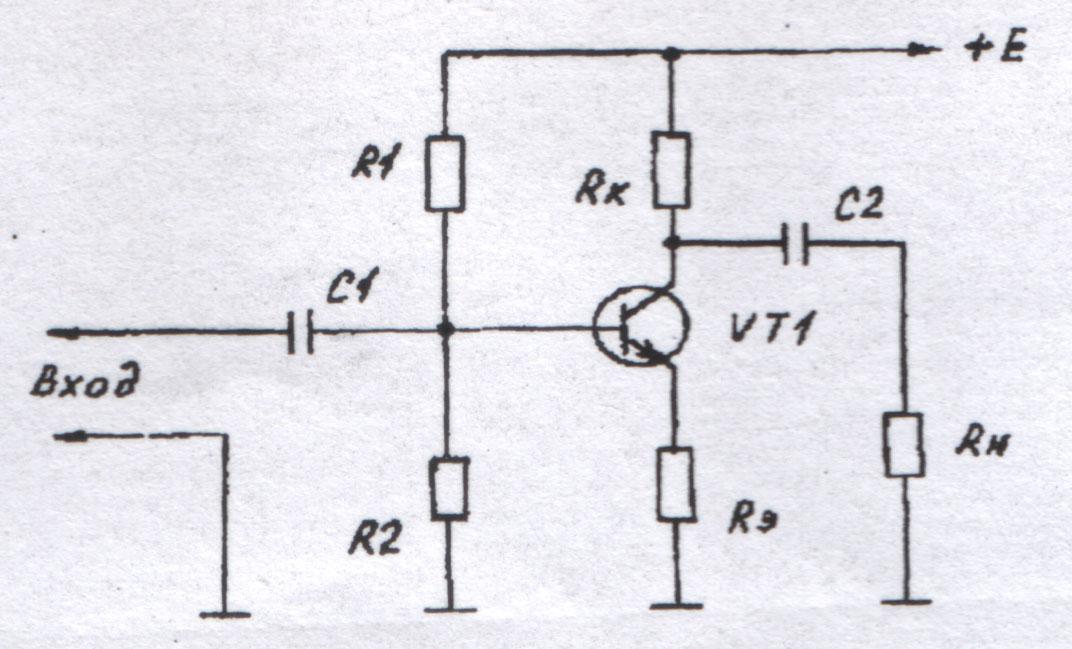 А вот коэффициент усиления по напряжению, определяемый соотношением (5.4), изменяется очень сильно. Действительно, стоящее в этом соотношении в знаменателе входное сопротивление Rвх, как мы уже выяснили, здорово увеличивается, что означает пропорциональное падение коэффициента усиления по напряжению. Учет ряда допущений привел нас к формуле (5.5), в которой уже явно видна зависимость \({K_I}_\sim\) от величины сопротивления в цепи эмиттера \(R_Э\).
А вот коэффициент усиления по напряжению, определяемый соотношением (5.4), изменяется очень сильно. Действительно, стоящее в этом соотношении в знаменателе входное сопротивление Rвх, как мы уже выяснили, здорово увеличивается, что означает пропорциональное падение коэффициента усиления по напряжению. Учет ряда допущений привел нас к формуле (5.5), в которой уже явно видна зависимость \({K_I}_\sim\) от величины сопротивления в цепи эмиттера \(R_Э\).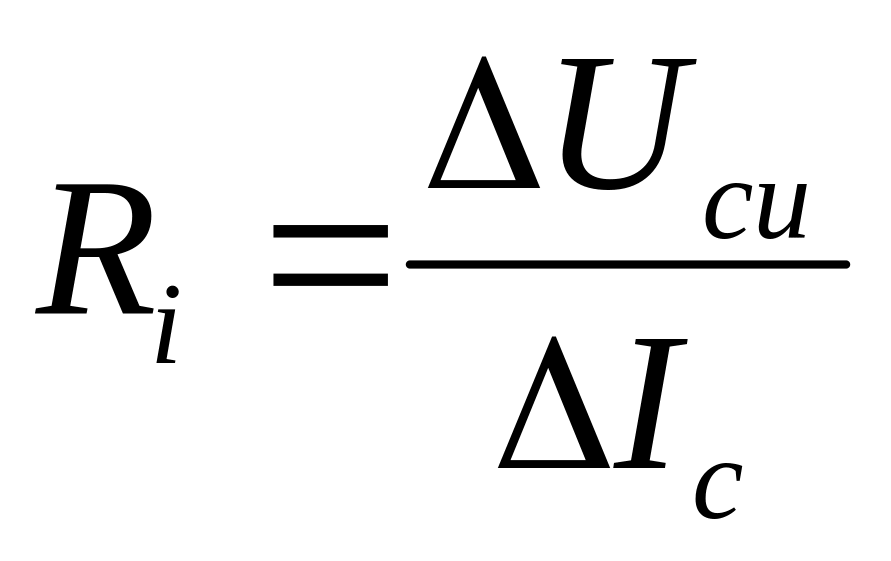 Истина как всегда лежит где-то посередине, и в зависимости от условий применения и назначения усилителя приходится искать некий компромисс между двумя крайностями. И вот здесь пришло время снова вспомнить о конденсаторе \(C_Э\), показанном на рис. 5.1, 5.2 пунктиром.
Истина как всегда лежит где-то посередине, и в зависимости от условий применения и назначения усилителя приходится искать некий компромисс между двумя крайностями. И вот здесь пришло время снова вспомнить о конденсаторе \(C_Э\), показанном на рис. 5.1, 5.2 пунктиром.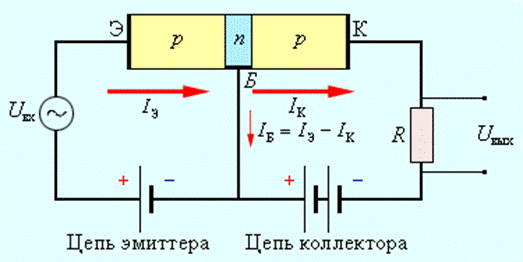 Но, как мы уже выяснили ранее, иногда нам могут оказаться нужны те полезные эффекты, которые привносит влияние обратной связи. Чтобы снова не бросаться в крайности, мы можем разделить сопротивление \(R_Э\) на два сопротивления, включенных последовательно, а шунтирующий конденсатор подключить только к одному из них, как показано на рис. 5.3,а. Теперь по постоянному току обратная связь обеспечивается через два последовательно включенных резистора \(R_{Э 1} + R_{Э 2}\), а по переменному току в рабочей полосе частот — только через резистор \(R_{Э 1}\), поскольку суммарное сопротивление цепочки \(R_{Э 2} C_{бл}\) в рабочей полосе частот ничтожно мало. Варьируя соотношение сопротивлений \(R_{Э 1}\) и \(R_{Э 2}\) (но оставляя постоянной их сумму), мы можем установить необходимую нам глубину ООС в рабочей полосе частот, оставляя неизменным режим работы каскада по постоянному току. Возможен и еще один вариант, показанный на рис. 5.3,б. По своим параметрам он ничем не отличается от варианта на рис.
Но, как мы уже выяснили ранее, иногда нам могут оказаться нужны те полезные эффекты, которые привносит влияние обратной связи. Чтобы снова не бросаться в крайности, мы можем разделить сопротивление \(R_Э\) на два сопротивления, включенных последовательно, а шунтирующий конденсатор подключить только к одному из них, как показано на рис. 5.3,а. Теперь по постоянному току обратная связь обеспечивается через два последовательно включенных резистора \(R_{Э 1} + R_{Э 2}\), а по переменному току в рабочей полосе частот — только через резистор \(R_{Э 1}\), поскольку суммарное сопротивление цепочки \(R_{Э 2} C_{бл}\) в рабочей полосе частот ничтожно мало. Варьируя соотношение сопротивлений \(R_{Э 1}\) и \(R_{Э 2}\) (но оставляя постоянной их сумму), мы можем установить необходимую нам глубину ООС в рабочей полосе частот, оставляя неизменным режим работы каскада по постоянному току. Возможен и еще один вариант, показанный на рис. 5.3,б. По своим параметрам он ничем не отличается от варианта на рис. 5.3,а, только пути протекания токов в нем другие. По постоянному току здесь задействовано только сопротивление \(R_{Э 1}\), а по переменному — параллельное включение сопротивлений \(R_{Э 1}\) и \(R_{Э 2}\).
5.3,а, только пути протекания токов в нем другие. По постоянному току здесь задействовано только сопротивление \(R_{Э 1}\), а по переменному — параллельное включение сопротивлений \(R_{Э 1}\) и \(R_{Э 2}\).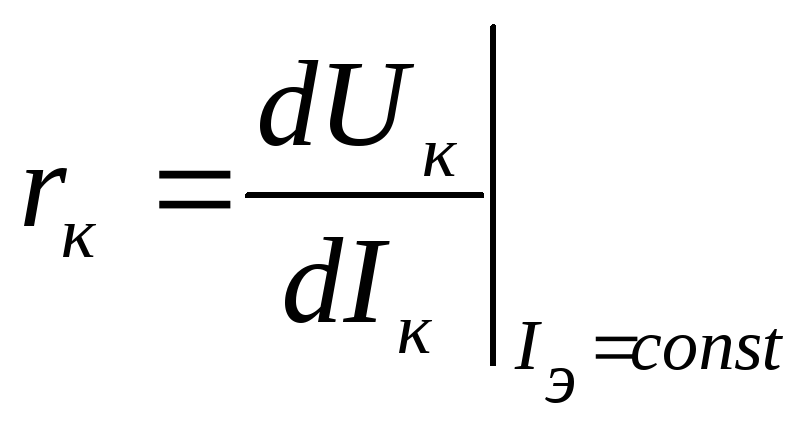 Тогда по мере уменьшения частоты сигнала общее эквивалентное сопротивление в цепи обратной связи будет заметно расти, соответственно будет изменяться в сторону уменьшения теоретический коэффициент усиления по напряжению. Реальная частотная характеристика усилительного каскада перестает плавно убывать с ростом частоты, выпрямляется и становится линейной (естественно, максимальной линеаризации можно добиться только при правильном подборе емкости блокировочного конденсатора).
Тогда по мере уменьшения частоты сигнала общее эквивалентное сопротивление в цепи обратной связи будет заметно расти, соответственно будет изменяться в сторону уменьшения теоретический коэффициент усиления по напряжению. Реальная частотная характеристика усилительного каскада перестает плавно убывать с ростом частоты, выпрямляется и становится линейной (естественно, максимальной линеаризации можно добиться только при правильном подборе емкости блокировочного конденсатора).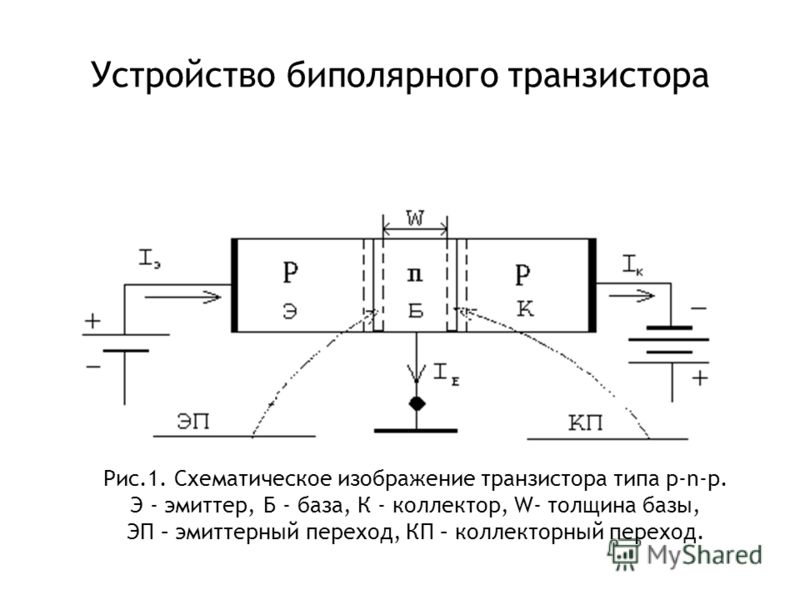 Таким образом, частотная характеристика всего усилительного каскада будет в основном определяться частотной характеристикой примененного в цепи обратной связи колебательного контура (ее ширина будет зависеть от добротности контура). На рис. 5.4 представлен пример такого усилительного каскада, являющегося выходным каскадом усилителя записи кассетного магнитофона.
Таким образом, частотная характеристика всего усилительного каскада будет в основном определяться частотной характеристикой примененного в цепи обратной связи колебательного контура (ее ширина будет зависеть от добротности контура). На рис. 5.4 представлен пример такого усилительного каскада, являющегося выходным каскадом усилителя записи кассетного магнитофона.