ЗАКОН ОМА
Электроника сейчас получила большое распространение, у всех дома много радиоприёмников, телефонов, компьютеров, планшетов, телевизоров фонариков и т.д. Это всё радиоэлектроника, поэтому некоторые люди заинтересовываются этим хобби, но не знают с чего начать. Наша цель рассказать в данном материале всё о Законе Ома.

Обозначения напряжения, тока, сопротивления
Всё же многие радиолюбители начинают с закона Ома. В закон Ома входят три единицы: напряжение, ток, сопротивление.
- Напряжение измеряется в вольтах (В) и обозначается U.
- Сопротивление измеряется в Омах (Ом) и обозначается R.
- Ток в Амперах (А) и обозначается I.
Расчёт напряжения, тока и сопротивления
Закон Ома предназначен для того, чтобы найти неизвестную третью, если известны первая и вторая. С этого по подробней, чтобы облегчить закон Ома, будем пользоваться треугольником Ома. Вот этот треугольник:

Давайте разберёмся с напряжением, чтобы найти напряжение, используя треугольник Ома, надо закрыть рукой напряжение – U, остались только I-ток и R-сопротивление, передними стоит вертикальная черта, вертикальная это черта снизу вверх, это вертикальная линия обозначает умножение, значит, чтобы найти напряжение надо ток умножить на сопротивление.
Вот такая формула получилась: U=I*R, где U-напряжение, I-ток, R-сопротивление.
Теперь давайте попробуем найти ток, прикроем рукой I, теперь перед напряжением и сопротивление стоит горизонтальная черта, горизонтальная, это та черта, которая идёт слева направо. Горизонтальная черта означает деление. Значит, чтобы найти ток, надо напряжение разделить на сопротивление.
Формула получилась следующая: I= U\R
, где I-ток, U-напряжение, R-сопротивление.Найдём сопротивление, закроем рукой R, то получим опять горизонтальную черту перед напряжением и током, значит нужно делить.
Формула получилась для расчёта сопротивления: R=U\I, где R-сопротивление, U-напряжение, I-ток. Итак, мы научились пользовать треугольником Ома и узнали о Законе Ома. Теперь, пожалуй, поучимся на примерах.
Примеры расчётов закона Ома

Давайте, найдём напряжение, если ток равен 0,9 Ампер, а сопротивление 100 Ом, пользуясь треугольником, прикрываем напряжение рукой, смотрим, вертикальная черта, значит умножить. Опять пользуемся той формулой, только подставляем числа, U = 0,9 А * 100 Ом, считаем, получиться 90, значит U = 90 вольт.
Теперь рассчитываем сопротивление, берём те же единицы, только убираем сопротивление, получиться вот такая формула: R = 90 В \ 0,9 А, получим 100 Ом.
Чтобы рассчитать ток, опять же убираем ток, получаем эту формулу I = 90 В \ 100 Ом, получаем 0,9 Ампер. Итак, на этом всё, кстати, закон Ома действует там, где нет катушек индуктивности и конденсаторов, не забивайте голову конденсаторами и катушками индуктивности, просто, запомните, что закон Ома действует, там, где нет катушек индуктивности и конденсаторов. Надеюсь, моя статья была полезной, всем удачи, с вами был Дмитрий Цывцын.
Справочники радиодеталейelwo.ru
Как найти силу тока через мощность, сопротивление и напряжение
Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.
Если известна мощность и напряжение
Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:
P=UI
После несложных мы получаем формулу для вычислений
I=P/U
Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:
Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:
Р1 = Р2/η
Здесь P2 – активная полезная мощность на валу,

Находим полную мощность с учетом cosФ (он также указывается на шильдике):
S = P1/cosφ
Определяем потребляемый ток по формуле:
Iном = S/(1,73·U)
Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.
Если известно напряжение или мощность и сопротивление
Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.
I=U/R
Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:
P=UI
При этом согласно тому же закону Ома:
U=IR
То:
P=I2*R
Значит расчёт проводим по формуле:
I2=P/R
Или возьмем выражение в правой части выражения под корень:
I=(P/R)1/2
Если известно ЭДС, внутреннее сопротивление и нагрузка
Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:
I=E/(R+r)
Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.
Закон Джоуля-Ленца
Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником. Для этого вспомним закон Джоуля-Ленца.
Его формула выглядит так:
Q=I2Rt
Тогда расчет проводите так:
I2=QRt
Или внесите правую часть уравнения под корень:
I=(Q/Rt)1/2
Несколько примеров
В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.
1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.
Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.
R1+R2=1+2=3 Ома
Тогда рассчитать силу тока можно по закону Ома:
I=U/R=12/3=4 Ампера
При параллельном соединении двух элементов Rобщее можно рассчитать так:
Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67
Тогда дальнейшие вычисления можно проводить так:
I=12*0,67=18А
2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.
Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома
Теперь схема примет вид:

Далее находим ток по тому же закону Ома:
I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер
Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!
Наверняка вы не знаете:
samelectrik.ru
Закон Ома – физика процесса на примере движения воды. Формулы зависимости сопротивления, напряжения, силы тока и мощности
Существует всего 2 базовых формулы которые помогут вам понять взаимосвязь между силой тока(Амер), напряжением(Вольт), сопротивлением (Ом) и мощностью (Ватт).
Зная хотя бы два из перечисленных параметра вы всегда можете рассчитать два других.
ЗАКОН ОМА
| Базовая формула | P=I*E | E=I*R | |
| Расчет напряжения | E=P/I | E=I*R | E=SQR(P*R) |
| Расчет силы тока | I=P/E | I=E/R | I=SQR(P/R) |
| Расчет мощности | P=I*E | P=E 2 /R | P=I 2 *R |
| Расчет сопротивления | R=E 2 /P | R=E/I | R=P/I 2 |
E – Напряжение (Вольт)
I – Сила тока (Ампер)
R – Электрическое сопротивление (Ом)
SQR – квадратный корень
Для справки:
Мы используем переменную E для обозначения напряжения, иногда вы можете встретить обозначение V для напряжения. Не дайте себя запутать названиям переменных.
Изменение сопротивления:
На следующей схеме вы видите разность сопротивлений между системами изображенными на правой и левой стороне рисунка. Сопротивление давлению воды в кране противодействует задвижка, в зависимости от степени открытия задвижки изменяется сопротивление.
Сопротивление в проводнике изображено в виде сужения проводника, чем более узкий проводник тем больше он противодействует прохождению тока.
Вы можете заметить что на правой и на левой стороне схемы напряжение и давление воды одинаково.
Вам необходимо обратить внимание на самый важный факт.
В зависимости от сопротивления увеличивается и уменьшается сила тока.
Слева при полностью открытой задвижке мы видим самый большой поток воды. И при самом низком сопротивлении, видим самый большой поток электронов (Ампераж) в проводнике.
Справа задвижка закрыта намного больше и поток воды тоже стал намного больше.
ужение проводника тоже уменьшилось вдвое, я значит вдвое увеличилось сопротивление протеканию тока. Как мы видим через проводник из за выского сопротивления протекает в два раза меньше электронов.
Для справки
Обратите внимание что сужение проводника изображенное на схеме используется только для примера сопротивления протеканию тока. В реальных условиях сужения проводника не сильно влияет на протекающий ток. Значительно большее сопротивление могут оказывать полупроводники и диэлектрики.
Сужающийся проводник на схеме изображен лишь для примера, для понимания сути происходящего процесса.
Формула закона Ома – зависимость сопротивления и силы тока
I = E/R
Как вы видите из формулы, сила тока обратнапропорциональна сопротивлению цепи.
Больше сопротивление = Меньше ток
* при условии что напряжение постоянно.
Изменение напряжения.
На изображенной схеме во всех системах сопротивление имеет одинаковую величину.
В этот раз на картинке изменяется сопротивление/давление.
Вы можете увидеть что при увеличении напряжения приводит к увеличению протекающего тока даже при постоянном сопротивлении.
Формула закона Ома – зависимость напряжения и силы тока
I = E/R
Обратите внимание что сила тока протекающего в проводнике прямопропорциональна напряжению.
Больше напряжение = Больше сила тока
* при условии что сопротивление постоянно.
Математический рассчет
Рассмотрим пример.
У нас есть аккумуляторная батарея с напряжением питания 12 Вольт. К ней напрямую подключен резистор (сопротивление) 10 Ом. Для того что бы рассчитать какая мощность приложена к нашему резистору, можно воспользоваться формулой.
P = E2/R
P = 122/10
P = 144/10.
P = 14.4 watts
Мощность рассеиваемая на резисторе состовляет 14,4 Ватта.
Если вы хотите определить величину тока протекающего через проводник, мы используем другую формулу
I = E/R
I = 12/10
I = 1.2 amps
Сила тока протекающего через цепь составляет 1,2 Ампера
—————-
Калькуляторы зависимости напряжения, силы тока и сопротивления.
1. Калькулятор рассеиваемой мощности и протекающей силы тока в зависимости от сопротивления и приложенного напряжения.
Демо закона Ома в реальном времени.
Для справки
В данном примере вы можете увеличивать напряжение и сопротивление цепи. Данные изменения в реальном времени будут изменять силу тока протекающего в цепи и мощность рассеиваемую на сопротивлении.
Если рассматривать аудио системы – вы должны помнить что усилитель выдает определенное напряжение на определенную нагрузку (сопротивление). Соотношение двух этих величин определяет мощность.
Усилитель может выдать ограниченную величину напряжения в зависимости от внутреннего блока питания и источника тока. Так же точно ограничена и мощность которую может подать усилитель на определенную нагрузку (к примеру 4 Ома).
Для того что бы получить больше мощности, вы можете подключить к усилителю нагрузку с меньшим сопротивлением (к примеру 2 Ома). Учтите что при использовании нагрузки с меньшим сопротивлением – скажем в два раза (было 4 Ома, стало 2 Ома) – мощность тоже возрастет в два раза.(при условии что данную мощность может обеспечить внутренний блок питания и источник тока).
Если мы возьмем для примера моно усилитель мощностью 100 Ватт на нагрузку 4 Ома, зная что он может выдать напряжение не более 20 Вольт на нагрузку.
Если вы поставите на нашем калькуляторе бегунки
Напряжение 20 Вольт
Сопротивление 4 Ома
Вы получите
Мощность 100 Ватт
Если вы сдвинете бегунок сопротивления на величину 2 Ома, вы увидите как мощность удвоится и составит 200 Ватт.
В общем примере источником тока является аккумуляторная батарея (а не усилитель звука) но зависимости силы тока, напряжения, сопротивления и сопротивления одинаковы во всех цепях.
www.insidecarelectronics.com
Электрическое сопротивление источника силы тока формула в Омах
Каждый человек знает, что по проводам течет электрический ток, за счет чего горит свет или работает прибор, потребляющий электрическую энергию. Это настолько прочно вошло в обычную жизнь, что никто не задумывается о физической составляющей данного явления. Человек, чья профессиональная деятельность не связана с физикой, слышал про электрическое сопротивление, силу тока или мощность последний раз в разрезе школьного курса физики.
Физика очень сложная наука, которая базируется не только на формулах и вычислениях, но в большей степени на понятиях. Особенно ярко это проявляется в разделе «электричество», которое само по себе не является материальной субстанцией, его не возможно «пощупать» или увидеть, но при этом оно занимает важную нишу в человеческой жизни.
Что есть сила сопротивления? Что такое электрическая цепь? Почему ток обладает силой? Для человека, который давно окончил школу, вопросов больше, чем ответов и немногие обладают хотя бы общим представлением, что на самом деле происходит под изоляцией электрического провода.
Какие процессы протекают в проводниках при прохождении через них тока?
Если некое тело, обладающее способностью проводить электрический ток, поместить таким образом, что с одной стороны будет находиться положительный полюс, а с другой отрицательный, то по нему начинает проходить электрический ток. Ток представляет собой в очень упрощенном виде движение отрицательных электронов, имеющее направленность. При этом частицы, имеющие отрицательный заряд, притягиваются к положительному полюсу. Именно за счет этого принято различать полярность электрической цепи, что легко заметить при подключении элементов питания, которые устанавливаются с учетом плюса и минуса.
При движении электроны встречают на своем пути атомы вещества, которым передается часть энергии в результате столкновения, что приводит к нагреву тела, пропускающее ток. При этом при столкновении происходит подтормаживание электронов. Появляющееся электрическое поле имеет способность заново ускорять замедленные электроны, которые снова начинают свое движение к положительному полюсу. Весь этот процесс будет бесконечным, пока тело подключено к источнику электрического поля. Именно движущиеся электроны испытывают на себе сопротивление поля, при этом существует прямая связь между количеством препятствий на пути заряженных частиц и значением данной величины. Сопротивление тока в цепи увеличивается при увеличении количества столкновении электронов.Сопротивление цепи — что это?
Существует два вида определения сопротивления. Первое базируется на законе Ома. Согласно данному определению сопротивление цепи есть численная величина, определяемая как результат деления значения напряжения, создаваемого в проводнике на силу тока, который протекает через него. Формула сопротивления в данном случае будет иметь вид:
R=U:I, где
R — сопротивление;
U — напряжение;
I — сила тока.
Второе определение формулы сопротивления базируется на физических особенностях токопроводящего материала. Сопротивление источника есть также числовая величина, указывающая на способность тела превращать электрическую энергию в тепловую. Формула сопротивления в Омах для второго случая выглядит следующим образом:
R=(p*l)/S, где
R — сопротивление;
p — удельное сопротивление;
l — длина проводника;
S — площадь сечения.
 При этом оба определения являются правильными и имеют право быть, но преимущественно в школьном курсе изучают лишь первый постулат. Единицы, определяющие сопротивление — Ом, названы так по имени ученого, который открыл сам факт существования данного явления и описал его природу.
При этом оба определения являются правильными и имеют право быть, но преимущественно в школьном курсе изучают лишь первый постулат. Единицы, определяющие сопротивление — Ом, названы так по имени ученого, который открыл сам факт существования данного явления и описал его природу.
Закон Ома или что есть сила в Омах
Одним очень важным открытием для понимания физической сущности электричества является открытый Омом закон, который выводит зависимость силы тока от напряжения. В основе закона лежит простой эксперимент. Представим, что существует простейшая цепь, которая состоит из обычной лампочки и амперметра. При добавлении в цепь большого гальванического элемента можно наблюдать, что нить накаливания лампы не нагревается и в сети практически отсутствует ток. Но если имеющийся гальванический элемент заменить свежим аккумулятором или элементом питания, то лампочка моментально загорается и ток в сети увеличивается. Замерив ток на обоих концах сети можно заметить, что при включении в сеть элемента питания напряжение значительно возрастает.

Закон Ома для участка цепи
Из проведенного опыта вытекает сформулированный Омом закон, который гласит, что сила тока в проводящем электрический ток теле увеличивается при увеличении напряжения, подаваемого к концам цепи или проводника. При этом сила тока находится в прямо пропорциональной зависимости от напряжения и обратно пропорциональной связи с сопротивлением. Закон Ома — это зависимая связь, в которой принимают участие сила тока, сопротивление и напряжение.
Виды сопротивлений
Физика выделяет несколько видов электрического сопротивления:
- Удельное. Под удельным сопротивлением понимается способность металла или иного тела противостоять прохождению электрического тела. Высокая величина удельного сопротивления будет означать, что данный материал является плохим проводником;
- Сопротивление провода. В данном случае формула сопротивления в Омах будет включать в себя диаметр сечения провода, удельное сопротивление конкретного металла и длину провода;
- Поверхностное сопротивление. Этот вид применяется для расчета удельного сопротивления тонких материалов, в частности пленок. В случае поверхностного сопротивления диаметр сечения в формуле представлен в виде габаритных размеров (толщина, длина, ширина).
Электрическое сопротивление является важным понятием, сделавшее возможным создание резистора, главная задача которого является осуществление контроля и ограничения действия электрического тока. Применение резисторов сводится к препятствованию возрастанию напряжения, поскольку эта деталь способна рассеивать тепло. Также резистор, который является неотъемлемой частью любой современной платы и схемы, применяется для разделения напряжения, понижая данную характеристику.
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
madenergy.ru
Внутреннее сопротивление источника тока – формула
Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.
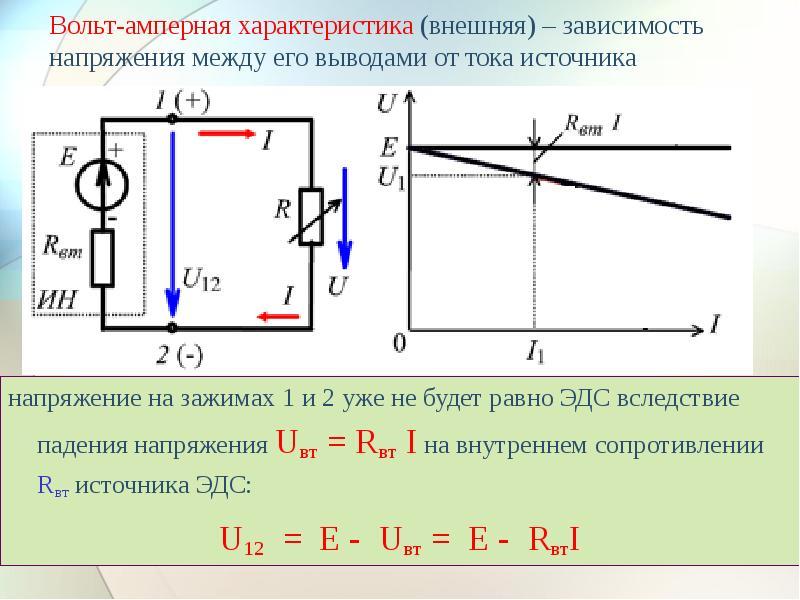
Зависимость напряжения между его выводами от тока источника
Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.
У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.
Измерение сопротивления петли фаза-нуль
Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).
Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.
Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.
На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:
- заменяются участки провода, не отвечающие требованиям по диаметру сечения;
- перекручиваются болтовые соединения с обязательной установкой врезных шайб;
- вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
- при необходимости в контур защитного заземления добавляются дополнительные элементы;
- исключается последовательное подключение корпусов устройств к общей шине заземления.
После выполнения комплекса мероприятий измерения проводятся повторно.
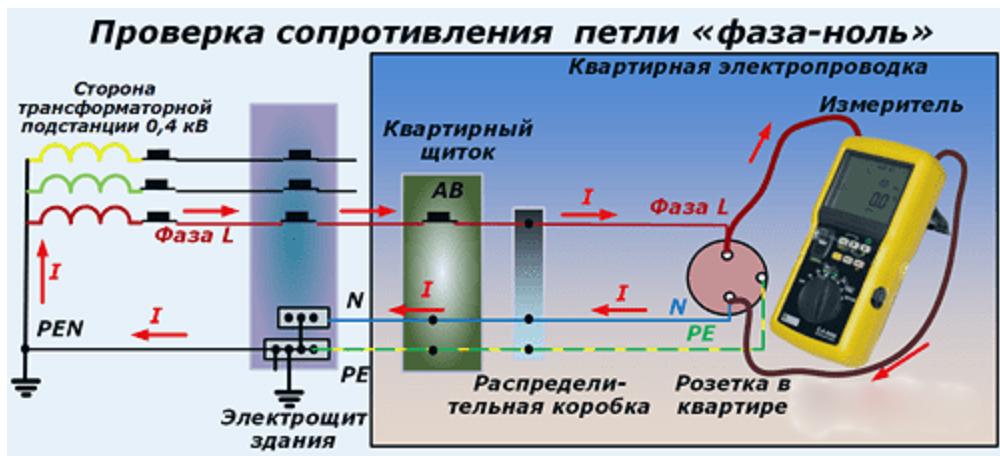
Проверка сопротивления петли «фаза – ноль»
Нахождение внутреннего сопротивления
Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.
Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:
I = ε / (r + R).
Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.
Выразив отсюда r, получают формулу для его вычисления:
r = (ε / I) – R,
где:
- r – внутреннее сопротивление источника;
- ε – ЭДС источника;
- I – сила тока в полной цепи;
- R – сопротивление в полной цепи.
Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.
Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.
В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.
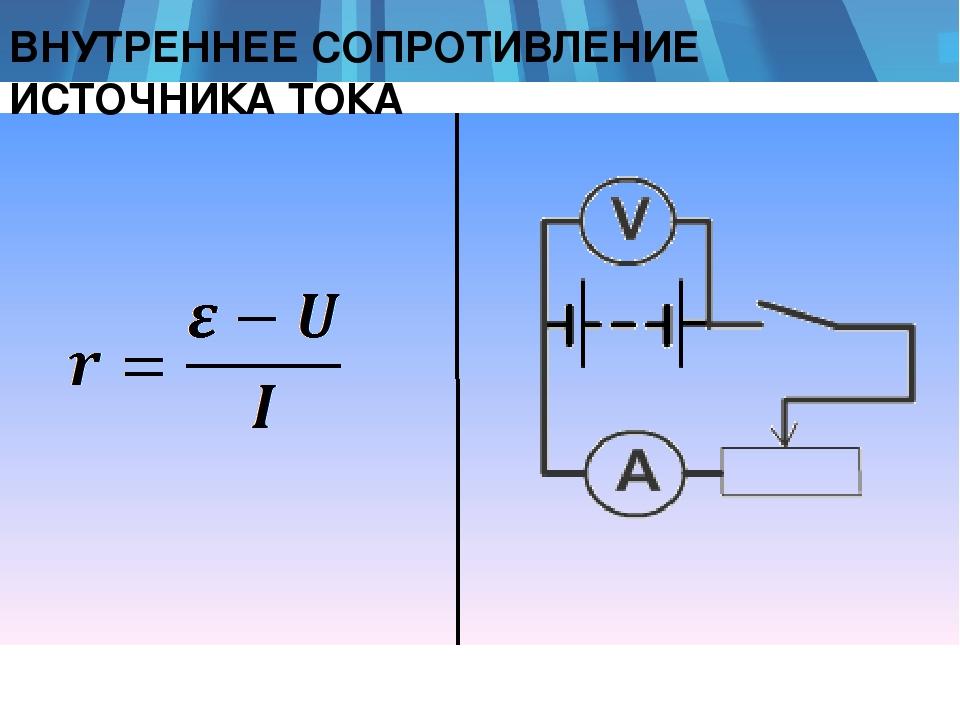
Внутреннее сопротивление источника тока
Малое внутреннее сопротивление
Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.
Реактивное внутреннее сопротивление
Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.
Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.
На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.
Большое внутреннее сопротивление
Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.
Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.
Внутреннее сопротивление и импеданс
Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.
Слагаемые полного сопротивления – импеданса
Двухполюсник и его эквивалентная схема
Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:
- цепи, содержащие источник тока или напряжения;
- двухполюсники, не являющиеся источниками.
Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.
Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.
Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.
Влияние внутреннего сопротивления на свойства двухполюсника
Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:
PR = E2/(r+R)2*R,
где:
- E – напряжение ЭДС;
- R – сопротивление нагрузки;
- r – активное внутреннее сопротивление двухполюсника.
Формула применима к двухполюсникам, не отдающим энергию.
К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.
Разрядная емкость источника
Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.
Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Разрядная ёмкость автомобильного аккумулятора
Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.
Видео
amperof.ru
Закон Ома для полной цепи
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название “закон Ома для полной цепи”

где
Е – ЭДС источника питания, В
R – сопротивление всех внешних элементов в цепи, Ом
I – сила ток в цепи, А
r – внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Резюме
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
www.ruselectronic.com
Формула связи между ЭДС (электродвижущей силой) и напряжением.
В задачах на электрический ток в качестве дано или найти присутствуют напряжение и ЭДС (электродвижущая сила). Есть достаточно простая связь между этими параметрами. Введём любую цепь (рис. 1).

Рис. 1. Связь между ЭДС и напряжением
Пусть дан источник с ЭДС
, напряжение во внешней цепи . Внутреннее сопротивление источника — , а сопротивление внешней цепи — . В данной системе течёт электрический ток . Тогда: (1) (2)Логично предположить, что количество электронов, сгенерированных источником, равно количеству электронов, ушедших в цепь, тогда приравниваем (1) и (2):
Откуда:
(3)Соотношение (3) — связь между ЭДС и напряжением в полной цепи постоянного тока.
В условиях идеальной цепи (внутреннее сопротивление источника равно нулю
), ЭДС численно равно напряжению.Вывод: приведенные соотношения помогают в ряде задач, в которых даны параметры источника тока/напряжения, а необходимо найти силу тока или напряжения на каком-либо элементе цепи (резистор, катушка, лампа и т.д.), и наоборот.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
www.abitur.by


