Спектральная плотность шума: Загадка фликкер-шума разгадана / Хабр

Загадка фликкер-шума разгадана / Хабр

Известно, что дельта-функция обладает равномерным спектром. Определим её спектральную плотность мощности по частоте и по периоду.

Коэффициенты ряда Фурье в комплексной форме определяются по формуле:

где ω1 – основная частота.
Если s(t) является дельта-функцией, то все коэффициенты Ck будут принимать одно и то же значение, независимо от k, причём значение основной частоты может быть любым.

Но ничто не мешает использовать вместо последовательности целых чисел любую другую последовательность. Если взять, например, последовательность чисел, обратную целым:

то формула (В.1) примет вид

где T1 – основной период,
и будет получен дискретный спектр с равномерным шагом по периоду. В данном случае для дельта-функции значение коэффициентов Ck также принимает одно и то же значение, и значение периода основной гармоники также может быть любым.

Если перейти к непрерывным спектрам мощности по частоте и по периоду, то получим, что и тот и другой спектр мощности является независимым от своего аргумента функцией, что противоречит формуле (4).

Получается, что спектр мощности дельта-функции зависит от метода его определения.

Попробуем определить, какие значения частот и периодов вообще возможны. Частота и период могут принимать любое значение от 0 до бесконечности по двум причинам:
1) Ось времени непрерывна – частоту можно увеличивать в бесконечное число раз, соответственно период можно уменьшать в бесконечное число раз.
2) Ось времени бесконечна – частоту можно уменьшать в бесконечное число раз, соответственно период можно увеличивать в бесконечное число раз.

Определим сначала спектр ограниченной во времени периодически продолженной и дискретной во временной области дельта-функции. Затем устремим к нулю шаг дискретизации и к бесконечности период повторения дельта-функции, в результате получим непрерывный спектр дельта-функции.

Известно, что периодический во временной области сигнал обладает дискретным спектром. Спектр такого сигнала представляется в виде сетки частот, полученных умножением частоты, равной f0 = 1 / (период сигнала) на целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по частоте с одинаковыми амплитудами.

Известно, что дискретный во временной области сигнал обладает периодическим спектром. Никаких ограничений на возможные значения частот нет (кроме условия, что частота в спектре должна быть меньше частоты Найквиста для восстановления).

Рассмотрим периодические дискретные сигналы:
a) Если сигнал является дискретным, то он определён только в некоторых конкретных точках: tn = n * Δt, где n – целое число, Δt – шаг дискретизации.
b) Если сигнал является периодическим, то все его значения повторяются через период времени: s(t) = s(t + T), где T – период сигнала.

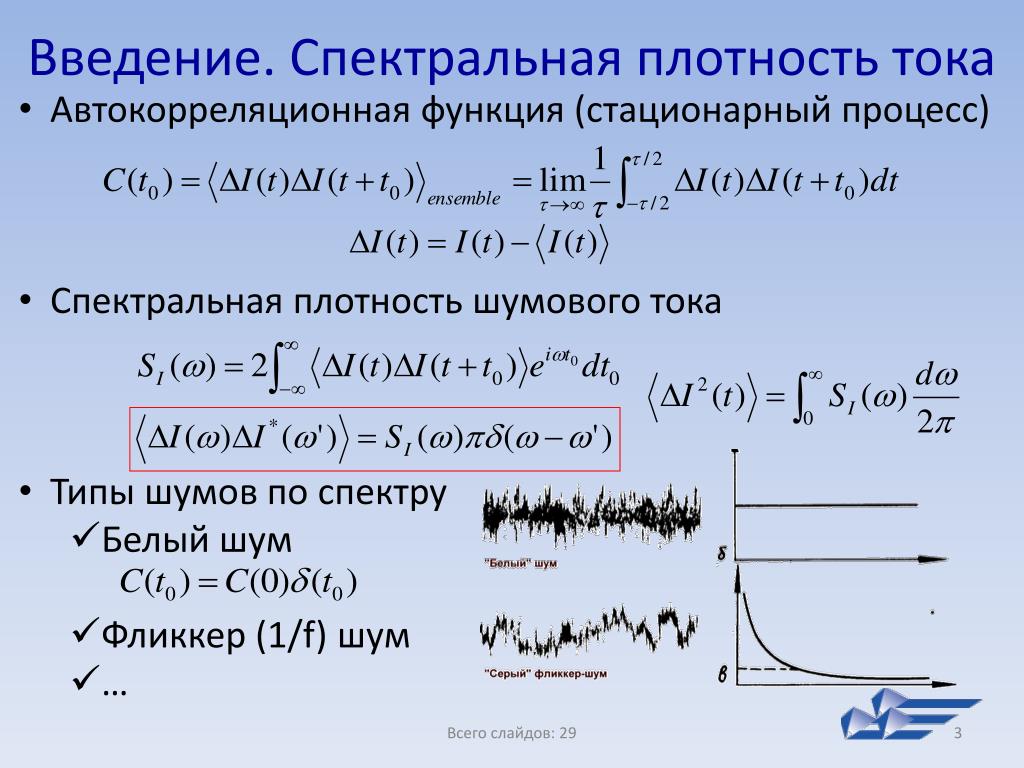c) Если сигнал является дискретным и периодическим, то все его значения повторяются через период времени, кратный шагу дискретизации s(tn) = s(tn + Td), где Td – период сигнала, являющийся суммой целого числа Δt. Это объясняется тем, что сигнал с периодом, состоящим из дробного числа Δt, через период не повторит своего значения, так как попадёт на несуществующее время. Получается, что ограничение на возможные значения частот всё же есть.

Например, если гармонический сигнал с частотой 1,5 Гц оцифровать с частотой дискретизации 10 Гц, то получается периодический сигнал с частотой 0,5 Гц.

Таким образом, дискретный во времени сигнал может быть периодическим только с периодом, кратным шагу дискретизации Δt, и спектр такого сигнала может состоять только из периодов Tn = n * Δt, где n – целое число. В случае дельта-функции получаем набор гармоник с равномерным шагом по периоду с одинаковыми амплитудами.

Теперь определим спектр ограниченной во времени периодически продолженной и дискретной во времени дельта-функции. Такой спектр может состоять только из частот fn, кратных f0 и периодов Tn, кратных Δt. Если какая-то из частот fn не совпадает ни с одной из 1/Tn, то это уже не частота fn, а какая-то другая из набора 1/Tn. Таким образом, если частотe fn не удаётся сопоставить ни один из периодов из набора Tn, то её следует удалить из набора fn, так как сигнал с такой частотой нереализуем при заданном шаге дискретизации. Если удалить из сетки частот все частоты, которым невозможно сопоставить период, то получаем новый неравномерный по частоте шаг, равный неравномерному шагу по периоду. Таким неравномерным шагом является равномерный шаг по логарифму частоты. Сигналом с равномерным по логарифму частоты спектром является фликкер-шум. Если устремить к нулю шаг дискретизации и к бесконечности период повторения дельта-функций, то получаем непрерывный спектр дельта-функции, совпадающий со спектром фликкер-шума.

4.4.2 Спектральная плотность мощности и корреляционная функция случайного процесса на выходе линейной цепи

Спектральная плотность мощности на выходе определяется аналогично тому, как это делалось при определении спектра выходного детерминированного сигнала.

Если входной сигнал обладает спектром мощности W_вх(w ), то на выходе сигнал будет иметь спектральную плотность мощности

W_вых (w )=W_вх(w ) H²(w ).

Корреляционную функцию определим как обратное преобразование Фурье

Аналогичные записи можно провести на основе знания импульсной характеристики цепи. Поскольку спектральной функции W_вх(w ) соответствует корреляционная функция

а спектральной функции H²(w ) соответствует

                    

то произведению W_вх(w ) H²(w ) соответствует свертка

                    

и

В случае белого шума на входе с W_вх(w )=W₀имеем W_вых(w )=  W₀H², а

                    

Это же выражение можно применить и для случая, когда спектральная плотность мощности случайного стационарного процесса на входе цепи равномерна лишь в полосе прозрачности цепи.

Лазерный опто-электронный автогенератор с малым уровнем спектральной плотности мощности фазового шума

Введение

Опто-электронный генератор (рис.1) или лазерный автогенератор (ЛАГ) с

волоконно-оптической линией задержки (ВОЛЗ) является перспективным источником

СВЧ и КВЧ колебаний. ЛАГ может использоваться в качестве задающего генератора в

устройствах радио- и оптических локационных комплексах, а также в системах

формирования и обработки оптических и электронных прецизионных сигналов, например,

с длительностью импульса порядка пикосекунды [1-7]. ЛАГ (или оптоэлектронный

автогенератор), выполненный на базе оптических микрорезонаторов [ 8 ] имеет малые

габариты, вес и стоимость. Экспериментальные результаты измерений спектральной

плотности фазовых шумов такого автогенератора, равные -147 Дб/Гц на частоте

генерации 10 ГГц при стандартной отстройке 1 кГц, позволяют заключить, что ЛАГ

конкурирует с малошумящими СВЧ генераторами с диэлектрическими резонаторами на

кристаллах сапфира на частотах генерации 8 – 70 ГГц [10].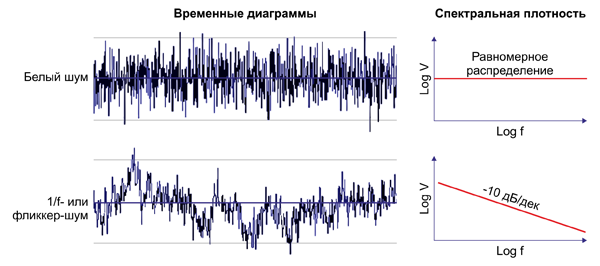 Разрабатываются методы

фазовой стабилизации автоколебаний ЛАГ [6,7] .

Для сравнения на рис.1, представлены нагруженные добротности резонаторов

традиционных автогенераторов и эквивалентная добротность волоконно-оптической

линии задержки (ВОЛЗ), применяемой в ЛАГ, а также размеры их резонаторов на рис.2,

и на рис.3 экспериментальные «рекордные» спектральные плотности мощности фазового

шума традиционных автогенераторов ЛАГ. На рис.1, рис.2 и рис.3 введены следующие

обозначения: 1-КР-кварцевый резонатор, 2-ПАВР- резонатор на поверхностных

акустических волнах, 3 ОбР-объемный резонатор электро-магнитных волн, 4- ДКР-

дисковый диэлектрический резонатор из керамических сплавах, 5- ДДРлС-дисковый

диэлектрический резонатор из лейкосапфира, 6 –ЖИГР-резонатор, 7-ВОЛЗ –волоконно-

оптическая линия задержки(50 мкс), 8- ОДР – оптический дисковый резонатор.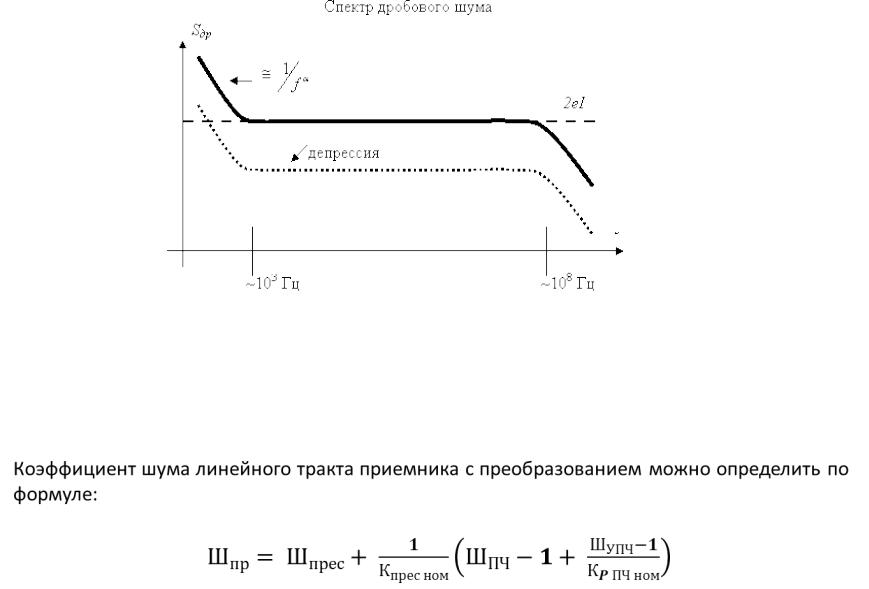 9-

ДДРстР – Дисковый диэлектрический специально стабилизированный резонатор , 10-

ФСК – фемто секундный синтезатор, на базе высоко стабилизированного лазера и

делителя частоты.

По типу механизмов задержки автоколебаний и аккумулирования энергии

резонаторы автогенераторов можно разделить на акустические (КР и ПАВР), электро-

магнитные (ЖИГР, ДКР, ОбР и ДДРлС [ 10 ]) и опто-электронные (ВОЛЗ и ОДР[ 3,8]).

Периодограммная оценка спектральной плотности мощности на основе бинарно-знакового стохастического квантования сигналов с использованием оконных функций

• Владимир Николаевич Якимов Самарский государственный технический университет

Аннотация

Спектральный анализ сигналов используется как один из основных методов исследования систем и объектов различной физической природы. В условиях статистической неопределенности сигналы подвергаются случайным изменениям и зашумлениям. Анализ таких сигналов приводит к необходимости оценивания спектральной плотности мощности (СПМ). На практике для её оценивания широко используется периодограммный метод. Основу цифровых алгоритмов, реализующих этот метод, составляет дискретное преобразование Фурье. В этих алгоритмах операции цифрового умножения являются массовыми операциями. Применение оконных функций ведет к увеличению числа этих операций. Операции умножения относятся к наиболее трудоемким операциям. Они являются доминирующим фактором при определении вычислительных возможностей алгоритма и определяют его мультипликативную сложность.

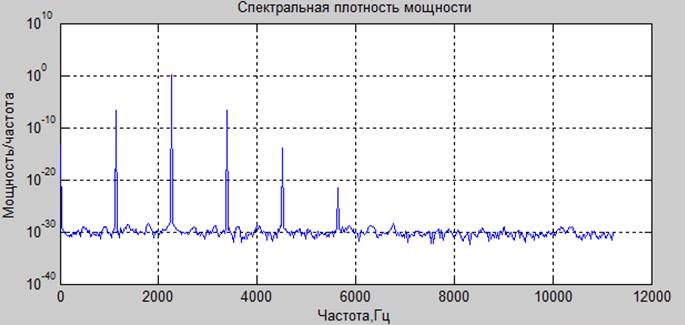
В статье рассматривается задача снижения мультипликативной сложности вычисления периодограммной оценки СПМ с применением оконных функций. Задача решается на основе использования бинарно-знакового стохастического квантования для преобразования сигнала в цифровую форму. Такое двухуровневое квантование сигналов осуществляется без систематической погрешности.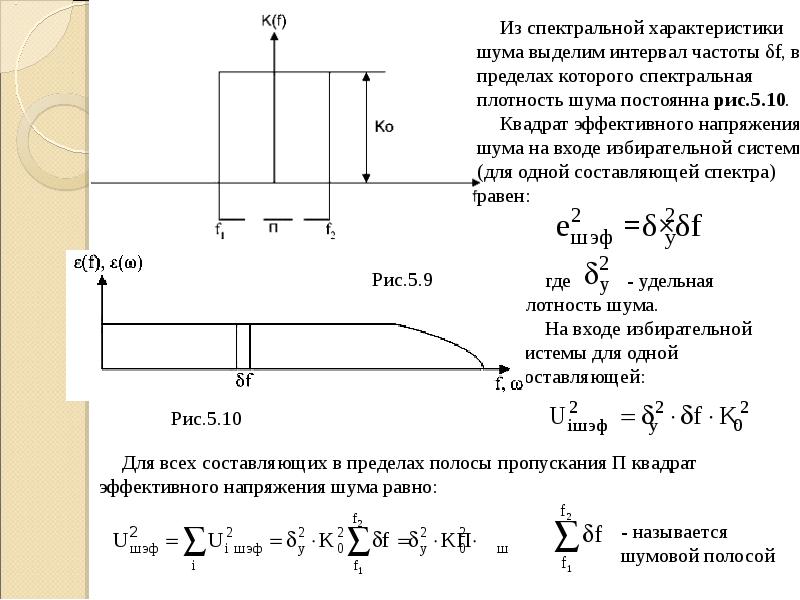

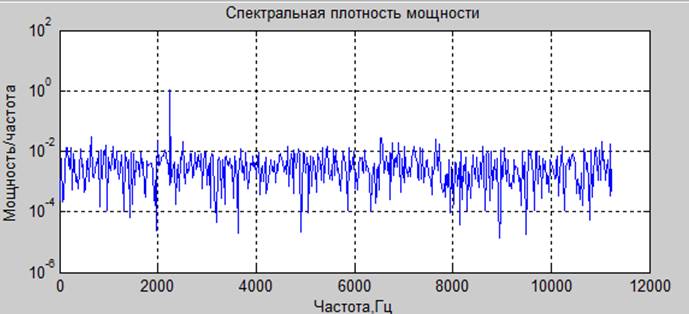На основе теории дискретно-событийного моделирования, результат бинарно-знакового стохастического квантования во времени рассматривается как хронологическая последовательность существенных событий, определяемых сменой его значений. Использование дискретно-событийной модели для результата бинарно-знакового стохастического квантования обеспечило аналитическое вычисление операций интегрирования при переходе от аналоговой формы периодограммной оценки СПМ к математическим процедурам ее вычисления в дискретном виде. Эти процедуры стали основой для разработки цифрового алгоритма. Основными вычислительными операциями алгоритма являются арифметические операции сложения и вычитания. Уменьшение количества операций умножения снижает общую вычислительную трудоемкость оценивания СПМ. С целью исследования работы алгоритма были проведены численные эксперименты. Они осуществлялись на основе имитационного моделирования дискретно-событийной процедуры бинарно-знакового стохастического квантования. В качестве примера приведены результаты вычисления оценок СПМ с применением ряда наиболее известных оконных функций. Полученные результаты свидетельствуют, что использование разработанного алгоритма позволяет вычислять периодограммные оценки СПМ с высокой точностью и частотным разрешением в условиях присутствия аддитивного белого шума при низком отношении сигнал/шум. Практическая реализация алгоритма осуществлена в виде функционально самостоятельного программного модуля. Данный модуль может использоваться как отдельный компонент в составе комплексного метрологически значимого программного обеспечения для оперативного анализа частотного состава сложных сигналов.

Литература

1. Шахтарин Б.И., Ковригин В.А. Методы спектрального оценивания случайных процессов // М.: Горячая линия-Телеком. 2011. 256 с.

2. Marple Jr.S.L. Digital Spectral Analysis with Applications: Second edition // Dover Publications Inc. 2019. 432 p.
3. Oppenheim A.V., Schafer R.W. Discrete-Time Signal Processing: Third edition // Pearson Higher Education. 2010. 1108 p.
4. Bendat J.S., Piersol A.G. Random Data: Analysis and Measurement Procedures. Fourth edition // Wiley. 2010. 621 p
5. Alessio S.M. Digital Signal Processing and Spectral Analysis for Scientists: Concepts and Applications // Springer. 2016. 900 p.
6. Stoica P., Moses R.L. Spectral Analysis of Signals // Pearson Prentice Hall. Upper Saddle River. 2005. 452 p.
7. Percival D.B., Walden A.T. Spectral Analysis for Univariate Time Series // Cambridge University Press. 2020. 692 p.
8. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.2. 8-изд. // М.: Физматлит. 2003. 864 с.
9. Oberguggenberger M., Ostermann A. Analysis for Computer Scientists Foundations, Methods and Algorithms // Springer. 2018. 378 p.
10. Ульянов М.В. Ресурсно-эффективные компьютерные алгоритмы. Разработка и анализ // М.: Физматлит. 2008. 304 с.
11. Kleinberg J., Tardos E. Algorithm Design // Pearson. 2006. 838 p.
12. Blahut R.E. Fast Algorithms for Signal Processing // Cambridge University Press. 2010. 453 p.
13. Bi G., Zeng Y. Transforms and Fast Algorithms for Signal Analysis and Representations // Birkhauser. 2004. 422 p.
14. Britanak V., Rao K.R. Cosine-/Sine-Modulated Filter Banks: General Properties, Fast Algorithms and Integer Approximations // Springer. 2018. 645 p.
15. Chu E. Discrete and Continuous Fourier Transforms: Analysis, Applications and Fast Algorithms // CRC Press, Taylor and Francis Group. 2008. 398 p.
16. Madisetti V.K. (editor-in-chief). The Digital Signal Processing Handbook, Second edition: Digital Signal Processing Fundamentals // CRC Press, Taylor and Francis Group. 2010. 904 p.
17. Stepanov A.A. Rose D.E. From Mathematics to Generic Programming // Addison-Wesley Professional. 2015. 292 p. 310.
18. Kester W. (Editor). Analog-Digital Conversion // Analog Devices. 2004. 1138 p.
19. Pelgrom M. Analog-to-Digital Conversion // Springer. 2017. 548 p.
20. Bhattacharyya S.S., Deprettere E.F., Leupers R., Takala J. (Eds.) Handbook of Signal Processing Systems // Springer. 2019. 1200 p.
21. Горбунов Ю.Н., Куликов Г.В., Шпак А.В. Радиолокация: стохастический подход / Под ред. Ю.Н. Горбунова // М.: Горячая линия-Телеком. 2016. 520 с.
22. Мирский Г.Я. Характеристики стохастической взаимосвязи и их измерения // М.: Энергоиздат. 1982. 320 с.
23. Max J. Methodes et techniques de traitement du signal et applications aux mesures physiques. Tome 1: Principes generaux et methodes classiques // Masson, Paris. 1996. 354 p.
24. Papadopoulos H.C., Wornell G.W., Oppenheim A.V. Sequential Signal Encoding From Noisy Measurements Using Quantizers with Dynamic Bias Control // IEEE Transactions on information theory. 2001. vol. 47. no. 3. pp. 978-1002.
25. Yakimov V.N. Direct Spectral Power Density Estimation from a Discrete-Time Representation of Stochastic Analog Quantization for an Analog Random Process // Measurement Techniques. 2009. vol. 52. no. 3. pp. 223-230.
26. Якимов В.Н. Цифровой комплексный статистический анализ на основе знакового представления случайных процессов // Известия самарского научного центра РАН. 2016. Т.18. №4(7). С. 1346-1353.
27. Isla J., Celga F. The Use of Binary Quantization for the Acquisition of Low SNR Ultrasonic Signals: a Study of the Input Dynamic Range // IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control. 2016. vol. 63. no. 9. pp. 1474-1482.
28. Zhai Q., Wang Y. Noise Effect on Signal Quantization in an Array of Binary Quantizers // Signal Processing. 2018. vol. 152. pp. 265-272.
29. Diao J.-D., Guo J., Sun C.-Y. Event-Triggered Identification of Fir Systems with Binary-Valued Output Observations // Automatica. 2018. vol. 98. pp. 95-102.
30. Law A.M. Simulation Modeling and Analysis: Fifth edition // McGraw-Hill Education. 2015. 804 p.
31. Zeigler B.P., Muzy A., Kofman E. Theory of Modeling and Simulation Discrete Event and Iterative System Computational Foundations // Academic Press. 2019. 667 p.
32. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т.1. 8-изд. // М.: Физматлит. 2003. 680 с.
33. Дворкович В.П., Дворкович А.В. Оконные функции для гармонического анализа сигналов. Изд. 2-е. // М.: Техносфера. 2016. 208 с.
34. Prabhu K.M.M. Window Functions and Their Applications in Signal Processing // CRC Press, Taylor and Francis Group. 2014. 382 p.
35. Poularikas A.D. The Handbook of Formulas and Tables for Signal Processing // CRC Press, IEEE Press. 1999. 838 p.
36. Allen R.L., Mills D.W. Signal Analysis: Time, Frequency, Scale, and Structure // Wiley-IEEE Press. 2004. 937 p.
37. Yakimov V.N., Zaberzhinskij B.E., Mashkov A.V. Bukanova Yu.V. Multi-threaded Approach to Software High-speed Algorithms for Spectral Analysis of Multi-component Signals // Proceedings of IEEE XXI International Conference on Complex Systems: Control and Modeling Problems (CSCMP). 2019. pp. 698-701.
38. Yakimov V. N., Gorbachev O.V. Firmware of the Amplitude Spectrum Evaluating System for Multicomponent Processes // Instruments and Experimental Techniques. 2013. vol. 56. no. 5. pp. 540-545.

Опубликован

2021-03-30

Статистика

Просмотры	243
Скачивания	185

Как цитировать

Якимов, В. Н. (2021). Периодограммная оценка спектральной плотности мощности на основе бинарно-знакового стохастического квантования сигналов с использованием оконных функций. Информатика и автоматизация, 20(2), 341-370. https://doi.org/10.15622/ia.2021.20.2.4

Другие форматы библиографических ссылок

Скачать ссылку

Раздел

Цифровые информационно-телекоммуникационные технологии

Copyright (c) Владимир Николаевич Якимов

Это произведение доступно по лицензии Creative Commons «Attribution» («Атрибуция») 4. 0 Всемирная.

Авторы, которые публикуются в данном журнале, соглашаются со следующими условиями: Авторы сохраняют за собой авторские права на работу и передают журналу право первой публикации вместе с работой, одновременно лицензируя ее на условиях Creative Commons Attribution License, которая позволяет другим распространять данную работу с обязательным указанием авторства данной работы и ссылкой на оригинальную публикацию в этом журнале. Авторы сохраняют право заключать отдельные, дополнительные контрактные соглашения на неэксклюзивное распространение версии работы, опубликованной этим журналом (например, разместить ее в университетском хранилище или опубликовать ее в книге), со ссылкой на оригинальную публикацию в этом журнале. Авторам разрешается размещать их работу в сети Интернет (например, в университетском хранилище или на их персональном веб-сайте) до и во время процесса рассмотрения ее данным журналом, так как это может привести к продуктивному обсуждению, а также к большему количеству ссылок на данную опубликованную работу (Смотри The Effect of Open Access).

Фазовые шумы КИПиА | Серния Инжиниринг

Что такое фазовый шум? 

Выходной сигнал реального источника отличается от идеальной синусоиды. Шумы оказывают влияние на амплитуду и мгновенную фазу сигнала, то есть такой сигнал на самом деле имеет амплитудную и фазовую шумовую модуляцию. Большинство современных генераторов сигналов, в том числе гетеродины приемников, работают в режиме насыщения, что позволяет пренебречь амплитудной составляющая шума, поскольку она обычно на 20 дБ ниже фазовой составляющей. По этой причине шум генератора называют фазовым шумом. 

Производители радиоэлектронной аппаратуры указывают значения фазового шума затем, чтобы охарактеризовать стабильность источника сигнала по частоте за короткие промежутки времени. В общем случае частотная стабильность показывает, насколько точно конкретный источник выдает одну и ту же выходную частоту в определенном временном интервале, и может быть как долгосрочной, так и кратковременной. Долгосрочная стабильность, как следует из названия, описывает изменение частоты источника в течение длительного интервала времени – обычно указывают отношение ухода частоты к ее номинальному значению за год. Кратковременная стабильность оценивается по изменению частоты сигнала за секунды. 

На осциллограмме фазовый шум проявляется в виде «дрожания» синусоидального колебания, что можно обнаружить по изменению точки пересечения сигналом нуля. Такое дрожание очень трудно обнаружить в случае применения современных генераторов с высокой стабильностью частоты, однако в частотной области фазовый шум все же заметен – в виде боковых полос около несущей частоты.

Фазовый шум обычно описывают в одной боковой полосе. Однополосный фазовый шум характеризуют относительной СПМ, под которой понимают отношение мощности шума в полосе 1 Гц при отстройке Δf от несущей к мощности на несущей частоте, в децибелах на герц (дБн/Гц или относительно сигнала – дБс/Гц). Спектральная плотность мощности является непрерывной функцией отстройки по частоте, и ее представляют в виде графика или указывают одно или несколько значений при конкретных значениях отстроек.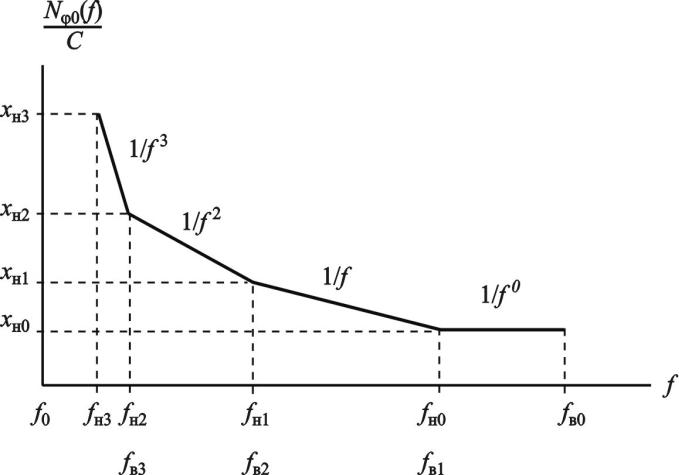   

Рис.1. Идеальный и реальный РЧ сигнал 

Типы шумов КИПиА

Существуют два типа шумовых сигналов — детерминированные и случайные. 

1. Детерминированные шумы – это дискретные сигналы в боковых полосах спектра. Эти сигналы точно соотносятся с определенными параметрами каждого конкретного источника сигнала, например, частота линии питания, частота вибрации, комбинационные продукты смешения. Уровень таких сигналов известен заранее и указывается в децибелах относительно уровня несущей. Детерминированные составляющие не относят к фазовому шуму, а учитывают только случайный шум. 

2. Случайные фазовые шумы складываются из теплового шума, дробового шума и фликкер-шума в полупроводниковых элементах.

• Тепловой шум возникает в резисторах и транзисторах. Такой шум имеет постоянную спектральную плотность мощности (СПМ) до нескольких сотен гигагерц и гауссовскую плотность распределения мгновенных значений.
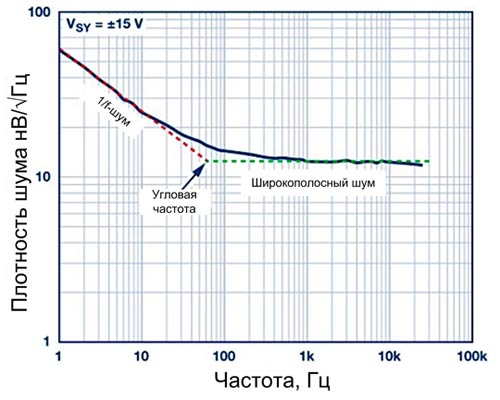
• Дробовый шум связан с током, протекающим через p-n переходы полупроводников. Сила тока зависит от величины заряда, проходящего через сечение проводящего элемента в секунду. Число частиц, несущих заряд, является величиной случайной. Поэтому появляются отклонения текущих значений тока от его среднего значения. Шумовой ток, протекая через сопротивление нагрузки, вызывает мгновенные изменения мощности – дробовый шум. Спектральная плотность мощности дробового шума плоская до нескольких гигагерц, а плотность распределения мгновенных значений – гауссовская.
• Фликкер-шум, или шум мерцания, связан с постоянным током и присутствует во всех активных и некоторых пассивных элементах. Фликкер-шум имеет спектральную плотность мощности, которая изменяется обратно пропорционально значению частоты.

Тепловой и дробовый шум являются основными составляющими фазового шума генератора при больших отстройках по частоте, фликкер-шум – при малых отстройках.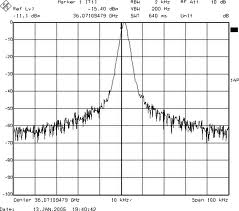  

Почему важен низкий фазовый шум? 

• В аналоговых системах связи полезная информация передается при помощи модуляции несущего сигнала. Частота модуляции, как правило, отличается от несущей частоты на нескольких сотен килогерц. При приеме несущая переносится на более высокую частоту при помощи конвертеров или смесителей. Если гетеродин в системе переноса частоты имеет плохую стабильность, то его фазовый шум будет ухудшать отношение сигнал-шум и может даже маскировать полезный сигнал. Такой гетеродин приведет к значительному уменьшению чувствительности и избирательности всей системы. 

• Доплеровские радиолокационные системы (РЛС) определяют расстояние до цели и скорость ее перемещения, измеряя изменения в частоте отраженного от цели сигнала. Однако на практике отраженный полезный сигнал часто поступает на радиолокационный приемник вместе с сигналом, отразившимся от земной поверхности. Причем отражения от земной поверхности имеют значительно большую амплитуду, чем полезный сигнал. Если гетеродин приемника имеет высокий фазовый шум, то сравнение исходного сигнала с принятым становится затруднительным, поскольку отраженный от поверхности земли сигнал скроет его. Уровень фазовых шумов гетеродина приемника определяет, таким образом, точность и возможности по обнаружению всей РЛС. 

  
  Рис. 2. Влияние шума на работу РЛС

• В цифровых системах передачи информации применяется фазовая манипуляция, и ухудшение отношения сигнал/шум за счет фазового шума гетеродина увеличивает вероятность ошибочного приема или не приема бита информации.  
• В радиопередающих устройствах фазовый шум также играет важную роль. Фазовый шум генератора передающего устройства усиливается вместе с полезным сигналом последующими каскадами и может оказывать значительное влияние на работу радиоприемных устройств, работающих поблизости. 

Выводы 

К аппаратуре, применяемой при разработке и отладке современных цифровых и аналоговых приемников и передатчиков, предъявляются довольно жесткие требования по фазовому шуму. В первую очередь это касается генераторов сигналов и анализаторов спектра. 

В современных анализаторах спектра гетеродины выполнены как синтезаторы частоты, синхронизированные высокоточным опорным сигналом через систему фазовой автоподстройки частоты (ФАПЧ). Полоса захвата системы ФАПЧ оказывает серьезное влияние на величину фазового шума. В анализаторах спектра эта полоса обычно является регулируемой, чтобы можно было адаптироваться к специфике задач измерений. Переключение режима часто происходит неявно, полоса системы ФАПЧ связывается или с анализируемым частотным диапазоном, или с выбранной полосой разрешения. Например, если требуется отображать большие частотные диапазоны, то важен минимальный фазовый шум вдали от несущей. Для таких задач автоматически выбирается узкая полоса захвата системы ФАПЧ. 

Для оптимального выбора параметров режима измерений в добавление к фазовому шуму при различных отстройках от несущей часто указываются рекомендуемые полосы разрешения или настройки диапазона качаний. Установка параметров, отличных от рекомендуемых, может привести к значительному увеличению уровня фазовых шумов. 

Сигнал любого источника содержит фазовый шум, который может быть более или менее четко определен. Выбирая соответствующий режим работы прибора, фазовый шум может быть минимизирован до определенного уровня, но никогда не может быть полностью исключен.

Корреляционная функция и спектральная плотность мощности шума

Корреляционная функция является детерминированной характеристикой случайного процесса (шума), которая связывает значение случайной величины (сигнала) x(t₁) в данный момент времени t₁ со значением этой величины (сигнала) x(t₂) в любой более поздний момент времени t₂= t₁ + t.

Важно заметить, что для стационарного случайного сигнала выбор конкретного значения момента времени t₁не имеет значения. Здесь имеет значение лишь значение t.

Корреляционная функция К(t) определяется как среднее значение произведения случайных величин в рассмотренные моменты времени: , где Т – время наблюдения.

Важно заметить, что для стационарного случайного процесса корреляционная функция зависит только от одного аргумента — временного интервала t.

Для одинаковых моментов времени t₁=t₂(t= 0) корреляционная функция, как это следует из формулы (1), с учетом того, что среднее значение <x(t)>=0, совпадает с дисперсией случайного процесса: .

В определœении функции К(t) фигурирует квадрат сигнала x(t). Квадраты сигналов пропорциональны интенсивности или мощности соответствующих физических величин.По этой причине корреляционная функция характеризует интенсивность случайного процесса.

Исследователœей интересует не только вопрос интенсивности флуктуаций, но и реакция приборов на эти флуктуации. Как известно, реакция прибора на любой сигнал может характеризоваться частотной характеристикой прибора, или его переходной характеристикой, или его импульсной характеристикой. Эти характеристики однозначно связаны между собой. Очевидно, что достаточно знать одну из них.

Внутренний шум, как правило, представляет собой хаотически изменяющийся сигнал, многократно изменяющий свою величину и (или) знак за время измерений. В этом смысле он напоминает периодический сигнал. По этой причине его взаимодействие с прибором удобно сравнивать с взаимодействием прибора с периодическим сигналом. Это взаимодействие, чаще всœего, описывают, используя понятия “частотная характеристика прибора” и “спектральная плотность сигнала”. Спектральная плотность сигнала находится с помощью преобразования Фурье. Зная частотную характеристику прибора и спектральную плотность сигнала на его входе , можно очень просто найти спектральную плотность сигнала на выходе прибора, умножив одну на другую: (см. рис.).

Далее, взяв обратное преобразование Фурье от функции , можно установить зависимость сигнала от времени на выходе прибора: .

В связи с этим можно ставить вопрос о спектральной плотности шумового сигнала. К сожалению, для случайных сигналов x(t). преобразование Фурье не существует, поскольку не существует интеграл . При этом, существует преобразование Фурье для квадратов случайных сигналов – x²(t). И поскольку квадраты сигналов пропорциональны мощности соответствующих физических величин, то можно говорить о спектральной плотности мощности соответствующих сигналов. Эту функцию будем обозначать как . В этом случае связь между спектральными плотностями мощности шумовых сигналов на выходе и входе прибора дается равенством .

Спектральная плотность S²(w) мощности шума тоже является детерминированной характеристикой случайного процесса и определяется как прямое преобразование Фурье корреляционной функции: . Используя обратное преобразование Фурье, отсюда можно выразить спектральную плотность шумового сигнала через спектральную плотность мощности: .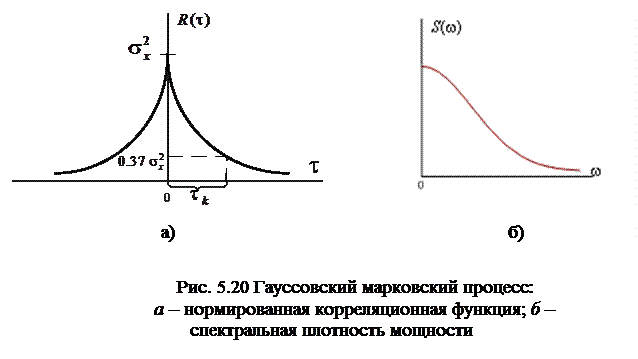 (5). Из предыдущих формул найдем: . Отсюда и из (2) следует очень важная формула, связывающая дисперсию случайной величины x со спектральной плотностью соответствующего случайного процесса:

.

Из этой формулы следует, что дисперсия шума является интегральной характеристикой интенсивности случайного процесса, усредненного по бесконечному частотному интервалу.

Замечание! Приведенная выше спектральная теория шумов годится не только для тепловых флуктуаций, но и для стационарных шумов любой природы.

Спектральная плотность шума

: новая метрика АЦП?

За последние десятилетия показатель производительности высокоскоростного аналого-цифрового преобразователя (АЦП), который имел большое значение, изменился, хотя и медленно, в результате постоянно растущих и ненасытных требований систем сбора данных к полосе пропускания. Изменился и способ измерения производительности АЦП.

В 1980-х годах мы оценивали АЦП в основном по его характеристикам постоянного тока, таким как дифференциальная и интегральная нелинейность (DNL и INL). В 1990-х годах мы в первую очередь оценивали АЦП по его отношению сигнал / шум (SNR). В то время как динамический диапазон без паразитных составляющих (SFDR) также является важным параметром АЦП, спектральная плотность шума (NSD) является еще одной всеобъемлющей характеристикой, которую современные высокоскоростные АЦП и АЦП с частотой гигасэмплов в секунду (GSPS) могут использовать для определения своих характеристик.

Хотя NSD долгое время использовался для определения шума преобразователя, он может быть новым для многих разработчиков систем как основная спецификация нового высокоскоростного АЦП.NSD также может быть совершенно чуждым понятием для некоторых инженеров, которые при выборе высокоскоростного АЦП сосредоточились на других спецификациях. Вот несколько ответов на типичные вопросы инженеров, которые помогают продемонстрировать, почему им следует больше узнать об этой метрике производительности АЦП:

Я и раньше видел спецификацию NSD в листе данных АЦП Найквиста, но никогда толком не понимал, что это значит и почему это важно.

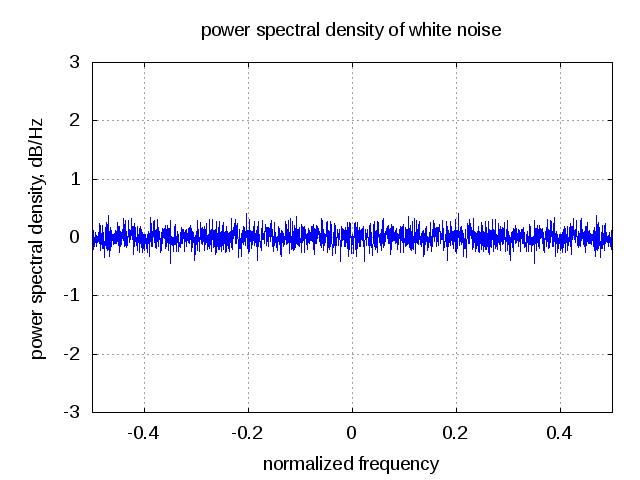Что такое спектральная плотность шума?

NSD в течение многих лет использовался в качестве параметра производительности на первых страницах многих технических паспортов АЦП.Вы могли заметить, что это относительно большое отрицательное число, определяемое либо в дБFS / Гц, либо в дБм / Гц. Типичный диапазон, который можно наблюдать в таблице данных для NSD АЦП, может быть где угодно от –140 дБ полной шкалы / Гц до –165 дБ полной шкалы / Гц. Однако это в конечном итоге определяется характеристиками SNR АЦП и частотой дискретизации, как будет описано далее в этой статье.

SNR от АЦП определяется как логарифмическое отношение мощности сигнала к общей несигнальной мощности, которая наблюдается на входе в АЦП.Относительно входа полной шкалы АЦП отношение сигнал / шум описывается как SNRFS. Есть несколько компонентов несигнальной мощности, таких как шум квантования, тепловой шум и небольшие ошибки в самой конструкции АЦП. Поскольку АЦП преобразует непрерывный сигнал в дискретные уровни с помощью нелинейного процесса, по своей сути создается шум квантования. Шум квантования – это разница между фактическим аналоговым входом, который обычно представлен синусоидой, и значением наименьшего дискретного шага или наименее значимого бита (LSB).

NSD определяет полную мощность шума на единицу полосы пропускания, дискретизированную на входе АЦП. Для АЦП с частотой дискретизации Найквиста этот шум распространяется по всей полосе частот Найквиста, которая равна половине fs, частоты дискретизации, или fs / 2.

Что обозначают единицы для НРД?

Термин дБFS / Гц означает, что шум определяется в единицах мощности (дБ) относительно полной шкалы АЦП, наблюдаемой в пределах диапазона частот 1 Гц. 1 Гц, спросите вы? Почему такой маленький? 1 Гц – это базовая единица ширины полосы шума, установленная для определения ширины интервала наблюдения по частоте, используемой для определения NSD.

Для абсолютной ссылки NSD может также определяться входной мощностью АЦП в абсолютных единицах дБм / Гц. В этом случае абсолютная полная входная мощность АЦП должна быть известна или измерена на основе входного напряжения и импеданса.

Как спецификация NSD помогает мне дифференцировать АЦП для использования в моей системе?

По мере удвоения частоты дискретизации АЦП с частотой дискретизации Найквиста плотность шума уменьшается соответственно на 3 дБ, поскольку он распространяется по более широкой полосе частот Найквиста.При 2-кратной частоте дискретизации такая же мощность входного шума теперь будет распределяться по удвоенной полосе пропускания, что увеличивает SNR. Это можно проверить, удвоив значение частоты дискретизации (fs) в следующей формуле, чтобы получить снижение на –3 дБ:

Поскольку частота дискретизации для высокоскоростных АЦП продолжает увеличиваться до диапазона ГГц, может быть достигнуто преимущество увеличения отношения сигнал / шум из-за передискретизации. При сравнении показателей производительности двух АЦП можно рассмотреть возможность выборки на более высокой частоте с учетом более низкой плотности шума.

Чем NSD отличается от минимального уровня шума моего быстрого преобразования Фурье (БПФ)?

Типичное БПФ берется с использованием десятков или сотен тысяч точек выборки – возможно, даже нескольких миллионов. Для большинства частот дискретизации АЦП это означает, что размер элемента дискретизации представляет собой диапазон в сотни Гц или несколько кГц. Размер ячейки БПФ определяется как спектр Найквиста (fs / 2), деленный на количество выборок БПФ с единицами частоты. Например, АЦП с 131 MSPS и 2 ¹⁶ (65.5 МГц) выборка БПФ имеет размер ячейки:

Итак, шум АЦП распространяется по зоне Найквиста с относительно большой шириной бина, которая в 1000 раз больше ширины бина, определенной в NSD. Это включает больше энергии шума в одном бине БПФ.

Для приведенного выше примера, если бы теперь для нашего АЦП с 131 MSPS использовалось очень большое 65,5 MS FFT, ширина бина была бы:

В этом случае минимальный уровень шума БПФ будет равен спектральной плотности шума АЦП, но общая мощность шума никогда не менялась.Такая же мощность шума распространяется только на более мелкие полосы частотных элементов, как показано на рисунке 1.

Рисунок 1. Шум квантования АЦП Найквиста и минимальный уровень шума БПФ в зоне Найквиста сравниваются по величине с его NSD. Шум БПФ на ячейку будет определяться количеством выборок, используемых в БПФ, в то время как NSD определяется с шириной полосы 1 Гц.

Сравните это с определением NSD, в котором единица шума имеет полосу пропускания или размер ячейки БПФ, равный 1 Гц. Теперь вы можете понять, почему типичный минимальный уровень шума БПФ почти всегда выше, чем спектральная плотность шума.Немногие инженеры используют в системе достаточно большой размер БПФ, чтобы получить ширину бина всего в 1 Гц. Вот почему кажется, что шум уменьшается, когда количество отсчетов в БПФ увеличивается.

Однако общий шум не меняется. Он все еще распространяется по тому же спектру Найквиста. Вместо использования приращений частотных интервалов, которые определяются размером выборки, определение NSD использует меньшие приращения частотных интервалов в 1 Гц, которые улавливают меньше энергии шума в одном интервале.

Как измеряется и рассчитывается НРД?

Для идеального АЦП:

Где N – разрешение АЦП, это определяет уровень шума квантования АЦП. Настоящий АЦП не сможет достичь этих показателей производительности, поскольку нелинейность его конструкции ограничит его практическое значение SNR ниже идеального. С другой стороны, если мы вычтем мощность сигнала из полной входной мощности АЦП, остальное будет просто полной мощностью шума. Если мы просуммируем все интервалы шума 1 Гц из нашего числа NSD, мы получим одно число шума мощности.

Чтобы определить значение NSD для АЦП с частотой Найквиста, необходимо вычислить, как шум распространяется по зоне Найквиста, и вычесть его из полной мощности сигнала.Для начала мы должны знать частоту дискретизации. Возьмем идеальный 12-разрядный АЦП с быстродействием 200 MSPS, который имеет идеальный сигнал полной шкалы:

Его шум распространяется по зоне Найквиста 100 МГц (fs / 2). Шум на интервал 1 Гц можно рассчитать с помощью функции журнала

.

Для этого 12-битного идеального преобразователя NSD будет:

Поскольку мы живем в неидеальном мире с неидеальными АЦП, мы должны найти фактическое SNRFS АЦП. Его можно измерить напрямую или извлечь из паспорта производителя.

Полномасштабный уровень мощности входного сигнала АЦП вычисляется с использованием известного полномасштабного пикового напряжения или полного среднеквадратичного напряжения и входного сопротивления АЦП. Мы можем вычислить полную мощность в дБм, если известны входное напряжение и входное сопротивление, где:

Для полной мощности сигнала в двм:

Какова форма спектра шума квантования АЦП? Всегда ли он плоский?

Рис. 2. Шум квантования АЦП с частотой Найквиста будет равномерным по всей полосе частот Найквиста.АЦП

с частотой Найквиста работают на минимальной частоте дискретизации, необходимой для захвата всей информации обо всей полосе пропускания входного сигнала. Большинство АЦП с частотой Найквиста, которые используют конвейер, регистр последовательного приближения (SAR) или тип флэш-памяти, будут иметь шум квантования, который по существу является плоским от постоянного тока до частоты Найквиста. Таким образом, они будут равноправными приемниками шума и будут принимать шум квантования конечной мощности одинаково по всему спектру fs / 2, как показано на рисунке 2.

Рисунок 3. Архитектура АЦП CTSD основана на петлевом фильтре и децимационном фильтре, которые формируют выходной шум.

Для приложений, в которых не требуется полная полоса пропускания Найквиста, могут быть реализованы альтернативные архитектуры АЦП. Полосовые АЦП с непрерывным временем Σ-Δ (CTΣΔ или CTSD) используют функцию формирования шума, которая по существу выталкивает или фильтрует шум внутриполосного квантования из интересующей полосы частот (рисунок 3). Это приводит к тому, что передаточная функция шума имеет неплоскую форму, которая имеет более низкий вырез в узкой интересующей полосе, меньшей, чем ширина полосы Найквиста.В этом диапазоне АЦП CTSD работает с максимальной производительностью, при которой SNRFS является самым высоким, что показано на рисунке 4.

Рисунок 4. Шум архитектуры CTSD ADC не будет плоским.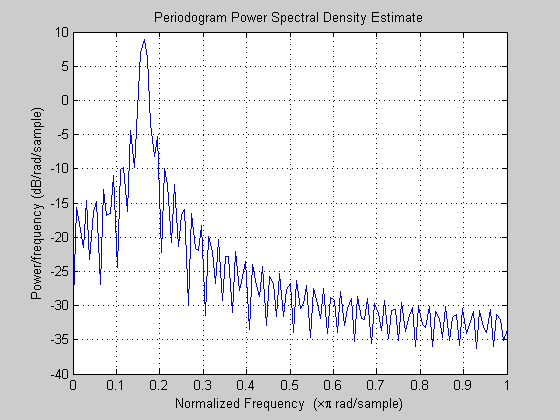 Он будет сформирован на основе отклика петлевого фильтра внутри модулятора, чтобы вытолкнуть шум за пределы интересующей полосы.

Поскольку одним из основных преимуществ архитектуры CTSD является ее способность обнаруживать сигналы в узкой полосе частот, широкополосный NSD не представляет особого интереса. Вместо этого динамический диапазон в узкой полосе пропускания будет выделен как показатель производительности АЦП CTSD.Передаточная функция формирования шума будет определяться на основе порядка петлевого фильтра, используемого в конструкции модулятора.

Как коэффициент усиления обработки АЦП влияет на плотность шума и SNR?

Существует несколько приложений, в которых интересующий первичный сигнал находится только в пределах небольшой полосы пропускания, которая намного меньше полной полосы пропускания Найквиста. В этом случае цифровая фильтрация может использоваться для фильтрации шума за пределами меньшей полосы пропускания. Эта обработка может быть выполнена с использованием каскада цифрового преобразования с понижением частоты для прореживания, настройки и фильтрации данных перед их выводом из АЦП Найквиста. Наш расчет SNR должен затем включать поправочный коэффициент для этой фильтрации, который учитывает выигрыш при обработке отфильтрованного шума, как показано на рисунке 5:

Рис. 5. Путем цифровой фильтрации выходного сигнала для наблюдения только за меньшим интересующим спектром BW может быть реализовано повышение выигрыша при обработке в отношении SNR, поскольку внеполосный шум теперь фильтруется.

Предположим, мы используем АЦП Найквиста с частотой дискретизации 100 MSPS, но нашему системному приложению не требуется соблюдать всю полосу Найквиста 50 МГц преобразователя.Вместо этого мы хотим наблюдать только меньшую, 1/8 Найквиста, в полосе пропускания 6,25 МГц, между 20 МГц и 26,25 МГц. Если мы реализуем алгоритм цифровой фильтрации и настроим фильтр на эту интересующую полосу пропускания, можно будет вычислить выигрыш при обработке в 9 дБ из-за передискретизации:

Для каждого уменьшения ширины полосы на степень двойки выигрыш обработки из-за фильтрованного шума увеличивается на 3 дБ.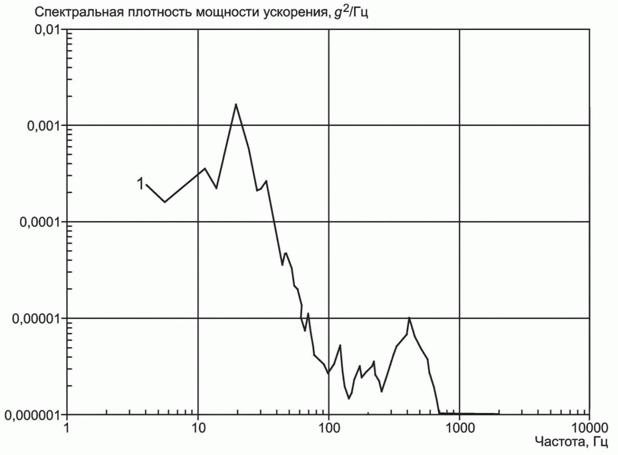 Это можно увидеть в приведенном выше примере с уменьшением полосы пропускания на 1/2 ³ , что дает выигрыш при обработке 3 дБ × 3 дБ.

Какие другие вспомогательные компоненты могут повлиять на производительность NSD ADC в моей системе?

Многие внешние факторы могут ухудшить производительность высокоскоростного АЦП. Это может привести к более низкому SNR и более высокой эффективной плотности шума. Любой дополнительный компонент, который влияет на SNRFS или частоту дискретизации ADC, может потенциально повлиять на его NSD в системе. Давайте сосредоточимся на джиттере тактового сигнала, который является одной из распространенных причин ухудшения отношения сигнал / шум для высоких частот дискретизации АЦП.

Высокоскоростные АЦП с высоким разрешением чувствительны к качеству входного тактового сигнала. Для достижения превосходного отношения сигнал / шум в высокоскоростном АЦП необходимо тщательно учитывать среднеквадратичное (среднеквадратичное) джиттер тактового сигнала, исходя из требований к входной частоте приложения. Среднеквадратичный джиттер тактового сигнала потенциально может ограничить отношение сигнал / шум даже самого высокопроизводительного АЦП, что усугубляется при более высоких входных частотах. Хотя это не изменит потенциал NSD АЦП, это ограничит его практические характеристики SNR в системе с высоким тактовым джиттером.

Поскольку аналоговая входная частота АЦП увеличивается втрое с использованием того же среднеквадратичного джиттера синхросигнала, наилучшее соотношение сигнал / шум снижается на 10 дБ. Ухудшение отношения сигнал / шум при заданной входной частоте (fA) только из-за дрожания апертуры (tJ) можно рассчитать по формуле:

Рисунок 6. Ограниченное ОСШ по тактовому джиттеру может быть нанесено на график в зависимости от частоты аналогового входа для различных профилей тактового джиттера.

На рисунке 6 показаны характеристики, ограниченные отношением сигнал / шум для различных входных частот в различных среднеквадратичных профилях джиттера синхросигнала в единицах фемтосекунд.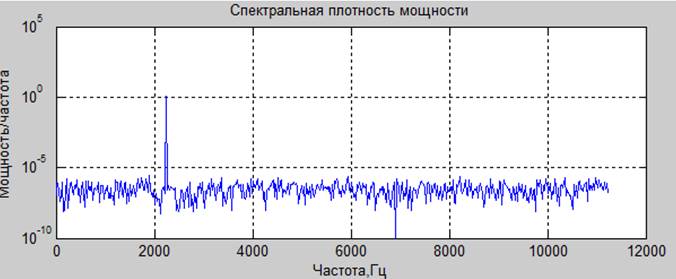 По мере увеличения входной частоты потребуется более низкий среднеквадратичный джиттер синхросигнала для достижения того же предела SNR, как это видно на более низких входных частотах. Например, среднеквадратичное значение джиттера тактового сигнала в 200 фемтосекунд ограничивает характеристику отношения сигнал / шум АЦП до уровня не выше 70 дБ на частоте 250 МГц. Однако для входного сигнала с частотой 1 ГГц потребуется среднеквадратичное значение джиттера тактовой частоты 50 фемтосекунд или лучше, чтобы достичь того же отношения сигнал / шум 70 дБ.

Спектральную плотность шума АЦП можно легко определить как полную мощность сигнала АЦП за вычетом мощности шума, распределенную по единице ширины полосы 1 Гц.Изменение глубины дискретизации БПФ не влияет на спектральную плотность шума АЦП. Он только распределяет шум по разным частотным полосам.

Форма шума может варьироваться в зависимости от архитектуры АЦП и от того, используется ли цифровая фильтрация для фильтрации внеполосного шума.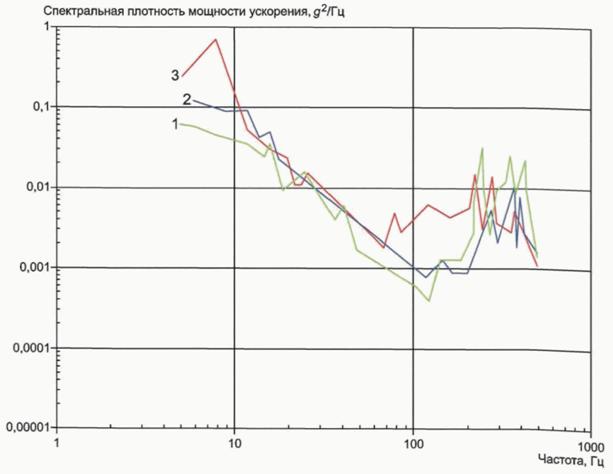 Выигрыш от обработки может увеличить динамический диапазон в пределах интересующей полосы пропускания для АЦП с частотой Найквиста, которые имеют гораздо более широкую полосу пропускания, чем требуется системе.

От спектральной плотности шума к среднеквадратичному шуму

Некоторые файлы cookie необходимы для безопасного входа в систему, но другие необязательны для функциональной деятельности.Сбор наших данных используется для улучшения наших продуктов и услуг. Мы рекомендуем вам принять наши файлы cookie, чтобы обеспечить максимальную производительность и функциональность нашего сайта. Для получения дополнительной информации вы можете просмотреть сведения о файлах cookie. Узнайте больше о нашей политике конфиденциальности.

Принять и продолжить Принять и продолжить

Файлы cookie, которые мы используем, можно разделить на следующие категории:

Строго необходимые файлы cookie:

Это файлы cookie, которые необходимы для работы аналога. com или предлагаемые конкретные функции. Они либо служат единственной цели передачи данных по сети, либо строго необходимы для предоставления онлайн-услуг, явно запрошенных вами.

Аналитические / рабочие файлы cookie:

Эти файлы cookie позволяют нам выполнять веб-аналитику или другие формы измерения аудитории, такие как распознавание и подсчет количества посетителей и наблюдение за тем, как посетители перемещаются по нашему веб-сайту. Это помогает нам улучшить работу веб-сайта, например, за счет того, что пользователи легко находят то, что ищут.

Функциональные файлы cookie:

Эти файлы cookie используются для распознавания вас, когда вы возвращаетесь на наш веб-сайт. Это позволяет нам персонализировать наш контент для вас, приветствовать вас по имени и запоминать ваши предпочтения (например, ваш выбор языка или региона). Потеря информации в этих файлах cookie может сделать наши службы менее функциональными, но не помешает работе веб-сайта.

Файлы cookie для таргетинга / профилирования:

Эти файлы cookie записывают ваше посещение нашего веб-сайта и / или использование вами услуг, страницы, которые вы посетили, и ссылки, по которым вы переходили.Мы будем использовать эту информацию, чтобы сделать веб-сайт и отображаемую на нем рекламу более соответствующими вашим интересам. Мы также можем передавать эту информацию третьим лицам с этой целью.

Отклонить файлы cookie

Spectral Noise – обзор

Введение

ACPR (коэффициент мощности соседнего канала), AltCPR (коэффициент мощности альтернативного канала) и шум являются важными показателями производительности для систем цифровой связи, которые используют, например, WCDMA (широкополосный множественный доступ с кодовым разделением каналов) модуляция.ACPR и AltCPR являются показателями спектрального возобновления роста. Мощность в несущей WCDMA измеряется с использованием полосы измерения 5 МГц; см. Рисунок 40.1. В случае ACPR общая мощность в полосе частот 3,84 МГц с центром на 5 МГц (разнос несущих) от центра самой удаленной несущей измеряется и сравнивается с мощностью несущей. Результат выражается в дБн. Для AltCPR процедура такая же, за исключением того, что мы центрируем измерение на 10 МГц от центра самой удаленной несущей.

Рисунок 40.1. Пределы ACPR WCDMA, согласно 3GPP TS 25.104, раздел 6.6.2.2.1

Для измерения ACPR и AltCPR см. Схему тестирования, показанную на рисунке 40.2. DUT (тестируемое устройство) – это LT5528, который представляет собой прямой I / Q-модулятор с высокой линейностью. Он принимает модуляцию WCDMA на входах основной полосы частот и генерирует модулированный сигнал WCDMA на выходе RF. Обратите внимание, что свободно работающий ВЧ-генератор обеспечивает сигнал гетеродина. Этот тип генератора используется из-за его превосходных шумовых характеристик.Это очень важно, поскольку зашумленный сигнал гетеродина может испортить выходной сигнал модулятора и, как следствие, измерение ACPR. Для показанного генератора автоматическая регулировка уровня должна быть отключена, чтобы избежать снижения его уровня широкополосного шума. Кроме того, рабочая частота может незначительно изменяться, поэтому может потребоваться ручная коррекция частоты.

Рисунок 40.2. ACPR Measurement Setup

Анализатор спектра должен иметь широкий динамический диапазон. Это означает высокую входную точку пересечения 3-го порядка и низкий уровень шума.Анализатор, показанный на рисунке 40.2, удовлетворяет обоим этим требованиям.

В общем, источник основной полосы частот не будет идеальным. Он генерирует спектральный рост и шум, которые могут снизить производительность тестируемого устройства. Фильтры нижних частот, показанные на выходах генератора модулирующих сигналов, снижают эти ухудшения до допустимого уровня. Предлагаемые для этой цели фильтры перечислены ниже:

•

1-канальное измерение ACPR Номер детали фильтра LE1182 2.5M-50-720B, от TTE Engineering Rejection на 2.6 МГц> 20 дБ Подавление на 3,08 МГц> 80 дБ

•

2-канальное измерение ACPR Номер фильтра LE1182 5M-50-720B, от TTE

Техническое подавление на 5,2 МГц> 20 дБ Подавление на 8,08 МГц> 80 дБ

•

4-канальное измерение ACPR Номер детали фильтра LE1182 10M-50-720B, от TTE Engineering Rejection на 10,4 МГц> 20 дБ Подавление на 13,08 МГц> 80 дБ

Точное измерение спектрального возобновления высоколинейного такое устройство, как LT5528, сложно, потому что его динамический диапазон может соперничать с диапазоном измерительного оборудования.По этой причине важно учитывать шум измерительной системы; т.е. анализатор спектра. См. Рисунок 40.3.

Рисунок 40.3. Спектр ACPR для сигнала WCDMA с одной несущей

Для этого сначала измерьте минимальный уровень шума анализатора спектра с входной нагрузкой 50 Ом. Входное ослабление анализатора должно быть установлено на 0 дБ. Это минимизирует входную точку пересечения 3-го порядка измерительной системы, а также коэффициент шума. Используется полоса разрешения 30 кГц, потому что показанный анализатор спектра имеет самый низкий коэффициент шума (около 24 дБ) при этой полосе разрешения.Этот анализатор спектра включает режим детектора отображения RMS, который специально разработан для измерения шумоподобных сигналов. Для анализаторов спектра, которые не предлагают этот режим, важно установить полосу пропускания видеосигнала, по крайней мере, в 3 раза превышающую полосу разрешения. В этом случае используйте полосу пропускания видео 100 кГц. Если отношение полосы пропускания видео к разрешению слишком низкое, измерение мощности будет неточным. Например, если соотношение составляет 1: 1, измеренная мощность может быть на 0,35 дБ ниже истинной мощности.Обратите внимание, что время развертки должно быть увеличено примерно в 10 раз, чтобы использовать большее количество выборок в этом режиме. Усреднение видео помогает сгладить результат; 100 средних значений дают хорошие результаты. Утилита мощности канала анализатора используется для определения полной мощности в полосе частот 3,84 МГц.

Затем измерьте выходной спектр тестируемого устройства, используя те же настройки. Для ACPR центрируйте полосу измерения на 5 МГц выше центра самой высокой несущей. Чтобы найти истинную спектральную мощность восстановления, преобразуйте измеренные уровни спектральной мощности в мВт и вычтите уровень шума анализатора спектра из измеренной мощности ИУ.Преобразуйте в дБм, чтобы получить истинный спектральный рост. Сделайте то же самое для полосы на 5 МГц ниже центра самой низкой несущей. Возьмите среднее значение двух значений дБн, чтобы получить среднее значение спектрального восстановления.

ACPR / AltCPR равно разнице в дБн между мощностью сигнала и спектральным восстановлением.

Показанный анализатор спектра также предлагает утилиту измерения ACPR. Однако эта утилита не даст точных результатов для высоколинейных устройств, так как не компенсирует минимальный уровень шума системы измерения.

Для измерения шума при отстройке 30 МГц испытательная установка изменена, как показано на рисунке 40.4. К выходу DUT добавлен настраиваемый полосовой фильтр. Этот фильтр должен быть настроен так, чтобы подавлять основной сигнал, но не ослаблять шум на 30 МГц выше крайнего канала. Измерения шума без использования этого метода фильтрации приведут к ухудшению результатов для сильных уровней радиочастотного сигнала. Причина в том, что динамического диапазона анализатора спектра недостаточно для приема мощности основного сигнала при точном измерении шума.Таким образом, основной сигнал будет иметь тенденцию к перегрузке входного высокочастотного интерфейса анализатора. Полосовой фильтр помогает уменьшить количество сигнала, достигающего анализатора, примерно на 20 дБ, добавляя при этом лишь около 1 дБ коэффициента шума к частоте измерения.

Рисунок 40.4. Установка для измерения шума со смещением 30 МГц

Продолжая это измерение, измерьте минимальный уровень шума анализатора спектра с входной нагрузкой 50 Ом. Можно использовать узкий диапазон 100 кГц при установке разрешения и полосы пропускания видео на 30 кГц.Входное ослабление анализатора должно быть установлено на 0 дБ. Здесь снова установите режим детектора на RMS. Используйте функцию шума маркера и усреднение видео, чтобы получить результат в дБм / Гц.

Затем подключите испытательную установку, как показано на рисунке 40.4. Измерьте шум на 30 МГц от центра частоты сигнала, используя те же настройки, что и выше. Чтобы найти истинный уровень шума, преобразуйте мощность шума и минимальный уровень шума в мВт и вычтите минимальный уровень шума анализатора спектра из выходной мощности шума ИУ.Преобразуйте в дБм / Гц, чтобы получить истинный уровень шума.

ACPR и AltCPR зависят от уровня выходного сигнала. Для низких уровней выходной мощности РЧ они ограничиваются минимальным уровнем выходного шума ИУ. При высоких уровнях выходной мощности РЧ они определяются линейностью ИУ. Максимальные ACPR / AltCPR наблюдаются между этими крайними значениями, где спектральный рост равен минимальному уровню шума DUT.

Некоторые примеры результатов этих измерений показаны, чтобы проиллюстрировать это на Рисунках 40.5 и 40.6. Рисунок 40.5 представляет собой график зависимости ACPR, AltCPR и шума от уровня возбуждения основной полосы частот для сигнала WCDMA с 4 несущими. На рисунке 40.6 показаны те же результаты для одной несущей WCDMA.

Рисунок 40.5. LT5528 4-канальный WCDMA смежный и альтернативный CPR и измерение минимального уровня шума 30 МГц в зависимости от мощности канала

Рисунок 40.6. LT5528 1-канальный WCDMA, соседний и альтернативный CPR и измерение минимального уровня шума 30 МГц в зависимости от мощности канала

Расчет отношения

сигнал-шум с использованием анализатора спектра

Уровень минимального шума, наблюдаемый на анализаторе спектра, частично зависит от выбранной полосы пропускания измерения.Чем шире полоса пропускания, тем больше шума измеряется для каждой точки данных. Если прибор может отображать плотность шума, он просто нормализует измерения мощности до полосы пропускания 1 Гц; отображаемая функция эквивалентна спектральной плотности мощности.

Если минимальный уровень шума изменяется при изменении полосы пропускания, это означает, что измеряется спектр мощности, то есть полная мощность в полосе разрешения в каждой частотной точке. Следовательно, уровень кажущегося шума будет изменяться с изменением разрешения по полосе пропускания независимо от того, измеряется ли шум тестируемого устройства или прибора.

Для всех измерений отношения сигнал / шум измерьте абсолютный уровень мощности сигнала с помощью маркера. Затем измерьте (или вычислите) мощность шума. Отношение сигнал / шум – это отношение этих двух показаний мощности (с учетом линейных единиц мощности, таких как ватты или милливатты). Чтобы выразить это в дБ, рассчитайте: 10 x log (S / N)

Иногда трудная часть этого измерения общей мощности шума в интересующей полосе пропускания.

Один из способов – измерить плотность шума, например, в милливаттах / Гц, в номинальной точке минимального уровня шума, а затем оценить общую мощность шума, умножив плотность шума на интересующую полосу пропускания.Обратите внимание, что результат в этом случае будет в единицах мощности милливатт.

Способ оценки плотности минимального шума состоит в том, чтобы измерить минимальный уровень шума с помощью маркера в линейных единицах мощности (например, милливаттах), а затем разделить это число на полосу разрешения. Опять же, чтобы оценить общую мощность шума, нужно будет умножить на общую интересующую полосу пропускания в Гц.

Способ оценки полной мощности шума в интересующей полосе пропускания в дБм состоит в том, чтобы добавить плотность мощности шума (мощность шума в полосе пропускания 1 Гц) к 10 x log (диапазон частот).

Короче говоря, отношения сигнал / шум действительно имеют значение только тогда, когда определена полная интересующая полоса пропускания.

Спектр и спектральная плотность БПФ – одинаковые данные, разное масштабирование

Анализ быстрого преобразования Фурье (БПФ), который преобразует сигналы из временной области в их эквивалент в частотной области, невероятно полезен при тестировании звука. Точные оценки многих основных показателей качества звука, таких как частота, уровень, гармонические искажения, интермодуляционные искажения, перекрестные помехи и т. Д., все можно получить из анализа БПФ. Фактически, все, кроме нескольких из сотен результатов, доступных в режиме последовательности в программном обеспечении APx500, получены из анализа БПФ.

Большинство пользователей знакомы с результатом FFT Spectrum, обычно используемым для анализа сигналов с дискретными частотными компонентами (например, синусоидальных волн). Но многие могут быть менее знакомы с результатами спектральной плотности мощности и амплитудной спектральной плотности, которые обычно используются при анализе шума. Этот пост объясняет разницу между этими результатами спектральной плотности и более часто используемым спектром БПФ.

FFT Spectrum
В целях иллюстрации на рисунке 1 показан сигнал, который содержит как дискретную частотную составляющую, так и относительно высокий уровень широкополосного шума. Шум создавался с помощью цифрового интерфейса с применением дизеринга с глубиной цвета всего 8 бит. Показаны результаты осциллографа (осциллограмма, слева) и спектра БПФ (справа) для этого синусоидального сигнала на частоте 1125 Гц с уровнем -20 дБ полной шкалы (или 0,10 полной шкалы).

Рис. 1. Форма волны и спектр БПФ 16k цифрового синусоидального сигнала 48 кГц Fs с 8-битным дизерингом (уровень = -20 дБFS; частота = 1125 Гц).

Результат спектра БПФ (иногда называемый линейным спектром или среднеквадратичным спектром) получается из автоматического спектра БПФ, при этом спектр масштабируется для представления среднеквадратичного уровня на каждой частоте. В результате спектр БПФ чистого синуса содержит пик на частоте синусоидального сигнала с амплитудой, равной его среднеквадратичному уровню. Например, пик в спектре БПФ на рисунке 1 в точности соответствует ожидаемому уровню сигнала -20 дБ полной шкалы. Спектр БПФ идеально подходит для анализа сигналов с дискретными компонентами или тонами.

Но что, если нас интересует количественная оценка уровня шума в этом сигнале? При случайном наблюдении за спектром на Рисунке 1 у нас может возникнуть соблазн сказать, что «минимальный уровень шума в этом измерении составляет -80 дБ полной шкалы» или «отношение сигнал / шум составляет 60 дБ». Но эти утверждения неверны из-за масштабирования спектра БПФ для чистых тонов. Это очевидно, если вы посмотрите на рисунок 2, на котором показан тот же сигнал, что и на рисунке 1, проанализированный с тремя различными настройками длины БПФ: 256, 16k и 1M точек.Обратите внимание, что пик остается на уровне -20 dBFS, но уровень плато кажущегося шума существенно снижается по мере увеличения количества элементов разрешения FFT.

Рис. 2. Линейные спектры БПФ сигнала на рис. 1 с длинами БПФ 256 (слева), 16k (в центре) и 1M выборок (справа). Обратите внимание на то, что амплитуда пика на частоте 1125 Гц постоянна, но уровень кажущегося плато шума уменьшается по мере увеличения длины БПФ.

Изменение уровня плато шума на Рисунке 2 является результатом изменения ширины интервала БПФ.Шум распределяется по всему частотному диапазону, поэтому чем шире интервалы БПФ, тем больше шума будет содержать каждый интервал. Фактически, каждый раз, когда ширина бина удваивается, мощность шума на бин также удваивается, что приводит к увеличению среднеквадратичного уровня на 3 дБ. При сглаживании, примененном к спектрам на рисунке 2, плато кажущегося шума составляет -62, -80 и -98 дБ полной шкалы для настроек длины БПФ 256, 16k и 1M, соответственно (т. Е. Изменение -18 дБ для каждого из два шага). Каждое увеличение длины БПФ с 256 до 16k и с 16k до 1M соответствует уменьшению ширины ячейки FFT в 64 раза, или в 2-6 раз.В результате среднеквадратичный уровень шума на ячейку уменьшается на 18 дБ (т. Е. На 6 x 3 дБ) в каждом случае.

Результаты спектральной плотности
Спектральная плотность мощности также выводится из автоспектра БПФ, но она масштабируется для правильного отображения плотности мощности шума (уровня в квадрате сигнала), эквивалентной мощности шума на каждой частоте измерено с фильтром шириной ровно 1 Гц. Он имеет единицы измерения V ² / Гц в аналоговой области и FS ² / Гц в цифровой области.

На рисунке 3 показаны результаты спектральной плотности мощности, соответствующие данным на рисунке 2. Обратите внимание, что плато кажущегося шума сигнала остается постоянным при изменении ширины бина БПФ, однако уровень дискретного пика на частоте 1125 Гц действительно изменяется с Длина БПФ. В этом случае утверждение о том, что «минимальный уровень шума в этом сигнале составляет приблизительно 1 нВ ² / Гц», является правильным.

Рисунок 3. Те же данные, что и на рисунке 3, выраженные в виде графиков спектральной плотности мощности.Обратите внимание на то, что плато шума является постоянным, но уровень пика увеличивается с увеличением длины БПФ.

Амплитуда спектральной плотности также используется для анализа шумовых сигналов. Он имеет единицы измерения В / √ Гц в аналоговой области и
FS / √ Гц в цифровой области. Спектральная плотность амплитуды – это просто квадратный корень из спектральной плотности мощности.

Окна БПФ и эквивалентная ширина полосы частот (ENBW)
При проведении анализа БПФ, как правило, оконная функция применяется к данным перед преобразованием Фурье, чтобы обеспечить необходимое условие, что сигнал является периодическим в пределах выбранного временного блока. .Существует много типов окон БПФ, и каждое из них имеет уникальные характеристики, которые предлагают определенные преимущества и недостатки, зависящие от приложения. Окно по умолчанию, используемое в программном обеспечении APx500, – это окно AP Equiripple. Среди других распространенных окон – окна Hann и Flat Top.

Следствием использования окна БПФ является то, что оно распределяет энергию сигнала из каждого бина БПФ на соседние бины, эффективно увеличивая ширину бина БПФ. Относительное увеличение ширины бина характеризуется свойством, известным как эквивалентная ширина полосы шума (ENBW).Каждое окно имеет определенный ENBW, который необходимо учитывать при масштабировании спектра БПФ. Например, ENBW окон AP Equiripple и Hann составляет 2,63 и 1,5 соответственно. Если окно не выбрано (иногда называемое прямоугольным окном), ENBW равно 1.0.

Спектр БПФ и спектральная плотность мощности связаны ENBW, как показано в уравнении (1).

Где PSD, представляет собой спектральную плотность мощности, S представляет среднеквадратичный (или линейный) спектр, j – это номер ячейки БПФ, а Δf – ширина ячейки БПФ.

Расчет уровня

Часто требуется рассчитать среднеквадратичный уровень шума в заданном диапазоне частот. Это может быть сделано путем интегрирования спектра БПФ или PSD между интересующими частотами. Другое общее требование – оценить среднеквадратичный уровень дискретной частотной составляющей, например гармоники. Как правило, это делается путем интегрирования БПФ по 3 ячейкам БПФ по обе стороны от ячейки, содержащей интересующую частоту, для учета эффекта расширения окна.Уравнения (2) и (3) могут использоваться для вычисления среднеквадратичного уровня из спектра БПФ и PSD, где каждое суммирование применяется по элементам разрешения БПФ, охватывающим интересующий частотный диапазон.

Преимущество использования PSD для этого вычисления (уравнение 3) состоит в том, что не требуется знать, какое окно FFT использовалось, поскольку ENBW встроен в масштабирование PSD.

Номер ссылки

Хайнцель, Г., Рюдигер, А., и Шиллинг, Р. (2002). Оценка спектра и спектральной плотности с помощью дискретного преобразования Фурье (ДПФ), включая исчерпывающий список оконных функций и несколько новых верхних окон.

Спектральная плотность мощности, объясненная энциклопедией RP Photonics; PSD, лазерный шум, анализаторы спектра, теорема Винера-Хинчина

В оптических технологиях и фотонике спектральные плотности мощности (также иногда называемые просто плотностями мощности) встречаются в основном в двух различных формах:

Далее обсуждаются оба типа величин. .

Когда спектральное распределение оптической мощности, например некоторого лазерного источника или другого источника света измеряется e.грамм. с анализатором оптического спектра (например, спектрографом) результат обычно выражается в виде некоторых спектральных величин. Например, можно указать лучистый поток на единицу оптической частоты или длины волны, который называется спектральным потоком . В других случаях указывается спектральная интенсивность (интенсивность излучения на единицу оптической частоты или длины волны) или некоторые другие спектральные величины. Все упомянутые величины являются величинами из области радиометрии; аналогичные спектральные величины используются и в фотометрии.

Спектральные величины излучения в принципе также можно интерпретировать как спектральные плотности мощности. В некоторых случаях они математически вычисляются как спектральная плотность мощности некоторой амплитуды, например с использованием статистических моделей. Во многих других случаях они вычисляются из общей оптической мощности в сочетании с известной спектральной формой или непосредственно измеряются, например с каким-то оптическим спектрометром.

Спектральные плотности оптической мощности также необходимы для визуализации e.грамм. формы импульсов со спектрограммами. В этом случае спектральные плотности мощности вычисляются для ограниченных интервалов времени путем применения преобразований Фурье к разделам данных, извлеченных с использованием некоторой оконной функции.

В случае мощности шума PSD всегда относится к усредненным уровням мощности, относящимся к интервалам шумовой частоты (а не оптической частоты). Такие PSD шума могут возникать в контексте любых оптических или электрических сигналов. Их можно использовать не только вместе с оптической мощностью (→ , интенсивность шума, ), но и e.грамм. для фазового шума, частотного шума, шума длительности импульса, энергии импульса или временного дрожания, например лазера с синхронизацией мод Точно так же PSD могут применяться к электрическим напряжениям или токам.

Рисунок 1: Спектр шумов интенсивности твердотельного лазера. Здесь отображается спектральная плотность мощности относительно дробового шума.

PSD могут быть определены через квадрат модуля преобразования Фурье интересующей величины, но прямой подход работает только для функций, которые имеют существенно ненулевые значения только в конечном интервале времени.Для часто встречающегося случая флуктуаций около долгосрочного среднего значения (например, в отношении флуктуаций мощности или фазы непрерывного лазера) такое определение, как

может использоваться для (двусторонней) PSD переменной X ( t ). Здесь интеграл ограничен конечным интервалом времени (таким образом достигается сходимость интеграла), а среднеквадратичный модуль преобразования Фурье делится на длину T временного интервала.Наконец, рассчитывается предел для больших интервалов времени T . Это определение концептуально понятно, но не всегда удобно (в особенности для аналитических расчетов). Поэтому обычно используется теорема Винера – Хинчина (или теорема Винера – Хинчина ), которая утверждает, что

где

– это автокорреляционная функция X ( t ).

В любом случае важно отметить, что спектральные плотности мощности являются статистическими показателями, которые можно оценить на основе реальных данных с помощью усреднения по результатам многих измерений.Выполнение единственной измерительной трассы дает лишь очень приблизительную оценку PSD.

Спектральные плотности мощности могут быть заданы как односторонних функций только положительных частот или как (в два раза меньше) двусторонних функций положительных и отрицательных частот. Плотности оптической мощности обычно односторонние и могут быть измерены, например, с анализатором оптического спектра. Шумовые PSD в основном односторонние в инженерных дисциплинах, но часто двусторонние в физике. Плотность мощности шума может быть измерена с помощью электронных анализаторов спектра или рассчитана на основе данных, записанных во временной области.Они указаны, например, в дБн / Гц (дБ относительно несущей в полосе пропускания 1 Гц) для шума относительной интенсивности или в рад ² / Гц для фазового шума. Иногда указываются квадратные корни из таких плотностей мощности с особыми единицами измерения, например рад на корень квадратный из герца.

Дисперсия величины (например, оптической фазы) в определенном диапазоне частот шума задается как интеграл по (односторонней) PSD:

Квадратный корень из такого значения является среднеквадратическим (r.м.с.) значение. Обратите внимание, однако, что такие интегралы не всегда сходятся (например, когда PSD имеет особенность при f = 0). В случае фазового шума такое расхождение связано с конечной шириной линии. Интегралы шума также часто используются для вычисления отношения сигнал / шум .

К сожалению, измерение или расчет спектральной плотности мощности подвержено множеству ошибок. Некоторые частые ошибки:

• путают односторонние и двусторонние PSD или неясно, какие из них используются
• неподходящие настройки электронных анализаторов спектра, e.грамм. о режиме детектора и методе усреднения
• Неспособность применить определенные поправочные коэффициенты (например, для эффективной ширины полосы шума) к данным, полученным с помощью электронных анализаторов спектра
• Невозможность удаления артефактов с помощью правильного управления окнами, когда PSD вычисляются из данных во временной области

Для правильной работы с спектральными плотностями мощности в лабораторных условиях требуется соответствующая подготовка по математическим основам, физическим эффектам и деталям электронного спектрального анализа.{\ alpha} \) (с \ (0.5 \ lesssim \ alpha \ lesssim 1.5 \)) поведение спектров мощности на низких частотах \ (f \) наблюдали в физике, технологии, биологии, астрофизике, геофизике, экономике, психологии. , язык и даже музыка (см. обзоры Press 1978, Hooge et al. 1981, Dutta and Horn 1981, Kogan 1985, Weissman 1988, West and Shlesinger 1990, Van Vliet 1991, Жигальский 1997, Milotti 2002 и Wong 2003).

Введение

Шум

\ (1 / f \) является промежуточным звеном между хорошо изученным белым шумом без корреляции во времени и шумом случайного блуждания (броуновское движение) без корреляции между приращениями.Броуновское движение является интегралом белого шума, и интегрирование сигнала увеличивает показатель \ (\ alpha \) на 2, тогда как обратная операция дифференцирования уменьшает его на 2. Следовательно, \ (1 / f \) шум не может быть получен простой процедурой интегрирования или дифференцирования таких удобных сигналов. Более того, не существует простых, даже линейных стохастических дифференциальных уравнений, генерирующих сигналы с шумом \ (1 / f \). Широкое распространение сигналов, демонстрирующих такое поведение, предполагает, что может существовать общее математическое объяснение.Однако, за исключением некоторых формальных математических описаний, таких как дробное броуновское движение , (половинный интеграл сигнала белого шума), общепризнанного физического объяснения шума \ (1 / f \) предложено не было. Следовательно, повсеместное распространение шума \ (1 / f \) – одна из самых старых загадок современной физики и науки в целом.

Случай \ (\ alpha = 1 \, \) или розовый шум является каноническим случаем, и наиболее интересная, но более общая форма, где \ (0 <\ alpha \ leq 3 \, \) иногда обозначается просто как \ (1 / f \.\ alpha \) шум представляет интерес, потому что он встречается во многих различных системах, как в мире природы, так и в искусственных процессах.

Выражение «зависимость на больших расстояниях», иногда используемое для обозначения шума \ (1 / f \), также использовалось в различных контекстах с несколько другими значениями. Так же иногда используются «долгая память» и другие варианты. Например, Вагенмакерс, Фаррелл и Ратклифф (2004) использовали выражения «дальнодействующая зависимость» и \ (1 / f \) шум как синонимы.С другой стороны, в статье Грейнджера и Динга (1988) некоторые модели длинной памяти изучаются в окрестности \ (f = 0 \. \). Но наборы данных конечны, и сколь угодно малые \ (f \) не могут быть реализованным. По этой причине мы ограничиваем наше обсуждение поведением вне окрестности \ (f = 0 \. \)

Часто открытие шума \ (1 / f \) в системе подразумевает существование какой-то другой специальной структуры, такой как самоорганизованная критичность или мультипликативный шум. Этот вывод необоснован, поскольку наше обсуждение различных моделей и их контекстов станет ясным.{\ alpha} \) спектр мощности – прямая линия, наклон которой \ (- \ alpha \, \) легко оценить. Ясно, что для таких природных систем, наблюдаемых людьми, нельзя зарегистрировать ни сколь угодно малые, ни сколь угодно большие частоты. Далее мы опишем выборку моделей, относящихся к таким физически вероятным ситуациям.

Рисунок 1: Слева: цветовая кодировка временных рядов различных шумов. Справа: соответствующие спектры мощности шумов. 2} & \ textrm {if} \ 0 \ ll \ lambda_1 \ ll \ lambda_2 \ ll f \ end {array} \ right.\. \]

Другими словами, \ (S (f) \) пропорционален \ (1 / f \) для \ (\ lambda_1 \ ll f \ ll \ lambda_2 \. \). Несколько позже Маквортер (1957) разработал более сложный модель, в которой шум приписывался захвату и удалению поверхностных состояний.

В отход от предыдущих теорий, которые подчеркивали физические свойства, Белл (1960) предположил, что такой шум является кооперативным явлением, возникающим из статистики очереди электронов, протекающих по проводу.Согласно теории Белла, электроны, текущие в проводе, случайным образом колеблются между связанным и возбужденным состояниями, выстраиваясь в очередь для доступа к узлам на атомах провода. Распределение вероятностей времени ожидания в очереди для зоны проводимости возбужденных свободных электронов, текущих по проводу, представляет собой суперпозицию экспоненциальных распределений с приблизительно равным весом их широко меняющихся постоянных времени, что приводит к уравнению, приведенному выше для спектральной плотности мощности. Белл (1960) также показал, что различные отклонения спектров мощности от \ (1 / f \, \), в частности, зависимость наклона спектра мощности от конкретного проводника или полупроводника, могут быть объяснены вариациями того, как суммирование возникает или в пределах, в которых это происходит.

Рисунок 2: Примеры шумов \ (1 / f \). Кривые являются иллюстративными на основе данных из указанных источников. Смежные пары отметок на горизонтальной оси под каждым числом указывают одну декаду частоты.

Примеры 1 / f-шума

1 / f шум в твердых телах, конденсированных средах и электронных устройствах

Низкочастотный шум или фликкер-шум был обнаружен во многих системах и стал горячей темой исследований на протяжении более восьми десятилетий. Большинство исследований шума \ (1 / f \) проводилось на резисторах, операционных усилителях или другом электронном оборудовании и системах (http: // www.nslij-genetics.org/wli/1fnoise/index.html). Для электронной системы легче производить образцы с различным шумовым поведением с помощью различных процессов производства или различных условий измерения, таких как температура, напряжение, смещение и т. 2} = \ frac {\ alpha _H} {N_Cf}, \]

где \ (\ alpha _H \) – безразмерная постоянная (параметр Хуге), а \ (N_C \) – количество носителей заряда в проводнике.Хотя эта формулировка оказала влияние и дает полезное приближение к спектру мощности электрического шума во многих материалах, Вайсман (1988) рассмотрел доказательства и аргументы, что она и связанные с ней формулировки не могут привести к правильной общей теории \ (1 / е \) шум. Это связано с тем, что в подходе Хоуге флуктуации связаны с независимыми подвижными носителями заряда, которые не сохраняются в образце материала достаточно долго, чтобы генерировать низкочастотный конец спектра мощности \ (1 / f \).{-6.3} \) Гц (рисунок 2B). Для этого требовалось регистрировать напряжение в течение 3 месяцев, а не 2,5 года, которое можно было бы снизить с помощью различных хитроумных устройств. Он также значительно усовершенствовал процесс вычисления спектра мощности для таких шумов и предложил модель шума \ (1 / f \), аналогичную модели Маквортера (1957).

Самоорганизованная критичность

«Самоорганизованная критичность» относится к явлению, при котором диссипативная динамическая система со многими степенями свободы работает вблизи конфигурации с минимальной стабильностью, критической конфигурации, и делает это без какой-либо точной настройки под воздействием внешнего управляющего воздействия.{1+ \ gamma} \ приблизительно s \]

где \ (\ gamma \) – скорость, с которой событие распространяется по системе. Было обнаружено, что эта конкретная модель и многие из ее последователей имеют некоторые тонкие несоответствия, включая путаницу между параметрами порядка и управления, и был разработан более общий подход среднего поля, который исправил большинство этих несоответствий (Vespignani & Zapperi , 1998). Важно отметить, что настоящие, почти одномерные “кучи” рисовых зерен действительно демонстрируют шум \ (1 / f \) (Maslov, Tang & Zhang, 1999).Более того, непрерывная диссипативная версия модели Бака, Танга и Визенфельда (1987) с направленным распространением возмущений ясно демонстрирует шум \ (1 / f \) как в 1-, так и в 2-мерной форме (De Los Rios & Zhang, 1999). {\ delta x } \) – характерное время, за которое энергия распространяется к узлу \ (x \) от начала решетки.Таким образом, в этой модели шум \ (1 / f \), характеризующий всю решетку, возникает в результате линейной суперпозиции (некоррелированных) спектров мощности независимых элементов, которые, в свою очередь, состоят из экспонент с диапазоном значений параметров, которые зависят от их расположение в решетке, как и в более ранних моделях, описанных выше.

Сердце бьется и покачивается

Один из мостов между неживыми и живыми системами – это наличие розового шума в обеих. Несколько примеров розового шума в живых системах представлены Musha (1981).Временной ряд, состоящий из интервалов между последовательными пиками R (отражающими мышечные сокращения) электрокардиограммы человеческого сердца, имеет спектр мощности приблизительно \ (1 / f \); Наклон логарифмического графика на Рисунке 2C составляет около 1,075 для нескольких десятилетий частоты. Муша (1981) также сообщил об исследовании покачивания человека, стоящего на платформе. Спектральная плотность мощности была приблизительно \ (1 / f \) для частот ниже 1 Гц, а \ (\ alpha \) была немного больше 1 для более высоких частот.Муша правильно считал, что спектр мощности \ (1 / f \) связан с механизмом контроля позы (Lauk, et al. 1998).

1 / f шум в головном мозге

Среди живых систем, производящих шум \ (1 / f \), есть мозг. В некоторых исследованиях «шум канала» в нейронах, который, как считается, возникает из-за случайного открытия и закрытия ионных каналов в клеточной мембране, рассматривается как \ (1 / f \. \). Одним из возможных механизмов этого является: модель колебания углеводородных цепей в липидах клеточной мембраны, которая влияет на проводимость ионов калия (Lundström and McQueen 1974).Муша (1981) показал, что ряд флуктуаций плотности времени (обратной скорости передачи) потенциалов действия, движущихся вниз по аксону гигантского кальмара, имеет спектр мощности примерно \ (1 / f \) ниже примерно 10 Гц (рис. 2D). . Новиков и др. (1997) обнаружили, что активность ансамблей нейронов в головном мозге, записанная у расслабленных людей с помощью магнитоэнцефалограммы, показывает спектр мощности \ (1 / f \) (рис. 2E). Спектр логарифма на рисунке 2E имеет наклон -1,03 в диапазоне 0.От 4 до 40 Гц. Записи электроэнцефалограммы также показывают шум \ (1 / f \) в головном мозге. Уорд (2002) описал неопубликованное исследование Макдональда и Уорда (1998), в котором серия больших связанных с событием потенциалов была вызвана 50-миллисекундной тональной вспышкой 1000 Гц с частотой 80 дБ от человека, сидящего в очень тихой ( 35 дБ фоновый шум) шумопоглощающее помещение. Спектр мощности серии, полученной путем выборки записи ЭЭГ в момент времени в период до стимула, и спектр мощности, полученный путем выборки записи ЭЭГ на пике самого раннего компонента потенциала, связанного с негативным событием, были приблизительно \ (1 / f \) (Рисунок 2F).

Аналогично, Linkenkaer-Hansen at el. (2001) показали, что как МЭГ, так и записи ЭЭГ спонтанной нервной активности у людей отображают \ (1 / f \) – подобные спектры мощности в \ (\ alpha \, \) \ (\ mu \, \) и \ (\ бета \) частотных диапазонов, хотя показатели степени, как правило, были несколько меньше 1 и различались в частотных диапазонах. Они предположили, что наблюдаемое ими степенное масштабирование возникло из-за самоорганизованной критичности, возникающей в нейронных сетях в мозгу. Однако возможно, что этот вывод необязательно обоснован.Одно недавнее исследование (Bedard et al., 2006) показало, что \ (1 / f \) масштабирование потенциалов локального поля мозга, по-видимому, не связано с критическими состояниями в одновременно регистрируемых нейронах активности, а скорее возникает из-за фильтрации нейронного сигнала через корковая ткань.

Фондовые рынки и ВНП

Шум

\ (1 / f \) в экономических данных обычно изучается как дальнодействующая зависимость или длинная память. Неоднократно было показано, что автокорреляционные функции экономических временных рядов, таких как ряды курсов акций за дни, недели или месяцы или ВНП различных стран за годы, не убывают экспоненциально, как если бы процесс, генерирующий ряды, был простой процесс авторегрессии (AR) (см. Baillie, 1996, для обзора длинной памяти в экономических данных).Вместо этого автокорреляционные функции многих экономических временных рядов достигают ненулевой асимптоты и остаются там на протяжении всего ряда, хотя часто и с низким значением, что указывает на то, что экономические события на некотором расстоянии в прошлом продолжают оказывать влияние на текущие цены или производство. . Такие процессы с длительной памятью обычно моделируются в экономике как процессы дробно-интегрированного белого шума в сочетании с процессами AR (параметр \ (p \)) и скользящего среднего (MA, параметр \ (q \)) для формирования ARFIMA (\ (p, d , q \)) модели, представленные Хоскингом (1981) как модели ARIMA (\ (p, d, q \)) (с интегрирующим параметром \ (d \) разрешено использовать действительное число вместо целого, как это есть в подходе Бокса-Дженкинса) и позже будет обсуждаться в разделе «Определение шума \ (1 / f \).«Но это не единственный возможный подход. Например, Грейнджер (1980) был первым, кто показал, что длинная память может быть результатом агрегации бесконечного числа процессов AR со случайными параметрами, а Грейнджер и Динг (1996) показали, что это может произойти для более реалистичных агрегаций конечного числа процессов AR. В разделе «Математика \ (1 / f \) шума» ниже есть дополнительная информация об агрегации процессов AR.

Модель мультипликативного точечного процесса (см. Раздел «Математика шума 1 / f») торговой активности, включая обобщения и расширения модели, объясняющие изменчивость долгосрочной памяти, была предложена Гонтисом и Каулакисом (2004, 2007). .

Музыка, восприятие времени, память и время реакции

Восс и Кларк (1975) показали, что спектр мощности для флуктуаций интенсивности в записи Бранденбургского концерта № 1 Баха (рис. 2G), а также во многих других случаях записанной музыки и человеческих голосов, слышимых по радио, был приблизительно равен \ ( 1 / f \) примерно за 3 декады частоты. Муша (1981) также резюмировал несколько своих собственных исследований, которые установили, что шум \ (1 / f \) в области пространственных частот характерен для некоторых мультфильмов и картин, и что чрескожное уменьшение боли более эффективно, когда применяется в соответствии с \ (1 / е \) последовательность.Гилден, Торнтон и Маллон (1995) сообщили о спектрах мощности примерно \ (1 / f \) для временных рядов, состоящих из ошибок, сделанных людьми при оценке различных временных интервалов (рис. 2H). Подобные спектры мощности также были обнаружены для времени реакции человека при выполнении задания на запоминание (Clayton & Frey, 1995), во многих других традиционных задачах, используемых в экспериментальной психологии (Gilden, 1997), в координации касания пальцем с метрономом (Chen, Ding & Kelso, 1997), и даже в простых реакциях обнаружения (Van Orden, Holden and Turvey, 2005).В психологических данных колебания зависимой переменной, которые не могут быть объяснены изменениями независимой (ых) переменной (ей), называются «ошибкой» в смысле остатков линейной регрессии. Обычно считается, что такая ошибка возникает из-за процесса белого шума. Gilden et al. (1995) смоделировали ошибки оценки времени линейной комбинацией шума \ (1 / f \) от внутренних часов и белого шума от моторного процесса, производящего нажатие клавиши. Гилден (1997) распространил эту модель на другие времена реакции и тем самым разделил необъяснимые флуктуации зависимой переменной или ошибку на две составляющие \ [1 / f \] и белый.Он обнаружил, что значительная часть остаточной ошибки составляет \ (1 / f \. \). Уорд и Ричард (описанные в Ward, 2002) смоделировали шумовую составляющую \ (1 / f \) путем объединения трех процессов AR (1). с различными параметрами и показали, что манипуляция нагрузкой принятия решения в задаче классификации, которая изменяет наклон спектра мощности, больше всего влияет на процесс со средним параметром.

Математика 1 / f-шума

Хотя \ (1 / f \) шум появляется во многих природных системах, как обобщено выше, и интенсивно изучается в течение десятилетий с многочисленными попытками описать это явление математически, исследователи до сих пор не смогли прийти к единому объяснению.{2 (1- \ beta)}}. \]

Когда \ (\ beta = 1/2 \, \), мы получаем \ (S (f) \ приблизительно1 / f \) (Lowen & Teich 2005).

Точечный процесс Пуассона кластеризации

Другой пример, основанный на точечном процессе Пуассона, – это кластеризация Пуассона. К каждой точке Пуассона \ (t_k \, \) присоединяется дополнительный набор точек, называемый кластером, который располагается после нее; кластеры могут перекрывать друг друга. Число точек в каждом кластере \ (m \, \) – это случайная величина, распределение которой \ (p_m \, \) сосредоточено на конечном наборе целых чисел.2 \) получаем \ (S (f) \ propto1 / f \) (Gruneis & Musha 1986). Несколько другая формулировка – это процесс стробирования, при котором кластеры не перекрываются. Здесь точечный процесс Пуассона умножается на процесс стробирования, который равен 1 на случайном интервале, затем 0 на случайном интервале и так далее. Чтобы получить шум \ (1 / f \), пусть интервалы 1 будут распределены экспоненциально, а интервалы 0 распределены геометрически, или наоборот. Затем примерно такие же вычисления, как только что обобщенные, дают приближение \ (1 / f \) (Gruneis 2001).Обратите внимание, что для процессов дробового шума, процессов кластера и стробирования, а также агрегации AR (1) вычисление спектральной плотности мощности дает сумму лоренцевых или лоренцевых функций.

Повторяющиеся модели

Недавно были предложены и обобщены модели точечных стохастических процессов шума \ (1 / f \) (Каулакис и Мешкаускас, 1998) (Каулакис и др., 2005). В этих моделях сигнал состоит из импульсов или событий.

\ [x (t) = a \ sum_k \ delta (t-t_k). \]

Здесь \ (\ delta (t) \) – дельта-функция Дирака, \ (\ {t_k \} \) – это набор моментов времени, когда частицы или импульсы пересекают сечение наблюдения, а \ (a \) – вклад в сигнал одного импульса или частицы.{\ mu} \ varepsilon _ {k}, \]

, где \ (\ epsilon_k \) – i.i.d. Гауссов шум, \ (\ gamma \) очень мал, и \ (\ sigma \, \) стандартное отклонение шума также мало, в то время как \ (\ mu \) представляет степень мультипликативности процесса. Частной формой модели является процесс AR (1)

\ [(\ tau_k – \ bar {\ tau}) = (1- \ gamma) (\ tau_k – \ bar {\ tau}) + \ sigma \ epsilon_k, \]

где \ (\ bar {\ tau} \) – среднее значение интервалов между событиями. 2 \) на длинном интервале, когда \ (\ gamma \) мало, и, следовательно, этот спектр мощности не такой, как у точечного процесса (чьи точки \ (t_k \) генерируют временной ряд) на этом интервале.2 & \ textrm {if} \ 1- \ theta_ {min} \ ll f \ ll 1 \ end {array} \ right. \. \]

(Эрланд и Гринвуд 2007). Также обратите внимание, что \ (S_m (f) \) является лоренцевой функцией.

Если коэффициенты \ (\ theta_m \) в процессах AR (1) равномерно распределены \ ((\ alpha = 1) \, \), можно получить хорошее приближение шума \ (1 / f \) просто путем усреднения индивидуальная серия. Это соответствует классическому результату о том, что спектр мощности однородной смеси экспоненциально убывающих автокорреляционных функций имеет форму \ (1 / f \) (Bell, 1960).\ alpha \, \) собирать или моделировать данные, относящиеся к модели, а затем оценивать параметр \ (\ alpha \) с помощью линейной регрессии или аналогичного метода (Pilgram & Kaplan, 1998) на основе логарифмически преобразованного спектра мощности данных. . Чаще всего физики (такие как Bell, 1960), биологи, инженеры, психологи и т. Д. Замечают, нанося спектр мощности на логарифмический график, что шум, производимый в конкретной экспериментальной ситуации, равен \ (1 / f \) – вроде. Затем они приступили, часто в отсутствие конкретной модели, к оценке \ (\ alpha \) с использованием линейной аппроксимации.Они также часто проверяют эту оценку против нулевой гипотезы \ (\ alpha = 0 \) или \ (\ alpha = 1 \. \)

Если кто-то имеет в виду конкретную модель, такую ​​как одна из описанных в предыдущем разделе, лучшей процедурой будет оценка параметров этой модели на основе собственных данных и определение того, подразумевают ли эти оценки \ (1 / f \) шум в контексте этой модели. Это может быть трудно выполнить из-за отсутствия соответствующей схемы оценки. Вагенмакерс, Фаррелл и Ратклифф (2004) предложили в контексте оценки наличия долгосрочной зависимости и / или шума \ (1 / f \) в психологических данных, что в отсутствие модели можно использовать схему, основанную на по оценке параметров модели, в которой свойство \ (1 / f \) возникает из-за дробно-разностного белого шума (Beran, 1994).Это модель ARFIMA (Hosking, 1981), где AR означает авторегрессивный процесс, MA означает процесс скользящего среднего, а FI означает частично интегрированный процесс белого шума. В схеме Wagenmakers et al. (2004) модель ARMA (1,1) тестируется против модели ARFIMA (1, \ (d \, \) 1), где \ (d \) – показатель степени оператора дробного разложения. Тест проводится с помощью процедуры, основанной на информационном критерии Акаике (AIC) (Akaike, 1974; Burnham, Anderson, 2002).k, \]

где \ (B \) – оператор обратного сдвига, определенный в последовательности \ (X_t \) как \ (BX_t = X_ {t-1} \, \), а \ (d \) – параметр дробной разности. Модель ARFIMA (1, \ (d \, \) 1) строится, сначала применяя оператор дробного разложения к шуму, \ (\ epsilon_t \, \), а затем используя полученный шум для построения процесса ARMA. Если \ (d \) может принимать только целые значения, у нас есть модель ARIMA, которая не отображает шум \ (1 / f \) для малых значений \ (p \) и \ (q \.{2d}}, \]

и если \ (0 \ le d \ le 1/2 \, \), то процесс называется стационарным с дальнодействующей зависимостью. Если \ (d = 1/2 \), то спектр мощности в точности равен \ (1 / f \. \). Процедура Wagenmakers et al. (2004) использует алгоритм Doornik and Ooms (2003) для оценки \ (\ hat {d}, \) \ (\ hat {\ theta_1}, \) и \ (\ hat {\ phi_1} \) для временного ряда и на основе этих оценок проверяет ARFIMA (1, \ (d \, \) 1) модель против модели ARMA (1,1). Считается, что предпочтение модели ARFIMA указывает на наличие дальнодействующей зависимости и шума \ (1 / f \) во временном ряду.\ alpha \) в связанном точечном процессе.

Существуют и другие подходы к описанию данных временных рядов способами, относящимися к шуму \ (1 / f \). К ним относятся анализ масштабированного диапазона (например, Chen, Ding & Kelso, 1997) и показатель Херста (например, Schroeder, 1991), которые оба включают оценку параметров, связанных с показателем степени спектра мощности, \ (\ alpha \. \) Например, для показателя Херста \ (H = (1+ \ alpha) / 2 \. \). Анализ данных временного ряда с нескольких точек зрения дает очевидные преимущества, но канонической процедуры пока не существует.

Список литературы

• Акаике Х. (1974) Новый взгляд на идентификацию статистической модели. IEEE Transactions on Automatic Control, 19: 716-723.
• Baillie R.T. (1996) Процессы с длительной памятью и дробная интеграция в эконометрике. J. Economet., 73: 5-59.
• Бак П. Тан К. Визенфельд К. (1987) Самоорганизованная критичность: объяснение шума 1 / f. Phys. Rev. Lett., 59: 381–384.
• Bedard C. Kroger H. Destexhe A. (2006) Отражает ли частотное масштабирование сигналов мозга 1 / f самоорганизованные критические состояния? Phys.Rev. Lett., 97: 118102.
• Белл Д.А. (1960) Электрический шум. Лондон: Ван Ностранд.
• Беран Дж. (1994). Статистика для процессов с длинной памятью. Нью-Йорк: Чепмен и Холл.
• Бернамонт Дж. (1937) Колебания потенциала, возникающие при металлическом проводнике, по объему, паркуру по номиналу. Анна. Phys. (Лейпциг), 7: 71-140.
• Бернхэм К. П. Андерсон Д. Р. (2002). Выбор модели и многомодельный вывод: практический теоретико-информационный подход.\ alpha \) type) в координации человека. Phys. Rev. Lett., 79: 4501-4504.
• Клейтон К. Фрей Б. (1997) Исследования ментального «шума». Нелин. Dynam. Psychol. Life Sci., 1: 173–180.
• Калояннидес М.А. (1974) Микроциклические спектральные оценки 1 / f-шума в полупроводниках. J. Appl. Phys., 45: 307–316.
• Де Лос Риос П. Чжан-И-К. (1999) Универсальный 1 / f-шум из моделей диссипативной самоорганизованной критичности. Phys. Rev. Lett., 82: 472-475.
• Дорник Я.А. и Оомс М.\ alpha \) шум от обратимых цепей Маркова. Phys. Ред. E, 76:
• Гилден Д.Л. (1997) Колебания времени, необходимого для принятия элементарных решений. Psychol. Sci., 8: 296-301.
• Гилден Д.Л. Торнтон Т. Мэллон М.В. (1995) 1 / f-шум в человеческом познании. Наука, 267: 1837-1839.
• Гонтис В. Каулакис Б. (2004) Мультипликативный точечный процесс как модель торговой деятельности. Physica A, 343: 505-514; конд-мат / 0303089.
• Гонтис В. Каулакис Б. (2007) Моделирование торговой активности с долговременной памятью с помощью стохастических дифференциальных уравнений.Physica A, 382 (1): 114-120; физика / 0608036.
• Granger C.W.J. (1980) Отношения с длительной памятью и агрегирование динамических моделей. J. Economet., 14: 227-238.
• Granger C.W.J. Дин З. (1996) Разновидности моделей с длинной памятью. J. Economet., 73: 61–77.
• Gruneis F. (2001) 1 / f-шум, перемежаемость и кластеризация Пуассоновский процесс. Fluct. Noise Lett., 1: R119 – R130.
• Gruneis F. Musha T. (1986) Кластерный процесс Пуассона и 1 / f-шум. Яп. J. Applied Phys., 25: 1504–1509.
• Hooge F. N. (1976) 1 / f шумы. Physica A&C, 83: 14-23.
• Hooge F. N., Kleinpenning T. G. M., Vandamme L. K. J. (1981) Экспериментальные исследования 1 / f-шума. Rep. Prog. Phys., 44: 479-532.
• Hooge F. N. (1994) 1 / f-источники шума. IEEE Trans. Электрон. Девич., 41: 1926-1935.
• Hosking J.R.M. (1981) Дробное разложение. Биометрика, 68: 165-176.
• Джонсон Дж. Б. (1925) Эффект Шоттки в низкочастотных цепях. Phys. Ред., 26: 71-85.
• Каулакис Б. Мешкаускас Т. (1998) Моделирование 1 / f-шума. Phys. Откровение E, 58: 7013-7019.
• Каулакис Б. Гонтис В. Алабурда М. (2005) Модель точечного процесса 1 / f-шума в сравнении с суммой лоренцевых. Phys. Rev. E, 71: 051105; конд-мат / 0504025.
• Каулакис Б. Русецкас Дж. Гонтис В. Алабурда М. (2006) Нелинейные стохастические модели 1 / f-шума и степенные распределения. Physica A, 365: 217-221; конд-мат / 0509626.
• Коган С. М. (1985) 1 / f-шум тока низкой частоты в твердых телах.Успехи физических наук, 145: 285-328; Сов. Phys. Усп. 28: 170.
• Лаук М. Чоу C.C. Павлик А.Э. Коллинз Дж. Дж. (1998) Человеческий баланс из равновесия: неравновесная статистическая механика в контроле позы. Phys. Rev. Lett., 80: 413-416.
• Линкенкаер-Хансен, К. Никулин, В.В. Palva, J.M. Ilmoniemi, R.J. (2001). Долгосрочные временные корреляции и масштабное поведение в колебаниях человеческого мозга. J. Neurosci., 21: 1370-1377.
• Lowen, B. & Teich, M.C. 2005 Точечные процессы, основанные на фрактале.Хобокен, Нью-Джерси: Уайли.
• Lundström I. McQueen D. (1974) Предложенный механизм шума 1 / f в мембранах нервных клеток. J. Теорет. Биол., 45: 405-409.
• Мандельброт Б. (1998) Мультифракталы и 1 / f-шум: дикая самоаффинность в физике. Нью-Йорк: Спрингер.
• Маслов С. Тан К. Чжан Ю.С. (1999) 1 / f-шум в моделях Бак-Танга-Визенфельда на узких полосах. Phys. Rev. Lett., 83: 2449–2452.
• McWhorter A. L. (1957) 1 / f-шум и свойства поверхности германия. В физике поверхности полупроводников, под редакцией Р.Х. Кингстон, Пенсильванский университет, Филадельфия, стр. 207-228.
• Милотти, Э. (2002) Педагогический обзор 1 / f-шума. Препринт Arxiv по физике / 0204033, 2002 – arxiv.org.
• Муша Т. (1981) 1 / ф колебания в биологических системах. В P.H.E. Мейер, Р.Д. Маунтин и Р.Дж. Сулен младший (ред.), Шестая международная конференция по шуму в физических системах (стр. 143–146). Вашингтон, округ Колумбия: Министерство торговли США и Национальное бюро стандартов.
• Новиков Е. Новиков А.Шаннахофф-Халса Д. Шварц Б. Райт Дж. (1997) Масштабная активность мозга. Phys. Ред. E, 56: R2387-R2389.
• Пилграм, Б. Каплан, Д.Т. (1998) Сравнение оценок для шума 1 / f. Physica D, 114: 108-122.
• Press W. H. 1978 Мерцающие шумы в астрономии и других местах. Комментарии о астрофизике, 7: 103-119.
• Schottky W. (1918) Über spontane Stromschwankungen in verschiedenen Elektrizitätsleitern. Анна. дер Phys., 57: 541-567.
• Шоттки В. (1926) Эффект мелкого выстрела и эффект мерцания.Phys. Rev., 28: 74-103.
• Шредер М. (1991) Фракталы, хаос, степенные законы: минуты из бесконечного рая. Нью-Йорк: Фриман.
• Ван Орден Г.Дж. Холден Дж. Турви М.Т. (2005) Человеческое познание и масштабирование 1 / f. J. Exper. Психол .: Быт., 132: 331-350.
• Ван Влит К. М. (1991) Обзор результатов и будущих перспектив квантового 1 / f-шума и 1 / f-шума в целом. Твердотельная электроника, 34: 1–21.
• Веспиньяни А. Заппери С. (1998) Как работает самоорганизованная критичность.\ alpha \) шум в человеческом познании. Психоном. Бык. Rev., 11: 579-615.
• Вайсман М. Б. (1988) 1 / f-шум и другая медленная неэкспоненциальная кинетика в конденсированных средах. Ред. Мод. Phys., 60: 537–571.
• Уорд Л.М. (2002) Динамическая когнитивная наука. Кембридж, Массачусетс: MIT Press.
• Вест Б. Дж. Шлезингер М.Ф. (1990) Шум в природных явлениях, American Scientist, 78: 40-45.
• Вонг Х. (2003) Исследование низкочастотного шума в электронных устройствах: обзор и обновление. Микроэлектрон.Достоверн., 43: 585-599.
• Жигальский Г. П. (1997) 1 / f-шум и нелинейные эффекты в тонких металлических пленках. Успехи физических наук, 167: 623-648; Phys. Усп., 40, 599.

Внутренние ссылки

• Ян А. Сандерс (2006) Усреднение. Академия наук, 1 (11): 1760.
• Валентино Брайтенберг (2007) Мозг. Академия наук, 2 (11): 2918.
• Ижикевич Евгений Михайлович (2006) Взрыв. Академия наук, 1 (3): 1300.
• Грегуар Николис и Катрин Рувас-Николис (2007) Сложные системы.Академия наук, 2 (11): 1473.
• Джеймс Мейсс (2007) Динамические системы. Scholarpedia, 2 (2): 1629.
• Пол Л. Нуньес и Рамеш Сринивасан (2007) Электроэнцефалограмма. Академия наук, 2 (2): 1348.
• Марк Аронофф (2007) Язык. Академия наук, 2 (5): 3175.
• Джефф Мохлис, Кресимир Йосич, Эрик Т. Ши-Браун (2006) Периодическая орбита. Академия наук, 1 (7): 1358.
• Филип Холмс и Эрик Т. Ши-Браун (2006) Стабильность. Scholarpedia, 1 (10): 1838.

Внешние ссылки

• 1 / f noise, Википедия [1]
• Розовый шум, Википедия [2]
• A Библиография по шуму 1 / f [3]
• Буквы флуктуации и шума (FNL) [4]
• Генерация DSP розового (1 / f) шума [5]
• Ассоциация науки, искусства и технологий колебаний: ASATeF [6]
• Вариация Аллана [7]
• Лаборатория надежности и контроля шума [8]
• Анализатор спектра с вейвлет-преобразованием в реальном времени для исследования шума 1 / f α [9]
• ОБЩАЯ БИБЛИОГРАФИЯ КВАНТОВОГО 1 / f ШУМА, стр.Х. Гендель [10]
• Труды Международной конференции по шуму в физических системах и 1 / f флуктуациям [11]

Рекомендуемая литература

• Беран Дж. (1994). Статистика для процессов с длинной памятью. Нью-Йорк: Чепмен и Холл.
• Hosking J.R.M. (1981) Дробное разложение. Биометрика, 68: 165-176.
• Мандельброт Б. (1998) Мультифракталы и 1 / f-шум: дикая самоаффинность в физике. Нью-Йорк: Спрингер.
• Милотти, Э.(2002) Педагогический обзор 1 / f-шума. Препринт arxiv по физике / 0204033, 2002 – arxiv.org
• Шредер М. (1991) Фракталы, хаос, степенные законы: минуты из бесконечного рая. Нью-Йорк: Фриман
• Уорд Л.М. (2002) Динамическая когнитивная наука. Кембридж, Массачусетс: MIT Press

См. Также

Хаос, фракталы, шум, куча песка, самоорганизованная критичность

.