Среднеквадратичное значение напряжения – , ,

Параметры переменного напряжения | Практическая электроника

Как вы помните из предыдущей статьи, переменное напряжение – это напряжение, которое меняется со временем. Оно может меняться с каким-то периодом, а может быть хаотичным. Но не стоит также забывать, что и переменное напряжение обладает своими особенными параметрами.

Среднее значение напряжения

Среднее значение переменного напряжения Uср – это, грубо говоря, площадь под осциллограммой относительно нуля за какой-то промежуток времени. Чтобы это понять, давайте рассмотрим вот такую осциллограмму.

среднее значение напряжения за период

Например,чему равняется среднее значение напряжения за эти два полупериода? В данном случае ноль вольт. Почему так? Площади S1 и S2 равны. Но все дело в том, что площадь S2 берется со знаком “минус”. А так как площади равны, то в сумме они дают ноль: S1+(-S2)=S1-S2=0. Для бесконечного по времени синусоидального сигнала среднее значение напряжения также равняется нулю.

То же самое касается и других сигналов, например, двухполярного меандра. Меандр – это прямоугольный сигнал, у которого длительности паузы и импульса равны. В этом случае его среднее напряжение также будет равняться нулю.

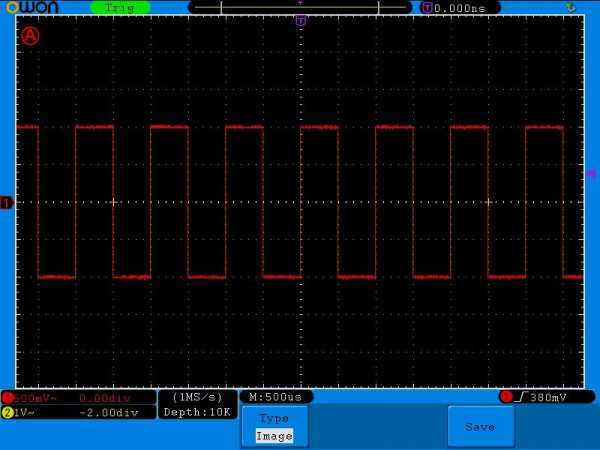меандр

Средневыпрямленное значение напряжения

Чаще всего используют средневыпрямленное значение напряжения Uср. выпр. То есть площадь сигнала, которая “пробивает пол” берут не с отрицательным знаком, а с положительным.

средневыпрямленное значение напряжения будет уже равняться не нулю, а S1+S2=2S1=2S2. Здесь мы суммируем площади, независимо от того, с каким они знаком.

На практике средневыпрямленное значение напряжения получить легко, использовав диодный мост. После выпрямления синусоидального сигнала, график будет выглядеть вот так:

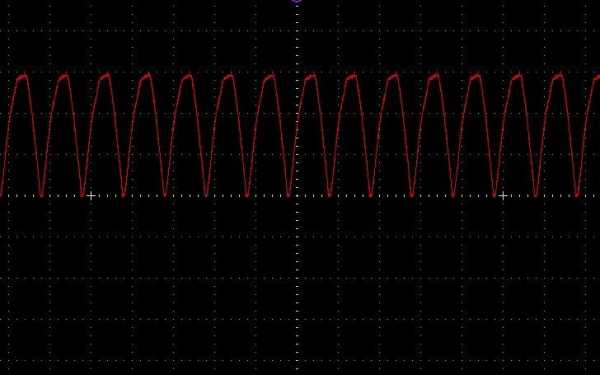выпрямленное переменное напряжение после диодного моста

Для того, чтобы примерно узнать, чему равняется средневыпрямленное напряжение, достаточно узнать максимальную амплитуду синусоидального сигнала Umax и сосчитать ее по формуле:

Среднеквадратичное значение напряжения

Чаще всего используют среднеквадратичное значение напряжения или его еще по-другому называют действующим. В литературе обозначается просто буквой U. Чтобы его вычислить, тут уже  простым графиком не отделаешься. Среднеквадратичное значение –  это значение постоянного напряжения, который, проходя через  нагрузку (скажем, лампу накаливания), выделяет за тот же промежуток времени такое же количество мощности, какое выделит в этой нагрузке переменное напряжение. В английском языке среднеквадратичное напряжение  обозначается так: RMS (rms) – root mean square.

Связь между амплитудным и среднеквадратическим значением устанавливается через коэффициент амплитуды K_a:

Вот некоторые значения коэффициента амплитуды K_a для некоторых сигналов переменного напряжения:

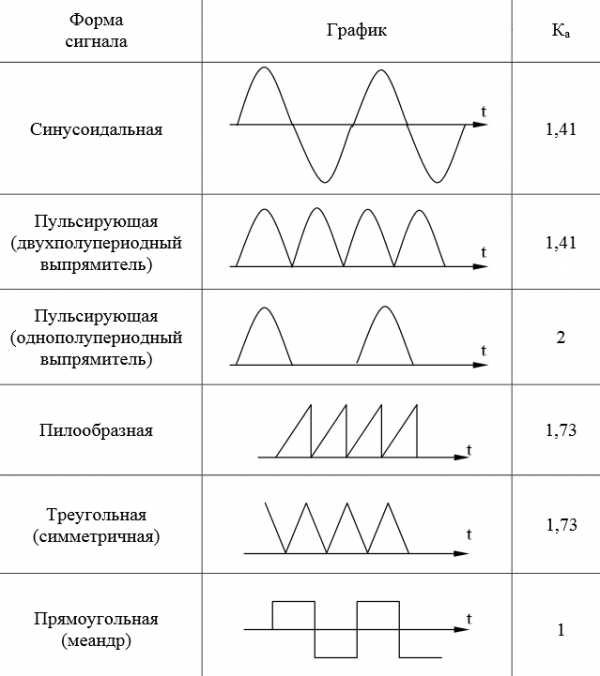
Более точные значения 1,41 и 1,73 – это √2 и √3 соответственно.

Как измерить среднеквадратичное значение напряжения

Для правильного замера среднеквадратического значения напряжения у нас должен быть мультиметр с логотипом T-RMS. RMS – как вы уже знаете – это среднеквадратическое значение. А что за буква “T” впереди? Думаю, вы помните, как раньше была мода на одно словечко: “тру”. “Она вся такая тру…”, “Ты тру или не тру?” и тд. Тру (true) – с англ. правильный, верный.

Так вот, T-RMS  расшифровывается как True RMS –  “правильное среднеквадратическое значение”. Мои токоизмерительные клещи могут замерять этот параметр без труда, так как на них есть логотип “T-RMS”.

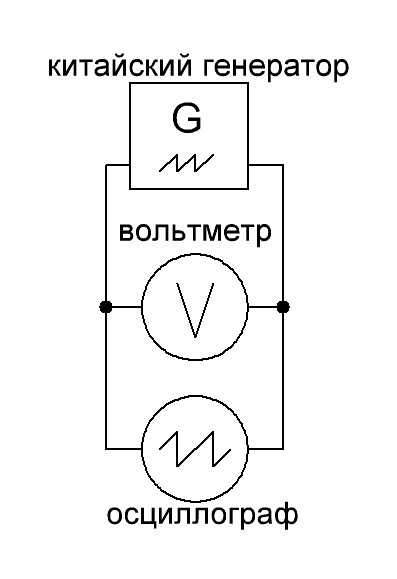
мультиметр с True RMS

Проведем небольшой опыт. Давайте соберем вот такую схемку:

Выставим на моем китайском генераторе частоты треугольный сигнал с частотой, ну скажем, 100 Герц

генератор частоты

А вот осциллограмма этого сигнала. Внизу, в красной рамке, можно посмотреть его параметры

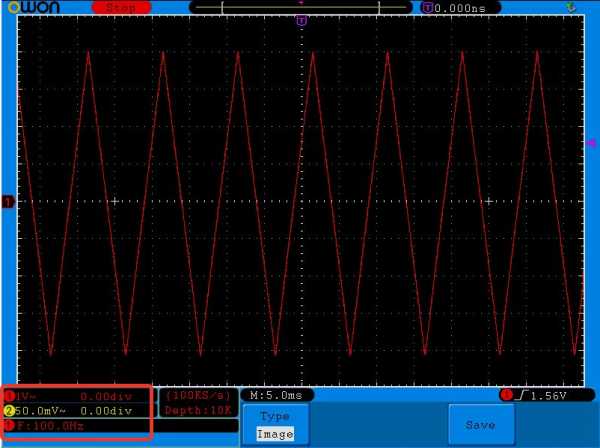треугольный сигнал

И теперь вопрос: чему будет равно среднеквадратическое напряжение этого сигнала?

Так как один квадратик у нас равняется 1 Вольт (мы это видим внизу осциллограммы в красной рамке), то получается, что амплитуда Umax этого треугольного сигнала равняется 4 Вольта. Для того, чтобы рассчитать среднеквадратическое напряжение, мы воспользуемся формулой:

Итак, смотрим нашу табличку и находим интересующий нас сигнал:

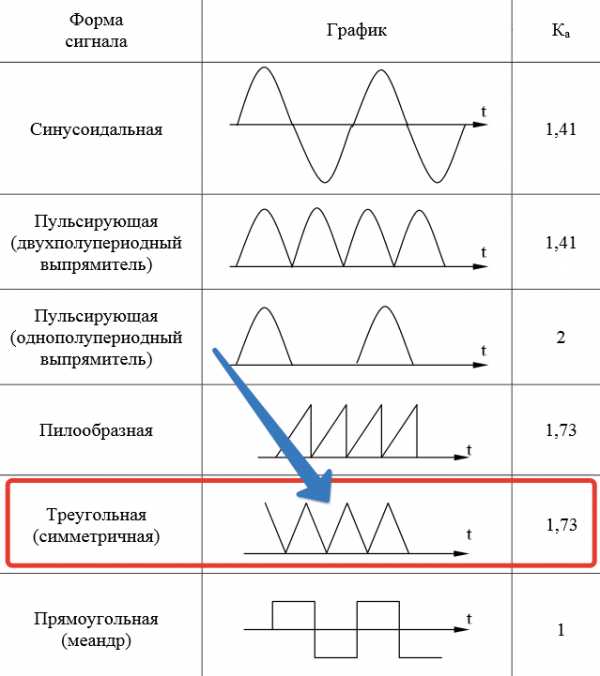
Для нас не важно, пробивает ли сигнал “пол” или нет, главное, чтобы сохранялась форма сигнала. Видим, что наш коэффициент амплитуды K_a= 1,73.

Подставляем его в формулу и вычисляем среднеквадратическое значение нашего треугольного сигнала

Проверяем нашим прибором, так ли оно на самом деле?

Супер! И в правду Тrue RMS.

Замеряем это же самое напряжение с помощью моего китайского мультиметра

Он меня обманул :-(. Он умеет измерять только среднеквадратическое значение синусоидального сигнала, а у нас сигнал треугольный.

Самый интересный сигнал в плане расчетов – это двуполярный меандр, ну тот есть тот, который “пробивает пол”.

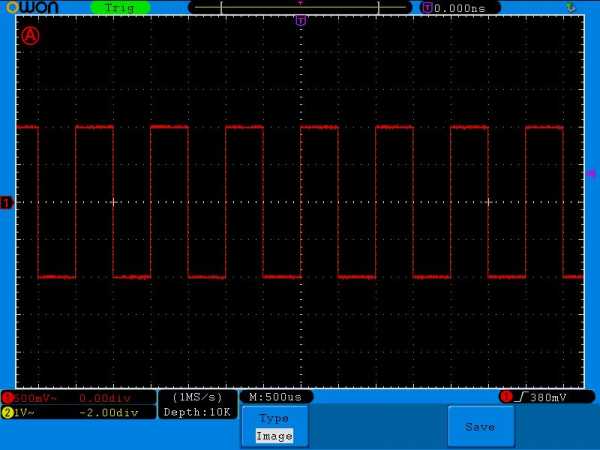
Его амплитудное Umax, средневыпрямленное Uср.выпр. и среднеквадратичное напряжение U равняется одному и тому же значению. В данном случае это 1 Вольт.

Вот вам небольшая картинка, чтобы не путаться

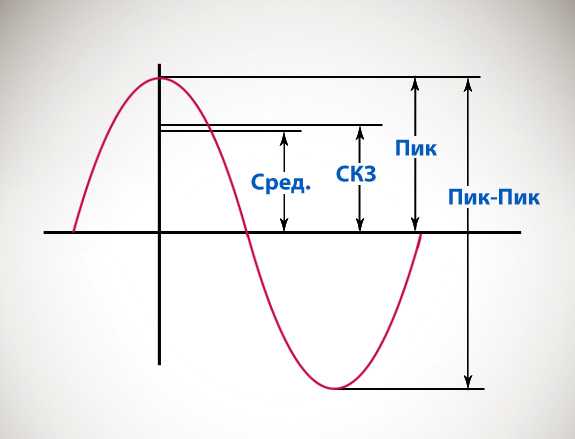среднее, среднеквадратичное и пиковое значения напряжения

• Сред.  – средневыпрямленное значение сигнала. Это и есть площадь под кривой
• СКЗ – среднеквадратичное напряжение. Как мы видим, для синусоидальных сигналов, оно будет больше, чем средневыпрямленное.
• Пик. – амплитудное значение сигнала
• Пик-пик. – размах или двойная амплитаду. Или иначе, амплитуда от пика до пика.

Так что же все-таки показывает мультиметр при измерении переменного напряжения? Показывает он НЕ амплитудное, НЕ среднее  и НЕ среднее выпрямленное напряжение, а среднее квадратическое, то есть действующее напряжение! Об этом всегда помним.

www.ruselectronic.com

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение
Истинное среднеквадратичное значение (ИСКЗ)

Root-mean-square (RMS) − среднеквадратичное значение – англ.
True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.

 

Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:

Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)

то действующее значение периодической несинусоидальной функции выражается формулой

Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.

Например если, несинусоидальный ток выражается формулой:

то среднеквадратичное значение тока равно:

 

Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.

 

Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)

Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения  только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным. Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.

Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.

Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.

 

Замечания

Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:

UСКЗ_ф = Uмакс_ф / (√2)

 

Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:

UСКЗ_л = Uмакс_л / (√2)

 

Соотношение между фазным и линейным напряжением:

UСКЗ

л = UСКЗ_ф * √3

 

Обозначения:

ф – линейное (напряжение)

л – фазное (напряжение)

СКЗ – среднеквадратичное значение

макс – максимальное или амплитудное значение (напряжения)

 

Примеры:

Фазному напряжению 220 В соответствует линейное напряжение 380 В

Фазному напряжению 230 В соответствует линейное напряжение 400 В

Фазному напряжению 240 В соответствует линейное напряжение 415 В

 

Фазное напряжение:

Напряжение в сети 220 В (СКЗ), – амплитудное значение напряжения около ±310 В

Напряжение в сети 230 В (СКЗ), – амплитудное значение напряжения около ±325 В

Напряжение в сети 240 В (СКЗ), – амплитудное значение напряжения около ±340 В

 

Линейное напряжение:

Напряжение в сети 380 В (СКЗ), – амплитудное значение напряжения около ±537 В

Напряжение в сети 400 В (СКЗ), – амплитудное значение напряжения около ±565 В

Напряжение в сети 415 В (СКЗ), – амплитудное значение напряжения около ±587 В

 

 

Ниже приведён обычный пример фазных напряжений в 3-фазной сети:

 

 

---

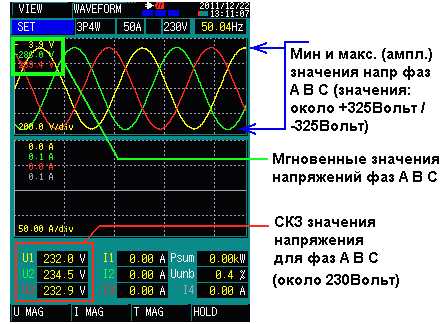[1] Г.И. Атабеков Основы Теории Цепей с.176, 434 с.

www.xn--80aacyeau1asblh.xn--p1ai

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение. Root-mean-square (RMS)

Среднеквадратичное значение (СКЗ). Действующее или эффективное значение
Истинное среднеквадратичное значение (ИСКЗ)

Root-mean-square (RMS) − среднеквадратичное значение – англ.
True Root-Mean-Square (TRMS) − истинное среднеквадратичное значение – англ.

 

Для любой периодической функции (например, тока или напряжения) вида f = f(t) среднеквадратичное значение функции определяется как:

Если функция задана в виде суммы гармоник (как например в случае тока нелинейной нагрузки)

то действующее значение периодической несинусоидальной функции выражается формулой

Поскольку Fn − амплитуда n-ой гармоники, то Fn / √2 − действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.

Например если, несинусоидальный ток выражается формулой:

то среднеквадратичное значение тока равно:

 

Все приведённые выше соотношения используются при вычислении в тестерах измеряющих ИСКЗ, в цепях измерения тока ИБП, в анализаторах сети и в др. оборудовании.

 

Истинное среднеквадратичное значение (ИСКЗ), True Root-Mean-Square (TRMS)

Большинство простых тестеров не могут точно измерять среднеквадратичное значение несинусоидального сигнала (то есть сигнала с большими гармоническими искажениями, например, прямоугольной формы). Они правильно определяют СКЗ напряжения  только для синусоидальных сигналов. Если таким прибором измерить СКЗ напряжения прямоугольной формы, то показание будет ошибочным. Причина ошибки – обычные тестеры при вычислении учитывают основную гармонику (для обычной сети – 50 Гц), но не берут в расчет высшие гармоники сигнала.

Для решения данной проблемы существуют особые приборы, точно измеряющие СКЗ с учётом высших гармоник (обычно до 30-50 гармоник). Они маркируются символом TRMS или ИСКЗ (true root-mean-square) – истинное среднеквадратичное значение, True RMS, истинное СКЗ.

Так, например, обычный тестер может измерить с ошибкой напряжение на выходе ИБП с аппроксимированной синусоидой, в то время как тестер «APPA 106 TRUE RMS MULTIMETER» измеряет напряжение (СКЗ) правильно.

 

Замечания

Для синусоидального сигнала, фазное напряжение в сети (нейтраль – фаза, phase voltage) равно:

UСКЗ_ф = Uмакс_ф / (√2)

 

Для синусоидального сигнала, линейное напряжение в сети (фаза – фаза, interlinear voltage) равно:

UСКЗ_л = Uмакс_л / (√2)

 

Соотношение между фазным и линейным напряжением:

UСКЗ_л = UСКЗ_ф * √3

 

Обозначения:

ф – линейное (напряжение)

л – фазное (напряжение)

СКЗ – среднеквадратичное значение

макс – максимальное или амплитудное значение (напряжения)

 

Примеры:

Фазному напряжению 220 В соответствует линейное напряжение 380 В

Фазному напряжению 230 В соответствует линейное напряжение 400 В

Фазному напряжению 240 В соответствует линейное напряжение 415 В

 

Фазное напряжение:

Напряжение в сети 220 В (СКЗ), – амплитудное значение напряжения около ±310 В

Напряжение в сети 230 В (СКЗ), – амплитудное значение напряжения около ±325 В

Напряжение в сети 240 В (СКЗ), – амплитудное значение напряжения около ±340 В

 

Линейное напряжение:

Напряжение в сети 380 В (СКЗ), – амплитудное значение напряжения около ±537 В

Напряжение в сети 400 В (СКЗ), – амплитудное значение напряжения около ±565 В

Напряжение в сети 415 В (СКЗ), – амплитудное значение напряжения около ±587 В

 

 

Ниже приведён обычный пример фазных напряжений в 3-фазной сети:

 

 

---

[1] Г.И. Атабеков Основы Теории Цепей с.176, 434 с.

www.xn--80aacyeau1asblh.xn--p1ai

Расчет среднего и среднеквадратичного значений тока/напряжения

.
.
Вот здесь есть расширенный и углубленный вариант данной заметки
.
.

Будучи в очень недавнем прошлом яростным разработчиком всевозможных импульсных источников питания, интересовался всяким по данной теме. В частности – вычислением среднего (AVG, Average) и среднеквадратичного (действующего, эффективного, RMS) значений напряжений и (особенно) токов, живущих в разрабатываемом источнике. Для тех, кто не помнит/не знает – напомню определение среднеквадратичного значения тока/напряжения из Википедии:

Действующим (эффективным) значением силы переменного тока называют величину постоянного тока, действие которого произведёт такую же работу (тепловой или электродинамический эффект), что и рассматриваемый переменный ток за время одного периода. В современной литературе чаще используется математическое определение этой величины — среднеквадратичное значение силы переменного тока

Посему, хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. И про выпрямители во вторичной цепи – та же песня. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.

Или, например, делаем могучий источник с высоким КПД. Чтобы оптимально спроектировать обмотку магнитного элемента требуются уже среднее значение тока и среднеквадратичное значение переменной составляющей. В общем – куда ни плюнь, везде фигурируют RMS и AVG (среднее значение, а не антивирус, это важно). Поэтому было принято решение сделать себе некий инструмент, упрощающий жизнь разработчика импульсных источников питания. Вот этим инструментом я и хочу поделиться с общественностью – вдруг кому пригодится.

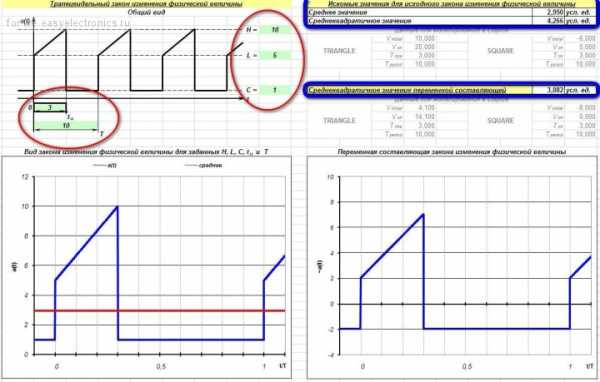
Как нетрудно заметить, данный инструмент («программа») представляет собой обычный Экселовский файл, поскольку в «компьютерном» программировании я вообще ничего не понимаю. В задачу рассматриваемой «программы» входит отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период) и отрисовка формы переменной составляющей заданного сигнала. Также «программа» умеет вычислять среднее и среднеквадратичное значения заданного сигнала и RMS-значение его переменной составляющей. Исходные данные вводятся слева в ячейки, выделенные зеленым цветом (на рисунке обведены красным). Рассчитанные значения AVG и RMS, а также среднеквадратичное значение переменной составляющей заданного сигнала отображаются в правой стороне экрана (обведены синим). Ну а картинки рисуются в нижней части экрана: слева – исходный сигнал, справа – его переменная составляющая.

В нагрузку к «программе» идет короткая заметка, в которой выводятся (а не берутся невесть откуда) расчетные формулы для основных форм сигналов в импульсных источниках питания (трапеции, прямоугольника, треугольника, пилы). Также в этой короткой заметке рассмотрен пример расчета AVG и RMS значений сложного сигнала.

Почему в качестве основы взята именно трапеция? Потому, что из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник

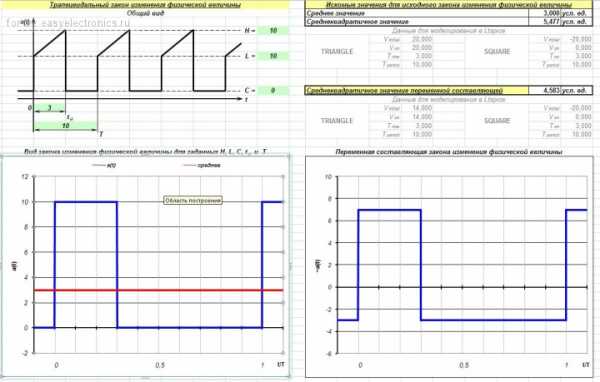
и треугольник

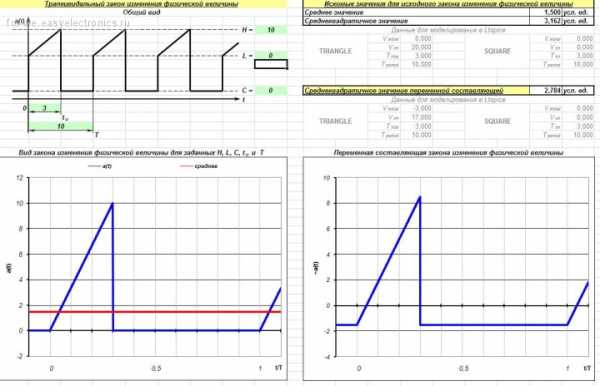
А уж на основе этих базовых сигналов можно сляпать и пилу

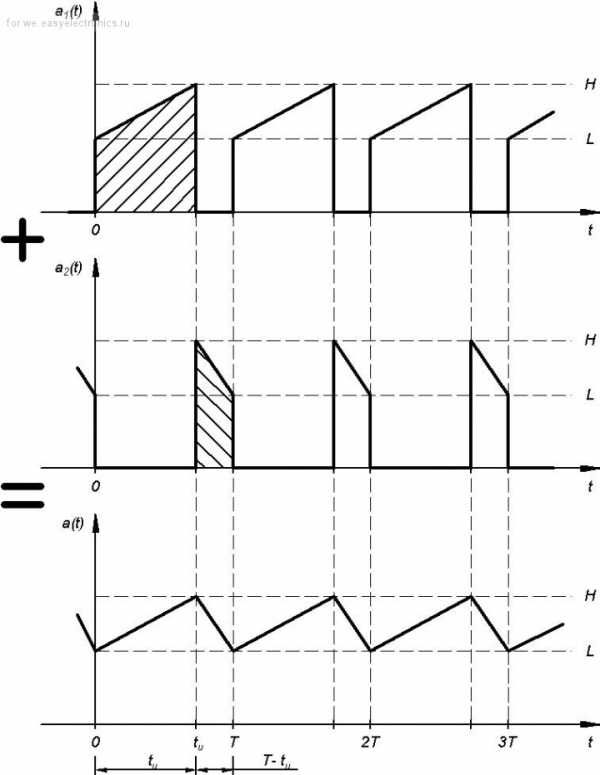
и даже то, что творится на вторичке пушпула:

И еще много чего. Пример же расчета среднего и среднеквадратичных значений для сложных (т.е., составленных из простейших) сигналов, повторюсь, есть в короткой заметке-нагрузке. Хотя, если кого-то заинтересует данный аспект, могу впоследствие осветить его и в этом топике.

Вот, в принципе, и всё описание представленной «программы». Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Примечание: все вопросы лучше валить в камменты после заметки, так как не факт, что я смогу на них на все ответить. А вот шансы на то, что в сообществе найдется более прошаренный человек по твоей теме — довольно хорошие. Но уж если зарегистрироваться на сайте совсем никак — можно воспользоваться возможностями электрической почты: [email protected]

Содержание архива (также прилеплен к заметке):
AVG_RMS.zip:
Среднее_и_среднеквадратичное_Трапеция.xls – собственно, «программа» для расчета AVG и RMS в формате Microsoft Excel;
Среднее и среднеквадратичное.pdf – короткая заметка-нагрузка с выводом расчетных формул и с примером расчета AVG и RMS значений сложного сигнала.

we.easyelectronics.ru

OWON SDS6062. Среднеквадратичное значение напряжения

Что же из себя представляет среднеквадратичное значение напряжения и как его замерить? Давайте разберем значение этого термина. Поможет нам в этих делах наш осциллограф OWON SDS6062 , Блок питания, а также ЛАТР (Лабораторный автотрансформатор).

 

Для опытов нам также понадобится простая автомобильная лампа накаливания на напряжение 12 Вольт:

 

 

 

Вот ее характеристики:  рабочее напряжение U=12 Вольт, мощность Р = 21 Ватт.

Следовательно, зная мощность и напряжение лампы, можно узнать, какую силу тока будет потреблять лампочка. Из формулы P=IU, где I — сила тока,  можно найти I. Значит  I=P/U=21/12=1,75 Ампер.

 

Ладно, с лампочкой разобрались. Давайте ее зажгем. Для этого на нашем блоке питания выставляем рабочее напряжение для нашей лампы

 

 

Подаем напряжение с блока питания на лампу и вуаля!

 

 

Замеряем напряжение на  клеммах-крокодилах блока питания с помощью Мультиметра . Ровненько 12 Вольт, как и предполагалось.

 

 

К этим же клеммах цепляем и наш осцил

 

 

Смотрим осциллограмму на осцилле:

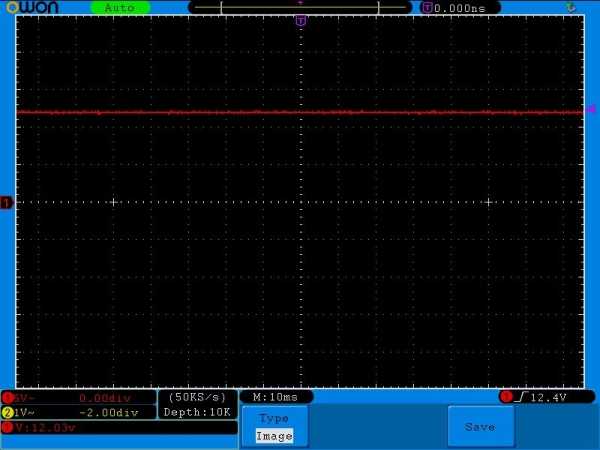
Видите прямую линию? Это и есть осциллограмма постоянного напряжения. В течение времени  у нас напряжение остается  таким, каким и было и не меняется. Если посчитать, то можно вычислить, чему равняется напряжение. Так как одна клеточка у нас 5 Вольт (на фото внизу слева), то  значит, наше напряжение 12 Вольт. Я также вывел это значение на дисплей осциллографа в самом нижнем левом углу: 12,03 Вольт. Все верно.

 

 

Замеряем  Силу тока, как правильно замерить силу тока в цепи, можно узнать, прочитав статью Как измерить ток и напряжение мультиметром?.

Получили 1,72 Ампер. А как вы помните, наше расчетное значение было 1,75 Ампер. Думаю, вину можно переложить  на погрешность прибора  или на лампочку ;-).

 

 

Теперь начинается самое интересное. Берем наш ЛАТР

 

 

Ставим прибор на измерение переменного напряжения и выставляем с помощью  крутилки ЛАТРа напряжение в 12 Вольт. Обратите внимание, что крутилка на мультиметре  находится в диапазоне измерения переменного напряжения. Забегая вперед, скажу, что мультиметр измеряет среднеквадратичное напряжение.

 

 

Цепляем осциллограф к клеммах ЛАТРа, не забывая на осцилле выставить замеры переменного напряжения и смотрим получившуюся осциллограмму:

 

 

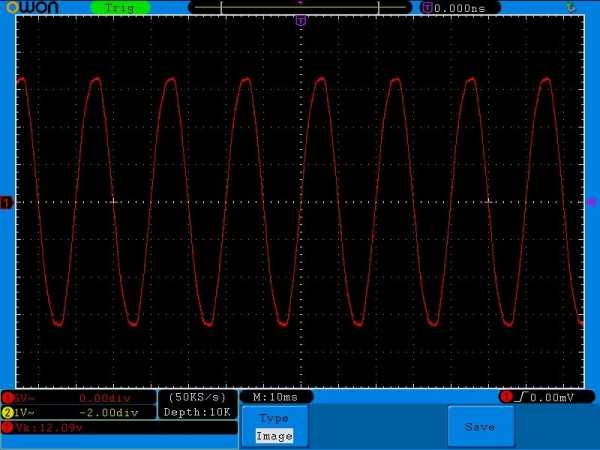
Смотрим, сколько  силы тока кушает наша лампочка. Все как положено, 1,71 Ампер.

 

 

 

Итак, что же у нас получилось? Как и постоянное напряжение, так и переменное напряжение  зажигали одну и ту же лампочку, которая кушала одну и ту же мощность.  Значит эта осциллограмма

 

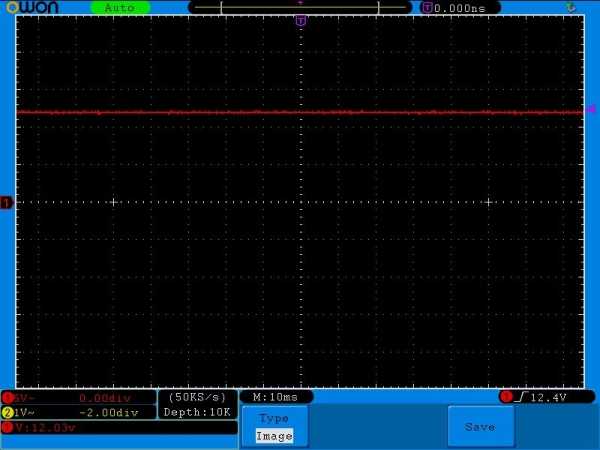
и вот эта осциллограмма

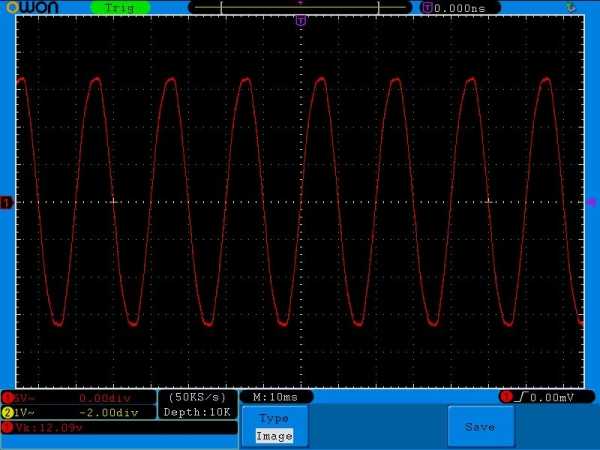
Значит они чем то похожи? Но чем??? 

 

Cреднеквадратичное значение напряжения  — это такое  значение переменного напряжения, при котором нагрузка потребляет столько же силы тока, как и при постоянном напряжении.  То есть лампочка у нас потребляла 1,71 Ампер и при постоянном токе и при переменном.  То есть, в двух этих случаях, мощность, которую потребляла лампочка, была одинакова.

 

Также среднеквадратичное напряжение еще называют действующим или эффективным значением напряжения. С помощью несложных умозаключений, инженеры-электрики пришли к выводу действующее (оно же среднеквадратичное) напряжение  синусоидального сигнала  любой частоты равняется максимальной его амплитуде, поделенной  на корень из двух

 

Стоп! Мы ведь не разобрали, что такое максимальная амлитуда! Давайте взглянем на осциллограмму и  сразу все поймем:

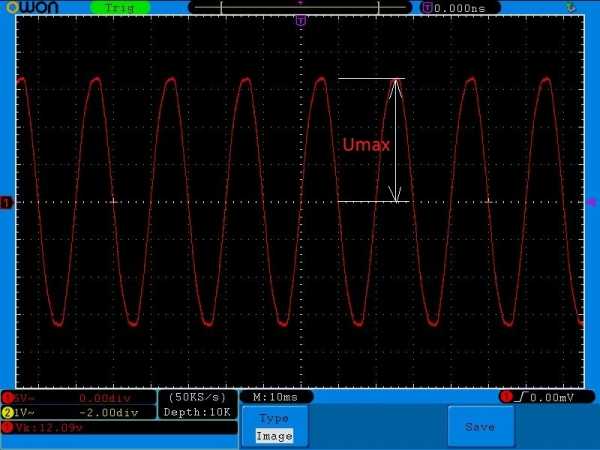
Ну что, догнали, что такое Umax? Если даже посчитать по клеточкам и глянуть, чему равняется одна клеточка по вертикали (смотрим внизу слева, она равняется 5 Вольт), то Umax=17 Вольт. Делим это значение на корень из двух. Я беру это значение как 1,41. Получаем, что среднеквадратичное значение равняется 17/1,41=12,06 Вольт. Ну что, все верно 😉

 

Значит, когда нам говорят, что напряжение в розетке равняется 220 Вольт, то мы то знаем, что на самом деле это среднеквадратичное напряжение.  Максимальная амплитуда этих  220 Вольт равняется 220х1,41=310 Вольт.

 

 Где же  среднеквадратичное напряжение и максимальная амплитуда сигнала прячутся на табличке измерений? Да вот  же они!

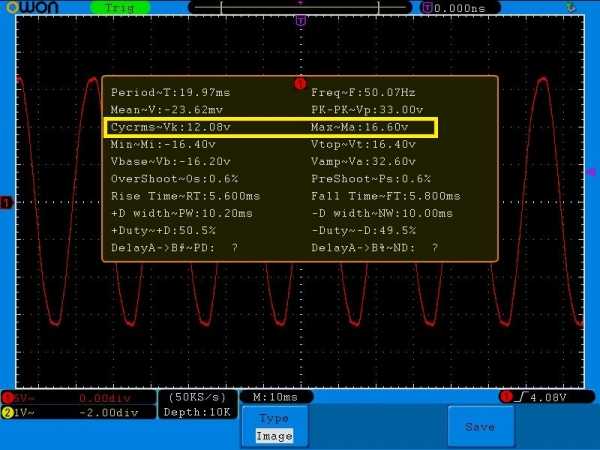
Vk — это и есть среднеквадратичное напряжение этого сигнала.

Ma — это  и есть Umax.

Конечно, 16,6/1,41=11,8  Вольт, а он пишет 12,08 Вольт. Думаю, это связано с тем, что в синусоиде есть небольшие искажения, поэтому измерения немного неточные.

 

Итак, внимание! Кто первый напишет среднеквадратичное значение  напряжения этого сигнала, получит 100 руб на мобилу 😉

 

 

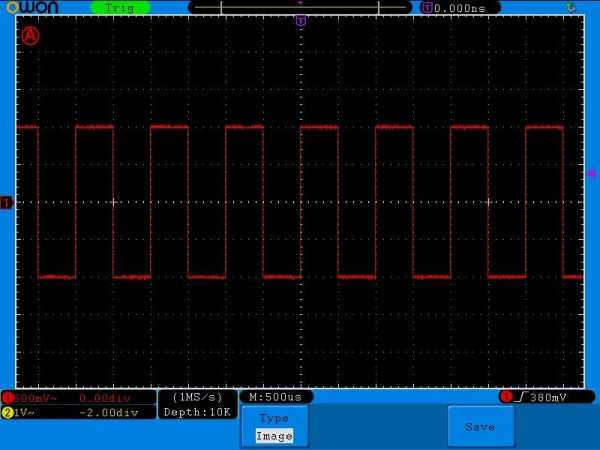
Конкурс уже давненько прошел и первая в комментах ответила Ирина Молчалина и выиграла 100 руб ;-). Правильный  ответ 1 Вольт. Почему именно так, читаем эту статью.

 

Читайте также:

Осциллограф. Основы эксплуатации

 

Цифровой осциллограф OWON SDS6062. Подготовка к работе.

 

 Параметры переменного напряжения

 

 

Назад
Источник

picofarad.ru

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

Расчет среднего и среднеквадратичного значений тока и напряжения: формулы и калькулятор

03.04.18

Данный текст является расширенным и углубленным вариантом моей старой заметки на сайте we.easyelectronics.ru.

Введение

В рамках данной заметки рассмотрим способы вычисления среднего и среднеквадратичного значений тока и напряжения. При этом для простоты ограничимся формами сигнала, характерными для импульсных источников питания. Обращаю ваше внимание – все формулы, приводимые в заметке, даются без выводов, дабы не забивать головы читателей мутной и не особо нужной херней. С другой стороны, если кому-то интересно, откуда данные формулы взялись – можно скачать файл, в котором приведены все необходимые выводы с пояснениями.

Основные определения

Будучи в недавнем прошлом яростным разработчиком всевозможных импульсных источников питания (ИИП), интересовался всяким по данной теме (да и сейчас, бывает, трясу стариной). В частности, весьма важными мне всегда казались такие характеристики сигнала, как среднее и среднеквадратичное значение токов и напряжений в различных точках схемы, поскольку при расчетах ИИП данные параметры используются сплошь и рядом. Чтобы понять, где могут быть полезны данные характеристики, сначала определимся с тем, что мы под ними понимаем.

Естественно, существуют строгие «математические» определения как для среднего, так и для среднеквадратичного значений физических величин, периодически изменяющихся во времени по некоторому закону. Однако, больно уж они мутные и абстрактные, и, на мой взгляд, нужны только при выводе формул. Разработчику же гораздо важнее понимать физический смысл используемых в расчетах величин, поэтому приводимые ниже определения среднего и среднеквадратичного значений будут носить сугубо прикладной характер.

Среднее значение переменного тока или напряжения (во вражеских терминах AVG) – это просто их постоянная составляющая. Поэтому вполне очевидно, что среднее значение широко применяется при расчетах схем, выделяющих из переменного сигнала постоянный уровень. Простейший понижающий преобразователь (Step-Down) с LC-фильтром на выходе, RC-цепочка, призванная выделить постоянное напряжение из поступающего на вход ШИМ-сигнала – всё это примеры того, где без использования среднего значения физической величины ничего толком не посчитаешь.

Среднеквадратичное (действующее, эффективное) значение определяется немного сложнее. Как известно, любой переменный ток (напряжение), проходя через активную линейную нагрузку (например, резистор), выделяет на ней некоторое количество тепла. Но так поступает не только переменный сигнал – постоянный ток тоже будет греть резистор.

Так вот, среднеквадратичное значение переменного тока или напряжения (во вражеских терминах RMS) – это такой постоянный ток (напряжение), который за одинаковый промежуток времени нагреет один и тот же резистор точно так же, как и исходный переменный сигнал. Поэтому одно из важнейших применений среднеквадратичного значения – расчет потерь и соответствующего нагрева для различных элементов силовых цепей ИИП. Хочешь узнать статические потери на ключе флайбэка – будь добр посчитать среднеквадратичное значение тока первички. Надо узнать мощность токосчитывающего резистора – туда же. Даже потери (и приблизительный нагрев) в обмотках трансов и дросселей для хиленьких источников и невысоких частот преобразования в первом приближении можно посчитать при помощи среднеквадратичного значения тока, через эти обмотки протекающего.

В общем, среднее и среднеквадратичное значения используются довольно часто. Поэтому неплохо было бы уметь их рассчитывать для любого сигнала, который может нам встретиться в импульсном источнике питания. При этом лично я разделяю токи и напряжения в ИИП на две большие группы: сигналы с простой формой (элементарные) и сигналы со сложной формой (т.е. те, которые могут быть представлены в виде суммы нескольких элементарных). И поскольку принципы расчета среднего и среднеквадратичного значений для этих двух групп немного отличаются, предлагаю рассмотреть их по отдельности.

Сигналы простой формы

У сигналов простой формы вычислить среднее и среднеквадратичное значение довольно легко – для этого надо всего лишь взять соответствующую формулу и подставить в нее нужные значения. Чтобы постоянно не шариться по различным справочникам, я завел себе специальную табличку, в которую свел расчетные формулы для наиболее часто встречающихся элементарных сигналов:

•  прямоугольника:

•  треугольника:

•  трапеции:

•  и пилы:

(данные формулы, кстати, взяты не с потолка – их вывод при желании можно посмотреть в специальной заметке-пояснении).

Здесь хотелось бы заострить внимание на нескольких моментах. Во-первых, на приведенных выше рисунках рассматривается по два варианта каждого из простейших сигналов: «в общем виде» и «без смещения». При этом с точки зрения разработчика импульсных источников питания наиболее интересным обычно является именно второй вариант, поэтому для него и даны отдельные формулы (чтобы постоянно не подставлять С=0 в «общие» выражения). Во-вторых, пилообразное напряжение, вообще говоря, является сложным сигналом, поскольку может быть представлено в виде суммы двух простых (либо трапеций, либо треугольников). Однако, пила настолько часто встречается при расчетах ИИП, а выражения AVG и RMS для нее настолько лаконичны и красивы, что я в результате включил-таки ее в список сигналов, среднее и среднеквадратичное значение которых вычисляется тупо всего по одной формуле. Ну и в-третьих, вышеприведенная таблица, в принципе, могла бы состоять всего из одной трапеции, ибо из нее легко получить как прямоугольник, так и треугольник, поставляя соответствующие значения «H», «L» и «C». Однако практика показала, что постоянно этим заниматься весьма муторно, ибо мы рассчитываем источник, а не тренируем математические навыки. Поэтому в итоге я себе выписал готовые формулы AVG и RMS для прямоугольника и треугольника, что оказалось весьма и весьма удобным. Ну а в целом – как ни странно, представленные выше формулы для элементарных сигналов покрывают, наверное, 75-80% всех потребностей разработчика импульсных источников питания, что весьма немало. Однако, всё многообразие токов и напряжений в ИИП отнюдь не ограничивается вышеупомянутыми четырьмя (и даже тремя, если не учитывать пилу) формами. Поэтому рано или поздно любой разработчик импульсников сталкивается с необходимостью вычисления среднего и среднеквадратичного значения сложного сигнала (яркий пример – расчет пуш-пула).

Сигналы сложной формы

Как было сказано выше, сигналы сложной формы – это такие, которые могут быть представлены в виде суммы нескольких элементарных сигналов. Применительно к импульсным источникам питания в качестве последних выступают прямоугольник, треугольник или трапеция, и значительно реже – синус, косинус и прочая «плавная» херня. Отметим, что в данном случае, в отличие от простейших форм, нахождение аналитических выражений для среднего и среднеквадратичного значений обычно превращается в неблагодарное занятие. Например, для вывода «среднеквадратичной» формулы нам надо разбить сложный сигнал на несколько простейших, а затем извлечь квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений (думаю, даже понять, о чем говорится в данном предложении, у вас получится далеко не сразу). Найти среднее значение сложного сигнала немного проще (надо просто просуммировать средние «элементарные» значения), однако поверьте – сделать из этого удобоваримую формулу в подавляющем большинстве случаев не удается:

К счастью, готовая формула для нахождения AVG и RMS сложного сигнала обычно не требуется. Чаще всего нам надо просто узнать среднее или среднеквадратичное значение тока (напряжения) именно для нашего конкретного случая, а не вывести аналитическое выражение на все случаи жизни. А это существенно упрощает задачу, ибо посчитать числовое значение AVG или RMS для каждого элементарного сигнала на соответствующем временно́м интервале не так уж и сложно. В качестве примера можно рассмотреть нахождение среднего и среднеквадратичного значения напряжения, характерного для пушпульной, полумостовой и полномостовой схем (данный расчет есть и в специальной заметке-пояснении):

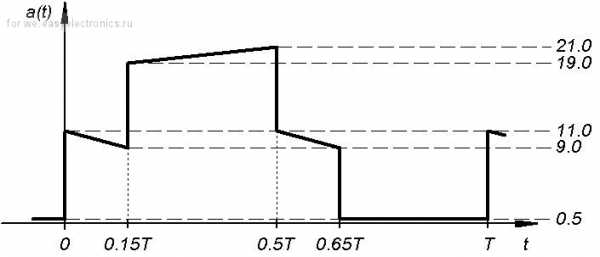
Как следует из предпоследнего рисунка, для начала нам надо разбить исходный сигнал на элементарные. Очевидно, что это будут три трапеции и один прямоугольник:

Дальше нам надо посчитать среднее и среднеквадратичное значение каждого из четырех элементарных сигналов, для чего воспользуемся формулами из вышеприведенной таблицы. Начнем с первого из них – трапеции №1. Как видно из последнего рисунка, это трапеция без смещения с параметрами

H₁=11;
L₁=9;
C₁=0;
t_И1=0,15∙T.

Поэтому в соответствии с формулами для трапеции, приведенными выше, будем иметь:

Сигнал №2 – это тоже трапеция без смещения. Параметры данной трапеции будут таковы:

H₂=21;
L₂=19;
C₂=0;
t_И2=0,50∙T – 0,15∙T = 0,35∙T.

Поэтому среднее и среднеквадратичное значение второго сигнала составят соответственно

Трапеция №3 полностью совпадает с трапецией №1, просто она сдвинута вправо на полпериода. Поэтому как параметры третьего сигнала, так и его среднее и среднеквадратичное значения будут равны соответствующим значениям первого сигнала:

H₃= H₁=11;
L₃= L₁=9;
C₃= C₁=0;
t_И3= t_И1= 0,65∙T – 0,50∙T = 0,15∙T.

Ну и остался сигнал №4. Данный сигнал представляет собой прямоугольник с параметрами

H₄=0,5;
C₄=0;
t_И4=1,00∙T – 0,65∙T = 0,35∙T.

И после использования формул для вычисления среднего и среднеквадратичного значения сигнала №4, получим следующее:

Теперь у нас есть все данные для нахождения AVG и RMS исходного сигнала. Как было сказано выше, среднее значение находится как сумма средних значений элементарных сигналов, на которые был разложен «исходник», а среднеквадратичное – как квадратный корень из суммы квадратов «элементарных» среднеквадратичных значений. То есть в нашем случае будем иметь

Для проверки полученного результата используем широко распространенное бесплатное ПО LTSpice IV от компании Linear Technology Corporation (LTC). Сгенерировав сигнал с требуемыми параметрами, измерим в эмуляторе среднее и среднеквадратичное его значение за 5 периодов:

Как видим, результаты работы эмулятора полностью совпадают с расчетными AVG и RMS, т.е. предложенный способ вычисления среднего и среднеквадратичного значений для сложного сигнала вполне имеет право на жизнь. Более того, способ этот довольно прост и не требует от разработчика ИИП никаких особых математических навыков. С другой стороны, муторность рассмотренного алгоритма также налицо. Лично меня дичайше бесит постоянно считать на калькуляторе и выписывать на бумажку средние и среднеквадратичные значения для всех элементарных сигналов, на которые раскладывается исходный, а пото́м складывать их на том же калькуляторе (и это в лучшем случае, ибо если требуется RMS, всё становится еще волшебнее). Поэтому я принял решение сделать себе некий инструмент, упрощающий жизнь разработчика ИИП, которым и хотел бы поделиться с читателями.

Калькулятор

Данный инструмент – это такая специальная «программа» (cko4aTb бесплатно). «Программа» представляет собой обычный экселовский файл (т.к. программист я тот еще), поэтому для работы нам потребуется «Excel» (у меня вот такой: Microsoft® Excel 2002 (10.4302.2625)). Изначальная и основная задача рассматриваемой «программы» – отрисовка формы трапецеидального сигнала с заданными параметрами (рисуется один период), а также вычисление среднего и среднеквадратичного значений для этого сигнала. Также «программа» умеет рисовать переменную составляющую заданной трапеции (она получается если из исходного сигнала вычесть постоянную составляющую) и вычислять ее RMS-значение (это уж так, чисто на всякий случай). Ну и еще предлагаемый софт позволяет быстро посчитать среднее и среднеквадратичное значения для сложного сигнала, состоящего максимум из 16-ти различных элементарных (большее количество в реальной жизни вряд ли потребуется):

Почему в качестве основы взята именно трапеция? Потому что, как было сказано выше, из нее легко получить все основные формы сигналов, встречающихся в импульсных источниках питания, а именно – прямоугольник и треугольник:

Ну а уж на основе этих базовых сигналов можно сляпать и пилу, и напряжение на стоке ключа во флайбэке, и то, что творится на вторичке пушпула и многое другое.

Пользоваться «программой» очень просто. Исходные данные для трапеции вводятся слева в ячейки, выделенные зеленым цветом. После этого чуть ниже можно посмотреть на форму сигнала с введенными параметрами, а еще ниже отобразятся рассчитанные среднее и среднеквадратичное значения этого сигнала. За переменную составляющую трапеции отвечает правый нижний угол экрана (здесь рисуется ее график и рассчитывается значение RMS). Ну а для работы со сложным сигналом предназначен правый верхний угол. Здесь в ячейки, выделенные зеленым цветом, вводятся средние и среднеквадратичные значения элементарных сигналов, из которых состоит «исходник», а ниже рассчитываются уже́ его собственные AVG и RMS.

Отмечу, что на всю «программу» наложена магическая защита, позволяющая редактировать только те ячейки, которые можно. При необходимости защита снимается элементарно («Сервис» => «Защита» => «Снять защиту листа»), однако делать это не рекомендую: можно по дури снести какую-нибудь нужную формулу, восстанавливать которую – лишний геморрой.

Вот, в принципе, и всё описание представленной «программы». Несмотря на свою простоту и очевидность, данный софт довольно существенно помогает и экономит время при расчетах ИИП (ну, во всяком случае, у меня происходит именно так). Например, на расчет среднего и среднеквадратичного значения сложного сигнала, приведенного в предыдущем пункте, понадобится менее минуты. Последовательность действий проста – вводим параметры первой трапеции, затем переписываем рассчитанные для нее значения AVG и RMS в ячейки секции сложного сигнала. Затем то же самое проделываем для остальных трех элементарных функций, из которых состоит «исходник». Всё, остальное «программа» сделает сама, не надо никаких шаманств с бумажками и калькуляторами:

Ну а у меня на сегодня всё. Желаю удачи при проектировании и изготовлении импульсных (и не только) источников питания!

Обсудить эту заметку можно здесь

Ссылки по теме, документация

Заметка-пояснение с выводом формул и примером расчета среднего и среднеквадратичного значений сложного сигнала:

•  AVG_RMS.pdf;

Калькулятор для упрощения вычислений среднего и среднеквадратичного значений простых и сложных сигналов:

•  AVG_RMS_Calc.xls;

kmpu.ru

Список параметров напряжения и силы электрического тока — Википедия

В связи с тем, что электрические сигналы представляют собой изменяющиеся во времени величины, в электротехнике и радиоэлектронике используются по необходимости разные способы представлений напряжения и силы электрического тока

Значения переменного напряжения (тока)

Далее для определенности будем говорить большей частью о параметрах напряжения, хотя они справедливы и для токов.

Мгновенное значение

Мгновенное значение — это значение сигнала в определённый момент времени, функцией которого является (  u(t) ,i(t){\displaystyle u(t)~,\quad i(t)}    ). Мгновенные значения медленно изменяющегося сигнала можно определить с помощью малоинерционного вольтметра постоянного тока, самописца или шлейфового осциллографа, для периодических быстротекущих процессов используется электронно-лучевой или цифровой осциллограф.

Амплитудное значение

• Амплитудное (пиковое) значение, иногда называемое просто «амплитуда» — наибольшее мгновенное значение напряжения или силы тока за период (без учёта знака):

UM=max(|u(t)|) ,IM=max(|i(t)|){\displaystyle U_{M}=\max(|u(t)|)~,\qquad I_{M}=\max(|i(t)|)}

Пиковое значение напряжения измеряется с помощью импульсного вольтметра или осциллографа.

Среднеквадратичное значение

Среднеквадратичное значение (устар. действующее, эффективное) — корень квадратный из среднего значения квадрата напряжения или тока.

U=1T∫0Tu2(t)dt ,I=1T∫0Ti2(t)dt{\displaystyle U={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}u^{2}(t)dt}}~,\qquad I={\sqrt {{\frac {1}{T}}\int \limits _{0}^{T}i^{2}(t)dt}}}

Среднеквадратичные значения являются самыми распространёнными, так как они наиболее удобны для практических расчётов, поскольку в линейных цепях с чисто активной нагрузкой переменный ток с действующими значениями I{\displaystyle I} и U{\displaystyle U} совершает ту же работу, что и постоянный ток с теми же значениями тока и напряжения. Например, лампа накаливания или кипятильник, включённые в сеть с переменным напряжением с действующим значением 220 В, работают (светят, греют) точно так же, как и будучи подключенными к источнику постоянного напряжения с тем же значением напряжения.

Когда не оговаривают особо, то обычно имеют в виду именно среднеквадратичные значения величины напряжения или силы тока.

В среднеквадратичных значениях проградуированы показывающие устройства большинства вольтметров и амперметров переменного тока, за исключением специальных приборов, однако эти обычные приборы дают правильные показания для среднеквадратических значений только при форме сигнала синусоидальной формы. Некритичны к форме сигнала приборы с термопреобразователем, в которых измеряемый ток или напряжение с помощью нагревателя, представляющим собой активное сопротивление, преобразуется в далее измеряемую температуру, которая и характеризует величину электрического сигнала. Также нечувствительны к форме сигнала специальные устройства, возводящие мгновенное значение сигнала в квадрат с последующим усреднением во времени (с квадратичным детектором) или АЦП, возводящие в входной сигнал в квадрат тоже с усреднением по времени. Квадратный корень из выходного сигнала таких устройств как раз и является среднеквадратическим значением.

Квадрат среднеквадратичного значения напряжения, выраженного в вольтах, численно равен средней рассеиваемой мощности в ваттах на резисторе с сопротивлением 1 Ом.

Среднее значение

Среднее значение (смещение) — постоянная составляющая напряжения или силы тока

U=1T∫0Tu(t)dt ,I=1T∫0Ti(t)dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}u(t)dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}i(t)dt}

В электротехнике используется редко, но сравнительно часто используется в радиотехнике (ток смещения и напряжение смещения). Геометрически это разность площадей под и над осью времени, делённая на период. Для синусоидального сигнала смещение равно нулю.

Средневыпрямленное значение

Средневыпрямленное значение — среднее значение модуля сигнала

U=1T∫0T∣u(t)∣dt ,I=1T∫0T∣i(t)∣dt{\displaystyle U={\frac {1}{T}}\int \limits _{0}^{T}\mid u(t)\mid dt~,\qquad I={\frac {1}{T}}\int \limits _{0}^{T}\mid i(t)\mid dt}

На практике используется редко, однако большинство измерительных приборов переменного тока – магнитоэлектрической системы (т. е., в которых ток перед измерением выпрямляется) фактически измеряют именно эту величину, хотя их шкала проградуирована по среднеквадратичным значениям для синусоидальной формы сигнала. Если сигнал заметно отличается от синусоидального, показания приборов магнитоэлектрической системы имеют систематическую ошибку. В отличие от приборов магнитоэлектрической системы, приборы электромагнитной, электродинамической и тепловой систем измерения всегда реагируют на действующее значение, независимо от формы электрического тока.

Геометрически это сумма площадей, ограниченная кривой над и под осью времени за время измерения. При однополярном измеряемом напряжении среднее и средневыпрямленное значения равны между собой.

Коэффициенты пересчёта значений

• Коэффициент формы кривой переменного напряжения (тока) — величина, равная отношению действующего значения периодического напряжения (тока) к его средневыпрямленному значению. Для синусоидального напряжения (тока) равен π/22≈1.11{\displaystyle {\frac {{\pi }/2}{\sqrt {2}}}\approx 1.11}.

• Коэффициент амплитуды кривой переменного напряжения (тока) — величина, равная отношению максимального по модулю за период значения напряжения (тока) к действующему значению периодического напряжения (тока). Для синусоидального напряжения (тока) равен 2{\displaystyle {\sqrt {2}}}.

Параметры постоянного тока

• Размах пульсации напряжения (тока) — величина, равная разности между наибольшим и наименьшим значениями пульсирующего напряжения (тока) за определенный интервал времени

• Коэффициент пульсации напряжения (тока) — величина, равная отношению наибольшего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей.
  • Коэффициент пульсации напряжения (тока) по действующему значению — величина, равная отношению действующего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей
  • Коэффициент пульсации напряжения (тока) пo среднему значению — величина, равная отношению среднего значения переменной составляющей пульсирующего напряжения (тока) к его постоянной составляющей

Параметры пульсации определяются по осциллографу, либо с помощью двух вольтметров или амперметров (постоянного и переменного тока)

Литература и документация

Литература

Нормативно-техническая документация

Ссылки

См. также

wikipedia.green