принцип работы, схемы и т.д.
Однополупериодный выпрямитель — это устройство или контур, проводящее во время одной половины цикла переменного тока. Однополупериодный выпрямитель состоит из трансформатора, полупроводникового диода (D1) и сопротивления (RL).
Обратите внимание на основы электричества и на приборы электроники.
Принцип действия однополупериодного выпрямителя
В этом примере сопротивление RL представляет нагрузку, хотя, на самом деле, нагрузкой может быть любой элемент или группа элементов, которая может вызвать падение напряжения.
Схема однополупериодного выпрямителяВ течение первой половины цикла переменного тока диод D1 находится в состоянии прямого подключения — положительный электрический потенциал воздействует на его анод, а отрицательный потенциал воздействует на его катод. Когда D1 находится в состоянии прямого подключения, ток протекает от отрицательной стороны вторичной обмотки трансформатора, через сопротивление нагрузки, через диод, обратно к положительной стороне вторичной обмотки.
В течение второй половины цикла переменного тока диод D1 находится в состоянии обратного подключения — на его анод воздействует отрицательный электрический потенциал, а положительный электрический потенциал воздействует на его катод. Этот диод не проводит, поэтому в сопротивлении нагрузки RL никакое напряжение не присутствует.
Однополупериодный выпрямитель в состоянии обратной проводимости D1Как видно по форме кривой, у однополупериодных выпрямителей только одна полуволна постоянного тока на выходе при каждом полном цикле переменного тока на входе. По этой причине в оборудованиях обычно не применяются однополупериодные выпрямители; когда они используются, они обычно устанавливаются в оборудовании или контурах, где требуется ток невысокого напряжения и где колебания напряжения не бывают причиной для беспокойства.
Однополупериодный выпрямитель тока. Схема и принцип работы.
Выпрямитель тока – это устройство, позволяющее выполнить преобразование тока переменного направления в ток постоянного направления. И сегодня мы рассмотрим базовую схему выпрямителя – однополупериодный выпрямитель. Разберем схему, принцип работы, а также достоинства и недостатки.
Однополупериодный выпрямитель.
Схема однополупериодного выпрямителя выглядит следующим образом:
Пусть на входе у нас переменное напряжение, меняющееся по синусоидальному закону:
Резистор же R_н играет роль нагрузки. То есть мы должны обеспечить протекание через него постоянного тока. Давайте разберемся как эта простейшая схема сможет решить нашу задачу!
Итак, диод D_1 пропускает ток только в одном направлении, в те моменты, когда к нему приложено прямое смещение, что соответствует положительным полупериодам (U_{вх}\gt0) входного сигнала.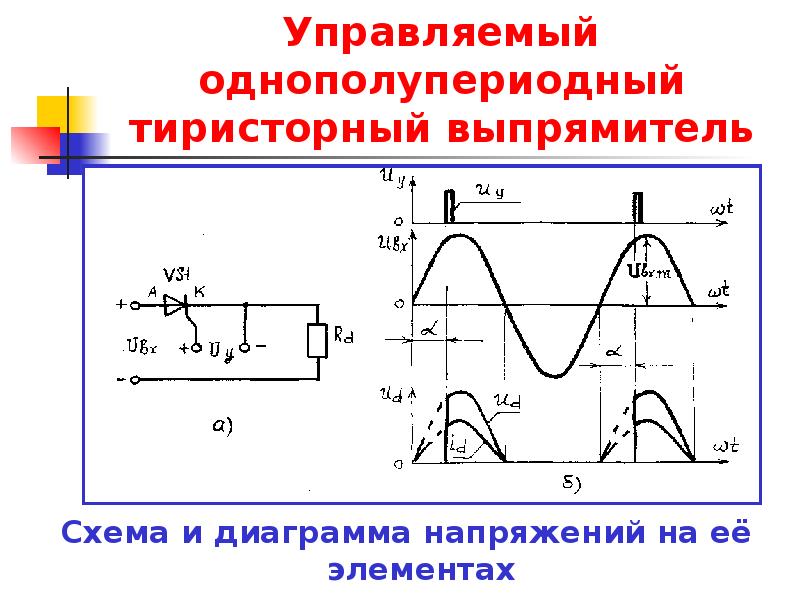 Когда к диоду будет приложено обратное смещение (отрицательные полупериоды), он будет закрыт и по цепи будет протекать только незначительный обратный ток. И в результате сигнал на нагрузке будет выглядеть так:
Когда к диоду будет приложено обратное смещение (отрицательные полупериоды), он будет закрыт и по цепи будет протекать только незначительный обратный ток. И в результате сигнал на нагрузке будет выглядеть так:
Обратным током обычно можно пренебречь, поэтому в итоге мы получаем, что ток через нагрузку протекает только в одном направлении. Но назвать его постоянным не представляется возможным 🙂 Ток через нагрузку хоть и является выпрямленным (протекает только в одном направлении), но носит пульсирующий
характер.Для сглаживания этих пульсаций в схему выпрямителя тока обычно добавляется конденсатор:
Идея заключается в том, что во время положительного полупериода, конденсатор заряжается (запасает энергию). А во время отрицательного полупериода конденсатор, напротив, разряжается (отдает энергию в нагрузку).
Таким образом, за счет накопленной энергии конденсатор обеспечивает протекание тока через нагрузку и в отрицательные полупериоды входного сигнала. При этом емкость конденсатора должна быть достаточной для того, чтобы он не успевал разряжаться за время, равное половине периода.
При этом емкость конденсатора должна быть достаточной для того, чтобы он не успевал разряжаться за время, равное половине периода.
Проверяем напряжение на нагрузке для этой схемы:
В точке 1 конденсатор заряжен до напряжения U_1. Далее входное напряжение понижается, а конденсатор, в свою очередь, начинает разряжаться на нагрузку. Поэтому выходное напряжение не падает до нуля вслед за входным.
В точке 2 конденсатор успел разрядиться до напряжения U_2. В то же время значение входного сигнала также становится равным этой же величине, поэтому конденсатор снова начинает заряжаться. И эти процессы в дальнейшем циклически повторяются.
А теперь поэкспериментируем и используем в схеме однополупериодного выпрямителя конденсатор меньшей емкости:
И здесь мы видим, что конденсатор из-за меньшей емкости успевает разрядиться гораздо сильнее, и это приводит к увеличению пульсаций, а следовательно к ухудшению работы всей схемы.
На промышленных частотах 50 – 60 Гц однополупериодный выпрямитель практически не применяется из-за того, что для таких частот потребуются конденсаторы с очень большой емкостью (а значит и внушительными габаритами).
Смотрите сами, чем ниже частота, тем больше период сигнала (а вместе с тем, и длительности положительного и отрицательного полупериодов). А чем больше длительность отрицательного полупериода, тем дольше конденсатор должен быть способен разряжаться на нагрузку. А это уже требует большей емкости.
Таким образом, на более низких частотах в силу своих ограничений эта схема не нашла широкого применения. Однако, на частотах в несколько десятков КГц однополупериодный выпрямитель используется вполне успешно.
Рассмотрим преимущества и недостатки однополупериодного выпрямителя:
- К основным достоинствам схемы, в первую очередь, конечно же, можно отнести простоту и, соответственно, небольшую себестоимость – используется всего один диод.

- Кроме того, снижено падение напряжения. Как вы помните, при протекании тока через диод на нем самом падает определенное напряжение. По сравнению с мостовой схемой (которую мы разберем в следующей статье), ток протекает только через один диод (а не через два), а значит и падение напряжения меньше.
Основных недостатков также можно выделить несколько:
- Схема использует энергию только положительного полупериода входного сигнала. То есть половина полезной энергии, которую также можно было бы использовать, уходит просто в никуда. В связи с этим КПД выпрямителя крайне низок.
- И даже с использованием сглаживающих конденсаторов величина пульсаций довольно-таки значительна, что также является очень серьезным недостатком.
Итак, давайте резюмируем! Мы разобрали схему и принцип работы однофазного однополупериодного выпрямителя тока, а в следующей статье перейдем к более сложным схемам выпрямителей, не пропустите!
Однофазный однополупериодный выпрямитель
Выпрямитель – это устройство, преобразующее электрическую энергию переменного тока в постоянный.
Основой выпрямителя являются полупроводниковые приборы: диоды, тиристоры, транзисторы. В зависимости от используемых полупроводников выпрямитель может быть неуправляемым и управляемым.
Неуправляемый однополупериодный выпрямитель
Простейший выпрямитель состоит из одного диода и называется однофазным однополупериодным выпрямителем.
На данной схеме к выпрямителю подключена активная нагрузка в виде резистора R, а на первичную обмотку трансформатора подано переменное синусоидальное напряжение. На вторичной обмотке трансформатора, также образуется синусоидальное напряжение Uab.
В момент, когда потенциал точки a выше, чем точки b (данный процесс соответствует точкам на диаграмме 0,2π,4π…), к аноду диода приложено положительное напряжение Uab, что вызывает ток id, который проходит через диод и нагрузка R оказывается под напряжением U
Когда потенциал точки a меньше, чем точки b (соответствует точкам на диаграмме 3π, 5π…), к аноду диода приложено отрицательное напряжение Uab, что вызывает запирание диода. Ток id становится равным нулю.
Ток id становится равным нулю.
Таким образом, диод пропускает ток только одну половину периода, отсюда и название – однополупериодный выпрямитель.
Среднее значение выпрямленного напряжения Ud равно интегралу функции взятой за период 2π, но так как одну половину периода диод не пропускает ток, она равна нулю, значит Ud принимает вид:
где U2 действующее значение напряжения на вторичной обмотке трансформатора.
На диаграмме среднее значение выпрямленного напряжения Ud представлено в виде площади прямоугольника (оранжевая штриховка) с высотой U d и основанием 2π. Эта площадь равна площади выпрямленной полуволны (зеленая штриховка).
Ток id повторяет по форме напряжение ud, потому как нагрузка в данном случае активная.
Среднее значение выпрямленного тока:
Управляемый однополупериодный выпрямитель
Для реализации управления величиной выпрямленного напряжения в схеме вместо диода используют тиристор.
Работа схема во многом аналогична схеме с диодом. В данном случае ток через нагрузку R будет проходить только при открытии тиристора VS. Открытие тиристора VS происходит при подаче на него управляющего импульса, и при условии, что к аноду тиристора приложено положительное (относительно катода) напряжение uab.
Задерживая подачу управляющего импульса на угол α относительно нулевого значения напряжения u
Однофазная однополупериодная схема выпрямителя на практике не получила широкого распространения. Это связано с тем, что в результате выпрямления диодом тока во вторичной обмотке, образуется постоянная составляющая Id, которая оказывает подмагничивающее действие на магнитопровод трансформатора.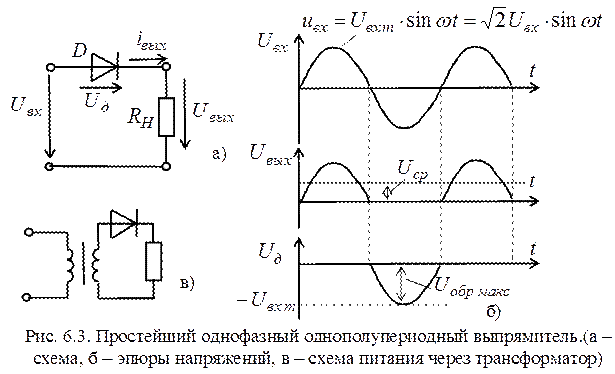 В результате этого, при расчетах приходилось выбирать трансформатор завышенной мощности, что приводило к увеличению его массы и габаритов, и было нецелесообразно экономически.
В результате этого, при расчетах приходилось выбирать трансформатор завышенной мощности, что приводило к увеличению его массы и габаритов, и было нецелесообразно экономически.
Однополупериодный выпрямитель Принцип работы выпрямителя кратко Электроника,…
Сразу хочу сказать, что здесь никакой воды про однополупериодный выпрямитель, и только нужная информация. Для того чтобы лучше понимать что такое однополупериодный выпрямитель , настоятельно рекомендую прочитать все из категории Электроника, Микроэлектроника , Элементная база
Считается, что трансформатор и выпрямительный диод – идеальны, то есть у трансформатора активное сопротивление обмоток равно нулю, у диода Rпр = 0 и Rобр = ∞.
Рис.2 Схема однополупериодного выпрямителя
Принцип работы выпрямителя
Рассмотрим временные диаграммы однополупериодного выпрямителя (рис.3) в интервале времени 0 – T/2 диод VD1 открыт φА > φВ, в нагрузке течет ток iн .
В интервале времени T/2 – T диод закрыт φА < φВ, к диоду приложено U2m.
Рис.3 . Об этом говорит сайт https://intellect.icu . Временные диаграммы однополупериодного выпрямителя
Ток и напряжение в нагрузке имеют пульсирующий характер и как следствие значительно отличаются от постоянных составляющих
Основные электрические параметры выпрямителя
Диод в выпрямителях является основным элементом и во многом определяет основные показатели выпрямителей.
1. Uнср и Iнср – средние значения выпрямленных напряжения и тока в нагрузочном устройстве
2. Мощность нагрузочного устройства Pнср = Uнср•Iнср
3. Амплитуда основной гармоники Uоснг
4. Коэффициент пульсаций выпрямленного напряжения
5. КПД выпрямителя
6. Обратное максимально напряжение на запертом диоде Uобрmax
Определим среднее значение выпрямленного напряжения и тока в нагрузке.
В однополупериодном выпрямителе теряется больше половины входного напряжения!
Входное напряжение (напряжение на вторичной обмотке трансформатора):
Среднее значение выпрямленного тока, средневыпрямленный ток равен току через диод:
Частота пульсаций выпрямленного напряжения равна частоте сетевого напряжения:
fп = fосн
Выпрямленное напряжение имеет несинусоидальную форму сигнала, поэтому может быть разложено в ряд Фурье:
Так как частота пульсаций выпрямленного напряжения равна частоте сети, то при расчете коэффициента пульсаций берут напряжение основной первой гармоники:
р = 1,57 – очень большой коэффициент пульсаций – это является недостатком схемы.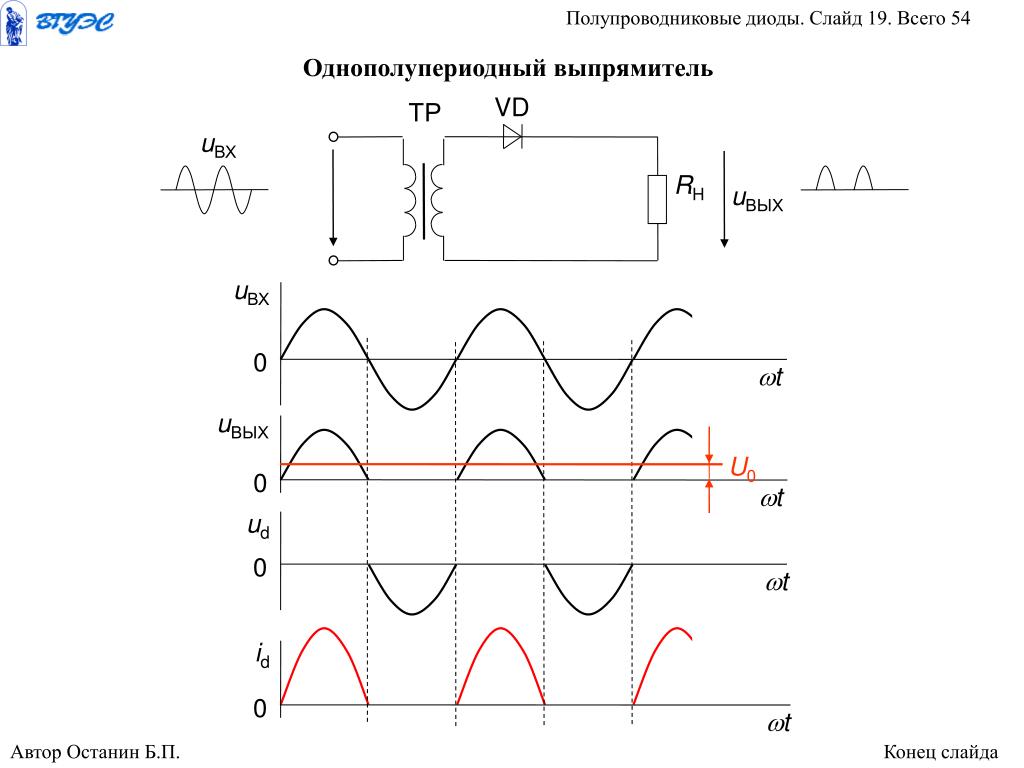
Обратное максимальное напряжение на запертом диоде равно амплитуде входного напряжения:
При выборе выпрямительных диодов используются максимально допустимые параметры: ток прямой максимально допустимый и напряжение обратное максимально допустимое: Iпрmax, Uобрmax.
Диод в выпрямителях является основным элементом, и его параметры во многом определяют основные параметры выпрямителей
См. также
А как ты думаешь, при улучшении однополупериодный выпрямитель, будет лучше нам? Надеюсь, что теперь ты понял что такое однополупериодный выпрямитель и для чего все это нужно, а если не понял, или есть замечания, то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории Электроника, Микроэлектроника , Элементная база
Выпрямители: Однофазный однополупериодный выпрямитель – Club155.ru
Простейшим выпрямителем является схема однофазного однополупериодного выпрямителя (рис. 2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
Отношение среднего значения выпрямленного напряжения \(U_{н ср}\) к действующему значению входного переменного напряжения \(U_{вх д}\) называется коэффициентом выпрямления (\(K_{вып}\)). Для рассматриваемой схемы \(K_{вып} = {0,45}\).
Максимальное обратное напряжение на диоде \(U_{обр max} = U_{вх max} = \pi U_{н ср}\) , т.е. более чем в три раза превышает среднее выпрямленное напряжение (это следует учитывать при выборе диода для выпрямителя).
Спектральный состав выпрямленного напряжения имеет вид (разложение в ряд Фурье):
\(U_н = \cfrac{1}{\pi} U_{вх max} + \cfrac{1}{2} U_{вх max} \sin{\left( \omega t \right)} – \cfrac{2}{3 \pi} \cos{\left( 2 \omega t \right)} – \)
\( – \cfrac{2}{15 \pi} U_{вх max} \cos{\left( 4 \omega t \right)} – {…} \)
Коэффициент пульсаций, равный отношению амплитуды низшей (основной) гармоники пульсаций к среднему значению выпрямленного напряжения, для описываемой схемы однополупериодного выпрямителя равен:
\(K_п = \cfrac{U_{пульс max 01}}{U_{н ср}} = \cfrac{\pi}{2} = {1,57}\).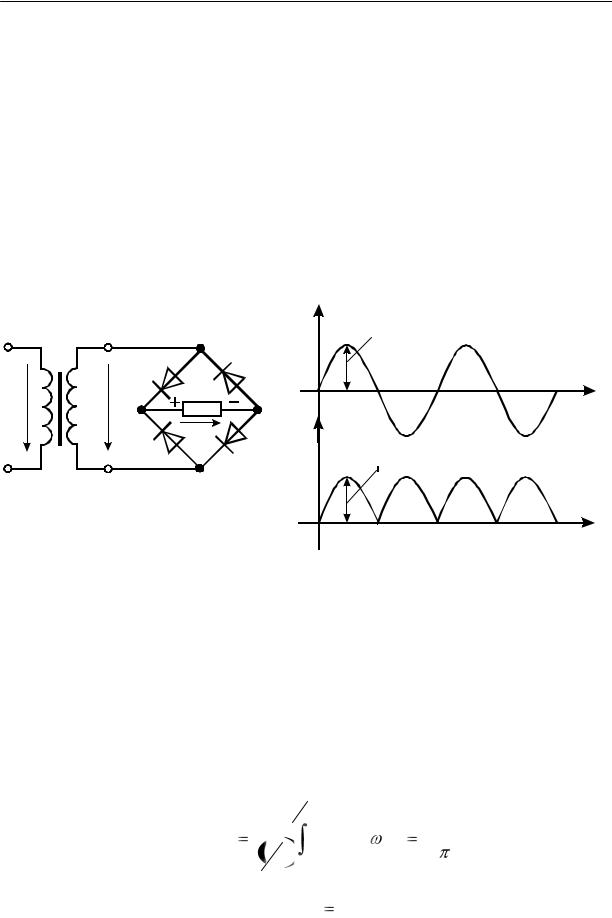
Как видно, однополупериодное выпрямление имеет низкую эффективность из-за высокой пульсации выпрямленного напряжения.
Еще один отрицательный аспект однополупериодного выпрямления связан с неэффективным использованием силового трансформатора, с которого берется переменное напряжение. Это обусловлено тем, что в токе вторичной обмотки трансформатора существует постоянная составляющая, равная среднему значению выпрямленного тока. Такая составляющая не трансформируется, т.е.:
\(I_1 \cdot w_1 = \left( I_2 – I_{н ср} \right) w_2\) ,
где \(I_1\), \(I_2\) — токи первичной и вторичной обмоток, а \(w_1\), \(w_2\) — число витков первичной и вторичной обмоток трансформатора.
Временнáя диаграмма тока первичной обмотки трансформатора (рис. 3.4-2) подобна диаграмме тока вторичной обмотки, но смещена на величину \(I_{н ср} \cfrac{w_2}{w_1}\).
Рис. 3.4-2. Временная диаграмма токов в первичной и вторичной обмотках силового трансформатора, нагруженного на схему однофазного однополупериодного выпрямителя
3.4-2. Временная диаграмма токов в первичной и вторичной обмотках силового трансформатора, нагруженного на схему однофазного однополупериодного выпрямителя
В сердечнике трансформатора за счет постоянной составляющей тока вторичной обмотки создается постоянный магнитный поток \(\Phi_0 = w_2 \cdot I_0\). Это явление принято называть вынужденным намагничиванием сердечника трансформатора. Оно может вызвать насыщение магнитной системы трансформатора, т.е. увеличение тока холостого хода, действующего значения первичного тока и следовательно, расчетной мощности первичной обмотки трансформатора, что обусловливает увеличение необходимых размеров трансформатора в целом.
Дополнительный минус однополупериодного выпрямления состоит в наличии участка стабильного тока, что также снижает эффективность использования трансформатора по мощности. Максимальный коэффициент использования трансформатора по мощности для такой схемы не превышает \(k_{тр P} \approx {0,48}\).
Для снижения уровня пульсаций на выходе выпрямителя включаются разнообразные индуктивно-емкостные фильтры. Наличие конденсаторов и индуктивностей в цепи нагрузки оказывает значительное влияние на работу выпрямителя.
В маломощных выпрямителях обычно применяют простейший емкостный фильтр, который представляет собой конденсатор, включенный параллельно нагрузке (рис. 3.4-3).
Рис. 3.4-3. Схема однофазного однополупериодного выпрямителя с емкостным фильтром (а) и временные диаграммы, поясняющие его работу (б)
В установившемся режиме работы, когда напряжение на входе выпрямителя \(U_{вх}\) больше напряжения на нагрузке \(U_н\) и диод выпрямителя открыт, конденсатор будет подзаряжаться, накапливая энергию, поступающую от внешнего источника. Когда же напряжение на входе выпрямителя упадет ниже уровня открывания диода и он закроется, конденсатор начнет разряжаться через \(R_н\), предотвращая при этом быстрое падение уровня напряжения на нагрузке. Таким образом, результирующее напряжение на выходе выпрямителя (на нагрузке) окажется уже не таким пульсирующим, а будет значительно сглажено, причем тем сильнее, чем большую емкость будет иметь применяемый конденсатор.
Таким образом, результирующее напряжение на выходе выпрямителя (на нагрузке) окажется уже не таким пульсирующим, а будет значительно сглажено, причем тем сильнее, чем большую емкость будет иметь применяемый конденсатор.
Обычно, емкость конденсатора фильтра выбирают такой, чтобы его реактивное сопротивление было намного меньше сопротивления нагрузки (\(1/ \omega C \ll R_н\)). В этом случае пульсации напряжения на нагрузке малы и допустимо предполагать, что это напряжение постоянно (\(U_н \approx {const}\)). Примем: \(U_н = U_{вх max} \cos{\beta}\), где \(\beta\) — некоторая константа, определяющая значение напряжения на нагрузке. Очевидно, что в общем случае \(\beta\) зависит от емкости конденсатора, сопротивления нагрузки, частоты входного напряжения и т.п. Физический смысл этой величины можно понять из временных диаграмм, приведенных на рис. 3.4-4. Как видно, \(\beta\) отражает длительность временного интервала в одном периоде колебаний внешнего напряжения, когда диод выпрямителя находится в открытом состоянии (\(\beta = \omega \cdot t_{откр}/2\)).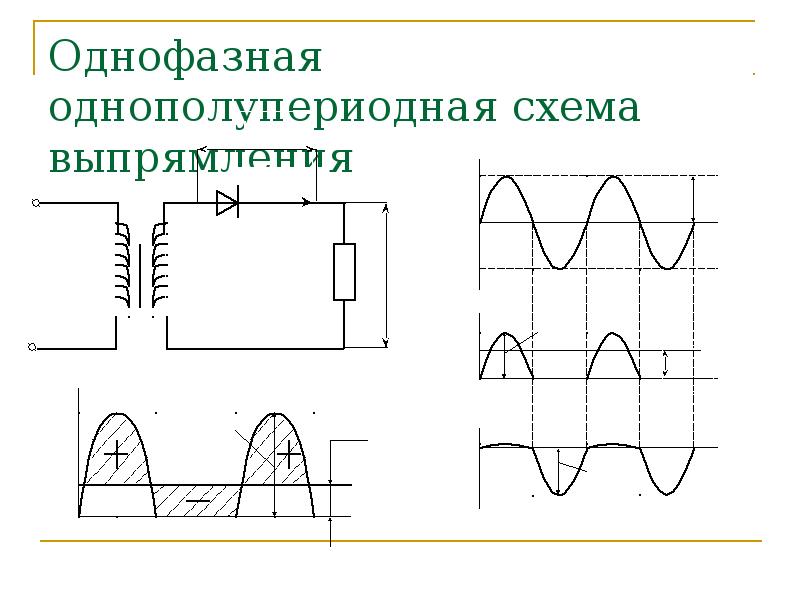 Угол \( \beta\) принято называть углом отсечки.
Угол \( \beta\) принято называть углом отсечки.
Рис. 3.4-4. График зависимости \(A(\beta)\)
Для тока, протекающего через диод в открытом состоянии, можно записать:
\( I_д = \cfrac{U_{вх} – U_н}{r} \) ,
где \(r\) — активное сопротивление, обусловленное сопротивлением диода в открытом состоянии и сопротивлением вторичной обмотки трансформатора (иногда его называют сопротивлением фазы выпрямителя).
Учитывая, что \(U_{вх} = U_{вх max} \sin{\left( \omega t \right)} \):
\(I_д = \cfrac{U_{вх max}}{r} \left( \sin{\left( \omega t \right)} – \cos{\left( \beta \right)} \right) = \cfrac{U_{вх max}}{r} \left(\sin{\left(\varphi \right)} – \cos{\left( \beta \right)} \right)\) (3.4.1)
Среднее за период значение выпрямленного тока диода (учитывая, что диод открыт только на участке \(\varphi = \left[\pi/2 – \beta ; \pi/2 + \beta \right]\):
\(I_{д ср} =\cfrac{1}{2 \pi} {\huge \int \normalsize}_{\frac{\pi}{2} – \beta}^{\frac{\pi}{2} + \beta} \cfrac{U_{вх max}}{r} \left( \sin{ \left( \varphi \right)} – \cos{\left( \beta \right)} \right) \operatorname{d} \varphi =\)
\(= \cfrac{U_{вх max}}{\pi r} \left( \sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)} \right) \)
Поскольку \(U_{вх max} = \cfrac{U_н}{\cos{\left( \beta \right)}} \):
\(I_{д ср} =\cfrac{U_н}{\pi r} \cdot \cfrac{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)} } = \cfrac{U_н}{\pi r} A \left( \beta \right) \),
где \( A \left( \beta \right) = \cfrac{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}} = \operatorname{tg} \left( \beta \right) – \beta \) (3. 4.2)
4.2)
Формула (3.4.2) очень важна при расчете выпрямителя. Ведь угол отсечки \(\beta\) не является заранее известным исходным параметром, как правило, его приходится вычислять на основании заданных выходного напряжения (\(U_н\)), сопротивления (\(R_н\)) или тока нагрузки (\(I_н\)), а также параметров применяемого диода и трансформатора (которые определяют сопротивление фазы \(r\)). Располагая этими данными и учитывая (3.4.2) можно определить значение коэффициента \(A\):
\(A \left( \beta \right) = \cfrac{I_{д ср} \pi r}{U_н} \)
Средний ток через диод \(I_{д ср}\) равен среднему току нагрузки \(I_{н ср}\), а учитывая, что напряжение на нагрузке предполагается неизменным, то и мгновенное значение тока через нагрузку равно току диода: \(I_н = I_{д ср}\). Таким образом:
\(A \left( \beta \right) = \cfrac{I_{н} \pi r}{U_н} = \cfrac{\pi r}{R_н} \)
Для нахождения угла отсечки \(\beta\) при известном коэффициенте \(A(\beta)\) на практике обычно пользуются графиком (рис.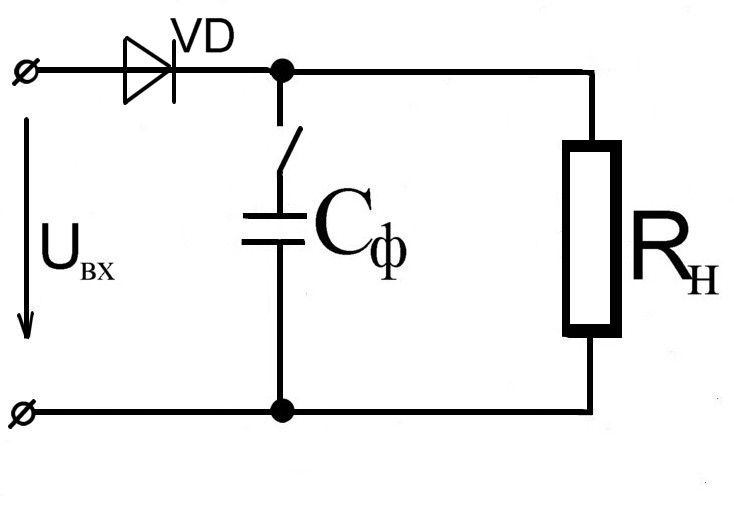 3.4-4).
3.4-4).
Максимальное значение тока диода достигается при \(U_{вх} = U_{вх max}\) в момент времени, когда \(\varphi = \pi/2 \), т.е. согласно выражения (3.4.1):
\( I_{д max} = \cfrac{U_{вх max}}{r} \left( 1 – \cos{\left( \beta \right)} \right) = \cfrac{U_н}{r} \cdot \cfrac{\pi \left( 1 – \cos{\left( \beta \right)} \right)}{\cos{\left( \beta \right)}} \)
И далее, учитывая (3.4.2) получим:
\( I_{д max} = \cfrac{I_{д ср} \cdot \pi}{A \left( \beta \right)} \cdot \cfrac{1- \cos{\left( \beta \right)}}{\cos{\left( \beta \right)}}\), где \(F \left( \beta \right) = \cfrac{\pi \cdot \left( 1 – \cos{\left( \beta \right)} \right)}{\sin{\left( \beta \right)} – \beta \cos{\left( \beta \right)}}\)
График функции \(F(\beta)\) представлен на рис. 3.4-5. Из него видно, что с уменьшением угла отсечки \(\beta\) существенно увеличивается амплитуда тока через вентили.
Рис.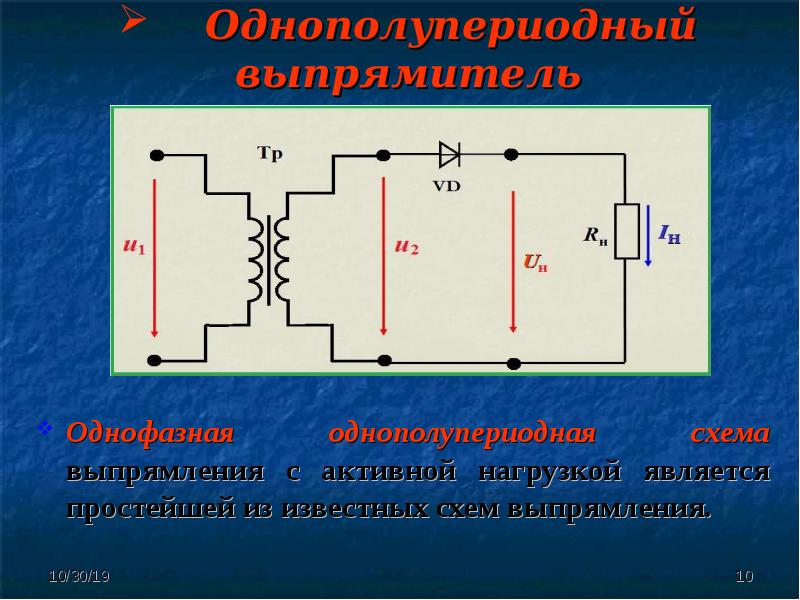 3.4-5. График зависимости \(F(\beta)\)
3.4-5. График зависимости \(F(\beta)\)
Таким образом, емкостный характер нагрузки выпрямителя приводит к тому, что выпрямительный диод оказывается открытым в течение меньшего промежутка времени, а амплитуда тока, проходящего в это время через диод, оказывается больше, чем в аналогичной схеме, работающей на чисто активную нагрузку. Этот факт необходимо учитывать при выборе диода, который должен выдерживать повторяющийся ток соответствующей амплитуды и более того, нормально переносить первоначальный всплеск тока при включении, когда происходит первоначальная зарядка конденсатора.
Указанная закономерность справедлива не только для описываемой схемы однофазного однополупериодного выпрямления. Аналогичным образом будет происходить работа и других рассматриваемых далее схем, имеющих нагрузку емкостного характера.
Требуемый коэффициент пульсаций на выходе однофазного однополупериодного выпрямителя с емкостным фильтром \(K_п\) может быть получен при правильном выборе емкости сглаживающего конденсатора.
\( С = \cfrac{H(\beta)}{r \cdot K_п}\),
где \(H(\beta)\) — это еще один вспомогательный коэффициент, значение которого находится по графику (рис. 3.4-6).
Рис. 3.4-6. График зависимости \(H(\beta)\)
Емкостный фильтр характерен для выпрямителей, рассчитанных на малые токи нагрузки. При больших токах обычно применяют индуктивные фильтры. Такой фильтр представляет собой катушку индуктивности (обычно с ферромагнитным сердечником), включенную последовательно с нагрузкой (рис. 3.4-7). Наличие индуктивности в цепи нагрузки также как и емкость оказывает значительное влияние на режим работы вентилей выпрямителя.
Рис. 3.4-7. Схема однофазного однополупериодного выпрямителя с индуктивным фильтром (а) и временные диаграммы, поясняющие его работу (б)
Работа схемы на рис. {- \cfrac{R_н t}{L}} \sin{( \theta )} \right) \),
{- \cfrac{R_н t}{L}} \sin{( \theta )} \right) \),
где \( \theta = \operatorname{arctg} \left( \cfrac{\omega L}{R_н} \right) \)
Временная диаграмма, отражающая эту зависимость приведена на рис. 3.4-7(б). По ней хорошо виден физический смысл константы \(\theta\). Она представляет собой угол, на который запаздывает основной всплеск тока в нагрузке относительно инициирующего его всплеска напряжения на входе выпрямителя.
Если проанализировать зависимость тока нагрузки \(I_н(t)\), можно заметить, что его амплитуда с увеличением индуктивности катушки падает (соответственно падает и его среднее значение). Т.е. среднее значение напряжения на нагрузке оказывается меньшим, чем в случае отсутствия индуктивности, уменьшаются также пульсации выходного напряжения. Сами колебания тока оказываются сдвинутыми относительно колебаний входного напряжения на угол \(\theta\). Это является причиной скачкообразного приложения к диоду в момент его запирания отрицательного обратного напряжения величиною до \(U_{обр} = U_{вх max}\).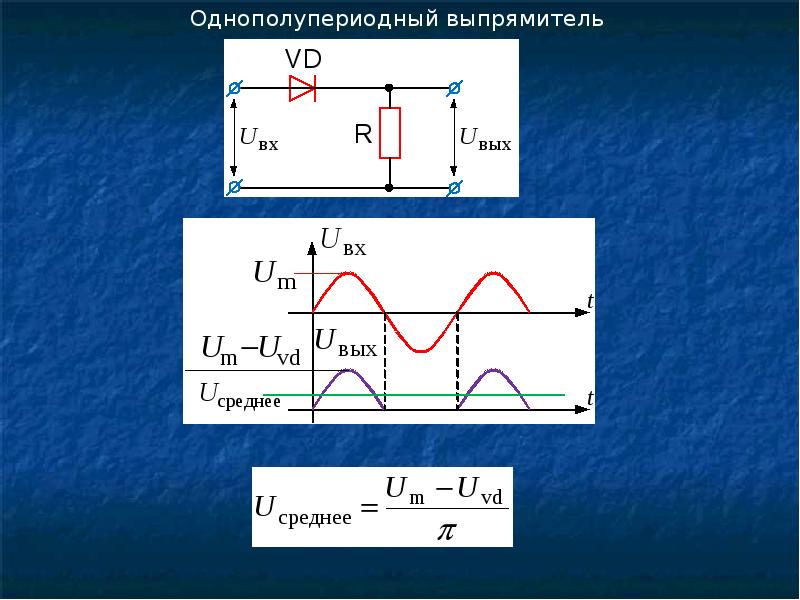
Описанный режим работы вентилей (затягивание тока, уменьшение его амплитуды, скачкообразное приложение обратного напряжения) при наличии индуктивного фильтра характерен для всех схем выпрямителей. Индуктивный фильтр обычно применяют в схемах мощных выпрямителей, поскольку в этом случае требуемая для существенного изменения параметров выходного напряжения индуктивность оказывается незначительной.
Наиболее эффективно сглаживание пульсаций выпрямленного напряжения осуществляется с помощью сложных многозвенных фильтров, в состав которых входят и катушки индуктивности и конденсаторы (основой таких фильтров являются т.н. Г- или П-образные звенья).
| < Предыдущая | Следующая > |
|---|
Однополупериодный выпрямитель схема. Расчет выпрямителей напряжения
В этой статье мы разберем какие бывают выпрямители, для какой цели служат, в чем заключаются особенности того или иного выпрямителя. Если мы решаем собрать какое-либо устройство или просто необходимо запитать готовое, то мы можем использовать питание от гальванических элементов (батареек), либо воспользоваться для этих целей аккумуляторами. Но как быть, если радиоустройство не планируется носить с собой и оно потребляет значительный ток? В таких случаях запитывают устройство от сети 220 вольт.
Если мы решаем собрать какое-либо устройство или просто необходимо запитать готовое, то мы можем использовать питание от гальванических элементов (батареек), либо воспользоваться для этих целей аккумуляторами. Но как быть, если радиоустройство не планируется носить с собой и оно потребляет значительный ток? В таких случаях запитывают устройство от сети 220 вольт.Напрямую запитать от 220 вольт, разумеется, мы не можем, напряжение слишком высокое и ток переменный, а для питания электронных устройств почти всегда необходим постоянный ток и более низкое напряжение. Необходим так называемый сетевой адаптер .
Фотография трансформатора
Понизить напряжение мы можем с помощью трансформатора, о нем мы поговорим в одной из следующих статей, пока нам достаточно знать, что с помощью трансформатора мы можем понизить или повысить напряжение при переменном токе. Далее нам необходимо сделать из переменного тока постоянный, для этих целей и служит выпрямитель.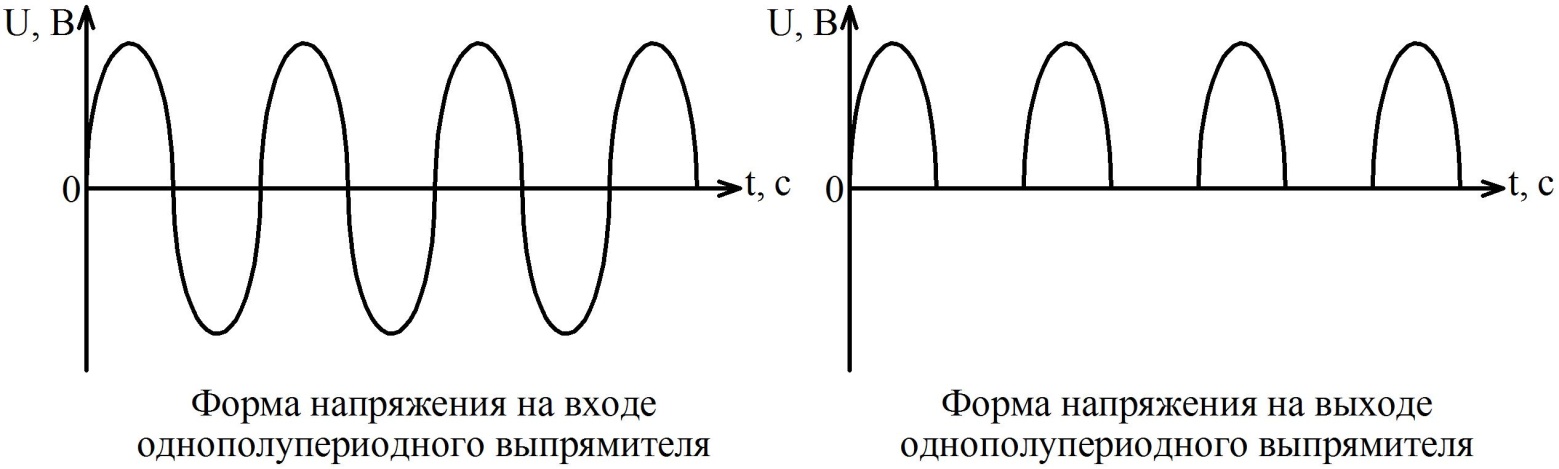 Существуют три основных типа выпрямителей.
Существуют три основных типа выпрямителей.
Однополупериодный выпрямитель
Этот выпрямитель работает только в течение положительного полупериода синусоиды. Это можно видеть на следующем графике:
На выходе после диода мы получаем пульсирующее напряжение, нам нужно сделать из него постоянное, то есть из пульсирующего тока получить постоянный. Для этих целей служит электролитический конденсатор большой емкости, подключенный параллельно выходу питания в соответствии с полярностью. На фотографии ниже можно увидеть внешний вид подобного конденсатора:
Такой конденсатор благодаря большой емкости разряжается в течении отрицательного полупериода синусоиды. Обычно для фильтрации напряжения в выпрямителях применяют электролитические конденсаторы от 2200 микрофарад. В усилителях и других устройствах, где важно чтобы напряжение не проседало при увеличении мощности нагрузки, ставят конденсаторы на большую емкость, чем 2200 микрофарад. Для устройств питающих бытовую аппаратуру обычно конденсаторов такой емкости бывает достаточно. На следующем графике (выделено красным), мы можем видеть, как конденсатор поддерживает напряжение стабильным во время прохождения отрицательной полуволны.
Для устройств питающих бытовую аппаратуру обычно конденсаторов такой емкости бывает достаточно. На следующем графике (выделено красным), мы можем видеть, как конденсатор поддерживает напряжение стабильным во время прохождения отрицательной полуволны.
Двухполупериодный выпрямитель со средней точкой
Для этой схемы необходим трансформатор, с двумя вторичными обмотками. Напряжение на диодах в два раза выше, чем при включении схемы с однополупериодным выпрямителем или при включении мостовой схемы. В этой схеме попеременно работают оба полупериода. В течении положительного полупериода работает одна часть схемы обозначенная В1 , во время отрицательного полупериода работает вторая часть схемы обозначенная В2 . Эта схема является менее экономичной, чем мостовая схема, в частности у неё более низкий коэффициент использования трансформатора. В этой схеме после диодов получается также пульсирующее напряжение, но частота пульсаций в два раза выше.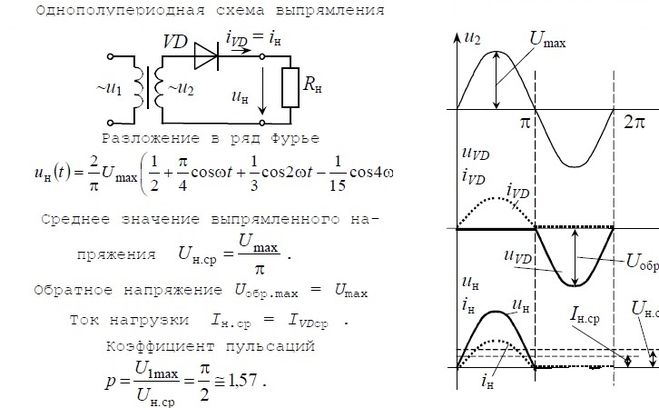 Что мы и можем видеть на следующем графике:
Что мы и можем видеть на следующем графике:
Двухполупериодный выпрямитель, мостовая схема
И наконец, рассмотрим схему мостового выпрямителя, самую распространенную схему, по которой сделана большая часть всех выпущенных трансформаторных блоков питания. Сейчас объясню принцип работы :
Ток у нас на выходе с трансформатора переменный, а переменный ток, как известно, в течение периода дважды меняет свое направление. Говоря другими словам, конечно же упрощенно, при переменном токе с частотой 50 герц, ток у нас 100 раз в секунду меняет свое направление. То есть сначала он течет от вывода диодного моста под цифрой один , ко второму, потом в течение другой полуволны он течет от вывода под номером два к первому.
Рассмотрим, что происходит с диодным мостом при подаче напряжения, мы видим, на рисунке обозначен красным путь тока, напрямую пройти к выводу диодного моста соединенного с переменным током не позволит диод, который получается у нас включенный в обратном включении, а в обратном включении, как мы помним, диоды не пропускают ток.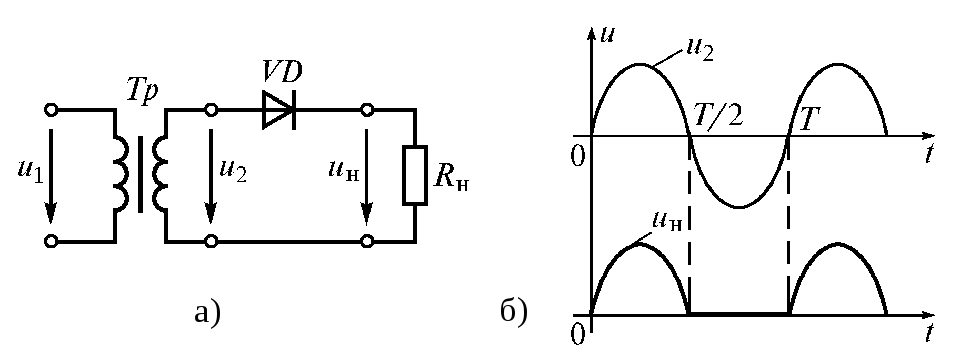 Току остается только один путь (выделено на рисунке синим), через нагрузку и через диод уйти в провод соединенный с выводом переменного тока. Когда у нас ток меняет свое направление, то вступает в действие вторая часть диодного моста, которая действует аналогично той, что описал выше. В итоге у нас получается на выходе такой же график напряжения, как и у двухполупериодного выпрямителя со средней точкой:
Току остается только один путь (выделено на рисунке синим), через нагрузку и через диод уйти в провод соединенный с выводом переменного тока. Когда у нас ток меняет свое направление, то вступает в действие вторая часть диодного моста, которая действует аналогично той, что описал выше. В итоге у нас получается на выходе такой же график напряжения, как и у двухполупериодного выпрямителя со средней точкой:
При сборке выпрямителя нужно учитывать полярность на выходе диодного моста, если мы подключим электролитический конденсатор неправильно, то рискуем испортить конденсатор и можно считать, что повезло, если этим все ограничится. Поэтому при сборке диодного моста важно помнить одно правило, плюс на выходе с моста всегда будет в точке соединения 2 катодов диодов, а минус в точке соединения анодов. Встречается и такое обозначение на схемах диодного моста:
Диодный мост можно собрать как из отдельных диодов, так и взять специальную сборку из 4 диодов, уже соединенных по мостовой схеме, и имеющий 4 вывода. В таком случае остается только подать переменный ток, идущий обычно с вторичной обмотки трансформатора на два вывода моста, а с оставшихся двух выводов снимать плюс и минус. Обычно на самой детали бывает обозначено, где какой вывод у моста. Так выглядит импортный диодный мост:
В таком случае остается только подать переменный ток, идущий обычно с вторичной обмотки трансформатора на два вывода моста, а с оставшихся двух выводов снимать плюс и минус. Обычно на самой детали бывает обозначено, где какой вывод у моста. Так выглядит импортный диодный мост:
Фото диодный мост кц405
Трехфазные выпрямители
Существуют и трехфазные трансформаторы. Обычным однофазным диодным мостом с такого трансформатора не получится на выходе постоянный ток. Конечно, если нагрузка небольшая можно подключиться к одной фазе и к нулевому проводу трансформатора, но экономичным такое решение не назовешь.
Для трехфазного тока существуют специальные схемы выпрямителей, две таких схемы приведены на рисунках ниже. Первая, известная как схема Миткевича , имеет низкий коэффициент габаритной мощности трансформатора. Эта схема применяется при небольших мощностях нагрузки.
Вторая схема, известная как , нашла широкое применение в электротехнике, так как имеет лучшие технико-экономические показатели по сравнению со схемой Миткевича.
Схема Ларионова может использоваться как “звезда-Ларионов” и “треугольник-Ларионов”. Вид подключения зависит от схемы подключения трансформатора, либо генератора, с выходом которого соединен этот выпрямитель. Автор статьи – AKV .
Обсудить статью ВЫПРЯМИТЕЛИ
В осветительной электрической сети, от которой получают питание все бытовые электроприборы, как правило, течёт переменный ток. Редкое исключение составляют небольшие сельские посёлки, где электростанции дают постоянный ток.
Радиоприемники, магнитофоны, электропроигрыватели и другие устройства работают на электронновакуумных лампах или полупроводниковых приборах, на электроды которых необходимо подавать напряжение постоянного тока. Зарядка аккумуляторов может быть произведена только постоянным током. Ряд производственных процессов на заводах, как например, хромирование, невозможно осуществить, если не имеется постоянного напряжения.
Почему же наши электростанции дают переменный ток? Ведь электронагревательные приборы и электромоторы так же хорошо будут работать и на постоянном токе? Объясняется это главным образом тем, что переменный ток можно легко трансформировать (преобразовать) в различные напряжения, что нельзя делать с постоянным током.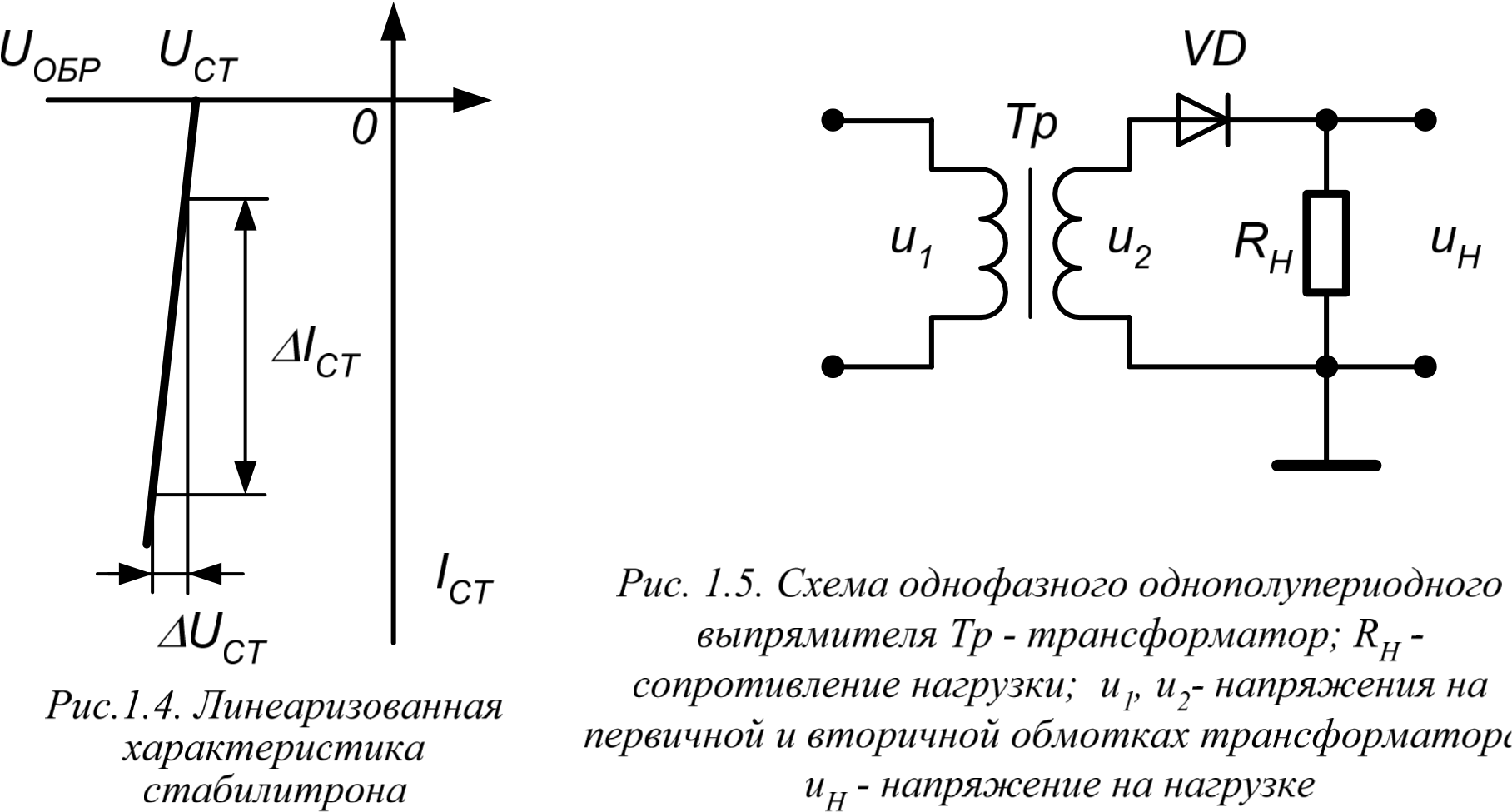 Передачу энергии переменного тока по линии электропередачи можно осуществить со значительно меньшими потерями, чем при постоянном токе, вследствие того, что напряжение в линии в этом случае может составлять десятки и сотни тысяч вольт. В месте потребления напряжение понижается на трансформаторных подстанциях и в наши квартиры и на заводы подается переменное напряжение 127 или 220 в.
Передачу энергии переменного тока по линии электропередачи можно осуществить со значительно меньшими потерями, чем при постоянном токе, вследствие того, что напряжение в линии в этом случае может составлять десятки и сотни тысяч вольт. В месте потребления напряжение понижается на трансформаторных подстанциях и в наши квартиры и на заводы подается переменное напряжение 127 или 220 в.
Как же получить постоянное напряжение, необходимое для нормальной работы некоторых приборов?
Для преобразования переменных напряжений в постоянные служит выпрямитель. Понять, как работает выпрямитель, можно, только ясно представляя, что такое переменный ток. Переменным током называется такой ток, направление и величина которого меняются во времени.
В осветительной сети, по принятому в нашей стране стандарту, направление тока меняется 50 раз в секунду, или, как говорят, частота промышленного тока равна 50 периодам (герцам). Это означает, что в какой-то период времени ток в сети равен 0, затем ток начинает плавно возрастать, достигает максимального (амплитудного) значения, после чего ток в сети постепенно уменьшается и становится равным нулю. После этого направление тока снова изменяется и ток опять плавно возрастает до максимального значения, а затем вновь уменьшается до нуля. Этот процесс напоминает качели, которые, качаясь около положения равновесия (нулевое значение тока), поднимаются на максимальную высоту (максимальное значение тока), затем опускаются, опять поднимаются и т. д. Такой процесс изменения тока называют периодическим. В нашей электросети такой процесс повторяется пятьдесят раз в секунду, т. е. ток (напряжение) имеет пятьдесят периодов в секунду, изменяя своё значение по синусоидальному закону.
После этого направление тока снова изменяется и ток опять плавно возрастает до максимального значения, а затем вновь уменьшается до нуля. Этот процесс напоминает качели, которые, качаясь около положения равновесия (нулевое значение тока), поднимаются на максимальную высоту (максимальное значение тока), затем опускаются, опять поднимаются и т. д. Такой процесс изменения тока называют периодическим. В нашей электросети такой процесс повторяется пятьдесят раз в секунду, т. е. ток (напряжение) имеет пятьдесят периодов в секунду, изменяя своё значение по синусоидальному закону.
Графически картина изменения тока в сети представлена на рис. 1. Такой график получается, если на вертикальной оси откладывать значения тока или напряжения, а по горизонтальной оси – отрезки времени, отсчитываемые от какого-то момента, принимаемого за начало отсчёта.
Задачей выпрямителя является получение постоянного напряжения из переменного; Постоянное напряжение графически можно изобразить так, как это показано на рис. 2. Постоянный ток не меняет ни своего направления, ни своей величины.
2. Постоянный ток не меняет ни своего направления, ни своей величины.
Процесс выпрямления переменного тока (напряжения) заключается в том, что на пути тока в электрической цепи включается элемент – вентиль, который пропускает ток только в одном направлении (одного знака). Схематично электрическая цепь переменного тока с вентилем представлена на рис. 3. Односторонняя проводимость вентиля приводит к тому, что только в положительные полупериоды ток проходит через вентиль, а в отрицательные полупериоды (отмеченные на рис. 1 знаком “-“) тока в цепи нет. Графически ток в такой цепи можно изобразить так, как это показа но на рис. 4. При положительной полуволне сопротивление вентиля мало и ток свободно проходит через него. При отрицательной полуволне ток встречает большое сопротивление, так как в обратном направлении сопротивление вентиля в сотни и даже тысячи раз больше и ток через него не проходит. Таким образом, включив в электрическую цепь переменного тока вентиль, мы уже не получаем в этой цепи переменного тока. Ток в этой цепи будет меняться только по величине и не будет изменять своего направления. Такой ток называют пульсирующим. Использовать его можно, например, для зарядки аккумуляторов. Для питания радиоаппаратуры такой ток не годится. Требуется дальнейшее его сглаживание, с тем чтобы ток превратился из пульсирующего в постоянный. Это достигается применением фильтра.
Ток в этой цепи будет меняться только по величине и не будет изменять своего направления. Такой ток называют пульсирующим. Использовать его можно, например, для зарядки аккумуляторов. Для питания радиоаппаратуры такой ток не годится. Требуется дальнейшее его сглаживание, с тем чтобы ток превратился из пульсирующего в постоянный. Это достигается применением фильтра.
В простейшем случае роль фильтра может выполнять конденсатор достаточно большой ёмкости. На рис. 5 показана схема цепи с вентилем и конденсатором С, являющимся фильтром. Сглаживание пульсаций (фильтрация) выпрямленного тока осуществляется вследствие того, что конденсатор заряжается током, проходящим через вентиль, и запасает электрическую энергию. Как только ток через вентиль начнет уменьшаться и напряжение на нагрузке Rн выпрямителя начнет падать, – а это происходит в конце каждого положительного полупериода, – конденсатор отдаёт накопленную им за положительный полупериод энергию. Графически это изображено на рис 6. Как видно из рисунка, ток ещё не стал совсем постоянным и заметны резкие пульсации. Необходим более совершенный фильтр, который на нагрузке обеспечил бы постоянный ток с очень незначительными пульсациями, которые не будут оказывать существенного влияния на работу устройства, питаемого от выпрямителя.
Как видно из рисунка, ток ещё не стал совсем постоянным и заметны резкие пульсации. Необходим более совершенный фильтр, который на нагрузке обеспечил бы постоянный ток с очень незначительными пульсациями, которые не будут оказывать существенного влияния на работу устройства, питаемого от выпрямителя.
Существует несколько типов выпрямителей. Наиболее простым из них является однополупериодный, схема которого изображена на рис. 7. В таком выпрямителе используются только положительные полупериоды выпрямленного тока. Частота пульсаций этого тока равна частоте сетевого напряжения и для сглаживания пульсаций выпрямитель, собранный по однополупериодной схеме, требует хорошего фильтра. Такие выпрямители используются для питания аппаратуры, потребляющей незначительный ток, так как при возрастании тока необходимо будет усложнять фильтр выпрямителя.
Более распространена двухполупериодная схема выпрямления, где (см. рис. 8) используются два вентиля В1 и В2. Ток в нагрузке протекает всё время в одном направлении.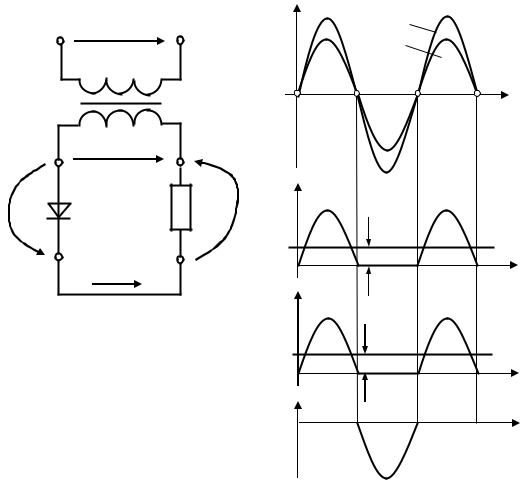 Выпрямление напряжения происходит следующим образом. В какой-то момент времени на одном (верхнем, по схеме} выводе вторичной обмотки трансформатора Тр1 будет положительное напряжение по отношению ко второму (нижнему) концу. Ток пойдёт через вентиль В1, и имеющий в прямом направлении маленькое сопротивление, затем через нагрузку на среднюю точку вторичной обмотки трансформатора. На рис. 8 прохождение тока показано сплошной стрелкой. Так будет продолжаться в течение первого положительного полупериода. При изменении направления тока в сети на верхнем конце трансформатора будет уже отрицательное напряжение и ток через вентиль B1 не пойдёт, так как вентиль будет иметь очень большое сопротивление. На нижнем конце вторичной обмотки трансформатора теперь будет положительное напряжение и ток пойдёт уже через вентиль В2, нагрузку и на среднюю точку вторичной обмотки – трансформатор Тр1.
Выпрямление напряжения происходит следующим образом. В какой-то момент времени на одном (верхнем, по схеме} выводе вторичной обмотки трансформатора Тр1 будет положительное напряжение по отношению ко второму (нижнему) концу. Ток пойдёт через вентиль В1, и имеющий в прямом направлении маленькое сопротивление, затем через нагрузку на среднюю точку вторичной обмотки трансформатора. На рис. 8 прохождение тока показано сплошной стрелкой. Так будет продолжаться в течение первого положительного полупериода. При изменении направления тока в сети на верхнем конце трансформатора будет уже отрицательное напряжение и ток через вентиль B1 не пойдёт, так как вентиль будет иметь очень большое сопротивление. На нижнем конце вторичной обмотки трансформатора теперь будет положительное напряжение и ток пойдёт уже через вентиль В2, нагрузку и на среднюю точку вторичной обмотки – трансформатор Тр1.
При таком включении вентилей используются уже оба полупериода выпрямляемого напряжения. Частота пульсаций в таком выпрямителе в два раза больше и поэтому значительно облегчается фильтрация выпрямленного напряжения. По двухполупериодной схеме собраны почти все выпрямители для радиоприёмников, телевизоров и магнитофонов.
По двухполупериодной схеме собраны почти все выпрямители для радиоприёмников, телевизоров и магнитофонов.
Существует ещё мостовая схема включения выпрямителя. В этом случае выпрямление происходит по двухполупериодной схеме, но трансформатор имеет более простую конструкцию, вторичная обмотка его содержит в два раза меньше витков и не требуется вывода от средней точки. Однако в выпрямителе, собранном по мостовой схеме, необходимо в два раза больше вентилей, чем при двухполупериодной схеме. Схема мостового выпрямителя изображена на рис. 9. Стрелками указано прохождение тока в оба полупериода.
В качестве вентиля для выпрямления переменного тока могут быть использованы селеновые или купроксные шайбы , кенотроны, газотроны или полупроводниковые диоды.
Для питания массовой радиоаппаратуры наибольшее распространение получили кенотронные и селеновые выпрямители. За последнее время начинают всё шире использоваться германиевые силовые диоды типа ДГ-Ц21-27.
Кенотрон представляет собой вакуумную, обычно стеклянную, радиолампу, имеющую два электрода – анод и катод. Двуханодный кенотрон имеет два анода. Вентильное свойство кенотрона проявляется в том, что ток через кенотрон может идти только в одном направлении – от анода к катоду. В обратном направлении – ток не пойдет, так как электроны вылетают только с поверхности нагретого катода и могут двигаться только на анод, если на нём в данный момент имеется положительное напряжение по отношению к катоду.
Двуханодный кенотрон имеет два анода. Вентильное свойство кенотрона проявляется в том, что ток через кенотрон может идти только в одном направлении – от анода к катоду. В обратном направлении – ток не пойдет, так как электроны вылетают только с поверхности нагретого катода и могут двигаться только на анод, если на нём в данный момент имеется положительное напряжение по отношению к катоду.
Простейшая однополупериодная схема выпрямителя с использованием в качестве вентиля кенотрона изображена на рис. 10. Направление тока I показано стрелкой. Конденсаторы С1 и С2 и дроссель Др1 составляют фильтр для сглаживания пульсаций. Подробно о фильтрах будет рассказано ниже.
Существует много различных типов кенотронов, каждый из которых рассчитан на определенные условия работы: одни позволяют получить большой выпрямленный ток при относительно низком напряжении, другие, наоборот, работают в выпрямителе, дающем высокое напряжение при ничтожно малом токе.
При конструировании выпрямителя прежде всего необходимо правильно выбрать тип кенотрона. Для этого нужно знать, какой ток и напряжение потребляет нагрузка, питающаяся от выпрямителя, и в соответствии с этими данными выбирать по справочнику подходящий тип кенотрона. Пусть требуется выбрать кенотрон, который предполагается установить в выпрямитель для питания приёмника. Приёмник имеет четыре лампы, не считая кенотрона.
Для этого нужно знать, какой ток и напряжение потребляет нагрузка, питающаяся от выпрямителя, и в соответствии с этими данными выбирать по справочнику подходящий тип кенотрона. Пусть требуется выбрать кенотрон, который предполагается установить в выпрямитель для питания приёмника. Приёмник имеет четыре лампы, не считая кенотрона.
Постоянное напряжение, потребное для питания радиоламп приёмника, равно 250 в. Общий ток, потребляемый анодно-экранными цепями всех ламп приемника, составляет около 40 мА.
Наиболее подходящим для нашего выпрямителя будет кенотрон 6Ц4П, который, по справочным данным, может обеспечить ток до 70 мА при двухполупериодной схеме выпрямления. По напряжению этот кенотрон также вполне подходит, так как для двухполупериодной схемы выпрямления обратное напряжение, возникающее в выпрямителе, не превышает тройного напряжения на нагрузке и равно 250х3 = 750 В, а кенотрон 6Ц4П выдерживает до 1000 В обратного напряжения.
В селеновом выпрямителе в качестве вентиля используют селеновые шайбы.
Селеновая шайба представляет собой железный диск или прямоугольную железную пластину, на которой с одной стороны нанесён тонкий слой полупроводника – селена. Сверху слой селена покрыт, для создания контакта, тонким слоем легкоплавкого металла.
Вентильные свойства селена проявляются в том, что он обладает односторонней проводимостью. Когда на железную пластину подан положительный полюс источника тока, селеновая шайба обладает ничтожно малым сопротивлением, и, наоборот, при смене полярности сопротивление шайбы возрастает в сотни раз.
Выбор селенового вентиля для выпрямителя производится также по току и напряжению, потребному для нагрузки. Необходимо помнить, что одна селеновая шайба выдерживает напряжение до 20 В, следовательно, если на нагрузке развивается напряжение больше этой величины, то селеновые шайбы нужно соединять последовательно.
Для нашего примера достаточно в каждое плечо двухполупериодного выпрямителя поставить по 13 шайб, так как напряжение на нагрузке равно 250 В и число шайб получится, если 250 В разделить на 20 В.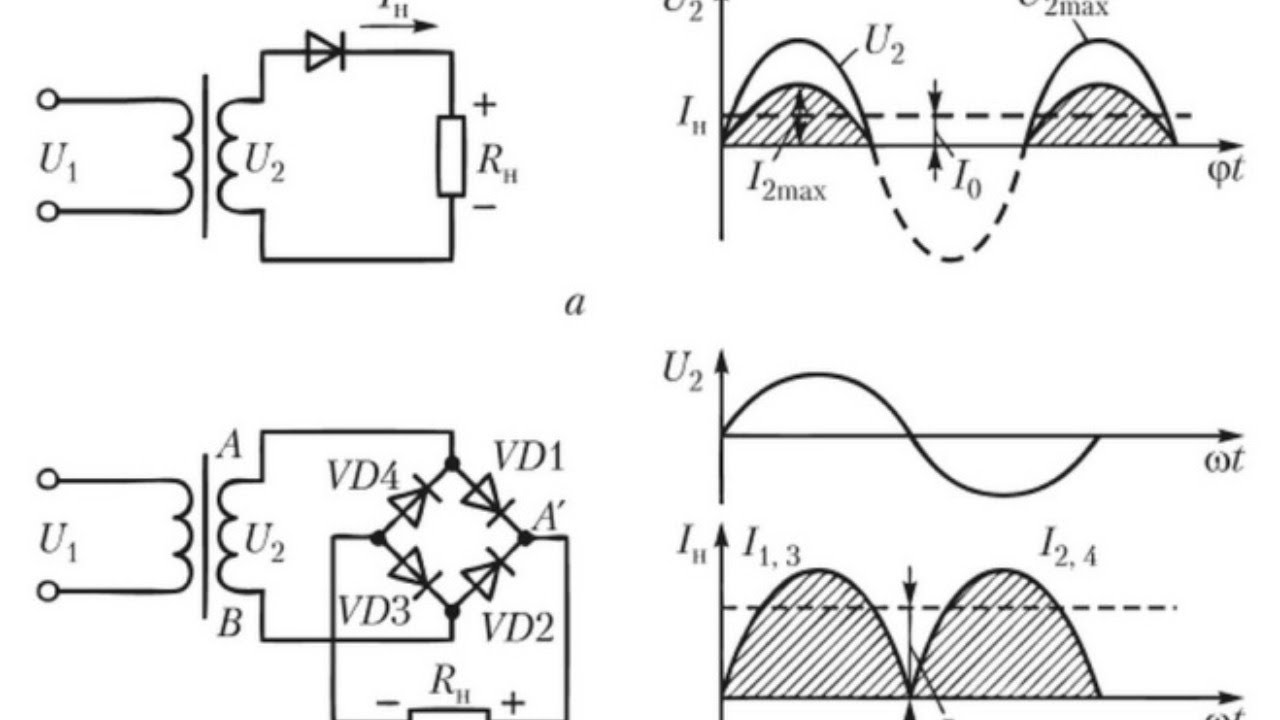 Получившееся дробное число необходимо округлить до ближайшего целого. Чтобы определить, какого диаметра нужно поставить шайбы, необходимо помнить, что на один квадратный сантиметр поверхности селеновой шайбы допускается ток, равный 30 мА. Следовательно, чтобы определить площадь селеновых шайб для нашего выпрямителя, нужно разделить величину тока, потребляемого приемником, на допустимую плотность тока (величину тока, допустимую на 1 см 2). Площадь шайбы равна 40/30 = 1,33 см. Диаметр шайбы легко определить по известной формуле площади окружности
Получившееся дробное число необходимо округлить до ближайшего целого. Чтобы определить, какого диаметра нужно поставить шайбы, необходимо помнить, что на один квадратный сантиметр поверхности селеновой шайбы допускается ток, равный 30 мА. Следовательно, чтобы определить площадь селеновых шайб для нашего выпрямителя, нужно разделить величину тока, потребляемого приемником, на допустимую плотность тока (величину тока, допустимую на 1 см 2). Площадь шайбы равна 40/30 = 1,33 см. Диаметр шайбы легко определить по известной формуле площади окружности
Sплощ = 0,25*π*D 2 ,
откуда диаметр шайбы равен
D = (4*S/π) 0,5 = (4*1,33/3,14) 0,5 ≈ 1,3 см.
Можно такого расчёта не производить и диаметр шайбы брать непосредственно из справочника. В случае, если у радиолюбителя имеются шайбы какого-то другого диаметра, то их можно использовать в этом выпрямителе. Если шайбы имеют больший диаметр, чем получился по расчету, их можно установить в качестве вентиля без всяких изменений в схеме выпрямителя, помня только, что допустимое напряжение на каждую шайбу не должно превышать 20 В.
В случае если диаметр имеющихся шайб меньше, чем получился по расчету, то шайбы можно соединить параллельно с таким расчетом, чтобы общая площадь двух параллельно соединённых шайб была равна или больше получившейся по расчету. При параллельном соединении шайб число их удваивается, так как необходимо соблюдать условие допустимого напряжения на каждую шайбу.
Расчёт вентиля, в качестве которого используется германиевый диод (рис. 11), производится аналогично. Зная ток нагрузки и напряжение на ней, выбирают по справочнику подходящий тип диода. Может случиться, что имеющиеся германиевые диоды типа ДГ-Ц не подходят по допустимому току или напряжению. Если диоды не подходят по току (ток нагрузки больше допустимого), то необходимо поставить несколько диодов, соединенных параллельно. Если диоды не подходят по напряжению, их соединяют последовательно. Расчёт числа последовательно соединенных диодов сводится к тому, чтобы выбрать такое количество диодов, при котором падение напряжения на каждом из них не превысило допустимого.
При последовательном соединении диодов типа ДГ-Ц каждый из них следует зашунтировать сопротивлением не менее 100 кОм мощностью до 1 Вт. Шунтировать диоды необходимо для выравнивания падения напряжения на каждом из них. Выпускаемые диоды имеют значительный разброс параметров, и может быть такой случай, когда на одном из них падение напряжения будет в несколько раз больше, чем на другом, что выводит диоды из строя. Этого не произойдет, если каждый диод будет зашунтирован сопротивлением и падение напряжения распределится равномерно между каждым диодом.
При параллельном соединении полупроводниковых диодов типа ДГ-Ц количество их рассчитывается по несложным формулам. Так, для диодов типа ДГ-Ц21 – 24 число параллельно соединённых диодов будет равно
Для диодов типа ДГ-Ц25 – 27 число параллельно соединённых диодов
n = 15,4I0 – 0,54.
В этих формулах I0 означает выпрямленный ток в амперах. Может случиться так, что число диодов n, рассчитанное по этим формулам, получается дробным.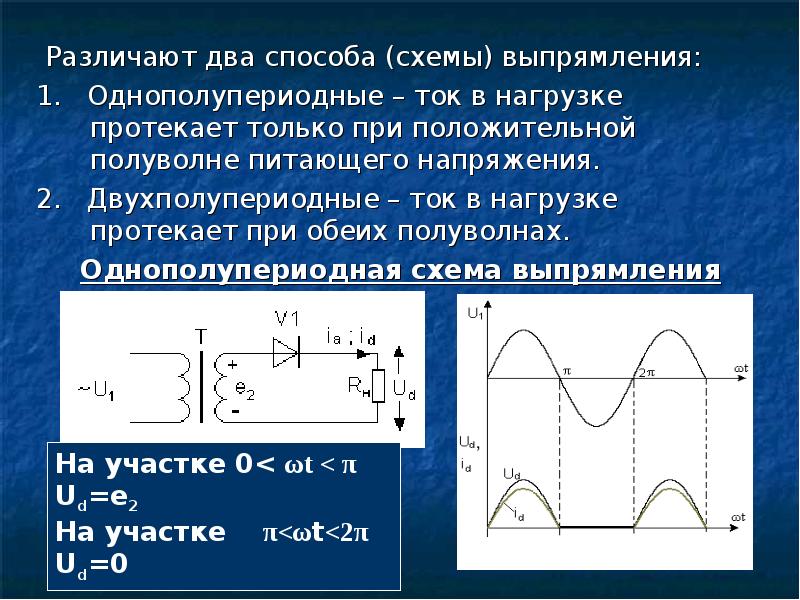 Тогда следует округлить это число до ближайшего большего целого числа. Иногда в расчете получается 0 или отрицательное число. Это означает, что необходимо поставить только один диод и никаких параллельных соединений делать не нужно, так как выбранный диод обеспечит требуемую величину выпрямленного тока.
Тогда следует округлить это число до ближайшего большего целого числа. Иногда в расчете получается 0 или отрицательное число. Это означает, что необходимо поставить только один диод и никаких параллельных соединений делать не нужно, так как выбранный диод обеспечит требуемую величину выпрямленного тока.
Сглаживающий фильтр
Как указывалось выше, для сглаживания пульсаций после выпрямителя на его выходе включается фильтр. Обычно фильтр состоит из дросселя фильтра Др1 (рис. 12), обмотка которого, выполненная из нескольких тысяч витков тонкой проволоки, располагается на стальном сердечнике. В фильтр входит также два и более конденсаторов фильтра. На месте этих конденсаторов в подавляющем большинстве случаев применяются электролитические конденсаторы, имеющие сравнительно небольшие габариты и большую ёмкость (10…50 мкф}.
Фильтр значительно ослабляет переменную составляющую выпрямленного напряжения и мало влияет на постоянную составляющую, идущую на питание анодно-экранных цепей приёмника.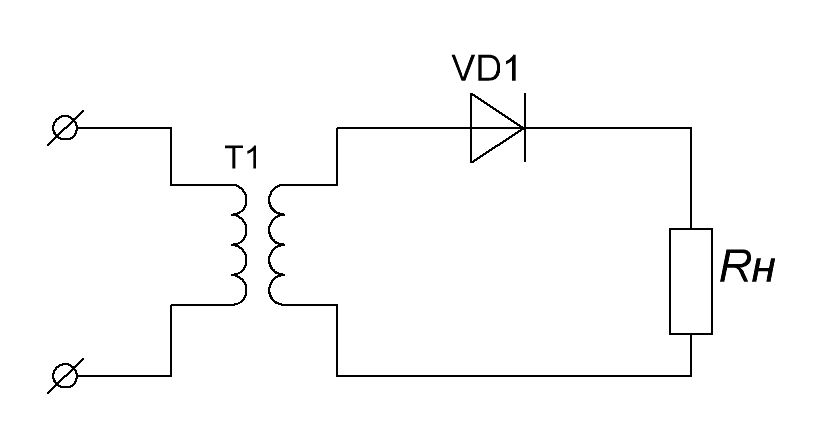
Качество фильтра определяется его коэффициентом фильтрации, который показывает, во сколько раз переменная составляющая на выходе фильтра ослабляется относительно переменной составляющей на его входе.
Допустимая величина переменной составляющей на выходе фильтра зависит от аппаратуры, которая питается от данного выпрямителя. Для усилителей низкой частоты амплитуда пульсаций анодного напряжения не должна превышать 0,5-1% от напряжения полезного сигнала, измеренного в анодной цепи данного каскада. Для каскадов усиления высокой и промежуточной частоты эта амплитуда не должна превышать 0,05-0,1% (0,1-0,2 В).
Работа фильтра зависит от произведения индуктивности дросселя на ёмкость конденсатора фильтра на выходе. Ёмкость этого конденсатора обычно берут в пределах 10-40 мкф. Индуктивность дросселя для маломощного выпрямителя обычно не превышает 20-30 Гн.
При прикидке данных фильтра можно пользоваться следующим правилом: произведение индуктивности катушки дросселя фильтра, выраженное в генри, на ёмкость конденсатора на выходе фильтра, выраженное в микофарадах, должно равняться 200.
Для улучшения фильтрации можно составлять сглаживающий фильтр из нескольких звеньев. Улучшения фильтрации можно также добиться путём применения настроенного дросселя, для этого параллельно дросселю фильтра подсоединяется конденсатор постоянной ёмкости (на рис. 12 это подключение показано пунктиром).
Ёмкость конденсатора берётся в пределах 0,05-0,1 мкф и в каждом отдельном случае находится опытным путём.
Дроссель фильтра можно включить как в «+», так и в «-» выпрямителя, это не скажется на качестве работы фильтра. В некоторых случаях, когда желательно воспользоваться падением напряжения на обмотке дросселя фильтра для подачи отрицательного смещения на управляющие сетки ламп усилителя приёмника, дроссель включают в минусовую цепь выпрямителя.
При питании малоламповых приемников вместо дросселя фильтра можно включить обмотки (или обмотку) трансформатора низкой частоты.
Конструктивно дроссель для сглаживающих фильтров аналогичен маломощному силовому трансформатору. Разница заключается в том, что трансформатор имеет несколько обмоток, дроссель только одну. Сердечник дросселя обязательно должен иметь воздушный зазор, который устраняет возможность магнитного насыщения сердечника постоянным током, протекающим по обмотке дросселя.
Разница заключается в том, что трансформатор имеет несколько обмоток, дроссель только одну. Сердечник дросселя обязательно должен иметь воздушный зазор, который устраняет возможность магнитного насыщения сердечника постоянным током, протекающим по обмотке дросселя.
Магнитное насыщение уменьшает индуктивность дросселя, что ухудшает работу фильтра.
Конструктивно дроссель фильтра и силовой трансформатор выпрямителя можно рассчитать, руководствуясь статьей, напечатанной в приложении № 1 для начинающих, «Расчет и изготовление силового трансформатора» (разослано с журналом «Радио» № 5 за 1957 год). Следует только учитывать, что, задаваясь напряжением на выходе выпрямителя, нужно принять во внимание падение напряжения на дросселе фильтра и что в случае применения двухполупериодного кенотронного выпрямителя с конденсаторным фильтром эффективное напряжение и ток повышающей обмотки связаны с напряжением и током на выходе выпрямителя следующими соотношениями: напряжение на вторичной обмотке берётся в 2. .2,2 раза больше напряжения на выходе выпрямителя, а ток в обмотке 1..1,2 I0. Токи и напряжения обмоток для накала ламп и кенотрона определяются данными накала кенотрона и ламп, для питания которых предназначен рассчитываемый выпрямитель.
.2,2 раза больше напряжения на выходе выпрямителя, а ток в обмотке 1..1,2 I0. Токи и напряжения обмоток для накала ламп и кенотрона определяются данными накала кенотрона и ламп, для питания которых предназначен рассчитываемый выпрямитель.
Вместо дросселя фильтра иногда применяют активное сопротивление, которое для получения хорошей фильтрации должно иметь значительную величину.
Недостатком такого фильтра является большое падение напряжения на сопротивлении фильтра, поэтому применять такой фильтр можно только в маломощных усилителях. При расчёте выпрямителя с таким фильтром задаются допустимым падением выпрямленного напряжения на сопротивлении, включенном в фильтр, Uпад, после чего величину этого сопротивления R находят по формуле
где I0 – ток в мА, снимаемый с выпрямителя.
Очень часто для питания той или иной аппаратуры применяются различные постоянные напряжения. Для того чтобы использовать для этой цели один и тот же выпрямитель, на его вход включают цепочку из нескольких последовательно соединённых постоянных сопротивлений величиной по нескольку тысяч Ом. Эти сопротивления не должны быть очень большими, так как в противном случае напряжение, снимаемое с делителя, будет сильно зависеть от величины нагрузки. Они также не должны быть очень малыми, чтобы не перегружать выпрямитель.
Эти сопротивления не должны быть очень большими, так как в противном случае напряжение, снимаемое с делителя, будет сильно зависеть от величины нагрузки. Они также не должны быть очень малыми, чтобы не перегружать выпрямитель.
Однополупериодный выпрямитель или четвертьмост является простейшим выпрямителем и включает в себя один вентиль (диод или тиристор).
Допущения: нагрузка чисто активная, вентиль – идеальный электрический ключ.
Напряжение со вторичной обмотки трансформатора проходит через вентиль на нагрузку только в положительные полупериоды переменного напряжения. В отрицательные полупериоды вентиль закрыт, всё падение напряжения происходит на вентиле, а напряжение на нагрузке Uн равно нулю. Среднее значение переменного тока по отношению к подведенному действующему составит:
Эта величина вдвое меньше, чем в полномостовом. Важно отметить, что среднеквадратичное (устар. эффективное, действующее) значение напряжения на выходе однополупериодного выпрямителя будет в корень из 2 меньше подведенного действующего, а потребляемая нагрузкой мощность в 2 раза меньше (для синусоидальной формы сигнала)
Отношение
среднего значения выпрямленного
напряжения Uн ср к действующему значению
входного переменного напряжения Uвх д
называется коэффициентом выпрямления
(Kвып). Для рассматриваемой схемы
Kвып=0,45.
Максимальное обратное напряжение на диоде Uобр max=Uвх max=πUн ср, т.е. более чем в три раза превышает среднее выпрямленное напряжение (это следует учитывать при выборе диода для выпрямителя).
Коэффициент пульсаций, равный отношению амплитуды низшей (основной) гармоники пульсаций к среднему значению выпрямленного напряжения, для описываемой схемы однополупериодного выпрямителя равен:
Kп=Uпульс max01Uн ср=π2=1,57.
27. Двуполупериодный выпрямитель со средней точкой. Диаграммы работы. Принцип действия. Основные параметры.
На интервале времени под действием напряжения Uвх1 диод VD1 смещен в прямом направлении (диод VD2 при этом смещен в обратном направлении) и поэтому ток в нагрузочном резисторе определяется только напряжением Uвх1. На интервале диод VD1 смещен в обратном направлении, а ток нагрузки протекает через прямосмещенный диод VD2 и определяется напряжением Uвх2. Таким образом, средние значения тока и напряжения на нагрузочном резисторе в случае двухполупериодного выпрямления будут в два раза превышать аналогичные показатели для однополупериодной схемы:
Uвх max и Iвх max – максимальные амплитудные значения входного напряжения и тока выпрямителя (по одному из напряжений питания),
Uвх
д и Iвх д – действующие значения входного
напряжения и тока выпрямителя.
Отрицательным свойством двухполупериодной схемы выпрямления со средней точкой является то, что во время прохождения тока через один из диодов обратное напряжение на другом (закрытом) диоде в пике достигает удвоенного максимального входного напряжения: Uобр max=2Umax. Этого нельзя забывать при выборе диодов для выпрямителя.
Основная частота пульсаций выпрямленного напряжения в данной схеме будет равна удвоенной частоте входного напряжения. Коэффициент пульсаций рассчитанный по методике, аналогичной описанной для схемы однофазного однополупериодного выпрямителя (разложение в ряд Фурье и выделение первой составляющей пульсаций) будет равен: Kп=0,67.
параметры смотреть в предыдущем пункте.
28. Однофазный мостовой выпрямитель. Диаграммы работы и принцип действия. Основные параметры выпрямителя.
Диаграммы работы:
Принцип работы:
В
однофазной мостовой схеме к одной из
диагоналей моста подключается источник
переменного напряжения (вторичная
обмотка трансформатора), а к другой –
нагрузка.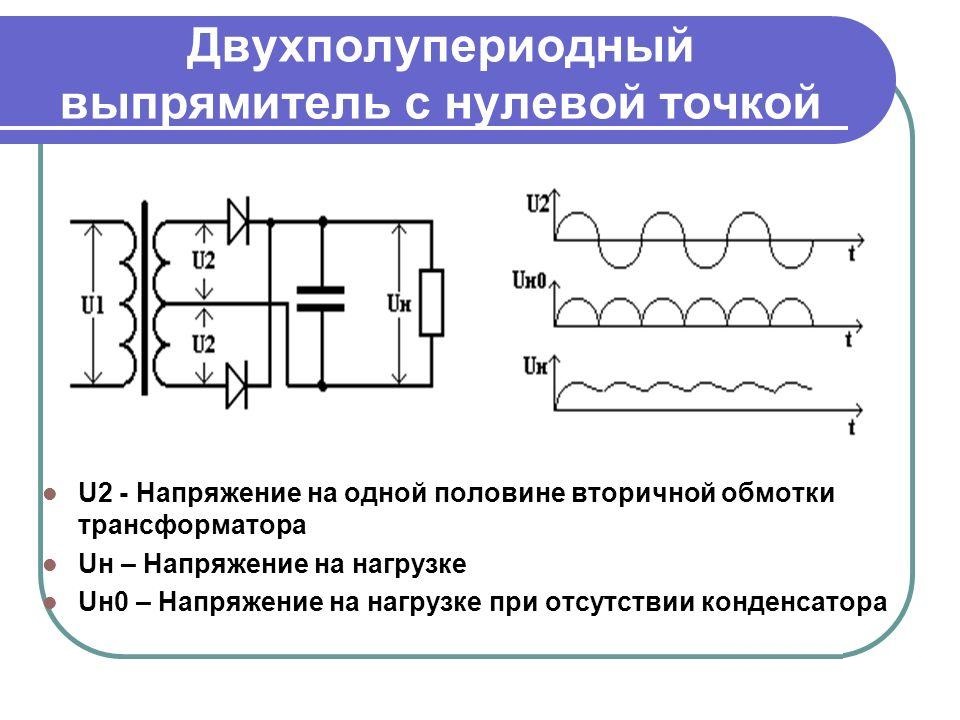
В мостовой схеме диоды работают попарно: в течение одной половины периода сетевого напряжения ток протекает от вторичной обмотки трансформатора по цепи VD1, RН, VD2, а на втором полупериоде – по цепи VD3, RН, VD4, причем в каждом полупериоде через нагрузку ток проходит в одном направлении, что и обеспечивает выпрямление. Коммутация диодов происходит в моменты перехода переменного напряжения через нуль.
где U2 ─ действующее значение переменного напряжения на входе выпрямителя.
Параметры:
Среднее значение тока через диод в два раза меньше среднего значения тока нагрузки Id:
Максимальное значение тока, протекающего через диод
Действующее значение переменного тока на входе выпрямителя
следовательно,
Мощность первичной и вторичной обмоток вентильного трансформатора
29.
Назначение сглаживающих фильтров. Схема
однофазного однополупериодного
выпрямителя с емкостным фильтром. Особенности работы. Внешние характеристики
выпрямителей с фильтрами
Особенности работы. Внешние характеристики
выпрямителей с фильтрами
Сглаживающий фильтр – устройство, предназначенное для уменьшения переменной составляющей выпрямленного напряжения до величины, при которой обеспечивается нормальная работа питаемой аппаратуры или её каскадов.
Схема однофазного однополупериодного выпрямителя с емкостным фильтром .
Особенности работы.
Для снижения уровня пульсаций на выходе выпрямителя включаются разнообразные индуктивно-емкостные фильтры. Наличие конденсаторов и индуктивностей в цепи нагрузки оказывает значительное влияние на работу выпрямителя. В маломощных выпрямителях обычно применяют простейший емкостный фильтр, который представляет собой конденсатор, включенный параллельно нагрузке.
В
установившемся режиме работы, когда
напряжение на входе выпрямителя U вх больше
напряжения на нагрузке U н и
диод выпрямителя открыт, конденсатор
будет подзаряжаться, накапливая энергию,
поступающую от внешнего источника.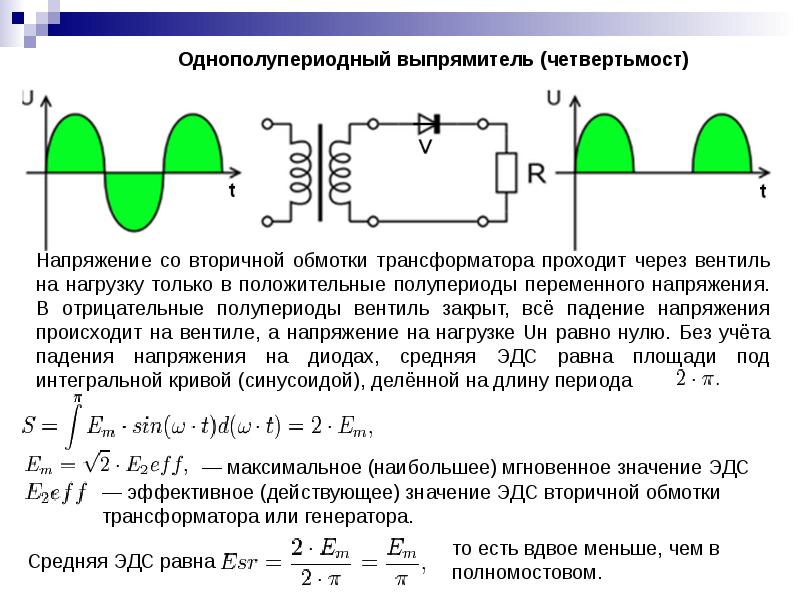 Когда же напряжение на входе выпрямителя
упадет ниже уровня открывания диода и
он закроется, конденсатор начнет
разряжаться через R н,
предотвращая при этом быстрое падение
уровня напряжения на нагрузке. Таким
образом, результирующее напряжение на
выходе выпрямителя (на нагрузке) окажется
уже не таким пульсирующим, а будет
значительно сглажено, причем тем сильнее,
чем большую емкость будет иметь
применяемый конденсатор.
Когда же напряжение на входе выпрямителя
упадет ниже уровня открывания диода и
он закроется, конденсатор начнет
разряжаться через R н,
предотвращая при этом быстрое падение
уровня напряжения на нагрузке. Таким
образом, результирующее напряжение на
выходе выпрямителя (на нагрузке) окажется
уже не таким пульсирующим, а будет
значительно сглажено, причем тем сильнее,
чем большую емкость будет иметь
применяемый конденсатор.
Обычно, емкость конденсатора фильтра выбирают такой, чтобы его реактивное сопротивление было намного меньше сопротивления нагрузки (1/ωC ≪R н). В этом случае пульсации напряжения на нагрузке малы и допустимо предполагать, что это напряжение постоянно (U н ≈const ).
30. Основные параметры стабилизаторов напряжения. Параметрические стабилизаторы.
Основные
параметры стабилизатора: 1. Коэффициент
стабилизации ,
равный отношению приращений входного
и выходного напряжений. Коэффициент
стабилизации характеризует качество
работы стабилизатора.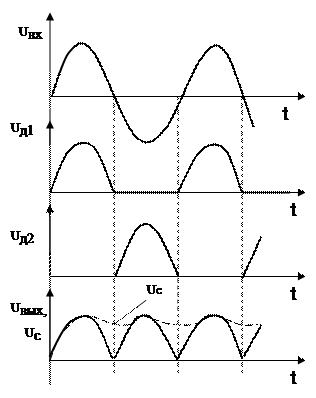
2. Выходное сопротивление стабилизатора Rвых = Rдиф Для нахождения Кст и Rвых рассматривается схема замещения стабилизатора для приращений. Нелинейный элемент работает на участке стабилизации, где его сопротивление переменному току Rдиф является параметром стабилизатора.
Дифференциальное сопротивление Rдиф определяется из уравнения:
Для схемы замещения получаем коэффициент стабилизации с учетом, что Rн >> Rдиф и Rбал >> Rдиф,:
Параметрический стабилизатор:
В
приведенной схеме, при изменении входного
напряжения или тока нагрузки – напряжение
на нагрузке практически не меняется
(оно остаётся таким же, как и на
стабилитроне), вместо этого изменяется
ток через стабилитрон (в случае изменения
входного напряжения и ток через балластный
резистор тоже). То есть, излишки входного
напряжения гасятся балластным резистором,
величина падения напряжения на этом
резисторе зависит от тока через него,
а ток через него зависит в том числе от
тока через стабилитрон, и таким образом,
получается, что изменение тока через
стабилитрон регулирует величину падения
напряжения на балластном резисторе.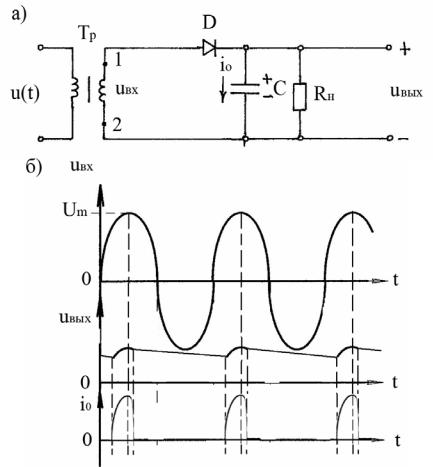
Коэффициент стабилизации параметрического стабилизатора напряжения
Кст = 5 ÷ 30 Для получения повышения стабилизированного напряжения применяют последовательное включение стабилитронов. Параллельное включение стабилитронов не допускается. С целью увеличения коэффициента стабилизации возможно каскадное включение нескольких параметрических стабилизаторов напряжения.
31. Структурные схемы компенсационных стабилизаторов. Принципиальная схема непрерывного стабилизатора напряжения. Получить выражение для выходного напряжения. Недостатки таких стабилизаторов.
Компенсационный
стабилизатор напряжения, по сути,
является устройством, в котором
автоматически происходит регулирование
выходной величины, то есть он поддерживает
напряжение на нагрузке в заданных
пределах при изменении входного
напряжения и выходного тока. По сравнению
с параметрическими компенсационные
стабилизаторы отличаются большими
выходными токами, меньшими выходными
сопротивлениями, большими коэффициентами
стабилизации.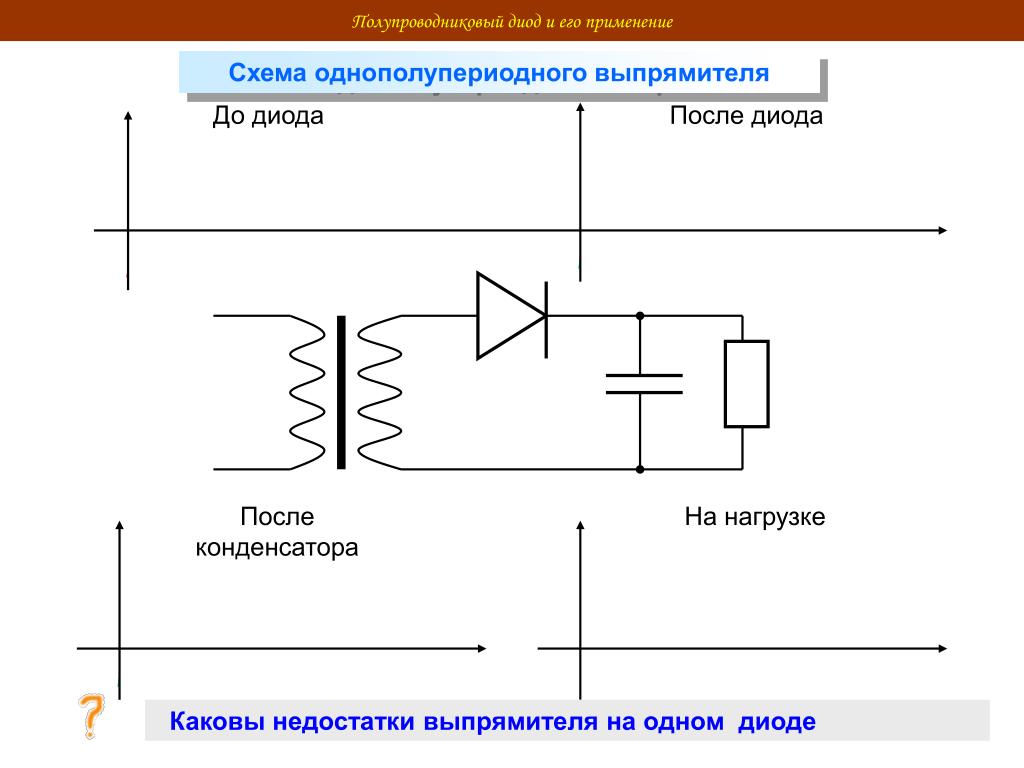
Непрерывный
Принципиальная схема стабилизатора напряжения непрерывного действия приведена на рис. б . Здесь роль ИЭ выполняет делитель напряжения на резисторах R 1 и R 2 . Балластный резистор R б и стабилитрон VD представляют собой маломощный параметрический стабилизатор, выполняющий роль ИОН. Операционный усилитель (ОУ) DA , включенный по схеме дифференциального усилителя, выполняет роль УС. ТранзисторVT является РЭ стабилизатора.
Выходное напряжение стабилизатора можно регулировать, меняя соотношение сопротивлений делителя R 1 и R 2 :
Простейшим выпрямителем является схема однофазного однополупериодного выпрямителя (рис. 3.4-1а). Графики, поясняющие его работу при синусоидальном входном напряжении \(U_{вх} = U_{вх max} \sin{\left(\omega t \right)}\) , представлены на рис. 2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
2 \operatorname{d} t} = \cfrac{I_{max}}{2} = {0,5} \cdot I_{max} \)
Отношение среднего значения выпрямленного напряжения \(U_{н ср}\) к действующему значению входного переменного напряжения \(U_{вх д}\) называется коэффициентом выпрямления (\(K_{вып}\)). Для рассматриваемой схемы \(K_{вып} = {0,45}\).
Максимальное обратное напряжение на диоде \(U_{обр max} = U_{вх max} = \pi U_{н ср}\) , т.е. более чем в три раза превышает среднее выпрямленное напряжение (это следует учитывать при выборе диода для выпрямителя).
Спектральный состав выпрямленного напряжения имеет вид (разложение в ряд Фурье):
\(U_н = \cfrac{1}{\pi} U_{вх max} + \cfrac{1}{2} U_{вх max} \sin{\left(\omega t \right)} – \cfrac{2}{3 \pi} \cos{\left(2 \omega t \right)} – \)
\(- \cfrac{2}{15 \pi} U_{вх max} \cos{\left(4 \omega t \right)} – {…} \)
Коэффициент пульсаций , равный отношению амплитуды низшей (основной) гармоники пульсаций к среднему значению выпрямленного напряжения, для описываемой схемы однополупериодного выпрямителя равен:
\(K_п = \cfrac{U_{пульс max 01}}{U_{н ср}} = \cfrac{\pi}{2} = {1,57}\).
Как видно, однополупериодное выпрямление имеет низкую эффективность из-за высокой пульсации выпрямленного напряжения.
Еще один отрицательный аспект однополупериодного выпрямления связан с неэффективным использованием силового трансформатора, с которого берется переменное напряжение. Это обусловлено тем, что в токе вторичной обмотки трансформатора существует постоянная составляющая, равная среднему значению выпрямленного тока. Такая составляющая не трансформируется, т.е.:
\(I_1 \cdot w_1 = \left(I_2 – I_{н ср} \right) w_2\) ,
где \(I_1\), \(I_2\) – токи первичной и вторичной обмоток, а \(w_1\), \(w_2\) – число витков первичной и вторичной обмоток трансформатора.
Временнáя диаграмма тока первичной обмотки трансформатора (рис. 3.4-2) подобна диаграмме тока вторичной обмотки, но смещена на величину \(I_{н ср} \cfrac{w_2}{w_1}\).
Рис. 3.4-2. Временная диаграмма токов в первичной и вторичной обмотках силового трансформатора, нагруженного на схему однофазного однополупериодного выпрямителя
В сердечнике трансформатора за счет постоянной составляющей тока вторичной обмотки создается постоянный магнитный поток \(\Phi_0 = w_2 \cdot I_0\).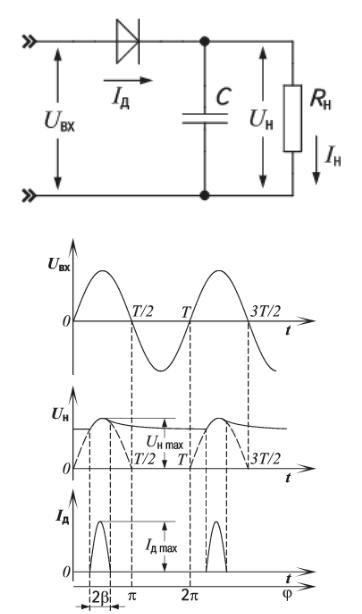 Это явление принято называть вынужденным намагничиванием сердечника трансформатора . Оно может вызвать насыщение магнитной системы трансформатора, т.е. увеличение тока холостого хода, действующего значения первичного тока и следовательно, расчетной мощности первичной обмотки трансформатора, что обусловливает увеличение необходимых размеров трансформатора в целом.
Это явление принято называть вынужденным намагничиванием сердечника трансформатора . Оно может вызвать насыщение магнитной системы трансформатора, т.е. увеличение тока холостого хода, действующего значения первичного тока и следовательно, расчетной мощности первичной обмотки трансформатора, что обусловливает увеличение необходимых размеров трансформатора в целом.
Дополнительный минус однополупериодного выпрямления состоит в наличии участка стабильного тока, что также снижает эффективность использования трансформатора по мощности. Максимальный коэффициент использования трансформатора по мощности для такой схемы не превышает \(k_{тр P} \approx {0,48}\).
Для снижения уровня пульсаций на выходе выпрямителя включаются разнообразные индуктивно-емкостные фильтры. Наличие конденсаторов и индуктивностей в цепи нагрузки оказывает значительное влияние на работу выпрямителя.
В маломощных выпрямителях обычно применяют простейший емкостный фильтр, который представляет собой конденсатор, включенный параллельно нагрузке (рис.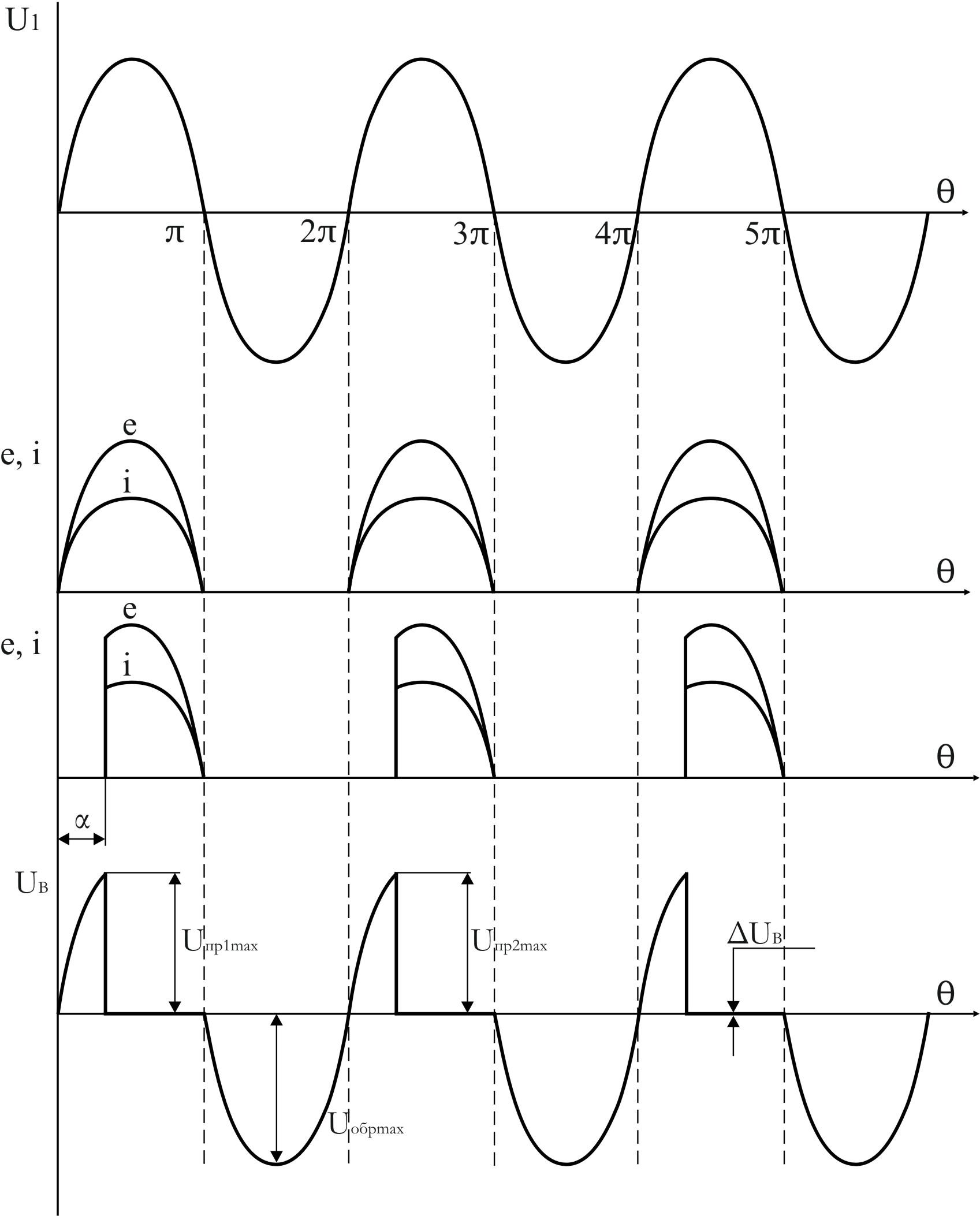 3.4-3).
3.4-3).
Рис. 3.4-3. Схема однофазного однополупериодного выпрямителя с емкостным фильтром (а) и временные диаграммы, поясняющие его работу (б)
В установившемся режиме работы, когда напряжение на входе выпрямителя \(U_{вх}\) больше напряжения на нагрузке \(U_н\) и диод выпрямителя открыт, конденсатор будет подзаряжаться, накапливая энергию, поступающую от внешнего источника. Когда же напряжение на входе выпрямителя упадет ниже уровня открывания диода и он закроется, конденсатор начнет разряжаться через \(R_н\), предотвращая при этом быстрое падение уровня напряжения на нагрузке. Таким образом, результирующее напряжение на выходе выпрямителя (на нагрузке) окажется уже не таким пульсирующим, а будет значительно сглажено, причем тем сильнее, чем большую емкость будет иметь применяемый конденсатор.
Обычно, емкость конденсатора фильтра выбирают такой, чтобы его реактивное сопротивление было намного меньше сопротивления нагрузки (\(1/ \omega C \ll R_н\)). В этом случае пульсации напряжения на нагрузке малы и допустимо предполагать, что это напряжение постоянно (\(U_н \approx {const}\)). Примем: \(U_н = U_{вх max} \cos{\beta}\), где \(\beta\) – некоторая константа, определяющая значение напряжения на нагрузке. Очевидно, что в общем случае \(\beta\) зависит от емкости конденсатора, сопротивления нагрузки, частоты входного напряжения и т.п. Физический смысл этой величины можно понять из временных диаграмм, приведенных на рис. 3.4-4. Как видно, \(\beta\) отражает длительность временного интервала в одном периоде колебаний внешнего напряжения, когда диод выпрямителя находится в открытом состоянии (\(\beta = \omega \cdot t_{откр}/2\)). Угол \(\beta\) принято называть углом отсечки .
Рис. 3.4-4. График зависимости \(A(\beta)\)
Для тока, протекающего через диод в открытом состоянии, можно записать:
\(I_д = \cfrac{U_{вх} – U_н}{r} \) ,
где \(r\) – активное сопротивление, обусловленное сопротивлением диода в открытом состоянии и сопротивлением вторичной обмотки трансформатора (иногда его называют сопротивлением фазы выпрямителя ).{\frac{\pi}{2} + \beta} \cfrac{U_{вх max}}{r} \left(\sin{ \left(\varphi \right)} – \cos{\left(\beta \right)} \right) \operatorname{d} \varphi =\)
\(= \cfrac{U_{вх max}}{\pi r} \left(\sin{\left(\beta \right)} – \beta \cos{\left(\beta \right)} \right) \)
Поскольку \(U_{вх max} = \cfrac{U_н}{\cos{\left(\beta \right)}} \):
\(I_{д ср} =\cfrac{U_н}{\pi r} \cdot \cfrac{\sin{\left(\beta \right)} – \beta \cos{\left(\beta \right)}}{\cos{\left(\beta \right)} } = \cfrac{U_н}{\pi r} A \left(\beta \right) \),
где \(A \left(\beta \right) = \cfrac{\sin{\left(\beta \right)} – \beta \cos{\left(\beta \right)}}{\cos{\left(\beta \right)}} = \operatorname{tg} \left(\beta \right) – \beta \) (3.4.2)
Формула (3.4.2) очень важна при расчете выпрямителя. Ведь угол отсечки \(\beta\) не является заранее известным исходным параметром, как правило, его приходится вычислять на основании заданных выходного напряжения (\(U_н\)), сопротивления (\(R_н\)) или тока нагрузки (\(I_н\)), а также параметров применяемого диода и трансформатора (которые определяют сопротивление фазы \(r\)). Располагая этими данными и учитывая (3.4.2) можно определить значение коэффициента \(A\):
\(A \left(\beta \right) = \cfrac{I_{д ср} \pi r}{U_н} \)
Средний ток через диод \(I_{д ср}\) равен среднему току нагрузки \(I_{н ср}\), а учитывая, что напряжение на нагрузке предполагается неизменным, то и мгновенное значение тока через нагрузку равно току диода: \(I_н = I_{д ср}\). Таким образом:
\(A \left(\beta \right) = \cfrac{I_{н} \pi r}{U_н} = \cfrac{\pi r}{R_н} \)
Для нахождения угла отсечки \(\beta\) при известном коэффициенте \(A(\beta)\) на практике обычно пользуются графиком (рис. 3.4-4).
Максимальное значение тока диода достигается при \(U_{вх} = U_{вх max}\) в момент времени, когда \(\varphi = \pi/2 \), т.е. согласно выражения (3.4.1):
\(I_{д max} = \cfrac{U_{вх max}}{r} \left(1 – \cos{\left(\beta \right)} \right) = \cfrac{U_н}{r} \cdot \cfrac{\pi \left(1 – \cos{\left(\beta \right)} \right)}{\cos{\left(\beta \right)}} \)
\(I_{д max} = \cfrac{I_{д ср} \cdot \pi}{A \left(\beta \right)} \cdot \cfrac{1- \cos{\left(\beta \right)}}{\cos{\left(\beta \right)}}\), где \(F \left(\beta \right) = \cfrac{\pi \cdot \left(1 – \cos{\left(\beta \right)} \right)}{\sin{\left(\beta \right)} – \beta \cos{\left(\beta \right)}}\)
График функции \(F(\beta)\) представлен на рис. 3.4-5. Из него видно, что с уменьшением угла отсечки \(\beta\) существенно увеличивается амплитуда тока через вентили.
Рис. 3.4-5. График зависимости \(F(\beta)\)
Таким образом, емкостный характер нагрузки выпрямителя приводит к тому, что выпрямительный диод оказывается открытым в течение меньшего промежутка времени, а амплитуда тока, проходящего в это время через диод, оказывается больше, чем в аналогичной схеме, работающей на чисто активную нагрузку. Этот факт необходимо учитывать при выборе диода, который должен выдерживать повторяющийся ток соответствующей амплитуды и более того, нормально переносить первоначальный всплеск тока при включении, когда происходит первоначальная зарядка конденсатора.
Указанная закономерность справедлива не только для описываемой схемы однофазного однополупериодного выпрямления. Аналогичным образом будет происходить работа и других рассматриваемых далее схем, имеющих нагрузку емкостного характера.
Требуемый коэффициент пульсаций на выходе однофазного однополупериодного выпрямителя с емкостным фильтром \(K_п\) может быть получен при правильном выборе емкости сглаживающего конденсатора. Для ее нахождения используется следующая формула:
\(С = \cfrac{H(\beta)}{r \cdot K_п}\),
где \(H(\beta)\) – это еще один вспомогательный коэффициент, значение которого находится по графику (рис. 3.4-6).
Рис. 3.4-6. График зависимости \(H(\beta)\)
Емкостный фильтр характерен для выпрямителей, рассчитанных на малые токи нагрузки. При больших токах обычно применяют индуктивные фильтры. Такой фильтр представляет собой катушку индуктивности (обычно с ферромагнитным сердечником), включенную последовательно с нагрузкой (рис. 3.4-7). Наличие индуктивности в цепи нагрузки также как и емкость оказывает значительное влияние на режим работы вентилей выпрямителя.
Рис. 3.4-7. Схема однофазного однополупериодного выпрямителя с индуктивным фильтром (а) и временные диаграммы, поясняющие его работу (б)
Работа схемы на рис. 3.4-7 описывается уравнением:
\(U_{вх max} \sin{\left(\omega t \right)} = L \cfrac{\operatorname{d} I_н}{\operatorname{d} t} + I_н R_н \)
Приняв ток в цепи в начальный момент времени \((t = 0)\) равным нулю, решив данное уравнение получим следующее выражение для тока в цепи нагрузки:
\(I_н(t) = \cfrac{U_{вх max}}{\sqrt{R_н^2 + {\left(\omega L \right)}^2}} \left(\sin{\left(\omega t – \theta \right)} + e^{- \cfrac{R_н t}{L}} \sin{(\theta)} \right) \),
где \(\theta = \operatorname{arctg} \left(\cfrac{\omega L}{R_н} \right) \)
Временная диаграмма, отражающая эту зависимость приведена на рис. 3.4-7(б). По ней хорошо виден физический смысл константы \(\theta\). Она представляет собой угол, на который запаздывает основной всплеск тока в нагрузке относительно инициирующего его всплеска напряжения на входе выпрямителя.
Если проанализировать зависимость тока нагрузки \(I_н(t)\), можно заметить, что его амплитуда с увеличением индуктивности катушки падает (соответственно падает и его среднее значение). Т.е. среднее значение напряжения на нагрузке оказывается меньшим, чем в случае отсутствия индуктивности, уменьшаются также пульсации выходного напряжения. Сами колебания тока оказываются сдвинутыми относительно колебаний входного напряжения на угол \(\theta\). Это является причиной скачкообразного приложения к диоду в момент его запирания отрицательного обратного напряжения величиною до \(U_{обр} = U_{вх max}\).
Описанный режим работы вентилей (затягивание тока, уменьшение его амплитуды, скачкообразное приложение обратного напряжения) при наличии индуктивного фильтра характерен для всех схем выпрямителей. Индуктивный фильтр обычно применяют в схемах мощных выпрямителей, поскольку в этом случае требуемая для существенного изменения параметров выходного напряжения индуктивность оказывается незначительной.
Наиболее эффективно сглаживание пульсаций выпрямленного напряжения осуществляется с помощью сложных многозвенных фильтров, в состав которых входят и катушки индуктивности и конденсаторы (основой таких фильтров являются т.н. Г- или П-образные звенья).
Однополупериодный выпрямитель: принцип работы и применение
Однополупериодный выпрямитель – это самый простой вид выпрямителя напряжения. Он берет на себя ровно половину от синусоидального переменного напряжения. По своим техническим характеристикам и принципам работы такой тип выпрямителя не подходит для очень многих сфер электрики и электроники.
В сигнале на выходе слишком много гармоник, которые трудно технически и практически отфильтровать. В настоящей статье будет рассмотрено строение, структура этого типы выпрямителя, а также где они могут быть использованы. Дополнением служат два ролика по данной теме, а также она подробная техническая лекция по данным типам выпрямления напряжения.
Как устроен выпрямитель тока
Схема однополупериодного выпрямителя
При подаче переменного sin-идального напряжения на первичную обмотку трансформатора напряжение на зажимах вторичной его обмотки также будет переменным синусоидальным и будет равноU2=U2msinwt. Диод проводит электрический ток только в том случае, когда его анод относительно катода будет иметь положительный потенциал. Поэтому ток в цепи – вторичная обмотка, диод и нагрузка – будет протекать только в одном направлении, то есть в течение одной половины периода переменного напряженияU2. В результате этого ток, протекающий в цепи нагрузки, оказывается пульсирующим. Максимальное значение тока:
Im=U2m/RH, гдеRH– сопротивление потребителя постоянного тока.
Кривая получаемого в процессе однополупериодного выпрямления пульсирующего тока может быть разложена в гармонический ряд Фурье:
i=Im(1/π+1/2 sinwt-2/3π∙1 cos2wt-…).
Пульсирующий ток, как видно из выражения, кроме переменных составляющих содержит также и постоянную I=Im/π. Отсюда постоянная составляющая напряжения
U=IRH=Im/π∙RH=U2m/π.
Через действующее значение напряжения: U=√2 ∙U2/π.
Переменные составляющие характеризуют величину пульсаций тока и напряжения.
График работы однополупериодного выпрямителя
Для оценки пульсаций при какой-либо схеме выпрямления вводится понятие коэффициента пульсаций q, под которым понимается отношение амплитуды Am наиболее резко выраженной гармонической составляющей, входящей в кривые выпрямленного тока или напряжения, к постоянной составляющей Aв тока\напряжения в выходной цепи выпрямителя:q=Am/AB.
Для схемы однополупериодного выпрямителя: q=0.5Im/(1/π ∙Im)=π/2. В течение половины периода, когда анод диода имеет отрицательный относительно катода потенциал, диод тока не проводит. Напряжение, воспринимаемое диодом в непроводящий полупериод, называется обратным напряжением Uобр. Обратное напряжение на диоде будет определяться напряжением на вторичной обмотке. Максимальное значение напряженияUобрm=U2m. Значит, вентиль надо выбирать так, чтобы [Umax обр]>=U2m.
Недостатки такой схемы выпрямления: большие пульсации выпрямленного тока и напряжения, а также плохое использование трансформатора, поскольку по его вторичной обмотке протекает ток только в течение половины периода. Такую установку используют в маломощных системах, когда выпрямленный ток мал.
Как устроен выпрямитель
Напряжение с вторичной обмотки силового трансформатора подаётся на один единственный диод. Поэтому выпрямитель и назван однополупериодным. Выпрямляется только один полупериод и на выходе получается импульсное напряжение. Схема проста и не требует большого количества элементов. Это и сказывается на качестве выпрямленного напряжения. При низких частотах переменного напряжения (например, как в электросети – 50 Гц) выпрямленное напряжение получается сильно пульсирующим. А это очень плохо.
Для того чтобы снизить величину пульсации выпрямленного напряжения приходится брать величину конденсатора С1 очень большую, порядка 2000 – 5000 микрофарад, что увеличивает размер блока питания, так как электролиты на 2000 – 5000 мкф имеют довольно большие размеры. Поэтому на низких частотах эта схема практически не используется. Зато однополупериодные выпрямители прекрасно зарекомендовали себя в импульсных блоках питания работающих на частотах 10 – 15 кГц (килогерц).
На таких частотах величина ёмкости фильтра может быть очень небольшой, а простота схемы уже не столь сильно влияет на качество выпрямленного напряжения.
Примером использования однополупериодного выпрямителя может служить простой зарядник от сотового телефона. Так как зарядник сам по себе маломощный, то в нём применяется однополупериодная схема, причём как во входном сетевом выпрямителе 220V (50Гц), так и в выходном, где требуется выпрямить переменное напряжение высокой частоты со вторичной обмотки импульсного трансформатора. К несомненным достоинствам такого выпрямителя следует отнести минимум деталей, низкую стоимость и простые схемные решения. В обычных (не импульсных) блоках питания многие десятилетия успешно работают двухполупериодные выпрямители.
Двухполупериодные выпрямители
Они бывают двух схемных решений: выпрямитель со средней точкой и мостовая схема, известная, как схема Гретца. Выпрямитель со средней точкой требует более сложного в исполнении силового трансформатора, хотя диодов там используется в два раза меньше чем в мостовой схеме. К недостаткам двухполупериодного выпрямителя со средней точкой можно отнести то, что для получения одинакового напряжения, число витков во вторичной обмотке трансформатора должно быть в два раза больше, чем при использовании мостовой схемы. А это уже не совсем экономично с точки зрения расходования медного провода.
Далее на рисунке показана типовая схема двухполупериодного выпрямителя со средней точкой. Величина пульсаций выпрямленного напряжения меньше чем у однополупериодного выпрямителя и величину конденсатора фильтра так же можно использовать гораздо меньшую. Как видим, на выходе выпрямителя уже в два раза меньше “провалов” напряжения – тех самых пульсаций.
Интересно почитать: что такое клистроны.
Активно применяется схема выпрямителя со средней точкой в выходных выпрямителях импульсных блоков питания для ПК. Так как во вторичной обмотке высокочастотного трансформатора требуется меньшее число витков медного провода, то гораздо эффективнее применять именно эту схему. Диоды же применяются сдвоенные, т.е. такие, у которых общий корпус и три вывода (два диода внутри). Один из выводов – общий (как правило катод). По виду сдвоенный диод очень похож на транзистор.
Выпрямитель напряжения
Наибольшую популярность приобрела в бытовой и промышленной аппаратуре мостовая схема. Можно без преувеличения сказать, что это самая распространённая схема. На практике вы с ней ещё не раз встретитесь. Она содержит четыре полупроводниковых диода, а на выходе, как правило, ставится RC-фильтр или только электролитический конденсатор для сглаживания пульсаций напряжения. О данной схеме уже рассказывалось на странице про диодный мост. Стоит отметить, что и у мостовой схемы есть недостатки. Как известно, у любого полупроводникового диода есть так называемое прямое падение напряжения (Forward voltage drop – VF).
Для обычных выпрямительных диодов оно может быть 1 – 1,2 V (зависит от типа диода). Так вот, при использовании мостовой схемы на диодах теряется напряжение, равное 2 x VF, т.е. около 2 вольт. Это происходит потому, что в выпрямлении одной полуволны переменного тока участвуют 2 диода (затем другие 2). Получается, что на диодном мосте теряется часть напряжения, которое мы снимаем со вторичной обмотки трансформатора, а это явные потери. Поэтому в некоторых случаях в составе диодного моста применяются диоды Шоттки, у которых прямое падение напряжения невелико (около 0,5 вольта). Правда, стоит учесть, что диод Шоттки не рассчитан на большое обратное напряжение и очень чувствителен к его превышению.
Трансформатор с однополупериодным выпрямителем
Наиболее распространенные схемы
Выпрямителем называется электронное устройство, предназначенное для преобразования электрической энергии переменного тока в постоянный. В основе выпрямителей лежат полупроводниковые приборы с односторонней проводимостью – диоды и тиристоры. При небольшой мощности нагрузки (до нескольких сотен ватт) преобразование переменного тока в постоянный осуществляют с помощью однофазных выпрямителей. Такие выпрямители предназначены для питания постоянным током различных электронных устройств, обмоток возбуждения двигателей постоянного тока небольшой и средней мощности и т.д.
Это интересно! Все о полупроводниковых диодах.
Для упрощения понимания работы схем выпрямления будем исходить из расчета, что выпрямитель работает на активную нагрузку. Схема содержит один выпрямительный диод, включенный между вторичной обмоткой трансформатора и нагрузкой. Напряжение u2 изменяется по синусоидальному закону, т.е. содержит положительные и отрицательные полуволны (полупериоды). Ток в цепи нагрузки проходит только в положительные полупериоды, когда к аноду диода VD прикладывается положительный потенциал. При обратной полярности напряжения u2 диод закрыт, ток в нагрузке не протекает, но к диоду прикладывается обратное напряжение Uобр.
Т.о. на нагрузке выделяется только одна полуволна напряжения вторичной обмотки. Ток в нагрузке протекает только в одном направлении и представляет собой выпрямленный ток, хотя носит пульсирующий характер. Такую форму напряжения (тока) называют постоянно-импульсная.
Выпрямленные напряжения и ток содержат постоянную (полезную) составляющую и переменную составляющую (пульсации). Качественная сторона работы выпрямителя оценивается соотношениями между полезной составляющей и пульсациями напряжения и тока. Коэффициент пульсаций данной схемы составляет 1,57. Среднее за период значение выпрямленного напряжения Uн = 0,45U2. Максимальное значение обратного напряжения на диоде Uобр.max = 3,14Uн.
Достоинством данной схемы является простота, недостатки: плохое использование трансформатора, большое обратное напряжение на диоде, большой коэффициент пульсации выпрямленного напряжения. Состоит из четырех диодов, включенных по мостовой схеме. В одну диагональ моста включается вторичная обмотка трансформатора, в другую – нагрузка. Общая точка катодов диодов VD2, VD4 является положительным полюсом выпрямителя, общая точка анодов диодов VD1, VD3 – отрицательным полюсом.
Выпрямитель электрического тока
Его электронная схема, предназначенная для преобразования переменного электрического тока в постоянный (одно полярный) электрический ток. В полупроводниковой аппаратуре выпрямители исполняются на полупроводниковых диодах. В более старой и высоковольтной аппаратуре выпрямители исполняются на электровакуумных приборах – кенотронах. Раньше широко использовались – селеновые выпрямители.
Для начала вспомним, что собой представляет переменный электрический ток. Это гармонический сигнал, меняющий свою амплитуду и полярность по синусоидальному закону. В переменном электрическом токе можно условно выделить положительные и отрицательные полупериоды. Всё то, что больше нулевого значения относится к положительным полупериодам (положительная полуволна – красным цветом), а всё, что меньше (ниже) нулевого значения – к отрицательным полупериодам (отрицательная полуволна – синим цветом).
Выпрямитель, в зависимости от его конструкции «отсекает», или «переворачивает» одну из полуволн переменного тока, делая направление тока односторонним. Схемы построения выпрямителей сетевого напряжения можно поделить на однофазные и трёхфазные, однополупериодные и двухполупериодные.
Однофазная мостовая схема выпрямления
Для удобства мы будем считать, что выпрямляемый переменный электрический ток поступает с вторичной обмотки трансформатора. Это соответствует истине и потому, что даже электрический ток в домашние розетки квартир домов приходит с трансформатора понижающей подстанции. Кроме того, поскольку сила тока – величина, напрямую зависящая от нагрузки, то при рассмотрении схем выпрямления мы будем оперировать не понятием силы тока, а понятием – напряжение, амплитуда которого напрямую не зависит от нагрузки.
Из сземы видно, что диод отсекает отрицательную полуволну. Если мы перевернём диод, поменяв его выводы – анод и катод местами, то на выходе окажется, что отсечена не отрицательная, а положительная полуволна. Среднее значение напряжения на выходе однополупериодного выпрямителя соответствует значению:
Uср = Umax / π = 0,318 Umax
где: π — константа равная 3,14.
Однополупериодные выпрямители используются в качестве выпрямителей сетевого напряжения в схемах, потребляющих слабый ток, а также в качестве выпрямителей импульсных источников питания. Они абсолютно не годятся в качестве выпрямителей сетевого напряжения синусоидальной формы для устройств, потребляющих большой ток. Наиболее распространёнными являются однофазные двухполупериодные выпрямители. Существуют две схемы таких выпрямителей – мостовая схема и балансная.
Работа выпрямительного диода
Заключение
Рейтинг автора
Автор статьи
Инженер по специальности “Программное обеспечение вычислительной техники и автоматизированных систем”, МИФИ, 2005–2010 гг.
Написано статей
Более подробно о том, что однополупериодный выпрямитель, рассказано в исследовательской работе по выпрямителям. Если у вас остались вопросы, можно задать их в комментариях на сайте. А также в нашей группе ВК можно задавать вопросы и получать на них подробные ответы от профессионалов. Для этого приглашаем читателей подписаться и вступить в группу.
В завершение статьи хочу выразить благодарность источникам, откуда мы черпали информацию во время подготовки материала:
www.meanders.ru
www.electricalschool.info
www.radioprog.ru
www.go-radio.ru
www.studfile.net
ПредыдущаяТеорияКак работает выпрямитель напряжения
СледующаяТеорияЧто такое мостовой выпрямитель и как он устроен
Полуволновой выпрямитель – инженеры в последнюю минуту
Большинству электронных систем, таких как телевизоры, аудиосистемы и компьютеры, для правильной работы требуется постоянное напряжение. Поскольку напряжение в сети переменное, нам необходимо преобразовать его в относительно постоянное выходное напряжение постоянного тока. Цепи, преобразующие переменное напряжение (AC) в постоянное (DC), называются выпрямителями .
Как известно, диод проводит ток только в одном направлении от анода к его катоду. Эта особенность делает их идеальными для исправления.
Диоды соединяются вместе, образуя различные типы выпрямительных схем, такие как «полуволновые», «двухполупериодные» или «мостовые» выпрямители.
Самым простым из всех выпрямителей является полупериодный выпрямитель .
Полупериодный выпрямитель
На следующем рисунке показана схема полуволнового выпрямителя.
Когда на диод подается переменное напряжение, положительный полупериод напряжения источника смещает диод в прямом направлении. В этом случае диод будет выглядеть как замкнутый переключатель , а положительный полупериод напряжения источника появится на нагрузочном резисторе.
Во время отрицательного полупериода диод смещен в обратном направлении. В этом случае диод будет выглядеть как разомкнутый переключатель , и на нагрузочном резисторе не будет напряжения.
В однополупериодном выпрямителе диод проводит в течение положительных полупериодов, а не отрицательных полупериодов. Из-за этого однополупериодный выпрямитель отсекает отрицательные полупериоды. Такой сигнал называется полуволновым сигналом .
Если диод перевернут, он станет смещенным в прямом направлении при отрицательном входном напряжении.В результате выходные импульсы будут отрицательными.
Это полуволновое напряжение создает ток нагрузки, который течет только в одном направлении, делая схему однонаправленной.
Значение постоянного тока полуволнового сигнала
Значение постоянного тока полуволнового сигнала такое же, как среднее значение.
Среднее значение сигнала за один цикл вычисляется по следующей формуле:
Это уравнение говорит нам, что значение постоянного тока полуволнового сигнала составляет около 31,8% от пикового значения.Например, если пиковое напряжение полуволнового сигнала составляет 10 В, напряжение постоянного тока будет 3,18 В
Когда вы измеряете полуволновой сигнал с помощью вольтметра постоянного тока, показания будут равны среднему значению постоянного тока.
A Приближение второго порядка
В действительности мы не можем получить идеальное полуволны напряжения на нагрузочном резисторе.
Из-за барьерного потенциала диод не включается, пока напряжение источника не достигнет примерно 0,7 В . Итак, выходное напряжение равно 0.На 7 В ниже пикового напряжения источника.
Например, если пиковое напряжение источника составляет всего 10 В, напряжение нагрузки будет иметь пиковое значение только 9,3 В.
Следовательно, более точная формула для расчета значения постоянного тока полуволнового сигнала:
Выходная частота
Изменение выпрямленного выходного сигнала во время положительного и отрицательного полупериодов дает форму волны с большим количеством Пульсация (колеблющаяся часть).
Результирующая пульсация имеет ту же частоту, что и входной переменный ток.
Следовательно, мы можем написать:
Фильтрация выхода выпрямителя
Выход, который мы получаем от полуволнового выпрямителя, представляет собой пульсирующее напряжение постоянного тока, которое увеличивается до максимума, а затем уменьшается до нуля.
Нам не нужно такое постоянное напряжение. Что нам нужно, так это стабильное и постоянное напряжение постоянного тока, без каких-либо колебаний или пульсаций напряжения, которые мы получаем от батареи.
Чтобы получить такое напряжение, нам нужно отфильтровать полуволновой сигнал. Один из способов сделать это – подключить конденсатор, известный как сглаживающий конденсатор , через нагрузочный резистор, как показано ниже.
Изначально конденсатор не заряжен. В течение первой четверти цикла диод смещен в прямом направлении, поэтому конденсатор начинает заряжаться. Зарядка продолжается до тех пор, пока входной сигнал не достигнет пикового значения. В этот момент напряжение на конденсаторе равно Vp.
После того, как входное напряжение достигает пика, оно начинает уменьшаться. Как только входное напряжение становится меньше Vp, напряжение на конденсаторе превышает входное напряжение, в результате чего диод отключается.
Когда диод выключен, конденсатор разряжается через нагрузочный резистор и обеспечивает ток нагрузки, пока не будет достигнут следующий пик.
Когда наступает следующий пик, диод ненадолго проводит ток и заряжает конденсатор до максимального значения.
Ограничения
Если резистор нагрузки мал для данного номинала конденсатора, через нагрузку будет протекать большой ток, который быстрее разряжает конденсатор (из-за постоянной времени RC) и приводит к увеличению пульсаций. Пока постоянная времени RC намного больше периода, конденсатор остается почти полностью заряженным, и мы получаем идеальное выходное напряжение постоянного тока.Чтобы иметь большую постоянную времени RC, нам нужен конденсатор большей емкости . Это непрактично, поскольку существуют ограничения как по стоимости, так и по размеру конденсатора.
Также нет выхода во время отрицательного полупериода, поэтому половина мощности тратится впустую , что приводит к более низкой выходной амплитуде.
Однополупериодные выпрямители из-за своих основных недостатков используются редко. Было бы более практично использовать двухполупериодный выпрямитель, как описано в следующем руководстве.
NEXTПолноволновой выпрямитель
Цепь полуволнового выпрямителясо схемой
Принципиальная схема полуволнового выпрямителяПростой полуволновой выпрямитель – это не что иное, как диод с одинарным pn-переходом, подключенный последовательно к нагрузочному резистору. Как вы знаете, диод относится к электрическому току, как односторонний клапан – к воде, он позволяет электрическому току течь только в одном направлении. Это свойство диода очень полезно при создании простых выпрямителей, которые используются для преобразования переменного тока в постоянный.
Если вы посмотрите на диаграмму выше, мы подаем переменный ток в качестве входа. Входное напряжение подается на понижающий трансформатор, а результирующее уменьшенное выходное напряжение трансформатора передается на диод «D» и нагрузочный резистор RL. Выходное напряжение измеряется на нагрузочном резисторе RL.
В рамках серии «Учебное пособие по базовой электронике» мы увидели, что выпрямление является наиболее важным применением диода с PN переходом. Процесс выпрямления – это преобразование переменного тока (AC) в постоянный (DC).
Работа полуволнового выпрямителя
Проще говоря, полуволновой выпрямитель удаляет отрицательный полупериод переменного тока на входе и позволяет проходить только положительным циклам, создавая поток постоянного тока.
Чтобы полностью понять принцип работы полуволнового выпрямителя, вы должны хорошо знать теоретическую часть . Если вы плохо знакомы с концепцией PN-перехода и его характеристиками, я рекомендую вам сначала прочитать часть теории полуволнового выпрямителя.
Работа полуволнового выпрямителя довольно проста.С теоретической части вы должны знать, что диод с pn переходом проводит ток только в одном направлении. Другими словами, диод с pn переходом проводит ток только тогда, когда он смещен в прямом направлении. Тот же принцип используется в полуволновом выпрямителе для преобразования переменного тока в постоянный. Здесь вводится переменный ток. Это входное напряжение понижается с помощью трансформатора. Пониженное напряжение подается на диод «D» и сопротивление нагрузки RL. Во время положительных полупериодов входной волны диод «D» будет смещен в прямом направлении, а во время отрицательных полупериодов входной волны диод «D» будет смещен в обратном направлении.Возьмем выход через резистор нагрузки RL. Поскольку диод пропускает ток только в течение половины периода входной волны, мы получаем выходной сигнал, как показано на диаграмме. Выход является положительным и значительным во время положительных полупериодов входной волны. При этом выход равен нулю или незначителен во время отрицательных полупериодов входной волны. Это называется полуволновым выпрямлением .
Объяснение полуволнового выпрямления академическими словами!
Когда одиночный выпрямительный диодный блок включен последовательно с нагрузкой на источнике переменного тока, он преобразует переменное напряжение в однонаправленное пульсирующее напряжение, используя половину цикла приложенного напряжения, а другой полупериод подавляется, потому что он проводит только в одном направлении.Следовательно, если в цепи нет индуктивности или батареи, ток будет нулевым в течение половины времени. Это называется полуволновым выпрямлением . Как уже говорилось, диод – это электронное устройство, состоящее из двух элементов, известных как катод и анод. Поскольку в диоде электроны могут течь только в одном направлении , то есть от катода к аноду, диод обеспечивает одностороннюю проводимость, необходимую для выпрямления. Это справедливо для диодов всех типов – вакуумных, газонаполненных, кристаллических или полупроводниковых, металлических (типа оксида меди и селена) диодов. Полупроводниковые диоды, из-за присущих им преимуществ обычно используются в качестве выпрямительного устройства. Однако для очень высоких напряжений можно использовать вакуумные диоды.
Работа однополупериодного выпрямителя
Схема однополупериодного выпрямителя с полупроводниковым диодом (D) с сопротивлением нагрузки R L , но без сглаживающего фильтра, не представлена на рисунке. Диод включен последовательно с вторичной обмоткой трансформатора и сопротивлением нагрузки R L. Первичная обмотка трансформатора подключается к сети переменного тока.
Переменное напряжение на вторичной обмотке меняет полярность после каждого полупериода входной волны. Во время положительных полупериодов входного переменного напряжения , то есть , когда верхний конец вторичной обмотки положительный относительно нижний конец диода смещен в прямом направлении и, следовательно, проводит ток. Если прямое сопротивление диода предполагается равным нулю (на практике, однако, существует небольшое сопротивление), входное напряжение во время положительных полупериодов прикладывается непосредственно к сопротивлению нагрузки R L , делая его верхний конец положительным. ш.r.t. его нижний конец. Формы сигналов выходного тока и выходного напряжения имеют ту же форму, что и входное переменное напряжение.
Во время отрицательных полупериодов входного переменного напряжения , т. Е. , когда нижний конец вторичной обмотки положительный по отношению к его верхний конец диод имеет обратное смещение и поэтому не проводит. Таким образом, во время отрицательных полупериодов входного переменного напряжения ток и напряжение на нагрузке остаются равными нулю. Обратный ток, будучи очень малым по величине, не учитывается.Таким образом, в течение отрицательных полупериодов питание на нагрузку не подается.
Таким образом, выходное напряжение (VL), возникающее на сопротивлении нагрузки R L , представляет собой серию положительных полупериодов переменного напряжения с промежуточными очень небольшими постоянными уровнями отрицательного напряжения. Из рисунка очевидно, что выход не является постоянным постоянным током. , но только пульсирующая волна постоянного тока. Чтобы сделать выходную волну гладкой и полезной в источнике питания постоянного тока, мы должны использовать фильтр по нагрузке.Поскольку используются только полупериоды входной волны, он называется полуволновым выпрямителем .
Теория полуволнового выпрямителя
Выпрямление – это применение диода с pn переходом. Полуволновой выпрямитель – это устройство, в котором используются основные свойства диода с pn переходом. Итак, чтобы понять основную теорию, лежащую в основе полуволнового выпрямителя, вам необходимо понять pn-переход и характеристики диода pn-перехода. Мы разработали две статьи, чтобы помочь вам понять их обе.
1) Понимание PN-перехода – Эта статья поможет вам понять pn-переход и основную теорию, лежащую в основе использования PN-перехода в качестве выпрямителя.
2) Характеристики диода с pn переходом – Эта статья поможет вам разобраться в характеристиках диода с pn переходом с помощью графиков. Вы можете понять поведение диода при различных уровнях напряжения и его проводимость.
Примечание: – За изобретением диода с PN переходом стоит интересная история .История вращается вокруг настойчивости молодого ученого из Bell Laboratories в США, г-на Рассела Ола. В этом рассказе вы узнаете, как происходят великие изобретения и как некоторые яркие умы 1930-х годов, такие как Уолтер Браттейн (один из трех изобретателей транзисторов), работали вместе, чтобы воплотить великие изобретения в нашу жизнь
Характеристики блока питания выпрямителяНаиболее важными характеристиками, которые необходимо указать для источника питания, являются требуемое выходное постоянное напряжение, средний и пиковый токи в диоде, пиковое обратное напряжение (PIV) диода, регулирование и коэффициент пульсации.
Преимущества и недостатки однополупериодного выпрямителя:
Однополупериодный выпрямитель на практике используется редко. Его никогда не используют в качестве источника питания аудиосхемы из-за очень высокого коэффициента пульсаций. Высокий коэффициент пульсации приведет к появлению шумов во входном аудиосигнале, что, в свою очередь, повлияет на качество звука.
Преимущество полуволнового выпрямителя только в том, что он дешев, прост и прост в изготовлении. Это дешево из-за небольшого количества задействованных компонентов.Просто благодаря прямолинейности схемотехники. Кроме того, у однополупериодного выпрямителя больше недостатков, чем достоинств!
Недостатки однополупериодного выпрямителя1. Выходной ток в нагрузке содержит, помимо постоянной составляющей, составляющие переменного тока основной частоты, равной частоте входного напряжения. Коэффициент пульсаций высок, поэтому для обеспечения стабильного выхода постоянного тока требуется сложная фильтрация.
2.Выходная мощность и, следовательно, эффективность выпрямления довольно низкие. Это связано с тем, что мощность подается только в течение половины цикла входного переменного напряжения.
3. Низкий коэффициент использования трансформатора.
4. Насыщение сердечника трансформатора постоянным током, приводящее к току намагничивания, гистерезисным потерям и генерации гармоник.
Выход постоянного тока от однополупериодного выпрямителя не подходит для обычного источника питания. Однако его можно использовать для некоторых приложений, например для зарядки аккумулятора.
Полуволновой выпрямитель с конденсаторным фильтром
Выход полуволнового выпрямителя не является постоянным напряжением постоянного тока. Из выходной диаграммы видно, что это пульсирующее постоянное напряжение с пульсациями переменного тока. В реальных приложениях нам нужен источник питания с плавной формой волны. Другими словами, нам нужен источник питания постоянного тока с постоянным выходным напряжением. Постоянное выходное напряжение от источника постоянного тока очень важно, поскольку оно напрямую влияет на надежность электронного устройства, которое мы подключаем к источнику питания.
Мы можем сделать выход полуволнового выпрямителя плавным, используя фильтр (конденсаторный фильтр или индуктивный фильтр) на диоде. В некоторых случаях также используется резистивно-конденсаторный фильтр (RC). На схеме ниже показан полуволновой выпрямитель с конденсаторным фильтром.
Полуволновой выпрямитель с конденсаторным фильтром – принципиальная схема и форма выходного сигналаАнализ полуволнового выпрямителя
Следующие параметры будут объяснены для анализа полуволнового выпрямителя: –
1. Пиковое обратное напряжение (PIV)Пиковое обратное напряжение (PIV) диода важно на этапах его проектирования. Это максимальное напряжение, которое выпрямительный диод должен выдерживать в течение периода обратного смещения.
Когда диод смещен в обратном направлении, в течение отрицательного полупериода ток через нагрузочный резистор RL не протекает. Следовательно, на сопротивлении нагрузки RL не будет падения напряжения, которое приведет к появлению всего входного напряжения на диоде.Таким образом, на диоде появляется пиковое вторичное напряжение V SMAX . Следовательно,
Пиковое обратное напряжение (PIV) однополупериодного выпрямителя = В SMAX
2. Средние и пиковые токи в диодеЕсли предположить, что напряжение на вторичной обмотке трансформатора синусоидально пиковых значений V SMAX , мгновенное значение напряжения, подаваемого на выпрямитель, может быть записано как
Мгновенное значение напряжения, приложенного к полуволновому выпрямителюПредполагая, что диод имеет прямое сопротивление ВЧ Ом и бесконечное значение обратного сопротивления, ток, протекающий через выходное сопротивление нагрузки RL, равен
. Ток, протекающий через диодI MAX = V SMAX / (R F + R L )
3. Выходной постоянный токВыходной постоянный ток равен
. Выходной постоянный ток полуволнового выпрямителяПодставив значение I MAX в уравнение I MAX = V SMAX / (R F + R ), имеем
I пост. 4. Выходное напряжение постоянного тока Значение постоянного напряжения на нагрузке равно В постоянного тока = I постоянного тока R L = В SMAX / pi (R F + R F + R L) 34 В SMAX / {1 + R F / R L } Если R L >> R F , V dc = V SMAX / pi Действующее значение тока, протекающего через диод, равно Действующее значение напряжения на нагрузке равно V Lrms = I rms R L = V SMAX R L /2 (R F ) = V SMAX /2 {1 + R F / R L } Если R L >> R F , V Lrms = V SMAX /2 Эффективность выпрямления определяется как отношение выходной мощности к входной мощности переменного тока. КПД, Ƞ = мощность постоянного тока, подаваемая на нагрузку / мощность переменного тока на входе от трансформатора = P постоянного тока / P переменного тока Мощность постоянного тока, подаваемая на нагрузку, P dc = I 2 dc R L = (I max / pi ) л
Входная мощность переменного тока на трансформатор, P ac = мощность, рассеиваемая на диодном переходе + мощность, рассеиваемая в сопротивлении нагрузки R L
= I 2 среднеквадратическое значение R F + I 2 среднеквадратичное значение R L = {I 5 МАКС. R F + R L ]
Итак, эффективность выпрямления, Ƞ = P dc / P ac = {4/ 2 } [ R L / (R F + L ) ] = 0.406/ {1+ R F / R L }
Максимальный КПД, который может быть получен с помощью полуволнового выпрямителя, составляет 40,6%. Это получается, если пренебречь R F .
8. Коэффициент пульсацииФактически коэффициент пульсаций является мерой оставшихся переменных компонентов на выходе выпрямителя с фильтром. Это отношение действующего значения составляющих переменного напряжения (или тока), присутствующих на выходе выпрямителя, к составляющей постоянного тока в выходном напряжении (или токе).
Действующее значение тока нагрузки равно
.I 2 = I 2 пост. I 2 постоянного тока + I 2 ac
Где, I 1 , I 2 , I 4 и т. Д. – среднеквадратичные значения основной, второй, четвертой и т. Д. Гармоник и I 2 ac – это сумма квадратов среднеквадратичных значений компонентов переменного тока.
Итак, коэффициент пульсации, γ = I ac / I dc = I 2 – I 2 dc ) / I dc4 (I = dc4 I = rms / I dc 2 ) -1} = K f 2 – 1)
Где K f – форм-фактор входного напряжения. Для однополупериодного выпрямителя форм-фактор равен
.K f = I среднеквадратичное значение / I среднеквадратичное значение = (I max / 2 ) / (I max / pi) = pi / 2 = 1.57
Итак, коэффициент пульсации, γ = (1,57 2 – 1) = 1,21
9. ПостановлениеИзменение выходного напряжения в зависимости от постоянного тока нагрузки называется регулированием. Регулирование в процентах составляет
.% Регулировка = {(Vno-load – Vfull-load) / Vfull-load} * 100
В случае идеального источника питания выходное напряжение не должно зависеть от тока нагрузки, а регулировка в процентах должна быть равна нулю.
Применение полупериодного выпрямителяДля построения источников постоянного тока используется любой выпрямитель.Практическое применение любого выпрямителя (будь то полуволновой или двухполупериодный) должно использоваться в качестве компонента в построении источников питания постоянного тока. Полупериодный выпрямитель ничем не отличается от двухполупериодного выпрямителя. Для создания эффективного и бесперебойного источника питания постоянного тока всегда предпочтительнее двухполупериодный выпрямитель. Однако для приложений, в которых постоянное напряжение постоянного тока не очень важно, вы можете использовать блоки питания с полуволновым выпрямителем.
Полупериодный выпрямитель– обзор
В этом подразделе характеристики упомянутых выше выпрямителей будут оцениваться по следующим параметрам.
10.2.3.1 Взаимосвязь напряжений
Среднее значение напряжения нагрузки В L , составляет В постоянного тока и определяется как
(10,1) В постоянного тока = 1T∫0TvL (t) dt
В случае однополупериодного выпрямителя на рис. 10.2 показано, что напряжение нагрузки v L ( t ) = 0 для отрицательного полупериода. Обратите внимание, что угловая частота источника ω = 2 π = T , и уравнение.(10.1) можно переписать как
(10.2) Vdc = 12π∫0Tvmsin ω t d (ωt)
Следовательно,
(10.3) Полуволна Vdc = Vmπ = 0,318 Вм
В случае двухполупериодный выпрямитель, рис. 10.4 и 10.6 показывают, что v L ( t ) = V m | sin ωt | как для положительного, так и для отрицательного полупериода. Следовательно, уравнение. (10.1) можно переписать как
(10.4) Vdc = 1π∫0πVmsinωt d (ω t)
Следовательно,
(10.5) Двухполупериодный Vdc = 2Vmπ = 0,636Vm
Среднеквадратичное значение напряжения нагрузки В L , составляет В L , что определяется как
( 10.6) VL = [1T∫0πvL2 (t) dt] 1/2
В случае полуволнового выпрямителя v L ( t ) = 0 для отрицательного полупериода, поэтому уравнение. (10.6) можно переписать как
(10.7) VL = 12π∫0π (Vmsin ω t) 2d (ωt)
или
(10.8) Полуволна VL = Vm2 = 0.5 Вм
В случае двухполупериодного выпрямителя В L ( t ) = V m | sin ω t | как для положительного, так и для отрицательного полупериода. Следовательно, уравнение. (10.6) можно переписать как
(10.9) VL = 1π∫0π (Vmsin ω t) 2d (ωt)
или
(10.10) Двухполупериодная VL = Vm2 = 0,707 Vm
Результат Уравнение (10.10) соответствует ожидаемому, потому что действующее значение двухполупериодного выпрямленного напряжения должно быть равно значению исходного переменного напряжения.
10.2.3.2 Текущие отношения
Среднее значение тока нагрузки i L составляет I dc , а поскольку нагрузка R является чисто резистивной, его можно найти как
(10.11) Idc = VdcR
Действующее значение тока нагрузки i L составляет I L , и его можно найти как
(10,12) IL = VLR
В случае полуволнового выпрямителя из уравнения. (10,3)
(10.13) Полуволна Idc = 0,318 VmR
и из уравнения. (10,8)
(10,14) Полупериодный IL = 0,5 ВмР
В случае двухполупериодного выпрямителя из уравнения. (10,5)
(10,15) Двухполупериодный Idc = 0,636 VmR
и из уравнения. (10.10)
(10.16) Двухполупериодный IL = 0,707 VmR
10.2.3.3 Коэффициент выпрямления
Коэффициент выпрямления, который является показателем качества для сравнения эффективности исправления, определяется как
(10,17) σ = PdcPL = VdcTdcVLIL
В случае полуволнового диодного выпрямителя коэффициент выпрямления можно определить, подставив уравнения(10.3), (10.13), (10.8) и (10.14) в уравнение. (10.17).
(10,18) Полуволна σ = (0,318 Вм) 2 (0,5 Вм) 2 = 40,5%
В случае двухполупериодного выпрямителя коэффициент выпрямления получается заменой уравнений. (10.5), (10.15), (10.10) и (10.16) в уравнение. (10.17).
(10,19) Двухполупериодный σ = (0,318 Вм) 2 (0,707 Вм) 2 = 81%
10.2.3.4 Форм-фактор
Форм-фактор (FF) определяется как отношение среднеквадратичного значение (нагревательная составляющая) напряжения или тока до его среднего значения,
(10.20) FF = VLVdc или ILIdc
В случае полуволнового выпрямителя FF можно найти, подставив уравнения (10.8) и (10.3) в уравнение. (10.20).
(10.21) Полупериодный FF = 0,5 Vm0,318 Vm = 1,57
В случае двухполупериодного выпрямителя FF можно найти, подставив уравнения (10.16) и (10.15) в уравнение. (10.20).
(10,22) Полноволновой FF = 0,707 Вм 0,636 Вм = 1,11
10.2.3.5 Коэффициент пульсаций
Коэффициент пульсаций (RF), который является мерой содержания пульсаций, определяется как
(10.23) RF = VacVdc
, где V ac – эффективное (среднеквадратичное) значение переменной составляющей напряжения нагрузки v L .
Подставляя уравнение. (10.24) в уравнение. (10,23) RF может быть выражен как
(10,25) RF = (VLVdc) 2-1 = FF2-1
В случае полуволнового выпрямителя
(10,26) Полупериодный RF = 1,572- 1 = 1,21
В случае двухполупериодного выпрямителя
(10,27) Двухполупериодный RF = 1,112-1 = 0,482
10.2.3.6 Коэффициент использования трансформатора
Коэффициент использования трансформатора (TUF), который является мерой качества выпрямительной схемы, определяется как отношение выходной мощности постоянного тока к номинальной мощности трансформатора, требуемой вторичная обмотка,
(10,28) TUF = PdcVsIs = VdcIdcVsIs
, где В, с и I с – номинальные значения действующего напряжения и действующего тока вторичного трансформатора.
Действующее значение вторичного тока трансформатора I с такое же, как у тока нагрузки I L .Для однополупериодного выпрямителя I s можно найти из уравнения. (10.14).
(10.30) Полупериодное Is = 0,5 ВмР
Для двухполупериодного выпрямителя I с находится из уравнения. (10.16).
(10.31) Двухполупериодный Is = 0,707 ВмР
Следовательно, TUF полуволнового выпрямителя можно получить, подставив уравнения (10.3), (10.13), (10.29) и (10.30) в уравнение. (10.28).
(10,32) Полуволновый TUF = 0,31820,707 × 0,5 = 0,286
Плохой TUF полуволнового выпрямителя означает, что используемый трансформатор должен иметь коэффициент 3.Номинальная мощность 496 (1 / 0,286) ВА для обеспечения выходной мощности 1 Вт постоянного тока на нагрузку. Кроме того, вторичная обмотка трансформатора должна пропускать постоянный ток, который может вызвать насыщение магнитопровода. В результате однополупериодные выпрямители используются только тогда, когда потребность в токе невелика.
В случае двухполупериодного выпрямителя с трансформатором с центральным отводом, схему можно рассматривать как два полуволновых выпрямителя, работающих вместе. Следовательно, номинальная мощность вторичной обмотки трансформатора, В с I с , вдвое больше, чем у полуволнового выпрямителя, но выходная мощность постоянного тока увеличивается в четыре раза из-за более высокого коэффициента выпрямления, как показано Уравнения.(10.5) и (10.15). Следовательно, TUF двухполупериодного выпрямителя с трансформатором с центральным отводом можно найти из уравнения. (10,32)
(10,33) Full-wavw TUF = 4 × 0,31822 × 0,707 × 0,5 = 0,572
В случае мостового выпрямителя он имеет самый высокий TUF в цепях однофазного выпрямителя, потому что токи, протекающие в обоих первичная и вторичная обмотки представляют собой сплошные синусоидальные волны. Подставляя уравнения. (10.5), (10.15), (10.29) и (10.31) в уравнение. (10.28) можно найти TUF мостового выпрямителя.
(10,34) Мост TUF = 0,6362 (0,707) 2 = 0,81
Номинальная мощность двухполупериодного выпрямителя в первичной обмотке трансформатора равна номинальной мощности мостового выпрямителя, поскольку ток, протекающий в первичной обмотке, также является непрерывным синусоидальным колебанием.
Шахрам Маривани – ДИОДНЫЙ ХАРАКТЕРИСТИК И ПОЛУВолновой выпрямитель
ДИОДНЫЙ ХАРАКТЕРИСТИК И ПОЛУВолновой выпрямитель
Цель:
Целью этого эксперимента является изучение характеристики постоянного тока кремниевого выпрямительного диода.Также будут изучены и измерены характеристики однополупериодного выпрямителя.
Введение:
Диод на полупроводниковом переходе – очень полезное устройство, которое используется во многих электронных схемах. Диод – это однонаправленное устройство, которое позволяет протекать электрическому току в одном направлении с небольшим сопротивлением, и в то же время обеспечивает относительно более высокое сопротивление, когда ток течет в противоположном направлении. Диод находится во включенном состоянии, когда он показывает низкое сопротивление, и выключен, когда он находится в режиме высокого сопротивления.
Ток будет течь в прямом направлении, когда напряжение прямого смещения достигнет напряжения включения 0,7 В в случае кремниевых диодов и около 0,3 В в случае германиевых диодов. Напряжение включения 0,7 В обусловлено равновесным барьерным потенциалом, также известным как встроенное напряжение. Для определения равновесного барьерного потенциала используются сложные соображения и уравнения энергии электронов. Однако его легко измерить по напряжению прямого включения кремниевого переходного диода.Типичная вольт-амперная характеристика маломощного кремниевого переходного диода показана на рисунке 1. Схема, используемая для получения этой кривой, состоит из переменного напряжения постоянного тока, приложенного к двум клеммам диода. Напряжение увеличивается с отрицательного значения до положительного. Прямой и обратный токи измеряются и отображаются в зависимости от напряжения.
Нелинейная характеристика диода может использоваться для преобразования переменного тока в однонаправленный, но пульсирующий ток в процессе, называемом выпрямлением.В выпрямительных схемах используется один или несколько диодов для обеспечения различной степени эффективности и действенности выпрямления. При анализе пульсирующих токов на выходе выпрямителя будет очевидно, что этот ток состоит из составляющей постоянного тока в дополнение ко многим гармоникам, которые являются целым числом, кратным основной гармонике входного переменного тока. Эти гармоники уменьшаются за счет использования некоторых реактивных компонентов, которые отфильтровывают гармоники и позволяют компоненту постоянного тока проходить на нагрузку.
На этом лабораторном занятии будет измерена и изучена ВАХ кремниевого диода. Полуволновой выпрямитель будет протестирован, и будет продемонстрировано влияние простого фильтра на выпрямленную форму волны.
Рисунок 1 – Вольт-амперная характеристика кремниевого выпрямительного диода.
Подготовительные работы:
Схема однополупериодного выпрямителя показана на рисунке 2. Диод в этой схеме будет обеспечивать низкое сопротивление, когда входная мощность переменного тока проходит через положительную полярность.Сопротивление диода будет значительно выше, когда цикл переменного тока проходит через отрицательную полярность. Следовательно, формы входных и выходных сигналов в этой схеме показаны на рисунке 3.
Рисунок 2 – Принципиальная схема простого однополупериодного выпрямителя
Выпрямленное выходное напряжение может быть связано с входным переменным напряжением как,
Уравнение 1
, где
В, p-out, – пиковое напряжение выпрямленного сигнала. V p-in – пиковое напряжение на входе
Напряжение переменного тока.r d – прямое сопротивление выпрямительного диода, V ton – напряжение включения диода, а R L – сопротивление нагрузки. См. Рисунки 2 и 3.
Рисунок 3 – Форма входного и выходного сигнала однополупериодного выпрямителя.
Средняя составляющая постоянного тока в полуволновом выпрямленном сигнале определяется как,
Уравнение2
Фактически, выпрямительный диод преобразует переменный ток в последовательность напряжения одной полярности, приложенную к импедансу нагрузки, которая на самом деле представляет собой последовательность периодических импульсов, как ясно показано на рисунке 3.Эти однополярные импульсы содержат постоянную составляющую в дополнение к большому количеству нежелательных гармоник. Значительного улучшения сглаживания этих импульсов можно достичь, разместив большой конденсатор поперек импеданса нагрузки, как показано на рисунке 2. Форма выходного сигнала с конденсатором, подключенным к нагрузке, показана на рисунке 4.
Рисунок 4 – Влияние сглаживающего конденсатора на выпрямленную мощность, подаваемую на нагрузку.
Лабораторные работы:
- Измерение характеристики постоянного тока переходного диода
- Установите напряжение постоянного тока источника питания на 0 В.
- Подключите диодную схему, как показано на рисунке 5.
- Измените напряжение питания постоянного тока с шагом 0,3 В или более. Используйте цифровой вольтметр, измерьте V в , V R и V D , как показано на рисунке 5. Сведите данные измерений в таблицу.
- Для каждого шага вычислите постоянный ток через диод, который равен (V R /10).
- НЕ ДОПУСКАЙТЕ Vin ПРЕВЫШАТЬ 9 В постоянного тока.
- Поменяйте полярность источника питания постоянного тока, как показано на рис. 5, и измените сопротивление на 4.7 МОм. Повторите шаги измерения с 1.a до 1.d.
- НЕ ДОПУСКАЙТЕ Vin ПРЕВЫШАТЬ 30 В постоянного тока.
Рисунок 5 – Схема подключения для измерения характеристики постоянного тока переходного диода - Характеристика однополупериодного выпрямителя
- Подключите схему однополупериодного выпрямителя, как показано на рисунке 2, на котором R L = 1 кОм. Не подключайте конденсатор C к нагрузке.
- Контролируйте на осциллографе одновременно V s и V o (см. Рисунок 3). Измерьте V на входе и V на выходе .Нарисуйте отображаемые осциллограммы. С помощью цифрового вольтметра измерьте напряжение постоянного тока на R L .
- Рассчитайте значение прямого сопротивления диода rd, зная, что диод, используемый при измерении, представляет собой кремниевый диод, в котором V ton = 0,7 В.
- Подключите 47 мкФ к R L . Наблюдайте за V s и Vo на осциллографе и нарисуйте обе формы сигнала как можно точнее. Повторите измерение с конденсатором 10 мкФ.Сравните две формы выпрямленного сигнала, полученные с разными конденсаторами.
Результаты и обсуждения:
- Постройте вольт-амперную характеристику выпрямительного диода.
- Какое значение прямого сопротивления диода?
- Какое значение имеет сопротивление обратного смещения диода? (Подсказка: используйте измеренную кривую V-I для вычисления этого значения).
- Оцените напряжение включения диода по кривой ВАХ.
- Заметили ли вы какое-либо изменение выходного постоянного напряжения при подключении конденсатора к сопротивлению нагрузки? Если да, то сколько?
- Сравните измеренное напряжение постоянного тока на RL с рассчитанным по уравнению. В чем разница между двумя значениями? Почему есть разница (если есть)?
Схема работы и ее характеристики
В 1880-х годах началась идентификация и уникальность выпрямителей.Развитие выпрямителей привело к появлению различных подходов в области силовой электроники. Первоначальный диод, который использовался в выпрямителе, был разработан в 1883 году. С развитием вакуумных диодов, впервые появившихся в начале 1900-х годов, возникли ограничения для выпрямителей. В то время как с модификациями ртутных дуговых трубок использование выпрямителей было расширено до различных мегаваттных диапазонов. И один тип выпрямителя – это полупериодный выпрямитель.
Усовершенствование вакуумных диодов показало эволюцию ртутных дуговых трубок, и эти ртутные дуговые трубки были названы выпрямительными трубками.С развитием выпрямителей были впервые применены многие другие материалы. Итак, это краткое объяснение того, как развивались выпрямители и как они развивались. Давайте иметь четкое и подробное объяснение того, что такое полуволновой выпрямитель, его схема, принцип работы и характеристики.
Что такое полуволновой выпрямитель?
Выпрямитель – это электронное устройство, преобразующее переменное напряжение в постоянное. Другими словами, он преобразует переменный ток в постоянный.Выпрямитель используется практически во всех электронных устройствах. В основном он используется для преобразования сетевого напряжения в постоянное напряжение в блоке питания. При питании от постоянного тока работают электронные устройства. По периоду проводимости выпрямители делятся на две категории: полуволновые выпрямители и полноволновые выпрямители
.Строительство
По сравнению с двухполупериодным выпрямителем, HWR является самым простым выпрямителем в конструкции. Только с одним диодом можно построить устройство.
HWR ConstructionОднополупериодный выпрямитель состоит из следующих компонентов:
- Источник переменного тока
- Резистор на участке нагрузки
- А диод
- Понижающий трансформатор
Источник переменного тока
Этот источник тока подает переменный ток на всю цепь. Этот переменный ток обычно представляется как синусоидальный сигнал.
Понижающий трансформатор
Для увеличения или уменьшения переменного напряжения обычно используется трансформатор.Поскольку здесь используется понижающий трансформатор, он снижает напряжение переменного тока, а когда используется повышающий трансформатор, он увеличивает напряжение переменного тока с минимального уровня до высокого уровня. В HWR используется в основном понижающий трансформатор, поскольку необходимое напряжение для диода очень минимально. Когда трансформатор не используется, большое количество переменного напряжения вызовет повреждение диода. В некоторых случаях также можно использовать повышающий трансформатор.
В понижающем устройстве вторичная обмотка имеет минимальное количество витков, чем первичная обмотка.Из-за этого понижающий трансформатор снижает уровень напряжения от первичной до вторичной обмотки.
Диод
Использование диода в однополупериодном выпрямителе позволяет току течь только в одном направлении, тогда как он останавливает ток в другом направлении.
Резистор
Это устройство, которое блокирует прохождение электрического тока только до определенного уровня.
Это конструкция полуволнового выпрямителя серии .
Работа полуволнового выпрямителя
Во время положительного полупериода диод находится в состоянии прямого смещения и проводит ток до RL (сопротивление нагрузки). На нагрузке возникает напряжение, такое же, как входной сигнал переменного тока положительного полупериода.
В качестве альтернативы, во время отрицательного полупериода диод находится в состоянии обратного смещения, и ток через диод не протекает. На нагрузке появляется только входное напряжение переменного тока, и это общий результат, который возможен в течение положительного полупериода.Выходное напряжение пульсирует постоянным напряжением.
Выпрямительные схемы
Однофазные цепи или многофазные цепи входят в состав выпрямительных цепей. Для бытовых применений используются однофазные выпрямительные схемы малой мощности, а для промышленных применений HVDC требуется трехфазное выпрямление. Наиболее важным применением диодов с PN переходом является выпрямление, и это процесс преобразования переменного тока в постоянный.
Полуволновое выпрямление
В однофазном однополупериодном выпрямителе течет либо отрицательная, либо положительная половина переменного напряжения, а другая половина переменного напряжения блокируется.Следовательно, выход принимает только половину волны переменного тока. Один диод требуется для однофазного полуволнового выпрямления и три диода для трехфазного питания. Полупериодный выпрямитель создает большее количество пульсаций, чем двухполупериодный выпрямитель, и для устранения гармоник он требует гораздо большей фильтрации.
Однофазный полуволновой выпрямительДля синусоидального входного напряжения выходное постоянное напряжение холостого хода для идеального полуволнового выпрямителя составляет
Vrms = Vpeak / 2
Vdc = Vpeak / ᴨ
Где
- Vdc, Vav – выходное напряжение постоянного тока или среднее выходное напряжение
- Vpeak – пиковое значение входного фазного напряжения
- Vrms – выходное напряжение среднеквадратичного значения
Работа полуволнового выпрямителя
PN-переходный диод работает только в состоянии прямого смещения.Полупериодный выпрямитель использует тот же принцип, что и диод с PN переходом, и, таким образом, преобразует переменный ток в постоянный. В схеме однополупериодного выпрямителя сопротивление нагрузки включено последовательно с диодом с PN переходом. Переменный ток – это вход однополупериодного выпрямителя. Понижающий трансформатор принимает входное напряжение, а выходной сигнал трансформатора передается на нагрузочный резистор и диод.
Работа HWR объясняется в двух фазах:
- Положительный полуволновой процесс
- Отрицательный полуволновой процесс
Положительная полуволна
Если входное напряжение переменного тока составляет 60 Гц, понижающий трансформатор снижает его до минимального напряжения.Таким образом, на вторичной обмотке трансформатора создается минимальное напряжение. Это напряжение на вторичной обмотке называется вторичным напряжением (Vs). Минимальное напряжение подается как входное напряжение на диод.
Когда входное напряжение достигает диода, во время положительного полупериода диод переходит в состояние прямого смещения и пропускает электрический ток, тогда как во время отрицательного полупериода диод переходит в отрицательное смещение. состояние и препятствует прохождению электрического тока.Положительная сторона входного сигнала, подаваемого на диод, совпадает с прямым постоянным напряжением, подаваемым на диод P-N. Таким же образом, отрицательная сторона входного сигнала, который подается на диод, совпадает с обратным напряжением постоянного тока, которое подается на диод P-N
.Итак, было известно, что диод проводит ток в состоянии прямого смещения и препятствует прохождению тока в состоянии обратного смещения. Таким же образом в цепи переменного тока диод пропускает ток в течение цикла + ve и блокирует ток во время цикла -ve.Переходя к + ve HWR, он не будет полностью блокировать полупериоды -ve, он допускает несколько сегментов полупериодов -ve или допускает минимальный отрицательный ток. Это генерация тока из-за неосновных носителей заряда, находящихся в диоде.
Генерация тока через эти неосновные носители заряда очень минимальна, поэтому им можно пренебречь. Эту минимальную часть полупериодов -ve невозможно наблюдать в секции нагрузки. В практических диодах считается, что отрицательный ток равен «0».
Резистор в секции нагрузки использует постоянный ток, который вырабатывается диодом. Таким образом, резистор называется резистором электрической нагрузки, где напряжение / ток постоянного тока рассчитываются на этом резисторе (R L ). Электрическая мощность считается электрическим коэффициентом схемы, в которой используется электрический ток. В HWR резистор использует ток, вырабатываемый диодом. Из-за этого резистор называют нагрузочным резистором. R L в HWR используется для ограничения или ограничения дополнительного постоянного тока, генерируемого диодом.
Таким образом, был сделан вывод, что выходной сигнал в полуволновом выпрямителе представляет собой непрерывный положительный полупериод, имеющий синусоидальную форму.
Отрицательная полуволна
Работа и конструкция однополупериодного выпрямителя в отрицательном направлении почти идентична положительному полуволновому выпрямителю. Единственный сценарий, который здесь будет изменен, – это направление диода.
Если входное напряжение переменного тока составляет 60 Гц, понижающий трансформатор снижает его до минимального напряжения.Таким образом, на вторичной обмотке трансформатора создается минимальное напряжение. Это напряжение на вторичной обмотке называется вторичным напряжением (Vs). Минимальное напряжение подается как входное напряжение на диод.
Когда входное напряжение достигает диода, во время отрицательного полупериода диод переходит в состояние прямого смещения и пропускает электрический ток, тогда как во время положительного полупериода диод переходит в отрицательное смещение. состояние и препятствует прохождению электрического тока.Отрицательная сторона входного сигнала, который подается на диод, совпадает с прямым напряжением постоянного тока, которое подается на диод P-N. Таким же образом положительная сторона входного сигнала, подаваемого на диод, совпадает с обратным постоянным напряжением, подаваемым на диод P-N
.Итак, было известно, что диод проводит ток в состоянии обратного смещения и препятствует прохождению тока в состоянии прямого смещения. Таким же образом в цепи переменного тока диод пропускает ток в течение цикла -ve и блокирует прохождение тока во время цикла + ve.Переходя к -ve HWR, он не будет полностью препятствовать положительным полупериодам, он допускает несколько сегментов положительных полупериодов или допускает минимальный положительный ток. Это генерация тока из-за неосновных носителей заряда, находящихся в диоде.
Генерация тока через эти неосновные носители заряда очень минимальна, поэтому им можно пренебречь. Эту минимальную часть положительных полупериодов невозможно наблюдать в секции нагрузки. В практических диодах считается, что положительный ток равен «0».
Резистор в секции нагрузки использует постоянный ток, который вырабатывается диодом. Таким образом, резистор называется резистором электрической нагрузки, где напряжение / ток постоянного тока рассчитываются на этом резисторе (R L ). Электрическая мощность считается электрическим коэффициентом схемы, в которой используется электрический ток. В HWR резистор использует ток, вырабатываемый диодом. Из-за этого резистор называют нагрузочным резистором. R L в HWR используется для ограничения или ограничения дополнительного постоянного тока, генерируемого диодом.
В идеальном диоде полупериоды + ve и -ve на выходе кажутся аналогичными полупериодам + ve и -ve Но в практических сценариях полупериоды + ve и -ve несколько отличаются от входных. циклов, и это ничтожно мало.
Таким образом, был сделан вывод, что выходной сигнал в полуволновом выпрямителе представляет собой непрерывные полупериоды, которые имеют синусоидальную форму. Таким образом, выходной сигнал полуволнового выпрямителя представляет собой непрерывные синусоидальные сигналы с положительной и отрицательной полярностью, но не чистый сигнал постоянного тока и в пульсирующей форме.
Работа полуволнового выпрямителяЭто пульсирующее значение постоянного тока изменяется в течение короткого периода времени.
Работа полуволнового выпрямителя
Во время положительного полупериода, когда вторичная обмотка верхнего конца положительна относительно нижнего конца, диод находится в состоянии прямого смещения и проводит ток. Во время положительных полупериодов входное напряжение прикладывается непосредственно к сопротивлению нагрузки, когда прямое сопротивление диода предполагается равным нулю.Формы выходного напряжения и выходного тока такие же, как у входного переменного напряжения.
Во время отрицательного полупериода, когда вторичная обмотка нижнего конца положительна относительно верхнего конца, диод находится в состоянии обратного смещения и не проводит ток. Во время отрицательного полупериода напряжение и ток на нагрузке остаются нулевыми. Величина обратного тока очень мала и им пренебрегают. Таким образом, в течение отрицательного полупериода мощность не передается.
Серия положительных полупериодов – это выходное напряжение, возникающее на сопротивлении нагрузки. Выходной сигнал представляет собой пульсирующую волну постоянного тока, и для создания плавных выходных волновых фильтров используются фильтры, которые должны проходить через нагрузку. Если входная волна имеет полупериод, то он известен как полуволновой выпрямитель.
Трехфазные однополупериодные схемы выпрямителя
Трехфазный полуволновой неуправляемый выпрямитель требует трех диодов, каждый из которых подключен к одной фазе. Схема трехфазного выпрямителя страдает от высокого уровня гармонических искажений как в цепях постоянного, так и переменного тока.Выходное напряжение на стороне постоянного тока выдает три различных импульса за цикл.
Трехфазный HWR в основном используется для преобразования трехфазной мощности переменного тока в трехфазную мощность постоянного тока. При этом вместо диодов используются переключаемые, которые называются неуправляемыми переключателями. Здесь неуправляемые переключатели соответствуют тому, что не существует подхода к регулированию времени включения и выключения переключателей. Это устройство построено с использованием трехфазного источника питания, подключенного к трехфазному трансформатору, причем вторичная обмотка трансформатора всегда соединена звездой.
Здесь используется только соединение звездой по той причине, что нейтральная точка необходима для повторного подключения нагрузки ко вторичной обмотке трансформатора, обеспечивая тем самым обратное направление для потока мощности.
Общая конструкция трехфазного HWR, обеспечивающего исключительно резистивную нагрузку, показана на рисунке ниже. Конструктивно каждая фаза трансформатора обозначена как отдельный источник переменного тока.
Коэффициент полезного действия трехфазного трансформатора составляет почти 96.8%. Хотя эффективность трехфазного HWR больше, чем у однофазного HWR, она меньше, чем эффективность трехфазного двухполупериодного выпрямителя.
Характеристики трехфазного однополупериодного выпрямителя HWRХарактеристики однополупериодного выпрямителя по параметрам
PIV (пиковое обратное напряжение)
В условиях обратного смещения диод должен выдерживать максимальное напряжение. Во время отрицательного полупериода ток через нагрузку не протекает.Таким образом, полное напряжение появляется на диоде, потому что нет падения напряжения через сопротивление нагрузки.
PIV однополупериодного выпрямителя = V SMAX
Это PIV полуволнового выпрямителя .
Средние и пиковые токи в диоде
Предположим, что напряжение на вторичной обмотке трансформатора синусоидально, а его пиковое значение равно V SMAX . Мгновенное напряжение, которое подается на однополупериодный выпрямитель, составляет
Vs = V SMAX Sin wt
Ток, протекающий через сопротивление нагрузки, составляет
.I MAX = V SMAX / (R F + R L )
Постановление
Регулировка – это разница между напряжением холостого хода и напряжением полной нагрузки по отношению к напряжению полной нагрузки, а регулировка напряжения в процентах дается как
.% Регулировка = {(Vno-load – Vfull-load) / Vfull-load} * 100
КПД
Отношение входного переменного тока к выходному постоянному току известно как КПД (?).
? = Pdc / Pac
Мощность постоянного тока, подаваемая на нагрузку, составляет
Pdc = I 2 dc R L = (I MAX / ᴨ) 2 R L
Входная мощность переменного тока к трансформатору,
Pac = рассеиваемая мощность в сопротивлении нагрузки + рассеиваемая мощность на переходном диоде
= I 2 RMS R F + I 2 RMS R L = {I 2 MAX /4} [R F + R L ]
? = Pdc / Pac = 0.406 / {1 + R F / R L }
КПД полуволнового выпрямителя без учета R F составляет 40,6%.
Коэффициент пульсации (γ)
Содержание пульсаций определяется как количество переменного тока, присутствующего в выходном постоянном токе. Если коэффициент пульсаций меньше, производительность выпрямителя будет больше. Значение коэффициента пульсаций для полуволнового выпрямителя составляет 1,21.
Мощность постоянного тока, генерируемая HWR, является не точным сигналом постоянного тока, а пульсирующим сигналом постоянного тока, а в форме пульсирующего постоянного тока существуют пульсации.Эти колебания можно уменьшить, используя фильтрующие устройства, такие как катушки индуктивности и конденсаторы.
Для вычисления количества пульсаций в сигнале постоянного тока используется коэффициент, который называется коэффициентом пульсаций и обозначается как γ . Когда коэффициент пульсации высокий, он показывает расширенную пульсирующую волну постоянного тока, тогда как минимальный коэффициент пульсации показывает минимальную пульсирующую волну постоянного тока,
Когда значение γ очень минимально, это означает, что выходной постоянный ток почти такой же, как чистый постоянный сигнал.Таким образом, можно утверждать, что чем ниже коэффициент пульсаций, тем более плавный сигнал постоянного тока.
В математической форме этот коэффициент пульсаций обозначается как пропорция среднеквадратичного значения участка переменного тока к участку постоянного тока выходного напряжения.
Коэффициент пульсаций = действующее значение секции переменного тока / среднеквадратичное значение секции постоянного тока
I 2 = I 2 dc + I 2 1 + I 2 2 + I 2 4 = I 2 dc 9024 2 905 + I 905 ac
γ = I ac / I dc = (I 2 – I 2 dc ) / I dc = {(I rms / I 2 dc ) / Idc = {(I rms / I 2 dc ) -1} = k f 2 -1)
Где kf – форм-фактор
kf = Irms / Iavg = (Imax / 2) / (Imax / ᴨ) = ᴨ / 2 = 1.57
Итак, γ = (1,572 – 1) = 1,21
Коэффициент использования трансформатора (TUF)
Определяется как отношение мощности переменного тока, подаваемой к нагрузке, и номинальной мощности переменного тока вторичной обмотки трансформатора. TUF однополупериодного выпрямителя составляет около 0,287.
HWR с конденсаторным фильтром
Согласно общей теории, которая обсуждалась выше, выход полуволнового выпрямителя представляет собой пульсирующий сигнал постоянного тока. Это получается, когда HWR работает без фильтра.Фильтры – это устройство, которое используется для преобразования пульсирующего сигнала постоянного тока в устойчивые сигналы постоянного тока, что означает (преобразование пульсирующего сигнала в плавный сигнал). Это может быть достигнуто путем подавления пульсаций постоянного тока, которые возникают в сигнале.
Хотя эти устройства теоретически можно использовать без фильтров, но предполагается, что они могут быть реализованы для любых практических приложений. Поскольку устройству постоянного тока потребуется устойчивый сигнал, пульсирующий сигнал должен быть преобразован в плавный, чтобы его можно было использовать в реальных приложениях.Это причина того, что HWR используется с фильтром в практических сценариях. Вместо фильтра можно использовать катушку индуктивности или конденсатор, но чаще всего используется HWR с конденсатором.
Рисунок ниже поясняет принципиальную схему конструкции полуволнового выпрямителя с конденсаторным фильтром и то, как он сглаживает пульсирующий сигнал постоянного тока.
Преимущества и недостатки
По сравнению с двухполупериодным выпрямителем, однополупериодный выпрямитель не так часто используется в приложениях.Хотя у этого устройства мало преимуществ. Преимущества полуволнового выпрямителя : :
.- Дешево – поскольку используется минимальное количество компонентов
- Простой – из-за того, что схема очень проста
- Простота использования – простая конструкция упрощает использование устройства
- Низкое количество компонентов
Недостатки полуволнового выпрямителя :
- В секции нагрузки выходная мощность включается в компоненты постоянного и переменного тока, где базовый уровень частоты аналогичен уровню частоты входного напряжения.Кроме того, будет увеличиваться коэффициент пульсации, что означает, что шум будет высоким, и потребуется расширенная фильтрация для обеспечения постоянного выходного сигнала постоянного тока.
- Поскольку подача мощности будет только во время одного полупериода входного переменного напряжения, их выпрямительная способность минимальна, а также будет меньше выходная мощность.
- Однополупериодный выпрямитель с минимальным коэффициентом использования трансформатора
- В сердечнике трансформатора происходит насыщение по постоянному току, что приводит к току намагничивания, гистерезисным потерям, а также развитию гармоник.
- Мощность постоянного тока, поступающая от полуволнового выпрямителя, недостаточна для генерации даже общего количества энергии. Принимая во внимание, что это может быть использовано для нескольких приложений, таких как зарядка аккумулятора.
Приложения
Основное применение полуволнового выпрямителя серии – получение мощности переменного тока от источника постоянного тока. Выпрямители в основном используются для внутренних цепей источников питания почти в каждом электронном устройстве. В источниках питания выпрямитель обычно размещается последовательно, таким образом, он состоит из трансформатора, сглаживающего фильтра и регулятора напряжения.Некоторые из других приложений HWR:
- Использование выпрямителя в блоке питания позволяет преобразовывать переменный ток в постоянный. Мостовые выпрямители широко используются в огромных приложениях, где они обладают способностью преобразовывать высокое переменное напряжение в минимальное постоянное напряжение.
- Реализация HWR помогает получить требуемый уровень постоянного напряжения через понижающие или повышающие трансформаторы.
- Это устройство также используется при сварке металлических цепей, а также в репеллентах от комаров, чтобы выталкивать провод для паров.
- Используется в радиоустройстве AM для обнаружения
- Используются как цепи зажигания и генерации импульсов
- Применяется в усилителях напряжения и устройствах модуляции.
Речь идет о схеме полуволнового выпрямителя и работе с ее характеристиками. Мы считаем, что информация, представленная в этой статье, поможет вам лучше понять этот проект. Кроме того, по любым вопросам, касающимся этой статьи, или любой помощи в реализации проектов в области электротехники и электроники, вы можете свободно обращаться к нам, оставляя комментарии в разделе комментариев ниже.Вот вам вопрос, какова основная функция однополупериодного выпрямителя?
Что такое полуволновой и полнополупериодный выпрямители? – Принцип работы и электрическая схема
В полуволновом выпрямителе , когда на вход подается питание переменного тока, на нагрузке появляется положительный полупериод, тогда как отрицательный полупериод подавляется. Это можно сделать с помощью полупроводникового диода с PN переходом. Диод пропускает ток только в одном направлении .Таким образом преобразует напряжение переменного тока в напряжение постоянного тока.
Принципиальная схема полуволнового выпрямителяВ полуволновом выпрямлении используется только один кристаллический диод. Он подключается в схему, как показано ниже.
Электропитание переменного тока, подлежащее выпрямлению, обычно подается через трансформатор. Трансформатор используется для понижения или повышения основного напряжения питания в соответствии с требованиями. Он также изолирует выпрямитель от линий электропередач и, таким образом, снижает риск поражения электрическим током.
Работа полуволнового выпрямителя
При включении питания переменного тока на клемме AB вторичной обмотки появляется переменное напряжение (V в ), показанное на рисунке ниже.
Во время положительного полупериода клемма A является положительной по отношению к B, а кристаллический диод смещен в прямом направлении. Следовательно, он проводит, и ток течет через нагрузочный резистор R L . Этот ток варьируется по величине, как показано на волновой диаграмме, показанной ниже.
Таким образом, положительный полупериод выходного напряжения (V out = i RL ) появляется на нагрузочном резисторе R L , показанном на рисунке ниже.
Пиковое обратное напряжение
Во время отрицательного полупериода, когда диод смещен в обратном направлении, максимальное значение напряжения, приходящего на диод, называется пиковым обратным напряжением . Поскольку ток протекает через нагрузочный резистор RL только в одном направлении, т.е.е. от M к L. Следовательно, через RL получается выходной сигнал постоянного тока, который по своей природе является пульсирующим.
Недостатки полуволнового выпрямителя
Недостатки однополупериодного выпрямителя следующие:
- Выходной сигнал низкий, потому что источник переменного тока обеспечивает питание только половину времени.
- Выходные данные содержат дополнительные переменные компоненты (рябь). Следовательно, для сглаживания выходного сигнала требуется мощная схема фильтра.
Полноволновой выпрямитель
В Full Wave Rectification , когда на входе подается переменный ток, в течение обоих полупериодов (т.е.е., как положительный, так и отрицательный) ток течет через нагрузку в одном и том же направлении. Этого можно добиться, используя два кристаллических диода. Два диода поочередно проводят ток.
Чтобы получить одинаковое направление протекания тока в нагрузочных резисторах R L как во время положительного, так и отрицательного полупериода входа, используются две цепи. Они имеют следующие названия: –
Чтобы получить подробное описание двух типов двухполупериодных выпрямителей, перейдите по ссылкам, приведенным выше.
Схема полуволнового выпрямителя»Электроника
Схема полуволнового выпрямителя работает с использованием диода, предотвращающего прохождение половины формы волны переменного тока. В результате проходит только часть (обычно половина) сигнала, и он выпрямляется.
Цепи диодного выпрямителя Включают:
Цепи диодного выпрямителя
Полупериодный выпрямитель
Двухполупериодный выпрямитель
Двухдиодный двухполупериодный выпрямитель
Двухполупериодный мостовой выпрямитель
Синхронный выпрямитель
Схема однополупериодного выпрямителя – это простейшая форма выпрямительной схемы, которую можно использовать, и хотя она может не обеспечивать наивысший уровень производительности в некоторых аспектах, тем не менее, она очень широко используется.
Применение полуволнового диодного выпрямителя
Полупериодный диодный выпрямитель используется по-разному и в самых разных схемах.
- Выпрямитель мощности: Один из наиболее очевидных способов использования полуволнового диодного выпрямителя – это выпрямитель мощности. Входная мощность линии или сети обычно проходит через трансформатор для преобразования напряжения до необходимого уровня.
- Демодуляция сигнала: Простой полуволновой диодный выпрямитель может использоваться для демодуляции сигналов с амплитудной модуляцией.Процесс выпрямления позволяет восстановить амплитудную модуляцию.
- Детектор пикового сигнала: Простой полуволновой диодный детектор можно использовать в качестве пикового детектора, обнаруживая пики входящей формы волны.
Базовая схема однополупериодного выпрямителя
Основы работы схемы однополупериодного выпрямителя довольно просты. Входящий сигнал проходит через диод. Поскольку он может пропускать ток только в одном направлении, он пропускает только ту часть формы волны, для которой диод смещен в прямом направлении.
Выпрямляющее действие диодаодиночный диод пропускает только половину формы волны
В схеме полуволнового выпрямителя обычно используется единственный диод. Входящий сигнал подключается непосредственно к диоду, а диод, в свою очередь, подключается к нагрузке, как показано на схеме полуволнового выпрямителя ниже.
Базовая схема однополупериодного выпрямителяСхема полуволнового диода
Хотя в схеме полуволнового диодного выпрямителя в основном используется один диод, существует несколько различий в схемах вокруг диода в зависимости от применения.
- Силовой выпрямитель: При использовании для выпрямления мощности, схема однополупериодного выпрямителя используется с трансформатором, если он будет использоваться для питания оборудования каким-либо образом. Обычно в этом приложении переменный сигнал на входе подается через трансформатор. Он используется для обеспечения необходимого входного напряжения.
Полупериодный выпрямитель с трансформаторным входом - AM демодуляция: Когда полуволновой выпрямитель используется для обнаружения амплитудной модуляции, очевидно, что схема требует взаимодействия с другими схемами в радиостанции.Типичная схема может быть такой, как показано ниже. Однополупериодный выпрямитель с трансформаторным входом
- Пиковый детектор: Полуволновая диодная схема часто используется как простой детектор пикового напряжения. Поместив конденсатор на выходную нагрузку, конденсатор будет заряжаться до пикового напряжения (& sqrt; 2 x среднеквадратичное напряжение синусоидальной волны). При условии, что постоянная времени цепи CR, конденсатора и сопротивления нагрузки намного больше периода формы сигнала или достаточна для захвата пика изменяющейся формы сигнала, схема будет удерживать пик напряжения.
Трансформатор обеспечивает изоляцию от сети или сети, а также позволяет входному напряжению на диод быть на требуемом уровне. Обратите внимание, что пиковое напряжение равно & sqrt; 2 или 1,414 раза больше среднеквадратичного значения.
Требования к полупериодному выпрямительному диоду
При разработке схемы однополупериодного выпрямителя необходимо убедиться, что диод способен обеспечить требуемые характеристики. Несмотря на то, что существует очень много параметров, которые определяют отдельные диоды, и их, возможно, необходимо учитывать для данной конструкции, некоторые из основных параметров подробно описаны ниже:
Меры предосторожности в цепи однополупериодного выпрямителя
При проектировании схемы однополупериодного выпрямителя необходимо убедиться, что в цепи присутствует возврат постоянного тока.Часто при использовании диодного выпрямителя для обнаружения сигнала или пика легко пропустить возврат постоянного тока. Он должен быть включен либо как резистор, либо как часть трансформатора или дросселя. Примеры приведены ниже.
Возврат постоянного тока, включенный в полуволновой диодный выпрямительЦепь полуволнового выпрямителя часто может быть полезной. В качестве выпрямителя мощности он обрабатывает только половину формы волны, что приводит к проблемам со сглаживанием позже. В результате для выпрямления мощности обычно используется двухполупериодная система.Полуволновой выпрямитель часто используется для обнаружения сигналов и пиков.
Другие схемы и схемотехника:
Основы операционных усилителей
Схемы операционных усилителей
Цепи питания
Конструкция транзистора
Транзистор Дарлингтона
Транзисторные схемы
Схемы на полевых транзисторах
Условные обозначения схем
Вернуться в меню «Конструкция схемы». . .


